code
stringlengths 2.5k
6.36M
| kind
stringclasses 2
values | parsed_code
stringlengths 0
404k
| quality_prob
float64 0
0.98
| learning_prob
float64 0.03
1
|
|---|---|---|---|---|
# Basics of Deep Learning
In this notebook, we will cover the basics behind Deep Learning. I'm talking about building a brain....

Only kidding. Deep learning is a fascinating new field that has exploded over the last few years. From being used as facial recognition in apps such as Snapchat or challenger banks, to more advanced use cases such as being used in [protein-folding](https://www.independent.co.uk/life-style/gadgets-and-tech/protein-folding-ai-deepmind-google-cancer-covid-b1764008.html).
In this notebook we will:
- Explain the building blocks of neural networks
- Go over some applications of Deep Learning
## Building blocks of Neural Networks
I have no doubt that you have heard/seen how similar neural networks are to....our brains.
### The Perceptron
The building block of neural networks. The perceptron has a rich history (covered in the background section of this book). The perceptron was created in 1958 by Frank Rosenblatt (I love that name) in Cornell, however, that story is for another day....or section in this book (backgrounds!),
The perceptron is an algorithm that can learn a binary classifier (e.g. is that a cat or dog?). This is known as a threshold function, which maps an input vector *x* to an output decision *$f(x)$ = output*. Here is the formal maths to better explain my verbal fluff:
$ f(x) = { 1 (if: w.x+b > 0), 0 (otherwise) $
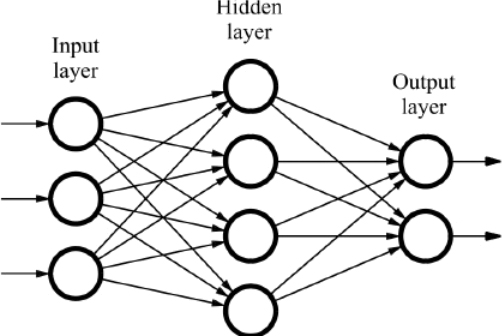
### The Artificial neural network
Lets take a look at the high level architecture first.

The gif above of a neural network classifying images is one of the best visual ways of understanding how neural networks, work. The neural network is made up of a few key concepts:
- An input: this is the data you pass into the network. For example, data relating to a customer (e.g. height, weight etc) or the pixels of an image
- An output: this is the prediction of the neural network
- A hidden layer: more on this later
- Neuron: the network is made up of neurons, that take an input, and give an output
Now, we have a slightly better understanding of what a neuron is. Lets look at a very simple neuron:
From the above image, you can clearly see the three components listed above together.
### But Abdi, what is the goal of a neural network?
Isn't it obvious? To me, it definitely was not when I first started to learn about neural networks. Neural networks are beautifully complex to understand, but with enough time and lots of youtube videos, you'll be able to master this topic.
The goal of a neural network is to make a pretty good guess of something. For example, a phone may have a face unlock feature. The phone probably got you to take a short video/images of yourself in order to set up this security feature, and when it **learned** your face, you were then able to use it to unlock your phone. This is pretty much what we do with neural networks. We teach it by giving it data, and making sure it gets better at making predictions by adjusting the weights between neurons. More on this soon.
## Gradient Descent Algo
One of the best videos on neural networks, by 3Blue1Brown:
<figure class="video_container">
<iframe src="https://www.youtube.com/watch?v=aircAruvnKk" frameborder="0" allowfullscreen="true"> </iframe>
</figure>
His series on Neural networks and Linear algebra are golden sources for learning Deep Learning.
### Simple Gradient Descent Implementation
with the help from our friends over at Udacity, please view below an implementation of the Gradient Descent Algo. This is a very basic neural network that only has its inputs linked directly to the outputs.
We begin by defining some functions.
```
import numpy as np
# We will be using a sigmoid activation function
def sigmoid(x):
return 1/(1+np.exp(-x))
# derivation of sigmoid(x) - will be used for backpropagating errors through the network
def sigmoid_prime(x):
return sigmoid(x)*(1-sigmoid(x))
```
We begin by defining a simple neural network:
- two input neurons: x1 and x2
- one output neuron: y1
```
x = np.array([1,5])
y = 0.4
```
We now define the weights, w1 and w2 for the two input neurons; x1 and x2. Also, we define a learning rate that will help us control our gradient descent step
```
weights = np.array([-0.2,0.4])
learnrate = 0.5
```
we now start moving forwards through the network, known as feed forward. We can combine the input vector with the weight vector using numpy's dot product
```
# linear combination
# h = x[0]*weights[0] + x[1]*weights[1]
h = np.dot(x, weights)
```
We now apply our non-linearity, this will provide us with our output.
```
# apply non-linearity
output = sigmoid(h)
```
Now that we have our prediction, we are able to determine the error of our neural network. Here, we will use the difference between our actual and predicted.
```
error = y - output
```
The goal now is to determine how to change our weights in order to reduce the error above. This is where our good friend gradient descent and the chain rule come into play:
- we determine the derivative of our error with respect to our input weights. Hence:
- change in weights = $ \frac{d}{dw_{i}} \frac{1}{2}{(y - \hat{y})^2}$
- simplifies to = learning rate * error term * $ x_{i}$
- where:
- learning rate = $ n $
- error term = $ (y - \hat{y}) * f'(h) $
- h = $ \sum_{i} W_{i} x_{i} $
We begin by calculating our f'(h)
```
# output gradient - derivative of activation function
output_gradient = sigmoid_prime(h)
```
Now, we can calcualte our error term
```
error_trm = error * output_gradient
```
With that, we can update our weights by combining the error term, learning rate and our x
```
#gradient desc step - updating the weights
dsc_step = [
learnrate * error_trm * x[0],
learnrate * error_trm * x[1]
]
```
Which leaves...
```
print(f'Actual: {y}')
print(f'NN output: {output}')
print(f'Error: {error}')
print(f'Weight change: {dsc_step}')
```
### More in depth...
Lets now build our own end to end example. we will begin by creating some fake data, followed by implementing our neural network.
```
x = np.random.rand(200,2)
y = np.random.randint(low=0, high=2, size=(200,1))
no_data_points, no_features = x.shape
def sig(x):
'''Calc for sigmoid'''
return 1 / (1+np.exp(-x))
weights = np.random.normal(scale=1/no_features**.5, size=no_features)
epochs = 1000
learning_rate = 0.5
last_loss = None
for single_data_pass in range(epochs):
# Creating a weight change tracker
change_in_weights = np.zeros(weights.shape)
for x_i, y_i in zip(x, y):
h = np.dot(x_i, weights)
y_hat = sigmoid(h)
error = y_i - y_hat
# error term = error * f'(h)
error_term = error * (y_hat * (1-y_hat))
# now multiply this by the current x & add to our weight update
change_in_weights += (error_term * x_i)
# now update the actual weights
weights += (learning_rate * change_in_weights / no_data_points)
# print the loss every 100th pass
if single_data_pass % (epochs/10) == 0:
# use current weights in NN to determine outputs
output = sigmoid(np.dot(x_i,weights))
# find the loss
loss = np.mean((output-y_i)**2)
#
if last_loss and last_loss < loss:
print(f'Train loss: {loss}, WARNING - Loss is inscreasing')
else:
print(f'Training loss: {loss}')
last_loss = loss
```
## Multilayer NN
Now, lets build upon our neural network, but this time, we have a hidden layer.
Lets first see how to build the network to make predictions.
```
X = np.random.randn(4)
weights_input_to_hidden = np.random.normal(0, scale=0.1, size=(4, 3))
weights_hidden_to_output = np.random.normal(0, scale=0.1, size=(3, 2))
sum_input = np.dot(X, weights_input_to_hidden)
h = sigmoid(sum_input)
sum_h = np.dot(h, weights_hidden_to_output)
y_pred = sigmoid(sum_h)
```
## Backpropa what?
Ok, so now, how do we refine our weights? Well, this is where **backpropagation** comes in. After feeding our data forwards through the network, using feed forward, we propagate our errors backwards, making use of things such as the chain rule.
Lets do an implementation.
```
# we have three input nodes
x = np.array([0.5, 0.2, -0.3])
# one output node
y = 0.7
learnrate = 0.5
# 2 nodes in hidden layer
weights_input_hidden = np.array(
[
[0.5, -0.6], [0.1, -0.2], [0.1, 0.7]
]
)
weights_hidden_output = np.array([
0.1,-0.3
])
# feeding data forwards through the network
hidden_layer_input = np.dot(x, weights_input_hidden)
hidden_layer_output = sigmoid(hidden_layer_input)
#---
output_layer_input = np.dot(hidden_layer_output, weights_hidden_output)
y_hat = sigmoid(output_layer_input)
# backward propagate the errors to tune the weights
# 1. calculate errors
error = y - y_hat
output_node_error_term = error * (y_hat * (1-y_hat))
#----
hidden_node_error_term = weights_hidden_output * output_node_error_term *(hidden_layer_output * (1-hidden_layer_output))
# 2. calculate weight changes
delta_w_output_node = learnrate * output_node_error_term * hidden_layer_output
#-----
delta_w_hidden_node = learnrate * hidden_node_error_term * x[:,None]
print(f'Original weights:\n{weights_input_hidden}\n{weights_hidden_output}')
print()
print('Change in weights for hidden layer to output layer:')
print(delta_w_output_node)
print('Change in weights for input layer to hidden layer:')
print(delta_w_hidden_node)
```
## Putting it all together
```
features = np.random.rand(200,2)
target = np.random.randint(low=0, high=2, size=(200,1))
def complete_backprop(x,y):
'''Complete implementation of backpropagation'''
n_hidden_units = 2
epochs = 900
learnrate = 0.005
n_records, n_features = features.shape
last_loss = None
w_input_to_hidden = np.random.normal(scale=1/n_features**.5,size=(n_features, n_hidden_units))
w_hidden_to_output = np.random.normal(scale=1/n_features**.5, size=n_hidden_units)
for single_epoch in range(epochs):
delw_input_to_hidden = np.zeros(w_input_to_hidden.shape)
delw_hidden_to_output = np.zeros(w_hidden_to_output.shape)
for x,y in zip(features, target):
# ----------------------
# 1. Feed data forwards
# ----------------------
hidden_layer_input = np.dot(x,w_input_to_hidden)
hidden_layer_output = sigmoid(hidden_layer_input)
output_layer_input = np.dot(hidden_layer_output, w_hidden_to_output)
output_layer_output = sigmoid(output_layer_input)
# ----------------------
# 2. Backpropagate the errors
# ----------------------
# error at output layer
prediction_error = y - output_layer_output
output_error_term = prediction_error * (output_layer_output * (1-output_layer_output))
# error at hidden layer (propagated from output layer)
# scale error from output layer by weights
hidden_layer_error = np.multiply(output_error_term, w_hidden_to_output)
hidden_error_term = hidden_layer_error * (hidden_layer_output * (1-hidden_layer_output))
# ----------------------
# 3. Find change of weights for each data point
# ----------------------
delw_hidden_to_output += output_error_term * hidden_layer_output
delw_input_to_hidden += hidden_error_term * x[:,None]
# Now update the actual weights
w_hidden_to_output += learnrate * delw_hidden_to_output / n_records
w_input_to_hidden += learnrate * delw_input_to_hidden / n_records
# Printing out the mean square error on the training set
if single_epoch % (epochs / 10) == 0:
hidden_output = sigmoid(np.dot(x, w_input_to_hidden))
out = sigmoid(np.dot(hidden_output,
w_hidden_to_output))
loss = np.mean((out - target) ** 2)
if last_loss and last_loss < loss:
print("Train loss: ", loss, " WARNING - Loss Increasing")
else:
print("Train loss: ", loss)
last_loss = loss
complete_backprop(features,target)
```
|
github_jupyter
|
import numpy as np
# We will be using a sigmoid activation function
def sigmoid(x):
return 1/(1+np.exp(-x))
# derivation of sigmoid(x) - will be used for backpropagating errors through the network
def sigmoid_prime(x):
return sigmoid(x)*(1-sigmoid(x))
x = np.array([1,5])
y = 0.4
weights = np.array([-0.2,0.4])
learnrate = 0.5
# linear combination
# h = x[0]*weights[0] + x[1]*weights[1]
h = np.dot(x, weights)
# apply non-linearity
output = sigmoid(h)
error = y - output
# output gradient - derivative of activation function
output_gradient = sigmoid_prime(h)
error_trm = error * output_gradient
#gradient desc step - updating the weights
dsc_step = [
learnrate * error_trm * x[0],
learnrate * error_trm * x[1]
]
print(f'Actual: {y}')
print(f'NN output: {output}')
print(f'Error: {error}')
print(f'Weight change: {dsc_step}')
x = np.random.rand(200,2)
y = np.random.randint(low=0, high=2, size=(200,1))
no_data_points, no_features = x.shape
def sig(x):
'''Calc for sigmoid'''
return 1 / (1+np.exp(-x))
weights = np.random.normal(scale=1/no_features**.5, size=no_features)
epochs = 1000
learning_rate = 0.5
last_loss = None
for single_data_pass in range(epochs):
# Creating a weight change tracker
change_in_weights = np.zeros(weights.shape)
for x_i, y_i in zip(x, y):
h = np.dot(x_i, weights)
y_hat = sigmoid(h)
error = y_i - y_hat
# error term = error * f'(h)
error_term = error * (y_hat * (1-y_hat))
# now multiply this by the current x & add to our weight update
change_in_weights += (error_term * x_i)
# now update the actual weights
weights += (learning_rate * change_in_weights / no_data_points)
# print the loss every 100th pass
if single_data_pass % (epochs/10) == 0:
# use current weights in NN to determine outputs
output = sigmoid(np.dot(x_i,weights))
# find the loss
loss = np.mean((output-y_i)**2)
#
if last_loss and last_loss < loss:
print(f'Train loss: {loss}, WARNING - Loss is inscreasing')
else:
print(f'Training loss: {loss}')
last_loss = loss
X = np.random.randn(4)
weights_input_to_hidden = np.random.normal(0, scale=0.1, size=(4, 3))
weights_hidden_to_output = np.random.normal(0, scale=0.1, size=(3, 2))
sum_input = np.dot(X, weights_input_to_hidden)
h = sigmoid(sum_input)
sum_h = np.dot(h, weights_hidden_to_output)
y_pred = sigmoid(sum_h)
# we have three input nodes
x = np.array([0.5, 0.2, -0.3])
# one output node
y = 0.7
learnrate = 0.5
# 2 nodes in hidden layer
weights_input_hidden = np.array(
[
[0.5, -0.6], [0.1, -0.2], [0.1, 0.7]
]
)
weights_hidden_output = np.array([
0.1,-0.3
])
# feeding data forwards through the network
hidden_layer_input = np.dot(x, weights_input_hidden)
hidden_layer_output = sigmoid(hidden_layer_input)
#---
output_layer_input = np.dot(hidden_layer_output, weights_hidden_output)
y_hat = sigmoid(output_layer_input)
# backward propagate the errors to tune the weights
# 1. calculate errors
error = y - y_hat
output_node_error_term = error * (y_hat * (1-y_hat))
#----
hidden_node_error_term = weights_hidden_output * output_node_error_term *(hidden_layer_output * (1-hidden_layer_output))
# 2. calculate weight changes
delta_w_output_node = learnrate * output_node_error_term * hidden_layer_output
#-----
delta_w_hidden_node = learnrate * hidden_node_error_term * x[:,None]
print(f'Original weights:\n{weights_input_hidden}\n{weights_hidden_output}')
print()
print('Change in weights for hidden layer to output layer:')
print(delta_w_output_node)
print('Change in weights for input layer to hidden layer:')
print(delta_w_hidden_node)
features = np.random.rand(200,2)
target = np.random.randint(low=0, high=2, size=(200,1))
def complete_backprop(x,y):
'''Complete implementation of backpropagation'''
n_hidden_units = 2
epochs = 900
learnrate = 0.005
n_records, n_features = features.shape
last_loss = None
w_input_to_hidden = np.random.normal(scale=1/n_features**.5,size=(n_features, n_hidden_units))
w_hidden_to_output = np.random.normal(scale=1/n_features**.5, size=n_hidden_units)
for single_epoch in range(epochs):
delw_input_to_hidden = np.zeros(w_input_to_hidden.shape)
delw_hidden_to_output = np.zeros(w_hidden_to_output.shape)
for x,y in zip(features, target):
# ----------------------
# 1. Feed data forwards
# ----------------------
hidden_layer_input = np.dot(x,w_input_to_hidden)
hidden_layer_output = sigmoid(hidden_layer_input)
output_layer_input = np.dot(hidden_layer_output, w_hidden_to_output)
output_layer_output = sigmoid(output_layer_input)
# ----------------------
# 2. Backpropagate the errors
# ----------------------
# error at output layer
prediction_error = y - output_layer_output
output_error_term = prediction_error * (output_layer_output * (1-output_layer_output))
# error at hidden layer (propagated from output layer)
# scale error from output layer by weights
hidden_layer_error = np.multiply(output_error_term, w_hidden_to_output)
hidden_error_term = hidden_layer_error * (hidden_layer_output * (1-hidden_layer_output))
# ----------------------
# 3. Find change of weights for each data point
# ----------------------
delw_hidden_to_output += output_error_term * hidden_layer_output
delw_input_to_hidden += hidden_error_term * x[:,None]
# Now update the actual weights
w_hidden_to_output += learnrate * delw_hidden_to_output / n_records
w_input_to_hidden += learnrate * delw_input_to_hidden / n_records
# Printing out the mean square error on the training set
if single_epoch % (epochs / 10) == 0:
hidden_output = sigmoid(np.dot(x, w_input_to_hidden))
out = sigmoid(np.dot(hidden_output,
w_hidden_to_output))
loss = np.mean((out - target) ** 2)
if last_loss and last_loss < loss:
print("Train loss: ", loss, " WARNING - Loss Increasing")
else:
print("Train loss: ", loss)
last_loss = loss
complete_backprop(features,target)
| 0.678753 | 0.989712 |
```
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import requests
import time
from config import weatherKey
from citipy import citipy
from scipy.stats import linregress
weatherAPIurl = f"http://api.openweathermap.org/data/2.5/weather?units=Imperial&APPID={weatherKey}&q="
outputPath = "./output/cities.csv"
citiesTargetTotal = 500
cityCoordinateList = []
cityUsedList = []
#generate random list of coordinates
cityLatRand = np.random.uniform(low = -90, high = 90, size = (citiesTargetTotal*3))
cityLongRand = np.random.uniform(low = -90, high = 90, size = (citiesTargetTotal*3))
cityCoordinateList = zip(cityLatRand, cityLongRand)
#associate each coordinate with nearest city
for x in cityCoordinateList:
city = citipy.nearest_city(x[0], x[1]).city_name
if city not in cityUsedList:
cityUsedList.append(city)
cityWeather = []
print("Retrieving data from openweathermap.org")
print("---------------------------------------")
recordCount = 1
setCount = 1
for index, city in enumerate(cityUsedList):
if(index % 50 == 0 and index >= 50):
recordCount = 0
setCount += 1
lookupURL = weatherAPIurl + city
print(f'Gathering Record {recordCount} of Set {setCount} |{city}')
recordCount += 1
try:
response = requests.get(lookupURL).json()
latitude = response["coord"]["lat"]
longitude = response["coord"]["lon"]
maxTemperature = response["main"]["temp_max"]
humidity = response["main"]["humidity"]
cloudCoverage = response["clouds"]["all"]
wind = response["wind"]["speed"]
country = response["sys"]["country"]
date = response["dt"]
cityWeather.append({"City:" : city,
"Latitude:" : latitude,
"Longitude:" : longitude,
"Max Temp:" : maxTemperature,
"Humidity:" : humidity,
"Cloud Coverage:" : cloudCoverage,
"Wind:" : wind,
"Country:" : country,
"Date:" : date,
})
except:
print(f'{city} not found in data set')
continue
print("---------------------------------------")
print("Data retrieval complete!")
cityWeather_df = pd.DataFrame(cityWeather)
latitude = cityWeather_df["Latitude:"]
maxTemperature = cityWeather_df["Max Temp:"]
humidity = cityWeather_df["Humidity:"]
cloudCoverage = cityWeather_df["Cloud Coverage:"]
wind = cityWeather_df["Wind:"]
cityWeather_df.to_csv(outputPath)
plt.scatter(latitude, maxTemperature, marker = "o", label = "Cities", edgecolor = "orange")
plt.title(f"City Latitude vs Highest Temperature {time.strftime('%x')}")
plt.xlabel("Latitude")
plt.ylabel("Temperature (F)")
plt.savefig("./output/Lat vs. Temp.png")
plt.show()
#it was hottest around 35 latitude and gets colder the further you get away from that latitude
plt.scatter(latitude, humidity, marker = "o", edgecolor = "pink", color = "green")
plt.title(f"City Latitude vs Humidity {time.strftime('%x')}")
plt.xlabel("Latitude")
plt.ylabel("Humidity (%)")
plt.savefig("./output/Lat vs. Humidity.png")
plt.show()
#little change in humidity with change in latitude
plt.scatter(latitude, wind, marker = "o", edgecolor = "green", color = "pink")
plt.title(f"City Latitude vs Wind Speed {time.strftime('%x')}")
plt.xlabel("Latitude")
plt.ylabel("Wind Speed (mph)")
plt.savefig("./output/Lat vs. Wind Speed.png")
plt.show()
#little change in windspeed with change in latitude
plt.scatter(latitude, cloudCoverage, marker = "o", edgecolor = "blue", color = "red")
plt.title(f"City Latitude vs Cloud Coverage {time.strftime('%x')}")
plt.xlabel("Latitude")
plt.ylabel("Cloudiness (%)")
plt.savefig("./output/Lat vs. Cloudiness.png")
plt.show()
#there were a lot of clouds just above the equator on this day
#northern and southern hemisphere dataframes
north_df = cityWeather_df.loc[(cityWeather_df["Latitude:"] >= 0)]
south_df = cityWeather_df.loc[(cityWeather_df["Latitude:"] < 0)]
def plotLinearRegression(x_values, y_values, yLabel, text_coordinates):
(slope, intercept, rvalue, pvalue, stderr) = linregress(x_values, y_values)
regress_values = x_values * slope + intercept
line_eq = "y = " + str(round(slope, 2)) + " x + " + str(round(intercept, 2))
plt.scatter(x_values, y_values)
plt.plot(x_values, regress_values, "r-")
plt.annotate(line_eq, text_coordinates, fontsize = 15, color = "red")
plt.xlabel("Latitude")
plt.ylabel(yLabel)
print(f"The r-squared is : {rvalue}")
plt.show()
#northern hemisphere - Lat vs Max Temp
x_values = north_df["Latitude:"]
y_values = north_df["Max Temp:"]
plotLinearRegression(x_values, y_values, "Max Temp", (20,40))
#the further north lower the max temp
#southern hemisphere - Lat vs Max Temp
x_values = south_df["Latitude:"]
y_values = south_df["Max Temp:"]
plotLinearRegression(x_values, y_values, "Max Temp", (-50,80))
#temperature rises the closer you get to the equator
#northern hemisphere - Lat vs Humidity
x_values = north_df["Latitude:"]
y_values = north_df["Humidity:"]
plotLinearRegression(x_values, y_values, "Humidity", (45,10))
#no relationship between humidity and latitude based off the information in this plot
#southern hemisphere - Lat vs Humidity
x_values = south_df["Latitude:"]
y_values = south_df["Humidity:"]
plotLinearRegression(x_values, y_values, "Humidity", (-55,10))
#little relationship between latitude and humidity in the southern hemisphere on this day.
#northern hemisphere - Lat vs Cloudiness
x_values = north_df["Latitude:"]
y_values = north_df["Cloud Coverage:"]
plotLinearRegression(x_values, y_values, "Cloudiness (%)", (45,10))
#small decrease in reported clouds the further north you go in the Northern Hemisphere.
#southern hemisphere - Lat vs Cloudiness
x_values = south_df["Latitude:"]
y_values = south_df["Cloud Coverage:"]
plotLinearRegression(x_values, y_values, "Cloudiness (%)", (-50,70))
#increase in reported clouds the closer to equator
#northern hemisphere - Lat vs Wind Speed
x_values = north_df["Latitude:"]
y_values = north_df["Wind:"]
plotLinearRegression(x_values, y_values, "Wind Speed (%)", (45,20))
#little relationship between windspeed and latitude in the northern hemisphere
#southern hemisphere - Lat vs Wind Speed
x_values = south_df["Latitude:"]
y_values = south_df["Wind:"]
plotLinearRegression(x_values, y_values, "Wind Speed (%)", (-30,30))
#higher reported wind speed the closer to the equator within the southern hemisphere
```
|
github_jupyter
|
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import requests
import time
from config import weatherKey
from citipy import citipy
from scipy.stats import linregress
weatherAPIurl = f"http://api.openweathermap.org/data/2.5/weather?units=Imperial&APPID={weatherKey}&q="
outputPath = "./output/cities.csv"
citiesTargetTotal = 500
cityCoordinateList = []
cityUsedList = []
#generate random list of coordinates
cityLatRand = np.random.uniform(low = -90, high = 90, size = (citiesTargetTotal*3))
cityLongRand = np.random.uniform(low = -90, high = 90, size = (citiesTargetTotal*3))
cityCoordinateList = zip(cityLatRand, cityLongRand)
#associate each coordinate with nearest city
for x in cityCoordinateList:
city = citipy.nearest_city(x[0], x[1]).city_name
if city not in cityUsedList:
cityUsedList.append(city)
cityWeather = []
print("Retrieving data from openweathermap.org")
print("---------------------------------------")
recordCount = 1
setCount = 1
for index, city in enumerate(cityUsedList):
if(index % 50 == 0 and index >= 50):
recordCount = 0
setCount += 1
lookupURL = weatherAPIurl + city
print(f'Gathering Record {recordCount} of Set {setCount} |{city}')
recordCount += 1
try:
response = requests.get(lookupURL).json()
latitude = response["coord"]["lat"]
longitude = response["coord"]["lon"]
maxTemperature = response["main"]["temp_max"]
humidity = response["main"]["humidity"]
cloudCoverage = response["clouds"]["all"]
wind = response["wind"]["speed"]
country = response["sys"]["country"]
date = response["dt"]
cityWeather.append({"City:" : city,
"Latitude:" : latitude,
"Longitude:" : longitude,
"Max Temp:" : maxTemperature,
"Humidity:" : humidity,
"Cloud Coverage:" : cloudCoverage,
"Wind:" : wind,
"Country:" : country,
"Date:" : date,
})
except:
print(f'{city} not found in data set')
continue
print("---------------------------------------")
print("Data retrieval complete!")
cityWeather_df = pd.DataFrame(cityWeather)
latitude = cityWeather_df["Latitude:"]
maxTemperature = cityWeather_df["Max Temp:"]
humidity = cityWeather_df["Humidity:"]
cloudCoverage = cityWeather_df["Cloud Coverage:"]
wind = cityWeather_df["Wind:"]
cityWeather_df.to_csv(outputPath)
plt.scatter(latitude, maxTemperature, marker = "o", label = "Cities", edgecolor = "orange")
plt.title(f"City Latitude vs Highest Temperature {time.strftime('%x')}")
plt.xlabel("Latitude")
plt.ylabel("Temperature (F)")
plt.savefig("./output/Lat vs. Temp.png")
plt.show()
#it was hottest around 35 latitude and gets colder the further you get away from that latitude
plt.scatter(latitude, humidity, marker = "o", edgecolor = "pink", color = "green")
plt.title(f"City Latitude vs Humidity {time.strftime('%x')}")
plt.xlabel("Latitude")
plt.ylabel("Humidity (%)")
plt.savefig("./output/Lat vs. Humidity.png")
plt.show()
#little change in humidity with change in latitude
plt.scatter(latitude, wind, marker = "o", edgecolor = "green", color = "pink")
plt.title(f"City Latitude vs Wind Speed {time.strftime('%x')}")
plt.xlabel("Latitude")
plt.ylabel("Wind Speed (mph)")
plt.savefig("./output/Lat vs. Wind Speed.png")
plt.show()
#little change in windspeed with change in latitude
plt.scatter(latitude, cloudCoverage, marker = "o", edgecolor = "blue", color = "red")
plt.title(f"City Latitude vs Cloud Coverage {time.strftime('%x')}")
plt.xlabel("Latitude")
plt.ylabel("Cloudiness (%)")
plt.savefig("./output/Lat vs. Cloudiness.png")
plt.show()
#there were a lot of clouds just above the equator on this day
#northern and southern hemisphere dataframes
north_df = cityWeather_df.loc[(cityWeather_df["Latitude:"] >= 0)]
south_df = cityWeather_df.loc[(cityWeather_df["Latitude:"] < 0)]
def plotLinearRegression(x_values, y_values, yLabel, text_coordinates):
(slope, intercept, rvalue, pvalue, stderr) = linregress(x_values, y_values)
regress_values = x_values * slope + intercept
line_eq = "y = " + str(round(slope, 2)) + " x + " + str(round(intercept, 2))
plt.scatter(x_values, y_values)
plt.plot(x_values, regress_values, "r-")
plt.annotate(line_eq, text_coordinates, fontsize = 15, color = "red")
plt.xlabel("Latitude")
plt.ylabel(yLabel)
print(f"The r-squared is : {rvalue}")
plt.show()
#northern hemisphere - Lat vs Max Temp
x_values = north_df["Latitude:"]
y_values = north_df["Max Temp:"]
plotLinearRegression(x_values, y_values, "Max Temp", (20,40))
#the further north lower the max temp
#southern hemisphere - Lat vs Max Temp
x_values = south_df["Latitude:"]
y_values = south_df["Max Temp:"]
plotLinearRegression(x_values, y_values, "Max Temp", (-50,80))
#temperature rises the closer you get to the equator
#northern hemisphere - Lat vs Humidity
x_values = north_df["Latitude:"]
y_values = north_df["Humidity:"]
plotLinearRegression(x_values, y_values, "Humidity", (45,10))
#no relationship between humidity and latitude based off the information in this plot
#southern hemisphere - Lat vs Humidity
x_values = south_df["Latitude:"]
y_values = south_df["Humidity:"]
plotLinearRegression(x_values, y_values, "Humidity", (-55,10))
#little relationship between latitude and humidity in the southern hemisphere on this day.
#northern hemisphere - Lat vs Cloudiness
x_values = north_df["Latitude:"]
y_values = north_df["Cloud Coverage:"]
plotLinearRegression(x_values, y_values, "Cloudiness (%)", (45,10))
#small decrease in reported clouds the further north you go in the Northern Hemisphere.
#southern hemisphere - Lat vs Cloudiness
x_values = south_df["Latitude:"]
y_values = south_df["Cloud Coverage:"]
plotLinearRegression(x_values, y_values, "Cloudiness (%)", (-50,70))
#increase in reported clouds the closer to equator
#northern hemisphere - Lat vs Wind Speed
x_values = north_df["Latitude:"]
y_values = north_df["Wind:"]
plotLinearRegression(x_values, y_values, "Wind Speed (%)", (45,20))
#little relationship between windspeed and latitude in the northern hemisphere
#southern hemisphere - Lat vs Wind Speed
x_values = south_df["Latitude:"]
y_values = south_df["Wind:"]
plotLinearRegression(x_values, y_values, "Wind Speed (%)", (-30,30))
#higher reported wind speed the closer to the equator within the southern hemisphere
| 0.397588 | 0.468851 |
<a href="https://colab.research.google.com/github/mghendi/feedbackclassifier/blob/main/Feedback_and_Question_Classifier.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## CCI508 - Language Technology Project
### Name: Samuel Mwamburi Mghendi
### Admission Number: P52/37621/2020
### Email: [email protected]
### Course: Language Technology – CCI 508
#### Applying Natural Language Processing (NLP) in the Classification of Bugs, Tasks and Improvements for feedback and questions received by Software Developers.
#### This report is organised as follows.
1. Data Description
* Data Loading and Preparation
* Exploratory Data Analysis
2. Data Preprocessing and Modelling
* Data Preprocessing
* Modelling
3. Model Evaluation
4. Conclusion
### 1. Data Description
#### Data Loading and Preparation
#### Initialization
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import pymysql
import os
import datetime
```
#### Import Data from Database
```
database = pymysql.connect (host="localhost", user = "root", passwd = "password", db = "helpdesk")
cursor1 = database.cursor()
cursor1.execute("select * from issues limit 5;")
results = cursor1.fetchall()
print(results)
import pandas as pd
df = pd.read_sql_query("select * from issues limit 70;", database)
df
from sklearn import preprocessing
from nltk.corpus import stopwords
from nltk.stem.snowball import SnowballStemmer
import matplotlib
from matplotlib import pyplot as plt
```
#### Exploratory Data Analysis
```
df.describe()
df.info()
df['issue_type'].astype(str)
del df['id']
del df['created']
del df['user']
df.groupby(['issue_type']).count().plot.bar(ylim=0)
plt.show()
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
```
#### Remove StopWords from issues
```
import nltk
nltk.download('stopwords')
sw = stopwords.words('english')
def stopwords(summary):
summary = [word.lower() for word in summary.split() if word.lower() not in sw]
return " ".join(summary)
df['summary'] = df['summary'].apply(stopwords)
df
```
#### Replacing non-ASCII characters with spaces
```
from unidecode import unidecode
def remove_non_ascii(summary):
return ''.join([i if ord(i) < 128 else ' ' for i in summary])
df['summary'] = df['summary'].apply(remove_non_ascii)
df
```
#### Removing HTML tags from issues
```
def remove_html_tags(summary):
import re
clean = re.compile('<.*?>')
return re.sub(clean, '', summary)
df['summary'] = df['summary'].apply(remove_html_tags)
df
```
#### Removing punctuations from issues
```
def remove_punctuation(summary):
import string
for c in string.punctuation:
summary = summary.replace(c," ")
return summary
df['summary'] = df['summary'].apply(remove_punctuation)
df
```
#### Lowercase all issues
```
def lowercase(summary):
import string
for c in string:
summary = summary.lower(c)
return summary
```
#### Removing emoticons from issues
```
def remove_emoticons(summary):
import re
regrex_pattern = re.compile(pattern = "["
u"\U0001F600-\U0001F64F" # emoticons
u"\U0001F300-\U0001F5FF" # symbols & pictographs
u"\U0001F680-\U0001F6FF" # transport & map symbols
u"\U0001F1E0-\U0001F1FF" # flags (iOS)
"]+", flags = re.UNICODE)
return regrex_pattern.sub(r'',summary)
df['summary'] = df['summary'].apply(remove_emoticons)
df
```
### 2. Data Preprocessing and Modelling
#### Converting Text to Numerical Vector
```
import pandas as pd
import numpy as np
import nltk
import string
import math
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import SGDClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn import metrics
import re
import string
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
from nltk.stem.wordnet import WordNetLemmatizer
df["issue_type"].replace({"Bug": "0", "Task": "1", "Improvement": "2"}, inplace=True)
print(df)
df["issue_type"].value_counts(normalize= True)
```
#### Vectorize sentences
```
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer(min_df=0, lowercase=False)
vectorizer.fit(df["summary"])
vectorizer.vocabulary_
```
#### Creating a Bag of Words model
```
vectorizer.transform(df["summary"]).toarray()
```
#### Split the data into train and test sets
```
from sklearn.model_selection import train_test_split
summaries = df["summary"].values
y = df["issue_type"].values
summaries_train, summaries_test, y_train, y_test = train_test_split(summaries, y, test_size=0.25, random_state=1000)
```
#### Using the BOW model to vectorize the questions
```
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer()
vectorizer.fit(summaries_train)
X_train = vectorizer.transform(summaries_train)
X_test = vectorizer.transform(summaries_test)
X_train
```
#### The resulting feature vectors have 52 samples which are the number of training samples after the train-test split. Each sample has 172 dimensions which is the size of the vocabulary.
### 3. Model Evaluation
```
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression()
classifier.fit(X_train, y_train)
score = classifier.score(X_test, y_test)
print("Accuracy:", score)
```
### 4. Conclusion
#### Logistic regression classifies the data by considering outcome variables on extreme ends and consequently forms a line to distinguish them.
#### This algorithm provides great efficiency, works well in the segmentation and categorization of a small number of categorical variables.
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import pymysql
import os
import datetime
database = pymysql.connect (host="localhost", user = "root", passwd = "password", db = "helpdesk")
cursor1 = database.cursor()
cursor1.execute("select * from issues limit 5;")
results = cursor1.fetchall()
print(results)
import pandas as pd
df = pd.read_sql_query("select * from issues limit 70;", database)
df
from sklearn import preprocessing
from nltk.corpus import stopwords
from nltk.stem.snowball import SnowballStemmer
import matplotlib
from matplotlib import pyplot as plt
df.describe()
df.info()
df['issue_type'].astype(str)
del df['id']
del df['created']
del df['user']
df.groupby(['issue_type']).count().plot.bar(ylim=0)
plt.show()
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import nltk
nltk.download('stopwords')
sw = stopwords.words('english')
def stopwords(summary):
summary = [word.lower() for word in summary.split() if word.lower() not in sw]
return " ".join(summary)
df['summary'] = df['summary'].apply(stopwords)
df
from unidecode import unidecode
def remove_non_ascii(summary):
return ''.join([i if ord(i) < 128 else ' ' for i in summary])
df['summary'] = df['summary'].apply(remove_non_ascii)
df
def remove_html_tags(summary):
import re
clean = re.compile('<.*?>')
return re.sub(clean, '', summary)
df['summary'] = df['summary'].apply(remove_html_tags)
df
def remove_punctuation(summary):
import string
for c in string.punctuation:
summary = summary.replace(c," ")
return summary
df['summary'] = df['summary'].apply(remove_punctuation)
df
def lowercase(summary):
import string
for c in string:
summary = summary.lower(c)
return summary
def remove_emoticons(summary):
import re
regrex_pattern = re.compile(pattern = "["
u"\U0001F600-\U0001F64F" # emoticons
u"\U0001F300-\U0001F5FF" # symbols & pictographs
u"\U0001F680-\U0001F6FF" # transport & map symbols
u"\U0001F1E0-\U0001F1FF" # flags (iOS)
"]+", flags = re.UNICODE)
return regrex_pattern.sub(r'',summary)
df['summary'] = df['summary'].apply(remove_emoticons)
df
import pandas as pd
import numpy as np
import nltk
import string
import math
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import SGDClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn import metrics
import re
import string
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
from nltk.stem.wordnet import WordNetLemmatizer
df["issue_type"].replace({"Bug": "0", "Task": "1", "Improvement": "2"}, inplace=True)
print(df)
df["issue_type"].value_counts(normalize= True)
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer(min_df=0, lowercase=False)
vectorizer.fit(df["summary"])
vectorizer.vocabulary_
vectorizer.transform(df["summary"]).toarray()
from sklearn.model_selection import train_test_split
summaries = df["summary"].values
y = df["issue_type"].values
summaries_train, summaries_test, y_train, y_test = train_test_split(summaries, y, test_size=0.25, random_state=1000)
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer()
vectorizer.fit(summaries_train)
X_train = vectorizer.transform(summaries_train)
X_test = vectorizer.transform(summaries_test)
X_train
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression()
classifier.fit(X_train, y_train)
score = classifier.score(X_test, y_test)
print("Accuracy:", score)
| 0.422981 | 0.861247 |
# Project : Advanced Lane Finding
The Goal of this Project
In this project, your goal is to write a software pipeline to identify the lane boundaries in a video from a front-facing camera on a car. The camera calibration images, test road images, and project videos are available in the project repository.
### The goals / steps of this project are the following:
- Compute the camera calibration matrix and distortion coefficients given a set of chessboard images.
- Apply a distortion correction to raw images.
- Use color transforms, gradients, etc., to create a thresholded binary image.
- Apply a perspective transform to rectify binary image ("birds-eye view").
- Detect lane pixels and fit to find the lane boundary.
- Determine the curvature of the lane and vehicle position with respect to center.
- Warp the detected lane boundaries back onto the original image.
- Output visual display of the lane boundaries and numerical estimation of lane curvature and vehicle position.
The images for camera calibration are stored in the folder called camera_cal. The images in test_images are for testing your pipeline on single frames. If you want to extract more test images from the videos, you can simply use an image writing method like cv2.imwrite(), i.e., you can read the video in frame by frame as usual, and for frames you want to save for later you can write to an image file.
To help the reviewer examine your work, please save examples of the output from each stage of your pipeline in the folder called output_images, and include a description in your writeup for the project of what each image shows. The video called project_video.mp4 is the video your pipeline should work well on.
The challenge_video.mp4 video is an extra (and optional) challenge for you if you want to test your pipeline under somewhat trickier conditions. The harder_challenge.mp4 video is another optional challenge and is brutal!
If you're feeling ambitious (again, totally optional though), don't stop there! We encourage you to go out and take video of your own, calibrate your camera and show us how you would implement this project from scratch!
## Import Packages
```
#importing packages
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import numpy as np
import cv2
import os
import collections as clx
from moviepy.editor import VideoFileClip
from IPython.display import HTML
%matplotlib inline
#%config InlineBackend.figure_format = 'retina'
```
## Configurations
```
# configurations Start
cameracal = "camera_cal/"
outputimages = "output_images/"
outputvideos = "output_videos/"
testimages = "test_images/"
testvideos = "test_videos/"
```
## The Camera Calibration
```
# prepare object points
nx = 9 #the number of inside corners in x
ny = 6 #the number of inside corners in y
def getchess(filepath=""):
# Preparing object points
objp = np.zeros((nx * ny, 3), np.float32)
objp[:,:2] = np.mgrid[0:nx, 0:ny].T.reshape(-1, 2)
objpoints = []
imgpoints = []
chessimgs = []
images = []
for filename in images:
img = plt.imread(filename)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, corners = cv2.findChessboardCorners(gray, (nx, ny), None)
if ret == True:
objpoints.append(objp)
imgpoints.append(corners)
chessimgs.append(cv2.drawChessboardCorners(img, (nx, ny), corners, ret))
return objpoints, imgpoints, chessimgs
imagePathList = [x for x in os.listdir("camera_cal") if x.endswith(".jpg")]
print(imagePathList)
```
|
github_jupyter
|
#importing packages
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import numpy as np
import cv2
import os
import collections as clx
from moviepy.editor import VideoFileClip
from IPython.display import HTML
%matplotlib inline
#%config InlineBackend.figure_format = 'retina'
# configurations Start
cameracal = "camera_cal/"
outputimages = "output_images/"
outputvideos = "output_videos/"
testimages = "test_images/"
testvideos = "test_videos/"
# prepare object points
nx = 9 #the number of inside corners in x
ny = 6 #the number of inside corners in y
def getchess(filepath=""):
# Preparing object points
objp = np.zeros((nx * ny, 3), np.float32)
objp[:,:2] = np.mgrid[0:nx, 0:ny].T.reshape(-1, 2)
objpoints = []
imgpoints = []
chessimgs = []
images = []
for filename in images:
img = plt.imread(filename)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, corners = cv2.findChessboardCorners(gray, (nx, ny), None)
if ret == True:
objpoints.append(objp)
imgpoints.append(corners)
chessimgs.append(cv2.drawChessboardCorners(img, (nx, ny), corners, ret))
return objpoints, imgpoints, chessimgs
imagePathList = [x for x in os.listdir("camera_cal") if x.endswith(".jpg")]
print(imagePathList)
| 0.247351 | 0.987424 |
# VacationPy
----
#### Note
* Keep an eye on your API usage. Use https://developers.google.com/maps/reporting/gmp-reporting as reference for how to monitor your usage and billing.
* Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.
```
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import gmaps
import os
# Import API key
from api_keys import g_key
```
### Store Part I results into DataFrame
* Load the csv exported in Part I to a DataFrame
```
city_data_df = pd.read_csv("output_data/cities.csv")
city_data_df.head()
```
### Humidity Heatmap
* Configure gmaps.
* Use the Lat and Lng as locations and Humidity as the weight.
* Add Heatmap layer to map.
```
#configure gmaps
gmaps.configure(api_key=g_key)
#Heamap of humidity
locations = city_data_df[["Lat", "Lng"]]
humidity = city_data_df["Humidity"]
fig = gmaps.figure()
heat_layer = gmaps.heatmap_layer(locations, weights=humidity, dissipating=False, max_intensity=300, point_radius=5)
fig.add_layer(heat_layer)
fig
```
### Create new DataFrame fitting weather criteria
* Narrow down the cities to fit weather conditions.
* Drop any rows will null values.
```
#Narrowing down cities that fit criteria and drop any results with null values
narrowed_city_df = city_data_df.loc[(city_data_df["Max Temp"] < 80) & (city_data_df["Max Temp"] > 70)\
& (city_data_df["Wind Speed"] < 10)\
& (city_data_df["Cloudiness"] == 0)].dropna()
narrowed_city_df
```
### Hotel Map
* Store into variable named `hotel_df`.
* Add a "Hotel Name" column to the DataFrame.
* Set parameters to search for hotels with 5000 meters.
* Hit the Google Places API for each city's coordinates.
* Store the first Hotel result into the DataFrame.
* Plot markers on top of the heatmap.
```
#Create a Dataframe called hotel_df to store hotel name along with city
hotel_df = narrowed_city_df[["City", "Country", "Lat", "Lng"]].copy()
hotel_df["Hotel Name"]=""
hotel_df
params={
"radius": 5000,
"types": "lodging",
"key": g_key
}
for index, row in hotel_df.iterrows():
#get lat and lng
lat = row["Lat"]
lng = row["Lng"]
params["location"] = f"{lat},{lng}"
#use the search term: hotel and out lat/lng
base_url = "https://maps.googleapis.com/maps/api/place/nearbysearch/json"
name_address = requests.get(base_url, params=params).json()
try:
hotel_df.loc[index, "Hotel Name"] = name_address["results"][0]["name"]
except(KeyError, IndexError):
print("Missing field/result...skipping")
hotel_df
# NOTE: Do not change any of the code in this cell
# Using the template add the hotel marks to the heatmap
info_box_template = """
<dl>
<dt>Name</dt><dd>{Hotel Name}</dd>
<dt>City</dt><dd>{City}</dd>
<dt>Country</dt><dd>{Country}</dd>
</dl>
"""
# Store the DataFrame Row
# NOTE: be sure to update with your DataFrame name
hotel_info = [info_box_template.format(**row) for index, row in hotel_df.iterrows()]
locations = hotel_df[["Lat", "Lng"]]
# Add marker layer ontop of heat map
marker_layer = gmaps.marker_layer(locations, info_box_content=hotel_info)
fig.add_layer(marker_layer)
# Display figure
fig
```
|
github_jupyter
|
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import gmaps
import os
# Import API key
from api_keys import g_key
city_data_df = pd.read_csv("output_data/cities.csv")
city_data_df.head()
#configure gmaps
gmaps.configure(api_key=g_key)
#Heamap of humidity
locations = city_data_df[["Lat", "Lng"]]
humidity = city_data_df["Humidity"]
fig = gmaps.figure()
heat_layer = gmaps.heatmap_layer(locations, weights=humidity, dissipating=False, max_intensity=300, point_radius=5)
fig.add_layer(heat_layer)
fig
#Narrowing down cities that fit criteria and drop any results with null values
narrowed_city_df = city_data_df.loc[(city_data_df["Max Temp"] < 80) & (city_data_df["Max Temp"] > 70)\
& (city_data_df["Wind Speed"] < 10)\
& (city_data_df["Cloudiness"] == 0)].dropna()
narrowed_city_df
#Create a Dataframe called hotel_df to store hotel name along with city
hotel_df = narrowed_city_df[["City", "Country", "Lat", "Lng"]].copy()
hotel_df["Hotel Name"]=""
hotel_df
params={
"radius": 5000,
"types": "lodging",
"key": g_key
}
for index, row in hotel_df.iterrows():
#get lat and lng
lat = row["Lat"]
lng = row["Lng"]
params["location"] = f"{lat},{lng}"
#use the search term: hotel and out lat/lng
base_url = "https://maps.googleapis.com/maps/api/place/nearbysearch/json"
name_address = requests.get(base_url, params=params).json()
try:
hotel_df.loc[index, "Hotel Name"] = name_address["results"][0]["name"]
except(KeyError, IndexError):
print("Missing field/result...skipping")
hotel_df
# NOTE: Do not change any of the code in this cell
# Using the template add the hotel marks to the heatmap
info_box_template = """
<dl>
<dt>Name</dt><dd>{Hotel Name}</dd>
<dt>City</dt><dd>{City}</dd>
<dt>Country</dt><dd>{Country}</dd>
</dl>
"""
# Store the DataFrame Row
# NOTE: be sure to update with your DataFrame name
hotel_info = [info_box_template.format(**row) for index, row in hotel_df.iterrows()]
locations = hotel_df[["Lat", "Lng"]]
# Add marker layer ontop of heat map
marker_layer = gmaps.marker_layer(locations, info_box_content=hotel_info)
fig.add_layer(marker_layer)
# Display figure
fig
| 0.367043 | 0.858896 |
<center>
<img src="images/meme.png">
</center>
# Машинное обучение
> Компьютерная программа обучается на основе опыта $E$ по отношению к некоторому классу задач $T$ и меры качества $P$, если качество решения задач из $T$, измеренное на основе $P$, улучшается с приобретением опыта $E$. (Т. М. Митчелл)
### Формулировка задачи:
$X$ $-$ множество объектов
$Y$ $-$ множество меток классов
$f: X \rightarrow Y$ $-$ неизвестная зависимость
**Дано**:
$x_1, \dots, x_n \subset X$ $-$ обучающая выборка
$y_i = f(x_i), i=1, \dots n$ $-$ известные метки классов
**Найти**:
$a∶ X \rightarrow Y$ $-$ алгоритм, решающую функцию, приближающую $f$ на всём множестве $X$.
```
!conda install -c intel scikit-learn -y
import numpy
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
import warnings
warnings.simplefilter('ignore')
numpy.random.seed(7)
%matplotlib inline
iris = load_iris()
X = iris.data
Y = iris.target
print(X.shape)
random_sample = numpy.random.choice(X.shape[0], 10)
for i in random_sample:
print(f"{X[i]}: {iris.target_names[Y[i]]}")
```
## Типы задач
### Задача классификации
$Y = \{ -1, +1 \}$ $-$ классификация на 2 класса;
$Y = \{1, \dots , K \}$ $-$ на $K$ непересекающихся классов;
$Y = \{0, 1 \}^K$ $-$ на $K$ классов, которые могут пересекаться.
Примеры: распознавание текста по рукописному вводу, определение предмета на фотографии.
### Задача регрессии
$Y = \mathbb{R}$ или $Y = \mathbb{R}^k$.
Примеры: предсказание стоимости акции через полгода, предсказание прибыли магазина в следующем месяце.
### Задача ранжирования
$Y$ $-$ конечное упорядоченное множество.
Пример: выдача поискового запроса.
### Задачи уменьшения размерности
Научиться описывать данные не $M$ признаками, а меньшим числом для повышения точности модели или последующей визуализации. В качестве примера помимо необходимости для визуализации можно привести сжатие данных.
### Задачи кластеризации
Разбиение данных множества объектов на подмножества (кластеры) таким образом, чтобы объекты из одного кластера были более похожи друг на друга, чем на объекты из других кластеров по какому-либо критерию.
<center>
<img src="images/ml_map.png">
</center>
```
from sklearn.svm import SVC
model = SVC(random_state=7)
model.fit(X, Y)
y_pred = model.predict(X)
for i in random_sample:
print(f"predicted: {iris.target_names[y_pred[i]]}, actual: {iris.target_names[Y[i]]}")
f"differences in {(Y != y_pred).sum()} samples"
```
# Оценка качества
## Метрика
### Задача классификации
Определим матрицу ошибок. Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов, тогда матрица ошибок классификации будет выглядеть следующим образом:
| $ $ | $y=1$ | $y=0$ |
|-------------|---------------------|---------------------|
| $\hat{y}=1$ | True Positive (TP) | False Positive (FP) |
| $\hat{y}=0$ | False Negative (FN) | True Negative (TN) |
Здесь $\hat{y}$ $-$ это ответ алгоритма на объекте, а $y$ $-$ истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: *False Negative (FN)* и *False Positive (FP)*.
- $\textit{accuracy} = \frac{TP + TN}{TP + FP + FN + TN}$
- $\textit{recall} = \frac{TP}{TP + FN}$
- $\textit{precision} = \frac{TP}{TP + FP}$
- $\textit{f1-score} = \frac{2 \cdot \textit{recall} \cdot \textit{precision}}{\textit{precision} + \textit{recall}}$
### Задача регрессии
- $MSE = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2$
- $RMSE = \sqrt{MSE}$
- $MAE = \frac{1}{n} \sum_{i=1}^n |y_i - \hat{y}_i|$
## Отложенная выборка
$X \rightarrow X_{train}, X_{val}, X_{test}$
- $X_{train}$ $-$ используется для обучения модели
- $X_{val}$ $-$ подбор гиперпараметров ($ \approx{30\%}$ от тренировочной части)
- $X_{test}$ $-$ оценка качества конечной модели
```
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, f1_score
# 1/3 всего датасета возьмём для тестовой выборки
# затем 30% от тренировочной будет валидационной
test_index = numpy.random.choice(X.shape[0], X.shape[0] // 3)
train_index = [i for i in range(X.shape[0]) if i not in test_index]
X_test = X[test_index]
Y_test = Y[test_index]
X_train, X_val, Y_train, Y_val = train_test_split(X[train_index], Y[train_index], test_size=0.3, shuffle=True, random_state=7)
print(f"train size: {X_train.shape[0]}")
print(f"val size: {X_val.shape[0]}")
print(f"test size: {X_test.shape[0]}")
best_score = -1
best_c = None
for c in [0.01, 0.1, 1, 10]:
model = SVC(C=c, random_state=7)
model.fit(X_train, Y_train)
y_pred = model.predict(X_val)
cur_score = f1_score(Y_val, y_pred, average='micro')
if cur_score > best_score:
best_score = cur_score
best_c = c
f"best score is {best_score} for C {best_c}"
full_model = SVC(C=1.0, random_state=7)
full_model.fit(X[train_index], Y[train_index])
y_pred = full_model.predict(X_test)
f"test score is {f1_score(Y_test, y_pred, average='micro')}"
```
# Алгоритмы классификации
## Линейный классификатор
Построение разделяющей гиперплоскости
$$
y = \textit{sign}(Wx + b)
$$
<center>
<img src="images/linear_classifier.png">
</center>
### Стандартизация величин
При использование линейных моделей, иногда полезно стандартизировать их значения, например, оценки пользователей.
$$
X_{stand} = \frac{X - X_{mean}}{X_{std}}
$$
Для этого в `sklearn` есть класс $-$ `StandartScaler`
### Логистическая регрессия
Использование функции логита для получения вероятности
<center>
<img src="images/logit.png">
</center>
## Метод опорных векторов (Support vector machine)
Построение "полоски" максимальной ширины, которая разделяет выборку
<center>
<img src="images/svm.png">
</center>
## Дерево решений (Decision tree)
В каждой вершине определяется критерий, по которому разбивается подвыборка.
<center>
<img src="images/decision_tree.png">
</center>
## Случайный лес (Random forest)
Множество деревьев решений, каждое из которых обучается на случайной подвыборке.
<center>
<img src="images/random_forest.png">
</center>
## Метод ближайших соседей (K-neighbors)
Решение базируется на основе $k$ ближайших известных примеров.
<center>
<img src="images/knn.png">
</center>
```
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=1000, n_features=50, n_informative=20)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, shuffle=True, random_state=7)
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
models = [
LogisticRegression(random_state=7, n_jobs=6),
SVC(random_state=7),
DecisionTreeClassifier(random_state=7),
RandomForestClassifier(random_state=7),
KNeighborsClassifier(n_jobs=6)
]
for model in models:
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print(f"model {model.__class__.__name__} scores {round(f1_score(y_test, y_pred, average='micro'), 2)}")
from sklearn.preprocessing import StandardScaler
standart_scaler = StandardScaler()
standart_scaler.fit(X_train)
X_train_scaled = standart_scaler.transform(X_train)
X_test_scaled = standart_scaler.transform(X_test)
model = SVC(random_state=7)
model.fit(X_train_scaled, y_train)
y_pred = model.predict(X_test_scaled)
f"test score is {f1_score(y_test, y_pred, average='micro')}"
```
# Inclass task #1
Реализуйте модель, которая классифицирует цифры по рисунку.
Ваша задача получить f1-score $0.98$ на тестовом датасете.
Можете пользоваться как алгоритмами выше, так и любыми другими реализованными в `sklearn`.
```
from sklearn.datasets import fetch_openml
# Load data from https://www.openml.org/d/554
X, Y = fetch_openml('mnist_784', return_X_y=True)
print(f"shape of X is {X.shape}")
plt.gray()
fig, axes = plt.subplots(2, 5, figsize=(15, 5))
for i, num in enumerate(numpy.random.choice(X.shape[0], 10)):
axes[i // 5, i % 5].matshow(X[num].reshape(28, 28))
axes[i // 5, i % 5].set_title(Y[num])
axes[i // 5, i % 5].axis('off')
plt.show()
test_shuffle = numpy.random.permutation(X.shape[0])
X_test, X_train = X[test_shuffle[:10000]], X[test_shuffle[10000:]]
Y_test, Y_train = Y[test_shuffle[:10000]], Y[test_shuffle[10000:]]
print(f"train size: {X_train.shape[0]}")
print(f"test size: {X_test.shape[0]}")
model = SVC(random_state=5)
model.fit(X_train, Y_train)
y_pred = model.predict(X_test)
print(f"test score is {f1_score(Y_test, y_pred, average='micro')}")
# test score is 0.9810000000000001
```
# Алгоритмы регрессии
Деревья решений, случайный лес и метод ближайших соседей легко обобщаются на случай регрессии. Ответ, как правило, это среднее из полученных значений (например, среднее значение ближайших примеров).
## Линейная регрессия
$y$ линейно зависим от $x$, т.е. имеет место уравнение
$$
y = Wx + b = W <x; 1>
$$
Такой подход имеет аналитическое решение, однако он требует вычисление обратной матрицы $X$, что не всегда возможно.
Другой подход $-$ минимизация функции ошибки, например $MSE$, с помощью техники градиентного спуска.
## Регуляризация
Чтобы избегать переобучения (когда модель хорошо работает только на тренировочных данных) используют различные техники *регуляризации*.
Один из признаков переобучения $-$ модель имеет большие веса, это можно контролировать путём добавления $L1$ или $L2$ нормы весов к функции ошибки.
То есть, итоговая ошибка, которая будет распространятся на веса модели, считается по формуле:
$$
Error(W) = MSE(W, X, y) + \lambda ||W||
$$
Такие модели, так же реализованы в `sklearn`:
- Lasso
- Ridge
```
from sklearn.datasets import load_boston
X, y = load_boston(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, shuffle=True, random_state=7)
from sklearn.linear_model import Lasso, Ridge, LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.svm import SVR
from sklearn.metrics import mean_squared_error
models = [
Lasso(random_state=7),
Ridge(random_state=7),
LinearRegression(n_jobs=6),
RandomForestRegressor(random_state=7, n_jobs=6),
KNeighborsRegressor(n_jobs=6),
SVR()
]
for model in models:
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print(f"model {model.__class__.__name__} scores {round(mean_squared_error(y_test, y_pred), 2)}")
```
# Inclass task #2
Реализуйте модель, которая предсказывает стоимость медицинской страховки. В данных есть текстовые бинарные признаки (`sex` и `smoker`), не забудьте конвертировать их в `0` и `1`. Признак `region` имеет $4$ разных значения, вы можете конвертировать их в числа $0-4$ или создать $4$ бинарных признака. Для этого вам может помочь `sklearn.preprocessing.LabelEncoder` и `pandas.get_dummies`.
Ваша задача получить RMSE-score меньше $5000$ на тестовом датасете.
Можете пользоваться как алгоритмами выше, так и любыми другими реализованными в `sklearn`.
```
def rmse(y_true, y_pred):
return numpy.sqrt(mean_squared_error(y_true, y_pred))
!conda install pandas -y
import pandas
from sklearn import preprocessing
data = pandas.read_csv('data/insurance.csv')
le = preprocessing.LabelEncoder()
data['sex'] = preprocessing.LabelEncoder().fit_transform(data['sex'])
data['smoker'] = preprocessing.LabelEncoder().fit_transform(data['smoker'])
data['region'] = preprocessing.LabelEncoder().fit_transform(data['region'])
data.head()
X = data.drop(['charges'], axis=1)
y = data['charges'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, shuffle=True, random_state=7)
print(f"train size: {X_train.shape[0]}")
print(f"test size: {X_test.shape[0]}")
model = RandomForestRegressor(random_state=5, n_jobs=6)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print(f"test score is {rmse(y_test, y_pred)}")
# test score is 4939.426892574252
```
|
github_jupyter
|
!conda install -c intel scikit-learn -y
import numpy
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
import warnings
warnings.simplefilter('ignore')
numpy.random.seed(7)
%matplotlib inline
iris = load_iris()
X = iris.data
Y = iris.target
print(X.shape)
random_sample = numpy.random.choice(X.shape[0], 10)
for i in random_sample:
print(f"{X[i]}: {iris.target_names[Y[i]]}")
from sklearn.svm import SVC
model = SVC(random_state=7)
model.fit(X, Y)
y_pred = model.predict(X)
for i in random_sample:
print(f"predicted: {iris.target_names[y_pred[i]]}, actual: {iris.target_names[Y[i]]}")
f"differences in {(Y != y_pred).sum()} samples"
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, f1_score
# 1/3 всего датасета возьмём для тестовой выборки
# затем 30% от тренировочной будет валидационной
test_index = numpy.random.choice(X.shape[0], X.shape[0] // 3)
train_index = [i for i in range(X.shape[0]) if i not in test_index]
X_test = X[test_index]
Y_test = Y[test_index]
X_train, X_val, Y_train, Y_val = train_test_split(X[train_index], Y[train_index], test_size=0.3, shuffle=True, random_state=7)
print(f"train size: {X_train.shape[0]}")
print(f"val size: {X_val.shape[0]}")
print(f"test size: {X_test.shape[0]}")
best_score = -1
best_c = None
for c in [0.01, 0.1, 1, 10]:
model = SVC(C=c, random_state=7)
model.fit(X_train, Y_train)
y_pred = model.predict(X_val)
cur_score = f1_score(Y_val, y_pred, average='micro')
if cur_score > best_score:
best_score = cur_score
best_c = c
f"best score is {best_score} for C {best_c}"
full_model = SVC(C=1.0, random_state=7)
full_model.fit(X[train_index], Y[train_index])
y_pred = full_model.predict(X_test)
f"test score is {f1_score(Y_test, y_pred, average='micro')}"
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=1000, n_features=50, n_informative=20)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, shuffle=True, random_state=7)
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
models = [
LogisticRegression(random_state=7, n_jobs=6),
SVC(random_state=7),
DecisionTreeClassifier(random_state=7),
RandomForestClassifier(random_state=7),
KNeighborsClassifier(n_jobs=6)
]
for model in models:
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print(f"model {model.__class__.__name__} scores {round(f1_score(y_test, y_pred, average='micro'), 2)}")
from sklearn.preprocessing import StandardScaler
standart_scaler = StandardScaler()
standart_scaler.fit(X_train)
X_train_scaled = standart_scaler.transform(X_train)
X_test_scaled = standart_scaler.transform(X_test)
model = SVC(random_state=7)
model.fit(X_train_scaled, y_train)
y_pred = model.predict(X_test_scaled)
f"test score is {f1_score(y_test, y_pred, average='micro')}"
from sklearn.datasets import fetch_openml
# Load data from https://www.openml.org/d/554
X, Y = fetch_openml('mnist_784', return_X_y=True)
print(f"shape of X is {X.shape}")
plt.gray()
fig, axes = plt.subplots(2, 5, figsize=(15, 5))
for i, num in enumerate(numpy.random.choice(X.shape[0], 10)):
axes[i // 5, i % 5].matshow(X[num].reshape(28, 28))
axes[i // 5, i % 5].set_title(Y[num])
axes[i // 5, i % 5].axis('off')
plt.show()
test_shuffle = numpy.random.permutation(X.shape[0])
X_test, X_train = X[test_shuffle[:10000]], X[test_shuffle[10000:]]
Y_test, Y_train = Y[test_shuffle[:10000]], Y[test_shuffle[10000:]]
print(f"train size: {X_train.shape[0]}")
print(f"test size: {X_test.shape[0]}")
model = SVC(random_state=5)
model.fit(X_train, Y_train)
y_pred = model.predict(X_test)
print(f"test score is {f1_score(Y_test, y_pred, average='micro')}")
# test score is 0.9810000000000001
from sklearn.datasets import load_boston
X, y = load_boston(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, shuffle=True, random_state=7)
from sklearn.linear_model import Lasso, Ridge, LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.svm import SVR
from sklearn.metrics import mean_squared_error
models = [
Lasso(random_state=7),
Ridge(random_state=7),
LinearRegression(n_jobs=6),
RandomForestRegressor(random_state=7, n_jobs=6),
KNeighborsRegressor(n_jobs=6),
SVR()
]
for model in models:
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print(f"model {model.__class__.__name__} scores {round(mean_squared_error(y_test, y_pred), 2)}")
def rmse(y_true, y_pred):
return numpy.sqrt(mean_squared_error(y_true, y_pred))
!conda install pandas -y
import pandas
from sklearn import preprocessing
data = pandas.read_csv('data/insurance.csv')
le = preprocessing.LabelEncoder()
data['sex'] = preprocessing.LabelEncoder().fit_transform(data['sex'])
data['smoker'] = preprocessing.LabelEncoder().fit_transform(data['smoker'])
data['region'] = preprocessing.LabelEncoder().fit_transform(data['region'])
data.head()
X = data.drop(['charges'], axis=1)
y = data['charges'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, shuffle=True, random_state=7)
print(f"train size: {X_train.shape[0]}")
print(f"test size: {X_test.shape[0]}")
model = RandomForestRegressor(random_state=5, n_jobs=6)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print(f"test score is {rmse(y_test, y_pred)}")
# test score is 4939.426892574252
| 0.501709 | 0.954095 |
```
import numpy as np
import matplotlib.pyplot as pl
import pickle5 as pickle
rad_ratio = 7.860 / 9.449
temp_ratio = 315 / 95
scale = rad_ratio * temp_ratio
output_dir = '/Users/tgordon/research/exomoons_jwst/JexoSim/output/'
filename = 'OOT_SNR_NIRSpec_BOTS_PRISM_Kepler-1513 b_2020_11_23_2232_57.pickle'
result = pickle.load(open(output_dir + filename, 'rb'))
result['noise_dic']['All noise']['fracNoT14_mean'] * np.sqrt(2)
#std = result['noise_dic']['All noise']['signal_std_mean'] / result['noise_dic']['All noise']['signal_mean_mean']
wl = result['noise_dic']['All noise']['wl']
inwl = result['input_spec_wl']
inspec = result['input_spec']
inspec_interp = np.interp(wl, inwl.value, inspec.value)
saturn = np.loadtxt('../data/saturn.txt', skiprows=13)
saturn_interp = np.interp(wl, saturn[:, 0], saturn[:, 1])
dense_wl = np.linspace(wl[0], wl[-1], 1000)
saturn_smooth_interp = np.interp(dense_wl, saturn[:, 0], saturn[:, 1])
spec = (saturn_interp - np.mean(saturn_interp)) * scale + (0.08 ** 2)
smooth_spec = (saturn_smooth_interp - np.mean(saturn_interp)) * scale + (0.08 ** 2)
pl.figure(figsize=(10, 6))
pl.plot(dense_wl, smooth_spec, 'k')
rand_spec = np.random.randn(len(spec)) * onesig*1e-6 + spec
pl.errorbar(wl, rand_spec, yerr=onesig*1e-6, fmt='ro')
pl.ylim(0.0061, 0.0067)
pl.xlim(0.9, 5.5)
pl.annotate(r'$\mathrm{CH}_4$', xy=(1.0, 0.00653), xycoords='data', fontsize=15, bbox=dict(fc="white", lw=0.5, pad=5))
pl.annotate(r'$\mathrm{CH}_4$', xy=(1.3, 0.0065), xycoords='data', fontsize=15, bbox=dict(fc="white", lw=0.5, pad=5))
pl.annotate(r'$\mathrm{CH}_4$', xy=(1.7, 0.0065), xycoords='data', fontsize=15, bbox=dict(fc="white", lw=0.5, pad=5))
pl.annotate(r'$\mathrm{CH}_4$', xy=(2.2, 0.00655), xycoords='data', fontsize=15, bbox=dict(fc="white", lw=0.5, pad=5))
#pl.annotate(r'$\mathrm{CH}_4$', xy=(3.0, 0.0066), xycoords='data', fontsize=15, bbox=dict(fc="white", lw=0.5, pad=5))
pl.annotate(r'$\mathrm{C}_2\mathrm{H}_6$ + unknown hydrocarbon', xy=(3.0, 0.00665), xycoords='data', fontsize=15, bbox=dict(fc="white", lw=0.5, pad=5))
pl.ylabel('transit depth', fontsize=20)
pl.xlabel(r'$\mu$m', fontsize=20)
pl.xticks(fontsize=12)
pl.yticks(fontsize=12)
pl.savefig('/Users/tgordon/Desktop/saturn_spec_scaled.pdf')
pl.figure(figsize=(10, 8))
pl.plot(dense_wl, smooth_spec, 'k')
rand_spec = np.random.randn(len(spec)) * onesig*1e-6 + spec
pl.errorbar(wl, rand_spec, yerr=onesig*1e-6, fmt='ro')
pl.ylim(0.0062, 0.0066)
pl.xlim(0.9, 2)
pl.savefig('/Users/tgordon/Desktop/saturn_spec_scaled_zoomed.pdf')
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as pl
import pickle5 as pickle
rad_ratio = 7.860 / 9.449
temp_ratio = 315 / 95
scale = rad_ratio * temp_ratio
output_dir = '/Users/tgordon/research/exomoons_jwst/JexoSim/output/'
filename = 'OOT_SNR_NIRSpec_BOTS_PRISM_Kepler-1513 b_2020_11_23_2232_57.pickle'
result = pickle.load(open(output_dir + filename, 'rb'))
result['noise_dic']['All noise']['fracNoT14_mean'] * np.sqrt(2)
#std = result['noise_dic']['All noise']['signal_std_mean'] / result['noise_dic']['All noise']['signal_mean_mean']
wl = result['noise_dic']['All noise']['wl']
inwl = result['input_spec_wl']
inspec = result['input_spec']
inspec_interp = np.interp(wl, inwl.value, inspec.value)
saturn = np.loadtxt('../data/saturn.txt', skiprows=13)
saturn_interp = np.interp(wl, saturn[:, 0], saturn[:, 1])
dense_wl = np.linspace(wl[0], wl[-1], 1000)
saturn_smooth_interp = np.interp(dense_wl, saturn[:, 0], saturn[:, 1])
spec = (saturn_interp - np.mean(saturn_interp)) * scale + (0.08 ** 2)
smooth_spec = (saturn_smooth_interp - np.mean(saturn_interp)) * scale + (0.08 ** 2)
pl.figure(figsize=(10, 6))
pl.plot(dense_wl, smooth_spec, 'k')
rand_spec = np.random.randn(len(spec)) * onesig*1e-6 + spec
pl.errorbar(wl, rand_spec, yerr=onesig*1e-6, fmt='ro')
pl.ylim(0.0061, 0.0067)
pl.xlim(0.9, 5.5)
pl.annotate(r'$\mathrm{CH}_4$', xy=(1.0, 0.00653), xycoords='data', fontsize=15, bbox=dict(fc="white", lw=0.5, pad=5))
pl.annotate(r'$\mathrm{CH}_4$', xy=(1.3, 0.0065), xycoords='data', fontsize=15, bbox=dict(fc="white", lw=0.5, pad=5))
pl.annotate(r'$\mathrm{CH}_4$', xy=(1.7, 0.0065), xycoords='data', fontsize=15, bbox=dict(fc="white", lw=0.5, pad=5))
pl.annotate(r'$\mathrm{CH}_4$', xy=(2.2, 0.00655), xycoords='data', fontsize=15, bbox=dict(fc="white", lw=0.5, pad=5))
#pl.annotate(r'$\mathrm{CH}_4$', xy=(3.0, 0.0066), xycoords='data', fontsize=15, bbox=dict(fc="white", lw=0.5, pad=5))
pl.annotate(r'$\mathrm{C}_2\mathrm{H}_6$ + unknown hydrocarbon', xy=(3.0, 0.00665), xycoords='data', fontsize=15, bbox=dict(fc="white", lw=0.5, pad=5))
pl.ylabel('transit depth', fontsize=20)
pl.xlabel(r'$\mu$m', fontsize=20)
pl.xticks(fontsize=12)
pl.yticks(fontsize=12)
pl.savefig('/Users/tgordon/Desktop/saturn_spec_scaled.pdf')
pl.figure(figsize=(10, 8))
pl.plot(dense_wl, smooth_spec, 'k')
rand_spec = np.random.randn(len(spec)) * onesig*1e-6 + spec
pl.errorbar(wl, rand_spec, yerr=onesig*1e-6, fmt='ro')
pl.ylim(0.0062, 0.0066)
pl.xlim(0.9, 2)
pl.savefig('/Users/tgordon/Desktop/saturn_spec_scaled_zoomed.pdf')
| 0.261991 | 0.404507 |
```
#VOTING
import nltk
import random
from nltk.corpus import movie_reviews
from nltk.classify import ClassifierI
from statistics import mode
from nltk.tokenize import word_tokenize
import pickle
class VoteClassifier(ClassifierI):
def __init__(self, *classifiers):
self._classifiers = classifiers
def classify(self,features):
votes=[]
for c in self._classifiers:
v=c.classify(features)
votes.append(v)
return mode(votes)
def confidence(self,features):
votes=[]
for c in self._classifiers:
v=c.classify(features)
votes.append(v)
choice_votes = votes.count(mode(votes)) #count how many occurences of most popular votes.
conf = choice_votes / len(votes)
return conf
documents_f = open("C:\\Data_jupyter\\pickled_algos\\documents.pickle","rb")
document=pickle.load(documents_f)
documents_f.close()
word_feature_f = open("C:\\Data_jupyter\\pickled_algos\\word_features5k.pickle","rb")
word_features = pickle.load(word_feature_f)
word_feature_f.close()
def find_features(document):
words=word_tokenize(document)
features = {}
for w in word_features:
features[w] = (w in words)
return features
open_features = open("C:\\Data_jupyter\\pickled_algos\\feature_set.pickle","rb")
featuresets=pickle.load(open_features)
open_features.close()
random.shuffle(featuresets)
#only positive testing set
training_set = featuresets[:10000]
testing_set = featuresets[10000:]
print(len(featuresets))
classifier_open=open("C:\\Data_jupyter\\pickled_algos\\originalnaivebayes5k.pickle","rb")
classifier = pickle.load(classifier_open)
classifier_open.close()
open_file = open("C:\\Data_jupyter\\pickled_algos\\MNB_classifier5k.pickle", "rb")
MNB_classifier = pickle.load(open_file)
open_file.close()
open_file = open("C:\\Data_jupyter\\pickled_algos\\BernoulliNB_classifier5k.pickle", "rb")
BernoulliNB_classifier = pickle.load(open_file)
open_file.close()
open_file = open("C:\\Data_jupyter\\pickled_algos\\Logistic_Regression_classifier5k.pickle", "rb")
LogisticRegression_classifier = pickle.load(open_file)
open_file.close()
open_file = open("C:\\Data_jupyter\\pickled_algos\\LinearSVC_classifier5k.pickle", "rb")
LinearSVC_classifier = pickle.load(open_file)
open_file.close()
open_file = open("C:\\Data_jupyter\\pickled_algos\\SGDClassifier_classifier5k.pickle", "rb")
SGDC_classifier = pickle.load(open_file)
open_file.close()
voted_classifier = VoteClassifier(
classifier,
LinearSVC_classifier,
MNB_classifier,
BernoulliNB_classifier,
LogisticRegression_classifier)
def sentiment(text):
feats = find_features(text)
return voted_classifier.classify(feats),voted_classifier.confidence(feats)
print(sentiment("This movie was awesome! The acting was great, plot was wonderful, and there were pythons...so yea!"))
print(sentiment("This movie was utter junk. There were absolutely 0 pythons. I don't see what the point was at all. Horrible movie, 0/10"))
```
|
github_jupyter
|
#VOTING
import nltk
import random
from nltk.corpus import movie_reviews
from nltk.classify import ClassifierI
from statistics import mode
from nltk.tokenize import word_tokenize
import pickle
class VoteClassifier(ClassifierI):
def __init__(self, *classifiers):
self._classifiers = classifiers
def classify(self,features):
votes=[]
for c in self._classifiers:
v=c.classify(features)
votes.append(v)
return mode(votes)
def confidence(self,features):
votes=[]
for c in self._classifiers:
v=c.classify(features)
votes.append(v)
choice_votes = votes.count(mode(votes)) #count how many occurences of most popular votes.
conf = choice_votes / len(votes)
return conf
documents_f = open("C:\\Data_jupyter\\pickled_algos\\documents.pickle","rb")
document=pickle.load(documents_f)
documents_f.close()
word_feature_f = open("C:\\Data_jupyter\\pickled_algos\\word_features5k.pickle","rb")
word_features = pickle.load(word_feature_f)
word_feature_f.close()
def find_features(document):
words=word_tokenize(document)
features = {}
for w in word_features:
features[w] = (w in words)
return features
open_features = open("C:\\Data_jupyter\\pickled_algos\\feature_set.pickle","rb")
featuresets=pickle.load(open_features)
open_features.close()
random.shuffle(featuresets)
#only positive testing set
training_set = featuresets[:10000]
testing_set = featuresets[10000:]
print(len(featuresets))
classifier_open=open("C:\\Data_jupyter\\pickled_algos\\originalnaivebayes5k.pickle","rb")
classifier = pickle.load(classifier_open)
classifier_open.close()
open_file = open("C:\\Data_jupyter\\pickled_algos\\MNB_classifier5k.pickle", "rb")
MNB_classifier = pickle.load(open_file)
open_file.close()
open_file = open("C:\\Data_jupyter\\pickled_algos\\BernoulliNB_classifier5k.pickle", "rb")
BernoulliNB_classifier = pickle.load(open_file)
open_file.close()
open_file = open("C:\\Data_jupyter\\pickled_algos\\Logistic_Regression_classifier5k.pickle", "rb")
LogisticRegression_classifier = pickle.load(open_file)
open_file.close()
open_file = open("C:\\Data_jupyter\\pickled_algos\\LinearSVC_classifier5k.pickle", "rb")
LinearSVC_classifier = pickle.load(open_file)
open_file.close()
open_file = open("C:\\Data_jupyter\\pickled_algos\\SGDClassifier_classifier5k.pickle", "rb")
SGDC_classifier = pickle.load(open_file)
open_file.close()
voted_classifier = VoteClassifier(
classifier,
LinearSVC_classifier,
MNB_classifier,
BernoulliNB_classifier,
LogisticRegression_classifier)
def sentiment(text):
feats = find_features(text)
return voted_classifier.classify(feats),voted_classifier.confidence(feats)
print(sentiment("This movie was awesome! The acting was great, plot was wonderful, and there were pythons...so yea!"))
print(sentiment("This movie was utter junk. There were absolutely 0 pythons. I don't see what the point was at all. Horrible movie, 0/10"))
| 0.279238 | 0.118487 |
# Guide for Authors
```
print('Welcome to "Generating Software Tests"!')
```
This notebook compiles the most important conventions for all chapters (notebooks) of "Generating Software Tests".
## Organization of this Book
### Chapters as Notebooks
Each chapter comes in its own _Jupyter notebook_. A single notebook (= a chapter) should cover the material (text and code, possibly slides) for a 90-minute lecture.
A chapter notebook should be named `Topic.ipynb`, where `Topic` is the topic. `Topic` must be usable as a Python module and should characterize the main contribution. If the main contribution of your chapter is a class `FooFuzzer`, for instance, then your topic (and notebook name) should be `FooFuzzer`, such that users can state
```python
from FooFuzzer import FooFuzzer
```
Since class and module names should start with uppercase letters, all non-notebook files and folders start with lowercase letters. this may make it easier to differentiate them. The special notebook `index.ipynb` gets converted into the home pages `index.html` (on fuzzingbook.org) and `README.md` (on GitHub).
Notebooks are stored in the `notebooks` folder.
### Output Formats
The notebooks by themselves can be used by instructors and students to toy around with. They can edit code (and text) as they like and even run them as a slide show.
The notebook can be _exported_ to multiple (non-interactive) formats:
* HTML – for placing this material online.
* PDF – for printing
* Python – for coding
* Slides – for presenting
The included Makefile can generate all of these automatically.
At this point, we mostly focus on HTML and Python, as we want to get these out quickly; but you should also occasionally ensure that your notebooks can (still) be exported into PDF. Other formats (Word, Markdown) are experimental.
## Sites
All sources for the book end up on the [Github project page](https://github.com/uds-se/fuzzingbook). This holds the sources (notebooks), utilities (Makefiles), as well as an issue tracker.
The derived material for the book ends up in the `docs/` folder, from where it is eventually pushed to the [fuzzingbook website](http://www.fuzzingbook.org/). This site allows to read the chapters online, can launch Jupyter notebooks using the binder service, and provides access to code and slide formats. Use `make publish` to create and update the site.
### The Book PDF
The book PDF is compiled automatically from the individual notebooks. Each notebook becomes a chapter; references are compiled in the final chapter. Use `make book` to create the book.
## Creating and Building
### Tools you will need
To work on the notebook files, you need the following:
1. Jupyter notebook. The easiest way to install this is via the [Anaconda distribution](https://www.anaconda.com/download/).
2. Once you have the Jupyter notebook installed, you can start editing and coding right away by starting `jupyter notebook` (or `jupyter lab`) in the topmost project folder.
3. If (like me) you don't like the Jupyter Notebook interface, I recommend [Jupyter Lab](https://jupyterlab.readthedocs.io/en/stable/), the designated successor to Jupyter Notebook. Invoke it as `jupyter lab`. It comes with a much more modern interface, but misses autocompletion and a couple of extensions. I am running it [as a Desktop application](http://christopherroach.com/articles/jupyterlab-desktop-app/) which gets rid of all the browser toolbars.
On the Mac, there is also the [Pineapple app](https://nwhitehead.github.io/pineapple/), which integrates a nice editor with a local server. This is easy to use, but misses a few features; also, it hasn't seen updates since 2015.
4. To create the entire book (with citations, references, and all), you also need the [ipybublish](https://github.com/chrisjsewell/ipypublish) package. This allows you to create the HTML files, merge multiple chapters into a single PDF or HTML file, create slides, and more. The Makefile provides the essential tools for creation.
### Version Control
We use git in a single strand of revisions. Feel free branch for features, but eventually merge back into the main "master" branch. Sync early; sync often. Only push if everything ("make all") builds and passes.
The Github repo thus will typically reflect work in progress. If you reach a stable milestone, you can push things on the fuzzingbook.org web site, using `make publish`.
#### nbdime
The [nbdime](https://github.com/jupyter/nbdime) package gives you tools such as `nbdiff` (and even better, `nbdiff-web`) to compare notebooks against each other; this ensures that cell _contents_ are compared rather than the binary format.
`nbdime config-git --enable` integrates nbdime with git such that `git diff` runs the above tools; merging should also be notebook-specific.
#### nbstripout
Notebooks in version control _should not contain output cells,_ as these tend to change a lot. (Hey, we're talking random output generation here!) To have output cells automatically stripped during commit, install the [nbstripout](https://github.com/kynan/nbstripout) package and use
```
nbstripout --install --attributes .gitattributes
```
in the `notebooks` folder to set it up as a git filter. As an example, the following cell should not have its output included in the git repo:
```
import random
random.random()
```
### Inkscape and GraphViz
Creating derived files uses [Inkscape](https://inkscape.org/en/) and [Graphviz](https://www.graphviz.org/) - through its [Python wrapper](https://pypi.org/project/graphviz/) - to process SVG images. These tools are not automatically installed, but are available on pip, _brew_ and _apt-get_ for all major distributions.
### LaTeX Fonts
By default, creating PDF uses XeLaTeX with a couple of special fonts, which you can find in the `fonts/` folder; install these fonts system-wide to make them accessible to XeLaTeX.
You can also run `make LATEX=pdflatex` to use `pdflatex` and standard LaTeX fonts instead.
### Creating Derived Formats (HTML, PDF, code, ...)
The [Makefile](../Makefile) provides rules for all targets. Type `make help` for instructions.
The Makefile should work with GNU make and a standard Jupyter Notebook installation. To create the multi-chapter book and BibTeX citation support, you need to install the [iPyPublish](https://github.com/chrisjsewell/ipypublish) package (which includes the `nbpublish` command).
### Creating a New Chapter
To create a new chapter for the book,
1. Set up a new `.ipynb` notebook file as copy of [Template.ipynb](Template.ipynb).
2. Include it in the `CHAPTERS` list in the `Makefile`.
3. Add it to the git repository.
## Teaching a Topic
Each chapter should be devoted to a central concept and a small set of lessons to be learned. I recommend the following structure:
* Introduce the problem ("We want to parse inputs")
* Illustrate it with some code examples ("Here's some input I'd like to parse")
* Develop a first (possibly quick and dirty) solution ("A PEG parser is short and often does the job"_
* Show that it works and how it works ("Here's a neat derivation tree. Look how we can use this to mutate and combine expressions!")
* Develop a second, more elaborated solution, which should then become the main contribution. ("Here's a general LR(1) parser that does not require a special grammar format. (You can skip it if you're not interested)")
* Offload non-essential extensions to later sections or to exercises. ("Implement a universal parser, using the Dragon Book")
The key idea is that readers should be able to grasp the essentials of the problem and the solution in the beginning of the chapter, and get further into details as they progress through it. Make it easy for readers to be drawn in, providing insights of value quickly. If they are interested to understand how things work, they will get deeper into the topic. If they just want to use the technique (because they may be more interested in later chapters), having them read only the first few examples should be fine for them, too.
Whatever you introduce should be motivated first, and illustrated after. Motivate the code you'll be writing, and use plenty of examples to show what the code just introduced is doing. Remember that readers should have fun interacting with your code and your examples. Show and tell again and again and again.
## Coding
### Set up
The first code block in each notebook should be
```
import fuzzingbook_utils
```
This sets up stuff such that notebooks can import each other's code (see below). This import statement is removed in the exported Python code, as the .py files would import each other directly.
Importing `fuzzingbook_utils` also sets a fixed _seed_ for random number generation. This way, whenever you execute a notebook from scratch (restarting the kernel), you get the exact same results; these results will also end up in the derived HTML and PDF files. (If you run a notebook or a cell for the second time, you will get more random results.)
### Coding Style and Consistency
We use Python 3 (specifically, Python 3.6) for all code. If you can, try to write code that can be easily backported to Python 2.
We use standard Python coding conventions according to [PEP 8](https://www.python.org/dev/peps/pep-0008/).
Use one cell for each definition or example. During importing, this makes it easier to decide which cells to import (see below).
Your code must pass the `pycodestyle` style checks which you get by invoking `make style`. A very easy way to meet this goal is to invoke `make reformat`, which reformats all code accordingly. The `code prettify` notebook extension also allows you to automatically make your code adhere to PEP 8.
In the book, this is how we denote `variables`, `functions()` and `methods()`, `Classes`, `Notebooks`, `variables_and_constants`, `EXPORTED_CONSTANTS`, `'characters'`, `"strings"`, `files`, `folders/`, and `<grammar-elements>`.
Beyond simple syntactical things, here's a [very nice guide](https://docs.python-guide.org/writing/style/) to get you started writing "pythonic" code.
### Importing Code from Notebooks
To import the code of individual notebooks, you can import directly from .ipynb notebook files.
```
from Fuzzer import fuzzer
fuzzer(100, ord('0'), 10)
```
**Important**: When importing a notebook, the module loader will **only** load cells that start with
* a function definition (`def`)
* a class definition (`class`)
* a variable definition if all uppercase (`ABC = 123`)
* `import` and `from` statements
All other cells are _ignored_ to avoid recomputation of notebooks and clutter of `print()` output.
The exported Python code will import from the respective .py file instead. (There's no filtering here as with notebooks, so you'll see plenty of output when importing.)
Import modules only as you need them, such that you can motivate them well in the text.
### Design and Architecture
Stick to simple functions and data types. We want our readers to focus on functionality, not Python. You are encouraged to write in a "pythonic" style, making use of elegant Python features such as list comprehensions, sets, and more; however, if you do so, be sure to explain the code such that readers familiar with, say, C or Java can still understand things.
### Introducing Classes
Defining _classes_ can be a bit tricky, since all of a class must fit into a single cell. This defeats the incremental style preferred for notebooks. By defining a class _as a subclass of itself_, though, you can avoid this problem.
Here's an example. We introduce a class `Foo`:
```
class Foo:
def __init__(self):
pass
def bar(self):
pass
```
Now we could discuss what `__init__()` and `bar()` do, or give an example of how to use them:
```
f = Foo()
f.bar()
```
We now can introduce a new `Foo` method by subclassing from `Foo` into a class which is _also_ called `Foo`:
```
class Foo(Foo):
def baz(self):
pass
```
This is the same as if we had subclassed `Foo` into `Foo_1` with `Foo` then becoming an alias for `Foo_1`. The original `Foo` class is overshadowed by the new one:
```
new_f = Foo()
new_f.baz()
```
Note, though, that _existing_ objects keep their original class:
```
from ExpectError import ExpectError
with ExpectError():
f.baz()
```
## Helpers
There's a couple of notebooks with helpful functions, including [Timer](Timer.ipynb), [ExpectError and ExpectTimeout](ExpectError.ipynb). Also check out the [Coverage](Coverage.ipynb) class.
### Quality Assurance
In your code, make use of plenty of assertions that allow to catch errors quickly. These assertions also help your readers understand the code.
### Issue Tracker
The [Github project page](https://github.com/uds-se/fuzzingbook) allows to enter and track issues.
## Writing Text
Text blocks use Markdown syntax. [Here is a handy guide](https://github.com/adam-p/markdown-here/wiki/Markdown-Cheatsheet).
### Sections
Any chapter notebook must begin with `# TITLE`, and sections and subsections should then follow by `## SECTION` and `### SUBSECTION`.
Sections should start with their own block, to facilitate cross-referencing.
### Highlighting
Use
* _emphasis_ (`_emphasis_`) for highlighting,
* `backticks` for code and other verbatim elements.
### Hyphens and Dashes
Use "–" for em-dashes, "-" for hyphens, and "$-$" for minus.
### Quotes
Use standard typewriter quotes (`"quoted string"`) for quoted text. The PDF version will automatically convert these to "smart" (e.g. left and right) quotes.
### Lists and Enumerations
You can use bulleted lists:
* Item A
* Item B
and enumerations:
1. item 1
1. item 2
For description lists, use a combination of bulleted lists and highlights:
* **PDF** is great for reading offline
* **HTML** is great for reading online
### Math
LaTeX math formatting works, too.
`$x = \sum_{n = 1}^{\infty}\frac{1}{n}$` gets you
$x = \sum_{n = 1}^{\infty}\frac{1}{n}$.
### Inline Code
Python code normally goes into its own cells, but you can also have it in the text:
```python
s = "Python syntax highlighting"
print(s)
```
## Images
To insert images, use Markdown syntax `{width=100%}` inserts a picture from the `PICS` folder.
{width=100%}
All pictures go to `PICS/`, both in source as well as derived formats; both are stored in git, too. (Not all of us have all tools to recreate diagrams, etc.)
## Floating Elements and References
\todo[inline]{I haven't gotten this to work yet -- AZ}
To produce floating elements in LaTeX and PDF, edit the metadata of the cell which contains it. (In the Jupyter Notebook Toolbar go to View -> Cell Toolbar -> Edit Metadata and a button will appear above each cell.) This allows you to control placement and create labels.
### Floating Figures
Edit metadata as follows:
```json
{
"ipub": {
"figure": {
"caption": "Figure caption.",
"label": "fig:flabel",
"placement": "H",
"height":0.4,
"widefigure": false,
}
}
}
```
- all tags are optional
- height/width correspond to the fraction of the page height/width, only one should be used (aspect ratio will be maintained automatically)
- `placement` is optional and constitutes using a placement arguments for the figure (e.g. \begin{figure}[H]). See [Positioning_images_and_tables](https://www.sharelatex.com/learn/Positioning_images_and_tables).
- `widefigure` is optional and constitutes expanding the figure to the page width (i.e. \begin{figure*}) (placement arguments will then be ignored)
### Floating Tables
For **tables** (e.g. those output by `pandas`), enter in cell metadata:
```json
{
"ipub": {
"table": {
"caption": "Table caption.",
"label": "tbl:tlabel",
"placement": "H",
"alternate": "gray!20"
}
}
}
```
- `caption` and `label` are optional
- `placement` is optional and constitutes using a placement arguments for the table (e.g. \begin{table}[H]). See [Positioning_images_and_tables](https://www.sharelatex.com/learn/Positioning_images_and_tables).
- `alternate` is optional and constitutes using alternating colors for the table rows (e.g. \rowcolors{2}{gray!25}{white}). See (https://tex.stackexchange.com/a/5365/107738)[https://tex.stackexchange.com/a/5365/107738].
- if tables exceed the text width, in latex, they will be shrunk to fit
### Floating Equations
For **equations** (e.g. those output by `sympy`), enter in cell metadata:
```json
{
"ipub": {
"equation": {
"environment": "equation",
"label": "eqn:elabel"
}
}
}
```
- environment is optional and can be 'none' or any of those available in [amsmath](https://www.sharelatex.com/learn/Aligning_equations_with_amsmath); 'equation', 'align','multline','gather', or their \* variants. Additionaly, 'breqn' or 'breqn\*' will select the experimental [breqn](https://ctan.org/pkg/breqn) environment to *smart* wrap long equations.
- label is optional and will only be used if the equation is in an environment
### References
To reference to a floating object, use `\cref`, e.g. \cref{eq:texdemo}
## Cross-Referencing
### Section References
* To refer to sections in the same notebook, use the header name as anchor, e.g.
`[Code](#Code)` gives you [Code](#Code). For multi-word titles, replace spaces by hyphens (`-`), as in [Using Notebooks as Modules](#Using-Notebooks-as-Modules).
* To refer to cells (e.g. equations or figures), you can define a label as cell metadata. See [Floating Elements and References](#Floating-Elements-and-References) for details.
* To refer to other notebooks, use a Markdown cross-reference to the notebook file, e.g. [the "Fuzzing" chapter](Fuzzer.ipynb). A special script will be run to take care of these links. Reference chapters by name, not by number.
### Citations
To cite papers, cite in LaTeX style. The text
```
print(r"\cite{Purdom1972}")
```
is expanded to \cite{Purdom1972}, which in HTML and PDF should be a nice reference.
The keys refer to BibTeX entries in [fuzzingbook.bib](fuzzingbook.bib).
* LaTeX/PDF output will have a "References" section appended.
* HTML output will link to the URL field from the BibTeX entry. Be sure it points to the DOI.
## Todo's
* To mark todo's, use `\todo{Thing to be done}.` \todo{Expand this}
## Tables
Tables with fixed contents can be produced using Markdown syntax:
| Tables | Are | Cool |
| ------ | ---:| ----:|
| Zebra | 2 | 30 |
| Gnu | 20 | 400 |
If you want to produce tables from Python data, the `PrettyTable` package (included in the book) allows to [produce tables with LaTeX-style formatting.](http://blog.juliusschulz.de/blog/ultimate-ipython-notebook)
```
import numpy as np
import fuzzingbook_utils.PrettyTable as pt
data = np.array([[1, 2, 30], [2, 3, 400]])
pt.PrettyTable(data, [r"$\frac{a}{b}$", r"$b$",
r"$c$"], print_latex_longtable=False)
```
## Plots and Data
It is possible to include plots in notebooks. Here is an example of plotting a function:
```
%matplotlib inline
import matplotlib.pyplot as plt
x = np.linspace(0, 3 * np.pi, 500)
plt.plot(x, np.sin(x ** 2))
plt.title('A simple chirp');
```
And here's an example of plotting data:
```
%matplotlib inline
import matplotlib.pyplot as plt
data = [25, 36, 57]
plt.plot(data)
plt.title('Increase in data');
```
Plots are available in all derived versions (HTML, PDF, etc.) Plots with `plotly` are even nicer (and interactive, even in HTML), However, at this point, we cannot export them to PDF, so `matplotlib` it is.
## Slides
You can set up the notebooks such that they also can be presented as slides. In the browser, select View -> Cell Toolbar -> Slideshow. You can then select a slide type for each cell:
* `New slide` starts a new slide with the cell (typically, every `## SECTION` in the chapter)
* `Sub-slide` starts a new sub-slide which you navigate "down" to (anything in the section)
* `Fragment` is a cell that gets revealed after a click (on the same slide)
* `Skip` is skipped during the slide show (e.g. `import` statements; navigation guides)
* `Notes` goes into presenter notes
To create slides, do `make slides`; to view them, change into the `slides/` folder and open the created HTML files. (The `reveal.js` package has to be in the same folder as the slide to be presented.)
The ability to use slide shows is a compelling argument for teachers and instructors in our audience.
(Hint: In a slide presentation, type `s` to see presenter notes.)
## Writing Tools
When you're editing in the browser, you may find these extensions helpful:
### Jupyter Notebook
[Jupyter Notebook Extensions](https://github.com/ipython-contrib/jupyter_contrib_nbextensions) is a collection of productivity-enhancing tools (including spellcheckers).
I found these extensions to be particularly useful:
* Spell Checker (while you're editing)
* Table of contents (for quick navigation)
* Code prettify (to produce "nice" syntax)
* Codefolding
* Live Markdown Preview (while you're editing)
### Jupyter Lab
Extensions for _Jupyter Lab_ are much less varied and less supported, but things get better. I am running
* [Spell Checker](https://github.com/ijmbarr/jupyterlab_spellchecker)
* [Table of Contents](https://github.com/jupyterlab/jupyterlab-toc)
## Interaction
It is possible to include interactive elements in a notebook, as in the following example:
```python
try:
from ipywidgets import interact, interactive, fixed, interact_manual
x = interact(fuzzer, char_start=(32, 128), char_range=(0, 96))
except ImportError:
pass
```
Note that such elements will be present in the notebook versions only, but not in the HTML and PDF versions, so use them sparingly (if at all). To avoid errors during production of derived files, protect against `ImportError` exceptions as in the above example.
## Read More
Here is some documentation on the tools we use:
1. [Markdown Cheatsheet](https://github.com/adam-p/markdown-here/wiki/Markdown-Cheatsheet) - general introduction to Markdown
1. [iPyPublish](https://github.com/chrisjsewell/ipypublish) - rich set of tools to create documents with citations and references
## Alternative Tool Sets
We don't currently use these, but they are worth learning:
1. [Making Publication-Ready Python Notebooks](http://blog.juliusschulz.de/blog/ultimate-ipython-notebook) - Another tool set on how to produce book chapters from notebooks
1. [Writing academic papers in plain text with Markdown and Jupyter notebook](https://sylvaindeville.net/2015/07/17/writing-academic-papers-in-plain-text-with-markdown-and-jupyter-notebook/) - Alternate ways on how to generate citations
1. [A Jupyter LaTeX template](https://gist.github.com/goerz/d5019bedacf5956bcf03ca8683dc5217#file-revtex-tplx) - How to define a LaTeX template
1. [Boost Your Jupyter Notebook Productivity](https://towardsdatascience.com/jupyter-notebook-hints-1f26b08429ad) - a collection of hints for debugging and profiling Jupyter notebooks
|
github_jupyter
|
print('Welcome to "Generating Software Tests"!')
from FooFuzzer import FooFuzzer
nbstripout --install --attributes .gitattributes
import random
random.random()
import fuzzingbook_utils
from Fuzzer import fuzzer
fuzzer(100, ord('0'), 10)
class Foo:
def __init__(self):
pass
def bar(self):
pass
f = Foo()
f.bar()
class Foo(Foo):
def baz(self):
pass
new_f = Foo()
new_f.baz()
from ExpectError import ExpectError
with ExpectError():
f.baz()
s = "Python syntax highlighting"
print(s)
{
"ipub": {
"figure": {
"caption": "Figure caption.",
"label": "fig:flabel",
"placement": "H",
"height":0.4,
"widefigure": false,
}
}
}
{
"ipub": {
"table": {
"caption": "Table caption.",
"label": "tbl:tlabel",
"placement": "H",
"alternate": "gray!20"
}
}
}
{
"ipub": {
"equation": {
"environment": "equation",
"label": "eqn:elabel"
}
}
}
print(r"\cite{Purdom1972}")
import numpy as np
import fuzzingbook_utils.PrettyTable as pt
data = np.array([[1, 2, 30], [2, 3, 400]])
pt.PrettyTable(data, [r"$\frac{a}{b}$", r"$b$",
r"$c$"], print_latex_longtable=False)
%matplotlib inline
import matplotlib.pyplot as plt
x = np.linspace(0, 3 * np.pi, 500)
plt.plot(x, np.sin(x ** 2))
plt.title('A simple chirp');
%matplotlib inline
import matplotlib.pyplot as plt
data = [25, 36, 57]
plt.plot(data)
plt.title('Increase in data');
try:
from ipywidgets import interact, interactive, fixed, interact_manual
x = interact(fuzzer, char_start=(32, 128), char_range=(0, 96))
except ImportError:
pass
| 0.412648 | 0.954774 |
# Getting started with the practicals
***These notebooks are best viewed in Jupyter. GitHub might not display all content of the notebook properly.***
## Goal of the practical exercises
The exercises have two goals:
1. Give you the opportunity to obtain 'hands-on' experience in implementing, training and evaluation machine learning models in Python. This experience will also help you better understand the theory covered during the lectures.
2. Occasionally demonstrate some 'exam-style' questions that you can use as a reference when studying for the exam. Note however that the example questions are (as the name suggests) only examples and do not constitute a complete and sufficient list of 'things that you have to learn for the exam'. You can recognize example questions as (parts of) exercises by <font color="#770a0a">this font color</font>.
For each set of exercises (one Python notebook such as this one $==$ one set of exercises) you have to submit deliverables that will then be graded and constitute 25% of the final grade. Thus, the work that you do during the practicals has double contribution towards the final grade: as 30% direct contribution and as a preparation for the exam that will define the other 65% of the grade.
## Deliverables
For each set of exercises, you have to submit:
1. Python functions and/or classes (`.py` files) that implement basic functionalities (e.g. a $k$-NN classifier) and
2. A *single* Python notebook that contains the experiments, visualization and answer to the questions and math problems. *Do not submit your answers as Word or PDF documents (they will not be graded)*. The submitted code and notebook should run without errors and be able to fully reproduce the reported results.
We recommend that you clone the provided notebooks (such as this one) and write your code in them. The following rubric will be used when grading the practical work:
Component | Insufficient | Satisfactory | Excellent
--- | --- | --- | ---
**Code** | Missing or incomplete code structure, runs with errors, lacks documentation | Self-contained, does not result in errors, contains some documentation, can be easily used to reproduce the reported results | User-friendly, well-structured (good separation of general functionality and experiments, i.e. between `.py` files and the Pyhthon notebook), detailed documentation, optimized for speed, use of a version control system (such as GitHub)
**Answers to questions** | Incorrect, does not convey understanding of the material, appears to be copied from another source | Correct, conveys good understanding of the material, description in own words | Correct, conveys excellent level of understanding, makes connections between topics
## A word on notation
When we refer to Python variables, we will use a monospace font. For example, `X` is a Python variable that contains the data matrix. When we refer to mathematical variables, we will use the de-facto standard notation: $a$ or $\lambda$ is a scalar variable, $\boldsymbol{\mathrm{w}}$ is a vector and $\boldsymbol{\mathrm{X}}$ is a matrix (e.g. a data matrix from the example above). You should use the same notation when writing your answers and solutions.
# Two simple machine learning models
## Preliminaries
Throughout the practical curriculum of this course, we will use the Python programming language and its ecosystem of libraries for scientific computing (such as `numpy`, `scipy`, `matplotlib`, `scikit-learn` etc). The practicals for the deep learning part of the course will use the `keras` deep learning framework. If you are not sufficiently familiar with this programming language and/or the listed libraries and packages, you are strongly advised to go over the corresponding tutorials from the ['Essential skills'](https://github.com/tueimage/essential-skills) module (the `scikit-learn` library is not covered by the tutorial, however, an extensive documentation is available [here](https://scikit-learn.org/stable/documentation.html).
In this first set of exercises, we will use two toy datasets that ship together with `scikit-learn`.
The first dataset is named `diabetes` and contains 442 patients described with 10 features: age, sex, body mass index, average blood pressure, and six blood serum measurements. The target variable is a continuous quantitative measure of the disease (diabetes) progression one year after the baseline measurements were recorded. More information is available [here](https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/datasets/descr/diabetes.rst) and [here](https://www4.stat.ncsu.edu/~boos/var.select/diabetes.html).
The second dataset is named `breast_cancer` and is a copy of the UCI ML Breast Cancer Wisconsin (Diagnostic) datasets (more infortmation is available [here](https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/datasets/descr/breast_cancer.rst) and [here](https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Diagnostic)). The datasets contains of 569 instances represented with 30 features that are computed from a images of a fine needle aspirate of a breast mass. The features describe characteristics of the cell nuclei present in the image. Each instance is associated with a binary target variable ('malignant' or 'benign').
You can load the two datasets in the following way:
```
import numpy as np
from sklearn.datasets import load_diabetes, load_breast_cancer
diabetes = load_diabetes()
breast_cancer = load_breast_cancer()
```
In the majority of the exercises in this course, we will use higher-level libraries and packages such as `scikit-learn` and `keras` to implement, train and evaluate machine learning models. However, the goal of this first set of exercises is to illustrate basic mathematical tools and machine learning concepts. Because of this, we will impose a restriction of only using basic `numpy` functionality. Furthermore, you should as much as possible restrict the use of for-loops (e.g. use a vector-to-matrix product instead of a for loop when appropriate).
If `X` is a 2D data matrix, we will use the convention that the rows of the matrix contain the samples (or instances) and the columns contain the features (inputs to the model). That means that a data matrix with a shape `(122, 13)` represents a dataset with 122 samples, each represented with 13 features. Similarly, if `Y` is a 2D matrix containing the targets, the rows correspond to the samples and the columns to the different targets (outputs of the model). Thus, if the shape of `Y` is `(122, 3)` that means that there are 122 samples and each sample is has 3 targets (note that in the majority of the examples we will only have a single target and thus the number of columns of `Y` will be 1).
You can obtain the data and target matrices from the two datasets in the following way:
```
X = diabetes.data
Y = diabetes.target[:, np.newaxis]
print(X.shape)
print(Y.shape)
```
If you want to only use a subset of the available features, you can obtain a reduced data matrix in the following way:
```
# use only the fourth feature
X = diabetes.data[:, np.newaxis, 3]
print(X.shape)
# use the third, and tenth features
X = diabetes.data[:, (3,9)]
print(X.shape)
```
***Question***: Why we need to use the `np.newaxis` expression in the examples above?
Note that in all your experiments in the exercises, you should use and independent training and testing sets. You can split the dataset into a training and testing subsets in the following way:
```
# use the fourth feature
# use the first 300 training samples for training, and the rest for testing
X_train = diabetes.data[:300, np.newaxis, 3]
y_train = diabetes.target[:300, np.newaxis]
X_test = diabetes.data[300:, np.newaxis, 3]
y_test = diabetes.target[300:, np.newaxis]
print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
print(y_test.shape)
```
## Exercises
### Linear regression
Implement training and evaluation of a linear regression model on the diabetes dataset using only matrix multiplication, inversion and transpose operations. Report the mean squared error of the model.
To get you started we have implemented the first part of this exercise (fitting of the model) as an example.
```
# add subfolder that contains all the function implementations
# to the system path so we can import them
import sys
sys.path.append('code/')
# the actual implementation is in linear_regression.py,
# here we will just use it to fit a model
from linear_regression import *
# load the dataset
# same as before, but now we use all features
X_train = diabetes.data[:300, :]
y_train = diabetes.target[:300, np.newaxis]
X_test = diabetes.data[300:, :]
y_lest = diabetes.target[300:, np.newaxis]
beta = lsq(X_train, y_train)
# print the parameters
print(beta)
```
### Weighted linear regression
Assume that in the dataset that you use to train a linear regression model, there are identical versions of some samples. This problem can be reformulated to a weighted linear regression problem where the matrices $\boldsymbol{\mathrm{X}}$ and $\boldsymbol{\mathrm{Y}}$ (or the vector $\boldsymbol{\mathrm{y}}$ if there is only a single target/output variable) contain only the unique data samples, and a vector $\boldsymbol{\mathrm{d}}$ is introduced that gives more weight to samples that appear multiple times in the original dataset (for example, the sample that appears 3 times has a corresponding weight of 3).
<p><font color='#770a0a'>Derive the expression for the least-squares solution of a weighted linear regression model (note that in addition to the matrices $\boldsymbol{\mathrm{X}}$ and $\boldsymbol{\mathrm{Y}}$, the solution should include a vector of weights $\boldsymbol{\mathrm{d}}$).</font></p>
### $k$-NN classification
Implement a $k$-Nearest neighbors classifier from scratch in Python using only basic matrix operations with `numpy` and `scipy`. Train and evaluate the classifier on the breast cancer dataset, using all features. Show the performance of the classifier for different values of $k$ (plot the results in a graph). Note that for optimal results, you should normalize the features (e.g. to the $[0, 1]$ range or to have a zero mean and unit standard deviation).
### $k$-NN regression
Modify the $k$-NN implementation to do regression instead of classification. Compare the performance of the linear regression model and the $k$-NN regression model on the diabetes dataset for different values of $k$..
### Class-conditional probability
Compute and visualize the class-conditional probability (conditional probability where the class label is the conditional variable, i.e. $P(X = x \mid Y = y)$ for all features in the breast cancer dataset. Assume a Gaussian distribution.
<p><font color='#770a0a'>Based on visual analysis of the plots, which individual feature can best discriminate between the two classes? Motivate your answer.</font></p>
|
github_jupyter
|
import numpy as np
from sklearn.datasets import load_diabetes, load_breast_cancer
diabetes = load_diabetes()
breast_cancer = load_breast_cancer()
X = diabetes.data
Y = diabetes.target[:, np.newaxis]
print(X.shape)
print(Y.shape)
# use only the fourth feature
X = diabetes.data[:, np.newaxis, 3]
print(X.shape)
# use the third, and tenth features
X = diabetes.data[:, (3,9)]
print(X.shape)
# use the fourth feature
# use the first 300 training samples for training, and the rest for testing
X_train = diabetes.data[:300, np.newaxis, 3]
y_train = diabetes.target[:300, np.newaxis]
X_test = diabetes.data[300:, np.newaxis, 3]
y_test = diabetes.target[300:, np.newaxis]
print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
print(y_test.shape)
# add subfolder that contains all the function implementations
# to the system path so we can import them
import sys
sys.path.append('code/')
# the actual implementation is in linear_regression.py,
# here we will just use it to fit a model
from linear_regression import *
# load the dataset
# same as before, but now we use all features
X_train = diabetes.data[:300, :]
y_train = diabetes.target[:300, np.newaxis]
X_test = diabetes.data[300:, :]
y_lest = diabetes.target[300:, np.newaxis]
beta = lsq(X_train, y_train)
# print the parameters
print(beta)
| 0.279337 | 0.993301 |
## Definição do *dataset*
O *dataset* utilizado será o "Electromyogram (EMG) Feature Reduction Using Mutual ComponentsAnalysis for Multifunction Prosthetic Fingers Control" [1]. Maiores informações podem ser vistas no site: https://www.rami-khushaba.com/electromyogram-emg-repository.html
De acordo com a figura seguinte, neste *dataset* existem 15 movimentos de 8 pessoas diferentes. Algumas questões de projetos foram levadas em consideração:
1. Cada pessoa possui uma pasta com 45 arquivos .csv, cada arquivo refere-se à 1 movimento. Cada movimento possui 3 tentativas.
2. São 8 eletrodos no total e cada movimento possui 80.000 samples por eletrodo.

[1] Rami N. Khushaba, Sarath Kodagoda, Dikai Liu, and Gamini Dissanayake "Electromyogram (EMG) Feature Reduction Using Mutual ComponentsAnalysis for Multifunction Prosthetic Fingers Control". https://onedrive.live.com/?authkey=%21Ar1wo75HiU9RrLM&cid=AAA78954F15E6559&id=AAA78954F15E6559%21316&parId=AAA78954F15E6559%21312&o=OneUp
### Dependências
```
import numpy as np
from numpy import genfromtxt
import math
from librosa import stft
from scipy.signal import stft
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
```
### Carregando dataset
Shape da matriz: 15 movimentos, 3 tentativas, 8 eletrodos, 80.000 samples
```
from glob import glob
# Obtendo lista dos arquivos
arquivos = list()
for num in range(1,9):
s = "./Delsys_8Chans_15Classes/S{}-Delsys-15Class/*.csv".format(num)
arquivos.append(glob(s))
# Ordenando por ordem alfabética
for i in range(8):
arquivos[i].sort()
# Criando matriz do dataset
data = list()
for k in range(8):
i = 0
X1 = list()
while(i < 45):
listaTrial = list()
for j in range(3):
listaTrial.append(genfromtxt(arquivos[k][i], delimiter=',', unpack=True))
i+=1
X1.append(listaTrial)
data.append(X1)
data = np.asarray(data)
print(data.shape)
```
### Segmentação dos dados
```
data = data[:,:,:,:,0:20000]
print(data.shape)
# Definição do salto e do tamanho do segmento (segmento - salto = sobreposição)
salto = 470
segmento = 1024
n_win = int((data.shape[-1] - segmento) / salto) + 1
ids = np.arange(n_win) * salto
x = np.array([data[:,:,:,:,k:(k + segmento)] for k in ids]).transpose(1, 2, 3, 4, 0, 5)
print(x.shape)
```
### Extraindo características no domínio do tempo
* `Mean Absolute Value (MAV)`:
> $\frac{1}{N}\sum_{i=1}^{N}|x_i|$
```
print(x.shape)
mav = np.sum(abs(x)/segmento, axis=-1)
print(mav.shape)
```
* `Variance of EMG (VAR)`:
> $\frac{1}{N-1}\sum_{i=1}^{N}x_i^2$
```
print(x.shape)
var = np.sum(np.power(x, 2)/(segmento-1), axis=-1)
print(var.shape)
```
* `Simple Square Integral (SSI)`:
> $\sum_{i=1}^{N}|x_i|^2$
```
print(x.shape)
ssi = np.sum(np.power(abs(x), 2), axis=-1)
print(ssi.shape)
```
* `Root Mean Square (RMS)`:
> $\sqrt{\frac{1}{N}\sum_{i=1}^{N}|x_i|^2}$
```
print(x.shape)
rms = np.sqrt(np.sum((np.power(abs(x), 2))/segmento, axis=-1))
print(rms.shape)
```
### Extraindo características no domínio da frequência
#### Transformação para o domínio da frequência
Aplicando stft no último eixo de data (3), com janela de 1024 e sobreposição de 512.
```
print(data.shape)
_, _, w = stft(data, fs=4000, nperseg=1024, noverlap=512)
w = np.swapaxes(w, 4, 5)
print(w.shape)
```
#### Power Spectrum Density (PSD)
Quadrado do valor absoluto de FFT.
```
psd = np.power(abs(w), 2)
print(psd.shape)
```
* `Frequency Median (FMD)`:
> $\frac{1}{2}\sum_{i=1}^{M}PSD$
```
fmd = np.sum(psd/2, axis=-1)
print(fmd.shape)
```
* `Frequency Mean (FMN)`:
> $FMN = \frac{\sum_{i=1}^{M}f_i PSD}{\sum_{i=1}^{M}PSD_i}$
> $f_i = \frac{i * SampleRate}{2M}$
```
sampleRate = 4000
M = 513
f = np.array([(i*sampleRate)/(2*M) for i in range(1,M+1)])
fmn = np.divide((np.sum(np.multiply(psd,f), axis = -1)), (np.sum(psd, axis=-1)))
print(fmn.shape)
```
#### Criando vetor de características
```
X = list()
for i in range(8):
features = list()
for feature in (mav[i], var[i], ssi[i], rms[i], fmd[i], fmn[i]):
feature = feature.transpose(0, 1, 3, 2)
feature = feature.reshape(15 * 3 * 41, 8)
features.append(feature)
X.append(np.concatenate(features, axis=-1))
X = np.asarray(X)
print(X.shape)
```
#### Criando vetor de labels
```
y = np.array([[str(i)] * int(X[0].shape[0] / 15) for i in range(15)])
y = y.reshape(y.shape[0] * y.shape[1])
y.shape
```
#### Classificação
Aplicando classificador SVC e testando acurácia para os diferentes valores de kernel, c e gamma.
```
# dividindo as porções de dados em treino e teste (70 e 30% respectivamente)
C = 1
gamma = 0.001
kernel = 'rbf'
pessoas = list()
acuracias = list()
print('Kernel:', kernel, ', Gamma:', gamma, ', C:', C)
print('Acurácias:')
for i in range(8):
X_train, X_test, y_train, y_test = train_test_split(X[i], y, test_size=0.3, shuffle=True)
clf = SVC(C=C, gamma=gamma, kernel=kernel)
clf.fit(X_train, y_train)
res = clf.predict(X_test)
tot_hit = sum([1 for i in range(len(res)) if res[i] == y_test[i]])
pessoas.append(str(i+1))
acuracias.append(tot_hit / X_test.shape[0] * 100)
print('Pessoa', i+1, ': {:.2f}%'.format(acuracias[i]))
# Plotando grafico
plt.bar(pessoas, acuracias, color='blue')
plt.xticks(labels)
plt.ylabel('Acurácia (%)')
plt.xlabel('Pessoa')
plt.title('Análise das 8 pessoas')
plt.show()
```
|
github_jupyter
|
import numpy as np
from numpy import genfromtxt
import math
from librosa import stft
from scipy.signal import stft
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
from glob import glob
# Obtendo lista dos arquivos
arquivos = list()
for num in range(1,9):
s = "./Delsys_8Chans_15Classes/S{}-Delsys-15Class/*.csv".format(num)
arquivos.append(glob(s))
# Ordenando por ordem alfabética
for i in range(8):
arquivos[i].sort()
# Criando matriz do dataset
data = list()
for k in range(8):
i = 0
X1 = list()
while(i < 45):
listaTrial = list()
for j in range(3):
listaTrial.append(genfromtxt(arquivos[k][i], delimiter=',', unpack=True))
i+=1
X1.append(listaTrial)
data.append(X1)
data = np.asarray(data)
print(data.shape)
data = data[:,:,:,:,0:20000]
print(data.shape)
# Definição do salto e do tamanho do segmento (segmento - salto = sobreposição)
salto = 470
segmento = 1024
n_win = int((data.shape[-1] - segmento) / salto) + 1
ids = np.arange(n_win) * salto
x = np.array([data[:,:,:,:,k:(k + segmento)] for k in ids]).transpose(1, 2, 3, 4, 0, 5)
print(x.shape)
print(x.shape)
mav = np.sum(abs(x)/segmento, axis=-1)
print(mav.shape)
print(x.shape)
var = np.sum(np.power(x, 2)/(segmento-1), axis=-1)
print(var.shape)
print(x.shape)
ssi = np.sum(np.power(abs(x), 2), axis=-1)
print(ssi.shape)
print(x.shape)
rms = np.sqrt(np.sum((np.power(abs(x), 2))/segmento, axis=-1))
print(rms.shape)
print(data.shape)
_, _, w = stft(data, fs=4000, nperseg=1024, noverlap=512)
w = np.swapaxes(w, 4, 5)
print(w.shape)
psd = np.power(abs(w), 2)
print(psd.shape)
fmd = np.sum(psd/2, axis=-1)
print(fmd.shape)
sampleRate = 4000
M = 513
f = np.array([(i*sampleRate)/(2*M) for i in range(1,M+1)])
fmn = np.divide((np.sum(np.multiply(psd,f), axis = -1)), (np.sum(psd, axis=-1)))
print(fmn.shape)
X = list()
for i in range(8):
features = list()
for feature in (mav[i], var[i], ssi[i], rms[i], fmd[i], fmn[i]):
feature = feature.transpose(0, 1, 3, 2)
feature = feature.reshape(15 * 3 * 41, 8)
features.append(feature)
X.append(np.concatenate(features, axis=-1))
X = np.asarray(X)
print(X.shape)
y = np.array([[str(i)] * int(X[0].shape[0] / 15) for i in range(15)])
y = y.reshape(y.shape[0] * y.shape[1])
y.shape
# dividindo as porções de dados em treino e teste (70 e 30% respectivamente)
C = 1
gamma = 0.001
kernel = 'rbf'
pessoas = list()
acuracias = list()
print('Kernel:', kernel, ', Gamma:', gamma, ', C:', C)
print('Acurácias:')
for i in range(8):
X_train, X_test, y_train, y_test = train_test_split(X[i], y, test_size=0.3, shuffle=True)
clf = SVC(C=C, gamma=gamma, kernel=kernel)
clf.fit(X_train, y_train)
res = clf.predict(X_test)
tot_hit = sum([1 for i in range(len(res)) if res[i] == y_test[i]])
pessoas.append(str(i+1))
acuracias.append(tot_hit / X_test.shape[0] * 100)
print('Pessoa', i+1, ': {:.2f}%'.format(acuracias[i]))
# Plotando grafico
plt.bar(pessoas, acuracias, color='blue')
plt.xticks(labels)
plt.ylabel('Acurácia (%)')
plt.xlabel('Pessoa')
plt.title('Análise das 8 pessoas')
plt.show()
| 0.319758 | 0.884139 |
1. Read in the split sequences.
2. Get the alphabets and add in a padding character (' '), a stop character ('.'), and a start character ('$').
3. Save n x L x c arrays as h5py files. X is the mature sequence. y is the signal peptide.
4. Check that saved sequences decode correctly.
5. Save n x L arrays as h5py files.
6. Check that saved sequences decode correctly.
7. Save the character tables
**For dataset that removes sequences at least 99% similar to the protein sequences in Zach's excel "initial_enzymes_1." Rerun on 6-14-18 for just training and validation sets.**
```
import pickle
import h5py
import itertools
import numpy as np
from tools import CharacterTable
# read in data from pickle files
with open('../data/filtered_datasets/train_augmented_99.pkl', 'rb') as f:
train_99 = pickle.load(f)
with open('../data/filtered_datasets/validate_99.pkl', 'rb') as f:
validate_99 = pickle.load(f)
train_small_99 = train_99[:1000]
alphabet = ''.join(sorted(set(itertools.chain.from_iterable([t[1] for t in train_99]))))
alphabet = ' .$' + alphabet
alphabet
max_len_in = 107 # max length of prot seq (105 aa) + 2 for tokens
max_len_out = 72
n_chars = len(alphabet)
ctable = CharacterTable(alphabet)
encoded = ctable.encode('$ACZ.', 7, reverse=False)
decoded = ctable.decode(encoded, reverse=False)
print(encoded)
print(decoded + '|')
def encode(seqs, max_len, ctable):
if ctable.one_hot:
X = np.zeros((len(seqs), max_len, n_chars))
else:
X = np.zeros((len(seqs), max_len))
seqs = ['$' + seq + '.' for seq in seqs]
seqs = [seq + ' ' * ((max_len) - len(seq))for seq in seqs]
for i, seq in enumerate(seqs):
X[i] = ctable.encode(seq, max_len)
return X
def to_h5py(seqs, fname, ctable):
chunksize = 500
with h5py.File('../../6-14-18_filtered_data/' + fname + '.hdf5', 'w') as f:
if ctable.one_hot:
X = f.create_dataset('X', (len(seqs), max_len_in, n_chars))
y = f.create_dataset('y', (len(seqs), max_len_out, n_chars))
else:
X = f.create_dataset('X', (len(seqs), max_len_in))
y = f.create_dataset('y', (len(seqs), max_len_out))
for i in range(0, len(seqs), chunksize):
X[i:i + chunksize, :] = encode([seq[1] for seq in seqs[i:i+chunksize]], max_len_in, ctable)
y[i:i + chunksize, :] = encode([seq[0] for seq in seqs[i:i+chunksize]], max_len_out, ctable)
left = len(seqs) % chunksize
if left > 0:
X[-left:, :] = encode([seq[1] for seq in seqs[-left:]], max_len_in, ctable)
y[-left:, :] = encode([seq[0] for seq in seqs[-left:]], max_len_out, ctable)
to_h5py(train_99, 'train_augmented_99', ctable)
to_h5py(validate_99, 'validate_99', ctable)
to_h5py(train_small_99, 'train_small_augmented_99', ctable)
with open('../../6-14-18_filtered_data/outputs/ctable_onehot_99.pkl', 'wb') as f:
pickle.dump(ctable, f)
ctable = CharacterTable(alphabet, one_hot=False)
encoded = ctable.encode('$ACZ.', 7, reverse=False)
decoded = ctable.decode(encoded, reverse=False)
print(encoded)
print(decoded + '|')
to_h5py(train_99, 'train_tokens_augmented_99', ctable)
to_h5py(validate_99, 'validate_tokens_99', ctable)
to_h5py(train_small_99, 'train_small_tokens_augmented_99', ctable)
with open('../../6-14-18_filtered_data/outputs/ctable_token_99.pkl', 'wb') as f:
pickle.dump(ctable, f)
import torch
import torch.nn as nn
from torch.autograd import Variable
from torch import optim
import torch.nn.functional as F
with h5py.File('../data/validate.hdf5', 'r') as f:
src = Variable(torch.Tensor(f['X'][:100]))
tgt = f['y'][:100].astype(int)
tgt = Variable(torch.LongTensor(tgt))
src = src.transpose(2, 1)
src = src.cuda()
tgt = tgt.cuda()
tgt.size()
#validate src: torch.Size([100, 26, 107]), tgt: torch.Size([100, 72, 26])
```
|
github_jupyter
|
import pickle
import h5py
import itertools
import numpy as np
from tools import CharacterTable
# read in data from pickle files
with open('../data/filtered_datasets/train_augmented_99.pkl', 'rb') as f:
train_99 = pickle.load(f)
with open('../data/filtered_datasets/validate_99.pkl', 'rb') as f:
validate_99 = pickle.load(f)
train_small_99 = train_99[:1000]
alphabet = ''.join(sorted(set(itertools.chain.from_iterable([t[1] for t in train_99]))))
alphabet = ' .$' + alphabet
alphabet
max_len_in = 107 # max length of prot seq (105 aa) + 2 for tokens
max_len_out = 72
n_chars = len(alphabet)
ctable = CharacterTable(alphabet)
encoded = ctable.encode('$ACZ.', 7, reverse=False)
decoded = ctable.decode(encoded, reverse=False)
print(encoded)
print(decoded + '|')
def encode(seqs, max_len, ctable):
if ctable.one_hot:
X = np.zeros((len(seqs), max_len, n_chars))
else:
X = np.zeros((len(seqs), max_len))
seqs = ['$' + seq + '.' for seq in seqs]
seqs = [seq + ' ' * ((max_len) - len(seq))for seq in seqs]
for i, seq in enumerate(seqs):
X[i] = ctable.encode(seq, max_len)
return X
def to_h5py(seqs, fname, ctable):
chunksize = 500
with h5py.File('../../6-14-18_filtered_data/' + fname + '.hdf5', 'w') as f:
if ctable.one_hot:
X = f.create_dataset('X', (len(seqs), max_len_in, n_chars))
y = f.create_dataset('y', (len(seqs), max_len_out, n_chars))
else:
X = f.create_dataset('X', (len(seqs), max_len_in))
y = f.create_dataset('y', (len(seqs), max_len_out))
for i in range(0, len(seqs), chunksize):
X[i:i + chunksize, :] = encode([seq[1] for seq in seqs[i:i+chunksize]], max_len_in, ctable)
y[i:i + chunksize, :] = encode([seq[0] for seq in seqs[i:i+chunksize]], max_len_out, ctable)
left = len(seqs) % chunksize
if left > 0:
X[-left:, :] = encode([seq[1] for seq in seqs[-left:]], max_len_in, ctable)
y[-left:, :] = encode([seq[0] for seq in seqs[-left:]], max_len_out, ctable)
to_h5py(train_99, 'train_augmented_99', ctable)
to_h5py(validate_99, 'validate_99', ctable)
to_h5py(train_small_99, 'train_small_augmented_99', ctable)
with open('../../6-14-18_filtered_data/outputs/ctable_onehot_99.pkl', 'wb') as f:
pickle.dump(ctable, f)
ctable = CharacterTable(alphabet, one_hot=False)
encoded = ctable.encode('$ACZ.', 7, reverse=False)
decoded = ctable.decode(encoded, reverse=False)
print(encoded)
print(decoded + '|')
to_h5py(train_99, 'train_tokens_augmented_99', ctable)
to_h5py(validate_99, 'validate_tokens_99', ctable)
to_h5py(train_small_99, 'train_small_tokens_augmented_99', ctable)
with open('../../6-14-18_filtered_data/outputs/ctable_token_99.pkl', 'wb') as f:
pickle.dump(ctable, f)
import torch
import torch.nn as nn
from torch.autograd import Variable
from torch import optim
import torch.nn.functional as F
with h5py.File('../data/validate.hdf5', 'r') as f:
src = Variable(torch.Tensor(f['X'][:100]))
tgt = f['y'][:100].astype(int)
tgt = Variable(torch.LongTensor(tgt))
src = src.transpose(2, 1)
src = src.cuda()
tgt = tgt.cuda()
tgt.size()
#validate src: torch.Size([100, 26, 107]), tgt: torch.Size([100, 72, 26])
| 0.323487 | 0.794265 |
# Convolutional Neural Network Example
Build a convolutional neural network with TensorFlow.
This example is using TensorFlow layers API, see 'convolutional_network_raw' example
for a raw TensorFlow implementation with variables.
- Author: Aymeric Damien
- Project: https://github.com/aymericdamien/TensorFlow-Examples/
## CNN Overview
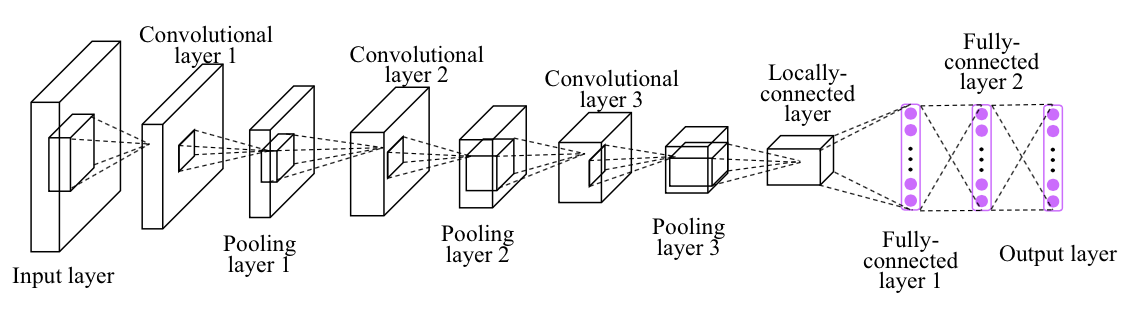
## MNIST Dataset Overview
This example is using MNIST handwritten digits. The dataset contains 60,000 examples for training and 10,000 examples for testing. The digits have been size-normalized and centered in a fixed-size image (28x28 pixels) with values from 0 to 1. For simplicity, each image has been flattened and converted to a 1-D numpy array of 784 features (28*28).

More info: http://yann.lecun.com/exdb/mnist/
```
from __future__ import division, print_function, absolute_import
# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=False)
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
# Training Parameters
learning_rate = 0.001
num_steps = 2000
batch_size = 128
# Network Parameters
num_input = 784 # MNIST data input (img shape: 28*28)
num_classes = 10 # MNIST total classes (0-9 digits)
dropout = 0.25 # Dropout, probability to drop a unit
# Create the neural network
def conv_net(x_dict, n_classes, dropout, reuse, is_training):
# Define a scope for reusing the variables
with tf.variable_scope('ConvNet', reuse=reuse):
# TF Estimator input is a dict, in case of multiple inputs
x = x_dict['images']
# MNIST data input is a 1-D vector of 784 features (28*28 pixels)
# Reshape to match picture format [Height x Width x Channel]
# Tensor input become 4-D: [Batch Size, Height, Width, Channel]
x = tf.reshape(x, shape=[-1, 28, 28, 1])
# Convolution Layer with 32 filters and a kernel size of 5
conv1 = tf.layers.conv2d(x, 32, 5, activation=tf.nn.relu)
# Max Pooling (down-sampling) with strides of 2 and kernel size of 2
conv1 = tf.layers.max_pooling2d(conv1, 2, 2)
# Convolution Layer with 64 filters and a kernel size of 3
conv2 = tf.layers.conv2d(conv1, 64, 3, activation=tf.nn.relu)
# Max Pooling (down-sampling) with strides of 2 and kernel size of 2
conv2 = tf.layers.max_pooling2d(conv2, 2, 2)
# Flatten the data to a 1-D vector for the fully connected layer
fc1 = tf.contrib.layers.flatten(conv2)
# Fully connected layer (in tf contrib folder for now)
fc1 = tf.layers.dense(fc1, 1024)
# Apply Dropout (if is_training is False, dropout is not applied)
fc1 = tf.layers.dropout(fc1, rate=dropout, training=is_training)
# Output layer, class prediction
out = tf.layers.dense(fc1, n_classes)
return out
# Define the model function (following TF Estimator Template)
def model_fn(features, labels, mode):
# Build the neural network
# Because Dropout have different behavior at training and prediction time, we
# need to create 2 distinct computation graphs that still share the same weights.
logits_train = conv_net(features, num_classes, dropout, reuse=False, is_training=True)
logits_test = conv_net(features, num_classes, dropout, reuse=True, is_training=False)
# Predictions
pred_classes = tf.argmax(logits_test, axis=1)
pred_probas = tf.nn.softmax(logits_test)
# If prediction mode, early return
if mode == tf.estimator.ModeKeys.PREDICT:
return tf.estimator.EstimatorSpec(mode, predictions=pred_classes)
# Define loss and optimizer
loss_op = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(
logits=logits_train, labels=tf.cast(labels, dtype=tf.int32)))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
train_op = optimizer.minimize(loss_op, global_step=tf.train.get_global_step())
# Evaluate the accuracy of the model
acc_op = tf.metrics.accuracy(labels=labels, predictions=pred_classes)
# TF Estimators requires to return a EstimatorSpec, that specify
# the different ops for training, evaluating, ...
estim_specs = tf.estimator.EstimatorSpec(
mode=mode,
predictions=pred_classes,
loss=loss_op,
train_op=train_op,
eval_metric_ops={'accuracy': acc_op})
return estim_specs
# Build the Estimator
model = tf.estimator.Estimator(model_fn)
# Define the input function for training
input_fn = tf.estimator.inputs.numpy_input_fn(
x={'images': mnist.train.images}, y=mnist.train.labels,
batch_size=batch_size, num_epochs=None, shuffle=True)
# Train the Model
model.train(input_fn, steps=num_steps)
# Evaluate the Model
# Define the input function for evaluating
input_fn = tf.estimator.inputs.numpy_input_fn(
x={'images': mnist.test.images}, y=mnist.test.labels,
batch_size=batch_size, shuffle=False)
# Use the Estimator 'evaluate' method
model.evaluate(input_fn)
# Predict single images
n_images = 4
# Get images from test set
test_images = mnist.test.images[:n_images]
# Prepare the input data
input_fn = tf.estimator.inputs.numpy_input_fn(
x={'images': test_images}, shuffle=False)
# Use the model to predict the images class
preds = list(model.predict(input_fn))
# Display
for i in range(n_images):
plt.imshow(np.reshape(test_images[i], [28, 28]), cmap='gray')
plt.show()
print("Model prediction:", preds[i])
```
|
github_jupyter
|
from __future__ import division, print_function, absolute_import
# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=False)
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
# Training Parameters
learning_rate = 0.001
num_steps = 2000
batch_size = 128
# Network Parameters
num_input = 784 # MNIST data input (img shape: 28*28)
num_classes = 10 # MNIST total classes (0-9 digits)
dropout = 0.25 # Dropout, probability to drop a unit
# Create the neural network
def conv_net(x_dict, n_classes, dropout, reuse, is_training):
# Define a scope for reusing the variables
with tf.variable_scope('ConvNet', reuse=reuse):
# TF Estimator input is a dict, in case of multiple inputs
x = x_dict['images']
# MNIST data input is a 1-D vector of 784 features (28*28 pixels)
# Reshape to match picture format [Height x Width x Channel]
# Tensor input become 4-D: [Batch Size, Height, Width, Channel]
x = tf.reshape(x, shape=[-1, 28, 28, 1])
# Convolution Layer with 32 filters and a kernel size of 5
conv1 = tf.layers.conv2d(x, 32, 5, activation=tf.nn.relu)
# Max Pooling (down-sampling) with strides of 2 and kernel size of 2
conv1 = tf.layers.max_pooling2d(conv1, 2, 2)
# Convolution Layer with 64 filters and a kernel size of 3
conv2 = tf.layers.conv2d(conv1, 64, 3, activation=tf.nn.relu)
# Max Pooling (down-sampling) with strides of 2 and kernel size of 2
conv2 = tf.layers.max_pooling2d(conv2, 2, 2)
# Flatten the data to a 1-D vector for the fully connected layer
fc1 = tf.contrib.layers.flatten(conv2)
# Fully connected layer (in tf contrib folder for now)
fc1 = tf.layers.dense(fc1, 1024)
# Apply Dropout (if is_training is False, dropout is not applied)
fc1 = tf.layers.dropout(fc1, rate=dropout, training=is_training)
# Output layer, class prediction
out = tf.layers.dense(fc1, n_classes)
return out
# Define the model function (following TF Estimator Template)
def model_fn(features, labels, mode):
# Build the neural network
# Because Dropout have different behavior at training and prediction time, we
# need to create 2 distinct computation graphs that still share the same weights.
logits_train = conv_net(features, num_classes, dropout, reuse=False, is_training=True)
logits_test = conv_net(features, num_classes, dropout, reuse=True, is_training=False)
# Predictions
pred_classes = tf.argmax(logits_test, axis=1)
pred_probas = tf.nn.softmax(logits_test)
# If prediction mode, early return
if mode == tf.estimator.ModeKeys.PREDICT:
return tf.estimator.EstimatorSpec(mode, predictions=pred_classes)
# Define loss and optimizer
loss_op = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(
logits=logits_train, labels=tf.cast(labels, dtype=tf.int32)))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
train_op = optimizer.minimize(loss_op, global_step=tf.train.get_global_step())
# Evaluate the accuracy of the model
acc_op = tf.metrics.accuracy(labels=labels, predictions=pred_classes)
# TF Estimators requires to return a EstimatorSpec, that specify
# the different ops for training, evaluating, ...
estim_specs = tf.estimator.EstimatorSpec(
mode=mode,
predictions=pred_classes,
loss=loss_op,
train_op=train_op,
eval_metric_ops={'accuracy': acc_op})
return estim_specs
# Build the Estimator
model = tf.estimator.Estimator(model_fn)
# Define the input function for training
input_fn = tf.estimator.inputs.numpy_input_fn(
x={'images': mnist.train.images}, y=mnist.train.labels,
batch_size=batch_size, num_epochs=None, shuffle=True)
# Train the Model
model.train(input_fn, steps=num_steps)
# Evaluate the Model
# Define the input function for evaluating
input_fn = tf.estimator.inputs.numpy_input_fn(
x={'images': mnist.test.images}, y=mnist.test.labels,
batch_size=batch_size, shuffle=False)
# Use the Estimator 'evaluate' method
model.evaluate(input_fn)
# Predict single images
n_images = 4
# Get images from test set
test_images = mnist.test.images[:n_images]
# Prepare the input data
input_fn = tf.estimator.inputs.numpy_input_fn(
x={'images': test_images}, shuffle=False)
# Use the model to predict the images class
preds = list(model.predict(input_fn))
# Display
for i in range(n_images):
plt.imshow(np.reshape(test_images[i], [28, 28]), cmap='gray')
plt.show()
print("Model prediction:", preds[i])
| 0.828973 | 0.987017 |
```
%load_ext autoreload
%autoreload 2
import gust # library for loading graph data
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import scipy.sparse as sp
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.distributions as dist
import time
import random
from scipy.spatial.distance import squareform
torch.set_default_tensor_type('torch.cuda.FloatTensor')
%matplotlib inline
sns.set_style('whitegrid')
# Load the dataset using `gust` library
# graph.standardize() makes the graph unweighted, undirected and selects
# the largest connected component
# graph.unpack() returns the necessary vectors / matrices
A, X, _, y = gust.load_dataset('cora').standardize().unpack()
# A - adjacency matrix
# X - attribute matrix - not needed
# y - node labels
A=A[:10,:10]
if (A != A.T).sum() > 0:
raise RuntimeError("The graph must be undirected!")
if (A.data != 1).sum() > 0:
raise RuntimeError("The graph must be unweighted!")
adj = torch.FloatTensor(A.toarray()).cuda()
# Make it stochastic
adj = torch.FloatTensor(A.toarray()).cuda()
'''
from the paper Sampling from Large Graphs:
We first choose node v uniformly at random. We then generate a random number x that is geometrically distributed
with mean pf /(1 − pf ). Node v selects x out-links incident
to nodes that were not yet visited. Let w1, w2, . . . , wx denote the other ends of these selected links. We then apply
this step recursively to each of w1, w2, . . . , wx until enough
nodes have been burned. As the process continues, nodes
cannot be visited a second time, preventing the construction
from cycling. If the fire dies, then we restart it, i.e. select
new node v uniformly at random. We call the parameter pf
the forward burning probability.
'''
#1. choose first node v uniformly at random and store it
v_new = np.random.randint(len(adj))
nodes = torch.tensor([v_new])
print('nodes: ', nodes)
#2. generate random number x from geometrix distribution with mean pf/(1-pf)
pf=0.3 #burning probability, evaluated as best from the given paper
x = np.random.geometric(pf/(1-pf))
#3. let idx choose x out-links
w = (adj[v_new]==1).nonzero()
if w.shape[0]>x:
idx_w = random.sample(range(0, w.shape[0]), x)
w=w[idx_w]
#4. loop until 15% of the dataset is covered
while len(nodes)<20:
v_new = w[0].item()
w = (adj[v_new]==1).nonzero()
for i in w:
for j in nodes:
if w[i]==nodes[j]:
w[i]=0
w = w.remove(0)
if w.shape[0]>x:
idx_w = random.sample(range(0, w.shape[0]), x)
v_new = torch.tensor([v_new])
nodes = torch.cat((nodes,v_new),0)
print(nodes)
num_nodes = A.shape[0]
num_edges = A.sum()
# Convert adjacency matrix to a CUDA Tensor
adj = torch.FloatTensor(A.toarray()).cuda()
#torch.manual_seed(123)
# Define the embedding matrix
embedding_dim = 64
emb = nn.Parameter(torch.empty(num_nodes, embedding_dim).normal_(0.0, 1.0))
# Initialize the bias
# The bias is initialized in such a way that if the dot product between two embedding vectors is 0
# (i.e. z_i^T z_j = 0), then their connection probability is sigmoid(b) equals to the
# background edge probability in the graph. This significantly speeds up training
edge_proba = num_edges / (num_nodes**2 - num_nodes)
bias_init = np.log(edge_proba / (1 - edge_proba))
b = nn.Parameter(torch.Tensor([bias_init]))
# Regularize the embeddings but don't regularize the bias
# The value of weight_decay has a significant effect on the performance of the model (don't set too high!)
opt = torch.optim.Adam([
{'params': [emb], 'weight_decay': 1e-7}, {'params': [b]}],
lr=1e-2)
def compute_loss_ber_sig(adj, emb, b=0.1):
#kernel: theta(z_i,z_j)=sigma(z_i^Tz_j+b)
# Initialization
N,d=emb.shape
#compute f(z_i, z_j) = sigma(z_i^Tz_j+b)
dot=torch.matmul(emb,emb.T)
logits =dot+b
#transform adj
ind=torch.triu_indices(N,N,offset=1)
logits = logits[ind[0], ind[1]]
labels = adj[ind[0],ind[1]]
#compute p(A|Z)
loss = F.binary_cross_entropy_with_logits(logits, labels, weight=None, size_average=None, reduce=None, reduction='mean')
return loss
def compute_loss_d1(adj, emb, b=0.0):
"""Compute the rdf distance of the Bernoulli model."""
# Initialization
start_time = time.time()
N,d=emb.shape
squared_euclidian = torch.zeros(N,N).cuda()
gamma= 0.1
end_time= time.time()
duration= end_time -start_time
#print(f' Time for initialization = {duration:.5f}')
# Compute squared euclidian
start_time = time.time()
for index, embedding in enumerate(emb):
sub = embedding-emb + 10e-9
squared_euclidian[index,:]= torch.sum(torch.pow(sub,2),1)
end_time= time.time()
duration= end_time -start_time
#print(f' Time for euclidian = {duration:.5f}')
# Compute exponentianl
start_time = time.time()
radial_exp = torch.exp (-gamma * torch.sqrt(squared_euclidian))
loss = F.binary_cross_entropy(radial_exp, adj, reduction='none')
loss[np.diag_indices(adj.shape[0])] = 0.0
end_time= time.time()
duration= end_time -start_time
#print(f' Time for loss = {duration:.5f}')
return loss.mean()
def compute_loss_ber_exp2(adj, emb, b=0.1):
#Init
N,d=emb.shape
#get indices of upper triangular matrix
ind=torch.triu_indices(N,N,offset=1)
#compute f(z_i, z_j) = sigma(z_i^Tz_j+b)
dot=torch.matmul(emb,emb.T)
print('dist: ', dot, dot.size(), type(dot))
logits=1-torch.exp(-dot)
logits=logits[ind[0],ind[1]]
labels = adj[ind[0],ind[1]]
print('logits: ', logits, logits.size(), type(logits))
#compute loss
loss = F.binary_cross_entropy_with_logits(logits, labels, reduction='mean')
return loss
def compute_loss_KL(adj, emb, b=0.0):
#adj = torch.FloatTensor(A.toarray()).cuda()
degree= torch.from_numpy(adj.sum(axis=1))
print('degree: ', degree, type(degree), degree.size())
inv_degree=torch.diagflat(1/degree).cuda()
print('invdegree: ', invdegree, type(invdegree), invdegree.size())
P = inv_degree.mm(adj)
print('P: ', invdegree, type(invdegree), invdegree.size())
loss = -(P*torch.log( 10e-9+ F.softmax(emb.mm(emb.t() ),dim=1,dtype=torch.float)))
return loss.mean()
max_epochs = 1000
display_step = 250
compute_loss = compute_loss_KL
for epoch in range(max_epochs):
opt.zero_grad()
loss = compute_loss(adj, emb, b)
loss.backward()
opt.step()
# Training loss is printed every display_step epochs
if epoch == 0 or (epoch + 1) % display_step == 0:
print(f'Epoch {epoch+1:4d}, loss = {loss.item():.5f}')
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
import gust # library for loading graph data
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import scipy.sparse as sp
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.distributions as dist
import time
import random
from scipy.spatial.distance import squareform
torch.set_default_tensor_type('torch.cuda.FloatTensor')
%matplotlib inline
sns.set_style('whitegrid')
# Load the dataset using `gust` library
# graph.standardize() makes the graph unweighted, undirected and selects
# the largest connected component
# graph.unpack() returns the necessary vectors / matrices
A, X, _, y = gust.load_dataset('cora').standardize().unpack()
# A - adjacency matrix
# X - attribute matrix - not needed
# y - node labels
A=A[:10,:10]
if (A != A.T).sum() > 0:
raise RuntimeError("The graph must be undirected!")
if (A.data != 1).sum() > 0:
raise RuntimeError("The graph must be unweighted!")
adj = torch.FloatTensor(A.toarray()).cuda()
# Make it stochastic
adj = torch.FloatTensor(A.toarray()).cuda()
'''
from the paper Sampling from Large Graphs:
We first choose node v uniformly at random. We then generate a random number x that is geometrically distributed
with mean pf /(1 − pf ). Node v selects x out-links incident
to nodes that were not yet visited. Let w1, w2, . . . , wx denote the other ends of these selected links. We then apply
this step recursively to each of w1, w2, . . . , wx until enough
nodes have been burned. As the process continues, nodes
cannot be visited a second time, preventing the construction
from cycling. If the fire dies, then we restart it, i.e. select
new node v uniformly at random. We call the parameter pf
the forward burning probability.
'''
#1. choose first node v uniformly at random and store it
v_new = np.random.randint(len(adj))
nodes = torch.tensor([v_new])
print('nodes: ', nodes)
#2. generate random number x from geometrix distribution with mean pf/(1-pf)
pf=0.3 #burning probability, evaluated as best from the given paper
x = np.random.geometric(pf/(1-pf))
#3. let idx choose x out-links
w = (adj[v_new]==1).nonzero()
if w.shape[0]>x:
idx_w = random.sample(range(0, w.shape[0]), x)
w=w[idx_w]
#4. loop until 15% of the dataset is covered
while len(nodes)<20:
v_new = w[0].item()
w = (adj[v_new]==1).nonzero()
for i in w:
for j in nodes:
if w[i]==nodes[j]:
w[i]=0
w = w.remove(0)
if w.shape[0]>x:
idx_w = random.sample(range(0, w.shape[0]), x)
v_new = torch.tensor([v_new])
nodes = torch.cat((nodes,v_new),0)
print(nodes)
num_nodes = A.shape[0]
num_edges = A.sum()
# Convert adjacency matrix to a CUDA Tensor
adj = torch.FloatTensor(A.toarray()).cuda()
#torch.manual_seed(123)
# Define the embedding matrix
embedding_dim = 64
emb = nn.Parameter(torch.empty(num_nodes, embedding_dim).normal_(0.0, 1.0))
# Initialize the bias
# The bias is initialized in such a way that if the dot product between two embedding vectors is 0
# (i.e. z_i^T z_j = 0), then their connection probability is sigmoid(b) equals to the
# background edge probability in the graph. This significantly speeds up training
edge_proba = num_edges / (num_nodes**2 - num_nodes)
bias_init = np.log(edge_proba / (1 - edge_proba))
b = nn.Parameter(torch.Tensor([bias_init]))
# Regularize the embeddings but don't regularize the bias
# The value of weight_decay has a significant effect on the performance of the model (don't set too high!)
opt = torch.optim.Adam([
{'params': [emb], 'weight_decay': 1e-7}, {'params': [b]}],
lr=1e-2)
def compute_loss_ber_sig(adj, emb, b=0.1):
#kernel: theta(z_i,z_j)=sigma(z_i^Tz_j+b)
# Initialization
N,d=emb.shape
#compute f(z_i, z_j) = sigma(z_i^Tz_j+b)
dot=torch.matmul(emb,emb.T)
logits =dot+b
#transform adj
ind=torch.triu_indices(N,N,offset=1)
logits = logits[ind[0], ind[1]]
labels = adj[ind[0],ind[1]]
#compute p(A|Z)
loss = F.binary_cross_entropy_with_logits(logits, labels, weight=None, size_average=None, reduce=None, reduction='mean')
return loss
def compute_loss_d1(adj, emb, b=0.0):
"""Compute the rdf distance of the Bernoulli model."""
# Initialization
start_time = time.time()
N,d=emb.shape
squared_euclidian = torch.zeros(N,N).cuda()
gamma= 0.1
end_time= time.time()
duration= end_time -start_time
#print(f' Time for initialization = {duration:.5f}')
# Compute squared euclidian
start_time = time.time()
for index, embedding in enumerate(emb):
sub = embedding-emb + 10e-9
squared_euclidian[index,:]= torch.sum(torch.pow(sub,2),1)
end_time= time.time()
duration= end_time -start_time
#print(f' Time for euclidian = {duration:.5f}')
# Compute exponentianl
start_time = time.time()
radial_exp = torch.exp (-gamma * torch.sqrt(squared_euclidian))
loss = F.binary_cross_entropy(radial_exp, adj, reduction='none')
loss[np.diag_indices(adj.shape[0])] = 0.0
end_time= time.time()
duration= end_time -start_time
#print(f' Time for loss = {duration:.5f}')
return loss.mean()
def compute_loss_ber_exp2(adj, emb, b=0.1):
#Init
N,d=emb.shape
#get indices of upper triangular matrix
ind=torch.triu_indices(N,N,offset=1)
#compute f(z_i, z_j) = sigma(z_i^Tz_j+b)
dot=torch.matmul(emb,emb.T)
print('dist: ', dot, dot.size(), type(dot))
logits=1-torch.exp(-dot)
logits=logits[ind[0],ind[1]]
labels = adj[ind[0],ind[1]]
print('logits: ', logits, logits.size(), type(logits))
#compute loss
loss = F.binary_cross_entropy_with_logits(logits, labels, reduction='mean')
return loss
def compute_loss_KL(adj, emb, b=0.0):
#adj = torch.FloatTensor(A.toarray()).cuda()
degree= torch.from_numpy(adj.sum(axis=1))
print('degree: ', degree, type(degree), degree.size())
inv_degree=torch.diagflat(1/degree).cuda()
print('invdegree: ', invdegree, type(invdegree), invdegree.size())
P = inv_degree.mm(adj)
print('P: ', invdegree, type(invdegree), invdegree.size())
loss = -(P*torch.log( 10e-9+ F.softmax(emb.mm(emb.t() ),dim=1,dtype=torch.float)))
return loss.mean()
max_epochs = 1000
display_step = 250
compute_loss = compute_loss_KL
for epoch in range(max_epochs):
opt.zero_grad()
loss = compute_loss(adj, emb, b)
loss.backward()
opt.step()
# Training loss is printed every display_step epochs
if epoch == 0 or (epoch + 1) % display_step == 0:
print(f'Epoch {epoch+1:4d}, loss = {loss.item():.5f}')
| 0.79158 | 0.604487 |
# Analyzing Portfolio Risk and Return
In this Challenge, you'll assume the role of a quantitative analyst for a FinTech investing platform. This platform aims to offer clients a one-stop online investment solution for their retirement portfolios that’s both inexpensive and high quality. (Think about [Wealthfront](https://www.wealthfront.com/) or [Betterment](https://www.betterment.com/)). To keep the costs low, the firm uses algorithms to build each client's portfolio. The algorithms choose from various investment styles and options.
You've been tasked with evaluating four new investment options for inclusion in the client portfolios. Legendary fund and hedge-fund managers run all four selections. (People sometimes refer to these managers as **whales**, because of the large amount of money that they manage). You’ll need to determine the fund with the most investment potential based on key risk-management metrics: the daily returns, standard deviations, Sharpe ratios, and betas.
## Instructions
### Import the Data
Use the `whale_analysis.ipynb` file to complete the following steps:
1. Import the required libraries and dependencies.
2. Use the `read_csv` function and the `Path` module to read the `whale_navs.csv` file into a Pandas DataFrame. Be sure to create a `DateTimeIndex`. Review the first five rows of the DataFrame by using the `head` function.
3. Use the Pandas `pct_change` function together with `dropna` to create the daily returns DataFrame. Base this DataFrame on the NAV prices of the four portfolios and on the closing price of the S&P 500 Index. Review the first five rows of the daily returns DataFrame.
### Analyze the Performance
Analyze the data to determine if any of the portfolios outperform the broader stock market, which the S&P 500 represents. To do so, complete the following steps:
1. Use the default Pandas `plot` function to visualize the daily return data of the four fund portfolios and the S&P 500. Be sure to include the `title` parameter, and adjust the figure size if necessary.
2. Use the Pandas `cumprod` function to calculate the cumulative returns for the four fund portfolios and the S&P 500. Review the last five rows of the cumulative returns DataFrame by using the Pandas `tail` function.
3. Use the default Pandas `plot` to visualize the cumulative return values for the four funds and the S&P 500 over time. Be sure to include the `title` parameter, and adjust the figure size if necessary.
4. Answer the following question: Based on the cumulative return data and the visualization, do any of the four fund portfolios outperform the S&P 500 Index?
### Analyze the Volatility
Analyze the volatility of each of the four fund portfolios and of the S&P 500 Index by using box plots. To do so, complete the following steps:
1. Use the Pandas `plot` function and the `kind="box"` parameter to visualize the daily return data for each of the four portfolios and for the S&P 500 in a box plot. Be sure to include the `title` parameter, and adjust the figure size if necessary.
2. Use the Pandas `drop` function to create a new DataFrame that contains the data for just the four fund portfolios by dropping the S&P 500 column. Visualize the daily return data for just the four fund portfolios by using another box plot. Be sure to include the `title` parameter, and adjust the figure size if necessary.
> **Hint** Save this new DataFrame—the one that contains the data for just the four fund portfolios. You’ll use it throughout the analysis.
3. Answer the following question: Based on the box plot visualization of just the four fund portfolios, which fund was the most volatile (with the greatest spread) and which was the least volatile (with the smallest spread)?
### Analyze the Risk
Evaluate the risk profile of each portfolio by using the standard deviation and the beta. To do so, complete the following steps:
1. Use the Pandas `std` function to calculate the standard deviation for each of the four portfolios and for the S&P 500. Review the standard deviation calculations, sorted from smallest to largest.
2. Calculate the annualized standard deviation for each of the four portfolios and for the S&P 500. To do that, multiply the standard deviation by the square root of the number of trading days. Use 252 for that number.
3. Use the daily returns DataFrame and a 21-day rolling window to plot the rolling standard deviations of the four fund portfolios and of the S&P 500 index. Be sure to include the `title` parameter, and adjust the figure size if necessary.
4. Use the daily returns DataFrame and a 21-day rolling window to plot the rolling standard deviations of only the four fund portfolios. Be sure to include the `title` parameter, and adjust the figure size if necessary.
5. Answer the following three questions:
* Based on the annualized standard deviation, which portfolios pose more risk than the S&P 500?
* Based on the rolling metrics, does the risk of each portfolio increase at the same time that the risk of the S&P 500 increases?
* Based on the rolling standard deviations of only the four fund portfolios, which portfolio poses the most risk? Does this change over time?
### Analyze the Risk-Return Profile
To determine the overall risk of an asset or portfolio, quantitative analysts and investment managers consider not only its risk metrics but also its risk-return profile. After all, if you have two portfolios that each offer a 10% return but one has less risk, you’d probably invest in the smaller-risk portfolio. For this reason, you need to consider the Sharpe ratios for each portfolio. To do so, complete the following steps:
1. Use the daily return DataFrame to calculate the annualized average return data for the four fund portfolios and for the S&P 500. Use 252 for the number of trading days. Review the annualized average returns, sorted from lowest to highest.
2. Calculate the Sharpe ratios for the four fund portfolios and for the S&P 500. To do that, divide the annualized average return by the annualized standard deviation for each. Review the resulting Sharpe ratios, sorted from lowest to highest.
3. Visualize the Sharpe ratios for the four funds and for the S&P 500 in a bar chart. Be sure to include the `title` parameter, and adjust the figure size if necessary.
4. Answer the following question: Which of the four portfolios offers the best risk-return profile? Which offers the worst?
#### Diversify the Portfolio
Your analysis is nearing completion. Now, you need to evaluate how the portfolios react relative to the broader market. Based on your analysis so far, choose two portfolios that you’re most likely to recommend as investment options. To start your analysis, complete the following step:
* Use the Pandas `var` function to calculate the variance of the S&P 500 by using a 60-day rolling window. Visualize the last five rows of the variance of the S&P 500.
Next, for each of the two portfolios that you chose, complete the following steps:
1. Using the 60-day rolling window, the daily return data, and the S&P 500 returns, calculate the covariance. Review the last five rows of the covariance of the portfolio.
2. Calculate the beta of the portfolio. To do that, divide the covariance of the portfolio by the variance of the S&P 500.
3. Use the Pandas `mean` function to calculate the average value of the 60-day rolling beta of the portfolio.
4. Plot the 60-day rolling beta. Be sure to include the `title` parameter, and adjust the figure size if necessary.
Finally, answer the following two questions:
* Which of the two portfolios seem more sensitive to movements in the S&P 500?
* Which of the two portfolios do you recommend for inclusion in your firm’s suite of fund offerings?
### Import the Data
#### Step 1: Import the required libraries and dependencies.
```
# Import the required libraries and dependencies
import pandas as pd
from pathlib import Path
%matplotlib inline
import numpy as np
import os
#understanding where we are in the dir in order to have Path work correctly
os.getcwd()
```
#### Step 2: Use the `read_csv` function and the `Path` module to read the `whale_navs.csv` file into a Pandas DataFrame. Be sure to create a `DateTimeIndex`. Review the first five rows of the DataFrame by using the `head` function.
```
# Import the data by reading in the CSV file and setting the DatetimeIndex
# Review the first 5 rows of the DataFrame
whale_df = pd.read_csv(
Path('Resources/whale_navs.csv'),
index_col = 'date',
parse_dates = True,
infer_datetime_format = True
)
whale_df.head()
```
#### Step 3: Use the Pandas `pct_change` function together with `dropna` to create the daily returns DataFrame. Base this DataFrame on the NAV prices of the four portfolios and on the closing price of the S&P 500 Index. Review the first five rows of the daily returns DataFrame.
```
# Prepare for the analysis by converting the dataframe of NAVs and prices to daily returns
# Drop any rows with all missing values
# Review the first five rows of the daily returns DataFrame.
whale_daily_returns = whale_df.pct_change().dropna()
whale_daily_returns.head(5)
```
---
## Quantative Analysis
The analysis has several components: performance, volatility, risk, risk-return profile, and portfolio diversification. You’ll analyze each component one at a time.
### Analyze the Performance
Analyze the data to determine if any of the portfolios outperform the broader stock market, which the S&P 500 represents.
#### Step 1: Use the default Pandas `plot` function to visualize the daily return data of the four fund portfolios and the S&P 500. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Plot the daily return data of the 4 funds and the S&P 500
# Include a title parameter and adjust the figure size
whale_daily_returns.plot(figsize =(15,5), title = 'Daily returns of the whales and S&P 500')
```
#### Step 2: Use the Pandas `cumprod` function to calculate the cumulative returns for the four fund portfolios and the S&P 500. Review the last five rows of the cumulative returns DataFrame by using the Pandas `tail` function.
```
# Calculate and plot the cumulative returns of the 4 fund portfolios and the S&P 500
# Review the last 5 rows of the cumulative returns DataFrame
whale_cumulative_returns = (1 + whale_daily_returns).cumprod()
whale_cumulative_returns.tail()
```
#### Step 3: Use the default Pandas `plot` to visualize the cumulative return values for the four funds and the S&P 500 over time. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Visualize the cumulative returns using the Pandas plot function
# Include a title parameter and adjust the figure size
whale_cumulative_returns.plot(figsize =(20,10), title = 'Cumulative returns of whales and the S&P 500')
```
#### Step 4: Answer the following question: Based on the cumulative return data and the visualization, do any of the four fund portfolios outperform the S&P 500 Index?
**Question** Based on the cumulative return data and the visualization, do any of the four fund portfolios outperform the S&P 500 Index?
**Answer** # No they do not. In fact, the S&P 500 outperforms every whale fund by a signifigant amount
---
### Analyze the Volatility
Analyze the volatility of each of the four fund portfolios and of the S&P 500 Index by using box plots.
#### Step 1: Use the Pandas `plot` function and the `kind="box"` parameter to visualize the daily return data for each of the four portfolios and for the S&P 500 in a box plot. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Use the daily return data to create box plots to visualize the volatility of the 4 funds and the S&P 500
# Include a title parameter and adjust the figure size
whale_daily_returns.plot(kind ='box', title = 'Box plot of daily returns of the whales and SPX')
```
#### Step 2: Use the Pandas `drop` function to create a new DataFrame that contains the data for just the four fund portfolios by dropping the S&P 500 column. Visualize the daily return data for just the four fund portfolios by using another box plot. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Create a new DataFrame containing only the 4 fund portfolios by dropping the S&P 500 column from the DataFrame
# Create box plots to reflect the return data for only the 4 fund portfolios
# Include a title parameter and adjust the figure size
whales_only = whale_daily_returns.drop(['S&P 500'], axis = 1)
whales_only.plot(kind = 'box', figsize =(15, 7), title = 'Whale only data ex-SPX')
```
#### Step 3: Answer the following question: Based on the box plot visualization of just the four fund portfolios, which fund was the most volatile (with the greatest spread) and which was the least volatile (with the smallest spread)?
**Question** Based on the box plot visualization of just the four fund portfolios, which fund was the most volatile (with the greatest spread) and which was the least volatile (with the smallest spread)?
**Answer** # It appears that Berkshire Hathaway has the largest spread as per the box spread daily return data.
---
### Analyze the Risk
Evaluate the risk profile of each portfolio by using the standard deviation and the beta.
#### Step 1: Use the Pandas `std` function to calculate the standard deviation for each of the four portfolios and for the S&P 500. Review the standard deviation calculations, sorted from smallest to largest.
```
# Calculate and sort the standard deviation for all 4 portfolios and the S&P 500
# Review the standard deviations sorted smallest to largest
whale_std = whale_daily_returns.std()
whale_std.sort_values()
```
#### Step 2: Calculate the annualized standard deviation for each of the four portfolios and for the S&P 500. To do that, multiply the standard deviation by the square root of the number of trading days. Use 252 for that number.
```
# Calculate and sort the annualized standard deviation (252 trading days) of the 4 portfolios and the S&P 500
# Review the annual standard deviations smallest to largest
whale_std_annualized = whale_std *np.sqrt(252)
whale_std_annualized.sort_values()
```
#### Step 3: Use the daily returns DataFrame and a 21-day rolling window to plot the rolling standard deviations of the four fund portfolios and of the S&P 500 index. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Using the daily returns DataFrame and a 21-day rolling window,
# plot the rolling standard deviation of the 4 portfolios and the S&P 500
# Include a title parameter and adjust the figure size
whale_std_21d = whale_daily_returns.rolling(window = 21).std()
whale_std_21d.plot(figsize=(15,10), title = 'Rolling 21d std deviations of Whales and SPX')
```
#### Step 4: Use the daily returns DataFrame and a 21-day rolling window to plot the rolling standard deviations of only the four fund portfolios. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Using the daily return data and a 21-day rolling window, plot the rolling standard deviation of just the 4 portfolios.
# Include a title parameter and adjust the figure size
rolling_std_deviaton_21d = whales_only.rolling(21).std()
rolling_std_deviaton_21d.plot(figsize = (15,7), title = 'Rolling Std Deviations -- 21d using daily return data')
```
#### Step 5: Answer the following three questions:
1. Based on the annualized standard deviation, which portfolios pose more risk than the S&P 500?
2. Based on the rolling metrics, does the risk of each portfolio increase at the same time that the risk of the S&P 500 increases?
3. Based on the rolling standard deviations of only the four fund portfolios, which portfolio poses the most risk? Does this change over time?
**Question 1** Based on the annualized standard deviation, which portfolios pose more risk than the S&P 500?
**Answer 1** # Based on the std deviations, Berkshire and Tiger pose more risk with annualized std deviations of 66 and 11.9 respectvly.
**Question 2** Based on the rolling metrics, does the risk of each portfolio increase at the same time that the risk of the S&P 500 increases?
**Answer 2** # Most of the time yes though the SPX has considerably higher spikes in standard deviation.
**Question 3** Based on the rolling standard deviations of only the four fund portfolios, which portfolio poses the most risk? Does this change over time?
**Answer 3** # The Berkshire fund poses the most risk out of the 4 funds. Since 2019, the Paulson fund has increased risk and std deviations close to Berkshire.
---
### Analyze the Risk-Return Profile
To determine the overall risk of an asset or portfolio, quantitative analysts and investment managers consider not only its risk metrics but also its risk-return profile. After all, if you have two portfolios that each offer a 10% return but one has less risk, you’d probably invest in the smaller-risk portfolio. For this reason, you need to consider the Sharpe ratios for each portfolio.
#### Step 1: Use the daily return DataFrame to calculate the annualized average return data for the four fund portfolios and for the S&P 500. Use 252 for the number of trading days. Review the annualized average returns, sorted from lowest to highest.
```
# Calculate the annual average return data for the for fund portfolios and the S&P 500
# Use 252 as the number of trading days in the year
# Review the annual average returns sorted from lowest to highest
annualized_average_returns = whale_daily_returns.mean()*(252)
annualized_average_returns.sort_values()
```
#### Step 2: Calculate the Sharpe ratios for the four fund portfolios and for the S&P 500. To do that, divide the annualized average return by the annualized standard deviation for each. Review the resulting Sharpe ratios, sorted from lowest to highest.
```
# Calculate the annualized Sharpe Ratios for each of the 4 portfolios and the S&P 500.
# Review the Sharpe ratios sorted lowest to highest
sharpe = annualized_average_returns / whale_std_annualized
sharpe.sort_values()
```
#### Step 3: Visualize the Sharpe ratios for the four funds and for the S&P 500 in a bar chart. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Visualize the Sharpe ratios as a bar chart
# Include a title parameter and adjust the figure size
sharpe.plot(kind = 'bar', figsize = (12,5), title = 'Sharpe Ratios of the Whales and the SPX')
```
#### Step 4: Answer the following question: Which of the four portfolios offers the best risk-return profile? Which offers the worst?
**Question** Which of the four portfolios offers the best risk-return profile? Which offers the worst?
**Answer** # Tiger Global offeres the best risk return profile (per the Sharpe Ratio) while Paulson offers the wors risk return profile.
---
### Diversify the Portfolio
Your analysis is nearing completion. Now, you need to evaluate how the portfolios react relative to the broader market. Based on your analysis so far, choose two portfolios that you’re most likely to recommend as investment options.
#### Use the Pandas `var` function to calculate the variance of the S&P 500 by using a 60-day rolling window. Visualize the last five rows of the variance of the S&P 500.
```
# Calculate the variance of the S&P 500 using a rolling 60-day window.
spx_var_60d = whale_daily_returns['S&P 500'].rolling(window = 60).var()
spx_var_60d.tail()
```
#### For each of the two portfolios that you chose, complete the following steps:
1. Using the 60-day rolling window, the daily return data, and the S&P 500 returns, calculate the covariance. Review the last five rows of the covariance of the portfolio.
2. Calculate the beta of the portfolio. To do that, divide the covariance of the portfolio by the variance of the S&P 500.
3. Use the Pandas `mean` function to calculate the average value of the 60-day rolling beta of the portfolio.
4. Plot the 60-day rolling beta. Be sure to include the `title` parameter, and adjust the figure size if necessary.
##### Portfolio 1 - Step 1: Using the 60-day rolling window, the daily return data, and the S&P 500 returns, calculate the covariance. Review the last five rows of the covariance of the portfolio.
```
# Calculate the covariance using a 60-day rolling window
# Review the last five rows of the covariance data
berkshire_spx_cov_60d = whale_daily_returns['BERKSHIRE HATHAWAY INC'].rolling (window = 60).cov(whale_daily_returns['S&P 500'].rolling(window=60))
berkshire_spx_cov_60d.tail()
```
##### Portfolio 1 - Step 2: Calculate the beta of the portfolio. To do that, divide the covariance of the portfolio by the variance of the S&P 500.
```
# Calculate the beta based on the 60-day rolling covariance compared to the market (S&P 500)
# Review the last five rows of the beta information
berkshire_beta = berkshire_spx_cov_60d / spx_var_60d
berkshire_beta.tail()
#covariance = whale_daily_returns['BERKSHIRE HATHAWAY INC'].cov(whale_daily_returns['S&P 500'])
#variance = whale_daily_returns['S&P 500'].var()
#beta = covariance/variance
#beta
```
##### Portfolio 1 - Step 3: Use the Pandas `mean` function to calculate the average value of the 60-day rolling beta of the portfolio.
```
# Calculate the average of the 60-day rolling beta
berkshire_average_60d_beta = berkshire_beta.mean()
berkshire_average_60d_beta
```
##### Portfolio 1 - Step 4: Plot the 60-day rolling beta. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Plot the rolling beta
# Include a title parameter and adjust the figure size
berkshire_beta.plot(figsize =(15,7), title = 'Berkshire 60d rolling beta')
```
##### Portfolio 2 - Step 1: Using the 60-day rolling window, the daily return data, and the S&P 500 returns, calculate the covariance. Review the last five rows of the covariance of the portfolio.
```
# Calculate the covariance using a 60-day rolling window
# Review the last five rows of the covariance data
tiger_spx_cov_60d = whale_daily_returns['TIGER GLOBAL MANAGEMENT LLC'].rolling (window = 60).cov(whale_daily_returns['S&P 500'].rolling(window=60))
tiger_spx_cov_60d.tail()
```
##### Portfolio 2 - Step 2: Calculate the beta of the portfolio. To do that, divide the covariance of the portfolio by the variance of the S&P 500.
```
# Calculate the beta based on the 60-day rolling covariance compared to the market (S&P 500)
# Review the last five rows of the beta information
tiger_beta = tiger_spx_cov_60d / spx_var_60d
```
##### Portfolio 2 - Step 3: Use the Pandas `mean` function to calculate the average value of the 60-day rolling beta of the portfolio.
```
# Calculate the average of the 60-day rolling beta
tiger_average_60d_beta = tiger_beta.mean()
tiger_average_60d_beta
```
##### Portfolio 2 - Step 4: Plot the 60-day rolling beta. Be sure to include the `title` parameter, and adjust the figure size if necessary.
```
# Plot the rolling beta
# Include a title parameter and adjust the figure size
tiger_beta.plot(figsize =(15,7), title = 'Tiger 60d rolling beta')
```
#### Answer the following two questions:
1. Which of the two portfolios seem more sensitive to movements in the S&P 500?
2. Which of the two portfolios do you recommend for inclusion in your firm’s suite of fund offerings?
**Question 1** Which of the two portfolios seem more sensitive to movements in the S&P 500?
**Answer 1** # It appears that the Berkshuire Hathway portfolio is more seneitive to the S&P 500
**Question 2** Which of the two portfolios do you recommend for inclusion in your firm’s suite of fund offerings?
**Answer 2** # Despite the increased risk I would recommend the Berkshire portfolio. This is largely due to the higher Sharpe ratio for berkshire is 0.71 vs Tiger which is 0.57.
---
|
github_jupyter
|
# Import the required libraries and dependencies
import pandas as pd
from pathlib import Path
%matplotlib inline
import numpy as np
import os
#understanding where we are in the dir in order to have Path work correctly
os.getcwd()
# Import the data by reading in the CSV file and setting the DatetimeIndex
# Review the first 5 rows of the DataFrame
whale_df = pd.read_csv(
Path('Resources/whale_navs.csv'),
index_col = 'date',
parse_dates = True,
infer_datetime_format = True
)
whale_df.head()
# Prepare for the analysis by converting the dataframe of NAVs and prices to daily returns
# Drop any rows with all missing values
# Review the first five rows of the daily returns DataFrame.
whale_daily_returns = whale_df.pct_change().dropna()
whale_daily_returns.head(5)
# Plot the daily return data of the 4 funds and the S&P 500
# Include a title parameter and adjust the figure size
whale_daily_returns.plot(figsize =(15,5), title = 'Daily returns of the whales and S&P 500')
# Calculate and plot the cumulative returns of the 4 fund portfolios and the S&P 500
# Review the last 5 rows of the cumulative returns DataFrame
whale_cumulative_returns = (1 + whale_daily_returns).cumprod()
whale_cumulative_returns.tail()
# Visualize the cumulative returns using the Pandas plot function
# Include a title parameter and adjust the figure size
whale_cumulative_returns.plot(figsize =(20,10), title = 'Cumulative returns of whales and the S&P 500')
# Use the daily return data to create box plots to visualize the volatility of the 4 funds and the S&P 500
# Include a title parameter and adjust the figure size
whale_daily_returns.plot(kind ='box', title = 'Box plot of daily returns of the whales and SPX')
# Create a new DataFrame containing only the 4 fund portfolios by dropping the S&P 500 column from the DataFrame
# Create box plots to reflect the return data for only the 4 fund portfolios
# Include a title parameter and adjust the figure size
whales_only = whale_daily_returns.drop(['S&P 500'], axis = 1)
whales_only.plot(kind = 'box', figsize =(15, 7), title = 'Whale only data ex-SPX')
# Calculate and sort the standard deviation for all 4 portfolios and the S&P 500
# Review the standard deviations sorted smallest to largest
whale_std = whale_daily_returns.std()
whale_std.sort_values()
# Calculate and sort the annualized standard deviation (252 trading days) of the 4 portfolios and the S&P 500
# Review the annual standard deviations smallest to largest
whale_std_annualized = whale_std *np.sqrt(252)
whale_std_annualized.sort_values()
# Using the daily returns DataFrame and a 21-day rolling window,
# plot the rolling standard deviation of the 4 portfolios and the S&P 500
# Include a title parameter and adjust the figure size
whale_std_21d = whale_daily_returns.rolling(window = 21).std()
whale_std_21d.plot(figsize=(15,10), title = 'Rolling 21d std deviations of Whales and SPX')
# Using the daily return data and a 21-day rolling window, plot the rolling standard deviation of just the 4 portfolios.
# Include a title parameter and adjust the figure size
rolling_std_deviaton_21d = whales_only.rolling(21).std()
rolling_std_deviaton_21d.plot(figsize = (15,7), title = 'Rolling Std Deviations -- 21d using daily return data')
# Calculate the annual average return data for the for fund portfolios and the S&P 500
# Use 252 as the number of trading days in the year
# Review the annual average returns sorted from lowest to highest
annualized_average_returns = whale_daily_returns.mean()*(252)
annualized_average_returns.sort_values()
# Calculate the annualized Sharpe Ratios for each of the 4 portfolios and the S&P 500.
# Review the Sharpe ratios sorted lowest to highest
sharpe = annualized_average_returns / whale_std_annualized
sharpe.sort_values()
# Visualize the Sharpe ratios as a bar chart
# Include a title parameter and adjust the figure size
sharpe.plot(kind = 'bar', figsize = (12,5), title = 'Sharpe Ratios of the Whales and the SPX')
# Calculate the variance of the S&P 500 using a rolling 60-day window.
spx_var_60d = whale_daily_returns['S&P 500'].rolling(window = 60).var()
spx_var_60d.tail()
# Calculate the covariance using a 60-day rolling window
# Review the last five rows of the covariance data
berkshire_spx_cov_60d = whale_daily_returns['BERKSHIRE HATHAWAY INC'].rolling (window = 60).cov(whale_daily_returns['S&P 500'].rolling(window=60))
berkshire_spx_cov_60d.tail()
# Calculate the beta based on the 60-day rolling covariance compared to the market (S&P 500)
# Review the last five rows of the beta information
berkshire_beta = berkshire_spx_cov_60d / spx_var_60d
berkshire_beta.tail()
#covariance = whale_daily_returns['BERKSHIRE HATHAWAY INC'].cov(whale_daily_returns['S&P 500'])
#variance = whale_daily_returns['S&P 500'].var()
#beta = covariance/variance
#beta
# Calculate the average of the 60-day rolling beta
berkshire_average_60d_beta = berkshire_beta.mean()
berkshire_average_60d_beta
# Plot the rolling beta
# Include a title parameter and adjust the figure size
berkshire_beta.plot(figsize =(15,7), title = 'Berkshire 60d rolling beta')
# Calculate the covariance using a 60-day rolling window
# Review the last five rows of the covariance data
tiger_spx_cov_60d = whale_daily_returns['TIGER GLOBAL MANAGEMENT LLC'].rolling (window = 60).cov(whale_daily_returns['S&P 500'].rolling(window=60))
tiger_spx_cov_60d.tail()
# Calculate the beta based on the 60-day rolling covariance compared to the market (S&P 500)
# Review the last five rows of the beta information
tiger_beta = tiger_spx_cov_60d / spx_var_60d
# Calculate the average of the 60-day rolling beta
tiger_average_60d_beta = tiger_beta.mean()
tiger_average_60d_beta
# Plot the rolling beta
# Include a title parameter and adjust the figure size
tiger_beta.plot(figsize =(15,7), title = 'Tiger 60d rolling beta')
| 0.851089 | 0.995805 |
```
# install: tqdm (progress bars)
!pip install tqdm
import torch
import torch.nn as nn
import numpy as np
from tqdm.auto import tqdm
from torch.utils.data import DataLoader, Dataset, TensorDataset
import torchvision.datasets as ds
```
## Load the data (CIFAR-10)
```
def load_cifar(datadir='./data_cache'): # will download ~400MB of data into this dir. Change the dir if neccesary. If using paperspace, you can make this /storage
train_ds = ds.CIFAR10(root=datadir, train=True,
download=True, transform=None)
test_ds = ds.CIFAR10(root=datadir, train=False,
download=True, transform=None)
def to_xy(dataset):
X = torch.Tensor(np.transpose(dataset.data, (0, 3, 1, 2))).float() / 255.0 # [0, 1]
Y = torch.Tensor(np.array(dataset.targets)).long()
return X, Y
X_tr, Y_tr = to_xy(train_ds)
X_te, Y_te = to_xy(test_ds)
return X_tr, Y_tr, X_te, Y_te
def make_loader(dataset, batch_size=128):
return torch.utils.data.DataLoader(dataset, batch_size=batch_size,
shuffle=True, num_workers=4, pin_memory=True)
X_tr, Y_tr, X_te, Y_te = load_cifar()
train_dl = make_loader(TensorDataset(X_tr, Y_tr))
test_dl = make_loader(TensorDataset(X_te, Y_te))
```
## Training helper functions
```
def train_epoch(model, train_dl : DataLoader, opt, k = 50):
''' Trains model for one epoch on the provided dataloader, with optimizer opt. Logs stats every k batches.'''
loss_func = nn.CrossEntropyLoss()
model.train()
model.cuda()
netLoss = 0.0
nCorrect = 0
nTotal = 0
for i, (xB, yB) in enumerate(tqdm(train_dl)):
opt.zero_grad()
xB, yB = xB.cuda(), yB.cuda()
outputs = model(xB)
loss = loss_func(outputs, yB)
loss.backward()
opt.step()
netLoss += loss.item() * len(xB)
with torch.no_grad():
_, preds = torch.max(outputs, dim=1)
nCorrect += (preds == yB).float().sum()
nTotal += preds.size(0)
if (i+1) % k == 0:
train_acc = nCorrect/nTotal
avg_loss = netLoss/nTotal
print(f'\t [Batch {i+1} / {len(train_dl)}] Train Loss: {avg_loss:.3f} \t Train Acc: {train_acc:.3f}')
train_acc = nCorrect/nTotal
avg_loss = netLoss/nTotal
return avg_loss, train_acc
def evaluate(model, test_dl, loss_func=nn.CrossEntropyLoss().cuda()):
''' Returns loss, acc'''
model.eval()
model.cuda()
nCorrect = 0.0
nTotal = 0
net_loss = 0.0
with torch.no_grad():
for (xb, yb) in test_dl:
xb, yb = xb.cuda(), yb.cuda()
outputs = model(xb)
loss = len(xb) * loss_func(outputs, yb)
_, preds = torch.max(outputs, dim=1)
nCorrect += (preds == yb).float().sum()
net_loss += loss
nTotal += preds.size(0)
acc = nCorrect.cpu().item() / float(nTotal)
loss = net_loss.cpu().item() / float(nTotal)
return loss, acc
## Define model
## 5-Layer CNN for CIFAR
## This is the Myrtle5 network by David Page (https://myrtle.ai/learn/how-to-train-your-resnet-4-architecture/)
class Flatten(nn.Module):
def forward(self, x): return x.view(x.size(0), x.size(1))
def make_cnn(c=64, num_classes=10):
''' Returns a 5-layer CNN with width parameter c. '''
return nn.Sequential(
# Layer 0
nn.Conv2d(3, c, kernel_size=3, stride=1,
padding=1, bias=True),
nn.BatchNorm2d(c),
nn.ReLU(),
# Layer 1
nn.Conv2d(c, c*2, kernel_size=3,
stride=1, padding=1, bias=True),
nn.BatchNorm2d(c*2),
nn.ReLU(),
nn.MaxPool2d(2),
# Layer 2
nn.Conv2d(c*2, c*4, kernel_size=3,
stride=1, padding=1, bias=True),
nn.BatchNorm2d(c*4),
nn.ReLU(),
nn.MaxPool2d(2),
# Layer 3
nn.Conv2d(c*4, c*8, kernel_size=3,
stride=1, padding=1, bias=True),
nn.BatchNorm2d(c*8),
nn.ReLU(),
nn.MaxPool2d(2),
# Layer 4
nn.MaxPool2d(4),
Flatten(),
nn.Linear(c*8, num_classes, bias=True)
)
## Train
model = make_cnn()
opt = torch.optim.SGD(model.parameters(), lr=0.1)
epochs = 20
for i in range(epochs):
print(f'Starting Epoch {i}')
train_loss, train_acc = train_epoch(model, train_dl, opt)
test_loss, test_acc = evaluate(model, test_dl)
print(f'Epoch {i}:\t Train Loss: {train_loss:.3f} \t Train Acc: {train_acc:.3f}\t Test Acc: {test_acc:.3f}')
```
|
github_jupyter
|
# install: tqdm (progress bars)
!pip install tqdm
import torch
import torch.nn as nn
import numpy as np
from tqdm.auto import tqdm
from torch.utils.data import DataLoader, Dataset, TensorDataset
import torchvision.datasets as ds
def load_cifar(datadir='./data_cache'): # will download ~400MB of data into this dir. Change the dir if neccesary. If using paperspace, you can make this /storage
train_ds = ds.CIFAR10(root=datadir, train=True,
download=True, transform=None)
test_ds = ds.CIFAR10(root=datadir, train=False,
download=True, transform=None)
def to_xy(dataset):
X = torch.Tensor(np.transpose(dataset.data, (0, 3, 1, 2))).float() / 255.0 # [0, 1]
Y = torch.Tensor(np.array(dataset.targets)).long()
return X, Y
X_tr, Y_tr = to_xy(train_ds)
X_te, Y_te = to_xy(test_ds)
return X_tr, Y_tr, X_te, Y_te
def make_loader(dataset, batch_size=128):
return torch.utils.data.DataLoader(dataset, batch_size=batch_size,
shuffle=True, num_workers=4, pin_memory=True)
X_tr, Y_tr, X_te, Y_te = load_cifar()
train_dl = make_loader(TensorDataset(X_tr, Y_tr))
test_dl = make_loader(TensorDataset(X_te, Y_te))
def train_epoch(model, train_dl : DataLoader, opt, k = 50):
''' Trains model for one epoch on the provided dataloader, with optimizer opt. Logs stats every k batches.'''
loss_func = nn.CrossEntropyLoss()
model.train()
model.cuda()
netLoss = 0.0
nCorrect = 0
nTotal = 0
for i, (xB, yB) in enumerate(tqdm(train_dl)):
opt.zero_grad()
xB, yB = xB.cuda(), yB.cuda()
outputs = model(xB)
loss = loss_func(outputs, yB)
loss.backward()
opt.step()
netLoss += loss.item() * len(xB)
with torch.no_grad():
_, preds = torch.max(outputs, dim=1)
nCorrect += (preds == yB).float().sum()
nTotal += preds.size(0)
if (i+1) % k == 0:
train_acc = nCorrect/nTotal
avg_loss = netLoss/nTotal
print(f'\t [Batch {i+1} / {len(train_dl)}] Train Loss: {avg_loss:.3f} \t Train Acc: {train_acc:.3f}')
train_acc = nCorrect/nTotal
avg_loss = netLoss/nTotal
return avg_loss, train_acc
def evaluate(model, test_dl, loss_func=nn.CrossEntropyLoss().cuda()):
''' Returns loss, acc'''
model.eval()
model.cuda()
nCorrect = 0.0
nTotal = 0
net_loss = 0.0
with torch.no_grad():
for (xb, yb) in test_dl:
xb, yb = xb.cuda(), yb.cuda()
outputs = model(xb)
loss = len(xb) * loss_func(outputs, yb)
_, preds = torch.max(outputs, dim=1)
nCorrect += (preds == yb).float().sum()
net_loss += loss
nTotal += preds.size(0)
acc = nCorrect.cpu().item() / float(nTotal)
loss = net_loss.cpu().item() / float(nTotal)
return loss, acc
## Define model
## 5-Layer CNN for CIFAR
## This is the Myrtle5 network by David Page (https://myrtle.ai/learn/how-to-train-your-resnet-4-architecture/)
class Flatten(nn.Module):
def forward(self, x): return x.view(x.size(0), x.size(1))
def make_cnn(c=64, num_classes=10):
''' Returns a 5-layer CNN with width parameter c. '''
return nn.Sequential(
# Layer 0
nn.Conv2d(3, c, kernel_size=3, stride=1,
padding=1, bias=True),
nn.BatchNorm2d(c),
nn.ReLU(),
# Layer 1
nn.Conv2d(c, c*2, kernel_size=3,
stride=1, padding=1, bias=True),
nn.BatchNorm2d(c*2),
nn.ReLU(),
nn.MaxPool2d(2),
# Layer 2
nn.Conv2d(c*2, c*4, kernel_size=3,
stride=1, padding=1, bias=True),
nn.BatchNorm2d(c*4),
nn.ReLU(),
nn.MaxPool2d(2),
# Layer 3
nn.Conv2d(c*4, c*8, kernel_size=3,
stride=1, padding=1, bias=True),
nn.BatchNorm2d(c*8),
nn.ReLU(),
nn.MaxPool2d(2),
# Layer 4
nn.MaxPool2d(4),
Flatten(),
nn.Linear(c*8, num_classes, bias=True)
)
## Train
model = make_cnn()
opt = torch.optim.SGD(model.parameters(), lr=0.1)
epochs = 20
for i in range(epochs):
print(f'Starting Epoch {i}')
train_loss, train_acc = train_epoch(model, train_dl, opt)
test_loss, test_acc = evaluate(model, test_dl)
print(f'Epoch {i}:\t Train Loss: {train_loss:.3f} \t Train Acc: {train_acc:.3f}\t Test Acc: {test_acc:.3f}')
| 0.879858 | 0.832475 |
# 선형계획법 Linear Programming
```
import matplotlib.pyplot as plt
import numpy as np
import numpy.linalg as nl
import scipy.optimize as so
```
ref :
* Wikipedia [link](https://en.wikipedia.org/wiki/Linear_programming)
* Stackoverflow [link](https://stackoverflow.com/questions/62571092/)
* Tips & Tricks on Linux, Matlab, vim, LaTex, etc [link](http://tipstrickshowtos.blogspot.com/2012/04/how-to-render-argmax-argmin-operator-in.html)
## Problem description<br>문제 설명
* Area of the farm 농장의 넓이 : $L = 10 (km^2)$
* Types of crops : wheat or rice<br>작물의 종류 : 밀 또는 쌀
* Available fertilizer 사용 가능한 비료의 양 : $F = 10 (kg)$
* Available pesticide 사용 가능한 살충제의 양 : $P = 5 (kg)$
| | Wheat 밀 | rice 쌀 |
|:-----:|:-----:|:-----:|
| Needed Fertilizer per unit area $(kg/km^2)$<br>단위면적 당 필요 비료 양 $(kg/km^2)$ | $F_1$ | $F_2$ |
| Needed Pesticide per unit area $(kg/km^2)$<br>단위면적 당 필요 살충제 양 $(kg/km^2)$ | $P_1$ | $P_2$ |
| Selling price per unit area $(\$/km^2)$<br>단위면적 당 매출 $(\$/km^2)$ | $S_1$ | $S_2$ |
| Planting area $(km^2)$<br>재배 면적 $(km^2)$ | $x_1$ | $x_2$ |
* Under the constraints, what are the areas of wheat and rice maximizing the overall selling price?<br>제한조건 하에서 매출을 최대로 하는 밀과 쌀의 재배 면적?
$$
\underset{x_1, x_2}{\arg\max} \left(S_1 x_1 + S_2 x_2\right)
$$
subject to 제한조건
$$
\begin{align}
x_1 + x_2 & \le L \\
F_1 x_1 + F_2 x_2 & \le F \\
P_1 x_1 + P_2 x_2 & \le P \\
x_1, x_2 & \ge 0
\end{align}
$$
In matrix form 행렬 형태로는:
$$
\underset{x_1, x_2}{\arg\max} \begin{bmatrix} S_1 & S_2 \end{bmatrix}\begin{pmatrix} x_1 \\ x_2 \end{pmatrix}
$$
subject to 제한조건
$$
\begin{align}
\begin{bmatrix}
1 & 1 \\
F_1 & F_2 \\
P_1 & P_2 \\
\end{bmatrix}
\begin{pmatrix}
x_1 \\
x_2
\end{pmatrix} & \le
\begin{pmatrix}
L \\
F \\
P
\end{pmatrix} \\
\begin{pmatrix}
x_1 \\
x_2
\end{pmatrix}& \ge 0
\end{align}
$$
## Parameters Example<br>매개변수 예
```
L = 10
F = 10
F1 = 2
F2 = 3
P = 5
P1 = 2
P2 = 1
S1 = 20
S2 = 25
```
## Visualization 시각화
$$
\begin{align}
x_1 + x_2 & \le L \\
F_1 x_1 + F_2 x_2 & \le F \\
P_1 x_1 + P_2 x_2 & \le P \\
x_1, x_2 & \ge 0
\end{align}
$$
$$
\begin{align}
x_2 & \le -x_1 + L \\
x_2 & \le -\frac{F_1}{F_2} x_1 + \frac{F}{F_2} \\
x_2 & \le -\frac{P_1}{P_2} x_1 + \frac{P}{P_2} \\
x_1 & \ge 0 \\
x_2 & \ge 0
\end{align}
$$
```
x1 = np.linspace(0, 2.5, 101)
x2 = np.linspace(0, 5, 101)
X1, X2 = np.meshgrid(x1, x2)
C = S1 * X1 + S2 * X2
C[X2 > (-F1 * X1 + F) / F2] = np.nan
C[X2 > (-P1 * X1 + P) / P2] = np.nan
plt.pcolor(X1, X2, C, shading="auto")
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.title("$S_1 x_1 + S_2 x_2$")
plt.colorbar()
plt.grid(True)
```
## `scipy.optimize.linprog()`
```
c_T = -np.array((S1, S2))
A_ub = np.array(
(
(1, 1),
(F1, F2),
(P1, P2),
)
)
b_ub = np.array(
((L, F, P),)
).T
bounds = (
(0, None),
(0, None),
)
result = so.linprog(c_T, A_ub, b_ub, bounds=bounds)
result
```
|
github_jupyter
|
import matplotlib.pyplot as plt
import numpy as np
import numpy.linalg as nl
import scipy.optimize as so
L = 10
F = 10
F1 = 2
F2 = 3
P = 5
P1 = 2
P2 = 1
S1 = 20
S2 = 25
x1 = np.linspace(0, 2.5, 101)
x2 = np.linspace(0, 5, 101)
X1, X2 = np.meshgrid(x1, x2)
C = S1 * X1 + S2 * X2
C[X2 > (-F1 * X1 + F) / F2] = np.nan
C[X2 > (-P1 * X1 + P) / P2] = np.nan
plt.pcolor(X1, X2, C, shading="auto")
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.title("$S_1 x_1 + S_2 x_2$")
plt.colorbar()
plt.grid(True)
c_T = -np.array((S1, S2))
A_ub = np.array(
(
(1, 1),
(F1, F2),
(P1, P2),
)
)
b_ub = np.array(
((L, F, P),)
).T
bounds = (
(0, None),
(0, None),
)
result = so.linprog(c_T, A_ub, b_ub, bounds=bounds)
result
| 0.305076 | 0.989265 |
```
import pandas as pd
df = pd.read_csv("Poblacion_Ocupada_Condicion_Informalidad.csv",encoding='cp1252')
```
<p> Datos obtenidos en <b> <a href="https://datos.gob.mx/busca/dataset/indicadores-estrategicos-poblacion-ocupada-por-condicion-de-informalidad">Indicadores Estratégicos/Población Ocupada por Condición De Informalidad </a><b> </p>
```
list(df.columns)
df
Per = df['Periodo']
pd.unique(Per)
col = list(df.columns)
nom = ["Per", "EntFed", "Sex", "Edad", "Cond", "Cantidad"]
Dict = {}
for i in range(0, len(col)):
var = list(pd.unique(df[col[i]]))
Dict[nom[i]] = var
del var
Dict['EntFed']
```
<b> En el año 2019 y principios del 2020</b>
```
data = df[(df['Periodo'] >= 20190301)]
data
AG = data[data.Entidad_Federativa == "Aguascalientes"]
AG
```
<b> Tasa [Informal] / [Formal] por Estado </b>
```
edos = pd.read_csv("edos.csv",encoding='utf-8')
len(edos)
edos['Estado'][1]
x = AG.groupby(['Condicion_informalidad']).sum()
x
x['Numero_personas'][0]
x['Numero_personas'][1]
tasa = x['Numero_personas'][1] / x['Numero_personas'][0]
tasa
edo = edos['Estado']
edo[1]
TasaEdos = {}
for i in range(0, len(edos)):
x = data[data.Entidad_Federativa == Dict['EntFed'][i]]
z = x.groupby(['Condicion_informalidad']).sum()
tasa = z['Numero_personas'][1] / z['Numero_personas'][0]
TasaEdos[Dict['EntFed'][i]] = tasa
del tasa
TasaEdos = {}
for i in range(0, len(edos)):
x = data[data.Entidad_Federativa == Dict['EntFed'][i]].groupby(['Condicion_informalidad']).sum()
tasa = x['Numero_personas'][1] / x['Numero_personas'][0]
TasaEdos[Dict['EntFed'][i]] = tasa
del tasa
TasaEdos['México'] = TasaEdos.pop('Estado de México')
x = data[data.Entidad_Federativa == Dict['EntFed'][i]]
x
!pip install geopandas
!git clone https://github.com/jschleuss/mexican-states.git
import geopandas as gpd
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
mex=gpd.read_file("mexican-states/mexican-states.shp")
#!pip install descartes
type(mex)
#Configurando el canvas en matplotlib y
#creando un objeto "axes"
fig,ax = plt.subplots(1,1,figsize=(10,8))
mex.plot(ax=ax)
plt.show()
TasaEdos
del TasaEdos['Nacional']
len(TasaEdos)
new = pd.DataFrame(list(TasaEdos.items()),columns = ['Estados','tasa'])
new
new.sort_values(["Estados"], axis=0,
ascending=True, inplace=True)
new
len(new)
mex
mex2 = mex.sort_values(by=['name'])
#mex2
list1 = mex2['name']
list2 = mex2['geometry']
#list3 = list(TasaEdos.keys())
list3 = new['Estados'] ### Checar cambio con new
list4 = new['tasa']
list3.pop(32)
#list3
list4 = list(TasaEdos.values())
list4.pop(32)
len(list4)
list3 == list1
list3[1],list1[1]
a = [1,1,2,3,5]
a[0] = 10
a
a = [10,1,2,3,5]
b = [1,1,30,3,5]
for i in range(len(a)):
if a[i]!=b[i]:
active = True
newval = input("EL valor de %s es %f \nIngrese el valor de reemplazo " %("columna", a[i]))
a[i] = newval
active = False
print(a,b)
list3
list1 = str(list1)
del list1
list1 = mex2['name']
type(list1)
type(list3)
list1 = list1.tolist()
type(list1)
list2 = list2.tolist()
type(list2)
for i in range(len(list3)):
if list1[i]!=list3[i]:
active = True
newval = input("list3 = %s list1 = %s \nIngrese el nombre de reemplazo " %(list3[i],list1[i]))
list1[i] = newval
active = False
for i in range(len(list3)):
if list1[i]!=list3[i]:
active = True
newval = input("list3 = %s list1 = %s \nIngrese el nombre de reemplazo " %(list3[i],list1[i]))
list1[i] = newval
active = False
#list3
i = 0
list1[0] = 1
df = pd.DataFrame(list(zip(list1, list3, list4, list2)),
columns =['geopandas_name', 'Tasas_name', 'Tasas', 'geometry'])
df
import mapclassify
#gpd_per_person = world['gdp_md_est'] / world['pop_est']
scheme = mapclassify.Quantiles(df['Tasas'], k=5)
# Note: this code sample requires geoplot>=0.4.0.
geoplot.choropleth(
world, hue=gpd_per_person, scheme=scheme,
cmap='Greens', figsize=(8, 4)
)
!pip install mapclassify
import mapclassify
scheme = mapclassify.Quantiles(df['Tasas'], k=5)
geoplot.choropleth(
df, hue=gpd_per_person, scheme=scheme,
cmap='Greens', figsize=(8, 4)
)
#Configurando el canvas en matplotlib y
#creando un objeto "axes"
fig,ax = plt.subplots(1,1,figsize=(10,8))
mex.plot(ax=ax, scheme=scheme)
plt.show()
type(mex)
gdf1 = geopandas.GeoDataFrame(df)
import matplotlib.pyplot as plt
#Configurando el canvas en matplotlib y
#creando un objeto "axes"
#figure,ax = plt.subplots(1,1,figsize=(10,8))
fig, ax = plt.subplots(1, 1, figsize=(15,12))
#gdf1.plot(ax=ax)
#gdf1.plot(column='Tasas');
gdf1.plot(column='Tasas', cmap='OrRd', ax=ax, legend=True)
plt.show()
#Configurando el canvas en matplotlib y
#creando un objeto "axes"
#figure,ax = plt.subplots(1,1,figsize=(10,8))
fig, ax = plt.subplots(1, 1, figsize=(15,12))
#gdf1.plot(ax=ax)
#gdf1.plot(column='Tasas');
gdf1.plot(column='Tasas', cmap='YlOrRd', ax=ax, legend=True)
plt.show()
```
|
github_jupyter
|
import pandas as pd
df = pd.read_csv("Poblacion_Ocupada_Condicion_Informalidad.csv",encoding='cp1252')
list(df.columns)
df
Per = df['Periodo']
pd.unique(Per)
col = list(df.columns)
nom = ["Per", "EntFed", "Sex", "Edad", "Cond", "Cantidad"]
Dict = {}
for i in range(0, len(col)):
var = list(pd.unique(df[col[i]]))
Dict[nom[i]] = var
del var
Dict['EntFed']
data = df[(df['Periodo'] >= 20190301)]
data
AG = data[data.Entidad_Federativa == "Aguascalientes"]
AG
edos = pd.read_csv("edos.csv",encoding='utf-8')
len(edos)
edos['Estado'][1]
x = AG.groupby(['Condicion_informalidad']).sum()
x
x['Numero_personas'][0]
x['Numero_personas'][1]
tasa = x['Numero_personas'][1] / x['Numero_personas'][0]
tasa
edo = edos['Estado']
edo[1]
TasaEdos = {}
for i in range(0, len(edos)):
x = data[data.Entidad_Federativa == Dict['EntFed'][i]]
z = x.groupby(['Condicion_informalidad']).sum()
tasa = z['Numero_personas'][1] / z['Numero_personas'][0]
TasaEdos[Dict['EntFed'][i]] = tasa
del tasa
TasaEdos = {}
for i in range(0, len(edos)):
x = data[data.Entidad_Federativa == Dict['EntFed'][i]].groupby(['Condicion_informalidad']).sum()
tasa = x['Numero_personas'][1] / x['Numero_personas'][0]
TasaEdos[Dict['EntFed'][i]] = tasa
del tasa
TasaEdos['México'] = TasaEdos.pop('Estado de México')
x = data[data.Entidad_Federativa == Dict['EntFed'][i]]
x
!pip install geopandas
!git clone https://github.com/jschleuss/mexican-states.git
import geopandas as gpd
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
mex=gpd.read_file("mexican-states/mexican-states.shp")
#!pip install descartes
type(mex)
#Configurando el canvas en matplotlib y
#creando un objeto "axes"
fig,ax = plt.subplots(1,1,figsize=(10,8))
mex.plot(ax=ax)
plt.show()
TasaEdos
del TasaEdos['Nacional']
len(TasaEdos)
new = pd.DataFrame(list(TasaEdos.items()),columns = ['Estados','tasa'])
new
new.sort_values(["Estados"], axis=0,
ascending=True, inplace=True)
new
len(new)
mex
mex2 = mex.sort_values(by=['name'])
#mex2
list1 = mex2['name']
list2 = mex2['geometry']
#list3 = list(TasaEdos.keys())
list3 = new['Estados'] ### Checar cambio con new
list4 = new['tasa']
list3.pop(32)
#list3
list4 = list(TasaEdos.values())
list4.pop(32)
len(list4)
list3 == list1
list3[1],list1[1]
a = [1,1,2,3,5]
a[0] = 10
a
a = [10,1,2,3,5]
b = [1,1,30,3,5]
for i in range(len(a)):
if a[i]!=b[i]:
active = True
newval = input("EL valor de %s es %f \nIngrese el valor de reemplazo " %("columna", a[i]))
a[i] = newval
active = False
print(a,b)
list3
list1 = str(list1)
del list1
list1 = mex2['name']
type(list1)
type(list3)
list1 = list1.tolist()
type(list1)
list2 = list2.tolist()
type(list2)
for i in range(len(list3)):
if list1[i]!=list3[i]:
active = True
newval = input("list3 = %s list1 = %s \nIngrese el nombre de reemplazo " %(list3[i],list1[i]))
list1[i] = newval
active = False
for i in range(len(list3)):
if list1[i]!=list3[i]:
active = True
newval = input("list3 = %s list1 = %s \nIngrese el nombre de reemplazo " %(list3[i],list1[i]))
list1[i] = newval
active = False
#list3
i = 0
list1[0] = 1
df = pd.DataFrame(list(zip(list1, list3, list4, list2)),
columns =['geopandas_name', 'Tasas_name', 'Tasas', 'geometry'])
df
import mapclassify
#gpd_per_person = world['gdp_md_est'] / world['pop_est']
scheme = mapclassify.Quantiles(df['Tasas'], k=5)
# Note: this code sample requires geoplot>=0.4.0.
geoplot.choropleth(
world, hue=gpd_per_person, scheme=scheme,
cmap='Greens', figsize=(8, 4)
)
!pip install mapclassify
import mapclassify
scheme = mapclassify.Quantiles(df['Tasas'], k=5)
geoplot.choropleth(
df, hue=gpd_per_person, scheme=scheme,
cmap='Greens', figsize=(8, 4)
)
#Configurando el canvas en matplotlib y
#creando un objeto "axes"
fig,ax = plt.subplots(1,1,figsize=(10,8))
mex.plot(ax=ax, scheme=scheme)
plt.show()
type(mex)
gdf1 = geopandas.GeoDataFrame(df)
import matplotlib.pyplot as plt
#Configurando el canvas en matplotlib y
#creando un objeto "axes"
#figure,ax = plt.subplots(1,1,figsize=(10,8))
fig, ax = plt.subplots(1, 1, figsize=(15,12))
#gdf1.plot(ax=ax)
#gdf1.plot(column='Tasas');
gdf1.plot(column='Tasas', cmap='OrRd', ax=ax, legend=True)
plt.show()
#Configurando el canvas en matplotlib y
#creando un objeto "axes"
#figure,ax = plt.subplots(1,1,figsize=(10,8))
fig, ax = plt.subplots(1, 1, figsize=(15,12))
#gdf1.plot(ax=ax)
#gdf1.plot(column='Tasas');
gdf1.plot(column='Tasas', cmap='YlOrRd', ax=ax, legend=True)
plt.show()
| 0.17774 | 0.769297 |
```
reset
# IMPORT PACKAGES
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.ticker as mticker
from netCDF4 import Dataset
import cartopy.crs as ccrs
import cartopy.feature as feature
import cmocean.cm
import pandas as pd
import xarray as xr
from scipy import signal
import collections
from windspharm.xarray import VectorWind
# fix to cartopy issue right now
from matplotlib.axes import Axes
from cartopy.mpl.geoaxes import GeoAxes
GeoAxes._pcolormesh_patched = Axes.pcolormesh
# PATHS TO DATA FILES
direc = '/tigress/GEOCLIM/janewb/MODEL_OUT'
files = collections.defaultdict(dict)
florruns = ['ctrl','hitopo','cam']
cesmruns = ['cesm_ctrl','cesm_cam']
diags = ['u', 'v']
files['ctrl']['u'] = direc+'/CTL1860_newdiag_tigercpu_intelmpi_18_576PE_coldstart/TIMESERIES/tau_x.00010101-03000101.ocean.nc'
files['cam']['u'] = '/tigress/janewb/MODEL_OUT_HERE/CTL1860_newdiag_tigercpu_intelmpi_18_576PE_coldstart_HiTopo1_CAM/TIMESERIES/tau_x.00010101-02050101.ocean.nc'
files['hitopo']['u'] = direc+'/CTL1860_newdiag_tigercpu_intelmpi_18_576PE_coldstart_HiTopo1/TIMESERIES/tau_x.00010101-06000101.ocean.nc'
files['obs']['u'] = '/tigress/janewb/OBS/MERRA2/MERRA2.tauxy.nc'
files['cesm_ctrl']['u'] = '/tigress/janewb/HiTopo/FROM_ALYSSA/CESM_data/b40.1850.track1.1deg.006.pop.h.TAUXregrid.120001-130012.nc'
files['cesm_cam']['u'] = '/tigress/janewb/HiTopo/FROM_ALYSSA/CESM_data/ccsm4pi_topo2.cam2.h0.TAUX.000101-029912.nc'
files['ctrl']['v'] = direc+'/CTL1860_newdiag_tigercpu_intelmpi_18_576PE_coldstart/TIMESERIES/tau_y.00010101-03000101.ocean.nc'
files['cam']['v'] = '/tigress/janewb/MODEL_OUT_HERE/CTL1860_newdiag_tigercpu_intelmpi_18_576PE_coldstart_HiTopo1_CAM/TIMESERIES/tau_y.00010101-02050101.ocean.nc'
files['hitopo']['v'] = direc+'/CTL1860_newdiag_tigercpu_intelmpi_18_576PE_coldstart_HiTopo1/TIMESERIES/tau_y.00010101-06000101.ocean.nc'
files['obs']['v'] = '/tigress/janewb/OBS/MERRA2/MERRA2.tauxy.nc'
files['cesm_ctrl']['v'] = '/tigress/janewb/HiTopo/FROM_ALYSSA/CESM_data/b40.1850.track1.1deg.006.pop.h.TAUYregrid.120001-130012.nc'
files['cesm_cam']['v'] = '/tigress/janewb/HiTopo/FROM_ALYSSA/CESM_data/ccsm4pi_topo2.cam2.h0.TAUY.000101-029912.nc'
# DATA CLEANING
dat0 = collections.defaultdict(dict)
dat = collections.defaultdict(dict)
tsel = collections.defaultdict(dict)
x = 'lon'
y = 'lat'
model_tmin = '0031'
model_tmax = '0200'
obs_tmin = '1980'
obs_tmax = '2019'
# FLOR Runs N/m^2
for run in florruns:
for diag in diags:
dat0[run][diag] = xr.open_dataset(files[run][diag])
dat0[run][diag] = dat0[run][diag].rename({'xu_ocean': 'lon','yu_ocean': 'lat'})
tsel[run][diag] = dat0[run][diag].sel(time = slice(model_tmin,model_tmax))
# CESM Runs
for run in ['cesm_cam']:
for diag in diags:
dat0[run][diag] = xr.open_dataset(files[run][diag])
if diag=='u':
tsel[run][diag] = dat0[run][diag].rename({'TAUX': 'tau_x'})
tsel[run][diag] = -tsel[run][diag].tau_x
if diag=='v':
tsel[run][diag] = dat0[run][diag].rename({'TAUY': 'tau_y'})
tsel[run][diag] = -tsel[run][diag].tau_y
for run in ['cesm_ctrl']:
for diag in diags:
dat0[run][diag] = xr.open_dataset(files[run][diag])
if diag=='u':
tsel[run][diag] = dat0[run][diag].rename({'TAUX_regrid': 'tau_x'})
tsel[run][diag] = tsel[run][diag].tau_x/10
if diag=='v':
tsel[run][diag] = dat0[run][diag].rename({'TAUY_regrid': 'tau_y'})
tsel[run][diag] = tsel[run][diag].tau_y/10
# OBSERVED data N/m^2
for diag in diags:
dat0['obs'][diag] = xr.open_dataset(files['obs'][diag])
tsel['obs'][diag] = dat0['obs'][diag].sel(time = slice(obs_tmin,obs_tmax)).rename({'TAUXWTR': 'tau_x','TAUYWTR': 'tau_y'})
# Calculate time mean wind stres x and y and save out
taux_tmean = {}
tauy_tmean = {}
vectorwind = {}
curl = {}
for run in ['ctrl','hitopo', 'cam','obs','cesm_cam','cesm_ctrl']:
taux_tmean[run] = tsel[run]['u'].mean(dim='time')
tauy_tmean[run] = tsel[run]['v'].mean(dim='time')
# ALTERNATIVE WAY OF CALCULATING CURL THAT DOESN'T WORK FOR ICOADS DATA WHICH HAS MISSING VALUES
#vectorwind[run] = VectorWind(taux_tmean[run],tauy_tmean[run])
#curl[run] = vectorwind[run].vorticity()
taux_tmean['ctrl'].to_netcdf('WINDSTRESS/taux_ctrl.nc')
taux_tmean['hitopo'].to_netcdf('WINDSTRESS/taux_hitopo.nc')
taux_tmean['cam'].to_netcdf('WINDSTRESS/taux_cam.nc')
taux_tmean['obs'].to_netcdf('WINDSTRESS/taux_merra2.nc')
taux_tmean['cesm_cam'].to_netcdf('WINDSTRESS/taux_cesm_cam.nc')
taux_tmean['cesm_ctrl'].to_netcdf('WINDSTRESS/taux_cesm_ctrl.nc')
tauy_tmean['ctrl'].to_netcdf('WINDSTRESS/tauy_ctrl.nc')
tauy_tmean['hitopo'].to_netcdf('WINDSTRESS/tauy_hitopo.nc')
tauy_tmean['cam'].to_netcdf('WINDSTRESS/tauy_cam.nc')
tauy_tmean['obs'].to_netcdf('WINDSTRESS/tauy_merra2.nc')
tauy_tmean['cesm_cam'].to_netcdf('WINDSTRESS/tauy_cesm_cam.nc')
tauy_tmean['cesm_ctrl'].to_netcdf('WINDSTRESS/tauy_cesm_ctrl.nc')
# NOW CALCULATE CURL USING PYFERRET BACK IN TERMINAL.
# cd /tigress/janewb/HiTopo/WINDSTRESS/
# module load pyferret
# pyferret
# --> go curl.nc icoads
# --> go curl.nc ctrl
# --> go curl.nc hitopo
# --> go curl.n cam
# --> go curl.nc cesm_ctrl
# --> go curl.n cesm_cam
# LOAD CURL DATA CALCULATED FROM PYFERRET
curl = {}
curl['obs'] = xr.open_dataset('WINDSTRESS/curl_merra2.nc').CURL
curl['ctrl'] = xr.open_dataset('WINDSTRESS/curl_ctrl.nc').CURL
curl['hitopo'] = xr.open_dataset('WINDSTRESS/curl_hitopo.nc').CURL
curl['cam'] = xr.open_dataset('WINDSTRESS/curl_cam.nc').CURL
curl['cesm_ctrl'] = xr.open_dataset('WINDSTRESS/curl_cesm_ctrl.nc').CURL
curl['cesm_cam'] = xr.open_dataset('WINDSTRESS/curl_cesm_cam.nc').CURL
# REGION BOUNDS FOR PLOTTING
xmin = 100
xmax = 300
ymin = -23.5
ymax = 23.5
# Plot wind stress curl
fig = plt.figure(figsize=(10,16))
proj = ccrs.Mercator(central_longitude=200)
clevs = np.arange(-0.8e-7,1e-7,2e-8)
ax1 = plt.subplot(611, projection=proj)
fill_vort = curl['obs'].plot(ax=ax1, levels=clevs, cmap=plt.cm.RdBu_r,
transform=ccrs.PlateCarree(), extend='both',
add_colorbar=False)
ax1.add_feature(feature.LAND, color = 'k',zorder=1)
ax1.set_title('e) Obs.')
ax1.set_extent([xmin, xmax, ymin, ymax], ccrs.PlateCarree())
gl = ax1.gridlines(crs=ccrs.PlateCarree(), draw_labels=True,
linewidth=2, color='gray', alpha=0.5, linestyle='--')
gl.xlabels_top = False
gl.xlabels_bottom = False
gl.ylabels_right = False
gl.xlocator = mticker.FixedLocator([140,190,-170,-120,-70,0])
gl.ylocator = mticker.FixedLocator([-30,-20,-10,0,10,20,30])
ax2 = plt.subplot(612, projection=proj)
im2 = curl['ctrl'].plot(ax=ax2, levels=clevs, cmap=plt.cm.RdBu_r,
transform=ccrs.PlateCarree(), extend='both',
add_colorbar=False)
ax2.add_feature(feature.LAND, color = 'k',zorder=1)
ax2.set_title('f) FLOR Control')
ax2.set_extent([xmin, xmax, ymin, ymax], ccrs.PlateCarree())
gl = ax2.gridlines(crs=ccrs.PlateCarree(), draw_labels=True,
linewidth=2, color='gray', alpha=0.5, linestyle='--')
gl.xlabels_top = False
gl.xlabels_bottom = False
gl.ylabels_right = False
gl.xlocator = mticker.FixedLocator([140,190,-170,-120,-70,0])
gl.ylocator = mticker.FixedLocator([-30,-20,-10,0,10,20,30])
ax3 = plt.subplot(613, projection=proj)
fill_vort = curl['hitopo'].plot(ax=ax3, levels=clevs, cmap=plt.cm.RdBu_r,
transform=ccrs.PlateCarree(), extend='both',
add_colorbar=False)
ax3.add_feature(feature.LAND, color = 'k',zorder=1)
ax3.set_title('g) FLOR HiTopo')
ax3.set_extent([xmin, xmax, ymin, ymax], ccrs.PlateCarree())
gl = ax3.gridlines(crs=ccrs.PlateCarree(), draw_labels=True,
linewidth=2, color='gray', alpha=0.5, linestyle='--')
gl.xlabels_top = False
gl.xlabels_bottom = False
gl.ylabels_right = False
gl.xlocator = mticker.FixedLocator([140,190,-170,-120,-70,0])
gl.ylocator = mticker.FixedLocator([-30,-20,-10,0,10,20,30])
ax4 = plt.subplot(614, projection=proj)
fill_vort = curl['cam'].plot(ax=ax4, levels=clevs, cmap=plt.cm.RdBu_r,
transform=ccrs.PlateCarree(), extend='both',
add_colorbar=False)
ax4.add_feature(feature.LAND, color = 'k',zorder=1)
ax4.set_title('h) FLOR CAm')
ax4.set_extent([xmin, xmax, ymin, ymax], ccrs.PlateCarree())
gl = ax4.gridlines(crs=ccrs.PlateCarree(), draw_labels=True,
linewidth=2, color='gray', alpha=0.5, linestyle='--')
gl.xlabels_top = False
gl.xlabels_bottom = False
gl.ylabels_right = False
gl.xlocator = mticker.FixedLocator([140,190,-170,-120,-70,0])
gl.ylocator = mticker.FixedLocator([-30,-20,-10,0,10,20,30])
ax5 = plt.subplot(615, projection=proj)
fill_vort = curl['cesm_ctrl'].plot(ax=ax5, levels=clevs, cmap=plt.cm.RdBu_r,
transform=ccrs.PlateCarree(), extend='both',
add_colorbar=False)
ax5.add_feature(feature.LAND, color = 'k',zorder=1)
ax5.set_title('i) CESM Control')
ax5.set_extent([xmin, xmax, ymin, ymax], ccrs.PlateCarree())
gl = ax5.gridlines(crs=ccrs.PlateCarree(), draw_labels=True,
linewidth=2, color='gray', alpha=0.5, linestyle='--')
gl.xlabels_top = False
gl.xlabels_bottom = False
gl.ylabels_right = False
gl.xlocator = mticker.FixedLocator([140,190,-170,-120,-70,0])
gl.ylocator = mticker.FixedLocator([-30,-20,-10,0,10,20,30])
ax6 = plt.subplot(616, projection=proj)
fill_vort = curl['cesm_cam'].plot(ax=ax6, levels=clevs, cmap=plt.cm.RdBu_r,
transform=ccrs.PlateCarree(), extend='both',
add_colorbar=False)
ax6.add_feature(feature.LAND, color = 'k',zorder=1)
ax6.set_title('j) CESM Ideal CAm')
ax6.set_extent([xmin, xmax, ymin, ymax], ccrs.PlateCarree())
gl = ax6.gridlines(crs=ccrs.PlateCarree(), draw_labels=True,
linewidth=2, color='gray', alpha=0.5, linestyle='--')
gl.xlabels_top = False
gl.ylabels_right = False
gl.xlocator = mticker.FixedLocator([140,190,-170,-120,-70,0])
gl.ylocator = mticker.FixedLocator([-30,-20,-10,0,10,20,30])
#plt.colorbar(fill_vort, orientation='horizontal')
#plt.title('Wind Stress Curl [N/m$^{3}$]', fontsize=16)
#fig.subplots_adjust(wspace=0.7)
cb1_ax = fig.add_axes([0.9, 0.1, 0.025, 0.8])
cb1 = fig.colorbar(im2, cax=cb1_ax)
cb1.ax.set_ylabel('wind stress curl [N/m$^{3}$]', rotation=90, fontsize=12)
#plt.tight_layout()
plt.savefig('windstresscurl.png')
fig = plt.figure(figsize=(8,7.5))
plt.rcParams.update({'font.size': 16})
fig.subplots_adjust(wspace=0.5, hspace = 0.38)
y1 = 0.0
y2 = 15.0
deriv = {}
deriv['obs'] = curl['obs'].sel(LAT=slice(y1,y2)).sel(LON=slice(-170,-110)).integrate('LON').differentiate('LAT')
deriv['ctrl'] = curl['ctrl'].sel(LAT=slice(y1,y2)).sel(LON=slice(-170,-110)).integrate('LON').differentiate('LAT')
deriv['hitopo'] = curl['hitopo'].sel(LAT=slice(y1,y2)).sel(LON=slice(-170,-110)).integrate('LON').differentiate('LAT')
deriv['cam'] = curl['cam'].sel(LAT=slice(y1,y2)).sel(LON=slice(-170,-110)).integrate('LON').differentiate('LAT')
deriv['cesm_ctrl'] = curl['cesm_ctrl'].sel(LAT=slice(y1,y2)).sel(LON=slice(-170+360,-110+360)).integrate('LON').differentiate('LAT')
deriv['cesm_cam'] = curl['cesm_cam'].sel(LAT=slice(y1,y2)).sel(LON=slice(-170+360,-110+360)).integrate('LON').differentiate('LAT')
lats_o = deriv['obs'].LAT
lats_m = deriv['ctrl'].LAT
lats_mc = deriv['cesm_cam'].LAT
ax = plt.subplot(121)
plt.plot(deriv['obs']*1e7,lats_o,color='k',label='Obs.: MERRA2')
plt.plot(deriv['ctrl']*1e7,lats_m,color='b',label='FLOR Control')
plt.plot(deriv['hitopo']*1e7,lats_m,color='r',label='FLOR HiTopo')
plt.plot(deriv['cam']*1e7,lats_m,color='r',dashes=[1,1,1,1],label='FLOR CAm')
plt.xlabel('Meridional Derivative of Zonal\nIntergral of Wind Stress Curl\n[-170 to -110$^{\circ}$E; $10^{-7}$ N/m$^{3}$]')
#plt.ylabel('Latitude [$^{\circ}$N]')
plt.title('f)')
plt.legend(fontsize=12)
plt.xlim([-11.5,15])
plt.axvline(x=0,color='k',linewidth=1)
ax = plt.subplot(122)
plt.plot(deriv['obs']*1e7,lats_o,color='k',label='Obs.: MERRA2')
plt.plot(deriv['cesm_ctrl']*1e7,lats_mc,color='b',label='CESM Control')
plt.plot(deriv['cesm_cam']*1e7,lats_mc,color='r',dashes=[1,1,1,1],label='CESM Ideal CAm')
plt.xlabel('Meridional Derivative of Zonal\nIntergral of Wind Stress Curl\n[-170 to -110$^{\circ}$E; $10^{-7}$ N/m$^{3}$]')
#plt.ylabel('Latitude [$^{\circ}$N]')
plt.title('e)')
plt.legend(fontsize=12)
plt.xlim([-11.5,15])
plt.axvline(x=0,color='k',linewidth=1)
plt.savefig('windstresscurlintderiv.pdf')
```
|
github_jupyter
|
reset
# IMPORT PACKAGES
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.ticker as mticker
from netCDF4 import Dataset
import cartopy.crs as ccrs
import cartopy.feature as feature
import cmocean.cm
import pandas as pd
import xarray as xr
from scipy import signal
import collections
from windspharm.xarray import VectorWind
# fix to cartopy issue right now
from matplotlib.axes import Axes
from cartopy.mpl.geoaxes import GeoAxes
GeoAxes._pcolormesh_patched = Axes.pcolormesh
# PATHS TO DATA FILES
direc = '/tigress/GEOCLIM/janewb/MODEL_OUT'
files = collections.defaultdict(dict)
florruns = ['ctrl','hitopo','cam']
cesmruns = ['cesm_ctrl','cesm_cam']
diags = ['u', 'v']
files['ctrl']['u'] = direc+'/CTL1860_newdiag_tigercpu_intelmpi_18_576PE_coldstart/TIMESERIES/tau_x.00010101-03000101.ocean.nc'
files['cam']['u'] = '/tigress/janewb/MODEL_OUT_HERE/CTL1860_newdiag_tigercpu_intelmpi_18_576PE_coldstart_HiTopo1_CAM/TIMESERIES/tau_x.00010101-02050101.ocean.nc'
files['hitopo']['u'] = direc+'/CTL1860_newdiag_tigercpu_intelmpi_18_576PE_coldstart_HiTopo1/TIMESERIES/tau_x.00010101-06000101.ocean.nc'
files['obs']['u'] = '/tigress/janewb/OBS/MERRA2/MERRA2.tauxy.nc'
files['cesm_ctrl']['u'] = '/tigress/janewb/HiTopo/FROM_ALYSSA/CESM_data/b40.1850.track1.1deg.006.pop.h.TAUXregrid.120001-130012.nc'
files['cesm_cam']['u'] = '/tigress/janewb/HiTopo/FROM_ALYSSA/CESM_data/ccsm4pi_topo2.cam2.h0.TAUX.000101-029912.nc'
files['ctrl']['v'] = direc+'/CTL1860_newdiag_tigercpu_intelmpi_18_576PE_coldstart/TIMESERIES/tau_y.00010101-03000101.ocean.nc'
files['cam']['v'] = '/tigress/janewb/MODEL_OUT_HERE/CTL1860_newdiag_tigercpu_intelmpi_18_576PE_coldstart_HiTopo1_CAM/TIMESERIES/tau_y.00010101-02050101.ocean.nc'
files['hitopo']['v'] = direc+'/CTL1860_newdiag_tigercpu_intelmpi_18_576PE_coldstart_HiTopo1/TIMESERIES/tau_y.00010101-06000101.ocean.nc'
files['obs']['v'] = '/tigress/janewb/OBS/MERRA2/MERRA2.tauxy.nc'
files['cesm_ctrl']['v'] = '/tigress/janewb/HiTopo/FROM_ALYSSA/CESM_data/b40.1850.track1.1deg.006.pop.h.TAUYregrid.120001-130012.nc'
files['cesm_cam']['v'] = '/tigress/janewb/HiTopo/FROM_ALYSSA/CESM_data/ccsm4pi_topo2.cam2.h0.TAUY.000101-029912.nc'
# DATA CLEANING
dat0 = collections.defaultdict(dict)
dat = collections.defaultdict(dict)
tsel = collections.defaultdict(dict)
x = 'lon'
y = 'lat'
model_tmin = '0031'
model_tmax = '0200'
obs_tmin = '1980'
obs_tmax = '2019'
# FLOR Runs N/m^2
for run in florruns:
for diag in diags:
dat0[run][diag] = xr.open_dataset(files[run][diag])
dat0[run][diag] = dat0[run][diag].rename({'xu_ocean': 'lon','yu_ocean': 'lat'})
tsel[run][diag] = dat0[run][diag].sel(time = slice(model_tmin,model_tmax))
# CESM Runs
for run in ['cesm_cam']:
for diag in diags:
dat0[run][diag] = xr.open_dataset(files[run][diag])
if diag=='u':
tsel[run][diag] = dat0[run][diag].rename({'TAUX': 'tau_x'})
tsel[run][diag] = -tsel[run][diag].tau_x
if diag=='v':
tsel[run][diag] = dat0[run][diag].rename({'TAUY': 'tau_y'})
tsel[run][diag] = -tsel[run][diag].tau_y
for run in ['cesm_ctrl']:
for diag in diags:
dat0[run][diag] = xr.open_dataset(files[run][diag])
if diag=='u':
tsel[run][diag] = dat0[run][diag].rename({'TAUX_regrid': 'tau_x'})
tsel[run][diag] = tsel[run][diag].tau_x/10
if diag=='v':
tsel[run][diag] = dat0[run][diag].rename({'TAUY_regrid': 'tau_y'})
tsel[run][diag] = tsel[run][diag].tau_y/10
# OBSERVED data N/m^2
for diag in diags:
dat0['obs'][diag] = xr.open_dataset(files['obs'][diag])
tsel['obs'][diag] = dat0['obs'][diag].sel(time = slice(obs_tmin,obs_tmax)).rename({'TAUXWTR': 'tau_x','TAUYWTR': 'tau_y'})
# Calculate time mean wind stres x and y and save out
taux_tmean = {}
tauy_tmean = {}
vectorwind = {}
curl = {}
for run in ['ctrl','hitopo', 'cam','obs','cesm_cam','cesm_ctrl']:
taux_tmean[run] = tsel[run]['u'].mean(dim='time')
tauy_tmean[run] = tsel[run]['v'].mean(dim='time')
# ALTERNATIVE WAY OF CALCULATING CURL THAT DOESN'T WORK FOR ICOADS DATA WHICH HAS MISSING VALUES
#vectorwind[run] = VectorWind(taux_tmean[run],tauy_tmean[run])
#curl[run] = vectorwind[run].vorticity()
taux_tmean['ctrl'].to_netcdf('WINDSTRESS/taux_ctrl.nc')
taux_tmean['hitopo'].to_netcdf('WINDSTRESS/taux_hitopo.nc')
taux_tmean['cam'].to_netcdf('WINDSTRESS/taux_cam.nc')
taux_tmean['obs'].to_netcdf('WINDSTRESS/taux_merra2.nc')
taux_tmean['cesm_cam'].to_netcdf('WINDSTRESS/taux_cesm_cam.nc')
taux_tmean['cesm_ctrl'].to_netcdf('WINDSTRESS/taux_cesm_ctrl.nc')
tauy_tmean['ctrl'].to_netcdf('WINDSTRESS/tauy_ctrl.nc')
tauy_tmean['hitopo'].to_netcdf('WINDSTRESS/tauy_hitopo.nc')
tauy_tmean['cam'].to_netcdf('WINDSTRESS/tauy_cam.nc')
tauy_tmean['obs'].to_netcdf('WINDSTRESS/tauy_merra2.nc')
tauy_tmean['cesm_cam'].to_netcdf('WINDSTRESS/tauy_cesm_cam.nc')
tauy_tmean['cesm_ctrl'].to_netcdf('WINDSTRESS/tauy_cesm_ctrl.nc')
# NOW CALCULATE CURL USING PYFERRET BACK IN TERMINAL.
# cd /tigress/janewb/HiTopo/WINDSTRESS/
# module load pyferret
# pyferret
# --> go curl.nc icoads
# --> go curl.nc ctrl
# --> go curl.nc hitopo
# --> go curl.n cam
# --> go curl.nc cesm_ctrl
# --> go curl.n cesm_cam
# LOAD CURL DATA CALCULATED FROM PYFERRET
curl = {}
curl['obs'] = xr.open_dataset('WINDSTRESS/curl_merra2.nc').CURL
curl['ctrl'] = xr.open_dataset('WINDSTRESS/curl_ctrl.nc').CURL
curl['hitopo'] = xr.open_dataset('WINDSTRESS/curl_hitopo.nc').CURL
curl['cam'] = xr.open_dataset('WINDSTRESS/curl_cam.nc').CURL
curl['cesm_ctrl'] = xr.open_dataset('WINDSTRESS/curl_cesm_ctrl.nc').CURL
curl['cesm_cam'] = xr.open_dataset('WINDSTRESS/curl_cesm_cam.nc').CURL
# REGION BOUNDS FOR PLOTTING
xmin = 100
xmax = 300
ymin = -23.5
ymax = 23.5
# Plot wind stress curl
fig = plt.figure(figsize=(10,16))
proj = ccrs.Mercator(central_longitude=200)
clevs = np.arange(-0.8e-7,1e-7,2e-8)
ax1 = plt.subplot(611, projection=proj)
fill_vort = curl['obs'].plot(ax=ax1, levels=clevs, cmap=plt.cm.RdBu_r,
transform=ccrs.PlateCarree(), extend='both',
add_colorbar=False)
ax1.add_feature(feature.LAND, color = 'k',zorder=1)
ax1.set_title('e) Obs.')
ax1.set_extent([xmin, xmax, ymin, ymax], ccrs.PlateCarree())
gl = ax1.gridlines(crs=ccrs.PlateCarree(), draw_labels=True,
linewidth=2, color='gray', alpha=0.5, linestyle='--')
gl.xlabels_top = False
gl.xlabels_bottom = False
gl.ylabels_right = False
gl.xlocator = mticker.FixedLocator([140,190,-170,-120,-70,0])
gl.ylocator = mticker.FixedLocator([-30,-20,-10,0,10,20,30])
ax2 = plt.subplot(612, projection=proj)
im2 = curl['ctrl'].plot(ax=ax2, levels=clevs, cmap=plt.cm.RdBu_r,
transform=ccrs.PlateCarree(), extend='both',
add_colorbar=False)
ax2.add_feature(feature.LAND, color = 'k',zorder=1)
ax2.set_title('f) FLOR Control')
ax2.set_extent([xmin, xmax, ymin, ymax], ccrs.PlateCarree())
gl = ax2.gridlines(crs=ccrs.PlateCarree(), draw_labels=True,
linewidth=2, color='gray', alpha=0.5, linestyle='--')
gl.xlabels_top = False
gl.xlabels_bottom = False
gl.ylabels_right = False
gl.xlocator = mticker.FixedLocator([140,190,-170,-120,-70,0])
gl.ylocator = mticker.FixedLocator([-30,-20,-10,0,10,20,30])
ax3 = plt.subplot(613, projection=proj)
fill_vort = curl['hitopo'].plot(ax=ax3, levels=clevs, cmap=plt.cm.RdBu_r,
transform=ccrs.PlateCarree(), extend='both',
add_colorbar=False)
ax3.add_feature(feature.LAND, color = 'k',zorder=1)
ax3.set_title('g) FLOR HiTopo')
ax3.set_extent([xmin, xmax, ymin, ymax], ccrs.PlateCarree())
gl = ax3.gridlines(crs=ccrs.PlateCarree(), draw_labels=True,
linewidth=2, color='gray', alpha=0.5, linestyle='--')
gl.xlabels_top = False
gl.xlabels_bottom = False
gl.ylabels_right = False
gl.xlocator = mticker.FixedLocator([140,190,-170,-120,-70,0])
gl.ylocator = mticker.FixedLocator([-30,-20,-10,0,10,20,30])
ax4 = plt.subplot(614, projection=proj)
fill_vort = curl['cam'].plot(ax=ax4, levels=clevs, cmap=plt.cm.RdBu_r,
transform=ccrs.PlateCarree(), extend='both',
add_colorbar=False)
ax4.add_feature(feature.LAND, color = 'k',zorder=1)
ax4.set_title('h) FLOR CAm')
ax4.set_extent([xmin, xmax, ymin, ymax], ccrs.PlateCarree())
gl = ax4.gridlines(crs=ccrs.PlateCarree(), draw_labels=True,
linewidth=2, color='gray', alpha=0.5, linestyle='--')
gl.xlabels_top = False
gl.xlabels_bottom = False
gl.ylabels_right = False
gl.xlocator = mticker.FixedLocator([140,190,-170,-120,-70,0])
gl.ylocator = mticker.FixedLocator([-30,-20,-10,0,10,20,30])
ax5 = plt.subplot(615, projection=proj)
fill_vort = curl['cesm_ctrl'].plot(ax=ax5, levels=clevs, cmap=plt.cm.RdBu_r,
transform=ccrs.PlateCarree(), extend='both',
add_colorbar=False)
ax5.add_feature(feature.LAND, color = 'k',zorder=1)
ax5.set_title('i) CESM Control')
ax5.set_extent([xmin, xmax, ymin, ymax], ccrs.PlateCarree())
gl = ax5.gridlines(crs=ccrs.PlateCarree(), draw_labels=True,
linewidth=2, color='gray', alpha=0.5, linestyle='--')
gl.xlabels_top = False
gl.xlabels_bottom = False
gl.ylabels_right = False
gl.xlocator = mticker.FixedLocator([140,190,-170,-120,-70,0])
gl.ylocator = mticker.FixedLocator([-30,-20,-10,0,10,20,30])
ax6 = plt.subplot(616, projection=proj)
fill_vort = curl['cesm_cam'].plot(ax=ax6, levels=clevs, cmap=plt.cm.RdBu_r,
transform=ccrs.PlateCarree(), extend='both',
add_colorbar=False)
ax6.add_feature(feature.LAND, color = 'k',zorder=1)
ax6.set_title('j) CESM Ideal CAm')
ax6.set_extent([xmin, xmax, ymin, ymax], ccrs.PlateCarree())
gl = ax6.gridlines(crs=ccrs.PlateCarree(), draw_labels=True,
linewidth=2, color='gray', alpha=0.5, linestyle='--')
gl.xlabels_top = False
gl.ylabels_right = False
gl.xlocator = mticker.FixedLocator([140,190,-170,-120,-70,0])
gl.ylocator = mticker.FixedLocator([-30,-20,-10,0,10,20,30])
#plt.colorbar(fill_vort, orientation='horizontal')
#plt.title('Wind Stress Curl [N/m$^{3}$]', fontsize=16)
#fig.subplots_adjust(wspace=0.7)
cb1_ax = fig.add_axes([0.9, 0.1, 0.025, 0.8])
cb1 = fig.colorbar(im2, cax=cb1_ax)
cb1.ax.set_ylabel('wind stress curl [N/m$^{3}$]', rotation=90, fontsize=12)
#plt.tight_layout()
plt.savefig('windstresscurl.png')
fig = plt.figure(figsize=(8,7.5))
plt.rcParams.update({'font.size': 16})
fig.subplots_adjust(wspace=0.5, hspace = 0.38)
y1 = 0.0
y2 = 15.0
deriv = {}
deriv['obs'] = curl['obs'].sel(LAT=slice(y1,y2)).sel(LON=slice(-170,-110)).integrate('LON').differentiate('LAT')
deriv['ctrl'] = curl['ctrl'].sel(LAT=slice(y1,y2)).sel(LON=slice(-170,-110)).integrate('LON').differentiate('LAT')
deriv['hitopo'] = curl['hitopo'].sel(LAT=slice(y1,y2)).sel(LON=slice(-170,-110)).integrate('LON').differentiate('LAT')
deriv['cam'] = curl['cam'].sel(LAT=slice(y1,y2)).sel(LON=slice(-170,-110)).integrate('LON').differentiate('LAT')
deriv['cesm_ctrl'] = curl['cesm_ctrl'].sel(LAT=slice(y1,y2)).sel(LON=slice(-170+360,-110+360)).integrate('LON').differentiate('LAT')
deriv['cesm_cam'] = curl['cesm_cam'].sel(LAT=slice(y1,y2)).sel(LON=slice(-170+360,-110+360)).integrate('LON').differentiate('LAT')
lats_o = deriv['obs'].LAT
lats_m = deriv['ctrl'].LAT
lats_mc = deriv['cesm_cam'].LAT
ax = plt.subplot(121)
plt.plot(deriv['obs']*1e7,lats_o,color='k',label='Obs.: MERRA2')
plt.plot(deriv['ctrl']*1e7,lats_m,color='b',label='FLOR Control')
plt.plot(deriv['hitopo']*1e7,lats_m,color='r',label='FLOR HiTopo')
plt.plot(deriv['cam']*1e7,lats_m,color='r',dashes=[1,1,1,1],label='FLOR CAm')
plt.xlabel('Meridional Derivative of Zonal\nIntergral of Wind Stress Curl\n[-170 to -110$^{\circ}$E; $10^{-7}$ N/m$^{3}$]')
#plt.ylabel('Latitude [$^{\circ}$N]')
plt.title('f)')
plt.legend(fontsize=12)
plt.xlim([-11.5,15])
plt.axvline(x=0,color='k',linewidth=1)
ax = plt.subplot(122)
plt.plot(deriv['obs']*1e7,lats_o,color='k',label='Obs.: MERRA2')
plt.plot(deriv['cesm_ctrl']*1e7,lats_mc,color='b',label='CESM Control')
plt.plot(deriv['cesm_cam']*1e7,lats_mc,color='r',dashes=[1,1,1,1],label='CESM Ideal CAm')
plt.xlabel('Meridional Derivative of Zonal\nIntergral of Wind Stress Curl\n[-170 to -110$^{\circ}$E; $10^{-7}$ N/m$^{3}$]')
#plt.ylabel('Latitude [$^{\circ}$N]')
plt.title('e)')
plt.legend(fontsize=12)
plt.xlim([-11.5,15])
plt.axvline(x=0,color='k',linewidth=1)
plt.savefig('windstresscurlintderiv.pdf')
| 0.270866 | 0.259567 |
# TL;DR *OCaml from the Very Beginning* by John Whitington
Notes, examples, answers etc. from the book, and some things that I wanted to check while reading the book.
## Chapter 1
1. OCaml uses this funny `;;` for marking end of statement.
2. Single `=` is used for checking equality (`2 = 2` is true).
3. Unlike Haskell, Ocaml "knows" negative numbers, so `2 * -5 = -10`.
4. Other then `=`, the rest of comparison operators work as usual. `<>` is used for *not equal*, but `!=` seems to work as well (?).
5. `'a'` is for char, `"hello world!"` is for string.
6. `&&` and `||` are the boolean operators.
## Chapter 2
To assign variables, you need to use `let` statement.
```
let x = 2 ;;
x + 2
```
You can use `let ... in ...` to use the variable right away. Apparently, there is some kind of local scoping when using braces `(...)`.
```
let result = (let x = 6 in x * x) ;;
result
x
```
`let` is also used to define functions.
```
let square x = x * x ;;
square 2
```
But negative numbers seem to be a little bit more tricky...
```
square -2
square (-2)
let doublePlusTwo x =
let y = x + 2 in
x + y ;;
doublePlusTwo 5
```
Recursive functions need to be defined explicitely.
```
let rec factorial a =
if a = 1 then 1 else a * factorial (a - 1)
factorial 5
let rec addToN n =
if n = 1 then 1 else (addToN (n-1)) + n
addToN 2 = 3
addToN 5 = (1 + 2 + 3 + 4 + 5)
let x = 1 in let x = 2 in x + x
```
## Chapter 3
There is pattern matching with `match ... with ...` (like `case` statements in many languages?).
```
let rec factorial a =
match a with
1 -> 1
| _ -> a * factorial (a - 1)
factorial 5
```
`_` is the wildchart by convention, but it seems mere convention (?).
```
let isNot42 x =
match x with
42 -> true
| xyz -> false ;;
assert (isNot42 5 = false)
let isvowel c =
match c with
'a' | 'e' | 'i' | 'o' | 'u' -> true
| _ -> false ;;
assert (isvowel 'u') ;;
assert (not (isvowel 'z')) ;;
```
## Chapter 4
`::` inserts element into list, `@` appends list to list.
```
1 :: [2;3]
[1;2] @ [3;4;5]
1 @ [2;3]
```
## Chapter 5
```
let rec insert x l =
match l with
[] -> [x]
| h::t ->
if x <= h
then x :: h :: t
else h :: insert x t
let rec sort l =
match l with
[] -> []
| h::t -> insert h (sort t)
sort [5;2;3;1;4;1;1;3]
```
## Chapter 6
```
let rec map f l =
match l with
[] -> []
| h::t -> f h :: map f t
```
Using anonymous function (`(\x -> x / 2)` in Haskell):
```
map (fun x -> x / 2) [2;4;1;5;7]
```
We can as well implement Haskell's `foldl`.
```
let rec foldl f prev lst =
match lst with
[] -> prev
| [x] -> f prev x
| h::t -> foldl f (f prev h) t ;;
assert (foldl (+) 0 [] = 0) ;;
assert (foldl (+) 0 [1] = 1) ;;
assert (foldl (+) 0 [1;2;3] = 1 + 2 + 3) ;;
foldl (+) 0 [1;2;3]
```
The Haskell magic works:
```
let sum = foldl (+) 0 ;;
sum [1;2;3] ;;
```
> Q4. Write a function apply which, given another function, a number of times to apply it, and an initial
> argument for the function, will return the cumulative effect of repeatedly applying the function. For
> instance, `apply f 6 4` should return `f (f (f (f (f (f 4))))))`. What is the type of your function?
```
let rec apply f n x =
match n with
1 -> f x
| _ -> apply f (n-1) (f x) ;;
assert (apply (fun x -> x * 2) 4 3 = 3 * 2 * 2 * 2 * 2)
```
## Chapter 7, 8, 9
- OCaml handles exceptions in similar way as in Python, where you raise them using `raise Exception` and handle using `try ... with ... -> ...` (as compared to `try ... except ...` in Python).
- Pairs (a.k.a. tuples) `(x, y)` are supported.
- Partial matching works as in Haskell (e.g. the `foldl` function to greate `sum` as above).
## Chapter 10
It describes definig own types using `type` declarations. The types can be defined in terms `of` subtypes that create them.
```
type coin = Heads | Tails ;;
let c = Heads ;;
type expr =
| Num of int
| Add of expr * expr
| Sub of expr * expr
| Mul of expr * expr
| Div of expr * expr ;;
let rec evaluate e =
match e with
| Num x -> x
| Add (e, e') -> evaluate e + evaluate e'
| Sub (e, e') -> evaluate e - evaluate e'
| Mul (e, e') -> evaluate e * evaluate e'
| Div (e, e') -> evaluate e / evaluate e' ;;
evaluate ( Add (Num 1, Mul (Num 2, Num 3)) ) ;;
```
## Chapter 11
```
type 'a tree =
| Br of 'a * 'a tree * 'a tree
| Lf of 'a ;;
let tree = Br (1, Lf 2, Lf 3) ;;
let rec size tr =
match tr with
| Br (_, l, r) -> 1 + size l + size r
| Lf _ -> 0 ;;
size (Br (1, Br (2, Lf 3, Lf 5), Br (6, Lf 7, Lf 8))) ;;
let max x y = if x > y then x else y ;;
let rec maxdepth tr =
match tr with
| Br (_, l, r) -> 1 + max (maxdepth l) (maxdepth r)
| Lf _ -> 0 ;;
maxdepth (Br (1, Br (2, Lf 3, Lf 5), Lf 6)) ;;
```
## Chapter 12 and further
*Here be dragons.* I/O, pointers, arrays, for loops. Many goodies as compared to Haskell.
|
github_jupyter
|
let x = 2 ;;
x + 2
let result = (let x = 6 in x * x) ;;
result
x
let square x = x * x ;;
square 2
square -2
square (-2)
let doublePlusTwo x =
let y = x + 2 in
x + y ;;
doublePlusTwo 5
let rec factorial a =
if a = 1 then 1 else a * factorial (a - 1)
factorial 5
let rec addToN n =
if n = 1 then 1 else (addToN (n-1)) + n
addToN 2 = 3
addToN 5 = (1 + 2 + 3 + 4 + 5)
let x = 1 in let x = 2 in x + x
let rec factorial a =
match a with
1 -> 1
| _ -> a * factorial (a - 1)
factorial 5
let isNot42 x =
match x with
42 -> true
| xyz -> false ;;
assert (isNot42 5 = false)
let isvowel c =
match c with
'a' | 'e' | 'i' | 'o' | 'u' -> true
| _ -> false ;;
assert (isvowel 'u') ;;
assert (not (isvowel 'z')) ;;
1 :: [2;3]
[1;2] @ [3;4;5]
1 @ [2;3]
let rec insert x l =
match l with
[] -> [x]
| h::t ->
if x <= h
then x :: h :: t
else h :: insert x t
let rec sort l =
match l with
[] -> []
| h::t -> insert h (sort t)
sort [5;2;3;1;4;1;1;3]
let rec map f l =
match l with
[] -> []
| h::t -> f h :: map f t
map (fun x -> x / 2) [2;4;1;5;7]
let rec foldl f prev lst =
match lst with
[] -> prev
| [x] -> f prev x
| h::t -> foldl f (f prev h) t ;;
assert (foldl (+) 0 [] = 0) ;;
assert (foldl (+) 0 [1] = 1) ;;
assert (foldl (+) 0 [1;2;3] = 1 + 2 + 3) ;;
foldl (+) 0 [1;2;3]
let sum = foldl (+) 0 ;;
sum [1;2;3] ;;
let rec apply f n x =
match n with
1 -> f x
| _ -> apply f (n-1) (f x) ;;
assert (apply (fun x -> x * 2) 4 3 = 3 * 2 * 2 * 2 * 2)
type coin = Heads | Tails ;;
let c = Heads ;;
type expr =
| Num of int
| Add of expr * expr
| Sub of expr * expr
| Mul of expr * expr
| Div of expr * expr ;;
let rec evaluate e =
match e with
| Num x -> x
| Add (e, e') -> evaluate e + evaluate e'
| Sub (e, e') -> evaluate e - evaluate e'
| Mul (e, e') -> evaluate e * evaluate e'
| Div (e, e') -> evaluate e / evaluate e' ;;
evaluate ( Add (Num 1, Mul (Num 2, Num 3)) ) ;;
type 'a tree =
| Br of 'a * 'a tree * 'a tree
| Lf of 'a ;;
let tree = Br (1, Lf 2, Lf 3) ;;
let rec size tr =
match tr with
| Br (_, l, r) -> 1 + size l + size r
| Lf _ -> 0 ;;
size (Br (1, Br (2, Lf 3, Lf 5), Br (6, Lf 7, Lf 8))) ;;
let max x y = if x > y then x else y ;;
let rec maxdepth tr =
match tr with
| Br (_, l, r) -> 1 + max (maxdepth l) (maxdepth r)
| Lf _ -> 0 ;;
maxdepth (Br (1, Br (2, Lf 3, Lf 5), Lf 6)) ;;
| 0.370225 | 0.935993 |
# Introduction to Deep Learning with PyTorch
In this notebook, you will get an introduction to [PyTorch](http://pytorch.org/), which is a framework for building and training neural networks (NN). ``PyTorch`` in a lot of ways behaves like the arrays you know and love from Numpy. These Numpy arrays, after all, are just *tensors*. PyTorch takes these tensors and makes it simple to move them to GPUs for the faster processing needed when training neural networks. It also provides a module that automatically calculates gradients (for backpropagation!) and another module specifically for building neural networks. All together, PyTorch ends up being more coherent with **Python** and the ``Numpy/Scipy`` stack compared to *TensorFlow* and other frameworks.
## Neural Networks
Deep Learning is based on artificial neural networks which have been around in some form since the late 1950s. The networks are built from individual parts approximating neurons, typically called units or simply "neurons." Each unit has some number of weighted inputs. These weighted inputs are summed together (a linear combination) then passed through an activation function to get the unit's output.
<img src="assets/simple_neuron.png" width=400px>
Mathematically this looks like:
$$
\begin{align}
y &= f(w_1 x_1 + w_2 x_2 + b) \\
y &= f\left(\sum_i w_i x_i +b \right)
\end{align}
$$
With vectors this is the dot/inner product of two vectors:
$$
h = \begin{bmatrix}
x_1 \, x_2 \cdots x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_1 \\
w_2 \\
\vdots \\
w_n
\end{bmatrix}
$$
## Tensors
It turns out neural network computations are just a bunch of linear algebra operations on *tensors*, a generalization of matrices. A vector is a 1-dimensional tensor, a matrix is a 2-dimensional tensor, an array with three indices is a 3-dimensional tensor (RGB color images for example). The fundamental data structure for neural networks are tensors and PyTorch (as well as pretty much every other deep learning framework) is built around tensors.
<img src="assets/tensor_examples.svg" width=600px>
With the basics covered, it's time to explore how we can use PyTorch to build a simple neural network.
```
# First, import PyTorch
!pip install torch==1.10.1
!pip install matplotlib==3.5.0
!pip install numpy==1.21.4
!pip install omegaconf==2.1.1
!pip install optuna==2.10.0
!pip install Pillow==9.0.0
!pip install scikit_learn==1.0.2
!pip install torchvision==0.11.2
!pip install transformers==4.15.0
# First, import PyTorch
import torch
def activation(x):
""" Sigmoid activation function
Arguments
---------
x: torch.Tensor
"""
return 1/(1+torch.exp(-x))
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 5 random normal variables
features = torch.randn((1, 5))
# True weights for our data, random normal variables again
weights = torch.randn_like(features)
# and a true bias term
bias = torch.randn((1, 1))
print(bias)
```
Above I generated data we can use to get the output of our simple network. This is all just random for now, going forward we'll start using normal data. Going through each relevant line:
`features = torch.randn((1, 5))` creates a tensor with shape `(1, 5)`, one row and five columns, that contains values randomly distributed according to the normal distribution with a mean of zero and standard deviation of one.
`weights = torch.randn_like(features)` creates another tensor with the same shape as `features`, again containing values from a normal distribution.
Finally, `bias = torch.randn((1, 1))` creates a single value from a normal distribution.
PyTorch tensors can be added, multiplied, subtracted, etc, just like Numpy arrays. In general, you'll use PyTorch tensors pretty much the same way you'd use Numpy arrays. They come with some nice benefits though such as GPU acceleration which we'll get to later. For now, use the generated data to calculate the output of this simple single layer network.
> **Exercise**: Calculate the output of the network with input features `features`, weights `weights`, and bias `bias`. Similar to Numpy, PyTorch has a [`torch.sum()`](https://pytorch.org/docs/stable/torch.html#torch.sum) function, as well as a `.sum()` method on tensors, for taking sums. Use the function `activation` defined above as the activation function.
```
## Calculate the output of this network using the weights and bias tensors
```
You can do the multiplication and sum in the same operation using a matrix multiplication. In general, you'll want to use matrix multiplications since they are more efficient and accelerated using modern libraries and high-performance computing on GPUs.
Here, we want to do a matrix multiplication of the features and the weights. For this we can use [`torch.mm()`](https://pytorch.org/docs/stable/torch.html#torch.mm) or [`torch.matmul()`](https://pytorch.org/docs/stable/torch.html#torch.matmul) which is somewhat more complicated and supports broadcasting. If we try to do it with `features` and `weights` as they are, we'll get an error
```python
>> torch.mm(features, weights)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-13-15d592eb5279> in <module>()
----> 1 torch.mm(features, weights)
RuntimeError: size mismatch, m1: [1 x 5], m2: [1 x 5] at /Users/soumith/minicondabuild3/conda-bld/pytorch_1524590658547/work/aten/src/TH/generic/THTensorMath.c:2033
```
As you're building neural networks in any framework, you'll see this often. Really often. What's happening here is our tensors aren't the correct shapes to perform a matrix multiplication. Remember that for matrix multiplications, the number of columns in the first tensor must equal to the number of rows in the second tensor. Both `features` and `weights` have the same shape, `(1, 5)`. This means we need to change the shape of `weights` to get the matrix multiplication to work.
**Note:** To see the shape of a tensor called `tensor`, use `tensor.shape`. If you're building neural networks, you'll be using this method often.
There are a few options here: [`weights.reshape()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.reshape), [`weights.resize_()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.resize_), [`weights.view()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.view) and [`torch.transpose(weights,0,1)`](https://pytorch.org/docs/master/generated/torch.transpose.html).
* `weights.reshape(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)` sometimes, and sometimes a clone, as in it copies the data to another part of memory.
* `weights.resize_(a, b)` returns the same tensor with a different shape. However, if the new shape results in fewer elements than the original tensor, some elements will be removed from the tensor (but not from memory). If the new shape results in more elements than the original tensor, new elements will be uninitialized in memory. Here I should note that the underscore at the end of the method denotes that this method is performed **in-place**. Here is a great forum thread to [read more about in-place operations](https://discuss.pytorch.org/t/what-is-in-place-operation/16244) in PyTorch.
* `weights.view(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)`.
* `torch.transpose(weights,0,1)` will return transposed weights tensor. This returns transposed version of inpjut tensor along dim 0 and dim 1. This is efficient since we do not specify to actual dimesions of weights.
I usually use `.view()`, but any of the three methods will work for this. So, now we can reshape `weights` to have five rows and one column with something like `weights.view(5, 1)`.
One more approach is to use `.t()` to transpose vector of weights, in our case from (1,5) to (5,1) shape.
> **Exercise**: Calculate the output of our little network using matrix multiplication.
```
## Calculate the output of this network using matrix multiplication
print('Hello pycharm')
```
### Stack them up!
That's how you can calculate the output for a single neuron. The real power of this algorithm happens when you start stacking these individual units into layers and stacks of layers, into a network of neurons. The output of one layer of neurons becomes the input for the next layer. With multiple input units and output units, we now need to express the weights as a matrix.
<img src='assets/multilayer_diagram_weights.png' width=450px>
The first layer shown on the bottom here are the inputs, understandably called the **input layer**. The middle layer is called the **hidden layer**, and the final layer (on the right) is the **output layer**. We can express this network mathematically with matrices again and use matrix multiplication to get linear combinations for each unit in one operation. For example, the hidden layer ($h_1$ and $h_2$ here) can be calculated
$$
\vec{h} = [h_1 \, h_2] =
\begin{bmatrix}
x_1 \, x_2 \cdots \, x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} &w_{22} \\
\vdots &\vdots \\
w_{n1} &w_{n2}
\end{bmatrix}
$$
The output for this small network is found by treating the hidden layer as inputs for the output unit. The network output is expressed simply
$$
y = f_2 \! \left(\, f_1 \! \left(\vec{x} \, \mathbf{W_1}\right) \mathbf{W_2} \right)
$$
```
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 3))
# Define the size of each layer in our network
n_input = features.shape[1] # Number of input units, must match number of input features
n_hidden = 2 # Number of hidden units
n_output = 1 # Number of output units
# Weights for inputs to hidden layer
W1 = torch.randn(n_input, n_hidden)
# Weights for hidden layer to output layer
W2 = torch.randn(n_hidden, n_output)
# and bias terms for hidden and output layers
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
```
> **Exercise:** Calculate the output for this multi-layer network using the weights `W1` & `W2`, and the biases, `B1` & `B2`.
```
## Your solution here
```
If you did this correctly, you should see the output `tensor([[ 0.3171]])`.
The number of hidden units are a parameter of the network, often called a **hyperparameter** to differentiate it from the weights and biases parameters. As you'll see later when we discuss training a neural network, the more hidden units a network has, and the more layers, the better able it is to learn from data and make accurate predictions.
## Numpy to Torch and back
Special bonus section! PyTorch has a great feature for converting between Numpy arrays and Torch tensors. To create a tensor from a Numpy array, use `torch.from_numpy()`. To convert a tensor to a Numpy array, use the `.numpy()` method.
```
import numpy as np
np.set_printoptions(precision=8)
a = np.random.rand(4,3)
a
torch.set_printoptions(precision=8)
b = torch.from_numpy(a)
b
b.numpy()
```
The memory is shared between the Numpy array and Torch tensor, so if you change the values in-place of one object, the other will change as well.
```
# Multiply PyTorch Tensor by 2, in place
b.mul_(2)
# Numpy array matches new values from Tensor
a
```
|
github_jupyter
|
# First, import PyTorch
!pip install torch==1.10.1
!pip install matplotlib==3.5.0
!pip install numpy==1.21.4
!pip install omegaconf==2.1.1
!pip install optuna==2.10.0
!pip install Pillow==9.0.0
!pip install scikit_learn==1.0.2
!pip install torchvision==0.11.2
!pip install transformers==4.15.0
# First, import PyTorch
import torch
def activation(x):
""" Sigmoid activation function
Arguments
---------
x: torch.Tensor
"""
return 1/(1+torch.exp(-x))
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 5 random normal variables
features = torch.randn((1, 5))
# True weights for our data, random normal variables again
weights = torch.randn_like(features)
# and a true bias term
bias = torch.randn((1, 1))
print(bias)
## Calculate the output of this network using the weights and bias tensors
>> torch.mm(features, weights)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-13-15d592eb5279> in <module>()
----> 1 torch.mm(features, weights)
RuntimeError: size mismatch, m1: [1 x 5], m2: [1 x 5] at /Users/soumith/minicondabuild3/conda-bld/pytorch_1524590658547/work/aten/src/TH/generic/THTensorMath.c:2033
## Calculate the output of this network using matrix multiplication
print('Hello pycharm')
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 3))
# Define the size of each layer in our network
n_input = features.shape[1] # Number of input units, must match number of input features
n_hidden = 2 # Number of hidden units
n_output = 1 # Number of output units
# Weights for inputs to hidden layer
W1 = torch.randn(n_input, n_hidden)
# Weights for hidden layer to output layer
W2 = torch.randn(n_hidden, n_output)
# and bias terms for hidden and output layers
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
## Your solution here
import numpy as np
np.set_printoptions(precision=8)
a = np.random.rand(4,3)
a
torch.set_printoptions(precision=8)
b = torch.from_numpy(a)
b
b.numpy()
# Multiply PyTorch Tensor by 2, in place
b.mul_(2)
# Numpy array matches new values from Tensor
a
| 0.708616 | 0.988949 |
```
import json
import re
import urllib
import pandas as pd
import numpy as np
pd.set_option('display.max_columns', 50)
pd.set_option('display.max_colwidth', 100)
erasmus_plus_mobility = pd.concat([
pd.read_excel(file)
for file in [
'input/ErasmusPlus_KA1_2014_LearningMobilityOfIndividuals_Projects_Overview_2018-09-18.xls',
'input/ErasmusPlus_KA1_2015_LearningMobilityOfIndividuals_Projects_Overview_2018-09-18.xls',
'input/ErasmusPlus_KA1_2016_LearningMobilityOfIndividuals_Projects_Overview_2018-09-18.xls',
'input/ErasmusPlus_KA1_2017_LearningMobilityOfIndividuals_Projects_Overview_2018-09-15.xls',
'input/ErasmusPlus_KA1_2018_LearningMobilityOfIndividuals_Projects_Overview_2018-09-18.xls',
'input/ErasmusPlus_KA2_CooperationForInnovationAndTheExchangeOfGoodPractices_Projects_Overview_2018-09-21.xls',
'input/ErasmusPlus_Sports_Projects_Overview_2018-09-10.xls',
'input/ErasmusPlus_JeanMonnet_Projects_Overview_2018-09-10.xls'
]
], ignore_index=True)
erasmus_plus_mobility.shape
erasmus_plus_mobility.head()
list(erasmus_plus_mobility)
erasmus_plus_mobility = erasmus_plus_mobility.rename(columns={
'Programme': 'funds',
'Call year': 'call_year',
'Project Identifier': 'project_identifier',
'Project Title': 'project',
'Project Summary': 'summary',
'Project Status': 'project_status',
"EU Grant award in euros (This amount represents the grant awarded after the selection stage and is indicative. Please note that any changes made during or after the project's lifetime will not be reflected here.)": 'max_contribution_eur',
'Project Website': 'project_url',
'Results Available': 'results_available',
'Results Platform Project Card': 'results_url',
'Participating countries': 'participating_countries',
'Coordinating organisation name': 'coord_name',
'Coordinating organisation type': 'coord_org_type',
"Coordinator's address": 'coord_address',
"Coordinator's region": 'coord_region',
"Coordinator's country": 'coord_country',
"Coordinator's website": 'coord_website',
'Key Action': 'key_action',
'Action Type': 'action_type',
'Is Good Practice': 'is_good_practice',
'Is Success Story': 'is_success_story',
'Results Platform Project Card': 'results_platform_project_card',
'Topics': 'topics'
}).copy()
erasmus_plus_mobility.head()
```
Let's check if these projects are on the map already - looked at the first few, and they don't seem to be there
```
erasmus_plus_mobility_check = erasmus_plus_mobility[erasmus_plus_mobility.coord_country == 'UK'].copy()
erasmus_plus_mobility_check = erasmus_plus_mobility_check[['coord_address', 'project', 'coord_country']].copy()
erasmus_plus_mobility_check.head()
```
### Unnamed Column
Apparently a placeholder for projects with more than 38 partners.
```
[erasmus_plus_mobility.shape, erasmus_plus_mobility['Unnamed: 250'].isna().sum()]
erasmus_plus_mobility['Unnamed: 250'][~erasmus_plus_mobility['Unnamed: 250'].isna()]
erasmus_plus_mobility.rename(columns={'Unnamed: 250': 'extra_partners'}, inplace=True)
```
### Project Identifier
Fortunately, this looks to be an ID.
```
erasmus_plus_mobility.project_identifier.isna().sum()
(erasmus_plus_mobility.project_identifier.str.strip() != erasmus_plus_mobility.project_identifier).sum()
[
erasmus_plus_mobility.shape,
erasmus_plus_mobility.project_identifier.nunique(),
erasmus_plus_mobility.project_identifier.str.upper().nunique()
]
```
## Extract Projects from Partners and Coordinators
```
projects = erasmus_plus_mobility[[
'project_identifier', 'funds',
'call_year',
'project', 'summary', 'project_status',
'max_contribution_eur', 'project_url',
'participating_countries', 'extra_partners'
]].copy()
projects.shape
```
### Funds
```
projects.funds.isna().sum()
projects.funds.unique()
```
### Call Year
```
projects.call_year.isna().sum()
projects.call_year.unique()
projects.call_year = projects.call_year.astype('int32')
```
### Project
```
projects.project.isna().sum()
(projects.project != projects.project.str.strip()).sum()
projects.project = projects.project.str.strip()
```
### Summary
```
projects.summary.isna().sum()
projects[projects.summary.isna()]
projects.summary[projects.summary.str.strip() != projects.summary] # lots
projects.summary = projects.summary.str.strip()
```
### Project Status
```
projects.project_status.isna().sum()
projects.project_status.unique()
```
### EU Investment
```
projects.max_contribution_eur.isna().sum()
projects.max_contribution_eur = projects.max_contribution_eur.map(str).str.strip()
max_contribution_eur_bad = projects.max_contribution_eur.str.match(re.compile(r'.*[^0-9.].*'))
projects.max_contribution_eur[max_contribution_eur_bad]
projects.max_contribution_eur = projects.max_contribution_eur.astype('float')
projects.max_contribution_eur.describe()
(projects.max_contribution_eur < 1000).value_counts()
projects = projects[projects.max_contribution_eur >= 1000]
projects.shape
```
### Project URL
```
(~projects.project_url.isna()).sum()
projects.project_url[~projects.project_url.isna()].head()
def is_valid_url(url):
result = urllib.parse.urlparse(str(url))
return bool(result.scheme and result.netloc)
(~projects.project_url.isna() & ~projects.project_url.apply(is_valid_url)).sum()
```
### Participating Countries
```
projects.participating_countries.isna().sum()
projects.participating_countries.head()
```
## Extract Coordinators
The coordinator is like a special partner, so make the names consistent, and we can treat partners and coordinators the same for cleaning purposes.
```
coordinators = erasmus_plus_mobility[[
'project_identifier',
'coord_name',
'coord_org_type',
'coord_address',
'coord_region',
'coord_country',
'coord_website'
]].copy()
coordinators.shape
coordinators.rename(columns={
'coord_name': 'name',
'coord_org_type': 'type',
'coord_address': 'address',
'coord_region': 'region',
'coord_country': 'country',
'coord_website': 'website',
}, inplace=True)
coordinators['coordinator'] = True
coordinators.head()
coordinators.count()
```
### Name
```
(coordinators.name.str.strip() != coordinators.name).sum()
coordinators.name = coordinators.name.str.strip()
coordinators.name.unique().shape
```
### Type
```
coordinators.type.isna().sum()
(coordinators.type[~coordinators.type.isna()] != coordinators.type[~coordinators.type.isna()].str.strip()).sum()
coordinators[~coordinators.type.isna()].type.sort_values().unique()[0:10]
```
### Country
```
coordinators.country.isna().sum()
[
coordinators.shape[0],
(coordinators.country != coordinators.country.str.strip()).sum(),
(coordinators.country != coordinators.country.str.upper()).sum(),
(coordinators.country.str.match('[A-Z]{2}')).sum()
]
```
### Website
```
(~coordinators.website.isna() & ~coordinators.website.apply(is_valid_url)).sum()
[
coordinators.website.str.startswith('http').sum(),
(~coordinators.website.isna() & coordinators.website.apply(is_valid_url)).sum()
]
coordinators.head()
coordinators.website[~coordinators.website.isna() & ~coordinators.website.apply(is_valid_url)].head()
coordinators.loc[
~coordinators.website.isna() &
~coordinators.website.apply(is_valid_url), 'website'] = 'http://' + coordinators.website
(~coordinators.website.isna() & ~coordinators.website.apply(is_valid_url)).sum()
coordinators.website[~coordinators.website.isna() & ~coordinators.website.apply(is_valid_url)]
coordinators.website = coordinators.website.str.replace(r'^(https?://)/', r'\1')
(~coordinators.website.isna() & ~coordinators.website.apply(is_valid_url)).sum()
coordinators.website.head()
```
### Postcodes for UK Coordinators
Some people have switched 'O' for '0' - could clean this up later
```
coordinators_uk = coordinators[coordinators.country == 'UK'].copy()
[coordinators_uk.shape[0], coordinators.shape[0]]
ukpostcodes = pd.read_csv('../postcodes/input/ukpostcodes.csv.gz')
ukpostcodes.shape
VALID_POSTCODE_RE = re.compile(
r'([A-Za-z][A-Ha-hJ-Yj-y]?[0-9][A-Za-z0-9]? ?[0-9][A-Za-z]{2}|[Gg][Ii][Rr] ?0[Aa]{2})'
)
assert ukpostcodes.postcode.str.match(VALID_POSTCODE_RE).sum() == ukpostcodes.shape[0]
coordinators_uk['raw_postcode'] = \
coordinators_uk.address.str.extract(VALID_POSTCODE_RE)[0]
coordinators_uk.raw_postcode.head()
coordinators_uk[coordinators_uk.raw_postcode.isna()]
[
(~coordinators_uk.raw_postcode.isna()).sum(),
coordinators_uk.raw_postcode.isin(ukpostcodes.postcode).sum(),
]
def find_postcode_from_raw_postcode(raw_postcode):
return raw_postcode.\
str.upper().\
str.strip().\
str.replace(r'[^A-Z0-9]', '').\
str.replace(r'^(\S+)([0-9][A-Z]{2})$', r'\1 \2')
coordinators_uk['postcode'] = find_postcode_from_raw_postcode(coordinators_uk.raw_postcode)
coordinators_uk.postcode.isin(ukpostcodes.postcode).sum()
coordinators_uk.postcode[~coordinators_uk.postcode.isin(ukpostcodes.postcode)].unique()
coordinators_uk[~coordinators_uk.postcode.isin(ukpostcodes.postcode)]
clean_coordinators_uk = coordinators_uk[
coordinators_uk.postcode.isin(ukpostcodes.postcode)
].copy()
clean_coordinators_uk.drop('raw_postcode', axis=1, inplace=True)
clean_coordinators_uk.shape
```
## Extract Partners
```
erasmus_plus_mobility.columns = [
re.sub(r'^Partner (\d+) (.+)$', r'Partner_\2_\1', column)
for column in erasmus_plus_mobility.columns
]
erasmus_plus_mobility.head()
partner_columns = [
column for column in erasmus_plus_mobility.columns
if column.startswith('Partner_')
]
partners_wide = erasmus_plus_mobility[['project_identifier'] + partner_columns]
partners_wide.head()
partners = pd.wide_to_long(
partners_wide,
['Partner_name','Partner_organisation type', 'Partner_address', 'Partner_country', 'Partner_region', 'Partner_website'],
'project_identifier', 'partner_number',
sep='_'
)
partners.head()
partners = partners.rename(columns={
'Partner_name': 'name',
'Partner_organisation type': 'type',
'Partner_address': 'address',
'Partner_country': 'country',
'Partner_region': 'region',
'Partner_website': 'website'
}).copy()
partners['coordinator'] = False
partners.head()
partners.count()
partners = partners[~partners.name.isna()].copy()
partners.count()
```
### Name
```
(partners.name.str.strip() != partners.name).sum()
partners.name = partners.name.str.strip()
partners.name.unique().shape
```
### Type
```
partners.type.isna().sum()
(partners.type[~partners.type.isna()] != partners.type[~partners.type.isna()].str.strip()).sum()
partners[~partners.type.isna()].type.sort_values().unique()[0:10]
```
### Country
```
partners.country.isna().sum()
[
partners.shape[0],
(partners.country != partners.country.str.strip()).sum(),
(partners.country != partners.country.str.upper()).sum(),
(partners.country.str.match('[A-Z]{2}')).sum()
]
```
### Website
```
(~partners.website.isna() & ~partners.website.apply(is_valid_url)).sum()
[
partners.website.str.startswith('http').sum(),
(~partners.website.isna() & partners.website.apply(is_valid_url)).sum()
]
partners_copy = partners.copy()
partners = partners_copy.copy()
partners.website[
partners.website.str.startswith('http') &
~partners.website.apply(is_valid_url)]
partners.website = partners.website.str.replace(r'^http:\\', 'http://')
partners.website = partners.website.str.replace(r'^http:://', 'http://')
partners.website = partners.website.str.replace(r'^http: //', 'http://')
partners.website = partners.website.str.replace(r'^http:/[^/]', 'http://')
partners.website = partners.website.str.replace(r'^http:[^/][^/]', 'http://')
partners.website = partners.website.str.replace(r'^http//:', 'http://')
partners.website = partners.website.str.replace(r'^http//', 'http://')
partners.website = partners.website.str.replace(r'^http/', 'http://')
partners.website = partners.website.str.replace(r'^http.www', 'http://www')
partners.loc[
~partners.website.isna() &
~partners.website.apply(is_valid_url), 'website'] = 'http://' + partners.website
(~partners.website.isna() & ~partners.website.apply(is_valid_url)).sum()
partners.website.head()
```
### Separating out UK partners
```
partners_uk = partners[partners.country == 'UK'].copy()
[partners_uk.shape, partners.shape]
partners_uk['raw_postcode'] = \
partners_uk.address.str.extract(VALID_POSTCODE_RE)[0]
partners_uk.raw_postcode.head()
partners_uk[partners_uk.raw_postcode.isna()]
```
Quite a few here
```
partners_uk.raw_postcode.isin(ukpostcodes.postcode).sum()
partners_uk['postcode'] = find_postcode_from_raw_postcode(partners_uk.raw_postcode)
partners_uk.postcode.isin(ukpostcodes.postcode).sum()
partners_uk.postcode[~partners_uk.postcode.isin(ukpostcodes.postcode)].unique()
partners_uk[~partners_uk.postcode.isna() & ~partners_uk.postcode.isin(ukpostcodes.postcode)]
clean_partners_uk = partners_uk[partners_uk.postcode.isin(ukpostcodes.postcode)].copy()
clean_partners_uk.drop('raw_postcode', axis=1, inplace=True)
clean_partners_uk.reset_index(inplace=True)
clean_partners_uk.shape
```
## Count Organisations and Countries
It is useful to know the total number of organisations and the number of countries involved, to deal with cases where the contribution of each organisation is unknown.
```
organisations = pd.concat([
partners.reset_index()[['project_identifier', 'country']],
coordinators.reset_index()[['project_identifier', 'country']]
])
organisations.shape
project_num_organisations = organisations.groupby('project_identifier').\
country.count().reset_index().rename(columns={'country': 'num_organisations'})
[projects.shape[0], project_num_organisations.shape]
```
Cross-check with partner numbers:
```
project_num_organisations_check = \
(partners.reset_index().groupby('project_identifier').partner_number.max() + 1).\
reset_index().rename(columns={'partner_number': 'num_organisations'})
[projects.shape[0], project_num_organisations_check.shape]
def compare_project_num_organisations():
c = pd.merge(project_num_organisations, project_num_organisations_check,
on='project_identifier', how='left')
c.loc[c.num_organisations_y.isna(), 'num_organisations_y'] = 1
return (c.num_organisations_x != c.num_organisations_y).sum()
compare_project_num_organisations()
project_num_countries = organisations.groupby('project_identifier').\
country.nunique().reset_index().rename(columns={'country': 'num_countries'})
[projects.shape[0], project_num_countries.shape]
project_num_organisations_and_countries = pd.merge(
project_num_countries, project_num_organisations,
on='project_identifier', validate='1:1'
)
project_num_organisations_and_countries.shape
project_num_organisations_and_countries.head()
projects = pd.merge(projects, project_num_organisations_and_countries,
on='project_identifier', validate='1:1')
projects.head()
```
## Save Data
### Organisations
```
organisations_uk = pd.concat([clean_coordinators_uk, clean_partners_uk], sort=True)
[
organisations_uk.shape,
clean_coordinators_uk.shape,
clean_partners_uk.shape
]
organisations_uk.rename(columns={
'name': 'organisation_name',
'type': 'organisation_type',
'address': 'organisation_address',
'country': 'organisation_country',
'region': 'organisation_region',
'website': 'organisation_website',
'coordinator': 'organisation_coordinator'
}, inplace=True)
organisations_uk
organisations_uk.project_identifier.unique().shape
organisations_uk.to_pickle('output/erasmus_mobility_organisations.pkl.gz')
```
### Projects in the UK
```
projects_uk_full = pd.merge(projects, organisations_uk, on='project_identifier', validate='1:m')
projects_uk_full.shape
projects_uk_full.head()
projects_uk = projects[projects.project_identifier.isin(organisations_uk.project_identifier)].copy()
projects_uk.shape
```
#### Convert to GBP
```
eur_gbp = pd.read_pickle('../exchange_rates/output/exchange_rates.pkl.gz')
eur_gbp.tail()
def find_average_eur_gbp_rate(row):
# create timeseries from start to end
year_start = str(row.call_year) +'-01-01'
year_end = str(row.call_year) +'-12-31'
days = pd.date_range(year_start, year_end, closed='left')
daily = pd.DataFrame({
'month_start': days,
'weight': 1.0 / days.shape[0]
})
monthly = daily.resample('MS', on='month_start').sum()
monthly = pd.merge(monthly, eur_gbp, on='month_start', validate='1:1')
return (monthly.weight * monthly.rate).sum()
projects_uk['eur_gbp'] = projects_uk.apply(
find_average_eur_gbp_rate, axis=1, result_type='reduce')
projects_uk.head()
projects_uk.to_pickle('output/erasmus_mobility_projects.pkl.gz')
```
|
github_jupyter
|
import json
import re
import urllib
import pandas as pd
import numpy as np
pd.set_option('display.max_columns', 50)
pd.set_option('display.max_colwidth', 100)
erasmus_plus_mobility = pd.concat([
pd.read_excel(file)
for file in [
'input/ErasmusPlus_KA1_2014_LearningMobilityOfIndividuals_Projects_Overview_2018-09-18.xls',
'input/ErasmusPlus_KA1_2015_LearningMobilityOfIndividuals_Projects_Overview_2018-09-18.xls',
'input/ErasmusPlus_KA1_2016_LearningMobilityOfIndividuals_Projects_Overview_2018-09-18.xls',
'input/ErasmusPlus_KA1_2017_LearningMobilityOfIndividuals_Projects_Overview_2018-09-15.xls',
'input/ErasmusPlus_KA1_2018_LearningMobilityOfIndividuals_Projects_Overview_2018-09-18.xls',
'input/ErasmusPlus_KA2_CooperationForInnovationAndTheExchangeOfGoodPractices_Projects_Overview_2018-09-21.xls',
'input/ErasmusPlus_Sports_Projects_Overview_2018-09-10.xls',
'input/ErasmusPlus_JeanMonnet_Projects_Overview_2018-09-10.xls'
]
], ignore_index=True)
erasmus_plus_mobility.shape
erasmus_plus_mobility.head()
list(erasmus_plus_mobility)
erasmus_plus_mobility = erasmus_plus_mobility.rename(columns={
'Programme': 'funds',
'Call year': 'call_year',
'Project Identifier': 'project_identifier',
'Project Title': 'project',
'Project Summary': 'summary',
'Project Status': 'project_status',
"EU Grant award in euros (This amount represents the grant awarded after the selection stage and is indicative. Please note that any changes made during or after the project's lifetime will not be reflected here.)": 'max_contribution_eur',
'Project Website': 'project_url',
'Results Available': 'results_available',
'Results Platform Project Card': 'results_url',
'Participating countries': 'participating_countries',
'Coordinating organisation name': 'coord_name',
'Coordinating organisation type': 'coord_org_type',
"Coordinator's address": 'coord_address',
"Coordinator's region": 'coord_region',
"Coordinator's country": 'coord_country',
"Coordinator's website": 'coord_website',
'Key Action': 'key_action',
'Action Type': 'action_type',
'Is Good Practice': 'is_good_practice',
'Is Success Story': 'is_success_story',
'Results Platform Project Card': 'results_platform_project_card',
'Topics': 'topics'
}).copy()
erasmus_plus_mobility.head()
erasmus_plus_mobility_check = erasmus_plus_mobility[erasmus_plus_mobility.coord_country == 'UK'].copy()
erasmus_plus_mobility_check = erasmus_plus_mobility_check[['coord_address', 'project', 'coord_country']].copy()
erasmus_plus_mobility_check.head()
[erasmus_plus_mobility.shape, erasmus_plus_mobility['Unnamed: 250'].isna().sum()]
erasmus_plus_mobility['Unnamed: 250'][~erasmus_plus_mobility['Unnamed: 250'].isna()]
erasmus_plus_mobility.rename(columns={'Unnamed: 250': 'extra_partners'}, inplace=True)
erasmus_plus_mobility.project_identifier.isna().sum()
(erasmus_plus_mobility.project_identifier.str.strip() != erasmus_plus_mobility.project_identifier).sum()
[
erasmus_plus_mobility.shape,
erasmus_plus_mobility.project_identifier.nunique(),
erasmus_plus_mobility.project_identifier.str.upper().nunique()
]
projects = erasmus_plus_mobility[[
'project_identifier', 'funds',
'call_year',
'project', 'summary', 'project_status',
'max_contribution_eur', 'project_url',
'participating_countries', 'extra_partners'
]].copy()
projects.shape
projects.funds.isna().sum()
projects.funds.unique()
projects.call_year.isna().sum()
projects.call_year.unique()
projects.call_year = projects.call_year.astype('int32')
projects.project.isna().sum()
(projects.project != projects.project.str.strip()).sum()
projects.project = projects.project.str.strip()
projects.summary.isna().sum()
projects[projects.summary.isna()]
projects.summary[projects.summary.str.strip() != projects.summary] # lots
projects.summary = projects.summary.str.strip()
projects.project_status.isna().sum()
projects.project_status.unique()
projects.max_contribution_eur.isna().sum()
projects.max_contribution_eur = projects.max_contribution_eur.map(str).str.strip()
max_contribution_eur_bad = projects.max_contribution_eur.str.match(re.compile(r'.*[^0-9.].*'))
projects.max_contribution_eur[max_contribution_eur_bad]
projects.max_contribution_eur = projects.max_contribution_eur.astype('float')
projects.max_contribution_eur.describe()
(projects.max_contribution_eur < 1000).value_counts()
projects = projects[projects.max_contribution_eur >= 1000]
projects.shape
(~projects.project_url.isna()).sum()
projects.project_url[~projects.project_url.isna()].head()
def is_valid_url(url):
result = urllib.parse.urlparse(str(url))
return bool(result.scheme and result.netloc)
(~projects.project_url.isna() & ~projects.project_url.apply(is_valid_url)).sum()
projects.participating_countries.isna().sum()
projects.participating_countries.head()
coordinators = erasmus_plus_mobility[[
'project_identifier',
'coord_name',
'coord_org_type',
'coord_address',
'coord_region',
'coord_country',
'coord_website'
]].copy()
coordinators.shape
coordinators.rename(columns={
'coord_name': 'name',
'coord_org_type': 'type',
'coord_address': 'address',
'coord_region': 'region',
'coord_country': 'country',
'coord_website': 'website',
}, inplace=True)
coordinators['coordinator'] = True
coordinators.head()
coordinators.count()
(coordinators.name.str.strip() != coordinators.name).sum()
coordinators.name = coordinators.name.str.strip()
coordinators.name.unique().shape
coordinators.type.isna().sum()
(coordinators.type[~coordinators.type.isna()] != coordinators.type[~coordinators.type.isna()].str.strip()).sum()
coordinators[~coordinators.type.isna()].type.sort_values().unique()[0:10]
coordinators.country.isna().sum()
[
coordinators.shape[0],
(coordinators.country != coordinators.country.str.strip()).sum(),
(coordinators.country != coordinators.country.str.upper()).sum(),
(coordinators.country.str.match('[A-Z]{2}')).sum()
]
(~coordinators.website.isna() & ~coordinators.website.apply(is_valid_url)).sum()
[
coordinators.website.str.startswith('http').sum(),
(~coordinators.website.isna() & coordinators.website.apply(is_valid_url)).sum()
]
coordinators.head()
coordinators.website[~coordinators.website.isna() & ~coordinators.website.apply(is_valid_url)].head()
coordinators.loc[
~coordinators.website.isna() &
~coordinators.website.apply(is_valid_url), 'website'] = 'http://' + coordinators.website
(~coordinators.website.isna() & ~coordinators.website.apply(is_valid_url)).sum()
coordinators.website[~coordinators.website.isna() & ~coordinators.website.apply(is_valid_url)]
coordinators.website = coordinators.website.str.replace(r'^(https?://)/', r'\1')
(~coordinators.website.isna() & ~coordinators.website.apply(is_valid_url)).sum()
coordinators.website.head()
coordinators_uk = coordinators[coordinators.country == 'UK'].copy()
[coordinators_uk.shape[0], coordinators.shape[0]]
ukpostcodes = pd.read_csv('../postcodes/input/ukpostcodes.csv.gz')
ukpostcodes.shape
VALID_POSTCODE_RE = re.compile(
r'([A-Za-z][A-Ha-hJ-Yj-y]?[0-9][A-Za-z0-9]? ?[0-9][A-Za-z]{2}|[Gg][Ii][Rr] ?0[Aa]{2})'
)
assert ukpostcodes.postcode.str.match(VALID_POSTCODE_RE).sum() == ukpostcodes.shape[0]
coordinators_uk['raw_postcode'] = \
coordinators_uk.address.str.extract(VALID_POSTCODE_RE)[0]
coordinators_uk.raw_postcode.head()
coordinators_uk[coordinators_uk.raw_postcode.isna()]
[
(~coordinators_uk.raw_postcode.isna()).sum(),
coordinators_uk.raw_postcode.isin(ukpostcodes.postcode).sum(),
]
def find_postcode_from_raw_postcode(raw_postcode):
return raw_postcode.\
str.upper().\
str.strip().\
str.replace(r'[^A-Z0-9]', '').\
str.replace(r'^(\S+)([0-9][A-Z]{2})$', r'\1 \2')
coordinators_uk['postcode'] = find_postcode_from_raw_postcode(coordinators_uk.raw_postcode)
coordinators_uk.postcode.isin(ukpostcodes.postcode).sum()
coordinators_uk.postcode[~coordinators_uk.postcode.isin(ukpostcodes.postcode)].unique()
coordinators_uk[~coordinators_uk.postcode.isin(ukpostcodes.postcode)]
clean_coordinators_uk = coordinators_uk[
coordinators_uk.postcode.isin(ukpostcodes.postcode)
].copy()
clean_coordinators_uk.drop('raw_postcode', axis=1, inplace=True)
clean_coordinators_uk.shape
erasmus_plus_mobility.columns = [
re.sub(r'^Partner (\d+) (.+)$', r'Partner_\2_\1', column)
for column in erasmus_plus_mobility.columns
]
erasmus_plus_mobility.head()
partner_columns = [
column for column in erasmus_plus_mobility.columns
if column.startswith('Partner_')
]
partners_wide = erasmus_plus_mobility[['project_identifier'] + partner_columns]
partners_wide.head()
partners = pd.wide_to_long(
partners_wide,
['Partner_name','Partner_organisation type', 'Partner_address', 'Partner_country', 'Partner_region', 'Partner_website'],
'project_identifier', 'partner_number',
sep='_'
)
partners.head()
partners = partners.rename(columns={
'Partner_name': 'name',
'Partner_organisation type': 'type',
'Partner_address': 'address',
'Partner_country': 'country',
'Partner_region': 'region',
'Partner_website': 'website'
}).copy()
partners['coordinator'] = False
partners.head()
partners.count()
partners = partners[~partners.name.isna()].copy()
partners.count()
(partners.name.str.strip() != partners.name).sum()
partners.name = partners.name.str.strip()
partners.name.unique().shape
partners.type.isna().sum()
(partners.type[~partners.type.isna()] != partners.type[~partners.type.isna()].str.strip()).sum()
partners[~partners.type.isna()].type.sort_values().unique()[0:10]
partners.country.isna().sum()
[
partners.shape[0],
(partners.country != partners.country.str.strip()).sum(),
(partners.country != partners.country.str.upper()).sum(),
(partners.country.str.match('[A-Z]{2}')).sum()
]
(~partners.website.isna() & ~partners.website.apply(is_valid_url)).sum()
[
partners.website.str.startswith('http').sum(),
(~partners.website.isna() & partners.website.apply(is_valid_url)).sum()
]
partners_copy = partners.copy()
partners = partners_copy.copy()
partners.website[
partners.website.str.startswith('http') &
~partners.website.apply(is_valid_url)]
partners.website = partners.website.str.replace(r'^http:\\', 'http://')
partners.website = partners.website.str.replace(r'^http:://', 'http://')
partners.website = partners.website.str.replace(r'^http: //', 'http://')
partners.website = partners.website.str.replace(r'^http:/[^/]', 'http://')
partners.website = partners.website.str.replace(r'^http:[^/][^/]', 'http://')
partners.website = partners.website.str.replace(r'^http//:', 'http://')
partners.website = partners.website.str.replace(r'^http//', 'http://')
partners.website = partners.website.str.replace(r'^http/', 'http://')
partners.website = partners.website.str.replace(r'^http.www', 'http://www')
partners.loc[
~partners.website.isna() &
~partners.website.apply(is_valid_url), 'website'] = 'http://' + partners.website
(~partners.website.isna() & ~partners.website.apply(is_valid_url)).sum()
partners.website.head()
partners_uk = partners[partners.country == 'UK'].copy()
[partners_uk.shape, partners.shape]
partners_uk['raw_postcode'] = \
partners_uk.address.str.extract(VALID_POSTCODE_RE)[0]
partners_uk.raw_postcode.head()
partners_uk[partners_uk.raw_postcode.isna()]
partners_uk.raw_postcode.isin(ukpostcodes.postcode).sum()
partners_uk['postcode'] = find_postcode_from_raw_postcode(partners_uk.raw_postcode)
partners_uk.postcode.isin(ukpostcodes.postcode).sum()
partners_uk.postcode[~partners_uk.postcode.isin(ukpostcodes.postcode)].unique()
partners_uk[~partners_uk.postcode.isna() & ~partners_uk.postcode.isin(ukpostcodes.postcode)]
clean_partners_uk = partners_uk[partners_uk.postcode.isin(ukpostcodes.postcode)].copy()
clean_partners_uk.drop('raw_postcode', axis=1, inplace=True)
clean_partners_uk.reset_index(inplace=True)
clean_partners_uk.shape
organisations = pd.concat([
partners.reset_index()[['project_identifier', 'country']],
coordinators.reset_index()[['project_identifier', 'country']]
])
organisations.shape
project_num_organisations = organisations.groupby('project_identifier').\
country.count().reset_index().rename(columns={'country': 'num_organisations'})
[projects.shape[0], project_num_organisations.shape]
project_num_organisations_check = \
(partners.reset_index().groupby('project_identifier').partner_number.max() + 1).\
reset_index().rename(columns={'partner_number': 'num_organisations'})
[projects.shape[0], project_num_organisations_check.shape]
def compare_project_num_organisations():
c = pd.merge(project_num_organisations, project_num_organisations_check,
on='project_identifier', how='left')
c.loc[c.num_organisations_y.isna(), 'num_organisations_y'] = 1
return (c.num_organisations_x != c.num_organisations_y).sum()
compare_project_num_organisations()
project_num_countries = organisations.groupby('project_identifier').\
country.nunique().reset_index().rename(columns={'country': 'num_countries'})
[projects.shape[0], project_num_countries.shape]
project_num_organisations_and_countries = pd.merge(
project_num_countries, project_num_organisations,
on='project_identifier', validate='1:1'
)
project_num_organisations_and_countries.shape
project_num_organisations_and_countries.head()
projects = pd.merge(projects, project_num_organisations_and_countries,
on='project_identifier', validate='1:1')
projects.head()
organisations_uk = pd.concat([clean_coordinators_uk, clean_partners_uk], sort=True)
[
organisations_uk.shape,
clean_coordinators_uk.shape,
clean_partners_uk.shape
]
organisations_uk.rename(columns={
'name': 'organisation_name',
'type': 'organisation_type',
'address': 'organisation_address',
'country': 'organisation_country',
'region': 'organisation_region',
'website': 'organisation_website',
'coordinator': 'organisation_coordinator'
}, inplace=True)
organisations_uk
organisations_uk.project_identifier.unique().shape
organisations_uk.to_pickle('output/erasmus_mobility_organisations.pkl.gz')
projects_uk_full = pd.merge(projects, organisations_uk, on='project_identifier', validate='1:m')
projects_uk_full.shape
projects_uk_full.head()
projects_uk = projects[projects.project_identifier.isin(organisations_uk.project_identifier)].copy()
projects_uk.shape
eur_gbp = pd.read_pickle('../exchange_rates/output/exchange_rates.pkl.gz')
eur_gbp.tail()
def find_average_eur_gbp_rate(row):
# create timeseries from start to end
year_start = str(row.call_year) +'-01-01'
year_end = str(row.call_year) +'-12-31'
days = pd.date_range(year_start, year_end, closed='left')
daily = pd.DataFrame({
'month_start': days,
'weight': 1.0 / days.shape[0]
})
monthly = daily.resample('MS', on='month_start').sum()
monthly = pd.merge(monthly, eur_gbp, on='month_start', validate='1:1')
return (monthly.weight * monthly.rate).sum()
projects_uk['eur_gbp'] = projects_uk.apply(
find_average_eur_gbp_rate, axis=1, result_type='reduce')
projects_uk.head()
projects_uk.to_pickle('output/erasmus_mobility_projects.pkl.gz')
| 0.46952 | 0.349977 |
# 3D Spectral Image
**Suhas Somnath**
10/12/2018
**This example illustrates how a 3D spectral image would be represented in the Universal Spectroscopy and
Imaging Data (USID) schema and stored in a Hierarchical Data Format (HDF5) file, also referred to as the h5USID file.**
This document is intended as a supplement to the explanation about the [USID model](../../usid_model.html)
Please consider downloading this document as a Jupyter notebook using the button at the bottom of this document.
Prerequisites:
--------------
We recommend that you read about the [USID model](../../usid_model.html)
We will be making use of the ``pyUSID`` package at multiple places to illustrate the central point. While it is
recommended / a bonus, it is not absolutely necessary that the reader understands how the specific ``pyUSID`` functions
work or why they were used in order to understand the data representation itself.
Examples about these functions can be found in other documentation on pyUSID and the reader is encouraged to read the
supplementary documents.
### Import all necessary packages
The main packages necessary for this example are ``h5py``, ``matplotlib``, and ``sidpy``, in addition to ``pyUSID``:
```
import subprocess
import sys
import os
import matplotlib.pyplot as plt
from warnings import warn
import h5py
%matplotlib notebook
def install(package):
subprocess.call([sys.executable, "-m", "pip", "install", package])
try:
# This package is not part of anaconda and may need to be installed.
import wget
except ImportError:
warn('wget not found. Will install with pip.')
import pip
install('wget')
import wget
# Finally import pyUSID.
try:
import pyUSID as usid
import sidpy
except ImportError:
warn('pyUSID not found. Will install with pip.')
import pip
install('pyUSID')
import sidpy
import pyUSID as usid
```
h5USID File
-----------
For this example, we will be working with a `Band Excitation Piezoresponse Force Microscopy (BE-PFM)` imaging dataset
acquired from advanced atomic force microscopes. In this dataset, a spectra was collected for each position in a two
dimensional grid of spatial locations. Thus, this is a three dimensional dataset that has been flattened to a two
dimensional matrix in accordance with **Universal Spectroscopy and Imaging Data (USID)** model.
As mentioned earlier, this dataset is available on the USID repository and can be accessed directly as well.
Here, we will simply download the file using ``wget``:
## Download from GitHub
Similarly the corresponding h5USID dataset is also available on the USID repository.
Here, we will simply download the file using ``wget``:
```
h5_path = 'temp.h5'
url = 'https://raw.githubusercontent.com/pycroscopy/USID/master/data/BELine_0004.h5'
if os.path.exists(h5_path):
os.remove(h5_path)
_ = wget.download(url, h5_path, bar=None)
```
Look at file contents
---------------------
Lets open the file and look at its contents using
[sidpy.hdf_utils.print_tree()](https://pycroscopy.github.io/sidpy/notebooks/03_hdf5/hdf_utils_read.html#print_tree())
```
h5_file = h5py.File(h5_path, mode='r')
sidpy.hdf_utils.print_tree(h5_file)
```
## Access the ``Main`` Dataset
We can access the first Main dataset by searching for a dataset that matches its given name using the convenient
function - [pyUSID.hdf_utils.find_dataset()](https://pycroscopy.github.io/sidpy/notebooks/03_hdf5/hdf_utils_read.html#find_dataset()).
Knowing that there is only one dataset with the name `USID_Alternate`, this is a safe operation.
```
h5_main = usid.hdf_utils.get_all_main(h5_file)[-1]
print(h5_main)
```
Here, ``h5_main`` is a [USIDataset](../user_guide/usi_dataset.html), which can be thought of as a supercharged
HDF5 Dataset that is not only aware of the contents of the plain ``USID_Alternate`` dataset but also its links to the
[Ancillary Datasets](https://pycroscopy.github.io/USID/usid_model.html#ancillary-datasets) that make it a ``Main Dataset``.
Understanding Dimensionality
----------------------------
What is more is that the above print statement shows that this ``Main`` Dataset has two ``Position Dimensions`` -
``X`` and ``Y`` each of size ``128`` and at each of these locations, data was recorded as a function of ``119``
values of the single ``Spectroscopic Dimension`` - ``Frequency``.
Therefore, this dataset is a 3D dataset with two position dimensions and one spectroscopic dimension.
To verify this, we can easily get the N-dimensional form of this dataset by invoking the
[get_n_dim_form()](h../user_guide/usi_dataset.html#Reshaping-to-N-dimensions)`_ of the
``USIDataset`` object:
```
print(h5_main.get_n_dim_form().shape)
print(h5_main.n_dim_labels)
```
## Understanding shapes and flattening
The print statement above shows that the original data is of shape ``(128, 128, 119)``. Let's see if we can arrive at
the shape of the ``Main`` dataset in USID representation.
Recall that USID requires all position dimensions to be flattened along the first axis and all spectroscopic
dimensions to be flattened along the second axis of the ``Main Dataset``. In other words, the data collected at each
location can be laid out along the horizontal direction as is since this dataset only has a single spectroscopic
dimension - ``Frequency``. The ``X`` and ``Y`` position dimensions however need to be collapsed along the vertical
axis of the ``Main`` dataset such that the positions are arranged column-by-column and then row-by-row (assuming that
the columns are the faster varying dimension).
### Visualize the ``Main`` Dataset
Now lets visualize the contents within this ``Main Dataset`` using the ``USIDataset's`` built-in
[visualize()](../user_guide/usi_dataset.html#Interactive-Visualization) function.
Note that the visualization below is static. However, if this document were downloaded as a jupyter notebook, you
would be able to interactively visualize this dataset.
```
usid.plot_utils.use_nice_plot_params()
h5_main.visualize()
```
Here is a visualization of the spectra at evenly spaced positions:
```
fig, axes = sidpy.plot_utils.plot_complex_spectra(h5_main[()], num_comps=6, amp_units='V',
subtitle_prefix='Position', evenly_spaced=True,
x_label=h5_main.spec_dim_descriptors[0])
```
Alternatively, the spectral image dataset can be visualized via slices across the spectroscopic axis as:
```
fig, axes = sidpy.plot_utils.plot_map_stack(np.abs(h5_main.get_n_dim_form()), reverse_dims=True, pad_mult=(0.15, 0.15),
title='Spatial maps at different frequencies', stdevs=2,
color_bar_mode='single', num_ticks=3,
x_vec=h5_main.get_pos_values('X'), y_vec=h5_main.get_pos_values('Y'),
evenly_spaced=True, fig_mult=(3, 3), title_yoffset=0.95)
freq_vals = h5_main.get_spec_values(h5_main.spec_dim_labels[0]) *1E-3
for axis, freq_ind in zip(axes, np.linspace(0, h5_main.spec_dim_sizes[0], 9, endpoint=False, dtype=np.uint)):
axis.set_title('{} = {}'.format(h5_main.spec_dim_labels[0], np.rint(freq_vals[freq_ind])))
```
Ancillary Datasets
------------------
As mentioned in the documentation on USID, ``Ancillary Datasets`` are required to complete the information for any
dataset. Specifically, these datasets need to provide information about the values against which measurements were
acquired, in addition to explaining the original dimensionality (2 in this case) of the original dataset. Let's look
at the ancillary datasets and see what sort of information they provide. We can access the ``Ancillary Datasets``
linked to the ``Main Dataset`` (``h5_main``) just like a property of the object.
Ancillary Position Datasets
---------------------------
```
print('Position Indices:')
print('-------------------------')
print(h5_main.h5_pos_inds)
print('\nPosition Values:')
print('-------------------------')
print(h5_main.h5_pos_vals)
```
Recall from the USID definition that the shape of the Position Ancillary datasets is ``(N, P)`` where ``N`` is the
number of Position dimensions and the ``P`` is the number of locations over which data was recorded. Here, we have
two position dimensions. Therefore ``N`` is ``2``. ``P`` matches with the first axis of the shape of ``h5_main``
which is ``16384``. Generally, there is no need to remember these rules or construct these ancillary datasets
manually since pyUSID has several functions that automatically simplify this process.
### Visualize the contents of the Position Ancillary Datasets
Notice below that there are two sets of lines, one for each dimension. The blue lines on the left-hand column
appear solid simply because this dimension (``X`` or columns) varies much faster than the other dimension (``Y`` or
rows). The first few rows of the dataset are visualized on the right-hand column.
```
fig, all_axes = plt.subplots(ncols=2, nrows=2, figsize=(8, 8))
for axes, h5_pos_dset, dset_name in zip(all_axes,
[h5_main.h5_pos_inds, h5_main.h5_pos_vals],
['Position Indices', 'Position Values']):
axes[0].plot(h5_pos_dset[()])
axes[0].set_title('Full dataset')
axes[1].set_title('First 512 rows only')
axes[1].plot(h5_pos_dset[:512])
for axis in axes.flat:
axis.set_xlabel('Row in ' + dset_name)
axis.set_ylabel(dset_name)
axis.legend(h5_main.pos_dim_labels)
for axis in all_axes[1]:
usid.plot_utils.use_scientific_ticks(axis, is_x=False, formatting='%1.e')
axis.legend(h5_main.pos_dim_descriptors)
fig.tight_layout()
```
### Making sense of the visualization
Given that the columns vary faster
than the rows means that the contents of each row of the image have been stored end-to-end in the ``Main Dataset``
as opposed to on top of each other as in the original 3D dataset.
### Attributes associated with the Position Indices Dataset
Just looking at the shape and values of the Position ancillary datasets does not provide all the information.
Recall that the ancillary datasets need to have some mandatory attributes like ``labels`` and ``units`` that
describe the quantity and units for each of the dimensions:
```
for key, val in sidpy.hdf_utils.get_attributes(h5_main.h5_pos_inds).items():
print('{} : {}'.format(key, val))
```
Ancillary Spectroscopic Datasets
--------------------------------
Recall that the spectrum at each location was acquired as a function of ``119`` values of the single Spectroscopic
dimension - ``Frequency``. Therefore, according to USID, we should expect the Spectroscopic Dataset to be of shape
``(M, S)`` where M is the number of spectroscopic dimensions (``1`` in this case) and S is the total number of
spectroscopic values against which data was acquired at each location (``119`` in this case).
```
print('Spectroscopic Indices:')
print('-------------------------')
print(h5_main.h5_spec_inds)
print('\nSpectroscopic Values:')
print('-------------------------')
print(h5_main.h5_spec_vals)
```
### Visualize the contents of the Spectroscopic Datasets
Observe the single curve that is associated with the single spectroscopic variable ``Frequency``. Also note that the contents
of the ``Spectroscopic Indices`` dataset are just a linearly increasing set of numbers starting from ``0`` according
to the definition of the ``Indices`` datasets which just count the nth value of independent variable that was varied.
```
fig, axes = plt.subplots(ncols=2, figsize=(8, 4))
for axis, data, title, y_lab in zip(axes.flat,
[h5_main.h5_spec_inds[()].T, h5_main.h5_spec_vals[()].T],
['Spectroscopic Indices', 'Spectroscopic Values'],
['Index', h5_main.spec_dim_descriptors[0]]):
axis.plot(data)
axis.set_title(title)
axis.set_xlabel('Row in ' + title)
axis.set_ylabel(y_lab)
sidpy.plot_utils.use_scientific_ticks(axis, is_x=False, formatting='%.1e')
# fig.suptitle('Ancillary Spectroscopic Datasets', y=1.05)
fig.tight_layout()
```
### Attributes within the Spectroscopic Indices Dataset
Again, the attributes of Spectroscopic Datasets show mandatory information about the Spectroscopic dimensions such as
the quantity (``labels``) and ``units``:
```
for key, val in sidpy.hdf_utils.get_attributes(h5_main.h5_spec_inds).items():
print('{} : {}'.format(key, val))
```
Clean up
--------
Finally lets close the HDF5 file.
```
h5_file.close()
```
Here, we will even delete the HDF5 file. Please comment out the line below if you want to look at the HDF5 file using
software like HDFView.
```
os.remove(h5_path)
```
|
github_jupyter
|
import subprocess
import sys
import os
import matplotlib.pyplot as plt
from warnings import warn
import h5py
%matplotlib notebook
def install(package):
subprocess.call([sys.executable, "-m", "pip", "install", package])
try:
# This package is not part of anaconda and may need to be installed.
import wget
except ImportError:
warn('wget not found. Will install with pip.')
import pip
install('wget')
import wget
# Finally import pyUSID.
try:
import pyUSID as usid
import sidpy
except ImportError:
warn('pyUSID not found. Will install with pip.')
import pip
install('pyUSID')
import sidpy
import pyUSID as usid
h5_path = 'temp.h5'
url = 'https://raw.githubusercontent.com/pycroscopy/USID/master/data/BELine_0004.h5'
if os.path.exists(h5_path):
os.remove(h5_path)
_ = wget.download(url, h5_path, bar=None)
h5_file = h5py.File(h5_path, mode='r')
sidpy.hdf_utils.print_tree(h5_file)
h5_main = usid.hdf_utils.get_all_main(h5_file)[-1]
print(h5_main)
print(h5_main.get_n_dim_form().shape)
print(h5_main.n_dim_labels)
usid.plot_utils.use_nice_plot_params()
h5_main.visualize()
fig, axes = sidpy.plot_utils.plot_complex_spectra(h5_main[()], num_comps=6, amp_units='V',
subtitle_prefix='Position', evenly_spaced=True,
x_label=h5_main.spec_dim_descriptors[0])
fig, axes = sidpy.plot_utils.plot_map_stack(np.abs(h5_main.get_n_dim_form()), reverse_dims=True, pad_mult=(0.15, 0.15),
title='Spatial maps at different frequencies', stdevs=2,
color_bar_mode='single', num_ticks=3,
x_vec=h5_main.get_pos_values('X'), y_vec=h5_main.get_pos_values('Y'),
evenly_spaced=True, fig_mult=(3, 3), title_yoffset=0.95)
freq_vals = h5_main.get_spec_values(h5_main.spec_dim_labels[0]) *1E-3
for axis, freq_ind in zip(axes, np.linspace(0, h5_main.spec_dim_sizes[0], 9, endpoint=False, dtype=np.uint)):
axis.set_title('{} = {}'.format(h5_main.spec_dim_labels[0], np.rint(freq_vals[freq_ind])))
print('Position Indices:')
print('-------------------------')
print(h5_main.h5_pos_inds)
print('\nPosition Values:')
print('-------------------------')
print(h5_main.h5_pos_vals)
fig, all_axes = plt.subplots(ncols=2, nrows=2, figsize=(8, 8))
for axes, h5_pos_dset, dset_name in zip(all_axes,
[h5_main.h5_pos_inds, h5_main.h5_pos_vals],
['Position Indices', 'Position Values']):
axes[0].plot(h5_pos_dset[()])
axes[0].set_title('Full dataset')
axes[1].set_title('First 512 rows only')
axes[1].plot(h5_pos_dset[:512])
for axis in axes.flat:
axis.set_xlabel('Row in ' + dset_name)
axis.set_ylabel(dset_name)
axis.legend(h5_main.pos_dim_labels)
for axis in all_axes[1]:
usid.plot_utils.use_scientific_ticks(axis, is_x=False, formatting='%1.e')
axis.legend(h5_main.pos_dim_descriptors)
fig.tight_layout()
for key, val in sidpy.hdf_utils.get_attributes(h5_main.h5_pos_inds).items():
print('{} : {}'.format(key, val))
print('Spectroscopic Indices:')
print('-------------------------')
print(h5_main.h5_spec_inds)
print('\nSpectroscopic Values:')
print('-------------------------')
print(h5_main.h5_spec_vals)
fig, axes = plt.subplots(ncols=2, figsize=(8, 4))
for axis, data, title, y_lab in zip(axes.flat,
[h5_main.h5_spec_inds[()].T, h5_main.h5_spec_vals[()].T],
['Spectroscopic Indices', 'Spectroscopic Values'],
['Index', h5_main.spec_dim_descriptors[0]]):
axis.plot(data)
axis.set_title(title)
axis.set_xlabel('Row in ' + title)
axis.set_ylabel(y_lab)
sidpy.plot_utils.use_scientific_ticks(axis, is_x=False, formatting='%.1e')
# fig.suptitle('Ancillary Spectroscopic Datasets', y=1.05)
fig.tight_layout()
for key, val in sidpy.hdf_utils.get_attributes(h5_main.h5_spec_inds).items():
print('{} : {}'.format(key, val))
h5_file.close()
os.remove(h5_path)
| 0.217836 | 0.948489 |
This notebook works out the expected hillslope sediment flux, topography, and soil thickness for steady state on a 4x7 grid. This provides "ground truth" values for tests.
Let the hillslope erosion rate be $E$, the flux coefficient $D$, critical gradient $S_c$, and slope gradient $S$. The regolith thickness is $H$, with bare-bedrock production rate $P_0$ and depth-decay $H_*$. Finally, we set the transport decay scale the same as the production depth-decay scale. Then we have the hillslope flux as a function of distance from ridgetop, $x$, as
$q_s = E x = \left( DSH^* + \frac{DH^*}{S_c^2} S^3 \right) \left(1 - e^{ -H/H_*} \right)$
Parameter values: let $D = 0.01 m^2 y^{-1}$, $S_c = 0.8$, $H_* = 0.5 m$, $P_0 = 0.0002$, and $E = 0.0001 m y^{-1}$:
```
D = 0.01
Sc = 0.8
Hstar = 0.5
E = 0.0001
P0 = 0.0002
```
With that, calculate the expected equilibrium $H$:
$E = P_0 e^{-H/H_*}$
$H = -H_* \ln (E/P_0)$
Plugging in the numbers:
```
import math
H = -Hstar * math.log(E / P0)
H
```
Double check: if we plug this $H$ back in, do we recover $E$?
```
P0 * math.exp(-H / Hstar)
```
Yes, good.
Now, our geometry consists of a hillslope discretized into seven nodes. The two on either end are zero-elevation fixed boundaries, so we have to find the elevations of the five interior ones. But the hillslope should be symmetrical, so we really only have to find 1, 2, and 3 as in
0 --- 1 --- 2 --- 3 --- etc.
where node 3 is the top of the hill.
The slope between nodes 1 and 0 must be positive (uphill to right). It must be just steep enough to carry all the sediment from its own cell plus the sediment from node 2's cell, plus half the sediment from node 3's cell. We'll assume all cells have width $dx = 10 m$. Therefore, we have to transport sediment produced in strip 25 m x 1 m, or 25 m2. Our expected flux is then:
```
qs = 25 * E
qs
```
In fact, for each interface between cells, the slope at that interface is given by the following polynomial:
$f\frac{D}{S_c^2} S^3 + 0 S^2 + fDS - qs = 0$
Here the $f$ is shorthand for $H^*[1 - \exp (-H/H_*)]$. I've included the zero in front of the $S^2$ term just to make it explicit.
So, for the slope between nodes 0 and 1, we need first to define our polynomial coefficients, $p$. Then we'll invoke numpy's *roots* function to solve for $S$. To be consistent with *roots* usage, we'll call the coefficient of the highest (cubic) term $p_0$, the next highest (square) $p_1$, etc. So:
$p_0 S^3 + p_1 S^2 + p_2 S + p_3 = 0$
Clearly, we'll need $f$, so let's calculate that first:
```
f = Hstar*(1.0 - math.exp(-H / Hstar))
f
```
Now, let's calculate the coefficients:
$p_0 = f D / S_c^2$
$p_1 = 0$
$p_2 = f D$
$p_3 = -q_s$
Clearly, only $p_3$ will vary from node to node. Here are the numbers:
```
import numpy as np
p = np.zeros(4)
p[0] = (f * D) / (Sc ** 2)
p[1] = 0.0
p[2] = f * D
p[3] = -qs
p
```
Now let's find the roots of this cubic polynomial:
```
my_roots = np.roots(p)
my_roots
```
There's just one real root here: $S \approx 1.33$. Let's plug that back in and see if we recapture the correct $qs$:
```
Spred = 0.6227
qspred = (D*Hstar * Spred + (D*Hstar / (Sc * Sc)) * (Spred ** 3)) * (1.0 - np.exp(-H / Hstar))
qspred
```
Great! That's extremely close. Let's try with the slope between nodes 1 and 2. The only difference here is that the flux $qs$ now derives from just $15 m^2$, so $qs = 0.0015:
```
p[3] = -0.0015
my_roots = np.roots(p)
my_roots
```
Once again, let's test:
```
Spred = 0.453
qspred = (D*Hstar * Spred + (D*Hstar / (Sc * Sc)) * (Spred ** 3)) * (1.0 - np.exp(-H / Hstar))
qspred
```
Finally, the slope between 2 and 3, which needs to carry half a cell's worth of sediment, or $qs = 0.0005$:
```
p[3] = -0.0005
my_roots = np.roots(p)
my_roots
```
And check this:
```
Spred = 0.189
qspred = (D*Hstar * Spred + (D*Hstar / (Sc * Sc)) * (Spred ** 3)) * (1.0 - np.exp(-H / Hstar))
qspred
```
Fabulous. Now to find the predicted elevations: just add up slope x distance for each node, going inward from the boundaries:
```
elev = np.zeros(7)
elev[1] = 0.6227 * 10.0
elev[5] = elev[1]
elev[2] = elev[1] + 0.453 * 10.0
elev[4] = elev[2]
elev[3] = elev[2] + 0.189 * 10.0
elev
```
So, at equilibrium, our model should create a symmetrical hill with a peak elevation a little over 12 m and a soil thickness of 0.347 m.
What time step size would be reasonable? Start by defining an "effective D" parameter, which is the linearized coefficient in front of the cubic term:
$D_{eff} = D (S / S_c)^2$
Then take the steepest steady state slope:
```
S = 0.6227
Deff = D*Hstar * ((S / Sc) ** 2)
Deff
```
Now, maximum time step size should be $\Delta x^2 / 2 D_{eff}$:
```
10.0*10.0/(2.0*Deff)
```
There's also a constraint for the weathering piece. The characteristic time scale is $T = H_* / P_0$, which in this case is:
```
Hstar / P0
```
So, this calculation suggests that weathering is the limiting factor on time-step size. We might choose 250 years for a reasonably smooth solution.
The time it would take for baselevel fall to bring the crest of the hill up to its ten times its equilibrium elevation of 8 m:
```
80.0 / E
```
So let's say we run for 800,000 years at 250 year time steps:
```
8.0e5/250.
```
So, make it 3200 iterations of 250 years each.
|
github_jupyter
|
D = 0.01
Sc = 0.8
Hstar = 0.5
E = 0.0001
P0 = 0.0002
import math
H = -Hstar * math.log(E / P0)
H
P0 * math.exp(-H / Hstar)
qs = 25 * E
qs
f = Hstar*(1.0 - math.exp(-H / Hstar))
f
import numpy as np
p = np.zeros(4)
p[0] = (f * D) / (Sc ** 2)
p[1] = 0.0
p[2] = f * D
p[3] = -qs
p
my_roots = np.roots(p)
my_roots
Spred = 0.6227
qspred = (D*Hstar * Spred + (D*Hstar / (Sc * Sc)) * (Spred ** 3)) * (1.0 - np.exp(-H / Hstar))
qspred
p[3] = -0.0015
my_roots = np.roots(p)
my_roots
Spred = 0.453
qspred = (D*Hstar * Spred + (D*Hstar / (Sc * Sc)) * (Spred ** 3)) * (1.0 - np.exp(-H / Hstar))
qspred
p[3] = -0.0005
my_roots = np.roots(p)
my_roots
Spred = 0.189
qspred = (D*Hstar * Spred + (D*Hstar / (Sc * Sc)) * (Spred ** 3)) * (1.0 - np.exp(-H / Hstar))
qspred
elev = np.zeros(7)
elev[1] = 0.6227 * 10.0
elev[5] = elev[1]
elev[2] = elev[1] + 0.453 * 10.0
elev[4] = elev[2]
elev[3] = elev[2] + 0.189 * 10.0
elev
S = 0.6227
Deff = D*Hstar * ((S / Sc) ** 2)
Deff
10.0*10.0/(2.0*Deff)
Hstar / P0
80.0 / E
8.0e5/250.
| 0.245718 | 0.988503 |
<h1>PCA Training with BotNet (02-03-2018)</h1>
```
import os
import tensorflow as tf
import numpy as np
import itertools
import matplotlib.pyplot as plt
import gc
from datetime import datetime
from sklearn.utils import shuffle
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.metrics import confusion_matrix
input_label = []
output_label = []
a,b = 0,0
ficheiro = open("..\\DatasetTratado\\02-03-2018.csv", "r")
nome_label = ficheiro.readline().split(",")
ficheiro.readline()
ficheiro.readline()
linha = ficheiro.readline()
while(linha != ""):
linha = linha.split(",")
out = linha.pop(37)
if(out == "Benign"):
out = 0
b += 1
else:
out = 1
a += 1
output_label.append(out)
input_label.append(linha)
linha = ficheiro.readline()
ficheiro.close()
print(str(a) + " " + str(b))
backup_input_label = input_label[:]
backup_output_label = output_label[:]
input_label = backup_input_label[:]
output_label = backup_output_label[:]
```
## "STANDARDIZATION"
```
scaler = MinMaxScaler(feature_range=(0,1))
scaler.fit(input_label)
input_label = scaler.transform(input_label)
input_label
```
<h2>NUMBER OF PARAMETERS WITH PCA</h2>
```
from sklearn.decomposition import PCA
pca=PCA(n_components=18)
pca.fit(input_label)
x_pca = pca.transform(input_label)
input_label.shape
x_pca.shape
input_label
x_pca
# plt.figure(figsize=(8,6))
# plt.scatter(range(1000), x_pca[:,0][:1000])
# plt.scatter(range(1000), x_pca[:,1][:1000], c="red")
# plt.xlabel('First principle component')
# plt.ylabel('Second principle component')
```
<h2>MATPLOTLIB</h2>
```
plt.figure(figsize=(8,6))
plt.scatter(x_pca[:,0][:200000],x_pca[:,1][:200000])
plt.xlabel('First principle component')
plt.ylabel('Second principle component')
```
<h2>MODEL TRAINING</h2>
```
x_pca = x_pca.reshape(len(x_pca), 18, 1)
y_pca = np.array(output_label)
x_pca, y_pca = shuffle(x_pca, y_pca)
inp_train, inp_test, out_train, out_test = train_test_split(x_pca, y_pca, test_size = 0.2)
model = keras.Sequential([
layers.Input(shape = (18, 1)),
layers.Conv1D(filters = 32, kernel_size = 3, padding = "same", activation = "relu", use_bias = True),
layers.MaxPool1D(pool_size = 3),
layers.Conv1D(filters = 16, kernel_size = 3, padding = "same", activation = "relu", use_bias = True),
layers.MaxPool1D(pool_size = 3),
layers.Flatten(),
layers.Dense(units = 2, activation = "softmax")
])
model.compile(optimizer= keras.optimizers.SGD(learning_rate= 0.08), loss="sparse_categorical_crossentropy", metrics=['accuracy'])
treino = model.fit(x = inp_train, y = out_train, validation_split= 0.1, epochs = 5, shuffle = True,verbose = 1)
res = [np.argmax(resu) for resu in model.predict(inp_test)]
cm = confusion_matrix(y_true = out_test.reshape(len(out_test)), y_pred = np.array(res))
def plot_confusion_matrix(cm, classes, normaliza = False, title = "Confusion matrix", cmap = plt.cm.Blues):
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
if normaliza:
cm = cm.astype('float') / cm.sum(axis = 1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print("Confusion matrix, without normalization")
print(cm)
thresh = cm.max() / 2
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i,j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
labels = ["Benign", "Bot"]
plot_confusion_matrix(cm = cm, classes = labels, title = "Bot IDS")
model.save("CNN1BotNet(02-03-2018)PCA2.h5")
```
|
github_jupyter
|
import os
import tensorflow as tf
import numpy as np
import itertools
import matplotlib.pyplot as plt
import gc
from datetime import datetime
from sklearn.utils import shuffle
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.metrics import confusion_matrix
input_label = []
output_label = []
a,b = 0,0
ficheiro = open("..\\DatasetTratado\\02-03-2018.csv", "r")
nome_label = ficheiro.readline().split(",")
ficheiro.readline()
ficheiro.readline()
linha = ficheiro.readline()
while(linha != ""):
linha = linha.split(",")
out = linha.pop(37)
if(out == "Benign"):
out = 0
b += 1
else:
out = 1
a += 1
output_label.append(out)
input_label.append(linha)
linha = ficheiro.readline()
ficheiro.close()
print(str(a) + " " + str(b))
backup_input_label = input_label[:]
backup_output_label = output_label[:]
input_label = backup_input_label[:]
output_label = backup_output_label[:]
scaler = MinMaxScaler(feature_range=(0,1))
scaler.fit(input_label)
input_label = scaler.transform(input_label)
input_label
from sklearn.decomposition import PCA
pca=PCA(n_components=18)
pca.fit(input_label)
x_pca = pca.transform(input_label)
input_label.shape
x_pca.shape
input_label
x_pca
# plt.figure(figsize=(8,6))
# plt.scatter(range(1000), x_pca[:,0][:1000])
# plt.scatter(range(1000), x_pca[:,1][:1000], c="red")
# plt.xlabel('First principle component')
# plt.ylabel('Second principle component')
plt.figure(figsize=(8,6))
plt.scatter(x_pca[:,0][:200000],x_pca[:,1][:200000])
plt.xlabel('First principle component')
plt.ylabel('Second principle component')
x_pca = x_pca.reshape(len(x_pca), 18, 1)
y_pca = np.array(output_label)
x_pca, y_pca = shuffle(x_pca, y_pca)
inp_train, inp_test, out_train, out_test = train_test_split(x_pca, y_pca, test_size = 0.2)
model = keras.Sequential([
layers.Input(shape = (18, 1)),
layers.Conv1D(filters = 32, kernel_size = 3, padding = "same", activation = "relu", use_bias = True),
layers.MaxPool1D(pool_size = 3),
layers.Conv1D(filters = 16, kernel_size = 3, padding = "same", activation = "relu", use_bias = True),
layers.MaxPool1D(pool_size = 3),
layers.Flatten(),
layers.Dense(units = 2, activation = "softmax")
])
model.compile(optimizer= keras.optimizers.SGD(learning_rate= 0.08), loss="sparse_categorical_crossentropy", metrics=['accuracy'])
treino = model.fit(x = inp_train, y = out_train, validation_split= 0.1, epochs = 5, shuffle = True,verbose = 1)
res = [np.argmax(resu) for resu in model.predict(inp_test)]
cm = confusion_matrix(y_true = out_test.reshape(len(out_test)), y_pred = np.array(res))
def plot_confusion_matrix(cm, classes, normaliza = False, title = "Confusion matrix", cmap = plt.cm.Blues):
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
if normaliza:
cm = cm.astype('float') / cm.sum(axis = 1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print("Confusion matrix, without normalization")
print(cm)
thresh = cm.max() / 2
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i,j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
labels = ["Benign", "Bot"]
plot_confusion_matrix(cm = cm, classes = labels, title = "Bot IDS")
model.save("CNN1BotNet(02-03-2018)PCA2.h5")
| 0.623377 | 0.711042 |
```
import os, requests
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
import pandas as pd
import tensorflow as tf
import tensorflow_hub as hub
from tensorflow.keras import layers
from tensorflow.keras import Model
from tensorflow.keras.models import load_model, Sequential
from keras.preprocessing import image
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.applications.resnet import ResNet101
from google.colab import drive
drive.mount('/content/drive')
BUCKET = 9
IMAGE_SIZE = (224, 224)
VALIDATION_SPLIT = 0.2
BATCH_SIZE = 64
gdrive_dir = "/content/drive/MyDrive"
working_dir = os.path.join(gdrive_dir, "CS3244 Project")
data_root_dir = os.path.join(working_dir, "landmarks/international/data_split")
data_dir = os.path.join(data_root_dir, str(BUCKET))
model_root_dir = os.path.join(working_dir, "models/KhengHun")
print('number of international labels:', len(os.listdir(data_dir)))
#dataflow_kwargs = dict(target_size=IMAGE_SIZE, batch_size=BATCH_SIZE, interpolation="bilinear")
train_datagen = tf.keras.preprocessing.image.ImageDataGenerator(
rescale = 1./255,
validation_split = VALIDATION_SPLIT,
rotation_range = 30,
width_shift_range = 0.1,
height_shift_range = 0.1,
shear_range = 0.1,
zoom_range = 0.1,
brightness_range = [0.9,1.1],
fill_mode = 'nearest'
)
train_generator = train_datagen.flow_from_directory(
data_dir,
subset = "training",
shuffle = True,
target_size = IMAGE_SIZE,
batch_size = BATCH_SIZE,
class_mode = 'categorical',
)
validation_datagen = ImageDataGenerator(
rescale=1./255,
validation_split = VALIDATION_SPLIT
)
validation_generator = validation_datagen.flow_from_directory(
data_dir,
subset = "validation",
shuffle = False,
target_size = IMAGE_SIZE,
batch_size = BATCH_SIZE,
class_mode = 'categorical'
)
#resnet_model = ResNet101();
#resnet_model.summary()
last_layer = resnet_model.get_layer("predictions")
last_output = last_layer.output
x = layers.Flatten()(last_output)
x = layers.Dense(512, activation='relu')(x)
x = layers.Dropout(0.2)(x)
x = layers.Dense(256, activation='relu')(x)
x = layers.BatchNormalization(momentum=0.95, name="batch_norm_pre-output")(x)
x = layers.Dense(200, activation='softmax')(x)
model = Model(resnet_model.input, x)
#save_model_dir = os.path.join(model_root_dir, "international1")
#model.save(save_model_dir)
model.summary()
load_model_dir = os.path.join(model_root_dir, "finali9")
model = tf.keras.models.load_model(load_model_dir)
model.compile(
loss = 'categorical_crossentropy',
optimizer = tf.keras.optimizers.Adam(lr=0.001),
metrics = ['accuracy']
)
steps_per_epoch = int(train_generator.samples / BATCH_SIZE)
validation_steps = int(validation_generator.samples / BATCH_SIZE)
print("Steps per epoch:", steps_per_epoch)
print("Validation steps:", validation_steps)
model.summary()
history = model.fit(
train_generator,
steps_per_epoch = steps_per_epoch,
epochs = 20,
validation_data = validation_generator,
validation_steps = validation_steps
)
save_model_dir = os.path.join(model_root_dir, "finali10")
model.save(save_model_dir)
df = pd.DataFrame(history.history)
hist_dir = os.path.join(model_root_dir, "history/finali10.csv")
df.to_csv(hist_dir)
save_model_dir = os.path.join(model_root_dir, "international0")
model.save(save_model_dir)
df = pd.DataFrame(history.history)
hist_dir = os.path.join(model_root_dir, "history/int0.csv")
df.to_csv(hist_dir)
model.summary()
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'r', label='Training accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.legend(loc=0)
plt.figure()
plt.plot(epochs, loss, 'r', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
url = "https://i1.wp.com/couldhavestayedhome.com/wp-content/uploads/2019/09/Supertree-Grove-Gardens-by-the-Bay.jpeg?fit=1632%2C1224&ssl=1"
try:
image_data = requests.get(url, stream=True).raw
except Exception as e:
print('Warning: Could not download image from %s' % url)
print('Error: %s' %e)
raise
try:
pil_image = Image.open(image_data)
except Exception as e:
print('Warning: Failed to parse image')
print('Error: %s' %e)
raise
try:
img = pil_image.convert('RGB').resize(IMAGE_SIZE)
except:
print('Warning: Failed to format image')
raise
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
classes = model.predict(x)
labels = list(train_generator.class_indices.keys())
for i in range(len(classes[0])):
print("%s: %s" % (labels[i], classes[0][i]))
```
|
github_jupyter
|
import os, requests
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
import pandas as pd
import tensorflow as tf
import tensorflow_hub as hub
from tensorflow.keras import layers
from tensorflow.keras import Model
from tensorflow.keras.models import load_model, Sequential
from keras.preprocessing import image
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.applications.resnet import ResNet101
from google.colab import drive
drive.mount('/content/drive')
BUCKET = 9
IMAGE_SIZE = (224, 224)
VALIDATION_SPLIT = 0.2
BATCH_SIZE = 64
gdrive_dir = "/content/drive/MyDrive"
working_dir = os.path.join(gdrive_dir, "CS3244 Project")
data_root_dir = os.path.join(working_dir, "landmarks/international/data_split")
data_dir = os.path.join(data_root_dir, str(BUCKET))
model_root_dir = os.path.join(working_dir, "models/KhengHun")
print('number of international labels:', len(os.listdir(data_dir)))
#dataflow_kwargs = dict(target_size=IMAGE_SIZE, batch_size=BATCH_SIZE, interpolation="bilinear")
train_datagen = tf.keras.preprocessing.image.ImageDataGenerator(
rescale = 1./255,
validation_split = VALIDATION_SPLIT,
rotation_range = 30,
width_shift_range = 0.1,
height_shift_range = 0.1,
shear_range = 0.1,
zoom_range = 0.1,
brightness_range = [0.9,1.1],
fill_mode = 'nearest'
)
train_generator = train_datagen.flow_from_directory(
data_dir,
subset = "training",
shuffle = True,
target_size = IMAGE_SIZE,
batch_size = BATCH_SIZE,
class_mode = 'categorical',
)
validation_datagen = ImageDataGenerator(
rescale=1./255,
validation_split = VALIDATION_SPLIT
)
validation_generator = validation_datagen.flow_from_directory(
data_dir,
subset = "validation",
shuffle = False,
target_size = IMAGE_SIZE,
batch_size = BATCH_SIZE,
class_mode = 'categorical'
)
#resnet_model = ResNet101();
#resnet_model.summary()
last_layer = resnet_model.get_layer("predictions")
last_output = last_layer.output
x = layers.Flatten()(last_output)
x = layers.Dense(512, activation='relu')(x)
x = layers.Dropout(0.2)(x)
x = layers.Dense(256, activation='relu')(x)
x = layers.BatchNormalization(momentum=0.95, name="batch_norm_pre-output")(x)
x = layers.Dense(200, activation='softmax')(x)
model = Model(resnet_model.input, x)
#save_model_dir = os.path.join(model_root_dir, "international1")
#model.save(save_model_dir)
model.summary()
load_model_dir = os.path.join(model_root_dir, "finali9")
model = tf.keras.models.load_model(load_model_dir)
model.compile(
loss = 'categorical_crossentropy',
optimizer = tf.keras.optimizers.Adam(lr=0.001),
metrics = ['accuracy']
)
steps_per_epoch = int(train_generator.samples / BATCH_SIZE)
validation_steps = int(validation_generator.samples / BATCH_SIZE)
print("Steps per epoch:", steps_per_epoch)
print("Validation steps:", validation_steps)
model.summary()
history = model.fit(
train_generator,
steps_per_epoch = steps_per_epoch,
epochs = 20,
validation_data = validation_generator,
validation_steps = validation_steps
)
save_model_dir = os.path.join(model_root_dir, "finali10")
model.save(save_model_dir)
df = pd.DataFrame(history.history)
hist_dir = os.path.join(model_root_dir, "history/finali10.csv")
df.to_csv(hist_dir)
save_model_dir = os.path.join(model_root_dir, "international0")
model.save(save_model_dir)
df = pd.DataFrame(history.history)
hist_dir = os.path.join(model_root_dir, "history/int0.csv")
df.to_csv(hist_dir)
model.summary()
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'r', label='Training accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.legend(loc=0)
plt.figure()
plt.plot(epochs, loss, 'r', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
url = "https://i1.wp.com/couldhavestayedhome.com/wp-content/uploads/2019/09/Supertree-Grove-Gardens-by-the-Bay.jpeg?fit=1632%2C1224&ssl=1"
try:
image_data = requests.get(url, stream=True).raw
except Exception as e:
print('Warning: Could not download image from %s' % url)
print('Error: %s' %e)
raise
try:
pil_image = Image.open(image_data)
except Exception as e:
print('Warning: Failed to parse image')
print('Error: %s' %e)
raise
try:
img = pil_image.convert('RGB').resize(IMAGE_SIZE)
except:
print('Warning: Failed to format image')
raise
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
classes = model.predict(x)
labels = list(train_generator.class_indices.keys())
for i in range(len(classes[0])):
print("%s: %s" % (labels[i], classes[0][i]))
| 0.431944 | 0.283471 |
<a href="https://colab.research.google.com/github/awikner/CHyPP/blob/master/TREND_Logistic_Regression.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Import libraries and sklearn and skimage modules.
```
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from skimage.util import invert
```
## Load in the mnist handwritten number dataset from the openml library. The X array contains images of handwritten numbers, while the y array contains their known classification.
```
X, y = fetch_openml('mnist_784', version=1, return_X_y=True)
```
## We plot a few of the number images and their known classifications in greyscale.
```
plt.imshow(invert(X[0].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title(str(y[0]))
plt.show()
plt.imshow(invert(X[1].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title(str(y[1]))
plt.show()
plt.imshow(invert(X[2].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title(str(y[2]))
plt.show()
```
## Before we can begin classification, we must train our model. We begin by breaking up our data set into training and testing sets.
```
train_samples = 800
# train_samples = 8000
test_samples = 10000
X_train, X_test, y_train, y_test = train_test_split(X,y,train_size = train_samples, test_size = test_samples)
```
## We use sklearn to create our logistic regression classifier. We then fit it to our training data.
```
classifier = LogisticRegression(solver = 'saga', penalty = 'l1', tol = 1e-2)
classifier.fit(X_train, y_train)
```
## We test the accuracy of our trained classifier using the accuracy score method on the training and testing data sets. This computes the number of accurately predicted classes over the total number of samples. Note that the in-sample (training) accuracy is much higher than the out-of-sample (test) accuracy.
```
score_train = classifier.score(X_train,y_train)
score_test = classifier.score(X_test,y_test)
print('Accuracy score for training data: ',score_train)
print('Accuracy score for test data: ',score_test)
```
## Finally, we plot a few test images to show how our classifier has classified them.
```
offset = 23
y0_test = classifier.predict(X_test[0 + offset].reshape(-1,X_test.shape[1]))
plt.imshow(invert(X_test[0 + offset].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title('Predicted number: '+y0_test+', True number: '+y_test[0+offset])
plt.show()
y1_test = classifier.predict(X_test[1 + offset ].reshape(-1,X_test.shape[1]))
plt.imshow(invert(X_test[1 + offset].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title('Predicted number: '+y1_test+', True number: '+y_test[1+offset])
plt.show()
y2_test = classifier.predict(X_test[2 + offset].reshape(-1,X_test.shape[1]))
plt.imshow(invert(X_test[2 + offset].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title('Predicted number: '+y2_test+', True number: '+y_test[2+offset])
plt.show()
```
|
github_jupyter
|
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from skimage.util import invert
X, y = fetch_openml('mnist_784', version=1, return_X_y=True)
plt.imshow(invert(X[0].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title(str(y[0]))
plt.show()
plt.imshow(invert(X[1].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title(str(y[1]))
plt.show()
plt.imshow(invert(X[2].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title(str(y[2]))
plt.show()
train_samples = 800
# train_samples = 8000
test_samples = 10000
X_train, X_test, y_train, y_test = train_test_split(X,y,train_size = train_samples, test_size = test_samples)
classifier = LogisticRegression(solver = 'saga', penalty = 'l1', tol = 1e-2)
classifier.fit(X_train, y_train)
score_train = classifier.score(X_train,y_train)
score_test = classifier.score(X_test,y_test)
print('Accuracy score for training data: ',score_train)
print('Accuracy score for test data: ',score_test)
offset = 23
y0_test = classifier.predict(X_test[0 + offset].reshape(-1,X_test.shape[1]))
plt.imshow(invert(X_test[0 + offset].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title('Predicted number: '+y0_test+', True number: '+y_test[0+offset])
plt.show()
y1_test = classifier.predict(X_test[1 + offset ].reshape(-1,X_test.shape[1]))
plt.imshow(invert(X_test[1 + offset].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title('Predicted number: '+y1_test+', True number: '+y_test[1+offset])
plt.show()
y2_test = classifier.predict(X_test[2 + offset].reshape(-1,X_test.shape[1]))
plt.imshow(invert(X_test[2 + offset].reshape(28,28)),interpolation='nearest',cmap="gray")
plt.title('Predicted number: '+y2_test+', True number: '+y_test[2+offset])
plt.show()
| 0.611034 | 0.99066 |
# Organization
Data analysis projects can quickly get out of hand and learning to manage them best will come with experience.
A few suggestions:
## Project Directory - Git Repository
When starting a new project create a directory that will contain everything pertaining to that project. Initialize it as a git repository so that all changes are tracked and can be backed up at github, bitbucket, or other such online repository.
Make use of a `.gitignore` file to prevent git from tracking large data files or any files in which credentials (passwords, cryptographic keys, etc) or other sensitive information are stored. Example `.gitignore` files can be found that will come preconfigured to ignore extra accessory files that are created such as `.ipynb_checkpoints` which doesn't hold the original code for jupyter notebook files but helps with the autosave features.
For example I set up a `.gitignore` file for this project that contains the following:
```
data/
venv/
.ipynb_checkpoints/
```
This will keep all the data and accessory files out of the git repository.
## Environment Management - python virtual environment
If you're working in python you should make it a habit to use virtual environments for each project. A virtual environment is like an isolated clean python install when you create it. Then you can add just the packages that are needed for your work.
There are several ways to do this depending on whether you're using python alone or anaconda. The general steps if using python on linux:
1) Create the virtual environment (using python 3.8 into a directory called `venv`)
`virtualenv -p python3.8 venv`
2) Activate virtual environment
`. venv/bin/activate`
3) Install things
`pip install pandas`
Environment management is a recurring concern in computational work and you'll encounter many ways to achieve similar things in different ways and for different purposes. The main ideas is to let you specify which versions of tools you need for a particular task while also letting them coexist on the same system as different versions of the same tools that are needed for a separate task. Additionally since these tools can be boiled down to a list of tool names and versions you can use this to recreate the same enviornment elsewhere.
Using `pip` the convention is to create a file called `requirements.txt` like so:
`pip freeze > requirements.txt`
This captures a list of packages installed in the current environment. It can be used to reconstitute the environment like so:
`pip install -r requirements.txt`
It's a good idea to add the `requirements.txt` or equivalent to the git repository so this travels along with your code.
## Notebooks
Just try to give them good names and use subdirectories to organize them as best you can.
## Reuseable Code
Code you develop in one notebook that you want to use in other notebooks is best moved to a python file or package. It's easier to find and any bugs you find and fix are done in one central location instead of having to remember to fix it in multiple notebooks.
|
github_jupyter
|
data/
venv/
.ipynb_checkpoints/
| 0.246533 | 0.874238 |
# 成為初級資料分析師 | R 程式設計與資料科學應用
> 流程控制:`while` 迴圈
## 郭耀仁
> When you’ve given the same in-person advice 3 times, write a blog post.
>
> David Robinson
## 大綱
- 邏輯值的應用場景
- `while` 迴圈
## 邏輯值的應用場景
## 邏輯值會出現在
- 條件判斷
- **`while` 迴圈**
- 資料篩選
## 迴圈是用來解決需要反覆執行、大量手動複製貼上程式碼的任務
## 將介於 1 至 100 的偶數印出
```r
2
4
# ...
100
```
## `while` 迴圈
## `while` 迴圈的 Code Block
- 保留字 `while`
- 起始值(start)
- 終止值(stop):被評估為 `logical` 的 `EXPR`
- 間隔(step)
```r
i <- 1 # start
while (EXPR) { # stop
# do something iteratively until EXPR is evaluated as FALSE
i <- i + 1 # step
}
```
```
i <- 2
while (i <= 100) {
print(i)
i <- i + 2
}
```
## 常見的迴圈任務
- `print()`
- 加總(Summation)
- 計數(Counter)
- 合併(Combine):在後面章節討論
## 計算 1 到 100 之間的偶數總和:[The Story of Gauss](https://www.nctm.org/Publications/Teaching-Children-Mathematics/Blog/The-Story-of-Gauss/)
```
i <- 2
even_summation <- 0
while (i <= 100) {
even_summation <- even_summation + i
i <- i + 2
}
even_summation
```
## 計算 x 到 y 之間的偶數個數(包含 x 或 y 如果它們為偶數)
```
x <- 55
y <- 66
i <- x
even_counter <- 0
while (i <= y) {
if (i %% 2 == 0) {
even_counter <- even_counter + 1
}
i <- i + 1
}
even_counter
```
## 隨堂練習:判斷質數
在大於 1 的正整數中,除了 1 和該數自身外,無法被其他正整數整除的數字
```
x <- 89
i <- 1
divisor_counter <- 0
while (i <= x**0.5) {
if (x %% i == 0) {
divisor_counter <- divisor_counter + 1
}
i <- i + 1
}
if (x == 1) {
ans <- sprintf("%s 不是質數", x)
} else if (divisor_counter == 1) {
ans <- sprintf("%s 是質數", x)
} else {
ans <- sprintf("%s 不是質數", x)
}
ans
x <- 56
i <- 1
divisor_counter <- 0
while (i <= x**0.5) {
if (x %% i == 0) {
divisor_counter <- divisor_counter + 1
}
i <- i + 1
}
if (x == 1) {
ans <- sprintf("%s 不是質數", x)
} else if (divisor_counter == 1) {
ans <- sprintf("%s 是質數", x)
} else {
ans <- sprintf("%s 不是質數", x)
}
ans
```
## 可搭配使用的保留字
- `break`
- `next`
## 更快地判斷質數
```
x <- 56
i <- 1
divisor_counter <- 0
while (i <= x**0.5) {
print(sprintf("第 %s 次檢查因數", i))
if (x %% i == 0) {
divisor_counter <- divisor_counter + 1
}
i <- i + 1
}
if (x == 1) {
ans <- sprintf("%s 不是質數", x)
} else if (divisor_counter == 1) {
ans <- sprintf("%s 是質數", x)
} else {
ans <- sprintf("%s 不是質數", x)
}
ans
x <- 56
i <- 1
divisor_counter <- 0
while (i <= x**0.5) {
print(sprintf("第 %s 次檢查因數", i))
if (x %% i == 0) {
divisor_counter <- divisor_counter + 1
}
i <- i + 1
if (divisor_counter > 1) {
break
}
}
if (x == 1) {
ans <- sprintf("%s 不是質數", x)
} else if (divisor_counter == 1) {
ans <- sprintf("%s 是質數", x)
} else {
ans <- sprintf("%s 不是質數", x)
}
ans
```
## 樓層的忌諱
```
i <- 1
n_floors <- 10
while (i <= n_floors) {
if (i == 4) {
i <- i + 1
next
}
print(sprintf("%s 樓", i))
i <- i + 1
}
```
## 隨堂練習:判斷介於 x 與 y 之間的質數個數(包含 x 與 y 如果他們也是質數)
```
x <- 1
y <- 5
primes_counter <- 0
i <- x
while (i <= y) {
if (i == 1) {
i <- i + 1
next
}
j <- 1
divisors_counter <- 0
while (j <= i**0.5) {
if (i %% j == 0) {
divisors_counter <- divisors_counter + 1
}
j <- j + 1
if (divisors_counter > 1) {
break
}
}
if (divisors_counter == 1) {
primes_counter <- primes_counter + 1
}
i <- i + 1
}
msg <- sprintf("介於 %s 與 %s 之間的質數有 %s 個", x, y, primes_counter)
msg
x <- 5
y <- 19
primes_counter <- 0
i <- x
while (i <= y) {
if (i == 1) {
i <- i + 1
next
}
j <- 1
divisors_counter <- 0
while (j <= i**0.5) {
if (i %% j == 0) {
divisors_counter <- divisors_counter + 1
}
j <- j + 1
if (divisors_counter > 1) {
break
}
}
if (divisors_counter == 1) {
primes_counter <- primes_counter + 1
}
i <- i + 1
}
msg <- sprintf("介於 %s 與 %s 之間的質數有 %s 個", x, y, primes_counter)
msg
```
|
github_jupyter
|
2
4
# ...
100
i <- 1 # start
while (EXPR) { # stop
# do something iteratively until EXPR is evaluated as FALSE
i <- i + 1 # step
}
i <- 2
while (i <= 100) {
print(i)
i <- i + 2
}
i <- 2
even_summation <- 0
while (i <= 100) {
even_summation <- even_summation + i
i <- i + 2
}
even_summation
x <- 55
y <- 66
i <- x
even_counter <- 0
while (i <= y) {
if (i %% 2 == 0) {
even_counter <- even_counter + 1
}
i <- i + 1
}
even_counter
x <- 89
i <- 1
divisor_counter <- 0
while (i <= x**0.5) {
if (x %% i == 0) {
divisor_counter <- divisor_counter + 1
}
i <- i + 1
}
if (x == 1) {
ans <- sprintf("%s 不是質數", x)
} else if (divisor_counter == 1) {
ans <- sprintf("%s 是質數", x)
} else {
ans <- sprintf("%s 不是質數", x)
}
ans
x <- 56
i <- 1
divisor_counter <- 0
while (i <= x**0.5) {
if (x %% i == 0) {
divisor_counter <- divisor_counter + 1
}
i <- i + 1
}
if (x == 1) {
ans <- sprintf("%s 不是質數", x)
} else if (divisor_counter == 1) {
ans <- sprintf("%s 是質數", x)
} else {
ans <- sprintf("%s 不是質數", x)
}
ans
x <- 56
i <- 1
divisor_counter <- 0
while (i <= x**0.5) {
print(sprintf("第 %s 次檢查因數", i))
if (x %% i == 0) {
divisor_counter <- divisor_counter + 1
}
i <- i + 1
}
if (x == 1) {
ans <- sprintf("%s 不是質數", x)
} else if (divisor_counter == 1) {
ans <- sprintf("%s 是質數", x)
} else {
ans <- sprintf("%s 不是質數", x)
}
ans
x <- 56
i <- 1
divisor_counter <- 0
while (i <= x**0.5) {
print(sprintf("第 %s 次檢查因數", i))
if (x %% i == 0) {
divisor_counter <- divisor_counter + 1
}
i <- i + 1
if (divisor_counter > 1) {
break
}
}
if (x == 1) {
ans <- sprintf("%s 不是質數", x)
} else if (divisor_counter == 1) {
ans <- sprintf("%s 是質數", x)
} else {
ans <- sprintf("%s 不是質數", x)
}
ans
i <- 1
n_floors <- 10
while (i <= n_floors) {
if (i == 4) {
i <- i + 1
next
}
print(sprintf("%s 樓", i))
i <- i + 1
}
x <- 1
y <- 5
primes_counter <- 0
i <- x
while (i <= y) {
if (i == 1) {
i <- i + 1
next
}
j <- 1
divisors_counter <- 0
while (j <= i**0.5) {
if (i %% j == 0) {
divisors_counter <- divisors_counter + 1
}
j <- j + 1
if (divisors_counter > 1) {
break
}
}
if (divisors_counter == 1) {
primes_counter <- primes_counter + 1
}
i <- i + 1
}
msg <- sprintf("介於 %s 與 %s 之間的質數有 %s 個", x, y, primes_counter)
msg
x <- 5
y <- 19
primes_counter <- 0
i <- x
while (i <= y) {
if (i == 1) {
i <- i + 1
next
}
j <- 1
divisors_counter <- 0
while (j <= i**0.5) {
if (i %% j == 0) {
divisors_counter <- divisors_counter + 1
}
j <- j + 1
if (divisors_counter > 1) {
break
}
}
if (divisors_counter == 1) {
primes_counter <- primes_counter + 1
}
i <- i + 1
}
msg <- sprintf("介於 %s 與 %s 之間的質數有 %s 個", x, y, primes_counter)
msg
| 0.086859 | 0.776369 |
```
#source: https://www.kaggle.com/bhaveshsk/getting-started-with-titanic-dataset/data
#data analysis and wrangling
import pandas as pd
import numpy as np
import random as rnd
#data visualization
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
#machine learning packages
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn import metrics
train_df = pd.read_csv("../input/train.csv")
test_df = pd.read_csv("../input/test.csv")
df = pd.concat([train_df,test_df])
df.head()
df = df.drop(['Ticket', 'Cabin'], axis=1)
df['Title'] = df.Name.str.extract(' ([A-Za-z]+)\.', expand=False)
df['Title'] = df['Title'].replace(['Lady', 'Countess','Capt', 'Col',\
'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
df['Title'] = df['Title'].replace('Mlle', 'Miss')
df['Title'] = df['Title'].replace('Ms', 'Miss')
df['Title'] = df['Title'].replace('Mme', 'Mrs')
title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Rare": 5}
df['Title'] = df['Title'].map(title_mapping)
df['Title'] = df['Title'].fillna(0)
df = df.drop(['Name', 'PassengerId'], axis=1)
df['Sex'] = df['Sex'].map( {'female': 1, 'male': 0} ).astype(int)
df['Age'] = df['Age'].fillna(df['Age'].dropna().median())
df['AgeBand'] = pd.cut(df['Age'], 5)
df.loc[ df['Age'] <= 16, 'Age'] = 0
df.loc[(df['Age'] > 16) & (df['Age'] <= 32), 'Age'] = 1
df.loc[(df['Age'] > 32) & (df['Age'] <= 48), 'Age'] = 2
df.loc[(df['Age'] > 48) & (df['Age'] <= 64), 'Age'] = 3
df = df.drop(['AgeBand'], axis=1)
df['FamilySize'] = df['SibSp'] + df['Parch'] + 1
df['IsAlone'] = 0
df.loc[df['FamilySize'] == 1, 'IsAlone'] = 1
df = df.drop(['Parch', 'SibSp', 'FamilySize'], axis=1)
df['Age*Class'] = df.Age * df.Pclass
freq_port = df.Embarked.dropna().mode()[0]
df['Embarked'] = df['Embarked'].fillna(freq_port)
df['Embarked'] = df['Embarked'].map( {'S': 0, 'C': 1, 'Q': 2} ).astype(int)
df['Fare'] = df['Fare'].fillna(df['Fare'].dropna().median())
df['FareBand'] = pd.qcut(df['Fare'], 4)
df.loc[ df['Fare'] <= 7.91, 'Fare'] = 0
df.loc[(df['Fare'] > 7.91) & (df['Fare'] <= 14.454), 'Fare'] = 1
df.loc[(df['Fare'] > 14.454) & (df['Fare'] <= 31), 'Fare'] = 2
df.loc[ df['Fare'] > 31, 'Fare'] = 3
df['Fare'] = df['Fare'].astype(int)
df = df.drop(['FareBand'], axis=1)
train_df = df[-df['Survived'].isna()]
test_df = df[df['Survived'].isna()]
test_df = test_df.drop('Survived', axis=1)
X_train = train_df.drop("Survived", axis=1)
Y_train = train_df["Survived"]
X_test = test_df.copy()
svc = SVC()
svc.fit(X_train, Y_train)
Y_pred = svc.predict(X_test)
acc_svc = round(svc.score(X_train, Y_train) * 100, 2)
acc_svc
knn = KNeighborsClassifier()
knn.fit(X_train, Y_train)
Y_pred = knn.predict(X_test)
acc_knn = round(knn.score(X_train, Y_train) * 100, 2)
acc_knn
gaussian = GaussianNB()
gaussian.fit(X_train, Y_train)
Y_pred = gaussian.predict(X_test)
acc_gaussian = round(gaussian.score(X_train, Y_train) * 100, 2)
acc_gaussian
perceptron = Perceptron()
perceptron.fit(X_train, Y_train)
Y_pred = perceptron.predict(X_test)
acc_perceptron = round(perceptron.score(X_train, Y_train) * 100, 2)
acc_perceptron
sgd = SGDClassifier()
sgd.fit(X_train, Y_train)
Y_pred = sgd.predict(X_test)
acc_sgd = round(sgd.score(X_train, Y_train) * 100, 2)
acc_sgd
decision_tree = DecisionTreeClassifier()
decision_tree.fit(X_train, Y_train)
Y_pred = decision_tree.predict(X_test)
acc_decision_tree = round(decision_tree.score(X_train, Y_train) * 100, 2)
acc_decision_tree
random_forest = RandomForestClassifier(n_estimators=100)
random_forest.fit(X_train, Y_train)
Y_pred = random_forest.predict(X_test)
random_forest.score(X_train, Y_train)
acc_random_forest = round(random_forest.score(X_train, Y_train) * 100, 2)
acc_random_forest
models = pd.DataFrame({
'Model': ['Support Vector Machines', 'KNN',
'Random Forest', 'Naive Bayes', 'Perceptron',
'Stochastic Gradient Decent',
'Decision Tree'],
'Score': [acc_svc, acc_knn,
acc_random_forest, acc_gaussian, acc_perceptron,
acc_sgd, acc_decision_tree]})
models.sort_values(by='Score', ascending=False)
```
|
github_jupyter
|
#source: https://www.kaggle.com/bhaveshsk/getting-started-with-titanic-dataset/data
#data analysis and wrangling
import pandas as pd
import numpy as np
import random as rnd
#data visualization
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
#machine learning packages
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn import metrics
train_df = pd.read_csv("../input/train.csv")
test_df = pd.read_csv("../input/test.csv")
df = pd.concat([train_df,test_df])
df.head()
df = df.drop(['Ticket', 'Cabin'], axis=1)
df['Title'] = df.Name.str.extract(' ([A-Za-z]+)\.', expand=False)
df['Title'] = df['Title'].replace(['Lady', 'Countess','Capt', 'Col',\
'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
df['Title'] = df['Title'].replace('Mlle', 'Miss')
df['Title'] = df['Title'].replace('Ms', 'Miss')
df['Title'] = df['Title'].replace('Mme', 'Mrs')
title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Rare": 5}
df['Title'] = df['Title'].map(title_mapping)
df['Title'] = df['Title'].fillna(0)
df = df.drop(['Name', 'PassengerId'], axis=1)
df['Sex'] = df['Sex'].map( {'female': 1, 'male': 0} ).astype(int)
df['Age'] = df['Age'].fillna(df['Age'].dropna().median())
df['AgeBand'] = pd.cut(df['Age'], 5)
df.loc[ df['Age'] <= 16, 'Age'] = 0
df.loc[(df['Age'] > 16) & (df['Age'] <= 32), 'Age'] = 1
df.loc[(df['Age'] > 32) & (df['Age'] <= 48), 'Age'] = 2
df.loc[(df['Age'] > 48) & (df['Age'] <= 64), 'Age'] = 3
df = df.drop(['AgeBand'], axis=1)
df['FamilySize'] = df['SibSp'] + df['Parch'] + 1
df['IsAlone'] = 0
df.loc[df['FamilySize'] == 1, 'IsAlone'] = 1
df = df.drop(['Parch', 'SibSp', 'FamilySize'], axis=1)
df['Age*Class'] = df.Age * df.Pclass
freq_port = df.Embarked.dropna().mode()[0]
df['Embarked'] = df['Embarked'].fillna(freq_port)
df['Embarked'] = df['Embarked'].map( {'S': 0, 'C': 1, 'Q': 2} ).astype(int)
df['Fare'] = df['Fare'].fillna(df['Fare'].dropna().median())
df['FareBand'] = pd.qcut(df['Fare'], 4)
df.loc[ df['Fare'] <= 7.91, 'Fare'] = 0
df.loc[(df['Fare'] > 7.91) & (df['Fare'] <= 14.454), 'Fare'] = 1
df.loc[(df['Fare'] > 14.454) & (df['Fare'] <= 31), 'Fare'] = 2
df.loc[ df['Fare'] > 31, 'Fare'] = 3
df['Fare'] = df['Fare'].astype(int)
df = df.drop(['FareBand'], axis=1)
train_df = df[-df['Survived'].isna()]
test_df = df[df['Survived'].isna()]
test_df = test_df.drop('Survived', axis=1)
X_train = train_df.drop("Survived", axis=1)
Y_train = train_df["Survived"]
X_test = test_df.copy()
svc = SVC()
svc.fit(X_train, Y_train)
Y_pred = svc.predict(X_test)
acc_svc = round(svc.score(X_train, Y_train) * 100, 2)
acc_svc
knn = KNeighborsClassifier()
knn.fit(X_train, Y_train)
Y_pred = knn.predict(X_test)
acc_knn = round(knn.score(X_train, Y_train) * 100, 2)
acc_knn
gaussian = GaussianNB()
gaussian.fit(X_train, Y_train)
Y_pred = gaussian.predict(X_test)
acc_gaussian = round(gaussian.score(X_train, Y_train) * 100, 2)
acc_gaussian
perceptron = Perceptron()
perceptron.fit(X_train, Y_train)
Y_pred = perceptron.predict(X_test)
acc_perceptron = round(perceptron.score(X_train, Y_train) * 100, 2)
acc_perceptron
sgd = SGDClassifier()
sgd.fit(X_train, Y_train)
Y_pred = sgd.predict(X_test)
acc_sgd = round(sgd.score(X_train, Y_train) * 100, 2)
acc_sgd
decision_tree = DecisionTreeClassifier()
decision_tree.fit(X_train, Y_train)
Y_pred = decision_tree.predict(X_test)
acc_decision_tree = round(decision_tree.score(X_train, Y_train) * 100, 2)
acc_decision_tree
random_forest = RandomForestClassifier(n_estimators=100)
random_forest.fit(X_train, Y_train)
Y_pred = random_forest.predict(X_test)
random_forest.score(X_train, Y_train)
acc_random_forest = round(random_forest.score(X_train, Y_train) * 100, 2)
acc_random_forest
models = pd.DataFrame({
'Model': ['Support Vector Machines', 'KNN',
'Random Forest', 'Naive Bayes', 'Perceptron',
'Stochastic Gradient Decent',
'Decision Tree'],
'Score': [acc_svc, acc_knn,
acc_random_forest, acc_gaussian, acc_perceptron,
acc_sgd, acc_decision_tree]})
models.sort_values(by='Score', ascending=False)
| 0.498535 | 0.427935 |
# Load Packages
```
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
```
# Load Data Points (Do not modify the following block)
```
with open('training_data.npz', 'rb') as f:
data = np.load(f)
x_list = data['x_list']
y_list = data['y_list']
x_data = data['x_data']
y_data = data['y_data']
n_data = len(x_data)
w = data['w']
original_degree = data['order']
# Print information of original function.
print("=================================")
print("We have", n_data, "number of data")
print("=================================")
weight_info_string = ''
for d in range(original_degree):
weight_info_string += 'w'+str(d)+':'+str(round(w[d],ndigits=3))+' '
print("Coefficients of the original polynomial")
print(weight_info_string)
print("=================================")
plt.plot(x_list, y_list, 'b:', linewidth=2, label="Original Function")
plt.scatter(x_data, y_data, s=50, c='r', label="Data Points")
plt.xlim([np.min(x_list),np.max(x_list)])
plt.ylim([np.min(y_data),np.max(y_data)])
plt.legend(prop={'size': 12})
plt.title("Data Plot")
plt.show()
```
# Polynomial Regression (Programming Assignment)
### Variable Explanation (Do not change variable names)
- 'w' is true coefficients of the original polynomial function
- 'original_degree' is the order of the original polynomial function
- 'x_list' is a list of the points at $x$-axis
- 'y_list' is a list of function value $f(x)$ corresponding to 'x_list'. In other words, y_list = $f($x_list$)$
- 'x_data' is an input data
- 'y_data' is an output data
- 'n_data' is the number of data points
### Our goal is to estimate 'w' from data points, 'x_data' and 'y_data'. Answer the following problems.
### 1. Compute a Vandermonde matrix when the degree of polynomial is $4$ (30pt)
- The variable 'degree' is the order of polynomial. In this problem, we set degree=$4$
- Use the variable 'A' for the Vandermonde matrix. Now, 'A' is initialized as a zero matrix whose elements are all zero. Fill in the element of the Vandermonde matrix by using power operator (\*\*), for loop, and np.concatenation.
```
degree = 4
A = np.zeros((n_data, degree+1)) # Dummy initialization
print(A)
k = np.ones((1,5), dtype=int)
for i in range(2,n_data+1):
g = np.array([[1,i,i**2,i**3,i**4]])
k = np.append(k, g, axis=0)
A = np.array(k)
print(A)
```
### Print results (do not modify the following block)
```
print(A)
```
### 2. Compute the coefficients of polynomial regression using a $4$ degree polynomial (40pt)
- Use the variable 'degree' and the Vandermonde matrix 'A' in Problem 1.
- The variable 'w_est' is the coefficients of polynomial regression. Now, 'w_est' is initialized as a zero vector. Compute the 'w_est' from 'A' and 'y'
- The variable 'y_est' is an estimated function value corresponding to the input points 'x_list'. Now, it is a zero list and fill the list by computing the estimated function values. In other words, y_est = $\hat{f}($x_list$)$
```
y_est = np.zeros_like(x_list)
w_est = np.zeros((est_order+1,1))
```
### Print results (do not modify the following block)
```
plt.plot(x_list, y_list, 'b:', linewidth=2, label="Original Function")
plt.plot(x_list, y_est, 'm-', linewidth=2, label="Polynomial Regression (d={})".format(degree))
plt.scatter(x_data, y_data, s=50, c='r', label="Data Points")
plt.xlim([np.min(x_list),np.max(x_list)])
plt.ylim([np.min(y_data),np.max(y_data)])
plt.legend(prop={'size': 12})
plt.title("Data Plot")
plt.show()
```
### 3. Compute the polynomial regression with $1$ degree polynomials (15pt)
- Repeat Problem 1 and Problem 2 with degree $1$.
- Use the following variables.
> degree1, A1, w_est1, y_est1
```
degree1 = 1
A1 = np.zeros((n_data, degree1+1))
w_est1 = np.zeros((degree1+1,1))
y_est1 = np.zeros_like(x_list)
m = np.ones((1,2), dtype=int)
for i in range(2,n_data+1):
n = np.array([[1,i]])
m = np.append(m, n, axis=0)
A1 = np.array(m)
A1
```
### Print results (do not modify the following block)
```
plt.plot(x_list, y_list, 'b:', linewidth=2, label="Original Function")
plt.plot(x_list, y_est1, 'g-', linewidth=2, label="Polynomial Regression (d={})".format(degree1))
plt.scatter(x_data, y_data, s=50, c='r', label="Data Points")
plt.xlim([np.min(x_list),np.max(x_list)])
plt.ylim([np.min(y_data),np.max(y_data)])
plt.legend(prop={'size': 12})
plt.title("Data Plot")
plt.show()
```
### 4. Compute the polynomial regression with $10$ degree polynomials (15pt)
- Repeat Problem 1 and Problem 2 with degree $10$.
- Use the following variables.
> degree2, A2, w_est2, y_est2
```
degree2 = 1
A2 = np.zeros((n_data, degree2+1))
w_est2 = np.zeros((degree2+1,1))
y_est2 = np.zeros_like(x_list)
t = np.ones((1,11), dtype=int)
for i in range(2,n_data+1):
j = np.array([[1,i,i**2,i**3,i**4,i**5,i**6,i**7,i**8,i**9,i**10]])
t = np.append(t, j, axis=0)
A2 = np.array(t)
A2
```
### Print results (do not modify the following block)
```
plt.plot(x_list, y_list, 'b:', linewidth=2, label="Original Function")
plt.plot(x_list, y_est2, 'c-', linewidth=2, label="Polynomial Regression (d={})".format(degree2))
plt.scatter(x_data, y_data, s=50, c='r', label="Data Points")
plt.xlim([np.min(x_list),np.max(x_list)])
plt.ylim([np.min(y_data),np.max(y_data)])
plt.legend(prop={'size': 12})
plt.title("Data Plot")
plt.show()
```
### 5. [Challenging Problem] Explain the effect of degree (20pt)
- By solving the above problems, we can observe the behaviors of polynomial regression with different degrees (1, 4, 10)
- Explain pros and cons of high degree polynomial
- Explain pros and cons of low degree polynomial
- What is this phenomenon called in machine learning?
```
#차수가 높으면 오차가 적어집니다 특성이 많을 수록 정답에 가까워지듯이요 단점은 오버피팅(과대적합)이 발생할 수 있습니다.
#차수가 낮으면 오버피팅(과대적합)을 면할 수 있겠지만 차수가 높을 때보다 정답을 맞추기 힘들어집니다. 언더피팅(과소적합)이 발생할 수 있습니다.
#학습곡선에서 차수가 높아 일어나는 검증문제를 과대적합이라 하고 훈련,학습 둘다 성능이 낮은 문제를 과소적합이라 합니다.
```
### The following figure shows all regression results with different degrees.
```
plt.plot(x_list, y_list, 'b:', linewidth=2, label="Original Function")
plt.plot(x_list, y_est, 'm-', linewidth=2, label="Polynomial Regression (d={})".format(1))
plt.plot(x_list, y_est1, 'g-', linewidth=2, label="Polynomial Regression (d={})".format(4))
plt.plot(x_list, y_est2, 'c-', linewidth=2, label="Polynomial Regression (d={})".format(10))
plt.scatter(x_data, y_data, s=50, c='r', label="Data Points")
plt.xlim([np.min(x_list),np.max(x_list)])
plt.ylim([np.min(y_data),np.max(y_data)])
plt.legend(prop={'size': 12})
plt.title("Data Plot")
plt.show()
```
Write your answer!!!
|
github_jupyter
|
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
with open('training_data.npz', 'rb') as f:
data = np.load(f)
x_list = data['x_list']
y_list = data['y_list']
x_data = data['x_data']
y_data = data['y_data']
n_data = len(x_data)
w = data['w']
original_degree = data['order']
# Print information of original function.
print("=================================")
print("We have", n_data, "number of data")
print("=================================")
weight_info_string = ''
for d in range(original_degree):
weight_info_string += 'w'+str(d)+':'+str(round(w[d],ndigits=3))+' '
print("Coefficients of the original polynomial")
print(weight_info_string)
print("=================================")
plt.plot(x_list, y_list, 'b:', linewidth=2, label="Original Function")
plt.scatter(x_data, y_data, s=50, c='r', label="Data Points")
plt.xlim([np.min(x_list),np.max(x_list)])
plt.ylim([np.min(y_data),np.max(y_data)])
plt.legend(prop={'size': 12})
plt.title("Data Plot")
plt.show()
degree = 4
A = np.zeros((n_data, degree+1)) # Dummy initialization
print(A)
k = np.ones((1,5), dtype=int)
for i in range(2,n_data+1):
g = np.array([[1,i,i**2,i**3,i**4]])
k = np.append(k, g, axis=0)
A = np.array(k)
print(A)
print(A)
y_est = np.zeros_like(x_list)
w_est = np.zeros((est_order+1,1))
plt.plot(x_list, y_list, 'b:', linewidth=2, label="Original Function")
plt.plot(x_list, y_est, 'm-', linewidth=2, label="Polynomial Regression (d={})".format(degree))
plt.scatter(x_data, y_data, s=50, c='r', label="Data Points")
plt.xlim([np.min(x_list),np.max(x_list)])
plt.ylim([np.min(y_data),np.max(y_data)])
plt.legend(prop={'size': 12})
plt.title("Data Plot")
plt.show()
degree1 = 1
A1 = np.zeros((n_data, degree1+1))
w_est1 = np.zeros((degree1+1,1))
y_est1 = np.zeros_like(x_list)
m = np.ones((1,2), dtype=int)
for i in range(2,n_data+1):
n = np.array([[1,i]])
m = np.append(m, n, axis=0)
A1 = np.array(m)
A1
plt.plot(x_list, y_list, 'b:', linewidth=2, label="Original Function")
plt.plot(x_list, y_est1, 'g-', linewidth=2, label="Polynomial Regression (d={})".format(degree1))
plt.scatter(x_data, y_data, s=50, c='r', label="Data Points")
plt.xlim([np.min(x_list),np.max(x_list)])
plt.ylim([np.min(y_data),np.max(y_data)])
plt.legend(prop={'size': 12})
plt.title("Data Plot")
plt.show()
degree2 = 1
A2 = np.zeros((n_data, degree2+1))
w_est2 = np.zeros((degree2+1,1))
y_est2 = np.zeros_like(x_list)
t = np.ones((1,11), dtype=int)
for i in range(2,n_data+1):
j = np.array([[1,i,i**2,i**3,i**4,i**5,i**6,i**7,i**8,i**9,i**10]])
t = np.append(t, j, axis=0)
A2 = np.array(t)
A2
plt.plot(x_list, y_list, 'b:', linewidth=2, label="Original Function")
plt.plot(x_list, y_est2, 'c-', linewidth=2, label="Polynomial Regression (d={})".format(degree2))
plt.scatter(x_data, y_data, s=50, c='r', label="Data Points")
plt.xlim([np.min(x_list),np.max(x_list)])
plt.ylim([np.min(y_data),np.max(y_data)])
plt.legend(prop={'size': 12})
plt.title("Data Plot")
plt.show()
#차수가 높으면 오차가 적어집니다 특성이 많을 수록 정답에 가까워지듯이요 단점은 오버피팅(과대적합)이 발생할 수 있습니다.
#차수가 낮으면 오버피팅(과대적합)을 면할 수 있겠지만 차수가 높을 때보다 정답을 맞추기 힘들어집니다. 언더피팅(과소적합)이 발생할 수 있습니다.
#학습곡선에서 차수가 높아 일어나는 검증문제를 과대적합이라 하고 훈련,학습 둘다 성능이 낮은 문제를 과소적합이라 합니다.
plt.plot(x_list, y_list, 'b:', linewidth=2, label="Original Function")
plt.plot(x_list, y_est, 'm-', linewidth=2, label="Polynomial Regression (d={})".format(1))
plt.plot(x_list, y_est1, 'g-', linewidth=2, label="Polynomial Regression (d={})".format(4))
plt.plot(x_list, y_est2, 'c-', linewidth=2, label="Polynomial Regression (d={})".format(10))
plt.scatter(x_data, y_data, s=50, c='r', label="Data Points")
plt.xlim([np.min(x_list),np.max(x_list)])
plt.ylim([np.min(y_data),np.max(y_data)])
plt.legend(prop={'size': 12})
plt.title("Data Plot")
plt.show()
| 0.495117 | 0.921922 |
# Quantum Key Distribution
## 1. Introduction
When Alice and Bob want to communicate a secret message (such as Bob’s online banking details) over an insecure channel (such as the internet), it is essential to encrypt the message. Since cryptography is a large area and almost all of it is outside the scope of this textbook, we will have to believe that Alice and Bob having a secret key that no one else knows is useful and allows them to communicate using symmetric-key cryptography.
If Alice and Bob want to use Eve’s classical communication channel to share their key, it is impossible to tell if Eve has made a copy of this key for herself- they must place complete trust in Eve that she is not listening. If, however, Eve provides a quantum communication channel, Alice and Bob no longer need to trust Eve at all- they will know if she tries to read Bob’s message before it gets to Alice.
For some readers, it may be useful to give an idea of how a quantum channel may be physically implemented. An example of a classical channel could be a telephone line; we send electric signals through the line that represent our message (or bits). A proposed example of a quantum communication channel could be some kind of fiber-optic cable, through which we can send individual photons (particles of light). Photons have a property called _polarisation,_ and this polarisation can be one of two states. We can use this to represent a qubit.
## 2. Protocol Overview
The protocol makes use of the fact that measuring a qubit can change its state. If Alice sends Bob a qubit, and an eavesdropper (Eve) tries to measure it before Bob does, there is a chance that Eve’s measurement will change the state of the qubit and Bob will not receive the qubit state Alice sent.
```
from qiskit import QuantumCircuit, Aer, transpile
from qiskit.visualization import plot_histogram, plot_bloch_multivector
from numpy.random import randint
import numpy as np
```
If Alice prepares a qubit in the state $|+\rangle$ (`0` in the $X$-basis), and Bob measures it in the $X$-basis, Bob is sure to measure `0`:
```
qc = QuantumCircuit(1,1)
# Alice prepares qubit in state |+>
qc.h(0)
qc.barrier()
# Alice now sends the qubit to Bob
# who measures it in the X-basis
qc.h(0)
qc.measure(0,0)
# Draw and simulate circuit
display(qc.draw())
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(qc)
plot_histogram(job.result().get_counts())
```
But if Eve tries to measure this qubit in the $Z$-basis before it reaches Bob, she will change the qubit's state from $|+\rangle$ to either $|0\rangle$ or $|1\rangle$, and Bob is no longer certain to measure `0`:
```
qc = QuantumCircuit(1,1)
# Alice prepares qubit in state |+>
qc.h(0)
# Alice now sends the qubit to Bob
# but Eve intercepts and tries to read it
qc.measure(0, 0)
qc.barrier()
# Eve then passes this on to Bob
# who measures it in the X-basis
qc.h(0)
qc.measure(0,0)
# Draw and simulate circuit
display(qc.draw())
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(qc)
plot_histogram(job.result().get_counts())
```
We can see here that Bob now has a 50% chance of measuring `1`, and if he does, he and Alice will know there is something wrong with their channel.
The quantum key distribution protocol involves repeating this process enough times that an eavesdropper has a negligible chance of getting away with this interception. It is roughly as follows:
**- Step 1**
Alice chooses a string of random bits, e.g.:
`1000101011010100`
And a random choice of basis for each bit:
`ZZXZXXXZXZXXXXXX`
Alice keeps these two pieces of information private to herself.
**- Step 2**
Alice then encodes each bit onto a string of qubits using the basis she chose; this means each qubit is in one of the states $|0\rangle$, $|1\rangle$, $|+\rangle$ or $|-\rangle$, chosen at random. In this case, the string of qubits would look like this:
$$ |1\rangle|0\rangle|+\rangle|0\rangle|-\rangle|+\rangle|-\rangle|0\rangle|-\rangle|1\rangle|+\rangle|-\rangle|+\rangle|-\rangle|+\rangle|+\rangle
$$
This is the message she sends to Bob.
**- Step 3**
Bob then measures each qubit at random, for example, he might use the bases:
`XZZZXZXZXZXZZZXZ`
And Bob keeps the measurement results private.
**- Step 4**
Bob and Alice then publicly share which basis they used for each qubit. If Bob measured a qubit in the same basis Alice prepared it in, they use this to form part of their shared secret key, otherwise they discard the information for that bit.
**- Step 5**
Finally, Bob and Alice share a random sample of their keys, and if the samples match, they can be sure (to a small margin of error) that their transmission is successful.
## 3. Qiskit Example: Without Interception
Let’s first see how the protocol works when no one is listening in, then we can see how Alice and Bob are able to detect an eavesdropper. As always, let's start by importing everything we need:
To generate pseudo-random keys, we will use the `randint` function from numpy. To make sure you can reproduce the results on this page, we will set the seed to 0:
```
np.random.seed(seed=0)
```
We will call the length of Alice's initial message `n`. In this example, Alice will send a message 100 qubits long:
```
n = 100
```
### 3.1 Step 1:
Alice generates her random set of bits:
```
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
print(alice_bits)
```
At the moment, the set of bits '`alice_bits`' is only known to Alice. We will keep track of what information is only known to Alice, what information is only known to Bob, and what has been sent over Eve's channel in a table like this:
| Alice's Knowledge |Over Eve's Channel| Bob's Knowledge |
|:-----------------:|:----------------:|:---------------:|
| alice_bits | | |
### 3.2 Step 2:
Alice chooses to encode each bit on qubit in the $X$ or $Z$-basis at random, and stores the choice for each qubit in `alice_bases`. In this case, a `0` means "prepare in the $Z$-basis", and a `1` means "prepare in the $X$-basis":
```
np.random.seed(seed=0)
n = 100
## Step 1
#Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
print(alice_bases)
```
Alice also keeps this knowledge private:
| Alice's Knowledge |Over Eve's Channel| Bob's Knowledge |
|:-----------------:|:----------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
The function `encode_message` below, creates a list of `QuantumCircuit`s, each representing a single qubit in Alice's message:
```
def encode_message(bits, bases):
message = []
for i in range(n):
qc = QuantumCircuit(1,1)
if bases[i] == 0: # Prepare qubit in Z-basis
if bits[i] == 0:
pass
else:
qc.x(0)
else: # Prepare qubit in X-basis
if bits[i] == 0:
qc.h(0)
else:
qc.x(0)
qc.h(0)
qc.barrier()
message.append(qc)
return message
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
```
We can see that the first bit in `alices_bits` is `0`, and the basis she encodes this in is the $X$-basis (represented by `1`):
```
print('bit = %i' % alice_bits[0])
print('basis = %i' % alice_bases[0])
```
And if we view the first circuit in `message` (representing the first qubit in Alice's message), we can verify that Alice has prepared a qubit in the state $|+\rangle$:
```
message[0].draw()
```
As another example, we can see that the fourth bit in `alice_bits` is `1`, and it is encoded in the $Z$-basis, Alice prepares the corresponding qubit in the state $|1\rangle$:
```
print('bit = %i' % alice_bits[4])
print('basis = %i' % alice_bases[4])
message[4].draw()
```
This message of qubits is then sent to Bob over Eve's quantum channel:
| Alice's Knowledge |Over Eve's Channel| Bob's Knowledge |
|:-----------------:|:----------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
### 3.3 Step 3:
Bob then measures each qubit in the $X$ or $Z$-basis at random and stores this information:
```
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
print(bob_bases)
```
`bob_bases` stores Bob's choice for which basis he measures each qubit in.
| Alice's Knowledge |Over Eve's Channel| Bob's Knowledge |
|:-----------------:|:----------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
Below, the function `measure_message` applies the corresponding measurement and simulates the result of measuring each qubit. We store the measurement results in `bob_results`.
```
def measure_message(message, bases):
backend = Aer.get_backend('aer_simulator')
measurements = []
for q in range(n):
if bases[q] == 0: # measuring in Z-basis
message[q].measure(0,0)
if bases[q] == 1: # measuring in X-basis
message[q].h(0)
message[q].measure(0,0)
aer_sim = Aer.get_backend('aer_simulator')
result = aer_sim.run(message[q], shots=1, memory=True).result()
measured_bit = int(result.get_memory()[0])
measurements.append(measured_bit)
return measurements
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
```
We can see that the circuit in `message[0]` (representing the 0th qubit) has had an $X$-measurement added to it by Bob:
```
message[0].draw()
```
Since Bob has by chance chosen to measure in the same basis Alice encoded the qubit in, Bob is guaranteed to get the result `0`. For the 6th qubit (shown below), Bob's random choice of measurement is not the same as Alice's, and Bob's result has only a 50% chance of matching Alices'.
```
message[6].draw()
print(bob_results)
```
Bob keeps his results private.
| Alice's Knowledge | Over Eve's Channel | Bob's Knowledge |
|:-----------------:|:------------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
| | | bob_results |
### 3.4 Step 4:
After this, Alice reveals (through Eve's channel) which qubits were encoded in which basis:
| Alice's Knowledge | Over Eve's Channel | Bob's Knowledge |
|:-----------------:|:------------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
| | | bob_results |
| | alice_bases | alice_bases |
And Bob reveals which basis he measured each qubit in:
| Alice's Knowledge | Over Eve's Channel | Bob's Knowledge |
|:-----------------:|:------------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
| | | bob_results |
| | alice_bases | alice_bases |
| bob_bases | bob_bases | |
If Bob happened to measure a bit in the same basis Alice prepared it in, this means the entry in `bob_results` will match the corresponding entry in `alice_bits`, and they can use that bit as part of their key. If they measured in different bases, Bob's result is random, and they both throw that entry away. Here is a function `remove_garbage` that does this for us:
```
def remove_garbage(a_bases, b_bases, bits):
good_bits = []
for q in range(n):
if a_bases[q] == b_bases[q]:
# If both used the same basis, add
# this to the list of 'good' bits
good_bits.append(bits[q])
return good_bits
```
Alice and Bob both discard the useless bits, and use the remaining bits to form their secret keys:
```
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
print(alice_key)
```
| Alice's Knowledge | Over Eve's Channel | Bob's Knowledge |
|:-----------------:|:------------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
| | | bob_results |
| | alice_bases | alice_bases |
| bob_bases | bob_bases | |
| alice_key | | |
```
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
print(bob_key)
```
| Alice's Knowledge | Over Eve's Channel | Bob's Knowledge |
|:-----------------:|:------------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
| | | bob_results |
| | alice_bases | alice_bases |
| bob_bases | bob_bases | |
| alice_key | | bob_key |
### 3.5 Step 5:
Finally, Bob and Alice compare a random selection of the bits in their keys to make sure the protocol has worked correctly:
```
def sample_bits(bits, selection):
sample = []
for i in selection:
# use np.mod to make sure the
# bit we sample is always in
# the list range
i = np.mod(i, len(bits))
# pop(i) removes the element of the
# list at index 'i'
sample.append(bits.pop(i))
return sample
```
Alice and Bob both broadcast these publicly, and remove them from their keys as they are no longer secret:
```
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
## Step 5
sample_size = 15
bit_selection = randint(n, size=sample_size)
bob_sample = sample_bits(bob_key, bit_selection)
print(" bob_sample = " + str(bob_sample))
alice_sample = sample_bits(alice_key, bit_selection)
print("alice_sample = "+ str(alice_sample))
```
| Alice's Knowledge | Over Eve's Channel | Bob's Knowledge |
|:-----------------:|:------------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
| | | bob_results |
| | alice_bases | alice_bases |
| bob_bases | bob_bases | |
| alice_key | | bob_key |
| bob_sample | bob_sample | bob_sample |
| alice_sample | alice_sample | alice_sample |
If the protocol has worked correctly without interference, their samples should match:
```
bob_sample == alice_sample
```
If their samples match, it means (with high probability) `alice_key == bob_key`. They now share a secret key they can use to encrypt their messages!
| Alice's Knowledge | Over Eve's Channel | Bob's Knowledge |
|:-----------------:|:------------------:|:---------------:|
| alice_bits | | |
| alice_bases | | |
| message | message | message |
| | | bob_bases |
| | | bob_results |
| | alice_bases | alice_bases |
| bob_bases | bob_bases | |
| alice_key | | bob_key |
| bob_sample | bob_sample | bob_sample |
| alice_sample | alice_sample | alice_sample |
| shared_key | | shared_key |
```
print(bob_key)
print(alice_key)
print("key length = %i" % len(alice_key))
```
## 4. Qiskit Example: *With* Interception
Let’s now see how Alice and Bob can tell if Eve has been trying to listen in on their quantum message. We repeat the same steps as without interference, but before Bob receives his qubits, Eve will try and extract some information from them. Let's set a different seed so we get a specific set of reproducible 'random' results:
```
np.random.seed(seed=3)
```
### 4.1 Step 1:
Alice generates her set of random bits:
```
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
print(alice_bits)
```
### 4.2 Step 2:
Alice encodes these in the $Z$ and $X$-bases at random, and sends these to Bob through Eve's quantum channel:
```
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
print(alice_bases)
```
In this case, the first qubit in Alice's message is in the state $|+\rangle$:
```
message[0].draw()
```
### Interception!
Oh no! Eve intercepts the message as it passes through her channel. She tries to measure the qubits in a random selection of bases, in the same way Bob will later.
```
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
print(intercepted_message)
```
We can see the case of qubit 0 below; Eve's random choice of basis is not the same as Alice's, and this will change the qubit state from $|+\rangle$, to a random state in the $Z$-basis, with 50% probability of $|0\rangle$ or $|1\rangle$:
```
message[0].draw()
```
### 4.3 Step 3:
Eve then passes on the qubits to Bob, who measures them at random. In this case, Bob chose (by chance) to measure in the same basis Alice prepared the qubit in. Without interception, Bob would be guaranteed to measure `0`, but because Eve tried to read the message he now has a 50% chance of measuring `1` instead.
```
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
message[0].draw()
```
### 4.4 Step 4:
Bob and Alice reveal their basis choices, and discard the useless bits:
```
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
```
### 4.5 Step 5:
Bob and Alice compare the same random selection of their keys to see if the qubits were intercepted:
```
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
## Step 5
sample_size = 15
bit_selection = randint(n, size=sample_size)
bob_sample = sample_bits(bob_key, bit_selection)
print(" bob_sample = " + str(bob_sample))
alice_sample = sample_bits(alice_key, bit_selection)
print("alice_sample = "+ str(alice_sample))
bob_sample == alice_sample
```
Oh no! Bob's key and Alice's key do not match. We know this is because Eve tried to read the message between steps 2 and 3, and changed the qubits' states. For all Alice and Bob know, this could be due to noise in the channel, but either way they must throw away all their results and try again- Eve's interception attempt has failed.
## 5. Risk Analysis
For this type of interception, in which Eve measures all the qubits, there is a small chance that Bob and Alice's samples could match, and Alice sends her vulnerable message through Eve's channel. Let's calculate that chance and see how risky quantum key distribution is.
- For Alice and Bob to use a qubit's result, they must both have chosen the same basis. If Eve chooses this basis too, she will successfully intercept this bit without introducing any error. There is a 50% chance of this happening.
- If Eve chooses the *wrong* basis, i.e. a different basis to Alice and Bob, there is still a 50% chance Bob will measure the value Alice was trying to send. In this case, the interception also goes undetected.
- But if Eve chooses the *wrong* basis, i.e. a different basis to Alice and Bob, there is a 50% chance Bob will not measure the value Alice was trying to send, and this *will* introduce an error into their keys.
<img src="images/qkd_risk.svg">
If Alice and Bob compare 1 bit from their keys, the probability the bits will match is $0.75$, and if so they will not notice Eve's interception. If they measure 2 bits, there is a $0.75^2 = 0.5625$ chance of the interception not being noticed. We can see that the probability of Eve going undetected can be calculated from the number of bits ($x$) Alice and Bob chose to compare:
$$ P(\text{undetected}) = 0.75^x $$
If we decide to compare 15 bits as we did above, there is a 1.3% chance Eve will be undetected. If this is too risky for us, we could compare 50 bits instead, and have a 0.00006% chance of being spied upon unknowingly.
You can retry the protocol again by running the cell below. Try changing `sample_size` to something low and see how easy it is for Eve to intercept Alice and Bob's keys.
```
n = 100
# Step 1
alice_bits = randint(2, size=n)
alice_bases = randint(2, size=n)
# Step 2
message = encode_message(alice_bits, alice_bases)
# Interception!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
# Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
# Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
# Step 5
sample_size = 15 # Change this to something lower and see if
# Eve can intercept the message without Alice
# and Bob finding out
bit_selection = randint(n, size=sample_size)
bob_sample = sample_bits(bob_key, bit_selection)
alice_sample = sample_bits(alice_key, bit_selection)
if bob_sample != alice_sample:
print("Eve's interference was detected.")
else:
print("Eve went undetected!")
import qiskit.tools.jupyter
%qiskit_version_table
```
|
github_jupyter
|
from qiskit import QuantumCircuit, Aer, transpile
from qiskit.visualization import plot_histogram, plot_bloch_multivector
from numpy.random import randint
import numpy as np
qc = QuantumCircuit(1,1)
# Alice prepares qubit in state |+>
qc.h(0)
qc.barrier()
# Alice now sends the qubit to Bob
# who measures it in the X-basis
qc.h(0)
qc.measure(0,0)
# Draw and simulate circuit
display(qc.draw())
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(qc)
plot_histogram(job.result().get_counts())
qc = QuantumCircuit(1,1)
# Alice prepares qubit in state |+>
qc.h(0)
# Alice now sends the qubit to Bob
# but Eve intercepts and tries to read it
qc.measure(0, 0)
qc.barrier()
# Eve then passes this on to Bob
# who measures it in the X-basis
qc.h(0)
qc.measure(0,0)
# Draw and simulate circuit
display(qc.draw())
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(qc)
plot_histogram(job.result().get_counts())
np.random.seed(seed=0)
n = 100
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
print(alice_bits)
np.random.seed(seed=0)
n = 100
## Step 1
#Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
print(alice_bases)
def encode_message(bits, bases):
message = []
for i in range(n):
qc = QuantumCircuit(1,1)
if bases[i] == 0: # Prepare qubit in Z-basis
if bits[i] == 0:
pass
else:
qc.x(0)
else: # Prepare qubit in X-basis
if bits[i] == 0:
qc.h(0)
else:
qc.x(0)
qc.h(0)
qc.barrier()
message.append(qc)
return message
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
print('bit = %i' % alice_bits[0])
print('basis = %i' % alice_bases[0])
message[0].draw()
print('bit = %i' % alice_bits[4])
print('basis = %i' % alice_bases[4])
message[4].draw()
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
print(bob_bases)
def measure_message(message, bases):
backend = Aer.get_backend('aer_simulator')
measurements = []
for q in range(n):
if bases[q] == 0: # measuring in Z-basis
message[q].measure(0,0)
if bases[q] == 1: # measuring in X-basis
message[q].h(0)
message[q].measure(0,0)
aer_sim = Aer.get_backend('aer_simulator')
result = aer_sim.run(message[q], shots=1, memory=True).result()
measured_bit = int(result.get_memory()[0])
measurements.append(measured_bit)
return measurements
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
message[0].draw()
message[6].draw()
print(bob_results)
def remove_garbage(a_bases, b_bases, bits):
good_bits = []
for q in range(n):
if a_bases[q] == b_bases[q]:
# If both used the same basis, add
# this to the list of 'good' bits
good_bits.append(bits[q])
return good_bits
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
print(alice_key)
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
print(bob_key)
def sample_bits(bits, selection):
sample = []
for i in selection:
# use np.mod to make sure the
# bit we sample is always in
# the list range
i = np.mod(i, len(bits))
# pop(i) removes the element of the
# list at index 'i'
sample.append(bits.pop(i))
return sample
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
## Step 5
sample_size = 15
bit_selection = randint(n, size=sample_size)
bob_sample = sample_bits(bob_key, bit_selection)
print(" bob_sample = " + str(bob_sample))
alice_sample = sample_bits(alice_key, bit_selection)
print("alice_sample = "+ str(alice_sample))
bob_sample == alice_sample
print(bob_key)
print(alice_key)
print("key length = %i" % len(alice_key))
np.random.seed(seed=3)
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
print(alice_bits)
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
print(alice_bases)
message[0].draw()
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
print(intercepted_message)
message[0].draw()
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
message[0].draw()
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
## Step 5
sample_size = 15
bit_selection = randint(n, size=sample_size)
bob_sample = sample_bits(bob_key, bit_selection)
print(" bob_sample = " + str(bob_sample))
alice_sample = sample_bits(alice_key, bit_selection)
print("alice_sample = "+ str(alice_sample))
bob_sample == alice_sample
n = 100
# Step 1
alice_bits = randint(2, size=n)
alice_bases = randint(2, size=n)
# Step 2
message = encode_message(alice_bits, alice_bases)
# Interception!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
# Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
# Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
# Step 5
sample_size = 15 # Change this to something lower and see if
# Eve can intercept the message without Alice
# and Bob finding out
bit_selection = randint(n, size=sample_size)
bob_sample = sample_bits(bob_key, bit_selection)
alice_sample = sample_bits(alice_key, bit_selection)
if bob_sample != alice_sample:
print("Eve's interference was detected.")
else:
print("Eve went undetected!")
import qiskit.tools.jupyter
%qiskit_version_table
| 0.555435 | 0.990404 |
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Algorithms/Segmentation/segmentation_snic.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Algorithms/Segmentation/segmentation_snic.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Algorithms/Segmentation/segmentation_snic.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Algorithms/Segmentation/segmentation_snic.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
**Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
```
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
# imageCollection = ee.ImageCollection("USDA/NAIP/DOQQ"),
# geometry = ee.Geometry.Polygon(
# [[[-121.89511299133301, 38.98496606984683],
# [-121.89511299133301, 38.909335196675435],
# [-121.69358253479004, 38.909335196675435],
# [-121.69358253479004, 38.98496606984683]]], {}, False),
# geometry2 = ee.Geometry.Polygon(
# [[[-108.34304809570307, 36.66975278349341],
# [-108.34225416183466, 36.66977859999848],
# [-108.34226489067072, 36.67042400981031],
# [-108.34308028221125, 36.670380982657925]]]),
# imageCollection2 = ee.ImageCollection("USDA/NASS/CDL"),
# cdl2016 = ee.Image("USDA/NASS/CDL/2016")
# Map.centerObject(geometry, {}, 'roi')
# # Map.addLayer(ee.Image(1), {'palette': "white"})
# cdl2016 = cdl2016.select(0).clip(geometry)
# function erode(img, distance) {
# d = (img.Not().unmask(1) \
# .fastDistanceTransform(30).sqrt() \
# .multiply(ee.Image.pixelArea().sqrt()))
# return img.updateMask(d.gt(distance))
# }
# function dilate(img, distance) {
# d = (img.fastDistanceTransform(30).sqrt() \
# .multiply(ee.Image.pixelArea().sqrt()))
# return d.lt(distance)
# }
# function expandSeeds(seeds) {
# seeds = seeds.unmask(0).focal_max()
# return seeds.updateMask(seeds)
# }
# bands = ["R", "G", "B", "N"]
# img = imageCollection \
# .filterDate('2015-01-01', '2017-01-01') \
# .filterBounds(geometry) \
# .mosaic()
# img = ee.Image(img).clip(geometry).divide(255).select(bands)
# Map.addLayer(img, {'gamma': 0.8}, "RGBN", False)
# seeds = ee.Algorithms.Image.Segmentation.seedGrid(36)
# # Apply a softening.
# kernel = ee.Kernel.gaussian(3)
# img = img.convolve(kernel)
# Map.addLayer(img, {'gamma': 0.8}, "RGBN blur", False)
# # Compute and display NDVI, NDVI slices and NDVI gradient.
# ndvi = img.normalizedDifference(["N", "R"])
# # print(ui.Chart.image.histogram(ndvi, geometry, 10))
# Map.addLayer(ndvi, {'min':0, 'max':1, 'palette': ["black", "tan", "green", "darkgreen"]}, "NDVI", False)
# Map.addLayer(ndvi.gt([0, 0.2, 0.40, 0.60, 0.80, 1.00]).reduce('sum'), {'min':0, 'max': 6}, "NDVI steps", False)
# ndviGradient = ndvi.gradient().pow(2).reduce('sum').sqrt()
# Map.addLayer(ndviGradient, {'min':0, 'max':0.01}, "NDVI gradient", False)
# gradient = img.spectralErosion().spectralGradient('emd')
# Map.addLayer(gradient, {'min':0, 'max': 0.3}, "emd", False)
# # Run SNIC on the regular square grid.
# snic = ee.Algorithms.Image.Segmentation.SNIC({
# 'image': img,
# 'size': 32,
# compactness: 5,
# connectivity: 8,
# neighborhoodSize:256,
# seeds: seeds
# }).select(["R_mean", "G_mean", "B_mean", "N_mean", "clusters"], ["R", "G", "B", "N", "clusters"])
# clusters = snic.select("clusters")
# Map.addLayer(clusters.randomVisualizer(), {}, "clusters")
# Map.addLayer(snic, {'bands': ["R", "G", "B"], 'min':0, 'max':1, 'gamma': 0.8}, "means", False)
# Map.addLayer(expandSeeds(seeds))
# # Compute per-cluster stdDev.
# stdDev = img.addBands(clusters).reduceConnectedComponents(ee.Reducer.stdDev(), "clusters", 256)
# Map.addLayer(stdDev, {'min':0, 'max':0.1}, "StdDev")
# # Display outliers as transparent
# outliers = stdDev.reduce('sum').gt(0.25)
# Map.addLayer(outliers.updateMask(outliers.Not()), {}, "Outliers", False)
# # Within each outlier, find most distant member.
# distance = img.select(bands).spectralDistance(snic.select(bands), "sam").updateMask(outliers)
# maxDistance = distance.addBands(clusters).reduceConnectedComponents(ee.Reducer.max(), "clusters", 256)
# Map.addLayer(distance, {'min':0, 'max':0.3}, "max distance")
# Map.addLayer(expandSeeds(expandSeeds(distance.eq(maxDistance))), {'palette': ["red"]}, "second seeds")
# newSeeds = seeds.unmask(0).add(distance.eq(maxDistance).unmask(0))
# newSeeds = newSeeds.updateMask(newSeeds)
# # Run SNIC again with both sets of seeds.
# snic2 = ee.Algorithms.Image.Segmentation.SNIC({
# 'image': img,
# 'size': 32,
# compactness: 5,
# connectivity: 8,
# neighborhoodSize: 256,
# seeds: newSeeds
# }).select(["R_mean", "G_mean", "B_mean", "N_mean", "clusters"], ["R", "G", "B", "N", "clusters"])
# clusters2 = snic2.select("clusters")
# Map.addLayer(clusters2.randomVisualizer(), {}, "clusters 2")
# Map.addLayer(snic2, {'bands': ["R", "G", "B"], 'min':0, 'max':1, 'gamma': 0.8}, "means", False)
# # Compute outliers again.
# stdDev2 = img.addBands(clusters2).reduceConnectedComponents(ee.Reducer.stdDev(), "clusters", 256)
# Map.addLayer(stdDev2, {'min':0, 'max':0.1}, "StdDev 2")
# outliers2 = stdDev2.reduce('sum').gt(0.25)
# outliers2 = outliers2.updateMask(outliers2.Not())
# Map.addLayer(outliers2, {}, "Outliers 2", False)
# # Show the final set of seeds.
# Map.addLayer(expandSeeds(newSeeds), {'palette': "white"}, "newSeeds")
# Map.addLayer(expandSeeds(distance.eq(maxDistance)), {'palette': ["red"]}, "second seeds")
# # Area, Perimeter, Width and Height (using snic1 for speed)
# area = ee.Image.pixelArea().addBands(clusters).reduceConnectedComponents(ee.Reducer.sum(), "clusters", 256)
# Map.addLayer(area, {'min':50000, 'max': 500000}, "Cluster Area")
# minMax = clusters.reduceNeighborhood(ee.Reducer.minMax(), ee.Kernel.square(1))
# perimeterPixels = minMax.select(0).neq(minMax.select(1)).rename('perimeter')
# Map.addLayer(perimeterPixels, {'min': 0, 'max': 1}, 'perimeterPixels')
# perimeter = perimeterPixels.addBands(clusters) \
# .reduceConnectedComponents(ee.Reducer.sum(), 'clusters', 256)
# Map.addLayer(perimeter, {'min': 100, 'max': 400}, 'Perimeter size', False)
# sizes = ee.Image.pixelLonLat().addBands(clusters).reduceConnectedComponents(ee.Reducer.minMax(), "clusters", 256)
# width = sizes.select("longitude_max").subtract(sizes.select("longitude_min"))
# height = sizes.select("latitude_max").subtract(sizes.select("latitude_min"))
# Map.addLayer(width, {'min':0, 'max':0.02}, "Cluster width")
# Map.addLayer(height, {'min':0, 'max':0.02}, "Cluster height")
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
|
github_jupyter
|
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
# Add Earth Engine dataset
# imageCollection = ee.ImageCollection("USDA/NAIP/DOQQ"),
# geometry = ee.Geometry.Polygon(
# [[[-121.89511299133301, 38.98496606984683],
# [-121.89511299133301, 38.909335196675435],
# [-121.69358253479004, 38.909335196675435],
# [-121.69358253479004, 38.98496606984683]]], {}, False),
# geometry2 = ee.Geometry.Polygon(
# [[[-108.34304809570307, 36.66975278349341],
# [-108.34225416183466, 36.66977859999848],
# [-108.34226489067072, 36.67042400981031],
# [-108.34308028221125, 36.670380982657925]]]),
# imageCollection2 = ee.ImageCollection("USDA/NASS/CDL"),
# cdl2016 = ee.Image("USDA/NASS/CDL/2016")
# Map.centerObject(geometry, {}, 'roi')
# # Map.addLayer(ee.Image(1), {'palette': "white"})
# cdl2016 = cdl2016.select(0).clip(geometry)
# function erode(img, distance) {
# d = (img.Not().unmask(1) \
# .fastDistanceTransform(30).sqrt() \
# .multiply(ee.Image.pixelArea().sqrt()))
# return img.updateMask(d.gt(distance))
# }
# function dilate(img, distance) {
# d = (img.fastDistanceTransform(30).sqrt() \
# .multiply(ee.Image.pixelArea().sqrt()))
# return d.lt(distance)
# }
# function expandSeeds(seeds) {
# seeds = seeds.unmask(0).focal_max()
# return seeds.updateMask(seeds)
# }
# bands = ["R", "G", "B", "N"]
# img = imageCollection \
# .filterDate('2015-01-01', '2017-01-01') \
# .filterBounds(geometry) \
# .mosaic()
# img = ee.Image(img).clip(geometry).divide(255).select(bands)
# Map.addLayer(img, {'gamma': 0.8}, "RGBN", False)
# seeds = ee.Algorithms.Image.Segmentation.seedGrid(36)
# # Apply a softening.
# kernel = ee.Kernel.gaussian(3)
# img = img.convolve(kernel)
# Map.addLayer(img, {'gamma': 0.8}, "RGBN blur", False)
# # Compute and display NDVI, NDVI slices and NDVI gradient.
# ndvi = img.normalizedDifference(["N", "R"])
# # print(ui.Chart.image.histogram(ndvi, geometry, 10))
# Map.addLayer(ndvi, {'min':0, 'max':1, 'palette': ["black", "tan", "green", "darkgreen"]}, "NDVI", False)
# Map.addLayer(ndvi.gt([0, 0.2, 0.40, 0.60, 0.80, 1.00]).reduce('sum'), {'min':0, 'max': 6}, "NDVI steps", False)
# ndviGradient = ndvi.gradient().pow(2).reduce('sum').sqrt()
# Map.addLayer(ndviGradient, {'min':0, 'max':0.01}, "NDVI gradient", False)
# gradient = img.spectralErosion().spectralGradient('emd')
# Map.addLayer(gradient, {'min':0, 'max': 0.3}, "emd", False)
# # Run SNIC on the regular square grid.
# snic = ee.Algorithms.Image.Segmentation.SNIC({
# 'image': img,
# 'size': 32,
# compactness: 5,
# connectivity: 8,
# neighborhoodSize:256,
# seeds: seeds
# }).select(["R_mean", "G_mean", "B_mean", "N_mean", "clusters"], ["R", "G", "B", "N", "clusters"])
# clusters = snic.select("clusters")
# Map.addLayer(clusters.randomVisualizer(), {}, "clusters")
# Map.addLayer(snic, {'bands': ["R", "G", "B"], 'min':0, 'max':1, 'gamma': 0.8}, "means", False)
# Map.addLayer(expandSeeds(seeds))
# # Compute per-cluster stdDev.
# stdDev = img.addBands(clusters).reduceConnectedComponents(ee.Reducer.stdDev(), "clusters", 256)
# Map.addLayer(stdDev, {'min':0, 'max':0.1}, "StdDev")
# # Display outliers as transparent
# outliers = stdDev.reduce('sum').gt(0.25)
# Map.addLayer(outliers.updateMask(outliers.Not()), {}, "Outliers", False)
# # Within each outlier, find most distant member.
# distance = img.select(bands).spectralDistance(snic.select(bands), "sam").updateMask(outliers)
# maxDistance = distance.addBands(clusters).reduceConnectedComponents(ee.Reducer.max(), "clusters", 256)
# Map.addLayer(distance, {'min':0, 'max':0.3}, "max distance")
# Map.addLayer(expandSeeds(expandSeeds(distance.eq(maxDistance))), {'palette': ["red"]}, "second seeds")
# newSeeds = seeds.unmask(0).add(distance.eq(maxDistance).unmask(0))
# newSeeds = newSeeds.updateMask(newSeeds)
# # Run SNIC again with both sets of seeds.
# snic2 = ee.Algorithms.Image.Segmentation.SNIC({
# 'image': img,
# 'size': 32,
# compactness: 5,
# connectivity: 8,
# neighborhoodSize: 256,
# seeds: newSeeds
# }).select(["R_mean", "G_mean", "B_mean", "N_mean", "clusters"], ["R", "G", "B", "N", "clusters"])
# clusters2 = snic2.select("clusters")
# Map.addLayer(clusters2.randomVisualizer(), {}, "clusters 2")
# Map.addLayer(snic2, {'bands': ["R", "G", "B"], 'min':0, 'max':1, 'gamma': 0.8}, "means", False)
# # Compute outliers again.
# stdDev2 = img.addBands(clusters2).reduceConnectedComponents(ee.Reducer.stdDev(), "clusters", 256)
# Map.addLayer(stdDev2, {'min':0, 'max':0.1}, "StdDev 2")
# outliers2 = stdDev2.reduce('sum').gt(0.25)
# outliers2 = outliers2.updateMask(outliers2.Not())
# Map.addLayer(outliers2, {}, "Outliers 2", False)
# # Show the final set of seeds.
# Map.addLayer(expandSeeds(newSeeds), {'palette': "white"}, "newSeeds")
# Map.addLayer(expandSeeds(distance.eq(maxDistance)), {'palette': ["red"]}, "second seeds")
# # Area, Perimeter, Width and Height (using snic1 for speed)
# area = ee.Image.pixelArea().addBands(clusters).reduceConnectedComponents(ee.Reducer.sum(), "clusters", 256)
# Map.addLayer(area, {'min':50000, 'max': 500000}, "Cluster Area")
# minMax = clusters.reduceNeighborhood(ee.Reducer.minMax(), ee.Kernel.square(1))
# perimeterPixels = minMax.select(0).neq(minMax.select(1)).rename('perimeter')
# Map.addLayer(perimeterPixels, {'min': 0, 'max': 1}, 'perimeterPixels')
# perimeter = perimeterPixels.addBands(clusters) \
# .reduceConnectedComponents(ee.Reducer.sum(), 'clusters', 256)
# Map.addLayer(perimeter, {'min': 100, 'max': 400}, 'Perimeter size', False)
# sizes = ee.Image.pixelLonLat().addBands(clusters).reduceConnectedComponents(ee.Reducer.minMax(), "clusters", 256)
# width = sizes.select("longitude_max").subtract(sizes.select("longitude_min"))
# height = sizes.select("latitude_max").subtract(sizes.select("latitude_min"))
# Map.addLayer(width, {'min':0, 'max':0.02}, "Cluster width")
# Map.addLayer(height, {'min':0, 'max':0.02}, "Cluster height")
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
| 0.665845 | 0.958654 |
# Introduction to XGBoost Spark with GPU
Taxi is an example of xgboost regressor. In this notebook, we will show you how to load data, train the xgboost model and use this model to predict "fare_amount" of your taxi trip.
A few libraries are required:
1. NumPy
2. cudf jar
3. xgboost4j jar
4. xgboost4j-spark jar
#### Import All Libraries
```
from ml.dmlc.xgboost4j.scala.spark import XGBoostRegressionModel, XGBoostRegressor
from ml.dmlc.xgboost4j.scala.spark.rapids import GpuDataReader
from pyspark.ml.evaluation import RegressionEvaluator
from pyspark.sql import SparkSession
from pyspark.sql.types import FloatType, IntegerType, StructField, StructType
from time import time
```
Note on CPU version: `GpuDataReader` is not necessary, but two extra libraries are required.
```Python
from pyspark.ml.feature import VectorAssembler
from pyspark.sql.functions import col
```
#### Create Spark Session
```
spark = SparkSession.builder.getOrCreate()
```
#### Specify the Data Schema and Load the Data
```
label = 'fare_amount'
schema = StructType([
StructField('vendor_id', FloatType()),
StructField('passenger_count', FloatType()),
StructField('trip_distance', FloatType()),
StructField('pickup_longitude', FloatType()),
StructField('pickup_latitude', FloatType()),
StructField('rate_code', FloatType()),
StructField('store_and_fwd', FloatType()),
StructField('dropoff_longitude', FloatType()),
StructField('dropoff_latitude', FloatType()),
StructField(label, FloatType()),
StructField('hour', FloatType()),
StructField('year', IntegerType()),
StructField('month', IntegerType()),
StructField('day', FloatType()),
StructField('day_of_week', FloatType()),
StructField('is_weekend', FloatType()),
])
features = [ x.name for x in schema if x.name != label ]
train_data = GpuDataReader(spark).schema(schema).option('header', True).csv('/data/datasets/taxi-small/train')
eval_data = GpuDataReader(spark).schema(schema).option('header', True).csv('/data/datasets/taxi-small/eval')
```
Note on CPU version: Data reader is created with `spark.read` instead of `GpuDataReader(spark)`. Also vectorization is required, which means you need to assemble all feature columns into one column.
```Python
def vectorize(data_frame):
to_floats = [ col(x.name).cast(FloatType()) for x in data_frame.schema ]
return (VectorAssembler()
.setInputCols(features)
.setOutputCol('features')
.transform(data_frame.select(to_floats))
.select(col('features'), col(label)))
train_data = spark.read.schema(schema).option('header', True).csv('/data/datasets/taxi-small/train')
eval_data = spark.read.schema(schema).option('header', True).csv('/data/datasets/taxi-small/eval')
train_data = vectorize(train_data)
eval_data = vectorize(eval_data)
```
#### Create XGBoostRegressor
```
params = {
'eta': 0.05,
'treeMethod': 'gpu_hist',
'maxDepth': 8,
'subsample': 0.8,
'gamma': 1.0,
'numRound': 100,
'numWorkers': 1,
}
regressor = XGBoostRegressor(**params).setLabelCol(label).setFeaturesCols(features)
```
Note on CPU version: The CPU version provides the `setFeaturesCol` function, that's why vectorization is required. The parameter `num_workers` should be set to the number of machines with GPU in Spark cluster in GPU version, while it can be set to the number of your CPU cores in CPU version. The tree method `gpu_hist` is designed for GPU training, while tree method `hist` is designed for CPU training.
```Python
regressor = XGBoostRegressor(**params).setLabelCol(label).setFeaturesCol('features')
```
#### Train the Data with Benchmark
```
def with_benchmark(phrase, action):
start = time()
result = action()
end = time()
print('{} takes {} seconds'.format(phrase, round(end - start, 2)))
return result
model = with_benchmark('Training', lambda: regressor.fit(train_data))
```
#### Save and Reload the Model
```
model.write().overwrite().save('/data/new-model-path')
loaded_model = XGBoostRegressionModel().load('/data/new-model-path')
```
#### Transformation and Show Result Sample
```
def transform():
result = loaded_model.transform(eval_data).cache()
result.foreachPartition(lambda _: None)
return result
result = with_benchmark('Transformation', transform)
result.select('vendor_id', 'passenger_count', 'trip_distance', label, 'prediction').show(5)
```
Note on CPU version: You cannot `select` the feature columns after vectorization. So please use `result.show(5)` instead.
#### Evaluation
```
accuracy = with_benchmark(
'Evaluation',
lambda: RegressionEvaluator().setLabelCol(label).evaluate(result))
print('RMSI is ' + str(accuracy))
```
#### Stop
```
spark.stop()
```
|
github_jupyter
|
from ml.dmlc.xgboost4j.scala.spark import XGBoostRegressionModel, XGBoostRegressor
from ml.dmlc.xgboost4j.scala.spark.rapids import GpuDataReader
from pyspark.ml.evaluation import RegressionEvaluator
from pyspark.sql import SparkSession
from pyspark.sql.types import FloatType, IntegerType, StructField, StructType
from time import time
from pyspark.ml.feature import VectorAssembler
from pyspark.sql.functions import col
spark = SparkSession.builder.getOrCreate()
label = 'fare_amount'
schema = StructType([
StructField('vendor_id', FloatType()),
StructField('passenger_count', FloatType()),
StructField('trip_distance', FloatType()),
StructField('pickup_longitude', FloatType()),
StructField('pickup_latitude', FloatType()),
StructField('rate_code', FloatType()),
StructField('store_and_fwd', FloatType()),
StructField('dropoff_longitude', FloatType()),
StructField('dropoff_latitude', FloatType()),
StructField(label, FloatType()),
StructField('hour', FloatType()),
StructField('year', IntegerType()),
StructField('month', IntegerType()),
StructField('day', FloatType()),
StructField('day_of_week', FloatType()),
StructField('is_weekend', FloatType()),
])
features = [ x.name for x in schema if x.name != label ]
train_data = GpuDataReader(spark).schema(schema).option('header', True).csv('/data/datasets/taxi-small/train')
eval_data = GpuDataReader(spark).schema(schema).option('header', True).csv('/data/datasets/taxi-small/eval')
def vectorize(data_frame):
to_floats = [ col(x.name).cast(FloatType()) for x in data_frame.schema ]
return (VectorAssembler()
.setInputCols(features)
.setOutputCol('features')
.transform(data_frame.select(to_floats))
.select(col('features'), col(label)))
train_data = spark.read.schema(schema).option('header', True).csv('/data/datasets/taxi-small/train')
eval_data = spark.read.schema(schema).option('header', True).csv('/data/datasets/taxi-small/eval')
train_data = vectorize(train_data)
eval_data = vectorize(eval_data)
params = {
'eta': 0.05,
'treeMethod': 'gpu_hist',
'maxDepth': 8,
'subsample': 0.8,
'gamma': 1.0,
'numRound': 100,
'numWorkers': 1,
}
regressor = XGBoostRegressor(**params).setLabelCol(label).setFeaturesCols(features)
regressor = XGBoostRegressor(**params).setLabelCol(label).setFeaturesCol('features')
def with_benchmark(phrase, action):
start = time()
result = action()
end = time()
print('{} takes {} seconds'.format(phrase, round(end - start, 2)))
return result
model = with_benchmark('Training', lambda: regressor.fit(train_data))
model.write().overwrite().save('/data/new-model-path')
loaded_model = XGBoostRegressionModel().load('/data/new-model-path')
def transform():
result = loaded_model.transform(eval_data).cache()
result.foreachPartition(lambda _: None)
return result
result = with_benchmark('Transformation', transform)
result.select('vendor_id', 'passenger_count', 'trip_distance', label, 'prediction').show(5)
accuracy = with_benchmark(
'Evaluation',
lambda: RegressionEvaluator().setLabelCol(label).evaluate(result))
print('RMSI is ' + str(accuracy))
spark.stop()
| 0.730001 | 0.960731 |
<!--BOOK_INFORMATION-->
<img align="left" style="padding-right:10px;" src="figures/PDSH-cover-small.png">
*This notebook contains an excerpt from the [Python Data Science Handbook](http://shop.oreilly.com/product/0636920034919.do) by Jake VanderPlas; the content is available [on GitHub](https://github.com/jakevdp/PythonDataScienceHandbook).*
*The text is released under the [CC-BY-NC-ND license](https://creativecommons.org/licenses/by-nc-nd/3.0/us/legalcode), and code is released under the [MIT license](https://opensource.org/licenses/MIT). If you find this content useful, please consider supporting the work by [buying the book](http://shop.oreilly.com/product/0636920034919.do)!*
*No changes were made to the contents of this notebook from the original.*
<!--NAVIGATION-->
< [Geographic Data with Basemap](04.13-Geographic-Data-With-Basemap.ipynb) | [Contents](Index.ipynb) | [Further Resources](04.15-Further-Resources.ipynb) >
# Visualization with Seaborn
Matplotlib has proven to be an incredibly useful and popular visualization tool, but even avid users will admit it often leaves much to be desired.
There are several valid complaints about Matplotlib that often come up:
- Prior to version 2.0, Matplotlib's defaults are not exactly the best choices. It was based off of MATLAB circa 1999, and this often shows.
- Matplotlib's API is relatively low level. Doing sophisticated statistical visualization is possible, but often requires a *lot* of boilerplate code.
- Matplotlib predated Pandas by more than a decade, and thus is not designed for use with Pandas ``DataFrame``s. In order to visualize data from a Pandas ``DataFrame``, you must extract each ``Series`` and often concatenate them together into the right format. It would be nicer to have a plotting library that can intelligently use the ``DataFrame`` labels in a plot.
An answer to these problems is [Seaborn](http://seaborn.pydata.org/). Seaborn provides an API on top of Matplotlib that offers sane choices for plot style and color defaults, defines simple high-level functions for common statistical plot types, and integrates with the functionality provided by Pandas ``DataFrame``s.
To be fair, the Matplotlib team is addressing this: it has recently added the ``plt.style`` tools discussed in [Customizing Matplotlib: Configurations and Style Sheets](04.11-Settings-and-Stylesheets.ipynb), and is starting to handle Pandas data more seamlessly.
The 2.0 release of the library will include a new default stylesheet that will improve on the current status quo.
But for all the reasons just discussed, Seaborn remains an extremely useful addon.
## Seaborn Versus Matplotlib
Here is an example of a simple random-walk plot in Matplotlib, using its classic plot formatting and colors.
We start with the typical imports:
```
import matplotlib.pyplot as plt
plt.style.use('classic')
%matplotlib inline
import numpy as np
import pandas as pd
```
Now we create some random walk data:
```
# Create some data
rng = np.random.RandomState(0)
x = np.linspace(0, 10, 500)
y = np.cumsum(rng.randn(500, 6), 0)
```
And do a simple plot:
```
# Plot the data with Matplotlib defaults
plt.plot(x, y)
plt.legend('ABCDEF', ncol=2, loc='upper left');
```
Although the result contains all the information we'd like it to convey, it does so in a way that is not all that aesthetically pleasing, and even looks a bit old-fashioned in the context of 21st-century data visualization.
Now let's take a look at how it works with Seaborn.
As we will see, Seaborn has many of its own high-level plotting routines, but it can also overwrite Matplotlib's default parameters and in turn get even simple Matplotlib scripts to produce vastly superior output.
We can set the style by calling Seaborn's ``set()`` method.
By convention, Seaborn is imported as ``sns``:
```
import seaborn as sns
sns.set()
```
Now let's rerun the same two lines as before:
```
# same plotting code as above!
plt.plot(x, y)
plt.legend('ABCDEF', ncol=2, loc='upper left');
```
Ah, much better!
## Exploring Seaborn Plots
The main idea of Seaborn is that it provides high-level commands to create a variety of plot types useful for statistical data exploration, and even some statistical model fitting.
Let's take a look at a few of the datasets and plot types available in Seaborn. Note that all of the following *could* be done using raw Matplotlib commands (this is, in fact, what Seaborn does under the hood) but the Seaborn API is much more convenient.
### Histograms, KDE, and densities
Often in statistical data visualization, all you want is to plot histograms and joint distributions of variables.
We have seen that this is relatively straightforward in Matplotlib:
```
data = np.random.multivariate_normal([0, 0], [[5, 2], [2, 2]], size=2000)
data = pd.DataFrame(data, columns=['x', 'y'])
for col in 'xy':
plt.hist(data[col], normed=True, alpha=0.5)
```
Rather than a histogram, we can get a smooth estimate of the distribution using a kernel density estimation, which Seaborn does with ``sns.kdeplot``:
```
for col in 'xy':
sns.kdeplot(data[col], shade=True)
```
Histograms and KDE can be combined using ``distplot``:
```
sns.distplot(data['x'])
sns.distplot(data['y']);
```
If we pass the full two-dimensional dataset to ``kdeplot``, we will get a two-dimensional visualization of the data:
```
sns.kdeplot(data);
```
We can see the joint distribution and the marginal distributions together using ``sns.jointplot``.
For this plot, we'll set the style to a white background:
```
with sns.axes_style('white'):
sns.jointplot("x", "y", data, kind='kde');
```
There are other parameters that can be passed to ``jointplot``—for example, we can use a hexagonally based histogram instead:
```
with sns.axes_style('white'):
sns.jointplot("x", "y", data, kind='hex')
```
### Pair plots
When you generalize joint plots to datasets of larger dimensions, you end up with *pair plots*. This is very useful for exploring correlations between multidimensional data, when you'd like to plot all pairs of values against each other.
We'll demo this with the well-known Iris dataset, which lists measurements of petals and sepals of three iris species:
```
iris = sns.load_dataset("iris")
iris.head()
```
Visualizing the multidimensional relationships among the samples is as easy as calling ``sns.pairplot``:
```
sns.pairplot(iris, hue='species', size=2.5);
```
### Faceted histograms
Sometimes the best way to view data is via histograms of subsets. Seaborn's ``FacetGrid`` makes this extremely simple.
We'll take a look at some data that shows the amount that restaurant staff receive in tips based on various indicator data:
```
tips = sns.load_dataset('tips')
tips.head()
tips['tip_pct'] = 100 * tips['tip'] / tips['total_bill']
grid = sns.FacetGrid(tips, row="sex", col="time", margin_titles=True)
grid.map(plt.hist, "tip_pct", bins=np.linspace(0, 40, 15));
```
### Factor plots
Factor plots can be useful for this kind of visualization as well. This allows you to view the distribution of a parameter within bins defined by any other parameter:
```
with sns.axes_style(style='ticks'):
g = sns.factorplot("day", "total_bill", "sex", data=tips, kind="box")
g.set_axis_labels("Day", "Total Bill");
```
### Joint distributions
Similar to the pairplot we saw earlier, we can use ``sns.jointplot`` to show the joint distribution between different datasets, along with the associated marginal distributions:
```
with sns.axes_style('white'):
sns.jointplot("total_bill", "tip", data=tips, kind='hex')
```
The joint plot can even do some automatic kernel density estimation and regression:
```
sns.jointplot("total_bill", "tip", data=tips, kind='reg');
```
### Bar plots
Time series can be plotted using ``sns.factorplot``. In the following example, we'll use the Planets data that we first saw in [Aggregation and Grouping](03.08-Aggregation-and-Grouping.ipynb):
```
planets = sns.load_dataset('planets')
planets.head()
with sns.axes_style('white'):
g = sns.factorplot("year", data=planets, aspect=2,
kind="count", color='steelblue')
g.set_xticklabels(step=5)
```
We can learn more by looking at the *method* of discovery of each of these planets:
```
with sns.axes_style('white'):
g = sns.factorplot("year", data=planets, aspect=4.0, kind='count',
hue='method', order=range(2001, 2015))
g.set_ylabels('Number of Planets Discovered')
```
For more information on plotting with Seaborn, see the [Seaborn documentation](http://seaborn.pydata.org/), a [tutorial](http://seaborn.pydata.org/
tutorial.htm), and the [Seaborn gallery](http://seaborn.pydata.org/examples/index.html).
## Example: Exploring Marathon Finishing Times
Here we'll look at using Seaborn to help visualize and understand finishing results from a marathon.
I've scraped the data from sources on the Web, aggregated it and removed any identifying information, and put it on GitHub where it can be downloaded
(if you are interested in using Python for web scraping, I would recommend [*Web Scraping with Python*](http://shop.oreilly.com/product/0636920034391.do) by Ryan Mitchell).
We will start by downloading the data from
the Web, and loading it into Pandas:
```
#!curl -O https://raw.githubusercontent.com/jakevdp/marathon-data/master/marathon-data.csv
data = pd.read_csv('marathon-data.csv')
data.head()
```
By default, Pandas loaded the time columns as Python strings (type ``object``); we can see this by looking at the ``dtypes`` attribute of the DataFrame:
```
data.dtypes
```
Let's fix this by providing a converter for the times:
```
import datetime as dt #pd.datatools.timedelta deprecated
def convert_time(s):
h, m, s = map(int, s.split(':'))
return dt.timedelta(hours=h, minutes=m, seconds=s)
data = pd.read_csv('marathon-data.csv',
converters={'split':convert_time, 'final':convert_time})
data.head()
data.dtypes
```
That looks much better. For the purpose of our Seaborn plotting utilities, let's next add columns that give the times in seconds:
```
data['split_sec'] = data['split'].astype(int) / 1E9
data['final_sec'] = data['final'].astype(int) / 1E9
data.head()
```
To get an idea of what the data looks like, we can plot a ``jointplot`` over the data:
```
with sns.axes_style('white'):
g = sns.jointplot("split_sec", "final_sec", data, kind='hex')
g.ax_joint.plot(np.linspace(4000, 16000),
np.linspace(8000, 32000), ':k')
```
The dotted line shows where someone's time would lie if they ran the marathon at a perfectly steady pace. The fact that the distribution lies above this indicates (as you might expect) that most people slow down over the course of the marathon.
If you have run competitively, you'll know that those who do the opposite—run faster during the second half of the race—are said to have "negative-split" the race.
Let's create another column in the data, the split fraction, which measures the degree to which each runner negative-splits or positive-splits the race:
```
data['split_frac'] = 1 - 2 * data['split_sec'] / data['final_sec']
data.head()
```
Where this split difference is less than zero, the person negative-split the race by that fraction.
Let's do a distribution plot of this split fraction:
```
sns.distplot(data['split_frac'], kde=False);
plt.axvline(0, color="k", linestyle="--");
sum(data.split_frac < 0)
```
Out of nearly 40,000 participants, there were only 250 people who negative-split their marathon.
Let's see whether there is any correlation between this split fraction and other variables. We'll do this using a ``pairgrid``, which draws plots of all these correlations:
```
g = sns.PairGrid(data, vars=['age', 'split_sec', 'final_sec', 'split_frac'],
hue='gender', palette='RdBu_r')
g.map(plt.scatter, alpha=0.8)
g.add_legend();
```
It looks like the split fraction does not correlate particularly with age, but does correlate with the final time: faster runners tend to have closer to even splits on their marathon time.
(We see here that Seaborn is no panacea for Matplotlib's ills when it comes to plot styles: in particular, the x-axis labels overlap. Because the output is a simple Matplotlib plot, however, the methods in [Customizing Ticks](04.10-Customizing-Ticks.ipynb) can be used to adjust such things if desired.)
The difference between men and women here is interesting. Let's look at the histogram of split fractions for these two groups:
```
sns.kdeplot(data.split_frac[data.gender=='M'], label='men', shade=True)
sns.kdeplot(data.split_frac[data.gender=='W'], label='women', shade=True)
plt.xlabel('split_frac');
```
The interesting thing here is that there are many more men than women who are running close to an even split!
This almost looks like some kind of bimodal distribution among the men and women. Let's see if we can suss-out what's going on by looking at the distributions as a function of age.
A nice way to compare distributions is to use a *violin plot*
```
sns.violinplot("gender", "split_frac", data=data,
palette=["lightblue", "lightpink"]);
```
This is yet another way to compare the distributions between men and women.
Let's look a little deeper, and compare these violin plots as a function of age. We'll start by creating a new column in the array that specifies the decade of age that each person is in:
```
data['age_dec'] = data.age.map(lambda age: 10 * (age // 10))
data.head()
men = (data.gender == 'M')
women = (data.gender == 'W')
with sns.axes_style(style=None):
sns.violinplot("age_dec", "split_frac", hue="gender", data=data,
split=True, inner="quartile",
palette=["lightblue", "lightpink"]);
```
Looking at this, we can see where the distributions of men and women differ: the split distributions of men in their 20s to 50s show a pronounced over-density toward lower splits when compared to women of the same age (or of any age, for that matter).
Also surprisingly, the 80-year-old women seem to outperform *everyone* in terms of their split time. This is probably due to the fact that we're estimating the distribution from small numbers, as there are only a handful of runners in that range:
```
(data.age > 80).sum()
```
Back to the men with negative splits: who are these runners? Does this split fraction correlate with finishing quickly? We can plot this very easily. We'll use ``regplot``, which will automatically fit a linear regression to the data:
```
g = sns.lmplot('final_sec', 'split_frac', col='gender', data=data,
markers=".", scatter_kws=dict(color='c'))
g.map(plt.axhline, y=0.1, color="k", ls=":");
```
Apparently the people with fast splits are the elite runners who are finishing within ~15,000 seconds, or about 4 hours. People slower than that are much less likely to have a fast second split.
<!--NAVIGATION-->
< [Geographic Data with Basemap](04.13-Geographic-Data-With-Basemap.ipynb) | [Contents](Index.ipynb) | [Further Resources](04.15-Further-Resources.ipynb) >
|
github_jupyter
|
import matplotlib.pyplot as plt
plt.style.use('classic')
%matplotlib inline
import numpy as np
import pandas as pd
# Create some data
rng = np.random.RandomState(0)
x = np.linspace(0, 10, 500)
y = np.cumsum(rng.randn(500, 6), 0)
# Plot the data with Matplotlib defaults
plt.plot(x, y)
plt.legend('ABCDEF', ncol=2, loc='upper left');
import seaborn as sns
sns.set()
# same plotting code as above!
plt.plot(x, y)
plt.legend('ABCDEF', ncol=2, loc='upper left');
data = np.random.multivariate_normal([0, 0], [[5, 2], [2, 2]], size=2000)
data = pd.DataFrame(data, columns=['x', 'y'])
for col in 'xy':
plt.hist(data[col], normed=True, alpha=0.5)
for col in 'xy':
sns.kdeplot(data[col], shade=True)
sns.distplot(data['x'])
sns.distplot(data['y']);
sns.kdeplot(data);
with sns.axes_style('white'):
sns.jointplot("x", "y", data, kind='kde');
with sns.axes_style('white'):
sns.jointplot("x", "y", data, kind='hex')
iris = sns.load_dataset("iris")
iris.head()
sns.pairplot(iris, hue='species', size=2.5);
tips = sns.load_dataset('tips')
tips.head()
tips['tip_pct'] = 100 * tips['tip'] / tips['total_bill']
grid = sns.FacetGrid(tips, row="sex", col="time", margin_titles=True)
grid.map(plt.hist, "tip_pct", bins=np.linspace(0, 40, 15));
with sns.axes_style(style='ticks'):
g = sns.factorplot("day", "total_bill", "sex", data=tips, kind="box")
g.set_axis_labels("Day", "Total Bill");
with sns.axes_style('white'):
sns.jointplot("total_bill", "tip", data=tips, kind='hex')
sns.jointplot("total_bill", "tip", data=tips, kind='reg');
planets = sns.load_dataset('planets')
planets.head()
with sns.axes_style('white'):
g = sns.factorplot("year", data=planets, aspect=2,
kind="count", color='steelblue')
g.set_xticklabels(step=5)
with sns.axes_style('white'):
g = sns.factorplot("year", data=planets, aspect=4.0, kind='count',
hue='method', order=range(2001, 2015))
g.set_ylabels('Number of Planets Discovered')
#!curl -O https://raw.githubusercontent.com/jakevdp/marathon-data/master/marathon-data.csv
data = pd.read_csv('marathon-data.csv')
data.head()
data.dtypes
import datetime as dt #pd.datatools.timedelta deprecated
def convert_time(s):
h, m, s = map(int, s.split(':'))
return dt.timedelta(hours=h, minutes=m, seconds=s)
data = pd.read_csv('marathon-data.csv',
converters={'split':convert_time, 'final':convert_time})
data.head()
data.dtypes
data['split_sec'] = data['split'].astype(int) / 1E9
data['final_sec'] = data['final'].astype(int) / 1E9
data.head()
with sns.axes_style('white'):
g = sns.jointplot("split_sec", "final_sec", data, kind='hex')
g.ax_joint.plot(np.linspace(4000, 16000),
np.linspace(8000, 32000), ':k')
data['split_frac'] = 1 - 2 * data['split_sec'] / data['final_sec']
data.head()
sns.distplot(data['split_frac'], kde=False);
plt.axvline(0, color="k", linestyle="--");
sum(data.split_frac < 0)
g = sns.PairGrid(data, vars=['age', 'split_sec', 'final_sec', 'split_frac'],
hue='gender', palette='RdBu_r')
g.map(plt.scatter, alpha=0.8)
g.add_legend();
sns.kdeplot(data.split_frac[data.gender=='M'], label='men', shade=True)
sns.kdeplot(data.split_frac[data.gender=='W'], label='women', shade=True)
plt.xlabel('split_frac');
sns.violinplot("gender", "split_frac", data=data,
palette=["lightblue", "lightpink"]);
data['age_dec'] = data.age.map(lambda age: 10 * (age // 10))
data.head()
men = (data.gender == 'M')
women = (data.gender == 'W')
with sns.axes_style(style=None):
sns.violinplot("age_dec", "split_frac", hue="gender", data=data,
split=True, inner="quartile",
palette=["lightblue", "lightpink"]);
(data.age > 80).sum()
g = sns.lmplot('final_sec', 'split_frac', col='gender', data=data,
markers=".", scatter_kws=dict(color='c'))
g.map(plt.axhline, y=0.1, color="k", ls=":");
| 0.669096 | 0.988906 |
# Object Detection Demo
Welcome to the object detection inference walkthrough! This notebook will walk you step by step through the process of using a pre-trained model to detect objects in an image. Make sure to follow the [installation instructions](https://github.com/tensorflow/models/blob/master/research/object_detection/g3doc/installation.md) before you start.
# Imports
```
import numpy as np
import os
import six.moves.urllib as urllib
import sys
import tarfile
import tensorflow as tf
import zipfile
import time
from collections import defaultdict
from io import StringIO
from matplotlib import pyplot as plt
from PIL import Image
print("Hello")
```
## Env setup
```
# This is needed to display the images.
%matplotlib inline
# This is needed since the notebook is stored in the object_detection folder.
sys.path.append("..")
print("Hello")
```
## Object detection imports
Here are the imports from the object detection module.
```
import label_map_util
import visualization_utils as vis_util
print("Hello")
```
# Model preparation
## Variables
Any model exported using the `export_inference_graph.py` tool can be loaded here simply by changing `PATH_TO_CKPT` to point to a new .pb file.
By default we use an "SSD with Mobilenet" model here. See the [detection model zoo](https://github.com/tensorflow/models/blob/master/research/object_detection/g3doc/detection_model_zoo.md) for a list of other models that can be run out-of-the-box with varying speeds and accuracies.
```
# What model to download.
MODEL_NAME = 'mask_rcnn_inception_v2_coco_2018_01_28'
MODEL_FILE = MODEL_NAME + '.tar.gz'
DOWNLOAD_BASE = 'http://download.tensorflow.org/models/object_detection/'
# Path to frozen detection graph. This is the actual model that is used for the object detection.
PATH_TO_CKPT = MODEL_NAME + '/frozen_inference_graph.pb'
# List of the strings that is used to add correct label for each box.
PATH_TO_LABELS = os.path.join('data', 'mscoco_label_map.pbtxt')
NUM_CLASSES = 90
print("DONE")
```
## Download Model
```
#opener = urllib.request.URLopener()
#opener.retrieve(DOWNLOAD_BASE + MODEL_FILE, MODEL_FILE)
tar_file = tarfile.open(MODEL_FILE)
for file in tar_file.getmembers():
file_name = os.path.basename(file.name)
if 'frozen_inference_graph.pb' in file_name:
tar_file.extract(file, os.getcwd())
print("DONE")
```
## Load a (frozen) Tensorflow model into memory.
```
detection_graph = tf.Graph()
with detection_graph.as_default():
od_graph_def = tf.GraphDef()
with tf.gfile.GFile(PATH_TO_CKPT, 'rb') as fid:
serialized_graph = fid.read()
od_graph_def.ParseFromString(serialized_graph)
tf.import_graph_def(od_graph_def, name='')
print("DONE")
```
## Loading label map
Label maps map indices to category names, so that when our convolution network predicts `5`, we know that this corresponds to `airplane`. Here we use internal utility functions, but anything that returns a dictionary mapping integers to appropriate string labels would be fine
```
label_map = label_map_util.load_labelmap(PATH_TO_LABELS)
categories = label_map_util.convert_label_map_to_categories(label_map, max_num_classes=NUM_CLASSES, use_display_name=True)
category_index = label_map_util.create_category_index(categories)
print("DONE")
```
## Helper code
```
def load_image_into_numpy_array(image):
(im_width, im_height) = image.size
return np.array(image.getdata()).reshape(
(im_height, im_width, 3)).astype(np.uint8)
print("DONE")
```
# Detection
```
# For the sake of simplicity we will use only 2 images:
# image1.jpg
# image2.jpg
# If you want to test the code with your images, just add path to the images to the TEST_IMAGE_PATHS.
PATH_TO_TEST_IMAGES_DIR = 'test_images'
TEST_IMAGE_PATHS = [ os.path.join(PATH_TO_TEST_IMAGES_DIR, 'image{}.jpg'.format(i)) for i in range(1,4)]
#print("Total no of images = ",i)
# Size, in inches, of the output images.
IMAGE_SIZE = (8,8)
print("Hello")
initial_time = time.time()
with detection_graph.as_default():
with tf.Session(graph=detection_graph) as sess:
# Definite input and output Tensors for detection_graph
image_tensor = detection_graph.get_tensor_by_name('image_tensor:0')
# Each box represents a part of the image where a particular object was detected.
detection_boxes = detection_graph.get_tensor_by_name('detection_boxes:0')
# Each score represent how level of confidence for each of the objects.
# Score is shown on the result image, together with the class label.
detection_scores = detection_graph.get_tensor_by_name('detection_scores:0')
detection_classes = detection_graph.get_tensor_by_name('detection_classes:0')
num_detections = detection_graph.get_tensor_by_name('num_detections:0')
for image_path in TEST_IMAGE_PATHS:
image = Image.open(image_path)
# the array based representation of the image will be used later in order to prepare the
# result image with boxes and labels on it.
image_np = load_image_into_numpy_array(image)
# Expand dimensions since the model expects images to have shape: [1, None, None, 3]
image_np_expanded = np.expand_dims(image_np, axis=0)
# Actual detection.
(boxes, scores, classes, num) = sess.run(
[detection_boxes, detection_scores, detection_classes, num_detections],
feed_dict={image_tensor: image_np_expanded})
# Visualization of the results of a detection.
vis_util.visualize_boxes_and_labels_on_image_array(
image_np,
np.squeeze(boxes),
np.squeeze(classes).astype(np.int32),
np.squeeze(scores),
category_index,
use_normalized_coordinates=True,
line_thickness=4)
plt.figure(figsize=IMAGE_SIZE)
plt.imshow(image_np)
final_time = time.time()
#print "Time taken is",final_time - initial_time
```
|
github_jupyter
|
import numpy as np
import os
import six.moves.urllib as urllib
import sys
import tarfile
import tensorflow as tf
import zipfile
import time
from collections import defaultdict
from io import StringIO
from matplotlib import pyplot as plt
from PIL import Image
print("Hello")
# This is needed to display the images.
%matplotlib inline
# This is needed since the notebook is stored in the object_detection folder.
sys.path.append("..")
print("Hello")
import label_map_util
import visualization_utils as vis_util
print("Hello")
# What model to download.
MODEL_NAME = 'mask_rcnn_inception_v2_coco_2018_01_28'
MODEL_FILE = MODEL_NAME + '.tar.gz'
DOWNLOAD_BASE = 'http://download.tensorflow.org/models/object_detection/'
# Path to frozen detection graph. This is the actual model that is used for the object detection.
PATH_TO_CKPT = MODEL_NAME + '/frozen_inference_graph.pb'
# List of the strings that is used to add correct label for each box.
PATH_TO_LABELS = os.path.join('data', 'mscoco_label_map.pbtxt')
NUM_CLASSES = 90
print("DONE")
#opener = urllib.request.URLopener()
#opener.retrieve(DOWNLOAD_BASE + MODEL_FILE, MODEL_FILE)
tar_file = tarfile.open(MODEL_FILE)
for file in tar_file.getmembers():
file_name = os.path.basename(file.name)
if 'frozen_inference_graph.pb' in file_name:
tar_file.extract(file, os.getcwd())
print("DONE")
detection_graph = tf.Graph()
with detection_graph.as_default():
od_graph_def = tf.GraphDef()
with tf.gfile.GFile(PATH_TO_CKPT, 'rb') as fid:
serialized_graph = fid.read()
od_graph_def.ParseFromString(serialized_graph)
tf.import_graph_def(od_graph_def, name='')
print("DONE")
label_map = label_map_util.load_labelmap(PATH_TO_LABELS)
categories = label_map_util.convert_label_map_to_categories(label_map, max_num_classes=NUM_CLASSES, use_display_name=True)
category_index = label_map_util.create_category_index(categories)
print("DONE")
def load_image_into_numpy_array(image):
(im_width, im_height) = image.size
return np.array(image.getdata()).reshape(
(im_height, im_width, 3)).astype(np.uint8)
print("DONE")
# For the sake of simplicity we will use only 2 images:
# image1.jpg
# image2.jpg
# If you want to test the code with your images, just add path to the images to the TEST_IMAGE_PATHS.
PATH_TO_TEST_IMAGES_DIR = 'test_images'
TEST_IMAGE_PATHS = [ os.path.join(PATH_TO_TEST_IMAGES_DIR, 'image{}.jpg'.format(i)) for i in range(1,4)]
#print("Total no of images = ",i)
# Size, in inches, of the output images.
IMAGE_SIZE = (8,8)
print("Hello")
initial_time = time.time()
with detection_graph.as_default():
with tf.Session(graph=detection_graph) as sess:
# Definite input and output Tensors for detection_graph
image_tensor = detection_graph.get_tensor_by_name('image_tensor:0')
# Each box represents a part of the image where a particular object was detected.
detection_boxes = detection_graph.get_tensor_by_name('detection_boxes:0')
# Each score represent how level of confidence for each of the objects.
# Score is shown on the result image, together with the class label.
detection_scores = detection_graph.get_tensor_by_name('detection_scores:0')
detection_classes = detection_graph.get_tensor_by_name('detection_classes:0')
num_detections = detection_graph.get_tensor_by_name('num_detections:0')
for image_path in TEST_IMAGE_PATHS:
image = Image.open(image_path)
# the array based representation of the image will be used later in order to prepare the
# result image with boxes and labels on it.
image_np = load_image_into_numpy_array(image)
# Expand dimensions since the model expects images to have shape: [1, None, None, 3]
image_np_expanded = np.expand_dims(image_np, axis=0)
# Actual detection.
(boxes, scores, classes, num) = sess.run(
[detection_boxes, detection_scores, detection_classes, num_detections],
feed_dict={image_tensor: image_np_expanded})
# Visualization of the results of a detection.
vis_util.visualize_boxes_and_labels_on_image_array(
image_np,
np.squeeze(boxes),
np.squeeze(classes).astype(np.int32),
np.squeeze(scores),
category_index,
use_normalized_coordinates=True,
line_thickness=4)
plt.figure(figsize=IMAGE_SIZE)
plt.imshow(image_np)
final_time = time.time()
#print "Time taken is",final_time - initial_time
| 0.330579 | 0.907763 |
# SMARTS selection and depiction
## Depict molecular components selected by a particular SMARTS
This notebook focuses on selecting molecules containing fragments matching a particular SMARTS query, and then depicting the components (i.e. bonds, angles, torsions) matching that particular query.
```
import openeye.oechem as oechem
import openeye.oedepict as oedepict
from IPython.display import display
import os
from __future__ import print_function
def depictMatch(mol, match, width=500, height=200):
"""Take in an OpenEye molecule and a substructure match and display the results
with (optionally) specified resolution."""
from IPython.display import Image
dopt = oedepict.OEPrepareDepictionOptions()
dopt.SetDepictOrientation( oedepict.OEDepictOrientation_Horizontal)
dopt.SetSuppressHydrogens(True)
oedepict.OEPrepareDepiction(mol, dopt)
opts = oedepict.OE2DMolDisplayOptions(width, height, oedepict.OEScale_AutoScale)
disp = oedepict.OE2DMolDisplay(mol, opts)
hstyle = oedepict.OEHighlightStyle_Color
hcolor = oechem.OEColor(oechem.OELightBlue)
oedepict.OEAddHighlighting(disp, hcolor, hstyle, match)
ofs = oechem.oeosstream()
oedepict.OERenderMolecule(ofs, 'png', disp)
ofs.flush()
return Image(data = "".join(ofs.str()))
import parmed
def createOpenMMSystem(mol):
"""
Generate OpenMM System and positions from an OEMol.
Parameters
----------
mol : OEMol
The molecule
Returns
-------
system : simtk.openmm.System
The OpenMM System
positions : simtk.unit.Quantity wrapped
Positions of the molecule
"""
# write mol2 file
ofsmol2 = oechem.oemolostream('molecule.mol2')
ofsmol2.SetFlavor( oechem.OEFormat_MOL2, oechem.OEOFlavor_MOL2_Forcefield );
oechem.OEWriteConstMolecule(ofsmol2, mol)
ofsmol2.close()
# write tleap input file
leap_input = """
lig = loadMol2 molecule.mol2
saveAmberParm lig prmtop inpcrd
quit
"""
outfile = open('leap.in', 'w')
outfile.write(leap_input)
outfile.close()
# run tleap
leaprc = 'leaprc.Frosst_AlkEthOH'
os.system( 'tleap -f %s -f leap.in > leap.out' % leaprc )
# check if param file was not saved (implies parameterization problems)
paramsNotSaved = 'Parameter file was not saved'
leaplog = open( 'leap.out', 'r' ).read()
if paramsNotSaved in leaplog:
raise Exception('Parameter file was not saved.')
# Read prmtop and inpcrd
amberparm = parmed.amber.AmberParm( 'prmtop', 'inpcrd' )
system = amberparm.createSystem()
return (system, amberparm.positions)
import copy
from simtk import openmm, unit
def getValenceEnergyComponent(system, positions, atoms):
"""
Get the OpenMM valence energy corresponding to a specified set of atoms (bond, angle, torsion).
Parameters
----------
system : simtk.openmm.System
The OpenMM System object for the molecule
positions : simtk.unit.Quantity of dimension (natoms,3) with units compatible with angstroms
The positions of the molecule
atoms : list or set of int
The set of atoms in the bond, angle, or torsion.
Returns
-------
potential : simtk.unit.Quantity with units compatible with kilocalories_per_mole
The energy of the valence component.
"""
atoms = set(atoms)
natoms = len(atoms) # number of atoms
# Create a copy of the original System object so we can manipulate it
system = copy.deepcopy(system)
# Determine Force types to keep
if natoms == 2:
forcename = 'HarmonicBondForce'
elif natoms == 3:
forcename = 'HarmonicAngleForce'
elif natoms == 4:
forcename = 'PeriodicTorsionForce'
else:
raise Exception('len(atoms) = %d, but must be in [2,3,4] for bond, angle, or torsion' % len(atoms))
# Discard Force objects we don't need
for force_index in reversed(range(system.getNumForces())):
if system.getForce(force_index).__class__.__name__ != forcename:
system.removeForce(force_index)
# Report on constraints
if forcename == 'HarmonicBondForce':
for constraint_index in range(system.getNumConstraints()):
[i, j, r0] = system.getConstraintParameters(constraint_index)
if set([i,j]) == atoms:
print('Bond is constrained')
# Zero out force components that don't involve the atoms
for force_index in range(system.getNumForces()):
force = system.getForce(force_index)
if forcename == 'HarmonicBondForce':
for param_index in range(force.getNumBonds()):
[i, j, r0, K] = force.getBondParameters(param_index)
if set([i,j]) != atoms:
K *= 0
else:
print('Match found: bond parameter %d : r0 = %s, K = %s' % (param_index, str(r0), str(K)))
force.setBondParameters(param_index, i, j, r0, K)
elif forcename == 'HarmonicAngleForce':
for param_index in range(force.getNumAngles()):
[i, j, k, theta0, K] = force.getAngleParameters(param_index)
if set([i,j,k]) != atoms:
K *= 0
else:
print('Match found: angle parameter %d : theta0 = %s, K = %s' % (param_index, str(theta0), str(K)))
force.setAngleParameters(param_index, i, j, k, theta0, K)
elif forcename == 'PeriodicTorsionForce':
for param_index in range(force.getNumTorsions()):
[i, j, k, l, periodicity, phase, K] = force.getTorsionParameters(param_index)
if set([i,j,k,l]) != atoms:
K *= 0
else:
print('Match found: torsion parameter %d : periodicity = %s, phase = %s, K = %s' % (param_index, str(periodicity), str(phase), str(K)))
force.setTorsionParameters(param_index, i, j, k, l, periodicity, phase, K)
# Compute energy
platform = openmm.Platform.getPlatformByName('Reference')
integrator = openmm.VerletIntegrator(1.0 * unit.femtoseconds)
context = openmm.Context(system, integrator, platform)
context.setPositions(positions)
potential = context.getState(getEnergy=True).getPotentialEnergy()
del context, integrator, system
# Return energy
return potential
#SMARTS query defining your search (and potentially forcefield term of interest)
#Note currently this must specify an angle term for the OpenMM energy to be
Smarts = '[#6X4]-[#6X4]-[#8X2]' # angle example
Smarts = '[a,A]-[#6X4]-[#8X2]-[#1]' # torsion example
Smarts = '[#6X4]-[#6X4]' # bond example
#Set up substructure query
qmol = oechem.OEQMol()
if not oechem.OEParseSmarts( qmol, Smarts ):
print( 'OEParseSmarts failed')
ss = oechem.OESubSearch( qmol)
#File to search for this substructure
fileprefix= 'AlkEthOH_dvrs1'
ifs = oechem.oemolistream(fileprefix+'.oeb')
#Do substructure search and depiction
mol = oechem.OEMol()
#Loop over molecules in file
for mol in ifs.GetOEMols():
# Get OpenMM System and positions.
[system, positions] = createOpenMMSystem(mol)
goodMol = True
oechem.OEPrepareSearch(mol, ss)
unique = True
#Loop over matches within this molecule in file and depict
for match in ss.Match(mol, unique):
display( depictMatch(mol, match))
atoms = list()
for ma in match.GetAtoms():
print(ma.target.GetIdx(), end=" ")
#print(ma.pattern.GetIdx(), end=" ")
atoms.append( ma.target.GetIdx() )
print('')
#Get OpenMM angle energy and print IF it's an angle term
potential = getValenceEnergyComponent(system, positions, atoms)
print('%16.10f kcal/mol' % (potential / unit.kilocalories_per_mole))
ifs.close()
```
|
github_jupyter
|
import openeye.oechem as oechem
import openeye.oedepict as oedepict
from IPython.display import display
import os
from __future__ import print_function
def depictMatch(mol, match, width=500, height=200):
"""Take in an OpenEye molecule and a substructure match and display the results
with (optionally) specified resolution."""
from IPython.display import Image
dopt = oedepict.OEPrepareDepictionOptions()
dopt.SetDepictOrientation( oedepict.OEDepictOrientation_Horizontal)
dopt.SetSuppressHydrogens(True)
oedepict.OEPrepareDepiction(mol, dopt)
opts = oedepict.OE2DMolDisplayOptions(width, height, oedepict.OEScale_AutoScale)
disp = oedepict.OE2DMolDisplay(mol, opts)
hstyle = oedepict.OEHighlightStyle_Color
hcolor = oechem.OEColor(oechem.OELightBlue)
oedepict.OEAddHighlighting(disp, hcolor, hstyle, match)
ofs = oechem.oeosstream()
oedepict.OERenderMolecule(ofs, 'png', disp)
ofs.flush()
return Image(data = "".join(ofs.str()))
import parmed
def createOpenMMSystem(mol):
"""
Generate OpenMM System and positions from an OEMol.
Parameters
----------
mol : OEMol
The molecule
Returns
-------
system : simtk.openmm.System
The OpenMM System
positions : simtk.unit.Quantity wrapped
Positions of the molecule
"""
# write mol2 file
ofsmol2 = oechem.oemolostream('molecule.mol2')
ofsmol2.SetFlavor( oechem.OEFormat_MOL2, oechem.OEOFlavor_MOL2_Forcefield );
oechem.OEWriteConstMolecule(ofsmol2, mol)
ofsmol2.close()
# write tleap input file
leap_input = """
lig = loadMol2 molecule.mol2
saveAmberParm lig prmtop inpcrd
quit
"""
outfile = open('leap.in', 'w')
outfile.write(leap_input)
outfile.close()
# run tleap
leaprc = 'leaprc.Frosst_AlkEthOH'
os.system( 'tleap -f %s -f leap.in > leap.out' % leaprc )
# check if param file was not saved (implies parameterization problems)
paramsNotSaved = 'Parameter file was not saved'
leaplog = open( 'leap.out', 'r' ).read()
if paramsNotSaved in leaplog:
raise Exception('Parameter file was not saved.')
# Read prmtop and inpcrd
amberparm = parmed.amber.AmberParm( 'prmtop', 'inpcrd' )
system = amberparm.createSystem()
return (system, amberparm.positions)
import copy
from simtk import openmm, unit
def getValenceEnergyComponent(system, positions, atoms):
"""
Get the OpenMM valence energy corresponding to a specified set of atoms (bond, angle, torsion).
Parameters
----------
system : simtk.openmm.System
The OpenMM System object for the molecule
positions : simtk.unit.Quantity of dimension (natoms,3) with units compatible with angstroms
The positions of the molecule
atoms : list or set of int
The set of atoms in the bond, angle, or torsion.
Returns
-------
potential : simtk.unit.Quantity with units compatible with kilocalories_per_mole
The energy of the valence component.
"""
atoms = set(atoms)
natoms = len(atoms) # number of atoms
# Create a copy of the original System object so we can manipulate it
system = copy.deepcopy(system)
# Determine Force types to keep
if natoms == 2:
forcename = 'HarmonicBondForce'
elif natoms == 3:
forcename = 'HarmonicAngleForce'
elif natoms == 4:
forcename = 'PeriodicTorsionForce'
else:
raise Exception('len(atoms) = %d, but must be in [2,3,4] for bond, angle, or torsion' % len(atoms))
# Discard Force objects we don't need
for force_index in reversed(range(system.getNumForces())):
if system.getForce(force_index).__class__.__name__ != forcename:
system.removeForce(force_index)
# Report on constraints
if forcename == 'HarmonicBondForce':
for constraint_index in range(system.getNumConstraints()):
[i, j, r0] = system.getConstraintParameters(constraint_index)
if set([i,j]) == atoms:
print('Bond is constrained')
# Zero out force components that don't involve the atoms
for force_index in range(system.getNumForces()):
force = system.getForce(force_index)
if forcename == 'HarmonicBondForce':
for param_index in range(force.getNumBonds()):
[i, j, r0, K] = force.getBondParameters(param_index)
if set([i,j]) != atoms:
K *= 0
else:
print('Match found: bond parameter %d : r0 = %s, K = %s' % (param_index, str(r0), str(K)))
force.setBondParameters(param_index, i, j, r0, K)
elif forcename == 'HarmonicAngleForce':
for param_index in range(force.getNumAngles()):
[i, j, k, theta0, K] = force.getAngleParameters(param_index)
if set([i,j,k]) != atoms:
K *= 0
else:
print('Match found: angle parameter %d : theta0 = %s, K = %s' % (param_index, str(theta0), str(K)))
force.setAngleParameters(param_index, i, j, k, theta0, K)
elif forcename == 'PeriodicTorsionForce':
for param_index in range(force.getNumTorsions()):
[i, j, k, l, periodicity, phase, K] = force.getTorsionParameters(param_index)
if set([i,j,k,l]) != atoms:
K *= 0
else:
print('Match found: torsion parameter %d : periodicity = %s, phase = %s, K = %s' % (param_index, str(periodicity), str(phase), str(K)))
force.setTorsionParameters(param_index, i, j, k, l, periodicity, phase, K)
# Compute energy
platform = openmm.Platform.getPlatformByName('Reference')
integrator = openmm.VerletIntegrator(1.0 * unit.femtoseconds)
context = openmm.Context(system, integrator, platform)
context.setPositions(positions)
potential = context.getState(getEnergy=True).getPotentialEnergy()
del context, integrator, system
# Return energy
return potential
#SMARTS query defining your search (and potentially forcefield term of interest)
#Note currently this must specify an angle term for the OpenMM energy to be
Smarts = '[#6X4]-[#6X4]-[#8X2]' # angle example
Smarts = '[a,A]-[#6X4]-[#8X2]-[#1]' # torsion example
Smarts = '[#6X4]-[#6X4]' # bond example
#Set up substructure query
qmol = oechem.OEQMol()
if not oechem.OEParseSmarts( qmol, Smarts ):
print( 'OEParseSmarts failed')
ss = oechem.OESubSearch( qmol)
#File to search for this substructure
fileprefix= 'AlkEthOH_dvrs1'
ifs = oechem.oemolistream(fileprefix+'.oeb')
#Do substructure search and depiction
mol = oechem.OEMol()
#Loop over molecules in file
for mol in ifs.GetOEMols():
# Get OpenMM System and positions.
[system, positions] = createOpenMMSystem(mol)
goodMol = True
oechem.OEPrepareSearch(mol, ss)
unique = True
#Loop over matches within this molecule in file and depict
for match in ss.Match(mol, unique):
display( depictMatch(mol, match))
atoms = list()
for ma in match.GetAtoms():
print(ma.target.GetIdx(), end=" ")
#print(ma.pattern.GetIdx(), end=" ")
atoms.append( ma.target.GetIdx() )
print('')
#Get OpenMM angle energy and print IF it's an angle term
potential = getValenceEnergyComponent(system, positions, atoms)
print('%16.10f kcal/mol' % (potential / unit.kilocalories_per_mole))
ifs.close()
| 0.676086 | 0.783119 |
## Summary
We face the problem of predicting tweets sentiment.
We have coded the text as Bag of Words and applied an SVM model. We have built a pipeline to check different hyperparameters using cross-validation. At the end, we have obtained a good model which achieve an AUC of **0.92**
## Data loading and cleaning
```
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
from bs4 import BeautifulSoup
import matplotlib.pyplot as plt
import seaborn as sns
import nltk
from nltk.corpus import stopwords
from nltk.stem import SnowballStemmer
from nltk.tokenize import TweetTokenizer
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split, StratifiedKFold, cross_val_score
from sklearn.pipeline import make_pipeline, Pipeline
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer, accuracy_score, f1_score
from sklearn.metrics import roc_curve, auc
from sklearn.metrics import confusion_matrix, roc_auc_score, recall_score, precision_score
data = pd.read_csv("./twitter-airline-sentiment/Tweets.csv")
```
We take only the tweets we are very confident with. We use the BeautifulSoup library to process html encoding present in some tweets because scrapping.
```
data_clean = data.copy()
data_clean = data_clean[data_clean['airline_sentiment_confidence'] > 0.65]
data_clean['sentiment'] = data_clean['airline_sentiment'].\
apply(lambda x: 1 if x=='negative' else 0)
data_clean['text_clean'] = data_clean['text'].apply(lambda x: BeautifulSoup(x, "lxml").text)
```
We are going to distinguish two cases: tweets with negative sentiment and tweets with non-negative sentiment
```
data_clean['sentiment'] = data_clean['airline_sentiment'].apply(lambda x: 1 if x=='negative' else 0)
data_clean = data_clean.loc[:, ['text_clean', 'sentiment']]
data_clean.head()
```
## Machine Learning Model
We split the data into training and testing set:
```
train, test = train_test_split(data_clean, test_size=0.2, random_state=1)
X_train = train['text_clean'].values
X_test = test['text_clean'].values
y_train = train['sentiment']
y_test = test['sentiment']
def tokenize(text):
tknzr = TweetTokenizer()
return tknzr.tokenize(text)
def stem(doc):
return (stemmer.stem(w) for w in analyzer(doc))
en_stopwords = set(stopwords.words("english"))
vectorizer = CountVectorizer(
analyzer = 'word',
tokenizer = tokenize,
lowercase = True,
ngram_range=(1, 1),
stop_words = en_stopwords)
```
We are going to use cross validation and grid search to find good hyperparameters for our SVM model. We need to build a pipeline to don't get features from the validation folds when building each training model.
```
kfolds = StratifiedKFold(n_splits=5, shuffle=True, random_state=1)
np.random.seed(1)
pipeline_svm = make_pipeline(vectorizer,
SVC(probability=True, kernel="linear", class_weight="balanced"))
grid_svm = GridSearchCV(pipeline_svm,
param_grid = {'svc__C': [0.01, 0.1, 1]},
cv = kfolds,
scoring="roc_auc",
verbose=1,
n_jobs=-1)
grid_svm.fit(X_train, y_train)
grid_svm.score(X_test, y_test)
grid_svm.best_params_
grid_svm.best_score_
def report_results(model, X, y):
pred_proba = model.predict_proba(X)[:, 1]
pred = model.predict(X)
auc = roc_auc_score(y, pred_proba)
acc = accuracy_score(y, pred)
f1 = f1_score(y, pred)
prec = precision_score(y, pred)
rec = recall_score(y, pred)
result = {'auc': auc, 'f1': f1, 'acc': acc, 'precision': prec, 'recall': rec}
return result
```
Let's see how the model (with the best hyperparameters) works on the test data:
```
report_results(grid_svm.best_estimator_, X_test, y_test)
def get_roc_curve(model, X, y):
pred_proba = model.predict_proba(X)[:, 1]
fpr, tpr, _ = roc_curve(y, pred_proba)
return fpr, tpr
roc_svm = get_roc_curve(grid_svm.best_estimator_, X_test, y_test)
fpr, tpr = roc_svm
plt.figure(figsize=(14,8))
plt.plot(fpr, tpr, color="red")
plt.plot([0, 1], [0, 1], color='black', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Roc curve')
plt.show()
```
Let's see if our model has some bias or variance problem ploting its learning curve:
```
from sklearn.model_selection import learning_curve
train_sizes, train_scores, test_scores = \
learning_curve(grid_svm.best_estimator_, X_train, y_train, cv=5, n_jobs=-1,
scoring="roc_auc", train_sizes=np.linspace(.1, 1.0, 10), random_state=1)
def plot_learning_curve(X, y, train_sizes, train_scores, test_scores, title='', ylim=None, figsize=(14,8)):
plt.figure(figsize=figsize)
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel("Training examples")
plt.ylabel("Score")
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Cross-validation score")
plt.legend(loc="lower right")
return plt
plot_learning_curve(X_train, y_train, train_sizes,
train_scores, test_scores, ylim=(0.7, 1.01), figsize=(14,6))
plt.show()
```
It looks like there isn't a big bias or variance problem, but it is clear that our model would work better with more data:. if we can get more labeled data the model performance will increase.
## Examples
We are going to apply the obtained machine learning model to some example text. If the output is **1** it means that the text has a negative sentiment associated:
```
grid_svm.predict(["flying with @united is always a great experience"])
grid_svm.predict(["flying with @united is always a great experience. If you don't lose your luggage"])
grid_svm.predict(["I love @united. Sorry, just kidding!"])
grid_svm.predict(["@united very bad experience!"])
grid_svm.predict(["@united very bad experience!"])
import pickle
pickle_out = open("modelSVM.pickle","wb")
pickle.dump(grid_svm,pickle_out)
pickle_out.close()
```
|
github_jupyter
|
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
from bs4 import BeautifulSoup
import matplotlib.pyplot as plt
import seaborn as sns
import nltk
from nltk.corpus import stopwords
from nltk.stem import SnowballStemmer
from nltk.tokenize import TweetTokenizer
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split, StratifiedKFold, cross_val_score
from sklearn.pipeline import make_pipeline, Pipeline
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer, accuracy_score, f1_score
from sklearn.metrics import roc_curve, auc
from sklearn.metrics import confusion_matrix, roc_auc_score, recall_score, precision_score
data = pd.read_csv("./twitter-airline-sentiment/Tweets.csv")
data_clean = data.copy()
data_clean = data_clean[data_clean['airline_sentiment_confidence'] > 0.65]
data_clean['sentiment'] = data_clean['airline_sentiment'].\
apply(lambda x: 1 if x=='negative' else 0)
data_clean['text_clean'] = data_clean['text'].apply(lambda x: BeautifulSoup(x, "lxml").text)
data_clean['sentiment'] = data_clean['airline_sentiment'].apply(lambda x: 1 if x=='negative' else 0)
data_clean = data_clean.loc[:, ['text_clean', 'sentiment']]
data_clean.head()
train, test = train_test_split(data_clean, test_size=0.2, random_state=1)
X_train = train['text_clean'].values
X_test = test['text_clean'].values
y_train = train['sentiment']
y_test = test['sentiment']
def tokenize(text):
tknzr = TweetTokenizer()
return tknzr.tokenize(text)
def stem(doc):
return (stemmer.stem(w) for w in analyzer(doc))
en_stopwords = set(stopwords.words("english"))
vectorizer = CountVectorizer(
analyzer = 'word',
tokenizer = tokenize,
lowercase = True,
ngram_range=(1, 1),
stop_words = en_stopwords)
kfolds = StratifiedKFold(n_splits=5, shuffle=True, random_state=1)
np.random.seed(1)
pipeline_svm = make_pipeline(vectorizer,
SVC(probability=True, kernel="linear", class_weight="balanced"))
grid_svm = GridSearchCV(pipeline_svm,
param_grid = {'svc__C': [0.01, 0.1, 1]},
cv = kfolds,
scoring="roc_auc",
verbose=1,
n_jobs=-1)
grid_svm.fit(X_train, y_train)
grid_svm.score(X_test, y_test)
grid_svm.best_params_
grid_svm.best_score_
def report_results(model, X, y):
pred_proba = model.predict_proba(X)[:, 1]
pred = model.predict(X)
auc = roc_auc_score(y, pred_proba)
acc = accuracy_score(y, pred)
f1 = f1_score(y, pred)
prec = precision_score(y, pred)
rec = recall_score(y, pred)
result = {'auc': auc, 'f1': f1, 'acc': acc, 'precision': prec, 'recall': rec}
return result
report_results(grid_svm.best_estimator_, X_test, y_test)
def get_roc_curve(model, X, y):
pred_proba = model.predict_proba(X)[:, 1]
fpr, tpr, _ = roc_curve(y, pred_proba)
return fpr, tpr
roc_svm = get_roc_curve(grid_svm.best_estimator_, X_test, y_test)
fpr, tpr = roc_svm
plt.figure(figsize=(14,8))
plt.plot(fpr, tpr, color="red")
plt.plot([0, 1], [0, 1], color='black', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Roc curve')
plt.show()
from sklearn.model_selection import learning_curve
train_sizes, train_scores, test_scores = \
learning_curve(grid_svm.best_estimator_, X_train, y_train, cv=5, n_jobs=-1,
scoring="roc_auc", train_sizes=np.linspace(.1, 1.0, 10), random_state=1)
def plot_learning_curve(X, y, train_sizes, train_scores, test_scores, title='', ylim=None, figsize=(14,8)):
plt.figure(figsize=figsize)
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel("Training examples")
plt.ylabel("Score")
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Cross-validation score")
plt.legend(loc="lower right")
return plt
plot_learning_curve(X_train, y_train, train_sizes,
train_scores, test_scores, ylim=(0.7, 1.01), figsize=(14,6))
plt.show()
grid_svm.predict(["flying with @united is always a great experience"])
grid_svm.predict(["flying with @united is always a great experience. If you don't lose your luggage"])
grid_svm.predict(["I love @united. Sorry, just kidding!"])
grid_svm.predict(["@united very bad experience!"])
grid_svm.predict(["@united very bad experience!"])
import pickle
pickle_out = open("modelSVM.pickle","wb")
pickle.dump(grid_svm,pickle_out)
pickle_out.close()
| 0.545044 | 0.930205 |
# <span style="color:red">Seaborn | Part-14: FacetGrid:</span>
Welcome to another lecture on *Seaborn*! Our journey began with assigning *style* and *color* to our plots as per our requirement. Then we moved on to *visualize distribution of a dataset*, and *Linear relationships*, and further we dived into topics covering *plots for Categorical data*. Every now and then, we've also roughly touched customization aspects using underlying Matplotlib code. That indeed is the end of the types of plots offered by Seaborn, and only leaves us with widening the scope of usage of all the plots that we have learnt till now.
Our discussion in upcoming lectures is majorly going to focus on using the core of Seaborn, based on which, *Seaborn* allows us to plot these amazing figures, that we had been detailing previously. This ofcourse isn't going to be a brand new topic because every now & then I have used these in previous lectures but hereon we're going to specifically deal with each one of those.
To introduce our new topic, i.e. **<span style="color:red">Grids</span>**, we shall at first list the options available. Majorly, there are just two aspects to our discussion on *Grids* that includes:
- **<span style="color:red">FacetGrid</span>**
- **<span style="color:red">PairGrid</span>**
Additionally, we also have a companion function for *PairGrid* to enhance execution speed of *PairGrid*, i.e.
- **<span style="color:red">Pairplot</span>**
Our discourse shall detail each one of these topics in-length for better understanding. As we have already covered the statistical inference of each type of plot, our emphasis shall mostly be on scaling and parameter variety of known plots on these grids. So let us commence our journey with **FacetGrid** in this lecture.
## <span style="color:red">FacetGrid:</span>
The term **Facet** here refers to *a dimension* or say, an *aspect* or a feature of a *multi-dimensional dataset*. This analysis is extremely useful when working with a multi-variate dataset which has a varied blend of datatypes, specially in *Data Science* & *Machine Learning* domain, where generally you would be dealing with huge datasets. If you're a *working pofessional*, you know what I am talking about. And if you're a *fresher* or a *student*, just to give you an idea, in this era of *Big Data*, an average *CSV file* (which is generally the most common form), or even a RDBMS size would vary from Gigabytes to Terabytes of data. If you are dealing with *Image/Video/Audio datasets*, then you may easily expect those to be in *hundreds of gigabyte*.
On the other hand, the term **Grid** refers to any *framework with spaced bars that are parallel to or cross each other, to form a series of squares or rectangles*. Statistically, these *Grids* are also used to represent and understand an entire *population* or just a *sample space* out of it. In general, these are pretty powerful tool for presentation, to describe our dataset and to study the *interrelationship*, or *correlation* between *each facet* of any *environment*.
To kill our curiousity, let us plot a simple **<span style="color:red">FacetGrid</span>** before continuing on with our discussion. And to do that, we shall once again quickly import our package dependencies and set the aesthetics for future use with built-in datasets.
```
# Importing intrinsic libraries:
import numpy as np
import pandas as pd
np.random.seed(101)
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set(style="whitegrid", palette="rocket")
import warnings
warnings.filterwarnings("ignore")
# Let us also get tableau colors we defined earlier:
tableau_20 = [(31, 119, 180), (174, 199, 232), (255, 127, 14), (255, 187, 120),
(44, 160, 44), (152, 223, 138), (214, 39, 40), (255, 152, 150),
(148, 103, 189), (197, 176, 213), (140, 86, 75), (196, 156, 148),
(227, 119, 194), (247, 182, 210), (127, 127, 127), (199, 199, 199),
(188, 189, 34), (219, 219, 141), (23, 190, 207), (158, 218, 229)]
# Scaling above RGB values to [0, 1] range, which is Matplotlib acceptable format:
for i in range(len(tableau_20)):
r, g, b = tableau_20[i]
tableau_20[i] = (r / 255., g / 255., b / 255.)
# Loading built-in Tips dataset:
tips = sns.load_dataset("tips")
# Plotting a basic FacetGrid with Scatterplot representation:
ax = sns.FacetGrid(tips, col="sex", hue="smoker", size=6.5)
ax.map(plt.scatter, "total_bill", "tip", alpha=.6)
ax.add_legend()
```
This is a combined scatter representation of Tips dataset that we have seen earlier as well, where Total tip generated against Total Bill amount is drawn in accordance with their Gender and Smoking practice. With this we can conclude how **FacetGrid** helps us visualize distribution of a variable or the relationship between multiple variables separately within subsets of our dataset. Important to note here is that Seaborn FacetGrid can only support upto **3-Dimensional figures**, using `row`, `column` and `hue` dimensions of the grid for *Categorical* and *Discrete* variables within our dataset.
Let us now have a look at the *parameters* offered or supported by Seaborn for a **FacetGrid**:
`seaborn.FacetGrid(data, row=None, col=None, hue=None, col_wrap=None, sharex=True, sharey=True, size=3, aspect=1, palette=None, row_order=None, col_order=None, hue_order=None, hue_kws=None, dropna=True, legend_out=True, despine=True, margin_titles=False, xlim=None, ylim=None, subplot_kws=None, gridspec_kws=None`
There seems to be few new parameters out here for us, so let us one-by-one understand their scope before we start experimenting with those on our plots:
- We are well acquainted with mandatory `data`, `row`, `col` and `hue` parameters.
- Next is `col_wrap` that defines the **width of our variable** selected as `col` dimension, so that the *column facets* can span multiple rows.
- `sharex` helps us **draft dedicated Y-axis** for each sub-plot, if declared `False`. Same concept holds good for `sharey` as well.
- `size` helps us determine the size of our grid-frame.
- We may also declare `hue_kws` parameter that lets us **control other aesthetics** of our plot.
- `dropna` drops all the **NULL variables** from the selected features; and `legend_out` places the Legend either inside or outside our plot, as we've already seen.
- `margin_titles` fetch the **feature names** from our dataset; and `xlim` & `ylim` additionally offers Matplotlib style limitation to each of our axes on the grid.
That pretty much seems to cover *intrinsic parameters* so let us now try to use them one-by-one with slight modifications:
Let us begin by pulling the *Legend inside* our FacetGrid and *creating a Header* for our grid:
```
ax = sns.FacetGrid(tips, col="sex", hue="smoker", size=6.5, legend_out=False)
ax.map(plt.scatter, "total_bill", "tip", alpha=.6)
ax.add_legend()
plt.suptitle('Tip Collection based on Gender and Smoking', fontsize=11)
```
So declaring `legend_out` as `False` and creating a **Superhead title** using *Matplotlib* seems to be working great on our Grid. Customization on *Header size* gives us an add-on capability as well. Right now, we are going by default `palette` for **marker colors** which can be customized by setting to a different one. Let us try other parameters as well:
Actually, before we jump further into utilization of other parameters, let me quickly take you behind the curtain of this plot. As visible, we assigned `ax` as a variable to our **FacetGrid** for creating a visualizaion figure, and then plotted a **Scatterplot** on top of it, before decorating further with a *Legend* and a *Super Title*. So when we initialized the assignment of `ax`, the grid actually gets created using backend *Matplotlib figure and axes*, though doesn't plot anything on top of it. This is when we call Scatterplot on our sample data, that in turn at the backend calls `FacetGrid.map()` function to map this grid to our Scatterplot. We intended to draw a linear relation plot, and thus entered multiple variable names, i.e. `Total Bill` and associated `Tip` to form *facets*, or dimensions of our grid.
Also important to note is the use the [matplotlib.pyplot.gca()](https://matplotlib.org/api/_as_gen/matplotlib.pyplot.gca.html) function, if required to *set the current axes* on our Grid. This shall fetch the current Axes instance on our current figure matching the given keyword arguments or params, & if unavailable, it shall even create one.
```
# Let us create a dummy DataFrame:
football = pd.DataFrame({
"Wins": [76, 64, 38, 78, 63, 45, 32, 46, 13, 40, 59, 80],
"Loss": [55, 67, 70, 56, 59, 69, 72, 24, 45, 21, 58, 22],
"Team": ["Arsenal"] * 4 + ["Liverpool"] * 4 + ["Chelsea"] * 4,
"Year": ["2015", "2016", "2017", "2018"] * 3})
```
Before I begin illustration using this DataFrame, on a lighter note, I would add a disclosure that this is a dummy dataset and holds no resemblance whatsoever to actual records of respective Soccer clubs. So if you're one among those die-hard fans of any of these clubs, kindly excuse me if the numbers don't tally, as they are all fabricated.
Here, **football** is kind of a *Time-series Pandas DataFrame* that in entirety reflects 4 features, where `Wins` and `Loss` variables represent the quarterly Scorecard of three soccer `Teams` for last four `Years`, from 2015 to 2018. Let us check how this DataFrame looks like:
```
football
```
This looks pretty good for our purpose so now let us initialize our FacetGrid on top of it and try to obtain a time-indexed with further plotting. In production environment, to keep our solution scalable, this is generally done by defining a function for data manipulation so we shall try that in this example:
```
# Defining a customizable function to be precise with our requirements & shall discuss it a little later:
# We shall be using a new type of plot here that I shall discuss in detail later on.
def football_plot(data, color):
sns.heatmap(data[["Wins", "Loss"]])
# 'margin_titles' won't necessarily guarantee desired results so better to be cautious:
ax = sns.FacetGrid(football, col="Team", size=5, margin_titles=True)
ax.map_dataframe(football_plot)
ax = sns.FacetGrid(football, col="Team", size=5)
ax.map(sns.kdeplot, "Wins", "Year", hist=True, lw=2)
```
As visible, **Heatmap** plots rectangular boxes for data points as a color-encoded matrix, and this is a topic we shall be discussing in detail in another Lecture but for now, I just wanted you to have a preview of it, and hence used it on top of our **FacetGrid**. Another good thing to know with *FacetGrid* is **gridspec** module which allows Matplotlib params to be passed for drawing attention to a particular facet by increasing its size. To better understand, let us try to use this module now:
```
# Loading built-in Titanic Dataset:
titanic = sns.load_dataset("titanic")
# Assigning reformed `deck` column:
titanic = titanic.assign(deck=titanic.deck.astype(object)).sort_values("deck")
# Creating Grid and Plot:
ax = sns.FacetGrid(titanic, col="class", sharex=False, size=7,
gridspec_kws={"width_ratios": [3.5, 2, 2]})
ax.map(sns.boxplot, "deck", "age")
ax.set_titles(fontweight='bold', size=17)
```
Breaking it down, at first we import our built-in Titanic dataset, and then assign a new column, i.e. `deck` using Pandas `.assign()` function. Here we declare this new column as a component of pre-existing `deck` column from Titanic dataset, but as a sorted object. Then we create our *FacetGrid* mentioning the DataFrame, the column on which Grids get segregated but with shared across *Y-axis*; for `chosen deck` against `Age` of passengers. Next in action is our **grid keyword specifications**, where we decide the *width ratio* of the plot that shall be passed on to these grids. Finally, we have our **Box Plot** representing values of `Age` feature across respective decks.
Now let us try to use different axes with same size for multivariate plotting on Tips dataset:
```
# Loading built-in Tips dataset:
tips = sns.load_dataset("tips")
# Mapping a Scatterplot to our FacetGrid:
ax = sns.FacetGrid(tips, col="smoker", row="sex", size=3.5)
ax = (ax.map(plt.scatter, "total_bill", "tip", color=tableau_20[6]).set_axis_labels("Total Bill Generated (USD)", "Tip Amount"))
# Increasing size for subplot Titles & making it appear Bolder:
ax.set_titles(fontweight='bold', size=11)
```
**Scatterplot** dealing with data that has multiple variables is no new science for us so instead let me highlight what `.map()` does for us. This function actually allows us to project our figure axes, in accordance to which our Scatterplot spreads the feature datapoints across the grids, depending upon the segregators. Here we have `sex` and `smoker` as our segregators (When I use the general term "segregator", it just refers to the columns on which we decide to determine the layout). This comes in really handy as we can pass *Matplotlib parrameters* for further customization of our plot. At the end, when we add `.set_axis_labels()` it gets easy for us to label our axes but please note that this method shall work for you only when you're dealing with grids, hence you didn't observe me adapting to this function, while detailing various other plots.
- Let us now talk about the `football_plot` function we defined earlier with **football** DataFrame. The only reason I didn't speak of it then was because I wanted you to go through a few more parameter implementation before getting into this. There are **3 important rules for defining such functions** that are supported by [FacetGrid.map](http://xarray.pydata.org/en/stable/generated/xarray.plot.FacetGrid.map.html):
-They must take array-like inputs as positional arguments, with the first argument corresponding to the `X-Axis`, and the second argument corresponding to `y-Axis`.
-They must also accept two keyword arguments: `color`, and `label`. If you want to use a `hue` variable, than these should get passed to the underlying plotting function (As a side note: You may just catch `**kwargs` and not do anything with them, if it's not relevant to the specific plot you're making.
-Lastly, when called, they must draw a plot on the "currently active" matplotlib Axes.
- Important to note is that there may be cases where your function draws a plot that looks correct without taking `x`, `y`, positional inputs and then it is better to just call the plot, like: `ax.set_axis_labels("Column_1", "Column_2")` after you use `.map()`, which should rename your axes properly. Alternatively, you may also want to do something like `ax.set(xticklabels=)` to get more meaningful ticks.
- Well I am also quite stoked to mention another important function (though not that comonly used), that is [FacetGrid.map_dataframe()](http://nullege.com/codes/search/axisgrid.FacetGrid.map_dataframe). The rules here are similar to `FacetGrid.map()`, but the function you pass must accept a DataFrame input in a parameter called `data`, and instead of taking *array-like positional* inputs it takes *strings* that correspond to variables in that dataframe. Then on each iteration through the *facets*, the function will be called with the *Input dataframe*, masked to just the values for that combination of `row`, `col`, and `hue` levels.
**Another important to note with both the above-mentioned functions is that the `return` value is ignored so you don't really have to worry about it.** Just for illustration purpose, let us consider drafting a function that just *draws a horizontal line in each `facet` at `y=2` and ignores all the Input data*:
```
# That is all you require in your function:
def plot_func(x, y, color=None, label=None):
ax.map(plt.axhline, y=2)
```
I know this function concept might look little hazy at the moment but once you have covered more on dates and maptplotlib syntax in particular, the picture shall get much more clearer for you.
Let us look at one more example of `FacetGrid()` and this time let us again create a synthetic DataFrame for this demonstration:
```
# Creating synthetic Data (Don't focus on how it's getting created):
units = np.linspace(0, 50)
A = [1., 18., 40., 100.]
df = []
for i in A:
V1 = np.sin(i * units)
V2 = np.cos(i * units)
df.append(pd.DataFrame({"units": units, "V_1": V1, "V_2": V2, "A": i}))
sample = pd.concat(df, axis=0)
# Previewing DataFrame:
sample.head(10)
sample.describe()
# Melting our sample DataFrame:
sample_melt = sample.melt(id_vars=['A', 'units'], value_vars=['V_1', 'V_2'])
# Creating plot:
ax = sns.FacetGrid(sample_melt, col='A', hue='A', palette="icefire", row='variable', sharey='row', margin_titles=True)
ax.map(plt.plot, 'units', 'value')
ax.add_legend()
```
This process shall come in handy if you ever wish to vertically stack rows of subplots on top of one another. You do not really have to focus on the process of creating dataset, as generally you will have your dataset provided with a problem statement. For our plot, yu may just consider these visual variations as [Sinusoidal waves](https://en.wikipedia.org/wiki/Sine_wave). I shall attach a link in our notebook, if you wish to dig deeper into what these are and how are they actually computed.
Our next lecture would be pretty much a small follow up to this lecture, where we would try to bring more of *Categorical data* to our **FacetGrid()**. Meanwhile, I would again suggest you to play around with analyzing and plotting datasets, as much as you can because visualization is a very important facet of *Data Science & Research*. And, I shall see you in our next lecture.
|
github_jupyter
|
# Importing intrinsic libraries:
import numpy as np
import pandas as pd
np.random.seed(101)
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set(style="whitegrid", palette="rocket")
import warnings
warnings.filterwarnings("ignore")
# Let us also get tableau colors we defined earlier:
tableau_20 = [(31, 119, 180), (174, 199, 232), (255, 127, 14), (255, 187, 120),
(44, 160, 44), (152, 223, 138), (214, 39, 40), (255, 152, 150),
(148, 103, 189), (197, 176, 213), (140, 86, 75), (196, 156, 148),
(227, 119, 194), (247, 182, 210), (127, 127, 127), (199, 199, 199),
(188, 189, 34), (219, 219, 141), (23, 190, 207), (158, 218, 229)]
# Scaling above RGB values to [0, 1] range, which is Matplotlib acceptable format:
for i in range(len(tableau_20)):
r, g, b = tableau_20[i]
tableau_20[i] = (r / 255., g / 255., b / 255.)
# Loading built-in Tips dataset:
tips = sns.load_dataset("tips")
# Plotting a basic FacetGrid with Scatterplot representation:
ax = sns.FacetGrid(tips, col="sex", hue="smoker", size=6.5)
ax.map(plt.scatter, "total_bill", "tip", alpha=.6)
ax.add_legend()
ax = sns.FacetGrid(tips, col="sex", hue="smoker", size=6.5, legend_out=False)
ax.map(plt.scatter, "total_bill", "tip", alpha=.6)
ax.add_legend()
plt.suptitle('Tip Collection based on Gender and Smoking', fontsize=11)
# Let us create a dummy DataFrame:
football = pd.DataFrame({
"Wins": [76, 64, 38, 78, 63, 45, 32, 46, 13, 40, 59, 80],
"Loss": [55, 67, 70, 56, 59, 69, 72, 24, 45, 21, 58, 22],
"Team": ["Arsenal"] * 4 + ["Liverpool"] * 4 + ["Chelsea"] * 4,
"Year": ["2015", "2016", "2017", "2018"] * 3})
football
# Defining a customizable function to be precise with our requirements & shall discuss it a little later:
# We shall be using a new type of plot here that I shall discuss in detail later on.
def football_plot(data, color):
sns.heatmap(data[["Wins", "Loss"]])
# 'margin_titles' won't necessarily guarantee desired results so better to be cautious:
ax = sns.FacetGrid(football, col="Team", size=5, margin_titles=True)
ax.map_dataframe(football_plot)
ax = sns.FacetGrid(football, col="Team", size=5)
ax.map(sns.kdeplot, "Wins", "Year", hist=True, lw=2)
# Loading built-in Titanic Dataset:
titanic = sns.load_dataset("titanic")
# Assigning reformed `deck` column:
titanic = titanic.assign(deck=titanic.deck.astype(object)).sort_values("deck")
# Creating Grid and Plot:
ax = sns.FacetGrid(titanic, col="class", sharex=False, size=7,
gridspec_kws={"width_ratios": [3.5, 2, 2]})
ax.map(sns.boxplot, "deck", "age")
ax.set_titles(fontweight='bold', size=17)
# Loading built-in Tips dataset:
tips = sns.load_dataset("tips")
# Mapping a Scatterplot to our FacetGrid:
ax = sns.FacetGrid(tips, col="smoker", row="sex", size=3.5)
ax = (ax.map(plt.scatter, "total_bill", "tip", color=tableau_20[6]).set_axis_labels("Total Bill Generated (USD)", "Tip Amount"))
# Increasing size for subplot Titles & making it appear Bolder:
ax.set_titles(fontweight='bold', size=11)
# That is all you require in your function:
def plot_func(x, y, color=None, label=None):
ax.map(plt.axhline, y=2)
# Creating synthetic Data (Don't focus on how it's getting created):
units = np.linspace(0, 50)
A = [1., 18., 40., 100.]
df = []
for i in A:
V1 = np.sin(i * units)
V2 = np.cos(i * units)
df.append(pd.DataFrame({"units": units, "V_1": V1, "V_2": V2, "A": i}))
sample = pd.concat(df, axis=0)
# Previewing DataFrame:
sample.head(10)
sample.describe()
# Melting our sample DataFrame:
sample_melt = sample.melt(id_vars=['A', 'units'], value_vars=['V_1', 'V_2'])
# Creating plot:
ax = sns.FacetGrid(sample_melt, col='A', hue='A', palette="icefire", row='variable', sharey='row', margin_titles=True)
ax.map(plt.plot, 'units', 'value')
ax.add_legend()
| 0.677581 | 0.986071 |
# MIST101 Pratical 1: Introduction to Tensorflow (Basics of Tensorflow)
## What is Tensor
The central unit of data in TensorFlow is the tensor. A tensor consists of a set of primitive values shaped into an array of any number of dimensions. A tensor's rank is its number of dimensions. Here are some examples of tensors:
```
3 # a rank 0 tensor; this is a scalar with shape []
[1., 2., 3.] # a rank 1 tensor; this is a vector with shape [3]
[[1., 2., 3.], [4., 5., 6.]] # a rank 2 tensor; a matrix with shape [2, 3]
[[[1., 2., 3.]], [[7., 8., 9.]]] # a rank 3 tensor with shape [2, 1, 3]
```
## What is Tensorflow - Building and Running the Computational Graph
The canonical import statement for TensorFlow programs is as follows:
```
import tensorflow as tf
```
This gives Python access to all of TensorFlow's classes, methods, and symbols.
You might think of TensorFlow Core programs as consisting of two discrete sections:
1. Building the computational graph.
2. Running the computational graph.
A computational graph is a series of TensorFlow operations arranged into a graph of nodes. Now, we are going to introduce some basic nodes.
## Basic Nodes
Let's start with building a simple computational graph. Each node takes zero or more tensors as inputs and produces a tensor as an output. One type of node is a constant. Like all TensorFlow constants, it takes no inputs, and it outputs a value it stores internally. We can create two floating point Tensors node1 and node2 as follows:
```
node1 = tf.constant(3.0, dtype=tf.float32)
node2 = tf.constant(4.0) # also tf.float32 implicitly
print(node1, node2)
```
Notice that printing the nodes does not output the values 3.0 and 4.0 as you might expect. Instead, they are nodes that, when evaluated, would produce 3.0 and 4.0, respectively. To actually evaluate the nodes, we must run the computational graph within a session. A session encapsulates the control and state of the TensorFlow runtime.
The following code creates a **Session** object and then invokes its run method to run enough of the computational graph to evaluate node1 and node2. By running the computational graph in a session as follows:
```
sess = tf.Session()
print(sess.run([node1, node2]))
```
We can build more complicated computations by combining Tensor nodes with operations (Operations are also nodes). For example, we can add our two constant nodes and produce a new graph as follows:
```
node3 = tf.add(node1, node2)
print(node3)
print(sess.run(node3))
```
This graph is not especially interesting because it always produces a constant result. A graph can be modified to accept external inputs, known as **placeholders**. A placeholder is a promise to provide a value later.
```
a = tf.placeholder(tf.float32)
b = tf.placeholder(tf.float32)
adder_node = a + b # + provides a shortcut for tf.add(a, b)
# This will give an error because the placeholders are not provided with any values
print(sess.run(adder_node))
```
To feed values to the placeholders, we need to add a dictionary to the "sess.run" function. In this dictionary, we pair up the placeholder nodes and the values we want to feed in.
```
print(sess.run(adder_node, {a: 3, b: 4.5}))
# Feeding multiple values for multiple runs
print(sess.run(adder_node, {a: [1, 3], b: [2, 4]}))
```
In machine learning we will typically want a model that can take arbitrary inputs, such as the one above. To make the model trainable, we need to be able to modify the graph to get new outputs with the same input. **Variables** allow us to add trainable parameters to a graph. They are constructed with a type and initial value:
```
W = tf.Variable([0.3], dtype=tf.float32)
b = tf.Variable([-0.3], dtype=tf.float32)
x = tf.placeholder(tf.float32)
linear_model = W * x + b
```
Constants are initialized when you call tf.constant, and their value can never change. By contrast, variables are not initialized when you call tf.Variable.
```
# This will give you an error when the variables are not yet initialized
sess.run(W)
```
To initialize all the variables in a TensorFlow program, you must explicitly call a special operation as follows:
```
init = tf.global_variables_initializer()
sess.run(init)
```
It is important to realize init is a handle to the TensorFlow sub-graph that initializes all the global variables. Until we call sess.run, the variables are uninitialized.
```
# This will not you an error after the variables are initialized
sess.run([W, b])
```
Since x is a placeholder, we can evaluate linear_model for several values of x simultaneously as follows:
```
# Evaluate the values from the linear model
print(sess.run(linear_model, {x: [1, 2, 3, 4]}))
```
We've created a model, but we don't know how good it is yet. To evaluate the model on training data, we need another placeholder (**y**) to provide the desired values, and we need to write a loss function.
A loss function measures how far apart the current model is from the provided data. We'll use a standard loss model for linear regression, which sums the squares of the deltas between the current model and the provided data. **linear_model - y** creates a vector where each element is the corresponding example's error delta. We call **tf.square** to square that error. Then, we sum all the squared errors to create a single scalar that abstracts the error of all examples using **tf.reduce_sum**:
```
# The desired values
y = tf.placeholder(tf.float32)
# Loss function
squared_deltas = tf.square(linear_model - y)
loss = tf.reduce_sum(squared_deltas)
# Evaluate the model
print(sess.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]}))
```
We could improve this manually by reassigning the values of W and b to the perfect values of -1 and 1. A variable is initialized to the value provided to **tf.Variable** but can be changed using operations like **tf.assign**. For example, W=-1 and b=1 are the optimal parameters for our model. We can change W and b accordingly:
```
# Define the assign nodes for both variables
fixW = tf.assign(W, [-1.])
fixb = tf.assign(b, [1.])
# Reassign the values of W and b
sess.run([fixW, fixb])
# Re-evaluate the model
print(sess.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]}))
```
We have encountered several tensor nodes in this tutorial. In summary:
#### Tensor Nodes
Tensor nodes provide a tensor as output.
1. tf.Placeholder: A promise to provide a value
2. tf.Variable: The value can be changed after initialization
3. tf.Constant: The value never changes
### Training Nodes
Manually changing the variables to improve the model is not ideal. Luckily, TensorFlow provides optimizers that slowly change each variable in order to minimize the loss function. The simplest optimizer is gradient descent. It modifies each variable according to the magnitude of the derivative of loss with respect to that variable. In general, computing symbolic derivatives manually is tedious and error-prone. Consequently, TensorFlow can automatically produce derivatives given only a description of the model using the function **tf.gradients**. For simplicity, optimizers typically do this for you. For example,
```
# Create nodes for optimizer and training
optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(loss)
# Reset variable values to incorrect defaults.
sess.run(init)
# Show the initial variable values
print("Variables Before training: " + str(sess.run([W, b])))
# Run the training node for 1000 times
for i in range(1000):
sess.run(train, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]})
# Show the new variable values
print("Variables After training: " + str(sess.run([W, b])))
# Loss re-evaluation
print("Loss After training: " + str(sess.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]})))
```
*This tutorial is modified from https://www.tensorflow.org/get_started/*
|
github_jupyter
|
3 # a rank 0 tensor; this is a scalar with shape []
[1., 2., 3.] # a rank 1 tensor; this is a vector with shape [3]
[[1., 2., 3.], [4., 5., 6.]] # a rank 2 tensor; a matrix with shape [2, 3]
[[[1., 2., 3.]], [[7., 8., 9.]]] # a rank 3 tensor with shape [2, 1, 3]
import tensorflow as tf
node1 = tf.constant(3.0, dtype=tf.float32)
node2 = tf.constant(4.0) # also tf.float32 implicitly
print(node1, node2)
sess = tf.Session()
print(sess.run([node1, node2]))
node3 = tf.add(node1, node2)
print(node3)
print(sess.run(node3))
a = tf.placeholder(tf.float32)
b = tf.placeholder(tf.float32)
adder_node = a + b # + provides a shortcut for tf.add(a, b)
# This will give an error because the placeholders are not provided with any values
print(sess.run(adder_node))
print(sess.run(adder_node, {a: 3, b: 4.5}))
# Feeding multiple values for multiple runs
print(sess.run(adder_node, {a: [1, 3], b: [2, 4]}))
W = tf.Variable([0.3], dtype=tf.float32)
b = tf.Variable([-0.3], dtype=tf.float32)
x = tf.placeholder(tf.float32)
linear_model = W * x + b
# This will give you an error when the variables are not yet initialized
sess.run(W)
init = tf.global_variables_initializer()
sess.run(init)
# This will not you an error after the variables are initialized
sess.run([W, b])
# Evaluate the values from the linear model
print(sess.run(linear_model, {x: [1, 2, 3, 4]}))
# The desired values
y = tf.placeholder(tf.float32)
# Loss function
squared_deltas = tf.square(linear_model - y)
loss = tf.reduce_sum(squared_deltas)
# Evaluate the model
print(sess.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]}))
# Define the assign nodes for both variables
fixW = tf.assign(W, [-1.])
fixb = tf.assign(b, [1.])
# Reassign the values of W and b
sess.run([fixW, fixb])
# Re-evaluate the model
print(sess.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]}))
# Create nodes for optimizer and training
optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(loss)
# Reset variable values to incorrect defaults.
sess.run(init)
# Show the initial variable values
print("Variables Before training: " + str(sess.run([W, b])))
# Run the training node for 1000 times
for i in range(1000):
sess.run(train, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]})
# Show the new variable values
print("Variables After training: " + str(sess.run([W, b])))
# Loss re-evaluation
print("Loss After training: " + str(sess.run(loss, {x: [1, 2, 3, 4], y: [0, -1, -2, -3]})))
| 0.872836 | 0.996264 |
<!--NOTEBOOK_HEADER-->
*This notebook contains material from [cbe61622](https://jckantor.github.io/cbe61622);
content is available [on Github](https://github.com/jckantor/cbe61622.git).*
<!--NAVIGATION-->
< [4.0 Chemical Instrumentation](https://jckantor.github.io/cbe61622/04.00-Chemical_Instrumentation.html) | [Contents](toc.html) | [5.0 Raspberry Pi Pico](https://jckantor.github.io/cbe61622/05.00-Raspberry-Pi-Pico.html) ><p><a href="https://colab.research.google.com/github/jckantor/cbe61622/blob/master/docs/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a><p><a href="https://jckantor.github.io/cbe61622/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://img.shields.io/badge/Github-Download-blue.svg" alt="Download" title="Download Notebook"></a>
# 4.10 Potentiostats and Galvanostats
## 4.10.1 References
---
Adams, Scott D., et al. "MiniStat: Development and evaluation of a mini-potentiostat for electrochemical measurements." Ieee Access 7 (2019): 31903-31912. https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=8657694
---
Ainla, Alar, et al. "Open-source potentiostat for wireless electrochemical detection with smartphones." Analytical chemistry 90.10 (2018): 6240-6246. https://gmwgroup.harvard.edu/files/gmwgroup/files/1308.pdf
---
Bianchi, Valentina, et al. "A Wi-Fi cloud-based portable potentiostat for electrochemical biosensors." IEEE Transactions on Instrumentation and Measurement 69.6 (2019): 3232-3240.
---
Dobbelaere, Thomas, Philippe M. Vereecken, and Christophe Detavernier. "A USB-controlled potentiostat/galvanostat for thin-film battery characterization." HardwareX 2 (2017): 34-49. https://doi.org/10.1016/j.ohx.2017.08.001
---
Hoilett, Orlando S., et al. "KickStat: A coin-sized potentiostat for high-resolution electrochemical analysis." Sensors 20.8 (2020): 2407. https://www.mdpi.com/1424-8220/20/8/2407/htm
---
Irving, P., R. Cecil, and M. Z. Yates. "MYSTAT: A compact potentiostat/galvanostat for general electrochemistry measurements." HardwareX 9 (2021): e00163. https://www.sciencedirect.com/science/article/pii/S2468067220300729
> 2, 3, and 4 wire cell configurations with +/- 12 volts at 200ma.
---
Lopin, Prattana, and Kyle V. Lopin. "PSoC-Stat: A single chip open source potentiostat based on a Programmable System on a Chip." PloS one 13.7 (2018): e0201353. https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0201353
---
Matsubara, Yasuo. "A Small yet Complete Framework for a Potentiostat, Galvanostat, and Electrochemical Impedance Spectrometer." (2021): 3362-3370. https://pubs.acs.org/doi/full/10.1021/acs.jchemed.1c00228
> Elegant 2 omp amp current source for a galvanostat.
---
## 4.10.2 Application to Electrical Impedence Spectroscopy
---
Wang, Shangshang, et al. "Electrochemical impedance spectroscopy." Nature Reviews Methods Primers 1.1 (2021): 1-21. https://www.nature.com/articles/s43586-021-00039-w.pdf
> Tutorial presentation of EIS, including instrumentation and data analysis.
---
Magar, Hend S., Rabeay YA Hassan, and Ashok Mulchandani. "Electrochemical Impedance Spectroscopy (EIS): Principles, Construction, and Biosensing Applications." Sensors 21.19 (2021): 6578. https://www.mdpi.com/1424-8220/21/19/6578/pdf
> Tutorial introduction with descriptions of application to solutions and reactions at surfaces.
---
Instruments, Gamry. "Basics of electrochemical impedance spectroscopy." G. Instruments, Complex impedance in Corrosion (2007): 1-30. https://www.c3-analysentechnik.eu/downloads/applikationsberichte/gamry/5657-Application-Note-EIS.pdf
> Tutorial introduction to EIS with extensive modeling discussion.
---
<!--NAVIGATION-->
< [4.0 Chemical Instrumentation](https://jckantor.github.io/cbe61622/04.00-Chemical_Instrumentation.html) | [Contents](toc.html) | [5.0 Raspberry Pi Pico](https://jckantor.github.io/cbe61622/05.00-Raspberry-Pi-Pico.html) ><p><a href="https://colab.research.google.com/github/jckantor/cbe61622/blob/master/docs/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a><p><a href="https://jckantor.github.io/cbe61622/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://img.shields.io/badge/Github-Download-blue.svg" alt="Download" title="Download Notebook"></a>
|
github_jupyter
|
<!--NOTEBOOK_HEADER-->
*This notebook contains material from [cbe61622](https://jckantor.github.io/cbe61622);
content is available [on Github](https://github.com/jckantor/cbe61622.git).*
<!--NAVIGATION-->
< [4.0 Chemical Instrumentation](https://jckantor.github.io/cbe61622/04.00-Chemical_Instrumentation.html) | [Contents](toc.html) | [5.0 Raspberry Pi Pico](https://jckantor.github.io/cbe61622/05.00-Raspberry-Pi-Pico.html) ><p><a href="https://colab.research.google.com/github/jckantor/cbe61622/blob/master/docs/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a><p><a href="https://jckantor.github.io/cbe61622/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://img.shields.io/badge/Github-Download-blue.svg" alt="Download" title="Download Notebook"></a>
# 4.10 Potentiostats and Galvanostats
## 4.10.1 References
---
Adams, Scott D., et al. "MiniStat: Development and evaluation of a mini-potentiostat for electrochemical measurements." Ieee Access 7 (2019): 31903-31912. https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=8657694
---
Ainla, Alar, et al. "Open-source potentiostat for wireless electrochemical detection with smartphones." Analytical chemistry 90.10 (2018): 6240-6246. https://gmwgroup.harvard.edu/files/gmwgroup/files/1308.pdf
---
Bianchi, Valentina, et al. "A Wi-Fi cloud-based portable potentiostat for electrochemical biosensors." IEEE Transactions on Instrumentation and Measurement 69.6 (2019): 3232-3240.
---
Dobbelaere, Thomas, Philippe M. Vereecken, and Christophe Detavernier. "A USB-controlled potentiostat/galvanostat for thin-film battery characterization." HardwareX 2 (2017): 34-49. https://doi.org/10.1016/j.ohx.2017.08.001
---
Hoilett, Orlando S., et al. "KickStat: A coin-sized potentiostat for high-resolution electrochemical analysis." Sensors 20.8 (2020): 2407. https://www.mdpi.com/1424-8220/20/8/2407/htm
---
Irving, P., R. Cecil, and M. Z. Yates. "MYSTAT: A compact potentiostat/galvanostat for general electrochemistry measurements." HardwareX 9 (2021): e00163. https://www.sciencedirect.com/science/article/pii/S2468067220300729
> 2, 3, and 4 wire cell configurations with +/- 12 volts at 200ma.
---
Lopin, Prattana, and Kyle V. Lopin. "PSoC-Stat: A single chip open source potentiostat based on a Programmable System on a Chip." PloS one 13.7 (2018): e0201353. https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0201353
---
Matsubara, Yasuo. "A Small yet Complete Framework for a Potentiostat, Galvanostat, and Electrochemical Impedance Spectrometer." (2021): 3362-3370. https://pubs.acs.org/doi/full/10.1021/acs.jchemed.1c00228
> Elegant 2 omp amp current source for a galvanostat.
---
## 4.10.2 Application to Electrical Impedence Spectroscopy
---
Wang, Shangshang, et al. "Electrochemical impedance spectroscopy." Nature Reviews Methods Primers 1.1 (2021): 1-21. https://www.nature.com/articles/s43586-021-00039-w.pdf
> Tutorial presentation of EIS, including instrumentation and data analysis.
---
Magar, Hend S., Rabeay YA Hassan, and Ashok Mulchandani. "Electrochemical Impedance Spectroscopy (EIS): Principles, Construction, and Biosensing Applications." Sensors 21.19 (2021): 6578. https://www.mdpi.com/1424-8220/21/19/6578/pdf
> Tutorial introduction with descriptions of application to solutions and reactions at surfaces.
---
Instruments, Gamry. "Basics of electrochemical impedance spectroscopy." G. Instruments, Complex impedance in Corrosion (2007): 1-30. https://www.c3-analysentechnik.eu/downloads/applikationsberichte/gamry/5657-Application-Note-EIS.pdf
> Tutorial introduction to EIS with extensive modeling discussion.
---
<!--NAVIGATION-->
< [4.0 Chemical Instrumentation](https://jckantor.github.io/cbe61622/04.00-Chemical_Instrumentation.html) | [Contents](toc.html) | [5.0 Raspberry Pi Pico](https://jckantor.github.io/cbe61622/05.00-Raspberry-Pi-Pico.html) ><p><a href="https://colab.research.google.com/github/jckantor/cbe61622/blob/master/docs/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a><p><a href="https://jckantor.github.io/cbe61622/04.10-Potentiostats-and-Galvanostats.ipynb"> <img align="left" src="https://img.shields.io/badge/Github-Download-blue.svg" alt="Download" title="Download Notebook"></a>
| 0.672762 | 0.703193 |
<a href="https://colab.research.google.com/github/linked0/deep-learning/blob/master/AAMY/cifar10_cnn_my.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
'''
#Train a simple deep CNN on the CIFAR10 small images dataset.
It gets to 75% validation accuracy in 25 epochs, and 79% after 50 epochs.
(It's still underfitting at that point, though).
'''
from __future__ import print_function
import keras
from keras.datasets import cifar10
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
import os
batch_size = 32
num_classes = 10
epochs = 100
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
print(x_train.shape)
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3,3), padding='same', input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3,3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3,3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3,3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_aumentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size = batch_size,
epochs = epochs,
validation_data = (x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set imput mean to 0 over the dataset
samplewise_center=False, # set each samle mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_ntd_normalization=False, # divide each input by tis std
)
```
|
github_jupyter
|
'''
#Train a simple deep CNN on the CIFAR10 small images dataset.
It gets to 75% validation accuracy in 25 epochs, and 79% after 50 epochs.
(It's still underfitting at that point, though).
'''
from __future__ import print_function
import keras
from keras.datasets import cifar10
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
import os
batch_size = 32
num_classes = 10
epochs = 100
data_augmentation = True
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
print(x_train.shape)
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3,3), padding='same', input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3,3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3,3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3,3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
if not data_aumentation:
print('Not using data augmentation.')
model.fit(x_train, y_train,
batch_size = batch_size,
epochs = epochs,
validation_data = (x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
# This will do preprocessing and realtime data augmentation:
datagen = ImageDataGenerator(
featurewise_center=False, # set imput mean to 0 over the dataset
samplewise_center=False, # set each samle mean to 0
featurewise_std_normalization=False, # divide inputs by std of the dataset
samplewise_ntd_normalization=False, # divide each input by tis std
)
| 0.873701 | 0.925634 |
# Hello Image Segmentation
A very basic introduction to using segmentation models with OpenVINO.
We use the pre-trained [road-segmentation-adas-0001](https://docs.openvinotoolkit.org/latest/omz_models_model_road_segmentation_adas_0001.html) model from the [Open Model Zoo](https://github.com/openvinotoolkit/open_model_zoo/). ADAS stands for Advanced Driver Assistance Services. The model recognizes four classes: background, road, curb and mark.
## Imports
```
import cv2
import matplotlib.pyplot as plt
import numpy as np
import sys
from openvino.runtime import Core
sys.path.append("../utils")
from notebook_utils import segmentation_map_to_image
```
## Load the Model
```
ie = Core()
model = ie.read_model(model="model/road-segmentation-adas-0001.xml")
compiled_model = ie.compile_model(model=model, device_name="CPU")
input_layer_ir = compiled_model.input(0)
output_layer_ir = compiled_model.output(0)
```
## Load an Image
A sample image from the [Mapillary Vistas](https://www.mapillary.com/dataset/vistas) dataset is provided.
```
# The segmentation network expects images in BGR format
image = cv2.imread("data/empty_road_mapillary.jpg")
rgb_image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
image_h, image_w, _ = image.shape
# N,C,H,W = batch size, number of channels, height, width
N, C, H, W = input_layer_ir.shape
# OpenCV resize expects the destination size as (width, height)
resized_image = cv2.resize(image, (W, H))
# reshape to network input shape
input_image = np.expand_dims(
resized_image.transpose(2, 0, 1), 0
)
plt.imshow(rgb_image)
```
## Do Inference
```
# Run the inference
result = compiled_model([input_image])[output_layer_ir]
# Prepare data for visualization
segmentation_mask = np.argmax(result, axis=1)
plt.imshow(segmentation_mask.transpose(1, 2, 0))
```
## Prepare Data for Visualization
```
# Define colormap, each color represents a class
colormap = np.array([[68, 1, 84], [48, 103, 141], [53, 183, 120], [199, 216, 52]])
# Define the transparency of the segmentation mask on the photo
alpha = 0.3
# Use function from notebook_utils.py to transform mask to an RGB image
mask = segmentation_map_to_image(segmentation_mask, colormap)
resized_mask = cv2.resize(mask, (image_w, image_h))
# Create image with mask put on
image_with_mask = cv2.addWeighted(resized_mask, alpha, rgb_image, 1 - alpha, 0)
```
## Visualize data
```
# Define titles with images
data = {"Base Photo": rgb_image, "Segmentation": mask, "Masked Photo": image_with_mask}
# Create subplot to visualize images
fig, axs = plt.subplots(1, len(data.items()), figsize=(15, 10))
# Fill subplot
for ax, (name, image) in zip(axs, data.items()):
ax.axis('off')
ax.set_title(name)
ax.imshow(image)
# Display image
plt.show(fig)
```
|
github_jupyter
|
import cv2
import matplotlib.pyplot as plt
import numpy as np
import sys
from openvino.runtime import Core
sys.path.append("../utils")
from notebook_utils import segmentation_map_to_image
ie = Core()
model = ie.read_model(model="model/road-segmentation-adas-0001.xml")
compiled_model = ie.compile_model(model=model, device_name="CPU")
input_layer_ir = compiled_model.input(0)
output_layer_ir = compiled_model.output(0)
# The segmentation network expects images in BGR format
image = cv2.imread("data/empty_road_mapillary.jpg")
rgb_image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
image_h, image_w, _ = image.shape
# N,C,H,W = batch size, number of channels, height, width
N, C, H, W = input_layer_ir.shape
# OpenCV resize expects the destination size as (width, height)
resized_image = cv2.resize(image, (W, H))
# reshape to network input shape
input_image = np.expand_dims(
resized_image.transpose(2, 0, 1), 0
)
plt.imshow(rgb_image)
# Run the inference
result = compiled_model([input_image])[output_layer_ir]
# Prepare data for visualization
segmentation_mask = np.argmax(result, axis=1)
plt.imshow(segmentation_mask.transpose(1, 2, 0))
# Define colormap, each color represents a class
colormap = np.array([[68, 1, 84], [48, 103, 141], [53, 183, 120], [199, 216, 52]])
# Define the transparency of the segmentation mask on the photo
alpha = 0.3
# Use function from notebook_utils.py to transform mask to an RGB image
mask = segmentation_map_to_image(segmentation_mask, colormap)
resized_mask = cv2.resize(mask, (image_w, image_h))
# Create image with mask put on
image_with_mask = cv2.addWeighted(resized_mask, alpha, rgb_image, 1 - alpha, 0)
# Define titles with images
data = {"Base Photo": rgb_image, "Segmentation": mask, "Masked Photo": image_with_mask}
# Create subplot to visualize images
fig, axs = plt.subplots(1, len(data.items()), figsize=(15, 10))
# Fill subplot
for ax, (name, image) in zip(axs, data.items()):
ax.axis('off')
ax.set_title(name)
ax.imshow(image)
# Display image
plt.show(fig)
| 0.636466 | 0.988414 |
[Table of Contents](http://nbviewer.ipython.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb)
# Gaussian Probabilities
```
#format the book
%matplotlib notebook
from __future__ import division, print_function
from book_format import load_style
load_style()
```
## Introduction
The last chapter ended by discussing some of the drawbacks of the Discrete Bayesian filter. For many tracking and filtering problems our desire is to have a filter that is *unimodal* and *continuous*. That is, we want to model our system using floating point math (continuous) and to have only one belief represented (unimodal). For example, we want to say an aircraft is at (12.34, -95.54, 2389.5) where that is latitude, longitude, and altitude. We do not want our filter to tell us "it might be at (1.65, -78.01, 2100.45) or it might be at (34.36, -98.23, 2543.79)." That doesn't match our physical intuition of how the world works, and as we discussed, it can be prohibitively expensive to compute the multimodal case. And, of course, multiple position estimates makes navigating impossible.
We desire a unimodal, continuous way to represent probabilities that models how the real world works, and that is computationally efficient to calculate. As you might guess from the chapter name, Gaussian distributions provide all of these features.
## Mean, Variance, and Standard Deviations
### Random Variables
Each time you roll a die the *outcome* will be between 1 and 6. If we rolled a fair die a million times we'd expect to get 1 1/6 of the time. Thus we say the *probability*, or *odds* of the outcome 1 is 1/6. Likewise, if I asked you the chance of 1 being the result of the next roll you'd reply 1/6.
This combination of values and associated probabilities is called a [*random variable*](https://en.wikipedia.org/wiki/Random_variable). *Random* does not mean the process is nondeterministic, only that we lack information. The result of a die toss is deterministic, but we lack enough information to compute the result. We don't know what will happen, except probabilistically.
While we are defining things, the range of values is called the [*sample space*](https://en.wikipedia.org/wiki/Sample_space). For a die the sample space is {1, 2, 3, 4, 5, 6}. For a coin the sample space is {H, T}. *Space* is a mathematical term which means a set with structure. The sample space for the die is a subset of the natural numbers in the range of 1 to 6.
Another example of a random variable is the heights of students in a university. Here the sample space is a range of values in the real numbers between two limits defined by biology.
Random variables such as coin tosses and die rolls are *discrete random variables*. This means their sample space is represented by either a finite number of values or a countably infinite number of values such as the natural numbers. Heights of humans are called *continuous random variables* since they can take on any real value between two limits.
Do not confuse the *measurement* of the random variable with the actual value. If we can only measure the height of a person to 0.1 meters we would only record values from 0.1, 0.2, 0.3...2.7, yielding 27 discrete choices. Nonetheless a person's height can vary between any arbitrary real value between those ranges, and so height is a continuous random variable.
In statistics capital letters are used for random variables, usually from the latter half of the alphabet. So, we might say that $X$ is the random variable representing the die toss, or $Y$ are the heights of the students in the freshmen poetry class. In later chapters we will follow the convention of using lower case for vectors, and upper case for matrices. Unfortunately these conventions clash, and you will have to determine which an author is using from context.
## Probability Distribution
The [*probability distribution*](https://en.wikipedia.org/wiki/Probability_distribution) gives the probability for the random variable to take any value in a sample space. For example, for a fair six sided die we might say:
|Value|Probability|
|-----|-----------|
|1|1/6|
|2|1/6|
|3|1/6|
|4|1/6|
|5|1/6|
|6|1/6|
Some sources call this the *probability function*. Using ordinary function notation, we would write:
$$P(X{=}4) = f(4) = \frac{1}{6}$$
This states that the probability of the die landing on 4 is $\frac{1}{6}$. $P(X{=}x_k)$ is notation for "the probability of $X$ being $x_k$. Some texts use $Pr$ or $Prob$ instead of $P$.
Another example is a fair coin. It has the sample space {H, T}. The coin is fair, so the probability for heads (H) is 50%, and the probability for tails (T) is 50%. We write this as
$$\begin{gathered}P(X{=}H) = 0.5\\P(X{=}T)=0.5\end{gathered}$$
Sample spaces are not unique. One sample space for a die is {1, 2, 3, 4, 5, 6}. Another valid sample space would be {even, odd}. Another might be {dots in all corners, not dots in all corners}. A sample space is valid so long as it covers all possibilities, and any single event is described by only one element. {even, 1, 3, 4, 5} is not a valid sample space for a die since a value of 4 is matched both by 'even' and '4'.
The probabilities for all values of a *discrete random value* is known as the *discrete probability distribution* and the probabilities for all values of a *continuous random value* is known as the *continuous probability distribution*.
To be a probability distribution the probability of each value $x_i$ must be $x_i \ge 0$, since no probability can be less than zero. Secondly, the sum of the probabilities for all values must equal one. This should be intuitively clear for a coin toss: if the odds of getting heads is 70%, then the odds of getting tails must be 30%. We formulize this requirement as
$$\sum\limits_u P(X{=}u)= 1$$
for discrete distributions, and as
$$\int P(X{=}u) \,du= 1$$
for continuous distributions.
### The Mean, Median, and Mode of a Random Variable
Given a set of data we often want to know a representative or average value for that set. There are many measures for this, and the concept is called a [*measure of central tendency*](https://en.wikipedia.org/wiki/Central_tendency). For example we will want to know the *average* height of the students. We all know how to find the average, but let me belabor the point so I can introduce more formal notation and terminology. Another word for average is the *mean*. We compute the mean by summing the values and dividing by the number of values. If the heights of the students in meters is
$$X = \{1.8, 2.0, 1.7, 1.9, 1.6\}$$
we compute the mean as
$$\mu = \frac{1.8 + 2.0 + 1.7 + 1.9 + 1.6}{5} = 1.8$$
It is traditional to use the symbol $\mu$ (mu) to denote the mean.
We can formalize this computation with the equation
$$ \mu = \frac{1}{n}\sum^n_{i=1} x_i$$
NumPy provides `numpy.mean()` for computing the mean.
```
import numpy as np
x = [1.85, 2.0, 1.7, 1.9, 1.6]
print(np.mean(x))
```
The *mode* of a set of numbers is the number that occurs most often. If only one number occurs most often we say it is a *unimodal* set, and if two or more numbers occur the most with equal frequency than te set is *multimodal*. For example the set {1, 2, 2, 2, 3, 4, 4, 4} has modes 2 and 4, which is multimodal, and the set {5, 7, 7, 13} has the mode 7, and so it is unimodal. We will not be computing the mode in this manner in this book, but we do use the concepts of unimodal and multimodal in a more general sense. For example, in the **Discrete Bayes** chapter we talked about our belief in the dog's position as a *multimodal distribution* because we assigned different probabilities to different positions.
Finally, the *median* of a set of numbers is the middle point of the set so that half the values are below the median and half are above the median. Here, above and below is in relation to the set being sorted. If the set contains an even number of values then the two middle numbers are averaged together.
Numpy provides `numpy.median()` to compute the median. As you can see the median of {1.85, 2.0, 1.7, 1.9, 1.6} is 1.85, because 1.85 is the third element of this set after being sorted.
```
print(np.median(x))
```
## Expected Value of a Random Variable
The [*expected value*](https://en.wikipedia.org/wiki/Expected_value) of a random variable is the average value it would have if we took an infinite number of samples of it and then averaged those samples together. Let's say we have $x=[1,3,5]$ and each value is equally probable. What would we *expect* $x$ to have, on average?
It would be the average of 1, 3, and 5, of course, which is 3. That should make sense; we would expect equal numbers of 1, 3, and 5 to occur, so $(1+3+5)/3=3$ is clearly the average of that infinite series of samples. In other words, here the expected value is the *mean* of the sample space.
Now suppose that each value has a different probability of happening. Say 1 has an 80% chance of occurring, 3 has an 15% chance, and 5 has only a 5% chance. In this case we compute the expected value by multiplying each value of $x$ by the percent chance of it occurring, and summing the result. For this case we could compute
$$\mathbb E[X] = (1)(0.8) + (3)(0.15) + (5)(0.05) = 1.5$$
Here I have introduced the notation $\mathbb E[X]$ for the expected value of $x$. Some texts use $E(x)$. The value 1.5 for $x$ makes intuitive sense because $x$ is far more likely to be 1 than 3 or 5, and 3 is more likely than 5 as well.
We can formalize this by letting $x_i$ be the $i^{th}$ value of $X$, and $p_i$ be the probability of its occurrence. This gives us
$$\mathbb E[X] = \sum_{i=1}^n p_ix_i$$
A trivial bit of algebra shows that if the probabilities are all equal, the expected value is the same as the mean:
$$\mathbb E[X] = \sum_{i=1}^n p_ix_i = \sum_{i=1}^n \frac{1}{n}x_i = \mu_x$$
If $x$ is continuous we substitute the sum for an integral, like so
$$\mathbb E[X] = \int_{-\infty}^\infty x\, f(x) \,dx$$
where $f(x)$ is the probability distribution function of $x$. We won't be using this equation yet, but we will be using it in the next chapter.
### Variance of a Random Variable
The computation above tells us the average height of the students, but it doesn't tell us everything we might want to know. For example, suppose we have three classes of students, which we label $X$, $Y$, and $Z$, with these heights:
```
X = [1.8, 2.0, 1.7, 1.9, 1.6]
Y = [2.2, 1.5, 2.3, 1.7, 1.3]
Z = [1.8, 1.8, 1.8, 1.8, 1.8]
```
Using NumPy we see that the mean height of each class is the same.
```
print(np.mean(X))
print(np.mean(Y))
print(np.mean(Z))
```
The mean of each class is 1.8 meters, but notice that there is a much greater amount of variation in the heights in the second class than in the first class, and that there is no variation at all in the third class.
The mean tells us something about the data, but not the whole story. We want to be able to specify how much *variation* there is between the heights of the students. You can imagine a number of reasons for this. Perhaps a school district needs to order 5,000 desks, and they want to be sure they buy sizes that accommodate the range of heights of the students.
Statistics has formalized this concept of measuring variation into the notion of [*standard deviation*](https://en.wikipedia.org/wiki/Standard_deviation) and [*variance*](https://en.wikipedia.org/wiki/Variance). The equation for computing the variance is
$$\mathit{VAR}(X) = E[(X - \mu)^2]$$
Ignoring the squared terms for a moment, you can see that the variance is the *expected value* for how much the sample space ($X$) varies from the mean (squared, of course). We have the formula for the expected value $E[X] = \sum\limits_{i=1}^n p_ix_i$, and we will assume that any height is equally probable, so we can substitute that into the equation above to get
$$\mathit{VAR}(X) = \frac{1}{n}\sum_{i=1}^n (x_i - \mu)^2$$
Let's compute the variance of the three classes to see what values we get and to become familiar with this concept.
The mean of $X$ is 1.8 ($\mu_x = 1.8$) so we compute
$$
\begin{aligned}
\mathit{VAR}(X) &=\frac{(1.8-1.8)^2 + (2-1.8)^2 + (1.7-1.8)^2 + (1.9-1.8)^2 + (1.6-1.8)^2} {5} \\
&= \frac{0 + 0.04 + 0.01 + 0.01 + 0.04}{5} \\
\mathit{VAR}(X)&= 0.02 \, m^2
\end{aligned}$$
NumPy provides the function `var()` to compute the variance:
```
print(np.var(X), "meters squared")
```
This is perhaps a bit hard to interpret. Heights are in meters, yet the variance is meters squared. Thus we have a more commonly used measure, the *standard deviation*, which is defined as the square root of the variance:
$$\sigma = \sqrt{\mathit{VAR}(X)}=\sqrt{\frac{1}{n}\sum_{i=1}^n(x_i - \mu)^2}$$
It is typical to use $\sigma$ for the *standard deviation* and $\sigma^2$ for the *variance*. In most of this book I will be using $\sigma^2$ instead of $\mathit{VAR}(X)$ for the variance; they symbolize the same thing.
For the first class we compute the standard deviation with
$$
\begin{aligned}
\sigma_x &=\sqrt{\frac{(1.8-1.8)^2 + (2-1.8)^2 + (1.7-1.8)^2 + (1.9-1.8)^2 + (1.6-1.8)^2} {5}} \\
&= \sqrt{\frac{0 + 0.04 + 0.01 + 0.01 + 0.04}{5}} \\
\sigma_x&= 0.1414
\end{aligned}$$
We can verify this computation with the NumPy method `numpy.std()` which computes the standard deviation. 'std' is a common abbreviation for standard deviation.
```
print('std {:.4f}'.format(np.std(X)))
print('var {:.4f}'.format(np.std(X)**2))
```
And, of course, $0.1414^2 = 0.02$, which agrees with our earlier computation of the variance.
What does the standard deviation signify? It tells us how much the heights vary amongst themselves. "How much" is not a mathematical term. We will be able to define it much more precisely once we introduce the concept of a Gaussian in the next section. For now I'll say that for many things 68% of all values lie within one standard deviation of the mean. In other words we can conclude that for a random class 68% of the students will have heights between 1.66 (1.8-0.1414) meters and 1.94 (1.8+0.1414) meters.
We can view this in a plot:
```
from book_format import set_figsize, figsize
from code.book_plots import interactive_plot
from code.gaussian_internal import plot_height_std
import matplotlib.pyplot as plt
with interactive_plot():
plot_height_std(X)
```
For only 5 students we obviously will not get exactly 68% within one standard deviation. We do see that 3 out of 5 students are within $\pm1\sigma$, or 60%, which is as close as you can get to 68% with only 5 samples. I haven't yet introduced enough math or Python for you to fully understand the next bit of code, but let's look at the results for a class with 100 students.
> We write one standard deviation as $1\sigma$, which is pronounced "one standard deviation", not "one sigma". Two standard deviations is $2\sigma$, and so on.
```
from numpy.random import randn
data = [1.8 + .1414*randn() for i in range(100)]
with interactive_plot():
plot_height_std(data, lw=2)
print('mean = {:.3f}'.format(np.mean(data)))
print('std = {:.3f}'.format(np.std(data)))
```
We can see by eye that roughly 68% of the heights lie within $\pm1\sigma$ of the mean 1.8.
We'll discuss this in greater depth soon. For now let's compute the standard deviation for
$$Y = [2.2, 1.5, 2.3, 1.7, 1.3]$$
The mean of $Y$ is $\mu=1.8$ m, so
$$
\begin{aligned}
\sigma_y &=\sqrt{\frac{(2.2-1.8)^2 + (1.5-1.8)^2 + (2.3-1.8)^2 + (1.7-1.8)^2 + (1.3-1.8)^2} {5}} \\
&= \sqrt{0.152} = 0.39 \ m
\end{aligned}$$
We will verify that with NumPy with
```
print('std of Y is {:.4f} m'.format(np.std(Y)))
```
This corresponds with what we would expect. There is more variation in the heights for $Y$, and the standard deviation is larger.
Finally, let's compute the standard deviation for $Z$. There is no variation in the values, so we would expect the standard deviation to be zero. We show this to be true with
$$
\begin{aligned}
\sigma_z &=\sqrt{\frac{(1.8-1.8)^2 + (1.8-1.8)^2 + (1.8-1.8)^2 + (1.8-1.8)^2 + (1.8-1.8)^2} {5}} \\
&= \sqrt{\frac{0+0+0+0+0}{5}} \\
\sigma_z&= 0.0 \ m
\end{aligned}$$
```
print(np.std(Z))
```
Before we continue I need to point out that I'm ignoring that on average men are taller than women. In general the height variance of a class that contains only men or women will be smaller than a class with both sexes. This is true for other factors as well. Well nourished children are taller than malnourished children. Scandinavians are taller than Italians. When designing experiments statisticians need to take these factors into account.
I suggested we might be performing this analysis to order desks for a school district. For each age group there are likely to be two different means - one clustered around the mean height of the females, and a second mean clustered around the mean heights of the males. The mean of the entire class will be somewhere between the two. If we bought desks for the mean of all students we are likely to end up with desks that fit neither the males or females in the school!
It's too early to understand why, but we will not normally be faced with these problems in this book. Consult any standard probability text if you need to learn techniques to deal with these issues.
### Why the Square of the Differences
Why are we taking the *square* of the differences for the variance? I could go into a lot of math, but let's look at this in a simple way. Here is a chart of the values of $X$ plotted against the mean for $X=[3,-3,3,-3]$
```
with interactive_plot():
X = [3, -3, 3, -3]
mean = np.average(X)
for i in range(len(X)):
plt.plot([i ,i], [mean, X[i]], color='k')
plt.axhline(mean)
plt.xlim(-1, len(X))
plt.tick_params(axis='x', labelbottom='off')
```
If we didn't take the square of the differences the signs would cancel everything out:
$$\frac{(3-0) + (-3-0) + (3-0) + (-3-0)}{4} = 0$$
This is clearly incorrect, as there is more than 0 variance in the data.
Maybe we can use the absolute value? We can see by inspection that the result is $12/4=3$ which is certainly correct — each value varies by 3 from the mean. But what if we have $Y=[6, -2, -3, 1]$? In this case we get $12/4=3$. $Y$ is clearly more spread out than $X$, but the computation yields the same variance. If we use the correct formula we get a variance of 3.5 for $Y$, which reflects its larger variation.
This is not a proof of correctness. Indeed, Carl Friedrich Gauss, the inventor of the technique, recognized that is is somewhat arbitrary. If there are outliers then squaring the difference gives disproportionate weight to that term. For example, let's see what happens if we have $X = [1,-1,1,-2,3,2,100]$.
```
X = [1, -1, 1, -2, 3, 2, 100]
print('Variance of X = {:.2f}'.format(np.var(X)))
```
Is this "correct"? You tell me. Without the outlier of 100 we get $\sigma^2=2.89$, which accurately reflects how $X$ is varying absent the outlier. The one outlier swamps the computation. I will not continue down this path; if you are interested you might want to look at the work that James Berger has done on this problem, in a field called *Bayesian robustness*, or the excellent publications on *robust statistics* by Peter J. Huber [3].
## Gaussians
We are now ready to learn about [Gaussians](https://en.wikipedia.org/wiki/Gaussian_function). Let's remind ourselves of the motivation for this chapter.
> We desire a unimodal, continuous way to represent probabilities that models how the real world works, and that is computationally efficient to calculate.
Let's look at a graph of a Gaussian distribution to get a sense of what we are talking about.
```
from filterpy.stats import plot_gaussian_pdf
plt.figure()
ax = plot_gaussian_pdf(mean=1.8, variance=0.1414**2,
xlabel='Student Height', ylabel='pdf')
```
This curve is a [*probability density function*](https://en.wikipedia.org/wiki/Probability_density_function) or *pdf* for short. It shows the relative likelihood for the random variable to take on a value. In the chart above, a student is somewhat more likely to have a height near 1.8 m than 1.7 m, and far more likely to have a height of 1.9 m vs 1.1 m.
> I explain how to plot Gaussians, and much more, in the Notebook *Computing_and_Plotting_PDFs* in the
Supporting_Notebooks folder. You can read it online [here](https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/Supporting_Notebooks/Computing_and_plotting_PDFs.ipynb) [1].
This may be recognizable to you as a 'bell curve'. This curve is ubiquitous because under real world conditions many observations are distributed in such a manner. In fact, this is the curve for the student heights given earlier. I will not use the term 'bell curve' to refer to a Gaussian because many probability distributions have a similar bell curve shape. Non-mathematical sources might not be as precise, so be judicious in what you conclude when you see the term used without definition.
This curve is not unique to heights — a vast amount of natural phenomena exhibits this sort of distribution, including the sensors that we use in filtering problems. As we will see, it also has all the attributes that we are looking for — it represents a unimodal belief or value as a probability, it is continuous, and it is computationally efficient. We will soon discover that it also has other desirable qualities which we may not realize we desire.
To further motivate you, recall the shapes of the probability distributions in the *Discrete Bayes* chapter. They were not perfect Gaussian curves, but they were similar, as in the plot below. We will be using Gaussians to replace the discrete probabilities used in that chapter!
```
import code.book_plots as book_plots
belief = [ 0.,0., 0., 0.1, 0.15, 0.5, 0.2, .15, 0, 0]
with interactive_plot():
book_plots.bar_plot(belief)
```
## Nomenclature
A bit of nomenclature before we continue - this chart depicts the *probability density* of a *random variable* having any value between ($-\infty..\infty)$. What does that mean? Imagine we take an infinite number of infinitely precise measurements of the speed of automobiles on a section of highway. We could then plot the results by showing the relative number of cars going past at any given speed. If the average was 120 kph, it might look like this:
```
with interactive_plot():
ax = plot_gaussian_pdf(mean=120, variance=17**2, xlabel='speed(kph)')
```
The y-axis depicts the *probability density* — the relative amount of cars that are going the speed at the corresponding x-axis.
You may object that human heights or automobile speeds cannot be less than zero, let alone $-\infty$ or $\infty$. This is true, but this is a common limitation of mathematical modeling. “The map is not the territory” is a common expression, and it is true for Bayesian filtering and statistics. The Gaussian distribution above models the distribution of the measured automobile speeds, but being a model it is necessarily imperfect. The difference between model and reality will come up again and again in these filters. Gaussians are used in many branches of mathematics, not because they perfectly model reality, but because they are easier to use than any other relatively accurate choice. However, even in this book Gaussians will fail to model reality, forcing us to use computationally expensive alternatives.
You will see these distributions called *Gaussian distributions* or *normal distributions*. *Gaussian* and *normal* both mean the same thing in this context, and are used interchangeably. I will use both throughout this book as different sources will use either term, and I want you to be used to seeing both. Finally, as in this paragraph, it is typical to shorten the name and talk about a *Gaussian* or *normal* — these are both typical shortcut names for the *Gaussian distribution*.
## Gaussian Distributions
Let's explore how Gaussians work. A Gaussian is a *continuous probability distribution* that is completely described with two parameters, the mean ($\mu$) and the variance ($\sigma^2$). It is defined as:
$$
f(x, \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}} \exp\big [{-\frac{(x-\mu)^2}{2\sigma^2} }\big ]
$$
$\exp[x]$ is notation for $e^x$.
<p> Don't be dissuaded by the equation if you haven't seen it before; you will not need to memorize or manipulate it. The computation of this function is stored in `stats.py` with the function `gaussian(x, mean, var)`.
> **Optional:** Let's remind ourselves how to look at a function stored in a file by using the *%load* magic. If you type *%load -s gaussian stats.py* into a code cell and then press CTRL-Enter, the notebook will create a new input cell and load the function into it.
```python
%load -s gaussian stats.py
def gaussian(x, mean, var):
"""returns normal distribution for x given a
gaussian with the specified mean and variance.
"""
return (np.exp((-0.5*(np.asarray(x)-mean)**2)/var) /
math.sqrt(2*math.pi*var))
```
<p><p><p><p>We will plot a Gaussian with a mean of 22 $(\mu=22)$, with a variance of 4 $(\sigma^2=4)$, and then discuss what this means.
```
from filterpy.stats import gaussian, norm_cdf
with interactive_plot():
ax = plot_gaussian_pdf(22, 4, mean_line=True, xlabel='$^{\circ}C$')
```
What does this curve *mean*? Assume we have a thermometer which reads 22°C. No thermometer is perfectly accurate, and so we expect that each reading will be slightly off the actual value. However, a theorem called [*Central Limit Theorem*](https://en.wikipedia.org/wiki/Central_limit_theorem) states that if we make many measurements that the measurements will be normally distributed. When we look at this chart we can "sort of" think of it as representing the probability of the thermometer reading a particular value given the actual temperature of 22°C.
Recall that a Gaussian distribution is *continuous*. Think of an infinitely long straight line - what is the probability that a point you pick randomly is at 2. Clearly 0%, as there is an infinite number of choices to choose from. The same is true for normal distributions; in the graph above the probability of being *exactly* 2°C is 0% because there are an infinite number of values the reading can take.
What is this curve? It is something we call the *probability density function.* The area under the curve at any region gives you the probability of those values. So, for example, if you compute the area under the curve between 20 and 22 the resulting area will be the probability of the temperature reading being between those two temperatures.
We can think of this in Bayesian terms or frequentist terms. As a Bayesian, if the thermometer reads exactly 22°C, then our belief is described by the curve - our belief that the actual (system) temperature is near 22 is very high, and our belief that the actual temperature is near 18 is very low. As a frequentist we would say that if we took 1 billion temperature measurements of a system at exactly 22°C, then a histogram of the measurements would look like this curve.
How do you compute the probability, or area under the curve? You integrate the equation for the Gaussian
$$ \int^{x_1}_{x_0} \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}{(x-\mu)^2}/\sigma^2 } dx$$
I wrote `filterpy.stats.norm_cdf` which computes the integral for you. For example, we can compute
```
print('Probability of range 21.5 to 22.5 is {:.2f}%'.format(
norm_cdf((21.5, 22.5), 22,4)*100))
print('Probability of range 23.5 to 24.5 is {:.2f}%'.format(
norm_cdf((23.5, 24.5), 22,4)*100))
```
The mean ($\mu$) is what it sounds like — the average of all possible probabilities. Because of the symmetric shape of the curve it is also the tallest part of the curve. The thermometer reads 22°C, so that is what we used for the mean.
The notation for a normal distribution for a random variable $X$ is $X \sim\ \mathcal{N}(\mu,\sigma^2)$ where $\sim$ means *distributed according to*. This means I can express the temperature reading of our thermometer as
$$\text{temp} \sim \mathcal{N}(22,4)$$
This is an extremely important result. Gaussians allow me to capture an infinite number of possible values with only two numbers! With the values $\mu=22$ and $\sigma^2=4$ I can compute the distribution of measurements for over any range.
> Some sources use $\mathcal N (\mu, \sigma)$ instead of $\mathcal N (\mu, \sigma^2)$. Either is fine, they are both conventions. You need to keep in mind which form is being used if you see a term such as $\mathcal{N}(22,4)$. In this book I always use $\mathcal N (\mu, \sigma^2)$, so $\sigma=2$, $\sigma^2=4$ for this example.
## The Variance and Belief
Since this is a probability density distribution it is required that the area under the curve always equals one. This should be intuitively clear — the area under the curve represents all possible outcomes, *something* happened, and the probability of *something happening* is one, so the density must sum to one. We can prove this ourselves with a bit of code. (If you are mathematically inclined, integrate the Gaussian equation from $-\infty$ to $\infty$)
```
print(norm_cdf((-1e8, 1e8), mu=0, var=4))
```
This leads to an important insight. If the variance is small the curve will be narrow. this is because the variance is a measure of *how much* the samples vary from the mean. To keep the area equal to 1, the curve must also be tall. On the other hand if the variance is large the curve will be wide, and thus it will also have to be short to make the area equal to 1.
Let's look at that graphically:
```
import numpy as np
import matplotlib.pyplot as plt
xs = np.arange(15, 30, 0.05)
with interactive_plot():
plt.plot(xs, gaussian(xs, 23, 0.05), label='$\sigma^2$=0.05', c='b')
plt.plot(xs, gaussian(xs, 23, 1), label='$\sigma^2$=1', ls=':', c='b')
plt.plot(xs, gaussian(xs, 23, 5), label='$\sigma^2$=5', ls='--', c='b')
plt.legend()
```
What is this telling us? The Gaussian with $\sigma^2=0.05$ is very narrow. It is saying that we believe $x=23$, and that we are very sure about that. In contrast, the Gaussian with $\sigma^2=5$ also believes that $x=23$, but we are much less sure about that. Our believe that $x=23$ is lower, and so our belief about the likely possible values for $x$ is spread out — we think it is quite likely that $x=20$ or $x=26$, for example. $\sigma^2=0.05$ has almost completely eliminated $22$ or $24$ as possible values, whereas $\sigma^2=5$ considers them nearly as likely as $23$.
If we think back to the thermometer, we can consider these three curves as representing the readings from three different thermometers. The curve for $\sigma^2=0.05$ represents a very accurate thermometer, and curve for $\sigma^2=5$ represents a fairly inaccurate one. Note the very powerful property the Gaussian distribution affords us — we can entirely represent both the reading and the error of a thermometer with only two numbers — the mean and the variance.
An equivalent formation for a Gaussian is $\mathcal{N}(\mu,1/\tau)$ where $\mu$ is the *mean* and $\tau$ the *precision*. $1/\tau = \sigma^2$; it is the reciprocal of the variance. While we do not use this formulation in this book, it underscores that the variance is a measure of how precise our data is. A small variance yields large precision — our measurement is very precise. Conversely, a large variance yields low precision — our belief is spread out across a large area. You should become comfortable with thinking about Gaussians in these equivalent forms. In Bayesian terms Gaussians reflect our *belief* about a measurement, they express the *precision* of the measurement, and they express how much *variance* there is in the measurements. These are all different ways of stating the same fact.
I'm getting ahead of myself, but in the next chapters we will use Gaussians to express our belief in things like the estimated position of the object we are tracking, or the accuracy of the sensors we are using.
## The 68-95-99.7 Rule
It is worth spending a few words on standard deviation now. The standard deviation is a measure of how much variation from the mean exists. For Gaussian distributions, 68% of all the data falls within one standard deviation ($\pm1\sigma$) of the mean, 95% falls within two standard deviations ($\pm2\sigma$), and 99.7% within three ($\pm3\sigma$). This is often called the [68-95-99.7 rule](https://en.wikipedia.org/wiki/68%E2%80%9395%E2%80%9399.7_rule). If you were told that the average test score in a class was 71 with a standard deviation of 9.4, you could conclude that 95% of the students received a score between 52.2 and 89.8 if the distribution is normal (that is calculated with $71 \pm (2 * 9.4)$).
Finally, these are not arbitrary numbers. If the Gaussian for our position is $\mu=22$ meters, then the standard deviation also has units meters. Thus $\sigma=0.2$ implies that 68% of the measurements range from 21.8 to 22.2 meters. Variance is the standard deviation squared, thus $\sigma^2 = .04$ meters$^2$.
The following graph depicts the relationship between the standard deviation and the normal distribution.
```
from code.gaussian_internal import display_stddev_plot
with interactive_plot():
display_stddev_plot()
```
## Interactive Gaussians
For those that are reading this in a Jupyter Notebook, here is an interactive version of the Gaussian plots. Use the sliders to modify $\mu$ and $\sigma^2$. Adjusting $\mu$ will move the graph to the left and right because you are adjusting the mean, and adjusting $\sigma^2$ will make the bell curve thicker and thinner.
```
import math
from IPython.html.widgets import interact, interactive, fixed
set_figsize(y=3)
def plt_g(mu,variance):
plt.figure()
xs = np.arange(2, 8, 0.1)
ys = gaussian(xs, mu, variance)
plt.plot(xs, ys)
plt.ylim((0, 1))
interact (plt_g, mu=(0., 10), variance = (.2, 1.));
```
Finally, if you are reading this online, here is an animation of a Gaussian. First, the mean is shifted to the right. Then the mean is centered at $\mu=5$ and the variance is modified.
<img src='animations/04_gaussian_animate.gif'>
## Computational Properties of Gaussians
A remarkable property of Gaussians is that the product of two independent Gaussians is another Gaussian! The sum is not Gaussian, but proportional to a Gaussian.
The discrete Bayes filter works by multiplying and adding probabilities. I'm getting ahead of myself, but the Kalman filter uses Gaussians instead of probabilities, but the rest of the algorithm remains the same. This means we will need to multiply and add Gaussians.
The Gaussian is a nonlinear function, and typically if you multiply a nonlinear equation with itself you end up with a different equation. For example, the shape of `sin(x)sin(x)` is very different from `sin(x)`. But the result of multiplying two Gaussians is yet another Gaussian. This is a fundamental property, and a key reason why Kalman filters are computationally feasible. Said another way, Kalman filters use Gaussians *because* they are computationally nice.
The remainder of this section is optional. I will derive the equations for the sum and product of two Gaussians. You will not need to understand this material to understand the rest of the book, so long as you accept the results.
### Product of Gaussians
The product of two independent Gaussians is given by:
$$\begin{aligned}\mu &=\frac{\sigma_1^2\mu_2 + \sigma_2^2\mu_1}{\sigma_1^2+\sigma_2^2}\\
\sigma^2 &=\frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2}
\end{aligned}$$
You can find this result by multiplying the equation for two Gaussians together and combining terms. The algebra gets messy. I will derive it using Bayes theorem. We can state the problem as: let the prior be $N(\bar\mu, \bar\sigma^2)$, and measurement be $z \propto N(z, \sigma_z^2)$. What is the posterior x given the measurement z?
Write the posterior as $P(x \mid z)$. Now we can use Bayes Theorem to state
$$P(x \mid z) = \frac{P(z \mid x)P(x)}{P(z)}$$
$P(z)$ is a normalizing constant, so we can create a proportinality
$$P(x \mid z) \propto P(z|x)P(x)$$
Now we subtitute in the equations for the Gaussians, which are
$$P(z \mid x) = \frac{1}{\sqrt{2\pi\sigma_z^2}}\exp \Big[-\frac{(z-x)^2}{2\sigma_z^2}\Big]$$
$$P(x) = \frac{1}{\sqrt{2\pi\bar\sigma^2}}\exp \Big[-\frac{(x-\bar\mu)^2}{2\bar\sigma^2}\Big]$$
We can drop the leading terms, as they are constants, giving us
$$\begin{aligned}
P(x \mid z) &\propto \exp \Big[-\frac{(z-x)^2}{2\sigma_z^2}\Big]\exp \Big[-\frac{(x-\bar\mu)^2}{2\bar\sigma^2}\Big]\\
&\propto \exp \Big[-\frac{(z-x)^2}{2\sigma_z^2}-\frac{(x-\bar\mu)^2}{2\bar\sigma^2}\Big] \\
&\propto \exp \Big[-\frac{1}{2\sigma_z^2\bar\sigma^2}[\bar\sigma^2(z-x)^2-\sigma_z^2(x-\bar\mu)^2]\Big]
\end{aligned}$$
Now we multiply out the squared terms and group in terms of the posterior $x$.
$$\begin{aligned}
P(x \mid z) &\propto \exp \Big[-\frac{1}{2\sigma_z^2\bar\sigma^2}[\bar\sigma^2(z^2 -2xz + x^2) + \sigma_z^2(x^2 - 2x\bar\mu+\bar\mu^2)]\Big ] \\
&\propto \exp \Big[-\frac{1}{2\sigma_z^2\bar\sigma^2}[x^2(\bar\sigma^2+\sigma_z^2)-2x(\sigma_z^2\bar\mu + \bar\sigma^2z) + (\bar\sigma^2z^2+\sigma_z^2\bar\mu^2)]\Big ]
\end{aligned}$$
The last parentheses do not contain the posterior $x$, so it can be treated as a constant and discarded.
$$P(x \mid z) \propto \exp \Big[-\frac{1}{2}\frac{x^2(\bar\sigma^2+\sigma_z^2)-2x(\sigma_z^2\bar\mu + \bar\sigma^2z)}{\sigma_z^2\bar\sigma^2}\Big ]
$$
Divide numerator and denominator by $\bar\sigma^2+\sigma_z^2$ to get
$$P(x \mid z) \propto \exp \Big[-\frac{1}{2}\frac{x^2-2x(\frac{\sigma_z^2\bar\mu + \bar\sigma^2z}{\bar\sigma^2+\sigma_z^2})}{\frac{\sigma_z^2\bar\sigma^2}{\bar\sigma^2+\sigma_z^2}}\Big ]
$$
Proportionality lets us create or delete constants at will, so we can factor this into
$$P(x \mid z) \propto \exp \Big[-\frac{1}{2}\frac{(x-\frac{\sigma_z^2\bar\mu + \bar\sigma^2z}{\bar\sigma^2+\sigma_z^2})^2}{\frac{\sigma_z^2\bar\sigma^2}{\bar\sigma^2+\sigma_z^2}}\Big ]
$$
A Gaussian is
$$N(\mu,\, \sigma^2) \propto \exp\Big [-\frac{1}{2}\frac{(x - \mu)^2}{\sigma^2}\Big ]$$
So we can see that $P(x \mid z)$ has a mean of
$$\mu_\mathtt{posterior} = \frac{\sigma_z^2\bar\mu + \bar\sigma^2z}{\bar\sigma^2+\sigma_z^2}$$
and a variance of
$$
\sigma_\mathtt{posterior} = \frac{\sigma_z^2\bar\sigma^2}{\bar\sigma^2+\sigma_z^2}
$$
I've dropped the constants, and so the result is not a normal, but proportional to one. Bayes theorem normalizes with the $P(z)$ divisor, ensuring that the result is normal. We normalize in the update step of our filters, ensuring the filter estimate is Gaussian.
$$\mathcal N_1 = \| \mathcal N_2\cdot \mathcal N_3\|$$
### Sum of Gaussians
The sum of two Gaussians is given by
$$\begin{gathered}\mu = \mu_1 + \mu_2 \\
\sigma^2 = \sigma^2_1 + \sigma^2_2
\end{gathered}$$
There are several proofs for this. I will use convolution since we used convolution in the previous chapter for the histograms of probabilities.
To find the density function of the sum of two Gaussian random variables we sum the density functions of each. They are nonlinear, continuous functions, so we need to compute the sum with an integral. If the random variables $p$ and $z$ (e.g. prior and measurement) are independent we can compute this with
$p(x) = \int\limits_{-\infty}^\infty f_p(x-z)f_z(z)\, dx$
This is the equation for a convolution. Now we just do some math:
$p(x) = \int\limits_{-\infty}^\infty f_2(x-x_1)f_1(x_1)\, dx$
$= \int\limits_{-\infty}^\infty
\frac{1}{\sqrt{2\pi}\sigma_z}\exp\left[-\frac{x - z - \mu_z}{2\sigma^2_z}\right]
\frac{1}{\sqrt{2\pi}\sigma_p}\exp\left[-\frac{x - \mu_p}{2\sigma^2_p}\right] \, dx$
$= \int\limits_{-\infty}^\infty
\frac{1}{\sqrt{2\pi}\sqrt{\sigma_p^2 + \sigma_z^2}} \exp\left[ -\frac{(x - (\mu_p + \mu_z)))^2}{2(\sigma_z^2+\sigma_p^2)}\right]
\frac{1}{\sqrt{2\pi}\frac{\sigma_p\sigma_z}{\sqrt{\sigma_p^2 + \sigma_z^2}}} \exp\left[ -\frac{(x - \frac{\sigma_p^2(x-\mu_z) + \sigma_z^2\mu_p}{}))^2}{2\left(\frac{\sigma_p\sigma_x}{\sqrt{\sigma_z^2+\sigma_p^2}}\right)^2}\right] \, dx$
$= \frac{1}{\sqrt{2\pi}\sqrt{\sigma_p^2 + \sigma_z^2}} \exp\left[ -\frac{(x - (\mu_p + \mu_z)))^2}{2(\sigma_z^2+\sigma_p^2)}\right] \int\limits_{-\infty}^\infty
\frac{1}{\sqrt{2\pi}\frac{\sigma_p\sigma_z}{\sqrt{\sigma_p^2 + \sigma_z^2}}} \exp\left[ -\frac{(x - \frac{\sigma_p^2(x-\mu_z) + \sigma_z^2\mu_p}{}))^2}{2\left(\frac{\sigma_p\sigma_x}{\sqrt{\sigma_z^2+\sigma_p^2}}\right)^2}\right] \, dx$
The expression inside the integral is a normal distribution. The sum of a normal distribution is one, hence the integral is one. This gives us
$$p(x) = \frac{1}{\sqrt{2\pi}\sqrt{\sigma_p^2 + \sigma_z^2}} \exp\left[ -\frac{(x - (\mu_p + \mu_z)))^2}{2(\sigma_z^2+\sigma_p^2)}\right]$$
This is in the form of a normal, where
$$\begin{gathered}\mu_x = \mu_p + \mu_z \\
\sigma_x^2 = \sigma_z^2+\sigma_p^2\, \square\end{gathered}$$
## Computing Probabilities with scipy.stats
In this chapter I used code from [FilterPy](https://github.com/rlabbe/filterpy) to compute and plot Gaussians. I did that to give you a chance to look at the code and see how these functions are implemented. However, Python comes with "batteries included" as the saying goes, and it comes with a wide range of statistics functions in the module `scipy.stats`. So let's walk through how to use scipy.stats to compute statistics and probabilities.
The `scipy.stats` module contains a number of objects which you can use to compute attributes of various probability distributions. The full documentation for this module is here: http://docs.scipy.org/doc/scipy/reference/stats.html. We will focus on the norm variable, which implements the normal distribution. Let's look at some code that uses `scipy.stats.norm` to compute a Gaussian, and compare its value to the value returned by the `gaussian()` function from FilterPy.
```
from scipy.stats import norm
import filterpy.stats
print(norm(2, 3).pdf(1.5))
print(filterpy.stats.gaussian(x=1.5, mean=2, var=3*3))
```
The call `norm(2, 3)` creates what scipy calls a 'frozen' distribution - it creates and returns an object with a mean of 2 and a standard deviation of 3. You can then use this object multiple times to get the probability density of various values, like so:
```
n23 = norm(2, 3)
print('pdf of 1.5 is %.4f' % n23.pdf(1.5))
print('pdf of 2.5 is also %.4f' % n23.pdf(2.5))
print('pdf of 2 is %.4f' % n23.pdf(2))
```
The documentation for [scipy.stats.norm](http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.norm.html#scipy.stats.normfor) [2] lists many other functions. For example, we can generate $n$ samples from the distribution with the `rvs()` function.
```
np.set_printoptions(precision=3, linewidth=50)
print(n23.rvs(size=15))
```
We can get the [*cumulative distribution function (CDF)*](https://en.wikipedia.org/wiki/Cumulative_distribution_function), which is the probability that a randomly drawn value from the distribution is less than or equal to $x$.
```
# probability that a random value is less than the mean 2
print(n23.cdf(2))
```
We can get various properties of the distribution:
```
print('variance is', n23.var())
print('standard deviation is', n23.std())
print('mean is', n23.mean())
```
## Fat Tails
Earlier I mentioned the *central limit theorem*, which states that under certain conditions the arithmetic sum of any independent random variable will be normally distributed, regardless of how the random variables are distributed. This is important to us because nature is full of distributions which are not normal, but when we apply the central limit theorem over large populations we end up with normal distributions.
However, a key part of the proof is “under certain conditions”. These conditions often do not hold for the physical world. The resulting distributions are called *fat tailed*. Tails is a colloquial term for the far left and right side parts of the curve where the probability density is close to zero.
Let's consider a trivial example. We think of things like test scores as being normally distributed. If you have ever had a professor “grade on a curve” you have been subject to this assumption. But of course test scores cannot follow a normal distribution. This is because the distribution assigns a nonzero probability distribution for *any* value, no matter how far from the mean. So, for example, say your mean is 90 and the standard deviation is 13. The normal distribution assumes that there is a large chance of somebody getting a 90, and a small chance of somebody getting a 40. However, it also implies that there is a tiny chance of somebody getting a grade of -10, or 150. It assigns an infinitesimal chance of getting a score of $-10^{300}$ or $10^{32986}$. The *tails* of a Gaussian distribution are infinitely long.
But for a test we know this is not true. Ignoring extra credit, you cannot get less than 0, or more than 100. Let's plot this range of values using a normal distribution.
```
xs = np.arange(10,100, 0.05)
ys = [gaussian(x, 90, 30) for x in xs]
with interactive_plot():
plt.plot(xs, ys, label='var=0.2')
plt.xlim((0,120))
plt.ylim(0, 0.09);
```
The area under the curve cannot equal 1, so it is not a probability distribution. What actually happens is that more students than predicted by a normal distribution get scores nearer the upper end of the range (for example), and that tail becomes “fat”. Also, the test is probably not able to perfectly distinguish incredibly minute differences in skill in the students, so the distribution to the left of the mean is also probably a bit bunched up in places. The resulting distribution is called a [*fat tail distribution*](https://en.wikipedia.org/wiki/Fat-tailed_distribution).
Kalman filters use sensors to measure the world. The errors in a sensor's measurements are rarely truly Gaussian. It is far too early to be talking about the difficulties that this presents to the Kalman filter designer. It is worth keeping in the back of your mind the fact that the Kalman filter math is based on an idealized model of the world. For now I will present a bit of code that I will be using later in the book to form fat tail distributions to simulate various processes and sensors. This distribution is called the [*Student's $t$-distribution*](https://en.wikipedia.org/wiki/Student%27s_t-distribution).
Let's say I want to model a sensor that has some white noise in the output. For simplicity, let's say the signal is a constant 10, and the standard deviation of the noise is 2. We can use the function `numpy.random.randn()` to get a random number with a mean of 0 and a standard deviation of 1. I can simulate this with:
```
from numpy.random import randn
def sense():
return 10 + randn()*2
```
Let's plot that signal and see what it looks like.
```
zs = [sense() for i in range(5000)]
with interactive_plot():
plt.plot(zs, lw=1)
```
That looks like I would expect. The signal is centered around 10. A standard deviation of 2 means that 68% of the measurements will be within $\pm$ 2 of 10, and 99% will be within $\pm$ 6 of 10, and that looks like what is happening.
Now let's look at a fat tailed distribution generated with the Student's $t$-distribution. I will not go into the math, but just give you the source code for it and then plot a distribution using it.
```
import random
import math
def rand_student_t(df, mu=0, std=1):
"""return random number distributed by Student's t
distribution with `df` degrees of freedom with the
specified mean and standard deviation.
"""
x = random.gauss(0, std)
y = 2.0*random.gammavariate(0.5*df, 2.0)
return x / (math.sqrt(y / df)) + mu
def sense_t():
return 10 + rand_student_t(7)*2
zs = [sense_t() for i in range(5000)]
with interactive_plot():
plt.plot(zs, lw=1)
```
We can see from the plot that while the output is similar to the normal distribution there are outliers that go far more than 3 standard deviations from the mean (7 to 13). This is what causes the 'fat tail'.
It is unlikely that the Student's $t$-distribution is an accurate model of how your sensor (say, a GPS or Doppler) performs, and this is not a book on how to model physical systems. However, it does produce reasonable data to test your filter's performance when presented with real world noise. We will be using distributions like these throughout the rest of the book in our simulations and tests.
This is not an idle concern. The Kalman filter equations assume the noise is normally distributed, and perform sub-optimally if this is not true. Designers for mission critical filters, such as the filters on spacecraft, need to master a lot of theory and empirical knowledge about the performance of the sensors on their spacecraft.
The code for rand_student_t is included in `filterpy.stats`. You may use it with
```python
from filterpy.stats import rand_student_t
```
## Summary and Key Points
This chapter is a poor introduction to statistics in general. I've only covered the concepts that needed to use Gaussians in the remainder of the book, no more. What I've covered will not get you very far if you intend to read the Kalman filter literature. If this is a new topic to you I suggest reading a statistics textbook. I've always liked the Schaum series for self study, and Alan Downey's *Think Stats* [5] is also very good.
The following points **must** be understood by you before we continue:
* Normals express a continuous probability distribution
* They are completely described by two parameters: the mean ($\mu$) and variance ($\sigma^2$)
* $\mu$ is the average of all possible values
* The variance $\sigma^2$ represents how much our measurements vary from the mean
* The standard deviation ($\sigma$) is the square root of the variance ($\sigma^2$)
* Many things in nature approximate a normal distribution
## References
[1] https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/Supporting_Notebooks/Computing_and_plotting_PDFs.ipynb
[2] http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.norm.html
[3] http://docs.scipy.org/doc/scipy/reference/tutorial/stats.html
[4] Huber, Peter J. *Robust Statistical Procedures*, Second Edition. Society for Industrial and Applied Mathematics, 1996.
[5] Downey, Alan. *Think Stats*, Second Edition. O'Reilly Media.
https://github.com/AllenDowney/ThinkStats2
http://greenteapress.com/thinkstats/
|
github_jupyter
|
#format the book
%matplotlib notebook
from __future__ import division, print_function
from book_format import load_style
load_style()
import numpy as np
x = [1.85, 2.0, 1.7, 1.9, 1.6]
print(np.mean(x))
print(np.median(x))
X = [1.8, 2.0, 1.7, 1.9, 1.6]
Y = [2.2, 1.5, 2.3, 1.7, 1.3]
Z = [1.8, 1.8, 1.8, 1.8, 1.8]
print(np.mean(X))
print(np.mean(Y))
print(np.mean(Z))
print(np.var(X), "meters squared")
print('std {:.4f}'.format(np.std(X)))
print('var {:.4f}'.format(np.std(X)**2))
from book_format import set_figsize, figsize
from code.book_plots import interactive_plot
from code.gaussian_internal import plot_height_std
import matplotlib.pyplot as plt
with interactive_plot():
plot_height_std(X)
from numpy.random import randn
data = [1.8 + .1414*randn() for i in range(100)]
with interactive_plot():
plot_height_std(data, lw=2)
print('mean = {:.3f}'.format(np.mean(data)))
print('std = {:.3f}'.format(np.std(data)))
print('std of Y is {:.4f} m'.format(np.std(Y)))
print(np.std(Z))
with interactive_plot():
X = [3, -3, 3, -3]
mean = np.average(X)
for i in range(len(X)):
plt.plot([i ,i], [mean, X[i]], color='k')
plt.axhline(mean)
plt.xlim(-1, len(X))
plt.tick_params(axis='x', labelbottom='off')
X = [1, -1, 1, -2, 3, 2, 100]
print('Variance of X = {:.2f}'.format(np.var(X)))
from filterpy.stats import plot_gaussian_pdf
plt.figure()
ax = plot_gaussian_pdf(mean=1.8, variance=0.1414**2,
xlabel='Student Height', ylabel='pdf')
import code.book_plots as book_plots
belief = [ 0.,0., 0., 0.1, 0.15, 0.5, 0.2, .15, 0, 0]
with interactive_plot():
book_plots.bar_plot(belief)
with interactive_plot():
ax = plot_gaussian_pdf(mean=120, variance=17**2, xlabel='speed(kph)')
%load -s gaussian stats.py
def gaussian(x, mean, var):
"""returns normal distribution for x given a
gaussian with the specified mean and variance.
"""
return (np.exp((-0.5*(np.asarray(x)-mean)**2)/var) /
math.sqrt(2*math.pi*var))
from filterpy.stats import gaussian, norm_cdf
with interactive_plot():
ax = plot_gaussian_pdf(22, 4, mean_line=True, xlabel='$^{\circ}C$')
print('Probability of range 21.5 to 22.5 is {:.2f}%'.format(
norm_cdf((21.5, 22.5), 22,4)*100))
print('Probability of range 23.5 to 24.5 is {:.2f}%'.format(
norm_cdf((23.5, 24.5), 22,4)*100))
print(norm_cdf((-1e8, 1e8), mu=0, var=4))
import numpy as np
import matplotlib.pyplot as plt
xs = np.arange(15, 30, 0.05)
with interactive_plot():
plt.plot(xs, gaussian(xs, 23, 0.05), label='$\sigma^2$=0.05', c='b')
plt.plot(xs, gaussian(xs, 23, 1), label='$\sigma^2$=1', ls=':', c='b')
plt.plot(xs, gaussian(xs, 23, 5), label='$\sigma^2$=5', ls='--', c='b')
plt.legend()
from code.gaussian_internal import display_stddev_plot
with interactive_plot():
display_stddev_plot()
import math
from IPython.html.widgets import interact, interactive, fixed
set_figsize(y=3)
def plt_g(mu,variance):
plt.figure()
xs = np.arange(2, 8, 0.1)
ys = gaussian(xs, mu, variance)
plt.plot(xs, ys)
plt.ylim((0, 1))
interact (plt_g, mu=(0., 10), variance = (.2, 1.));
from scipy.stats import norm
import filterpy.stats
print(norm(2, 3).pdf(1.5))
print(filterpy.stats.gaussian(x=1.5, mean=2, var=3*3))
n23 = norm(2, 3)
print('pdf of 1.5 is %.4f' % n23.pdf(1.5))
print('pdf of 2.5 is also %.4f' % n23.pdf(2.5))
print('pdf of 2 is %.4f' % n23.pdf(2))
np.set_printoptions(precision=3, linewidth=50)
print(n23.rvs(size=15))
# probability that a random value is less than the mean 2
print(n23.cdf(2))
print('variance is', n23.var())
print('standard deviation is', n23.std())
print('mean is', n23.mean())
xs = np.arange(10,100, 0.05)
ys = [gaussian(x, 90, 30) for x in xs]
with interactive_plot():
plt.plot(xs, ys, label='var=0.2')
plt.xlim((0,120))
plt.ylim(0, 0.09);
from numpy.random import randn
def sense():
return 10 + randn()*2
zs = [sense() for i in range(5000)]
with interactive_plot():
plt.plot(zs, lw=1)
import random
import math
def rand_student_t(df, mu=0, std=1):
"""return random number distributed by Student's t
distribution with `df` degrees of freedom with the
specified mean and standard deviation.
"""
x = random.gauss(0, std)
y = 2.0*random.gammavariate(0.5*df, 2.0)
return x / (math.sqrt(y / df)) + mu
def sense_t():
return 10 + rand_student_t(7)*2
zs = [sense_t() for i in range(5000)]
with interactive_plot():
plt.plot(zs, lw=1)
from filterpy.stats import rand_student_t
| 0.68056 | 0.992386 |
<h1>KRUSKAL'S ALGORITHM</h1>
```
import math
import pandas as pd
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
from collections import defaultdict
import timeit as time
print('Kruskal\'s Algorithm For Undirected Graphs\n')
print('1. Input 1 - Undirected Graph')
print('2. Input 2 - Undirected Graph')
print('3. Input 3 - Undirected Graph')
print('4. Input 4 - Undirected Graph')
input_selection = int(input('Please Choose an Input : '))
if input_selection==1:
file_name='Input1_UndirectedGraph.txt'
elif input_selection==2:
file_name='i1.txt'
elif input_selection==3:
file_name='Input3_UndirectedGraph.txt'
elif input_selection==4:
file_name='Input4_UndirectedGraph.txt'
else:
print('\nPlease Enter a Valid Input')
f = open(file_name, "r")
data = [x.split() for x in f]
#information on number of vertices,edges and whether graph is directed or not
no_of_vertices = int(data[0][0])
no_of_edges = int(data[0][1])
directed = data[0][2]!='U'
#checking if source is given in the text file and rewriting data accordingly
if len(data[-1])==1 :
source = ''.join(data[-1])
data=data[1:-1]
else:
source = None
data=data[1:]
#Functions for Graph Visualisation
def DrawGraph(from_vertices,to_vertices):
# Build a dataframe with 4 connections
df = pd.DataFrame({ 'from':from_vertices, 'to':to_vertices})
# Build your graph
G=nx.from_pandas_edgelist(df, 'from', 'to')
# Plot it
nx.draw(G, with_labels=True)
plt.show()
def PreProcess(drawedge):
if drawedge==None:
DrawGraph(vertices,vertices)
else:
for i in range(len(vertices)):
fullstring = drawedge
substring = vertices[i]
try:
index = fullstring.index(substring)
except ValueError:
___
#print ("Not found!")
else:
vertices.append(drawedge[index])
if index==0:
index=1
else:
index=0
to.append(drawedge[index])
DrawGraph(vertices,to)
#storing data into dictionary
vertices = dict()
def getAllNodePaths(data):
d = dict()
for i in data:
vertices[i[0]]=True
vertices[i[1]]=True
node= i[0]+i[1]
if d.get(node,None)!=None:
d[node]+=int(i[2])
else:
d[node]=int(i[2])
return d
d = getAllNodePaths(data)
d = dict(sorted(d.items(), key=lambda item: item[1])) #sorted dictionary according to values
V=vertices
to = [k for k,v in vertices.items()]
vertices =[k for k,v in vertices.items()]
#storing Alphabetical nodes as integers into a hash table
d1=dict()
d2=dict()
for i,v in enumerate(sorted(set(vertices))):
d1[v]=i
d2[i]=v
class Kruskals:
def __init__(self, vertices):
self.SET = vertices # The Total Number of Vertices
self.graph = [] #inorder to store graph
# function to add an edge to graph
def addEdge(self, start, end, w):
self.graph.append([start, end, w])
def search_for_parent(self, parent, i):
if parent[i] == i:
return i
return self.search_for_parent(parent, parent[i])
def combine(self, parent, position, x, y):
r_x = self.search_for_parent(parent, x)
r_y = self.search_for_parent(parent, y)
if position[r_x] < position[r_y]:
parent[r_x] = r_y
elif position[r_x] > position[r_y]:
parent[r_y] = r_x
else:
parent[r_y] = r_x
position[r_x] += 1
# The main function to construct M using Kruskal's algorithm
def KruskalsAlgorithm(self):
final_res = [] # This will store the resultant MST
i = 0
no_edges = 0
self.graph = sorted(self.graph,
key=lambda item: item[2])
parent = []
position = []
for node in range(self.SET):
parent.append(node)
position.append(0)
while no_edges < self.SET - 1:
start, end, w = self.graph[i]
i = i + 1
x = self.search_for_parent(parent, start)
y = self.search_for_parent(parent, end)
if x != y:
no_edges = no_edges + 1
final_res.append([start, end, w])
self.combine(parent, position, x, y)
print("Edge Added : {} = {}".format(d2[start]+d2[end],w))
else:
print("Edge Considered But not Added : {} = {}".format(d2[start]+d2[end],w))
min_cost = 0
print ("\nThe Edges in the Minimum Spanning Tree are")
for start, end, weight in final_res:
min_cost += weight
print("For Edge From {} ------> {} , The Path Cost is = {}".format(d2[start], d2[end], weight))
loss_time_start=time.default_timer()
PreProcess(d2[start]+d2[end])
loss_time_end=time.default_timer()
global lost_time
lost_time+=(loss_time_end-loss_time_start)
print("So The Minimum Spanning Tree Has a Cost of {}".format(min_cost));
g=Kruskals(len(d1))
for k,val in d.items():
g.addEdge(int(d1[k[0]]),int(d1[k[-1]]),val)
lost_time=0
start_time = time.default_timer()
g.KruskalsAlgorithm()
end_time=time.default_timer()
total_time=(end_time-start_time-lost_time)*(10**9)
print('\n\nSo The Total Execution Time in Nano Seconds = {}'.format(round(total_time,1)))
```
|
github_jupyter
|
import math
import pandas as pd
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
from collections import defaultdict
import timeit as time
print('Kruskal\'s Algorithm For Undirected Graphs\n')
print('1. Input 1 - Undirected Graph')
print('2. Input 2 - Undirected Graph')
print('3. Input 3 - Undirected Graph')
print('4. Input 4 - Undirected Graph')
input_selection = int(input('Please Choose an Input : '))
if input_selection==1:
file_name='Input1_UndirectedGraph.txt'
elif input_selection==2:
file_name='i1.txt'
elif input_selection==3:
file_name='Input3_UndirectedGraph.txt'
elif input_selection==4:
file_name='Input4_UndirectedGraph.txt'
else:
print('\nPlease Enter a Valid Input')
f = open(file_name, "r")
data = [x.split() for x in f]
#information on number of vertices,edges and whether graph is directed or not
no_of_vertices = int(data[0][0])
no_of_edges = int(data[0][1])
directed = data[0][2]!='U'
#checking if source is given in the text file and rewriting data accordingly
if len(data[-1])==1 :
source = ''.join(data[-1])
data=data[1:-1]
else:
source = None
data=data[1:]
#Functions for Graph Visualisation
def DrawGraph(from_vertices,to_vertices):
# Build a dataframe with 4 connections
df = pd.DataFrame({ 'from':from_vertices, 'to':to_vertices})
# Build your graph
G=nx.from_pandas_edgelist(df, 'from', 'to')
# Plot it
nx.draw(G, with_labels=True)
plt.show()
def PreProcess(drawedge):
if drawedge==None:
DrawGraph(vertices,vertices)
else:
for i in range(len(vertices)):
fullstring = drawedge
substring = vertices[i]
try:
index = fullstring.index(substring)
except ValueError:
___
#print ("Not found!")
else:
vertices.append(drawedge[index])
if index==0:
index=1
else:
index=0
to.append(drawedge[index])
DrawGraph(vertices,to)
#storing data into dictionary
vertices = dict()
def getAllNodePaths(data):
d = dict()
for i in data:
vertices[i[0]]=True
vertices[i[1]]=True
node= i[0]+i[1]
if d.get(node,None)!=None:
d[node]+=int(i[2])
else:
d[node]=int(i[2])
return d
d = getAllNodePaths(data)
d = dict(sorted(d.items(), key=lambda item: item[1])) #sorted dictionary according to values
V=vertices
to = [k for k,v in vertices.items()]
vertices =[k for k,v in vertices.items()]
#storing Alphabetical nodes as integers into a hash table
d1=dict()
d2=dict()
for i,v in enumerate(sorted(set(vertices))):
d1[v]=i
d2[i]=v
class Kruskals:
def __init__(self, vertices):
self.SET = vertices # The Total Number of Vertices
self.graph = [] #inorder to store graph
# function to add an edge to graph
def addEdge(self, start, end, w):
self.graph.append([start, end, w])
def search_for_parent(self, parent, i):
if parent[i] == i:
return i
return self.search_for_parent(parent, parent[i])
def combine(self, parent, position, x, y):
r_x = self.search_for_parent(parent, x)
r_y = self.search_for_parent(parent, y)
if position[r_x] < position[r_y]:
parent[r_x] = r_y
elif position[r_x] > position[r_y]:
parent[r_y] = r_x
else:
parent[r_y] = r_x
position[r_x] += 1
# The main function to construct M using Kruskal's algorithm
def KruskalsAlgorithm(self):
final_res = [] # This will store the resultant MST
i = 0
no_edges = 0
self.graph = sorted(self.graph,
key=lambda item: item[2])
parent = []
position = []
for node in range(self.SET):
parent.append(node)
position.append(0)
while no_edges < self.SET - 1:
start, end, w = self.graph[i]
i = i + 1
x = self.search_for_parent(parent, start)
y = self.search_for_parent(parent, end)
if x != y:
no_edges = no_edges + 1
final_res.append([start, end, w])
self.combine(parent, position, x, y)
print("Edge Added : {} = {}".format(d2[start]+d2[end],w))
else:
print("Edge Considered But not Added : {} = {}".format(d2[start]+d2[end],w))
min_cost = 0
print ("\nThe Edges in the Minimum Spanning Tree are")
for start, end, weight in final_res:
min_cost += weight
print("For Edge From {} ------> {} , The Path Cost is = {}".format(d2[start], d2[end], weight))
loss_time_start=time.default_timer()
PreProcess(d2[start]+d2[end])
loss_time_end=time.default_timer()
global lost_time
lost_time+=(loss_time_end-loss_time_start)
print("So The Minimum Spanning Tree Has a Cost of {}".format(min_cost));
g=Kruskals(len(d1))
for k,val in d.items():
g.addEdge(int(d1[k[0]]),int(d1[k[-1]]),val)
lost_time=0
start_time = time.default_timer()
g.KruskalsAlgorithm()
end_time=time.default_timer()
total_time=(end_time-start_time-lost_time)*(10**9)
print('\n\nSo The Total Execution Time in Nano Seconds = {}'.format(round(total_time,1)))
| 0.276105 | 0.632942 |
```
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='whitegrid', font_scale=1.5)
%matplotlib inline
```
In order to test a number of GradeIT features including the "bridge builder", a trip segment from San Franciso Bay Area was identified. The GPS data from the trip shows the vehicle traversing the San Mateo - Hayward Bridge (very long) and the Alfred Zampa Memorial Bridge just south of Vallejo, CA (medium). The data also includes grade data collected by vehicles instrumented with inclinometers and differential GPS - this is the closest to "ground truth" grade data available for this work. A QGIS screenshot of part of the trip segment is shown below:

<!-- <img src="../docs/imgs/caltrans_SF_bridge_trip_2.png" style="width: 500px;"/> -->
```
df = pd.read_csv('data/SF_bridge_trip_segment.csv')
```
|Column|Description|
|------|-----------|
|sampno| household identifier |
|vehno|vehicle identifier|
|time_local|date/timestamp in the local timezone|
|time_rel|relative within vehcile or trip|
|gpsspeed|GPS logger recorded vehicle speed (miles/hour)|
|elev_ft|USGS derived elevation from a GradeIT predecessor (feet)|
|grade|Road grade derived from USGS elevation (%/100)|
|net_id|link ID in the TomTom Multinet road network|
|geom|PostGIS hex-format point geometry|
|grdsrc1|boolean indicator whether the instrumented truck grade data came from the highest quality source|
|tt_grade|road grade data from instrumented trucks 10(%) - divide this value by 1000 to compare to USGS value which is (change in elevation/change in distance)|
```
df.head()
fig, ax = plt.subplots(figsize=(9,5))
df.plot(x='longitude', y='latitude',ax=ax)
plt.ylabel('latitude');
fig, ax = plt.subplots(figsize=(9,5))
df.elev_ft.plot(ax=ax)
plt.ylabel('Elevation (ft)');
```
__Note__ the bridge events where elevation hits 0 feet (USGS elevation representing sea-level) around 2500-8000 and 24000.
```
fig, ax = plt.subplots(figsize=(9,5))
df.grade.plot(ax=ax)
(df.tt_grade/1000).plot(ax=ax)
plt.ylabel('Grade (%/100)');
from gradeit.gradeit import gradeit
db_path = "/datasets/USGS/NED_13/"
general_filter = True
sg_val = 5
df_grade = gradeit(df=df, lat_col='latitude', lon_col='longitude',
filtering=general_filter, source='usgs-local',
usgs_db_path=db_path, des_sg=sg_val)
fig, ax = plt.subplots(figsize=(9,5))
df.elev_ft.plot(ax=ax, label='Tomtom')
df_grade.elevation_ft.plot(ax=ax, label='GradeIT unfilter')
df_grade.elevation_ft_filtered.plot(ax=ax, label='GradeIT filter')
plt.ylabel('elevation_ft');
plt.legend()
fig, ax = plt.subplots(figsize=(9,5))
(df.tt_grade/1000).plot(ax=ax)
df_grade.grade_dec_unfiltered.plot(ax = ax)
df_grade.grade_dec_filtered.plot(ax = ax)
```
|
github_jupyter
|
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='whitegrid', font_scale=1.5)
%matplotlib inline
df = pd.read_csv('data/SF_bridge_trip_segment.csv')
df.head()
fig, ax = plt.subplots(figsize=(9,5))
df.plot(x='longitude', y='latitude',ax=ax)
plt.ylabel('latitude');
fig, ax = plt.subplots(figsize=(9,5))
df.elev_ft.plot(ax=ax)
plt.ylabel('Elevation (ft)');
fig, ax = plt.subplots(figsize=(9,5))
df.grade.plot(ax=ax)
(df.tt_grade/1000).plot(ax=ax)
plt.ylabel('Grade (%/100)');
from gradeit.gradeit import gradeit
db_path = "/datasets/USGS/NED_13/"
general_filter = True
sg_val = 5
df_grade = gradeit(df=df, lat_col='latitude', lon_col='longitude',
filtering=general_filter, source='usgs-local',
usgs_db_path=db_path, des_sg=sg_val)
fig, ax = plt.subplots(figsize=(9,5))
df.elev_ft.plot(ax=ax, label='Tomtom')
df_grade.elevation_ft.plot(ax=ax, label='GradeIT unfilter')
df_grade.elevation_ft_filtered.plot(ax=ax, label='GradeIT filter')
plt.ylabel('elevation_ft');
plt.legend()
fig, ax = plt.subplots(figsize=(9,5))
(df.tt_grade/1000).plot(ax=ax)
df_grade.grade_dec_unfiltered.plot(ax = ax)
df_grade.grade_dec_filtered.plot(ax = ax)
| 0.537041 | 0.929376 |
## Introduction
(You can also read this article on our website, [easy-tensorFlow](http://www.easy-tensorflow.com/basics/graph-and-session))
Why do we need tensorflow? Why are people crazy about it? In a way, it is lazy computing and offers flexibility in the way you run your code. What is this thing with flexbility and laze computing? We are glad, you asked!
Lazy Computing: TensorFlow is a way of representing computation without actually performing it until asked. The first step to learn Tensorflow is to understand its main key feature, the __"computational graph"__ approach. Basically, all Tensorflow codes contain two important parts:
__Part 1:__ building the __GRAPH__, it represents the data flow of the computations
__Part 2:__ running a __SESSION__, it executes the operations in the graph
First step you create the graph i.e. what you want to do with the data, then you run it seperately using a session (don't struggle to wrap your head around it, it will come to you eventually).
Flexibility: When you create a graph, you are not bound to run the whole graph and can control the parts of the graph that are executed separately. This provides a huge flexibility with your models.
Bonus: One of the biggest advantages of TensorFlow is its visualizations of the computation graph. Its called TensorBoard and will be discussed in future. Now that we have discussed what and why about TensorFlow, lets dive in to the actual thing.
TensorFlow separates the definition of computations from their execution. These two parts are explained in more detail in the following sections. Before that, remember that the first step is to import the Tensorflow library!
```
import tensorflow as tf
```
This gives Python access to all of TensorFlow's classes, methods, and symbols. Using this command, TensorFlow library will be imported under the alias __tf__ so that later we can use it instead of typing the whole term __tensorflow__ each time.
__What is a Tensor?__
TensorFlow programs use a data structure called tensor to represent all the data. Any type of data you plan to use for your model can be stored in Tensors. Simply put, a Tensor is a multi-dimensional array (0-D tensor: scalar, 1-D tensor: vector, 2-D tensor: matrix, and so on). Hence, TensorFlow is simply referring to the flow of the Tensors in the computational graph.
<img src="files/files/1_1.gif">
___Fig1. ___ A sample computational graph in TensorFlow (Source: TensorFlow website)
## GRAPH
The biggest idea about Tensorflow is that all the numerical computations are expressed as a computational graph. In other words, the backbone of any Tensorflow program is a __Graph__. Anything that happens in your model is represented by the computational graph. This makes it, the to go place for anything related to your model. Quoted from the TensorFlow website, "A __computational graph__ (or graph in short) is a series of TensorFlow operations arranged into a graph of nodes". Basically, it means a graph is just an arrangement of nodes that represent the operations in your model.
So First let's see what does a node and operation mean? The best way to explain it is by looking at a simple example. Suppose we want to write the code for function $f(x,y)=x^2y+y+2$. The Graph in TensorFlow will be something like:
<img src="files/files/1_2.png" width="500" height="1000" >
___Fig2. ___ Schematic of the constructed computational graph in TensorFlow
The graph is composed of a series of nodes connected to each other by edges (from the image above). Each __node__ in the graph is called __op__ (short for operation). So we'll have one node for each operation; either for operations on tensors (like math operations) or generating tensors (like variables and constants). Each node takes zero or more tensors as inputs and produces a tensor as an output.
Now Let's build a simple computational graph.
### Example 1:
Let's start with a basic arithmatic operation like addition to demonstrate a graph. The code adds two values, say a=2 and b=3, using TensorFlow. To do so, we need to call __tf.add()__. From here on, we recommend you to check out the documentation of each method/class to get a clear idea of what it can do(documentation can be found at tensorflow.org or you can just use google to get to the required page in the documentation). The __tf.add()__ has three arugments 'x', 'y', and 'name' where x and y are the values to be added together and __name__ is the operation name, i.e. the name associated to the addition node on the graph.
If we call the operation __"Add"__, the code will be as follows:
```
import tensorflow as tf
a = 2
b = 3
c = tf.add(a, b, name='Add')
print(c)
```
The generated graph and variables are:
__*Note__: The graph is generated using __Tensorboard__. As discussed earlier, it is a visualization tool for the graph and will be discussed in detail in future.
<img src="files/files/1_3.png" width="800" height="1500">
___Fig3. ___ __Left:__ generated graph visualized in Tensorboard, __Right:__ generated variables (screenshot captured from PyCharm debugger when running in debug mode)
This code creates two input nodes (for inputs a=2 and b=3) and one output node for the addition operation (named Add). When we print out the variable __c__ (i.e. the output Tensor of the addition operation), it prints out the Tensor information; its name (Add), shape (__()__ means scalar), and type (32-bit integer). However, It does not spit out the result (2+3=5). Why?!
Remember earlier in this post, we talked about the two parts of a TensorFlow code. First step is to create a graph and to actually evaluate the nodes, we must run the computational graph within a __Session__. In simple words, the written code only generates the graph which only determines the expected sizes of Tensors and operations to be executed on them. However, it doesn't assign a numeric value to any of the Tensors i.e. TensorFlow does not execute the graph unless it is specified to do so with a session. Hence, to assign these values and make them flow through the graph, we need to create and run a session.
Therefore a TensorFlow Graph is something like a function definition in Python. It __WILL NOT__ do any computation for you (just like a function definition will not have any execution result). It __ONLY__ defines computation operations.
## Session
To compute anything, a graph must be launched in a session. Technically, session places the graph ops on hardware such as CPUs or GPUs and provides methods to execute them. In our example, to run the graph and get the value for c the following code will create a session and execute the graph by running 'c':
```
sess = tf.Session()
print(sess.run(c))
sess.close()
```
This code creates a Session object (assigned to __sess__), and then (the second line) invokes its run method to run enough of the computational graph to evaluate __c__. This means that it only runs that part of the graph which is necessary to get the value of __c__ (remember the flexibility of using TensorFlow? In this simple example, it runs the whole graph). Remember to close the session at the end of the session. That is done using the last line in the above code.
The following code does the same thing and is more commonly used. The only difference is that there is no need to close the session at the end as it gets closed automatically.
```
with tf.Session() as sess:
print(sess.run(c))
```
Now let's look at the created graph one more time. Don't you see anything weird?
<img src="files/files/1_4.png" width="500" height="1000">
___Fig4. ___ The generated graph visualized by Tensorboard
Exactly! What is x and y?! Where did these two thing come from? We didn't define any x or y variables!
Well... To explain clearly, let's make up two names; say __"Python-name"__ and __"TensorFlow-name"__. In this piece of code, we generated 3 variables (look at the right panel of Fig. 3) with __"Python-name"__s of _a_, _b_, and _c_. Here, _a_ and _b_ are Python variables, thus have no __"TensorFlow-name"__; while _c_ is a Tensor with ___Add___ as its __"TensorFlow-name"__.
Clear? Okay, let's get back to our question, what is x and y then?
In an ideal Tensorflow case, __tf.add()__ receives two __Tensors__ with defined __"TensorFlow-name"__ as input (these names are separate from __Python-name__). For example, by writing $c = tf.add(a, b, name='Add')$, we're actually creating a variable (or Tensor) with __c__ as its Python-name and __Add__ as the TensorFlow-name.
In the above code, we passed two Python variables (a=2 and b=3) which only have Python-names (a and b), but they have no TensorFlow-names. TensorFlow uses the TensorFlow-names for visualizing the graphs. Since a and b have no TensorFlow-names, it uses some default names, x and y.
__*Note:__ This name mismatch can easily be solved by using tf.constant() for creating the input variables as Tensors instead of simply using Python variables (a=2, b=3). This is explained thoroughly in the next tutorial where we talk about TensorFlow DataTypes.
For now, we'll continue using Python variables and change the Python variable names __a__ and __b__ into __x__ and __y__ to solve the name mismatch temporarily.
Now let's look at a more complicated example.
### Example 2:
Creating a graph with multiple math operations
```
import tensorflow as tf
x = 2
y = 3
add_op = tf.add(x, y, name='Add')
mul_op = tf.multiply(x, y, name='Multiply')
pow_op = tf.pow(add_op, mul_op, name='Power')
useless_op = tf.multiply(x, add_op, name='Useless')
with tf.Session() as sess:
pow_out, useless_out = sess.run([pow_op, useless_op])
```
The created graph and the defined variables (Tensors and Python variables) are:
<img src="files/files/1_5.png" width="1000" height="2000">
___Fig5. ___ __Left:__ generated graph visualized in Tensorboard, __Right:__ generated variables (screenshot captured from PyCharm debugger when running in debug mode)
I called one of the operations useless_op because it's output is not used by other operations. Lets talk about an __IMPORTANT__ point. Given this graph, if we fetch the __pow_op__ operation, it will first run the __add_op__ and __mul_op__ to get their output tensor and then run __pow_op__ on them to compute the required output value. In other words __useless_op__ will not be executed as it's output tensor is not used in executing the __pow_op__ operation.
__This is one of the advantages of defining a graph and running a session on it! It helps running only the required operations of the graph and skip the rest (remember flexibility). This specially saves a significant amount of time for us when dealing with huge networks with hundreds and thousands of operations.__
In the above code, in the defined session, we're fetching the value of two tensors (i.e. output tensors of __pow_op__ and __useless_op__) at the same time. This will run the whole graph to get the required output tensors.
I hope this post has helped you to understand the concept of __Graph__ and __Session__ in TensorFlow. Thank you so much for reading! If you have any questions, feel free to leave a comment in our [webpage](http://www.easy-tensorflow.com/basics/graph-and-session). You can also send us feedback through the [__contacts__](http://www.easy-tensorflow.com/contacts) page.
|
github_jupyter
|
import tensorflow as tf
import tensorflow as tf
a = 2
b = 3
c = tf.add(a, b, name='Add')
print(c)
sess = tf.Session()
print(sess.run(c))
sess.close()
with tf.Session() as sess:
print(sess.run(c))
import tensorflow as tf
x = 2
y = 3
add_op = tf.add(x, y, name='Add')
mul_op = tf.multiply(x, y, name='Multiply')
pow_op = tf.pow(add_op, mul_op, name='Power')
useless_op = tf.multiply(x, add_op, name='Useless')
with tf.Session() as sess:
pow_out, useless_out = sess.run([pow_op, useless_op])
| 0.495361 | 0.992697 |
# Example Layer 2/3 Microcircuit Simulation
```
#===============================================================================================================
# 2021 Hay lab, Krembil Centre for Neuroinformatics, Summer School. Code available for educational purposes only
#===============================================================================================================
#====================================================================
# Import Modules and load relevant files
#====================================================================
import os
import time
tic = time.perf_counter()
from os.path import join
import sys
import zipfile
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.collections import LineCollection
from matplotlib.collections import PolyCollection
import numpy as np
np.seterr(divide='ignore', invalid='ignore')
import scipy
from scipy import signal as ss
from scipy import stats as st
from mpi4py import MPI
import math
import neuron
from neuron import h, gui
import LFPy
from LFPy import NetworkCell, Network, Synapse, RecExtElectrode, StimIntElectrode
from net_params import *
import warnings
warnings.filterwarnings('ignore')
print('Mechanisms found: ', os.path.isfile('mod/x86_64/special'))
neuron.h('forall delete_section()')
neuron.load_mechanisms('mod/')
h.load_file('net_functions.hoc')
h.load_file('models/biophys_HL23PN1.hoc')
h.load_file('models/biophys_HL23MN1.hoc')
h.load_file('models/biophys_HL23BN1.hoc')
h.load_file('models/biophys_HL23VN1.hoc')
#====================================================================
# Parameters
#====================================================================
N_HL23PN = 800
N_HL23MN = 50
N_HL23BN = 70
N_HL23VN = 89
dt = 2**-4
tstart = 0.
tmid = 0.
tstop = 30000.
celsius = 34.
v_init = -80.
L23_pop_args = {'radius':250,
'loc':-800,
'scale':500,
'cap': float(200)}
rotations = {'HL23PN1':{'x':1.57,'y':2.62},
'HL23MN1':{'x':1.77,'y':2.77},
'HL23BN1':{'x':1.26,'y':2.57},
'HL23VN1':{'x':-1.57,'y':3.57}}
networkParams = {
'dt' : dt,
'tstart': tstart,
'tstop' : tstop,
'v_init' : v_init,
'celsius' : celsius,
'verbose' : False,
'OUTPUTPATH': 'Circuit_output/E3_1/'}
#method Network.simulate() parameters
simargs = {'rec_imem': False,
'rec_vmem': False,
'rec_ipas': False,
'rec_icap': False,
'rec_isyn': False,
'rec_vmemsyn': False,
'rec_istim': False,
'rec_current_dipole_moment':True,
'rec_pop_contributions': False,
'rec_variables': [],
'to_memory': False,
'to_file': False,
'file_name':'OUTPUT.h5',
'dotprodcoeffs': None}
#====================================================================
# Create Population Function
#====================================================================
def generateSubPop(popsize,mname,popargs,Gou,Gtonic):
print('Initiating ' + mname + ' population...')
morphpath = 'morphologies/' + mname + '.swc'
templatepath = 'models/NeuronTemplate.hoc'
templatename = 'NeuronTemplate'
cellParams = {
'morphology': morphpath,
'templatefile': templatepath,
'templatename': templatename,
'templateargs': morphpath,
'v_init': v_init,
'passive': False,
'dt': dt,
'tstart': 0.,
'tstop': tstop,#defaults to 100
'nsegs_method': None,
'pt3d': False,
'delete_sections': False,
'verbose': False}
rotation = rotations.get(mname)
popParams = {
'CWD': None,
'CELLPATH': None,
'Cell' : LFPy.NetworkCell,
'POP_SIZE': popsize,
'name': mname,
'cell_args' : cellParams,
'pop_args' : popargs,
'rotation_args' : rotation}
network.create_population(**popParams)
# Add biophys, OU processes, & tonic inhibition to cells
for cellind in range(0,len(network.populations[mname].cells)): #0 is redundant?
biophys = 'h.biophys_' + mname + '(network.populations[\'' + mname + '\'].cells[' + str(cellind) + '].template)'
exec(biophys)
rseed = 1234
h.createArtificialSyn(rseed,network.populations[mname].cells[cellind].template,Gou)
h.addTonicInhibition(network.populations[mname].cells[cellind].template,Gtonic,Gtonic)
#====================================================================
# Run Simulation
#====================================================================
network = Network(**networkParams)
generateSubPop(N_HL23PN,'HL23PN1',L23_pop_args,0.00004,0.000827)
generateSubPop(N_HL23MN,'HL23MN1',L23_pop_args,0.00005,0.000827)
generateSubPop(N_HL23BN,'HL23BN1',L23_pop_args,0.00045,0.000827)
generateSubPop(N_HL23VN,'HL23VN1',L23_pop_args,0.00009,0.000827)
E_syn = neuron.h.ProbAMPANMDA
I_syn = neuron.h.ProbUDFsyn
weightFunction = np.random.normal
WP = {'loc':1, 'scale':0.0000001}
PN_WP = {'loc':connection_strength, 'scale':0.0000001}
delayFunction = np.random.normal
delayParams = {'loc':.5, 'scale':0.0000001}
mindelay=0.5
multapseFunction = np.random.normal
connectionProbability = [[connection_prob['HL23PN1HL23PN1'],connection_prob['HL23PN1HL23MN1'],connection_prob['HL23PN1HL23BN1'],connection_prob['HL23PN1HL23VN1']],
[connection_prob['HL23MN1HL23PN1'],connection_prob['HL23MN1HL23MN1'],connection_prob['HL23MN1HL23BN1'],connection_prob['HL23MN1HL23VN1']],
[connection_prob['HL23BN1HL23PN1'],connection_prob['HL23BN1HL23MN1'],connection_prob['HL23BN1HL23BN1'],connection_prob['HL23BN1HL23VN1']],
[connection_prob['HL23VN1HL23PN1'],connection_prob['HL23VN1HL23MN1'],connection_prob['HL23VN1HL23BN1'],connection_prob['HL23VN1HL23VN1']]]
synapseParameters = [[syn_params['HL23PN1HL23PN1'],syn_params['HL23PN1HL23MN1'],syn_params['HL23PN1HL23BN1'],syn_params['HL23PN1HL23VN1']],
[syn_params['HL23MN1HL23PN1'],syn_params['HL23MN1HL23MN1'],syn_params['HL23MN1HL23BN1'],syn_params['HL23MN1HL23VN1']],
[syn_params['HL23BN1HL23PN1'],syn_params['HL23BN1HL23MN1'],syn_params['HL23BN1HL23BN1'],syn_params['HL23BN1HL23VN1']],
[syn_params['HL23VN1HL23PN1'],syn_params['HL23VN1HL23MN1'],syn_params['HL23VN1HL23BN1'],syn_params['HL23VN1HL23VN1']]]
weightArguments = [[WP, WP, WP, WP],
[WP, WP, WP, WP],
[WP, WP, WP, WP],
[WP, WP, WP, WP]]
minweight = [[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]]
delayArguments = np.full([4, 4], delayParams)
multapseArguments = [[mult_syns['HL23PN1HL23PN1'],mult_syns['HL23PN1HL23MN1'],mult_syns['HL23PN1HL23BN1'],mult_syns['HL23PN1HL23VN1']],
[mult_syns['HL23MN1HL23PN1'],mult_syns['HL23MN1HL23MN1'],mult_syns['HL23MN1HL23BN1'],mult_syns['HL23MN1HL23VN1']],
[mult_syns['HL23BN1HL23PN1'],mult_syns['HL23BN1HL23MN1'],mult_syns['HL23BN1HL23BN1'],mult_syns['HL23BN1HL23VN1']],
[mult_syns['HL23VN1HL23PN1'],mult_syns['HL23VN1HL23MN1'],mult_syns['HL23VN1HL23BN1'],mult_syns['HL23VN1HL23VN1']]]
synapsePositionArguments = [[pos_args['HL23PN1HL23PN1'],pos_args['HL23PN1HL23MN1'],pos_args['HL23PN1HL23BN1'],pos_args['HL23PN1HL23VN1']],
[pos_args['HL23MN1HL23PN1'],pos_args['HL23MN1HL23MN1'],pos_args['HL23MN1HL23BN1'],pos_args['HL23MN1HL23VN1']],
[pos_args['HL23BN1HL23PN1'],pos_args['HL23BN1HL23MN1'],pos_args['HL23BN1HL23BN1'],pos_args['HL23BN1HL23VN1']],
[pos_args['HL23VN1HL23PN1'],pos_args['HL23VN1HL23MN1'],pos_args['HL23VN1HL23BN1'],pos_args['HL23VN1HL23VN1']]]
for i, pre in enumerate(network.population_names):
for j, post in enumerate(network.population_names):
connectivity = network.get_connectivity_rand(
pre=pre,
post=post,
connprob=connectionProbability[i][j])
(conncount, syncount) = network.connect(
pre=pre, post=post,
connectivity=connectivity,
syntype=E_syn if pre=='HL23PN1' else I_syn,
synparams=synapseParameters[i][j],
weightfun=weightFunction,
weightargs=weightArguments[i][j],
minweight=minweight[i][j],
delayfun=delayFunction,
delayargs=delayArguments[i][j],
mindelay=mindelay,
multapsefun=multapseFunction,
multapseargs=multapseArguments[i][j],
syn_pos_args=synapsePositionArguments[i][j])
SPIKES,DIPOLEMOMENT = network.simulate(**simargs)
np.save('SPIKES.npy',SPIKES)
np.save('DIPOLEMOMENT.npy',DIPOLEMOMENT)
```
|
github_jupyter
|
#===============================================================================================================
# 2021 Hay lab, Krembil Centre for Neuroinformatics, Summer School. Code available for educational purposes only
#===============================================================================================================
#====================================================================
# Import Modules and load relevant files
#====================================================================
import os
import time
tic = time.perf_counter()
from os.path import join
import sys
import zipfile
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.collections import LineCollection
from matplotlib.collections import PolyCollection
import numpy as np
np.seterr(divide='ignore', invalid='ignore')
import scipy
from scipy import signal as ss
from scipy import stats as st
from mpi4py import MPI
import math
import neuron
from neuron import h, gui
import LFPy
from LFPy import NetworkCell, Network, Synapse, RecExtElectrode, StimIntElectrode
from net_params import *
import warnings
warnings.filterwarnings('ignore')
print('Mechanisms found: ', os.path.isfile('mod/x86_64/special'))
neuron.h('forall delete_section()')
neuron.load_mechanisms('mod/')
h.load_file('net_functions.hoc')
h.load_file('models/biophys_HL23PN1.hoc')
h.load_file('models/biophys_HL23MN1.hoc')
h.load_file('models/biophys_HL23BN1.hoc')
h.load_file('models/biophys_HL23VN1.hoc')
#====================================================================
# Parameters
#====================================================================
N_HL23PN = 800
N_HL23MN = 50
N_HL23BN = 70
N_HL23VN = 89
dt = 2**-4
tstart = 0.
tmid = 0.
tstop = 30000.
celsius = 34.
v_init = -80.
L23_pop_args = {'radius':250,
'loc':-800,
'scale':500,
'cap': float(200)}
rotations = {'HL23PN1':{'x':1.57,'y':2.62},
'HL23MN1':{'x':1.77,'y':2.77},
'HL23BN1':{'x':1.26,'y':2.57},
'HL23VN1':{'x':-1.57,'y':3.57}}
networkParams = {
'dt' : dt,
'tstart': tstart,
'tstop' : tstop,
'v_init' : v_init,
'celsius' : celsius,
'verbose' : False,
'OUTPUTPATH': 'Circuit_output/E3_1/'}
#method Network.simulate() parameters
simargs = {'rec_imem': False,
'rec_vmem': False,
'rec_ipas': False,
'rec_icap': False,
'rec_isyn': False,
'rec_vmemsyn': False,
'rec_istim': False,
'rec_current_dipole_moment':True,
'rec_pop_contributions': False,
'rec_variables': [],
'to_memory': False,
'to_file': False,
'file_name':'OUTPUT.h5',
'dotprodcoeffs': None}
#====================================================================
# Create Population Function
#====================================================================
def generateSubPop(popsize,mname,popargs,Gou,Gtonic):
print('Initiating ' + mname + ' population...')
morphpath = 'morphologies/' + mname + '.swc'
templatepath = 'models/NeuronTemplate.hoc'
templatename = 'NeuronTemplate'
cellParams = {
'morphology': morphpath,
'templatefile': templatepath,
'templatename': templatename,
'templateargs': morphpath,
'v_init': v_init,
'passive': False,
'dt': dt,
'tstart': 0.,
'tstop': tstop,#defaults to 100
'nsegs_method': None,
'pt3d': False,
'delete_sections': False,
'verbose': False}
rotation = rotations.get(mname)
popParams = {
'CWD': None,
'CELLPATH': None,
'Cell' : LFPy.NetworkCell,
'POP_SIZE': popsize,
'name': mname,
'cell_args' : cellParams,
'pop_args' : popargs,
'rotation_args' : rotation}
network.create_population(**popParams)
# Add biophys, OU processes, & tonic inhibition to cells
for cellind in range(0,len(network.populations[mname].cells)): #0 is redundant?
biophys = 'h.biophys_' + mname + '(network.populations[\'' + mname + '\'].cells[' + str(cellind) + '].template)'
exec(biophys)
rseed = 1234
h.createArtificialSyn(rseed,network.populations[mname].cells[cellind].template,Gou)
h.addTonicInhibition(network.populations[mname].cells[cellind].template,Gtonic,Gtonic)
#====================================================================
# Run Simulation
#====================================================================
network = Network(**networkParams)
generateSubPop(N_HL23PN,'HL23PN1',L23_pop_args,0.00004,0.000827)
generateSubPop(N_HL23MN,'HL23MN1',L23_pop_args,0.00005,0.000827)
generateSubPop(N_HL23BN,'HL23BN1',L23_pop_args,0.00045,0.000827)
generateSubPop(N_HL23VN,'HL23VN1',L23_pop_args,0.00009,0.000827)
E_syn = neuron.h.ProbAMPANMDA
I_syn = neuron.h.ProbUDFsyn
weightFunction = np.random.normal
WP = {'loc':1, 'scale':0.0000001}
PN_WP = {'loc':connection_strength, 'scale':0.0000001}
delayFunction = np.random.normal
delayParams = {'loc':.5, 'scale':0.0000001}
mindelay=0.5
multapseFunction = np.random.normal
connectionProbability = [[connection_prob['HL23PN1HL23PN1'],connection_prob['HL23PN1HL23MN1'],connection_prob['HL23PN1HL23BN1'],connection_prob['HL23PN1HL23VN1']],
[connection_prob['HL23MN1HL23PN1'],connection_prob['HL23MN1HL23MN1'],connection_prob['HL23MN1HL23BN1'],connection_prob['HL23MN1HL23VN1']],
[connection_prob['HL23BN1HL23PN1'],connection_prob['HL23BN1HL23MN1'],connection_prob['HL23BN1HL23BN1'],connection_prob['HL23BN1HL23VN1']],
[connection_prob['HL23VN1HL23PN1'],connection_prob['HL23VN1HL23MN1'],connection_prob['HL23VN1HL23BN1'],connection_prob['HL23VN1HL23VN1']]]
synapseParameters = [[syn_params['HL23PN1HL23PN1'],syn_params['HL23PN1HL23MN1'],syn_params['HL23PN1HL23BN1'],syn_params['HL23PN1HL23VN1']],
[syn_params['HL23MN1HL23PN1'],syn_params['HL23MN1HL23MN1'],syn_params['HL23MN1HL23BN1'],syn_params['HL23MN1HL23VN1']],
[syn_params['HL23BN1HL23PN1'],syn_params['HL23BN1HL23MN1'],syn_params['HL23BN1HL23BN1'],syn_params['HL23BN1HL23VN1']],
[syn_params['HL23VN1HL23PN1'],syn_params['HL23VN1HL23MN1'],syn_params['HL23VN1HL23BN1'],syn_params['HL23VN1HL23VN1']]]
weightArguments = [[WP, WP, WP, WP],
[WP, WP, WP, WP],
[WP, WP, WP, WP],
[WP, WP, WP, WP]]
minweight = [[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]]
delayArguments = np.full([4, 4], delayParams)
multapseArguments = [[mult_syns['HL23PN1HL23PN1'],mult_syns['HL23PN1HL23MN1'],mult_syns['HL23PN1HL23BN1'],mult_syns['HL23PN1HL23VN1']],
[mult_syns['HL23MN1HL23PN1'],mult_syns['HL23MN1HL23MN1'],mult_syns['HL23MN1HL23BN1'],mult_syns['HL23MN1HL23VN1']],
[mult_syns['HL23BN1HL23PN1'],mult_syns['HL23BN1HL23MN1'],mult_syns['HL23BN1HL23BN1'],mult_syns['HL23BN1HL23VN1']],
[mult_syns['HL23VN1HL23PN1'],mult_syns['HL23VN1HL23MN1'],mult_syns['HL23VN1HL23BN1'],mult_syns['HL23VN1HL23VN1']]]
synapsePositionArguments = [[pos_args['HL23PN1HL23PN1'],pos_args['HL23PN1HL23MN1'],pos_args['HL23PN1HL23BN1'],pos_args['HL23PN1HL23VN1']],
[pos_args['HL23MN1HL23PN1'],pos_args['HL23MN1HL23MN1'],pos_args['HL23MN1HL23BN1'],pos_args['HL23MN1HL23VN1']],
[pos_args['HL23BN1HL23PN1'],pos_args['HL23BN1HL23MN1'],pos_args['HL23BN1HL23BN1'],pos_args['HL23BN1HL23VN1']],
[pos_args['HL23VN1HL23PN1'],pos_args['HL23VN1HL23MN1'],pos_args['HL23VN1HL23BN1'],pos_args['HL23VN1HL23VN1']]]
for i, pre in enumerate(network.population_names):
for j, post in enumerate(network.population_names):
connectivity = network.get_connectivity_rand(
pre=pre,
post=post,
connprob=connectionProbability[i][j])
(conncount, syncount) = network.connect(
pre=pre, post=post,
connectivity=connectivity,
syntype=E_syn if pre=='HL23PN1' else I_syn,
synparams=synapseParameters[i][j],
weightfun=weightFunction,
weightargs=weightArguments[i][j],
minweight=minweight[i][j],
delayfun=delayFunction,
delayargs=delayArguments[i][j],
mindelay=mindelay,
multapsefun=multapseFunction,
multapseargs=multapseArguments[i][j],
syn_pos_args=synapsePositionArguments[i][j])
SPIKES,DIPOLEMOMENT = network.simulate(**simargs)
np.save('SPIKES.npy',SPIKES)
np.save('DIPOLEMOMENT.npy',DIPOLEMOMENT)
| 0.246806 | 0.582521 |
```
import numpy as np
import logging
import torch
import torch.nn.functional as F
import numpy as np
from tqdm import trange
from pytorch_pretrained_bert import GPT2Tokenizer, GPT2Model, GPT2LMHeadModel
# Load pre-trained model tokenizer (vocabulary)
tokenizer = GPT2Tokenizer.from_pretrained('gpt2')
text_1 = "It was nearly two weeks later when the cosmonaut was jolted out of sleep, "
text_2 = "snug against"
indexed_tokens_1 = tokenizer.encode(text_1)
indexed_tokens_2 = tokenizer.encode(text_2)
# Convert inputs to PyTorch tensors
tokens_tensor_1 = torch.tensor([indexed_tokens_1])
tokens_tensor_2 = torch.tensor([indexed_tokens_2])
# Load pre-trained model (weights)
model = GPT2LMHeadModel.from_pretrained('gpt2')
model.eval()
# If you have a GPU, put everything on cuda
tokens_tensor_1 = tokens_tensor_1.to('cuda')
tokens_tensor_2 = tokens_tensor_2.to('cuda')
model.to('cuda')
# Predict all tokens
with torch.no_grad():
predictions_1, past = model(tokens_tensor_1)
# past can be used to reuse precomputed hidden state in a subsequent predictions
# (see beam-search examples in the run_gpt2.py example).
predictions_2, past = model(tokens_tensor_2, past=past)
# get the predicted last token
predicted_index = torch.argmax(predictions_2[0, -1, :]).item()
predicted_token = tokenizer.decode([predicted_index])
predicted_token
```
lol
```
logging.basicConfig(format = '%(asctime)s - %(levelname)s - %(name)s - %(message)s',
datefmt = '%m/%d/%Y %H:%M:%S',
level = logging.INFO)
logger = logging.getLogger(__name__)
def top_k_logits(logits, k):
"""
Masks everything but the k top entries as -infinity (1e10).
Used to mask logits such that e^-infinity -> 0 won't contribute to the
sum of the denominator.
"""
if k == 0:
return logits
else:
values = torch.topk(logits, k)[0]
batch_mins = values[:, -1].view(-1, 1).expand_as(logits)
return torch.where(logits < batch_mins, torch.ones_like(logits) * -1e10, logits)
def sample_sequence(model, length, start_token=None, batch_size=None, context=None, temperature=1, top_k=0, device='cuda', sample=True):
if start_token is None:
assert context is not None, 'Specify exactly one of start_token and context!'
context = torch.tensor(context, device=device, dtype=torch.long).unsqueeze(0).repeat(batch_size, 1)
else:
assert context is None, 'Specify exactly one of start_token and context!'
context = torch.full((batch_size, 1), start_token, device=device, dtype=torch.long)
prev = context
output = context
past = None
with torch.no_grad():
for i in trange(length):
logits, past = model(prev, past=past)
logits = logits[:, -1, :] / temperature
logits = top_k_logits(logits, k=top_k)
log_probs = F.softmax(logits, dim=-1)
if sample:
prev = torch.multinomial(log_probs, num_samples=1)
else:
_, prev = torch.topk(log_probs, k=1, dim=-1)
output = torch.cat((output, prev), dim=1)
return output
def run_model(input_text, length=-1, nsamples=1, batch_size=1, temperature=1.0, top_k=0, seed=0):
assert nsamples % batch_size == 0
np.random.seed(seed)
torch.random.manual_seed(seed)
torch.cuda.manual_seed(seed)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
enc = GPT2Tokenizer.from_pretrained('gpt2')
model = GPT2LMHeadModel.from_pretrained('gpt2')
model.to(device)
model.eval()
if length == -1:
length = model.config.n_ctx // 2
elif length > model.config.n_ctx:
raise ValueError("Can't get samples longer than window size: %s" % model.config.n_ctx)
while True:
context_tokens = []
if input_text:
context_tokens = enc.encode(input_text)
generated = 0
for _ in range(nsamples // batch_size):
out = sample_sequence(
model=model, length=length,
context=context_tokens,
start_token=None,
batch_size=batch_size,
temperature=temperature, top_k=top_k, device=device
)
out = out[:, len(context_tokens):].tolist()
for i in range(batch_size):
generated += 1
text = enc.decode(out[i])
print("=" * 40 + " SAMPLE " + str(generated) + " " + "=" * 40)
print(text)
print("=" * 80)
else:
generated = 0
for _ in range(nsamples // batch_size):
out = sample_sequence(
model=model, length=length,
context=None,
start_token=enc.encoder['<|endoftext|>'],
batch_size=batch_size,
temperature=temperature, top_k=top_k, device=device
)
out = out[:,1:].tolist()
for i in range(batch_size):
generated += 1
text = enc.decode(out[i])
print("=" * 40 + " SAMPLE " + str(generated) + " " + "=" * 40)
print(text)
print("=" * 80)
run_model("It was nearly two weeks later when the cosmonaut was jolted out of sleep, jolted by")
```
|
github_jupyter
|
import numpy as np
import logging
import torch
import torch.nn.functional as F
import numpy as np
from tqdm import trange
from pytorch_pretrained_bert import GPT2Tokenizer, GPT2Model, GPT2LMHeadModel
# Load pre-trained model tokenizer (vocabulary)
tokenizer = GPT2Tokenizer.from_pretrained('gpt2')
text_1 = "It was nearly two weeks later when the cosmonaut was jolted out of sleep, "
text_2 = "snug against"
indexed_tokens_1 = tokenizer.encode(text_1)
indexed_tokens_2 = tokenizer.encode(text_2)
# Convert inputs to PyTorch tensors
tokens_tensor_1 = torch.tensor([indexed_tokens_1])
tokens_tensor_2 = torch.tensor([indexed_tokens_2])
# Load pre-trained model (weights)
model = GPT2LMHeadModel.from_pretrained('gpt2')
model.eval()
# If you have a GPU, put everything on cuda
tokens_tensor_1 = tokens_tensor_1.to('cuda')
tokens_tensor_2 = tokens_tensor_2.to('cuda')
model.to('cuda')
# Predict all tokens
with torch.no_grad():
predictions_1, past = model(tokens_tensor_1)
# past can be used to reuse precomputed hidden state in a subsequent predictions
# (see beam-search examples in the run_gpt2.py example).
predictions_2, past = model(tokens_tensor_2, past=past)
# get the predicted last token
predicted_index = torch.argmax(predictions_2[0, -1, :]).item()
predicted_token = tokenizer.decode([predicted_index])
predicted_token
logging.basicConfig(format = '%(asctime)s - %(levelname)s - %(name)s - %(message)s',
datefmt = '%m/%d/%Y %H:%M:%S',
level = logging.INFO)
logger = logging.getLogger(__name__)
def top_k_logits(logits, k):
"""
Masks everything but the k top entries as -infinity (1e10).
Used to mask logits such that e^-infinity -> 0 won't contribute to the
sum of the denominator.
"""
if k == 0:
return logits
else:
values = torch.topk(logits, k)[0]
batch_mins = values[:, -1].view(-1, 1).expand_as(logits)
return torch.where(logits < batch_mins, torch.ones_like(logits) * -1e10, logits)
def sample_sequence(model, length, start_token=None, batch_size=None, context=None, temperature=1, top_k=0, device='cuda', sample=True):
if start_token is None:
assert context is not None, 'Specify exactly one of start_token and context!'
context = torch.tensor(context, device=device, dtype=torch.long).unsqueeze(0).repeat(batch_size, 1)
else:
assert context is None, 'Specify exactly one of start_token and context!'
context = torch.full((batch_size, 1), start_token, device=device, dtype=torch.long)
prev = context
output = context
past = None
with torch.no_grad():
for i in trange(length):
logits, past = model(prev, past=past)
logits = logits[:, -1, :] / temperature
logits = top_k_logits(logits, k=top_k)
log_probs = F.softmax(logits, dim=-1)
if sample:
prev = torch.multinomial(log_probs, num_samples=1)
else:
_, prev = torch.topk(log_probs, k=1, dim=-1)
output = torch.cat((output, prev), dim=1)
return output
def run_model(input_text, length=-1, nsamples=1, batch_size=1, temperature=1.0, top_k=0, seed=0):
assert nsamples % batch_size == 0
np.random.seed(seed)
torch.random.manual_seed(seed)
torch.cuda.manual_seed(seed)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
enc = GPT2Tokenizer.from_pretrained('gpt2')
model = GPT2LMHeadModel.from_pretrained('gpt2')
model.to(device)
model.eval()
if length == -1:
length = model.config.n_ctx // 2
elif length > model.config.n_ctx:
raise ValueError("Can't get samples longer than window size: %s" % model.config.n_ctx)
while True:
context_tokens = []
if input_text:
context_tokens = enc.encode(input_text)
generated = 0
for _ in range(nsamples // batch_size):
out = sample_sequence(
model=model, length=length,
context=context_tokens,
start_token=None,
batch_size=batch_size,
temperature=temperature, top_k=top_k, device=device
)
out = out[:, len(context_tokens):].tolist()
for i in range(batch_size):
generated += 1
text = enc.decode(out[i])
print("=" * 40 + " SAMPLE " + str(generated) + " " + "=" * 40)
print(text)
print("=" * 80)
else:
generated = 0
for _ in range(nsamples // batch_size):
out = sample_sequence(
model=model, length=length,
context=None,
start_token=enc.encoder['<|endoftext|>'],
batch_size=batch_size,
temperature=temperature, top_k=top_k, device=device
)
out = out[:,1:].tolist()
for i in range(batch_size):
generated += 1
text = enc.decode(out[i])
print("=" * 40 + " SAMPLE " + str(generated) + " " + "=" * 40)
print(text)
print("=" * 80)
run_model("It was nearly two weeks later when the cosmonaut was jolted out of sleep, jolted by")
| 0.871297 | 0.707859 |
```
# matplotlib inline plotting
%matplotlib inline
# make inline plotting higher resolution
%config InlineBackend.figure_format = 'svg'
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import re
from sklearn.ensemble import RandomForestClassifier
from statsmodels.api import OLS
from statsmodels.api import add_constant
plt.style.use('dark_background')
```
## Kaggle Knowledge Competition: Titanic - Machine Learning from Disaster
My solution attempt at predicting which passengers survived the Titanic shipwreck.
Data and additional information is available at [Kaggle](https://www.kaggle.com/c/titanic)
### 1: Read data
```
train = pd.read_csv('train.csv', index_col='PassengerId')
train.index.name = None
train.head()
test = pd.read_csv('test.csv', index_col='PassengerId')
test.index.name = None
test.head()
# I will need to do the same operations for each data-set - thus combining them in an iterable list.
combined = [train, test]
```
### 2: Missing Data
#### 2.1 Cabin is missing
There's so few observations on the `Cabin` column. I'll drop this one.
```
print(f'{train.Cabin.shape[0] - train.Cabin.dropna().shape[0]} missing observations for Cabin.')
for df in combined:
df.drop(columns='Cabin', inplace=True)
```
#### 2.2 Age has a lot of missing observations
There's a lot of missing observations on `Age`. This is however not as severe as for the `Cabin` column.
I think we can use the cross-section, taking into account number of siblings/parents etc. to fill these `NaN`s using OLS.
This poses a few issues however:
- The $R^2$ of the regressions are relatively low. However one can reasonable assume that this method is more exact than filling based on median/averages.
- The models are however significant (joint f-test).
- OLS can predict negative ages. For any here I'll assume that they're babies and fix age at 1. I also fix ages as integer to stay consistent with existing data.
```
for df in combined:
# train-data
X_train = df.loc[df['Age'].dropna().index]
X_train = X_train.dropna(how='any')
X_train = add_constant(X_train)
Y_train = X_train['Age']
X_train = X_train.drop(columns=['Name', 'Age', 'Ticket'])
X_train = pd.get_dummies(X_train, drop_first=True) # one-hot encoding
# test-data
X_test = df.loc[df['Age'].isnull()]
X_test = add_constant(X_test)
Y_test = X_test['Age']
X_test = X_test.drop(columns=['Name', 'Age', 'Ticket'])
X_test = pd.get_dummies(X_test, drop_first=True) # one-hot encoding
mdl = OLS(endog=Y_train, exog=X_train)
mdl = mdl.fit()
# Predict and fill age data from OLS model
fillData = mdl.predict(X_test)
df['Age'].fillna(fillData, inplace=True)
print(f'Dataset has {df.shape[0] - X_train.shape[0]} missing values.')
print(f'OLS R2: {np.round(mdl.rsquared, 2)}, Joint f-statistic: {np.round(mdl.fvalue, 2)}')
print('\n')
# OLS can predict non-integer and negative ages
for df in combined:
df['Age'] = df['Age'].apply(np.round)
df['Age'] = df['Age'].apply(lambda x: 1 if x < 1 else x)
```
#### 2.3 Last NaN's in `Embarked` and `Fare`
These values are so rare and sparse that I'll simply fill with most likely observation.
```
for df in combined:
df['Fare'].fillna(df['Fare'].mean(), inplace=True)
df['Embarked'].fillna(df['Embarked'].value_counts().sort_values().index[-1], inplace=True)
```
### 3: Feature Engineering
Now that we've dealt with all missing values, it is time to scale and engineer our values for our `RandomForrest` model.
The goal here is to extract as much information as possible from the supplied data.
#### 3.1 There's more to a name
To be able to distinguish the passengers in more sub-categories, we'll use the title in their name. There's probably a lot more to be done here - fx. looking at the ethnicity of passengers based on their names. We'll keep it simple for now though.
As we see, there's a lot of _less-frequent_ titles. I'll bulk these into `Royal` or `Professional` depending on their role in society.
```
for df in combined:
df['Title'] = df['Name'].apply(lambda x: re.search(string=x, pattern=' ([A-Z][a-z]+)\.').group(1))
sns.countplot(data=train, x='Title', hue='Survived')
plt.xticks(rotation=45)
plt.legend(loc='upper right')
plt.show()
SocialClass = {'Mr': 'Mr',
'Mrs': 'Mrs',
'Miss': 'Miss',
'Master': 'Royal',
'Don': 'Royal',
'Rev': 'Professional',
'Dr': 'Professional',
'Mme': 'Mrs',
'Ms': 'Mrs',
'Major': 'Professional',
'Lady': 'Royal',
'Sir': 'Royal',
'Mlle': 'Miss',
'Col': 'Professional',
'Capt': 'Professional',
'Countess': 'Royal',
'Jonkheer': 'Royal'}
for df in combined:
df['SocialClass'] = df['Title'].map(SocialClass)
sns.countplot(data=train, x='SocialClass', hue='Survived')
plt.xticks(rotation=45)
plt.legend(loc='upper right')
plt.show()
```
#### 3.2 Families who travel together, survive together (?!)
One could reasonable assume, that larger families would stick together and possible be able to secure a lifeboat together. To investigate this, I'll create a `FamSize` feature consisting of `SibSp + Parch + 1`. This feature will of cause overlap across the data.
- We see in the plot that there tends to be higher survivability for family-sizes from 2-4.
```
for df in combined:
df['FamSize'] = df['SibSp'] + df['Parch'] + 1
sns.countplot(data=train, x='FamSize', hue='Survived')
plt.xticks(rotation=45)
plt.legend(loc='upper right')
plt.show()
```
#### 3.3 Old and young of the boat!
We see in the density, that there are _some_ differences in terms of whom survives depending on age.
To better explain this variation we'll group passengers into age groups.
- There is probably some intuition behind this result. Passengers in the group 20-30 would likely have been either staff (very likely) or somehow wealthy.
```
sns.displot(x='Age', hue='Survived', data=train, kde=True)
plt.show()
intervals = [0, 5, 12, 20, 30, 55, 120]
category = ['Babies', 'Children', 'Young', 'Young-Adult', 'Adult', 'Senior']
for df in combined:
df['AgeCategory'] = pd.cut(df['Age'], intervals, labels=category)
sns.countplot(data=train, x='AgeCategory', hue='Survived')
plt.xticks(rotation=45)
plt.legend(loc='upper right')
plt.show()
```
#### 3.4 Even rich people are mortal
This is probably the saddest graph in this notebook. However we see a very strong trend that survivability increases with ticket-price.
```
for df in combined:
intervals = [
-1,
1,
np.quantile(df['Fare'], q=.10),
np.quantile(df['Fare'], q=.20),
np.quantile(df['Fare'], q=.30),
np.quantile(df['Fare'], q=.40),
np.quantile(df['Fare'], q=.50),
np.quantile(df['Fare'], q=.60),
np.quantile(df['Fare'], q=.80),
np.quantile(df['Fare'], q=.90),
np.quantile(df['Fare'], q=1) +1
]
category = [f'Q{i}' for i in range(len(intervals) -1)]
df['FareQ'] = pd.cut(df['Fare'], intervals, labels=category)
sns.countplot(data=train, x='FareQ', hue='Survived')
plt.xticks(rotation=45)
plt.legend(loc='upper right')
plt.show()
```
### 4: Drop and encode datasets
```
# drop irrelevant columns
for df in combined:
df = df.drop(columns=['Name', 'Ticket', 'Fare', 'Age', 'Title'], inplace=True)
# use one-hot encoding
train = pd.get_dummies(train, drop_first=True)
test = pd.get_dummies(test, drop_first=True)
X_train = train.drop(columns='Survived')
Y_train = train['Survived']
X_test = test
```
### 5: Model fit and prediction
```
mdl = RandomForestClassifier()
mdl.fit(X_train, Y_train)
Y_pred = mdl.predict(X_test)
print(f'RandomForest cross-validation score: {np.round(mdl.score(X_train, Y_train), 4) * 100}%')
pd.DataFrame({'PassengerId': test.index, 'Survived': Y_pred}).to_csv('submission.csv', index=False)
```
|
github_jupyter
|
# matplotlib inline plotting
%matplotlib inline
# make inline plotting higher resolution
%config InlineBackend.figure_format = 'svg'
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import re
from sklearn.ensemble import RandomForestClassifier
from statsmodels.api import OLS
from statsmodels.api import add_constant
plt.style.use('dark_background')
train = pd.read_csv('train.csv', index_col='PassengerId')
train.index.name = None
train.head()
test = pd.read_csv('test.csv', index_col='PassengerId')
test.index.name = None
test.head()
# I will need to do the same operations for each data-set - thus combining them in an iterable list.
combined = [train, test]
print(f'{train.Cabin.shape[0] - train.Cabin.dropna().shape[0]} missing observations for Cabin.')
for df in combined:
df.drop(columns='Cabin', inplace=True)
for df in combined:
# train-data
X_train = df.loc[df['Age'].dropna().index]
X_train = X_train.dropna(how='any')
X_train = add_constant(X_train)
Y_train = X_train['Age']
X_train = X_train.drop(columns=['Name', 'Age', 'Ticket'])
X_train = pd.get_dummies(X_train, drop_first=True) # one-hot encoding
# test-data
X_test = df.loc[df['Age'].isnull()]
X_test = add_constant(X_test)
Y_test = X_test['Age']
X_test = X_test.drop(columns=['Name', 'Age', 'Ticket'])
X_test = pd.get_dummies(X_test, drop_first=True) # one-hot encoding
mdl = OLS(endog=Y_train, exog=X_train)
mdl = mdl.fit()
# Predict and fill age data from OLS model
fillData = mdl.predict(X_test)
df['Age'].fillna(fillData, inplace=True)
print(f'Dataset has {df.shape[0] - X_train.shape[0]} missing values.')
print(f'OLS R2: {np.round(mdl.rsquared, 2)}, Joint f-statistic: {np.round(mdl.fvalue, 2)}')
print('\n')
# OLS can predict non-integer and negative ages
for df in combined:
df['Age'] = df['Age'].apply(np.round)
df['Age'] = df['Age'].apply(lambda x: 1 if x < 1 else x)
for df in combined:
df['Fare'].fillna(df['Fare'].mean(), inplace=True)
df['Embarked'].fillna(df['Embarked'].value_counts().sort_values().index[-1], inplace=True)
for df in combined:
df['Title'] = df['Name'].apply(lambda x: re.search(string=x, pattern=' ([A-Z][a-z]+)\.').group(1))
sns.countplot(data=train, x='Title', hue='Survived')
plt.xticks(rotation=45)
plt.legend(loc='upper right')
plt.show()
SocialClass = {'Mr': 'Mr',
'Mrs': 'Mrs',
'Miss': 'Miss',
'Master': 'Royal',
'Don': 'Royal',
'Rev': 'Professional',
'Dr': 'Professional',
'Mme': 'Mrs',
'Ms': 'Mrs',
'Major': 'Professional',
'Lady': 'Royal',
'Sir': 'Royal',
'Mlle': 'Miss',
'Col': 'Professional',
'Capt': 'Professional',
'Countess': 'Royal',
'Jonkheer': 'Royal'}
for df in combined:
df['SocialClass'] = df['Title'].map(SocialClass)
sns.countplot(data=train, x='SocialClass', hue='Survived')
plt.xticks(rotation=45)
plt.legend(loc='upper right')
plt.show()
for df in combined:
df['FamSize'] = df['SibSp'] + df['Parch'] + 1
sns.countplot(data=train, x='FamSize', hue='Survived')
plt.xticks(rotation=45)
plt.legend(loc='upper right')
plt.show()
sns.displot(x='Age', hue='Survived', data=train, kde=True)
plt.show()
intervals = [0, 5, 12, 20, 30, 55, 120]
category = ['Babies', 'Children', 'Young', 'Young-Adult', 'Adult', 'Senior']
for df in combined:
df['AgeCategory'] = pd.cut(df['Age'], intervals, labels=category)
sns.countplot(data=train, x='AgeCategory', hue='Survived')
plt.xticks(rotation=45)
plt.legend(loc='upper right')
plt.show()
for df in combined:
intervals = [
-1,
1,
np.quantile(df['Fare'], q=.10),
np.quantile(df['Fare'], q=.20),
np.quantile(df['Fare'], q=.30),
np.quantile(df['Fare'], q=.40),
np.quantile(df['Fare'], q=.50),
np.quantile(df['Fare'], q=.60),
np.quantile(df['Fare'], q=.80),
np.quantile(df['Fare'], q=.90),
np.quantile(df['Fare'], q=1) +1
]
category = [f'Q{i}' for i in range(len(intervals) -1)]
df['FareQ'] = pd.cut(df['Fare'], intervals, labels=category)
sns.countplot(data=train, x='FareQ', hue='Survived')
plt.xticks(rotation=45)
plt.legend(loc='upper right')
plt.show()
# drop irrelevant columns
for df in combined:
df = df.drop(columns=['Name', 'Ticket', 'Fare', 'Age', 'Title'], inplace=True)
# use one-hot encoding
train = pd.get_dummies(train, drop_first=True)
test = pd.get_dummies(test, drop_first=True)
X_train = train.drop(columns='Survived')
Y_train = train['Survived']
X_test = test
mdl = RandomForestClassifier()
mdl.fit(X_train, Y_train)
Y_pred = mdl.predict(X_test)
print(f'RandomForest cross-validation score: {np.round(mdl.score(X_train, Y_train), 4) * 100}%')
pd.DataFrame({'PassengerId': test.index, 'Survived': Y_pred}).to_csv('submission.csv', index=False)
| 0.433262 | 0.917191 |
```
import fnmatch
import os
import numpy
import pandas
import seaborn
# generate an empty dataframe
df = pandas.DataFrame(columns = ["business_id", "url", "name", "open_precovid", "open_postcovid", "address", "city", "state", "postal_code"])
# loop over all files in the directory and concatenate the scrape output files
for file in os.listdir("data"):
if fnmatch.fnmatch(file, "output*to*.csv"):
df = pandas.concat([df, pandas.read_csv("data/" + file, index_col = "Unnamed: 0")])
df.head()
df.shape
pandas.read_csv("../data/even.csv")
# For emilys df
# df = pandas.read_csv("../data/odd.csv", index_col="Unnamed: 0")
# df.drop(["open_precovid", "open_postcovid"], inplace=True, axis=1)
# df.rename({"is_open": "open_precovid", "open": "open_postcovid"}, axis=1, inplace=True)
# df.head()
errors = df[df["open_postcovid"] == -1]
df = df[df["open_postcovid"] != -1]
print("okay: " + str(df.shape[0]))
print("errors: " + str(errors.shape[0]))
print("error %: " + str(int(errors.shape[0] / (df.shape[0] + errors.shape[0]) * 100)) + "%")
ct = pandas.crosstab(df["open_precovid"], df["open_postcovid"])
print("was open and stayed open: " + str(ct.loc[1][1]) + " (" + str(int(round(ct.loc[1][1] / df.shape[0] * 100))) + "%)")
print("was open and then closed: " + str(ct.loc[1][0]) + " (" + str(round(ct.loc[1][0] / df.shape[0] * 100, 1)) + "%)")
print("was closed and stayed closed: " + str(ct.loc[0][0]) + " (" + str(round(ct.loc[0][0] / df.shape[0] * 100, 1)) + "%)")
print("was closed and then opened: " + str(ct.loc[0][1]) + " (" + str(int(round(ct.loc[0][1] / df.shape[0] * 100))) + "%)")
errors[["url", "name"]]
df.groupby(["state", "postal_code"]).count()
df[(df["state"].isin(["CA", "AZ"])) & (df["postal_code"] == 89109)]
len(df["postal_code"].unique())
# removes zips with insufficient number of businesses
df = df[df["postal_code"] != 28202]
df_agg = df[["postal_code"]].groupby("postal_code").count()
df_agg["n_businesses"] = df.groupby("postal_code")["business_id"].count()
df_agg["open_precovid"] = df.groupby("postal_code")["open_precovid"].sum()
df_agg["open_postcovid"] = df.groupby("postal_code")["open_postcovid"].sum()
df_agg["perc_open_precovid"] = df_agg["open_precovid"] / df_agg["n_businesses"]
df_agg["perc_open_postcovid"] = df_agg["open_postcovid"] / df_agg["n_businesses"]
df_agg["perc_open_abschange"] = df_agg["perc_open_postcovid"] - df_agg["perc_open_precovid"]
df_agg["perc_open_relchaneg"] = (df_agg["perc_open_postcovid"] - df_agg["perc_open_precovid"]) / df_agg["perc_open_precovid"]
df["stayed_open"] = numpy.where((df["open_precovid"] == 1) & (df["open_postcovid"] == 1), True, False)
df["became_open"] = numpy.where((df["open_precovid"] == 0) & (df["open_postcovid"] == 1), True, False)
df_agg["stayed_open"] = df.groupby("postal_code")["stayed_open"].sum()
df_agg["perc_stayed_open"] = df_agg["stayed_open"] / df_agg["open_precovid"]
df_agg["became_open"] = df.groupby("postal_code")["became_open"].sum()
df_agg["perc_became_opened"] = df_agg["became_open"] / (df_agg["n_businesses"] - df_agg["open_precovid"])
df_agg = df_agg.reset_index()
even = pandas.read_csv("../data/even.csv")
pandas.concat([even, df_agg], axis=0).reset_index().drop("index", axis=1).to_csv("even_and_odd.csv")
seaborn.heatmap(df_agg.corr())
```
|
github_jupyter
|
import fnmatch
import os
import numpy
import pandas
import seaborn
# generate an empty dataframe
df = pandas.DataFrame(columns = ["business_id", "url", "name", "open_precovid", "open_postcovid", "address", "city", "state", "postal_code"])
# loop over all files in the directory and concatenate the scrape output files
for file in os.listdir("data"):
if fnmatch.fnmatch(file, "output*to*.csv"):
df = pandas.concat([df, pandas.read_csv("data/" + file, index_col = "Unnamed: 0")])
df.head()
df.shape
pandas.read_csv("../data/even.csv")
# For emilys df
# df = pandas.read_csv("../data/odd.csv", index_col="Unnamed: 0")
# df.drop(["open_precovid", "open_postcovid"], inplace=True, axis=1)
# df.rename({"is_open": "open_precovid", "open": "open_postcovid"}, axis=1, inplace=True)
# df.head()
errors = df[df["open_postcovid"] == -1]
df = df[df["open_postcovid"] != -1]
print("okay: " + str(df.shape[0]))
print("errors: " + str(errors.shape[0]))
print("error %: " + str(int(errors.shape[0] / (df.shape[0] + errors.shape[0]) * 100)) + "%")
ct = pandas.crosstab(df["open_precovid"], df["open_postcovid"])
print("was open and stayed open: " + str(ct.loc[1][1]) + " (" + str(int(round(ct.loc[1][1] / df.shape[0] * 100))) + "%)")
print("was open and then closed: " + str(ct.loc[1][0]) + " (" + str(round(ct.loc[1][0] / df.shape[0] * 100, 1)) + "%)")
print("was closed and stayed closed: " + str(ct.loc[0][0]) + " (" + str(round(ct.loc[0][0] / df.shape[0] * 100, 1)) + "%)")
print("was closed and then opened: " + str(ct.loc[0][1]) + " (" + str(int(round(ct.loc[0][1] / df.shape[0] * 100))) + "%)")
errors[["url", "name"]]
df.groupby(["state", "postal_code"]).count()
df[(df["state"].isin(["CA", "AZ"])) & (df["postal_code"] == 89109)]
len(df["postal_code"].unique())
# removes zips with insufficient number of businesses
df = df[df["postal_code"] != 28202]
df_agg = df[["postal_code"]].groupby("postal_code").count()
df_agg["n_businesses"] = df.groupby("postal_code")["business_id"].count()
df_agg["open_precovid"] = df.groupby("postal_code")["open_precovid"].sum()
df_agg["open_postcovid"] = df.groupby("postal_code")["open_postcovid"].sum()
df_agg["perc_open_precovid"] = df_agg["open_precovid"] / df_agg["n_businesses"]
df_agg["perc_open_postcovid"] = df_agg["open_postcovid"] / df_agg["n_businesses"]
df_agg["perc_open_abschange"] = df_agg["perc_open_postcovid"] - df_agg["perc_open_precovid"]
df_agg["perc_open_relchaneg"] = (df_agg["perc_open_postcovid"] - df_agg["perc_open_precovid"]) / df_agg["perc_open_precovid"]
df["stayed_open"] = numpy.where((df["open_precovid"] == 1) & (df["open_postcovid"] == 1), True, False)
df["became_open"] = numpy.where((df["open_precovid"] == 0) & (df["open_postcovid"] == 1), True, False)
df_agg["stayed_open"] = df.groupby("postal_code")["stayed_open"].sum()
df_agg["perc_stayed_open"] = df_agg["stayed_open"] / df_agg["open_precovid"]
df_agg["became_open"] = df.groupby("postal_code")["became_open"].sum()
df_agg["perc_became_opened"] = df_agg["became_open"] / (df_agg["n_businesses"] - df_agg["open_precovid"])
df_agg = df_agg.reset_index()
even = pandas.read_csv("../data/even.csv")
pandas.concat([even, df_agg], axis=0).reset_index().drop("index", axis=1).to_csv("even_and_odd.csv")
seaborn.heatmap(df_agg.corr())
| 0.142441 | 0.140366 |
# Module 1. Dataset Cleaning and Analysis
이 실습에서는 MovieLens 데이터 세트에서 수집된 데이터를 기반으로, 영화 추천 모델을 작성하는 법을 안내합니다.<br/>Module 1 에서는 MovieLens 데이터 세트를 가져와 각 피처들을 확인하고 데이터 클린징 및 분석 작업을 진행합니다.
## Notebook 사용법
코드는 여러 코드 셀들로 구성됩니다. 이 페이지의 상단에 삼각형으로 된 실행 단추를 마우스로 클릭하여 각 셀을 실행하고 다음 셀로 이동할 수 있습니다. 또는 셀에서 키보드 단축키 `Shift + Enter`를 눌러 셀을 실행하고 다음 셀로 이동할 수도 있습니다.
셀이 실행되면 셀이 실행되는 동안 측면에 줄이 * 표시되어 있거나 셀 내의 모든 코드를 예측한 후 실행이 완료된 마지막 셀을 나타내기 위해 숫자로 업데이트됩니다.
아래 지침을 따르고 셀을 실행하세요.
## Library Import
파이썬에는 광범위한 라이브러리 모음이 포함되어 있으며, 본 LAB을 위해서 핵심 Data Scientist용 Tool 인 boto3 (AWS SDK) 및 Pandas/Numpy와 같은 라이브러리를 가져와야 합니다.
```
import boto3
import json
import numpy as np
import pandas as pd
import time
import jsonlines
import os
from datetime import datetime
import sagemaker
import time
import warnings
import matplotlib.pyplot as plt
from matplotlib.dates import DateFormatter
import matplotlib.dates as mdate
from botocore.exceptions import ClientError
```
다음으로 여러분의 환경이 Amazon Personalize와 성공적으로 통신할 수 있는지 확인해야 합니다.
```
# Configure the SDK to Personalize:
personalize = boto3.client('personalize')
personalize_runtime = boto3.client('personalize-runtime')
s3 = boto3.resource('s3')
## Please fill the information below
#WORK_DATE="<working date that will be used for prefix of solution names"
#data_dir = "<local data path>"
#BUCKET_NAME = "<your_bucket_name>"
#PREFIX="<prefix used for data stroage>"
WORK_DATE="20201215"
data_dir = "poc-data"
os.makedirs(data_dir+'/'+WORK_DATE,exist_ok=True)
account_id = "870180618679"
BUCKET_NAME = "jihys-personalize-ap-northeast-2"
PREFIX=WORK_DATE
INTERACTION_FILE="interation"
USER_FILE="user"
ITEM_FILE="item"
```
## 파일 다운로드
이번 HoL에 사용할 데이터 셋의 압축을 풉니다. 해당 데이터 셋은 [Movie Lense 데이터 셋](http://files.grouplens.org/datasets/movielens/ml-1m.zip) 을 변형한 데이터 입니다.
```
!unzip -o ml-1m-modified.zip
```
## 데이터 확인하기
Personalize 에서는 3종류의 데이터 셋을 인풋으로 사용 합니다.
1) **User**: 이 데이터 세트는 사용자에 대한 메타데이터를 저장합니다. 여기에는 맞춤화 시스템에서 중요한 신호가 될 수 있는 연령, 성별 및 충성도 멤버십 등의 정보가 포함될 수 있습니다.
2) **Item:** 이 데이터 세트는 항목에 대한 메타데이터를 저장합니다. 여기에는 가격, SKU 유형 또는 가용성과 같은 정보가 포함될 수 있습니다.
3) **Interaction:** 이 데이터 세트는 사용자와 항목 간의 상호 작용에서 나온 과거 및 실시간 데이터를 저장합니다. 이 데이터에는 사용자의 위치 또는 디바이스(모바일, 태블릿, 데스크톱 등)와 같은 사용자의 검색 컨텍스트에 대한 노출 데이터와 컨텍스트 메타데이터가 포함될 수 있습니다. Interaction 데이터셋은 모든 알고리즘에서 필수로 제공 해야하는 데이터 입니다.
이번 실습에 사용할 파일의 컬럼에 대한 정보는 아래 README 파일을 통해 확인합니다.
```
!cat data_ml_1m/README
df=pd.read_csv('data_ml_1m/ratings.csv')
df.columns=["USER_ID","ITEM_ID","EVENT_VALUE", "TIMESTAMP"]
df['EVENT_TYPE']='RATING'
df.head()
item=pd.read_csv('data_ml_1m/movies.csv')
item.columns=['ITEM_ID', 'TITLE', 'GENRE']
item.head()
user=pd.read_csv('data_ml_1m/users.dat',sep='::',encoding='latin1',names=['USER_ID', 'GENDER','AGE', 'OCCUPATION','ZIPCODE'])
user.head()
```
## 데이터 클린징
여기에서는 아래와 같은 데이터 클린징 작업을 합니다.
- Null/Duplicated 데이터 정리
- 인터렉션 데이터중 메타데이터에 없는 데이터 삭제
### NULL Data 및 Duplicated Data 확인 및 삭제
인터렉션 데이터를 조사해 보면 많은 중복 데이터가 존재합니다. 특히나 Interaction data 로그에서 이러한 패턴을 많이 보입니다.
여기서는 불필요한 중복 데이터를 삭제합니다. 또한 TIMESTAMP와 USER_ID, ITEM_ID와 같이 필수 데이터가 null 인 데이터를 제거하도록 합니다.
단 Amazon Personalize에서는 Amazon Personalize 솔루션에서 생성할 때 일부 메타데이터에 한 해 "null"을 허용된 메타데이터 값으로 정의할 수 있습니다. 예를 들어 interaction data의 EVENT_TYPE, item 혹은 user data의 메타 데이터 값에서는 "null"을 허용합니다. "null" 을 허용된 값으로 사용하기 위해서는 스키마 정의시 null 을 허용하도록 세팅 하여야 합니다.
~~~
{
"type": "record",
"name": "Items",
"namespace": "com.amazonaws.personalize.schema",
"fields": [
{
"name": "ITEM_ID",
"type": "string"
},
{
"name": "GENRES",
"type": [
"null",
"string"
],
"categorical": true
},
{
"name": "CREATION_TIMESTAMP",
"type": "long"
}
],
"version": "1.0"
}
~~~
Amazon Personalize는 솔루션을 생성하면서 누락된 메타데이터가 있는 필드를 자동으로 인식하고 기계 학습 모델을 훈련할 때 적절하게 처리합니다.자세한 내용은 [여기](https://docs.aws.amazon.com/personalize/latest/dg/how-it-works-dataset-schema.html#dataset-requirements) 를 참고해 주세요.
```
#interactin data null 데이터 확인
print("# of rows of Null TimeStamp : {}".format(df['TIMESTAMP'].isnull().sum()))
print("# of rows of Null User ID : {}".format(df['USER_ID'].isnull().sum()))
print("# of rows of Null Item ID : {}".format(df['ITEM_ID'].isnull().sum()))
# interaction null 데이터 삭제
df=df.dropna(subset=['TIMESTAMP','USER_ID','ITEM_ID'])
#interaction 중복 데이터 확인
print("duplicated rows:", len(df[df.duplicated(keep=False)]))
#interaction 중복 데이터 제거
df=df.drop_duplicates()
#item에서 ITEM_ID가 null 인 행을 제거
print("# of rows of Null Item ID : {}".format(item['ITEM_ID'].isnull().sum()))
item=item.dropna(subset=['ITEM_ID'])
#item meta 중복 데이터 확인
print("duplicated rows:", len(item[item.duplicated(keep=False)]))
#item meta 중복 데이터 제거
item=item.drop_duplicates()
#user에서 USER_ID가 null 인 행을 제거
print("# of rows of Null User ID : {}".format(df['USER_ID'].isnull().sum()))
user=user.dropna(subset=['USER_ID'])
#user meta 중복 데이터 확인
print("duplicated rows:", len(user[user.duplicated(keep=False)]))
#user meta 중복 데이터 제거
user=user.drop_duplicates()
```
### 인터렉션 데이터중 메타데이터에 없는 데이터 삭제
#### Item Metadata 에 없는 인터렉션 삭제하기
- Item metadata에 없는 아이템 아이디를 제외한 인터렉션 테이블을 추려냅니다.<br/> (이번 샘플 데이터 셋에는 위같은 데이터가 존재하진 않습니다.)<br/>
`unique_item_from_df=df['ITEM_ID'].unique()`<br/>
`unique_item_from_meta=item['ITEM_ID'].unique()`
- 아래 코드를 실행하여 Item metadata에 없는 인터렉션 정보를 확인합니다. <br/>
`assert(len(df[- df['ITEM_ID'].isin(unique_item_from_meta)])==0)`
- 해당 인터렉션 라인을 삭제 합니다. <br/>
`df= df[df['ITEM_ID'].isin(unique_item_from_meta)] `
비슷한 방식으로 User metadata에 없는 사용자를 제거 할수도 있습니다.<br/>
* `unique_user_from_df=df['USER_ID'].unique()`<br/>
* `unique_user_from_meta=user['USER_ID'].unique()`<br/>
* `assert(len(df[- df['USER_ID'].isin(unique_user_from_meta)])==0)`<br/>
* `df= df[df['USER_ID'].isin(unique_user_from_meta)] `<p/>
```
unique_item_from_df=df["ITEM_ID"].unique()
unique_item_from_meta=item['ITEM_ID'].unique()
print("Unique items from interaction:",len(unique_item_from_df))
print("Unique items from item metadata:", len(unique_item_from_meta))
assert(len(df[- df['ITEM_ID'].isin(unique_item_from_meta)])==0)
#df=df[df['ITEM_ID'].isin(unique_item_from_meta)]
```
### Multi-Category 데이터 준비
영화 장르와 같이 여러 장르로 구분할 수 있는 데이터는 '|'로 구분되어 표기되어야 합니다. <br/>
아래 코드는 '.'으로 구분되어 있는 구분자를 '|'로 대체 할 수 있습니다.
자세한 내용은 [여기](https://docs.aws.amazon.com/ko_kr/personalize/latest/dg/data-prep-formatting.html)를 클릭하여 확인합니다.

```
#Multi label
for idx,i in enumerate(item["GENRE"]):
item["GENRE"][idx]=i.replace('.', '|')
item.head()
```
## INTERACTION DATA 정보 확인
Personalize에서 학습을 수행하기 위해서는 다음과 [official limits](https://docs.aws.amazon.com/personalize/latest/dg/limits.html)같은 데이터 요구사항을 맞추어야 합니다.
* 최소 25명 고유 사용자
* 최소 100개 고유 아이템
* 사용자 당 2개 이상의 Interaction(예. 구매,평가 등) 기록
하지만 일반적으로 다음과 같은 데이터가 준비 되어 있는것이 좋습니다.
* 최소 50명 고유 사용자
* 최소 100개 고유 아이템
* 사용자 당 24 이상의 Interaction(예. 구매,평가 등) 기록
### 사용자 평점 분포하기
여기에서는 사용자 평점 분포를 확인합니다.
사용자 평점이 1,2 인 경우 사용자가 선호하는 아이템으로 확인하기 어렵기 때문에 여기 핸즈온에서는 3점 이상인 벨류만 사용하도록 합니다.
```
# Print User Rating Value counts
df.EVENT_VALUE.value_counts().plot(kind='bar')
plt.title("EVENT_VALUE: USer Ratings count")
plt.show()
df=df[df['EVENT_VALUE']>=3]
```
### 인터렉션의 사용자 정보 분석
User personalization 계열의 추천 알고리즘에서는 학습에 포함할 Percentile을 조정할 수 있는 파라메터(min_user_history_length_percentile, max_user_history_length_percentile)가 있습니다.
너무 인터렉션이 많은 사용자는 데이터에 노이즈를 포함되는 경우가 있기 때문에 제외하는 것이 좋습니다. 또한 너무 인터렉션이 적은 사용자 또한 제대로된 추천 기록을 받기 어렵기 때문에 제외하는것이 좋습니다. Default로는 min max 값은 0과 0.99로 세팅되어 있습니다.
예를 들어 min_user_history_length_percentile to 0.05 및 max_user_history_length_percentile to 0.95 설정에는 기록 길이가 하위 또는 상위 5%에 해당하는 사용자를 제외한 모든 사용자가 포함됩니다.
```
## checkout the unique number of users and items in the interaction
unique_user_from_df=df['USER_ID'].unique()
unique_item_from_df=df['ITEM_ID'].unique()
print("Unique User from interaction:", len(unique_user_from_df))
print("Unique Item from interaction:",len(unique_item_from_df))
unique_user_from_meta=user["USER_ID"].unique()
unique_item_from_meta=item["ITEM_ID"].unique()
print("Unique User from usermeta", len(unique_user_from_meta))
print("Unique Item from itemmeta:",len(unique_item_from_meta))
user_activity_counts = df.groupby("USER_ID").count().loc[:,["EVENT_VALUE"]].rename(columns={"EVENT_VALUE":"INTERACTION_COUNTS"})
user_activity_counts
user_activity_counts.quantile([0.01,0.05,.1,.2,.3,.4,.5,.6,.8,.9,.95,.99,.999,.9999,1.0])
user_activity_counts=user_activity_counts.reset_index()
activities = user_activity_counts.groupby('INTERACTION_COUNTS').count()
activities.columns=['NUM_USERS']
activities['NUM_USERS'].sum()
assert (len(unique_user_from_df)==activities['NUM_USERS'].sum())
activities.plot(kind='bar',figsize=(15,5))
#activities.loc[:,:].plot(kind='bar', figsize=(15,5), ylim=(0,5496))
plt.title("activities users group")
plt.show()
print("Number of Users in Activities counts @Max Frequency of {}:".format(activities['NUM_USERS'].idxmax()),activities['NUM_USERS'].max())
activities[activities.index > 24].NUM_USERS.sum()
```
### 인터렉션의 아이템 분석
```
print(df.head())
df.ITEM_ID = df.ITEM_ID.astype(str)
def draw_long_tails(df, is_in_event_types, groupby_column_name, count_name, range1=100, range2=1000, range3=3000):
filtered_df = df.loc[df["EVENT_VALUE"].isin(is_in_event_types)]
#print(filtered_df.head())
groupby_df = filtered_df.groupby(groupby_column_name).count().loc[:,["EVENT_VALUE"]].rename(columns={"EVENT_VALUE":count_name})
#print(groupby_df.head())
sorted_df = groupby_df.sort_values([count_name], ascending=False)
#print(sorted_df.head())
sorted_df.plot(kind='line', figsize=(15,5))
plt.title(count_name + " per " + groupby_column_name)
plt.show()
sorted_df[:range1].plot(kind='line', figsize=(15,5))
plt.title(count_name + " per " + groupby_column_name + "/ 1 ~" + str(range1) + "th")
plt.show()
sorted_df[range1:range2].plot(kind='line', figsize=(15,5))
plt.title(count_name + " per " + groupby_column_name + " / " + str(range1) + "th ~ "+ str(range2) + "th")
plt.show()
sorted_df[range2:range3].plot(kind='line', figsize=(15,5))
plt.title(count_name + " per " + groupby_column_name + " / " + str(range2) + "th ~ "+ str(range3) + "th")
plt.show()
sorted_df[range3:].plot(kind='line', figsize=(15,5))
plt.title(count_name + " per " + groupby_column_name + " / " + str(range3) + "th ~ ")
plt.show()
#draw_long_tails(df, ["ORDER","VIEW_DETAIL","ADD_CART"], "ITEM_ID", "ALL_EVENTS", 100, 1000, 3000)
draw_long_tails(df, ["5","4","3"], "ITEM_ID", "ALL_EVENTS", 100, 1000, 3000)
```
## 사용자 메타 데이터 분석
```
print(user.head())
user.describe()
user_GENDER_counts = user.groupby('GENDER').count().loc[:,["USER_ID"]].rename(columns={"USER_ID":"GENDER_COUNTS"})
user_GENDER_counts
user_AGE_counts = user.groupby('AGE').count().loc[:,["USER_ID"]].rename(columns={"USER_ID":"AGE_COUNTS"})
user_AGE_counts
user_OCCUPATION_counts = user.groupby('OCCUPATION').count().loc[:,["USER_ID"]].rename(columns={"USER_ID":"OCCUPATION_COUNTS"})
user_OCCUPATION_counts
user_ZIPCODE_counts = user.groupby('ZIPCODE').count().loc[:,["USER_ID"]].rename(columns={"USER_ID":"ZIPCODE_COUNTS"})
user_ZIPCODE_counts
```
AGE,GENDER,OCCUPATION은 전체 사용자 수 6023명 대비 비교적낮은 캐터고리 개수(Cardinality)가 존배합니다.
하지만 zipcode 경우 3439개로 너무 높습니다. 따라서 이후 학습시에는 사용하지 않도록 합니다.
```
user=user.drop(['ZIPCODE'],axis=1)
user.head()
```
## ITEM 메타 데이터 분석
```
item.head()
item.ITEM_ID = item.ITEM_ID.astype(str)
item_genre_counts = item.groupby('GENRE').count().loc[:,["ITEM_ID"]].rename(columns={"ITEM_ID":"GENRE_COUNTS"})
item_genre_counts
sorted_item = item_genre_counts.sort_values("GENRE_COUNTS", ascending=False)
sorted_item[:10].plot(kind='bar',figsize=(15,5))
plt.title("Top 10 frequent movie genres in item data")
plt.show()
item_file=data_dir+'/'+WORK_DATE+'/'+'item.csv'
user_file=data_dir+'/'+WORK_DATE+'/'+'user.csv'
inter_file=data_dir+'/'+WORK_DATE+'/'+'intercation.csv'
item.to_csv(item_file,index=False)
user.to_csv(user_file,index=False)
df.to_csv(inter_file,index=False)
%store WORK_DATE
%store data_dir
%store account_id
%store BUCKET_NAME
%store PREFIX
%store item_file
%store user_file
%store inter_file
```
|
github_jupyter
|
import boto3
import json
import numpy as np
import pandas as pd
import time
import jsonlines
import os
from datetime import datetime
import sagemaker
import time
import warnings
import matplotlib.pyplot as plt
from matplotlib.dates import DateFormatter
import matplotlib.dates as mdate
from botocore.exceptions import ClientError
# Configure the SDK to Personalize:
personalize = boto3.client('personalize')
personalize_runtime = boto3.client('personalize-runtime')
s3 = boto3.resource('s3')
## Please fill the information below
#WORK_DATE="<working date that will be used for prefix of solution names"
#data_dir = "<local data path>"
#BUCKET_NAME = "<your_bucket_name>"
#PREFIX="<prefix used for data stroage>"
WORK_DATE="20201215"
data_dir = "poc-data"
os.makedirs(data_dir+'/'+WORK_DATE,exist_ok=True)
account_id = "870180618679"
BUCKET_NAME = "jihys-personalize-ap-northeast-2"
PREFIX=WORK_DATE
INTERACTION_FILE="interation"
USER_FILE="user"
ITEM_FILE="item"
!unzip -o ml-1m-modified.zip
!cat data_ml_1m/README
df=pd.read_csv('data_ml_1m/ratings.csv')
df.columns=["USER_ID","ITEM_ID","EVENT_VALUE", "TIMESTAMP"]
df['EVENT_TYPE']='RATING'
df.head()
item=pd.read_csv('data_ml_1m/movies.csv')
item.columns=['ITEM_ID', 'TITLE', 'GENRE']
item.head()
user=pd.read_csv('data_ml_1m/users.dat',sep='::',encoding='latin1',names=['USER_ID', 'GENDER','AGE', 'OCCUPATION','ZIPCODE'])
user.head()
#interactin data null 데이터 확인
print("# of rows of Null TimeStamp : {}".format(df['TIMESTAMP'].isnull().sum()))
print("# of rows of Null User ID : {}".format(df['USER_ID'].isnull().sum()))
print("# of rows of Null Item ID : {}".format(df['ITEM_ID'].isnull().sum()))
# interaction null 데이터 삭제
df=df.dropna(subset=['TIMESTAMP','USER_ID','ITEM_ID'])
#interaction 중복 데이터 확인
print("duplicated rows:", len(df[df.duplicated(keep=False)]))
#interaction 중복 데이터 제거
df=df.drop_duplicates()
#item에서 ITEM_ID가 null 인 행을 제거
print("# of rows of Null Item ID : {}".format(item['ITEM_ID'].isnull().sum()))
item=item.dropna(subset=['ITEM_ID'])
#item meta 중복 데이터 확인
print("duplicated rows:", len(item[item.duplicated(keep=False)]))
#item meta 중복 데이터 제거
item=item.drop_duplicates()
#user에서 USER_ID가 null 인 행을 제거
print("# of rows of Null User ID : {}".format(df['USER_ID'].isnull().sum()))
user=user.dropna(subset=['USER_ID'])
#user meta 중복 데이터 확인
print("duplicated rows:", len(user[user.duplicated(keep=False)]))
#user meta 중복 데이터 제거
user=user.drop_duplicates()
unique_item_from_df=df["ITEM_ID"].unique()
unique_item_from_meta=item['ITEM_ID'].unique()
print("Unique items from interaction:",len(unique_item_from_df))
print("Unique items from item metadata:", len(unique_item_from_meta))
assert(len(df[- df['ITEM_ID'].isin(unique_item_from_meta)])==0)
#df=df[df['ITEM_ID'].isin(unique_item_from_meta)]
#Multi label
for idx,i in enumerate(item["GENRE"]):
item["GENRE"][idx]=i.replace('.', '|')
item.head()
# Print User Rating Value counts
df.EVENT_VALUE.value_counts().plot(kind='bar')
plt.title("EVENT_VALUE: USer Ratings count")
plt.show()
df=df[df['EVENT_VALUE']>=3]
## checkout the unique number of users and items in the interaction
unique_user_from_df=df['USER_ID'].unique()
unique_item_from_df=df['ITEM_ID'].unique()
print("Unique User from interaction:", len(unique_user_from_df))
print("Unique Item from interaction:",len(unique_item_from_df))
unique_user_from_meta=user["USER_ID"].unique()
unique_item_from_meta=item["ITEM_ID"].unique()
print("Unique User from usermeta", len(unique_user_from_meta))
print("Unique Item from itemmeta:",len(unique_item_from_meta))
user_activity_counts = df.groupby("USER_ID").count().loc[:,["EVENT_VALUE"]].rename(columns={"EVENT_VALUE":"INTERACTION_COUNTS"})
user_activity_counts
user_activity_counts.quantile([0.01,0.05,.1,.2,.3,.4,.5,.6,.8,.9,.95,.99,.999,.9999,1.0])
user_activity_counts=user_activity_counts.reset_index()
activities = user_activity_counts.groupby('INTERACTION_COUNTS').count()
activities.columns=['NUM_USERS']
activities['NUM_USERS'].sum()
assert (len(unique_user_from_df)==activities['NUM_USERS'].sum())
activities.plot(kind='bar',figsize=(15,5))
#activities.loc[:,:].plot(kind='bar', figsize=(15,5), ylim=(0,5496))
plt.title("activities users group")
plt.show()
print("Number of Users in Activities counts @Max Frequency of {}:".format(activities['NUM_USERS'].idxmax()),activities['NUM_USERS'].max())
activities[activities.index > 24].NUM_USERS.sum()
print(df.head())
df.ITEM_ID = df.ITEM_ID.astype(str)
def draw_long_tails(df, is_in_event_types, groupby_column_name, count_name, range1=100, range2=1000, range3=3000):
filtered_df = df.loc[df["EVENT_VALUE"].isin(is_in_event_types)]
#print(filtered_df.head())
groupby_df = filtered_df.groupby(groupby_column_name).count().loc[:,["EVENT_VALUE"]].rename(columns={"EVENT_VALUE":count_name})
#print(groupby_df.head())
sorted_df = groupby_df.sort_values([count_name], ascending=False)
#print(sorted_df.head())
sorted_df.plot(kind='line', figsize=(15,5))
plt.title(count_name + " per " + groupby_column_name)
plt.show()
sorted_df[:range1].plot(kind='line', figsize=(15,5))
plt.title(count_name + " per " + groupby_column_name + "/ 1 ~" + str(range1) + "th")
plt.show()
sorted_df[range1:range2].plot(kind='line', figsize=(15,5))
plt.title(count_name + " per " + groupby_column_name + " / " + str(range1) + "th ~ "+ str(range2) + "th")
plt.show()
sorted_df[range2:range3].plot(kind='line', figsize=(15,5))
plt.title(count_name + " per " + groupby_column_name + " / " + str(range2) + "th ~ "+ str(range3) + "th")
plt.show()
sorted_df[range3:].plot(kind='line', figsize=(15,5))
plt.title(count_name + " per " + groupby_column_name + " / " + str(range3) + "th ~ ")
plt.show()
#draw_long_tails(df, ["ORDER","VIEW_DETAIL","ADD_CART"], "ITEM_ID", "ALL_EVENTS", 100, 1000, 3000)
draw_long_tails(df, ["5","4","3"], "ITEM_ID", "ALL_EVENTS", 100, 1000, 3000)
print(user.head())
user.describe()
user_GENDER_counts = user.groupby('GENDER').count().loc[:,["USER_ID"]].rename(columns={"USER_ID":"GENDER_COUNTS"})
user_GENDER_counts
user_AGE_counts = user.groupby('AGE').count().loc[:,["USER_ID"]].rename(columns={"USER_ID":"AGE_COUNTS"})
user_AGE_counts
user_OCCUPATION_counts = user.groupby('OCCUPATION').count().loc[:,["USER_ID"]].rename(columns={"USER_ID":"OCCUPATION_COUNTS"})
user_OCCUPATION_counts
user_ZIPCODE_counts = user.groupby('ZIPCODE').count().loc[:,["USER_ID"]].rename(columns={"USER_ID":"ZIPCODE_COUNTS"})
user_ZIPCODE_counts
user=user.drop(['ZIPCODE'],axis=1)
user.head()
item.head()
item.ITEM_ID = item.ITEM_ID.astype(str)
item_genre_counts = item.groupby('GENRE').count().loc[:,["ITEM_ID"]].rename(columns={"ITEM_ID":"GENRE_COUNTS"})
item_genre_counts
sorted_item = item_genre_counts.sort_values("GENRE_COUNTS", ascending=False)
sorted_item[:10].plot(kind='bar',figsize=(15,5))
plt.title("Top 10 frequent movie genres in item data")
plt.show()
item_file=data_dir+'/'+WORK_DATE+'/'+'item.csv'
user_file=data_dir+'/'+WORK_DATE+'/'+'user.csv'
inter_file=data_dir+'/'+WORK_DATE+'/'+'intercation.csv'
item.to_csv(item_file,index=False)
user.to_csv(user_file,index=False)
df.to_csv(inter_file,index=False)
%store WORK_DATE
%store data_dir
%store account_id
%store BUCKET_NAME
%store PREFIX
%store item_file
%store user_file
%store inter_file
| 0.148448 | 0.957437 |
# Loading Image Data
So far we've been working with fairly artificial datasets that you wouldn't typically be using in real projects. Instead, you'll likely be dealing with full-sized images like you'd get from smart phone cameras. In this notebook, we'll look at how to load images and use them to train neural networks.
We'll be using a [dataset of cat and dog photos](https://www.kaggle.com/c/dogs-vs-cats) available from Kaggle. Here are a couple example images:
<img src='assets/dog_cat.png'>
We'll use this dataset to train a neural network that can differentiate between cats and dogs. These days it doesn't seem like a big accomplishment, but five years ago it was a serious challenge for computer vision systems.
```
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import torch
from torchvision import datasets, transforms
import helper
```
The easiest way to load image data is with `datasets.ImageFolder` from `torchvision` ([documentation](http://pytorch.org/docs/master/torchvision/datasets.html#imagefolder)). In general you'll use `ImageFolder` like so:
```python
dataset = datasets.ImageFolder('path/to/data', transform=transform)
```
where `'path/to/data'` is the file path to the data directory and `transform` is a list of processing steps built with the [`transforms`](http://pytorch.org/docs/master/torchvision/transforms.html) module from `torchvision`. ImageFolder expects the files and directories to be constructed like so:
```
root/dog/xxx.png
root/dog/xxy.png
root/dog/xxz.png
root/cat/123.png
root/cat/nsdf3.png
root/cat/asd932_.png
```
where each class has it's own directory (`cat` and `dog`) for the images. The images are then labeled with the class taken from the directory name. So here, the image `123.png` would be loaded with the class label `cat`. You can download the dataset already structured like this [from here](https://s3.amazonaws.com/content.udacity-data.com/nd089/Cat_Dog_data.zip). I've also split it into a training set and test set.
### Transforms
When you load in the data with `ImageFolder`, you'll need to define some transforms. For example, the images are different sizes but we'll need them to all be the same size for training. You can either resize them with `transforms.Resize()` or crop with `transforms.CenterCrop()`, `transforms.RandomResizedCrop()`, etc. We'll also need to convert the images to PyTorch tensors with `transforms.ToTensor()`. Typically you'll combine these transforms into a pipeline with `transforms.Compose()`, which accepts a list of transforms and runs them in sequence. It looks something like this to scale, then crop, then convert to a tensor:
```python
transform = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()])
```
There are plenty of transforms available, I'll cover more in a bit and you can read through the [documentation](http://pytorch.org/docs/master/torchvision/transforms.html).
### Data Loaders
With the `ImageFolder` loaded, you have to pass it to a [`DataLoader`](http://pytorch.org/docs/master/data.html#torch.utils.data.DataLoader). The `DataLoader` takes a dataset (such as you would get from `ImageFolder`) and returns batches of images and the corresponding labels. You can set various parameters like the batch size and if the data is shuffled after each epoch.
```python
dataloader = torch.utils.data.DataLoader(dataset, batch_size=32, shuffle=True)
```
Here `dataloader` is a [generator](https://jeffknupp.com/blog/2013/04/07/improve-your-python-yield-and-generators-explained/). To get data out of it, you need to loop through it or convert it to an iterator and call `next()`.
```python
# Looping through it, get a batch on each loop
for images, labels in dataloader:
pass
# Get one batch
images, labels = next(iter(dataloader))
```
>**Exercise:** Load images from the `Cat_Dog_data/train` folder, define a few transforms, then build the dataloader.
```
data_dir = 'Cat_Dog_data/train'
transform = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()])
dataset =
dataloader = # TODO: use the ImageFolder dataset to create the DataLoader
# Run this to test your data loader
images, labels = next(iter(dataloader))
helper.imshow(images[0], normalize=False)
```
If you loaded the data correctly, you should see something like this (your image will be different):
<img src='assets/cat_cropped.png' width=244>
## Data Augmentation
A common strategy for training neural networks is to introduce randomness in the input data itself. For example, you can randomly rotate, mirror, scale, and/or crop your images during training. This will help your network generalize as it's seeing the same images but in different locations, with different sizes, in different orientations, etc.
To randomly rotate, scale and crop, then flip your images you would define your transforms like this:
```python
train_transforms = transforms.Compose([transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize([0.5, 0.5, 0.5],
[0.5, 0.5, 0.5])])
```
You'll also typically want to normalize images with `transforms.Normalize`. You pass in a list of means and list of standard deviations, then the color channels are normalized like so
```input[channel] = (input[channel] - mean[channel]) / std[channel]```
Subtracting `mean` centers the data around zero and dividing by `std` squishes the values to be between -1 and 1. Normalizing helps keep the network work weights near zero which in turn makes backpropagation more stable. Without normalization, networks will tend to fail to learn.
You can find a list of all [the available transforms here](http://pytorch.org/docs/0.3.0/torchvision/transforms.html). When you're testing however, you'll want to use images that aren't altered (except you'll need to normalize the same way). So, for validation/test images, you'll typically just resize and crop.
>**Exercise:** Define transforms for training data and testing data below.
```
data_dir = 'Cat_Dog_data'
# TODO: Define transforms for the training data and testing data
train_transforms =
test_transforms =
# Pass transforms in here, then run the next cell to see how the transforms look
train_data = datasets.ImageFolder(data_dir + '/train', transform=train_transforms)
test_data = datasets.ImageFolder(data_dir + '/test', transform=test_transforms)
trainloader = torch.utils.data.DataLoader(train_data, batch_size=32)
testloader = torch.utils.data.DataLoader(test_data, batch_size=32)
# change this to the trainloader or testloader
data_iter = iter(testloader)
images, labels = next(data_iter)
fig, axes = plt.subplots(figsize=(10,4), ncols=4)
for ii in range(4):
ax = axes[ii]
helper.imshow(images[ii], ax=ax, normalize=False)
```
Your transformed images should look something like this.
<center>Training examples:</center>
<img src='assets/train_examples.png' width=500px>
<center>Testing examples:</center>
<img src='assets/test_examples.png' width=500px>
At this point you should be able to load data for training and testing. Now, you should try building a network that can classify cats vs dogs. This is quite a bit more complicated than before with the MNIST and Fashion-MNIST datasets. To be honest, you probably won't get it to work with a fully-connected network, no matter how deep. These images have three color channels and at a higher resolution (so far you've seen 28x28 images which are tiny).
In the next part, I'll show you how to use a pre-trained network to build a model that can actually solve this problem.
```
# Optional TODO: Attempt to build a network to classify cats vs dogs from this dataset
```
|
github_jupyter
|
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import torch
from torchvision import datasets, transforms
import helper
dataset = datasets.ImageFolder('path/to/data', transform=transform)
root/dog/xxx.png
root/dog/xxy.png
root/dog/xxz.png
root/cat/123.png
root/cat/nsdf3.png
root/cat/asd932_.png
transform = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()])
dataloader = torch.utils.data.DataLoader(dataset, batch_size=32, shuffle=True)
# Looping through it, get a batch on each loop
for images, labels in dataloader:
pass
# Get one batch
images, labels = next(iter(dataloader))
data_dir = 'Cat_Dog_data/train'
transform = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()])
dataset =
dataloader = # TODO: use the ImageFolder dataset to create the DataLoader
# Run this to test your data loader
images, labels = next(iter(dataloader))
helper.imshow(images[0], normalize=False)
train_transforms = transforms.Compose([transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize([0.5, 0.5, 0.5],
[0.5, 0.5, 0.5])])
Subtracting `mean` centers the data around zero and dividing by `std` squishes the values to be between -1 and 1. Normalizing helps keep the network work weights near zero which in turn makes backpropagation more stable. Without normalization, networks will tend to fail to learn.
You can find a list of all [the available transforms here](http://pytorch.org/docs/0.3.0/torchvision/transforms.html). When you're testing however, you'll want to use images that aren't altered (except you'll need to normalize the same way). So, for validation/test images, you'll typically just resize and crop.
>**Exercise:** Define transforms for training data and testing data below.
Your transformed images should look something like this.
<center>Training examples:</center>
<img src='assets/train_examples.png' width=500px>
<center>Testing examples:</center>
<img src='assets/test_examples.png' width=500px>
At this point you should be able to load data for training and testing. Now, you should try building a network that can classify cats vs dogs. This is quite a bit more complicated than before with the MNIST and Fashion-MNIST datasets. To be honest, you probably won't get it to work with a fully-connected network, no matter how deep. These images have three color channels and at a higher resolution (so far you've seen 28x28 images which are tiny).
In the next part, I'll show you how to use a pre-trained network to build a model that can actually solve this problem.
| 0.532911 | 0.990422 |
# Analyzing Simulation Trajectories
- toc: false
- branch: master
- badges: true
- comments: false
- categories: [grad school, molecular modeling, scientific computing]
Let's say you've conducted a simulation.
Everything up to that point (parametrization, initialization, actually running the simulation) will be assumed
and probably discussed another day.
What you have from a simulation is a **trajectory** (*timeseries of coordinates*), and now we have to derive some
meaningful properties from this trajectory.
Many meaningful properties can be derived from these coordinates, be it how atomic coordinates are related to each other, the sorts of geometries or larger structures we see, or how these coordinates are correlated over time.
Whatever it is you're interested in, it all starts with the coordinates
There are many analysis packages:
* [**MDTraj**] (http://mdtraj.org/1.9.3/)
* [**MDAnalysis**] (https://www.mdanalysis.org/docs/)
* [**Freud**] (https://freud.readthedocs.io/en/stable/)
* [**Pytraj**] (https://amber-md.github.io/pytraj/latest/index.html)
* [**Cpptraj**] (https://amber-md.github.io/cpptraj/CPPTRAJ.xhtml)
* and many, many others (this is what happens when a open-source software goes rampant with different desired functionality and starts from independent research groups)
While each has a variety of different built-in/common analysis routines, some are more common
(like radial distribution functions).
What EVERY modeller will use, though, is the coordinates.
The *most important* function in these analysis packages is the ability to turn
a large trajectory file, written to disk, and read it into memory as a data structure whose XYZ coordinates we can access.
Every simulation engine has different file formats and data encodings, but many of these analysis packages can support a wide range of file formats and pump out the same `Trajectory` data structure core to each package.
For example, we can use **MDtraj** to read in some simulation files from GROMACS.
We obtain information about the XYZ coordinates and *molecular topology*
(atoms, elements, atom names/types, residues, chemical bonding)
In general, there's a sort of hierarchy/classification to groups of atoms.
At the base, you have an *atom*, which is as it sounds, or a coarse-grained particle depending on your simulation.
Groups of atoms can form a *chain*, which is pretty much just a bonded network of atoms.
Groups of atoms and chains form a *residue*. This derives from protein amino acid residues, where each monomer was a residue. In other applications, this can also refer to a closed-loop bonded network of atoms (a singular molecule).
All of these different entities/groupings form your *topology*
```
import mdtraj
traj = mdtraj.load('trajectory.xtc', top='em.gro')
traj
```
Most analysis packages have some way to access each *atom* in your topology
```
traj.topology.atom(0)
```
If designed well, you can access *residue information* from each *atom*
```
traj.topology.atom(0).residue
```
Or, you could acess each *residue* in your topology
```
traj.topology.residue(0)
```
And then access each *atom* from within that *residue*
```
traj.topology.residue(0).atom(2)
```
Every *atom* has an *index*, which is often used for accessing the different arrays
```
traj.topology.atom(100).index
```
Some analysis packages also have an *atom-selection language*, which returns various atom indices
```
traj.topology.select("element N")
```
Now we can get to the important numbers, the coordinates
```
traj.xyz
```
This is a multi-dimensional array, but off the bat you can start seeing these 3-tuples for XYZ.
This is a `numpy array`, though, so we can use some numpy functions
```
traj.xyz.shape
```
1501 frames, 18546 atoms, 3 spatial coordinates.
We can also snip out a frame to get all of the coordinates for all the atoms in that one frame
```
traj.xyz[0].shape
```
Snip out an atom (or collection of atoms) - based on index - to get all frames and all the coordinates of that collection of atoms
```
traj.xyz[:, [1,2,3],:].shape
```
Snip out just one dimension to get all frames and all atoms and just one dimension
```
traj.xyz[:,:,0].shape
```
Since a trajectory is just a collection of frames, one after another, you can also snip out frames from a trajectory
```
traj[0]
```
This is still a `Trajectory` object, just 1 frame. XYZ coordinates are still accessible as earlier
All simulations occur within a unitcell to define the boundaries of the simulation.
```
traj.unitcell_vectors
traj.unitcell_vectors.shape
```
For each frame, there is a 3x3 array to describe the simulation box vectors
I won't go into how you should analyze a trajectory, but every molecular modeller should be familiar with what analysis routines exist in which packages, and which analysis routines you should design yourself
## Comments
There is a whole zoo of trajectory file formats that simulation engines produce - each analysis package can accommodate a subset of those file formats, each analysis package has different built-in analysis routines. Sometimes it's a mix-and-match game where you need to use package A to read a trajectory, and convert to package B representation because it has some particular analysis routine you need.
You could use an analysis package to read in one file format but write in another file format, or use an analysis package to manipulate coordinates/toplogy. Because these packages are designed intuitively and very similar to other structures in the SciPy ecosystem, there is a lot of room for creativity
Recent developments in the SciPy ecosystem look at out-of-memory or GPU representations of `numpy array` or `pandas DataFrame`, and this is a growing issue in our field - sometimes loading an entire Trajectory into memory is just not possible, so *chunking* is necessary to break the whole Trajectory into memory-manageable data
## Summary
There are a variety of analysis packages out there, but they all start out the same way: read a simulation trajectory file and create an in-memory data representation that contains trajectory (coordinates) and topology (atoms, bonds) information.
|
github_jupyter
|
import mdtraj
traj = mdtraj.load('trajectory.xtc', top='em.gro')
traj
traj.topology.atom(0)
traj.topology.atom(0).residue
traj.topology.residue(0)
traj.topology.residue(0).atom(2)
traj.topology.atom(100).index
traj.topology.select("element N")
traj.xyz
traj.xyz.shape
traj.xyz[0].shape
traj.xyz[:, [1,2,3],:].shape
traj.xyz[:,:,0].shape
traj[0]
traj.unitcell_vectors
traj.unitcell_vectors.shape
| 0.446736 | 0.988668 |
```
import dpkt
import os
import struct
import numpy as np
from collections import defaultdict
from pprint import pprint
try:
from Memoizer import memoize_to_folder
memoize = memoize_to_folder("e2e_memoization")
except:
# In case Memoizer isn't present, this decorator will just do nothing
memoize = lambda x : x
KEYLEN=8
def read_pcap(out_dir, dst_mac_is_ts = True, try_compare_counters = True):
counters = {
'set': 0,
'miss': 0,
'get': 0,
'value': 0,
'unreach': 0,
'other': 0,
'stored': 0
}
gets = defaultdict(list)
vals = defaultdict(list)
sets = defaultdict(list)
storeds = defaultdict(list)
misses = []
pcfs = [os.path.join(out_dir, 'pcap_dump', 'mcd_c_to_tofino1.pcap'),
os.path.join(out_dir, 'pcap_dump', 'tofino1_to_mcd_c.pcap'),]
for pcf in pcfs:
f = open(pcf, 'rb')
print("Reading {}".format(pcf))
pcap=dpkt.pcap.Reader(f)
total_size = 0
start_ts = None
for i, (ts, buf) in enumerate(pcap):
try:
eth=dpkt.ethernet.Ethernet(buf)
ip=eth.data
if type(ip) != dpkt.ip.IP:
counters['other'] += 1
continue
udp = ip.data
spkt = udp.data
except Exception as e:
print("Exception parsing packet {} : {}".format(buf, e))
Ether(buf).show2()
raise
if start_ts is None:
start_ts = ts
ts -= start_ts
if type(spkt) == dpkt.icmp.ICMP.Unreach:
counters['unreach'] += 1
continue
get_start = spkt.find(b'get ')
if get_start >= 0:
key = spkt[:2] + spkt[get_start+4:get_start+4+KEYLEN]
gets[key].append(ts)
counters['get'] += 1
continue
val_start = spkt.find(b'VALUE ')
if val_start >= 0:
key = spkt[:2] + spkt[val_start+6:val_start+6+KEYLEN]
vals[key].append((ts, ip.id))
counters['value'] += 1
total_size += udp.ulen + 44
continue
if b'set ' in spkt:
key = spkt[:2]
sets[key].append(ts)
counters['set'] += 1
elif b'STORED' in spkt:
key = spkt[:2]
storeds[key].append((ts, ip.id))
counters['stored'] += 1
total_size += udp.ulen + 44
continue
elif b'END' in spkt:
counters['miss'] += 1
total_size += udp.ulen + 44
misses.append(ts)
else:
counters['other'] += 1
print('Unknown packet load: {}'.format(buf))
print("Finished reading pcap: ")
pprint(counters)
return gets, vals, sets, storeds, total_size, misses, counters
import itertools
def calculate_success(reqs, resps, start, end, extra_resps = {}, interval = 5):
starts = np.arange(start, end, interval)
ends = np.arange(start + interval, end + interval, interval)
n_reqs = [0. for _ in starts]
n_resp = [0. for _ in starts]
for k, v in reqs.items():
for time in v:
idx = np.nonzero((time >= starts) & (time < ends))
if len(idx[0]) == 0:
continue
if len(idx[0]) != 1:
print("WEIRD!")
n_reqs[idx[0][0]] += 1
if k in resps:
n_resp[idx[0][0]] += float(len(resps[k])) / len(v)
return np.array(n_resp) / np.array(n_reqs)
def calculate_tds(reqs, resps, hits_only = False, misses_only = False):
print("Getting TDs")
req_keys = set(reqs.keys())
resp_keys = set(resps.keys())
missing_resps = 0
for k in req_keys - resp_keys:
missing_resps += len(reqs[k])
missing_reqs = 0
for k in resp_keys - req_keys:
missing_reqs += len(resps[k])
mismatched_length_reqs = 0
mismatched_length_resps = 0
tds = []
for k in req_keys & resp_keys:
resp = resps[k]
mask = (np.ones(len(resp)) == 1)
if misses_only:
mask &= np.array([v[1] != 1 for v in resp])
if hits_only:
mask &= np.array([v[1] == 1 for v in resp])
resp_times = np.array([v[0] for v in resp])
req_times = np.array(reqs[k])
lendiff = len(resp_times) - len(req_times)
if lendiff != 0:
mismatched_length_resps += len(resp_times)
mismatched_length_reqs += len(req_times)
continue
new_tds = resp_times[mask] - req_times[mask]
tds.extend([gt, td] for gt, td in zip(req_times[mask], new_tds))
print("Missing {} requests".format(missing_reqs))
print("Discarded {} requests".format(mismatched_length_reqs))
print("Missing {} responses".format(missing_resps))
print("Discarded {} responses".format(mismatched_length_resps))
print("\n*** Got {} Latencies ***\n".format(len(tds)))
return np.array(tds)
def experiment_success_rate(directory):
_, _, _, _, _, _, counters = read_pcap(directory)
return (counters['value'] + counters['miss']) * 100.0 / counters['get'], \
(counters['stored'] * 100.0) / counters['set']
return get_success_percent(gets, vals), get_success_percent(sets, storeds)
@memoize
def experiment_tds(directory, start, end):
gets, vals, sets, storeds, total_length, misses, _ = read_pcap(directory)
get_succ = calculate_success(gets, vals, start, end, misses)
set_succ = calculate_success(sets, storeds, start, end)
get_tds = calculate_tds(gets, vals)
set_tds = calculate_tds(sets, storeds)
print(get_tds[:,0].max(), get_tds[:,0].min())
print(set_tds[:,0].max(), set_tds[:,0].min())
get_tds = get_tds[(get_tds[:,0] > start) & (get_tds[:,0] < end)]
set_tds = set_tds[(set_tds[:,0] > start) & (set_tds[:,0] < end)]
return get_tds, set_tds, get_succ, set_succ
import json
from glob import glob
DIV = 1e6
def lenient_read_json(file):
try:
return json.load(open(file))
except Exception as e:
print("Malformed json {}: {}".format(file, e))
lines = '\n'.join(open(file).readlines()[1:])
return json.loads(lines)
def read_iperf_ts_directory(directory):
client_file = os.path.join(directory,'log_files','iperf_c_prog_5.log')
client = lenient_read_json(client_file)
client_bps = []
for interval in client['intervals']:
interval = interval['sum']
client_bps.append(interval['bits_per_second'])
summed_bps = np.array(client_bps)[5:]
print(np.mean(summed_bps) / DIV)
return summed_bps / DIV
MCD_START = 55
MCD_END = 245
def aggregate_iperf_data(experiments):
y = []
for exp in experiments:
print(exp)
y.append(read_iperf_ts_directory(exp))
return y
def aggregate_mcd_data(experiments):
y = []
for exp in experiments:
gets, sets, _, _ = experiment_tds(exp, MCD_START, MCD_END)
all_tds = np.array([[], []]).T
all_tds = np.append(all_tds, gets, 0)
all_tds = np.append(all_tds, sets, 0)
y.append(all_tds)
return y
def aggregate_more_mcd_data(experiments):
y = defaultdict(list)
for exp in experiments:
gets, sets, get_succ, set_succ = experiment_tds(exp, MCD_START, MCD_END)
y['get'].append(gets)
y['set'].append(sets)
y['get_s'].append(get_succ)
y['set_s'].append(set_succ)
return y
from collections import OrderedDict
base_dir = '../bmv2//test_output/tclust_e2e_bw_10_tclust_'
experiments = ['noop', 'compression', 'drop_compression', 'fec_and_hc', 'complete']
exp_dirs = [base_dir + e for e in experiments]
exp_dirs
iperf_data = aggregate_iperf_data(exp_dirs)
iperf_data[1]
more_mcd_data = aggregate_more_mcd_data(exp_dirs)
for i in range(len(experiments)):
more_mcd_data['get_s'][i] *= 100
more_mcd_data['set_s'][i] *= 100
more_mcd_data['set_s'][0]
len(more_mcd_data['get_s'][0]), len(iperf_data[0])
import matplotlib.pyplot as plt
BOX_WIDTH = .5
def boxplot(ax, data, pos, facecolor, linecolor, textfile, labels, width=BOX_WIDTH * .8, line='-'):
pl = ax.plot(pos, [np.median(y) for y in data], line, color=facecolor, linewidth=2, zorder=1)
bp = ax.boxplot(data, positions=pos, widths=width,showfliers=False, showmeans=True, patch_artist=True, whis=[10,90], boxprops=dict(facecolor=facecolor), whiskerprops=dict(linewidth=2),medianprops=dict(color=linecolor), zorder=10)
plt.xticks(np.arange(len(pos)))
ax.set_xticklabels(labels, fontsize=14)
if textfile:
with open(textfile,'w') as f:
f.write("ft.\t10%\t25%\t50%\t75%\t90%\n")
for x, y in zip(mcdx, data):
f.write("{}\t{:.2f}\t{:.2f}\t{:.2f}\t{:.2f}\t{:.2f}\n"
.format(x, *[np.percentile(y, p) for p in [10,25,50,75,90]]))
return pl
def make_iperf_boxplot(labels, y, ax, color_labels=True, textfile=None, width=BOX_WIDTH, offset = BOX_WIDTH/2.5):
x = np.arange(len(labels)) + offset
print(len(x), len(y))
c = 'r'
parts = boxplot(ax, y, x, c, [1,1,0], textfile, labels, line='--', width=width)
ax.legend(parts, ['Iperf Throughput'],loc='upper right')
ax.set_ylabel('Throughput (Mbps)', color=c if color_labels else 'k')
ax.set_yscale('linear')
ax.yaxis.set_label_position('left')
ax.yaxis.tick_left()
if color_labels:
plt.setp(ax.get_yticklabels(), color=c)
ax.tick_params(axis='y', colors=c)
ax.spines['right'].set_color(c)
plt.xlim([-.5, 4.5])
return parts
def make_mcd_boxplot(labels, data, ax, color_labels=True, textfile=None,
color = None, width=BOX_WIDTH, offset = -BOX_WIDTH/2.5,
legend = 'Cache Latency'):
pos = np.arange(len(labels)) + offset
try:
y = [d[:,1] for d in data]
except:
y = data
if color is not None:
c = color
else:
c = 'b'
parts = boxplot(ax, y, pos,c, [.7,.9,.7], textfile, labels, width=width)
ax.legend(parts, [legend], loc='lower left')
ax.set_ylabel(r"Latency ($s$)", color=c if color_labels else 'k')
ax.yaxis.set_label_position('left')
ax.yaxis.tick_left()
if color_labels:
plt.setp(ax.get_yticklabels(), color=c)
ax.tick_params(axis='y', colors=c)
ax.spines['left'].set_color(c)
# ax.set_yscale('log')
plt.xlim([-.5, 4.5])
return parts
def make_figure(experiments, iperf_data, more_mcd_data):
plt.figure()
ax= plt.subplot(311)
s = make_iperf_boxplot(experiments, iperf_data, ax, width=.5, offset = 0)
for x in .5, 1.5, 2.5, 3.5:
ax.axvline(x, color=[.2,.2,.2], linewidth=.5)
ax.set_xticks([])
ax.legend(s, ['iperf Throughput'], loc=(.57, .7))
ax= plt.subplot(312)
s = make_mcd_boxplot(experiments, more_mcd_data['set'], ax, color='green', width=.3, offset = -.15)
g = make_mcd_boxplot(experiments, more_mcd_data['get'], ax, width=.3, offset = .15)
# plt.yscale('linear')
for x in .5, 1.5, 2.5, 3.5:
ax.axvline(x, color=[.2,.2,.2], linewidth=.5)
ax.set_xticks([])
ax.legend(g+s, ['Get latency', 'Set Latency'], loc=(.6, .6))
ax= plt.subplot(313)
s = make_mcd_boxplot(experiments, more_mcd_data['set_s'], ax, color='green', width=.3, offset = -.15)
g = make_mcd_boxplot(experiments, more_mcd_data['get_s'], ax, width=.3, offset = .3)
for x in .5, 1.5, 2.5, 3.5:
ax.axvline(x, color=[.2,.2,.2], linewidth=.5)
ax.legend(g+s, ['Get Success', 'Set Success'], loc=(.2, .2))
plt.yscale('linear')
plt.ylabel("Success (%)")
plt.tight_layout(h_pad=-.2)
# plt.yscale('linear')
%matplotlib notebook
make_figure(['noop', 'HC', 'Drop', 'FEC', "KV"], iperf_data, more_mcd_data)
plt.suptitle("No Bounds")
```
|
github_jupyter
|
import dpkt
import os
import struct
import numpy as np
from collections import defaultdict
from pprint import pprint
try:
from Memoizer import memoize_to_folder
memoize = memoize_to_folder("e2e_memoization")
except:
# In case Memoizer isn't present, this decorator will just do nothing
memoize = lambda x : x
KEYLEN=8
def read_pcap(out_dir, dst_mac_is_ts = True, try_compare_counters = True):
counters = {
'set': 0,
'miss': 0,
'get': 0,
'value': 0,
'unreach': 0,
'other': 0,
'stored': 0
}
gets = defaultdict(list)
vals = defaultdict(list)
sets = defaultdict(list)
storeds = defaultdict(list)
misses = []
pcfs = [os.path.join(out_dir, 'pcap_dump', 'mcd_c_to_tofino1.pcap'),
os.path.join(out_dir, 'pcap_dump', 'tofino1_to_mcd_c.pcap'),]
for pcf in pcfs:
f = open(pcf, 'rb')
print("Reading {}".format(pcf))
pcap=dpkt.pcap.Reader(f)
total_size = 0
start_ts = None
for i, (ts, buf) in enumerate(pcap):
try:
eth=dpkt.ethernet.Ethernet(buf)
ip=eth.data
if type(ip) != dpkt.ip.IP:
counters['other'] += 1
continue
udp = ip.data
spkt = udp.data
except Exception as e:
print("Exception parsing packet {} : {}".format(buf, e))
Ether(buf).show2()
raise
if start_ts is None:
start_ts = ts
ts -= start_ts
if type(spkt) == dpkt.icmp.ICMP.Unreach:
counters['unreach'] += 1
continue
get_start = spkt.find(b'get ')
if get_start >= 0:
key = spkt[:2] + spkt[get_start+4:get_start+4+KEYLEN]
gets[key].append(ts)
counters['get'] += 1
continue
val_start = spkt.find(b'VALUE ')
if val_start >= 0:
key = spkt[:2] + spkt[val_start+6:val_start+6+KEYLEN]
vals[key].append((ts, ip.id))
counters['value'] += 1
total_size += udp.ulen + 44
continue
if b'set ' in spkt:
key = spkt[:2]
sets[key].append(ts)
counters['set'] += 1
elif b'STORED' in spkt:
key = spkt[:2]
storeds[key].append((ts, ip.id))
counters['stored'] += 1
total_size += udp.ulen + 44
continue
elif b'END' in spkt:
counters['miss'] += 1
total_size += udp.ulen + 44
misses.append(ts)
else:
counters['other'] += 1
print('Unknown packet load: {}'.format(buf))
print("Finished reading pcap: ")
pprint(counters)
return gets, vals, sets, storeds, total_size, misses, counters
import itertools
def calculate_success(reqs, resps, start, end, extra_resps = {}, interval = 5):
starts = np.arange(start, end, interval)
ends = np.arange(start + interval, end + interval, interval)
n_reqs = [0. for _ in starts]
n_resp = [0. for _ in starts]
for k, v in reqs.items():
for time in v:
idx = np.nonzero((time >= starts) & (time < ends))
if len(idx[0]) == 0:
continue
if len(idx[0]) != 1:
print("WEIRD!")
n_reqs[idx[0][0]] += 1
if k in resps:
n_resp[idx[0][0]] += float(len(resps[k])) / len(v)
return np.array(n_resp) / np.array(n_reqs)
def calculate_tds(reqs, resps, hits_only = False, misses_only = False):
print("Getting TDs")
req_keys = set(reqs.keys())
resp_keys = set(resps.keys())
missing_resps = 0
for k in req_keys - resp_keys:
missing_resps += len(reqs[k])
missing_reqs = 0
for k in resp_keys - req_keys:
missing_reqs += len(resps[k])
mismatched_length_reqs = 0
mismatched_length_resps = 0
tds = []
for k in req_keys & resp_keys:
resp = resps[k]
mask = (np.ones(len(resp)) == 1)
if misses_only:
mask &= np.array([v[1] != 1 for v in resp])
if hits_only:
mask &= np.array([v[1] == 1 for v in resp])
resp_times = np.array([v[0] for v in resp])
req_times = np.array(reqs[k])
lendiff = len(resp_times) - len(req_times)
if lendiff != 0:
mismatched_length_resps += len(resp_times)
mismatched_length_reqs += len(req_times)
continue
new_tds = resp_times[mask] - req_times[mask]
tds.extend([gt, td] for gt, td in zip(req_times[mask], new_tds))
print("Missing {} requests".format(missing_reqs))
print("Discarded {} requests".format(mismatched_length_reqs))
print("Missing {} responses".format(missing_resps))
print("Discarded {} responses".format(mismatched_length_resps))
print("\n*** Got {} Latencies ***\n".format(len(tds)))
return np.array(tds)
def experiment_success_rate(directory):
_, _, _, _, _, _, counters = read_pcap(directory)
return (counters['value'] + counters['miss']) * 100.0 / counters['get'], \
(counters['stored'] * 100.0) / counters['set']
return get_success_percent(gets, vals), get_success_percent(sets, storeds)
@memoize
def experiment_tds(directory, start, end):
gets, vals, sets, storeds, total_length, misses, _ = read_pcap(directory)
get_succ = calculate_success(gets, vals, start, end, misses)
set_succ = calculate_success(sets, storeds, start, end)
get_tds = calculate_tds(gets, vals)
set_tds = calculate_tds(sets, storeds)
print(get_tds[:,0].max(), get_tds[:,0].min())
print(set_tds[:,0].max(), set_tds[:,0].min())
get_tds = get_tds[(get_tds[:,0] > start) & (get_tds[:,0] < end)]
set_tds = set_tds[(set_tds[:,0] > start) & (set_tds[:,0] < end)]
return get_tds, set_tds, get_succ, set_succ
import json
from glob import glob
DIV = 1e6
def lenient_read_json(file):
try:
return json.load(open(file))
except Exception as e:
print("Malformed json {}: {}".format(file, e))
lines = '\n'.join(open(file).readlines()[1:])
return json.loads(lines)
def read_iperf_ts_directory(directory):
client_file = os.path.join(directory,'log_files','iperf_c_prog_5.log')
client = lenient_read_json(client_file)
client_bps = []
for interval in client['intervals']:
interval = interval['sum']
client_bps.append(interval['bits_per_second'])
summed_bps = np.array(client_bps)[5:]
print(np.mean(summed_bps) / DIV)
return summed_bps / DIV
MCD_START = 55
MCD_END = 245
def aggregate_iperf_data(experiments):
y = []
for exp in experiments:
print(exp)
y.append(read_iperf_ts_directory(exp))
return y
def aggregate_mcd_data(experiments):
y = []
for exp in experiments:
gets, sets, _, _ = experiment_tds(exp, MCD_START, MCD_END)
all_tds = np.array([[], []]).T
all_tds = np.append(all_tds, gets, 0)
all_tds = np.append(all_tds, sets, 0)
y.append(all_tds)
return y
def aggregate_more_mcd_data(experiments):
y = defaultdict(list)
for exp in experiments:
gets, sets, get_succ, set_succ = experiment_tds(exp, MCD_START, MCD_END)
y['get'].append(gets)
y['set'].append(sets)
y['get_s'].append(get_succ)
y['set_s'].append(set_succ)
return y
from collections import OrderedDict
base_dir = '../bmv2//test_output/tclust_e2e_bw_10_tclust_'
experiments = ['noop', 'compression', 'drop_compression', 'fec_and_hc', 'complete']
exp_dirs = [base_dir + e for e in experiments]
exp_dirs
iperf_data = aggregate_iperf_data(exp_dirs)
iperf_data[1]
more_mcd_data = aggregate_more_mcd_data(exp_dirs)
for i in range(len(experiments)):
more_mcd_data['get_s'][i] *= 100
more_mcd_data['set_s'][i] *= 100
more_mcd_data['set_s'][0]
len(more_mcd_data['get_s'][0]), len(iperf_data[0])
import matplotlib.pyplot as plt
BOX_WIDTH = .5
def boxplot(ax, data, pos, facecolor, linecolor, textfile, labels, width=BOX_WIDTH * .8, line='-'):
pl = ax.plot(pos, [np.median(y) for y in data], line, color=facecolor, linewidth=2, zorder=1)
bp = ax.boxplot(data, positions=pos, widths=width,showfliers=False, showmeans=True, patch_artist=True, whis=[10,90], boxprops=dict(facecolor=facecolor), whiskerprops=dict(linewidth=2),medianprops=dict(color=linecolor), zorder=10)
plt.xticks(np.arange(len(pos)))
ax.set_xticklabels(labels, fontsize=14)
if textfile:
with open(textfile,'w') as f:
f.write("ft.\t10%\t25%\t50%\t75%\t90%\n")
for x, y in zip(mcdx, data):
f.write("{}\t{:.2f}\t{:.2f}\t{:.2f}\t{:.2f}\t{:.2f}\n"
.format(x, *[np.percentile(y, p) for p in [10,25,50,75,90]]))
return pl
def make_iperf_boxplot(labels, y, ax, color_labels=True, textfile=None, width=BOX_WIDTH, offset = BOX_WIDTH/2.5):
x = np.arange(len(labels)) + offset
print(len(x), len(y))
c = 'r'
parts = boxplot(ax, y, x, c, [1,1,0], textfile, labels, line='--', width=width)
ax.legend(parts, ['Iperf Throughput'],loc='upper right')
ax.set_ylabel('Throughput (Mbps)', color=c if color_labels else 'k')
ax.set_yscale('linear')
ax.yaxis.set_label_position('left')
ax.yaxis.tick_left()
if color_labels:
plt.setp(ax.get_yticklabels(), color=c)
ax.tick_params(axis='y', colors=c)
ax.spines['right'].set_color(c)
plt.xlim([-.5, 4.5])
return parts
def make_mcd_boxplot(labels, data, ax, color_labels=True, textfile=None,
color = None, width=BOX_WIDTH, offset = -BOX_WIDTH/2.5,
legend = 'Cache Latency'):
pos = np.arange(len(labels)) + offset
try:
y = [d[:,1] for d in data]
except:
y = data
if color is not None:
c = color
else:
c = 'b'
parts = boxplot(ax, y, pos,c, [.7,.9,.7], textfile, labels, width=width)
ax.legend(parts, [legend], loc='lower left')
ax.set_ylabel(r"Latency ($s$)", color=c if color_labels else 'k')
ax.yaxis.set_label_position('left')
ax.yaxis.tick_left()
if color_labels:
plt.setp(ax.get_yticklabels(), color=c)
ax.tick_params(axis='y', colors=c)
ax.spines['left'].set_color(c)
# ax.set_yscale('log')
plt.xlim([-.5, 4.5])
return parts
def make_figure(experiments, iperf_data, more_mcd_data):
plt.figure()
ax= plt.subplot(311)
s = make_iperf_boxplot(experiments, iperf_data, ax, width=.5, offset = 0)
for x in .5, 1.5, 2.5, 3.5:
ax.axvline(x, color=[.2,.2,.2], linewidth=.5)
ax.set_xticks([])
ax.legend(s, ['iperf Throughput'], loc=(.57, .7))
ax= plt.subplot(312)
s = make_mcd_boxplot(experiments, more_mcd_data['set'], ax, color='green', width=.3, offset = -.15)
g = make_mcd_boxplot(experiments, more_mcd_data['get'], ax, width=.3, offset = .15)
# plt.yscale('linear')
for x in .5, 1.5, 2.5, 3.5:
ax.axvline(x, color=[.2,.2,.2], linewidth=.5)
ax.set_xticks([])
ax.legend(g+s, ['Get latency', 'Set Latency'], loc=(.6, .6))
ax= plt.subplot(313)
s = make_mcd_boxplot(experiments, more_mcd_data['set_s'], ax, color='green', width=.3, offset = -.15)
g = make_mcd_boxplot(experiments, more_mcd_data['get_s'], ax, width=.3, offset = .3)
for x in .5, 1.5, 2.5, 3.5:
ax.axvline(x, color=[.2,.2,.2], linewidth=.5)
ax.legend(g+s, ['Get Success', 'Set Success'], loc=(.2, .2))
plt.yscale('linear')
plt.ylabel("Success (%)")
plt.tight_layout(h_pad=-.2)
# plt.yscale('linear')
%matplotlib notebook
make_figure(['noop', 'HC', 'Drop', 'FEC', "KV"], iperf_data, more_mcd_data)
plt.suptitle("No Bounds")
| 0.218086 | 0.200499 |
In support of the World Bank's ongoing support to the CoVID response in Africa, the INFRA-SAP team has partnered with the Chief Economist of HD to analyze the preparedness of the health system to respond to CoVID, focusing on ideas around infrastructure: access to facilities, demographics, electrification, and connectivity.
https://github.com/worldbank/INFRA_SAP/wiki/Kenya-CoVID-response
```
import os, sys, importlib
import rasterio, affine, gdal
import networkx as nx
import geopandas as gpd
import pandas as pd
import numpy as np
import skimage.graph as graph
from shapely.geometry import Point, shape, box
from shapely.wkt import loads
from shapely.ops import cascaded_union
from rasterio import features
import GOSTnets as gn
import GOSTnets.load_osm as losm
sys.path.append("/home/wb411133/Code/GOST")
import GOSTRocks.rasterMisc as rMisc
import GOSTRocks.misc as misc
import GOSTRocks.Urban.UrbanRaster as urban
sys.path.append("../")
import infrasap.market_access as ma
country = "KEN"
iso2 = "KE"
out_folder = "/home/wb411133/data/Country/%s" % country
travel_folder = os.path.join(out_folder, 'TRAVEL_TIMES')
road_network = "/home/wb411133/data/Country/KEN/INFRA/KEN_OSM_OSMLR_1_3.osm.pbf"
network_map = os.path.join(travel_folder, "road_network.tif")
all_hospitals = "/home/public/Data/COUNTRY/KEN/HD_INF/merged_hospitals.shp"
critical_facilities = "/home/wb411133/data/Country/KEN/INFRA/HEALTH_INF/KEN_Critical_Care_Facilities.csv"
pop_layer = "/home/public/Data/GLOBAL/Population/WorldPop_PPP_2020/MOSAIC_ppp_prj_2020/ppp_prj_2020_%s.tif" % country
vul_map = "/home/public/Data/COUNTRY/KEN/HD_INF/KEN_vulnerability_map.tif"
urbanPop = os.path.join(out_folder, "wp_urban_pop.tif")
gsm_folder = "/home/public/Data/GLOBAL/INFRA/GSMA/2019/MCE/Data_MCE/Global"
gsm_2g = os.path.join(gsm_folder, "MCE_Global2G_2020.tif")
gsm_3g = os.path.join(gsm_folder, "MCE_Global3G_2020.tif")
gsm_4g = os.path.join(gsm_folder, "MCE_Global4G_2020.tif")
energy_folder = "/home/public/Data/COUNTRY/%s/GEP" % country
energy_settlements = os.path.join(energy_folder, "Kenya_final_clusters.shp")
energy_scenario = os.path.join(energy_folder, "ke-1-1_1_1_1_1_0.csv")
in_wards = "/home/public/Data/COUNTRY/KEN/ADMIN/KEN_adm4.shp"
inH = gpd.read_file(all_hospitals)
inW = gpd.read_file(in_wards)
pop_data = rasterio.open(pop_layer)
if not os.path.exists(critical_facilities.replace(".csv",".shp")):
critical_h = pd.read_csv(critical_facilities)
c_geom = [Point(x) for x in zip(critical_h['Long'], critical_h['Lat'])]
in_c = gpd.GeoDataFrame(critical_h, geometry=c_geom, crs={'init':'epsg:4326'})
in_c.to_file(critical_facilities.replace(".csv",".shp"))
else:
in_c = gpd.read_file(critical_facilities.replace(".csv",".shp"))
inH.shape
all_facilities = "/home/public/Data/GLOBAL/HEALTH/HealthsitesIO/20201023/World-node.shp"
in_bounds = "/home/public/Data/COUNTRY/KEN/ADMIN/KEN_adm1.shp"
in_b = gpd.read_file(in_bounds)
in_facilities = gpd.read_file(all_facilities)
sidx = in_facilities.sindex
if in_b.crs != in_facilities.crs:
in_b = in_b.to_crs(in_facilities.crs)
sel_facilities = in_facilities.loc[sidx.intersection(in_b.total_bounds)]
sel_facilities.shape
sel_facilities['amenity'].value_counts()
inH.shape
inH['type'].value_counts()
```
# Clean Data
```
bad_facilities = ["VCT Centre","Blood Centre","Facility Type","Radiology Unit","Hospice"]
inH = inH.loc[~inH['type'].isin(bad_facilities)]
bedH = inH.loc[inH['Beds'] > 0]
onlyH = inH.loc[inH['type'] == "Hospital"]
inH['type'].value_counts()
```
# Measure access to facilitites
```
# Create the traversal time map
if not os.path.exists(network_map):
loadOSM = losm.OSM_to_network(road_network)
loadOSM.generateRoadsGDF()
roads = loadOSM.roadsGPD
roads['speed'] = roads['infra_type'].map(ma.speed_dict)
roads['geometry'] = roads['Wkt']
traversal_time = ma.generate_network_raster(pop_data, roads)
meta = pop_data.meta.copy()
meta.update(dtype=traversal_time.dtype)
with rasterio.open(network_map, 'w', **meta) as outR:
outR.write_band(1, traversal_time)
else:
network_r = rasterio.open(network_map)
meta = network_r.meta.copy()
traversal_time = network_r.read()[0,:,:]
mcp = graph.MCP_Geometric(traversal_time)
# calculate minimum travel time to nearest facility with a bed
travel_time = os.path.join(travel_folder, "bed_tt.tif")
if not os.path.exists(travel_time):
dests = list(set([pop_data.index(x.x, x.y) for x in bedH['geometry']]))
dests = [(d) for d in dests if (d[0] > 0 and d[1] > 0)]
costs, traceback = mcp.find_costs(dests)
costs = costs.astype(pop_data.meta['dtype'])
with rasterio.open(travel_time, 'w', **pop_data.meta) as out_f:
out_f.write_band(1, costs)
# calculate minimum travel time to nearest facility
travel_time = os.path.join(travel_folder, "all_facilities_tt.tif")
if not os.path.exists(travel_time):
dests = list(set([pop_data.index(x.x, x.y) for x in good_f['geometry']]))
dests = [(d) for d in dests if (d[0] > 0 and d[1] > 0)]
dests = [(d) for d in dests if (d[0] <= traversal_time.shape[0] and d[1] <= traversal_time.shape[1])]
costs, traceback = mcp.find_costs(dests)
costs = costs.astype(pop_data.meta['dtype'])
with rasterio.open(travel_time, 'w', **pop_data.meta) as out_f:
out_f.write_band(1, costs)
# calculate minimum travel time to critical care facility
travel_time = os.path.join(travel_folder, "cc_facilities_tt.tif")
if not os.path.exists(travel_time):
dests = list(set([pop_data.index(x.x, x.y) for x in in_c['geometry']]))
dests = [(d) for d in dests if (d[0] > 0 and d[1] > 0)]
dests = [(d) for d in dests if (d[0] <= traversal_time.shape[0] and d[1] <= traversal_time.shape[1])]
costs, traceback = mcp.find_costs(dests)
costs = costs.astype(pop_data.meta['dtype'])
with rasterio.open(travel_time, 'w', **pop_data.meta) as out_f:
out_f.write_band(1, costs)
# calculate minimum travel time to nearest hospital
travel_time = os.path.join(travel_folder, "hospital_tt.tif")
if not os.path.exists(travel_time):
dests = list(set([pop_data.index(x.x, x.y) for x in inH['geometry']]))
dests = [(d) for d in dests if (d[0] > 0 and d[1] > 0)]
costs, traceback = mcp.find_costs(dests)
costs = costs.astype(pop_data.meta['dtype'])
with rasterio.open(travel_time, 'w', **pop_data.meta) as out_f:
out_f.write_band(1, costs)
```
# Summarize Wards
```
# Population zonal stats
res = rMisc.zonalStats(inW, pop_layer, minVal=0, allTouched = True)
res = pd.DataFrame(res, columns=["SUM","MIN",'MAX',"SUM"])
inW['Pop'] = 0
inW['Pop'] = res['SUM']
# Calculate urban population
urb_calculator = urban.urbanGriddedPop(pop_layer)
if not os.path.exists(urbanPop):
urban_res = urb_calculator.calculateUrban(densVal = 3, totalPopThresh=5000,
smooth=False, raster_pop = urbanPop)
res = rMisc.zonalStats(inW, urbanPop, minVal=0, allTouched = True)
res = pd.DataFrame(res, columns=["SUM","MIN",'MAX',"SUM"])
inW['URB_POP'] = 0
inW['URB_POP'] = res['SUM']
#Summarize vulnerable population
res = rMisc.zonalStats(inW, vul_map, minVal=0)
res = pd.DataFrame(res, columns=['SUM','MIN','MAX','MEAN'])
inW["VUL_POP"] = res['SUM']
# Summarize Population within driving times
in_files = ['bed_tt.tif','hospital_tt.tif','cc_facilities_tt.tif','all_facilities_tt.tif']
pop_data = rasterio.open(pop_layer).read()[0,:,:]
for tt_file in in_files:
tt = rasterio.open(os.path.join(travel_folder, tt_file))
tt_data = tt.read()[0,:,:]
for min_thresh in [1800, 3600, 7200, 14400]:
out_file = os.path.join(travel_folder, tt_file.replace(".tif", "_%s_pop.tif" % (min_thresh)))
if not os.path.exists(out_file):
tt_thresh = (tt_data < (min_thresh)).astype(int)
thresh_pop = tt_thresh * pop_data
thresh_pop = thresh_pop.astype(tt.meta['dtype'])
with rasterio.open(out_file, 'w', **tt.meta) as outR:
outR.write_band(1, thresh_pop)
res = rMisc.zonalStats(inW, out_file, minVal=0, allTouched = True)
res = pd.DataFrame(res, columns=["SUM","MIN",'MAX',"SUM"])
column_name = "%s_%s" % (tt_file.split("_")[0], min_thresh)
inW[column_name] = 0
inW[column_name] = res['SUM']
misc.tPrint("%s : %s" % (column_name, min_thresh))
# create risk index based on hospital access, urbanization, and vulnerability
inW['VUL_IDX'] = (inW['VUL_POP'].rank() > (inW.shape[0] * 0.8)).astype(int)
inW['URB_IDX'] = (inW['URB_POP'] / inW['Pop']) > 0.7
inW['ACC_IDX'] = (inW['all_3600'] / inW['Pop']) > 0.5
in_settlements = gpd.read_file(energy_settlements)
in_scenario = pd.read_csv(energy_scenario)
in_settlements = pd.merge(in_settlements, in_scenario, on="id")
settlement_index = in_settlements.sindex
inW['sPop'] = 0
inW['ePop'] = 0
inW['ePop2'] = 0
for idx, row in inW.iterrows():
# find possible settlements
possible_matches_index = list(settlement_index.intersection(row['geometry'].bounds))
possible_matches = in_settlements.iloc[possible_matches_index]
precise_matches = possible_matches[possible_matches.intersects(row['geometry'])]
inW.loc[idx, 'sPop'] = precise_matches['Population'].sum()
inW.loc[idx, 'ePop'] = precise_matches['ElecPop_x'].sum()
inW.loc[idx, 'ePop2'] = precise_matches.loc[precise_matches['ElecStart'] == 1, 'Population'].sum()
inW.to_file(os.path.join(out_folder, "Wards.shp"))
```
# Summarizing facilities
```
sindex = inW.sindex
#attach WARD ID to the facilities
inH['MYWARD'] = 0
allVals = []
for idx, row in inH.iterrows():
selW = inW.loc[list(sindex.nearest((row['geometry'].x, row['geometry'].y)))[0]]
try:
inH.loc[idx, "MYWARD"] = selW['ID_4']
except:
break
# summarize facility access to other facilities (CC, hospitals, and all facilities)
for raster_defs in [
['BED_ACC', 'bed_tt.tif'],
['CCF_ACC', "cc_facilities_tt.tif"],
['HOS_ACC', "hospital_tt.tif"],
]:
cc_tt = rasterio.open(os.path.join(travel_folder, raster_defs[1]))
inH[raster_defs[0]] = 0
for idx, row in inH.iterrows():
try:
val = list(cc_tt.sample([(row['geometry'].x, row['geometry'].y)]))[0][0]
except:
val = 0
inH.loc[idx, raster_defs[0]] = val
# Attribute facilities with GSM coverage
inR_2g = rasterio.open(gsm_2g)
inR_3g = rasterio.open(gsm_3g)
inR_4g = rasterio.open(gsm_4g)
inH = inH.to_crs(inR_2g.crs)
inH_pts = [[x.x, x.y] for x in inH['geometry']]
vals = [x[0] for x in list(inR_2g.sample(inH_pts))]
print(sum(vals))
inH.loc[:,'gsm2g'] = 0
inH.loc[:,'gsm2g'] = vals
vals = [x[0] for x in list(inR_3g.sample(inH_pts))]
print(sum(vals))
inH.loc[:,'gsm3g'] = 0
inH.loc[:,'gsm3g'] = vals
vals = [x[0] for x in list(inR_4g.sample(inH_pts))]
print(sum(vals))
inH.loc[:,'gsm4g'] = 0
inH.loc[:,'gsm4g'] = vals
inH = inH.to_crs({'init':'epsg:4326'})
# Attribute facilities with electrification
inH['sPop'] = 0
inH['sEPop'] = 0
inH['sElec'] = 0
inH = inH.to_crs(in_settlements.crs)
for idx, row in inH.iterrows():
# identify settlement and store electrification information
select_settlement = in_settlements.loc[list(settlement_index.nearest([row['geometry'].x, row['geometry'].y]))]
pop = select_settlement['Population'].values[0]
elecPop = select_settlement['ElecPop_y'].values[0]
startElec = select_settlement['ElecStart'].values[0]
inH.loc[idx, 'sPop'] = pop
inH.loc[idx, 'sEPop'] = elecPop
inH.loc[idx, 'sElec'] = startElec
inH = inH.to_crs({'init':'epsg:4326'})
inH.to_file(os.path.join(out_folder, "attributed_hospitals.shp"))
inW.head()
```
|
github_jupyter
|
import os, sys, importlib
import rasterio, affine, gdal
import networkx as nx
import geopandas as gpd
import pandas as pd
import numpy as np
import skimage.graph as graph
from shapely.geometry import Point, shape, box
from shapely.wkt import loads
from shapely.ops import cascaded_union
from rasterio import features
import GOSTnets as gn
import GOSTnets.load_osm as losm
sys.path.append("/home/wb411133/Code/GOST")
import GOSTRocks.rasterMisc as rMisc
import GOSTRocks.misc as misc
import GOSTRocks.Urban.UrbanRaster as urban
sys.path.append("../")
import infrasap.market_access as ma
country = "KEN"
iso2 = "KE"
out_folder = "/home/wb411133/data/Country/%s" % country
travel_folder = os.path.join(out_folder, 'TRAVEL_TIMES')
road_network = "/home/wb411133/data/Country/KEN/INFRA/KEN_OSM_OSMLR_1_3.osm.pbf"
network_map = os.path.join(travel_folder, "road_network.tif")
all_hospitals = "/home/public/Data/COUNTRY/KEN/HD_INF/merged_hospitals.shp"
critical_facilities = "/home/wb411133/data/Country/KEN/INFRA/HEALTH_INF/KEN_Critical_Care_Facilities.csv"
pop_layer = "/home/public/Data/GLOBAL/Population/WorldPop_PPP_2020/MOSAIC_ppp_prj_2020/ppp_prj_2020_%s.tif" % country
vul_map = "/home/public/Data/COUNTRY/KEN/HD_INF/KEN_vulnerability_map.tif"
urbanPop = os.path.join(out_folder, "wp_urban_pop.tif")
gsm_folder = "/home/public/Data/GLOBAL/INFRA/GSMA/2019/MCE/Data_MCE/Global"
gsm_2g = os.path.join(gsm_folder, "MCE_Global2G_2020.tif")
gsm_3g = os.path.join(gsm_folder, "MCE_Global3G_2020.tif")
gsm_4g = os.path.join(gsm_folder, "MCE_Global4G_2020.tif")
energy_folder = "/home/public/Data/COUNTRY/%s/GEP" % country
energy_settlements = os.path.join(energy_folder, "Kenya_final_clusters.shp")
energy_scenario = os.path.join(energy_folder, "ke-1-1_1_1_1_1_0.csv")
in_wards = "/home/public/Data/COUNTRY/KEN/ADMIN/KEN_adm4.shp"
inH = gpd.read_file(all_hospitals)
inW = gpd.read_file(in_wards)
pop_data = rasterio.open(pop_layer)
if not os.path.exists(critical_facilities.replace(".csv",".shp")):
critical_h = pd.read_csv(critical_facilities)
c_geom = [Point(x) for x in zip(critical_h['Long'], critical_h['Lat'])]
in_c = gpd.GeoDataFrame(critical_h, geometry=c_geom, crs={'init':'epsg:4326'})
in_c.to_file(critical_facilities.replace(".csv",".shp"))
else:
in_c = gpd.read_file(critical_facilities.replace(".csv",".shp"))
inH.shape
all_facilities = "/home/public/Data/GLOBAL/HEALTH/HealthsitesIO/20201023/World-node.shp"
in_bounds = "/home/public/Data/COUNTRY/KEN/ADMIN/KEN_adm1.shp"
in_b = gpd.read_file(in_bounds)
in_facilities = gpd.read_file(all_facilities)
sidx = in_facilities.sindex
if in_b.crs != in_facilities.crs:
in_b = in_b.to_crs(in_facilities.crs)
sel_facilities = in_facilities.loc[sidx.intersection(in_b.total_bounds)]
sel_facilities.shape
sel_facilities['amenity'].value_counts()
inH.shape
inH['type'].value_counts()
bad_facilities = ["VCT Centre","Blood Centre","Facility Type","Radiology Unit","Hospice"]
inH = inH.loc[~inH['type'].isin(bad_facilities)]
bedH = inH.loc[inH['Beds'] > 0]
onlyH = inH.loc[inH['type'] == "Hospital"]
inH['type'].value_counts()
# Create the traversal time map
if not os.path.exists(network_map):
loadOSM = losm.OSM_to_network(road_network)
loadOSM.generateRoadsGDF()
roads = loadOSM.roadsGPD
roads['speed'] = roads['infra_type'].map(ma.speed_dict)
roads['geometry'] = roads['Wkt']
traversal_time = ma.generate_network_raster(pop_data, roads)
meta = pop_data.meta.copy()
meta.update(dtype=traversal_time.dtype)
with rasterio.open(network_map, 'w', **meta) as outR:
outR.write_band(1, traversal_time)
else:
network_r = rasterio.open(network_map)
meta = network_r.meta.copy()
traversal_time = network_r.read()[0,:,:]
mcp = graph.MCP_Geometric(traversal_time)
# calculate minimum travel time to nearest facility with a bed
travel_time = os.path.join(travel_folder, "bed_tt.tif")
if not os.path.exists(travel_time):
dests = list(set([pop_data.index(x.x, x.y) for x in bedH['geometry']]))
dests = [(d) for d in dests if (d[0] > 0 and d[1] > 0)]
costs, traceback = mcp.find_costs(dests)
costs = costs.astype(pop_data.meta['dtype'])
with rasterio.open(travel_time, 'w', **pop_data.meta) as out_f:
out_f.write_band(1, costs)
# calculate minimum travel time to nearest facility
travel_time = os.path.join(travel_folder, "all_facilities_tt.tif")
if not os.path.exists(travel_time):
dests = list(set([pop_data.index(x.x, x.y) for x in good_f['geometry']]))
dests = [(d) for d in dests if (d[0] > 0 and d[1] > 0)]
dests = [(d) for d in dests if (d[0] <= traversal_time.shape[0] and d[1] <= traversal_time.shape[1])]
costs, traceback = mcp.find_costs(dests)
costs = costs.astype(pop_data.meta['dtype'])
with rasterio.open(travel_time, 'w', **pop_data.meta) as out_f:
out_f.write_band(1, costs)
# calculate minimum travel time to critical care facility
travel_time = os.path.join(travel_folder, "cc_facilities_tt.tif")
if not os.path.exists(travel_time):
dests = list(set([pop_data.index(x.x, x.y) for x in in_c['geometry']]))
dests = [(d) for d in dests if (d[0] > 0 and d[1] > 0)]
dests = [(d) for d in dests if (d[0] <= traversal_time.shape[0] and d[1] <= traversal_time.shape[1])]
costs, traceback = mcp.find_costs(dests)
costs = costs.astype(pop_data.meta['dtype'])
with rasterio.open(travel_time, 'w', **pop_data.meta) as out_f:
out_f.write_band(1, costs)
# calculate minimum travel time to nearest hospital
travel_time = os.path.join(travel_folder, "hospital_tt.tif")
if not os.path.exists(travel_time):
dests = list(set([pop_data.index(x.x, x.y) for x in inH['geometry']]))
dests = [(d) for d in dests if (d[0] > 0 and d[1] > 0)]
costs, traceback = mcp.find_costs(dests)
costs = costs.astype(pop_data.meta['dtype'])
with rasterio.open(travel_time, 'w', **pop_data.meta) as out_f:
out_f.write_band(1, costs)
# Population zonal stats
res = rMisc.zonalStats(inW, pop_layer, minVal=0, allTouched = True)
res = pd.DataFrame(res, columns=["SUM","MIN",'MAX',"SUM"])
inW['Pop'] = 0
inW['Pop'] = res['SUM']
# Calculate urban population
urb_calculator = urban.urbanGriddedPop(pop_layer)
if not os.path.exists(urbanPop):
urban_res = urb_calculator.calculateUrban(densVal = 3, totalPopThresh=5000,
smooth=False, raster_pop = urbanPop)
res = rMisc.zonalStats(inW, urbanPop, minVal=0, allTouched = True)
res = pd.DataFrame(res, columns=["SUM","MIN",'MAX',"SUM"])
inW['URB_POP'] = 0
inW['URB_POP'] = res['SUM']
#Summarize vulnerable population
res = rMisc.zonalStats(inW, vul_map, minVal=0)
res = pd.DataFrame(res, columns=['SUM','MIN','MAX','MEAN'])
inW["VUL_POP"] = res['SUM']
# Summarize Population within driving times
in_files = ['bed_tt.tif','hospital_tt.tif','cc_facilities_tt.tif','all_facilities_tt.tif']
pop_data = rasterio.open(pop_layer).read()[0,:,:]
for tt_file in in_files:
tt = rasterio.open(os.path.join(travel_folder, tt_file))
tt_data = tt.read()[0,:,:]
for min_thresh in [1800, 3600, 7200, 14400]:
out_file = os.path.join(travel_folder, tt_file.replace(".tif", "_%s_pop.tif" % (min_thresh)))
if not os.path.exists(out_file):
tt_thresh = (tt_data < (min_thresh)).astype(int)
thresh_pop = tt_thresh * pop_data
thresh_pop = thresh_pop.astype(tt.meta['dtype'])
with rasterio.open(out_file, 'w', **tt.meta) as outR:
outR.write_band(1, thresh_pop)
res = rMisc.zonalStats(inW, out_file, minVal=0, allTouched = True)
res = pd.DataFrame(res, columns=["SUM","MIN",'MAX',"SUM"])
column_name = "%s_%s" % (tt_file.split("_")[0], min_thresh)
inW[column_name] = 0
inW[column_name] = res['SUM']
misc.tPrint("%s : %s" % (column_name, min_thresh))
# create risk index based on hospital access, urbanization, and vulnerability
inW['VUL_IDX'] = (inW['VUL_POP'].rank() > (inW.shape[0] * 0.8)).astype(int)
inW['URB_IDX'] = (inW['URB_POP'] / inW['Pop']) > 0.7
inW['ACC_IDX'] = (inW['all_3600'] / inW['Pop']) > 0.5
in_settlements = gpd.read_file(energy_settlements)
in_scenario = pd.read_csv(energy_scenario)
in_settlements = pd.merge(in_settlements, in_scenario, on="id")
settlement_index = in_settlements.sindex
inW['sPop'] = 0
inW['ePop'] = 0
inW['ePop2'] = 0
for idx, row in inW.iterrows():
# find possible settlements
possible_matches_index = list(settlement_index.intersection(row['geometry'].bounds))
possible_matches = in_settlements.iloc[possible_matches_index]
precise_matches = possible_matches[possible_matches.intersects(row['geometry'])]
inW.loc[idx, 'sPop'] = precise_matches['Population'].sum()
inW.loc[idx, 'ePop'] = precise_matches['ElecPop_x'].sum()
inW.loc[idx, 'ePop2'] = precise_matches.loc[precise_matches['ElecStart'] == 1, 'Population'].sum()
inW.to_file(os.path.join(out_folder, "Wards.shp"))
sindex = inW.sindex
#attach WARD ID to the facilities
inH['MYWARD'] = 0
allVals = []
for idx, row in inH.iterrows():
selW = inW.loc[list(sindex.nearest((row['geometry'].x, row['geometry'].y)))[0]]
try:
inH.loc[idx, "MYWARD"] = selW['ID_4']
except:
break
# summarize facility access to other facilities (CC, hospitals, and all facilities)
for raster_defs in [
['BED_ACC', 'bed_tt.tif'],
['CCF_ACC', "cc_facilities_tt.tif"],
['HOS_ACC', "hospital_tt.tif"],
]:
cc_tt = rasterio.open(os.path.join(travel_folder, raster_defs[1]))
inH[raster_defs[0]] = 0
for idx, row in inH.iterrows():
try:
val = list(cc_tt.sample([(row['geometry'].x, row['geometry'].y)]))[0][0]
except:
val = 0
inH.loc[idx, raster_defs[0]] = val
# Attribute facilities with GSM coverage
inR_2g = rasterio.open(gsm_2g)
inR_3g = rasterio.open(gsm_3g)
inR_4g = rasterio.open(gsm_4g)
inH = inH.to_crs(inR_2g.crs)
inH_pts = [[x.x, x.y] for x in inH['geometry']]
vals = [x[0] for x in list(inR_2g.sample(inH_pts))]
print(sum(vals))
inH.loc[:,'gsm2g'] = 0
inH.loc[:,'gsm2g'] = vals
vals = [x[0] for x in list(inR_3g.sample(inH_pts))]
print(sum(vals))
inH.loc[:,'gsm3g'] = 0
inH.loc[:,'gsm3g'] = vals
vals = [x[0] for x in list(inR_4g.sample(inH_pts))]
print(sum(vals))
inH.loc[:,'gsm4g'] = 0
inH.loc[:,'gsm4g'] = vals
inH = inH.to_crs({'init':'epsg:4326'})
# Attribute facilities with electrification
inH['sPop'] = 0
inH['sEPop'] = 0
inH['sElec'] = 0
inH = inH.to_crs(in_settlements.crs)
for idx, row in inH.iterrows():
# identify settlement and store electrification information
select_settlement = in_settlements.loc[list(settlement_index.nearest([row['geometry'].x, row['geometry'].y]))]
pop = select_settlement['Population'].values[0]
elecPop = select_settlement['ElecPop_y'].values[0]
startElec = select_settlement['ElecStart'].values[0]
inH.loc[idx, 'sPop'] = pop
inH.loc[idx, 'sEPop'] = elecPop
inH.loc[idx, 'sElec'] = startElec
inH = inH.to_crs({'init':'epsg:4326'})
inH.to_file(os.path.join(out_folder, "attributed_hospitals.shp"))
inW.head()
| 0.250638 | 0.639483 |
```
from typing import Tuple, Dict, Callable, Iterator, Union, Optional, List
import os
import sys
import yaml
import numpy as np
import torch
from torch import Tensor
import gym
# To import module code.
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
from src.environment_api import EnvironmentObjective, manipulate_reward
from src.policy_parameterizations import MLP, discretize
from src.evaluate import (
offline_reward_evaluation,
postprocessing_interpolate_x,
plot_rewards_over_calls,
)
import matplotlib.pyplot as plt
%config Completer.use_jedi = False
plt.style.use('seaborn-whitegrid')
tex_fonts = {
# Use LaTeX to write all text
"text.usetex": True,
"font.family": "serif",
# Use 10pt font in plots, to match 10pt font in document
"axes.labelsize": 9,
"font.size": 9,
# Make the legend/label fonts a little smaller
"legend.fontsize": 8,
"xtick.labelsize": 8,
"ytick.labelsize": 8
}
plt.rcParams.update(tex_fonts)
def plot_rewards_over_calls(
rewards_optimizer: List[torch.tensor],
names_optimizer: List[str],
title: str,
marker: List[str] = ["o", ">"],
steps: int = 100,
markevery: int = 5,
figsize: Tuple[float] = (2.8, 1.7),
path_savefig: Optional[str] = None,
):
"""Generate plot showing rewards over objective calls for multiple optimizer.
Args:
rewards_optimizer: List of torch tensors for every optimizer.
title: Plot title.
marker: Plot marker.
steps: Number which defines the x-th reward that should be plotted.
markevery: Number which defines the x-th reward which should be marked (after steps).
path_savefig: Path where to save the resulting figure.
"""
plt.figure(figsize=figsize)
for index_optimizer, rewards in enumerate(rewards_optimizer):
max_calls = rewards.shape[-1]
m = torch.mean(rewards, dim=0)[::steps]
std = torch.std(rewards, dim=0)[::steps]
plt.plot(
torch.linspace(0, max_calls, max_calls // steps),
m,
marker=marker[index_optimizer],
markevery=markevery,
markersize=3,
label=names_optimizer[index_optimizer],
)
plt.fill_between(
torch.linspace(0, max_calls, max_calls // steps),
m - std,
m + std,
alpha=0.2,
)
plt.xlabel("\# of evaluations")
plt.ylabel("Average Reward")
plt.legend(loc="lower right")
plt.title(title)
plt.xlim([0, max_calls])
if path_savefig:
plt.savefig(path_savefig, bbox_inches="tight")
def postprocess_data(configs: List[str], postprocess: bool = True):
method_to_name = {'gibo': 'GIBO', 'rs': 'ARS', 'vbo': 'Vanilla BO'}
list_interpolated_rewards = []
list_names_optimizer = []
for cfg_str in configs:
with open(cfg_str, 'r') as f:
cfg = yaml.load(f, Loader=yaml.Loader)
directory = '.' + cfg['out_dir']
if postprocess:
print('Postprocess tracked parameters over optimization procedure.')
# Usecase 1: optimizing policy for a reinforcement learning environment.
mlp = MLP(*cfg['mlp']['layers'], add_bias=cfg['mlp']['add_bias'])
len_params = mlp.len_params
# In evaluation mode manipulation of state and reward is always None.
objective_env = EnvironmentObjective(
env=gym.make(cfg['environment_name']),
policy=mlp,
manipulate_state=None,
manipulate_reward=None,
)
# Load data.
print(f'Load data from {directory}.')
parameters = np.load(
os.path.join(directory, 'parameters.npy'), allow_pickle=True
).item()
calls = np.load(
os.path.join(directory, 'calls.npy'), allow_pickle=True
).item()
# Postprocess data (offline evaluation and interpolation).
print('Postprocess data: offline evaluation and interpolation.')
offline_rewards = offline_reward_evaluation(parameters, objective_env)
interpolated_rewards = postprocessing_interpolate_x(
offline_rewards, calls, max_calls=cfg['max_objective_calls']
)
# Save postprocessed data.
print(f'Save postprocessed data in {directory}.')
torch.save(
interpolated_rewards, os.path.join(directory, 'interpolated_rewards.pt')
)
torch.save(offline_rewards, os.path.join(directory, 'offline_rewards.pt'))
else:
interpolated_rewards = torch.load(
os.path.join(directory, 'interpolated_rewards.pt')
)
list_names_optimizer.append(method_to_name[cfg['method']])
list_interpolated_rewards.append(interpolated_rewards)
return list_names_optimizer, list_interpolated_rewards
(list_names_optimizer,
list_interpolated_rewards) = postprocess_data(configs=['../configs/rl_experiment/cartpole/rs_10runs.yaml',
'../configs/rl_experiment/cartpole/gibo_10runs.yaml',
],
postprocess = False)
plt.rcParams['lines.linewidth'] = 1.
plot_rewards_over_calls(
rewards_optimizer=list_interpolated_rewards,
names_optimizer=list_names_optimizer,
title='Cartpole-v1',
marker=['o', '>'],
steps=10,
markevery=1,
figsize = (1.92, 1.19),
path_savefig=None #'../experiments/rl_experiments/cartpole/cartpole_v1_10runs.pdf',
)
(list_names_optimizer,
list_interpolated_rewards) = postprocess_data(configs=['../configs/rl_experiment/swimmer/rs_10runs.yaml',
'../configs/rl_experiment/swimmer/gibo_10runs.yaml',
],
postprocess = False)
plt.rcParams['lines.linewidth'] = 1.
plot_rewards_over_calls(
rewards_optimizer=list_interpolated_rewards,
names_optimizer=list_names_optimizer,
title='Swimmer-v1',
marker=['o', '>'],
steps=50,
markevery=5,
figsize = (1.92, 1.19),
path_savefig=None #'../experiments/rl_experiments/swimmer/swimmer_v1_10runs.pdf',
)
(list_names_optimizer,
list_interpolated_rewards) = postprocess_data(configs=['../configs/rl_experiment/hopper/rs_10runs.yaml',
'../configs/rl_experiment/hopper/gibo_10runs.yaml',
],
postprocess = False)
plt.rcParams['lines.linewidth'] = 1.
plot_rewards_over_calls(
rewards_optimizer=list_interpolated_rewards,
names_optimizer=list_names_optimizer,
title='Hopper-v1',
marker=['o', '>'],
steps=200,
markevery=5,
figsize = (1.92, 1.19),
path_savefig=None #'../experiments/rl_experiments/hopper/hopper_v1_10runs.pdf',
)
```
|
github_jupyter
|
from typing import Tuple, Dict, Callable, Iterator, Union, Optional, List
import os
import sys
import yaml
import numpy as np
import torch
from torch import Tensor
import gym
# To import module code.
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
from src.environment_api import EnvironmentObjective, manipulate_reward
from src.policy_parameterizations import MLP, discretize
from src.evaluate import (
offline_reward_evaluation,
postprocessing_interpolate_x,
plot_rewards_over_calls,
)
import matplotlib.pyplot as plt
%config Completer.use_jedi = False
plt.style.use('seaborn-whitegrid')
tex_fonts = {
# Use LaTeX to write all text
"text.usetex": True,
"font.family": "serif",
# Use 10pt font in plots, to match 10pt font in document
"axes.labelsize": 9,
"font.size": 9,
# Make the legend/label fonts a little smaller
"legend.fontsize": 8,
"xtick.labelsize": 8,
"ytick.labelsize": 8
}
plt.rcParams.update(tex_fonts)
def plot_rewards_over_calls(
rewards_optimizer: List[torch.tensor],
names_optimizer: List[str],
title: str,
marker: List[str] = ["o", ">"],
steps: int = 100,
markevery: int = 5,
figsize: Tuple[float] = (2.8, 1.7),
path_savefig: Optional[str] = None,
):
"""Generate plot showing rewards over objective calls for multiple optimizer.
Args:
rewards_optimizer: List of torch tensors for every optimizer.
title: Plot title.
marker: Plot marker.
steps: Number which defines the x-th reward that should be plotted.
markevery: Number which defines the x-th reward which should be marked (after steps).
path_savefig: Path where to save the resulting figure.
"""
plt.figure(figsize=figsize)
for index_optimizer, rewards in enumerate(rewards_optimizer):
max_calls = rewards.shape[-1]
m = torch.mean(rewards, dim=0)[::steps]
std = torch.std(rewards, dim=0)[::steps]
plt.plot(
torch.linspace(0, max_calls, max_calls // steps),
m,
marker=marker[index_optimizer],
markevery=markevery,
markersize=3,
label=names_optimizer[index_optimizer],
)
plt.fill_between(
torch.linspace(0, max_calls, max_calls // steps),
m - std,
m + std,
alpha=0.2,
)
plt.xlabel("\# of evaluations")
plt.ylabel("Average Reward")
plt.legend(loc="lower right")
plt.title(title)
plt.xlim([0, max_calls])
if path_savefig:
plt.savefig(path_savefig, bbox_inches="tight")
def postprocess_data(configs: List[str], postprocess: bool = True):
method_to_name = {'gibo': 'GIBO', 'rs': 'ARS', 'vbo': 'Vanilla BO'}
list_interpolated_rewards = []
list_names_optimizer = []
for cfg_str in configs:
with open(cfg_str, 'r') as f:
cfg = yaml.load(f, Loader=yaml.Loader)
directory = '.' + cfg['out_dir']
if postprocess:
print('Postprocess tracked parameters over optimization procedure.')
# Usecase 1: optimizing policy for a reinforcement learning environment.
mlp = MLP(*cfg['mlp']['layers'], add_bias=cfg['mlp']['add_bias'])
len_params = mlp.len_params
# In evaluation mode manipulation of state and reward is always None.
objective_env = EnvironmentObjective(
env=gym.make(cfg['environment_name']),
policy=mlp,
manipulate_state=None,
manipulate_reward=None,
)
# Load data.
print(f'Load data from {directory}.')
parameters = np.load(
os.path.join(directory, 'parameters.npy'), allow_pickle=True
).item()
calls = np.load(
os.path.join(directory, 'calls.npy'), allow_pickle=True
).item()
# Postprocess data (offline evaluation and interpolation).
print('Postprocess data: offline evaluation and interpolation.')
offline_rewards = offline_reward_evaluation(parameters, objective_env)
interpolated_rewards = postprocessing_interpolate_x(
offline_rewards, calls, max_calls=cfg['max_objective_calls']
)
# Save postprocessed data.
print(f'Save postprocessed data in {directory}.')
torch.save(
interpolated_rewards, os.path.join(directory, 'interpolated_rewards.pt')
)
torch.save(offline_rewards, os.path.join(directory, 'offline_rewards.pt'))
else:
interpolated_rewards = torch.load(
os.path.join(directory, 'interpolated_rewards.pt')
)
list_names_optimizer.append(method_to_name[cfg['method']])
list_interpolated_rewards.append(interpolated_rewards)
return list_names_optimizer, list_interpolated_rewards
(list_names_optimizer,
list_interpolated_rewards) = postprocess_data(configs=['../configs/rl_experiment/cartpole/rs_10runs.yaml',
'../configs/rl_experiment/cartpole/gibo_10runs.yaml',
],
postprocess = False)
plt.rcParams['lines.linewidth'] = 1.
plot_rewards_over_calls(
rewards_optimizer=list_interpolated_rewards,
names_optimizer=list_names_optimizer,
title='Cartpole-v1',
marker=['o', '>'],
steps=10,
markevery=1,
figsize = (1.92, 1.19),
path_savefig=None #'../experiments/rl_experiments/cartpole/cartpole_v1_10runs.pdf',
)
(list_names_optimizer,
list_interpolated_rewards) = postprocess_data(configs=['../configs/rl_experiment/swimmer/rs_10runs.yaml',
'../configs/rl_experiment/swimmer/gibo_10runs.yaml',
],
postprocess = False)
plt.rcParams['lines.linewidth'] = 1.
plot_rewards_over_calls(
rewards_optimizer=list_interpolated_rewards,
names_optimizer=list_names_optimizer,
title='Swimmer-v1',
marker=['o', '>'],
steps=50,
markevery=5,
figsize = (1.92, 1.19),
path_savefig=None #'../experiments/rl_experiments/swimmer/swimmer_v1_10runs.pdf',
)
(list_names_optimizer,
list_interpolated_rewards) = postprocess_data(configs=['../configs/rl_experiment/hopper/rs_10runs.yaml',
'../configs/rl_experiment/hopper/gibo_10runs.yaml',
],
postprocess = False)
plt.rcParams['lines.linewidth'] = 1.
plot_rewards_over_calls(
rewards_optimizer=list_interpolated_rewards,
names_optimizer=list_names_optimizer,
title='Hopper-v1',
marker=['o', '>'],
steps=200,
markevery=5,
figsize = (1.92, 1.19),
path_savefig=None #'../experiments/rl_experiments/hopper/hopper_v1_10runs.pdf',
)
| 0.727782 | 0.433382 |
```
%reload_ext blackcellmagic
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from qflow.wavefunctions import (
JastrowMcMillian,
JastrowPade,
JastrowOrion,
SimpleGaussian,
WavefunctionProduct,
FixedWavefunction,
Dnn,
SumPooling,
)
from qflow.wavefunctions.nn.layers import DenseLayer
from qflow.wavefunctions.nn.activations import sigmoid, tanh, relu, identity, exponential
from qflow.hamiltonians import LennardJones, HDFHE2
from qflow.samplers import BoxImportanceSampler, BoxMetropolisSampler
from qflow.optimizers import AdamOptimizer, SgdOptimizer
from qflow.training import train, EnergyCallback, SymmetryCallback, ParameterCallback
from qflow.statistics import compute_statistics_for_series
from qflow import DistanceCache
def plot_training(energies, symmetries, parameters):
fig, (eax, sax, pax) = plt.subplots(ncols=3, figsize=(16, 4))
eax.plot(energies, label=r"$\langle E_L\rangle$ [a.u]")
sax.semilogx(symmetries, label=r"$S(\Psi)$")
pax.semilogx(parameters)
eax.legend()
sax.legend()
H = LennardJones()
x = np.linspace(2.4, 5, 100)
plt.plot(x, [H.internal_potential(np.array([[0, 0], [1, 0]])*x_) for x_ in x])
plt.hlines(0, min(x), max(x), linestyles='dashed')
rho = 0.0196 # Å^-3
P, D = 64, 3 # Particles, dimensions
L = (P / rho)**(1/3)
system = np.empty((P, D))
L
psi = JastrowMcMillian(5, 2.51)
psi_sampler = BoxMetropolisSampler(system, psi, L, 5)
s = psi_sampler.next_configuration()
np.min([np.linalg.norm(s[i]-s[j]) for i in range(P) for j in range(P) if i!=j])
with DistanceCache(system, L):
psi = JastrowMcMillian(5, 2.51)
psi_sampler = BoxMetropolisSampler(system, psi, L, 5)
psi_sampler.thermalize(10000)
s = psi_sampler.next_configuration()
print(psi_sampler.acceptance_rate)
print(H.internal_potential(s))
print(H.kinetic_energy(s, psi))
print(H.local_energy(s, psi))
print(np.min([np.linalg.norm(s[i]-s[j]) for i in range(P) for j in range(P) if i!=j]))
psi_energies = EnergyCallback(samples=5000, verbose=True)
psi_symmetries = SymmetryCallback(samples=100)
psi_parameters = ParameterCallback()
with DistanceCache(system, L):
train(
psi,
H,
psi_sampler,
iters=15000,
samples=1000,
gamma=0,
optimizer=AdamOptimizer(len(psi.parameters)),
call_backs=(psi_energies, psi_symmetries, psi_parameters),
)
plot_training(np.array(psi_energies)/P, psi_symmetries, psi_parameters)
psi_sampler.acceptance_rate
```
|
github_jupyter
|
%reload_ext blackcellmagic
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from qflow.wavefunctions import (
JastrowMcMillian,
JastrowPade,
JastrowOrion,
SimpleGaussian,
WavefunctionProduct,
FixedWavefunction,
Dnn,
SumPooling,
)
from qflow.wavefunctions.nn.layers import DenseLayer
from qflow.wavefunctions.nn.activations import sigmoid, tanh, relu, identity, exponential
from qflow.hamiltonians import LennardJones, HDFHE2
from qflow.samplers import BoxImportanceSampler, BoxMetropolisSampler
from qflow.optimizers import AdamOptimizer, SgdOptimizer
from qflow.training import train, EnergyCallback, SymmetryCallback, ParameterCallback
from qflow.statistics import compute_statistics_for_series
from qflow import DistanceCache
def plot_training(energies, symmetries, parameters):
fig, (eax, sax, pax) = plt.subplots(ncols=3, figsize=(16, 4))
eax.plot(energies, label=r"$\langle E_L\rangle$ [a.u]")
sax.semilogx(symmetries, label=r"$S(\Psi)$")
pax.semilogx(parameters)
eax.legend()
sax.legend()
H = LennardJones()
x = np.linspace(2.4, 5, 100)
plt.plot(x, [H.internal_potential(np.array([[0, 0], [1, 0]])*x_) for x_ in x])
plt.hlines(0, min(x), max(x), linestyles='dashed')
rho = 0.0196 # Å^-3
P, D = 64, 3 # Particles, dimensions
L = (P / rho)**(1/3)
system = np.empty((P, D))
L
psi = JastrowMcMillian(5, 2.51)
psi_sampler = BoxMetropolisSampler(system, psi, L, 5)
s = psi_sampler.next_configuration()
np.min([np.linalg.norm(s[i]-s[j]) for i in range(P) for j in range(P) if i!=j])
with DistanceCache(system, L):
psi = JastrowMcMillian(5, 2.51)
psi_sampler = BoxMetropolisSampler(system, psi, L, 5)
psi_sampler.thermalize(10000)
s = psi_sampler.next_configuration()
print(psi_sampler.acceptance_rate)
print(H.internal_potential(s))
print(H.kinetic_energy(s, psi))
print(H.local_energy(s, psi))
print(np.min([np.linalg.norm(s[i]-s[j]) for i in range(P) for j in range(P) if i!=j]))
psi_energies = EnergyCallback(samples=5000, verbose=True)
psi_symmetries = SymmetryCallback(samples=100)
psi_parameters = ParameterCallback()
with DistanceCache(system, L):
train(
psi,
H,
psi_sampler,
iters=15000,
samples=1000,
gamma=0,
optimizer=AdamOptimizer(len(psi.parameters)),
call_backs=(psi_energies, psi_symmetries, psi_parameters),
)
plot_training(np.array(psi_energies)/P, psi_symmetries, psi_parameters)
psi_sampler.acceptance_rate
| 0.423577 | 0.695984 |
## Deliverable 2. Create a Customer Travel Destinations Map.
```
# Dependencies and Setup
import pandas as pd
import requests
import gmaps
# Import API key
from config import g_key
# Configure gmaps API key
gmaps.configure(api_key=g_key)
# 1. Import the WeatherPy_database.csv file.
city_data_df = pd.read_csv("../Weather_Database/Weather_Database.csv")
city_data_df.head()
# 2. Prompt the user to enter minimum and maximum temperature criteria
min_temp=int(input("Please enter the mininum temperature you wish for your trip"))
max_temp=int(input("Please enter the maximum temperature you wish for your trip"))
# 3. Filter the city_data_df DataFrame using the input statements to create a new DataFrame using the loc method.
ideal_city_data_df=city_data_df.loc[(city_data_df["Max Temp"]<=max_temp)&(city_data_df["Max Temp"]>=min_temp)].copy()
# 4a. Determine if there are any empty rows.
ideal_city_data_df.count()
# 4b. Drop any empty rows and create a new DataFrame that doesn’t have empty rows.
preferred_cities=ideal_city_data_df.dropna()
preferred_cities.isnull().sum()
# 5a. Create DataFrame called hotel_df to store hotel names along with city, country, max temp, and coordinates.
hotel_df = preferred_cities[["City", "Country", "Max Temp", "Current Description", "Lat", "Lng"]].copy()
# 5b. Create a new column "Hotel Name"
hotel_df["Hotel Name"] = ""
hotel_df.head(10)
# 6a. Set parameters to search for hotels with 5000 meters.
params = {
"radius": 5000,
"type": "lodging",
"key": g_key
}
# 6b. Iterate through the hotel DataFrame.
for index,row in hotel_df.iterrows():
# 6c. Get latitude and longitude from DataFrame
lat=row["Lat"]
lng=row["Lng"]
# 6d. Set up the base URL for the Google Directions API to get JSON data.
base_url="https://maps.googleapis.com/maps/api/place/nearbysearch/json"
params["location"]=f"{lat},{lng}"
# 6e. Make request and retrieve the JSON data from the search.
hotel=requests.get(base_url,params=params).json()
# 6f. Get the first hotel from the results and store the name, if a hotel isn't found skip the city.
try:
hotel_df.loc[index,"Hotel Name"]=hotel["results"][0]["name"]
except:
print("Hotel not found. Skipping...")
# 7. Drop the rows where there is no Hotel Name.
clean_hotel_df=hotel_df.dropna()
# 8a. Create the output File (CSV)
output_data_file="WeatherPy_vacation.csv"
# 8b. Export the City_Data into a csv
clean_hotel_df.to_csv(output_data_file, index_label="City_ID")
# 9. Using the template add city name, the country code, the weather description and maximum temperature for the city.
info_box_template = """
<dl>
<dt>Hotel Name</dt><dd>{Hotel Name}</dd>
<dt>City</dt><dd>{City}</dd>
<dt>Country</dt><dd>{Country}</dd>
<dt>Current Weather</dt><dd>{Current Description} and {Max Temp} °F</dd>
</dl>
"""
# 10a. Get the data from each row and add it to the formatting template and store the data in a list.
hotel_info = [info_box_template.format(**row) for index, row in clean_hotel_df.iterrows()]
# 10b. Get the latitude and longitude from each row and store in a new DataFrame.
locations = clean_hotel_df[["Lat", "Lng"]]
# 11a. Add a marker layer for each city to the map.
fig=gmaps.figure(center=(30.0, 31.0), zoom_level=1.5)
marker_layer=gmaps.marker_layer(locations,info_box_content=hotel_info)
fig.add_layer(marker_layer)
# 11b. Display the figure
fig
```
|
github_jupyter
|
# Dependencies and Setup
import pandas as pd
import requests
import gmaps
# Import API key
from config import g_key
# Configure gmaps API key
gmaps.configure(api_key=g_key)
# 1. Import the WeatherPy_database.csv file.
city_data_df = pd.read_csv("../Weather_Database/Weather_Database.csv")
city_data_df.head()
# 2. Prompt the user to enter minimum and maximum temperature criteria
min_temp=int(input("Please enter the mininum temperature you wish for your trip"))
max_temp=int(input("Please enter the maximum temperature you wish for your trip"))
# 3. Filter the city_data_df DataFrame using the input statements to create a new DataFrame using the loc method.
ideal_city_data_df=city_data_df.loc[(city_data_df["Max Temp"]<=max_temp)&(city_data_df["Max Temp"]>=min_temp)].copy()
# 4a. Determine if there are any empty rows.
ideal_city_data_df.count()
# 4b. Drop any empty rows and create a new DataFrame that doesn’t have empty rows.
preferred_cities=ideal_city_data_df.dropna()
preferred_cities.isnull().sum()
# 5a. Create DataFrame called hotel_df to store hotel names along with city, country, max temp, and coordinates.
hotel_df = preferred_cities[["City", "Country", "Max Temp", "Current Description", "Lat", "Lng"]].copy()
# 5b. Create a new column "Hotel Name"
hotel_df["Hotel Name"] = ""
hotel_df.head(10)
# 6a. Set parameters to search for hotels with 5000 meters.
params = {
"radius": 5000,
"type": "lodging",
"key": g_key
}
# 6b. Iterate through the hotel DataFrame.
for index,row in hotel_df.iterrows():
# 6c. Get latitude and longitude from DataFrame
lat=row["Lat"]
lng=row["Lng"]
# 6d. Set up the base URL for the Google Directions API to get JSON data.
base_url="https://maps.googleapis.com/maps/api/place/nearbysearch/json"
params["location"]=f"{lat},{lng}"
# 6e. Make request and retrieve the JSON data from the search.
hotel=requests.get(base_url,params=params).json()
# 6f. Get the first hotel from the results and store the name, if a hotel isn't found skip the city.
try:
hotel_df.loc[index,"Hotel Name"]=hotel["results"][0]["name"]
except:
print("Hotel not found. Skipping...")
# 7. Drop the rows where there is no Hotel Name.
clean_hotel_df=hotel_df.dropna()
# 8a. Create the output File (CSV)
output_data_file="WeatherPy_vacation.csv"
# 8b. Export the City_Data into a csv
clean_hotel_df.to_csv(output_data_file, index_label="City_ID")
# 9. Using the template add city name, the country code, the weather description and maximum temperature for the city.
info_box_template = """
<dl>
<dt>Hotel Name</dt><dd>{Hotel Name}</dd>
<dt>City</dt><dd>{City}</dd>
<dt>Country</dt><dd>{Country}</dd>
<dt>Current Weather</dt><dd>{Current Description} and {Max Temp} °F</dd>
</dl>
"""
# 10a. Get the data from each row and add it to the formatting template and store the data in a list.
hotel_info = [info_box_template.format(**row) for index, row in clean_hotel_df.iterrows()]
# 10b. Get the latitude and longitude from each row and store in a new DataFrame.
locations = clean_hotel_df[["Lat", "Lng"]]
# 11a. Add a marker layer for each city to the map.
fig=gmaps.figure(center=(30.0, 31.0), zoom_level=1.5)
marker_layer=gmaps.marker_layer(locations,info_box_content=hotel_info)
fig.add_layer(marker_layer)
# 11b. Display the figure
fig
| 0.441191 | 0.701713 |
Lambda School Data Science
*Unit 2, Sprint 2, Module 3*
---
# Cross-Validation
- Do **cross-validation** with independent test set
- Use scikit-learn for **hyperparameter optimization**
### Setup
Run the code cell below. You can work locally (follow the [local setup instructions](https://lambdaschool.github.io/ds/unit2/local/)) or on Colab.
Libraries
- **category_encoders**
- matplotlib
- numpy
- pandas
- **pandas-profiling**
- scikit-learn
- scipy.stats
```
%%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Kaggle-Challenge/master/data/'
!pip install category_encoders==2.*
!pip install pandas-profiling==2.*
# If you're working locally:
else:
DATA_PATH = '../data/'
```
# Do cross-validation with independent test set
## Overview
### Predict rent in NYC 🏠
We're going back to one of our New York City real estate datasets.
```
import numpy as np
import pandas as pd
# Read New York City apartment rental listing data
df = pd.read_csv(DATA_PATH+'apartments/renthop-nyc.csv')
assert df.shape == (49352, 34)
# Remove the most extreme 1% prices,
# the most extreme .1% latitudes, &
# the most extreme .1% longitudes
df = df[(df['price'] >= np.percentile(df['price'], 0.5)) &
(df['price'] <= np.percentile(df['price'], 99.5)) &
(df['latitude'] >= np.percentile(df['latitude'], 0.05)) &
(df['latitude'] < np.percentile(df['latitude'], 99.95)) &
(df['longitude'] >= np.percentile(df['longitude'], 0.05)) &
(df['longitude'] <= np.percentile(df['longitude'], 99.95))]
# Do train/test split
# Use data from April & May 2016 to train
# Use data from June 2016 to test
df['created'] = pd.to_datetime(df['created'], infer_datetime_format=True)
cutoff = pd.to_datetime('2016-06-01')
train = df[df.created < cutoff]
test = df[df.created >= cutoff]
# Wrangle train & test sets in the same way
def engineer_features(df):
# Avoid SettingWithCopyWarning
df = df.copy()
# Does the apartment have a description?
df['description'] = df['description'].str.strip().fillna('')
df['has_description'] = df['description'] != ''
# How long is the description?
df['description_length'] = df['description'].str.len()
# How many total perks does each apartment have?
perk_cols = ['elevator', 'cats_allowed', 'hardwood_floors', 'dogs_allowed',
'doorman', 'dishwasher', 'no_fee', 'laundry_in_building',
'fitness_center', 'pre-war', 'laundry_in_unit', 'roof_deck',
'outdoor_space', 'dining_room', 'high_speed_internet', 'balcony',
'swimming_pool', 'new_construction', 'exclusive', 'terrace',
'loft', 'garden_patio', 'common_outdoor_space',
'wheelchair_access']
df['perk_count'] = df[perk_cols].sum(axis=1)
# Are cats or dogs allowed?
df['cats_or_dogs'] = (df['cats_allowed']==1) | (df['dogs_allowed']==1)
# Are cats and dogs allowed?
df['cats_and_dogs'] = (df['cats_allowed']==1) & (df['dogs_allowed']==1)
# Total number of rooms (beds + baths)
df['rooms'] = df['bedrooms'] + df['bathrooms']
# Extract number of days elapsed in year, and drop original date feature
df['days'] = (df['created'] - pd.to_datetime('2016-01-01')).dt.days
df = df.drop(columns='created')
return df
train = engineer_features(train)
test = engineer_features(test)
# Pandas Profiling can be very slow with medium & large datasets.
# These parameters will make it faster.
# https://github.com/pandas-profiling/pandas-profiling/issues/222
import pandas_profiling
profile_report = train.profile_report(
check_correlation_pearson=False,
correlations={
'pearson': False,
'spearman': False,
'kendall': False,
'phi_k': False,
'cramers': False,
'recoded': False,
},
plot={'histogram': {'bayesian_blocks_bins': False}},
)
profile_report
```
### Validation options
Let's take another look at [Sebastian Raschka's diagram of model evaluation methods.](https://sebastianraschka.com/blog/2018/model-evaluation-selection-part4.html) So far we've been using "**train/validation/test split**", but we have more options.
Today we'll learn about "k-fold **cross-validation** with independent test set", for "model selection (**hyperparameter optimization**) and performance estimation."
<img src="https://sebastianraschka.com/images/blog/2018/model-evaluation-selection-part4/model-eval-conclusions.jpg" width="600">
<sup>Source: https://sebastianraschka.com/blog/2018/model-evaluation-selection-part4.html</sup>
### Cross-validation: What & Why?
The Scikit-Learn docs show a diagram of how k-fold cross-validation works, and explain the pros & cons of cross-validation versus train/validate/test split.
#### [Scikit-Learn User Guide, 3.1 Cross-validation](https://scikit-learn.org/stable/modules/cross_validation.html)
> When evaluating different settings (“hyperparameters”) for estimators, there is still a risk of overfitting on the test set because the parameters can be tweaked until the estimator performs optimally. This way, knowledge about the test set can “leak” into the model and evaluation metrics no longer report on generalization performance. To solve this problem, yet another part of the dataset can be held out as a so-called “validation set”: training proceeds on the training set, after which evaluation is done on the validation set, and when the experiment seems to be successful, final evaluation can be done on the test set.
>
> However, **by partitioning the available data into three sets, we drastically reduce the number of samples which can be used for learning the model, and the results can depend on a particular random choice for the pair of (train, validation) sets.**
>
> **A solution to this problem is a procedure called cross-validation (CV for short). A test set should still be held out for final evaluation, but the validation set is no longer needed when doing CV.**
<img src="https://scikit-learn.org/stable/_images/grid_search_cross_validation.png" width="600">
> In the basic approach, called k-fold CV, the training set is split into k smaller sets. The following procedure is followed for each of the k “folds”:
>
> - A model is trained using $k-1$ of the folds as training data;
> - the resulting model is validated on the remaining part of the data (i.e., it is used as a test set to compute a performance measure such as accuracy).
>
> The performance measure reported by k-fold cross-validation is then the average of the values computed in the loop. **This approach can be computationally expensive, but does not waste too much data (as is the case when fixing an arbitrary validation set).**
## Follow Along
### cross_val_score
How do we get started? According to the [Scikit-Learn User Guide](https://scikit-learn.org/stable/modules/cross_validation.html#computing-cross-validated-metrics),
> The simplest way to use cross-validation is to call the [**`cross_val_score`**](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_score.html) helper function
But, there's a quirk: For scikit-learn's cross-validation [**scoring**](https://scikit-learn.org/stable/modules/model_evaluation.html#scoring-parameter), higher is better. But for regression error metrics, lower is better. So scikit-learn multiplies regression error metrics by -1 to make them negative. That's why the value of the `scoring` parameter is `'neg_mean_absolute_error'`.
So, k-fold cross-validation with this dataset looks like this:
### Linear Model
```
import category_encoders as ce
import numpy as np
from sklearn.feature_selection import f_regression, SelectKBest
from sklearn.impute import SimpleImputer
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
target = 'price'
high_cardinality = ['display_address', 'street_address', 'description']
features = train.columns.drop([target] + high_cardinality)
X_train = train[features]
y_train = train[target]
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(strategy='mean'),
StandardScaler(),
SelectKBest(f_regression, k=20),
Ridge(alpha=1.0)
)
k = 3
scores = cross_val_score(pipeline, X_train, y_train, cv=k,
scoring='neg_mean_absolute_error')
print(f'MAE for {k} folds:', -scores)
-scores.mean()
```
### Random Forest
```
from sklearn.ensemble import RandomForestRegressor
features = train.columns.drop(target)
X_train = train[features]
y_train = train[target]
pipeline = make_pipeline(
ce.TargetEncoder(min_samples_leaf=1, smoothing=1),
SimpleImputer(strategy='median'),
RandomForestRegressor(n_estimators=100, n_jobs=-1, random_state=42)
)
k = 3
scores = cross_val_score(pipeline, X_train, y_train, cv=k,
scoring='neg_mean_absolute_error')
print(f'MAE for {k} folds:', -scores)
-scores.mean()
```
But the Random Forest has many hyperparameters. We mostly used the defaults, and arbitrarily chose `n_estimators`. Is it too high? Too low? Just right? How do we know?
```
print('Model Hyperparameters:')
print(pipeline.named_steps['randomforestregressor'])
```
## Challenge
You will continue to participate in our Kaggle challenge. Use cross-validation and submit new predictions.
# Use scikit-learn for hyperparameter optimization
## Overview
"The universal tension in machine learning is between optimization and generalization; the ideal model is one that stands right at the border between underfitting and overfitting; between undercapacity and overcapacity. To figure out where this border lies, first you must cross it." —[Francois Chollet](https://books.google.com/books?id=dadfDwAAQBAJ&pg=PA114)
### Validation Curve
Let's try different parameter values, and visualize "the border between underfitting and overfitting."
Using scikit-learn, we can make [validation curves](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.validation_curve.html), "to determine training and test scores for varying parameter values. This is similar to grid search with one parameter."
<img src="https://jakevdp.github.io/PythonDataScienceHandbook/figures/05.03-validation-curve.png">
<sup>Source: https://jakevdp.github.io/PythonDataScienceHandbook/05.03-hyperparameters-and-model-validation.html#Validation-curves-in-Scikit-Learn</sup>
Validation curves are awesome for learning about overfitting and underfitting. (But less useful in real-world projects, because we usually want to vary more than one parameter.)
For this example, let's see what happens when we vary the depth of a decision tree. (This will be faster than varying the number of estimators in a random forest.)
```
%matplotlib inline
import matplotlib.pyplot as plt
from sklearn.model_selection import validation_curve
from sklearn.tree import DecisionTreeRegressor
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(),
DecisionTreeRegressor()
)
depth = range(1, 30, 3)
train_scores, val_scores = validation_curve(
pipeline, X_train, y_train,
param_name='decisiontreeregressor__max_depth',
param_range=depth, scoring='neg_mean_absolute_error',
cv=3,
n_jobs=-1
)
plt.figure(dpi=150)
plt.plot(depth, np.mean(-train_scores, axis=1), color='blue', label='training error')
plt.plot(depth, np.mean(-val_scores, axis=1), color='red', label='validation error')
plt.title('Validation Curve')
plt.xlabel('model complexity: DecisionTreeRegressor max_depth')
plt.ylabel('model score: Mean Absolute Error')
plt.legend();
plt.figure(dpi=150)
plt.plot(depth, np.mean(-train_scores, axis=1), color='blue', label='training error')
plt.plot(depth, np.mean(-val_scores, axis=1), color='red', label='validation error')
plt.title('Validation Curve, Zoomed In')
plt.xlabel('model complexity: DecisionTreeRegressor max_depth')
plt.ylabel('model score: Mean Absolute Error')
plt.ylim((500, 700)) # Zoom in
plt.legend();
```
## Follow Along
To vary multiple hyperparameters and find their optimal values, let's try **Randomized Search CV.**
#### [Scikit-Learn User Guide, 3.2 Tuning the hyper-parameters of an estimator](https://scikit-learn.org/stable/modules/grid_search.html)
> Hyper-parameters are parameters that are not directly learnt within estimators. In scikit-learn they are passed as arguments to the constructor of the estimator classes.
>
> It is possible and recommended to search the hyper-parameter space for the best cross validation score.
>
> [`GridSearchCV`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html#sklearn.model_selection.GridSearchCV) exhaustively considers all parameter combinations, while [`RandomizedSearchCV`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RandomizedSearchCV.html) can sample a given number of candidates from a parameter space with a specified distribution.
>
> While using a grid of parameter settings is currently the most widely used method for parameter optimization, other search methods have more favourable properties. [`RandomizedSearchCV`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RandomizedSearchCV.html) implements a randomized search over parameters, where each setting is sampled from a distribution over possible parameter values.
>
> Specifying how parameters should be sampled is done using a dictionary. Additionally, a computation budget, being the number of sampled candidates or sampling iterations, is specified using the `n_iter` parameter.
>
> For each parameter, either a distribution over possible values or a list of discrete choices (which will be sampled uniformly) can be specified.
Here's a good blog post to explain more: [**A Comparison of Grid Search and Randomized Search Using Scikit Learn**](https://blog.usejournal.com/a-comparison-of-grid-search-and-randomized-search-using-scikit-learn-29823179bc85).
<img src="https://miro.medium.com/max/2500/1*9W1MrRkHi0YFmBoHi9Y2Ow.png" width="50%">
### Linear Model
```
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
features = train.columns.drop([target] + high_cardinality)
X_train = train[features]
y_train = train[target]
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
SelectKBest(f_regression),
Ridge()
)
param_distributions = {
'simpleimputer__strategy': ['mean', 'median'],
'selectkbest__k': range(1, len(X_train.columns)+1),
'ridge__alpha': [0.1, 1, 10],
}
# If you're on Colab, decrease n_iter & cv parameters
search = RandomizedSearchCV(
pipeline,
param_distributions=param_distributions,
n_iter=100,
cv=5,
scoring='neg_mean_absolute_error',
verbose=10,
return_train_score=True,
n_jobs=-1
)
search.fit(X_train, y_train);
print('Best hyperparameters', search.best_params_)
print('Cross-validation MAE', -search.best_score_)
# If we used GridSearchCV instead of RandomizedSearchCV,
# how many candidates would there be?
# 2 imputation strategies * n columns * 3 Ridge alphas
2 * len(X_train.columns) * 3
```
### "Fitting X folds for each of Y candidates, totalling Z fits" ?
What did that mean? What do you think?
### Random Forest
#### [Scikit-Learn User Guide, 3.2 Tuning the hyper-parameters of an estimator](https://scikit-learn.org/stable/modules/grid_search.html)
> [`RandomizedSearchCV`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RandomizedSearchCV.html) implements a randomized search over parameters, where each setting is sampled from a distribution over possible parameter values.
>
> For each parameter, either a distribution over possible values or a list of discrete choices (which will be sampled uniformly) can be specified.
>
> This example uses the `scipy.stats` module, which contains many useful distributions for sampling parameters.
```
from scipy.stats import randint, uniform
features = train.columns.drop(target)
X_train = train[features]
y_train = train[target]
pipeline = make_pipeline(
ce.TargetEncoder(),
SimpleImputer(),
RandomForestRegressor(random_state=42)
)
param_distributions = {
'targetencoder__min_samples_leaf': randint(1, 1000),
'targetencoder__smoothing': uniform(1, 1000),
'simpleimputer__strategy': ['mean', 'median'],
'randomforestregressor__n_estimators': randint(50, 500),
'randomforestregressor__max_depth': [5, 10, 15, 20, None],
'randomforestregressor__max_features': uniform(0, 1),
}
# If you're on Colab, decrease n_iter & cv parameters
search = RandomizedSearchCV(
pipeline,
param_distributions=param_distributions,
n_iter=10,
cv=3,
scoring='neg_mean_absolute_error',
verbose=10,
return_train_score=True,
n_jobs=-1
)
search.fit(X_train, y_train);
print('Best hyperparameters', search.best_params_)
print('Cross-validation MAE', -search.best_score_)
```
### See detailed results
```
pd.DataFrame(search.cv_results_).sort_values(by='rank_test_score').T
```
### Make predictions for test set
```
search_best_model = search.best_estimator_
from sklearn.metrics import mean_absolute_error
X_test = test[features]
y_test = test[target]
y_pred = search_best_model.predict(X_test)
mae = mean_absolute_error(y_test, y_pred)
print(f'Test MAE: ${mae:,.0f}')
```
Here's what the [`RandomizdSearchCV` documentation](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RandomizedSearchCV.html) says about the `best_estimator_` attribute:
> **best_estimator_** : ***estimator***
> Estimator that was chosen by the search, i.e. estimator which gave highest score (or smallest loss if specified) on the left out data. Not available if `refit=False`. ... See `refit` parameter for more information ...
So let's look at the `refit` parameter too:
> **refit** : ***boolean, string, or callable, default=True***
> Refit an estimator using the best found parameters on the whole dataset.
By default, scikit-learn cross-validation will _"refit an estimator using the best found parameters on the whole dataset",_ which means, use **all** the training data:
<img src="https://scikit-learn.org/stable/_images/grid_search_workflow.png" width="50%">
***Tip: If you're doing 3-way train/validation/split, you should do this too!*** After you've optimized your hyperparameters and selected your final model, then manually refit on both the training and validation data.
## Challenge
For your assignment, use scikit-learn for hyperparameter optimization with RandomizedSearchCV.
# Review
Continue to participate in our Kaggle Challenge, and practice these objectives:
- Do **cross-validation** with independent test set
- Use scikit-learn for **hyperparameter optimization**
You can refer to these suggestions when you do hyperparameter optimization, now and in future projects:
### Tree Ensemble hyperparameter suggestions
#### Random Forest
- class_weight (for imbalanced classes)
- max_depth (usually high, can try decreasing)
- n_estimators (too low underfits, too high wastes time)
- min_samples_leaf (increase if overfitting)
- max_features (decrease for more diverse trees)
#### XGBoost
- scale_pos_weight (for imbalanced classes)
- max_depth (usually low, can try increasing)
- n_estimators (too low underfits, too high wastes time/overfits) — _I recommend using early stopping instead of cross-validation_
- learning_rate (too low underfits, too high overfits)
- See [Notes on Parameter Tuning](https://xgboost.readthedocs.io/en/latest/tutorials/param_tuning.html) and [DART booster](https://xgboost.readthedocs.io/en/latest/tutorials/dart.html) for more ideas
### Linear Model hyperparameter suggestions
#### Logistic Regression
- C
- class_weight (for imbalanced classes)
- penalty
#### Ridge / Lasso Regression
- alpha
#### ElasticNet Regression
- alpha
- l1_ratio
For more explanation, see [**Aaron Gallant's 9 minute video on Ridge Regression**](https://www.youtube.com/watch?v=XK5jkedy17w)!
# Sources
- Jake VanderPlas, [Python Data Science Handbook, Chapter 5.3,](https://jakevdp.github.io/PythonDataScienceHandbook/05.03-hyperparameters-and-model-validation.html) Hyperparameters and Model Validation
- Peter Worcester, [A Comparison of Grid Search and Randomized Search Using Scikit Learn](https://blog.usejournal.com/a-comparison-of-grid-search-and-randomized-search-using-scikit-learn-29823179bc85)
- Ron Zacharski, [A Programmer’s Guide to Data Mining, Chapter 5,](http://guidetodatamining.com/chapter5/) first 10 pages, for a great explanation of cross-validation with examples and pictures
- Sebastian Raschka, [Model Evaluation](https://sebastianraschka.com/blog/2018/model-evaluation-selection-part4.html)
- [Scikit-Learn User Guide, 3.1 Cross-validation](https://scikit-learn.org/stable/modules/cross_validation.html)
- [Scikit-Learn User Guide, 3.2 Tuning the hyper-parameters of an estimator](https://scikit-learn.org/stable/modules/grid_search.html)
- [sklearn.model_selection.cross_val_score](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_score.html)
- [sklearn.model_selection.RandomizedSearchCV](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RandomizedSearchCV.html)
- [xgboost, Notes on Parameter Tuning](https://xgboost.readthedocs.io/en/latest/tutorials/param_tuning.html)
|
github_jupyter
|
%%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Kaggle-Challenge/master/data/'
!pip install category_encoders==2.*
!pip install pandas-profiling==2.*
# If you're working locally:
else:
DATA_PATH = '../data/'
import numpy as np
import pandas as pd
# Read New York City apartment rental listing data
df = pd.read_csv(DATA_PATH+'apartments/renthop-nyc.csv')
assert df.shape == (49352, 34)
# Remove the most extreme 1% prices,
# the most extreme .1% latitudes, &
# the most extreme .1% longitudes
df = df[(df['price'] >= np.percentile(df['price'], 0.5)) &
(df['price'] <= np.percentile(df['price'], 99.5)) &
(df['latitude'] >= np.percentile(df['latitude'], 0.05)) &
(df['latitude'] < np.percentile(df['latitude'], 99.95)) &
(df['longitude'] >= np.percentile(df['longitude'], 0.05)) &
(df['longitude'] <= np.percentile(df['longitude'], 99.95))]
# Do train/test split
# Use data from April & May 2016 to train
# Use data from June 2016 to test
df['created'] = pd.to_datetime(df['created'], infer_datetime_format=True)
cutoff = pd.to_datetime('2016-06-01')
train = df[df.created < cutoff]
test = df[df.created >= cutoff]
# Wrangle train & test sets in the same way
def engineer_features(df):
# Avoid SettingWithCopyWarning
df = df.copy()
# Does the apartment have a description?
df['description'] = df['description'].str.strip().fillna('')
df['has_description'] = df['description'] != ''
# How long is the description?
df['description_length'] = df['description'].str.len()
# How many total perks does each apartment have?
perk_cols = ['elevator', 'cats_allowed', 'hardwood_floors', 'dogs_allowed',
'doorman', 'dishwasher', 'no_fee', 'laundry_in_building',
'fitness_center', 'pre-war', 'laundry_in_unit', 'roof_deck',
'outdoor_space', 'dining_room', 'high_speed_internet', 'balcony',
'swimming_pool', 'new_construction', 'exclusive', 'terrace',
'loft', 'garden_patio', 'common_outdoor_space',
'wheelchair_access']
df['perk_count'] = df[perk_cols].sum(axis=1)
# Are cats or dogs allowed?
df['cats_or_dogs'] = (df['cats_allowed']==1) | (df['dogs_allowed']==1)
# Are cats and dogs allowed?
df['cats_and_dogs'] = (df['cats_allowed']==1) & (df['dogs_allowed']==1)
# Total number of rooms (beds + baths)
df['rooms'] = df['bedrooms'] + df['bathrooms']
# Extract number of days elapsed in year, and drop original date feature
df['days'] = (df['created'] - pd.to_datetime('2016-01-01')).dt.days
df = df.drop(columns='created')
return df
train = engineer_features(train)
test = engineer_features(test)
# Pandas Profiling can be very slow with medium & large datasets.
# These parameters will make it faster.
# https://github.com/pandas-profiling/pandas-profiling/issues/222
import pandas_profiling
profile_report = train.profile_report(
check_correlation_pearson=False,
correlations={
'pearson': False,
'spearman': False,
'kendall': False,
'phi_k': False,
'cramers': False,
'recoded': False,
},
plot={'histogram': {'bayesian_blocks_bins': False}},
)
profile_report
import category_encoders as ce
import numpy as np
from sklearn.feature_selection import f_regression, SelectKBest
from sklearn.impute import SimpleImputer
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
target = 'price'
high_cardinality = ['display_address', 'street_address', 'description']
features = train.columns.drop([target] + high_cardinality)
X_train = train[features]
y_train = train[target]
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(strategy='mean'),
StandardScaler(),
SelectKBest(f_regression, k=20),
Ridge(alpha=1.0)
)
k = 3
scores = cross_val_score(pipeline, X_train, y_train, cv=k,
scoring='neg_mean_absolute_error')
print(f'MAE for {k} folds:', -scores)
-scores.mean()
from sklearn.ensemble import RandomForestRegressor
features = train.columns.drop(target)
X_train = train[features]
y_train = train[target]
pipeline = make_pipeline(
ce.TargetEncoder(min_samples_leaf=1, smoothing=1),
SimpleImputer(strategy='median'),
RandomForestRegressor(n_estimators=100, n_jobs=-1, random_state=42)
)
k = 3
scores = cross_val_score(pipeline, X_train, y_train, cv=k,
scoring='neg_mean_absolute_error')
print(f'MAE for {k} folds:', -scores)
-scores.mean()
print('Model Hyperparameters:')
print(pipeline.named_steps['randomforestregressor'])
%matplotlib inline
import matplotlib.pyplot as plt
from sklearn.model_selection import validation_curve
from sklearn.tree import DecisionTreeRegressor
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(),
DecisionTreeRegressor()
)
depth = range(1, 30, 3)
train_scores, val_scores = validation_curve(
pipeline, X_train, y_train,
param_name='decisiontreeregressor__max_depth',
param_range=depth, scoring='neg_mean_absolute_error',
cv=3,
n_jobs=-1
)
plt.figure(dpi=150)
plt.plot(depth, np.mean(-train_scores, axis=1), color='blue', label='training error')
plt.plot(depth, np.mean(-val_scores, axis=1), color='red', label='validation error')
plt.title('Validation Curve')
plt.xlabel('model complexity: DecisionTreeRegressor max_depth')
plt.ylabel('model score: Mean Absolute Error')
plt.legend();
plt.figure(dpi=150)
plt.plot(depth, np.mean(-train_scores, axis=1), color='blue', label='training error')
plt.plot(depth, np.mean(-val_scores, axis=1), color='red', label='validation error')
plt.title('Validation Curve, Zoomed In')
plt.xlabel('model complexity: DecisionTreeRegressor max_depth')
plt.ylabel('model score: Mean Absolute Error')
plt.ylim((500, 700)) # Zoom in
plt.legend();
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
features = train.columns.drop([target] + high_cardinality)
X_train = train[features]
y_train = train[target]
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
SelectKBest(f_regression),
Ridge()
)
param_distributions = {
'simpleimputer__strategy': ['mean', 'median'],
'selectkbest__k': range(1, len(X_train.columns)+1),
'ridge__alpha': [0.1, 1, 10],
}
# If you're on Colab, decrease n_iter & cv parameters
search = RandomizedSearchCV(
pipeline,
param_distributions=param_distributions,
n_iter=100,
cv=5,
scoring='neg_mean_absolute_error',
verbose=10,
return_train_score=True,
n_jobs=-1
)
search.fit(X_train, y_train);
print('Best hyperparameters', search.best_params_)
print('Cross-validation MAE', -search.best_score_)
# If we used GridSearchCV instead of RandomizedSearchCV,
# how many candidates would there be?
# 2 imputation strategies * n columns * 3 Ridge alphas
2 * len(X_train.columns) * 3
from scipy.stats import randint, uniform
features = train.columns.drop(target)
X_train = train[features]
y_train = train[target]
pipeline = make_pipeline(
ce.TargetEncoder(),
SimpleImputer(),
RandomForestRegressor(random_state=42)
)
param_distributions = {
'targetencoder__min_samples_leaf': randint(1, 1000),
'targetencoder__smoothing': uniform(1, 1000),
'simpleimputer__strategy': ['mean', 'median'],
'randomforestregressor__n_estimators': randint(50, 500),
'randomforestregressor__max_depth': [5, 10, 15, 20, None],
'randomforestregressor__max_features': uniform(0, 1),
}
# If you're on Colab, decrease n_iter & cv parameters
search = RandomizedSearchCV(
pipeline,
param_distributions=param_distributions,
n_iter=10,
cv=3,
scoring='neg_mean_absolute_error',
verbose=10,
return_train_score=True,
n_jobs=-1
)
search.fit(X_train, y_train);
print('Best hyperparameters', search.best_params_)
print('Cross-validation MAE', -search.best_score_)
pd.DataFrame(search.cv_results_).sort_values(by='rank_test_score').T
search_best_model = search.best_estimator_
from sklearn.metrics import mean_absolute_error
X_test = test[features]
y_test = test[target]
y_pred = search_best_model.predict(X_test)
mae = mean_absolute_error(y_test, y_pred)
print(f'Test MAE: ${mae:,.0f}')
| 0.501221 | 0.927495 |
```
import pandas as pd
import panel as pn
pn.extension()
```
The ``DataFrame`` pane renders pandas, dask and streamz ``DataFrame`` and ``Series`` types as an HTML table. If you need to edit the values of a `DataFrame` use the `DataFrame` widget instead. The Pane supports all the arguments to the `DataFrame.to_html` function.
#### Parameters:
For layout and styling related parameters see the [customization user guide](../../user_guide/Customization.ipynb).
* **``bold_rows``** (boolean, default=True): Make the row labels bold in the output.
* **``border``** (int, default=0): Width of the border included in the opening ``table`` tag.
* **``classes``** (list[str]): CSS class(es) to apply to the resulting html table.
* **``col_space``** (int or str): The minimum width of each column in CSS length units. An int is assumed to be px units.
* **``decimal``** (str, default='.'): Character recognized as decimal separator, e.g. ',' in Europe.
* **``escape``** (boolean, default=False): Convert the characters <, >, and & to HTML-safe sequences.
* **``float_format``** (function): Formatter function to apply to columns' elements if they are floats. The result of this function must be a unicode string.
* **``formatters``** (dict or list): Formatter functions to apply to columns' elements by position or name. The result of each function must be a unicode string.
* **``object``** (object): The HoloViews object being displayed
* **``header``** (boolean, default=True): Whether to print column labels.
* **``index``** (boolean, default=True): Whether to print index (row) labels.
* **``index_names``** (boolean, default=True): Whether to print the names of the indexes.
* **``justify``** (str): How to justify the column labels ('left', 'right', 'center', 'justify', 'justify-all', 'start', 'end', 'inherit', 'match-parent', 'initial', 'unset')
* **``max_rows``** (int): Maximum number of rows to display.
* **``max_rows``** (int): Maximum number of rows to display.
* **``max_cols``** (int): Maximum number of columns to display.
* **``na_rep``** (str, default='NaN'): String representation of NAN to use.
* **``render_links``** (boolean, default=False): Convert URLs to HTML links.
* **``show_dimensions``** (boolean, default=False): Display DataFrame dimensions (number of rows by number of columns).
* **``sparsify``** (boolean, default=True): Set to False for a DataFrame with a hierarchical index to print every multi-index key at each row.
___
The `DataFrame` uses the inbuilt HTML repr to render the underlying DataFrame:
```
df = pd.util.testing.makeMixedDataFrame()
df_pane = pn.pane.DataFrame(df)
df_pane
```
Like all other Panel objects changing a parameter will update the view allowing us to control the styling of the dataframe. In this example we will control these parameters using a set of widgets created directly from Pane:
```
pn.panel(df_pane.param, parameters=['bold_rows', 'index', 'header', 'max_rows', 'show_dimensions'],
widgets={'max_rows': {'start': 1, 'end': len(df), 'value': len(df)}})
```
In addition to rendering standard pandas `DataFrame` and `Series` types the `DataFrame` pane will also render updating `streamz` types (Note: in a live kernel you should see the dataframe update every 0.5 seconds):
```
from streamz.dataframe import Random
sdf = Random(interval='200ms', freq='50ms')
pn.pane.DataFrame(sdf, width=500)
type(sdf.groupby('y').sum().x)
```
|
github_jupyter
|
import pandas as pd
import panel as pn
pn.extension()
df = pd.util.testing.makeMixedDataFrame()
df_pane = pn.pane.DataFrame(df)
df_pane
pn.panel(df_pane.param, parameters=['bold_rows', 'index', 'header', 'max_rows', 'show_dimensions'],
widgets={'max_rows': {'start': 1, 'end': len(df), 'value': len(df)}})
from streamz.dataframe import Random
sdf = Random(interval='200ms', freq='50ms')
pn.pane.DataFrame(sdf, width=500)
type(sdf.groupby('y').sum().x)
| 0.301876 | 0.954351 |
Packages instalation:
```
pip install eli5
import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import cross_val_score
import eli5
from eli5.sklearn import PermutationImportance
from ast import literal_eval
from tqdm import tqdm_notebook
cd "/content/drive/My Drive/Colab Notebooks"
cd "Dataworshop_matrix"
ls data
```
Import data:
```
df = pd.read_csv('data/men_shoes.csv',low_memory=False)
```
Define run_model() funstion:
```
def run_model(feats, model= DecisionTreeRegressor(max_depth=5)):
X = df[feats].values
y = df['price_amountmin'].values
scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error')
return np.mean(scores), np.std(scores)
```
Feature Engineering:
<br>
- data normalization
```
df['brand_cat'] = df['brand'].map(lambda x: str(x).lower()).factorize()[0]
```
- parse features
```
def parse_features(x):
output_dict = {}
if str(x) == 'nan': return output_dict
features = literal_eval(x.replace('\\"', '"'))
for item in features:
key = item['key'].lower().strip()
value = item['value'][0].lower().strip()
output_dict[key] = value
return output_dict
df['features_parsed'] = df['features'].map(parse_features)
df['features_parsed'].head().values
```
- Different types of attributes
```
keys = set()
df['features_parsed'].map(lambda x: keys.update(x.keys()))
len(keys)
def get_name_feat(key):
return 'feat_' + key
for key in tqdm_notebook(keys):
df[get_name_feat(key)] = df.features_parsed.map(
lambda feats: feats[key] if key in feats else np.nan)
```
Verify the importance of variables:
```
keys_stat = {}
for key in tqdm_notebook(keys):
keys_stat[key] = df[False == df[get_name_feat(key)].isnull()].shape[0] / df.shape[0] * 100
{k:v for k,v in keys_stat.items() if v > 30}
df['feat_brand_cat'] = df['feat_brand'].factorize()[0]
df['feat_color_cat'] = df['feat_color'].factorize()[0]
df['feat_gender_cat'] = df['feat_gender'].factorize()[0]
df['feat_manufacturer part number_cat'] = df['feat_manufacturer part number'].factorize()[0]
df['feat_material_cat'] = df['feat_material'].factorize()[0]
df['feat_sport_cat'] = df['feat_sport'].factorize()[0]
df['feat_style_cat'] = df['feat_style'].factorize()[0]
df['feat_season_cat'] = df['feat_season'].factorize()[0]
df['feat_metal type_cat'] = df['feat_metal type'].factorize()[0]
df['feat_shape_cat'] = df['feat_shape'].factorize()[0]
for key in tqdm_notebook(keys):
df[get_name_feat(key) + '_cat'] = df[get_name_feat(key)].factorize()[0]
df['brand'] = df['brand'].map(lambda x: str(x).lower())
df[df.brand == df.feat_brand].shape
feats = ['brand_cat', 'feat_brand_cat', 'feat_color_cat', 'feat_gender_cat', 'feat_material_cat', 'feat_style_cat', 'feat_metal type_cat', 'feat_shape_cat']
feats_cat = [x for x in df.columns if 'cat' in x]
feats_cat
```
DecisionTreeRegressor:
```
run_model(['brand_cat'])
```
RandomForestRegressor:
```
model = RandomForestRegressor(max_depth=5, n_estimators=100, random_state=123)
results = run_model(feats, model)
```
Features importances:
```
X = df[feats].values
y = df['price_amountmin'].values
m = RandomForestRegressor(max_depth=5, n_estimators=100, random_state=123)
m.fit(X, y)
print(results)
perm = PermutationImportance(m, random_state=1).fit(X, y);
eli5.show_weights(perm, feature_names=feats)
df['brand'].value_counts(normalize=True)
df[df['brand'] == 'nike'].features_parsed.sample(10).values
!git add matrix_one/1_day5.ipynb
!git commit -m "Predict Men's Shoes Prices - second part"
```
|
github_jupyter
|
pip install eli5
import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import cross_val_score
import eli5
from eli5.sklearn import PermutationImportance
from ast import literal_eval
from tqdm import tqdm_notebook
cd "/content/drive/My Drive/Colab Notebooks"
cd "Dataworshop_matrix"
ls data
df = pd.read_csv('data/men_shoes.csv',low_memory=False)
def run_model(feats, model= DecisionTreeRegressor(max_depth=5)):
X = df[feats].values
y = df['price_amountmin'].values
scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error')
return np.mean(scores), np.std(scores)
df['brand_cat'] = df['brand'].map(lambda x: str(x).lower()).factorize()[0]
def parse_features(x):
output_dict = {}
if str(x) == 'nan': return output_dict
features = literal_eval(x.replace('\\"', '"'))
for item in features:
key = item['key'].lower().strip()
value = item['value'][0].lower().strip()
output_dict[key] = value
return output_dict
df['features_parsed'] = df['features'].map(parse_features)
df['features_parsed'].head().values
keys = set()
df['features_parsed'].map(lambda x: keys.update(x.keys()))
len(keys)
def get_name_feat(key):
return 'feat_' + key
for key in tqdm_notebook(keys):
df[get_name_feat(key)] = df.features_parsed.map(
lambda feats: feats[key] if key in feats else np.nan)
keys_stat = {}
for key in tqdm_notebook(keys):
keys_stat[key] = df[False == df[get_name_feat(key)].isnull()].shape[0] / df.shape[0] * 100
{k:v for k,v in keys_stat.items() if v > 30}
df['feat_brand_cat'] = df['feat_brand'].factorize()[0]
df['feat_color_cat'] = df['feat_color'].factorize()[0]
df['feat_gender_cat'] = df['feat_gender'].factorize()[0]
df['feat_manufacturer part number_cat'] = df['feat_manufacturer part number'].factorize()[0]
df['feat_material_cat'] = df['feat_material'].factorize()[0]
df['feat_sport_cat'] = df['feat_sport'].factorize()[0]
df['feat_style_cat'] = df['feat_style'].factorize()[0]
df['feat_season_cat'] = df['feat_season'].factorize()[0]
df['feat_metal type_cat'] = df['feat_metal type'].factorize()[0]
df['feat_shape_cat'] = df['feat_shape'].factorize()[0]
for key in tqdm_notebook(keys):
df[get_name_feat(key) + '_cat'] = df[get_name_feat(key)].factorize()[0]
df['brand'] = df['brand'].map(lambda x: str(x).lower())
df[df.brand == df.feat_brand].shape
feats = ['brand_cat', 'feat_brand_cat', 'feat_color_cat', 'feat_gender_cat', 'feat_material_cat', 'feat_style_cat', 'feat_metal type_cat', 'feat_shape_cat']
feats_cat = [x for x in df.columns if 'cat' in x]
feats_cat
run_model(['brand_cat'])
model = RandomForestRegressor(max_depth=5, n_estimators=100, random_state=123)
results = run_model(feats, model)
X = df[feats].values
y = df['price_amountmin'].values
m = RandomForestRegressor(max_depth=5, n_estimators=100, random_state=123)
m.fit(X, y)
print(results)
perm = PermutationImportance(m, random_state=1).fit(X, y);
eli5.show_weights(perm, feature_names=feats)
df['brand'].value_counts(normalize=True)
df[df['brand'] == 'nike'].features_parsed.sample(10).values
!git add matrix_one/1_day5.ipynb
!git commit -m "Predict Men's Shoes Prices - second part"
| 0.498291 | 0.797162 |
```
%%sh
pip install -q pip --upgrade
pip install -q sagemaker smdebug awscli --upgrade --user
```
## Download the Fashion-MNIST dataset
```
import os
import numpy as np
from tensorflow.keras.datasets import fashion_mnist
(x_train, y_train), (x_val, y_val) = fashion_mnist.load_data()
os.makedirs("./data", exist_ok = True)
np.savez('./data/training', image=x_train, label=y_train)
np.savez('./data/validation', image=x_val, label=y_val)
!pygmentize fmnist-5.py
```
## Upload Fashion-MNIST data to S3
```
import sagemaker, smdebug
print(sagemaker.__version__)
sess = sagemaker.Session()
role = sagemaker.get_execution_role()
bucket = sess.default_bucket()
prefix = 'keras2-fashion-mnist'
training_input_path = sess.upload_data('data/training.npz', key_prefix=prefix+'/training')
validation_input_path = sess.upload_data('data/validation.npz', key_prefix=prefix+'/validation')
output_path = 's3://{}/{}/output/'.format(bucket, prefix)
chk_path = 's3://{}/{}/checkpoints/'.format(bucket, prefix)
print(training_input_path)
print(validation_input_path)
print(output_path)
print(chk_path)
```
## Train with Tensorflow
```
from sagemaker.tensorflow import TensorFlow
from sagemaker.debugger import rule_configs, Rule, DebuggerHookConfig, CollectionConfig
save_interval = '100'
tf_estimator = TensorFlow(entry_point='fmnist-5.py',
role=role,
train_instance_count=1,
train_instance_type='ml.p3.2xlarge',
framework_version='2.1.0',
py_version='py3',
hyperparameters={'epochs': 30},
output_path=output_path,
train_use_spot_instances=True,
train_max_run=3600,
train_max_wait=7200,
debugger_hook_config=DebuggerHookConfig(
s3_output_path='s3://{}/{}/debug'.format(bucket, prefix),
collection_configs=[
CollectionConfig(name='metrics', parameters={"save_interval": save_interval}),
CollectionConfig(name='losses', parameters={"save_interval": save_interval}),
CollectionConfig(name='outputs', parameters={"save_interval": save_interval}),
CollectionConfig(name='weights', parameters={"save_interval": save_interval}),
CollectionConfig(name='gradients', parameters={"save_interval": save_interval})
],
),
rules=[
Rule.sagemaker(rule_configs.poor_weight_initialization()),
Rule.sagemaker(rule_configs.dead_relu()),
Rule.sagemaker(rule_configs.check_input_images(), rule_parameters={"channel": '3'})
]
)
tf_estimator.fit({'training': training_input_path, 'validation': validation_input_path})
description = tf_estimator.latest_training_job.rule_job_summary()
for rule in description:
rule.pop('LastModifiedTime')
rule.pop('RuleEvaluationJobArn')
print(rule)
from smdebug.trials import create_trial
s3_output_path = tf_estimator.latest_job_debugger_artifacts_path()
trial = create_trial(s3_output_path)
trial.tensor_names()
%matplotlib inline
import matplotlib.pyplot as plt
loss = trial.tensor('val_f1_score')
plt.autoscale()
values = [loss.value(s) for s in loss.steps()]
plt.plot(loss.steps(), values)
w = trial.tensor('conv2d/weights/conv2d/kernel:0')
print(w.value(0).shape)
g = trial.tensor('training/Adam/gradients/gradients/conv2d/Conv2D_grad/Conv2DBackpropFilter:0')
print(g.value(0).shape)
def plot_conv_filter(tensor_name, filter_num, min_step=0):
tensor = trial.tensor(tensor_name)
steps = [s for s in tensor.steps() if s >= min_step]
plt.autoscale()
for i in range(0,3):
for j in range(0,3):
values = [tensor.value(s)[:,:,0,filter_num][i][j] for s in steps]
label='({},{})'.format(i,j)
plt.plot(steps, values, label=label)
plt.legend(loc='upper left')
plt.show()
plot_conv_filter('conv2d/weights/conv2d/kernel:0', 63)
plot_conv_filter('training/Adam/gradients/gradients/conv2d/Conv2D_grad/Conv2DBackpropFilter:0', 63, min_step=15000)
```
## Deploy
```
import time
tf_endpoint_name = 'keras-tf-fmnist-'+time.strftime("%Y-%m-%d-%H-%M-%S", time.gmtime())
tf_predictor = tf_estimator.deploy(
initial_instance_count=1,
instance_type='ml.m5.large',
endpoint_name=tf_endpoint_name)
```
## Predict
```
%matplotlib inline
import random
import matplotlib.pyplot as plt
num_samples = 5
indices = random.sample(range(x_val.shape[0] - 1), num_samples)
images = x_val[indices]/255
labels = y_val[indices]
for i in range(num_samples):
plt.subplot(1,num_samples,i+1)
plt.imshow(images[i].reshape(28, 28), cmap='gray')
plt.title(labels[i])
plt.axis('off')
payload = images.reshape(num_samples, 28, 28, 1)
# Default format for inference is JSON
from sagemaker.predictor import json_serializer
tf_predictor.content_type = 'application/json'
tf_predictor.serializer = json_serializer
response = tf_predictor.predict(payload)
prediction = np.array(response['predictions'])
predicted_label = prediction.argmax(axis=1)
print('Predicted labels are: {}'.format(predicted_label))
```
## Clean up
```
tf_predictor.delete_endpoint()
```
|
github_jupyter
|
%%sh
pip install -q pip --upgrade
pip install -q sagemaker smdebug awscli --upgrade --user
import os
import numpy as np
from tensorflow.keras.datasets import fashion_mnist
(x_train, y_train), (x_val, y_val) = fashion_mnist.load_data()
os.makedirs("./data", exist_ok = True)
np.savez('./data/training', image=x_train, label=y_train)
np.savez('./data/validation', image=x_val, label=y_val)
!pygmentize fmnist-5.py
import sagemaker, smdebug
print(sagemaker.__version__)
sess = sagemaker.Session()
role = sagemaker.get_execution_role()
bucket = sess.default_bucket()
prefix = 'keras2-fashion-mnist'
training_input_path = sess.upload_data('data/training.npz', key_prefix=prefix+'/training')
validation_input_path = sess.upload_data('data/validation.npz', key_prefix=prefix+'/validation')
output_path = 's3://{}/{}/output/'.format(bucket, prefix)
chk_path = 's3://{}/{}/checkpoints/'.format(bucket, prefix)
print(training_input_path)
print(validation_input_path)
print(output_path)
print(chk_path)
from sagemaker.tensorflow import TensorFlow
from sagemaker.debugger import rule_configs, Rule, DebuggerHookConfig, CollectionConfig
save_interval = '100'
tf_estimator = TensorFlow(entry_point='fmnist-5.py',
role=role,
train_instance_count=1,
train_instance_type='ml.p3.2xlarge',
framework_version='2.1.0',
py_version='py3',
hyperparameters={'epochs': 30},
output_path=output_path,
train_use_spot_instances=True,
train_max_run=3600,
train_max_wait=7200,
debugger_hook_config=DebuggerHookConfig(
s3_output_path='s3://{}/{}/debug'.format(bucket, prefix),
collection_configs=[
CollectionConfig(name='metrics', parameters={"save_interval": save_interval}),
CollectionConfig(name='losses', parameters={"save_interval": save_interval}),
CollectionConfig(name='outputs', parameters={"save_interval": save_interval}),
CollectionConfig(name='weights', parameters={"save_interval": save_interval}),
CollectionConfig(name='gradients', parameters={"save_interval": save_interval})
],
),
rules=[
Rule.sagemaker(rule_configs.poor_weight_initialization()),
Rule.sagemaker(rule_configs.dead_relu()),
Rule.sagemaker(rule_configs.check_input_images(), rule_parameters={"channel": '3'})
]
)
tf_estimator.fit({'training': training_input_path, 'validation': validation_input_path})
description = tf_estimator.latest_training_job.rule_job_summary()
for rule in description:
rule.pop('LastModifiedTime')
rule.pop('RuleEvaluationJobArn')
print(rule)
from smdebug.trials import create_trial
s3_output_path = tf_estimator.latest_job_debugger_artifacts_path()
trial = create_trial(s3_output_path)
trial.tensor_names()
%matplotlib inline
import matplotlib.pyplot as plt
loss = trial.tensor('val_f1_score')
plt.autoscale()
values = [loss.value(s) for s in loss.steps()]
plt.plot(loss.steps(), values)
w = trial.tensor('conv2d/weights/conv2d/kernel:0')
print(w.value(0).shape)
g = trial.tensor('training/Adam/gradients/gradients/conv2d/Conv2D_grad/Conv2DBackpropFilter:0')
print(g.value(0).shape)
def plot_conv_filter(tensor_name, filter_num, min_step=0):
tensor = trial.tensor(tensor_name)
steps = [s for s in tensor.steps() if s >= min_step]
plt.autoscale()
for i in range(0,3):
for j in range(0,3):
values = [tensor.value(s)[:,:,0,filter_num][i][j] for s in steps]
label='({},{})'.format(i,j)
plt.plot(steps, values, label=label)
plt.legend(loc='upper left')
plt.show()
plot_conv_filter('conv2d/weights/conv2d/kernel:0', 63)
plot_conv_filter('training/Adam/gradients/gradients/conv2d/Conv2D_grad/Conv2DBackpropFilter:0', 63, min_step=15000)
import time
tf_endpoint_name = 'keras-tf-fmnist-'+time.strftime("%Y-%m-%d-%H-%M-%S", time.gmtime())
tf_predictor = tf_estimator.deploy(
initial_instance_count=1,
instance_type='ml.m5.large',
endpoint_name=tf_endpoint_name)
%matplotlib inline
import random
import matplotlib.pyplot as plt
num_samples = 5
indices = random.sample(range(x_val.shape[0] - 1), num_samples)
images = x_val[indices]/255
labels = y_val[indices]
for i in range(num_samples):
plt.subplot(1,num_samples,i+1)
plt.imshow(images[i].reshape(28, 28), cmap='gray')
plt.title(labels[i])
plt.axis('off')
payload = images.reshape(num_samples, 28, 28, 1)
# Default format for inference is JSON
from sagemaker.predictor import json_serializer
tf_predictor.content_type = 'application/json'
tf_predictor.serializer = json_serializer
response = tf_predictor.predict(payload)
prediction = np.array(response['predictions'])
predicted_label = prediction.argmax(axis=1)
print('Predicted labels are: {}'.format(predicted_label))
tf_predictor.delete_endpoint()
| 0.454714 | 0.818918 |
# Evolutionary Path Relinking
In Evolutionary Path Relinking we **relink solutions in the elite set**
> This operation can be completed periodically (e.g. every 10 iterations) or as a post processing step when the all iterations of the algorithm are complete or a time limit has been reached.
----
## Imports
```
from itertools import combinations
import numpy as np
import sys
```
## `metapy` imports
```
# install metapy if running in Google Colab
if 'google.colab' in sys.modules:
!pip install meta-py
from metapy.tsp import tsp_io as io
from metapy.tsp.euclidean import gen_matrix, plot_tour
from metapy.tsp.objective import OptimisedSimpleTSPObjective
from metapy.local_search.hill_climbing import (HillClimber, TweakTwoOpt)
from metapy.tsp.grasp import (SemiGreedyConstructor,
FixedRCLSizer,
RandomRCLSizer,
MonitoredLocalSearch,
GRASP,
EliteSet,
GRASPPlusPathRelinking,
TSPPathRelinker)
```
## Load problem
```
#load file
file_path = 'https://raw.githubusercontent.com/TomMonks/meta-py/main/data/st70.tsp'
#number of rows in the file that are meta_data
md_rows = 6
#read the coordinates
cities = io.read_coordinates(file_path, md_rows)
matrix = gen_matrix(cities, as_integer=True)
```
## Post processing step implementation
We add two (more!) classes to our GRASP+PR framework:
* `EvolutionaryPathRelinker`: a simple class that generates all pairwise combinations of solutions in `EliteSet`. The class accepts a `relinker` argument that provides the logic for relinking all solutions.
* `GRASPPlusEvoPathRelinking` extends `GRASPPlusPathRelinking`. It simply delegates the standard GRASP+PR to its super class and then calls the evolutionary path relinking logic as a post processing step.
```
class EvolutionaryPathRelinker:
'''
Creates all pairwise combinations of solutions in
the elite set and runs path relinking on all combinations.
'''
def __init__(self, tracker, relinker):
self.tracker = tracker
self.relinker = relinker
self.best = None
self.best_solution = None
def relink(self, best_solution, best_cost):
self.best = best_cost
self.best_solution = best_solution
pairwise = self.generate_pairwise_combinations()
for s1, s2 in pairwise:
new_s, new_cost = self.relinker.relink(s1, s2)
# update elite set
self.tracker.update(new_s, new_cost)
if new_cost > self.best:
self.best = new_cost
self.best_solution = new_s
elite_solution, elite_best = self.tracker.get_best_solution()
if elite_best > self.best:
print('Evo PR found a better better solution')
self.best = elite_best
self.best_solution = elite_solution
def generate_pairwise_combinations(self):
return [c for c in combinations(self.tracker.solutions, 2)]
class GRASPPlusEvoPathRelinking(GRASPPlusPathRelinking):
'''
Evolutionary path relinking as post processing step.
'''
def __init__(self, constructor, local_search, relinker, evo_relinker,
elite_tracker, max_iter=1000, time_limit=np.inf):
'''
Constructor
Params:
------
constructor: object
semi-greedy construction logic
local_search: object
local search logic for 2nd phase of GRASP
relinker: object
TSP path relinking logic
evo_relinker: object
Evolutionary path relinking logic
elite_tracker: object
logic to track and update the elite set
max_iter: int, optional, (default=1000)
maximum number of iterations
time_limit: float, optional (default = np.inf)
algorithm time limit. Will override max_iter
'''
super().__init__(constructor, local_search, relinker,
elite_tracker, max_iter, time_limit)
self.evo_relinker = evo_relinker
self.tracker = elite_tracker
self.best = None
self.best_solution = None
def solve(self):
'''
Run GRASP with evolutionary path relinking
'''
# run GRASP with path relinking
super().solve()
self.n_updates_before_evo = self.elite_tracker.n_updates
self.elite_tracker.n_updates = 0
print('GRASP complete => running evolutionary path relinking')
# run evolutionary path relinking
self.evo_relinker.relink(self.best_solution, self.best)
if self.evo_relinker.best > self.best:
self.best = self.evo_relinker.best
self.best_solution = solf.evo_relinker.best_solution
def compose_grasp(tour, matrix, rcl_size=10, max_iter=50, elite_set_size=10, pr_trunc=10,
seeds=(None, None)):
'''
Create a GRASP with EVO path relinking algorithm.
'''
# objective function
obj = OptimisedSimpleTSPObjective(-matrix)
# Two-opt tweaks
tweaker = TweakTwoOpt()
# local search for main GRASP = first improvement hill climbing
ls1 = HillClimber(obj, tour, tweaker)
# local search for path relinking = first improvement hill climbing
ls2 = HillClimber(obj, tour, tweaker)
# semi-greedy constructor and RCL sizer
sizer = FixedRCLSizer(rcl_size)
constructor = SemiGreedyConstructor(sizer, tour, -matrix,
random_seed=seeds[0])
# elite set tracker
tracker = EliteSet(min_delta=1, max_size=elite_set_size)
# path relinking logic
relinker = TSPPathRelinker(ls2, tracker, obj, trunc=pr_trunc,
random_seed=seeds[1])
# evo path relinking logic
evo_relinker = EvolutionaryPathRelinker(tracker, relinker)
# GRASP + EVO PR framework
solver = GRASPPlusEvoPathRelinking(constructor, ls1, relinker, evo_relinker,
tracker, max_iter=max_iter)
return solver
tour = np.arange(len(cities))
solver = compose_grasp(tour, matrix, max_iter=50, seeds=(42, 1966), rcl_size=10)
print("\nRunning GRASP+EvPR")
solver.solve()
print("\n** GRASP OUTPUT ***")
print(f"best cost:\t{solver.best}")
print("best solutions:")
print(solver.best_solution)
fig, ax = plot_tour(solver.best_solution, cities, figsize=(12,9))
```
|
github_jupyter
|
from itertools import combinations
import numpy as np
import sys
# install metapy if running in Google Colab
if 'google.colab' in sys.modules:
!pip install meta-py
from metapy.tsp import tsp_io as io
from metapy.tsp.euclidean import gen_matrix, plot_tour
from metapy.tsp.objective import OptimisedSimpleTSPObjective
from metapy.local_search.hill_climbing import (HillClimber, TweakTwoOpt)
from metapy.tsp.grasp import (SemiGreedyConstructor,
FixedRCLSizer,
RandomRCLSizer,
MonitoredLocalSearch,
GRASP,
EliteSet,
GRASPPlusPathRelinking,
TSPPathRelinker)
#load file
file_path = 'https://raw.githubusercontent.com/TomMonks/meta-py/main/data/st70.tsp'
#number of rows in the file that are meta_data
md_rows = 6
#read the coordinates
cities = io.read_coordinates(file_path, md_rows)
matrix = gen_matrix(cities, as_integer=True)
class EvolutionaryPathRelinker:
'''
Creates all pairwise combinations of solutions in
the elite set and runs path relinking on all combinations.
'''
def __init__(self, tracker, relinker):
self.tracker = tracker
self.relinker = relinker
self.best = None
self.best_solution = None
def relink(self, best_solution, best_cost):
self.best = best_cost
self.best_solution = best_solution
pairwise = self.generate_pairwise_combinations()
for s1, s2 in pairwise:
new_s, new_cost = self.relinker.relink(s1, s2)
# update elite set
self.tracker.update(new_s, new_cost)
if new_cost > self.best:
self.best = new_cost
self.best_solution = new_s
elite_solution, elite_best = self.tracker.get_best_solution()
if elite_best > self.best:
print('Evo PR found a better better solution')
self.best = elite_best
self.best_solution = elite_solution
def generate_pairwise_combinations(self):
return [c for c in combinations(self.tracker.solutions, 2)]
class GRASPPlusEvoPathRelinking(GRASPPlusPathRelinking):
'''
Evolutionary path relinking as post processing step.
'''
def __init__(self, constructor, local_search, relinker, evo_relinker,
elite_tracker, max_iter=1000, time_limit=np.inf):
'''
Constructor
Params:
------
constructor: object
semi-greedy construction logic
local_search: object
local search logic for 2nd phase of GRASP
relinker: object
TSP path relinking logic
evo_relinker: object
Evolutionary path relinking logic
elite_tracker: object
logic to track and update the elite set
max_iter: int, optional, (default=1000)
maximum number of iterations
time_limit: float, optional (default = np.inf)
algorithm time limit. Will override max_iter
'''
super().__init__(constructor, local_search, relinker,
elite_tracker, max_iter, time_limit)
self.evo_relinker = evo_relinker
self.tracker = elite_tracker
self.best = None
self.best_solution = None
def solve(self):
'''
Run GRASP with evolutionary path relinking
'''
# run GRASP with path relinking
super().solve()
self.n_updates_before_evo = self.elite_tracker.n_updates
self.elite_tracker.n_updates = 0
print('GRASP complete => running evolutionary path relinking')
# run evolutionary path relinking
self.evo_relinker.relink(self.best_solution, self.best)
if self.evo_relinker.best > self.best:
self.best = self.evo_relinker.best
self.best_solution = solf.evo_relinker.best_solution
def compose_grasp(tour, matrix, rcl_size=10, max_iter=50, elite_set_size=10, pr_trunc=10,
seeds=(None, None)):
'''
Create a GRASP with EVO path relinking algorithm.
'''
# objective function
obj = OptimisedSimpleTSPObjective(-matrix)
# Two-opt tweaks
tweaker = TweakTwoOpt()
# local search for main GRASP = first improvement hill climbing
ls1 = HillClimber(obj, tour, tweaker)
# local search for path relinking = first improvement hill climbing
ls2 = HillClimber(obj, tour, tweaker)
# semi-greedy constructor and RCL sizer
sizer = FixedRCLSizer(rcl_size)
constructor = SemiGreedyConstructor(sizer, tour, -matrix,
random_seed=seeds[0])
# elite set tracker
tracker = EliteSet(min_delta=1, max_size=elite_set_size)
# path relinking logic
relinker = TSPPathRelinker(ls2, tracker, obj, trunc=pr_trunc,
random_seed=seeds[1])
# evo path relinking logic
evo_relinker = EvolutionaryPathRelinker(tracker, relinker)
# GRASP + EVO PR framework
solver = GRASPPlusEvoPathRelinking(constructor, ls1, relinker, evo_relinker,
tracker, max_iter=max_iter)
return solver
tour = np.arange(len(cities))
solver = compose_grasp(tour, matrix, max_iter=50, seeds=(42, 1966), rcl_size=10)
print("\nRunning GRASP+EvPR")
solver.solve()
print("\n** GRASP OUTPUT ***")
print(f"best cost:\t{solver.best}")
print("best solutions:")
print(solver.best_solution)
fig, ax = plot_tour(solver.best_solution, cities, figsize=(12,9))
| 0.436622 | 0.807461 |
<a href="https://colab.research.google.com/github/gandalf1819/SF-Opioid-Crisis/blob/master/SF_drug_Random_forest.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from google.colab import drive
drive.mount('/content/gdrive')
import numpy as np
import pandas as pd
import os
d_crime = pd.read_csv("/content/gdrive/My Drive/SF dataset/Police_Department_Incident_Reports__Historical_2003_to_May_2018.csv")
d_crime.columns
np.random.seed(100)
random_d_crime=d_crime.sample(2215024)
train_size=int(0.67 *2215024)
train_df=random_d_crime[:train_size]
test_df=random_d_crime[train_size:]
train_df['DateTime'] = train_df.Date + " " + train_df.Time
train_df['DateTime'] = pd.to_datetime(train_df['DateTime'], format='%m/%d/%Y %H:%M')
test_df['DateTime'] = test_df.Date + " " + test_df.Time
test_df['DateTime'] = pd.to_datetime(test_df['DateTime'], format='%m/%d/%Y %H:%M')
train_df.columns
test_df.columns
train_df.shape
target = train_df["Category"].unique()
print(target.shape)
target
# X = train_df.drop(train_df.columns[[1, 2, 5, 6]], axis = 1)
X = train_df[['DateTime', 'DayOfWeek', 'PdDistrict', 'X', 'Y']]
X.head()
y = train_df.iloc[:, 1]
y.head()
def preprocess_data(dataset):
dataset['DateTime'] = pd.to_datetime(dataset['DateTime'])
dataset['Month'] = dataset.DateTime.apply(lambda x: x.month)
dataset['Day'] = dataset.DateTime.apply(lambda x: x.day)
dataset['Hour'] = dataset.DateTime.apply(lambda x: x.hour)
dataset['Minute'] = dataset.DateTime.apply(lambda x: x.minute)
dataset = dataset.drop('DateTime', 1)
dataset = pd.get_dummies(data=dataset, columns=['DayOfWeek', 'PdDistrict'])
return dataset
X = preprocess_data(X)
X.head()
from sklearn.preprocessing import LabelEncoder
y = y.to_frame()
le = LabelEncoder()
y["Category"] = le.fit_transform(y["Category"])
print(y.head())
keys = le.classes_
values = le.transform(le.classes_)
dictionary = dict(zip(keys, values))
print(dictionary)
# Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
# print(type(X_train), type(y_train))
print(X_train.head())
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(max_depth = 10, n_estimators = 256)
rf.fit(X_train.values, y_train.values.ravel())
y_pred = rf.predict(X_test)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_test, y_pred)
print ("Accuracy for Random Forest: %.2f%%" % (accuracy * 100.0))
# Computer precision score across multiple classes
from sklearn.metrics import precision_score
precision = precision_score(y_test, y_pred, average='micro')
print("Precision for Random Forest: %.2f%%" % precision)
# Compute recall over multiple classes
from sklearn.metrics import recall_score
recall = recall_score(y_test, y_pred, average='micro')
print("Recall for Random Forest: %.2f%%" % recall)
# Compute f1 score across multiple classes
from sklearn.metrics import f1_score
f1 = f1_score(y_test, y_pred, average='micro')
print("F1 score for Random Forest: %.2f%%" % f1)
from sklearn.metrics import classification_report, confusion_matrix
import seaborn as sns
cm = confusion_matrix(y_test, y_pred)
cm = pd.DataFrame(cm)
sns.heatmap(cm, cmap="YlGnBu", square=True)
```
### **Preprocess test_df dataframe**
```
test_data = test_df[['DateTime', 'DayOfWeek', 'PdDistrict', 'Address', 'X', 'Y']]
test_data.head()
test_data = preprocess_data(test_data)
test_data.head()
test_data.head()
y_pred_proba = rf.predict_proba(test_data)
colmn = ["ARSON","ASSAULT","BAD CHECKS","BRIBERY","BURGLARY","DISORDERLY CONDUCT","DRIVING UNDER THE INFLUENCE","DRUG/NARCOTIC","DRUNKENNESS","EMBEZZLEMENT","EXTORTION","FAMILY OFFENSES","FORGERY/COUNTERFEITING","FRAUD","GAMBLING","KIDNAPPING","LARCENY/THEFT","LIQUOR LAWS","LOITERING","MISSING PERSON","NON-CRIMINAL","OTHER OFFENSES","PORNOGRAPHY/OBSCENE MAT","PROSTITUTION","RECOVERED VEHICLE","ROBBERY","RUNAWAY","SECONDARY CODES","SEX OFFENSES FORCIBLE","SEX OFFENSES NON FORCIBLE","STOLEN PROPERTY","SUICIDE","SUSPICIOUS OCC","TREA","TRESPASS","VANDALISM","VEHICLE THEFT","WARRANTS","WEAPON LAWS"]
result = pd.DataFrame(y_pred_proba, columns=colmn)
result
```
|
github_jupyter
|
from google.colab import drive
drive.mount('/content/gdrive')
import numpy as np
import pandas as pd
import os
d_crime = pd.read_csv("/content/gdrive/My Drive/SF dataset/Police_Department_Incident_Reports__Historical_2003_to_May_2018.csv")
d_crime.columns
np.random.seed(100)
random_d_crime=d_crime.sample(2215024)
train_size=int(0.67 *2215024)
train_df=random_d_crime[:train_size]
test_df=random_d_crime[train_size:]
train_df['DateTime'] = train_df.Date + " " + train_df.Time
train_df['DateTime'] = pd.to_datetime(train_df['DateTime'], format='%m/%d/%Y %H:%M')
test_df['DateTime'] = test_df.Date + " " + test_df.Time
test_df['DateTime'] = pd.to_datetime(test_df['DateTime'], format='%m/%d/%Y %H:%M')
train_df.columns
test_df.columns
train_df.shape
target = train_df["Category"].unique()
print(target.shape)
target
# X = train_df.drop(train_df.columns[[1, 2, 5, 6]], axis = 1)
X = train_df[['DateTime', 'DayOfWeek', 'PdDistrict', 'X', 'Y']]
X.head()
y = train_df.iloc[:, 1]
y.head()
def preprocess_data(dataset):
dataset['DateTime'] = pd.to_datetime(dataset['DateTime'])
dataset['Month'] = dataset.DateTime.apply(lambda x: x.month)
dataset['Day'] = dataset.DateTime.apply(lambda x: x.day)
dataset['Hour'] = dataset.DateTime.apply(lambda x: x.hour)
dataset['Minute'] = dataset.DateTime.apply(lambda x: x.minute)
dataset = dataset.drop('DateTime', 1)
dataset = pd.get_dummies(data=dataset, columns=['DayOfWeek', 'PdDistrict'])
return dataset
X = preprocess_data(X)
X.head()
from sklearn.preprocessing import LabelEncoder
y = y.to_frame()
le = LabelEncoder()
y["Category"] = le.fit_transform(y["Category"])
print(y.head())
keys = le.classes_
values = le.transform(le.classes_)
dictionary = dict(zip(keys, values))
print(dictionary)
# Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
# print(type(X_train), type(y_train))
print(X_train.head())
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(max_depth = 10, n_estimators = 256)
rf.fit(X_train.values, y_train.values.ravel())
y_pred = rf.predict(X_test)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_test, y_pred)
print ("Accuracy for Random Forest: %.2f%%" % (accuracy * 100.0))
# Computer precision score across multiple classes
from sklearn.metrics import precision_score
precision = precision_score(y_test, y_pred, average='micro')
print("Precision for Random Forest: %.2f%%" % precision)
# Compute recall over multiple classes
from sklearn.metrics import recall_score
recall = recall_score(y_test, y_pred, average='micro')
print("Recall for Random Forest: %.2f%%" % recall)
# Compute f1 score across multiple classes
from sklearn.metrics import f1_score
f1 = f1_score(y_test, y_pred, average='micro')
print("F1 score for Random Forest: %.2f%%" % f1)
from sklearn.metrics import classification_report, confusion_matrix
import seaborn as sns
cm = confusion_matrix(y_test, y_pred)
cm = pd.DataFrame(cm)
sns.heatmap(cm, cmap="YlGnBu", square=True)
test_data = test_df[['DateTime', 'DayOfWeek', 'PdDistrict', 'Address', 'X', 'Y']]
test_data.head()
test_data = preprocess_data(test_data)
test_data.head()
test_data.head()
y_pred_proba = rf.predict_proba(test_data)
colmn = ["ARSON","ASSAULT","BAD CHECKS","BRIBERY","BURGLARY","DISORDERLY CONDUCT","DRIVING UNDER THE INFLUENCE","DRUG/NARCOTIC","DRUNKENNESS","EMBEZZLEMENT","EXTORTION","FAMILY OFFENSES","FORGERY/COUNTERFEITING","FRAUD","GAMBLING","KIDNAPPING","LARCENY/THEFT","LIQUOR LAWS","LOITERING","MISSING PERSON","NON-CRIMINAL","OTHER OFFENSES","PORNOGRAPHY/OBSCENE MAT","PROSTITUTION","RECOVERED VEHICLE","ROBBERY","RUNAWAY","SECONDARY CODES","SEX OFFENSES FORCIBLE","SEX OFFENSES NON FORCIBLE","STOLEN PROPERTY","SUICIDE","SUSPICIOUS OCC","TREA","TRESPASS","VANDALISM","VEHICLE THEFT","WARRANTS","WEAPON LAWS"]
result = pd.DataFrame(y_pred_proba, columns=colmn)
result
| 0.404155 | 0.795102 |
```
import pandas as pd
df = pd.read_csv( '/Users/jun/Downloads/body.csv', encoding="utf_8")
# display( df )
values = df.values
```
## ウエスト分布を描く
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.optimize import curve_fit
def func(x, a, mu, sigma):
return a*np.exp( -(x-mu)**2 / ( 2*sigma**2 ) )
data = values[:, 4].astype( float )
# 読み込んだ分布を描く
plt.figure( figsize=( 5, 5 ), dpi=100 )
fig, ax = plt.subplots( figsize=(5, 5), dpi=100 )
ax.grid( True )
plt.ylabel( 'person'); plt.xlabel( 'Waist(cm)' )
plt.xlim( [45, 75] )
ax.hist( data, bins=75-45+1, range=( 44.5, 75.5 ),
facecolor='green', alpha=0.75 )
# フィッテイング
hist, bins = np.histogram( data, 75-45, range=(45, 75))
# フィッテイング分布を描く
bins = bins[:-1]
paramIni = [ 1, 60, 10 ]
popt, pcov = curve_fit( func, bins, hist, p0=paramIni )
x = np.linspace(45, 75, 1000)
fitCurve = func( x, popt[0], popt[1], popt[2] )
plt.plot( x, fitCurve, 'r-' )
```
## バスト分布を描く
```
data = values[:, 3].astype( float )
# 読み込んだ分布を描く
plt.figure( figsize=( 5, 5 ), dpi=100 )
fig, ax = plt.subplots( figsize=(5, 5), dpi=100 )
ax.grid( True )
plt.ylabel( 'person'); plt.xlabel( 'Bust(cm)' )
plt.xlim( [70, 100] )
ax.hist( data, bins=100-70+1, range=( 69.5, 100.5 ),
facecolor='green', alpha=0.75 )
# フィッテイング
hist, bins = np.histogram( data, 100-70, range=(70, 100))
bins = bins[:-1]
paramIni = [ 1, 80, 10 ]
popt, pcov = curve_fit( func, bins, hist, p0=paramIni )
x = np.linspace(70, 100, 1000)
fitCurve = func( x, popt[0], popt[1], popt[2] )
plt.plot( x, fitCurve, 'r-' )
```
## ヒップ情報を描く
```
data = values[:, 5].astype( float )
# 読み込んだ分布を描画する
plt.figure( figsize=( 5, 5 ), dpi=100 )
fig, ax = plt.subplots( figsize=(5, 5), dpi=100 )
ax.grid( True )
plt.ylabel( 'person'); plt.xlabel( 'Hip(cm)' )
plt.xlim( [100, 70] )
ax.hist( data.astype( float ), bins=100-70+1, range=( 70, 100 ),
facecolor='green', alpha=0.75 )
# フィッテイング
hist, bins = np.histogram( data, 100-70, range=(70, 100))
bins = bins[:-1]
paramIni = [ 1, 90, 10 ]
popt, pcov = curve_fit( func, bins, hist, p0=paramIni )
x = np.linspace(70, 100, 1000)
fitCurve = func( x, popt[0], popt[1], popt[2] )
plt.plot( x, fitCurve, 'r-' )
plt.figure( figsize=( 5, 5 ), dpi=100 )
fig, ax = plt.subplots( figsize=( 5, 5 ), dpi=100 )
ax.hist2d( values[:, 3].astype( float ),
values[:, 4].astype( float ),
bins=[ np.linspace(74.5,100.5,100.5-74.5+1),
np.linspace(44.5,75.5,75.5-44.5+1) ]
)
ax.grid( True )
ax.set_xlabel('Bust(cm)')
ax.set_ylabel('Waist(cm)')
ax.set_xticks( np.linspace(75,100,100-75+1), minor=True )
ax.set_yticks( np.linspace(45,75,75-45+1), minor=True )
plt.figure( figsize=( 5, 5 ), dpi=100 )
fig, ax = plt.subplots( figsize=( 5, 5 ), dpi=100 )
ax.hist2d( values[:, 3].astype( float ),
values[:, 4].astype( float ),
bins=[ np.linspace(74.5,100.5,100.5-74.5+1),
np.linspace(44.5,75.5,75.5-44.5+1) ]
)
ax.grid( True )
ax.set_xlabel('Bust(cm)')
ax.set_ylabel('Waist(cm)')
ax.set_xticks( np.linspace(75,100,100-75+1), minor=True )
ax.set_yticks( np.linspace(45,75,75-45+1), minor=True )
```
|
github_jupyter
|
import pandas as pd
df = pd.read_csv( '/Users/jun/Downloads/body.csv', encoding="utf_8")
# display( df )
values = df.values
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.optimize import curve_fit
def func(x, a, mu, sigma):
return a*np.exp( -(x-mu)**2 / ( 2*sigma**2 ) )
data = values[:, 4].astype( float )
# 読み込んだ分布を描く
plt.figure( figsize=( 5, 5 ), dpi=100 )
fig, ax = plt.subplots( figsize=(5, 5), dpi=100 )
ax.grid( True )
plt.ylabel( 'person'); plt.xlabel( 'Waist(cm)' )
plt.xlim( [45, 75] )
ax.hist( data, bins=75-45+1, range=( 44.5, 75.5 ),
facecolor='green', alpha=0.75 )
# フィッテイング
hist, bins = np.histogram( data, 75-45, range=(45, 75))
# フィッテイング分布を描く
bins = bins[:-1]
paramIni = [ 1, 60, 10 ]
popt, pcov = curve_fit( func, bins, hist, p0=paramIni )
x = np.linspace(45, 75, 1000)
fitCurve = func( x, popt[0], popt[1], popt[2] )
plt.plot( x, fitCurve, 'r-' )
data = values[:, 3].astype( float )
# 読み込んだ分布を描く
plt.figure( figsize=( 5, 5 ), dpi=100 )
fig, ax = plt.subplots( figsize=(5, 5), dpi=100 )
ax.grid( True )
plt.ylabel( 'person'); plt.xlabel( 'Bust(cm)' )
plt.xlim( [70, 100] )
ax.hist( data, bins=100-70+1, range=( 69.5, 100.5 ),
facecolor='green', alpha=0.75 )
# フィッテイング
hist, bins = np.histogram( data, 100-70, range=(70, 100))
bins = bins[:-1]
paramIni = [ 1, 80, 10 ]
popt, pcov = curve_fit( func, bins, hist, p0=paramIni )
x = np.linspace(70, 100, 1000)
fitCurve = func( x, popt[0], popt[1], popt[2] )
plt.plot( x, fitCurve, 'r-' )
data = values[:, 5].astype( float )
# 読み込んだ分布を描画する
plt.figure( figsize=( 5, 5 ), dpi=100 )
fig, ax = plt.subplots( figsize=(5, 5), dpi=100 )
ax.grid( True )
plt.ylabel( 'person'); plt.xlabel( 'Hip(cm)' )
plt.xlim( [100, 70] )
ax.hist( data.astype( float ), bins=100-70+1, range=( 70, 100 ),
facecolor='green', alpha=0.75 )
# フィッテイング
hist, bins = np.histogram( data, 100-70, range=(70, 100))
bins = bins[:-1]
paramIni = [ 1, 90, 10 ]
popt, pcov = curve_fit( func, bins, hist, p0=paramIni )
x = np.linspace(70, 100, 1000)
fitCurve = func( x, popt[0], popt[1], popt[2] )
plt.plot( x, fitCurve, 'r-' )
plt.figure( figsize=( 5, 5 ), dpi=100 )
fig, ax = plt.subplots( figsize=( 5, 5 ), dpi=100 )
ax.hist2d( values[:, 3].astype( float ),
values[:, 4].astype( float ),
bins=[ np.linspace(74.5,100.5,100.5-74.5+1),
np.linspace(44.5,75.5,75.5-44.5+1) ]
)
ax.grid( True )
ax.set_xlabel('Bust(cm)')
ax.set_ylabel('Waist(cm)')
ax.set_xticks( np.linspace(75,100,100-75+1), minor=True )
ax.set_yticks( np.linspace(45,75,75-45+1), minor=True )
plt.figure( figsize=( 5, 5 ), dpi=100 )
fig, ax = plt.subplots( figsize=( 5, 5 ), dpi=100 )
ax.hist2d( values[:, 3].astype( float ),
values[:, 4].astype( float ),
bins=[ np.linspace(74.5,100.5,100.5-74.5+1),
np.linspace(44.5,75.5,75.5-44.5+1) ]
)
ax.grid( True )
ax.set_xlabel('Bust(cm)')
ax.set_ylabel('Waist(cm)')
ax.set_xticks( np.linspace(75,100,100-75+1), minor=True )
ax.set_yticks( np.linspace(45,75,75-45+1), minor=True )
| 0.434461 | 0.851459 |
Universidade Federal do Rio Grande do Sul (UFRGS)
Programa de Pós-Graduação em Engenharia Civil (PPGEC)
# Project PETROBRAS (2018/00147-5):
## Attenuation of dynamic loading along mooring lines embedded in clay
---
_Prof. Marcelo M. Rocha, Dr.techn._ [(ORCID)](https://orcid.org/0000-0001-5640-1020)
Porto Alegre, RS, Brazil
___
[1. Introduction](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/01_Introduction.ipynb?flush_cache=true)
[2. Reduced model scaling](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/02_Reduced_model.ipynb?flush_cache=true)
[3. Typical soil](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/03_Typical_soil.ipynb?flush_cache=true)
[4. The R4 studless 120mm chain](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/04_R4_studless_chain.ipynb?flush_cache=true)
[5. Dynamic load definition](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/05_Dynamic_load.ipynb?flush_cache=true)
[6. Design of chain anchoring system](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/06_Chain_anchor.ipynb?flush_cache=true)
[7. Design of uniaxial load cell with inclinometer](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/07_Load_cell.ipynb?flush_cache=true)
[8. Location of experimental sites](https://nbviewer.jupyter.org/github/mmaiarocha/Attenuation/blob/master/08_Experimental_sites.ipynb?flush_cache=true)
```
# Importing Python modules required for this notebook
# (this cell must be executed with "shift+enter" before any other Python cell)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Importing "pandas dataframe" with dimension exponents for scales calculation
DimData = pd.read_excel('resources/DimData.xlsx', sheet_name='DimData', index_col=0)
print(DimData)
```
## 2. Reduced model scaling
[(Link for PEC00144 class on Dimensional Analysis)](https://nbviewer.jupyter.org/github/mmaiarocha/PEC00144/blob/master/2_Dimensional_analysis.ipynb)
Experiments must be designed with a reduced length scale specified as $\lambda_L = 1:10$.
By considering that the soil in the experimental field satisfactorily resembles the
specified _typical soil_ (see [section 3](https://nbviewer.jupyter.org/urls/dl.dropbox.com/s/z35uz1iz5be4mq2/03_Typical_soil.ipynb?flush_cache=true)), the further scale-restricted
quantities are the soil density, $\rho_{\rm soil} = 1600{\rm kg/m^3}$ with scale $\lambda_\rho = 1:1$,
and the gravity acceleration, $g = 9.81{\rm m/s^2}$ also with scale $\lambda_g = 1:1$.
All other quantities have derived scales that must be calculated and used for the
interpretation of experimental results.
The choice of these three control quantities, $L$, $\rho$, and $g$, is based on the very
basic assumption that _the most important parameter governing the soil reaction for large
displacements is the undrained shear resistance_, $s_{\rm u}$. This parameter is assumed
to have the general form:
$$ s_{\rm u} = k\rho_{\rm soil} g z $$
where $k$ is a non-dimensional factor and $z$ the depth measured from soil surface.
Under this assumption, the scale of $s_{\rm u}$ will be correct at any depth $z$.
The three control quantities allow the definition of an new dimensional base to be used
for calculating the derived scales of further relevant quantities.
Dimension exponents are read from ``pandas`` dataframe ``DimData``:
```
ABC = ['L', 'ρ', 'a'] # control quantities are length, density and acceleration
LMT = ['L', 'M', 'T'] # dimension exponents (last three columns of DimData dataframe)
base = DimData.loc[ABC, LMT]
print(base)
```
Scales calculation requires the inversion of this new base, what is carried out with
``numpy`` method ``linalg.inv``:
```
i_base = np.linalg.inv(base)
print(i_base)
```
Now we specify a list of all quantities for which derived scales are to be calculated.
We choose, for instance:
* Force, $F$, (for chain tension),
* Frequency, $f$, (for dynamic loading spectral density),
* Mass per unit length, $\mu_L$, (for specifying the grade of model chain),
* Stress, $\sigma$, (for soil resistance)
A list with the identifiers of these quantities is used to read their dimension
exponents from ``DimData`` dataframe, given the problem dimension matrix also as
a dataframe:
```
param = ['F', 'f', 'μL', 'σ'] # parameters which scales must be calculated
npar = len(param) # number of parameters in the previous list
DimMat = DimData.loc[param, LMT]
print(DimMat)
```
The code snipet below calculates a new dimension matrix with the dimension exponents
corresponding to the new base. This new matrix is directly formatted as a ``pandas`` dataframe:
```
NewMat = pd.DataFrame(data = np.dot(DimMat,i_base),
index = DimMat.index,
columns = ABC)
print(NewMat)
```
To check the results above, let us take a look in the force dimensions:
\begin{align*}
[F] &= [L]^3 \, [\rho]^1 \, [a]^1 \\
&= {\rm (m)^3 \, (kg/m^3)^1 \, (m/s^2)^1} \\
&= {\rm kg \, m \, / \, s^2} \\
&= {\rm N}
\end{align*}
where $[\cdot]$ means ''unit of''. One may conclude that the computational procedure is _ok_,
despite its conciseness.
The next step is the especification of experimental scales for the control quantities, as
previously discussed:
```
λ_L = 1/10 # length scale for the reduced model
λ_ρ = 1/1 # same soil, with same density
λ_a = 1/1 # gravity will not be changed!
scales = np.tile([λ_L, λ_ρ, λ_a],(npar,1))
```
A last code line calculates the derived scales and includes them as an additional column in
dataframe ``NewMat``:
```
NewMat['scale'] = np.prod(scales**NewMat[ABC], axis=1)
print(NewMat)
```
where it can be seen, for instance, that the forces in the reduced model will be
one thousandth of the real scale forces. On the other hand, model time passes $\approx$3.16 times
faster, what makes frequencies the same amount higher.
The stress scale calculated above applies to the undrained soil shear resistance, $s_{\rm u}$,
for this resistance depends on the product of the base quantities. However, elastic stresses
and stiffness properties (Young's and shear modulae) _are not expected to follow this
scale_. It is important to keep in mind that these quantities are not likely to be relevant
for the experimental results, for large plastic displacements are to dominate the process.
These scales will be used in the following sections to design all experimental features.
|
github_jupyter
|
# Importing Python modules required for this notebook
# (this cell must be executed with "shift+enter" before any other Python cell)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Importing "pandas dataframe" with dimension exponents for scales calculation
DimData = pd.read_excel('resources/DimData.xlsx', sheet_name='DimData', index_col=0)
print(DimData)
ABC = ['L', 'ρ', 'a'] # control quantities are length, density and acceleration
LMT = ['L', 'M', 'T'] # dimension exponents (last three columns of DimData dataframe)
base = DimData.loc[ABC, LMT]
print(base)
i_base = np.linalg.inv(base)
print(i_base)
param = ['F', 'f', 'μL', 'σ'] # parameters which scales must be calculated
npar = len(param) # number of parameters in the previous list
DimMat = DimData.loc[param, LMT]
print(DimMat)
NewMat = pd.DataFrame(data = np.dot(DimMat,i_base),
index = DimMat.index,
columns = ABC)
print(NewMat)
λ_L = 1/10 # length scale for the reduced model
λ_ρ = 1/1 # same soil, with same density
λ_a = 1/1 # gravity will not be changed!
scales = np.tile([λ_L, λ_ρ, λ_a],(npar,1))
NewMat['scale'] = np.prod(scales**NewMat[ABC], axis=1)
print(NewMat)
| 0.626238 | 0.941007 |
<center>
<img src="https://raw.githubusercontent.com/Yorko/mlcourse.ai/master/img/ods_stickers.jpg" />
## [mlcourse.ai](https://mlcourse.ai) - Open Machine Learning Course
<center>
Auteur: [Yury Kashnitskiy](https://yorko.github.io). Traduit par Anna Larionova et [Ousmane Cissé](https://fr.linkedin.com/in/ousmane-cisse).
Ce matériel est soumis aux termes et conditions de la licence [Creative Commons CC BY-NC-SA 4.0](https://creativecommons.org/licenses/by-nc-sa/4.0/).
L'utilisation gratuite est autorisée à des fins non commerciales.
# <center> Sujet 6. Régression</center>
## <center>Lasso et Regression Ridge</center>
*Le programme du cours diffère cette semaine du plan de l'article, car le sujet 4 (modèles linéaires) est trop vaste et important, nous couvrons donc la régression cette semaine.*
```
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
%config InlineBackend.figure_format = 'retina'
import seaborn as sns
sns.set() # just to use the seaborn theme
from sklearn.datasets import load_boston
from sklearn.linear_model import Lasso, LassoCV, Ridge, RidgeCV
from sklearn.model_selection import KFold, cross_val_score
```
**Nous travaillerons avec les données sur les prix des logements à Boston (référentiel UCI).**
**Téléchargez les données.**
```
boston = load_boston()
X, y = boston["data"], boston["target"]
```
**Description des données:**
```
print(boston.DESCR)
boston.feature_names
```
**Regardons les deux premiers enregistrements.**
```
X[:2]
```
## Régression Lasso
La régression Lasso minimise l'erreur quadratique moyenne avec la régularisation L1:
$$\Large error(X, y, w) = \frac{1}{2} \sum_{i=1}^\ell {(y_i - w^Tx_i)}^2 + \alpha \sum_{i=1}^d |w_i|$$
où l'équation d'hyperplan $y = w^Tx$ en fonction des paramètres du modèle $w$, $\ell$ est le nombre d'observations dans les données $X$, $d$ est le nombre d'entités, valeurs cibles $y$, coefficient de régularisation $\alpha$.
**Ajustons la régression Lasso avec le petit coefficient $\alpha$ (régularisation faible). Le coefficient lié à la caractéristique NOX (concentration en oxydes nitriques) sera nul. Cela signifie que cette caractéristique est la moins importante pour la prévision des prix médians des logements dans cette région.**
```
lasso = Lasso(alpha=0.1)
lasso.fit(X, y)
lasso.coef_
```
**Entraînons la régression Lasso avec $\alpha=10$. Tous les coefficients sont égaux à zéro, à l'exception des caractéristiques ZN (proportion de terrains résidentiels zonés pour des lots de plus de 25 000 pieds carrés), TAXE (taux de taxe foncière de pleine valeur), B (proportion de Noirs par ville) et LSTAT (% de statut inférieur de la population).**
```
lasso = Lasso(alpha=10)
lasso.fit(X, y)
lasso.coef_
```
**Cela signifie que la régression Lasso peut servir de méthode de sélection des caractéristiques.**
```
n_alphas = 200
alphas = np.linspace(0.1, 10, n_alphas)
model = Lasso()
coefs = []
for a in alphas:
model.set_params(alpha=a)
model.fit(X, y)
coefs.append(model.coef_)
plt.rcParams["figure.figsize"] = (12, 8)
ax = plt.gca()
# ax.set_color_cycle(['b', 'r', 'g', 'c', 'k', 'y', 'm'])
ax.plot(alphas, coefs)
ax.set_xscale("log")
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
plt.xlabel("alpha")
plt.ylabel("weights")
plt.title("Lasso coefficients as a function of the regularization")
plt.axis("tight")
plt.show();
```
**Maintenant, trouvons la meilleure valeur de $\alpha$ lors de la validation croisée.**
```
lasso_cv = LassoCV(alphas=alphas, cv=3, random_state=17)
lasso_cv.fit(X, y)
lasso_cv.coef_
lasso_cv.alpha_
```
**Dans Scikit-learn, les métriques sont généralement * maximisées *, donc pour MSE il y a une solution: `neg_mean_squared_error` est plutôt minimisé. Pas vraiment pratique.**
```
cross_val_score(Lasso(lasso_cv.alpha_), X, y, cv=3, scoring="neg_mean_squared_error")
abs(
cross_val_score(
Lasso(lasso_cv.alpha_), X, y, cv=3, scoring="neg_mean_squared_error"
).mean()
)
abs(np.mean(cross_val_score(Lasso(9.95), X, y, cv=3, scoring="neg_mean_squared_error")))
```
**Encore un point ambigu: LassoCV trie les valeurs des paramètres par ordre décroissant pour faciliter l'optimisation. Il peut sembler que l’optimisation $\alpha$ ne fonctionne pas correctement.**
```
lasso_cv.alphas[:10]
lasso_cv.alphas_[:10]
plt.plot(lasso_cv.alphas, lasso_cv.mse_path_.mean(1)) # incorrect
plt.axvline(lasso_cv.alpha_, c="g");
plt.plot(lasso_cv.alphas_, lasso_cv.mse_path_.mean(1)) # correct
plt.axvline(lasso_cv.alpha_, c="g");
```
## Régression Ridge
La régression Ridge minimise l'erreur quadratique moyenne avec la régularisation L2:
$$\Large error(X, y, w) = \frac{1}{2} \sum_{i=1}^\ell {(y_i - w^Tx_i)}^2 + \alpha \sum_{i=1}^d w_i^2$$
où l'équation d'hyperplan $y = w^Tx$ en fonction des paramètres du modèle $w$, $\ell$ est le nombre d'observations dans les données $X$, $d$ est le nombre d'entités, valeurs cibles $y$, coefficient de régularisation $\alpha$.
Il existe une classe spéciale [RidgeCV](http://scikit-learn.org/stable/modules/generated/sklearn.linear _model.RidgeCV.html # sklearn.linear_ model.RidgeCV) pour la régression Ridge validation croisée.
```
n_alphas = 200
ridge_alphas = np.logspace(-2, 6, n_alphas)
ridge_cv = RidgeCV(alphas=ridge_alphas, scoring="neg_mean_squared_error", cv=3)
ridge_cv.fit(X, y)
ridge_cv.alpha_
```
**En cas de régression Ridge, aucun des paramètres ne se réduit à zéro. La valeur peut être petite mais non nulle.**
```
ridge_cv.coef_
n_alphas = 200
ridge_alphas = np.logspace(-2, 6, n_alphas)
model = Ridge()
coefs = []
for a in ridge_alphas:
model.set_params(alpha=a)
model.fit(X, y)
coefs.append(model.coef_)
ax = plt.gca()
# ax.set_color_cycle(['b', 'r', 'g', 'c', 'k', 'y', 'm'])
ax.plot(ridge_alphas, coefs)
ax.set_xscale("log")
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
plt.xlabel("alpha")
plt.ylabel("weights")
plt.title("Ridge coefficients as a function of the regularization")
plt.axis("tight")
plt.show()
```
## Références
- [Generalized linear models](http://scikit-learn.org/stable/modules/linear_model.html) (Generalized Linear Models, GLM) in Scikit-learn
- [LinearRegression](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression), [Lasso](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html#sklearn.linear_model.Lasso), [LassoCV](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LassoCV.html#sklearn.linear_model.LassoCV), [Ridge](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html) and [RidgeCV](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.RidgeCV.html#sklearn.linear_model.RidgeCV) in Scikit-learn
|
github_jupyter
|
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
%config InlineBackend.figure_format = 'retina'
import seaborn as sns
sns.set() # just to use the seaborn theme
from sklearn.datasets import load_boston
from sklearn.linear_model import Lasso, LassoCV, Ridge, RidgeCV
from sklearn.model_selection import KFold, cross_val_score
boston = load_boston()
X, y = boston["data"], boston["target"]
print(boston.DESCR)
boston.feature_names
X[:2]
lasso = Lasso(alpha=0.1)
lasso.fit(X, y)
lasso.coef_
lasso = Lasso(alpha=10)
lasso.fit(X, y)
lasso.coef_
n_alphas = 200
alphas = np.linspace(0.1, 10, n_alphas)
model = Lasso()
coefs = []
for a in alphas:
model.set_params(alpha=a)
model.fit(X, y)
coefs.append(model.coef_)
plt.rcParams["figure.figsize"] = (12, 8)
ax = plt.gca()
# ax.set_color_cycle(['b', 'r', 'g', 'c', 'k', 'y', 'm'])
ax.plot(alphas, coefs)
ax.set_xscale("log")
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
plt.xlabel("alpha")
plt.ylabel("weights")
plt.title("Lasso coefficients as a function of the regularization")
plt.axis("tight")
plt.show();
lasso_cv = LassoCV(alphas=alphas, cv=3, random_state=17)
lasso_cv.fit(X, y)
lasso_cv.coef_
lasso_cv.alpha_
cross_val_score(Lasso(lasso_cv.alpha_), X, y, cv=3, scoring="neg_mean_squared_error")
abs(
cross_val_score(
Lasso(lasso_cv.alpha_), X, y, cv=3, scoring="neg_mean_squared_error"
).mean()
)
abs(np.mean(cross_val_score(Lasso(9.95), X, y, cv=3, scoring="neg_mean_squared_error")))
lasso_cv.alphas[:10]
lasso_cv.alphas_[:10]
plt.plot(lasso_cv.alphas, lasso_cv.mse_path_.mean(1)) # incorrect
plt.axvline(lasso_cv.alpha_, c="g");
plt.plot(lasso_cv.alphas_, lasso_cv.mse_path_.mean(1)) # correct
plt.axvline(lasso_cv.alpha_, c="g");
n_alphas = 200
ridge_alphas = np.logspace(-2, 6, n_alphas)
ridge_cv = RidgeCV(alphas=ridge_alphas, scoring="neg_mean_squared_error", cv=3)
ridge_cv.fit(X, y)
ridge_cv.alpha_
ridge_cv.coef_
n_alphas = 200
ridge_alphas = np.logspace(-2, 6, n_alphas)
model = Ridge()
coefs = []
for a in ridge_alphas:
model.set_params(alpha=a)
model.fit(X, y)
coefs.append(model.coef_)
ax = plt.gca()
# ax.set_color_cycle(['b', 'r', 'g', 'c', 'k', 'y', 'm'])
ax.plot(ridge_alphas, coefs)
ax.set_xscale("log")
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
plt.xlabel("alpha")
plt.ylabel("weights")
plt.title("Ridge coefficients as a function of the regularization")
plt.axis("tight")
plt.show()
| 0.764716 | 0.984094 |
# The Physics of Sound, Part I
[return to main page](index.ipynb)
## Preparations
For this exercise we need the [Sound Field Synthesis Toolbox for Python](http://python.sfstoolbox.org);
```
import sfs
```
And some other stuff:
```
# remove "inline" to get a separate plotting window:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from numpy.core.umath_tests import inner1d
```
A grid for computation and plotting:
```
grid = sfs.util.xyz_grid([-2, 2], [-2, 2], 0, spacing=0.01)
```
*Exercise:* Use the help functionality of Python to find out what the function parameters mean. What does the third argument mean in our case? How many dimensions does our grid have?
## Physical Quantities
### Sound Pressure $p(\mathbf x, t)$
The acoustic sound pressure $p(\mathbf x, t)$ is the fluaction of the static pressure inside a medium (e.g. air) and hence changes the distribution of the atoms/molecules (sound particles) in a deterministic manner. Let's plot this an illustration of this distribution.
```
### create 10000 randomly distributed particles
particles = [np.random.uniform(-2, 2, 10000), np.random.uniform(-2, 2, 10000), 0];
# particles without displacement
plt.subplot(1,2,1) # define left subplot
sfs.plot.particles(particles, facecolor='black', s=2)
plt.ylim(-2,2)
plt.xlim(-2,2)
plt.title('Particles wo displacement')
# particles with displacement
n = [np.sqrt(2), np.sqrt(2), 0]; # direction of plane wave
f = 300; # temporal frequency
omega = 2*np.pi*f; # angular frequency
amplitude = 4e4 # unrealistically large to see an effect
v = sfs.mono.source.plane_velocity(omega, [0, 0, 0], n, particles)
particles = particles + amplitude * sfs.util.displacement(v, omega)
plt.subplot(1,2,2) # define right subplot
sfs.plot.particles(particles, facecolor='black', s=2)
plt.ylim(-2,2)
plt.xlim(-2,2)
plt.title('Particles with displacement')
plt.ylabel('');
```
### Particle Velocity $\mathbf v(\mathbf x, t)$
The particle velocity $\mathbf v(\mathbf x, t)$ describes the instantaneous velocity of a particle moving in the medium. Contrary to the sound pressure, the particle velocity is a vector field.
*Exercise*: What is main difference between a scalar and vector field?
## Relations between the Quantities
### The Equation of State
The Equation of State follows from the so-called *conservation of mass* principle combined with the idialized properties of the medium. It reads
$$ -\frac{\partial p(\mathbf x, t)}{\partial t} = \varrho_0 c^2 \nabla \cdot \mathbf v(\mathbf x, t)\,,$$
with $\varrho_0$ and $c$ denoting the static volumentric density and speed of sound of the medium, respectively.
*Exercise*: How does the speed of sound change $c$, if the medium is changed from air to water? Find the correct relation.
$$c_{\mathrm{air}}\,?\,c_{\mathrm{water}}$$
*Exercise*: How is the $\nabla$-operator defined in Cartesian coordinates?
$$ \nabla = ??? $$
*Exercise*: What is its meaning when applied to a vector field?
$$ \nabla \mathbf f(\mathbf x) = ??? $$
*Exercise*: What is the physical meaning of the Equation of State?
### Euler's Equation
Euler's Equation follows from the so-called *conservation of momentum* principle and reads
$$ -\varrho_0 \frac{\partial \mathbf v(\mathbf x, t)}{\partial t} = \nabla p(\mathbf x, t) $$
*Exercise*: What is the meaning of $\nabla$-operator when being applied to a scalar or a scalar field?
$$ \nabla f(\mathbf x) = ??? $$
*Exercise*: What is the physical meaning of Euler's Equation?
## The Wave Equation
In linear acoustics, a sound pressure field $p(\mathbf x, t)$ fulfils the wave equation
$$\Delta p(\mathbf x, t) - \frac{1}{c^2} \frac{\partial^2}{\partial t^2} p(\mathbf x, t) = -q(\mathbf x, t)$$
*Exercise*: How is the $\Delta$-operator defined?
$$ \Delta =\,???$$
If we apply the temporal Fourier transform to the wave equation, we get the Helmholtz equation
$$\Delta P(\mathbf x, \omega) + \left(\frac{\omega}{c}\right)^2 P(\mathbf x, \omega) = -Q(\mathbf x, \omega)$$
*Exercise*: How is the temporal Fourier transform defined?
$$ F(\mathbf x, \omega) = \,???\, f(\mathbf x, t) \,???\, $$
*Exercise*: What do the terms *homogeneous* and *inhomogeneous* mean in the context of the wave equation and the Helmholtz equation?
homogeneous:
inhomogeneous:
## Selected Solutions of the Wave Equation (Acoustic Sources)
### Plane Wave
A plane wave
$$p_{pw}(\mathbf x, t) = \delta \left(t - \dfrac{\mathbf n_{\mathrm {pw}} \cdot \mathbf x}{c} \right)$$
with its direction of progation defined by the vector $\mathbf n_{\mathrm {pw}}$ with $|\mathbf n_{\mathrm {pw}}| = 1$ is a solution of the homogeneous wave equation.
*Exercise*: What the is temporal Fourier transform of the above equation? Hind: Keep the Fourier transform of a dirac impulse and the shift theorem in mind.
$$P_{pw}(\mathbf x, \omega) = ??? $$
Let's plot a [plane wave](http://python.sfstoolbox.org/#sfs.mono.source.plane) with a frequency of 1000 Hertz which propagates in the direction of the negative y-axis.
```
x0 = 0, 0, 0 # point of zero phase (metre)
npw = 0, -1, 0 # propagation vector (unit length)
f = 1000 # time-frequency (Hz)
omega = 2 * np.pi * f # angular frequency (rad/s)
p_plane = sfs.mono.source.plane(omega, x0, npw, grid); # compute sound pressure field
sfs.plot.soundfield(p_plane, grid); # plotting command
plt.title("Plane wave with $n_{{pw}} = {}$".format(npw)); # set title of plot
```
*Exercise:* How can you see that the plane wave in the plot travels down and not up?
*Exercise:* Try different propagation angles and different frequencies.
*Exercise*: How does the sound field change, if we change the speed of sound? BTW, you can get (and set) the speed of sound currently used by the SFS toolbox via the variable `sfs.defs.c`. How are speed of sound, frequency and wave length related?
*Exercise:* How does the level of the plane wave decay over distance? Use the corresponding function to plot the level.
```
sfs.plot.level?
```
### Point Source
The density $q_{ps}(\mathbf x, t) = \delta(t)\delta(x-x_s)\delta(y-y_s)\delta(z-z_s)$ corresponds to a point source
$$p_{ps}(\mathbf x, t) = \delta \left(t - \dfrac{|\mathbf x-\mathbf x_{\mathrm s}|}{c}\right)$$
with its position defined by the vector $\mathbf x_{\mathrm {s}} = [x_s,y_s,z_s]^{\mathrm T}$.
*Exercise*: What the is temporal Fourier transform of the above equation
$$P_{ps}(\mathbf x, \omega) = ???$$
Let's plot a [point source](http://python.sfstoolbox.org/#sfs.mono.source.point) at the position $(0, 1.5, 0)$ metres with a frequency of 1000 Hertz.
```
xs = 0, 1.5, 0 # position (metre)
f = 1000 # time-frequency (Hz)
omega = 2 * np.pi * f # angular frequency (rad/s)
p_point = sfs.mono.source.point(omega, xs, None, grid)
sfs.plot.soundfield(p_point, grid)
plt.title("Point Source at {} m".format(xs));
```
The amplitude of the sound field is a bit weak ...
*Exercise:* Multiply the sound pressure field by a scaling factor of $4\pi$ to get an appropriate amplitude.
```
scaling_factor_point_source = 4 * np.pi
```
*Exercise:* Try different source positions and different frequencies.
*Exercise:* Compare the amplitude decay of a point source and a plane wave.
### Line Source
$q_{ls}(\mathbf x, t) = \delta(t)\delta(x-x_s)\delta(y-y_s)$ corresponds to a line source parallel to the $z$-axis with its position defined by the vector $\mathbf x_{\mathrm {s}} = [x_s, y_s, 0]^{\mathrm T}$. Its temporal Fourier spectrum is given as:
$$ P_{ls}(\mathbf x, \omega) = -\frac{j}{4} H_0\left(\frac{\omega}{c}\sqrt{(x-x_s)^2 + (y-y_s)^2}\right) $$
Let's plot a [line source](http://python.sfstoolbox.org/#sfs.mono.source.line) (parallel to the z-axis) at the position $(0, 1.5)$ metres with a frequency of 1000 Hertz.
```
xs = 0, 1.5 # position (metre)
f = 1000 # time-frequency (Hz)
omega = 2 * np.pi * f # angular frequency (rad/s)
p_line = sfs.mono.source.line(omega, xs, None, grid)
sfs.plot.soundfield(p_line, grid)
plt.title("Line Source at {} m".format(xs[:2]));
```
Again, the amplitude is a bit weak, let's scale it up!
This time, the scaling factor is a bit more involved:
```
scaling_factor_line_source = np.sqrt(8 * np.pi * omega / sfs.defs.c) * np.exp(1j * np.pi / 4)
```
*Exercise:* Scale the sound field by the given factor.
*Exercise:* Again, try different source positions and different frequencies.
*Exercise:* What's the difference between the sound fields of a point source and a line source?
### Dipole Source
This time, we start with the exercises and derive the sound field of the dipole source afterwards.
*Exercise*: Compute the sound field of two point sources lying on a axis with orientation $\mathbf n_s$ with a distance $2h=0.2$ m between them. Normalize the resulting sound field by $2h$. The two point sources should have the opposite polarity (opposite sign).
```
h = 0.1 # half distance between the two sources
xs = np.array([0,0,0]) # coordinate between the two sources
ns = np.array([1,0,0]) # orientation of the axis between the two sources
f = 500 # time-frequency (Hz)
omega = 2 * np.pi * f # angular frequency (rad/s)
# xs1 = ??? # position of the first point source
# xs2 = ??? # position of the second point source
# p_point1 = ???
# p_point2 = ???
# p_res = ???
# sfs.plot.soundfield(p_res*scaling_factor_point_source, grid)
```
*Exercise*: Reduce the distance between the point source. What can you observe?
The exact sound field of the Dipole Source is the limiting case of the above example.
$$P_{dps}(\mathbf x, \omega) = \lim_{h \rightarrow \infty} \frac{
P_{ps}(\mathbf x - h\,\mathbf n_s) - P_{ps}(\mathbf x + h\,\mathbf n_s)
}
{2h} $$
*Exercise*: Any idea what mathematically meaning this limit has?
*Exercise*: Plot the the exact sound field of a dipole source.
```
sfs.mono.source.point_dipole?
```
## Solutions
If you had problems solving some of the exercises, don't despair!
Have a look at the [example solutions](physics_of_sound_I-solutions.ipynb).
<p xmlns:dct="http://purl.org/dc/terms/">
<a rel="license"
href="http://creativecommons.org/publicdomain/zero/1.0/">
<img src="http://i.creativecommons.org/p/zero/1.0/88x31.png" style="border-style: none;" alt="CC0" />
</a>
<br />
To the extent possible under law,
<span rel="dct:publisher" resource="[_:publisher]">the person who associated CC0</span>
with this work has waived all copyright and related or neighboring
rights to this work.
</p>
|
github_jupyter
|
import sfs
# remove "inline" to get a separate plotting window:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from numpy.core.umath_tests import inner1d
grid = sfs.util.xyz_grid([-2, 2], [-2, 2], 0, spacing=0.01)
### create 10000 randomly distributed particles
particles = [np.random.uniform(-2, 2, 10000), np.random.uniform(-2, 2, 10000), 0];
# particles without displacement
plt.subplot(1,2,1) # define left subplot
sfs.plot.particles(particles, facecolor='black', s=2)
plt.ylim(-2,2)
plt.xlim(-2,2)
plt.title('Particles wo displacement')
# particles with displacement
n = [np.sqrt(2), np.sqrt(2), 0]; # direction of plane wave
f = 300; # temporal frequency
omega = 2*np.pi*f; # angular frequency
amplitude = 4e4 # unrealistically large to see an effect
v = sfs.mono.source.plane_velocity(omega, [0, 0, 0], n, particles)
particles = particles + amplitude * sfs.util.displacement(v, omega)
plt.subplot(1,2,2) # define right subplot
sfs.plot.particles(particles, facecolor='black', s=2)
plt.ylim(-2,2)
plt.xlim(-2,2)
plt.title('Particles with displacement')
plt.ylabel('');
x0 = 0, 0, 0 # point of zero phase (metre)
npw = 0, -1, 0 # propagation vector (unit length)
f = 1000 # time-frequency (Hz)
omega = 2 * np.pi * f # angular frequency (rad/s)
p_plane = sfs.mono.source.plane(omega, x0, npw, grid); # compute sound pressure field
sfs.plot.soundfield(p_plane, grid); # plotting command
plt.title("Plane wave with $n_{{pw}} = {}$".format(npw)); # set title of plot
sfs.plot.level?
xs = 0, 1.5, 0 # position (metre)
f = 1000 # time-frequency (Hz)
omega = 2 * np.pi * f # angular frequency (rad/s)
p_point = sfs.mono.source.point(omega, xs, None, grid)
sfs.plot.soundfield(p_point, grid)
plt.title("Point Source at {} m".format(xs));
scaling_factor_point_source = 4 * np.pi
xs = 0, 1.5 # position (metre)
f = 1000 # time-frequency (Hz)
omega = 2 * np.pi * f # angular frequency (rad/s)
p_line = sfs.mono.source.line(omega, xs, None, grid)
sfs.plot.soundfield(p_line, grid)
plt.title("Line Source at {} m".format(xs[:2]));
scaling_factor_line_source = np.sqrt(8 * np.pi * omega / sfs.defs.c) * np.exp(1j * np.pi / 4)
h = 0.1 # half distance between the two sources
xs = np.array([0,0,0]) # coordinate between the two sources
ns = np.array([1,0,0]) # orientation of the axis between the two sources
f = 500 # time-frequency (Hz)
omega = 2 * np.pi * f # angular frequency (rad/s)
# xs1 = ??? # position of the first point source
# xs2 = ??? # position of the second point source
# p_point1 = ???
# p_point2 = ???
# p_res = ???
# sfs.plot.soundfield(p_res*scaling_factor_point_source, grid)
sfs.mono.source.point_dipole?
| 0.577019 | 0.995291 |
# GCP Dataflow Component Sample
A Kubeflow Pipeline component that prepares data by submitting an Apache Beam job (authored in Python) to Cloud Dataflow for execution. The Python Beam code is run with Cloud Dataflow Runner.
## Intended use
Use this component to run a Python Beam code to submit a Cloud Dataflow job as a step of a Kubeflow pipeline.
## Runtime arguments
Name | Description | Optional | Data type| Accepted values | Default |
:--- | :----------| :----------| :----------| :----------| :---------- |
python_file_path | The path to the Cloud Storage bucket or local directory containing the Python file to be run. | | GCSPath | | |
project_id | The ID of the Google Cloud Platform (GCP) project containing the Cloud Dataflow job.| | String | | |
region | The Google Cloud Platform (GCP) region to run the Cloud Dataflow job.| | String | | |
staging_dir | The path to the Cloud Storage directory where the staging files are stored. A random subdirectory will be created under the staging directory to keep the job information.This is done so that you can resume the job in case of failure. `staging_dir` is passed as the command line arguments (`staging_location` and `temp_location`) of the Beam code. | Yes | GCSPath | | None |
requirements_file_path | The path to the Cloud Storage bucket or local directory containing the pip requirements file. | Yes | GCSPath | | None |
args | The list of arguments to pass to the Python file. | No | List | A list of string arguments | None |
wait_interval | The number of seconds to wait between calls to get the status of the job. | Yes | Integer | | 30 |
## Input data schema
Before you use the component, the following files must be ready in a Cloud Storage bucket:
- A Beam Python code file.
- A `requirements.txt` file which includes a list of dependent packages.
The Beam Python code should follow the [Beam programming guide](https://beam.apache.org/documentation/programming-guide/) as well as the following additional requirements to be compatible with this component:
- It accepts the command line arguments `--project`, `--region`, `--temp_location`, `--staging_location`, which are [standard Dataflow Runner options](https://cloud.google.com/dataflow/docs/guides/specifying-exec-params#setting-other-cloud-pipeline-options).
- It enables `info logging` before the start of a Cloud Dataflow job in the Python code. This is important to allow the component to track the status and ID of the job that is created. For example, calling `logging.getLogger().setLevel(logging.INFO)` before any other code.
## Output
Name | Description
:--- | :----------
job_id | The id of the Cloud Dataflow job that is created.
## Cautions & requirements
To use the components, the following requirements must be met:
- Cloud Dataflow API is enabled.
- The component is running under a secret Kubeflow user service account in a Kubeflow Pipeline cluster. For example:
```
component_op(...)
```
The Kubeflow user service account is a member of:
- `roles/dataflow.developer` role of the project.
- `roles/storage.objectViewer` role of the Cloud Storage Objects `python_file_path` and `requirements_file_path`.
- `roles/storage.objectCreator` role of the Cloud Storage Object `staging_dir`.
## Detailed description
The component does several things during the execution:
- Downloads `python_file_path` and `requirements_file_path` to local files.
- Starts a subprocess to launch the Python program.
- Monitors the logs produced from the subprocess to extract the Cloud Dataflow job information.
- Stores the Cloud Dataflow job information in `staging_dir` so the job can be resumed in case of failure.
- Waits for the job to finish.
# Setup
```
project = 'Input your PROJECT ID'
region = 'Input GCP region' # For example, 'us-central1'
output = 'Input your GCS bucket name' # No ending slash
```
## Install Pipeline SDK
```
!python3 -m pip install 'kfp>=0.1.31' --quiet
```
## Load the component using KFP SDK
```
import kfp.components as comp
dataflow_python_op = comp.load_component_from_url(
'https://raw.githubusercontent.com/kubeflow/pipelines/master/components/gcp/dataflow/launch_python/component.yaml')
help(dataflow_python_op)
```
## Use the wordcount python sample
In this sample, we run a wordcount sample code in a Kubeflow Pipeline. The output will be stored in a Cloud Storage bucket. Here is the sample code:
```
!gsutil cat gs://ml-pipeline-playground/samples/dataflow/wc/wc.py
```
## Example pipeline that uses the component
```
import kfp
import kfp.dsl as dsl
import json
output_file = '{}/wc/wordcount.out'.format(output)
@dsl.pipeline(
name='dataflow-launch-python-pipeline',
description='Dataflow launch python pipeline'
)
def pipeline(
python_file_path = 'gs://ml-pipeline/sample-pipeline/word-count/wc.py',
project_id = project,
region = region,
staging_dir = output,
requirements_file_path = 'gs://ml-pipeline/sample-pipeline/word-count/requirements.txt',
args = json.dumps([
'--output', output_file
]),
wait_interval = 30
):
dataflow_python_op(
python_file_path = python_file_path,
project_id = project_id,
region = region,
staging_dir = staging_dir,
requirements_file_path = requirements_file_path,
args = args,
wait_interval = wait_interval)
```
## Submit the pipeline for execution
```
kfp.Client().create_run_from_pipeline_func(pipeline, arguments={})
```
#### Inspect the output
```
!gsutil cat $output_file
```
## References
* [Component python code](https://github.com/kubeflow/pipelines/blob/master/components/gcp/container/component_sdk/python/kfp_component/google/dataflow/_launch_python.py)
* [Component docker file](https://github.com/kubeflow/pipelines/blob/master/components/gcp/container/Dockerfile)
* [Sample notebook](https://github.com/kubeflow/pipelines/blob/master/components/gcp/dataflow/launch_python/sample.ipynb)
* [Dataflow Python Quickstart](https://cloud.google.com/dataflow/docs/quickstarts/quickstart-python)
|
github_jupyter
|
component_op(...)
project = 'Input your PROJECT ID'
region = 'Input GCP region' # For example, 'us-central1'
output = 'Input your GCS bucket name' # No ending slash
!python3 -m pip install 'kfp>=0.1.31' --quiet
import kfp.components as comp
dataflow_python_op = comp.load_component_from_url(
'https://raw.githubusercontent.com/kubeflow/pipelines/master/components/gcp/dataflow/launch_python/component.yaml')
help(dataflow_python_op)
!gsutil cat gs://ml-pipeline-playground/samples/dataflow/wc/wc.py
import kfp
import kfp.dsl as dsl
import json
output_file = '{}/wc/wordcount.out'.format(output)
@dsl.pipeline(
name='dataflow-launch-python-pipeline',
description='Dataflow launch python pipeline'
)
def pipeline(
python_file_path = 'gs://ml-pipeline/sample-pipeline/word-count/wc.py',
project_id = project,
region = region,
staging_dir = output,
requirements_file_path = 'gs://ml-pipeline/sample-pipeline/word-count/requirements.txt',
args = json.dumps([
'--output', output_file
]),
wait_interval = 30
):
dataflow_python_op(
python_file_path = python_file_path,
project_id = project_id,
region = region,
staging_dir = staging_dir,
requirements_file_path = requirements_file_path,
args = args,
wait_interval = wait_interval)
kfp.Client().create_run_from_pipeline_func(pipeline, arguments={})
!gsutil cat $output_file
| 0.342572 | 0.951278 |
```
!pip install gluoncv # -i https://opentuna.cn/pypi/web/simple
%matplotlib inline
```
4. Transfer Learning with Your Own Image Dataset
=======================================================
Dataset size is a big factor in the performance of deep learning models.
``ImageNet`` has over one million labeled images, but
we often don't have so much labeled data in other domains.
Training a deep learning models on small datasets may lead to severe overfitting.
Transfer learning is a technique that addresses this problem.
The idea is simple: we can start training with a pre-trained model,
instead of starting from scratch.
As Isaac Newton said, "If I have seen further it is by standing on the
shoulders of Giants".
In this tutorial, we will explain the basics of transfer
learning, and apply it to the ``MINC-2500`` dataset.
Data Preparation
----------------
`MINC <http://opensurfaces.cs.cornell.edu/publications/minc/>`__ is
short for Materials in Context Database, provided by Cornell.
``MINC-2500`` is a resized subset of ``MINC`` with 23 classes, and 2500
images in each class. It is well labeled and has a moderate size thus is
perfect to be our example.
|image-minc|
To start, we first download ``MINC-2500`` from
`here <http://opensurfaces.cs.cornell.edu/publications/minc/>`__.
Suppose we have the data downloaded to ``~/data/`` and
extracted to ``~/data/minc-2500``.
After extraction, it occupies around 2.6GB disk space with the following
structure:
::
minc-2500
├── README.txt
├── categories.txt
├── images
└── labels
The ``images`` folder has 23 sub-folders for 23 classes, and ``labels``
folder contains five different splits for training, validation, and test.
We have written a script to prepare the data for you:
:download:`Download prepare_minc.py<../../../scripts/classification/finetune/prepare_minc.py>`
Run it with
::
python prepare_minc.py --data ~/data/minc-2500 --split 1
Now we have the following structure:
::
minc-2500
├── categories.txt
├── images
├── labels
├── README.txt
├── test
├── train
└── val
In order to go through this tutorial within a reasonable amount of time,
we have prepared a small subset of the ``MINC-2500`` dataset,
but you should substitute it with the original dataset for your experiments.
We can download and extract it with:
Hyperparameters
----------
First, let's import all other necessary libraries.
```
import mxnet as mx
import numpy as np
import os, time, shutil
from mxnet import gluon, image, init, nd
from mxnet import autograd as ag
from mxnet.gluon import nn
from mxnet.gluon.data.vision import transforms
from gluoncv.utils import makedirs
from gluoncv.model_zoo import get_model
```
We set the hyperparameters as following:
```
classes = 5
epochs = 100
lr = 0.001
per_device_batch_size = 32
momentum = 0.9
wd = 0.0001
lr_factor = 0.75
lr_steps = [10, 20, 30, np.inf]
num_gpus = 1
num_workers = 8
ctx = [mx.gpu(i) for i in range(num_gpus)] if num_gpus > 0 else [mx.cpu()]
batch_size = per_device_batch_size * max(num_gpus, 1)
```
Things to keep in mind:
1. ``epochs = 5`` is just for this tutorial with the tiny dataset. please change it to a larger number in your experiments, for instance 40.
2. ``per_device_batch_size`` is also set to a small number. In your experiments you can try larger number like 64.
3. remember to tune ``num_gpus`` and ``num_workers`` according to your machine.
4. A pre-trained model is already in a pretty good status. So we can start with a small ``lr``.
Data Augmentation
-----------------
In transfer learning, data augmentation can also help.
We use the following augmentation in training:
2. Randomly crop the image and resize it to 224x224
3. Randomly flip the image horizontally
4. Randomly jitter color and add noise
5. Transpose the data from height*width*num_channels to num_channels*height*width, and map values from [0, 255] to [0, 1]
6. Normalize with the mean and standard deviation from the ImageNet dataset.
```
jitter_param = 0.4
lighting_param = 0.1
transform_train = transforms.Compose([
transforms.RandomResizedCrop(224),
transforms.RandomFlipLeftRight(),
transforms.RandomColorJitter(brightness=jitter_param, contrast=jitter_param,
saturation=jitter_param),
transforms.RandomLighting(lighting_param),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])
transform_test = transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])
```
With the data augmentation functions, we can define our data loaders:
```
!wget -O image_classification.zip "https://datalab.s3.amazonaws.com/data/image_classification.zip?AWSAccessKeyId=AKIAYNUCDPLSDWHHQJ7Y&Signature=LV6WeQbTIHylCBov79KW8iRigPg%3D&Expires=1637340066"
!unzip -q image_classification.zip
!mkdir -p data/train
!mkdir -p data/test
import os
base_dir = 'image_classification'
filenames = os.listdir(base_dir)
class_names = []
for filename in filenames:
if os.path.isdir(os.path.join(base_dir, filename)) and not filename.startswith('.'):
class_names.append(filename)
if not os.path.exists(os.path.join('data/train/', filename)):
os.mkdir(os.path.join('data/train/', filename))
os.mkdir(os.path.join('data/test/', filename))
from sklearn.model_selection import train_test_split
for name in class_names:
filenames = os.listdir(os.path.join(base_dir, name))
print(name, len(filenames))
train_filenames, test_filenames = train_test_split(filenames, test_size=0.3)
for filename in train_filenames:
os.system('cp '+os.path.join(base_dir, name, filename)+' '+os.path.join('data/train/', name, filename))
for filename in test_filenames:
os.system('cp '+os.path.join(base_dir, name, filename)+' '+os.path.join('data/test/', name, filename))
path = './data'
train_path = os.path.join(path, 'train')
val_path = os.path.join(path, 'test')
test_path = os.path.join(path, 'test')
train_data = gluon.data.DataLoader(
gluon.data.vision.ImageFolderDataset(train_path).transform_first(transform_train),
batch_size=batch_size, shuffle=True, num_workers=num_workers)
val_data = gluon.data.DataLoader(
gluon.data.vision.ImageFolderDataset(val_path).transform_first(transform_test),
batch_size=batch_size, shuffle=False, num_workers = num_workers)
test_data = gluon.data.DataLoader(
gluon.data.vision.ImageFolderDataset(test_path).transform_first(transform_test),
batch_size=batch_size, shuffle=False, num_workers = num_workers)
print(gluon.data.vision.ImageFolderDataset(train_path).synsets)
print(gluon.data.vision.ImageFolderDataset(val_path).synsets)
print(gluon.data.vision.ImageFolderDataset(test_path).synsets)
```
Note that only ``train_data`` uses ``transform_train``, while
``val_data`` and ``test_data`` use ``transform_test`` to produce deterministic
results for evaluation.
Model and Trainer
-----------------
We use a pre-trained ``ResNet50_v2`` model, which has balanced accuracy and
computation cost.
```
model_name = 'ResNet50_v2'
# model_name = 'ResNet152_v1d'
finetune_net = get_model(model_name, pretrained=True)
with finetune_net.name_scope():
finetune_net.output = nn.Dense(classes)
finetune_net.output.initialize(init.Xavier(), ctx = ctx)
finetune_net.collect_params().reset_ctx(ctx)
finetune_net.hybridize()
trainer = gluon.Trainer(finetune_net.collect_params(), 'sgd', {
'learning_rate': lr, 'momentum': momentum, 'wd': wd})
metric = mx.metric.Accuracy()
L = gluon.loss.SoftmaxCrossEntropyLoss()
```
Here's an illustration of the pre-trained model
and our newly defined model:
|image-model|
Specifically, we define the new model by::
1. load the pre-trained model
2. re-define the output layer for the new task
3. train the network
This is called "fine-tuning", i.e. we have a model trained on another task,
and we would like to tune it for the dataset we have in hand.
We define a evaluation function for validation and testing.
```
def test(net, val_data, ctx):
metric = mx.metric.Accuracy()
for i, batch in enumerate(val_data):
data = gluon.utils.split_and_load(batch[0], ctx_list=ctx, batch_axis=0, even_split=False)
label = gluon.utils.split_and_load(batch[1], ctx_list=ctx, batch_axis=0, even_split=False)
outputs = [net(X) for X in data]
metric.update(label, outputs)
# print(label, outputs)
return metric.get()
```
Training Loop
-------------
Following is the main training loop. It is the same as the loop in
`CIFAR10 <dive_deep_cifar10.html>`__
and ImageNet.
<div class="alert alert-info"><h4>Note</h4><p>Once again, in order to go through the tutorial faster, we are training on a small
subset of the original ``MINC-2500`` dataset, and for only 5 epochs. By training on the
full dataset with 40 epochs, it is expected to get accuracy around 80% on test data.</p></div>
```
lr_counter = 0
num_batch = len(train_data)
for epoch in range(epochs):
if epoch == lr_steps[lr_counter]:
trainer.set_learning_rate(trainer.learning_rate*lr_factor)
lr_counter += 1
tic = time.time()
train_loss = 0
metric.reset()
for i, batch in enumerate(train_data):
# print(i)
data = gluon.utils.split_and_load(batch[0], ctx_list=ctx, batch_axis=0, even_split=False)
label = gluon.utils.split_and_load(batch[1], ctx_list=ctx, batch_axis=0, even_split=False)
# print(label)
with ag.record():
outputs = [finetune_net(X) for X in data]
loss = [L(yhat, y) for yhat, y in zip(outputs, label)]
for l in loss:
l.backward()
trainer.step(batch_size)
train_loss += sum([l.mean().asscalar() for l in loss]) / len(loss)
metric.update(label, outputs)
_, train_acc = metric.get()
train_loss /= num_batch
_, val_acc = test(finetune_net, val_data, ctx)
print('[Epoch %d] Train-acc: %.3f, loss: %.3f | Val-acc: %.3f | time: %.1f' %
(epoch, train_acc, train_loss, val_acc, time.time() - tic))
_, test_acc = test(finetune_net, test_data, ctx)
print('[Finished] Test-acc: %.3f' % (test_acc))
print('[Finished] Test-acc: %.3f' % (test_acc))
!mkdir endpoint/model
finetune_net.save_parameters('endpoint/model/model-0000.params')
```
Next
----
Now that you have learned to muster the power of transfer
learning, to learn more about training a model on
ImageNet, please read `this tutorial <dive_deep_imagenet.html>`__.
The idea of transfer learning is the basis of
`object detection <../examples_detection/index.html>`_ and
`semantic segmentation <../examples_segmentation/index.html>`_,
the next two chapters of our tutorial.
.. |image-minc| image:: https://raw.githubusercontent.com/dmlc/web-data/master/gluoncv/datasets/MINC-2500.png
.. |image-model| image:: https://zh.gluon.ai/_images/fine-tuning.svg
|
github_jupyter
|
!pip install gluoncv # -i https://opentuna.cn/pypi/web/simple
%matplotlib inline
import mxnet as mx
import numpy as np
import os, time, shutil
from mxnet import gluon, image, init, nd
from mxnet import autograd as ag
from mxnet.gluon import nn
from mxnet.gluon.data.vision import transforms
from gluoncv.utils import makedirs
from gluoncv.model_zoo import get_model
classes = 5
epochs = 100
lr = 0.001
per_device_batch_size = 32
momentum = 0.9
wd = 0.0001
lr_factor = 0.75
lr_steps = [10, 20, 30, np.inf]
num_gpus = 1
num_workers = 8
ctx = [mx.gpu(i) for i in range(num_gpus)] if num_gpus > 0 else [mx.cpu()]
batch_size = per_device_batch_size * max(num_gpus, 1)
jitter_param = 0.4
lighting_param = 0.1
transform_train = transforms.Compose([
transforms.RandomResizedCrop(224),
transforms.RandomFlipLeftRight(),
transforms.RandomColorJitter(brightness=jitter_param, contrast=jitter_param,
saturation=jitter_param),
transforms.RandomLighting(lighting_param),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])
transform_test = transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
])
!wget -O image_classification.zip "https://datalab.s3.amazonaws.com/data/image_classification.zip?AWSAccessKeyId=AKIAYNUCDPLSDWHHQJ7Y&Signature=LV6WeQbTIHylCBov79KW8iRigPg%3D&Expires=1637340066"
!unzip -q image_classification.zip
!mkdir -p data/train
!mkdir -p data/test
import os
base_dir = 'image_classification'
filenames = os.listdir(base_dir)
class_names = []
for filename in filenames:
if os.path.isdir(os.path.join(base_dir, filename)) and not filename.startswith('.'):
class_names.append(filename)
if not os.path.exists(os.path.join('data/train/', filename)):
os.mkdir(os.path.join('data/train/', filename))
os.mkdir(os.path.join('data/test/', filename))
from sklearn.model_selection import train_test_split
for name in class_names:
filenames = os.listdir(os.path.join(base_dir, name))
print(name, len(filenames))
train_filenames, test_filenames = train_test_split(filenames, test_size=0.3)
for filename in train_filenames:
os.system('cp '+os.path.join(base_dir, name, filename)+' '+os.path.join('data/train/', name, filename))
for filename in test_filenames:
os.system('cp '+os.path.join(base_dir, name, filename)+' '+os.path.join('data/test/', name, filename))
path = './data'
train_path = os.path.join(path, 'train')
val_path = os.path.join(path, 'test')
test_path = os.path.join(path, 'test')
train_data = gluon.data.DataLoader(
gluon.data.vision.ImageFolderDataset(train_path).transform_first(transform_train),
batch_size=batch_size, shuffle=True, num_workers=num_workers)
val_data = gluon.data.DataLoader(
gluon.data.vision.ImageFolderDataset(val_path).transform_first(transform_test),
batch_size=batch_size, shuffle=False, num_workers = num_workers)
test_data = gluon.data.DataLoader(
gluon.data.vision.ImageFolderDataset(test_path).transform_first(transform_test),
batch_size=batch_size, shuffle=False, num_workers = num_workers)
print(gluon.data.vision.ImageFolderDataset(train_path).synsets)
print(gluon.data.vision.ImageFolderDataset(val_path).synsets)
print(gluon.data.vision.ImageFolderDataset(test_path).synsets)
model_name = 'ResNet50_v2'
# model_name = 'ResNet152_v1d'
finetune_net = get_model(model_name, pretrained=True)
with finetune_net.name_scope():
finetune_net.output = nn.Dense(classes)
finetune_net.output.initialize(init.Xavier(), ctx = ctx)
finetune_net.collect_params().reset_ctx(ctx)
finetune_net.hybridize()
trainer = gluon.Trainer(finetune_net.collect_params(), 'sgd', {
'learning_rate': lr, 'momentum': momentum, 'wd': wd})
metric = mx.metric.Accuracy()
L = gluon.loss.SoftmaxCrossEntropyLoss()
def test(net, val_data, ctx):
metric = mx.metric.Accuracy()
for i, batch in enumerate(val_data):
data = gluon.utils.split_and_load(batch[0], ctx_list=ctx, batch_axis=0, even_split=False)
label = gluon.utils.split_and_load(batch[1], ctx_list=ctx, batch_axis=0, even_split=False)
outputs = [net(X) for X in data]
metric.update(label, outputs)
# print(label, outputs)
return metric.get()
lr_counter = 0
num_batch = len(train_data)
for epoch in range(epochs):
if epoch == lr_steps[lr_counter]:
trainer.set_learning_rate(trainer.learning_rate*lr_factor)
lr_counter += 1
tic = time.time()
train_loss = 0
metric.reset()
for i, batch in enumerate(train_data):
# print(i)
data = gluon.utils.split_and_load(batch[0], ctx_list=ctx, batch_axis=0, even_split=False)
label = gluon.utils.split_and_load(batch[1], ctx_list=ctx, batch_axis=0, even_split=False)
# print(label)
with ag.record():
outputs = [finetune_net(X) for X in data]
loss = [L(yhat, y) for yhat, y in zip(outputs, label)]
for l in loss:
l.backward()
trainer.step(batch_size)
train_loss += sum([l.mean().asscalar() for l in loss]) / len(loss)
metric.update(label, outputs)
_, train_acc = metric.get()
train_loss /= num_batch
_, val_acc = test(finetune_net, val_data, ctx)
print('[Epoch %d] Train-acc: %.3f, loss: %.3f | Val-acc: %.3f | time: %.1f' %
(epoch, train_acc, train_loss, val_acc, time.time() - tic))
_, test_acc = test(finetune_net, test_data, ctx)
print('[Finished] Test-acc: %.3f' % (test_acc))
print('[Finished] Test-acc: %.3f' % (test_acc))
!mkdir endpoint/model
finetune_net.save_parameters('endpoint/model/model-0000.params')
| 0.679179 | 0.925769 |
## Diffusion Tensor Imaging (DTI)
Diffusion tensor imaging or "DTI" refers to images describing diffusion with a tensor model. DTI is derived from preprocessed diffusion weighted imaging (DWI) data. First proposed by Basser and colleagues ([Basser, 1994](https://www.ncbi.nlm.nih.gov/pubmed/8130344)), the diffusion tensor model describes diffusion characteristics within an imaging voxel. This model has been very influential in demonstrating the utility of the diffusion MRI in characterizing the microstructure of white matter and the biophysical properties (inferred from local diffusion properties). The DTI model is still a commonly used model to investigate white matter.
The tensor models the diffusion signal mathematically as:

Where  is a unit vector in 3D space indicating the direction of measurement and b are the parameters of the measurement, such as the strength and duration of diffusion-weighting gradient.  is the diffusion-weighted signal measured and  is the signal conducted in a measurement with no diffusion weighting.  is a positive-definite quadratic form, which contains six free parameters to be fit. These six parameters are:

The diffusion matrix is a variance-covariance matrix of the diffusivity along the three spatial dimensions. Note that we can assume that the diffusivity has antipodal symmetry, so elements across the diagonal of the matrix are equal. For example: . This is why there are only 6 free parameters to estimate here.
Tensors are represented by ellipsoids characterized by calculated eigenvalues () and eigenvectors () from the previously described matrix. The computed eigenvalues and eigenvectors are normally sorted in descending magnitude (i.e. ). Eigenvalues are always strictly positive in the context of dMRI and are measured in mm^2/s. In the DTI model, the largest eigenvalue gives the principal direction of the diffusion tensor, and the other two eigenvectors span the orthogonal plane to the former direction.

_Adapted from Jelison et al., 2004_
In the following example, we will walk through how to model a diffusion dataset. While there are a number of diffusion models, many of which are implemented in `DIPY`. However, for the purposes of this lesson, we will focus on the tensor model described above.
### Reconstruction with the `dipy.reconst` module
The `reconst` module contains implementations of the following models:
* Tensor (Basser et al., 1994)
* Constrained Spherical Deconvolution (Tournier et al. 2007)
* Diffusion Kurtosis (Jensen et al. 2005)
* DSI (Wedeen et al. 2008)
* DSI with deconvolution (Canales-Rodriguez et al. 2010)
* Generalized Q Imaging (Yeh et al. 2010)
* MAPMRI (Özarslan et al. 2013)
* SHORE (Özarslan et al. 2008)
* CSA (Aganj et al. 2009)
* Q ball (Descoteaux et al. 2007)
* OPDT (Tristan-Vega et al. 2010)
* Sparse Fascicle Model (Rokem et al. 2015)
The different algorithms implemented in the module all share a similar conceptual structure:
* `ReconstModel` objects (e.g. `TensorModel`) carry the parameters that are required in order to fit a model. For example, the directions and magnitudes of the gradients that were applied in the experiment. `TensorModel` objects have a `fit` method, which takes in data, and returns a `ReconstFit` object. This is where a lot of the heavy lifting of the processing will take place.
* `ReconstFit` objects carry the model that was used to generate the object. They also include the parameters that were estimated during fitting of the data. They have methods to calculate derived statistics, which can differ from model to model. All objects also have an orientation distribution function (`odf`), and most (but not all) contain a `predict` method, which enables the prediction of another dataset based on the current gradient table.
### Reconstruction with the DTI model
Let's get started! First, we will need to grab **preprocessed** DWI files and load them! We will also load in the anatomical image to use as a reference later on!
```
import bids
from bids.layout import BIDSLayout
from dipy.io.gradients import read_bvals_bvecs
from dipy.core.gradients import gradient_table
from nilearn import image as img
import nibabel as nib
bids.config.set_option('extension_initial_dot', True)
deriv_layout = BIDSLayout("../../../data/ds000221/derivatives", validate=False)
subj = "010006"
# Grab the transformed t1 file for reference
t1 = deriv_layout.get(subject=subj, space="dwi",
extension='nii.gz', return_type='file')[0]
# Recall the preprocessed data is no longer in BIDS - we will directly grab these files
dwi = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.nii.gz" % subj
bval = "../../../data/ds000221/sub-%s/ses-01/dwi/sub-%s_ses-01_dwi.bval" % (
subj, subj)
bvec = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.eddy_rotated_bvecs" % subj
t1_data = img.load_img(t1)
dwi_data = img.load_img(dwi)
gt_bvals, gt_bvecs = read_bvals_bvecs(bval, bvec)
gtab = gradient_table(gt_bvals, gt_bvecs)
```
Next, we need to create the tensor model using our gradient table and then fit the model using our data! We will start by creating a mask from our data and apply it to avoid calculating tensors on the background! This can be done using `DIPY`'s mask module. Then, we will our data!
```
import dipy.reconst.dti as dti
from dipy.segment.mask import median_otsu
dwi_data = dwi_data.get_fdata() # We re-use the variable for memory purposes
dwi_data, dwi_mask = median_otsu(dwi_data, vol_idx=[0], numpass=1) # Specify the volume index to the b0 volumes
dti_model = dti.TensorModel(gtab)
dti_fit = dti_model.fit(dwi_data, mask=dwi_mask) # This step may take a while
```
The fit method creates a <code>TensorFit</code> object which contains the fitting parameters and other attributes of the model. A number of quantitative scalar metrics can be derived from the eigenvalues! In this tutorial, we will cover fractional anisotropy, mean diffusivity, axial diffusivity, and radial diffusivity. Each of these scalar, rotationally invariant metrics were calculated in the previous fitting step!
### Fractional anisotropy (FA)
Fractional anisotropy (FA) characterizes the degree to which the distribution of diffusion in an imaging voxel is directional. That is, whether there is relatively unrestricted diffusion in a particular direction.
Mathematically, FA is defined as the normalized variance of the eigenvalues of the tensor:

Values of FA vary between 0 and 1 (unitless). In the cases of perfect, isotropic diffusion, , the diffusion tensor is a sphere and FA = 0. If the first two eigenvalues are equal the tensor will be oblate or planar, whereas if the first eigenvalue is larger than the other two, it will have the mentioned ellipsoid shape: as diffusion progressively becomes more anisotropic, eigenvalues become more unequal, causing the tensor to be elongated, with FA approaching 1. Note that FA should be interpreted carefully. It may be an indication of the density of packing fibers in a voxel and the amount of myelin wrapped around those axons, but it is not always a measure of "tissue integrity".
Let's take a look at what the FA map looks like! An FA map is a gray-scale image, where higher intensities reflect more anisotropic diffuse regions.
_Note: we will have to first create the image from the array, making use of the reference anatomical_
```
from nilearn import plotting as plot
import matplotlib.pyplot as plt # To enable plotting
%matplotlib inline
fa_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.fa)
plot.plot_anat(fa_img, cut_coords=(0, -29, 20))
```
Derived from partial volume effects in imaging voxels due to the presence of different tissues, noise in the measurements and numerical errors, the DTI model estimation may yield negative eigenvalues. Such *degenerate* case is not physically meaningful. These values are usually revealed as black or 0-valued pixels in FA maps.
FA is a central value in dMRI: large FA values imply that the underlying fiber populations have a very coherent orientation, whereas lower FA values point to voxels containing multiple fiber crossings. Lowest FA values are indicative of non-white matter tissue in healthy brains (see, for example, Alexander et al.'s "Diffusion Tensor Imaging of the Brain". Neurotherapeutics 4, 316-329 (2007), and Jeurissen et al.'s "Investigating the Prevalence of Complex Fiber Configurations in White Matter Tissue with Diffusion Magnetic Resonance Imaging". Hum. Brain Mapp. 2012, 34(11) pp. 2747-2766).
### Mean diffusivity (MD)
An often used complimentary measure to FA is mean diffusivity (MD). MD is a measure of the degree of diffusion, independent of direction. This is sometimes known as the apparent diffusion coefficient (ADC). Mathematically, MD is computed as the mean eigenvalues of the tensor and is measured in mm^2/s.

Similar to the previous FA image, let's take a look at what the MD map looks like. Again, higher intensities reflect higher mean diffusivity!
```
%matplotlib inline
md_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.md)
# Arbitrarily set min and max of color bar
plot.plot_anat(md_img, cut_coords=(0, -29, 20), vmin=0, vmax=0.01)
```
### Axial and radial diffusivity (AD & RD)
The final two metrics we will discuss are axial diffusivity (AD) and radial diffusivity (RD). Two tensors with different shapes may yield the same FA values, and additional measures such as AD and RD are required to further characterize the tensor. AD describes the diffusion rate along the primary axis of diffusion, along , or parallel to the axon (and hence, some works refer to it as the *parallel diffusivity*). On the other hand, RD reflects the average diffusivity along the other two minor axes (being named as *perpendicular diffusivity* in some works) (). Both are measured in mm^2/s.

### Tensor visualizations
There are several ways of visualizing tensors. One way is using an RGB map, which overlays the primary diffusion orientation on an FA map. The colours of this map encodes the diffusion orientation. Note that this map provides no directional information (e.g. whether the diffusion flows from right-to-left or vice-versa). To do this with <code>DIPY</code>, we can use the <code>color_fa</code> function. The colours map to the following orientations:
* Red = Left / Right
* Green = Anterior / Posterior
* Blue = Superior / Inferior
_Note: The plotting functions in <code>nilearn</code> are unable to visualize these RGB maps. However, we can use the <code>matplotlib</code> library to view these images._
```
from scipy import ndimage # To rotate image for visualization purposes
from dipy.reconst.dti import color_fa
%matplotlib inline
RGB_map = color_fa(dti_fit.fa, dti_fit.evecs)
fig, ax = plt.subplots(1, 3, figsize=(10, 10))
ax[0].imshow(ndimage.rotate(
RGB_map[:, RGB_map.shape[1]//2, :, :], 90, reshape=False))
ax[1].imshow(ndimage.rotate(
RGB_map[RGB_map.shape[0]//2, :, :, :], 90, reshape=False))
ax[2].imshow(ndimage.rotate(
RGB_map[:, :, RGB_map.shape[2]//2, :], 90, reshape=False))
```
Another way of viewing the tensors is to visualize the diffusion tensor in each imaging voxel with colour encoding (we will refer you to the [`Dipy` documentation](https://dipy.org/tutorials/) for the steps to perform this type of visualization as it can be memory intensive). Below is an example image of such tensor visualization.

### Some notes on DTI
DTI is only one of many models and is one of the simplest models available for modelling diffusion. While it is used for many studies, there are also some drawbacks (e.g. ability to distinguish multiple fibre orientations in an imaging voxel). Examples of this can be seen below!

_Sourced from Sotiropoulos and Zalesky (2017). Building connectomes using diffusion MRI: why, how, and but. NMR in Biomedicine. 4(32). e3752. doi:10.1002/nbm.3752._
Though other models are outside the scope of this lesson, we recommend looking into some of the pros and cons of each model (listed previously) to choose one best suited for your data!
## Exercise 1
Plot the axial and radial diffusivity maps of the example given. Start from fitting the preprocessed diffusion image.
## Solution
```
from bids.layout import BIDSLayout
from dipy.io.gradients import read_bvals_bvecs
from dipy.core.gradients import gradient_table
import dipy.reconst.dti as dti
from dipy.segment.mask import median_otsu
from nilearn import image as img
import nibabel as nib
deriv_layout = BIDSLayout("../../../data/ds000221/derivatives", validate=False)
subj = "010006"
t1 = deriv_layout.get(subject=subj, space="dwi",
extension='nii.gz', return_type='file')[0]
dwi = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.nii.gz" % subj
bval = "../../../data/ds000221/sub-%s/ses-01/dwi/sub-%s_ses-01_dwi.bval" % (
subj, subj)
bvec = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.eddy_rotated_bvecs" % subj
t1_data = img.load_img(t1)
dwi_data = img.load_img(dwi)
gt_bvals, gt_bvecs = read_bvals_bvecs(bval, bvec)
gtab = gradient_table(gt_bvals, gt_bvecs)
dwi_data = dwi_data.get_fdata()
dwi_data, dwi_mask = median_otsu(dwi_data, vol_idx=[0], numpass=1)
# Fit dti model
dti_model = dti.TensorModel(gtab)
dti_fit = dti_model.fit(dwi_data, mask=dwi_mask) # This step may take a while
# Plot axial diffusivity map
ad_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.ad)
plot.plot_anat(ad_img, cut_coords=(0, -29, 20), vmin=0, vmax=0.01)
# Plot radial diffusivity map
rd_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.rd)
plot.plot_anat(rd_img, cut_coords=(0, -29, 20), vmin=0, vmax=0.01)
```
|
github_jupyter
|
import bids
from bids.layout import BIDSLayout
from dipy.io.gradients import read_bvals_bvecs
from dipy.core.gradients import gradient_table
from nilearn import image as img
import nibabel as nib
bids.config.set_option('extension_initial_dot', True)
deriv_layout = BIDSLayout("../../../data/ds000221/derivatives", validate=False)
subj = "010006"
# Grab the transformed t1 file for reference
t1 = deriv_layout.get(subject=subj, space="dwi",
extension='nii.gz', return_type='file')[0]
# Recall the preprocessed data is no longer in BIDS - we will directly grab these files
dwi = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.nii.gz" % subj
bval = "../../../data/ds000221/sub-%s/ses-01/dwi/sub-%s_ses-01_dwi.bval" % (
subj, subj)
bvec = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.eddy_rotated_bvecs" % subj
t1_data = img.load_img(t1)
dwi_data = img.load_img(dwi)
gt_bvals, gt_bvecs = read_bvals_bvecs(bval, bvec)
gtab = gradient_table(gt_bvals, gt_bvecs)
import dipy.reconst.dti as dti
from dipy.segment.mask import median_otsu
dwi_data = dwi_data.get_fdata() # We re-use the variable for memory purposes
dwi_data, dwi_mask = median_otsu(dwi_data, vol_idx=[0], numpass=1) # Specify the volume index to the b0 volumes
dti_model = dti.TensorModel(gtab)
dti_fit = dti_model.fit(dwi_data, mask=dwi_mask) # This step may take a while
from nilearn import plotting as plot
import matplotlib.pyplot as plt # To enable plotting
%matplotlib inline
fa_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.fa)
plot.plot_anat(fa_img, cut_coords=(0, -29, 20))
%matplotlib inline
md_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.md)
# Arbitrarily set min and max of color bar
plot.plot_anat(md_img, cut_coords=(0, -29, 20), vmin=0, vmax=0.01)
from scipy import ndimage # To rotate image for visualization purposes
from dipy.reconst.dti import color_fa
%matplotlib inline
RGB_map = color_fa(dti_fit.fa, dti_fit.evecs)
fig, ax = plt.subplots(1, 3, figsize=(10, 10))
ax[0].imshow(ndimage.rotate(
RGB_map[:, RGB_map.shape[1]//2, :, :], 90, reshape=False))
ax[1].imshow(ndimage.rotate(
RGB_map[RGB_map.shape[0]//2, :, :, :], 90, reshape=False))
ax[2].imshow(ndimage.rotate(
RGB_map[:, :, RGB_map.shape[2]//2, :], 90, reshape=False))
from bids.layout import BIDSLayout
from dipy.io.gradients import read_bvals_bvecs
from dipy.core.gradients import gradient_table
import dipy.reconst.dti as dti
from dipy.segment.mask import median_otsu
from nilearn import image as img
import nibabel as nib
deriv_layout = BIDSLayout("../../../data/ds000221/derivatives", validate=False)
subj = "010006"
t1 = deriv_layout.get(subject=subj, space="dwi",
extension='nii.gz', return_type='file')[0]
dwi = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.nii.gz" % subj
bval = "../../../data/ds000221/sub-%s/ses-01/dwi/sub-%s_ses-01_dwi.bval" % (
subj, subj)
bvec = "../../../data/ds000221/derivatives/uncorrected_topup_eddy/sub-%s/ses-01/dwi/dwi.eddy_rotated_bvecs" % subj
t1_data = img.load_img(t1)
dwi_data = img.load_img(dwi)
gt_bvals, gt_bvecs = read_bvals_bvecs(bval, bvec)
gtab = gradient_table(gt_bvals, gt_bvecs)
dwi_data = dwi_data.get_fdata()
dwi_data, dwi_mask = median_otsu(dwi_data, vol_idx=[0], numpass=1)
# Fit dti model
dti_model = dti.TensorModel(gtab)
dti_fit = dti_model.fit(dwi_data, mask=dwi_mask) # This step may take a while
# Plot axial diffusivity map
ad_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.ad)
plot.plot_anat(ad_img, cut_coords=(0, -29, 20), vmin=0, vmax=0.01)
# Plot radial diffusivity map
rd_img = img.new_img_like(ref_niimg=t1_data, data=dti_fit.rd)
plot.plot_anat(rd_img, cut_coords=(0, -29, 20), vmin=0, vmax=0.01)
| 0.68616 | 0.99153 |
**Introduction and Workspace setting**
We collected a valueble dataset just before the election from random street interviews in kaduwela Colombo area in Sri Lanka in order to predict the winnning presidential election candidate of Sri Lanka in 2019 polls and collected people's rationale behind their decision and try to come up with policies that the people think the winner should bring forward. In order to collect above date, we have prepared a questionnaire with 12 questions and offered them to randomly selected persons at public places. The participation to the survey was completely on their preference and there was no persuation to get the data from individuals. Other than to road interviews, we have done the same survey on social media with the same questions and collected those responses separately.
> Dataset contains,
> 1. Road interviews data (face_to_face_road_interviews.csv)
> 2. Social media data (social_media_votes.csv)
Please go to our [github repo](https://github.com/PraAnj/srilanka-election-prediction-2019) for more information. This repo contains the questionnaire and the dataset along with analysis scripts. This dataset is publicly available so that anyone can use it for academic work.
```
library(tidyverse) # metapackage with lots of helpful functions
list.files(path = "../input/srilankanpresidentialelectionprediction2019")
```
### Loading data
```
roadInterviewData <- read.csv(file="../input/srilankanpresidentialelectionprediction2019/face_to_face_road_interviews.csv", header=TRUE, sep=",")
head(roadInterviewData)
summary(roadInterviewData$firstVote)
tabEducationVsCandidate <- table(roadInterviewData$education, roadInterviewData$firstVote)
ftable(tabEducationVsCandidate)
par(las=2, mar=c(12,5,5,5))
counts <- table(roadInterviewData$firstVote)
barplot(counts, main="Votes for Candidates", col=
c("red","maroon", "black", "yellow", "white", "green"), cex.main=2)
par(las=2, mar=c(1,1,1,1))
slices <- c(counts)
lbls <- c(colnames(tabEducationVsCandidate))
pct <- round(slices/sum(slices)*100)
lbls <- paste(lbls, pct) # add percents to labels
lbls <- paste(lbls,"%",sep="") # ad % to labels
pie(slices, labels = lbls, col=rainbow(length(slices)), main="Pie charts for Votes as a percentage", radius=1.5, cex.main=1.7, cex=1)
```
### Education Level of people vs selected Candidate
```
par(las=2, mar=c(12,5,5,5))
barplot(tabEducationVsCandidate, main="Education Level Vs Presidential Candidate", col=c("darkblue","red", "green", "yellow"),
legend = rownames(tabEducationVsCandidate), cex.lab=1, cex.main=1.7, args.legend = list(x = 'topright', bty='n'))
png(file = "test.jpg")
```
### Policies vs Candidates
```
tabPolicyVsCandidate <- table(roadInterviewData$policyInclination, roadInterviewData$firstVote)
ftable(tabPolicyVsCandidate)
par(las=2,mar=c(12,5,5,5))
barplot(tabPolicyVsCandidate, main="Policy Changes Vs Presidential Candidate",
col=c("darkblue","green", "red", "yellow", "black", "purple", "white", "blue"), cex.lab=2, cex.main=1.7,
legend = rownames(tabPolicyVsCandidate), args.legend = list(x='topright', bty='n'), ylim=c(0,30) )
```
### Income vs candidate
```
tabIncomeVsCandidate <- table(roadInterviewData$income, roadInterviewData$firstVote)
par(las=2,mar=c(12,5,5,5))
barplot(tabIncomeVsCandidate, main="Income Vs Presidential Candidate",
col=c("darkblue","white", "red", "yellow", "green"), cex.lab=2, cex.main=1.7,
legend = rownames(tabIncomeVsCandidate), args.legend = list(x='topright', bty='n'), ylim=c(0,30) )
```
### Age vs Candidate
```
tabAgeVsCandidate <- table(roadInterviewData$age, roadInterviewData$firstVote)
par(las=2,mar=c(12,5,5,5))
barplot(tabAgeVsCandidate, main="Age Vs Presidential Candidate",
col=c("darkblue","white", "red", "yellow", "green"), cex.lab=2, cex.main=1.7,
legend = rownames(tabAgeVsCandidate), args.legend = list(x='topright', bty='n'), ylim=c(0,30) )
```
### Gender vs Candidate
```
tabGenderVsCandidate <- table(roadInterviewData$gender, roadInterviewData$firstVote)
par(las=2,mar=c(12,5,5,5))
barplot(tabGenderVsCandidate, main="Gender Vs Presidential Candidate",
col=c("pink","blue"), cex.lab=2, cex.main=1.7,
legend = rownames(tabGenderVsCandidate), args.legend = list(x='topright', bty='n'), ylim=c(0,30) )
```
### Religion vs candidate
```
tabReligionVsCandidate <- table(roadInterviewData$religion, roadInterviewData$firstVote)
par(las=2,mar=c(12,5,5,5))
barplot(tabReligionVsCandidate, main="Religion Vs Presidential Candidate",
col=c("green","blue", "yellow"), cex.lab=2, cex.main=1.7,
legend = rownames(tabReligionVsCandidate), args.legend = list(x='topright', bty='n'), ylim=c(0,30) )
```
### Ethnicity vs candidate
```
tabEthnicityVsCandidate <- table(roadInterviewData$ethnicity, roadInterviewData$firstVote)
par(las=2,mar=c(12,5,5,5))
barplot(tabEthnicityVsCandidate, main="Ethnicity Vs Presidential Candidate",
col=c("green","blue", "yellow"), cex.lab=2, cex.main=1.7,
legend = rownames(tabEthnicityVsCandidate), args.legend = list(x='topright', bty='n'), ylim=c(0,30) )
# percentage <- round(counts/sum(counts)*100)
tableExecPresidency <- table(roadInterviewData$isExecutivePresidencyRequired, roadInterviewData$isExecutivePresidencyRequired)
counts <- table(roadInterviewData$isExecutivePresidencyRequired)
par(las=2, mar=c(1,5,1,3))
slices <- c(counts)
lbls <- c(colnames(tableExecPresidency))
pct <- round(slices/sum(slices)*100)
lbls <- paste(lbls, pct) # add percents to labels
lbls <- paste(lbls,"%",sep="") # ad % to labels
pie(slices, labels = lbls, col=rainbow(length(slices)), main="Does country needs an Executive presidency?", radius=1.5, cex.main=1.7, cex=1)
```
## Bootstrapping testing on winning candidate
#### Removing votes marked as "Not voting" and "Not Decided yet"
```
socialdataCleaned <- subset(roadInterviewData, (firstVote != 'Not voting' ))
socialdataCleaned <- subset(socialdataCleaned, (firstVote != 'Not Decided yet' ))
foo <- function(data, indices){
dt <- data[indices,]
tbl <- table(dt$firstVote)
t = as.data.frame(tbl)
t[,2] <- t[,2]/sum(t[,2])*100
c(mean(t[2,2]))
}
```
### Running bootstraping on data set with 1000 repititions
```
library(boot)
set.seed(12345)
myBootstrap <- boot(socialdataCleaned, foo, R=1000)
plot(myBootstrap, index=1)
```
### Calculate 95% confident interval for the percentage Gotabaya Rajapaksha will get
```
boot.ci(myBootstrap, index=1, type='norm')
```
**Threfore we can be 95% confident that Gotabaya Rajapaksha will get 48.27% to 78.67% in this presidential election and become the president !!**
### Combining Social media data
```
socialdata <- read.csv(file="../input/srilankanpresidentialelectionprediction2019/social_media_votes.csv", header=TRUE, sep=",")
head(socialdata)
```
### Combining road interviewed data frames and social media data
```
combined = rbind(roadInterviewData, socialdata)
combined <- subset(combined, firstVote != 'Not voting')
combined <- subset(combined, (firstVote != 'Not Decided yet' ))
tabEducationVsCandidate <- table(combined$education, combined$firstVote)
ftable(tabEducationVsCandidate)
par(las=2, mar=c(12,5,5,5))
barplot(tabEducationVsCandidate, main="Education Level Vs Presidential Candidate", col=c("darkblue","red", "green", "yellow"),
legend = rownames(tabEducationVsCandidate), cex.lab=1, cex.main=1.7, args.legend = list(x = 'topright', bty='n'))
```
**It can vishually be seen that most of the graduated people are voting Gotabaya Rajapaksha**
Lets do a Bootstrap experiment on how many graduated people will vote for Gotabaya Rajapaksha
### Running a bootstrapping on graguated people percentage voting for GR
```
graduatedPercentage <- function(data, indices){
dt <- data[indices,]
tbl <- table(dt$education, dt$firstVote)
tbl[2,] = tbl[2,]/sum(tbl[2,]) * 100
c(mean(tbl[2,2]))
}
set.seed(12345)
graduatedBootstrap <- boot(combined, graduatedPercentage, R=1000)
plot(graduatedBootstrap, index=1)
```
### Getting 95% Confidence interval
```
boot.ci(graduatedBootstrap, index=1, type='norm')
```
### Therefore we can be 95% confident that 47.86% to 75.11% of Graduated people will be voting for Gotabaya Rajapaska!
|
github_jupyter
|
library(tidyverse) # metapackage with lots of helpful functions
list.files(path = "../input/srilankanpresidentialelectionprediction2019")
roadInterviewData <- read.csv(file="../input/srilankanpresidentialelectionprediction2019/face_to_face_road_interviews.csv", header=TRUE, sep=",")
head(roadInterviewData)
summary(roadInterviewData$firstVote)
tabEducationVsCandidate <- table(roadInterviewData$education, roadInterviewData$firstVote)
ftable(tabEducationVsCandidate)
par(las=2, mar=c(12,5,5,5))
counts <- table(roadInterviewData$firstVote)
barplot(counts, main="Votes for Candidates", col=
c("red","maroon", "black", "yellow", "white", "green"), cex.main=2)
par(las=2, mar=c(1,1,1,1))
slices <- c(counts)
lbls <- c(colnames(tabEducationVsCandidate))
pct <- round(slices/sum(slices)*100)
lbls <- paste(lbls, pct) # add percents to labels
lbls <- paste(lbls,"%",sep="") # ad % to labels
pie(slices, labels = lbls, col=rainbow(length(slices)), main="Pie charts for Votes as a percentage", radius=1.5, cex.main=1.7, cex=1)
par(las=2, mar=c(12,5,5,5))
barplot(tabEducationVsCandidate, main="Education Level Vs Presidential Candidate", col=c("darkblue","red", "green", "yellow"),
legend = rownames(tabEducationVsCandidate), cex.lab=1, cex.main=1.7, args.legend = list(x = 'topright', bty='n'))
png(file = "test.jpg")
tabPolicyVsCandidate <- table(roadInterviewData$policyInclination, roadInterviewData$firstVote)
ftable(tabPolicyVsCandidate)
par(las=2,mar=c(12,5,5,5))
barplot(tabPolicyVsCandidate, main="Policy Changes Vs Presidential Candidate",
col=c("darkblue","green", "red", "yellow", "black", "purple", "white", "blue"), cex.lab=2, cex.main=1.7,
legend = rownames(tabPolicyVsCandidate), args.legend = list(x='topright', bty='n'), ylim=c(0,30) )
tabIncomeVsCandidate <- table(roadInterviewData$income, roadInterviewData$firstVote)
par(las=2,mar=c(12,5,5,5))
barplot(tabIncomeVsCandidate, main="Income Vs Presidential Candidate",
col=c("darkblue","white", "red", "yellow", "green"), cex.lab=2, cex.main=1.7,
legend = rownames(tabIncomeVsCandidate), args.legend = list(x='topright', bty='n'), ylim=c(0,30) )
tabAgeVsCandidate <- table(roadInterviewData$age, roadInterviewData$firstVote)
par(las=2,mar=c(12,5,5,5))
barplot(tabAgeVsCandidate, main="Age Vs Presidential Candidate",
col=c("darkblue","white", "red", "yellow", "green"), cex.lab=2, cex.main=1.7,
legend = rownames(tabAgeVsCandidate), args.legend = list(x='topright', bty='n'), ylim=c(0,30) )
tabGenderVsCandidate <- table(roadInterviewData$gender, roadInterviewData$firstVote)
par(las=2,mar=c(12,5,5,5))
barplot(tabGenderVsCandidate, main="Gender Vs Presidential Candidate",
col=c("pink","blue"), cex.lab=2, cex.main=1.7,
legend = rownames(tabGenderVsCandidate), args.legend = list(x='topright', bty='n'), ylim=c(0,30) )
tabReligionVsCandidate <- table(roadInterviewData$religion, roadInterviewData$firstVote)
par(las=2,mar=c(12,5,5,5))
barplot(tabReligionVsCandidate, main="Religion Vs Presidential Candidate",
col=c("green","blue", "yellow"), cex.lab=2, cex.main=1.7,
legend = rownames(tabReligionVsCandidate), args.legend = list(x='topright', bty='n'), ylim=c(0,30) )
tabEthnicityVsCandidate <- table(roadInterviewData$ethnicity, roadInterviewData$firstVote)
par(las=2,mar=c(12,5,5,5))
barplot(tabEthnicityVsCandidate, main="Ethnicity Vs Presidential Candidate",
col=c("green","blue", "yellow"), cex.lab=2, cex.main=1.7,
legend = rownames(tabEthnicityVsCandidate), args.legend = list(x='topright', bty='n'), ylim=c(0,30) )
# percentage <- round(counts/sum(counts)*100)
tableExecPresidency <- table(roadInterviewData$isExecutivePresidencyRequired, roadInterviewData$isExecutivePresidencyRequired)
counts <- table(roadInterviewData$isExecutivePresidencyRequired)
par(las=2, mar=c(1,5,1,3))
slices <- c(counts)
lbls <- c(colnames(tableExecPresidency))
pct <- round(slices/sum(slices)*100)
lbls <- paste(lbls, pct) # add percents to labels
lbls <- paste(lbls,"%",sep="") # ad % to labels
pie(slices, labels = lbls, col=rainbow(length(slices)), main="Does country needs an Executive presidency?", radius=1.5, cex.main=1.7, cex=1)
socialdataCleaned <- subset(roadInterviewData, (firstVote != 'Not voting' ))
socialdataCleaned <- subset(socialdataCleaned, (firstVote != 'Not Decided yet' ))
foo <- function(data, indices){
dt <- data[indices,]
tbl <- table(dt$firstVote)
t = as.data.frame(tbl)
t[,2] <- t[,2]/sum(t[,2])*100
c(mean(t[2,2]))
}
library(boot)
set.seed(12345)
myBootstrap <- boot(socialdataCleaned, foo, R=1000)
plot(myBootstrap, index=1)
boot.ci(myBootstrap, index=1, type='norm')
socialdata <- read.csv(file="../input/srilankanpresidentialelectionprediction2019/social_media_votes.csv", header=TRUE, sep=",")
head(socialdata)
combined = rbind(roadInterviewData, socialdata)
combined <- subset(combined, firstVote != 'Not voting')
combined <- subset(combined, (firstVote != 'Not Decided yet' ))
tabEducationVsCandidate <- table(combined$education, combined$firstVote)
ftable(tabEducationVsCandidate)
par(las=2, mar=c(12,5,5,5))
barplot(tabEducationVsCandidate, main="Education Level Vs Presidential Candidate", col=c("darkblue","red", "green", "yellow"),
legend = rownames(tabEducationVsCandidate), cex.lab=1, cex.main=1.7, args.legend = list(x = 'topright', bty='n'))
graduatedPercentage <- function(data, indices){
dt <- data[indices,]
tbl <- table(dt$education, dt$firstVote)
tbl[2,] = tbl[2,]/sum(tbl[2,]) * 100
c(mean(tbl[2,2]))
}
set.seed(12345)
graduatedBootstrap <- boot(combined, graduatedPercentage, R=1000)
plot(graduatedBootstrap, index=1)
boot.ci(graduatedBootstrap, index=1, type='norm')
| 0.319227 | 0.948489 |
```
import pandas as pd
import numpy as np
import statsmodels.api as sm
from scipy.stats import norm
# Getting the database
df_data = pd.read_excel('proshares_analysis_data.xlsx', header=0, index_col=0, sheet_name='merrill_factors')
df_data.head()
```
# Section 1 - Short answer
1.1 Mean-variance optimization goes long the highest Sharpe-Ratio assets and shorts the lowest Sharpe-ratio assets.
False. The mean-variance optimization takes into account not only the mean returns and volatilities but also the correlation structure among assets. If an asset has low covariance with other assets it can have a high weight even if its sharpe ratio is not so big.
1.2 Investing in an ETF makes more sense for a long-term horizon than a short-term horizon.
True. An ETF is a portfolio of stocks. It should show better performance metrics over long horizons then short horizons.
1.3 Do you suggest that we (in a year) estimate the regression with an intercept or without an
intercept? Why?
We should include the intercept in the regression. As we have a small sample of data the estimate of mean returns will not be trustable. As a result, we should not force the betas of the regression to try to replicate both the trend and the variation of the asset returns.
1.4 Is HDG effective at tracking HFRI in-sample? And out of sample?
Yes, the out-of-sample replication performs very well in comparison to the target. In terms of the in-sample comparison, the annualized tracking error is 0.023 which is acceptable.
1.5 A hedge fund claims to beat the market by having a very high alpha. After regressing the hedge fund returns on the
6 Merrill-Lynch style factors, you find the alpha to be negative. Explain why this discrepancy can happen.
The difference can be in terms of the benchmark you are comparing the returns. If for example, the hedge fund is comparing its returns with a smaller set of factors, the regression can show a positive and high alpha. But in this case is just because you have ommited variables.
# Section 2 - Allocation
```
# 2.1 What are the weights of the tangency portfolio, wtan?
rf_lab = 'USGG3M Index'
df_excess = df_data.apply(lambda x: x - df_data.loc[:, rf_lab]).drop(rf_lab, axis=1)
df_excess.head()
mu = df_excess.mean()
cov_matrix = df_excess.cov()
inv_cov = np.linalg.inv(cov_matrix)
wtan = (1 / (np.ones(len(mu)) @ inv_cov @ mu)) * (inv_cov @ mu)
df_wtan = pd.DataFrame(wtan, index = df_excess.columns.values, columns=['Weights'])
df_wtan
# 2.2 What are the weights of the optimal portfolio, w* with a targeted excess mean return of .02 per month?
# Is the optimal portfolio, w*, invested in the risk-free rate?
mu_target = 0.02
k = len(mu)
delta = mu_target * ((np.ones((1, k)) @ inv_cov @ mu) / (mu.T @ inv_cov @ mu))
wstar = delta * wtan
df_wstar = pd.DataFrame(wstar, index = df_excess.columns.values, columns=['Weights'])
df_wstar
print('The optimal mean-variance portfolio is positioned by {:.2f}% in the risk free rate.'.format(100 * (1 - delta[0])))
# 2.3 Report the mean, volatility, and Sharpe ratio of the optimized portfolio. Annualize all three statistics
df_retstar = pd.DataFrame(df_excess.values @ wstar, index=df_excess.index, columns=['Mean-variance'])
df_stats = pd.DataFrame(index = ['MV portfolio'], columns=['Mean', 'Volatility', 'Sharpe'])
df_stats['Mean'] = 12 * df_retstar.mean().values
df_stats['Volatility'] = np.sqrt(12) * df_retstar.std().values
df_stats['Sharpe'] = df_stats['Mean'].values / df_stats['Volatility'].values
df_stats
# 2.4 Re-calculate the optimal portfolio, w∗ with target excess mean of .02 per month. But this time only use data through
# 2018 in doing the calculation. Calculate the return in 2019-2021 based on those optimal weights.
df_excess_IS = df_excess.loc['2018', :]
df_excess_OOS = df_excess.loc['2019':, :]
mu_IS = df_excess_IS.mean()
cov_matrix_IS = df_excess_IS.cov()
inv_cov_IS = np.linalg.inv(cov_matrix_IS)
wtan_IS = (1 / (np.ones(len(mu_IS)) @ inv_cov_IS @ mu_IS)) * (inv_cov_IS @ mu_IS)
delta_IS = mu_target * ((np.ones((1, len(mu_IS))) @ inv_cov_IS @ mu_IS) / (mu_IS.T @ inv_cov_IS @ mu_IS))
wstar_IS = delta_IS * wtan_IS
pd.DataFrame(wstar_IS, index=df_excess_IS.columns.values, columns=['MV portfolio'])
# Report the mean, volatility, and Sharpe ratio of the 2019-2021 performance.
df_retstar_OOS = pd.DataFrame(df_excess_OOS.values @ wstar_IS, index=df_excess_OOS.index, columns=['MV portfolio'])
df_stats_OOS = pd.DataFrame(index=['MV portfolio'], columns=['Mean', 'Volatility', 'Sharpe'])
df_stats_OOS['Mean'] = 12 * df_retstar_OOS.mean().values
df_stats_OOS['Volatility'] = np.sqrt(12) * df_retstar_OOS.std().values
df_stats_OOS['Sharpe'] = df_stats_OOS['Mean'] / df_stats_OOS['Volatility']
df_stats_OOS
```
2.5 Suppose that instead of optimizing these 5 risky assets, we optimized 5 commodity futures: oil, coffee, cocoa, lumber, cattle, and gold. Do you think the out-of-sample fragility problem would be better or worse than what we have seen optimizing equities?
It will depend on how accurate is our estimate for the parameters of mean and covariance matrix of those assets. The weak out-of-sample performance of the mean-variance approach is driven by the fact that the mean and covariance matrix are not robust statistics and both change over time. In my opinion the out-of-sample fragility would be even worse in the case of the commodity futures because we will have very correlated assets. The determinant of the covariance matrix should be very low, which will make the weights very sensitive to any change in the mean return.
# Section 3 - Hedging and replication
```
# Suppose we want to invest in EEM, but hedge out SPY. Do this by estimating a regression of EEM on SPY
y = df_excess.loc[:, 'EEM US Equity']
x = df_excess.loc[:, 'SPY US Equity']
model_factor = sm.OLS(y, x).fit()
print(model_factor.summary())
```
3.1 What is the optimal hedge ratio over the full sample of data? That is, for every dollar invested in EEM, what would you invest in SPY?
The optimal hedge ratio will be the beta parameter of the above regression. As a result, the optimal hedge ratio will be 0.9257 invested in S&P for every dollar you invested in EEM.
```
# 3.2 What is the mean, volatility, and Sharpe ratio of the hedged position, had we applied that hedge throughout the
# full sample?
beta = model_factor.params[0]
df_position = pd.DataFrame(y.values - beta * x.values, index=y.index, columns=['Hedged position'])
df_stats_hedged = pd.DataFrame(index=['Hedged position'], columns=['Mean', 'Volatility', 'Sharpe'])
df_stats_hedged['Mean'] = 12 * df_position.mean().values
df_stats_hedged['Volatility'] = np.sqrt(12) * df_position.std().values
df_stats_hedged['Sharpe'] = df_stats_hedged['Mean'] / df_stats_hedged['Volatility']
df_stats_hedged
```
3.3 Does it have the same mean as EEM? Why or why not?
No it does not have the same mean as EEM. As we are hedging against the S&P, our position is shorting the S&P index so that we can hedge against market movements. As a result, our hedged position will subtract the beta multiplied by the mean of the S&P returns.
3.4 Suppose we estimated a multifactor regression where in addition to SPY, we had IWM as a regressor. Why might this regression be difficult to use for attribution or even hedging?
Because our regressors will be very correlated. As the IWM is an ETF of stocks, its correlation with the S&P should be very high.
# Section 4 - Modeling Risk
```
df_total = df_data.loc[:, ['SPY US Equity', 'EFA US Equity']]
df_total.head()
df_total['Diff'] = df_total['EFA US Equity'] - df_total['SPY US Equity']
mu = 12 * np.log(1 + df_total['Diff']).mean()
sigma = np.sqrt(12) * np.log(1 + df_total['Diff']).std()
threshold = 0
h = 10
# Calculatiing the probability
prob = norm.cdf((threshold - mu) / (sigma / np.sqrt(h)))
print('The probability that the S&P will outperform EFA is: {:.2f}%.'.format(100 * prob))
# 4.2 Calculate the 60-month rolling volatility of EFA
vol_rolling = ((df_total.loc[:, 'EFA US Equity'].shift(1) ** 2).rolling(window=60).mean()) ** 0.5
vol_current = vol_rolling.values[-1]
# Use the latest estimate of the volatility (Sep 2021), along with the normality formula, to calculate a Sep 2021 estimate
# of the 1-month, 1% VaR. In using the VaR formula, assume that the mean is zero.
var_5 = -2.33 * vol_current
print('The estimated 1% VaR is {:.3f}%.'.format(var_5 * 100))
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import statsmodels.api as sm
from scipy.stats import norm
# Getting the database
df_data = pd.read_excel('proshares_analysis_data.xlsx', header=0, index_col=0, sheet_name='merrill_factors')
df_data.head()
# 2.1 What are the weights of the tangency portfolio, wtan?
rf_lab = 'USGG3M Index'
df_excess = df_data.apply(lambda x: x - df_data.loc[:, rf_lab]).drop(rf_lab, axis=1)
df_excess.head()
mu = df_excess.mean()
cov_matrix = df_excess.cov()
inv_cov = np.linalg.inv(cov_matrix)
wtan = (1 / (np.ones(len(mu)) @ inv_cov @ mu)) * (inv_cov @ mu)
df_wtan = pd.DataFrame(wtan, index = df_excess.columns.values, columns=['Weights'])
df_wtan
# 2.2 What are the weights of the optimal portfolio, w* with a targeted excess mean return of .02 per month?
# Is the optimal portfolio, w*, invested in the risk-free rate?
mu_target = 0.02
k = len(mu)
delta = mu_target * ((np.ones((1, k)) @ inv_cov @ mu) / (mu.T @ inv_cov @ mu))
wstar = delta * wtan
df_wstar = pd.DataFrame(wstar, index = df_excess.columns.values, columns=['Weights'])
df_wstar
print('The optimal mean-variance portfolio is positioned by {:.2f}% in the risk free rate.'.format(100 * (1 - delta[0])))
# 2.3 Report the mean, volatility, and Sharpe ratio of the optimized portfolio. Annualize all three statistics
df_retstar = pd.DataFrame(df_excess.values @ wstar, index=df_excess.index, columns=['Mean-variance'])
df_stats = pd.DataFrame(index = ['MV portfolio'], columns=['Mean', 'Volatility', 'Sharpe'])
df_stats['Mean'] = 12 * df_retstar.mean().values
df_stats['Volatility'] = np.sqrt(12) * df_retstar.std().values
df_stats['Sharpe'] = df_stats['Mean'].values / df_stats['Volatility'].values
df_stats
# 2.4 Re-calculate the optimal portfolio, w∗ with target excess mean of .02 per month. But this time only use data through
# 2018 in doing the calculation. Calculate the return in 2019-2021 based on those optimal weights.
df_excess_IS = df_excess.loc['2018', :]
df_excess_OOS = df_excess.loc['2019':, :]
mu_IS = df_excess_IS.mean()
cov_matrix_IS = df_excess_IS.cov()
inv_cov_IS = np.linalg.inv(cov_matrix_IS)
wtan_IS = (1 / (np.ones(len(mu_IS)) @ inv_cov_IS @ mu_IS)) * (inv_cov_IS @ mu_IS)
delta_IS = mu_target * ((np.ones((1, len(mu_IS))) @ inv_cov_IS @ mu_IS) / (mu_IS.T @ inv_cov_IS @ mu_IS))
wstar_IS = delta_IS * wtan_IS
pd.DataFrame(wstar_IS, index=df_excess_IS.columns.values, columns=['MV portfolio'])
# Report the mean, volatility, and Sharpe ratio of the 2019-2021 performance.
df_retstar_OOS = pd.DataFrame(df_excess_OOS.values @ wstar_IS, index=df_excess_OOS.index, columns=['MV portfolio'])
df_stats_OOS = pd.DataFrame(index=['MV portfolio'], columns=['Mean', 'Volatility', 'Sharpe'])
df_stats_OOS['Mean'] = 12 * df_retstar_OOS.mean().values
df_stats_OOS['Volatility'] = np.sqrt(12) * df_retstar_OOS.std().values
df_stats_OOS['Sharpe'] = df_stats_OOS['Mean'] / df_stats_OOS['Volatility']
df_stats_OOS
# Suppose we want to invest in EEM, but hedge out SPY. Do this by estimating a regression of EEM on SPY
y = df_excess.loc[:, 'EEM US Equity']
x = df_excess.loc[:, 'SPY US Equity']
model_factor = sm.OLS(y, x).fit()
print(model_factor.summary())
# 3.2 What is the mean, volatility, and Sharpe ratio of the hedged position, had we applied that hedge throughout the
# full sample?
beta = model_factor.params[0]
df_position = pd.DataFrame(y.values - beta * x.values, index=y.index, columns=['Hedged position'])
df_stats_hedged = pd.DataFrame(index=['Hedged position'], columns=['Mean', 'Volatility', 'Sharpe'])
df_stats_hedged['Mean'] = 12 * df_position.mean().values
df_stats_hedged['Volatility'] = np.sqrt(12) * df_position.std().values
df_stats_hedged['Sharpe'] = df_stats_hedged['Mean'] / df_stats_hedged['Volatility']
df_stats_hedged
df_total = df_data.loc[:, ['SPY US Equity', 'EFA US Equity']]
df_total.head()
df_total['Diff'] = df_total['EFA US Equity'] - df_total['SPY US Equity']
mu = 12 * np.log(1 + df_total['Diff']).mean()
sigma = np.sqrt(12) * np.log(1 + df_total['Diff']).std()
threshold = 0
h = 10
# Calculatiing the probability
prob = norm.cdf((threshold - mu) / (sigma / np.sqrt(h)))
print('The probability that the S&P will outperform EFA is: {:.2f}%.'.format(100 * prob))
# 4.2 Calculate the 60-month rolling volatility of EFA
vol_rolling = ((df_total.loc[:, 'EFA US Equity'].shift(1) ** 2).rolling(window=60).mean()) ** 0.5
vol_current = vol_rolling.values[-1]
# Use the latest estimate of the volatility (Sep 2021), along with the normality formula, to calculate a Sep 2021 estimate
# of the 1-month, 1% VaR. In using the VaR formula, assume that the mean is zero.
var_5 = -2.33 * vol_current
print('The estimated 1% VaR is {:.3f}%.'.format(var_5 * 100))
| 0.777638 | 0.904777 |
# Curso de introducción al análisis y modelado de datos con Python
<img src="../images/cacheme.png" alt="logo" style="width: 150px;"/>
<img src="../images/aeropython_logo.png" alt="logo" style="width: 115px;"/>
---
# Pandas: Carga y manipulación básica de datos
_Hasta ahora hemos visto las diferentes estructuras para almacenamiento de datos que nos ofrece Python, como; integer, real, complex, boolen, list, tuple, dictionary... Sin embargo, también se pueden utilizar arrays a través del paquete `NumPy`, matrices dispersas que nos proporciona el paquete `sparse` de `SciPy`, y otros tipos de estructuras._
_En este notebook, vamos a presentar y empezar a trabajar con el paquete `pandas`. En concreto, nos basaremos en algunos problemas para ver las características de sus estructuras de datos, y para aprender a cargar datos y empezar a manipularnos._
---
## ¿Qué es pandas?
`pandas` es una libreria que nos proporciona estructuras de datos y herramientas para realizar análisis de grandes volúmenes de datos de manera rápida.
Se articula sobre la librería `NumPy`, y nos permite enfrentarnos a situaciones en las que tenemos que manejar datos reales, que requieren seguir un proceso de carga, limpieza, filtrado y reducción, y su posterior análisis y representación.
Es de gran utilidad en la industria del Big Data, pues un grandísmo porcentaje del tiempo de trabajo de un Data Scientist, está asociado a la limpieza y preparación de los datos (ver [artículo](https://www.forbes.com/sites/gilpress/2016/03/23/data-preparation-most-time-consuming-least-enjoyable-data-science-task-survey-says/#a5231076f637)), y pandas nos ayuda mucho en esta tarea.
De manera estándar y por convenio, pandas se importa de la siguiente forma:
## Cargando los datos
Trabajaremos sobre un fichero de datos metereológicos de AEMET obtenido de su portal de datos abiertos a través de la API (ver notebook adjunto). https://opendata.aemet.es/centrodedescargas/inicio
```
# preserve
from IPython.display import HTML
HTML('<iframe src="https://opendata.aemet.es/centrodedescargas/inicio" width="700" height="400"></iframe>')
```
Vemos que pinta tiene el fichero:
```
# en linux
#!head ../data/alicante_city_climate_aemet.csv
# en windows
# !more ..\data\alicante_city_climate_aemet.csv
```
Vemos que los datos no están en formato CSV, aunque sí que tienen algo de estructura.
¿Qué sucede si intentamos cargarlos con pandas?
Tenemos que hacer los siguientes cambios:
* Separar los campos por tabuladores.
* Saltar las primeras lineas.
* Descartar columnas que no nos interesan.
* Dar nombre a las nuevas columnas.
* Convertir las fechas al formato correcto.
* Definir la fecha como índice.
<div class="alert alert-info">Para acordarnos de cómo parsear las fechas: http://strftime.org/</div>
## Explorando los datos
```
# recuperar los tipos de datos de cada columna
# recuperar los índices
# muestro solo las primers 4 líneas
# muestro sólo las últimas 6 líneas
# muestro sólo determinadas líneas (slicing)
# ordeno de índice más antiguo a más moderno
# ordeno de mayor a menor la temperatura media
# información general del dataset.
# cuidado, para cada columna son las filas con elementos
# numero de filas y columnas en el dataset
# contamos cuantos elementos tenemos sin valor
# contamos cuantos elementos tenemos con valor
```
### Descripción estadística
Se pueden pedir los datos estadísticos asociados al dataframe.
```
# descripción estadística
```
Por defecto, los elementos con NA no se tienen en cuenta a la hora de calcular los valores. Se puede comprobar viendo como cambian los datos cuando se sustitiyen con ceros.
```
# cambiar na por ceros y volver a ver la descripción estadística
# recuerda que esto no cambia data en realidad, porque no lo hemos guardado
```
Otra forma de acceder a los datos estadísticos, es pedirlos de forma directa.
```
# media
# cuantil
```
## Accediendo a los datos.
Tenemos dos funciones principales para acceder a los datos, que son `.loc` que permite acceder por etiquetas, y `.iloc`que permite acceder por índices.
##### columnas
Hay varias formas de acceder a las columnas: por nombre o por atributo (si no contienen espacios ni caracteres especiales). Además, también se puede usar `.loc` (basado en etiquetas), `.iloc` (basado en posiciones enteras).
```
# accediendo a una columna por el nombre (label) y obteniendo una serie
# accediendo a una columna por el nombre (label) y obteniendo un dataframe.
# accediendo a varias columnas por el nombre (label)
# accediendo a una columna por el atributo
# accediendo a una columna por índice y obteniendo una serie
# accediendo a una columna por índice y obteniendo un dataframe
# accediendo a varias columnas por índice
# accediendo a una columna por el label y obteniendo una serie
# accediendo a una columna por el label y obteniendo un dataframe
# accediendo a varias columnas por le label
```
##### filas
Para acceder a las filas tenemos dos métodos: `.loc` (basado en etiquetas), `.iloc` (basado en posiciones enteras).
```
# accediendo a una fila por etiqueta y obteniendo una serie
# accediendo a una fila por etiqueta y obteniendo un dataframe
# accediendo a varias filas por etiqueta
# accediendo a una fila por posición entera y obteniendo una serie
# accediendo a una fila por posición entera y obteniendo un dataframe
# accediendo a varias filas por posición entera
```
##### filas y columnas
```
# accediendo a files y columnas por etiquetas
# accediendo a filas y columnas por posiciones enteras
```
## Filtrado de datos
```
# busco duplicados en las fechas
# tmax > 37
# 0<tmin< 2
# busqueda de valores nulos
```
## Representaciones de datos
```
# importamos matplotlib
```
#### Líneas
```
# pintar la temperatura máx, min, med
```
Pintar datos para una fecha.
```
# crear widget
```
#### barras
#### cajas
### Visualizaciones especiales
#### scatter
```
# scatter_matrix
```
---
Hemos aprendido:
* Como leer un CSV con distintos formatos utilizando la librería pandas.
* Como extraer información de la librería los datos cargados.
* Como acceder a los datos cargados.
* Como representar datos con pandas.
###### Juan Luis Cano, Alejandro Sáez, Mabel Delgado
---
_Las siguientes celdas contienen configuración del Notebook_
_Para visualizar y utlizar los enlaces a Twitter el notebook debe ejecutarse como [seguro](http://ipython.org/ipython-doc/dev/notebook/security.html)_
File > Trusted Notebook
```
#preserve
# Esta celda da el estilo al notebook
from IPython.core.display import HTML
css_file = '../style/style.css'
HTML(open(css_file, "r").read())
```
|
github_jupyter
|
# preserve
from IPython.display import HTML
HTML('<iframe src="https://opendata.aemet.es/centrodedescargas/inicio" width="700" height="400"></iframe>')
# en linux
#!head ../data/alicante_city_climate_aemet.csv
# en windows
# !more ..\data\alicante_city_climate_aemet.csv
# recuperar los tipos de datos de cada columna
# recuperar los índices
# muestro solo las primers 4 líneas
# muestro sólo las últimas 6 líneas
# muestro sólo determinadas líneas (slicing)
# ordeno de índice más antiguo a más moderno
# ordeno de mayor a menor la temperatura media
# información general del dataset.
# cuidado, para cada columna son las filas con elementos
# numero de filas y columnas en el dataset
# contamos cuantos elementos tenemos sin valor
# contamos cuantos elementos tenemos con valor
# descripción estadística
# cambiar na por ceros y volver a ver la descripción estadística
# recuerda que esto no cambia data en realidad, porque no lo hemos guardado
# media
# cuantil
# accediendo a una columna por el nombre (label) y obteniendo una serie
# accediendo a una columna por el nombre (label) y obteniendo un dataframe.
# accediendo a varias columnas por el nombre (label)
# accediendo a una columna por el atributo
# accediendo a una columna por índice y obteniendo una serie
# accediendo a una columna por índice y obteniendo un dataframe
# accediendo a varias columnas por índice
# accediendo a una columna por el label y obteniendo una serie
# accediendo a una columna por el label y obteniendo un dataframe
# accediendo a varias columnas por le label
# accediendo a una fila por etiqueta y obteniendo una serie
# accediendo a una fila por etiqueta y obteniendo un dataframe
# accediendo a varias filas por etiqueta
# accediendo a una fila por posición entera y obteniendo una serie
# accediendo a una fila por posición entera y obteniendo un dataframe
# accediendo a varias filas por posición entera
# accediendo a files y columnas por etiquetas
# accediendo a filas y columnas por posiciones enteras
# busco duplicados en las fechas
# tmax > 37
# 0<tmin< 2
# busqueda de valores nulos
# importamos matplotlib
# pintar la temperatura máx, min, med
# crear widget
# scatter_matrix
#preserve
# Esta celda da el estilo al notebook
from IPython.core.display import HTML
css_file = '../style/style.css'
HTML(open(css_file, "r").read())
| 0.342791 | 0.988142 |
```
# importing required packages
from pyspark.sql import SparkSession
from pyspark.ml.feature import HashingTF, IDF, Normalizer, Word2Vec
from pyspark.ml.linalg import DenseVector, Vectors, VectorUDT
from pyspark.sql.functions import col, explode, udf, concat_ws, collect_list, split
from pyspark.ml.recommendation import ALS
from pyspark.sql.types import DoubleType
# Setting a spark session
spark = SparkSession \
.builder \
.appName("Workload-2") \
.getOrCreate()
# spark.conf.set("spark.sql.shuffle.partitions", 100)
sc = spark.sparkContext
sc.defaultParallelism
sc.getConf().getAll()
spark.conf.set('spark.sql.adaptive.enabled',True)
# reading data
data = spark.read.option("multiline","true").json('tweets.json')
# data.cache()spark.conf
# data.show(truncate=False)
# Data formatting for collaborative filtering
data2_formatting = data.withColumn("user_mentions", explode("user_mentions")).select(
col('user_id'), col("user_mentions")["id"].alias("mention_users")).cache()
# data2_formatting.show()
data2_required = data2_formatting.groupBy("user_id", "mention_users").count().withColumnRenamed("count","rating").cache()
# data2_required.show()
# data2_required.dtypes
data2_formatting.unpersist()
# Mapping large id values to integer range values
distinct_tweet_uids = data2_required.select("user_id").distinct()
distinct_mention_uids = data2_required.select("mention_users").distinct()
# distinct_user_id.show()
distinct_ids_total = distinct_tweet_uids.union(distinct_mention_uids).distinct()
# distinct_ids_total.show()
indices_for_ids = distinct_ids_total.rdd.zipWithIndex().toDF()
# indices_for_ids.show()
mapping_df_for_uid = indices_for_ids.select("_1.*", "_2").withColumnRenamed("user_id","uid").withColumnRenamed("_2","new_uid").cache()
mapping_df_for_mid = mapping_df_for_uid.withColumnRenamed("new_uid","new_mid")
# print(mapping_df_for_uid.dtypes)
# print(mapping_df_for_mid.dtypes)
# Preparing data with the mapped values
data_with_new_uid = data2_required.join(mapping_df_for_uid,data2_required.user_id==mapping_df_for_uid.uid,how='inner').drop('uid').cache()
# data_with_new_uid.show()
data_with_new_mid = data_with_new_uid.join(mapping_df_for_mid,data_with_new_uid.mention_users==mapping_df_for_mid.uid).drop('uid')
# data_with_new_mid.show()
# Building the recommendation model
als = ALS(rank=8,maxIter=20,regParam=0.01, implicitPrefs=True,userCol="new_uid", itemCol="new_mid", ratingCol="rating",coldStartStrategy="drop")
als_model = als.fit(data_with_new_mid)
# Recommending 5 items for each user
user_recommendations = als_model.recommendForAllUsers(5)
output = user_recommendations.join(mapping_df_for_uid,user_recommendations.new_uid==mapping_df_for_uid.new_uid).select(col('uid').alias('tweet_users'),col('recommendations').alias('mention_users'))
# output.dtypes
final_output = output.select('tweet_users','mention_users.new_mid')
# final_output.show()
# Re-mapping and getting back the original ids
mapping_dictionary = mapping_df_for_uid.rdd.map(lambda x: (x.new_uid, x.uid)).collectAsMap()
# type(mapping_dictionary)
# mapping_dictionary
mapping_array = udf(lambda x: [mapping_dictionary[key] for key in x])
final_required_output = final_output.withColumn('original_mids', mapping_array(final_output['new_mid']))
# Recommended mention users for each tweet user
final_required_output.cache()
final_required_output.select('tweet_users',col('original_mids').alias('mention_users')).show(truncate=False)
# sc.getConf().getAll()
```
|
github_jupyter
|
# importing required packages
from pyspark.sql import SparkSession
from pyspark.ml.feature import HashingTF, IDF, Normalizer, Word2Vec
from pyspark.ml.linalg import DenseVector, Vectors, VectorUDT
from pyspark.sql.functions import col, explode, udf, concat_ws, collect_list, split
from pyspark.ml.recommendation import ALS
from pyspark.sql.types import DoubleType
# Setting a spark session
spark = SparkSession \
.builder \
.appName("Workload-2") \
.getOrCreate()
# spark.conf.set("spark.sql.shuffle.partitions", 100)
sc = spark.sparkContext
sc.defaultParallelism
sc.getConf().getAll()
spark.conf.set('spark.sql.adaptive.enabled',True)
# reading data
data = spark.read.option("multiline","true").json('tweets.json')
# data.cache()spark.conf
# data.show(truncate=False)
# Data formatting for collaborative filtering
data2_formatting = data.withColumn("user_mentions", explode("user_mentions")).select(
col('user_id'), col("user_mentions")["id"].alias("mention_users")).cache()
# data2_formatting.show()
data2_required = data2_formatting.groupBy("user_id", "mention_users").count().withColumnRenamed("count","rating").cache()
# data2_required.show()
# data2_required.dtypes
data2_formatting.unpersist()
# Mapping large id values to integer range values
distinct_tweet_uids = data2_required.select("user_id").distinct()
distinct_mention_uids = data2_required.select("mention_users").distinct()
# distinct_user_id.show()
distinct_ids_total = distinct_tweet_uids.union(distinct_mention_uids).distinct()
# distinct_ids_total.show()
indices_for_ids = distinct_ids_total.rdd.zipWithIndex().toDF()
# indices_for_ids.show()
mapping_df_for_uid = indices_for_ids.select("_1.*", "_2").withColumnRenamed("user_id","uid").withColumnRenamed("_2","new_uid").cache()
mapping_df_for_mid = mapping_df_for_uid.withColumnRenamed("new_uid","new_mid")
# print(mapping_df_for_uid.dtypes)
# print(mapping_df_for_mid.dtypes)
# Preparing data with the mapped values
data_with_new_uid = data2_required.join(mapping_df_for_uid,data2_required.user_id==mapping_df_for_uid.uid,how='inner').drop('uid').cache()
# data_with_new_uid.show()
data_with_new_mid = data_with_new_uid.join(mapping_df_for_mid,data_with_new_uid.mention_users==mapping_df_for_mid.uid).drop('uid')
# data_with_new_mid.show()
# Building the recommendation model
als = ALS(rank=8,maxIter=20,regParam=0.01, implicitPrefs=True,userCol="new_uid", itemCol="new_mid", ratingCol="rating",coldStartStrategy="drop")
als_model = als.fit(data_with_new_mid)
# Recommending 5 items for each user
user_recommendations = als_model.recommendForAllUsers(5)
output = user_recommendations.join(mapping_df_for_uid,user_recommendations.new_uid==mapping_df_for_uid.new_uid).select(col('uid').alias('tweet_users'),col('recommendations').alias('mention_users'))
# output.dtypes
final_output = output.select('tweet_users','mention_users.new_mid')
# final_output.show()
# Re-mapping and getting back the original ids
mapping_dictionary = mapping_df_for_uid.rdd.map(lambda x: (x.new_uid, x.uid)).collectAsMap()
# type(mapping_dictionary)
# mapping_dictionary
mapping_array = udf(lambda x: [mapping_dictionary[key] for key in x])
final_required_output = final_output.withColumn('original_mids', mapping_array(final_output['new_mid']))
# Recommended mention users for each tweet user
final_required_output.cache()
final_required_output.select('tweet_users',col('original_mids').alias('mention_users')).show(truncate=False)
# sc.getConf().getAll()
| 0.38318 | 0.556641 |
<a href="https://colab.research.google.com/github/TarekAzzouni/Baterries-ML-Lithium-Ions-01/blob/main/Data_Driven_model_for_HNEI_DATASET_(_Machine_learning_part).ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Description of the dataset :
A batch of fifty-one 18650-format lithium ion cells was purchased from a commercial vendor. These cells were manufactured by LG Chemical Limited, (Seoul, Korea), under the model denomination “ICR18650 C2” and intended for notebook PC applications. The negative electrode (NE) was made of a graphitic intercalation compound (GIC), while the positive electrode (PE) was a blend of LiCoO2 (LCO) and LiNi4Co4Mn2O2 (NMC). The electrolyte composition was not disclosed. The recommended charge cut-off voltage was 4.30 V (associated with a 50 mA cut-off current). The recommended charge rate was C/2 and the maximum charge rate was 1 C. The recommended discharge cut-off voltage was 3.00 V and the maximum discharge rate was 2 C at ambient temperatures (5 to 45 °C). The nominal capacity was 2800 mAh and the maximum weight was 50 grams. The calculated energy density was approximately 208 Wh/kg classifying it as a high-energy cell by current standards.
# Packages
```
import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib.colors import ListedColormap
from sklearn.metrics import plot_confusion_matrix
from scipy.stats import norm, boxcox
from sklearn.metrics import confusion_matrix, classification_report, accuracy_score
from collections import Counter
from scipy import stats
import tensorflow as tf
import matplotlib.pyplot as plt
import io
import requests
from warnings import simplefilter
import warnings
# ignore all warnings
simplefilter(action='ignore')
```
# Reading Data & Data leaning / processing
```
url="https://www.batteryarchive.org/data/HNEI_18650_NMC_LCO_25C_0-100_0.5-1.5C_a_timeseries.csv"
s = requests.get(url).content
df = pd.read_csv(io.StringIO(s.decode('utf-8')))
df_0 = df.replace(to_replace = np.nan, value =25)
df_0
df.info()
#new_df = df_0[df['Cycle_Index'] < 2 ]
#new_df
Train = df_0[df_0['Cycle_Index'] == 2 ]
Train.shape
# Test = df_0[df_0['Cycle_Index'] == 1 ]
#Test.shape
Train_1 = Train.drop(['Test_Time (s)','Environment_Temperature (C)','Cell_Temperature (C)','Date_Time','Cycle_Index'],axis=1)
#Test_1 = Test.drop(['Test_Time (s)','Environment_Temperature (C)','Cell_Temperature (C)'],axis=1)
```
# Feature selection can be done in multiple ways but there are broadly 2 categories of it:
1. Correlation Coefficient ( filter Method )
2. Wrapper Methods (if we can get the tangent and set it as target we can you this operation )
## 1/ Correlation Coefficient
description : Correlation is a measure of the linear relationship of 2 or more variables. Through correlation, we can predict one variable from the other. The logic behind using correlation for feature selection is that the good variables are highly correlated with the target. Furthermore, variables should be correlated with the target but should be uncorrelated among themselves.
We need to set an absolute value, say 0.5 as the threshold for selecting the variables. If we find that the predictor variables are correlated among themselves, we can drop the variable which has a lower correlation coefficient value with the target variable. We can also compute multiple correlation coefficients to check whether more than two variables are correlated to each other. This phenomenon is known as multicollinearity.
```
plt.subplots(figsize=(20,15))
cor = Train_1.corr()
sns.heatmap(cor, annot = True,square=True)
#Correlation with output variable
cor_target = abs(cor["Charge_Capacity (Ah)"])
#Selecting highly correlated features
relevant_features = cor_target[cor_target>0.5]
relevant_features
```
Interpretation of the correlation heatmap :
As we set the charge capacity as a correlation target and we say what are the features that influence the Charge Capacity:
those features are :
* Test time & The Voltage (V) have a high correlation of 0.978678 and 0,940138 respectively we can see that they increase at the same time (verification in Data visualization part )
* Charge_Energy (Wh) has a highest correlation.
* Discharge Energy (Wh) and Discharge Capacity (Ah) have a negative correlation ( see the heat map and in the data visualization part) which means that : one variable increases as the other decreases, and vice versa .
## 2/ Wrapper Methods
Description : Wrappers require some method to search the space of all possible subsets of features, assessing their quality by learning and evaluating a classifier with that feature subset. The feature selection process is based on a specific machine learning algorithm that we are trying to fit on a given dataset. It follows a greedy search approach by evaluating all the possible combinations of features against the evaluation criterion. The wrapper methods usually result in better predictive accuracy than filter methods.
*Forward Feature Selection :* This is an iterative method wherein we start with the best performing variable against the target. Next, we select another variable that gives the best performance in combination with the first selected variable. This process continues until the preset criterion is achieved
link 1: https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.SequentialFeatureSelector.html?highlight=sequentialfeatureselector#sklearn.feature_selection.SequentialFeatureSelector
link 2 : https://www.analyticsvidhya.com/blog/2020/10/feature-selection-techniques-in-machine-learning/
# Data visualization over the charge capacity
```
graph1 = df_0[df_0['Cycle_Index'] == 1 ]
graph2 = df_0[df_0['Cycle_Index'] == 450 ]
graph3 = df_0[df_0['Cycle_Index'] == 1100]
ax = plt.gca()
graph1.plot(kind='line',x='Voltage (V)',y='Charge_Capacity (Ah)',ax=ax, label='Voltage at Cycle = 1')
graph2.plot(kind='line',x='Voltage (V)',y='Charge_Capacity (Ah)',ax=ax, label='Voltage at Cycle = 450')
graph3.plot(kind='line',x='Voltage (V)',y='Charge_Capacity (Ah)',ax=ax, label='Voltage at Cycle = 1100')
#ax.set_ylabel('Charge_Capacity (Ah)',color='navy',fontsize=17)
plt.title("")
plt.show()
ax = plt.gca()
df_0.plot(kind='line',x='Cycle_Index',y='Charge_Capacity (Ah)',ax=ax, label='Charge_Capacity (Ah)')
#graph2.plot(kind='line',x='Charge_Capacity (Ah)',y='Voltage (V)',ax=ax, label='Voltage at Cycle = 450')
#graph3.plot(kind='line',x='Charge_Capacity (Ah)',y='Voltage (V)',ax=ax, label='Voltage at Cycle = 1100')
#ax.set_ylabel('Charge_Capacity (Ah)',color='navy',fontsize=17)
plt.title("")
plt.show()
import datetime as dt
graph1['Date_Time']= pd.to_datetime(Train['Date_Time'],format='%Y-%m-%d %H:%M:%S')
df_gen=graph1.groupby('Date_Time').sum().reset_index()
df_gen['time']=df_gen['Date_Time'].dt.time
fig,ax = plt.subplots(ncols=2,nrows=1,dpi=100,figsize=(20,5))
# Charge capacity plot
df_gen.plot(x='Date_Time',y='Charge_Capacity (Ah)',color='navy',ax=ax[0])
# Charge energy plot
df_gen.set_index('time').drop('Date_Time',1)[['Voltage (V)']].plot(ax=ax[1])
ax[0].set_title('time dependant of the charge capacity',)
ax[1].set_title('Time dependant of the charge energy ')
ax[0].set_ylabel('Charge_Capacity (Ah)',color='navy',fontsize=17)
ax[1].set_ylabel('Voltage (V)', color = 'navy',fontsize=17)
plt.show()
import datetime as dt
graph2['Date_Time']= pd.to_datetime(graph2['Date_Time'],format='%Y-%m-%d %H:%M')
df_gen=graph2.groupby('Date_Time').sum().reset_index()
df_gen['time']=df_gen['Date_Time'].dt.time
fig,ax = plt.subplots(ncols=2,nrows=1,dpi=100,figsize=(20,5))
# Charge capacity plot
df_gen.plot(x='Date_Time',y='Charge_Capacity (Ah)',color='navy',ax=ax[0])
# Charge energy plot
df_gen.set_index('time').drop('Date_Time',1)[['Voltage (V)']].plot(ax=ax[1])
ax[0].set_title('time dependant of the charge capacity',)
ax[1].set_title('Time dependant of the charge energy ')
ax[0].set_ylabel('Charge_Capacity (Ah)',color='navy',fontsize=17)
ax[1].set_ylabel('Voltage (V)', color = 'navy',fontsize=17)
plt.show()
fig,ax = plt.subplots(ncols=2,nrows=1,dpi=100,figsize=(20,5))
# Charge capacity plot
graph1.plot(x='Charge_Capacity (Ah)',y='Voltage (V)',color='navy',ax=ax[0])
# Charge energy plot
graph1.plot(x='Charge_Capacity (Ah)',y='Current (A)',color='navy',ax=ax[1])
# Charge energy plot
ax[0].set_title('Voltage in function of the charge capacity',)
ax[1].set_title('Current in function of the charge capacity')
ax[0].set_ylabel('Voltage (V)',color='navy',fontsize=17)
ax[1].set_ylabel('Current (A)', color = 'navy',fontsize=17)
plt.show()
```
this is the evidence of the non correlation between the current and charge capacity.
Therefor we can see the relationship between voltage and the charge capacity
```
#Test.shape
```
observation of the cycles on the battery.
# Neural Network model
## 1/ Test diffirent models of machine learning for a regression.
```
Train_1.info()
#Train_1['charge_capacity_per'] = (Train_1['Charge_Capacity (Ah)']/
# Train_1['Charge_Capacity (Ah)'].sum())*100000
ax = plt.gca()
Train_1.plot(kind='line',x='Charge_Capacity (Ah)',y='Voltage (V)',ax=ax, label='Voltage at Cycle = 1')
#ax.set_ylabel('Charge_Capacity (Ah)',color='navy',fontsize=17)
plt.title("")
plt.show()
#Test['charge_capacity_per'] = (Test['Charge_Capacity (Ah)']/
# Test['Charge_Capacity (Ah)'].sum())*100000
Train_1
```
### The logic behind the charge capacity percentage
Once we have tried the LTSM ( see below ) which is a forcasting model, we thought that it would be better to creat a new column that will look like the SOC. so as in the Data vizualization part, the bihaviour of the CC is similar to the SOC.
### Machine Learning model Supervised model
```
Train_1.columns
Col_feature = ["Voltage (V)","Discharge_Capacity (Ah)","Charge_Energy (Wh)","Current (A)"]
Col_target = ["Charge_Capacity (Ah)"]
feature = Train_1[Col_feature]
target = Train_1[Col_target]
#Split training dataset into independent and dependent varibales
train_X = Train_1[feature.columns]
y = Train_1[target.columns]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(Train_1, y, test_size=0.2)
print (X_train.shape, y_train.shape)
print (X_test.shape, y_test.shape)
#Split testing dataset into independent and dependent varibales
#test_X = Test[feature.columns]
#test_y = Test[target.columns]
from sklearn.linear_model import Lasso , Ridge
from sklearn.ensemble import RandomForestRegressor, ExtraTreesRegressor , GradientBoostingRegressor
from sklearn.neural_network import MLPRegressor
import xgboost as xgb
from sklearn import neighbors
from sklearn.svm import SVR
models = [
['Lasso: ', Lasso()],
['Ridge: ', Ridge()],
['KNeighborsRegressor: ', neighbors.KNeighborsRegressor()],
['SVR:' , SVR(kernel='rbf')],
['RandomForest ',RandomForestRegressor()],
['ExtraTreeRegressor :',ExtraTreesRegressor()],
['GradientBoostingClassifier: ', GradientBoostingRegressor()] ,
['XGBRegressor: ', xgb.XGBRegressor()] ,
['MLPRegressor: ', MLPRegressor( activation='relu', solver='adam',learning_rate='adaptive',max_iter=1000,learning_rate_init=0.01,alpha=0.01)]
]
import time
from math import sqrt
from sklearn.metrics import mean_squared_error
from sklearn import preprocessing, model_selection, metrics
model_data = []
for name,curr_model in models :
curr_model_data = {}
curr_model.random_state = 78
curr_model_data["Name"] = name
start = time.time()
curr_model.fit(X_train,y_train)
end = time.time()
curr_model_data["Train_Time"] = end - start
curr_model_data["Train_R2_Score"] = metrics.r2_score(y_train,curr_model.predict(X_train))
curr_model_data["Test_R2_Score"] = metrics.r2_score(y_test,curr_model.predict(X_test))
curr_model_data["Test_RMSE_Score"] = sqrt(mean_squared_error(y_test,curr_model.predict(X_test)))
model_data.append(curr_model_data)
model_data
models
Train_2 = pd.DataFrame(model_data)
Train_2.plot(x="Name", y=['Test_R2_Score' , 'Train_R2_Score' , 'Test_RMSE_Score'], kind="bar" , title = 'R2 Score Results' , figsize= (10,10)) ;
Train_2
```
### Evaluating Machine Learning Models using Hyperparameter Tuning
```
from sklearn.model_selection import GridSearchCV
param_grid = [{
'max_depth': [80, 150, 200,250],
'n_estimators' : [100,150,200,250],
'max_features': ["auto", "sqrt", "log2"]
}]
reg = ExtraTreesRegressor(random_state=40)
# Instantiate the grid search model
grid_search = GridSearchCV(estimator = reg, param_grid = param_grid, cv = 5, n_jobs = -1 , scoring='r2' , verbose=2)
grid_search.fit(X_train,y_train)
grid_search.best_params_
grid_search.best_estimator_
# R2 score on training set with tuned parameters
grid_search.best_estimator_.score(X_train,y_train)
# R2 score on test set with tuned parameters
grid_search.best_estimator_.score(X_test,y_test)
```
exploring the random forest ML method prediction.
In this part we are going to go deeper in the Random forest method as we saw that it gave us a Test R² score of : 0.9472581168453291
```
# test regression dataset
from sklearn.datasets import make_regression
# define dataset
train_X, train_y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=2)
# summarize the dataset
print(train_X.shape, train_y.shape)
# evaluate random forest ensemble for regression
from numpy import mean
from numpy import std
from sklearn.datasets import make_regression
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedKFold
from sklearn.ensemble import RandomForestRegressor
# define dataset
train_X, train_y= make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=2)
# define the model
model = RandomForestRegressor()
# evaluate the model
cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, train_X, train_y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('MAE: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))
```
In this case, we can see the random forest ensemble with default hyperparameters achieves a MAE of about 90.
|
github_jupyter
|
import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib.colors import ListedColormap
from sklearn.metrics import plot_confusion_matrix
from scipy.stats import norm, boxcox
from sklearn.metrics import confusion_matrix, classification_report, accuracy_score
from collections import Counter
from scipy import stats
import tensorflow as tf
import matplotlib.pyplot as plt
import io
import requests
from warnings import simplefilter
import warnings
# ignore all warnings
simplefilter(action='ignore')
url="https://www.batteryarchive.org/data/HNEI_18650_NMC_LCO_25C_0-100_0.5-1.5C_a_timeseries.csv"
s = requests.get(url).content
df = pd.read_csv(io.StringIO(s.decode('utf-8')))
df_0 = df.replace(to_replace = np.nan, value =25)
df_0
df.info()
#new_df = df_0[df['Cycle_Index'] < 2 ]
#new_df
Train = df_0[df_0['Cycle_Index'] == 2 ]
Train.shape
# Test = df_0[df_0['Cycle_Index'] == 1 ]
#Test.shape
Train_1 = Train.drop(['Test_Time (s)','Environment_Temperature (C)','Cell_Temperature (C)','Date_Time','Cycle_Index'],axis=1)
#Test_1 = Test.drop(['Test_Time (s)','Environment_Temperature (C)','Cell_Temperature (C)'],axis=1)
plt.subplots(figsize=(20,15))
cor = Train_1.corr()
sns.heatmap(cor, annot = True,square=True)
#Correlation with output variable
cor_target = abs(cor["Charge_Capacity (Ah)"])
#Selecting highly correlated features
relevant_features = cor_target[cor_target>0.5]
relevant_features
graph1 = df_0[df_0['Cycle_Index'] == 1 ]
graph2 = df_0[df_0['Cycle_Index'] == 450 ]
graph3 = df_0[df_0['Cycle_Index'] == 1100]
ax = plt.gca()
graph1.plot(kind='line',x='Voltage (V)',y='Charge_Capacity (Ah)',ax=ax, label='Voltage at Cycle = 1')
graph2.plot(kind='line',x='Voltage (V)',y='Charge_Capacity (Ah)',ax=ax, label='Voltage at Cycle = 450')
graph3.plot(kind='line',x='Voltage (V)',y='Charge_Capacity (Ah)',ax=ax, label='Voltage at Cycle = 1100')
#ax.set_ylabel('Charge_Capacity (Ah)',color='navy',fontsize=17)
plt.title("")
plt.show()
ax = plt.gca()
df_0.plot(kind='line',x='Cycle_Index',y='Charge_Capacity (Ah)',ax=ax, label='Charge_Capacity (Ah)')
#graph2.plot(kind='line',x='Charge_Capacity (Ah)',y='Voltage (V)',ax=ax, label='Voltage at Cycle = 450')
#graph3.plot(kind='line',x='Charge_Capacity (Ah)',y='Voltage (V)',ax=ax, label='Voltage at Cycle = 1100')
#ax.set_ylabel('Charge_Capacity (Ah)',color='navy',fontsize=17)
plt.title("")
plt.show()
import datetime as dt
graph1['Date_Time']= pd.to_datetime(Train['Date_Time'],format='%Y-%m-%d %H:%M:%S')
df_gen=graph1.groupby('Date_Time').sum().reset_index()
df_gen['time']=df_gen['Date_Time'].dt.time
fig,ax = plt.subplots(ncols=2,nrows=1,dpi=100,figsize=(20,5))
# Charge capacity plot
df_gen.plot(x='Date_Time',y='Charge_Capacity (Ah)',color='navy',ax=ax[0])
# Charge energy plot
df_gen.set_index('time').drop('Date_Time',1)[['Voltage (V)']].plot(ax=ax[1])
ax[0].set_title('time dependant of the charge capacity',)
ax[1].set_title('Time dependant of the charge energy ')
ax[0].set_ylabel('Charge_Capacity (Ah)',color='navy',fontsize=17)
ax[1].set_ylabel('Voltage (V)', color = 'navy',fontsize=17)
plt.show()
import datetime as dt
graph2['Date_Time']= pd.to_datetime(graph2['Date_Time'],format='%Y-%m-%d %H:%M')
df_gen=graph2.groupby('Date_Time').sum().reset_index()
df_gen['time']=df_gen['Date_Time'].dt.time
fig,ax = plt.subplots(ncols=2,nrows=1,dpi=100,figsize=(20,5))
# Charge capacity plot
df_gen.plot(x='Date_Time',y='Charge_Capacity (Ah)',color='navy',ax=ax[0])
# Charge energy plot
df_gen.set_index('time').drop('Date_Time',1)[['Voltage (V)']].plot(ax=ax[1])
ax[0].set_title('time dependant of the charge capacity',)
ax[1].set_title('Time dependant of the charge energy ')
ax[0].set_ylabel('Charge_Capacity (Ah)',color='navy',fontsize=17)
ax[1].set_ylabel('Voltage (V)', color = 'navy',fontsize=17)
plt.show()
fig,ax = plt.subplots(ncols=2,nrows=1,dpi=100,figsize=(20,5))
# Charge capacity plot
graph1.plot(x='Charge_Capacity (Ah)',y='Voltage (V)',color='navy',ax=ax[0])
# Charge energy plot
graph1.plot(x='Charge_Capacity (Ah)',y='Current (A)',color='navy',ax=ax[1])
# Charge energy plot
ax[0].set_title('Voltage in function of the charge capacity',)
ax[1].set_title('Current in function of the charge capacity')
ax[0].set_ylabel('Voltage (V)',color='navy',fontsize=17)
ax[1].set_ylabel('Current (A)', color = 'navy',fontsize=17)
plt.show()
#Test.shape
Train_1.info()
#Train_1['charge_capacity_per'] = (Train_1['Charge_Capacity (Ah)']/
# Train_1['Charge_Capacity (Ah)'].sum())*100000
ax = plt.gca()
Train_1.plot(kind='line',x='Charge_Capacity (Ah)',y='Voltage (V)',ax=ax, label='Voltage at Cycle = 1')
#ax.set_ylabel('Charge_Capacity (Ah)',color='navy',fontsize=17)
plt.title("")
plt.show()
#Test['charge_capacity_per'] = (Test['Charge_Capacity (Ah)']/
# Test['Charge_Capacity (Ah)'].sum())*100000
Train_1
Train_1.columns
Col_feature = ["Voltage (V)","Discharge_Capacity (Ah)","Charge_Energy (Wh)","Current (A)"]
Col_target = ["Charge_Capacity (Ah)"]
feature = Train_1[Col_feature]
target = Train_1[Col_target]
#Split training dataset into independent and dependent varibales
train_X = Train_1[feature.columns]
y = Train_1[target.columns]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(Train_1, y, test_size=0.2)
print (X_train.shape, y_train.shape)
print (X_test.shape, y_test.shape)
#Split testing dataset into independent and dependent varibales
#test_X = Test[feature.columns]
#test_y = Test[target.columns]
from sklearn.linear_model import Lasso , Ridge
from sklearn.ensemble import RandomForestRegressor, ExtraTreesRegressor , GradientBoostingRegressor
from sklearn.neural_network import MLPRegressor
import xgboost as xgb
from sklearn import neighbors
from sklearn.svm import SVR
models = [
['Lasso: ', Lasso()],
['Ridge: ', Ridge()],
['KNeighborsRegressor: ', neighbors.KNeighborsRegressor()],
['SVR:' , SVR(kernel='rbf')],
['RandomForest ',RandomForestRegressor()],
['ExtraTreeRegressor :',ExtraTreesRegressor()],
['GradientBoostingClassifier: ', GradientBoostingRegressor()] ,
['XGBRegressor: ', xgb.XGBRegressor()] ,
['MLPRegressor: ', MLPRegressor( activation='relu', solver='adam',learning_rate='adaptive',max_iter=1000,learning_rate_init=0.01,alpha=0.01)]
]
import time
from math import sqrt
from sklearn.metrics import mean_squared_error
from sklearn import preprocessing, model_selection, metrics
model_data = []
for name,curr_model in models :
curr_model_data = {}
curr_model.random_state = 78
curr_model_data["Name"] = name
start = time.time()
curr_model.fit(X_train,y_train)
end = time.time()
curr_model_data["Train_Time"] = end - start
curr_model_data["Train_R2_Score"] = metrics.r2_score(y_train,curr_model.predict(X_train))
curr_model_data["Test_R2_Score"] = metrics.r2_score(y_test,curr_model.predict(X_test))
curr_model_data["Test_RMSE_Score"] = sqrt(mean_squared_error(y_test,curr_model.predict(X_test)))
model_data.append(curr_model_data)
model_data
models
Train_2 = pd.DataFrame(model_data)
Train_2.plot(x="Name", y=['Test_R2_Score' , 'Train_R2_Score' , 'Test_RMSE_Score'], kind="bar" , title = 'R2 Score Results' , figsize= (10,10)) ;
Train_2
from sklearn.model_selection import GridSearchCV
param_grid = [{
'max_depth': [80, 150, 200,250],
'n_estimators' : [100,150,200,250],
'max_features': ["auto", "sqrt", "log2"]
}]
reg = ExtraTreesRegressor(random_state=40)
# Instantiate the grid search model
grid_search = GridSearchCV(estimator = reg, param_grid = param_grid, cv = 5, n_jobs = -1 , scoring='r2' , verbose=2)
grid_search.fit(X_train,y_train)
grid_search.best_params_
grid_search.best_estimator_
# R2 score on training set with tuned parameters
grid_search.best_estimator_.score(X_train,y_train)
# R2 score on test set with tuned parameters
grid_search.best_estimator_.score(X_test,y_test)
# test regression dataset
from sklearn.datasets import make_regression
# define dataset
train_X, train_y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=2)
# summarize the dataset
print(train_X.shape, train_y.shape)
# evaluate random forest ensemble for regression
from numpy import mean
from numpy import std
from sklearn.datasets import make_regression
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedKFold
from sklearn.ensemble import RandomForestRegressor
# define dataset
train_X, train_y= make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=2)
# define the model
model = RandomForestRegressor()
# evaluate the model
cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, train_X, train_y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('MAE: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))
| 0.58166 | 0.955026 |
```
try:
import openmdao.api as om
except ImportError:
!python -m pip install openmdao[notebooks]
import openmdao.api as om
```
# BoundsEnforceLS
The BoundsEnforceLS only backtracks until variables violate their upper and lower bounds.
Here is a simple example where BoundsEnforceLS is used to backtrack during the Newton solver's iteration on
a system that contains an implicit component with 3 states that are confined to a small range of values.
```
import numpy as np
import openmdao.api as om
from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays
top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])
top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()
top.model.nonlinear_solver.linesearch = om.BoundsEnforceLS()
top.setup()
top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))
# Test lower bounds: should go to the lower bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()
for ind in range(3):
print(top.get_val('comp.z', indices=ind))
from openmdao.utils.assert_utils import assert_near_equal
for ind in range(3):
assert_near_equal(top.get_val('comp.z', indices=ind), [1.5], 1e-8)
```
## BoundsEnforceLS Options
```
om.show_options_table("openmdao.solvers.linesearch.backtracking.BoundsEnforceLS")
```
## BoundsEnforceLS Constructor
The call signature for the `BoundsEnforceLS` constructor is:
```{eval-rst}
.. automethod:: openmdao.solvers.linesearch.backtracking.BoundsEnforceLS.__init__
:noindex:
```
## BoundsEnforceLS Option Examples
**bound_enforcement**
BoundsEnforceLS includes the `bound_enforcement` option in its options dictionary. This option has a dual role:
1. Behavior of the non-bounded variables when the bounded ones are capped.
2. Direction of the further backtracking.
There are three difference bounds enforcement schemes available in this option.
With "scalar" bounds enforcement, only the variables that violate their bounds are pulled back to feasible values; the
remaining values are kept at the Newton-stepped point. This changes the direction of the backtracking vector so that
it still moves in the direction of the initial point. This is the default bounds enforcement for `BoundsEnforceLS`.

With "vector" bounds enforcement, the solution in the output vector is pulled back in unison to a point where none of the
variables violate any upper or lower bounds. Further backtracking continues along the Newton gradient direction vector back towards the
initial point.

With "wall" bounds enforcement, only the variables that violate their bounds are pulled back to feasible values; the remaining values are kept at the Newton-stepped point. Further backtracking only occurs in the direction of the non-violating variables, so that it will move along the wall.
```{Note}
When using BoundsEnforceLS linesearch, the `scalar` and `wall` methods are exactly the same because no further
backtracking is performed.
```

Here are a few examples of this option:
- bound_enforcement: vector
The `bound_enforcement` option in the options dictionary is used to specify how the output bounds
are enforced. When this is set to "vector", the output vector is rolled back along the computed gradient until
it reaches a point where the earliest bound violation occurred. The backtracking continues along the original
computed gradient.
```
from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays
top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])
top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()
top.model.nonlinear_solver.linesearch = om.BoundsEnforceLS(bound_enforcement='vector')
top.setup()
top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))
# Test lower bounds: should go to the lower bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()
for ind in range(3):
print(top.get_val('comp.z', indices=ind))
for ind in range(3):
assert_near_equal(top.get_val('comp.z', indices=ind), [1.5], 1e-8)
```
- bound_enforcement: scalar
The `bound_enforcement` option in the options dictionary is used to specify how the output bounds
are enforced. When this is set to "scaler", then the only indices in the output vector that are rolled back
are the ones that violate their upper or lower bounds. The backtracking continues along the modified gradient.
```
from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays
top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])
top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()
top.model.nonlinear_solver.linesearch = om.BoundsEnforceLS(bound_enforcement='scalar')
top.setup()
top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))
top.run_model()
# Test lower bounds: should stop just short of the lower bound
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()
```
- bound_enforcement: wall
The `bound_enforcement` option in the options dictionary is used to specify how the output bounds
are enforced. When this is set to "wall", then the only indices in the output vector that are rolled back
are the ones that violate their upper or lower bounds. The backtracking continues along a modified gradient
direction that follows the boundary of the violated output bounds.
```
from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays
top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])
top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()
top.model.nonlinear_solver.linesearch = om.BoundsEnforceLS(bound_enforcement='wall')
top.setup()
top.set_val('x', np.array([0.5, 0.5, 0.5]).reshape(3, 1))
# Test upper bounds: should go to the upper bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 2.4)
top.run_model()
print(top.get_val('comp.z', indices=0))
print(top.get_val('comp.z', indices=1))
print(top.get_val('comp.z', indices=2))
assert_near_equal(top.get_val('comp.z', indices=0), [2.6], 1e-8)
assert_near_equal(top.get_val('comp.z', indices=1), [2.5], 1e-8)
assert_near_equal(top.get_val('comp.z', indices=2), [2.65], 1e-8)
```
|
github_jupyter
|
try:
import openmdao.api as om
except ImportError:
!python -m pip install openmdao[notebooks]
import openmdao.api as om
import numpy as np
import openmdao.api as om
from openmdao.test_suite.components.implicit_newton_linesearch import ImplCompTwoStatesArrays
top = om.Problem()
top.model.add_subsystem('comp', ImplCompTwoStatesArrays(), promotes_inputs=['x'])
top.model.nonlinear_solver = om.NewtonSolver(solve_subsystems=False)
top.model.nonlinear_solver.options['maxiter'] = 10
top.model.linear_solver = om.ScipyKrylov()
top.model.nonlinear_solver.linesearch = om.BoundsEnforceLS()
top.setup()
top.set_val('x', np.array([2., 2, 2]).reshape(3, 1))
# Test lower bounds: should go to the lower bound and stall
top.set_val('comp.y', 0.)
top.set_val('comp.z', 1.6)
top.run_model()
for ind in range(3):
print(top.get_val('comp.z', indices=ind))
from openmdao.utils.assert_utils import assert_near_equal
for ind in range(3):
assert_near_equal(top.get_val('comp.z', indices=ind), [1.5], 1e-8)
om.show_options_table("openmdao.solvers.linesearch.backtracking.BoundsEnforceLS")
## BoundsEnforceLS Option Examples
**bound_enforcement**
BoundsEnforceLS includes the `bound_enforcement` option in its options dictionary. This option has a dual role:
1. Behavior of the non-bounded variables when the bounded ones are capped.
2. Direction of the further backtracking.
There are three difference bounds enforcement schemes available in this option.
With "scalar" bounds enforcement, only the variables that violate their bounds are pulled back to feasible values; the
remaining values are kept at the Newton-stepped point. This changes the direction of the backtracking vector so that
it still moves in the direction of the initial point. This is the default bounds enforcement for `BoundsEnforceLS`.

With "vector" bounds enforcement, the solution in the output vector is pulled back in unison to a point where none of the
variables violate any upper or lower bounds. Further backtracking continues along the Newton gradient direction vector back towards the
initial point.

With "wall" bounds enforcement, only the variables that violate their bounds are pulled back to feasible values; the remaining values are kept at the Newton-stepped point. Further backtracking only occurs in the direction of the non-violating variables, so that it will move along the wall.

Here are a few examples of this option:
- bound_enforcement: vector
The `bound_enforcement` option in the options dictionary is used to specify how the output bounds
are enforced. When this is set to "vector", the output vector is rolled back along the computed gradient until
it reaches a point where the earliest bound violation occurred. The backtracking continues along the original
computed gradient.
- bound_enforcement: scalar
The `bound_enforcement` option in the options dictionary is used to specify how the output bounds
are enforced. When this is set to "scaler", then the only indices in the output vector that are rolled back
are the ones that violate their upper or lower bounds. The backtracking continues along the modified gradient.
- bound_enforcement: wall
The `bound_enforcement` option in the options dictionary is used to specify how the output bounds
are enforced. When this is set to "wall", then the only indices in the output vector that are rolled back
are the ones that violate their upper or lower bounds. The backtracking continues along a modified gradient
direction that follows the boundary of the violated output bounds.
| 0.825379 | 0.8059 |
```
import pyspark
from pyspark import SparkConf
from pyspark import SparkContext, SQLContext
import pandas as pd
import seaborn as sns
# You can configure the SparkContext
conf = SparkConf()
conf.set('spark.sql.shuffle.partitions', '2100')
conf.set("spark.executor.cores", "5")
SparkContext.setSystemProperty('spark.executor.memory', '10g')
SparkContext.setSystemProperty('spark.driver.memory', '10g')
sc = SparkContext(appName='mm_exp', conf=conf)
sqlContext = pyspark.SQLContext(sc)
metadata = sqlContext.read.json('/amazon/data/metadata.json.gz')
metadata.show()
review_data = sqlContext.read.json('/amazon/data/item_dedup.json.gz')
review_data.show()
metadata_pandas_df = metadata.limit(100).toPandas()
review_data_pandas_df = review_data.limit(100).toPandas()
review_data_pandas_df.to_csv('review_data_cutted.csv')
metadata_pandas_df.to_csv('metadata_cutted.csv')
df = pd.merge(review_data_pandas_df, metadata_pandas_df, on='asin', how='inner')
df
flat_categories_df = pd.DataFrame(columns=['asin','category', 'reviewTime', 'overall', 'reviewerID', 'price', 'title'])
for index, row in df.iterrows():
if row['categories'] is None:
flat_categories_df = flat_categories_df.append({'asin': row['asin'],
'category': None,
'reviewTime': row['reviewTime'],
'overall': row['overall'],
'reviewerID': row['reviewerID'],
'price': row['price'],
'title': row['title']},
ignore_index=True)
continue
for category in row['categories'][0]:
flat_categories_df = flat_categories_df.append({'asin': row['asin'],
'category': category,
'reviewTime': row['reviewTime'],
'overall': row['overall'],
'reviewerID': row['reviewerID'],
'price': row['price'],
'title': row['title']},
ignore_index=True)
flat_categories_df['reviewTime'] = pd.to_datetime(flat_categories_df['reviewTime']).dt.to_period('M')
flat_categories_df
g = sns.countplot(data=flat_categories_df, x='category')
g.set_xticklabels(g.get_xticklabels(),rotation=90)
final = pd.DataFrame(flat_categories_df.groupby(['category','reviewTime'])['overall'].mean())
final
```
|
github_jupyter
|
import pyspark
from pyspark import SparkConf
from pyspark import SparkContext, SQLContext
import pandas as pd
import seaborn as sns
# You can configure the SparkContext
conf = SparkConf()
conf.set('spark.sql.shuffle.partitions', '2100')
conf.set("spark.executor.cores", "5")
SparkContext.setSystemProperty('spark.executor.memory', '10g')
SparkContext.setSystemProperty('spark.driver.memory', '10g')
sc = SparkContext(appName='mm_exp', conf=conf)
sqlContext = pyspark.SQLContext(sc)
metadata = sqlContext.read.json('/amazon/data/metadata.json.gz')
metadata.show()
review_data = sqlContext.read.json('/amazon/data/item_dedup.json.gz')
review_data.show()
metadata_pandas_df = metadata.limit(100).toPandas()
review_data_pandas_df = review_data.limit(100).toPandas()
review_data_pandas_df.to_csv('review_data_cutted.csv')
metadata_pandas_df.to_csv('metadata_cutted.csv')
df = pd.merge(review_data_pandas_df, metadata_pandas_df, on='asin', how='inner')
df
flat_categories_df = pd.DataFrame(columns=['asin','category', 'reviewTime', 'overall', 'reviewerID', 'price', 'title'])
for index, row in df.iterrows():
if row['categories'] is None:
flat_categories_df = flat_categories_df.append({'asin': row['asin'],
'category': None,
'reviewTime': row['reviewTime'],
'overall': row['overall'],
'reviewerID': row['reviewerID'],
'price': row['price'],
'title': row['title']},
ignore_index=True)
continue
for category in row['categories'][0]:
flat_categories_df = flat_categories_df.append({'asin': row['asin'],
'category': category,
'reviewTime': row['reviewTime'],
'overall': row['overall'],
'reviewerID': row['reviewerID'],
'price': row['price'],
'title': row['title']},
ignore_index=True)
flat_categories_df['reviewTime'] = pd.to_datetime(flat_categories_df['reviewTime']).dt.to_period('M')
flat_categories_df
g = sns.countplot(data=flat_categories_df, x='category')
g.set_xticklabels(g.get_xticklabels(),rotation=90)
final = pd.DataFrame(flat_categories_df.groupby(['category','reviewTime'])['overall'].mean())
final
| 0.358465 | 0.288636 |
# Classroom exercise: energy calculation
## Diffusion model in 1D
Description: A one-dimensional diffusion model. (Could be a gas of particles, or a bunch of crowded people in a corridor, or animals in a valley habitat...)
- Agents are on a 1d axis
- Agents do not want to be where there are other agents
- This is represented as an 'energy': the higher the energy, the more unhappy the agents.
Implementation:
- Given a vector $n$ of positive integers, and of arbitrary length
- Compute the energy, $E(n) = \sum_i n_i(n_i - 1)$
- Later, we will have the likelyhood of an agent moving depend on the change in energy.
```
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
density = np.array([0, 0, 3, 5, 8, 4, 2, 1])
fig, ax = plt.subplots()
ax.bar(np.arange(len(density)) - 0.5, density)
ax.xrange = [-0.5, len(density) - 0.5]
ax.set_ylabel("Particle count $n_i$")
ax.set_xlabel("Position $i$")
```
Here, the total energy due to position 2 is $3 (3-1)=6$, and due to column 7 is $1 (1-1)=0$. We need to sum these to get the
total energy.
## Starting point
Create a Python module:
```
%%bash
rm -rf diffusion
mkdir diffusion
install -m 644 /dev/null diffusion/__init__.py
```
**Windows:** You will need to run the following instead
```cmd
%%cmd
rmdir /s diffusion
mkdir diffusion
type nul > diffusion/__init__.py
```
**NB.** If you are using the Windows command prompt, you will also have to replace all subsequent `%%bash` directives with `%%cmd`
* Implementation file: diffusion_model.py
```
%%writefile diffusion/model.py
def energy(density, coeff=1.0):
"""Energy associated with the diffusion model
Parameters
----------
density: array of positive integers
Number of particles at each position i in the array
coeff: float
Diffusion coefficient.
"""
# implementation goes here
```
* Testing file: test_diffusion_model.py
```
%%writefile diffusion/test_model.py
from .model import energy
def test_energy():
"""Optional description for nose reporting."""
# Test something
```
Invoke the tests:
```
%%bash
cd diffusion
py.test
```
Now, write your code (in `model.py`), and tests (in `test_model.py`), testing as you do.
## Solution
Don't look until after you've tried!
In the spirit of test-driven development let's first consider our tests.
```
%%writefile diffusion/test_model.py
"""Unit tests for a diffusion model."""
from pytest import raises
from .model import energy
def test_energy_fails_on_non_integer_density():
with raises(TypeError) as exception:
energy([1.0, 2, 3])
def test_energy_fails_on_negative_density():
with raises(ValueError) as exception:
energy([-1, 2, 3])
def test_energy_fails_ndimensional_density():
with raises(ValueError) as exception:
energy([[1, 2, 3], [3, 4, 5]])
def test_zero_energy_cases():
# Zero energy at zero density
densities = [[], [0], [0, 0, 0]]
for density in densities:
assert energy(density) == 0
def test_derivative():
from numpy.random import randint
# Loop over vectors of different sizes (but not empty)
for vector_size in randint(1, 1000, size=30):
# Create random density of size N
density = randint(50, size=vector_size)
# will do derivative at this index
element_index = randint(vector_size)
# modified densities
density_plus_one = density.copy()
density_plus_one[element_index] += 1
# Compute and check result
# d(n^2-1)/dn = 2n
expected = 2.0 * density[element_index] if density[element_index] > 0 else 0
actual = energy(density_plus_one) - energy(density)
assert expected == actual
def test_derivative_no_self_energy():
"""If particle is alone, then its participation to energy is zero."""
from numpy import array
density = array([1, 0, 1, 10, 15, 0])
density_plus_one = density.copy()
density[1] += 1
expected = 0
actual = energy(density_plus_one) - energy(density)
assert expected == actual
```
Now let's write an implementation that passes the tests.
```
%%writefile diffusion/model.py
"""Simplistic 1-dimensional diffusion model."""
from numpy import array, any, sum
def energy(density):
"""Energy associated with the diffusion model
:Parameters:
density: array of positive integers
Number of particles at each position i in the array/geometry
"""
# Make sure input is an numpy array
density = array(density)
# ...of the right kind (integer). Unless it is zero length,
# in which case type does not matter.
if density.dtype.kind != "i" and len(density) > 0:
raise TypeError("Density should be a array of *integers*.")
# and the right values (positive or null)
if any(density < 0):
raise ValueError("Density should be an array of *positive* integers.")
if density.ndim != 1:
raise ValueError(
"Density should be an a *1-dimensional*" + "array of positive integers."
)
return sum(density * (density - 1))
%%bash
cd diffusion
py.test
```
## Coverage
With py.test, you can use the ["pytest-cov" plugin](https://github.com/pytest-dev/pytest-cov) to measure test coverage
```
%%bash
cd diffusion
py.test --cov
```
Or an html report:
```
%%bash
#%%cmd (windows)
cd diffusion
py.test --cov --cov-report html
```
Look at the [coverage results](./diffusion/htmlcov/index.html)
|
github_jupyter
|
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
density = np.array([0, 0, 3, 5, 8, 4, 2, 1])
fig, ax = plt.subplots()
ax.bar(np.arange(len(density)) - 0.5, density)
ax.xrange = [-0.5, len(density) - 0.5]
ax.set_ylabel("Particle count $n_i$")
ax.set_xlabel("Position $i$")
%%bash
rm -rf diffusion
mkdir diffusion
install -m 644 /dev/null diffusion/__init__.py
%%cmd
rmdir /s diffusion
mkdir diffusion
type nul > diffusion/__init__.py
%%writefile diffusion/model.py
def energy(density, coeff=1.0):
"""Energy associated with the diffusion model
Parameters
----------
density: array of positive integers
Number of particles at each position i in the array
coeff: float
Diffusion coefficient.
"""
# implementation goes here
%%writefile diffusion/test_model.py
from .model import energy
def test_energy():
"""Optional description for nose reporting."""
# Test something
%%bash
cd diffusion
py.test
%%writefile diffusion/test_model.py
"""Unit tests for a diffusion model."""
from pytest import raises
from .model import energy
def test_energy_fails_on_non_integer_density():
with raises(TypeError) as exception:
energy([1.0, 2, 3])
def test_energy_fails_on_negative_density():
with raises(ValueError) as exception:
energy([-1, 2, 3])
def test_energy_fails_ndimensional_density():
with raises(ValueError) as exception:
energy([[1, 2, 3], [3, 4, 5]])
def test_zero_energy_cases():
# Zero energy at zero density
densities = [[], [0], [0, 0, 0]]
for density in densities:
assert energy(density) == 0
def test_derivative():
from numpy.random import randint
# Loop over vectors of different sizes (but not empty)
for vector_size in randint(1, 1000, size=30):
# Create random density of size N
density = randint(50, size=vector_size)
# will do derivative at this index
element_index = randint(vector_size)
# modified densities
density_plus_one = density.copy()
density_plus_one[element_index] += 1
# Compute and check result
# d(n^2-1)/dn = 2n
expected = 2.0 * density[element_index] if density[element_index] > 0 else 0
actual = energy(density_plus_one) - energy(density)
assert expected == actual
def test_derivative_no_self_energy():
"""If particle is alone, then its participation to energy is zero."""
from numpy import array
density = array([1, 0, 1, 10, 15, 0])
density_plus_one = density.copy()
density[1] += 1
expected = 0
actual = energy(density_plus_one) - energy(density)
assert expected == actual
%%writefile diffusion/model.py
"""Simplistic 1-dimensional diffusion model."""
from numpy import array, any, sum
def energy(density):
"""Energy associated with the diffusion model
:Parameters:
density: array of positive integers
Number of particles at each position i in the array/geometry
"""
# Make sure input is an numpy array
density = array(density)
# ...of the right kind (integer). Unless it is zero length,
# in which case type does not matter.
if density.dtype.kind != "i" and len(density) > 0:
raise TypeError("Density should be a array of *integers*.")
# and the right values (positive or null)
if any(density < 0):
raise ValueError("Density should be an array of *positive* integers.")
if density.ndim != 1:
raise ValueError(
"Density should be an a *1-dimensional*" + "array of positive integers."
)
return sum(density * (density - 1))
%%bash
cd diffusion
py.test
%%bash
cd diffusion
py.test --cov
%%bash
#%%cmd (windows)
cd diffusion
py.test --cov --cov-report html
| 0.724188 | 0.982305 |
```
import pandas as pd
import sklearn
from sklearn import model_selection
from sklearn.metrics import accuracy_score
from sklearn.neighbors import KNeighborsClassifier
from tkinter import *
import tkinter as tk
from tkinter import filedialog
root= tk.Tk()
root.resizable(0, 0)
root.title("Iris Prediction")
canvas1 = tk.Canvas(root, width = 600, height = 400, relief = 'raised', bg="white")
canvas1.pack()
input_text = StringVar()
input_text1 = StringVar()
input_text2 = StringVar()
input_text3 = StringVar()
result = StringVar()
label1 = tk.Label(root, text='Iris Prediction')
label1.config(font=('helvetica', 16),bg="white")
canvas1.create_window(300, 30, window=label1)
label2 = tk.Label(root, text='Sepal-length :')
label2.config(font=('helvetica', 12),bg="white")
canvas1.create_window(130, 90, window=label2)
entry1 = tk.Entry(root, font = ('helvetica', 12, 'bold'), textvariable = input_text, borderwidth=2)
canvas1.create_window(380, 90, window=entry1)
label3 = tk.Label(root, text='Sepal-width :')
label3.config(font=('helvetica', 12),bg="white")
canvas1.create_window(130, 130, window=label3)
entry2 = tk.Entry (root, font = ('helvetica', 12, 'bold'), textvariable = input_text1, borderwidth=2)
canvas1.create_window(380, 130, window=entry2)
label4 = tk.Label(root, text='Petal-length :')
label4.config(font=('helvetica', 12),bg="white")
canvas1.create_window(130, 170, window=label4)
entry3 = tk.Entry (root, font = ('helvetica', 12, 'bold'), textvariable = input_text2, borderwidth=2)
canvas1.create_window(380, 170, window=entry3)
label5 = tk.Label(root, text='Petal-width :')
label5.config(font=('helvetica', 12),bg="white")
canvas1.create_window(130, 210, window=label5)
entry4 = tk.Entry (root, font = ('helvetica', 12, 'bold'), textvariable = input_text3, borderwidth=2)
canvas1.create_window(380, 210, window=entry4)
label6 = tk.Label(root, text= 'Predictin is ' ,font=('helvetica', 14),bg="white")
canvas1.create_window(170, 330, window=label6)
entry5 = tk.Entry (root, font = ('helvetica', 12, 'bold'), textvariable = result, borderwidth=2)
canvas1.create_window(380, 330, window=entry5)
def btnclear():
input_text.set("")
input_text1.set("")
input_text2.set("")
input_text3.set("")
result.set("")
def getCSV ():
global df
import_file_path = filedialog.askopenfilename()
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
df = pd.read_csv (import_file_path, names=names)
print (df)
def getPredict ():
x1 = entry1.get()
x2 = entry2.get()
x3 = entry3.get()
x4 = entry4.get()
list1=[x1,x2,x3,x4]
# print(df.groupby("class").size())
# Split-out validation dataset
array = df.values
X = array[:, 0:4]
Y = array[:, 4]
# print(X)
validation_size = 0.20
seed = 7
X_train, X_validation, Y_train, Y_validation = model_selection.train_test_split(X, Y, test_size=validation_size,
random_state=seed)
# Make predictions on validation dataset
knn = KNeighborsClassifier()
# train
knn.fit(X_train, Y_train)
X1=[list1]
predictions = knn.predict(X1)
result.set(predictions)
browseButton_CSV = tk.Button(text=" Import CSV File ", command=getCSV, bg='white', fg='black', font=('helvetica', 12, 'bold'),borderwidth=3)
canvas1.create_window(140, 270, window=browseButton_CSV)
predictButton = tk.Button(text=" Predict ", command=getPredict, bg='white', fg='black', font=('helvetica', 12, 'bold'), borderwidth=3)
canvas1.create_window(320, 270, window=predictButton)
clear = tk.Button(text=" Clear ", command=btnclear, bg='white', fg='black', font=('helvetica', 12, 'bold'),borderwidth=3)
canvas1.create_window(460, 270, window=clear)
root.mainloop()
```
|
github_jupyter
|
import pandas as pd
import sklearn
from sklearn import model_selection
from sklearn.metrics import accuracy_score
from sklearn.neighbors import KNeighborsClassifier
from tkinter import *
import tkinter as tk
from tkinter import filedialog
root= tk.Tk()
root.resizable(0, 0)
root.title("Iris Prediction")
canvas1 = tk.Canvas(root, width = 600, height = 400, relief = 'raised', bg="white")
canvas1.pack()
input_text = StringVar()
input_text1 = StringVar()
input_text2 = StringVar()
input_text3 = StringVar()
result = StringVar()
label1 = tk.Label(root, text='Iris Prediction')
label1.config(font=('helvetica', 16),bg="white")
canvas1.create_window(300, 30, window=label1)
label2 = tk.Label(root, text='Sepal-length :')
label2.config(font=('helvetica', 12),bg="white")
canvas1.create_window(130, 90, window=label2)
entry1 = tk.Entry(root, font = ('helvetica', 12, 'bold'), textvariable = input_text, borderwidth=2)
canvas1.create_window(380, 90, window=entry1)
label3 = tk.Label(root, text='Sepal-width :')
label3.config(font=('helvetica', 12),bg="white")
canvas1.create_window(130, 130, window=label3)
entry2 = tk.Entry (root, font = ('helvetica', 12, 'bold'), textvariable = input_text1, borderwidth=2)
canvas1.create_window(380, 130, window=entry2)
label4 = tk.Label(root, text='Petal-length :')
label4.config(font=('helvetica', 12),bg="white")
canvas1.create_window(130, 170, window=label4)
entry3 = tk.Entry (root, font = ('helvetica', 12, 'bold'), textvariable = input_text2, borderwidth=2)
canvas1.create_window(380, 170, window=entry3)
label5 = tk.Label(root, text='Petal-width :')
label5.config(font=('helvetica', 12),bg="white")
canvas1.create_window(130, 210, window=label5)
entry4 = tk.Entry (root, font = ('helvetica', 12, 'bold'), textvariable = input_text3, borderwidth=2)
canvas1.create_window(380, 210, window=entry4)
label6 = tk.Label(root, text= 'Predictin is ' ,font=('helvetica', 14),bg="white")
canvas1.create_window(170, 330, window=label6)
entry5 = tk.Entry (root, font = ('helvetica', 12, 'bold'), textvariable = result, borderwidth=2)
canvas1.create_window(380, 330, window=entry5)
def btnclear():
input_text.set("")
input_text1.set("")
input_text2.set("")
input_text3.set("")
result.set("")
def getCSV ():
global df
import_file_path = filedialog.askopenfilename()
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
df = pd.read_csv (import_file_path, names=names)
print (df)
def getPredict ():
x1 = entry1.get()
x2 = entry2.get()
x3 = entry3.get()
x4 = entry4.get()
list1=[x1,x2,x3,x4]
# print(df.groupby("class").size())
# Split-out validation dataset
array = df.values
X = array[:, 0:4]
Y = array[:, 4]
# print(X)
validation_size = 0.20
seed = 7
X_train, X_validation, Y_train, Y_validation = model_selection.train_test_split(X, Y, test_size=validation_size,
random_state=seed)
# Make predictions on validation dataset
knn = KNeighborsClassifier()
# train
knn.fit(X_train, Y_train)
X1=[list1]
predictions = knn.predict(X1)
result.set(predictions)
browseButton_CSV = tk.Button(text=" Import CSV File ", command=getCSV, bg='white', fg='black', font=('helvetica', 12, 'bold'),borderwidth=3)
canvas1.create_window(140, 270, window=browseButton_CSV)
predictButton = tk.Button(text=" Predict ", command=getPredict, bg='white', fg='black', font=('helvetica', 12, 'bold'), borderwidth=3)
canvas1.create_window(320, 270, window=predictButton)
clear = tk.Button(text=" Clear ", command=btnclear, bg='white', fg='black', font=('helvetica', 12, 'bold'),borderwidth=3)
canvas1.create_window(460, 270, window=clear)
root.mainloop()
| 0.25488 | 0.12603 |
```
import itertools
from skyscanner import FlightsCache
service = FlightsCache('se893794935794863942245517499220')
params = dict(
market='US',
currency='USD',
locale='en-US',
destinationplace='US',
outbounddate='2016-08',
inbounddate='2016-08')
user1_params = dict(originplace='DTW-sky')
user2_params = dict(originplace='SFO-sky')
user1_result = service.get_cheapest_quotes(**params, **user1_params).parsed
user2_result = service.get_cheapest_quotes(**params, **user2_params).parsed
import sqlite3
DB_SCHEMA = """
PRAGMA foreign_keys = ON;
CREATE TABLE place
( id INTEGER PRIMARY KEY
, name TEXT NOT NULL
, type TEXT NOT NULL
);
CREATE TABLE quote
( query_id INTEGER
, quote_id INTEGER
, direct BOOLEAN NOT NULL
, minimum_price FLOAT NOT NULL
, quote_datetime DATETIME NOT NULL
, outbound_departure_date DATETIME NOT NULL
, outbound_origin_id INTEGER NOT NULL REFERENCES place(id)
, outbound_destination_id INTEGER NOT NULL REFERENCES place(id)
, outbound_carriers TEXT NOT NULL
, inbound_departure_date DATETIME NOT NULL
, inbound_origin_id INTEGER NOT NULL REFERENCES place(id)
, inbound_destination_id INTEGER NOT NULL REFERENCES place(id)
, inbound_carriers TEXT NOT NULL
, PRIMARY KEY (query_id, quote_id)
);
"""
sqlite3.enable_callback_tracebacks(True)
db = sqlite3.connect(':memory:')
db.executescript(DB_SCHEMA)
places = [(d['PlaceId'], d['Name'], d['Type'])
for d in itertools.chain(user1_result['Places'],
user2_result['Places'])]
db.executemany('INSERT INTO place VALUES (?,?,?)', set(places))
quotes1 = [(1, d['QuoteId'], d['Direct'], d['MinPrice'], d['QuoteDateTime'],
d['OutboundLeg']['DepartureDate'], d['OutboundLeg']['OriginId'],
d['OutboundLeg']['DestinationId'], str(d['OutboundLeg']['CarrierIds']),
d['InboundLeg']['DepartureDate'], d['InboundLeg']['OriginId'],
d['InboundLeg']['DestinationId'], str(d['InboundLeg']['CarrierIds']))
for d in user1_result['Quotes']]
db.executemany('INSERT INTO quote VALUES (?,?,?,?,?,?,?,?,?,?,?,?,?)', quotes1)
quotes2 = [(2, d['QuoteId'], d['Direct'], d['MinPrice'], d['QuoteDateTime'],
d['OutboundLeg']['DepartureDate'], d['OutboundLeg']['OriginId'],
d['OutboundLeg']['DestinationId'], str(d['OutboundLeg']['CarrierIds']),
d['InboundLeg']['DepartureDate'], d['InboundLeg']['OriginId'],
d['InboundLeg']['DestinationId'], str(d['InboundLeg']['CarrierIds']))
for d in user2_result['Quotes']]
db.executemany('INSERT INTO quote VALUES (?,?,?,?,?,?,?,?,?,?,?,?,?)', quotes2)
import pandas as pd
place_table = pd.read_sql('SELECT * FROM place', con=db)
place_map = dict(zip(place_table.id, place_table.name))
query = """
SELECT
quote1.minimum_price + quote2.minimum_price AS minimum_total_price
, quote1.outbound_origin_id AS quote1_origin
, quote2.outbound_origin_id AS quote2_origin
, quote1.outbound_destination_id AS destination
, quote1.outbound_departure_date AS quote1_outbound_date
, quote2.outbound_departure_date AS quote2_outbound_date
, quote1.inbound_departure_date AS quote1_inbound_date
, quote2.inbound_departure_date AS quote2_inbound_date
FROM (SELECT * FROM quote where query_id = 1) AS quote1
JOIN (SELECT * FROM quote where query_id = 2) AS quote2
ON quote1.outbound_destination_id = quote2.outbound_destination_id
-- AND JULIANDAY(quote1.outbound_departure_date) = JULIANDAY(quote2.outbound_departure_date)
"""
data = pd.read_sql(query, con=db, parse_dates=['quote1_outbound_date', 'quote2_outbound_date', 'quote1_inbound_date', 'quote2_inbound_date'])
data.quote1_origin = data.quote1_origin.map(place_map)
data.quote2_origin = data.quote2_origin.map(place_map)
data.destination = data.destination.map(place_map)
data[(abs((data.quote1_inbound_date - data.quote2_inbound_date).dt.days) <= 0) &
(abs((data.quote1_outbound_date - data.quote2_outbound_date).dt.days) <= 0)].sort_values('minimum_total_price').head()
```
|
github_jupyter
|
import itertools
from skyscanner import FlightsCache
service = FlightsCache('se893794935794863942245517499220')
params = dict(
market='US',
currency='USD',
locale='en-US',
destinationplace='US',
outbounddate='2016-08',
inbounddate='2016-08')
user1_params = dict(originplace='DTW-sky')
user2_params = dict(originplace='SFO-sky')
user1_result = service.get_cheapest_quotes(**params, **user1_params).parsed
user2_result = service.get_cheapest_quotes(**params, **user2_params).parsed
import sqlite3
DB_SCHEMA = """
PRAGMA foreign_keys = ON;
CREATE TABLE place
( id INTEGER PRIMARY KEY
, name TEXT NOT NULL
, type TEXT NOT NULL
);
CREATE TABLE quote
( query_id INTEGER
, quote_id INTEGER
, direct BOOLEAN NOT NULL
, minimum_price FLOAT NOT NULL
, quote_datetime DATETIME NOT NULL
, outbound_departure_date DATETIME NOT NULL
, outbound_origin_id INTEGER NOT NULL REFERENCES place(id)
, outbound_destination_id INTEGER NOT NULL REFERENCES place(id)
, outbound_carriers TEXT NOT NULL
, inbound_departure_date DATETIME NOT NULL
, inbound_origin_id INTEGER NOT NULL REFERENCES place(id)
, inbound_destination_id INTEGER NOT NULL REFERENCES place(id)
, inbound_carriers TEXT NOT NULL
, PRIMARY KEY (query_id, quote_id)
);
"""
sqlite3.enable_callback_tracebacks(True)
db = sqlite3.connect(':memory:')
db.executescript(DB_SCHEMA)
places = [(d['PlaceId'], d['Name'], d['Type'])
for d in itertools.chain(user1_result['Places'],
user2_result['Places'])]
db.executemany('INSERT INTO place VALUES (?,?,?)', set(places))
quotes1 = [(1, d['QuoteId'], d['Direct'], d['MinPrice'], d['QuoteDateTime'],
d['OutboundLeg']['DepartureDate'], d['OutboundLeg']['OriginId'],
d['OutboundLeg']['DestinationId'], str(d['OutboundLeg']['CarrierIds']),
d['InboundLeg']['DepartureDate'], d['InboundLeg']['OriginId'],
d['InboundLeg']['DestinationId'], str(d['InboundLeg']['CarrierIds']))
for d in user1_result['Quotes']]
db.executemany('INSERT INTO quote VALUES (?,?,?,?,?,?,?,?,?,?,?,?,?)', quotes1)
quotes2 = [(2, d['QuoteId'], d['Direct'], d['MinPrice'], d['QuoteDateTime'],
d['OutboundLeg']['DepartureDate'], d['OutboundLeg']['OriginId'],
d['OutboundLeg']['DestinationId'], str(d['OutboundLeg']['CarrierIds']),
d['InboundLeg']['DepartureDate'], d['InboundLeg']['OriginId'],
d['InboundLeg']['DestinationId'], str(d['InboundLeg']['CarrierIds']))
for d in user2_result['Quotes']]
db.executemany('INSERT INTO quote VALUES (?,?,?,?,?,?,?,?,?,?,?,?,?)', quotes2)
import pandas as pd
place_table = pd.read_sql('SELECT * FROM place', con=db)
place_map = dict(zip(place_table.id, place_table.name))
query = """
SELECT
quote1.minimum_price + quote2.minimum_price AS minimum_total_price
, quote1.outbound_origin_id AS quote1_origin
, quote2.outbound_origin_id AS quote2_origin
, quote1.outbound_destination_id AS destination
, quote1.outbound_departure_date AS quote1_outbound_date
, quote2.outbound_departure_date AS quote2_outbound_date
, quote1.inbound_departure_date AS quote1_inbound_date
, quote2.inbound_departure_date AS quote2_inbound_date
FROM (SELECT * FROM quote where query_id = 1) AS quote1
JOIN (SELECT * FROM quote where query_id = 2) AS quote2
ON quote1.outbound_destination_id = quote2.outbound_destination_id
-- AND JULIANDAY(quote1.outbound_departure_date) = JULIANDAY(quote2.outbound_departure_date)
"""
data = pd.read_sql(query, con=db, parse_dates=['quote1_outbound_date', 'quote2_outbound_date', 'quote1_inbound_date', 'quote2_inbound_date'])
data.quote1_origin = data.quote1_origin.map(place_map)
data.quote2_origin = data.quote2_origin.map(place_map)
data.destination = data.destination.map(place_map)
data[(abs((data.quote1_inbound_date - data.quote2_inbound_date).dt.days) <= 0) &
(abs((data.quote1_outbound_date - data.quote2_outbound_date).dt.days) <= 0)].sort_values('minimum_total_price').head()
| 0.267408 | 0.092401 |
# 元组
元组不可变
---
「元组」定义语法为:(元素1, 元素2, ..., 元素n)
- 小括号把所有元素绑在一起
- 逗号将每个元素一一分开
## 1. 创建和访问一个元组
- Python 的元组与列表类似,不同之处在于tuple被创建后就不能对其进行修改,类似字符串。
- 元组使用小括号,列表使用方括号。
- 元组与列表类似,也用整数来对它进行**索引 (indexing) 和切片 (slicing)**。
```
t1 = (1, 10.31, 'python')
t2 = 1, 10.31, 'python'
print(t1, type(t1))
# (1, 10.31, 'python') <class 'tuple'>
print(t2, type(t2))
# (1, 10.31, 'python') <class 'tuple'>
tuple1 = (1, 2, 3, 4, 5, 6, 7, 8)
print(tuple1[1]) # 2
print(tuple1[5:]) # (6, 7, 8)
print(tuple1[:5]) # (1, 2, 3, 4, 5)
tuple2 = tuple1[:]
print(tuple2) # (1, 2, 3, 4, 5, 6, 7, 8)
```
创建元组可以用小括号 (),也可以什么都不用,为了可读性,建议还是用 ()。
元组中**只包含一个元素**时,需要在元素后面添加逗号,否则括号会被当作运算符使用。
```
x = (1)
print(type(x)) # <class 'int'>
x = 2, 3, 4, 5
print(type(x)) # <class 'tuple'>
x = []
print(type(x)) # <class 'list'>
x = ()
print(type(x)) # <class 'tuple'>
x = (1,)
print(type(x)) # <class 'tuple'>
print(8 * (8)) # 64
print(8 * (8,)) # (8, 8, 8, 8, 8, 8, 8, 8)
x = (1, 10.31, 'python'), ('data', 11)
print(x)
# ((1, 10.31, 'python'), ('data', 11))
print(x[0])
# (1, 10.31, 'python')
print(x[0][0], x[0][1], x[0][2])
# 1 10.31 python
print(x[0][0:2])
# (1, 10.31)
```
## 2. 更新和删除一个元组
**此处应该是新建了一个元组, 只不过也是取名叫做week**
```
week = ('Monday', 'Tuesday', 'Thursday', 'Friday')
week = week[:2] + ('Wednesday',) + week[2:]
print(week) # ('Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday')
```
元组有不可更改 (immutable) 的性质,因此不能直接给元组的元素赋值,但是只要元组中的元素可更改 (mutable),那么我们可以直接更改其元素,注意这跟赋值其元素不同。
```
t1 = (1, 2, 3, [4, 5, 6])
print(t1) # (1, 2, 3, [4, 5, 6])
t1[3][0] = 9
print(t1) # (1, 2, 3, [9, 5, 6])
```
## 3. 元组相关的操作符
- 等号操作符:==
- 连接操作符 +
- 重复操作符 *
- 成员关系操作符 in、not in
「等号 ==」,只有成员、成员位置都相同时才返回True。
元组拼接有两种方式,用「加号 +」和「乘号 *」,前者首尾拼接,后者复制拼接。
```
t1 = (123, 456)
t2 = (456, 123)
t3 = (123, 456)
print(t1 == t2) # False
print(t1 == t3) # True
t4 = t1 + t2
print(t4) # (123, 456, 456, 123)
t5 = t3 * 3
print(t5) # (123, 456, 123, 456, 123, 456)
t3 *= 3
print(t3) # (123, 456, 123, 456, 123, 456)
print(123 in t3) # True
print(456 not in t3) # False
```
## 4. 内置方法
元组大小和内容都不可更改,因此只有 **count** 和 **index** 两种方法。
```
t = (1, 10.31, 'python')
print(t.count('python')) # 1
print(t.index(10.31)) # 1
```
- count('python') 是记录在元组 t 中该元素出现几次,显然是 1 次
- index(10.31) 是找到该元素在元组 t 的索引,显然是 1
## 5. 解压元组
解压(unpack)一维元组(有几个元素左边括号定义几个变量)
```
t = (1, 10.31, 'python')
(a, b, c) = t
print(a, b, c)
# 1 10.31 python
```
解压二维元组(按照元组里的元组结构来定义变量)
```
t = (1, 10.31, ('OK', 'python'))
(a, b, (c, d)) = t
print(a, b, c, d)
# 1 10.31 OK python
```
如果你只想要元组其中几个元素,用通配符「*」,英文叫 wildcard,在计算机语言中代表一个或多个元素。下例就是把多个元素丢给了 rest 变量。
```
t = 1, 2, 3, 4, 5
a, b, *rest, c = t
print(a, b, c) # 1 2 5
print(rest) # [3, 4]
```
如果你根本不在乎 rest 变量,那么就用通配符「*」加上下划线「_」
```
t = 1, 2, 3, 4, 5
a, b, *_ = t
print(a, b) # 1 2
```
## 练习题
### 1、元组概念
写出下面代码的执行结果和最终结果的类型
```
(1, 2)*2
# (1,2)是元组
# (1, 2, 1, 2)
(1, )*2
# (1, )是元组,因为有,
# (1, 1,)
(1)*2
# (1)被当成是int数据,因为没有, 所以输出为2
# 2
```
### 2、拆包过程是什么?
不属于,因为a, b 都是单个变量,不是元组。
使用 *- 的通配符来匹配给占位符
|
github_jupyter
|
t1 = (1, 10.31, 'python')
t2 = 1, 10.31, 'python'
print(t1, type(t1))
# (1, 10.31, 'python') <class 'tuple'>
print(t2, type(t2))
# (1, 10.31, 'python') <class 'tuple'>
tuple1 = (1, 2, 3, 4, 5, 6, 7, 8)
print(tuple1[1]) # 2
print(tuple1[5:]) # (6, 7, 8)
print(tuple1[:5]) # (1, 2, 3, 4, 5)
tuple2 = tuple1[:]
print(tuple2) # (1, 2, 3, 4, 5, 6, 7, 8)
x = (1)
print(type(x)) # <class 'int'>
x = 2, 3, 4, 5
print(type(x)) # <class 'tuple'>
x = []
print(type(x)) # <class 'list'>
x = ()
print(type(x)) # <class 'tuple'>
x = (1,)
print(type(x)) # <class 'tuple'>
print(8 * (8)) # 64
print(8 * (8,)) # (8, 8, 8, 8, 8, 8, 8, 8)
x = (1, 10.31, 'python'), ('data', 11)
print(x)
# ((1, 10.31, 'python'), ('data', 11))
print(x[0])
# (1, 10.31, 'python')
print(x[0][0], x[0][1], x[0][2])
# 1 10.31 python
print(x[0][0:2])
# (1, 10.31)
week = ('Monday', 'Tuesday', 'Thursday', 'Friday')
week = week[:2] + ('Wednesday',) + week[2:]
print(week) # ('Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday')
t1 = (1, 2, 3, [4, 5, 6])
print(t1) # (1, 2, 3, [4, 5, 6])
t1[3][0] = 9
print(t1) # (1, 2, 3, [9, 5, 6])
t1 = (123, 456)
t2 = (456, 123)
t3 = (123, 456)
print(t1 == t2) # False
print(t1 == t3) # True
t4 = t1 + t2
print(t4) # (123, 456, 456, 123)
t5 = t3 * 3
print(t5) # (123, 456, 123, 456, 123, 456)
t3 *= 3
print(t3) # (123, 456, 123, 456, 123, 456)
print(123 in t3) # True
print(456 not in t3) # False
t = (1, 10.31, 'python')
print(t.count('python')) # 1
print(t.index(10.31)) # 1
t = (1, 10.31, 'python')
(a, b, c) = t
print(a, b, c)
# 1 10.31 python
t = (1, 10.31, ('OK', 'python'))
(a, b, (c, d)) = t
print(a, b, c, d)
# 1 10.31 OK python
t = 1, 2, 3, 4, 5
a, b, *rest, c = t
print(a, b, c) # 1 2 5
print(rest) # [3, 4]
t = 1, 2, 3, 4, 5
a, b, *_ = t
print(a, b) # 1 2
(1, 2)*2
# (1,2)是元组
# (1, 2, 1, 2)
(1, )*2
# (1, )是元组,因为有,
# (1, 1,)
(1)*2
# (1)被当成是int数据,因为没有, 所以输出为2
# 2
| 0.078212 | 0.828106 |
<a href="https://colab.research.google.com/github/Tessellate-Imaging/monk_v1/blob/master/study_roadmaps/1_getting_started_roadmap/8_expert_mode/2)%20Create%20experiment%20from%20scratch%20-%20Pytorch%20backend%20-%20train%2C%20validate%2C%20infer.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Goals
### Learn how to use full potential of monk in it's expert mode
# Table of Contents
## [0. Install](#0)
## [1. Load data, setup model, select params, and Train](#1)
## [2. Run validation on trained classifier](#2)
## [3. Run inferencing on trained classifier](#3)
<a id='0'></a>
# Install Monk
- git clone https://github.com/Tessellate-Imaging/monk_v1.git
- cd monk_v1/installation/Linux && pip install -r requirements_cu9.txt
- (Select the requirements file as per OS and CUDA version)
```
!git clone https://github.com/Tessellate-Imaging/monk_v1.git
# If using Colab install using the commands below
!cd monk_v1/installation/Misc && pip install -r requirements_colab.txt
# If using Kaggle uncomment the following command
#!cd monk_v1/installation/Misc && pip install -r requirements_kaggle.txt
# Select the requirements file as per OS and CUDA version when using a local system or cloud
#!cd monk_v1/installation/Linux && pip install -r requirements_cu9.txt
```
## Dataset - Natural Images Classification
- https://www.kaggle.com/prasunroy/natural-images
```
! wget --load-cookies /tmp/cookies.txt "https://docs.google.com/uc?export=download&confirm=$(wget --save-cookies /tmp/cookies.txt --keep-session-cookies --no-check-certificate 'https://docs.google.com/uc?export=download&id=1sbQ_KaEDd7kRrTvna-4odLqxM2G0QT0Z' -O- | sed -rn 's/.*confirm=([0-9A-Za-z_]+).*/\1\n/p')&id=1sbQ_KaEDd7kRrTvna-4odLqxM2G0QT0Z" -O natural-images.zip && rm -rf /tmp/cookies.txt
! unzip -qq natural-images.zip
```
# Imports
```
# Monk
import os
import sys
sys.path.append("monk_v1/monk/");
#Using pytorch backend
from pytorch_prototype import prototype
```
<a id='1'></a>
# Load data, setup model, select params, and Train
```
gtf = prototype(verbose=1);
gtf.Prototype("project", "expert_mode");
```
## Set Data params
```
gtf.Dataset_Params(dataset_path="natural-images/train",
split=0.9,
input_size=224,
batch_size=16,
shuffle_data=True,
num_processors=3);
```
## Apply Transforms
```
gtf.apply_random_horizontal_flip(train=True, val=True);
gtf.apply_normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225], train=True, val=True, test=True);
```
## Load Dataset
```
gtf.Dataset();
```
## Set Model Params
```
gtf.Model_Params(model_name="resnet18",
freeze_base_network=True,
use_gpu=True,
use_pretrained=True);
```
## Append Custom layers to transfer learning base model
```
gtf.append_dropout(probability=0.1);
gtf.append_linear(final_layer=True);
```
## Load Model
```
gtf.Model();
```
## Freeze first few layers
```
gtf.Freeze_Layers(num=10);
```
## Set Training params
```
gtf.Training_Params(num_epochs=10,
display_progress=True,
display_progress_realtime=True,
save_intermediate_models=True,
intermediate_model_prefix="intermediate_model_",
save_training_logs=True);
## Set Optimizer, losses and learning rate schedulers
gtf.optimizer_sgd(0.001);
gtf.lr_fixed();
gtf.loss_softmax_crossentropy()
#Start Training
gtf.Train();
#Read the training summary generated once you run the cell and training is completed
```
<a id='2'></a>
# Validating the trained classifier
```
gtf = prototype(verbose=1);
gtf.Prototype("project", "expert_mode", eval_infer=True);
# Just for example purposes, validating on the training set itself
gtf.Dataset_Params(dataset_path="natural-images/train");
gtf.Dataset();
accuracy, class_based_accuracy = gtf.Evaluate();
```
<a id='3'></a>
# Running inference on test images
```
gtf = prototype(verbose=1);
gtf.Prototype("project", "expert_mode", eval_infer=True);
img_name = "natural-images/test/test1.jpg";
predictions = gtf.Infer(img_name=img_name);
#Display
from IPython.display import Image
Image(filename=img_name)
img_name = "natural-images/test/test2.jpg";
predictions = gtf.Infer(img_name=img_name);
#Display
from IPython.display import Image
Image(filename=img_name)
img_name = "natural-images/test/test3.jpg";
predictions = gtf.Infer(img_name=img_name);
#Display
from IPython.display import Image
Image(filename=img_name)
```
|
github_jupyter
|
!git clone https://github.com/Tessellate-Imaging/monk_v1.git
# If using Colab install using the commands below
!cd monk_v1/installation/Misc && pip install -r requirements_colab.txt
# If using Kaggle uncomment the following command
#!cd monk_v1/installation/Misc && pip install -r requirements_kaggle.txt
# Select the requirements file as per OS and CUDA version when using a local system or cloud
#!cd monk_v1/installation/Linux && pip install -r requirements_cu9.txt
! wget --load-cookies /tmp/cookies.txt "https://docs.google.com/uc?export=download&confirm=$(wget --save-cookies /tmp/cookies.txt --keep-session-cookies --no-check-certificate 'https://docs.google.com/uc?export=download&id=1sbQ_KaEDd7kRrTvna-4odLqxM2G0QT0Z' -O- | sed -rn 's/.*confirm=([0-9A-Za-z_]+).*/\1\n/p')&id=1sbQ_KaEDd7kRrTvna-4odLqxM2G0QT0Z" -O natural-images.zip && rm -rf /tmp/cookies.txt
! unzip -qq natural-images.zip
# Monk
import os
import sys
sys.path.append("monk_v1/monk/");
#Using pytorch backend
from pytorch_prototype import prototype
gtf = prototype(verbose=1);
gtf.Prototype("project", "expert_mode");
gtf.Dataset_Params(dataset_path="natural-images/train",
split=0.9,
input_size=224,
batch_size=16,
shuffle_data=True,
num_processors=3);
gtf.apply_random_horizontal_flip(train=True, val=True);
gtf.apply_normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225], train=True, val=True, test=True);
gtf.Dataset();
gtf.Model_Params(model_name="resnet18",
freeze_base_network=True,
use_gpu=True,
use_pretrained=True);
gtf.append_dropout(probability=0.1);
gtf.append_linear(final_layer=True);
gtf.Model();
gtf.Freeze_Layers(num=10);
gtf.Training_Params(num_epochs=10,
display_progress=True,
display_progress_realtime=True,
save_intermediate_models=True,
intermediate_model_prefix="intermediate_model_",
save_training_logs=True);
## Set Optimizer, losses and learning rate schedulers
gtf.optimizer_sgd(0.001);
gtf.lr_fixed();
gtf.loss_softmax_crossentropy()
#Start Training
gtf.Train();
#Read the training summary generated once you run the cell and training is completed
gtf = prototype(verbose=1);
gtf.Prototype("project", "expert_mode", eval_infer=True);
# Just for example purposes, validating on the training set itself
gtf.Dataset_Params(dataset_path="natural-images/train");
gtf.Dataset();
accuracy, class_based_accuracy = gtf.Evaluate();
gtf = prototype(verbose=1);
gtf.Prototype("project", "expert_mode", eval_infer=True);
img_name = "natural-images/test/test1.jpg";
predictions = gtf.Infer(img_name=img_name);
#Display
from IPython.display import Image
Image(filename=img_name)
img_name = "natural-images/test/test2.jpg";
predictions = gtf.Infer(img_name=img_name);
#Display
from IPython.display import Image
Image(filename=img_name)
img_name = "natural-images/test/test3.jpg";
predictions = gtf.Infer(img_name=img_name);
#Display
from IPython.display import Image
Image(filename=img_name)
| 0.483892 | 0.904017 |
<a href="https://colab.research.google.com/github/krakowiakpawel9/convnet-course/blob/master/02_mnist_cnn.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Trenowanie prostej sieci neuronowej na zbiorze MNIST
```
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
import warnings
warnings.filterwarnings('ignore')
```
### Załadowanie danych
```
# zdefiniowanie wymiarów obrazu wejsciowego
img_rows, img_cols = 28, 28
(X_train, y_train), (X_test, y_test) = mnist.load_data()
```
### Eksploracja danych
```
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
print('Liczba dabych treningowych:', X_train.shape[0])
print('Liczba danych testowych:', X_test.shape[0])
print('Rozmiar pojedynczego obrazka:', X_train[0].shape)
```
### Wyświetlenie obrazka
```
import matplotlib.pyplot as plt
plt.imshow(X_train[0], cmap='Greys')
plt.axis('off')
```
### Wyświetlenie kilku obrazków
```
plt.figure(figsize=(13, 13))
for i in range(1, 11):
plt.subplot(1, 10, i)
plt.axis('off')
plt.imshow(X_train[i], cmap='Greys')
plt.show()
```
### Wyświetlenie danych
```
print(X_train[0][10])
# dolna połówka obrazka
plt.imshow(X_train[0][14:], cmap='Greys')
# górna połówka obrazka
plt.imshow(X_train[0][:14], cmap='Greys')
```
### Przycinanie obrazka
```
plt.imshow(X_train[0][5:20, 5:20], cmap='Greys')
```
### Obsługa problemu zapisu obrazów wejściowych - channel first vs. channel last
```
print(K.image_data_format())
if K.image_data_format() == 'channel_first':
X_train = X_train.reshape(X_train.shape[0], 1, img_rows, img_cols)
X_test = X_test.reshape(X_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
X_train = X_train.reshape(X_train.shape[0], img_rows, img_cols, 1)
X_test = X_test.reshape(X_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
print(input_shape)
```
### Wyświetlenie etykiet
```
print('y_train:', y_train)
print('y_train shape:', y_train.shape)
```
## Przygotowanie danych
```
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
print(X_train.shape)
print(X_test.shape)
```
### Przygotowanie etykiet
```
y_train = keras.utils.to_categorical(y_train, num_classes=10)
y_test = keras.utils.to_categorical(y_test, num_classes=10)
print(y_train.shape)
print(y_test.shape)
print(y_train[0])
```
### Budowa modelu
```
model = Sequential()
model.add(Conv2D(filters=32, kernel_size=(3, 3), activation='relu', input_shape=input_shape))
model.add(Conv2D(filters=64, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(units=128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax'))
model.summary()
```
### Kompilacja modelu
```
model.compile(optimizer='adadelta',
loss='categorical_crossentropy',
metrics=['accuracy'])
```
### Trenowanie modelu
```
history = model.fit(X_train, y_train,
batch_size=128,
epochs=20,
validation_data=(X_test, y_test))
```
### Ocena modelu
```
score = model.evaluate(X_test, y_test)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
```
### Wykres dokładności
```
def make_accuracy_plot(history):
"""
Funkcja zwraca wykres dokładności (accuracy) modelu na zbiorze treningowym
i walidacyjnym.
"""
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
acc, val_acc = history.history['acc'], history.history['val_acc']
epochs = range(1, len(acc) + 1)
plt.figure(figsize=(10, 8))
plt.plot(epochs, acc, label='Dokładność trenowania', marker='o')
plt.plot(epochs, val_acc, label='Dokładność walidacji', marker='o')
plt.legend()
plt.title('Dokładność trenowania i walidacji')
plt.xlabel('Epoki')
plt.ylabel('Dokładność')
plt.show()
def make_loss_plot(history):
"""
Funkcja zwraca wykres straty (loss) modelu na zbiorze treningowym
i walidacyjnym.
"""
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
loss, val_loss = history.history['loss'], history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.figure(figsize=(10, 8))
plt.plot(epochs, loss, label='Strata trenowania', marker='o')
plt.plot(epochs, val_loss, label='Strata walidacji', marker='o')
plt.legend()
plt.title('Strata trenowania i walidacji')
plt.xlabel('Epoki')
plt.ylabel('Strata')
plt.show()
make_accuracy_plot(history)
make_loss_plot(history)
```
|
github_jupyter
|
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
import warnings
warnings.filterwarnings('ignore')
# zdefiniowanie wymiarów obrazu wejsciowego
img_rows, img_cols = 28, 28
(X_train, y_train), (X_test, y_test) = mnist.load_data()
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
print('Liczba dabych treningowych:', X_train.shape[0])
print('Liczba danych testowych:', X_test.shape[0])
print('Rozmiar pojedynczego obrazka:', X_train[0].shape)
import matplotlib.pyplot as plt
plt.imshow(X_train[0], cmap='Greys')
plt.axis('off')
plt.figure(figsize=(13, 13))
for i in range(1, 11):
plt.subplot(1, 10, i)
plt.axis('off')
plt.imshow(X_train[i], cmap='Greys')
plt.show()
print(X_train[0][10])
# dolna połówka obrazka
plt.imshow(X_train[0][14:], cmap='Greys')
# górna połówka obrazka
plt.imshow(X_train[0][:14], cmap='Greys')
plt.imshow(X_train[0][5:20, 5:20], cmap='Greys')
print(K.image_data_format())
if K.image_data_format() == 'channel_first':
X_train = X_train.reshape(X_train.shape[0], 1, img_rows, img_cols)
X_test = X_test.reshape(X_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
X_train = X_train.reshape(X_train.shape[0], img_rows, img_cols, 1)
X_test = X_test.reshape(X_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
print(input_shape)
print('y_train:', y_train)
print('y_train shape:', y_train.shape)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
print(X_train.shape)
print(X_test.shape)
y_train = keras.utils.to_categorical(y_train, num_classes=10)
y_test = keras.utils.to_categorical(y_test, num_classes=10)
print(y_train.shape)
print(y_test.shape)
print(y_train[0])
model = Sequential()
model.add(Conv2D(filters=32, kernel_size=(3, 3), activation='relu', input_shape=input_shape))
model.add(Conv2D(filters=64, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(units=128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax'))
model.summary()
model.compile(optimizer='adadelta',
loss='categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(X_train, y_train,
batch_size=128,
epochs=20,
validation_data=(X_test, y_test))
score = model.evaluate(X_test, y_test)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
def make_accuracy_plot(history):
"""
Funkcja zwraca wykres dokładności (accuracy) modelu na zbiorze treningowym
i walidacyjnym.
"""
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
acc, val_acc = history.history['acc'], history.history['val_acc']
epochs = range(1, len(acc) + 1)
plt.figure(figsize=(10, 8))
plt.plot(epochs, acc, label='Dokładność trenowania', marker='o')
plt.plot(epochs, val_acc, label='Dokładność walidacji', marker='o')
plt.legend()
plt.title('Dokładność trenowania i walidacji')
plt.xlabel('Epoki')
plt.ylabel('Dokładność')
plt.show()
def make_loss_plot(history):
"""
Funkcja zwraca wykres straty (loss) modelu na zbiorze treningowym
i walidacyjnym.
"""
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
loss, val_loss = history.history['loss'], history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.figure(figsize=(10, 8))
plt.plot(epochs, loss, label='Strata trenowania', marker='o')
plt.plot(epochs, val_loss, label='Strata walidacji', marker='o')
plt.legend()
plt.title('Strata trenowania i walidacji')
plt.xlabel('Epoki')
plt.ylabel('Strata')
plt.show()
make_accuracy_plot(history)
make_loss_plot(history)
| 0.728941 | 0.950915 |
```
import pandas as pd
import numpy as np
from os import path
import matplotlib.pyplot as plt
import seaborn as sns
import librosa
from matplotlib.ticker import (MultipleLocator, FormatStrFormatter,
AutoMinorLocator)
import matplotlib as mpl
metadata = pd.read_csv('metadata.csv')
plt.style.use('seaborn')
```
### Plotting the gender distribution
```
gender_labels = metadata['g'].unique()[::-1] # getiing the genders
gender_count = []
for i in range(len(gender_labels)):
gender_count.append(len(metadata[(metadata['g'] == gender_labels[i])])) # counting each label and storing in a list
fig, ax = plt.subplots(figsize=(2, 6))
ax.bar(2,gender_count[0], align='center',alpha=1,capsize=5,width=.6)
ax.bar(4,gender_count[1], align='center',alpha=1,capsize=5,width=.6)
for i, v in enumerate(gender_count):
ax.text(2*(i+1)-.3,v + 3, str(v), color='black', fontweight='bold',fontsize=14) # ploting the exact count
plt.xticks([2,4], ['MALE','FEMALE'])
plt.ylabel('COUNT', fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
ax.set_xlim(1,5)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
plt.show()
```
### Plotting the age distribution
```
age_labels = metadata['a'].unique() # storing every unique age
age_count_male = []
age_count_female = []
for i in range(len(age_labels)): # storing count of each age for male and female
if age_labels[i] == 'X':
age_labels[i] = 0
age_count_male.append(len(metadata[(metadata['a'] == age_labels[i]) & (metadata['g']=='male')]))
age_count_female.append(len(metadata[(metadata['a'] == age_labels[i]) & (metadata['g']=='female')]))
age_count_male = metadata[(metadata['g']=='male')]['a'].values
age_count_female = metadata[(metadata['g']=='female')]['a'].values
age_labels = ['0-10','10-20', '20-30', '30-40', '40-50', '50-60', '60-70', '70-80'] # taking 8 age groups
age_grouped_male = []
age_grouped_female = []
for i in age_labels: # storing count for age group for male and female
age_grouped_male.append(len(age_count_male[(age_count_male > (int(i.split('-')[0])-1)) & \
(age_count_male < int(i.split('-')[1]))]))
age_grouped_female.append(len(age_count_female[(age_count_female > (int(i.split('-')[0])-1)) & \
(age_count_female < int(i.split('-')[1]))]))
fig, ax = plt.subplots(figsize=(7, 6))
ax.bar(np.arange(0,len(age_labels)),age_grouped_male, align='center',alpha=1,width=.3,label='MALE')
ax.bar(np.arange(0,len(age_labels))+.3,age_grouped_female, align='center',alpha=1,width=.3,label='FEMALE')
ax.legend(frameon=False,loc='upper right',fontsize=14)
plt.ylabel('COUNT', fontsize=12)
plt.xlabel('AGE GROUP', fontsize=12)
plt.xticks(np.arange(0,len(age_labels)), age_labels,rotation=0,fontsize=12)
plt.yticks(fontsize=12)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
plt.show()
```
### Plotting the health status
```
df = metadata.replace('None', np.nan)
df= metadata.replace(np.nan, False)
df['healthy'] = False
df['covid'] = 0.0
df['unhealthy_but_no_covid'] = False
for i in range(len(df)):
# taking the following as healthy
if (df.at[i,'covid_status']=='healthy') & (df.at[i,'asthma']==False) &\
(df.at[i,'cld']==False) & (df.at[i,'cold']==False) &\
(df.at[i,'cough']==False) & (df.at[i,'pneumonia']==False) &\
(df.at[i,'fever']==False):
df.at[i,'healthy'] = True
# taking these class as having covid
if (df.at[i,'covid_status']=='positive_asymp'):
df.at[i,'covid'] = 1
if (df.at[i,'covid_status']=='positive_mild'):
df.at[i,'covid'] = 2
if (df.at[i,'covid_status']=='positive_moderate'):
df.at[i,'covid'] = 3
# following these are unhealthy but don't have covid
if (df.at[i,'covid_status']=='resp_illness_not_identified') & ((df.at[i,'asthma']==True) |\
(df.at[i,'cld']==True) | (df.at[i,'cold']==True) |\
(df.at[i,'cough']==True) | (df.at[i,'pneumonia']==True)):
df.at[i,'unhealthy_but_no_covid'] = True
health_count = []
health_count.append(len(df[(df['healthy']==True)]))
health_count.append(len(df[(df['covid']>0)]))
health_count.append(len(df[(df['unhealthy_but_no_covid']==True)]))
fig, ax = plt.subplots(figsize=(5, 6))
ax.bar(2, health_count[0], align='center',alpha=1,width=.3)
ax.bar(4, health_count[1], align='center',alpha=1,width=.3)
ax.bar(6, health_count[2], align='center',alpha=1,width=.3)
plt.xticks([2,4,6],['HEALTHY','COVID-19','RESP. AIL \n (NOT COVID)'],rotation=0,fontsize=12)
for i, v in enumerate(health_count):
ax.text(2*(i+1)-.1,v + 3, str(v), color='black', fontweight='bold',fontsize=12)
plt.ylabel('COUNT', fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
plt.xlim(1,7)
plt.show()
```
|
github_jupyter
|
import pandas as pd
import numpy as np
from os import path
import matplotlib.pyplot as plt
import seaborn as sns
import librosa
from matplotlib.ticker import (MultipleLocator, FormatStrFormatter,
AutoMinorLocator)
import matplotlib as mpl
metadata = pd.read_csv('metadata.csv')
plt.style.use('seaborn')
gender_labels = metadata['g'].unique()[::-1] # getiing the genders
gender_count = []
for i in range(len(gender_labels)):
gender_count.append(len(metadata[(metadata['g'] == gender_labels[i])])) # counting each label and storing in a list
fig, ax = plt.subplots(figsize=(2, 6))
ax.bar(2,gender_count[0], align='center',alpha=1,capsize=5,width=.6)
ax.bar(4,gender_count[1], align='center',alpha=1,capsize=5,width=.6)
for i, v in enumerate(gender_count):
ax.text(2*(i+1)-.3,v + 3, str(v), color='black', fontweight='bold',fontsize=14) # ploting the exact count
plt.xticks([2,4], ['MALE','FEMALE'])
plt.ylabel('COUNT', fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
ax.set_xlim(1,5)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
plt.show()
age_labels = metadata['a'].unique() # storing every unique age
age_count_male = []
age_count_female = []
for i in range(len(age_labels)): # storing count of each age for male and female
if age_labels[i] == 'X':
age_labels[i] = 0
age_count_male.append(len(metadata[(metadata['a'] == age_labels[i]) & (metadata['g']=='male')]))
age_count_female.append(len(metadata[(metadata['a'] == age_labels[i]) & (metadata['g']=='female')]))
age_count_male = metadata[(metadata['g']=='male')]['a'].values
age_count_female = metadata[(metadata['g']=='female')]['a'].values
age_labels = ['0-10','10-20', '20-30', '30-40', '40-50', '50-60', '60-70', '70-80'] # taking 8 age groups
age_grouped_male = []
age_grouped_female = []
for i in age_labels: # storing count for age group for male and female
age_grouped_male.append(len(age_count_male[(age_count_male > (int(i.split('-')[0])-1)) & \
(age_count_male < int(i.split('-')[1]))]))
age_grouped_female.append(len(age_count_female[(age_count_female > (int(i.split('-')[0])-1)) & \
(age_count_female < int(i.split('-')[1]))]))
fig, ax = plt.subplots(figsize=(7, 6))
ax.bar(np.arange(0,len(age_labels)),age_grouped_male, align='center',alpha=1,width=.3,label='MALE')
ax.bar(np.arange(0,len(age_labels))+.3,age_grouped_female, align='center',alpha=1,width=.3,label='FEMALE')
ax.legend(frameon=False,loc='upper right',fontsize=14)
plt.ylabel('COUNT', fontsize=12)
plt.xlabel('AGE GROUP', fontsize=12)
plt.xticks(np.arange(0,len(age_labels)), age_labels,rotation=0,fontsize=12)
plt.yticks(fontsize=12)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
plt.show()
df = metadata.replace('None', np.nan)
df= metadata.replace(np.nan, False)
df['healthy'] = False
df['covid'] = 0.0
df['unhealthy_but_no_covid'] = False
for i in range(len(df)):
# taking the following as healthy
if (df.at[i,'covid_status']=='healthy') & (df.at[i,'asthma']==False) &\
(df.at[i,'cld']==False) & (df.at[i,'cold']==False) &\
(df.at[i,'cough']==False) & (df.at[i,'pneumonia']==False) &\
(df.at[i,'fever']==False):
df.at[i,'healthy'] = True
# taking these class as having covid
if (df.at[i,'covid_status']=='positive_asymp'):
df.at[i,'covid'] = 1
if (df.at[i,'covid_status']=='positive_mild'):
df.at[i,'covid'] = 2
if (df.at[i,'covid_status']=='positive_moderate'):
df.at[i,'covid'] = 3
# following these are unhealthy but don't have covid
if (df.at[i,'covid_status']=='resp_illness_not_identified') & ((df.at[i,'asthma']==True) |\
(df.at[i,'cld']==True) | (df.at[i,'cold']==True) |\
(df.at[i,'cough']==True) | (df.at[i,'pneumonia']==True)):
df.at[i,'unhealthy_but_no_covid'] = True
health_count = []
health_count.append(len(df[(df['healthy']==True)]))
health_count.append(len(df[(df['covid']>0)]))
health_count.append(len(df[(df['unhealthy_but_no_covid']==True)]))
fig, ax = plt.subplots(figsize=(5, 6))
ax.bar(2, health_count[0], align='center',alpha=1,width=.3)
ax.bar(4, health_count[1], align='center',alpha=1,width=.3)
ax.bar(6, health_count[2], align='center',alpha=1,width=.3)
plt.xticks([2,4,6],['HEALTHY','COVID-19','RESP. AIL \n (NOT COVID)'],rotation=0,fontsize=12)
for i, v in enumerate(health_count):
ax.text(2*(i+1)-.1,v + 3, str(v), color='black', fontweight='bold',fontsize=12)
plt.ylabel('COUNT', fontsize=12)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
plt.xlim(1,7)
plt.show()
| 0.124519 | 0.653085 |
# Overview of the nmrsim Top-Level API
This notebook gives a tour of the top level classes the nmrsim API provides. These are conveniences that abstract away lower-level API functions. Users wanting more control can consult the full API documentation.
```
import os
import sys
import numpy as np
import matplotlib as mpl
mpl.rcParams['figure.dpi']= 300
%matplotlib inline
%config InlineBackend.figure_format = 'svg' # makes inline plot look less blurry
home_path = os.path.abspath(os.path.join('..', '..', '..'))
if home_path not in sys.path:
sys.path.append(home_path)
tests_path = os.path.abspath(os.path.join('..', '..', '..', 'tests'))
if tests_path not in sys.path:
sys.path.append(tests_path)
```
## Definitions
In naming classes, functions, methods, data types etc. certain phrases, taken from NMR nomenclature, have the following interpretations:
* **multiplet** (e.g. the `nmrsim.Multiplet` class): a first-order simulation for one signal (i.e. one or more chemical shift-equivalent nuclei). Examples: doublet, triplet, doublet of triplets, but **not** an AB quartet (which is a second-order pattern for two nuclei).
* **spin system** (e.g. the `SpinSystem` class): a simulation of a set of coupled nuclei.
* **spectrum** (e.g. the `Spectrum` class): a complete collection of first- and/or second-order components for simulating a total NMR spectrum. 'Spectrum' can also refer in general to the simulation results for the system, e.g a peaklist or lineshape (see below).
* **peak**: a pair of frequency (Hz), intensity values corresponding to a resonance in an NMR spectrum. For example, a 1H triplet centered at 100 Hz with J = 10 Hz would have the following peaks: (110, 0.25), (100, 0.5), (90, 0.25).
* **peaklist**: a list of peaks (e.g. \[(110, 0.25), (100, 0.5), (90, 0.25)] for the above triplet).
* **lineshape**: a pair of \[x_coordinates...], \[y_coordinates] arrays for plotting the lineshape of a spectrum.
In this notebook the term **list** is interchangeable with other iterables such as numpy arrays or tuples. As much as possible, nmrsim relies on <"duck typing">(https://en.wikipedia.org/wiki/Duck_typing) to accept a variety of iterables as inputs, converting them to specific types such as numpy arrays as needed. The term **matrix** refers to a 2D array-like object in general, e.g. a list of lists or a 2D numpy array. It does *not* refer specifically to the (marked-for-deprecation) `numpy.matrix` class.
The following idioms are used for arguments:
* **v** for a frequency or list of frequencies (similar to $\nu$ ).
* **I** for a signal intensity
* **J** for coupling constant data (exact format depends on the implementation).
## Scenario: user wants to plot a spectrum for an ABX 3-spin system.
A spin system can be described using a list of frequencies v and J (coupling constant) data . For this example, a function from nmrsim's test suite will provide some example data:
```
# This dataset is for the vinyl group of vinyl acetate, as used in:
# http://www.users.csbsju.edu/~frioux/nmr/ABC-NMR-Tensor.pdf
def rioux():
v = np.array([430.0, 265.0, 300.0])
J = np.zeros((3, 3))
J[0, 1] = 7.0
J[0, 2] = 15.0
J[1, 2] = 1.50
J = J + J.T
return v, J
v, J = rioux()
print('v: ', v) # frequencies in Hz
print('J: \n', J) # matrix of coupling constants
```
The J matrix is constructed so that J[a, b] is the coupling constant between v[a] and v[b]. The diagonal elements should be 0.
The `SpinSystem` class can be used to model a set of coupled nuclei.
```
from nmrsim import SpinSystem
abx_system = SpinSystem(v, J)
```
The `SpinSystem.peaklist()` method returns the peaklist for the simulation:
```
abx_system.peaklist()
```
You can plot this data with the visualization library of your choice. However, the `nmrsim.plt` library has functions for convenient plotting of common nmrsim data types. The `plt.mplplot` function will take a peaklist and use matplotlib to plot the corresponding lineshape. The optional keyword argument `y_max` can be used to set the maximum for the y-axis (and `y_min` for the minimum).
```
from nmrsim.plt import mplplot
mplplot(abx_system.peaklist(), y_max=0.2);
```
To plot the spectra as a "stick" style plot (single lines for each peak, rather than a simulated lineshape), you can use the mplplot_stick function instead of mplplot:
```
from nmrsim.plt import mplplot_stick
# The range of the x axis can be specified using the 'limits' keyword argument:
mplplot_stick(abx_system.peaklist(), y_max=0.3, limits=(250, 320));
```
SpinSystem defaults to second-order simulation of a spin system. If the SpinSystem object is instantiated with the `second_order=False` keyword argument, or if the SpinSystem.second_order attribute is set to `False`, first-order simulation will be performed instead.
```
abx_system.second_order = False
mplplot(abx_system.peaklist(), y_max=0.2);
```
Depending on the resolution of the plot and how the data points for the lineshape are interpolated, the peak heights may not look identical. The correct relative intensities can be seen in the stick plot, however:
```
mplplot_stick(abx_system.peaklist(), y_max=0.3);
```
## Scenario: User wants to simulate individual first-order multiplets
The Multiplet class can be used to represent an individual first-order multiplet.
```
from nmrsim import Multiplet
```
Required arguments for Multiplet are the central frequency `v`, the intensity `I` ("integration") in the absence of coupling, and a list of coupling data `J`. These arguments become attributes of Multiplet. Each list entry is a tuple of (J value in Hz, number of nuclei causing the coupling). For example, the following Multiplet represents: 1200 Hz, 2H, td, J = 7.1, 1.1 Hz.
```
# 1200 Hz, 2H, td, J= 7.1, 1.1 Hz
td = Multiplet(1200.0, 2, [(7.1, 2), (1.1, 1)])
print(td.v)
print(td.I)
print(td.J)
```
The `Multiplet.peaklist()` method returns the peaklist for the multiplet:
```
mplplot_stick(td.peaklist());
mplplot(td.peaklist());
```
Multiplet attributes can be modified.
```
td2 = Multiplet(1200.0, 2, [(7.1, 2), (1.1, 1)])
td2.v = 1100
mplplot(td2.peaklist());
```
If a Multiplet is multiplied by a scalar, a new Multiplet is returned that has all intensities multiplied by the scalar. In-place multiplication (`*=`) modifies the original Multiplet object.
```
td3 = td2 * 2
td2 *= 2
assert td2 is not td3
mplplot(td2.peaklist());
```
Multiplets are equal to each other if their peaklists are equal.
```
assert td2 == td3
```
Division and division in place is also possible:
```
td4 = td2 / 2
td2 /= 2
assert td4 == td2
```
If two multiplets are added together, the result is a `Spectrum` object. See the next Scenario for the usage of `Spectrum`.
## Scenario: User wants to simulate a spectrum built from individual components
Any object that has a `.peaklist()` method can be used to create a Spectrum object.
A Spectrum object can be specifically created by providing a list of components as the first argument:
```
from nmrsim import Spectrum
two_td = Spectrum([td, td3])
mplplot(two_td.peaklist());
```
A Spectrum object is also returned from certain binary operations, such as addition:
```
td3.v = 1000
td4.v = 900
all_tds = td + td2 + td3 + td4
mplplot(all_tds.peaklist());
```
A Spectrum can be composed from both first- and second-order components:
```
combo_spectrum = abx_system + td3 + td4
# mplplot has an optional y_max keyword argument to set the max range of the y-axis
mplplot(combo_spectrum.peaklist(), y_max=0.4);
```
## Scenario: User wants to model a specific spin system using an explicit (non-qm) solution
The nmrsim.partial module contains "canned" mathematical solutions for second-order systems.
Example: simulate the AB part of an ABX<sub>3</sub> system
```
from nmrsim.discrete import ABX3
help(ABX3)
abx3_peaklist = ABX3(-12, 7, 7, 14, 150)
mplplot(abx3_peaklist, y_max=0.25);
```
Here is an alternate, non-qm simulation for the ABX system from the SpinSystem demonstration:
```
from nmrsim.discrete import ABX
help(ABX)
abx_peaklist = ABX(1.5, 7, 15, 35, 282.5, 430)
mplplot(abx_peaklist, y_max=0.4);
```
## Scenario: User wants to model DNMR two-spin exchange, without and with coupling
The nmrsim.dnmr library provides functions for calculating DNMR lineshapes, and classes to describe these systems. Currently, models for two uncoupled nuclei and two coupled nuclei are provided.
```
from nmrsim.dnmr import DnmrTwoSinglets, DnmrAB
```
For: v<sub>a</sub> = 165 Hz, v<sub>b</sub> = 135 Hz, k = 65.9 s<sup>-1</sup>, line widths (at the slow exchange limit) w<sub>a</sub> and w<sub>b</sub> = 0.5 Hz, and population of state a = 0.5 (i.e. 50%):
```
two_singlet_system = DnmrTwoSinglets(165.00, 135.00, 65.9, 0.50, 0.50, 0.50)
from nmrsim.plt import mplplot_lineshape
mplplot_lineshape(*two_singlet_system.lineshape());
```
Class attributes can be changed. In the previous case, k = 65.9 <sup>-1</sup> corresponds to the point of coalescence. When the rate of exchange is lower, two separate peaks are observed.
```
two_singlet_system.k = 5
mplplot_lineshape(*two_singlet_system.lineshape());
```
What if the relative populations of states a and b are 75% and 25%, respectively?
```
two_singlet_system.pa = 0.75
mplplot_lineshape(*two_singlet_system.lineshape());
```
To model an AB-like system of two coupled nuclei undergoing exchange, use the DnmrAB class. In the following example, the frequencies are the same as for the previous system. J = 5 Hz, k = 12 <sup>-1</sup>, and the line width (at the slow exchange limit) is 0.5 Hz.
```
from nmrsim.dnmr import DnmrAB
AB = DnmrAB(165, 135, 5, 10, 0.5)
mplplot_lineshape(*AB.lineshape());
```
|
github_jupyter
|
import os
import sys
import numpy as np
import matplotlib as mpl
mpl.rcParams['figure.dpi']= 300
%matplotlib inline
%config InlineBackend.figure_format = 'svg' # makes inline plot look less blurry
home_path = os.path.abspath(os.path.join('..', '..', '..'))
if home_path not in sys.path:
sys.path.append(home_path)
tests_path = os.path.abspath(os.path.join('..', '..', '..', 'tests'))
if tests_path not in sys.path:
sys.path.append(tests_path)
# This dataset is for the vinyl group of vinyl acetate, as used in:
# http://www.users.csbsju.edu/~frioux/nmr/ABC-NMR-Tensor.pdf
def rioux():
v = np.array([430.0, 265.0, 300.0])
J = np.zeros((3, 3))
J[0, 1] = 7.0
J[0, 2] = 15.0
J[1, 2] = 1.50
J = J + J.T
return v, J
v, J = rioux()
print('v: ', v) # frequencies in Hz
print('J: \n', J) # matrix of coupling constants
from nmrsim import SpinSystem
abx_system = SpinSystem(v, J)
abx_system.peaklist()
from nmrsim.plt import mplplot
mplplot(abx_system.peaklist(), y_max=0.2);
from nmrsim.plt import mplplot_stick
# The range of the x axis can be specified using the 'limits' keyword argument:
mplplot_stick(abx_system.peaklist(), y_max=0.3, limits=(250, 320));
abx_system.second_order = False
mplplot(abx_system.peaklist(), y_max=0.2);
mplplot_stick(abx_system.peaklist(), y_max=0.3);
from nmrsim import Multiplet
# 1200 Hz, 2H, td, J= 7.1, 1.1 Hz
td = Multiplet(1200.0, 2, [(7.1, 2), (1.1, 1)])
print(td.v)
print(td.I)
print(td.J)
mplplot_stick(td.peaklist());
mplplot(td.peaklist());
td2 = Multiplet(1200.0, 2, [(7.1, 2), (1.1, 1)])
td2.v = 1100
mplplot(td2.peaklist());
td3 = td2 * 2
td2 *= 2
assert td2 is not td3
mplplot(td2.peaklist());
assert td2 == td3
td4 = td2 / 2
td2 /= 2
assert td4 == td2
from nmrsim import Spectrum
two_td = Spectrum([td, td3])
mplplot(two_td.peaklist());
td3.v = 1000
td4.v = 900
all_tds = td + td2 + td3 + td4
mplplot(all_tds.peaklist());
combo_spectrum = abx_system + td3 + td4
# mplplot has an optional y_max keyword argument to set the max range of the y-axis
mplplot(combo_spectrum.peaklist(), y_max=0.4);
from nmrsim.discrete import ABX3
help(ABX3)
abx3_peaklist = ABX3(-12, 7, 7, 14, 150)
mplplot(abx3_peaklist, y_max=0.25);
from nmrsim.discrete import ABX
help(ABX)
abx_peaklist = ABX(1.5, 7, 15, 35, 282.5, 430)
mplplot(abx_peaklist, y_max=0.4);
from nmrsim.dnmr import DnmrTwoSinglets, DnmrAB
two_singlet_system = DnmrTwoSinglets(165.00, 135.00, 65.9, 0.50, 0.50, 0.50)
from nmrsim.plt import mplplot_lineshape
mplplot_lineshape(*two_singlet_system.lineshape());
two_singlet_system.k = 5
mplplot_lineshape(*two_singlet_system.lineshape());
two_singlet_system.pa = 0.75
mplplot_lineshape(*two_singlet_system.lineshape());
from nmrsim.dnmr import DnmrAB
AB = DnmrAB(165, 135, 5, 10, 0.5)
mplplot_lineshape(*AB.lineshape());
| 0.289472 | 0.98882 |
# Think Bayes: Chapter 7
This notebook presents code and exercises from Think Bayes, second edition.
Copyright 2016 Allen B. Downey
MIT License: https://opensource.org/licenses/MIT
```
from __future__ import print_function, division
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
import math
import numpy as np
from thinkbayes2 import Pmf, Cdf, Suite, Joint
import thinkbayes2
import thinkplot
```
## Warm-up exercises
**Exercise:** Suppose that goal scoring in hockey is well modeled by a
Poisson process, and that the long-run goal-scoring rate of the
Boston Bruins against the Vancouver Canucks is 2.9 goals per game.
In their next game, what is the probability
that the Bruins score exactly 3 goals? Plot the PMF of `k`, the number
of goals they score in a game.
```
### Solution
```
**Exercise:** Assuming again that the goal scoring rate is 2.9, what is the probability of scoring a total of 9 goals in three games? Answer this question two ways:
1. Compute the distribution of goals scored in one game and then add it to itself twice to find the distribution of goals scored in 3 games.
2. Use the Poisson PMF with parameter $\lambda t$, where $\lambda$ is the rate in goals per game and $t$ is the duration in games.
```
### Solution
```
**Exercise:** Suppose that the long-run goal-scoring rate of the
Canucks against the Bruins is 2.6 goals per game. Plot the distribution
of `t`, the time until the Canucks score their first goal.
In their next game, what is the probability that the Canucks score
during the first period (that is, the first third of the game)?
Hint: `thinkbayes2` provides `MakeExponentialPmf` and `EvalExponentialCdf`.
```
### Solution
```
**Exercise:** Assuming again that the goal scoring rate is 2.8, what is the probability that the Canucks get shut out (that is, don't score for an entire game)? Answer this question two ways, using the CDF of the exponential distribution and the PMF of the Poisson distribution.
```
### Solution
```
## The Boston Bruins problem
The `Hockey` suite contains hypotheses about the goal scoring rate for one team against the other. The prior is Gaussian, with mean and variance based on previous games in the league.
The Likelihood function takes as data the number of goals scored in a game.
```
from thinkbayes2 import MakeNormalPmf
from thinkbayes2 import EvalPoissonPmf
class Hockey(thinkbayes2.Suite):
"""Represents hypotheses about the scoring rate for a team."""
def __init__(self, label=None):
"""Initializes the Hockey object.
label: string
"""
mu = 2.8
sigma = 0.3
pmf = MakeNormalPmf(mu, sigma, num_sigmas=4, n=101)
thinkbayes2.Suite.__init__(self, pmf, label=label)
def Likelihood(self, data, hypo):
"""Computes the likelihood of the data under the hypothesis.
Evaluates the Poisson PMF for lambda k.
hypo: goal scoring rate in goals per game
data: goals scored in one game
"""
lam = hypo
k = data
like = EvalPoissonPmf(k, lam)
return like
```
Now we can initialize a suite for each team:
```
suite1 = Hockey('bruins')
suite2 = Hockey('canucks')
```
Here's what the priors look like:
```
thinkplot.PrePlot(num=2)
thinkplot.Pdf(suite1)
thinkplot.Pdf(suite2)
thinkplot.Config(xlabel='Goals per game',
ylabel='Probability')
```
And we can update each suite with the scores from the first 4 games.
```
suite1.UpdateSet([0, 2, 8, 4])
suite2.UpdateSet([1, 3, 1, 0])
thinkplot.PrePlot(num=2)
thinkplot.Pdf(suite1)
thinkplot.Pdf(suite2)
thinkplot.Config(xlabel='Goals per game',
ylabel='Probability')
suite1.Mean(), suite2.Mean()
```
To predict the number of goals scored in the next game we can compute, for each hypothetical value of $\lambda$, a Poisson distribution of goals scored, then make a weighted mixture of Poissons:
```
from thinkbayes2 import MakeMixture
from thinkbayes2 import MakePoissonPmf
def MakeGoalPmf(suite, high=10):
"""Makes the distribution of goals scored, given distribution of lam.
suite: distribution of goal-scoring rate
high: upper bound
returns: Pmf of goals per game
"""
metapmf = Pmf()
for lam, prob in suite.Items():
pmf = MakePoissonPmf(lam, high)
metapmf.Set(pmf, prob)
mix = MakeMixture(metapmf, label=suite.label)
return mix
```
Here's what the results look like.
```
goal_dist1 = MakeGoalPmf(suite1)
goal_dist2 = MakeGoalPmf(suite2)
thinkplot.PrePlot(num=2)
thinkplot.Pmf(goal_dist1)
thinkplot.Pmf(goal_dist2)
thinkplot.Config(xlabel='Goals',
ylabel='Probability',
xlim=[-0.7, 11.5])
goal_dist1.Mean(), goal_dist2.Mean()
```
Now we can compute the probability that the Bruins win, lose, or tie in regulation time.
```
diff = goal_dist1 - goal_dist2
p_win = diff.ProbGreater(0)
p_loss = diff.ProbLess(0)
p_tie = diff.Prob(0)
print('Prob win, loss, tie:', p_win, p_loss, p_tie)
```
If the game goes into overtime, we have to compute the distribution of `t`, the time until the first goal, for each team. For each hypothetical value of $\lambda$, the distribution of `t` is exponential, so the predictive distribution is a mixture of exponentials.
```
from thinkbayes2 import MakeExponentialPmf
def MakeGoalTimePmf(suite):
"""Makes the distribution of time til first goal.
suite: distribution of goal-scoring rate
returns: Pmf of goals per game
"""
metapmf = Pmf()
for lam, prob in suite.Items():
pmf = MakeExponentialPmf(lam, high=2.5, n=1001)
metapmf.Set(pmf, prob)
mix = MakeMixture(metapmf, label=suite.label)
return mix
```
Here's what the predictive distributions for `t` look like.
```
time_dist1 = MakeGoalTimePmf(suite1)
time_dist2 = MakeGoalTimePmf(suite2)
thinkplot.PrePlot(num=2)
thinkplot.Pmf(time_dist1)
thinkplot.Pmf(time_dist2)
thinkplot.Config(xlabel='Games until goal',
ylabel='Probability')
time_dist1.Mean(), time_dist2.Mean()
```
In overtime the first team to score wins, so the probability of winning is the probability of generating a smaller value of `t`:
```
p_win_in_overtime = time_dist1.ProbLess(time_dist2)
p_adjust = time_dist1.ProbEqual(time_dist2)
p_win_in_overtime += p_adjust / 2
print('p_win_in_overtime', p_win_in_overtime)
```
Finally, we can compute the overall chance that the Bruins win, either in regulation or overtime.
```
p_win_overall = p_win + p_tie * p_win_in_overtime
print('p_win_overall', p_win_overall)
```
## Exercises
**Exercise:** To make the model of overtime more correct, we could update both suites with 0 goals in one game, before computing the predictive distribution of `t`. Make this change and see what effect it has on the results.
```
### Solution
```
**Exercise:** In the final match of the 2014 FIFA World Cup, Germany defeated Argentina 1-0. What is the probability that Germany had the better team? What is the probability that Germany would win a rematch?
For a prior distribution on the goal-scoring rate for each team, use a gamma distribution with parameter 1.3.
```
from thinkbayes2 import MakeGammaPmf
xs = np.linspace(0, 8, 101)
pmf = MakeGammaPmf(xs, 1.3)
thinkplot.Pdf(pmf)
thinkplot.Config(xlabel='Goals per game')
pmf.Mean()
### Solution
```
**Exercise:** In the 2014 FIFA World Cup, Germany played Brazil in a semifinal match. Germany scored after 11 minutes and again at the 23 minute mark. At that point in the match, how many goals would you expect Germany to score after 90 minutes? What was the probability that they would score 5 more goals (as, in fact, they did)?
Note: for this one you will need a new suite that provides a Likelihood function that takes as data the time between goals, rather than the number of goals in a game.
```
### Solution
```
**Exercise:** Which is a better way to break a tie: overtime or penalty shots?
**Exercise:** Suppose that you are an ecologist sampling the insect population in a new environment. You deploy 100 traps in a test area and come back the next day to check on them. You find that 37 traps have been triggered, trapping an insect inside. Once a trap triggers, it cannot trap another insect until it has been reset.
If you reset the traps and come back in two days, how many traps do you expect to find triggered? Compute a posterior predictive distribution for the number of traps.
```
### Solution
```
|
github_jupyter
|
from __future__ import print_function, division
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
import math
import numpy as np
from thinkbayes2 import Pmf, Cdf, Suite, Joint
import thinkbayes2
import thinkplot
### Solution
### Solution
### Solution
### Solution
from thinkbayes2 import MakeNormalPmf
from thinkbayes2 import EvalPoissonPmf
class Hockey(thinkbayes2.Suite):
"""Represents hypotheses about the scoring rate for a team."""
def __init__(self, label=None):
"""Initializes the Hockey object.
label: string
"""
mu = 2.8
sigma = 0.3
pmf = MakeNormalPmf(mu, sigma, num_sigmas=4, n=101)
thinkbayes2.Suite.__init__(self, pmf, label=label)
def Likelihood(self, data, hypo):
"""Computes the likelihood of the data under the hypothesis.
Evaluates the Poisson PMF for lambda k.
hypo: goal scoring rate in goals per game
data: goals scored in one game
"""
lam = hypo
k = data
like = EvalPoissonPmf(k, lam)
return like
suite1 = Hockey('bruins')
suite2 = Hockey('canucks')
thinkplot.PrePlot(num=2)
thinkplot.Pdf(suite1)
thinkplot.Pdf(suite2)
thinkplot.Config(xlabel='Goals per game',
ylabel='Probability')
suite1.UpdateSet([0, 2, 8, 4])
suite2.UpdateSet([1, 3, 1, 0])
thinkplot.PrePlot(num=2)
thinkplot.Pdf(suite1)
thinkplot.Pdf(suite2)
thinkplot.Config(xlabel='Goals per game',
ylabel='Probability')
suite1.Mean(), suite2.Mean()
from thinkbayes2 import MakeMixture
from thinkbayes2 import MakePoissonPmf
def MakeGoalPmf(suite, high=10):
"""Makes the distribution of goals scored, given distribution of lam.
suite: distribution of goal-scoring rate
high: upper bound
returns: Pmf of goals per game
"""
metapmf = Pmf()
for lam, prob in suite.Items():
pmf = MakePoissonPmf(lam, high)
metapmf.Set(pmf, prob)
mix = MakeMixture(metapmf, label=suite.label)
return mix
goal_dist1 = MakeGoalPmf(suite1)
goal_dist2 = MakeGoalPmf(suite2)
thinkplot.PrePlot(num=2)
thinkplot.Pmf(goal_dist1)
thinkplot.Pmf(goal_dist2)
thinkplot.Config(xlabel='Goals',
ylabel='Probability',
xlim=[-0.7, 11.5])
goal_dist1.Mean(), goal_dist2.Mean()
diff = goal_dist1 - goal_dist2
p_win = diff.ProbGreater(0)
p_loss = diff.ProbLess(0)
p_tie = diff.Prob(0)
print('Prob win, loss, tie:', p_win, p_loss, p_tie)
from thinkbayes2 import MakeExponentialPmf
def MakeGoalTimePmf(suite):
"""Makes the distribution of time til first goal.
suite: distribution of goal-scoring rate
returns: Pmf of goals per game
"""
metapmf = Pmf()
for lam, prob in suite.Items():
pmf = MakeExponentialPmf(lam, high=2.5, n=1001)
metapmf.Set(pmf, prob)
mix = MakeMixture(metapmf, label=suite.label)
return mix
time_dist1 = MakeGoalTimePmf(suite1)
time_dist2 = MakeGoalTimePmf(suite2)
thinkplot.PrePlot(num=2)
thinkplot.Pmf(time_dist1)
thinkplot.Pmf(time_dist2)
thinkplot.Config(xlabel='Games until goal',
ylabel='Probability')
time_dist1.Mean(), time_dist2.Mean()
p_win_in_overtime = time_dist1.ProbLess(time_dist2)
p_adjust = time_dist1.ProbEqual(time_dist2)
p_win_in_overtime += p_adjust / 2
print('p_win_in_overtime', p_win_in_overtime)
p_win_overall = p_win + p_tie * p_win_in_overtime
print('p_win_overall', p_win_overall)
### Solution
from thinkbayes2 import MakeGammaPmf
xs = np.linspace(0, 8, 101)
pmf = MakeGammaPmf(xs, 1.3)
thinkplot.Pdf(pmf)
thinkplot.Config(xlabel='Goals per game')
pmf.Mean()
### Solution
### Solution
### Solution
| 0.772788 | 0.983738 |
# [Метрики качества классификации](https://www.coursera.org/learn/vvedenie-mashinnoe-obuchenie/programming/vfD6M/mietriki-kachiestva-klassifikatsii)
## Введение
В задачах классификации может быть много особенностей, влияющих на подсчет качества: различные цены ошибок, несбалансированность классов и т.д. Из-за этого существует большое количество метрик качества — каждая из них рассчитана на определенное сочетание свойств задачи и требований к ее решению.
Меры качества классификации можно разбить на две большие группы: предназначенные для алгоритмов, выдающих номера классов, и для алгоритмов, выдающих оценки принадлежности к классам. К первой группе относятся доля правильных ответов, точность, полнота, F-мера. Ко второй — площади под ROC- или PR-кривой.
```
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
data = pd.read_csv('./data/classification.csv', sep=",")
true = data['true']
pred = data['pred']
data.head()
```
## 2. Заполните таблицу ошибок классификации:
```
TP = len(data[(data['pred'] == 1) & (data['true'] == 1)])
FP = len(data[(data['pred'] == 1) & (data['true'] == 0)])
FN = len(data[(data['pred'] == 0) & (data['true'] == 1)])
TN = len(data[(data['pred'] == 0) & (data['true'] == 0)])
print(f"TP: {TP} FP: {FP} FN: {FN} TN: {TN}")
pd.DataFrame({'Actual Positive': [TP, FN], 'Actual Negative': [FP, TN]}, index=['Predicted Positive', 'Predicted Negative'])
```
## 3. Посчитайте основные метрики качества классификатора:
### Accuracy (доля верно угаданных) — sklearn.metrics.accuracy_score
```
from sklearn.metrics import accuracy_score
_ = accuracy_score(true, pred)
round(_, 2)
```
### Precision (точность) — sklearn.metrics.precision_score
```
from sklearn.metrics import precision_score
round(precision_score(true, pred), 2)
```
### Recall (полнота) — sklearn.metrics.recall_score
```
from sklearn.metrics import recall_score
round(recall_score(true, pred), 2)
```
### F-мера — sklearn.metrics.f1_score
```
from sklearn.metrics import f1_score
round(f1_score(true, pred), 2)
```
## 4. Имеется четыре обученных классификатора. В файле scores.csv записаны истинные классы и значения степени принадлежности положительному классу для каждого классификатора на некоторой выборке:
* для логистической регрессии — вероятность положительного класса (колонка score_logreg),
* для SVM — отступ от разделяющей поверхности (колонка score_svm),
* для метрического алгоритма — взвешенная сумма классов соседей (колонка score_knn),
* для решающего дерева — доля положительных объектов в листе (колонка score_tree).
```
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score
data = pd.read_csv('./data/scores.csv', sep=",")
true = data['true']
score_logreg = data['score_logreg']
score_svm = data['score_svm']
score_knn = data['score_knn']
score_tree = data['score_tree']
data.head()
```
## 5. Посчитайте площадь под ROC-кривой для каждого классификатора. Какой классификатор имеет наибольшее значение метрики AUC-ROC (укажите название столбца)? Воспользуйтесь функцией sklearn.metrics.roc_auc_score.
```
roc_auc_score(true, score_logreg)
roc_auc_score(true, score_svm)
roc_auc_score(true, score_knn)
roc_auc_score(true, score_tree)
```
## 6. Какой классификатор достигает наибольшей точности (Precision) при полноте (Recall) не менее 70% ?
Чтобы получить ответ на этот вопрос, найдите все точки precision-recall-кривой с помощью функции sklearn.metrics.precision_recall_curve. Она возвращает три массива: precision, recall, thresholds. В них записаны точность и полнота при определенных порогах, указанных в массиве thresholds. Найдите максимальной значение точности среди тех записей, для которых полнота не меньше, чем 0.7.
```
from sklearn.metrics import precision_recall_curve, auc
import matplotlib.pyplot as plt
precision, recall, thresholds = precision_recall_curve(true, score_logreg)
data = pd.DataFrame({'precision': precision , 'recall': recall})
print(data[data['recall'] >= 0.7]['precision'].idxmax())
print(data.loc[78])
# data.head()
data[70:80]
# max(data[data['recall'] >= 0.7]['precision'])
precision, recall, thresholds = precision_recall_curve(true, score_svm)
data = pd.DataFrame({'precision': precision , 'recall': recall})
print(data[data['recall'] >= 0.7]['precision'].idxmax())
print(data.loc[85])
data.head()
precision, recall, thresholds = precision_recall_curve(true, score_knn)
data = pd.DataFrame({'precision': precision , 'recall': recall})
print(data[data['recall'] >= 0.7]['precision'].idxmax())
print(data.loc[34])
# data.head()
data[20:40]
precision, recall, thresholds = precision_recall_curve(true, score_tree)
data = pd.DataFrame({'precision': precision , 'recall': recall})
print(data[data['recall'] >= 0.7]['precision'].idxmax())
print(data.loc[5])
data.head()
```
|
github_jupyter
|
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
data = pd.read_csv('./data/classification.csv', sep=",")
true = data['true']
pred = data['pred']
data.head()
TP = len(data[(data['pred'] == 1) & (data['true'] == 1)])
FP = len(data[(data['pred'] == 1) & (data['true'] == 0)])
FN = len(data[(data['pred'] == 0) & (data['true'] == 1)])
TN = len(data[(data['pred'] == 0) & (data['true'] == 0)])
print(f"TP: {TP} FP: {FP} FN: {FN} TN: {TN}")
pd.DataFrame({'Actual Positive': [TP, FN], 'Actual Negative': [FP, TN]}, index=['Predicted Positive', 'Predicted Negative'])
from sklearn.metrics import accuracy_score
_ = accuracy_score(true, pred)
round(_, 2)
from sklearn.metrics import precision_score
round(precision_score(true, pred), 2)
from sklearn.metrics import recall_score
round(recall_score(true, pred), 2)
from sklearn.metrics import f1_score
round(f1_score(true, pred), 2)
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score
data = pd.read_csv('./data/scores.csv', sep=",")
true = data['true']
score_logreg = data['score_logreg']
score_svm = data['score_svm']
score_knn = data['score_knn']
score_tree = data['score_tree']
data.head()
roc_auc_score(true, score_logreg)
roc_auc_score(true, score_svm)
roc_auc_score(true, score_knn)
roc_auc_score(true, score_tree)
from sklearn.metrics import precision_recall_curve, auc
import matplotlib.pyplot as plt
precision, recall, thresholds = precision_recall_curve(true, score_logreg)
data = pd.DataFrame({'precision': precision , 'recall': recall})
print(data[data['recall'] >= 0.7]['precision'].idxmax())
print(data.loc[78])
# data.head()
data[70:80]
# max(data[data['recall'] >= 0.7]['precision'])
precision, recall, thresholds = precision_recall_curve(true, score_svm)
data = pd.DataFrame({'precision': precision , 'recall': recall})
print(data[data['recall'] >= 0.7]['precision'].idxmax())
print(data.loc[85])
data.head()
precision, recall, thresholds = precision_recall_curve(true, score_knn)
data = pd.DataFrame({'precision': precision , 'recall': recall})
print(data[data['recall'] >= 0.7]['precision'].idxmax())
print(data.loc[34])
# data.head()
data[20:40]
precision, recall, thresholds = precision_recall_curve(true, score_tree)
data = pd.DataFrame({'precision': precision , 'recall': recall})
print(data[data['recall'] >= 0.7]['precision'].idxmax())
print(data.loc[5])
data.head()
| 0.494385 | 0.915205 |
# Diseño de software para cómputo científico
----
## Unidad 3: Object Relational Mappers
## Python + RBMS
```python
import MySQLdb
db = MySQLdb.connect(host='localhost',user='root',
passwd='',db='Prueba')
cursor = db.cursor()
cursor.execute('Select * From usuarios')
resultado = cursor.fetchall()
print('Datos de Usuarios')
for registro in resultado:
print(registro[0], '->', registro[1])
```
**out**
```console
Datos de Usuarios
USU01 -> Young Neil
USU02 -> Knives Chau
```
## Como estamos?
- Si te gusta *SQL*.
- Pero *SQL* no esta implementado igual en los distintos motores.
- Y nada garantiza que ese motor no cambie con el tiempo (sobre todo en empresas
grandes donde el que decide poco tiene que ver con el desarrolla)
- Lo que devuelve los conectores son set de datos y no objetos ``User``
propiamente.
- La diferencias entre el modelo de objetos y relacional.
- Pero esto es rápido.
## Que opciones tenemos?
- Usar ORM
El mapeo objeto-relacional es una
técnica de programación para convertir datos entre el sistema de tipos
utilizado en un lenguaje de programación OO y el utilizado
en una base de datos relacional, utilizando un motor de persistencia. En la
práctica esto crea una base de datos orientada a objetos virtual, sobre la
base de datos relacional. Esto posibilita el uso de las características
propias de la orientación a objetos (básicamente herencia y polimorfismo)
`Wikipedia: ORM <http://es.wikipedia.org/wiki/Mapeo_objeto-relacional>`_
- Alternativas en Pyhon: SqlAlchemy, Storm, **Peewee**, Django-ORM
## Una evidencia de la diferencia de modelos
Si necesitamos modelar la lógica **un usuario tiene muchos autos.**, y trataramos de extraer todos los autos por usuario.
- En diagramas Entity-Relational (ER) - Modelo Relacional

```python
c_x_u = {}
for c in cars:
if c.user not in c_x_u:
c_x_u[c.user] = []
c_x_u[c.user].append(c)
```
- En diagrama de Clases - Modelo OO

```python
c_x_u = {u: u.cars for u in user}
```
## Vamos con **Peewee**
- No es el mejor orm que existe (SQLAlchemy es el mejor que existe, pero no tenemos 3 hs).
- Es Django-like.
- Lo he usando para ordenar datos data minining y varias otras cosas.
- http://docs.peewee-orm.com/

Declarando las tablas y las clases
----------------------------------
```
!pip install peewee
from peewee import *
example_db = SqliteDatabase('03_orm/example.db')
class ExampleModel(Model):
class Meta:
database = example_db
class User(ExampleModel):
name = CharField()
age = IntegerField()
class Car(ExampleModel):
model = CharField(null=True)
plate = CharField(unique=True)
user = ForeignKeyField(User, related_name="cars")
User.create_table(fail_silently=True)
Car.create_table(fail_silently=True)
```
Un poco mas de los Fields
-------------------------
* ``null=False``: boolean indicating whether null values are allowed to be
stored
* ``index=False``: boolean indicating whether to create an index on this column
* ``unique=False``: boolean indicating whether to create a unique index on this
column
* ``verbose_name=None``: string representing the "user-friendly" name of this
field
* ``help_text=None``: string representing any helpful text for this field
* ``db_column=None``: string representing the underlying column to use if
different, useful for legacy databases
* ``default=None``: any value to use as a default for uninitialized models
* ``choices=None``: an optional iterable containing 2-tuples of ``value``,
``display``
* ``primary_key=False``: whether this field is the primary key for the table
Mas todavia de los Fields
-------------------------

Creamos registros
-----------------
```
u0 = User()
u0.name = "Ramona Flowers"
u0.age = 24
u0.save()
u1 = User(name="Stephen Stills", age=24)
u1.save()
u2 = User(name="Scott Pilgrim", age=23)
u2.save()
```
## Queries 1
```sql
SELECT * FROM user
```
```
print("Todos los Usuarios")
for u in User.select():
print(u.id, u.name, u.age)
```
Queries 2
---------
```sql
SELECT * FROM user WHERE id = 1
```
```
print("Con ID=1")
user = User.get(User.id == 1)
print(type(user), user.id, user.name)
```
Queries 3
---------
```sql
SELECT * FROM user WHERE name = 'Stephen Stills'
```
```
print("Con nombre 'Stephen Stills'")
usr = User.get(User.name == "Stephen Stills")
print(usr)
```
Queries 4
---------
```sql
SELECT * FROM user WHERE age <= 24
```
```
print("Con edad <= 24")
for u in User.filter(User.age <= 24):
print(u.name)
```
Queries 5
---------
```
print("Con nombre que empieza con 'S'")
for u in User.filter(fn.Substr(User.name, 1, 1) == "S"):
print(u.id, u.name)
```
Queries 6 (Entran los autos)
----------------------------
```
# u0 -> Ramona Flowers
car = Car(model="2012", plate="aac 2502", user=u0)
car.save()
print("Autos de u0")
for c in u0.cars: # Car.filter(Car.user == u0)
print("{} -> {}".format(c.plate, c.user.name))
```
Queries 7
---------
```
print("Cantidad de autos de personas con 24 años")
print(
Car.select().join(
User
).where(
User.age == 24
).count()
)
```
Queries 8
---------
```
print("Autos con modelo 2012 de usuarios de 24 años")
for car in Car.select().join(User).where(User.age == 24, Car.model=="2012"):
print(car.plate, "--", car.model)
```
Update and Delete
-----------------
**UPDATE**
```
print("Una actualización")
c = Car.get(plate="jbc 2502")
c.plate = "AAC 6666"
c.save()
```
**DELETE**
```
print(u0.cars.count())
car0.delete_instance()
print(u0.cars.count())
```
Cosas en el tintero
-------------------
- ``.order_by``
- ``.having``
- ``.group_by``
|
github_jupyter
|
import MySQLdb
db = MySQLdb.connect(host='localhost',user='root',
passwd='',db='Prueba')
cursor = db.cursor()
cursor.execute('Select * From usuarios')
resultado = cursor.fetchall()
print('Datos de Usuarios')
for registro in resultado:
print(registro[0], '->', registro[1])
Datos de Usuarios
USU01 -> Young Neil
USU02 -> Knives Chau
c_x_u = {}
for c in cars:
if c.user not in c_x_u:
c_x_u[c.user] = []
c_x_u[c.user].append(c)
c_x_u = {u: u.cars for u in user}
!pip install peewee
from peewee import *
example_db = SqliteDatabase('03_orm/example.db')
class ExampleModel(Model):
class Meta:
database = example_db
class User(ExampleModel):
name = CharField()
age = IntegerField()
class Car(ExampleModel):
model = CharField(null=True)
plate = CharField(unique=True)
user = ForeignKeyField(User, related_name="cars")
User.create_table(fail_silently=True)
Car.create_table(fail_silently=True)
u0 = User()
u0.name = "Ramona Flowers"
u0.age = 24
u0.save()
u1 = User(name="Stephen Stills", age=24)
u1.save()
u2 = User(name="Scott Pilgrim", age=23)
u2.save()
SELECT * FROM user
print("Todos los Usuarios")
for u in User.select():
print(u.id, u.name, u.age)
SELECT * FROM user WHERE id = 1
print("Con ID=1")
user = User.get(User.id == 1)
print(type(user), user.id, user.name)
SELECT * FROM user WHERE name = 'Stephen Stills'
print("Con nombre 'Stephen Stills'")
usr = User.get(User.name == "Stephen Stills")
print(usr)
SELECT * FROM user WHERE age <= 24
print("Con edad <= 24")
for u in User.filter(User.age <= 24):
print(u.name)
print("Con nombre que empieza con 'S'")
for u in User.filter(fn.Substr(User.name, 1, 1) == "S"):
print(u.id, u.name)
# u0 -> Ramona Flowers
car = Car(model="2012", plate="aac 2502", user=u0)
car.save()
print("Autos de u0")
for c in u0.cars: # Car.filter(Car.user == u0)
print("{} -> {}".format(c.plate, c.user.name))
print("Cantidad de autos de personas con 24 años")
print(
Car.select().join(
User
).where(
User.age == 24
).count()
)
print("Autos con modelo 2012 de usuarios de 24 años")
for car in Car.select().join(User).where(User.age == 24, Car.model=="2012"):
print(car.plate, "--", car.model)
print("Una actualización")
c = Car.get(plate="jbc 2502")
c.plate = "AAC 6666"
c.save()
print(u0.cars.count())
car0.delete_instance()
print(u0.cars.count())
| 0.174305 | 0.773302 |
# Neural Network Q Learning Part 2: Looking at what went wrong and becoming less greedy
In the previous part, we created a simple Neural Network based player and had it play against the Random Player, the Min Max Player, and the non-deterministic Min Max player. While we had some success, overall results were underwhelming:
| Player | NN Player 1st | NN Player 2nd |
| --- | --- | --- |
| Random | Not bad but not perfect | Kind of but not really |
| Min Max | Mixed - All or nothing | Mixed - All or nothing |
| Rnd Min Max | Sometimes / Mixed | Nope |
## What could have gone wrong?
Let's start by looking at our code and try to identify possible reasons why things may have gone less than optimal:
* Bugs in the code or other fundamental screw-ups.
* The network we defined is not suitable for this task: Input features not optimal, not enough layers, layers not big enough, sub-optimal activation function, sub-optimal optimizer, sub-optimal weight initialization, sub-optimal loss function.
* Bad values for other hyper-parameters: Optimizer learning rate, reward discount, win/loss/draw rewards.
* The training data wasn't optimal.
* The Tic Tac Toe Q function is fundamentally unlearnable by Neural Networks.
Well, this is quite a list. Randomly tweaking and seeing what happens is not really feasible. Too many possible ways to do so and each of them would take a long time to evaluate - at least on my computer.
Let's make a quick assessment and come up with some hypotheses about each of the above. Hopefully we can identify some more likely candidates and discard some others.
### Bugs in the code or other fundamental screw ups.
Possible, but hard to confirm. Maybe we calculate the rewards incorrectly, or we feed the training data into the network incorrectly, or we use TensorFlow incorrectly, maybe we don't even create the graph correctly? We know that we didn't screw up completely as the Neural Netwok does learn quite well in some scenarios / cases. This doesn't mean we don't have some nasty bugs in there, but for the moment this might not be the most promising avenue to pursue. Maybe some bugs will surface while we look close at some of the other options.
### Our network itself.
#### Input features
We encode the board state as 3x9=27 bits indicating naughts, crosses, and empty fields on the board. There are other possible ways we could do this:
1. We could use an array of 9 integers encoding crosses, naughts, and empty spaces.
2. We could feed in our board hash value as a single integer input.
3. We could create and add some hand-crafted features: Another array indicating moves that would win the game or lose the game; mark potential forks etc.
4. We could feed the board in as 2D features planes instead of 1D feature vectors.
Option 1) is possible, but as far as I remember the consensus seems to be that bit features are better than value-encoded features for cases like game board states. It's also what the professionals seem to use, e.g. DeepMind for [AplhaZero](https://deepmind.com/documents/119/agz_unformatted_nature.pdf). There are significant differences in other parts of our approach and the one used in AlphaZero, and I don't seem to be able to find any hard references for bit vs value encoding right now, but I'm reasonably confident we're probably not too wrong in what we do here. Option 2) should be even worse in this case.
Options 3) would almost certainly improve things, but I explicitly don't want to do this. The goal here really is to train a Neural Network to play Tic Tac Toe based on reinforcement alone, i.e. with no prior human game strategy knowledge built into the system. By suggesting that certain features like win/lose in one move, or forks are important would artificially add such information. So, while it may work, we won't do this.
Option 4) is an interesting one. The fact that we use a 1D vector certainly loses some of the obviously existing 2D features on the board. For a human, it would be very hard to play Tic Tac Toe if presented with a board in this way, especially if they have to do so without transforming it back to a 2D representation in their head. On the other hand, I don't see how our particular network would be able to exploit the 2D representation. If we would be using a [Convolutional Neural Network](https://en.wikipedia.org/wiki/Convolutional_neural_network), this would be different, but for our simple network I don't think it would make a difference. Feel encouraged however to give it a try and report back. Especially if it worked!
In summary, while there is some uncertainty about our input feature vector, it's probably OK I think.
#### The network itself
We only use 1 hidden layer and this layer is not particularly large. Maybe we should try bigger or more hidden layers.
We use `ReLu` as activation function and there are other options we could try, such as `tanh`, `leaky relu`, `sigmoid`, etc. Might be worth trying, but `ReLu` seems to be generally regarded as an all-rounder to be used unless you have a particular reason not to. Based on my very limited understanding of what I'm doing here, I don't really see a good reason to use any of the others, so we'll leave that one alone as well for the time being. If you want to play around with this, maybe give the `leaky ReLu` a go and let us know how it went.
Similar to the activation function, the [GradientDescentOptimizer](https://www.tensorflow.org/api_docs/python/tf/train/GradientDescentOptimizer) should be a good all-rounder to be used here. But again, there are many other options one could try, e.g. the popular [AdamOptimizer](https://www.tensorflow.org/api_docs/python/tf/train/AdamOptimizer).
Regarding the loss function, I'm reasonably confident here. We want to approximate a function (the Q function of Tic Tac Toe), so this should make it a regression problem, which as I understand it should mean that [Mean Squared Error](tf.losses.mean_squared_error) should be a good choice.
Weight initialization is in my limited experience surprisingly important, and can significantly impact performance. E.g. in the worst case of initializing all weights with the same number it basically collapses the layer widths to 1 as all nodes in a layer would always have the same value. We use the [Variance Scaling initializer](tf.contrib.layers.variance_scaling_initializer) which shouldn't be a bad choice as far as I can tell - especially if we want to add more layers to our network, but again, there are many other options we could try.
We have already discussed the input feature above.
There are also various other, more sophisticated network topologies we can use to try to train a Neural Network how to play Tic Tac Toe: Double Q Network, Deep Q Network, Dueling Q Network, Policy Gradient, Asynchronous Actor-Critic Agents (A3C), etc.
#### Other Hyper Parameters
Then there are the hyper-parameters that let us tune the network without changing its topology: Learning rate, reward discount, win/loss/draw rewards are all values we can be changed and which potentially will make performance better or worse. We'll have to see if we can get some clues on whether we need to make changes here.
### Training data
The training data is pretty much determined by our use of the Reinforcement Learning approach. I.e. making the current network play games using its current Q function approximation and then update its weights based on the outcome. There are some things we could do a bit differently however, and potentially better:
* We currently always chose the move that we estimate is the best one. This is called a *greedy* strategy. This carries the risk that we get stuck in a particular pattern and never take a risk and investigate some other potential moves. E.g. in the worst case this might mean that due random weight initialization the move that would be best ends up with an estimated Q value that is so bad that it would never be chosen. Since we will never ever chose this move it will never get a chance to cause a positive reward and thus get a chance to have its Q value estimate corrected. A potential solution for this is to use a *$\epsilon$ - greedy* strategy, where we *most of the time* use the move with the highest Q value, but occasionally (with probability $\epsilon$ - thus the name) chose a sub-optimal move to encourage better exploration of our possible action-space.
* Another limitation of our current approach is that we only feed the last game into the training step. The risk here is that if a network loses a lot it will mostly get losses as training input. This could potentially cause a self-reinforcing situation where the lack of any positive rewards will lead the network to predict that, no matter what it does, it will always lose, thus all moves are just bad. We should test this hypothesis, and if true might need to add a cache of previously played games to feed back into the network, potentially artificially boosting the number of samples with positive reward outcomes.
We will give this a try and see if it helps.
### The Tic Tac Toe Q function is fundamentally unlearnable by Neural Networks
Yeah, nah. Theoretically possible maybe, but extremely unlikely. Given the success others have with Neural Networks in related and much more complex tasks, this is probably not it.
Most serious approaches do however use a slightly different approach than we do by combining a Neural Network with other techniques such as variations of Tree Search, e.g. [Monte Carlo tree search](https://en.wikipedia.org/wiki/Monte_Carlo_tree_search). This wouldn't make much sense in our Tic Tac Toe scenario since we have seen in the Min Max Player part that a tree search on its own can master Tic Tac Toe already without breaking a sweat. There is not much a Neural Network could contribute here even if we severely restrict the search depth.
# Becoming less greedy
Based on our investigation above, it looks like a promising first step might be to use a less greedy action policy.
Becoming less greedy is quite straight forward. We simply add a parameter $\epsilon$, and with probability $\epsilon$ we don't chose what we think is the best move, but a random, different move.
In the beginning of our training we want to be quite adventurous and try all kinds of moves. The more our training advances the more confident we should be in our Q value estimates and thus the less likely we should be to try random other moves. This means we will also need a second parameter to continuously decrease $\epsilon$ over time.
This is implemented in [EGreedyNNQPlayer.py](https://github.com/fcarsten/tic-tac-toe/blob/master/tic_tac_toe/EGreedyNNQPlayer.py).
It is very similar to our previous version, with the following changes. When we select a move, instead of
```Python
move = np.argmax(probs)
```
we now do
```Python
if self.training is True and np.random.rand(1) < self.random_move_prob:
move = board.random_empty_spot()
else:
move = np.argmax(probs)
```
and during training we reduce the probability of making a random move:
```Python
self.random_move_prob *= self.random_move_decrease
```
Let's see how it goes. We will use the new $\epsilon$-greedy strategy and also play a bit with the other hyper-parameters:
```
%matplotlib inline
import tensorflow as tf
import matplotlib.pyplot as plt
from util import evaluate_players
from tic_tac_toe.TFSessionManager import TFSessionManager
from tic_tac_toe.RandomPlayer import RandomPlayer
from tic_tac_toe.EGreedyNNQPlayer import EGreedyNNQPlayer
from tic_tac_toe.MinMaxAgent import MinMaxAgent
tf.reset_default_graph()
nnplayer = EGreedyNNQPlayer("QLearner1", learning_rate=0.001, reward_discount=0.99, random_move_decrease=0.99)
mm_player = MinMaxAgent()
rndplayer = RandomPlayer()
TFSessionManager.set_session(tf.Session())
TFSessionManager.get_session().run(tf.global_variables_initializer())
game_number, p1_wins, p2_wins, draws = evaluate_players(nnplayer, mm_player, num_battles=50)
p = plt.plot(game_number, draws, 'r-', game_number, p1_wins, 'g-', game_number, p2_wins, 'b-')
plt.show()
TFSessionManager.set_session(None)
```
Feel encouraged to play with the example above and try out different combinations. Overall I didn't notice much change - on occasion however it seemed to be able to break out of a complete losing streak and find a strategy that resulted in 100% draws. To see if this is statistically significant however would require a lot of runs. Many more than I have time or patience for. Especially since it is still losing badly gogin second against the non-deterministic Min Max player. Clearly, it didn't actually solve the problem to a degree that is acceptable.
In the next part we will look at using a more sophisticated network topology.
|
github_jupyter
|
move = np.argmax(probs)
if self.training is True and np.random.rand(1) < self.random_move_prob:
move = board.random_empty_spot()
else:
move = np.argmax(probs)
self.random_move_prob *= self.random_move_decrease
%matplotlib inline
import tensorflow as tf
import matplotlib.pyplot as plt
from util import evaluate_players
from tic_tac_toe.TFSessionManager import TFSessionManager
from tic_tac_toe.RandomPlayer import RandomPlayer
from tic_tac_toe.EGreedyNNQPlayer import EGreedyNNQPlayer
from tic_tac_toe.MinMaxAgent import MinMaxAgent
tf.reset_default_graph()
nnplayer = EGreedyNNQPlayer("QLearner1", learning_rate=0.001, reward_discount=0.99, random_move_decrease=0.99)
mm_player = MinMaxAgent()
rndplayer = RandomPlayer()
TFSessionManager.set_session(tf.Session())
TFSessionManager.get_session().run(tf.global_variables_initializer())
game_number, p1_wins, p2_wins, draws = evaluate_players(nnplayer, mm_player, num_battles=50)
p = plt.plot(game_number, draws, 'r-', game_number, p1_wins, 'g-', game_number, p2_wins, 'b-')
plt.show()
TFSessionManager.set_session(None)
| 0.387574 | 0.980581 |
<a href="https://colab.research.google.com/github/Nirzu97/pyprobml/blob/matrix-factorization/notebooks/matrix_factorization_recommender.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Matrix Factorization for Movie Lens Recommendations
This notebook is based on code from Nick Becker
https://github.com/beckernick/matrix_factorization_recommenders/blob/master/matrix_factorization_recommender.ipynb
# Setting Up the Ratings Data
We read the data directly from MovieLens website, since they don't allow redistribution. We want to include the metadata (movie titles, etc), not just the ratings matrix.
```
import pandas as pd
import numpy as np
import os
import matplotlib.pyplot as plt
!wget http://files.grouplens.org/datasets/movielens/ml-100k.zip
!ls
!unzip ml-100k
folder = "ml-100k"
!wget http://files.grouplens.org/datasets/movielens/ml-1m.zip
!unzip ml-1m
!ls
folder = "ml-1m"
ratings_list = [
[int(x) for x in i.strip().split("::")] for i in open(os.path.join(folder, "ratings.dat"), "r").readlines()
]
users_list = [i.strip().split("::") for i in open(os.path.join(folder, "users.dat"), "r").readlines()]
movies_list = [
i.strip().split("::") for i in open(os.path.join(folder, "movies.dat"), "r", encoding="latin-1").readlines()
]
ratings_df = pd.DataFrame(ratings_list, columns=["UserID", "MovieID", "Rating", "Timestamp"], dtype=int)
movies_df = pd.DataFrame(movies_list, columns=["MovieID", "Title", "Genres"])
movies_df["MovieID"] = movies_df["MovieID"].apply(pd.to_numeric)
movies_df.head()
def get_movie_name(movies_df, movie_id_str):
ndx = movies_df["MovieID"] == int(movie_id_str)
name = movies_df["Title"][ndx].to_numpy()[0]
return name
print(get_movie_name(movies_df, 1))
print(get_movie_name(movies_df, "527"))
def get_movie_genres(movies_df, movie_id_str):
ndx = movies_df["MovieID"] == int(movie_id_str)
name = movies_df["Genres"][ndx].to_numpy()[0]
return name
print(get_movie_genres(movies_df, 1))
print(get_movie_genres(movies_df, "527"))
ratings_df.head()
```
These look good, but I want the format of my ratings matrix to be one row per user and one column per movie. I'll `pivot` `ratings_df` to get that and call the new variable `R`.
```
R_df = ratings_df.pivot(index="UserID", columns="MovieID", values="Rating").fillna(0)
R_df.head()
```
The last thing I need to do is de-mean the data (normalize by each users mean) and convert it from a dataframe to a numpy array.
```
R = R_df.to_numpy()
user_ratings_mean = np.mean(R, axis=1)
R_demeaned = R - user_ratings_mean.reshape(-1, 1)
print(R.shape)
print(np.count_nonzero(R))
```
# Singular Value Decomposition
Scipy and Numpy both have functions to do the singular value decomposition. I'm going to use the Scipy function `svds` because it let's me choose how many latent factors I want to use to approximate the original ratings matrix (instead of having to truncate it after).
```
from scipy.sparse.linalg import svds
U, sigma, Vt = svds(R_demeaned, k=50)
sigma = np.diag(sigma)
latents = [10, 20, 50]
errors = []
for latent_dim in latents:
U, sigma, Vt = svds(R_demeaned, k=latent_dim)
sigma = np.diag(sigma)
Rpred = np.dot(np.dot(U, sigma), Vt) + user_ratings_mean.reshape(-1, 1)
Rpred[Rpred < 0] = 0
Rpred[Rpred > 5] = 5
err = np.sqrt(np.sum(np.power(R - Rpred, 2)))
errors.append(err)
print(errors)
```
# Making Predictions from the Decomposed Matrices
I now have everything I need to make movie ratings predictions for every user. I can do it all at once by following the math and matrix multiply $U$, $\Sigma$, and $V^{T}$ back to get the rank $k=50$ approximation of $R$.
I also need to add the user means back to get the actual star ratings prediction.
```
all_user_predicted_ratings = np.dot(np.dot(U, sigma), Vt) + user_ratings_mean.reshape(-1, 1)
```
# Making Movie Recommendations
Finally, it's time. With the predictions matrix for every user, I can build a function to recommend movies for any user. All I need to do is return the movies with the highest predicted rating that the specified user hasn't already rated. Though I didn't use actually use any explicit movie content features (such as genre or title), I'll merge in that information to get a more complete picture of the recommendations.
I'll also return the list of movies the user has already rated, for the sake of comparison.
```
preds_df = pd.DataFrame(all_user_predicted_ratings, columns=R_df.columns)
preds_df.head()
def recommend_movies(preds_df, userID, movies_df, original_ratings_df, num_recommendations=5):
# Get and sort the user's predictions
user_row_number = userID - 1 # UserID starts at 1, not 0
sorted_user_predictions = preds_df.iloc[user_row_number].sort_values(ascending=False) # UserID starts at 1
# Get the user's data and merge in the movie information.
user_data = original_ratings_df[original_ratings_df.UserID == (userID)]
user_full = user_data.merge(movies_df, how="left", left_on="MovieID", right_on="MovieID").sort_values(
["Rating"], ascending=False
)
print("User {0} has already rated {1} movies.".format(userID, user_full.shape[0]))
print("Recommending highest {0} predicted ratings movies not already rated.".format(num_recommendations))
# Recommend the highest predicted rating movies that the user hasn't seen yet.
recommendations = (
movies_df[~movies_df["MovieID"].isin(user_full["MovieID"])]
.merge(pd.DataFrame(sorted_user_predictions).reset_index(), how="left", left_on="MovieID", right_on="MovieID")
.rename(columns={user_row_number: "Predictions"})
.sort_values("Predictions", ascending=False)
.iloc[:num_recommendations, :-1]
)
return user_full, recommendations
already_rated, predictions = recommend_movies(preds_df, 837, movies_df, ratings_df, 10)
```
So, how'd I do?
```
already_rated.head(10)
df = already_rated[["MovieID", "Title", "Genres"]].copy()
df.head(10)
predictions
```
Pretty cool! These look like pretty good recommendations. It's also good to see that, though I didn't actually use the genre of the movie as a feature, the truncated matrix factorization features "picked up" on the underlying tastes and preferences of the user. I've recommended some film-noirs, crime, drama, and war movies - all of which were genres of some of this user's top rated movies.
# Visualizing true and predicted ratings matrix
```
Rpred = all_user_predicted_ratings
Rpred[Rpred < 0] = 0
Rpred[Rpred > 5] = 5
print(np.linalg.norm(R - Rpred, ord="fro"))
print(np.sqrt(np.sum(np.power(R - Rpred, 2))))
import matplotlib.pyplot as plt
nusers = 20
nitems = 20
plt.figure(figsize=(10, 10))
plt.imshow(R[:nusers, :nitems], cmap="jet")
plt.xlabel("item")
plt.ylabel("user")
plt.title("True ratings")
plt.colorbar()
plt.figure(figsize=(10, 10))
plt.imshow(Rpred[:nusers, :nitems], cmap="jet")
plt.xlabel("item")
plt.ylabel("user")
plt.title("Predcted ratings")
plt.colorbar()
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import os
import matplotlib.pyplot as plt
!wget http://files.grouplens.org/datasets/movielens/ml-100k.zip
!ls
!unzip ml-100k
folder = "ml-100k"
!wget http://files.grouplens.org/datasets/movielens/ml-1m.zip
!unzip ml-1m
!ls
folder = "ml-1m"
ratings_list = [
[int(x) for x in i.strip().split("::")] for i in open(os.path.join(folder, "ratings.dat"), "r").readlines()
]
users_list = [i.strip().split("::") for i in open(os.path.join(folder, "users.dat"), "r").readlines()]
movies_list = [
i.strip().split("::") for i in open(os.path.join(folder, "movies.dat"), "r", encoding="latin-1").readlines()
]
ratings_df = pd.DataFrame(ratings_list, columns=["UserID", "MovieID", "Rating", "Timestamp"], dtype=int)
movies_df = pd.DataFrame(movies_list, columns=["MovieID", "Title", "Genres"])
movies_df["MovieID"] = movies_df["MovieID"].apply(pd.to_numeric)
movies_df.head()
def get_movie_name(movies_df, movie_id_str):
ndx = movies_df["MovieID"] == int(movie_id_str)
name = movies_df["Title"][ndx].to_numpy()[0]
return name
print(get_movie_name(movies_df, 1))
print(get_movie_name(movies_df, "527"))
def get_movie_genres(movies_df, movie_id_str):
ndx = movies_df["MovieID"] == int(movie_id_str)
name = movies_df["Genres"][ndx].to_numpy()[0]
return name
print(get_movie_genres(movies_df, 1))
print(get_movie_genres(movies_df, "527"))
ratings_df.head()
R_df = ratings_df.pivot(index="UserID", columns="MovieID", values="Rating").fillna(0)
R_df.head()
R = R_df.to_numpy()
user_ratings_mean = np.mean(R, axis=1)
R_demeaned = R - user_ratings_mean.reshape(-1, 1)
print(R.shape)
print(np.count_nonzero(R))
from scipy.sparse.linalg import svds
U, sigma, Vt = svds(R_demeaned, k=50)
sigma = np.diag(sigma)
latents = [10, 20, 50]
errors = []
for latent_dim in latents:
U, sigma, Vt = svds(R_demeaned, k=latent_dim)
sigma = np.diag(sigma)
Rpred = np.dot(np.dot(U, sigma), Vt) + user_ratings_mean.reshape(-1, 1)
Rpred[Rpred < 0] = 0
Rpred[Rpred > 5] = 5
err = np.sqrt(np.sum(np.power(R - Rpred, 2)))
errors.append(err)
print(errors)
all_user_predicted_ratings = np.dot(np.dot(U, sigma), Vt) + user_ratings_mean.reshape(-1, 1)
preds_df = pd.DataFrame(all_user_predicted_ratings, columns=R_df.columns)
preds_df.head()
def recommend_movies(preds_df, userID, movies_df, original_ratings_df, num_recommendations=5):
# Get and sort the user's predictions
user_row_number = userID - 1 # UserID starts at 1, not 0
sorted_user_predictions = preds_df.iloc[user_row_number].sort_values(ascending=False) # UserID starts at 1
# Get the user's data and merge in the movie information.
user_data = original_ratings_df[original_ratings_df.UserID == (userID)]
user_full = user_data.merge(movies_df, how="left", left_on="MovieID", right_on="MovieID").sort_values(
["Rating"], ascending=False
)
print("User {0} has already rated {1} movies.".format(userID, user_full.shape[0]))
print("Recommending highest {0} predicted ratings movies not already rated.".format(num_recommendations))
# Recommend the highest predicted rating movies that the user hasn't seen yet.
recommendations = (
movies_df[~movies_df["MovieID"].isin(user_full["MovieID"])]
.merge(pd.DataFrame(sorted_user_predictions).reset_index(), how="left", left_on="MovieID", right_on="MovieID")
.rename(columns={user_row_number: "Predictions"})
.sort_values("Predictions", ascending=False)
.iloc[:num_recommendations, :-1]
)
return user_full, recommendations
already_rated, predictions = recommend_movies(preds_df, 837, movies_df, ratings_df, 10)
already_rated.head(10)
df = already_rated[["MovieID", "Title", "Genres"]].copy()
df.head(10)
predictions
Rpred = all_user_predicted_ratings
Rpred[Rpred < 0] = 0
Rpred[Rpred > 5] = 5
print(np.linalg.norm(R - Rpred, ord="fro"))
print(np.sqrt(np.sum(np.power(R - Rpred, 2))))
import matplotlib.pyplot as plt
nusers = 20
nitems = 20
plt.figure(figsize=(10, 10))
plt.imshow(R[:nusers, :nitems], cmap="jet")
plt.xlabel("item")
plt.ylabel("user")
plt.title("True ratings")
plt.colorbar()
plt.figure(figsize=(10, 10))
plt.imshow(Rpred[:nusers, :nitems], cmap="jet")
plt.xlabel("item")
plt.ylabel("user")
plt.title("Predcted ratings")
plt.colorbar()
| 0.451568 | 0.913754 |
+ This notebook is part of lecture 31 *Change of basis and image compression* in the OCW MIT course 18.06 by Prof Gilbert Strang [1]
+ Created by me, Dr Juan H Klopper
+ Head of Acute Care Surgery
+ Groote Schuur Hospital
+ University Cape Town
+ <a href="mailto:[email protected]">Email me with your thoughts, comments, suggestions and corrections</a>
<a rel="license" href="http://creativecommons.org/licenses/by-nc/4.0/"><img alt="Creative Commons Licence" style="border-width:0" src="https://i.creativecommons.org/l/by-nc/4.0/88x31.png" /></a><br /><span xmlns:dct="http://purl.org/dc/terms/" href="http://purl.org/dc/dcmitype/InteractiveResource" property="dct:title" rel="dct:type">Linear Algebra OCW MIT18.06</span> <span xmlns:cc="http://creativecommons.org/ns#" property="cc:attributionName">IPython notebook [2] study notes by Dr Juan H Klopper</span> is licensed under a <a rel="license" href="http://creativecommons.org/licenses/by-nc/4.0/">Creative Commons Attribution-NonCommercial 4.0 International License</a>.
+ [1] <a href="http://ocw.mit.edu/courses/mathematics/18-06sc-linear-algebra-fall-2011/index.htm">OCW MIT 18.06</a>
+ [2] Fernando Pérez, Brian E. Granger, IPython: A System for Interactive Scientific Computing, Computing in Science and Engineering, vol. 9, no. 3, pp. 21-29, May/June 2007, doi:10.1109/MCSE.2007.53. URL: http://ipython.org
```
from IPython.core.display import HTML, Image
css_file = 'style.css'
HTML(open(css_file, 'r').read())
from sympy import init_printing, Matrix, symbols, sqrt, Rational
from warnings import filterwarnings
init_printing(use_latex = 'mathjax')
filterwarnings('ignore')
```
# Image compression and change of basis
## Lossy image compression
+ Consider a 2<sup>9</sup> × 2<sup>9</sup> monochrome image
+ Every pixel in this 512×512 image can take a value of 0 ≤ *x*<sub>i</sub> < 255 (this is 8-bit)
+ This make **x** a vector in ℝ<sup>n</sup>, with *n* = 512<sup>2</sup> (for color images this would be 3×n)
```
# Just look at what 512 square is
512 ** 2
```
+ This is a very large, unwieldy basis
+ Consider the standard basis
$$ \begin{bmatrix} 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix},\begin{bmatrix} 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix},\cdots ,\begin{bmatrix} 0 \\ 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix} $$
+ Consider now the better basis
$$ \begin{bmatrix} 1 \\ 1 \\ 1 \\ \vdots \\ 1 \end{bmatrix},\begin{bmatrix} 1 \\ \vdots \\ 1 \\ -1 \\ \vdots \\ -1 \end{bmatrix},\begin{bmatrix} 1 \\ -1 \\ 1 \\ -1 \\ \vdots \end{bmatrix},\cdots $$
+ Indeed, there are many options
+ JPEG uses an 8 × 8 Fourier basis
+ This means that an image is broken up into 64 × 64 pixel blocks
+ See the lectures on the Fourier basis
$$ \begin{bmatrix} 1 \\ 1 \\ 1 \\ \vdots \\ 1 \end{bmatrix},\begin{bmatrix} 1 \\ W \\ { W }^{ 2 } \\ \vdots \\ { W }^{ n-1 } \end{bmatrix},\cdots $$
+ This gives us a vector **x** in ℝ<sup>64</sup> (i.e. with 64 coefficients)
+ Up until this point the compression is lossless
+ Now comes the compression (of which there are many such as thresholding)
+ Thresholding
+ Get rid of values more or less than set values (now there a less coefficients)
$$ \hat{x}=\sum{\hat{c}_{i}{v}_{i}} $$
* Video is a sequence of images that are highly correlated (not big changes from one image to the next) and you can predict future changes from previous changes
+ There are newer basis such as *wavelets*
+ Here is an example
$$ \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{bmatrix},\begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \\ -1 \\ -1 \\ -1 \\ -1 \end{bmatrix},\begin{bmatrix} 1 \\ 1 \\ -1 \\ -1 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix},\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 \\ 1 \end{bmatrix},\begin{bmatrix} 1 \\ -1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix},\begin{bmatrix} 0 \\ 0 \\ 1 \\ -1 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix},\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ -1 \\ 0 \\ 0 \end{bmatrix},\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ -1 \end{bmatrix} $$
+ Every vector in ℝ<sup>8</sup> is a linear combination of these 8 basis vectors
+ Let's do some linear algebra
+ Consider only a top row of 8 pixels
+ The standard vector of the values will be as follows (with 0 ≤ *p*<sub>i</sub> < 255)
$$ \begin{bmatrix} { p }_{ 1 } \\ { p }_{ 2 } \\ { p }_{ 3 } \\ { p }_{ 4 } \\ { p }_{ 5 } \\ { p }_{ 6 } \\ { p }_{ 7 } \\ { p }_{ 8 } \end{bmatrix} $$
+ We have to write this as a linear combination of the wavelet basis vectors *w*<sub>i</sub> (the lossless step)
$$ {P}={c}_{1}{w}_{1}+{c}_{2}{w}_{2}+\dots+{c}_{8}{w}_{8} $$
+ In vector form we have the following
$$ P=\begin{bmatrix} \vdots & \cdots & \vdots \\ { w }_{ 1 } & \cdots & { w }_{ 8 } \\ \vdots & \cdots & \vdots \end{bmatrix}\begin{bmatrix} { c }_{ 1 } \\ \vdots \\ { c }_{ 8 } \end{bmatrix} \\ P=Wc \\ c={W}^{-1}{P}$$
+ Let's bring some reality to this
+ For fast computation, W must be as easy to invert as possible
+ There is great competition to come up with *better* compression matrices
+ A *good* matrix must have the following
+ Be fast, i.e. the fast Fourier transform (FFT)
+ The wavelet basis above is fast
+ The basis vectors are orthogonal (and can be made orthonormal)
+ **If they are orthonormal then the inverse is equal to the transpose**
+ Good compression
+ If we threw away some of the *p*<sub>i</sub> values, we would just have a dark image
+ We we threw away, say the last two *c*<sub>i</sub> values (last two basis vectors) that won't lose us so much quality
## Change of basis
+ Let's look at this change in basis
+ Above, we had the following
$$ x=Wc $$
+ Here W is the matrix that takes us from the vector **x** in the old basis to the vector **c** in the new basis
+ Consider any transformation T (such as a rotation transformation)
+ With respect to *v*<sub>1</sub>,...,*v*<sub>8</sub> it has a matrix A
+ With respect to *w*<sub>1</sub>,...,*w*<sub>8</sub> it has a matrix B
+ Turns out that matrices A and B are similar
$$ B={M}^{-1}AM $$
+ Here M is the matrix that transforms the basis
+ What is A then, using the basis *v*<sub>1</sub>,...,*v*<sub>8</sub>?
+ We know T completely from T(*v*<sub>i</sub>)...
+ ... because if every **x**=Σ*c*<sub>i</sub>*v*<sub>i</sub>
+ ... then T(**x**)=Σ*c*<sub>i</sub>T(*v*<sub>i</sub>)
+ Constructing A
+ Write down all the transformations
$$ T\left( { v }_{ 1 } \right) ={ a }_{ 11 }{ v }_{ 1 }+{ a }_{ 21 }{ v }_{ 2 }+\dots +{ a }_{ 81 }{ v }_{ 8 }\\ T\left( { v }_{ 2 } \right) ={ a }_{ 12 }{ v }_{ 1 }+{ a }_{ 22 }{ v }_{ 2 }+\dots +{ a }_{ 82 }{ v }_{ 8 }\\ \vdots \\ T\left( { v }_{ 8 } \right) ={ a }_{ 18 }{ v }_{ 1 }+{ a }_{ 28 }{ v }_{ 2 }+\dots +{ a }_{ 88 }{ v }_{ 8 } $$
+ Now we know A
$$ A=\begin{bmatrix} { a }_{ 11 } & \cdots & { a }_{ 18 } \\ \vdots & \cdots & \vdots \\ { a }_{ 81 } & \cdots & { a }_{ 88 } \end{bmatrix} $$
+ Let's consider the linear transformation T(*v*<sub>i</sub>)=λ<sub>i</sub>
+ This makes A the following
$$ A=\begin{bmatrix} { \lambda }_{ 1 } & 0 & \cdots & \cdots & 0 \\ 0 & { \lambda }_{ 2 } & 0 & \cdots & \vdots \\ \vdots & 0 & \ddots & \cdots & \vdots \\ \vdots & \vdots & \vdots & \ddots & 0 \\ 0 & \cdots & \cdots & 0 & { \lambda }_{ 8 } \end{bmatrix} $$
## Example problems
### Example problem 1
+ The vector space of all polynomials in *x* (of degree ≤ 2) has the basis 1, *x*, *x*<sup>2</sup>
+ Consider a different basis *w*<sub>1</sub>, *w*<sub>2</sub>, *w*<sub>3</sub> whose values at *x* = -1, 0, and 1 are given by the following
$$ x=-1\rightarrow 1{ w }_{ 1 }+{ 0w }_{ 2 }+{ 0w }_{ 3 }\\ x=0\rightarrow 0{ w }_{ 1 }+1{ w }_{ 2 }+{ 0w }_{ 3 }\\ x=1\rightarrow 0{ w }_{ 1 }+{ 0w }_{ 2 }+{ 1w }_{ 3 } $$
+ Express *y*(*x*)=-*x*+5 in the new basis
+ Find the change of basis matrices
+ Find the matrix of taking derivatives in both of the basis
#### Solution
$$ y\left( x \right) =5-x\\ y\left( x \right) =\alpha { w }_{ 1 }+\beta { w }_{ 2 }+\gamma { w }_{ 3 } \\ y\left( -1 \right) =6 \\ y\left( 0 \right) =5\\ y\left( 1 \right) =4\\ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} \alpha \\ \beta \\ \gamma \end{bmatrix}=\begin{bmatrix} 6 \\ 5 \\ 4 \end{bmatrix} \\ \alpha =6,\beta =5,\gamma =4 \\ y=6{w}_{1}+5{w}_{2}+4{w}_{3} $$
+ For the second part let's look at what happens at *x* for the various values at 1 (which is *x*<sup>0</sup>), *x*, and *x*<sup>2</sup>
+ For -1 we have 1, -1, and 1
+ For 0 we have 1, 0, and 0
+ For 1 we have 1, 1, and 1
+ From this we can conclude the following
$$ 1={w}_{1}+{w}_{2}+{w}_{3} \\ x=-{w}_{1}+{w}_{3} \\ {x}^{2}={w}_{1}+{w}_{3} $$
+ Now we have the following matrix
$$ A=\begin{bmatrix}1&-1&1\\1&0&0\\1&1&1\end{bmatrix} $$
+ This converts the first basis to the second
+ To convert the second basis to the original we just need A<sup>-1</sup>
```
A = Matrix([[1, -1, 1], [1, 0, 0], [1, 1, 1]])
A.inv()
```
+ Now for derivative matrices
+ For the original basis, this is easy
$$ {D}_{x}=\begin{bmatrix}0&1&0\\0&0&2\\0&0&0\end{bmatrix} $$
+ For the second basis we need the following
$$ {D}_{w}=AD{A}^{-1} $$
```
Dx = Matrix([[0, 1, 0], [0, 0, 2], [0, 0, 0]])
Dw = A * Dx * A.inv()
Dw
```
+ Just to conclude we can write the values for *w*<sub>i</sub> from the inverse of A (the columns)
$$ {w}_{1}=\frac{-1}{2}{x}+\frac{1}{2}{x}^{2} \\ {w}_{2}=1-{x}^{2} \\ {w}_{3}=\frac{1}{2}x+\frac{1}{2}{x}^{2} $$
|
github_jupyter
|
from IPython.core.display import HTML, Image
css_file = 'style.css'
HTML(open(css_file, 'r').read())
from sympy import init_printing, Matrix, symbols, sqrt, Rational
from warnings import filterwarnings
init_printing(use_latex = 'mathjax')
filterwarnings('ignore')
# Just look at what 512 square is
512 ** 2
A = Matrix([[1, -1, 1], [1, 0, 0], [1, 1, 1]])
A.inv()
Dx = Matrix([[0, 1, 0], [0, 0, 2], [0, 0, 0]])
Dw = A * Dx * A.inv()
Dw
| 0.391988 | 0.94366 |
# 基于注意力的神经机器翻译
此笔记本训练一个将鞑靼语翻译为英语的序列到序列(sequence to sequence,简写为 seq2seq)模型。此例子难度较高,需要对序列到序列模型的知识有一定了解。
训练完此笔记本中的模型后,你将能够输入一个鞑靼语句子,例如 *"Әйдәгез!"*,并返回其英语翻译 *"Let's go!"*
对于一个简单的例子来说,翻译质量令人满意。但是更有趣的可能是生成的注意力图:它显示在翻译过程中,输入句子的哪些部分受到了模型的注意。
<img src="https://tensorflow.google.cn/images/spanish-english.png" alt="spanish-english attention plot">
请注意:运行这个例子用一个 P100 GPU 需要花大约 10 分钟。
```
import tensorflow as tf
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from sklearn.model_selection import train_test_split
import unicodedata
import re
import numpy as np
import os
import io
import time
```
## 下载和准备数据集
我们将使用 http://www.manythings.org/anki/ 提供的一个语言数据集。这个数据集包含如下格式的语言翻译对:
```
May I borrow this book? ¿Puedo tomar prestado este libro?
```
这个数据集中有很多种语言可供选择。我们将使用英语 - 鞑靼语数据集。为方便使用,我们在谷歌云上提供了此数据集的一份副本。但是你也可以自己下载副本。下载完数据集后,我们将采取下列步骤准备数据:
1. 给每个句子添加一个 *开始* 和一个 *结束* 标记(token)。
2. 删除特殊字符以清理句子。
3. 创建一个单词索引和一个反向单词索引(即一个从单词映射至 id 的词典和一个从 id 映射至单词的词典)。
4. 将每个句子填充(pad)到最大长度。
```
'''
# 下载文件
path_to_zip = tf.keras.utils.get_file(
'spa-eng.zip', origin='http://storage.googleapis.com/download.tensorflow.org/data/spa-eng.zip',
extract=True)
path_to_file = os.path.dirname(path_to_zip)+"/spa-eng/spa.txt"
'''
path_to_file = "./lan/tat.txt"
# 将 unicode 文件转换为 ascii
def unicode_to_ascii(s):
return ''.join(c for c in unicodedata.normalize('NFD', s)
if unicodedata.category(c) != 'Mn')
def preprocess_sentence(w):
w = unicode_to_ascii(w.lower().strip())
# 在单词与跟在其后的标点符号之间插入一个空格
# 例如: "he is a boy." => "he is a boy ."
# 参考:https://stackoverflow.com/questions/3645931/python-padding-punctuation-with-white-spaces-keeping-punctuation
w = re.sub(r"([?.!,¿])", r" \1 ", w)
w = re.sub(r'[" "]+', " ", w)
# 除了 (a-z, A-Z, ".", "?", "!", ","),将所有字符替换为空格
w = re.sub(r"[^a-zA-Z?.!,¿]+", " ", w)
w = w.rstrip().strip()
# 给句子加上开始和结束标记
# 以便模型知道何时开始和结束预测
w = '<start> ' + w + ' <end>'
return w
en_sentence = u"May I borrow this book?"
sp_sentence = u"¿Puedo tomar prestado este libro?"
print(preprocess_sentence(en_sentence))
print(preprocess_sentence(sp_sentence).encode('utf-8'))
# 1. 去除重音符号
# 2. 清理句子
# 3. 返回这样格式的单词对:[ENGLISH, SPANISH]
def create_dataset(path, num_examples):
lines = io.open(path, encoding='UTF-8').read().strip().split('\n')
word_pairs = [[preprocess_sentence(w) for w in l.split('\t')] for l in lines[:num_examples]]
return zip(*word_pairs)
en, sp = create_dataset(path_to_file, None)
print(en[-1])
print(sp[-1])
def max_length(tensor):
return max(len(t) for t in tensor)
def tokenize(lang):
lang_tokenizer = tf.keras.preprocessing.text.Tokenizer(
filters='')
lang_tokenizer.fit_on_texts(lang)
tensor = lang_tokenizer.texts_to_sequences(lang)
tensor = tf.keras.preprocessing.sequence.pad_sequences(tensor,
padding='post')
return tensor, lang_tokenizer
def load_dataset(path, num_examples=None):
# 创建清理过的输入输出对
targ_lang, inp_lang = create_dataset(path, num_examples)
input_tensor, inp_lang_tokenizer = tokenize(inp_lang)
target_tensor, targ_lang_tokenizer = tokenize(targ_lang)
return input_tensor, target_tensor, inp_lang_tokenizer, targ_lang_tokenizer
```
### 限制数据集的大小以加快实验速度(可选)
在超过 10 万个句子的完整数据集上训练需要很长时间。为了更快地训练,我们可以将数据集的大小限制为 3 万个句子(当然,翻译质量也会随着数据的减少而降低):
```
# 尝试实验不同大小的数据集
num_examples = 30000
input_tensor, target_tensor, inp_lang, targ_lang = load_dataset(path_to_file, num_examples)
# 计算目标张量的最大长度 (max_length)
max_length_targ, max_length_inp = max_length(target_tensor), max_length(input_tensor)
# 采用 80 - 20 的比例切分训练集和验证集
input_tensor_train, input_tensor_val, target_tensor_train, target_tensor_val = train_test_split(input_tensor, target_tensor, test_size=0.2)
# 显示长度
print(len(input_tensor_train), len(target_tensor_train), len(input_tensor_val), len(target_tensor_val))
def convert(lang, tensor):
for t in tensor:
if t!=0:
print ("%d ----> %s" % (t, lang.index_word[t]))
print ("Input Language; index to word mapping")
convert(inp_lang, input_tensor_train[0])
print ()
print ("Target Language; index to word mapping")
convert(targ_lang, target_tensor_train[0])
```
### 创建一个 tf.data 数据集
```
BUFFER_SIZE = len(input_tensor_train)
BATCH_SIZE = 64
steps_per_epoch = len(input_tensor_train)//BATCH_SIZE
embedding_dim = 256
units = 1024
vocab_inp_size = len(inp_lang.word_index)+1
vocab_tar_size = len(targ_lang.word_index)+1
dataset = tf.data.Dataset.from_tensor_slices((input_tensor_train, target_tensor_train)).shuffle(BUFFER_SIZE)
dataset = dataset.batch(BATCH_SIZE, drop_remainder=True)
example_input_batch, example_target_batch = next(iter(dataset))
example_input_batch.shape, example_target_batch.shape
```
## 编写编码器 (encoder) 和解码器 (decoder) 模型
实现一个基于注意力的编码器 - 解码器模型。关于这种模型,你可以阅读 TensorFlow 的 [神经机器翻译 (序列到序列) 教程](https://github.com/tensorflow/nmt)。本示例采用一组更新的 API。此笔记本实现了上述序列到序列教程中的 [注意力方程式](https://github.com/tensorflow/nmt#background-on-the-attention-mechanism)。下图显示了注意力机制为每个输入单词分配一个权重,然后解码器将这个权重用于预测句子中的下一个单词。下图和公式是 [Luong 的论文](https://arxiv.org/abs/1508.04025v5)中注意力机制的一个例子。
<img src="https://tensorflow.google.cn/images/seq2seq/attention_mechanism.jpg" width="500" alt="attention mechanism">
输入经过编码器模型,编码器模型为我们提供形状为 *(批大小,最大长度,隐藏层大小)* 的编码器输出和形状为 *(批大小,隐藏层大小)* 的编码器隐藏层状态。
下面是所实现的方程式:
<img src="https://tensorflow.google.cn/images/seq2seq/attention_equation_0.jpg" alt="attention equation 0" width="800">
<img src="https://tensorflow.google.cn/images/seq2seq/attention_equation_1.jpg" alt="attention equation 1" width="800">
本教程的编码器采用 [Bahdanau 注意力](https://arxiv.org/pdf/1409.0473.pdf)。在用简化形式编写之前,让我们先决定符号:
* FC = 完全连接(密集)层
* EO = 编码器输出
* H = 隐藏层状态
* X = 解码器输入
以及伪代码:
* `score = FC(tanh(FC(EO) + FC(H)))`
* `attention weights = softmax(score, axis = 1)`。 Softmax 默认被应用于最后一个轴,但是这里我们想将它应用于 *第一个轴*, 因为分数 (score) 的形状是 *(批大小,最大长度,隐藏层大小)*。最大长度 (`max_length`) 是我们的输入的长度。因为我们想为每个输入分配一个权重,所以 softmax 应该用在这个轴上。
* `context vector = sum(attention weights * EO, axis = 1)`。选择第一个轴的原因同上。
* `embedding output` = 解码器输入 X 通过一个嵌入层。
* `merged vector = concat(embedding output, context vector)`
* 此合并后的向量随后被传送到 GRU
每个步骤中所有向量的形状已在代码的注释中阐明:
```
class Encoder(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, enc_units, batch_sz):
super(Encoder, self).__init__()
self.batch_sz = batch_sz
self.enc_units = enc_units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.enc_units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
def call(self, x, hidden):
x = self.embedding(x)
output, state = self.gru(x, initial_state = hidden)
return output, state
def initialize_hidden_state(self):
return tf.zeros((self.batch_sz, self.enc_units))
encoder = Encoder(vocab_inp_size, embedding_dim, units, BATCH_SIZE)
# 样本输入
sample_hidden = encoder.initialize_hidden_state()
sample_output, sample_hidden = encoder(example_input_batch, sample_hidden)
print ('Encoder output shape: (batch size, sequence length, units) {}'.format(sample_output.shape))
print ('Encoder Hidden state shape: (batch size, units) {}'.format(sample_hidden.shape))
class BahdanauAttention(tf.keras.layers.Layer):
def __init__(self, units):
super(BahdanauAttention, self).__init__()
self.W1 = tf.keras.layers.Dense(units)
self.W2 = tf.keras.layers.Dense(units)
self.V = tf.keras.layers.Dense(1)
def call(self, query, values):
# 隐藏层的形状 == (批大小,隐藏层大小)
# hidden_with_time_axis 的形状 == (批大小,1,隐藏层大小)
# 这样做是为了执行加法以计算分数
hidden_with_time_axis = tf.expand_dims(query, 1)
# 分数的形状 == (批大小,最大长度,1)
# 我们在最后一个轴上得到 1, 因为我们把分数应用于 self.V
# 在应用 self.V 之前,张量的形状是(批大小,最大长度,单位)
score = self.V(tf.nn.tanh(
self.W1(values) + self.W2(hidden_with_time_axis)))
# 注意力权重 (attention_weights) 的形状 == (批大小,最大长度,1)
attention_weights = tf.nn.softmax(score, axis=1)
# 上下文向量 (context_vector) 求和之后的形状 == (批大小,隐藏层大小)
context_vector = attention_weights * values
context_vector = tf.reduce_sum(context_vector, axis=1)
return context_vector, attention_weights
attention_layer = BahdanauAttention(10)
attention_result, attention_weights = attention_layer(sample_hidden, sample_output)
print("Attention result shape: (batch size, units) {}".format(attention_result.shape))
print("Attention weights shape: (batch_size, sequence_length, 1) {}".format(attention_weights.shape))
class Decoder(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, dec_units, batch_sz):
super(Decoder, self).__init__()
self.batch_sz = batch_sz
self.dec_units = dec_units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.dec_units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
self.fc = tf.keras.layers.Dense(vocab_size)
# 用于注意力
self.attention = BahdanauAttention(self.dec_units)
def call(self, x, hidden, enc_output):
# 编码器输出 (enc_output) 的形状 == (批大小,最大长度,隐藏层大小)
context_vector, attention_weights = self.attention(hidden, enc_output)
# x 在通过嵌入层后的形状 == (批大小,1,嵌入维度)
x = self.embedding(x)
# x 在拼接 (concatenation) 后的形状 == (批大小,1,嵌入维度 + 隐藏层大小)
x = tf.concat([tf.expand_dims(context_vector, 1), x], axis=-1)
# 将合并后的向量传送到 GRU
output, state = self.gru(x)
# 输出的形状 == (批大小 * 1,隐藏层大小)
output = tf.reshape(output, (-1, output.shape[2]))
# 输出的形状 == (批大小,vocab)
x = self.fc(output)
return x, state, attention_weights
decoder = Decoder(vocab_tar_size, embedding_dim, units, BATCH_SIZE)
sample_decoder_output, _, _ = decoder(tf.random.uniform((64, 1)),
sample_hidden, sample_output)
print ('Decoder output shape: (batch_size, vocab size) {}'.format(sample_decoder_output.shape))
```
## 定义优化器和损失函数
```
optimizer = tf.keras.optimizers.Adam()
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(
from_logits=True, reduction='none')
def loss_function(real, pred):
mask = tf.math.logical_not(tf.math.equal(real, 0))
loss_ = loss_object(real, pred)
mask = tf.cast(mask, dtype=loss_.dtype)
loss_ *= mask
return tf.reduce_mean(loss_)
```
## 检查点(基于对象保存)
```
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(optimizer=optimizer,
encoder=encoder,
decoder=decoder)
```
## 训练
1. 将 *输入* 传送至 *编码器*,编码器返回 *编码器输出* 和 *编码器隐藏层状态*。
2. 将编码器输出、编码器隐藏层状态和解码器输入(即 *开始标记*)传送至解码器。
3. 解码器返回 *预测* 和 *解码器隐藏层状态*。
4. 解码器隐藏层状态被传送回模型,预测被用于计算损失。
5. 使用 *教师强制 (teacher forcing)* 决定解码器的下一个输入。
6. *教师强制* 是将 *目标词* 作为 *下一个输入* 传送至解码器的技术。
7. 最后一步是计算梯度,并将其应用于优化器和反向传播。
```
@tf.function
def train_step(inp, targ, enc_hidden):
loss = 0
with tf.GradientTape() as tape:
enc_output, enc_hidden = encoder(inp, enc_hidden)
dec_hidden = enc_hidden
dec_input = tf.expand_dims([targ_lang.word_index['<start>']] * BATCH_SIZE, 1)
# 教师强制 - 将目标词作为下一个输入
for t in range(1, targ.shape[1]):
# 将编码器输出 (enc_output) 传送至解码器
predictions, dec_hidden, _ = decoder(dec_input, dec_hidden, enc_output)
loss += loss_function(targ[:, t], predictions)
# 使用教师强制
dec_input = tf.expand_dims(targ[:, t], 1)
batch_loss = (loss / int(targ.shape[1]))
variables = encoder.trainable_variables + decoder.trainable_variables
gradients = tape.gradient(loss, variables)
optimizer.apply_gradients(zip(gradients, variables))
return batch_loss
EPOCHS = 10
for epoch in range(EPOCHS):
start = time.time()
enc_hidden = encoder.initialize_hidden_state()
total_loss = 0
for (batch, (inp, targ)) in enumerate(dataset.take(steps_per_epoch)):
batch_loss = train_step(inp, targ, enc_hidden)
total_loss += batch_loss
if batch % 100 == 0:
print('Epoch {} Batch {} Loss {:.4f}'.format(epoch + 1,
batch,
batch_loss.numpy()))
# 每 2 个周期(epoch),保存(检查点)一次模型
if (epoch + 1) % 2 == 0:
checkpoint.save(file_prefix = checkpoint_prefix)
print('Epoch {} Loss {:.4f}'.format(epoch + 1,
total_loss / steps_per_epoch))
print('Time taken for 1 epoch {} sec\n'.format(time.time() - start))
```
## 翻译
* 评估函数类似于训练循环,不同之处在于在这里我们不使用 *教师强制*。每个时间步的解码器输入是其先前的预测、隐藏层状态和编码器输出。
* 当模型预测 *结束标记* 时停止预测。
* 存储 *每个时间步的注意力权重*。
请注意:对于一个输入,编码器输出仅计算一次。
```
def evaluate(sentence):
attention_plot = np.zeros((max_length_targ, max_length_inp))
sentence = preprocess_sentence(sentence)
inputs = [inp_lang.word_index[i] for i in sentence.split(' ')]
inputs = tf.keras.preprocessing.sequence.pad_sequences([inputs],
maxlen=max_length_inp,
padding='post')
inputs = tf.convert_to_tensor(inputs)
result = ''
hidden = [tf.zeros((1, units))]
enc_out, enc_hidden = encoder(inputs, hidden)
dec_hidden = enc_hidden
dec_input = tf.expand_dims([targ_lang.word_index['<start>']], 0)
for t in range(max_length_targ):
predictions, dec_hidden, attention_weights = decoder(dec_input,
dec_hidden,
enc_out)
# 存储注意力权重以便后面制图
attention_weights = tf.reshape(attention_weights, (-1, ))
attention_plot[t] = attention_weights.numpy()
predicted_id = tf.argmax(predictions[0]).numpy()
result += targ_lang.index_word[predicted_id] + ' '
if targ_lang.index_word[predicted_id] == '<end>':
return result, sentence, attention_plot
# 预测的 ID 被输送回模型
dec_input = tf.expand_dims([predicted_id], 0)
return result, sentence, attention_plot
# 注意力权重制图函数
def plot_attention(attention, sentence, predicted_sentence):
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(1, 1, 1)
ax.matshow(attention, cmap='viridis')
fontdict = {'fontsize': 14}
ax.set_xticklabels([''] + sentence, fontdict=fontdict, rotation=90)
ax.set_yticklabels([''] + predicted_sentence, fontdict=fontdict)
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.yaxis.set_major_locator(ticker.MultipleLocator(1))
plt.show()
def translate(sentence):
result, sentence, attention_plot = evaluate(sentence)
print('Input: %s' % (sentence))
print('Predicted translation: {}'.format(result))
attention_plot = attention_plot[:len(result.split(' ')), :len(sentence.split(' '))]
plot_attention(attention_plot, sentence.split(' '), result.split(' '))
```
## 恢复最新的检查点并验证
```
# 恢复检查点目录 (checkpoint_dir) 中最新的检查点
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
translate(u'hace mucho frio aqui.')
translate(u'esta es mi vida.')
translate(u'¿todavia estan en casa?')
# 错误的翻译
translate(u'trata de averiguarlo.')
```
|
github_jupyter
|
import tensorflow as tf
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from sklearn.model_selection import train_test_split
import unicodedata
import re
import numpy as np
import os
import io
import time
May I borrow this book? ¿Puedo tomar prestado este libro?
'''
# 下载文件
path_to_zip = tf.keras.utils.get_file(
'spa-eng.zip', origin='http://storage.googleapis.com/download.tensorflow.org/data/spa-eng.zip',
extract=True)
path_to_file = os.path.dirname(path_to_zip)+"/spa-eng/spa.txt"
'''
path_to_file = "./lan/tat.txt"
# 将 unicode 文件转换为 ascii
def unicode_to_ascii(s):
return ''.join(c for c in unicodedata.normalize('NFD', s)
if unicodedata.category(c) != 'Mn')
def preprocess_sentence(w):
w = unicode_to_ascii(w.lower().strip())
# 在单词与跟在其后的标点符号之间插入一个空格
# 例如: "he is a boy." => "he is a boy ."
# 参考:https://stackoverflow.com/questions/3645931/python-padding-punctuation-with-white-spaces-keeping-punctuation
w = re.sub(r"([?.!,¿])", r" \1 ", w)
w = re.sub(r'[" "]+', " ", w)
# 除了 (a-z, A-Z, ".", "?", "!", ","),将所有字符替换为空格
w = re.sub(r"[^a-zA-Z?.!,¿]+", " ", w)
w = w.rstrip().strip()
# 给句子加上开始和结束标记
# 以便模型知道何时开始和结束预测
w = '<start> ' + w + ' <end>'
return w
en_sentence = u"May I borrow this book?"
sp_sentence = u"¿Puedo tomar prestado este libro?"
print(preprocess_sentence(en_sentence))
print(preprocess_sentence(sp_sentence).encode('utf-8'))
# 1. 去除重音符号
# 2. 清理句子
# 3. 返回这样格式的单词对:[ENGLISH, SPANISH]
def create_dataset(path, num_examples):
lines = io.open(path, encoding='UTF-8').read().strip().split('\n')
word_pairs = [[preprocess_sentence(w) for w in l.split('\t')] for l in lines[:num_examples]]
return zip(*word_pairs)
en, sp = create_dataset(path_to_file, None)
print(en[-1])
print(sp[-1])
def max_length(tensor):
return max(len(t) for t in tensor)
def tokenize(lang):
lang_tokenizer = tf.keras.preprocessing.text.Tokenizer(
filters='')
lang_tokenizer.fit_on_texts(lang)
tensor = lang_tokenizer.texts_to_sequences(lang)
tensor = tf.keras.preprocessing.sequence.pad_sequences(tensor,
padding='post')
return tensor, lang_tokenizer
def load_dataset(path, num_examples=None):
# 创建清理过的输入输出对
targ_lang, inp_lang = create_dataset(path, num_examples)
input_tensor, inp_lang_tokenizer = tokenize(inp_lang)
target_tensor, targ_lang_tokenizer = tokenize(targ_lang)
return input_tensor, target_tensor, inp_lang_tokenizer, targ_lang_tokenizer
# 尝试实验不同大小的数据集
num_examples = 30000
input_tensor, target_tensor, inp_lang, targ_lang = load_dataset(path_to_file, num_examples)
# 计算目标张量的最大长度 (max_length)
max_length_targ, max_length_inp = max_length(target_tensor), max_length(input_tensor)
# 采用 80 - 20 的比例切分训练集和验证集
input_tensor_train, input_tensor_val, target_tensor_train, target_tensor_val = train_test_split(input_tensor, target_tensor, test_size=0.2)
# 显示长度
print(len(input_tensor_train), len(target_tensor_train), len(input_tensor_val), len(target_tensor_val))
def convert(lang, tensor):
for t in tensor:
if t!=0:
print ("%d ----> %s" % (t, lang.index_word[t]))
print ("Input Language; index to word mapping")
convert(inp_lang, input_tensor_train[0])
print ()
print ("Target Language; index to word mapping")
convert(targ_lang, target_tensor_train[0])
BUFFER_SIZE = len(input_tensor_train)
BATCH_SIZE = 64
steps_per_epoch = len(input_tensor_train)//BATCH_SIZE
embedding_dim = 256
units = 1024
vocab_inp_size = len(inp_lang.word_index)+1
vocab_tar_size = len(targ_lang.word_index)+1
dataset = tf.data.Dataset.from_tensor_slices((input_tensor_train, target_tensor_train)).shuffle(BUFFER_SIZE)
dataset = dataset.batch(BATCH_SIZE, drop_remainder=True)
example_input_batch, example_target_batch = next(iter(dataset))
example_input_batch.shape, example_target_batch.shape
class Encoder(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, enc_units, batch_sz):
super(Encoder, self).__init__()
self.batch_sz = batch_sz
self.enc_units = enc_units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.enc_units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
def call(self, x, hidden):
x = self.embedding(x)
output, state = self.gru(x, initial_state = hidden)
return output, state
def initialize_hidden_state(self):
return tf.zeros((self.batch_sz, self.enc_units))
encoder = Encoder(vocab_inp_size, embedding_dim, units, BATCH_SIZE)
# 样本输入
sample_hidden = encoder.initialize_hidden_state()
sample_output, sample_hidden = encoder(example_input_batch, sample_hidden)
print ('Encoder output shape: (batch size, sequence length, units) {}'.format(sample_output.shape))
print ('Encoder Hidden state shape: (batch size, units) {}'.format(sample_hidden.shape))
class BahdanauAttention(tf.keras.layers.Layer):
def __init__(self, units):
super(BahdanauAttention, self).__init__()
self.W1 = tf.keras.layers.Dense(units)
self.W2 = tf.keras.layers.Dense(units)
self.V = tf.keras.layers.Dense(1)
def call(self, query, values):
# 隐藏层的形状 == (批大小,隐藏层大小)
# hidden_with_time_axis 的形状 == (批大小,1,隐藏层大小)
# 这样做是为了执行加法以计算分数
hidden_with_time_axis = tf.expand_dims(query, 1)
# 分数的形状 == (批大小,最大长度,1)
# 我们在最后一个轴上得到 1, 因为我们把分数应用于 self.V
# 在应用 self.V 之前,张量的形状是(批大小,最大长度,单位)
score = self.V(tf.nn.tanh(
self.W1(values) + self.W2(hidden_with_time_axis)))
# 注意力权重 (attention_weights) 的形状 == (批大小,最大长度,1)
attention_weights = tf.nn.softmax(score, axis=1)
# 上下文向量 (context_vector) 求和之后的形状 == (批大小,隐藏层大小)
context_vector = attention_weights * values
context_vector = tf.reduce_sum(context_vector, axis=1)
return context_vector, attention_weights
attention_layer = BahdanauAttention(10)
attention_result, attention_weights = attention_layer(sample_hidden, sample_output)
print("Attention result shape: (batch size, units) {}".format(attention_result.shape))
print("Attention weights shape: (batch_size, sequence_length, 1) {}".format(attention_weights.shape))
class Decoder(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, dec_units, batch_sz):
super(Decoder, self).__init__()
self.batch_sz = batch_sz
self.dec_units = dec_units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.dec_units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
self.fc = tf.keras.layers.Dense(vocab_size)
# 用于注意力
self.attention = BahdanauAttention(self.dec_units)
def call(self, x, hidden, enc_output):
# 编码器输出 (enc_output) 的形状 == (批大小,最大长度,隐藏层大小)
context_vector, attention_weights = self.attention(hidden, enc_output)
# x 在通过嵌入层后的形状 == (批大小,1,嵌入维度)
x = self.embedding(x)
# x 在拼接 (concatenation) 后的形状 == (批大小,1,嵌入维度 + 隐藏层大小)
x = tf.concat([tf.expand_dims(context_vector, 1), x], axis=-1)
# 将合并后的向量传送到 GRU
output, state = self.gru(x)
# 输出的形状 == (批大小 * 1,隐藏层大小)
output = tf.reshape(output, (-1, output.shape[2]))
# 输出的形状 == (批大小,vocab)
x = self.fc(output)
return x, state, attention_weights
decoder = Decoder(vocab_tar_size, embedding_dim, units, BATCH_SIZE)
sample_decoder_output, _, _ = decoder(tf.random.uniform((64, 1)),
sample_hidden, sample_output)
print ('Decoder output shape: (batch_size, vocab size) {}'.format(sample_decoder_output.shape))
optimizer = tf.keras.optimizers.Adam()
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(
from_logits=True, reduction='none')
def loss_function(real, pred):
mask = tf.math.logical_not(tf.math.equal(real, 0))
loss_ = loss_object(real, pred)
mask = tf.cast(mask, dtype=loss_.dtype)
loss_ *= mask
return tf.reduce_mean(loss_)
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(optimizer=optimizer,
encoder=encoder,
decoder=decoder)
@tf.function
def train_step(inp, targ, enc_hidden):
loss = 0
with tf.GradientTape() as tape:
enc_output, enc_hidden = encoder(inp, enc_hidden)
dec_hidden = enc_hidden
dec_input = tf.expand_dims([targ_lang.word_index['<start>']] * BATCH_SIZE, 1)
# 教师强制 - 将目标词作为下一个输入
for t in range(1, targ.shape[1]):
# 将编码器输出 (enc_output) 传送至解码器
predictions, dec_hidden, _ = decoder(dec_input, dec_hidden, enc_output)
loss += loss_function(targ[:, t], predictions)
# 使用教师强制
dec_input = tf.expand_dims(targ[:, t], 1)
batch_loss = (loss / int(targ.shape[1]))
variables = encoder.trainable_variables + decoder.trainable_variables
gradients = tape.gradient(loss, variables)
optimizer.apply_gradients(zip(gradients, variables))
return batch_loss
EPOCHS = 10
for epoch in range(EPOCHS):
start = time.time()
enc_hidden = encoder.initialize_hidden_state()
total_loss = 0
for (batch, (inp, targ)) in enumerate(dataset.take(steps_per_epoch)):
batch_loss = train_step(inp, targ, enc_hidden)
total_loss += batch_loss
if batch % 100 == 0:
print('Epoch {} Batch {} Loss {:.4f}'.format(epoch + 1,
batch,
batch_loss.numpy()))
# 每 2 个周期(epoch),保存(检查点)一次模型
if (epoch + 1) % 2 == 0:
checkpoint.save(file_prefix = checkpoint_prefix)
print('Epoch {} Loss {:.4f}'.format(epoch + 1,
total_loss / steps_per_epoch))
print('Time taken for 1 epoch {} sec\n'.format(time.time() - start))
def evaluate(sentence):
attention_plot = np.zeros((max_length_targ, max_length_inp))
sentence = preprocess_sentence(sentence)
inputs = [inp_lang.word_index[i] for i in sentence.split(' ')]
inputs = tf.keras.preprocessing.sequence.pad_sequences([inputs],
maxlen=max_length_inp,
padding='post')
inputs = tf.convert_to_tensor(inputs)
result = ''
hidden = [tf.zeros((1, units))]
enc_out, enc_hidden = encoder(inputs, hidden)
dec_hidden = enc_hidden
dec_input = tf.expand_dims([targ_lang.word_index['<start>']], 0)
for t in range(max_length_targ):
predictions, dec_hidden, attention_weights = decoder(dec_input,
dec_hidden,
enc_out)
# 存储注意力权重以便后面制图
attention_weights = tf.reshape(attention_weights, (-1, ))
attention_plot[t] = attention_weights.numpy()
predicted_id = tf.argmax(predictions[0]).numpy()
result += targ_lang.index_word[predicted_id] + ' '
if targ_lang.index_word[predicted_id] == '<end>':
return result, sentence, attention_plot
# 预测的 ID 被输送回模型
dec_input = tf.expand_dims([predicted_id], 0)
return result, sentence, attention_plot
# 注意力权重制图函数
def plot_attention(attention, sentence, predicted_sentence):
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(1, 1, 1)
ax.matshow(attention, cmap='viridis')
fontdict = {'fontsize': 14}
ax.set_xticklabels([''] + sentence, fontdict=fontdict, rotation=90)
ax.set_yticklabels([''] + predicted_sentence, fontdict=fontdict)
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.yaxis.set_major_locator(ticker.MultipleLocator(1))
plt.show()
def translate(sentence):
result, sentence, attention_plot = evaluate(sentence)
print('Input: %s' % (sentence))
print('Predicted translation: {}'.format(result))
attention_plot = attention_plot[:len(result.split(' ')), :len(sentence.split(' '))]
plot_attention(attention_plot, sentence.split(' '), result.split(' '))
# 恢复检查点目录 (checkpoint_dir) 中最新的检查点
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
translate(u'hace mucho frio aqui.')
translate(u'esta es mi vida.')
translate(u'¿todavia estan en casa?')
# 错误的翻译
translate(u'trata de averiguarlo.')
| 0.469763 | 0.928409 |
# **¿Qué es una simulación?**
> Introducción a la materia y descripción de las herramientas computacionales que se van a utilizar a lo largo del curso.
___
### Simulación
- Es una técnica o conjunto de técnicas que ayudan a entender el comportamiento de un _sistema_ real o hipotético.
<img style="center" src="https://upload.wikimedia.org/wikipedia/commons/thumb/c/c8/Crowd_simulation%2C_Covent_Garden.jpg/640px-Crowd_simulation%2C_Covent_Garden.jpg" width="500px" height="200px" alt="atom" />
**¿Qué es un sistema? **
- Colección de objetos, partes, componentes, etc., que interactúan entre si, dentro de una cierta frontera, para producir un patrón particular o comportamiento.
- Frontera: Es necesaria esta idea para separar al sistema del resto del universo.
**¿Qué es un modelo? **
- Físicos (replicas) - Abstractos (Modelos matemáticos)
_Tipos_
- Deterministas o Estocásticos.
- Dinámicos o estacionarios.
**¿Porqué hacer simulación?**
- Reducción de costos: la simulación es mucho menos costosa que la experimentación en la vida real.
- Se pueden probar diferentes ideas en un mismo escenario.
- Se puede determinar el impacto potencial de eventos aleatorios (inversión).
- Evaluar si ciertos procesos son viables (determinar el impacto a largo plazo).
- ...
<img style="center" src="https://upload.wikimedia.org/wikipedia/commons/4/4a/FAE_visualization.jpg" width="250px" height="200px" alt="atom" />
_Referencia:_
_Simulation Fundamentals, B. S. Bennett_
### Herramientas computacionales
### - [python](https://www.python.org) - [anaconda](https://www.continuum.io/downloads) - [jupyter](http://jupyter.org)
<div>
<img style="float: left; margin: 0px 0px 15px 15px;" src="https://www.python.org/static/community_logos/python-logo.png" width="200px" height="200px" alt="atom" />
<img style="float: left; margin: 0px 0px 15px 15px;" src="https://upload.wikimedia.org/wikipedia/en/c/cd/Anaconda_Logo.png" width="120" />
<img style="float: left; margin: 0px 0px 15px 15px;" src="http://jupyter.org/assets/main-logo.svg" width="80" />
¿Porqué Python?
- https://www.economist.com/graphic-detail/2018/07/26/python-is-becoming-the-worlds-most-popular-coding-language
- https://www.economist.com/science-and-technology/2018/07/19/python-has-brought-computer-programming-to-a-vast-new-audience
## Instalar ANACONDA... ¡No confundir Anaconda con esto!
```
from IPython.display import YouTubeVideo
YouTubeVideo('LDZX4ooRsWs')
```
## Herramientas adicionales
- [Markdown](https://confluence.atlassian.com/bitbucketserver/markdown-syntax-guide-776639995.html)
- [git](https://git-scm.com)
- [GitHub](https://github.com)
### Encabezado
- **1**
- *1.1*
- *1.2*
- **2**
- *2.1*
- *2.2*
### jupyter notebook
- Aprender a usar el jupyter notebook
- Los notebooks tienen celdas de entrada y generalmente celdas de salida, así como celdas de texto. Las celdas de texto es lo que estas leyendo ahora. Las celdas de código inician con "In []:" con algún numero en los brackets. Si te colocas sobre una salda de entrada y presionas Shift-Enter, el código correrá en el ** interprete ** de python y el resultado se imprimirá en la celda de salida.
**Trabajando con el notebook de jupyter**
Además de poder realizar progrmación, tiene otras ventajas. Como ya se dieron cuenta toda esta presentación esta hecha con el notebook. Además de eso, también se puede incluir directamente dentro de este documento, código <font color="blue"> HTML </font>.
Uno de los atractivos más relevantes (personalmente) es que puedes escribir ecuaciones estilo $\LaTeX$, esto es gracias al proyecto [MathJax](https://www.mathjax.org) el cual se especializa en que podamos publicar matemáticas en línea. A continuación, se muestra una ejemplo.
___
>Ecuaciones de Maxwell:
>$$\nabla\cdot \mathbf{D}=\rho\quad \nabla\cdot \mathbf{B}=0\quad \nabla\times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}\quad \nabla\times \mathbf{H} = \mathbf{J} +\frac{\partial \mathbf{D}}{\partial t}$$
___
___
>Ecuación de Bernoulli:
>$$P_1+\frac{1}{2}\rho v_1^2+\rho g h_1=P_2+\frac{1}{2}\rho v_2^2+\rho g h_2,$$
>donde:
>- $P_1$, $v_1$ y $h_1$ es la presión, la velocidad y la altura en el punto 1,
>- $P_2$, $v_2$ y $h_2$ es la presión, la velocidad y la altura en el punto 2,
>- $\rho$ es la densidad del fluido, y
>- $g$ es la aceleración de gravedad.
___
https://es.khanacademy.org/science/physics/fluids/fluid-dynamics/a/what-is-bernoullis-equation
___
>Capitalización por *interés compuesto*:
>$$C_k=C_0(1+i)^k,$$
>donde:
>- $C_k$ es el capital al final del $k$-ésimo periodo,
>- $C_0$ es el capital inicial,
>- $i$ es la tasa de interés pactada, y
>- $k$ es el número de periodos.
___
https://es.wikipedia.org/wiki/Inter%C3%A9s_compuesto
#### Archivos de python (script)
- Estos son simplemente archivos de texto con la extensión .py
- user $ python miprograma.py
- Cada linea en el archivo es una declaración de código en python, o parte del código.
#### Programa de bienvenida.
welcome.py
```
%run welcome.py
```
> **Actividad:** <font color = blue>** Realizar una presentación personal haciendo uso de la sintaxis `Markdown`. En ella deben incluir un resumen de uno de los artículos de The Economist.** </font>
<script>
$(document).ready(function(){
$('div.prompt').hide();
$('div.back-to-top').hide();
$('nav#menubar').hide();
$('.breadcrumb').hide();
$('.hidden-print').hide();
});
</script>
<footer id="attribution" style="float:right; color:#808080; background:#fff;">
Created with Jupyter by Esteban Jiménez Rodríguez.
</footer>
|
github_jupyter
|
from IPython.display import YouTubeVideo
YouTubeVideo('LDZX4ooRsWs')
%run welcome.py
| 0.301671 | 0.955858 |
# pyPCGA stwave inversion example
```
%matplotlib inline
```
- import relevant python packages after installing pyPCGA
- stwave.py includes python wrapper to stwave model
```
import matplotlib.pyplot as plt
from scipy.io import savemat, loadmat
import numpy as np
import stwave as st
from pyPCGA import PCGA
import math
import datetime as dt
```
- model domain and discretization
```
N = np.array([110,83])
m = np.prod(N)
dx = np.array([5.,5.])
xmin = np.array([0. + dx[0]/2., 0. + dx[1]/2.])
xmax = np.array([110.*5. - dx[0]/2., 83.*5. - dx[1]/2.])
```
- covariance kernel and scale parameters following Hojat's CSKF paper
```
prior_std = 1.5
prior_cov_scale = np.array([18.*5., 18.*5.])
def kernel(r): return (prior_std**2)*np.exp(-r**2)
```
- grid coordinates for plotting purposes
```
x = np.linspace(0. + dx[0]/2., 110*5 - dx[0]/2., N[0])
y = np.linspace(0. + dx[1]/2., 83*5 - dx[0]/2., N[1])
XX, YY = np.meshgrid(x, y)
pts = np.hstack((XX.ravel()[:,np.newaxis], YY.ravel()[:,np.newaxis]))
```
- load data, true field is optional
```
obs = np.loadtxt('obs.txt')
s_true = np.loadtxt('true_depth.txt')
```
- define domain extent, discretization and measurement collection time
```
nx = 110
ny = 83
Lx = 550
Ly = 415
x0, y0 = (62.0, 568.0)
t1 = dt.datetime(2015, 10, 07, 20, 00)
t2 = dt.datetime(2015, 10, 07, 21, 00)
stwave_params = {'nx': nx, 'ny': ny, 'Lx': Lx, 'Ly': Ly, 'x0': x0, 'y0': y0, 't1': t1, 't2': t2,
'offline_dataloc': "./input_files/8m-array_2015100718_2015100722.nc"}
```
- prepare interface to run stwave as a function
```
def forward_model(s,parallelization,ncores = None):
# initialize stwave
model = st.Model(stwave_params)
if parallelization:
simul_obs = model.run(s,parallelization,ncores)
else:
simul_obs = model.run(s,parallelization)
return simul_obs
```
- PCGA inversion parameters
```
params = {'R':(0.1)**2, 'n_pc':50,
'maxiter':10, 'restol':0.01,
'matvec':'FFT','xmin':xmin, 'xmax':xmax, 'N':N,
'prior_std':prior_std,'prior_cov_scale':prior_cov_scale,
'kernel':kernel, 'post_cov':"diag",
'precond':True, 'LM': True,
'parallel':True, 'linesearch' : True,
'forward_model_verbose': False, 'verbose': False,
'iter_save': True}
```
- initial guess
```
s_init = np.mean(s_true)*np.ones((m,1))
```
- initialize PCGA object
```
prob = PCGA(forward_model, s_init = s_init, pts = pts, params = params, s_true = s_true, obs = obs)
```
- run PCGA inversion
```
s_hat, simul_obs, post_diagv, iter_best = prob.Run()
# converting to 2d array for plotting
s_hat2d = s_hat.reshape(N[1],N[0])
s_true2d = s_true.reshape(N[1],N[0])
post_diagv[post_diagv <0.] = 0. # just in case
post_std = np.sqrt(post_diagv)
post_std2d = post_std.reshape(N[1],N[0])
```
- plot results
```
minv = s_true.min()
maxv = s_true.max()
fig, axes = plt.subplots(1,2, figsize=(15,5))
plt.suptitle('prior var.: (%g)^2, n_pc : %d' % (prior_std,params['n_pc']))
im = axes[0].imshow(np.flipud(np.fliplr(-s_true2d)), extent=[0, 110, 0, 83], vmin=-7., vmax=0., cmap=plt.get_cmap('jet'))
axes[0].set_title('(a) True', loc='left')
axes[0].set_aspect('equal')
axes[0].set_xlabel('Offshore distance (px)')
axes[0].set_ylabel('Alongshore distance (px)')
axes[1].imshow(np.flipud(np.fliplr(-s_hat2d)), extent=[0, 110, 0, 83], vmin=-7., vmax=0., cmap=plt.get_cmap('jet'))
axes[1].set_title('(b) Estimate', loc='left')
axes[1].set_xlabel('Offshore distance (px)')
axes[1].set_aspect('equal')
fig.subplots_adjust(right=0.8)
cbar_ax = fig.add_axes([0.85, 0.15, 0.05, 0.7])
fig.colorbar(im, cax=cbar_ax)
```
- plot transect at y = 25 px and 45 px
```
fig = plt.figure()
im = plt.imshow(np.flipud(np.fliplr(post_std2d)), extent=[0, 110, 0, 83], cmap=plt.get_cmap('jet'))
plt.title('Uncertainty (std)', loc='left')
plt.xlabel('Offshore distance (px)')
plt.ylabel('Alongshore distance (px)')
plt.gca().set_aspect('equal', adjustable='box')
fig.colorbar(im)
fig, axes = plt.subplots(1,2)
fig.suptitle('transect with prior var.: (%g)^2, n_pc : %d, lx = %f m, ly = %f m' % (prior_std, params['n_pc'],prior_cov_scale[0],prior_cov_scale[1]))
linex = np.arange(1,111)*5.0
line1_true = s_true2d[83-25+1,:]
line1 = s_hat2d[83-25+1,:]
line1_u = s_hat2d[83-25+1,:] + 1.96*post_std2d[83-25+1,:]
line1_l = s_hat2d[83-25+1,:] - 1.96*post_std2d[83-25+1,:]
#line1_X = Xbeta2d[83-25+1,:]
line2_true = s_true2d[83-45+1,:]
line2 = s_hat2d[83-45+1,:]
line2_u = s_hat2d[83-45+1,:] + 1.96*post_std2d[83-45+1,:]
line2_l = s_hat2d[83-45+1,:] - 1.96*post_std2d[83-45+1,:]
#line2_X = Xbeta2d[83-45+1,:]
axes[0].plot(linex, np.flipud(-line1_true),'r-', label='True')
axes[0].plot(linex, np.flipud(-line1),'k-', label='Estimated')
axes[0].plot(linex, np.flipud(-line1_u),'k--', label='95% credible interval')
axes[0].plot(linex, np.flipud(-line1_l),'k--')
#axes[0].plot(linex, np.flipud(-line1_X),'b--', label='Drift/Trend')
axes[0].set_title('(a) 125 m', loc='left')
#axes[0].set_title('(a) 25 px', loc='left')
handles, labels = axes[0].get_legend_handles_labels()
axes[0].legend(handles, labels)
axes[1].plot(linex, np.flipud(-line2_true),'r-', label='True')
axes[1].plot(linex, np.flipud(-line2),'k-', label='Estimated')
axes[1].plot(linex, np.flipud(-line2_u),'k--', label='95% credible interval')
axes[1].plot(linex, np.flipud(-line2_l),'k--')
#axes[1].plot(linex, np.flipud(-line2_X),'b--', label='Drift/Trend')
axes[1].set_title('(b) 225 m', loc='left')
#axes[1].set_title('(b) 45 px', loc='left')
handles, labels = axes[1].get_legend_handles_labels()
axes[1].legend(handles, labels)
nobs = prob.obs.shape[0]
fig = plt.figure()
plt.title('obs. vs simul.')
plt.plot(prob.obs,simul_obs,'.')
plt.xlabel('observation')
plt.ylabel('simulation')
minobs = np.vstack((prob.obs,simul_obs)).min(0)
maxobs = np.vstack((prob.obs,simul_obs)).max(0)
plt.plot(np.linspace(minobs,maxobs,20),np.linspace(minobs,maxobs,20),'k-')
plt.axis('equal')
axes = plt.gca()
axes.set_xlim([math.floor(minobs),math.ceil(maxobs)])
axes.set_ylim([math.floor(minobs),math.ceil(maxobs)])
plt.semilogy(range(len(prob.objvals)),prob.objvals,'r-')
plt.title('obj values over iterations')
plt.axis('tight')
fig, axes = plt.subplots(4,4, sharex = True, sharey = True)
fig.suptitle('n_pc : %d' % params['n_pc'])
for i in range(4):
for j in range(4):
axes[i,j].imshow(prob.priorU[:,(i*4+j)*2].reshape(N[1],N[0]), extent=[0, 110, 0, 83])
axes[i,j].set_title('%d-th eigv' %((i*4+j)*2))
fig = plt.figure()
plt.semilogy(prob.priord,'o')
```
|
github_jupyter
|
%matplotlib inline
import matplotlib.pyplot as plt
from scipy.io import savemat, loadmat
import numpy as np
import stwave as st
from pyPCGA import PCGA
import math
import datetime as dt
N = np.array([110,83])
m = np.prod(N)
dx = np.array([5.,5.])
xmin = np.array([0. + dx[0]/2., 0. + dx[1]/2.])
xmax = np.array([110.*5. - dx[0]/2., 83.*5. - dx[1]/2.])
prior_std = 1.5
prior_cov_scale = np.array([18.*5., 18.*5.])
def kernel(r): return (prior_std**2)*np.exp(-r**2)
x = np.linspace(0. + dx[0]/2., 110*5 - dx[0]/2., N[0])
y = np.linspace(0. + dx[1]/2., 83*5 - dx[0]/2., N[1])
XX, YY = np.meshgrid(x, y)
pts = np.hstack((XX.ravel()[:,np.newaxis], YY.ravel()[:,np.newaxis]))
obs = np.loadtxt('obs.txt')
s_true = np.loadtxt('true_depth.txt')
nx = 110
ny = 83
Lx = 550
Ly = 415
x0, y0 = (62.0, 568.0)
t1 = dt.datetime(2015, 10, 07, 20, 00)
t2 = dt.datetime(2015, 10, 07, 21, 00)
stwave_params = {'nx': nx, 'ny': ny, 'Lx': Lx, 'Ly': Ly, 'x0': x0, 'y0': y0, 't1': t1, 't2': t2,
'offline_dataloc': "./input_files/8m-array_2015100718_2015100722.nc"}
def forward_model(s,parallelization,ncores = None):
# initialize stwave
model = st.Model(stwave_params)
if parallelization:
simul_obs = model.run(s,parallelization,ncores)
else:
simul_obs = model.run(s,parallelization)
return simul_obs
params = {'R':(0.1)**2, 'n_pc':50,
'maxiter':10, 'restol':0.01,
'matvec':'FFT','xmin':xmin, 'xmax':xmax, 'N':N,
'prior_std':prior_std,'prior_cov_scale':prior_cov_scale,
'kernel':kernel, 'post_cov':"diag",
'precond':True, 'LM': True,
'parallel':True, 'linesearch' : True,
'forward_model_verbose': False, 'verbose': False,
'iter_save': True}
s_init = np.mean(s_true)*np.ones((m,1))
prob = PCGA(forward_model, s_init = s_init, pts = pts, params = params, s_true = s_true, obs = obs)
s_hat, simul_obs, post_diagv, iter_best = prob.Run()
# converting to 2d array for plotting
s_hat2d = s_hat.reshape(N[1],N[0])
s_true2d = s_true.reshape(N[1],N[0])
post_diagv[post_diagv <0.] = 0. # just in case
post_std = np.sqrt(post_diagv)
post_std2d = post_std.reshape(N[1],N[0])
minv = s_true.min()
maxv = s_true.max()
fig, axes = plt.subplots(1,2, figsize=(15,5))
plt.suptitle('prior var.: (%g)^2, n_pc : %d' % (prior_std,params['n_pc']))
im = axes[0].imshow(np.flipud(np.fliplr(-s_true2d)), extent=[0, 110, 0, 83], vmin=-7., vmax=0., cmap=plt.get_cmap('jet'))
axes[0].set_title('(a) True', loc='left')
axes[0].set_aspect('equal')
axes[0].set_xlabel('Offshore distance (px)')
axes[0].set_ylabel('Alongshore distance (px)')
axes[1].imshow(np.flipud(np.fliplr(-s_hat2d)), extent=[0, 110, 0, 83], vmin=-7., vmax=0., cmap=plt.get_cmap('jet'))
axes[1].set_title('(b) Estimate', loc='left')
axes[1].set_xlabel('Offshore distance (px)')
axes[1].set_aspect('equal')
fig.subplots_adjust(right=0.8)
cbar_ax = fig.add_axes([0.85, 0.15, 0.05, 0.7])
fig.colorbar(im, cax=cbar_ax)
fig = plt.figure()
im = plt.imshow(np.flipud(np.fliplr(post_std2d)), extent=[0, 110, 0, 83], cmap=plt.get_cmap('jet'))
plt.title('Uncertainty (std)', loc='left')
plt.xlabel('Offshore distance (px)')
plt.ylabel('Alongshore distance (px)')
plt.gca().set_aspect('equal', adjustable='box')
fig.colorbar(im)
fig, axes = plt.subplots(1,2)
fig.suptitle('transect with prior var.: (%g)^2, n_pc : %d, lx = %f m, ly = %f m' % (prior_std, params['n_pc'],prior_cov_scale[0],prior_cov_scale[1]))
linex = np.arange(1,111)*5.0
line1_true = s_true2d[83-25+1,:]
line1 = s_hat2d[83-25+1,:]
line1_u = s_hat2d[83-25+1,:] + 1.96*post_std2d[83-25+1,:]
line1_l = s_hat2d[83-25+1,:] - 1.96*post_std2d[83-25+1,:]
#line1_X = Xbeta2d[83-25+1,:]
line2_true = s_true2d[83-45+1,:]
line2 = s_hat2d[83-45+1,:]
line2_u = s_hat2d[83-45+1,:] + 1.96*post_std2d[83-45+1,:]
line2_l = s_hat2d[83-45+1,:] - 1.96*post_std2d[83-45+1,:]
#line2_X = Xbeta2d[83-45+1,:]
axes[0].plot(linex, np.flipud(-line1_true),'r-', label='True')
axes[0].plot(linex, np.flipud(-line1),'k-', label='Estimated')
axes[0].plot(linex, np.flipud(-line1_u),'k--', label='95% credible interval')
axes[0].plot(linex, np.flipud(-line1_l),'k--')
#axes[0].plot(linex, np.flipud(-line1_X),'b--', label='Drift/Trend')
axes[0].set_title('(a) 125 m', loc='left')
#axes[0].set_title('(a) 25 px', loc='left')
handles, labels = axes[0].get_legend_handles_labels()
axes[0].legend(handles, labels)
axes[1].plot(linex, np.flipud(-line2_true),'r-', label='True')
axes[1].plot(linex, np.flipud(-line2),'k-', label='Estimated')
axes[1].plot(linex, np.flipud(-line2_u),'k--', label='95% credible interval')
axes[1].plot(linex, np.flipud(-line2_l),'k--')
#axes[1].plot(linex, np.flipud(-line2_X),'b--', label='Drift/Trend')
axes[1].set_title('(b) 225 m', loc='left')
#axes[1].set_title('(b) 45 px', loc='left')
handles, labels = axes[1].get_legend_handles_labels()
axes[1].legend(handles, labels)
nobs = prob.obs.shape[0]
fig = plt.figure()
plt.title('obs. vs simul.')
plt.plot(prob.obs,simul_obs,'.')
plt.xlabel('observation')
plt.ylabel('simulation')
minobs = np.vstack((prob.obs,simul_obs)).min(0)
maxobs = np.vstack((prob.obs,simul_obs)).max(0)
plt.plot(np.linspace(minobs,maxobs,20),np.linspace(minobs,maxobs,20),'k-')
plt.axis('equal')
axes = plt.gca()
axes.set_xlim([math.floor(minobs),math.ceil(maxobs)])
axes.set_ylim([math.floor(minobs),math.ceil(maxobs)])
plt.semilogy(range(len(prob.objvals)),prob.objvals,'r-')
plt.title('obj values over iterations')
plt.axis('tight')
fig, axes = plt.subplots(4,4, sharex = True, sharey = True)
fig.suptitle('n_pc : %d' % params['n_pc'])
for i in range(4):
for j in range(4):
axes[i,j].imshow(prob.priorU[:,(i*4+j)*2].reshape(N[1],N[0]), extent=[0, 110, 0, 83])
axes[i,j].set_title('%d-th eigv' %((i*4+j)*2))
fig = plt.figure()
plt.semilogy(prob.priord,'o')
| 0.417865 | 0.868437 |
### **Heavy Machinery Image Recognition**
We are going to build a Machine Learning which can recognize a heavy machinery images, whether it is a truck or an excavator
```
from IPython.display import display
import os
import requests
from PIL import Image
from io import BytesIO
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras.preprocessing.image import load_img, img_to_array
from keras.layers.convolutional import Conv2D, MaxPooling2D
from keras.layers import Dense, Dropout, Flatten, Activation
from sklearn.svm import SVC
from matplotlib import pyplot as plt
```
## **Connect to Google Drive**
Our data is stored in Google Drive, so we need to mount/connect our Google Colab session to Google Drive folder
```
from google.colab import drive
drive.mount('/content/gdrive')
```
**Define the path of the folder in our Google Drive**
```
DATA_SOURCE = "/content/gdrive/My Drive/Colab Notebooks/images_data/"
PATH_TRUCK_IMAGES = DATA_SOURCE + "Trucks/"
PATH_EXCAVATOR_IMAGES = DATA_SOURCE + "Excavators/"
```
## **Let's try to read and image and do Some Processing**
```
HEIGHT = 200
WIDTH = 300
IMAGE_SIZE = (HEIGHT, WIDTH, 1)
img = load_img(PATH_TRUCK_IMAGES + "6-image-Komatsu-960E-1.jpg", target_size=IMAGE_SIZE)
display(img)
```
An image is actually just an array. Our photos above is a colored image, or we can call it an RGB image.
RGB image is a 3D array, which first dimension indicates height, second dimension indicates width, and the third dimension indicates th intensity of color red, green, and blue
```
img_array = img_to_array(img)
img_array.shape
```
**Converting to Grayscale**
In our case, we can clearly see that trucks and excavators have very different shape. Also, most of them are colored yellow (or yellow-ish). Therefore, it is okay to ignore colors and convert our image to grayscale to save some resources.
Converting RGB image to Grayscale image means we reduce data-size to 1/3, thus saving a lot computing resources
```
img_array_grayscale = tf.image.rgb_to_grayscale(img_array, name=None)[:,:,0]/255
img_array_grayscale.shape
plt.imshow(img_array_grayscale, cmap='gray', vmin=0, vmax=1)
plt.show()
img_array_grayscale_flat = img_array.flatten()
img_array_grayscale_flat.shape
img_array_grayscale_flat
```
## **Building The Machine Learning**
## **Load images from directory**
```
train_data = tf.keras.preprocessing.image_dataset_from_directory(
directory=DATA_SOURCE,
class_names=["Excavators", "Trucks"],
subset="training", validation_split=0.2,
seed=100,
label_mode="binary",
color_mode='grayscale' if IMAGE_SIZE[-1]==1 else "rgb", # <-------------------------------------------- automatically set the image to grayscale
image_size=IMAGE_SIZE[0:-1],
)
validation_data = tf.keras.preprocessing.image_dataset_from_directory(
directory=DATA_SOURCE,
class_names=["Excavators", "Trucks"],
subset="validation", validation_split=0.2,
seed=100,
label_mode="binary",
color_mode='grayscale' if IMAGE_SIZE[-1]==1 else "rgb", # <-------------------------------------------- automatically set the image to grayscale
image_size=IMAGE_SIZE[0:-1],
)
```
## Design our Machine Learning
## 1. Simple Flattened Image + Support Vector Machine (SVM)
```
simple_ML = tf.keras.Sequential()
simple_ML.add(tf.keras.layers.experimental.preprocessing.Rescaling(1/255, input_shape=IMAGE_SIZE))
simple_ML.add(tf.keras.layers.Flatten())
simple_ML.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
simple_ML.summary()
for images, labels in train_data.take(1):
X_train = images.numpy()
train_labels = labels.numpy()
X_train = simple_ML.predict(X_train)
train_labels = train_labels.flatten()
for images, labels in validation_data.take(1):
X_validation = images.numpy()
validation_labels = labels.numpy()
X_validation = simple_ML.predict(X_validation)
validation_labels = validation_labels.flatten()
SVC_classifier = SVC()
SVC_classifier.fit(X=X_train, y=train_labels)
y_training = SVC_classifier.predict(X_train)
y_predict = SVC_classifier.predict(X_validation)
accuracy_t = np.sum([y_training == train_labels])/len(train_labels)
accuracy_v = np.sum([y_predict == validation_labels])/len(validation_labels)
print("Accuracy on Training Set: {}".format(accuracy_t))
print("Accuracy on Validation Set: {}".format(accuracy_v))
```
## 2. Convolutional Neural Network (CNN)
```
CNN_model = tf.keras.Sequential()
CNN_model.add(tf.keras.layers.experimental.preprocessing.Rescaling(1/255, input_shape=IMAGE_SIZE))
CNN_model.add(Conv2D(30, (5,5), input_shape=IMAGE_SIZE, activation='relu'))
CNN_model.add(MaxPooling2D(pool_size=(2,2)))
CNN_model.add(Conv2D(30, (3,3), activation='relu'))
CNN_model.add(MaxPooling2D(pool_size=(2,2)))
CNN_model.add(Dropout(0.2))
CNN_model.add(Flatten())
CNN_model.add(Dense(100, activation='relu'))
CNN_model.add(Dense(20, activation='relu'))
CNN_model.add(Dense(1, activation='sigmoid'))
CNN_model.compile(optimizer='adam', loss="binary_crossentropy", metrics=['accuracy'])
CNN_model.summary()
training = CNN_model.fit(train_data, validation_data=validation_data, batch_size=80, epochs=10)
def predict_image(url, model):
response = requests.get(url)
img = Image.open(BytesIO(response.content))
img_resize = img.resize((IMAGE_SIZE[1], IMAGE_SIZE[0]))
img_resize_display = img.resize((IMAGE_SIZE[1], IMAGE_SIZE[0]), Image.ANTIALIAS)
img_array = tf.keras.preprocessing.image.img_to_array(
img_resize, data_format=None, dtype=None
)
img_array_grayscale = tf.image.rgb_to_grayscale(img_array, name=None).numpy()
img_array_grayscale.shape
img_array_grayscale =img_array_grayscale.reshape(1, 200, 300, 1)
prediction = model.predict(img_array_grayscale)[0][0]
predict_label = "Excavator" if prediction < 0.5 else "Dump Truck"
predict_score = 1-prediction if prediction < 0.5 else prediction
print("{0} (Confidence: {1:.2f}%)".format(predict_label, predict_score*100))
display(img_resize_display)
url = "https://baumaschinen-modelle.net/de/sammlung/Dresser_730E.jpg"
predict_image(url=url, model=CNN_model)
```
|
github_jupyter
|
from IPython.display import display
import os
import requests
from PIL import Image
from io import BytesIO
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras.preprocessing.image import load_img, img_to_array
from keras.layers.convolutional import Conv2D, MaxPooling2D
from keras.layers import Dense, Dropout, Flatten, Activation
from sklearn.svm import SVC
from matplotlib import pyplot as plt
from google.colab import drive
drive.mount('/content/gdrive')
DATA_SOURCE = "/content/gdrive/My Drive/Colab Notebooks/images_data/"
PATH_TRUCK_IMAGES = DATA_SOURCE + "Trucks/"
PATH_EXCAVATOR_IMAGES = DATA_SOURCE + "Excavators/"
HEIGHT = 200
WIDTH = 300
IMAGE_SIZE = (HEIGHT, WIDTH, 1)
img = load_img(PATH_TRUCK_IMAGES + "6-image-Komatsu-960E-1.jpg", target_size=IMAGE_SIZE)
display(img)
img_array = img_to_array(img)
img_array.shape
img_array_grayscale = tf.image.rgb_to_grayscale(img_array, name=None)[:,:,0]/255
img_array_grayscale.shape
plt.imshow(img_array_grayscale, cmap='gray', vmin=0, vmax=1)
plt.show()
img_array_grayscale_flat = img_array.flatten()
img_array_grayscale_flat.shape
img_array_grayscale_flat
train_data = tf.keras.preprocessing.image_dataset_from_directory(
directory=DATA_SOURCE,
class_names=["Excavators", "Trucks"],
subset="training", validation_split=0.2,
seed=100,
label_mode="binary",
color_mode='grayscale' if IMAGE_SIZE[-1]==1 else "rgb", # <-------------------------------------------- automatically set the image to grayscale
image_size=IMAGE_SIZE[0:-1],
)
validation_data = tf.keras.preprocessing.image_dataset_from_directory(
directory=DATA_SOURCE,
class_names=["Excavators", "Trucks"],
subset="validation", validation_split=0.2,
seed=100,
label_mode="binary",
color_mode='grayscale' if IMAGE_SIZE[-1]==1 else "rgb", # <-------------------------------------------- automatically set the image to grayscale
image_size=IMAGE_SIZE[0:-1],
)
simple_ML = tf.keras.Sequential()
simple_ML.add(tf.keras.layers.experimental.preprocessing.Rescaling(1/255, input_shape=IMAGE_SIZE))
simple_ML.add(tf.keras.layers.Flatten())
simple_ML.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
simple_ML.summary()
for images, labels in train_data.take(1):
X_train = images.numpy()
train_labels = labels.numpy()
X_train = simple_ML.predict(X_train)
train_labels = train_labels.flatten()
for images, labels in validation_data.take(1):
X_validation = images.numpy()
validation_labels = labels.numpy()
X_validation = simple_ML.predict(X_validation)
validation_labels = validation_labels.flatten()
SVC_classifier = SVC()
SVC_classifier.fit(X=X_train, y=train_labels)
y_training = SVC_classifier.predict(X_train)
y_predict = SVC_classifier.predict(X_validation)
accuracy_t = np.sum([y_training == train_labels])/len(train_labels)
accuracy_v = np.sum([y_predict == validation_labels])/len(validation_labels)
print("Accuracy on Training Set: {}".format(accuracy_t))
print("Accuracy on Validation Set: {}".format(accuracy_v))
CNN_model = tf.keras.Sequential()
CNN_model.add(tf.keras.layers.experimental.preprocessing.Rescaling(1/255, input_shape=IMAGE_SIZE))
CNN_model.add(Conv2D(30, (5,5), input_shape=IMAGE_SIZE, activation='relu'))
CNN_model.add(MaxPooling2D(pool_size=(2,2)))
CNN_model.add(Conv2D(30, (3,3), activation='relu'))
CNN_model.add(MaxPooling2D(pool_size=(2,2)))
CNN_model.add(Dropout(0.2))
CNN_model.add(Flatten())
CNN_model.add(Dense(100, activation='relu'))
CNN_model.add(Dense(20, activation='relu'))
CNN_model.add(Dense(1, activation='sigmoid'))
CNN_model.compile(optimizer='adam', loss="binary_crossentropy", metrics=['accuracy'])
CNN_model.summary()
training = CNN_model.fit(train_data, validation_data=validation_data, batch_size=80, epochs=10)
def predict_image(url, model):
response = requests.get(url)
img = Image.open(BytesIO(response.content))
img_resize = img.resize((IMAGE_SIZE[1], IMAGE_SIZE[0]))
img_resize_display = img.resize((IMAGE_SIZE[1], IMAGE_SIZE[0]), Image.ANTIALIAS)
img_array = tf.keras.preprocessing.image.img_to_array(
img_resize, data_format=None, dtype=None
)
img_array_grayscale = tf.image.rgb_to_grayscale(img_array, name=None).numpy()
img_array_grayscale.shape
img_array_grayscale =img_array_grayscale.reshape(1, 200, 300, 1)
prediction = model.predict(img_array_grayscale)[0][0]
predict_label = "Excavator" if prediction < 0.5 else "Dump Truck"
predict_score = 1-prediction if prediction < 0.5 else prediction
print("{0} (Confidence: {1:.2f}%)".format(predict_label, predict_score*100))
display(img_resize_display)
url = "https://baumaschinen-modelle.net/de/sammlung/Dresser_730E.jpg"
predict_image(url=url, model=CNN_model)
| 0.652795 | 0.90261 |
# Grouping for Aggregation, Filtration, and Transformation
```
import pandas as pd
import numpy as np
pd.set_option('max_columns', 4, 'max_rows', 10, 'max_colwidth', 12)
```
## Introduction
### Defining an Aggregation
### How to do it...
```
flights = pd.read_csv('data/flights.csv')
flights.head()
(flights
.groupby('AIRLINE')
.agg({'ARR_DELAY':'mean'})
)
(flights
.groupby('AIRLINE')
['ARR_DELAY']
.agg('mean')
)
(flights
.groupby('AIRLINE')
['ARR_DELAY']
.agg(np.mean)
)
(flights
.groupby('AIRLINE')
['ARR_DELAY']
.mean()
)
```
### How it works...
```
grouped = flights.groupby('AIRLINE')
type(grouped)
```
### There's more...
```
(flights
.groupby('AIRLINE')
['ARR_DELAY']
.agg(np.sqrt)
)
```
## Grouping and aggregating with multiple columns and functions
### How to do it...
```
(flights
.groupby(['AIRLINE', 'WEEKDAY'])
['CANCELLED']
.agg('sum')
)
(flights
.groupby(['AIRLINE', 'WEEKDAY'])
['CANCELLED', 'DIVERTED']
.agg(['sum', 'mean'])
)
(flights
.groupby(['ORG_AIR', 'DEST_AIR'])
.agg({'CANCELLED':['sum', 'mean', 'size'],
'AIR_TIME':['mean', 'var']})
)
(flights
.groupby(['ORG_AIR', 'DEST_AIR'])
.agg(sum_cancelled=pd.NamedAgg(column='CANCELLED', aggfunc='sum'),
mean_cancelled=pd.NamedAgg(column='CANCELLED', aggfunc='mean'),
size_cancelled=pd.NamedAgg(column='CANCELLED', aggfunc='size'),
mean_air_time=pd.NamedAgg(column='AIR_TIME', aggfunc='mean'),
var_air_time=pd.NamedAgg(column='AIR_TIME', aggfunc='var'))
)
```
### How it works...
### There's more...
```
res = (flights
.groupby(['ORG_AIR', 'DEST_AIR'])
.agg({'CANCELLED':['sum', 'mean', 'size'],
'AIR_TIME':['mean', 'var']})
)
res.columns = ['_'.join(x) for x in
res.columns.to_flat_index()]
res
def flatten_cols(df):
df.columns = ['_'.join(x) for x in
df.columns.to_flat_index()]
return df
res = (flights
.groupby(['ORG_AIR', 'DEST_AIR'])
.agg({'CANCELLED':['sum', 'mean', 'size'],
'AIR_TIME':['mean', 'var']})
.pipe(flatten_cols)
)
res
res = (flights
.assign(ORG_AIR=flights.ORG_AIR.astype('category'))
.groupby(['ORG_AIR', 'DEST_AIR'])
.agg({'CANCELLED':['sum', 'mean', 'size'],
'AIR_TIME':['mean', 'var']})
)
res
res = (flights
.assign(ORG_AIR=flights.ORG_AIR.astype('category'))
.groupby(['ORG_AIR', 'DEST_AIR'], observed=True)
.agg({'CANCELLED':['sum', 'mean', 'size'],
'AIR_TIME':['mean', 'var']})
)
res
```
## Removing the MultiIndex after grouping
```
flights = pd.read_csv('data/flights.csv')
airline_info = (flights
.groupby(['AIRLINE', 'WEEKDAY'])
.agg({'DIST':['sum', 'mean'],
'ARR_DELAY':['min', 'max']})
.astype(int)
)
airline_info
airline_info.columns.get_level_values(0)
airline_info.columns.get_level_values(1)
airline_info.columns.to_flat_index()
airline_info.columns = ['_'.join(x) for x in
airline_info.columns.to_flat_index()]
airline_info
airline_info.reset_index()
(flights
.groupby(['AIRLINE', 'WEEKDAY'])
.agg(dist_sum=pd.NamedAgg(column='DIST', aggfunc='sum'),
dist_mean=pd.NamedAgg(column='DIST', aggfunc='mean'),
arr_delay_min=pd.NamedAgg(column='ARR_DELAY', aggfunc='min'),
arr_delay_max=pd.NamedAgg(column='ARR_DELAY', aggfunc='max'))
.astype(int)
.reset_index()
)
```
### How it works...
### There's more...
```
(flights
.groupby(['AIRLINE'], as_index=False)
['DIST']
.agg('mean')
.round(0)
)
```
## Grouping with a custom aggregation function
### How to do it...
```
college = pd.read_csv('data/college.csv')
(college
.groupby('STABBR')
['UGDS']
.agg(['mean', 'std'])
.round(0)
)
def max_deviation(s):
std_score = (s - s.mean()) / s.std()
return std_score.abs().max()
(college
.groupby('STABBR')
['UGDS']
.agg(max_deviation)
.round(1)
)
```
### How it works...
### There's more...
```
(college
.groupby('STABBR')
['UGDS', 'SATVRMID', 'SATMTMID']
.agg(max_deviation)
.round(1)
)
(college
.groupby(['STABBR', 'RELAFFIL'])
['UGDS', 'SATVRMID', 'SATMTMID']
.agg([max_deviation, 'mean', 'std'])
.round(1)
)
max_deviation.__name__
max_deviation.__name__ = 'Max Deviation'
(college
.groupby(['STABBR', 'RELAFFIL'])
['UGDS', 'SATVRMID', 'SATMTMID']
.agg([max_deviation, 'mean', 'std'])
.round(1)
)
```
## Customizing aggregating functions with *args and **kwargs
### How to do it...
```
def pct_between_1_3k(s):
return (s
.between(1_000, 3_000)
.mean()
* 100
)
(college
.groupby(['STABBR', 'RELAFFIL'])
['UGDS']
.agg(pct_between_1_3k)
.round(1)
)
def pct_between(s, low, high):
return s.between(low, high).mean() * 100
(college
.groupby(['STABBR', 'RELAFFIL'])
['UGDS']
.agg(pct_between, 1_000, 10_000)
.round(1)
)
```
### How it works...
### There's more...
```
def between_n_m(n, m):
def wrapper(ser):
return pct_between(ser, n, m)
wrapper.__name__ = f'between_{n}_{m}'
return wrapper
(college
.groupby(['STABBR', 'RELAFFIL'])
['UGDS']
.agg([between_n_m(1_000, 10_000), 'max', 'mean'])
.round(1)
)
```
## Examining the groupby object
### How to do it...
```
college = pd.read_csv('data/college.csv')
grouped = college.groupby(['STABBR', 'RELAFFIL'])
type(grouped)
print([attr for attr in dir(grouped) if not
attr.startswith('_')])
grouped.ngroups
groups = list(grouped.groups)
groups[:6]
grouped.get_group(('FL', 1))
from IPython.display import display
for name, group in grouped:
print(name)
display(group.head(3))
for name, group in grouped:
print(name)
print(group)
break
grouped.head(2)
```
### How it works...
### There's more...
```
grouped.nth([1, -1])
```
## Filtering for states with a minority majority
### How to do it...
```
college = pd.read_csv('data/college.csv', index_col='INSTNM')
grouped = college.groupby('STABBR')
grouped.ngroups
college['STABBR'].nunique() # verifying the same number
def check_minority(df, threshold):
minority_pct = 1 - df['UGDS_WHITE']
total_minority = (df['UGDS'] * minority_pct).sum()
total_ugds = df['UGDS'].sum()
total_minority_pct = total_minority / total_ugds
return total_minority_pct > threshold
college_filtered = grouped.filter(check_minority, threshold=.5)
college_filtered
college.shape
college_filtered.shape
college_filtered['STABBR'].nunique()
```
### How it works...
### There's more...
```
college_filtered_20 = grouped.filter(check_minority, threshold=.2)
college_filtered_20.shape
college_filtered_20['STABBR'].nunique()
college_filtered_70 = grouped.filter(check_minority, threshold=.7)
college_filtered_70.shape
college_filtered_70['STABBR'].nunique()
```
## Transforming through a weight loss bet
### How to do it...
```
weight_loss = pd.read_csv('data/weight_loss.csv')
weight_loss.query('Month == "Jan"')
def percent_loss(s):
return ((s - s.iloc[0]) / s.iloc[0]) * 100
(weight_loss
.query('Name=="Bob" and Month=="Jan"')
['Weight']
.pipe(percent_loss)
)
(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
)
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)))
.query('Name=="Bob" and Month in ["Jan", "Feb"]')
)
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)))
.query('Week == "Week 4"')
)
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)))
.query('Week == "Week 4"')
.pivot(index='Month', columns='Name',
values='percent_loss')
)
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)))
.query('Week == "Week 4"')
.pivot(index='Month', columns='Name',
values='percent_loss')
.assign(winner=lambda df_:
np.where(df_.Amy < df_.Bob, 'Amy', 'Bob'))
)
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)))
.query('Week == "Week 4"')
.pivot(index='Month', columns='Name',
values='percent_loss')
.assign(winner=lambda df_:
np.where(df_.Amy < df_.Bob, 'Amy', 'Bob'))
.style.highlight_min(axis=1)
)
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)))
.query('Week == "Week 4"')
.pivot(index='Month', columns='Name',
values='percent_loss')
.assign(winner=lambda df_:
np.where(df_.Amy < df_.Bob, 'Amy', 'Bob'))
.winner
.value_counts()
)
```
### How it works...
```
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)))
.query('Week == "Week 4"')
.groupby(['Month', 'Name'])
['percent_loss']
.first()
.unstack()
)
```
### There's more...
```
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)),
Month=pd.Categorical(weight_loss.Month,
categories=['Jan', 'Feb', 'Mar', 'Apr'],
ordered=True))
.query('Week == "Week 4"')
.pivot(index='Month', columns='Name',
values='percent_loss')
)
```
## Calculating weighted mean SAT scores per state with apply
### How to do it...
```
college = pd.read_csv('data/college.csv')
subset = ['UGDS', 'SATMTMID', 'SATVRMID']
college2 = college.dropna(subset=subset)
college.shape
college2.shape
def weighted_math_average(df):
weighted_math = df['UGDS'] * df['SATMTMID']
return int(weighted_math.sum() / df['UGDS'].sum())
college2.groupby('STABBR').apply(weighted_math_average)
(college2
.groupby('STABBR')
.agg(weighted_math_average)
)
(college2
.groupby('STABBR')
['SATMTMID']
.agg(weighted_math_average)
)
def weighted_average(df):
weight_m = df['UGDS'] * df['SATMTMID']
weight_v = df['UGDS'] * df['SATVRMID']
wm_avg = weight_m.sum() / df['UGDS'].sum()
wv_avg = weight_v.sum() / df['UGDS'].sum()
data = {'w_math_avg': wm_avg,
'w_verbal_avg': wv_avg,
'math_avg': df['SATMTMID'].mean(),
'verbal_avg': df['SATVRMID'].mean(),
'count': len(df)
}
return pd.Series(data)
(college2
.groupby('STABBR')
.apply(weighted_average)
.astype(int)
)
```
### How it works...
```
(college
.groupby('STABBR')
.apply(weighted_average)
)
```
### There's more...
```
from scipy.stats import gmean, hmean
def calculate_means(df):
df_means = pd.DataFrame(index=['Arithmetic', 'Weighted',
'Geometric', 'Harmonic'])
cols = ['SATMTMID', 'SATVRMID']
for col in cols:
arithmetic = df[col].mean()
weighted = np.average(df[col], weights=df['UGDS'])
geometric = gmean(df[col])
harmonic = hmean(df[col])
df_means[col] = [arithmetic, weighted,
geometric, harmonic]
df_means['count'] = len(df)
return df_means.astype(int)
(college2
.groupby('STABBR')
.apply(calculate_means)
)
```
## Grouping by continuous variables
### How to do it...
```
flights = pd.read_csv('data/flights.csv')
flights
bins = [-np.inf, 200, 500, 1000, 2000, np.inf]
cuts = pd.cut(flights['DIST'], bins=bins)
cuts
cuts.value_counts()
(flights
.groupby(cuts)
['AIRLINE']
.value_counts(normalize=True)
.round(3)
)
```
### How it works...
### There's more...
```
(flights
.groupby(cuts)
['AIR_TIME']
.quantile(q=[.25, .5, .75])
.div(60)
.round(2)
)
labels=['Under an Hour', '1 Hour', '1-2 Hours',
'2-4 Hours', '4+ Hours']
cuts2 = pd.cut(flights['DIST'], bins=bins, labels=labels)
(flights
.groupby(cuts2)
['AIRLINE']
.value_counts(normalize=True)
.round(3)
.unstack()
)
```
## Counting the total number of flights between cities
### How to do it...
```
flights = pd.read_csv('data/flights.csv')
flights_ct = flights.groupby(['ORG_AIR', 'DEST_AIR']).size()
flights_ct
flights_ct.loc[[('ATL', 'IAH'), ('IAH', 'ATL')]]
f_part3 = (flights # doctest: +SKIP
[['ORG_AIR', 'DEST_AIR']]
.apply(lambda ser:
ser.sort_values().reset_index(drop=True),
axis='columns')
)
f_part3
rename_dict = {0:'AIR1', 1:'AIR2'}
(flights # doctest: +SKIP
[['ORG_AIR', 'DEST_AIR']]
.apply(lambda ser:
ser.sort_values().reset_index(drop=True),
axis='columns')
.rename(columns=rename_dict)
.groupby(['AIR1', 'AIR2'])
.size()
)
(flights # doctest: +SKIP
[['ORG_AIR', 'DEST_AIR']]
.apply(lambda ser:
ser.sort_values().reset_index(drop=True),
axis='columns')
.rename(columns=rename_dict)
.groupby(['AIR1', 'AIR2'])
.size()
.loc[('ATL', 'IAH')]
)
(flights # doctest: +SKIP
[['ORG_AIR', 'DEST_AIR']]
.apply(lambda ser:
ser.sort_values().reset_index(drop=True),
axis='columns')
.rename(columns=rename_dict)
.groupby(['AIR1', 'AIR2'])
.size()
.loc[('IAH', 'ATL')]
)
```
### How it works...
### There's more ...
```
data_sorted = np.sort(flights[['ORG_AIR', 'DEST_AIR']])
data_sorted[:10]
flights_sort2 = pd.DataFrame(data_sorted, columns=['AIR1', 'AIR2'])
flights_sort2.equals(f_part3.rename(columns={'ORG_AIR':'AIR1',
'DEST_AIR':'AIR2'}))
```
```
%%timeit
data_sorted = np.sort(flights[['ORG_AIR', 'DEST_AIR']])
flights_sort2 = pd.DataFrame(data_sorted,
columns=['AIR1', 'AIR2'])
```
## Finding the longest streak of on-time flights
### How to do it...
```
s = pd.Series([0, 1, 1, 0, 1, 1, 1, 0])
s
s1 = s.cumsum()
s1
s.mul(s1)
s.mul(s1).diff()
(s
.mul(s.cumsum())
.diff()
.where(lambda x: x < 0)
)
(s
.mul(s.cumsum())
.diff()
.where(lambda x: x < 0)
.ffill()
)
(s
.mul(s.cumsum())
.diff()
.where(lambda x: x < 0)
.ffill()
.add(s.cumsum(), fill_value=0)
)
flights = pd.read_csv('data/flights.csv')
(flights
.assign(ON_TIME=flights['ARR_DELAY'].lt(15).astype(int))
[['AIRLINE', 'ORG_AIR', 'ON_TIME']]
)
def max_streak(s):
s1 = s.cumsum()
return (s
.mul(s1)
.diff()
.where(lambda x: x < 0)
.ffill()
.add(s1, fill_value=0)
.max()
)
(flights
.assign(ON_TIME=flights['ARR_DELAY'].lt(15).astype(int))
.sort_values(['MONTH', 'DAY', 'SCHED_DEP'])
.groupby(['AIRLINE', 'ORG_AIR'])
['ON_TIME']
.agg(['mean', 'size', max_streak])
.round(2)
)
```
### How it works...
### There's more...
```
def max_delay_streak(df):
df = df.reset_index(drop=True)
late = 1 - df['ON_TIME']
late_sum = late.cumsum()
streak = (late
.mul(late_sum)
.diff()
.where(lambda x: x < 0)
.ffill()
.add(late_sum, fill_value=0)
)
last_idx = streak.idxmax()
first_idx = last_idx - streak.max() + 1
res = (df
.loc[[first_idx, last_idx], ['MONTH', 'DAY']]
.assign(streak=streak.max())
)
res.index = ['first', 'last']
return res
(flights
.assign(ON_TIME=flights['ARR_DELAY'].lt(15).astype(int))
.sort_values(['MONTH', 'DAY', 'SCHED_DEP'])
.groupby(['AIRLINE', 'ORG_AIR'])
.apply(max_delay_streak)
.sort_values('streak', ascending=False)
)
```
|
github_jupyter
|
import pandas as pd
import numpy as np
pd.set_option('max_columns', 4, 'max_rows', 10, 'max_colwidth', 12)
flights = pd.read_csv('data/flights.csv')
flights.head()
(flights
.groupby('AIRLINE')
.agg({'ARR_DELAY':'mean'})
)
(flights
.groupby('AIRLINE')
['ARR_DELAY']
.agg('mean')
)
(flights
.groupby('AIRLINE')
['ARR_DELAY']
.agg(np.mean)
)
(flights
.groupby('AIRLINE')
['ARR_DELAY']
.mean()
)
grouped = flights.groupby('AIRLINE')
type(grouped)
(flights
.groupby('AIRLINE')
['ARR_DELAY']
.agg(np.sqrt)
)
(flights
.groupby(['AIRLINE', 'WEEKDAY'])
['CANCELLED']
.agg('sum')
)
(flights
.groupby(['AIRLINE', 'WEEKDAY'])
['CANCELLED', 'DIVERTED']
.agg(['sum', 'mean'])
)
(flights
.groupby(['ORG_AIR', 'DEST_AIR'])
.agg({'CANCELLED':['sum', 'mean', 'size'],
'AIR_TIME':['mean', 'var']})
)
(flights
.groupby(['ORG_AIR', 'DEST_AIR'])
.agg(sum_cancelled=pd.NamedAgg(column='CANCELLED', aggfunc='sum'),
mean_cancelled=pd.NamedAgg(column='CANCELLED', aggfunc='mean'),
size_cancelled=pd.NamedAgg(column='CANCELLED', aggfunc='size'),
mean_air_time=pd.NamedAgg(column='AIR_TIME', aggfunc='mean'),
var_air_time=pd.NamedAgg(column='AIR_TIME', aggfunc='var'))
)
res = (flights
.groupby(['ORG_AIR', 'DEST_AIR'])
.agg({'CANCELLED':['sum', 'mean', 'size'],
'AIR_TIME':['mean', 'var']})
)
res.columns = ['_'.join(x) for x in
res.columns.to_flat_index()]
res
def flatten_cols(df):
df.columns = ['_'.join(x) for x in
df.columns.to_flat_index()]
return df
res = (flights
.groupby(['ORG_AIR', 'DEST_AIR'])
.agg({'CANCELLED':['sum', 'mean', 'size'],
'AIR_TIME':['mean', 'var']})
.pipe(flatten_cols)
)
res
res = (flights
.assign(ORG_AIR=flights.ORG_AIR.astype('category'))
.groupby(['ORG_AIR', 'DEST_AIR'])
.agg({'CANCELLED':['sum', 'mean', 'size'],
'AIR_TIME':['mean', 'var']})
)
res
res = (flights
.assign(ORG_AIR=flights.ORG_AIR.astype('category'))
.groupby(['ORG_AIR', 'DEST_AIR'], observed=True)
.agg({'CANCELLED':['sum', 'mean', 'size'],
'AIR_TIME':['mean', 'var']})
)
res
flights = pd.read_csv('data/flights.csv')
airline_info = (flights
.groupby(['AIRLINE', 'WEEKDAY'])
.agg({'DIST':['sum', 'mean'],
'ARR_DELAY':['min', 'max']})
.astype(int)
)
airline_info
airline_info.columns.get_level_values(0)
airline_info.columns.get_level_values(1)
airline_info.columns.to_flat_index()
airline_info.columns = ['_'.join(x) for x in
airline_info.columns.to_flat_index()]
airline_info
airline_info.reset_index()
(flights
.groupby(['AIRLINE', 'WEEKDAY'])
.agg(dist_sum=pd.NamedAgg(column='DIST', aggfunc='sum'),
dist_mean=pd.NamedAgg(column='DIST', aggfunc='mean'),
arr_delay_min=pd.NamedAgg(column='ARR_DELAY', aggfunc='min'),
arr_delay_max=pd.NamedAgg(column='ARR_DELAY', aggfunc='max'))
.astype(int)
.reset_index()
)
(flights
.groupby(['AIRLINE'], as_index=False)
['DIST']
.agg('mean')
.round(0)
)
college = pd.read_csv('data/college.csv')
(college
.groupby('STABBR')
['UGDS']
.agg(['mean', 'std'])
.round(0)
)
def max_deviation(s):
std_score = (s - s.mean()) / s.std()
return std_score.abs().max()
(college
.groupby('STABBR')
['UGDS']
.agg(max_deviation)
.round(1)
)
(college
.groupby('STABBR')
['UGDS', 'SATVRMID', 'SATMTMID']
.agg(max_deviation)
.round(1)
)
(college
.groupby(['STABBR', 'RELAFFIL'])
['UGDS', 'SATVRMID', 'SATMTMID']
.agg([max_deviation, 'mean', 'std'])
.round(1)
)
max_deviation.__name__
max_deviation.__name__ = 'Max Deviation'
(college
.groupby(['STABBR', 'RELAFFIL'])
['UGDS', 'SATVRMID', 'SATMTMID']
.agg([max_deviation, 'mean', 'std'])
.round(1)
)
def pct_between_1_3k(s):
return (s
.between(1_000, 3_000)
.mean()
* 100
)
(college
.groupby(['STABBR', 'RELAFFIL'])
['UGDS']
.agg(pct_between_1_3k)
.round(1)
)
def pct_between(s, low, high):
return s.between(low, high).mean() * 100
(college
.groupby(['STABBR', 'RELAFFIL'])
['UGDS']
.agg(pct_between, 1_000, 10_000)
.round(1)
)
def between_n_m(n, m):
def wrapper(ser):
return pct_between(ser, n, m)
wrapper.__name__ = f'between_{n}_{m}'
return wrapper
(college
.groupby(['STABBR', 'RELAFFIL'])
['UGDS']
.agg([between_n_m(1_000, 10_000), 'max', 'mean'])
.round(1)
)
college = pd.read_csv('data/college.csv')
grouped = college.groupby(['STABBR', 'RELAFFIL'])
type(grouped)
print([attr for attr in dir(grouped) if not
attr.startswith('_')])
grouped.ngroups
groups = list(grouped.groups)
groups[:6]
grouped.get_group(('FL', 1))
from IPython.display import display
for name, group in grouped:
print(name)
display(group.head(3))
for name, group in grouped:
print(name)
print(group)
break
grouped.head(2)
grouped.nth([1, -1])
college = pd.read_csv('data/college.csv', index_col='INSTNM')
grouped = college.groupby('STABBR')
grouped.ngroups
college['STABBR'].nunique() # verifying the same number
def check_minority(df, threshold):
minority_pct = 1 - df['UGDS_WHITE']
total_minority = (df['UGDS'] * minority_pct).sum()
total_ugds = df['UGDS'].sum()
total_minority_pct = total_minority / total_ugds
return total_minority_pct > threshold
college_filtered = grouped.filter(check_minority, threshold=.5)
college_filtered
college.shape
college_filtered.shape
college_filtered['STABBR'].nunique()
college_filtered_20 = grouped.filter(check_minority, threshold=.2)
college_filtered_20.shape
college_filtered_20['STABBR'].nunique()
college_filtered_70 = grouped.filter(check_minority, threshold=.7)
college_filtered_70.shape
college_filtered_70['STABBR'].nunique()
weight_loss = pd.read_csv('data/weight_loss.csv')
weight_loss.query('Month == "Jan"')
def percent_loss(s):
return ((s - s.iloc[0]) / s.iloc[0]) * 100
(weight_loss
.query('Name=="Bob" and Month=="Jan"')
['Weight']
.pipe(percent_loss)
)
(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
)
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)))
.query('Name=="Bob" and Month in ["Jan", "Feb"]')
)
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)))
.query('Week == "Week 4"')
)
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)))
.query('Week == "Week 4"')
.pivot(index='Month', columns='Name',
values='percent_loss')
)
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)))
.query('Week == "Week 4"')
.pivot(index='Month', columns='Name',
values='percent_loss')
.assign(winner=lambda df_:
np.where(df_.Amy < df_.Bob, 'Amy', 'Bob'))
)
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)))
.query('Week == "Week 4"')
.pivot(index='Month', columns='Name',
values='percent_loss')
.assign(winner=lambda df_:
np.where(df_.Amy < df_.Bob, 'Amy', 'Bob'))
.style.highlight_min(axis=1)
)
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)))
.query('Week == "Week 4"')
.pivot(index='Month', columns='Name',
values='percent_loss')
.assign(winner=lambda df_:
np.where(df_.Amy < df_.Bob, 'Amy', 'Bob'))
.winner
.value_counts()
)
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)))
.query('Week == "Week 4"')
.groupby(['Month', 'Name'])
['percent_loss']
.first()
.unstack()
)
(weight_loss
.assign(percent_loss=(weight_loss
.groupby(['Name', 'Month'])
['Weight']
.transform(percent_loss)
.round(1)),
Month=pd.Categorical(weight_loss.Month,
categories=['Jan', 'Feb', 'Mar', 'Apr'],
ordered=True))
.query('Week == "Week 4"')
.pivot(index='Month', columns='Name',
values='percent_loss')
)
college = pd.read_csv('data/college.csv')
subset = ['UGDS', 'SATMTMID', 'SATVRMID']
college2 = college.dropna(subset=subset)
college.shape
college2.shape
def weighted_math_average(df):
weighted_math = df['UGDS'] * df['SATMTMID']
return int(weighted_math.sum() / df['UGDS'].sum())
college2.groupby('STABBR').apply(weighted_math_average)
(college2
.groupby('STABBR')
.agg(weighted_math_average)
)
(college2
.groupby('STABBR')
['SATMTMID']
.agg(weighted_math_average)
)
def weighted_average(df):
weight_m = df['UGDS'] * df['SATMTMID']
weight_v = df['UGDS'] * df['SATVRMID']
wm_avg = weight_m.sum() / df['UGDS'].sum()
wv_avg = weight_v.sum() / df['UGDS'].sum()
data = {'w_math_avg': wm_avg,
'w_verbal_avg': wv_avg,
'math_avg': df['SATMTMID'].mean(),
'verbal_avg': df['SATVRMID'].mean(),
'count': len(df)
}
return pd.Series(data)
(college2
.groupby('STABBR')
.apply(weighted_average)
.astype(int)
)
(college
.groupby('STABBR')
.apply(weighted_average)
)
from scipy.stats import gmean, hmean
def calculate_means(df):
df_means = pd.DataFrame(index=['Arithmetic', 'Weighted',
'Geometric', 'Harmonic'])
cols = ['SATMTMID', 'SATVRMID']
for col in cols:
arithmetic = df[col].mean()
weighted = np.average(df[col], weights=df['UGDS'])
geometric = gmean(df[col])
harmonic = hmean(df[col])
df_means[col] = [arithmetic, weighted,
geometric, harmonic]
df_means['count'] = len(df)
return df_means.astype(int)
(college2
.groupby('STABBR')
.apply(calculate_means)
)
flights = pd.read_csv('data/flights.csv')
flights
bins = [-np.inf, 200, 500, 1000, 2000, np.inf]
cuts = pd.cut(flights['DIST'], bins=bins)
cuts
cuts.value_counts()
(flights
.groupby(cuts)
['AIRLINE']
.value_counts(normalize=True)
.round(3)
)
(flights
.groupby(cuts)
['AIR_TIME']
.quantile(q=[.25, .5, .75])
.div(60)
.round(2)
)
labels=['Under an Hour', '1 Hour', '1-2 Hours',
'2-4 Hours', '4+ Hours']
cuts2 = pd.cut(flights['DIST'], bins=bins, labels=labels)
(flights
.groupby(cuts2)
['AIRLINE']
.value_counts(normalize=True)
.round(3)
.unstack()
)
flights = pd.read_csv('data/flights.csv')
flights_ct = flights.groupby(['ORG_AIR', 'DEST_AIR']).size()
flights_ct
flights_ct.loc[[('ATL', 'IAH'), ('IAH', 'ATL')]]
f_part3 = (flights # doctest: +SKIP
[['ORG_AIR', 'DEST_AIR']]
.apply(lambda ser:
ser.sort_values().reset_index(drop=True),
axis='columns')
)
f_part3
rename_dict = {0:'AIR1', 1:'AIR2'}
(flights # doctest: +SKIP
[['ORG_AIR', 'DEST_AIR']]
.apply(lambda ser:
ser.sort_values().reset_index(drop=True),
axis='columns')
.rename(columns=rename_dict)
.groupby(['AIR1', 'AIR2'])
.size()
)
(flights # doctest: +SKIP
[['ORG_AIR', 'DEST_AIR']]
.apply(lambda ser:
ser.sort_values().reset_index(drop=True),
axis='columns')
.rename(columns=rename_dict)
.groupby(['AIR1', 'AIR2'])
.size()
.loc[('ATL', 'IAH')]
)
(flights # doctest: +SKIP
[['ORG_AIR', 'DEST_AIR']]
.apply(lambda ser:
ser.sort_values().reset_index(drop=True),
axis='columns')
.rename(columns=rename_dict)
.groupby(['AIR1', 'AIR2'])
.size()
.loc[('IAH', 'ATL')]
)
data_sorted = np.sort(flights[['ORG_AIR', 'DEST_AIR']])
data_sorted[:10]
flights_sort2 = pd.DataFrame(data_sorted, columns=['AIR1', 'AIR2'])
flights_sort2.equals(f_part3.rename(columns={'ORG_AIR':'AIR1',
'DEST_AIR':'AIR2'}))
%%timeit
data_sorted = np.sort(flights[['ORG_AIR', 'DEST_AIR']])
flights_sort2 = pd.DataFrame(data_sorted,
columns=['AIR1', 'AIR2'])
s = pd.Series([0, 1, 1, 0, 1, 1, 1, 0])
s
s1 = s.cumsum()
s1
s.mul(s1)
s.mul(s1).diff()
(s
.mul(s.cumsum())
.diff()
.where(lambda x: x < 0)
)
(s
.mul(s.cumsum())
.diff()
.where(lambda x: x < 0)
.ffill()
)
(s
.mul(s.cumsum())
.diff()
.where(lambda x: x < 0)
.ffill()
.add(s.cumsum(), fill_value=0)
)
flights = pd.read_csv('data/flights.csv')
(flights
.assign(ON_TIME=flights['ARR_DELAY'].lt(15).astype(int))
[['AIRLINE', 'ORG_AIR', 'ON_TIME']]
)
def max_streak(s):
s1 = s.cumsum()
return (s
.mul(s1)
.diff()
.where(lambda x: x < 0)
.ffill()
.add(s1, fill_value=0)
.max()
)
(flights
.assign(ON_TIME=flights['ARR_DELAY'].lt(15).astype(int))
.sort_values(['MONTH', 'DAY', 'SCHED_DEP'])
.groupby(['AIRLINE', 'ORG_AIR'])
['ON_TIME']
.agg(['mean', 'size', max_streak])
.round(2)
)
def max_delay_streak(df):
df = df.reset_index(drop=True)
late = 1 - df['ON_TIME']
late_sum = late.cumsum()
streak = (late
.mul(late_sum)
.diff()
.where(lambda x: x < 0)
.ffill()
.add(late_sum, fill_value=0)
)
last_idx = streak.idxmax()
first_idx = last_idx - streak.max() + 1
res = (df
.loc[[first_idx, last_idx], ['MONTH', 'DAY']]
.assign(streak=streak.max())
)
res.index = ['first', 'last']
return res
(flights
.assign(ON_TIME=flights['ARR_DELAY'].lt(15).astype(int))
.sort_values(['MONTH', 'DAY', 'SCHED_DEP'])
.groupby(['AIRLINE', 'ORG_AIR'])
.apply(max_delay_streak)
.sort_values('streak', ascending=False)
)
| 0.367724 | 0.743354 |
# Searchligh Analysis
* A classification problem
* Two conditions: positive / negative
### Data description
* Three subjects
* sub-01, sub-02, sub-03
* Images
* aligned in MNI space
* beta-values
* Run in ROI mask
* Left precentral gyrus in AAL atlas
```
# initialize data
data_dir = '/home/ubuntu/data/'
result_dir = '/home/ubuntu/results/'
subj_list = ['sub-01', 'sub-02', 'sub-03']
num_subj = len(subj_list)
# initialize headers
import nilearn.decoding
import nilearn.image
import pandas as pd
import time
from sklearn.model_selection import KFold
```
* If you got import error in 'pandas', run `!pip3 install pandas`
### Check data structure
* `*_bold*.nii.gz`: beta value time-series data
* `*_event*.csv`: behavioral table
* `l_precentral_mask.nii.gz`: the roi mask
```
!ls $data_dir
```
### Check behavioral data
* degree: The class which I want to classify
* order: time index in beta-value time series images
```
labels = pd.read_csv(data_dir + 'sub-01_event1.csv')
labels.head()
```
## Run SVC searchlight
* See here: https://nilearn.github.io/decoding/searchlight.html
```
mask_img = nilearn.image.load_img(data_dir + 'l_precentral_mask.nii.gz')
cv = KFold(n_splits=2)
for subj in subj_list:
print('running %s ...' % subj, end='')
# initializing searchlight instance
searchlight = nilearn.decoding.SearchLight(
mask_img,
radius=5,
estimator='svc',
n_jobs=2,
verbose=False,
cv=cv
)
# loading behavioral data
label1 = pd.read_csv(data_dir + '%s_event1.csv' % subj)
label2 = pd.read_csv(data_dir + '%s_event2.csv' % subj)
# loading fMRI images
run1_img = nilearn.image.load_img(data_dir + '%s_bold1.nii.gz' % subj)
run2_img = nilearn.image.load_img(data_dir + '%s_bold2.nii.gz' % subj)
# slicing images with order
run1_img = nilearn.image.index_img(run1_img, label1['order']-1)
run2_img = nilearn.image.index_img(run2_img, label2['order']-1)
# preparing data
X = nilearn.image.concat_imgs([run1_img, run2_img])
y = list(label1['degree']) + list(label2['degree'])
group = [1 for _ in label1['degree']] + [2 for _ in label2['degree']]
# run searchlight
searchlight.fit(X, y, group)
# save result image
result_img = nilearn.image.new_img_like(mask_img, searchlight.scores_)
result_img.to_filename(result_dir + '%s_result.nii.gz' % subj)
print('done.')
```
# Comparing results
* Run group analysis with one sample t-test
* See here: https://nilearn.github.io/modules/generated/nilearn.mass_univariate.permuted_ols.html
```
!ls $result_dir
# initialize header
import numpy as np
import nilearn.mass_univariate
# load data
scores_each_subject = []
for subj in subj_list:
score = nilearn.image.load_img(result_dir + '%s_result.nii.gz' % subj).get_data()
scores_each_subject.append(score)
scores_each_subject = np.array(scores_each_subject)
# show data summary
shape = scores_each_subject[1, :, :, :].shape
for i, subj in enumerate(subj_list):
data = scores_each_subject[i, :, :, :].flat
mean = np.mean(data[np.nonzero(data)])
std = np.std(data[np.nonzero(data)])
median = np.median(data[np.nonzero(data)])
print('%s: mean %.2f, median %.2f, std %.2f' % (subj, mean, median, std))
# sub chance level
scores_each_subject[i, :, :, :] = (scores_each_subject[i, :, :, :] - 0.5)
# perform statistical test and save t map
t_img = np.zeros(shape)
p_img = np.zeros(shape)
for j in range(shape[0]):
for k in range(shape[1]):
for l in range(shape[2]):
# check voxel is in group mask
if scores_each_subject[0, j, k, l] != 0:
# perform permuted OLS
p_score, t_score, _ = nilearn.mass_univariate.permuted_ols(
np.ones((num_subj, 1)), # one group
scores_each_subject[:, j, k, l].reshape(-1, 1), # make data (num_subject, data vector)
n_perm=100,
two_sided_test=True,
n_jobs=2)
# save results as image
t_img[j, k, l] = t_score
p_img[j, k, l] = p_score
print('%d, %d, ..., ' % (j, k), end='\r')
t_img = nilearn.image.new_img_like(mask_img, t_img)
t_img.to_filename(result_dir + 'tstat.nii.gz')
p_img = nilearn.image.new_img_like(mask_img, p_img)
p_img.to_filename(result_dir + 'pstat.nii.gz')
```
|
github_jupyter
|
# initialize data
data_dir = '/home/ubuntu/data/'
result_dir = '/home/ubuntu/results/'
subj_list = ['sub-01', 'sub-02', 'sub-03']
num_subj = len(subj_list)
# initialize headers
import nilearn.decoding
import nilearn.image
import pandas as pd
import time
from sklearn.model_selection import KFold
!ls $data_dir
labels = pd.read_csv(data_dir + 'sub-01_event1.csv')
labels.head()
mask_img = nilearn.image.load_img(data_dir + 'l_precentral_mask.nii.gz')
cv = KFold(n_splits=2)
for subj in subj_list:
print('running %s ...' % subj, end='')
# initializing searchlight instance
searchlight = nilearn.decoding.SearchLight(
mask_img,
radius=5,
estimator='svc',
n_jobs=2,
verbose=False,
cv=cv
)
# loading behavioral data
label1 = pd.read_csv(data_dir + '%s_event1.csv' % subj)
label2 = pd.read_csv(data_dir + '%s_event2.csv' % subj)
# loading fMRI images
run1_img = nilearn.image.load_img(data_dir + '%s_bold1.nii.gz' % subj)
run2_img = nilearn.image.load_img(data_dir + '%s_bold2.nii.gz' % subj)
# slicing images with order
run1_img = nilearn.image.index_img(run1_img, label1['order']-1)
run2_img = nilearn.image.index_img(run2_img, label2['order']-1)
# preparing data
X = nilearn.image.concat_imgs([run1_img, run2_img])
y = list(label1['degree']) + list(label2['degree'])
group = [1 for _ in label1['degree']] + [2 for _ in label2['degree']]
# run searchlight
searchlight.fit(X, y, group)
# save result image
result_img = nilearn.image.new_img_like(mask_img, searchlight.scores_)
result_img.to_filename(result_dir + '%s_result.nii.gz' % subj)
print('done.')
!ls $result_dir
# initialize header
import numpy as np
import nilearn.mass_univariate
# load data
scores_each_subject = []
for subj in subj_list:
score = nilearn.image.load_img(result_dir + '%s_result.nii.gz' % subj).get_data()
scores_each_subject.append(score)
scores_each_subject = np.array(scores_each_subject)
# show data summary
shape = scores_each_subject[1, :, :, :].shape
for i, subj in enumerate(subj_list):
data = scores_each_subject[i, :, :, :].flat
mean = np.mean(data[np.nonzero(data)])
std = np.std(data[np.nonzero(data)])
median = np.median(data[np.nonzero(data)])
print('%s: mean %.2f, median %.2f, std %.2f' % (subj, mean, median, std))
# sub chance level
scores_each_subject[i, :, :, :] = (scores_each_subject[i, :, :, :] - 0.5)
# perform statistical test and save t map
t_img = np.zeros(shape)
p_img = np.zeros(shape)
for j in range(shape[0]):
for k in range(shape[1]):
for l in range(shape[2]):
# check voxel is in group mask
if scores_each_subject[0, j, k, l] != 0:
# perform permuted OLS
p_score, t_score, _ = nilearn.mass_univariate.permuted_ols(
np.ones((num_subj, 1)), # one group
scores_each_subject[:, j, k, l].reshape(-1, 1), # make data (num_subject, data vector)
n_perm=100,
two_sided_test=True,
n_jobs=2)
# save results as image
t_img[j, k, l] = t_score
p_img[j, k, l] = p_score
print('%d, %d, ..., ' % (j, k), end='\r')
t_img = nilearn.image.new_img_like(mask_img, t_img)
t_img.to_filename(result_dir + 'tstat.nii.gz')
p_img = nilearn.image.new_img_like(mask_img, p_img)
p_img.to_filename(result_dir + 'pstat.nii.gz')
| 0.362969 | 0.782039 |
## Stable Model Training
#### NOTES:
* This is "NoGAN" based training, described in the DeOldify readme.
* This model prioritizes stable and reliable renderings. It does particularly well on portraits and landscapes. It's not as colorful as the artistic model.
```
import os
os.environ['CUDA_VISIBLE_DEVICES']='0'
import fastai
from fastai import *
from fastai.vision import *
from fastai.callbacks.tensorboard import *
from fastai.vision.gan import *
from fasterai.generators import *
from fasterai.critics import *
from fasterai.dataset import *
from fasterai.loss import *
from fasterai.save import *
from PIL import Image, ImageDraw, ImageFont
from PIL import ImageFile
```
## Setup
```
path = Path('data/imagenet/ILSVRC/Data/CLS-LOC')
path_hr = path
path_lr = path/'bandw'
proj_id = 'StableModel'
gen_name = proj_id + '_gen'
pre_gen_name = gen_name + '_0'
crit_name = proj_id + '_crit'
name_gen = proj_id + '_image_gen'
path_gen = path/name_gen
TENSORBOARD_PATH = Path('data/tensorboard/' + proj_id)
nf_factor = 2
pct_start = 1e-8
def get_data(bs:int, sz:int, keep_pct:float):
return get_colorize_data(sz=sz, bs=bs, crappy_path=path_lr, good_path=path_hr,
random_seed=None, keep_pct=keep_pct)
def get_crit_data(classes, bs, sz):
src = ImageList.from_folder(path, include=classes, recurse=True).random_split_by_pct(0.1, seed=42)
ll = src.label_from_folder(classes=classes)
data = (ll.transform(get_transforms(max_zoom=2.), size=sz)
.databunch(bs=bs).normalize(imagenet_stats))
return data
def create_training_images(fn,i):
dest = path_lr/fn.relative_to(path_hr)
dest.parent.mkdir(parents=True, exist_ok=True)
img = PIL.Image.open(fn).convert('LA').convert('RGB')
img.save(dest)
def save_preds(dl):
i=0
names = dl.dataset.items
for b in dl:
preds = learn_gen.pred_batch(batch=b, reconstruct=True)
for o in preds:
o.save(path_gen/names[i].name)
i += 1
def save_gen_images():
if path_gen.exists(): shutil.rmtree(path_gen)
path_gen.mkdir(exist_ok=True)
data_gen = get_data(bs=bs, sz=sz, keep_pct=0.085)
save_preds(data_gen.fix_dl)
PIL.Image.open(path_gen.ls()[0])
```
## Create black and white training images
Only runs if the directory isn't already created.
```
if not path_lr.exists():
il = ImageList.from_folder(path_hr)
parallel(create_training_images, il.items)
```
## Pre-train generator
#### NOTE
Most of the training takes place here in pretraining for NoGAN. The goal here is to take the generator as far as possible with conventional training, as that is much easier to control and obtain glitch-free results compared to GAN training.
### 64px
```
bs=88
sz=64
keep_pct=1.0
data_gen = get_data(bs=bs, sz=sz, keep_pct=keep_pct)
learn_gen = gen_learner_wide(data=data_gen, gen_loss=FeatureLoss(), nf_factor=nf_factor)
learn_gen.callback_fns.append(partial(ImageGenTensorboardWriter, base_dir=TENSORBOARD_PATH, name='GenPre'))
learn_gen.fit_one_cycle(1, pct_start=0.8, max_lr=slice(1e-3))
learn_gen.save(pre_gen_name)
learn_gen.unfreeze()
learn_gen.fit_one_cycle(1, pct_start=pct_start, max_lr=slice(3e-7, 3e-4))
learn_gen.save(pre_gen_name)
```
### 128px
```
bs=20
sz=128
keep_pct=1.0
learn_gen.data = get_data(sz=sz, bs=bs, keep_pct=keep_pct)
learn_gen.unfreeze()
learn_gen.fit_one_cycle(1, pct_start=pct_start, max_lr=slice(1e-7,1e-4))
learn_gen.save(pre_gen_name)
```
### 192px
```
bs=8
sz=192
keep_pct=0.50
learn_gen.data = get_data(sz=sz, bs=bs, keep_pct=keep_pct)
learn_gen.unfreeze()
learn_gen.fit_one_cycle(1, pct_start=pct_start, max_lr=slice(5e-8,5e-5))
learn_gen.save(pre_gen_name)
```
## Repeatable GAN Cycle
#### NOTE
Best results so far have been based on repeating the cycle below a few times (about 5-8?), until diminishing returns are hit (no improvement in image quality). Each time you repeat the cycle, you want to increment that old_checkpoint_num by 1 so that new check points don't overwrite the old.
```
old_checkpoint_num = 0
checkpoint_num = old_checkpoint_num + 1
gen_old_checkpoint_name = gen_name + '_' + str(old_checkpoint_num)
gen_new_checkpoint_name = gen_name + '_' + str(checkpoint_num)
crit_old_checkpoint_name = crit_name + '_' + str(old_checkpoint_num)
crit_new_checkpoint_name= crit_name + '_' + str(checkpoint_num)
```
### Save Generated Images
```
bs=8
sz=192
learn_gen = gen_learner_wide(data=data_gen, gen_loss=FeatureLoss(), nf_factor=nf_factor).load(gen_old_checkpoint_name, with_opt=False)
save_gen_images()
```
### Pretrain Critic
##### Only need full pretraining of critic when starting from scratch. Otherwise, just finetune!
```
if old_checkpoint_num == 0:
bs=64
sz=128
learn_gen=None
gc.collect()
data_crit = get_crit_data([name_gen, 'test'], bs=bs, sz=sz)
data_crit.show_batch(rows=3, ds_type=DatasetType.Train, imgsize=3)
learn_critic = colorize_crit_learner(data=data_crit, nf=256)
learn_critic.callback_fns.append(partial(LearnerTensorboardWriter, base_dir=TENSORBOARD_PATH, name='CriticPre'))
learn_critic.fit_one_cycle(6, 1e-3)
learn_critic.save(crit_old_checkpoint_name)
bs=16
sz=192
data_crit = get_crit_data([name_gen, 'test'], bs=bs, sz=sz)
data_crit.show_batch(rows=3, ds_type=DatasetType.Train, imgsize=3)
learn_critic = colorize_crit_learner(data=data_crit, nf=256).load(crit_old_checkpoint_name, with_opt=False)
learn_critic.callback_fns.append(partial(LearnerTensorboardWriter, base_dir=TENSORBOARD_PATH, name='CriticPre'))
learn_critic.fit_one_cycle(4, 1e-4)
learn_critic.save(crit_new_checkpoint_name)
```
### GAN
```
learn_crit=None
learn_gen=None
gc.collect()
lr=2e-5
sz=192
bs=5
data_crit = get_crit_data([name_gen, 'test'], bs=bs, sz=sz)
learn_crit = colorize_crit_learner(data=data_crit, nf=256).load(crit_new_checkpoint_name, with_opt=False)
learn_gen = gen_learner_wide(data=data_gen, gen_loss=FeatureLoss(), nf_factor=nf_factor).load(gen_old_checkpoint_name, with_opt=False)
switcher = partial(AdaptiveGANSwitcher, critic_thresh=0.65)
learn = GANLearner.from_learners(learn_gen, learn_crit, weights_gen=(1.0,1.5), show_img=False, switcher=switcher,
opt_func=partial(optim.Adam, betas=(0.,0.9)), wd=1e-3)
learn.callback_fns.append(partial(GANDiscriminativeLR, mult_lr=5.))
learn.callback_fns.append(partial(GANTensorboardWriter, base_dir=TENSORBOARD_PATH, name='GanLearner', visual_iters=100))
learn.callback_fns.append(partial(GANSaveCallback, learn_gen=learn_gen, filename=gen_new_checkpoint_name, save_iters=100))
```
#### Instructions:
Find the checkpoint just before where glitches start to be introduced. This is all very new so you may need to play around with just how far you go here with keep_pct.
```
learn.data = get_data(sz=sz, bs=bs, keep_pct=0.03)
learn_gen.freeze_to(-1)
learn.fit(1,lr)
```
|
github_jupyter
|
import os
os.environ['CUDA_VISIBLE_DEVICES']='0'
import fastai
from fastai import *
from fastai.vision import *
from fastai.callbacks.tensorboard import *
from fastai.vision.gan import *
from fasterai.generators import *
from fasterai.critics import *
from fasterai.dataset import *
from fasterai.loss import *
from fasterai.save import *
from PIL import Image, ImageDraw, ImageFont
from PIL import ImageFile
path = Path('data/imagenet/ILSVRC/Data/CLS-LOC')
path_hr = path
path_lr = path/'bandw'
proj_id = 'StableModel'
gen_name = proj_id + '_gen'
pre_gen_name = gen_name + '_0'
crit_name = proj_id + '_crit'
name_gen = proj_id + '_image_gen'
path_gen = path/name_gen
TENSORBOARD_PATH = Path('data/tensorboard/' + proj_id)
nf_factor = 2
pct_start = 1e-8
def get_data(bs:int, sz:int, keep_pct:float):
return get_colorize_data(sz=sz, bs=bs, crappy_path=path_lr, good_path=path_hr,
random_seed=None, keep_pct=keep_pct)
def get_crit_data(classes, bs, sz):
src = ImageList.from_folder(path, include=classes, recurse=True).random_split_by_pct(0.1, seed=42)
ll = src.label_from_folder(classes=classes)
data = (ll.transform(get_transforms(max_zoom=2.), size=sz)
.databunch(bs=bs).normalize(imagenet_stats))
return data
def create_training_images(fn,i):
dest = path_lr/fn.relative_to(path_hr)
dest.parent.mkdir(parents=True, exist_ok=True)
img = PIL.Image.open(fn).convert('LA').convert('RGB')
img.save(dest)
def save_preds(dl):
i=0
names = dl.dataset.items
for b in dl:
preds = learn_gen.pred_batch(batch=b, reconstruct=True)
for o in preds:
o.save(path_gen/names[i].name)
i += 1
def save_gen_images():
if path_gen.exists(): shutil.rmtree(path_gen)
path_gen.mkdir(exist_ok=True)
data_gen = get_data(bs=bs, sz=sz, keep_pct=0.085)
save_preds(data_gen.fix_dl)
PIL.Image.open(path_gen.ls()[0])
if not path_lr.exists():
il = ImageList.from_folder(path_hr)
parallel(create_training_images, il.items)
bs=88
sz=64
keep_pct=1.0
data_gen = get_data(bs=bs, sz=sz, keep_pct=keep_pct)
learn_gen = gen_learner_wide(data=data_gen, gen_loss=FeatureLoss(), nf_factor=nf_factor)
learn_gen.callback_fns.append(partial(ImageGenTensorboardWriter, base_dir=TENSORBOARD_PATH, name='GenPre'))
learn_gen.fit_one_cycle(1, pct_start=0.8, max_lr=slice(1e-3))
learn_gen.save(pre_gen_name)
learn_gen.unfreeze()
learn_gen.fit_one_cycle(1, pct_start=pct_start, max_lr=slice(3e-7, 3e-4))
learn_gen.save(pre_gen_name)
bs=20
sz=128
keep_pct=1.0
learn_gen.data = get_data(sz=sz, bs=bs, keep_pct=keep_pct)
learn_gen.unfreeze()
learn_gen.fit_one_cycle(1, pct_start=pct_start, max_lr=slice(1e-7,1e-4))
learn_gen.save(pre_gen_name)
bs=8
sz=192
keep_pct=0.50
learn_gen.data = get_data(sz=sz, bs=bs, keep_pct=keep_pct)
learn_gen.unfreeze()
learn_gen.fit_one_cycle(1, pct_start=pct_start, max_lr=slice(5e-8,5e-5))
learn_gen.save(pre_gen_name)
old_checkpoint_num = 0
checkpoint_num = old_checkpoint_num + 1
gen_old_checkpoint_name = gen_name + '_' + str(old_checkpoint_num)
gen_new_checkpoint_name = gen_name + '_' + str(checkpoint_num)
crit_old_checkpoint_name = crit_name + '_' + str(old_checkpoint_num)
crit_new_checkpoint_name= crit_name + '_' + str(checkpoint_num)
bs=8
sz=192
learn_gen = gen_learner_wide(data=data_gen, gen_loss=FeatureLoss(), nf_factor=nf_factor).load(gen_old_checkpoint_name, with_opt=False)
save_gen_images()
if old_checkpoint_num == 0:
bs=64
sz=128
learn_gen=None
gc.collect()
data_crit = get_crit_data([name_gen, 'test'], bs=bs, sz=sz)
data_crit.show_batch(rows=3, ds_type=DatasetType.Train, imgsize=3)
learn_critic = colorize_crit_learner(data=data_crit, nf=256)
learn_critic.callback_fns.append(partial(LearnerTensorboardWriter, base_dir=TENSORBOARD_PATH, name='CriticPre'))
learn_critic.fit_one_cycle(6, 1e-3)
learn_critic.save(crit_old_checkpoint_name)
bs=16
sz=192
data_crit = get_crit_data([name_gen, 'test'], bs=bs, sz=sz)
data_crit.show_batch(rows=3, ds_type=DatasetType.Train, imgsize=3)
learn_critic = colorize_crit_learner(data=data_crit, nf=256).load(crit_old_checkpoint_name, with_opt=False)
learn_critic.callback_fns.append(partial(LearnerTensorboardWriter, base_dir=TENSORBOARD_PATH, name='CriticPre'))
learn_critic.fit_one_cycle(4, 1e-4)
learn_critic.save(crit_new_checkpoint_name)
learn_crit=None
learn_gen=None
gc.collect()
lr=2e-5
sz=192
bs=5
data_crit = get_crit_data([name_gen, 'test'], bs=bs, sz=sz)
learn_crit = colorize_crit_learner(data=data_crit, nf=256).load(crit_new_checkpoint_name, with_opt=False)
learn_gen = gen_learner_wide(data=data_gen, gen_loss=FeatureLoss(), nf_factor=nf_factor).load(gen_old_checkpoint_name, with_opt=False)
switcher = partial(AdaptiveGANSwitcher, critic_thresh=0.65)
learn = GANLearner.from_learners(learn_gen, learn_crit, weights_gen=(1.0,1.5), show_img=False, switcher=switcher,
opt_func=partial(optim.Adam, betas=(0.,0.9)), wd=1e-3)
learn.callback_fns.append(partial(GANDiscriminativeLR, mult_lr=5.))
learn.callback_fns.append(partial(GANTensorboardWriter, base_dir=TENSORBOARD_PATH, name='GanLearner', visual_iters=100))
learn.callback_fns.append(partial(GANSaveCallback, learn_gen=learn_gen, filename=gen_new_checkpoint_name, save_iters=100))
learn.data = get_data(sz=sz, bs=bs, keep_pct=0.03)
learn_gen.freeze_to(-1)
learn.fit(1,lr)
| 0.483648 | 0.693116 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.