code
stringlengths 2.5k
6.36M
| kind
stringclasses 2
values | parsed_code
stringlengths 0
404k
| quality_prob
float64 0
0.98
| learning_prob
float64 0.03
1
|
|---|---|---|---|---|
# Custom Estimator
**Learning Objectives:**
* Use a custom estimator of the `Estimator` class in TensorFlow to predict median housing price
The data is based on 1990 census data from California. This data is at the city block level, so these features reflect the total number of rooms in that block, or the total number of people who live on that block, respectively.
<p>
Let's use a set of features to predict house value.
## Set Up
In this first cell, we'll load the necessary libraries.
```
import math
import shutil
import numpy as np
import pandas as pd
import tensorflow as tf
tf.logging.set_verbosity(tf.logging.INFO)
pd.options.display.max_rows = 10
pd.options.display.float_format = '{:.1f}'.format
```
Next, we'll load our data set.
```
df = pd.read_csv("https://storage.googleapis.com/ml_universities/california_housing_train.csv", sep = ",")
```
## Examine the data
It's a good idea to get to know your data a little bit before you work with it.
We'll print out a quick summary of a few useful statistics on each column.
This will include things like mean, standard deviation, max, min, and various quantiles.
```
df.head()
df.describe()
```
This data is at the city block level, so these features reflect the total number of rooms in that block, or the total number of people who live on that block, respectively. Let's create a different, more appropriate feature. Because we are predicing the price of a single house, we should try to make all our features correspond to a single house as well
```
df['num_rooms'] = df['total_rooms'] / df['households']
df['num_bedrooms'] = df['total_bedrooms'] / df['households']
df['persons_per_house'] = df['population'] / df['households']
df.describe()
df.drop(['total_rooms', 'total_bedrooms', 'population', 'households'], axis = 1, inplace = True)
df.describe()
```
## Build a custom estimator linear regressor
In this exercise, we'll be trying to predict `median_house_value`. It will be our label. We'll use the remaining columns as our input features.
To train our model, we'll use the Estimator API and create a custom estimator for linear regression.
Note that we don't actually need a custom estimator for linear regression since there is a canned estimator for it, however we're keeping it simple so you can practice creating a custom estimator function.
```
# Define feature columns
feature_columns = {
colname : tf.feature_column.numeric_column(colname) \
for colname in ['housing_median_age','median_income','num_rooms','num_bedrooms','persons_per_house']
}
# Bucketize lat, lon so it's not so high-res; California is mostly N-S, so more lats than lons
feature_columns['longitude'] = tf.feature_column.bucketized_column(tf.feature_column.numeric_column('longitude'), np.linspace(-124.3, -114.3, 5).tolist())
feature_columns['latitude'] = tf.feature_column.bucketized_column(tf.feature_column.numeric_column('latitude'), np.linspace(32.5, 42, 10).tolist())
# Split into train and eval and create input functions
msk = np.random.rand(len(df)) < 0.8
traindf = df[msk]
evaldf = df[~msk]
SCALE = 100000
BATCH_SIZE=128
train_input_fn = tf.estimator.inputs.pandas_input_fn(x = traindf[list(feature_columns.keys())],
y = traindf["median_house_value"] / SCALE,
num_epochs = None,
batch_size = BATCH_SIZE,
shuffle = True)
eval_input_fn = tf.estimator.inputs.pandas_input_fn(x = evaldf[list(feature_columns.keys())],
y = evaldf["median_house_value"] / SCALE, # note the scaling
num_epochs = 1,
batch_size = len(evaldf),
shuffle=False)
# Create the custom estimator
def custom_estimator(features, labels, mode, params):
# 0. Extract data from feature columns
input_layer = tf.feature_column.input_layer(features, params['feature_columns'])
# 1. Define Model Architecture
predictions = tf.layers.dense(input_layer,1,activation=None)
# 2. Loss function, training/eval ops
if mode == tf.estimator.ModeKeys.TRAIN or mode == tf.estimator.ModeKeys.EVAL:
labels = tf.expand_dims(tf.cast(labels, dtype=tf.float32), -1)
loss = tf.losses.mean_squared_error(labels, predictions)
optimizer = tf.train.FtrlOptimizer(learning_rate=0.2)
train_op = optimizer.minimize(
loss = loss,
global_step = tf.train.get_global_step())
eval_metric_ops = {
"rmse": tf.metrics.root_mean_squared_error(labels*SCALE, predictions*SCALE)
}
else:
loss = None
train_op = None
eval_metric_ops = None
# 3. Create predictions
predictions_dict = {"predicted": predictions}
# 4. Create export outputs
export_outputs = {"regression_export_outputs": tf.estimator.export.RegressionOutput(value = predictions)}
# 5. Return EstimatorSpec
return tf.estimator.EstimatorSpec(
mode = mode,
predictions = predictions_dict,
loss = loss,
train_op = train_op,
eval_metric_ops = eval_metric_ops,
export_outputs = export_outputs)
# Create serving input function
def serving_input_fn():
feature_placeholders = {
colname : tf.placeholder(tf.float32, [None]) for colname in 'housing_median_age,median_income,num_rooms,num_bedrooms,persons_per_house'.split(',')
}
feature_placeholders['longitude'] = tf.placeholder(tf.float32, [None])
feature_placeholders['latitude'] = tf.placeholder(tf.float32, [None])
features = {
key: tf.expand_dims(tensor, -1)
for key, tensor in feature_placeholders.items()
}
return tf.estimator.export.ServingInputReceiver(features, feature_placeholders)
# Create custom estimator's train and evaluate function
def train_and_evaluate(output_dir):
estimator = tf.estimator.Estimator(
model_fn = custom_estimator,
model_dir = output_dir,
params={'feature_columns': list(feature_columns.values())})
train_spec = tf.estimator.TrainSpec(input_fn = train_input_fn,
max_steps = 1000)
exporter = tf.estimator.LatestExporter('exporter', serving_input_fn)
eval_spec = tf.estimator.EvalSpec(input_fn = eval_input_fn,
steps = None,
exporters = exporter)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
#Run Training
OUTDIR = 'custom_estimator_trained_model'
shutil.rmtree(OUTDIR, ignore_errors = True) # start fresh each time
train_and_evaluate(OUTDIR)
```
## Challenge Excercise
Modify the custom_estimator function to be a neural network with one hidden layer, instead of a linear regressor
```
def custom_estimator(features, labels, mode, params):
# 0. Extract data from feature columns
input_layer = tf.feature_column.input_layer(features, params['feature_columns'])
# 1. Define Model Architecture
predictions = tf.layers.dense(input_layer,10,activation=tf.nn.relu)
predictions = tf.layers.dense(input_layer,1,activation=None)
# 2. Loss function, training/eval ops
if mode == tf.estimator.ModeKeys.TRAIN or mode == tf.estimator.ModeKeys.EVAL:
labels = tf.expand_dims(tf.cast(labels, dtype=tf.float32), -1)
loss = tf.losses.mean_squared_error(labels, predictions)
optimizer = tf.train.FtrlOptimizer(learning_rate=0.2)
train_op = optimizer.minimize(
loss = loss,
global_step = tf.train.get_global_step())
eval_metric_ops = {
"rmse": tf.metrics.root_mean_squared_error(labels*SCALE, predictions*SCALE)
}
else:
loss = None
train_op = None
eval_metric_ops = None
# 3. Create predictions
predictions_dict = {"predicted": predictions}
# 4. Create export outputs
export_outputs = {"regression_export_outputs": tf.estimator.export.RegressionOutput(value = predictions)}
# 5. Return EstimatorSpec
return tf.estimator.EstimatorSpec(
mode = mode,
predictions = predictions_dict,
loss = loss,
train_op = train_op,
eval_metric_ops = eval_metric_ops,
export_outputs = export_outputs)
# Create serving input function
def serving_input_fn():
feature_placeholders = {
colname : tf.placeholder(tf.float32, [None]) for colname in 'housing_median_age,median_income,num_rooms,num_bedrooms,persons_per_house'.split(',')
}
feature_placeholders['longitude'] = tf.placeholder(tf.float32, [None])
feature_placeholders['latitude'] = tf.placeholder(tf.float32, [None])
features = {
key: tf.expand_dims(tensor, -1)
for key, tensor in feature_placeholders.items()
}
return tf.estimator.export.ServingInputReceiver(features, feature_placeholders)
# Create custom estimator's train and evaluate function
def train_and_evaluate(output_dir):
estimator = tf.estimator.Estimator(
model_fn = custom_estimator,
model_dir = output_dir,
params={'feature_columns': list(feature_columns.values())})
train_spec = tf.estimator.TrainSpec(input_fn = train_input_fn,
max_steps = 1000)
exporter = tf.estimator.LatestExporter('exporter', serving_input_fn)
eval_spec = tf.estimator.EvalSpec(input_fn = eval_input_fn,
steps = None,
exporters = exporter)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
#Run Training
OUTDIR = 'custom_estimator_trained_model'
shutil.rmtree(OUTDIR, ignore_errors = True) # start fresh each time
train_and_evaluate(OUTDIR)
```
|
github_jupyter
|
import math
import shutil
import numpy as np
import pandas as pd
import tensorflow as tf
tf.logging.set_verbosity(tf.logging.INFO)
pd.options.display.max_rows = 10
pd.options.display.float_format = '{:.1f}'.format
df = pd.read_csv("https://storage.googleapis.com/ml_universities/california_housing_train.csv", sep = ",")
df.head()
df.describe()
df['num_rooms'] = df['total_rooms'] / df['households']
df['num_bedrooms'] = df['total_bedrooms'] / df['households']
df['persons_per_house'] = df['population'] / df['households']
df.describe()
df.drop(['total_rooms', 'total_bedrooms', 'population', 'households'], axis = 1, inplace = True)
df.describe()
# Define feature columns
feature_columns = {
colname : tf.feature_column.numeric_column(colname) \
for colname in ['housing_median_age','median_income','num_rooms','num_bedrooms','persons_per_house']
}
# Bucketize lat, lon so it's not so high-res; California is mostly N-S, so more lats than lons
feature_columns['longitude'] = tf.feature_column.bucketized_column(tf.feature_column.numeric_column('longitude'), np.linspace(-124.3, -114.3, 5).tolist())
feature_columns['latitude'] = tf.feature_column.bucketized_column(tf.feature_column.numeric_column('latitude'), np.linspace(32.5, 42, 10).tolist())
# Split into train and eval and create input functions
msk = np.random.rand(len(df)) < 0.8
traindf = df[msk]
evaldf = df[~msk]
SCALE = 100000
BATCH_SIZE=128
train_input_fn = tf.estimator.inputs.pandas_input_fn(x = traindf[list(feature_columns.keys())],
y = traindf["median_house_value"] / SCALE,
num_epochs = None,
batch_size = BATCH_SIZE,
shuffle = True)
eval_input_fn = tf.estimator.inputs.pandas_input_fn(x = evaldf[list(feature_columns.keys())],
y = evaldf["median_house_value"] / SCALE, # note the scaling
num_epochs = 1,
batch_size = len(evaldf),
shuffle=False)
# Create the custom estimator
def custom_estimator(features, labels, mode, params):
# 0. Extract data from feature columns
input_layer = tf.feature_column.input_layer(features, params['feature_columns'])
# 1. Define Model Architecture
predictions = tf.layers.dense(input_layer,1,activation=None)
# 2. Loss function, training/eval ops
if mode == tf.estimator.ModeKeys.TRAIN or mode == tf.estimator.ModeKeys.EVAL:
labels = tf.expand_dims(tf.cast(labels, dtype=tf.float32), -1)
loss = tf.losses.mean_squared_error(labels, predictions)
optimizer = tf.train.FtrlOptimizer(learning_rate=0.2)
train_op = optimizer.minimize(
loss = loss,
global_step = tf.train.get_global_step())
eval_metric_ops = {
"rmse": tf.metrics.root_mean_squared_error(labels*SCALE, predictions*SCALE)
}
else:
loss = None
train_op = None
eval_metric_ops = None
# 3. Create predictions
predictions_dict = {"predicted": predictions}
# 4. Create export outputs
export_outputs = {"regression_export_outputs": tf.estimator.export.RegressionOutput(value = predictions)}
# 5. Return EstimatorSpec
return tf.estimator.EstimatorSpec(
mode = mode,
predictions = predictions_dict,
loss = loss,
train_op = train_op,
eval_metric_ops = eval_metric_ops,
export_outputs = export_outputs)
# Create serving input function
def serving_input_fn():
feature_placeholders = {
colname : tf.placeholder(tf.float32, [None]) for colname in 'housing_median_age,median_income,num_rooms,num_bedrooms,persons_per_house'.split(',')
}
feature_placeholders['longitude'] = tf.placeholder(tf.float32, [None])
feature_placeholders['latitude'] = tf.placeholder(tf.float32, [None])
features = {
key: tf.expand_dims(tensor, -1)
for key, tensor in feature_placeholders.items()
}
return tf.estimator.export.ServingInputReceiver(features, feature_placeholders)
# Create custom estimator's train and evaluate function
def train_and_evaluate(output_dir):
estimator = tf.estimator.Estimator(
model_fn = custom_estimator,
model_dir = output_dir,
params={'feature_columns': list(feature_columns.values())})
train_spec = tf.estimator.TrainSpec(input_fn = train_input_fn,
max_steps = 1000)
exporter = tf.estimator.LatestExporter('exporter', serving_input_fn)
eval_spec = tf.estimator.EvalSpec(input_fn = eval_input_fn,
steps = None,
exporters = exporter)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
#Run Training
OUTDIR = 'custom_estimator_trained_model'
shutil.rmtree(OUTDIR, ignore_errors = True) # start fresh each time
train_and_evaluate(OUTDIR)
def custom_estimator(features, labels, mode, params):
# 0. Extract data from feature columns
input_layer = tf.feature_column.input_layer(features, params['feature_columns'])
# 1. Define Model Architecture
predictions = tf.layers.dense(input_layer,10,activation=tf.nn.relu)
predictions = tf.layers.dense(input_layer,1,activation=None)
# 2. Loss function, training/eval ops
if mode == tf.estimator.ModeKeys.TRAIN or mode == tf.estimator.ModeKeys.EVAL:
labels = tf.expand_dims(tf.cast(labels, dtype=tf.float32), -1)
loss = tf.losses.mean_squared_error(labels, predictions)
optimizer = tf.train.FtrlOptimizer(learning_rate=0.2)
train_op = optimizer.minimize(
loss = loss,
global_step = tf.train.get_global_step())
eval_metric_ops = {
"rmse": tf.metrics.root_mean_squared_error(labels*SCALE, predictions*SCALE)
}
else:
loss = None
train_op = None
eval_metric_ops = None
# 3. Create predictions
predictions_dict = {"predicted": predictions}
# 4. Create export outputs
export_outputs = {"regression_export_outputs": tf.estimator.export.RegressionOutput(value = predictions)}
# 5. Return EstimatorSpec
return tf.estimator.EstimatorSpec(
mode = mode,
predictions = predictions_dict,
loss = loss,
train_op = train_op,
eval_metric_ops = eval_metric_ops,
export_outputs = export_outputs)
# Create serving input function
def serving_input_fn():
feature_placeholders = {
colname : tf.placeholder(tf.float32, [None]) for colname in 'housing_median_age,median_income,num_rooms,num_bedrooms,persons_per_house'.split(',')
}
feature_placeholders['longitude'] = tf.placeholder(tf.float32, [None])
feature_placeholders['latitude'] = tf.placeholder(tf.float32, [None])
features = {
key: tf.expand_dims(tensor, -1)
for key, tensor in feature_placeholders.items()
}
return tf.estimator.export.ServingInputReceiver(features, feature_placeholders)
# Create custom estimator's train and evaluate function
def train_and_evaluate(output_dir):
estimator = tf.estimator.Estimator(
model_fn = custom_estimator,
model_dir = output_dir,
params={'feature_columns': list(feature_columns.values())})
train_spec = tf.estimator.TrainSpec(input_fn = train_input_fn,
max_steps = 1000)
exporter = tf.estimator.LatestExporter('exporter', serving_input_fn)
eval_spec = tf.estimator.EvalSpec(input_fn = eval_input_fn,
steps = None,
exporters = exporter)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
#Run Training
OUTDIR = 'custom_estimator_trained_model'
shutil.rmtree(OUTDIR, ignore_errors = True) # start fresh each time
train_and_evaluate(OUTDIR)
| 0.651687 | 0.975577 |
```
#hide
#skip
! [ -e /content ] && pip install -Uqq fastai # upgrade fastai on colab
# all_cuda
#export
from fastai.basics import *
from fastai.callback.progress import *
from torch.cuda.amp import GradScaler,autocast
from torch.cuda.amp.grad_scaler import OptState
#default_exp callback.fp16
#hide
from fastai.test_utils import *
from nbdev.showdoc import *
```
# Mixed precision training
> Callback and utility functions to allow mixed precision training
## A little bit of theory
A very nice and clear introduction to mixed precision training is [this video from NVIDIA](https://on-demand.gputechconf.com/gtc/2019/video/_/S9143/).
### What's half precision?
In neural nets, all the computations are usually done in single precision, which means all the floats in all the arrays that represent inputs, activations, weights... are 32-bit floats (FP32 in the rest of this post). An idea to reduce memory usage (and avoid those annoying cuda errors) has been to try and do the same thing in half-precision, which means using 16-bits floats (or FP16 in the rest of this post). By definition, they take half the space in RAM, and in theory could allow you to double the size of your model and double your batch size.
Another very nice feature is that NVIDIA developed its latest GPUs (the Volta generation) to take fully advantage of half-precision tensors. Basically, if you give half-precision tensors to those, they'll stack them so that each core can do more operations at the same time, and theoretically gives an 8x speed-up (sadly, just in theory).
So training at half precision is better for your memory usage, way faster if you have a Volta GPU (still a tiny bit faster if you don't since the computations are easiest). How do we do it? Super easily in pytorch, we just have to put .half() everywhere: on the inputs of our model and all the parameters. Problem is that you usually won't see the same accuracy in the end (so it happens sometimes) because half-precision is... well... not as precise ;).
### Problems with half-precision:
To understand the problems with half precision, let's look briefly at what an FP16 looks like (more information [here](https://en.wikipedia.org/wiki/Half-precision_floating-point_format)).

The sign bit gives us +1 or -1, then we have 5 bits to code an exponent between -14 and 15, while the fraction part has the remaining 10 bits. Compared to FP32, we have a smaller range of possible values (2e-14 to 2e15 roughly, compared to 2e-126 to 2e127 for FP32) but also a smaller *offset*.
For instance, between 1 and 2, the FP16 format only represents the number 1, 1+2e-10, 1+2*2e-10... which means that 1 + 0.0001 = 1 in half precision. That's what will cause a certain numbers of problems, specifically three that can occur and mess up your training.
1. The weight update is imprecise: inside your optimizer, you basically do w = w - lr * w.grad for each weight of your network. The problem in performing this operation in half precision is that very often, w.grad is several orders of magnitude below w, and the learning rate is also small. The situation where w=1 and lr*w.grad is 0.0001 (or lower) is therefore very common, but the update doesn't do anything in those cases.
2. Your gradients can underflow. In FP16, your gradients can easily be replaced by 0 because they are too low.
3. Your activations or loss can overflow. The opposite problem from the gradients: it's easier to hit nan (or infinity) in FP16 precision, and your training might more easily diverge.
### The solution: mixed precision training
To address those three problems, we don't fully train in FP16 precision. As the name mixed training implies, some of the operations will be done in FP16, others in FP32. This is mainly to take care of the first problem listed above. For the next two there are additional tricks.
The main idea is that we want to do the forward pass and the gradient computation in half precision (to go fast) but the update in single precision (to be more precise). It's okay if w and grad are both half floats, but when we do the operation w = w - lr * grad, we need to compute it in FP32. That way our 1 + 0.0001 is going to be 1.0001.
This is why we keep a copy of the weights in FP32 (called master model). Then, our training loop will look like:
1. compute the output with the FP16 model, then the loss
2. back-propagate the gradients in half-precision.
3. copy the gradients in FP32 precision
4. do the update on the master model (in FP32 precision)
5. copy the master model in the FP16 model.
Note that we lose precision during step 5, and that the 1.0001 in one of the weights will go back to 1. But if the next update corresponds to add 0.0001 again, since the optimizer step is done on the master model, the 1.0001 will become 1.0002 and if we eventually go like this up to 1.0005, the FP16 model will be able to tell the difference.
That takes care of problem 1. For the second problem, we use something called gradient scaling: to avoid the gradients getting zeroed by the FP16 precision, we multiply the loss by a scale factor (scale=512 for instance). That way we can push the gradients to the right in the next figure, and have them not become zero.

Of course we don't want those 512-scaled gradients to be in the weight update, so after converting them into FP32, we can divide them by this scale factor (once they have no risks of becoming 0). This changes the loop to:
1. compute the output with the FP16 model, then the loss.
2. multiply the loss by scale then back-propagate the gradients in half-precision.
3. copy the gradients in FP32 precision then divide them by scale.
4. do the update on the master model (in FP32 precision).
5. copy the master model in the FP16 model.
For the last problem, the tricks offered by NVIDIA are to leave the batchnorm layers in single precision (they don't have many weights so it's not a big memory challenge) and compute the loss in single precision (which means converting the last output of the model in single precision before passing it to the loss).

### Dynamic loss scaling
The only annoying thing with the previous implementation of mixed precision training is that it introduces one new hyper-parameter to tune, the value of the loss scaling. Fortunately for us, there is a way around this. We want the loss scaling to be as high as possible so that our gradients can use the whole range of representation, so let's first try a really high value. In all likelihood, this will cause our gradients or our loss to overflow, and we will try again with half that big value, and again, until we get to the largest loss scale possible that doesn't make our gradients overflow.
This value will be perfectly fitted to our model and can continue to be dynamically adjusted as the training goes, if it's still too high, by just halving it each time we overflow. After a while though, training will converge and gradients will start to get smaller, so we al
so need a mechanism to get this dynamic loss scale larger if it's safe to do so. The strategy used in the Apex library is to multiply the loss scale by 2 each time we had a given number of iterations without overflowing.
## MixedPrecision -
```
#export
@delegates(GradScaler)
class MixedPrecision(Callback):
"Mixed precision training using Pytorch's `autocast` and `GradScaler`"
order = 10
def __init__(self, **kwargs): self.kwargs,self.autocast = kwargs,autocast()
def before_fit(self): self.learn.scaler,self.scales = GradScaler(**self.kwargs),L()
def before_batch(self): self.autocast.__enter__()
def after_pred(self):
if listify(self.pred)[0].dtype==torch.float16: self.learn.pred = to_float(self.pred)
def after_loss(self): self.autocast.__exit__()
def before_backward(self): self.learn.loss_grad = self.scaler.scale(self.loss_grad)
def before_step(self):
self.skipped=True
self.scaler.step(self)
if self.skipped: raise CancelStepException()
self.scales.append(self.scaler.get_scale())
def after_step(self): self.learn.scaler.update()
@property # pretend to be an optimizer for `GradScaler`
def param_groups(self): return self.opt.param_groups
def step(self, *args, **kwargs): self.skipped=False
#export
class FP16TestCallback(Callback):
"Asserts that predictions are `float16` values"
order = 9
def after_pred(self): assert listify(self.pred)[0].dtype==torch.float16
#cuda
set_seed(99, True)
learn = synth_learner(cbs=[MixedPrecision,FP16TestCallback], cuda=True)
learn.model = nn.Sequential(nn.Linear(1,1), nn.Linear(1,1)).cuda()
learn.opt_func = partial(SGD, mom=0.)
learn.splitter = lambda m: [list(m[0].parameters()), list(m[1].parameters())]
learn.fit(3)
assert learn.recorder.values[-1][-1]<learn.recorder.values[0][-1]
#hide
#cuda
#Multioutput version
set_seed(99, True)
learn = synth_learner(cbs=[MixedPrecision,FP16TestCallback], cuda=True)
class MultiOutputModel(Module):
def __init__(self): self.linear1, self.linear2 = nn.Linear(1,1) , nn.Linear(1,1)
def forward(self,x): return self.linear1(x), self.linear2(x)
def multioutputloss(pred, val): return ((val-pred[0]).abs() + 0.5 * (val-pred[1]).abs()).sum()
learn.model = MultiOutputModel()
learn.opt_func = partial(SGD, mom=0.)
learn.splitter = lambda m: [list(m.linear1.parameters()), list(m.linear2.parameters())]
learn.loss_func=multioutputloss
learn.fit(3)
assert learn.recorder.values[-1][-1]<learn.recorder.values[0][-1]
#export
@patch
@delegates(GradScaler)
def to_fp16(self:Learner, **kwargs): return self.add_cb(MixedPrecision(**kwargs))
#export
@patch
def to_fp32(self:Learner): return self.remove_cb(MixedPrecision)
```
## Util functions
Before going in the main `Callback` we will need some helper functions. We use the ones from the [APEX library](https://github.com/NVIDIA/apex).
```
# export
from fastai.fp16_utils import convert_network, model_grads_to_master_grads, master_params_to_model_params
```
### Converting the model to FP16
We will need a function to convert all the layers of the model to FP16 precision except the BatchNorm-like layers (since those need to be done in FP32 precision to be stable). In Apex, the function that does this for us is `convert_network`. We can use it to put the model in FP16 or back to FP32.
```
model = nn.Sequential(nn.Linear(10,30), nn.BatchNorm1d(30), nn.Linear(30,2)).cuda()
model = convert_network(model, torch.float16)
for i,t in enumerate([torch.float16, torch.float32, torch.float16]):
test_eq(model[i].weight.dtype, t)
test_eq(model[i].bias.dtype, t)
model = nn.Sequential(nn.Linear(10,30), BatchNorm(30, ndim=1), nn.Linear(30,2)).cuda()
model = convert_network(model, torch.float16)
for i,t in enumerate([torch.float16, torch.float32, torch.float16]):
test_eq(model[i].weight.dtype, t)
test_eq(model[i].bias.dtype, t)
```
### Creating the master copy of the parameters
From our model parameters (mostly in FP16), we'll want to create a copy in FP32 (master parameters) that we will use for the step in the optimizer. Optionally, we concatenate all the parameters to do one flat big tensor, which can make that step a little bit faster.
We can't use the FP16 util function here as it doesn't handle multiple parameter groups, which is the thing we use to
- do transfer learning and freeze some layers
- apply discriminative learning rates
- don't apply weight decay to some layers (like BatchNorm) or the bias terms
```
#export
from torch.nn.utils import parameters_to_vector
#export
def get_master(opt, flat_master=False):
model_params = [[param for param in pg if getattr(param, 'requires_grad', False) and hasattr(param, 'data')] for pg in opt.param_lists]
if flat_master:
master_params = []
for pg in model_params:
mp = parameters_to_vector([param.data.float() for param in pg])
mp = nn.Parameter(mp, requires_grad=True)
if mp.grad is None: mp.grad = mp.new(*mp.size())
master_params.append([mp])
else:
master_params = [[nn.Parameter(param.data.clone().float().detach(), requires_grad=True) for param in pg] for pg in model_params]
return model_params, master_params
#hide
#cuda
learn = synth_learner()
learn.model = convert_network(nn.Sequential(nn.Linear(1,1), nn.Linear(1,1)), torch.float16).cuda()
learn.splitter = lambda m: [list(m[0].parameters()), list(m[1].parameters())]
learn.opt = learn.opt_func(learn.splitter(learn.model), learn.lr)
model_p,master_p = get_master(learn.opt)
test_eq(len(model_p), 2) #2 pqrqm groups
test_eq(len(master_p), 2)
for pg1,pg2 in zip(model_p,master_p):
test_eq([p.float() for p in pg1], pg2) #Same values but different types
for p in pg1: assert p.dtype == torch.float16
#hide
#cuda
#Flattened version
model_pf,master_pf = get_master(learn.opt, flat_master=True)
test_eq(len(model_pf), 2) #2 pqrqm groups
test_eq(len(master_pf), 2)
for pg1,pg2 in zip(model_pf,master_pf):
test_eq(len(pg2), 1) #One flattened tensor
test_eq([p.float().squeeze() for p in pg1], [p for p in pg2[0]]) #Same values but different types
for p in pg1: assert p.dtype == torch.float16
```
### Copy the gradients from model params to master params
After the backward pass, all gradients must be copied to the master params before the optimizer step can be done in FP32. The corresponding function in the Apex utils is `model_grads_to_master_grads` but we need to adapt it to work with param groups.
```
# export
def to_master_grads(model_pgs, master_pgs, flat_master=False):
for (model_params,master_params) in zip(model_pgs,master_pgs):
model_grads_to_master_grads(model_params, master_params, flat_master=flat_master)
#hide
#cuda
xb,yb = learn.dls.one_batch()
pred = learn.model.cuda()(xb.cuda().half())
loss = F.mse_loss(pred, yb.cuda().half())
loss.backward()
to_master_grads(model_p, master_p)
to_master_grads(model_pf, master_pf, flat_master=True)
test_eq([[p.grad.float() for p in pg] for pg in model_p],
[[p.grad for p in pg] for pg in master_p])
test_eq([[p.grad.float().squeeze() for p in pg] for pg in model_pf],
[[p for p in pg[0].grad] for pg in master_pf])
xb.shape
```
### Copy the master params to the model params
After the step, we need to copy back the master parameters to the model parameters for the next update. The corresponding function in Apex is `master_params_to_model_params`.
```
# export
def to_model_params(model_pgs, master_pgs, flat_master=False)->None:
for (model_params,master_params) in zip(model_pgs,master_pgs):
master_params_to_model_params(model_params, master_params, flat_master=flat_master)
#hide
#cuda
learn.opt.params = master_p
learn.opt.step()
to_model_params(model_p, master_p)
test_close([p.float() for pg in model_p for p in pg], [p for pg in master_p for p in pg], eps=1e-3)
#hide
#cuda
learn.opt.params = master_pf
learn.opt.step()
to_model_params(model_pf, master_pf, flat_master=True)
test_close([p.float().squeeze() for pg in model_pf for p in pg], [p for pg in master_pf for p in pg[0]], eps=1e-3)
```
### Checking for overflow
For dynamic loss scaling, we need to know when the gradients have gone up to infinity. It's faster to check it on the sum than to do `torch.isinf(x).any()`.
```
# export
def test_overflow(x):
s = float(x.float().sum())
return (s == float('inf') or s == float('-inf') or s != s)
x = torch.randn(3,4)
assert not test_overflow(x)
x[1,2] = float('inf')
assert test_overflow(x)
```
Then we can use it in the following function that checks for gradient overflow:
```
# export
def grad_overflow(pgs):
for pg in pgs:
for p in pg:
if p.grad is not None and test_overflow(p.grad.data): return True
return False
#hide
#cuda
assert not grad_overflow(model_p)
assert not grad_overflow(model_pf)
model_p[1][0].grad.data[0,0] = float('inf')
model_pf[0][1].grad.data[0] = float('inf')
assert grad_overflow(model_p)
assert grad_overflow(model_pf)
```
## NonNativeMixedPrecision -
```
# export
def copy_clone(d):
return {k:(v.detach().clone().float() if isinstance(v,Tensor) else v) for k,v in d.items()}
# export
def _copy_state(opt, pgs1, pgs2):
opt.param_lists = pgs2
for pg1,pg2 in zip(pgs1, pgs2):
for p1,p2 in zip(pg1, pg2): opt.state[p2] = copy_clone(opt.state.pop(p1, {}))
# export
class ModelToHalf(Callback):
"Use with NonNativeMixedPrecision callback (but it needs to run at the very beginning)"
order=-50
def before_fit(self): self.learn.model = convert_network(self.model, dtype=torch.float16)
def after_fit (self): self.learn.model = convert_network(self.model, dtype=torch.float32)
#export
@docs
class NonNativeMixedPrecision(Callback):
"Run training in mixed precision"
order=10
def __init__(self, loss_scale=512, flat_master=False, dynamic=True, max_loss_scale=2.**24,
div_factor=2., scale_wait=500, clip=None):
assert torch.backends.cudnn.enabled, "Mixed precision training requires cudnn."
self.flat_master,self.dynamic,self.max_loss_scale = flat_master,dynamic,max_loss_scale
self.div_factor,self.scale_wait,self.clip = div_factor,scale_wait,clip
self.loss_scale = max_loss_scale if dynamic else loss_scale
def before_fit(self):
assert self.dls.device.type == 'cuda', "Mixed-precision training requires a GPU, remove the call `to_fp16`"
if self.learn.opt is None: self.learn.create_opt()
self.model_pgs,self.master_pgs = get_master(self.opt, self.flat_master)
self.old_pgs = self.opt.param_lists
#Changes the optimizer so that the optimization step is done in FP32.
_copy_state(self.learn.opt, self.model_pgs, self.master_pgs)
if self.dynamic: self.count = 0
def before_batch(self): self.learn.xb = to_half(self.xb)
def after_pred(self): self.learn.pred = to_float(self.pred)
def before_backward(self): self.learn.loss_grad *= self.loss_scale
def before_step(self):
#First, check for an overflow
if self.dynamic and grad_overflow(self.model_pgs):
self.loss_scale /= self.div_factor
self.learn.loss_grad /= self.div_factor #to record correct loss
self.model.zero_grad()
raise CancelBatchException() #skip step and zero_grad
to_master_grads(self.model_pgs, self.master_pgs, self.flat_master)
for master_params in self.master_pgs:
for param in master_params:
if param.grad is not None: param.grad.div_(self.loss_scale)
if self.clip is not None:
for group in self.master_pgs: nn.utils.clip_grad_norm_(group, self.clip)
# Check if it's been long enough without overflow
if self.dynamic:
self.count += 1
if self.count == self.scale_wait:
self.count = 0
self.loss_scale *= self.div_factor
def after_step(self):
self.model.zero_grad() #Zero the gradients of the model manually (optimizer disconnected)
to_model_params(self.model_pgs, self.master_pgs, self.flat_master)
def after_batch(self):
if self.training: self.learn.loss_grad /= self.loss_scale #Log correct loss
def after_fit(self):
if not hasattr(self,'master_pgs'): return
_copy_state(self.learn.opt, self.master_pgs, self.model_pgs)
self.learn.opt.param_lists = self.old_pgs
delattr(self, "master_pgs")
delattr(self, "model_pgs")
delattr(self, "old_pgs")
_docs = dict(before_fit="Put the model in FP16 and prepare the two copies of the parameters",
before_batch="Put the input in FP16",
after_pred="Put the output back to FP32 so that the loss is computed in FP32",
before_backward="Apply loss scaling to avoid gradient underflow",
before_step="Copy the gradients to the master param and undo the loss scaling",
after_step="Copy the master params to the model params",
after_batch="Ensure loss is logged correctly",
after_fit="Put the model back in FP32")
#hide
class TestBeforeMixedPrecision(Callback):
order=-55
def before_fit(self): test_eq(first(self.model.parameters()).dtype, torch.float32)
def before_batch(self): test_eq(self.x.dtype, torch.float32)
def after_pred(self): test_eq(self.pred.dtype, torch.float16)
def after_loss(self): self.tst_loss = self.learn.loss_grad.detach().clone()
def before_step(self):
self.learn.has_overflown = grad_overflow(self.non_native_mixed_precision.model_pgs)
self.grads = [p.grad.data.clone() for p in self.model.parameters()]
self.old_params = [p.data.clone() for p in self.model.parameters()]
def after_cancel_step(self): assert self.has_overflown
class TestAfterMixedPrecision(Callback):
order=65
def before_fit(self): test_eq(first(self.model.parameters()).dtype, torch.float16)
def after_fit(self): test_eq(first(self.model.parameters()).dtype, torch.float32)
def before_batch(self): test_eq(self.x.dtype, torch.float16)
def after_pred(self): test_eq(self.pred.dtype, torch.float32)
def before_backward(self):
loss_scale = self.non_native_mixed_precision.loss_scale if self.training else 1.
test_eq(self.loss_grad, self.test_before_mixed_precision.tst_loss * loss_scale)
def before_step(self):
tbmp = self.test_before_mixed_precision
test_eq(self.loss_grad, tbmp.loss_grad)
#Test gradients have been copied and scaled back
test_close(sum([[p.grad.data for p in pg] for pg in self.non_native_mixed_precision.master_pgs], []),
[g.float()/self.non_native_mixed_precision.loss_scale for g in tbmp.grads])
def after_batch(self):
if self.has_overflown: return
tbmp,mp =self.test_before_mixed_precision,self.non_native_mixed_precision
#Test master params have been copied to model
test_close(sum([[p.data for p in pg] for pg in mp.master_pgs], []),
[p.data.float() for p in self.model.parameters()], eps=1e-3)
#Test update has been done properly
for p,g,op in zip(self.model.parameters(), tbmp.grads, tbmp.old_params):
test_close(p.data.float(), op.float() - self.lr*g.float()/self.non_native_mixed_precision.loss_scale, eps=1e-3)
#hide
#cuda
learn = synth_learner(cbs=[ModelToHalf(), NonNativeMixedPrecision()], cuda=True)
learn.model = nn.Sequential(nn.Linear(1,1), nn.Linear(1,1)).cuda()
learn.opt_func = partial(SGD, mom=0.)
learn.splitter = lambda m: [list(m[0].parameters()), list(m[1].parameters())]
learn.fit(3, cbs=[TestAfterMixedPrecision(), TestBeforeMixedPrecision()])
#Check loss scale did change
assert 1 < learn.non_native_mixed_precision.loss_scale < 2**24
#Check the model did train
for v1,v2 in zip(learn.recorder.values[0], learn.recorder.values[-1]): assert v2<v1
#hide
#cuda
learn = synth_learner(cbs=[ModelToHalf(), NonNativeMixedPrecision(dynamic=False)], cuda=True)
learn.model = nn.Sequential(nn.Linear(1,1), nn.Linear(1,1)).cuda()
learn.opt_func = partial(SGD, mom=0.)
learn.splitter = lambda m: [list(m[0].parameters()), list(m[1].parameters())]
learn.fit(3, cbs=[TestAfterMixedPrecision(), TestBeforeMixedPrecision()])
#Check loss scale did mot change
test_eq(learn.non_native_mixed_precision.loss_scale,512)
#Check the model did train
for v1,v2 in zip(learn.recorder.values[0], learn.recorder.values[-1]): assert v2<v1
#export
@patch
@delegates(NonNativeMixedPrecision.__init__)
def to_non_native_fp16(self:Learner, **kwargs): return self.add_cbs([ModelToHalf(), NonNativeMixedPrecision(**kwargs)])
#cuda
learn = synth_learner(cuda=True)
learn.model = nn.Sequential(nn.Linear(1,1), nn.Linear(1,1)).cuda()
learn.opt_func = partial(SGD, mom=0.)
learn.splitter = lambda m: [list(m[0].parameters()), list(m[1].parameters())]
learn.to_non_native_fp16()
learn.fit(3, cbs=[TestAfterMixedPrecision(), TestBeforeMixedPrecision()])
#Check the model did train
for v1,v2 in zip(learn.recorder.values[0], learn.recorder.values[-1]): assert v2<v1
#hide
#cuda
learn = synth_learner(cuda=True)
learn.model = nn.Sequential(nn.Linear(1,1), nn.Linear(1,1)).cuda()
learn.opt_func = partial(SGD, mom=0.9)
learn.splitter = lambda m: [list(m[0].parameters()), list(m[1].parameters())]
learn.to_non_native_fp16()
learn.freeze()
learn.create_opt()
init_ps = [p for pg in learn.opt.param_groups for p in pg]
learn.fit(3)
final_ps = [p for pg in learn.opt.param_groups for p in pg]
for p1,p2 in zip(init_ps, final_ps): test_is(p1, p2)
#First param groups has no state because not trained
test_eq([learn.opt.state[p] for p in learn.opt.param_lists[0]], [{}, {'do_wd': False}])
#Second param groups has state
for p in learn.opt.param_lists[1]: assert 'grad_avg' in learn.opt.state[p]
#export
@patch
def to_non_native_fp32(self: Learner): return self.remove_cbs([ModelToHalf, NonNativeMixedPrecision])
#cuda
learn = learn.to_non_native_fp32()
```
## Export -
```
#hide
from nbdev.export import *
notebook2script()
```
|
github_jupyter
|
#hide
#skip
! [ -e /content ] && pip install -Uqq fastai # upgrade fastai on colab
# all_cuda
#export
from fastai.basics import *
from fastai.callback.progress import *
from torch.cuda.amp import GradScaler,autocast
from torch.cuda.amp.grad_scaler import OptState
#default_exp callback.fp16
#hide
from fastai.test_utils import *
from nbdev.showdoc import *
#export
@delegates(GradScaler)
class MixedPrecision(Callback):
"Mixed precision training using Pytorch's `autocast` and `GradScaler`"
order = 10
def __init__(self, **kwargs): self.kwargs,self.autocast = kwargs,autocast()
def before_fit(self): self.learn.scaler,self.scales = GradScaler(**self.kwargs),L()
def before_batch(self): self.autocast.__enter__()
def after_pred(self):
if listify(self.pred)[0].dtype==torch.float16: self.learn.pred = to_float(self.pred)
def after_loss(self): self.autocast.__exit__()
def before_backward(self): self.learn.loss_grad = self.scaler.scale(self.loss_grad)
def before_step(self):
self.skipped=True
self.scaler.step(self)
if self.skipped: raise CancelStepException()
self.scales.append(self.scaler.get_scale())
def after_step(self): self.learn.scaler.update()
@property # pretend to be an optimizer for `GradScaler`
def param_groups(self): return self.opt.param_groups
def step(self, *args, **kwargs): self.skipped=False
#export
class FP16TestCallback(Callback):
"Asserts that predictions are `float16` values"
order = 9
def after_pred(self): assert listify(self.pred)[0].dtype==torch.float16
#cuda
set_seed(99, True)
learn = synth_learner(cbs=[MixedPrecision,FP16TestCallback], cuda=True)
learn.model = nn.Sequential(nn.Linear(1,1), nn.Linear(1,1)).cuda()
learn.opt_func = partial(SGD, mom=0.)
learn.splitter = lambda m: [list(m[0].parameters()), list(m[1].parameters())]
learn.fit(3)
assert learn.recorder.values[-1][-1]<learn.recorder.values[0][-1]
#hide
#cuda
#Multioutput version
set_seed(99, True)
learn = synth_learner(cbs=[MixedPrecision,FP16TestCallback], cuda=True)
class MultiOutputModel(Module):
def __init__(self): self.linear1, self.linear2 = nn.Linear(1,1) , nn.Linear(1,1)
def forward(self,x): return self.linear1(x), self.linear2(x)
def multioutputloss(pred, val): return ((val-pred[0]).abs() + 0.5 * (val-pred[1]).abs()).sum()
learn.model = MultiOutputModel()
learn.opt_func = partial(SGD, mom=0.)
learn.splitter = lambda m: [list(m.linear1.parameters()), list(m.linear2.parameters())]
learn.loss_func=multioutputloss
learn.fit(3)
assert learn.recorder.values[-1][-1]<learn.recorder.values[0][-1]
#export
@patch
@delegates(GradScaler)
def to_fp16(self:Learner, **kwargs): return self.add_cb(MixedPrecision(**kwargs))
#export
@patch
def to_fp32(self:Learner): return self.remove_cb(MixedPrecision)
# export
from fastai.fp16_utils import convert_network, model_grads_to_master_grads, master_params_to_model_params
model = nn.Sequential(nn.Linear(10,30), nn.BatchNorm1d(30), nn.Linear(30,2)).cuda()
model = convert_network(model, torch.float16)
for i,t in enumerate([torch.float16, torch.float32, torch.float16]):
test_eq(model[i].weight.dtype, t)
test_eq(model[i].bias.dtype, t)
model = nn.Sequential(nn.Linear(10,30), BatchNorm(30, ndim=1), nn.Linear(30,2)).cuda()
model = convert_network(model, torch.float16)
for i,t in enumerate([torch.float16, torch.float32, torch.float16]):
test_eq(model[i].weight.dtype, t)
test_eq(model[i].bias.dtype, t)
#export
from torch.nn.utils import parameters_to_vector
#export
def get_master(opt, flat_master=False):
model_params = [[param for param in pg if getattr(param, 'requires_grad', False) and hasattr(param, 'data')] for pg in opt.param_lists]
if flat_master:
master_params = []
for pg in model_params:
mp = parameters_to_vector([param.data.float() for param in pg])
mp = nn.Parameter(mp, requires_grad=True)
if mp.grad is None: mp.grad = mp.new(*mp.size())
master_params.append([mp])
else:
master_params = [[nn.Parameter(param.data.clone().float().detach(), requires_grad=True) for param in pg] for pg in model_params]
return model_params, master_params
#hide
#cuda
learn = synth_learner()
learn.model = convert_network(nn.Sequential(nn.Linear(1,1), nn.Linear(1,1)), torch.float16).cuda()
learn.splitter = lambda m: [list(m[0].parameters()), list(m[1].parameters())]
learn.opt = learn.opt_func(learn.splitter(learn.model), learn.lr)
model_p,master_p = get_master(learn.opt)
test_eq(len(model_p), 2) #2 pqrqm groups
test_eq(len(master_p), 2)
for pg1,pg2 in zip(model_p,master_p):
test_eq([p.float() for p in pg1], pg2) #Same values but different types
for p in pg1: assert p.dtype == torch.float16
#hide
#cuda
#Flattened version
model_pf,master_pf = get_master(learn.opt, flat_master=True)
test_eq(len(model_pf), 2) #2 pqrqm groups
test_eq(len(master_pf), 2)
for pg1,pg2 in zip(model_pf,master_pf):
test_eq(len(pg2), 1) #One flattened tensor
test_eq([p.float().squeeze() for p in pg1], [p for p in pg2[0]]) #Same values but different types
for p in pg1: assert p.dtype == torch.float16
# export
def to_master_grads(model_pgs, master_pgs, flat_master=False):
for (model_params,master_params) in zip(model_pgs,master_pgs):
model_grads_to_master_grads(model_params, master_params, flat_master=flat_master)
#hide
#cuda
xb,yb = learn.dls.one_batch()
pred = learn.model.cuda()(xb.cuda().half())
loss = F.mse_loss(pred, yb.cuda().half())
loss.backward()
to_master_grads(model_p, master_p)
to_master_grads(model_pf, master_pf, flat_master=True)
test_eq([[p.grad.float() for p in pg] for pg in model_p],
[[p.grad for p in pg] for pg in master_p])
test_eq([[p.grad.float().squeeze() for p in pg] for pg in model_pf],
[[p for p in pg[0].grad] for pg in master_pf])
xb.shape
# export
def to_model_params(model_pgs, master_pgs, flat_master=False)->None:
for (model_params,master_params) in zip(model_pgs,master_pgs):
master_params_to_model_params(model_params, master_params, flat_master=flat_master)
#hide
#cuda
learn.opt.params = master_p
learn.opt.step()
to_model_params(model_p, master_p)
test_close([p.float() for pg in model_p for p in pg], [p for pg in master_p for p in pg], eps=1e-3)
#hide
#cuda
learn.opt.params = master_pf
learn.opt.step()
to_model_params(model_pf, master_pf, flat_master=True)
test_close([p.float().squeeze() for pg in model_pf for p in pg], [p for pg in master_pf for p in pg[0]], eps=1e-3)
# export
def test_overflow(x):
s = float(x.float().sum())
return (s == float('inf') or s == float('-inf') or s != s)
x = torch.randn(3,4)
assert not test_overflow(x)
x[1,2] = float('inf')
assert test_overflow(x)
# export
def grad_overflow(pgs):
for pg in pgs:
for p in pg:
if p.grad is not None and test_overflow(p.grad.data): return True
return False
#hide
#cuda
assert not grad_overflow(model_p)
assert not grad_overflow(model_pf)
model_p[1][0].grad.data[0,0] = float('inf')
model_pf[0][1].grad.data[0] = float('inf')
assert grad_overflow(model_p)
assert grad_overflow(model_pf)
# export
def copy_clone(d):
return {k:(v.detach().clone().float() if isinstance(v,Tensor) else v) for k,v in d.items()}
# export
def _copy_state(opt, pgs1, pgs2):
opt.param_lists = pgs2
for pg1,pg2 in zip(pgs1, pgs2):
for p1,p2 in zip(pg1, pg2): opt.state[p2] = copy_clone(opt.state.pop(p1, {}))
# export
class ModelToHalf(Callback):
"Use with NonNativeMixedPrecision callback (but it needs to run at the very beginning)"
order=-50
def before_fit(self): self.learn.model = convert_network(self.model, dtype=torch.float16)
def after_fit (self): self.learn.model = convert_network(self.model, dtype=torch.float32)
#export
@docs
class NonNativeMixedPrecision(Callback):
"Run training in mixed precision"
order=10
def __init__(self, loss_scale=512, flat_master=False, dynamic=True, max_loss_scale=2.**24,
div_factor=2., scale_wait=500, clip=None):
assert torch.backends.cudnn.enabled, "Mixed precision training requires cudnn."
self.flat_master,self.dynamic,self.max_loss_scale = flat_master,dynamic,max_loss_scale
self.div_factor,self.scale_wait,self.clip = div_factor,scale_wait,clip
self.loss_scale = max_loss_scale if dynamic else loss_scale
def before_fit(self):
assert self.dls.device.type == 'cuda', "Mixed-precision training requires a GPU, remove the call `to_fp16`"
if self.learn.opt is None: self.learn.create_opt()
self.model_pgs,self.master_pgs = get_master(self.opt, self.flat_master)
self.old_pgs = self.opt.param_lists
#Changes the optimizer so that the optimization step is done in FP32.
_copy_state(self.learn.opt, self.model_pgs, self.master_pgs)
if self.dynamic: self.count = 0
def before_batch(self): self.learn.xb = to_half(self.xb)
def after_pred(self): self.learn.pred = to_float(self.pred)
def before_backward(self): self.learn.loss_grad *= self.loss_scale
def before_step(self):
#First, check for an overflow
if self.dynamic and grad_overflow(self.model_pgs):
self.loss_scale /= self.div_factor
self.learn.loss_grad /= self.div_factor #to record correct loss
self.model.zero_grad()
raise CancelBatchException() #skip step and zero_grad
to_master_grads(self.model_pgs, self.master_pgs, self.flat_master)
for master_params in self.master_pgs:
for param in master_params:
if param.grad is not None: param.grad.div_(self.loss_scale)
if self.clip is not None:
for group in self.master_pgs: nn.utils.clip_grad_norm_(group, self.clip)
# Check if it's been long enough without overflow
if self.dynamic:
self.count += 1
if self.count == self.scale_wait:
self.count = 0
self.loss_scale *= self.div_factor
def after_step(self):
self.model.zero_grad() #Zero the gradients of the model manually (optimizer disconnected)
to_model_params(self.model_pgs, self.master_pgs, self.flat_master)
def after_batch(self):
if self.training: self.learn.loss_grad /= self.loss_scale #Log correct loss
def after_fit(self):
if not hasattr(self,'master_pgs'): return
_copy_state(self.learn.opt, self.master_pgs, self.model_pgs)
self.learn.opt.param_lists = self.old_pgs
delattr(self, "master_pgs")
delattr(self, "model_pgs")
delattr(self, "old_pgs")
_docs = dict(before_fit="Put the model in FP16 and prepare the two copies of the parameters",
before_batch="Put the input in FP16",
after_pred="Put the output back to FP32 so that the loss is computed in FP32",
before_backward="Apply loss scaling to avoid gradient underflow",
before_step="Copy the gradients to the master param and undo the loss scaling",
after_step="Copy the master params to the model params",
after_batch="Ensure loss is logged correctly",
after_fit="Put the model back in FP32")
#hide
class TestBeforeMixedPrecision(Callback):
order=-55
def before_fit(self): test_eq(first(self.model.parameters()).dtype, torch.float32)
def before_batch(self): test_eq(self.x.dtype, torch.float32)
def after_pred(self): test_eq(self.pred.dtype, torch.float16)
def after_loss(self): self.tst_loss = self.learn.loss_grad.detach().clone()
def before_step(self):
self.learn.has_overflown = grad_overflow(self.non_native_mixed_precision.model_pgs)
self.grads = [p.grad.data.clone() for p in self.model.parameters()]
self.old_params = [p.data.clone() for p in self.model.parameters()]
def after_cancel_step(self): assert self.has_overflown
class TestAfterMixedPrecision(Callback):
order=65
def before_fit(self): test_eq(first(self.model.parameters()).dtype, torch.float16)
def after_fit(self): test_eq(first(self.model.parameters()).dtype, torch.float32)
def before_batch(self): test_eq(self.x.dtype, torch.float16)
def after_pred(self): test_eq(self.pred.dtype, torch.float32)
def before_backward(self):
loss_scale = self.non_native_mixed_precision.loss_scale if self.training else 1.
test_eq(self.loss_grad, self.test_before_mixed_precision.tst_loss * loss_scale)
def before_step(self):
tbmp = self.test_before_mixed_precision
test_eq(self.loss_grad, tbmp.loss_grad)
#Test gradients have been copied and scaled back
test_close(sum([[p.grad.data for p in pg] for pg in self.non_native_mixed_precision.master_pgs], []),
[g.float()/self.non_native_mixed_precision.loss_scale for g in tbmp.grads])
def after_batch(self):
if self.has_overflown: return
tbmp,mp =self.test_before_mixed_precision,self.non_native_mixed_precision
#Test master params have been copied to model
test_close(sum([[p.data for p in pg] for pg in mp.master_pgs], []),
[p.data.float() for p in self.model.parameters()], eps=1e-3)
#Test update has been done properly
for p,g,op in zip(self.model.parameters(), tbmp.grads, tbmp.old_params):
test_close(p.data.float(), op.float() - self.lr*g.float()/self.non_native_mixed_precision.loss_scale, eps=1e-3)
#hide
#cuda
learn = synth_learner(cbs=[ModelToHalf(), NonNativeMixedPrecision()], cuda=True)
learn.model = nn.Sequential(nn.Linear(1,1), nn.Linear(1,1)).cuda()
learn.opt_func = partial(SGD, mom=0.)
learn.splitter = lambda m: [list(m[0].parameters()), list(m[1].parameters())]
learn.fit(3, cbs=[TestAfterMixedPrecision(), TestBeforeMixedPrecision()])
#Check loss scale did change
assert 1 < learn.non_native_mixed_precision.loss_scale < 2**24
#Check the model did train
for v1,v2 in zip(learn.recorder.values[0], learn.recorder.values[-1]): assert v2<v1
#hide
#cuda
learn = synth_learner(cbs=[ModelToHalf(), NonNativeMixedPrecision(dynamic=False)], cuda=True)
learn.model = nn.Sequential(nn.Linear(1,1), nn.Linear(1,1)).cuda()
learn.opt_func = partial(SGD, mom=0.)
learn.splitter = lambda m: [list(m[0].parameters()), list(m[1].parameters())]
learn.fit(3, cbs=[TestAfterMixedPrecision(), TestBeforeMixedPrecision()])
#Check loss scale did mot change
test_eq(learn.non_native_mixed_precision.loss_scale,512)
#Check the model did train
for v1,v2 in zip(learn.recorder.values[0], learn.recorder.values[-1]): assert v2<v1
#export
@patch
@delegates(NonNativeMixedPrecision.__init__)
def to_non_native_fp16(self:Learner, **kwargs): return self.add_cbs([ModelToHalf(), NonNativeMixedPrecision(**kwargs)])
#cuda
learn = synth_learner(cuda=True)
learn.model = nn.Sequential(nn.Linear(1,1), nn.Linear(1,1)).cuda()
learn.opt_func = partial(SGD, mom=0.)
learn.splitter = lambda m: [list(m[0].parameters()), list(m[1].parameters())]
learn.to_non_native_fp16()
learn.fit(3, cbs=[TestAfterMixedPrecision(), TestBeforeMixedPrecision()])
#Check the model did train
for v1,v2 in zip(learn.recorder.values[0], learn.recorder.values[-1]): assert v2<v1
#hide
#cuda
learn = synth_learner(cuda=True)
learn.model = nn.Sequential(nn.Linear(1,1), nn.Linear(1,1)).cuda()
learn.opt_func = partial(SGD, mom=0.9)
learn.splitter = lambda m: [list(m[0].parameters()), list(m[1].parameters())]
learn.to_non_native_fp16()
learn.freeze()
learn.create_opt()
init_ps = [p for pg in learn.opt.param_groups for p in pg]
learn.fit(3)
final_ps = [p for pg in learn.opt.param_groups for p in pg]
for p1,p2 in zip(init_ps, final_ps): test_is(p1, p2)
#First param groups has no state because not trained
test_eq([learn.opt.state[p] for p in learn.opt.param_lists[0]], [{}, {'do_wd': False}])
#Second param groups has state
for p in learn.opt.param_lists[1]: assert 'grad_avg' in learn.opt.state[p]
#export
@patch
def to_non_native_fp32(self: Learner): return self.remove_cbs([ModelToHalf, NonNativeMixedPrecision])
#cuda
learn = learn.to_non_native_fp32()
#hide
from nbdev.export import *
notebook2script()
| 0.794106 | 0.926037 |
# ¿Cómo funciona `git`?
<img src="http://conociendogithub.readthedocs.io/en/latest/_images/Git.png" title="git" width="200" height="50" align="center">
___
### Descargar `git`
https://git-scm.com/downloads
**Control de versiones**
<p align = "justify"> `Git` es un software de control de versiones diseñado por Linus Torvalds, pensando en la eficiencia y la confiabilidad del mantenimiento de versiones de aplicaciones cuando éstas tienen un gran número de archivos de código fuente.</p>
<p align = "justify"> Se llama control de versiones a la gestión de los diversos cambios que se realizan sobre los elementos de algún producto o una configuración del mismo. Una versión, revisión o edición de un producto, es el estado en el que se encuentra el mismo en un momento dado de su desarrollo o modificación.</p>
### Set up `git`
- https://help.github.com/articles/set-up-git/
Referencias:
- https://git-scm.com/doc
- https://es.wikipedia.org/wiki/Git
- https://try.github.io/
- http://learngitbranching.js.org
- https://es.wikipedia.org/wiki/Control_de_versiones
### !git init
Sirve para crear el directorio ".git/", localmente. En ese directorio está todo lo importante relacionado con **git**. Si se borra este directorio se pierde toda la información del repositorio.
```
!git init
```
**Nota:** En el shell(prompt, terminal) solo es necesario escribir **git init**
Si deseamos saber en que directorio estamos actualmente usamos:
```
pwd
```
Borrar un directorio _rm -r mydir_
Y si queremos ver el contenido en dicho directorio
```
ls
```
Veamos lo que contiene todo el directorio **git**
```
ls -alp .git
```
### `git` clone
Este comando clona un repositorio remoto de `git` en un directorio local. Este comando configura el repositorio para notar los cambios que se hacen en el repositorio remoto.
Como ejemplo de este comando, para clonar este curso deben usar la instrucción
> ```git clone https://github.com/LazarusA/Simulacion2017```
lo que creará el directorio (local, respecto al lugar donde ejecuten el comando) Simulacion2017
### !`git` help
```
!git help
```
**Para obtener el manual correspondiente a cada comando se usa**
> ```git help <command>```
```
!git help mv
```
### !git status
Muestra el estado del repositorio, por ejemplo: la rama en la que se está trabajando, los cambios en los archivos que se siguen y los que no se están siguiendo.
```
!git status
```
### !git log
```
!git log
```
### git add
Este es uno de los comandos más importantes: agrega el contenido del archivo a la lista de archivos cuyos cambios se segurán en el repositorio:
> ```git add <file>```
### git commit
Este comando "compromete" los cambios hechos y agregados con git add, es decir, los incluye en el historial del repositorio. Es un comando muy importante, en el sentido que no usarlo puede llevar a pérdida del trabajo realizado.
### git checkout
Este comando tiene varias aplicaciones.
> ```git checkout my_branch```
sirve para cambiarse de rama, a la rama "my_branch". También permite crear ramas, por ejemplo la rama "other_branch", usando
> ```git checkout -b other_branch```
También permite revertir ciertos cambios en archivos. Por ejemplo,
> ```git checkout -- file```
revierte los cambios hecho en el archivo "file", es decir, vuelve a la versión del archivo (o de directorios) que está almacenada en el historial de git.
### Configuración de `git`
Los comandos básicos de configuración son:
>
```
git config --global user.name "Tu nombre"
git config --global user.email "tu_usuario@email_real.com"
git config --global color.ui "auto"
git config --global github.user "Usuario_GitHub"
```
> `git` config --list
Si su configuración es local, por ejemplo, por que comparten la cuenta en la máquina en la que trabajan, en lugar de usar --global deben usar --local.
## `git` colaborativo
### Ramas (*branches*)
Un punto esencial para hacer de `git` una herramienta colaborativa es el uso de ramas (*branches*).
La idea es trabajar en una rama independiente. En esa rama uno hace un desarrollo específico, que eventualmente se envía para ser considerado a incluirse en el proyecto.
Para crear una rama, uno usa el comando
> ```
git branch <nombre_rama>
```
Ejemplos de posibles nombres de ramas son "tutorial_git" o "LazarusA/GitTutorial".
El comando anterior *crea* la rama, pero no nos cambia a esa rama. Para cambiarnos, utilizamos (ver arriba) el comando `git checkout <nombre_rama>`. Para ver qué ramas hay en el proyecto, uno usa el comando `git branch -v`.
Una manera más corta de crear la rama y cambiarnos a ella es usar el comando
```
git checkout -b <nombre_rama>
```
Es importante señalar que uno puede crear tantas ramas como se quiera.
La idea de las ramas es hacer todos los ensayos posibles sin que esto afecte el desarrollo del proyecto (cuya rama principal es `master`); eventualmente uno hace (desde su propio *fork* en GitHub un *Pull Request* para que los cambios se incluyan en el proyecto.
### Servidores remotos
Uno debe tener claro que uno tiene una copia íntegra del repositorio en su disco duro. El repositorio, además de estar en cada una de nuestras máquinas está en GitHub. Como se dijo más arriba, `git clone` permite clonar un repositorio *remoto* (por ejemplo, en GitHub, aunque no exclusivamente) a un directorio local. `git` permite de hecho poder seguir los cambios de distintos repositorios remotos, por ejemplo el proyecto oficial, y el de nuestro *fork* propio.
Para ver qué configuración se tiene de los repositorios remotos, uno ejecuta `git remove -v`:
Si uno quiere agregar un nuevo servidor para seguir los cambios, por ejemplo, el de su *fork*, lo que se necesita hacer es usar el comando:
>
```
git remote add <alias> <url_de_su_fork>
```
donde `<url_de_su_fork>` es la dirección donde está su *fork* en GitHub, y `<alias>` es la abreviación que le darán (por ejemplo, "fork" o "mifork"; este último es el que usaré).
Las abreviaciones (o alias) de los repositorios son muy útiles. Por ejemplo, ustedes *sólamente* van a poder subir los cambios que hagan en un proyecto a su propio *fork* (o también a los repositorios donde estén declarados como colaboradores del proyecto). El comando
> ```
git push mifork
```
*empuja* sus cambios a `mifork`.
De igual manera, ustedes quieren tener actualizada la rama `master` con el proyecto del curso. Lo que deben hacer para esto es:
>
```
git checkout master
git pull origin
git push mifork
```
La primer instrucción hace el cambio de rama a `master`, y la segunda *jala* los cambios (si es que hay en master) a la rama que tenemos localmente. Vale la pena notar que, si bien tenemos la copia *local* actualizada, la copia en el *fork* aún no lo está; esa es la razón de la tercer instrucción.
<img src="https://raw.githubusercontent.com/louim/in-case-of-fire/master/in_case_of_fire.png" title="In case of fire (https://github.com/louim/in-case-of-fire)" width="200" height="50" align="center">
> Tarea
<script>
$(document).ready(function(){
$('div.prompt').hide();
$('div.back-to-top').hide();
$('nav#menubar').hide();
$('.breadcrumb').hide();
$('.hidden-print').hide();
});
</script>
<footer id="attribution" style="float:right; color:#808080; background:#fff;">
Created with Jupyter by Lázaro Alonso.
</footer>
|
github_jupyter
|
!git init
pwd
ls
ls -alp .git
lo que creará el directorio (local, respecto al lugar donde ejecuten el comando) Simulacion2017
### !`git` help
**Para obtener el manual correspondiente a cada comando se usa**
> ```git help <command>```
### !git status
Muestra el estado del repositorio, por ejemplo: la rama en la que se está trabajando, los cambios en los archivos que se siguen y los que no se están siguiendo.
### !git log
### git add
Este es uno de los comandos más importantes: agrega el contenido del archivo a la lista de archivos cuyos cambios se segurán en el repositorio:
> ```git add <file>```
### git commit
Este comando "compromete" los cambios hechos y agregados con git add, es decir, los incluye en el historial del repositorio. Es un comando muy importante, en el sentido que no usarlo puede llevar a pérdida del trabajo realizado.
### git checkout
Este comando tiene varias aplicaciones.
> ```git checkout my_branch```
sirve para cambiarse de rama, a la rama "my_branch". También permite crear ramas, por ejemplo la rama "other_branch", usando
> ```git checkout -b other_branch```
También permite revertir ciertos cambios en archivos. Por ejemplo,
> ```git checkout -- file```
revierte los cambios hecho en el archivo "file", es decir, vuelve a la versión del archivo (o de directorios) que está almacenada en el historial de git.
### Configuración de `git`
Los comandos básicos de configuración son:
>
> `git` config --list
Si su configuración es local, por ejemplo, por que comparten la cuenta en la máquina en la que trabajan, en lugar de usar --global deben usar --local.
## `git` colaborativo
### Ramas (*branches*)
Un punto esencial para hacer de `git` una herramienta colaborativa es el uso de ramas (*branches*).
La idea es trabajar en una rama independiente. En esa rama uno hace un desarrollo específico, que eventualmente se envía para ser considerado a incluirse en el proyecto.
Para crear una rama, uno usa el comando
> ```
git branch <nombre_rama>
git checkout -b <nombre_rama>
git remote add <alias> <url_de_su_fork>
git push mifork
git checkout master
git pull origin
git push mifork
| 0.417034 | 0.908456 |
Thinking back to the previous examples for tokenization and lexical counting, there is an obvious shortcoming, that it does not assimilate lexically identical words with one another. For example, we may want to count "est" and "sunt" as instances of "esse".
Lemmatization is the non-trivial process of reconciling inflected forms to their dictionary headword. The CLTK offers several methods. We'll show here one of the less sophisticated approaches. (Documentation for a new statistical method is in the works.)
Note: You may have heard of stemming, which is similar in purpose, however it does not convert a word to a dictionary form, but only reduces commonly related forms into a new, unambiguous string (e.g., 'amicitia' --> 'amiciti'). This is not what we need for Greek and Latin.
# Latin
```
cato_agri_praef = "Est interdum praestare mercaturis rem quaerere, nisi tam periculosum sit, et item foenerari, si tam honestum. Maiores nostri sic habuerunt et ita in legibus posiverunt: furem dupli condemnari, foeneratorem quadrupli. Quanto peiorem civem existimarint foeneratorem quam furem, hinc licet existimare. Et virum bonum quom laudabant, ita laudabant: bonum agricolam bonumque colonum; amplissime laudari existimabatur qui ita laudabatur. Mercatorem autem strenuum studiosumque rei quaerendae existimo, verum, ut supra dixi, periculosum et calamitosum. At ex agricolis et viri fortissimi et milites strenuissimi gignuntur, maximeque pius quaestus stabilissimusque consequitur minimeque invidiosus, minimeque male cogitantes sunt qui in eo studio occupati sunt. Nunc, ut ad rem redeam, quod promisi institutum principium hoc erit."
# First import a repository: the CLTK data models for Latin
from cltk.corpus.utils.importer import CorpusImporter
corpus_importer = CorpusImporter('latin')
corpus_importer.import_corpus('latin_models_cltk')
# Replace j/v and tokenize
from cltk.stem.latin.j_v import JVReplacer
from cltk.tokenize.word import WordTokenizer
jv_replacer = JVReplacer()
cato_agri_praef = jv_replacer.replace(cato_agri_praef.lower())
word_tokenizer = WordTokenizer('latin')
cato_word_tokens = word_tokenizer.tokenize(cato_agri_praef.lower())
cato_word_tokens = [token for token in cato_word_tokens if token not in ['.', ',', ':', ';']]
from cltk.stem.lemma import LemmaReplacer
lemmatizer = LemmaReplacer('latin')
lemmata = lemmatizer.lemmatize(cato_word_tokens)
print(lemmata)
# Now we do the same but also return the original form
# This is useful for checking accuracy
lemmata_orig = lemmatizer.lemmatize(cato_word_tokens, return_raw=True)
print(lemmata_orig)
# Let's count again
# Count all words
print(len(lemmata))
# Count unique words
print(len(set(lemmata)))
# Finally, measure lexical diversity, using lemmata
print(len(set(lemmata)) / len(lemmata))
```
Greek
```
athenaeus_incipit = "Ἀθήναιος μὲν ὁ τῆς βίβλου πατήρ· ποιεῖται δὲ τὸν λόγον πρὸς Τιμοκράτην· Δειπνοσοφιστὴς δὲ ταύτῃ τὸ ὄνομα. Ὑπόκειται δὲ τῷ λόγῳ Λαρήνσιος Ῥωμαῖος, ἀνὴρ τῇ τύχῃ περιφανής, τοὺς κατὰ πᾶσαν παιδείαν ἐμπειροτάτους ἐν αὑτοῦ δαιτυμόνας ποιούμενος· ἐν οἷς οὐκ ἔσθ᾽ οὗτινος τῶν καλλίστων οὐκ ἐμνημόνευσεν. Ἰχθῦς τε γὰρ τῇ βίβλῳ ἐνέθετο καὶ τὰς τούτων χρείας καὶ τὰς τῶν ὀνομάτων ἀναπτύξεις καὶ λαχάνων γένη παντοῖα καὶ ζῴων παντοδαπῶν καὶ ἄνδρας ἱστορίας συγγεγραφότας καὶ ποιητὰς καὶ φιλοσόφους καὶ ὄργανα μουσικὰ καὶ σκωμμάτων εἴδη μυρία καὶ ἐκπωμάτων διαφορὰς καὶ πλούτους βασιλέων διηγήσατο καὶ νηῶν μεγέθη καὶ ὅσα ἄλλα οὐδ᾽ ἂν εὐχερῶς ἀπομνημονεύσαιμι, ἢ ἐπιλίποι μ᾽ ἂν ἡ ἡμέρα κατ᾽ εἶδος διεξερχόμενον. Καί ἐστιν ἡ τοῦ λόγου οἰκονομία μίμημα τῆς τοῦ δείπνου πολυτελείας καὶ ἡ τῆς βίβλου διασκευὴ τῆς ἐν τῷ δείπνῳ παρασκευῆς. Τοιοῦτον ὁ θαυμαστὸς οὗτος τοῦ λόγου οἰκονόμος Ἀθήναιος ἥδιστον λογόδειπνον εἰσηγεῖται κρείττων τε αὐτὸς ἑαυτοῦ γινόμενος, ὥσπερ οἱ Ἀθήνησι ῥήτορες, ὑπὸ τῆς ἐν τῷ λέγειν θερμότητος πρὸς τὰ ἑπόμενα τῆς βίβλου βαθμηδὸν ὑπεράλλεται."
from cltk.corpus.utils.importer import CorpusImporter
corpus_importer = CorpusImporter('greek')
corpus_importer.import_corpus('greek_models_cltk')
from cltk.tokenize.word import WordTokenizer
word_tokenizer = WordTokenizer('greek')
athenaeus_word_tokens = word_tokenizer.tokenize(athenaeus_incipit.lower())
athenaeus_word_tokens = [token for token in athenaeus_word_tokens if token not in ['.', ',', ':', ';']]
from cltk.stem.lemma import LemmaReplacer
lemmatizer = LemmaReplacer('greek')
lemmata = lemmatizer.lemmatize(athenaeus_word_tokens)
print(lemmata)
lemmata_orig = lemmatizer.lemmatize(athenaeus_word_tokens, return_raw=True)
print(lemmata_orig)
print(len(lemmata))
print(len(set(lemmata)))
print(len(set(lemmata)) / len(lemmata))
```
|
github_jupyter
|
cato_agri_praef = "Est interdum praestare mercaturis rem quaerere, nisi tam periculosum sit, et item foenerari, si tam honestum. Maiores nostri sic habuerunt et ita in legibus posiverunt: furem dupli condemnari, foeneratorem quadrupli. Quanto peiorem civem existimarint foeneratorem quam furem, hinc licet existimare. Et virum bonum quom laudabant, ita laudabant: bonum agricolam bonumque colonum; amplissime laudari existimabatur qui ita laudabatur. Mercatorem autem strenuum studiosumque rei quaerendae existimo, verum, ut supra dixi, periculosum et calamitosum. At ex agricolis et viri fortissimi et milites strenuissimi gignuntur, maximeque pius quaestus stabilissimusque consequitur minimeque invidiosus, minimeque male cogitantes sunt qui in eo studio occupati sunt. Nunc, ut ad rem redeam, quod promisi institutum principium hoc erit."
# First import a repository: the CLTK data models for Latin
from cltk.corpus.utils.importer import CorpusImporter
corpus_importer = CorpusImporter('latin')
corpus_importer.import_corpus('latin_models_cltk')
# Replace j/v and tokenize
from cltk.stem.latin.j_v import JVReplacer
from cltk.tokenize.word import WordTokenizer
jv_replacer = JVReplacer()
cato_agri_praef = jv_replacer.replace(cato_agri_praef.lower())
word_tokenizer = WordTokenizer('latin')
cato_word_tokens = word_tokenizer.tokenize(cato_agri_praef.lower())
cato_word_tokens = [token for token in cato_word_tokens if token not in ['.', ',', ':', ';']]
from cltk.stem.lemma import LemmaReplacer
lemmatizer = LemmaReplacer('latin')
lemmata = lemmatizer.lemmatize(cato_word_tokens)
print(lemmata)
# Now we do the same but also return the original form
# This is useful for checking accuracy
lemmata_orig = lemmatizer.lemmatize(cato_word_tokens, return_raw=True)
print(lemmata_orig)
# Let's count again
# Count all words
print(len(lemmata))
# Count unique words
print(len(set(lemmata)))
# Finally, measure lexical diversity, using lemmata
print(len(set(lemmata)) / len(lemmata))
athenaeus_incipit = "Ἀθήναιος μὲν ὁ τῆς βίβλου πατήρ· ποιεῖται δὲ τὸν λόγον πρὸς Τιμοκράτην· Δειπνοσοφιστὴς δὲ ταύτῃ τὸ ὄνομα. Ὑπόκειται δὲ τῷ λόγῳ Λαρήνσιος Ῥωμαῖος, ἀνὴρ τῇ τύχῃ περιφανής, τοὺς κατὰ πᾶσαν παιδείαν ἐμπειροτάτους ἐν αὑτοῦ δαιτυμόνας ποιούμενος· ἐν οἷς οὐκ ἔσθ᾽ οὗτινος τῶν καλλίστων οὐκ ἐμνημόνευσεν. Ἰχθῦς τε γὰρ τῇ βίβλῳ ἐνέθετο καὶ τὰς τούτων χρείας καὶ τὰς τῶν ὀνομάτων ἀναπτύξεις καὶ λαχάνων γένη παντοῖα καὶ ζῴων παντοδαπῶν καὶ ἄνδρας ἱστορίας συγγεγραφότας καὶ ποιητὰς καὶ φιλοσόφους καὶ ὄργανα μουσικὰ καὶ σκωμμάτων εἴδη μυρία καὶ ἐκπωμάτων διαφορὰς καὶ πλούτους βασιλέων διηγήσατο καὶ νηῶν μεγέθη καὶ ὅσα ἄλλα οὐδ᾽ ἂν εὐχερῶς ἀπομνημονεύσαιμι, ἢ ἐπιλίποι μ᾽ ἂν ἡ ἡμέρα κατ᾽ εἶδος διεξερχόμενον. Καί ἐστιν ἡ τοῦ λόγου οἰκονομία μίμημα τῆς τοῦ δείπνου πολυτελείας καὶ ἡ τῆς βίβλου διασκευὴ τῆς ἐν τῷ δείπνῳ παρασκευῆς. Τοιοῦτον ὁ θαυμαστὸς οὗτος τοῦ λόγου οἰκονόμος Ἀθήναιος ἥδιστον λογόδειπνον εἰσηγεῖται κρείττων τε αὐτὸς ἑαυτοῦ γινόμενος, ὥσπερ οἱ Ἀθήνησι ῥήτορες, ὑπὸ τῆς ἐν τῷ λέγειν θερμότητος πρὸς τὰ ἑπόμενα τῆς βίβλου βαθμηδὸν ὑπεράλλεται."
from cltk.corpus.utils.importer import CorpusImporter
corpus_importer = CorpusImporter('greek')
corpus_importer.import_corpus('greek_models_cltk')
from cltk.tokenize.word import WordTokenizer
word_tokenizer = WordTokenizer('greek')
athenaeus_word_tokens = word_tokenizer.tokenize(athenaeus_incipit.lower())
athenaeus_word_tokens = [token for token in athenaeus_word_tokens if token not in ['.', ',', ':', ';']]
from cltk.stem.lemma import LemmaReplacer
lemmatizer = LemmaReplacer('greek')
lemmata = lemmatizer.lemmatize(athenaeus_word_tokens)
print(lemmata)
lemmata_orig = lemmatizer.lemmatize(athenaeus_word_tokens, return_raw=True)
print(lemmata_orig)
print(len(lemmata))
print(len(set(lemmata)))
print(len(set(lemmata)) / len(lemmata))
| 0.243103 | 0.734024 |
<a href="https://colab.research.google.com/github/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_02_2_pandas_cat.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# T81-558: Applications of Deep Neural Networks
**Module 2: Python for Machine Learning**
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), McKelvey School of Engineering, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# Module 2 Material
Main video lecture:
* Part 2.1: Introduction to Pandas [[Video]](https://www.youtube.com/watch?v=bN4UuCBdpZc&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_02_1_python_pandas.ipynb)
* **Part 2.2: Categorical Values** [[Video]](https://www.youtube.com/watch?v=4a1odDpG0Ho&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_02_2_pandas_cat.ipynb)
* Part 2.3: Grouping, Sorting, and Shuffling in Python Pandas [[Video]](https://www.youtube.com/watch?v=YS4wm5gD8DM&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_02_3_pandas_grouping.ipynb)
* Part 2.4: Using Apply and Map in Pandas for Keras [[Video]](https://www.youtube.com/watch?v=XNCEZ4WaPBY&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_02_4_pandas_functional.ipynb)
* Part 2.5: Feature Engineering in Pandas for Deep Learning in Keras [[Video]](https://www.youtube.com/watch?v=BWPTj4_Mi9E&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_02_5_pandas_features.ipynb)
# Google CoLab Instructions
The following code ensures that Google CoLab is running the correct version of TensorFlow.
```
try:
%tensorflow_version 2.x
COLAB = True
print("Note: using Google CoLab")
except:
print("Note: not using Google CoLab")
COLAB = False
```
# Part 2.2: Categorical and Continuous Values
Neural networks require their input to be a fixed number of columns. This is very similar to spreadsheet data. This input must be completely numeric.
It is important to represent the data in a way that the neural network can train from it. In class 6, we will see even more ways to preprocess data. For now, we will look at several of the most basic ways to transform data for a neural network.
Before we look at specific ways to preprocess data, it is important to consider four basic types of data, as defined by [Stanley Smith Stevens](https://en.wikipedia.org/wiki/Stanley_Smith_Stevens). These are commonly referred to as the [levels of measure](https://en.wikipedia.org/wiki/Level_of_measurement):
* Character Data (strings)
* **Nominal** - Individual discrete items, no order. For example: color, zip code, shape.
* **Ordinal** - Individual discrete items that can be ordered. For example: grade level, job title, Starbucks(tm) coffee size (tall, vente, grande)
* Numeric Data
* **Interval** - Numeric values, no defined start. For example, temperature. You would never say "yesterday was twice as hot as today".
* **Ratio** - Numeric values, clearly defined start. For example, speed. You would say that "The first car is going twice as fast as the second."
### Encoding Continuous Values
One common transformation is to normalize the inputs. It is sometimes valuable to normalization numeric inputs to be put in a standard form so that two values can easily be compared. Consider if a friend told you that he received a $10 discount. Is this a good deal? Maybe. But the value is not normalized. If your friend purchased a car, then the discount is not that good. If your friend purchased dinner, this is a very good discount!
Percentages are a very common form of normalization. If your friend tells you they got 10% off, we know that this is a better discount than 5%. It does not matter how much the purchase price was. One very common machine learning normalization is the Z-Score:
$z = \frac{x - \mu}{\sigma} $
To calculate the Z-Score you need to also calculate the mean($\mu$) and the standard deviation ($\sigma$). The mean is calculated as follows:
$\mu = \bar{x} = \frac{x_1+x_2+\cdots +x_n}{n}$
The standard deviation is calculated as follows:
$\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2}, {\rm \ \ where\ \ } \mu = \frac{1}{N} \sum_{i=1}^N x_i$
The following Python code replaces the mpg with a z-score. Cars with average MPG will be near zero, above zero is above average, and below zero is below average. Z-Scores above/below -3/3 are very rare, these are outliers.
```
import os
import pandas as pd
from scipy.stats import zscore
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/auto-mpg.csv",
na_values=['NA','?'])
df['mpg'] = zscore(df['mpg'])
display(df[0:5])
```
### Encoding Categorical Values as Dummies
The classic means of encoding categorical values is to make them dummy variables. This is also called one-hot-encoding. Consider the following data set.
```
import pandas as pd
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/jh-simple-dataset.csv",
na_values=['NA','?'])
display(df[0:5])
areas = list(df['area'].unique())
print(f'Number of areas: {len(areas)}')
print(f'Areas: {areas}')
```
There are four unique values in the areas column. To encode these to dummy variables we would use four columns, each of which would represent one of the areas. For each row, one column would have a value of one, the rest zeros. This is why this type of encoding is sometimes called one-hot encoding. The following code shows how you might encode the values "a" through "d". The value A becomes [1,0,0,0] and the value B becomes [0,1,0,0].
```
dummies = pd.get_dummies(['a','b','c','d'],prefix='area')
print(dummies)
```
To encode the "area" column, we use the following.
It is necessary to merge these dummies back into the data frame.
```
dummies = pd.get_dummies(df['area'],prefix='area')
print(dummies[0:10]) # Just show the first 10
df = pd.concat([df,dummies],axis=1)
```
Displaying select columns from the dataset we can see the dummy variables added.
```
display(df[0:10][['id','job','area','income','area_a',
'area_b','area_c','area_d']])
```
Usually, you will remove the original column ('area'), because it is the goal to get the dataframe to be entirely numeric for the neural network.
```
df.drop('area', axis=1, inplace=True)
display(df[0:10][['id','job','income','area_a',
'area_b','area_c','area_d']])
```
### Target Encoding for Categoricals
Target encoding can sometimes increase the predictive power of a machine learning model. However, it also greatly increases the risk of overfitting. Because of this risk, care must be take if you are going to use this method. It is a popular technique for Kaggle competitions.
Generally, target encoding can only be used on a categorical feature when the output of the machine learning model is numeric (regression).
The concept of target encoding is actually very simple. For each value
```
# Create a small sample dataset
import pandas as pd
import numpy as np
np.random.seed(43)
df = pd.DataFrame({
'cont_9': np.random.rand(10)*100,
'cat_0': ['dog'] * 5 + ['cat'] * 5,
'cat_1': ['wolf'] * 9 + ['tiger'] * 1,
'y': [1, 0, 1, 1, 1, 1, 0, 0, 0, 0]
})
display(df)
```
Rather than creating dummy variables for dog and cat, we would like to change it to a number. We could just use 0 for cat, 1 for dog. However, we can encode more information than just that. The simple 0 or 1 would also only work for one animal. Consider what the mean target value is for cat and dog.
```
means0 = df.groupby('cat_0')['y'].mean().to_dict()
means0
```
The danger is that we are now using the target value for training. This will potentially overfit. The possibility of overfitting is even greater if there are a small number of a particular category. To prevent this from happening, we use a weighting factor. The stronger the weight the more than categories with a small number of values will tend towards the overall average of y, which is calculated as follows.
```
df['y'].mean()
```
The complete function for target encoding is given here.
```
# Source: https://maxhalford.github.io/blog/target-encoding-done-the-right-way/
def calc_smooth_mean(df1, df2, cat_name, target, weight):
# Compute the global mean
mean = df[target].mean()
# Compute the number of values and the mean of each group
agg = df.groupby(cat_name)[target].agg(['count', 'mean'])
counts = agg['count']
means = agg['mean']
# Compute the "smoothed" means
smooth = (counts * means + weight * mean) / (counts + weight)
# Replace each value by the according smoothed mean
if df2 is None:
return df1[cat_name].map(smooth)
else:
return df1[cat_name].map(smooth),df2[cat_name].map(smooth.to_dict())
```
The following code encodes these two categories.
```
WEIGHT = 5
df['cat_0_enc'] = calc_smooth_mean(df1=df, df2=None, cat_name='cat_0', target='y', weight=WEIGHT)
df['cat_1_enc'] = calc_smooth_mean(df1=df, df2=None, cat_name='cat_1', target='y', weight=WEIGHT)
display(df)
```
### Encoding Categorical Values as Ordinal
Typically categoricals will be encoded as dummy variables. However, there might be other techniques to convert categoricals to numeric. Any time there is an order to the categoricals, a number should be used. Consider if you had a categorical that described the current education level of an individual.
* Kindergarten (0)
* First Grade (1)
* Second Grade (2)
* Third Grade (3)
* Fourth Grade (4)
* Fifth Grade (5)
* Sixth Grade (6)
* Seventh Grade (7)
* Eighth Grade (8)
* High School Freshman (9)
* High School Sophomore (10)
* High School Junior (11)
* High School Senior (12)
* College Freshman (13)
* College Sophomore (14)
* College Junior (15)
* College Senior (16)
* Graduate Student (17)
* PhD Candidate (18)
* Doctorate (19)
* Post Doctorate (20)
The above list has 21 levels. This would take 21 dummy variables. However, simply encoding this to dummies would lose the order information. Perhaps the easiest approach would be to assign simply number them and assign the category a single number that is equal to the value in parenthesis above. However, we might be able to do even better. Graduate student is likely more than a year, so you might increase more than just one value.
|
github_jupyter
|
try:
%tensorflow_version 2.x
COLAB = True
print("Note: using Google CoLab")
except:
print("Note: not using Google CoLab")
COLAB = False
import os
import pandas as pd
from scipy.stats import zscore
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/auto-mpg.csv",
na_values=['NA','?'])
df['mpg'] = zscore(df['mpg'])
display(df[0:5])
import pandas as pd
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/jh-simple-dataset.csv",
na_values=['NA','?'])
display(df[0:5])
areas = list(df['area'].unique())
print(f'Number of areas: {len(areas)}')
print(f'Areas: {areas}')
dummies = pd.get_dummies(['a','b','c','d'],prefix='area')
print(dummies)
dummies = pd.get_dummies(df['area'],prefix='area')
print(dummies[0:10]) # Just show the first 10
df = pd.concat([df,dummies],axis=1)
display(df[0:10][['id','job','area','income','area_a',
'area_b','area_c','area_d']])
df.drop('area', axis=1, inplace=True)
display(df[0:10][['id','job','income','area_a',
'area_b','area_c','area_d']])
# Create a small sample dataset
import pandas as pd
import numpy as np
np.random.seed(43)
df = pd.DataFrame({
'cont_9': np.random.rand(10)*100,
'cat_0': ['dog'] * 5 + ['cat'] * 5,
'cat_1': ['wolf'] * 9 + ['tiger'] * 1,
'y': [1, 0, 1, 1, 1, 1, 0, 0, 0, 0]
})
display(df)
means0 = df.groupby('cat_0')['y'].mean().to_dict()
means0
df['y'].mean()
# Source: https://maxhalford.github.io/blog/target-encoding-done-the-right-way/
def calc_smooth_mean(df1, df2, cat_name, target, weight):
# Compute the global mean
mean = df[target].mean()
# Compute the number of values and the mean of each group
agg = df.groupby(cat_name)[target].agg(['count', 'mean'])
counts = agg['count']
means = agg['mean']
# Compute the "smoothed" means
smooth = (counts * means + weight * mean) / (counts + weight)
# Replace each value by the according smoothed mean
if df2 is None:
return df1[cat_name].map(smooth)
else:
return df1[cat_name].map(smooth),df2[cat_name].map(smooth.to_dict())
WEIGHT = 5
df['cat_0_enc'] = calc_smooth_mean(df1=df, df2=None, cat_name='cat_0', target='y', weight=WEIGHT)
df['cat_1_enc'] = calc_smooth_mean(df1=df, df2=None, cat_name='cat_1', target='y', weight=WEIGHT)
display(df)
| 0.430387 | 0.993372 |
```
import h5py
import pandas as pd
import numpy as np
import torch
from torch.utils.data import DataLoader,Dataset
#This is the dataloader that is called for each minibatch of data in the main training loop
def LoadTCGA(data_root, batch_size=32, split='train', cancer='brca', attr = None,
shuffle=True, load_first_n = None):
data_root = data_root+'tcga.h5'
key = '/'.join(['tcga',split,cancer])
print(key)
tcga_dataset = TCGA(data_root,key,load_first_n)
return DataLoader(tcga_dataset,batch_size=batch_size,shuffle=shuffle,drop_last=True)
#This is an extension of the Dataset class for our TCGA data
#The private variable 'expression' was original named data but
#I think since we have the __getitem___ method that it should be ok to change this name
#to something more meaningful
class TCGA(Dataset):
def __init__(self, root, key, load_first_n = None):
with h5py.File(root,'r') as f:
data = f[key][()]
if load_first_n:
data = data[:load_first_n]
self.expression = data
def __getitem__(self, index):
return self.expression[index]
def __len__(self):
return len(self.expression)
#Testing that the dataloader works
test_loader = LoadTCGA('')
# #Creating the tiny TCGA test dataset
# #load the csvs into pandas dataframes
# dlbc = pd.read_csv('dlbc.csv', index_col=0)
# gbm = pd.read_csv('gbm.csv', index_col=0)
# brca = pd.read_csv('brca.csv', index_col=0)
### Make the tiny h5 file for testing
### 10 training samples that are (20501,) and 5 test samples (20501,)
# tcga = h5py.File('tcga.h5', mode='a')
# tcga.create_dataset('tcga/train/dlbc', data=dlbc.values.T[:10])
# tcga.create_dataset('tcga/test/dlbc', data=dlbc.values.T[10:15])
# tcga.create_dataset('tcga/train/gbm', data=gbm.values.T[:10])
# tcga.create_dataset('tcga/test/gbm', data=gbm.values.T[10:15])
# tcga.create_dataset('tcga/train/brca', data=brca.values.T[:10])
# tcga.create_dataset('tcga/test/brca', data=brca.values.T[10:15])
```
## Try out loading the data
```
#utility function for walking the h5 file
def print_name(name):
print(name)
tcga = h5py.File('tcga.h5', mode='r')
tcga.visit(print_name)
list(tcga['tcga/train'])
tcga['tcga/train/brca'][()].shape
tcga['tcga/train/dlbc'][()]
```
tcga.close()
## Select most variable genes across training data
Pick the `n_genes` with the largest median absolute deiviation (MAD)
```
tcga = h5py.File('tcga.h5', mode='r')
n_genes = 1000 # Number of genes
# Cancers to include
cancers = list(tcga['tcga/train'])
# Compute MAD for each cancer type
def mad(X, axis=0):
'Median absolute deviation'
return(np.median(np.abs(X - np.median(X,axis=axis)),axis=axis))
mad_cancer = np.vstack(list(map(lambda cancer: mad(tcga['tcga/train/'+cancer][()]), cancers)))
# Average MAD over cancer types
mad_avg = np.mean(mad_cancer,axis=0)
# Take the n_genes with the largest average MAD
id_genes_keep = np.sort(np.argsort(mad_avg)[::-1][:n_genes])
# Create dataset
tcga_mad = h5py.File('tcga_mad.h5', mode='a')
for c in cancers:
tcga_mad.create_dataset('tcga/train/'+c, data=tcga['tcga/train/'+c][:,id_genes_keep])
tcga_mad.create_dataset('tcga/test/'+c, data=tcga['tcga/test/'+c][:,id_genes_keep])
tcga_mad.close()
```
## Face dataset
```
def LoadFace(data_root, batch_size=32, split='train', style='photo', attr = None,
shuffle=True, load_first_n = None):
data_root = data_root+'face.h5'
key = '/'.join(['CelebA',split,style])
celeba_dataset = Face(data_root,key,load_first_n)
return DataLoader(celeba_dataset,batch_size=batch_size,shuffle=shuffle,drop_last=True)
class Face(Dataset):
def __init__(self, root, key, load_first_n = None):
with h5py.File(root,'r') as f:
data = f[key][()]
if load_first_n:
data = data[:load_first_n]
self.imgs = (data/255.0)*2 -1
def __getitem__(self, index):
return self.imgs[index]
def __len__(self):
return len(self.imgs)
face = h5py.File('../UFDN/data/face.h5', mode='r')
face.visit(print_name)
list(face.keys())
face['CelebA/train/paint'][()].shape
face['CelebA/train/photo'][()].shape
face['CelebA/train/sketch'][()].shape
face['CelebA/test/paint'][()].shape
face.close()
(64-4+2)/2+1
```
#### Create smaller face dataset
```
ntrain = 10
ntest = 5
domains = list(face['CelebA/train'])
# Create dataset
face_small = h5py.File('face_small.h5', mode='a')
for d in domains:
face_small.create_dataset('CelebA/train/'+d, data=face['CelebA/train/'+d][:ntrain,:])
face_small.create_dataset('CelebA/test/'+d, data=face['CelebA/test/'+d][:ntest,:])
face_small.close()
face_small = h5py.File('face_small.h5', mode='r')
face_small.visit(print_name)
face_small['CelebA/train/paint'][()].shape
```
|
github_jupyter
|
import h5py
import pandas as pd
import numpy as np
import torch
from torch.utils.data import DataLoader,Dataset
#This is the dataloader that is called for each minibatch of data in the main training loop
def LoadTCGA(data_root, batch_size=32, split='train', cancer='brca', attr = None,
shuffle=True, load_first_n = None):
data_root = data_root+'tcga.h5'
key = '/'.join(['tcga',split,cancer])
print(key)
tcga_dataset = TCGA(data_root,key,load_first_n)
return DataLoader(tcga_dataset,batch_size=batch_size,shuffle=shuffle,drop_last=True)
#This is an extension of the Dataset class for our TCGA data
#The private variable 'expression' was original named data but
#I think since we have the __getitem___ method that it should be ok to change this name
#to something more meaningful
class TCGA(Dataset):
def __init__(self, root, key, load_first_n = None):
with h5py.File(root,'r') as f:
data = f[key][()]
if load_first_n:
data = data[:load_first_n]
self.expression = data
def __getitem__(self, index):
return self.expression[index]
def __len__(self):
return len(self.expression)
#Testing that the dataloader works
test_loader = LoadTCGA('')
# #Creating the tiny TCGA test dataset
# #load the csvs into pandas dataframes
# dlbc = pd.read_csv('dlbc.csv', index_col=0)
# gbm = pd.read_csv('gbm.csv', index_col=0)
# brca = pd.read_csv('brca.csv', index_col=0)
### Make the tiny h5 file for testing
### 10 training samples that are (20501,) and 5 test samples (20501,)
# tcga = h5py.File('tcga.h5', mode='a')
# tcga.create_dataset('tcga/train/dlbc', data=dlbc.values.T[:10])
# tcga.create_dataset('tcga/test/dlbc', data=dlbc.values.T[10:15])
# tcga.create_dataset('tcga/train/gbm', data=gbm.values.T[:10])
# tcga.create_dataset('tcga/test/gbm', data=gbm.values.T[10:15])
# tcga.create_dataset('tcga/train/brca', data=brca.values.T[:10])
# tcga.create_dataset('tcga/test/brca', data=brca.values.T[10:15])
#utility function for walking the h5 file
def print_name(name):
print(name)
tcga = h5py.File('tcga.h5', mode='r')
tcga.visit(print_name)
list(tcga['tcga/train'])
tcga['tcga/train/brca'][()].shape
tcga['tcga/train/dlbc'][()]
tcga = h5py.File('tcga.h5', mode='r')
n_genes = 1000 # Number of genes
# Cancers to include
cancers = list(tcga['tcga/train'])
# Compute MAD for each cancer type
def mad(X, axis=0):
'Median absolute deviation'
return(np.median(np.abs(X - np.median(X,axis=axis)),axis=axis))
mad_cancer = np.vstack(list(map(lambda cancer: mad(tcga['tcga/train/'+cancer][()]), cancers)))
# Average MAD over cancer types
mad_avg = np.mean(mad_cancer,axis=0)
# Take the n_genes with the largest average MAD
id_genes_keep = np.sort(np.argsort(mad_avg)[::-1][:n_genes])
# Create dataset
tcga_mad = h5py.File('tcga_mad.h5', mode='a')
for c in cancers:
tcga_mad.create_dataset('tcga/train/'+c, data=tcga['tcga/train/'+c][:,id_genes_keep])
tcga_mad.create_dataset('tcga/test/'+c, data=tcga['tcga/test/'+c][:,id_genes_keep])
tcga_mad.close()
def LoadFace(data_root, batch_size=32, split='train', style='photo', attr = None,
shuffle=True, load_first_n = None):
data_root = data_root+'face.h5'
key = '/'.join(['CelebA',split,style])
celeba_dataset = Face(data_root,key,load_first_n)
return DataLoader(celeba_dataset,batch_size=batch_size,shuffle=shuffle,drop_last=True)
class Face(Dataset):
def __init__(self, root, key, load_first_n = None):
with h5py.File(root,'r') as f:
data = f[key][()]
if load_first_n:
data = data[:load_first_n]
self.imgs = (data/255.0)*2 -1
def __getitem__(self, index):
return self.imgs[index]
def __len__(self):
return len(self.imgs)
face = h5py.File('../UFDN/data/face.h5', mode='r')
face.visit(print_name)
list(face.keys())
face['CelebA/train/paint'][()].shape
face['CelebA/train/photo'][()].shape
face['CelebA/train/sketch'][()].shape
face['CelebA/test/paint'][()].shape
face.close()
(64-4+2)/2+1
ntrain = 10
ntest = 5
domains = list(face['CelebA/train'])
# Create dataset
face_small = h5py.File('face_small.h5', mode='a')
for d in domains:
face_small.create_dataset('CelebA/train/'+d, data=face['CelebA/train/'+d][:ntrain,:])
face_small.create_dataset('CelebA/test/'+d, data=face['CelebA/test/'+d][:ntest,:])
face_small.close()
face_small = h5py.File('face_small.h5', mode='r')
face_small.visit(print_name)
face_small['CelebA/train/paint'][()].shape
| 0.460532 | 0.606207 |
# Support Vector Machines (SVM)
Le __[Support Vector Machines](https://it.wikipedia.org/wiki/Macchine_a_vettori_di_supporto)__ sono un **algoritmo di machine learning supervisionato in grado sia di fare classificazione binaria e di fare regressione, risulta anche essere in grado di essere robusto agli** __[outliers](https://en.wikipedia.org/wiki/Outlier)__ **ovvero dati che sono molto diversi dalle altre osservazioni precedenti per possibili errori o condizioni diversi**.<br>
Il funzionamento di queste macchine su basa su un principio piuttosto semplice, quando noi effettuiamo una classificazione binaria quello che definiamo è un sottospazio detto __[iperpiano](https://it.wikipedia.org/wiki/Iperpiano)__ attraverso cui riusciamo a definire due regioni dello spazio a cui noi possiamo associare una delle due classi, se per esempio siamo in uno spazio 2d con dei dati quello che possiamo fare è associare una linea in grado di dirci che se i punti sono a sinistra o a destra di esso allora abbiamo una classe determinabile dai punti usati per definire l'iperpiano attraverso il training.<br>
Ora però abbiamo un problema, **qualora fosse possibile definire un'iperpiano(*hyperplane in inglese*) quello che potremmo trovarci è che ne esiste più di uno, allora come fare a scegliere il migliore?**<br>
<center> <img src = "../img/hyperplane.png" width ="800" /> </center>
## Maximum Margin Optimization
In genere l'iperpiano migliore è quello che riesce a massimizzare la distanza dall'iperpiano ai punti della classi, detto anche margine in matematica, abbiamo quindi un problema di __[massimizzazione margine dell'iperpiano](https://www.sciencedirect.com/topics/computer-science/maximum-margin-hyperplane)__, in genere per risolvere questo problema si usano i **vettori di supporto(support vectors) ovvero i vettori ottenuti dalla distanza dell'iperpiano ai punti più vicini ad esso**.<br>
Tradotto in fotmule matematiche noi abbiamo:
\begin{equation}
\Large w^{T}x + b = 0 \quad Hyperplane\\
\Large \frac{1}{\Vert w \Vert} \quad Margin (\Vert w \Vert \;is\; the\; norm\; of\; w)\\
\Large |w^{T}x + b| = 1 \quad classification
\end{equation}
Ora utilizzando la condizione di massimizzare il margine dell'iperpiano contando la capacità di classificare otteniamo il seguente problema:
\begin{equation}
\Large Maximize \quad \frac{1}{\Vert w \Vert} \, subject \, to \, \min_{n = 1,2,..,N} |w^{T}x + b| = 1
\end{equation}
che è possibile tradurre in:
\begin{equation}
\Large Minimize \quad \frac{w^{T}w}{2} \, subject \, to \, y_n(w^{T}x_n + b) \geqslant 1 \quad with \; n = 1,2,..,N \, and \, y_n \in [-1,1]
\end{equation}
Usando le condizioni di __[KKT](https://it.wikipedia.org/wiki/Condizioni_di_Karush-Kuhn-Tucker)__ e imponendo la minimizzazione si ottiene la seguente formula di massimizzazione:
\begin{equation}
\Large Maximize \; \mathcal{L}(\alpha) = \sum_{n=1}^{N} \alpha_n -\frac{1}{2} \sum_{n=1}^{N} \sum_{m=1}^{N} y_n y_m \alpha_n \alpha_m x^{T}_{n} x_{m}\\
\Large subject\, to \ , \alpha_n \geqslant 0 \, for \, n = 1,..N \, and \, \sum_{n=1}^{N} \alpha_n y_n = 0 \\
\Large If \; y_n(w^{T}x_n + b) = 1 \; then \; x_n \; is \; a \; support \; vector
\end{equation}
quindi il termine $\alpha$ sarebbe un termine che influisce sulla creazione del margine ed è definibile dal training sui dati.
## Il problema degli outlier
Abbiamo però il problema che fino ad ora abbiamo ipotizzato che non ci fossero outlier e che quindi non ci fosser dati "strani", **se però per esempio ipotizziamo che un dato è stato classificato male, ovvero è un outlier, ma poichè presenta tutte le caratteristiche dell'altra classe sappiamo che è stato classificato male, dobbiamo allora fare in modo che l'algoritmo ne tenga conto al fine di poter generalizzare meglio in seguito**, in tal caso quello che possiamo fare è introdurre un ***termine di violazione del margine tale che il nostro margine diventi "soft" ovvero permetta la sua violazione, in tal modo avremo la possibilità di permettere ad alcuni punti di essere outliers".
Dal punto di vista matematico quello che succede è:
\begin{equation}
\Large Minimize \quad \frac{w^{T}w}{2} + C \sum_{i=1}^{N} \xi_n \quad subject \; to \; y_n(w^{T}x_n + b) \geqslant 1 - \xi_n, \; \xi_n \geqslant 0
\end{equation}
dove il termine $\xi$ rappresenta la violazione del dato nella violazione del margine, ora dal punto di vista della loss function essa diventa usando sempre __[KKT](https://it.wikipedia.org/wiki/Condizioni_di_Karush-Kuhn-Tucker)__:
\begin{equation}
\Large Maximize \; \mathcal{L}(\alpha) = \sum_{n=1}^{N} \alpha_n -\frac{1}{2} \sum_{n=1}^{N} \sum_{m=1}^{N} y_n y_m \alpha_n \alpha_m x^{T}_{n} x_{m}\\
\Large subject\, to \ , 0 \geqslant \alpha_n \geqslant C \, for \, n = 1,..N \, and \, \sum_{n=1}^{N} \alpha_n y_n = 0 \\
\end{equation}
Notate bene che in questa formula $\alpha$ non deve essere solo positiva come nel caso precedente, ma deve essere superiormente limitata da $C$ che ora è diventato il nostro termine di regoralizzazione sulla quale abbiamo imposto quanto pesa la nostra violazione dei dati.<br>
In __[scikit](https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html#sklearn.svm.SVC)__ il parametro $C$ controlla effettivamente se vogliamo pesare molto le misclassification oppure no, in genere se imponente **un $C$ non nullo e non troppo grande dite all'algoritmo che permettete la possibilità di misclassification e state definendo un "soft margin"**, mentre se imponete **un $C$ tendente ad infinite state dicendo di non fare misclassification e quindi non accettate violazioni del margine detto "hard margin"**, a qui un __[esempio di scikit](https://scikit-learn.org/stable/auto_examples/svm/plot_svm_margin.html#sphx-glr-auto-examples-svm-plot-svm-margin-py)__.<br>
## Dati non lineari e il Kernel
Ora il problema è che non sempre i dati sono classificabili in maniera lineare, in tal caso è necessario effettuare una trasformazione non lineare che possiamo definire come $z = \Phi(x)$, ora se noi applicassimo la formula di minimizzazione precedente avremmo:
\begin{equation}
\Large Maximize \; \mathcal{L}(\alpha) = \sum_{n=1}^{N} \alpha_n -\frac{1}{2} \sum_{n=1}^{N} \sum_{m=1}^{N} y_n y_m \alpha_n \alpha_m z^{T}_{n} z_{m}\\
\Large subject\, to \ , 0 \geqslant \alpha_n \geqslant C \, for \, n = 1,..N \, and \, \sum_{n=1}^{N} \alpha_n y_n = 0 \\
\end{equation}
Ora abbiamo che il kernel è definito come(ho usato z vettorizzato):
\begin{equation}
\Large Kernel \quad K(x,x') = z^{T}z'
\end{equation}
Ora se volessimo ad esempio una trasformazione polinomiale di grado 2 ad uno spazio 2D avremmo:
\begin{equation}
\Large x = (x_1, x_2) \quad \rightarrow \quad z = \Phi(x) = (1, x_1, x_2, x_{1}^{2}, x_{2}^{2}, x_1 x_2)\\
\Large K(x,x') = z^{T}z' = 1 + x_1 x'_{1} + x_2 x'_{2} + x^{2}_{1} x'^{2}_{1} + x^{2}_{2} x'^{2}_{2} + x_1 x'_{1} x_2 x'_{2}
\end{equation}
Ora se potete notare calcolare in questa maniera è molto dispendioso visto che devo trasformare e poi applicare un prodotto scalare che porta numerosi termini, un trucco per ridurre il calcolo computazionale è usare il __[kernel trick](https://towardsdatascience.com/the-kernel-trick-c98cdbcaeb3f)__, per vederlo potete notare che:
\begin{equation}
\Large K(x,x') = (1 + x^{T}x')^2 = 1 + 2x_1 x'_{1} + 2x_2 x'_{2} + x^{2}_{1} x'^{2}_{1} + x^{2}_{2} x'^{2}_{2} + 2x_1 x'_{1} x_2 x'_{2}\\
\end{equation}
Questa formula aparte dei coefficienti che non ci interessano poichè non influiscono sulla definizione del nuovo spazio, il prodotto scalare precedente è esattamente uguale al prodotto scalare delle trasformazioni dello spazio lineare come definito primo, in poche parole il kernel trick ci dice che:
\begin{equation}
K(x,x') = < \Phi(x), \Phi(x')> = \Phi(<x,x'>)
\end{equation}
**Il simbolo $<,>$ inidica il prodotto scalare, grazie a questo a questo è possibile usare la __[radial basis function](https://scikit-learn.org/stable/modules/generated/sklearn.gaussian_process.kernels.RBF.html?highlight=rbf#sklearn.gaussian_process.kernels.RBF)__ attraverso cui possiamo fare una classificazione lineare in uno spazio infinito dimensionale in tempo finito! Not Bad!**.
## Il Support Vector Regression (SVR)
Il __[Support Vector Regression](https://www.educba.com/support-vector-regression/)__ è la SVM applicata nel contesto di regressione, **la differenza fondamentale con la classificazione è che in questo caso voi cercate di mantenere i punti della regressione all'interno dei margini della nostra SVM**, questo ci dice che l'algoritmo considererà outliers i punti al di fuori del margine, pe averne una visione completa guardate questi __[esempi scikit](https://scikit-learn.org/stable/auto_examples/svm/plot_svm_regression.html#sphx-glr-auto-examples-svm-plot-svm-regression-py)__.
<div class="alert alert-block alert-warning">
La trattazione che ho cercato di fare è quanto più completa possibile, ma so che potrei non essere stato molto chiaro, pertanto vi rimando a questo <a href="https://www.lorenzogovoni.com/support-vector-machine/">link in italiano</a> che lo spiega in maniera più semplice e meno matematica.
</div>
Qui sotto metto invece un link youtube video in cui potete visualzzare i concetti appena visti, sono 3 video, ma non posso linkare una playlist cercate comunque su youtube.
```
from IPython.display import YouTubeVideo
#put link yotube video, only final part
YouTubeVideo("efR1C6CvhmE")
import pandas as pd
import matplotlib.pyplot as plt
import time
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import plot_confusion_matrix, classification_report
from sklearn.svm import SVC, SVR
#regression data
boston = load_boston()
X_boston, y_boston = boston.data, boston.target
#classification data
diabetes = pd.read_csv('../data/diabetes2.csv')
X_diabetes, y_diabetes = diabetes.drop('Outcome', axis = 1).values, diabetes.Outcome.values
feature_diabetes = diabetes.columns.values[:-1]
target_names = ["Not Diabetes", "Diabetes"]
#divide the data in training and testing
X_boston_train, X_boston_test, y_boston_train, y_boston_test = train_test_split(
X_boston, y_boston, random_state=0, test_size = 0.2)
X_diabetes_train, X_diabetes_test, y_diabetes_train, y_diabetes_test = train_test_split(
X_diabetes, y_diabetes, random_state=0, test_size = 0.2)
print("SVM FOR REGRESSION TESTED ON BOSTON DATASET")
print('R^2 score training and testing using SVR with C = 1 kernel:')
svr = SVR(kernel = "poly", degree=3)
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- polynomial of degree 3, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
svr = SVR(kernel = "linear")
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- linear, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
svr = SVR(kernel = "rbf")
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- Radial basis function, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
svr = SVR(kernel = "sigmoid")
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- Sigmoid, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
print('-'*80)
print('R^2 score training and testing using SVR with C = 1000 kernel:')
svr = SVR(C = 1e3, kernel = "poly", degree=3)
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- polynomial of degree 3, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
svr = SVR(C = 1e3, kernel = "linear")
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- linear, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
svr = SVR(C = 1e3,kernel = "rbf")
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- Radial basis function, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
svr = SVR(C = 1e3, kernel = "sigmoid")
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- Sigmoid, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
#let's use now svm for classification
svcs = [SVC(C = 1, kernel = 'poly', degree = 3), SVC(C = 1, kernel = 'rbf'),
SVC(C = 1, kernel = 'linear'), SVC(C = 1, kernel = 'sigmoid')]
#lets train the models
for svc in svcs:
start = time.time()
svc.fit(X_diabetes_train, y_diabetes_train)
print(f"Time taken to train {str(svc)}: {time.time() - start}s \t")
#lets make a confusion matrix for every single one
#confusion matrixes plots
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(16,10))
for svc, ax in zip(svcs, axes.flatten()):
plot_confusion_matrix(svc,
X_diabetes_test,
y_diabetes_test,
ax=ax,
display_labels=target_names,
colorbar= False)
ax.title.set_text(str(svc))
plt.tight_layout()
plt.show()
#lets use a classification report
for svc in svcs:
print(f"Classification report of {str(svc)}\n")
print(classification_report(y_diabetes_test, svc.predict(X_diabetes_test),
target_names=target_names))
#let's use now svm for classification
svcs = [SVC(C = 1e3, kernel = 'poly', degree = 3), SVC(C = 1e3, kernel = 'rbf'),
SVC(C = 1e3, kernel = 'linear'), SVC(C = 1e3, kernel = 'sigmoid')]
#lets train the models
for svc in svcs:
start = time.time()
svc.fit(X_diabetes_train, y_diabetes_train)
print(f"Time taken to train {str(svc)}: {time.time() - start}s \t")
#lets make a confusion matrix for every single one
#confusion matrixes plots
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(16,10))
for svc, ax in zip(svcs, axes.flatten()):
plot_confusion_matrix(svc,
X_diabetes_test,
y_diabetes_test,
ax=ax,
display_labels=target_names,
colorbar= False)
ax.title.set_text(str(svc))
plt.tight_layout()
plt.show()
#lets use a classification report
for svc in svcs:
print(f"Classification report of {str(svc)}\n")
print(classification_report(y_diabetes_test, svc.predict(X_diabetes_test),
target_names=target_names))
```
Qualora voleste provare altri algoritmi andate alla __[guida scikit](https://scikit-learn.org/stable/modules/svm.html)__ che offre un enorme varietà e esempi a tal proposito.
***
COMPLIMENTI AVETE FINITO LA LEZIONE DI SVM!
|
github_jupyter
|
from IPython.display import YouTubeVideo
#put link yotube video, only final part
YouTubeVideo("efR1C6CvhmE")
import pandas as pd
import matplotlib.pyplot as plt
import time
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import plot_confusion_matrix, classification_report
from sklearn.svm import SVC, SVR
#regression data
boston = load_boston()
X_boston, y_boston = boston.data, boston.target
#classification data
diabetes = pd.read_csv('../data/diabetes2.csv')
X_diabetes, y_diabetes = diabetes.drop('Outcome', axis = 1).values, diabetes.Outcome.values
feature_diabetes = diabetes.columns.values[:-1]
target_names = ["Not Diabetes", "Diabetes"]
#divide the data in training and testing
X_boston_train, X_boston_test, y_boston_train, y_boston_test = train_test_split(
X_boston, y_boston, random_state=0, test_size = 0.2)
X_diabetes_train, X_diabetes_test, y_diabetes_train, y_diabetes_test = train_test_split(
X_diabetes, y_diabetes, random_state=0, test_size = 0.2)
print("SVM FOR REGRESSION TESTED ON BOSTON DATASET")
print('R^2 score training and testing using SVR with C = 1 kernel:')
svr = SVR(kernel = "poly", degree=3)
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- polynomial of degree 3, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
svr = SVR(kernel = "linear")
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- linear, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
svr = SVR(kernel = "rbf")
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- Radial basis function, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
svr = SVR(kernel = "sigmoid")
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- Sigmoid, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
print('-'*80)
print('R^2 score training and testing using SVR with C = 1000 kernel:')
svr = SVR(C = 1e3, kernel = "poly", degree=3)
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- polynomial of degree 3, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
svr = SVR(C = 1e3, kernel = "linear")
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- linear, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
svr = SVR(C = 1e3,kernel = "rbf")
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- Radial basis function, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
svr = SVR(C = 1e3, kernel = "sigmoid")
start = time.time()
svr.fit(X_boston_train, y_boston_train)
end = time.time()
print(f"- Sigmoid, training score:{svr.score(X_boston_train, y_boston_train)},"
f" testing score : {svr.score(X_boston_test, y_boston_test)}, time taken :{end-start}s")
#let's use now svm for classification
svcs = [SVC(C = 1, kernel = 'poly', degree = 3), SVC(C = 1, kernel = 'rbf'),
SVC(C = 1, kernel = 'linear'), SVC(C = 1, kernel = 'sigmoid')]
#lets train the models
for svc in svcs:
start = time.time()
svc.fit(X_diabetes_train, y_diabetes_train)
print(f"Time taken to train {str(svc)}: {time.time() - start}s \t")
#lets make a confusion matrix for every single one
#confusion matrixes plots
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(16,10))
for svc, ax in zip(svcs, axes.flatten()):
plot_confusion_matrix(svc,
X_diabetes_test,
y_diabetes_test,
ax=ax,
display_labels=target_names,
colorbar= False)
ax.title.set_text(str(svc))
plt.tight_layout()
plt.show()
#lets use a classification report
for svc in svcs:
print(f"Classification report of {str(svc)}\n")
print(classification_report(y_diabetes_test, svc.predict(X_diabetes_test),
target_names=target_names))
#let's use now svm for classification
svcs = [SVC(C = 1e3, kernel = 'poly', degree = 3), SVC(C = 1e3, kernel = 'rbf'),
SVC(C = 1e3, kernel = 'linear'), SVC(C = 1e3, kernel = 'sigmoid')]
#lets train the models
for svc in svcs:
start = time.time()
svc.fit(X_diabetes_train, y_diabetes_train)
print(f"Time taken to train {str(svc)}: {time.time() - start}s \t")
#lets make a confusion matrix for every single one
#confusion matrixes plots
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(16,10))
for svc, ax in zip(svcs, axes.flatten()):
plot_confusion_matrix(svc,
X_diabetes_test,
y_diabetes_test,
ax=ax,
display_labels=target_names,
colorbar= False)
ax.title.set_text(str(svc))
plt.tight_layout()
plt.show()
#lets use a classification report
for svc in svcs:
print(f"Classification report of {str(svc)}\n")
print(classification_report(y_diabetes_test, svc.predict(X_diabetes_test),
target_names=target_names))
| 0.372848 | 0.92976 |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import researchpy as rp
plt.rcParams['figure.figsize'] = 12,8
plt.rcParams['font.size'] = 16
plt.rcParams['font.size'] = 16
plt.rcParams['font.family'] = 'sans-serif'
# read clean data again
df = pd.read_csv('../data/diabetes_cleaned_data.csv')
df.head()
```
# Demographic Summary(Counts, Percentage)
```
rp.codebook(df['Age_of_Participant'])
# summary stats of demographics variables
demographics_summary = rp.summary_cat(df[['Gender', 'Age_Group', 'Marital_status', 'Education_Level',
'Occupation']])
# demographics_summary.to_csv('../results/demographics_summary.csv', index=False)
demographics_summary
```
# Estimation of probable diabetes type(Counts, Percentage)
```
estimation = rp.summary_cat(df[['At_which_age_you_diagnosed_diabetes?',
'What_type_of_diabetes_do_you_have?',
'Did_you_inject_insulin_within_the_first_3_months_of_being_diagnosed_?',
'Did_you_continue_injecting_for_more_than_one_year_after_you_first_injected_insulin?']])
# estimation.to_csv('../results/estimation_of_probable_diabetes_type.csv', index=False)
estimation
# Cross-tabulation test
pd.crosstab(df['Did_you_inject_insulin_within_the_first_3_months_of_being_diagnosed_?'],
df['What_type_of_diabetes_do_you_have?'], normalize=True) * 100
# Comparison between self-reported type with those from the c
rp.crosstab(df['Did_you_inject_insulin_within_the_first_3_months_of_being_diagnosed_?'],
df['What_type_of_diabetes_do_you_have?'],
prop='cell')
# Comparison between self-reported type with those from the derived variable
rp.crosstab(df['Did_you_continue_injecting_for_more_than_one_year_after_you_first_injected_insulin?'],
df['What_type_of_diabetes_do_you_have?'],
prop='cell')
# Participants self-reported type of diabetes, by derived diabetes(bar chart)
sns.countplot(data=df, y='Did_you_inject_insulin_within_the_first_3_months_of_being_diagnosed_?',
hue='What_type_of_diabetes_do_you_have?',
orient='h',
palette='viridis')
plt.xlabel("Count")
plt.ylabel('')
plt.legend(['Type 1', 'Type 2', "Don't Know"], loc='lower right')
plt.tight_layout()
plt.savefig('../results/probable_type1.jpeg', dpi = 300)
plt.show()
# Participants self-reported type of diabetes, by derived diabetes(bar chart)
sns.countplot(data=df, y='Did_you_continue_injecting_for_more_than_one_year_after_you_first_injected_insulin?',
hue='What_type_of_diabetes_do_you_have?',
orient='h',
palette='Set2')
plt.xlabel("Count")
plt.ylabel('')
plt.legend(['Type 1', 'Type 2', "Don't Know"], loc='lower right')
plt.tight_layout()
plt.savefig('../results/probable_type2.jpeg', dpi = 300)
plt.show()
df.groupby('Did_you_inject_insulin_within_the_first_3_months_of_being_diagnosed_?')['Age_of_Participant'].mean()
df.groupby('Did_you_continue_injecting_for_more_than_one_year_after_you_first_injected_insulin?')['Age_of_Participant'].mean()
```
# Health Status of Diabetic Patients(Counts, Percentage)
```
health_status = rp.summary_cat(df[['Overall_health_in_the_past_4_weeks_?',
'Does_diabetes_affect_day_to_day_activities_?',
'Whether_stayed_in_hospital_overnight',
'Reason_for_most_recent__stay_in_hospital',
'Where_do__you__go_for_diabetes_check-up',
'Number_of_diabetes_check-ups_in_the_last__12_month',
'Family_history_of_diabetes']])
# health_status.to_csv('../results/health_status.csv', index=False)
health_status
rp.crosstab(df['Does_diabetes_affect_day_to_day_activities_?'],
df['What_type_of_diabetes_do_you_have?'], prop='cell')
rp.crosstab(df['Overall_health_in_the_past_4_weeks_?'],
df['What_type_of_diabetes_do_you_have?'], prop='cell')
# self-reported health status, by diabetes type and age
sns.countplot(data=df,
hue='Overall_health_in_the_past_4_weeks_?',
y='What_type_of_diabetes_do_you_have?',
orient='h',
palette='coolwarm')
plt.xlabel("Count")
plt.ylabel('')
plt.legend(loc='lower right')
plt.tight_layout()
plt.savefig('../results/self-reported_health_status_by_diabetes_type.jpeg', dpi = 300)
plt.show()
rp.crosstab(df['Does_diabetes_affect_day_to_day_activities_?'],
df['At_which_age_you_diagnosed_diabetes?'], prop='cell')
rp.crosstab(df['Overall_health_in_the_past_4_weeks_?'],
df['At_which_age_you_diagnosed_diabetes?'], prop='cell')
# self-reported health status, by diabetes type and age
sns.countplot(data=df,
hue='Overall_health_in_the_past_4_weeks_?',
y='At_which_age_you_diagnosed_diabetes?',
orient='h',
palette='magma')
plt.xlabel("Count")
plt.ylabel('')
plt.legend(loc='lower right')
plt.tight_layout()
plt.savefig('../results/self-reported_health_status_by_age.jpeg', dpi = 300)
plt.show()
```
# Self Management of Diabetes(Counts, Percentage)
```
df[]
self_management_results = rp.summary_cat(df[['How_do_you_control_your_diabetes_now_?',
'Do_you_take_any_medication_for_any_other_condition_?',
'What_type_of_medication_do_you_take_?',
'How_often_do_you_test_your_own_blood_glucose_level_?',
'Do_you_take_any_medication_for_any_other_condition_?']])
# self_management_results.to_csv('../results/self_management_results.csv', index=False)
self_management_results
```
# Knowledge of Partcipants regarding diabetes
```
knowledge_status = rp.summary_cat(df[[
'Do_you_know_enough_about_when_to_take_your_medication_?',
'Do_you_know_enough_about_what_you_should_eat_to_help_you_manage_your_diabetes_?',
'Do_you_know_about_the_role_of_Physical_activity_in_managing_your_diabetes_?',
'Do_you_smoke_?']])
# knowledge_status.to_csv('../results/knowledge_status.csv', index=False)
knowledge_status
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import researchpy as rp
plt.rcParams['figure.figsize'] = 12,8
plt.rcParams['font.size'] = 16
plt.rcParams['font.size'] = 16
plt.rcParams['font.family'] = 'sans-serif'
# read clean data again
df = pd.read_csv('../data/diabetes_cleaned_data.csv')
df.head()
rp.codebook(df['Age_of_Participant'])
# summary stats of demographics variables
demographics_summary = rp.summary_cat(df[['Gender', 'Age_Group', 'Marital_status', 'Education_Level',
'Occupation']])
# demographics_summary.to_csv('../results/demographics_summary.csv', index=False)
demographics_summary
estimation = rp.summary_cat(df[['At_which_age_you_diagnosed_diabetes?',
'What_type_of_diabetes_do_you_have?',
'Did_you_inject_insulin_within_the_first_3_months_of_being_diagnosed_?',
'Did_you_continue_injecting_for_more_than_one_year_after_you_first_injected_insulin?']])
# estimation.to_csv('../results/estimation_of_probable_diabetes_type.csv', index=False)
estimation
# Cross-tabulation test
pd.crosstab(df['Did_you_inject_insulin_within_the_first_3_months_of_being_diagnosed_?'],
df['What_type_of_diabetes_do_you_have?'], normalize=True) * 100
# Comparison between self-reported type with those from the c
rp.crosstab(df['Did_you_inject_insulin_within_the_first_3_months_of_being_diagnosed_?'],
df['What_type_of_diabetes_do_you_have?'],
prop='cell')
# Comparison between self-reported type with those from the derived variable
rp.crosstab(df['Did_you_continue_injecting_for_more_than_one_year_after_you_first_injected_insulin?'],
df['What_type_of_diabetes_do_you_have?'],
prop='cell')
# Participants self-reported type of diabetes, by derived diabetes(bar chart)
sns.countplot(data=df, y='Did_you_inject_insulin_within_the_first_3_months_of_being_diagnosed_?',
hue='What_type_of_diabetes_do_you_have?',
orient='h',
palette='viridis')
plt.xlabel("Count")
plt.ylabel('')
plt.legend(['Type 1', 'Type 2', "Don't Know"], loc='lower right')
plt.tight_layout()
plt.savefig('../results/probable_type1.jpeg', dpi = 300)
plt.show()
# Participants self-reported type of diabetes, by derived diabetes(bar chart)
sns.countplot(data=df, y='Did_you_continue_injecting_for_more_than_one_year_after_you_first_injected_insulin?',
hue='What_type_of_diabetes_do_you_have?',
orient='h',
palette='Set2')
plt.xlabel("Count")
plt.ylabel('')
plt.legend(['Type 1', 'Type 2', "Don't Know"], loc='lower right')
plt.tight_layout()
plt.savefig('../results/probable_type2.jpeg', dpi = 300)
plt.show()
df.groupby('Did_you_inject_insulin_within_the_first_3_months_of_being_diagnosed_?')['Age_of_Participant'].mean()
df.groupby('Did_you_continue_injecting_for_more_than_one_year_after_you_first_injected_insulin?')['Age_of_Participant'].mean()
health_status = rp.summary_cat(df[['Overall_health_in_the_past_4_weeks_?',
'Does_diabetes_affect_day_to_day_activities_?',
'Whether_stayed_in_hospital_overnight',
'Reason_for_most_recent__stay_in_hospital',
'Where_do__you__go_for_diabetes_check-up',
'Number_of_diabetes_check-ups_in_the_last__12_month',
'Family_history_of_diabetes']])
# health_status.to_csv('../results/health_status.csv', index=False)
health_status
rp.crosstab(df['Does_diabetes_affect_day_to_day_activities_?'],
df['What_type_of_diabetes_do_you_have?'], prop='cell')
rp.crosstab(df['Overall_health_in_the_past_4_weeks_?'],
df['What_type_of_diabetes_do_you_have?'], prop='cell')
# self-reported health status, by diabetes type and age
sns.countplot(data=df,
hue='Overall_health_in_the_past_4_weeks_?',
y='What_type_of_diabetes_do_you_have?',
orient='h',
palette='coolwarm')
plt.xlabel("Count")
plt.ylabel('')
plt.legend(loc='lower right')
plt.tight_layout()
plt.savefig('../results/self-reported_health_status_by_diabetes_type.jpeg', dpi = 300)
plt.show()
rp.crosstab(df['Does_diabetes_affect_day_to_day_activities_?'],
df['At_which_age_you_diagnosed_diabetes?'], prop='cell')
rp.crosstab(df['Overall_health_in_the_past_4_weeks_?'],
df['At_which_age_you_diagnosed_diabetes?'], prop='cell')
# self-reported health status, by diabetes type and age
sns.countplot(data=df,
hue='Overall_health_in_the_past_4_weeks_?',
y='At_which_age_you_diagnosed_diabetes?',
orient='h',
palette='magma')
plt.xlabel("Count")
plt.ylabel('')
plt.legend(loc='lower right')
plt.tight_layout()
plt.savefig('../results/self-reported_health_status_by_age.jpeg', dpi = 300)
plt.show()
df[]
self_management_results = rp.summary_cat(df[['How_do_you_control_your_diabetes_now_?',
'Do_you_take_any_medication_for_any_other_condition_?',
'What_type_of_medication_do_you_take_?',
'How_often_do_you_test_your_own_blood_glucose_level_?',
'Do_you_take_any_medication_for_any_other_condition_?']])
# self_management_results.to_csv('../results/self_management_results.csv', index=False)
self_management_results
knowledge_status = rp.summary_cat(df[[
'Do_you_know_enough_about_when_to_take_your_medication_?',
'Do_you_know_enough_about_what_you_should_eat_to_help_you_manage_your_diabetes_?',
'Do_you_know_about_the_role_of_Physical_activity_in_managing_your_diabetes_?',
'Do_you_smoke_?']])
# knowledge_status.to_csv('../results/knowledge_status.csv', index=False)
knowledge_status
| 0.186132 | 0.72688 |
# EfficientNet Explained:
Main intution behind Efficient is to perform scaling on three paramenters:
+ **Resolution:**
If resolution of picture is high it contains more information.
+ With higher resolution input images, ConvNets can potentially capture more fine-grained patterns. However, for very high resolutions, the accuracy gains disminishes.
+ **Depth:**
Depth of a network is responsible for models accuracy.
+ Deeper ConvNets capture more complex features and generalize well. However, more difficult to train due to vanishing gradient. Although techniques such as “skip connections” and “batch normalization” are alleviating the training problem, the accuracy gain diminishes for very deep network.
+ **Width:**
Width scaling refers to wider networks (more channels) to capture more features
+ Wider networks tend to capture more fined-grained features and are easier to train. However, accuracy for such network tends to quickly saturate.

Some observations made by the authors of paper: " Rethinking Model Scaling for Convolutional Neural Networks"
+ Scaling up any dimension of network width, depth or resolution improves accuracy, but the accuracy gains dimnishes for bigger models.
+ In order to pursue better accuracy and efficiency, It is critical to balance all dimensions of the network width, depth, and resolution during scaling.
We can then think about scaling multiple dimension at one time. It is possible to scale two or three dimensions arbitrarily, requiring manual tuning which often yields to sub-optimal accuracy and efficiency.
In this paper, they are trying to address the following issue:
+ “Is there a principled method to scale up ConvNets that can achieve better accuracy and efficiency ?”
Their empirical study shows that it is critical to balance all dimensions of network (width/depth/resolution) at the same time.
Such balance can be achieved by scaling each of them by a constant ratio. This method is called “compound scaling method”, which consists of uniformly scales the network width, depth and resolution with a set of fixed scaling coefficients.
The intuition comes from the following fact:
+ If the input image is bigger (resolution), then there is more complex-features and fine-grained patterns. To capture more complex-feature, the network needs bigger receptive field which is achieved by adding more layers (depth). To capture more fine-grained patterns, the network needs more channels.
## **Baseline Model: EfficientNet B0**
Before even understanding and performing compound scaling we need to have a baseline model to work with.
Here the baseline model is Efficientnet-B0

The baseline network is developed by performing a neural architecture search using the AutoML MNAS framework, which optimizes both accuracy and efficiency (FLOPS). The resulting architecture uses mobile inverted bottleneck convolution (MBConv), similar to MobileNetV2 and MnasNet, but is slightly larger due to an increased FLOP budget. Then we scale up the baseline network to obtain a family of models, called EfficientNets.
### **EfficientNet-B0 Architecture**

The main building block of this network consists of MBConv to which squeeze-and-excitation optimization is added. MBConv is similar to the inverted residual blocks used in MobileNet v2. These form a shortcut connection between the beginning and end of a convolutional block. The input activation maps are first expanded using 1x1 convolutions to increase the depth of the feature maps. This is followed by 3x3 Depth-wise convolutions and Point-wise convolutions that reduce the number of channels in the output feature map. The shortcut connections connect the narrow layers whilst the wider layers are present between the skip connections. This structure helps in decreasing the overall number of operations required as well as the model size.

### **EfficientNet Performance**
In general, the EfficientNet models achieve both higher accuracy and better efficiency over existing CNNs, reducing parameter size and FLOPS by an order of magnitude. Below you can see the comparisions.

### **Compound Model Scaling: A Better Way to Scale Up CNNs**
While scaling individual dimensions improves model performance, we observed that balancing all dimensions of the network—width, depth, and image resolution—against the available resources would best improve overall performance.The first step in the compound scaling method is to perform a grid search to find the relationship between different scaling dimensions of the baseline network under a fixed resource constraint (e.g., 2x more FLOPS).his determines the appropriate scaling coefficient for each of the dimensions mentioned above. We then apply those coefficients to scale up the baseline network to the desired target model size or computational budget.
Finding a set of good coefficients to scale these dimensions for each layer is impossible, since the search space is huge. So, in order to restrict the search space, the authors lay down a set of ground rules.
+ All the layers/stages in the scaled models will use the same convolution operations as the baseline network
+ All layers must be scaled uniformly with constant ratio

Intuitively, $\phi$ is a user-defined coeffecient that determines how much extra resources are available. The constants $\alpha, \beta, \gamma$ determine how to distribute these extra resources accross networks depth(d), width(w) and input resolution(r).
Given that we have some extra resources $\alpha, \beta, \gamma$ can be determined using a small grid search and thus we can scale networks depth, width and input resolution to get a bigger network.
Starting from the baseline EfficientNet-B0, we apply our compound scaling method to scale it up with two steps:
+ STEP 1: we first fix φ = 1, assuming twice more resources available, and do a small grid search of α, β, γ. In particular, we find the best values for EfficientNet-B0 are α = 1.2, β = 1.1, γ = 1.15, under constraint of α * β2 * γ2 ≈ 2.
+ STEP 2: we then fix α, β, γ as constants and scale up baseline network with different φ, to obtain EfficientNet-B1 to B7.
|
github_jupyter
|
# EfficientNet Explained:
Main intution behind Efficient is to perform scaling on three paramenters:
+ **Resolution:**
If resolution of picture is high it contains more information.
+ With higher resolution input images, ConvNets can potentially capture more fine-grained patterns. However, for very high resolutions, the accuracy gains disminishes.
+ **Depth:**
Depth of a network is responsible for models accuracy.
+ Deeper ConvNets capture more complex features and generalize well. However, more difficult to train due to vanishing gradient. Although techniques such as “skip connections” and “batch normalization” are alleviating the training problem, the accuracy gain diminishes for very deep network.
+ **Width:**
Width scaling refers to wider networks (more channels) to capture more features
+ Wider networks tend to capture more fined-grained features and are easier to train. However, accuracy for such network tends to quickly saturate.

Some observations made by the authors of paper: " Rethinking Model Scaling for Convolutional Neural Networks"
+ Scaling up any dimension of network width, depth or resolution improves accuracy, but the accuracy gains dimnishes for bigger models.
+ In order to pursue better accuracy and efficiency, It is critical to balance all dimensions of the network width, depth, and resolution during scaling.
We can then think about scaling multiple dimension at one time. It is possible to scale two or three dimensions arbitrarily, requiring manual tuning which often yields to sub-optimal accuracy and efficiency.
In this paper, they are trying to address the following issue:
+ “Is there a principled method to scale up ConvNets that can achieve better accuracy and efficiency ?”
Their empirical study shows that it is critical to balance all dimensions of network (width/depth/resolution) at the same time.
Such balance can be achieved by scaling each of them by a constant ratio. This method is called “compound scaling method”, which consists of uniformly scales the network width, depth and resolution with a set of fixed scaling coefficients.
The intuition comes from the following fact:
+ If the input image is bigger (resolution), then there is more complex-features and fine-grained patterns. To capture more complex-feature, the network needs bigger receptive field which is achieved by adding more layers (depth). To capture more fine-grained patterns, the network needs more channels.
## **Baseline Model: EfficientNet B0**
Before even understanding and performing compound scaling we need to have a baseline model to work with.
Here the baseline model is Efficientnet-B0

The baseline network is developed by performing a neural architecture search using the AutoML MNAS framework, which optimizes both accuracy and efficiency (FLOPS). The resulting architecture uses mobile inverted bottleneck convolution (MBConv), similar to MobileNetV2 and MnasNet, but is slightly larger due to an increased FLOP budget. Then we scale up the baseline network to obtain a family of models, called EfficientNets.
### **EfficientNet-B0 Architecture**

The main building block of this network consists of MBConv to which squeeze-and-excitation optimization is added. MBConv is similar to the inverted residual blocks used in MobileNet v2. These form a shortcut connection between the beginning and end of a convolutional block. The input activation maps are first expanded using 1x1 convolutions to increase the depth of the feature maps. This is followed by 3x3 Depth-wise convolutions and Point-wise convolutions that reduce the number of channels in the output feature map. The shortcut connections connect the narrow layers whilst the wider layers are present between the skip connections. This structure helps in decreasing the overall number of operations required as well as the model size.

### **EfficientNet Performance**
In general, the EfficientNet models achieve both higher accuracy and better efficiency over existing CNNs, reducing parameter size and FLOPS by an order of magnitude. Below you can see the comparisions.

### **Compound Model Scaling: A Better Way to Scale Up CNNs**
While scaling individual dimensions improves model performance, we observed that balancing all dimensions of the network—width, depth, and image resolution—against the available resources would best improve overall performance.The first step in the compound scaling method is to perform a grid search to find the relationship between different scaling dimensions of the baseline network under a fixed resource constraint (e.g., 2x more FLOPS).his determines the appropriate scaling coefficient for each of the dimensions mentioned above. We then apply those coefficients to scale up the baseline network to the desired target model size or computational budget.
Finding a set of good coefficients to scale these dimensions for each layer is impossible, since the search space is huge. So, in order to restrict the search space, the authors lay down a set of ground rules.
+ All the layers/stages in the scaled models will use the same convolution operations as the baseline network
+ All layers must be scaled uniformly with constant ratio

Intuitively, $\phi$ is a user-defined coeffecient that determines how much extra resources are available. The constants $\alpha, \beta, \gamma$ determine how to distribute these extra resources accross networks depth(d), width(w) and input resolution(r).
Given that we have some extra resources $\alpha, \beta, \gamma$ can be determined using a small grid search and thus we can scale networks depth, width and input resolution to get a bigger network.
Starting from the baseline EfficientNet-B0, we apply our compound scaling method to scale it up with two steps:
+ STEP 1: we first fix φ = 1, assuming twice more resources available, and do a small grid search of α, β, γ. In particular, we find the best values for EfficientNet-B0 are α = 1.2, β = 1.1, γ = 1.15, under constraint of α * β2 * γ2 ≈ 2.
+ STEP 2: we then fix α, β, γ as constants and scale up baseline network with different φ, to obtain EfficientNet-B1 to B7.
| 0.894973 | 0.995408 |
# WES|WGS Pipeline
## Be sure to install paramiko and scp with pip before using this notebook
## 1. Configure AWS key pair, data location on S3 and the project information
This cell only contains information that you, the user, should input.
#### String Fields
**s3_input_files_address**: This is an s3 path to where your input fastq files are found. This shouldn't be the path to the actual fastq files, just to the directory containing all of them. All fastq files must be in the same s3 bucket.
**s3_output_files_address**: This is an s3 path to where you would like the outputs from your project to be uploaded. This will only be the root directory, please see the README for information about exactly how outputs are structured
**design_file**: This is a path to your design file for this project. Please see the README for the format specification for the design files.
**your_cluster_name**: This is the name given to your cluster when it was created using ParallelCluster.
**private_key**: The path to your private key needed to access your cluster.
**project_name**: Name of your project. There should be no whitespace.
**workflow**: The workflow you want to run for this project. For the DNASeq pipeline the possible workflows are "bwa_gatk" and "bwa_mutect".
**genome**: The name of the reference you want to use for your project. Currently only "hg19" and "GRCm38" are supported here.
#### analysis_steps
This is a set of strings that contains the steps you would like to run. The order of the steps does not matter.
posible bwa_gatk steps: "fastqc", "trim", "align", "multiqc", "sort", "dedup", "split", "postalignment", "haplotype", "merge", "combine_vcf"
possible bwa_mutect steps: "fastqc", "trim" , "align", "multiqc", "sort", "dedup", "split", "postalignment",
"somatic_variant_calling", "merge"
```
import os
import sys
sys.path.append("../../src/cirrus_ngs")
from awsCluster import ClusterManager, ConnectionManager
from util import PipelineManager
from util import DesignFileLoader
from util import ConfigParser
#s3 address of input files and output files
s3_input_files_address = "s3://path/to/fastq"
s3_output_files_address = "s3://path/to/output"
## ParallelCluster name
your_cluster_name = "clustername"
## The private key pair for accessing cluster.
private_key = "/path/to/your_aws_key.pem"
## Project information
project_name = "test_project"
#bwa_gatk, bwa_mutect, bwa_sv
workflow = "bwa_mutect"
#hg19, hg38 or GRCm38
genome = "GRCm38"
## Possible analysis_steps inputs for the two workflows. Order of input does not matter.
##bwa_gatk: "fastqc", "trim", "align", "multiqc","sort", "split", "postalignment",
#"haplotype", "merge", "group_vcf", "filter"
##bwa_mutect: "fastqc", "trim" , "align", "multiqc", "sort", "split", "postalignment",
#"somatic_variant_calling", "merge"
##bwa_sv: "fastqc", "trim" , "align", "multiqc", "sort", "split", "postalignment",
#"haplotype", "merge", "group_vcf", "filter", "sv_calling"
analysis_steps = {
"fastqc"
,"trim"
,"align"
,"multiqc"
,"sort"
,"dedup"
,"split"
}
#add design file path here
#examples in cirrus_root/data/cirrus-ngs/
design_file = design_file = "../../data/cirrus-ngs/dnaseq_design_example.txt"
print("variables set")
```
## 2. Create ParallelCluster
Following cell connects to your cluster. Run before step 3.
```
## Create a new cluster
master_ip_address = ClusterManager.create_aws_cluster(cluster_name=your_cluster_name)
ssh_client = ConnectionManager.connect_master(hostname=master_ip_address,
username="ec2-user",
private_key_file=private_key)
```
## 3. Run the pipeline
This cell actually executes your pipeline. Make sure that steps 1 and 2 have been completed before running.
```
## DO NOT EDIT BELOW
## print the analysis information
reference_list, tool_list = ConfigParser.parse(os.getcwd())
ConfigParser.print_software_info("DNASeq", workflow, genome, reference_list, tool_list)
print (analysis_steps)
sample_list, group_list, pairs_list = DesignFileLoader.load_design_file(design_file)
PipelineManager.execute("DNASeq", ssh_client, project_name, workflow, analysis_steps, s3_input_files_address,
sample_list, group_list, s3_output_files_address, genome, "NA", pairs_list)
```
## 4. Check status of pipeline
This allows you to check the status of your pipeline. You can specify a step or set the step variable to "all". If you specify a step it should be one that is in your analysis_steps set. You can toggle how verbose the status checking is by setting the verbose flag (at the end of the second line) to False.
```
step = "all"
PipelineManager.check_status(ssh_client, step, "DNASeq", workflow, project_name, analysis_steps,verbose=False)
```
If your pipeline is finished run this cell just in case there's some processes still running.
This is only relevant if you plan on doing another run on the same cluster afterwards.
```
PipelineManager.stop_pipeline(ssh_client)
```
## 5. Display MultiQC report
### Note: Run the cells below after the multiqc step is done
```
# Download the multiqc html file to local
notebook_dir = os.getcwd().split("notebooks")[0] + "data/"
!aws s3 cp $s3_output_files_address/$project_name/$workflow/multiqc_report.html $notebook_dir
from IPython.display import IFrame
IFrame(os.path.relpath("{}multiqc_report.html".format(notebook_dir)), width="100%", height=1000)
```
|
github_jupyter
|
import os
import sys
sys.path.append("../../src/cirrus_ngs")
from awsCluster import ClusterManager, ConnectionManager
from util import PipelineManager
from util import DesignFileLoader
from util import ConfigParser
#s3 address of input files and output files
s3_input_files_address = "s3://path/to/fastq"
s3_output_files_address = "s3://path/to/output"
## ParallelCluster name
your_cluster_name = "clustername"
## The private key pair for accessing cluster.
private_key = "/path/to/your_aws_key.pem"
## Project information
project_name = "test_project"
#bwa_gatk, bwa_mutect, bwa_sv
workflow = "bwa_mutect"
#hg19, hg38 or GRCm38
genome = "GRCm38"
## Possible analysis_steps inputs for the two workflows. Order of input does not matter.
##bwa_gatk: "fastqc", "trim", "align", "multiqc","sort", "split", "postalignment",
#"haplotype", "merge", "group_vcf", "filter"
##bwa_mutect: "fastqc", "trim" , "align", "multiqc", "sort", "split", "postalignment",
#"somatic_variant_calling", "merge"
##bwa_sv: "fastqc", "trim" , "align", "multiqc", "sort", "split", "postalignment",
#"haplotype", "merge", "group_vcf", "filter", "sv_calling"
analysis_steps = {
"fastqc"
,"trim"
,"align"
,"multiqc"
,"sort"
,"dedup"
,"split"
}
#add design file path here
#examples in cirrus_root/data/cirrus-ngs/
design_file = design_file = "../../data/cirrus-ngs/dnaseq_design_example.txt"
print("variables set")
## Create a new cluster
master_ip_address = ClusterManager.create_aws_cluster(cluster_name=your_cluster_name)
ssh_client = ConnectionManager.connect_master(hostname=master_ip_address,
username="ec2-user",
private_key_file=private_key)
## DO NOT EDIT BELOW
## print the analysis information
reference_list, tool_list = ConfigParser.parse(os.getcwd())
ConfigParser.print_software_info("DNASeq", workflow, genome, reference_list, tool_list)
print (analysis_steps)
sample_list, group_list, pairs_list = DesignFileLoader.load_design_file(design_file)
PipelineManager.execute("DNASeq", ssh_client, project_name, workflow, analysis_steps, s3_input_files_address,
sample_list, group_list, s3_output_files_address, genome, "NA", pairs_list)
step = "all"
PipelineManager.check_status(ssh_client, step, "DNASeq", workflow, project_name, analysis_steps,verbose=False)
PipelineManager.stop_pipeline(ssh_client)
# Download the multiqc html file to local
notebook_dir = os.getcwd().split("notebooks")[0] + "data/"
!aws s3 cp $s3_output_files_address/$project_name/$workflow/multiqc_report.html $notebook_dir
from IPython.display import IFrame
IFrame(os.path.relpath("{}multiqc_report.html".format(notebook_dir)), width="100%", height=1000)
| 0.301259 | 0.764144 |
# PADRÕES DE PROJETO EM PYTHON
[](https://colab.research.google.com/github/python-joinville/workshops/blob/master/padroes-de-projeto/1-decorator.ipynb) [launch](https://colab.research.google.com/github/python-joinville/workshops/blob/master/padroes-de-projeto/1-decorator.ipynb)
Os [padrões de projeto](https://pt.wikipedia.org/wiki/Padr%C3%A3o_de_projeto_de_software) foram documentados pela primeira vez pelo grupo GoF ([Gang of Four](https://en.wikipedia.org/wiki/Design_Patterns)). Inicialmente foram descobertos 23 padrões de projeto e documentados foco nas linguagens C++ e Java. Desde então, as linguagens de programação evoluíram e vários desses padrões foram implementados em nível de linguagem, como é feito em Python.
Os padrões podem ser divididos em 3 categorias.
**Padrões de criação**: funcionam com base no modo como os objetos podem ser criados isolando os detalhes da criação dos objetos. O código é independente do tipo do objeto a ser criado.
**Padrões estruturais**: determinam o design da estrutura de objetos e classes para que estes possam ser compostos. O foco está em simplificar a estrutura e identificar o relacionamento entre classes e objetos. Está focado na herança e composição de classes.
**Padrões comportamentais**: estão preocupados com a interação entre os objetos e suas responsabilidades. Os objetos deve ser capazes de interagir e, mesmo assim, devem ter baixo acoplamento.
Em linguagens dinâmicas como Python os tipos e classes são objetos criados em tempo de execução. As variáveis podem ter seu tipo definido a partir de um valor atribuído e podem ser modificadas em tempo de execução. Por exemplo, se definirmos a variável `variavel = 42`, podemos modificarmos p seu valor para `variavel = 'Quarenta e Dois` em tempo de execução, isso também muda o tipo da variável.
No geral, linguagens dinâmicas também são mais flexíveis em relação às restrições na contrução de classes. Por exemplo, em Python o polimorfismo está embutido na linguagem e não existem palavras reservadas como `private` e `protected`.
O uso de Padrões de Projetos nos fornecem algumas vantagens:
* Fornecem uma linguagem comum para todos os desenvolvedores do projeto;
* Os Padrões são reutilizáveis em vários projetos;
* Nos ajudam a solucionar problemas de arquitetura;
* São confiáveis;
* Diminuem a carga mental ao tentar solucionar problemas.
Nem todo código pode virar um Padrão de Projeto. Alguns códigos são apenas trechos que servem a determinado propósito como por exemplo realizar uma conexão com o banco de dados. Outros códigos podem ser apenas uma convensão. Um padrão é uma solução eficiente e escalável, resistente ao teste do tempo que resolverá toda uma classe de problemas conhecidos.
Padrões de Projetos são independentes de linguagem e podem ser implementados em linguagens diferentes. Eles podem ser personalizados de forma a se tornarem mais úteis aos desenvolvedores e não têm por objetivo resolver todos os problemas.
Descubra mais sobre Design Patterns:
* https://www.industriallogic.com/xp/refactoring/catalog.html
* https://sourcemaking.com
* https://github.com/faif/python-patterns
* https://github.com/iluwatar/java-design-patterns
* https://www.toptal.com/python/python-design-patterns
## PADRÃO DECORATOR
Decorators permitem adicionar um comportamento a funções, métodos e objetos já existentes em tempo de execução, ou seja, agregar dinamicamente responsabilidades adicionais. Decorators oferecem uma alternativa flexível ao uso de herança para estender uma funcionalidade, com isso adiciona-se uma responsabilidade ao objeto e não à classe [[*]](https://pt.wikipedia.org/wiki/Decorator). O uso de Decorators nos ajuda a adicionar funcionalidades à um objeto sem a necessidade de usar herança.

Em Python Decorators são implementados usando funções, então antes de entender o que é e como usar o Decorator, vamos entender um pouco mais sobre funções.
Funções são trechos de código que recebem parâmetros, realizam operações e retornam algum valor. Abaixo uma função que implementa a soma de dois números:
```python
def sum(one, two):
return (one + two)
```
Em Python. funções são "objetos de primeira classe". Isso significa que funções podem ser passadas como parâmetro, utilizadas como retorno de outras funções, assim como qualquer outro time (string, int, float).
Vamos ver como usar este poder! Atribuindo funções à variáveis:
```
def greet(name):
return f"Hello {name}"
greet_someone = greet
print(greet_someone("World"))
```
Definindo funções dentro de outras funções:
```
def greet(name):
def get_message():
return "Hello"
result = f"{get_message()} {name}"
return result
print(greet("World"))
```
Passando funções como parâmetro para outra função:
```
def greet(name):
return f"Hello {name}"
def call_func(func):
other_name = "World"
return func(other_name)
print(call_func(greet))
```
Funções podem ser definidas dentro de outras funções e retornadas. Estas funções são chamadas de "nested functions":
```
def compose_greet_func():
def get_message():
return "Hello World!"
return get_message
greet = compose_greet_func()
print(greet())
```
Funções definidas dentro de outras funções tem acesso ao escopo onde estão incluídas. Este comportamento é conhecido como "closure". Em Python temos acesso apenas a leitura de valores do escopo, não à escrita:
```
def compose_greet_func(name):
def get_message():
return f"Hello there {name}!"
return get_message
greet = compose_greet_func("World")
print(greet())
```
Agora que aprendemos um pouco mais sobre funções, vamos entender os Decorators. Decorators nada mais são do que funções para envolver outras funções, wrappers, modificando seu comportamento.
```
def decorator(funcao):
def wrapper():
print("Before function")
funcao()
print("After function")
return wrapper
def other_function():
print("Function")
decorated_function = decorator(other_function)
decorated_function()
```
Dessa forma, conseguimos adicionar qualquer comportamento antes e depois da execução de uma função qualquer. Vamos fazer agora um exemplo mais útil, algo que todo mundo que desenvolve software teve que fazer alguma vez vida: calcular o tempo de execução de determinada função [[*]](https://pythonacademy.com.br/blog/domine-decorators-em-python):
```
import time
def duration(function):
def wrapper():
initial_time = time.time()
function()
final_time = time.time()
total_time = str(final_time - initial_time)
print(f"[{function.__name__}] Total time: {total_time}")
return wrapper
def test_function_one():
for n in range(0, 10000000):
pass
test_function_one = duration(test_function_one)
def test_function_two():
for n in range(0, 100000000):
pass
test_function_two = duration(test_function_two)
test_function_one()
test_function_two()
```
Python torna a criação e uso de Decorators mais simples através de um ["syntactic sugar"](https://en.wikipedia.org/wiki/Syntactic_sugar). Para decorar `test_function_one` não precisamos fazer a atribuição `test_function_one = decorator(test_function_one)`. Uma notação especial representada pelo símbolo `@` foi definida na [PEP 318](https://www.python.org/dev/peps/pep-0318/):
```
@duration
def test_function_one():
for n in range(0, 10000000):
pass
@duration
def test_function_two():
for n in range(0, 100000000):
pass
test_function_one()
test_function_two()
```
Este padrão é muito importante no universo Python e também em outras linguagens. Em Java, por exemplo, este padrão é chamado de "Anotation". Usamos Decorators por exemplo no framework [Flask](http://flask.pocoo.org/) para definir as rotas de um servidor de aplicação web:
```python
@app.route('/api/users')
def users_list():
users = [1, 2, 3]
return jsonify(users)
```
Toda vez que uma requisição for feita para o endpoint `/api/users` a lista de usuários será retornada.
É possível ainda criar um Decorator que recebe parâmetros:
```
import functools
def repeat(num_times):
def decorator_repeat(func):
@functools.wraps(func)
def wrapper_repeat(*args, **kwargs):
for _ in range(num_times):
value = func(*args, **kwargs)
return value
return wrapper_repeat
return decorator_repeat
@repeat(num_times=4)
def greet(name):
print(f"Hello {name}")
greet("World")
```
Veja que introduzimos aqui uma nova função, a `functools.wraps`. Usamos esta função para nos ajudar a definir um Decorator que pode receber parâmetros. Quer entender melhor como isso funciona? Veja a [documentação do Python](https://docs.python.org/3.7/library/functools.html).
É possível ainda guardar estado dentro de Decorators. Podemos usar esta habilidade para criar por exemplo uma função de cache e evitar chamadas repetidas de um a determinada função:
```
import functools
def cache(func):
@functools.wraps(func)
def wrapper_cache(*args, **kwargs):
cache_key = args + tuple(kwargs.items())
if cache_key not in wrapper_cache.cache:
wrapper_cache.cache[cache_key] = func(*args, **kwargs)
return wrapper_cache.cache[cache_key]
else:
print(f"[cache] Getting value from cache {wrapper_cache.cache[cache_key]}")
return wrapper_cache.cache[cache_key]
wrapper_cache.cache = dict()
return wrapper_cache
def fibonacci_call(num):
if num < 2:
return num
return fibonacci_call(num - 1) + fibonacci_call(num - 2)
@cache
def fibonacci(num):
return fibonacci_call(num)
print(fibonacci(10))
print(fibonacci(10))
print(fibonacci(8))
print(fibonacci(8))
```
Podemos ainda definir uma classe como um Decorator:
```
import functools
class CountCalls:
def __init__(self, func):
functools.update_wrapper(self, func)
self.func = func
self.num_calls = 0
def __call__(self, *args, **kwargs):
self.num_calls += 1
print(f"Call {self.num_calls} of {self.func.__name__!r}")
return self.func(*args, **kwargs)
@CountCalls
def say_whee():
print("Whee!")
say_whee()
say_whee()
say_whee()
say_whee()
say_whee()
```
Descubra mais sober o padrão Decorator:
* https://realpython.com/primer-on-python-decorators
* https://en.wikipedia.org/wiki/Decorator_pattern
* https://docs.python.org/3.7/library/functools.html
* https://docs.python.org/3/glossary.html#term-decorator
* https://www.thecodeship.com/patterns/guide-to-python-function-decorators
* https://docs.python.org/3/library/functions.html
* https://docs.python.org/3/library/functools.html
|
github_jupyter
|
def sum(one, two):
return (one + two)
def greet(name):
return f"Hello {name}"
greet_someone = greet
print(greet_someone("World"))
def greet(name):
def get_message():
return "Hello"
result = f"{get_message()} {name}"
return result
print(greet("World"))
def greet(name):
return f"Hello {name}"
def call_func(func):
other_name = "World"
return func(other_name)
print(call_func(greet))
def compose_greet_func():
def get_message():
return "Hello World!"
return get_message
greet = compose_greet_func()
print(greet())
def compose_greet_func(name):
def get_message():
return f"Hello there {name}!"
return get_message
greet = compose_greet_func("World")
print(greet())
def decorator(funcao):
def wrapper():
print("Before function")
funcao()
print("After function")
return wrapper
def other_function():
print("Function")
decorated_function = decorator(other_function)
decorated_function()
import time
def duration(function):
def wrapper():
initial_time = time.time()
function()
final_time = time.time()
total_time = str(final_time - initial_time)
print(f"[{function.__name__}] Total time: {total_time}")
return wrapper
def test_function_one():
for n in range(0, 10000000):
pass
test_function_one = duration(test_function_one)
def test_function_two():
for n in range(0, 100000000):
pass
test_function_two = duration(test_function_two)
test_function_one()
test_function_two()
@duration
def test_function_one():
for n in range(0, 10000000):
pass
@duration
def test_function_two():
for n in range(0, 100000000):
pass
test_function_one()
test_function_two()
@app.route('/api/users')
def users_list():
users = [1, 2, 3]
return jsonify(users)
import functools
def repeat(num_times):
def decorator_repeat(func):
@functools.wraps(func)
def wrapper_repeat(*args, **kwargs):
for _ in range(num_times):
value = func(*args, **kwargs)
return value
return wrapper_repeat
return decorator_repeat
@repeat(num_times=4)
def greet(name):
print(f"Hello {name}")
greet("World")
import functools
def cache(func):
@functools.wraps(func)
def wrapper_cache(*args, **kwargs):
cache_key = args + tuple(kwargs.items())
if cache_key not in wrapper_cache.cache:
wrapper_cache.cache[cache_key] = func(*args, **kwargs)
return wrapper_cache.cache[cache_key]
else:
print(f"[cache] Getting value from cache {wrapper_cache.cache[cache_key]}")
return wrapper_cache.cache[cache_key]
wrapper_cache.cache = dict()
return wrapper_cache
def fibonacci_call(num):
if num < 2:
return num
return fibonacci_call(num - 1) + fibonacci_call(num - 2)
@cache
def fibonacci(num):
return fibonacci_call(num)
print(fibonacci(10))
print(fibonacci(10))
print(fibonacci(8))
print(fibonacci(8))
import functools
class CountCalls:
def __init__(self, func):
functools.update_wrapper(self, func)
self.func = func
self.num_calls = 0
def __call__(self, *args, **kwargs):
self.num_calls += 1
print(f"Call {self.num_calls} of {self.func.__name__!r}")
return self.func(*args, **kwargs)
@CountCalls
def say_whee():
print("Whee!")
say_whee()
say_whee()
say_whee()
say_whee()
say_whee()
| 0.471467 | 0.926103 |
# Laboratorio 3
En este laboratorio nuevamente utilizaremos los datos de COVID-19 disponibilizados por el Ministerio de Ciencias, Tecnología, Conocimiento e Innovación de Chile ([info](https://github.com/MinCiencia/Datos-COVID19/tree/master/output/producto1)).
```
import pandas as pd
covid = pd.read_csv("https://raw.githubusercontent.com/MinCiencia/Datos-COVID19/master/output/producto1/Covid-19_std.csv")
covid.head(20)
```
## Ejercicio 1
(1 pto)
¿Cuál es la región que tiene menos registros (filas)?
```
print(f"La Region de {covid['Region'].value_counts().index[15]}, con {covid['Region'].value_counts().min()} registros")
```
__Respuesta:__ La región de Arica y Parinacota
## Ejercicio 2
(2 puntos)
1. Define la serie `casos` tal que:
* Solo sean los registros de la región Valparaíso.
* Los _index_ deben ser la _Fecha_ pero en formato `datetime`. Hint: `pd.to_datetime()`
* Los _values_ deben ser los _Casos confirmados_.
2. Define la serie `casos_not_null` filtrando los calores `NaN` de la serie `casos`.
3. Obtén el mínimo, máximo y suma y promedio de la serie `casos_not_null`.
```
covid_valpo = covid.loc[covid.loc[:,"Region"] == "Valparaíso"]
indices = pd.to_datetime(covid_valpo.loc[:,"Fecha"], format='%Y-%m-%d')
values = covid_valpo.loc[:,"Casos confirmados"].values
casos = pd.Series(values,indices)
casos.head()
casos_not_null = casos.loc[lambda x: x.notnull()]
type(casos_not_null)
casos_min = casos_not_null.min()
casos_max = casos_not_null.max()
casos_sum = casos_not_null.sum()
casos_mean = casos_sum/len(casos_not_null)
print(f"Mínimo casos: {casos_min}")
print(f"Máximo casos: {casos_max}")
print(f"Suma de casos: {casos_sum}")
print(f"Promedio de casos: {casos_mean}")
```
## Ejercicio 3
* Define el dataframe `covid_full` uniendo (`merge`) los dataframes `covid_total` y `covid_death` utilizando la _Fecha_ como _key_ y de tal forma de unir solo los registros que se encuentren en ambos conjuntos de datos. Hint: Escoger sabiamente entre _left_, _right_, _inner_ u _outer join_.
* Filtra el dataframe `covid_full` tal que:
- Fechas con por lo menos 1000 casos totales.
- Fechas con por lo menos 100 casos nuevos con síntomas.
- Fechas con más de 20 muertes en el grupo etárea `70-79`.
¿Cuál es la fecha máxima y mínima? ¿Cuántos registros quedan finalmente?
```
covid_total = pd.read_csv("https://raw.githubusercontent.com/MinCiencia/Datos-COVID19/master/output/producto5/TotalesNacionales_T.csv", usecols=range(3))
covid_total.head()
covid_death = pd.read_csv("https://raw.githubusercontent.com/MinCiencia/Datos-COVID19/master/output/producto10/FallecidosEtario_T.csv").rename(columns={"Grupo de edad": "Fecha"})
covid_death.head()
covid_full = covid_total.merge(covid_death, how="inner", on="Fecha")
covid_full.head()
mask1 = covid_full['Casos totales'] >999
mask2 = covid_full["Casos nuevos con sintomas"] >99
mask3 = covid_full['70-79'] >20
covid_full_filtered = covid_full[mask1 & mask2 & mask3]
covid_full_filtered
print(f"Fecha mínima: {covid_full_filtered.loc[:,'Fecha'].min()}")
print(f"Fecha máxima: {covid_full_filtered.loc[:,'Fecha'].max()}")
print(f"Cantidad de registros finalmente:{len(covid_full_filtered)}")
```
|
github_jupyter
|
import pandas as pd
covid = pd.read_csv("https://raw.githubusercontent.com/MinCiencia/Datos-COVID19/master/output/producto1/Covid-19_std.csv")
covid.head(20)
print(f"La Region de {covid['Region'].value_counts().index[15]}, con {covid['Region'].value_counts().min()} registros")
covid_valpo = covid.loc[covid.loc[:,"Region"] == "Valparaíso"]
indices = pd.to_datetime(covid_valpo.loc[:,"Fecha"], format='%Y-%m-%d')
values = covid_valpo.loc[:,"Casos confirmados"].values
casos = pd.Series(values,indices)
casos.head()
casos_not_null = casos.loc[lambda x: x.notnull()]
type(casos_not_null)
casos_min = casos_not_null.min()
casos_max = casos_not_null.max()
casos_sum = casos_not_null.sum()
casos_mean = casos_sum/len(casos_not_null)
print(f"Mínimo casos: {casos_min}")
print(f"Máximo casos: {casos_max}")
print(f"Suma de casos: {casos_sum}")
print(f"Promedio de casos: {casos_mean}")
covid_total = pd.read_csv("https://raw.githubusercontent.com/MinCiencia/Datos-COVID19/master/output/producto5/TotalesNacionales_T.csv", usecols=range(3))
covid_total.head()
covid_death = pd.read_csv("https://raw.githubusercontent.com/MinCiencia/Datos-COVID19/master/output/producto10/FallecidosEtario_T.csv").rename(columns={"Grupo de edad": "Fecha"})
covid_death.head()
covid_full = covid_total.merge(covid_death, how="inner", on="Fecha")
covid_full.head()
mask1 = covid_full['Casos totales'] >999
mask2 = covid_full["Casos nuevos con sintomas"] >99
mask3 = covid_full['70-79'] >20
covid_full_filtered = covid_full[mask1 & mask2 & mask3]
covid_full_filtered
print(f"Fecha mínima: {covid_full_filtered.loc[:,'Fecha'].min()}")
print(f"Fecha máxima: {covid_full_filtered.loc[:,'Fecha'].max()}")
print(f"Cantidad de registros finalmente:{len(covid_full_filtered)}")
| 0.253953 | 0.826502 |
# Machine Learning Engineer Nanodegree
## Supervised Learning
## Project: Finding Donors for *CharityML*
Welcome to the second project of the Machine Learning Engineer Nanodegree! In this notebook, some template code has already been provided for you, and it will be your job to implement the additional functionality necessary to successfully complete this project. Sections that begin with **'Implementation'** in the header indicate that the following block of code will require additional functionality which you must provide. Instructions will be provided for each section and the specifics of the implementation are marked in the code block with a `'TODO'` statement. Please be sure to read the instructions carefully!
In addition to implementing code, there will be questions that you must answer which relate to the project and your implementation. Each section where you will answer a question is preceded by a **'Question X'** header. Carefully read each question and provide thorough answers in the following text boxes that begin with **'Answer:'**. Your project submission will be evaluated based on your answers to each of the questions and the implementation you provide.
>**Note:** Code and Markdown cells can be executed using the **Shift + Enter** keyboard shortcut. In addition, Markdown cells can be edited by typically double-clicking the cell to enter edit mode.
## Getting Started
In this project, you will employ several supervised algorithms of your choice to accurately model individuals' income using data collected from the 1994 U.S. Census. You will then choose the best candidate algorithm from preliminary results and further optimize this algorithm to best model the data. Your goal with this implementation is to construct a model that accurately predicts whether an individual makes more than $50,000. This sort of task can arise in a non-profit setting, where organizations survive on donations. Understanding an individual's income can help a non-profit better understand how large of a donation to request, or whether or not they should reach out to begin with. While it can be difficult to determine an individual's general income bracket directly from public sources, we can (as we will see) infer this value from other publically available features.
The dataset for this project originates from the [UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/datasets/Census+Income). The datset was donated by Ron Kohavi and Barry Becker, after being published in the article _"Scaling Up the Accuracy of Naive-Bayes Classifiers: A Decision-Tree Hybrid"_. You can find the article by Ron Kohavi [online](https://www.aaai.org/Papers/KDD/1996/KDD96-033.pdf). The data we investigate here consists of small changes to the original dataset, such as removing the `'fnlwgt'` feature and records with missing or ill-formatted entries.
----
## Exploring the Data
Run the code cell below to load necessary Python libraries and load the census data. Note that the last column from this dataset, `'income'`, will be our target label (whether an individual makes more than, or at most, $50,000 annually). All other columns are features about each individual in the census database.
```
# Import libraries necessary for this project
import numpy as np
import pandas as pd
from time import time
from IPython.display import display # Allows the use of display() for DataFrames
# Import supplementary visualization code visuals.py
import visuals as vs
# Pretty display for notebooks
%matplotlib inline
# Load the Census dataset
data = pd.read_csv("census.csv")
# Success - Display the first record
display(data.head(n=1))
```
### Implementation: Data Exploration
A cursory investigation of the dataset will determine how many individuals fit into either group, and will tell us about the percentage of these individuals making more than \$50,000. In the code cell below, you will need to compute the following:
- The total number of records, `'n_records'`
- The number of individuals making more than \$50,000 annually, `'n_greater_50k'`.
- The number of individuals making at most \$50,000 annually, `'n_at_most_50k'`.
- The percentage of individuals making more than \$50,000 annually, `'greater_percent'`.
**Hint:** You may need to look at the table above to understand how the `'income'` entries are formatted.
```
# TODO: Total number of records
n_records = len(data)
# TODO: Number of records where individual's income is more than $50,000
n_greater_50k = 0
for entry in data.income:
if entry == '>50K':
n_greater_50k = n_greater_50k+1
# TODO: Number of records where individual's income is at most $50,000
n_at_most_50k = 0
for entry in data.income:
if entry == '<=50K':
n_at_most_50k = n_at_most_50k + 1
# TODO: Percentage of individuals whose income is more than $50,000
greater_percent = (float(n_greater_50k)/n_records)*100
# Print the results
print "Total number of records: {}".format(n_records)
print "Individuals making more than $50,000: {}".format(n_greater_50k)
print "Individuals making at most $50,000: {}".format(n_at_most_50k)
print "Percentage of individuals making more than $50,000: {:.2f}%".format(greater_percent)
```
----
## Preparing the Data
Before data can be used as input for machine learning algorithms, it often must be cleaned, formatted, and restructured — this is typically known as **preprocessing**. Fortunately, for this dataset, there are no invalid or missing entries we must deal with, however, there are some qualities about certain features that must be adjusted. This preprocessing can help tremendously with the outcome and predictive power of nearly all learning algorithms.
### Transforming Skewed Continuous Features
A dataset may sometimes contain at least one feature whose values tend to lie near a single number, but will also have a non-trivial number of vastly larger or smaller values than that single number. Algorithms can be sensitive to such distributions of values and can underperform if the range is not properly normalized. With the census dataset two features fit this description: '`capital-gain'` and `'capital-loss'`.
Run the code cell below to plot a histogram of these two features. Note the range of the values present and how they are distributed.
```
# Split the data into features and target label
income_raw = data['income']
features_raw = data.drop('income', axis = 1)
# Visualize skewed continuous features of original data
vs.distribution(data)
```
For highly-skewed feature distributions such as `'capital-gain'` and `'capital-loss'`, it is common practice to apply a <a href="https://en.wikipedia.org/wiki/Data_transformation_(statistics)">logarithmic transformation</a> on the data so that the very large and very small values do not negatively affect the performance of a learning algorithm. Using a logarithmic transformation significantly reduces the range of values caused by outliers. Care must be taken when applying this transformation however: The logarithm of `0` is undefined, so we must translate the values by a small amount above `0` to apply the the logarithm successfully.
Run the code cell below to perform a transformation on the data and visualize the results. Again, note the range of values and how they are distributed.
```
# Log-transform the skewed features
skewed = ['capital-gain', 'capital-loss']
features_raw[skewed] = data[skewed].apply(lambda x: np.log(x + 1))
# Visualize the new log distributions
vs.distribution(features_raw, transformed = True)
```
### Normalizing Numerical Features
In addition to performing transformations on features that are highly skewed, it is often good practice to perform some type of scaling on numerical features. Applying a scaling to the data does not change the shape of each feature's distribution (such as `'capital-gain'` or `'capital-loss'` above); however, normalization ensures that each feature is treated equally when applying supervised learners. Note that once scaling is applied, observing the data in its raw form will no longer have the same original meaning, as exampled below.
Run the code cell below to normalize each numerical feature. We will use [`sklearn.preprocessing.MinMaxScaler`](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html) for this.
```
# Import sklearn.preprocessing.StandardScaler
from sklearn.preprocessing import MinMaxScaler
# Initialize a scaler, then apply it to the features
scaler = MinMaxScaler()
numerical = ['age', 'education-num', 'capital-gain', 'capital-loss', 'hours-per-week']
features_raw[numerical] = scaler.fit_transform(data[numerical])
# Show an example of a record with scaling applied
display(features_raw.head(n = 1))
```
### Implementation: Data Preprocessing
From the table in **Exploring the Data** above, we can see there are several features for each record that are non-numeric. Typically, learning algorithms expect input to be numeric, which requires that non-numeric features (called *categorical variables*) be converted. One popular way to convert categorical variables is by using the **one-hot encoding** scheme. One-hot encoding creates a _"dummy"_ variable for each possible category of each non-numeric feature. For example, assume `someFeature` has three possible entries: `A`, `B`, or `C`. We then encode this feature into `someFeature_A`, `someFeature_B` and `someFeature_C`.
| | someFeature | | someFeature_A | someFeature_B | someFeature_C |
| :-: | :-: | | :-: | :-: | :-: |
| 0 | B | | 0 | 1 | 0 |
| 1 | C | ----> one-hot encode ----> | 0 | 0 | 1 |
| 2 | A | | 1 | 0 | 0 |
Additionally, as with the non-numeric features, we need to convert the non-numeric target label, `'income'` to numerical values for the learning algorithm to work. Since there are only two possible categories for this label ("<=50K" and ">50K"), we can avoid using one-hot encoding and simply encode these two categories as `0` and `1`, respectively. In code cell below, you will need to implement the following:
- Use [`pandas.get_dummies()`](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.get_dummies.html?highlight=get_dummies#pandas.get_dummies) to perform one-hot encoding on the `'features_raw'` data.
- Convert the target label `'income_raw'` to numerical entries.
- Set records with "<=50K" to `0` and records with ">50K" to `1`.
```
from sklearn.preprocessing import LabelEncoder
import pandas as pd
# TODO: One-hot encode the 'features_raw' data using pandas.get_dummies()
features = pd.get_dummies(features_raw)
le = LabelEncoder()
le.fit(income_raw)
# TODO: Encode the 'income_raw' data to numerical values
income = le.transform(income_raw)
# Print the number of features after one-hot encoding
encoded = list(features.columns)
print "{} total features after one-hot encoding.".format(len(encoded))
# Uncomment the following line to see the encoded feature names
print encoded
```
### Shuffle and Split Data
Now all _categorical variables_ have been converted into numerical features, and all numerical features have been normalized. As always, we will now split the data (both features and their labels) into training and test sets. 80% of the data will be used for training and 20% for testing.
Run the code cell below to perform this split.
```
# Import train_test_split
from sklearn.cross_validation import train_test_split
# Split the 'features' and 'income' data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(features, income, test_size = 0.2, random_state = 0)
# Show the results of the split
print "Training set has {} samples.".format(X_train.shape[0])
print "Testing set has {} samples.".format(X_test.shape[0])
```
----
## Evaluating Model Performance
In this section, we will investigate four different algorithms, and determine which is best at modeling the data. Three of these algorithms will be supervised learners of your choice, and the fourth algorithm is known as a *naive predictor*.
### Metrics and the Naive Predictor
*CharityML*, equipped with their research, knows individuals that make more than \$50,000 are most likely to donate to their charity. Because of this, *UdacityML* is particularly interested in predicting who makes more than \$50,000 accurately. It would seem that using **accuracy** as a metric for evaluating a particular model's performace would is appropriate. Additionally, identifying someone that *does not* make more than \$50,000 as someone who does would be detrimental to *UdacityML*, since they are looking to find individuals willing to donate. Therefore, a model's ability to precisely predict those that make more than \$50,000 is *more important* than the model's ability to **recall** those individuals. We can use **F-beta score** as a metric that considers both precision and recall:
$$ F_{\beta} = (1 + \beta^2) \cdot \frac{precision \cdot recall}{\left( \beta^2 \cdot precision \right) + recall} $$
In particular, when $\beta = 0.5$, more emphasis is placed on precision. This is called the **F$_{0.5}$ score** (or F-score for simplicity).
Looking at the distribution of classes (those who make at most \$50,000, and those who make more), it's clear most individuals do not make more than \$50,000. This can greatly affect **accuracy**, since we could simply say *"this person does not make more than \$50,000"* and generally be right, without ever looking at the data! Making such a statement would be called **naive**, since we have not considered any information to substantiate the claim. It is always important to consider the *naive prediction* for your data, to help establish a benchmark for whether a model is performing well. That been said, using that prediction would be pointless: If we predicted all people made less than \$50,000, *UdacityML* would identify no one as donors.
### Question 1 - Naive Predictor Performace
*If we chose a model that always predicted an individual made more than \$50,000, what would that model's accuracy and F-score be on this dataset?*
**Note:** You must use the code cell below and assign your results to `'accuracy'` and `'fscore'` to be used later.
```
# TODO: Calculate accuracy
accuracy = 0.2478
# TODO: Calculate F-score using the formula above for beta = 0.5
fscore = (1+0.5**2)*(0.2478*1)/(((0.5**2)*0.2478)+1)
# Print the results
print "Naive Predictor: [Accuracy score: {:.4f}, F-score: {:.4f}]".format(accuracy, fscore)
```
### Supverised Learning Models
**The following supervised learning models are currently available in** [`scikit-learn`](http://scikit-learn.org/stable/supervised_learning.html) **that you may choose from:**
- Gaussian Naive Bayes (GaussianNB)
- Decision Trees
- Ensemble Methods (Bagging, AdaBoost, Random Forest, Gradient Boosting)
- K-Nearest Neighbors (KNeighbors)
- Stochastic Gradient Descent Classifier (SGDC)
- Support Vector Machines (SVM)
- Logistic Regression
### Question 2 - Model Application
List three of the supervised learning models above that are appropriate for this problem that you will test on the census data. For each model chosen
- *Describe one real-world application in industry where the model can be applied.* (You may need to do research for this — give references!)
- *What are the strengths of the model; when does it perform well?*
- *What are the weaknesses of the model; when does it perform poorly?*
- *What makes this model a good candidate for the problem, given what you know about the data?*
**Answer: **
As this is a classification problem, the models that I think are appropriate for this are
1. Gaussian Naive Bayes
2. Decision Tree
3. Support Vector Machine
Applications:
1.Naive Bayes for spam detection of emails
2.Tree based classification has been used recently for recognizing three dimensional objects
3.SVM for Protein Fold and Remote Homology Detection
References:
Quora.com, http://www.cbcb.umd.edu/~salzberg/docs/murthy_thesis/survey, http://www.clopinet.com/SVM.applications.html
Strengths and Weaknesses:
Naive Bayes is fast to train, so it performs well on discrete data.
Weakness is that it assumes independence of features.
Decision Trees give you a lot of possibilities, so it will perform well when you have to make more than one decision.
Weakness is overfitting i.e, if you consider all possibilities you might be overfitting the data.
SVM has many kernel tricks and regularisation parameter.
SVMs cannot represent all features as a simple parametric function since its dimension may be very high.
As the problem is a classification problem, all of these make good candidates to solve it.
### Implementation - Creating a Training and Predicting Pipeline
To properly evaluate the performance of each model you've chosen, it's important that you create a training and predicting pipeline that allows you to quickly and effectively train models using various sizes of training data and perform predictions on the testing data. Your implementation here will be used in the following section.
In the code block below, you will need to implement the following:
- Import `fbeta_score` and `accuracy_score` from [`sklearn.metrics`](http://scikit-learn.org/stable/modules/classes.html#sklearn-metrics-metrics).
- Fit the learner to the sampled training data and record the training time.
- Perform predictions on the test data `X_test`, and also on the first 300 training points `X_train[:300]`.
- Record the total prediction time.
- Calculate the accuracy score for both the training subset and testing set.
- Calculate the F-score for both the training subset and testing set.
- Make sure that you set the `beta` parameter!
```
# TODO: Import two metrics from sklearn - fbeta_score and accuracy_score
from sklearn.metrics import fbeta_score, accuracy_score
def train_predict(learner, sample_size, X_train, y_train, X_test, y_test):
'''
inputs:
- learner: the learning algorithm to be trained and predicted on
- sample_size: the size of samples (number) to be drawn from training set
- X_train: features training set
- y_train: income training set
- X_test: features testing set
- y_test: income testing set
'''
results = {}
# TODO: Fit the learner to the training data using slicing with 'sample_size'
start = time() # Get start time
learner.fit(X_train[:sample_size], y_train[:sample_size])
end = time() # Get end time
# TODO: Calculate the training time
results['train_time'] = end-start
# TODO: Get the predictions on the test set,
# then get predictions on the first 300 training samples
start = time() # Get start time
predictions_test = learner.predict(X_test)
predictions_train = learner.predict(X_train[:300])
end = time() # Get end time
# TODO: Calculate the total prediction time
results['pred_time'] = end-start
# TODO: Compute accuracy on the first 300 training samples
results['acc_train'] = accuracy_score(y_train[:300],predictions_train)
# TODO: Compute accuracy on test set
results['acc_test'] = accuracy_score(y_test,predictions_test)
# TODO: Compute F-score on the the first 300 training samples
results['f_train'] = fbeta_score(y_train[:300],predictions_train, beta = 0.5)
# TODO: Compute F-score on the test set
results['f_test'] = fbeta_score(y_test,predictions_test,beta =0.5)
# Success
print "{} trained on {} samples.".format(learner.__class__.__name__, sample_size)
# Return the results
return results
```
### Implementation: Initial Model Evaluation
In the code cell, you will need to implement the following:
- Import the three supervised learning models you've discussed in the previous section.
- Initialize the three models and store them in `'clf_A'`, `'clf_B'`, and `'clf_C'`.
- Use a `'random_state'` for each model you use, if provided.
- **Note:** Use the default settings for each model — you will tune one specific model in a later section.
- Calculate the number of records equal to 1%, 10%, and 100% of the training data.
- Store those values in `'samples_1'`, `'samples_10'`, and `'samples_100'` respectively.
**Note:** Dependent on which algorithms you chose, the following implementation may take some time to run!
```
# TODO: Import the three supervised learning models from sklearn
from sklearn.naive_bayes import GaussianNB
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
# TODO: Initialize the three models
clf_A = GaussianNB()
clf_B = DecisionTreeClassifier()
clf_C = SVC()
# TODO: Calculate the number of samples for 1%, 10%, and 100% of the training data
samples_1 = len(X_train)/100
samples_10 = len(X_train)/10
samples_100 = len(X_train)/1
# Collect results on the learners
results = {}
for clf in [clf_A, clf_B, clf_C]:
clf_name = clf.__class__.__name__
results[clf_name] = {}
for i, samples in enumerate([samples_1, samples_10, samples_100]):
results[clf_name][i] = \
train_predict(clf, samples, X_train, y_train, X_test, y_test)
# Run metrics visualization for the three supervised learning models chosen
vs.evaluate(results, accuracy, fscore)
```
----
## Improving Results
In this final section, you will choose from the three supervised learning models the *best* model to use on the student data. You will then perform a grid search optimization for the model over the entire training set (`X_train` and `y_train`) by tuning at least one parameter to improve upon the untuned model's F-score.
### Question 3 - Choosing the Best Model
*Based on the evaluation you performed earlier, in one to two paragraphs, explain to *CharityML* which of the three models you believe to be most appropriate for the task of identifying individuals that make more than \$50,000.*
**Hint:** Your answer should include discussion of the metrics, prediction/training time, and the algorithm's suitability for the data.
**Answer: **
Based on the evaluation graphs, A DecisionTreeClassifier will be most appropriate for identifying individuals that make more than $50,000.
As we can see the time taken for training is very less in both Naive Bayes and Decision Tree Classifier. But it is very much high in the case of SVC as the data grows bigger. So, SVC gets out of the scenario.
Then if we check both our evaluation metrics fbeta_score and accuracy, then Decision Tree Classifier gives accuracy and fbeta_score of almost 1 while training which is much higher when compared to Naive Bayes.
In case of testing as well , accuracy of Decision Tree Classifier is almost 0.8 and fbeta_score is almost 0.6
So, taking into consideration all these factors I think that Decision Tree Classifier is the best model for this problem.
### Question 4 - Describing the Model in Layman's Terms
*In one to two paragraphs, explain to *CharityML*, in layman's terms, how the final model chosen is supposed to work. Be sure that you are describing the major qualities of the model, such as how the model is trained and how the model makes a prediction. Avoid using advanced mathematical or technical jargon, such as describing equations or discussing the algorithm implementation.*
**Answer: **
Our final model is Decision Tree Classifier.
So based on our set of features, we ask questions about the feature and have different route for every answer to the question. So, a series of questions about our features bring us to some conclusion about the dataset. These conclusions are our labels.
So, if you'll give this model a set of features to predict the output, it'll just ask the questions about the feature and finally get to some conclusion i.e, label.
### Implementation: Model Tuning
Fine tune the chosen model. Use grid search (`GridSearchCV`) with at least one important parameter tuned with at least 3 different values. You will need to use the entire training set for this. In the code cell below, you will need to implement the following:
- Import [`sklearn.grid_search.GridSearchCV`](http://scikit-learn.org/0.17/modules/generated/sklearn.grid_search.GridSearchCV.html) and [`sklearn.metrics.make_scorer`](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.make_scorer.html).
- Initialize the classifier you've chosen and store it in `clf`.
- Set a `random_state` if one is available to the same state you set before.
- Create a dictionary of parameters you wish to tune for the chosen model.
- Example: `parameters = {'parameter' : [list of values]}`.
- **Note:** Avoid tuning the `max_features` parameter of your learner if that parameter is available!
- Use `make_scorer` to create an `fbeta_score` scoring object (with $\beta = 0.5$).
- Perform grid search on the classifier `clf` using the `'scorer'`, and store it in `grid_obj`.
- Fit the grid search object to the training data (`X_train`, `y_train`), and store it in `grid_fit`.
**Note:** Depending on the algorithm chosen and the parameter list, the following implementation may take some time to run!
```
# TODO: Import 'GridSearchCV', 'make_scorer', and any other necessary libraries
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer
# TODO: Initialize the classifier
clf = DecisionTreeClassifier()
# TODO: Create the parameters list you wish to tune
parameters = {}
# TODO: Make an fbeta_score scoring object
scorer = make_scorer(fbeta_score, beta = 0.5)
# TODO: Perform grid search on the classifier using 'scorer' as the scoring method
grid_obj = GridSearchCV(clf, parameters)
# TODO: Fit the grid search object to the training data and find the optimal parameters
grid_fit = grid_obj.fit(X_train,y_train)
# Get the estimator
best_clf = grid_fit.best_estimator_
# Make predictions using the unoptimized and model
predictions = (clf.fit(X_train, y_train)).predict(X_test)
best_predictions = best_clf.predict(X_test)
# Report the before-and-afterscores
print "Unoptimized model\n------"
print "Accuracy score on testing data: {:.4f}".format(accuracy_score(y_test, predictions))
print "F-score on testing data: {:.4f}".format(fbeta_score(y_test, predictions, beta = 0.5))
print "\nOptimized Model\n------"
print "Final accuracy score on the testing data: {:.4f}".format(accuracy_score(y_test, best_predictions))
print "Final F-score on the testing data: {:.4f}".format(fbeta_score(y_test, best_predictions, beta = 0.5))
```
### Question 5 - Final Model Evaluation
_What is your optimized model's accuracy and F-score on the testing data? Are these scores better or worse than the unoptimized model? How do the results from your optimized model compare to the naive predictor benchmarks you found earlier in **Question 1**?_
**Note:** Fill in the table below with your results, and then provide discussion in the **Answer** box.
#### Results:
| Metric | Benchmark Predictor | Unoptimized Model | Optimized Model |
| :------------: | :-----------------: | :---------------: | :-------------: |
| Accuracy Score | 0.2478 | 0.8153 | 0.8181 |
| F-score | 0.2917 | 0.6210 | 0.6270 |
**Answer: **
My accuracy for optimized model is 0.8181, whereas F-score is 0.6270
These are slightly better than the unoptimized model because the model was already giving very good results.
But these results do a commendable job when compared to the naive predictor benchmarks.
----
## Feature Importance
An important task when performing supervised learning on a dataset like the census data we study here is determining which features provide the most predictive power. By focusing on the relationship between only a few crucial features and the target label we simplify our understanding of the phenomenon, which is most always a useful thing to do. In the case of this project, that means we wish to identify a small number of features that most strongly predict whether an individual makes at most or more than \$50,000.
Choose a scikit-learn classifier (e.g., adaboost, random forests) that has a `feature_importance_` attribute, which is a function that ranks the importance of features according to the chosen classifier. In the next python cell fit this classifier to training set and use this attribute to determine the top 5 most important features for the census dataset.
### Question 6 - Feature Relevance Observation
When **Exploring the Data**, it was shown there are thirteen available features for each individual on record in the census data.
_Of these thirteen records, which five features do you believe to be most important for prediction, and in what order would you rank them?_
**Answer:**
1. Occupation
2. hours per week
3. Work class
4. Education level
5. Capital_gain
### Implementation - Extracting Feature Importance
Choose a `scikit-learn` supervised learning algorithm that has a `feature_importance_` attribute availble for it. This attribute is a function that ranks the importance of each feature when making predictions based on the chosen algorithm.
In the code cell below, you will need to implement the following:
- Import a supervised learning model from sklearn if it is different from the three used earlier.
- Train the supervised model on the entire training set.
- Extract the feature importances using `'.feature_importances_'`.
```
# TODO: Import a supervised learning model that has 'feature_importances_'
# TODO: Train the supervised model on the training set
model = DecisionTreeClassifier()
model.fit(X_train , y_train)
# TODO: Extract the feature importances
importances = model.feature_importances_
# Plot
vs.feature_plot(importances, X_train, y_train)
```
### Question 7 - Extracting Feature Importance
Observe the visualization created above which displays the five most relevant features for predicting if an individual makes at most or above \$50,000.
_How do these five features compare to the five features you discussed in **Question 6**? If you were close to the same answer, how does this visualization confirm your thoughts? If you were not close, why do you think these features are more relevant?_
**Answer:**
I predicted only 2 of the above 5 features, which are capital-gain and hours per week.
I think that marital status is important because if he is a family person there's a tendency that he earns more.
Age is also a factor because with experience there's a chance of higher salary.
similar is the case with education-num
### Feature Selection
How does a model perform if we only use a subset of all the available features in the data? With less features required to train, the expectation is that training and prediction time is much lower — at the cost of performance metrics. From the visualization above, we see that the top five most important features contribute more than half of the importance of **all** features present in the data. This hints that we can attempt to *reduce the feature space* and simplify the information required for the model to learn. The code cell below will use the same optimized model you found earlier, and train it on the same training set *with only the top five important features*.
```
# Import functionality for cloning a model
from sklearn.base import clone
# Reduce the feature space
X_train_reduced = X_train[X_train.columns.values[(np.argsort(importances)[::-1])[:5]]]
X_test_reduced = X_test[X_test.columns.values[(np.argsort(importances)[::-1])[:5]]]
# Train on the "best" model found from grid search earlier
clf = (clone(best_clf)).fit(X_train_reduced, y_train)
# Make new predictions
reduced_predictions = clf.predict(X_test_reduced)
# Report scores from the final model using both versions of data
print "Final Model trained on full data\n------"
print "Accuracy on testing data: {:.4f}".format(accuracy_score(y_test, best_predictions))
print "F-score on testing data: {:.4f}".format(fbeta_score(y_test, best_predictions, beta = 0.5))
print "\nFinal Model trained on reduced data\n------"
print "Accuracy on testing data: {:.4f}".format(accuracy_score(y_test, reduced_predictions))
print "F-score on testing data: {:.4f}".format(fbeta_score(y_test, reduced_predictions, beta = 0.5))
```
### Question 8 - Effects of Feature Selection
*How does the final model's F-score and accuracy score on the reduced data using only five features compare to those same scores when all features are used?*
*If training time was a factor, would you consider using the reduced data as your training set?*
**Answer:**
The final model's accuracy score and f-score were better on the reduced data compared to all the features used.
I would definitely like to train on the reduce data if training time was a factor.
> **Note**: Once you have completed all of the code implementations and successfully answered each question above, you may finalize your work by exporting the iPython Notebook as an HTML document. You can do this by using the menu above and navigating to
**File -> Download as -> HTML (.html)**. Include the finished document along with this notebook as your submission.
|
github_jupyter
|
# Import libraries necessary for this project
import numpy as np
import pandas as pd
from time import time
from IPython.display import display # Allows the use of display() for DataFrames
# Import supplementary visualization code visuals.py
import visuals as vs
# Pretty display for notebooks
%matplotlib inline
# Load the Census dataset
data = pd.read_csv("census.csv")
# Success - Display the first record
display(data.head(n=1))
# TODO: Total number of records
n_records = len(data)
# TODO: Number of records where individual's income is more than $50,000
n_greater_50k = 0
for entry in data.income:
if entry == '>50K':
n_greater_50k = n_greater_50k+1
# TODO: Number of records where individual's income is at most $50,000
n_at_most_50k = 0
for entry in data.income:
if entry == '<=50K':
n_at_most_50k = n_at_most_50k + 1
# TODO: Percentage of individuals whose income is more than $50,000
greater_percent = (float(n_greater_50k)/n_records)*100
# Print the results
print "Total number of records: {}".format(n_records)
print "Individuals making more than $50,000: {}".format(n_greater_50k)
print "Individuals making at most $50,000: {}".format(n_at_most_50k)
print "Percentage of individuals making more than $50,000: {:.2f}%".format(greater_percent)
# Split the data into features and target label
income_raw = data['income']
features_raw = data.drop('income', axis = 1)
# Visualize skewed continuous features of original data
vs.distribution(data)
# Log-transform the skewed features
skewed = ['capital-gain', 'capital-loss']
features_raw[skewed] = data[skewed].apply(lambda x: np.log(x + 1))
# Visualize the new log distributions
vs.distribution(features_raw, transformed = True)
# Import sklearn.preprocessing.StandardScaler
from sklearn.preprocessing import MinMaxScaler
# Initialize a scaler, then apply it to the features
scaler = MinMaxScaler()
numerical = ['age', 'education-num', 'capital-gain', 'capital-loss', 'hours-per-week']
features_raw[numerical] = scaler.fit_transform(data[numerical])
# Show an example of a record with scaling applied
display(features_raw.head(n = 1))
from sklearn.preprocessing import LabelEncoder
import pandas as pd
# TODO: One-hot encode the 'features_raw' data using pandas.get_dummies()
features = pd.get_dummies(features_raw)
le = LabelEncoder()
le.fit(income_raw)
# TODO: Encode the 'income_raw' data to numerical values
income = le.transform(income_raw)
# Print the number of features after one-hot encoding
encoded = list(features.columns)
print "{} total features after one-hot encoding.".format(len(encoded))
# Uncomment the following line to see the encoded feature names
print encoded
# Import train_test_split
from sklearn.cross_validation import train_test_split
# Split the 'features' and 'income' data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(features, income, test_size = 0.2, random_state = 0)
# Show the results of the split
print "Training set has {} samples.".format(X_train.shape[0])
print "Testing set has {} samples.".format(X_test.shape[0])
# TODO: Calculate accuracy
accuracy = 0.2478
# TODO: Calculate F-score using the formula above for beta = 0.5
fscore = (1+0.5**2)*(0.2478*1)/(((0.5**2)*0.2478)+1)
# Print the results
print "Naive Predictor: [Accuracy score: {:.4f}, F-score: {:.4f}]".format(accuracy, fscore)
# TODO: Import two metrics from sklearn - fbeta_score and accuracy_score
from sklearn.metrics import fbeta_score, accuracy_score
def train_predict(learner, sample_size, X_train, y_train, X_test, y_test):
'''
inputs:
- learner: the learning algorithm to be trained and predicted on
- sample_size: the size of samples (number) to be drawn from training set
- X_train: features training set
- y_train: income training set
- X_test: features testing set
- y_test: income testing set
'''
results = {}
# TODO: Fit the learner to the training data using slicing with 'sample_size'
start = time() # Get start time
learner.fit(X_train[:sample_size], y_train[:sample_size])
end = time() # Get end time
# TODO: Calculate the training time
results['train_time'] = end-start
# TODO: Get the predictions on the test set,
# then get predictions on the first 300 training samples
start = time() # Get start time
predictions_test = learner.predict(X_test)
predictions_train = learner.predict(X_train[:300])
end = time() # Get end time
# TODO: Calculate the total prediction time
results['pred_time'] = end-start
# TODO: Compute accuracy on the first 300 training samples
results['acc_train'] = accuracy_score(y_train[:300],predictions_train)
# TODO: Compute accuracy on test set
results['acc_test'] = accuracy_score(y_test,predictions_test)
# TODO: Compute F-score on the the first 300 training samples
results['f_train'] = fbeta_score(y_train[:300],predictions_train, beta = 0.5)
# TODO: Compute F-score on the test set
results['f_test'] = fbeta_score(y_test,predictions_test,beta =0.5)
# Success
print "{} trained on {} samples.".format(learner.__class__.__name__, sample_size)
# Return the results
return results
# TODO: Import the three supervised learning models from sklearn
from sklearn.naive_bayes import GaussianNB
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
# TODO: Initialize the three models
clf_A = GaussianNB()
clf_B = DecisionTreeClassifier()
clf_C = SVC()
# TODO: Calculate the number of samples for 1%, 10%, and 100% of the training data
samples_1 = len(X_train)/100
samples_10 = len(X_train)/10
samples_100 = len(X_train)/1
# Collect results on the learners
results = {}
for clf in [clf_A, clf_B, clf_C]:
clf_name = clf.__class__.__name__
results[clf_name] = {}
for i, samples in enumerate([samples_1, samples_10, samples_100]):
results[clf_name][i] = \
train_predict(clf, samples, X_train, y_train, X_test, y_test)
# Run metrics visualization for the three supervised learning models chosen
vs.evaluate(results, accuracy, fscore)
# TODO: Import 'GridSearchCV', 'make_scorer', and any other necessary libraries
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer
# TODO: Initialize the classifier
clf = DecisionTreeClassifier()
# TODO: Create the parameters list you wish to tune
parameters = {}
# TODO: Make an fbeta_score scoring object
scorer = make_scorer(fbeta_score, beta = 0.5)
# TODO: Perform grid search on the classifier using 'scorer' as the scoring method
grid_obj = GridSearchCV(clf, parameters)
# TODO: Fit the grid search object to the training data and find the optimal parameters
grid_fit = grid_obj.fit(X_train,y_train)
# Get the estimator
best_clf = grid_fit.best_estimator_
# Make predictions using the unoptimized and model
predictions = (clf.fit(X_train, y_train)).predict(X_test)
best_predictions = best_clf.predict(X_test)
# Report the before-and-afterscores
print "Unoptimized model\n------"
print "Accuracy score on testing data: {:.4f}".format(accuracy_score(y_test, predictions))
print "F-score on testing data: {:.4f}".format(fbeta_score(y_test, predictions, beta = 0.5))
print "\nOptimized Model\n------"
print "Final accuracy score on the testing data: {:.4f}".format(accuracy_score(y_test, best_predictions))
print "Final F-score on the testing data: {:.4f}".format(fbeta_score(y_test, best_predictions, beta = 0.5))
# TODO: Import a supervised learning model that has 'feature_importances_'
# TODO: Train the supervised model on the training set
model = DecisionTreeClassifier()
model.fit(X_train , y_train)
# TODO: Extract the feature importances
importances = model.feature_importances_
# Plot
vs.feature_plot(importances, X_train, y_train)
# Import functionality for cloning a model
from sklearn.base import clone
# Reduce the feature space
X_train_reduced = X_train[X_train.columns.values[(np.argsort(importances)[::-1])[:5]]]
X_test_reduced = X_test[X_test.columns.values[(np.argsort(importances)[::-1])[:5]]]
# Train on the "best" model found from grid search earlier
clf = (clone(best_clf)).fit(X_train_reduced, y_train)
# Make new predictions
reduced_predictions = clf.predict(X_test_reduced)
# Report scores from the final model using both versions of data
print "Final Model trained on full data\n------"
print "Accuracy on testing data: {:.4f}".format(accuracy_score(y_test, best_predictions))
print "F-score on testing data: {:.4f}".format(fbeta_score(y_test, best_predictions, beta = 0.5))
print "\nFinal Model trained on reduced data\n------"
print "Accuracy on testing data: {:.4f}".format(accuracy_score(y_test, reduced_predictions))
print "F-score on testing data: {:.4f}".format(fbeta_score(y_test, reduced_predictions, beta = 0.5))
| 0.424889 | 0.992725 |
## Deliverable 2. Create a Customer Travel Destinations Map.
```
# Dependencies and Setup
import pandas as pd
import requests
import gmaps
# Import API key
from config3 import g_key
# Configure gmaps API key
gmaps.configure(api_key=g_key)
# 1. Import the WeatherPy_database.csv file.
city_data_df = pd.read_csv("../Weather_Database/WeatherPy_database.csv")
city_data_df.head()
# Get the data types of my dataframe file.
city_data_df.dtypes
# 2. Prompt the user to enter minimum and maximum temperature criteria
min_temp = float(input("Please enter the minimum temperature you would like for your trip? "))
max_temp = float(input("Please enter the maximum temperature you would like for your trip? "))
# 3. Filter the city_data_df DataFrame using the input statements to create a new DataFrame using the loc method.
ideal_cities_df = city_data_df.loc[(city_data_df["Max Temp"] <= max_temp) &
(city_data_df["Max Temp"] >= min_temp)].dropna()
ideal_cities_df.head()
# 4a. Determine if there are any empty rows.
ideal_cities_df.count()
# 4b. Drop any empty rows and create a new DataFrame that doesn’t have empty rows.
# See Step 3 as I added a dropna() at the end of my filtering statement for my new dataframe.
# 5a. Create DataFrame called hotel_df to store hotel names along with city, country, max temp, and coordinates.
hotel_df = ideal_cities_df[["City", "Country", "Max Temp", "Weather Description", "Lat", "Lng"]].copy()
# 5b. Create a new column "Hotel Name"
hotel_df["Hotel Name"] = ""
hotel_df.head(10)
from config3 import g_key
# 6a. Set parameters to search for hotels within 5000 meters.
params = {
"radius": 5000,
"type": "lodging",
"key": g_key,
}
# 6b. Iterate through the hotel DataFrame.
for index, row in hotel_df.iterrows():
# 6c. Get latitude and longitude from DataFrame
lat = row["Lat"]
lng = row["Lng"]
#Add the latitude and longitude to location key for the params dictionary.
params["location"] = f"{lat},{lng}"
# 6d. Set up the base URL for the Google Directions API to get JSON data.
base_url = "https://maps.googleapis.com/maps/api/place/nearbysearch/json"
# 6e. Make request and retrieve the JSON data from the search.
hotels = requests.get(base_url, params=params).json()
# 6f. Get the first hotel from the results and store the name, if a hotel isn't found skip the city.
try:
hotel_df.loc[index, "Hotel Name"] = hotels["results"][0]["name"]
except IndexError:
print("Hotel not found... skipping.")
hotel_df
hotel_df.dtypes
import numpy as np
# 7. Drop the rows where there is no Hotel Name.
hotel_df["Hotel Name"].replace("", np.nan, inplace=True)
hotel_df.dropna(inplace=True)
hotel_df
# 8a. Create the output File (CSV)
output_data_file = "WeatherPy_vacation.csv"
# 8b. Export the City_Data into a csv
hotel_df.to_csv(output_data_file, index_label="City_ID")
# Read CSV file.
vacation_df = pd.read_csv("WeatherPy_Vacation.csv")
vacation_df.head(10)
# 9. Using the template add city name, the country code, the weather description and maximum temperature for the city.
info_box_template = """
<dl>
<dt>Hotel Name</dt><dd>{Hotel Name}</dd>
<dt>City</dt><dd>{City}</dd>
<dt>Country</dt><dd>{Country}</dd>
<dt>Weather Description</dt><dd>{Weather Description}</dd>
<dt>Max Temp</dt><dd>{Max Temp}</dd>
"""
# 10a. Get the data from each row and add it to the formatting template and store the data in a list.
hotel_info = [info_box_template.format(**row) for index, row in vacation_df.iterrows()]
# 10b. Get the latitude and longitude from each row and store in a new DataFrame.
locations = vacation_df[["Lat", "Lng"]]
# 11a. Add a marker layer for each city to the map.
marker_layer = gmaps.marker_layer(locations, info_box_content=hotel_info)
fig = gmaps.figure(center=(30.0, 31.0), zoom_level=1.5)
fig.add_layer(marker_layer)
# 11b. Display the figure
fig
```
|
github_jupyter
|
# Dependencies and Setup
import pandas as pd
import requests
import gmaps
# Import API key
from config3 import g_key
# Configure gmaps API key
gmaps.configure(api_key=g_key)
# 1. Import the WeatherPy_database.csv file.
city_data_df = pd.read_csv("../Weather_Database/WeatherPy_database.csv")
city_data_df.head()
# Get the data types of my dataframe file.
city_data_df.dtypes
# 2. Prompt the user to enter minimum and maximum temperature criteria
min_temp = float(input("Please enter the minimum temperature you would like for your trip? "))
max_temp = float(input("Please enter the maximum temperature you would like for your trip? "))
# 3. Filter the city_data_df DataFrame using the input statements to create a new DataFrame using the loc method.
ideal_cities_df = city_data_df.loc[(city_data_df["Max Temp"] <= max_temp) &
(city_data_df["Max Temp"] >= min_temp)].dropna()
ideal_cities_df.head()
# 4a. Determine if there are any empty rows.
ideal_cities_df.count()
# 4b. Drop any empty rows and create a new DataFrame that doesn’t have empty rows.
# See Step 3 as I added a dropna() at the end of my filtering statement for my new dataframe.
# 5a. Create DataFrame called hotel_df to store hotel names along with city, country, max temp, and coordinates.
hotel_df = ideal_cities_df[["City", "Country", "Max Temp", "Weather Description", "Lat", "Lng"]].copy()
# 5b. Create a new column "Hotel Name"
hotel_df["Hotel Name"] = ""
hotel_df.head(10)
from config3 import g_key
# 6a. Set parameters to search for hotels within 5000 meters.
params = {
"radius": 5000,
"type": "lodging",
"key": g_key,
}
# 6b. Iterate through the hotel DataFrame.
for index, row in hotel_df.iterrows():
# 6c. Get latitude and longitude from DataFrame
lat = row["Lat"]
lng = row["Lng"]
#Add the latitude and longitude to location key for the params dictionary.
params["location"] = f"{lat},{lng}"
# 6d. Set up the base URL for the Google Directions API to get JSON data.
base_url = "https://maps.googleapis.com/maps/api/place/nearbysearch/json"
# 6e. Make request and retrieve the JSON data from the search.
hotels = requests.get(base_url, params=params).json()
# 6f. Get the first hotel from the results and store the name, if a hotel isn't found skip the city.
try:
hotel_df.loc[index, "Hotel Name"] = hotels["results"][0]["name"]
except IndexError:
print("Hotel not found... skipping.")
hotel_df
hotel_df.dtypes
import numpy as np
# 7. Drop the rows where there is no Hotel Name.
hotel_df["Hotel Name"].replace("", np.nan, inplace=True)
hotel_df.dropna(inplace=True)
hotel_df
# 8a. Create the output File (CSV)
output_data_file = "WeatherPy_vacation.csv"
# 8b. Export the City_Data into a csv
hotel_df.to_csv(output_data_file, index_label="City_ID")
# Read CSV file.
vacation_df = pd.read_csv("WeatherPy_Vacation.csv")
vacation_df.head(10)
# 9. Using the template add city name, the country code, the weather description and maximum temperature for the city.
info_box_template = """
<dl>
<dt>Hotel Name</dt><dd>{Hotel Name}</dd>
<dt>City</dt><dd>{City}</dd>
<dt>Country</dt><dd>{Country}</dd>
<dt>Weather Description</dt><dd>{Weather Description}</dd>
<dt>Max Temp</dt><dd>{Max Temp}</dd>
"""
# 10a. Get the data from each row and add it to the formatting template and store the data in a list.
hotel_info = [info_box_template.format(**row) for index, row in vacation_df.iterrows()]
# 10b. Get the latitude and longitude from each row and store in a new DataFrame.
locations = vacation_df[["Lat", "Lng"]]
# 11a. Add a marker layer for each city to the map.
marker_layer = gmaps.marker_layer(locations, info_box_content=hotel_info)
fig = gmaps.figure(center=(30.0, 31.0), zoom_level=1.5)
fig.add_layer(marker_layer)
# 11b. Display the figure
fig
| 0.484624 | 0.741276 |
# Bayesian Logistic Regression
In this notebook we demonstrate the use of the random walk Rosenbluth-Metropolis-Hasting algorithm on a simple logistic regression.
```
import jax
import jax.numpy as jnp
import jax.random as random
import matplotlib.pyplot as plt
from sklearn.datasets import make_biclusters
import blackjax
%config InlineBackend.figure_format = "retina"
plt.rcParams["axes.spines.right"] = False
plt.rcParams["axes.spines.top"] = False
plt.rcParams["figure.figsize"] = (12, 8)
%load_ext watermark
%watermark -d -m -v -p jax,jaxlib,blackjax
```
## The data
We create two clusters of points using [scikit-learn's `make_bicluster` function](https://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_biclusters.html?highlight=bicluster%20data#sklearn.datasets.make_biclusters).
```
num_points = 50
X, rows, cols = make_biclusters(
(num_points, 2), 2, noise=0.6, random_state=314, minval=-3, maxval=3
)
y = rows[0] * 1.0 # y[i] = whether point i belongs to cluster 1
colors = ["tab:red" if el else "tab:blue" for el in rows[0]]
plt.scatter(*X.T, edgecolors=colors, c="none")
plt.xlabel(r"$X_0$")
plt.ylabel(r"$X_1$")
plt.show()
```
## The model
We use a simple logistic regression model to infer to which cluster each of the points belongs. We note $y$ a binary variable that indicates whether a point belongs to the first cluster :
$$
y \sim \operatorname{Bernoulli}(p)
$$
The probability $p$ to belong to the first cluster commes from a logistic regression:
$$
p = \operatorname{logistic}(\Phi\,\boldsymbol{w})
$$
where $w$ is a vector of weights whose priors are a normal prior centered on 0:
$$
\boldsymbol{w} \sim \operatorname{Normal}(0, \sigma)
$$
And $\Phi$ is the matrix that contains the data, so each row $\Phi_{i,:}$ is the vector $\left[1, X_0^i, X_1^i\right]$
```
Phi = jnp.c_[jnp.ones(num_points)[:, None], X]
N, M = Phi.shape
def sigmoid(z):
return jnp.exp(z) / (1 + jnp.exp(z))
def log_sigmoid(z):
return z - jnp.log(1 + jnp.exp(z))
def logprob_fn(w, alpha=1.0):
"""The log-probability density function of the posterior distribution of the model."""
log_an = log_sigmoid(Phi @ w)
an = Phi @ w
log_likelihood_term = y * log_an + (1 - y) * jnp.log(1 - sigmoid(an))
prior_term = alpha * w @ w / 2
return -prior_term + log_likelihood_term.sum()
```
## Posterior sampling
We use `blackjax`'s Random Walk RMH kernel to sample from the posterior distribution.
```
rng_key = random.PRNGKey(314)
w0 = random.multivariate_normal(rng_key, 0.1 + jnp.zeros(M), jnp.eye(M))
rmh = blackjax.rmh(logprob_fn, sigma=jnp.ones(M) * 0.7)
initial_state = rmh.init(w0)
```
Since `blackjax` does not provide an inference loop we need to implement one ourselves:
```
def inference_loop(rng_key, kernel, initial_state, num_samples):
@jax.jit
def one_step(state, rng_key):
state, _ = kernel(rng_key, state)
return state, state
keys = jax.random.split(rng_key, num_samples)
_, states = jax.lax.scan(one_step, initial_state, keys)
return states
```
We can now run the inference:
```
_, rng_key = random.split(rng_key)
states = inference_loop(rng_key, rmh.step, initial_state, 5_000)
```
And display the trace:
```
burnin = 300
fig, ax = plt.subplots(1, 3, figsize=(12, 2))
for i, axi in enumerate(ax):
axi.plot(states.position[:, i])
axi.set_title(f"$w_{i}$")
axi.axvline(x=burnin, c="tab:red")
plt.show()
chains = states.position[burnin:, :]
nsamp, _ = chains.shape
```
### Predictive distribution
Having infered the posterior distribution of the regression's coefficients we can compute the probability to belong to the first cluster at each position $(X_0, X_1)$.
```
# Create a meshgrid
xmin, ymin = X.min(axis=0) - 0.1
xmax, ymax = X.max(axis=0) + 0.1
step = 0.1
Xspace = jnp.mgrid[xmin:xmax:step, ymin:ymax:step]
_, nx, ny = Xspace.shape
# Compute the average probability to belong to the first cluster at each point on the meshgrid
Phispace = jnp.concatenate([jnp.ones((1, nx, ny)), Xspace])
Z_mcmc = sigmoid(jnp.einsum("mij,sm->sij", Phispace, chains))
Z_mcmc = Z_mcmc.mean(axis=0)
plt.contourf(*Xspace, Z_mcmc)
plt.scatter(*X.T, c=colors)
plt.xlabel(r"$X_0$")
plt.ylabel(r"$X_1$")
plt.show()
```
|
github_jupyter
|
import jax
import jax.numpy as jnp
import jax.random as random
import matplotlib.pyplot as plt
from sklearn.datasets import make_biclusters
import blackjax
%config InlineBackend.figure_format = "retina"
plt.rcParams["axes.spines.right"] = False
plt.rcParams["axes.spines.top"] = False
plt.rcParams["figure.figsize"] = (12, 8)
%load_ext watermark
%watermark -d -m -v -p jax,jaxlib,blackjax
num_points = 50
X, rows, cols = make_biclusters(
(num_points, 2), 2, noise=0.6, random_state=314, minval=-3, maxval=3
)
y = rows[0] * 1.0 # y[i] = whether point i belongs to cluster 1
colors = ["tab:red" if el else "tab:blue" for el in rows[0]]
plt.scatter(*X.T, edgecolors=colors, c="none")
plt.xlabel(r"$X_0$")
plt.ylabel(r"$X_1$")
plt.show()
Phi = jnp.c_[jnp.ones(num_points)[:, None], X]
N, M = Phi.shape
def sigmoid(z):
return jnp.exp(z) / (1 + jnp.exp(z))
def log_sigmoid(z):
return z - jnp.log(1 + jnp.exp(z))
def logprob_fn(w, alpha=1.0):
"""The log-probability density function of the posterior distribution of the model."""
log_an = log_sigmoid(Phi @ w)
an = Phi @ w
log_likelihood_term = y * log_an + (1 - y) * jnp.log(1 - sigmoid(an))
prior_term = alpha * w @ w / 2
return -prior_term + log_likelihood_term.sum()
rng_key = random.PRNGKey(314)
w0 = random.multivariate_normal(rng_key, 0.1 + jnp.zeros(M), jnp.eye(M))
rmh = blackjax.rmh(logprob_fn, sigma=jnp.ones(M) * 0.7)
initial_state = rmh.init(w0)
def inference_loop(rng_key, kernel, initial_state, num_samples):
@jax.jit
def one_step(state, rng_key):
state, _ = kernel(rng_key, state)
return state, state
keys = jax.random.split(rng_key, num_samples)
_, states = jax.lax.scan(one_step, initial_state, keys)
return states
_, rng_key = random.split(rng_key)
states = inference_loop(rng_key, rmh.step, initial_state, 5_000)
burnin = 300
fig, ax = plt.subplots(1, 3, figsize=(12, 2))
for i, axi in enumerate(ax):
axi.plot(states.position[:, i])
axi.set_title(f"$w_{i}$")
axi.axvline(x=burnin, c="tab:red")
plt.show()
chains = states.position[burnin:, :]
nsamp, _ = chains.shape
# Create a meshgrid
xmin, ymin = X.min(axis=0) - 0.1
xmax, ymax = X.max(axis=0) + 0.1
step = 0.1
Xspace = jnp.mgrid[xmin:xmax:step, ymin:ymax:step]
_, nx, ny = Xspace.shape
# Compute the average probability to belong to the first cluster at each point on the meshgrid
Phispace = jnp.concatenate([jnp.ones((1, nx, ny)), Xspace])
Z_mcmc = sigmoid(jnp.einsum("mij,sm->sij", Phispace, chains))
Z_mcmc = Z_mcmc.mean(axis=0)
plt.contourf(*Xspace, Z_mcmc)
plt.scatter(*X.T, c=colors)
plt.xlabel(r"$X_0$")
plt.ylabel(r"$X_1$")
plt.show()
| 0.822902 | 0.986231 |
# KMeans Clustering
The $K$-means algorithm divides a set of $N$ samples $X$ into $K$ disjoint clusters $C$, each described by the mean $\mu_j$ of the samples in the cluster. The means are commonly called the **cluster “centroids”**; note that they are not, in general, points from $X$, although they live in the same space. The K-means algorithm aims to choose centroids that minimise the inertia, or within-cluster sum of squared criterion:
$$\sum_{i=0}^{n}\min_{\mu_j \in C}(||x_j - \mu_i||^2)$$
## How the algorithm works
The $Κ$-means clustering algorithm uses iterative refinement to produce a final result. The algorithm inputs are the number of clusters $Κ$ and the data set. The data set is a collection of features for each data point. The algorithms starts with initial estimates for the $Κ$ centroids, which can either be randomly generated or randomly selected from the data set. The algorithm then iterates between two steps:
**Data assigment step**: Each centroid defines one of the clusters. In this step, each data point is assigned to its nearest centroid, based on the squared Euclidean distance. More formally, if $c_i$ is the collection of centroids in set $C$, then each data point $x$ is assigned to a cluster based on
$$\underset{c_i \in C}{\arg\min} \; dist(c_i,x)^2$$
where dist( · ) is the standard ($L_2$) Euclidean distance. Let the set of data point assignments for each ith cluster centroid be $S_i$.
**Centroid update step**: In this step, the centroids are recomputed. This is done by taking the mean of all data points assigned to that centroid's cluster.
$$c_i=\frac{1}{|S_i|}\sum_{x_i \in S_i x_i}$$
The algorithm iterates between steps one and two until a stopping criteria is met (i.e., no data points change clusters, the sum of the distances is minimized, or some maximum number of iterations is reached).
### Convergence and random initialization
This algorithm is guaranteed to converge to a result. The result may be a local optimum (i.e. not necessarily the best possible outcome), meaning that assessing more than one run of the algorithm with randomized starting centroids may give a better outcome.
<img src=https://upload.wikimedia.org/wikipedia/commons/e/ea/K-means_convergence.gif style="width: 500px;"/>
## The Data
For this project we will attempt to use KMeans Clustering to cluster Universities into to two groups, Private and Public. We will use a data frame with 777 observations on the following 18 variables.
* Private A factor with levels No and Yes indicating private or public university
* Apps Number of applications received
* Accept Number of applications accepted
* Enroll Number of new students enrolled
* Top10perc Pct. new students from top 10% of H.S. class
* Top25perc Pct. new students from top 25% of H.S. class
* F.Undergrad Number of fulltime undergraduates
* P.Undergrad Number of parttime undergraduates
* Outstate Out-of-state tuition
* Room.Board Room and board costs
* Books Estimated book costs
* Personal Estimated personal spending
* PhD Pct. of faculty with Ph.D.’s
* Terminal Pct. of faculty with terminal degree
* S.F.Ratio Student/faculty ratio
* perc.alumni Pct. alumni who donate
* Expend Instructional expenditure per student
* Grad.Rate Graduation rate
## Setup
```
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.cluster import KMeans
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
%matplotlib inline
df = pd.read_csv('datasets/College_Data',
index_col=0)
df.head()
df.info()
df.describe()
```
## Exploratory Analysis
```
sns.set_style('whitegrid')
sns.lmplot('Room.Board',
'Grad.Rate',
data=df,
hue='Private',
palette='coolwarm',
size=6,
aspect=1,
fit_reg=True);
sns.boxplot(x='Private',
y='S.F.Ratio',
data=df);
sns.boxplot(x='Private',
y='perc.alumni',
data=df);
sns.set_style('darkgrid')
g = sns.FacetGrid(df,
hue='Private',
palette='coolwarm',
height=6,
aspect=2)
g = g.map(plt.hist,
'Outstate',
bins=20,
alpha=.7)
g = sns.FacetGrid(df,
hue='Private',
palette='coolwarm',
height=6,
aspect=2)
g = g.map(plt.hist,
'Grad.Rate',
bins=20,
alpha=.7)
```
There seems to be a private school with a graduation rate of higher than 100%
```
df[df['Grad.Rate'] > 100]
```
** Set that school's graduation rate to 100 so it makes sense. You may get a warning not an error) when doing this operation, so use dataframe operations or just re-do the histogram visualization to make sure it actually went through.**
```
df['Grad.Rate']['Cazenovia College'] = 100
df[df['Grad.Rate'] > 100]
g = sns.FacetGrid(df,
hue='Private',
palette='coolwarm',
height=6,
aspect=2)
g = g.map(plt.hist,
'Grad.Rate',
bins=20,
alpha=.7)
```
## $K$Means Cluster Creation
```
kmeans = KMeans(n_clusters=2,
verbose=0,
tol=1e-3,
max_iter=300,
n_init=20)
kmeans.fit(df.drop('Private',
axis=1))
```
** What are the cluster center vectors?**
```
kmeans.cluster_centers_
```
Now compare these cluster centers (for all dimensions/features) to the known means of labeled data.
```
df[df['Private']=='Yes'].describe()
df[df['Private']=='No'].describe()
```
Create a data frame with cluster centers and with column names borrowed from the original data frame
Is it clear from this data frame which label corresponds to private college (0 or 1)?
```
df_desc=pd.DataFrame(df.describe())
feat=list(df_desc.columns)
kmclus=pd.DataFrame(kmeans.cluster_centers_,
columns=feat)
kmclus
```
#### What are the cluster labels?
```
kmeans.labels_
```
## Evaluation
There is no perfect way to evaluate clustering if you don't have the labels, however since this is just an exercise, we do have the labels, so we take advantage of this to evaluate our clusters, keep in mind, you usually won't have this luxury in the real world.
** Create a new column for df called 'Cluster', which is a 1 for a Private school, and a 0 for a public school.**
```
df1 = df.copy()
df1['Cluster'] = df['Private'].map(dict(Yes=1, No=0))
df1.head()
print(confusion_matrix(df1['Cluster'], kmeans.labels_))
print(classification_report(df1['Cluster'], kmeans.labels_))
```
## Clustering performance (e.g. distance between centroids)
Create two data frames consisting of only private or public university data
```
df_pvt=df[df['Private']=='Yes']
df_pub=df[df['Private']=='No']
```
Play with parameters such as max_iter and n_init and calculate cluster centroid distances
```
kmeans = KMeans(n_clusters=2,verbose=0,tol=1e-3,max_iter=50,n_init=10)
kmeans.fit(df.drop('Private',axis=1))
clus_cent=kmeans.cluster_centers_
df_desc=pd.DataFrame(df.describe())
feat = list(df_desc.columns)
kmclus = pd.DataFrame(clus_cent,columns=feat)
a=np.array(kmclus.diff().iloc[1])
centroid_diff = pd.DataFrame(a,columns=['K-means cluster centroid-distance'],index=df_desc.columns)
centroid_diff['Mean of corresponding entity (private)']=np.array(df_pvt.mean())
centroid_diff['Mean of corresponding entity (public)']=np.array(df_pub.mean())
centroid_diff
```
|
github_jupyter
|
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.cluster import KMeans
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
%matplotlib inline
df = pd.read_csv('datasets/College_Data',
index_col=0)
df.head()
df.info()
df.describe()
sns.set_style('whitegrid')
sns.lmplot('Room.Board',
'Grad.Rate',
data=df,
hue='Private',
palette='coolwarm',
size=6,
aspect=1,
fit_reg=True);
sns.boxplot(x='Private',
y='S.F.Ratio',
data=df);
sns.boxplot(x='Private',
y='perc.alumni',
data=df);
sns.set_style('darkgrid')
g = sns.FacetGrid(df,
hue='Private',
palette='coolwarm',
height=6,
aspect=2)
g = g.map(plt.hist,
'Outstate',
bins=20,
alpha=.7)
g = sns.FacetGrid(df,
hue='Private',
palette='coolwarm',
height=6,
aspect=2)
g = g.map(plt.hist,
'Grad.Rate',
bins=20,
alpha=.7)
df[df['Grad.Rate'] > 100]
df['Grad.Rate']['Cazenovia College'] = 100
df[df['Grad.Rate'] > 100]
g = sns.FacetGrid(df,
hue='Private',
palette='coolwarm',
height=6,
aspect=2)
g = g.map(plt.hist,
'Grad.Rate',
bins=20,
alpha=.7)
kmeans = KMeans(n_clusters=2,
verbose=0,
tol=1e-3,
max_iter=300,
n_init=20)
kmeans.fit(df.drop('Private',
axis=1))
kmeans.cluster_centers_
df[df['Private']=='Yes'].describe()
df[df['Private']=='No'].describe()
df_desc=pd.DataFrame(df.describe())
feat=list(df_desc.columns)
kmclus=pd.DataFrame(kmeans.cluster_centers_,
columns=feat)
kmclus
kmeans.labels_
df1 = df.copy()
df1['Cluster'] = df['Private'].map(dict(Yes=1, No=0))
df1.head()
print(confusion_matrix(df1['Cluster'], kmeans.labels_))
print(classification_report(df1['Cluster'], kmeans.labels_))
df_pvt=df[df['Private']=='Yes']
df_pub=df[df['Private']=='No']
kmeans = KMeans(n_clusters=2,verbose=0,tol=1e-3,max_iter=50,n_init=10)
kmeans.fit(df.drop('Private',axis=1))
clus_cent=kmeans.cluster_centers_
df_desc=pd.DataFrame(df.describe())
feat = list(df_desc.columns)
kmclus = pd.DataFrame(clus_cent,columns=feat)
a=np.array(kmclus.diff().iloc[1])
centroid_diff = pd.DataFrame(a,columns=['K-means cluster centroid-distance'],index=df_desc.columns)
centroid_diff['Mean of corresponding entity (private)']=np.array(df_pvt.mean())
centroid_diff['Mean of corresponding entity (public)']=np.array(df_pub.mean())
centroid_diff
| 0.289071 | 0.98315 |
# Machine Learning & Statistics Project

# Introduction
We have been tasked with creating a web service that uses machine learning to make predictions based on the data set provided on power production taken from Moodle. The goal is to produce a model that accurately predicts wind turbine power output from wind speed values, as in the data set. We must then develop a web service that will respond with predicted power values based on speed values sent as HTTP requests. Below is a breakdown of the data and a description of the modelling methods used to determine the correct algorithm for to accurately model the power production on any given wind speed.
## Wind Power Description
Wind power is a form of renewable energy that generates electrical power through the turning of a turbine in an electrical generator with the use of the force provided by the wind. Wind is an intermittent energy source providing variable power availability if not paired with another energy storage solution. The quantity of power generation from year to year is consistent but can vary wildly in the short term. There are also on shore and off shore considerations when looking at the location for these systems. While off shore winds are steadier and stronger and reduce the visual impact the construction and maintenance costs are also much greater and must be considered.
Wind power is responsible for about 5% of the global power generation. The ability to predict the output of the turbine based on the predicted wind speed would be a large advantage in future energy projections and the ability to quantify how much mitigation of energy is required in times of low winds. Generally speaking turbines follow a curve as shown below so we would expect something similar in the data we have received.

We will be looking to create a model to provide reliable predictions based on the empirical data provided. The data collected consists of a single csv file populated with values. Below we will explore the data.
***
# Explore the data
First we will import the required libraries and start to explore the data to get a feel for what we're dealing with taking a look at the first and last few rows and providing decriptions of the data types, shape and if there is any sections of missing data in the form of null or na values.
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from pylab import rcParams
import sklearn
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import scale
import tensorflow.keras as kr
from collections import Counter
from sklearn.pipeline import Pipeline
# Matplotlib graph sizes
rcParams['figure.figsize']=20, 12
# Import the csv file containing the information
df = pd.read_csv('powerproduction.txt')
# Check first 10 rows to ensure we're getting correct data in as first 5 columns power outputt displayed as 0
print(f'{df.head(11)}\n')
print(f'{df.tail(15)}\n')
# Display dataframes information
print(f'{df.info()}\n')
print(f'{df.describe()}\n')
print(f'{df.shape}\n')
print(f'{df.isnull().sum()}\n')
print(f'{df.isna().sum()}')
```
From the above we can see that the information received is 2 colmuns of 500 rows populated by floats. The speed range is 0-25 and the power range is 0-113. No units are given in this table but for the purpose of this report it will be assumed the speed is measured in m/s and the power is in % of design output.
We can see that at the minimum and maximum speed values there is a value of 0 which is showing us a minimum wind speed required to start the power generation and a high point cut off switch. We will need to visualise the data to check for anymore 0 values scattered in the data as this could potentially throw off our calculations. This indicates the data will need to be cleaned before moving forward with the prediction model generation.
The data is sorted sequentially by speed with the power generation generally increasing with it within a certain range. This shows a relationship between the two variables. From the typical turbine output graph shown above it would appear that this is a polynomial relationship but we will need to visualise our data before we can be sure of this.
There appears to be no missing information in the data as shown by our `df.isnull().sum()` and `df.isna().sum()` check. This data will need to be cleaned before it will be useable. To determine if there are any other anomalies we'll plot some graphs to give a better visual representation of the data.
```
# Visualise dataset
sns.jointplot(data=df, x="speed", y="power",kind="reg", height=8)
#sns.relplot(data=df, x="speed", y="power", height=8, aspect=2)
sns.pairplot(df, height=4, aspect=2);
```
The above shows us that it is not a typical linear relationship between speed and power and matches what we expeted with the exception of the 0 values scattered throughout. It appears the speed power relationship follows a polynomial relationship as predicted. It shows that while the wind speed is below 10 m/s the power generation remains low. From 10 to around 18 m/s there is a much faster growth of power generation before peaking out around the 100% mark at about 18 m/s wind speed where it remains until the wind speed reaches 24.5 m/s when an automatic cut off takes effect dropping power generation to 0.
In relation to the zero values scattered throughout the data this could be due to a malfunction or maintenance period on the turbine itself so these will need to be removed before moving forward to determine an accurate algorithm. The zero values at the start and end will also be removed to ensure we hve an accurate model to work with based on the power generation timees only and not have the shut down periods affecting the data.
## Clean Data
```
# Check were majority of readings for 0 power generation values are located.
df_check= df[df['power'] == 0]
sns.histplot(data=df_check, x="speed", bins=25);
```
It appears the vast majority of the 0 readings are at both the low and high ends. From our inital look at the head and tail of the data we can see that the power generation doesn't start until 0.325 m/s wind speed and cuts out from 24.499 m/s wind speed. From our research we have found this to be a typical setup for the wind turbines.
We will now use this information to remove all values of 0 that this is due to a malfunction or a maintenance period and therefore should not have any influence on our alogrithm generation as it is an independent event that has no bearing on the data. The high and low end cut off also needs to be removed to ensure accuracy in our prerdictions.
```
# https://stackoverflow.com/questions/13851535/how-to-delete-rows-from-a-pandas-dataframe-based-on-a-conditional-expression
df = df.drop(df[df.power == 0.0].index)
# Plot scatter graph
plt.scatter(df.speed,df.power,s=15)
plt.xlabel('Speed (m/s)',fontsize=16)
plt.ylabel('Power (%)',fontsize=16)
plt.show()
# Confirm all zero valuees have been removed.
df_check= df[df['power'] == 0]
sns.histplot(data=df_check, x="speed", bins=25);
df.shape
```
Confirmation that all zero values have been removed. Now we have explored the data and we have an idea of what it is we are looking at we'll start to model the data using various models to determine the most accurate representation to use.
***
## Linear Regression
Linear regression is the approach of modelling the independent (also known as explanatory) and dependent variables by fitting a linear equation to some observed data. The equation for a simple linear regression model generally takes the form of-
\begin{gather*}
y = \alpha + \beta x_{i}\\
\alpha = the \hspace{1mm} intercept\\
\beta = the \hspace{1mm} slope\\
y = dependent \hspace{1mm} variable\\
x_{i} = independent \hspace{1mm} variable\\
\end{gather*}
This creates predictive values providing a straight line prediction of the curve as shown by the blue line below-

Looking at the graphs from our exploring the data section it does not look like this would be a good fit. I believe this will not lead to an accurate predictor model but afterwards we can look at polynomial linear regression to make the fit more suitable and compare the different models in terms of accuracy.
```
# https://www.analyticsvidhya.com/blog/2020/03/polynomial-regression-python/v
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
# Generate data and convert to arrays to prepare for use
y = df.power.to_numpy()
x = df.speed.to_numpy().reshape(-1, 1)
# Training Model
lm=LinearRegression()
lm.fit(x.reshape(-1,1),y.reshape(-1,1))
# Generate predition variable
y_pred=lm.predict(x.reshape(-1,1))
# Test refers to the wind power entered to provide a predicted value. Emp refers to the empirical data from csv file received
test1, emp1 = df.at[12,'speed'], df.at[12,'power']
test2, emp2 = df.at[97,'speed'] , df.at[97,'power']
test3, emp3 = df.at[201,'speed'], df.at[201,'power']
test4, emp4 = df.at[253,'speed'], df.at[253,'power']
test5, emp5 = df.at[293,'speed'], df.at[293,'power']
test6, emp6 = df.at[357,'speed'], df.at[357,'power']
test7, emp7 = df.at[425,'speed'], df.at[425,'power']
# Function ot give a positive percentage difference value
def Accuracy_L (test, emp):
if (((lm.predict([[test]]))/emp)*100 < 100):
return f"Undershot by {int(100 - ((lm.predict([[test]]))/emp)*100)}%"
else:
return f"Overshot by {int((((lm.predict([[test]]))/emp) * 100) - 100)}%"
print(f'\nTest 1 (Linear)-\nWind Speed: {test1} m/s\nEmpirical data: {emp1}\nPredicted value: {float((lm.predict([[test1]]))):.2f}\nActual Difference: {float(abs(emp1-lm.predict([[test1]]))):.2f}\nAccuracy: {Accuracy_L (test1, emp1)}')
print(f'\nTest 2 (Linear)-\nWind Speed: {test2} m/s\nEmpirical data: {emp2}\nPredicted value: {float((lm.predict([[test2]]))):.2f}\nActual Difference: {float(abs(emp2-lm.predict([[test2]]))):.2f}\nAccuracy: {Accuracy_L (test2, emp2)}')
print(f'\nTest 3 (Linear)-\nWind Speed: {test3} m/s\nEmpirical data: {emp3}\nPredicted value: {float((lm.predict([[test3]]))):.2f}\nActual Difference: {float(abs(emp3-lm.predict([[test3]]))):.2f}\nAccuracy: {Accuracy_L (test3, emp3)}')
print(f'\nTest 4 (Linear)-\nWind Speed: {test4} m/s\nEmpirical data: {emp4}\nPredicted value: {float((lm.predict([[test4]]))):.2f}\nActual Difference: {float(abs(emp4-lm.predict([[test4]]))):.2f}\nAccuracy: {Accuracy_L (test4, emp4)}')
print(f'\nTest 5 (Linear)-\nWind Speed: {test5} m/s\nEmpirical data: {emp5}\nPredicted value: {float((lm.predict([[test5]]))):.2f}\nActual Difference: {float(abs(emp5-lm.predict([[test5]]))):.2f}\nAccuracy: {Accuracy_L (test5, emp5)}')
print(f'\nTest 6 (Linear)-\nWind Speed: {test6} m/s\nEmpirical data: {emp6}\nPredicted value: {float((lm.predict([[test6]]))):.2f}\nActual Difference: {float(abs(emp6-lm.predict([[test6]]))):.2f}\nAccuracy: {Accuracy_L (test6, emp6)}')
print(f'\nTest 7 (Linear)-\nWind Speed: {test7} m/s\nEmpirical data: {emp7}\nPredicted value: {float((lm.predict([[test7]]))):.2f}\nActual Difference: {float(abs(emp7-lm.predict([[test7]]))):.2f}\nAccuracy: {Accuracy_L (test7, emp7)}')
```
We can see above that while the higher value numbers are only off by about 10& the lower value numbers have a much great discrepancy between the predicted values and the actual empirically determined values. To get a better idea of why this we'll need to plot the data points with the predicted model overlaid.
```
# Plotting predictions
#plt.figure(figsize=(10,5))
plt.scatter(x,y,s=15)
plt.plot(x,y_pred,color='g')
plt.xlabel('Speed (m/s)',fontsize=16)
plt.ylabel('Power (%)',fontsize=16)
plt.show()
print(f'Root mean squared error for Linear Regression is {np.sqrt(mean_squared_error(y,y_pred))}')
print(f'The R2 value is {r2_score(y, y_pred)}')
```
From the above figures and corresponding graph we can see that there are large sections of the graph missed by a linear regression model. We can see very large differences particularly on the low end of the graph which explains the value we were getting for the low end test values.
While the linear regression model type in the above format would not be useable it does appear that the graph does have 3 distinct zones. If we split the graph into 3 sections and applied the model to each section we would greatly increase the accuracy though in that case it may be better to apply the polynomial regression model with greater degrees of accuracy as we go through below.
***
## Polynomial Linear Regression
Polynomial linear regression is a form of regression where the independent and dependent variables are modelled to the <i>n</i>th degree. This can be represented by thhe formula-
\begin{gather*}
y = \beta + \beta_{1} x + \beta_{2} x^{2} + \beta_{3} x^{3} + ... + \beta_{n} x^{n} + \epsilon\\
\alpha = the \hspace{1mm} intercept\\
\beta = the \hspace{1mm} slope\\
y = dependent \hspace{1mm} variable\\
x_{i} = independent \hspace{1mm} variable\\
\end{gather*}
A typical regression curve for polynomial linear regression can have multiple direction changes depending on the degree applied. Below is an example of a polynomialcurve-
<img src="./images/Poly_Reg.png" alt="Typical Polynomial Linear Regression Curve" style="width: 500px;"/>
This model will be a good fit for our data as from our initial inspections there are multiple changes of the slop in the graph.
```
# Check multiple degrees to validate which best fits the line
Input3=[('polynomial',PolynomialFeatures(degree=3)),('modal',LinearRegression())]
pipe3=Pipeline(Input3)
pipe3.fit(x.reshape(-1,1),y.reshape(-1,1))
poly_pred3=pipe3.predict(x.reshape(-1,1))
#sorting predicted values with respect to predictor
sorted_zip3 = sorted(zip(x,poly_pred3))
x_poly, poly_pred3 = zip(*sorted_zip3)
# creating pipeline and fitting it on data
Input4=[('polynomial',PolynomialFeatures(degree=4)),('modal',LinearRegression())]
pipe4=Pipeline(Input4)
pipe4.fit(x.reshape(-1,1),y.reshape(-1,1))
poly_pred4=pipe4.predict(x.reshape(-1,1))
#sorting predicted values with respect to predictor
sorted_zip4 = sorted(zip(x,poly_pred4))
x_poly, poly_pred4 = zip(*sorted_zip4)
# creating pipeline and fitting it on data
Input5=[('polynomial',PolynomialFeatures(degree=5)),('modal',LinearRegression())]
pipe5=Pipeline(Input5)
pipe5.fit(x.reshape(-1,1),y.reshape(-1,1))
poly_pred5=pipe5.predict(x.reshape(-1,1))
#sorting predicted values with respect to predictor
sorted_zip5 = sorted(zip(x,poly_pred5))
x_poly, poly_pred5 = zip(*sorted_zip5)
# creating pipeline and fitting it on data
Input6=[('polynomial',PolynomialFeatures(degree=6)),('modal',LinearRegression())]
pipe6=Pipeline(Input6)
pipe6.fit(x.reshape(-1,1),y.reshape(-1,1))
poly_pred6=pipe6.predict(x.reshape(-1,1))
#sorting predicted values with respect to predictor
sorted_zip6 = sorted(zip(x,poly_pred6))
x_poly, poly_pred6 = zip(*sorted_zip6)
#plotting predictions
plt.scatter(x,y,s=15)
plt.plot(x_poly,poly_pred3,color='r',label='Polynomial Regression Degree=3')
plt.plot(x_poly,poly_pred4,color='m',label='Polynomial Regression Degree=4')
plt.plot(x_poly,poly_pred5,color='k',label='Polynomial Regression Degree=5')
plt.plot(x_poly,poly_pred6,color='c',label='Polynomial Regression Degree=6')
plt.xlabel('Speed (m/s)',fontsize=16)
plt.ylabel('Power (%)',fontsize=16)
plt.legend(fontsize=12)
plt.show()
print(f'3rd degree polynomial regression-')
print(f'The RMSE is {np.sqrt(mean_squared_error(y,poly_pred3))}')
print(f'The R2 value is {r2_score(y, poly_pred3)}\n')
print(f'4th degree polynomial regression-')
print(f'The RMSE is {np.sqrt(mean_squared_error(y,poly_pred4))}')
print(f'The R2 value is {r2_score(y, poly_pred4)}\n')
print(f'5th degree polynomial regression-')
print(f'The RMSE is {np.sqrt(mean_squared_error(y,poly_pred5))}')
print(f'The R2 value is {r2_score(y, poly_pred5)}\n')
print(f'6th degree polynomial regression-')
print(f'The RMSE is {np.sqrt(mean_squared_error(y,poly_pred6))}')
print(f'The R2 value is {r2_score(y, poly_pred6)}\n')
# Function ot give a positive percentage difference value
def Accuracy_P (test, emp):
if ((pipe5.predict([[test]])/emp)*100 < 100):
return f"Undershot by {int(100 - (pipe5.predict([[test]])/emp)*100)}%"
else:
return f"Overshot by {int(((pipe5.predict([[test]])/emp) * 100) - 100)}%"
print(f'\nTest 1 (Polynomial)-\nWind Speed: {test1} m/s\nEmpirical data: {emp1}\nPredicted value: {float(pipe5.predict([[test1]])):.2f}\nActual Difference: {float(abs(emp1-pipe5.predict([[test1]]))):.2f}\nAccuracy: {Accuracy_P (test1, emp1)}')
print(f'\nTest 2 (Polynomial)-\nWind Speed: {test2} m/s\nEmpirical data: {emp2}\nPredicted value: {float(pipe5.predict([[test2]])):.2f}\nActual Difference: {float(abs(emp2-pipe5.predict([[test2]]))):.2f}\nAccuracy: {Accuracy_P (test2, emp2)}')
print(f'\nTest 3 (Polynomial)-\nWind Speed: {test3} m/s\nEmpirical data: {emp3}\nPredicted value: {float(pipe5.predict([[test3]])):.2f}\nActual Difference: {float(abs(emp3-pipe5.predict([[test3]]))):.2f}\nAccuracy: {Accuracy_P (test3, emp3)}')
print(f'\nTest 4 (Polynomial)-\nWind Speed: {test4} m/s\nEmpirical data: {emp4}\nPredicted value: {float(pipe5.predict([[test4]])):.2f}\nActual Difference: {float(abs(emp4-pipe5.predict([[test4]]))):.2f}\nAccuracy: {Accuracy_P (test4, emp4)}')
print(f'\nTest 5 (Polynomial)-\nWind Speed: {test5} m/s\nEmpirical data: {emp5}\nPredicted value: {float(pipe5.predict([[test5]])):.2f}\nActual Difference: {float(abs(emp5-pipe5.predict([[test5]]))):.2f}\nAccuracy: {Accuracy_P (test5, emp5)}')
print(f'\nTest 6 (Polynomial)-\nWind Speed: {test6} m/s\nEmpirical data: {emp6}\nPredicted value: {float(pipe5.predict([[test6]])):.2f}\nActual Difference: {float(abs(emp6-pipe5.predict([[test6]]))):.2f}\nAccuracy: {Accuracy_P (test6, emp6)}')
print(f'\nTest 7 (Polynomial)-\nWind Speed: {test7} m/s\nEmpirical data: {emp7}\nPredicted value: {float(pipe5.predict([[test7]])):.2f}\nActual Difference: {float(abs(emp7-pipe5.predict([[test7]]))):.2f}\nAccuracy: {Accuracy_P (test7, emp7)}')
```
We can see from the data and graph above the increasing degrees leads us to a better overall fit of the data. The 5th and 6th degree models are very close to be almost indistinguishable from the graph so to avoid unneccesary complexity we can use the 5th degree polynomial for our model as it gives an R2 value of 0.988 and matches closely with our empirical data received. This is a claer improvement over the simple linear regression model which has an R2 value of 0.898 and a root mean square error of 12.897. While these figures alone don't tell the full story of the fit in conjuntion with the graph we get a very strong idea of how confident we can be in the model created.
Then tested with values taken from the data we can see that the predictions are a good degree more accurate than the previously determined simple linear regression.
***
## Keras Neural Networks
Keras is an open source python library that utilises Tensorflow and Theano to train an artificial neural network model. It was created to be user friendly, modular, easy to expand and work with Python. It has broad adaptation and supports a wide array of production deployment options. The digram below gives an indication of the type of process that occurs during the neural network activation-
<img src="./images/neural_reg.jpg" alt="Neural Network Diagram" style="width: 500px;"/>
```
poly = df
test = df
# Train the model.
model = kr.models.Sequential()
model.add(kr.layers.Dense(20, input_shape=(1,), activation='sigmoid', kernel_initializer="glorot_uniform", bias_initializer="glorot_uniform"))
model.add(kr.layers.Dense(1, activation='linear', kernel_initializer="glorot_uniform", bias_initializer="glorot_uniform"))
model.compile('adam', loss='mean_squared_error')
# Fit the data.
model.fit(poly['speed'], poly['power'], epochs=500, batch_size=10)
# Function to give a positive percentage difference value
def Accuracy_N (test, emp):
if ((model.predict([test])/emp)*100 < 100):
return f"Undershot by {int((100 - ((model.predict([test]))/emp)*100))}%"
else:
return f"Overshot by {int((((model.predict([test]))/emp) * 100) - 100)}%"
print(f'\nTest 1 (Neural Network)-\nWind Speed: {test1} m/s\nEmpirical data: {emp1}\nPredicted value: {float(model.predict([test1])):.2f}\nActual Difference: {float(abs(emp1-model.predict([test1]))):.2f}\nAccuracy: {Accuracy_N (test1, emp1)}')
print(f'\nTest 2 (Neural Network)-\nWind Speed: {test2} m/s\nEmpirical data: {emp2}\nPredicted value: {float(model.predict([test2])):.2f}\nActual Difference: {float(abs(emp2-model.predict([test2]))):.2f}\nAccuracy: {Accuracy_N (test2, emp2)}')
print(f'\nTest 3 (Neural Network)-\nWind Speed: {test3} m/s\nEmpirical data: {emp3}\nPredicted value: {float(model.predict([test3])):.2f}\nActual Difference: {float(abs(emp3-model.predict([test3]))):.2f}\nAccuracy: {Accuracy_N (test3, emp3)}')
print(f'\nTest 4 (Neural Network)-\nWind Speed: {test4} m/s\nEmpirical data: {emp4}\nPredicted value: {float(model.predict([test4])):.2f}\nActual Difference: {float(abs(emp4-model.predict([test4]))):.2f}\nAccuracy: {Accuracy_N (test4, emp4)}')
print(f'\nTest 5 (Neural Network)-\nWind Speed: {test5} m/s\nEmpirical data: {emp5}\nPredicted value: {float(model.predict([test5])):.2f}\nActual Difference: {float(abs(emp5-model.predict([test5]))):.2f}\nAccuracy: {Accuracy_N (test5, emp5)}')
print(f'\nTest 6 (Neural Network)-\nWind Speed: {test6} m/s\nEmpirical data: {emp6}\nPredicted value: {float(model.predict([test6])):.2f}\nActual Difference: {float(abs(emp6-model.predict([test6]))):.2f}\nAccuracy: {Accuracy_N (test6, emp6)}')
print(f'\nTest 7 (Neural Network)-\nWind Speed: {test7} m/s\nEmpirical data: {emp7}\nPredicted value: {float(model.predict([test7])):.2f}\nActual Difference: {float(abs(emp7-model.predict([test7]))):.2f}\nAccuracy: {Accuracy_N (test7, emp7)}')
# Graph prediction
plt.scatter(x,y,s=15)
plt.plot(poly['speed'], poly['power'], label='Actual Values')
plt.plot(poly['speed'], model.predict(poly['speed']), label='Prediction Curve')
plt.xlabel('Speed (m/s)',fontsize=16)
plt.ylabel('Power (%)',fontsize=16)
plt.legend(fontsize=12)
plt.show()
```
From the neural network model and the values displayed above we can see that this gives us a very accurate model to base our predictions on. While the later predictions would be similar to the polynomial model accuracy levels thhe early predictions are much closer to the actual values determined.
### Models Compared
```
# Provide a breakdown of all models test results compared
print(f'Test 1 (Linear)-\nWind Speed: {test1} m/s\nEmpirical data: {emp1}\nPredicted value: {float((lm.predict([[test1]]))):.2f}\nActual Difference: {float(abs(emp1-lm.predict([[test1]]))):.2f}\nAccuracy: {Accuracy_L (test1, emp1)}')
print(f'\nTest 1 (Polynomial)-\nWind Speed: {test1} m/s\nEmpirical data: {emp1}\nPredicted value: {float(pipe5.predict([[test1]])):.2f}\nActual Difference: {float(abs(emp1-pipe5.predict([[test1]]))):.2f}\nAccuracy: {Accuracy_P (test1, emp1)}')
print(f'\nTest 1 (Neural Network)-\nWind Speed: {test1} m/s\nEmpirical data: {emp1}\nPredicted value: {float(model.predict([test1])):.2f}\nActual Difference: {float(abs(emp1-model.predict([test1]))):.2f}\nAccuracy: {Accuracy_N (test1, emp1)}')
print(f'\nTest 2 (Linear)-\nWind Speed: {test2} m/s\nEmpirical data: {emp2}\nPredicted value: {float((lm.predict([[test2]]))):.2f}\nActual Difference: {float(abs(emp2-lm.predict([[test2]]))):.2f}\nAccuracy: {Accuracy_L (test2, emp2)}')
print(f'\nTest 2 (Polynomial)-\nWind Speed: {test2} m/s\nEmpirical data: {emp2}\nPredicted value: {float(pipe5.predict([[test2]])):.2f}\nActual Difference: {float(abs(emp2-pipe5.predict([[test2]]))):.2f}\nAccuracy: {Accuracy_P (test2, emp2)}')
print(f'\nTest 2 (Neural Network)-\nWind Speed: {test2} m/s\nEmpirical data: {emp2}\nPredicted value: {float(model.predict([test2])):.2f}\nActual Difference: {float(abs(emp2-model.predict([test2]))):.2f}\nAccuracy: {Accuracy_N (test2, emp2)}')
print(f'\nTest 3 (Linear)-\nWind Speed: {test3} m/s\nEmpirical data: {emp3}\nPredicted value: {float((lm.predict([[test3]]))):.2f}\nActual Difference: {float(abs(emp3-lm.predict([[test3]]))):.2f}\nAccuracy: {Accuracy_L (test3, emp3)}')
print(f'\nTest 3 (Polynomial)-\nWind Speed: {test3} m/s\nEmpirical data: {emp3}\nPredicted value: {float(pipe5.predict([[test3]])):.2f}\nActual Difference: {float(abs(emp3-pipe5.predict([[test3]]))):.2f}\nAccuracy: {Accuracy_P (test3, emp3)}')
print(f'\nTest 3 (Neural Network)-\nWind Speed: {test3} m/s\nEmpirical data: {emp3}\nPredicted value: {float(model.predict([test3])):.2f}\nActual Difference: {float(abs(emp3-model.predict([test3]))):.2f}\nAccuracy: {Accuracy_N (test3, emp3)}')
print(f'\nTest 4 (Linear)-\nWind Speed: {test4} m/s\nEmpirical data: {emp4}\nPredicted value: {float((lm.predict([[test4]]))):.2f}\nActual Difference: {float(abs(emp4-lm.predict([[test4]]))):.2f}\nAccuracy: {Accuracy_L (test4, emp4)}')
print(f'\nTest 4 (Polynomial)-\nWind Speed: {test4} m/s\nEmpirical data: {emp4}\nPredicted value: {float(pipe5.predict([[test4]])):.2f}\nActual Difference: {float(abs(emp4-pipe5.predict([[test4]]))):.2f}\nAccuracy: {Accuracy_P (test4, emp4)}')
print(f'\nTest 4 (Neural Network)-\nWind Speed: {test4} m/s\nEmpirical data: {emp4}\nPredicted value: {float(model.predict([test4])):.2f}\nActual Difference: {float(abs(emp4-model.predict([test4]))):.2f}\nAccuracy: {Accuracy_N (test4, emp4)}')
print(f'\nTest 5 (Linear)-\nWind Speed: {test5} m/s\nEmpirical data: {emp5}\nPredicted value: {float((lm.predict([[test5]]))):.2f}\nActual Difference: {float(abs(emp5-lm.predict([[test5]]))):.2f}\nAccuracy: {Accuracy_L (test5, emp5)}')
print(f'\nTest 5 (Polynomial)-\nWind Speed: {test5} m/s\nEmpirical data: {emp5}\nPredicted value: {float(pipe5.predict([[test5]])):.2f}\nActual Difference: {float(abs(emp5-pipe5.predict([[test5]]))):.2f}\nAccuracy: {Accuracy_P (test5, emp5)}')
print(f'\nTest 5 (Neural Network)-\nWind Speed: {test5} m/s\nEmpirical data: {emp5}\nPredicted value: {float(model.predict([test5])):.2f}\nActual Difference: {float(abs(emp5-model.predict([test5]))):.2f}\nAccuracy: {Accuracy_N (test5, emp5)}')
print(f'\nTest 6 (Linear)-\nWind Speed: {test6} m/s\nEmpirical data: {emp6}\nPredicted value: {float((lm.predict([[test6]]))):.2f}\nActual Difference: {float(abs(emp6-lm.predict([[test6]]))):.2f}\nAccuracy: {Accuracy_L (test6, emp6)}')
print(f'\nTest 6 (Polynomial)-\nWind Speed: {test6} m/s\nEmpirical data: {emp6}\nPredicted value: {float(pipe5.predict([[test6]])):.2f}\nActual Difference: {float(abs(emp6-pipe5.predict([[test6]]))):.2f}\nAccuracy: {Accuracy_P (test6, emp6)}')
print(f'\nTest 6 (Neural Network)-\nWind Speed: {test6} m/s\nEmpirical data: {emp6}\nPredicted value: {float(model.predict([test6])):.2f}\nActual Difference: {float(abs(emp6-model.predict([test6]))):.2f}\nAccuracy: {Accuracy_N (test6, emp6)}')
print(f'\nTest 7 (Linear)-\nWind Speed: {test7} m/s\nEmpirical data: {emp7}\nPredicted value: {float((lm.predict([[test7]]))):.2f}\nActual Difference: {float(abs(emp7-lm.predict([[test7]]))):.2f}\nAccuracy: {Accuracy_L (test7, emp7)}')
print(f'\nTest 7 (Polynomial)-\nWind Speed: {test7} m/s\nEmpirical data: {emp7}\nPredicted value: {float(pipe5.predict([[test7]])):.2f}\nActual Difference: {float(abs(emp7-pipe5.predict([[test7]]))):.2f}\nAccuracy: {Accuracy_P (test7, emp7)}')
print(f'\nTest 7 (Neural Network)-\nWind Speed: {test7} m/s\nEmpirical data: {emp7}\nPredicted value: {float(model.predict([test7])):.2f}\nActual Difference: {float(abs(emp7-model.predict([test7]))):.2f}\nAccuracy: {Accuracy_N (test7, emp7)}')
#plotting all predictions
plt.scatter(x,y,s=15)
plt.plot(poly['speed'], model.predict(poly['speed']), color='k', label='Neural')
plt.plot(x,y_pred,color='g',label='Linear Regression')
plt.plot(x_poly,poly_pred5,color='r',label='Polynomial Regression')
plt.title('Combined Models Predictive Curve',fontsize=16)
plt.xlabel('Speed (m/s)',fontsize=16)
plt.ylabel('Power (%)',fontsize=16)
plt.legend(fontsize=12)
plt.show()
```
From the above we can see that for the vast majority of cases the neural network is the most accurate model used. It shows especially clear on the values beow 10 m/s wind speed.
### Save Neural Networks Model To JSON
```
# https://machinelearningmastery.com/save-load-keras-deep-learning-models/
# serialize model to JSON
model_json = model.to_json()
with open("model.json", "w") as json_file:
json_file.write(model_json)
# serialize weights to HDF5
model.save_weights("model.h5")
print("Saved model to disk")
```
### Load Neural Networks Model From JSON File
```
from tensorflow.keras.models import model_from_json
# load json and create model
json_file = open('model.json', 'r')
loaded_model_json = json_file.read()
json_file.close()
loaded_model = model_from_json(loaded_model_json)
# load weights into new model
loaded_model.load_weights("model.h5")
print("Loaded model from disk")
# Check data loaded correctly bycomparing below to above values
print(f'\nTest 1 (Loaded Neural Network)-\nWind Speed: {test1} m/s\nEmpirical data: {emp1}\nPredicted value: {float(loaded_model.predict([test1])):.2f}\nActual Difference: {float(abs(emp1-loaded_model.predict([test1]))):.2f}\nAccuracy: {Accuracy_N (test1, emp1)}')
print(f'\nTest 2 (Loaded Neural Network)-\nWind Speed: {test2} m/s\nEmpirical data: {emp2}\nPredicted value: {float(loaded_model.predict([test2])):.2f}\nActual Difference: {float(abs(emp2-loaded_model.predict([test2]))):.2f}\nAccuracy: {Accuracy_N (test2, emp2)}')
print(f'\nTest 3 (Loaded Neural Network)-\nWind Speed: {test3} m/s\nEmpirical data: {emp3}\nPredicted value: {float(loaded_model.predict([test3])):.2f}\nActual Difference: {float(abs(emp3-loaded_model.predict([test3]))):.2f}\nAccuracy: {Accuracy_N (test3, emp3)}')
print(f'\nTest 4 (Loaded Neural Network)-\nWind Speed: {test4} m/s\nEmpirical data: {emp4}\nPredicted value: {float(loaded_model.predict([test4])):.2f}\nActual Difference: {float(abs(emp4-loaded_model.predict([test4]))):.2f}\nAccuracy: {Accuracy_N (test4, emp4)}')
print(f'\nTest 5 (Loaded Neural Network)-\nWind Speed: {test5} m/s\nEmpirical data: {emp5}\nPredicted value: {float(loaded_model.predict([test5])):.2f}\nActual Difference: {float(abs(emp5-loaded_model.predict([test5]))):.2f}\nAccuracy: {Accuracy_N (test5, emp5)}')
print(f'\nTest 6 (Loaded Neural Network)-\nWind Speed: {test6} m/s\nEmpirical data: {emp6}\nPredicted value: {float(loaded_model.predict([test6])):.2f}\nActual Difference: {float(abs(emp6-loaded_model.predict([test6]))):.2f}\nAccuracy: {Accuracy_N (test6, emp6)}')
print(f'\nTest 7 (Loaded Neural Network)-\nWind Speed: {test7} m/s\nEmpirical data: {emp7}\nPredicted value: {float(loaded_model.predict([test7])):.2f}\nActual Difference: {float(abs(emp7-loaded_model.predict([test7]))):.2f}\nAccuracy: {Accuracy_N (test7, emp7)}')
```
## Sources
[1] wikipedia.org, "Wind power", [online], https://en.wikipedia.org/wiki/Wind_power
[2] sciencedirect.com, "Seasonal forecasts of wind power generation", [online], https://www.sciencedirect.com/science/article/pii/S0960148119306196
[3] wikipedia.org, "Polynomial regression", [online], https://en.wikipedia.org/wiki/Polynomial_regression
[4] geeksforgeeks.org, "Working with missing data in pandas", [online], https://www.geeksforgeeks.org/working-with-missing-data-in-pandas
[5] realypython.com, "linear regression in python", [online], https://realpython.com/linear-regression-in-python/
[6] towarddatascience.com, "Polynomial from scracthh in python", [onlone], https://towardsdatascience.com/polynomial-regression-from-scratch-in-python-1f34a3a5f373
[7] statisticsbyjim.com, "Curve fitting using linear and nonn linear regression", [onlone], https://statisticsbyjim.com/regression/curve-fitting-linear-nonlinear-regress
[8] statisticsbyjim.com, "Interpret r squared regression", [online], https://statisticsbyjim.com/regression/interpret-r-squared-regression/
[9] towarddatascience.com, "Polynomial regression", [online], https://towardsdatascience.com/polynomial-regression-bbe8b9d97491
[10] analyticsvidhya.com, "Introdution regression splines python codes", [online], https://www.analyticsvidhya.com/blog/2018/03/introduction-regression-splines-python-codes/
[11] datascienceplus.com, "Keras regression based neural networks", [online], https://datascienceplus.com/keras-regression-based-neural-networks/ (keras)
[12] machinelearningmastery.com, "Save load keras deep learning models", [online], https://machinelearningmastery.com/save-load-keras-deep-learning-models/ (saving keras result)
[13] towarddatascience.com, "Deploying a keras deep learning model as a web application", https://towardsdatascience.com/deploying-a-keras-deep-learning-model-as-a-web-application-in-p-fc0f2354a7ff
[14] vernier.com, "What are Mean Squared Error and Root Mean Squared Error?", [online], https://www.vernier.com/til/1014
[15] wikipedia.org, "Linear regression", [online], https://en.wikipedia.org/wiki/Linear_regression
[16] stat.yale.edu, "Linear regression", [online], http://www.stat.yale.edu/Courses/1997-98/101/linreg.htm
[17] github.com, "Latexsheet", [online], https://wch.github.io/latexsheet/
[18] analyticsvidhya.com, "Build your first Machine Learning pipeline using scikit-learn!", [online], https://www.analyticsvidhya.com/blog/2020/01/build-your-first-machine-learning-pipeline-using-scikit-learn/?utm_source=blog&utm_medium=polynomial-regression-python
|
github_jupyter
|
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from pylab import rcParams
import sklearn
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import scale
import tensorflow.keras as kr
from collections import Counter
from sklearn.pipeline import Pipeline
# Matplotlib graph sizes
rcParams['figure.figsize']=20, 12
# Import the csv file containing the information
df = pd.read_csv('powerproduction.txt')
# Check first 10 rows to ensure we're getting correct data in as first 5 columns power outputt displayed as 0
print(f'{df.head(11)}\n')
print(f'{df.tail(15)}\n')
# Display dataframes information
print(f'{df.info()}\n')
print(f'{df.describe()}\n')
print(f'{df.shape}\n')
print(f'{df.isnull().sum()}\n')
print(f'{df.isna().sum()}')
# Visualise dataset
sns.jointplot(data=df, x="speed", y="power",kind="reg", height=8)
#sns.relplot(data=df, x="speed", y="power", height=8, aspect=2)
sns.pairplot(df, height=4, aspect=2);
# Check were majority of readings for 0 power generation values are located.
df_check= df[df['power'] == 0]
sns.histplot(data=df_check, x="speed", bins=25);
# https://stackoverflow.com/questions/13851535/how-to-delete-rows-from-a-pandas-dataframe-based-on-a-conditional-expression
df = df.drop(df[df.power == 0.0].index)
# Plot scatter graph
plt.scatter(df.speed,df.power,s=15)
plt.xlabel('Speed (m/s)',fontsize=16)
plt.ylabel('Power (%)',fontsize=16)
plt.show()
# Confirm all zero valuees have been removed.
df_check= df[df['power'] == 0]
sns.histplot(data=df_check, x="speed", bins=25);
df.shape
# https://www.analyticsvidhya.com/blog/2020/03/polynomial-regression-python/v
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
# Generate data and convert to arrays to prepare for use
y = df.power.to_numpy()
x = df.speed.to_numpy().reshape(-1, 1)
# Training Model
lm=LinearRegression()
lm.fit(x.reshape(-1,1),y.reshape(-1,1))
# Generate predition variable
y_pred=lm.predict(x.reshape(-1,1))
# Test refers to the wind power entered to provide a predicted value. Emp refers to the empirical data from csv file received
test1, emp1 = df.at[12,'speed'], df.at[12,'power']
test2, emp2 = df.at[97,'speed'] , df.at[97,'power']
test3, emp3 = df.at[201,'speed'], df.at[201,'power']
test4, emp4 = df.at[253,'speed'], df.at[253,'power']
test5, emp5 = df.at[293,'speed'], df.at[293,'power']
test6, emp6 = df.at[357,'speed'], df.at[357,'power']
test7, emp7 = df.at[425,'speed'], df.at[425,'power']
# Function ot give a positive percentage difference value
def Accuracy_L (test, emp):
if (((lm.predict([[test]]))/emp)*100 < 100):
return f"Undershot by {int(100 - ((lm.predict([[test]]))/emp)*100)}%"
else:
return f"Overshot by {int((((lm.predict([[test]]))/emp) * 100) - 100)}%"
print(f'\nTest 1 (Linear)-\nWind Speed: {test1} m/s\nEmpirical data: {emp1}\nPredicted value: {float((lm.predict([[test1]]))):.2f}\nActual Difference: {float(abs(emp1-lm.predict([[test1]]))):.2f}\nAccuracy: {Accuracy_L (test1, emp1)}')
print(f'\nTest 2 (Linear)-\nWind Speed: {test2} m/s\nEmpirical data: {emp2}\nPredicted value: {float((lm.predict([[test2]]))):.2f}\nActual Difference: {float(abs(emp2-lm.predict([[test2]]))):.2f}\nAccuracy: {Accuracy_L (test2, emp2)}')
print(f'\nTest 3 (Linear)-\nWind Speed: {test3} m/s\nEmpirical data: {emp3}\nPredicted value: {float((lm.predict([[test3]]))):.2f}\nActual Difference: {float(abs(emp3-lm.predict([[test3]]))):.2f}\nAccuracy: {Accuracy_L (test3, emp3)}')
print(f'\nTest 4 (Linear)-\nWind Speed: {test4} m/s\nEmpirical data: {emp4}\nPredicted value: {float((lm.predict([[test4]]))):.2f}\nActual Difference: {float(abs(emp4-lm.predict([[test4]]))):.2f}\nAccuracy: {Accuracy_L (test4, emp4)}')
print(f'\nTest 5 (Linear)-\nWind Speed: {test5} m/s\nEmpirical data: {emp5}\nPredicted value: {float((lm.predict([[test5]]))):.2f}\nActual Difference: {float(abs(emp5-lm.predict([[test5]]))):.2f}\nAccuracy: {Accuracy_L (test5, emp5)}')
print(f'\nTest 6 (Linear)-\nWind Speed: {test6} m/s\nEmpirical data: {emp6}\nPredicted value: {float((lm.predict([[test6]]))):.2f}\nActual Difference: {float(abs(emp6-lm.predict([[test6]]))):.2f}\nAccuracy: {Accuracy_L (test6, emp6)}')
print(f'\nTest 7 (Linear)-\nWind Speed: {test7} m/s\nEmpirical data: {emp7}\nPredicted value: {float((lm.predict([[test7]]))):.2f}\nActual Difference: {float(abs(emp7-lm.predict([[test7]]))):.2f}\nAccuracy: {Accuracy_L (test7, emp7)}')
# Plotting predictions
#plt.figure(figsize=(10,5))
plt.scatter(x,y,s=15)
plt.plot(x,y_pred,color='g')
plt.xlabel('Speed (m/s)',fontsize=16)
plt.ylabel('Power (%)',fontsize=16)
plt.show()
print(f'Root mean squared error for Linear Regression is {np.sqrt(mean_squared_error(y,y_pred))}')
print(f'The R2 value is {r2_score(y, y_pred)}')
# Check multiple degrees to validate which best fits the line
Input3=[('polynomial',PolynomialFeatures(degree=3)),('modal',LinearRegression())]
pipe3=Pipeline(Input3)
pipe3.fit(x.reshape(-1,1),y.reshape(-1,1))
poly_pred3=pipe3.predict(x.reshape(-1,1))
#sorting predicted values with respect to predictor
sorted_zip3 = sorted(zip(x,poly_pred3))
x_poly, poly_pred3 = zip(*sorted_zip3)
# creating pipeline and fitting it on data
Input4=[('polynomial',PolynomialFeatures(degree=4)),('modal',LinearRegression())]
pipe4=Pipeline(Input4)
pipe4.fit(x.reshape(-1,1),y.reshape(-1,1))
poly_pred4=pipe4.predict(x.reshape(-1,1))
#sorting predicted values with respect to predictor
sorted_zip4 = sorted(zip(x,poly_pred4))
x_poly, poly_pred4 = zip(*sorted_zip4)
# creating pipeline and fitting it on data
Input5=[('polynomial',PolynomialFeatures(degree=5)),('modal',LinearRegression())]
pipe5=Pipeline(Input5)
pipe5.fit(x.reshape(-1,1),y.reshape(-1,1))
poly_pred5=pipe5.predict(x.reshape(-1,1))
#sorting predicted values with respect to predictor
sorted_zip5 = sorted(zip(x,poly_pred5))
x_poly, poly_pred5 = zip(*sorted_zip5)
# creating pipeline and fitting it on data
Input6=[('polynomial',PolynomialFeatures(degree=6)),('modal',LinearRegression())]
pipe6=Pipeline(Input6)
pipe6.fit(x.reshape(-1,1),y.reshape(-1,1))
poly_pred6=pipe6.predict(x.reshape(-1,1))
#sorting predicted values with respect to predictor
sorted_zip6 = sorted(zip(x,poly_pred6))
x_poly, poly_pred6 = zip(*sorted_zip6)
#plotting predictions
plt.scatter(x,y,s=15)
plt.plot(x_poly,poly_pred3,color='r',label='Polynomial Regression Degree=3')
plt.plot(x_poly,poly_pred4,color='m',label='Polynomial Regression Degree=4')
plt.plot(x_poly,poly_pred5,color='k',label='Polynomial Regression Degree=5')
plt.plot(x_poly,poly_pred6,color='c',label='Polynomial Regression Degree=6')
plt.xlabel('Speed (m/s)',fontsize=16)
plt.ylabel('Power (%)',fontsize=16)
plt.legend(fontsize=12)
plt.show()
print(f'3rd degree polynomial regression-')
print(f'The RMSE is {np.sqrt(mean_squared_error(y,poly_pred3))}')
print(f'The R2 value is {r2_score(y, poly_pred3)}\n')
print(f'4th degree polynomial regression-')
print(f'The RMSE is {np.sqrt(mean_squared_error(y,poly_pred4))}')
print(f'The R2 value is {r2_score(y, poly_pred4)}\n')
print(f'5th degree polynomial regression-')
print(f'The RMSE is {np.sqrt(mean_squared_error(y,poly_pred5))}')
print(f'The R2 value is {r2_score(y, poly_pred5)}\n')
print(f'6th degree polynomial regression-')
print(f'The RMSE is {np.sqrt(mean_squared_error(y,poly_pred6))}')
print(f'The R2 value is {r2_score(y, poly_pred6)}\n')
# Function ot give a positive percentage difference value
def Accuracy_P (test, emp):
if ((pipe5.predict([[test]])/emp)*100 < 100):
return f"Undershot by {int(100 - (pipe5.predict([[test]])/emp)*100)}%"
else:
return f"Overshot by {int(((pipe5.predict([[test]])/emp) * 100) - 100)}%"
print(f'\nTest 1 (Polynomial)-\nWind Speed: {test1} m/s\nEmpirical data: {emp1}\nPredicted value: {float(pipe5.predict([[test1]])):.2f}\nActual Difference: {float(abs(emp1-pipe5.predict([[test1]]))):.2f}\nAccuracy: {Accuracy_P (test1, emp1)}')
print(f'\nTest 2 (Polynomial)-\nWind Speed: {test2} m/s\nEmpirical data: {emp2}\nPredicted value: {float(pipe5.predict([[test2]])):.2f}\nActual Difference: {float(abs(emp2-pipe5.predict([[test2]]))):.2f}\nAccuracy: {Accuracy_P (test2, emp2)}')
print(f'\nTest 3 (Polynomial)-\nWind Speed: {test3} m/s\nEmpirical data: {emp3}\nPredicted value: {float(pipe5.predict([[test3]])):.2f}\nActual Difference: {float(abs(emp3-pipe5.predict([[test3]]))):.2f}\nAccuracy: {Accuracy_P (test3, emp3)}')
print(f'\nTest 4 (Polynomial)-\nWind Speed: {test4} m/s\nEmpirical data: {emp4}\nPredicted value: {float(pipe5.predict([[test4]])):.2f}\nActual Difference: {float(abs(emp4-pipe5.predict([[test4]]))):.2f}\nAccuracy: {Accuracy_P (test4, emp4)}')
print(f'\nTest 5 (Polynomial)-\nWind Speed: {test5} m/s\nEmpirical data: {emp5}\nPredicted value: {float(pipe5.predict([[test5]])):.2f}\nActual Difference: {float(abs(emp5-pipe5.predict([[test5]]))):.2f}\nAccuracy: {Accuracy_P (test5, emp5)}')
print(f'\nTest 6 (Polynomial)-\nWind Speed: {test6} m/s\nEmpirical data: {emp6}\nPredicted value: {float(pipe5.predict([[test6]])):.2f}\nActual Difference: {float(abs(emp6-pipe5.predict([[test6]]))):.2f}\nAccuracy: {Accuracy_P (test6, emp6)}')
print(f'\nTest 7 (Polynomial)-\nWind Speed: {test7} m/s\nEmpirical data: {emp7}\nPredicted value: {float(pipe5.predict([[test7]])):.2f}\nActual Difference: {float(abs(emp7-pipe5.predict([[test7]]))):.2f}\nAccuracy: {Accuracy_P (test7, emp7)}')
poly = df
test = df
# Train the model.
model = kr.models.Sequential()
model.add(kr.layers.Dense(20, input_shape=(1,), activation='sigmoid', kernel_initializer="glorot_uniform", bias_initializer="glorot_uniform"))
model.add(kr.layers.Dense(1, activation='linear', kernel_initializer="glorot_uniform", bias_initializer="glorot_uniform"))
model.compile('adam', loss='mean_squared_error')
# Fit the data.
model.fit(poly['speed'], poly['power'], epochs=500, batch_size=10)
# Function to give a positive percentage difference value
def Accuracy_N (test, emp):
if ((model.predict([test])/emp)*100 < 100):
return f"Undershot by {int((100 - ((model.predict([test]))/emp)*100))}%"
else:
return f"Overshot by {int((((model.predict([test]))/emp) * 100) - 100)}%"
print(f'\nTest 1 (Neural Network)-\nWind Speed: {test1} m/s\nEmpirical data: {emp1}\nPredicted value: {float(model.predict([test1])):.2f}\nActual Difference: {float(abs(emp1-model.predict([test1]))):.2f}\nAccuracy: {Accuracy_N (test1, emp1)}')
print(f'\nTest 2 (Neural Network)-\nWind Speed: {test2} m/s\nEmpirical data: {emp2}\nPredicted value: {float(model.predict([test2])):.2f}\nActual Difference: {float(abs(emp2-model.predict([test2]))):.2f}\nAccuracy: {Accuracy_N (test2, emp2)}')
print(f'\nTest 3 (Neural Network)-\nWind Speed: {test3} m/s\nEmpirical data: {emp3}\nPredicted value: {float(model.predict([test3])):.2f}\nActual Difference: {float(abs(emp3-model.predict([test3]))):.2f}\nAccuracy: {Accuracy_N (test3, emp3)}')
print(f'\nTest 4 (Neural Network)-\nWind Speed: {test4} m/s\nEmpirical data: {emp4}\nPredicted value: {float(model.predict([test4])):.2f}\nActual Difference: {float(abs(emp4-model.predict([test4]))):.2f}\nAccuracy: {Accuracy_N (test4, emp4)}')
print(f'\nTest 5 (Neural Network)-\nWind Speed: {test5} m/s\nEmpirical data: {emp5}\nPredicted value: {float(model.predict([test5])):.2f}\nActual Difference: {float(abs(emp5-model.predict([test5]))):.2f}\nAccuracy: {Accuracy_N (test5, emp5)}')
print(f'\nTest 6 (Neural Network)-\nWind Speed: {test6} m/s\nEmpirical data: {emp6}\nPredicted value: {float(model.predict([test6])):.2f}\nActual Difference: {float(abs(emp6-model.predict([test6]))):.2f}\nAccuracy: {Accuracy_N (test6, emp6)}')
print(f'\nTest 7 (Neural Network)-\nWind Speed: {test7} m/s\nEmpirical data: {emp7}\nPredicted value: {float(model.predict([test7])):.2f}\nActual Difference: {float(abs(emp7-model.predict([test7]))):.2f}\nAccuracy: {Accuracy_N (test7, emp7)}')
# Graph prediction
plt.scatter(x,y,s=15)
plt.plot(poly['speed'], poly['power'], label='Actual Values')
plt.plot(poly['speed'], model.predict(poly['speed']), label='Prediction Curve')
plt.xlabel('Speed (m/s)',fontsize=16)
plt.ylabel('Power (%)',fontsize=16)
plt.legend(fontsize=12)
plt.show()
# Provide a breakdown of all models test results compared
print(f'Test 1 (Linear)-\nWind Speed: {test1} m/s\nEmpirical data: {emp1}\nPredicted value: {float((lm.predict([[test1]]))):.2f}\nActual Difference: {float(abs(emp1-lm.predict([[test1]]))):.2f}\nAccuracy: {Accuracy_L (test1, emp1)}')
print(f'\nTest 1 (Polynomial)-\nWind Speed: {test1} m/s\nEmpirical data: {emp1}\nPredicted value: {float(pipe5.predict([[test1]])):.2f}\nActual Difference: {float(abs(emp1-pipe5.predict([[test1]]))):.2f}\nAccuracy: {Accuracy_P (test1, emp1)}')
print(f'\nTest 1 (Neural Network)-\nWind Speed: {test1} m/s\nEmpirical data: {emp1}\nPredicted value: {float(model.predict([test1])):.2f}\nActual Difference: {float(abs(emp1-model.predict([test1]))):.2f}\nAccuracy: {Accuracy_N (test1, emp1)}')
print(f'\nTest 2 (Linear)-\nWind Speed: {test2} m/s\nEmpirical data: {emp2}\nPredicted value: {float((lm.predict([[test2]]))):.2f}\nActual Difference: {float(abs(emp2-lm.predict([[test2]]))):.2f}\nAccuracy: {Accuracy_L (test2, emp2)}')
print(f'\nTest 2 (Polynomial)-\nWind Speed: {test2} m/s\nEmpirical data: {emp2}\nPredicted value: {float(pipe5.predict([[test2]])):.2f}\nActual Difference: {float(abs(emp2-pipe5.predict([[test2]]))):.2f}\nAccuracy: {Accuracy_P (test2, emp2)}')
print(f'\nTest 2 (Neural Network)-\nWind Speed: {test2} m/s\nEmpirical data: {emp2}\nPredicted value: {float(model.predict([test2])):.2f}\nActual Difference: {float(abs(emp2-model.predict([test2]))):.2f}\nAccuracy: {Accuracy_N (test2, emp2)}')
print(f'\nTest 3 (Linear)-\nWind Speed: {test3} m/s\nEmpirical data: {emp3}\nPredicted value: {float((lm.predict([[test3]]))):.2f}\nActual Difference: {float(abs(emp3-lm.predict([[test3]]))):.2f}\nAccuracy: {Accuracy_L (test3, emp3)}')
print(f'\nTest 3 (Polynomial)-\nWind Speed: {test3} m/s\nEmpirical data: {emp3}\nPredicted value: {float(pipe5.predict([[test3]])):.2f}\nActual Difference: {float(abs(emp3-pipe5.predict([[test3]]))):.2f}\nAccuracy: {Accuracy_P (test3, emp3)}')
print(f'\nTest 3 (Neural Network)-\nWind Speed: {test3} m/s\nEmpirical data: {emp3}\nPredicted value: {float(model.predict([test3])):.2f}\nActual Difference: {float(abs(emp3-model.predict([test3]))):.2f}\nAccuracy: {Accuracy_N (test3, emp3)}')
print(f'\nTest 4 (Linear)-\nWind Speed: {test4} m/s\nEmpirical data: {emp4}\nPredicted value: {float((lm.predict([[test4]]))):.2f}\nActual Difference: {float(abs(emp4-lm.predict([[test4]]))):.2f}\nAccuracy: {Accuracy_L (test4, emp4)}')
print(f'\nTest 4 (Polynomial)-\nWind Speed: {test4} m/s\nEmpirical data: {emp4}\nPredicted value: {float(pipe5.predict([[test4]])):.2f}\nActual Difference: {float(abs(emp4-pipe5.predict([[test4]]))):.2f}\nAccuracy: {Accuracy_P (test4, emp4)}')
print(f'\nTest 4 (Neural Network)-\nWind Speed: {test4} m/s\nEmpirical data: {emp4}\nPredicted value: {float(model.predict([test4])):.2f}\nActual Difference: {float(abs(emp4-model.predict([test4]))):.2f}\nAccuracy: {Accuracy_N (test4, emp4)}')
print(f'\nTest 5 (Linear)-\nWind Speed: {test5} m/s\nEmpirical data: {emp5}\nPredicted value: {float((lm.predict([[test5]]))):.2f}\nActual Difference: {float(abs(emp5-lm.predict([[test5]]))):.2f}\nAccuracy: {Accuracy_L (test5, emp5)}')
print(f'\nTest 5 (Polynomial)-\nWind Speed: {test5} m/s\nEmpirical data: {emp5}\nPredicted value: {float(pipe5.predict([[test5]])):.2f}\nActual Difference: {float(abs(emp5-pipe5.predict([[test5]]))):.2f}\nAccuracy: {Accuracy_P (test5, emp5)}')
print(f'\nTest 5 (Neural Network)-\nWind Speed: {test5} m/s\nEmpirical data: {emp5}\nPredicted value: {float(model.predict([test5])):.2f}\nActual Difference: {float(abs(emp5-model.predict([test5]))):.2f}\nAccuracy: {Accuracy_N (test5, emp5)}')
print(f'\nTest 6 (Linear)-\nWind Speed: {test6} m/s\nEmpirical data: {emp6}\nPredicted value: {float((lm.predict([[test6]]))):.2f}\nActual Difference: {float(abs(emp6-lm.predict([[test6]]))):.2f}\nAccuracy: {Accuracy_L (test6, emp6)}')
print(f'\nTest 6 (Polynomial)-\nWind Speed: {test6} m/s\nEmpirical data: {emp6}\nPredicted value: {float(pipe5.predict([[test6]])):.2f}\nActual Difference: {float(abs(emp6-pipe5.predict([[test6]]))):.2f}\nAccuracy: {Accuracy_P (test6, emp6)}')
print(f'\nTest 6 (Neural Network)-\nWind Speed: {test6} m/s\nEmpirical data: {emp6}\nPredicted value: {float(model.predict([test6])):.2f}\nActual Difference: {float(abs(emp6-model.predict([test6]))):.2f}\nAccuracy: {Accuracy_N (test6, emp6)}')
print(f'\nTest 7 (Linear)-\nWind Speed: {test7} m/s\nEmpirical data: {emp7}\nPredicted value: {float((lm.predict([[test7]]))):.2f}\nActual Difference: {float(abs(emp7-lm.predict([[test7]]))):.2f}\nAccuracy: {Accuracy_L (test7, emp7)}')
print(f'\nTest 7 (Polynomial)-\nWind Speed: {test7} m/s\nEmpirical data: {emp7}\nPredicted value: {float(pipe5.predict([[test7]])):.2f}\nActual Difference: {float(abs(emp7-pipe5.predict([[test7]]))):.2f}\nAccuracy: {Accuracy_P (test7, emp7)}')
print(f'\nTest 7 (Neural Network)-\nWind Speed: {test7} m/s\nEmpirical data: {emp7}\nPredicted value: {float(model.predict([test7])):.2f}\nActual Difference: {float(abs(emp7-model.predict([test7]))):.2f}\nAccuracy: {Accuracy_N (test7, emp7)}')
#plotting all predictions
plt.scatter(x,y,s=15)
plt.plot(poly['speed'], model.predict(poly['speed']), color='k', label='Neural')
plt.plot(x,y_pred,color='g',label='Linear Regression')
plt.plot(x_poly,poly_pred5,color='r',label='Polynomial Regression')
plt.title('Combined Models Predictive Curve',fontsize=16)
plt.xlabel('Speed (m/s)',fontsize=16)
plt.ylabel('Power (%)',fontsize=16)
plt.legend(fontsize=12)
plt.show()
# https://machinelearningmastery.com/save-load-keras-deep-learning-models/
# serialize model to JSON
model_json = model.to_json()
with open("model.json", "w") as json_file:
json_file.write(model_json)
# serialize weights to HDF5
model.save_weights("model.h5")
print("Saved model to disk")
from tensorflow.keras.models import model_from_json
# load json and create model
json_file = open('model.json', 'r')
loaded_model_json = json_file.read()
json_file.close()
loaded_model = model_from_json(loaded_model_json)
# load weights into new model
loaded_model.load_weights("model.h5")
print("Loaded model from disk")
# Check data loaded correctly bycomparing below to above values
print(f'\nTest 1 (Loaded Neural Network)-\nWind Speed: {test1} m/s\nEmpirical data: {emp1}\nPredicted value: {float(loaded_model.predict([test1])):.2f}\nActual Difference: {float(abs(emp1-loaded_model.predict([test1]))):.2f}\nAccuracy: {Accuracy_N (test1, emp1)}')
print(f'\nTest 2 (Loaded Neural Network)-\nWind Speed: {test2} m/s\nEmpirical data: {emp2}\nPredicted value: {float(loaded_model.predict([test2])):.2f}\nActual Difference: {float(abs(emp2-loaded_model.predict([test2]))):.2f}\nAccuracy: {Accuracy_N (test2, emp2)}')
print(f'\nTest 3 (Loaded Neural Network)-\nWind Speed: {test3} m/s\nEmpirical data: {emp3}\nPredicted value: {float(loaded_model.predict([test3])):.2f}\nActual Difference: {float(abs(emp3-loaded_model.predict([test3]))):.2f}\nAccuracy: {Accuracy_N (test3, emp3)}')
print(f'\nTest 4 (Loaded Neural Network)-\nWind Speed: {test4} m/s\nEmpirical data: {emp4}\nPredicted value: {float(loaded_model.predict([test4])):.2f}\nActual Difference: {float(abs(emp4-loaded_model.predict([test4]))):.2f}\nAccuracy: {Accuracy_N (test4, emp4)}')
print(f'\nTest 5 (Loaded Neural Network)-\nWind Speed: {test5} m/s\nEmpirical data: {emp5}\nPredicted value: {float(loaded_model.predict([test5])):.2f}\nActual Difference: {float(abs(emp5-loaded_model.predict([test5]))):.2f}\nAccuracy: {Accuracy_N (test5, emp5)}')
print(f'\nTest 6 (Loaded Neural Network)-\nWind Speed: {test6} m/s\nEmpirical data: {emp6}\nPredicted value: {float(loaded_model.predict([test6])):.2f}\nActual Difference: {float(abs(emp6-loaded_model.predict([test6]))):.2f}\nAccuracy: {Accuracy_N (test6, emp6)}')
print(f'\nTest 7 (Loaded Neural Network)-\nWind Speed: {test7} m/s\nEmpirical data: {emp7}\nPredicted value: {float(loaded_model.predict([test7])):.2f}\nActual Difference: {float(abs(emp7-loaded_model.predict([test7]))):.2f}\nAccuracy: {Accuracy_N (test7, emp7)}')
| 0.752922 | 0.994336 |
<a href="https://colab.research.google.com/github/lalitpagaria/obsei/blob/master/example/Obsei_playstore_classification_logger_example.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Install latest Obsei
```
!pip install git+https://github.com/lalitpagaria/obsei.git
```
## Configure Play Store Scrapper Source
```
from obsei.source.playstore_scrapper import PlayStoreScrapperConfig, PlayStoreScrapperSource
# initialize play store source config
source_config = PlayStoreScrapperConfig(
# Need two parameters package_name and country.
# `package_name` can be found at the end of the url of app in play store.
# For example - https://play.google.com/store/apps/details?id=com.google.android.gm&hl=en&gl=US
# `com.google.android.gm` is the package_name for xcode and `us` is country.
countries=["us"],
package_name="com.google.android.gm",
max_count=10, # Number of reviews to fetch
lookup_period="1h" # Lookup period from current time, format: `<number><d|h|m>` (day|hour|minute)
)
# initialize play store reviews retriever
source = PlayStoreScrapperSource()
```
## Configure Text Classification Analyzer
```
from obsei.analyzer.classification_analyzer import ClassificationAnalyzerConfig, ZeroShotClassificationAnalyzer
# initialize classification analyzer config
# It can also detect sentiments if "positive" and "negative" labels are added.
analyzer_config=ClassificationAnalyzerConfig(
labels=["interface", "crash", "performance"],
)
# initialize classification analyzer
# For supported models refer https://huggingface.co/models?filter=zero-shot-classification
text_analyzer = ZeroShotClassificationAnalyzer(
model_name_or_path="typeform/mobilebert-uncased-mnli",
device="auto" # change to "cuda:0" for using gpu
)
```
## Configure Logger Sink
```
from obsei.sink.logger_sink import LoggerSink, LoggerSinkConfig
import logging
import sys
logger = logging.getLogger("Obsei")
logging.basicConfig(stream=sys.stdout, level=logging.INFO)
# initialize logger sink config
sink_config = LoggerSinkConfig(
logger=logger,
level=logging.INFO
)
# initialize logger sink
sink = LoggerSink()
```
## Execute Workflow/Pipeline
```
# This will fetch information from configured source
source_response_list = source.lookup(source_config)
# This will execute analyzer
analyzer_response_list = text_analyzer.analyze_input(
source_response_list=source_response_list,
analyzer_config=analyzer_config
)
# This will send analyzed output to sink
sink.send_data(analyzer_response_list, sink_config)
```
|
github_jupyter
|
!pip install git+https://github.com/lalitpagaria/obsei.git
from obsei.source.playstore_scrapper import PlayStoreScrapperConfig, PlayStoreScrapperSource
# initialize play store source config
source_config = PlayStoreScrapperConfig(
# Need two parameters package_name and country.
# `package_name` can be found at the end of the url of app in play store.
# For example - https://play.google.com/store/apps/details?id=com.google.android.gm&hl=en&gl=US
# `com.google.android.gm` is the package_name for xcode and `us` is country.
countries=["us"],
package_name="com.google.android.gm",
max_count=10, # Number of reviews to fetch
lookup_period="1h" # Lookup period from current time, format: `<number><d|h|m>` (day|hour|minute)
)
# initialize play store reviews retriever
source = PlayStoreScrapperSource()
from obsei.analyzer.classification_analyzer import ClassificationAnalyzerConfig, ZeroShotClassificationAnalyzer
# initialize classification analyzer config
# It can also detect sentiments if "positive" and "negative" labels are added.
analyzer_config=ClassificationAnalyzerConfig(
labels=["interface", "crash", "performance"],
)
# initialize classification analyzer
# For supported models refer https://huggingface.co/models?filter=zero-shot-classification
text_analyzer = ZeroShotClassificationAnalyzer(
model_name_or_path="typeform/mobilebert-uncased-mnli",
device="auto" # change to "cuda:0" for using gpu
)
from obsei.sink.logger_sink import LoggerSink, LoggerSinkConfig
import logging
import sys
logger = logging.getLogger("Obsei")
logging.basicConfig(stream=sys.stdout, level=logging.INFO)
# initialize logger sink config
sink_config = LoggerSinkConfig(
logger=logger,
level=logging.INFO
)
# initialize logger sink
sink = LoggerSink()
# This will fetch information from configured source
source_response_list = source.lookup(source_config)
# This will execute analyzer
analyzer_response_list = text_analyzer.analyze_input(
source_response_list=source_response_list,
analyzer_config=analyzer_config
)
# This will send analyzed output to sink
sink.send_data(analyzer_response_list, sink_config)
| 0.725551 | 0.817647 |
### Tutorial: Using adipocyte U-net to predict adipocyte areas from images.
In this notebook, we'll use ten example images of adipocytes, obtain their segmentation masks from the U-net and calculate some predicted areas.
```
import matplotlib.pyplot as plt
import numpy as np
import tifffile as tiff
import keras.backend as K
from keras.metrics import binary_crossentropy
from math import sqrt
from skimage.transform import resize
import logging
import sys
import tensorflow as tf
import sys; #sys.path.append('../')
from src.models.clr_callback import *
from src.models.adipocyte_unet import UNet
from src.utils.runtime import gpu_selection
from src.utils.data import random_transforms
from src.utils.model import dice_coef, jaccard_coef
import cv2
import numpy as np
import cv2
import glob
import random
from matplotlib.image import imsave
import mahotas as mh
from scipy import ndimage
from skimage.measure import regionprops
import matplotlib.pyplot as plt
import seaborn as sns
from src.utils.model import dice_coef, jaccard_coef,tru_pos,fls_pos,tru_neg,fls_neg
sns.set_style("whitegrid", {'axes.grid' : False})
def metric_wrapper(yt, yp, metric):
return K.get_value(metric(K.variable(yt), K.variable(yp)))
```
**Instantiate the Unet model:**
```
#model = UNet()
model = UNet('unet')
model.config['data_path'] = '.'
#model.load_data()
```
**We will be using a GPU. select the appropriate GPU. If you have a single GPU, this will be:**
`visible_devices=0`
If you run this without a GPU it will just be ignored
```
gpu_selection(visible_devices="3")
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
session = tf.Session(config=config)
config = tf.ConfigProto()
config.gpu_options.per_process_gpu_memory_fraction = 1
session = tf.Session(config=config)
```
**Load the trained model weights**
```
model.compile()
model.net.load_weights('checkpoints/unet_1024_dilation/weights_loss_val.weights')
```
**This is the structure of the adipocyte U-net**
```
model.net.summary()
```
**Images need to be standardised to make predictions, we load and normalise the images with the following function:**
```python
process_tiles(img_dir)
```
```
def process_tiles(img_dir):
tiles = glob.glob(img_dir +'*')
samples = []
for i in tiles:
s = cv2.imread(i,0)
s = np.array(s,np.float32) /255
#_mean, _std = np.mean(s), np.std(s)
normalised_img = np.expand_dims((s - np.mean(s)) / np.std(s),0)
#s = normalize(s)
samples.append(normalised_img)
samples=np.array(samples)
return samples
example_imgs = process_tiles('example_tiles/')
```
**Lets have a look at an example image we would like to segment**
```
plt.figure(figsize=(10,10))
plt.imshow(example_imgs[2][0,:,:],cmap='gray')
plt.show()
```
**Here I have defined a small function to loop over images and predict the corresponding segmentation for each image:**
```python
generate_predictions(example_imgs)
```
```
def generate_predictions(example_imgs):
preds_bool = []
preds = []
for img in example_imgs:
pred = model.net.predict(img,batch_size=1)
preds.append(pred)
img = np.array(pred* 255,dtype='uint8')
T = mh.thresholding.otsu(img)
img = img[0,:,:] > T
preds_bool.append(img)
return preds, preds_bool
```
*This will be a bit slow if you're not using a GPU (i.e. running it on your laptop!) (~1 min)*
```
preds, preds_bool = generate_predictions(example_imgs)
```
**Lets plot the corresponding segmentation prediction for the image. Looks good!**
```
plt.figure(figsize=(10,10))
plt.imshow(preds_bool[2],cmap='gray')
plt.show()
```
** Lets take the segmentation masks from Adipocyte U-net and calculate the cell areas **
```
def predict_areas(prd_batch):
blobs = np.where(prd_batch[0,:,:] > 0.80, 0, 1)
blobs = np.array(cv2.erode((blobs *1.0).astype(np.float32),np.ones((3,3))),dtype='int8')
blobs = ndimage.morphology.binary_fill_holes(blobs,structure=np.ones((5,5))).astype(int)
labels, no_objects = ndimage.label(blobs)
props = regionprops(labels)
size={i:props[i].area for i in range (0, no_objects)}
no_of_cells=(sum(i > 200 and i < 100000 for i in size.values()))
areas=[i for i in size.values() if i >= 200 and i <= 100000]
areas= np.array(areas) * 0.495
return(blobs,areas, np.median(areas),np.mean(areas),no_of_cells)
blob_img,areas, median_area, mean_area, no_of_cells = predict_areas(preds[2])
plt.figure(figsize=(10,10))
plt.imshow(blob_img,cmap='gray')
plt.show()
plt.hist(areas, bins=20)
plt.title('Distribution of adipocyte areas ($\mu m^{2}$)')
plt.xlabel('adipocyte areas ($\mu m^{2}$)')
plt.ylabel('Frequency')
print("Number of cells in image {:}".format(no_of_cells))
print("Median cell area in image {:.2f}um^2".format(median_area))
```
|
github_jupyter
|
import matplotlib.pyplot as plt
import numpy as np
import tifffile as tiff
import keras.backend as K
from keras.metrics import binary_crossentropy
from math import sqrt
from skimage.transform import resize
import logging
import sys
import tensorflow as tf
import sys; #sys.path.append('../')
from src.models.clr_callback import *
from src.models.adipocyte_unet import UNet
from src.utils.runtime import gpu_selection
from src.utils.data import random_transforms
from src.utils.model import dice_coef, jaccard_coef
import cv2
import numpy as np
import cv2
import glob
import random
from matplotlib.image import imsave
import mahotas as mh
from scipy import ndimage
from skimage.measure import regionprops
import matplotlib.pyplot as plt
import seaborn as sns
from src.utils.model import dice_coef, jaccard_coef,tru_pos,fls_pos,tru_neg,fls_neg
sns.set_style("whitegrid", {'axes.grid' : False})
def metric_wrapper(yt, yp, metric):
return K.get_value(metric(K.variable(yt), K.variable(yp)))
#model = UNet()
model = UNet('unet')
model.config['data_path'] = '.'
#model.load_data()
gpu_selection(visible_devices="3")
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
session = tf.Session(config=config)
config = tf.ConfigProto()
config.gpu_options.per_process_gpu_memory_fraction = 1
session = tf.Session(config=config)
model.compile()
model.net.load_weights('checkpoints/unet_1024_dilation/weights_loss_val.weights')
model.net.summary()
process_tiles(img_dir)
def process_tiles(img_dir):
tiles = glob.glob(img_dir +'*')
samples = []
for i in tiles:
s = cv2.imread(i,0)
s = np.array(s,np.float32) /255
#_mean, _std = np.mean(s), np.std(s)
normalised_img = np.expand_dims((s - np.mean(s)) / np.std(s),0)
#s = normalize(s)
samples.append(normalised_img)
samples=np.array(samples)
return samples
example_imgs = process_tiles('example_tiles/')
plt.figure(figsize=(10,10))
plt.imshow(example_imgs[2][0,:,:],cmap='gray')
plt.show()
generate_predictions(example_imgs)
def generate_predictions(example_imgs):
preds_bool = []
preds = []
for img in example_imgs:
pred = model.net.predict(img,batch_size=1)
preds.append(pred)
img = np.array(pred* 255,dtype='uint8')
T = mh.thresholding.otsu(img)
img = img[0,:,:] > T
preds_bool.append(img)
return preds, preds_bool
preds, preds_bool = generate_predictions(example_imgs)
plt.figure(figsize=(10,10))
plt.imshow(preds_bool[2],cmap='gray')
plt.show()
def predict_areas(prd_batch):
blobs = np.where(prd_batch[0,:,:] > 0.80, 0, 1)
blobs = np.array(cv2.erode((blobs *1.0).astype(np.float32),np.ones((3,3))),dtype='int8')
blobs = ndimage.morphology.binary_fill_holes(blobs,structure=np.ones((5,5))).astype(int)
labels, no_objects = ndimage.label(blobs)
props = regionprops(labels)
size={i:props[i].area for i in range (0, no_objects)}
no_of_cells=(sum(i > 200 and i < 100000 for i in size.values()))
areas=[i for i in size.values() if i >= 200 and i <= 100000]
areas= np.array(areas) * 0.495
return(blobs,areas, np.median(areas),np.mean(areas),no_of_cells)
blob_img,areas, median_area, mean_area, no_of_cells = predict_areas(preds[2])
plt.figure(figsize=(10,10))
plt.imshow(blob_img,cmap='gray')
plt.show()
plt.hist(areas, bins=20)
plt.title('Distribution of adipocyte areas ($\mu m^{2}$)')
plt.xlabel('adipocyte areas ($\mu m^{2}$)')
plt.ylabel('Frequency')
print("Number of cells in image {:}".format(no_of_cells))
print("Median cell area in image {:.2f}um^2".format(median_area))
| 0.55929 | 0.89419 |
# WORD2VEC GENERATOR
This script is for generating multiple gensim word2vec models having different sized windows and vectors
**Import packages and modules**
```
import time
import os
import pandas as pd
from gensim.models import Word2Vec
```
**Get the number of processors**
```
import multiprocessing
WORKERS = multiprocessing.cpu_count()
print("Number of workers:",WORKERS)
```
**Extract the total number of examples in combined train and test set**
```
input_dir = "../input/yelp_review_polarity_csv/"
train_data = pd.read_csv(input_dir+"train_data_processed.csv")
test_data = pd.read_csv(input_dir+"test_data_processed.csv")
total_examples = train_data.shape[0]+test_data.shape[0]
del(train_data, test_data)
```
## 1. Function to generate and save gensim word2vec models
**Class module to load sentences from files containing chunks of reviews**
```
class MySentences(object):
def __init__(self, dirname):
self.dirname = dirname
def __iter__(self):
for fname in os.listdir(self.dirname):
if fname.endswith(".csv"):
for line in open(os.path.join(self.dirname, fname)):
yield line.split()
```
**Create an object of the senntence loader with the given data path**
```
sentences = MySentences('../input/yelp_review_processed_chunks/')
```
**A function to generate and save gensim word2vec models**
```
def word2vec_generator(sentences, size, window, total_examples, workers, destination_folder = "./word2vec_models/"):
'''
A function to generate word2vec model
'''
# create a word2vec model
model = Word2Vec(sentences, size=size, window=window, sg= 1, min_count=1, workers=workers)
# train model
model.train(sentences, total_examples=total_examples, epochs=5)
# file path
fname = destination_folder + "word2vec_size_" + str(size) + "_window_" + str(window) + ".mdl"
# save the model
model. wv.save_word2vec_format(fname)
```
## 2. Generate multiple word2vec models having different sized windows and vectors
**size = 100; window = 5**
```
t_start = time.time()
size = 100
window = 5
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 1: {:.2f} mins".format((t_end-t_start)/60))
```
**size = 100; window = 10**
```
t_start = time.time()
size = 100
window = 10
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 2: {:.2f} mins".format((t_end-t_start)/60))
```
**size = 100; window = 15**
```
t_start = time.time()
size = 100
window = 15
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 3: {:.2f} mins".format((t_end-t_start)/60))
```
**size = 100; window = 20**
```
t_start = time.time()
size = 100
window = 20
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 4: {:.2f} mins".format((t_end-t_start)/60))
```
**size = 100; window = 25**
```
t_start = time.time()
size = 100
window = 25
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 5: {:.2f} mins".format((t_end-t_start)/60))
```
**size = 200; window = 5**
```
t_start = time.time()
size = 200
window = 5
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 6: {:.2f} mins".format((t_end-t_start)/60))
```
**size = 200; window = 10**
```
t_start = time.time()
size = 200
window = 10
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 7: {:.2f} mins".format((t_end-t_start)/60))
```
**size = 200; window = 15**
```
t_start = time.time()
size = 200
window = 15
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 8: {:.2f} mins".format((t_end-t_start)/60))
```
**size = 200; window = 20**
```
t_start = time.time()
size = 200
window = 20
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 9: {:.2f} mins".format((t_end-t_start)/60))
```
**size = 200; window = 25**
```
t_start = time.time()
size = 200
window = 25
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 10: {:.2f} mins".format((t_end-t_start)/60))
```
**size = 300; window = 5**
```
t_start = time.time()
size = 300
window = 5
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 11: {:.2f} mins".format((t_end-t_start)/60))
```
**size = 300; window = 10**
```
t_start = time.time()
size = 300
window = 10
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 12: {:.2f} mins".format((t_end-t_start)/60))
```
**size = 300; window = 15**
```
t_start = time.time()
size = 300
window = 15
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 13: {:.2f} mins".format((t_end-t_start)/60))
```
**size = 300; window = 20**
```
t_start = time.time()
size = 300
window = 20
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 14: {:.2f} mins".format((t_end-t_start)/60))
```
**size = 300; window = 25**
```
t_start = time.time()
size = 300
window = 25
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 15: {:.2f} mins".format((t_end-t_start)/60))
```
|
github_jupyter
|
import time
import os
import pandas as pd
from gensim.models import Word2Vec
import multiprocessing
WORKERS = multiprocessing.cpu_count()
print("Number of workers:",WORKERS)
input_dir = "../input/yelp_review_polarity_csv/"
train_data = pd.read_csv(input_dir+"train_data_processed.csv")
test_data = pd.read_csv(input_dir+"test_data_processed.csv")
total_examples = train_data.shape[0]+test_data.shape[0]
del(train_data, test_data)
class MySentences(object):
def __init__(self, dirname):
self.dirname = dirname
def __iter__(self):
for fname in os.listdir(self.dirname):
if fname.endswith(".csv"):
for line in open(os.path.join(self.dirname, fname)):
yield line.split()
sentences = MySentences('../input/yelp_review_processed_chunks/')
def word2vec_generator(sentences, size, window, total_examples, workers, destination_folder = "./word2vec_models/"):
'''
A function to generate word2vec model
'''
# create a word2vec model
model = Word2Vec(sentences, size=size, window=window, sg= 1, min_count=1, workers=workers)
# train model
model.train(sentences, total_examples=total_examples, epochs=5)
# file path
fname = destination_folder + "word2vec_size_" + str(size) + "_window_" + str(window) + ".mdl"
# save the model
model. wv.save_word2vec_format(fname)
t_start = time.time()
size = 100
window = 5
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 1: {:.2f} mins".format((t_end-t_start)/60))
t_start = time.time()
size = 100
window = 10
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 2: {:.2f} mins".format((t_end-t_start)/60))
t_start = time.time()
size = 100
window = 15
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 3: {:.2f} mins".format((t_end-t_start)/60))
t_start = time.time()
size = 100
window = 20
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 4: {:.2f} mins".format((t_end-t_start)/60))
t_start = time.time()
size = 100
window = 25
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 5: {:.2f} mins".format((t_end-t_start)/60))
t_start = time.time()
size = 200
window = 5
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 6: {:.2f} mins".format((t_end-t_start)/60))
t_start = time.time()
size = 200
window = 10
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 7: {:.2f} mins".format((t_end-t_start)/60))
t_start = time.time()
size = 200
window = 15
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 8: {:.2f} mins".format((t_end-t_start)/60))
t_start = time.time()
size = 200
window = 20
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 9: {:.2f} mins".format((t_end-t_start)/60))
t_start = time.time()
size = 200
window = 25
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 10: {:.2f} mins".format((t_end-t_start)/60))
t_start = time.time()
size = 300
window = 5
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 11: {:.2f} mins".format((t_end-t_start)/60))
t_start = time.time()
size = 300
window = 10
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 12: {:.2f} mins".format((t_end-t_start)/60))
t_start = time.time()
size = 300
window = 15
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 13: {:.2f} mins".format((t_end-t_start)/60))
t_start = time.time()
size = 300
window = 20
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 14: {:.2f} mins".format((t_end-t_start)/60))
t_start = time.time()
size = 300
window = 25
word2vec_generator(sentences, size, window, total_examples, WORKERS)
t_end = time.time()
print("Time taken to save model 15: {:.2f} mins".format((t_end-t_start)/60))
| 0.28398 | 0.943815 |
<img style="float: right;" src="http://www.gislk.com/images/science_of_where.png" height="64" width="64">
# Raster Analytics Dashboard
Using this Dashboard, you can distribute your raster processing algorithms using ArcGIS Image Server and Raster Analytics.
## Import IPython Widgets and Display
```
from ipywidgets import widgets
from IPython.display import clear_output
```
## Connect to ArcGIS Online and Access the Landsat Services
```
from arcgis.gis import GIS
from arcgis.raster.functions import *
gis = GIS()
landsat_item = gis.content.search('Landsat Multispectral', 'Imagery Layer')[0]
landsat = landsat_item.layers[0]
```
## Create a Map and Add Landsat Layers
```
map1 = gis.map("California, USA")
map1
map1.add_layer(landsat)
```
## Get RFTs from Landsat Service
```
rfts = []
#print(landsat.properties['rasterFunctionInfos'])
for idx,props in enumerate(landsat.properties['rasterFunctionInfos']):
rfts.append(landsat.properties['rasterFunctionInfos'][idx]['name'])
```
## Create a Dropdown from the RFTs
```
rft_select = widgets.Dropdown(
options=rfts,
value='None',
description='Raster Function',
disabled=False,
)
def on_rft_change(change):
if change['type'] == 'change' and change['name'] == 'value':
map1.remove_layers()
map1.add_layer(landsat, {"imageServiceParameters" :{ "renderingRule": { "rasterFunction": rft_select.value}}})
#print("changed to %s" % change['new'])
rft_select.observe(on_rft_change)
display(rft_select)
```
## Create a List of AOIs or Study Areas We Might Want to Run Raster Analytics Over and Add Them to a Dropdown
```
from arcgis.geocoding import geocode
from arcgis.features import FeatureLayer
study_area_dict = {'California':'http://services.arcgis.com/PpEMp4p6SBYbe0zW/arcgis/rest/services/California_Counties/FeatureServer/0',
'Montana':'http://services.arcgis.com/iTQUx5ZpNUh47Geb/arcgis/rest/services/Montana_Mask/FeatureServer/0',
'Nevada':'http://services.arcgis.com/pGfbNJoYypmNq86F/arcgis/rest/services/28R04_Nevada_Region/FeatureServer/5',
'Oregon':'https://services.arcgis.com/uUvqNMGPm7axC2dD/arcgis/rest/services/Oregon_Boundary_generalized/FeatureServer/0',
'Texas':'http://services2.arcgis.com/5MVN2jsqIrNZD4tP/arcgis/rest/services/Texas_Outline/FeatureServer/0'}
study_areas = ['California',
'Montana',
'Nevada',
'Oregon',
'Texas']
country = widgets.Dropdown(
options=study_areas,
value='California',
description='Region to Process:',
disabled=False,
)
def on_change(change):
if change['type'] == 'change' and change['name'] == 'value':
location = geocode(str(country.value) + ', USA')[0]
map1.extent = location['extent']
#fl = FeatureLayer(study_area_dict[country.value])
#map1.extent = fl.properties['extent']
#print("changed to %s" % change['new'])
country.observe(on_change)
display(country)
```
## Add A Button for Initializting a Raster Analytics Process
```
from datetime import datetime
def on_button_click(b):
#map1.extentx = getextent
clear_output()
print("Job submitted at " + f"{datetime.now():%Y-%m-%d %H:%M:%S}")
button = widgets.Button(description="Run Raster Analytics",
disabled=False,
button_style='success',
tooltip='Kick Off A Raster Analytics Job',
icon='check')
display(button)
button.on_click(on_button_click)
```
|
github_jupyter
|
from ipywidgets import widgets
from IPython.display import clear_output
from arcgis.gis import GIS
from arcgis.raster.functions import *
gis = GIS()
landsat_item = gis.content.search('Landsat Multispectral', 'Imagery Layer')[0]
landsat = landsat_item.layers[0]
map1 = gis.map("California, USA")
map1
map1.add_layer(landsat)
rfts = []
#print(landsat.properties['rasterFunctionInfos'])
for idx,props in enumerate(landsat.properties['rasterFunctionInfos']):
rfts.append(landsat.properties['rasterFunctionInfos'][idx]['name'])
rft_select = widgets.Dropdown(
options=rfts,
value='None',
description='Raster Function',
disabled=False,
)
def on_rft_change(change):
if change['type'] == 'change' and change['name'] == 'value':
map1.remove_layers()
map1.add_layer(landsat, {"imageServiceParameters" :{ "renderingRule": { "rasterFunction": rft_select.value}}})
#print("changed to %s" % change['new'])
rft_select.observe(on_rft_change)
display(rft_select)
from arcgis.geocoding import geocode
from arcgis.features import FeatureLayer
study_area_dict = {'California':'http://services.arcgis.com/PpEMp4p6SBYbe0zW/arcgis/rest/services/California_Counties/FeatureServer/0',
'Montana':'http://services.arcgis.com/iTQUx5ZpNUh47Geb/arcgis/rest/services/Montana_Mask/FeatureServer/0',
'Nevada':'http://services.arcgis.com/pGfbNJoYypmNq86F/arcgis/rest/services/28R04_Nevada_Region/FeatureServer/5',
'Oregon':'https://services.arcgis.com/uUvqNMGPm7axC2dD/arcgis/rest/services/Oregon_Boundary_generalized/FeatureServer/0',
'Texas':'http://services2.arcgis.com/5MVN2jsqIrNZD4tP/arcgis/rest/services/Texas_Outline/FeatureServer/0'}
study_areas = ['California',
'Montana',
'Nevada',
'Oregon',
'Texas']
country = widgets.Dropdown(
options=study_areas,
value='California',
description='Region to Process:',
disabled=False,
)
def on_change(change):
if change['type'] == 'change' and change['name'] == 'value':
location = geocode(str(country.value) + ', USA')[0]
map1.extent = location['extent']
#fl = FeatureLayer(study_area_dict[country.value])
#map1.extent = fl.properties['extent']
#print("changed to %s" % change['new'])
country.observe(on_change)
display(country)
from datetime import datetime
def on_button_click(b):
#map1.extentx = getextent
clear_output()
print("Job submitted at " + f"{datetime.now():%Y-%m-%d %H:%M:%S}")
button = widgets.Button(description="Run Raster Analytics",
disabled=False,
button_style='success',
tooltip='Kick Off A Raster Analytics Job',
icon='check')
display(button)
button.on_click(on_button_click)
| 0.228243 | 0.915507 |
## Working with SBML Ids
Usually basico uses the COPASI display names, to work with model elements. That way a consistent naming scheme between the COPASI graphical user interface, and the scripts can be easily maintained. However, for someone inspecting an SBML model, it might be convenient to also look at the SBML ids and identify elements that way. For this reason the data frames returned for compartments, events, parameters, species and reactions now also contain a column `sbml_id`.
Lets start as usual with the common imports:
```
import sys
if '../..' not in sys.path:
sys.path.append('../..')
from basico import *
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
Next lets load a model from the BioModels Database, and look at the elments:
```
load_biomodel(64);
```
Now we have not just the element name availabe, but also their respective `sbml_id`:
```
get_species()[['sbml_id', 'initial_concentration']]
```
similarly we can get the elements by SBML id as well:
```
get_species(sbml_id='ATP')
```
Whereas in COPASI each element has a concentration and a particle number, in SBML usually elements deal only with concentrations and amounts. To make it easy to access them, it is convenient to add the expressions for the amount to the model, so that they can be accessed at any point in time. For that a utility function exists. If `use_sbml_ids` is specified, the sbml id of the species will be used in the name (i.e: `amount(sbml_id)`), otherwise it will be named `amount(display name)`. In case `ignore_fixed` is specified, no expressions for fixed species will be created, and similarly assignment expressions can be ignored:
```
add_amount_expressions(use_sbml_ids=True, ignore_fixed=True)
```
lets look at the expressions created, we see it is just the concentration multiplied with the compartment size the species is in:
```
get_parameters(name='amount(')[['initial_value', 'expression']]
```
the `run_time_course` function now also takes a parameter to use sbml id's if they are present (it will still use the display names in case an element has no sbml id.
```
run_time_course(use_sbml_id=True)
df = run_time_course()
```
so lets plot just the amounts we got:
```
amount_columns = list(df.columns)
amount_columns = [name for name in amount_columns if 'amount(' in name]
df[amount_columns].plot();
```
of course the added global parameters can be easily removed:
```
remove_amount_expressions()
```
and now we can plot the concentrations:
```
run_time_course(use_sbml_id=True).plot();
```
|
github_jupyter
|
import sys
if '../..' not in sys.path:
sys.path.append('../..')
from basico import *
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
load_biomodel(64);
get_species()[['sbml_id', 'initial_concentration']]
get_species(sbml_id='ATP')
add_amount_expressions(use_sbml_ids=True, ignore_fixed=True)
get_parameters(name='amount(')[['initial_value', 'expression']]
run_time_course(use_sbml_id=True)
df = run_time_course()
amount_columns = list(df.columns)
amount_columns = [name for name in amount_columns if 'amount(' in name]
df[amount_columns].plot();
remove_amount_expressions()
run_time_course(use_sbml_id=True).plot();
| 0.117458 | 0.896795 |
```
# Imports
import pandas as pd
import numpy as np
from warnings import filterwarnings
from sklearn.metrics import accuracy_score
from math import log
# Disable warnings from being printed
filterwarnings('ignore')
fileN = 800
fileM = 100000
def read_data(filename):
data = pd.DataFrame(columns=range(fileM))
with open(filename, 'r') as datafile:
lines = datafile.readlines()
for i in range(len(lines)):
record = np.fromstring(lines[i], dtype=int, sep=' ')
record_bool = [0 for i in range(fileM)]
for col in record:
record_bool[col-1] = 1
data.loc[i] = record_bool
return data
def read_labels(filename):
labels = []
with open(filename, 'r') as datafile:
lines = datafile.readlines()
for line in lines:
labels.append(np.fromstring(line, dtype=int, sep=' ')[0])
return labels
# Read the data into dataframe
train_data = read_data("dorothea/dorothea_train.data")
valid_data = read_data("dorothea/dorothea_valid.data")
# Get the labels of the train data
train_data_labels = read_labels("dorothea/dorothea_train.labels")
valid_data_labels = read_labels("dorothea/dorothea_valid.labels")
# Compute data which is constant in different runs of pca, i.e. eigenvectors
def compute_eigenvectors(data):
# Center the data around mean
data_centered = data - np.mean(data, axis=0)
# Compute the covariance matrix (xx' i.e nXn), and find eigenvalues and eigenvectors
cov_matrix = np.cov(data_centered)
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
# Now eigenvectors of x'x matrix can be obtained from these by multiplying by x', eigenvalues remain same
eigenvectors = np.dot(np.transpose(data_centered), eigenvectors)
# Sort the eigenvectors in decreasing order of eigenvalues
sort_order = np.argsort(eigenvalues)[::-1]
new_eigenvectors = np.zeros(eigenvectors.shape)
for i in range(eigenvalues.shape[0]):
new_eigenvectors[:, i] = eigenvectors[:, sort_order[i]]
return new_eigenvectors
# Get data in the new feature space of reduced dimensionality.
def pca_(data, new_eigenvectors, k):
# Get first K eigenvectors
eigenvectors_firstK = new_eigenvectors[:, :k]
# Get data in reduced dimension space
projected_data = np.dot(data, eigenvectors_firstK)
return pd.DataFrame(projected_data)
def GNBC(train, valid):
# Separate the classes
class_m = train[train["labels"] == -1]
class_p = train[train["labels"] == 1]
# Calculate prior probabilities for both classes
prior_m = class_m.shape[0]/train.shape[0]
prior_p = class_p.shape[0]/train.shape[0]
# Calculate variances for all features
var_m = np.var(class_m, axis=0)
var_p = np.var(class_p, axis=0)
# Calculate mean for all features
mean_m = np.mean(class_m, axis=0)
mean_p = np.mean(class_p, axis=0)
# Predict
results = []
for i in range(valid.shape[0]):
posterior_m = log(prior_m)
posterior_p = log(prior_p)
for j in range(valid.shape[1]-1):
cur_x = valid.loc[i, j]
posterior_m = posterior_m + (-0.5 * (((cur_x - mean_m[j])**2) / var_m[j])) - 0.5*log(var_m[j])
posterior_p = posterior_p + (-0.5 * (((cur_x - mean_p[j])**2) / var_p[j])) - 0.5*log(var_p[j])
if posterior_m >= posterior_p:
cur_class = -1
else:
cur_class = 1
results.append(cur_class)
# Calculate accuracy
return accuracy_score(valid["labels"], results)
def iterate_pca(train_data, valid_data, train_data_labels, valid_data_labels):
accuracies = []
kl = [100, 500, 800]
new_eigenvectors_train = compute_eigenvectors(train_data)
new_eigenvectors_valid = compute_eigenvectors(valid_data)
for k in kl:
projected_train = pca_(train_data, new_eigenvectors_train, k)
projected_valid = pca_(valid_data, new_eigenvectors_valid, k)
projected_train["labels"] = train_data_labels
projected_valid["labels"] = valid_data_labels
cur_accuracy = GNBC_pca(projected_train, projected_valid)
accuracies.append(cur_accuracy)
print("Statistics")
print(100, accuracies[0])
print(500, accuracies[1])
print(800, accuracies[2])
iterate_pca(train_data, valid_data, train_data_labels, valid_data_labels)
def lda_(data):
# Separate the train data classwise.
class_m = data[data["labels"] == -1]
class_p = data[data["labels"] == 1]
# Drop the last labels column for matrix calculations
class_m = class_m.drop("labels", axis=1)
class_p = class_p.drop("labels", axis=1)
# Get scatter matrices for each class separately
scatter_m = np.cov(np.transpose(class_m))
scatter_p = np.cov(np.transpose(class_p))
# Compute means for each feature.
mean_m = np.mean(class_m, axis=0)
mean_p = np.mean(class_p, axis=0)
mean_t = np.mean(data, axis=0)
mean_t = mean_t.drop("labels")
# Compute with class and between class scatter matrices
sw = scatter_m + scatter_p
swin = np.linalg.inv(sw)
wstar = np.dot(swin, (mean_m - mean_p))
# Find new projected data
new_projected_data = data.drop("labels", axis=1)
new_projected_data = np.dot(np.transpose(wstar), new_projected_data)
return pd.DataFrame(new_projected_data)
def iterate_lda(train_data, valid_data, train_data_labels, valid_data_labels):
# Get projected data as input for LDA
new_eigenvectors_train = compute_eigenvectors(train_data)
new_eigenvectors_valid = compute_eigenvectors(valid_data)
projected_train = pca_(train_data, new_eigenvectors_train, 800)
projected_valid = pca_(valid_data, new_eigenvectors_valid, 800)
projected_train["labels"] = train_data_labels
projected_valid["labels"] = valid_data_labels
# Get LDA applied projected data
new_projected_train = lda_(projected_train)
new_projected_valid = lda_(projected_valid)
new_projected_train["labels"] = train_data_labels
new_projected_valid["labels"] = valid_data_labels
accuracy = GNBC(new_projected_train, new_projected_valid)
print("Accuracy: ", accuracy)
iterate_lda(train_data, valid_data, train_data_labels, valid_data_labels)
```
|
github_jupyter
|
# Imports
import pandas as pd
import numpy as np
from warnings import filterwarnings
from sklearn.metrics import accuracy_score
from math import log
# Disable warnings from being printed
filterwarnings('ignore')
fileN = 800
fileM = 100000
def read_data(filename):
data = pd.DataFrame(columns=range(fileM))
with open(filename, 'r') as datafile:
lines = datafile.readlines()
for i in range(len(lines)):
record = np.fromstring(lines[i], dtype=int, sep=' ')
record_bool = [0 for i in range(fileM)]
for col in record:
record_bool[col-1] = 1
data.loc[i] = record_bool
return data
def read_labels(filename):
labels = []
with open(filename, 'r') as datafile:
lines = datafile.readlines()
for line in lines:
labels.append(np.fromstring(line, dtype=int, sep=' ')[0])
return labels
# Read the data into dataframe
train_data = read_data("dorothea/dorothea_train.data")
valid_data = read_data("dorothea/dorothea_valid.data")
# Get the labels of the train data
train_data_labels = read_labels("dorothea/dorothea_train.labels")
valid_data_labels = read_labels("dorothea/dorothea_valid.labels")
# Compute data which is constant in different runs of pca, i.e. eigenvectors
def compute_eigenvectors(data):
# Center the data around mean
data_centered = data - np.mean(data, axis=0)
# Compute the covariance matrix (xx' i.e nXn), and find eigenvalues and eigenvectors
cov_matrix = np.cov(data_centered)
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
# Now eigenvectors of x'x matrix can be obtained from these by multiplying by x', eigenvalues remain same
eigenvectors = np.dot(np.transpose(data_centered), eigenvectors)
# Sort the eigenvectors in decreasing order of eigenvalues
sort_order = np.argsort(eigenvalues)[::-1]
new_eigenvectors = np.zeros(eigenvectors.shape)
for i in range(eigenvalues.shape[0]):
new_eigenvectors[:, i] = eigenvectors[:, sort_order[i]]
return new_eigenvectors
# Get data in the new feature space of reduced dimensionality.
def pca_(data, new_eigenvectors, k):
# Get first K eigenvectors
eigenvectors_firstK = new_eigenvectors[:, :k]
# Get data in reduced dimension space
projected_data = np.dot(data, eigenvectors_firstK)
return pd.DataFrame(projected_data)
def GNBC(train, valid):
# Separate the classes
class_m = train[train["labels"] == -1]
class_p = train[train["labels"] == 1]
# Calculate prior probabilities for both classes
prior_m = class_m.shape[0]/train.shape[0]
prior_p = class_p.shape[0]/train.shape[0]
# Calculate variances for all features
var_m = np.var(class_m, axis=0)
var_p = np.var(class_p, axis=0)
# Calculate mean for all features
mean_m = np.mean(class_m, axis=0)
mean_p = np.mean(class_p, axis=0)
# Predict
results = []
for i in range(valid.shape[0]):
posterior_m = log(prior_m)
posterior_p = log(prior_p)
for j in range(valid.shape[1]-1):
cur_x = valid.loc[i, j]
posterior_m = posterior_m + (-0.5 * (((cur_x - mean_m[j])**2) / var_m[j])) - 0.5*log(var_m[j])
posterior_p = posterior_p + (-0.5 * (((cur_x - mean_p[j])**2) / var_p[j])) - 0.5*log(var_p[j])
if posterior_m >= posterior_p:
cur_class = -1
else:
cur_class = 1
results.append(cur_class)
# Calculate accuracy
return accuracy_score(valid["labels"], results)
def iterate_pca(train_data, valid_data, train_data_labels, valid_data_labels):
accuracies = []
kl = [100, 500, 800]
new_eigenvectors_train = compute_eigenvectors(train_data)
new_eigenvectors_valid = compute_eigenvectors(valid_data)
for k in kl:
projected_train = pca_(train_data, new_eigenvectors_train, k)
projected_valid = pca_(valid_data, new_eigenvectors_valid, k)
projected_train["labels"] = train_data_labels
projected_valid["labels"] = valid_data_labels
cur_accuracy = GNBC_pca(projected_train, projected_valid)
accuracies.append(cur_accuracy)
print("Statistics")
print(100, accuracies[0])
print(500, accuracies[1])
print(800, accuracies[2])
iterate_pca(train_data, valid_data, train_data_labels, valid_data_labels)
def lda_(data):
# Separate the train data classwise.
class_m = data[data["labels"] == -1]
class_p = data[data["labels"] == 1]
# Drop the last labels column for matrix calculations
class_m = class_m.drop("labels", axis=1)
class_p = class_p.drop("labels", axis=1)
# Get scatter matrices for each class separately
scatter_m = np.cov(np.transpose(class_m))
scatter_p = np.cov(np.transpose(class_p))
# Compute means for each feature.
mean_m = np.mean(class_m, axis=0)
mean_p = np.mean(class_p, axis=0)
mean_t = np.mean(data, axis=0)
mean_t = mean_t.drop("labels")
# Compute with class and between class scatter matrices
sw = scatter_m + scatter_p
swin = np.linalg.inv(sw)
wstar = np.dot(swin, (mean_m - mean_p))
# Find new projected data
new_projected_data = data.drop("labels", axis=1)
new_projected_data = np.dot(np.transpose(wstar), new_projected_data)
return pd.DataFrame(new_projected_data)
def iterate_lda(train_data, valid_data, train_data_labels, valid_data_labels):
# Get projected data as input for LDA
new_eigenvectors_train = compute_eigenvectors(train_data)
new_eigenvectors_valid = compute_eigenvectors(valid_data)
projected_train = pca_(train_data, new_eigenvectors_train, 800)
projected_valid = pca_(valid_data, new_eigenvectors_valid, 800)
projected_train["labels"] = train_data_labels
projected_valid["labels"] = valid_data_labels
# Get LDA applied projected data
new_projected_train = lda_(projected_train)
new_projected_valid = lda_(projected_valid)
new_projected_train["labels"] = train_data_labels
new_projected_valid["labels"] = valid_data_labels
accuracy = GNBC(new_projected_train, new_projected_valid)
print("Accuracy: ", accuracy)
iterate_lda(train_data, valid_data, train_data_labels, valid_data_labels)
| 0.705379 | 0.569553 |
## Final Notebook Submission
Please fill out:
* Student name:
* Student pace: self paced / part time / full time
* Scheduled project review date/time:
* Instructor name:
* Blog post URL:
```
import pandas as pd
import numpy as np
import seaborn as sns
from sklearn.preprocessing import OneHotEncoder
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
%matplotlib inline
housing_df = pd.read_csv('data/kc_house_data.csv')
housing_df.info()
housing_df.isna().sum()
housing_df['datetime'] = pd.to_datetime(housing_df['date'])
housing_df['soldyear'] = housing_df['datetime'].dt.year
housing_df['age_when_sold'] = housing_df['soldyear'] - housing_df['yr_built']
housing_df['grade_num'] = housing_df['grade'].str.split()
housing_df['grade_num'] = housing_df['grade_num'].str[0]
housing_df['grade_num'] = housing_df['grade_num'].astype(int)
housing_df['sqft_basement'] = housing_df['sqft_living'] - housing_df['sqft_above']
housing_df['Basement'] = None
housing_df['Basement'] = housing_df['sqft_basement'].map(lambda x: False if x == 0 else True)
housing_df['Basement'] = housing_df['Basement'].astype(int)
housing_df.condition.value_counts()
replace_dict2 = {'Poor': 1, 'Fair': 2, 'Average': 3, 'Good': 4, 'Very Good': 5}
housing_df['condition'] = housing_df['condition'].replace(replace_dict2)
from sklearn.impute import SimpleImputer
wtr_col = housing_df[['waterfront']]
imputer = SimpleImputer(strategy='constant', fill_value = 'NO')
imputer.fit(wtr_col)
waterfront_imputed = imputer.transform(wtr_col)
housing_df.waterfront = waterfront_imputed
from sklearn.preprocessing import OrdinalEncoder
wtr_col = housing_df[['waterfront']]
encoder_wtr = OrdinalEncoder()
encoder_wtr.fit(wtr_col)
encoded_wtr = encoder_wtr.transform(wtr_col)
encoded_wtr = encoded_wtr.flatten()
housing_df.waterfront = encoded_wtr
from sklearn.impute import SimpleImputer
view_col = housing_df[['view']]
imputer = SimpleImputer(strategy='constant', fill_value = 'NONE')
imputer.fit(view_col)
view_imputed = imputer.transform(view_col)
housing_df.view = view_imputed
housing_df.isna().sum()
housing_ols = housing_df.drop(['datetime', 'date', 'soldyear', 'yr_built', 'lat', 'long',
'sqft_above', 'sqft_lot15', 'sqft_living15', 'grade', 'sqft_above', 'sqft_basement', 'yr_renovated'], axis = 1)
housing_ols
fig, (axes1, axes2, axes3) = plt.subplots(nrows=3, ncols=3, figsize=(12,12))
for xcol, ax in zip(['bedrooms', 'bathrooms', 'sqft_living'], axes1):
housing_ols.plot(kind='scatter', x=xcol, y='price', ax=ax, alpha=0.4, color='b')
for xcols, axs in zip(['sqft_lot', 'floors', 'view'], axes2):
housing_ols.plot(kind='scatter', x=xcols, y='price', ax=axs, alpha=0.4, color='b')
for xcolss, axss in zip(['condition', 'age_when_sold', 'grade_num'], axes3):
housing_ols.plot(kind='scatter', x=xcolss, y='price', ax=axss, alpha=0.4, color='b')
housing_pred = housing_ols.copy()
bedrooms_ohe = housing_pred[['bedrooms']]
ohe_bedrooms = OneHotEncoder(categories ='auto', sparse =False)
ohe_bedrooms.fit(bedrooms_ohe)
ohe_bedrooms_encoded = ohe_bedrooms.transform(bedrooms_ohe)
bedrooms_encoded_ohe = pd.DataFrame(ohe_bedrooms_encoded, columns = ohe_bedrooms.get_feature_names(['bedrooms']), index = housing_pred.index )
housing_pred1 = pd.concat([housing_pred, bedrooms_encoded_ohe ], axis =1)
grade_num_ohe = housing_pred[['grade_num']]
ohe_grade_num = OneHotEncoder(categories ='auto', sparse =False)
ohe_grade_num.fit(grade_num_ohe)
ohe_grade_num_encoded = ohe_grade_num.transform(grade_num_ohe)
grade_num_encoded_ohe = pd.DataFrame(ohe_grade_num_encoded, columns = ohe_grade_num.get_feature_names(['grade_num']), index = housing_pred.index )
housing_pred2 = pd.concat([housing_pred1, grade_num_encoded_ohe], axis =1)
condition_ohe = housing_pred[['condition']]
ohe = OneHotEncoder(categories="auto", sparse=False)
cond_encoded_ohe = pd.DataFrame (ohe.fit_transform(condition_ohe))
cond_encoded_ohe.columns = ohe.get_feature_names(['condition'])
housing_pred3 = pd.concat([housing_pred2, cond_encoded_ohe], axis = 1)
bathrooms_ohe = housing_pred[['bathrooms']]
ohe = OneHotEncoder(categories='auto', sparse=False, handle_unknown='ignore')
bathrooms_transform = ohe.fit_transform(bathrooms_ohe)
bathrooms_encoded_ohe = pd.DataFrame(bathrooms_transform, columns=ohe.get_feature_names(['bathrooms']), index=housing_pred.index)
housing_pred4 = pd.concat([housing_pred3, bathrooms_encoded_ohe], axis = 1)
view_ohe = housing_pred[['view']]
ohe = OneHotEncoder(categories="auto", sparse=False)
ohe.fit(view_ohe)
view_encoded = ohe.transform(view_ohe)
view_encoded_ohe =pd.DataFrame(view_encoded, columns=ohe.get_feature_names(['view']), index=housing_pred.index)
housing_pred5 = pd.concat([housing_pred4, view_encoded_ohe], axis = 1)
floors_ohe = housing_pred[['floors']]
ohe_floors = OneHotEncoder(categories ='auto', sparse =False)
ohe_floors.fit(floors_ohe)
ohe_floors_encoded = ohe_floors.transform(floors_ohe)
floors_encoded_ohe = pd.DataFrame(ohe_floors_encoded, columns = ohe_floors.get_feature_names(['floors']), index = housing_pred.index )
housing_pred6 = pd.concat([housing_pred5, floors_encoded_ohe ], axis =1)
zipcode_ohe = housing_pred[['zipcode']]
ohe = OneHotEncoder(categories="auto", sparse=False)
ohe.fit(zipcode_ohe)
zipcode_encoded = ohe.transform(zipcode_ohe)
zipcode_encoded_ohe =pd.DataFrame(zipcode_encoded, columns=ohe.get_feature_names(['zipcode']), index=housing_pred.index)
housing_pred_final = pd.concat([housing_pred6, zipcode_encoded_ohe ], axis =1)
housing_pred_final.columns
housing_pred_final.drop(['id', 'floors', 'bedrooms', 'bathrooms', 'view', 'condition', 'zipcode', 'grade_num'], axis = 1, inplace=True)
X_dummy = housing_pred_final['price']
y_dummy = housing_pred_final.drop('price', axis = 1)
from sklearn.model_selection import train_test_split
d_X_train, d_X_test, d_y_train, d_y_test = train_test_split(X_dummy, y_dummy, test_size=0.2, random_state=42)
from sklearn.dummy import DummyRegressor
dummy_regr = DummyRegressor(strategy="mean")
dummy_regr.fit(d_X_train, d_y_train)
print(dummy_regr.score(d_X_train, d_y_train))
print(dummy_regr.score(d_X_test, d_y_test))
simple_model_df = pd.concat([housing_pred_final['price'], housing_pred_final['sqft_living']], axis = 1)
X_simple = simple_model_df.drop('price', axis = 1)
y_simple = simple_model_df['price']
from sklearn.model_selection import train_test_split
s_X_train, s_X_test, s_y_train, s_y_test = train_test_split(X_simple, y_simple, test_size=0.2, random_state=42)
simple_reg = LinearRegression()
simple_reg.fit(s_X_train, s_y_train)
print(simple_reg.score(s_X_train, s_y_train))
print(simple_reg.score(s_X_test, s_y_test))
s_y_hat_train = simple_reg.predict(s_X_train)
s_y_hat_test = simple_reg.predict(s_X_test)
s_train_mse = mean_squared_error(s_y_train, s_y_hat_train)
s_test_mse = mean_squared_error(s_y_test, s_y_hat_test)
print('Train Mean Squarred Error:', s_train_mse)
print('Test Mean Squarred Error:', s_test_mse)
multi_model_1 = pd.concat([housing_pred_final['price'], housing_pred_final['sqft_living'], view_encoded_ohe], axis = 1)
X_multi1 = multi_model_1.drop('price', axis = 1)
y_multi1 = multi_model_1['price']
from sklearn.model_selection import train_test_split
m_one_X_train, m_one_X_test, m_one_y_train, m_one_y_test = train_test_split(X_multi1, y_multi1, test_size=0.2, random_state=42)
multi1_reg = LinearRegression()
multi1_reg.fit(m_one_X_train, m_one_y_train)
print(multi1_reg.score(m_one_X_train, m_one_y_train))
print(multi1_reg.score(m_one_X_test, m_one_y_test))
m_one_y_hat_train = multi1_reg.predict(m_one_X_train)
m_one_y_hat_test = multi1_reg.predict(m_one_X_test)
m_one_train_mse = mean_squared_error(m_one_y_train, m_one_y_hat_train)
m_one_test_mse = mean_squared_error(m_one_y_test, m_one_y_hat_test)
print('Train Mean Squarred Error:', m_one_train_mse)
print('Test Mean Squarred Error:', m_one_test_mse)
multi_model_2 = pd.concat([housing_pred_final['price'], housing_pred_final['sqft_living'], view_encoded_ohe, cond_encoded_ohe], axis = 1)
X_multi2 = multi_model_2.drop('price', axis = 1)
y_multi2 = multi_model_2['price']
from sklearn.model_selection import train_test_split
m_two_X_train, m_two_X_test, m_two_y_train, m_two_y_test = train_test_split(X_multi2, y_multi2, test_size=0.2, random_state=42)
multi2_reg = LinearRegression()
multi2_reg.fit(m_two_X_train, m_two_y_train)
print(multi2_reg.score(m_two_X_train, m_two_y_train))
print(multi2_reg.score(m_two_X_test, m_two_y_test))
m_two_y_hat_train = multi2_reg.predict(m_two_X_train)
m_two_y_hat_test = multi2_reg.predict(m_two_X_test)
m_two_train_mse = mean_squared_error(m_two_y_train, m_two_y_hat_train)
m_two_test_mse = mean_squared_error(m_two_y_test, m_two_y_hat_test)
print('Train Mean Squarred Error:', m_two_train_mse)
print('Test Mean Squarred Error:', m_two_test_mse)
multi_model_2
#baseline
#dummy_regr.score(X_train, y_train)
#dummy_regr.score(X_test, y_test)
#first simple model
#simple_reg.score(X_train, y_train)
#simple_reg.score(X_test, y_test)
#second multi model
#multi1_reg.score(X_train, y_train)
#multi1_reg.score(X_test, y_test)
#third multi model
#multi2_reg.score(X_train, y_train)
#multi2_reg.score(X_test, y_test)
column = ['baseline', '1st model', '2nd model', '3rd model']
index = ['train', 'test']
regression_score = pd.DataFrame(index=index, columns=column)
regression_score['baseline'] = [dummy_regr.score(d_X_train, d_y_train), dummy_regr.score(d_X_test, d_y_test)]
regression_score['1st model'] = [simple_reg.score(s_X_train, s_y_train),simple_reg.score(s_X_test, s_y_test)]
regression_score['2nd model'] = [multi1_reg.score(m_one_X_train, m_one_y_train),multi1_reg.score(m_one_X_test, m_one_y_test)]
regression_score['3rd model'] = [multi2_reg.score(m_two_X_train, m_two_y_train),multi2_reg.score(m_two_X_test, m_two_y_test)]
regression_score = regression_score.T
regression_score
import matplotlib.pyplot as plt
%matplotlib inline
ax = regression_score.plot.bar(color=["SkyBlue","IndianRed"], rot=0, title="Model Progression")
index = ['simple_r', 'multiple_1', 'multiple_2','multiple_3', 'multiple_4']
columns = ['test score']
regression_score = pd.DataFrame(index=index, columns=columns)
regression_score['test score'] = [0.493, 0.543, 0.545, 0.697, 0.782]
import matplotlib.pyplot as plt
%matplotlib inline
ax = regression_score.plot.bar(color=["SkyBlue"], rot=0, title="Model Progression")
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import seaborn as sns
from sklearn.preprocessing import OneHotEncoder
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
%matplotlib inline
housing_df = pd.read_csv('data/kc_house_data.csv')
housing_df.info()
housing_df.isna().sum()
housing_df['datetime'] = pd.to_datetime(housing_df['date'])
housing_df['soldyear'] = housing_df['datetime'].dt.year
housing_df['age_when_sold'] = housing_df['soldyear'] - housing_df['yr_built']
housing_df['grade_num'] = housing_df['grade'].str.split()
housing_df['grade_num'] = housing_df['grade_num'].str[0]
housing_df['grade_num'] = housing_df['grade_num'].astype(int)
housing_df['sqft_basement'] = housing_df['sqft_living'] - housing_df['sqft_above']
housing_df['Basement'] = None
housing_df['Basement'] = housing_df['sqft_basement'].map(lambda x: False if x == 0 else True)
housing_df['Basement'] = housing_df['Basement'].astype(int)
housing_df.condition.value_counts()
replace_dict2 = {'Poor': 1, 'Fair': 2, 'Average': 3, 'Good': 4, 'Very Good': 5}
housing_df['condition'] = housing_df['condition'].replace(replace_dict2)
from sklearn.impute import SimpleImputer
wtr_col = housing_df[['waterfront']]
imputer = SimpleImputer(strategy='constant', fill_value = 'NO')
imputer.fit(wtr_col)
waterfront_imputed = imputer.transform(wtr_col)
housing_df.waterfront = waterfront_imputed
from sklearn.preprocessing import OrdinalEncoder
wtr_col = housing_df[['waterfront']]
encoder_wtr = OrdinalEncoder()
encoder_wtr.fit(wtr_col)
encoded_wtr = encoder_wtr.transform(wtr_col)
encoded_wtr = encoded_wtr.flatten()
housing_df.waterfront = encoded_wtr
from sklearn.impute import SimpleImputer
view_col = housing_df[['view']]
imputer = SimpleImputer(strategy='constant', fill_value = 'NONE')
imputer.fit(view_col)
view_imputed = imputer.transform(view_col)
housing_df.view = view_imputed
housing_df.isna().sum()
housing_ols = housing_df.drop(['datetime', 'date', 'soldyear', 'yr_built', 'lat', 'long',
'sqft_above', 'sqft_lot15', 'sqft_living15', 'grade', 'sqft_above', 'sqft_basement', 'yr_renovated'], axis = 1)
housing_ols
fig, (axes1, axes2, axes3) = plt.subplots(nrows=3, ncols=3, figsize=(12,12))
for xcol, ax in zip(['bedrooms', 'bathrooms', 'sqft_living'], axes1):
housing_ols.plot(kind='scatter', x=xcol, y='price', ax=ax, alpha=0.4, color='b')
for xcols, axs in zip(['sqft_lot', 'floors', 'view'], axes2):
housing_ols.plot(kind='scatter', x=xcols, y='price', ax=axs, alpha=0.4, color='b')
for xcolss, axss in zip(['condition', 'age_when_sold', 'grade_num'], axes3):
housing_ols.plot(kind='scatter', x=xcolss, y='price', ax=axss, alpha=0.4, color='b')
housing_pred = housing_ols.copy()
bedrooms_ohe = housing_pred[['bedrooms']]
ohe_bedrooms = OneHotEncoder(categories ='auto', sparse =False)
ohe_bedrooms.fit(bedrooms_ohe)
ohe_bedrooms_encoded = ohe_bedrooms.transform(bedrooms_ohe)
bedrooms_encoded_ohe = pd.DataFrame(ohe_bedrooms_encoded, columns = ohe_bedrooms.get_feature_names(['bedrooms']), index = housing_pred.index )
housing_pred1 = pd.concat([housing_pred, bedrooms_encoded_ohe ], axis =1)
grade_num_ohe = housing_pred[['grade_num']]
ohe_grade_num = OneHotEncoder(categories ='auto', sparse =False)
ohe_grade_num.fit(grade_num_ohe)
ohe_grade_num_encoded = ohe_grade_num.transform(grade_num_ohe)
grade_num_encoded_ohe = pd.DataFrame(ohe_grade_num_encoded, columns = ohe_grade_num.get_feature_names(['grade_num']), index = housing_pred.index )
housing_pred2 = pd.concat([housing_pred1, grade_num_encoded_ohe], axis =1)
condition_ohe = housing_pred[['condition']]
ohe = OneHotEncoder(categories="auto", sparse=False)
cond_encoded_ohe = pd.DataFrame (ohe.fit_transform(condition_ohe))
cond_encoded_ohe.columns = ohe.get_feature_names(['condition'])
housing_pred3 = pd.concat([housing_pred2, cond_encoded_ohe], axis = 1)
bathrooms_ohe = housing_pred[['bathrooms']]
ohe = OneHotEncoder(categories='auto', sparse=False, handle_unknown='ignore')
bathrooms_transform = ohe.fit_transform(bathrooms_ohe)
bathrooms_encoded_ohe = pd.DataFrame(bathrooms_transform, columns=ohe.get_feature_names(['bathrooms']), index=housing_pred.index)
housing_pred4 = pd.concat([housing_pred3, bathrooms_encoded_ohe], axis = 1)
view_ohe = housing_pred[['view']]
ohe = OneHotEncoder(categories="auto", sparse=False)
ohe.fit(view_ohe)
view_encoded = ohe.transform(view_ohe)
view_encoded_ohe =pd.DataFrame(view_encoded, columns=ohe.get_feature_names(['view']), index=housing_pred.index)
housing_pred5 = pd.concat([housing_pred4, view_encoded_ohe], axis = 1)
floors_ohe = housing_pred[['floors']]
ohe_floors = OneHotEncoder(categories ='auto', sparse =False)
ohe_floors.fit(floors_ohe)
ohe_floors_encoded = ohe_floors.transform(floors_ohe)
floors_encoded_ohe = pd.DataFrame(ohe_floors_encoded, columns = ohe_floors.get_feature_names(['floors']), index = housing_pred.index )
housing_pred6 = pd.concat([housing_pred5, floors_encoded_ohe ], axis =1)
zipcode_ohe = housing_pred[['zipcode']]
ohe = OneHotEncoder(categories="auto", sparse=False)
ohe.fit(zipcode_ohe)
zipcode_encoded = ohe.transform(zipcode_ohe)
zipcode_encoded_ohe =pd.DataFrame(zipcode_encoded, columns=ohe.get_feature_names(['zipcode']), index=housing_pred.index)
housing_pred_final = pd.concat([housing_pred6, zipcode_encoded_ohe ], axis =1)
housing_pred_final.columns
housing_pred_final.drop(['id', 'floors', 'bedrooms', 'bathrooms', 'view', 'condition', 'zipcode', 'grade_num'], axis = 1, inplace=True)
X_dummy = housing_pred_final['price']
y_dummy = housing_pred_final.drop('price', axis = 1)
from sklearn.model_selection import train_test_split
d_X_train, d_X_test, d_y_train, d_y_test = train_test_split(X_dummy, y_dummy, test_size=0.2, random_state=42)
from sklearn.dummy import DummyRegressor
dummy_regr = DummyRegressor(strategy="mean")
dummy_regr.fit(d_X_train, d_y_train)
print(dummy_regr.score(d_X_train, d_y_train))
print(dummy_regr.score(d_X_test, d_y_test))
simple_model_df = pd.concat([housing_pred_final['price'], housing_pred_final['sqft_living']], axis = 1)
X_simple = simple_model_df.drop('price', axis = 1)
y_simple = simple_model_df['price']
from sklearn.model_selection import train_test_split
s_X_train, s_X_test, s_y_train, s_y_test = train_test_split(X_simple, y_simple, test_size=0.2, random_state=42)
simple_reg = LinearRegression()
simple_reg.fit(s_X_train, s_y_train)
print(simple_reg.score(s_X_train, s_y_train))
print(simple_reg.score(s_X_test, s_y_test))
s_y_hat_train = simple_reg.predict(s_X_train)
s_y_hat_test = simple_reg.predict(s_X_test)
s_train_mse = mean_squared_error(s_y_train, s_y_hat_train)
s_test_mse = mean_squared_error(s_y_test, s_y_hat_test)
print('Train Mean Squarred Error:', s_train_mse)
print('Test Mean Squarred Error:', s_test_mse)
multi_model_1 = pd.concat([housing_pred_final['price'], housing_pred_final['sqft_living'], view_encoded_ohe], axis = 1)
X_multi1 = multi_model_1.drop('price', axis = 1)
y_multi1 = multi_model_1['price']
from sklearn.model_selection import train_test_split
m_one_X_train, m_one_X_test, m_one_y_train, m_one_y_test = train_test_split(X_multi1, y_multi1, test_size=0.2, random_state=42)
multi1_reg = LinearRegression()
multi1_reg.fit(m_one_X_train, m_one_y_train)
print(multi1_reg.score(m_one_X_train, m_one_y_train))
print(multi1_reg.score(m_one_X_test, m_one_y_test))
m_one_y_hat_train = multi1_reg.predict(m_one_X_train)
m_one_y_hat_test = multi1_reg.predict(m_one_X_test)
m_one_train_mse = mean_squared_error(m_one_y_train, m_one_y_hat_train)
m_one_test_mse = mean_squared_error(m_one_y_test, m_one_y_hat_test)
print('Train Mean Squarred Error:', m_one_train_mse)
print('Test Mean Squarred Error:', m_one_test_mse)
multi_model_2 = pd.concat([housing_pred_final['price'], housing_pred_final['sqft_living'], view_encoded_ohe, cond_encoded_ohe], axis = 1)
X_multi2 = multi_model_2.drop('price', axis = 1)
y_multi2 = multi_model_2['price']
from sklearn.model_selection import train_test_split
m_two_X_train, m_two_X_test, m_two_y_train, m_two_y_test = train_test_split(X_multi2, y_multi2, test_size=0.2, random_state=42)
multi2_reg = LinearRegression()
multi2_reg.fit(m_two_X_train, m_two_y_train)
print(multi2_reg.score(m_two_X_train, m_two_y_train))
print(multi2_reg.score(m_two_X_test, m_two_y_test))
m_two_y_hat_train = multi2_reg.predict(m_two_X_train)
m_two_y_hat_test = multi2_reg.predict(m_two_X_test)
m_two_train_mse = mean_squared_error(m_two_y_train, m_two_y_hat_train)
m_two_test_mse = mean_squared_error(m_two_y_test, m_two_y_hat_test)
print('Train Mean Squarred Error:', m_two_train_mse)
print('Test Mean Squarred Error:', m_two_test_mse)
multi_model_2
#baseline
#dummy_regr.score(X_train, y_train)
#dummy_regr.score(X_test, y_test)
#first simple model
#simple_reg.score(X_train, y_train)
#simple_reg.score(X_test, y_test)
#second multi model
#multi1_reg.score(X_train, y_train)
#multi1_reg.score(X_test, y_test)
#third multi model
#multi2_reg.score(X_train, y_train)
#multi2_reg.score(X_test, y_test)
column = ['baseline', '1st model', '2nd model', '3rd model']
index = ['train', 'test']
regression_score = pd.DataFrame(index=index, columns=column)
regression_score['baseline'] = [dummy_regr.score(d_X_train, d_y_train), dummy_regr.score(d_X_test, d_y_test)]
regression_score['1st model'] = [simple_reg.score(s_X_train, s_y_train),simple_reg.score(s_X_test, s_y_test)]
regression_score['2nd model'] = [multi1_reg.score(m_one_X_train, m_one_y_train),multi1_reg.score(m_one_X_test, m_one_y_test)]
regression_score['3rd model'] = [multi2_reg.score(m_two_X_train, m_two_y_train),multi2_reg.score(m_two_X_test, m_two_y_test)]
regression_score = regression_score.T
regression_score
import matplotlib.pyplot as plt
%matplotlib inline
ax = regression_score.plot.bar(color=["SkyBlue","IndianRed"], rot=0, title="Model Progression")
index = ['simple_r', 'multiple_1', 'multiple_2','multiple_3', 'multiple_4']
columns = ['test score']
regression_score = pd.DataFrame(index=index, columns=columns)
regression_score['test score'] = [0.493, 0.543, 0.545, 0.697, 0.782]
import matplotlib.pyplot as plt
%matplotlib inline
ax = regression_score.plot.bar(color=["SkyBlue"], rot=0, title="Model Progression")
| 0.493897 | 0.566678 |
```
import colormaps as cmaps
cmaps.bamako
cmaps.discrete_5_4_section_blue_orange
cmaps.Cat12
cmaps.MPL_Set1
cmaps.BkBlAqGrYeOrReViWh200
cmaps.drought_severity
cmaps.ice
cmaps.ice.discrete(10)
import numpy as np
import matplotlib.pyplot as plt
gradient = np.linspace(0, 1, 256)
gradient = np.vstack((gradient, gradient))
def plot_color_gradients(cname):
fig, axs = plt.subplots(nrows= 1, figsize=(8, 1.5))
axs.imshow(gradient, aspect='auto', cmap=eval("cmaps." + cname))
# Turn off *all* ticks & spines, not just the ones with colormaps.
axs.set_axis_off()
plot_color_gradients('ice.discrete(10)')
plt.savefig('/home/ghost/Documents/colormaps/colormaps_doc/assets/images/demo/ice_discrete_10.png')
cmaps.ice.shift(0.5)
plot_color_gradients('ice.shift(0.5)')
plt.savefig('/home/ghost/Documents/colormaps/colormaps_doc/assets/images/demo/ice_shift_0_5.png')
cmaps.ice.shift(0.5).discrete(10)
plot_color_gradients('ice.shift(0.5).discrete(10)')
plt.savefig('/home/ghost/Documents/colormaps/colormaps_doc/assets/images/demo/ice_shift_0_5_discrete_10.png')
cmaps.balance.discrete(11)
cmaps.ice.discrete(11).cut(0.25, 'left')
plot_color_gradients("ice.discrete(11).cut(0.25, 'left')")
plt.savefig('/home/ghost/Documents/colormaps/colormaps_doc/assets/images/demo/ice_discrete_11_cut_0.25.png')
from colormaps.utils import concat
concat1 = concat(["cmocean_ice", "BkBlAqGrYeOrReViWh200"])
fig, axs = plt.subplots(nrows= 1, figsize=(8, 1.5))
axs.imshow(gradient, aspect='auto', cmap=concat1)
axs.set_axis_off()
#plot_color_gradients("concat1")
plt.savefig('/home/ghost/Documents/colormaps/colormaps_doc/assets/images/demo/concat_1.png')
, ratios=[0.25,0.75]
import colormaps as cmaps
concat2 = concat([cmaps.cmocean_ice, cmaps.BkBlAqGrYeOrReViWh200], ratios=[0.25,0.75])
fig, axs = plt.subplots(nrows= 1, figsize=(8, 1.5))
axs.imshow(gradient, aspect='auto', cmap=concat2)
axs.set_axis_off()
#plot_color_gradients("concat1")
plt.savefig('/home/ghost/Documents/colormaps/colormaps_doc/assets/images/demo/concat_2.png')
from cycler import cycler
x = np.linspace(0, 2 * np.pi)
offsets = np.linspace(0, 2*np.pi, 4, endpoint=False)
# Create array with shifted-sine curve along each column
yy = np.transpose([np.sin(x + phi) for phi in offsets])
# 1. Setting prop cycle on default rc parameter
plt.rc('lines', linewidth=4)
plt.rc('axes', prop_cycle=(cycler('color', ['r', 'g', 'b', 'y']) +
cycler('linestyle', ['-', '--', ':', '-.'])))
fig, (ax0, ax1) = plt.subplots(nrows=2)
ax0.plot(yy)
ax0.set_title('Set default color cycle to rgby')
# 2. Define prop cycle for single set of axes
#ax1.set_prop_cycle(cycler('color', ['c', 'm', 'y', 'k']) +
# cycler('lw', [1, 2, 3, 4]))
ax1.set_prop_cycle(cycler('color', cmaps.dark2_8.colors))
ax1.plot(yy)
ax1.set_title('Set axes color cycle to cmyk')
# Tweak spacing between subplots to prevent labels from overlapping
fig.subplots_adjust(hspace=0.5)
plt.show()
```
|
github_jupyter
|
import colormaps as cmaps
cmaps.bamako
cmaps.discrete_5_4_section_blue_orange
cmaps.Cat12
cmaps.MPL_Set1
cmaps.BkBlAqGrYeOrReViWh200
cmaps.drought_severity
cmaps.ice
cmaps.ice.discrete(10)
import numpy as np
import matplotlib.pyplot as plt
gradient = np.linspace(0, 1, 256)
gradient = np.vstack((gradient, gradient))
def plot_color_gradients(cname):
fig, axs = plt.subplots(nrows= 1, figsize=(8, 1.5))
axs.imshow(gradient, aspect='auto', cmap=eval("cmaps." + cname))
# Turn off *all* ticks & spines, not just the ones with colormaps.
axs.set_axis_off()
plot_color_gradients('ice.discrete(10)')
plt.savefig('/home/ghost/Documents/colormaps/colormaps_doc/assets/images/demo/ice_discrete_10.png')
cmaps.ice.shift(0.5)
plot_color_gradients('ice.shift(0.5)')
plt.savefig('/home/ghost/Documents/colormaps/colormaps_doc/assets/images/demo/ice_shift_0_5.png')
cmaps.ice.shift(0.5).discrete(10)
plot_color_gradients('ice.shift(0.5).discrete(10)')
plt.savefig('/home/ghost/Documents/colormaps/colormaps_doc/assets/images/demo/ice_shift_0_5_discrete_10.png')
cmaps.balance.discrete(11)
cmaps.ice.discrete(11).cut(0.25, 'left')
plot_color_gradients("ice.discrete(11).cut(0.25, 'left')")
plt.savefig('/home/ghost/Documents/colormaps/colormaps_doc/assets/images/demo/ice_discrete_11_cut_0.25.png')
from colormaps.utils import concat
concat1 = concat(["cmocean_ice", "BkBlAqGrYeOrReViWh200"])
fig, axs = plt.subplots(nrows= 1, figsize=(8, 1.5))
axs.imshow(gradient, aspect='auto', cmap=concat1)
axs.set_axis_off()
#plot_color_gradients("concat1")
plt.savefig('/home/ghost/Documents/colormaps/colormaps_doc/assets/images/demo/concat_1.png')
, ratios=[0.25,0.75]
import colormaps as cmaps
concat2 = concat([cmaps.cmocean_ice, cmaps.BkBlAqGrYeOrReViWh200], ratios=[0.25,0.75])
fig, axs = plt.subplots(nrows= 1, figsize=(8, 1.5))
axs.imshow(gradient, aspect='auto', cmap=concat2)
axs.set_axis_off()
#plot_color_gradients("concat1")
plt.savefig('/home/ghost/Documents/colormaps/colormaps_doc/assets/images/demo/concat_2.png')
from cycler import cycler
x = np.linspace(0, 2 * np.pi)
offsets = np.linspace(0, 2*np.pi, 4, endpoint=False)
# Create array with shifted-sine curve along each column
yy = np.transpose([np.sin(x + phi) for phi in offsets])
# 1. Setting prop cycle on default rc parameter
plt.rc('lines', linewidth=4)
plt.rc('axes', prop_cycle=(cycler('color', ['r', 'g', 'b', 'y']) +
cycler('linestyle', ['-', '--', ':', '-.'])))
fig, (ax0, ax1) = plt.subplots(nrows=2)
ax0.plot(yy)
ax0.set_title('Set default color cycle to rgby')
# 2. Define prop cycle for single set of axes
#ax1.set_prop_cycle(cycler('color', ['c', 'm', 'y', 'k']) +
# cycler('lw', [1, 2, 3, 4]))
ax1.set_prop_cycle(cycler('color', cmaps.dark2_8.colors))
ax1.plot(yy)
ax1.set_title('Set axes color cycle to cmyk')
# Tweak spacing between subplots to prevent labels from overlapping
fig.subplots_adjust(hspace=0.5)
plt.show()
| 0.636127 | 0.380356 |
<img src="images/logodwengo.png" alt="Banner" width="150"/>
<div>
<font color=#690027 markdown="1">
<h1>NOTEBOOK DOORLOPEN</h1>
</font>
</div>
<div class="alert alert-box alert-success">
In deze notebook leer je uit welke onderdelen een notebook is opgebouwd en hoe je ermee omgaat.
</div>
<div>
<font color=#690027 markdown="1">
<h2>1. Soorten cellen</h2>
</font>
</div>
In de notebooks vind je twee soorten cellen terug: een *Markdown-cel* en een *code-cel*.
- Een **Markdown-cel** komt overeen met een vak waarin je tekst kan schrijven, maar ook hyperlinks en afbeeldingen kunt invoegen.
- Een **code-cel** dient om code in te geven. Je herkent een code-cel omdat ze altijd grijs is en voorafgegaan wordt door `In [ ]`. Bij het uitvoeren van de code verschijnt er een \* tussen de `[ ]`. Eens de code is uitgevoerd, staat er een getal tussen de `[ ]`.
<br><br>
**Alle tekst die hierboven staat, staat in Markdown-cellen.**
```
# Deze tekst staat in een code-cel.
```
Om bv. tekst te lay-outen wordt *Markdown-* of *html-code* gebruikt. Dit wordt ook gebruikt om afbeeldingen in te voeren.<br>
Wiskundige formules invoeren in een Markdown-cel gebeurt met de veelgebruikte LaTeX-code tussen $$.
### Opdracht 1.1
<div>
Dubbelklik eens <span style="color:#1E64C8"><b>hier</b></span>. De achterliggende instructies van deze Markdown-cel worden zichtbaar, evenals de contour van de cel.
</div>
Je zou deze cel nu kunnen bewerken.<br>
Keer terug naar de meer leesbare weergave door op **Ctrl + Enter** te drukken of op 'Run' in de werkbalk.
<img src="images/runknop.jpg" alt="Banner" align="right" width="80"/>
<div class="alert alert-block alert-success">
Soms wordt in de notebook gevraagd om een antwoord te formuleren bij een opdracht. Dat gebeurt steeds in een Markdown-cel. <br>Je dubbelklikt dan op de cel en voert het antwoord in. Met 'Ctrl + Enter' of 'Run' voer je tot slot de cel uit om terug te keren naar de meer leesbare weergave.
</div>
<div>
<img src="images/knipcopypasteknop.jpg" alt="Banner" align="left" width="100"/> of 'Insert' uit de werkbalk kan je gebruiken om cellen te verwijderen, toe te voegen, te kopiëren, te knippen en te plakken.
</div>
### Opdracht 1.2
<div>
<span style="color:#1E64C8"> <b>Klik</b> deze Markdown-cel aan.</span><br> <b>Voeg een cel in</b> door in de werkbalk bovenaan te kiezen voor: Insert > Insert Cell Below.<br>
Hieronder verschijnt een code-cel.
</div>
De aangemaakte cel is automatisch een code-cel. Verander die cel in een Markdown-cel door erin te klikken en in de werkbalk `Code` te veranderen naar `Markdown`.
Je kan ook een cel invoegen door een code-cel aan de linkerkant aan te klikken; vooraan verschijnt dan een blauwe lijn. Je kan dan een cel invoegen op dezelfde manier als bij een Markdown-cel.
### Opdracht 1.3
- Klik in de code-cel hieronder.
- Druk op 'Ctrl + Enter' of op 'Run' in de werkbalk om de code-cel uit te voeren.<br> Let op het \*-symbool en het getal die zullen verschijnen tussen de `[ ]`.<br> De uitvoer verschijnt onder de cel.
```
print("Welkom bij Python notebooks!")
```
<div>
<font color=#690027 markdown="1">
<h2>2. Modules</h2>
</font>
</div>
De notebooks zijn zo opgebouwd dat bij het begin van een notebook doorgaans eerst de nodige *modules* worden geïmporteerd. Dat houdt de notebooks overzichtelijk.
<div class="alert alert-block alert-info">
Modules zijn als het ware pakketten met bouwstenen die je kan gebruiken om je code te schrijven. Deze bouwstenen bevatten complexe code die voor jou reeds geschreven werd, zodat je dit zelf niet meer moet doen.
</div>
Besteed bij het invoeren van code aandacht aan een **leesbare programmeerstijl** en voeg de nodige **commentaar** toe om je stappen te verduidelijken!
<div class="alert alert-block alert-danger">
Interessant om te weten is dat in een notebook alle code samenhoort. De notebook onthoudt als het ware welke code reeds werd uitgevoerd, ongeacht in welke volgorde die werd ingetikt in de notebook.
<div>
<img src="images/cclic.png" alt="Banner" align="left" width="100"/><br><br>
Notebook Python in wiskunde en STEM, zie Computationeel denken - Programmeren in Python van <a href="http://www.aiopschool.be">AI Op School</a>, van F. wyffels, B. Van de Velde & N. Gesquière is in licentie gegeven volgens een <a href="http://creativecommons.org/licenses/by-nc-sa/4.0/">Creative Commons Naamsvermelding-NietCommercieel-GelijkDelen 4.0 Internationaal-licentie</a>.
|
github_jupyter
|
# Deze tekst staat in een code-cel.
print("Welkom bij Python notebooks!")
| 0.186206 | 0.8059 |
# Gradient Descent
:label:`sec_gd`
In this section we are going to introduce the basic concepts underlying *gradient descent*.
Although it is rarely used directly in deep learning, an understanding of gradient descent is key to understanding stochastic gradient descent algorithms.
For instance, the optimization problem might diverge due to an overly large learning rate. This phenomenon can already be seen in gradient descent. Likewise, preconditioning is a common technique in gradient descent and carries over to more advanced algorithms.
Let us start with a simple special case.
## One-Dimensional Gradient Descent
Gradient descent in one dimension is an excellent example to explain why the gradient descent algorithm may reduce the value of the objective function. Consider some continuously differentiable real-valued function $f: \mathbb{R} \rightarrow \mathbb{R}$. Using a Taylor expansion we obtain
$$f(x + \epsilon) = f(x) + \epsilon f'(x) + \mathcal{O}(\epsilon^2).$$
:eqlabel:`gd-taylor`
That is, in first-order approximation $f(x+\epsilon)$ is given by the function value $f(x)$ and the first derivative $f'(x)$ at $x$. It is not unreasonable to assume that for small $\epsilon$ moving in the direction of the negative gradient will decrease $f$. To keep things simple we pick a fixed step size $\eta > 0$ and choose $\epsilon = -\eta f'(x)$. Plugging this into the Taylor expansion above we get
$$f(x - \eta f'(x)) = f(x) - \eta f'^2(x) + \mathcal{O}(\eta^2 f'^2(x)).$$
:eqlabel:`gd-taylor-2`
If the derivative $f'(x) \neq 0$ does not vanish we make progress since $\eta f'^2(x)>0$. Moreover, we can always choose $\eta$ small enough for the higher-order terms to become irrelevant. Hence we arrive at
$$f(x - \eta f'(x)) \lessapprox f(x).$$
This means that, if we use
$$x \leftarrow x - \eta f'(x)$$
to iterate $x$, the value of function $f(x)$ might decline. Therefore, in gradient descent we first choose an initial value $x$ and a constant $\eta > 0$ and then use them to continuously iterate $x$ until the stop condition is reached, for example, when the magnitude of the gradient $|f'(x)|$ is small enough or the number of iterations has reached a certain value.
For simplicity we choose the objective function $f(x)=x^2$ to illustrate how to implement gradient descent. Although we know that $x=0$ is the solution to minimize $f(x)$, we still use this simple function to observe how $x$ changes.
```
%matplotlib inline
import numpy as np
import tensorflow as tf
from d2l import tensorflow as d2l
def f(x): # Objective function
return x ** 2
def f_grad(x): # Gradient (derivative) of the objective function
return 2 * x
```
Next, we use $x=10$ as the initial value and assume $\eta=0.2$. Using gradient descent to iterate $x$ for 10 times we can see that, eventually, the value of $x$ approaches the optimal solution.
```
def gd(eta, f_grad):
x = 10.0
results = [x]
for i in range(10):
x -= eta * f_grad(x)
results.append(float(x))
print(f'epoch 10, x: {x:f}')
return results
results = gd(0.2, f_grad)
```
The progress of optimizing over $x$ can be plotted as follows.
```
def show_trace(results, f):
n = max(abs(min(results)), abs(max(results)))
f_line = tf.range(-n, n, 0.01)
d2l.set_figsize()
d2l.plot([f_line, results], [[f(x) for x in f_line], [
f(x) for x in results]], 'x', 'f(x)', fmts=['-', '-o'])
show_trace(results, f)
```
### Learning Rate
:label:`subsec_gd-learningrate`
The learning rate $\eta$ can be set by the algorithm designer. If we use a learning rate that is too small, it will cause $x$ to update very slowly, requiring more iterations to get a better solution. To show what happens in such a case, consider the progress in the same optimization problem for $\eta = 0.05$. As we can see, even after 10 steps we are still very far from the optimal solution.
```
show_trace(gd(0.05, f_grad), f)
```
Conversely, if we use an excessively high learning rate, $\left|\eta f'(x)\right|$ might be too large for the first-order Taylor expansion formula. That is, the term $\mathcal{O}(\eta^2 f'^2(x))$ in :eqref:`gd-taylor-2` might become significant. In this case, we cannot guarantee that the iteration of $x$ will be able to lower the value of $f(x)$. For example, when we set the learning rate to $\eta=1.1$, $x$ overshoots the optimal solution $x=0$ and gradually diverges.
```
show_trace(gd(1.1, f_grad), f)
```
### Local Minima
To illustrate what happens for nonconvex functions consider the case of $f(x) = x \cdot \cos(cx)$ for some constant $c$. This function has infinitely many local minima. Depending on our choice of the learning rate and depending on how well conditioned the problem is, we may end up with one of many solutions. The example below illustrates how an (unrealistically) high learning rate will lead to a poor local minimum.
```
c = tf.constant(0.15 * np.pi)
def f(x): # Objective function
return x * tf.cos(c * x)
def f_grad(x): # Gradient of the objective function
return tf.cos(c * x) - c * x * tf.sin(c * x)
show_trace(gd(2, f_grad), f)
```
## Multivariate Gradient Descent
Now that we have a better intuition of the univariate case, let us consider the situation where $\mathbf{x} = [x_1, x_2, \ldots, x_d]^\top$. That is, the objective function $f: \mathbb{R}^d \to \mathbb{R}$ maps vectors into scalars. Correspondingly its gradient is multivariate, too. It is a vector consisting of $d$ partial derivatives:
$$\nabla f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_d}\bigg]^\top.$$
Each partial derivative element $\partial f(\mathbf{x})/\partial x_i$ in the gradient indicates the rate of change of $f$ at $\mathbf{x}$ with respect to the input $x_i$. As before in the univariate case we can use the corresponding Taylor approximation for multivariate functions to get some idea of what we should do. In particular, we have that
$$f(\mathbf{x} + \boldsymbol{\epsilon}) = f(\mathbf{x}) + \mathbf{\boldsymbol{\epsilon}}^\top \nabla f(\mathbf{x}) + \mathcal{O}(\|\boldsymbol{\epsilon}\|^2).$$
:eqlabel:`gd-multi-taylor`
In other words, up to second-order terms in $\boldsymbol{\epsilon}$ the direction of steepest descent is given by the negative gradient $-\nabla f(\mathbf{x})$. Choosing a suitable learning rate $\eta > 0$ yields the prototypical gradient descent algorithm:
$$\mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f(\mathbf{x}).$$
To see how the algorithm behaves in practice let us construct an objective function $f(\mathbf{x})=x_1^2+2x_2^2$ with a two-dimensional vector $\mathbf{x} = [x_1, x_2]^\top$ as input and a scalar as output. The gradient is given by $\nabla f(\mathbf{x}) = [2x_1, 4x_2]^\top$. We will observe the trajectory of $\mathbf{x}$ by gradient descent from the initial position $[-5, -2]$.
To begin with, we need two more helper functions. The first uses an update function and applies it 20 times to the initial value. The second helper visualizes the trajectory of $\mathbf{x}$.
```
def train_2d(trainer, steps=20, f_grad=None): #@save
"""Optimize a 2D objective function with a customized trainer."""
# `s1` and `s2` are internal state variables that will be used later
x1, x2, s1, s2 = -5, -2, 0, 0
results = [(x1, x2)]
for i in range(steps):
if f_grad:
x1, x2, s1, s2 = trainer(x1, x2, s1, s2, f_grad)
else:
x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
results.append((x1, x2))
print(f'epoch {i + 1}, x1: {float(x1):f}, x2: {float(x2):f}')
return results
def show_trace_2d(f, results): #@save
"""Show the trace of 2D variables during optimization."""
d2l.set_figsize()
d2l.plt.plot(*zip(*results), '-o', color='#ff7f0e')
x1, x2 = tf.meshgrid(tf.range(-5.5, 1.0, 0.1),
tf.range(-3.0, 1.0, 0.1))
d2l.plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
d2l.plt.xlabel('x1')
d2l.plt.ylabel('x2')
```
Next, we observe the trajectory of the optimization variable $\mathbf{x}$ for learning rate $\eta = 0.1$. We can see that after 20 steps the value of $\mathbf{x}$ approaches its minimum at $[0, 0]$. Progress is fairly well-behaved albeit rather slow.
```
def f_2d(x1, x2): # Objective function
return x1 ** 2 + 2 * x2 ** 2
def f_2d_grad(x1, x2): # Gradient of the objective function
return (2 * x1, 4 * x2)
def gd_2d(x1, x2, s1, s2, f_grad):
g1, g2 = f_grad(x1, x2)
return (x1 - eta * g1, x2 - eta * g2, 0, 0)
eta = 0.1
show_trace_2d(f_2d, train_2d(gd_2d, f_grad=f_2d_grad))
```
## Adaptive Methods
As we could see in :numref:`subsec_gd-learningrate`, getting the learning rate $\eta$ "just right" is tricky. If we pick it too small, we make little progress. If we pick it too large, the solution oscillates and in the worst case it might even diverge. What if we could determine $\eta$ automatically or get rid of having to select a learning rate at all?
Second-order methods that look not only at the value and gradient of the objective function
but also at its *curvature* can help in this case. While these methods cannot be applied to deep learning directly due to the computational cost, they provide useful intuition into how to design advanced optimization algorithms that mimic many of the desirable properties of the algorithms outlined below.
### Newton's Method
Reviewing the Taylor expansion of some function $f: \mathbb{R}^d \rightarrow \mathbb{R}$ there is no need to stop after the first term. In fact, we can write it as
$$f(\mathbf{x} + \boldsymbol{\epsilon}) = f(\mathbf{x}) + \boldsymbol{\epsilon}^\top \nabla f(\mathbf{x}) + \frac{1}{2} \boldsymbol{\epsilon}^\top \nabla^2 f(\mathbf{x}) \boldsymbol{\epsilon} + \mathcal{O}(\|\boldsymbol{\epsilon}\|^3).$$
:eqlabel:`gd-hot-taylor`
To avoid cumbersome notation we define $\mathbf{H} \stackrel{\mathrm{def}}{=} \nabla^2 f(\mathbf{x})$ to be the Hessian of $f$, which is a $d \times d$ matrix. For small $d$ and simple problems $\mathbf{H}$ is easy to compute. For deep neural networks, on the other hand, $\mathbf{H}$ may be prohibitively large, due to the cost of storing $\mathcal{O}(d^2)$ entries. Furthermore it may be too expensive to compute via backpropagation. For now let us ignore such considerations and look at what algorithm we would get.
After all, the minimum of $f$ satisfies $\nabla f = 0$.
Following calculus rules in :numref:`subsec_calculus-grad`,
by taking derivatives of :eqref:`gd-hot-taylor` with regard to $\boldsymbol{\epsilon}$ and ignoring higher-order terms we arrive at
$$\nabla f(\mathbf{x}) + \mathbf{H} \boldsymbol{\epsilon} = 0 \text{ and hence }
\boldsymbol{\epsilon} = -\mathbf{H}^{-1} \nabla f(\mathbf{x}).$$
That is, we need to invert the Hessian $\mathbf{H}$ as part of the optimization problem.
As a simple example, for $f(x) = \frac{1}{2} x^2$ we have $\nabla f(x) = x$ and $\mathbf{H} = 1$. Hence for any $x$ we obtain $\epsilon = -x$. In other words, a *single* step is sufficient to converge perfectly without the need for any adjustment! Alas, we got a bit lucky here: the Taylor expansion was exact since $f(x+\epsilon)= \frac{1}{2} x^2 + \epsilon x + \frac{1}{2} \epsilon^2$.
Let us see what happens in other problems.
Given a convex hyperbolic cosine function $f(x) = \cosh(cx)$ for some constant $c$, we can see that
the global minimum at $x=0$ is reached
after a few iterations.
```
c = tf.constant(0.5)
def f(x): # Objective function
return tf.cosh(c * x)
def f_grad(x): # Gradient of the objective function
return c * tf.sinh(c * x)
def f_hess(x): # Hessian of the objective function
return c**2 * tf.cosh(c * x)
def newton(eta=1):
x = 10.0
results = [x]
for i in range(10):
x -= eta * f_grad(x) / f_hess(x)
results.append(float(x))
print('epoch 10, x:', x)
return results
show_trace(newton(), f)
```
Now let us consider a *nonconvex* function, such as $f(x) = x \cos(c x)$ for some constant $c$. After all, note that in Newton's method we end up dividing by the Hessian. This means that if the second derivative is *negative* we may walk into the direction of *increasing* the value of $f$.
That is a fatal flaw of the algorithm.
Let us see what happens in practice.
```
c = tf.constant(0.15 * np.pi)
def f(x): # Objective function
return x * tf.cos(c * x)
def f_grad(x): # Gradient of the objective function
return tf.cos(c * x) - c * x * tf.sin(c * x)
def f_hess(x): # Hessian of the objective function
return - 2 * c * tf.sin(c * x) - x * c**2 * tf.cos(c * x)
show_trace(newton(), f)
```
This went spectacularly wrong. How can we fix it? One way would be to "fix" the Hessian by taking its absolute value instead. Another strategy is to bring back the learning rate. This seems to defeat the purpose, but not quite. Having second-order information allows us to be cautious whenever the curvature is large and to take longer steps whenever the objective function is flatter.
Let us see how this works with a slightly smaller learning rate, say $\eta = 0.5$. As we can see, we have quite an efficient algorithm.
```
show_trace(newton(0.5), f)
```
### Convergence Analysis
We only analyze the convergence rate of Newton's method for some convex and three times differentiable objective function $f$, where the second derivative is nonzero, i.e., $f'' > 0$. The multivariate proof is a straightforward extension of the one-dimensional argument below and omitted since it does not help us much in terms of intuition.
Denote by $x^{(k)}$ the value of $x$ at the $k^\mathrm{th}$ iteration and let $e^{(k)} \stackrel{\mathrm{def}}{=} x^{(k)} - x^*$ be the distance from optimality at the $k^\mathrm{th}$ iteration. By Taylor expansion we have that the condition $f'(x^*) = 0$ can be written as
$$0 = f'(x^{(k)} - e^{(k)}) = f'(x^{(k)}) - e^{(k)} f''(x^{(k)}) + \frac{1}{2} (e^{(k)})^2 f'''(\xi^{(k)}),$$
which holds for some $\xi^{(k)} \in [x^{(k)} - e^{(k)}, x^{(k)}]$. Dividing the above expansion by $f''(x^{(k)})$ yields
$$e^{(k)} - \frac{f'(x^{(k)})}{f''(x^{(k)})} = \frac{1}{2} (e^{(k)})^2 \frac{f'''(\xi^{(k)})}{f''(x^{(k)})}.$$
Recall that we have the update $x^{(k+1)} = x^{(k)} - f'(x^{(k)}) / f''(x^{(k)})$.
Plugging in this update equation and taking the absolute value of both sides, we have
$$\left|e^{(k+1)}\right| = \frac{1}{2}(e^{(k)})^2 \frac{\left|f'''(\xi^{(k)})\right|}{f''(x^{(k)})}.$$
Consequently, whenever we are in a region of bounded $\left|f'''(\xi^{(k)})\right| / (2f''(x^{(k)})) \leq c$, we have a quadratically decreasing error
$$\left|e^{(k+1)}\right| \leq c (e^{(k)})^2.$$
As an aside, optimization researchers call this *linear* convergence, whereas a condition such as $\left|e^{(k+1)}\right| \leq \alpha \left|e^{(k)}\right|$ would be called a *constant* rate of convergence.
Note that this analysis comes with a number of caveats.
First, we do not really have much of a guarantee when we will reach the region of rapid convergence. Instead, we only know that once we reach it, convergence will be very quick. Second, this analysis requires that $f$ is well-behaved up to higher-order derivatives. It comes down to ensuring that $f$ does not have any "surprising" properties in terms of how it might change its values.
### Preconditioning
Quite unsurprisingly computing and storing the full Hessian is very expensive. It is thus desirable to find alternatives. One way to improve matters is *preconditioning*. It avoids computing the Hessian in its entirety but only computes the *diagonal* entries. This leads to update algorithms of the form
$$\mathbf{x} \leftarrow \mathbf{x} - \eta \mathrm{diag}(\mathbf{H})^{-1} \nabla f(\mathbf{x}).$$
While this is not quite as good as the full Newton's method, it is still much better than not using it.
To see why this might be a good idea consider a situation where one variable denotes height in millimeters and the other one denotes height in kilometers. Assuming that for both the natural scale is in meters, we have a terrible mismatch in parameterizations. Fortunately, using preconditioning removes this. Effectively preconditioning with gradient descent amounts to selecting a different learning rate for each variable (coordinate of vector $\mathbf{x}$).
As we will see later, preconditioning drives some of the innovation in stochastic gradient descent optimization algorithms.
### Gradient Descent with Line Search
One of the key problems in gradient descent is that we might overshoot the goal or make insufficient progress. A simple fix for the problem is to use line search in conjunction with gradient descent. That is, we use the direction given by $\nabla f(\mathbf{x})$ and then perform binary search as to which learning rate $\eta$ minimizes $f(\mathbf{x} - \eta \nabla f(\mathbf{x}))$.
This algorithm converges rapidly (for an analysis and proof see e.g., :cite:`Boyd.Vandenberghe.2004`). However, for the purpose of deep learning this is not quite so feasible, since each step of the line search would require us to evaluate the objective function on the entire dataset. This is way too costly to accomplish.
## Summary
* Learning rates matter. Too large and we diverge, too small and we do not make progress.
* Gradient descent can get stuck in local minima.
* In high dimensions adjusting the learning rate is complicated.
* Preconditioning can help with scale adjustment.
* Newton's method is a lot faster once it has started working properly in convex problems.
* Beware of using Newton's method without any adjustments for nonconvex problems.
## Exercises
1. Experiment with different learning rates and objective functions for gradient descent.
1. Implement line search to minimize a convex function in the interval $[a, b]$.
1. Do you need derivatives for binary search, i.e., to decide whether to pick $[a, (a+b)/2]$ or $[(a+b)/2, b]$.
1. How rapid is the rate of convergence for the algorithm?
1. Implement the algorithm and apply it to minimizing $\log (\exp(x) + \exp(-2x -3))$.
1. Design an objective function defined on $\mathbb{R}^2$ where gradient descent is exceedingly slow. Hint: scale different coordinates differently.
1. Implement the lightweight version of Newton's method using preconditioning:
1. Use diagonal Hessian as preconditioner.
1. Use the absolute values of that rather than the actual (possibly signed) values.
1. Apply this to the problem above.
1. Apply the algorithm above to a number of objective functions (convex or not). What happens if you rotate coordinates by $45$ degrees?
[Discussions](https://discuss.d2l.ai/t/351)
|
github_jupyter
|
%matplotlib inline
import numpy as np
import tensorflow as tf
from d2l import tensorflow as d2l
def f(x): # Objective function
return x ** 2
def f_grad(x): # Gradient (derivative) of the objective function
return 2 * x
def gd(eta, f_grad):
x = 10.0
results = [x]
for i in range(10):
x -= eta * f_grad(x)
results.append(float(x))
print(f'epoch 10, x: {x:f}')
return results
results = gd(0.2, f_grad)
def show_trace(results, f):
n = max(abs(min(results)), abs(max(results)))
f_line = tf.range(-n, n, 0.01)
d2l.set_figsize()
d2l.plot([f_line, results], [[f(x) for x in f_line], [
f(x) for x in results]], 'x', 'f(x)', fmts=['-', '-o'])
show_trace(results, f)
show_trace(gd(0.05, f_grad), f)
show_trace(gd(1.1, f_grad), f)
c = tf.constant(0.15 * np.pi)
def f(x): # Objective function
return x * tf.cos(c * x)
def f_grad(x): # Gradient of the objective function
return tf.cos(c * x) - c * x * tf.sin(c * x)
show_trace(gd(2, f_grad), f)
def train_2d(trainer, steps=20, f_grad=None): #@save
"""Optimize a 2D objective function with a customized trainer."""
# `s1` and `s2` are internal state variables that will be used later
x1, x2, s1, s2 = -5, -2, 0, 0
results = [(x1, x2)]
for i in range(steps):
if f_grad:
x1, x2, s1, s2 = trainer(x1, x2, s1, s2, f_grad)
else:
x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
results.append((x1, x2))
print(f'epoch {i + 1}, x1: {float(x1):f}, x2: {float(x2):f}')
return results
def show_trace_2d(f, results): #@save
"""Show the trace of 2D variables during optimization."""
d2l.set_figsize()
d2l.plt.plot(*zip(*results), '-o', color='#ff7f0e')
x1, x2 = tf.meshgrid(tf.range(-5.5, 1.0, 0.1),
tf.range(-3.0, 1.0, 0.1))
d2l.plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
d2l.plt.xlabel('x1')
d2l.plt.ylabel('x2')
def f_2d(x1, x2): # Objective function
return x1 ** 2 + 2 * x2 ** 2
def f_2d_grad(x1, x2): # Gradient of the objective function
return (2 * x1, 4 * x2)
def gd_2d(x1, x2, s1, s2, f_grad):
g1, g2 = f_grad(x1, x2)
return (x1 - eta * g1, x2 - eta * g2, 0, 0)
eta = 0.1
show_trace_2d(f_2d, train_2d(gd_2d, f_grad=f_2d_grad))
c = tf.constant(0.5)
def f(x): # Objective function
return tf.cosh(c * x)
def f_grad(x): # Gradient of the objective function
return c * tf.sinh(c * x)
def f_hess(x): # Hessian of the objective function
return c**2 * tf.cosh(c * x)
def newton(eta=1):
x = 10.0
results = [x]
for i in range(10):
x -= eta * f_grad(x) / f_hess(x)
results.append(float(x))
print('epoch 10, x:', x)
return results
show_trace(newton(), f)
c = tf.constant(0.15 * np.pi)
def f(x): # Objective function
return x * tf.cos(c * x)
def f_grad(x): # Gradient of the objective function
return tf.cos(c * x) - c * x * tf.sin(c * x)
def f_hess(x): # Hessian of the objective function
return - 2 * c * tf.sin(c * x) - x * c**2 * tf.cos(c * x)
show_trace(newton(), f)
show_trace(newton(0.5), f)
| 0.702428 | 0.994631 |
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import local_config
import math
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import pandas as pd
import pygraphviz as pg
import re
def jgraph_from_links_filtered(df):
"""
Function to create a jgraph-readable dict from
networkx-readable DataFrame
Parameter
---------
df: DataFrame
three columns: source, destination, magnitude
Returns
-------
jdict: dictionary
dictionary of nodes and edges
"""
edges = []
for edge in df.iterrows():
edges.append(
{
"source": edge[1][
df.columns[0]
],
"target": edge[1][
df.columns[1]
],
"edge_size": abs(
edge[1][
df.columns[2]
]
)
}
)
jdict = {
"nodes": {
**{
node: {} for node in list(
df[
df.columns[0]
]
)
}, **{
node: {} for node in list(
df[
df.columns[1]
]
)
}
},
"edges": edges
}
return(jdict)
```
`local_config.collect_data()` takes an optional `in_dir` parameter.
The default is `data` for a folder in the same directory as this
notebook and `local_config.py` with that name containing one or
more \*.CSV files.
```
data = local_config.collect_data()
```
Subset individual questions:
```
data = data[[
c for c in data.columns if re.search(
r"_\d",
c
)
]].copy()
Pearson_ρ = data.corr('pearson')
Kendall_τ = data.corr('kendall')
Spearman_ρ = data.corr('spearman')
Pearson_ρ
Kendall_τ
Spearman_ρ
```
Adapted from *The Python Graph Gallery* "[#327 Network from correlation matrix](https://python-graph-gallery.com/327-network-from-correlation-matrix/)" bf [Yan Holtz](https://github.com/holtzy/):
```
# Transform it in a links data frame (3 columns only):
links = Pearson_ρ.stack().reset_index()
links.columns = ['q1', 'q2','corr']
# Remove self correlation (cor(A,A)=1)
links_filtered=links.loc[ (links['q1'] != links['q2']) ]
links_filtered=links_filtered.assign(
weight=links_filtered["corr"].apply(
lambda x: 1/abs(x) if x != 0 else np.inf
)
)
# Drop infinite-length edges
links_filtered = links_filtered.loc[links_filtered["weight"]!=np.inf].copy()
# Build your graph
G=nx.from_pandas_dataframe(links_filtered, 'q1', 'q2', 'weight')
# Plot the network:
nx.draw(
G,
with_labels=False,
node_size=26,
node_color='#0067a0',
edge_color='#a31c3f',
linewidths=1)
Gp = pg.AGraph()
jdict = jgraph_from_links_filtered(links_filtered)
edge_sizes = [i['edge_size'] for i in jdict['edges']]
edge_size_desc = pd.Series(edge_sizes).describe()
Gp.add_nodes_from(
list(
jdict[
"nodes"
]
),
label="",
shape="point",
color="#0067a0"
)
for node in Gp.nodes():
Gp.get_node(
node
).attr[
"color"
] = "#97e2ef" if "DMDD" in node else \
"#404341" if "MDD" in node else \
"#eeae30" if "SocAnx" in node else "#0067a0"
# add new edge with custom length (all others have length=2.0):
for edge in jdict["edges"]:
Gp.add_edge(
edge[
"source"
],
edge[
"target"
],
len=edge[
"edge_size"
],
color="#000000" if edge[
"edge_size"
] <= edge_size_desc["25%"] else "#f9e28a" if edge[
"edge_size"
] <= edge_size_desc["50%"] else "#e4e4e4" if edge[
"edge_size"
] <= edge_size_desc["75%"] else "#a31c3f",
width="1.0"
)
Gp.graph_attr.update(size="30!")
# and you can confirm that introspection by drawing & printing this graph:
Gp.draw(
'all_graphed.png',
format='png',
prog='neato'
)
```
Export for Cytoscape
```
nx.write_graphml(G, "Pearson_ρ.graphml")
graphs = list(nx.connected_component_subgraphs(G))
num_nodes = {}
for i, g in enumerate(graphs):
num_nodes[i] = len(
g.nodes
)
num_nodes_list = list(
num_nodes.values()
)
num_nodes_list.sort()
num_nodes
pd.Series(
num_nodes_list[:-1]
).describe()
graphs[9].nodes
for i, g in enumerate(graphs):
print("{0}: {1}".format(
str(i),
str(g.nodes)
))
nx.draw(
graphs[3],
with_labels=True,
node_size=32,
node_color='#0067a0',
edge_color='#a31c3f',
linewidths=1,
font_size=15
)
list(graphs[3].nodes)
Gp3 = pg.AGraph()
jdict3 = jgraph_from_links_filtered(links_filtered.loc[
links_filtered[
"q1"
].isin(
pd.Series(
list(
graphs[3].nodes
)
)
) | links_filtered[
"q2"
].isin(
pd.Series(
list(
graphs[3].nodes
)
)
)
])
edge_sizes3 = [i['edge_size'] for i in jdict3['edges']]
edge_size_desc3 = pd.Series(edge_sizes3).describe()
Gp3.add_nodes_from(
list(
jdict3[
"nodes"
]
),
label="",
shape="point",
)
for node in Gp3.nodes():
Gp3.get_node(
node
).attr[
"color"
] = "#97e2ef" if "DMDD" in node else \
"#404341" if "MDD" in node else \
"#eeae30" if "SocAnx" in node else "#0067a0"
for edge in jdict3["edges"]:
Gp3.add_edge(
edge[
"source"
],
edge[
"target"
],
len=edge[
"edge_size"
],
color="none",
width="0"
)
Gp3.graph_attr.update(size="30!")
# and you can confirm that introspection by drawing & printing this graph:
Gp3.draw(
'graph3.png',
format='png',
prog='neato'
)
```
---
Create legend for poster
```
from matplotlib.lines import Line2D
legend_elements = [
Line2D(
[0],
[0],
marker='o',
color='w',
label='ESWAN question about\nDisruptive Mood Dysregulation Disorder',
markerfacecolor='#97e2ef',
markersize=12
),
Line2D(
[0],
[0],
marker='o',
color='w',
label='ESWAN question about\nMajor Depressive Disorder',
markerfacecolor='#404341',
markersize=12
),
Line2D(
[0],
[0],
marker='o',
color='w',
label='ESWAN question about\nSocial Anxiety Disorder',
markerfacecolor='#eeae30',
markersize=12
),
Line2D(
[0],
[0],
marker='o',
color='w',
label='any other question\nfrom any questionnaire',
markerfacecolor='#0067a0',
markersize=12
),
Line2D(
[0],
[0],
color='#000000',
lw=2,
label='{0} < |1/ρ| ≤ {1}\n[25th percentile edge length]'.format(
format(
edge_size_desc["min"],
".3f"
),
format(
edge_size_desc["25%"],
".3f"
)
)
),
Line2D(
[0],
[0],
color='#f9e28a',
lw=2,
label='{0} < |1/ρ| ≤ {1}\n[50th percentile edge length]'.format(
format(
edge_size_desc["25%"],
".3f"
),
format(
edge_size_desc["50%"],
".3f"
)
)
),
Line2D(
[0],
[0],
color='#e4e4e4',
lw=2,
label='{0} < |1/ρ| ≤ {1}\n[75th percentile edge length]'.format(
format(
edge_size_desc["50%"],
".3f"
),
format(
edge_size_desc["75%"],
".3f"
)
)
),
Line2D(
[0],
[0],
color='#a31c3f',
lw=2,
label='{0} < |1/ρ| ≤ {1}\n[100th percentile edge length]'.format(
format(
edge_size_desc["75%"],
".3f"
),
format(
edge_size_desc["max"],
".3f"
)
)
)
]
# Create the figure
fig, ax = plt.subplots()
ax.legend(handles=legend_elements, loc='center')
plt.axis('off')
plt.savefig('legend.png', dpi=300)
plt.show()
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
%matplotlib inline
import local_config
import math
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import pandas as pd
import pygraphviz as pg
import re
def jgraph_from_links_filtered(df):
"""
Function to create a jgraph-readable dict from
networkx-readable DataFrame
Parameter
---------
df: DataFrame
three columns: source, destination, magnitude
Returns
-------
jdict: dictionary
dictionary of nodes and edges
"""
edges = []
for edge in df.iterrows():
edges.append(
{
"source": edge[1][
df.columns[0]
],
"target": edge[1][
df.columns[1]
],
"edge_size": abs(
edge[1][
df.columns[2]
]
)
}
)
jdict = {
"nodes": {
**{
node: {} for node in list(
df[
df.columns[0]
]
)
}, **{
node: {} for node in list(
df[
df.columns[1]
]
)
}
},
"edges": edges
}
return(jdict)
data = local_config.collect_data()
data = data[[
c for c in data.columns if re.search(
r"_\d",
c
)
]].copy()
Pearson_ρ = data.corr('pearson')
Kendall_τ = data.corr('kendall')
Spearman_ρ = data.corr('spearman')
Pearson_ρ
Kendall_τ
Spearman_ρ
# Transform it in a links data frame (3 columns only):
links = Pearson_ρ.stack().reset_index()
links.columns = ['q1', 'q2','corr']
# Remove self correlation (cor(A,A)=1)
links_filtered=links.loc[ (links['q1'] != links['q2']) ]
links_filtered=links_filtered.assign(
weight=links_filtered["corr"].apply(
lambda x: 1/abs(x) if x != 0 else np.inf
)
)
# Drop infinite-length edges
links_filtered = links_filtered.loc[links_filtered["weight"]!=np.inf].copy()
# Build your graph
G=nx.from_pandas_dataframe(links_filtered, 'q1', 'q2', 'weight')
# Plot the network:
nx.draw(
G,
with_labels=False,
node_size=26,
node_color='#0067a0',
edge_color='#a31c3f',
linewidths=1)
Gp = pg.AGraph()
jdict = jgraph_from_links_filtered(links_filtered)
edge_sizes = [i['edge_size'] for i in jdict['edges']]
edge_size_desc = pd.Series(edge_sizes).describe()
Gp.add_nodes_from(
list(
jdict[
"nodes"
]
),
label="",
shape="point",
color="#0067a0"
)
for node in Gp.nodes():
Gp.get_node(
node
).attr[
"color"
] = "#97e2ef" if "DMDD" in node else \
"#404341" if "MDD" in node else \
"#eeae30" if "SocAnx" in node else "#0067a0"
# add new edge with custom length (all others have length=2.0):
for edge in jdict["edges"]:
Gp.add_edge(
edge[
"source"
],
edge[
"target"
],
len=edge[
"edge_size"
],
color="#000000" if edge[
"edge_size"
] <= edge_size_desc["25%"] else "#f9e28a" if edge[
"edge_size"
] <= edge_size_desc["50%"] else "#e4e4e4" if edge[
"edge_size"
] <= edge_size_desc["75%"] else "#a31c3f",
width="1.0"
)
Gp.graph_attr.update(size="30!")
# and you can confirm that introspection by drawing & printing this graph:
Gp.draw(
'all_graphed.png',
format='png',
prog='neato'
)
nx.write_graphml(G, "Pearson_ρ.graphml")
graphs = list(nx.connected_component_subgraphs(G))
num_nodes = {}
for i, g in enumerate(graphs):
num_nodes[i] = len(
g.nodes
)
num_nodes_list = list(
num_nodes.values()
)
num_nodes_list.sort()
num_nodes
pd.Series(
num_nodes_list[:-1]
).describe()
graphs[9].nodes
for i, g in enumerate(graphs):
print("{0}: {1}".format(
str(i),
str(g.nodes)
))
nx.draw(
graphs[3],
with_labels=True,
node_size=32,
node_color='#0067a0',
edge_color='#a31c3f',
linewidths=1,
font_size=15
)
list(graphs[3].nodes)
Gp3 = pg.AGraph()
jdict3 = jgraph_from_links_filtered(links_filtered.loc[
links_filtered[
"q1"
].isin(
pd.Series(
list(
graphs[3].nodes
)
)
) | links_filtered[
"q2"
].isin(
pd.Series(
list(
graphs[3].nodes
)
)
)
])
edge_sizes3 = [i['edge_size'] for i in jdict3['edges']]
edge_size_desc3 = pd.Series(edge_sizes3).describe()
Gp3.add_nodes_from(
list(
jdict3[
"nodes"
]
),
label="",
shape="point",
)
for node in Gp3.nodes():
Gp3.get_node(
node
).attr[
"color"
] = "#97e2ef" if "DMDD" in node else \
"#404341" if "MDD" in node else \
"#eeae30" if "SocAnx" in node else "#0067a0"
for edge in jdict3["edges"]:
Gp3.add_edge(
edge[
"source"
],
edge[
"target"
],
len=edge[
"edge_size"
],
color="none",
width="0"
)
Gp3.graph_attr.update(size="30!")
# and you can confirm that introspection by drawing & printing this graph:
Gp3.draw(
'graph3.png',
format='png',
prog='neato'
)
from matplotlib.lines import Line2D
legend_elements = [
Line2D(
[0],
[0],
marker='o',
color='w',
label='ESWAN question about\nDisruptive Mood Dysregulation Disorder',
markerfacecolor='#97e2ef',
markersize=12
),
Line2D(
[0],
[0],
marker='o',
color='w',
label='ESWAN question about\nMajor Depressive Disorder',
markerfacecolor='#404341',
markersize=12
),
Line2D(
[0],
[0],
marker='o',
color='w',
label='ESWAN question about\nSocial Anxiety Disorder',
markerfacecolor='#eeae30',
markersize=12
),
Line2D(
[0],
[0],
marker='o',
color='w',
label='any other question\nfrom any questionnaire',
markerfacecolor='#0067a0',
markersize=12
),
Line2D(
[0],
[0],
color='#000000',
lw=2,
label='{0} < |1/ρ| ≤ {1}\n[25th percentile edge length]'.format(
format(
edge_size_desc["min"],
".3f"
),
format(
edge_size_desc["25%"],
".3f"
)
)
),
Line2D(
[0],
[0],
color='#f9e28a',
lw=2,
label='{0} < |1/ρ| ≤ {1}\n[50th percentile edge length]'.format(
format(
edge_size_desc["25%"],
".3f"
),
format(
edge_size_desc["50%"],
".3f"
)
)
),
Line2D(
[0],
[0],
color='#e4e4e4',
lw=2,
label='{0} < |1/ρ| ≤ {1}\n[75th percentile edge length]'.format(
format(
edge_size_desc["50%"],
".3f"
),
format(
edge_size_desc["75%"],
".3f"
)
)
),
Line2D(
[0],
[0],
color='#a31c3f',
lw=2,
label='{0} < |1/ρ| ≤ {1}\n[100th percentile edge length]'.format(
format(
edge_size_desc["75%"],
".3f"
),
format(
edge_size_desc["max"],
".3f"
)
)
)
]
# Create the figure
fig, ax = plt.subplots()
ax.legend(handles=legend_elements, loc='center')
plt.axis('off')
plt.savefig('legend.png', dpi=300)
plt.show()
| 0.527073 | 0.784402 |
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc" style="margin-top: 1em;"><ul class="toc-item"><li><span><a href="#Name" data-toc-modified-id="Name-1"><span class="toc-item-num">1 </span>Name</a></span></li><li><span><a href="#Search" data-toc-modified-id="Search-2"><span class="toc-item-num">2 </span>Search</a></span><ul class="toc-item"><li><span><a href="#Load-Cached-Results" data-toc-modified-id="Load-Cached-Results-2.1"><span class="toc-item-num">2.1 </span>Load Cached Results</a></span></li><li><span><a href="#Run-From-Scratch" data-toc-modified-id="Run-From-Scratch-2.2"><span class="toc-item-num">2.2 </span>Run From Scratch</a></span></li></ul></li><li><span><a href="#Analysis" data-toc-modified-id="Analysis-3"><span class="toc-item-num">3 </span>Analysis</a></span><ul class="toc-item"><li><span><a href="#Gender-Breakdown" data-toc-modified-id="Gender-Breakdown-3.1"><span class="toc-item-num">3.1 </span>Gender Breakdown</a></span></li><li><span><a href="#Face-Sizes" data-toc-modified-id="Face-Sizes-3.2"><span class="toc-item-num">3.2 </span>Face Sizes</a></span></li><li><span><a href="#Appearances-on-a-Single-Show" data-toc-modified-id="Appearances-on-a-Single-Show-3.3"><span class="toc-item-num">3.3 </span>Appearances on a Single Show</a></span></li><li><span><a href="#Screen-Time-Across-All-Shows" data-toc-modified-id="Screen-Time-Across-All-Shows-3.4"><span class="toc-item-num">3.4 </span>Screen Time Across All Shows</a></span></li></ul></li><li><span><a href="#Persist-to-Cloud" data-toc-modified-id="Persist-to-Cloud-4"><span class="toc-item-num">4 </span>Persist to Cloud</a></span><ul class="toc-item"><li><span><a href="#Save-Model-to-GCS" data-toc-modified-id="Save-Model-to-GCS-4.1"><span class="toc-item-num">4.1 </span>Save Model to GCS</a></span><ul class="toc-item"><li><span><a href="#Make-sure-the-GCS-file-is-valid" data-toc-modified-id="Make-sure-the-GCS-file-is-valid-4.1.1"><span class="toc-item-num">4.1.1 </span>Make sure the GCS file is valid</a></span></li></ul></li><li><span><a href="#Save-Labels-to-DB" data-toc-modified-id="Save-Labels-to-DB-4.2"><span class="toc-item-num">4.2 </span>Save Labels to DB</a></span><ul class="toc-item"><li><span><a href="#Commit-the-person-and-labeler" data-toc-modified-id="Commit-the-person-and-labeler-4.2.1"><span class="toc-item-num">4.2.1 </span>Commit the person and labeler</a></span></li><li><span><a href="#Commit-the-FaceIdentity-labels" data-toc-modified-id="Commit-the-FaceIdentity-labels-4.2.2"><span class="toc-item-num">4.2.2 </span>Commit the FaceIdentity labels</a></span></li></ul></li></ul></li></ul></div>
```
from esper.prelude import *
from esper.identity import *
from esper import embed_google_images
```
# Name
```
name = 'Don Lemon'
```
# Search
## Load Cached Results
```
assert name != ''
results = FaceIdentityModel.load(name=name)
imshow(np.hstack([cv2.resize(x[1][0], (200, 200)) for x in results.model_params['images']]))
plt.show()
plot_precision_and_cdf(results)
```
## Run From Scratch
Run this section if you do not have a cached model and precision curve estimates.
```
assert name != ''
img_dir = embed_google_images.fetch_images(name)
face_imgs = load_and_select_faces_from_images(img_dir)
face_embs = embed_google_images.embed_images(face_imgs)
assert(len(face_embs) == len(face_imgs))
imshow(np.hstack([cv2.resize(x[0], (200, 200)) for x in face_imgs if x]))
plt.show()
face_ids_by_bucket, face_ids_to_score = face_search_by_embeddings(face_embs)
precision_model = PrecisionModel(face_ids_by_bucket)
print('Select all MISTAKES. Ordered by DESCENDING score. Expecting {} frames'.format(precision_model.get_lower_count()))
lower_widget = precision_model.get_lower_widget()
lower_widget
print('Select all NON-MISTAKES. Ordered by ASCENDING distance. Expecting {} frames'.format(precision_model.get_upper_count()))
upper_widget = precision_model.get_upper_widget()
upper_widget
```
Run the following cell after labelling.
```
lower_precision = precision_model.compute_precision_for_lower_buckets(lower_widget.selected)
upper_precision = precision_model.compute_precision_for_upper_buckets(upper_widget.selected)
precision_by_bucket = {**lower_precision, **upper_precision}
results = FaceIdentityModel(
name=name,
face_ids_by_bucket=face_ids_by_bucket,
face_ids_to_score=face_ids_to_score,
precision_by_bucket=precision_by_bucket,
model_params={
'images': list(zip(face_embs, face_imgs))
}
)
plot_precision_and_cdf(results)
# Save the model
results.save()
```
# Analysis
## Gender Breakdown
```
gender_breakdown = compute_gender_breakdown(results)
print('Raw counts:')
for k, v in gender_breakdown.items():
print(' ', k, ':', v)
print()
print('Proportions:')
denominator = sum(v for v in gender_breakdown.values())
for k, v in gender_breakdown.items():
print(' ', k, ':', v / denominator)
print()
print('Showing examples:')
show_gender_examples(results)
```
## Face Sizes
```
plot_histogram_of_face_sizes(results)
```
## Appearances on a Single Show
```
show_name = 'CNN Tonight With Don Lemon'
screen_time_by_video_id = compute_screen_time_by_video(results, show_name)
plot_histogram_of_screen_times_by_video(name, show_name, screen_time_by_video_id)
plot_screentime_over_time(name, show_name, screen_time_by_video_id)
plot_distribution_of_appearance_times_by_video(results, show_name)
```
## Screen Time Across All Shows
```
screen_time_by_show = get_screen_time_by_show(results)
plot_screen_time_by_show(name, screen_time_by_show)
```
# Persist to Cloud
## Save Model to GCS
```
gcs_model_path = results.save_to_gcs()
```
### Make sure the GCS file is valid
```
gcs_results = FaceIdentityModel.load_from_gcs(name=name)
plot_precision_and_cdf(gcs_results)
```
## Save Labels to DB
```
from django.core.exceptions import ObjectDoesNotExist
def standardize_name(name):
return name.lower()
person_type = ThingType.objects.get(name='person')
try:
person = Thing.objects.get(name=standardize_name(name), type=person_type)
print('Found person:', person.name)
except ObjectDoesNotExist:
person = Thing(name=standardize_name(name), type=person_type)
print('Creating person:', person.name)
labeler = Labeler(name='face-identity-{}'.format(person.name), data_path=gcs_model_path)
```
### Commit the person and labeler
```
person.save()
labeler.save()
```
### Commit the FaceIdentity labels
```
commit_face_identities_to_db(results, person, labeler)
print('Committed {} labels to the db'.format(FaceIdentity.objects.filter(labeler=labeler).count()))
```
|
github_jupyter
|
from esper.prelude import *
from esper.identity import *
from esper import embed_google_images
name = 'Don Lemon'
assert name != ''
results = FaceIdentityModel.load(name=name)
imshow(np.hstack([cv2.resize(x[1][0], (200, 200)) for x in results.model_params['images']]))
plt.show()
plot_precision_and_cdf(results)
assert name != ''
img_dir = embed_google_images.fetch_images(name)
face_imgs = load_and_select_faces_from_images(img_dir)
face_embs = embed_google_images.embed_images(face_imgs)
assert(len(face_embs) == len(face_imgs))
imshow(np.hstack([cv2.resize(x[0], (200, 200)) for x in face_imgs if x]))
plt.show()
face_ids_by_bucket, face_ids_to_score = face_search_by_embeddings(face_embs)
precision_model = PrecisionModel(face_ids_by_bucket)
print('Select all MISTAKES. Ordered by DESCENDING score. Expecting {} frames'.format(precision_model.get_lower_count()))
lower_widget = precision_model.get_lower_widget()
lower_widget
print('Select all NON-MISTAKES. Ordered by ASCENDING distance. Expecting {} frames'.format(precision_model.get_upper_count()))
upper_widget = precision_model.get_upper_widget()
upper_widget
lower_precision = precision_model.compute_precision_for_lower_buckets(lower_widget.selected)
upper_precision = precision_model.compute_precision_for_upper_buckets(upper_widget.selected)
precision_by_bucket = {**lower_precision, **upper_precision}
results = FaceIdentityModel(
name=name,
face_ids_by_bucket=face_ids_by_bucket,
face_ids_to_score=face_ids_to_score,
precision_by_bucket=precision_by_bucket,
model_params={
'images': list(zip(face_embs, face_imgs))
}
)
plot_precision_and_cdf(results)
# Save the model
results.save()
gender_breakdown = compute_gender_breakdown(results)
print('Raw counts:')
for k, v in gender_breakdown.items():
print(' ', k, ':', v)
print()
print('Proportions:')
denominator = sum(v for v in gender_breakdown.values())
for k, v in gender_breakdown.items():
print(' ', k, ':', v / denominator)
print()
print('Showing examples:')
show_gender_examples(results)
plot_histogram_of_face_sizes(results)
show_name = 'CNN Tonight With Don Lemon'
screen_time_by_video_id = compute_screen_time_by_video(results, show_name)
plot_histogram_of_screen_times_by_video(name, show_name, screen_time_by_video_id)
plot_screentime_over_time(name, show_name, screen_time_by_video_id)
plot_distribution_of_appearance_times_by_video(results, show_name)
screen_time_by_show = get_screen_time_by_show(results)
plot_screen_time_by_show(name, screen_time_by_show)
gcs_model_path = results.save_to_gcs()
gcs_results = FaceIdentityModel.load_from_gcs(name=name)
plot_precision_and_cdf(gcs_results)
from django.core.exceptions import ObjectDoesNotExist
def standardize_name(name):
return name.lower()
person_type = ThingType.objects.get(name='person')
try:
person = Thing.objects.get(name=standardize_name(name), type=person_type)
print('Found person:', person.name)
except ObjectDoesNotExist:
person = Thing(name=standardize_name(name), type=person_type)
print('Creating person:', person.name)
labeler = Labeler(name='face-identity-{}'.format(person.name), data_path=gcs_model_path)
person.save()
labeler.save()
commit_face_identities_to_db(results, person, labeler)
print('Committed {} labels to the db'.format(FaceIdentity.objects.filter(labeler=labeler).count()))
| 0.500977 | 0.931525 |
```
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
from sklearn.preprocessing import StandardScaler
dane = pd.read_csv('cervical-cancer_csv.csv')
# usuwanie kolumn
dane = dane.drop(['STDs:cervical condylomatosis',
'STDs:vaginal condylomatosis',
'STDs:pelvic inflammatory disease',
'STDs:genital herpes',
'STDs:molluscum contagiosum',
'STDs:AIDS',
'STDs:Hepatitis B',
'STDs:HPV', 'Dx:CIN'], axis=1)
# uzupełnianie braków i kodowanie zmiennych kategorycznych
def column_nodata(df, column_name):
df[column_name + "_null"] = df[column_name].apply(lambda x: 1 if pd.isnull(x) else 0)
df[column_name] = df[column_name].fillna(0)
def replace_in_column(df, column_name, src, dst):
df[column_name] = df[column_name].replace(to_replace=src, value=dst)
replace_in_column(dane, 'STDs (number)', [3, 4], 2)
replace_in_column(dane, 'STDs: Number of diagnosis', [2,3], 1)
nodata_categories = [
'Smokes',
'Hormonal Contraceptives',
'IUD',
'STDs',
'STDs (number)',
'STDs:condylomatosis',
'STDs:vulvo-perineal condylomatosis',
'STDs:syphilis',
'STDs:HIV'
]
for category in nodata_categories:
column_nodata(dane, category)
dane = pd.concat([dane, pd.get_dummies(dane['STDs (number)'], prefix='STDs_')],axis=1)
dane.drop(['STDs (number)'],axis=1, inplace=True)
# standaryzacja
numerical = ['Age', 'Number of sexual partners', 'First sexual intercourse', 'Num of pregnancies', 'Smokes (years)',
'Smokes (packs/year)', 'Hormonal Contraceptives (years)', 'IUD (years)', 'STDs: Time since first diagnosis',
'STDs: Time since last diagnosis']
scaler = StandardScaler()
dane_scaled = scaler.fit_transform(dane[numerical])
d2 = pd.DataFrame(dane_scaled, columns = numerical)
dane[numerical] = d2[numerical]
# stworzenie jednego targetu
targets = ['Hinselmann', 'Schiller', 'Citology', 'Biopsy']
def has_cancer(row):
for target in targets:
if row[target] == 1:
return 1
return 0
dane['cancer'] = dane.apply(lambda row: has_cancer(row), axis=1)
dane = dane.drop(targets, axis=1)
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
from sklearn.metrics import roc_auc_score
# podzial zbioru na treningowy i testowy
def default_split(X, y):
return train_test_split(X, y, test_size=0.2, random_state=2137)
# scoring
def scoring(y_test, y_predicted):
print("ACC = ", accuracy_score(y_test, y_predicted))
print("PREC = ", precision_score(y_test, y_predicted))
print("RECALL = ", recall_score(y_test, y_predicted))
print("F1 = ", f1_score(y_test, y_predicted))
print("FPR = ", roc_auc_score(y_test, y_predicted))
# wyodrebnienie y
def extract_y(data):
y = data[["cancer"]]
return data.drop(["cancer"], axis=1), y
```
# GBM
```
# przygotowanie danych
X, y = extract_y(dane)
X = X.fillna(0)
X_train, X_test, y_train, y_test = default_split(X, y)
print(X.shape, X_train.shape, X_test.shape)
from sklearn.ensemble import GradientBoostingClassifier
model_gbm = GradientBoostingClassifier()
model_gbm.fit(X_train, y_train)
y_predicted_old = model_gbm.predict(X_test)
scoring(y_test, y_predicted_old)
```
# Strojenie parametrów
```
import sklearn
sorted(sklearn.metrics.SCORERS.keys())
from sklearn.model_selection import GridSearchCV
n_estimators = [100, 300, 500, 800]
max_depth = [1, 3, 5, 10]
min_samples_split = [2, 3, 5, 10]
learning_rate = [0.05, 0.1, 0.2]
gbm = GradientBoostingClassifier()
hyperF = dict(n_estimators = n_estimators, max_depth = max_depth,
min_samples_split = min_samples_split,
learning_rate = learning_rate)
gridF = GridSearchCV(gbm, hyperF, cv = 5, verbose = 1,
n_jobs = -1, scoring = 'average_precision')
bestF = gridF.fit(X_train, y_train)
y_predicted_new = bestF.predict(X_test)
scoring(y_test, y_predicted_new)
y_predicted_new
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
from sklearn.preprocessing import StandardScaler
dane = pd.read_csv('cervical-cancer_csv.csv')
# usuwanie kolumn
dane = dane.drop(['STDs:cervical condylomatosis',
'STDs:vaginal condylomatosis',
'STDs:pelvic inflammatory disease',
'STDs:genital herpes',
'STDs:molluscum contagiosum',
'STDs:AIDS',
'STDs:Hepatitis B',
'STDs:HPV', 'Dx:CIN'], axis=1)
# uzupełnianie braków i kodowanie zmiennych kategorycznych
def column_nodata(df, column_name):
df[column_name + "_null"] = df[column_name].apply(lambda x: 1 if pd.isnull(x) else 0)
df[column_name] = df[column_name].fillna(0)
def replace_in_column(df, column_name, src, dst):
df[column_name] = df[column_name].replace(to_replace=src, value=dst)
replace_in_column(dane, 'STDs (number)', [3, 4], 2)
replace_in_column(dane, 'STDs: Number of diagnosis', [2,3], 1)
nodata_categories = [
'Smokes',
'Hormonal Contraceptives',
'IUD',
'STDs',
'STDs (number)',
'STDs:condylomatosis',
'STDs:vulvo-perineal condylomatosis',
'STDs:syphilis',
'STDs:HIV'
]
for category in nodata_categories:
column_nodata(dane, category)
dane = pd.concat([dane, pd.get_dummies(dane['STDs (number)'], prefix='STDs_')],axis=1)
dane.drop(['STDs (number)'],axis=1, inplace=True)
# standaryzacja
numerical = ['Age', 'Number of sexual partners', 'First sexual intercourse', 'Num of pregnancies', 'Smokes (years)',
'Smokes (packs/year)', 'Hormonal Contraceptives (years)', 'IUD (years)', 'STDs: Time since first diagnosis',
'STDs: Time since last diagnosis']
scaler = StandardScaler()
dane_scaled = scaler.fit_transform(dane[numerical])
d2 = pd.DataFrame(dane_scaled, columns = numerical)
dane[numerical] = d2[numerical]
# stworzenie jednego targetu
targets = ['Hinselmann', 'Schiller', 'Citology', 'Biopsy']
def has_cancer(row):
for target in targets:
if row[target] == 1:
return 1
return 0
dane['cancer'] = dane.apply(lambda row: has_cancer(row), axis=1)
dane = dane.drop(targets, axis=1)
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
from sklearn.metrics import roc_auc_score
# podzial zbioru na treningowy i testowy
def default_split(X, y):
return train_test_split(X, y, test_size=0.2, random_state=2137)
# scoring
def scoring(y_test, y_predicted):
print("ACC = ", accuracy_score(y_test, y_predicted))
print("PREC = ", precision_score(y_test, y_predicted))
print("RECALL = ", recall_score(y_test, y_predicted))
print("F1 = ", f1_score(y_test, y_predicted))
print("FPR = ", roc_auc_score(y_test, y_predicted))
# wyodrebnienie y
def extract_y(data):
y = data[["cancer"]]
return data.drop(["cancer"], axis=1), y
# przygotowanie danych
X, y = extract_y(dane)
X = X.fillna(0)
X_train, X_test, y_train, y_test = default_split(X, y)
print(X.shape, X_train.shape, X_test.shape)
from sklearn.ensemble import GradientBoostingClassifier
model_gbm = GradientBoostingClassifier()
model_gbm.fit(X_train, y_train)
y_predicted_old = model_gbm.predict(X_test)
scoring(y_test, y_predicted_old)
import sklearn
sorted(sklearn.metrics.SCORERS.keys())
from sklearn.model_selection import GridSearchCV
n_estimators = [100, 300, 500, 800]
max_depth = [1, 3, 5, 10]
min_samples_split = [2, 3, 5, 10]
learning_rate = [0.05, 0.1, 0.2]
gbm = GradientBoostingClassifier()
hyperF = dict(n_estimators = n_estimators, max_depth = max_depth,
min_samples_split = min_samples_split,
learning_rate = learning_rate)
gridF = GridSearchCV(gbm, hyperF, cv = 5, verbose = 1,
n_jobs = -1, scoring = 'average_precision')
bestF = gridF.fit(X_train, y_train)
y_predicted_new = bestF.predict(X_test)
scoring(y_test, y_predicted_new)
y_predicted_new
| 0.431824 | 0.608856 |
```
import pandas as pd
import numpy as np
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from simpletransformers.ner import NERModel,NERArgs
import torch
class bert_training:
'''
__init__ : INPUT- BIO data format for BERT
WORKING- Splits into train and test
give_Args: INPUT- Model Arguments (no. of epochs, Learning rate, Training batch size, Evaluation batch size)
WORKING- Fine-tunes BERT uncased model, on the given data and display the results on test data
save_model: INPUT- Path to save the model(with name)
WORKING- Saves the model
'''
def __init__(self,bio_data_path):
self.data = pd.read_csv(bio_data_path,encoding="latin1" )
self.data = self.data.replace(r'^\s*$', np.nan, regex=True)
self.data = self.data.fillna(method ="ffill")
self.data["Sentence #"] = LabelEncoder().fit_transform(self.data["Sentence #"])
self.data.rename(columns={"Sentence #":"sentence_id","Word":"words","Tag":"labels"}, inplace =True)
X = self.data[["sentence_id","words"]]
Y = self.data["labels"]
x_train, x_test, y_train, y_test = train_test_split(X,Y, test_size =0.2)
#building up train and test data
self.train_data = pd.DataFrame({"sentence_id":x_train["sentence_id"],"words":x_train["words"],"labels":y_train})
self.test_data = pd.DataFrame({"sentence_id":x_test["sentence_id"],"words":x_test["words"],"labels":y_test})
self.label = self.data["labels"].unique().tolist()
def give_Args(self,num_epochs,learning_rate,train_batch_size,eval_batch_size):
args = NERArgs()
args.num_train_epochs = num_epochs
args.learning_rate = learning_rate
args.overwrite_output_dir =True
args.train_batch_size = train_batch_size
args.eval_batch_size = eval_batch_size
print("DOWNLOADING Model")
self.model = NERModel('bert', 'bert-base-uncased',labels=self.label,args =args)
print("TRAINING Begins")
self.model.train_model(self.train_data,eval_data =self.test_data,acc=accuracy_score)
print("TRAINING Ends")
result, model_outputs, preds_list = self.model.eval_model(self.test_data)
print(result) #after fine tuning on test data
def save_model(self,path):
torch.save(self.model,path)
print("Model Saved at given ",path)
print(bert_training.__doc__)
data_path = "/content/drive/MyDrive/2000_BIO_taggingdata_ALL_ROW_WISE.csv"
obj_name = bert_training(data_path) #DATA READ
obj_name.give_Args(2,1e-4,32,32)
obj_name.save_model("/content/drive/MyDrive/model_check")
```
|
github_jupyter
|
import pandas as pd
import numpy as np
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from simpletransformers.ner import NERModel,NERArgs
import torch
class bert_training:
'''
__init__ : INPUT- BIO data format for BERT
WORKING- Splits into train and test
give_Args: INPUT- Model Arguments (no. of epochs, Learning rate, Training batch size, Evaluation batch size)
WORKING- Fine-tunes BERT uncased model, on the given data and display the results on test data
save_model: INPUT- Path to save the model(with name)
WORKING- Saves the model
'''
def __init__(self,bio_data_path):
self.data = pd.read_csv(bio_data_path,encoding="latin1" )
self.data = self.data.replace(r'^\s*$', np.nan, regex=True)
self.data = self.data.fillna(method ="ffill")
self.data["Sentence #"] = LabelEncoder().fit_transform(self.data["Sentence #"])
self.data.rename(columns={"Sentence #":"sentence_id","Word":"words","Tag":"labels"}, inplace =True)
X = self.data[["sentence_id","words"]]
Y = self.data["labels"]
x_train, x_test, y_train, y_test = train_test_split(X,Y, test_size =0.2)
#building up train and test data
self.train_data = pd.DataFrame({"sentence_id":x_train["sentence_id"],"words":x_train["words"],"labels":y_train})
self.test_data = pd.DataFrame({"sentence_id":x_test["sentence_id"],"words":x_test["words"],"labels":y_test})
self.label = self.data["labels"].unique().tolist()
def give_Args(self,num_epochs,learning_rate,train_batch_size,eval_batch_size):
args = NERArgs()
args.num_train_epochs = num_epochs
args.learning_rate = learning_rate
args.overwrite_output_dir =True
args.train_batch_size = train_batch_size
args.eval_batch_size = eval_batch_size
print("DOWNLOADING Model")
self.model = NERModel('bert', 'bert-base-uncased',labels=self.label,args =args)
print("TRAINING Begins")
self.model.train_model(self.train_data,eval_data =self.test_data,acc=accuracy_score)
print("TRAINING Ends")
result, model_outputs, preds_list = self.model.eval_model(self.test_data)
print(result) #after fine tuning on test data
def save_model(self,path):
torch.save(self.model,path)
print("Model Saved at given ",path)
print(bert_training.__doc__)
data_path = "/content/drive/MyDrive/2000_BIO_taggingdata_ALL_ROW_WISE.csv"
obj_name = bert_training(data_path) #DATA READ
obj_name.give_Args(2,1e-4,32,32)
obj_name.save_model("/content/drive/MyDrive/model_check")
| 0.590189 | 0.522933 |
## Introduction
This notebook demonstrates how to scale the CIFAR-10 image classification task using multiple FPGAs.
In the first step, we connect to an existing Dask cluster using it's scheduler's IP address.
```
from dask.distributed import Client, progress, get_worker
import os
import binascii
# Replace with IP address of the Dask scheduler
client = Client("tcp://131.180.106.138:8786")
client
```
### Define experiment parameters:
BATCH_SIZES => A list of different batch sizes (number of images) we would like to run this experiment for.
PLATFORM => One of the two supported platforms by the driver (alveo/zynq-iodma)
XCLBIN_PATH_DEFAULT => Default path for the .xclbin file if one not provided via command line args
DEVICE_NAME_DEFAULT => Default name for the FPGA device if one not provided via command line args
```
BATCH_SIZES = [100, 500]
BATCH_SIZES = [100, 500, 1000, 1500, 2000]
PLATFORM = "alveo"
XCLBIN_PATH_DEFAULT = "a.xclbin"
DEVICE_NAME_DEFAULT = "xilinx_u50_gen3x16_xdma_201920_3"
```
### Download dataset
Download a numpy-array formatted CIFAR-10 dataset to the current directory:
```
!wget https://raw.githubusercontent.com/modestyachts/CIFAR-10.1/master/datasets/cifar10.1_v4_data.npy
```
### Define the worker method
Here, we define the Python method which will be executed on each of the Dask workers. This function calls the driver using the data partition it receives, and returns the output data (along with some performance statistics) to the caller (the Dask client)
The little dance with the forking logic is needed since Pynq (used internally by *FINNAccelDriver*) cannot run in a non-main thread, which is how a Dask worker runs.
```
def run_on_worker(ibuf_normal, index):
print("Received ", len(ibuf_normal), "images for classification")
from multiprocessing import Process,Queue
import numpy as np
import time
def forked_process(queue, ibuf_normal):
from driver import FINNAccelDriver
from pynq.ps import Clocks
batch_size = len(ibuf_normal)
device_name = os.environ.get('DEVICE_NAME', DEVICE_NAME_DEFAULT)
xclbin_path = os.environ.get('XCLBIN_PATH', XCLBIN_PATH_DEFAULT)
print("Using parameters: DEVICE_NAME =", device_name, " XCLBIN_PATH =", xclbin_path, " PLATFORM =", PLATFORM)
finnDriver = FINNAccelDriver(batch_size, xclbin_path, PLATFORM, device_name)
ibuf_folded = finnDriver.fold_input(ibuf_normal)
# ibuf_packed = finnDriver.pack_input(ibuf_folded) Do not pack for performance reasons
ibuf_packed = ibuf_folded
finnDriver.copy_input_data_to_device(ibuf_packed)
t0 = time.time()
finnDriver.execute()
t1 = time.time()
obuf_packed = np.empty_like(finnDriver.obuf_packed_device)
finnDriver.copy_output_data_from_device(obuf_packed)
obuf_folded = finnDriver.unpack_output(obuf_packed)
obuf_normal = finnDriver.unfold_output(obuf_folded)
if PLATFORM != "alveo":
fclk_mhz = Clocks.fclk0_mhz
else:
fclk_mhz = finnDriver.fclk_mhz
runtime = t1-t0
queue.put({
'data': obuf_normal,
'runtime': runtime,
'index': index,
'fclk_mhz': fclk_mhz,
'throughput': batch_size/runtime,
'bandwidth_in': np.prod(finnDriver.ishape_packed)*0.000001 / runtime,
'bandwidth_out': np.prod(finnDriver.oshape_packed)*0.000001 / runtime,
'N': batch_size
})
# We need to run the Pynq overlay in a new forked process since it cannot be run in a non-Main thread
t0_total = time.time()
queue = Queue()
p = Process(target=forked_process, args=(queue, ibuf_normal))
p.start()
result = queue.get()
p.join()
t1_total = time.time()
print("TOTAL EXECUTION TIME ON THIS WORKER (s): ", t1_total - t0_total)
return result
```
### Run the experiment
Now we can run the classification.
1. Partition the dataset into as many parts as the number of workers
2. Send each part to a separate worker (using the *scatter* function from Dask)
3. Submit the *run_on_worker* defined above to the scheduler, which will run it on all the workers.
4. Collect and merge the results
```
import time
import numpy as np
import json
num_of_workers = len(client.scheduler_info()["workers"])
full_cifar = np.load('cifar10.1_v4_data.npy')
execution_times = []
end_to_end_times = []
for BATCH_SIZE in BATCH_SIZES:
print("BATCH_SIZE:", BATCH_SIZE)
partial_cifar = full_cifar[:BATCH_SIZE]
t0 = time.time()
# Split up the file into equal sized chunks based on number of available Dask workers
data_split = []
start = 0
chunk_size = int(len(partial_cifar)/num_of_workers)
for i in range(num_of_workers - 1):
data_split.append(partial_cifar[start: start+chunk_size])
start += chunk_size
data_split.append(partial_cifar[start:]) #Last partition
# Scatter the data to the workers before calling run_on_worker on the workers
print("Sending data to workers, and triggering worker tasks...")
distributed_data = client.scatter(data_split)
futures = client.map(run_on_worker, distributed_data, range(num_of_workers))
results = client.gather(futures)
print("Received data from workers.")
# Reorder the response based on original input order
results.sort(key = lambda result: result['index'])
# Concatenate the result where each is an ndarray of the shape (BATCH_SIZE/num_of_workers, 1)
merged_result = np.concatenate([r['data'] for r in results]) # FINAL RESULTS (CLASS LABELS)
t1 = time.time()
max_fpga_runtime = max([r['runtime'] for r in results])
def avg(li):
return sum(li)/len(li)
print("TOTAL EXECUTION TIME:", t1-t0)
print("Maximum FPGA runtime[s]:", max_fpga_runtime) # Shown in the plot
print("Average throughput[images/s]:", avg([r['throughput'] for r in results]))
print("Average DRAM_in_bandwidth[Mb/s]:", avg([r['bandwidth_in'] for r in results]))
print("Average DRAM_out_bandwidth[Mb/s]:", avg([r['bandwidth_out'] for r in results]))
print("**************************")
execution_times.append(max_fpga_runtime)
end_to_end_times.append(t1-t0)
```
### Generate a performance plot
Plot the execution times for different batch sizes. Here, we plot the maximum FPGA execution times from all the workers. This time includes the data buffering time to/from the FPGA and the actual inference time. To plot the total end-to-end time instead, replace the *execution_times* variable below with the *end_to_end_times* variable.
```
import numpy as np
import matplotlib.pyplot as plt
f = plt.figure(figsize=(50,50))
x = BATCH_SIZES
f = plt.figure()
y2 = execution_times
plt.plot(x, y2, label = "2 FPGAs", marker='x')
plt.xlabel('Batch size (no. of images)')
plt.ylabel('Time taken to classify (in s)')
plt.title('FINN CNV + Cifar-10 performance demo')
plt.legend()
plt.grid()
f.savefig("cnv-1-vs-2.png", bbox_inches='tight', dpi=150)
```
### Measure scaling benefits
To measure the benefits of scaling, run this notebook again after creating or destroying one or more Dask workers. Then compare the plots above to see the speedup.
|
github_jupyter
|
from dask.distributed import Client, progress, get_worker
import os
import binascii
# Replace with IP address of the Dask scheduler
client = Client("tcp://131.180.106.138:8786")
client
BATCH_SIZES = [100, 500]
BATCH_SIZES = [100, 500, 1000, 1500, 2000]
PLATFORM = "alveo"
XCLBIN_PATH_DEFAULT = "a.xclbin"
DEVICE_NAME_DEFAULT = "xilinx_u50_gen3x16_xdma_201920_3"
!wget https://raw.githubusercontent.com/modestyachts/CIFAR-10.1/master/datasets/cifar10.1_v4_data.npy
def run_on_worker(ibuf_normal, index):
print("Received ", len(ibuf_normal), "images for classification")
from multiprocessing import Process,Queue
import numpy as np
import time
def forked_process(queue, ibuf_normal):
from driver import FINNAccelDriver
from pynq.ps import Clocks
batch_size = len(ibuf_normal)
device_name = os.environ.get('DEVICE_NAME', DEVICE_NAME_DEFAULT)
xclbin_path = os.environ.get('XCLBIN_PATH', XCLBIN_PATH_DEFAULT)
print("Using parameters: DEVICE_NAME =", device_name, " XCLBIN_PATH =", xclbin_path, " PLATFORM =", PLATFORM)
finnDriver = FINNAccelDriver(batch_size, xclbin_path, PLATFORM, device_name)
ibuf_folded = finnDriver.fold_input(ibuf_normal)
# ibuf_packed = finnDriver.pack_input(ibuf_folded) Do not pack for performance reasons
ibuf_packed = ibuf_folded
finnDriver.copy_input_data_to_device(ibuf_packed)
t0 = time.time()
finnDriver.execute()
t1 = time.time()
obuf_packed = np.empty_like(finnDriver.obuf_packed_device)
finnDriver.copy_output_data_from_device(obuf_packed)
obuf_folded = finnDriver.unpack_output(obuf_packed)
obuf_normal = finnDriver.unfold_output(obuf_folded)
if PLATFORM != "alveo":
fclk_mhz = Clocks.fclk0_mhz
else:
fclk_mhz = finnDriver.fclk_mhz
runtime = t1-t0
queue.put({
'data': obuf_normal,
'runtime': runtime,
'index': index,
'fclk_mhz': fclk_mhz,
'throughput': batch_size/runtime,
'bandwidth_in': np.prod(finnDriver.ishape_packed)*0.000001 / runtime,
'bandwidth_out': np.prod(finnDriver.oshape_packed)*0.000001 / runtime,
'N': batch_size
})
# We need to run the Pynq overlay in a new forked process since it cannot be run in a non-Main thread
t0_total = time.time()
queue = Queue()
p = Process(target=forked_process, args=(queue, ibuf_normal))
p.start()
result = queue.get()
p.join()
t1_total = time.time()
print("TOTAL EXECUTION TIME ON THIS WORKER (s): ", t1_total - t0_total)
return result
import time
import numpy as np
import json
num_of_workers = len(client.scheduler_info()["workers"])
full_cifar = np.load('cifar10.1_v4_data.npy')
execution_times = []
end_to_end_times = []
for BATCH_SIZE in BATCH_SIZES:
print("BATCH_SIZE:", BATCH_SIZE)
partial_cifar = full_cifar[:BATCH_SIZE]
t0 = time.time()
# Split up the file into equal sized chunks based on number of available Dask workers
data_split = []
start = 0
chunk_size = int(len(partial_cifar)/num_of_workers)
for i in range(num_of_workers - 1):
data_split.append(partial_cifar[start: start+chunk_size])
start += chunk_size
data_split.append(partial_cifar[start:]) #Last partition
# Scatter the data to the workers before calling run_on_worker on the workers
print("Sending data to workers, and triggering worker tasks...")
distributed_data = client.scatter(data_split)
futures = client.map(run_on_worker, distributed_data, range(num_of_workers))
results = client.gather(futures)
print("Received data from workers.")
# Reorder the response based on original input order
results.sort(key = lambda result: result['index'])
# Concatenate the result where each is an ndarray of the shape (BATCH_SIZE/num_of_workers, 1)
merged_result = np.concatenate([r['data'] for r in results]) # FINAL RESULTS (CLASS LABELS)
t1 = time.time()
max_fpga_runtime = max([r['runtime'] for r in results])
def avg(li):
return sum(li)/len(li)
print("TOTAL EXECUTION TIME:", t1-t0)
print("Maximum FPGA runtime[s]:", max_fpga_runtime) # Shown in the plot
print("Average throughput[images/s]:", avg([r['throughput'] for r in results]))
print("Average DRAM_in_bandwidth[Mb/s]:", avg([r['bandwidth_in'] for r in results]))
print("Average DRAM_out_bandwidth[Mb/s]:", avg([r['bandwidth_out'] for r in results]))
print("**************************")
execution_times.append(max_fpga_runtime)
end_to_end_times.append(t1-t0)
import numpy as np
import matplotlib.pyplot as plt
f = plt.figure(figsize=(50,50))
x = BATCH_SIZES
f = plt.figure()
y2 = execution_times
plt.plot(x, y2, label = "2 FPGAs", marker='x')
plt.xlabel('Batch size (no. of images)')
plt.ylabel('Time taken to classify (in s)')
plt.title('FINN CNV + Cifar-10 performance demo')
plt.legend()
plt.grid()
f.savefig("cnv-1-vs-2.png", bbox_inches='tight', dpi=150)
| 0.44071 | 0.829837 |
<a id="title_ID"></a>
# JWST Pipeline Validation Notebook:
# calwebb_detector1, rscd unit tests
<span style="color:red"> **Instruments Affected**</span>: MIRI
### Table of Contents
<div style="text-align: left">
<br> [Introduction](#intro)
<br> [JWST Unit Tests](#unit)
<br> [Defining Terms](#terms)
<br> [Test Description](#description)
<br> [Data Description](#data_descr)
<br> [Imports](#imports)
<br> [Convenience Functions](#functions)
<br> [Perform Tests](#testing)
<br> [About This Notebook](#about)
<br>
</div>
<a id="intro"></a>
# Introduction
This is the validation notebook that displays the unit tests for the RSCD step in calwebb_detector1. This notebook runs and displays the unit tests that are performed as a part of the normal software continuous integration process. For more information on the pipeline visit the links below.
* Pipeline description: https://jwst-pipeline.readthedocs.io/en/latest/jwst/rscd/index.html
* Pipeline code: https://github.com/spacetelescope/jwst/tree/master/jwst/
[Top of Page](#title_ID)
<a id="unit"></a>
# JWST Unit Tests
JWST unit tests are located in the "tests" folder for each pipeline step within the [GitHub repository](https://github.com/spacetelescope/jwst/tree/master/jwst/), e.g., ```jwst/rscd/tests```.
* Unit test README: https://github.com/spacetelescope/jwst#unit-tests
[Top of Page](#title_ID)
<a id="terms"></a>
# Defining Terms
These are terms or acronymns used in this notebook that may not be known a general audience.
* JWST: James Webb Space Telescope
* NIRCam: Near-Infrared Camera
[Top of Page](#title_ID)
<a id="description"></a>
# Test Description
Unit testing is a software testing method by which individual units of source code are tested to determine whether they are working sufficiently well. Unit tests do not require a separate data file; the test creates the necessary test data and parameters as a part of the test code.
[Top of Page](#title_ID)
<a id="data_descr"></a>
# Data Description
Data used for unit tests is created on the fly within the test itself, and is typically an array in the expected format of JWST data with added metadata needed to run through the pipeline.
[Top of Page](#title_ID)
<a id="imports"></a>
# Imports
* tempfile for creating temporary output products
* pytest for unit test functions
* jwst for the JWST Pipeline
* IPython.display for display pytest reports
[Top of Page](#title_ID)
```
import tempfile
import pytest
import jwst
from IPython.display import IFrame
```
<a id="functions"></a>
# Convenience Functions
Here we define any convenience functions to help with running the unit tests.
[Top of Page](#title_ID)
```
def display_report(fname):
'''Convenience function to display pytest report.'''
return IFrame(src=fname, width=700, height=600)
```
<a id="testing"></a>
# Perform Tests
Below we run the unit tests for the RSCD step.
[Top of Page](#title_ID)
```
with tempfile.TemporaryDirectory() as tmpdir:
!pytest jwst/rscd -v --ignore=jwst/associations --ignore=jwst/datamodels --ignore=jwst/stpipe --ignore=jwst/regtest --html=tmpdir/unit_report.html --self-contained-html
report = display_report('tmpdir/unit_report.html')
report
```
<a id="about"></a>
## About This Notebook
**Author:** Alicia Canipe, Staff Scientist, NIRCam
<br>**Updated On:** 01/07/2021
[Top of Page](#title_ID)
<img style="float: right;" src="./stsci_pri_combo_mark_horizonal_white_bkgd.png" alt="stsci_pri_combo_mark_horizonal_white_bkgd" width="200px"/>
|
github_jupyter
|
import tempfile
import pytest
import jwst
from IPython.display import IFrame
def display_report(fname):
'''Convenience function to display pytest report.'''
return IFrame(src=fname, width=700, height=600)
with tempfile.TemporaryDirectory() as tmpdir:
!pytest jwst/rscd -v --ignore=jwst/associations --ignore=jwst/datamodels --ignore=jwst/stpipe --ignore=jwst/regtest --html=tmpdir/unit_report.html --self-contained-html
report = display_report('tmpdir/unit_report.html')
report
| 0.189972 | 0.957952 |
## NLP model creation and training
```
from fastai.gen_doc.nbdoc import *
from fastai.text import *
```
The main thing here is [`RNNLearner`](/text.learner.html#RNNLearner). There are also some utility functions to help create and update text models.
## Quickly get a learner
```
show_doc(language_model_learner)
```
The model used is given by `arch` and `config`. It can be:
- an [`AWD_LSTM`](/text.models.awd_lstm.html#AWD_LSTM)([Merity et al.](https://arxiv.org/abs/1708.02182))
- a [`Transformer`](/text.models.transformer.html#Transformer) decoder ([Vaswani et al.](https://arxiv.org/abs/1706.03762))
- a [`TransformerXL`](/text.models.transformer.html#TransformerXL) ([Dai et al.](https://arxiv.org/abs/1901.02860))
They each have a default config for language modelling that is in <code>{lower_case_class_name}_lm_config</code> if you want to change the default parameter. At this stage, only the AWD LSTM support `pretrained=True` but we hope to add more pretrained models soon. `drop_mult` is applied to all the dropouts weights of the `config`, `learn_kwargs` are passed to the [`Learner`](/basic_train.html#Learner) initialization.
```
jekyll_note("Using QRNN (change the flag in the config of the AWD LSTM) requires to have cuda installed (same version as pytorch is using).")
path = untar_data(URLs.IMDB_SAMPLE)
data = TextLMDataBunch.from_csv(path, 'texts.csv')
learn = language_model_learner(data, AWD_LSTM, drop_mult=0.5)
show_doc(text_classifier_learner)
```
Here again, the backbone of the model is determined by `arch` and `config`. The input texts are fed into that model by bunch of `bptt` and only the last `max_len` activations are considered. This gives us the backbone of our model. The head then consists of:
- a layer that concatenates the final outputs of the RNN with the maximum and average of all the intermediate outputs (on the sequence length dimension),
- blocks of ([`nn.BatchNorm1d`](https://pytorch.org/docs/stable/nn.html#torch.nn.BatchNorm1d), [`nn.Dropout`](https://pytorch.org/docs/stable/nn.html#torch.nn.Dropout), [`nn.Linear`](https://pytorch.org/docs/stable/nn.html#torch.nn.Linear), [`nn.ReLU`](https://pytorch.org/docs/stable/nn.html#torch.nn.ReLU)) layers.
The blocks are defined by the `lin_ftrs` and `drops` arguments. Specifically, the first block will have a number of inputs inferred from the backbone arch and the last one will have a number of outputs equal to data.c (which contains the number of classes of the data) and the intermediate blocks have a number of inputs/outputs determined by `lin_ftrs` (of course a block has a number of inputs equal to the number of outputs of the previous block). The dropouts all have a the same value ps if you pass a float, or the corresponding values if you pass a list. Default is to have an intermediate hidden size of 50 (which makes two blocks model_activation -> 50 -> n_classes) with a dropout of 0.1.
```
path = untar_data(URLs.IMDB_SAMPLE)
data = TextClasDataBunch.from_csv(path, 'texts.csv')
learn = text_classifier_learner(data, AWD_LSTM, drop_mult=0.5)
show_doc(RNNLearner)
```
Handles the whole creation from <code>data</code> and a `model` with a text data using a certain `bptt`. The `split_func` is used to properly split the model in different groups for gradual unfreezing and differential learning rates. Gradient clipping of `clip` is optionally applied. `alpha` and `beta` are all passed to create an instance of [`RNNTrainer`](/callbacks.rnn.html#RNNTrainer). Can be used for a language model or an RNN classifier. It also handles the conversion of weights from a pretrained model as well as saving or loading the encoder.
```
show_doc(RNNLearner.get_preds)
```
If `ordered=True`, returns the predictions in the order of the dataset, otherwise they will be ordered by the sampler (from the longest text to the shortest). The other arguments are passed [`Learner.get_preds`](/basic_train.html#Learner.get_preds).
### Loading and saving
```
show_doc(RNNLearner.load_encoder)
show_doc(RNNLearner.save_encoder)
show_doc(RNNLearner.load_pretrained)
```
Opens the weights in the `wgts_fname` of `self.model_dir` and the dictionary in `itos_fname` then adapts the pretrained weights to the vocabulary of the <code>data</code>. The two files should be in the models directory of the `learner.path`.
## Utility functions
```
show_doc(convert_weights)
```
Uses the dictionary `stoi_wgts` (mapping of word to id) of the weights to map them to a new dictionary `itos_new` (mapping id to word).
## Get predictions
```
show_doc(LanguageLearner, title_level=3)
show_doc(LanguageLearner.predict)
```
If `no_unk=True` the unknown token is never picked. Words are taken randomly with the distribution of probabilities returned by the model. If `min_p` is not `None`, that value is the minimum probability to be considered in the pool of words. Lowering `temperature` will make the texts less randomized.
```
show_doc(LanguageLearner.beam_search)
```
## Basic functions to get a model
```
show_doc(get_language_model)
show_doc(get_text_classifier)
```
This model uses an encoder taken from the `arch` on `config`. This encoder is fed the sequence by successive bits of size `bptt` and we only keep the last `max_seq` outputs for the pooling layers.
The decoder use a concatenation of the last outputs, a `MaxPooling` of all the outputs and an `AveragePooling` of all the outputs. It then uses a list of `BatchNorm`, `Dropout`, `Linear`, `ReLU` blocks (with no `ReLU` in the last one), using a first layer size of `3*emb_sz` then following the numbers in `n_layers`. The dropouts probabilities are read in `drops`.
Note that the model returns a list of three things, the actual output being the first, the two others being the intermediate hidden states before and after dropout (used by the [`RNNTrainer`](/callbacks.rnn.html#RNNTrainer)). Most loss functions expect one output, so you should use a Callback to remove the other two if you're not using [`RNNTrainer`](/callbacks.rnn.html#RNNTrainer).
## Undocumented Methods - Methods moved below this line will intentionally be hidden
## New Methods - Please document or move to the undocumented section
```
show_doc(MultiBatchEncoder.forward)
show_doc(LanguageLearner.show_results)
show_doc(MultiBatchEncoder.concat)
show_doc(MultiBatchEncoder)
show_doc(decode_spec_tokens)
show_doc(MultiBatchEncoder.reset)
```
|
github_jupyter
|
from fastai.gen_doc.nbdoc import *
from fastai.text import *
show_doc(language_model_learner)
jekyll_note("Using QRNN (change the flag in the config of the AWD LSTM) requires to have cuda installed (same version as pytorch is using).")
path = untar_data(URLs.IMDB_SAMPLE)
data = TextLMDataBunch.from_csv(path, 'texts.csv')
learn = language_model_learner(data, AWD_LSTM, drop_mult=0.5)
show_doc(text_classifier_learner)
path = untar_data(URLs.IMDB_SAMPLE)
data = TextClasDataBunch.from_csv(path, 'texts.csv')
learn = text_classifier_learner(data, AWD_LSTM, drop_mult=0.5)
show_doc(RNNLearner)
show_doc(RNNLearner.get_preds)
show_doc(RNNLearner.load_encoder)
show_doc(RNNLearner.save_encoder)
show_doc(RNNLearner.load_pretrained)
show_doc(convert_weights)
show_doc(LanguageLearner, title_level=3)
show_doc(LanguageLearner.predict)
show_doc(LanguageLearner.beam_search)
show_doc(get_language_model)
show_doc(get_text_classifier)
show_doc(MultiBatchEncoder.forward)
show_doc(LanguageLearner.show_results)
show_doc(MultiBatchEncoder.concat)
show_doc(MultiBatchEncoder)
show_doc(decode_spec_tokens)
show_doc(MultiBatchEncoder.reset)
| 0.722135 | 0.939803 |
```
import sqlite3
import pandas as pd
def sql_two_tables_between_dates(df_a, df_b, query):
""" Example:
df_a = StudyPeriod,
df_b = Rx,
query = \"""select b.*
from a as a left join b as b
on a.ID = b.ID
where a.StartDT <= b.Date and b.Date <= a.EndDT
\""")
Rx = pd.DataFrame({"ID":[1, 2, 3, 1, 2, 3, 1, 2, 2],
"Drug": ["B", "O", "T", 'O', 'A', 'G', 'T', 'B', 'G'],
"Date":[pd.datetime(2020, 1, 1), pd.datetime(2020, 1, 1), pd.datetime(2020, 1, 1),
pd.datetime(2020, 2, 1), pd.datetime(2020, 4, 1), pd.datetime(2020, 8, 1),
pd.datetime(2020, 10, 1), pd.datetime(2020, 11, 1), pd.datetime(2020, 12, 1)]})
StudyPeriod = pd.DataFrame({'ID':[1,2,3],
'StartDT':[pd.datetime(2020, 1, 1), pd.datetime(2020, 4, 1), pd.datetime(2020, 7, 1)],
'EndDT':[pd.datetime(2020, 3, 1), pd.datetime(2020, 8, 1), pd.datetime(2020, 12, 1)]})
Rx.sort_values(['ID', 'Date'])
Out[26]:
ID Drug Date
0 1 B 2020-01-01
3 1 O 2020-02-01
6 1 T 2020-10-01
1 2 O 2020-01-01
4 2 A 2020-04-01
7 2 B 2020-11-01
8 2 G 2020-12-01
2 3 T 2020-01-01
5 3 G 2020-08-01
StudyPeriod
Out[27]:
ID StartDT EndDT
0 1 2020-01-01 2020-03-01
1 2 2020-04-01 2020-08-01
2 3 2020-07-01 2020-12-01
join_sql(df_a = StudyPeriod,
df_b = Rx,
query = \"""select b.*
from a as a left join b as b
on a.ID = b.ID
where a.StartDT <= b.Date and b.Date <= a.EndDT
\""")
Out[32]:
ID Drug Date
0 1 B 2020-01-01 00:00:00
1 1 O 2020-02-01 00:00:00
2 2 A 2020-04-01 00:00:00
3 3 G 2020-08-01 00:00:00
"""
#Make the db in memory
conn = sqlite3.connect(':memory:')
#write the tables
df_a.to_sql('a', conn, index=False)
df_b.to_sql('b', conn, index=False)
qry = query
df = pd.read_sql_query(qry, conn)
conn.close()
return df
Rx = pd.DataFrame({"ID":[1, 2, 3, 1, 2, 3, 1, 2, 2],
"Drug": ["B", "O", "T", 'O', 'A', 'G', 'T', 'B', 'G'],
"Date":[pd.datetime(2020, 1, 1), pd.datetime(2020, 1, 1), pd.datetime(2020, 1, 1),
pd.datetime(2020, 2, 1), pd.datetime(2020, 4, 1), pd.datetime(2020, 8, 1),
pd.datetime(2020, 10, 1), pd.datetime(2020, 11, 1), pd.datetime(2020, 12, 1)]})
StudyPeriod = pd.DataFrame({'ID':[1,2,3],
'StartDT':[pd.datetime(2020, 1, 1), pd.datetime(2020, 4, 1), pd.datetime(2020, 7, 1)],
'EndDT':[pd.datetime(2020, 3, 1), pd.datetime(2020, 8, 1), pd.datetime(2020, 12, 1)]})
Rx.sort_values(['ID', 'Date'])
StudyPeriod
sql_two_tables_between_dates(df_a = StudyPeriod,
df_b = Rx,
query = """select b.*
from a as a left join b as b
on a.ID = b.ID
where a.StartDT <= b.Date and b.Date <= a.EndDT
""")
```
|
github_jupyter
|
import sqlite3
import pandas as pd
def sql_two_tables_between_dates(df_a, df_b, query):
""" Example:
df_a = StudyPeriod,
df_b = Rx,
query = \"""select b.*
from a as a left join b as b
on a.ID = b.ID
where a.StartDT <= b.Date and b.Date <= a.EndDT
\""")
Rx = pd.DataFrame({"ID":[1, 2, 3, 1, 2, 3, 1, 2, 2],
"Drug": ["B", "O", "T", 'O', 'A', 'G', 'T', 'B', 'G'],
"Date":[pd.datetime(2020, 1, 1), pd.datetime(2020, 1, 1), pd.datetime(2020, 1, 1),
pd.datetime(2020, 2, 1), pd.datetime(2020, 4, 1), pd.datetime(2020, 8, 1),
pd.datetime(2020, 10, 1), pd.datetime(2020, 11, 1), pd.datetime(2020, 12, 1)]})
StudyPeriod = pd.DataFrame({'ID':[1,2,3],
'StartDT':[pd.datetime(2020, 1, 1), pd.datetime(2020, 4, 1), pd.datetime(2020, 7, 1)],
'EndDT':[pd.datetime(2020, 3, 1), pd.datetime(2020, 8, 1), pd.datetime(2020, 12, 1)]})
Rx.sort_values(['ID', 'Date'])
Out[26]:
ID Drug Date
0 1 B 2020-01-01
3 1 O 2020-02-01
6 1 T 2020-10-01
1 2 O 2020-01-01
4 2 A 2020-04-01
7 2 B 2020-11-01
8 2 G 2020-12-01
2 3 T 2020-01-01
5 3 G 2020-08-01
StudyPeriod
Out[27]:
ID StartDT EndDT
0 1 2020-01-01 2020-03-01
1 2 2020-04-01 2020-08-01
2 3 2020-07-01 2020-12-01
join_sql(df_a = StudyPeriod,
df_b = Rx,
query = \"""select b.*
from a as a left join b as b
on a.ID = b.ID
where a.StartDT <= b.Date and b.Date <= a.EndDT
\""")
Out[32]:
ID Drug Date
0 1 B 2020-01-01 00:00:00
1 1 O 2020-02-01 00:00:00
2 2 A 2020-04-01 00:00:00
3 3 G 2020-08-01 00:00:00
"""
#Make the db in memory
conn = sqlite3.connect(':memory:')
#write the tables
df_a.to_sql('a', conn, index=False)
df_b.to_sql('b', conn, index=False)
qry = query
df = pd.read_sql_query(qry, conn)
conn.close()
return df
Rx = pd.DataFrame({"ID":[1, 2, 3, 1, 2, 3, 1, 2, 2],
"Drug": ["B", "O", "T", 'O', 'A', 'G', 'T', 'B', 'G'],
"Date":[pd.datetime(2020, 1, 1), pd.datetime(2020, 1, 1), pd.datetime(2020, 1, 1),
pd.datetime(2020, 2, 1), pd.datetime(2020, 4, 1), pd.datetime(2020, 8, 1),
pd.datetime(2020, 10, 1), pd.datetime(2020, 11, 1), pd.datetime(2020, 12, 1)]})
StudyPeriod = pd.DataFrame({'ID':[1,2,3],
'StartDT':[pd.datetime(2020, 1, 1), pd.datetime(2020, 4, 1), pd.datetime(2020, 7, 1)],
'EndDT':[pd.datetime(2020, 3, 1), pd.datetime(2020, 8, 1), pd.datetime(2020, 12, 1)]})
Rx.sort_values(['ID', 'Date'])
StudyPeriod
sql_two_tables_between_dates(df_a = StudyPeriod,
df_b = Rx,
query = """select b.*
from a as a left join b as b
on a.ID = b.ID
where a.StartDT <= b.Date and b.Date <= a.EndDT
""")
| 0.359027 | 0.655991 |
# Day 14: Monte Carlo, Continued
---
Monte Carlo concepts
- Uncertainty propagation
- Estimating distributions
- Varying deterministic variables with `df_det`
- Random seeds / common random numbers
- Important for optimization; helps ensure smoothness
- Estimating probabilities
```
import pandas as pd
import grama as gr
import numpy as np
from plotnine import *
DF = gr.Intention()
```
## Monte Carlo on Grama Models
---
### Uncertainty Propagation
Remember from last time we looked at the example $F = Z^2$ where $Z \sim N(0, 1^2)$.
```
md_example = (
## Build a simple model
gr.Model()
>> gr.cp_vec_function(
fun=lambda df: gr.df_make(F=df.Z**2),
var=["Z"],
out=["F"],
)
>> gr.cp_marginals(Z=dict(dist="norm", loc=0, scale=1))
>> gr.cp_copula_independence()
)
(
md_example
## Approximate distribution using Monte Carlo
>> gr.ev_monte_carlo(n=1e4, df_det="nom")
## Do some data reshaping
>> gr.tf_gather("var", "value", ["F", "Z"])
## Visualize
>> ggplot(aes("value"))
+ geom_density()
# + geom_vline(xintercept=1, linetype="dashed")
+ facet_wrap("var")
+ theme_minimal()
+ labs(x="Quantity", y="Density")
)
```
Remind me: What observations did we have about these two random quantities $Z, F = Z^2$?
- ???
<br><br><br>
*Aside*: I did an exact comparison of $Z$ against $Z^2 \sim \chi^2_1$, and it turns out the point where $Z = Z^2 = 1$ has the same density. This somewhat endorses the "stretch-squeeze around 1" idea we discussed before.

<br><br><br>
> A function $f$ with random inputs $X$ will produce a random output $F$.
Note that if the inputs $X \in \mathbb{R}^d$ are *random* $X \sim \rho$, then any function of those random inputs is itself random $F = f(X) \sim \psi$. As we saw above, the distribution for $F \sim \psi$ can be weird and complicated.
> Random inputs are said to *induce* randomness on outputs.
Calling`gr.ev_monte_carlo()` on a Grama model draws random values for the `inputs` and computes values for each `output`.
```
(
md_example
>> gr.ev_monte_carlo(n=4, df_det="nom")
)
```
> `gr.ev_monte_carlo()` draws random inputs, and evaluates the model functions to produce random outputs.
We can do all kinds of useful work with these samples; let's look at that work in-context:
### Cantilever Beam model
As a running example, let's look at the cantilever beam model. The cantilever beam has a width $w$ and thickness $t$, elasticity $E$, yield strength $Y$, and is subjected to loads $H, V$.

Figure credit: [Richard W. Fenrich](https://arc.aiaa.org/doi/abs/10.2514/1.J058345).
There's a fair bit going on in this model, so the primary features I want you to concentrate on are the *limit state functions* `g_disp` and `g_stress`.
> For limit state functions $g$
> $$g > 0\text{ corresponds to success}$$
> $$g \leq 0\text{ corresponds to failure}$$
The beam limit states are
$$g_{\text{disp}} = \delta_{\max} - \delta_{tip}$$
$$g_{\text{stress}} = \sigma_{\max} - \sigma_{\text{applied}}$$
```
from grama.models import make_cantilever_beam
md_beam = make_cantilever_beam()
md_beam.printpretty()
```
### Estimating distributions
We talked about Monte Carlo as a way to approximate the mean of a random variable:
```
(
md_beam
>> gr.ev_monte_carlo(n=1e3, df_det="nom")
>> gr.tf_summarize(
g_disp_mean=gr.mean(DF.g_disp),
g_stress_mean=gr.mean(DF.g_stress),
)
)
```
These mean values are greater than zero, which is a positive indication. We want $g > 0$, so *on average* the structure seems safe. But remember that the mean is only a typical value; what if we want a beam that isn't just "typically" safe?
> For a critical failure mode, we don't just want it to *typically* work! Therefore the mean of a limit state $g$ isn't the right quantity to study.
When we want more than just the mean; calling `gr.plot_auto()` on the output of `gr.eval_monte_carlo()` will automatically plot a histogram for each output:
```
(
md_beam
>> gr.ev_monte_carlo(n=1e3, df_det="nom")
>> gr.pt_auto()
)
```
Remember that:
$$g > 0\text{ corresponds to success}$$
$$g \leq 0\text{ corresponds to failure}$$
Based on these histograms, how safe does the cantilever beam seem to be?
<br><br><br>
Now we can see that a small fraction of the distributions for `g_disp` and `g_stress` lie below zero; this indicates a small---but nonzero---probability of failure.
These histograms are an *approximation* of the real density for the outputs.
### Sweeping deterministic values
Let's take another look at the `printpretty()` output of `md_beam`; note that it has both deterministic and random variables:
```
md_beam.printpretty()
```
Note that the beam model has both *deterministic* and *random* variables:
| Input | Type | Meaning |
|---|---|---|
| `w` | Deterministic | Design variable: Width |
| `t` | Deterministic | Design variable: Thickness |
| `H` | Random | Uncertainty: Horizontal tip load |
| `V` | Random | Uncertainty: Vertical tip load |
| `E` | Random | Uncertainty: Material elasticity |
| `Y` | Random | Uncertainty: Material (yield) strength |
What happens to the deterministic variables `w, t` when we set `df_det="nom"`?
```
(
md_beam
>> gr.ev_monte_carlo(n=4, df_det="nom")
)
```
What values do `w, t` take?
<br><br><br>
Note that `w, t` take single, fixed values. Setting `df_det="nom"` sets *nominal* values for all the deterministic inputs. Note that if you want to set specific values for the deterministic variables, you can set `df_det` to a DataFrame of desired values.
> The `df_det` argument allows you to sweep deterministic variables with Monte Carlo
The helper `gr.df_make()` is a convenient way to make a DataFrame; in particular, you can hold one or more values constant and sweep one value. For instance, the line
`gr.df_make(w=3.0, t=np.linspace(2, 4))`
will set `w == 3.0` and sweep over values of `t`.
```
(
## Generate a Monte Carlo sample, sweep with values of t
md_beam
>> gr.ev_monte_carlo(
n=3,
df_det=gr.df_make(w=3.0, t=np.linspace(2, 4, num=4)),
)
## Summarize
>> gr.tf_summarize(
g_stress_mean=gr.mean(DF.g_stress),
g_stress_sd=gr.sd(DF.g_stress),
)
)
```
We swept over values of $t$, so why doesn't $t$ show up in these results?
<br><br><br>
In order to avoid summarizing over the different samples for different values of $t$, we need to `gr.tf_group_by(DF.t)` to compute each mean/sd within a *group* defined by unique values of $t$.
```
(
## Generate a Monte Carlo sample at values of t
md_beam
>> gr.ev_monte_carlo(
n=1e2,
df_det=gr.df_make(w=3.0, t=np.linspace(2, 4, num=6)),
)
## Define a grouping of the DataFrame
>> gr.tf_group_by(DF.t)
## Summarize at each value of t
>> gr.tf_summarize(
g_stress_mean=gr.mean(DF.g_stress),
g_stress_sd=gr.sd(DF.g_stress),
)
)
```
> When sweeping with `df_det`, we need to use a `gr.tf_group_by()` before summarizing.
Using a `gr.tf_group_by()` before the summary provides a mean and standard deviation at each value of `t`, which we can plot:
```
(
## Generate a Monte Carlo sample at values of t
md_beam
>> gr.ev_monte_carlo(
n=1e2,
df_det=gr.df_make(w=3.0, t=np.linspace(2, 4)),
)
## Summarize at each value of t
>> gr.tf_group_by(DF.t)
>> gr.tf_summarize(
g_stress_mean=gr.mean(DF.g_stress),
g_stress_sd=gr.sd(DF.g_stress),
)
## Visualize
>> ggplot(aes("t"))
+ geom_hline(yintercept=0, color="salmon")
+ geom_ribbon(
aes(
ymin="g_stress_mean - g_stress_sd",
ymax="g_stress_mean + g_stress_sd",
),
alpha=1/3,
)
+ geom_line(aes(y="g_stress_mean"))
+ labs(
x="Thickness (in)",
y="Limit State: Stress (-)",
)
)
```
This is great, because we can think of the standard deviation as a means to add a *principled* margin-of-safety to our design. We could---for instance---choose a thickness $t$ where the shaded band is above zero. We'll see a more principled way to use this information for design when we talk about *reliability* later.
### Random seeds
One of the key arguments to `gr.eval_monte_carlo()` is `seed`; this sets the [random seed](https://en.wikipedia.org/wiki/Random_seed) for [pseudorandom](https://en.wikipedia.org/wiki/Pseudorandomness) number generation. Setting a fixed seed will "fix" the values generated by `gr.eval_monte_carlo()`. This raises all kinds of questions about "what is random?" that we won't get into in this class....
*Aside*: Before the advent of modern computing and access to high-quality pseudorandom number generators, scientists would use dice, wheels, and [published tables of randomly-generated digits](https://en.wikipedia.org/wiki/A_Million_Random_Digits_with_100,000_Normal_Deviates). This has led to some humorous [Amazon reviews](https://www.amazon.com/product-reviews/0833030477/). There is, *astoundingly*, an [audiobook](http://amillionrandomdigits.com/index.html) version of this work as well.
```
# Reset the seed for this demo
np.random.seed()
# Note the difference between these two lines....
df_sample_rand = gr.eval_monte_carlo(md_beam, n=10, df_det="nom")
df_sample_fixed = gr.eval_monte_carlo(md_beam, n=10, df_det="nom", seed=101)
# Visualize both samples
(
df_sample_rand
>> gr.tf_mutate(source="seed: reset")
>> gr.tf_bind_rows(
df_sample_fixed
>> gr.tf_mutate(source="seed: fixed")
)
>> ggplot(aes("H", "V"))
+ geom_point()
+ coord_cartesian(
xlim=(300, 650),
ylim=(850, 1250),
)
+ facet_wrap("source")
+ labs(x="H: Horizontal load", y="V: Vertical load")
)
```
Note that with a fixed seed the random numbers don't change. Setting the seed gives us a fixed sample. Here's a rough rule-of-thumb on setting seeds:
> - When testing the statistical properties of a random algorithm, it's important to test a variety of seeds.
> - When using a random algorithm to do design, it's best to fix a single seed.
Fixing a random seed allows us to generate *common random numbers*.
### Common random numbers
Remember how we did a sweep over `t` with the beam model? The response looks smooth. That's because `gr.eval_monte_carlo()` uses a single sample (set of realizations) for each setting of the deterministic variables. If we plot each realization $t$, we'll see points that appear to form curves:
```
(
## Generate a Monte Carlo sample at values of t
md_beam
>> gr.ev_monte_carlo(
n=25,
df_det=gr.df_make(w=3.0, t=np.linspace(2, 4)),
)
## Visualize each realization; we get smooth sweeps across `t`
>> ggplot(aes("t", "g_stress"))
+ geom_line(aes(group="E"), color="grey", size=0.1, alpha=1/3)
+ geom_point(size=0.1)
+ theme_minimal()
+ labs(
x="Thickness (in)",
y="Limit State: Stress (-)"
)
)
```
If we *instead* draw an independent sample for each value of $t$, we will no longer see a "smooth" response:
```
## Purposefully draw an independent sample for each t value
df_sweep_t = gr.df_make(w=3.0, t=np.linspace(2, 4))
df_sweep = pd.DataFrame()
for i in range(df_sweep_t.shape[0]):
df_tmp = (
md_beam
>> gr.ev_monte_carlo(
n=25,
df_det=df_sweep_t.iloc[[i]],
# seed=101, # Set seed for common random numbers
)
)
df_sweep = pd.concat((df_tmp, df_sweep), axis=0)
(
df_sweep
>> ggplot(aes("t", "g_stress"))
+ geom_point(aes(group="E"), size=0.1)
+ theme_minimal()
+ labs(
x="Thickness (in)",
y="Limit State: Stress (-)"
)
)
```
Where this really matters is in using these results to do *optimization*; imagine we aim to find the point in `t` where the mean of `g_stress` crosses zero. The following curve shows us that using independent samples will give us a jagged curve, which will in turn make optimization using this result challenging:
```
(
df_sweep
## Summarize at each value of t
>> gr.tf_group_by(DF.t)
>> gr.tf_summarize(
g_stress_mean=gr.mean(DF.g_stress),
g_stress_sd=gr.sd(DF.g_stress),
)
>> ggplot(aes("t"))
+ geom_hline(yintercept=0, color="salmon")
+ geom_ribbon(aes(ymin="g_stress_mean - g_stress_sd", ymax="g_stress_mean + g_stress_sd"), alpha=1/3)
+ geom_line(aes(y="g_stress_mean"))
+ labs(
x="Thickness (in)",
y="Limit State: Stress (-)",
title="Method: Independent Samples"
)
)
```
The *one simple change* you can make to deal with this is give an integer value for `seed` when calling `gr.eval_monte_carlo()`. This will give you *common random numbers* across different values of the deterministic variables.
```
## Purposefully draw an independent sample for each t value
df_sweep_t = gr.df_make(w=3.0, t=np.linspace(2, 4))
df_sweep_com = pd.DataFrame()
for i in range(df_sweep_t.shape[0]):
df_tmp = (
md_beam
>> gr.ev_monte_carlo(
n=25,
df_det=df_sweep_t.iloc[[i]],
seed=101, # Set seed for common random numbers
)
)
df_sweep_com = pd.concat((df_tmp, df_sweep_com), axis=0)
## Visualize
(
# Summarize the data
df_sweep_com
>> gr.tf_group_by(DF.t)
>> gr.tf_summarize(
g_stress_mean=gr.mean(DF.g_stress),
g_stress_sd=gr.sd(DF.g_stress),
)
>> gr.tf_mutate(method="Method: Common Random Numbers")
# Bind previous results for comparison
>> gr.tf_bind_rows(
df_sweep
>> gr.tf_group_by(DF.t)
>> gr.tf_summarize(
g_stress_mean=gr.mean(DF.g_stress),
g_stress_sd=gr.sd(DF.g_stress),
)
>> gr.tf_mutate(method="Method: Independent Samples")
)
# Make the visual
>> ggplot(aes("t"))
+ geom_hline(yintercept=0, color="salmon")
+ geom_ribbon(aes(ymin="g_stress_mean - g_stress_sd", ymax="g_stress_mean + g_stress_sd"), alpha=1/3)
+ geom_line(aes(y="g_stress_mean"))
+ facet_wrap("method")
+ labs(
x="Thickness (in)",
y="Limit State: Stress (-)",
)
)
```
> Common random numbers are important when doing sweeps or optimization.
> You can set a fixed seed in Monte Carlo to use common random numbers.
## Estimating Probabilities
---
Remember that probability is the area under the PDF; this is an integral over a desired set $A$.
$$\mathbb{P}[X \in A] = \int_A \rho(x)dx$$
We're going to re-express probability in terms of a mean (expectation); this will allow us to use Monte Carlo to estimate probabilities. First, let's define the *indicator function* $1(x \in A)$, which is the function
$$1(x \in A) = \left\{\begin{array}{ll} 1 & x \in A \\ 0 & x \not\in A\end{array}\right.$$
This allows us to re-express an integral over a set $A$ to an integral over the entire domain
$$\int_A \rho(x)dx = \int_{\mathbb{R}^d} 1(x \in A)\rho(x) dx.$$
But remember that an integral of a random variable against its density is nothing more than the mean:
$$\int_{\mathbb{R}^d} 1(x \in A)\rho(x) dx = \mathbb{E}[1(X \in A)]$$
Chaining all these expressions together, we can state
$$\mathbb{P}[X \in A] = \mathbb{E}[1(X \in A)].$$
We can estimate a probability using Monte Carlo by using this framing as a mean:
$$\mathbb{E}[1(X \in A)] \approx \frac{1}{n}\sum_{i=1}^n 1(X_i \in A)$$
> The probability of an event $X \in A$ can be approximated using Monte Carlo. To do this, you must use an indicator function $I = 1(X \in A)$ and approximate the mean of $I$.
### Using the Indicator Function
For us to make use of the Monte Carlo estimator $\mathbb{E}[1(X \in A)] \approx \frac{1}{n}\sum_{i=1}^n 1(X_i \in A)$, we need to define a set $A$, and construct an indicator to reflect that set. For example, with the cantilever beam problem, we have
$$g > 0\text{ corresponds to success}$$
$$g \leq 0\text{ corresponds to failure}$$
So if we wanted to compute the probability of failure, we would define $A = \{x\,|\,g(x) \leq 0\}$.
In Python, we can directly use inequalities to implement an indicator function; for instance, the code
`df.g_stress <= 0`
will return a Series (column) which will take the value `True` when `g_stress <=0`, and the value `False` when `g_stress > 0`.
### Boolean Arithmetic
You might be wondering how we can *possibly* do math with `True` and `False` values. Something important to know is that Python treats `True == 1` and `False == 0`. This means we can do math with boolean values:
```
True == 1
False == 0
0 + True
```
Importantly, this means we can compute the proportion of `True`'s in a boolean array by taking its mean:
```
np.mean([True, False])
```
### Computing probabilities of failure with the beam model
Let's use this idea to approximate the probabilities of failure for the cantilever beam model.
```
## TODO: Someone help me write this code!
(
md_beam
)
(
md_beam
>> gr.ev_monte_carlo(n=1e3, df_det="nom")
>> gr.tf_mutate(
fail_stress=DF.g_stress <= 0,
fail_disp=DF.g_disp <= 0,
)
>> gr.tf_summarize(
pof_stress_mu=gr.mean(DF.fail_stress),
pof_disp_mu=gr.mean(DF.fail_disp),
)
)
```
We can use `gr.binomial_ci()` to compute lower and upper confidence bounds for a probability:
```
(
md_beam
>> gr.ev_monte_carlo(n=1e3, df_det="nom")
>> gr.tf_mutate(
fail_stress=DF.g_stress <= 0,
fail_disp=DF.g_disp <= 0,
)
>> gr.tf_summarize(
pof_stress_lo=gr.binomial_ci(DF.fail_stress, side="lo"),
pof_stress_mu=gr.mean(DF.fail_stress),
pof_stress_up=gr.binomial_ci(DF.fail_stress, side="up"),
pof_disp_lo=gr.binomial_ci(DF.fail_disp, side="lo"),
pof_disp_mu=gr.mean(DF.fail_disp),
pof_disp_up=gr.binomial_ci(DF.fail_disp, side="up"),
)
)
```
Let's visualize the results; how do they change with Monte Carlo sample size $n$?
```
(
md_beam
>> gr.ev_monte_carlo(n=10, df_det="nom")
# >> gr.ev_monte_carlo(n=1e3, df_det="nom")
>> gr.tf_mutate(
fail_stress=DF.g_stress <= 0,
fail_disp=DF.g_disp <= 0,
)
>> gr.tf_summarize(
pof_stress_lo=gr.binomial_ci(DF.fail_stress, side="lo"),
pof_stress_mu=gr.mean(DF.fail_stress),
pof_stress_up=gr.binomial_ci(DF.fail_stress, side="up"),
pof_disp_lo=gr.binomial_ci(DF.fail_disp, side="lo"),
pof_disp_mu=gr.mean(DF.fail_disp),
pof_disp_up=gr.binomial_ci(DF.fail_disp, side="up"),
)
## Data reshaping
>> gr.tf_gather(
"key",
"value",
gr.everything(),
)
>> gr.tf_mutate(
stat=gr.str_sub(DF.key, start=-2),
mode=gr.str_sub(DF.key, start=4, end=-3),
)
>> gr.tf_select("value", "stat", "mode")
>> gr.tf_spread("stat", "value")
## Visualize
>> ggplot(aes("mode"))
+ geom_point(aes(y="mu"))
+ geom_errorbar(aes(ymin="lo", ymax="up"))
+ coord_cartesian(ylim=(0, 1))
+ labs(
x="Failure Modes",
y="Probability of Failure",
)
)
```
|
github_jupyter
|
import pandas as pd
import grama as gr
import numpy as np
from plotnine import *
DF = gr.Intention()
md_example = (
## Build a simple model
gr.Model()
>> gr.cp_vec_function(
fun=lambda df: gr.df_make(F=df.Z**2),
var=["Z"],
out=["F"],
)
>> gr.cp_marginals(Z=dict(dist="norm", loc=0, scale=1))
>> gr.cp_copula_independence()
)
(
md_example
## Approximate distribution using Monte Carlo
>> gr.ev_monte_carlo(n=1e4, df_det="nom")
## Do some data reshaping
>> gr.tf_gather("var", "value", ["F", "Z"])
## Visualize
>> ggplot(aes("value"))
+ geom_density()
# + geom_vline(xintercept=1, linetype="dashed")
+ facet_wrap("var")
+ theme_minimal()
+ labs(x="Quantity", y="Density")
)
(
md_example
>> gr.ev_monte_carlo(n=4, df_det="nom")
)
from grama.models import make_cantilever_beam
md_beam = make_cantilever_beam()
md_beam.printpretty()
(
md_beam
>> gr.ev_monte_carlo(n=1e3, df_det="nom")
>> gr.tf_summarize(
g_disp_mean=gr.mean(DF.g_disp),
g_stress_mean=gr.mean(DF.g_stress),
)
)
(
md_beam
>> gr.ev_monte_carlo(n=1e3, df_det="nom")
>> gr.pt_auto()
)
md_beam.printpretty()
(
md_beam
>> gr.ev_monte_carlo(n=4, df_det="nom")
)
(
## Generate a Monte Carlo sample, sweep with values of t
md_beam
>> gr.ev_monte_carlo(
n=3,
df_det=gr.df_make(w=3.0, t=np.linspace(2, 4, num=4)),
)
## Summarize
>> gr.tf_summarize(
g_stress_mean=gr.mean(DF.g_stress),
g_stress_sd=gr.sd(DF.g_stress),
)
)
(
## Generate a Monte Carlo sample at values of t
md_beam
>> gr.ev_monte_carlo(
n=1e2,
df_det=gr.df_make(w=3.0, t=np.linspace(2, 4, num=6)),
)
## Define a grouping of the DataFrame
>> gr.tf_group_by(DF.t)
## Summarize at each value of t
>> gr.tf_summarize(
g_stress_mean=gr.mean(DF.g_stress),
g_stress_sd=gr.sd(DF.g_stress),
)
)
(
## Generate a Monte Carlo sample at values of t
md_beam
>> gr.ev_monte_carlo(
n=1e2,
df_det=gr.df_make(w=3.0, t=np.linspace(2, 4)),
)
## Summarize at each value of t
>> gr.tf_group_by(DF.t)
>> gr.tf_summarize(
g_stress_mean=gr.mean(DF.g_stress),
g_stress_sd=gr.sd(DF.g_stress),
)
## Visualize
>> ggplot(aes("t"))
+ geom_hline(yintercept=0, color="salmon")
+ geom_ribbon(
aes(
ymin="g_stress_mean - g_stress_sd",
ymax="g_stress_mean + g_stress_sd",
),
alpha=1/3,
)
+ geom_line(aes(y="g_stress_mean"))
+ labs(
x="Thickness (in)",
y="Limit State: Stress (-)",
)
)
# Reset the seed for this demo
np.random.seed()
# Note the difference between these two lines....
df_sample_rand = gr.eval_monte_carlo(md_beam, n=10, df_det="nom")
df_sample_fixed = gr.eval_monte_carlo(md_beam, n=10, df_det="nom", seed=101)
# Visualize both samples
(
df_sample_rand
>> gr.tf_mutate(source="seed: reset")
>> gr.tf_bind_rows(
df_sample_fixed
>> gr.tf_mutate(source="seed: fixed")
)
>> ggplot(aes("H", "V"))
+ geom_point()
+ coord_cartesian(
xlim=(300, 650),
ylim=(850, 1250),
)
+ facet_wrap("source")
+ labs(x="H: Horizontal load", y="V: Vertical load")
)
(
## Generate a Monte Carlo sample at values of t
md_beam
>> gr.ev_monte_carlo(
n=25,
df_det=gr.df_make(w=3.0, t=np.linspace(2, 4)),
)
## Visualize each realization; we get smooth sweeps across `t`
>> ggplot(aes("t", "g_stress"))
+ geom_line(aes(group="E"), color="grey", size=0.1, alpha=1/3)
+ geom_point(size=0.1)
+ theme_minimal()
+ labs(
x="Thickness (in)",
y="Limit State: Stress (-)"
)
)
## Purposefully draw an independent sample for each t value
df_sweep_t = gr.df_make(w=3.0, t=np.linspace(2, 4))
df_sweep = pd.DataFrame()
for i in range(df_sweep_t.shape[0]):
df_tmp = (
md_beam
>> gr.ev_monte_carlo(
n=25,
df_det=df_sweep_t.iloc[[i]],
# seed=101, # Set seed for common random numbers
)
)
df_sweep = pd.concat((df_tmp, df_sweep), axis=0)
(
df_sweep
>> ggplot(aes("t", "g_stress"))
+ geom_point(aes(group="E"), size=0.1)
+ theme_minimal()
+ labs(
x="Thickness (in)",
y="Limit State: Stress (-)"
)
)
(
df_sweep
## Summarize at each value of t
>> gr.tf_group_by(DF.t)
>> gr.tf_summarize(
g_stress_mean=gr.mean(DF.g_stress),
g_stress_sd=gr.sd(DF.g_stress),
)
>> ggplot(aes("t"))
+ geom_hline(yintercept=0, color="salmon")
+ geom_ribbon(aes(ymin="g_stress_mean - g_stress_sd", ymax="g_stress_mean + g_stress_sd"), alpha=1/3)
+ geom_line(aes(y="g_stress_mean"))
+ labs(
x="Thickness (in)",
y="Limit State: Stress (-)",
title="Method: Independent Samples"
)
)
## Purposefully draw an independent sample for each t value
df_sweep_t = gr.df_make(w=3.0, t=np.linspace(2, 4))
df_sweep_com = pd.DataFrame()
for i in range(df_sweep_t.shape[0]):
df_tmp = (
md_beam
>> gr.ev_monte_carlo(
n=25,
df_det=df_sweep_t.iloc[[i]],
seed=101, # Set seed for common random numbers
)
)
df_sweep_com = pd.concat((df_tmp, df_sweep_com), axis=0)
## Visualize
(
# Summarize the data
df_sweep_com
>> gr.tf_group_by(DF.t)
>> gr.tf_summarize(
g_stress_mean=gr.mean(DF.g_stress),
g_stress_sd=gr.sd(DF.g_stress),
)
>> gr.tf_mutate(method="Method: Common Random Numbers")
# Bind previous results for comparison
>> gr.tf_bind_rows(
df_sweep
>> gr.tf_group_by(DF.t)
>> gr.tf_summarize(
g_stress_mean=gr.mean(DF.g_stress),
g_stress_sd=gr.sd(DF.g_stress),
)
>> gr.tf_mutate(method="Method: Independent Samples")
)
# Make the visual
>> ggplot(aes("t"))
+ geom_hline(yintercept=0, color="salmon")
+ geom_ribbon(aes(ymin="g_stress_mean - g_stress_sd", ymax="g_stress_mean + g_stress_sd"), alpha=1/3)
+ geom_line(aes(y="g_stress_mean"))
+ facet_wrap("method")
+ labs(
x="Thickness (in)",
y="Limit State: Stress (-)",
)
)
True == 1
False == 0
0 + True
np.mean([True, False])
## TODO: Someone help me write this code!
(
md_beam
)
(
md_beam
>> gr.ev_monte_carlo(n=1e3, df_det="nom")
>> gr.tf_mutate(
fail_stress=DF.g_stress <= 0,
fail_disp=DF.g_disp <= 0,
)
>> gr.tf_summarize(
pof_stress_mu=gr.mean(DF.fail_stress),
pof_disp_mu=gr.mean(DF.fail_disp),
)
)
(
md_beam
>> gr.ev_monte_carlo(n=1e3, df_det="nom")
>> gr.tf_mutate(
fail_stress=DF.g_stress <= 0,
fail_disp=DF.g_disp <= 0,
)
>> gr.tf_summarize(
pof_stress_lo=gr.binomial_ci(DF.fail_stress, side="lo"),
pof_stress_mu=gr.mean(DF.fail_stress),
pof_stress_up=gr.binomial_ci(DF.fail_stress, side="up"),
pof_disp_lo=gr.binomial_ci(DF.fail_disp, side="lo"),
pof_disp_mu=gr.mean(DF.fail_disp),
pof_disp_up=gr.binomial_ci(DF.fail_disp, side="up"),
)
)
(
md_beam
>> gr.ev_monte_carlo(n=10, df_det="nom")
# >> gr.ev_monte_carlo(n=1e3, df_det="nom")
>> gr.tf_mutate(
fail_stress=DF.g_stress <= 0,
fail_disp=DF.g_disp <= 0,
)
>> gr.tf_summarize(
pof_stress_lo=gr.binomial_ci(DF.fail_stress, side="lo"),
pof_stress_mu=gr.mean(DF.fail_stress),
pof_stress_up=gr.binomial_ci(DF.fail_stress, side="up"),
pof_disp_lo=gr.binomial_ci(DF.fail_disp, side="lo"),
pof_disp_mu=gr.mean(DF.fail_disp),
pof_disp_up=gr.binomial_ci(DF.fail_disp, side="up"),
)
## Data reshaping
>> gr.tf_gather(
"key",
"value",
gr.everything(),
)
>> gr.tf_mutate(
stat=gr.str_sub(DF.key, start=-2),
mode=gr.str_sub(DF.key, start=4, end=-3),
)
>> gr.tf_select("value", "stat", "mode")
>> gr.tf_spread("stat", "value")
## Visualize
>> ggplot(aes("mode"))
+ geom_point(aes(y="mu"))
+ geom_errorbar(aes(ymin="lo", ymax="up"))
+ coord_cartesian(ylim=(0, 1))
+ labs(
x="Failure Modes",
y="Probability of Failure",
)
)
| 0.674265 | 0.957078 |
# 라이브러리 임포트
```
import sys
# 예제 파일 경로로 수정한 다음 주석 해제
# sys.path.append(r'/to/your/example_code/path/lincoln')
# imports
from typing import Tuple, List
from collections import deque
import torch
import torch.optim as optim
from torch.optim import lr_scheduler
from torch.optim import Optimizer
import numpy as np
from torch import Tensor
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.modules.loss import _Loss
from lincoln.pytorch.layers import PyTorchLayer, DenseLayer
from lincoln.pytorch.model import PyTorchModel
from lincoln.pytorch.train import PyTorchTrainer
from lincoln.pytorch.preprocessor import ConvNetPreprocessor
from lincoln.pytorch.utils import assert_dim, permute_data
torch.manual_seed(20190325);
%load_ext autoreload
%autoreload 2
```
# 주택가격 데이터셋
```
from sklearn.datasets import load_boston
boston = load_boston()
data = boston.data
target = boston.target
features = boston.feature_names
from sklearn.preprocessing import StandardScaler
s = StandardScaler()
data = s.fit_transform(data)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=0.3, random_state=80718)
y_train, y_test = y_train.reshape(-1, 1), y_test.reshape(-1, 1)
X_train, X_test, y_train, y_test = Tensor(X_train), Tensor(X_test), Tensor(y_train), Tensor(y_test)
```
## 주택가격 예측 모델 정의
```
class BostonModel(PyTorchModel):
def __init__(self,
hidden_size: int = 13,
hidden_dropout: float = 1.0):
super().__init__()
self.dense1 = DenseLayer(13, hidden_size,
activation=nn.Tanh(),
dropout = hidden_dropout)
self.dense2 = DenseLayer(hidden_size, 1)
def forward(self, x: Tensor,
inference: bool = False) -> Tensor:
assert_dim(x, 2)
assert x.shape[1] == 13
x = self.dense1(x, inference)
return self.dense2(x, inference),
```
## 학습률 감쇠 구현
```
# model, optimizer, loss
pytorch_boston_model = BostonModel(hidden_size=13, hidden_dropout=0.8)
optimizer = optim.SGD(pytorch_boston_model.parameters(), lr=0.001, momentum=0.9)
criterion = nn.MSELoss()
trainer = PyTorchTrainer(pytorch_boston_model, optimizer, criterion)
trainer.fit(X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test,
epochs=100,
eval_every=10,
final_lr_exp = 0.001)
torch.mean(torch.pow(pytorch_boston_model(X_test, inference=True)[0] - y_test, 2)).item()
test_pred = pytorch_boston_model(X_test)[0].view(-1)
test_actual = y_test
test_pred = test_pred.detach().numpy()
test_actual = test_actual.detach().numpy()
```
## 주택 가격 데이터 - 데이터 탐색
```
import matplotlib.pyplot as plt
%matplotlib inline
plt.scatter(test_pred, test_actual)
```
# 파이토치로 CNN 구현하기
`DataLoader`를 사용한 예와 사용하지 않은 예의 순서대로 살펴보자.
```
import torchvision
from torchvision.datasets import MNIST
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
img_transforms = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1305,), (0.3081,))
])
# https://pytorch.org/docs/stable/data.html
train_dataset = MNIST(root='../mnist_data/',
train=True,
download=True,
transform=img_transforms)
test_dataset = MNIST(root='../mnist_data/',
train=False,
download=True,
transform=img_transforms)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=60,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=60,
shuffle=False)
class ConvLayer(PyTorchLayer):
def __init__(self,
in_channels: int,
out_channels: int,
filter_size: int,
activation: nn.Module = None,
dropout: float = 1.0,
flatten: bool = False) -> None:
super().__init__()
self.conv = nn.Conv2d(in_channels, out_channels, filter_size,
padding=filter_size // 2)
self.activation = activation
self.flatten = flatten
if dropout < 1.0:
self.dropout = nn.Dropout(1 - dropout)
def forward(self, x: Tensor) -> Tensor:
x = self.conv(x)
if self.activation:
x = self.activation(x)
if self.flatten:
x = x.view(x.shape[0], x.shape[1] * x.shape[2] * x.shape[3])
if hasattr(self, "dropout"):
x = self.dropout(x)
return x
class MNIST_ConvNet(PyTorchModel):
def __init__(self):
super().__init__()
self.conv1 = ConvLayer(1, 14, 5, activation=nn.Tanh(),
dropout=0.8)
self.conv2 = ConvLayer(14, 7, 5, activation=nn.Tanh(), flatten=True,
dropout=0.8)
self.dense1 = DenseLayer(28 * 28 * 7, 32, activation=nn.Tanh(),
dropout=0.8)
self.dense2 = DenseLayer(32, 10)
def forward(self, x: Tensor) -> Tensor:
assert_dim(x, 4)
x = self.conv1(x)
x = self.conv2(x)
x = self.dense1(x)
x = self.dense2(x)
return x,
model = MNIST_ConvNet()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
```
### `Dataloader`를 사용한 경우
```
trainer = PyTorchTrainer(model, optimizer, criterion)
trainer.fit(train_dataloader = train_loader,
test_dataloader = test_loader,
epochs = 1,
eval_every = 1)
```
## `DataLoader`를 사용했을 때 정확도
```
def test_accuracy(model):
model.eval()
accuracies = []
for X_batch, y_batch in test_loader:
output = model(X_batch)[0]
accuracy_batch = (torch.max(output, dim=1)[1] == y_batch).type(torch.float32).mean().item()
accuracies.append(accuracy_batch)
return torch.Tensor(accuracies).mean().item()
test_accuracy(model)
```
## `DataLoader`를 사용하지 않은 경우
### 전처리
```
mnist_train = ((train_dataset.data.type(torch.float32).unsqueeze(3).permute(0, 3, 1, 2) / 255.0) - 0.1305) / 0.3081
mnist_test = ((test_dataset.data.type(torch.float32).unsqueeze(3).permute(0, 3, 1, 2) / 255.0) - 0.1305) / 0.3081
mnist_train.min(), mnist_train.max(), mnist_test.min(), mnist_test.max()
```
### 학습
```
trainer = PyTorchTrainer(model, optimizer, criterion)
trainer.fit(X_train=mnist_train, y_train=train_dataset.targets,
X_test=mnist_test, y_test=test_dataset.targets,
epochs=1,
eval_every=1)
```
### 성능 측정
```
def test_accuracy_no_dataloader(model, mnist_test):
model.eval()
output = model(mnist_test)[0]
return (torch.max(output, dim=1)[1] == test_dataset.test_labels).type(torch.float32).mean().item()
test_accuracy_no_dataloader(model, mnist_test)
```
~97.3% 정확도
# LSTM
## `LSTMLayer`
```
class LSTMLayer(PyTorchLayer):
def __init__(self,
sequence_length: int,
input_size: int,
hidden_size: int,
output_size: int,
dropout: float = 1.0) -> None:
super().__init__()
self.hidden_size = hidden_size
self.h_init = torch.zeros((1, hidden_size))
self.c_init = torch.zeros((1, hidden_size))
self.lstm = nn.LSTM(input_size, hidden_size, batch_first=True)
self.fc = DenseLayer(hidden_size, output_size)
if dropout < 1.0:
self.dropout = nn.Dropout(1 - dropout)
def _transform_hidden_batch(self, hidden: Tensor,
batch_size: int,
before_layer: bool) -> Tensor:
if before_layer:
return (hidden
.repeat(batch_size, 1)
.view(batch_size, 1, self.hidden_size)
.permute(1,0,2))
else:
return (hidden
.permute(1,0,2)
.mean(dim=0))
def forward(self, x: Tensor) -> Tensor:
batch_size = x.shape[0]
h_layer = self._transform_hidden_batch(self.h_init, batch_size, before_layer=True)
c_layer = self._transform_hidden_batch(self.c_init, batch_size, before_layer=True)
x, (h_out, c_out) = self.lstm(x, (h_layer, c_layer))
self.h_init, self.c_init = (
self._transform_hidden_batch(h_out, batch_size, before_layer=False).detach(),
self._transform_hidden_batch(c_out, batch_size, before_layer=False).detach()
)
x = self.fc(x)
if hasattr(self, "dropout"):
x = self.dropout(x)
return x
lay = LSTMLayer(sequence_length=25,
input_size=62,
hidden_size=100,
output_size=128)
x = torch.randn(32, 25, 62)
lay(x).shape
```
## `NextCharacterModel`
```
class NextCharacterModel(PyTorchModel):
def __init__(self,
vocab_size: int,
hidden_size: int = 256,
sequence_length: int = 25):
super().__init__()
self.vocab_size = vocab_size
self.sequence_length = sequence_length
# 이 모델에는 층이 하나 뿐이며
# 이 층의 출력은 입력과 모양이 같다
self.lstm = LSTMLayer(self.sequence_length, self.vocab_size, hidden_size, self.vocab_size)
def forward(self,
inputs: Tensor):
assert_dim(inputs, 3) # batch_size, sequence_length, vocab_size
out = self.lstm(inputs)
return out.permute(0, 2, 1),
```
## `LSTMTrainer`
```
class LSTMTrainer(PyTorchTrainer):
def __init__(self,
model: NextCharacterModel,
optim: Optimizer,
criterion: _Loss):
super().__init__(model, optim, criterion)
self.vocab_size = self.model.vocab_size
self.max_len = self.model.sequence_length
def fit(self,
data: str,
epochs: int=10,
eval_every: int=1,
batch_size: int=32,
seed: int = 121718)-> None:
self.data = data
self.train_data, self.test_data = self._train_test_split_text()
self.chars = list(set(self.data))
self.char_to_idx = {ch: i for i, ch in enumerate(self.chars)}
self.idx_to_char = {i: ch for i, ch in enumerate(self.chars)}
torch.manual_seed(seed)
losses = deque(maxlen=50)
for e in range(epochs):
batch_generator = self.generate_batches_next_char(batch_size)
for ii, (X_batch, y_batch) in enumerate(batch_generator):
self.optim.zero_grad()
outputs = self.model(X_batch)[0]
loss = self.loss(outputs, y_batch)
losses.append(loss.item())
loss.backward()
self.optim.step()
if (e+1) % eval_every == 0:
X_test, y_test = self.generate_test_data()
test_preds = self.model.forward(X_test)[0]
loss = self.loss.forward(test_preds, y_test)
print(f"{e+1}에폭에서 검증 데이터에 대한 손실값: {loss.item():.3f}")
def _train_test_split_text(self, pct=0.8) -> Tuple[str]:
n = len(self.data)
return self.data[:int(n * pct)], self.data[int(n * pct):]
def generate_batches_next_char(self,
batch_size: int) -> Tuple[Tensor]:
N = len(self.train_data)
# add batch size
for ii in range(0, N, batch_size):
features_tensors = []
target_indices = []
for char in range(batch_size):
features_str, target_str =\
self.train_data[ii+char:ii+char+self.max_len],\
self.train_data[ii+char+1:ii+char+self.max_len+1]
features_array = self._string_to_one_hot_array(features_str)
target_indices_seq = [self.char_to_idx[char] for char in target_str]
features_tensors.append(features_array)
target_indices.append(target_indices_seq)
if len(features_str) != len(target_str):
break
yield torch.stack(features_tensors), torch.LongTensor(target_indices)
def _string_to_one_hot_array(self, input_string: str) -> Tuple[Tensor]:
ind = [self.char_to_idx[ch] for ch in input_string]
array = self._one_hot_text_data(ind)
return array
def _one_hot_text_data(self,
sequence: List):
sequence_length = len(sequence)
batch = torch.zeros(sequence_length, self.vocab_size)
for i in range(sequence_length):
batch[i, sequence[i]] = 1.0
return Tensor(batch)
def generate_test_data(self) -> Tuple[Tensor]:
features_str, target_str = self.test_data[:-1], self.test_data[1:]
X_tensors = []
y_tensors = []
N = len(self.test_data)
for start in range(0, N, self.max_len):
features_str, target_str =\
self.test_data[start:start+self.max_len],\
self.test_data[start+1:start+self.max_len+1]
if len(features_str) != len(target_str):
break
features_array = self._string_to_one_hot_array(features_str)
target_indices_seq = [self.char_to_idx[char] for char in target_str]
X_tensors.append(features_array)
y_tensors.append(torch.LongTensor(target_indices_seq))
return torch.stack(X_tensors), torch.stack(y_tensors)
#data = open('data/input.txt', 'r').read()
data = open('../06_rnns/input.txt', 'r').read()
vocab_size = len(set(data))
model = NextCharacterModel(vocab_size, hidden_size=vocab_size, sequence_length=50)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001,
weight_decay=1e-5)
lstm_trainer = LSTMTrainer(model, optimizer, criterion)
lstm_trainer.fit(data, epochs=1)
```
# 오토인코더를 활용한 비지도 학습
## `DeconvLayer`
```
class DeconvLayer(PyTorchLayer):
def __init__(self,
in_channels: int,
out_channels: int,
filter_size: int,
activation: nn.Module = None,
dropout: float = 1.0,
flatten: bool = False) -> None:
super().__init__()
self.deconv = nn.ConvTranspose2d(in_channels, out_channels, filter_size,
padding=filter_size // 2)
self.activation = activation
self.flatten = flatten
if dropout < 1.0:
self.dropout = nn.Dropout(1 - dropout)
def forward(self, x: Tensor) -> Tensor:
x = self.deconv(x)
if self.activation:
x = self.activation(x)
if self.flatten:
x = x.view(x.shape[0], x.shape[1] * x.shape[2] * x.shape[3])
if hasattr(self, "dropout"):
x = self.dropout(x)
return x
```
## `Autoencoder`
```
class Autoencoder(PyTorchModel):
def __init__(self,
hidden_dim: int = 28):
super(Autoencoder, self).__init__()
self.conv1 = ConvLayer(1, 14, 5, activation=nn.Tanh())
self.conv2 = ConvLayer(14, 7, 5, activation=nn.Tanh(), flatten=True)
self.dense1 = DenseLayer(7 * 28 * 28, hidden_dim, activation=nn.Tanh())
self.dense2 = DenseLayer(hidden_dim, 7 * 28 * 28, activation=nn.Tanh())
self.conv3 = ConvLayer(7, 14, 5, activation=nn.Tanh())
self.conv4 = ConvLayer(14, 1, 5, activation=nn.Tanh())
def forward(self, x: Tensor) -> Tensor:
assert_dim(x, 4)
x = self.conv1(x)
x = self.conv2(x)
# import pdb; pdb.set_trace()
encoding = self.dense1(x)
x = self.dense2(encoding)
x = x.view(-1, 7, 28, 28)
x = self.conv3(x)
x = self.conv4(x)
return x, encoding
```
## 데이터 전처리
```
X_train = mnist_train
X_test = mnist_test
X_train_auto = (X_train - X_train.min()) / (X_train.max() - X_train.min()) * 2 - 1
X_test_auto = (X_test - X_train.min()) / (X_train.max() - X_train.min()) * 2 - 1
model = Autoencoder()
model = Autoencoder(hidden_dim=28)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
trainer = PyTorchTrainer(model, optimizer, criterion)
trainer.fit(X_train_auto, X_train_auto,
X_test_auto, X_test_auto,
epochs=1,
batch_size=60)
reconstructed_images, image_representations = model(X_test_auto)
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
%matplotlib inline
# matplotlib 폰트설정
#plt.rc('font', family='NanumGothicOTF') # For MacOS
matplotlib.rcParams['axes.unicode_minus'] = False
plt.rc('font', family='NanumGothic') # For Windows
print(plt.rcParams['font.family'])
def display_image(ax,
t: Tensor):
n = t.detach().numpy()
ax.imshow(n.reshape(28, 28))
np.random.seed(20190504)
a = np.random.randint(0, 10000)
X_test[a].shape
f, axarr = plt.subplots(1,2)
display_image(axarr[0], X_test[a])
display_image(axarr[1], reconstructed_images[a])
axarr[0].set_title("원래 이미지")
axarr[1].set_title("오토인코더로 복원한 이미지")
axarr[0].axis('off')
axarr[1].axis('off');
# f.savefig("../../01_deep-learning-from-scratch/images/07_pytorch/03_autoencoder_example_image.png")
```
# t-SNE를 이용한 시각화
```
from sklearn.manifold import TSNE
tsne_result = TSNE(n_components=2, random_state=20190405).fit_transform(image_representations.detach().numpy())
```
## 시각화
```
import pandas as pd
tsne_df = pd.DataFrame({'tsne_dim_1': tsne_result[:,0],
'tsne_dim_2': tsne_result[:,1],
'category': test_dataset.targets})
groups = tsne_df.groupby('category')
# Plot
fig, ax = plt.subplots(figsize=(25,25))
ax.set_title('''MNIST 데이터 집합 중 테스트 집합의 10000개 관찰을 대상으로 한다.
색은 해당 관찰이 어떤 숫자를 쓴 것인지 가리키며
위치는 합성곱 오토인코더로 압축된 28차원값을 재차 t-SNE로 차원축소한 결과다.''')
ax.margins(0.05) # 자동 스케일링을 위한 5% 패딩 추가
for name, group in groups:
ax.scatter(group['tsne_dim_1'], group['tsne_dim_2'], marker='o', label=name)
ax.legend();
# fig.savefig("../../01_deep-learning-from-scratch/images/07_pytorch/00_tsne.png")
```
|
github_jupyter
|
import sys
# 예제 파일 경로로 수정한 다음 주석 해제
# sys.path.append(r'/to/your/example_code/path/lincoln')
# imports
from typing import Tuple, List
from collections import deque
import torch
import torch.optim as optim
from torch.optim import lr_scheduler
from torch.optim import Optimizer
import numpy as np
from torch import Tensor
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.modules.loss import _Loss
from lincoln.pytorch.layers import PyTorchLayer, DenseLayer
from lincoln.pytorch.model import PyTorchModel
from lincoln.pytorch.train import PyTorchTrainer
from lincoln.pytorch.preprocessor import ConvNetPreprocessor
from lincoln.pytorch.utils import assert_dim, permute_data
torch.manual_seed(20190325);
%load_ext autoreload
%autoreload 2
from sklearn.datasets import load_boston
boston = load_boston()
data = boston.data
target = boston.target
features = boston.feature_names
from sklearn.preprocessing import StandardScaler
s = StandardScaler()
data = s.fit_transform(data)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=0.3, random_state=80718)
y_train, y_test = y_train.reshape(-1, 1), y_test.reshape(-1, 1)
X_train, X_test, y_train, y_test = Tensor(X_train), Tensor(X_test), Tensor(y_train), Tensor(y_test)
class BostonModel(PyTorchModel):
def __init__(self,
hidden_size: int = 13,
hidden_dropout: float = 1.0):
super().__init__()
self.dense1 = DenseLayer(13, hidden_size,
activation=nn.Tanh(),
dropout = hidden_dropout)
self.dense2 = DenseLayer(hidden_size, 1)
def forward(self, x: Tensor,
inference: bool = False) -> Tensor:
assert_dim(x, 2)
assert x.shape[1] == 13
x = self.dense1(x, inference)
return self.dense2(x, inference),
# model, optimizer, loss
pytorch_boston_model = BostonModel(hidden_size=13, hidden_dropout=0.8)
optimizer = optim.SGD(pytorch_boston_model.parameters(), lr=0.001, momentum=0.9)
criterion = nn.MSELoss()
trainer = PyTorchTrainer(pytorch_boston_model, optimizer, criterion)
trainer.fit(X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test,
epochs=100,
eval_every=10,
final_lr_exp = 0.001)
torch.mean(torch.pow(pytorch_boston_model(X_test, inference=True)[0] - y_test, 2)).item()
test_pred = pytorch_boston_model(X_test)[0].view(-1)
test_actual = y_test
test_pred = test_pred.detach().numpy()
test_actual = test_actual.detach().numpy()
import matplotlib.pyplot as plt
%matplotlib inline
plt.scatter(test_pred, test_actual)
import torchvision
from torchvision.datasets import MNIST
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
img_transforms = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1305,), (0.3081,))
])
# https://pytorch.org/docs/stable/data.html
train_dataset = MNIST(root='../mnist_data/',
train=True,
download=True,
transform=img_transforms)
test_dataset = MNIST(root='../mnist_data/',
train=False,
download=True,
transform=img_transforms)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=60,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=60,
shuffle=False)
class ConvLayer(PyTorchLayer):
def __init__(self,
in_channels: int,
out_channels: int,
filter_size: int,
activation: nn.Module = None,
dropout: float = 1.0,
flatten: bool = False) -> None:
super().__init__()
self.conv = nn.Conv2d(in_channels, out_channels, filter_size,
padding=filter_size // 2)
self.activation = activation
self.flatten = flatten
if dropout < 1.0:
self.dropout = nn.Dropout(1 - dropout)
def forward(self, x: Tensor) -> Tensor:
x = self.conv(x)
if self.activation:
x = self.activation(x)
if self.flatten:
x = x.view(x.shape[0], x.shape[1] * x.shape[2] * x.shape[3])
if hasattr(self, "dropout"):
x = self.dropout(x)
return x
class MNIST_ConvNet(PyTorchModel):
def __init__(self):
super().__init__()
self.conv1 = ConvLayer(1, 14, 5, activation=nn.Tanh(),
dropout=0.8)
self.conv2 = ConvLayer(14, 7, 5, activation=nn.Tanh(), flatten=True,
dropout=0.8)
self.dense1 = DenseLayer(28 * 28 * 7, 32, activation=nn.Tanh(),
dropout=0.8)
self.dense2 = DenseLayer(32, 10)
def forward(self, x: Tensor) -> Tensor:
assert_dim(x, 4)
x = self.conv1(x)
x = self.conv2(x)
x = self.dense1(x)
x = self.dense2(x)
return x,
model = MNIST_ConvNet()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
trainer = PyTorchTrainer(model, optimizer, criterion)
trainer.fit(train_dataloader = train_loader,
test_dataloader = test_loader,
epochs = 1,
eval_every = 1)
def test_accuracy(model):
model.eval()
accuracies = []
for X_batch, y_batch in test_loader:
output = model(X_batch)[0]
accuracy_batch = (torch.max(output, dim=1)[1] == y_batch).type(torch.float32).mean().item()
accuracies.append(accuracy_batch)
return torch.Tensor(accuracies).mean().item()
test_accuracy(model)
mnist_train = ((train_dataset.data.type(torch.float32).unsqueeze(3).permute(0, 3, 1, 2) / 255.0) - 0.1305) / 0.3081
mnist_test = ((test_dataset.data.type(torch.float32).unsqueeze(3).permute(0, 3, 1, 2) / 255.0) - 0.1305) / 0.3081
mnist_train.min(), mnist_train.max(), mnist_test.min(), mnist_test.max()
trainer = PyTorchTrainer(model, optimizer, criterion)
trainer.fit(X_train=mnist_train, y_train=train_dataset.targets,
X_test=mnist_test, y_test=test_dataset.targets,
epochs=1,
eval_every=1)
def test_accuracy_no_dataloader(model, mnist_test):
model.eval()
output = model(mnist_test)[0]
return (torch.max(output, dim=1)[1] == test_dataset.test_labels).type(torch.float32).mean().item()
test_accuracy_no_dataloader(model, mnist_test)
class LSTMLayer(PyTorchLayer):
def __init__(self,
sequence_length: int,
input_size: int,
hidden_size: int,
output_size: int,
dropout: float = 1.0) -> None:
super().__init__()
self.hidden_size = hidden_size
self.h_init = torch.zeros((1, hidden_size))
self.c_init = torch.zeros((1, hidden_size))
self.lstm = nn.LSTM(input_size, hidden_size, batch_first=True)
self.fc = DenseLayer(hidden_size, output_size)
if dropout < 1.0:
self.dropout = nn.Dropout(1 - dropout)
def _transform_hidden_batch(self, hidden: Tensor,
batch_size: int,
before_layer: bool) -> Tensor:
if before_layer:
return (hidden
.repeat(batch_size, 1)
.view(batch_size, 1, self.hidden_size)
.permute(1,0,2))
else:
return (hidden
.permute(1,0,2)
.mean(dim=0))
def forward(self, x: Tensor) -> Tensor:
batch_size = x.shape[0]
h_layer = self._transform_hidden_batch(self.h_init, batch_size, before_layer=True)
c_layer = self._transform_hidden_batch(self.c_init, batch_size, before_layer=True)
x, (h_out, c_out) = self.lstm(x, (h_layer, c_layer))
self.h_init, self.c_init = (
self._transform_hidden_batch(h_out, batch_size, before_layer=False).detach(),
self._transform_hidden_batch(c_out, batch_size, before_layer=False).detach()
)
x = self.fc(x)
if hasattr(self, "dropout"):
x = self.dropout(x)
return x
lay = LSTMLayer(sequence_length=25,
input_size=62,
hidden_size=100,
output_size=128)
x = torch.randn(32, 25, 62)
lay(x).shape
class NextCharacterModel(PyTorchModel):
def __init__(self,
vocab_size: int,
hidden_size: int = 256,
sequence_length: int = 25):
super().__init__()
self.vocab_size = vocab_size
self.sequence_length = sequence_length
# 이 모델에는 층이 하나 뿐이며
# 이 층의 출력은 입력과 모양이 같다
self.lstm = LSTMLayer(self.sequence_length, self.vocab_size, hidden_size, self.vocab_size)
def forward(self,
inputs: Tensor):
assert_dim(inputs, 3) # batch_size, sequence_length, vocab_size
out = self.lstm(inputs)
return out.permute(0, 2, 1),
class LSTMTrainer(PyTorchTrainer):
def __init__(self,
model: NextCharacterModel,
optim: Optimizer,
criterion: _Loss):
super().__init__(model, optim, criterion)
self.vocab_size = self.model.vocab_size
self.max_len = self.model.sequence_length
def fit(self,
data: str,
epochs: int=10,
eval_every: int=1,
batch_size: int=32,
seed: int = 121718)-> None:
self.data = data
self.train_data, self.test_data = self._train_test_split_text()
self.chars = list(set(self.data))
self.char_to_idx = {ch: i for i, ch in enumerate(self.chars)}
self.idx_to_char = {i: ch for i, ch in enumerate(self.chars)}
torch.manual_seed(seed)
losses = deque(maxlen=50)
for e in range(epochs):
batch_generator = self.generate_batches_next_char(batch_size)
for ii, (X_batch, y_batch) in enumerate(batch_generator):
self.optim.zero_grad()
outputs = self.model(X_batch)[0]
loss = self.loss(outputs, y_batch)
losses.append(loss.item())
loss.backward()
self.optim.step()
if (e+1) % eval_every == 0:
X_test, y_test = self.generate_test_data()
test_preds = self.model.forward(X_test)[0]
loss = self.loss.forward(test_preds, y_test)
print(f"{e+1}에폭에서 검증 데이터에 대한 손실값: {loss.item():.3f}")
def _train_test_split_text(self, pct=0.8) -> Tuple[str]:
n = len(self.data)
return self.data[:int(n * pct)], self.data[int(n * pct):]
def generate_batches_next_char(self,
batch_size: int) -> Tuple[Tensor]:
N = len(self.train_data)
# add batch size
for ii in range(0, N, batch_size):
features_tensors = []
target_indices = []
for char in range(batch_size):
features_str, target_str =\
self.train_data[ii+char:ii+char+self.max_len],\
self.train_data[ii+char+1:ii+char+self.max_len+1]
features_array = self._string_to_one_hot_array(features_str)
target_indices_seq = [self.char_to_idx[char] for char in target_str]
features_tensors.append(features_array)
target_indices.append(target_indices_seq)
if len(features_str) != len(target_str):
break
yield torch.stack(features_tensors), torch.LongTensor(target_indices)
def _string_to_one_hot_array(self, input_string: str) -> Tuple[Tensor]:
ind = [self.char_to_idx[ch] for ch in input_string]
array = self._one_hot_text_data(ind)
return array
def _one_hot_text_data(self,
sequence: List):
sequence_length = len(sequence)
batch = torch.zeros(sequence_length, self.vocab_size)
for i in range(sequence_length):
batch[i, sequence[i]] = 1.0
return Tensor(batch)
def generate_test_data(self) -> Tuple[Tensor]:
features_str, target_str = self.test_data[:-1], self.test_data[1:]
X_tensors = []
y_tensors = []
N = len(self.test_data)
for start in range(0, N, self.max_len):
features_str, target_str =\
self.test_data[start:start+self.max_len],\
self.test_data[start+1:start+self.max_len+1]
if len(features_str) != len(target_str):
break
features_array = self._string_to_one_hot_array(features_str)
target_indices_seq = [self.char_to_idx[char] for char in target_str]
X_tensors.append(features_array)
y_tensors.append(torch.LongTensor(target_indices_seq))
return torch.stack(X_tensors), torch.stack(y_tensors)
#data = open('data/input.txt', 'r').read()
data = open('../06_rnns/input.txt', 'r').read()
vocab_size = len(set(data))
model = NextCharacterModel(vocab_size, hidden_size=vocab_size, sequence_length=50)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001,
weight_decay=1e-5)
lstm_trainer = LSTMTrainer(model, optimizer, criterion)
lstm_trainer.fit(data, epochs=1)
class DeconvLayer(PyTorchLayer):
def __init__(self,
in_channels: int,
out_channels: int,
filter_size: int,
activation: nn.Module = None,
dropout: float = 1.0,
flatten: bool = False) -> None:
super().__init__()
self.deconv = nn.ConvTranspose2d(in_channels, out_channels, filter_size,
padding=filter_size // 2)
self.activation = activation
self.flatten = flatten
if dropout < 1.0:
self.dropout = nn.Dropout(1 - dropout)
def forward(self, x: Tensor) -> Tensor:
x = self.deconv(x)
if self.activation:
x = self.activation(x)
if self.flatten:
x = x.view(x.shape[0], x.shape[1] * x.shape[2] * x.shape[3])
if hasattr(self, "dropout"):
x = self.dropout(x)
return x
class Autoencoder(PyTorchModel):
def __init__(self,
hidden_dim: int = 28):
super(Autoencoder, self).__init__()
self.conv1 = ConvLayer(1, 14, 5, activation=nn.Tanh())
self.conv2 = ConvLayer(14, 7, 5, activation=nn.Tanh(), flatten=True)
self.dense1 = DenseLayer(7 * 28 * 28, hidden_dim, activation=nn.Tanh())
self.dense2 = DenseLayer(hidden_dim, 7 * 28 * 28, activation=nn.Tanh())
self.conv3 = ConvLayer(7, 14, 5, activation=nn.Tanh())
self.conv4 = ConvLayer(14, 1, 5, activation=nn.Tanh())
def forward(self, x: Tensor) -> Tensor:
assert_dim(x, 4)
x = self.conv1(x)
x = self.conv2(x)
# import pdb; pdb.set_trace()
encoding = self.dense1(x)
x = self.dense2(encoding)
x = x.view(-1, 7, 28, 28)
x = self.conv3(x)
x = self.conv4(x)
return x, encoding
X_train = mnist_train
X_test = mnist_test
X_train_auto = (X_train - X_train.min()) / (X_train.max() - X_train.min()) * 2 - 1
X_test_auto = (X_test - X_train.min()) / (X_train.max() - X_train.min()) * 2 - 1
model = Autoencoder()
model = Autoencoder(hidden_dim=28)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
trainer = PyTorchTrainer(model, optimizer, criterion)
trainer.fit(X_train_auto, X_train_auto,
X_test_auto, X_test_auto,
epochs=1,
batch_size=60)
reconstructed_images, image_representations = model(X_test_auto)
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
%matplotlib inline
# matplotlib 폰트설정
#plt.rc('font', family='NanumGothicOTF') # For MacOS
matplotlib.rcParams['axes.unicode_minus'] = False
plt.rc('font', family='NanumGothic') # For Windows
print(plt.rcParams['font.family'])
def display_image(ax,
t: Tensor):
n = t.detach().numpy()
ax.imshow(n.reshape(28, 28))
np.random.seed(20190504)
a = np.random.randint(0, 10000)
X_test[a].shape
f, axarr = plt.subplots(1,2)
display_image(axarr[0], X_test[a])
display_image(axarr[1], reconstructed_images[a])
axarr[0].set_title("원래 이미지")
axarr[1].set_title("오토인코더로 복원한 이미지")
axarr[0].axis('off')
axarr[1].axis('off');
# f.savefig("../../01_deep-learning-from-scratch/images/07_pytorch/03_autoencoder_example_image.png")
from sklearn.manifold import TSNE
tsne_result = TSNE(n_components=2, random_state=20190405).fit_transform(image_representations.detach().numpy())
import pandas as pd
tsne_df = pd.DataFrame({'tsne_dim_1': tsne_result[:,0],
'tsne_dim_2': tsne_result[:,1],
'category': test_dataset.targets})
groups = tsne_df.groupby('category')
# Plot
fig, ax = plt.subplots(figsize=(25,25))
ax.set_title('''MNIST 데이터 집합 중 테스트 집합의 10000개 관찰을 대상으로 한다.
색은 해당 관찰이 어떤 숫자를 쓴 것인지 가리키며
위치는 합성곱 오토인코더로 압축된 28차원값을 재차 t-SNE로 차원축소한 결과다.''')
ax.margins(0.05) # 자동 스케일링을 위한 5% 패딩 추가
for name, group in groups:
ax.scatter(group['tsne_dim_1'], group['tsne_dim_2'], marker='o', label=name)
ax.legend();
# fig.savefig("../../01_deep-learning-from-scratch/images/07_pytorch/00_tsne.png")
| 0.773131 | 0.90261 |
This notebook explores the confidence the model has in errors compared to right answers.
```
BARS_PATH = "../bars/test/"
```
# Import & Load the Bar Categorization Model
```
import time
import tensorflow as tf
print('Loading categorization model...', end='')
start_time = time.time()
cat_model = tf.keras.models.load_model('./exported-models/bar_cat_EfficientNetB2_9723')
end_time = time.time()
elapsed_time = end_time - start_time
print('Done! Took {} seconds'.format(elapsed_time))
```
## Model evaluation
```
from os import listdir
from os.path import isfile, join
paths = [BARS_PATH + f for f in listdir(BARS_PATH) if isfile(join(BARS_PATH, f))]
paths
import pandas as pd
test_df = pd.DataFrame({'path': paths})
test_df["dec"] = test_df.apply(lambda x: int(x['path'].split("/")[-1].split("_")[0]), axis=1)
test_df["bin"] = test_df.apply(lambda x: bin(x['dec']), axis=1)
test_df["class"] = test_df.apply(lambda x: [i for i in reversed(range(20)) if (x['dec'] & 1 << i) != 0], axis=1)
print(test_df.shape)
test_df.head()
from tensorflow.keras.preprocessing.image import ImageDataGenerator
target_size = (450, 100)
test_datagen = ImageDataGenerator()
test_generator = test_datagen.flow_from_dataframe(
dataframe = test_df,
directory = ".",
target_size = target_size,
shuffle = False,
x_col = 'path',
y_col = 'class',
class_mode = 'categorical')
cat_model.evaluate(test_generator)
```
# Explore Errors and Confidence Classifying Bars
```
prediction = cat_model.predict(test_generator)
prediction
# prediction in binary
test_df["pred_bin"] = ["{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}"
.format(round(x[19]),round(x[18]),round(x[17]),round(x[16]),round(x[15]),
round(x[14]),round(x[13]),round(x[12]),round(x[11]),round(x[10]),
round(x[9]), round(x[8]), round(x[7]), round(x[6]), round(x[5]),
round(x[4]), round(x[3]), round(x[2]), round(x[1]), round(x[0])) for x in prediction]
#prediction in decimal
vals = []
for p in prediction:
val = 0
for i in range(20):
val += round(p[i]) << i
vals.append(val)
test_df["pred_dec"] = vals
# number of errors
test_df["errors"] = test_df.apply(lambda x: bin(x["dec"] ^ x["pred_dec"]).count("1"), axis=1)
test_df
test_df["pred_class"] = [[cl for cl, x in enumerate(prediction[i]) if x>0.5] for i in range(len(prediction))]
test_df["error_classes"] = [list(set(test_df["pred_class"][i]).symmetric_difference(set(test_df["class"][i]))) for i in range(len(test_df))]
test_df[["dec", "errors", "class", "pred_class", "error_classes"]]
from numpy import nan
# Average confidence of correct predictions
avg_conf_corr = []
avg_conf_err = []
lowest_err_conf = []
sec_lowest_err_conf = []
lowest_corr_conf = []
for idx, pred in enumerate(prediction):
errors = test_df["errors"][idx]
conf_corr = 0
conf_err = 0
l_err_conf = 2
l2_err_conf = 2
l_corr_conf = 2
for i in range(len(pred)):
conf = 1 - min(abs(pred[i]-1), pred[i])
if i in test_df["error_classes"][idx]:
conf_err += conf/errors
if conf < l_err_conf:
l_err_conf = conf
elif conf < l2_err_conf:
l2_err_conf = conf
else:
conf_corr += conf/(len(pred) - errors)
if conf < l_corr_conf:
l_corr_conf = conf
avg_conf_corr.append(conf_corr)
avg_conf_err.append(conf_err)
lowest_err_conf.append(l_err_conf)
sec_lowest_err_conf.append(l2_err_conf)
lowest_corr_conf.append(l_corr_conf)
test_df["avg_conf_corr"] = avg_conf_corr
test_df["avg_conf_err"] = avg_conf_err
test_df["lowest_err_conf"] = lowest_err_conf
test_df["sec_lowest_err_conf"] = sec_lowest_err_conf
test_df["lowest_corr_conf"] = lowest_corr_conf
test_df.loc[test_df["sec_lowest_err_conf"] == 2,"sec_lowest_err_conf"] = nan
test_df.loc[test_df["lowest_err_conf"] == 2,"lowest_err_conf"] = nan
test_df[["errors", "class", "pred_class", "error_classes", "avg_conf_corr", "avg_conf_err", "lowest_corr_conf", "lowest_err_conf", "sec_lowest_err_conf"]]
test_df["succ_corr"] = test_df["lowest_err_conf"]<test_df["lowest_corr_conf"]
test_df["succ_corr"][test_df["errors"]>0][test_df["errors"]<6].value_counts(normalize=True)
test_df["succ_2corr"] = test_df["sec_lowest_err_conf"]<test_df["lowest_corr_conf"]
test_df["succ_2corr"][test_df["errors"]>1][test_df["errors"]<6].value_counts(normalize=True)
```
|
github_jupyter
|
BARS_PATH = "../bars/test/"
import time
import tensorflow as tf
print('Loading categorization model...', end='')
start_time = time.time()
cat_model = tf.keras.models.load_model('./exported-models/bar_cat_EfficientNetB2_9723')
end_time = time.time()
elapsed_time = end_time - start_time
print('Done! Took {} seconds'.format(elapsed_time))
from os import listdir
from os.path import isfile, join
paths = [BARS_PATH + f for f in listdir(BARS_PATH) if isfile(join(BARS_PATH, f))]
paths
import pandas as pd
test_df = pd.DataFrame({'path': paths})
test_df["dec"] = test_df.apply(lambda x: int(x['path'].split("/")[-1].split("_")[0]), axis=1)
test_df["bin"] = test_df.apply(lambda x: bin(x['dec']), axis=1)
test_df["class"] = test_df.apply(lambda x: [i for i in reversed(range(20)) if (x['dec'] & 1 << i) != 0], axis=1)
print(test_df.shape)
test_df.head()
from tensorflow.keras.preprocessing.image import ImageDataGenerator
target_size = (450, 100)
test_datagen = ImageDataGenerator()
test_generator = test_datagen.flow_from_dataframe(
dataframe = test_df,
directory = ".",
target_size = target_size,
shuffle = False,
x_col = 'path',
y_col = 'class',
class_mode = 'categorical')
cat_model.evaluate(test_generator)
prediction = cat_model.predict(test_generator)
prediction
# prediction in binary
test_df["pred_bin"] = ["{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}"
.format(round(x[19]),round(x[18]),round(x[17]),round(x[16]),round(x[15]),
round(x[14]),round(x[13]),round(x[12]),round(x[11]),round(x[10]),
round(x[9]), round(x[8]), round(x[7]), round(x[6]), round(x[5]),
round(x[4]), round(x[3]), round(x[2]), round(x[1]), round(x[0])) for x in prediction]
#prediction in decimal
vals = []
for p in prediction:
val = 0
for i in range(20):
val += round(p[i]) << i
vals.append(val)
test_df["pred_dec"] = vals
# number of errors
test_df["errors"] = test_df.apply(lambda x: bin(x["dec"] ^ x["pred_dec"]).count("1"), axis=1)
test_df
test_df["pred_class"] = [[cl for cl, x in enumerate(prediction[i]) if x>0.5] for i in range(len(prediction))]
test_df["error_classes"] = [list(set(test_df["pred_class"][i]).symmetric_difference(set(test_df["class"][i]))) for i in range(len(test_df))]
test_df[["dec", "errors", "class", "pred_class", "error_classes"]]
from numpy import nan
# Average confidence of correct predictions
avg_conf_corr = []
avg_conf_err = []
lowest_err_conf = []
sec_lowest_err_conf = []
lowest_corr_conf = []
for idx, pred in enumerate(prediction):
errors = test_df["errors"][idx]
conf_corr = 0
conf_err = 0
l_err_conf = 2
l2_err_conf = 2
l_corr_conf = 2
for i in range(len(pred)):
conf = 1 - min(abs(pred[i]-1), pred[i])
if i in test_df["error_classes"][idx]:
conf_err += conf/errors
if conf < l_err_conf:
l_err_conf = conf
elif conf < l2_err_conf:
l2_err_conf = conf
else:
conf_corr += conf/(len(pred) - errors)
if conf < l_corr_conf:
l_corr_conf = conf
avg_conf_corr.append(conf_corr)
avg_conf_err.append(conf_err)
lowest_err_conf.append(l_err_conf)
sec_lowest_err_conf.append(l2_err_conf)
lowest_corr_conf.append(l_corr_conf)
test_df["avg_conf_corr"] = avg_conf_corr
test_df["avg_conf_err"] = avg_conf_err
test_df["lowest_err_conf"] = lowest_err_conf
test_df["sec_lowest_err_conf"] = sec_lowest_err_conf
test_df["lowest_corr_conf"] = lowest_corr_conf
test_df.loc[test_df["sec_lowest_err_conf"] == 2,"sec_lowest_err_conf"] = nan
test_df.loc[test_df["lowest_err_conf"] == 2,"lowest_err_conf"] = nan
test_df[["errors", "class", "pred_class", "error_classes", "avg_conf_corr", "avg_conf_err", "lowest_corr_conf", "lowest_err_conf", "sec_lowest_err_conf"]]
test_df["succ_corr"] = test_df["lowest_err_conf"]<test_df["lowest_corr_conf"]
test_df["succ_corr"][test_df["errors"]>0][test_df["errors"]<6].value_counts(normalize=True)
test_df["succ_2corr"] = test_df["sec_lowest_err_conf"]<test_df["lowest_corr_conf"]
test_df["succ_2corr"][test_df["errors"]>1][test_df["errors"]<6].value_counts(normalize=True)
| 0.213705 | 0.802168 |
special credits : https://github.com/worasom/aqi_thailand
```
import sys
import math
from pathlib import Path
import seaborn as sns
import pandas as pd
import statsmodels.api as sm
import datetime
import matplotlib.dates as mdates
import matplotlib as mpl
from matplotlib.gridspec import GridSpec
import matplotlib.pyplot as plt
from statsmodels.sandbox.regression.predstd import wls_prediction_std
from mpl_toolkits.axes_grid1.axes_divider import make_axes_locatable
from mpl_toolkits.axes_grid1.colorbar import colorbar
from bokeh.io import output_file, output_notebook, show,curdoc, reset_output,export_png
from bokeh.models import (
GMapPlot, GMapOptions, ColumnDataSource, Circle, LogColorMapper, BasicTicker, ColorBar,
DataRange1d, PanTool, WheelZoomTool, BoxSelectTool, CategoricalColorMapper, Slider, DateRangeSlider,
DateSlider, SingleIntervalTicker, LinearAxis,Legend, LegendItem, Label
)
from bokeh.models.markers import Asterisk
from bokeh.models.mappers import ColorMapper, LinearColorMapper
from bokeh.palettes import Viridis5
from bokeh.plotting import figure, show, output_file
from bokeh.tile_providers import STAMEN_TERRAIN,CARTODBPOSITRON_RETINA
from bokeh.layouts import widgetbox,row, column, gridplot
fire = pd.read_csv('data/thaifirenew.csv')
fire = fire.drop(['latitude','longitude'],axis=1)
fire['distbkk'] = fire.apply(lambda fire : math.sqrt((fire.merlat-1535855.81)**2+(fire.merlong-11187764.67)**2)/1000,axis=1)
fire = fire.drop(['scan','track','satellite','instrument','version','type',],axis=1)
def ttt(test):
if len(str(test))==3:
test11 = '0'+str(int(str(test)[0:1]))+":"+str(test)[-2:]+':00'
return(test11)
else:
test3 = str(test)[0:2]+':'+str(test)[-2:]+':00'
return(test3)
fire['T'] = fire.apply(lambda fire : ttt(fire.acq_time),axis=1)
fire['D'] = fire.apply(lambda fire : str(fire.acq_date)[:-4],axis=1)
fire['dc']= fire.apply(lambda fire : str(fire['D'])+''+str(fire['T']),axis=1)
fire['datetime'] = pd.to_datetime(fire['dc'])
fire = fire.drop(['T','D','dc','daynight','acq_date','acq_time',],axis=1)
fire['datetime'] = fire['datetime'].dt.tz_localize('UTC').dt.tz_convert('Asia/Bangkok')
fire['datetime'] = fire['datetime'] .dt.tz_localize(None)
fire.set_index('datetime',inplace=True)
fire.head()
# find active fire with in 250 km from bkk
fireclose240 = fire[fire['distbkk'].values < 250]
# count the number of hotspot by hour
fireclose240 = fireclose240.resample('H').agg({'frp':['count']})
fireclose240.columns = ['fire0-240km']
# collect the amount of fire in the past 24 hours
fireclose240['fire0-240km'] = fireclose240['fire0-240km'].rolling(window=24).sum()
#fireclose240new = fireclose240.dropna()
fireclose240 = fireclose240.dropna()
fireclose240
pm251819 = pd.read_csv("data/bangkok/bkk_pm25_sec1819.csv",index_col=0)
pm251819
pm_fire = fireclose240.merge(pm251819['PM2.5'],left_index=True,
right_index=True, how='left' )
pm_fire
import matplotlib.dates as mdates
temp = pm_fire['2018-01':'2019-12'].copy()
temp['color'] = pd.cut(temp['PM2.5'],bins = [0, 35.5, 55.5, 150.4],
labels=['green', 'orange','red'])
temp['level'] = pd.cut(temp['PM2.5'],bins = [0, 35.5, 55.5, 150.4],
labels=['satisfactory', 'moderate', 'unhealthy'])
fig,(ax1,ax2) = plt.subplots(2,1,figsize=(9, 6),sharex=True)
# make legend
for legend in ['satisfactory', 'moderate', 'unhealthy']:
toplot = temp[temp['level']==legend]
# plot the data for each pollution level
ax1.scatter(toplot.index, toplot['PM2.5'],
c=toplot['color'],s=8, label=legend)
ax1.legend(loc='upper right')
ax1.set_title("PM2.5 level in Bangkok ($\mu$g/m$^3$)")
ax1.xaxis.set_major_formatter(mdates.DateFormatter("%b\n%Y"))
ax2.scatter(x=temp.index,y=temp['fire0-240km'],s=8,c='darkblue')
ax2.set_title("hot spots count within 240 km distance for filed servey period")
plt.xlim(temp.index.min(), temp.index.max())
fig.savefig('C:\\Users\\chath\\Desktop\\figouts\\hotspot1819.png')
```
|
github_jupyter
|
import sys
import math
from pathlib import Path
import seaborn as sns
import pandas as pd
import statsmodels.api as sm
import datetime
import matplotlib.dates as mdates
import matplotlib as mpl
from matplotlib.gridspec import GridSpec
import matplotlib.pyplot as plt
from statsmodels.sandbox.regression.predstd import wls_prediction_std
from mpl_toolkits.axes_grid1.axes_divider import make_axes_locatable
from mpl_toolkits.axes_grid1.colorbar import colorbar
from bokeh.io import output_file, output_notebook, show,curdoc, reset_output,export_png
from bokeh.models import (
GMapPlot, GMapOptions, ColumnDataSource, Circle, LogColorMapper, BasicTicker, ColorBar,
DataRange1d, PanTool, WheelZoomTool, BoxSelectTool, CategoricalColorMapper, Slider, DateRangeSlider,
DateSlider, SingleIntervalTicker, LinearAxis,Legend, LegendItem, Label
)
from bokeh.models.markers import Asterisk
from bokeh.models.mappers import ColorMapper, LinearColorMapper
from bokeh.palettes import Viridis5
from bokeh.plotting import figure, show, output_file
from bokeh.tile_providers import STAMEN_TERRAIN,CARTODBPOSITRON_RETINA
from bokeh.layouts import widgetbox,row, column, gridplot
fire = pd.read_csv('data/thaifirenew.csv')
fire = fire.drop(['latitude','longitude'],axis=1)
fire['distbkk'] = fire.apply(lambda fire : math.sqrt((fire.merlat-1535855.81)**2+(fire.merlong-11187764.67)**2)/1000,axis=1)
fire = fire.drop(['scan','track','satellite','instrument','version','type',],axis=1)
def ttt(test):
if len(str(test))==3:
test11 = '0'+str(int(str(test)[0:1]))+":"+str(test)[-2:]+':00'
return(test11)
else:
test3 = str(test)[0:2]+':'+str(test)[-2:]+':00'
return(test3)
fire['T'] = fire.apply(lambda fire : ttt(fire.acq_time),axis=1)
fire['D'] = fire.apply(lambda fire : str(fire.acq_date)[:-4],axis=1)
fire['dc']= fire.apply(lambda fire : str(fire['D'])+''+str(fire['T']),axis=1)
fire['datetime'] = pd.to_datetime(fire['dc'])
fire = fire.drop(['T','D','dc','daynight','acq_date','acq_time',],axis=1)
fire['datetime'] = fire['datetime'].dt.tz_localize('UTC').dt.tz_convert('Asia/Bangkok')
fire['datetime'] = fire['datetime'] .dt.tz_localize(None)
fire.set_index('datetime',inplace=True)
fire.head()
# find active fire with in 250 km from bkk
fireclose240 = fire[fire['distbkk'].values < 250]
# count the number of hotspot by hour
fireclose240 = fireclose240.resample('H').agg({'frp':['count']})
fireclose240.columns = ['fire0-240km']
# collect the amount of fire in the past 24 hours
fireclose240['fire0-240km'] = fireclose240['fire0-240km'].rolling(window=24).sum()
#fireclose240new = fireclose240.dropna()
fireclose240 = fireclose240.dropna()
fireclose240
pm251819 = pd.read_csv("data/bangkok/bkk_pm25_sec1819.csv",index_col=0)
pm251819
pm_fire = fireclose240.merge(pm251819['PM2.5'],left_index=True,
right_index=True, how='left' )
pm_fire
import matplotlib.dates as mdates
temp = pm_fire['2018-01':'2019-12'].copy()
temp['color'] = pd.cut(temp['PM2.5'],bins = [0, 35.5, 55.5, 150.4],
labels=['green', 'orange','red'])
temp['level'] = pd.cut(temp['PM2.5'],bins = [0, 35.5, 55.5, 150.4],
labels=['satisfactory', 'moderate', 'unhealthy'])
fig,(ax1,ax2) = plt.subplots(2,1,figsize=(9, 6),sharex=True)
# make legend
for legend in ['satisfactory', 'moderate', 'unhealthy']:
toplot = temp[temp['level']==legend]
# plot the data for each pollution level
ax1.scatter(toplot.index, toplot['PM2.5'],
c=toplot['color'],s=8, label=legend)
ax1.legend(loc='upper right')
ax1.set_title("PM2.5 level in Bangkok ($\mu$g/m$^3$)")
ax1.xaxis.set_major_formatter(mdates.DateFormatter("%b\n%Y"))
ax2.scatter(x=temp.index,y=temp['fire0-240km'],s=8,c='darkblue')
ax2.set_title("hot spots count within 240 km distance for filed servey period")
plt.xlim(temp.index.min(), temp.index.max())
fig.savefig('C:\\Users\\chath\\Desktop\\figouts\\hotspot1819.png')
| 0.277082 | 0.813424 |
# WeatherPy
----
```
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import time
from scipy.stats import linregress
from pprint import pprint
# Import API key
#weather1_url=('https://api.openweathermap.org/data/2.5/onecall?lat={lat}&lon={lon}&appid={YOUR API KEY}')
#weather_url=('https://api.openweathermap.org/data/2.5/weather?q={city name}&appid={your api key}')
from api_keys import weather_api_key
# Incorporated citipy to determine city based on latitude and longitude
from citipy import citipy
# Output File (CSV)
output_data_file = "output_data/cities.csv"
# Range of latitudes and longitudes
lat_range = (-90, 90)
lng_range = (-180, 180)
```
## Generate Cities List
```
# List for holding lat_lngs and cities
lat_lngs = []
cities = []
# df for information
column_names1 = ["city", "lat", "long", "country"]
city_info_df = pd.DataFrame(columns = column_names1)
city_info_df.info()
# Create a set of random lat and lng combinations
lats = np.random.uniform(low=-90.000, high=90.000, size=1500)
lngs = np.random.uniform(low=-180.000, high=180.000, size=1500)
lat_lngs = zip(lats, lngs)
# Identify nearest city for each lat, lng combination
for lat_lng in lat_lngs:
city = citipy.nearest_city(lat_lng[0], lat_lng[1]).city_name
# If the city is unique, then add it to a our cities list
if city not in cities:
cities.append(city)
# Print the city count to confirm sufficient count
len(cities)
```
### Perform API Calls
* Perform a weather check on each city using a series of successive API calls.
* Include a print log of each city as it'sbeing processed (with the city number and city name).
```
print('Beginning Data Retrieval')
print('-----------------------------')
for i in range(len(cities)):
weather_url=(f'https://api.openweathermap.org/data/2.5/weather?q={cities[i]}&appid={weather_api_key}')
# print(weather_url)
resp = requests.get(weather_url)
response = resp.json()
if resp.status_code != 200:
print('City not found. Skipping...')
else:
print(f'Processing Record {i+1} | {cities[i]}')
city_info_df.loc[i,'cloudiness'] = response['clouds']['all']
city_info_df.loc[i,'date'] = response['dt']
city_info_df.loc[i,'humidity'] = response['main']['humidity']
calc_max_temp = response['main']['temp_max']
calc_max_temp = calc_max_temp - 273.15
city_info_df.loc[i,'max_temp'] = calc_max_temp * 9 / 5 + 32
city_info_df.loc[i,'wind_speed'] = response['wind']['speed']
city_info_df.loc[i,'lat'] = response['coord']['lat']
city_info_df.loc[i,'long'] = response['coord']['lon']
city_info_df.loc[i,'city'] = response['name']
city_info_df.loc[i,'country'] = response['sys']['country']
print('-----------------------------')
print('Data Retrieval Complete')
print('-----------------------------')
```
### Convert Raw Data to DataFrame
* Export the city data into a .csv.
* Display the DataFrame
```
city_info_df.to_csv(output_data_file, index=False)
city_info_df = city_info_df.reset_index()
city_info_df.info()
```
### Plotting the Data
* Use proper labeling of the plots using plot titles (including date of analysis) and axes labels.
* Save the plotted figures as .pngs.
#### Latitude vs. Temperature Plot
```
city_info_df.plot.scatter(x='lat', y='max_temp', c='blue', marker='o')
plt.xlabel("Latitude")
plt.ylabel("Max. Temperature")
plt.title("Latitude vs. Temperature")
plt.grid()
# Save the Figure
plt.savefig("../Images/lat_vs_temp.png")
# Show the Figure
plt.show()
plt.tight_layout();
```
#### Latitude vs. Humidity Plot
```
city_info_df.plot.scatter(x='lat', y='humidity', c='green', marker='o')
plt.xlabel("Latitude")
plt.ylabel("Humidity")
plt.title("Latitude vs. Humidity")
plt.grid()
# Save the Figure
plt.savefig("../Images/lat_vs_humidity.png")
# Show the Figure
plt.show()
plt.tight_layout();
```
#### Latitude vs. Cloudiness Plot
```
city_info_df.plot.scatter(x='lat', y='cloudiness', c='yellow', marker='o')
plt.xlabel("Latitude")
plt.ylabel("Cloudiness")
plt.title("Latitude vs. Cloudiness")
plt.grid()
# Save the Figure
plt.savefig("../Images/lat_vs_cloudiness.png")
# Show the Figure
plt.show()
plt.tight_layout();
```
#### Latitude vs. Wind Speed Plot
```
city_info_df.plot.scatter(x='lat', y='wind_speed', c='purple', marker='o')
plt.xlabel("Latitude")
plt.ylabel("Wind Speed")
plt.title("Latitude vs. Wind Speed")
plt.grid()
# Save the Figure
plt.savefig("../Images/lat_vs_windspeed.png")
# Show the Figure
plt.show()
plt.tight_layout();
```
## Linear Regression
```
# OPTIONAL: Create a function to create Linear Regression plots
# Create Northern and Southern Hemisphere DataFrames
no_city_info_df = city_info_df[(city_info_df['lat'] >= 0)]
no_city_info_df
so_city_info_df = city_info_df[(city_info_df['lat'] < 0)]
so_city_info_df
```
#### Northern Hemisphere - Max Temp vs. Latitude Linear Regression
#### Southern Hemisphere - Max Temp vs. Latitude Linear Regression
#### Northern Hemisphere - Humidity (%) vs. Latitude Linear Regression
#### Southern Hemisphere - Humidity (%) vs. Latitude Linear Regression
#### Northern Hemisphere - Cloudiness (%) vs. Latitude Linear Regression
#### Southern Hemisphere - Cloudiness (%) vs. Latitude Linear Regression
#### Northern Hemisphere - Wind Speed (mph) vs. Latitude Linear Regression
#### Southern Hemisphere - Wind Speed (mph) vs. Latitude Linear Regression
|
github_jupyter
|
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import time
from scipy.stats import linregress
from pprint import pprint
# Import API key
#weather1_url=('https://api.openweathermap.org/data/2.5/onecall?lat={lat}&lon={lon}&appid={YOUR API KEY}')
#weather_url=('https://api.openweathermap.org/data/2.5/weather?q={city name}&appid={your api key}')
from api_keys import weather_api_key
# Incorporated citipy to determine city based on latitude and longitude
from citipy import citipy
# Output File (CSV)
output_data_file = "output_data/cities.csv"
# Range of latitudes and longitudes
lat_range = (-90, 90)
lng_range = (-180, 180)
# List for holding lat_lngs and cities
lat_lngs = []
cities = []
# df for information
column_names1 = ["city", "lat", "long", "country"]
city_info_df = pd.DataFrame(columns = column_names1)
city_info_df.info()
# Create a set of random lat and lng combinations
lats = np.random.uniform(low=-90.000, high=90.000, size=1500)
lngs = np.random.uniform(low=-180.000, high=180.000, size=1500)
lat_lngs = zip(lats, lngs)
# Identify nearest city for each lat, lng combination
for lat_lng in lat_lngs:
city = citipy.nearest_city(lat_lng[0], lat_lng[1]).city_name
# If the city is unique, then add it to a our cities list
if city not in cities:
cities.append(city)
# Print the city count to confirm sufficient count
len(cities)
print('Beginning Data Retrieval')
print('-----------------------------')
for i in range(len(cities)):
weather_url=(f'https://api.openweathermap.org/data/2.5/weather?q={cities[i]}&appid={weather_api_key}')
# print(weather_url)
resp = requests.get(weather_url)
response = resp.json()
if resp.status_code != 200:
print('City not found. Skipping...')
else:
print(f'Processing Record {i+1} | {cities[i]}')
city_info_df.loc[i,'cloudiness'] = response['clouds']['all']
city_info_df.loc[i,'date'] = response['dt']
city_info_df.loc[i,'humidity'] = response['main']['humidity']
calc_max_temp = response['main']['temp_max']
calc_max_temp = calc_max_temp - 273.15
city_info_df.loc[i,'max_temp'] = calc_max_temp * 9 / 5 + 32
city_info_df.loc[i,'wind_speed'] = response['wind']['speed']
city_info_df.loc[i,'lat'] = response['coord']['lat']
city_info_df.loc[i,'long'] = response['coord']['lon']
city_info_df.loc[i,'city'] = response['name']
city_info_df.loc[i,'country'] = response['sys']['country']
print('-----------------------------')
print('Data Retrieval Complete')
print('-----------------------------')
city_info_df.to_csv(output_data_file, index=False)
city_info_df = city_info_df.reset_index()
city_info_df.info()
city_info_df.plot.scatter(x='lat', y='max_temp', c='blue', marker='o')
plt.xlabel("Latitude")
plt.ylabel("Max. Temperature")
plt.title("Latitude vs. Temperature")
plt.grid()
# Save the Figure
plt.savefig("../Images/lat_vs_temp.png")
# Show the Figure
plt.show()
plt.tight_layout();
city_info_df.plot.scatter(x='lat', y='humidity', c='green', marker='o')
plt.xlabel("Latitude")
plt.ylabel("Humidity")
plt.title("Latitude vs. Humidity")
plt.grid()
# Save the Figure
plt.savefig("../Images/lat_vs_humidity.png")
# Show the Figure
plt.show()
plt.tight_layout();
city_info_df.plot.scatter(x='lat', y='cloudiness', c='yellow', marker='o')
plt.xlabel("Latitude")
plt.ylabel("Cloudiness")
plt.title("Latitude vs. Cloudiness")
plt.grid()
# Save the Figure
plt.savefig("../Images/lat_vs_cloudiness.png")
# Show the Figure
plt.show()
plt.tight_layout();
city_info_df.plot.scatter(x='lat', y='wind_speed', c='purple', marker='o')
plt.xlabel("Latitude")
plt.ylabel("Wind Speed")
plt.title("Latitude vs. Wind Speed")
plt.grid()
# Save the Figure
plt.savefig("../Images/lat_vs_windspeed.png")
# Show the Figure
plt.show()
plt.tight_layout();
# OPTIONAL: Create a function to create Linear Regression plots
# Create Northern and Southern Hemisphere DataFrames
no_city_info_df = city_info_df[(city_info_df['lat'] >= 0)]
no_city_info_df
so_city_info_df = city_info_df[(city_info_df['lat'] < 0)]
so_city_info_df
| 0.310276 | 0.71469 |
```
%matplotlib inline
```
PyTorch에서 데이터 불러오기
=======================
PyTorch는 인공신경망을 만드는데 필요한 다양한 기본 요소를 간단하고 직관적이며
안정적인 API로 제공합니다. PyTorch는 공용 데이터셋을 쉽게 사용할 수 있도록
도와주는 패키지를 포함하고 있습니다.
개요
------------
PyTorch 데이터 불러오기 기능의 핵심은
`torch.utils.data.DataLoader <https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader>`__
클래스입니다. 데이터를 파이썬 iterable로써 접근할 수 있게 해주는 클래스입니다.
또한, `torch.utils.data.Dataset <https://pytorch.org/docs/stable/data.html#torch.utils.data.Dataset>`__
클래스를 통해 PyTorch에 내장된 다양한 고품질 데이터셋을 이용하실 수 있습니다.
개별 데이터셋은 아래 패키지에서 확인하실 수 있으며, 데이터셋은 계속해서 추가될 예정입니다.
* `torchvision <https://pytorch.org/vision/stable/datasets.html>`__
* `torchaudio <https://pytorch.org/audio/stable/datasets.html>`__
* `torchtext <https://pytorch.org/text/stable/datasets.html>`__
이번 레시피에서는 ``torchaudio.datasets.YESNO`` 데이터셋을 살펴보면서,
PyTorch ``Dataset`` 에서 PyTorch ``DataLoader`` 로 데이터를 효과적이고 효율적으로
불러오는 방법을 살펴보겠습니다.
초기 설정(Setup)
-----------------------------------------------------------------
시작하기 전에, 데이터셋이 포함된 ``torchaudio`` 패키지를 설치합니다.
```
# pip install torchaudio
```
Google Colab에서는 아래와 같이 실행합니다:
```
# !pip install torchaudio
```
단계(Steps)
-----------------------------------------------------------------
1. 데이터를 불러오는데 필요한 라이브러리 import하기
2. 데이터 접근하기
3. 데이터 불러오기
4. 데이터 순회하기
5. [선택 사항] 데이터 시각화하기
1. 데이터를 불러오는데 필요한 라이브러리 import하기
-----------------------------------------------------------------
이번 레시피는 ``torch`` 와 ``torchaudio`` 를 사용합니다. 다른 내장 데이터셋이
필요하다면 ``torchvision`` 혹은 ``torchtext`` 를 설치해서 사용해도 됩니다.
```
import torch
import torchaudio
```
2. 데이터에 접근하기
-----------------------------------------------------------------
``torchaudio`` 의 YesNo 데이터셋은 한 사람이 히브리어로 yes 혹은
no를 녹음한 오디오 클립 60개로 구성되어 있습니다. 오디오 클립 각각의 길이는 단어 8개입니다.
(`더 알아보기 <https://www.openslr.org/1/>`__).
``torchaudio.datasets.YESNO`` 클래스를 사용하여 YesNo 데이터셋을 생성합니다.
```
torchaudio.datasets.YESNO(
root,
url='http://www.openslr.org/resources/1/waves_yesno.tar.gz',
folder_in_archive='waves_yesno',
download=False,
transform=None,
target_transform=None)
```
각각의 데이터 항목 (item)은 튜플 형태 (waveform: 파형, sample_rate: 샘플 속도, labels: 라벨)를 갖습니다.
YesNo 데이터셋을 불러올 때 ``root`` 매개변수는 꼭 지정해주셔야 합니다. ``root`` 는
학습(training) 및 테스트(testing) 데이터셋이 존재하는 위치를 가르켜야 합니다.
그 외의 매개변수는 선택 사항이며, 위 예시에서 기본값을 확인하실 있습니다. 아래와
같은 매개변수도 사용 가능합니다.
* ``download``: 참인 경우, 데이터셋 파일을 인터넷에서 다운받고 root 폴더에 저장합니다. 파일이 이미 존재하면 다시 다운받지 않습니다.
* ``transform``: 데이터를 변환하여 학습에 사용할 수 있도록 이어붙이고 비정규화된 형태로 불러오실 수 있습니다. 라이브러리마다 다양한 transformation을 지원하고 있으며, 앞으로도 추가될 예정입니다.
* ``target_transform``: 타겟 데이터를 변환하기 위한 함수 혹은 transform입니다.
이제 YesNo 데이터를 확인해봅시다:
```
# YesNo 안에 각각의 데이터 항목은 튜플 형태 (파형, 샘플 속도, 라벨)를 가지며,
# 이때 labels는 0(no)과 1(yes)을 담은 리스트 형태로 되어 있습니다.
yesno_data = torchaudio.datasets.YESNO('./', download=True)
# 실제 데이터에 접근해서 yesno_data의 형태를 확인합니다. 세 번째 항목을 예시로 살펴봅니다.
n = 3
waveform, sample_rate, labels = yesno_data[n]
print("Waveform: {}\nSample rate: {}\nLabels: {}".format(waveform, sample_rate, labels))
```
실제 상황에서는 데이터를 "학습(training)" 데이터셋과 "테스트(testing)" 데이터셋으로 나누는 것이
권장됩니다. 모델의 성능을 제대로 평가하려면 학습에 쓰이지 않은 out-of-sample
데이터를 이용해야 하기 때문입니다.
3. 데이터 불러오기
-----------------------------------------------------------------
데이터셋에 성공적으로 접근했으니, 이제 데이터셋을 ``torch.utils.data.DataLoader`` 로 넘겨줍니다.
``DataLoader`` 는 데이터셋을 sampler와 조합시켜 데이터셋을 순회할 수 있는 iterable을 만들어줍니다.
```
data_loader = torch.utils.data.DataLoader(yesno_data,
batch_size=1,
shuffle=True)
```
4. 데이터 순회하기
-----------------------------------------------------------------
이제 ``data_loader`` 를 이용해서 데이터를 순회할 수 있습니다. 모델을 학습하려면 이처럼
데이터를 순회할 수 있어야 합니다. 아래 예시를 보시면 ``data_loader`` 안에 있는 각각의
데이터 항목이 파형, 샘플 속도, 라벨을 담은 텐서로 바뀌었음을 확인할 수 있습니다.
```
for data in data_loader:
print("Data: ", data)
print("Waveform: {}\nSample rate: {}\nLabels: {}".format(data[0], data[1], data[2]))
break
```
5. [선택 사항] 데이터 시각화하기
-----------------------------------------------------------------
``DataLoader`` 의 데이터를 시각화해서 더 자세히 확인해보실 수 있습니다.
```
import matplotlib.pyplot as plt
print(data[0][0].numpy())
plt.figure()
plt.plot(waveform.t().numpy())
```
축하드립니다! PyTorch에서 데이터를 불러오는데 성공하셨습니다.
더 알아보기
-----------------------------------------------------------------
다른 레시피를 둘러보고 계속 배워보세요:
- :doc:`/recipes/recipes/defining_a_neural_network`
- :doc:`/recipes/recipes/what_is_state_dict`
|
github_jupyter
|
%matplotlib inline
# pip install torchaudio
# !pip install torchaudio
import torch
import torchaudio
torchaudio.datasets.YESNO(
root,
url='http://www.openslr.org/resources/1/waves_yesno.tar.gz',
folder_in_archive='waves_yesno',
download=False,
transform=None,
target_transform=None)
# YesNo 안에 각각의 데이터 항목은 튜플 형태 (파형, 샘플 속도, 라벨)를 가지며,
# 이때 labels는 0(no)과 1(yes)을 담은 리스트 형태로 되어 있습니다.
yesno_data = torchaudio.datasets.YESNO('./', download=True)
# 실제 데이터에 접근해서 yesno_data의 형태를 확인합니다. 세 번째 항목을 예시로 살펴봅니다.
n = 3
waveform, sample_rate, labels = yesno_data[n]
print("Waveform: {}\nSample rate: {}\nLabels: {}".format(waveform, sample_rate, labels))
data_loader = torch.utils.data.DataLoader(yesno_data,
batch_size=1,
shuffle=True)
for data in data_loader:
print("Data: ", data)
print("Waveform: {}\nSample rate: {}\nLabels: {}".format(data[0], data[1], data[2]))
break
import matplotlib.pyplot as plt
print(data[0][0].numpy())
plt.figure()
plt.plot(waveform.t().numpy())
| 0.495117 | 0.984826 |
# Luther - Linear Regression Model
This is where I work with the merged dataframe to fit a linear regression model in order to predict the opening box office gross
```
# all of the imports
import pandas as pd
import numpy as np
import pickle
import patsy
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import ElasticNetCV
from sklearn.linear_model import LassoCV
from sklearn import metrics
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
from scipy.stats import boxcox
from sklearn.pipeline import make_pipeline
from sklearn.cross_validation import train_test_split
from sklearn.cross_validation import KFold
from sklearn.cross_validation import cross_val_score
% matplotlib inline
%config InlineBackend.figure_format = 'png'
import matplotlib as mpl
mpl.rcParams['figure.dpi']= 300
import warnings
warnings.filterwarnings('ignore')
# Import merged dataframe
merged_df = pd.read_pickle('data/merged_df.pkl')
test_2018 = pd.read_pickle('data/merged_2018.pkl')
merged_df.head(7)
# add these columns to account for whether the actors/directors were identified
merged_df["dirgross_bin"] = merged_df.dir_gross.apply(lambda x: x/x if x > 0 else x)
merged_df["actgross_bin"] = merged_df.act_gross.apply(lambda x: x/x if x > 0 else x)
test_2018["dirgross_bin"] = merged_df.dir_gross.apply(lambda x: x/x if x > 0 else x)
test_2018["actgross_bin"] = merged_df.act_gross.apply(lambda x: x/x if x > 0 else x)
merged_df.head()
# Test on entire 2013-2017 dataset
merged_test = test_2018
merged_train = merged_df
merged_test.columns
#merged2.columns
#drop unnecessary/duplicate columns
merged_test = merged_test.drop(["movie","movie_name","tick", "year",
"tot_gross","op_gross","date_time"],1)
merged_train = merged_train.drop(["movie","movie_name","tick", "year",
"tot_gross","op_gross","date_time"],1)
X_train = patsy.dmatrix('rated',data=merged_train,return_type='dataframe')
X_test = patsy.dmatrix('rated',data=merged_test,return_type='dataframe')
X_train.head()
merged2_test = merged_test.join(X_test)
merged2_test = merged_test.drop(["rated"],1)
merged2_train = merged_train.join(X_train)
merged2_train = merged_train.drop(["rated"],1)
#sns.pairplot(merged2)
#sns.regplot(merged2.unemp_rate, merged2.est_tick)
# Add 1 to the comments, director gross and actor gross in order to normalize data with
# log or boxcox
merged2_test['Ycom_adj'] = merged2_test.Ycom_adj.apply(lambda x: x + 1)
merged2_test['dir_gross'] = merged2_test.dir_gross.apply(lambda x: x + 1)
merged2_test['act_gross'] = merged2_test.act_gross.apply(lambda x: x + 1)
merged2_test['act_nmovies'] = merged2_test.act_gross.apply(lambda x: x + 1)
merged2_test['dir_nmovies'] = merged2_test.act_gross.apply(lambda x: x + 1)
merged2_train['Ycom_adj'] = merged2_train.Ycom_adj.apply(lambda x: x + 1)
merged2_train['dir_gross'] = merged2_train.dir_gross.apply(lambda x: x + 1)
merged2_train['act_gross'] = merged2_train.act_gross.apply(lambda x: x + 1)
merged2_train['act_nmovies'] = merged2_train.act_gross.apply(lambda x: x + 1)
merged2_train['dir_nmovies'] = merged2_train.act_gross.apply(lambda x: x + 1)
# Normalize dataset with log transformation
merged2_train["tick_log"] = np.log(merged2_train.est_tick)
merged2_train["Ylikes_log"] = np.log(merged2_train.Ylikes_adj)
merged2_train["Yviews_log"] = np.log(merged2_train.Yviews_adj)
merged2_train["Ydis_log"] = np.log(merged2_train.Ydis_adj)
merged2_train["runtime_log"] = np.log(merged2_train.runtime)
merged2_train["dir_gross"] = np.log(merged2_train.dir_gross)
merged2_train["act_gross"] = np.log(merged2_train.act_gross)
merged2_train["Ycom_log"] = np.log(merged2_train.Ycom_adj)
merged3_train = merged2_train.drop(["est_tick","Ylikes_adj","Yviews_adj","Ydis_adj","runtime",
"act_gross","dir_gross","Ycom_adj"], 1)
merged2_test["tick_log"] = np.log(merged2_test.est_tick)
merged2_test["Ylikes_log"] = np.log(merged2_test.Ylikes_adj)
merged2_test["Yviews_log"] = np.log(merged2_test.Yviews_adj)
merged2_test["Ydis_log"] = np.log(merged2_test.Ydis_adj)
merged2_test["runtime_log"] = np.log(merged2_test.runtime)
merged2_test["dir_gross"] = np.log(merged2_test.dir_gross)
merged2_test["act_gross"] = np.log(merged2_test.act_gross)
merged2_test["Ycom_log"] = np.log(merged2_test.Ycom_adj)
merged3_test = merged2_test.drop(["est_tick","Ylikes_adj","Yviews_adj","Ydis_adj","runtime",
"act_gross","dir_gross","Ycom_adj"], 1)
sns.heatmap(merged3_train.corr(), cmap = "seismic")
merged3_train.columns
y_train = merged3_train.tick_log
X_train = merged3_train.drop(['tick_log'],1)
y_test = merged3_test.tick_log
X_test = merged3_test.drop(['tick_log'],1)
#model= LinearRegression()
#fit = model.fit(X,y)
# Split train test set
#X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.2, random_state = 42)
# The Xtrain and Ytrain will be used to train the data & cross validate
# X test and Y test will be used to assess the performance after CV
#Split CV
X_trainCV, X_CV, y_trainCV, y_CV = train_test_split(X_train,y_train,test_size = 0.3,
random_state= 32)
# alphas = [0,1e-8,1e-7,1e-6,1e-5,1e-4,1e-3,1e-2,1e-1]
# elas_model = ElasticNetCV(alphas=alphas, l1_ratio=[1e-8, 1e-6, 1e-4, 1e-2, .5, 1])
# fit = elas_model.fit(X_train,y_train)
# #fit.predict(X_train)
# fit.alpha_
# fit.l1_ratio_
# Linear model without polyfit
alphas = [0,1e-8,1e-7,1e-6,1e-5,1e-4,1e-3,1e-2,1e-1]
l1 = [0, 1e-8, 1e-6, 1e-4, 1e-2, .5, .9, 1]
degree = 2
lin_model = make_pipeline(ElasticNetCV(alphas=alphas, l1_ratio = l1,cv=10))
lin_model.fit(X_trainCV,y_trainCV)
print("alpha =", lin_model.named_steps.elasticnetcv.alpha_)
print("l1_ratio =", lin_model.named_steps.elasticnetcv.l1_ratio_)
print("R^2 on CV =", lin_model.score(X_CV,y_CV))
# Polyfit model
alphas = [1e-4,1e-3,1e-2,1e-1,1,10,30,60,90,100,300,600]
l1 = [0, .1, .5, .7, .9, .95, .99, 1]
degree = 2
poly_model = make_pipeline(PolynomialFeatures(degree),
ElasticNetCV(alphas=alphas, l1_ratio = l1,cv=10))
poly_model.fit(X_trainCV,y_trainCV)
print("alpha =", poly_model.named_steps.elasticnetcv.alpha_)
print("l1_ratio =", poly_model.named_steps.elasticnetcv.l1_ratio_)
print("R^2 on CV =", poly_model.score(X_CV,y_CV))
# Polyfit model
alphas = [1e-4,1e-3,1e-2,1e-1,1,10,30,60,90,100,300,600]
l1 = [0, .1, .5, .7, .9, .95, .99, 1]
degree = 2
poly_model_lasso = make_pipeline(PolynomialFeatures(degree),
LassoCV(alphas=alphas,cv=10))
poly_model_lasso.fit(X_trainCV,y_trainCV)
print("alpha =", poly_model_lasso.named_steps.lassocv.alpha_)
#print("l1_ratio =", poly_model_lasso.named_steps.elasticnetcv.l1_ratio_)
print("R^2 on CV =", poly_model_lasso.score(X_CV,y_CV))
import math
from sklearn.metrics import mean_squared_error
rms = math.exp(math.sqrt(mean_squared_error(y_test, poly_model.predict(X_test))))
r_squared = poly_model.score(X_test,y_test)
print("R^2 =", r_squared)
print("rms =", rms)
#poly_model.predict(X_CV)
def diagnostic_plot(x, y, model):
plt.figure(figsize=(20,5))
rgr = model
model.fit(x,y)
pred = model.predict(x)
# plt.subplot(1, 3, 1)
# plt.scatter(x,y)
# plt.plot(x, pred, color='blue',linewidth=1)
# plt.title("Regression fit")
# plt.xlabel("x")
# plt.ylabel("y")
plt.subplot(1, 3, 2)
res = y - pred
plt.scatter(pred, res)
plt.title("Residual plot")
plt.xlabel("prediction")
plt.ylabel("residuals")
plt.subplot(1, 3, 3)
#Generates a probability plot of sample data against the quantiles of a
# specified theoretical distribution
stats.probplot(res, dist="norm", plot=plt)
plt.title("Normal Q-Q plot")
diagnostic_plot(X_train, y_train, poly_model)
# Plot your predicted values on the x-axis, and your residuals on the y-axis
merged4 = merged3_train
merged4['predict']=poly_model.predict(X_train)
merged4['resid']=merged3_train.tick_log-merged4_train.predict
with sns.axes_style('white'):
plot=merged4.plot(kind='scatter',
x='predict',y='resid',alpha=0.2,figsize=(10,6))
```
## See how well the linear regression performs on 2017 data
```
prediction = poly_model.predict(X_test)
math.exp(16.854)
test_2018 = test_2018.drop(["movie","date_time","theaters","unemp_rate",
"imdb","metacritic","Ycom_adj","Ylikes_adj",
"Ydis_adj","rotten_tomatoes","runtime",
"dir_nmovies","dirgross_bin","actgross_bin",
"dir_gross","act_gross","act_nmovies"],1)
test_2018["predict_tick"] = prediction
test_2018["predict_tick"] = test_2018.predict_tick.apply(lambda x: math.exp(x))
test_2018["predict_gross"] = test_2018.predict_tick.multiply(test_2018.tick)
test_2018["predict_gross_error"] = test_2018.op_gross.subtract(test_2018.predict_gross)
test_2018["predict_tick_error"] = test_2018.est_tick.subtract(test_2018.predict_tick)
test_2018["percent_gross_error"] = test_2018.predict_gross_error.divide(
test_2018.op_gross)
test_2018["percent_gross_error"] = test_2018.percent_gross_error.apply(lambda x: abs(x))
test_2018.head()
test_2018.percent_gross_error.describe()
print(test_2018.predict_gross_error.quantile([0.25,0.5,0.75]))
sns.boxplot(test_2018.predict_gross_error.apply(lambda x: x/1e6),color="maroon")
#plt.xlim(0, None)
plt.xlabel("Opening Gross Error ($million)")
#plt.xlabel("Actual Gross ($million)")
plt.title("Absolute Gross Error On 2017 Movies")
#plt.ticklabel_format(style='plain')
plt.xticks(rotation=30)
print(test_2018.percent_gross_error.quantile([0.25,0.5,0.75]))
sns.boxplot(test_2018.percent_gross_error*100,color="maroon")
plt.xlim(0, 500)
plt.xlabel("Percent Error on Opening Gross (%)")
plt.title("Percent Error On 2017 Movies")
plt.xticks(rotation=30)
import matplotlib.pyplot as plt
sns.regplot(test_2018.op_gross/1e6, test_2018.percent_gross_error*100,fit_reg=False,
color="maroon")
# plt.ylim(0, 500)
# plt.xlim(0, None)
plt.ylabel("Opening Gross Percent Error (%)")
plt.xlabel("Actual Gross on Opening Week ($million)")
plt.title("Percent Error On 2017 Movies")
plt.ticklabel_format(style='plain')
plt.xticks(rotation=30)
import matplotlib.pyplot as plt
sns.regplot(test_2018.op_gross/1e6, test_2018.predict_gross_error/1e6,fit_reg=False,
color="maroon")
plt.ylim(0, None)
plt.xlim(0, None)
plt.ylabel("Opening Gross Error ($million)")
plt.xlabel("Actual Gross on Opening Week ($million)")
plt.title("Opening Gross Error On 2018 Movies")
plt.ticklabel_format(style='plain')
plt.xticks(rotation=30)
pd.set_option('display.float_format', lambda x: '%.3f' % x)
test_2018.sort_values(by="percent_gross_error",ascending=False).head()
test_2018.iloc[1,:]
# Check the coefficients for the features in the final model
poly_coeff = pd.DataFrame({"feature" : poly_model.named_steps.polynomialfeatures.get_feature_names(),
"coefficients" : poly_model.named_steps.elasticnetcv.coef_})
poly_coeff.sort_values(by="coefficients",ascending=False).head(7)
#merged2.iloc[393,:]
# # Statsmodel
# model = sm.OLS(y,X)
# # Fit your model to your training set
# fit = model.fit()
# # Print summary statistics of the model's performance
# fit.summary()
```
|
github_jupyter
|
# all of the imports
import pandas as pd
import numpy as np
import pickle
import patsy
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import ElasticNetCV
from sklearn.linear_model import LassoCV
from sklearn import metrics
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
from scipy.stats import boxcox
from sklearn.pipeline import make_pipeline
from sklearn.cross_validation import train_test_split
from sklearn.cross_validation import KFold
from sklearn.cross_validation import cross_val_score
% matplotlib inline
%config InlineBackend.figure_format = 'png'
import matplotlib as mpl
mpl.rcParams['figure.dpi']= 300
import warnings
warnings.filterwarnings('ignore')
# Import merged dataframe
merged_df = pd.read_pickle('data/merged_df.pkl')
test_2018 = pd.read_pickle('data/merged_2018.pkl')
merged_df.head(7)
# add these columns to account for whether the actors/directors were identified
merged_df["dirgross_bin"] = merged_df.dir_gross.apply(lambda x: x/x if x > 0 else x)
merged_df["actgross_bin"] = merged_df.act_gross.apply(lambda x: x/x if x > 0 else x)
test_2018["dirgross_bin"] = merged_df.dir_gross.apply(lambda x: x/x if x > 0 else x)
test_2018["actgross_bin"] = merged_df.act_gross.apply(lambda x: x/x if x > 0 else x)
merged_df.head()
# Test on entire 2013-2017 dataset
merged_test = test_2018
merged_train = merged_df
merged_test.columns
#merged2.columns
#drop unnecessary/duplicate columns
merged_test = merged_test.drop(["movie","movie_name","tick", "year",
"tot_gross","op_gross","date_time"],1)
merged_train = merged_train.drop(["movie","movie_name","tick", "year",
"tot_gross","op_gross","date_time"],1)
X_train = patsy.dmatrix('rated',data=merged_train,return_type='dataframe')
X_test = patsy.dmatrix('rated',data=merged_test,return_type='dataframe')
X_train.head()
merged2_test = merged_test.join(X_test)
merged2_test = merged_test.drop(["rated"],1)
merged2_train = merged_train.join(X_train)
merged2_train = merged_train.drop(["rated"],1)
#sns.pairplot(merged2)
#sns.regplot(merged2.unemp_rate, merged2.est_tick)
# Add 1 to the comments, director gross and actor gross in order to normalize data with
# log or boxcox
merged2_test['Ycom_adj'] = merged2_test.Ycom_adj.apply(lambda x: x + 1)
merged2_test['dir_gross'] = merged2_test.dir_gross.apply(lambda x: x + 1)
merged2_test['act_gross'] = merged2_test.act_gross.apply(lambda x: x + 1)
merged2_test['act_nmovies'] = merged2_test.act_gross.apply(lambda x: x + 1)
merged2_test['dir_nmovies'] = merged2_test.act_gross.apply(lambda x: x + 1)
merged2_train['Ycom_adj'] = merged2_train.Ycom_adj.apply(lambda x: x + 1)
merged2_train['dir_gross'] = merged2_train.dir_gross.apply(lambda x: x + 1)
merged2_train['act_gross'] = merged2_train.act_gross.apply(lambda x: x + 1)
merged2_train['act_nmovies'] = merged2_train.act_gross.apply(lambda x: x + 1)
merged2_train['dir_nmovies'] = merged2_train.act_gross.apply(lambda x: x + 1)
# Normalize dataset with log transformation
merged2_train["tick_log"] = np.log(merged2_train.est_tick)
merged2_train["Ylikes_log"] = np.log(merged2_train.Ylikes_adj)
merged2_train["Yviews_log"] = np.log(merged2_train.Yviews_adj)
merged2_train["Ydis_log"] = np.log(merged2_train.Ydis_adj)
merged2_train["runtime_log"] = np.log(merged2_train.runtime)
merged2_train["dir_gross"] = np.log(merged2_train.dir_gross)
merged2_train["act_gross"] = np.log(merged2_train.act_gross)
merged2_train["Ycom_log"] = np.log(merged2_train.Ycom_adj)
merged3_train = merged2_train.drop(["est_tick","Ylikes_adj","Yviews_adj","Ydis_adj","runtime",
"act_gross","dir_gross","Ycom_adj"], 1)
merged2_test["tick_log"] = np.log(merged2_test.est_tick)
merged2_test["Ylikes_log"] = np.log(merged2_test.Ylikes_adj)
merged2_test["Yviews_log"] = np.log(merged2_test.Yviews_adj)
merged2_test["Ydis_log"] = np.log(merged2_test.Ydis_adj)
merged2_test["runtime_log"] = np.log(merged2_test.runtime)
merged2_test["dir_gross"] = np.log(merged2_test.dir_gross)
merged2_test["act_gross"] = np.log(merged2_test.act_gross)
merged2_test["Ycom_log"] = np.log(merged2_test.Ycom_adj)
merged3_test = merged2_test.drop(["est_tick","Ylikes_adj","Yviews_adj","Ydis_adj","runtime",
"act_gross","dir_gross","Ycom_adj"], 1)
sns.heatmap(merged3_train.corr(), cmap = "seismic")
merged3_train.columns
y_train = merged3_train.tick_log
X_train = merged3_train.drop(['tick_log'],1)
y_test = merged3_test.tick_log
X_test = merged3_test.drop(['tick_log'],1)
#model= LinearRegression()
#fit = model.fit(X,y)
# Split train test set
#X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.2, random_state = 42)
# The Xtrain and Ytrain will be used to train the data & cross validate
# X test and Y test will be used to assess the performance after CV
#Split CV
X_trainCV, X_CV, y_trainCV, y_CV = train_test_split(X_train,y_train,test_size = 0.3,
random_state= 32)
# alphas = [0,1e-8,1e-7,1e-6,1e-5,1e-4,1e-3,1e-2,1e-1]
# elas_model = ElasticNetCV(alphas=alphas, l1_ratio=[1e-8, 1e-6, 1e-4, 1e-2, .5, 1])
# fit = elas_model.fit(X_train,y_train)
# #fit.predict(X_train)
# fit.alpha_
# fit.l1_ratio_
# Linear model without polyfit
alphas = [0,1e-8,1e-7,1e-6,1e-5,1e-4,1e-3,1e-2,1e-1]
l1 = [0, 1e-8, 1e-6, 1e-4, 1e-2, .5, .9, 1]
degree = 2
lin_model = make_pipeline(ElasticNetCV(alphas=alphas, l1_ratio = l1,cv=10))
lin_model.fit(X_trainCV,y_trainCV)
print("alpha =", lin_model.named_steps.elasticnetcv.alpha_)
print("l1_ratio =", lin_model.named_steps.elasticnetcv.l1_ratio_)
print("R^2 on CV =", lin_model.score(X_CV,y_CV))
# Polyfit model
alphas = [1e-4,1e-3,1e-2,1e-1,1,10,30,60,90,100,300,600]
l1 = [0, .1, .5, .7, .9, .95, .99, 1]
degree = 2
poly_model = make_pipeline(PolynomialFeatures(degree),
ElasticNetCV(alphas=alphas, l1_ratio = l1,cv=10))
poly_model.fit(X_trainCV,y_trainCV)
print("alpha =", poly_model.named_steps.elasticnetcv.alpha_)
print("l1_ratio =", poly_model.named_steps.elasticnetcv.l1_ratio_)
print("R^2 on CV =", poly_model.score(X_CV,y_CV))
# Polyfit model
alphas = [1e-4,1e-3,1e-2,1e-1,1,10,30,60,90,100,300,600]
l1 = [0, .1, .5, .7, .9, .95, .99, 1]
degree = 2
poly_model_lasso = make_pipeline(PolynomialFeatures(degree),
LassoCV(alphas=alphas,cv=10))
poly_model_lasso.fit(X_trainCV,y_trainCV)
print("alpha =", poly_model_lasso.named_steps.lassocv.alpha_)
#print("l1_ratio =", poly_model_lasso.named_steps.elasticnetcv.l1_ratio_)
print("R^2 on CV =", poly_model_lasso.score(X_CV,y_CV))
import math
from sklearn.metrics import mean_squared_error
rms = math.exp(math.sqrt(mean_squared_error(y_test, poly_model.predict(X_test))))
r_squared = poly_model.score(X_test,y_test)
print("R^2 =", r_squared)
print("rms =", rms)
#poly_model.predict(X_CV)
def diagnostic_plot(x, y, model):
plt.figure(figsize=(20,5))
rgr = model
model.fit(x,y)
pred = model.predict(x)
# plt.subplot(1, 3, 1)
# plt.scatter(x,y)
# plt.plot(x, pred, color='blue',linewidth=1)
# plt.title("Regression fit")
# plt.xlabel("x")
# plt.ylabel("y")
plt.subplot(1, 3, 2)
res = y - pred
plt.scatter(pred, res)
plt.title("Residual plot")
plt.xlabel("prediction")
plt.ylabel("residuals")
plt.subplot(1, 3, 3)
#Generates a probability plot of sample data against the quantiles of a
# specified theoretical distribution
stats.probplot(res, dist="norm", plot=plt)
plt.title("Normal Q-Q plot")
diagnostic_plot(X_train, y_train, poly_model)
# Plot your predicted values on the x-axis, and your residuals on the y-axis
merged4 = merged3_train
merged4['predict']=poly_model.predict(X_train)
merged4['resid']=merged3_train.tick_log-merged4_train.predict
with sns.axes_style('white'):
plot=merged4.plot(kind='scatter',
x='predict',y='resid',alpha=0.2,figsize=(10,6))
prediction = poly_model.predict(X_test)
math.exp(16.854)
test_2018 = test_2018.drop(["movie","date_time","theaters","unemp_rate",
"imdb","metacritic","Ycom_adj","Ylikes_adj",
"Ydis_adj","rotten_tomatoes","runtime",
"dir_nmovies","dirgross_bin","actgross_bin",
"dir_gross","act_gross","act_nmovies"],1)
test_2018["predict_tick"] = prediction
test_2018["predict_tick"] = test_2018.predict_tick.apply(lambda x: math.exp(x))
test_2018["predict_gross"] = test_2018.predict_tick.multiply(test_2018.tick)
test_2018["predict_gross_error"] = test_2018.op_gross.subtract(test_2018.predict_gross)
test_2018["predict_tick_error"] = test_2018.est_tick.subtract(test_2018.predict_tick)
test_2018["percent_gross_error"] = test_2018.predict_gross_error.divide(
test_2018.op_gross)
test_2018["percent_gross_error"] = test_2018.percent_gross_error.apply(lambda x: abs(x))
test_2018.head()
test_2018.percent_gross_error.describe()
print(test_2018.predict_gross_error.quantile([0.25,0.5,0.75]))
sns.boxplot(test_2018.predict_gross_error.apply(lambda x: x/1e6),color="maroon")
#plt.xlim(0, None)
plt.xlabel("Opening Gross Error ($million)")
#plt.xlabel("Actual Gross ($million)")
plt.title("Absolute Gross Error On 2017 Movies")
#plt.ticklabel_format(style='plain')
plt.xticks(rotation=30)
print(test_2018.percent_gross_error.quantile([0.25,0.5,0.75]))
sns.boxplot(test_2018.percent_gross_error*100,color="maroon")
plt.xlim(0, 500)
plt.xlabel("Percent Error on Opening Gross (%)")
plt.title("Percent Error On 2017 Movies")
plt.xticks(rotation=30)
import matplotlib.pyplot as plt
sns.regplot(test_2018.op_gross/1e6, test_2018.percent_gross_error*100,fit_reg=False,
color="maroon")
# plt.ylim(0, 500)
# plt.xlim(0, None)
plt.ylabel("Opening Gross Percent Error (%)")
plt.xlabel("Actual Gross on Opening Week ($million)")
plt.title("Percent Error On 2017 Movies")
plt.ticklabel_format(style='plain')
plt.xticks(rotation=30)
import matplotlib.pyplot as plt
sns.regplot(test_2018.op_gross/1e6, test_2018.predict_gross_error/1e6,fit_reg=False,
color="maroon")
plt.ylim(0, None)
plt.xlim(0, None)
plt.ylabel("Opening Gross Error ($million)")
plt.xlabel("Actual Gross on Opening Week ($million)")
plt.title("Opening Gross Error On 2018 Movies")
plt.ticklabel_format(style='plain')
plt.xticks(rotation=30)
pd.set_option('display.float_format', lambda x: '%.3f' % x)
test_2018.sort_values(by="percent_gross_error",ascending=False).head()
test_2018.iloc[1,:]
# Check the coefficients for the features in the final model
poly_coeff = pd.DataFrame({"feature" : poly_model.named_steps.polynomialfeatures.get_feature_names(),
"coefficients" : poly_model.named_steps.elasticnetcv.coef_})
poly_coeff.sort_values(by="coefficients",ascending=False).head(7)
#merged2.iloc[393,:]
# # Statsmodel
# model = sm.OLS(y,X)
# # Fit your model to your training set
# fit = model.fit()
# # Print summary statistics of the model's performance
# fit.summary()
| 0.452778 | 0.843122 |
```
# Import dependencies
import pandas as pd
import numpy as np
import time
from itertools import islice
# Create DataFrame from CSV
t0 = time.time()
filtered_cooccurring_df = pd.read_csv('../../Data/filtered_cooccurring_TF.csv')
filtered_cooccurring_df.index = filtered_cooccurring_df.index - 1
t1 = time.time()
print(f'Run time: {t1-t0} seconds')
filtered_cooccurring_df.head(3)
# Create a dictionary of category names and ids
cat_name_id = {}
category_list = ['blues', 'classical', 'country', 'funk', 'hiphop', 'indie_alt', 'jazz',
'metal', 'pop', 'punk', 'rnb', 'rock', 'romance', 'soul']
for cat in category_list:
cat_id = list(filtered_cooccurring_df[filtered_cooccurring_df['category_name']==cat]['category_id'])[0]
cat_name_id[cat] = cat_id
print(cat, cat_id)
# Create a new DataFrame with co-occurring word columns
new_lyric_TF_df = filtered_cooccurring_df.drop([-1])
new_lyric_TF_df = new_lyric_TF_df.drop(columns=new_lyric_TF_df.columns[17:14144])
new_lyric_TF_df.head(3)
# Create a list of the overall top ten words
word_count_df = filtered_cooccurring_df.drop(columns=filtered_cooccurring_df.columns[:14144])#[:1]
word_count_df = word_count_df.sort_values(by=[-1], axis=1, ascending=False)
total_count = len(word_count_df) - 1
top_words = list(word_count_df.columns[0:10])
word_count_df = word_count_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(word_count_df[word_count_df[word]!=0])-1) / total_count * 100
top_ten[word] = round(percent, 1)
top_word_counts = list(word_count_df.loc[-1])[0:10]
index = 0
for word in top_ten:
print(word)
print('Frequency & percent: (', top_word_counts[index], ',', top_ten[word], ')')
index+=1
# Create a dictionary of the top ten co-occurring words for each category
t0 = time.time()
df_rows = []
blues_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='blues'].copy()
count_blues = len(blues_df)
blues_df.loc[0] = blues_df.sum(numeric_only=True)
blues_words = blues_df.sort_index()[blues_df.columns[17:]][0:1]
blues_words = blues_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(blues_words.columns[0:10])
blues_df = blues_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(blues_df[blues_df[word]!=0])-1) / count_blues * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(blues_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
classical_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='classical'].copy()
count_classical = len(classical_df)
classical_df.loc[0] = classical_df.sum(numeric_only=True)
classical_words = classical_df.sort_index()[classical_df.columns[18:]][0:1]
classical_words = classical_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(classical_words.columns[0:10])
classical_df = classical_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(classical_df[classical_df[word]!=0])-1) / count_classical * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(classical_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
country_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='country'].copy()
count_country = len(country_df)
country_df.loc[0] = country_df.sum(numeric_only=True)
country_words = country_df.sort_index()[country_df.columns[18:]][0:1]
country_words = country_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(country_words.columns[0:10])
country_df = country_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(country_df[country_df[word]!=0])-1) / count_country * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(country_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
funk_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='funk'].copy()
count_funk = len(funk_df)
funk_df.loc[0] = funk_df.sum(numeric_only=True)
funk_words = funk_df.sort_index()[funk_df.columns[18:]][0:1]
funk_words = funk_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(funk_words.columns[0:10])
funk_df = funk_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(funk_df[funk_df[word]!=0])-1) / count_funk * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(funk_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
hiphop_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='hiphop'].copy()
count_hiphop = len(hiphop_df)
hiphop_df.loc[0] = hiphop_df.sum(numeric_only=True)
hiphop_words = hiphop_df.sort_index()[hiphop_df.columns[18:]][0:1]
hiphop_words = hiphop_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(hiphop_words.columns[0:10])
hiphop_df = hiphop_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(hiphop_df[hiphop_df[word]!=0])-1) / count_hiphop * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(hiphop_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
indie_alt_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='indie_alt'].copy()
count_indie_alt = len(indie_alt_df)
indie_alt_df.loc[0] = indie_alt_df.sum(numeric_only=True)
indie_alt_words = indie_alt_df.sort_index()[indie_alt_df.columns[18:]][0:1]
indie_alt_words = indie_alt_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(indie_alt_words.columns[0:10])
indie_alt_df = indie_alt_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(indie_alt_df[indie_alt_df[word]!=0])-1) / count_indie_alt * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(indie_alt_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
jazz_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='jazz'].copy()
count_jazz = len(jazz_df)
jazz_df.loc[0] = jazz_df.sum(numeric_only=True)
jazz_words = jazz_df.sort_index()[jazz_df.columns[18:]][0:1]
jazz_words = jazz_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(jazz_words.columns[0:10])
jazz_df = jazz_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(jazz_df[jazz_df[word]!=0])-1) / count_jazz * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(jazz_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
metal_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='metal'].copy()
count_metal = len(metal_df)
metal_df.loc[0] = metal_df.sum(numeric_only=True)
metal_words = metal_df.sort_index()[metal_df.columns[18:]][0:1]
metal_words = metal_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(metal_words.columns[0:10])
metal_df = metal_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(metal_df[metal_df[word]!=0])-1) / count_metal * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(metal_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
pop_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='pop'].copy()
count_pop = len(pop_df)
pop_df.loc[-1] = pop_df.sum(numeric_only=True)
pop_words = pop_df.sort_index()[pop_df.columns[18:]][:1]
pop_words = pop_words.sort_values(by=[-1], axis=1, ascending=False)
top_words = list(pop_words.columns[0:10])
pop_df = pop_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(pop_df[pop_df[word]!=0])-1) / count_pop * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(pop_words.loc[-1])[0:10])
df_rows.append(list(top_ten.values()))
punk_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='punk'].copy()
count_punk = len(punk_df)
punk_df.loc[0] = punk_df.sum(numeric_only=True)
punk_words = punk_df.sort_index()[punk_df.columns[18:]][0:1]
punk_words = punk_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(punk_words.columns[0:10])
punk_df = punk_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(punk_df[punk_df[word]!=0])-1) / count_punk * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(punk_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
rnb_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='rnb'].copy()
count_rnb = len(rnb_df)
rnb_df.loc[0] = rnb_df.sum(numeric_only=True)
rnb_words = rnb_df.sort_index()[rnb_df.columns[18:]][0:1]
rnb_words = rnb_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(rnb_words.columns[0:10])
rnb_df = rnb_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(rnb_df[rnb_df[word]!=0])-1) / count_rnb * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(rnb_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
rock_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='rock'].copy()
count_rock = len(rock_df)
rock_df.loc[0] = rock_df.sum(numeric_only=True)
rock_words = rock_df.sort_index()[rock_df.columns[18:]][0:1]
rock_words = rock_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(rock_words.columns[0:10])
rock_df = rock_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(rock_df[rock_df[word]!=0])-1) / count_rock * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(rock_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
romance_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='romance'].copy()
count_romance = len(romance_df)
romance_df.loc[0] = romance_df.sum(numeric_only=True)
romance_words = romance_df.sort_index()[romance_df.columns[18:]][0:1]
romance_words = romance_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(romance_words.columns[0:10])
romance_df = romance_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(romance_df[romance_df[word]!=0])-1) / count_romance * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(romance_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
soul_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='soul'].copy()
count_soul = len(soul_df)
soul_df.loc[0] = soul_df.sum(numeric_only=True)
soul_words = soul_df.sort_index()[soul_df.columns[18:]][0:1]
soul_words = soul_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(soul_words.columns[0:10])
soul_df = soul_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(soul_df[soul_df[word]!=0])-1) / count_soul * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(soul_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
t1 = time.time()
print(f'Run time: {t1-t0} seconds')
# Create dictionary of top word frequencies
unique_top_words = []
for i in range(len(df_rows)):
if i%3 == 0:
unique_top_words.extend(df_rows[i])
unique_top_words = list(set(unique_top_words))
top_word_freq = dict.fromkeys(unique_top_words, 0)
for i in range(len(df_rows)):
if i%3 == 0:
for word in df_rows[i]:
top_word_freq[word]+=1
print(len(top_word_freq))
top_word_freq
# Print top words that are unique to one genre
unique_to_one = dict(filter(lambda key: key[1] == 1, top_word_freq.items()))
print(len(unique_to_one))
unique_to_one
# Print top words that are unique to two genre
unique_to_two = dict(filter(lambda key: key[1] == 2, top_word_freq.items()))
print(len(unique_to_two))
unique_to_two
# Create DataFrame of top ten words
categories = np.array(['blues', 'blues', 'blues', 'classical', 'classical', 'classical', 'country', 'country', 'country',
'funk', 'funk', 'funk', 'hiphop', 'hiphop', 'hiphop', 'indie_alt', 'indie_alt', 'indie_alt',
'jazz', 'jazz', 'jazz', 'metal', 'metal', 'metal', 'pop', 'pop', 'pop', 'punk', 'punk', 'punk',
'rnb', 'rnb', 'rnb', 'rock', 'rock', 'rock', 'romance', 'romance', 'romance', 'soul', 'soul', 'soul'])
arrays = [categories, np.array(['words', 'frequencies', 'percents', 'words', 'frequencies', 'percents', 'words',
'frequencies', 'percents', 'words', 'frequencies', 'percents', 'words', 'frequencies',
'percents', 'words', 'frequencies', 'percents', 'words', 'frequencies', 'percents', 'words',
'frequencies', 'percents', 'words', 'frequencies', 'percents', 'words', 'frequencies',
'percents', 'words', 'frequencies', 'percents', 'words', 'frequencies', 'percents', 'words',
'frequencies', 'percents', 'words', 'frequencies', 'percents'])]
tuples = list(zip(*arrays))
index = pd.MultiIndex.from_tuples(tuples)
top_cooccurring_df = pd.DataFrame(df_rows, index=arrays, columns=range(1,11))
top_cooccurring_df
# Save DataFrame to CSV
top_cooccurring_df.to_csv('../../Data/Analysis/top_cooccurring_words.csv')
```
# Conclusions about top co-occurring words
- From the total 140 top ten co-occurring words from each of the 14 genres, 46 were unique
- 25 of the top ten co-occurring words are unique to one genre
- 2 of the top ten co-occurring words are unique to two genres
- 'dont know' is in the top ten co-occurring words for 13 out of 14 genres
|
github_jupyter
|
# Import dependencies
import pandas as pd
import numpy as np
import time
from itertools import islice
# Create DataFrame from CSV
t0 = time.time()
filtered_cooccurring_df = pd.read_csv('../../Data/filtered_cooccurring_TF.csv')
filtered_cooccurring_df.index = filtered_cooccurring_df.index - 1
t1 = time.time()
print(f'Run time: {t1-t0} seconds')
filtered_cooccurring_df.head(3)
# Create a dictionary of category names and ids
cat_name_id = {}
category_list = ['blues', 'classical', 'country', 'funk', 'hiphop', 'indie_alt', 'jazz',
'metal', 'pop', 'punk', 'rnb', 'rock', 'romance', 'soul']
for cat in category_list:
cat_id = list(filtered_cooccurring_df[filtered_cooccurring_df['category_name']==cat]['category_id'])[0]
cat_name_id[cat] = cat_id
print(cat, cat_id)
# Create a new DataFrame with co-occurring word columns
new_lyric_TF_df = filtered_cooccurring_df.drop([-1])
new_lyric_TF_df = new_lyric_TF_df.drop(columns=new_lyric_TF_df.columns[17:14144])
new_lyric_TF_df.head(3)
# Create a list of the overall top ten words
word_count_df = filtered_cooccurring_df.drop(columns=filtered_cooccurring_df.columns[:14144])#[:1]
word_count_df = word_count_df.sort_values(by=[-1], axis=1, ascending=False)
total_count = len(word_count_df) - 1
top_words = list(word_count_df.columns[0:10])
word_count_df = word_count_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(word_count_df[word_count_df[word]!=0])-1) / total_count * 100
top_ten[word] = round(percent, 1)
top_word_counts = list(word_count_df.loc[-1])[0:10]
index = 0
for word in top_ten:
print(word)
print('Frequency & percent: (', top_word_counts[index], ',', top_ten[word], ')')
index+=1
# Create a dictionary of the top ten co-occurring words for each category
t0 = time.time()
df_rows = []
blues_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='blues'].copy()
count_blues = len(blues_df)
blues_df.loc[0] = blues_df.sum(numeric_only=True)
blues_words = blues_df.sort_index()[blues_df.columns[17:]][0:1]
blues_words = blues_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(blues_words.columns[0:10])
blues_df = blues_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(blues_df[blues_df[word]!=0])-1) / count_blues * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(blues_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
classical_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='classical'].copy()
count_classical = len(classical_df)
classical_df.loc[0] = classical_df.sum(numeric_only=True)
classical_words = classical_df.sort_index()[classical_df.columns[18:]][0:1]
classical_words = classical_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(classical_words.columns[0:10])
classical_df = classical_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(classical_df[classical_df[word]!=0])-1) / count_classical * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(classical_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
country_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='country'].copy()
count_country = len(country_df)
country_df.loc[0] = country_df.sum(numeric_only=True)
country_words = country_df.sort_index()[country_df.columns[18:]][0:1]
country_words = country_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(country_words.columns[0:10])
country_df = country_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(country_df[country_df[word]!=0])-1) / count_country * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(country_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
funk_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='funk'].copy()
count_funk = len(funk_df)
funk_df.loc[0] = funk_df.sum(numeric_only=True)
funk_words = funk_df.sort_index()[funk_df.columns[18:]][0:1]
funk_words = funk_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(funk_words.columns[0:10])
funk_df = funk_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(funk_df[funk_df[word]!=0])-1) / count_funk * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(funk_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
hiphop_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='hiphop'].copy()
count_hiphop = len(hiphop_df)
hiphop_df.loc[0] = hiphop_df.sum(numeric_only=True)
hiphop_words = hiphop_df.sort_index()[hiphop_df.columns[18:]][0:1]
hiphop_words = hiphop_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(hiphop_words.columns[0:10])
hiphop_df = hiphop_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(hiphop_df[hiphop_df[word]!=0])-1) / count_hiphop * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(hiphop_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
indie_alt_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='indie_alt'].copy()
count_indie_alt = len(indie_alt_df)
indie_alt_df.loc[0] = indie_alt_df.sum(numeric_only=True)
indie_alt_words = indie_alt_df.sort_index()[indie_alt_df.columns[18:]][0:1]
indie_alt_words = indie_alt_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(indie_alt_words.columns[0:10])
indie_alt_df = indie_alt_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(indie_alt_df[indie_alt_df[word]!=0])-1) / count_indie_alt * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(indie_alt_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
jazz_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='jazz'].copy()
count_jazz = len(jazz_df)
jazz_df.loc[0] = jazz_df.sum(numeric_only=True)
jazz_words = jazz_df.sort_index()[jazz_df.columns[18:]][0:1]
jazz_words = jazz_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(jazz_words.columns[0:10])
jazz_df = jazz_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(jazz_df[jazz_df[word]!=0])-1) / count_jazz * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(jazz_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
metal_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='metal'].copy()
count_metal = len(metal_df)
metal_df.loc[0] = metal_df.sum(numeric_only=True)
metal_words = metal_df.sort_index()[metal_df.columns[18:]][0:1]
metal_words = metal_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(metal_words.columns[0:10])
metal_df = metal_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(metal_df[metal_df[word]!=0])-1) / count_metal * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(metal_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
pop_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='pop'].copy()
count_pop = len(pop_df)
pop_df.loc[-1] = pop_df.sum(numeric_only=True)
pop_words = pop_df.sort_index()[pop_df.columns[18:]][:1]
pop_words = pop_words.sort_values(by=[-1], axis=1, ascending=False)
top_words = list(pop_words.columns[0:10])
pop_df = pop_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(pop_df[pop_df[word]!=0])-1) / count_pop * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(pop_words.loc[-1])[0:10])
df_rows.append(list(top_ten.values()))
punk_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='punk'].copy()
count_punk = len(punk_df)
punk_df.loc[0] = punk_df.sum(numeric_only=True)
punk_words = punk_df.sort_index()[punk_df.columns[18:]][0:1]
punk_words = punk_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(punk_words.columns[0:10])
punk_df = punk_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(punk_df[punk_df[word]!=0])-1) / count_punk * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(punk_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
rnb_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='rnb'].copy()
count_rnb = len(rnb_df)
rnb_df.loc[0] = rnb_df.sum(numeric_only=True)
rnb_words = rnb_df.sort_index()[rnb_df.columns[18:]][0:1]
rnb_words = rnb_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(rnb_words.columns[0:10])
rnb_df = rnb_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(rnb_df[rnb_df[word]!=0])-1) / count_rnb * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(rnb_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
rock_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='rock'].copy()
count_rock = len(rock_df)
rock_df.loc[0] = rock_df.sum(numeric_only=True)
rock_words = rock_df.sort_index()[rock_df.columns[18:]][0:1]
rock_words = rock_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(rock_words.columns[0:10])
rock_df = rock_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(rock_df[rock_df[word]!=0])-1) / count_rock * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(rock_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
romance_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='romance'].copy()
count_romance = len(romance_df)
romance_df.loc[0] = romance_df.sum(numeric_only=True)
romance_words = romance_df.sort_index()[romance_df.columns[18:]][0:1]
romance_words = romance_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(romance_words.columns[0:10])
romance_df = romance_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(romance_df[romance_df[word]!=0])-1) / count_romance * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(romance_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
soul_df = new_lyric_TF_df[new_lyric_TF_df['category_name']=='soul'].copy()
count_soul = len(soul_df)
soul_df.loc[0] = soul_df.sum(numeric_only=True)
soul_words = soul_df.sort_index()[soul_df.columns[18:]][0:1]
soul_words = soul_words.sort_values(by=[0], axis=1, ascending=False)
top_words = list(soul_words.columns[0:10])
soul_df = soul_df[top_words]
top_ten = {}
for word in top_words:
percent = (len(soul_df[soul_df[word]!=0])-1) / count_soul * 100
top_ten[word] = round(percent, 1)
df_rows.append(top_words)
df_rows.append(list(soul_words.loc[0])[0:10])
df_rows.append(list(top_ten.values()))
t1 = time.time()
print(f'Run time: {t1-t0} seconds')
# Create dictionary of top word frequencies
unique_top_words = []
for i in range(len(df_rows)):
if i%3 == 0:
unique_top_words.extend(df_rows[i])
unique_top_words = list(set(unique_top_words))
top_word_freq = dict.fromkeys(unique_top_words, 0)
for i in range(len(df_rows)):
if i%3 == 0:
for word in df_rows[i]:
top_word_freq[word]+=1
print(len(top_word_freq))
top_word_freq
# Print top words that are unique to one genre
unique_to_one = dict(filter(lambda key: key[1] == 1, top_word_freq.items()))
print(len(unique_to_one))
unique_to_one
# Print top words that are unique to two genre
unique_to_two = dict(filter(lambda key: key[1] == 2, top_word_freq.items()))
print(len(unique_to_two))
unique_to_two
# Create DataFrame of top ten words
categories = np.array(['blues', 'blues', 'blues', 'classical', 'classical', 'classical', 'country', 'country', 'country',
'funk', 'funk', 'funk', 'hiphop', 'hiphop', 'hiphop', 'indie_alt', 'indie_alt', 'indie_alt',
'jazz', 'jazz', 'jazz', 'metal', 'metal', 'metal', 'pop', 'pop', 'pop', 'punk', 'punk', 'punk',
'rnb', 'rnb', 'rnb', 'rock', 'rock', 'rock', 'romance', 'romance', 'romance', 'soul', 'soul', 'soul'])
arrays = [categories, np.array(['words', 'frequencies', 'percents', 'words', 'frequencies', 'percents', 'words',
'frequencies', 'percents', 'words', 'frequencies', 'percents', 'words', 'frequencies',
'percents', 'words', 'frequencies', 'percents', 'words', 'frequencies', 'percents', 'words',
'frequencies', 'percents', 'words', 'frequencies', 'percents', 'words', 'frequencies',
'percents', 'words', 'frequencies', 'percents', 'words', 'frequencies', 'percents', 'words',
'frequencies', 'percents', 'words', 'frequencies', 'percents'])]
tuples = list(zip(*arrays))
index = pd.MultiIndex.from_tuples(tuples)
top_cooccurring_df = pd.DataFrame(df_rows, index=arrays, columns=range(1,11))
top_cooccurring_df
# Save DataFrame to CSV
top_cooccurring_df.to_csv('../../Data/Analysis/top_cooccurring_words.csv')
| 0.121594 | 0.266691 |
```
import urllib
import pandas as pd
from bs4 import BeautifulSoup
import numpy as np
import matplotlib.pyplot as plt
import string as st
import seaborn as sns
import scipy as sci
import json
def load_data(url):
r = urllib.request.urlopen(url)
soup = BeautifulSoup(r)
data2 = soup.find_all('tr')
labels = []
for h in data2[0].find_all('th'):
labels.append(h.get_text().strip().lower())
final = []
for data in data2[1:]:
data_list = []
for d in data.find_all('td'):
d_str = d.get_text().replace(',','')
if d_str.isnumeric():
data_list.append(int(d_str))
else:
data_list.append(d_str)
final.append(data_list)
df = pd.DataFrame(final, columns = labels)
df['submit date'] = pd.to_datetime(df['submit date'])
df['start date'] = pd.to_datetime(df['start date'])
df['state'] = df['location'].str.split().str[-1]
df['year'] = df['submit date'].dt.year
df['month'] = df['submit date'].dt.month
return df
bs = load_data('https://h1bdata.info/index.php?em=&job=&city=NEW+YORK&year=All+Years')
bsbs = load_data('https://h1bdata.info/index.php?em=&job=&city=LOS+ANGELES&year=All+Years')
bsbs1 = load_data('https://h1bdata.info/index.php?em=&job=&city=SAN+FRANCISCO&year=All+Years')
bs4 = load_data('https://h1bdata.info/index.php?em=&job=&city=HOUSTON&year=All+Years')
bs5=load_data('https://h1bdata.info/index.php?em=&job=&city=CHICAGO&year=All+Years')
bs4['location']='Houston'
bs5['location']='Chicago'
bs['location']='New York'
bsbs['location']='Los Angeles'
bsbs1['location']='San Francisco'
base = pd.concat([bs5, bs4,bsbs1,bsbs,bs ])
base = base.replace(r'^\s*$', np.nan, regex=True)
base=base.dropna()
base=base[ base['year'] >2015 ]
por_año=base.groupby(['year']).count()
por_ciudad=base.groupby(['location']).count()
por_añociudad = basee.groupby(['year', 'location']).count()
base.to_excel(r'a.xlsx')
por_añociudad = base.groupby(['year', 'location']).count()
año_empleador= base.groupby(['year', 'employer']).count()
empleador_ciuda= base.groupby(['location', 'employer']).count()
base6=base[ base['year']==2016 ]
base7=base[ base['year']==2017 ]
base8=base[ base['year']==2018 ]
base9=base[ base['year']==2019 ]
base0=base[ base['year']==2020 ]
año_empleador6= base6.groupby(['year', 'employer']).count()
año_empleador7= base7.groupby(['year', 'employer']).count()
año_empleador8= base8.groupby(['year', 'employer']).count()
año_empleador9= base9.groupby(['year', 'employer']).count()
año_empleador0= base0.groupby(['year', 'employer']).count()
año_empleador6=año_empleador6.sort_values(by=['job title'])
año_empleador7=año_empleador7.sort_values(by=['job title'])
año_empleador8=año_empleador8.sort_values(by=['job title'])
año_empleador9=año_empleador9.sort_values(by=['job title'])
año_empleador0=año_empleador0.sort_values(by=['job title'])
año_empleador6.tail()
año_empleador7.tail()
año_empleador8.tail()
año_empleador9.tail()
año_empleador0.tail()
fig = plt.figure()
ax = plt.axes()
plt.plot( por_año.index,por_año.month,':b')
plt.legend()
plt.title('Número de solicitudes por año (2016-2020)')
plt.xlabel("Numero de solicitudes")
plt.ylabel("Año");
plt.bar(por_ciudad.index, por_ciudad.month)
# Organización de la base de datos
bs_york = bs[ bs['year'] ==2020 ]
bs_york = bs_york[ bs_york['location'] == "New York" ]
bs_bla = bs_york.groupby('employer').agg({'base salary': ['std', 'count', 'mean']})
df = bs_bla['base salary']
df['std_2'] = df['std'].fillna(df['std'].mean())
df['std'] = df['std'].fillna(10**-13)
# Define likelihood function
def normal_v(params):
m, t = params[0], params[1]
v = df['mean']
negLL = -np.sum(sci.stats.norm.logpdf(v, loc=m, scale=t))
return(negLL)
# Optimizamos la función de verosimilitud
guess = np.array([0,1])
estimadores = sci.optimize.fmin(normal_v, guess)
# Estos son miu y tau estiamdos de la distribución prior
estimadores
# Cálculo del estimador Bayesiano desviación estandar igual a 0
df['eb estimator'] = ((df['count']/df['std']**2)/((df['count']/df['std']**2) + (1/estimadores[1]**2)))*df['mean'] + ((1/estimadores[1]**2)/((df['count']/df['std']**2) + (1/estimadores[1]**2)))*estimadores[0]
# Cálculo del estimador Bayesiano desviación estandar igual al maximo de las desviaciones
df['eb estimator 2'] = ((df['count']/df['std_2']**2)/((df['count']/df['std_2']**2) + (1/estimadores[1]**2)))*df['mean'] + ((1/estimadores[1]**2)/((df['count']/df['std_2']**2) + (1/estimadores[1]**2)))*estimadores[0]
df['total mean'] = df['mean'].mean()
df_sub = df.loc[np.random.choice(df.index, 15, replace=False)]
df_sub_t_1 = df_sub[['mean', 'eb estimator', 'total mean']].T
df_sub_t_2 = df_sub[['mean', 'eb estimator 2', 'total mean']].T
# Gráfica se shrink
x = np.array([0,1,2])
my_xticks = np.array(['Media v', 'Estimador EB', 'Media total'])
plt.xticks(x, my_xticks)
for i in range(0,15):
plt.plot(x, np.array(df_sub_t_1.iloc[:,i]), marker='o', color='grey')
plt.ylabel('Valores')
plt.grid(True)
# Gráfica se shrink
x = np.array([0,1,2])
my_xticks = np.array(['Media v', 'Estimador EB', 'Media total'])
plt.xticks(x, my_xticks)
for i in range(0,15):
plt.plot(x, np.array(df_sub_t_2.iloc[:,i]), marker='o', color='grey')
plt.ylabel('Valores')
plt.grid(True)
bs.head()
bs['employer'].nunique()
bs['location'].unique()
bs.groupby('location')['base salary'].describe()
bs['base salary'].describe()
```
|
github_jupyter
|
import urllib
import pandas as pd
from bs4 import BeautifulSoup
import numpy as np
import matplotlib.pyplot as plt
import string as st
import seaborn as sns
import scipy as sci
import json
def load_data(url):
r = urllib.request.urlopen(url)
soup = BeautifulSoup(r)
data2 = soup.find_all('tr')
labels = []
for h in data2[0].find_all('th'):
labels.append(h.get_text().strip().lower())
final = []
for data in data2[1:]:
data_list = []
for d in data.find_all('td'):
d_str = d.get_text().replace(',','')
if d_str.isnumeric():
data_list.append(int(d_str))
else:
data_list.append(d_str)
final.append(data_list)
df = pd.DataFrame(final, columns = labels)
df['submit date'] = pd.to_datetime(df['submit date'])
df['start date'] = pd.to_datetime(df['start date'])
df['state'] = df['location'].str.split().str[-1]
df['year'] = df['submit date'].dt.year
df['month'] = df['submit date'].dt.month
return df
bs = load_data('https://h1bdata.info/index.php?em=&job=&city=NEW+YORK&year=All+Years')
bsbs = load_data('https://h1bdata.info/index.php?em=&job=&city=LOS+ANGELES&year=All+Years')
bsbs1 = load_data('https://h1bdata.info/index.php?em=&job=&city=SAN+FRANCISCO&year=All+Years')
bs4 = load_data('https://h1bdata.info/index.php?em=&job=&city=HOUSTON&year=All+Years')
bs5=load_data('https://h1bdata.info/index.php?em=&job=&city=CHICAGO&year=All+Years')
bs4['location']='Houston'
bs5['location']='Chicago'
bs['location']='New York'
bsbs['location']='Los Angeles'
bsbs1['location']='San Francisco'
base = pd.concat([bs5, bs4,bsbs1,bsbs,bs ])
base = base.replace(r'^\s*$', np.nan, regex=True)
base=base.dropna()
base=base[ base['year'] >2015 ]
por_año=base.groupby(['year']).count()
por_ciudad=base.groupby(['location']).count()
por_añociudad = basee.groupby(['year', 'location']).count()
base.to_excel(r'a.xlsx')
por_añociudad = base.groupby(['year', 'location']).count()
año_empleador= base.groupby(['year', 'employer']).count()
empleador_ciuda= base.groupby(['location', 'employer']).count()
base6=base[ base['year']==2016 ]
base7=base[ base['year']==2017 ]
base8=base[ base['year']==2018 ]
base9=base[ base['year']==2019 ]
base0=base[ base['year']==2020 ]
año_empleador6= base6.groupby(['year', 'employer']).count()
año_empleador7= base7.groupby(['year', 'employer']).count()
año_empleador8= base8.groupby(['year', 'employer']).count()
año_empleador9= base9.groupby(['year', 'employer']).count()
año_empleador0= base0.groupby(['year', 'employer']).count()
año_empleador6=año_empleador6.sort_values(by=['job title'])
año_empleador7=año_empleador7.sort_values(by=['job title'])
año_empleador8=año_empleador8.sort_values(by=['job title'])
año_empleador9=año_empleador9.sort_values(by=['job title'])
año_empleador0=año_empleador0.sort_values(by=['job title'])
año_empleador6.tail()
año_empleador7.tail()
año_empleador8.tail()
año_empleador9.tail()
año_empleador0.tail()
fig = plt.figure()
ax = plt.axes()
plt.plot( por_año.index,por_año.month,':b')
plt.legend()
plt.title('Número de solicitudes por año (2016-2020)')
plt.xlabel("Numero de solicitudes")
plt.ylabel("Año");
plt.bar(por_ciudad.index, por_ciudad.month)
# Organización de la base de datos
bs_york = bs[ bs['year'] ==2020 ]
bs_york = bs_york[ bs_york['location'] == "New York" ]
bs_bla = bs_york.groupby('employer').agg({'base salary': ['std', 'count', 'mean']})
df = bs_bla['base salary']
df['std_2'] = df['std'].fillna(df['std'].mean())
df['std'] = df['std'].fillna(10**-13)
# Define likelihood function
def normal_v(params):
m, t = params[0], params[1]
v = df['mean']
negLL = -np.sum(sci.stats.norm.logpdf(v, loc=m, scale=t))
return(negLL)
# Optimizamos la función de verosimilitud
guess = np.array([0,1])
estimadores = sci.optimize.fmin(normal_v, guess)
# Estos son miu y tau estiamdos de la distribución prior
estimadores
# Cálculo del estimador Bayesiano desviación estandar igual a 0
df['eb estimator'] = ((df['count']/df['std']**2)/((df['count']/df['std']**2) + (1/estimadores[1]**2)))*df['mean'] + ((1/estimadores[1]**2)/((df['count']/df['std']**2) + (1/estimadores[1]**2)))*estimadores[0]
# Cálculo del estimador Bayesiano desviación estandar igual al maximo de las desviaciones
df['eb estimator 2'] = ((df['count']/df['std_2']**2)/((df['count']/df['std_2']**2) + (1/estimadores[1]**2)))*df['mean'] + ((1/estimadores[1]**2)/((df['count']/df['std_2']**2) + (1/estimadores[1]**2)))*estimadores[0]
df['total mean'] = df['mean'].mean()
df_sub = df.loc[np.random.choice(df.index, 15, replace=False)]
df_sub_t_1 = df_sub[['mean', 'eb estimator', 'total mean']].T
df_sub_t_2 = df_sub[['mean', 'eb estimator 2', 'total mean']].T
# Gráfica se shrink
x = np.array([0,1,2])
my_xticks = np.array(['Media v', 'Estimador EB', 'Media total'])
plt.xticks(x, my_xticks)
for i in range(0,15):
plt.plot(x, np.array(df_sub_t_1.iloc[:,i]), marker='o', color='grey')
plt.ylabel('Valores')
plt.grid(True)
# Gráfica se shrink
x = np.array([0,1,2])
my_xticks = np.array(['Media v', 'Estimador EB', 'Media total'])
plt.xticks(x, my_xticks)
for i in range(0,15):
plt.plot(x, np.array(df_sub_t_2.iloc[:,i]), marker='o', color='grey')
plt.ylabel('Valores')
plt.grid(True)
bs.head()
bs['employer'].nunique()
bs['location'].unique()
bs.groupby('location')['base salary'].describe()
bs['base salary'].describe()
| 0.247532 | 0.208139 |
### Heroes Of Pymoli Data Analysis
* Of the 1163 active players, the vast majority are male (84%). There also exists, a smaller, but notable proportion of female players (14%).
* Our peak age demographic falls between 20-24 (44.8%) with secondary groups falling between 15-19 (18.60%) and 25-29 (13.4%).
-----
### Note
* Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.
```
# Dependencies and Setup
import pandas as pd
# File to Load (Remember to Change These)
file_to_load = "Resources/purchase_data.csv"
# Read Purchasing File and store into Pandas data frame
purchase_data = pd.read_csv(file_to_load)
```
## Player Count
* Display the total number of players
## Purchasing Analysis (Total)
* Run basic calculations to obtain number of unique items, average price, etc.
* Create a summary data frame to hold the results
* Optional: give the displayed data cleaner formatting
* Display the summary data frame
## Gender Demographics
* Percentage and Count of Male Players
* Percentage and Count of Female Players
* Percentage and Count of Other / Non-Disclosed
## Purchasing Analysis (Gender)
* Run basic calculations to obtain purchase count, avg. purchase price, avg. purchase total per person etc. by gender
* Create a summary data frame to hold the results
* Optional: give the displayed data cleaner formatting
* Display the summary data frame
## Age Demographics
* Establish bins for ages
* Categorize the existing players using the age bins. Hint: use pd.cut()
* Calculate the numbers and percentages by age group
* Create a summary data frame to hold the results
* Optional: round the percentage column to two decimal points
* Display Age Demographics Table
## Purchasing Analysis (Age)
* Bin the purchase_data data frame by age
* Run basic calculations to obtain purchase count, avg. purchase price, avg. purchase total per person etc. in the table below
* Create a summary data frame to hold the results
* Optional: give the displayed data cleaner formatting
* Display the summary data frame
## Top Spenders
* Run basic calculations to obtain the results in the table below
* Create a summary data frame to hold the results
* Sort the total purchase value column in descending order
* Optional: give the displayed data cleaner formatting
* Display a preview of the summary data frame
## Most Popular Items
* Retrieve the Item ID, Item Name, and Item Price columns
* Group by Item ID and Item Name. Perform calculations to obtain purchase count, item price, and total purchase value
* Create a summary data frame to hold the results
* Sort the purchase count column in descending order
* Optional: give the displayed data cleaner formatting
* Display a preview of the summary data frame
## Most Profitable Items
* Sort the above table by total purchase value in descending order
* Optional: give the displayed data cleaner formatting
* Display a preview of the data frame
|
github_jupyter
|
# Dependencies and Setup
import pandas as pd
# File to Load (Remember to Change These)
file_to_load = "Resources/purchase_data.csv"
# Read Purchasing File and store into Pandas data frame
purchase_data = pd.read_csv(file_to_load)
| 0.372505 | 0.9357 |
# Navigation
---
In this notebook, you will learn how to use the Unity ML-Agents environment for the first project of the [Deep Reinforcement Learning Nanodegree](https://www.udacity.com/course/deep-reinforcement-learning-nanodegree--nd893).
### 1. Start the Environment
We begin by importing some necessary packages. If the code cell below returns an error, please revisit the project instructions to double-check that you have installed [Unity ML-Agents](https://github.com/Unity-Technologies/ml-agents/blob/master/docs/Installation.md) and [NumPy](http://www.numpy.org/).
```
from unityagents import UnityEnvironment
import numpy as np
from collections import deque
import matplotlib.pyplot as plt
import double_dqn_agent
import torch
%matplotlib inline
```
Next, we will start the environment! **_Before running the code cell below_**, change the `file_name` parameter to match the location of the Unity environment that you downloaded.
- **Mac**: `"path/to/Banana.app"`
- **Windows** (x86): `"path/to/Banana_Windows_x86/Banana.exe"`
- **Windows** (x86_64): `"path/to/Banana_Windows_x86_64/Banana.exe"`
- **Linux** (x86): `"path/to/Banana_Linux/Banana.x86"`
- **Linux** (x86_64): `"path/to/Banana_Linux/Banana.x86_64"`
- **Linux** (x86, headless): `"path/to/Banana_Linux_NoVis/Banana.x86"`
- **Linux** (x86_64, headless): `"path/to/Banana_Linux_NoVis/Banana.x86_64"`
For instance, if you are using a Mac, then you downloaded `Banana.app`. If this file is in the same folder as the notebook, then the line below should appear as follows:
```
env = UnityEnvironment(file_name="Banana.app")
```
```
visual = False # this parameter regulates if we train from pixels or from the info coming directly from the environment
env = UnityEnvironment(file_name="/Users/manuelsh/code/deep-reinforcement-learning/p1_navigation/Banana.app")
```
Environments contain **_brains_** which are responsible for deciding the actions of their associated agents. Here we check for the first brain available, and set it as the default brain we will be controlling from Python.
```
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
```
### 2. Examine the State and Action Spaces
The simulation contains a single agent that navigates a large environment. At each time step, it has four actions at its disposal:
- `0` - walk forward
- `1` - walk backward
- `2` - turn left
- `3` - turn right
The state space has `37` dimensions and contains the agent's velocity, along with ray-based perception of objects around agent's forward direction. A reward of `+1` is provided for collecting a yellow banana, and a reward of `-1` is provided for collecting a blue banana.
Run the code cell below to print some information about the environment.
```
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents in the environment
print('Number of agents:', len(env_info.agents))
# number of actions
action_size = brain.vector_action_space_size
print('Number of actions:', action_size)
# examine the state space
state = env_info.vector_observations[0]
print('States look like:\n', state)
state_size = len(state)
print('States have length:', state_size)
```
### 3. Training a deep Q-Network agent
```
env_info = env.reset(train_mode=True)[brain_name]
agent = double_dqn_agent.Agent(state_size, action_size, 0, visual)
def dqn(n_episodes=2000, max_t=1000, eps_start=1.0, eps_end=0.01, eps_decay=0.995):
"""Deep Q-Learning.
Params
======
n_episodes (int): maximum number of training episodes
max_t (int): maximum number of timesteps per episode
eps_start (float): starting value of epsilon, for epsilon-greedy action selection
eps_end (float): minimum value of epsilon
eps_decay (float): multiplicative factor (per episode) for decreasing epsilon
"""
scores = [] # list containing scores from each episode
scores_window = deque(maxlen=100) # last 100 scores
eps = eps_start # initialize epsilon
for i_episode in range(1, n_episodes+1):
#Pdb().set_trace()
env_info = env.reset(train_mode=True)[brain_name]
if visual:
state = env_info.visual_observations[0]
else:
state = env_info.vector_observations[0]
score = 0
for t in range(max_t):
action = agent.act(state, eps)
state_info = env.step(action)[brain_name]
if visual:
next_state = state_info.visual_observations[0]
else:
next_state = state_info.vector_observations[0]
reward = state_info.rewards[0]
done = state_info.local_done[0]
agent.step(state, action, reward, next_state, done)
state = next_state
score += reward
if done:
break
scores_window.append(score) # save most recent score
scores.append(score) # save most recent score
eps = max(eps_end, eps_decay*eps) # decrease epsilon
print('\rEpisode {}\tMean Score: {:.2f}\tMax score: {:.2f}'.format(i_episode,
np.mean(scores_window),
np.max(scores_window)), end="")
if i_episode % 100 == 0:
print('\rEpisode {}\tAverage Score: {:.2f} \tLoss: {:.2f}'.format(i_episode,
np.mean(scores_window),
agent.loss))
if np.mean(scores_window)>=200.0:
print('\nEnvironment solved in {:d} episodes!\tMean score: {:.2f}\tMax score: {:.2f}'.format(i_episode-100, np.mean(scores_window), np.max(scores_window)))
torch.save(agent.qnetwork_local.state_dict(), 'checkpoint.pth')
break
return scores
scores = dqn()
# plot the scores
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(len(scores)), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
torch.save(agent.qnetwork_local.state_dict(), 'Q_network_parameters.pt')
# env.close()
```
|
github_jupyter
|
from unityagents import UnityEnvironment
import numpy as np
from collections import deque
import matplotlib.pyplot as plt
import double_dqn_agent
import torch
%matplotlib inline
env = UnityEnvironment(file_name="Banana.app")
visual = False # this parameter regulates if we train from pixels or from the info coming directly from the environment
env = UnityEnvironment(file_name="/Users/manuelsh/code/deep-reinforcement-learning/p1_navigation/Banana.app")
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents in the environment
print('Number of agents:', len(env_info.agents))
# number of actions
action_size = brain.vector_action_space_size
print('Number of actions:', action_size)
# examine the state space
state = env_info.vector_observations[0]
print('States look like:\n', state)
state_size = len(state)
print('States have length:', state_size)
env_info = env.reset(train_mode=True)[brain_name]
agent = double_dqn_agent.Agent(state_size, action_size, 0, visual)
def dqn(n_episodes=2000, max_t=1000, eps_start=1.0, eps_end=0.01, eps_decay=0.995):
"""Deep Q-Learning.
Params
======
n_episodes (int): maximum number of training episodes
max_t (int): maximum number of timesteps per episode
eps_start (float): starting value of epsilon, for epsilon-greedy action selection
eps_end (float): minimum value of epsilon
eps_decay (float): multiplicative factor (per episode) for decreasing epsilon
"""
scores = [] # list containing scores from each episode
scores_window = deque(maxlen=100) # last 100 scores
eps = eps_start # initialize epsilon
for i_episode in range(1, n_episodes+1):
#Pdb().set_trace()
env_info = env.reset(train_mode=True)[brain_name]
if visual:
state = env_info.visual_observations[0]
else:
state = env_info.vector_observations[0]
score = 0
for t in range(max_t):
action = agent.act(state, eps)
state_info = env.step(action)[brain_name]
if visual:
next_state = state_info.visual_observations[0]
else:
next_state = state_info.vector_observations[0]
reward = state_info.rewards[0]
done = state_info.local_done[0]
agent.step(state, action, reward, next_state, done)
state = next_state
score += reward
if done:
break
scores_window.append(score) # save most recent score
scores.append(score) # save most recent score
eps = max(eps_end, eps_decay*eps) # decrease epsilon
print('\rEpisode {}\tMean Score: {:.2f}\tMax score: {:.2f}'.format(i_episode,
np.mean(scores_window),
np.max(scores_window)), end="")
if i_episode % 100 == 0:
print('\rEpisode {}\tAverage Score: {:.2f} \tLoss: {:.2f}'.format(i_episode,
np.mean(scores_window),
agent.loss))
if np.mean(scores_window)>=200.0:
print('\nEnvironment solved in {:d} episodes!\tMean score: {:.2f}\tMax score: {:.2f}'.format(i_episode-100, np.mean(scores_window), np.max(scores_window)))
torch.save(agent.qnetwork_local.state_dict(), 'checkpoint.pth')
break
return scores
scores = dqn()
# plot the scores
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(len(scores)), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
torch.save(agent.qnetwork_local.state_dict(), 'Q_network_parameters.pt')
# env.close()
| 0.584627 | 0.979235 |
# Predicting medical appointments using Python
In this notebook, I'll use Python and its libraries to predict whether someone would show up for a medical appointment or not. I'll develop an Artificial Neural Network and train my model on the data.
## Import libraries
I'll import the necessary deep learning libraries, Keras and Tensorflow along with some metrics.
```
import pandas as pd
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
import os
import tensorflow
os.environ['KERAS_BACKEND'] = 'tensorflow'
import keras
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras import metrics
```
## Import dataset
```
dataset = pd.read_csv('data/dataset_modified.csv')
dataset.head(5)
```
## Data engineering
I'll remove unnecessary columns, map some categorical columns to seprate columns. Then, I'll split the data into test and train data.
I'll use `StandardScaler` function to scale the data as well.
If a person has missed an appointment before, there are chances he/she might miss again. Let's see if that is correlated.
I found this idea from a kernel on [Kaggle](https://www.kaggle.com/belagoesr/predicting-no-show-downsampling-approach-with-rf).
```
missed_appointment = dataset.groupby('PatientId')['Showed_up'].sum()
missed_appointment = missed_appointment.to_dict()
dataset['missed_appointment_before'] = dataset.PatientId.map(lambda x: 1 if missed_appointment[x]>0 else 0)
dataset['missed_appointment_before'].corr(dataset['Showed_up'])
```
Surprisingly the correlation is really high and we should keep this column.
As we don't need all the columns, I'll start ommiting them.
```
dataset = dataset.drop(['PatientId', 'AppointmentID', 'ScheduledDay', 'AppointmentDay'], axis = 1)
print("Columns: {}".format(dataset.columns))
```
Let's great dummy columns to accomodate all neighborhoods.
```
dataset = pd.concat([dataset.drop('Neighbourhood', axis = 1),
pd.get_dummies(dataset['Neighbourhood'])], axis=1)
```
Now, let's map the Gender column to random values, here 'M' as 0 and 'F' as 1.
```
gender_map = {'M': 0, 'F': 1}
dataset['Gender'] = dataset['Gender'].map(gender_map)
```
Next, I'll split the dataset into train and test data.
```
y = dataset.loc[:, 'Showed_up']
X = dataset.drop(['Showed_up'], axis = 1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.33, random_state = 42)
print("Final shape: {}".format(X_train.shape))
```
Let's now scale the data to make it ready for the Neural Network.
```
standardScaler = StandardScaler()
X_train = standardScaler.fit_transform(X_train)
X_test = standardScaler.transform(X_test)
```
## Model generation
I'll develop an Artificial Neural Network to map the data to find patterns and eventually learn from it.
```
classifier = Sequential()
classifier.add(Dense(units = 512, activation = 'relu', input_dim = 91))
classifier.add(Dropout(rate = 0.6))
classifier.add(Dense(units = 1024, activation = 'relu'))
classifier.add(Dropout(rate = 0.6))
classifier.add(Dense(units = 2048, activation = 'relu'))
classifier.add(Dropout(rate = 0.6))
classifier.add(Dense(units = 1, activation = 'sigmoid'))
classifier.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])
classifier.summary()
history = classifier.fit(X_train, y_train, epochs = 5, validation_split = 0.1)
```
## Model prediction
As the model is now ready and trained, let's test on the test data.
For a baseline, I'll also write the difference between the two classes in the test data.
```
y_pred = classifier.predict(X_test)
y_pred = y_pred > 0.5
print("Test data description:")
print("{}".format(y_test.value_counts()))
print("-"*50)
print("Confusion matrix:")
print(confusion_matrix(y_test, y_pred))
print("Accuracy: {:.2f}%".format(accuracy_score(y_test, y_pred)*100))
```
## Conclusion
Using `ANN` with data engineering, I was able to achieve an accuracy of over 88% in predicting whether someone would show up or not for their appointment.
|
github_jupyter
|
import pandas as pd
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
import os
import tensorflow
os.environ['KERAS_BACKEND'] = 'tensorflow'
import keras
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras import metrics
dataset = pd.read_csv('data/dataset_modified.csv')
dataset.head(5)
missed_appointment = dataset.groupby('PatientId')['Showed_up'].sum()
missed_appointment = missed_appointment.to_dict()
dataset['missed_appointment_before'] = dataset.PatientId.map(lambda x: 1 if missed_appointment[x]>0 else 0)
dataset['missed_appointment_before'].corr(dataset['Showed_up'])
dataset = dataset.drop(['PatientId', 'AppointmentID', 'ScheduledDay', 'AppointmentDay'], axis = 1)
print("Columns: {}".format(dataset.columns))
dataset = pd.concat([dataset.drop('Neighbourhood', axis = 1),
pd.get_dummies(dataset['Neighbourhood'])], axis=1)
gender_map = {'M': 0, 'F': 1}
dataset['Gender'] = dataset['Gender'].map(gender_map)
y = dataset.loc[:, 'Showed_up']
X = dataset.drop(['Showed_up'], axis = 1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.33, random_state = 42)
print("Final shape: {}".format(X_train.shape))
standardScaler = StandardScaler()
X_train = standardScaler.fit_transform(X_train)
X_test = standardScaler.transform(X_test)
classifier = Sequential()
classifier.add(Dense(units = 512, activation = 'relu', input_dim = 91))
classifier.add(Dropout(rate = 0.6))
classifier.add(Dense(units = 1024, activation = 'relu'))
classifier.add(Dropout(rate = 0.6))
classifier.add(Dense(units = 2048, activation = 'relu'))
classifier.add(Dropout(rate = 0.6))
classifier.add(Dense(units = 1, activation = 'sigmoid'))
classifier.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])
classifier.summary()
history = classifier.fit(X_train, y_train, epochs = 5, validation_split = 0.1)
y_pred = classifier.predict(X_test)
y_pred = y_pred > 0.5
print("Test data description:")
print("{}".format(y_test.value_counts()))
print("-"*50)
print("Confusion matrix:")
print(confusion_matrix(y_test, y_pred))
print("Accuracy: {:.2f}%".format(accuracy_score(y_test, y_pred)*100))
| 0.549641 | 0.96853 |
## How to complete a Kaggle Competition with Machine Learning
In this code along session, you'll build several algorithms of increasing complexity that predict whether any given passenger on the Titanic survived or not, given data on them such as the fare they paid, where they embarked and their age.
<img src="img/nytimes.jpg" width="500">
In particular, you'll build _supervised learning_ models. _Supervised learning_ is the branch of machine learning (ML) that involves predicting labels, such as 'Survived' or 'Not'. Such models:
* it learns from labelled data, e.g. data that includes whether a passenger survived (called model training).
* and then predicts on unlabelled data.
On Kaggle, a platform for predictive modelling and analytics competitions, these are called train and test sets because
* You want to build a model that learns patterns in the training set
* You _then_ use the model to make predictions on the test set!
Kaggle then tells you the **percentage that you got correct**: this is known as the _accuracy_ of your model.
## Approach
A good way to approach supervised learning:
* Exploratory Data Analysis (EDA);
* Build a quick and dirty model (baseline);
* Iterate;
* Engineer features;
* Get model that performs better.
In this code along session, we'll do all of these! We also have free courses that get you up and running with machine learning for the Titanic dataset in [Python](https://campus.datacamp.com/courses/kaggle-python-tutorial-on-machine-learning) and [R](https://campus.datacamp.com/courses/kaggle-r-tutorial-on-machine-learning).
**Note:** We may move quickly at some points in order to get a bit further along. I'll answer questions in the live event but also feel free to chime in and help each other in the comments.
## Import you data and check it out
```
# Import modules
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import tree
from sklearn.metrics import accuracy_score
# Figures inline and set visualization style
%matplotlib inline
sns.set()
# Import test and train datasets
df_train = pd.read_csv('data/train.csv')
df_test = pd.read_csv('data/test.csv')
# View first lines of training data
df_train.head()
```
* What are all these features? Check out the Kaggle data documentation [here](https://www.kaggle.com/c/titanic/data).
**Important note on terminology:**
* The _target variable_ is the one you are trying to predict;
* Other variables are known as _features_ (or _predictor variables_).
```
# View first lines of test data
df_test.head()
```
* Use the DataFrame `.info()` method to check out datatypes, missing values and more (of `df_train`).
```
df_train.info()
```
* Use the DataFrame `.describe()` method to check out summary statistics of numeric columns (of `df_train`).
```
df_train.describe()
```
**Recap:**
* you've loaded your data and had a look at it.
**Up next:** Explore your data visually and build a first model!
For more on `pandas`, check out our [Data Manipulation with Python track](https://www.datacamp.com/tracks/data-manipulation-with-python).
If you're enoying this session, retweet or share on FB now and follow us on Twitter: [@hugobowne](https://twitter.com/hugobowne) & [@DataCamp](https://twitter.com/datacamp).
## Visual exploratory data analysis and your first model
* Use `seaborn` to build a bar plot of Titanic survival (your _target variable_).
```
sns.countplot(x='Survived', data=df_train); #case sensative in Survived
```
**Take-away:** In the training set, less people survived than didn't. Let's then build a first model that **predict that nobody survived**.
This is a bad model as we know that people survived. But it gives us a _baseline_: any model that we build later needs to do better than this one.
* Create a column 'Survived' for `df_test` that encodes 'did not survive' for all rows;
* Save 'PassengerId' and 'Survived' columns of `df_test` to a .csv and submit to Kaggle.
```
df_test['Survived'] = 0 #assume nobody survived
df_test[['PassengerId', 'Survived']].to_csv('data/predictions/no_survivors.csv', index=False)
```
* What accuracy did this give you?
Accuracy on Kaggle = 0.622
**Essential note!** There are metrics other than accuracy that you may want to use.
**Recap:**
* you've loaded your data and had a look at it.
* you've explored your target variable visually and made your first predictions.
**Up next:** More EDA and you'll build another model.
## EDA on feature variables
* Use `seaborn` to build a bar plot of the Titanic dataset feature 'Sex' (of `df_train`).
```
sns.countplot(x="Sex", data=df_train);
```
* Use `seaborn` to build bar plots of the Titanic dataset feature 'Survived' split (faceted) over the feature 'Sex'.
```
sns.catplot(x='Survived', col='Sex', kind="count", data=df_train);
```
**Take-away:** Women were more likely to survive than men.
* Use `pandas` to figure out how many women and how many men survived.
```
female_S = df_train[df_train.Sex == 'female'].Survived.sum()
male_S = df_train[df_train.Sex == 'male'].Survived.sum()
print("female Survivors", female_S)
print("Male Survivors", male_S)
# another way using groupby
df_train.groupby(['Sex']).Survived.sum() #count will count who survived and who didnt survive
```
* Use `pandas` to figure out the proportion of women that survived, along with the proportion of men:
```
print(df_train[df_train.Sex == 'female'].Survived.sum()/df_train[df_train.Sex == 'female'].Survived.count())
print(df_train[df_train.Sex == 'male'].Survived.sum()/df_train[df_train.Sex == 'male'].Survived.count())
```
74% of women survived, while 18% of men survived.
Let's now build a second model and predict that all women survived and all men didn't. Once again, this is an unrealistic model, but it will provide a baseline against which to compare future models.
* Create a column 'Survived' for `df_test` that encodes the above prediction.
* Save 'PassengerId' and 'Survived' columns of `df_test` to a .csv and submit to Kaggle.
```
i=0
while i<df_test.Sex.count():
if (df_test.Sex[i] == 'female'):
df_test['Survived'][i] = 1
else:
df_test['Survived'][i] = 0
i +=1
df_test['Survived']
# df_test.Sex
df_test['Survived'] = df_test.Sex == 'female'
df_test.tail()
df_test['Survived'] = df_test.Survived.apply(lambda x: int(x)) #apply function turns true =1 & false = 0
df_test.head()
df_test[['PassengerId', 'Survived']].to_csv('data/predictions/women_survive.csv', index=False)
```
* What accuracy did this give you?
Accuracy on Kaggle = 0.76555
**Recap:**
* you've loaded your data and had a look at it.
* you've explored your target variable visually and made your first predictions.
* you've explored some of your feature variables visually and made more predictions that did better based on your EDA.
**Up next:** EDA of other feature variables, categorical and numeric.
For more on `pandas`, check out our [Data Manipulation with Python track](https://www.datacamp.com/tracks/data-manipulation-with-python).
For more on `seaborn`, check out Chapter 3 of our [Intro. to Datavis with Python course](https://www.datacamp.com/courses/introduction-to-data-visualization-with-python).
If you're enoying this session, retweet or share on FB now and follow us on Twitter: [@hugobowne](https://twitter.com/hugobowne) & [@DataCamp](https://twitter.com/datacamp).
## Explore your data more!
* Use `seaborn` to build bar plots of the Titanic dataset feature 'Survived' split (faceted) over the feature 'Pclass'.
```
____
```
**Take-away:** [Include take-away from figure here]
* Use `seaborn` to build bar plots of the Titanic dataset feature 'Survived' split (faceted) over the feature 'Embarked'.
```
____
```
**Take-away:** [Include take-away from figure here]
## EDA with numeric variables
* Use `seaborn` to plot a histogram of the 'Fare' column of `df_train`.
```
____
```
**Take-away:** [Include take-away from figure here]
* Use a `pandas` plotting method to plot the column 'Fare' for each value of 'Survived' on the same plot.
```
____
```
**Take-away:** [Include take-away from figure here]
* Use `seaborn` to plot a histogram of the 'Age' column of `df_train`. _Hint_: you may need to drop null values before doing so.
```
df_train_drop = ____
____
```
**Take-away:** [Include take-away from figure here]
* Plot a strip plot & a swarm plot of 'Fare' with 'Survived' on the x-axis.
```
____
____
```
**Take-away:** [Include take-away from figure here]
* Use the DataFrame method `.describe()` to check out summary statistics of 'Fare' as a function of survival.
```
____
```
* Use `seaborn` to plot a scatter plot of 'Age' against 'Fare', colored by 'Survived'.
```
____
```
**Take-away:** [Include take-away from figure here]
* Use `seaborn` to create a pairplot of `df_train`, colored by 'Survived'.
```
____
```
**Take-away:** [Include take-away from figure here]
**Recap:**
* you've loaded your data and had a look at it.
* you've explored your target variable visually and made your first predictions.
* you've explored some of your feature variables visually and made more predictions that did better based on your EDA.
* you've done some serious EDA of feature variables, categorical and numeric.
**Up next:** Time to build some Machine Learning models, based on what you've learnt from your EDA here. Open the notebook `2-titanic_first_ML-model.ipynb`.
For more on `pandas`, check out our [Data Manipulation with Python track](https://www.datacamp.com/tracks/data-manipulation-with-python).
For more on `seaborn`, check out Chapter 3 of our [Intro. to Datavis with Python course](https://www.datacamp.com/courses/introduction-to-data-visualization-with-python).
If you're enoying this session, retweet or share on FB now and follow us on Twitter: [@hugobowne](https://twitter.com/hugobowne) & [@DataCamp](https://twitter.com/datacamp).
|
github_jupyter
|
# Import modules
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import tree
from sklearn.metrics import accuracy_score
# Figures inline and set visualization style
%matplotlib inline
sns.set()
# Import test and train datasets
df_train = pd.read_csv('data/train.csv')
df_test = pd.read_csv('data/test.csv')
# View first lines of training data
df_train.head()
# View first lines of test data
df_test.head()
df_train.info()
df_train.describe()
sns.countplot(x='Survived', data=df_train); #case sensative in Survived
df_test['Survived'] = 0 #assume nobody survived
df_test[['PassengerId', 'Survived']].to_csv('data/predictions/no_survivors.csv', index=False)
sns.countplot(x="Sex", data=df_train);
sns.catplot(x='Survived', col='Sex', kind="count", data=df_train);
female_S = df_train[df_train.Sex == 'female'].Survived.sum()
male_S = df_train[df_train.Sex == 'male'].Survived.sum()
print("female Survivors", female_S)
print("Male Survivors", male_S)
# another way using groupby
df_train.groupby(['Sex']).Survived.sum() #count will count who survived and who didnt survive
print(df_train[df_train.Sex == 'female'].Survived.sum()/df_train[df_train.Sex == 'female'].Survived.count())
print(df_train[df_train.Sex == 'male'].Survived.sum()/df_train[df_train.Sex == 'male'].Survived.count())
i=0
while i<df_test.Sex.count():
if (df_test.Sex[i] == 'female'):
df_test['Survived'][i] = 1
else:
df_test['Survived'][i] = 0
i +=1
df_test['Survived']
# df_test.Sex
df_test['Survived'] = df_test.Sex == 'female'
df_test.tail()
df_test['Survived'] = df_test.Survived.apply(lambda x: int(x)) #apply function turns true =1 & false = 0
df_test.head()
df_test[['PassengerId', 'Survived']].to_csv('data/predictions/women_survive.csv', index=False)
____
____
____
____
df_train_drop = ____
____
____
____
____
____
____
| 0.264168 | 0.969556 |
<p style="text-align: right;"> ✅ Put your name here</p>
# <p style="text-align: center;"> Pre-Class Assignment 23: Background for Quantum Computing </p>
This notebook starts a unit introducing a different model of computation, a model that plays by the rules of <i>quantum</i> physics rather than <i>classical</i> physics.
I hope you're not intimidated! Unfortunately, quantum physics gets a bad rap of being inherently confusing. This is not at all the case! Quantum physics sounds strange due to some weird consequences that we'll see shortly, but it's actually really easy to <i>do</i>, involving some simple mathematics that you have probably seen before. And it doesn't require you to know any classical physics! (If you do, you'll see why quantum physics is a strange theory.)
Quantum computing is a relatively new field that started in the 1980s and 1990s. Due to recent advances in experimental physics and engineering, we have today some of the world's first quantum computers, and the field has received a lot of attention recently. At the end of this unit, you'll have the opportunity to program a quantum computer!
## <p style="text-align: center;"> Itinerary for Quantum Computing Unit </p>
<table align="center" style="width:50%">
<tr>
<td style="text-align:center"><b>Assignment</b></td>
<td style="text-align:center"><b>Topic</b></td>
<td style="text-align:center"><b>Description</b></td>
</tr>
<tr>
<td bgcolor="yellow" style="text-align:center">Pre Class 23</td>
<td bgcolor="yellow" style="text-align:center">Background for Quantum Computing</td>
<td bgcolor="yellow" style="text-align:center">How Computers Store Information</td>
</tr>
<tr>
<td style="text-align:center">In Class 23</td>
<td style="text-align:center">Classsical and Quantum Bits</td>
<td style="text-align:center">Information in Quantum States</td>
</tr>
<tr>
<td style="text-align:center">Pre Class 24</td>
<td style="text-align:center">Software for Quantum Computing</td>
<td style="text-align:center">High Level Software and the Circuit Model</td>
</tr>
<tr>
<td style="text-align:center">In Class 24</td>
<td style="text-align:center">Programming Quantum Computers</td>
<td style="text-align:center">Manipulating Quantum Bits to Perform Useful Computations</td>
</tr>
</table>
### <p style="text-align: center;"> Before you start... </p>
Take ten seconds to answer these survey questions:
```
from IPython.display import HTML
HTML(
"""
<iframe
src="https://goo.gl/forms/aTOqrX354o9n52r92"
width="80%"
height="1200px"
frameborder="0"
marginheight="0"
marginwidth="0">
Loading...
</iframe>
"""
)
```
## <p style="text-align: center;"> Learning Goals for Today's Pre-Class Assignment </p>
By the end of today's pre-class assignment, you should be able to:
1. Describe how computers store information using binary digits.
1. State the fundamental difference between classical and quantum computers in terms of how they store information.
1. Review/learn <b><font color="green">complex numbers</font></b>, <b><font color="red">probability</font></b> distributions, and <b><font color="blue">vectors</font></b> to more deeply understand quantum binary digits.
# <p style="text-align: center;"> How Computers Store Information </p>
Watch the following video to learn about <b>binary digits</b>, or <b>bits</b>, the fundamental unit of information for all data in a computer.
```
"""How computers work: binary & data."""
from IPython.display import YouTubeVideo
YouTubeVideo("USCBCmwMCDA", width=640, height=360)
```
<b>Question:</b> What are the possible values of a bit?
<font size=8 color="#009600">✎</font> **Answer:** Erase the contents of this cell and put your answer here!
The video mentioned that 1001 in binary is equal to 9 in decimal. You should understand how to convert from binary to decimal ($1001$ means $1 \cdot 2^3 + 0 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 2^0 = 9$). There's a cool trick for doing this in Python, shown below.
```
"""Cool trick! Converting from binary to decimal."""
int("1001", 2)
```
Here, the first argument to `int` is what gets converted to a number. The second argument to `int` represents the base of the number system to use (binary = base 2). You can change the first argument to get different resulting numbers and test your understanding of binary.
<b>Question:</b> All data on a computer--including text, images, and sound--is stored in bits. Pick one of these (text, images, or sound) and explain how bits are used to represent this information.
<font size=8 color="#009600">✎</font> **Answer:** Erase the contents of this cell and put your answer here!
<b>Question:</b> What do we use to physically represent bits in computers?
<font size=8 color="#009600">✎</font> **Answer:** Erase the contents of this cell and put your answer here!
# <p style="text-align: center;"> How Quantum Computers Store Information </p>
Recall the last statement from the above video on bits and data:
<blockquote> <i> <font size="4"> "If you want to understand how computers work on the inside, it all comes down to these simple ones and zeros and the electrical signals in the circuits behind them." </font> </i> </blockquote>
In the same way, if you want to understand how <b>quantum</b> computers work, it all comes down to how information is stored.
<blockquote> <i> <font size="4"> Quantum computers store information in <b>quantum bits</b>, or <b>qubits</b> (pronounced "CUE bits") for short. </font> </i> </blockquote>
Watch the following short video to get introduced to qubits.
```
"""Introduction to qubits."""
from IPython.display import YouTubeVideo
YouTubeVideo("KBpYK3i3kDs",width=640,height=360)
```
# <p style="text-align: center;"> Understanding Qubits: Three Key Concepts </p>
To understand a qubit, we only have to understand three concepts.
1. <b><font color="green">Complex numbers.</font></b>
1. <b><font color="red">Probability.</font></b>
1. <b><font color="blue">Vectors.</font></b>
Watch the next three videos to see each concept in turn, and complete the exercises to test your understanding.
The goal of these concepts is to understand a qubit at a deeper level. Each may seem unrelated, but everything will tie together at the end of the notebook.
```
"""Imports for the notebook."""
import numpy as np
import matplotlib.pyplot as plt
```
## <p style="text-align: center;"> Concept #1: <font color="green">Complex Numbers</font> </p>
Watch the following video on complex numbers.
```
"""Complex numbers."""
from IPython.display import YouTubeVideo
YouTubeVideo("3AmdT0CsLbk",width=640,height=360)
```
### <p style="text-align: center;"> <font color="green">Video Recap</font> </p>
* The <b><font color="green">imaginary unit</font></b>, which we'll denote $i$, is defined by the property that $i^2 = -1$. (<b>Note:</b> In Python, `j` is used for the imaginary unit.)
* A <b><font color="green">complex number</font></b> has the form
\begin{equation}
\alpha = a + b i
\end{equation}
where $a$ and $b$ are real numbers. (The symbol $\alpha$ is the Greek letter alpha. We'll use Greek letters for complex numbers to not confuse them with real numbers.)
* The <b><font color="green">addition of two complex numbers</font></b> is defined by
\begin{equation}
\alpha + \beta = (a + b i) + (c + d i) := (a + c) + (b + d)i .
\end{equation}
* We define the <b><font color="green">complex conjugate</font></b> of a complex number $\alpha = a + bi$ to be
\begin{equation}
\alpha^* := a - bi .
\end{equation}
(That is, we flip the sign of the imaginary part.)
* The <b><font color="green">modulus squared</font></b> of $\alpha$ is defined to be the product of itself with its complex conjugate:
\begin{equation}
|\alpha|^2 := \alpha^* \alpha = a^2 + b^2
\end{equation}
As you might guess, the <b><font color="green">modulus</font></b> is just the square root of the modulus squared.
### <p style="text-align: center;"> <font color="green">Exercise: Working with Complex Numbers</font> </p>
<font size=8 color="#009600">✎</font> **Do this:** Run the cell below to see how to perform some operations on complex numbers in Python.
```
"""Working with complex numbers in Python."""
# define two complex numbers
alpha = 1 + 2j # note: j is used for the imaginary unit in Python
beta = 3 - 4j
print("alpha =", alpha)
print("beta =", beta)
# print out the type of alpha
print("\ntype(alpha) =", type(alpha))
# print out the real and imaginary part of alpha
print("\nThe real part of alpha is", alpha.real)
print("The imaginary part of alpha is", alpha.imag)
# print out the sum of alpha and beta
print("\nalpha + beta =", alpha + beta)
# print out the complex conjugate of alpha and beta
print("\nalpha* =", alpha.conjugate())
print("beta* =", beta.conjugate())
```
<font size=8 color="#009600">✎</font> **Do this:** Write a function called `modulus_squared` that inputs a complex number $\alpha$ and returns its modulus squared $|\alpha|^2 = \alpha^* \alpha$.
<b>Important:</b> Make sure your function returns a `float`, not a `complex` number. You can do this by using the `real` part of the modulus squared.
```
"""Put code for implementing your function here!"""
def modulus_squared(alpha):
pass
```
The next cell contains test cases for your function. If your function is correct, this cell will execute without error. (Note: `assert EXPRESSION` throws an error if the `EXPRESSION` is `False`. Otherwise, nothing happens. For this reason, it's often used to test code.)
```
"""Test cases: run this cell to ensure your function is correct."""
assert np.isclose(modulus_squared(3+4j), 25.0)
assert np.isclose(modulus_squared(1), 1.0)
assert np.isclose(modulus_squared(1j), 1.0)
assert np.isclose(modulus_squared(-3 - 4j), 25.0)
```
## <p style="text-align: center;"> Concept #2: <font color="red">Probability</font> </p>
Watch the following video on probability distributions.
```
"""Probability."""
from IPython.display import YouTubeVideo
YouTubeVideo("rfmmhXzi5lk",width=640,height=360)
```
### <p style="text-align: center;"> <font color="red">Video Recap</font> </p>
A <b><font color="red">probability distribution</font></b> is a list of numbers $p_1, ..., p_n$ that satisfy the following conditions:
* Each probability is non-negative.
\begin{equation}
p_i \ge 0
\end{equation}
* The sum over all probabilites is equal to one.
\begin{equation}
\sum_{i = 1}^{n} p_i = 1 .
\end{equation}
### <p style="text-align: center;"> <font color="red">Exercise: Working with Probabilities</font> </p>
**Question:** Could the following list of numbers be a probability distribution? Why or why not?
```
"""Potential probability distribution."""
distribution = np.array([0.1, 0.3, 0.2, 0.2, 0.1, 0.2])
```
<font size=8 color="#009600">✎</font> **Answer:** Erase the contents of this cell and put your answer here!
**Question:** Write a function, called `is_valid`, that inputs a numpy array and returns `True` if the list of numbers defines a valid probability distribution, else returns `False`.
```
"""Put code for implementing your function here!"""
def is_valid(array):
pass
```
Run the next cell to test your function. If your function is correct, no errors should be thrown.
```
"""Run this cell to test your function."""
assert is_valid(np.array([0.5, 0.3, 0.2]))
assert not is_valid(np.array([0.2, 0.4, 0.2]))
assert not is_valid(np.array([1.0, -1.0, 1.0]))
```
## <p style="text-align: center;"> Concept #3: <font color="blue">Linear Algebra & Vectors </font> </p>
Watch the following video on vectors.
```
"""Linear algebra and vectors."""
from IPython.display import YouTubeVideo
YouTubeVideo("klDm1eC1gxg",width=640,height=360)
```
### <p style="text-align: center;"> <font color="blue">Video Recap</font> </p>
* A <b><font color="blue">vector</font></b> is the formal mathematical term for a list of numbers. (You may understand vectors as objects with size and direction, which is an equally valid definition. For the purposes of quantum computing, it's more convenient to think of vectors as just lists of numbers.)
* An example of a vector is
\begin{equation}
|0\rangle := \left[ \begin{matrix}
1 \\
0 \\
\end{matrix} \right],
\end{equation}
and another example of a vector is
\begin{equation}
|1\rangle := \left[ \begin{matrix}
0 \\
1 \\
\end{matrix} \right]
\end{equation}
* The angled-bracket notation $|\rangle$ denotes that an object is a vector. The number inside of the angled brackets is a label for which vector it is. (You'll see why we label the vectors 0 and 1 in the next In Class Assignment. In principle, though, any symbol could be used to label the vector.)
* <font color="blue"><b>Vector addition</b></font> is defined component-wise. For example,
\begin{equation}
|0\rangle + |1\rangle = \left[ \begin{matrix}
1 \\
0 \\
\end{matrix} \right] +
\left[ \begin{matrix}
0 \\
1 \\
\end{matrix} \right]
=
\left[ \begin{matrix}
1 + 0 \\
0 + 1 \\
\end{matrix} \right]
=
\left[ \begin{matrix}
1 \\
1 \\
\end{matrix} \right]
\end{equation}
* We can also take <font color="blue"><b>scalar multiples</b></font> of vectors, for example
\begin{equation}
\alpha |0\rangle = \alpha \left[ \begin{matrix}
1 \\
0 \\
\end{matrix} \right]
=
\left[ \begin{matrix}
\alpha \cdot 1 \\
\alpha \cdot 0 \\
\end{matrix} \right]
=
\left[ \begin{matrix}
\alpha \\
0 \\
\end{matrix} \right].
\end{equation}
In general, we multiply each component of the vector by the number $\alpha$.
* This allows us to write <b>superpositions</b>, which are scalar multiples and sums of vectors. That is, equations of the form
\begin{equation}
\alpha |0\rangle + \beta |1\rangle
\end{equation}
* In Python, Numpy arrays handle vector operations for us.
### <p style="text-align: center;"> <font color="blue">Exercise: Working with Vectors</font> </p>
The following cell shows how we use Numpy arrays to work with vectors in Python.
```
"""Using numpy to perform vector operations."""
# the |0> == zero vector and |1> == one vector from above
zero = np.array([1, 0], dtype=np.complex64)
one = np.array([0, 1], dtype=np.complex64)
# print out the vectors
print("|0> =", zero)
print("|1> =", one)
# some complex numbers
alpha = 0.5 + 0.5j
beta = 1 - 2j
```
<font size=8 color="#009600">✎</font> **Do this:** Run the following code cell to see how Numpy arrays handle vector operations for us. Complete the last portion, labeled `TODO`.
```
"""Run this cell. Complete the last portion."""
# print out the sum of zero and one
print("|0> + |1> =", zero + one)
# compute and print out alpha * |0>
print("alpha |0> =", alpha * zero)
# compute and print out beta * |1>
print("beta |1>> =", beta * one)
# TODO: print out the superposition alpha |0> + beta |1>
```
<b>Question:</b> Is this output of the cell above what you expect based on the definition of vector addition and scalar multiples of vectors?
<font size=8 color="#009600">✎</font> **Answer:** Erase the contents of this cell and put your answer here!
# <p style="text-align: center;"> Tying Together the Concepts </p>
When we introduced a qubit, we said it could be the state $|0\rangle$, $|1\rangle$, or superpositions of $|0\rangle$ and $|1\rangle$. We can now fully understand this statement.
A <b>superposition</b> is a sum of scalar multiples of vectors. So, the most general state of a <b>qubit</b> can be written
\begin{equation}
|\psi\rangle = \alpha |0\rangle + \beta |1\rangle
=
\left[ \begin{matrix}
\alpha \\
\beta \\
\end{matrix} \right]
\end{equation}
where $|\alpha|^2 + |\beta|^2 = 1$.
That is, a <b>qubit</b> is a <b><font color="blue">vector</font></b> of <b><font color="green">complex numbers</font></b>. These complex numbers determine the <b><font color="red">probability</font></b> of measuring a particular state, as we'll discuss in upcoming assignments.
Unlike bits, which are only 0 or 1, qubits can exist in superposition states. This is the first idea that there is "more" processing power with qubits (quantum computers) than with bits (classical computers).
However, this isn't the entire story. <i>Teaser of what's to come:</i> When we measure qubits, we record either 0 with a probability that depends on $\alpha$, the coefficient of $|0\rangle$. In particular,
\begin{equation}
p(\text{measuring 0}) = |\alpha|^2
\end{equation}
Similarly for measuring 1:
\begin{equation}
p(\text{measuring 1}) = |\beta|^2
\end{equation}
This is why we requre $|\alpha|^2 + |\beta|^2 = 1$ for qubits. The next in class assignment will explore measurements further and give you more practice working with qubits.
(Brief remark for those interested: A qubit is an example of a wavefunction in quantum physics. A wavefunction is a mathematical description of a quantum system. In the discrete case (like a qubit), it consists of a vector of complex numbers which determine the probability of measuring particular states.)
# <p style="text-align: center;"> Assignment Wrapup </p>
## <p style="text-align: center;"> Survey </p>
```
from IPython.display import HTML
HTML(
"""
<iframe
src="https://goo.gl/forms/n00m87at8mHLAbZN2"
width="80%"
height="1200px"
frameborder="0"
marginheight="0"
marginwidth="0">
Loading...
</iframe>
"""
)
```
## <p style="text-align: center;"> Congrats, You're Finished! </p>
Now, you just need to submit this assignment by uploading it to the course <a href="https://d2l.msu.edu/">Desire2Learn</a> web page for today's submission folder. (Don't forget to add your name in the first cell.)
<p style="text-align: right;"><b>© Copyright 2019, Michigan State University Board of Trustees.</b></p>
|
github_jupyter
|
from IPython.display import HTML
HTML(
"""
<iframe
src="https://goo.gl/forms/aTOqrX354o9n52r92"
width="80%"
height="1200px"
frameborder="0"
marginheight="0"
marginwidth="0">
Loading...
</iframe>
"""
)
"""How computers work: binary & data."""
from IPython.display import YouTubeVideo
YouTubeVideo("USCBCmwMCDA", width=640, height=360)
"""Cool trick! Converting from binary to decimal."""
int("1001", 2)
"""Introduction to qubits."""
from IPython.display import YouTubeVideo
YouTubeVideo("KBpYK3i3kDs",width=640,height=360)
"""Imports for the notebook."""
import numpy as np
import matplotlib.pyplot as plt
"""Complex numbers."""
from IPython.display import YouTubeVideo
YouTubeVideo("3AmdT0CsLbk",width=640,height=360)
"""Working with complex numbers in Python."""
# define two complex numbers
alpha = 1 + 2j # note: j is used for the imaginary unit in Python
beta = 3 - 4j
print("alpha =", alpha)
print("beta =", beta)
# print out the type of alpha
print("\ntype(alpha) =", type(alpha))
# print out the real and imaginary part of alpha
print("\nThe real part of alpha is", alpha.real)
print("The imaginary part of alpha is", alpha.imag)
# print out the sum of alpha and beta
print("\nalpha + beta =", alpha + beta)
# print out the complex conjugate of alpha and beta
print("\nalpha* =", alpha.conjugate())
print("beta* =", beta.conjugate())
"""Put code for implementing your function here!"""
def modulus_squared(alpha):
pass
"""Test cases: run this cell to ensure your function is correct."""
assert np.isclose(modulus_squared(3+4j), 25.0)
assert np.isclose(modulus_squared(1), 1.0)
assert np.isclose(modulus_squared(1j), 1.0)
assert np.isclose(modulus_squared(-3 - 4j), 25.0)
"""Probability."""
from IPython.display import YouTubeVideo
YouTubeVideo("rfmmhXzi5lk",width=640,height=360)
"""Potential probability distribution."""
distribution = np.array([0.1, 0.3, 0.2, 0.2, 0.1, 0.2])
"""Put code for implementing your function here!"""
def is_valid(array):
pass
"""Run this cell to test your function."""
assert is_valid(np.array([0.5, 0.3, 0.2]))
assert not is_valid(np.array([0.2, 0.4, 0.2]))
assert not is_valid(np.array([1.0, -1.0, 1.0]))
"""Linear algebra and vectors."""
from IPython.display import YouTubeVideo
YouTubeVideo("klDm1eC1gxg",width=640,height=360)
"""Using numpy to perform vector operations."""
# the |0> == zero vector and |1> == one vector from above
zero = np.array([1, 0], dtype=np.complex64)
one = np.array([0, 1], dtype=np.complex64)
# print out the vectors
print("|0> =", zero)
print("|1> =", one)
# some complex numbers
alpha = 0.5 + 0.5j
beta = 1 - 2j
"""Run this cell. Complete the last portion."""
# print out the sum of zero and one
print("|0> + |1> =", zero + one)
# compute and print out alpha * |0>
print("alpha |0> =", alpha * zero)
# compute and print out beta * |1>
print("beta |1>> =", beta * one)
# TODO: print out the superposition alpha |0> + beta |1>
from IPython.display import HTML
HTML(
"""
<iframe
src="https://goo.gl/forms/n00m87at8mHLAbZN2"
width="80%"
height="1200px"
frameborder="0"
marginheight="0"
marginwidth="0">
Loading...
</iframe>
"""
)
| 0.57523 | 0.962321 |
# VacationPy
----
#### Note
* Keep an eye on your API usage. Use https://developers.google.com/maps/reporting/gmp-reporting as reference for how to monitor your usage and billing.
* Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.
```
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import gmaps
import os
# Import API key
from api_keys import g_key
```
### Store Part I results into DataFrame
* Load the csv exported in Part I to a DataFrame
```
# To get File Path
file_path = "../WeatherPy/output_data/cities.csv"
cities_df = pd.read_csv(file_path)
cities_df['Date'] = cities_df['Date'].astype(int)
cities_df
```
### Humidity Heatmap
* Configure gmaps.
* Use the Lat and Lng as locations and Humidity as the weight.
* Add Heatmap layer to map.
```
gmaps.configure(api_key=g_key)
locations = cities_df[['Lat','Lng']]
locations
humidity_cities = cities_df['Humidity']
humidity_cities
# cities_df['Humidity'].max()
max_humidity = humidity_cities.max()
# Plot Heatmap
fig = gmaps.figure(center=(0,0),zoom_level=2)
# Create heat layer
heat_layer = gmaps.heatmap_layer(locations, weights=humidity_cities,
dissipating=False, max_intensity=max_humidity,
point_radius=3, opacity=0.6)
# Add layer
fig.add_layer(heat_layer)
# Display figure
fig
```
### Create new DataFrame fitting weather criteria
* Narrow down the cities to fit weather conditions.
* Drop any rows will null values.
```
# A max temperature lower than 80 degrees but higher than 70.
# Wind speed less than 10 mph.
# Zero cloudiness.
# Drop any rows that don’t contain all three conditions. You want to be sure the weather is ideal.
weather_fit_df = cities_df.loc[(cities_df['Max Temp'] < 80) & (cities_df['Max Temp'] > 70) & (cities_df['Wind Speed'] < 10) & (cities_df['Cloudiness'] == 0)]
weather_fit_df
```
### Hotel Map
* Store into variable named `hotel_df`.
* Add a "Hotel Name" column to the DataFrame.
* Set parameters to search for hotels with 5000 meters.
* Hit the Google Places API for each city's coordinates.
* Store the first Hotel result into the DataFrame.
* Plot markers on top of the heatmap.
```
hotel_df = weather_fit_df[['City','Lat','Lng','Country']].copy()
# weather_fit_df
hotel_df["Hotel Name"]=""
hotel_df
from pprint import pprint
# To get Parameters for gmap
params={
"radius":5000,
"types":'lodging',
"key": g_key
}
base_url = "https://maps.googleapis.com/maps/api/place/nearbysearch/json"
# To get first Hotel Name nearby each city and add it to dataFrame
for index, row in weather_fit_df.iterrows():
params["location"] = f"{row['Lat']},{row['Lng']}"
response = requests.get(base_url, params=params)
json_response = response.json()
try:
hotel_df.loc[index, "Hotel Name"] = json_response["results"][0]["name"]
except:
print("Missing field/result... skipping.")
pass
hotel_df
# NOTE: Do not change any of the code in this cell
# Using the template add the hotel marks to the heatmap
info_box_template = """
<dl>
<dt>Name</dt><dd>{Hotel Name}</dd>
<dt>City</dt><dd>{City}</dd>
<dt>Country</dt><dd>{Country}</dd>
</dl>
"""
# Store the DataFrame Row
# NOTE: be sure to update with your DataFrame name
hotel_info = [info_box_template.format(**row) for index, row in hotel_df.iterrows()]
locations = hotel_df[["Lat", "Lng"]]
# Add marker layer ontop of heat map
markers = gmaps.marker_layer(locations)
hotel_layer = gmaps.symbol_layer(
locations, fill_color='rgba(0, 150, 0, 0.4)',
stroke_color='rgba(0, 0, 150, 0.4)', scale=4,
info_box_content=hotel_info
)
# Display figure
fig.add_layer(markers)
fig.add_layer(hotel_layer)
fig
```
|
github_jupyter
|
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import gmaps
import os
# Import API key
from api_keys import g_key
# To get File Path
file_path = "../WeatherPy/output_data/cities.csv"
cities_df = pd.read_csv(file_path)
cities_df['Date'] = cities_df['Date'].astype(int)
cities_df
gmaps.configure(api_key=g_key)
locations = cities_df[['Lat','Lng']]
locations
humidity_cities = cities_df['Humidity']
humidity_cities
# cities_df['Humidity'].max()
max_humidity = humidity_cities.max()
# Plot Heatmap
fig = gmaps.figure(center=(0,0),zoom_level=2)
# Create heat layer
heat_layer = gmaps.heatmap_layer(locations, weights=humidity_cities,
dissipating=False, max_intensity=max_humidity,
point_radius=3, opacity=0.6)
# Add layer
fig.add_layer(heat_layer)
# Display figure
fig
# A max temperature lower than 80 degrees but higher than 70.
# Wind speed less than 10 mph.
# Zero cloudiness.
# Drop any rows that don’t contain all three conditions. You want to be sure the weather is ideal.
weather_fit_df = cities_df.loc[(cities_df['Max Temp'] < 80) & (cities_df['Max Temp'] > 70) & (cities_df['Wind Speed'] < 10) & (cities_df['Cloudiness'] == 0)]
weather_fit_df
hotel_df = weather_fit_df[['City','Lat','Lng','Country']].copy()
# weather_fit_df
hotel_df["Hotel Name"]=""
hotel_df
from pprint import pprint
# To get Parameters for gmap
params={
"radius":5000,
"types":'lodging',
"key": g_key
}
base_url = "https://maps.googleapis.com/maps/api/place/nearbysearch/json"
# To get first Hotel Name nearby each city and add it to dataFrame
for index, row in weather_fit_df.iterrows():
params["location"] = f"{row['Lat']},{row['Lng']}"
response = requests.get(base_url, params=params)
json_response = response.json()
try:
hotel_df.loc[index, "Hotel Name"] = json_response["results"][0]["name"]
except:
print("Missing field/result... skipping.")
pass
hotel_df
# NOTE: Do not change any of the code in this cell
# Using the template add the hotel marks to the heatmap
info_box_template = """
<dl>
<dt>Name</dt><dd>{Hotel Name}</dd>
<dt>City</dt><dd>{City}</dd>
<dt>Country</dt><dd>{Country}</dd>
</dl>
"""
# Store the DataFrame Row
# NOTE: be sure to update with your DataFrame name
hotel_info = [info_box_template.format(**row) for index, row in hotel_df.iterrows()]
locations = hotel_df[["Lat", "Lng"]]
# Add marker layer ontop of heat map
markers = gmaps.marker_layer(locations)
hotel_layer = gmaps.symbol_layer(
locations, fill_color='rgba(0, 150, 0, 0.4)',
stroke_color='rgba(0, 0, 150, 0.4)', scale=4,
info_box_content=hotel_info
)
# Display figure
fig.add_layer(markers)
fig.add_layer(hotel_layer)
fig
| 0.615781 | 0.856632 |
# "Basra and Laura Nilva Paye"
> "This week we head back to Plot for a peach of a coffee from Peru, which makes some fantastic filter and espresso. Alongside we have the 1965 Blue Note recording 'Basra' from Pete La Roca"
- toc: false
- author: Lewis Cole (2021)
- branch: master
- badges: false
- comments: false
- categories: [Jazz, Coffee, Pete-La-Roca, 1960s, Plot, Peru, Washed, Bourbon]
- hide: false
- search_exclude: false
- image: https://github.com/jazzcoffeestuff/blog/raw/master/images/050-Basra/Basra.jpg
> youtube: https://youtu.be/390UPSAD0OI
This week on the blog we are yet again visiting Plot Coffee Roasters - a near constant feature in the blog as of late. This time we have a rather neat competition winning lot from Peru. The lot is from Laura Nilva Paye located in the Puno department of the country. In terms of location this is the south easterly corner of Peru, close to the border with Bolivia.
The cultivar of this coffee is Bourbon. I have been reminded that my sloppy use of the word "varietal" is technically incorrect when referring to coffee. In layman's terms the difference between "varietal" and "cultivar" is the presence of human intervention - in coffee (essentially) all coffee plants have been selectively bred, hence they should be referred to as "cultivar" as opposed to "varietal". This is something I often forget and end up referring to varietal but I'll try and be more precise in the future.
Plot label this coffee as a "washed" process, however looking into the details the coffee has been depulped and fermented for 20-24 hours before being washed. In that sense it is a little more "honey" than many washed coffees available. Following the washing stage the coffee is dried under shade.
Let's not hang around but get straight down to business: on the dry aroma I get sweet caramel and peaches, but they are very feint. Overall the coffee doesn't have a huge bouquet when compared to others, but it is very appealling I have a sense this will be a coffee I'll like. As I've said before the dry aroma (or lack thereof) doesn't necessarily align with what ends up in the cup.
Into the filter; it is clear to see how much quality is in this cup. It is very clean and clear, every flavour is well defined. The first thing that hits me is the sweetness, it has a very sticky-sweet vibe like a really ripe peach or even a peach syrup. After the intial stone fruit hit subsides you're left with a stunning floral finish which is clean and long lasting. The notes from Plot say: "a flavour profile more akin to Ethiopia than Peru" and it is very hard to argue with that. In terms of acidity I would describe it as a medium, or it may be that all the sweetness just offsets it. Eitherway it is a very easy cup to drink but also has layers of complexity to keep you entertained. I find it's best enjoyed at a slightly cooler temperature, straight out of the brewer the flavours get a bit too muddled for my tastes.
Onto espresso: I found it basically impossible to get a bad shot out of this. You can basically pull it however you like, with any grind setting and it'll be great. I was without electricity for a day and even pulled a shot on my cafelat robot and it was perhaps the best shot I had. I love the robot as a manual espresso maker, but I struggle with the lighter filter roasts I favour for espresso because it is hard to keep the temperature high enough. No problem with this coffee though, it still extracted perfectly. I found most enjoyment pulling the shots a little shorter that 1:2 to get a more luxurious caramel mouthfeel. The flavour profile in the cup is pure condensed peach and apricot. It is like a shot of peach syrup, incredibly high sweetness, just enough balancing acidity and no harshness at all. As much as I enjoyed this coffee in a filter, for me it really shone as an espresso - up there with the best of the year so far.
On the jazz side this week we're heading back to a classic Blue Note recording from 1965 - "Basra" by Pete La Roca.

Pete "La Roca" Sims is a drummer/percussionist - he is best known as a sideman having appeared alongside some of the all time greats: Sonny Rollins (Roca appeared albeit briefly on "Live at the Vanguard"), Joe Henderson (on "Page One"), Jackie McLean, Bill Evans, Sonny Clark and so on. He started his career however playing in latin bands, an influence that came through in his playing throughout his career. There are a few things interesting about Pete: firstly he despised the name "La Roca" - he came up with the moniker early in his career and it is how most people knew him, but he regretted it in later life. Secondly he was in some sense a "part timer" - throughout the 60s he made money as an NY taxi driver and later became a lawyer in the 70s returning to jazz just once after this.
> youtube: https://youtu.be/3M1O7InNT14
"La Roca" only has 3 albums under his own name, and one of those was erroniously labelled as a "Chick Corea" album by the record label initially. It's for that reason I consider "Basra" to be a bit of an "under the radar classic". I'm not a fan of labels like "under the radar" or "underrated" since they always bring out arguments of "XXXX is less well known, so this isn't underrated" eventually devolving into an excuse for showing how obscure ones musical tastes are. I consider "Basra" an "under the radar classic" however, because almost every "experienced" jazz fan I know loves the album but it will rarely (if ever) feature on a "top 100 albums" list and "La Roca" will never feature in a list of artists you "have to hear" - as a result this is an album that many do not discover until much later in their jazz journey.
So what makes the album so special? Firstly the line up:
- Pete "La Roca" - Drums
- Joe Henderson - Tenor Sax
- Steve Swallow - Bass
- Steve Kuhn - Piano
As with many Blue Note recordings from around this time: a true heavyweight line-up. But more than that: "Basra" features some truly explorative playing. It is not your typical "hard bop" album, the is a darker brooding attitude and vibe throughout. The players also lean into the avant-garde/free styles more than many other albums of the period. But more than that there are influences outside of the typical "jazz" paradigm.
This is perhaps most evident in the title track "Basra" (embedded at the start of the blog). A take on Middle Eastern classical music it is based around one chord and captures the "meditative" essence of the style. The "blank canvas" allows Joe to carve out any line he wants and it is some of the best lead playing you'll hear from Henderson.
There is also the firey "Malaguena" (above) which is a piece originally penned by Cuban composer Ernesto Lecuona (again "La Roca" tipping his hat towards the latin music he played in his early career.) Again Joe plays out of his skin and there are plenty of "Henderson-isms" throughout which is no bad thing. The piece manages to be energetic without being high tempo, the quartet masterfully keeps racheting up the tension as it goes on but somehow manages to swing.
> youtube: https://youtu.be/briljflpx2s
"Basra" also features the original recording of the Swallow tune: "Eiderdown" which later went on to be a Swallow signature tune and a standard in its own right. It is interesting to hear it in its "original" form here. It is perhaps the most "straight ahead" of all the tunes on the album and Swallow's bass keeps the tune driving forward in his own inimitable way. This is also one of the recordings shortly before Steve switched to electric bass entirely, so it is nice to hear him play with an acoustic instrument.
All in all "Basra" is, in my opinion, one of the greatest recordings on Blue Note. Definitely hunt out a copy through whatever medium you use to consume your music. It is a shame we have so few records of "La Roca" under his own name, it would have been great to see where he would have taken his music.
|
github_jupyter
|
# "Basra and Laura Nilva Paye"
> "This week we head back to Plot for a peach of a coffee from Peru, which makes some fantastic filter and espresso. Alongside we have the 1965 Blue Note recording 'Basra' from Pete La Roca"
- toc: false
- author: Lewis Cole (2021)
- branch: master
- badges: false
- comments: false
- categories: [Jazz, Coffee, Pete-La-Roca, 1960s, Plot, Peru, Washed, Bourbon]
- hide: false
- search_exclude: false
- image: https://github.com/jazzcoffeestuff/blog/raw/master/images/050-Basra/Basra.jpg
> youtube: https://youtu.be/390UPSAD0OI
This week on the blog we are yet again visiting Plot Coffee Roasters - a near constant feature in the blog as of late. This time we have a rather neat competition winning lot from Peru. The lot is from Laura Nilva Paye located in the Puno department of the country. In terms of location this is the south easterly corner of Peru, close to the border with Bolivia.
The cultivar of this coffee is Bourbon. I have been reminded that my sloppy use of the word "varietal" is technically incorrect when referring to coffee. In layman's terms the difference between "varietal" and "cultivar" is the presence of human intervention - in coffee (essentially) all coffee plants have been selectively bred, hence they should be referred to as "cultivar" as opposed to "varietal". This is something I often forget and end up referring to varietal but I'll try and be more precise in the future.
Plot label this coffee as a "washed" process, however looking into the details the coffee has been depulped and fermented for 20-24 hours before being washed. In that sense it is a little more "honey" than many washed coffees available. Following the washing stage the coffee is dried under shade.
Let's not hang around but get straight down to business: on the dry aroma I get sweet caramel and peaches, but they are very feint. Overall the coffee doesn't have a huge bouquet when compared to others, but it is very appealling I have a sense this will be a coffee I'll like. As I've said before the dry aroma (or lack thereof) doesn't necessarily align with what ends up in the cup.
Into the filter; it is clear to see how much quality is in this cup. It is very clean and clear, every flavour is well defined. The first thing that hits me is the sweetness, it has a very sticky-sweet vibe like a really ripe peach or even a peach syrup. After the intial stone fruit hit subsides you're left with a stunning floral finish which is clean and long lasting. The notes from Plot say: "a flavour profile more akin to Ethiopia than Peru" and it is very hard to argue with that. In terms of acidity I would describe it as a medium, or it may be that all the sweetness just offsets it. Eitherway it is a very easy cup to drink but also has layers of complexity to keep you entertained. I find it's best enjoyed at a slightly cooler temperature, straight out of the brewer the flavours get a bit too muddled for my tastes.
Onto espresso: I found it basically impossible to get a bad shot out of this. You can basically pull it however you like, with any grind setting and it'll be great. I was without electricity for a day and even pulled a shot on my cafelat robot and it was perhaps the best shot I had. I love the robot as a manual espresso maker, but I struggle with the lighter filter roasts I favour for espresso because it is hard to keep the temperature high enough. No problem with this coffee though, it still extracted perfectly. I found most enjoyment pulling the shots a little shorter that 1:2 to get a more luxurious caramel mouthfeel. The flavour profile in the cup is pure condensed peach and apricot. It is like a shot of peach syrup, incredibly high sweetness, just enough balancing acidity and no harshness at all. As much as I enjoyed this coffee in a filter, for me it really shone as an espresso - up there with the best of the year so far.
On the jazz side this week we're heading back to a classic Blue Note recording from 1965 - "Basra" by Pete La Roca.

Pete "La Roca" Sims is a drummer/percussionist - he is best known as a sideman having appeared alongside some of the all time greats: Sonny Rollins (Roca appeared albeit briefly on "Live at the Vanguard"), Joe Henderson (on "Page One"), Jackie McLean, Bill Evans, Sonny Clark and so on. He started his career however playing in latin bands, an influence that came through in his playing throughout his career. There are a few things interesting about Pete: firstly he despised the name "La Roca" - he came up with the moniker early in his career and it is how most people knew him, but he regretted it in later life. Secondly he was in some sense a "part timer" - throughout the 60s he made money as an NY taxi driver and later became a lawyer in the 70s returning to jazz just once after this.
> youtube: https://youtu.be/3M1O7InNT14
"La Roca" only has 3 albums under his own name, and one of those was erroniously labelled as a "Chick Corea" album by the record label initially. It's for that reason I consider "Basra" to be a bit of an "under the radar classic". I'm not a fan of labels like "under the radar" or "underrated" since they always bring out arguments of "XXXX is less well known, so this isn't underrated" eventually devolving into an excuse for showing how obscure ones musical tastes are. I consider "Basra" an "under the radar classic" however, because almost every "experienced" jazz fan I know loves the album but it will rarely (if ever) feature on a "top 100 albums" list and "La Roca" will never feature in a list of artists you "have to hear" - as a result this is an album that many do not discover until much later in their jazz journey.
So what makes the album so special? Firstly the line up:
- Pete "La Roca" - Drums
- Joe Henderson - Tenor Sax
- Steve Swallow - Bass
- Steve Kuhn - Piano
As with many Blue Note recordings from around this time: a true heavyweight line-up. But more than that: "Basra" features some truly explorative playing. It is not your typical "hard bop" album, the is a darker brooding attitude and vibe throughout. The players also lean into the avant-garde/free styles more than many other albums of the period. But more than that there are influences outside of the typical "jazz" paradigm.
This is perhaps most evident in the title track "Basra" (embedded at the start of the blog). A take on Middle Eastern classical music it is based around one chord and captures the "meditative" essence of the style. The "blank canvas" allows Joe to carve out any line he wants and it is some of the best lead playing you'll hear from Henderson.
There is also the firey "Malaguena" (above) which is a piece originally penned by Cuban composer Ernesto Lecuona (again "La Roca" tipping his hat towards the latin music he played in his early career.) Again Joe plays out of his skin and there are plenty of "Henderson-isms" throughout which is no bad thing. The piece manages to be energetic without being high tempo, the quartet masterfully keeps racheting up the tension as it goes on but somehow manages to swing.
> youtube: https://youtu.be/briljflpx2s
"Basra" also features the original recording of the Swallow tune: "Eiderdown" which later went on to be a Swallow signature tune and a standard in its own right. It is interesting to hear it in its "original" form here. It is perhaps the most "straight ahead" of all the tunes on the album and Swallow's bass keeps the tune driving forward in his own inimitable way. This is also one of the recordings shortly before Steve switched to electric bass entirely, so it is nice to hear him play with an acoustic instrument.
All in all "Basra" is, in my opinion, one of the greatest recordings on Blue Note. Definitely hunt out a copy through whatever medium you use to consume your music. It is a shame we have so few records of "La Roca" under his own name, it would have been great to see where he would have taken his music.
| 0.53777 | 0.692499 |
```
!pip install spacy spacy-pytorch-transformers farm
!python -m spacy download de_core_news_md
!python -m spacy download de_trf_bertbasecased_lg
!python -m spacy convert --converter ner /content/drive/MyDrive/Colab_Notebooks/Datasets/Gender_Dataset_100_Train_New.txt /content/drive/MyDrive/Colab_Notebooks/Datasets/data/train
!python -m spacy convert --converter ner /content/drive/MyDrive/Colab_Notebooks/Datasets/Gender_Dataset_100_Val.txt /content/drive/MyDrive/Colab_Notebooks/Datasets/data/val
!python -m spacy convert --converter ner /content/drive/MyDrive/Colab_Notebooks/Datasets/Gender_Dataset_100_Test_New.txt /content/drive/MyDrive/Colab_Notebooks/Datasets/data/test
!python -m spacy debug-data de /content/drive/MyDrive/Colab_Notebooks/Datasets/data/train /content/drive/MyDrive/Colab_Notebooks/Datasets/data/val -p ner -b de_trf_bertbasecased_lg
```
**Train Core News Model**
```
!python -m spacy train de /content/drive/MyDrive/Colab_Notebooks/Datasets/data/model /content/drive/MyDrive/Colab_Notebooks/Datasets/data/train/Gender_Dataset_100_Train_New.json /content/drive/MyDrive/Colab_Notebooks/Datasets/data/val/Gender_Dataset_100_Val.json --base-model de_core_news_md --pipeline 'ner' -R -n 20
```
**Evaluate Model**
```
!python -m spacy evaluate data/04_models/md/model-best data/03_val
```
**Train German BERT Model**
```
!python -m spacy train de /content/drive/MyDrive/Colab_Notebooks/Datasets/data/model /content/drive/MyDrive/Colab_Notebooks/Datasets/data/train/Gender_Dataset_100_Train_New.json /content/drive/MyDrive/Colab_Notebooks/Datasets/data/val/Gender_Dataset_100_Val.json \
--base-model de_trf_bertbasecased_lg --pipeline 'ner' -R -n 20
```
**Evaluate Model**
```
!python -m spacy evaluate /content/drive/MyDrive/Colab_Notebooks/Datasets/data/model/model-best /content/drive/MyDrive/Colab_Notebooks/Datasets/data/val
```
**Make Predictions**
```
import spacy
MODEL_PATH = '/content/drive/MyDrive/Colab_Notebooks/Datasets/data/model/model-best'
nlp = spacy.load(MODEL_PATH)
sample = """Der Arzt muss dem Mitarbeiter helfen."""
doc = nlp(sample)
for ent in doc.ents:
print(ent.label_, ':', ent.text)
```
Evaluate Model
```
from spacy.gold import GoldCorpus
VAL_FILENAME = '/content/drive/MyDrive/Colab_Notebooks/Datasets/data/val/Gender_Bias_Dataset_Val.json'
val_corpus = GoldCorpus(VAL_FILENAME, VAL_FILENAME)
docs_golds = list(val_corpus.train_docs(nlp))
docs, golds = zip(*docs_golds)
ner = nlp.pipeline[0][1]
predictions = list(ner.pipe(docs))
from spacy.scorer import Scorer
from collections import Counter
tag_counts = Counter()
scorer = Scorer()
for y_p, y_t in zip(predictions, golds):
scorer.score(y_p, y_t)
for tag in y_t.ner:
tag_counts[tag.split('-')[-1]] += 1
print(scorer.ents_p, scorer.ents_r, scorer.ents_f)
```
**Backup**
```
X_train = df["Word"]
y_train = df["Label"]
import pandas as pd
df = pd.read_csv('/content/gender_bias_dataset_train.txt', delimiter = "\t", encoding="utf-16", header = None)
df[['Word', 'Label']] = df[0].str.split(' ', 1, expand=True)
df = df.drop(df.columns[0], axis=1)
df.head()
from pathlib import Path
import re
file_path = Path("/content/drive/MyDrive/Colab Notebooks/Gender_Bias_Dataset.txt")
raw_text = file_path.read_text().strip()
raw_docs = re.split('\s+', raw_text)
raw_text.split()
raw_docs = re.split(r'\n', raw_text)
print(raw_docs)
#print(raw_text)
from flair.data import Corpus
from flair.datasets import ColumnCorpus
# define columns
columns = {0: 'text', 1: 'ner'}
# this is the folder in which train, test and dev files reside
data_folder = '/content'
# init a corpus using column format, data folder and the names of the train, dev and test files
corpus: Corpus = ColumnCorpus(data_folder, columns,
train_file='Gender_Detector_Dataset.txt')#,
#test_file='test.txt',
#dev_file='dev.txt')
from pathlib import Path
import re
file_path = Path(filepath)
raw_text = file_path.read_text().strip()
#print(raw_text)
raw_docs = re.split(r'\n\t?\n', raw_text)
token_docs = []
tag_docs = []
#print(raw_docs)
for doc in raw_docs:
print("doc " + doc)
tokens = []
tags = []
for line in doc.split('\t'):
print("line " + line[0])
#token, tag = re.split('\s+', line)
print(line.split('\t'))
#token, tag = line.split()
#print("token " + token)
#print("tag " + tag)
corpus.train
print(corpus.train[0].to_tagged_string('ner'))
print(corpus.train[1].to_tagged_string('ner'))
from transformers import AutoTokenizer
tokenizer = AutoTokenizer.from_pretrained(MODEL_NAME)
from flair.data import Sentence
from flair.models import SequenceTagger
# load tagger
tagger = SequenceTagger.load("ner-large")
# make example sentence
sentence = Sentence("Beide Athleten sind nun im Podcast zu hören.")
# predict NER tags
tagger.predict(sentence)
# print sentence
print(sentence)
# print predicted NER spans
print('The following NER tags are found:')
# iterate over entities and print
for entity in sentence.get_spans('ner'):
print(entity)
def load_data(filename: str):
with open(filename, 'rb') as file:
lines = [line[:-1].split() for line in file]
samples, start = [], 0
for end, parts in enumerate(lines):
if not parts:
sample = [(token, tag.split('-')[-1]) for token, tag in lines[start:end]]
samples.append(sample)
start = end + 1
if start < end:
samples.append(lines[start:end])
return samples
train_samples = load_data("/content/gender_bias.conll")
#val_samples = load_data('data/01_raw/bgh.conll')
#samples = train_samples + val_samples
schema = ['_'] + sorted({tag for sentence in train_samples
for _, tag in sentence})
```
|
github_jupyter
|
!pip install spacy spacy-pytorch-transformers farm
!python -m spacy download de_core_news_md
!python -m spacy download de_trf_bertbasecased_lg
!python -m spacy convert --converter ner /content/drive/MyDrive/Colab_Notebooks/Datasets/Gender_Dataset_100_Train_New.txt /content/drive/MyDrive/Colab_Notebooks/Datasets/data/train
!python -m spacy convert --converter ner /content/drive/MyDrive/Colab_Notebooks/Datasets/Gender_Dataset_100_Val.txt /content/drive/MyDrive/Colab_Notebooks/Datasets/data/val
!python -m spacy convert --converter ner /content/drive/MyDrive/Colab_Notebooks/Datasets/Gender_Dataset_100_Test_New.txt /content/drive/MyDrive/Colab_Notebooks/Datasets/data/test
!python -m spacy debug-data de /content/drive/MyDrive/Colab_Notebooks/Datasets/data/train /content/drive/MyDrive/Colab_Notebooks/Datasets/data/val -p ner -b de_trf_bertbasecased_lg
!python -m spacy train de /content/drive/MyDrive/Colab_Notebooks/Datasets/data/model /content/drive/MyDrive/Colab_Notebooks/Datasets/data/train/Gender_Dataset_100_Train_New.json /content/drive/MyDrive/Colab_Notebooks/Datasets/data/val/Gender_Dataset_100_Val.json --base-model de_core_news_md --pipeline 'ner' -R -n 20
!python -m spacy evaluate data/04_models/md/model-best data/03_val
!python -m spacy train de /content/drive/MyDrive/Colab_Notebooks/Datasets/data/model /content/drive/MyDrive/Colab_Notebooks/Datasets/data/train/Gender_Dataset_100_Train_New.json /content/drive/MyDrive/Colab_Notebooks/Datasets/data/val/Gender_Dataset_100_Val.json \
--base-model de_trf_bertbasecased_lg --pipeline 'ner' -R -n 20
!python -m spacy evaluate /content/drive/MyDrive/Colab_Notebooks/Datasets/data/model/model-best /content/drive/MyDrive/Colab_Notebooks/Datasets/data/val
import spacy
MODEL_PATH = '/content/drive/MyDrive/Colab_Notebooks/Datasets/data/model/model-best'
nlp = spacy.load(MODEL_PATH)
sample = """Der Arzt muss dem Mitarbeiter helfen."""
doc = nlp(sample)
for ent in doc.ents:
print(ent.label_, ':', ent.text)
from spacy.gold import GoldCorpus
VAL_FILENAME = '/content/drive/MyDrive/Colab_Notebooks/Datasets/data/val/Gender_Bias_Dataset_Val.json'
val_corpus = GoldCorpus(VAL_FILENAME, VAL_FILENAME)
docs_golds = list(val_corpus.train_docs(nlp))
docs, golds = zip(*docs_golds)
ner = nlp.pipeline[0][1]
predictions = list(ner.pipe(docs))
from spacy.scorer import Scorer
from collections import Counter
tag_counts = Counter()
scorer = Scorer()
for y_p, y_t in zip(predictions, golds):
scorer.score(y_p, y_t)
for tag in y_t.ner:
tag_counts[tag.split('-')[-1]] += 1
print(scorer.ents_p, scorer.ents_r, scorer.ents_f)
X_train = df["Word"]
y_train = df["Label"]
import pandas as pd
df = pd.read_csv('/content/gender_bias_dataset_train.txt', delimiter = "\t", encoding="utf-16", header = None)
df[['Word', 'Label']] = df[0].str.split(' ', 1, expand=True)
df = df.drop(df.columns[0], axis=1)
df.head()
from pathlib import Path
import re
file_path = Path("/content/drive/MyDrive/Colab Notebooks/Gender_Bias_Dataset.txt")
raw_text = file_path.read_text().strip()
raw_docs = re.split('\s+', raw_text)
raw_text.split()
raw_docs = re.split(r'\n', raw_text)
print(raw_docs)
#print(raw_text)
from flair.data import Corpus
from flair.datasets import ColumnCorpus
# define columns
columns = {0: 'text', 1: 'ner'}
# this is the folder in which train, test and dev files reside
data_folder = '/content'
# init a corpus using column format, data folder and the names of the train, dev and test files
corpus: Corpus = ColumnCorpus(data_folder, columns,
train_file='Gender_Detector_Dataset.txt')#,
#test_file='test.txt',
#dev_file='dev.txt')
from pathlib import Path
import re
file_path = Path(filepath)
raw_text = file_path.read_text().strip()
#print(raw_text)
raw_docs = re.split(r'\n\t?\n', raw_text)
token_docs = []
tag_docs = []
#print(raw_docs)
for doc in raw_docs:
print("doc " + doc)
tokens = []
tags = []
for line in doc.split('\t'):
print("line " + line[0])
#token, tag = re.split('\s+', line)
print(line.split('\t'))
#token, tag = line.split()
#print("token " + token)
#print("tag " + tag)
corpus.train
print(corpus.train[0].to_tagged_string('ner'))
print(corpus.train[1].to_tagged_string('ner'))
from transformers import AutoTokenizer
tokenizer = AutoTokenizer.from_pretrained(MODEL_NAME)
from flair.data import Sentence
from flair.models import SequenceTagger
# load tagger
tagger = SequenceTagger.load("ner-large")
# make example sentence
sentence = Sentence("Beide Athleten sind nun im Podcast zu hören.")
# predict NER tags
tagger.predict(sentence)
# print sentence
print(sentence)
# print predicted NER spans
print('The following NER tags are found:')
# iterate over entities and print
for entity in sentence.get_spans('ner'):
print(entity)
def load_data(filename: str):
with open(filename, 'rb') as file:
lines = [line[:-1].split() for line in file]
samples, start = [], 0
for end, parts in enumerate(lines):
if not parts:
sample = [(token, tag.split('-')[-1]) for token, tag in lines[start:end]]
samples.append(sample)
start = end + 1
if start < end:
samples.append(lines[start:end])
return samples
train_samples = load_data("/content/gender_bias.conll")
#val_samples = load_data('data/01_raw/bgh.conll')
#samples = train_samples + val_samples
schema = ['_'] + sorted({tag for sentence in train_samples
for _, tag in sentence})
| 0.344333 | 0.335405 |
# Computational psychrometric analysis of cooling systems as a control problem
**Note**: Numbers of chapters and figures of this notebook correspond to those from the accompaning paper:
> C. Ghiaus (2022) Computational psychrometric analysis of cooling systems as a control problem: case of cooling and dehumidification systems, *International Journal of Building Performance Simulation*, vol. 15, no. 1, p. 21-38
[DOI: 10.1080/19401493.2021.1995498](https://doi.org/10.1080/19401493.2021.1995498)
<img src="Figures/Legend.png" alt="Legend_figures" style="width: 600px;"/>
> Figure 3. Legend for figures 4 - 10
This legend is valid for all figures.
**Model of the HVAC system**
The HVAC system is composed of (see methods *lin_model* and *solve_lin* of class *MxCcRhTzBl* in file `cool.py` and Figures 2 and 4 in the accompaning paper Ghiaus (2022)):
- mixing recycled and outdoor air (MR block),
- cooling coil with by-pass (CC and MX blocks),
- reheating coil (HC block),
- thermal zone (TZ block) of the building (BL block).
<img src="Figures/AHU_model.png" alt="AHU_model" style="width: 600px;"/>
> Figure 4. Cooling and dehumidification: direct (or simulation) problem obtained by assembling elementary psychrometric processes.
**Types of systems** (see file `cool.py`):
- CAV: constant air volume - the mass flow rate is constant (see *CAV_wd* in `cool.py`).
- VBP: constant air volum (CAV) system with variable mix-air bypass (see *VBP_wd* in `cool.py`).
- VAV: variable air volume - the mass flow rate is variable (see *VAV_wd* in `cool.py`).
**Types of controls** (numbers correspond to the sections in the accompaning paper Ghiaus (2022)):
*- Linear control problem* (constant air volume (CAV) systems):
5.1 Control of indoor air temperature & humidity in constant air volume (CAV) systems with reheating
5.2 Control of indoor air temperature in constant air volume (CAV) systems without reheating
*- Non-linear parameter optimization problem:*
6.1 By-pass control in constant air volume (CAV) systems without reheating
6.1.1. Control of indoor air temperature & humidity in CAV systems
6.1.2. Control of indoor and supply air temperatures in CAV systems
6.2 Mass-flow control in variable air volume (VAV) systems
6.2.1 Control of indoor air temperature & humidity in VAV systems without reheating
6.2.2 Control of indoor and supply air temperatures in VAV systems without reheating
6.2.3 Control of indoor air temperature & humidity and of supply air temperature in VAV systems with reheating
```
import ipywidgets as wd
import matplotlib.pyplot as plt
import cool as cc
# %matplotlib inline # uncomment for inline figure
# %matplotlib qt # uncomment for figure in separate window
plt.rcParams["figure.figsize"] = (10, 7.7)
font = {'size': 16}
plt.rc('font', **font)
```
### Create *HVAC system* object
```
Kθ, Kw = 1e10, 0 # Gain factors of the P-controllers
β = 0.16 # By-pass factor of the cooling coil
m, mo = 3.1, 1. # kg/s, mass flow rate, supply and outdoor air
θo, φo = 32., 0.5 # °C, -, outdoor air temperature and relative humidity
θ5sp, φ5sp = 26., 0.5 # °C, -, indoor air set points
mi = 1.35 # kg/s, mass flow rate of infiltration air
UA = 675. # W/K, overall heat transfet coefficient
QsBL, QlBL = 34000., 4000. # W, sensible & latent auxiliar heat
parameters = m, mo, β, Kθ, Kw
inputs = θo, φo, θ5sp, φ5sp, mi, UA, QsBL, QlBL
```
# 5 Linear control problem: constant air volume (CAV) systems
## 5.1 Control of indoor air temperature & humidity in CAV systems with reheating
<img src="Figures/CAV_θ5_φ5.png" alt="CAV_θ5_φ5" style="width: 600px;"/>
> Figure 5. CAV system controling indoor temperature, $\theta_5$, and humidity, $\varphi_5$, by acting on the cooling coil [CC], $\dot{Q}_{tCC}$, and heating coil [HC], $\dot{Q}_{sHC}$, respectively.
> - The mass flow rate of supply air, $\dot{m}$, is given and constant (CAV system).
> - The supply air temperature, $\theta_4$, is not controlled.
```
cool0 = cc.MxCcRhTzBl(parameters, inputs)
Kw = 1e10
cool0.actual[4] = Kw
wd.interact(cool0.CAV_wd, θo=(26, 34), φo=(0.4, 1), θ5sp=(20, 28), φ5sp=(0.30, 1, 0.01),
mi=(0.1, 3, 0.1), UA=(500, 800, 10), QsBL=(0, 60_000, 500), QlBL=(0, 20_000, 500))
print()
```
> Figure 6. Psychrometric diagram for cooling and dehumidification of a single zone modelled by the block diagram given in Figure 5.
## 5.2 Control of indoor air temperature in CAV systems without reheating ($K_w = 0$)
<img src="Figures/CAV_θ5.png" alt="CAV_θ5" style="width: 600px;"/>
> Figure 7. CAV system controling the indoor temperature, $\theta_5$, by acting on the cooling coil [CC], $\dot{Q}_{tCC}$.
> - The heating coil is not operating, $\dot{Q}_{sHC}=0$; indoor humidity, $w_5$, is not controlled.
> - The mass flow rate of supply air, $\dot{m}$, is given and constant (CAV system).
> - The supply air temperature, $\theta_4 = \theta_3$, is not controlled.
*Note on widgets*:
- Acting on the set point of indoor humidity, $\varphi_{5sp}$ = `φ5sp`, has no effect.
```
cool1 = cc.MxCcRhTzBl(parameters, inputs)
wd.interact(cool1.CAV_wd, θo=(26, 34), φo=(0.4, 1), θ5sp=(20, 28), φI5sp=(0.4, 1, 0.01),
mi=(0.5, 3, 0.1), UA=(500, 8000, 10), QsBL=(0, 60_000, 500), QlBL=(0, 20_000, 500))
print()
```
> Figure 8. Psychrometric diagram with typical processes for cooling and dehumidification of a single zone modelled by the block diagram given in Figure 7.
# 6 Non-linear parameter optimization problem
## 6.1 By-pass control in constant air volume (CAV) systems without reheating
### 6.1.1 Control of indoor air temperature & humidity in CAV systems
<img src="Figures/CAV_β_θ5_φ5.png" alt="CAV_β_θ5_φ5" style="width: 600px;"/>
> Figure 9. CAV with mix-air bypass controlling the indoor temperature, $\theta_5$, by acting on the cooling coil [CC], $\dot{Q}_{tCC}$, and the indoor humidity, $\varphi_5$, by acting on the by-pass damper D, $\beta$.
> - The heating coil is not operating, $\dot{Q}_{sHC}=0$.
> - The mass flow rate of supply air, $\dot{m}$, is given and constant (CAV system).
> - The supply air temperature, $\theta_4 = \theta_3$, is not controlled.
*Notes on widgets*:
- `value`represents the controlled variable (i.e. φ5); `sp` is its set-point value.
- Acting on the set point of the indoor humidity, $\varphi_{5, sp}$ = `φ5sp`, has no effect (the heating coil does not operate).
```
cool4 = cc.MxCcRhTzBl(parameters, inputs)
wd.interact(cool4.VBP_wd, value='φ5', sp=(0.3, 0.9, 0.01), θo=(26, 34), φo=(0.4, 1),
θ5sp=(20, 28), φ5sp=(0.4, 0.8, 0.01),
mi=(0.5, 3, 0.1), UA=(500, 800, 10), Qsa=(0, 60_000, 500), Qla=(0, 20_000, 500))
print()
```
> Figure 10. Psychrometric diagram for cooling and dehumidification by a CAV system with mix-air bypass modelled by the block diagram given in Figure 9.
### 6.1.2 Control of indoor and supply air temperatures in CAV systems
Controlling the supply air temperature, $\theta_4$, by acting on the by-pass, $\beta$, has **no solution**.
Explanation:
In the sensible heat balace of the thermal zone [TZ],
$$\dot{m}c(\theta_4 - \theta_5) + \dot{Q}_{s, TZ} = 0$$
all valiables (i.e. $\dot{m}, \theta_4, \theta_5$ and $\dot{Q}_{s, TZ}$) are imposed. There is no way to control the supply air temperature, $\theta_4$, because the supply air mass flow rate, $\dot{m}$, is fixed in a CAV system. Given $\theta_5$ and $\dot{Q}_{sTZ}$:
- either $\dot{m}$ controls $\theta_4$,
- or $\theta_4$ controls $\dot{m}$.
```
# Executing the following code will generate an error: no solution for β
# cool = cc.MxCcRhTzBl(parameters, inputs)
# θ4sp = 11.77
# m = 3.162
# cool.actual[0] = m
# cool.VBP_wd('θS', θ4sp, θo, φo, θ5sp, φ5sp, mi, UA, QsBL, QlBL)
```
## 6.2 Mass-flow control in variable air volume (VAV) systems
### 6.2.1 Control of indoor air temperature & humidity in VAV systems without reheating
<img src="Figures/VAV_θ5_φ5.png" alt="VAV_θ5_φ5" style="width: 600px;"/>
> Figure 11. VAV system controling: the indoor temperature, $\theta_5$, by acting on the cooling coil [CC], $\dot{Q}_{tCC}$, and the indoor air humidity, $\varphi_5$, by acting on the supply air mass flow rate, $\dot{m}$.
> - The heating coil is not operating, $\dot{Q}_{sHC}=0$.
```
cool3 = cc.MxCcRhTzBl(parameters, inputs)
wd.interact(cool3.VAV_wd, value='φ5', sp=(0.4, 0.5, 0.05), θo=(26, 34), φo=(0.4, 1),
θ5sp=(20, 28), φ5sp=(0.4, 0.8),
mi=(0.7, 3, 0.1), UA=(500, 800, 10), QsBL=(0, 60_000, 500), QlBL=(0, 20_000, 500))
print()
```
> Figure 12. Psychrometric diagram for cooling and dehumidification by a VAV system controlling the thermal zone temperature and humidity modelled by the block diagram given in Figure 11.
### 6.2.2 Control of indoor and supply air temperatures in VAV systems without reheating
<img src="Figures/VAV_θ4_θ5.png" alt="VAV_θ4_θ5" style="width: 600px;"/>
> Figuer 13. VAV system controling: indoor temperature, $\theta_5$, by acting on the cooling coil [CC], $\dot{Q}_{t,CC}$, and the supply air temperature, $\theta_4$, by acting on the supply air mass flow rate, $\dot{m}$.
> - The heating coil is not operating, $\dot{Q}_{sHC}=0$.
```
cool6 = cc.MxCcRhTzBl(parameters, inputs)
Kw = 0
cool6.actual[4] = Kw
wd.interact(cool6.VAV_wd, value='θ4', sp=(14, 21), θo=(26, 34), φo=(0.4, 1),
θ5sp=(20, 28), φ5sp=(0.4, 0.8),
mi=(0.5, 3, 0.1), UA=(500, 800, 10), QsBL=(0, 60_000, 500), QlBL=(0, 20_000, 500))
print()
```
> Figure 14. Psychrometric diagram for cooling and dehumidification by a VAV system controlling the temperatures of the supply air and the thermal zone modelled by the block diagram given in Figure 13.
### 6.2.3 Control of indoor air temperature & humidity and of supply air temperature in VAV systems with reheating
<img src="Figures/VAV_θ4_θ5_φ5.png" alt="VAV_θ4_θ5_φ5" style="width: 600px;"/>
> Figure 15. VAV system controling: indoor temperature, $\theta_5$, by acting on the cooling coil [CC], $\dot{Q}_{tCC}$, indoor humidity, by acting on the heating coil [HC], $\dot{Q}_{s,HC}$, and supply air temperature, $\theta_4$, by acting on the supply air mass flow rate, $\dot{m}$.
```
cool6 = cc.MxCcRhTzBl(parameters, inputs)
Kw = 1e10
cool6.actual[4] = Kw
wd.interact(cool6.VAV_wd, value='θ4', sp=(14, 21), θo=(28, 36), φo=(0.4, 1),
θ5sp=(22, 26), φ5sp=(0.4, 0.8),
mi=(0.5, 3, 0.1), UA=(500, 800, 10), QsBL=(0, 60_000, 500), QlBL=(0, 20_000, 500))
print()
```
> Figure 16. Psychrometric diagram for a VAV system controlling the supply air temperature and the air temperature & humidity in the thermal zone modelled by the block diagram given in Figure 15.
|
github_jupyter
|
import ipywidgets as wd
import matplotlib.pyplot as plt
import cool as cc
# %matplotlib inline # uncomment for inline figure
# %matplotlib qt # uncomment for figure in separate window
plt.rcParams["figure.figsize"] = (10, 7.7)
font = {'size': 16}
plt.rc('font', **font)
Kθ, Kw = 1e10, 0 # Gain factors of the P-controllers
β = 0.16 # By-pass factor of the cooling coil
m, mo = 3.1, 1. # kg/s, mass flow rate, supply and outdoor air
θo, φo = 32., 0.5 # °C, -, outdoor air temperature and relative humidity
θ5sp, φ5sp = 26., 0.5 # °C, -, indoor air set points
mi = 1.35 # kg/s, mass flow rate of infiltration air
UA = 675. # W/K, overall heat transfet coefficient
QsBL, QlBL = 34000., 4000. # W, sensible & latent auxiliar heat
parameters = m, mo, β, Kθ, Kw
inputs = θo, φo, θ5sp, φ5sp, mi, UA, QsBL, QlBL
cool0 = cc.MxCcRhTzBl(parameters, inputs)
Kw = 1e10
cool0.actual[4] = Kw
wd.interact(cool0.CAV_wd, θo=(26, 34), φo=(0.4, 1), θ5sp=(20, 28), φ5sp=(0.30, 1, 0.01),
mi=(0.1, 3, 0.1), UA=(500, 800, 10), QsBL=(0, 60_000, 500), QlBL=(0, 20_000, 500))
print()
cool1 = cc.MxCcRhTzBl(parameters, inputs)
wd.interact(cool1.CAV_wd, θo=(26, 34), φo=(0.4, 1), θ5sp=(20, 28), φI5sp=(0.4, 1, 0.01),
mi=(0.5, 3, 0.1), UA=(500, 8000, 10), QsBL=(0, 60_000, 500), QlBL=(0, 20_000, 500))
print()
cool4 = cc.MxCcRhTzBl(parameters, inputs)
wd.interact(cool4.VBP_wd, value='φ5', sp=(0.3, 0.9, 0.01), θo=(26, 34), φo=(0.4, 1),
θ5sp=(20, 28), φ5sp=(0.4, 0.8, 0.01),
mi=(0.5, 3, 0.1), UA=(500, 800, 10), Qsa=(0, 60_000, 500), Qla=(0, 20_000, 500))
print()
# Executing the following code will generate an error: no solution for β
# cool = cc.MxCcRhTzBl(parameters, inputs)
# θ4sp = 11.77
# m = 3.162
# cool.actual[0] = m
# cool.VBP_wd('θS', θ4sp, θo, φo, θ5sp, φ5sp, mi, UA, QsBL, QlBL)
cool3 = cc.MxCcRhTzBl(parameters, inputs)
wd.interact(cool3.VAV_wd, value='φ5', sp=(0.4, 0.5, 0.05), θo=(26, 34), φo=(0.4, 1),
θ5sp=(20, 28), φ5sp=(0.4, 0.8),
mi=(0.7, 3, 0.1), UA=(500, 800, 10), QsBL=(0, 60_000, 500), QlBL=(0, 20_000, 500))
print()
cool6 = cc.MxCcRhTzBl(parameters, inputs)
Kw = 0
cool6.actual[4] = Kw
wd.interact(cool6.VAV_wd, value='θ4', sp=(14, 21), θo=(26, 34), φo=(0.4, 1),
θ5sp=(20, 28), φ5sp=(0.4, 0.8),
mi=(0.5, 3, 0.1), UA=(500, 800, 10), QsBL=(0, 60_000, 500), QlBL=(0, 20_000, 500))
print()
cool6 = cc.MxCcRhTzBl(parameters, inputs)
Kw = 1e10
cool6.actual[4] = Kw
wd.interact(cool6.VAV_wd, value='θ4', sp=(14, 21), θo=(28, 36), φo=(0.4, 1),
θ5sp=(22, 26), φ5sp=(0.4, 0.8),
mi=(0.5, 3, 0.1), UA=(500, 800, 10), QsBL=(0, 60_000, 500), QlBL=(0, 20_000, 500))
print()
| 0.380183 | 0.98881 |
# Data Analysis for Champions League Finals
> answering questions regarding champions league finals since 1955
- toc: true
- badges: true
- comments: true
- categories: [web scraping, data analysis, visualization]
```
import requests
from bs4 import BeautifulSoup
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import re
%matplotlib inline
```
## Retrieving Data
Data collected from [Wikipedia's Champions league finals' page](https://en.wikipedia.org/wiki/List_of_European_Cup_and_UEFA_Champions_League_finals)
```
html = requests.get("https://en.wikipedia.org/wiki/List_of_UEFA_Champions_League_finals")
soup = BeautifulSoup(html.content)
finals_table = soup.select("table.wikitable.plainrowheaders.sortable")[0]
finals_body = finals_table.tbody
# get all the tr with no classes (upcoming finals has class 'sortbottom')
matches = finals_body.find_all('tr', class_='')
# remove the first and second columns becuase they are columns names
matches.pop(0)
matches.pop(0)
# remove the 19th index from the matches array
# since it's just a score for a replayed match. will be edited in the dataframe
matches.pop(19)
def get_matches(matches):
df = pd.DataFrame(columns=['season', 'winner_nation', 'winner_team', 'score', 'runnerup_nation', 'runnerup_team', 'venue', 'attendence'])
for match in matches:
th = match.find_next('th')
tds = match.find_all('td')
season = th.a.text
winner_nationality = tds[0].span.a.text
winner_name = tds[1].a.text
# how the match ended
try:
if tds[2]['bgcolor'] == 'FBCEB1':
finished = 'extra time'
elif tds[2]['bgcolor'] == 'cedff2':
finished = 'penalties'
else:
finished = 'normal'
except:
finished = 'normal'
score = tds[2].a.text
runnerup_nationality = tds[3].span.a.text
runnerup_name = tds[4].a.text
venue = tds[5].text
attendance = tds[6].text
df = df.append({'season':season,
'winner_nation': winner_nationality,
'winner_team':winner_name,
'score': score,
'runnerup_nation': runnerup_nationality,
'runnerup_team': runnerup_name,
'venue': venue,
'attendence': attendance,
'finished': finished}, ignore_index=True)
return df
champions_finals = get_matches(matches)
champions_finals.head()
```
## Cleaning Data
### Remove unnecessary ends
in venue and attendance. [sol](https://stackoverflow.com/a/42324495/10438987)
```
# remove all the trailing white space (\n)
champions_finals[['venue', 'attendence']] = champions_finals[['venue', 'attendence']].apply(lambda x: x.str.strip(), )
champions_finals.tail(3)
pattern = r'\[.*?\]'
champions_finals['venue'] = champions_finals['venue'].apply(lambda x: re.sub(pattern, '', str(x)))
champions_finals['attendence'] = champions_finals['attendence'].apply(lambda x: re.sub(pattern, '', str(x)))
champions_finals.tail(3)
```
### split the score into two columns
split into winner_score and runnerup_score. [sol](https://www.geeksforgeeks.org/split-a-text-column-into-two-columns-in-pandas-dataframe/).
then merge them into the dataframe [sol](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.join.html)
```
scores = pd.DataFrame(champions_finals['score'].str.split('–').tolist(), columns=['winner_score', 'runnerup_score'])
champions_finals = champions_finals.join(scores).drop(columns=['score'], axis=1)
champions_finals.head(3)
```
### Convert columns into numerical
```
champions_finals.info()
```
attendence, winner_score, and runnerup_score need to be changed into numerical. But first we need to clean attendance column
```
champions_finals['attendence'] = champions_finals['attendence'].str.replace(',', '')
champions_finals.head(3)
champions_finals['attendence'] = champions_finals['attendence'].astype('int')
champions_finals['winner_score'] = champions_finals['winner_score'].astype('int')
champions_finals['runnerup_score'] = champions_finals['runnerup_score'].astype('int')
champions_finals.info()
```
## **Insights**
```
def barplotting(x, y, xticksrange=False, yticksrange=False, xticksstep=1, yticksstep=1, figsize=(8, 5), style='whitegrid'):
plt.figure(figsize=figsize)
sns.set_style(style)
if xticksrange:
plt.xticks(np.arange(0, xticksrange+1, xticksstep))
if yticksrange:
plt.yticks(np.arange(0, yticksrange+1, yticksstep))
sns.barplot(x=x, y=y, palette='Set1');
```
### Q1: Most winning teams
```
most_winning_teams = champions_finals['winner_team'].value_counts()
barplotting(x=most_winning_teams, y=most_winning_teams.index, xticksrange=max(most_winning_teams))
```
### Q2: Most Runner up teams
```
most_running_up = champions_finals['runnerup_team'].value_counts()
barplotting(x=most_running_up, y=most_running_up.index, xticksrange=max(most_running_up), figsize=(12,8))
```
### Q3: What is the most common scores?
```
finals_score = champions_finals.value_counts(subset=['winner_score', 'runnerup_score'])
finals_score.index = finals_score.index.map(lambda x: str(x[0]) + '-' + str(x[1]))
plt.pie(finals_score, labels=finals_score.index, autopct='%.1f%%', startangle=60, radius=2.5);
```
### Q4: How games ended
```
finished = champions_finals['finished'].value_counts()
barplotting(x=finished.index, y=finished, xticksrange=max(finished))
```
### Q5) Most playing nations
#### Most winning
```
most_wining_nations = champions_finals['winner_nation'].value_counts()
barplotting(x=most_wining_nations.index, y=most_wining_nations, yticksrange=max(most_wining_nations))
```
#### Most running up
```
most_runningup_nations = champions_finals['runnerup_nation'].value_counts()
barplotting(x=most_runningup_nations.index, y=most_runningup_nations, yticksrange=max(most_wining_nations))
```
#### Appearances
```
participation = champions_finals['winner_nation'].append(champions_finals['runnerup_nation'], ignore_index=True)
participation = participation.value_counts()
barplotting(x=participation.index, y=participation, yticksrange=max(participation), yticksstep=4)
```
### Q6: Most used Stadium in finals
```
most_used_stadiums = champions_finals['venue'].value_counts()
barplotting(x=most_used_stadiums, y=most_used_stadiums.index, yticksrange=max(most_used_stadiums), figsize=(12, 10))
```
### Q7: Average attendance in finals
line or dot at the mean of the graph. [sol](https://www.tutorialspoint.com/how-to-locate-the-median-in-a-seaborn-kde-plot)
```
attendance_mean = np.mean(champions_finals['attendence'])
plt.figure(figsize=(12,7))
sns.histplot(x='attendence', data=champions_finals)
plt.xticks(np.arange(0, 200_000, 10_000), rotation=90)
plt.xlim([0, 200000]);
```
### Q8: Most conceded goals and scored goals
```
total_goals = pd.DataFrame(columns=['team', 'scored', 'conceded'])
unique_teams = champions_finals['winner_team'].append(champions_finals['runnerup_team'], ignore_index=True).unique()
for team in unique_teams:
winning = champions_finals[champions_finals['winner_team'] == team][['winner_score', 'runnerup_score']].sum()
runningup = champions_finals[champions_finals['runnerup_team'] == team][['winner_score', 'runnerup_score']].sum()
total_scored = winning[0] + runningup[1]
total_conceded = winning[1] + runningup[0]
total_goals = total_goals.append({'team': team, 'scored': int(total_scored), 'conceded': int(total_conceded)}, ignore_index=True)
scoring_sorted = total_goals.sort_values(by='scored', ascending=False)
barplotting(x=scoring_sorted.team[:10], y=scoring_sorted.scored[:10], figsize=(10, 5))
plt.title('Most Scoring teams')
plt.xticks(rotation=60);
conceding_sorted = total_goals.sort_values(by='conceded', ascending=False)
barplotting(x=conceding_sorted.team[:10], y=conceding_sorted.conceded[:10], figsize=(10, 5))
plt.title('Most Conceding teams')
plt.xticks(rotation=60);
df = scoring_sorted[:10].melt(id_vars='team', var_name='kind', value_name='goals')
sns.catplot(x='team', y='goals', hue='kind', data=df, kind='bar', height=8, aspect=1.5)
plt.title('Scored and Conceded goals for Highest Scoring Teams')
plt.xlabel('Teams')
plt.ylabel('Goals')
plt.xticks(rotation=60)
plt.yticks(np.arange(0, 50, 2));
```
|
github_jupyter
|
import requests
from bs4 import BeautifulSoup
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import re
%matplotlib inline
html = requests.get("https://en.wikipedia.org/wiki/List_of_UEFA_Champions_League_finals")
soup = BeautifulSoup(html.content)
finals_table = soup.select("table.wikitable.plainrowheaders.sortable")[0]
finals_body = finals_table.tbody
# get all the tr with no classes (upcoming finals has class 'sortbottom')
matches = finals_body.find_all('tr', class_='')
# remove the first and second columns becuase they are columns names
matches.pop(0)
matches.pop(0)
# remove the 19th index from the matches array
# since it's just a score for a replayed match. will be edited in the dataframe
matches.pop(19)
def get_matches(matches):
df = pd.DataFrame(columns=['season', 'winner_nation', 'winner_team', 'score', 'runnerup_nation', 'runnerup_team', 'venue', 'attendence'])
for match in matches:
th = match.find_next('th')
tds = match.find_all('td')
season = th.a.text
winner_nationality = tds[0].span.a.text
winner_name = tds[1].a.text
# how the match ended
try:
if tds[2]['bgcolor'] == 'FBCEB1':
finished = 'extra time'
elif tds[2]['bgcolor'] == 'cedff2':
finished = 'penalties'
else:
finished = 'normal'
except:
finished = 'normal'
score = tds[2].a.text
runnerup_nationality = tds[3].span.a.text
runnerup_name = tds[4].a.text
venue = tds[5].text
attendance = tds[6].text
df = df.append({'season':season,
'winner_nation': winner_nationality,
'winner_team':winner_name,
'score': score,
'runnerup_nation': runnerup_nationality,
'runnerup_team': runnerup_name,
'venue': venue,
'attendence': attendance,
'finished': finished}, ignore_index=True)
return df
champions_finals = get_matches(matches)
champions_finals.head()
# remove all the trailing white space (\n)
champions_finals[['venue', 'attendence']] = champions_finals[['venue', 'attendence']].apply(lambda x: x.str.strip(), )
champions_finals.tail(3)
pattern = r'\[.*?\]'
champions_finals['venue'] = champions_finals['venue'].apply(lambda x: re.sub(pattern, '', str(x)))
champions_finals['attendence'] = champions_finals['attendence'].apply(lambda x: re.sub(pattern, '', str(x)))
champions_finals.tail(3)
scores = pd.DataFrame(champions_finals['score'].str.split('–').tolist(), columns=['winner_score', 'runnerup_score'])
champions_finals = champions_finals.join(scores).drop(columns=['score'], axis=1)
champions_finals.head(3)
champions_finals.info()
champions_finals['attendence'] = champions_finals['attendence'].str.replace(',', '')
champions_finals.head(3)
champions_finals['attendence'] = champions_finals['attendence'].astype('int')
champions_finals['winner_score'] = champions_finals['winner_score'].astype('int')
champions_finals['runnerup_score'] = champions_finals['runnerup_score'].astype('int')
champions_finals.info()
def barplotting(x, y, xticksrange=False, yticksrange=False, xticksstep=1, yticksstep=1, figsize=(8, 5), style='whitegrid'):
plt.figure(figsize=figsize)
sns.set_style(style)
if xticksrange:
plt.xticks(np.arange(0, xticksrange+1, xticksstep))
if yticksrange:
plt.yticks(np.arange(0, yticksrange+1, yticksstep))
sns.barplot(x=x, y=y, palette='Set1');
most_winning_teams = champions_finals['winner_team'].value_counts()
barplotting(x=most_winning_teams, y=most_winning_teams.index, xticksrange=max(most_winning_teams))
most_running_up = champions_finals['runnerup_team'].value_counts()
barplotting(x=most_running_up, y=most_running_up.index, xticksrange=max(most_running_up), figsize=(12,8))
finals_score = champions_finals.value_counts(subset=['winner_score', 'runnerup_score'])
finals_score.index = finals_score.index.map(lambda x: str(x[0]) + '-' + str(x[1]))
plt.pie(finals_score, labels=finals_score.index, autopct='%.1f%%', startangle=60, radius=2.5);
finished = champions_finals['finished'].value_counts()
barplotting(x=finished.index, y=finished, xticksrange=max(finished))
most_wining_nations = champions_finals['winner_nation'].value_counts()
barplotting(x=most_wining_nations.index, y=most_wining_nations, yticksrange=max(most_wining_nations))
most_runningup_nations = champions_finals['runnerup_nation'].value_counts()
barplotting(x=most_runningup_nations.index, y=most_runningup_nations, yticksrange=max(most_wining_nations))
participation = champions_finals['winner_nation'].append(champions_finals['runnerup_nation'], ignore_index=True)
participation = participation.value_counts()
barplotting(x=participation.index, y=participation, yticksrange=max(participation), yticksstep=4)
most_used_stadiums = champions_finals['venue'].value_counts()
barplotting(x=most_used_stadiums, y=most_used_stadiums.index, yticksrange=max(most_used_stadiums), figsize=(12, 10))
attendance_mean = np.mean(champions_finals['attendence'])
plt.figure(figsize=(12,7))
sns.histplot(x='attendence', data=champions_finals)
plt.xticks(np.arange(0, 200_000, 10_000), rotation=90)
plt.xlim([0, 200000]);
total_goals = pd.DataFrame(columns=['team', 'scored', 'conceded'])
unique_teams = champions_finals['winner_team'].append(champions_finals['runnerup_team'], ignore_index=True).unique()
for team in unique_teams:
winning = champions_finals[champions_finals['winner_team'] == team][['winner_score', 'runnerup_score']].sum()
runningup = champions_finals[champions_finals['runnerup_team'] == team][['winner_score', 'runnerup_score']].sum()
total_scored = winning[0] + runningup[1]
total_conceded = winning[1] + runningup[0]
total_goals = total_goals.append({'team': team, 'scored': int(total_scored), 'conceded': int(total_conceded)}, ignore_index=True)
scoring_sorted = total_goals.sort_values(by='scored', ascending=False)
barplotting(x=scoring_sorted.team[:10], y=scoring_sorted.scored[:10], figsize=(10, 5))
plt.title('Most Scoring teams')
plt.xticks(rotation=60);
conceding_sorted = total_goals.sort_values(by='conceded', ascending=False)
barplotting(x=conceding_sorted.team[:10], y=conceding_sorted.conceded[:10], figsize=(10, 5))
plt.title('Most Conceding teams')
plt.xticks(rotation=60);
df = scoring_sorted[:10].melt(id_vars='team', var_name='kind', value_name='goals')
sns.catplot(x='team', y='goals', hue='kind', data=df, kind='bar', height=8, aspect=1.5)
plt.title('Scored and Conceded goals for Highest Scoring Teams')
plt.xlabel('Teams')
plt.ylabel('Goals')
plt.xticks(rotation=60)
plt.yticks(np.arange(0, 50, 2));
| 0.306423 | 0.858896 |
# Sin regularizar
```
library('fastDummies')
set.seed(103783)
# Cargo el csv
mat <- read.csv("student-por.csv")
# Train y Test
sample <- sample.int(n = nrow(mat), size = floor(.75*nrow(mat)), replace = F)
train <- mat[sample, ]
test <- mat[-sample, ]
y_train <- c(train$G3)
x_train <- subset(train, select = -c(G3))
y_test <- c(test$G3)
x_test <- subset(test, select = -c(G3))
# Preproceso
preprocesar <- function(mat) {
mat_prepros <- dummy_cols(mat,remove_first_dummy = TRUE)
mat_prepros <- mat_prepros[-c(1,2,4,5,6,9,10,11,12,16,17,18,19,20,21,22,23)]
as.data.frame(scale(mat_prepros))
}
x_train <- preprocesar(x_train)
model <- lm(formula=y_train~.,data=x_train)
summary(model)
x_test <- preprocesar(x_test)
pred <- predict(model, x_test)
modelEval <- cbind(y_test, pred)
colnames(modelEval) <- c('Actual', 'Predicted')
modelEval <- as.data.frame(modelEval)
mse <- mean((modelEval$Actual - modelEval$Predicted)**2)
rmse <- sqrt(mse)
print(cat("Mean Squared Error:",mse))
print(cat("Mean Absolute Error:",rmse))
```
# Lasso
```
library("glmnet")
# Cargo el csv
mat <- read.csv("student-por.csv")
# Train y Test
sample <- sample.int(n = nrow(mat), size = floor(.75*nrow(mat)), replace = F)
train <- mat[sample, ]
test <- mat[-sample, ]
y_train <- c(train$G3)
x_train <- subset(train, select = -c(G3))
y_test <- c(test$G3)
x_test <- subset(test, select = -c(G3))
mat_prepros <- dummy_cols(x_train,remove_first_dummy = TRUE)
mat_prepros <- mat_prepros[-c(1,2,4,5,6,9,10,11,12,16,17,18,19,20,21,22,23)]
x_train <- scale(mat_prepros)
mat_prepros <- dummy_cols(x_test,remove_first_dummy = TRUE)
mat_prepros <- mat_prepros[-c(1,2,4,5,6,9,10,11,12,16,17,18,19,20,21,22,23)]
x_test <- scale(mat_prepros)
lambdas <- 10^seq(2, -3, by = -.1)
# Setting alpha = 1 implements lasso regression
lasso_reg <- cv.glmnet(x_train, y_train, alpha = 1, lambda = lambdas, standardize = TRUE, nfolds = 5)
# Best
lambda_best <- lasso_reg$lambda.min
lambda_best
eval_results <- function(true, predicted, df) {
SSE <- sum((predicted - true)^2)
SST <- sum((true - mean(true))^2)
R_square <- 1 - SSE / SST
RMSE = sqrt(SSE/nrow(df))
# Model performance metrics
data.frame(
RMSE = RMSE,
Rsquare = R_square
)
}
# Prediction and evaluation on train data
predictions_train <- predict(lasso_reg, s = lambda_best, newx = x_train)
eval_results(y_train, predictions_train, x_train)
predictions_test <- predict(lasso_reg, s = lambda_best, newx = x_test)
eval_results(y_test, predictions_test, x_test)
coef(lasso_reg, s = "lambda.min")
```
# Ridge
```
library("glmnet")
# Cargo el csv
mat <- read.csv("student-por.csv")
# Train y Test
sample <- sample.int(n = nrow(mat), size = floor(.75*nrow(mat)), replace = F)
train <- mat[sample, ]
test <- mat[-sample, ]
y_train <- c(train$G3)
x_train <- subset(train, select = -c(G3))
y_test <- c(test$G3)
x_test <- subset(test, select = -c(G3))
mat_prepros <- dummy_cols(x_train,remove_first_dummy = TRUE)
mat_prepros <- mat_prepros[-c(1,2,4,5,6,9,10,11,12,16,17,18,19,20,21,22,23)]
x_train <- scale(mat_prepros)
mat_prepros <- dummy_cols(x_test,remove_first_dummy = TRUE)
mat_prepros <- mat_prepros[-c(1,2,4,5,6,9,10,11,12,16,17,18,19,20,21,22,23)]
x_test <- scale(mat_prepros)
lambdas <- 10^seq(2, -3, by = -.1)
ridge_reg <- cv.glmnet(x_train, y_train, alpha = 0, lambda = lambdas)
optimal_lambda <- ridge_reg$lambda.min
optimal_lambda
# Prediction and evaluation on train data
predictions_train <- predict(ridge_reg, s = optimal_lambda, newx = x_train)
eval_results(y_train, predictions_train, x_train)
# Prediction and evaluation on test data
predictions_test <- predict(ridge_reg, s = optimal_lambda, newx = x_test)
eval_results(y_test, predictions_test, x_test)
coef(ridge_reg, s = "lambda.min")
```
|
github_jupyter
|
library('fastDummies')
set.seed(103783)
# Cargo el csv
mat <- read.csv("student-por.csv")
# Train y Test
sample <- sample.int(n = nrow(mat), size = floor(.75*nrow(mat)), replace = F)
train <- mat[sample, ]
test <- mat[-sample, ]
y_train <- c(train$G3)
x_train <- subset(train, select = -c(G3))
y_test <- c(test$G3)
x_test <- subset(test, select = -c(G3))
# Preproceso
preprocesar <- function(mat) {
mat_prepros <- dummy_cols(mat,remove_first_dummy = TRUE)
mat_prepros <- mat_prepros[-c(1,2,4,5,6,9,10,11,12,16,17,18,19,20,21,22,23)]
as.data.frame(scale(mat_prepros))
}
x_train <- preprocesar(x_train)
model <- lm(formula=y_train~.,data=x_train)
summary(model)
x_test <- preprocesar(x_test)
pred <- predict(model, x_test)
modelEval <- cbind(y_test, pred)
colnames(modelEval) <- c('Actual', 'Predicted')
modelEval <- as.data.frame(modelEval)
mse <- mean((modelEval$Actual - modelEval$Predicted)**2)
rmse <- sqrt(mse)
print(cat("Mean Squared Error:",mse))
print(cat("Mean Absolute Error:",rmse))
library("glmnet")
# Cargo el csv
mat <- read.csv("student-por.csv")
# Train y Test
sample <- sample.int(n = nrow(mat), size = floor(.75*nrow(mat)), replace = F)
train <- mat[sample, ]
test <- mat[-sample, ]
y_train <- c(train$G3)
x_train <- subset(train, select = -c(G3))
y_test <- c(test$G3)
x_test <- subset(test, select = -c(G3))
mat_prepros <- dummy_cols(x_train,remove_first_dummy = TRUE)
mat_prepros <- mat_prepros[-c(1,2,4,5,6,9,10,11,12,16,17,18,19,20,21,22,23)]
x_train <- scale(mat_prepros)
mat_prepros <- dummy_cols(x_test,remove_first_dummy = TRUE)
mat_prepros <- mat_prepros[-c(1,2,4,5,6,9,10,11,12,16,17,18,19,20,21,22,23)]
x_test <- scale(mat_prepros)
lambdas <- 10^seq(2, -3, by = -.1)
# Setting alpha = 1 implements lasso regression
lasso_reg <- cv.glmnet(x_train, y_train, alpha = 1, lambda = lambdas, standardize = TRUE, nfolds = 5)
# Best
lambda_best <- lasso_reg$lambda.min
lambda_best
eval_results <- function(true, predicted, df) {
SSE <- sum((predicted - true)^2)
SST <- sum((true - mean(true))^2)
R_square <- 1 - SSE / SST
RMSE = sqrt(SSE/nrow(df))
# Model performance metrics
data.frame(
RMSE = RMSE,
Rsquare = R_square
)
}
# Prediction and evaluation on train data
predictions_train <- predict(lasso_reg, s = lambda_best, newx = x_train)
eval_results(y_train, predictions_train, x_train)
predictions_test <- predict(lasso_reg, s = lambda_best, newx = x_test)
eval_results(y_test, predictions_test, x_test)
coef(lasso_reg, s = "lambda.min")
library("glmnet")
# Cargo el csv
mat <- read.csv("student-por.csv")
# Train y Test
sample <- sample.int(n = nrow(mat), size = floor(.75*nrow(mat)), replace = F)
train <- mat[sample, ]
test <- mat[-sample, ]
y_train <- c(train$G3)
x_train <- subset(train, select = -c(G3))
y_test <- c(test$G3)
x_test <- subset(test, select = -c(G3))
mat_prepros <- dummy_cols(x_train,remove_first_dummy = TRUE)
mat_prepros <- mat_prepros[-c(1,2,4,5,6,9,10,11,12,16,17,18,19,20,21,22,23)]
x_train <- scale(mat_prepros)
mat_prepros <- dummy_cols(x_test,remove_first_dummy = TRUE)
mat_prepros <- mat_prepros[-c(1,2,4,5,6,9,10,11,12,16,17,18,19,20,21,22,23)]
x_test <- scale(mat_prepros)
lambdas <- 10^seq(2, -3, by = -.1)
ridge_reg <- cv.glmnet(x_train, y_train, alpha = 0, lambda = lambdas)
optimal_lambda <- ridge_reg$lambda.min
optimal_lambda
# Prediction and evaluation on train data
predictions_train <- predict(ridge_reg, s = optimal_lambda, newx = x_train)
eval_results(y_train, predictions_train, x_train)
# Prediction and evaluation on test data
predictions_test <- predict(ridge_reg, s = optimal_lambda, newx = x_test)
eval_results(y_test, predictions_test, x_test)
coef(ridge_reg, s = "lambda.min")
| 0.477067 | 0.815526 |
<a href="https://colab.research.google.com/github/ayulockin/LossLandscape/blob/master/ResNet20v1_CIFAR10_Different_Inits.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Set up and imports
```
# TensorFlow Imports
import tensorflow as tf
print(tf.__version__)
# Which GPU?
!nvidia-smi
%%capture
!pip install wandb
import wandb
from wandb.keras import WandbCallback
wandb.login()
# Other imports
from tensorflow.keras.layers import *
from tensorflow.keras.models import *
import matplotlib.pyplot as plt
import tensorflow as tf
import numpy as np
import time
# Random seed fixation
tf.random.set_seed(666)
np.random.seed(666)
```
## Get the model from [keras-idiomatic-programmer](https://github.com/GoogleCloudPlatform/keras-idiomatic-programmer)
```
!wget https://raw.githubusercontent.com/GoogleCloudPlatform/keras-idiomatic-programmer/master/zoo/resnet/resnet_cifar10.py
import resnet_cifar10
```
## Utils
```
def get_training_model():
# ResNet20
n = 2
depth = n * 9 + 2
n_blocks = ((depth - 2) // 9) - 1
# The input tensor
inputs = Input(shape=(32, 32, 3))
# The Stem Convolution Group
x = resnet_cifar10.stem(inputs)
# The learner
x = resnet_cifar10.learner(x, n_blocks)
# The Classifier for 10 classes
outputs = resnet_cifar10.classifier(x, 10)
# Instantiate the Model
model = Model(inputs, outputs)
return model
```
## Construct data loaders
```
# Load the training set of CIFAR10
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
BATCH_SIZE = 128
def normalize(image, label):
return tf.image.convert_image_dtype(image, tf.float32), label
# Adding data augmentation
def augment(image,label):
image = tf.image.resize_with_crop_or_pad(image, 40, 40) # Add 8 pixels of padding
image = tf.image.random_crop(image, size=[32, 32, 3]) # Random crop back to 32x32
image = tf.image.random_brightness(image, max_delta=0.5) # Random brightness
image = tf.clip_by_value(image, 0., 1.)
return image, label
train_ds = tf.data.Dataset.from_tensor_slices((x_train, y_train))
train_ds = (
train_ds
.shuffle(1024)
.map(normalize, num_parallel_calls=tf.data.experimental.AUTOTUNE)
.map(augment, num_parallel_calls=tf.data.experimental.AUTOTUNE)
.batch(BATCH_SIZE)
.prefetch(tf.data.experimental.AUTOTUNE)
)
test_ds = tf.data.Dataset.from_tensor_slices((x_test, y_test))
test_ds = (
test_ds
.map(normalize, num_parallel_calls=tf.data.experimental.AUTOTUNE)
.batch(BATCH_SIZE)
.prefetch(tf.data.experimental.AUTOTUNE)
)
```
## Model sanity checks
```
model = get_training_model()
model.summary()
```
## Callbacks
```
# Custom LR schedule as mentioned in the LossLandscape paper
LR_SCHEDULE = [
# (epoch to start, learning rate) tuples
(0, 1.6*1e-3),
(9, (1.6*1e-3)/2),
(19, (1.6*1e-3)/4),
(29, (1.6*1e-3)/8),
]
def lr_schedule(epoch):
if (epoch >= 0) & (epoch < 9):
return LR_SCHEDULE[0][1]
elif (epoch >= 9) & (epoch < 19):
return LR_SCHEDULE[1][1]
elif (epoch >= 19) & (epoch < 29):
return LR_SCHEDULE[2][1]
else:
return LR_SCHEDULE[3][1]
lr_callback = tf.keras.callbacks.LearningRateScheduler(lambda epoch: lr_schedule(epoch), verbose=True)
rng = rng = [i for i in range(40)]
plt.plot([lr_schedule(x) for x in rng])
plt.show()
```
A custom callback to log confusion matrix batchwise (referred from this [tutorial](https://www.tensorflow.org/tensorboard/image_summaries)).
```
from sklearn.metrics import confusion_matrix
import itertools
import io
CLASS_NAMES = ["airplane", "automobile", "bird", "cat", "deer", "dog", "frog", "horse", "ship", "truck"]
def plot_confusion_matrix(cm, class_names):
figure = plt.figure(figsize=(8, 8))
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
plt.title("Confusion matrix")
plt.colorbar()
tick_marks = np.arange(len(class_names))
plt.xticks(tick_marks, class_names, rotation=45)
plt.yticks(tick_marks, class_names)
# Normalize the confusion matrix.
cm = np.around(cm.astype('float') / cm.sum(axis=1)[:, np.newaxis], decimals=2)
# Use white text if squares are dark; otherwise black.
threshold = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
color = "white" if cm[i, j] > threshold else "black"
plt.text(j, i, cm[i, j], horizontalalignment="center", color=color)
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
return figure
def plot_to_image(figure):
"""Converts the matplotlib plot specified by 'figure' to a PNG image and
returns it. The supplied figure is closed and inaccessible after this call."""
# Save the plot to a PNG in memory.
buf = io.BytesIO()
plt.savefig(buf, format='png')
# Closing the figure prevents it from being displayed directly inside
# the notebook.
plt.close(figure)
buf.seek(0)
# Convert PNG buffer to TF image
image = tf.image.decode_png(buf.getvalue(), channels=3)
# Convert back to NumPy
image = image.numpy()
return image
def log_confusion_matrix(epoch, logs):
# Use the model to predict the values from the validation dataset
test_pred_raw = model.predict(x_test)
test_pred = np.argmax(test_pred_raw, axis=1)
# Calculate the confusion matrix
cm = confusion_matrix(y_test, test_pred)
# Log the confusion matrix as an image to wandb
figure = plot_confusion_matrix(cm, class_names=CLASS_NAMES)
cm_image = plot_to_image(figure)
wandb.log({'confusion_matrix': wandb.Image(cm_image)})
cm_callback = tf.keras.callbacks.LambdaCallback(on_epoch_end=log_confusion_matrix, verbose=True)
```
## Model training
```
for i in range(10):
id = 'resnet20v1-aug-diff-inits-corrected' + str(i)
wandb.init(project='loss-landscape', id=id)
# Train model
model = get_training_model()
model.compile(loss="sparse_categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
start = time.time()
model.fit(train_ds,
validation_data=test_ds,
epochs=40,
callbacks=[lr_callback, WandbCallback(), cm_callback])
end = time.time()
print("Network takes {:.3f} seconds to train".format(end - start))
wandb.log({'training_time': end - start})
wandb.log({'nb_model_params': model.count_params()})
model_name = 'resnet20v1-aug-diff-inits-' + str(i) + '.h5'
model.save(model_name)
```
Outputs have been Omitted for brevity.
## Put the model weights in a GCS bucket
```
from google.colab import auth as google_auth
google_auth.authenticate_user()
!gsutil -m cp -r resnet20v1-aug-diff-inits-*.h5 gs://losslandscape/ResNet20v1_CIFAR10_Aug_Diff_Inits/
```
|
github_jupyter
|
# TensorFlow Imports
import tensorflow as tf
print(tf.__version__)
# Which GPU?
!nvidia-smi
%%capture
!pip install wandb
import wandb
from wandb.keras import WandbCallback
wandb.login()
# Other imports
from tensorflow.keras.layers import *
from tensorflow.keras.models import *
import matplotlib.pyplot as plt
import tensorflow as tf
import numpy as np
import time
# Random seed fixation
tf.random.set_seed(666)
np.random.seed(666)
!wget https://raw.githubusercontent.com/GoogleCloudPlatform/keras-idiomatic-programmer/master/zoo/resnet/resnet_cifar10.py
import resnet_cifar10
def get_training_model():
# ResNet20
n = 2
depth = n * 9 + 2
n_blocks = ((depth - 2) // 9) - 1
# The input tensor
inputs = Input(shape=(32, 32, 3))
# The Stem Convolution Group
x = resnet_cifar10.stem(inputs)
# The learner
x = resnet_cifar10.learner(x, n_blocks)
# The Classifier for 10 classes
outputs = resnet_cifar10.classifier(x, 10)
# Instantiate the Model
model = Model(inputs, outputs)
return model
# Load the training set of CIFAR10
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
BATCH_SIZE = 128
def normalize(image, label):
return tf.image.convert_image_dtype(image, tf.float32), label
# Adding data augmentation
def augment(image,label):
image = tf.image.resize_with_crop_or_pad(image, 40, 40) # Add 8 pixels of padding
image = tf.image.random_crop(image, size=[32, 32, 3]) # Random crop back to 32x32
image = tf.image.random_brightness(image, max_delta=0.5) # Random brightness
image = tf.clip_by_value(image, 0., 1.)
return image, label
train_ds = tf.data.Dataset.from_tensor_slices((x_train, y_train))
train_ds = (
train_ds
.shuffle(1024)
.map(normalize, num_parallel_calls=tf.data.experimental.AUTOTUNE)
.map(augment, num_parallel_calls=tf.data.experimental.AUTOTUNE)
.batch(BATCH_SIZE)
.prefetch(tf.data.experimental.AUTOTUNE)
)
test_ds = tf.data.Dataset.from_tensor_slices((x_test, y_test))
test_ds = (
test_ds
.map(normalize, num_parallel_calls=tf.data.experimental.AUTOTUNE)
.batch(BATCH_SIZE)
.prefetch(tf.data.experimental.AUTOTUNE)
)
model = get_training_model()
model.summary()
# Custom LR schedule as mentioned in the LossLandscape paper
LR_SCHEDULE = [
# (epoch to start, learning rate) tuples
(0, 1.6*1e-3),
(9, (1.6*1e-3)/2),
(19, (1.6*1e-3)/4),
(29, (1.6*1e-3)/8),
]
def lr_schedule(epoch):
if (epoch >= 0) & (epoch < 9):
return LR_SCHEDULE[0][1]
elif (epoch >= 9) & (epoch < 19):
return LR_SCHEDULE[1][1]
elif (epoch >= 19) & (epoch < 29):
return LR_SCHEDULE[2][1]
else:
return LR_SCHEDULE[3][1]
lr_callback = tf.keras.callbacks.LearningRateScheduler(lambda epoch: lr_schedule(epoch), verbose=True)
rng = rng = [i for i in range(40)]
plt.plot([lr_schedule(x) for x in rng])
plt.show()
from sklearn.metrics import confusion_matrix
import itertools
import io
CLASS_NAMES = ["airplane", "automobile", "bird", "cat", "deer", "dog", "frog", "horse", "ship", "truck"]
def plot_confusion_matrix(cm, class_names):
figure = plt.figure(figsize=(8, 8))
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
plt.title("Confusion matrix")
plt.colorbar()
tick_marks = np.arange(len(class_names))
plt.xticks(tick_marks, class_names, rotation=45)
plt.yticks(tick_marks, class_names)
# Normalize the confusion matrix.
cm = np.around(cm.astype('float') / cm.sum(axis=1)[:, np.newaxis], decimals=2)
# Use white text if squares are dark; otherwise black.
threshold = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
color = "white" if cm[i, j] > threshold else "black"
plt.text(j, i, cm[i, j], horizontalalignment="center", color=color)
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
return figure
def plot_to_image(figure):
"""Converts the matplotlib plot specified by 'figure' to a PNG image and
returns it. The supplied figure is closed and inaccessible after this call."""
# Save the plot to a PNG in memory.
buf = io.BytesIO()
plt.savefig(buf, format='png')
# Closing the figure prevents it from being displayed directly inside
# the notebook.
plt.close(figure)
buf.seek(0)
# Convert PNG buffer to TF image
image = tf.image.decode_png(buf.getvalue(), channels=3)
# Convert back to NumPy
image = image.numpy()
return image
def log_confusion_matrix(epoch, logs):
# Use the model to predict the values from the validation dataset
test_pred_raw = model.predict(x_test)
test_pred = np.argmax(test_pred_raw, axis=1)
# Calculate the confusion matrix
cm = confusion_matrix(y_test, test_pred)
# Log the confusion matrix as an image to wandb
figure = plot_confusion_matrix(cm, class_names=CLASS_NAMES)
cm_image = plot_to_image(figure)
wandb.log({'confusion_matrix': wandb.Image(cm_image)})
cm_callback = tf.keras.callbacks.LambdaCallback(on_epoch_end=log_confusion_matrix, verbose=True)
for i in range(10):
id = 'resnet20v1-aug-diff-inits-corrected' + str(i)
wandb.init(project='loss-landscape', id=id)
# Train model
model = get_training_model()
model.compile(loss="sparse_categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
start = time.time()
model.fit(train_ds,
validation_data=test_ds,
epochs=40,
callbacks=[lr_callback, WandbCallback(), cm_callback])
end = time.time()
print("Network takes {:.3f} seconds to train".format(end - start))
wandb.log({'training_time': end - start})
wandb.log({'nb_model_params': model.count_params()})
model_name = 'resnet20v1-aug-diff-inits-' + str(i) + '.h5'
model.save(model_name)
from google.colab import auth as google_auth
google_auth.authenticate_user()
!gsutil -m cp -r resnet20v1-aug-diff-inits-*.h5 gs://losslandscape/ResNet20v1_CIFAR10_Aug_Diff_Inits/
| 0.901686 | 0.938857 |
# Tutorial: Hand gesture classification with EMG data using Riemannian metrics
In this notebook we are using EMG time series collected by 8 electrodes placed on the arm skin. We are going to show how to
- Process these kind of signal into covariance matrices that we can manipulate with geomstats tools.
- How to apply ML algorithms on this data to classify four different hand gestures present in the data (Rock, Paper, Scissors, Ok).
- How do the different methods (using Riemanian metrics, projecting on tangent space, Euclidean metric) compare to each other.
<img src="figures/paper_rock_scissors.png" />
## Context
The data are acquired from somOS-interface: an sEMG armband that allows you to interact via bluetooth with an Android smartphone (you can contact Marius Guerard ([email protected]) or Renaud Renault ([email protected]) for more info on how to make this kind of armband yourself).
An example of application is to record static signs that are linked with different actions (moving a cursor and clicking, sign recognition for command based personal assistants, ...). In these experiments, we want to evaluate the difference in performance (measured as the accuracy of sign recognition) between three different real life situations where we change the conditions of training (when user record signs or "calibrate" the device) and testing (when the app guess what sign the user is doing):
- 1. What is the accuracy when doing sign recognition right after training?
- 2. What is the accuracy when calibrating, removing and replacing the armband at the same position and then testing?
- 3. What is the accuracy when calibrating, removing the armband and giving it to someone else that is testing it without calibration?
To simulate these situations, we record data from two different users (rr and mg) and in two different sessions (s1 or s2). The user put the bracelet before every session and remove it after every session.
Quick description of the data:
- Each row corresponds to one acquisition, there is an acquisition every ~4 ms for 8 electrodes which correspond to a 250Hz acquisition rate.
- The time column is in ms.
- The columns c0 to c7 correspond to the electrical value recorded at each of the 8 electrodes (arbitrary unit).
- The label correspond to the sign being recorded by the user at this time point ('rest', 'rock', 'paper', 'scissors', or 'ok). 'rest' correspond to a rested arm.
- the exp identify the user (rr and mg) and the session (s1 or s2)
Note: Another interesting use case, not explored in this notebook, would be to test what is the accruacy when calibrating, removing the armband and giving it to someone else that is calibrating it on its own arm before testing it. The idea being that transfer learning might help getting better results (or faster calibration) than calibrating on one user.
## Setup
Before starting this tutorial, we set the working directory to be the root of the geomstats repository. In order to have the code working on your machine, you need to change this path to the path of your geomstats repository.
```
import os
import subprocess
import matplotlib
matplotlib.interactive(True)
import matplotlib.pyplot as plt
geomstats_gitroot_path = subprocess.check_output(
['git', 'rev-parse', '--show-toplevel'],
universal_newlines=True)
os.chdir(geomstats_gitroot_path[:-1])
print('Working directory: ', os.getcwd())
import geomstats.backend as gs
gs.random.seed(2021)
```
## Parameters
```
N_ELECTRODES = 8
N_SIGNS = 4
```
## The Data
```
import geomstats.datasets.utils as data_utils
data = data_utils.load_emg()
data.head()
fig, ax = plt.subplots(N_SIGNS, figsize=(20, 20))
label_list = ['rock', 'scissors', 'paper', 'ok']
for i, label_i in enumerate(label_list):
sign_df = data[data.label==label_i].iloc[:100]
for electrode in range(N_ELECTRODES):
ax[i].plot(sign_df.iloc[:, 1 + electrode])
ax[i].title.set_text(label_i)
```
We are removing the sign 'rest' for the rest of the analysis.
```
data = data[data.label != 'rest']
```
### Preprocessing into covariance matrices
```
import numpy as np
import pandas as pd
### Parameters.
N_STEPS = 100
LABEL_MAP = {'rock': 0, 'scissors': 1, 'paper': 2, 'ok': 3}
MARGIN = 1000
```
Unpacking data into arrays for batching
```
data_dict = {
'time': gs.array(data.time),
'raw_data': gs.array(data[['c{}'.format(i) for i in range(N_ELECTRODES)]]),
'label': gs.array(data.label),
'exp': gs.array(data.exp)}
from geomstats.datasets.prepare_emg_data import TimeSeriesCovariance
cov_data = TimeSeriesCovariance(data_dict, N_STEPS, N_ELECTRODES, LABEL_MAP, MARGIN)
cov_data.transform()
```
We check that these matrics belong to the space of SPD matrices.
```
import geomstats.geometry.spd_matrices as spd
manifold = spd.SPDMatrices(N_ELECTRODES)
gs.all(manifold.belongs(cov_data.covs))
```
#### Covariances plot of the euclidean average
```
fig, ax = plt.subplots(2, 2, figsize=(20, 10))
for label_i, i in cov_data.label_map.items():
label_ids = np.where(cov_data.labels==i)[0]
sign_cov_mat = cov_data.covs[label_ids]
mean_cov = np.mean(sign_cov_mat, axis=0)
ax[i // 2, i % 2].matshow(mean_cov)
ax[i // 2, i % 2].title.set_text(label_i)
```
Looking at the euclidean average of the spd matrices for each sign, does not show a striking difference between 3 of our signs (scissors, paper, and ok). Minimum Distance to Mean (MDM) algorithm will probably performed poorly if using euclidean mean here.
#### Covariances plot of the Frechet Mean of the affine invariant metric
```
from geomstats.learning.frechet_mean import FrechetMean
from geomstats.geometry.spd_matrices import SPDMetricAffine
metric_affine = SPDMetricAffine(N_ELECTRODES)
mean_affine = FrechetMean(metric=metric_affine, point_type='matrix')
fig, ax = plt.subplots(2, 2, figsize=(20, 10))
for label_i, i in cov_data.label_map.items():
label_ids = np.where(cov_data.labels==i)[0]
sign_cov_mat = cov_data.covs[label_ids]
mean_affine.fit(X=sign_cov_mat)
mean_cov = mean_affine.estimate_
ax[i // 2, i % 2].matshow(mean_cov)
ax[i // 2, i % 2].title.set_text(label_i)
```
We see that the average matrices computed using the affine invariant metric are now more differenciated from each other and can potentially give better results, when using MDM to predict the sign linked to a matrix sample.
## Sign Classification
We are now going to train some classifiers on those matrices to see how we can accurately discriminate these 4 hand positions.
The baseline accuracy is defined as the accuracy we get by randomly guessing the signs. In our case, the baseline accuracy is 25%.
```
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_validate
from sklearn.preprocessing import StandardScaler
# Hiding the numerous sklearn warnings
import warnings
warnings.filterwarnings('ignore')
!pip install tensorflow
from tensorflow.keras.wrappers.scikit_learn import KerasClassifier
import tensorflow as tf
```
N_EPOCHS is the number of epochs on which to train the DNN. Recommended is ~100
```
N_EPOCHS = 10
N_FEATURES = int(N_ELECTRODES * (N_ELECTRODES + 1) / 2)
```
### A. Test on the same session and user as Training/Calibration
In this first part we are training our model on the same session that we are testing it on. In real life, it corresponds to a user calibrating his armband right before using it. To do this, we are splitting every session in k-folds, training on $(k-1)$ fold to test on the $k^{th}$ last fold.
```
class ExpResults:
"""Class handling the score collection and plotting among the different experiments.
"""
def __init__(self, exps):
self.exps = exps
self.results = {}
self.exp_ids = {}
# Compute the index corresponding to each session only once at initialization.
for exp in set(self.exps):
self.exp_ids[exp] = np.where(self.exps==exp)[0]
def add_result(self, model_name, model, X, y):
"""Add the results from the cross validated pipeline.
For the model 'pipeline', it will add the cross validated results of every session in the model_name
entry of self.results.
Parameters
----------
model_name : str
Name of the pipeline/model that we are adding results from.
model : sklearn.pipeline.Pipeline
sklearn pipeline that we are evaluating.
X : array
data that we are ingesting in the pipeline.
y : array
labels corresponding to the data.
"""
self.results[model_name] = {'fit_time': [], 'score_time': [], 'test_score': [], 'train_score': []}
for exp in self.exp_ids.keys():
ids = self.exp_ids[exp]
exp_result = cross_validate(pipeline, X[ids], y[ids])
for key in exp_result.keys():
self.results[model_name][key] += list(exp_result[key])
print('Average training score: {}, Average test score: {}'.format(np.mean(self.results[model_name]['train_score']),
np.mean(self.results[model_name]['test_score'])))
def plot_results(self, title, variables, err_bar=None, save_name=None, xlabel='Model', ylabel='Acc'):
"""Plot bar plot comparing the different pipelines' results.
Compare the results added previously using the 'add_result' method with bar plots.
Parameters
----------
title : str
Title of the plot.
variables : list of array
List of the variables to plot (e.g. train_score, test_score,...)
err_bar : list of float
list of error to use for plotting error bars. If None, std is used by default.
save_name : str
path to save the plot. If None, plot is not saved.
xlabel : str
Label of the x-axis.
ylabel : str
Label of the y-axis.
"""
### Some defaults parameters.
w = 0.5
colors = ['b', 'r', 'gray']
### Reshaping the results for plotting.
x_labels = self.results.keys()
list_vec = []
for variable in variables:
list_vec.append(np.array([self.results[model][variable] for model in x_labels]).transpose())
rand_m1 = lambda size: np.random.random(size) * 2 - 1
### Plots parameters.
label_loc = np.arange(len(x_labels))
center_bar = [w * (i - 0.5) for i in range(len(list_vec))]
### Plots values.
avg_vec = [np.nanmean(vec, axis=0) for vec in list_vec]
if err_bar is None:
err_bar = [np.nanstd(vec, axis=0) for vec in list_vec]
### Plotting the data.
fig, ax = plt.subplots(figsize=(20, 15))
for i, vec in enumerate(list_vec):
label_i = variable[i] + ' (n = {})'.format(len(vec))
rects = ax.bar(label_loc + center_bar[i], avg_vec[i], w, label=label_i,
yerr=err_bar[i], color=colors[i], alpha=0.6)
for j, x in enumerate(label_loc):
ax.scatter((x + center_bar[i]) + rand_m1(vec[:, j].size) * w/4,
vec[:, j], color=colors[i], edgecolor='k')
# Add some text for labels, title and custom x-axis tick labels, etc.
ax.set_xlabel(xlabel)
ax.set_ylabel(ylabel)
ax.set_title(title)
ax.set_xticks(label_loc)
ax.set_xticklabels(x_labels)
ax.legend()
plt.legend()
### Saving the figure with a timestamp as a name.
if save_name is not None:
plt.savefig(save_name)
exp_arr = data.exp.iloc[cov_data.batches]
intra_sessions_results = ExpResults(exp_arr)
```
#### A.0. Using Logistic Regression on the vectorized Matrix (Euclidean Method)
```
pipeline = Pipeline(
steps=[('standardize', StandardScaler()),
('logreg', LogisticRegression(solver='lbfgs', multi_class='multinomial'))])
intra_sessions_results.add_result(model_name='logreg_eucl', model=pipeline, X=cov_data.covecs, y=cov_data.labels)
```
#### A.1. Using DNN on the vectorized Matrix (Euclidean Method)
```
def create_model(weights='initial_weights.hd5', n_features=N_FEATURES, n_signs=N_SIGNS):
"""Function to create model, required for using KerasClassifier and wrapp a Keras model inside a
scikitlearn form.
We added a weight saving/loading to remove the randomness of the weight initialization (for better comparison).
"""
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(n_features, activation='relu', input_shape=(n_features,)),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(17, activation='relu'),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(n_signs, activation='softmax'),
])
model.compile(loss = 'sparse_categorical_crossentropy', optimizer='rmsprop', metrics=['accuracy'])
if weights is None:
model.save_weights('initial_weights.hd5')
else:
model.load_weights(weights)
return model
def create_model_covariance(weights='initial_weights.hd5'):
return create_model(weights=weights, n_features=N_FEATURES)
```
Use the line below to generate the 'initial_weights.hd5' file
```
generate_weights = create_model(weights=None)
pipeline = Pipeline(
steps=[('standardize', StandardScaler()),
('dnn', KerasClassifier(build_fn=create_model, epochs=N_EPOCHS, verbose=0))])
intra_sessions_results.add_result(model_name='dnn_eucl', model=pipeline, X=cov_data.covecs, y=cov_data.labels)
```
#### A.2. Using Tangent space projection + Logistic Regression
```
from geomstats.learning.preprocessing import ToTangentSpace
pipeline = Pipeline(
steps=[('feature_ext', ToTangentSpace(geometry=metric_affine)),
('standardize', StandardScaler()),
('logreg', LogisticRegression(solver='lbfgs', multi_class='multinomial'))])
intra_sessions_results.add_result(model_name='logreg_affinvariant_tangent', model=pipeline, X=cov_data.covs, y=cov_data.labels)
```
#### A.3. Using Tangent space projection + DNN
```
pipeline = Pipeline(
steps=[('feature_ext', ToTangentSpace(geometry=metric_affine)),
('standardize', StandardScaler()),
('dnn', KerasClassifier(build_fn=create_model_covariance, epochs=N_EPOCHS, verbose=0))])
intra_sessions_results.add_result(model_name='dnn_affinvariant_tangent', model=pipeline, X=cov_data.covs, y=cov_data.labels)
```
#### A.4. Using Euclidean MDM
#### A.5. Using MDM with a Riemannian metric
#### Summary plots
```
intra_sessions_results.plot_results('intra_sess', ['test_score'])
```
|
github_jupyter
|
import os
import subprocess
import matplotlib
matplotlib.interactive(True)
import matplotlib.pyplot as plt
geomstats_gitroot_path = subprocess.check_output(
['git', 'rev-parse', '--show-toplevel'],
universal_newlines=True)
os.chdir(geomstats_gitroot_path[:-1])
print('Working directory: ', os.getcwd())
import geomstats.backend as gs
gs.random.seed(2021)
N_ELECTRODES = 8
N_SIGNS = 4
import geomstats.datasets.utils as data_utils
data = data_utils.load_emg()
data.head()
fig, ax = plt.subplots(N_SIGNS, figsize=(20, 20))
label_list = ['rock', 'scissors', 'paper', 'ok']
for i, label_i in enumerate(label_list):
sign_df = data[data.label==label_i].iloc[:100]
for electrode in range(N_ELECTRODES):
ax[i].plot(sign_df.iloc[:, 1 + electrode])
ax[i].title.set_text(label_i)
data = data[data.label != 'rest']
import numpy as np
import pandas as pd
### Parameters.
N_STEPS = 100
LABEL_MAP = {'rock': 0, 'scissors': 1, 'paper': 2, 'ok': 3}
MARGIN = 1000
data_dict = {
'time': gs.array(data.time),
'raw_data': gs.array(data[['c{}'.format(i) for i in range(N_ELECTRODES)]]),
'label': gs.array(data.label),
'exp': gs.array(data.exp)}
from geomstats.datasets.prepare_emg_data import TimeSeriesCovariance
cov_data = TimeSeriesCovariance(data_dict, N_STEPS, N_ELECTRODES, LABEL_MAP, MARGIN)
cov_data.transform()
import geomstats.geometry.spd_matrices as spd
manifold = spd.SPDMatrices(N_ELECTRODES)
gs.all(manifold.belongs(cov_data.covs))
fig, ax = plt.subplots(2, 2, figsize=(20, 10))
for label_i, i in cov_data.label_map.items():
label_ids = np.where(cov_data.labels==i)[0]
sign_cov_mat = cov_data.covs[label_ids]
mean_cov = np.mean(sign_cov_mat, axis=0)
ax[i // 2, i % 2].matshow(mean_cov)
ax[i // 2, i % 2].title.set_text(label_i)
from geomstats.learning.frechet_mean import FrechetMean
from geomstats.geometry.spd_matrices import SPDMetricAffine
metric_affine = SPDMetricAffine(N_ELECTRODES)
mean_affine = FrechetMean(metric=metric_affine, point_type='matrix')
fig, ax = plt.subplots(2, 2, figsize=(20, 10))
for label_i, i in cov_data.label_map.items():
label_ids = np.where(cov_data.labels==i)[0]
sign_cov_mat = cov_data.covs[label_ids]
mean_affine.fit(X=sign_cov_mat)
mean_cov = mean_affine.estimate_
ax[i // 2, i % 2].matshow(mean_cov)
ax[i // 2, i % 2].title.set_text(label_i)
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_validate
from sklearn.preprocessing import StandardScaler
# Hiding the numerous sklearn warnings
import warnings
warnings.filterwarnings('ignore')
!pip install tensorflow
from tensorflow.keras.wrappers.scikit_learn import KerasClassifier
import tensorflow as tf
N_EPOCHS = 10
N_FEATURES = int(N_ELECTRODES * (N_ELECTRODES + 1) / 2)
class ExpResults:
"""Class handling the score collection and plotting among the different experiments.
"""
def __init__(self, exps):
self.exps = exps
self.results = {}
self.exp_ids = {}
# Compute the index corresponding to each session only once at initialization.
for exp in set(self.exps):
self.exp_ids[exp] = np.where(self.exps==exp)[0]
def add_result(self, model_name, model, X, y):
"""Add the results from the cross validated pipeline.
For the model 'pipeline', it will add the cross validated results of every session in the model_name
entry of self.results.
Parameters
----------
model_name : str
Name of the pipeline/model that we are adding results from.
model : sklearn.pipeline.Pipeline
sklearn pipeline that we are evaluating.
X : array
data that we are ingesting in the pipeline.
y : array
labels corresponding to the data.
"""
self.results[model_name] = {'fit_time': [], 'score_time': [], 'test_score': [], 'train_score': []}
for exp in self.exp_ids.keys():
ids = self.exp_ids[exp]
exp_result = cross_validate(pipeline, X[ids], y[ids])
for key in exp_result.keys():
self.results[model_name][key] += list(exp_result[key])
print('Average training score: {}, Average test score: {}'.format(np.mean(self.results[model_name]['train_score']),
np.mean(self.results[model_name]['test_score'])))
def plot_results(self, title, variables, err_bar=None, save_name=None, xlabel='Model', ylabel='Acc'):
"""Plot bar plot comparing the different pipelines' results.
Compare the results added previously using the 'add_result' method with bar plots.
Parameters
----------
title : str
Title of the plot.
variables : list of array
List of the variables to plot (e.g. train_score, test_score,...)
err_bar : list of float
list of error to use for plotting error bars. If None, std is used by default.
save_name : str
path to save the plot. If None, plot is not saved.
xlabel : str
Label of the x-axis.
ylabel : str
Label of the y-axis.
"""
### Some defaults parameters.
w = 0.5
colors = ['b', 'r', 'gray']
### Reshaping the results for plotting.
x_labels = self.results.keys()
list_vec = []
for variable in variables:
list_vec.append(np.array([self.results[model][variable] for model in x_labels]).transpose())
rand_m1 = lambda size: np.random.random(size) * 2 - 1
### Plots parameters.
label_loc = np.arange(len(x_labels))
center_bar = [w * (i - 0.5) for i in range(len(list_vec))]
### Plots values.
avg_vec = [np.nanmean(vec, axis=0) for vec in list_vec]
if err_bar is None:
err_bar = [np.nanstd(vec, axis=0) for vec in list_vec]
### Plotting the data.
fig, ax = plt.subplots(figsize=(20, 15))
for i, vec in enumerate(list_vec):
label_i = variable[i] + ' (n = {})'.format(len(vec))
rects = ax.bar(label_loc + center_bar[i], avg_vec[i], w, label=label_i,
yerr=err_bar[i], color=colors[i], alpha=0.6)
for j, x in enumerate(label_loc):
ax.scatter((x + center_bar[i]) + rand_m1(vec[:, j].size) * w/4,
vec[:, j], color=colors[i], edgecolor='k')
# Add some text for labels, title and custom x-axis tick labels, etc.
ax.set_xlabel(xlabel)
ax.set_ylabel(ylabel)
ax.set_title(title)
ax.set_xticks(label_loc)
ax.set_xticklabels(x_labels)
ax.legend()
plt.legend()
### Saving the figure with a timestamp as a name.
if save_name is not None:
plt.savefig(save_name)
exp_arr = data.exp.iloc[cov_data.batches]
intra_sessions_results = ExpResults(exp_arr)
pipeline = Pipeline(
steps=[('standardize', StandardScaler()),
('logreg', LogisticRegression(solver='lbfgs', multi_class='multinomial'))])
intra_sessions_results.add_result(model_name='logreg_eucl', model=pipeline, X=cov_data.covecs, y=cov_data.labels)
def create_model(weights='initial_weights.hd5', n_features=N_FEATURES, n_signs=N_SIGNS):
"""Function to create model, required for using KerasClassifier and wrapp a Keras model inside a
scikitlearn form.
We added a weight saving/loading to remove the randomness of the weight initialization (for better comparison).
"""
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(n_features, activation='relu', input_shape=(n_features,)),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(17, activation='relu'),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(n_signs, activation='softmax'),
])
model.compile(loss = 'sparse_categorical_crossentropy', optimizer='rmsprop', metrics=['accuracy'])
if weights is None:
model.save_weights('initial_weights.hd5')
else:
model.load_weights(weights)
return model
def create_model_covariance(weights='initial_weights.hd5'):
return create_model(weights=weights, n_features=N_FEATURES)
generate_weights = create_model(weights=None)
pipeline = Pipeline(
steps=[('standardize', StandardScaler()),
('dnn', KerasClassifier(build_fn=create_model, epochs=N_EPOCHS, verbose=0))])
intra_sessions_results.add_result(model_name='dnn_eucl', model=pipeline, X=cov_data.covecs, y=cov_data.labels)
from geomstats.learning.preprocessing import ToTangentSpace
pipeline = Pipeline(
steps=[('feature_ext', ToTangentSpace(geometry=metric_affine)),
('standardize', StandardScaler()),
('logreg', LogisticRegression(solver='lbfgs', multi_class='multinomial'))])
intra_sessions_results.add_result(model_name='logreg_affinvariant_tangent', model=pipeline, X=cov_data.covs, y=cov_data.labels)
pipeline = Pipeline(
steps=[('feature_ext', ToTangentSpace(geometry=metric_affine)),
('standardize', StandardScaler()),
('dnn', KerasClassifier(build_fn=create_model_covariance, epochs=N_EPOCHS, verbose=0))])
intra_sessions_results.add_result(model_name='dnn_affinvariant_tangent', model=pipeline, X=cov_data.covs, y=cov_data.labels)
intra_sessions_results.plot_results('intra_sess', ['test_score'])
| 0.616474 | 0.987532 |
<i>Copyright (c) Microsoft Corporation. All rights reserved.</i>
<i>Licensed under the MIT License.</i>
# Train SAR on MovieLens with Azure Machine Learning (Python, CPU)
---
## Introduction to Azure Machine Learning
The **[Azure Machine Learning service (AzureML)](https://docs.microsoft.com/azure/machine-learning/service/overview-what-is-azure-ml)** provides a cloud-based environment you can use to prep data, train, test, deploy, manage, and track machine learning models. By using Azure Machine Learning service, you can start training on your local machine and then scale out to the cloud. With many available compute targets, like [Azure Machine Learning Compute](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-set-up-training-targets#amlcompute) and [Azure Databricks](https://docs.microsoft.com/en-us/azure/azure-databricks/what-is-azure-databricks), and with [advanced hyperparameter tuning services](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-tune-hyperparameters), you can build better models faster by using the power of the cloud.
Data scientists and AI developers use the main [Azure Machine Learning Python SDK](https://docs.microsoft.com/en-us/python/api/overview/azure/ml/intro?view=azure-ml-py) to build and run machine learning workflows with the Azure Machine Learning service. You can interact with the service in any Python environment, including Jupyter Notebooks or your favorite Python IDE. The Azure Machine Learning SDK allows you the choice of using local or cloud compute resources, while managing and maintaining the complete data science workflow from the cloud.

This notebook provides an example of how to utilize and evaluate the Simple Algorithm for Recommendation (SAR) algorithm using the Azure Machine Learning service. It takes the content of the [SAR quickstart notebook](sar_movielens.ipynb) and demonstrates how to use the power of the cloud to manage data, switch to powerful GPU machines, and monitor runs while training a model.
See the hyperparameter tuning notebook for more advanced use cases with AzureML.
### Advantages of using AzureML:
- Manage cloud resources for monitoring, logging, and organizing your machine learning experiments.
- Train models either locally or by using cloud resources, including GPU-accelerated model training.
- Easy to scale out when dataset grows - by just creating and pointing to new compute target
---
## Details of SAR
<details>
<summary>Click to expand</summary>
SAR is a fast scalable adaptive algorithm for personalized recommendations based on user transaction history. It produces easily explainable / interpretable recommendations and handles "cold item" and "semi-cold user" scenarios. SAR is a kind of neighborhood based algorithm (as discussed in [Recommender Systems by Aggarwal](https://dl.acm.org/citation.cfm?id=2931100)) which is intended for ranking top items for each user.
SAR recommends items that are most ***similar*** to the ones that the user already has an existing ***affinity*** for. Two items are ***similar*** if the users who have interacted with one item are also likely to have interacted with another. A user has an ***affinity*** to an item if they have interacted with it in the past.
### Advantages of SAR:
- High accuracy for an easy to train and deploy algorithm
- Fast training, only requiring simple counting to construct matrices used at prediction time
- Fast scoring, only involving multiplication of the similarity matric with an affinity vector
### Notes to use SAR properly:
- SAR does not use item or user features, so cannot handle cold-start use cases
- SAR requires the creation of an $mxm$ dense matrix (where $m$ is the number of items). So memory consumption can be an issue with large numbers of items.
- SAR is best used for ranking items per user, as the scale of predicted ratings may be different from the input range and will differ across users.
For more details see the deep dive notebook on SAR here: [SAR Deep Dive Notebook](../02_model/sar_deep_dive.ipynb)</details>
---
## Prerequisities
- **Azure Subscription**
- If you don’t have an Azure subscription, create a free account before you begin. Try the [free or paid version of Azure Machine Learning service today](https://azure.microsoft.com/en-us/free/services/machine-learning/).
- You get credits to spend on Azure services, which will easily cover the cost of running this example notebook. After they're used up, you can keep the account and use [free Azure services](https://azure.microsoft.com/en-us/free/). Your credit card is never charged unless you explicitly change your settings and ask to be charged. Or [activate MSDN subscriber benefits](https://azure.microsoft.com/en-us/pricing/member-offers/credit-for-visual-studio-subscribers/), which give you credits every month that you can use for paid Azure services.
---
```
# set the environment path to find Recommenders
import sys
sys.path.append("../../")
import os
import shutil
from tempfile import TemporaryDirectory
import azureml
from azureml.core import Workspace, Run, Experiment
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.train.estimator import Estimator
from azureml.widgets import RunDetails
from reco_utils.azureml.azureml_utils import get_or_create_workspace
from reco_utils.dataset import movielens
print("azureml.core version: {}".format(azureml.core.VERSION))
# top k items to recommend
TOP_K = 10
# Select Movielens data size: 100k, 1m, 10m, or 20m
MOVIELENS_DATA_SIZE = '1m'
```
### Connect to an AzureML workspace
An [AzureML Workspace](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.workspace.workspace?view=azure-ml-py) is an Azure resource that organizes and coordinates the actions of many other Azure resources to assist in executing and sharing machine learning workflows. In particular, an Azure ML Workspace coordinates storage, databases, and compute resources providing added functionality for machine learning experimentation, deployment, inferencing, and the monitoring of deployed models.
The function below will get or create an AzureML Workspace and save the configuration to `aml_config/config.json`.
It defaults to use provided input parameters or environment variables for the Workspace configuration values. Otherwise, it will use an existing configuration file (either at `./aml_config/config.json` or a path specified by the config_path parameter).
Lastly, if the workspace does not exist, one will be created for you. See [this tutorial](https://docs.microsoft.com/en-us/azure/machine-learning/service/setup-create-workspace#portal) to locate information such as subscription id.
```
ws = get_or_create_workspace(
subscription_id="<SUBSCRIPTION_ID>",
resource_group="<RESOURCE_GROUP>",
workspace_name="<WORKSPACE_NAME>",
workspace_region="<WORKSPACE_REGION>"
)
```
### Create a Temporary Directory
This directory will house the data and scripts needed by the AzureML Workspace
```
tmp_dir = TemporaryDirectory()
```
### Download dataset and upload to datastore
Every workspace comes with a default [datastore](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-access-data) (and you can register more) which is backed by the Azure blob storage account associated with the workspace. We can use it to transfer data from local to the cloud, and access it from the compute target.
The data files are uploaded into a directory named `data` at the root of the datastore.
```
TARGET_DIR = 'movielens'
# download dataset
data = movielens.load_pandas_df(
size=MOVIELENS_DATA_SIZE,
header=['UserId','MovieId','Rating','Timestamp']
)
# upload dataset to workspace datastore
data_file_name = "movielens_" + MOVIELENS_DATA_SIZE + "_data.pkl"
data.to_pickle(os.path.join(tmp_dir.name, data_file_name))
ds = ws.get_default_datastore()
ds.upload(src_dir=tmp_dir.name, target_path=TARGET_DIR, overwrite=True, show_progress=True)
```
### Create or Attach Azure Machine Learning Compute
We create a cpu cluster as our **remote compute target**. If a cluster with the same name already exists in your workspace, the script will load it instead. You can read [Set up compute targets for model training](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-set-up-training-targets) to learn more about setting up compute target on different locations. You can also create GPU machines when larger machines are necessary to train the model.
According to Azure [Pricing calculator](https://azure.microsoft.com/en-us/pricing/calculator/), with example VM size `STANDARD_D2_V2`, it costs a few dollars to run this notebook, which is well covered by Azure new subscription credit. For billing and pricing questions, please contact [Azure support](https://azure.microsoft.com/en-us/support/options/).
**Note**:
- 10m and 20m dataset requires more capacity than `STANDARD_D2_V2`, such as `STANDARD_NC6` or `STANDARD_NC12`. See list of all available VM sizes [here](https://docs.microsoft.com/en-us/azure/templates/Microsoft.Compute/2018-10-01/virtualMachines?toc=%2Fen-us%2Fazure%2Fazure-resource-manager%2Ftoc.json&bc=%2Fen-us%2Fazure%2Fbread%2Ftoc.json#hardwareprofile-object).
- As with other Azure services, there are limits on certain resources (e.g. AzureML Compute quota) associated with the Azure Machine Learning service. Please read [these instructions](https://docs.microsoft.com/en-us/azure/azure-supportability/resource-manager-core-quotas-request) on the default limits and how to request more quota.
---
#### Learn more about Azure Machine Learning Compute
<details>
<summary>Click to learn more about compute types</summary>
[Azure Machine Learning Compute](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-set-up-training-targets#amlcompute) is managed compute infrastructure that allows the user to easily create single to multi-node compute of the appropriate VM Family. It is created within your workspace region and is a resource that can be used by other users in your workspace. It autoscales by default to the max_nodes, when a job is submitted, and executes in a containerized environment packaging the dependencies as specified by the user.
Since it is managed compute, job scheduling and cluster management are handled internally by Azure Machine Learning service.
You can provision a persistent AzureML Compute resource by simply defining two parameters thanks to smart defaults. By default it autoscales from 0 nodes and provisions dedicated VMs to run your job in a container. This is useful when you want to continously re-use the same target, debug it between jobs or simply share the resource with other users of your workspace.
In addition to vm_size and max_nodes, you can specify:
- **min_nodes**: Minimum nodes (default 0 nodes) to downscale to while running a job on AzureML Compute
- **vm_priority**: Choose between 'dedicated' (default) and 'lowpriority' VMs when provisioning AzureML Compute. Low Priority VMs use Azure's excess capacity and are thus cheaper but risk your run being pre-empted
- **idle_seconds_before_scaledown**: Idle time (default 120 seconds) to wait after run completion before auto-scaling to min_nodes
- **vnet_resourcegroup_name**: Resource group of the existing VNet within which Azure MLCompute should be provisioned
- **vnet_name**: Name of VNet
- **subnet_name**: Name of SubNet within the VNet
</details>
---
```
# Remote compute (cluster) configuration. If you want to save the cost more, set these to small.
VM_SIZE = 'STANDARD_D2_V2'
# Cluster nodes
MIN_NODES = 0
MAX_NODES = 2
CLUSTER_NAME = 'cpucluster'
try:
compute_target = ComputeTarget(workspace=ws, name=CLUSTER_NAME)
print("Found existing compute target")
except:
print("Creating a new compute target...")
# Specify the configuration for the new cluster
compute_config = AmlCompute.provisioning_configuration(
vm_size=VM_SIZE,
min_nodes=MIN_NODES,
max_nodes=MAX_NODES
)
# Create the cluster with the specified name and configuration
compute_target = ComputeTarget.create(ws, CLUSTER_NAME, compute_config)
# Wait for the cluster to complete, show the output log
compute_target.wait_for_completion(show_output=True, min_node_count=None, timeout_in_minutes=20)
```
# Prepare training script
### 1. Create a directory
Create a directory that will contain all the necessary code from your local machine that you will need access to on the remote resource. This includes the training script, and any additional files your training script depends on.
```
SCRIPT_DIR = os.path.join(tmp_dir.name, 'movielens-sar')
os.makedirs(SCRIPT_DIR, exist_ok=True)
TRAIN_FILE = os.path.join(SCRIPT_DIR, 'train.py')
```
### 2. Create a training script
To submit the job to the cluster, first create a training script. Run the following code to create the training script called `train.py` in temporary directory. This training adds a regularization rate to the training algorithm, so produces a slightly different model than the local version.
This code takes what is in the local quickstart and convert it to one single training script. We use run.log() to record parameters to the run. We will be able to review and compare these measures in the Azure Portal at a later time.
```
%%writefile $TRAIN_FILE
import argparse
import os
import numpy as np
import pandas as pd
import itertools
import logging
import time
from azureml.core import Run
from sklearn.externals import joblib
from reco_utils.dataset import movielens
from reco_utils.dataset.python_splitters import python_random_split
from reco_utils.evaluation.python_evaluation import map_at_k, ndcg_at_k, precision_at_k, recall_at_k
from reco_utils.recommender.sar.sar_singlenode import SARSingleNode
TARGET_DIR = 'movielens'
OUTPUT_FILE_NAME = 'outputs/movielens_sar_model.pkl'
MODEL_FILE_NAME = 'movielens_sar_model.pkl'
# get hold of the current run
run = Run.get_context()
# let user feed in 2 parameters, the location of the data files (from datastore), and the regularization rate of the logistic regression model
parser = argparse.ArgumentParser()
parser.add_argument('--data-folder', type=str, dest='data_folder', help='data folder mounting point')
parser.add_argument('--data-file', type=str, dest='data_file', help='data file name')
parser.add_argument('--top-k', type=int, dest='top_k', default=10, help='top k items to recommend')
parser.add_argument('--data-size', type=str, dest='data_size', default=10, help='Movielens data size: 100k, 1m, 10m, or 20m')
args = parser.parse_args()
data_pickle_path = os.path.join(args.data_folder, args.data_file)
data = pd.read_pickle(path=data_pickle_path)
# Log arguments to the run for tracking
run.log("top-k", args.top_k)
run.log("data-size", args.data_size)
train, test = python_random_split(data)
# instantiate the SAR algorithm and set the index
header = {
"col_user": "UserId",
"col_item": "MovieId",
"col_rating": "Rating",
"col_timestamp": "Timestamp",
}
logging.basicConfig(level=logging.DEBUG,
format='%(asctime)s %(levelname)-8s %(message)s')
model = SARSingleNode(
remove_seen=True, similarity_type="jaccard",
time_decay_coefficient=30, time_now=None, timedecay_formula=True, **header
)
# train the SAR model
start_time = time.time()
model.fit(train)
train_time = time.time() - start_time
run.log(name="Training time", value=train_time)
start_time = time.time()
top_k = model.recommend_k_items(test)
test_time = time.time() - start_time
run.log(name="Prediction time", value=test_time)
# TODO: remove this call when the model returns same type as input
top_k['UserId'] = pd.to_numeric(top_k['UserId'])
top_k['MovieId'] = pd.to_numeric(top_k['MovieId'])
# evaluate
eval_map = map_at_k(test, top_k, col_user="UserId", col_item="MovieId",
col_rating="Rating", col_prediction="prediction",
relevancy_method="top_k", k=args.top_k)
eval_ndcg = ndcg_at_k(test, top_k, col_user="UserId", col_item="MovieId",
col_rating="Rating", col_prediction="prediction",
relevancy_method="top_k", k=args.top_k)
eval_precision = precision_at_k(test, top_k, col_user="UserId", col_item="MovieId",
col_rating="Rating", col_prediction="prediction",
relevancy_method="top_k", k=args.top_k)
eval_recall = recall_at_k(test, top_k, col_user="UserId", col_item="MovieId",
col_rating="Rating", col_prediction="prediction",
relevancy_method="top_k", k=args.top_k)
run.log("map", eval_map)
run.log("ndcg", eval_ndcg)
run.log("precision", eval_precision)
run.log("recall", eval_recall)
# automatic upload of everything in ./output folder doesn't work for very large model file
# model file has to be saved to a temp location, then uploaded by upload_file function
joblib.dump(value=model, filename=MODEL_FILE_NAME)
run.upload_file(OUTPUT_FILE_NAME, MODEL_FILE_NAME)
# copy dependent python files
UTILS_DIR = os.path.join(SCRIPT_DIR, 'reco_utils')
shutil.copytree('../../reco_utils/', UTILS_DIR)
```
# Run training script
### 1. Create an estimator
An [estimator](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-train-ml-models) object is used to submit the run. You can create and use a generic Estimator to submit a training script using any learning framework you choose (such as scikit-learn) you want to run on any compute target, whether it's your local machine, a single VM in Azure, or a GPU cluster in Azure.
Create your estimator by running the following code to define:
* The name of the estimator object, `est`
* The directory that contains your scripts. All the files in this directory are uploaded into the cluster nodes for execution.
* The compute target. In this case you will use the AzureML Compute you created
* The training script name, train.py
* Parameters required from the training script
* Python packages needed for training
* Connect to the data files in the datastore
In this tutorial, this target is AzureML Compute. All files in the script folder are uploaded into the cluster nodes for execution. `ds.as_mount()` mounts a datastore on the remote compute and returns the folder. See documentation [here](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-access-data#access-datastores-during-training).
```
script_params = {
'--data-folder': ds.as_mount(),
'--data-file': 'movielens/' + data_file_name,
'--top-k': TOP_K,
'--data-size': MOVIELENS_DATA_SIZE
}
est = Estimator(source_directory=SCRIPT_DIR,
script_params=script_params,
compute_target=compute_target,
entry_script='train.py',
conda_packages=['pandas'],
pip_packages=['sklearn', 'tqdm'])
```
### 2. Submit the job to the cluster
An [experiment](https://docs.microsoft.com/en-us/python/api/overview/azure/ml/intro?view=azure-ml-py#experiment) is a logical container in an AzureML Workspace. It hosts run records which can include run metrics and output artifacts from your experiments. We access an experiment from our AzureML workspace by name, which will be created if it doesn't exist.
Then, run the experiment by submitting the estimator object.
```
# create experiment
EXPERIMENT_NAME = 'movielens-sar'
exp = Experiment(workspace=ws, name=EXPERIMENT_NAME)
run = exp.submit(config=est)
```
### 3. Monitor remote run
#### Jupyter widget
Jupyter widget can watch the progress of the run. Like the run submission, the widget is asynchronous and provides live updates every 10-15 seconds until the job completes.
```
RunDetails(run).show()
```
### 4. Viewing run results
Azure Machine Learning stores all the details about the run in the Azure cloud. Let's access those details by retrieving a link to the run using the default run output. Clicking on the resulting link will take you to an interactive page.
```
run
```
Above cell should output similar table as below.

After clicking "Link to Azure Portal", experiment run details tab looks like this with logged metrics.

```
# run below after run is complete, otherwise metrics is empty
metrics = run.get_metrics()
print(metrics)
```
# Deprovision compute resource
To avoid unnecessary charges, if you created compute target that doesn't scale down to 0, make sure the compute target is deprovisioned after use.
```
# delete () is used to deprovision and delete the AzureML Compute target.
# do not run below before experiment completes
# compute_target.delete()
# deletion will take a few minutes. You can check progress in Azure Portal / Computing tab
# clean up temporary directory
tmp_dir.cleanup()
```
|
github_jupyter
|
# set the environment path to find Recommenders
import sys
sys.path.append("../../")
import os
import shutil
from tempfile import TemporaryDirectory
import azureml
from azureml.core import Workspace, Run, Experiment
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.train.estimator import Estimator
from azureml.widgets import RunDetails
from reco_utils.azureml.azureml_utils import get_or_create_workspace
from reco_utils.dataset import movielens
print("azureml.core version: {}".format(azureml.core.VERSION))
# top k items to recommend
TOP_K = 10
# Select Movielens data size: 100k, 1m, 10m, or 20m
MOVIELENS_DATA_SIZE = '1m'
ws = get_or_create_workspace(
subscription_id="<SUBSCRIPTION_ID>",
resource_group="<RESOURCE_GROUP>",
workspace_name="<WORKSPACE_NAME>",
workspace_region="<WORKSPACE_REGION>"
)
tmp_dir = TemporaryDirectory()
TARGET_DIR = 'movielens'
# download dataset
data = movielens.load_pandas_df(
size=MOVIELENS_DATA_SIZE,
header=['UserId','MovieId','Rating','Timestamp']
)
# upload dataset to workspace datastore
data_file_name = "movielens_" + MOVIELENS_DATA_SIZE + "_data.pkl"
data.to_pickle(os.path.join(tmp_dir.name, data_file_name))
ds = ws.get_default_datastore()
ds.upload(src_dir=tmp_dir.name, target_path=TARGET_DIR, overwrite=True, show_progress=True)
# Remote compute (cluster) configuration. If you want to save the cost more, set these to small.
VM_SIZE = 'STANDARD_D2_V2'
# Cluster nodes
MIN_NODES = 0
MAX_NODES = 2
CLUSTER_NAME = 'cpucluster'
try:
compute_target = ComputeTarget(workspace=ws, name=CLUSTER_NAME)
print("Found existing compute target")
except:
print("Creating a new compute target...")
# Specify the configuration for the new cluster
compute_config = AmlCompute.provisioning_configuration(
vm_size=VM_SIZE,
min_nodes=MIN_NODES,
max_nodes=MAX_NODES
)
# Create the cluster with the specified name and configuration
compute_target = ComputeTarget.create(ws, CLUSTER_NAME, compute_config)
# Wait for the cluster to complete, show the output log
compute_target.wait_for_completion(show_output=True, min_node_count=None, timeout_in_minutes=20)
SCRIPT_DIR = os.path.join(tmp_dir.name, 'movielens-sar')
os.makedirs(SCRIPT_DIR, exist_ok=True)
TRAIN_FILE = os.path.join(SCRIPT_DIR, 'train.py')
%%writefile $TRAIN_FILE
import argparse
import os
import numpy as np
import pandas as pd
import itertools
import logging
import time
from azureml.core import Run
from sklearn.externals import joblib
from reco_utils.dataset import movielens
from reco_utils.dataset.python_splitters import python_random_split
from reco_utils.evaluation.python_evaluation import map_at_k, ndcg_at_k, precision_at_k, recall_at_k
from reco_utils.recommender.sar.sar_singlenode import SARSingleNode
TARGET_DIR = 'movielens'
OUTPUT_FILE_NAME = 'outputs/movielens_sar_model.pkl'
MODEL_FILE_NAME = 'movielens_sar_model.pkl'
# get hold of the current run
run = Run.get_context()
# let user feed in 2 parameters, the location of the data files (from datastore), and the regularization rate of the logistic regression model
parser = argparse.ArgumentParser()
parser.add_argument('--data-folder', type=str, dest='data_folder', help='data folder mounting point')
parser.add_argument('--data-file', type=str, dest='data_file', help='data file name')
parser.add_argument('--top-k', type=int, dest='top_k', default=10, help='top k items to recommend')
parser.add_argument('--data-size', type=str, dest='data_size', default=10, help='Movielens data size: 100k, 1m, 10m, or 20m')
args = parser.parse_args()
data_pickle_path = os.path.join(args.data_folder, args.data_file)
data = pd.read_pickle(path=data_pickle_path)
# Log arguments to the run for tracking
run.log("top-k", args.top_k)
run.log("data-size", args.data_size)
train, test = python_random_split(data)
# instantiate the SAR algorithm and set the index
header = {
"col_user": "UserId",
"col_item": "MovieId",
"col_rating": "Rating",
"col_timestamp": "Timestamp",
}
logging.basicConfig(level=logging.DEBUG,
format='%(asctime)s %(levelname)-8s %(message)s')
model = SARSingleNode(
remove_seen=True, similarity_type="jaccard",
time_decay_coefficient=30, time_now=None, timedecay_formula=True, **header
)
# train the SAR model
start_time = time.time()
model.fit(train)
train_time = time.time() - start_time
run.log(name="Training time", value=train_time)
start_time = time.time()
top_k = model.recommend_k_items(test)
test_time = time.time() - start_time
run.log(name="Prediction time", value=test_time)
# TODO: remove this call when the model returns same type as input
top_k['UserId'] = pd.to_numeric(top_k['UserId'])
top_k['MovieId'] = pd.to_numeric(top_k['MovieId'])
# evaluate
eval_map = map_at_k(test, top_k, col_user="UserId", col_item="MovieId",
col_rating="Rating", col_prediction="prediction",
relevancy_method="top_k", k=args.top_k)
eval_ndcg = ndcg_at_k(test, top_k, col_user="UserId", col_item="MovieId",
col_rating="Rating", col_prediction="prediction",
relevancy_method="top_k", k=args.top_k)
eval_precision = precision_at_k(test, top_k, col_user="UserId", col_item="MovieId",
col_rating="Rating", col_prediction="prediction",
relevancy_method="top_k", k=args.top_k)
eval_recall = recall_at_k(test, top_k, col_user="UserId", col_item="MovieId",
col_rating="Rating", col_prediction="prediction",
relevancy_method="top_k", k=args.top_k)
run.log("map", eval_map)
run.log("ndcg", eval_ndcg)
run.log("precision", eval_precision)
run.log("recall", eval_recall)
# automatic upload of everything in ./output folder doesn't work for very large model file
# model file has to be saved to a temp location, then uploaded by upload_file function
joblib.dump(value=model, filename=MODEL_FILE_NAME)
run.upload_file(OUTPUT_FILE_NAME, MODEL_FILE_NAME)
# copy dependent python files
UTILS_DIR = os.path.join(SCRIPT_DIR, 'reco_utils')
shutil.copytree('../../reco_utils/', UTILS_DIR)
script_params = {
'--data-folder': ds.as_mount(),
'--data-file': 'movielens/' + data_file_name,
'--top-k': TOP_K,
'--data-size': MOVIELENS_DATA_SIZE
}
est = Estimator(source_directory=SCRIPT_DIR,
script_params=script_params,
compute_target=compute_target,
entry_script='train.py',
conda_packages=['pandas'],
pip_packages=['sklearn', 'tqdm'])
# create experiment
EXPERIMENT_NAME = 'movielens-sar'
exp = Experiment(workspace=ws, name=EXPERIMENT_NAME)
run = exp.submit(config=est)
RunDetails(run).show()
run
# run below after run is complete, otherwise metrics is empty
metrics = run.get_metrics()
print(metrics)
# delete () is used to deprovision and delete the AzureML Compute target.
# do not run below before experiment completes
# compute_target.delete()
# deletion will take a few minutes. You can check progress in Azure Portal / Computing tab
# clean up temporary directory
tmp_dir.cleanup()
| 0.25992 | 0.961893 |
This notebook extends Kate's work on generating forcing files for the tides at Johnstone Strait. Kate's notebook is based on observations from Thomson and Huggett (1980). Unfortunately, their observations are not long enough to retrieve the smaller tidal constuents: O1, S2, N2, P1, Q1, K2.
To determine these constituents, we will calculate the amplitude and phase change of the M2/K1 harmonics between the Webtide point closest to our boundary and the Johnstone Strait harmonics that Kate has determined. We will apply the same change to the remaining constituents.
```
%matplotlib inline
from matplotlib import pylab
import matplotlib.pyplot as plt
import netCDF4 as NC
import numpy as np
from math import cos, sin, tan, radians
import math
import webtide_tools
TSin = {'North': {'M2': {'Amp': 1.2468500142849095, 'Pha': 5.8718032013900494}, 'Q1': {'Amp': 0.88018411744300051, 'Pha': 3.3676909436466511}, 'O1': {'Amp': 0.92187588787164776, 'Pha': -1.8419422569093058}, 'S2': {'Amp': 0.98646859951016619, 'Pha': -10.363961743466264}, 'K1': {'Amp': 1.056369887585026, 'Pha': -7.2574882761515624}, 'N2': {'Amp': 0.95930333678587432, 'Pha': -6.8740655239509989}}, 'West': {'M2': {'Amp': 0.8840061749307605, 'Pha': -7.8587198373167935}, 'Q1': {'Amp': 0.95936152535045738, 'Pha': 1.1445537519586795}, 'O1': {'Amp': 1.058133345863022, 'Pha': 0.92064288566727737}, 'S2': {'Amp': 1.0232932221404019, 'Pha': 0.7966194737248522}, 'K1': {'Amp': 1.0168859739167362, 'Pha': -3.8356999030330829}, 'N2': {'Amp': 1.0027750731988296, 'Pha': 2.5899670236940464}}}
# These are the corrections to be used.
code = 'N36_AF'
# Fine tuning corrections, note that these are relative to M2/K1 P1 and K2 calculated as fixed ratios (see below)
amp_corr = {
'O1': TSin['North']['O1']['Amp'],
'S2': TSin['North']['S2']['Amp'],
'P1': 0.,
'N2': TSin['North']['N2']['Amp'],
'Q1': TSin['North']['Q1']['Amp'],
'K2': 0.}
pha_corr = {
'O1': np.radians(TSin['North']['O1']['Pha']),
'S2': np.radians(TSin['North']['S2']['Pha']),
'P1': 0.*np.pi/180.,
'N2': np.radians(TSin['North']['N2']['Pha']),
'Q1': np.radians(TSin['North']['Q1']['Pha']),
'K2': 0.*np.pi/180.0}
```
Load the NETCDF tidal data from the north.
```
def get_files(constituent,code):
#returns the U, V, T netcdf handles for the tidal constiruents that Kate created for the northern boundary
#constituent = 'O1', 'M2', etc
filename = 'SalishSea_'+code+'_North_tide_' + constituent
fU=NC.Dataset(filename + '_grid_U.nc', 'r')
fV=NC.Dataset(filename + '_grid_V.nc', 'r')
fT=NC.Dataset(filename + '_grid_T.nc', 'r')
return fU, fV, fT
consts_full= {'M2': [], 'K1': [], 'O1': [], 'S2': [], 'N2': [], 'P1': [], 'Q1': [], 'K2': []}
consts_North= {'M2': [], 'K1': []}
fUs_North={}
fVs_North={}
fTs_North={}
for key in consts_North:
[fUs_North[key], fVs_North[key],fTs_North[key]]= get_files(key,code)
```
NEMO takes the harmonics as :
$Z_1 = A \cos(\phi)$
$Z_2 = A \sin(\phi)$
Where $A$ and $\phi$ are the amplitude and phase.
So: $A = \sqrt(Z_1^2+Z_2^2)$ and $ \phi = \arctan(Z_2/Z_1)$
```
def get_harmomincs(f, comp):
#returns the harmonics as vecotors
#f is the nertcdf handle
#comp is the component ('U','V','T')
import numpy as np
import math
if comp=='U':
x1='u1'; x2='u2';
elif comp == 'V':
x1='v1'; x2='v2';
elif comp == 'T':
x1='z1'; x2='z2';
X1=f.variables[x1]; X1=np.array(X1); X1=X1.flatten();
X2=f.variables[x2]; X2=np.array(X2); X2=X2.flatten();
amp = np.sqrt(X1[:]**2 + X2[:]**2);
pha=[]
for i in range(0,len(amp)):
pha.append(math.atan2(X2[i],X1[i]))
pha = np.array(pha)
pha = pha + (pha<0)*2*np.pi
return amp, pha
```
Open the NETCDF files and retrieve the constituents at the North. These are the ones that Kate calculated from Thomson and Huggett (1980). This data is relative to the NEMO grid rotation.
```
Us_North_amp = {}; Us_North_pha = {}
Vs_North_amp = {}; Vs_North_pha = {}
Ts_North_amp = {}; Ts_North_pha = {}
for key in consts_North:
[Us_North_amp[key], Us_North_pha[key]]= get_harmomincs(fUs_North[key],'U')
[Vs_North_amp[key], Vs_North_pha[key]]= get_harmomincs(fVs_North[key],'V')
[Ts_North_amp[key], Ts_North_pha[key]]= get_harmomincs(fTs_North[key],'T')
```
Get the tidal elevation constituents from the nearby Webtide point.
Note: Kate has the tidal elevation constituents from webtide saved in webtide_point_johnstone_strait.csv. I had to retrieve the current constituents.
To do this, I launched Webtide, created a tidal marker at the Lat/Lon from Kate's webtide point. Then I pressed "Get Harmonics" with currents selected. Webtide outputs an html file which I saved and then copied to a csv file.
The data is in:
Currents: /data/nsoontie/MEOPAR/tools/I_ForcingFiles/Tides/Webtide_Current_Constituents_North.csv
Elevation: /data/nsoontie/MEOPAR/tools/I_ForcingFiles/Tides/webtide_point_johnstone_strait.csv
```
def get_webtide_data(constituent):
# returns the phase and amplitude of a constituent from webtide. Takes into account the rotation of the grid.
# constituent is eg 'M2', 'K1', etc...
# this is based on Kate's function get_data_from_csv() in webtide_tools
# returns the T,U,V phase (radians) and amplitude for the NEMO grid (ie rotated)
# uses Kate's method of rotating the currents from webtide. See Data acquisition in docs
import pandas as pd
import math
import numpy as np
theta = math.radians(29);
webtide_curr = pd.read_csv('Webtide_Current_Constituents_North.csv',\
skiprows = 2)
webtide_curr = webtide_curr.rename(columns={'Constituent': 'const', 'Longitude': 'lon', 'Latitude': 'lat', \
'U Amplitude (m)': 'ewamp', 'U Phase (deg GMT)': 'ewpha',\
'V Amplitude (m)': 'nsamp', 'V Phase (deg GMT)': 'nspha'})
#Convert phase from north/south into grid co-ordinates (see docs/tides/tides_data_acquisition for details)
ua = webtide_curr[webtide_curr.const==(constituent)].ewamp
va = webtide_curr[webtide_curr.const==(constituent)].nsamp
uphi = math.radians(webtide_curr[webtide_curr.const==(constituent)].ewpha)
vphi = math.radians(webtide_curr[webtide_curr.const==(constituent)].nspha)
uZ1 = ua*math.cos(theta)*math.cos(uphi) - va*math.sin(theta)*math.sin(vphi)
uZ2 = ua*math.cos(theta)*math.sin(uphi) + va*math.sin(theta)*math.cos(vphi)
vZ1 = -ua*math.sin(theta)*math.cos(uphi) - va*math.cos(theta)*math.sin(vphi)
vZ2 = -ua*math.sin(theta)*math.sin(uphi) + va*math.cos(theta)*math.cos(vphi)
#Now get the phase and amplitude for U on NEMO grid
U_amp = math.sqrt(uZ1**2 +uZ2**2);
U_pha=math.atan2(uZ2,uZ1)
U_pha = U_pha + (U_pha<0)*2*np.pi;
#Now get the phase and amplitude for V on NEMO grid
V_amp = math.sqrt(vZ1**2 +vZ2**2);
V_pha=math.atan2(vZ2,vZ1)
V_pha = V_pha + (V_pha<0)*2*np.pi;
#Now get the webtide data for elevation. This is much easier since we don't have to worry about rotation.
webtide_elev = pd.read_csv('webtide_point_johnstone_strait.csv',\
skiprows = 2)
webtide_elev = webtide_elev.rename(columns={'Constituent': 'const', 'Longitude': 'lon', 'Latitude': 'lat', \
'Amplitude (m)': 'amp', 'Phase (deg GMT)': 'pha'})
T_amp = np.array(webtide_elev[webtide_elev.const==(constituent)].amp)[0]
T_pha = np.radians(np.array(webtide_elev[webtide_elev.const==(constituent)].pha)[0])
T_pha = T_pha + (T_pha<0)*2*np.pi;
return U_amp, U_pha, V_amp, V_pha, T_amp, T_pha
#Get all the webtide data
Us_web_amp={}
Us_web_pha={}
Vs_web_amp={}
Vs_web_pha={}
Ts_web_amp={}
Ts_web_pha={}
for key in consts_full:
[Us_web_amp[key], Us_web_pha[key], Vs_web_amp[key],
Vs_web_pha[key], Ts_web_amp[key], Ts_web_pha[key]] = get_webtide_data(key)
```
Check on the calculations from webtide and Northern tides by plotting.
```
#West
amp = [-20, 30, 0, 1.5]
pha = [-20, 30, 0, 360]
cols = {'M2':'r', 'K1': 'b','O1': 'm', 'S2': 'k','P1': 'g', 'N2': 'c', 'Q1': 'y', 'K2': '0.75'}
plt.figure(figsize=(18,14))
for key in consts_full:
pylab.subplot(3,2,1)
pylab.plot(Us_web_amp[key],cols[key],marker ='o',label=key + ' webtide')
pylab.title('U amp')
pylab.legend(loc=0)
pylab.subplot(3,2,2)
pylab.plot(np.degrees(Us_web_pha[key]),cols[key],marker ='o',label=key + ' webtide')
pylab.title('U pha')
pylab.legend(loc=0)
pylab.subplot(3,2,3)
pylab.plot(Vs_web_amp[key],cols[key], marker ='o',label=key + ' webtide')
pylab.title('V amp')
pylab.legend(loc=0)
pylab.subplot(3,2,4)
pylab.plot(np.degrees(Vs_web_pha[key]),cols[key], marker ='o',label=key + ' webtide')
pylab.title('V pha')
pylab.legend(loc=0)
pylab.subplot(3,2,5)
pylab.plot(Ts_web_amp[key],cols[key],marker ='o',label=key+ ' webtide')
pylab.title('T amp')
pylab.subplot(3,2,6)
pylab.plot(np.degrees(Ts_web_pha[key]),cols[key], marker ='o',label=key+ 'webtide')
pylab.title('T pha')
for key in consts_North:
pylab.subplot(3,2,1)
pylab.plot(Us_North_amp[key],cols[key],label=key + 'North')
pylab.title('U amp')
pylab.legend(loc=0)
pylab.axis(amp)
pylab.subplot(3,2,2)
pylab.plot(np.degrees(Us_North_pha[key]),cols[key],label=key + 'North')
pylab.title('U pha')
pylab.legend(loc=0)
pylab.axis(pha)
pylab.subplot(3,2,3)
pylab.plot(Vs_North_amp[key],cols[key], label=key + 'North')
pylab.title('V amp')
pylab.legend(loc=0)
pylab.axis(amp)
pylab.subplot(3,2,4)
pylab.plot(np.degrees(Vs_North_pha[key]),cols[key], label=key + 'North')
pylab.title('V pha')
pylab.legend(loc=0)
pylab.axis(pha)
pylab.subplot(3,2,5)
pylab.plot(Ts_North_amp[key],cols[key],label=key+ 'North')
pylab.title('T amp')
pylab.subplot(3,2,6)
pylab.plot(np.degrees(Ts_North_pha[key]),cols[key], label=key+ 'North')
pylab.title('T pha')
```
Now, we will see how much the amplitudes and phases have changed between webtide and our tuned values.
If the M2 tide amplitude has changed by a factor $R$, then we will assume the S2 tide ampltiude has changed by a factor $R$. So,
$\frac{M_{2 North}}{ M_{2 Webtide}} = \frac{S_{2 North}}{ S_{2 Webtide}}$.
This means
$S_{2 North} = S_{2 Webtide}\frac{M_{2 North}}{ M_{2 Webtide}}$
If the M2 tide phase has changed by $\Delta$ then we will assume that the S2 tide phase has also changed by $\Delta$. Or,
$M_{2 North} - M_{2 Webtide} = S_{2 North} - S_{2 Webtide}$.
This means
$S_{2 North} = S_{2 Webtide} + \Delta$,
where $\Delta =M_{2 North} - M_{2 Webtide}$.
```
Us_ratio_amp = {}
Vs_ratio_amp = {}
Ts_ratio_amp = {}
Us_diff_pha= {}
Vs_diff_pha = {}
Ts_diff_pha = {}
for key in consts_North: # M2 and K1
Us_ratio_amp[key] = Us_North_amp[key]/Us_web_amp[key];
Vs_ratio_amp[key] = Vs_North_amp[key]/Vs_web_amp[key];
Ts_ratio_amp[key] = Ts_North_amp[key]/Ts_web_amp[key];
Us_diff_pha[key] = Us_North_pha[key]- Us_web_pha[key];
Vs_diff_pha[key] = Vs_North_pha[key]- Vs_web_pha[key];
Ts_diff_pha[key] = Ts_North_pha[key]- Ts_web_pha[key];
print (Us_ratio_amp)
print (Us_diff_pha)
```
Compute the new Northern amplitudes and phases based on the ratios and make any fine-tuning changes here too.
```
consts_2 = {'S2': [], 'N2': []}
consts_1 = {'O1': [], 'Q1': []}
# Fine tuning corrections moved to top of notebook
# 2 tides
for key in consts_2:
Us_North_amp[key] = Us_web_amp[key]*Us_ratio_amp['M2']*amp_corr[key]
Vs_North_amp[key] = Vs_web_amp[key]*Vs_ratio_amp['M2']*amp_corr[key]
Ts_North_amp[key] = Ts_web_amp[key]*Ts_ratio_amp['M2']*amp_corr[key]
Us_North_pha[key] = Us_web_pha[key] + Us_diff_pha['M2'] + pha_corr[key]
Vs_North_pha[key] = Vs_web_pha[key] + Vs_diff_pha['M2'] + pha_corr[key]
Ts_North_pha[key] = Ts_web_pha[key] + Ts_diff_pha['M2'] + pha_corr[key]
# 1 tides
for key in consts_1:
Us_North_amp[key] = Us_web_amp[key]*Us_ratio_amp['K1']*amp_corr[key]
Vs_North_amp[key] = Vs_web_amp[key]*Vs_ratio_amp['K1']*amp_corr[key]
Ts_North_amp[key] = Ts_web_amp[key]*Ts_ratio_amp['K1']*amp_corr[key]
Us_North_pha[key] = Us_web_pha[key] + Us_diff_pha['K1'] + pha_corr[key]
Vs_North_pha[key] = Vs_web_pha[key] + Vs_diff_pha['K1'] + pha_corr[key]
Ts_North_pha[key] = Ts_web_pha[key] + Ts_diff_pha['K1'] + pha_corr[key]
# can't resolve K2, fix these
Us_North_amp['K2'] = Us_North_amp['S2'] * 0.28; Vs_North_amp['K2'] = Vs_North_amp['S2'] * 0.28
Ts_North_amp['K2'] = Ts_North_amp['S2'] * 0.28
Us_North_pha['K2'] = Us_North_pha['S2']-7*np.pi/180.; Vs_North_pha['K2'] = Vs_North_pha['S2']-7*np.pi/180.;
Ts_North_pha['K2'] = Ts_North_pha['S2']-7*np.pi/180.
# can't resolve P1, fix these
Us_North_amp['P1'] = Us_North_amp['K1'] * 0.306; Vs_North_amp['P1'] = Vs_North_amp['K1'] * 0.306
Ts_North_amp['P1'] = Ts_North_amp['K1'] * 0.306
Us_North_pha['P1'] = Us_North_pha['K1']-3*np.pi/180.; Vs_North_pha['P1'] = Vs_North_pha['K1']-3*np.pi/180.;
Ts_North_pha['P1'] = Ts_North_pha['K1']-3*np.pi/180.
```
Plot the results to check.
```
cols = {'M2':'r', 'K1': 'b','O1': 'm', 'S2': 'k','P1': 'g', 'N2': 'c', 'Q1': 'y', 'K2': '0.75'}
plt.figure(figsize=(14,10))
for key in consts_full:
pylab.subplot(3,2,1)
pylab.plot(Us_North_amp[key],cols[key],label=key)
pylab.title('U amp')
pylab.legend(loc=0)
pylab.subplot(3,2,2)
pylab.plot(np.degrees(Us_North_pha[key]),cols[key],label=key)
pylab.title('U pha')
pylab.legend(loc=0)
pylab.subplot(3,2,3)
pylab.plot(Vs_North_amp[key],cols[key],label=key)
pylab.title('V amp')
pylab.legend(loc=0)
pylab.subplot(3,2,4)
pylab.plot(np.degrees(Vs_North_pha[key]),cols[key],label=key)
pylab.title('V pha')
pylab.legend(loc=0)
pylab.subplot(3,2,5)
pylab.plot(Ts_North_amp[key],cols[key],label=key)
pylab.title('T amp')
pylab.legend(loc=0)
pylab.subplot(3,2,6)
pylab.plot(np.degrees(Ts_North_pha[key]),cols[key],label=key)
pylab.title('T pha')
pylab.legend(loc=0)
```
Now convert to the form that NEMO likes:
$Z_1 = A\cos(\phi)$ and $Z_2=A\sin(\phi)$
```
U1s = {}
U2s = {}
V1s = {}
V2s = {}
T1s = {}
T2s = {}
for key in consts_full:
U1s[key] = Us_North_amp[key]*np.cos(Us_North_pha[key]); X=np.array(U1s[key]); U1s[key]=np.reshape(X,(len(X),1))
U2s[key] = Us_North_amp[key]*np.sin(Us_North_pha[key]); X=np.array(U2s[key]); U2s[key]=np.reshape(X,(len(X),1))
V1s[key] = Vs_North_amp[key]*np.cos(Vs_North_pha[key]); X=np.array(V1s[key]); V1s[key]=np.reshape(X,(len(X),1))
V2s[key] = Vs_North_amp[key]*np.sin(Vs_North_pha[key]); X=np.array(V2s[key]); V2s[key]=np.reshape(X,(len(X),1))
T1s[key] = Ts_North_amp[key]*np.cos(Ts_North_pha[key]); X=np.array(T1s[key]); T1s[key]=np.reshape(X,(len(X),1))
T2s[key] = Ts_North_amp[key]*np.sin(Ts_North_pha[key]); X=np.array(T2s[key]); T2s[key]=np.reshape(X,(len(X),1))
```
Check with a plot
```
cols = {'M2':'r', 'K1': 'b','O1': 'm', 'S2': 'k','P1': 'g', 'N2': 'c', 'Q1': 'y', 'K2': '0.75'}
plt.figure(figsize=(14,10))
for key in consts_full:
pylab.subplot(3,2,1)
pylab.plot(U1s[key],cols[key],label=key)
pylab.title('U1')
pylab.legend(loc=0)
pylab.subplot(3,2,2)
pylab.plot(U2s[key],cols[key],label=key)
pylab.title('U2')
pylab.legend(loc=0)
pylab.subplot(3,2,3)
pylab.plot(V1s[key],cols[key],label=key)
pylab.title('V1')
pylab.legend(loc=0)
pylab.subplot(3,2,4)
pylab.plot(V2s[key],cols[key],label=key)
pylab.title('V2')
pylab.legend(loc=0)
pylab.subplot(3,2,5)
pylab.plot(T1s[key],cols[key],label=key)
pylab.title('T1')
pylab.legend(loc=0)
pylab.subplot(3,2,6)
pylab.plot(T2s[key],cols[key],label=key)
pylab.title('T2')
pylab.legend(loc=0)
```
Save N2, P1, Q1, K2 and the U/V components of O1, S2
```
#reload(webtide_tools)
#wait.... what about the U and V being on different grids?
#.... nothing really changes because we don't have great spatial resolution of measurements...
#... perhaps we'll need to make an extra cell for the V grid....
#currents
print (X.shape)
saves={'S2': [], 'O1': [], 'N2': [], 'P1': [], 'Q1': [], 'K2': []}
for key in saves:
webtide_tools.create_northern_tides_contd(U1s[key],U2s[key],'U',key,code, name='SalishSea')
webtide_tools.create_northern_tides_contd(V1s[key],V2s[key],'V',key,code, name='SalishSea')
webtide_tools.create_northern_tides_contd(T1s[key][0,0],T2s[key][0,0],'T',key,code, name='SalishSea')
```
Now that the files are created, I will copy them over to NEMO-forcing and commit.
|
github_jupyter
|
%matplotlib inline
from matplotlib import pylab
import matplotlib.pyplot as plt
import netCDF4 as NC
import numpy as np
from math import cos, sin, tan, radians
import math
import webtide_tools
TSin = {'North': {'M2': {'Amp': 1.2468500142849095, 'Pha': 5.8718032013900494}, 'Q1': {'Amp': 0.88018411744300051, 'Pha': 3.3676909436466511}, 'O1': {'Amp': 0.92187588787164776, 'Pha': -1.8419422569093058}, 'S2': {'Amp': 0.98646859951016619, 'Pha': -10.363961743466264}, 'K1': {'Amp': 1.056369887585026, 'Pha': -7.2574882761515624}, 'N2': {'Amp': 0.95930333678587432, 'Pha': -6.8740655239509989}}, 'West': {'M2': {'Amp': 0.8840061749307605, 'Pha': -7.8587198373167935}, 'Q1': {'Amp': 0.95936152535045738, 'Pha': 1.1445537519586795}, 'O1': {'Amp': 1.058133345863022, 'Pha': 0.92064288566727737}, 'S2': {'Amp': 1.0232932221404019, 'Pha': 0.7966194737248522}, 'K1': {'Amp': 1.0168859739167362, 'Pha': -3.8356999030330829}, 'N2': {'Amp': 1.0027750731988296, 'Pha': 2.5899670236940464}}}
# These are the corrections to be used.
code = 'N36_AF'
# Fine tuning corrections, note that these are relative to M2/K1 P1 and K2 calculated as fixed ratios (see below)
amp_corr = {
'O1': TSin['North']['O1']['Amp'],
'S2': TSin['North']['S2']['Amp'],
'P1': 0.,
'N2': TSin['North']['N2']['Amp'],
'Q1': TSin['North']['Q1']['Amp'],
'K2': 0.}
pha_corr = {
'O1': np.radians(TSin['North']['O1']['Pha']),
'S2': np.radians(TSin['North']['S2']['Pha']),
'P1': 0.*np.pi/180.,
'N2': np.radians(TSin['North']['N2']['Pha']),
'Q1': np.radians(TSin['North']['Q1']['Pha']),
'K2': 0.*np.pi/180.0}
def get_files(constituent,code):
#returns the U, V, T netcdf handles for the tidal constiruents that Kate created for the northern boundary
#constituent = 'O1', 'M2', etc
filename = 'SalishSea_'+code+'_North_tide_' + constituent
fU=NC.Dataset(filename + '_grid_U.nc', 'r')
fV=NC.Dataset(filename + '_grid_V.nc', 'r')
fT=NC.Dataset(filename + '_grid_T.nc', 'r')
return fU, fV, fT
consts_full= {'M2': [], 'K1': [], 'O1': [], 'S2': [], 'N2': [], 'P1': [], 'Q1': [], 'K2': []}
consts_North= {'M2': [], 'K1': []}
fUs_North={}
fVs_North={}
fTs_North={}
for key in consts_North:
[fUs_North[key], fVs_North[key],fTs_North[key]]= get_files(key,code)
def get_harmomincs(f, comp):
#returns the harmonics as vecotors
#f is the nertcdf handle
#comp is the component ('U','V','T')
import numpy as np
import math
if comp=='U':
x1='u1'; x2='u2';
elif comp == 'V':
x1='v1'; x2='v2';
elif comp == 'T':
x1='z1'; x2='z2';
X1=f.variables[x1]; X1=np.array(X1); X1=X1.flatten();
X2=f.variables[x2]; X2=np.array(X2); X2=X2.flatten();
amp = np.sqrt(X1[:]**2 + X2[:]**2);
pha=[]
for i in range(0,len(amp)):
pha.append(math.atan2(X2[i],X1[i]))
pha = np.array(pha)
pha = pha + (pha<0)*2*np.pi
return amp, pha
Us_North_amp = {}; Us_North_pha = {}
Vs_North_amp = {}; Vs_North_pha = {}
Ts_North_amp = {}; Ts_North_pha = {}
for key in consts_North:
[Us_North_amp[key], Us_North_pha[key]]= get_harmomincs(fUs_North[key],'U')
[Vs_North_amp[key], Vs_North_pha[key]]= get_harmomincs(fVs_North[key],'V')
[Ts_North_amp[key], Ts_North_pha[key]]= get_harmomincs(fTs_North[key],'T')
def get_webtide_data(constituent):
# returns the phase and amplitude of a constituent from webtide. Takes into account the rotation of the grid.
# constituent is eg 'M2', 'K1', etc...
# this is based on Kate's function get_data_from_csv() in webtide_tools
# returns the T,U,V phase (radians) and amplitude for the NEMO grid (ie rotated)
# uses Kate's method of rotating the currents from webtide. See Data acquisition in docs
import pandas as pd
import math
import numpy as np
theta = math.radians(29);
webtide_curr = pd.read_csv('Webtide_Current_Constituents_North.csv',\
skiprows = 2)
webtide_curr = webtide_curr.rename(columns={'Constituent': 'const', 'Longitude': 'lon', 'Latitude': 'lat', \
'U Amplitude (m)': 'ewamp', 'U Phase (deg GMT)': 'ewpha',\
'V Amplitude (m)': 'nsamp', 'V Phase (deg GMT)': 'nspha'})
#Convert phase from north/south into grid co-ordinates (see docs/tides/tides_data_acquisition for details)
ua = webtide_curr[webtide_curr.const==(constituent)].ewamp
va = webtide_curr[webtide_curr.const==(constituent)].nsamp
uphi = math.radians(webtide_curr[webtide_curr.const==(constituent)].ewpha)
vphi = math.radians(webtide_curr[webtide_curr.const==(constituent)].nspha)
uZ1 = ua*math.cos(theta)*math.cos(uphi) - va*math.sin(theta)*math.sin(vphi)
uZ2 = ua*math.cos(theta)*math.sin(uphi) + va*math.sin(theta)*math.cos(vphi)
vZ1 = -ua*math.sin(theta)*math.cos(uphi) - va*math.cos(theta)*math.sin(vphi)
vZ2 = -ua*math.sin(theta)*math.sin(uphi) + va*math.cos(theta)*math.cos(vphi)
#Now get the phase and amplitude for U on NEMO grid
U_amp = math.sqrt(uZ1**2 +uZ2**2);
U_pha=math.atan2(uZ2,uZ1)
U_pha = U_pha + (U_pha<0)*2*np.pi;
#Now get the phase and amplitude for V on NEMO grid
V_amp = math.sqrt(vZ1**2 +vZ2**2);
V_pha=math.atan2(vZ2,vZ1)
V_pha = V_pha + (V_pha<0)*2*np.pi;
#Now get the webtide data for elevation. This is much easier since we don't have to worry about rotation.
webtide_elev = pd.read_csv('webtide_point_johnstone_strait.csv',\
skiprows = 2)
webtide_elev = webtide_elev.rename(columns={'Constituent': 'const', 'Longitude': 'lon', 'Latitude': 'lat', \
'Amplitude (m)': 'amp', 'Phase (deg GMT)': 'pha'})
T_amp = np.array(webtide_elev[webtide_elev.const==(constituent)].amp)[0]
T_pha = np.radians(np.array(webtide_elev[webtide_elev.const==(constituent)].pha)[0])
T_pha = T_pha + (T_pha<0)*2*np.pi;
return U_amp, U_pha, V_amp, V_pha, T_amp, T_pha
#Get all the webtide data
Us_web_amp={}
Us_web_pha={}
Vs_web_amp={}
Vs_web_pha={}
Ts_web_amp={}
Ts_web_pha={}
for key in consts_full:
[Us_web_amp[key], Us_web_pha[key], Vs_web_amp[key],
Vs_web_pha[key], Ts_web_amp[key], Ts_web_pha[key]] = get_webtide_data(key)
#West
amp = [-20, 30, 0, 1.5]
pha = [-20, 30, 0, 360]
cols = {'M2':'r', 'K1': 'b','O1': 'm', 'S2': 'k','P1': 'g', 'N2': 'c', 'Q1': 'y', 'K2': '0.75'}
plt.figure(figsize=(18,14))
for key in consts_full:
pylab.subplot(3,2,1)
pylab.plot(Us_web_amp[key],cols[key],marker ='o',label=key + ' webtide')
pylab.title('U amp')
pylab.legend(loc=0)
pylab.subplot(3,2,2)
pylab.plot(np.degrees(Us_web_pha[key]),cols[key],marker ='o',label=key + ' webtide')
pylab.title('U pha')
pylab.legend(loc=0)
pylab.subplot(3,2,3)
pylab.plot(Vs_web_amp[key],cols[key], marker ='o',label=key + ' webtide')
pylab.title('V amp')
pylab.legend(loc=0)
pylab.subplot(3,2,4)
pylab.plot(np.degrees(Vs_web_pha[key]),cols[key], marker ='o',label=key + ' webtide')
pylab.title('V pha')
pylab.legend(loc=0)
pylab.subplot(3,2,5)
pylab.plot(Ts_web_amp[key],cols[key],marker ='o',label=key+ ' webtide')
pylab.title('T amp')
pylab.subplot(3,2,6)
pylab.plot(np.degrees(Ts_web_pha[key]),cols[key], marker ='o',label=key+ 'webtide')
pylab.title('T pha')
for key in consts_North:
pylab.subplot(3,2,1)
pylab.plot(Us_North_amp[key],cols[key],label=key + 'North')
pylab.title('U amp')
pylab.legend(loc=0)
pylab.axis(amp)
pylab.subplot(3,2,2)
pylab.plot(np.degrees(Us_North_pha[key]),cols[key],label=key + 'North')
pylab.title('U pha')
pylab.legend(loc=0)
pylab.axis(pha)
pylab.subplot(3,2,3)
pylab.plot(Vs_North_amp[key],cols[key], label=key + 'North')
pylab.title('V amp')
pylab.legend(loc=0)
pylab.axis(amp)
pylab.subplot(3,2,4)
pylab.plot(np.degrees(Vs_North_pha[key]),cols[key], label=key + 'North')
pylab.title('V pha')
pylab.legend(loc=0)
pylab.axis(pha)
pylab.subplot(3,2,5)
pylab.plot(Ts_North_amp[key],cols[key],label=key+ 'North')
pylab.title('T amp')
pylab.subplot(3,2,6)
pylab.plot(np.degrees(Ts_North_pha[key]),cols[key], label=key+ 'North')
pylab.title('T pha')
Us_ratio_amp = {}
Vs_ratio_amp = {}
Ts_ratio_amp = {}
Us_diff_pha= {}
Vs_diff_pha = {}
Ts_diff_pha = {}
for key in consts_North: # M2 and K1
Us_ratio_amp[key] = Us_North_amp[key]/Us_web_amp[key];
Vs_ratio_amp[key] = Vs_North_amp[key]/Vs_web_amp[key];
Ts_ratio_amp[key] = Ts_North_amp[key]/Ts_web_amp[key];
Us_diff_pha[key] = Us_North_pha[key]- Us_web_pha[key];
Vs_diff_pha[key] = Vs_North_pha[key]- Vs_web_pha[key];
Ts_diff_pha[key] = Ts_North_pha[key]- Ts_web_pha[key];
print (Us_ratio_amp)
print (Us_diff_pha)
consts_2 = {'S2': [], 'N2': []}
consts_1 = {'O1': [], 'Q1': []}
# Fine tuning corrections moved to top of notebook
# 2 tides
for key in consts_2:
Us_North_amp[key] = Us_web_amp[key]*Us_ratio_amp['M2']*amp_corr[key]
Vs_North_amp[key] = Vs_web_amp[key]*Vs_ratio_amp['M2']*amp_corr[key]
Ts_North_amp[key] = Ts_web_amp[key]*Ts_ratio_amp['M2']*amp_corr[key]
Us_North_pha[key] = Us_web_pha[key] + Us_diff_pha['M2'] + pha_corr[key]
Vs_North_pha[key] = Vs_web_pha[key] + Vs_diff_pha['M2'] + pha_corr[key]
Ts_North_pha[key] = Ts_web_pha[key] + Ts_diff_pha['M2'] + pha_corr[key]
# 1 tides
for key in consts_1:
Us_North_amp[key] = Us_web_amp[key]*Us_ratio_amp['K1']*amp_corr[key]
Vs_North_amp[key] = Vs_web_amp[key]*Vs_ratio_amp['K1']*amp_corr[key]
Ts_North_amp[key] = Ts_web_amp[key]*Ts_ratio_amp['K1']*amp_corr[key]
Us_North_pha[key] = Us_web_pha[key] + Us_diff_pha['K1'] + pha_corr[key]
Vs_North_pha[key] = Vs_web_pha[key] + Vs_diff_pha['K1'] + pha_corr[key]
Ts_North_pha[key] = Ts_web_pha[key] + Ts_diff_pha['K1'] + pha_corr[key]
# can't resolve K2, fix these
Us_North_amp['K2'] = Us_North_amp['S2'] * 0.28; Vs_North_amp['K2'] = Vs_North_amp['S2'] * 0.28
Ts_North_amp['K2'] = Ts_North_amp['S2'] * 0.28
Us_North_pha['K2'] = Us_North_pha['S2']-7*np.pi/180.; Vs_North_pha['K2'] = Vs_North_pha['S2']-7*np.pi/180.;
Ts_North_pha['K2'] = Ts_North_pha['S2']-7*np.pi/180.
# can't resolve P1, fix these
Us_North_amp['P1'] = Us_North_amp['K1'] * 0.306; Vs_North_amp['P1'] = Vs_North_amp['K1'] * 0.306
Ts_North_amp['P1'] = Ts_North_amp['K1'] * 0.306
Us_North_pha['P1'] = Us_North_pha['K1']-3*np.pi/180.; Vs_North_pha['P1'] = Vs_North_pha['K1']-3*np.pi/180.;
Ts_North_pha['P1'] = Ts_North_pha['K1']-3*np.pi/180.
cols = {'M2':'r', 'K1': 'b','O1': 'm', 'S2': 'k','P1': 'g', 'N2': 'c', 'Q1': 'y', 'K2': '0.75'}
plt.figure(figsize=(14,10))
for key in consts_full:
pylab.subplot(3,2,1)
pylab.plot(Us_North_amp[key],cols[key],label=key)
pylab.title('U amp')
pylab.legend(loc=0)
pylab.subplot(3,2,2)
pylab.plot(np.degrees(Us_North_pha[key]),cols[key],label=key)
pylab.title('U pha')
pylab.legend(loc=0)
pylab.subplot(3,2,3)
pylab.plot(Vs_North_amp[key],cols[key],label=key)
pylab.title('V amp')
pylab.legend(loc=0)
pylab.subplot(3,2,4)
pylab.plot(np.degrees(Vs_North_pha[key]),cols[key],label=key)
pylab.title('V pha')
pylab.legend(loc=0)
pylab.subplot(3,2,5)
pylab.plot(Ts_North_amp[key],cols[key],label=key)
pylab.title('T amp')
pylab.legend(loc=0)
pylab.subplot(3,2,6)
pylab.plot(np.degrees(Ts_North_pha[key]),cols[key],label=key)
pylab.title('T pha')
pylab.legend(loc=0)
U1s = {}
U2s = {}
V1s = {}
V2s = {}
T1s = {}
T2s = {}
for key in consts_full:
U1s[key] = Us_North_amp[key]*np.cos(Us_North_pha[key]); X=np.array(U1s[key]); U1s[key]=np.reshape(X,(len(X),1))
U2s[key] = Us_North_amp[key]*np.sin(Us_North_pha[key]); X=np.array(U2s[key]); U2s[key]=np.reshape(X,(len(X),1))
V1s[key] = Vs_North_amp[key]*np.cos(Vs_North_pha[key]); X=np.array(V1s[key]); V1s[key]=np.reshape(X,(len(X),1))
V2s[key] = Vs_North_amp[key]*np.sin(Vs_North_pha[key]); X=np.array(V2s[key]); V2s[key]=np.reshape(X,(len(X),1))
T1s[key] = Ts_North_amp[key]*np.cos(Ts_North_pha[key]); X=np.array(T1s[key]); T1s[key]=np.reshape(X,(len(X),1))
T2s[key] = Ts_North_amp[key]*np.sin(Ts_North_pha[key]); X=np.array(T2s[key]); T2s[key]=np.reshape(X,(len(X),1))
cols = {'M2':'r', 'K1': 'b','O1': 'm', 'S2': 'k','P1': 'g', 'N2': 'c', 'Q1': 'y', 'K2': '0.75'}
plt.figure(figsize=(14,10))
for key in consts_full:
pylab.subplot(3,2,1)
pylab.plot(U1s[key],cols[key],label=key)
pylab.title('U1')
pylab.legend(loc=0)
pylab.subplot(3,2,2)
pylab.plot(U2s[key],cols[key],label=key)
pylab.title('U2')
pylab.legend(loc=0)
pylab.subplot(3,2,3)
pylab.plot(V1s[key],cols[key],label=key)
pylab.title('V1')
pylab.legend(loc=0)
pylab.subplot(3,2,4)
pylab.plot(V2s[key],cols[key],label=key)
pylab.title('V2')
pylab.legend(loc=0)
pylab.subplot(3,2,5)
pylab.plot(T1s[key],cols[key],label=key)
pylab.title('T1')
pylab.legend(loc=0)
pylab.subplot(3,2,6)
pylab.plot(T2s[key],cols[key],label=key)
pylab.title('T2')
pylab.legend(loc=0)
#reload(webtide_tools)
#wait.... what about the U and V being on different grids?
#.... nothing really changes because we don't have great spatial resolution of measurements...
#... perhaps we'll need to make an extra cell for the V grid....
#currents
print (X.shape)
saves={'S2': [], 'O1': [], 'N2': [], 'P1': [], 'Q1': [], 'K2': []}
for key in saves:
webtide_tools.create_northern_tides_contd(U1s[key],U2s[key],'U',key,code, name='SalishSea')
webtide_tools.create_northern_tides_contd(V1s[key],V2s[key],'V',key,code, name='SalishSea')
webtide_tools.create_northern_tides_contd(T1s[key][0,0],T2s[key][0,0],'T',key,code, name='SalishSea')
| 0.513668 | 0.870377 |
# 优化与深度学习
本节将讨论优化与深度学习的关系,以及优化在深度学习中的挑战。在一个深度学习问题中,我们通常会预先定义一个损失函数。有了损失函数以后,我们就可以使用优化算法试图将其最小化。在优化中,这样的损失函数通常被称作优化问题的目标函数(objective function)。依据惯例,优化算法通常只考虑最小化目标函数。其实,任何最大化问题都可以很容易地转化为最小化问题,只需令目标函数的相反数为新的目标函数即可。
## 优化与深度学习的关系
虽然优化为深度学习提供了最小化损失函数的方法,但本质上,优化与深度学习的目标是有区别的。
在[“模型选择、欠拟合和过拟合”](../chapter_deep-learning-basics/underfit-overfit.ipynb)一节中,我们区分了训练误差和泛化误差。
由于优化算法的目标函数通常是一个基于训练数据集的损失函数,优化的目标在于降低训练误差。
而深度学习的目标在于降低泛化误差。为了降低泛化误差,除了使用优化算法降低训练误差以外,还需要注意应对过拟合。
本章中,我们只关注优化算法在最小化目标函数上的表现,而不关注模型的泛化误差。
## 优化在深度学习中的挑战
我们在[“线性回归”](../chapter_deep-learning-basics/linear-regression.ipynb)一节中对优化问题的解析解和数值解做了区分。深度学习中绝大多数目标函数都很复杂。因此,很多优化问题并不存在解析解,而需要使用基于数值方法的优化算法找到近似解,即数值解。本书中讨论的优化算法都是这类基于数值方法的算法。为了求得最小化目标函数的数值解,我们将通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。
优化在深度学习中有很多挑战。下面描述了其中的两个挑战,即局部最小值和鞍点。为了更好地描述问题,我们先导入本节中实验需要的包或模块。
```
%matplotlib inline
import d2lzh as d2l
from mpl_toolkits import mplot3d
import numpy as np
```
### 局部最小值
对于目标函数$f(x)$,如果$f(x)$在$x$上的值比在$x$邻近的其他点的值更小,那么$f(x)$可能是一个局部最小值(local minimum)。如果$f(x)$在$x$上的值是目标函数在整个定义域上的最小值,那么$f(x)$是全局最小值(global minimum)。
举个例子,给定函数
$$f(x) = x \cdot \text{cos}(\pi x), \qquad -1.0 \leq x \leq 2.0,$$
我们可以大致找出该函数的局部最小值和全局最小值的位置。需要注意的是,图中箭头所指示的只是大致位置。
```
def f(x):
return x * np.cos(np.pi * x)
d2l.set_figsize((4.5, 2.5))
x = np.arange(-1.0, 2.0, 0.1)
fig, = d2l.plt.plot(x, f(x)) # 逗号表示只取返回列表中的第一个元素
fig.axes.annotate('local minimum', xy=(-0.3, -0.25), xytext=(-0.77, -1.0),
arrowprops=dict(arrowstyle='->'))
fig.axes.annotate('global minimum', xy=(1.1, -0.95), xytext=(0.6, 0.8),
arrowprops=dict(arrowstyle='->'))
d2l.plt.xlabel('x')
d2l.plt.ylabel('f(x)');
```
深度学习模型的目标函数可能有若干局部最优值。当一个优化问题的数值解在局部最优解附近时,由于目标函数有关解的梯度接近或变成0,最终迭代求得的数值解可能只令目标函数局部最小化而非全局最小化。
### 鞍点
刚刚我们提到,梯度接近或变成0可能是由于当前解在局部最优解附近造成的。事实上,另一种可能性是当前解在鞍点(saddle point)附近。
举个例子,给定函数
$$f(x) = x^3,$$
我们可以找出该函数的鞍点位置。
```
x = np.arange(-2.0, 2.0, 0.1)
fig, = d2l.plt.plot(x, x**3)
fig.axes.annotate('saddle point', xy=(0, -0.2), xytext=(-0.52, -5.0),
arrowprops=dict(arrowstyle='->'))
d2l.plt.xlabel('x')
d2l.plt.ylabel('f(x)');
```
再举个定义在二维空间的函数的例子,例如:
$$f(x, y) = x^2 - y^2.$$
我们可以找出该函数的鞍点位置。也许你已经发现了,该函数看起来像一个马鞍,而鞍点恰好是马鞍上可坐区域的中心。
```
x, y = np.mgrid[-1: 1: 31j, -1: 1: 31j]
z = x**2 - y**2
ax = d2l.plt.figure().add_subplot(111, projection='3d')
ax.plot_wireframe(x, y, z, **{'rstride': 2, 'cstride': 2})
ax.plot([0], [0], [0], 'rx')
ticks = [-1, 0, 1]
d2l.plt.xticks(ticks)
d2l.plt.yticks(ticks)
ax.set_zticks(ticks)
d2l.plt.xlabel('x')
d2l.plt.ylabel('y');
```
在图的鞍点位置,目标函数在$x$轴方向上是局部最小值,但在$y$轴方向上是局部最大值。
假设一个函数的输入为$k$维向量,输出为标量,那么它的海森矩阵(Hessian matrix)有$k$个特征值(参见附录中[“数学基础”](../chapter_appendix/math.ipynb)一节)。该函数在梯度为0的位置上可能是局部最小值、局部最大值或者鞍点:
* 当函数的海森矩阵在梯度为0的位置上的特征值全为正时,该函数得到局部最小值。
* 当函数的海森矩阵在梯度为0的位置上的特征值全为负时,该函数得到局部最大值。
* 当函数的海森矩阵在梯度为0的位置上的特征值有正有负时,该函数得到鞍点。
随机矩阵理论告诉我们,对于一个大的高斯随机矩阵来说,任一特征值是正或者是负的概率都是0.5 [1]。那么,以上第一种情况的概率为 $0.5^k$。由于深度学习模型参数通常都是高维的($k$很大),目标函数的鞍点通常比局部最小值更常见。
在深度学习中,虽然找到目标函数的全局最优解很难,但这并非必要。我们将在本章接下来的几节中逐一介绍深度学习中常用的优化算法,它们在很多实际问题中都能够训练出十分有效的深度学习模型。
## 小结
* 由于优化算法的目标函数通常是一个基于训练数据集的损失函数,优化的目标在于降低训练误差。
* 由于深度学习模型参数通常都是高维的,目标函数的鞍点通常比局部最小值更常见。
## 练习
* 对于深度学习中的优化问题,你还能想到哪些其他的挑战?
## 参考文献
[1] Wigner, E. P. (1958). On the distribution of the roots of certain symmetric matrices. Annals of Mathematics, 325-327.
## 扫码直达[讨论区](https://discuss.gluon.ai/t/topic/1876)

|
github_jupyter
|
%matplotlib inline
import d2lzh as d2l
from mpl_toolkits import mplot3d
import numpy as np
def f(x):
return x * np.cos(np.pi * x)
d2l.set_figsize((4.5, 2.5))
x = np.arange(-1.0, 2.0, 0.1)
fig, = d2l.plt.plot(x, f(x)) # 逗号表示只取返回列表中的第一个元素
fig.axes.annotate('local minimum', xy=(-0.3, -0.25), xytext=(-0.77, -1.0),
arrowprops=dict(arrowstyle='->'))
fig.axes.annotate('global minimum', xy=(1.1, -0.95), xytext=(0.6, 0.8),
arrowprops=dict(arrowstyle='->'))
d2l.plt.xlabel('x')
d2l.plt.ylabel('f(x)');
x = np.arange(-2.0, 2.0, 0.1)
fig, = d2l.plt.plot(x, x**3)
fig.axes.annotate('saddle point', xy=(0, -0.2), xytext=(-0.52, -5.0),
arrowprops=dict(arrowstyle='->'))
d2l.plt.xlabel('x')
d2l.plt.ylabel('f(x)');
x, y = np.mgrid[-1: 1: 31j, -1: 1: 31j]
z = x**2 - y**2
ax = d2l.plt.figure().add_subplot(111, projection='3d')
ax.plot_wireframe(x, y, z, **{'rstride': 2, 'cstride': 2})
ax.plot([0], [0], [0], 'rx')
ticks = [-1, 0, 1]
d2l.plt.xticks(ticks)
d2l.plt.yticks(ticks)
ax.set_zticks(ticks)
d2l.plt.xlabel('x')
d2l.plt.ylabel('y');
| 0.437583 | 0.985963 |
# LeNet Lab

Source: Yan LeCun
## Load Data
Load the MNIST data, which comes pre-loaded with TensorFlow.
You do not need to modify this section.
```
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", reshape=False)
X_train, y_train = mnist.train.images, mnist.train.labels
X_validation, y_validation = mnist.validation.images, mnist.validation.labels
X_test, y_test = mnist.test.images, mnist.test.labels
assert(len(X_train) == len(y_train))
assert(len(X_validation) == len(y_validation))
assert(len(X_test) == len(y_test))
print()
print("Image Shape: {}".format(X_train[0].shape))
print()
print("Training Set: {} samples".format(len(X_train)))
print("Validation Set: {} samples".format(len(X_validation)))
print("Test Set: {} samples".format(len(X_test)))
```
The MNIST data that TensorFlow pre-loads comes as 28x28x1 images.
However, the LeNet architecture only accepts 32x32xC images, where C is the number of color channels.
In order to reformat the MNIST data into a shape that LeNet will accept, we pad the data with two rows of zeros on the top and bottom, and two columns of zeros on the left and right (28+2+2 = 32).
You do not need to modify this section.
```
import numpy as np
# Pad images with 0s
X_train = np.pad(X_train, ((0,0),(2,2),(2,2),(0,0)), 'constant')
X_validation = np.pad(X_validation, ((0,0),(2,2),(2,2),(0,0)), 'constant')
X_test = np.pad(X_test, ((0,0),(2,2),(2,2),(0,0)), 'constant')
print("Updated Image Shape: {}".format(X_train[0].shape))
```
## Visualize Data
View a sample from the dataset.
You do not need to modify this section.
```
import random
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
index = random.randint(0, len(X_train))
image = X_train[index].squeeze()
plt.figure(figsize=(1,1))
plt.imshow(image, cmap="gray")
print(y_train[index])
```
## Preprocess Data
Shuffle the training data.
You do not need to modify this section.
```
from sklearn.utils import shuffle
X_train, y_train = shuffle(X_train, y_train)
```
## Setup TensorFlow
The `EPOCH` and `BATCH_SIZE` values affect the training speed and model accuracy.
You do not need to modify this section.
```
import tensorflow as tf
EPOCHS = 10
BATCH_SIZE = 128
```
## TODO: Implement LeNet-5
Implement the [LeNet-5](http://yann.lecun.com/exdb/lenet/) neural network architecture.
This is the only cell you need to edit.
### Input
The LeNet architecture accepts a 32x32xC image as input, where C is the number of color channels. Since MNIST images are grayscale, C is 1 in this case.
### Architecture
**Layer 1: Convolutional.** The output shape should be 28x28x6.
**Activation.** Your choice of activation function.
**Pooling.** The output shape should be 14x14x6.
**Layer 2: Convolutional.** The output shape should be 10x10x16.
**Activation.** Your choice of activation function.
**Pooling.** The output shape should be 5x5x16.
**Flatten.** Flatten the output shape of the final pooling layer such that it's 1D instead of 3D. The easiest way to do is by using `tf.contrib.layers.flatten`, which is already imported for you.
**Layer 3: Fully Connected.** This should have 120 outputs.
**Activation.** Your choice of activation function.
**Layer 4: Fully Connected.** This should have 84 outputs.
**Activation.** Your choice of activation function.
**Layer 5: Fully Connected (Logits).** This should have 10 outputs.
### Output
Return the result of the 2nd fully connected layer.
```
def get_weights_biases(mu, sigma):
weights = {
'wc1' : tf.Variable(tf.truncated_normal([5, 5, 1, 6], mu, sigma)),
'wc2' : tf.Variable(tf.truncated_normal([5, 5, 6, 16], mu, sigma)),
'wd1' : tf.Variable(tf.truncated_normal([400, 120], mu, sigma)),
'wd2' : tf.Variable(tf.truncated_normal([120, 84], mu, sigma)),
'out' : tf.Variable(tf.truncated_normal([84, 10], mu, sigma))
}
biases = {
'bc1' : tf.Variable(tf.truncated_normal([6], mu, sigma)),
'bc2' : tf.Variable(tf.truncated_normal([16], mu, sigma)),
'bd1' : tf.Variable(tf.truncated_normal([120], mu, sigma)),
'bd2' : tf.Variable(tf.truncated_normal([84], mu, sigma)),
'out' : tf.Variable(tf.truncated_normal([10], mu, sigma))
}
return weights, biases
def conv2d(x, W, b, strides=1):
conv = tf.nn.conv2d(x, W, strides=[1, strides, strides, 1], padding='VALID')
conv = tf.nn.bias_add(conv, b)
return tf.nn.relu(conv)
def maxpooling2D(x, k=2):
return tf.nn.max_pool(x,
ksize=[1, k, k, 1],
strides=[1, k, k, 1],
padding="SAME")
from tensorflow.contrib.layers import flatten
def LeNet(x):
# Arguments used for tf.truncated_normal, randomly defines variables for the weights and biases for each layer
mu = 0
sigma = 0.1
weights, biases = get_weights_biases(mu, sigma)
# TODO: Layer 1: Convolutional. Input = 32x32x1. Output = 28x28x6.
# TODO: Activation.
conv1 = conv2d(x, weights['wc1'], biases['bc1'])
#print(conv1.get_shape().as_list())
# TODO: Pooling. Input = 28x28x6. Output = 14x14x6.
conv1 = maxpooling2D(conv1)
print(conv1.get_shape().as_list())
# TODO: Layer 2: Convolutional. Output = 10x10x16.
# TODO: Activation.
conv2 = conv2d(conv1, weights['wc2'], biases['bc2'])
#print(conv2.get_shape().as_list())
# TODO: Pooling. Input = 10x10x16. Output = 5x5x16.
conv2 = maxpooling2D(conv2)
#print(conv2.get_shape().as_list())
# TODO: Flatten. Input = 5x5x16. Output = 400.
f_conv2 = flatten(conv2)
print(f_conv2.get_shape().as_list())
# TODO: Layer 3: Fully Connected. Input = 400. Output = 120.
fc1 = tf.add(tf.matmul(f_conv2, weights['wd1']), biases['bd1'])
# TODO: Activation.
fc1 = tf.nn.relu(fc1)
# TODO: Layer 4: Fully Connected. Input = 120. Output = 84.
fc2 = tf.add(tf.matmul(fc1, weights['wd2']), biases['bd2'])
# TODO: Activation.
fc2 = tf.nn.relu(fc2)
# TODO: Layer 5: Fully Connected. Input = 84. Output = 10.
logits = tf.add(tf.matmul(fc2, weights['out']), biases['out'])
return logits
```
## Features and Labels
Train LeNet to classify [MNIST](http://yann.lecun.com/exdb/mnist/) data.
`x` is a placeholder for a batch of input images.
`y` is a placeholder for a batch of output labels.
You do not need to modify this section.
```
x = tf.placeholder(tf.float32, (None, 32, 32, 1))
y = tf.placeholder(tf.int32, (None))
one_hot_y = tf.one_hot(y, 10)
```
## Training Pipeline
Create a training pipeline that uses the model to classify MNIST data.
You do not need to modify this section.
```
rate = 0.001
logits = LeNet(x)
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=one_hot_y, logits=logits)
loss_operation = tf.reduce_mean(cross_entropy)
optimizer = tf.train.AdamOptimizer(learning_rate = rate)
training_operation = optimizer.minimize(loss_operation)
```
## Model Evaluation
Evaluate how well the loss and accuracy of the model for a given dataset.
You do not need to modify this section.
```
correct_prediction = tf.equal(tf.argmax(logits, 1), tf.argmax(one_hot_y, 1))
accuracy_operation = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
saver = tf.train.Saver()
def evaluate(X_data, y_data):
num_examples = len(X_data)
total_accuracy = 0
sess = tf.get_default_session()
for offset in range(0, num_examples, BATCH_SIZE):
batch_x, batch_y = X_data[offset:offset+BATCH_SIZE], y_data[offset:offset+BATCH_SIZE]
accuracy = sess.run(accuracy_operation, feed_dict={x: batch_x, y: batch_y})
total_accuracy += (accuracy * len(batch_x))
return total_accuracy / num_examples
```
## Train the Model
Run the training data through the training pipeline to train the model.
Before each epoch, shuffle the training set.
After each epoch, measure the loss and accuracy of the validation set.
Save the model after training.
You do not need to modify this section.
```
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
num_examples = len(X_train)
print("Training...")
print()
for i in range(EPOCHS):
X_train, y_train = shuffle(X_train, y_train)
for offset in range(0, num_examples, BATCH_SIZE):
end = offset + BATCH_SIZE
batch_x, batch_y = X_train[offset:end], y_train[offset:end]
sess.run(training_operation, feed_dict={x: batch_x, y: batch_y})
validation_accuracy = evaluate(X_validation, y_validation)
print("EPOCH {} ...".format(i+1))
print("Validation Accuracy = {:.3f}".format(validation_accuracy))
print()
saver.save(sess, './lenet')
print("Model saved")
```
## Evaluate the Model
Once you are completely satisfied with your model, evaluate the performance of the model on the test set.
Be sure to only do this once!
If you were to measure the performance of your trained model on the test set, then improve your model, and then measure the performance of your model on the test set again, that would invalidate your test results. You wouldn't get a true measure of how well your model would perform against real data.
You do not need to modify this section.
```
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('.'))
test_accuracy = evaluate(X_test, y_test)
print("Test Accuracy = {:.3f}".format(test_accuracy))
```
|
github_jupyter
|
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", reshape=False)
X_train, y_train = mnist.train.images, mnist.train.labels
X_validation, y_validation = mnist.validation.images, mnist.validation.labels
X_test, y_test = mnist.test.images, mnist.test.labels
assert(len(X_train) == len(y_train))
assert(len(X_validation) == len(y_validation))
assert(len(X_test) == len(y_test))
print()
print("Image Shape: {}".format(X_train[0].shape))
print()
print("Training Set: {} samples".format(len(X_train)))
print("Validation Set: {} samples".format(len(X_validation)))
print("Test Set: {} samples".format(len(X_test)))
import numpy as np
# Pad images with 0s
X_train = np.pad(X_train, ((0,0),(2,2),(2,2),(0,0)), 'constant')
X_validation = np.pad(X_validation, ((0,0),(2,2),(2,2),(0,0)), 'constant')
X_test = np.pad(X_test, ((0,0),(2,2),(2,2),(0,0)), 'constant')
print("Updated Image Shape: {}".format(X_train[0].shape))
import random
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
index = random.randint(0, len(X_train))
image = X_train[index].squeeze()
plt.figure(figsize=(1,1))
plt.imshow(image, cmap="gray")
print(y_train[index])
from sklearn.utils import shuffle
X_train, y_train = shuffle(X_train, y_train)
import tensorflow as tf
EPOCHS = 10
BATCH_SIZE = 128
def get_weights_biases(mu, sigma):
weights = {
'wc1' : tf.Variable(tf.truncated_normal([5, 5, 1, 6], mu, sigma)),
'wc2' : tf.Variable(tf.truncated_normal([5, 5, 6, 16], mu, sigma)),
'wd1' : tf.Variable(tf.truncated_normal([400, 120], mu, sigma)),
'wd2' : tf.Variable(tf.truncated_normal([120, 84], mu, sigma)),
'out' : tf.Variable(tf.truncated_normal([84, 10], mu, sigma))
}
biases = {
'bc1' : tf.Variable(tf.truncated_normal([6], mu, sigma)),
'bc2' : tf.Variable(tf.truncated_normal([16], mu, sigma)),
'bd1' : tf.Variable(tf.truncated_normal([120], mu, sigma)),
'bd2' : tf.Variable(tf.truncated_normal([84], mu, sigma)),
'out' : tf.Variable(tf.truncated_normal([10], mu, sigma))
}
return weights, biases
def conv2d(x, W, b, strides=1):
conv = tf.nn.conv2d(x, W, strides=[1, strides, strides, 1], padding='VALID')
conv = tf.nn.bias_add(conv, b)
return tf.nn.relu(conv)
def maxpooling2D(x, k=2):
return tf.nn.max_pool(x,
ksize=[1, k, k, 1],
strides=[1, k, k, 1],
padding="SAME")
from tensorflow.contrib.layers import flatten
def LeNet(x):
# Arguments used for tf.truncated_normal, randomly defines variables for the weights and biases for each layer
mu = 0
sigma = 0.1
weights, biases = get_weights_biases(mu, sigma)
# TODO: Layer 1: Convolutional. Input = 32x32x1. Output = 28x28x6.
# TODO: Activation.
conv1 = conv2d(x, weights['wc1'], biases['bc1'])
#print(conv1.get_shape().as_list())
# TODO: Pooling. Input = 28x28x6. Output = 14x14x6.
conv1 = maxpooling2D(conv1)
print(conv1.get_shape().as_list())
# TODO: Layer 2: Convolutional. Output = 10x10x16.
# TODO: Activation.
conv2 = conv2d(conv1, weights['wc2'], biases['bc2'])
#print(conv2.get_shape().as_list())
# TODO: Pooling. Input = 10x10x16. Output = 5x5x16.
conv2 = maxpooling2D(conv2)
#print(conv2.get_shape().as_list())
# TODO: Flatten. Input = 5x5x16. Output = 400.
f_conv2 = flatten(conv2)
print(f_conv2.get_shape().as_list())
# TODO: Layer 3: Fully Connected. Input = 400. Output = 120.
fc1 = tf.add(tf.matmul(f_conv2, weights['wd1']), biases['bd1'])
# TODO: Activation.
fc1 = tf.nn.relu(fc1)
# TODO: Layer 4: Fully Connected. Input = 120. Output = 84.
fc2 = tf.add(tf.matmul(fc1, weights['wd2']), biases['bd2'])
# TODO: Activation.
fc2 = tf.nn.relu(fc2)
# TODO: Layer 5: Fully Connected. Input = 84. Output = 10.
logits = tf.add(tf.matmul(fc2, weights['out']), biases['out'])
return logits
x = tf.placeholder(tf.float32, (None, 32, 32, 1))
y = tf.placeholder(tf.int32, (None))
one_hot_y = tf.one_hot(y, 10)
rate = 0.001
logits = LeNet(x)
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=one_hot_y, logits=logits)
loss_operation = tf.reduce_mean(cross_entropy)
optimizer = tf.train.AdamOptimizer(learning_rate = rate)
training_operation = optimizer.minimize(loss_operation)
correct_prediction = tf.equal(tf.argmax(logits, 1), tf.argmax(one_hot_y, 1))
accuracy_operation = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
saver = tf.train.Saver()
def evaluate(X_data, y_data):
num_examples = len(X_data)
total_accuracy = 0
sess = tf.get_default_session()
for offset in range(0, num_examples, BATCH_SIZE):
batch_x, batch_y = X_data[offset:offset+BATCH_SIZE], y_data[offset:offset+BATCH_SIZE]
accuracy = sess.run(accuracy_operation, feed_dict={x: batch_x, y: batch_y})
total_accuracy += (accuracy * len(batch_x))
return total_accuracy / num_examples
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
num_examples = len(X_train)
print("Training...")
print()
for i in range(EPOCHS):
X_train, y_train = shuffle(X_train, y_train)
for offset in range(0, num_examples, BATCH_SIZE):
end = offset + BATCH_SIZE
batch_x, batch_y = X_train[offset:end], y_train[offset:end]
sess.run(training_operation, feed_dict={x: batch_x, y: batch_y})
validation_accuracy = evaluate(X_validation, y_validation)
print("EPOCH {} ...".format(i+1))
print("Validation Accuracy = {:.3f}".format(validation_accuracy))
print()
saver.save(sess, './lenet')
print("Model saved")
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('.'))
test_accuracy = evaluate(X_test, y_test)
print("Test Accuracy = {:.3f}".format(test_accuracy))
| 0.584153 | 0.98347 |
<a href="https://colab.research.google.com/github/16A0/experiments/blob/master/Copy_of_ImageColorizerColab.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
### **<font color='blue'> Artistic Colorizer </font>**
#◢ DeOldify - Colorize your own photos!
####**Credits:**
Special thanks to:
Jason Antic for creating the DeOldify for training and inferencing.
Matt Robinson and María Benavente for pioneering the DeOldify image colab notebook.
Dana Kelley for doing things, breaking stuff & having an opinion on everything.
---
#◢ Verify Correct Runtime Settings
**<font color='#FF000'> IMPORTANT </font>**
In the "Runtime" menu for the notebook window, select "Change runtime type." Ensure that the following are selected:
* Runtime Type = Python 3
* Hardware Accelerator = GPU
```
import torch
if not torch.cuda.is_available():
print('GPU not available.')
```
#◢ Git clone and install DeOldify
```
!git clone https://github.com/Dakini/AnimeColorDeOldify.git DeOldify
cd DeOldify
```
#◢ Setup
```
!pip install -r colab_requirements.txt
import fastai
from deoldify.visualize import *
torch.backends.cudnn.benchmark = True
!mkdir 'models'
!wget https://www.dropbox.com/s/vtku6xx9dp8knw7/E4PKzf54BXzzenHR8qcujkMuwgZbs7gSRh6gLCf5N.pth?dl=0 -O ./models/ColorizeArtistic_gen.pth
stats = ([0.7137, 0.6628, 0.6519],[0.2970, 0.3017, 0.2979])
colorizer = get_image_colorizer(artistic=True,stats=stats)
```
#◢ Instructions
### source_url
Type in a url to a direct link of an image. Usually that means they'll end in .png, .jpg, etc. NOTE: If you want to use your own image, upload it first to a site like Imgur.
### render_factor
The default value of 12 has been carefully chosen and should work -ok- for most scenarios (but probably won't be the -best-). This determines resolution at which the color portion of the image is rendered. Lower resolution will render faster, and colors also tend to look more vibrant. Older and lower quality images in particular will generally benefit by lowering the render factor. Higher render factors are often better for higher quality images, but the colors may get slightly washed out.
### watermarked
Selected by default, this places a watermark icon of a palette at the bottom left corner of the image. This is intended to be a standard way to convey to others viewing the image that it is colorized by AI. We want to help promote this as a standard, especially as the technology continues to improve and the distinction between real and fake becomes harder to discern. This palette watermark practice was initiated and lead by the company MyHeritage in the MyHeritage In Color feature (which uses a newer version of DeOldify than what you're using here).
### post_process
Selected by default, this outputs the image without being postprocessed. The post processing usually works really well for images that contain some shading, however it does not work for images that are mainly line drawings (sketches). It is recommended to turn this off, if you are colorising a sketch.
#### How to Download a Copy
Simply right click on the displayed image and click "Save image as..."!
## Pro Tips
You can evaluate how well the image is rendered at each render_factor by using the code at the bottom (that cell under "See how well render_factor values perform on a frame here").
## Troubleshooting
If you get a 'CUDA out of memory' error, you probably have the render_factor too high.
#◢ Colorize!!
```
source_url = 'https://upload.wikimedia.org/wikipedia/commons/thumb/d/d7/Street_Craftsman_in_Olinda.jpg/271px-Street_Craftsman_in_Olinda.jpg' #@param {type:"string"}
render_factor = 26 #@param {type:"slider", min:7, max:45, step:1}
watermarked = True #@param {type:"boolean"}
if source_url is not None and source_url !='':
image_path = colorizer.plot_transformed_image_from_url(url=source_url, render_factor=render_factor, compare=True, post_process=False, watermarked=watermarked)
show_image_in_notebook(image_path)
else:
print('Provide an image url and try again.')
```
## See how well render_factor values perform on the image here
```
for i in range(10,45,2):
colorizer.plot_transformed_image('test_images/5694_.png', render_factor=i, display_render_factor=True, post_process=True, figsize=(8,8))
```
|
github_jupyter
|
import torch
if not torch.cuda.is_available():
print('GPU not available.')
!git clone https://github.com/Dakini/AnimeColorDeOldify.git DeOldify
cd DeOldify
!pip install -r colab_requirements.txt
import fastai
from deoldify.visualize import *
torch.backends.cudnn.benchmark = True
!mkdir 'models'
!wget https://www.dropbox.com/s/vtku6xx9dp8knw7/E4PKzf54BXzzenHR8qcujkMuwgZbs7gSRh6gLCf5N.pth?dl=0 -O ./models/ColorizeArtistic_gen.pth
stats = ([0.7137, 0.6628, 0.6519],[0.2970, 0.3017, 0.2979])
colorizer = get_image_colorizer(artistic=True,stats=stats)
source_url = 'https://upload.wikimedia.org/wikipedia/commons/thumb/d/d7/Street_Craftsman_in_Olinda.jpg/271px-Street_Craftsman_in_Olinda.jpg' #@param {type:"string"}
render_factor = 26 #@param {type:"slider", min:7, max:45, step:1}
watermarked = True #@param {type:"boolean"}
if source_url is not None and source_url !='':
image_path = colorizer.plot_transformed_image_from_url(url=source_url, render_factor=render_factor, compare=True, post_process=False, watermarked=watermarked)
show_image_in_notebook(image_path)
else:
print('Provide an image url and try again.')
for i in range(10,45,2):
colorizer.plot_transformed_image('test_images/5694_.png', render_factor=i, display_render_factor=True, post_process=True, figsize=(8,8))
| 0.466846 | 0.929376 |
# Temporal-Difference Methods
In this notebook, you will write your own implementations of many Temporal-Difference (TD) methods.
While we have provided some starter code, you are welcome to erase these hints and write your code from scratch.
---
### Part 0: Explore CliffWalkingEnv
We begin by importing the necessary packages.
```
import sys
import gym
import numpy as np
import random
import math
from collections import defaultdict, deque
import matplotlib.pyplot as plt
%matplotlib inline
import check_test
from plot_utils import plot_values
```
Use the code cell below to create an instance of the [CliffWalking](https://github.com/openai/gym/blob/master/gym/envs/toy_text/cliffwalking.py) environment.
```
env = gym.make('CliffWalking-v0')
```
The agent moves through a $4\times 12$ gridworld, with states numbered as follows:
```
[[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35],
[36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47]]
```
At the start of any episode, state `36` is the initial state. State `47` is the only terminal state, and the cliff corresponds to states `37` through `46`.
The agent has 4 potential actions:
```
UP = 0
RIGHT = 1
DOWN = 2
LEFT = 3
```
Thus, $\mathcal{S}^+=\{0, 1, \ldots, 47\}$, and $\mathcal{A} =\{0, 1, 2, 3\}$. Verify this by running the code cell below.
```
print(env.action_space)
print(env.observation_space)
```
In this mini-project, we will build towards finding the optimal policy for the CliffWalking environment. The optimal state-value function is visualized below. Please take the time now to make sure that you understand _why_ this is the optimal state-value function.
_**Note**: You can safely ignore the values of the cliff "states" as these are not true states from which the agent can make decisions. For the cliff "states", the state-value function is not well-defined._
```
# define the optimal state-value function
V_opt = np.zeros((4,12))
V_opt[0][0:13] = -np.arange(3, 15)[::-1]
V_opt[1][0:13] = -np.arange(3, 15)[::-1] + 1
V_opt[2][0:13] = -np.arange(3, 15)[::-1] + 2
V_opt[3][0] = -13
plot_values(V_opt)
```
### Part 1: TD Control: Sarsa
In this section, you will write your own implementation of the Sarsa control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def update_Q_sarsa(alpha, gamma, Q, state, action, reward, next_state=None, next_action=None):
"""Returns updated Q-value for the most recent experience."""
current = Q[state][action] # estimate in Q-table (for current state, action pair)
# get value of state, action pair at next time step
Qsa_next = Q[next_state][next_action] if next_state is not None else 0
target = reward + (gamma * Qsa_next) # construct TD target
new_value = current + (alpha * (target - current)) # get updated value
return new_value
def epsilon_greedy(Q, state, nA, eps):
"""Selects epsilon-greedy action for supplied state.
Params
======
Q (dictionary): action-value function
state (int): current state
nA (int): number actions in the environment
eps (float): epsilon
"""
if random.random() > eps: # select greedy action with probability epsilon
return np.argmax(Q[state])
else: # otherwise, select an action randomly
return random.choice(np.arange(env.action_space.n))
def sarsa(env, num_episodes, alpha, gamma=1.0, plot_every=100):
nA = env.action_space.n # number of actions
Q = defaultdict(lambda: np.zeros(nA)) # initialize empty dictionary of arrays
# monitor performance
tmp_scores = deque(maxlen=plot_every) # deque for keeping track of scores
avg_scores = deque(maxlen=num_episodes) # average scores over every plot_every episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
score = 0 # initialize score
state = env.reset() # start episode
eps = 1.0 / i_episode # set value of epsilon
action = epsilon_greedy(Q, state, nA, eps) # epsilon-greedy action selection
while True:
next_state, reward, done, info = env.step(action) # take action A, observe R, S'
score += reward # add reward to agent's score
if not done:
next_action = epsilon_greedy(Q, next_state, nA, eps) # epsilon-greedy action
Q[state][action] = update_Q_sarsa(alpha, gamma, Q, \
state, action, reward, next_state, next_action)
state = next_state # S <- S'
action = next_action # A <- A'
if done:
Q[state][action] = update_Q_sarsa(alpha, gamma, Q, \
state, action, reward)
tmp_scores.append(score) # append score
break
if (i_episode % plot_every == 0):
avg_scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(avg_scores),endpoint=False), np.asarray(avg_scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(avg_scores))
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_sarsa = sarsa(env, 10000, .01)
# print the estimated optimal policy
policy_sarsa = np.array([np.argmax(Q_sarsa[key]) if key in Q_sarsa else -1 for key in np.arange(48)]).reshape(4,12)
check_test.run_check('td_control_check', policy_sarsa)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_sarsa)
# plot the estimated optimal state-value function
V_sarsa = ([np.max(Q_sarsa[key]) if key in Q_sarsa else 0 for key in np.arange(48)])
plot_values(V_sarsa)
```
### Part 2: TD Control: Q-learning
In this section, you will write your own implementation of the Q-learning control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def update_Q_sarsamax(alpha, gamma, Q, state, action, reward, next_state=None):
"""Returns updated Q-value for the most recent experience."""
current = Q[state][action] # estimate in Q-table (for current state, action pair)
Qsa_next = np.max(Q[next_state]) if next_state is not None else 0 # value of next state
target = reward + (gamma * Qsa_next) # construct TD target
new_value = current + (alpha * (target - current)) # get updated value
return new_value
def q_learning(env, num_episodes, alpha, gamma=1.0, plot_every=100):
"""Q-Learning - TD Control
Params
======
num_episodes (int): number of episodes to run the algorithm
alpha (float): learning rate
gamma (float): discount factor
plot_every (int): number of episodes to use when calculating average score
"""
nA = env.action_space.n # number of actions
Q = defaultdict(lambda: np.zeros(nA)) # initialize empty dictionary of arrays
# monitor performance
tmp_scores = deque(maxlen=plot_every) # deque for keeping track of scores
avg_scores = deque(maxlen=num_episodes) # average scores over every plot_every episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
score = 0 # initialize score
state = env.reset() # start episode
eps = 1.0 / i_episode # set value of epsilon
while True:
action = epsilon_greedy(Q, state, nA, eps) # epsilon-greedy action selection
next_state, reward, done, info = env.step(action) # take action A, observe R, S'
score += reward # add reward to agent's score
Q[state][action] = update_Q_sarsamax(alpha, gamma, Q, \
state, action, reward, next_state)
state = next_state # S <- S'
if done:
tmp_scores.append(score) # append score
break
if (i_episode % plot_every == 0):
avg_scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(avg_scores),endpoint=False), np.asarray(avg_scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(avg_scores))
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_sarsamax = q_learning(env, 5000, .01)
# print the estimated optimal policy
policy_sarsamax = np.array([np.argmax(Q_sarsamax[key]) if key in Q_sarsamax else -1 for key in np.arange(48)]).reshape((4,12))
check_test.run_check('td_control_check', policy_sarsamax)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_sarsamax)
# plot the estimated optimal state-value function
plot_values([np.max(Q_sarsamax[key]) if key in Q_sarsamax else 0 for key in np.arange(48)])
```
### Part 3: TD Control: Expected Sarsa
In this section, you will write your own implementation of the Expected Sarsa control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def update_Q_expsarsa(alpha, gamma, nA, eps, Q, state, action, reward, next_state=None):
"""Returns updated Q-value for the most recent experience."""
current = Q[state][action] # estimate in Q-table (for current state, action pair)
policy_s = np.ones(nA) * eps / nA # current policy (for next state S')
policy_s[np.argmax(Q[next_state])] = 1 - eps + (eps / nA) # greedy action
Qsa_next = np.dot(Q[next_state], policy_s) # get value of state at next time step
target = reward + (gamma * Qsa_next) # construct target
new_value = current + (alpha * (target - current)) # get updated value
return new_value
def expected_sarsa(env, num_episodes, alpha, gamma=1.0, plot_every=100):
"""Expected SARSA - TD Control
Params
======
num_episodes (int): number of episodes to run the algorithm
alpha (float): step-size parameters for the update step
gamma (float): discount factor
plot_every (int): number of episodes to use when calculating average score
"""
nA = env.action_space.n # number of actions
Q = defaultdict(lambda: np.zeros(nA)) # initialize empty dictionary of arrays
# monitor performance
tmp_scores = deque(maxlen=plot_every) # deque for keeping track of scores
avg_scores = deque(maxlen=num_episodes) # average scores over every plot_every episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
score = 0 # initialize score
state = env.reset() # start episode
eps = 0.005 # set value of epsilon
while True:
action = epsilon_greedy(Q, state, nA, eps) # epsilon-greedy action selection
next_state, reward, done, info = env.step(action) # take action A, observe R, S'
score += reward # add reward to agent's score
# update Q
Q[state][action] = update_Q_expsarsa(alpha, gamma, nA, eps, Q, \
state, action, reward, next_state)
state = next_state # S <- S'
if done:
tmp_scores.append(score) # append score
break
if (i_episode % plot_every == 0):
avg_scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(avg_scores),endpoint=False), np.asarray(avg_scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(avg_scores))
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_expsarsa = expected_sarsa(env, 5000, 1)
# print the estimated optimal policy
policy_expsarsa = np.array([np.argmax(Q_expsarsa[key]) if key in Q_expsarsa else -1 for key in np.arange(48)]).reshape(4,12)
check_test.run_check('td_control_check', policy_expsarsa)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_expsarsa)
# plot the estimated optimal state-value function
plot_values([np.max(Q_expsarsa[key]) if key in Q_expsarsa else 0 for key in np.arange(48)])
```
|
github_jupyter
|
import sys
import gym
import numpy as np
import random
import math
from collections import defaultdict, deque
import matplotlib.pyplot as plt
%matplotlib inline
import check_test
from plot_utils import plot_values
env = gym.make('CliffWalking-v0')
[[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35],
[36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47]]
UP = 0
RIGHT = 1
DOWN = 2
LEFT = 3
print(env.action_space)
print(env.observation_space)
# define the optimal state-value function
V_opt = np.zeros((4,12))
V_opt[0][0:13] = -np.arange(3, 15)[::-1]
V_opt[1][0:13] = -np.arange(3, 15)[::-1] + 1
V_opt[2][0:13] = -np.arange(3, 15)[::-1] + 2
V_opt[3][0] = -13
plot_values(V_opt)
def update_Q_sarsa(alpha, gamma, Q, state, action, reward, next_state=None, next_action=None):
"""Returns updated Q-value for the most recent experience."""
current = Q[state][action] # estimate in Q-table (for current state, action pair)
# get value of state, action pair at next time step
Qsa_next = Q[next_state][next_action] if next_state is not None else 0
target = reward + (gamma * Qsa_next) # construct TD target
new_value = current + (alpha * (target - current)) # get updated value
return new_value
def epsilon_greedy(Q, state, nA, eps):
"""Selects epsilon-greedy action for supplied state.
Params
======
Q (dictionary): action-value function
state (int): current state
nA (int): number actions in the environment
eps (float): epsilon
"""
if random.random() > eps: # select greedy action with probability epsilon
return np.argmax(Q[state])
else: # otherwise, select an action randomly
return random.choice(np.arange(env.action_space.n))
def sarsa(env, num_episodes, alpha, gamma=1.0, plot_every=100):
nA = env.action_space.n # number of actions
Q = defaultdict(lambda: np.zeros(nA)) # initialize empty dictionary of arrays
# monitor performance
tmp_scores = deque(maxlen=plot_every) # deque for keeping track of scores
avg_scores = deque(maxlen=num_episodes) # average scores over every plot_every episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
score = 0 # initialize score
state = env.reset() # start episode
eps = 1.0 / i_episode # set value of epsilon
action = epsilon_greedy(Q, state, nA, eps) # epsilon-greedy action selection
while True:
next_state, reward, done, info = env.step(action) # take action A, observe R, S'
score += reward # add reward to agent's score
if not done:
next_action = epsilon_greedy(Q, next_state, nA, eps) # epsilon-greedy action
Q[state][action] = update_Q_sarsa(alpha, gamma, Q, \
state, action, reward, next_state, next_action)
state = next_state # S <- S'
action = next_action # A <- A'
if done:
Q[state][action] = update_Q_sarsa(alpha, gamma, Q, \
state, action, reward)
tmp_scores.append(score) # append score
break
if (i_episode % plot_every == 0):
avg_scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(avg_scores),endpoint=False), np.asarray(avg_scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(avg_scores))
return Q
# obtain the estimated optimal policy and corresponding action-value function
Q_sarsa = sarsa(env, 10000, .01)
# print the estimated optimal policy
policy_sarsa = np.array([np.argmax(Q_sarsa[key]) if key in Q_sarsa else -1 for key in np.arange(48)]).reshape(4,12)
check_test.run_check('td_control_check', policy_sarsa)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_sarsa)
# plot the estimated optimal state-value function
V_sarsa = ([np.max(Q_sarsa[key]) if key in Q_sarsa else 0 for key in np.arange(48)])
plot_values(V_sarsa)
def update_Q_sarsamax(alpha, gamma, Q, state, action, reward, next_state=None):
"""Returns updated Q-value for the most recent experience."""
current = Q[state][action] # estimate in Q-table (for current state, action pair)
Qsa_next = np.max(Q[next_state]) if next_state is not None else 0 # value of next state
target = reward + (gamma * Qsa_next) # construct TD target
new_value = current + (alpha * (target - current)) # get updated value
return new_value
def q_learning(env, num_episodes, alpha, gamma=1.0, plot_every=100):
"""Q-Learning - TD Control
Params
======
num_episodes (int): number of episodes to run the algorithm
alpha (float): learning rate
gamma (float): discount factor
plot_every (int): number of episodes to use when calculating average score
"""
nA = env.action_space.n # number of actions
Q = defaultdict(lambda: np.zeros(nA)) # initialize empty dictionary of arrays
# monitor performance
tmp_scores = deque(maxlen=plot_every) # deque for keeping track of scores
avg_scores = deque(maxlen=num_episodes) # average scores over every plot_every episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
score = 0 # initialize score
state = env.reset() # start episode
eps = 1.0 / i_episode # set value of epsilon
while True:
action = epsilon_greedy(Q, state, nA, eps) # epsilon-greedy action selection
next_state, reward, done, info = env.step(action) # take action A, observe R, S'
score += reward # add reward to agent's score
Q[state][action] = update_Q_sarsamax(alpha, gamma, Q, \
state, action, reward, next_state)
state = next_state # S <- S'
if done:
tmp_scores.append(score) # append score
break
if (i_episode % plot_every == 0):
avg_scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(avg_scores),endpoint=False), np.asarray(avg_scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(avg_scores))
return Q
# obtain the estimated optimal policy and corresponding action-value function
Q_sarsamax = q_learning(env, 5000, .01)
# print the estimated optimal policy
policy_sarsamax = np.array([np.argmax(Q_sarsamax[key]) if key in Q_sarsamax else -1 for key in np.arange(48)]).reshape((4,12))
check_test.run_check('td_control_check', policy_sarsamax)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_sarsamax)
# plot the estimated optimal state-value function
plot_values([np.max(Q_sarsamax[key]) if key in Q_sarsamax else 0 for key in np.arange(48)])
def update_Q_expsarsa(alpha, gamma, nA, eps, Q, state, action, reward, next_state=None):
"""Returns updated Q-value for the most recent experience."""
current = Q[state][action] # estimate in Q-table (for current state, action pair)
policy_s = np.ones(nA) * eps / nA # current policy (for next state S')
policy_s[np.argmax(Q[next_state])] = 1 - eps + (eps / nA) # greedy action
Qsa_next = np.dot(Q[next_state], policy_s) # get value of state at next time step
target = reward + (gamma * Qsa_next) # construct target
new_value = current + (alpha * (target - current)) # get updated value
return new_value
def expected_sarsa(env, num_episodes, alpha, gamma=1.0, plot_every=100):
"""Expected SARSA - TD Control
Params
======
num_episodes (int): number of episodes to run the algorithm
alpha (float): step-size parameters for the update step
gamma (float): discount factor
plot_every (int): number of episodes to use when calculating average score
"""
nA = env.action_space.n # number of actions
Q = defaultdict(lambda: np.zeros(nA)) # initialize empty dictionary of arrays
# monitor performance
tmp_scores = deque(maxlen=plot_every) # deque for keeping track of scores
avg_scores = deque(maxlen=num_episodes) # average scores over every plot_every episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
score = 0 # initialize score
state = env.reset() # start episode
eps = 0.005 # set value of epsilon
while True:
action = epsilon_greedy(Q, state, nA, eps) # epsilon-greedy action selection
next_state, reward, done, info = env.step(action) # take action A, observe R, S'
score += reward # add reward to agent's score
# update Q
Q[state][action] = update_Q_expsarsa(alpha, gamma, nA, eps, Q, \
state, action, reward, next_state)
state = next_state # S <- S'
if done:
tmp_scores.append(score) # append score
break
if (i_episode % plot_every == 0):
avg_scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(avg_scores),endpoint=False), np.asarray(avg_scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(avg_scores))
return Q
# obtain the estimated optimal policy and corresponding action-value function
Q_expsarsa = expected_sarsa(env, 5000, 1)
# print the estimated optimal policy
policy_expsarsa = np.array([np.argmax(Q_expsarsa[key]) if key in Q_expsarsa else -1 for key in np.arange(48)]).reshape(4,12)
check_test.run_check('td_control_check', policy_expsarsa)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_expsarsa)
# plot the estimated optimal state-value function
plot_values([np.max(Q_expsarsa[key]) if key in Q_expsarsa else 0 for key in np.arange(48)])
| 0.522689 | 0.960878 |
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from __future__ import print_function
import sklearn
from sklearn.ensemble import RandomForestClassifier
from sklearn import preprocessing
%matplotlib inline
%config InlineBackend.figure_format = 'png'
pd.set_option("max_columns",50)
# 해야하는 것
# User 10000명 random choice
# Feature 10개 random choice
# => randomforest 에 넣고 변하는지 안변하는지 확인해보기
# => 변한다면 데이터가 흔들린다는 증거
%%time
df = pd.read_csv("../data/train_2013.csv", index_col=0)
df = df.reset_index(drop=True)
```
랜덤 샘플링을 얼마나 해야되나.. 5개 집단
```
le = preprocessing.LabelEncoder()
%%time
df["date_time"] = pd.to_datetime(df["date_time"], errors="coerce")
df["date_time"] = df["date_time"].dt.date
df["srch_ci"] = pd.to_datetime(df["srch_ci"], errors="coerce")
df["srch_co"] = pd.to_datetime(df["srch_co"], errors="coerce")
df["date_time"] = le.fit_transform(df["date_time"])
df["srch_ci"] = le.fit_transform(df["srch_ci"])
df["srch_co"] = le.fit_transform(df["srch_co"])
df["orig_destination_distance"].fillna(0, inplace=True)
seed_list = [402,555, 666, 777, 888]
rank_df = pd.DataFrame()
%%time
for i in seed_list:
np.random.seed(i)
print("="*20)
print("seed값 : %d" %i)
df1 = df.ix[np.random.choice(df.index, 10000)]
trn_x1 = df1.ix[:,:-1]
trn_y1 = df1.ix[:,-1:]
model = RandomForestClassifier(max_depth=3, n_jobs=-1, random_state=402)
model.fit(trn_x1,trn_y1)
importances = model.feature_importances_
std = np.std([tree.feature_importances_ for tree in model.estimators_], axis=0)
indices = np.argsort(importances)[::-1]
print("Feature ranking:")
rank_series = pd.Series([])
for f in range(trn_x1.shape[1]):
print("%d. feature %d %s (%f)" % (f + 1, indices[f], trn_x1.columns[indices[f]], importances[indices[f]]))
rank_series = rank_series.append(pd.Series([trn_x1.columns[indices[f]], importances[indices[f]]]))
rank_df.insert(len(rank_df.columns), column=i ,value=rank_series)
plt.title("Feature importances")
plt.bar(range(trn_x1.shape[1]), importances[indices], color="r", yerr=std[indices], align="center")
plt.xticks(range(trn_x1.shape[1]), indices)
plt.xlim([-1, trn_x1.shape[1]])
plt.show()
rank_df
%%time
rank_df1 = pd.DataFrame()
for i in seed_list:
np.random.seed(i)
print("="*20)
print("seed값 : %d" %i)
df1 = df.ix[np.random.choice(df.index, 100000)]
trn_x1 = df1.ix[:,:-1]
trn_y1 = df1.ix[:,-1:]
model = RandomForestClassifier(max_depth=3, n_jobs=-1, random_state=402)
model.fit(trn_x1,trn_y1)
importances = model.feature_importances_
std = np.std([tree.feature_importances_ for tree in model.estimators_], axis=0)
indices = np.argsort(importances)[::-1]
print("Feature ranking:")
rank_series = pd.Series([])
for f in range(trn_x1.shape[1]):
print("%d. feature %d %s (%f)" % (f + 1, indices[f], trn_x1.columns[indices[f]], importances[indices[f]]))
rank_series = rank_series.append(pd.Series([trn_x1.columns[indices[f]], importances[indices[f]]]))
rank_df1.insert(len(rank_df1.columns), column=i ,value=rank_series)
plt.title("Feature importances")
plt.bar(range(trn_x1.shape[1]), importances[indices], color="r", yerr=std[indices], align="center")
plt.xticks(range(trn_x1.shape[1]), indices)
plt.xlim([-1, trn_x1.shape[1]])
plt.show()
rank_df1
%%time
rank_df2 = pd.DataFrame()
for i in seed_list:
np.random.seed(i)
print("="*20)
print("seed값 : %d" %i)
df1 = df.ix[np.random.choice(df.index, 100000)]
trn_x1 = df1.ix[:,:-1]
trn_y1 = df1.ix[:,-1:]
model = RandomForestClassifier(max_depth=3, n_jobs=-1, random_state=402)
model.fit(trn_x1,trn_y1)
importances = model.feature_importances_
std = np.std([tree.feature_importances_ for tree in model.estimators_], axis=0)
indices = np.argsort(importances)[::-1]
print("Feature ranking:")
rank_series = pd.Series([])
for f in range(trn_x1.shape[1]):
print("%d. feature %d %s (%f)" % (f + 1, indices[f], trn_x1.columns[indices[f]], importances[indices[f]]))
rank_series = rank_series.append(pd.Series([trn_x1.columns[indices[f]], importances[indices[f]]]))
rank_df2.insert(len(rank_df2.columns), column=i ,value=rank_series)
plt.title("Feature importances")
plt.bar(range(trn_x1.shape[1]), importances[indices], color="r", yerr=std[indices], align="center")
plt.xticks(range(trn_x1.shape[1]), indices)
plt.xlim([-1, trn_x1.shape[1]])
plt.show()
rank_df2
rank_df.head(10)
rank_df1.head(10)
rank_df2.head(10)
# hotel_continent, orig_destination_distance
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from __future__ import print_function
import sklearn
from sklearn.ensemble import RandomForestClassifier
from sklearn import preprocessing
%matplotlib inline
%config InlineBackend.figure_format = 'png'
pd.set_option("max_columns",50)
# 해야하는 것
# User 10000명 random choice
# Feature 10개 random choice
# => randomforest 에 넣고 변하는지 안변하는지 확인해보기
# => 변한다면 데이터가 흔들린다는 증거
%%time
df = pd.read_csv("../data/train_2013.csv", index_col=0)
df = df.reset_index(drop=True)
le = preprocessing.LabelEncoder()
%%time
df["date_time"] = pd.to_datetime(df["date_time"], errors="coerce")
df["date_time"] = df["date_time"].dt.date
df["srch_ci"] = pd.to_datetime(df["srch_ci"], errors="coerce")
df["srch_co"] = pd.to_datetime(df["srch_co"], errors="coerce")
df["date_time"] = le.fit_transform(df["date_time"])
df["srch_ci"] = le.fit_transform(df["srch_ci"])
df["srch_co"] = le.fit_transform(df["srch_co"])
df["orig_destination_distance"].fillna(0, inplace=True)
seed_list = [402,555, 666, 777, 888]
rank_df = pd.DataFrame()
%%time
for i in seed_list:
np.random.seed(i)
print("="*20)
print("seed값 : %d" %i)
df1 = df.ix[np.random.choice(df.index, 10000)]
trn_x1 = df1.ix[:,:-1]
trn_y1 = df1.ix[:,-1:]
model = RandomForestClassifier(max_depth=3, n_jobs=-1, random_state=402)
model.fit(trn_x1,trn_y1)
importances = model.feature_importances_
std = np.std([tree.feature_importances_ for tree in model.estimators_], axis=0)
indices = np.argsort(importances)[::-1]
print("Feature ranking:")
rank_series = pd.Series([])
for f in range(trn_x1.shape[1]):
print("%d. feature %d %s (%f)" % (f + 1, indices[f], trn_x1.columns[indices[f]], importances[indices[f]]))
rank_series = rank_series.append(pd.Series([trn_x1.columns[indices[f]], importances[indices[f]]]))
rank_df.insert(len(rank_df.columns), column=i ,value=rank_series)
plt.title("Feature importances")
plt.bar(range(trn_x1.shape[1]), importances[indices], color="r", yerr=std[indices], align="center")
plt.xticks(range(trn_x1.shape[1]), indices)
plt.xlim([-1, trn_x1.shape[1]])
plt.show()
rank_df
%%time
rank_df1 = pd.DataFrame()
for i in seed_list:
np.random.seed(i)
print("="*20)
print("seed값 : %d" %i)
df1 = df.ix[np.random.choice(df.index, 100000)]
trn_x1 = df1.ix[:,:-1]
trn_y1 = df1.ix[:,-1:]
model = RandomForestClassifier(max_depth=3, n_jobs=-1, random_state=402)
model.fit(trn_x1,trn_y1)
importances = model.feature_importances_
std = np.std([tree.feature_importances_ for tree in model.estimators_], axis=0)
indices = np.argsort(importances)[::-1]
print("Feature ranking:")
rank_series = pd.Series([])
for f in range(trn_x1.shape[1]):
print("%d. feature %d %s (%f)" % (f + 1, indices[f], trn_x1.columns[indices[f]], importances[indices[f]]))
rank_series = rank_series.append(pd.Series([trn_x1.columns[indices[f]], importances[indices[f]]]))
rank_df1.insert(len(rank_df1.columns), column=i ,value=rank_series)
plt.title("Feature importances")
plt.bar(range(trn_x1.shape[1]), importances[indices], color="r", yerr=std[indices], align="center")
plt.xticks(range(trn_x1.shape[1]), indices)
plt.xlim([-1, trn_x1.shape[1]])
plt.show()
rank_df1
%%time
rank_df2 = pd.DataFrame()
for i in seed_list:
np.random.seed(i)
print("="*20)
print("seed값 : %d" %i)
df1 = df.ix[np.random.choice(df.index, 100000)]
trn_x1 = df1.ix[:,:-1]
trn_y1 = df1.ix[:,-1:]
model = RandomForestClassifier(max_depth=3, n_jobs=-1, random_state=402)
model.fit(trn_x1,trn_y1)
importances = model.feature_importances_
std = np.std([tree.feature_importances_ for tree in model.estimators_], axis=0)
indices = np.argsort(importances)[::-1]
print("Feature ranking:")
rank_series = pd.Series([])
for f in range(trn_x1.shape[1]):
print("%d. feature %d %s (%f)" % (f + 1, indices[f], trn_x1.columns[indices[f]], importances[indices[f]]))
rank_series = rank_series.append(pd.Series([trn_x1.columns[indices[f]], importances[indices[f]]]))
rank_df2.insert(len(rank_df2.columns), column=i ,value=rank_series)
plt.title("Feature importances")
plt.bar(range(trn_x1.shape[1]), importances[indices], color="r", yerr=std[indices], align="center")
plt.xticks(range(trn_x1.shape[1]), indices)
plt.xlim([-1, trn_x1.shape[1]])
plt.show()
rank_df2
rank_df.head(10)
rank_df1.head(10)
rank_df2.head(10)
# hotel_continent, orig_destination_distance
| 0.253953 | 0.586316 |
<h1 align="center">Curso Introducción a Python</h1>
<h2 align="center">Universidad EAFIT - Bancolombia</h2>
<h3 align="center">MEDELLÍN - COLOMBIA </h3>
<h2 align="center">Sesión 05 - Estructuras de datos (Tuplas y Listas)</h2>
## Instructor:
> <strong> *Carlos Alberto Álvarez Henao, I.C. Ph.D.* </strong>
## Colecciones de datos
- Hasta ahora, cada variable que hemos creado se ha referido a un número simple o cadena de caracteres.
- En este capítulo se usaran colecciones de datos.
- Python posee diferentes tipos de colecciones de datos: *Tuplas*, *Listas* y *Diccionarios*.
- Estos tres tipos, pueden almacenar colecciones de datos de diversos tipos y se diferencian por su sintaxis y por la forma en la cual los datos pueden ser manipulados.
# Tuplas
- Una tupla es una variable que permite almacenar varios datos inmutables (no pueden ser modificados una vez creados) de tipos diferentes y separados por coma `,`.
- Aunque no es obligatorio, es usual juntar estos datos entre paréntesis.
```
mi_tupla = 1, "a", 2.5, "dato"
type(mi_tupla)
otra_tupla = (2, "Dato", 2.9, "Zammis", False, "otro dato")
print(otra_tupla)
type(otra_tupla)
```
Para referirnos a elementos de una tupla se usa el operador `[ ]`
```
dato_tupla = mi_tupla[3]
print(dato_tupla)
```
Para saber los métodos que se pueden realizar sobre tuplas se hace mediante el nombre de la tupla seguido por un punto `.` y mediante la opción de autocompletar (tabulador) se despliega una ventana con las diferentes opciones.
```
mi_tupla.
```
# Listas
Las listas se relacionan a arreglos (`arrays`) en lenguajes como `C`, `C++` o `Java`, pero en `Python` las listas son más fexibles y poderosas qe los clásicos arregos. Por ejemplo, los ítems en una lista no necesitan ser todos del mismo tipo, más aún, pueden crecer en la ejecución del programa, mientras que en `C` el tamaño de un arreglo es fijo.
Las principales propiedades de una lista son:
- Están ordenados
- Contienen una colección arbitraria de objetos (números, cadenas, booleanos, otras listas...)
- Los elementos de una lista pueden ser accesados por un índice
- Variable en tamaño
- Son mutables, es decir, los elementos en una lista pueden cambiar
para definir una lista basta ubicar los diferentes elementos que la compondrán, separados por coma y entre corchetes
```
mi_lista = ['dato', 15, 2.8, "otro dato", True, "98456226", 27]
print(type(mi_lista))
print(mi_lista)
```
> - La numeración de los índices siempre empieza en cero (`0`) si se acceden desde el primer elemento a la izquierda y se recorren hacia la derecha. O desde `-1`, si se acceden desde el último elemento a la derecha y se recorre hacia la izquierda.
```
# diferentes formas de acceder al primer elemento de la lista
print(mi_lista[0])
print(mi_lista[-7])
# acceder al último elemento de la lista
print(mi_lista[-1])
```
A continuación veamos algunos procedimientos que podemos realizar sobre listas
Podemos cambiar los valores en un elemento de la lista
```
mi_lista[2] = 3.8
print(mi_lista)
```
Con la función `len()` podemos determinar el tamaño de la lista (cantidad de elementos que la componen)
```
len(mi_lista)
```
Para saber cuáles métodos se aplican a una lista, se coloca el nombre de la lista seguido de un `.` y la opción autocompletar (tabulación). Se despliega un menú con los diferentes métodos:
```
mi_lista.
```
A las listas se les permiten agregar nuevos valores mediante el método `append`. El método `append` adiciona cada vez un elemento al final de la lista (es lo que en estructura de datos se conoce con el concepto de `pila`
```
mi_lista.append("último")
mi_lista
```
Cuando se quiere agregar un elemento en una posoción determinada por el usuario se emplea el método `insert`
```
mi_lista.insert(2,10)
mi_lista
lista = []
for i in range(100):
lista.append(i+1)
print(lista)
```
`Python` dispone de tres formas diferentes para eliminar elementos en una lista:
- `del`: Eliminación por índice
```
del mi_lista[5]
print(mi_lista)
```
- `remove`: Eliminación por valor
```
mi_lista.remove(10)
print (mi_lista)
```
- `pop`: Eliminación por índice, mostrando el elemento eliminado.
```
mi_lista.pop(2)
print(mi_lista)
```
***Slicing (o particionado):*** Permitir seleccionar porciones de la lista para generar sublistas.
- Si en lugar de un número escribimos dos números `start` y `stop` separados por dos puntos `lista[start:stop]`, `Python` interpretará que queremos una lista que vaya desde la posición `start` hasta la posición `stop`, sin incluir este último.
- Si escribimos tres números `lista[start:stop:step]` en lugar de dos, el tercero se utiliza para determinar cada cuantas posiciones añadir un elemento a la lista.
```
print(mi_lista)
Parte_lista = mi_lista[1:3]
print(Parte_lista)
Parte_lista = mi_lista[1:4:2]
print(Parte_lista)
```
A veces no es necesario indicar el principio y el final del slicing, sino que, si estos se omiten, se usarán por defecto las posiciones de inicio y fin de la lista, respectivamente.
```
mi_parte = mi_lista[1:]
print(mi_parte)
mi_parte = mi_lista[:3]
print(mi_parte)
mi_parte = mi_lista[:]
print(mi_parte)
mi_parte = mi_lista[::2]
print(mi_parte)
```
### Listas como cadenas de texto:
```
texto = "Listas y cadenas de caracteres pueden ser accesados vía índices"
print(texto[0], texto[9], texto[20])
```
### Listas anidadas
```
nestedlist = [["London","England", 7556900], ["Paris","France",2193031], ["Bern", "Switzerland", 123466]]
print(nestedlist)
print(nestedlist[1][1])
```
### Operaciones Básicas con Listas
```
len(mi_lista) # Longitud
[1, 2, 3] + [4 , 5, 6, 7] # Concatenación
["Hola!"]*4 # Repetición
"ñ" in ["h","o","l","a"] # Afiliación
lista=["hola","mundo","2018"]
lista[0][1]
for x in [1,2,3,4]: print(x) # Iteración
```
### Algunas Funciones y Métodos en Listas
```
lista1 = [1, 3, 5, 7]
lista2 = ((1, 2), 3, 4)
sum(lista1)
```
## List comprenhension
la comprensión de lista se incluyó en `Python`a partir de la versión `2.0`. Esencialmente, es la forma en que `Python` implementa una notación bien conocida para conjuntos como la usan los matemáticos.
En matemáticas, los números cuadrados de los números naturales son, por ejemplo, creados por {x2 | x ∈ ℕ} o el conjunto de enteros complejos {(x, y) | x ∈ ℤ ∧ y ∈ ℤ}.
La comprensión de listas es una forma elegante de definir y crear listas en `Python`. Estas listas tienen a menudo las cualidades de conjuntos, pero no son en todos los casos conjuntos.
### Ejemplos:
Veamos este ejemplo en donde se crea un código que convierte un dato dado en grados *Celsius* a *Fahrenheit*.
```
Celsius = [39.2, 36.5, 37.3, 37.8]
Fahrenheit = [ (9/5*x + 32) for x in Celsius ]
print(Fahrenheit)
```
Veamos ahora el caso de la tarna pitagórica, que consta de tres enteros positivos $a$, $b$ y $c$, de modo que $a^2 + b^2 = c^2$. Tal terna se escribe comúnmente $(a, b, c)$, y el ejemplo más conocido es $(3, 4, 5)$. La siguiente comprensión de lista crea la terna pitagórica
```
n = 20
[(x,y,z) for x in range(1,n) for y in range(x,n) for z in range(y,n) if x**2 + y**2 == z**2]
```
## Laboratorio
1. Para el programa de la $Secuencia$ $de$ $Fibonacci$, con $n = 25$, genere una lista que contega los elementos pares de dicha serie.
2. Escribir una función que tome un carácter y devuelva `True` si es una vocal, de lo contrario devuelve `False`.
3. Definir una función inversa() que calcule la inversión de una cadena. Por ejemplo la cadena "estoy probando" debería devolver la cadena "odnaborp yotse"
4. Crear una función contar_vocales(), que reciba una palabra y cuente cuantas letras "a" tiene, cuantas letras "e" tiene y así hasta completar todas las vocales. Se puede hacer que el usuario sea quien elija la palabra.
5. Realizar el ejercicio de la suma de los 100 p
|
github_jupyter
|
mi_tupla = 1, "a", 2.5, "dato"
type(mi_tupla)
otra_tupla = (2, "Dato", 2.9, "Zammis", False, "otro dato")
print(otra_tupla)
type(otra_tupla)
dato_tupla = mi_tupla[3]
print(dato_tupla)
mi_tupla.
mi_lista = ['dato', 15, 2.8, "otro dato", True, "98456226", 27]
print(type(mi_lista))
print(mi_lista)
# diferentes formas de acceder al primer elemento de la lista
print(mi_lista[0])
print(mi_lista[-7])
# acceder al último elemento de la lista
print(mi_lista[-1])
mi_lista[2] = 3.8
print(mi_lista)
len(mi_lista)
mi_lista.
mi_lista.append("último")
mi_lista
mi_lista.insert(2,10)
mi_lista
lista = []
for i in range(100):
lista.append(i+1)
print(lista)
del mi_lista[5]
print(mi_lista)
mi_lista.remove(10)
print (mi_lista)
mi_lista.pop(2)
print(mi_lista)
print(mi_lista)
Parte_lista = mi_lista[1:3]
print(Parte_lista)
Parte_lista = mi_lista[1:4:2]
print(Parte_lista)
mi_parte = mi_lista[1:]
print(mi_parte)
mi_parte = mi_lista[:3]
print(mi_parte)
mi_parte = mi_lista[:]
print(mi_parte)
mi_parte = mi_lista[::2]
print(mi_parte)
texto = "Listas y cadenas de caracteres pueden ser accesados vía índices"
print(texto[0], texto[9], texto[20])
nestedlist = [["London","England", 7556900], ["Paris","France",2193031], ["Bern", "Switzerland", 123466]]
print(nestedlist)
print(nestedlist[1][1])
len(mi_lista) # Longitud
[1, 2, 3] + [4 , 5, 6, 7] # Concatenación
["Hola!"]*4 # Repetición
"ñ" in ["h","o","l","a"] # Afiliación
lista=["hola","mundo","2018"]
lista[0][1]
for x in [1,2,3,4]: print(x) # Iteración
lista1 = [1, 3, 5, 7]
lista2 = ((1, 2), 3, 4)
sum(lista1)
Celsius = [39.2, 36.5, 37.3, 37.8]
Fahrenheit = [ (9/5*x + 32) for x in Celsius ]
print(Fahrenheit)
n = 20
[(x,y,z) for x in range(1,n) for y in range(x,n) for z in range(y,n) if x**2 + y**2 == z**2]
| 0.082731 | 0.937669 |
### 导入需要的库
```
from keras.layers import Bidirectional, Dense, Embedding, Input, Lambda, LSTM, RepeatVector, TimeDistributed, Layer, Activation, Dropout
from keras.preprocessing.sequence import pad_sequences
from keras.layers.advanced_activations import ELU
from keras.preprocessing.text import Tokenizer
from keras.callbacks import ModelCheckpoint
from keras.optimizers import Adam
from keras import backend as K
from keras.models import Model
from scipy import spatial
from random import shuffle
import tensorflow as tf
import pandas as pd
import numpy as np
import codecs
import os
```
## 加载目录和文档
首先,我们将设置主目录和一些有关文本特征的变量。我们将序列长度设置为5-20,将词汇表中的最大单词数设置为270000(原270054),我们将使用200维embeddings。最后,从txt加载文本。文本文件来源于新闻、网页、小说等,包含大约287万个句子(130万条符合长度要求)。
```
BASE_DIR = './data/'
TRAIN_DATA_FILE = BASE_DIR + 'train.txt'# 287+万条句子
GLOVE_EMBEDDING = BASE_DIR + 'Tencent_AILab_ChineseEmbedding.txt'#单词->200维embedding
VALIDATION_SPLIT = 0.2
MIN_SEQUENCE_LENGTH = 5 #最小序列长度5
MAX_SEQUENCE_LENGTH = 20 #最大序列长度20
MAX_NB_WORDS = 270000
EMBEDDING_DIM = 200 #embedding维度300
texts = [] #通过列表来存储句子
with codecs.open(TRAIN_DATA_FILE, encoding='utf-8') as f:
reader = f.readline()
while reader: #取出句子,存入texts
if (len(reader.split()) <= MAX_SEQUENCE_LENGTH) and (len(reader.split()) >= MIN_SEQUENCE_LENGTH):
texts.append(reader)
reader = f.readline()
f.close()
n_sents = len(texts)
print('Found %s texts in train.txt' % n_sents) #训练用句子个数
```
### 文本预处理
使用Keras的tokenizer和text_to_sequences函数预处理文本
```
tokenizer = Tokenizer(MAX_NB_WORDS+1, oov_token='unk') #Tokenizer是一个用于向量化文本,或将文本转换为序列(即单词在字典中的下标构成的列表,从1算起)的类
tokenizer.fit_on_texts(texts)
print('Found %s unique tokens' % len(tokenizer.word_index))
## **关键步骤** 若不能正常工作,丢弃OOV_Token
tokenizer.word_index = {e:i for e,i in tokenizer.word_index.items() if i <= MAX_NB_WORDS} # <= 从1开始
#tokenizer.word_index[tokenizer.oov_token] = MAX_NB_WORDS + 1
word_index = tokenizer.word_index #word到index的字典
index2word = {v: k for k, v in word_index.items()} #index到word的字典
sequences = tokenizer.texts_to_sequences(texts)#序列的列表,列表中每个序列对应于一段输入文本
shuffle(sequences) #打乱句子
data_1 = pad_sequences(sequences, maxlen=MAX_SEQUENCE_LENGTH) #序列全部填充到25维,尾补0
print('Shape of data tensor:', data_1.shape)
NB_WORDS = (min(tokenizer.num_words, len(word_index))+1) #+1 for zero padding
print('NB_WORDS:', NB_WORDS)
data_val = data_1[1000000:1200000]
data_train = data_1[:1000000]
print(word_index['unk'])
print(index2word[270000])
```
### Word embeddings
使用预训练的中文 word embeddings(355776个)。创建一个矩阵,在词汇表中为每个单词对应一个embedding,然后我们将这个矩阵作为权重传递给我们模型的embedding layer
```
embeddings_index = {}
unk_embedding = np.zeros(200)
#取出word及其对应的embeddings,存入字典embeddings_index
with codecs.open(GLOVE_EMBEDDING, encoding='utf-8') as f:
line = f.readline()
line = f.readline()
while line: #取出句子,存入texts
values = line.split()
if len(values)!=201:
line = f.readline()
continue
word = values[0]
#print(word)
coefs = np.asarray(values[1:], dtype='float32')
unk_embedding = unk_embedding + coefs
embeddings_index[word] = coefs
if len(embeddings_index)%100000==0:
print(len(embeddings_index))
line = f.readline()
f.close()
unk_embedding = unk_embedding / len(embeddings_index)
print('Found %s word vectors.' % len(embeddings_index))
#print(unk_embedding)
glove_embedding_matrix = np.zeros((NB_WORDS, EMBEDDING_DIM)) #申请0数组,(413501,300)
for word, i in word_index.items():
if i < NB_WORDS+1: #+1 for 'unk' oov token
embedding_vector = embeddings_index.get(word)
if embedding_vector is not None:
glove_embedding_matrix[i] = embedding_vector
else:
# 在embeddings索引中找不到的单词,将是unk的embeddings
#print('i=',i)
glove_embedding_matrix[i] = unk_embedding
print('Null word embeddings: %d' % np.sum(np.sum(glove_embedding_matrix, axis=1) == 0))
```
### VAE 模型
模型基于seq2seq架构,包含双向LSTM编码器和LSTM解码器。
通过 RepeatVector(max_len)函数,将每个时间步的潜在表示作为输入提供给解码器decoder。为了避免标签的独热码表示,我们使用tf.contrib.seq2seq.sequence_loss函数,它只需要单词索引作为标签(与embedding矩阵的输入相同)并在内部计算最终的softmax(所以 模型以具有线性激活的dense层结束)。
可选地,“sequence_loss”允许使用采样的softmax,这有助于处理大型词汇表(例如,具有50k字词汇),但在此没有使用。这里使用的解码器与文中实现的解码器不同; 不是将context vector作为解码器的初始状态和预测的单词作为输入,而是在每个时间步处输入潜在表示z作为输入。
```
batch_size = 100
max_len = MAX_SEQUENCE_LENGTH
emb_dim = EMBEDDING_DIM
latent_dim = 64
intermediate_dim = 256
epsilon_std = 1.0
kl_weight = 0.01
num_sampled=500
act = ELU()
x = Input(shape=(max_len,)) #输入是按批量的40维向量(句子)
x_embed = Embedding(NB_WORDS, emb_dim, weights=[glove_embedding_matrix], input_length=max_len, trainable=False)(x)
h = Bidirectional(LSTM(intermediate_dim, return_sequences=False, recurrent_dropout=0.2), merge_mode='concat')(x_embed)
#h = Bidirectional(LSTM(intermediate_dim, return_sequences=False), merge_mode='concat')(h)
#h = Dropout(0.2)(h)
#h = Dense(intermediate_dim, activation='linear')(h)
#h = act(h)
#h = Dropout(0.2)(h)
z_mean = Dense(latent_dim)(h)
z_log_var = Dense(latent_dim)(h)
def sampling(args):
z_mean, z_log_var = args
epsilon = K.random_normal(shape=(batch_size, latent_dim), mean=0.,
stddev=epsilon_std)
return z_mean + K.exp(z_log_var / 2) * epsilon
# note that "output_shape" isn't necessary with the TensorFlow backend
z = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])
# 分别实例化这些层,以便以后重用
repeated_context = RepeatVector(max_len)
decoder_h = LSTM(intermediate_dim, return_sequences=True, recurrent_dropout=0.2)
decoder_mean = Dense(NB_WORDS, activation='linear')#softmax is applied in the seq2seqloss by tf #TimeDistributed()
h_decoded = decoder_h(repeated_context(z))
x_decoded_mean = decoder_mean(h_decoded)
# placeholder loss
def zero_loss(y_true, y_pred):
return K.zeros_like(y_pred)
'''
#Sampled softmax
logits = tf.constant(np.random.randn(batch_size, max_len, NB_WORDS), tf.float32)
targets = tf.constant(np.random.randint(NB_WORDS, size=(batch_size, max_len)), tf.int32)
proj_w = tf.constant(np.random.randn(NB_WORDS, NB_WORDS), tf.float32)
proj_b = tf.constant(np.zeros(NB_WORDS), tf.float32)
def _sampled_loss(labels, logits):
labels = tf.cast(labels, tf.int64)
labels = tf.reshape(labels, [-1, 1])
logits = tf.cast(logits, tf.float32)
return tf.cast(
tf.nn.sampled_softmax_loss(
proj_w,
proj_b,
labels,
logits,
num_sampled=num_sampled,
num_classes=NB_WORDS),
tf.float32)
softmax_loss_f = _sampled_loss
'''
# 用于计算VAE损失的自定义层
class CustomVariationalLayer(Layer):
def __init__(self, **kwargs):
self.is_placeholder = True
super(CustomVariationalLayer, self).__init__(**kwargs)
self.target_weights = tf.constant(np.ones((batch_size, max_len)), tf.float32)
def vae_loss(self, x, x_decoded_mean):
#xent_loss = K.sum(metrics.categorical_crossentropy(x, x_decoded_mean), axis=-1)
labels = tf.cast(x, tf.int32)
xent_loss = K.sum(tf.contrib.seq2seq.sequence_loss(x_decoded_mean, labels,
weights=self.target_weights,
average_across_timesteps=False,
average_across_batch=False), axis=-1)
#softmax_loss_function=softmax_loss_f), axis=-1)#,
kl_loss = - 0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
xent_loss = K.mean(xent_loss)
kl_loss = K.mean(kl_loss)
return K.mean(xent_loss + kl_weight * kl_loss)
#编写一个call方法,来实现自定义层
def call(self, inputs):
x = inputs[0]
x_decoded_mean = inputs[1]
print(x.shape, x_decoded_mean.shape)
loss = self.vae_loss(x, x_decoded_mean)
self.add_loss(loss, inputs=inputs)
# we don't use this output, but it has to have the correct shape:
return K.ones_like(x)
def kl_loss(x, x_decoded_mean):
kl_loss = - 0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
kl_loss = kl_weight * kl_loss
return kl_loss
loss_layer = CustomVariationalLayer()([x, x_decoded_mean])
vae = Model(x, [loss_layer])
opt = Adam(lr=0.01)
vae.compile(optimizer='adam', loss=[zero_loss], metrics=[kl_loss])
vae.summary()
```
### 模型训练
通过keras.fit()训练100epochs。对于验证数据,传递相同的数组两次,因为此模型的输入和标签相同。
如果不使用“tf.contrib.seq2seq.sequence_loss”(或其他类似的函数),
将必须作为标签传递单词的one-hot码高维度序列(batch_size,seq_len,vocab_size)消耗大量内存。
```
def create_model_checkpoint(dir, model_name):
filepath = dir + '/' + model_name + ".h5"
directory = os.path.dirname(filepath)
try:
os.stat(directory)
except:
os.mkdir(directory)
checkpointer = ModelCheckpoint(filepath=filepath, verbose=1, save_best_only=True)
return checkpointer
checkpointer = create_model_checkpoint('models', 'vae_seq2seq_test_very_high_std')
vae.fit(data_train, data_train,
shuffle=True,
epochs=100,
batch_size=batch_size,
validation_data=(data_val, data_val), callbacks=[checkpointer])
#print(K.eval(vae.optimizer.lr))
#K.set_value(vae.optimizer.lr, 0.01)
vae.save('models/vae_lstm.h5')
#vae.load_weights('models/vae_lstm.h5')
```
|
github_jupyter
|
from keras.layers import Bidirectional, Dense, Embedding, Input, Lambda, LSTM, RepeatVector, TimeDistributed, Layer, Activation, Dropout
from keras.preprocessing.sequence import pad_sequences
from keras.layers.advanced_activations import ELU
from keras.preprocessing.text import Tokenizer
from keras.callbacks import ModelCheckpoint
from keras.optimizers import Adam
from keras import backend as K
from keras.models import Model
from scipy import spatial
from random import shuffle
import tensorflow as tf
import pandas as pd
import numpy as np
import codecs
import os
BASE_DIR = './data/'
TRAIN_DATA_FILE = BASE_DIR + 'train.txt'# 287+万条句子
GLOVE_EMBEDDING = BASE_DIR + 'Tencent_AILab_ChineseEmbedding.txt'#单词->200维embedding
VALIDATION_SPLIT = 0.2
MIN_SEQUENCE_LENGTH = 5 #最小序列长度5
MAX_SEQUENCE_LENGTH = 20 #最大序列长度20
MAX_NB_WORDS = 270000
EMBEDDING_DIM = 200 #embedding维度300
texts = [] #通过列表来存储句子
with codecs.open(TRAIN_DATA_FILE, encoding='utf-8') as f:
reader = f.readline()
while reader: #取出句子,存入texts
if (len(reader.split()) <= MAX_SEQUENCE_LENGTH) and (len(reader.split()) >= MIN_SEQUENCE_LENGTH):
texts.append(reader)
reader = f.readline()
f.close()
n_sents = len(texts)
print('Found %s texts in train.txt' % n_sents) #训练用句子个数
tokenizer = Tokenizer(MAX_NB_WORDS+1, oov_token='unk') #Tokenizer是一个用于向量化文本,或将文本转换为序列(即单词在字典中的下标构成的列表,从1算起)的类
tokenizer.fit_on_texts(texts)
print('Found %s unique tokens' % len(tokenizer.word_index))
## **关键步骤** 若不能正常工作,丢弃OOV_Token
tokenizer.word_index = {e:i for e,i in tokenizer.word_index.items() if i <= MAX_NB_WORDS} # <= 从1开始
#tokenizer.word_index[tokenizer.oov_token] = MAX_NB_WORDS + 1
word_index = tokenizer.word_index #word到index的字典
index2word = {v: k for k, v in word_index.items()} #index到word的字典
sequences = tokenizer.texts_to_sequences(texts)#序列的列表,列表中每个序列对应于一段输入文本
shuffle(sequences) #打乱句子
data_1 = pad_sequences(sequences, maxlen=MAX_SEQUENCE_LENGTH) #序列全部填充到25维,尾补0
print('Shape of data tensor:', data_1.shape)
NB_WORDS = (min(tokenizer.num_words, len(word_index))+1) #+1 for zero padding
print('NB_WORDS:', NB_WORDS)
data_val = data_1[1000000:1200000]
data_train = data_1[:1000000]
print(word_index['unk'])
print(index2word[270000])
embeddings_index = {}
unk_embedding = np.zeros(200)
#取出word及其对应的embeddings,存入字典embeddings_index
with codecs.open(GLOVE_EMBEDDING, encoding='utf-8') as f:
line = f.readline()
line = f.readline()
while line: #取出句子,存入texts
values = line.split()
if len(values)!=201:
line = f.readline()
continue
word = values[0]
#print(word)
coefs = np.asarray(values[1:], dtype='float32')
unk_embedding = unk_embedding + coefs
embeddings_index[word] = coefs
if len(embeddings_index)%100000==0:
print(len(embeddings_index))
line = f.readline()
f.close()
unk_embedding = unk_embedding / len(embeddings_index)
print('Found %s word vectors.' % len(embeddings_index))
#print(unk_embedding)
glove_embedding_matrix = np.zeros((NB_WORDS, EMBEDDING_DIM)) #申请0数组,(413501,300)
for word, i in word_index.items():
if i < NB_WORDS+1: #+1 for 'unk' oov token
embedding_vector = embeddings_index.get(word)
if embedding_vector is not None:
glove_embedding_matrix[i] = embedding_vector
else:
# 在embeddings索引中找不到的单词,将是unk的embeddings
#print('i=',i)
glove_embedding_matrix[i] = unk_embedding
print('Null word embeddings: %d' % np.sum(np.sum(glove_embedding_matrix, axis=1) == 0))
batch_size = 100
max_len = MAX_SEQUENCE_LENGTH
emb_dim = EMBEDDING_DIM
latent_dim = 64
intermediate_dim = 256
epsilon_std = 1.0
kl_weight = 0.01
num_sampled=500
act = ELU()
x = Input(shape=(max_len,)) #输入是按批量的40维向量(句子)
x_embed = Embedding(NB_WORDS, emb_dim, weights=[glove_embedding_matrix], input_length=max_len, trainable=False)(x)
h = Bidirectional(LSTM(intermediate_dim, return_sequences=False, recurrent_dropout=0.2), merge_mode='concat')(x_embed)
#h = Bidirectional(LSTM(intermediate_dim, return_sequences=False), merge_mode='concat')(h)
#h = Dropout(0.2)(h)
#h = Dense(intermediate_dim, activation='linear')(h)
#h = act(h)
#h = Dropout(0.2)(h)
z_mean = Dense(latent_dim)(h)
z_log_var = Dense(latent_dim)(h)
def sampling(args):
z_mean, z_log_var = args
epsilon = K.random_normal(shape=(batch_size, latent_dim), mean=0.,
stddev=epsilon_std)
return z_mean + K.exp(z_log_var / 2) * epsilon
# note that "output_shape" isn't necessary with the TensorFlow backend
z = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])
# 分别实例化这些层,以便以后重用
repeated_context = RepeatVector(max_len)
decoder_h = LSTM(intermediate_dim, return_sequences=True, recurrent_dropout=0.2)
decoder_mean = Dense(NB_WORDS, activation='linear')#softmax is applied in the seq2seqloss by tf #TimeDistributed()
h_decoded = decoder_h(repeated_context(z))
x_decoded_mean = decoder_mean(h_decoded)
# placeholder loss
def zero_loss(y_true, y_pred):
return K.zeros_like(y_pred)
'''
#Sampled softmax
logits = tf.constant(np.random.randn(batch_size, max_len, NB_WORDS), tf.float32)
targets = tf.constant(np.random.randint(NB_WORDS, size=(batch_size, max_len)), tf.int32)
proj_w = tf.constant(np.random.randn(NB_WORDS, NB_WORDS), tf.float32)
proj_b = tf.constant(np.zeros(NB_WORDS), tf.float32)
def _sampled_loss(labels, logits):
labels = tf.cast(labels, tf.int64)
labels = tf.reshape(labels, [-1, 1])
logits = tf.cast(logits, tf.float32)
return tf.cast(
tf.nn.sampled_softmax_loss(
proj_w,
proj_b,
labels,
logits,
num_sampled=num_sampled,
num_classes=NB_WORDS),
tf.float32)
softmax_loss_f = _sampled_loss
'''
# 用于计算VAE损失的自定义层
class CustomVariationalLayer(Layer):
def __init__(self, **kwargs):
self.is_placeholder = True
super(CustomVariationalLayer, self).__init__(**kwargs)
self.target_weights = tf.constant(np.ones((batch_size, max_len)), tf.float32)
def vae_loss(self, x, x_decoded_mean):
#xent_loss = K.sum(metrics.categorical_crossentropy(x, x_decoded_mean), axis=-1)
labels = tf.cast(x, tf.int32)
xent_loss = K.sum(tf.contrib.seq2seq.sequence_loss(x_decoded_mean, labels,
weights=self.target_weights,
average_across_timesteps=False,
average_across_batch=False), axis=-1)
#softmax_loss_function=softmax_loss_f), axis=-1)#,
kl_loss = - 0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
xent_loss = K.mean(xent_loss)
kl_loss = K.mean(kl_loss)
return K.mean(xent_loss + kl_weight * kl_loss)
#编写一个call方法,来实现自定义层
def call(self, inputs):
x = inputs[0]
x_decoded_mean = inputs[1]
print(x.shape, x_decoded_mean.shape)
loss = self.vae_loss(x, x_decoded_mean)
self.add_loss(loss, inputs=inputs)
# we don't use this output, but it has to have the correct shape:
return K.ones_like(x)
def kl_loss(x, x_decoded_mean):
kl_loss = - 0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
kl_loss = kl_weight * kl_loss
return kl_loss
loss_layer = CustomVariationalLayer()([x, x_decoded_mean])
vae = Model(x, [loss_layer])
opt = Adam(lr=0.01)
vae.compile(optimizer='adam', loss=[zero_loss], metrics=[kl_loss])
vae.summary()
def create_model_checkpoint(dir, model_name):
filepath = dir + '/' + model_name + ".h5"
directory = os.path.dirname(filepath)
try:
os.stat(directory)
except:
os.mkdir(directory)
checkpointer = ModelCheckpoint(filepath=filepath, verbose=1, save_best_only=True)
return checkpointer
checkpointer = create_model_checkpoint('models', 'vae_seq2seq_test_very_high_std')
vae.fit(data_train, data_train,
shuffle=True,
epochs=100,
batch_size=batch_size,
validation_data=(data_val, data_val), callbacks=[checkpointer])
#print(K.eval(vae.optimizer.lr))
#K.set_value(vae.optimizer.lr, 0.01)
vae.save('models/vae_lstm.h5')
#vae.load_weights('models/vae_lstm.h5')
| 0.462716 | 0.747501 |
```
# -*- coding: utf-8 -*-
import logging
from gensim.models import word2vec
def main():
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
sentences = word2vec.LineSentence("../Word_Segmentation/Spur10_preprocessed_20180614_20170510.segmentated")
model = word2vec.Word2Vec(sentences, size=50)
#保存模型,供日後使用
model.save("word2vec.model")
#模型讀取方式
# model = word2vec.Word2Vec.load("your_model_name")
if __name__ == "__main__":
main()
from gensim import models
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
model = models.Word2Vec.load('word2vec.model')
query_str = "舒適"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
#%run -i /Users/coslate/Word2Vec/Preprocess/preprocess.py
query_str = "坦"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
query_str = "馬刺"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
query_str = "LBJ"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
# -*- coding: utf-8 -*-
import logging
from gensim.models import word2vec
def main():
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
sentences = word2vec.LineSentence("../Word_Segmentation/Spur10_preprocessed_20180614_20150510.segmentated")
model = word2vec.Word2Vec(sentences, size=50)
#保存模型,供日後使用
model.save("word2vec.model")
#模型讀取方式
# model = word2vec.Word2Vec.load("your_model_name")
if __name__ == "__main__":
main()
from gensim import models
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
model = models.Word2Vec.load('word2vec.model')
query_str = "馬刺"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
# -*- coding: utf-8 -*-
import logging
from gensim.models import word2vec
def main():
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
sentences = word2vec.LineSentence("../Word_Segmentation/Total_20180614_20170510_preprocessed_20180614_20170510.segmentated")
model = word2vec.Word2Vec(sentences, size=50)
#保存模型,供日後使用
model.save("word2vec.model")
#模型讀取方式
# model = word2vec.Word2Vec.load("your_model_name")
if __name__ == "__main__":
main()
from gensim import models
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
model = models.Word2Vec.load('word2vec.model')
query_str = "馬刺"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
# -*- coding: utf-8 -*-
import logging
from gensim.models import word2vec
def main():
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
sentences = word2vec.LineSentence("../Word_Segmentation/Total_20180614_20170510_preprocessed_20180614_20170510.segmentated")
model = word2vec.Word2Vec(sentences, size=50, sg=1)
#保存模型,供日後使用
model.save("word2vec.model")
#模型讀取方式
# model = word2vec.Word2Vec.load("your_model_name")
if __name__ == "__main__":
main()
from gensim import models
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
model = models.Word2Vec.load('word2vec.model')
query_str = "馬刺"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
# -*- coding: utf-8 -*-
import logging
from gensim.models import word2vec
def main():
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
sentences = word2vec.LineSentence("../Word_Segmentation/Spur10_preprocessed_20180614_20170510.segmentated")
model = word2vec.Word2Vec(sentences, size=50, sg=0)
#保存模型,供日後使用
model.save("word2vec.model")
#模型讀取方式
# model = word2vec.Word2Vec.load("your_model_name")
if __name__ == "__main__":
main()
from gensim import models
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
model = models.Word2Vec.load('word2vec.model')
query_str = "馬刺"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
type(res)
a = "123, 456"
tuple(list(a))
res[0]
```
|
github_jupyter
|
# -*- coding: utf-8 -*-
import logging
from gensim.models import word2vec
def main():
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
sentences = word2vec.LineSentence("../Word_Segmentation/Spur10_preprocessed_20180614_20170510.segmentated")
model = word2vec.Word2Vec(sentences, size=50)
#保存模型,供日後使用
model.save("word2vec.model")
#模型讀取方式
# model = word2vec.Word2Vec.load("your_model_name")
if __name__ == "__main__":
main()
from gensim import models
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
model = models.Word2Vec.load('word2vec.model')
query_str = "舒適"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
#%run -i /Users/coslate/Word2Vec/Preprocess/preprocess.py
query_str = "坦"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
query_str = "馬刺"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
query_str = "LBJ"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
# -*- coding: utf-8 -*-
import logging
from gensim.models import word2vec
def main():
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
sentences = word2vec.LineSentence("../Word_Segmentation/Spur10_preprocessed_20180614_20150510.segmentated")
model = word2vec.Word2Vec(sentences, size=50)
#保存模型,供日後使用
model.save("word2vec.model")
#模型讀取方式
# model = word2vec.Word2Vec.load("your_model_name")
if __name__ == "__main__":
main()
from gensim import models
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
model = models.Word2Vec.load('word2vec.model')
query_str = "馬刺"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
# -*- coding: utf-8 -*-
import logging
from gensim.models import word2vec
def main():
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
sentences = word2vec.LineSentence("../Word_Segmentation/Total_20180614_20170510_preprocessed_20180614_20170510.segmentated")
model = word2vec.Word2Vec(sentences, size=50)
#保存模型,供日後使用
model.save("word2vec.model")
#模型讀取方式
# model = word2vec.Word2Vec.load("your_model_name")
if __name__ == "__main__":
main()
from gensim import models
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
model = models.Word2Vec.load('word2vec.model')
query_str = "馬刺"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
# -*- coding: utf-8 -*-
import logging
from gensim.models import word2vec
def main():
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
sentences = word2vec.LineSentence("../Word_Segmentation/Total_20180614_20170510_preprocessed_20180614_20170510.segmentated")
model = word2vec.Word2Vec(sentences, size=50, sg=1)
#保存模型,供日後使用
model.save("word2vec.model")
#模型讀取方式
# model = word2vec.Word2Vec.load("your_model_name")
if __name__ == "__main__":
main()
from gensim import models
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
model = models.Word2Vec.load('word2vec.model')
query_str = "馬刺"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
# -*- coding: utf-8 -*-
import logging
from gensim.models import word2vec
def main():
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
sentences = word2vec.LineSentence("../Word_Segmentation/Spur10_preprocessed_20180614_20170510.segmentated")
model = word2vec.Word2Vec(sentences, size=50, sg=0)
#保存模型,供日後使用
model.save("word2vec.model")
#模型讀取方式
# model = word2vec.Word2Vec.load("your_model_name")
if __name__ == "__main__":
main()
from gensim import models
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
model = models.Word2Vec.load('word2vec.model')
query_str = "馬刺"
print("相似詞前 100 排序")
res = model.most_similar(query_str,topn = 100)
for item in res:
print(item[0]+","+str(item[1]))
type(res)
a = "123, 456"
tuple(list(a))
res[0]
| 0.150496 | 0.165121 |
# RadarCOVID-Report
## Data Extraction
```
import datetime
import json
import logging
import os
import shutil
import tempfile
import textwrap
import uuid
import matplotlib.pyplot as plt
import matplotlib.ticker
import numpy as np
import pandas as pd
import pycountry
import retry
import seaborn as sns
%matplotlib inline
current_working_directory = os.environ.get("PWD")
if current_working_directory:
os.chdir(current_working_directory)
sns.set()
matplotlib.rcParams["figure.figsize"] = (15, 6)
extraction_datetime = datetime.datetime.utcnow()
extraction_date = extraction_datetime.strftime("%Y-%m-%d")
extraction_previous_datetime = extraction_datetime - datetime.timedelta(days=1)
extraction_previous_date = extraction_previous_datetime.strftime("%Y-%m-%d")
extraction_date_with_hour = datetime.datetime.utcnow().strftime("%Y-%m-%d@%H")
current_hour = datetime.datetime.utcnow().hour
are_today_results_partial = current_hour != 23
```
### Constants
```
from Modules.ExposureNotification import exposure_notification_io
spain_region_country_code = "ES"
germany_region_country_code = "DE"
default_backend_identifier = spain_region_country_code
backend_generation_days = 7 * 2
daily_summary_days = 7 * 4 * 3
daily_plot_days = 7 * 4
tek_dumps_load_limit = daily_summary_days + 1
```
### Parameters
```
environment_backend_identifier = os.environ.get("RADARCOVID_REPORT__BACKEND_IDENTIFIER")
if environment_backend_identifier:
report_backend_identifier = environment_backend_identifier
else:
report_backend_identifier = default_backend_identifier
report_backend_identifier
environment_enable_multi_backend_download = \
os.environ.get("RADARCOVID_REPORT__ENABLE_MULTI_BACKEND_DOWNLOAD")
if environment_enable_multi_backend_download:
report_backend_identifiers = None
else:
report_backend_identifiers = [report_backend_identifier]
report_backend_identifiers
environment_invalid_shared_diagnoses_dates = \
os.environ.get("RADARCOVID_REPORT__INVALID_SHARED_DIAGNOSES_DATES")
if environment_invalid_shared_diagnoses_dates:
invalid_shared_diagnoses_dates = environment_invalid_shared_diagnoses_dates.split(",")
else:
invalid_shared_diagnoses_dates = []
invalid_shared_diagnoses_dates
```
### COVID-19 Cases
```
report_backend_client = \
exposure_notification_io.get_backend_client_with_identifier(
backend_identifier=report_backend_identifier)
@retry.retry(tries=10, delay=10, backoff=1.1, jitter=(0, 10))
def download_cases_dataframe():
return pd.read_csv("https://raw.githubusercontent.com/owid/covid-19-data/master/public/data/owid-covid-data.csv")
confirmed_df_ = download_cases_dataframe()
confirmed_df_.iloc[0]
confirmed_df = confirmed_df_.copy()
confirmed_df = confirmed_df[["date", "new_cases", "iso_code"]]
confirmed_df.rename(
columns={
"date": "sample_date",
"iso_code": "country_code",
},
inplace=True)
def convert_iso_alpha_3_to_alpha_2(x):
try:
return pycountry.countries.get(alpha_3=x).alpha_2
except Exception as e:
logging.info(f"Error converting country ISO Alpha 3 code '{x}': {repr(e)}")
return None
confirmed_df["country_code"] = confirmed_df.country_code.apply(convert_iso_alpha_3_to_alpha_2)
confirmed_df.dropna(inplace=True)
confirmed_df["sample_date"] = pd.to_datetime(confirmed_df.sample_date, dayfirst=True)
confirmed_df["sample_date"] = confirmed_df.sample_date.dt.strftime("%Y-%m-%d")
confirmed_df.sort_values("sample_date", inplace=True)
confirmed_df.tail()
confirmed_days = pd.date_range(
start=confirmed_df.iloc[0].sample_date,
end=extraction_datetime)
confirmed_days_df = pd.DataFrame(data=confirmed_days, columns=["sample_date"])
confirmed_days_df["sample_date_string"] = \
confirmed_days_df.sample_date.dt.strftime("%Y-%m-%d")
confirmed_days_df.tail()
def sort_source_regions_for_display(source_regions: list) -> list:
if report_backend_identifier in source_regions:
source_regions = [report_backend_identifier] + \
list(sorted(set(source_regions).difference([report_backend_identifier])))
else:
source_regions = list(sorted(source_regions))
return source_regions
report_source_regions = report_backend_client.source_regions_for_date(
date=extraction_datetime.date())
report_source_regions = sort_source_regions_for_display(
source_regions=report_source_regions)
report_source_regions
def get_cases_dataframe(source_regions_for_date_function, columns_suffix=None):
source_regions_at_date_df = confirmed_days_df.copy()
source_regions_at_date_df["source_regions_at_date"] = \
source_regions_at_date_df.sample_date.apply(
lambda x: source_regions_for_date_function(date=x))
source_regions_at_date_df.sort_values("sample_date", inplace=True)
source_regions_at_date_df["_source_regions_group"] = source_regions_at_date_df. \
source_regions_at_date.apply(lambda x: ",".join(sort_source_regions_for_display(x)))
source_regions_at_date_df.tail()
#%%
source_regions_for_summary_df_ = \
source_regions_at_date_df[["sample_date", "_source_regions_group"]].copy()
source_regions_for_summary_df_.rename(columns={"_source_regions_group": "source_regions"}, inplace=True)
source_regions_for_summary_df_.tail()
#%%
confirmed_output_columns = ["sample_date", "new_cases", "covid_cases"]
confirmed_output_df = pd.DataFrame(columns=confirmed_output_columns)
for source_regions_group, source_regions_group_series in \
source_regions_at_date_df.groupby("_source_regions_group"):
source_regions_set = set(source_regions_group.split(","))
confirmed_source_regions_set_df = \
confirmed_df[confirmed_df.country_code.isin(source_regions_set)].copy()
confirmed_source_regions_group_df = \
confirmed_source_regions_set_df.groupby("sample_date").new_cases.sum() \
.reset_index().sort_values("sample_date")
confirmed_source_regions_group_df = \
confirmed_source_regions_group_df.merge(
confirmed_days_df[["sample_date_string"]].rename(
columns={"sample_date_string": "sample_date"}),
how="right")
confirmed_source_regions_group_df["new_cases"] = \
confirmed_source_regions_group_df["new_cases"].clip(lower=0)
confirmed_source_regions_group_df["covid_cases"] = \
confirmed_source_regions_group_df.new_cases.rolling(7, min_periods=0).mean().round()
confirmed_source_regions_group_df = \
confirmed_source_regions_group_df[confirmed_output_columns]
confirmed_source_regions_group_df = confirmed_source_regions_group_df.replace(0, np.nan)
confirmed_source_regions_group_df.fillna(method="ffill", inplace=True)
confirmed_source_regions_group_df = \
confirmed_source_regions_group_df[
confirmed_source_regions_group_df.sample_date.isin(
source_regions_group_series.sample_date_string)]
confirmed_output_df = confirmed_output_df.append(confirmed_source_regions_group_df)
result_df = confirmed_output_df.copy()
result_df.tail()
#%%
result_df.rename(columns={"sample_date": "sample_date_string"}, inplace=True)
result_df = confirmed_days_df[["sample_date_string"]].merge(result_df, how="left")
result_df.sort_values("sample_date_string", inplace=True)
result_df.fillna(method="ffill", inplace=True)
result_df.tail()
#%%
result_df[["new_cases", "covid_cases"]].plot()
if columns_suffix:
result_df.rename(
columns={
"new_cases": "new_cases_" + columns_suffix,
"covid_cases": "covid_cases_" + columns_suffix},
inplace=True)
return result_df, source_regions_for_summary_df_
confirmed_eu_df, source_regions_for_summary_df = get_cases_dataframe(
report_backend_client.source_regions_for_date)
confirmed_es_df, _ = get_cases_dataframe(
lambda date: [spain_region_country_code],
columns_suffix=spain_region_country_code.lower())
```
### Extract API TEKs
```
raw_zip_path_prefix = "Data/TEKs/Raw/"
base_backend_identifiers = [report_backend_identifier]
multi_backend_exposure_keys_df = \
exposure_notification_io.download_exposure_keys_from_backends(
backend_identifiers=report_backend_identifiers,
generation_days=backend_generation_days,
fail_on_error_backend_identifiers=base_backend_identifiers,
save_raw_zip_path_prefix=raw_zip_path_prefix)
multi_backend_exposure_keys_df["region"] = multi_backend_exposure_keys_df["backend_identifier"]
multi_backend_exposure_keys_df.rename(
columns={
"generation_datetime": "sample_datetime",
"generation_date_string": "sample_date_string",
},
inplace=True)
multi_backend_exposure_keys_df.head()
early_teks_df = multi_backend_exposure_keys_df[
multi_backend_exposure_keys_df.rolling_period < 144].copy()
early_teks_df["rolling_period_in_hours"] = early_teks_df.rolling_period / 6
early_teks_df[early_teks_df.sample_date_string != extraction_date] \
.rolling_period_in_hours.hist(bins=list(range(24)))
early_teks_df[early_teks_df.sample_date_string == extraction_date] \
.rolling_period_in_hours.hist(bins=list(range(24)))
multi_backend_exposure_keys_df = multi_backend_exposure_keys_df[[
"sample_date_string", "region", "key_data"]]
multi_backend_exposure_keys_df.head()
active_regions = \
multi_backend_exposure_keys_df.groupby("region").key_data.nunique().sort_values().index.unique().tolist()
active_regions
multi_backend_summary_df = multi_backend_exposure_keys_df.groupby(
["sample_date_string", "region"]).key_data.nunique().reset_index() \
.pivot(index="sample_date_string", columns="region") \
.sort_index(ascending=False)
multi_backend_summary_df.rename(
columns={"key_data": "shared_teks_by_generation_date"},
inplace=True)
multi_backend_summary_df.rename_axis("sample_date", inplace=True)
multi_backend_summary_df = multi_backend_summary_df.fillna(0).astype(int)
multi_backend_summary_df = multi_backend_summary_df.head(backend_generation_days)
multi_backend_summary_df.head()
def compute_keys_cross_sharing(x):
teks_x = x.key_data_x.item()
common_teks = set(teks_x).intersection(x.key_data_y.item())
common_teks_fraction = len(common_teks) / len(teks_x)
return pd.Series(dict(
common_teks=common_teks,
common_teks_fraction=common_teks_fraction,
))
multi_backend_exposure_keys_by_region_df = \
multi_backend_exposure_keys_df.groupby("region").key_data.unique().reset_index()
multi_backend_exposure_keys_by_region_df["_merge"] = True
multi_backend_exposure_keys_by_region_combination_df = \
multi_backend_exposure_keys_by_region_df.merge(
multi_backend_exposure_keys_by_region_df, on="_merge")
multi_backend_exposure_keys_by_region_combination_df.drop(
columns=["_merge"], inplace=True)
if multi_backend_exposure_keys_by_region_combination_df.region_x.nunique() > 1:
multi_backend_exposure_keys_by_region_combination_df = \
multi_backend_exposure_keys_by_region_combination_df[
multi_backend_exposure_keys_by_region_combination_df.region_x !=
multi_backend_exposure_keys_by_region_combination_df.region_y]
multi_backend_exposure_keys_cross_sharing_df = \
multi_backend_exposure_keys_by_region_combination_df \
.groupby(["region_x", "region_y"]) \
.apply(compute_keys_cross_sharing) \
.reset_index()
multi_backend_cross_sharing_summary_df = \
multi_backend_exposure_keys_cross_sharing_df.pivot_table(
values=["common_teks_fraction"],
columns="region_x",
index="region_y",
aggfunc=lambda x: x.item())
multi_backend_cross_sharing_summary_df
multi_backend_without_active_region_exposure_keys_df = \
multi_backend_exposure_keys_df[multi_backend_exposure_keys_df.region != report_backend_identifier]
multi_backend_without_active_region = \
multi_backend_without_active_region_exposure_keys_df.groupby("region").key_data.nunique().sort_values().index.unique().tolist()
multi_backend_without_active_region
exposure_keys_summary_df = multi_backend_exposure_keys_df[
multi_backend_exposure_keys_df.region == report_backend_identifier]
exposure_keys_summary_df.drop(columns=["region"], inplace=True)
exposure_keys_summary_df = \
exposure_keys_summary_df.groupby(["sample_date_string"]).key_data.nunique().to_frame()
exposure_keys_summary_df = \
exposure_keys_summary_df.reset_index().set_index("sample_date_string")
exposure_keys_summary_df.sort_index(ascending=False, inplace=True)
exposure_keys_summary_df.rename(columns={"key_data": "shared_teks_by_generation_date"}, inplace=True)
exposure_keys_summary_df.head()
```
### Dump API TEKs
```
tek_list_df = multi_backend_exposure_keys_df[
["sample_date_string", "region", "key_data"]].copy()
tek_list_df["key_data"] = tek_list_df["key_data"].apply(str)
tek_list_df.rename(columns={
"sample_date_string": "sample_date",
"key_data": "tek_list"}, inplace=True)
tek_list_df = tek_list_df.groupby(
["sample_date", "region"]).tek_list.unique().reset_index()
tek_list_df["extraction_date"] = extraction_date
tek_list_df["extraction_date_with_hour"] = extraction_date_with_hour
tek_list_path_prefix = "Data/TEKs/"
tek_list_current_path = tek_list_path_prefix + f"/Current/RadarCOVID-TEKs.json"
tek_list_daily_path = tek_list_path_prefix + f"Daily/RadarCOVID-TEKs-{extraction_date}.json"
tek_list_hourly_path = tek_list_path_prefix + f"Hourly/RadarCOVID-TEKs-{extraction_date_with_hour}.json"
for path in [tek_list_current_path, tek_list_daily_path, tek_list_hourly_path]:
os.makedirs(os.path.dirname(path), exist_ok=True)
tek_list_base_df = tek_list_df[tek_list_df.region == report_backend_identifier]
tek_list_base_df.drop(columns=["extraction_date", "extraction_date_with_hour"]).to_json(
tek_list_current_path,
lines=True, orient="records")
tek_list_base_df.drop(columns=["extraction_date_with_hour"]).to_json(
tek_list_daily_path,
lines=True, orient="records")
tek_list_base_df.to_json(
tek_list_hourly_path,
lines=True, orient="records")
tek_list_base_df.head()
```
### Load TEK Dumps
```
import glob
def load_extracted_teks(mode, region=None, limit=None) -> pd.DataFrame:
extracted_teks_df = pd.DataFrame(columns=["region"])
file_paths = list(reversed(sorted(glob.glob(tek_list_path_prefix + mode + "/RadarCOVID-TEKs-*.json"))))
if limit:
file_paths = file_paths[:limit]
for file_path in file_paths:
logging.info(f"Loading TEKs from '{file_path}'...")
iteration_extracted_teks_df = pd.read_json(file_path, lines=True)
extracted_teks_df = extracted_teks_df.append(
iteration_extracted_teks_df, sort=False)
extracted_teks_df["region"] = \
extracted_teks_df.region.fillna(spain_region_country_code).copy()
if region:
extracted_teks_df = \
extracted_teks_df[extracted_teks_df.region == region]
return extracted_teks_df
daily_extracted_teks_df = load_extracted_teks(
mode="Daily",
region=report_backend_identifier,
limit=tek_dumps_load_limit)
daily_extracted_teks_df.head()
exposure_keys_summary_df_ = daily_extracted_teks_df \
.sort_values("extraction_date", ascending=False) \
.groupby("sample_date").tek_list.first() \
.to_frame()
exposure_keys_summary_df_.index.name = "sample_date_string"
exposure_keys_summary_df_["tek_list"] = \
exposure_keys_summary_df_.tek_list.apply(len)
exposure_keys_summary_df_ = exposure_keys_summary_df_ \
.rename(columns={"tek_list": "shared_teks_by_generation_date"}) \
.sort_index(ascending=False)
exposure_keys_summary_df = exposure_keys_summary_df_
exposure_keys_summary_df.head()
```
### Daily New TEKs
```
tek_list_df = daily_extracted_teks_df.groupby("extraction_date").tek_list.apply(
lambda x: set(sum(x, []))).reset_index()
tek_list_df = tek_list_df.set_index("extraction_date").sort_index(ascending=True)
tek_list_df.head()
def compute_teks_by_generation_and_upload_date(date):
day_new_teks_set_df = tek_list_df.copy().diff()
try:
day_new_teks_set = day_new_teks_set_df[
day_new_teks_set_df.index == date].tek_list.item()
except ValueError:
day_new_teks_set = None
if pd.isna(day_new_teks_set):
day_new_teks_set = set()
day_new_teks_df = daily_extracted_teks_df[
daily_extracted_teks_df.extraction_date == date].copy()
day_new_teks_df["shared_teks"] = \
day_new_teks_df.tek_list.apply(lambda x: set(x).intersection(day_new_teks_set))
day_new_teks_df["shared_teks"] = \
day_new_teks_df.shared_teks.apply(len)
day_new_teks_df["upload_date"] = date
day_new_teks_df.rename(columns={"sample_date": "generation_date"}, inplace=True)
day_new_teks_df = day_new_teks_df[
["upload_date", "generation_date", "shared_teks"]]
day_new_teks_df["generation_to_upload_days"] = \
(pd.to_datetime(day_new_teks_df.upload_date) -
pd.to_datetime(day_new_teks_df.generation_date)).dt.days
day_new_teks_df = day_new_teks_df[day_new_teks_df.shared_teks > 0]
return day_new_teks_df
shared_teks_generation_to_upload_df = pd.DataFrame()
for upload_date in daily_extracted_teks_df.extraction_date.unique():
shared_teks_generation_to_upload_df = \
shared_teks_generation_to_upload_df.append(
compute_teks_by_generation_and_upload_date(date=upload_date))
shared_teks_generation_to_upload_df \
.sort_values(["upload_date", "generation_date"], ascending=False, inplace=True)
shared_teks_generation_to_upload_df.tail()
today_new_teks_df = \
shared_teks_generation_to_upload_df[
shared_teks_generation_to_upload_df.upload_date == extraction_date].copy()
today_new_teks_df.tail()
if not today_new_teks_df.empty:
today_new_teks_df.set_index("generation_to_upload_days") \
.sort_index().shared_teks.plot.bar()
generation_to_upload_period_pivot_df = \
shared_teks_generation_to_upload_df[
["upload_date", "generation_to_upload_days", "shared_teks"]] \
.pivot(index="upload_date", columns="generation_to_upload_days") \
.sort_index(ascending=False).fillna(0).astype(int) \
.droplevel(level=0, axis=1)
generation_to_upload_period_pivot_df.head()
new_tek_df = tek_list_df.diff().tek_list.apply(
lambda x: len(x) if not pd.isna(x) else None).to_frame().reset_index()
new_tek_df.rename(columns={
"tek_list": "shared_teks_by_upload_date",
"extraction_date": "sample_date_string",}, inplace=True)
new_tek_df.tail()
shared_teks_uploaded_on_generation_date_df = shared_teks_generation_to_upload_df[
shared_teks_generation_to_upload_df.generation_to_upload_days == 0] \
[["upload_date", "shared_teks"]].rename(
columns={
"upload_date": "sample_date_string",
"shared_teks": "shared_teks_uploaded_on_generation_date",
})
shared_teks_uploaded_on_generation_date_df.head()
estimated_shared_diagnoses_df = shared_teks_generation_to_upload_df \
.groupby(["upload_date"]).shared_teks.max().reset_index() \
.sort_values(["upload_date"], ascending=False) \
.rename(columns={
"upload_date": "sample_date_string",
"shared_teks": "shared_diagnoses",
})
invalid_shared_diagnoses_dates_mask = \
estimated_shared_diagnoses_df.sample_date_string.isin(invalid_shared_diagnoses_dates)
estimated_shared_diagnoses_df[invalid_shared_diagnoses_dates_mask] = 0
estimated_shared_diagnoses_df.head()
```
### Hourly New TEKs
```
hourly_extracted_teks_df = load_extracted_teks(
mode="Hourly", region=report_backend_identifier, limit=25)
hourly_extracted_teks_df.head()
hourly_new_tek_count_df = hourly_extracted_teks_df \
.groupby("extraction_date_with_hour").tek_list. \
apply(lambda x: set(sum(x, []))).reset_index().copy()
hourly_new_tek_count_df = hourly_new_tek_count_df.set_index("extraction_date_with_hour") \
.sort_index(ascending=True)
hourly_new_tek_count_df["new_tek_list"] = hourly_new_tek_count_df.tek_list.diff()
hourly_new_tek_count_df["new_tek_count"] = hourly_new_tek_count_df.new_tek_list.apply(
lambda x: len(x) if not pd.isna(x) else 0)
hourly_new_tek_count_df.rename(columns={
"new_tek_count": "shared_teks_by_upload_date"}, inplace=True)
hourly_new_tek_count_df = hourly_new_tek_count_df.reset_index()[[
"extraction_date_with_hour", "shared_teks_by_upload_date"]]
hourly_new_tek_count_df.head()
hourly_summary_df = hourly_new_tek_count_df.copy()
hourly_summary_df.set_index("extraction_date_with_hour", inplace=True)
hourly_summary_df = hourly_summary_df.fillna(0).astype(int).reset_index()
hourly_summary_df["datetime_utc"] = pd.to_datetime(
hourly_summary_df.extraction_date_with_hour, format="%Y-%m-%d@%H")
hourly_summary_df.set_index("datetime_utc", inplace=True)
hourly_summary_df = hourly_summary_df.tail(-1)
hourly_summary_df.head()
```
### Official Statistics
```
import requests
import pandas.io.json
official_stats_response = requests.get("https://radarcovid.covid19.gob.es/kpi/statistics/basics")
official_stats_response.raise_for_status()
official_stats_df_ = pandas.io.json.json_normalize(official_stats_response.json())
official_stats_df = official_stats_df_.copy()
official_stats_df["date"] = pd.to_datetime(official_stats_df["date"], dayfirst=True)
official_stats_df.head()
official_stats_column_map = {
"date": "sample_date",
"applicationsDownloads.totalAcummulated": "app_downloads_es_accumulated",
"communicatedContagions.totalAcummulated": "shared_diagnoses_es_accumulated",
}
accumulated_suffix = "_accumulated"
accumulated_values_columns = \
list(filter(lambda x: x.endswith(accumulated_suffix), official_stats_column_map.values()))
interpolated_values_columns = \
list(map(lambda x: x[:-len(accumulated_suffix)], accumulated_values_columns))
official_stats_df = \
official_stats_df[official_stats_column_map.keys()] \
.rename(columns=official_stats_column_map)
official_stats_df["extraction_date"] = extraction_date
official_stats_df.head()
official_stats_path = "Data/Statistics/Current/RadarCOVID-Statistics.json"
previous_official_stats_df = pd.read_json(official_stats_path, orient="records", lines=True)
previous_official_stats_df["sample_date"] = pd.to_datetime(previous_official_stats_df["sample_date"], dayfirst=True)
official_stats_df = official_stats_df.append(previous_official_stats_df)
official_stats_df.head()
official_stats_df = official_stats_df[~(official_stats_df.shared_diagnoses_es_accumulated == 0)]
official_stats_df.sort_values("extraction_date", ascending=False, inplace=True)
official_stats_df.drop_duplicates(subset=["sample_date"], keep="first", inplace=True)
official_stats_df.head()
official_stats_stored_df = official_stats_df.copy()
official_stats_stored_df["sample_date"] = official_stats_stored_df.sample_date.dt.strftime("%Y-%m-%d")
official_stats_stored_df.to_json(official_stats_path, orient="records", lines=True)
official_stats_df.drop(columns=["extraction_date"], inplace=True)
official_stats_df = confirmed_days_df.merge(official_stats_df, how="left")
official_stats_df.sort_values("sample_date", ascending=False, inplace=True)
official_stats_df.head()
official_stats_df[accumulated_values_columns] = \
official_stats_df[accumulated_values_columns] \
.astype(float).interpolate(limit_area="inside")
official_stats_df[interpolated_values_columns] = \
official_stats_df[accumulated_values_columns].diff(periods=-1)
official_stats_df.drop(columns="sample_date", inplace=True)
official_stats_df.head()
```
### Data Merge
```
result_summary_df = exposure_keys_summary_df.merge(
new_tek_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = result_summary_df.merge(
shared_teks_uploaded_on_generation_date_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = result_summary_df.merge(
estimated_shared_diagnoses_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = result_summary_df.merge(
official_stats_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = confirmed_eu_df.tail(daily_summary_days).merge(
result_summary_df, on=["sample_date_string"], how="left")
result_summary_df.head()
result_summary_df = confirmed_es_df.tail(daily_summary_days).merge(
result_summary_df, on=["sample_date_string"], how="left")
result_summary_df.head()
result_summary_df["sample_date"] = pd.to_datetime(result_summary_df.sample_date_string)
result_summary_df = result_summary_df.merge(source_regions_for_summary_df, how="left")
result_summary_df.set_index(["sample_date", "source_regions"], inplace=True)
result_summary_df.drop(columns=["sample_date_string"], inplace=True)
result_summary_df.sort_index(ascending=False, inplace=True)
result_summary_df.head()
with pd.option_context("mode.use_inf_as_na", True):
result_summary_df = result_summary_df.fillna(0).astype(int)
result_summary_df["teks_per_shared_diagnosis"] = \
(result_summary_df.shared_teks_by_upload_date / result_summary_df.shared_diagnoses).fillna(0)
result_summary_df["shared_diagnoses_per_covid_case"] = \
(result_summary_df.shared_diagnoses / result_summary_df.covid_cases).fillna(0)
result_summary_df["shared_diagnoses_per_covid_case_es"] = \
(result_summary_df.shared_diagnoses_es / result_summary_df.covid_cases_es).fillna(0)
result_summary_df.head(daily_plot_days)
def compute_aggregated_results_summary(days) -> pd.DataFrame:
aggregated_result_summary_df = result_summary_df.copy()
aggregated_result_summary_df["covid_cases_for_ratio"] = \
aggregated_result_summary_df.covid_cases.mask(
aggregated_result_summary_df.shared_diagnoses == 0, 0)
aggregated_result_summary_df["covid_cases_for_ratio_es"] = \
aggregated_result_summary_df.covid_cases_es.mask(
aggregated_result_summary_df.shared_diagnoses_es == 0, 0)
aggregated_result_summary_df = aggregated_result_summary_df \
.sort_index(ascending=True).fillna(0).rolling(days).agg({
"covid_cases": "sum",
"covid_cases_es": "sum",
"covid_cases_for_ratio": "sum",
"covid_cases_for_ratio_es": "sum",
"shared_teks_by_generation_date": "sum",
"shared_teks_by_upload_date": "sum",
"shared_diagnoses": "sum",
"shared_diagnoses_es": "sum",
}).sort_index(ascending=False)
with pd.option_context("mode.use_inf_as_na", True):
aggregated_result_summary_df = aggregated_result_summary_df.fillna(0).astype(int)
aggregated_result_summary_df["teks_per_shared_diagnosis"] = \
(aggregated_result_summary_df.shared_teks_by_upload_date /
aggregated_result_summary_df.covid_cases_for_ratio).fillna(0)
aggregated_result_summary_df["shared_diagnoses_per_covid_case"] = \
(aggregated_result_summary_df.shared_diagnoses /
aggregated_result_summary_df.covid_cases_for_ratio).fillna(0)
aggregated_result_summary_df["shared_diagnoses_per_covid_case_es"] = \
(aggregated_result_summary_df.shared_diagnoses_es /
aggregated_result_summary_df.covid_cases_for_ratio_es).fillna(0)
return aggregated_result_summary_df
aggregated_result_with_7_days_window_summary_df = compute_aggregated_results_summary(days=7)
aggregated_result_with_7_days_window_summary_df.head()
last_7_days_summary = aggregated_result_with_7_days_window_summary_df.to_dict(orient="records")[1]
last_7_days_summary
aggregated_result_with_14_days_window_summary_df = compute_aggregated_results_summary(days=13)
last_14_days_summary = aggregated_result_with_14_days_window_summary_df.to_dict(orient="records")[1]
last_14_days_summary
```
## Report Results
```
display_column_name_mapping = {
"sample_date": "Sample\u00A0Date\u00A0(UTC)",
"source_regions": "Source Countries",
"datetime_utc": "Timestamp (UTC)",
"upload_date": "Upload Date (UTC)",
"generation_to_upload_days": "Generation to Upload Period in Days",
"region": "Backend",
"region_x": "Backend\u00A0(A)",
"region_y": "Backend\u00A0(B)",
"common_teks": "Common TEKs Shared Between Backends",
"common_teks_fraction": "Fraction of TEKs in Backend (A) Available in Backend (B)",
"covid_cases": "COVID-19 Cases (Source Countries)",
"shared_teks_by_generation_date": "Shared TEKs by Generation Date (Source Countries)",
"shared_teks_by_upload_date": "Shared TEKs by Upload Date (Source Countries)",
"shared_teks_uploaded_on_generation_date": "Shared TEKs Uploaded on Generation Date (Source Countries)",
"shared_diagnoses": "Shared Diagnoses (Source Countries – Estimation)",
"teks_per_shared_diagnosis": "TEKs Uploaded per Shared Diagnosis (Source Countries)",
"shared_diagnoses_per_covid_case": "Usage Ratio (Source Countries)",
"covid_cases_es": "COVID-19 Cases (Spain)",
"app_downloads_es": "App Downloads (Spain – Official)",
"shared_diagnoses_es": "Shared Diagnoses (Spain – Official)",
"shared_diagnoses_per_covid_case_es": "Usage Ratio (Spain)",
}
summary_columns = [
"covid_cases",
"shared_teks_by_generation_date",
"shared_teks_by_upload_date",
"shared_teks_uploaded_on_generation_date",
"shared_diagnoses",
"teks_per_shared_diagnosis",
"shared_diagnoses_per_covid_case",
"covid_cases_es",
"app_downloads_es",
"shared_diagnoses_es",
"shared_diagnoses_per_covid_case_es",
]
summary_percentage_columns= [
"shared_diagnoses_per_covid_case_es",
"shared_diagnoses_per_covid_case",
]
```
### Daily Summary Table
```
result_summary_df_ = result_summary_df.copy()
result_summary_df = result_summary_df[summary_columns]
result_summary_with_display_names_df = result_summary_df \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping)
result_summary_with_display_names_df
```
### Daily Summary Plots
```
result_plot_summary_df = result_summary_df.head(daily_plot_days)[summary_columns] \
.droplevel(level=["source_regions"]) \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping)
summary_ax_list = result_plot_summary_df.sort_index(ascending=True).plot.bar(
title=f"Daily Summary",
rot=45, subplots=True, figsize=(15, 30), legend=False)
ax_ = summary_ax_list[0]
ax_.get_figure().tight_layout()
ax_.get_figure().subplots_adjust(top=0.95)
_ = ax_.set_xticklabels(sorted(result_plot_summary_df.index.strftime("%Y-%m-%d").tolist()))
for percentage_column in summary_percentage_columns:
percentage_column_index = summary_columns.index(percentage_column)
summary_ax_list[percentage_column_index].yaxis \
.set_major_formatter(matplotlib.ticker.PercentFormatter(1.0))
```
### Daily Generation to Upload Period Table
```
display_generation_to_upload_period_pivot_df = \
generation_to_upload_period_pivot_df \
.head(backend_generation_days)
display_generation_to_upload_period_pivot_df \
.head(backend_generation_days) \
.rename_axis(columns=display_column_name_mapping) \
.rename_axis(index=display_column_name_mapping)
fig, generation_to_upload_period_pivot_table_ax = plt.subplots(
figsize=(12, 1 + 0.6 * len(display_generation_to_upload_period_pivot_df)))
generation_to_upload_period_pivot_table_ax.set_title(
"Shared TEKs Generation to Upload Period Table")
sns.heatmap(
data=display_generation_to_upload_period_pivot_df
.rename_axis(columns=display_column_name_mapping)
.rename_axis(index=display_column_name_mapping),
fmt=".0f",
annot=True,
ax=generation_to_upload_period_pivot_table_ax)
generation_to_upload_period_pivot_table_ax.get_figure().tight_layout()
```
### Hourly Summary Plots
```
hourly_summary_ax_list = hourly_summary_df \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.plot.bar(
title=f"Last 24h Summary",
rot=45, subplots=True, legend=False)
ax_ = hourly_summary_ax_list[-1]
ax_.get_figure().tight_layout()
ax_.get_figure().subplots_adjust(top=0.9)
_ = ax_.set_xticklabels(sorted(hourly_summary_df.index.strftime("%Y-%m-%d@%H").tolist()))
```
### Publish Results
```
github_repository = os.environ.get("GITHUB_REPOSITORY")
if github_repository is None:
github_repository = "pvieito/Radar-STATS"
github_project_base_url = "https://github.com/" + github_repository
display_formatters = {
display_column_name_mapping["teks_per_shared_diagnosis"]: lambda x: f"{x:.2f}" if x != 0 else "",
display_column_name_mapping["shared_diagnoses_per_covid_case"]: lambda x: f"{x:.2%}" if x != 0 else "",
display_column_name_mapping["shared_diagnoses_per_covid_case_es"]: lambda x: f"{x:.2%}" if x != 0 else "",
}
general_columns = \
list(filter(lambda x: x not in display_formatters, display_column_name_mapping.values()))
general_formatter = lambda x: f"{x}" if x != 0 else ""
display_formatters.update(dict(map(lambda x: (x, general_formatter), general_columns)))
daily_summary_table_html = result_summary_with_display_names_df \
.head(daily_plot_days) \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.to_html(formatters=display_formatters)
multi_backend_summary_table_html = multi_backend_summary_df \
.head(daily_plot_days) \
.rename_axis(columns=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.rename_axis(index=display_column_name_mapping) \
.to_html(formatters=display_formatters)
def format_multi_backend_cross_sharing_fraction(x):
if pd.isna(x):
return "-"
elif round(x * 100, 1) == 0:
return ""
else:
return f"{x:.1%}"
multi_backend_cross_sharing_summary_table_html = multi_backend_cross_sharing_summary_df \
.rename_axis(columns=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.rename_axis(index=display_column_name_mapping) \
.to_html(
classes="table-center",
formatters=display_formatters,
float_format=format_multi_backend_cross_sharing_fraction)
multi_backend_cross_sharing_summary_table_html = \
multi_backend_cross_sharing_summary_table_html \
.replace("<tr>","<tr style=\"text-align: center;\">")
extraction_date_result_summary_df = \
result_summary_df[result_summary_df.index.get_level_values("sample_date") == extraction_date]
extraction_date_result_hourly_summary_df = \
hourly_summary_df[hourly_summary_df.extraction_date_with_hour == extraction_date_with_hour]
covid_cases = \
extraction_date_result_summary_df.covid_cases.item()
shared_teks_by_generation_date = \
extraction_date_result_summary_df.shared_teks_by_generation_date.item()
shared_teks_by_upload_date = \
extraction_date_result_summary_df.shared_teks_by_upload_date.item()
shared_diagnoses = \
extraction_date_result_summary_df.shared_diagnoses.item()
teks_per_shared_diagnosis = \
extraction_date_result_summary_df.teks_per_shared_diagnosis.item()
shared_diagnoses_per_covid_case = \
extraction_date_result_summary_df.shared_diagnoses_per_covid_case.item()
shared_teks_by_upload_date_last_hour = \
extraction_date_result_hourly_summary_df.shared_teks_by_upload_date.sum().astype(int)
display_source_regions = ", ".join(report_source_regions)
if len(report_source_regions) == 1:
display_brief_source_regions = report_source_regions[0]
else:
display_brief_source_regions = f"{len(report_source_regions)} 🇪🇺"
def get_temporary_image_path() -> str:
return os.path.join(tempfile.gettempdir(), str(uuid.uuid4()) + ".png")
def save_temporary_plot_image(ax):
if isinstance(ax, np.ndarray):
ax = ax[0]
media_path = get_temporary_image_path()
ax.get_figure().savefig(media_path)
return media_path
def save_temporary_dataframe_image(df):
import dataframe_image as dfi
df = df.copy()
df_styler = df.style.format(display_formatters)
media_path = get_temporary_image_path()
dfi.export(df_styler, media_path)
return media_path
summary_plots_image_path = save_temporary_plot_image(
ax=summary_ax_list)
summary_table_image_path = save_temporary_dataframe_image(
df=result_summary_with_display_names_df)
hourly_summary_plots_image_path = save_temporary_plot_image(
ax=hourly_summary_ax_list)
multi_backend_summary_table_image_path = save_temporary_dataframe_image(
df=multi_backend_summary_df)
generation_to_upload_period_pivot_table_image_path = save_temporary_plot_image(
ax=generation_to_upload_period_pivot_table_ax)
```
### Save Results
```
report_resources_path_prefix = "Data/Resources/Current/RadarCOVID-Report-"
result_summary_df.to_csv(
report_resources_path_prefix + "Summary-Table.csv")
result_summary_df.to_html(
report_resources_path_prefix + "Summary-Table.html")
hourly_summary_df.to_csv(
report_resources_path_prefix + "Hourly-Summary-Table.csv")
multi_backend_summary_df.to_csv(
report_resources_path_prefix + "Multi-Backend-Summary-Table.csv")
multi_backend_cross_sharing_summary_df.to_csv(
report_resources_path_prefix + "Multi-Backend-Cross-Sharing-Summary-Table.csv")
generation_to_upload_period_pivot_df.to_csv(
report_resources_path_prefix + "Generation-Upload-Period-Table.csv")
_ = shutil.copyfile(
summary_plots_image_path,
report_resources_path_prefix + "Summary-Plots.png")
_ = shutil.copyfile(
summary_table_image_path,
report_resources_path_prefix + "Summary-Table.png")
_ = shutil.copyfile(
hourly_summary_plots_image_path,
report_resources_path_prefix + "Hourly-Summary-Plots.png")
_ = shutil.copyfile(
multi_backend_summary_table_image_path,
report_resources_path_prefix + "Multi-Backend-Summary-Table.png")
_ = shutil.copyfile(
generation_to_upload_period_pivot_table_image_path,
report_resources_path_prefix + "Generation-Upload-Period-Table.png")
```
### Publish Results as JSON
```
def generate_summary_api_results(df: pd.DataFrame) -> list:
api_df = df.reset_index().copy()
api_df["sample_date_string"] = \
api_df["sample_date"].dt.strftime("%Y-%m-%d")
api_df["source_regions"] = \
api_df["source_regions"].apply(lambda x: x.split(","))
return api_df.to_dict(orient="records")
summary_api_results = \
generate_summary_api_results(df=result_summary_df)
today_summary_api_results = \
generate_summary_api_results(df=extraction_date_result_summary_df)[0]
summary_results = dict(
backend_identifier=report_backend_identifier,
source_regions=report_source_regions,
extraction_datetime=extraction_datetime,
extraction_date=extraction_date,
extraction_date_with_hour=extraction_date_with_hour,
last_hour=dict(
shared_teks_by_upload_date=shared_teks_by_upload_date_last_hour,
shared_diagnoses=0,
),
today=today_summary_api_results,
last_7_days=last_7_days_summary,
last_14_days=last_14_days_summary,
daily_results=summary_api_results)
summary_results = \
json.loads(pd.Series([summary_results]).to_json(orient="records"))[0]
with open(report_resources_path_prefix + "Summary-Results.json", "w") as f:
json.dump(summary_results, f, indent=4)
```
### Publish on README
```
with open("Data/Templates/README.md", "r") as f:
readme_contents = f.read()
readme_contents = readme_contents.format(
extraction_date_with_hour=extraction_date_with_hour,
github_project_base_url=github_project_base_url,
daily_summary_table_html=daily_summary_table_html,
multi_backend_summary_table_html=multi_backend_summary_table_html,
multi_backend_cross_sharing_summary_table_html=multi_backend_cross_sharing_summary_table_html,
display_source_regions=display_source_regions)
with open("README.md", "w") as f:
f.write(readme_contents)
```
### Publish on Twitter
```
enable_share_to_twitter = os.environ.get("RADARCOVID_REPORT__ENABLE_PUBLISH_ON_TWITTER")
github_event_name = os.environ.get("GITHUB_EVENT_NAME")
if enable_share_to_twitter and github_event_name == "schedule" and \
(shared_teks_by_upload_date_last_hour or not are_today_results_partial):
import tweepy
twitter_api_auth_keys = os.environ["RADARCOVID_REPORT__TWITTER_API_AUTH_KEYS"]
twitter_api_auth_keys = twitter_api_auth_keys.split(":")
auth = tweepy.OAuthHandler(twitter_api_auth_keys[0], twitter_api_auth_keys[1])
auth.set_access_token(twitter_api_auth_keys[2], twitter_api_auth_keys[3])
api = tweepy.API(auth)
summary_plots_media = api.media_upload(summary_plots_image_path)
summary_table_media = api.media_upload(summary_table_image_path)
generation_to_upload_period_pivot_table_image_media = api.media_upload(generation_to_upload_period_pivot_table_image_path)
media_ids = [
summary_plots_media.media_id,
summary_table_media.media_id,
generation_to_upload_period_pivot_table_image_media.media_id,
]
if are_today_results_partial:
today_addendum = " (Partial)"
else:
today_addendum = ""
def format_shared_diagnoses_per_covid_case(value) -> str:
if value == 0:
return "–"
return f"≤{value:.2%}"
display_shared_diagnoses_per_covid_case = \
format_shared_diagnoses_per_covid_case(value=shared_diagnoses_per_covid_case)
display_last_14_days_shared_diagnoses_per_covid_case = \
format_shared_diagnoses_per_covid_case(value=last_14_days_summary["shared_diagnoses_per_covid_case"])
display_last_14_days_shared_diagnoses_per_covid_case_es = \
format_shared_diagnoses_per_covid_case(value=last_14_days_summary["shared_diagnoses_per_covid_case_es"])
status = textwrap.dedent(f"""
#RadarCOVID – {extraction_date_with_hour}
Today{today_addendum}:
- Uploaded TEKs: {shared_teks_by_upload_date:.0f} ({shared_teks_by_upload_date_last_hour:+d} last hour)
- Shared Diagnoses: ≤{shared_diagnoses:.0f}
- Usage Ratio: {display_shared_diagnoses_per_covid_case}
Last 14 Days:
- Usage Ratio (Estimation): {display_last_14_days_shared_diagnoses_per_covid_case}
- Usage Ratio (Official): {display_last_14_days_shared_diagnoses_per_covid_case_es}
Info: {github_project_base_url}#documentation
""")
status = status.encode(encoding="utf-8")
api.update_status(status=status, media_ids=media_ids)
```
|
github_jupyter
|
import datetime
import json
import logging
import os
import shutil
import tempfile
import textwrap
import uuid
import matplotlib.pyplot as plt
import matplotlib.ticker
import numpy as np
import pandas as pd
import pycountry
import retry
import seaborn as sns
%matplotlib inline
current_working_directory = os.environ.get("PWD")
if current_working_directory:
os.chdir(current_working_directory)
sns.set()
matplotlib.rcParams["figure.figsize"] = (15, 6)
extraction_datetime = datetime.datetime.utcnow()
extraction_date = extraction_datetime.strftime("%Y-%m-%d")
extraction_previous_datetime = extraction_datetime - datetime.timedelta(days=1)
extraction_previous_date = extraction_previous_datetime.strftime("%Y-%m-%d")
extraction_date_with_hour = datetime.datetime.utcnow().strftime("%Y-%m-%d@%H")
current_hour = datetime.datetime.utcnow().hour
are_today_results_partial = current_hour != 23
from Modules.ExposureNotification import exposure_notification_io
spain_region_country_code = "ES"
germany_region_country_code = "DE"
default_backend_identifier = spain_region_country_code
backend_generation_days = 7 * 2
daily_summary_days = 7 * 4 * 3
daily_plot_days = 7 * 4
tek_dumps_load_limit = daily_summary_days + 1
environment_backend_identifier = os.environ.get("RADARCOVID_REPORT__BACKEND_IDENTIFIER")
if environment_backend_identifier:
report_backend_identifier = environment_backend_identifier
else:
report_backend_identifier = default_backend_identifier
report_backend_identifier
environment_enable_multi_backend_download = \
os.environ.get("RADARCOVID_REPORT__ENABLE_MULTI_BACKEND_DOWNLOAD")
if environment_enable_multi_backend_download:
report_backend_identifiers = None
else:
report_backend_identifiers = [report_backend_identifier]
report_backend_identifiers
environment_invalid_shared_diagnoses_dates = \
os.environ.get("RADARCOVID_REPORT__INVALID_SHARED_DIAGNOSES_DATES")
if environment_invalid_shared_diagnoses_dates:
invalid_shared_diagnoses_dates = environment_invalid_shared_diagnoses_dates.split(",")
else:
invalid_shared_diagnoses_dates = []
invalid_shared_diagnoses_dates
report_backend_client = \
exposure_notification_io.get_backend_client_with_identifier(
backend_identifier=report_backend_identifier)
@retry.retry(tries=10, delay=10, backoff=1.1, jitter=(0, 10))
def download_cases_dataframe():
return pd.read_csv("https://raw.githubusercontent.com/owid/covid-19-data/master/public/data/owid-covid-data.csv")
confirmed_df_ = download_cases_dataframe()
confirmed_df_.iloc[0]
confirmed_df = confirmed_df_.copy()
confirmed_df = confirmed_df[["date", "new_cases", "iso_code"]]
confirmed_df.rename(
columns={
"date": "sample_date",
"iso_code": "country_code",
},
inplace=True)
def convert_iso_alpha_3_to_alpha_2(x):
try:
return pycountry.countries.get(alpha_3=x).alpha_2
except Exception as e:
logging.info(f"Error converting country ISO Alpha 3 code '{x}': {repr(e)}")
return None
confirmed_df["country_code"] = confirmed_df.country_code.apply(convert_iso_alpha_3_to_alpha_2)
confirmed_df.dropna(inplace=True)
confirmed_df["sample_date"] = pd.to_datetime(confirmed_df.sample_date, dayfirst=True)
confirmed_df["sample_date"] = confirmed_df.sample_date.dt.strftime("%Y-%m-%d")
confirmed_df.sort_values("sample_date", inplace=True)
confirmed_df.tail()
confirmed_days = pd.date_range(
start=confirmed_df.iloc[0].sample_date,
end=extraction_datetime)
confirmed_days_df = pd.DataFrame(data=confirmed_days, columns=["sample_date"])
confirmed_days_df["sample_date_string"] = \
confirmed_days_df.sample_date.dt.strftime("%Y-%m-%d")
confirmed_days_df.tail()
def sort_source_regions_for_display(source_regions: list) -> list:
if report_backend_identifier in source_regions:
source_regions = [report_backend_identifier] + \
list(sorted(set(source_regions).difference([report_backend_identifier])))
else:
source_regions = list(sorted(source_regions))
return source_regions
report_source_regions = report_backend_client.source_regions_for_date(
date=extraction_datetime.date())
report_source_regions = sort_source_regions_for_display(
source_regions=report_source_regions)
report_source_regions
def get_cases_dataframe(source_regions_for_date_function, columns_suffix=None):
source_regions_at_date_df = confirmed_days_df.copy()
source_regions_at_date_df["source_regions_at_date"] = \
source_regions_at_date_df.sample_date.apply(
lambda x: source_regions_for_date_function(date=x))
source_regions_at_date_df.sort_values("sample_date", inplace=True)
source_regions_at_date_df["_source_regions_group"] = source_regions_at_date_df. \
source_regions_at_date.apply(lambda x: ",".join(sort_source_regions_for_display(x)))
source_regions_at_date_df.tail()
#%%
source_regions_for_summary_df_ = \
source_regions_at_date_df[["sample_date", "_source_regions_group"]].copy()
source_regions_for_summary_df_.rename(columns={"_source_regions_group": "source_regions"}, inplace=True)
source_regions_for_summary_df_.tail()
#%%
confirmed_output_columns = ["sample_date", "new_cases", "covid_cases"]
confirmed_output_df = pd.DataFrame(columns=confirmed_output_columns)
for source_regions_group, source_regions_group_series in \
source_regions_at_date_df.groupby("_source_regions_group"):
source_regions_set = set(source_regions_group.split(","))
confirmed_source_regions_set_df = \
confirmed_df[confirmed_df.country_code.isin(source_regions_set)].copy()
confirmed_source_regions_group_df = \
confirmed_source_regions_set_df.groupby("sample_date").new_cases.sum() \
.reset_index().sort_values("sample_date")
confirmed_source_regions_group_df = \
confirmed_source_regions_group_df.merge(
confirmed_days_df[["sample_date_string"]].rename(
columns={"sample_date_string": "sample_date"}),
how="right")
confirmed_source_regions_group_df["new_cases"] = \
confirmed_source_regions_group_df["new_cases"].clip(lower=0)
confirmed_source_regions_group_df["covid_cases"] = \
confirmed_source_regions_group_df.new_cases.rolling(7, min_periods=0).mean().round()
confirmed_source_regions_group_df = \
confirmed_source_regions_group_df[confirmed_output_columns]
confirmed_source_regions_group_df = confirmed_source_regions_group_df.replace(0, np.nan)
confirmed_source_regions_group_df.fillna(method="ffill", inplace=True)
confirmed_source_regions_group_df = \
confirmed_source_regions_group_df[
confirmed_source_regions_group_df.sample_date.isin(
source_regions_group_series.sample_date_string)]
confirmed_output_df = confirmed_output_df.append(confirmed_source_regions_group_df)
result_df = confirmed_output_df.copy()
result_df.tail()
#%%
result_df.rename(columns={"sample_date": "sample_date_string"}, inplace=True)
result_df = confirmed_days_df[["sample_date_string"]].merge(result_df, how="left")
result_df.sort_values("sample_date_string", inplace=True)
result_df.fillna(method="ffill", inplace=True)
result_df.tail()
#%%
result_df[["new_cases", "covid_cases"]].plot()
if columns_suffix:
result_df.rename(
columns={
"new_cases": "new_cases_" + columns_suffix,
"covid_cases": "covid_cases_" + columns_suffix},
inplace=True)
return result_df, source_regions_for_summary_df_
confirmed_eu_df, source_regions_for_summary_df = get_cases_dataframe(
report_backend_client.source_regions_for_date)
confirmed_es_df, _ = get_cases_dataframe(
lambda date: [spain_region_country_code],
columns_suffix=spain_region_country_code.lower())
raw_zip_path_prefix = "Data/TEKs/Raw/"
base_backend_identifiers = [report_backend_identifier]
multi_backend_exposure_keys_df = \
exposure_notification_io.download_exposure_keys_from_backends(
backend_identifiers=report_backend_identifiers,
generation_days=backend_generation_days,
fail_on_error_backend_identifiers=base_backend_identifiers,
save_raw_zip_path_prefix=raw_zip_path_prefix)
multi_backend_exposure_keys_df["region"] = multi_backend_exposure_keys_df["backend_identifier"]
multi_backend_exposure_keys_df.rename(
columns={
"generation_datetime": "sample_datetime",
"generation_date_string": "sample_date_string",
},
inplace=True)
multi_backend_exposure_keys_df.head()
early_teks_df = multi_backend_exposure_keys_df[
multi_backend_exposure_keys_df.rolling_period < 144].copy()
early_teks_df["rolling_period_in_hours"] = early_teks_df.rolling_period / 6
early_teks_df[early_teks_df.sample_date_string != extraction_date] \
.rolling_period_in_hours.hist(bins=list(range(24)))
early_teks_df[early_teks_df.sample_date_string == extraction_date] \
.rolling_period_in_hours.hist(bins=list(range(24)))
multi_backend_exposure_keys_df = multi_backend_exposure_keys_df[[
"sample_date_string", "region", "key_data"]]
multi_backend_exposure_keys_df.head()
active_regions = \
multi_backend_exposure_keys_df.groupby("region").key_data.nunique().sort_values().index.unique().tolist()
active_regions
multi_backend_summary_df = multi_backend_exposure_keys_df.groupby(
["sample_date_string", "region"]).key_data.nunique().reset_index() \
.pivot(index="sample_date_string", columns="region") \
.sort_index(ascending=False)
multi_backend_summary_df.rename(
columns={"key_data": "shared_teks_by_generation_date"},
inplace=True)
multi_backend_summary_df.rename_axis("sample_date", inplace=True)
multi_backend_summary_df = multi_backend_summary_df.fillna(0).astype(int)
multi_backend_summary_df = multi_backend_summary_df.head(backend_generation_days)
multi_backend_summary_df.head()
def compute_keys_cross_sharing(x):
teks_x = x.key_data_x.item()
common_teks = set(teks_x).intersection(x.key_data_y.item())
common_teks_fraction = len(common_teks) / len(teks_x)
return pd.Series(dict(
common_teks=common_teks,
common_teks_fraction=common_teks_fraction,
))
multi_backend_exposure_keys_by_region_df = \
multi_backend_exposure_keys_df.groupby("region").key_data.unique().reset_index()
multi_backend_exposure_keys_by_region_df["_merge"] = True
multi_backend_exposure_keys_by_region_combination_df = \
multi_backend_exposure_keys_by_region_df.merge(
multi_backend_exposure_keys_by_region_df, on="_merge")
multi_backend_exposure_keys_by_region_combination_df.drop(
columns=["_merge"], inplace=True)
if multi_backend_exposure_keys_by_region_combination_df.region_x.nunique() > 1:
multi_backend_exposure_keys_by_region_combination_df = \
multi_backend_exposure_keys_by_region_combination_df[
multi_backend_exposure_keys_by_region_combination_df.region_x !=
multi_backend_exposure_keys_by_region_combination_df.region_y]
multi_backend_exposure_keys_cross_sharing_df = \
multi_backend_exposure_keys_by_region_combination_df \
.groupby(["region_x", "region_y"]) \
.apply(compute_keys_cross_sharing) \
.reset_index()
multi_backend_cross_sharing_summary_df = \
multi_backend_exposure_keys_cross_sharing_df.pivot_table(
values=["common_teks_fraction"],
columns="region_x",
index="region_y",
aggfunc=lambda x: x.item())
multi_backend_cross_sharing_summary_df
multi_backend_without_active_region_exposure_keys_df = \
multi_backend_exposure_keys_df[multi_backend_exposure_keys_df.region != report_backend_identifier]
multi_backend_without_active_region = \
multi_backend_without_active_region_exposure_keys_df.groupby("region").key_data.nunique().sort_values().index.unique().tolist()
multi_backend_without_active_region
exposure_keys_summary_df = multi_backend_exposure_keys_df[
multi_backend_exposure_keys_df.region == report_backend_identifier]
exposure_keys_summary_df.drop(columns=["region"], inplace=True)
exposure_keys_summary_df = \
exposure_keys_summary_df.groupby(["sample_date_string"]).key_data.nunique().to_frame()
exposure_keys_summary_df = \
exposure_keys_summary_df.reset_index().set_index("sample_date_string")
exposure_keys_summary_df.sort_index(ascending=False, inplace=True)
exposure_keys_summary_df.rename(columns={"key_data": "shared_teks_by_generation_date"}, inplace=True)
exposure_keys_summary_df.head()
tek_list_df = multi_backend_exposure_keys_df[
["sample_date_string", "region", "key_data"]].copy()
tek_list_df["key_data"] = tek_list_df["key_data"].apply(str)
tek_list_df.rename(columns={
"sample_date_string": "sample_date",
"key_data": "tek_list"}, inplace=True)
tek_list_df = tek_list_df.groupby(
["sample_date", "region"]).tek_list.unique().reset_index()
tek_list_df["extraction_date"] = extraction_date
tek_list_df["extraction_date_with_hour"] = extraction_date_with_hour
tek_list_path_prefix = "Data/TEKs/"
tek_list_current_path = tek_list_path_prefix + f"/Current/RadarCOVID-TEKs.json"
tek_list_daily_path = tek_list_path_prefix + f"Daily/RadarCOVID-TEKs-{extraction_date}.json"
tek_list_hourly_path = tek_list_path_prefix + f"Hourly/RadarCOVID-TEKs-{extraction_date_with_hour}.json"
for path in [tek_list_current_path, tek_list_daily_path, tek_list_hourly_path]:
os.makedirs(os.path.dirname(path), exist_ok=True)
tek_list_base_df = tek_list_df[tek_list_df.region == report_backend_identifier]
tek_list_base_df.drop(columns=["extraction_date", "extraction_date_with_hour"]).to_json(
tek_list_current_path,
lines=True, orient="records")
tek_list_base_df.drop(columns=["extraction_date_with_hour"]).to_json(
tek_list_daily_path,
lines=True, orient="records")
tek_list_base_df.to_json(
tek_list_hourly_path,
lines=True, orient="records")
tek_list_base_df.head()
import glob
def load_extracted_teks(mode, region=None, limit=None) -> pd.DataFrame:
extracted_teks_df = pd.DataFrame(columns=["region"])
file_paths = list(reversed(sorted(glob.glob(tek_list_path_prefix + mode + "/RadarCOVID-TEKs-*.json"))))
if limit:
file_paths = file_paths[:limit]
for file_path in file_paths:
logging.info(f"Loading TEKs from '{file_path}'...")
iteration_extracted_teks_df = pd.read_json(file_path, lines=True)
extracted_teks_df = extracted_teks_df.append(
iteration_extracted_teks_df, sort=False)
extracted_teks_df["region"] = \
extracted_teks_df.region.fillna(spain_region_country_code).copy()
if region:
extracted_teks_df = \
extracted_teks_df[extracted_teks_df.region == region]
return extracted_teks_df
daily_extracted_teks_df = load_extracted_teks(
mode="Daily",
region=report_backend_identifier,
limit=tek_dumps_load_limit)
daily_extracted_teks_df.head()
exposure_keys_summary_df_ = daily_extracted_teks_df \
.sort_values("extraction_date", ascending=False) \
.groupby("sample_date").tek_list.first() \
.to_frame()
exposure_keys_summary_df_.index.name = "sample_date_string"
exposure_keys_summary_df_["tek_list"] = \
exposure_keys_summary_df_.tek_list.apply(len)
exposure_keys_summary_df_ = exposure_keys_summary_df_ \
.rename(columns={"tek_list": "shared_teks_by_generation_date"}) \
.sort_index(ascending=False)
exposure_keys_summary_df = exposure_keys_summary_df_
exposure_keys_summary_df.head()
tek_list_df = daily_extracted_teks_df.groupby("extraction_date").tek_list.apply(
lambda x: set(sum(x, []))).reset_index()
tek_list_df = tek_list_df.set_index("extraction_date").sort_index(ascending=True)
tek_list_df.head()
def compute_teks_by_generation_and_upload_date(date):
day_new_teks_set_df = tek_list_df.copy().diff()
try:
day_new_teks_set = day_new_teks_set_df[
day_new_teks_set_df.index == date].tek_list.item()
except ValueError:
day_new_teks_set = None
if pd.isna(day_new_teks_set):
day_new_teks_set = set()
day_new_teks_df = daily_extracted_teks_df[
daily_extracted_teks_df.extraction_date == date].copy()
day_new_teks_df["shared_teks"] = \
day_new_teks_df.tek_list.apply(lambda x: set(x).intersection(day_new_teks_set))
day_new_teks_df["shared_teks"] = \
day_new_teks_df.shared_teks.apply(len)
day_new_teks_df["upload_date"] = date
day_new_teks_df.rename(columns={"sample_date": "generation_date"}, inplace=True)
day_new_teks_df = day_new_teks_df[
["upload_date", "generation_date", "shared_teks"]]
day_new_teks_df["generation_to_upload_days"] = \
(pd.to_datetime(day_new_teks_df.upload_date) -
pd.to_datetime(day_new_teks_df.generation_date)).dt.days
day_new_teks_df = day_new_teks_df[day_new_teks_df.shared_teks > 0]
return day_new_teks_df
shared_teks_generation_to_upload_df = pd.DataFrame()
for upload_date in daily_extracted_teks_df.extraction_date.unique():
shared_teks_generation_to_upload_df = \
shared_teks_generation_to_upload_df.append(
compute_teks_by_generation_and_upload_date(date=upload_date))
shared_teks_generation_to_upload_df \
.sort_values(["upload_date", "generation_date"], ascending=False, inplace=True)
shared_teks_generation_to_upload_df.tail()
today_new_teks_df = \
shared_teks_generation_to_upload_df[
shared_teks_generation_to_upload_df.upload_date == extraction_date].copy()
today_new_teks_df.tail()
if not today_new_teks_df.empty:
today_new_teks_df.set_index("generation_to_upload_days") \
.sort_index().shared_teks.plot.bar()
generation_to_upload_period_pivot_df = \
shared_teks_generation_to_upload_df[
["upload_date", "generation_to_upload_days", "shared_teks"]] \
.pivot(index="upload_date", columns="generation_to_upload_days") \
.sort_index(ascending=False).fillna(0).astype(int) \
.droplevel(level=0, axis=1)
generation_to_upload_period_pivot_df.head()
new_tek_df = tek_list_df.diff().tek_list.apply(
lambda x: len(x) if not pd.isna(x) else None).to_frame().reset_index()
new_tek_df.rename(columns={
"tek_list": "shared_teks_by_upload_date",
"extraction_date": "sample_date_string",}, inplace=True)
new_tek_df.tail()
shared_teks_uploaded_on_generation_date_df = shared_teks_generation_to_upload_df[
shared_teks_generation_to_upload_df.generation_to_upload_days == 0] \
[["upload_date", "shared_teks"]].rename(
columns={
"upload_date": "sample_date_string",
"shared_teks": "shared_teks_uploaded_on_generation_date",
})
shared_teks_uploaded_on_generation_date_df.head()
estimated_shared_diagnoses_df = shared_teks_generation_to_upload_df \
.groupby(["upload_date"]).shared_teks.max().reset_index() \
.sort_values(["upload_date"], ascending=False) \
.rename(columns={
"upload_date": "sample_date_string",
"shared_teks": "shared_diagnoses",
})
invalid_shared_diagnoses_dates_mask = \
estimated_shared_diagnoses_df.sample_date_string.isin(invalid_shared_diagnoses_dates)
estimated_shared_diagnoses_df[invalid_shared_diagnoses_dates_mask] = 0
estimated_shared_diagnoses_df.head()
hourly_extracted_teks_df = load_extracted_teks(
mode="Hourly", region=report_backend_identifier, limit=25)
hourly_extracted_teks_df.head()
hourly_new_tek_count_df = hourly_extracted_teks_df \
.groupby("extraction_date_with_hour").tek_list. \
apply(lambda x: set(sum(x, []))).reset_index().copy()
hourly_new_tek_count_df = hourly_new_tek_count_df.set_index("extraction_date_with_hour") \
.sort_index(ascending=True)
hourly_new_tek_count_df["new_tek_list"] = hourly_new_tek_count_df.tek_list.diff()
hourly_new_tek_count_df["new_tek_count"] = hourly_new_tek_count_df.new_tek_list.apply(
lambda x: len(x) if not pd.isna(x) else 0)
hourly_new_tek_count_df.rename(columns={
"new_tek_count": "shared_teks_by_upload_date"}, inplace=True)
hourly_new_tek_count_df = hourly_new_tek_count_df.reset_index()[[
"extraction_date_with_hour", "shared_teks_by_upload_date"]]
hourly_new_tek_count_df.head()
hourly_summary_df = hourly_new_tek_count_df.copy()
hourly_summary_df.set_index("extraction_date_with_hour", inplace=True)
hourly_summary_df = hourly_summary_df.fillna(0).astype(int).reset_index()
hourly_summary_df["datetime_utc"] = pd.to_datetime(
hourly_summary_df.extraction_date_with_hour, format="%Y-%m-%d@%H")
hourly_summary_df.set_index("datetime_utc", inplace=True)
hourly_summary_df = hourly_summary_df.tail(-1)
hourly_summary_df.head()
import requests
import pandas.io.json
official_stats_response = requests.get("https://radarcovid.covid19.gob.es/kpi/statistics/basics")
official_stats_response.raise_for_status()
official_stats_df_ = pandas.io.json.json_normalize(official_stats_response.json())
official_stats_df = official_stats_df_.copy()
official_stats_df["date"] = pd.to_datetime(official_stats_df["date"], dayfirst=True)
official_stats_df.head()
official_stats_column_map = {
"date": "sample_date",
"applicationsDownloads.totalAcummulated": "app_downloads_es_accumulated",
"communicatedContagions.totalAcummulated": "shared_diagnoses_es_accumulated",
}
accumulated_suffix = "_accumulated"
accumulated_values_columns = \
list(filter(lambda x: x.endswith(accumulated_suffix), official_stats_column_map.values()))
interpolated_values_columns = \
list(map(lambda x: x[:-len(accumulated_suffix)], accumulated_values_columns))
official_stats_df = \
official_stats_df[official_stats_column_map.keys()] \
.rename(columns=official_stats_column_map)
official_stats_df["extraction_date"] = extraction_date
official_stats_df.head()
official_stats_path = "Data/Statistics/Current/RadarCOVID-Statistics.json"
previous_official_stats_df = pd.read_json(official_stats_path, orient="records", lines=True)
previous_official_stats_df["sample_date"] = pd.to_datetime(previous_official_stats_df["sample_date"], dayfirst=True)
official_stats_df = official_stats_df.append(previous_official_stats_df)
official_stats_df.head()
official_stats_df = official_stats_df[~(official_stats_df.shared_diagnoses_es_accumulated == 0)]
official_stats_df.sort_values("extraction_date", ascending=False, inplace=True)
official_stats_df.drop_duplicates(subset=["sample_date"], keep="first", inplace=True)
official_stats_df.head()
official_stats_stored_df = official_stats_df.copy()
official_stats_stored_df["sample_date"] = official_stats_stored_df.sample_date.dt.strftime("%Y-%m-%d")
official_stats_stored_df.to_json(official_stats_path, orient="records", lines=True)
official_stats_df.drop(columns=["extraction_date"], inplace=True)
official_stats_df = confirmed_days_df.merge(official_stats_df, how="left")
official_stats_df.sort_values("sample_date", ascending=False, inplace=True)
official_stats_df.head()
official_stats_df[accumulated_values_columns] = \
official_stats_df[accumulated_values_columns] \
.astype(float).interpolate(limit_area="inside")
official_stats_df[interpolated_values_columns] = \
official_stats_df[accumulated_values_columns].diff(periods=-1)
official_stats_df.drop(columns="sample_date", inplace=True)
official_stats_df.head()
result_summary_df = exposure_keys_summary_df.merge(
new_tek_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = result_summary_df.merge(
shared_teks_uploaded_on_generation_date_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = result_summary_df.merge(
estimated_shared_diagnoses_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = result_summary_df.merge(
official_stats_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = confirmed_eu_df.tail(daily_summary_days).merge(
result_summary_df, on=["sample_date_string"], how="left")
result_summary_df.head()
result_summary_df = confirmed_es_df.tail(daily_summary_days).merge(
result_summary_df, on=["sample_date_string"], how="left")
result_summary_df.head()
result_summary_df["sample_date"] = pd.to_datetime(result_summary_df.sample_date_string)
result_summary_df = result_summary_df.merge(source_regions_for_summary_df, how="left")
result_summary_df.set_index(["sample_date", "source_regions"], inplace=True)
result_summary_df.drop(columns=["sample_date_string"], inplace=True)
result_summary_df.sort_index(ascending=False, inplace=True)
result_summary_df.head()
with pd.option_context("mode.use_inf_as_na", True):
result_summary_df = result_summary_df.fillna(0).astype(int)
result_summary_df["teks_per_shared_diagnosis"] = \
(result_summary_df.shared_teks_by_upload_date / result_summary_df.shared_diagnoses).fillna(0)
result_summary_df["shared_diagnoses_per_covid_case"] = \
(result_summary_df.shared_diagnoses / result_summary_df.covid_cases).fillna(0)
result_summary_df["shared_diagnoses_per_covid_case_es"] = \
(result_summary_df.shared_diagnoses_es / result_summary_df.covid_cases_es).fillna(0)
result_summary_df.head(daily_plot_days)
def compute_aggregated_results_summary(days) -> pd.DataFrame:
aggregated_result_summary_df = result_summary_df.copy()
aggregated_result_summary_df["covid_cases_for_ratio"] = \
aggregated_result_summary_df.covid_cases.mask(
aggregated_result_summary_df.shared_diagnoses == 0, 0)
aggregated_result_summary_df["covid_cases_for_ratio_es"] = \
aggregated_result_summary_df.covid_cases_es.mask(
aggregated_result_summary_df.shared_diagnoses_es == 0, 0)
aggregated_result_summary_df = aggregated_result_summary_df \
.sort_index(ascending=True).fillna(0).rolling(days).agg({
"covid_cases": "sum",
"covid_cases_es": "sum",
"covid_cases_for_ratio": "sum",
"covid_cases_for_ratio_es": "sum",
"shared_teks_by_generation_date": "sum",
"shared_teks_by_upload_date": "sum",
"shared_diagnoses": "sum",
"shared_diagnoses_es": "sum",
}).sort_index(ascending=False)
with pd.option_context("mode.use_inf_as_na", True):
aggregated_result_summary_df = aggregated_result_summary_df.fillna(0).astype(int)
aggregated_result_summary_df["teks_per_shared_diagnosis"] = \
(aggregated_result_summary_df.shared_teks_by_upload_date /
aggregated_result_summary_df.covid_cases_for_ratio).fillna(0)
aggregated_result_summary_df["shared_diagnoses_per_covid_case"] = \
(aggregated_result_summary_df.shared_diagnoses /
aggregated_result_summary_df.covid_cases_for_ratio).fillna(0)
aggregated_result_summary_df["shared_diagnoses_per_covid_case_es"] = \
(aggregated_result_summary_df.shared_diagnoses_es /
aggregated_result_summary_df.covid_cases_for_ratio_es).fillna(0)
return aggregated_result_summary_df
aggregated_result_with_7_days_window_summary_df = compute_aggregated_results_summary(days=7)
aggregated_result_with_7_days_window_summary_df.head()
last_7_days_summary = aggregated_result_with_7_days_window_summary_df.to_dict(orient="records")[1]
last_7_days_summary
aggregated_result_with_14_days_window_summary_df = compute_aggregated_results_summary(days=13)
last_14_days_summary = aggregated_result_with_14_days_window_summary_df.to_dict(orient="records")[1]
last_14_days_summary
display_column_name_mapping = {
"sample_date": "Sample\u00A0Date\u00A0(UTC)",
"source_regions": "Source Countries",
"datetime_utc": "Timestamp (UTC)",
"upload_date": "Upload Date (UTC)",
"generation_to_upload_days": "Generation to Upload Period in Days",
"region": "Backend",
"region_x": "Backend\u00A0(A)",
"region_y": "Backend\u00A0(B)",
"common_teks": "Common TEKs Shared Between Backends",
"common_teks_fraction": "Fraction of TEKs in Backend (A) Available in Backend (B)",
"covid_cases": "COVID-19 Cases (Source Countries)",
"shared_teks_by_generation_date": "Shared TEKs by Generation Date (Source Countries)",
"shared_teks_by_upload_date": "Shared TEKs by Upload Date (Source Countries)",
"shared_teks_uploaded_on_generation_date": "Shared TEKs Uploaded on Generation Date (Source Countries)",
"shared_diagnoses": "Shared Diagnoses (Source Countries – Estimation)",
"teks_per_shared_diagnosis": "TEKs Uploaded per Shared Diagnosis (Source Countries)",
"shared_diagnoses_per_covid_case": "Usage Ratio (Source Countries)",
"covid_cases_es": "COVID-19 Cases (Spain)",
"app_downloads_es": "App Downloads (Spain – Official)",
"shared_diagnoses_es": "Shared Diagnoses (Spain – Official)",
"shared_diagnoses_per_covid_case_es": "Usage Ratio (Spain)",
}
summary_columns = [
"covid_cases",
"shared_teks_by_generation_date",
"shared_teks_by_upload_date",
"shared_teks_uploaded_on_generation_date",
"shared_diagnoses",
"teks_per_shared_diagnosis",
"shared_diagnoses_per_covid_case",
"covid_cases_es",
"app_downloads_es",
"shared_diagnoses_es",
"shared_diagnoses_per_covid_case_es",
]
summary_percentage_columns= [
"shared_diagnoses_per_covid_case_es",
"shared_diagnoses_per_covid_case",
]
result_summary_df_ = result_summary_df.copy()
result_summary_df = result_summary_df[summary_columns]
result_summary_with_display_names_df = result_summary_df \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping)
result_summary_with_display_names_df
result_plot_summary_df = result_summary_df.head(daily_plot_days)[summary_columns] \
.droplevel(level=["source_regions"]) \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping)
summary_ax_list = result_plot_summary_df.sort_index(ascending=True).plot.bar(
title=f"Daily Summary",
rot=45, subplots=True, figsize=(15, 30), legend=False)
ax_ = summary_ax_list[0]
ax_.get_figure().tight_layout()
ax_.get_figure().subplots_adjust(top=0.95)
_ = ax_.set_xticklabels(sorted(result_plot_summary_df.index.strftime("%Y-%m-%d").tolist()))
for percentage_column in summary_percentage_columns:
percentage_column_index = summary_columns.index(percentage_column)
summary_ax_list[percentage_column_index].yaxis \
.set_major_formatter(matplotlib.ticker.PercentFormatter(1.0))
display_generation_to_upload_period_pivot_df = \
generation_to_upload_period_pivot_df \
.head(backend_generation_days)
display_generation_to_upload_period_pivot_df \
.head(backend_generation_days) \
.rename_axis(columns=display_column_name_mapping) \
.rename_axis(index=display_column_name_mapping)
fig, generation_to_upload_period_pivot_table_ax = plt.subplots(
figsize=(12, 1 + 0.6 * len(display_generation_to_upload_period_pivot_df)))
generation_to_upload_period_pivot_table_ax.set_title(
"Shared TEKs Generation to Upload Period Table")
sns.heatmap(
data=display_generation_to_upload_period_pivot_df
.rename_axis(columns=display_column_name_mapping)
.rename_axis(index=display_column_name_mapping),
fmt=".0f",
annot=True,
ax=generation_to_upload_period_pivot_table_ax)
generation_to_upload_period_pivot_table_ax.get_figure().tight_layout()
hourly_summary_ax_list = hourly_summary_df \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.plot.bar(
title=f"Last 24h Summary",
rot=45, subplots=True, legend=False)
ax_ = hourly_summary_ax_list[-1]
ax_.get_figure().tight_layout()
ax_.get_figure().subplots_adjust(top=0.9)
_ = ax_.set_xticklabels(sorted(hourly_summary_df.index.strftime("%Y-%m-%d@%H").tolist()))
github_repository = os.environ.get("GITHUB_REPOSITORY")
if github_repository is None:
github_repository = "pvieito/Radar-STATS"
github_project_base_url = "https://github.com/" + github_repository
display_formatters = {
display_column_name_mapping["teks_per_shared_diagnosis"]: lambda x: f"{x:.2f}" if x != 0 else "",
display_column_name_mapping["shared_diagnoses_per_covid_case"]: lambda x: f"{x:.2%}" if x != 0 else "",
display_column_name_mapping["shared_diagnoses_per_covid_case_es"]: lambda x: f"{x:.2%}" if x != 0 else "",
}
general_columns = \
list(filter(lambda x: x not in display_formatters, display_column_name_mapping.values()))
general_formatter = lambda x: f"{x}" if x != 0 else ""
display_formatters.update(dict(map(lambda x: (x, general_formatter), general_columns)))
daily_summary_table_html = result_summary_with_display_names_df \
.head(daily_plot_days) \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.to_html(formatters=display_formatters)
multi_backend_summary_table_html = multi_backend_summary_df \
.head(daily_plot_days) \
.rename_axis(columns=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.rename_axis(index=display_column_name_mapping) \
.to_html(formatters=display_formatters)
def format_multi_backend_cross_sharing_fraction(x):
if pd.isna(x):
return "-"
elif round(x * 100, 1) == 0:
return ""
else:
return f"{x:.1%}"
multi_backend_cross_sharing_summary_table_html = multi_backend_cross_sharing_summary_df \
.rename_axis(columns=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.rename_axis(index=display_column_name_mapping) \
.to_html(
classes="table-center",
formatters=display_formatters,
float_format=format_multi_backend_cross_sharing_fraction)
multi_backend_cross_sharing_summary_table_html = \
multi_backend_cross_sharing_summary_table_html \
.replace("<tr>","<tr style=\"text-align: center;\">")
extraction_date_result_summary_df = \
result_summary_df[result_summary_df.index.get_level_values("sample_date") == extraction_date]
extraction_date_result_hourly_summary_df = \
hourly_summary_df[hourly_summary_df.extraction_date_with_hour == extraction_date_with_hour]
covid_cases = \
extraction_date_result_summary_df.covid_cases.item()
shared_teks_by_generation_date = \
extraction_date_result_summary_df.shared_teks_by_generation_date.item()
shared_teks_by_upload_date = \
extraction_date_result_summary_df.shared_teks_by_upload_date.item()
shared_diagnoses = \
extraction_date_result_summary_df.shared_diagnoses.item()
teks_per_shared_diagnosis = \
extraction_date_result_summary_df.teks_per_shared_diagnosis.item()
shared_diagnoses_per_covid_case = \
extraction_date_result_summary_df.shared_diagnoses_per_covid_case.item()
shared_teks_by_upload_date_last_hour = \
extraction_date_result_hourly_summary_df.shared_teks_by_upload_date.sum().astype(int)
display_source_regions = ", ".join(report_source_regions)
if len(report_source_regions) == 1:
display_brief_source_regions = report_source_regions[0]
else:
display_brief_source_regions = f"{len(report_source_regions)} 🇪🇺"
def get_temporary_image_path() -> str:
return os.path.join(tempfile.gettempdir(), str(uuid.uuid4()) + ".png")
def save_temporary_plot_image(ax):
if isinstance(ax, np.ndarray):
ax = ax[0]
media_path = get_temporary_image_path()
ax.get_figure().savefig(media_path)
return media_path
def save_temporary_dataframe_image(df):
import dataframe_image as dfi
df = df.copy()
df_styler = df.style.format(display_formatters)
media_path = get_temporary_image_path()
dfi.export(df_styler, media_path)
return media_path
summary_plots_image_path = save_temporary_plot_image(
ax=summary_ax_list)
summary_table_image_path = save_temporary_dataframe_image(
df=result_summary_with_display_names_df)
hourly_summary_plots_image_path = save_temporary_plot_image(
ax=hourly_summary_ax_list)
multi_backend_summary_table_image_path = save_temporary_dataframe_image(
df=multi_backend_summary_df)
generation_to_upload_period_pivot_table_image_path = save_temporary_plot_image(
ax=generation_to_upload_period_pivot_table_ax)
report_resources_path_prefix = "Data/Resources/Current/RadarCOVID-Report-"
result_summary_df.to_csv(
report_resources_path_prefix + "Summary-Table.csv")
result_summary_df.to_html(
report_resources_path_prefix + "Summary-Table.html")
hourly_summary_df.to_csv(
report_resources_path_prefix + "Hourly-Summary-Table.csv")
multi_backend_summary_df.to_csv(
report_resources_path_prefix + "Multi-Backend-Summary-Table.csv")
multi_backend_cross_sharing_summary_df.to_csv(
report_resources_path_prefix + "Multi-Backend-Cross-Sharing-Summary-Table.csv")
generation_to_upload_period_pivot_df.to_csv(
report_resources_path_prefix + "Generation-Upload-Period-Table.csv")
_ = shutil.copyfile(
summary_plots_image_path,
report_resources_path_prefix + "Summary-Plots.png")
_ = shutil.copyfile(
summary_table_image_path,
report_resources_path_prefix + "Summary-Table.png")
_ = shutil.copyfile(
hourly_summary_plots_image_path,
report_resources_path_prefix + "Hourly-Summary-Plots.png")
_ = shutil.copyfile(
multi_backend_summary_table_image_path,
report_resources_path_prefix + "Multi-Backend-Summary-Table.png")
_ = shutil.copyfile(
generation_to_upload_period_pivot_table_image_path,
report_resources_path_prefix + "Generation-Upload-Period-Table.png")
def generate_summary_api_results(df: pd.DataFrame) -> list:
api_df = df.reset_index().copy()
api_df["sample_date_string"] = \
api_df["sample_date"].dt.strftime("%Y-%m-%d")
api_df["source_regions"] = \
api_df["source_regions"].apply(lambda x: x.split(","))
return api_df.to_dict(orient="records")
summary_api_results = \
generate_summary_api_results(df=result_summary_df)
today_summary_api_results = \
generate_summary_api_results(df=extraction_date_result_summary_df)[0]
summary_results = dict(
backend_identifier=report_backend_identifier,
source_regions=report_source_regions,
extraction_datetime=extraction_datetime,
extraction_date=extraction_date,
extraction_date_with_hour=extraction_date_with_hour,
last_hour=dict(
shared_teks_by_upload_date=shared_teks_by_upload_date_last_hour,
shared_diagnoses=0,
),
today=today_summary_api_results,
last_7_days=last_7_days_summary,
last_14_days=last_14_days_summary,
daily_results=summary_api_results)
summary_results = \
json.loads(pd.Series([summary_results]).to_json(orient="records"))[0]
with open(report_resources_path_prefix + "Summary-Results.json", "w") as f:
json.dump(summary_results, f, indent=4)
with open("Data/Templates/README.md", "r") as f:
readme_contents = f.read()
readme_contents = readme_contents.format(
extraction_date_with_hour=extraction_date_with_hour,
github_project_base_url=github_project_base_url,
daily_summary_table_html=daily_summary_table_html,
multi_backend_summary_table_html=multi_backend_summary_table_html,
multi_backend_cross_sharing_summary_table_html=multi_backend_cross_sharing_summary_table_html,
display_source_regions=display_source_regions)
with open("README.md", "w") as f:
f.write(readme_contents)
enable_share_to_twitter = os.environ.get("RADARCOVID_REPORT__ENABLE_PUBLISH_ON_TWITTER")
github_event_name = os.environ.get("GITHUB_EVENT_NAME")
if enable_share_to_twitter and github_event_name == "schedule" and \
(shared_teks_by_upload_date_last_hour or not are_today_results_partial):
import tweepy
twitter_api_auth_keys = os.environ["RADARCOVID_REPORT__TWITTER_API_AUTH_KEYS"]
twitter_api_auth_keys = twitter_api_auth_keys.split(":")
auth = tweepy.OAuthHandler(twitter_api_auth_keys[0], twitter_api_auth_keys[1])
auth.set_access_token(twitter_api_auth_keys[2], twitter_api_auth_keys[3])
api = tweepy.API(auth)
summary_plots_media = api.media_upload(summary_plots_image_path)
summary_table_media = api.media_upload(summary_table_image_path)
generation_to_upload_period_pivot_table_image_media = api.media_upload(generation_to_upload_period_pivot_table_image_path)
media_ids = [
summary_plots_media.media_id,
summary_table_media.media_id,
generation_to_upload_period_pivot_table_image_media.media_id,
]
if are_today_results_partial:
today_addendum = " (Partial)"
else:
today_addendum = ""
def format_shared_diagnoses_per_covid_case(value) -> str:
if value == 0:
return "–"
return f"≤{value:.2%}"
display_shared_diagnoses_per_covid_case = \
format_shared_diagnoses_per_covid_case(value=shared_diagnoses_per_covid_case)
display_last_14_days_shared_diagnoses_per_covid_case = \
format_shared_diagnoses_per_covid_case(value=last_14_days_summary["shared_diagnoses_per_covid_case"])
display_last_14_days_shared_diagnoses_per_covid_case_es = \
format_shared_diagnoses_per_covid_case(value=last_14_days_summary["shared_diagnoses_per_covid_case_es"])
status = textwrap.dedent(f"""
#RadarCOVID – {extraction_date_with_hour}
Today{today_addendum}:
- Uploaded TEKs: {shared_teks_by_upload_date:.0f} ({shared_teks_by_upload_date_last_hour:+d} last hour)
- Shared Diagnoses: ≤{shared_diagnoses:.0f}
- Usage Ratio: {display_shared_diagnoses_per_covid_case}
Last 14 Days:
- Usage Ratio (Estimation): {display_last_14_days_shared_diagnoses_per_covid_case}
- Usage Ratio (Official): {display_last_14_days_shared_diagnoses_per_covid_case_es}
Info: {github_project_base_url}#documentation
""")
status = status.encode(encoding="utf-8")
api.update_status(status=status, media_ids=media_ids)
| 0.268749 | 0.215464 |
# Derivative Removal by Adiabatic Gate
*Copyright (c) 2021 Institute for Quantum Computing, Baidu Inc. All Rights Reserved.*
## Outline
This tutorial will demonstrate how to implement an X gate employing the DRAG (Derivative Reduction by Adiabatic Gate) technique using Quanlse. The outline of this tutorial is as follows:
- Introduction
- Preparation
- Define the waveform for DRAG
- Quanlse realization
- Summary
## Introduction
In superconducting circuits, one has to consider the leakage error due to the fact that superconducting circuits are not perfect two-level systems. For weakly anharmonic qubits, leakage into the third energy level takes the qubit out of the computational subspace. To overcome this issue, researchers proposed the DRAG procedure \[1\], which removes most of the leakage error by modifying the waveforms of the drive pulses.
## Preparation
After you have successfully installed Quanlse, you could run the Quanlse program below following this tutorial. To run this particular tutorial, you would need to import the following packages from Quanlse and other commonly-used Python libraries:
```
# Import numpy and scipy
import numpy as np
from scipy import integrate
# Import the Hamiltonian module
from Quanlse.Utils import Hamiltonian as qham
# Import the function for calculating infidelity
from Quanlse.Utils.Tools import unitaryInfidelity
# Import related operators
from Quanlse.Utils.Operator import driveX, driveY, number, duff
# Import waveforms and functions used to process the waveforms' data
from Quanlse.Utils.Waveforms import gaussian, dragY1
from Quanlse.Utils.Waveforms import makeWaveData, waveFuncToSeq
# Import simulator interface for Quanlse Cloud Service
from Quanlse.remoteSimulator import remoteSimulatorRunHamiltonian as runHamiltonian
# Import matplotlib for graphing purposes
import matplotlib.pyplot as plt
```
To use Quanlse Cloud Service, we need to acquire a token to get access to the cloud.
```
# Import Define class and set the token for cloud service
# Please visit http://quantum-hub.baidu.com
from Quanlse import Define
Define.hubToken = ""
```
## Define the waveform for DRAG
By performing a rotating wave approximation (RWA), the Hamiltonian in the rotating frame can be written as \[2\]:
$$
\hat H_R / \hbar = \delta_1 |1\rangle \langle 1|+\delta_2 |2\rangle \langle 2|+\alpha_q\hat a^{\dagger}\hat a^{\dagger}\hat a \hat a/2+\frac{\varepsilon_x(t)}{2}
\left[ \hat{a}^\dagger + \hat{a} \right]+\frac{\varepsilon_y(t)}{2}
i \left[\hat{a}^\dagger - \hat{a}\right]
,
$$
where $\omega_1$ and $\omega_2$ are the qubits' frequencies; and $\omega_d$ is the driving frequency. $\alpha_q = \omega_2 -2\omega_1$ is the anharmonicity of the system. $\delta_1 = \omega_1-\omega_d$ and $\delta_2 = \omega_2-\omega_d$ are the detunings of the transitions with respect to the drive frequency. $\varepsilon_x(t)$ and $\varepsilon_y(t)$ are the pulses' amplitudes of the two independent quadrature controls (XY control).
In the ideal case, we can ignore the higher energy levels of the qubit. To implement a $\theta$ rotation about the x-axis, we set $\delta _1$ to be zero and solve the equation directly:
$$
\int_0^{t_g}\varepsilon_x(t)dt=\theta.
$$
As for a Gaussian waveform $\varepsilon_G=Ae^{\frac{1}{2}(\frac{t-\tau}{\sigma})^2}-B$, we solve $\int_0^{t_g}\varepsilon_G(t)dt=\theta_x$ to determine the amplitude $A$ corresponding to a $\theta_x$ rotation about the x-axis:
$$
A=\theta_x/\left( \int_0^{t_g}e^{-(t-\tau)^2/2\sigma^2}dt-t_ge^{-\tau^2/2\sigma^2} \right),
$$
$$
B=Ae^{-\tau^2/2\sigma^2}.
$$
In the equations above, $A$ ensures that the desired magnitude of rotation is implemented; while $B$ enforces that the pulse's amplitude start and end on zero.
In the following code, we first define a couple of parameters to set the rotation angle and the anharmonicity of the system. Then, we define the functions for calculating parameters of the Gaussian waveform (commonly used waveform functions are available in Quanlse).
```
theta_x = np.pi # the angle of rotation
Delta = -0.4 * 2 * np.pi # the anharmonicity in GHz
# Calculate the parameters
def intTheta(tg):
y = integrate.quad(gaussian, 0, tg, {"a": 1, "tau": 0.5 * tg, "sigma": 0.25 * tg})
return y[0]
def calAx(tg):
return theta_x / (intTheta(tg) - gaussian(0, args={"a": 1, "tau": 0.5 * tg, "sigma": 0.25 * tg}) * tg)
def calBx(tg):
return calAx(tg) * gaussian(0, args={"a": 1, "tau": 0.5 * tg, "sigma": 0.25 * tg})
```
In the DRAG procedure, the waveforms and detunings are modified to:
$$
\varepsilon_y(t) = -\frac{\dot {\varepsilon_x}(t)}{\alpha_q},
$$
$$
\delta_1(t) = -\frac{\varepsilon_x^2(t)}{2\alpha_q}.
$$
Here, we build the control pulses $\varepsilon_x(t)$ and $\varepsilon_y(t)$ and set the drive detuning $\delta_1$ according to the equations above.
```
# Define the control waveforms
def epsilonX(t, params):
tg = params['tg']
a = calAx(tg)
b = calBx(tg)
return gaussian(t, args={"a": a, "tau": 0.5 * tg, "sigma": 0.25 * tg}) - b
def epsilonY(t, params):
tg = params['tg']
a = calAx(tg)
return dragY1(t, args={"a": a, "tau": 0.5 * tg, "sigma": 0.25 * tg}) / Delta
# Set the drive detuning
def delta1(t, params):
tg = params['tg']
lamda = np.sqrt(2)
return - epsilonX(t, {"tg": tg}) ** 2 / 2 / Delta
```
## Quanlse realization
Quanlse stores the system's information required for simulation and optimization in the Hamiltonian dictionaries. First of all, we create an empty Hamiltonian dictionary using the function `createHam()` and add terms to it using previously defined parameters and functions.
```
# Initiate the Hamiltonian dictionaries
ham = qham.createHam(title="no drag", dt=0.1, qubitNum=1, sysLevel=3)
ham_drag = qham.createHam(title="drag", dt=0.1, qubitNum=1, sysLevel=3)
```
For this particular task, the system Hamiltonian can be expressed in four terms:
$$
\hat H_R = \hat H_{\rm drift} + \hat H_{\rm xctrl} + \hat H_{\rm yctrl}+ \hat H_{\rm freq} ,
$$
where $\hat H_{\rm drift}= \alpha_q\hat a^{\dagger}\hat a^{\dagger}\hat a \hat a/2$ represents the anharmonicity of the qubit, which is intrinsic and time-independent. We add the drift terms by calling `addDrift()`. The operator $\hat a^{\dagger}a^{\dagger} \hat a \hat a$ is defined as `duff()` in Quanlse, which takes the system's dimension as a parameter.
```
# Add the anharmonic terms
qham.addDrift(ham, "drift", onQubits=0, matrices=duff(3), amp=Delta / 2.0)
qham.addDrift(ham_drag, "drift", onQubits=0, matrices=duff(3), amp=Delta / 2.0)
```
Next, the control terms $\hat H_{\rm xctrl}=\frac{1}{2}(\hat a +\hat a^{\dagger})$, $\hat H_{\rm yctrl}=\frac{i}{2}(\hat a -\hat a^{\dagger})$ and $ \hat H_{\rm freq}=\hat a^{\dagger}\hat a $ are added by calling the function `addControl()`. Their according operators are also available and can be found in `Utils.Operator`.
```
# Add the control terms
qham.addControl(ham, "ctrlx", onQubits=0, matrices=driveX(3))
qham.addControl(ham_drag, "ctrlx", onQubits=0, matrices=driveX(3))
qham.addControl(ham_drag, "ctrly", onQubits=0, matrices=driveY(3))
# Add the detuning term
qham.addControl(ham_drag, "detune", onQubits=0, matrices=number(3))
```
For a thorough comparison, we compute gate fidelities within a range of gate times. In fact, the task can be done very efficiently using Quanlse. In particular, `runHamiltonian()` supports batch-job simulation and returns a list of dictionaries with details of the result, and the unitary operator is stored under the key `"unitary"`.
The simulation may take a long time to process on local devices. However, Quanlse provides a cloud service that could speed up this process significantly. To use Quanlse Cloud Service, the users can get a token from http://quantum-hub.baidu.com and use the functions in `runHamiltonian()` module to submit the job onto Quanlse's server.
After the simulation, we assess the performance of the implemented gate using DRAG pulse by calculating the infidelity for various gate time defined as:
$$
{\rm infid} =1- \frac{1}{2}\left|{\rm Tr}(\hat{\sigma}_x P(U))\right|.
$$
Here, the projected evolution $P(U)$ ($U$ is the evolution of the system) in particular describes the evolution projected to the computational subspace consisting of the two lowest energy eigenstates $|0\rangle$ and $|1\rangle$; $\hat{\sigma}_x$ is the target gate we want to implement.
```
# Gate times at which to compute gate fidelities
t = np.arange(2., 9., 0.5)
# Create the arrays for storing gate infidelities
errorx = np.zeros(len(t))
errorxdrag = np.zeros(len(t))
# Intialize array index
jobList = []
jobList_drag = []
for tg in t:
jobWaves = []
jobWaves_drag = []
# Add Gaussian Wave of X control on the qubit 0
paraArgs = {"a": -0.5 * 2.0 * np.pi}
# Add wave for the job list without DRAG pulses
jobWaves.append(makeWaveData(ham, "ctrlx", f=epsilonX, para={"tg": tg}, t0=0, t=tg))
# Add wave for the job list with DRAG pulses
jobWaves_drag.append(makeWaveData(ham_drag, "ctrlx", f=epsilonX, para={"tg": tg}, t0=0, t=tg))
jobWaves_drag.append(makeWaveData(ham_drag, "ctrly", f=epsilonY, para={"tg": tg}, t0=0, t=tg))
jobWaves_drag.append(makeWaveData(ham_drag, "detune", f=delta1, para={"tg": tg}, t0=0, t=tg))
# Append this job to the job list
jobList.append(jobWaves)
jobList_drag.append(jobWaves_drag)
# Submit the job lists to Quanlse Cloud Service
result = runHamiltonian(ham, jobList=jobList)
result_drag = runHamiltonian(ham_drag, jobList=jobList_drag)
errorx = []
errorx_drag = []
for index in range(len(t)):
errorx.append(unitaryInfidelity(np.array([[0, 1], [1, 0]], dtype=complex), result[index]["unitary"], 1))
errorx_drag.append(unitaryInfidelity(np.array([[0, 1], [1, 0]], dtype=complex), result_drag[index]["unitary"], 1))
```
Finally, we can analyze and visualize the results using the Matplotlib library.
```
plt.semilogy(t, errorx_drag, label='With DRAG', marker='.')
plt.semilogy(t, errorx, label='Without DRAG', marker='.')
plt.xlabel('Gate Time (ns)')
plt.ylabel('Infidelity')
plt.title('X Gate')
plt.legend()
plt.show()
```
As demonstrated above, most of the leakage error is mitigated. The blue (DRAG optimized waveform) line illustrates that DRAG reduces the infidelity by orders of magnitude.
## Summary
This tutorial introduces the DRAG technique using Quanlse. The users are encouraged to explore other advanced research which are different from this tutorial.
## References
\[1\] [Motzoi, Felix, et al. "Simple pulses for elimination of leakage in weakly nonlinear qubits." *Physical review letters* 103.11 (2009): 110501.](https://link.aps.org/doi/10.1103/PhysRevLett.103.110501)
\[2\] [Krantz, Philip, et al. "A quantum engineer's guide to superconducting qubits." *Applied Physics Reviews* 6.2 (2019): 021318.](https://aip.scitation.org/doi/abs/10.1063/1.5089550)
|
github_jupyter
|
# Import numpy and scipy
import numpy as np
from scipy import integrate
# Import the Hamiltonian module
from Quanlse.Utils import Hamiltonian as qham
# Import the function for calculating infidelity
from Quanlse.Utils.Tools import unitaryInfidelity
# Import related operators
from Quanlse.Utils.Operator import driveX, driveY, number, duff
# Import waveforms and functions used to process the waveforms' data
from Quanlse.Utils.Waveforms import gaussian, dragY1
from Quanlse.Utils.Waveforms import makeWaveData, waveFuncToSeq
# Import simulator interface for Quanlse Cloud Service
from Quanlse.remoteSimulator import remoteSimulatorRunHamiltonian as runHamiltonian
# Import matplotlib for graphing purposes
import matplotlib.pyplot as plt
# Import Define class and set the token for cloud service
# Please visit http://quantum-hub.baidu.com
from Quanlse import Define
Define.hubToken = ""
theta_x = np.pi # the angle of rotation
Delta = -0.4 * 2 * np.pi # the anharmonicity in GHz
# Calculate the parameters
def intTheta(tg):
y = integrate.quad(gaussian, 0, tg, {"a": 1, "tau": 0.5 * tg, "sigma": 0.25 * tg})
return y[0]
def calAx(tg):
return theta_x / (intTheta(tg) - gaussian(0, args={"a": 1, "tau": 0.5 * tg, "sigma": 0.25 * tg}) * tg)
def calBx(tg):
return calAx(tg) * gaussian(0, args={"a": 1, "tau": 0.5 * tg, "sigma": 0.25 * tg})
# Define the control waveforms
def epsilonX(t, params):
tg = params['tg']
a = calAx(tg)
b = calBx(tg)
return gaussian(t, args={"a": a, "tau": 0.5 * tg, "sigma": 0.25 * tg}) - b
def epsilonY(t, params):
tg = params['tg']
a = calAx(tg)
return dragY1(t, args={"a": a, "tau": 0.5 * tg, "sigma": 0.25 * tg}) / Delta
# Set the drive detuning
def delta1(t, params):
tg = params['tg']
lamda = np.sqrt(2)
return - epsilonX(t, {"tg": tg}) ** 2 / 2 / Delta
# Initiate the Hamiltonian dictionaries
ham = qham.createHam(title="no drag", dt=0.1, qubitNum=1, sysLevel=3)
ham_drag = qham.createHam(title="drag", dt=0.1, qubitNum=1, sysLevel=3)
# Add the anharmonic terms
qham.addDrift(ham, "drift", onQubits=0, matrices=duff(3), amp=Delta / 2.0)
qham.addDrift(ham_drag, "drift", onQubits=0, matrices=duff(3), amp=Delta / 2.0)
# Add the control terms
qham.addControl(ham, "ctrlx", onQubits=0, matrices=driveX(3))
qham.addControl(ham_drag, "ctrlx", onQubits=0, matrices=driveX(3))
qham.addControl(ham_drag, "ctrly", onQubits=0, matrices=driveY(3))
# Add the detuning term
qham.addControl(ham_drag, "detune", onQubits=0, matrices=number(3))
# Gate times at which to compute gate fidelities
t = np.arange(2., 9., 0.5)
# Create the arrays for storing gate infidelities
errorx = np.zeros(len(t))
errorxdrag = np.zeros(len(t))
# Intialize array index
jobList = []
jobList_drag = []
for tg in t:
jobWaves = []
jobWaves_drag = []
# Add Gaussian Wave of X control on the qubit 0
paraArgs = {"a": -0.5 * 2.0 * np.pi}
# Add wave for the job list without DRAG pulses
jobWaves.append(makeWaveData(ham, "ctrlx", f=epsilonX, para={"tg": tg}, t0=0, t=tg))
# Add wave for the job list with DRAG pulses
jobWaves_drag.append(makeWaveData(ham_drag, "ctrlx", f=epsilonX, para={"tg": tg}, t0=0, t=tg))
jobWaves_drag.append(makeWaveData(ham_drag, "ctrly", f=epsilonY, para={"tg": tg}, t0=0, t=tg))
jobWaves_drag.append(makeWaveData(ham_drag, "detune", f=delta1, para={"tg": tg}, t0=0, t=tg))
# Append this job to the job list
jobList.append(jobWaves)
jobList_drag.append(jobWaves_drag)
# Submit the job lists to Quanlse Cloud Service
result = runHamiltonian(ham, jobList=jobList)
result_drag = runHamiltonian(ham_drag, jobList=jobList_drag)
errorx = []
errorx_drag = []
for index in range(len(t)):
errorx.append(unitaryInfidelity(np.array([[0, 1], [1, 0]], dtype=complex), result[index]["unitary"], 1))
errorx_drag.append(unitaryInfidelity(np.array([[0, 1], [1, 0]], dtype=complex), result_drag[index]["unitary"], 1))
plt.semilogy(t, errorx_drag, label='With DRAG', marker='.')
plt.semilogy(t, errorx, label='Without DRAG', marker='.')
plt.xlabel('Gate Time (ns)')
plt.ylabel('Infidelity')
plt.title('X Gate')
plt.legend()
plt.show()
| 0.673084 | 0.975414 |
<a href="https://colab.research.google.com/github/Jenn-mawia/State-of-Financial-Inclusion-in-East-Africa/blob/master/Moringa_Data_Science_Core_W2_Independent_Project_2020_08_Jenipher_Mawia_Python_Notebook.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Defining the question
## Specifiying the data analytic question
Research questions:
Find out how we can predict which individuals are most likely to have or use a bank account.
## Defining the metric for success
The objectives of this project will be met if the following can be determined:
- Insight into the state of financial inclusion in the countries: Kenya, Uganda, Rwanda, Tanzania
- Insight into some of the key demographic factos that might drive an individual's financial outcomes
- Prediction of individuals most likely to have or use a bank account
## Understanding the context
Financial Inclusion remains one of the main obstacles to economic and human development in Africa. For example, across Kenya, Rwanda, Tanzania, and Uganda only 9.1 million adults (or 13.9% of the adult population) have access to or use a commercial bank account.
Traditionally, access to bank accounts has been regarded as an indicator of financial inclusion. Despite the proliferation of mobile money in Africa and the growth of innovative fintech solutions, banks still play a pivotal role in facilitating access to financial services. Access to bank accounts enables households to save and facilitate payments while also helping businesses build up their credit-worthiness and improve their access to other financial services. Therefore, access to bank accounts is an essential contributor to long-term economic growth.
## Recording the experimental design taken
1. Loading dataset
2. Checking the dataset's shape, top, bottom, datatypes
3. External data source validation
4. Data Cleaning
- renaming column names & ensuring consistency in column names
- dropping unnecessary columns
- handling null values, duplicated records, outliers, anomalies
5. Exploratory Data Analysis
- Univariate EDA
- Bivariate EDA
- analysis by country
- analysis by demographic factors
- Multivariate EDA
## The appropriateness of the available data to answer the given question
The available data is deemed as appropriate as the data contains all variables that will be required to perform analysis by country and by either demographic factors such as: age, gender, level of education, income level, area or residence, employment, marital status among other factors that influence an individuals financial outcomes.
# Reading the data
```
# importing libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style()
```
The data used for the project contains demographic information and financial services used by individuals across East Africa. This data was extracted from various Finscope Surveys ranging from 2016-2018. More information about this surveys can be found here:
- FinAccess Kenya 2018. [Link](https://fsdkenya.org/publication/finaccess2019/)
- Finscope Rwanda 2016. [Link](http://www.statistics.gov.rw/publication/finscope-rwanda-2016)
- Finscope Tanzania 2017. [Link](http://www.fsdt.or.tz/finscope/)
- Finscope Uganda 2018. [Link](http://fsduganda.or.ug/finscope-2018-survey-report/)
To upload the dataset onto the environment, download the dataset [here](http://bit.ly/FinancialDataset) go to, Table of contents > files > upload on Colab.
```
# Attribute Information:
# country - country interviewee is in
# year - year survey was done
# uniqueid - unique identifier for each interviewee
# has_a_bank_account - if interviewee has a bank account : Yes/No
# location_type - type of location : Rural, Urban
# cellphone_access - if interviewee has access to cellphone: Yes/No
# household_size - number of people living in one house
# age_of_respondent - age of interviewee
# gender_of_respondent - gender of interviewee: Male, Female
# relationship_with_head - interviewee relationship with the head of the house: Head of Household, Spouse, Child, Parent, Other relative, Other non-relative, Don't know
# marital_status - marital status of interviewee: Married/Living together, Divorced/Separated, Widowed, Single/Never Married, Don't know
# education_level - highest level of education: No formal education, Primary education, Secondary education, Vocational/Specialised training, Tertiary education, Other/Don't know/RTA
# job_type - type of job interviewee has: Farming and Fishing, Formally employed Government, Formally employed Private, Informally employed, Remittance Dependent, Government Dependent, Self employed, Other Income, No Income, Don't know/Refused to answer
# reading the data
financial = pd.read_csv("Financial Dataset - 1.csv")
```
# Checking the data
```
# number of rows and columns
financial.shape
# preview the top of the dataset
financial.head()
# previewing the bottom of the dataset
financial.tail()
# checking whether each column has appropriate datatypes
financial.dtypes
```
# External Data Source Validation
The data available for analysis can be validated with the following [data](https://www.kaggle.com/bhrt97/machine-learning-starter-program-hackathon-dataset) from [Kaggle](https://www.kaggle.com/).
This data was compiled to analyse and predict the performances of a trainee based on the demographic information available. This would enable a client to strengthen its training problem by focusing on the most important factors that leading to better engagement and performance of a trainee.
Some of the demographic factors that were compiled for analysis include: gender of trainee, education level of trainee, city/area of residence, age of the trainee.
All these are very similar to what we have in our data so we can move on with analysis since we have the right data to answer our question.
# Data Cleaning
```
# rename column
financial.rename(columns={'The relathip with head': 'relationship_with_head', 'Level of Educuation':'level_of_education'}, inplace = True)
financial.columns
# making all column names consistent in the format
financial.columns = financial.columns.str.strip().str.lower().str.replace(" ", "_")
financial
# drop irrelevant fields
financial.drop(['uniqueid', 'year'], axis=1, inplace=True)
financial
# checking for null values
financial.isnull().sum()
# drop null values
fin = financial.dropna()
fin.isnull().sum()
# checking for duplicates
fin.duplicated().sum()
# drop duplicates
df1 = fin.drop_duplicates()
df1
# checking for outliers
df1.boxplot(figsize=(8, 6), fontsize=10)
# print size of the data with outliers present
print(df1.shape)
print("********************************************")
# removing outliers
Q1 = df1.quantile(0.25)
Q3 = df1.quantile(0.75)
IQR = Q3 - Q1
df = df1[~((df1 < (Q1 - 1.5 * IQR)) | (df1 > (Q3 + 1.5 * IQR))).any(axis=1)]
# print size of the data after removal of outliers
print(df.shape)
# plot of the new data, without ouliers
df.boxplot()
# checking for anomalies
# getting the quantiles
q1_house = df['household_size'].quantile(.25)
q3_house = df['household_size'].quantile(.75)
# calculating inter-quartile range using values from above
iqr_31_house = q3_house - q1_house
# another way is to find quantiles using the percentiles from the numpy library
q1_h, q3_h = np.percentile(df['household_size'], [25, 75])
# IQR
iqr_31_h = q3_h - q1_h
# compare if the two values are similar
print(iqr_31_house, iqr_31_h)
# getting to know more about the dataset
df.info()
```
# Exploratory Data Analysis
## Univariate Analysis
```
# how many individuals have or do not have bank accounts?
#
# plot a count plot for the variable
ax = sns.countplot(df['has_a_bank_account'], order = df['has_a_bank_account'].value_counts().index)
# formatting and labelling axes
plt.title('Count of indidviduals with and without a bank account')
plt.xlabel('Has a bank account?')
plt.ylabel('Frequency/count of individuals')
# plot count plot for the type of location
ax = sns.countplot(df['type_of_location'], order = df['type_of_location'].value_counts().index)
# formatting the plot, labelling axes
plt.title("Rural and Urban locations")
plt.xlabel('Rural or urban?')
plt.ylabel('Number of individuals')
# frequency table of the same for comparison
df['type_of_location'].value_counts()
# plot count plot of the access to cell phones by individual respondent
ax = sns.countplot(df['cell_phone_access'], order = df['cell_phone_access'].value_counts().index)
# formatting and labelling the plot
plt.title('Access to cell phone')
plt.xlabel('Has access to cell phone?')
plt.ylabel('Number of individuals')
# plot for the number of people living in one household
ax = sns.countplot(df['household_size'], order = df['household_size'].value_counts().index)
# formatting and labelling chart
plt.title('Distribution of number of people living in one household')
plt.xlabel('Number of individuals per household')
plt.ylabel('Frequency distribution across the population')
# plot age distribution of the respondents
# specify size of the figure since the values are so many-makes it easier to read the chart
plt.figure(figsize=(20,5))
ax = sns.countplot(df['respondent_age'], order = df['respondent_age'].value_counts().index)
# formatting and labelling the chart
plt.xticks(rotation = 90)
plt.title("Age distribution across the population")
plt.xlabel("Age")
plt.ylabel("Frequency/number of occurrences")
# count plot for the gender of the respondent
ax = sns.countplot(df['gender_of_respondent'], order = df['gender_of_respondent'].value_counts().index)
# formatting and labelling the plot
plt.title("Gender distribution across the interviewed population")
plt.xlabel("Gender")
plt.ylabel("Frequency")
# count plot of the relationship of the respondent to the head of the household
ax = sns.countplot(df['relationship_with_head'], order = df['relationship_with_head'].value_counts().index)
# formatting and labelling the chart
plt.title("Relationship of the respodent to the head of household")
plt.xlabel("Relation to household head")
plt.ylabel("Frequency of occur")
plt.xticks(rotation = 90)
# plot of the marital status of the respondents, order them in descending order
ax = sns.countplot(df['marital_status'], order = df['marital_status'].value_counts().index)
# formatting the chart and labelling axes
plt.title("Marital status of the interviewees")
plt.xlabel("Marital status")
plt.ylabel("Number of individuals in the population")
plt.xticks(rotation=90)
# plot of the level of education for the respondents who took part in the interview
df['level_of_education'].value_counts().plot(kind='bar')
# formatting and labelling the plot
plt.title("Highest level of education reached by interviewees in the population")
plt.xlabel("Highest level reached")
plt.ylabel("Number of respondents")
# notice an anomaly in the above plot.6 is represented yet it does not represent any thing related to level of education
# drop the anomaly 6 in the level of education
df = df[~(df['level_of_education']=='6')]
df['level_of_education'].value_counts()
# plot a new chart for the level of education after dropping the anomalies
ax = sns.countplot(df['level_of_education'], order = df['level_of_education'].value_counts().index)
# formatting and labelling the chart
plt.title("Highest level of education reached by interviewees in the population")
plt.xlabel("Highest level reached")
plt.ylabel("Number of respondents")
plt.xticks(rotation=90)
# count plot for the type of job
ax = sns.countplot(df['type_of_job'], order = df['type_of_job'].value_counts().index)
# formatting and labelling the chart
plt.title("Type of job respondent holds")
plt.xlabel("Type of job")
plt.ylabel("Number of respondents")
plt.xticks(rotation=90)
```
**Measures of central tendency**
```
print(df['respondent_age'].mean())
print(df['respondent_age'].median())
print(df['respondent_age'].mode())
print(df['household_size'].mean())
print(df['household_size'].median())
print(df['household_size'].mode())
```
## Bivariate Analysis
```
# rename/save the dataframe using a new name
finance = df
finance.head()
# checking the datatypes
finance.info()
```
**Analysis by Country**
```
# create a crosstab/frequency table for the countries and bank account possession
countries_bankacc= pd.crosstab(index=finance['country'], columns=finance['has_a_bank_account'])
print(countries_bankacc)
# plot chart for the frequencies represented in the crosstab dataframe
countries_bankacc.plot(kind="bar", figsize=(8,8),stacked=True)
# labelling axes and formatting chart
plt.title("Bank account possession by country")
plt.ylabel("Distribution across the population")
# create a crosstab/frequency table for the countries and accessibility to cell phone
countries_cellphone = pd.crosstab(index=finance['country'], columns=finance['cell_phone_access'])
print(countries_cellphone)
# plot chart for the frequencies represented in the crosstab dataframe
countries_cellphone.plot(kind="bar", figsize=(8,8),stacked=True)
# labelling axes and formatting chart
plt.title("Accessibility to cellphone by country")
plt.ylabel("Distribution across the population")
# create a crosstab/frequency table
countries_location = pd.crosstab(index=finance['country'], columns=finance['type_of_location'])
print(countries_location)
# plot chart for the frequencies represented in the crosstab dataframe
countries_location.plot(kind="bar", figsize=(8,8),stacked=True)
# labelling axes and formatting chart
plt.title("Locations of respondents by country")
plt.ylabel("Distribution across the population")
# create a frequency table dataframe
countries_housesize = pd.crosstab(index=finance['country'], columns=finance['household_size'])
print(countries_housesize)
# plot chart from the frequency table dataframe
countries_housesize.plot(kind="bar", figsize=(8,8),stacked=True)
# labelling axes and formatting chart
plt.title("Housesizes for the respondents by country")
plt.ylabel("Distribution across the population")
# create a crosstab dataframe
countries_gender = pd.crosstab(index=finance['country'], columns=finance['marital_status'])
print(countries_gender)
# plot chart from the dataframe
countries_gender.plot(kind="bar", figsize=(8,8))
# formatting and labelling chart
plt.title("Marital status of respondents by country")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
countries_job = pd.crosstab(index=finance['country'], columns=finance['type_of_job'])
print(countries_job)
# plot chart
countries_job.plot(kind="bar", figsize=(8,8))
# formatting
plt.title("Type of job respondent holds by country")
plt.ylabel("Distribution across the population")
```
**Demographic factor analysis**
```
# create crosstab
edu_bank = pd.crosstab(index=finance['level_of_education'], columns=finance['has_a_bank_account'])
print(edu_bank)
# plot chart
edu_bank.plot(kind="bar", figsize=(8,8))
# format & label chart
plt.title("Relation of respondents education level to bank account possession")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
age_bank = pd.crosstab(index=finance['respondent_age'], columns=finance['has_a_bank_account'])
print(age_bank)
# plot chart
age_bank.plot(kind="bar", figsize=(20,5))
# format and label chart
plt.title("Relation of respondent age and possession of bank account")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
gender_bank = pd.crosstab(index=finance['gender_of_respondent'], columns=finance['has_a_bank_account'])
print(gender_bank)
# plot of the relation of gender to individuals possession to bank account
gender_bank.plot(kind="bar", figsize=(8,8))
# formatting&labelling chart
plt.title("Relation of respondent age and possession of bank account")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
marital_bank = pd.crosstab(index=finance['marital_status'], columns=finance['has_a_bank_account'])
print(marital_bank)
# plot chart
marital_bank.plot(kind="bar", figsize=(8,8))
# formatting&labelling
plt.title("Effect of marital status and possession of bank account")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
employ_bank = pd.crosstab(index=finance['type_of_job'], columns=finance['has_a_bank_account'])
print(employ_bank)
# plot chart from the dataframe
employ_bank.plot(kind="bar", figsize=(8,8), stacked=True)
# labelling chart
plt.title("Effect of employment status to possession of bank account")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
location_bank = pd.crosstab(index=finance['type_of_location'], columns=finance['has_a_bank_account'])
print(location_bank)
# plot chart
location_bank.plot(kind="bar", figsize=(8,8))
# label chart
plt.title("Effect of area of residence to possession of bank account")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
housesize_bank = pd.crosstab(index=finance['household_size'], columns=finance['has_a_bank_account'])
print(housesize_bank)
# plot chart
housesize_bank.plot(kind="bar", figsize=(8,8), stacked=True)
# label chart
plt.title("Effect of household size to possession of bank account")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
cellphone_bank = pd.crosstab(index=finance['cell_phone_access'], columns=finance['has_a_bank_account'])
print(cellphone_bank)
# plot chart
cellphone_bank.plot(kind="bar", figsize=(8,8))
# labelling chart
plt.title("Effect of cell phone accessibility to possession of bank account")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
relation_withhead_bank = pd.crosstab(index=finance['relationship_with_head'], columns=finance['has_a_bank_account'])
print(relation_withhead_bank)
# plot chart
relation_withhead_bank.plot(kind="bar", figsize=(8,8), stacked=True)
# label chart
plt.title("Relation of respondent's relationship with head of household to possession of bank account")
plt.ylabel("Distribution across the population")
```
## Multivariate Analysis
# Findings
After univariate analysis, it was found that :
- a huge population of the respondents in the four countries did not have or use a bank account.
- most individuals live in rural areas
- the most popular family/household size is 2
- a huge number of the respondents are of age 30, while the mean of the ages of all respondents was 39.
- a large population of the respondents were female.
- huge number of the respondents were heads of the household, followed by spouses.
- most individuals in the population were married and the next most highest were single individuals.
- most respondents had only studied upto primary level of education. Very few had studied upto the tertiary level.
- a huge number of the respondent population were self-employed
After bivariate analysis by country, it was found that:
- Rwanda recorded a huge number of individuals without a bank account. Kenya however, recorded a relatively high number of individuals possessing a bank account.
- the distribution of accessibility to cell phone was fairly distributed across the countries with Tanzania having a relatively huge population with no access to a cell phone
- most respondents from Tanzania reside in urban areas, while in Rwanda a huge population live in rural areas
- in Tanzania, most respondents live in household sizes of 1 or 2 people
- most respondents in Kenya, Rwanda and Uganda are married while in Uganda, a huge population are single/never married
- a huge population of the respondents from Kenya and Rwanda do farming and fishing as their income source, while in Uganda and Tanzania,a huge population are self-employed
After bivariate analysis by demographic factors, it was found that:
- most individuals who had gone through higher education i.e. tertiary level or vocational training, have/use a bank account, hence the bars are almost equal
- a huge population of individuals of ages 30, 35, 40, 42 had bank accounts
- as much as females dominated the respondents population, males who have/use a bank account were relatively more than the females who use a bank account
- most respondents who are married have a bank account followed by those who are single
- more individuals that are self employed have a bank account, followed by farmers, formally employed privately and informally employed
- area of residence did not have a huge effect on bank account possession as more individuals living in the rural areas had a bank account compared to those in urban areas
- individuals who live in households with a smaller size tend to own a bank account
- more individuals that have access to a cell phone have a bank account. This could be due to the accessiblity of mobile banking, online banking services which can be done on the phone.
- more individuals that are head of household have a a bank account followed by spouses. This could be due to the responsibilities that generally fall onto the head of the household that leads them to budgeting, saving for the future and hence having a bank account to manage finances.
|
github_jupyter
|
# importing libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style()
# Attribute Information:
# country - country interviewee is in
# year - year survey was done
# uniqueid - unique identifier for each interviewee
# has_a_bank_account - if interviewee has a bank account : Yes/No
# location_type - type of location : Rural, Urban
# cellphone_access - if interviewee has access to cellphone: Yes/No
# household_size - number of people living in one house
# age_of_respondent - age of interviewee
# gender_of_respondent - gender of interviewee: Male, Female
# relationship_with_head - interviewee relationship with the head of the house: Head of Household, Spouse, Child, Parent, Other relative, Other non-relative, Don't know
# marital_status - marital status of interviewee: Married/Living together, Divorced/Separated, Widowed, Single/Never Married, Don't know
# education_level - highest level of education: No formal education, Primary education, Secondary education, Vocational/Specialised training, Tertiary education, Other/Don't know/RTA
# job_type - type of job interviewee has: Farming and Fishing, Formally employed Government, Formally employed Private, Informally employed, Remittance Dependent, Government Dependent, Self employed, Other Income, No Income, Don't know/Refused to answer
# reading the data
financial = pd.read_csv("Financial Dataset - 1.csv")
# number of rows and columns
financial.shape
# preview the top of the dataset
financial.head()
# previewing the bottom of the dataset
financial.tail()
# checking whether each column has appropriate datatypes
financial.dtypes
# rename column
financial.rename(columns={'The relathip with head': 'relationship_with_head', 'Level of Educuation':'level_of_education'}, inplace = True)
financial.columns
# making all column names consistent in the format
financial.columns = financial.columns.str.strip().str.lower().str.replace(" ", "_")
financial
# drop irrelevant fields
financial.drop(['uniqueid', 'year'], axis=1, inplace=True)
financial
# checking for null values
financial.isnull().sum()
# drop null values
fin = financial.dropna()
fin.isnull().sum()
# checking for duplicates
fin.duplicated().sum()
# drop duplicates
df1 = fin.drop_duplicates()
df1
# checking for outliers
df1.boxplot(figsize=(8, 6), fontsize=10)
# print size of the data with outliers present
print(df1.shape)
print("********************************************")
# removing outliers
Q1 = df1.quantile(0.25)
Q3 = df1.quantile(0.75)
IQR = Q3 - Q1
df = df1[~((df1 < (Q1 - 1.5 * IQR)) | (df1 > (Q3 + 1.5 * IQR))).any(axis=1)]
# print size of the data after removal of outliers
print(df.shape)
# plot of the new data, without ouliers
df.boxplot()
# checking for anomalies
# getting the quantiles
q1_house = df['household_size'].quantile(.25)
q3_house = df['household_size'].quantile(.75)
# calculating inter-quartile range using values from above
iqr_31_house = q3_house - q1_house
# another way is to find quantiles using the percentiles from the numpy library
q1_h, q3_h = np.percentile(df['household_size'], [25, 75])
# IQR
iqr_31_h = q3_h - q1_h
# compare if the two values are similar
print(iqr_31_house, iqr_31_h)
# getting to know more about the dataset
df.info()
# how many individuals have or do not have bank accounts?
#
# plot a count plot for the variable
ax = sns.countplot(df['has_a_bank_account'], order = df['has_a_bank_account'].value_counts().index)
# formatting and labelling axes
plt.title('Count of indidviduals with and without a bank account')
plt.xlabel('Has a bank account?')
plt.ylabel('Frequency/count of individuals')
# plot count plot for the type of location
ax = sns.countplot(df['type_of_location'], order = df['type_of_location'].value_counts().index)
# formatting the plot, labelling axes
plt.title("Rural and Urban locations")
plt.xlabel('Rural or urban?')
plt.ylabel('Number of individuals')
# frequency table of the same for comparison
df['type_of_location'].value_counts()
# plot count plot of the access to cell phones by individual respondent
ax = sns.countplot(df['cell_phone_access'], order = df['cell_phone_access'].value_counts().index)
# formatting and labelling the plot
plt.title('Access to cell phone')
plt.xlabel('Has access to cell phone?')
plt.ylabel('Number of individuals')
# plot for the number of people living in one household
ax = sns.countplot(df['household_size'], order = df['household_size'].value_counts().index)
# formatting and labelling chart
plt.title('Distribution of number of people living in one household')
plt.xlabel('Number of individuals per household')
plt.ylabel('Frequency distribution across the population')
# plot age distribution of the respondents
# specify size of the figure since the values are so many-makes it easier to read the chart
plt.figure(figsize=(20,5))
ax = sns.countplot(df['respondent_age'], order = df['respondent_age'].value_counts().index)
# formatting and labelling the chart
plt.xticks(rotation = 90)
plt.title("Age distribution across the population")
plt.xlabel("Age")
plt.ylabel("Frequency/number of occurrences")
# count plot for the gender of the respondent
ax = sns.countplot(df['gender_of_respondent'], order = df['gender_of_respondent'].value_counts().index)
# formatting and labelling the plot
plt.title("Gender distribution across the interviewed population")
plt.xlabel("Gender")
plt.ylabel("Frequency")
# count plot of the relationship of the respondent to the head of the household
ax = sns.countplot(df['relationship_with_head'], order = df['relationship_with_head'].value_counts().index)
# formatting and labelling the chart
plt.title("Relationship of the respodent to the head of household")
plt.xlabel("Relation to household head")
plt.ylabel("Frequency of occur")
plt.xticks(rotation = 90)
# plot of the marital status of the respondents, order them in descending order
ax = sns.countplot(df['marital_status'], order = df['marital_status'].value_counts().index)
# formatting the chart and labelling axes
plt.title("Marital status of the interviewees")
plt.xlabel("Marital status")
plt.ylabel("Number of individuals in the population")
plt.xticks(rotation=90)
# plot of the level of education for the respondents who took part in the interview
df['level_of_education'].value_counts().plot(kind='bar')
# formatting and labelling the plot
plt.title("Highest level of education reached by interviewees in the population")
plt.xlabel("Highest level reached")
plt.ylabel("Number of respondents")
# notice an anomaly in the above plot.6 is represented yet it does not represent any thing related to level of education
# drop the anomaly 6 in the level of education
df = df[~(df['level_of_education']=='6')]
df['level_of_education'].value_counts()
# plot a new chart for the level of education after dropping the anomalies
ax = sns.countplot(df['level_of_education'], order = df['level_of_education'].value_counts().index)
# formatting and labelling the chart
plt.title("Highest level of education reached by interviewees in the population")
plt.xlabel("Highest level reached")
plt.ylabel("Number of respondents")
plt.xticks(rotation=90)
# count plot for the type of job
ax = sns.countplot(df['type_of_job'], order = df['type_of_job'].value_counts().index)
# formatting and labelling the chart
plt.title("Type of job respondent holds")
plt.xlabel("Type of job")
plt.ylabel("Number of respondents")
plt.xticks(rotation=90)
print(df['respondent_age'].mean())
print(df['respondent_age'].median())
print(df['respondent_age'].mode())
print(df['household_size'].mean())
print(df['household_size'].median())
print(df['household_size'].mode())
# rename/save the dataframe using a new name
finance = df
finance.head()
# checking the datatypes
finance.info()
# create a crosstab/frequency table for the countries and bank account possession
countries_bankacc= pd.crosstab(index=finance['country'], columns=finance['has_a_bank_account'])
print(countries_bankacc)
# plot chart for the frequencies represented in the crosstab dataframe
countries_bankacc.plot(kind="bar", figsize=(8,8),stacked=True)
# labelling axes and formatting chart
plt.title("Bank account possession by country")
plt.ylabel("Distribution across the population")
# create a crosstab/frequency table for the countries and accessibility to cell phone
countries_cellphone = pd.crosstab(index=finance['country'], columns=finance['cell_phone_access'])
print(countries_cellphone)
# plot chart for the frequencies represented in the crosstab dataframe
countries_cellphone.plot(kind="bar", figsize=(8,8),stacked=True)
# labelling axes and formatting chart
plt.title("Accessibility to cellphone by country")
plt.ylabel("Distribution across the population")
# create a crosstab/frequency table
countries_location = pd.crosstab(index=finance['country'], columns=finance['type_of_location'])
print(countries_location)
# plot chart for the frequencies represented in the crosstab dataframe
countries_location.plot(kind="bar", figsize=(8,8),stacked=True)
# labelling axes and formatting chart
plt.title("Locations of respondents by country")
plt.ylabel("Distribution across the population")
# create a frequency table dataframe
countries_housesize = pd.crosstab(index=finance['country'], columns=finance['household_size'])
print(countries_housesize)
# plot chart from the frequency table dataframe
countries_housesize.plot(kind="bar", figsize=(8,8),stacked=True)
# labelling axes and formatting chart
plt.title("Housesizes for the respondents by country")
plt.ylabel("Distribution across the population")
# create a crosstab dataframe
countries_gender = pd.crosstab(index=finance['country'], columns=finance['marital_status'])
print(countries_gender)
# plot chart from the dataframe
countries_gender.plot(kind="bar", figsize=(8,8))
# formatting and labelling chart
plt.title("Marital status of respondents by country")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
countries_job = pd.crosstab(index=finance['country'], columns=finance['type_of_job'])
print(countries_job)
# plot chart
countries_job.plot(kind="bar", figsize=(8,8))
# formatting
plt.title("Type of job respondent holds by country")
plt.ylabel("Distribution across the population")
# create crosstab
edu_bank = pd.crosstab(index=finance['level_of_education'], columns=finance['has_a_bank_account'])
print(edu_bank)
# plot chart
edu_bank.plot(kind="bar", figsize=(8,8))
# format & label chart
plt.title("Relation of respondents education level to bank account possession")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
age_bank = pd.crosstab(index=finance['respondent_age'], columns=finance['has_a_bank_account'])
print(age_bank)
# plot chart
age_bank.plot(kind="bar", figsize=(20,5))
# format and label chart
plt.title("Relation of respondent age and possession of bank account")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
gender_bank = pd.crosstab(index=finance['gender_of_respondent'], columns=finance['has_a_bank_account'])
print(gender_bank)
# plot of the relation of gender to individuals possession to bank account
gender_bank.plot(kind="bar", figsize=(8,8))
# formatting&labelling chart
plt.title("Relation of respondent age and possession of bank account")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
marital_bank = pd.crosstab(index=finance['marital_status'], columns=finance['has_a_bank_account'])
print(marital_bank)
# plot chart
marital_bank.plot(kind="bar", figsize=(8,8))
# formatting&labelling
plt.title("Effect of marital status and possession of bank account")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
employ_bank = pd.crosstab(index=finance['type_of_job'], columns=finance['has_a_bank_account'])
print(employ_bank)
# plot chart from the dataframe
employ_bank.plot(kind="bar", figsize=(8,8), stacked=True)
# labelling chart
plt.title("Effect of employment status to possession of bank account")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
location_bank = pd.crosstab(index=finance['type_of_location'], columns=finance['has_a_bank_account'])
print(location_bank)
# plot chart
location_bank.plot(kind="bar", figsize=(8,8))
# label chart
plt.title("Effect of area of residence to possession of bank account")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
housesize_bank = pd.crosstab(index=finance['household_size'], columns=finance['has_a_bank_account'])
print(housesize_bank)
# plot chart
housesize_bank.plot(kind="bar", figsize=(8,8), stacked=True)
# label chart
plt.title("Effect of household size to possession of bank account")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
cellphone_bank = pd.crosstab(index=finance['cell_phone_access'], columns=finance['has_a_bank_account'])
print(cellphone_bank)
# plot chart
cellphone_bank.plot(kind="bar", figsize=(8,8))
# labelling chart
plt.title("Effect of cell phone accessibility to possession of bank account")
plt.ylabel("Distribution across the population")
# create crosstab dataframe
relation_withhead_bank = pd.crosstab(index=finance['relationship_with_head'], columns=finance['has_a_bank_account'])
print(relation_withhead_bank)
# plot chart
relation_withhead_bank.plot(kind="bar", figsize=(8,8), stacked=True)
# label chart
plt.title("Relation of respondent's relationship with head of household to possession of bank account")
plt.ylabel("Distribution across the population")
| 0.435902 | 0.982372 |
# Exercise 3: Parallel ETL
```
%load_ext sql
import boto3
import configparser
import matplotlib.pyplot as plt
import pandas as pd
from time import time
```
# STEP 1: Get the params of the created redshift cluster
- We need:
- The redshift cluster <font color='red'>endpoint</font>
- The <font color='red'>IAM role ARN</font> that give access to Redshift to read from S3
```
config = configparser.ConfigParser()
config.read_file(open('dwh.cfg'))
KEY=config.get('AWS','key')
SECRET= config.get('AWS','secret')
DWH_DB= config.get("DWH","DWH_DB")
DWH_DB_USER= config.get("DWH","DWH_DB_USER")
DWH_DB_PASSWORD= config.get("DWH","DWH_DB_PASSWORD")
DWH_PORT = config.get("DWH","DWH_PORT")
# FILL IN THE REDSHIFT ENPOINT HERE
# e.g. DWH_ENDPOINT="redshift-cluster-1.csmamz5zxmle.us-west-2.redshift.amazonaws.com"
DWH_ENDPOINT="dwhcluster.clye7s3564yq.us-west-2.redshift.amazonaws.com"
#FILL IN THE IAM ROLE ARN you got in step 2.2 of the previous exercise
#e.g DWH_ROLE_ARN="arn:aws:iam::988332130976:role/dwhRole"
DWH_ROLE_ARN="arn:aws:iam::878250915983:role/dwhRole"
```
# STEP 2: Connect to the Redshift Cluster
```
conn_string="postgresql://{}:{}@{}:{}/{}".format(DWH_DB_USER, DWH_DB_PASSWORD, DWH_ENDPOINT, DWH_PORT,DWH_DB)
print(conn_string)
%sql $conn_string
s3 = boto3.resource('s3',
region_name="us-west-2",
aws_access_key_id=KEY,
aws_secret_access_key=SECRET
)
sampleDbBucket = s3.Bucket("udacity-labs")# TODO: Create udacity-labs bucket
for obj in sampleDbBucket.objects.filter(Prefix="tickets"):
print(obj)
```
# STEP 3: Create Tables
```
%%sql
DROP TABLE IF EXISTS "sporting_event_ticket";
CREATE TABLE "sporting_event_ticket" (
"id" double precision DEFAULT nextval('sporting_event_ticket_seq') NOT NULL,
"sporting_event_id" double precision NOT NULL,
"sport_location_id" double precision NOT NULL,
"seat_level" numeric(1,0) NOT NULL,
"seat_section" character varying(15) NOT NULL,
"seat_row" character varying(10) NOT NULL,
"seat" character varying(10) NOT NULL,
"ticketholder_id" double precision,
"ticket_price" numeric(8,2) NOT NULL
);
```
# STEP 4: Load Partitioned data into the cluster
Use the COPY command to load data from `s3://udacity-labs/tickets/split/part` using your iam role credentials. Use gzip delimiter `;`.
```
%%time
qry = """
copy sporting_event_ticket from 's3://udacity-labs/tickets/split/part'
credentials 'aws_iam_role={}'
gzip delimiter ';' compupdate off region 'us-west-2';
""".format(DWH_ROLE_ARN)
%sql $qry
```
# STEP 5: Create Tables for the non-partitioned data
```
%%sql
DROP TABLE IF EXISTS "sporting_event_ticket_full";
CREATE TABLE "sporting_event_ticket_full" (
"id" double precision DEFAULT nextval('sporting_event_ticket_seq') NOT NULL,
"sporting_event_id" double precision NOT NULL,
"sport_location_id" double precision NOT NULL,
"seat_level" numeric(1,0) NOT NULL,
"seat_section" character varying(15) NOT NULL,
"seat_row" character varying(10) NOT NULL,
"seat" character varying(10) NOT NULL,
"ticketholder_id" double precision,
"ticket_price" numeric(8,2) NOT NULL
);
```
# STEP 6: Load non-partitioned data into the cluster
Use the COPY command to load data from `s3://udacity-labs/tickets/full/full.csv.gz` using your iam role credentials. Use gzip delimiter `;`.
- Note how it's slower than loading partitioned data
```
%%time
qry = """
copy sporting_event_ticket from 's3://udacity-labs/tickets/full/full.csv.gz'
credentials 'aws_iam_role={}'
gzip delimiter ';' compupdate off region 'us-west-2';
""".format(DWH_ROLE_ARN)
%sql $qry
```
|
github_jupyter
|
%load_ext sql
import boto3
import configparser
import matplotlib.pyplot as plt
import pandas as pd
from time import time
config = configparser.ConfigParser()
config.read_file(open('dwh.cfg'))
KEY=config.get('AWS','key')
SECRET= config.get('AWS','secret')
DWH_DB= config.get("DWH","DWH_DB")
DWH_DB_USER= config.get("DWH","DWH_DB_USER")
DWH_DB_PASSWORD= config.get("DWH","DWH_DB_PASSWORD")
DWH_PORT = config.get("DWH","DWH_PORT")
# FILL IN THE REDSHIFT ENPOINT HERE
# e.g. DWH_ENDPOINT="redshift-cluster-1.csmamz5zxmle.us-west-2.redshift.amazonaws.com"
DWH_ENDPOINT="dwhcluster.clye7s3564yq.us-west-2.redshift.amazonaws.com"
#FILL IN THE IAM ROLE ARN you got in step 2.2 of the previous exercise
#e.g DWH_ROLE_ARN="arn:aws:iam::988332130976:role/dwhRole"
DWH_ROLE_ARN="arn:aws:iam::878250915983:role/dwhRole"
conn_string="postgresql://{}:{}@{}:{}/{}".format(DWH_DB_USER, DWH_DB_PASSWORD, DWH_ENDPOINT, DWH_PORT,DWH_DB)
print(conn_string)
%sql $conn_string
s3 = boto3.resource('s3',
region_name="us-west-2",
aws_access_key_id=KEY,
aws_secret_access_key=SECRET
)
sampleDbBucket = s3.Bucket("udacity-labs")# TODO: Create udacity-labs bucket
for obj in sampleDbBucket.objects.filter(Prefix="tickets"):
print(obj)
%%sql
DROP TABLE IF EXISTS "sporting_event_ticket";
CREATE TABLE "sporting_event_ticket" (
"id" double precision DEFAULT nextval('sporting_event_ticket_seq') NOT NULL,
"sporting_event_id" double precision NOT NULL,
"sport_location_id" double precision NOT NULL,
"seat_level" numeric(1,0) NOT NULL,
"seat_section" character varying(15) NOT NULL,
"seat_row" character varying(10) NOT NULL,
"seat" character varying(10) NOT NULL,
"ticketholder_id" double precision,
"ticket_price" numeric(8,2) NOT NULL
);
%%time
qry = """
copy sporting_event_ticket from 's3://udacity-labs/tickets/split/part'
credentials 'aws_iam_role={}'
gzip delimiter ';' compupdate off region 'us-west-2';
""".format(DWH_ROLE_ARN)
%sql $qry
%%sql
DROP TABLE IF EXISTS "sporting_event_ticket_full";
CREATE TABLE "sporting_event_ticket_full" (
"id" double precision DEFAULT nextval('sporting_event_ticket_seq') NOT NULL,
"sporting_event_id" double precision NOT NULL,
"sport_location_id" double precision NOT NULL,
"seat_level" numeric(1,0) NOT NULL,
"seat_section" character varying(15) NOT NULL,
"seat_row" character varying(10) NOT NULL,
"seat" character varying(10) NOT NULL,
"ticketholder_id" double precision,
"ticket_price" numeric(8,2) NOT NULL
);
%%time
qry = """
copy sporting_event_ticket from 's3://udacity-labs/tickets/full/full.csv.gz'
credentials 'aws_iam_role={}'
gzip delimiter ';' compupdate off region 'us-west-2';
""".format(DWH_ROLE_ARN)
%sql $qry
| 0.21036 | 0.53692 |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import pickle
test = pd.read_csv('./data/test_set_all_a4.csv')
test.head()
texas_dogs = (test[(test['contact.address.state']=='TX')])
#texas_dogs = (test[(test['contact.address.state']=='TX') & test['cg_adpt_time']=='> 3 months'])
texas_dogs.head()
rand_texas_dogs = texas_dogs.sample(n=100, random_state=0)
rand_texas_dogs.head()
X_features = ['age', 'gender', 'size', 'breed_pop',
'breeds.primary',
'breeds.mixed',
'contact.address.state']
rtd_X = rand_texas_dogs[X_features]
rtd_X = rtd_X.reset_index()
rtd_X.head()
az = ['AZ'] * 100
co = ['CO'] * 100
mn = ['MN'] * 100
import random
random.seed = 0
rand_state = random.choice(['AZ','MN','CO'])
rand_state
rand_state = [random.choice(['AZ','MN','CO']) for i in range(100)]
print('AZ :{}, CO: {}, MN: {}'.format(rand_state.count('AZ'), rand_state.count('CO'), rand_state.count('MN')))
rtd_X['rand_state']=rand_state
rtd_X['state_az']=az
rtd_X['state_co']=co
rtd_X['state_mn']=mn
rtd_X.head()
rtd_X.head()
filename = './models/rfpipe_combined.pkl'
loaded_pipe = pickle.load(open(filename, 'rb'))
rand_times=loaded_pipe.predict(rtd_X.drop(['index','contact.address.state', 'state_az', 'state_co', 'state_mn'], axis=1))
rand_times=rand_times.tolist()
def convert_time(time):
if time == '< 1 week':
return 3.5
elif time == '1 - 2 weeks':
return 10
elif time == '< 1 month':
return 21.5
elif time == '< 3 months':
return 59.5
else:
return 100
rand_times
rand_times_conv = list(map(lambda x:convert_time(x), rand_times))
rtd_X['adoption_time_rand']=rand_times_conv
az_times=loaded_pipe.predict(rtd_X.drop(['index','contact.address.state', 'rand_state', 'state_co',
'state_mn', 'adoption_time_rand'], axis=1))
az_times=az_times.tolist()
az_times_conv = list(map(lambda x:convert_time(x), az_times))
co_times=loaded_pipe.predict(rtd_X.drop(['index','contact.address.state', 'rand_state', 'state_az',
'state_mn', 'adoption_time_rand'], axis=1))
co_times=co_times.tolist()
co_times_conv = list(map(lambda x:convert_time(x), co_times))
mn_times=loaded_pipe.predict(rtd_X.drop(['index','contact.address.state', 'rand_state', 'state_co',
'state_az', 'adoption_time_rand'], axis=1))
mn_times=mn_times.tolist()
mn_times_conv = list(map(lambda x:convert_time(x), mn_times))
list(zip(az_times_conv, co_times_conv, mn_times_conv))
min_time = [min(l1, l2, l3) for l1, l2, l3 in zip(az_times_conv, co_times_conv, mn_times_conv)]
rtd_X['adoption_time_min']=min_time
rtd_X.head()
rtd_X['adoption_time_rand'].mean()
rtd_X['adoption_time_min'].mean()
## saves 14 days (40% reduction) in adoption time. cost of keeping a dog at a shelter - 50/mo for food,20/mo for supplies, around 100/mo total
## 100/mo - 50/14 days. save 50 per dog. 40k relocations - 2 million
## Maddie's fund - 200 per month, 100/14 days, 40k relocations - 4 million
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import pickle
test = pd.read_csv('./data/test_set_all_a4.csv')
test.head()
texas_dogs = (test[(test['contact.address.state']=='TX')])
#texas_dogs = (test[(test['contact.address.state']=='TX') & test['cg_adpt_time']=='> 3 months'])
texas_dogs.head()
rand_texas_dogs = texas_dogs.sample(n=100, random_state=0)
rand_texas_dogs.head()
X_features = ['age', 'gender', 'size', 'breed_pop',
'breeds.primary',
'breeds.mixed',
'contact.address.state']
rtd_X = rand_texas_dogs[X_features]
rtd_X = rtd_X.reset_index()
rtd_X.head()
az = ['AZ'] * 100
co = ['CO'] * 100
mn = ['MN'] * 100
import random
random.seed = 0
rand_state = random.choice(['AZ','MN','CO'])
rand_state
rand_state = [random.choice(['AZ','MN','CO']) for i in range(100)]
print('AZ :{}, CO: {}, MN: {}'.format(rand_state.count('AZ'), rand_state.count('CO'), rand_state.count('MN')))
rtd_X['rand_state']=rand_state
rtd_X['state_az']=az
rtd_X['state_co']=co
rtd_X['state_mn']=mn
rtd_X.head()
rtd_X.head()
filename = './models/rfpipe_combined.pkl'
loaded_pipe = pickle.load(open(filename, 'rb'))
rand_times=loaded_pipe.predict(rtd_X.drop(['index','contact.address.state', 'state_az', 'state_co', 'state_mn'], axis=1))
rand_times=rand_times.tolist()
def convert_time(time):
if time == '< 1 week':
return 3.5
elif time == '1 - 2 weeks':
return 10
elif time == '< 1 month':
return 21.5
elif time == '< 3 months':
return 59.5
else:
return 100
rand_times
rand_times_conv = list(map(lambda x:convert_time(x), rand_times))
rtd_X['adoption_time_rand']=rand_times_conv
az_times=loaded_pipe.predict(rtd_X.drop(['index','contact.address.state', 'rand_state', 'state_co',
'state_mn', 'adoption_time_rand'], axis=1))
az_times=az_times.tolist()
az_times_conv = list(map(lambda x:convert_time(x), az_times))
co_times=loaded_pipe.predict(rtd_X.drop(['index','contact.address.state', 'rand_state', 'state_az',
'state_mn', 'adoption_time_rand'], axis=1))
co_times=co_times.tolist()
co_times_conv = list(map(lambda x:convert_time(x), co_times))
mn_times=loaded_pipe.predict(rtd_X.drop(['index','contact.address.state', 'rand_state', 'state_co',
'state_az', 'adoption_time_rand'], axis=1))
mn_times=mn_times.tolist()
mn_times_conv = list(map(lambda x:convert_time(x), mn_times))
list(zip(az_times_conv, co_times_conv, mn_times_conv))
min_time = [min(l1, l2, l3) for l1, l2, l3 in zip(az_times_conv, co_times_conv, mn_times_conv)]
rtd_X['adoption_time_min']=min_time
rtd_X.head()
rtd_X['adoption_time_rand'].mean()
rtd_X['adoption_time_min'].mean()
## saves 14 days (40% reduction) in adoption time. cost of keeping a dog at a shelter - 50/mo for food,20/mo for supplies, around 100/mo total
## 100/mo - 50/14 days. save 50 per dog. 40k relocations - 2 million
## Maddie's fund - 200 per month, 100/14 days, 40k relocations - 4 million
| 0.271735 | 0.525673 |
# 範例 : (Kaggle)房價預測
***
- 以下用房價預測資料, 觀察均值編碼的效果
```
# 做完特徵工程前的所有準備
import pandas as pd
import numpy as np
import copy, time
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.preprocessing import LabelEncoder
data_path = 'data/data2/'
df_train = pd.read_csv(data_path + 'house_train.csv.gz')
df_test = pd.read_csv(data_path + 'house_test.csv.gz')
train_Y = np.log1p(df_train['SalePrice'])
ids = df_test['Id']
df_train = df_train.drop(['Id', 'SalePrice'] , axis=1)
df_test = df_test.drop(['Id'] , axis=1)
df = pd.concat([df_train,df_test])
df.head()
#只取類別值 (object) 型欄位, 存於 object_features 中
object_features = []
for dtype, feature in zip(df.dtypes, df.columns):
if dtype == 'object':
object_features.append(feature)
print(f'{len(object_features)} Numeric Features : {object_features}\n')
# 只留類別型欄位
df = df[object_features]
df = df.fillna('None')
train_num = train_Y.shape[0]
df.head()
# 對照組 : 標籤編碼 + 線性迴歸
df_temp = pd.DataFrame()
for c in df.columns:
df_temp[c] = LabelEncoder().fit_transform(df[c])
train_X = df_temp[:train_num]
estimator = LinearRegression()
start = time.time()
print(f'shape : {train_X.shape}')
print(f'score : {cross_val_score(estimator, train_X, train_Y, cv=5).mean()}')
print(f'time : {time.time() - start} sec')
# 均值編碼 + 線性迴歸
data = pd.concat([df[:train_num], train_Y], axis=1)
for c in df.columns:
mean_df = data.groupby([c])['SalePrice'].mean().reset_index()
mean_df.columns = [c, f'{c}_mean']
data = pd.merge(data, mean_df, on=c, how='left')
data = data.drop([c] , axis=1)
data = data.drop(['SalePrice'] , axis=1)
estimator = LinearRegression()
start = time.time()
print(f'shape : {train_X.shape}')
print(f'score : {cross_val_score(estimator, data, train_Y, cv=5).mean()}')
print(f'time : {time.time() - start} sec')
# 對照組 : 標籤編碼 + 梯度提升樹
df_temp = pd.DataFrame()
for c in df.columns:
df_temp[c] = LabelEncoder().fit_transform(df[c])
train_X = df_temp[:train_num]
estimator = GradientBoostingRegressor()
start = time.time()
print(f'shape : {train_X.shape}')
print(f'score : {cross_val_score(estimator, train_X, train_Y, cv=5).mean()}')
print(f'time : {time.time() - start} sec')
# 均值編碼 + 梯度提升樹
data = pd.concat([df[:train_num], train_Y], axis=1)
for c in df.columns:
mean_df = data.groupby([c])['SalePrice'].mean().reset_index()
mean_df.columns = [c, f'{c}_mean']
data = pd.merge(data, mean_df, on=c, how='left')
data = data.drop([c] , axis=1)
data = data.drop(['SalePrice'] , axis=1)
estimator = GradientBoostingRegressor()
start = time.time()
print(f'shape : {train_X.shape}')
print(f'score : {cross_val_score(estimator, data, train_Y, cv=5).mean()}')
print(f'time : {time.time() - start} sec')
```
# 作業1
* 請仿照範例,將鐵達尼範例中的類別型特徵改用均值編碼實作一次
# 作業2
* 觀察鐵達尼生存預測中,均值編碼與標籤編碼兩者比較,哪一個效果比較好? 可能的原因是什麼?
|
github_jupyter
|
# 做完特徵工程前的所有準備
import pandas as pd
import numpy as np
import copy, time
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.preprocessing import LabelEncoder
data_path = 'data/data2/'
df_train = pd.read_csv(data_path + 'house_train.csv.gz')
df_test = pd.read_csv(data_path + 'house_test.csv.gz')
train_Y = np.log1p(df_train['SalePrice'])
ids = df_test['Id']
df_train = df_train.drop(['Id', 'SalePrice'] , axis=1)
df_test = df_test.drop(['Id'] , axis=1)
df = pd.concat([df_train,df_test])
df.head()
#只取類別值 (object) 型欄位, 存於 object_features 中
object_features = []
for dtype, feature in zip(df.dtypes, df.columns):
if dtype == 'object':
object_features.append(feature)
print(f'{len(object_features)} Numeric Features : {object_features}\n')
# 只留類別型欄位
df = df[object_features]
df = df.fillna('None')
train_num = train_Y.shape[0]
df.head()
# 對照組 : 標籤編碼 + 線性迴歸
df_temp = pd.DataFrame()
for c in df.columns:
df_temp[c] = LabelEncoder().fit_transform(df[c])
train_X = df_temp[:train_num]
estimator = LinearRegression()
start = time.time()
print(f'shape : {train_X.shape}')
print(f'score : {cross_val_score(estimator, train_X, train_Y, cv=5).mean()}')
print(f'time : {time.time() - start} sec')
# 均值編碼 + 線性迴歸
data = pd.concat([df[:train_num], train_Y], axis=1)
for c in df.columns:
mean_df = data.groupby([c])['SalePrice'].mean().reset_index()
mean_df.columns = [c, f'{c}_mean']
data = pd.merge(data, mean_df, on=c, how='left')
data = data.drop([c] , axis=1)
data = data.drop(['SalePrice'] , axis=1)
estimator = LinearRegression()
start = time.time()
print(f'shape : {train_X.shape}')
print(f'score : {cross_val_score(estimator, data, train_Y, cv=5).mean()}')
print(f'time : {time.time() - start} sec')
# 對照組 : 標籤編碼 + 梯度提升樹
df_temp = pd.DataFrame()
for c in df.columns:
df_temp[c] = LabelEncoder().fit_transform(df[c])
train_X = df_temp[:train_num]
estimator = GradientBoostingRegressor()
start = time.time()
print(f'shape : {train_X.shape}')
print(f'score : {cross_val_score(estimator, train_X, train_Y, cv=5).mean()}')
print(f'time : {time.time() - start} sec')
# 均值編碼 + 梯度提升樹
data = pd.concat([df[:train_num], train_Y], axis=1)
for c in df.columns:
mean_df = data.groupby([c])['SalePrice'].mean().reset_index()
mean_df.columns = [c, f'{c}_mean']
data = pd.merge(data, mean_df, on=c, how='left')
data = data.drop([c] , axis=1)
data = data.drop(['SalePrice'] , axis=1)
estimator = GradientBoostingRegressor()
start = time.time()
print(f'shape : {train_X.shape}')
print(f'score : {cross_val_score(estimator, data, train_Y, cv=5).mean()}')
print(f'time : {time.time() - start} sec')
| 0.311322 | 0.701291 |
# Bayes by Backprop from scratch (NN, classification)
We have already learned how to implement deep neural networks and how to use them for classification and regression tasks. In order to fight overfitting, we further introduced a concept called _dropout_, which randomly turns off a certain percentage of the weights during training.
Recall the classic architecture of a MLP (shown below, without bias terms). So far, when training a neural network, our goal was to find an optimal point estimate for the weights.

While networks trained using this approach usually perform well in regions with lots of data, they fail to express uncertainity in regions with little or no data, leading to overconfident decisions. This drawback motivates the application of Bayesian learning to neural networks, introducing probability distributions over the weights. These distributions can be of various nature in theory. To make our lifes easier and to have an intuitive understanding of the distribution at each weight, we will use a Gaussian distribution.

Unfortunately though, exact Bayesian inference on the parameters of a neural network is intractable. One promising way of addressing this problem is presented by the "Bayes by Backprop" algorithm (introduced by the "[Weight Uncertainity in Neural Networks](https://arxiv.org/abs/1505.05424)" paper) which derives a variational approximation to the true posterior. This algorithm does not only make networks more "honest" with respect to their overall uncertainity, but also automatically leads to regularization, thereby eliminating the need of using dropout in this model.
While we will try to explain the most important concepts of this algorithm in this notebook, we also encourage the reader to consult the paper for deeper insights.
Let's start implementing this idea and evaluate its performance on the MNIST classification problem. We start off with the usual set of imports.
```
from __future__ import print_function
import collections
import mxnet as mx
import numpy as np
from mxnet import nd, autograd
from matplotlib import pyplot as plt
```
For easy tuning and experimentation, we define a dictionary holding the hyper-parameters of our model.
```
config = {
"num_hidden_layers": 2,
"num_hidden_units": 400,
"batch_size": 128,
"epochs": 10,
"learning_rate": 0.001,
"num_samples": 1,
"pi": 0.25,
"sigma_p": 1.0,
"sigma_p1": 0.75,
"sigma_p2": 0.1,
}
```
Also, we specify the device context for MXNet.
```
ctx = mx.cpu()
```
## Load MNIST data
We will again train and evaluate the algorithm on the MNIST data set and therefore load the data set as follows:
```
def transform(data, label):
return data.astype(np.float32)/126.0, label.astype(np.float32)
mnist = mx.test_utils.get_mnist()
num_inputs = 784
num_outputs = 10
batch_size = config['batch_size']
train_data = mx.gluon.data.DataLoader(mx.gluon.data.vision.MNIST(train=True, transform=transform),
batch_size, shuffle=True)
test_data = mx.gluon.data.DataLoader(mx.gluon.data.vision.MNIST(train=False, transform=transform),
batch_size, shuffle=False)
num_train = sum([batch_size for i in train_data])
num_batches = num_train / batch_size
```
In order to reproduce and compare the results from the paper, we preprocess the pixels by dividing by 126.
## Model definition
### Activation function
As with lots of past examples, we will again use the ReLU as our activation function for the hidden units of our neural network.
```
def relu(X):
return nd.maximum(X, nd.zeros_like(X))
```
### Neural net modeling
As our model we are using a straightforward MLP and we are wiring up our network just as we are used to.
```
num_layers = config['num_hidden_layers']
# define function for evaluating MLP
def net(X, layer_params):
layer_input = X
for i in range(len(layer_params) // 2 - 2):
h_linear = nd.dot(layer_input, layer_params[2*i]) + layer_params[2*i + 1]
layer_input = relu(h_linear)
# last layer without ReLU
output = nd.dot(layer_input, layer_params[-2]) + layer_params[-1]
return output
# define network weight shapes
layer_param_shapes = []
num_hidden = config['num_hidden_units']
for i in range(num_layers + 1):
if i == 0: # input layer
W_shape = (num_inputs, num_hidden)
b_shape = (num_hidden,)
elif i == num_layers: # last layer
W_shape = (num_hidden, num_outputs)
b_shape = (num_outputs,)
else: # hidden layers
W_shape = (num_hidden, num_hidden)
b_shape = (num_hidden,)
layer_param_shapes.extend([W_shape, b_shape])
```
## Build objective/loss
As we briefly mentioned at the beginning of the notebook, we will use variational inference in order to make the prediction of the posterior tractable. While we can not model the posterior $P(\mathbf{w}\ |\ \mathcal{D})$ directly, we try to find the parameters $\mathbf{\theta}$ of a distribution on the weights $q(\mathbf{w}\ |\ \mathbf{\theta})$ (commly referred to as the _variational posterior_) that minimizes the KL divergence with the true posterior. Formally this can be expressed as:
\begin{equation*}
\begin{split}
\theta^{*} & = \arg\min_{\theta} \text{KL}[q(\mathbf{w}\ |\ \mathbf{\theta})\ ||\ P(\mathbf{w}\ |\ \mathcal{D}]\\
& = \arg\min_{\theta} \int q(\mathbf{w}\ |\ \mathbf{\theta}) \log \frac{q(\mathbf{w}\ |\ \mathbf{\theta})}{P(\mathbf{w}) P(\mathcal{D}\ |\ \mathbf{w})} d\mathbf{w} \\
& = \arg\min_{\theta} \text{KL}[q(\mathbf{w}\ |\ \mathbf{\theta})\ ||\ P(\mathbf{w})] - \mathbb{E}_{q(\mathbf{w}\ |\ \mathbf{\theta})}[\log P(\mathcal{D}\ |\ \mathbf{w})]
\end{split}
\end{equation*}
The resulting loss function, commonly referred to as either _variational free energy_ or _expected lower bound_ (_ELBO_), has to be minimized and is then given as follows:
\begin{equation*}
\mathcal{F}(\mathcal{D}, \mathbf{\theta}) = \text{KL}[q(\mathbf{w}\ |\ \mathbf{\theta})\ ||\ P(\mathbf{w})] - \mathbb{E}_{q(\mathbf{w}\ |\ \mathbf{\theta})}[\log P(\mathcal{D}\ |\ \mathbf{w})]
\end{equation*}
As one can easily see, the cost function tries to balance the complexity of the data $P(\mathcal{D}\ |\ \mathbf{w})$ and the simplicity of the prior $P(\mathbf{w})$.
We can approximate this exact cost through a Monte Carlo sampling procedure as follows
\begin{equation*}
\mathcal{F}(\mathcal{D}, \mathbf{\theta}) \approx \sum_{i = 1}^{n} \log q(\mathbf{w}^{(i)}\ |\ \mathbf{\theta}) - \log P(\mathbf{w}^{(i)}) - \log P(\mathcal{D}\ |\ \mathbf{w}^{(i)})
\end{equation*}
where $\mathbf{w}^{(i)}$ corresponds to the $i$-th Monte Carlo sample from the variational posterior. While writing this notebook, we noticed that even taking just one sample leads to good results and we will therefore stick to just sampling once throughout the notebook.
Since we will be working with mini-batches, the exact loss form on mini-batch $i$ we will be using looks as follows:
\begin{equation*}
\begin{split}
\mathcal{F}(\mathcal{D}_i, \mathbf{\theta}) & = \frac{1}{M} \text{KL}[\log q(\mathbf{w}\ |\ \mathbf{\theta})\ ||\ \log P(\mathbf{w})] - \mathbb{E}_{q(\mathbf{w}\ |\ \mathbf{\theta})}[\log P(\mathcal{D}_i\ |\ \mathbf{w})]\\
& \approx \frac{1}{M} (\log q(\mathbf{w}^{(1)}\ |\ \mathbf{\theta}) - \log P(\mathbf{w}^{(1)})) - \log P(\mathcal{D}_i\ |\ \mathbf{w}^{(1)})
\end{split}
\end{equation*}
where $M$ corresponds to the number of batches,
and $\mathcal{F}(\mathcal{D}, \mathbf{\theta}) = \sum_{i = 1}^{M} \mathcal{F}(\mathcal{D}_i, \mathbf{\theta})$
Let's now look at each of these single terms individually.
### Likelihood
As with lots of past examples, we will again use the softmax to define our likelihood $P(\mathcal{D}_i\ |\ \mathbf{w})$. Revisit the [MLP from scratch notebook](https://github.com/zackchase/mxnet-the-straight-dope/blob/master/chapter03_deep-neural-networks/mlp-scratch.ipynb) for a detailed motivation of this function.
```
def log_softmax_likelihood(yhat_linear, y):
return nd.nansum(y * nd.log_softmax(yhat_linear), axis=0, exclude=True)
```
### Prior
Since we are introducing a Bayesian treatment for the network, we need to define a Prior over the weights.
#### Gaussian prior
A popular and simple prior is the Gaussian distribution. The prior over the entire weight vector simply corresponds to the prodcut of the individual Gaussians:
\begin{equation*}
P(\mathbf{w}) = \prod_i \mathcal{N}(\mathbf{w}_i\ |\ 0,\sigma_p^2)
\end{equation*}
We can define the Gaussian distribution and our Gaussian prior as seen below. Note that we are ultimately intersted in the log-prior $\log P(\mathbf{w})$ and therefore compute the sum of the log-Gaussians.
\begin{equation*}
\log P(\mathbf{w}) = \sum_i \log \mathcal{N}(\mathbf{w}_i\ |\ 0,\sigma_p^2)
\end{equation*}
```
LOG2PI = np.log(2.0 * np.pi)
def log_gaussian(x, mu, sigma):
return -0.5 * LOG2PI - nd.log(sigma) - (x - mu) ** 2 / (2 * sigma ** 2)
def gaussian_prior(x):
sigma_p = nd.array([config['sigma_p']], ctx=ctx)
return nd.sum(log_gaussian(x, 0., sigma_p))
```
#### Scale mixture prior
Instead of a single Gaussian, the paper also suggests the usage of a scale mixture prior for $P(\mathbf{w})$ as an alternative:
\begin{equation*}
P(\mathbf{w}) = \prod_i \bigg ( \pi \mathcal{N}(\mathbf{w}_i\ |\ 0,\sigma_1^2) + (1 - \pi) \mathcal{N}(\mathbf{w}_i\ |\ 0,\sigma_2^2)\bigg )
\end{equation*}
where $\pi \in [0, 1]$, $\sigma_1 > \sigma_2$ and $\sigma_2 \ll 1$. Again we are intersted in the log-prior $\log P(\mathbf{w})$, which can be expressed as follows:
\begin{equation*}
\log P(\mathbf{w}) = \sum_i \log \bigg ( \pi \mathcal{N}(\mathbf{w}_i\ |\ 0,\sigma_1^2) + (1 - \pi) \mathcal{N}(\mathbf{w}_i\ |\ 0,\sigma_2^2)\bigg )
\end{equation*}
```
def gaussian(x, mu, sigma):
scaling = 1.0 / nd.sqrt(2.0 * np.pi * (sigma ** 2))
bell = nd.exp(- (x - mu) ** 2 / (2.0 * sigma ** 2))
return scaling * bell
def scale_mixture_prior(x):
sigma_p1 = nd.array([config['sigma_p1']], ctx=ctx)
sigma_p2 = nd.array([config['sigma_p2']], ctx=ctx)
pi = config['pi']
first_gaussian = pi * gaussian(x, 0., sigma_p1)
second_gaussian = (1 - pi) * gaussian(x, 0., sigma_p2)
return nd.log(first_gaussian + second_gaussian)
```
### Variational Posterior
The last missing piece in the equation is the variational posterior. Again, we choose a Gaussian disribution for this purpose. The variational posterior on the weights is centered on the mean vector $\mathbf{\mu}$ and has variance $\mathbf{\sigma}^2$:
\begin{equation*}
q(\mathbf{w}\ |\ \theta) = \prod_i \mathcal{N}(\mathbf{w}_i\ |\ \mathbf{\mu},\mathbf{\sigma}^2)
\end{equation*}
The log-posterior $\log q(\mathbf{w}\ |\ \theta)$ is given by:
\begin{equation*}
\log q(\mathbf{w}\ |\ \theta) = \sum_i \log \mathcal{N}(\mathbf{w}_i\ |\ \mathbf{\mu},\mathbf{\sigma}^2)
\end{equation*}
### Combined Loss
After introducing the data likelihood, the prior, and the variational posterior, we are now able to build our combined loss function: $\mathcal{F}(\mathcal{D}_i, \mathbf{\theta}) = \frac{1}{M} (\log q(\mathbf{w}\ |\ \mathbf{\theta}) - \log P(\mathbf{w})) - \log P(\mathcal{D}_i\ |\ \mathbf{w})$
```
def combined_loss(output, label_one_hot, params, mus, sigmas, log_prior, log_likelihood):
# Calculate data likelihood
log_likelihood_sum = nd.sum(log_likelihood(output, label_one_hot))
# Calculate prior
log_prior_sum = sum([nd.sum(log_prior(param)) for param in params])
# Calculate variational posterior
log_var_posterior_sum = sum([nd.sum(log_gaussian(params[i], mus[i], sigmas[i])) for i in range(len(params))])
# Calculate total loss
return 1.0 / num_batches * (log_var_posterior_sum - log_prior_sum) - log_likelihood_sum
```
## Optimizer
We use vanilla stochastic gradient descent to optimize the variational parameters. Note that this implements the updates described in the paper, as the gradient contribution due to the reparametrization trick is automatically included by taking the gradients of the combined loss function with respect to the variational parameters.
```
def SGD(params, lr):
for param in params:
param[:] = param - lr * param.grad
```
## Evaluation metric
In order to being able to assess our model performance we define a helper function which evaluates our accuracy on an ongoing basis.
```
def evaluate_accuracy(data_iterator, net, layer_params):
numerator = 0.
denominator = 0.
for i, (data, label) in enumerate(data_iterator):
data = data.as_in_context(ctx).reshape((-1, 784))
label = label.as_in_context(ctx)
output = net(data, layer_params)
predictions = nd.argmax(output, axis=1)
numerator += nd.sum(predictions == label)
denominator += data.shape[0]
return (numerator / denominator).asscalar()
```
## Parameter initialization
We are using a Gaussian distribution for each individual weight as our variational posterior, which means that we need to store two parameters, mean and variance, for each weight. For the variance we need to ensure that it is non-negative, which we will do by using the softplus function to express $\mathbf{\sigma}$ in terms of an unconstrained parameter $\mathbf{\rho}$. While gradient descent will be performed on $\theta = (\mathbf{\mu}, \mathbf{\rho})$, the distribution for each individual weight is represented as $w_i \sim \mathcal{N}(w_i\ |\ \mu_i,\sigma_i)$ with $\sigma_i = \text{softplus}(\mathbf{\rho}_i)$.
We initialize $\mathbf{\mu}$ with a Gaussian around $0$ (just as we would initialize standard weights of a neural network). It is important to initialize $\mathbf{\rho}$ (and hence $\sigma$) to a small value, otherwise learning might not work properly.
```
weight_scale = .1
rho_offset = -3
# initialize variational parameters; mean and variance for each weight
mus = []
rhos = []
for shape in layer_param_shapes:
mu = nd.random_normal(shape=shape, ctx=ctx, scale=weight_scale)
rho = rho_offset + nd.zeros(shape=shape, ctx=ctx)
mus.append(mu)
rhos.append(rho)
variational_params = mus + rhos
```
Since these are the parameters we wish to do gradient descent on, we need to allocate space for storing the gradients.
```
for param in variational_params:
param.attach_grad()
```
## Main training loop
The main training loop is pretty similar to the one we used in the MLP example. The only adaptation we need to make is to add the weight sampling which is performed during each optimization step. Generating a set of weights, which will subsequently be used in the neural network and the loss function, is a 3-step process:
1) Sample $\mathbf{\epsilon} \sim \mathcal{N}(\mathbf{0},\mathbf{I}^{d})$
```
def sample_epsilons(param_shapes):
epsilons = [nd.random_normal(shape=shape, loc=0., scale=1.0, ctx=ctx) for shape in param_shapes]
return epsilons
```
2) Transform $\mathbf{\rho}$ to a postive vector via the softplus function: $\mathbf{\sigma} = \text{softplus}(\mathbf{\rho}) = \log(1 + \exp(\mathbf{\rho}))$
```
def softplus(x):
return nd.log(1. + nd.exp(x))
def transform_rhos(rhos):
return [softplus(rho) for rho in rhos]
```
3) Compute $\mathbf{w}$: $\mathbf{w} = \mathbf{\mu} + \mathbf{\sigma} \circ \mathbf{\epsilon}$, where the $\circ$ operator represents the element-wise multiplication. This is the "reparametrization trick" for separating the randomness from the parameters of $q$.
```
def transform_gaussian_samples(mus, sigmas, epsilons):
samples = []
for j in range(len(mus)):
samples.append(mus[j] + sigmas[j] * epsilons[j])
return samples
```
### Complete loop
The complete training loop is given below.
```
epochs = config['epochs']
learning_rate = config['learning_rate']
smoothing_constant = .01
train_acc = []
test_acc = []
for e in range(epochs):
for i, (data, label) in enumerate(train_data):
data = data.as_in_context(ctx).reshape((-1, 784))
label = label.as_in_context(ctx)
label_one_hot = nd.one_hot(label, 10)
with autograd.record():
# sample epsilons from standard normal
epsilons = sample_epsilons(layer_param_shapes)
# compute softplus for variance
sigmas = transform_rhos(rhos)
# obtain a sample from q(w|theta) by transforming the epsilons
layer_params = transform_gaussian_samples(mus, sigmas, epsilons)
# forward-propagate the batch
output = net(data, layer_params)
# calculate the loss
loss = combined_loss(output, label_one_hot, layer_params, mus, sigmas, gaussian_prior, log_softmax_likelihood)
# backpropagate for gradient calculation
loss.backward()
# apply stochastic gradient descent to variational parameters
SGD(variational_params, learning_rate)
# calculate moving loss for monitoring convergence
curr_loss = nd.mean(loss).asscalar()
moving_loss = (curr_loss if ((i == 0) and (e == 0))
else (1 - smoothing_constant) * moving_loss + (smoothing_constant) * curr_loss)
test_accuracy = evaluate_accuracy(test_data, net, mus)
train_accuracy = evaluate_accuracy(train_data, net, mus)
train_acc.append(np.asscalar(train_accuracy))
test_acc.append(np.asscalar(test_accuracy))
print("Epoch %s. Loss: %s, Train_acc %s, Test_acc %s" %
(e, moving_loss, train_accuracy, test_accuracy))
plt.plot(train_acc)
plt.plot(test_acc)
plt.show()
```
For demonstration purposes, we can now take a look at one particular weight by plotting its distribution.
```
def show_weight_dist(mean, variance):
sigma = nd.sqrt(variance)
x = np.linspace(mean.asscalar() - 4*sigma.asscalar(), mean.asscalar() + 4*sigma.asscalar(), 100)
plt.plot(x, gaussian(nd.array(x, ctx=ctx), mean, sigma).asnumpy())
plt.show()
mu = mus[0][0][0]
var = softplus(rhos[0][0][0]) ** 2
show_weight_dist(mu, var)
```
Great! We have obtained a fully functional Bayesian neural network. However, the number of weights now is twice as high as for traditional neural networks. As we will see in the final section of this notebook, we are able to drastically reduce the number of weights our network uses for prediction with _weight pruning_.
## Weight pruning
To measure the degree of redundancy present in the trained network and to reduce the model's parameter count, we now want to examine the effect of setting some of the weights to $0$ and evaluate the test accuracy afterwards. We can achieve this by ordering the weights according to their signal-to-noise-ratio, $\frac{|\mu_i|}{\sigma_i}$, and setting a certain percentage of the weights with the lowest ratios to $0$.
We can calculate the signal-to-noise-ratio as follows:
```
def signal_to_noise_ratio(mus, sigmas):
sign_to_noise = []
for j in range(len(mus)):
sign_to_noise.extend([nd.abs(mus[j]) / sigmas[j]])
return sign_to_noise
```
We further introduce a few helper methods which turn our list of weights into a single vector containing all weights. This will make our subsequent actions easier.
```
def vectorize_matrices_in_vector(vec):
for i in range(0, (num_layers + 1) * 2, 2):
if i == 0:
vec[i] = nd.reshape(vec[i], num_inputs * num_hidden)
elif i == num_layers * 2:
vec[i] = nd.reshape(vec[i], num_hidden * num_outputs)
else:
vec[i] = nd.reshape(vec[i], num_hidden * num_hidden)
return vec
def concact_vectors_in_vector(vec):
concat_vec = vec[0]
for i in range(1, len(vec)):
concat_vec = nd.concat(concat_vec, vec[i], dim=0)
return concat_vec
def transform_vector_structure(vec):
vec = vectorize_matrices_in_vector(vec)
vec = concact_vectors_in_vector(vec)
return vec
```
In addition, we also have a helper method which transforms the pruned weight vector back to the original layered structure.
```
from functools import reduce
import operator
def prod(iterable):
return reduce(operator.mul, iterable, 1)
def restore_weight_structure(vec):
pruned_weights = []
index = 0
for shape in layer_param_shapes:
incr = prod(shape)
pruned_weights.extend([nd.reshape(vec[index : index + incr], shape)])
index += incr
return pruned_weights
```
The actual pruning of the vector happens in the following function. Note that this function accepts an ordered list of percentages to evaluate the performance at different pruning rates. In this setting, pruning at each iteration means extracting the index of the lowest signal-to-noise-ratio weight and setting the weight at this index to $0$.
```
def prune_weights(sign_to_noise_vec, prediction_vector, percentages):
pruning_indices = nd.argsort(sign_to_noise_vec, axis=0)
for percentage in percentages:
prediction_vector = mus_copy_vec.copy()
pruning_indices_percent = pruning_indices[0:int(len(pruning_indices)*percentage)]
for pr_ind in pruning_indices_percent:
prediction_vector[int(pr_ind.asscalar())] = 0
pruned_weights = restore_weight_structure(prediction_vector)
test_accuracy = evaluate_accuracy(test_data, net, pruned_weights)
print("%s --> %s" % (percentage, test_accuracy))
```
Putting the above functions together:
```
sign_to_noise = signal_to_noise_ratio(mus, sigmas)
sign_to_noise_vec = transform_vector_structure(sign_to_noise)
mus_copy = mus.copy()
mus_copy_vec = transform_vector_structure(mus_copy)
prune_weights(sign_to_noise_vec, mus_copy_vec, [0.1, 0.25, 0.5, 0.75, 0.95, 0.99, 1.0])
```
Depending on the number of units used in the original network and the number of training epochs, the highest achievable pruning percentages (without significantly reducing the predictive performance) can vary. The paper, for example, reports almost no change in the test accuracy when pruning 95% of the weights in a 2x1200 unit Bayesian neural network, which creates a significantly sparser network, leading to faster predictions and reduced memory requirements.
## Conclusion
We have taken a look at an efficient Bayesian treatment for neural networks using variational inference via the "Bayes by Backprop" algorithm (introduced by the "[Weight Uncertainity in Neural Networks](https://arxiv.org/abs/1505.05424)" paper). We have implemented a stochastic version of the variational lower bound and optimized it in order to find an approximation to the posterior distribution over the weights of a MLP network on the MNIST data set. As a result, we achieve regularization on the network's parameters and can quantify our uncertainty about the weights accurately. Finally, we saw that it is possible to significantly reduce the number of weights in the neural network after training while still keeping a high accuracy on the test set.
We also note that, given this model implementation, we were able to reproduce the paper's results on the MNIST data set, achieving a comparable test accuracy for all documented instances of the MNIST classification problem.
For whinges or inquiries, [open an issue on GitHub.](https://github.com/zackchase/mxnet-the-straight-dope)
|
github_jupyter
|
from __future__ import print_function
import collections
import mxnet as mx
import numpy as np
from mxnet import nd, autograd
from matplotlib import pyplot as plt
config = {
"num_hidden_layers": 2,
"num_hidden_units": 400,
"batch_size": 128,
"epochs": 10,
"learning_rate": 0.001,
"num_samples": 1,
"pi": 0.25,
"sigma_p": 1.0,
"sigma_p1": 0.75,
"sigma_p2": 0.1,
}
ctx = mx.cpu()
def transform(data, label):
return data.astype(np.float32)/126.0, label.astype(np.float32)
mnist = mx.test_utils.get_mnist()
num_inputs = 784
num_outputs = 10
batch_size = config['batch_size']
train_data = mx.gluon.data.DataLoader(mx.gluon.data.vision.MNIST(train=True, transform=transform),
batch_size, shuffle=True)
test_data = mx.gluon.data.DataLoader(mx.gluon.data.vision.MNIST(train=False, transform=transform),
batch_size, shuffle=False)
num_train = sum([batch_size for i in train_data])
num_batches = num_train / batch_size
def relu(X):
return nd.maximum(X, nd.zeros_like(X))
num_layers = config['num_hidden_layers']
# define function for evaluating MLP
def net(X, layer_params):
layer_input = X
for i in range(len(layer_params) // 2 - 2):
h_linear = nd.dot(layer_input, layer_params[2*i]) + layer_params[2*i + 1]
layer_input = relu(h_linear)
# last layer without ReLU
output = nd.dot(layer_input, layer_params[-2]) + layer_params[-1]
return output
# define network weight shapes
layer_param_shapes = []
num_hidden = config['num_hidden_units']
for i in range(num_layers + 1):
if i == 0: # input layer
W_shape = (num_inputs, num_hidden)
b_shape = (num_hidden,)
elif i == num_layers: # last layer
W_shape = (num_hidden, num_outputs)
b_shape = (num_outputs,)
else: # hidden layers
W_shape = (num_hidden, num_hidden)
b_shape = (num_hidden,)
layer_param_shapes.extend([W_shape, b_shape])
def log_softmax_likelihood(yhat_linear, y):
return nd.nansum(y * nd.log_softmax(yhat_linear), axis=0, exclude=True)
LOG2PI = np.log(2.0 * np.pi)
def log_gaussian(x, mu, sigma):
return -0.5 * LOG2PI - nd.log(sigma) - (x - mu) ** 2 / (2 * sigma ** 2)
def gaussian_prior(x):
sigma_p = nd.array([config['sigma_p']], ctx=ctx)
return nd.sum(log_gaussian(x, 0., sigma_p))
def gaussian(x, mu, sigma):
scaling = 1.0 / nd.sqrt(2.0 * np.pi * (sigma ** 2))
bell = nd.exp(- (x - mu) ** 2 / (2.0 * sigma ** 2))
return scaling * bell
def scale_mixture_prior(x):
sigma_p1 = nd.array([config['sigma_p1']], ctx=ctx)
sigma_p2 = nd.array([config['sigma_p2']], ctx=ctx)
pi = config['pi']
first_gaussian = pi * gaussian(x, 0., sigma_p1)
second_gaussian = (1 - pi) * gaussian(x, 0., sigma_p2)
return nd.log(first_gaussian + second_gaussian)
def combined_loss(output, label_one_hot, params, mus, sigmas, log_prior, log_likelihood):
# Calculate data likelihood
log_likelihood_sum = nd.sum(log_likelihood(output, label_one_hot))
# Calculate prior
log_prior_sum = sum([nd.sum(log_prior(param)) for param in params])
# Calculate variational posterior
log_var_posterior_sum = sum([nd.sum(log_gaussian(params[i], mus[i], sigmas[i])) for i in range(len(params))])
# Calculate total loss
return 1.0 / num_batches * (log_var_posterior_sum - log_prior_sum) - log_likelihood_sum
def SGD(params, lr):
for param in params:
param[:] = param - lr * param.grad
def evaluate_accuracy(data_iterator, net, layer_params):
numerator = 0.
denominator = 0.
for i, (data, label) in enumerate(data_iterator):
data = data.as_in_context(ctx).reshape((-1, 784))
label = label.as_in_context(ctx)
output = net(data, layer_params)
predictions = nd.argmax(output, axis=1)
numerator += nd.sum(predictions == label)
denominator += data.shape[0]
return (numerator / denominator).asscalar()
weight_scale = .1
rho_offset = -3
# initialize variational parameters; mean and variance for each weight
mus = []
rhos = []
for shape in layer_param_shapes:
mu = nd.random_normal(shape=shape, ctx=ctx, scale=weight_scale)
rho = rho_offset + nd.zeros(shape=shape, ctx=ctx)
mus.append(mu)
rhos.append(rho)
variational_params = mus + rhos
for param in variational_params:
param.attach_grad()
def sample_epsilons(param_shapes):
epsilons = [nd.random_normal(shape=shape, loc=0., scale=1.0, ctx=ctx) for shape in param_shapes]
return epsilons
def softplus(x):
return nd.log(1. + nd.exp(x))
def transform_rhos(rhos):
return [softplus(rho) for rho in rhos]
def transform_gaussian_samples(mus, sigmas, epsilons):
samples = []
for j in range(len(mus)):
samples.append(mus[j] + sigmas[j] * epsilons[j])
return samples
epochs = config['epochs']
learning_rate = config['learning_rate']
smoothing_constant = .01
train_acc = []
test_acc = []
for e in range(epochs):
for i, (data, label) in enumerate(train_data):
data = data.as_in_context(ctx).reshape((-1, 784))
label = label.as_in_context(ctx)
label_one_hot = nd.one_hot(label, 10)
with autograd.record():
# sample epsilons from standard normal
epsilons = sample_epsilons(layer_param_shapes)
# compute softplus for variance
sigmas = transform_rhos(rhos)
# obtain a sample from q(w|theta) by transforming the epsilons
layer_params = transform_gaussian_samples(mus, sigmas, epsilons)
# forward-propagate the batch
output = net(data, layer_params)
# calculate the loss
loss = combined_loss(output, label_one_hot, layer_params, mus, sigmas, gaussian_prior, log_softmax_likelihood)
# backpropagate for gradient calculation
loss.backward()
# apply stochastic gradient descent to variational parameters
SGD(variational_params, learning_rate)
# calculate moving loss for monitoring convergence
curr_loss = nd.mean(loss).asscalar()
moving_loss = (curr_loss if ((i == 0) and (e == 0))
else (1 - smoothing_constant) * moving_loss + (smoothing_constant) * curr_loss)
test_accuracy = evaluate_accuracy(test_data, net, mus)
train_accuracy = evaluate_accuracy(train_data, net, mus)
train_acc.append(np.asscalar(train_accuracy))
test_acc.append(np.asscalar(test_accuracy))
print("Epoch %s. Loss: %s, Train_acc %s, Test_acc %s" %
(e, moving_loss, train_accuracy, test_accuracy))
plt.plot(train_acc)
plt.plot(test_acc)
plt.show()
def show_weight_dist(mean, variance):
sigma = nd.sqrt(variance)
x = np.linspace(mean.asscalar() - 4*sigma.asscalar(), mean.asscalar() + 4*sigma.asscalar(), 100)
plt.plot(x, gaussian(nd.array(x, ctx=ctx), mean, sigma).asnumpy())
plt.show()
mu = mus[0][0][0]
var = softplus(rhos[0][0][0]) ** 2
show_weight_dist(mu, var)
def signal_to_noise_ratio(mus, sigmas):
sign_to_noise = []
for j in range(len(mus)):
sign_to_noise.extend([nd.abs(mus[j]) / sigmas[j]])
return sign_to_noise
def vectorize_matrices_in_vector(vec):
for i in range(0, (num_layers + 1) * 2, 2):
if i == 0:
vec[i] = nd.reshape(vec[i], num_inputs * num_hidden)
elif i == num_layers * 2:
vec[i] = nd.reshape(vec[i], num_hidden * num_outputs)
else:
vec[i] = nd.reshape(vec[i], num_hidden * num_hidden)
return vec
def concact_vectors_in_vector(vec):
concat_vec = vec[0]
for i in range(1, len(vec)):
concat_vec = nd.concat(concat_vec, vec[i], dim=0)
return concat_vec
def transform_vector_structure(vec):
vec = vectorize_matrices_in_vector(vec)
vec = concact_vectors_in_vector(vec)
return vec
from functools import reduce
import operator
def prod(iterable):
return reduce(operator.mul, iterable, 1)
def restore_weight_structure(vec):
pruned_weights = []
index = 0
for shape in layer_param_shapes:
incr = prod(shape)
pruned_weights.extend([nd.reshape(vec[index : index + incr], shape)])
index += incr
return pruned_weights
def prune_weights(sign_to_noise_vec, prediction_vector, percentages):
pruning_indices = nd.argsort(sign_to_noise_vec, axis=0)
for percentage in percentages:
prediction_vector = mus_copy_vec.copy()
pruning_indices_percent = pruning_indices[0:int(len(pruning_indices)*percentage)]
for pr_ind in pruning_indices_percent:
prediction_vector[int(pr_ind.asscalar())] = 0
pruned_weights = restore_weight_structure(prediction_vector)
test_accuracy = evaluate_accuracy(test_data, net, pruned_weights)
print("%s --> %s" % (percentage, test_accuracy))
sign_to_noise = signal_to_noise_ratio(mus, sigmas)
sign_to_noise_vec = transform_vector_structure(sign_to_noise)
mus_copy = mus.copy()
mus_copy_vec = transform_vector_structure(mus_copy)
prune_weights(sign_to_noise_vec, mus_copy_vec, [0.1, 0.25, 0.5, 0.75, 0.95, 0.99, 1.0])
| 0.791217 | 0.994708 |
# Training Neural Networks
The network we built in the previous part isn't so smart, it doesn't know anything about our handwritten digits. Neural networks with non-linear activations work like universal function approximators. There is some function that maps your input to the output. For example, images of handwritten digits to class probabilities. The power of neural networks is that we can train them to approximate this function, and basically any function given enough data and compute time.
<img src="assets/function_approx.png" width=500px>
At first the network is naive, it doesn't know the function mapping the inputs to the outputs. We train the network by showing it examples of real data, then adjusting the network parameters such that it approximates this function.
To find these parameters, we need to know how poorly the network is predicting the real outputs. For this we calculate a **loss function** (also called the cost), a measure of our prediction error. For example, the mean squared loss is often used in regression and binary classification problems
$$
\large \ell = \frac{1}{2n}\sum_i^n{\left(y_i - \hat{y}_i\right)^2}
$$
where $n$ is the number of training examples, $y_i$ are the true labels, and $\hat{y}_i$ are the predicted labels.
By minimizing this loss with respect to the network parameters, we can find configurations where the loss is at a minimum and the network is able to predict the correct labels with high accuracy. We find this minimum using a process called **gradient descent**. The gradient is the slope of the loss function and points in the direction of fastest change. To get to the minimum in the least amount of time, we then want to follow the gradient (downwards). You can think of this like descending a mountain by following the steepest slope to the base.
<img src='assets/gradient_descent.png' width=350px>
## Backpropagation
For single layer networks, gradient descent is straightforward to implement. However, it's more complicated for deeper, multilayer neural networks like the one we've built. Complicated enough that it took about 30 years before researchers figured out how to train multilayer networks.
Training multilayer networks is done through **backpropagation** which is really just an application of the chain rule from calculus. It's easiest to understand if we convert a two layer network into a graph representation.
<img src='assets/backprop_diagram.png' width=550px>
In the forward pass through the network, our data and operations go from bottom to top here. We pass the input $x$ through a linear transformation $L_1$ with weights $W_1$ and biases $b_1$. The output then goes through the sigmoid operation $S$ and another linear transformation $L_2$. Finally we calculate the loss $\ell$. We use the loss as a measure of how bad the network's predictions are. The goal then is to adjust the weights and biases to minimize the loss.
To train the weights with gradient descent, we propagate the gradient of the loss backwards through the network. Each operation has some gradient between the inputs and outputs. As we send the gradients backwards, we multiply the incoming gradient with the gradient for the operation. Mathematically, this is really just calculating the gradient of the loss with respect to the weights using the chain rule.
$$
\large \frac{\partial \ell}{\partial W_1} = \frac{\partial L_1}{\partial W_1} \frac{\partial S}{\partial L_1} \frac{\partial L_2}{\partial S} \frac{\partial \ell}{\partial L_2}
$$
**Note:** I'm glossing over a few details here that require some knowledge of vector calculus, but they aren't necessary to understand what's going on.
We update our weights using this gradient with some learning rate $\alpha$.
$$
\large W^\prime_1 = W_1 - \alpha \frac{\partial \ell}{\partial W_1}
$$
The learning rate $\alpha$ is set such that the weight update steps are small enough that the iterative method settles in a minimum.
## Losses in PyTorch
Let's start by seeing how we calculate the loss with PyTorch. Through the `nn` module, PyTorch provides losses such as the cross-entropy loss (`nn.CrossEntropyLoss`). You'll usually see the loss assigned to `criterion`. As noted in the last part, with a classification problem such as MNIST, we're using the softmax function to predict class probabilities. With a softmax output, you want to use cross-entropy as the loss. To actually calculate the loss, you first define the criterion then pass in the output of your network and the correct labels.
Something really important to note here. Looking at [the documentation for `nn.CrossEntropyLoss`](https://pytorch.org/docs/stable/nn.html#torch.nn.CrossEntropyLoss),
> This criterion combines `nn.LogSoftmax()` and `nn.NLLLoss()` in one single class.
>
> The input is expected to contain scores for each class.
This means we need to pass in the raw output of our network into the loss, not the output of the softmax function. This raw output is usually called the *logits* or *scores*. We use the logits because softmax gives you probabilities which will often be very close to zero or one but floating-point numbers can't accurately represent values near zero or one ([read more here](https://docs.python.org/3/tutorial/floatingpoint.html)). It's usually best to avoid doing calculations with probabilities, typically we use log-probabilities.
```
import torch
from torch import nn
import torch.nn.functional as F
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)),
])
# Download and load the training data
trainset = datasets.MNIST('~/.pytorch/MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
```
### Note
If you haven't seen `nn.Sequential` yet, please finish the end of the Part 2 notebook.
```
# Build a feed-forward network
model = nn.Sequential(nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10))
# Define the loss
criterion = nn.CrossEntropyLoss()
# Get our data
dataiter = iter(trainloader)
images, labels = next(dataiter)
# Flatten images
images = images.view(images.shape[0], -1)
# Forward pass, get our logits
logits = model(images)
# Calculate the loss with the logits and the labels
loss = criterion(logits, labels)
print(loss)
```
In my experience it's more convenient to build the model with a log-softmax output using `nn.LogSoftmax` or `F.log_softmax` ([documentation](https://pytorch.org/docs/stable/nn.html#torch.nn.LogSoftmax)). Then you can get the actual probabilities by taking the exponential `torch.exp(output)`. With a log-softmax output, you want to use the negative log likelihood loss, `nn.NLLLoss` ([documentation](https://pytorch.org/docs/stable/nn.html#torch.nn.NLLLoss)).
>**Exercise:** Build a model that returns the log-softmax as the output and calculate the loss using the negative log likelihood loss. Note that for `nn.LogSoftmax` and `F.log_softmax` you'll need to set the `dim` keyword argument appropriately. `dim=0` calculates softmax across the rows, so each column sums to 1, while `dim=1` calculates across the columns so each row sums to 1. Think about what you want the output to be and choose `dim` appropriately.
```
# TODO: Build a feed-forward network
model = nn.Sequential(nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.LogSoftmax(dim=0),
)
# TODO: Define the loss
criterion = nn.NLLLoss()
### Run this to check your work
# Get our data
dataiter = iter(trainloader)
images, labels = next(dataiter)
# Flatten images
images = images.view(images.shape[0], -1)
# Forward pass, get our logits
logits = model(images)
# Calculate the loss with the logits and the labels
loss = criterion(logits, labels)
print(loss)
```
## Autograd
Now that we know how to calculate a loss, how do we use it to perform backpropagation? Torch provides a module, `autograd`, for automatically calculating the gradients of tensors. We can use it to calculate the gradients of all our parameters with respect to the loss. Autograd works by keeping track of operations performed on tensors, then going backwards through those operations, calculating gradients along the way. To make sure PyTorch keeps track of operations on a tensor and calculates the gradients, you need to set `requires_grad = True` on a tensor. You can do this at creation with the `requires_grad` keyword, or at any time with `x.requires_grad_(True)`.
You can turn off gradients for a block of code with the `torch.no_grad()` content:
```python
x = torch.zeros(1, requires_grad=True)
>>> with torch.no_grad():
... y = x * 2
>>> y.requires_grad
False
```
Also, you can turn on or off gradients altogether with `torch.set_grad_enabled(True|False)`.
The gradients are computed with respect to some variable `z` with `z.backward()`. This does a backward pass through the operations that created `z`.
```
x = torch.randn(2,2, requires_grad=True)
print(x)
y = x**2
print(y)
```
Below we can see the operation that created `y`, a power operation `PowBackward0`.
```
## grad_fn shows the function that generated this variable
print(y.grad_fn)
```
The autograd module keeps track of these operations and knows how to calculate the gradient for each one. In this way, it's able to calculate the gradients for a chain of operations, with respect to any one tensor. Let's reduce the tensor `y` to a scalar value, the mean.
```
z = y.mean()
print(z)
```
You can check the gradients for `x` and `y` but they are empty currently.
```
print(x.grad)
```
To calculate the gradients, you need to run the `.backward` method on a Variable, `z` for example. This will calculate the gradient for `z` with respect to `x`
$$
\frac{\partial z}{\partial x} = \frac{\partial}{\partial x}\left[\frac{1}{n}\sum_i^n x_i^2\right] = \frac{x}{2}
$$
```
z.backward()
print(x.grad)
print(x/2)
```
These gradients calculations are particularly useful for neural networks. For training we need the gradients of the cost with respect to the weights. With PyTorch, we run data forward through the network to calculate the loss, then, go backwards to calculate the gradients with respect to the loss. Once we have the gradients we can make a gradient descent step.
## Loss and Autograd together
When we create a network with PyTorch, all of the parameters are initialized with `requires_grad = True`. This means that when we calculate the loss and call `loss.backward()`, the gradients for the parameters are calculated. These gradients are used to update the weights with gradient descent. Below you can see an example of calculating the gradients using a backwards pass.
```
# Build a feed-forward network
model = nn.Sequential(nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.LogSoftmax(dim=1))
criterion = nn.NLLLoss()
dataiter = iter(trainloader)
images, labels = next(dataiter)
images = images.view(images.shape[0], -1)
logits = model(images)
loss = criterion(logits, labels)
print('Before backward pass: \n', model[0].weight.grad)
loss.backward()
print('After backward pass: \n', model[0].weight.grad)
```
## Training the network!
There's one last piece we need to start training, an optimizer that we'll use to update the weights with the gradients. We get these from PyTorch's [`optim` package](https://pytorch.org/docs/stable/optim.html). For example we can use stochastic gradient descent with `optim.SGD`. You can see how to define an optimizer below.
```
from torch import optim
# Optimizers require the parameters to optimize and a learning rate
optimizer = optim.SGD(model.parameters(), lr=0.01)
```
Now we know how to use all the individual parts so it's time to see how they work together. Let's consider just one learning step before looping through all the data. The general process with PyTorch:
* Make a forward pass through the network
* Use the network output to calculate the loss
* Perform a backward pass through the network with `loss.backward()` to calculate the gradients
* Take a step with the optimizer to update the weights
Below I'll go through one training step and print out the weights and gradients so you can see how it changes. Note that I have a line of code `optimizer.zero_grad()`. When you do multiple backwards passes with the same parameters, the gradients are accumulated. This means that you need to zero the gradients on each training pass or you'll retain gradients from previous training batches.
```
print('Initial weights - ', model[0].weight)
dataiter = iter(trainloader)
images, labels = next(dataiter)
images.resize_(64, 784)
# Clear the gradients, do this because gradients are accumulated
optimizer.zero_grad()
# Forward pass, then backward pass, then update weights
output = model(images)
loss = criterion(output, labels)
loss.backward()
print('Gradient -', model[0].weight.grad)
# Take an update step and view the new weights
optimizer.step()
print('Updated weights - ', model[0].weight)
```
### Training for real
Now we'll put this algorithm into a loop so we can go through all the images. Some nomenclature, one pass through the entire dataset is called an *epoch*. So here we're going to loop through `trainloader` to get our training batches. For each batch, we'll doing a training pass where we calculate the loss, do a backwards pass, and update the weights.
>**Exercise:** Implement the training pass for our network. If you implemented it correctly, you should see the training loss drop with each epoch.
```
## Your solution here
model = nn.Sequential(nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.LogSoftmax(dim=1))
criterion = nn.NLLLoss()
optimizer = optim.SGD(model.parameters(), lr=0.003)
epochs = 5
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
# Flatten MNIST images into a 784 long vector
images = images.view(images.shape[0], -1)
# TODO: Training pass
optimizer.zero_grad()
output = model(images)
loss = criterion(output, labels)
running_loss += loss.item()
loss.backward()
optimizer.step()
else:
print(f"Training loss: {running_loss/len(trainloader)}")
```
With the network trained, we can check out it's predictions.
```
%matplotlib inline
import helper
dataiter = iter(trainloader)
images, labels = next(dataiter)
img = images[0].view(1, 784)
# Turn off gradients to speed up this part
with torch.no_grad():
logps = model(img)
# Output of the network are log-probabilities, need to take exponential for probabilities
ps = torch.exp(logps)
helper.view_classify(img.view(1, 28, 28), ps)
```
Now our network is (almost) brilliant (we train and "test" on the same data) . It can accurately predict the digits in our images. Next up you'll write the code for training a neural network on a more complex dataset.
|
github_jupyter
|
import torch
from torch import nn
import torch.nn.functional as F
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)),
])
# Download and load the training data
trainset = datasets.MNIST('~/.pytorch/MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# Build a feed-forward network
model = nn.Sequential(nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10))
# Define the loss
criterion = nn.CrossEntropyLoss()
# Get our data
dataiter = iter(trainloader)
images, labels = next(dataiter)
# Flatten images
images = images.view(images.shape[0], -1)
# Forward pass, get our logits
logits = model(images)
# Calculate the loss with the logits and the labels
loss = criterion(logits, labels)
print(loss)
# TODO: Build a feed-forward network
model = nn.Sequential(nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.LogSoftmax(dim=0),
)
# TODO: Define the loss
criterion = nn.NLLLoss()
### Run this to check your work
# Get our data
dataiter = iter(trainloader)
images, labels = next(dataiter)
# Flatten images
images = images.view(images.shape[0], -1)
# Forward pass, get our logits
logits = model(images)
# Calculate the loss with the logits and the labels
loss = criterion(logits, labels)
print(loss)
x = torch.zeros(1, requires_grad=True)
>>> with torch.no_grad():
... y = x * 2
>>> y.requires_grad
False
x = torch.randn(2,2, requires_grad=True)
print(x)
y = x**2
print(y)
## grad_fn shows the function that generated this variable
print(y.grad_fn)
z = y.mean()
print(z)
print(x.grad)
z.backward()
print(x.grad)
print(x/2)
# Build a feed-forward network
model = nn.Sequential(nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.LogSoftmax(dim=1))
criterion = nn.NLLLoss()
dataiter = iter(trainloader)
images, labels = next(dataiter)
images = images.view(images.shape[0], -1)
logits = model(images)
loss = criterion(logits, labels)
print('Before backward pass: \n', model[0].weight.grad)
loss.backward()
print('After backward pass: \n', model[0].weight.grad)
from torch import optim
# Optimizers require the parameters to optimize and a learning rate
optimizer = optim.SGD(model.parameters(), lr=0.01)
print('Initial weights - ', model[0].weight)
dataiter = iter(trainloader)
images, labels = next(dataiter)
images.resize_(64, 784)
# Clear the gradients, do this because gradients are accumulated
optimizer.zero_grad()
# Forward pass, then backward pass, then update weights
output = model(images)
loss = criterion(output, labels)
loss.backward()
print('Gradient -', model[0].weight.grad)
# Take an update step and view the new weights
optimizer.step()
print('Updated weights - ', model[0].weight)
## Your solution here
model = nn.Sequential(nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.LogSoftmax(dim=1))
criterion = nn.NLLLoss()
optimizer = optim.SGD(model.parameters(), lr=0.003)
epochs = 5
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
# Flatten MNIST images into a 784 long vector
images = images.view(images.shape[0], -1)
# TODO: Training pass
optimizer.zero_grad()
output = model(images)
loss = criterion(output, labels)
running_loss += loss.item()
loss.backward()
optimizer.step()
else:
print(f"Training loss: {running_loss/len(trainloader)}")
%matplotlib inline
import helper
dataiter = iter(trainloader)
images, labels = next(dataiter)
img = images[0].view(1, 784)
# Turn off gradients to speed up this part
with torch.no_grad():
logps = model(img)
# Output of the network are log-probabilities, need to take exponential for probabilities
ps = torch.exp(logps)
helper.view_classify(img.view(1, 28, 28), ps)
| 0.86094 | 0.994584 |
# Bank Simulator
Copyright 2019 IBM Corp.
# Load Trained Classifier
* This data was created by running the notebook train-on-core-features.ipynb
```
import pickle, os
home_dir = "../data"
charge_off_classifier_core_pkl = os.path.join(home_dir, "co_clf_core.pkl")
with open(charge_off_classifier_core_pkl,'rb') as f:
data_df, idx_train, idx_test, idx_validate, clf_core, core_features, analytics = pickle.load(f)
```
# Import packages
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
import warnings
import gc
warnings.simplefilter(action='ignore', category=FutureWarning)
warnings.simplefilter(action='ignore', category=DeprecationWarning)
%matplotlib inline
import matplotlib.ticker as tkr
from matplotlib import rcParams
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score, cross_val_predict
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
from sklearn.model_selection import train_test_split
```
# Useful functions
```
def print_score(clf, X_train, y_train, X_test, y_test, train=False, plot_features=False, features=None):
if train:
print("Train Result:\n")
print("accuracy score: {0:.4f}\n".format(accuracy_score(y_train, clf.predict(X_train))))
print("Classification Report: \n {}\n".format(classification_report(y_train, clf.predict(X_train))))
print("Confusion Matrix: \n {}\n".format(confusion_matrix(y_train, clf.predict(X_train))))
res = cross_val_score(clf, X_train, y_train, cv=10, scoring='accuracy')
print("Average Accuracy: \t {0:.4f}".format(np.mean(res)))
print("Accuracy SD: \t\t {0:.4f}".format(np.std(res)))
elif train==False:
print("Test Result:\n")
print("accuracy score: {0:.4f}\n".format(accuracy_score(y_test, clf.predict(X_test))))
print("Classification Report: \n {}\n".format(classification_report(y_test, clf.predict(X_test))))
print("Confusion Matrix: \n {}\n".format(confusion_matrix(y_test, clf.predict(X_test))))
if plot_features and features is not None:
# Get top features
feature_importances = pd.DataFrame(clf.feature_importances_,
index = features,
columns=['importance']).\
sort_values('importance',ascending=False)
# Plot
rcParams['figure.figsize'] = 20, 10
rcParams['font.size'] = 16
feature_importances.iloc[:10,:].plot(kind='barh')
plt.show()
def calc_threshold(X, gain_col, plot=False):
thrs = [0. , 0.025, 0.05 , 0.075, 0.1 , 0.125, 0.15 , 0.175, 0.2 ,
0.225, 0.25 , 0.275, 0.3 , 0.325, 0.35 , 0.375, 0.4 , 0.425,
0.45 , 0.475, 0.5 , 0.525, 0.55 , 0.575, 0.6 , 0.625, 0.65 ,
0.675, 0.7 , 0.725, 0.75 , 0.775, 0.8 , 0.825, 0.85 ]
gain = np.array([X.loc[X.score <= thr, gain_col].sum() for thr in thrs])
if plot:
plt.plot(thrs, gain)
plt.xlabel('Threshold')
plt.ylabel(gain_col)
plt.show()
b = np.argmax(gain)
optimal_threshold = thrs[b]
return optimal_threshold
def evaluate_invest(sample_df, invest_sum, optimal_threshold, plot=False ):
#eval_fields = [gain_col, 'loan_amnt', 'LoanStatus', 'recoveries', 'total_rec_prncp', 'total_rec_int']
# Apply the selection rule
selected_df = sample_df.loc[sample_df.score <= optimal_threshold, :]
# Buy the loans up to the investment sum
invested_df = selected_df.loc[selected_df['loan_amnt'].cumsum() <= invest_sum, :]
return invested_df, selected_df
def payments(row):
#message = ""
rate = float( row['int_rate']/100 )
rate /= float(12)
N = int(row['term'])
if N == 0:
N = 36
else:
N = 60
L = row['funded_amnt']
install = row['installment']
total_rec_int = row['total_rec_int']
total_rec_prncp = row['total_rec_prncp']
recoveries = row['recoveries']
total_pymnt = row['total_pymnt']
life_of_loan = int(row['LifeOfLoan'])
charged_off = (row['LoanStatus'] == 1.0)
int_rec = []
prn_rec = []
prn_rem = []
P = L
tot_int = 0
tot_prn = 0
tot_rec = 0
for n in range(N):
# Normal payments
int_pmnt = P*rate
prn_pmnt = install - int_pmnt
# End of interest payments is termination condition
if not (int_pmnt + tot_int) < total_rec_int:
#message = "Interest payments terminated"
int_pmnt = total_rec_int - tot_int
if (int_pmnt < 0):
# print("int neg 1")
int_rec[-1] += int_pmnt
break
prn_pmnt = total_rec_prncp - tot_prn
tot_int += int_pmnt
tot_prn += prn_pmnt
int_rec.append(int_pmnt)
prn_rec.append(prn_pmnt)
break
# In default, last few payments are considered interest?
if not (prn_pmnt + tot_prn) < total_rec_prncp:
prn_pmnt = total_rec_prncp - tot_prn
int_pmnt = install - prn_pmnt
tot_int += int_pmnt
tot_prn += prn_pmnt
P -= prn_pmnt
int_rec.append(int_pmnt)
prn_rec.append(prn_pmnt)
loss = L - tot_prn + recoveries
return int_rec, prn_rec, n, loss
def loss(row, loss, delay):
n = int( row["month"] + delay)
l = row["loss"]
loss[n] += l
def generate_series(invested_df, loss_delay, N=60):
df = pd.DataFrame(invested_df.apply(payments, axis=1).to_list(), columns=["int","prn","month", "loss"])
int_series = pd.DataFrame(df["int"].tolist()).fillna(value=0).aggregate(sum, axis=0).to_list()
prn_series = pd.DataFrame(df["prn"].tolist()).fillna(value=0).aggregate(sum, axis=0).to_list()
int_series += [0]*(N - len(int_series))
prn_series += [0]*(N - len(prn_series))
loss_series = np.zeros(N + loss_delay)
df.apply(loss, axis=1, args=(loss_series, loss_delay))
return int_series, prn_series, loss_series
def print_investment_analysis(invested_df, show_plot=False):
# Calculate the return, amount invested, loss, gain
invested_return = invested_df[gain_col] / invested_df['loan_amnt']
invested_amnt = invested_df['loan_amnt'].sum()
invested_loss = invested_df['loan_amnt'].sum() \
- invested_df['total_rec_prncp'].sum() - invested_df['recoveries'].sum()
invested_int = invested_df['total_rec_int'].sum()
invested_loss = max(invested_loss, 0)
invested_gain = invested_df[gain_col].sum()
return_on_investment = 100 * invested_gain / invested_amnt
# Collect some loan statistics
num_loans = invested_df.shape[0]
num_failed = invested_df.loc[invested_df['LoanStatus'] > 0, 'LoanStatus'].count()
print("\tInvested ${0:,.2f}".format(invested_amnt))
print("\tReturn {0:.4f}%".format(return_on_investment))
print("\t\tNumber loans: {0:}".format(num_loans))
print("\t\tNumber failed: {0:}".format(num_failed))
print("\t\tInterest paid: ${0:15,.2f}".format(invested_int))
print("\t\tLoss of principal: ${0:15,.2f}".format(invested_loss))
print("\t\tTotal gain: ${0:15,.2f}".format(invested_gain))
if show_plot:
invested_return.hist(bins=150)
plt.xlabel("Return of Loan")
plt.ylabel("Number of loans")
plt.show()
def print_payments(row, int_rec, prn_rec):
rate = float( row['int_rate']/100 )
rate /= float(12)
N = int(row['term'])
if N == 0:
N = 36
else:
N = 60
L = row['funded_amnt']
install = L * (rate * pow(1+rate,N))/(pow(1+rate,N) - 1)
print("Installment calculated: {0:,.2f} \t Installment from LC data: {1:,.2f}"
.format(install, row['installment']))
total_rec_int = row['total_rec_int']
total_rec_prncp = row['total_rec_prncp']
recoveries = row['recoveries']
total_pymnt = row['total_pymnt']
life_of_loan = int(row['LifeOfLoan'])
charged_off = (row['LoanStatus'] == 1.0)
print("Loan: ${1:,.0f}\tTerm of loan: {3:2d} months \tRate {2:.2f}% ".format(install, L, row['int_rate'], N))
print(" \tLife of loan: {0:2d} months \tCharged_off: {1:}"
.format(life_of_loan, charged_off))
print(" \tInterest: ${0:,.2f} Principal: ${1:,.2f} Total ${2:,.2f} Recoveries ${3:,.2f}"
.format(total_rec_int, total_rec_prncp, total_pymnt, recoveries))
tot_prn = 0
tot_int = 0
tot_rec = 0
P = L
for n in range(len(int_rec)):
P -= prn_rec[n]
tot_prn += prn_rec[n]
tot_int += int_rec[n]
print("month {3:4d} principal payment {0:8.2f} interest payment {2:8.2f} principal remaining {1:8.2f} principal paid {4:8.2f}"
.format(prn_rec[n], P, int_rec[n], n, tot_prn))
tot_rec = tot_prn + tot_int + recoveries
print("Interest: ${0:,.2f} Principal: ${1:,.2f} Total: ${3:,.2f} Net Loss: ${2:,.2f}"
.format(tot_int, tot_prn, L - tot_prn - recoveries, tot_rec))
def plot_bank_run(dyn_params, opt_params, capital, income, losses, assets, bankrupt):
# figure size in inches
rcParams['figure.figsize'] = 8,4.5
rcParams['font.size'] = 16
plt.tight_layout()
N = len(capital)
if bankrupt:
N -= 1
capital = capital[:N]
income = income[:N]
losses = losses[:N]
assets = assets[:N]
ax = plt.subplot()
ax.plot(range(N), capital, 'g', label='Capital', )
ax.plot(range(N), income, 'c', label='Income')
ax.plot(range(N), losses, 'r', label='Losses')
ax.yaxis.set_major_formatter(tkr.StrMethodFormatter('${x:,.0f}'))
ax.xaxis.set_major_locator(plt.MultipleLocator(4))
ax.legend()
plt.title("Lending Club bank: {0:.0f}Y performance \n Threshold {1:.3f}, leverage {2:2d}:1, Loss delay {3:d}M"
.format(N/4, opt_params['threshold'], opt_params['leverage_ratio'],
opt_params['loss_delay']))
skip_ratios = True
if skip_ratios:
ann_ret_exponent = float(12) / float(dyn_params['inv_cycle'])
ROA = (np.array(income) - np.array(losses)) / np.array(assets)
ROA = np.power(ROA + 1, ann_ret_exponent) - 1
prev_capital = np.zeros(N)
prev_capital[0] = opt_params['starting_capital']
prev_capital[1:] = capital[:N-1]
next_capital = np.array(capital)
ROC = (next_capital - prev_capital)/prev_capital
ROC = np.power(ROC+1, ann_ret_exponent) - 1
LR = np.array(losses) / np.array(assets)
LR = np.power(LR+1, ann_ret_exponent) - 1
#ax = plt.subplot(3,1,2)
#ax.plot(range(1,N), ROC[1:], label='Return on Capital')
#ax.yaxis.set_major_formatter(tkr.StrMethodFormatter('{x:,.4f}'))
#ax.xaxis.set_major_locator(plt.MultipleLocator(4))
#plt.legend()
#ax = plt.subplot(3,1,3)
#ax.plot(range(1,N), LR[1:], label='Loss Ratio')
#ax.plot(range(1,N), ROA[1:], label='Return on Assets')
#ax.yaxis.set_major_formatter(tkr.StrMethodFormatter('{x:,.4f}'))
#ax.xaxis.set_major_locator(plt.MultipleLocator(4))
#plt.legend()
plt.xlabel("Quarters")
plt.show()
def bank_run(dyn_params, dec_params, do_print=False, do_plot=False):
# sampled loans
df_list = dyn_params['sample_df_list']
# Initial cash
cash = dec_params['starting_capital']
# Initial assets
assets = 0
# Initial liabilities
liabilities = 0
# Initial capital
capital = cash + assets - liabilities
# Series to output
asset_series = []
capital_series = []
income_series = []
losses_series = []
# Monthly rate on loan
rate_3M = (dyn_params['inv_cycle'] / 12) * (dec_params['loan_interest_rate']/100 )
# Set up data structures
interest_income = np.zeros(3 * dyn_params['length_of_run'])
principal_pymnt = np.zeros(3 * dyn_params['length_of_run'])
loss_recognized = np.zeros(3 * dyn_params['length_of_run'] + dec_params['loss_delay'])
# Initial values for run
old_loan = 0
old_d = 0
n = 0
bankrupt = False
for d in range(dyn_params['inv_cycle'] ,1+dyn_params['length_of_run'],dyn_params['inv_cycle']):
# Borrow
new_loan = dec_params['leverage_ratio'] * capital
cash += new_loan
# Pay back old loan
cash -= old_loan
# Invest everything
to_invest = max(0, cash)
if to_invest > 0.0:
# Make investments
invested_df, selected_df = \
evaluate_invest(df_list[n], to_invest, dec_params['threshold'])
n+=1
# Total actually invested
invested = invested_df['loan_amnt'].sum()
# Update cash balance
cash -= invested
# Update assets
assets += invested
# Calculate outcomes of new investment
int_series, prn_series, lss_series = generate_series(invested_df, dec_params['loss_delay'])
# Add new outcomes to tails of old outcomes
interest_income[old_d: len(int_series) + old_d] += int_series
principal_pymnt[old_d: len(prn_series) + old_d] += prn_series
loss_recognized[old_d: len(lss_series) + old_d] += lss_series
if do_print:
print("Month: {0:2d} \t New investment ${1:,.2f} New loan ${2:,.2f}".format(d, invested, new_loan))
# Calculate interest, principal, losses from old_d to d
int_calc = interest_income[old_d:d].sum()
prn_calc = principal_pymnt[old_d:d].sum()
loss_calc = loss_recognized[old_d:d].sum()
# Loan interest due
int_loan = new_loan * (rate_3M)
# Update cash on hand
cash += int_calc
cash += prn_calc
cash -= int_loan
if do_print:
print(" \t Income: {1:,.2f} Expense: {2:,.2f} Net income: {3:,.2f} Cash: {4:,.2f}"
.format(d, int_calc, int_loan, int_calc - int_loan, cash))
print(" \t Loss ratio {0:,.2f}".format(loss_calc/assets))
# Update assets - deduct losses from assets
assets -= (loss_calc + prn_calc)
# Update liabilities
liabilities -= old_loan
liabilities += new_loan
# Balance sheet
capital = cash + assets - liabilities
if do_print:
print(" \t Assets: {1:,.2f} Liabilities: {2:,.2f} Capital: {3:,.2f} \n"
.format(d, assets, liabilities, capital))
# Record
asset_series.append(assets)
capital_series.append(capital)
income_series.append(int_calc - int_loan)
losses_series.append(loss_calc)
# Bankrupt!
if capital < 0:
bankrupt = True
print("Bankrupt!")
break
# Update
old_d = d
old_loan = new_loan
if do_plot:
plot_bank_run(dyn_params, dec_params, capital_series, income_series, losses_series, asset_series, bankrupt)
return capital_series, income_series, losses_series, asset_series, bankrupt
```
# Print scores
```
# Define train, test, and validate df
train_df = data_df.loc[idx_train, :]
test_df = data_df.loc[idx_test, :]
validate_df = data_df.loc[idx_validate, :]
print("Number of loans in Train set: {}".format(train_df.shape[0]))
print("Number of loans in Test set: {}".format(test_df.shape[0]))
print("Number of loans in Validate set: {}".format(validate_df.shape[0]))
# Just for sanity, print the scores and features for the classifier
print_score(clf_core, train_df[core_features], train_df['LoanStatus'], test_df[core_features], test_df['LoanStatus'],
plot_features=True, features=core_features)
```
# Calculate optimal thresholds
This is useful as an upper bound on thresholds
```
# select criterion
gain_col = 'TotalGain'
test_df['score'] = clf_core.predict_proba(test_df[core_features])[:,1]
opt_threshold = calc_threshold(test_df, gain_col)
print("Threshold is {0:.4f}".format(opt_threshold))
```
# Simulate lending
```
# Generate sample of loans
sample_params = {'inv_cycle': 3,
'sample_size': 2000,
'length_of_run': 120,
'sample_df_list': []
}
sample_df_list = sample_params['sample_df_list']
for d in range(sample_params['inv_cycle'] ,1 + sample_params['length_of_run'], sample_params['inv_cycle']):
# Generate sample from validate set
sample_df = validate_df.sample(sample_params['sample_size'], replace=True)
# Score sampled data
sample_df['score'] = clf_core.predict_proba(sample_df[core_features])[:,1]
sample_df_list.append(sample_df)
# Simulate the bank
opt_params = {'loss_delay': 3,
'starting_capital': 1e6,
'leverage_ratio': 10,
'loan_interest_rate': 3.0,
'threshold': opt_threshold - 0.1
}
capital, income, losses, assets, bankrupt = bank_run(sample_params, opt_params, do_print=False, do_plot=True)
```
|
github_jupyter
|
import pickle, os
home_dir = "../data"
charge_off_classifier_core_pkl = os.path.join(home_dir, "co_clf_core.pkl")
with open(charge_off_classifier_core_pkl,'rb') as f:
data_df, idx_train, idx_test, idx_validate, clf_core, core_features, analytics = pickle.load(f)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
import warnings
import gc
warnings.simplefilter(action='ignore', category=FutureWarning)
warnings.simplefilter(action='ignore', category=DeprecationWarning)
%matplotlib inline
import matplotlib.ticker as tkr
from matplotlib import rcParams
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score, cross_val_predict
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
from sklearn.model_selection import train_test_split
def print_score(clf, X_train, y_train, X_test, y_test, train=False, plot_features=False, features=None):
if train:
print("Train Result:\n")
print("accuracy score: {0:.4f}\n".format(accuracy_score(y_train, clf.predict(X_train))))
print("Classification Report: \n {}\n".format(classification_report(y_train, clf.predict(X_train))))
print("Confusion Matrix: \n {}\n".format(confusion_matrix(y_train, clf.predict(X_train))))
res = cross_val_score(clf, X_train, y_train, cv=10, scoring='accuracy')
print("Average Accuracy: \t {0:.4f}".format(np.mean(res)))
print("Accuracy SD: \t\t {0:.4f}".format(np.std(res)))
elif train==False:
print("Test Result:\n")
print("accuracy score: {0:.4f}\n".format(accuracy_score(y_test, clf.predict(X_test))))
print("Classification Report: \n {}\n".format(classification_report(y_test, clf.predict(X_test))))
print("Confusion Matrix: \n {}\n".format(confusion_matrix(y_test, clf.predict(X_test))))
if plot_features and features is not None:
# Get top features
feature_importances = pd.DataFrame(clf.feature_importances_,
index = features,
columns=['importance']).\
sort_values('importance',ascending=False)
# Plot
rcParams['figure.figsize'] = 20, 10
rcParams['font.size'] = 16
feature_importances.iloc[:10,:].plot(kind='barh')
plt.show()
def calc_threshold(X, gain_col, plot=False):
thrs = [0. , 0.025, 0.05 , 0.075, 0.1 , 0.125, 0.15 , 0.175, 0.2 ,
0.225, 0.25 , 0.275, 0.3 , 0.325, 0.35 , 0.375, 0.4 , 0.425,
0.45 , 0.475, 0.5 , 0.525, 0.55 , 0.575, 0.6 , 0.625, 0.65 ,
0.675, 0.7 , 0.725, 0.75 , 0.775, 0.8 , 0.825, 0.85 ]
gain = np.array([X.loc[X.score <= thr, gain_col].sum() for thr in thrs])
if plot:
plt.plot(thrs, gain)
plt.xlabel('Threshold')
plt.ylabel(gain_col)
plt.show()
b = np.argmax(gain)
optimal_threshold = thrs[b]
return optimal_threshold
def evaluate_invest(sample_df, invest_sum, optimal_threshold, plot=False ):
#eval_fields = [gain_col, 'loan_amnt', 'LoanStatus', 'recoveries', 'total_rec_prncp', 'total_rec_int']
# Apply the selection rule
selected_df = sample_df.loc[sample_df.score <= optimal_threshold, :]
# Buy the loans up to the investment sum
invested_df = selected_df.loc[selected_df['loan_amnt'].cumsum() <= invest_sum, :]
return invested_df, selected_df
def payments(row):
#message = ""
rate = float( row['int_rate']/100 )
rate /= float(12)
N = int(row['term'])
if N == 0:
N = 36
else:
N = 60
L = row['funded_amnt']
install = row['installment']
total_rec_int = row['total_rec_int']
total_rec_prncp = row['total_rec_prncp']
recoveries = row['recoveries']
total_pymnt = row['total_pymnt']
life_of_loan = int(row['LifeOfLoan'])
charged_off = (row['LoanStatus'] == 1.0)
int_rec = []
prn_rec = []
prn_rem = []
P = L
tot_int = 0
tot_prn = 0
tot_rec = 0
for n in range(N):
# Normal payments
int_pmnt = P*rate
prn_pmnt = install - int_pmnt
# End of interest payments is termination condition
if not (int_pmnt + tot_int) < total_rec_int:
#message = "Interest payments terminated"
int_pmnt = total_rec_int - tot_int
if (int_pmnt < 0):
# print("int neg 1")
int_rec[-1] += int_pmnt
break
prn_pmnt = total_rec_prncp - tot_prn
tot_int += int_pmnt
tot_prn += prn_pmnt
int_rec.append(int_pmnt)
prn_rec.append(prn_pmnt)
break
# In default, last few payments are considered interest?
if not (prn_pmnt + tot_prn) < total_rec_prncp:
prn_pmnt = total_rec_prncp - tot_prn
int_pmnt = install - prn_pmnt
tot_int += int_pmnt
tot_prn += prn_pmnt
P -= prn_pmnt
int_rec.append(int_pmnt)
prn_rec.append(prn_pmnt)
loss = L - tot_prn + recoveries
return int_rec, prn_rec, n, loss
def loss(row, loss, delay):
n = int( row["month"] + delay)
l = row["loss"]
loss[n] += l
def generate_series(invested_df, loss_delay, N=60):
df = pd.DataFrame(invested_df.apply(payments, axis=1).to_list(), columns=["int","prn","month", "loss"])
int_series = pd.DataFrame(df["int"].tolist()).fillna(value=0).aggregate(sum, axis=0).to_list()
prn_series = pd.DataFrame(df["prn"].tolist()).fillna(value=0).aggregate(sum, axis=0).to_list()
int_series += [0]*(N - len(int_series))
prn_series += [0]*(N - len(prn_series))
loss_series = np.zeros(N + loss_delay)
df.apply(loss, axis=1, args=(loss_series, loss_delay))
return int_series, prn_series, loss_series
def print_investment_analysis(invested_df, show_plot=False):
# Calculate the return, amount invested, loss, gain
invested_return = invested_df[gain_col] / invested_df['loan_amnt']
invested_amnt = invested_df['loan_amnt'].sum()
invested_loss = invested_df['loan_amnt'].sum() \
- invested_df['total_rec_prncp'].sum() - invested_df['recoveries'].sum()
invested_int = invested_df['total_rec_int'].sum()
invested_loss = max(invested_loss, 0)
invested_gain = invested_df[gain_col].sum()
return_on_investment = 100 * invested_gain / invested_amnt
# Collect some loan statistics
num_loans = invested_df.shape[0]
num_failed = invested_df.loc[invested_df['LoanStatus'] > 0, 'LoanStatus'].count()
print("\tInvested ${0:,.2f}".format(invested_amnt))
print("\tReturn {0:.4f}%".format(return_on_investment))
print("\t\tNumber loans: {0:}".format(num_loans))
print("\t\tNumber failed: {0:}".format(num_failed))
print("\t\tInterest paid: ${0:15,.2f}".format(invested_int))
print("\t\tLoss of principal: ${0:15,.2f}".format(invested_loss))
print("\t\tTotal gain: ${0:15,.2f}".format(invested_gain))
if show_plot:
invested_return.hist(bins=150)
plt.xlabel("Return of Loan")
plt.ylabel("Number of loans")
plt.show()
def print_payments(row, int_rec, prn_rec):
rate = float( row['int_rate']/100 )
rate /= float(12)
N = int(row['term'])
if N == 0:
N = 36
else:
N = 60
L = row['funded_amnt']
install = L * (rate * pow(1+rate,N))/(pow(1+rate,N) - 1)
print("Installment calculated: {0:,.2f} \t Installment from LC data: {1:,.2f}"
.format(install, row['installment']))
total_rec_int = row['total_rec_int']
total_rec_prncp = row['total_rec_prncp']
recoveries = row['recoveries']
total_pymnt = row['total_pymnt']
life_of_loan = int(row['LifeOfLoan'])
charged_off = (row['LoanStatus'] == 1.0)
print("Loan: ${1:,.0f}\tTerm of loan: {3:2d} months \tRate {2:.2f}% ".format(install, L, row['int_rate'], N))
print(" \tLife of loan: {0:2d} months \tCharged_off: {1:}"
.format(life_of_loan, charged_off))
print(" \tInterest: ${0:,.2f} Principal: ${1:,.2f} Total ${2:,.2f} Recoveries ${3:,.2f}"
.format(total_rec_int, total_rec_prncp, total_pymnt, recoveries))
tot_prn = 0
tot_int = 0
tot_rec = 0
P = L
for n in range(len(int_rec)):
P -= prn_rec[n]
tot_prn += prn_rec[n]
tot_int += int_rec[n]
print("month {3:4d} principal payment {0:8.2f} interest payment {2:8.2f} principal remaining {1:8.2f} principal paid {4:8.2f}"
.format(prn_rec[n], P, int_rec[n], n, tot_prn))
tot_rec = tot_prn + tot_int + recoveries
print("Interest: ${0:,.2f} Principal: ${1:,.2f} Total: ${3:,.2f} Net Loss: ${2:,.2f}"
.format(tot_int, tot_prn, L - tot_prn - recoveries, tot_rec))
def plot_bank_run(dyn_params, opt_params, capital, income, losses, assets, bankrupt):
# figure size in inches
rcParams['figure.figsize'] = 8,4.5
rcParams['font.size'] = 16
plt.tight_layout()
N = len(capital)
if bankrupt:
N -= 1
capital = capital[:N]
income = income[:N]
losses = losses[:N]
assets = assets[:N]
ax = plt.subplot()
ax.plot(range(N), capital, 'g', label='Capital', )
ax.plot(range(N), income, 'c', label='Income')
ax.plot(range(N), losses, 'r', label='Losses')
ax.yaxis.set_major_formatter(tkr.StrMethodFormatter('${x:,.0f}'))
ax.xaxis.set_major_locator(plt.MultipleLocator(4))
ax.legend()
plt.title("Lending Club bank: {0:.0f}Y performance \n Threshold {1:.3f}, leverage {2:2d}:1, Loss delay {3:d}M"
.format(N/4, opt_params['threshold'], opt_params['leverage_ratio'],
opt_params['loss_delay']))
skip_ratios = True
if skip_ratios:
ann_ret_exponent = float(12) / float(dyn_params['inv_cycle'])
ROA = (np.array(income) - np.array(losses)) / np.array(assets)
ROA = np.power(ROA + 1, ann_ret_exponent) - 1
prev_capital = np.zeros(N)
prev_capital[0] = opt_params['starting_capital']
prev_capital[1:] = capital[:N-1]
next_capital = np.array(capital)
ROC = (next_capital - prev_capital)/prev_capital
ROC = np.power(ROC+1, ann_ret_exponent) - 1
LR = np.array(losses) / np.array(assets)
LR = np.power(LR+1, ann_ret_exponent) - 1
#ax = plt.subplot(3,1,2)
#ax.plot(range(1,N), ROC[1:], label='Return on Capital')
#ax.yaxis.set_major_formatter(tkr.StrMethodFormatter('{x:,.4f}'))
#ax.xaxis.set_major_locator(plt.MultipleLocator(4))
#plt.legend()
#ax = plt.subplot(3,1,3)
#ax.plot(range(1,N), LR[1:], label='Loss Ratio')
#ax.plot(range(1,N), ROA[1:], label='Return on Assets')
#ax.yaxis.set_major_formatter(tkr.StrMethodFormatter('{x:,.4f}'))
#ax.xaxis.set_major_locator(plt.MultipleLocator(4))
#plt.legend()
plt.xlabel("Quarters")
plt.show()
def bank_run(dyn_params, dec_params, do_print=False, do_plot=False):
# sampled loans
df_list = dyn_params['sample_df_list']
# Initial cash
cash = dec_params['starting_capital']
# Initial assets
assets = 0
# Initial liabilities
liabilities = 0
# Initial capital
capital = cash + assets - liabilities
# Series to output
asset_series = []
capital_series = []
income_series = []
losses_series = []
# Monthly rate on loan
rate_3M = (dyn_params['inv_cycle'] / 12) * (dec_params['loan_interest_rate']/100 )
# Set up data structures
interest_income = np.zeros(3 * dyn_params['length_of_run'])
principal_pymnt = np.zeros(3 * dyn_params['length_of_run'])
loss_recognized = np.zeros(3 * dyn_params['length_of_run'] + dec_params['loss_delay'])
# Initial values for run
old_loan = 0
old_d = 0
n = 0
bankrupt = False
for d in range(dyn_params['inv_cycle'] ,1+dyn_params['length_of_run'],dyn_params['inv_cycle']):
# Borrow
new_loan = dec_params['leverage_ratio'] * capital
cash += new_loan
# Pay back old loan
cash -= old_loan
# Invest everything
to_invest = max(0, cash)
if to_invest > 0.0:
# Make investments
invested_df, selected_df = \
evaluate_invest(df_list[n], to_invest, dec_params['threshold'])
n+=1
# Total actually invested
invested = invested_df['loan_amnt'].sum()
# Update cash balance
cash -= invested
# Update assets
assets += invested
# Calculate outcomes of new investment
int_series, prn_series, lss_series = generate_series(invested_df, dec_params['loss_delay'])
# Add new outcomes to tails of old outcomes
interest_income[old_d: len(int_series) + old_d] += int_series
principal_pymnt[old_d: len(prn_series) + old_d] += prn_series
loss_recognized[old_d: len(lss_series) + old_d] += lss_series
if do_print:
print("Month: {0:2d} \t New investment ${1:,.2f} New loan ${2:,.2f}".format(d, invested, new_loan))
# Calculate interest, principal, losses from old_d to d
int_calc = interest_income[old_d:d].sum()
prn_calc = principal_pymnt[old_d:d].sum()
loss_calc = loss_recognized[old_d:d].sum()
# Loan interest due
int_loan = new_loan * (rate_3M)
# Update cash on hand
cash += int_calc
cash += prn_calc
cash -= int_loan
if do_print:
print(" \t Income: {1:,.2f} Expense: {2:,.2f} Net income: {3:,.2f} Cash: {4:,.2f}"
.format(d, int_calc, int_loan, int_calc - int_loan, cash))
print(" \t Loss ratio {0:,.2f}".format(loss_calc/assets))
# Update assets - deduct losses from assets
assets -= (loss_calc + prn_calc)
# Update liabilities
liabilities -= old_loan
liabilities += new_loan
# Balance sheet
capital = cash + assets - liabilities
if do_print:
print(" \t Assets: {1:,.2f} Liabilities: {2:,.2f} Capital: {3:,.2f} \n"
.format(d, assets, liabilities, capital))
# Record
asset_series.append(assets)
capital_series.append(capital)
income_series.append(int_calc - int_loan)
losses_series.append(loss_calc)
# Bankrupt!
if capital < 0:
bankrupt = True
print("Bankrupt!")
break
# Update
old_d = d
old_loan = new_loan
if do_plot:
plot_bank_run(dyn_params, dec_params, capital_series, income_series, losses_series, asset_series, bankrupt)
return capital_series, income_series, losses_series, asset_series, bankrupt
# Define train, test, and validate df
train_df = data_df.loc[idx_train, :]
test_df = data_df.loc[idx_test, :]
validate_df = data_df.loc[idx_validate, :]
print("Number of loans in Train set: {}".format(train_df.shape[0]))
print("Number of loans in Test set: {}".format(test_df.shape[0]))
print("Number of loans in Validate set: {}".format(validate_df.shape[0]))
# Just for sanity, print the scores and features for the classifier
print_score(clf_core, train_df[core_features], train_df['LoanStatus'], test_df[core_features], test_df['LoanStatus'],
plot_features=True, features=core_features)
# select criterion
gain_col = 'TotalGain'
test_df['score'] = clf_core.predict_proba(test_df[core_features])[:,1]
opt_threshold = calc_threshold(test_df, gain_col)
print("Threshold is {0:.4f}".format(opt_threshold))
# Generate sample of loans
sample_params = {'inv_cycle': 3,
'sample_size': 2000,
'length_of_run': 120,
'sample_df_list': []
}
sample_df_list = sample_params['sample_df_list']
for d in range(sample_params['inv_cycle'] ,1 + sample_params['length_of_run'], sample_params['inv_cycle']):
# Generate sample from validate set
sample_df = validate_df.sample(sample_params['sample_size'], replace=True)
# Score sampled data
sample_df['score'] = clf_core.predict_proba(sample_df[core_features])[:,1]
sample_df_list.append(sample_df)
# Simulate the bank
opt_params = {'loss_delay': 3,
'starting_capital': 1e6,
'leverage_ratio': 10,
'loan_interest_rate': 3.0,
'threshold': opt_threshold - 0.1
}
capital, income, losses, assets, bankrupt = bank_run(sample_params, opt_params, do_print=False, do_plot=True)
| 0.392686 | 0.742106 |
```
from tqdm.std import tqdm, trange
from tqdm import notebook
notebook.tqdm = tqdm
notebook.trange = trange
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch import nn
from torchvision import datasets
from torchvision.transforms import ToTensor
from torch.utils.data import DataLoader
# Load the data
training_data = datasets.MNIST(
root="data",
train=True,
download=True,
transform=ToTensor(),
)
test_data = datasets.MNIST(
root="data",
train=False,
download=True,
transform=ToTensor(),
)
class ThreeBlue(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.layers = nn.Sequential(
nn.Linear(784,10)
)
def forward(self,x):
y = self.flatten(x)
z = self.layers(y)
return z
wed = ThreeBlue()
class ThreeBlue(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.layers = nn.Sequential(
nn.Linear(784,16),
nn.Sigmoid(),
nn.Linear(16,16),
nn.Sigmoid(),
nn.Linear(16,10),
nn.Sigmoid()
)
def forward(self,x):
x = x/255
y = self.flatten(x)
z = self.layers(y)
return z
wed = ThreeBlue()
for p in wed.parameters():
print(p.shape)
for p in wed.parameters():
print(p.numel())
sum([p.numel() for p in wed.parameters()])
sum(p.numel() for p in wed.parameters())
wed
wed.layers
wed.layers[2]
wed.layers[2].weight.shape
wed.layers[2].bias.shape
wed(training_data.data)[:3]
y_pred = wed(training_data.data)
training_data.targets[:3]
from torch.nn.functional import one_hot
one_hot(training_data.targets[:3], num_classes=10).to(torch.float)
y_true = one_hot(training_data.targets, num_classes=10).to(torch.float)
y_true.shape
loss_fn = nn.MSELoss()
loss_fn(y_pred, y_true)
optimizer = torch.optim.SGD(wed.parameters(), lr=0.1)
for p in wed.parameters():
print(p.grad)
loss = loss_fn(y_pred, y_true)
for p in wed.parameters():
print(p.grad)
loss.backward()
for p in wed.parameters():
print(p.grad)
optimizer.step()
wed(training_data.data)[:3]
epochs = 10
for i in range(epochs):
y_true = one_hot(training_data.targets, num_classes=10).to(torch.float)
y_pred = wed(training_data.data)
loss = loss_fn(y_true,y_pred)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(loss)
epochs = 100
for i in range(epochs):
y_true = one_hot(training_data.targets, num_classes=10).to(torch.float)
y_pred = wed(training_data.data)
loss = loss_fn(y_true,y_pred)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if i%2 == 0:
print(loss)
wed = ThreeBlue()
optimizer = torch.optim.SGD(wed.parameters(), lr=500)
epochs = 10
for i in range(epochs):
y_true = one_hot(training_data.targets, num_classes=10).to(torch.float)
y_pred = wed(training_data.data)
loss = loss_fn(y_true,y_pred)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(loss)
```
|
github_jupyter
|
from tqdm.std import tqdm, trange
from tqdm import notebook
notebook.tqdm = tqdm
notebook.trange = trange
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch import nn
from torchvision import datasets
from torchvision.transforms import ToTensor
from torch.utils.data import DataLoader
# Load the data
training_data = datasets.MNIST(
root="data",
train=True,
download=True,
transform=ToTensor(),
)
test_data = datasets.MNIST(
root="data",
train=False,
download=True,
transform=ToTensor(),
)
class ThreeBlue(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.layers = nn.Sequential(
nn.Linear(784,10)
)
def forward(self,x):
y = self.flatten(x)
z = self.layers(y)
return z
wed = ThreeBlue()
class ThreeBlue(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.layers = nn.Sequential(
nn.Linear(784,16),
nn.Sigmoid(),
nn.Linear(16,16),
nn.Sigmoid(),
nn.Linear(16,10),
nn.Sigmoid()
)
def forward(self,x):
x = x/255
y = self.flatten(x)
z = self.layers(y)
return z
wed = ThreeBlue()
for p in wed.parameters():
print(p.shape)
for p in wed.parameters():
print(p.numel())
sum([p.numel() for p in wed.parameters()])
sum(p.numel() for p in wed.parameters())
wed
wed.layers
wed.layers[2]
wed.layers[2].weight.shape
wed.layers[2].bias.shape
wed(training_data.data)[:3]
y_pred = wed(training_data.data)
training_data.targets[:3]
from torch.nn.functional import one_hot
one_hot(training_data.targets[:3], num_classes=10).to(torch.float)
y_true = one_hot(training_data.targets, num_classes=10).to(torch.float)
y_true.shape
loss_fn = nn.MSELoss()
loss_fn(y_pred, y_true)
optimizer = torch.optim.SGD(wed.parameters(), lr=0.1)
for p in wed.parameters():
print(p.grad)
loss = loss_fn(y_pred, y_true)
for p in wed.parameters():
print(p.grad)
loss.backward()
for p in wed.parameters():
print(p.grad)
optimizer.step()
wed(training_data.data)[:3]
epochs = 10
for i in range(epochs):
y_true = one_hot(training_data.targets, num_classes=10).to(torch.float)
y_pred = wed(training_data.data)
loss = loss_fn(y_true,y_pred)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(loss)
epochs = 100
for i in range(epochs):
y_true = one_hot(training_data.targets, num_classes=10).to(torch.float)
y_pred = wed(training_data.data)
loss = loss_fn(y_true,y_pred)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if i%2 == 0:
print(loss)
wed = ThreeBlue()
optimizer = torch.optim.SGD(wed.parameters(), lr=500)
epochs = 10
for i in range(epochs):
y_true = one_hot(training_data.targets, num_classes=10).to(torch.float)
y_pred = wed(training_data.data)
loss = loss_fn(y_true,y_pred)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(loss)
| 0.923087 | 0.650044 |
#### libraries to be imported first
```
#importing libraries
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn import linear_model
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.model_selection import GridSearchCV
from matplotlib import pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
```
#### read data to a dataset
```
#read csv
train = pd.read_csv('train.csv')
train
#shape of the dataset imported
train.shape
#go through the dataset, mean and everything listed below in the results
train.describe()
#columns name, .keys() can be used as well for this
train.columns
#dropping duplicates if any?
train.drop_duplicates(keep='first')
```
##### looks like no duplicate record is there, thats awesome:)
```
#correlation matrix using corr() fuction; will have to look for any multicolinearity if any
corr = train.corr()
corr = corr.SalePrice.sort_values(ascending=False)
#filtering for "SalesPrice" columns by sorting it in descending order
corr
```
definatly there is correlations between few columns ....
#### Analysis of the data ; EDA; but first looking at the data, duplicates, missng values and all
For imputing we can impute using any method, like for numercial columns we can use mean,median kind of values to be imputed, so is used in the below approach.
Well as the data dictionary informs us regarding the categorical columns or features, that for some categories, the value "NaN" actually means something. So looking at that , we are going to fill in a value like 'none' for instance so that we can keep that information with us and do not make any changes in the analysis by dropping them.
```
#look at the null values as shown
train_data_nulls = pd.isnull(train).sum()
train_data_nulls = train_data_nulls.to_frame("Traning_data")
train_data_nulls
#as per the data dictionary we could find below mentioned features where the null means somehting
something_null_in_data = ["Alley", "BsmtQual", "BsmtCond", "BsmtExposure", "BsmtFinType1", "BsmtFinType2", "FireplaceQu", "GarageType", "GarageFinish", "GarageQual", "GarageCond", "PoolQC", "Fence", "MiscFeature"]
#as mentioned above we are imputing 'none', in place of NA in the dataset to make it more meaningful
for i in something_null_in_data:
train[i].fillna("None", inplace=True)
```
##### now look at more imputing of data
```
#using the imputer from sklearn as below for helping out with this
from sklearn.preprocessing import Imputer
imputer = Imputer(strategy="median")
#again checking the null values, as its important to find them out and make sure they are used properly, since they mean somehitng
train_null_data = pd.isnull(train).sum()
train_null_data = train_null_data.to_frame("TRaining_data")
train_null_data
#checking if there are many values missibg let say > 200
train_null_data[train_null_data.sum(axis=1) > 200]
```
###### LotFrontage has too many Null values(i.e. > 200), may be better to just drop it as it is a numerical value feature, can't do much about it, hence dropping it
```
#dropped
train.drop("LotFrontage", axis=1, inplace=True)
#looking at the null values which are not that greater than 200, may be called as less number of nulls
train_not_many_nulls = train_null_data[(train_null_data.sum(axis=1) > 0) & (train_null_data.sum(axis=1) < 200)]
train_not_many_nulls
#imputing them all..... to make sure they don't cause troubles while creating models
train.GarageYrBlt.fillna(train["GarageYrBlt"].median(), inplace=True)
train.MasVnrArea.fillna(train["MasVnrArea"].median(), inplace=True)
train.MasVnrType.fillna("None", inplace=True)
train.Electrical.fillna("None", inplace=True)
#handling fewer missing ones, first organising the features as per numeric and categorical manner
train_dtypes = train.dtypes
train_numeric_features = train_dtypes[(train_dtypes != object) ]
train_categorical_feature = train_dtypes[train_dtypes == object]
#Converting num_features to list and then traversing it to impute as shown.......
train_numeric_val = list(train_numeric_features.index)
train_filled_numercal_data = []
for i in train_numeric_val:
if i in list(train_not_many_nulls.index):
train_filled_numercal_data.append(i)
train_filled_numercal_data
for i in train_filled_numercal_data:
train[i].fillna(train[i].median(), inplace=True)
```
##### as we Imputed the numeric features doing the same with the Categorically one with the method mentioned earlier
```
categorical_value_train = list(train_categorical_feature.index)
train_filled_categorical_data = []
for x in categorical_value_train:
if x in list(train_not_many_nulls.index):
train_filled_categorical_data.append(x)
train_filled_categorical_data
```
well this must be it, now we can finally proceed towards model building....
```
# recheking again to make sure.... before we go with actual..
train_null_data = pd.isnull(train).sum()
train_null_data = train_null_data.to_frame("Training_data")
train_null_data[train_null_data.sum(axis=1) > 0]
```
now we can see that its not having any null data....
```
sns.distplot(train["SalePrice"]);
sns.distplot(np.log(train["SalePrice"]));
```
So looking at the graphs it seems tat we need to transform the prices that would make sure tha the model's performance is boosted. As its skewed, we are going to transform....
```
train["TransformedPrice"] = np.log(train["SalePrice"])
```
Categorical features awaits, we are goinging to look at them next...
```
#creating a list of them firts and look at them further
categorical_values_train = list(train_categorical_feature.index)
categorical_values_train
#changing categorical values to representative number
for x in categorical_values_train:
train_feature_set = set(train[x])
for y in train_feature_set:
feature_list = list(train_feature_set)
train.loc[train[x] == y, x] = feature_list.index(y)
train.head()
```
now we are finally going to model buildng, here we go.....
```
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_squared_error
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score, KFold
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge
from sklearn.tree import DecisionTreeRegressor
warnings.filterwarnings("ignore", category=DeprecationWarning)
```
##### working further on train and test sets further
```
X_t = train.drop(["Id", "SalePrice", "TransformedPrice"], axis=1).values
y_t = train["TransformedPrice"].values
```
#### Split for train and test
```
from sklearn.model_selection import train_test_split #to create test data set
# scale
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(X_t)
# split
X_train, X_test, y_train, y_test = train_test_split(X_t, y_t, test_size = 0.3,random_state = 1)
```
##### As learned in the program we need to have a Split into Validation set as well from train set...
for evaluating the model and to avoid the ovefitting phenomeon we are further going to split our training data into a small validation sets.
```
X_train, X_valid, y_train, y_valid = train_test_split(X_train, y_train, test_size=0.15, random_state=0)
```
##### Now lets get ti Linear Regression Model buildng
```
linreg = LinearRegression()
parameters_lin = {"fit_intercept" : [True, False], "normalize" : [True, False], "copy_X" : [True, False]}
grid_linreg = GridSearchCV(linreg, parameters_lin, verbose=1 , scoring = "r2")
grid_linreg.fit(X_train, y_train)
grid_linreg.best_estimator_
str(grid_linreg.best_score_)
linreg = grid_linreg.best_estimator_
linreg.fit(X_train, y_train)
lin_pred = linreg.predict(X_valid)
r2_lin = r2_score(y_valid, lin_pred)
rmse_lin = np.sqrt(mean_squared_error(y_valid, lin_pred))
str(rmse_lin)
str(r2_lin)
scores_lin = cross_val_score(linreg, X_train, y_train, cv=10, scoring="r2")
np.mean(scores_lin)
```
##### Let look at the Lasso Model(building and analysis)
```
folds = KFold(n_splits = 5, shuffle = True, random_state = 4)
#number of alphas to tune....
params = {'alpha': [0.0001, 0.001, 0.01, 0.05, 0.1]}
lasso = Lasso()
# cross validation
lasso_grid = GridSearchCV(estimator = lasso, param_grid = params,scoring= 'neg_mean_absolute_error', cv = folds, return_train_score=True,verbose = 1)
lasso_grid.fit(X_train, y_train)
lasso = lasso_grid.best_estimator_
lasso.fit(X_train, y_train)
lasso_pred = lasso.predict(X_valid)
r2_lasso = r2_score(y_valid, lasso_pred)
rmse_lasso = np.sqrt(mean_squared_error(y_valid, lasso_pred))
str(r2_lasso)
str(rmse_lasso)
scores_lasso = cross_val_score(lasso, X_train, y_train, cv=10, scoring="r2")
str(np.mean(scores_lasso))
cv_results = pd.DataFrame(lasso_grid.cv_results_)
cv_results.head()
# plotting mean test and train scoes with alpha
cv_results['param_alpha'] = cv_results['param_alpha'].astype('float32')
# plotting
plt.plot(cv_results['param_alpha'], cv_results['mean_train_score'])
plt.plot(cv_results['param_alpha'], cv_results['mean_test_score'])
plt.xlabel('alpha')
plt.ylabel('Neg. Mean Abs Err')
plt.title("Mean Absolute Error(Negative) and alpha")
plt.legend(['train score', 'test score'], loc='upper left')
plt.show()
alpha =0.001
lasso = Lasso(alpha=alpha)
lasso.fit(X_train, y_train)
lasso.coef_
# lasso model parameters
model_parameters = list(lasso.coef_)
model_parameters.insert(0, lasso.intercept_)
model_parameters = [round(x, 3) for x in model_parameters]
cols = train.columns
cols = cols.insert(0, "constant")
list(zip(cols, model_parameters))
```
HouseStyle,OverallQual,MasVnrArea,GrLivArea,Functional -- here are few features that can be selected
##### looking at the Ridge Model
```
# alfas to tune
params = {'alpha': [0.001, 0.01, 1.0, 5.0, 10.0]}
ridge = Ridge()
# cross validation .....
folds = KFold(n_splits = 5, shuffle = True, random_state = 4)
grid_ridge = GridSearchCV(estimator = ridge,
param_grid = params,
scoring= 'neg_mean_absolute_error',
cv = folds,
return_train_score=True,
verbose = 1)
grid_ridge.fit(X_train, y_train)
str(grid_ridge.best_estimator_)
str(grid_ridge.best_score_)
ridge = grid_ridge.best_estimator_
ridge.fit(X_train, y_train)
ridge_pred = ridge.predict(X_valid)
r2_ridge = r2_score(y_valid, ridge_pred)
rmse_ridge = np.sqrt(mean_squared_error(y_valid, ridge_pred))
str(r2_ridge)
str(rmse_ridge)
scores_ridge = cross_val_score(ridge, X_train, y_train, cv=10, scoring="r2")
#cross validatiopn score
np.mean(scores_ridge)
print("Sorted by R Squared:")
model_perfor.sort_values(by="R Squared", ascending=False)
cv_results = pd.DataFrame(grid_ridge.cv_results_)
cv_results = cv_results[cv_results['param_alpha']<=200]
cv_results.head()
# plotting mean test and train scoes with alpha
cv_results['param_alpha'] = cv_results['param_alpha'].astype('int32')
# plotting
plt.plot(cv_results['param_alpha'], cv_results['mean_train_score'])
plt.plot(cv_results['param_alpha'], cv_results['mean_test_score'])
plt.xlabel('alpha')
plt.ylabel('Negative Mean Abs Error')
plt.legend(['train score', 'test score'], loc='upper left')
plt.show()
#made choice from above
alpha =10
ridge = Ridge(alpha=alpha)
ridge.fit(X_train, y_train)
ridge.coef_
# R model parameters
model_parameters = list(ridge.coef_)
model_parameters.insert(0, ridge.intercept_)
model_parameters = [round(x, 3) for x in model_parameters]
cols = train.columns
cols = cols.insert(0, "constant")
list(zip(cols, model_parameters))
```
looking at the variables above we can choose the right ones, and the create a linear model to see the progress
|
github_jupyter
|
#importing libraries
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn import linear_model
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.model_selection import GridSearchCV
from matplotlib import pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
#read csv
train = pd.read_csv('train.csv')
train
#shape of the dataset imported
train.shape
#go through the dataset, mean and everything listed below in the results
train.describe()
#columns name, .keys() can be used as well for this
train.columns
#dropping duplicates if any?
train.drop_duplicates(keep='first')
#correlation matrix using corr() fuction; will have to look for any multicolinearity if any
corr = train.corr()
corr = corr.SalePrice.sort_values(ascending=False)
#filtering for "SalesPrice" columns by sorting it in descending order
corr
#look at the null values as shown
train_data_nulls = pd.isnull(train).sum()
train_data_nulls = train_data_nulls.to_frame("Traning_data")
train_data_nulls
#as per the data dictionary we could find below mentioned features where the null means somehting
something_null_in_data = ["Alley", "BsmtQual", "BsmtCond", "BsmtExposure", "BsmtFinType1", "BsmtFinType2", "FireplaceQu", "GarageType", "GarageFinish", "GarageQual", "GarageCond", "PoolQC", "Fence", "MiscFeature"]
#as mentioned above we are imputing 'none', in place of NA in the dataset to make it more meaningful
for i in something_null_in_data:
train[i].fillna("None", inplace=True)
#using the imputer from sklearn as below for helping out with this
from sklearn.preprocessing import Imputer
imputer = Imputer(strategy="median")
#again checking the null values, as its important to find them out and make sure they are used properly, since they mean somehitng
train_null_data = pd.isnull(train).sum()
train_null_data = train_null_data.to_frame("TRaining_data")
train_null_data
#checking if there are many values missibg let say > 200
train_null_data[train_null_data.sum(axis=1) > 200]
#dropped
train.drop("LotFrontage", axis=1, inplace=True)
#looking at the null values which are not that greater than 200, may be called as less number of nulls
train_not_many_nulls = train_null_data[(train_null_data.sum(axis=1) > 0) & (train_null_data.sum(axis=1) < 200)]
train_not_many_nulls
#imputing them all..... to make sure they don't cause troubles while creating models
train.GarageYrBlt.fillna(train["GarageYrBlt"].median(), inplace=True)
train.MasVnrArea.fillna(train["MasVnrArea"].median(), inplace=True)
train.MasVnrType.fillna("None", inplace=True)
train.Electrical.fillna("None", inplace=True)
#handling fewer missing ones, first organising the features as per numeric and categorical manner
train_dtypes = train.dtypes
train_numeric_features = train_dtypes[(train_dtypes != object) ]
train_categorical_feature = train_dtypes[train_dtypes == object]
#Converting num_features to list and then traversing it to impute as shown.......
train_numeric_val = list(train_numeric_features.index)
train_filled_numercal_data = []
for i in train_numeric_val:
if i in list(train_not_many_nulls.index):
train_filled_numercal_data.append(i)
train_filled_numercal_data
for i in train_filled_numercal_data:
train[i].fillna(train[i].median(), inplace=True)
categorical_value_train = list(train_categorical_feature.index)
train_filled_categorical_data = []
for x in categorical_value_train:
if x in list(train_not_many_nulls.index):
train_filled_categorical_data.append(x)
train_filled_categorical_data
# recheking again to make sure.... before we go with actual..
train_null_data = pd.isnull(train).sum()
train_null_data = train_null_data.to_frame("Training_data")
train_null_data[train_null_data.sum(axis=1) > 0]
sns.distplot(train["SalePrice"]);
sns.distplot(np.log(train["SalePrice"]));
train["TransformedPrice"] = np.log(train["SalePrice"])
#creating a list of them firts and look at them further
categorical_values_train = list(train_categorical_feature.index)
categorical_values_train
#changing categorical values to representative number
for x in categorical_values_train:
train_feature_set = set(train[x])
for y in train_feature_set:
feature_list = list(train_feature_set)
train.loc[train[x] == y, x] = feature_list.index(y)
train.head()
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_squared_error
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score, KFold
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge
from sklearn.tree import DecisionTreeRegressor
warnings.filterwarnings("ignore", category=DeprecationWarning)
X_t = train.drop(["Id", "SalePrice", "TransformedPrice"], axis=1).values
y_t = train["TransformedPrice"].values
from sklearn.model_selection import train_test_split #to create test data set
# scale
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(X_t)
# split
X_train, X_test, y_train, y_test = train_test_split(X_t, y_t, test_size = 0.3,random_state = 1)
X_train, X_valid, y_train, y_valid = train_test_split(X_train, y_train, test_size=0.15, random_state=0)
linreg = LinearRegression()
parameters_lin = {"fit_intercept" : [True, False], "normalize" : [True, False], "copy_X" : [True, False]}
grid_linreg = GridSearchCV(linreg, parameters_lin, verbose=1 , scoring = "r2")
grid_linreg.fit(X_train, y_train)
grid_linreg.best_estimator_
str(grid_linreg.best_score_)
linreg = grid_linreg.best_estimator_
linreg.fit(X_train, y_train)
lin_pred = linreg.predict(X_valid)
r2_lin = r2_score(y_valid, lin_pred)
rmse_lin = np.sqrt(mean_squared_error(y_valid, lin_pred))
str(rmse_lin)
str(r2_lin)
scores_lin = cross_val_score(linreg, X_train, y_train, cv=10, scoring="r2")
np.mean(scores_lin)
folds = KFold(n_splits = 5, shuffle = True, random_state = 4)
#number of alphas to tune....
params = {'alpha': [0.0001, 0.001, 0.01, 0.05, 0.1]}
lasso = Lasso()
# cross validation
lasso_grid = GridSearchCV(estimator = lasso, param_grid = params,scoring= 'neg_mean_absolute_error', cv = folds, return_train_score=True,verbose = 1)
lasso_grid.fit(X_train, y_train)
lasso = lasso_grid.best_estimator_
lasso.fit(X_train, y_train)
lasso_pred = lasso.predict(X_valid)
r2_lasso = r2_score(y_valid, lasso_pred)
rmse_lasso = np.sqrt(mean_squared_error(y_valid, lasso_pred))
str(r2_lasso)
str(rmse_lasso)
scores_lasso = cross_val_score(lasso, X_train, y_train, cv=10, scoring="r2")
str(np.mean(scores_lasso))
cv_results = pd.DataFrame(lasso_grid.cv_results_)
cv_results.head()
# plotting mean test and train scoes with alpha
cv_results['param_alpha'] = cv_results['param_alpha'].astype('float32')
# plotting
plt.plot(cv_results['param_alpha'], cv_results['mean_train_score'])
plt.plot(cv_results['param_alpha'], cv_results['mean_test_score'])
plt.xlabel('alpha')
plt.ylabel('Neg. Mean Abs Err')
plt.title("Mean Absolute Error(Negative) and alpha")
plt.legend(['train score', 'test score'], loc='upper left')
plt.show()
alpha =0.001
lasso = Lasso(alpha=alpha)
lasso.fit(X_train, y_train)
lasso.coef_
# lasso model parameters
model_parameters = list(lasso.coef_)
model_parameters.insert(0, lasso.intercept_)
model_parameters = [round(x, 3) for x in model_parameters]
cols = train.columns
cols = cols.insert(0, "constant")
list(zip(cols, model_parameters))
# alfas to tune
params = {'alpha': [0.001, 0.01, 1.0, 5.0, 10.0]}
ridge = Ridge()
# cross validation .....
folds = KFold(n_splits = 5, shuffle = True, random_state = 4)
grid_ridge = GridSearchCV(estimator = ridge,
param_grid = params,
scoring= 'neg_mean_absolute_error',
cv = folds,
return_train_score=True,
verbose = 1)
grid_ridge.fit(X_train, y_train)
str(grid_ridge.best_estimator_)
str(grid_ridge.best_score_)
ridge = grid_ridge.best_estimator_
ridge.fit(X_train, y_train)
ridge_pred = ridge.predict(X_valid)
r2_ridge = r2_score(y_valid, ridge_pred)
rmse_ridge = np.sqrt(mean_squared_error(y_valid, ridge_pred))
str(r2_ridge)
str(rmse_ridge)
scores_ridge = cross_val_score(ridge, X_train, y_train, cv=10, scoring="r2")
#cross validatiopn score
np.mean(scores_ridge)
print("Sorted by R Squared:")
model_perfor.sort_values(by="R Squared", ascending=False)
cv_results = pd.DataFrame(grid_ridge.cv_results_)
cv_results = cv_results[cv_results['param_alpha']<=200]
cv_results.head()
# plotting mean test and train scoes with alpha
cv_results['param_alpha'] = cv_results['param_alpha'].astype('int32')
# plotting
plt.plot(cv_results['param_alpha'], cv_results['mean_train_score'])
plt.plot(cv_results['param_alpha'], cv_results['mean_test_score'])
plt.xlabel('alpha')
plt.ylabel('Negative Mean Abs Error')
plt.legend(['train score', 'test score'], loc='upper left')
plt.show()
#made choice from above
alpha =10
ridge = Ridge(alpha=alpha)
ridge.fit(X_train, y_train)
ridge.coef_
# R model parameters
model_parameters = list(ridge.coef_)
model_parameters.insert(0, ridge.intercept_)
model_parameters = [round(x, 3) for x in model_parameters]
cols = train.columns
cols = cols.insert(0, "constant")
list(zip(cols, model_parameters))
| 0.541409 | 0.857351 |
### Importing Libraries
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import librosa
import tensorflow as tf
from tensorflow import keras
```
### Choosing Model
```
my_model = keras.Sequential([
keras.layers.Dense(units=313, activation='relu'),
keras.layers.Dense(units=192, activation='relu'),
keras.layers.Dense(units=128, activation='relu'),
keras.layers.Dense(units=3, activation='softmax')
])
my_model.load_weights('saved_model/dnn')
my_model.compile(optimizer='adam',
loss=tf.losses.CategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
```
### Inference
```
def evaluate(spectrogram_path):
spec = np.load(spectrogram_path)
spec = spec.T
output = []
for i in range(spec.shape[0]):
x = spec[i].reshape(1,-1)
y = my_model.predict(tf.convert_to_tensor(x))
if y[0][0] >= y[0][1] and y[0][0] >= y[0][2]:
output.append('Music')
elif y[0][1] >= y[0][0] and y[0][1] >= y[0][2]:
output.append('Speech')
elif y[0][2] >= y[0][1] and y[0][2] >= y[0][0]:
output.append('Silence')
return output
def erode_and_dillate(output):
res = output
for i in range(1, len(output)-1):
if output[i-1] == output[i+1]:
res[i] = output[i-1]
res[0] = res[1]
res[len(output)-1] = res[len(output)-2]
for i in range(1, len(output)-1):
if res[len(output)-2-i] == res[len(output)-i] :
res[len(output)-1-i] = res[len(output)-2-i]
return res
def detect_timestamps(output):
timestamps = []
events = []
curr = ""
start_frame = 0
end_frame = 0
for idx, class_ in enumerate(output):
if curr == class_:
end_frame += 1
elif curr == "":
curr = class_
start_frame = idx
end_frame = start_frame
else:
events.append(curr)
timestamps.append((start_frame, end_frame))
curr = class_
start_frame = idx
end_frame = start_frame
events.append(class_)
timestamps.append([start_frame, end_frame])
return events, timestamps
def filter_timestamps(events, timestamps, threshold=32):
assert len(events) == len(timestamps)
events_new = []
event_times = []
for i in range(len(events)):
if events[i] == 'silence' :
continue
elif timestamps[i][1] - timestamps[i][0] >= threshold:
event_times.append([(timestamps[i][0]/312)*10, (timestamps[i][1]/312)*10])
events_new.append(events[i])
return events_new, event_times
import os
test_spectrogram_file_path = "./Test Data_AED/"
filenames = os.listdir(test_spectrogram_file_path)
task1 = [['filename', 'event', 'onset', 'offset']]
task2 = [['filename', 'Music', 'Speech']]
for file in filenames:
output = evaluate(test_spectrogram_file_path + file)
output = erode_and_dillate(output)
events, timestamps = detect_timestamps(output)
events, event_times = filter_timestamps(events, timestamps, 32)
for i in range(len(events)):
y1 = [file.split('.')[0], events[i], event_times[i][0], event_times[i][1]]
task1.append(y1)
music_present = 0
speech_present = 0
for event in events :
if event == 'Music' :
music_present = 1
elif event == 'Speech' :
speech_present = 1
task2.append([file.split('.')[0], music_present, speech_present])
for i in range(len(task1)):
print(task1[i][0], ',', task1[i][1], ',', task1[i][2], ',', task1[i][3], sep='')
for i in range(len(task2)):
print(task2[i][0], ',', task2[i][1], ',', task2[i][2], sep='')
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import librosa
import tensorflow as tf
from tensorflow import keras
my_model = keras.Sequential([
keras.layers.Dense(units=313, activation='relu'),
keras.layers.Dense(units=192, activation='relu'),
keras.layers.Dense(units=128, activation='relu'),
keras.layers.Dense(units=3, activation='softmax')
])
my_model.load_weights('saved_model/dnn')
my_model.compile(optimizer='adam',
loss=tf.losses.CategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
def evaluate(spectrogram_path):
spec = np.load(spectrogram_path)
spec = spec.T
output = []
for i in range(spec.shape[0]):
x = spec[i].reshape(1,-1)
y = my_model.predict(tf.convert_to_tensor(x))
if y[0][0] >= y[0][1] and y[0][0] >= y[0][2]:
output.append('Music')
elif y[0][1] >= y[0][0] and y[0][1] >= y[0][2]:
output.append('Speech')
elif y[0][2] >= y[0][1] and y[0][2] >= y[0][0]:
output.append('Silence')
return output
def erode_and_dillate(output):
res = output
for i in range(1, len(output)-1):
if output[i-1] == output[i+1]:
res[i] = output[i-1]
res[0] = res[1]
res[len(output)-1] = res[len(output)-2]
for i in range(1, len(output)-1):
if res[len(output)-2-i] == res[len(output)-i] :
res[len(output)-1-i] = res[len(output)-2-i]
return res
def detect_timestamps(output):
timestamps = []
events = []
curr = ""
start_frame = 0
end_frame = 0
for idx, class_ in enumerate(output):
if curr == class_:
end_frame += 1
elif curr == "":
curr = class_
start_frame = idx
end_frame = start_frame
else:
events.append(curr)
timestamps.append((start_frame, end_frame))
curr = class_
start_frame = idx
end_frame = start_frame
events.append(class_)
timestamps.append([start_frame, end_frame])
return events, timestamps
def filter_timestamps(events, timestamps, threshold=32):
assert len(events) == len(timestamps)
events_new = []
event_times = []
for i in range(len(events)):
if events[i] == 'silence' :
continue
elif timestamps[i][1] - timestamps[i][0] >= threshold:
event_times.append([(timestamps[i][0]/312)*10, (timestamps[i][1]/312)*10])
events_new.append(events[i])
return events_new, event_times
import os
test_spectrogram_file_path = "./Test Data_AED/"
filenames = os.listdir(test_spectrogram_file_path)
task1 = [['filename', 'event', 'onset', 'offset']]
task2 = [['filename', 'Music', 'Speech']]
for file in filenames:
output = evaluate(test_spectrogram_file_path + file)
output = erode_and_dillate(output)
events, timestamps = detect_timestamps(output)
events, event_times = filter_timestamps(events, timestamps, 32)
for i in range(len(events)):
y1 = [file.split('.')[0], events[i], event_times[i][0], event_times[i][1]]
task1.append(y1)
music_present = 0
speech_present = 0
for event in events :
if event == 'Music' :
music_present = 1
elif event == 'Speech' :
speech_present = 1
task2.append([file.split('.')[0], music_present, speech_present])
for i in range(len(task1)):
print(task1[i][0], ',', task1[i][1], ',', task1[i][2], ',', task1[i][3], sep='')
for i in range(len(task2)):
print(task2[i][0], ',', task2[i][1], ',', task2[i][2], sep='')
| 0.444565 | 0.771757 |
# Image annotations for a batch of samples
Using this notebook, cardiologists are able to quickly view and annotate MRI images for a batch of samples. These annotated images become the training data for the next round of modeling.
# Setup
<div class="alert alert-block alert-warning">
This notebook assumes
<ul>
<li><b>Terra</b> is running custom Docker image <kbd>ghcr.io/broadinstitute/ml4h/ml4h_terra:20210928_221837</kbd>.</li>
<li><b>ml4h</b> is running custom Docker image <kbd>gcr.io/broad-ml4cvd/deeplearning:tf2-latest-gpu</kbd>.</li>
</ul>
</div>

```
# TODO(deflaux): remove this cell after gcr.io/broad-ml4cvd/deeplearning:tf2-latest-gpu has this preinstalled.
from ml4h.runtime_data_defines import determine_runtime
from ml4h.runtime_data_defines import Runtime
if Runtime.ML4H_VM == determine_runtime():
!pip3 install --user ipycanvas==0.7.0 ipyannotations==0.2.1
!jupyter nbextension install --user --py ipycanvas
!jupyter nbextension enable --user --py ipycanvas
# Be sure to restart the kernel if pip installs anything.
# Also, shift-reload the browser page after the notebook extension installation.
from ipyannotations import BoxAnnotator, PointAnnotator, PolygonAnnotator
from ml4h.visualization_tools.annotation_storage import BigQueryAnnotationStorage
from ml4h.visualization_tools.batch_image_annotations import BatchImageAnnotator
import pandas as pd
import tensorflow as tf
%%javascript
// Display cell outputs to full height (no vertical scroll bar)
IPython.OutputArea.auto_scroll_threshold = 9999;
pd.set_option('display.max_colwidth', -1)
BIG_QUERY_ANNOTATIONS_STORAGE = BigQueryAnnotationStorage('uk-biobank-sek-data.ml_results.annotations')
```
# Define the batch of samples to annotate
<div class="alert alert-block alert-info">
Edit the CSV file path below, if needed, to either a local file or one in Cloud Storage.
</div>
```
#---[ EDIT AND RUN THIS CELL TO READ FROM A LOCAL FILE OR A FILE IN CLOUD STORAGE ]---
SAMPLE_BATCH_FILE = None
if SAMPLE_BATCH_FILE:
samples_df = pd.read_csv(tf.io.gfile.GFile(SAMPLE_BATCH_FILE))
else:
# Normally these would all be the same or similar TMAP. We are using different ones here just to make it
# more obvious in this demo that we are processing different samples.
samples_df = pd.DataFrame(
columns=BatchImageAnnotator.EXPECTED_COLUMN_NAMES,
data=[
[1655349, 'cine_lax_3ch_192', 25, 'gs://ml4cvd/deflaux/ukbb_tensors/'],
[1655349, 't2_flair_sag_p2_1mm_fs_ellip_pf78_1', 50, 'gs://ml4cvd/deflaux/ukbb_tensors/'],
[1655349, 'cine_lax_4ch_192', 25, 'gs://ml4cvd/deflaux/ukbb_tensors/'],
[1655349, 't2_flair_sag_p2_1mm_fs_ellip_pf78_2', 50, 'gs://ml4cvd/deflaux/ukbb_tensors/'],
[2403657, 'cine_lax_3ch_192', 25, 'gs://ml4cvd/deflaux/ukbb_tensors/'],
])
samples_df.shape
samples_df.head(n = 10)
```
# Annotate the batch!
## Annotate with points
Use points to annotate landmarks within the images.
```
# Note: a zoom level of 1.0 displays the tensor as-is. For higher zoom levels, this code currently
# use the PIL library to scale the image.
annotator = BatchImageAnnotator(samples=samples_df,
zoom=2.0,
annotation_categories=['region_of_interest'],
annotation_storage=BIG_QUERY_ANNOTATIONS_STORAGE,
annotator=PointAnnotator)
annotator.annotate_images()
```
## Annotate with polygons
Use polygons to annotate arbitrarily shaped regions within the images.
```
# Note: a zoom level of 1.0 displays the tensor as-is. For higher zoom levels, this code currently
# use the PIL library to scale the image.
annotator = BatchImageAnnotator(samples=samples_df,
zoom=2.0,
annotation_categories=['region_of_interest'],
annotation_storage=BIG_QUERY_ANNOTATIONS_STORAGE,
annotator=PolygonAnnotator)
annotator.annotate_images()
```
## Annotate with rectangles
Use rectangles to annotate rectangular regions within the image.
```
# Note: a zoom level of 1.0 displays the tensor as-is. For higher zoom levels, this code currently
# use the PIL library to scale the image.
annotator = BatchImageAnnotator(samples=samples_df,
zoom=2.0,
annotation_categories=['region_of_interest'],
annotation_storage=BIG_QUERY_ANNOTATIONS_STORAGE,
annotator=BoxAnnotator)
annotator.annotate_images()
```
# View the stored annotations
```
annotator.view_recent_submissions(count=10)
```
# Provenance
```
import datetime
print(datetime.datetime.now())
%%bash
pip3 freeze
```
Questions about these particular notebooks? Join the discussion https://github.com/broadinstitute/ml4h/discussions.
|
github_jupyter
|
# TODO(deflaux): remove this cell after gcr.io/broad-ml4cvd/deeplearning:tf2-latest-gpu has this preinstalled.
from ml4h.runtime_data_defines import determine_runtime
from ml4h.runtime_data_defines import Runtime
if Runtime.ML4H_VM == determine_runtime():
!pip3 install --user ipycanvas==0.7.0 ipyannotations==0.2.1
!jupyter nbextension install --user --py ipycanvas
!jupyter nbextension enable --user --py ipycanvas
# Be sure to restart the kernel if pip installs anything.
# Also, shift-reload the browser page after the notebook extension installation.
from ipyannotations import BoxAnnotator, PointAnnotator, PolygonAnnotator
from ml4h.visualization_tools.annotation_storage import BigQueryAnnotationStorage
from ml4h.visualization_tools.batch_image_annotations import BatchImageAnnotator
import pandas as pd
import tensorflow as tf
%%javascript
// Display cell outputs to full height (no vertical scroll bar)
IPython.OutputArea.auto_scroll_threshold = 9999;
pd.set_option('display.max_colwidth', -1)
BIG_QUERY_ANNOTATIONS_STORAGE = BigQueryAnnotationStorage('uk-biobank-sek-data.ml_results.annotations')
#---[ EDIT AND RUN THIS CELL TO READ FROM A LOCAL FILE OR A FILE IN CLOUD STORAGE ]---
SAMPLE_BATCH_FILE = None
if SAMPLE_BATCH_FILE:
samples_df = pd.read_csv(tf.io.gfile.GFile(SAMPLE_BATCH_FILE))
else:
# Normally these would all be the same or similar TMAP. We are using different ones here just to make it
# more obvious in this demo that we are processing different samples.
samples_df = pd.DataFrame(
columns=BatchImageAnnotator.EXPECTED_COLUMN_NAMES,
data=[
[1655349, 'cine_lax_3ch_192', 25, 'gs://ml4cvd/deflaux/ukbb_tensors/'],
[1655349, 't2_flair_sag_p2_1mm_fs_ellip_pf78_1', 50, 'gs://ml4cvd/deflaux/ukbb_tensors/'],
[1655349, 'cine_lax_4ch_192', 25, 'gs://ml4cvd/deflaux/ukbb_tensors/'],
[1655349, 't2_flair_sag_p2_1mm_fs_ellip_pf78_2', 50, 'gs://ml4cvd/deflaux/ukbb_tensors/'],
[2403657, 'cine_lax_3ch_192', 25, 'gs://ml4cvd/deflaux/ukbb_tensors/'],
])
samples_df.shape
samples_df.head(n = 10)
# Note: a zoom level of 1.0 displays the tensor as-is. For higher zoom levels, this code currently
# use the PIL library to scale the image.
annotator = BatchImageAnnotator(samples=samples_df,
zoom=2.0,
annotation_categories=['region_of_interest'],
annotation_storage=BIG_QUERY_ANNOTATIONS_STORAGE,
annotator=PointAnnotator)
annotator.annotate_images()
# Note: a zoom level of 1.0 displays the tensor as-is. For higher zoom levels, this code currently
# use the PIL library to scale the image.
annotator = BatchImageAnnotator(samples=samples_df,
zoom=2.0,
annotation_categories=['region_of_interest'],
annotation_storage=BIG_QUERY_ANNOTATIONS_STORAGE,
annotator=PolygonAnnotator)
annotator.annotate_images()
# Note: a zoom level of 1.0 displays the tensor as-is. For higher zoom levels, this code currently
# use the PIL library to scale the image.
annotator = BatchImageAnnotator(samples=samples_df,
zoom=2.0,
annotation_categories=['region_of_interest'],
annotation_storage=BIG_QUERY_ANNOTATIONS_STORAGE,
annotator=BoxAnnotator)
annotator.annotate_images()
annotator.view_recent_submissions(count=10)
import datetime
print(datetime.datetime.now())
%%bash
pip3 freeze
| 0.344554 | 0.878314 |
```
%pylab inline
import matplotlib.pylab as plt
import math
import random
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')
```
## Линейная классификация
Ранее мы изучили задачу восстановления регрессии и способы её решения. В частности, для линейной модели с функционалом качества MSE решение данной задачи выписывается аналитически через матрицу "объект-признак" и вектор ответов обучающей выборки.
Процесс обучения линейного классификатора складывается из следующих шагов:
* Получение обучающей выборки $X = \{ \left( x_i, y_i \right) \}_{i=1}^l$
* Выбор верхней оценки для пороговой функции потерь — отсюда получаем общий вид оптимизируемого функционала $\widetilde{Q}(w, X^l)$
* Проводим оптимизацию при помощи некоторого метода оптимизации и получаем оптимальное значение $w^*$
* Предсказываем ответы для новых объектов по формуле $a(x) = \langle w^*, x\rangle$
### Логистическая регрессия
Рассмотрим в качестве верхней оценки пороговой функции потерь логистическую функцию:
$$\widetilde{L}(M) = \log_2(1 + \exp(-M)).$$
Таким образом, необходимо решить следующую оптимизационную задачу:
$$\frac{1}{l} \sum_{i=1}^l \widetilde{L} (M_i) = \frac{1}{l} \sum_{i=1}^l \log_2 (1 + \exp (-y_i \langle w, x_i \rangle)) \to \min_w$$
Получившийся метод обучения называется **логистической регрессией**.
Одно из полезных свойств логистической регрессии, которое будет изучено нами несколько позднее, — тот факт, что она позволяет предсказывать помимо метки класса ещё и вероятность принадлежности каждому из них, что может быть полезным в некоторых задачах.
**Пример**: Вы работаете в банке и хотите выдавать кредиты только тем клиентам, которые вернут его с вероятностью не меньше 0.9.
### Пример обучения логистической регрессии
#### Определение спама по тексту электронного письма
Попробуем при помощи моделей линейной классификации построить алгоритм, отделяющий спам от нормальной почты. Для экспериментов воспользуемся небольшим набором данных с [UCI](https://archive.ics.uci.edu/ml/datasets/spambase). Объекты в датасете соответствуют письмам, которые описаны признаками на основе текста письма, спам — положительный пример для классификации, хорошее письмо — отрицательный пример.
```
colums = []
with open("spambase.names", "r") as doc:
lines = doc.readlines()
for line in lines[33:]:
colums.append(line.split(":")[0])
print(colums)
spam_data = pd.read_csv("spambase.data", names=colums+['class'])
spam_data.head()
X, y = spam_data.iloc[:, :-1].values, spam_data.iloc[:, -1].values
spam_data.shape
spam_data.describe()
spam_data.isna().sum().sum()
spam_data['class'].value_counts(normalize=True)
```
### Обучение логистической регрессии
Разделим выборку на обучающую и тестовую в отношении 80/20 и обучим логистическую регрессию при помощи объекта [LogisticRegression](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html).
```
from sklearn.linear_model import LogisticRegression
# splitting data
train_part = 0.8
n_train = int(train_part * X.shape[0])
X_tr = X[:n_train]
X_test = X[n_train:]
y_tr = y[:n_train]
y_test = y[n_train:]
# training
lr = LogisticRegression()
lr = lr.fit(X_tr, y_tr)
```
Оценим долю верных прогнозов полученной модели (accuracy) при помощи соответствующей функции из модуля [sklearn.metrics](http://scikit-learn.org/stable/modules/classes.html#module-sklearn.metrics).
```
from sklearn import metrics
preds = lr.predict(X_test)
print('Accuracy =', metrics.accuracy_score(y_test, preds))
```
Сгенерируем двумерную искуственную выборку из 2 различных нормальных распределений:
```
plt.figure(figsize=(20,10))
mean0 = [10, 5]
cov0 = [[1, 0], [0, 5]] # diagonal covariance
data0 = np.random.multivariate_normal(mean0, cov0, 1000)
mean1 = [0, 0]
cov1 = [[3, 1], [0, 1]]
data1 = np.random.multivariate_normal(mean1, cov1, 1000)
data = np.vstack((data0, data1))
y_vis = np.hstack((-np.ones(1000), np.ones(1000)))
plt.scatter(data0[:, 0], data0[:, 1], c='red')
plt.scatter(data1[:, 0], data1[:, 1], c='green')
plt.legend(['y = -1', 'y = 1'])
axes = plt.gca()
axes.set_xlim([-5,15])
axes.set_ylim([-5,10])
plt.show()
```
Обучим логистическую регрессию:
```
X_train_vis, X_test_vis, y_train_vis, y_test_vis = train_test_split(
data, y_vis, test_size=0.2)
from sklearn import linear_model
logreg = linear_model.LogisticRegression(penalty='l2')
logreg.fit(X_train_vis, y_train_vis)
```
Полученные в результате оптимизации коэффициенты линейной модели содержатся в атрибутах coef\_ и intercept\_ соответствующего объекта. Визуализируем разделяющую гиперплоскость алгоритма и рассмотрим значения предсказанных моделью вероятностей принадлежности нового объекта каждому из классов в зависимости от его координат.
```
print(logreg.coef_, logreg.intercept_)
w_1 = logreg.coef_[0][0]
w_2 = logreg.coef_[0][1]
w_0 = logreg.intercept_[0]
plt.figure(figsize=(20,10))
plt.scatter(data0[:, 0], data0[:, 1], c='red')
plt.scatter(data1[:, 0], data1[:, 1], c='green')
plt.legend(['y = -1', 'y = 1'])
x_arr = np.linspace(-10, 15, 3000)
plt.plot(x_arr, -(w_0 + w_1 * x_arr) / w_2)
axes = plt.gca()
axes.set_xlim([-5,15])
axes.set_ylim([-5,10])
plt.show()
point = np.array([[10, 2]]) # изменяем только координаты объекта
plt.figure(figsize=(20,10))
plt.scatter(data0[:, 0], data0[:, 1], c='red')
plt.scatter(data1[:, 0], data1[:, 1], c='green')
plt.scatter(point[:, 0], point[:, 1], marker = '*', s = 300, color = 'magenta')
plt.legend(['y = -1', 'y = 1'])
x_arr = np.linspace(-10, 15, 3000)
plt.plot(x_arr, -(w_0 + w_1 * x_arr) / w_2)
axes = plt.gca()
axes.set_xlim([-5,15])
axes.set_ylim([-5,10])
prob = logreg.predict_proba(point)
print('P(y = -1|x) =', prob[0][0])
print('P(y = 1|x) =', prob[0][1])
plt.show()
logreg.predict_proba(point)
logreg.predict_proba(data)
data
```
### SGDClassifier
Объект [SGDClissifier](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.SGDClassifier.html) позволяет обучать линейные модели классификации и регрессии с помощью стохастического градиентного спуска.
Полезные параметры:
* loss - функция потерь (по факту то, какую модель обучаем): **hinge** (SVM), **log** (логистическая регрессия), **perceptron** (персептрон) и другие;
* penalty - тип регуляризации: **l1**, **l2**, **elasticnet** (смесь l1 и l2 регуляризации);
* alpha - коэффициент регуляризации;
* fit_intercept - необходимо ли добавлять в модель свободный член (True/False);
* n_iter - число эпох (полных проходов по выборке) при обучении;
* learning_rate - шаг градиентного спуска (оптимизируется по умолчанию).
```
from sklearn.linear_model import SGDClassifier
lr_sgd = SGDClassifier(loss="log", alpha=0.05,
max_iter=200, fit_intercept=True)
lr_sgd.fit(X_tr, y_tr)
preds_sgd = lr_sgd.predict(X_test)
print('Accuracy =', metrics.accuracy_score(y_test, preds_sgd))
lr_sgd = SGDClassifier(loss="hinge")
lr_sgd.fit(X_tr, y_tr)
preds_sgd = lr_sgd.predict(X_test)
print('Accuracy =', metrics.accuracy_score(y_test, preds_sgd))
```
## Оценка качества работы классификатора
### Бинарные метрики
Обучение и оценка качества модели производится на независимых множествах примеров. Как правило, имеющующиеся примеры разбивают на два подмножества: обучение (`train`) и контроль (`test`). Выбор пропорции разбиения — компромисс: большой размер обучения ведет к более богатым информацией и качественным алгоритмам, большой размер контрольной выборки ведет к менее шумной оценке качества.
Для оценки качества классификации рассматривают [матрицу ошибок](http://en.wikipedia.org/wiki/Confusion_matrix): строчки соответствуют прогнозу модели, столбцы — истинным ответам, ячейки содержат число примеров тестовой выборки. Если для некоторого алгоритма $a(\cdot)$ и объекта $x$ выполняется $a(x) = 1$, то говорят, что алгоритм $a$ _выделяет_ объект $x$.
| | y = +1 | y = -1 |
|------|------|
| **a(x) = +1** | TP| FP |
| **a(x) = -1**| FN | TN |
Диагональ матрицы ошибок содержит правильно классифицированные положительные (TP) и отрицательные (TN) примеры. False Positive (FP) — ошибки I рода (ложное срабатывание, положили в спам хорошее письмо), False Negative (FN) — ошибки II рода (не отфильтровали спам). Ошибки I и II рода могут иметь различную стоимость.
Часто рассматриваются следующие метрики качества бинарной классификации:
- Доля правильных ответов (Accuracy):
$$accuracy = \frac{TP + TN}{TP + TN + FP + FN}$$
- Точность/precision (доля действительно положительных объектов среди объектов, выделенных алгоритмом):
$$precision = \frac{TP}{TP + FP}$$
- Полнота/recall (доля выделенных алгоритмом объектов среди всех положительных объектов выборки):
$$recall = \frac{TP}{TP + FN}$$
- $F_1$-мера (среднее гармоническое между точностью и полнотой)
$$F_1 = \frac{2 \cdot Precision \cdot Recall}{Precision + Recall}$$
Подробнее про метрики качества бинарной классификации на Википедии: [Precision and Recall](http://en.wikipedia.org/wiki/Precision_and_recall).
### Выбор порога классификации
Многие модели классификации получают оценку принадлежности положительному классу $b(x) \in \mathbb{R}$, после чего принимается решение о классификации объекта путем сравнения оценки с некоторым порогом:
$a(x) = \begin{cases}
+1, \, b(x) \ge t,\\
-1, \, b(x) < t.
\end{cases}$
Матрица ошибок и все производные от нее метрики (Accuracy, Precision, Recall, etc.) зависят от порога $t$:

Поскольку иногда необходимо оценить качество модели $b(x),$ предсказывающей не конкретную метку класса, а степень принадлежности классу (т.е. вне зависимости от значения порога), рассматривают координатную плоскость, по осям которой отложены значения метрик, а качество работы классификатора представлено в виде кривой — траектории изменения соответствующих метрик при варьировании порога:

Наиболее распространены ROC-кривые и Precision/Recall кривые.
- По осям Ox и Oy ROC-кривой отложены соответственно False Positive Rate (FPR) и True Positive Rate (TPR):
$$FPR = \frac{FP}{FP + TN},$$
$$TPR = \frac{TP}{FN + TP}.$$
- По осям Ox и Oy PR-кривой отложены соответственно Recall и Precision.
Аббревиатура ROC ([Receiver Operating Characteristic](en.wikipedia.org/wiki/Receiver_operating_characteristic)) была унаследована из инженерного дела.

В случае, если необходимо сравнить качество классификаторов вне зависимости от порога, применяют интегральные числовые метрики, например AUC-ROC (**A**rea **U**nder RO**C**) — площадь под ROC-кривой классификатора. AUC-ROC идеально работающего классификатора равно 1. Идеальный случайный классификатор в среднем имеет AUC-ROC=0.5.
Построим описанные кривые для логистической регрессии, обученной на описанном выше датасете.
* PR-кривая проходит через точку (0,0).
* Если при каком-то значении порога $t$ алгоритм $a(x)$ идеально разделяет объекты 2 классов, то PR-кривая проходит через точку (1,1).
```
X_train_curve, X_test_curve, y_train_curve, y_test_curve = train_test_split(
X, y, test_size=0.2)
lr = LogisticRegression()
lr = lr.fit(X_train_curve, y_train_curve)
from sklearn.metrics import precision_recall_curve
precision, recall, thresholds = precision_recall_curve(
y_test_curve,
lr.predict_proba(X_test_curve)[:, 1])
plt.plot(recall, precision)
plt.xlabel('recall')
plt.ylabel('precision')
plt.show()
from sklearn.metrics import auc
auc(recall, precision)
```
* ROC проходит через точки (0,0) и (1,1)
* Если при каком-то значении порога $t$ алгоритм $a(x)$ идеально разделяет объекты 2 классов, то ROC проходит через точку (0,1).
```
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_test_curve,
lr.predict_proba(X_test_curve)[:, 1])
plt.plot(fpr, tpr)
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.show()
auc(fpr, tpr)
```
## Валидация
Чтобы оценить качество работы алгоритма, необходимо провести валидацию. Это один из самых важных шагов в процессе решения задачи. Оценим accuracy для модели логистической регрессии в задаче про спам-письма на тестовой выборке.
```
spam_data = pd.read_csv("spambase.data", names=colums+['class'])
X, y = spam_data.iloc[:, :-1].values, spam_data.iloc[:, -1].values
# обучающая выборка
X_tr = X[:n_train]
y_tr = y[:n_train]
# валидационная выборка
X_test = X[n_train:]
y_test = y[n_train:]
# обучим ещё раз логистическую регрессию
lr = LogisticRegression()
lr = lr.fit(X_tr, y_tr)
#посмотрим на точность классификации
preds = lr.predict(X_test)
print('Accuracy =', metrics.accuracy_score(y_test, preds))
```
А теперь попробуем перемешать объекты и повторим действия:
```
X_tr, X_test, y_tr, y_test = train_test_split(
X, y, test_size=train_part, random_state=123, shuffle=True)
# обучим ещё раз логистическую регрессию
lr = LogisticRegression()
lr = lr.fit(X_tr, y_tr)
# посмотрим на точность классификации
preds = lr.predict(X_test)
print('Accuracy =', metrics.accuracy_score(y_test, preds))
```
Как мы видим, качество классификации новых данных резко возросло. С чем это может быть связано? Рассмотрим вектор целевой переменной:
```
plt.plot(y, 'ro')
plt.xlabel('Object number')
plt.ylabel('Target')
```
Проблема заключалась в том, что в выборке примеры были упорядочены: сначала шли примеры положительного класса, а потом отрицательного. Поэтому нельзя забывать **перемешивать классы**.
Чтобы повысить устойчивость оценки качества, можно проводить разбиение выборки на обучающую и тестовую не один, $N$ раз, после чего усреднять результаты, полученные на $N$ контрольных выборках. Для этого можно использовать функцию [`sklearn.model_selection.ShuffleSplit`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.ShuffleSplit.html)
```
from sklearn.model_selection import ShuffleSplit
ss = ShuffleSplit(n_splits=5, test_size=0.1, random_state=123)
quals = []
lr = LogisticRegression()
for tr_ind, test_ind in ss.split(X):
lr.fit(X[tr_ind, :], y[tr_ind])
quals.append(
metrics.roc_auc_score(y[test_ind],
lr.predict_proba(X[test_ind, :])[:, 1]))
print('Mean AUC-ROC =', np.mean(quals))
print('AUC-ROC standart deviation =', np.std(quals))
```
Увеличим $N$:
```
ss = ShuffleSplit(n_splits=10, test_size=0.1, random_state=123)
quals = []
lr = LogisticRegression()
for tr_ind, test_ind in ss.split(X):
lr.fit(X[tr_ind, :], y[tr_ind])
quals.append(
metrics.roc_auc_score(y[test_ind],
lr.predict_proba(X[test_ind, :])[:, 1]))
print('Mean AUC-ROC =', np.mean(quals))
print('AUC-ROC standart deviation =', np.std(quals))
ss = ShuffleSplit(n_splits=10, test_size=0.1, random_state=123)
ss
ss.get_n_splits(X)
ss.split(X)
```
### Несбалансированные классы
Если объём выборки невелик, а объектов одного класса значительно меньше, чем другого, то может сложиться ситуация, когда при случайном разбиении объектов меньшего класса не окажется в тестовой выборке, в связи с чем результаты оценки качества будут неустойчивы.
**Пример**: задача кредитного скоринга. Поскольку случаи невозврата кредита довольно редки, количество объектов отрицательного класса будет значительно меньше, чем положительного.
```
df = pd.read_csv('data/givemesomecredit')
X = df.drop('SeriousDlqin2yrs', axis=1)
X = X.fillna(X.mean()).as_matrix()
y = df['SeriousDlqin2yrs']
print("Доля заемщиков, не вернувших кредит:", y.mean())
df
```
- Всего 0.7% выборки составляют объекты положительного класса
- В таком случае необходимо производить стратификацию, то есть разбивать отдельно объекты каждого класса на обучение и тест (сохраняя их доли).
Оценим влияние стратификации на оценку качества путем разбиения выборки $N=10$ раз на обучение и тест и последующего усреднения AUC-ROC на тестовой выборке:
```
ss = ShuffleSplit(n_splits=10, test_size=0.2, random_state=123)
quals = []
lr = LogisticRegression()
for tr_ind, test_ind in ss.split(X):
lr.fit(X[tr_ind, :], y[tr_ind])
quals.append(metrics.roc_auc_score(y[test_ind], lr.predict_proba(X[test_ind,:])[:,1]))
print("AUC-ROC w/o stratification = ", np.mean(quals))
print("AUC-ROC std w/o stratification = ", np.std(quals))
from sklearn.model_selection import StratifiedShuffleSplit
sss = StratifiedShuffleSplit(n_splits=10, test_size=0.2, random_state=124)
quals = []
lr = LogisticRegression()
for tr_ind, test_ind in sss.split(X, y):
lr.fit(X[tr_ind, :], y[tr_ind])
quals.append(metrics.roc_auc_score(y[test_ind], lr.predict_proba(X[test_ind,:])[:,1]))
print("AUC-ROC with stratification = ", np.mean(quals))
print("AUC-ROC std with stratification = ", np.std(quals))
```
Как мы видим, стратификация позволяет уменьшить дисперсию и более точно оценить качество
#### Кросс-валидация
Рассмотрим датасет о пациентах, больных бесплодием, содержащий около 100 объектов. Выборка небольшая, но из специфичной области, поэтому каждый объект может нести в себе важную информацию, влияющую на значение целевой переменной. В связи с этим при оценивании качества модели хотелось бы сделать обучающую выборку как можно больше. При этом из-за маленького объема всей выборки мы можем позволить себе обучать модель многократно. В данной ситуации для оценки качества можно использовать схему leave-one-out, реализованную в качестве объекта [`LeaveOneOut`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.LeaveOneOut.html).
Оценка качества производится следующим образом: каждый объект поочередно исключается из обучающей выборки, после чего модель обучается на всех остальных объектах, а качество измеряется на исключенном объекте (этот объект играет роль тестовой выборки); после того, как каждый объект был выкинут ровно по одному разу, итоговая оценка качества получается как среднее по всем полученным значениям функционала:
$$Q_{LOO}(X) = \frac{1}{l} \sum_{i=1}^l Q(\{x_i \}; a_{X \backslash \{x_i\} }),$$
где
* $X = \left\{ (x_i, y_i)\right\}_{i=1}^l$ — обучающая выборка;
* $Q(X^{test}; a)$ — значение функционала алгоритма $a$ на контрольной выборке $X^{test}$;
* $a_{X^{train}}(\cdot)$ — алгоритм, обученный на обучающей выборке $X^{train}.$
```
from sklearn.model_selection import LeaveOneOut
df = pd.read_csv('data/fertility', header=None)
X = df.ix[:, :8]
y = np.zeros(df.shape[0])
y[df[9].as_matrix() == 'N'] = 1
loo = LeaveOneOut()
qual = []
for tr_ids, test_ids in loo.split(X):
lr.fit(X.ix[tr_ids, :], y[tr_ids])
qual.append(lr.predict(X.ix[test_ids, :]) == y[test_ids])
print("LOO accuracy =", np.mean(qual))
df[9].value_counts()
```
С ростом размера выборки возрастают также и затраты на многократное обучение модели. Тем не менее, хотелось бы, чтобы каждый объект побывал и в обучающей, и в тестовой выборках, причём одинаковое количество раз. Чтобы удовлетворить этому условию, можно использовать схему K-fold кросс-валидации, реализованную в качестве объекта [`sklearn.cross_validation.KFold`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.KFold.html).
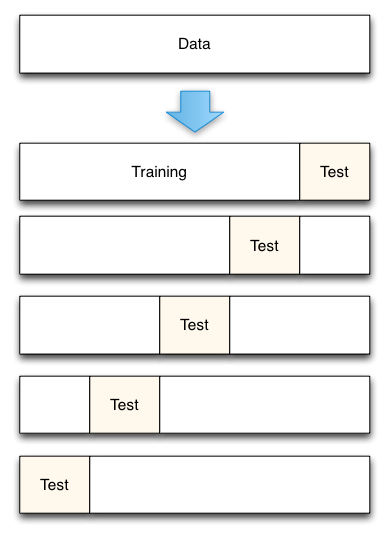
В данном случае выборка разбивается на $K$ (примерно) одинаковых блоков, каждый из которых поочередно выступает в качестве контрольной выборки, а оставшиеся $K-1$ — в качестве обучающей, после чего оценки качества усредняются:
$$Q_{K-fold}(X) = \frac{1}{K} \sum_{k=1}^K Q(X^k; a_{X \backslash X^k }),$$
где $X^k, k = \overline{1, K}$ — непересекающиеся блоки, на которые разбивается выборка $X$: $X = \sqcup_{k=1}^K X^k.$
```
from sklearn.model_selection import KFold
kf = KFold(n_splits=2, random_state=123, shuffle=True)
lr = LogisticRegression()
quals = []
for tr_ids, test_ids in kf.split(X):
lr.fit(X.ix[tr_ids, :], y[tr_ids])
quals.append(
metrics.accuracy_score(y[test_ids], lr.predict(X.ix[test_ids, :])))
print("K-fold accuracy =", np.mean(quals))
```
|
github_jupyter
|
%pylab inline
import matplotlib.pylab as plt
import math
import random
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')
colums = []
with open("spambase.names", "r") as doc:
lines = doc.readlines()
for line in lines[33:]:
colums.append(line.split(":")[0])
print(colums)
spam_data = pd.read_csv("spambase.data", names=colums+['class'])
spam_data.head()
X, y = spam_data.iloc[:, :-1].values, spam_data.iloc[:, -1].values
spam_data.shape
spam_data.describe()
spam_data.isna().sum().sum()
spam_data['class'].value_counts(normalize=True)
from sklearn.linear_model import LogisticRegression
# splitting data
train_part = 0.8
n_train = int(train_part * X.shape[0])
X_tr = X[:n_train]
X_test = X[n_train:]
y_tr = y[:n_train]
y_test = y[n_train:]
# training
lr = LogisticRegression()
lr = lr.fit(X_tr, y_tr)
from sklearn import metrics
preds = lr.predict(X_test)
print('Accuracy =', metrics.accuracy_score(y_test, preds))
plt.figure(figsize=(20,10))
mean0 = [10, 5]
cov0 = [[1, 0], [0, 5]] # diagonal covariance
data0 = np.random.multivariate_normal(mean0, cov0, 1000)
mean1 = [0, 0]
cov1 = [[3, 1], [0, 1]]
data1 = np.random.multivariate_normal(mean1, cov1, 1000)
data = np.vstack((data0, data1))
y_vis = np.hstack((-np.ones(1000), np.ones(1000)))
plt.scatter(data0[:, 0], data0[:, 1], c='red')
plt.scatter(data1[:, 0], data1[:, 1], c='green')
plt.legend(['y = -1', 'y = 1'])
axes = plt.gca()
axes.set_xlim([-5,15])
axes.set_ylim([-5,10])
plt.show()
X_train_vis, X_test_vis, y_train_vis, y_test_vis = train_test_split(
data, y_vis, test_size=0.2)
from sklearn import linear_model
logreg = linear_model.LogisticRegression(penalty='l2')
logreg.fit(X_train_vis, y_train_vis)
print(logreg.coef_, logreg.intercept_)
w_1 = logreg.coef_[0][0]
w_2 = logreg.coef_[0][1]
w_0 = logreg.intercept_[0]
plt.figure(figsize=(20,10))
plt.scatter(data0[:, 0], data0[:, 1], c='red')
plt.scatter(data1[:, 0], data1[:, 1], c='green')
plt.legend(['y = -1', 'y = 1'])
x_arr = np.linspace(-10, 15, 3000)
plt.plot(x_arr, -(w_0 + w_1 * x_arr) / w_2)
axes = plt.gca()
axes.set_xlim([-5,15])
axes.set_ylim([-5,10])
plt.show()
point = np.array([[10, 2]]) # изменяем только координаты объекта
plt.figure(figsize=(20,10))
plt.scatter(data0[:, 0], data0[:, 1], c='red')
plt.scatter(data1[:, 0], data1[:, 1], c='green')
plt.scatter(point[:, 0], point[:, 1], marker = '*', s = 300, color = 'magenta')
plt.legend(['y = -1', 'y = 1'])
x_arr = np.linspace(-10, 15, 3000)
plt.plot(x_arr, -(w_0 + w_1 * x_arr) / w_2)
axes = plt.gca()
axes.set_xlim([-5,15])
axes.set_ylim([-5,10])
prob = logreg.predict_proba(point)
print('P(y = -1|x) =', prob[0][0])
print('P(y = 1|x) =', prob[0][1])
plt.show()
logreg.predict_proba(point)
logreg.predict_proba(data)
data
from sklearn.linear_model import SGDClassifier
lr_sgd = SGDClassifier(loss="log", alpha=0.05,
max_iter=200, fit_intercept=True)
lr_sgd.fit(X_tr, y_tr)
preds_sgd = lr_sgd.predict(X_test)
print('Accuracy =', metrics.accuracy_score(y_test, preds_sgd))
lr_sgd = SGDClassifier(loss="hinge")
lr_sgd.fit(X_tr, y_tr)
preds_sgd = lr_sgd.predict(X_test)
print('Accuracy =', metrics.accuracy_score(y_test, preds_sgd))
X_train_curve, X_test_curve, y_train_curve, y_test_curve = train_test_split(
X, y, test_size=0.2)
lr = LogisticRegression()
lr = lr.fit(X_train_curve, y_train_curve)
from sklearn.metrics import precision_recall_curve
precision, recall, thresholds = precision_recall_curve(
y_test_curve,
lr.predict_proba(X_test_curve)[:, 1])
plt.plot(recall, precision)
plt.xlabel('recall')
plt.ylabel('precision')
plt.show()
from sklearn.metrics import auc
auc(recall, precision)
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_test_curve,
lr.predict_proba(X_test_curve)[:, 1])
plt.plot(fpr, tpr)
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.show()
auc(fpr, tpr)
spam_data = pd.read_csv("spambase.data", names=colums+['class'])
X, y = spam_data.iloc[:, :-1].values, spam_data.iloc[:, -1].values
# обучающая выборка
X_tr = X[:n_train]
y_tr = y[:n_train]
# валидационная выборка
X_test = X[n_train:]
y_test = y[n_train:]
# обучим ещё раз логистическую регрессию
lr = LogisticRegression()
lr = lr.fit(X_tr, y_tr)
#посмотрим на точность классификации
preds = lr.predict(X_test)
print('Accuracy =', metrics.accuracy_score(y_test, preds))
X_tr, X_test, y_tr, y_test = train_test_split(
X, y, test_size=train_part, random_state=123, shuffle=True)
# обучим ещё раз логистическую регрессию
lr = LogisticRegression()
lr = lr.fit(X_tr, y_tr)
# посмотрим на точность классификации
preds = lr.predict(X_test)
print('Accuracy =', metrics.accuracy_score(y_test, preds))
plt.plot(y, 'ro')
plt.xlabel('Object number')
plt.ylabel('Target')
from sklearn.model_selection import ShuffleSplit
ss = ShuffleSplit(n_splits=5, test_size=0.1, random_state=123)
quals = []
lr = LogisticRegression()
for tr_ind, test_ind in ss.split(X):
lr.fit(X[tr_ind, :], y[tr_ind])
quals.append(
metrics.roc_auc_score(y[test_ind],
lr.predict_proba(X[test_ind, :])[:, 1]))
print('Mean AUC-ROC =', np.mean(quals))
print('AUC-ROC standart deviation =', np.std(quals))
ss = ShuffleSplit(n_splits=10, test_size=0.1, random_state=123)
quals = []
lr = LogisticRegression()
for tr_ind, test_ind in ss.split(X):
lr.fit(X[tr_ind, :], y[tr_ind])
quals.append(
metrics.roc_auc_score(y[test_ind],
lr.predict_proba(X[test_ind, :])[:, 1]))
print('Mean AUC-ROC =', np.mean(quals))
print('AUC-ROC standart deviation =', np.std(quals))
ss = ShuffleSplit(n_splits=10, test_size=0.1, random_state=123)
ss
ss.get_n_splits(X)
ss.split(X)
df = pd.read_csv('data/givemesomecredit')
X = df.drop('SeriousDlqin2yrs', axis=1)
X = X.fillna(X.mean()).as_matrix()
y = df['SeriousDlqin2yrs']
print("Доля заемщиков, не вернувших кредит:", y.mean())
df
ss = ShuffleSplit(n_splits=10, test_size=0.2, random_state=123)
quals = []
lr = LogisticRegression()
for tr_ind, test_ind in ss.split(X):
lr.fit(X[tr_ind, :], y[tr_ind])
quals.append(metrics.roc_auc_score(y[test_ind], lr.predict_proba(X[test_ind,:])[:,1]))
print("AUC-ROC w/o stratification = ", np.mean(quals))
print("AUC-ROC std w/o stratification = ", np.std(quals))
from sklearn.model_selection import StratifiedShuffleSplit
sss = StratifiedShuffleSplit(n_splits=10, test_size=0.2, random_state=124)
quals = []
lr = LogisticRegression()
for tr_ind, test_ind in sss.split(X, y):
lr.fit(X[tr_ind, :], y[tr_ind])
quals.append(metrics.roc_auc_score(y[test_ind], lr.predict_proba(X[test_ind,:])[:,1]))
print("AUC-ROC with stratification = ", np.mean(quals))
print("AUC-ROC std with stratification = ", np.std(quals))
from sklearn.model_selection import LeaveOneOut
df = pd.read_csv('data/fertility', header=None)
X = df.ix[:, :8]
y = np.zeros(df.shape[0])
y[df[9].as_matrix() == 'N'] = 1
loo = LeaveOneOut()
qual = []
for tr_ids, test_ids in loo.split(X):
lr.fit(X.ix[tr_ids, :], y[tr_ids])
qual.append(lr.predict(X.ix[test_ids, :]) == y[test_ids])
print("LOO accuracy =", np.mean(qual))
df[9].value_counts()
from sklearn.model_selection import KFold
kf = KFold(n_splits=2, random_state=123, shuffle=True)
lr = LogisticRegression()
quals = []
for tr_ids, test_ids in kf.split(X):
lr.fit(X.ix[tr_ids, :], y[tr_ids])
quals.append(
metrics.accuracy_score(y[test_ids], lr.predict(X.ix[test_ids, :])))
print("K-fold accuracy =", np.mean(quals))
| 0.484624 | 0.912826 |
<a href="https://colab.research.google.com/github/siddharthtelang/Face-Detection/blob/main/k_NN.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import scipy.io as sio
import numpy as np
import matplotlib.pyplot as plt
import math
from sklearn.decomposition import PCA
import random
from google.colab import files
uploaded = files.upload()
# initialization
subjects = 68
types = 13
usePCA = True
useMDA = False
dataset_file = 'pose.mat'
# dataset_file = 'Data/data.mat'
# dataset_file = 'Data/illumination.mat'
dataset = ''
# load the dataset
data_ = sio.loadmat(dataset_file)
if 'pose' in dataset_file:
data = data_.get('pose')
dataset = 'pose'
elif 'illumination' in dataset_file:
data = data_.get('illum')
dataset = 'illum'
else:
data = data_.get('face')
dataset = 'face'
# flatten the dataset
if dataset == 'pose':
flattened = np.zeros(shape=(subjects*types, data.shape[0]*data.shape[1]))
elif dataset == 'illum':
flattened = np.zeros(shape=(subjects*types, data.shape[0]))
else:
flattened = np.zeros(shape=(subjects*types, data.shape[0]*data.shape[1]))
c = 0
d = 0
for i in range(flattened.shape[0]):
if c == types:
c = 0
d += 1
if dataset == 'pose':
temp = data[:,:,c,d]
flattened[i] = temp.flatten()
elif dataset == 'face':
temp = data[:,:,i]
flattened[i] = temp.flatten()
elif dataset == 'illum':
flattened[i] = data[:,c,d]
c += 1
def doPCA(flattened, dim):
pca = PCA(dim)
projected = pca.fit_transform(flattened)
return projected
# Perform PCA if true
if usePCA:
pca = PCA().fit(flattened)
plt.figure()
plt.xlabel('Dimensions')
plt.ylabel('Variance Retention')
plt.plot(pca.explained_variance_ratio_.cumsum(), lw=3)
min_dim = (np.where(pca.explained_variance_ratio_.cumsum() > 0.95))[0][0]
print('Minimum dimensions required for 95% retention ', min_dim)
projected = doPCA(flattened, min_dim)
print('Before dimension reduction shape = ', flattened.shape)
print('After dimension reduction shape = ', projected.shape)
# Split in training and testing data set
def genereate_training_testing_data(projected, subjects, types):
training_data = []
testing_data = []
train_per_subject = int(math.ceil(2*types/3))
test_per_subject = types - train_per_subject
print('Training data per subject=', train_per_subject)
print('Testing data per subject=', test_per_subject)
for i in range(subjects):
temp = []
start = i*types
end = (i+1)*types
# print(start, start+train_per_subject)
# print(start+train_per_subject, end)
# print('-----------------')
for j in range(start , start + test_per_subject):
testing_data.append(projected[j])
for j in range(start + test_per_subject , end):
training_data.append(projected[j])
# training_data.append(projected[start : start + train_per_subject])
# testing_data.append(projected[start + train_per_subject : end])
print('Size of training data = ', len(training_data))
print('Size of testing data = ', len(testing_data))
return training_data, testing_data, train_per_subject, test_per_subject
training_data, testing_data, train_per_subject, test_per_subject = genereate_training_testing_data(projected, subjects, types)
# Compute the mean and covariance for each training sample
def calculate_covariance_mean(training_data, dataset):
cov = []
mu = []
for i in range(len(training_data)):
sample = training_data[i]
size = sample.shape[0]
sample = sample.reshape(1, size)
cov_ = np.dot((sample - np.mean(sample)).T, (sample - np.mean(sample))) / size
# add noise to make determinant non-zero
if dataset == 'face':
noise = 0.24*np.identity(cov_.shape[0])
elif dataset == 'pose':
noise = 0.03*np.identity(cov_.shape[0])
else:
noise = 0.01*np.identity(cov_.shape[0])
cov_ = cov_ + noise
mu.append(np.mean(sample))
cov.append(cov_)
return cov, mu
cov, mu = calculate_covariance_mean(training_data, dataset)
np.linalg.det(cov[0])
# K-NN
k = 1
while (k<=8):
score = 0
actual_tests = len(testing_data)
for i in range(len(testing_data)):
test_class = int(i/test_per_subject)
dist = np.zeros(shape=(len(training_data)))
for j in range(len(training_data)):
# d = np.dot(testing_data[i] - mu[j], np.dot(np.linalg.inv(cov[j]), (testing_data[i] - mu[j]).T))
d = np.linalg.norm(testing_data[i] - training_data[j])
dist[j] = d
sort = np.argsort(dist)
predicted_nearest_class = np.zeros(shape=dist.shape[0])
votes_class = np.zeros(shape=subjects)
for l in range(k):
predicted_nearest_class[l] = int(sort[l]/train_per_subject)
temp_class = int(predicted_nearest_class[l])
# print(temp_class)
votes_class[temp_class] += 1
# print(sort[:k])
# print(votes_class)
# print(np.where(votes_class == np.max(votes_class)))
same_votes = (np.where(votes_class == np.max(votes_class)))[0]
if len(same_votes) > 1:
# print('Same votes, skip this sample')
actual_tests -= 1
continue
votes_class = -1*votes_class
predicted_class = np.argsort(votes_class)[0]
# print(predicted_class)
# print(test_class)
if predicted_class == test_class:
score += 1
# print('Correct, score = ', score)
# else:
# print('Incorrect')
# print('-------------------------------------------')
print('Accuracy of ',str(k),'-NN = ', (score*100/actual_tests))
k += 1
# When using NORM
accuracy = [89.7, 100.0, 96.29, 97.5, 95.86, 92.2, 90, 89.7]
neighbours = [1,2,3,4,5,6,7,8]
plt.xlabel('Number of Nearest Neighbours (k)')
plt.ylabel('Accuracy in %')
plt.plot(neighbours, accuracy)
# When distance is calculated as Mannhabolis Distance
accuracy = [92.64, 97.43, 94.52, 88.88, 85.13, 82.87, 79.72, 75.64]
neighbours = [1,2,3,4,5,6,7,8]
plt.xlabel('Number of Nearest Neighbours (k)')
plt.ylabel('Accuracy in %')
plt.plot(neighbours, accuracy)
```
|
github_jupyter
|
import scipy.io as sio
import numpy as np
import matplotlib.pyplot as plt
import math
from sklearn.decomposition import PCA
import random
from google.colab import files
uploaded = files.upload()
# initialization
subjects = 68
types = 13
usePCA = True
useMDA = False
dataset_file = 'pose.mat'
# dataset_file = 'Data/data.mat'
# dataset_file = 'Data/illumination.mat'
dataset = ''
# load the dataset
data_ = sio.loadmat(dataset_file)
if 'pose' in dataset_file:
data = data_.get('pose')
dataset = 'pose'
elif 'illumination' in dataset_file:
data = data_.get('illum')
dataset = 'illum'
else:
data = data_.get('face')
dataset = 'face'
# flatten the dataset
if dataset == 'pose':
flattened = np.zeros(shape=(subjects*types, data.shape[0]*data.shape[1]))
elif dataset == 'illum':
flattened = np.zeros(shape=(subjects*types, data.shape[0]))
else:
flattened = np.zeros(shape=(subjects*types, data.shape[0]*data.shape[1]))
c = 0
d = 0
for i in range(flattened.shape[0]):
if c == types:
c = 0
d += 1
if dataset == 'pose':
temp = data[:,:,c,d]
flattened[i] = temp.flatten()
elif dataset == 'face':
temp = data[:,:,i]
flattened[i] = temp.flatten()
elif dataset == 'illum':
flattened[i] = data[:,c,d]
c += 1
def doPCA(flattened, dim):
pca = PCA(dim)
projected = pca.fit_transform(flattened)
return projected
# Perform PCA if true
if usePCA:
pca = PCA().fit(flattened)
plt.figure()
plt.xlabel('Dimensions')
plt.ylabel('Variance Retention')
plt.plot(pca.explained_variance_ratio_.cumsum(), lw=3)
min_dim = (np.where(pca.explained_variance_ratio_.cumsum() > 0.95))[0][0]
print('Minimum dimensions required for 95% retention ', min_dim)
projected = doPCA(flattened, min_dim)
print('Before dimension reduction shape = ', flattened.shape)
print('After dimension reduction shape = ', projected.shape)
# Split in training and testing data set
def genereate_training_testing_data(projected, subjects, types):
training_data = []
testing_data = []
train_per_subject = int(math.ceil(2*types/3))
test_per_subject = types - train_per_subject
print('Training data per subject=', train_per_subject)
print('Testing data per subject=', test_per_subject)
for i in range(subjects):
temp = []
start = i*types
end = (i+1)*types
# print(start, start+train_per_subject)
# print(start+train_per_subject, end)
# print('-----------------')
for j in range(start , start + test_per_subject):
testing_data.append(projected[j])
for j in range(start + test_per_subject , end):
training_data.append(projected[j])
# training_data.append(projected[start : start + train_per_subject])
# testing_data.append(projected[start + train_per_subject : end])
print('Size of training data = ', len(training_data))
print('Size of testing data = ', len(testing_data))
return training_data, testing_data, train_per_subject, test_per_subject
training_data, testing_data, train_per_subject, test_per_subject = genereate_training_testing_data(projected, subjects, types)
# Compute the mean and covariance for each training sample
def calculate_covariance_mean(training_data, dataset):
cov = []
mu = []
for i in range(len(training_data)):
sample = training_data[i]
size = sample.shape[0]
sample = sample.reshape(1, size)
cov_ = np.dot((sample - np.mean(sample)).T, (sample - np.mean(sample))) / size
# add noise to make determinant non-zero
if dataset == 'face':
noise = 0.24*np.identity(cov_.shape[0])
elif dataset == 'pose':
noise = 0.03*np.identity(cov_.shape[0])
else:
noise = 0.01*np.identity(cov_.shape[0])
cov_ = cov_ + noise
mu.append(np.mean(sample))
cov.append(cov_)
return cov, mu
cov, mu = calculate_covariance_mean(training_data, dataset)
np.linalg.det(cov[0])
# K-NN
k = 1
while (k<=8):
score = 0
actual_tests = len(testing_data)
for i in range(len(testing_data)):
test_class = int(i/test_per_subject)
dist = np.zeros(shape=(len(training_data)))
for j in range(len(training_data)):
# d = np.dot(testing_data[i] - mu[j], np.dot(np.linalg.inv(cov[j]), (testing_data[i] - mu[j]).T))
d = np.linalg.norm(testing_data[i] - training_data[j])
dist[j] = d
sort = np.argsort(dist)
predicted_nearest_class = np.zeros(shape=dist.shape[0])
votes_class = np.zeros(shape=subjects)
for l in range(k):
predicted_nearest_class[l] = int(sort[l]/train_per_subject)
temp_class = int(predicted_nearest_class[l])
# print(temp_class)
votes_class[temp_class] += 1
# print(sort[:k])
# print(votes_class)
# print(np.where(votes_class == np.max(votes_class)))
same_votes = (np.where(votes_class == np.max(votes_class)))[0]
if len(same_votes) > 1:
# print('Same votes, skip this sample')
actual_tests -= 1
continue
votes_class = -1*votes_class
predicted_class = np.argsort(votes_class)[0]
# print(predicted_class)
# print(test_class)
if predicted_class == test_class:
score += 1
# print('Correct, score = ', score)
# else:
# print('Incorrect')
# print('-------------------------------------------')
print('Accuracy of ',str(k),'-NN = ', (score*100/actual_tests))
k += 1
# When using NORM
accuracy = [89.7, 100.0, 96.29, 97.5, 95.86, 92.2, 90, 89.7]
neighbours = [1,2,3,4,5,6,7,8]
plt.xlabel('Number of Nearest Neighbours (k)')
plt.ylabel('Accuracy in %')
plt.plot(neighbours, accuracy)
# When distance is calculated as Mannhabolis Distance
accuracy = [92.64, 97.43, 94.52, 88.88, 85.13, 82.87, 79.72, 75.64]
neighbours = [1,2,3,4,5,6,7,8]
plt.xlabel('Number of Nearest Neighbours (k)')
plt.ylabel('Accuracy in %')
plt.plot(neighbours, accuracy)
| 0.264074 | 0.841435 |
## Learning Objectives
Today we are going to learn about how to transform qualitative features into quantitative features and we do so using the most common representation: dummy varibles.
## Back to the data
So in this lesson we jump back to the data and talk about how we transform qualitative values into quantitative ones.
We have already seen this happen a couple of times when we were making random variables. A heads on a coin became a 1 and a tails 0. Getting a queen became a 1 and otherwise 0. Why did we choose the representations?
## Dummy variables
So in this lesson we will talk about the most common cannonical way to transform these variables: the dummy variable transform.
First let's get our data:
```
import pandas as pd
import numpy as np
df = pd.read_csv('../data/billionaires.csv')
del df['was founder']
del df['inherited']
del df['from emerging']
df.age.replace(-1, np.NaN, inplace=True)
df.founded.replace(0, np.NaN, inplace=True)
df.gdp.replace(0, np.NaN, inplace=True)
```
Now let's check out some of the qualitative columns:
```
%matplotlib inline
import seaborn as sns
df['wealth.type'].value_counts()
```
The above column has five types with a good spread over types. But let's say we wanted to transform this quantitatvie column into a qualitative one (for example we could be interested in creating a random variable).
What would we do?
One suggestion would be to just make them the numbers 1, 2, 3, 4, 5. But can you already see the problem here? What would happen if we averaged the column? We would get something around 3.1, but what does that mean? The average has lost its meaning. What about the implied relationship between the columns? In this case executive is five times inherited. Does that make any practical sense?
You may be getting the feeling that our problem is impossible. And it certainly is, if you only have one column...
## More dummies
The way to solve this problem is by adding more columns. For the dummy variable approach you can add one column for each type. That way you can't compare the types to each other. But what values do you fill the columns with?
Well we want the average to mean something right? So filling them with -42 is inherited and 99 is not inherited still leaves us in a situtation where the average still doesn't mean anything. Is there a value that we can use that will actually have meaning?
It turns out that 0 and 1 is pretty good for this. In the inherited column you put a 1 if they did inherit their wealth and a 0 otherwise. In this case what does the average mean?
You guessed it, now the average is the probability that the person is inherited!
## Panda time
So now that we understand what the transformation is, let's use it in practice:
```
df_new = pd.get_dummies(df, columns=['wealth.type'])
df_new.info()
```
Using the above command we get all our goodies. Notice that we no longer have our old wealth.type column but instead have 5 new ones, and we can do some interesting things with our data now:
```
wealth_type_columns = [col for col in df_new.columns if col.startswith('wealth')]
# get all the associated dummy columns
wealth_type_columns
df_new.groupby('gender')[wealth_type_columns].mean()
```
Now we can compare how wealth type is distributed over other qualitative variables.
```
sns.heatmap(df_new.groupby('gender')[wealth_type_columns].mean())
```
Or we can get the correlations due to wealth type:
```
sns.jointplot(x='wealth.type_inherited', y='worth in billions', data=df_new)
```
## One view
Once again this is just one way of transforming qualitative variables into quantitative variables, and once we do that we can do much of the traditional quantitative variable analysis on them. There are many ways of transforming these variables and if you interested in learning more, please tune in to my videos on patsy where I specifically go over the most common ones.
## Learning Objectives
Today we are going to learn about how to transform qualitative features into quantitative features and we do so using the most common representation: dummy varibles.
## Comprehension Questions
1. Are there other good representations that you can think of?
2. What are the properties of good representations?
|
github_jupyter
|
import pandas as pd
import numpy as np
df = pd.read_csv('../data/billionaires.csv')
del df['was founder']
del df['inherited']
del df['from emerging']
df.age.replace(-1, np.NaN, inplace=True)
df.founded.replace(0, np.NaN, inplace=True)
df.gdp.replace(0, np.NaN, inplace=True)
%matplotlib inline
import seaborn as sns
df['wealth.type'].value_counts()
df_new = pd.get_dummies(df, columns=['wealth.type'])
df_new.info()
wealth_type_columns = [col for col in df_new.columns if col.startswith('wealth')]
# get all the associated dummy columns
wealth_type_columns
df_new.groupby('gender')[wealth_type_columns].mean()
sns.heatmap(df_new.groupby('gender')[wealth_type_columns].mean())
sns.jointplot(x='wealth.type_inherited', y='worth in billions', data=df_new)
| 0.172102 | 0.988992 |
```
__author__ = 'Adam Scott <[email protected]>' # single string; emails in <>
__version__ = '20190103' # yyyymmdd; version datestamp of this notebook
__datasets__ = ['ls_dr5'] # datasets used in this notebook; for available datasets, see cell "Available datasets in Data Lab" further below
__keywords__ = ['tutorial','query'], # keywords relevant to this notebook, e.g. ['science case','dwarf galaxies'] Use only keywords from the master list: https://github.com/noaodatalab/notebooks_private/blob/master/internal/keywords.txt
```
# CStore Performance Vs. Row Store
*Adam Scott & NOAO Data Lab Team*
### Table of contents
* [Goals & notebook summary](#goals)
* [Disclaimer & Attribution](#attribution)
* [Imports & setup](#import)
* [Query against Rowstore](#rstore)
* [Query against CStore](#cstore)
* [Graph of results](#graph)
* [When should I use CStore tables in Data Lab?](#when)
<a class="anchor" id="goals"></a>
# Goals
* Learn the difference between column store (cstore) and row store database tables
* Understand the circumstances when you might want to use cstore tables
# Summary
At Data Lab, we ran performance tests of various scenarios against many open-source DBMSs. The cstore_fdw (for columnar store, foreign data wrapper), proved very fast for some applications. Below we compare the run time between both storage formats. (For more on cstore see https://github.com/citusdata/cstore_fdw)
<a class="anchor" id="attribution"></a>
# Disclaimer & attribution
If you use this notebook for your published science, please acknowledge the following:
* Data Lab concept paper: Fitzpatrick et al., "The NOAO Data Laboratory: a conceptual overview", SPIE, 9149, 2014, http://dx.doi.org/10.1117/12.2057445
* Data Lab disclaimer: http://datalab.noao.edu/disclaimers.php
<a class="anchor" id="import"></a>
# Basic Imports
```
# 3rd party
import matplotlib.pyplot as plt
%matplotlib inline
# Datalab
from dl import queryClient as qc
```
<a class="anchor" id="rstore"></a>
# Query against Rowstore
```
%%time
query = """SELECT min(flux_g), max(flux_g), avg(flux_g),
min(flux_r), max(flux_r), avg(flux_r),
min(flux_z), max(flux_z), avg(flux_z)
FROM ls_dr5.tractor
WHERE psfsize_r > 0.6635 and psfsize_r < 1.327"""
# Send the query to the Queryclient in SQL, with a comma-separated-value (csv) output
response = qc.query(sql=query, fmt='csv')
```
In this run, it took **5min 22s** to execute the query against the normal rowstore table in Postgres. Since `psfsize_r` is not indexed (only bold columns listed here are indexed: http://datalab.noao.edu/query.php?name=ls_dr5.tractor), the database has to read through every row in `ls_dr5.tractor` to find all rows satisfying the WHERE clause.
Compare this to the next run.
<a class="anchor" id="cstore"></a>
# Query Against CStore
```
%%time
query = """SELECT min(flux_g), max(flux_g), avg(flux_g),
min(flux_r), max(flux_r), avg(flux_r),
min(flux_z), max(flux_z), avg(flux_z)
FROM ls_dr5.tractor_cs
WHERE psfsize_r > 0.6635 and psfsize_r < 1.327"""
# Send the query to the Queryclient in SQL, with a comma-separated-value (csv) output
response = qc.query(sql=query, fmt='csv')
```
This time, we queried against a cstore table (denoted by the `_cs` in the table name in the query above), and it took significantly less time at **3min 44s**. Since cstore tables store the min/max values of each stripe, they have an inherent index **on every column** that requires litte extra space to store on disk.
<a class="anchor" id="graph"></a>
# Graph of results
```
x = [1,2]
y = [322,224]
ax = plt.subplot()
pr, pc = plt.bar(x,y)
pr.set_facecolor('b')
pc.set_facecolor('r')
ax.set_xticks(x)
ax.set_xticklabels(['Rowstore','CStore'])
ax.set_ylim([0,600])
ax.set_ylabel('seconds to execute query')
ax.set_title('Rowstore vs. CStore query time')
```
<a class="anchor" id="when"></a>
# When should I use CStore tables in Data Lab?
We recommend running your query against a cstore table when your query's WHERE clause is against unindexed columns.
~~~~
SELECT <...>
FROM <...>_cs
WHERE unindexed_column <...>
~~~~
If some columns in the WHERE clause are indexed and others are not, there is not a universal recommendation. A useful rule-of-thumb is when the number of rows to sample is > ~100,000 *after* applying the conditions of the indexed columns, you might try a cstore table to see if performance improves.
|
github_jupyter
|
__author__ = 'Adam Scott <[email protected]>' # single string; emails in <>
__version__ = '20190103' # yyyymmdd; version datestamp of this notebook
__datasets__ = ['ls_dr5'] # datasets used in this notebook; for available datasets, see cell "Available datasets in Data Lab" further below
__keywords__ = ['tutorial','query'], # keywords relevant to this notebook, e.g. ['science case','dwarf galaxies'] Use only keywords from the master list: https://github.com/noaodatalab/notebooks_private/blob/master/internal/keywords.txt
# 3rd party
import matplotlib.pyplot as plt
%matplotlib inline
# Datalab
from dl import queryClient as qc
%%time
query = """SELECT min(flux_g), max(flux_g), avg(flux_g),
min(flux_r), max(flux_r), avg(flux_r),
min(flux_z), max(flux_z), avg(flux_z)
FROM ls_dr5.tractor
WHERE psfsize_r > 0.6635 and psfsize_r < 1.327"""
# Send the query to the Queryclient in SQL, with a comma-separated-value (csv) output
response = qc.query(sql=query, fmt='csv')
%%time
query = """SELECT min(flux_g), max(flux_g), avg(flux_g),
min(flux_r), max(flux_r), avg(flux_r),
min(flux_z), max(flux_z), avg(flux_z)
FROM ls_dr5.tractor_cs
WHERE psfsize_r > 0.6635 and psfsize_r < 1.327"""
# Send the query to the Queryclient in SQL, with a comma-separated-value (csv) output
response = qc.query(sql=query, fmt='csv')
x = [1,2]
y = [322,224]
ax = plt.subplot()
pr, pc = plt.bar(x,y)
pr.set_facecolor('b')
pc.set_facecolor('r')
ax.set_xticks(x)
ax.set_xticklabels(['Rowstore','CStore'])
ax.set_ylim([0,600])
ax.set_ylabel('seconds to execute query')
ax.set_title('Rowstore vs. CStore query time')
| 0.788827 | 0.893588 |
```
import pandas as pd
import numpy as np
from collections import OrderedDict
%time
df = pd.read_csv('Base_11.csv', index_col = 0)
df.head()
df.tail()
df = df.drop(columns = ['PROVIDER_NAME'])
df.head()
df.shape
print('Type of Principal Diag Code Column: ', df.PRINC_DIAG_CODE.dtype)
print('Type of Principal Surg Proc Code Column: ', df.PRINC_SURG_PROC_CODE.dtype)
print('Type of Principal ICD9 Code Column: ', df.PRINC_ICD9_CODE.dtype)
print('Number of Null Values in Principal Diag Code Column: ', df.PRINC_DIAG_CODE.isnull().sum())
print('Number of Null Values in Principal Surg Proc Code Column: ', df.PRINC_SURG_PROC_CODE.isnull().sum())
print('Number of Null Values in Principal ICD9 Code Column: ', df.PRINC_ICD9_CODE.isnull().sum())
def changetype(elem):
try:
return int(elem)
except:
return 0
df.PRINC_DIAG_CODE = df['PRINC_DIAG_CODE'].map(lambda x: changetype(x))
df.PRINC_ICD9_CODE = df['PRINC_ICD9_CODE'].map(lambda x: changetype(x))
df.PRINC_SURG_PROC_CODE = df['PRINC_SURG_PROC_CODE'].map(lambda x: changetype(x))
print('Type of Principal Diag Code Column: ', df.PRINC_DIAG_CODE.dtype)
print('Type of Principal Surg Proc Code Column: ', df.PRINC_SURG_PROC_CODE.dtype)
print('Type of Principal ICD9 Code Column: ', df.PRINC_ICD9_CODE.dtype)
print('Number of Null Values in Principal Diag Code Column: ', df.PRINC_DIAG_CODE.isnull().sum())
print('Number of Null Values in Principal Surg Proc Code Column: ', df.PRINC_SURG_PROC_CODE.isnull().sum())
print('Number of Null Values in Principal ICD9 Code Column: ', df.PRINC_ICD9_CODE.isnull().sum())
proc_code = [362, 370, 387, 390, 391]
for x in range(3500, 4000):
proc_code.append(x)
proc_code
surg_count = df['PRINC_SURG_PROC_CODE'].value_counts().to_dict()
for s in list(surg_count.keys()):
if s not in proc_code:
del surg_count[s]
surg_code_count = pd.DataFrame(list(surg_count.items()), columns = ['Surg_Code_1', 'Surg_Count_1'])
surg_code_count.head()
surg_code_count.shape
proc_count = df['PRINC_ICD9_CODE'].value_counts().to_dict()
for p in list(proc_count.keys()):
if p not in proc_code:
del proc_count[p]
ICD9_code_count = pd.DataFrame(list(proc_count.items()), columns = ['ICD9_Code_1', 'ICD9_Count_1'])
ICD9_code_count.head()
ICD9_code_count.shape
df = df[df['PRINC_ICD9_CODE'].isin(proc_code) & df['PRINC_SURG_PROC_CODE'].isin(proc_code)]
df.head()
surg_count = df['PRINC_SURG_PROC_CODE'].value_counts().to_dict()
for s in list(surg_count.keys()):
if s not in proc_code:
del surg_count[s]
surg_code_count_2 = pd.DataFrame(list(surg_count.items()), columns = ['Surg_Code_2', 'Surg_Count_2'])
surg_code_count_2.head()
surg_code_count_2.shape
proc_count = df['PRINC_ICD9_CODE'].value_counts().to_dict()
for p in list(proc_count.keys()):
if p not in proc_code:
del proc_count[p]
ICD9_code_count_2 = pd.DataFrame(list(proc_count.items()), columns = ['ICD9_Code_2', 'ICD9_Count_2'])
ICD9_code_count_2.head()
ICD9_code_count_2.shape
diag_code = [390, 393, 412]
for x in range(3910, 3981):
diag_code.append(x)
for x in range(4110, 4290):
diag_code.append(x)
for x in range(39890, 40292):
diag_code.append(x)
for x in range(40400, 40494):
diag_code.append(x)
for x in range(41000, 42843):
diag_code.append(x)
diag_code
diag_count = df['PRINC_DIAG_CODE'].value_counts().to_dict()
for d in list(diag_count.keys()):
if d not in diag_code:
del diag_count[d]
diag_code_count = pd.DataFrame(list(diag_count.items()), columns = ['Diag_Code_1', 'Diag_Count_1'])
diag_code_count.head()
diag_code_count.shape
df = df[df['PRINC_DIAG_CODE'].isin(diag_code)]
df.head()
diag_count_check = df['PRINC_DIAG_CODE'].value_counts().to_dict()
for d in list(diag_count.keys()):
if d not in diag_code:
del diag_count[d]
diag_code_count_2 = pd.DataFrame(list(diag_count.items()), columns = ['Diag_Code_2', 'Diag_Count_2'])
diag_code_count_2.head()
diag_code_count_2.shape
df.shape
df.head()
df = df.reset_index(drop = True)
df.head()
df.to_csv('Base_11_Subset.csv')
```
|
github_jupyter
|
import pandas as pd
import numpy as np
from collections import OrderedDict
%time
df = pd.read_csv('Base_11.csv', index_col = 0)
df.head()
df.tail()
df = df.drop(columns = ['PROVIDER_NAME'])
df.head()
df.shape
print('Type of Principal Diag Code Column: ', df.PRINC_DIAG_CODE.dtype)
print('Type of Principal Surg Proc Code Column: ', df.PRINC_SURG_PROC_CODE.dtype)
print('Type of Principal ICD9 Code Column: ', df.PRINC_ICD9_CODE.dtype)
print('Number of Null Values in Principal Diag Code Column: ', df.PRINC_DIAG_CODE.isnull().sum())
print('Number of Null Values in Principal Surg Proc Code Column: ', df.PRINC_SURG_PROC_CODE.isnull().sum())
print('Number of Null Values in Principal ICD9 Code Column: ', df.PRINC_ICD9_CODE.isnull().sum())
def changetype(elem):
try:
return int(elem)
except:
return 0
df.PRINC_DIAG_CODE = df['PRINC_DIAG_CODE'].map(lambda x: changetype(x))
df.PRINC_ICD9_CODE = df['PRINC_ICD9_CODE'].map(lambda x: changetype(x))
df.PRINC_SURG_PROC_CODE = df['PRINC_SURG_PROC_CODE'].map(lambda x: changetype(x))
print('Type of Principal Diag Code Column: ', df.PRINC_DIAG_CODE.dtype)
print('Type of Principal Surg Proc Code Column: ', df.PRINC_SURG_PROC_CODE.dtype)
print('Type of Principal ICD9 Code Column: ', df.PRINC_ICD9_CODE.dtype)
print('Number of Null Values in Principal Diag Code Column: ', df.PRINC_DIAG_CODE.isnull().sum())
print('Number of Null Values in Principal Surg Proc Code Column: ', df.PRINC_SURG_PROC_CODE.isnull().sum())
print('Number of Null Values in Principal ICD9 Code Column: ', df.PRINC_ICD9_CODE.isnull().sum())
proc_code = [362, 370, 387, 390, 391]
for x in range(3500, 4000):
proc_code.append(x)
proc_code
surg_count = df['PRINC_SURG_PROC_CODE'].value_counts().to_dict()
for s in list(surg_count.keys()):
if s not in proc_code:
del surg_count[s]
surg_code_count = pd.DataFrame(list(surg_count.items()), columns = ['Surg_Code_1', 'Surg_Count_1'])
surg_code_count.head()
surg_code_count.shape
proc_count = df['PRINC_ICD9_CODE'].value_counts().to_dict()
for p in list(proc_count.keys()):
if p not in proc_code:
del proc_count[p]
ICD9_code_count = pd.DataFrame(list(proc_count.items()), columns = ['ICD9_Code_1', 'ICD9_Count_1'])
ICD9_code_count.head()
ICD9_code_count.shape
df = df[df['PRINC_ICD9_CODE'].isin(proc_code) & df['PRINC_SURG_PROC_CODE'].isin(proc_code)]
df.head()
surg_count = df['PRINC_SURG_PROC_CODE'].value_counts().to_dict()
for s in list(surg_count.keys()):
if s not in proc_code:
del surg_count[s]
surg_code_count_2 = pd.DataFrame(list(surg_count.items()), columns = ['Surg_Code_2', 'Surg_Count_2'])
surg_code_count_2.head()
surg_code_count_2.shape
proc_count = df['PRINC_ICD9_CODE'].value_counts().to_dict()
for p in list(proc_count.keys()):
if p not in proc_code:
del proc_count[p]
ICD9_code_count_2 = pd.DataFrame(list(proc_count.items()), columns = ['ICD9_Code_2', 'ICD9_Count_2'])
ICD9_code_count_2.head()
ICD9_code_count_2.shape
diag_code = [390, 393, 412]
for x in range(3910, 3981):
diag_code.append(x)
for x in range(4110, 4290):
diag_code.append(x)
for x in range(39890, 40292):
diag_code.append(x)
for x in range(40400, 40494):
diag_code.append(x)
for x in range(41000, 42843):
diag_code.append(x)
diag_code
diag_count = df['PRINC_DIAG_CODE'].value_counts().to_dict()
for d in list(diag_count.keys()):
if d not in diag_code:
del diag_count[d]
diag_code_count = pd.DataFrame(list(diag_count.items()), columns = ['Diag_Code_1', 'Diag_Count_1'])
diag_code_count.head()
diag_code_count.shape
df = df[df['PRINC_DIAG_CODE'].isin(diag_code)]
df.head()
diag_count_check = df['PRINC_DIAG_CODE'].value_counts().to_dict()
for d in list(diag_count.keys()):
if d not in diag_code:
del diag_count[d]
diag_code_count_2 = pd.DataFrame(list(diag_count.items()), columns = ['Diag_Code_2', 'Diag_Count_2'])
diag_code_count_2.head()
diag_code_count_2.shape
df.shape
df.head()
df = df.reset_index(drop = True)
df.head()
df.to_csv('Base_11_Subset.csv')
| 0.216012 | 0.335446 |
```
import pandas as pd
import panel as pn
import numpy as np
import holoviews as hv
from holoviews.streams import Buffer
from bokeh.models import Button, Slider, Spinner
import time
import asyncio
pn.extension(sizing_mode="stretch_width")
```
This app provides a simple example of a graphical interface for scientific instrument control using Panel for layout/interaction and [Holoviews](http://holoviews.org) for buffering and plotting data from the instrument.
First we make a mock instrument for this standalone example. The non-mock version of this class would communicate with the instrument (via serial/USB or NI-VISA, etc.)
```
class FakeInstrument(object):
def __init__(self, offset=0.0):
self.offset = offset
def set_offset(self, value):
self.offset = value
def read_data(self):
return np.random.random() + self.offset
instrument = FakeInstrument() # Instantiate your instrument
```
Now set up the buffer and plot to handle the streaming data. You could get by without making a Pandas Dataframe, but it does a good job of writing to a csv file. See [Working with Streaming Data](http://holoviews.org/user_guide/Streaming_Data.html) in the Holoviews documentation for other options.
Here we're only plotting one line of data, so we can create the DynamicMap simply by passing it hv.Curve. The Curve function is going to assume we want to plot the "Temperature (°C)" column versus the "Time (s)" column and generate the plot accordingly. If we wanted some other behavior, or if we had another column in our dataset and wanted to plot two lines at once, we could instead use functools.partial or define our own function that uses hv.Curve to plot the lines the way we want.
```
def make_df(time_sec=0.0, temperature_degC=0.0):
return pd.DataFrame({'Time (s)': time_sec, 'Temperature (°C)': temperature_degC}, index=[0])
example_df = pd.DataFrame(columns=make_df().columns)
buffer = Buffer(example_df, length=1000, index=False)
plot = hv.DynamicMap(hv.Curve, streams=[buffer]).opts(padding=0.1, height=600, xlim=(0, None), responsive=True)
```
Next we make our GUI components.
```
LABEL_START = 'Start'
LABEL_STOP = 'Stop'
LABEL_CSV_START = "Save to csv"
LABEL_CSV_STOP = "Stop save"
CSV_FILENAME = 'tmp.csv'
button_startstop = Button(label=LABEL_START, button_type="primary")
button_csv = Button(label=LABEL_CSV_START, button_type="success")
offset = Slider(title='Offset', start=-10.0, end=10.0, value=0.0, step=0.1)
interval = Spinner(title="Interval (sec)", value=0.1, step=0.01)
```
Now we define the functionality. As in the Holoviews documentation on [Working with Streaming Data](http://holoviews.org/user_guide/Streaming_Data.html), here we're using a coroutine to handle getting and plotting the data without blocking the GUI (although here we're using async/await rather than a decorator). This asychronous approach works fine if you are only trying to get data from your instrument once every ~50 ms or so. If you need to communicate with your instrument more frequently than that, then you'll want a separate thread (and maybe even separate hardware) to handle the communication, and you will want to update the plot with blocks of data points rather than with every individual point.
```
acquisition_task = None
save_to_csv = False
async def acquire_data(interval_sec=0.1):
global save_to_csv
t0 = time.time()
while True:
instrument.set_offset(offset.value)
time_elapsed = time.time() - t0
value = instrument.read_data()
b = make_df(time_elapsed, value)
buffer.send(b)
if save_to_csv:
b.to_csv(CSV_FILENAME, header=False, index=False, mode='a')
time_spent_buffering = time.time() - t0 - time_elapsed
if interval_sec > time_spent_buffering:
await asyncio.sleep(interval_sec - time_spent_buffering)
def toggle_csv(*events):
global save_to_csv
if button_csv.label == LABEL_CSV_START:
button_csv.label = LABEL_CSV_STOP
example_df.to_csv(CSV_FILENAME, index=False) # example_df is empty, so this just writes the header
save_to_csv = True
else:
save_to_csv = False
button_csv.label = LABEL_CSV_START
def start_stop(*events):
global acquisition_task, save_to_csv
if button_startstop.label == LABEL_START:
button_startstop.label = LABEL_STOP
buffer.clear()
acquisition_task = asyncio.get_running_loop().create_task(acquire_data(interval_sec=interval.value))
else:
acquisition_task.cancel()
button_startstop.label = LABEL_START
if save_to_csv:
toggle_csv()
button_startstop.on_click(start_stop)
button_csv.on_click(toggle_csv)
```
Finally, layout the GUI and start it. To run this in a notebook, we are using the .show method on a Panel object to start a Bokeh server and open the GUI in a new browser window. See [Depolying Bokeh Apps](http://holoviews.org/user_guide/Deploying_Bokeh_Apps.html) for more info and other options.
```
hv.extension('bokeh')
hv.renderer('bokeh').theme = 'caliber'
controls = pn.WidgetBox('# Controls',
button_startstop,
button_csv,
interval,
offset,
)
pn.Row(plot, controls)
```
## App
Lets wrap it into nice template that can be served via `panel serve hardware_automation.ipynb`
```
pn.template.FastListTemplate(
site="Panel",
title="Hardware Automation, IoT, Streaming and Async",
sidebar=[*controls],
main=[
"This app provides a simple example of a graphical interface for **scientific instrument control** using Panel for layout/interaction and [Holoviews](http://holoviews.org) for buffering and plotting data from the instrument.",
plot,
]
).servable();
```
|
github_jupyter
|
import pandas as pd
import panel as pn
import numpy as np
import holoviews as hv
from holoviews.streams import Buffer
from bokeh.models import Button, Slider, Spinner
import time
import asyncio
pn.extension(sizing_mode="stretch_width")
class FakeInstrument(object):
def __init__(self, offset=0.0):
self.offset = offset
def set_offset(self, value):
self.offset = value
def read_data(self):
return np.random.random() + self.offset
instrument = FakeInstrument() # Instantiate your instrument
def make_df(time_sec=0.0, temperature_degC=0.0):
return pd.DataFrame({'Time (s)': time_sec, 'Temperature (°C)': temperature_degC}, index=[0])
example_df = pd.DataFrame(columns=make_df().columns)
buffer = Buffer(example_df, length=1000, index=False)
plot = hv.DynamicMap(hv.Curve, streams=[buffer]).opts(padding=0.1, height=600, xlim=(0, None), responsive=True)
LABEL_START = 'Start'
LABEL_STOP = 'Stop'
LABEL_CSV_START = "Save to csv"
LABEL_CSV_STOP = "Stop save"
CSV_FILENAME = 'tmp.csv'
button_startstop = Button(label=LABEL_START, button_type="primary")
button_csv = Button(label=LABEL_CSV_START, button_type="success")
offset = Slider(title='Offset', start=-10.0, end=10.0, value=0.0, step=0.1)
interval = Spinner(title="Interval (sec)", value=0.1, step=0.01)
acquisition_task = None
save_to_csv = False
async def acquire_data(interval_sec=0.1):
global save_to_csv
t0 = time.time()
while True:
instrument.set_offset(offset.value)
time_elapsed = time.time() - t0
value = instrument.read_data()
b = make_df(time_elapsed, value)
buffer.send(b)
if save_to_csv:
b.to_csv(CSV_FILENAME, header=False, index=False, mode='a')
time_spent_buffering = time.time() - t0 - time_elapsed
if interval_sec > time_spent_buffering:
await asyncio.sleep(interval_sec - time_spent_buffering)
def toggle_csv(*events):
global save_to_csv
if button_csv.label == LABEL_CSV_START:
button_csv.label = LABEL_CSV_STOP
example_df.to_csv(CSV_FILENAME, index=False) # example_df is empty, so this just writes the header
save_to_csv = True
else:
save_to_csv = False
button_csv.label = LABEL_CSV_START
def start_stop(*events):
global acquisition_task, save_to_csv
if button_startstop.label == LABEL_START:
button_startstop.label = LABEL_STOP
buffer.clear()
acquisition_task = asyncio.get_running_loop().create_task(acquire_data(interval_sec=interval.value))
else:
acquisition_task.cancel()
button_startstop.label = LABEL_START
if save_to_csv:
toggle_csv()
button_startstop.on_click(start_stop)
button_csv.on_click(toggle_csv)
hv.extension('bokeh')
hv.renderer('bokeh').theme = 'caliber'
controls = pn.WidgetBox('# Controls',
button_startstop,
button_csv,
interval,
offset,
)
pn.Row(plot, controls)
pn.template.FastListTemplate(
site="Panel",
title="Hardware Automation, IoT, Streaming and Async",
sidebar=[*controls],
main=[
"This app provides a simple example of a graphical interface for **scientific instrument control** using Panel for layout/interaction and [Holoviews](http://holoviews.org) for buffering and plotting data from the instrument.",
plot,
]
).servable();
| 0.508056 | 0.857828 |
```
import warnings
from collections import Counter
warnings.filterwarnings("ignore")
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
import pickle
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from ctgan import CTGANSynthesizer
from sklearn.model_selection import train_test_split
from utils import *
MODELS_PATH = './models'
dataset = 'diabetes'
seed = 1
np.random.seed(seed)
```
# A. Load data, preprocess, and calculate accuracy
```
X, y, le = read_data(dataset)
# Append classifier to preprocessing pipeline.
# Now we have a full prediction pipeline.
categorical_features=[]
preprocessor = get_preprocessor(X, categorical_features)
rf = RandomForestClassifier(n_jobs=-1, random_state=seed)
clf = Pipeline(steps=[('preprocessor', preprocessor),
('classifier', rf)])
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=seed)
clf.fit(X_train, y_train)
print("model score: %.3f" % clf.score(X_test, y_test))
```
# B. Plot confidence scores for X_train
```
y_prob = rf.predict_proba(X_train)
y_conf_train = y_prob[:, 0] # confidence scores
plot_confidence_levels(y_conf_train, "Confidence scores for X_train")
```
# C. Train CTGAN and plot the training loss
```
z_features = get_noise_features(X_train, categorical_features)
z_rows = int(0.25 * X_train.shape[0])
z = gen_random_noise(shape=(z_rows, z_features))
batch_size = 50
epochs = 50
confidence_level = 0.9
gen_lr = 2e-5
loss = 'log'
rf_ctgan = CTGANSynthesizer(batch_size=batch_size,
blackbox_model=rf,
preprocessing_pipeline=preprocessor,
bb_loss=loss
)
hist = rf_ctgan.fit(train_data=z,
epochs=epochs,
confidence_level=confidence_level,
gen_lr=gen_lr,
verbose=False
)
# rf_ctgan.save(f"{MODELS_PATH}/{dataset}_ctgan_c_{confidence_level}.pkl")
plot_losses(hist, title=f'{dataset} loss, c = {confidence_level}')
print()
```
# D. Plot confidence scores for 100 generated samples
```
# check confidence for the generated samples
samples = 100
gen_data = rf_ctgan.sample(samples)
y_prob = rf.predict_proba(gen_data)
y_conf_gen = y_prob[:, 0] # confidence scores
plot_confidence_levels(y_conf_gen, f"Scores of generated {samples} samples (c={confidence_level})")
```
# E. Find generated samples above the confidence score
```
# find samples s such that s.confidence > c
indices = np.argwhere(y_conf_gen>confidence_level).squeeze()
print(f"indecies:\n\t{indices}\nconfidence levels:\n\t{y_conf_gen[indices]}")
gen_indices = indices if indices.shape != () else [indices] # avoide no shape arrays
# inverse the generated data
scaler = get_scaler(preprocessor)
gen_data_above_c_before = gen_data.iloc[gen_indices]
gen_data_above_c = scaler.inverse_transform(gen_data_above_c_before)
gen_data_above_c = pd.DataFrame(gen_data_above_c).set_index(gen_data_above_c_before.index)
```
# F. Print most similar examples (X_similiar)
```
similarities = calc_similarities(gen_data_above_c, X_train)
X_similiar_indices = [el[0] for el in similarities.values()]
print(f"gen_sample_above_c -> (most_similiar_sample_x_train, cosine_score)\n\n{similarities}")
```
# G. Print confidence scores for X_similiar
```
# extract X_similiar
X_train_pd = pd.DataFrame(X_train)
X_similiar = X_train_pd.iloc[X_similiar_indices]
# print confidence scores
# y_prob_similar = rf.predict_proba(X_similiar)
# y_conf_similar = y_prob_similar[:, 0]
print(f"confidence scores for similar samples:\n{y_conf_train[X_similiar_indices]}")
```
# Plot as table
```
data = []
for gen_idx, value in similarities.items():
similar_idx = value[0]
similarity = value[1]
gen_conf = y_conf_gen[gen_idx]
similar_conf = y_conf_train[similar_idx]
data.append([gen_idx, gen_conf, similar_idx, similar_conf, similarity])
columns = ['gen_idx', 'score', 'sim_idx', 'score', 'similarity']
results = pd.DataFrame(data, columns=columns)
results
plot_similarities_dist(gen_data_above_c, X_train)
```
|
github_jupyter
|
import warnings
from collections import Counter
warnings.filterwarnings("ignore")
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
import pickle
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from ctgan import CTGANSynthesizer
from sklearn.model_selection import train_test_split
from utils import *
MODELS_PATH = './models'
dataset = 'diabetes'
seed = 1
np.random.seed(seed)
X, y, le = read_data(dataset)
# Append classifier to preprocessing pipeline.
# Now we have a full prediction pipeline.
categorical_features=[]
preprocessor = get_preprocessor(X, categorical_features)
rf = RandomForestClassifier(n_jobs=-1, random_state=seed)
clf = Pipeline(steps=[('preprocessor', preprocessor),
('classifier', rf)])
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=seed)
clf.fit(X_train, y_train)
print("model score: %.3f" % clf.score(X_test, y_test))
y_prob = rf.predict_proba(X_train)
y_conf_train = y_prob[:, 0] # confidence scores
plot_confidence_levels(y_conf_train, "Confidence scores for X_train")
z_features = get_noise_features(X_train, categorical_features)
z_rows = int(0.25 * X_train.shape[0])
z = gen_random_noise(shape=(z_rows, z_features))
batch_size = 50
epochs = 50
confidence_level = 0.9
gen_lr = 2e-5
loss = 'log'
rf_ctgan = CTGANSynthesizer(batch_size=batch_size,
blackbox_model=rf,
preprocessing_pipeline=preprocessor,
bb_loss=loss
)
hist = rf_ctgan.fit(train_data=z,
epochs=epochs,
confidence_level=confidence_level,
gen_lr=gen_lr,
verbose=False
)
# rf_ctgan.save(f"{MODELS_PATH}/{dataset}_ctgan_c_{confidence_level}.pkl")
plot_losses(hist, title=f'{dataset} loss, c = {confidence_level}')
print()
# check confidence for the generated samples
samples = 100
gen_data = rf_ctgan.sample(samples)
y_prob = rf.predict_proba(gen_data)
y_conf_gen = y_prob[:, 0] # confidence scores
plot_confidence_levels(y_conf_gen, f"Scores of generated {samples} samples (c={confidence_level})")
# find samples s such that s.confidence > c
indices = np.argwhere(y_conf_gen>confidence_level).squeeze()
print(f"indecies:\n\t{indices}\nconfidence levels:\n\t{y_conf_gen[indices]}")
gen_indices = indices if indices.shape != () else [indices] # avoide no shape arrays
# inverse the generated data
scaler = get_scaler(preprocessor)
gen_data_above_c_before = gen_data.iloc[gen_indices]
gen_data_above_c = scaler.inverse_transform(gen_data_above_c_before)
gen_data_above_c = pd.DataFrame(gen_data_above_c).set_index(gen_data_above_c_before.index)
similarities = calc_similarities(gen_data_above_c, X_train)
X_similiar_indices = [el[0] for el in similarities.values()]
print(f"gen_sample_above_c -> (most_similiar_sample_x_train, cosine_score)\n\n{similarities}")
# extract X_similiar
X_train_pd = pd.DataFrame(X_train)
X_similiar = X_train_pd.iloc[X_similiar_indices]
# print confidence scores
# y_prob_similar = rf.predict_proba(X_similiar)
# y_conf_similar = y_prob_similar[:, 0]
print(f"confidence scores for similar samples:\n{y_conf_train[X_similiar_indices]}")
data = []
for gen_idx, value in similarities.items():
similar_idx = value[0]
similarity = value[1]
gen_conf = y_conf_gen[gen_idx]
similar_conf = y_conf_train[similar_idx]
data.append([gen_idx, gen_conf, similar_idx, similar_conf, similarity])
columns = ['gen_idx', 'score', 'sim_idx', 'score', 'similarity']
results = pd.DataFrame(data, columns=columns)
results
plot_similarities_dist(gen_data_above_c, X_train)
| 0.529993 | 0.728676 |
# Interpolation Comparison in 2D
Comparing `scipy.interpolate.interpn` with `method='linear'` and `method='splinef2d'`, and `scipy.ndimage.map_coordinates`.
We calculate the x-directed electric field due to a rotated, finite length electric dipole source in a homogeneous fullspcae with vertical transverse electrical isotropy (see below under the section `empymod` for the exact model parameters).
For the semi-analytical 1D calculation we use `empymod`, and for the full 3D calculation emg3d, see https://empymod.github.io for both.
The semi-analytical solution is calculated on a very fine grid every 5 meters, whereas the much more expensive 3D model is calculated on a stretched grid, starting with cell width of 20 meters which increases up to 200 m. Different interpolation methods available in `SciPy` are compared. Here, the problem is reduced to a 2D problem. However, in general this is a 3D problem, for which `scipy.interpolate.interpn` is ONLY AVAILABLE for the methods `linear` and `nearest`, BUT NOT for `spline`.
#### Requires
- ``emg3d``, ``discretize``, ``empymod``
- ``numpy``, ``scipy``, ``numba``, ``matplotlib``
Recommended:
```
pip install discretize
conda install -c prisae empymod emg3d
```
However, also possible is
```
pip install discretize empymod emg3d
```
```
import emg3d
import empymod
import discretize
import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate, ndimage
# Style adjustments
%matplotlib inline
plt.style.use('ggplot')
```
## `empymod`
Semi-analytical solution on a regular grid from -2560 meters to 2560 meters in x- and y-directions, calculated every 5 meters. (Analytical in the wavenumber-frequency domain, but then integrated with 5 points to get a finite length dipole and transformed to space-frequency domain with digital linear filters.)
```
# Survey parameters
x = (np.arange(1025))*5-2560
rx = np.repeat([x,],np.size(x),axis=0)
ry = rx.transpose()
# Model parameters
resh = 1. # Horizontal resistivity
aniso = np.sqrt(2.) # Anisotropy
resv = resh*aniso**2 # Vertical resistivity
src = [-50, 50, -30, 30, -320., -280.] # Source: [x1, x2, y1, y2, z1, z2]
src_c = np.mean(np.array(src).reshape(3, 2), 1).ravel() # Center points of course
zrec = -400. # Receiver depth
freq = 0.77 # Frequency
strength = np.pi # Source strength
# Input for empymod
model = { # empymod has positive z-down, so switch source-za
'src': [src[0], src[1], src[2], src[3], -src[4], -src[5]],
'depth': [],
'res': resh,
'aniso': aniso,
'strength': strength,
'srcpts': 5,
'freqtime': freq,
'htarg': {'pts_per_dec': -1},
}
```
Calculate the result and just get the real part for this comparison.
```
epm_fs = empymod.bipole(rec=[rx.ravel(), ry.ravel(), -zrec, 0, 0], verb=3, **model).reshape(np.shape(rx)).real
```
## `emg3d`
Smallest cell is 20x20x20 meters at source location. Cells are stretched; biggest cells are roughly 161x161x200 meters.
```
# Get calculation domain as a function of frequency (resp., skin depth)
hx_min, xdomain = emg3d.utils.get_domain(x0=src[0], freq=0.1, min_width=20)
hz_min, zdomain = emg3d.utils.get_domain(x0=src[2], freq=0.1, min_width=20)
# Create stretched grid
nx = 2**7
hx = emg3d.utils.get_stretched_h(hx_min, xdomain, nx, src_c[0])
hy = emg3d.utils.get_stretched_h(hx_min, xdomain, nx, src_c[1])
hz = emg3d.utils.get_stretched_h(hz_min, zdomain, nx, x0=-400, x1=0)
pgrid = discretize.TensorMesh([hx, hy, hz], x0=(xdomain[0], xdomain[0], zdomain[0]))
pgrid
# Get the model
pmodel = emg3d.utils.Model(pgrid, res_x=resh, res_z=resv, freq=freq)
# Get the source field
sfield = emg3d.utils.get_source_field(pgrid, src, freq, strength)
# Calculate the electric field
pfield = emg3d.solver.solver(pgrid, pmodel, sfield, verb=3)
```
Get the 2D slice at receiver depth, just the real part for this comparison.
```
ind = 53
print(np.allclose(pgrid.vectorNz[ind], zrec)) # Check it is at receiver depth.
data = pfield.fx[:, :, ind].real
```
## Interpolate
```
def interpn_ndimage(points, values, xi):
def spline1d(x, xnew):
fn = interpolate.interp1d(x, np.arange(len(x)), kind='cubic')
return fn(xnew.ravel())
i = spline1d(points[0], xi[0])
j = spline1d(points[1], xi[1])
coords = np.vstack([i, j])
return ndimage.map_coordinates(values, coords, order=3).reshape(rx.shape)
emg3d_ndimage = interpn_ndimage((pgrid.vectorCCx, pgrid.vectorNy), data, (rx, ry))
emg3d_linear = interpolate.interpn((pgrid.vectorCCx, pgrid.vectorNy), data, (rx, ry), method='linear')
emg3d_spline = interpolate.interpn((pgrid.vectorCCx, pgrid.vectorNy), data, (rx, ry), method='splinef2d')
emg3d_ndimage = interpn_ndimage((pgrid.vectorCCx, pgrid.vectorNy), data, (rx, ry))
```
## Plot
### Helper routines for plotting
```
def set_axis(ax, name, x):
"""Set axis."""
plt.sca(ax)
ax.set_title(name)
ax.set_xlim(min(x)/1000, max(x)/1000)
ax.set_ylim(min(x)/1000, max(x)/1000)
ax.axis("equal")
def plot_error(ax, data1, data2):
cf = ax.pcolormesh(
x/1000, x/1000, np.log10(np.abs((data1-data2)/data1)*100),
vmin=-2, vmax=2, linewidth=0, rasterized=True,
cmap=plt.cm.get_cmap("RdBu_r", 8))
return cf
```
### Actual comparison
```
fig, axs = plt.subplots(figsize=(11, 9), nrows=2, ncols=2)
# Plot DATA
set_axis(axs[0, 0], "(a) Semy-analytical Result", x)
cf0 = axs[0, 0].pcolormesh(
x/1000, x/1000, np.log10(np.abs(epm_fs)), linewidth=0,
rasterized=True, cmap="viridis", vmin=-12, vmax=-6)
# Plot Linear
set_axis(axs[0, 1], "(b) `interpn(method='linear')`", x)
plot_error(axs[0, 1], epm_fs, emg3d_linear)
# Plot Spline
set_axis(axs[1, 0], "(c) `interpn(method='splinef2d')`", x)
plot_error(axs[1, 0], epm_fs, emg3d_spline)
# Plot ndimage
set_axis(axs[1, 1], "(d) `ndimage.map_coordinates`", x)
cf1 = plot_error(axs[1, 1], epm_fs, emg3d_ndimage)
# Colorbars
fig.colorbar(cf0, ax=axs[0, :], label=r"$\log_{10}$ Amplitude (V/m)")
cbar = fig.colorbar(cf1, ax=axs[1, :], label=r"Relative Error")
cbar.set_ticks([-2, -1, 0, 1, 2])
cbar.ax.set_yticklabels([r"$0.01\,\%$", r"$0.1\,\%$", r"$1\,\%$", r"$10\,\%$", r"$100\,\%$"])
# Axis label
fig.text(0.4, 0.05, "Inline Offset (km)", fontsize=14)
fig.text(0.08, 0.6, "Crossline Offset (km)", rotation=90, fontsize=14)
plt.savefig('InterpolationComparison.png', bbox_inches='tight')
plt.show()
```
---
---
# Pure analytical example, same modeller for fined and coarse grid.
## Model parameters
```
model = {
'src': [0, 0, 300], # Source at (0, 0, 0)
'res': 1, # Resistivity 1 Ohm.m
'freqtime': 1, # Frequency 1 Hz
'verb': 1,
}
zrec = 100. # Receiver depth
```
## Calculate analytical solution for regular, fine grid
Calculate it on a 5m x 5m grid.
```
x1 = (np.arange(1025))*5-2560
r1x = np.repeat([x1,], np.size(x1), axis=0)
r1y = r1x.transpose()
epm_fs = empymod.analytical(
rec=[r1x.ravel(), r1y.ravel(), zrec], **model
).reshape(np.shape(r1x)).real
```
## Calculate analytical solution for stretched grid
Calculate it on a stretched grid, starting at 0.6 m up to 243 m cell width.
```
x2 = np.cumsum(1.1**np.arange(64))*.6
x2 = np.r_[-x2[::-1], 0.001, x2]
x2size = np.diff(x2)
print(f"Stretched grid; min: {np.round(np.abs(x2size).min(), 2)} m, max: {np.round(np.abs(x2size).max(), 2)}\n")
r2x = np.repeat([x2,],np.size(x2),axis=0)
r2y = r2x.transpose()
epm_fs2 = empymod.analytical(
rec=[r2x.ravel(), r2y.ravel(), zrec], **model
).reshape(np.shape(r2x)).real
```
# Interpolate
```
epm_fs_linear = interpolate.interpn((x2, x2), epm_fs2, (r1y, r1x), method='linear')
epm_fs_scubic = interpolate.interpn((x2, x2), epm_fs2, (r1y, r1x), method='splinef2d')
```
# Plot
```
fig, axs = plt.subplots(figsize=(14, 6))
# Plot DATA
plt.subplot(131)
plt.title("(a) Data (fine grid)")
cf0 = plt.pcolormesh(
x1/1000, x1/1000, np.log10(np.abs(epm_fs)), linewidth=0,
rasterized=True, cmap="viridis", vmin=-14, vmax=-8)
plt.ylabel("Crossline Offset (km)", fontsize=16)
plt.xlim(min(x1)/1000, max(x1)/1000)
plt.ylim(min(x1)/1000, max(x1)/1000)
plt.axis("equal")
fig.colorbar(cf0, label=r"$\log_{10}$ Amplitude (V/m)", orientation='horizontal')
# Plot Linear
plt.subplot(132)
plt.title("(b) Linear interpolation")
cf1 = plt.pcolormesh(
x1/1000, x1/1000, np.log10(np.abs((epm_fs-epm_fs_linear)/epm_fs)*100),
vmin=-2, vmax=2, linewidth=0, rasterized=True,
cmap=plt.cm.get_cmap("RdBu_r", 8))
plt.xlim(min(x1)/1000, max(x1)/1000)
plt.ylim(min(x1)/1000, max(x1)/1000)
plt.axis("equal")
plt.xlabel("Inline Offset (km)", fontsize=16)
cbar = fig.colorbar(cf1, label=r"Relative Error", orientation='horizontal')
cbar.set_ticks([-2, -1, 0, 1, 2])
cbar.ax.set_xticklabels([r"$0.01\,\%$", r"$0.1\,\%$", r"$1\,\%$", r"$10\,\%$", r"$100\,\%$"])
# Plot cubic
plt.subplot(133)
plt.title("(c) Cubic spline interpolation")
cf2 = plt.pcolormesh(
x1/1000, x1/1000, np.log10(np.abs((epm_fs-epm_fs_scubic)/epm_fs)*100),
vmin=-2, vmax=2, linewidth=0, rasterized=True,
cmap=plt.cm.get_cmap("RdBu_r", 8))
plt.xlim(min(x1)/1000, max(x1)/1000)
plt.ylim(min(x1)/1000, max(x1)/1000)
plt.axis("equal")
cbar = fig.colorbar(cf2, label=r"Relative Error", orientation='horizontal')
cbar.set_ticks([-2, -1, 0, 1, 2])
cbar.ax.set_xticklabels([r"$0.01\,\%$", r"$0.1\,\%$", r"$1\,\%$", r"$10\,\%$", r"$100\,\%$"])
plt.suptitle('Linear vs cubic spline interpolation for stretched grids.', fontsize=18, y=1.05)
plt.tight_layout()
plt.savefig('InterpolationComparison-analytical.png', bbox_inches='tight')
plt.show()
emg3d.Versions([empymod, discretize])
```
|
github_jupyter
|
pip install discretize
conda install -c prisae empymod emg3d
pip install discretize empymod emg3d
import emg3d
import empymod
import discretize
import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate, ndimage
# Style adjustments
%matplotlib inline
plt.style.use('ggplot')
# Survey parameters
x = (np.arange(1025))*5-2560
rx = np.repeat([x,],np.size(x),axis=0)
ry = rx.transpose()
# Model parameters
resh = 1. # Horizontal resistivity
aniso = np.sqrt(2.) # Anisotropy
resv = resh*aniso**2 # Vertical resistivity
src = [-50, 50, -30, 30, -320., -280.] # Source: [x1, x2, y1, y2, z1, z2]
src_c = np.mean(np.array(src).reshape(3, 2), 1).ravel() # Center points of course
zrec = -400. # Receiver depth
freq = 0.77 # Frequency
strength = np.pi # Source strength
# Input for empymod
model = { # empymod has positive z-down, so switch source-za
'src': [src[0], src[1], src[2], src[3], -src[4], -src[5]],
'depth': [],
'res': resh,
'aniso': aniso,
'strength': strength,
'srcpts': 5,
'freqtime': freq,
'htarg': {'pts_per_dec': -1},
}
epm_fs = empymod.bipole(rec=[rx.ravel(), ry.ravel(), -zrec, 0, 0], verb=3, **model).reshape(np.shape(rx)).real
# Get calculation domain as a function of frequency (resp., skin depth)
hx_min, xdomain = emg3d.utils.get_domain(x0=src[0], freq=0.1, min_width=20)
hz_min, zdomain = emg3d.utils.get_domain(x0=src[2], freq=0.1, min_width=20)
# Create stretched grid
nx = 2**7
hx = emg3d.utils.get_stretched_h(hx_min, xdomain, nx, src_c[0])
hy = emg3d.utils.get_stretched_h(hx_min, xdomain, nx, src_c[1])
hz = emg3d.utils.get_stretched_h(hz_min, zdomain, nx, x0=-400, x1=0)
pgrid = discretize.TensorMesh([hx, hy, hz], x0=(xdomain[0], xdomain[0], zdomain[0]))
pgrid
# Get the model
pmodel = emg3d.utils.Model(pgrid, res_x=resh, res_z=resv, freq=freq)
# Get the source field
sfield = emg3d.utils.get_source_field(pgrid, src, freq, strength)
# Calculate the electric field
pfield = emg3d.solver.solver(pgrid, pmodel, sfield, verb=3)
ind = 53
print(np.allclose(pgrid.vectorNz[ind], zrec)) # Check it is at receiver depth.
data = pfield.fx[:, :, ind].real
def interpn_ndimage(points, values, xi):
def spline1d(x, xnew):
fn = interpolate.interp1d(x, np.arange(len(x)), kind='cubic')
return fn(xnew.ravel())
i = spline1d(points[0], xi[0])
j = spline1d(points[1], xi[1])
coords = np.vstack([i, j])
return ndimage.map_coordinates(values, coords, order=3).reshape(rx.shape)
emg3d_ndimage = interpn_ndimage((pgrid.vectorCCx, pgrid.vectorNy), data, (rx, ry))
emg3d_linear = interpolate.interpn((pgrid.vectorCCx, pgrid.vectorNy), data, (rx, ry), method='linear')
emg3d_spline = interpolate.interpn((pgrid.vectorCCx, pgrid.vectorNy), data, (rx, ry), method='splinef2d')
emg3d_ndimage = interpn_ndimage((pgrid.vectorCCx, pgrid.vectorNy), data, (rx, ry))
def set_axis(ax, name, x):
"""Set axis."""
plt.sca(ax)
ax.set_title(name)
ax.set_xlim(min(x)/1000, max(x)/1000)
ax.set_ylim(min(x)/1000, max(x)/1000)
ax.axis("equal")
def plot_error(ax, data1, data2):
cf = ax.pcolormesh(
x/1000, x/1000, np.log10(np.abs((data1-data2)/data1)*100),
vmin=-2, vmax=2, linewidth=0, rasterized=True,
cmap=plt.cm.get_cmap("RdBu_r", 8))
return cf
fig, axs = plt.subplots(figsize=(11, 9), nrows=2, ncols=2)
# Plot DATA
set_axis(axs[0, 0], "(a) Semy-analytical Result", x)
cf0 = axs[0, 0].pcolormesh(
x/1000, x/1000, np.log10(np.abs(epm_fs)), linewidth=0,
rasterized=True, cmap="viridis", vmin=-12, vmax=-6)
# Plot Linear
set_axis(axs[0, 1], "(b) `interpn(method='linear')`", x)
plot_error(axs[0, 1], epm_fs, emg3d_linear)
# Plot Spline
set_axis(axs[1, 0], "(c) `interpn(method='splinef2d')`", x)
plot_error(axs[1, 0], epm_fs, emg3d_spline)
# Plot ndimage
set_axis(axs[1, 1], "(d) `ndimage.map_coordinates`", x)
cf1 = plot_error(axs[1, 1], epm_fs, emg3d_ndimage)
# Colorbars
fig.colorbar(cf0, ax=axs[0, :], label=r"$\log_{10}$ Amplitude (V/m)")
cbar = fig.colorbar(cf1, ax=axs[1, :], label=r"Relative Error")
cbar.set_ticks([-2, -1, 0, 1, 2])
cbar.ax.set_yticklabels([r"$0.01\,\%$", r"$0.1\,\%$", r"$1\,\%$", r"$10\,\%$", r"$100\,\%$"])
# Axis label
fig.text(0.4, 0.05, "Inline Offset (km)", fontsize=14)
fig.text(0.08, 0.6, "Crossline Offset (km)", rotation=90, fontsize=14)
plt.savefig('InterpolationComparison.png', bbox_inches='tight')
plt.show()
model = {
'src': [0, 0, 300], # Source at (0, 0, 0)
'res': 1, # Resistivity 1 Ohm.m
'freqtime': 1, # Frequency 1 Hz
'verb': 1,
}
zrec = 100. # Receiver depth
x1 = (np.arange(1025))*5-2560
r1x = np.repeat([x1,], np.size(x1), axis=0)
r1y = r1x.transpose()
epm_fs = empymod.analytical(
rec=[r1x.ravel(), r1y.ravel(), zrec], **model
).reshape(np.shape(r1x)).real
x2 = np.cumsum(1.1**np.arange(64))*.6
x2 = np.r_[-x2[::-1], 0.001, x2]
x2size = np.diff(x2)
print(f"Stretched grid; min: {np.round(np.abs(x2size).min(), 2)} m, max: {np.round(np.abs(x2size).max(), 2)}\n")
r2x = np.repeat([x2,],np.size(x2),axis=0)
r2y = r2x.transpose()
epm_fs2 = empymod.analytical(
rec=[r2x.ravel(), r2y.ravel(), zrec], **model
).reshape(np.shape(r2x)).real
epm_fs_linear = interpolate.interpn((x2, x2), epm_fs2, (r1y, r1x), method='linear')
epm_fs_scubic = interpolate.interpn((x2, x2), epm_fs2, (r1y, r1x), method='splinef2d')
fig, axs = plt.subplots(figsize=(14, 6))
# Plot DATA
plt.subplot(131)
plt.title("(a) Data (fine grid)")
cf0 = plt.pcolormesh(
x1/1000, x1/1000, np.log10(np.abs(epm_fs)), linewidth=0,
rasterized=True, cmap="viridis", vmin=-14, vmax=-8)
plt.ylabel("Crossline Offset (km)", fontsize=16)
plt.xlim(min(x1)/1000, max(x1)/1000)
plt.ylim(min(x1)/1000, max(x1)/1000)
plt.axis("equal")
fig.colorbar(cf0, label=r"$\log_{10}$ Amplitude (V/m)", orientation='horizontal')
# Plot Linear
plt.subplot(132)
plt.title("(b) Linear interpolation")
cf1 = plt.pcolormesh(
x1/1000, x1/1000, np.log10(np.abs((epm_fs-epm_fs_linear)/epm_fs)*100),
vmin=-2, vmax=2, linewidth=0, rasterized=True,
cmap=plt.cm.get_cmap("RdBu_r", 8))
plt.xlim(min(x1)/1000, max(x1)/1000)
plt.ylim(min(x1)/1000, max(x1)/1000)
plt.axis("equal")
plt.xlabel("Inline Offset (km)", fontsize=16)
cbar = fig.colorbar(cf1, label=r"Relative Error", orientation='horizontal')
cbar.set_ticks([-2, -1, 0, 1, 2])
cbar.ax.set_xticklabels([r"$0.01\,\%$", r"$0.1\,\%$", r"$1\,\%$", r"$10\,\%$", r"$100\,\%$"])
# Plot cubic
plt.subplot(133)
plt.title("(c) Cubic spline interpolation")
cf2 = plt.pcolormesh(
x1/1000, x1/1000, np.log10(np.abs((epm_fs-epm_fs_scubic)/epm_fs)*100),
vmin=-2, vmax=2, linewidth=0, rasterized=True,
cmap=plt.cm.get_cmap("RdBu_r", 8))
plt.xlim(min(x1)/1000, max(x1)/1000)
plt.ylim(min(x1)/1000, max(x1)/1000)
plt.axis("equal")
cbar = fig.colorbar(cf2, label=r"Relative Error", orientation='horizontal')
cbar.set_ticks([-2, -1, 0, 1, 2])
cbar.ax.set_xticklabels([r"$0.01\,\%$", r"$0.1\,\%$", r"$1\,\%$", r"$10\,\%$", r"$100\,\%$"])
plt.suptitle('Linear vs cubic spline interpolation for stretched grids.', fontsize=18, y=1.05)
plt.tight_layout()
plt.savefig('InterpolationComparison-analytical.png', bbox_inches='tight')
plt.show()
emg3d.Versions([empymod, discretize])
| 0.733547 | 0.979354 |
# Lists in Python
<p>
In most languages a collection of homogeneous (all of the same type)
entities is called an array. The size of the array is fixed at the
time of creation, however, the contents of the array can be changed
during the course of the execution of the program. Higher dimensional
arrays are also possible, where each element of an array is an array.
</p>
<p>
The analogue of an array in Python is a <i>list</i>. Even though a
list defines a collection of things it has different properties from
an array. A list could be a collection of heterogeneous (different
types) items. The size of a list is dynamic. It is not specified at
the time of creation and can grow or shrink as needed. A list could
have duplicate items. The order of the items in a list is important
and not their uniqueness. Python also provides built-in functions to
manipulate a list and its contents. A higher dimensional list has
elements that are themselves lists. Given the flexibility and the
associated functions, a Python list is a more powerful data structure
than an array.
</p>
<h3> List Creation </h3>
<p>
There are several ways in which to create a list. You can enumerate
all the elements of a list or create an empty list and then append
or insert items into the list. When you append an item to a list, that
item is added to the end of the list. To insert an item into a list
you must specify its position and then all the elements to the right
or below it are shifted to make space for it.
```
# Enumerate the items
a = [1, 2, 3]
a
# Create an empty list and append or insert
a = []
print(a)
a.append(1) # a = [1]
print(a)
a.append(2) # a = [1, 2]
print(a)
a.insert(1, 3) # a = [1, 3, 2]
print(a)
# Create a two dimensional list
b = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]
b
```
Note that the positions of items in a list start at an index value of 0.
You can also create a list by concatenating two or more lists together.
You can initialize a list with a predefined value.
```
a = [1, 2]
b = [4, 5]
c = a + b # c = [1, 2, 4, 5]
print(c)
d = [0] * 5 # d = [0, 0, 0, 0, 0]
print(d)
import numpy as np
a1 = np.array(a)
b1 = np.array(b)
print(a + b)
print(a1 + b1)
a1.shape
```
## Basic List Manipulations
To obtain the length of a list you can use the <i>len()</i> function.
```
a = [1, 2, 3]
length = len (a) # length = 3
length
```
#### Indexing
The items in a list are indexed starting at 0 and ending at index
<i>length - 1</i>. You can also use negative indices to access elements
in a list. For example a[-1] returns the last item on the list and
a[-length] returns the first. Unlike a string, a list is mutable, i.e.
its contents can be changed like so:
```
a = [1, 2, 3]
a[1] = 4 # a = [1, 4, 3]
a
```
To access or change an element in a 2-dimensional list specify the row
first and then the column.
```
b = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]
print(b)
d = b[1][2] # d = 6
print(d)
b[2][1] = b[1][2]*2
print(b)
```
Note that the positions of items in a list start at an index value of 0.
You can also create a list by concatenating two or more lists together.
You can initialize a list with a predefined value.
```
a = [1, 2]
b = [4, 5]
c = a + b # c = [1, 2, 4, 5]
print(c)
d = [0] * 5 # d = [0, 0, 0, 0, 0]
d
```
#### List Traversal
<p>
One of the most important operations that you can do with a list is to
traverse it, i.e. visit each and every element in the list in order.
There are several ways in which to do so:
<pre>
</pre>
</p>
```
a = [9, 2, 6, 4, 7]
print(a)
for item in a:
print (item, end = " ") # 9 2 6 4 7
# Doubles each item in the list
length = len (a)
for i in range(length):
a[i] = a[i] * 2
```
<a href = "https://docs.python.org/3/tutorial/datastructures.html">
Other List Functions </a>
<table border = "1" width = "75%">
<tr>
<th> Function </th><th> Meaning </th>
</tr>
<tr>
<td> list.sort() </td>
<td> Sorts a list in ascending order </td>
</tr>
<tr>
<td> list.reverse() </td>
<td> Reverses the elements in a list </td>
</tr>
<tr>
<td> <i>value</i> in list </td>
<td> Returns True if the <i>value</i> is in the list and False otherwise</td>
</tr>
<tr>
<td> list.index(x) </td>
<td> Returns the index of the first occurence of x. Use with the above
function to check if <i>x</i> is in the list before determining its position.
</td>
</tr>
<tr>
<td> list.count(x) </td>
<td> Returns the number of occurences of x in the list </td>
</tr>
<tr>
<td> list.remove(x) </td>
<td> Deletes the first occurence of x in list </td>
</tr>
<tr>
<td> list.pop(i) </td>
<td> Deletes the ith element in the list and returns its value </td>
</tr>
</table>
```
a = [9, 2, 6, 4, 7]
a.sort()
a
a = [9, 2, 6, 4, 7]
a.reverse()
a
for value in [9, 2, 6, 4, 7]:
print(value)
#index
a = [9, 2, 6, 4, 7]
a.index(6)
# count()
a = [9, 2, 6, 6, 4, 7]
a.count(6)
# remove
a = [9, 2, 6, 4,2, 7]
a.remove(2)
a
# pop
a = [9, 2, 6, 4, 7]
b = a.pop(2)
print(b)
a
```
# List Comprehensions
https://docs.python.org/3/tutorial/datastructures.html#list-comprehensions
```
# For example, we want to create a list p
a = [1, 2, 3, 4, 5, 6]
b = [1, -2, 3, -6]
p=[]
for item in b:
if item in a:
p.append(item)
else:
p.append(1000)
print(p)
# instead of the above we can write in python the following.
p = [item if item in a else 1000 for item in b]
print(p)
```
|
github_jupyter
|
# Enumerate the items
a = [1, 2, 3]
a
# Create an empty list and append or insert
a = []
print(a)
a.append(1) # a = [1]
print(a)
a.append(2) # a = [1, 2]
print(a)
a.insert(1, 3) # a = [1, 3, 2]
print(a)
# Create a two dimensional list
b = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]
b
a = [1, 2]
b = [4, 5]
c = a + b # c = [1, 2, 4, 5]
print(c)
d = [0] * 5 # d = [0, 0, 0, 0, 0]
print(d)
import numpy as np
a1 = np.array(a)
b1 = np.array(b)
print(a + b)
print(a1 + b1)
a1.shape
a = [1, 2, 3]
length = len (a) # length = 3
length
a = [1, 2, 3]
a[1] = 4 # a = [1, 4, 3]
a
b = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]
print(b)
d = b[1][2] # d = 6
print(d)
b[2][1] = b[1][2]*2
print(b)
a = [1, 2]
b = [4, 5]
c = a + b # c = [1, 2, 4, 5]
print(c)
d = [0] * 5 # d = [0, 0, 0, 0, 0]
d
a = [9, 2, 6, 4, 7]
print(a)
for item in a:
print (item, end = " ") # 9 2 6 4 7
# Doubles each item in the list
length = len (a)
for i in range(length):
a[i] = a[i] * 2
a = [9, 2, 6, 4, 7]
a.sort()
a
a = [9, 2, 6, 4, 7]
a.reverse()
a
for value in [9, 2, 6, 4, 7]:
print(value)
#index
a = [9, 2, 6, 4, 7]
a.index(6)
# count()
a = [9, 2, 6, 6, 4, 7]
a.count(6)
# remove
a = [9, 2, 6, 4,2, 7]
a.remove(2)
a
# pop
a = [9, 2, 6, 4, 7]
b = a.pop(2)
print(b)
a
# For example, we want to create a list p
a = [1, 2, 3, 4, 5, 6]
b = [1, -2, 3, -6]
p=[]
for item in b:
if item in a:
p.append(item)
else:
p.append(1000)
print(p)
# instead of the above we can write in python the following.
p = [item if item in a else 1000 for item in b]
print(p)
| 0.177847 | 0.978672 |
# Load monthly 5 by 5 degree WCPFC catch and effort data + define lon, lat
Variables defined are:
wf, wfbegdate, wfenddate, timemocatch, lon, lat
```
ncfile = dpath + 'WCPFC/5by5deg/ByMonth/PurseSeine_0/WCPFC_purseseine_bysettype_monthly_5deg.nc'
wf = xr.open_dataset(ncfile)
```
### Correct the time axis
```
# - Time goes from Jan 1967 - Dec 2017 --> 612 months
wfbegdate = datetime.date(year = 1967, month = 1, day = 1)
wfenddate = datetime.date(year = 2017, month = 12, day = 1)
timemocatch = pd.date_range(wfbegdate, wfenddate, freq='MS')
wf['time'] = timemocatch
```
### Get data from between -22.5 and 22.5 degs lat only
```
wf = wf.isel(lat=slice(6,16))
```
### Define lon, lat
```
lon = wf['lon']
lat = wf['lat']
```
# Load monthly ENSO time series
Variables loaded/calculated are:
oni, onien, oniln, onienln, onitime
```
# - Load ONI
dfoni = pd.read_csv(dpath+'ENSOindices/oni/oniindex1950_2018.txt',names=['Date','ONI']);
# - Month fractions corresp to jan, feb, mar, etc. in the ONI txt file
monthfracs = [0,0.0834,0.1666,0.25,0.3334,0.4166,0.5,0.5834,0.6666,0.75,0.8334,0.9166];
# - Get ONI ts over WCPFC dataset timeframe
onibegmoidx = dfoni.index[dfoni['Date'] == (wfbegdate.year + monthfracs[wfbegdate.month-1])][0]
oniendmoidx = dfoni.index[dfoni['Date'] == (wfenddate.year + monthfracs[wfenddate.month-1])][0]
oni = dfoni['ONI'].iloc[onibegmoidx:(oniendmoidx+1)].values
onitime = pd.date_range(wfbegdate, wfenddate, freq='MS') # should be 612 months long
# - Create EN/LN month classifications
onien = [0]*len(oni) # 1 = el nino month
oniln = [0]*len(oni) # 1 = la nina month
# - Classify El Nino months
cmcounter = 0; # consecutive months counter
for imonth in range(len(oni)):
if oni[imonth]>=0.5:
cmcounter=cmcounter+1;
elif oni[imonth]<0.5:
cmcounter=0;
if cmcounter>=5:
onien[imonth-cmcounter:imonth]=[1]*cmcounter;
# - Classify La Nina months
cmcounter = 0; # consecutive months counter
for imonth in range(len(oni)):
if oni[imonth]<=-0.5:
cmcounter=cmcounter+1;
elif oni[imonth]>-0.5:
cmcounter=0;
if cmcounter>=5:
oniln[imonth-cmcounter:imonth]=[1]*cmcounter;
# - Put everything in DataArrays
oni = xr.DataArray(oni, dims=('time'), coords={'time': onitime})
onien = xr.DataArray(onien, dims=('time'), coords={'time': onitime})
oniln = xr.DataArray(oniln, dims=('time'), coords={'time': onitime})
onienln = xr.zeros_like(onien, dtype='int')
onienln[onien==1]=1 # el nino = 1
onienln[oniln==1]=-1 # la nina = -1
plotensoidx=1
if plotensoidx==1:
fig = plt.figure(figsize=(11,4))
plt.plot(onitime,oni)
plt.plot(onitime,onien)
plt.plot(onitime,oniln)
#plt.plot(onitime,onienln)
plt.legend(["oni","onien","oniln","onienln"])
plt.title('ENSO index (ONI)')
```
# Calculate WCPFC total (over all set types) effort, SKJ + BET catch/CPUE, BET:SKJ CPUE ratio
Variables calced are:
skj_c_tot, bet_c_tot, sets_tot,
skj_cp_tot, bet_cp_tot, bettoskj_cp_tot
```
# - The following are 3-D (time, lon, lat):
if settypes=='afaddfad':
skj_c_tot = wf.skj_c_dfad + wf.skj_c_afad
bet_c_tot = wf.bet_c_dfad + wf.bet_c_afad
sets_tot = wf.sets_dfad + wf.sets_afad
elif settypes=='afaddfadlog':
skj_c_tot = wf.skj_c_log + wf.skj_c_dfad + wf.skj_c_afad
bet_c_tot = wf.bet_c_log + wf.bet_c_dfad + wf.bet_c_afad
sets_tot = wf.sets_log + wf.sets_dfad + wf.sets_afad
elif settypes=='unassociated':
skj_c_tot = wf.skj_c_una
bet_c_tot = wf.bet_c_una
sets_tot = wf.sets_una
elif settypes=='unassociatedother':
skj_c_tot = wf.skj_c_una + wf.skj_c_oth
bet_c_tot = wf.bet_c_una + wf.bet_c_oth
sets_tot = wf.sets_una + wf.sets_oth
elif settypes=='allsets':
skj_c_tot = wf.skj_c_una + wf.skj_c_log + wf.skj_c_dfad + wf.skj_c_afad + wf.skj_c_oth
bet_c_tot = wf.bet_c_una + wf.bet_c_log + wf.bet_c_dfad + wf.bet_c_afad + wf.bet_c_oth
sets_tot = wf.sets_una + wf.sets_log + wf.sets_dfad + wf.sets_afad + wf.sets_oth
if catchorcpue=='catch':
skj_cp_tot = skj_c_tot
bet_cp_tot = bet_c_tot
elif catchorcpue=='CPUE':
skj_cp_tot = skj_c_tot/sets_tot
bet_cp_tot = bet_c_tot/sets_tot
skj_cp_tot = skj_cp_tot.where(~np.isinf(skj_cp_tot), np.nan)
bet_cp_tot = bet_cp_tot.where(~np.isinf(bet_cp_tot), np.nan)
bettoskj_cp_tot = bet_cp_tot/skj_cp_tot
# - Name the dataarrays for later merging into datasets
skj_c_tot.name = 'skj_c_tot'
bet_c_tot.name = 'bet_c_tot'
skj_cp_tot.name = 'skj_cp_tot'
bet_cp_tot.name = 'bet_cp_tot'
bettoskj_cp_tot.name = 'bettoskj_cp_tot'
```
# Calculate WCPFC total (over all set types) effort, SKJ + BET CPUE, BET:SKJ CPUE ratio monthly climatology and anomalies
Variables calced are:
skj_cp_tot_seas, bet_cp_tot_seas, bettoskj_cp_tot_seas,
skj_cp_tot_clim, bet_cp_tot_clim, bettoskj_cp_tot_clim,
skj_cp_tot_anom, bet_cp_tot_anom, bettoskj_cp_tot_anom
```
# - The following are all 3-D (time, lon, lat):
skj_cp_tot_seas = skj_cp_tot.groupby('time.season').mean('time')
bet_cp_tot_seas = bet_cp_tot.groupby('time.season').mean('time')
bettoskj_cp_tot_seas = bettoskj_cp_tot.groupby('time.season').mean('time')
skj_cp_tot_clim = skj_cp_tot.groupby('time.month').mean('time')
bet_cp_tot_clim = bet_cp_tot.groupby('time.month').mean('time')
bettoskj_cp_tot_clim = bettoskj_cp_tot.groupby('time.month').mean('time')
skj_cp_tot_anom = skj_cp_tot.groupby('time.month') - skj_cp_tot_clim
bet_cp_tot_anom = bet_cp_tot.groupby('time.month') - bet_cp_tot_clim
bettoskj_cp_tot_anom = bettoskj_cp_tot.groupby('time.month') - bettoskj_cp_tot_clim
# - Name the dataarrays for later merging into datasets
skj_cp_tot_seas.name = 'skj_cp_tot_seas'
bet_cp_tot_seas.name = 'bet_cp_tot_seas'
bettoskj_cp_tot_seas.name = 'bettoskj_cp_tot_seas'
skj_cp_tot_clim.name = 'skj_cp_tot_clim'
bet_cp_tot_clim.name = 'bet_cp_tot_clim'
bettoskj_cp_tot_clim.name = 'bettoskj_cp_tot_clim'
skj_cp_tot_anom.name = 'skj_cp_tot_anom'
bet_cp_tot_anom.name = 'bet_cp_tot_anom'
bettoskj_cp_tot_anom.name = 'bettoskj_cp_tot_anom'
```
# Compute seasonal mean p-val maps
Variables calced are:
skj_cp_tot_seas_kw_pval, skj_cp_tot_seas_kw_ptf,
bet_cp_tot_seas_kw_pval, bet_cp_tot_seas_kw_ptf,
bettoskj_cp_tot_seas_kw_pval, bettoskj_cp_tot_seas_kw_ptf
```
alphafdr = 0.1
skj_cp_tot_seas_kw_pval = kwpvalmap_loop(
skj_cp_tot.sel(time=skj_cp_tot['time.season']=='DJF'),
skj_cp_tot.sel(time=skj_cp_tot['time.season']=='MAM'),
skj_cp_tot.sel(time=skj_cp_tot['time.season']=='JJA'),
skj_cp_tot.sel(time=skj_cp_tot['time.season']=='SON'),
'skj_cp_tot_seas')
skj_cp_tot_seas_kw_ptf = controlfdr2d(skj_cp_tot_seas_kw_pval,alphafdr)
bet_cp_tot_seas_kw_pval = kwpvalmap_loop(
bet_cp_tot.sel(time=bet_cp_tot['time.season']=='DJF'),
bet_cp_tot.sel(time=bet_cp_tot['time.season']=='MAM'),
bet_cp_tot.sel(time=bet_cp_tot['time.season']=='JJA'),
bet_cp_tot.sel(time=bet_cp_tot['time.season']=='SON'),
'bet_cp_tot_seas')
bet_cp_tot_seas_kw_ptf = controlfdr2d(bet_cp_tot_seas_kw_pval,alphafdr)
bettoskj_cp_tot_seas_kw_pval = kwpvalmap_loop(
bettoskj_cp_tot.sel(time=bettoskj_cp_tot['time.season']=='DJF'),
bettoskj_cp_tot.sel(time=bettoskj_cp_tot['time.season']=='MAM'),
bettoskj_cp_tot.sel(time=bettoskj_cp_tot['time.season']=='JJA'),
bettoskj_cp_tot.sel(time=bettoskj_cp_tot['time.season']=='SON'),
'bettoskj_cp_tot_seas')
bettoskj_cp_tot_seas_kw_ptf = controlfdr2d(bettoskj_cp_tot_seas_kw_pval,alphafdr)
```
# Calculate mean, ENSO anomaly composites, and ENSO composites of total (over all set types) SKJ + BET CPUE, BET:SKJ CPUE
Variables calced are:
skj_cp_tot_mean, bet_cp_tot_mean, bettoskj_cp_tot_mean,
skj_cp_tot_anom_en, bet_cp_tot_anom_en, bettoskj_cp_tot_anom_en,
skj_cp_tot_anom_ln, bet_cp_tot_anom_ln, bettoskj_cp_tot_anom_ln
skj_cp_tot_en, bet_cp_tot_en, bettoskj_cp_tot_en,
skj_cp_tot_ln, bet_cp_tot_ln, bettoskj_cp_tot_ln
```
# - The following are 2-D (lon, lat):
skj_cp_tot_mean = skj_cp_tot.mean('time')
bet_cp_tot_mean = bet_cp_tot.mean('time')
bettoskj_cp_tot_mean = bettoskj_cp_tot.mean('time')
skj_cp_tot_anom_en = skj_cp_tot_anom[onienln==1].mean(dim='time')
skj_cp_tot_anom_ln = skj_cp_tot_anom[onienln==-1].mean(dim='time')
bet_cp_tot_anom_en = bet_cp_tot_anom[onienln==1].mean(dim='time')
bet_cp_tot_anom_ln = bet_cp_tot_anom[onienln==-1].mean(dim='time')
bettoskj_cp_tot_anom_en = bettoskj_cp_tot_anom[onienln==1].mean(dim='time')
bettoskj_cp_tot_anom_ln = bettoskj_cp_tot_anom[onienln==-1].mean(dim='time')
skj_cp_tot_en = skj_cp_tot[onienln==1].mean(dim='time')
skj_cp_tot_ln = skj_cp_tot[onienln==-1].mean(dim='time')
bet_cp_tot_en = bet_cp_tot[onienln==1].mean(dim='time')
bet_cp_tot_ln = bet_cp_tot[onienln==-1].mean(dim='time')
bettoskj_cp_tot_en = bettoskj_cp_tot[onienln==1].mean(dim='time')
bettoskj_cp_tot_ln = bettoskj_cp_tot[onienln==-1].mean(dim='time')
```
# Compute EN vs. LN anomaly composite and composite p-val maps
Variables calced are:
skj_cp_tot_anom_enln_wrs_pval, skj_cp_tot_anom_enln_wrs_ptf,
bet_cp_tot_anom_enln_wrs_pval, bet_cp_tot_anom_enln_wrs_ptf,
bettoskj_cp_tot_anom_enln_wrs_pval, bettoskj_cp_tot_anom_enln_wrs_ptf,
skj_cp_tot_enln_wrs_pval, skj_cp_tot_enln_wrs_ptf,
bet_cp_tot_enln_wrs_pval, bet_cp_tot_enln_wrs_ptf,
bettoskj_cp_tot_enln_wrs_pval, bettoskj_cp_tot_enln_wrs_ptf
```
alphafdr = 0.1
skj_cp_tot_anom_enln_wrs_pval = wrspvalmap_loop(
skj_cp_tot_anom[onienln==1],skj_cp_tot_anom[onienln==-1],'skj_cp_tot_anom_enln')
skj_cp_tot_anom_enln_wrs_ptf = controlfdr2d(skj_cp_tot_anom_enln_wrs_pval,alphafdr)
bet_cp_tot_anom_enln_wrs_pval = wrspvalmap_loop(
bet_cp_tot_anom[onienln==1],bet_cp_tot_anom[onienln==-1],'bet_cp_tot_anom_enln')
bet_cp_tot_anom_enln_wrs_ptf = controlfdr2d(bet_cp_tot_anom_enln_wrs_pval,alphafdr)
bettoskj_cp_tot_anom_enln_wrs_pval = wrspvalmap_loop(
bettoskj_cp_tot_anom[onienln==1],bettoskj_cp_tot_anom[onienln==-1],'bettoskj_cp_tot_anom_enln')
bettoskj_cp_tot_anom_enln_wrs_ptf = controlfdr2d(bettoskj_cp_tot_anom_enln_wrs_pval,alphafdr)
skj_cp_tot_enln_wrs_pval = wrspvalmap_loop(
skj_cp_tot[onienln==1],skj_cp_tot[onienln==-1],'skj_cp_tot_enln')
skj_cp_tot_enln_wrs_ptf = controlfdr2d(skj_cp_tot_enln_wrs_pval,alphafdr)
bet_cp_tot_enln_wrs_pval = wrspvalmap_loop(
bet_cp_tot[onienln==1],bet_cp_tot[onienln==-1],'bet_cp_tot_enln')
bet_cp_tot_enln_wrs_ptf = controlfdr2d(bet_cp_tot_enln_wrs_pval,alphafdr)
bettoskj_cp_tot_enln_wrs_pval = wrspvalmap_loop(
bettoskj_cp_tot[onienln==1],bettoskj_cp_tot[onienln==-1],'bettoskj_cp_tot_enln')
bettoskj_cp_tot_enln_wrs_ptf = controlfdr2d(bettoskj_cp_tot_enln_wrs_pval,alphafdr)
```
# Calculate total and deseasonalized stdevs of total (over all set types) SKJ + BET CPUE, BET:SKJ CPUE
Variables calced are:
skj_cp_tot_std, bet_cp_tot_std, bettoskj_cp_tot_std,
skj_cp_tot_anom_std, bet_cp_tot_anom_std, bettoskj_cp_tot_anom_std
```
# - The following are 2-D (lon, lat):
skj_cp_tot_std = skj_cp_tot.std('time')
bet_cp_tot_std = bet_cp_tot.std('time')
bettoskj_cp_tot_std = bettoskj_cp_tot.std('time')
skj_cp_tot_clim_std = skj_cp_tot_clim.std('month')
bet_cp_tot_clim_std = bet_cp_tot_clim.std('month')
bettoskj_cp_tot_clim_std = bettoskj_cp_tot_clim.std('month')
skj_cp_tot_anom_std = skj_cp_tot_anom.std('time')
bet_cp_tot_anom_std = bet_cp_tot_anom.std('time')
bettoskj_cp_tot_anom_std = bettoskj_cp_tot_anom.std('time')
skj_cp_tot_anom_enln_std = skj_cp_tot_anom[onienln!=0].std('time')
bet_cp_tot_anom_enln_std = bet_cp_tot_anom[onienln!=0].std('time')
bettoskj_cp_tot_anom_enln_std = bettoskj_cp_tot_anom[onienln!=0].std('time')
```
|
github_jupyter
|
ncfile = dpath + 'WCPFC/5by5deg/ByMonth/PurseSeine_0/WCPFC_purseseine_bysettype_monthly_5deg.nc'
wf = xr.open_dataset(ncfile)
# - Time goes from Jan 1967 - Dec 2017 --> 612 months
wfbegdate = datetime.date(year = 1967, month = 1, day = 1)
wfenddate = datetime.date(year = 2017, month = 12, day = 1)
timemocatch = pd.date_range(wfbegdate, wfenddate, freq='MS')
wf['time'] = timemocatch
wf = wf.isel(lat=slice(6,16))
lon = wf['lon']
lat = wf['lat']
# - Load ONI
dfoni = pd.read_csv(dpath+'ENSOindices/oni/oniindex1950_2018.txt',names=['Date','ONI']);
# - Month fractions corresp to jan, feb, mar, etc. in the ONI txt file
monthfracs = [0,0.0834,0.1666,0.25,0.3334,0.4166,0.5,0.5834,0.6666,0.75,0.8334,0.9166];
# - Get ONI ts over WCPFC dataset timeframe
onibegmoidx = dfoni.index[dfoni['Date'] == (wfbegdate.year + monthfracs[wfbegdate.month-1])][0]
oniendmoidx = dfoni.index[dfoni['Date'] == (wfenddate.year + monthfracs[wfenddate.month-1])][0]
oni = dfoni['ONI'].iloc[onibegmoidx:(oniendmoidx+1)].values
onitime = pd.date_range(wfbegdate, wfenddate, freq='MS') # should be 612 months long
# - Create EN/LN month classifications
onien = [0]*len(oni) # 1 = el nino month
oniln = [0]*len(oni) # 1 = la nina month
# - Classify El Nino months
cmcounter = 0; # consecutive months counter
for imonth in range(len(oni)):
if oni[imonth]>=0.5:
cmcounter=cmcounter+1;
elif oni[imonth]<0.5:
cmcounter=0;
if cmcounter>=5:
onien[imonth-cmcounter:imonth]=[1]*cmcounter;
# - Classify La Nina months
cmcounter = 0; # consecutive months counter
for imonth in range(len(oni)):
if oni[imonth]<=-0.5:
cmcounter=cmcounter+1;
elif oni[imonth]>-0.5:
cmcounter=0;
if cmcounter>=5:
oniln[imonth-cmcounter:imonth]=[1]*cmcounter;
# - Put everything in DataArrays
oni = xr.DataArray(oni, dims=('time'), coords={'time': onitime})
onien = xr.DataArray(onien, dims=('time'), coords={'time': onitime})
oniln = xr.DataArray(oniln, dims=('time'), coords={'time': onitime})
onienln = xr.zeros_like(onien, dtype='int')
onienln[onien==1]=1 # el nino = 1
onienln[oniln==1]=-1 # la nina = -1
plotensoidx=1
if plotensoidx==1:
fig = plt.figure(figsize=(11,4))
plt.plot(onitime,oni)
plt.plot(onitime,onien)
plt.plot(onitime,oniln)
#plt.plot(onitime,onienln)
plt.legend(["oni","onien","oniln","onienln"])
plt.title('ENSO index (ONI)')
# - The following are 3-D (time, lon, lat):
if settypes=='afaddfad':
skj_c_tot = wf.skj_c_dfad + wf.skj_c_afad
bet_c_tot = wf.bet_c_dfad + wf.bet_c_afad
sets_tot = wf.sets_dfad + wf.sets_afad
elif settypes=='afaddfadlog':
skj_c_tot = wf.skj_c_log + wf.skj_c_dfad + wf.skj_c_afad
bet_c_tot = wf.bet_c_log + wf.bet_c_dfad + wf.bet_c_afad
sets_tot = wf.sets_log + wf.sets_dfad + wf.sets_afad
elif settypes=='unassociated':
skj_c_tot = wf.skj_c_una
bet_c_tot = wf.bet_c_una
sets_tot = wf.sets_una
elif settypes=='unassociatedother':
skj_c_tot = wf.skj_c_una + wf.skj_c_oth
bet_c_tot = wf.bet_c_una + wf.bet_c_oth
sets_tot = wf.sets_una + wf.sets_oth
elif settypes=='allsets':
skj_c_tot = wf.skj_c_una + wf.skj_c_log + wf.skj_c_dfad + wf.skj_c_afad + wf.skj_c_oth
bet_c_tot = wf.bet_c_una + wf.bet_c_log + wf.bet_c_dfad + wf.bet_c_afad + wf.bet_c_oth
sets_tot = wf.sets_una + wf.sets_log + wf.sets_dfad + wf.sets_afad + wf.sets_oth
if catchorcpue=='catch':
skj_cp_tot = skj_c_tot
bet_cp_tot = bet_c_tot
elif catchorcpue=='CPUE':
skj_cp_tot = skj_c_tot/sets_tot
bet_cp_tot = bet_c_tot/sets_tot
skj_cp_tot = skj_cp_tot.where(~np.isinf(skj_cp_tot), np.nan)
bet_cp_tot = bet_cp_tot.where(~np.isinf(bet_cp_tot), np.nan)
bettoskj_cp_tot = bet_cp_tot/skj_cp_tot
# - Name the dataarrays for later merging into datasets
skj_c_tot.name = 'skj_c_tot'
bet_c_tot.name = 'bet_c_tot'
skj_cp_tot.name = 'skj_cp_tot'
bet_cp_tot.name = 'bet_cp_tot'
bettoskj_cp_tot.name = 'bettoskj_cp_tot'
# - The following are all 3-D (time, lon, lat):
skj_cp_tot_seas = skj_cp_tot.groupby('time.season').mean('time')
bet_cp_tot_seas = bet_cp_tot.groupby('time.season').mean('time')
bettoskj_cp_tot_seas = bettoskj_cp_tot.groupby('time.season').mean('time')
skj_cp_tot_clim = skj_cp_tot.groupby('time.month').mean('time')
bet_cp_tot_clim = bet_cp_tot.groupby('time.month').mean('time')
bettoskj_cp_tot_clim = bettoskj_cp_tot.groupby('time.month').mean('time')
skj_cp_tot_anom = skj_cp_tot.groupby('time.month') - skj_cp_tot_clim
bet_cp_tot_anom = bet_cp_tot.groupby('time.month') - bet_cp_tot_clim
bettoskj_cp_tot_anom = bettoskj_cp_tot.groupby('time.month') - bettoskj_cp_tot_clim
# - Name the dataarrays for later merging into datasets
skj_cp_tot_seas.name = 'skj_cp_tot_seas'
bet_cp_tot_seas.name = 'bet_cp_tot_seas'
bettoskj_cp_tot_seas.name = 'bettoskj_cp_tot_seas'
skj_cp_tot_clim.name = 'skj_cp_tot_clim'
bet_cp_tot_clim.name = 'bet_cp_tot_clim'
bettoskj_cp_tot_clim.name = 'bettoskj_cp_tot_clim'
skj_cp_tot_anom.name = 'skj_cp_tot_anom'
bet_cp_tot_anom.name = 'bet_cp_tot_anom'
bettoskj_cp_tot_anom.name = 'bettoskj_cp_tot_anom'
alphafdr = 0.1
skj_cp_tot_seas_kw_pval = kwpvalmap_loop(
skj_cp_tot.sel(time=skj_cp_tot['time.season']=='DJF'),
skj_cp_tot.sel(time=skj_cp_tot['time.season']=='MAM'),
skj_cp_tot.sel(time=skj_cp_tot['time.season']=='JJA'),
skj_cp_tot.sel(time=skj_cp_tot['time.season']=='SON'),
'skj_cp_tot_seas')
skj_cp_tot_seas_kw_ptf = controlfdr2d(skj_cp_tot_seas_kw_pval,alphafdr)
bet_cp_tot_seas_kw_pval = kwpvalmap_loop(
bet_cp_tot.sel(time=bet_cp_tot['time.season']=='DJF'),
bet_cp_tot.sel(time=bet_cp_tot['time.season']=='MAM'),
bet_cp_tot.sel(time=bet_cp_tot['time.season']=='JJA'),
bet_cp_tot.sel(time=bet_cp_tot['time.season']=='SON'),
'bet_cp_tot_seas')
bet_cp_tot_seas_kw_ptf = controlfdr2d(bet_cp_tot_seas_kw_pval,alphafdr)
bettoskj_cp_tot_seas_kw_pval = kwpvalmap_loop(
bettoskj_cp_tot.sel(time=bettoskj_cp_tot['time.season']=='DJF'),
bettoskj_cp_tot.sel(time=bettoskj_cp_tot['time.season']=='MAM'),
bettoskj_cp_tot.sel(time=bettoskj_cp_tot['time.season']=='JJA'),
bettoskj_cp_tot.sel(time=bettoskj_cp_tot['time.season']=='SON'),
'bettoskj_cp_tot_seas')
bettoskj_cp_tot_seas_kw_ptf = controlfdr2d(bettoskj_cp_tot_seas_kw_pval,alphafdr)
# - The following are 2-D (lon, lat):
skj_cp_tot_mean = skj_cp_tot.mean('time')
bet_cp_tot_mean = bet_cp_tot.mean('time')
bettoskj_cp_tot_mean = bettoskj_cp_tot.mean('time')
skj_cp_tot_anom_en = skj_cp_tot_anom[onienln==1].mean(dim='time')
skj_cp_tot_anom_ln = skj_cp_tot_anom[onienln==-1].mean(dim='time')
bet_cp_tot_anom_en = bet_cp_tot_anom[onienln==1].mean(dim='time')
bet_cp_tot_anom_ln = bet_cp_tot_anom[onienln==-1].mean(dim='time')
bettoskj_cp_tot_anom_en = bettoskj_cp_tot_anom[onienln==1].mean(dim='time')
bettoskj_cp_tot_anom_ln = bettoskj_cp_tot_anom[onienln==-1].mean(dim='time')
skj_cp_tot_en = skj_cp_tot[onienln==1].mean(dim='time')
skj_cp_tot_ln = skj_cp_tot[onienln==-1].mean(dim='time')
bet_cp_tot_en = bet_cp_tot[onienln==1].mean(dim='time')
bet_cp_tot_ln = bet_cp_tot[onienln==-1].mean(dim='time')
bettoskj_cp_tot_en = bettoskj_cp_tot[onienln==1].mean(dim='time')
bettoskj_cp_tot_ln = bettoskj_cp_tot[onienln==-1].mean(dim='time')
alphafdr = 0.1
skj_cp_tot_anom_enln_wrs_pval = wrspvalmap_loop(
skj_cp_tot_anom[onienln==1],skj_cp_tot_anom[onienln==-1],'skj_cp_tot_anom_enln')
skj_cp_tot_anom_enln_wrs_ptf = controlfdr2d(skj_cp_tot_anom_enln_wrs_pval,alphafdr)
bet_cp_tot_anom_enln_wrs_pval = wrspvalmap_loop(
bet_cp_tot_anom[onienln==1],bet_cp_tot_anom[onienln==-1],'bet_cp_tot_anom_enln')
bet_cp_tot_anom_enln_wrs_ptf = controlfdr2d(bet_cp_tot_anom_enln_wrs_pval,alphafdr)
bettoskj_cp_tot_anom_enln_wrs_pval = wrspvalmap_loop(
bettoskj_cp_tot_anom[onienln==1],bettoskj_cp_tot_anom[onienln==-1],'bettoskj_cp_tot_anom_enln')
bettoskj_cp_tot_anom_enln_wrs_ptf = controlfdr2d(bettoskj_cp_tot_anom_enln_wrs_pval,alphafdr)
skj_cp_tot_enln_wrs_pval = wrspvalmap_loop(
skj_cp_tot[onienln==1],skj_cp_tot[onienln==-1],'skj_cp_tot_enln')
skj_cp_tot_enln_wrs_ptf = controlfdr2d(skj_cp_tot_enln_wrs_pval,alphafdr)
bet_cp_tot_enln_wrs_pval = wrspvalmap_loop(
bet_cp_tot[onienln==1],bet_cp_tot[onienln==-1],'bet_cp_tot_enln')
bet_cp_tot_enln_wrs_ptf = controlfdr2d(bet_cp_tot_enln_wrs_pval,alphafdr)
bettoskj_cp_tot_enln_wrs_pval = wrspvalmap_loop(
bettoskj_cp_tot[onienln==1],bettoskj_cp_tot[onienln==-1],'bettoskj_cp_tot_enln')
bettoskj_cp_tot_enln_wrs_ptf = controlfdr2d(bettoskj_cp_tot_enln_wrs_pval,alphafdr)
# - The following are 2-D (lon, lat):
skj_cp_tot_std = skj_cp_tot.std('time')
bet_cp_tot_std = bet_cp_tot.std('time')
bettoskj_cp_tot_std = bettoskj_cp_tot.std('time')
skj_cp_tot_clim_std = skj_cp_tot_clim.std('month')
bet_cp_tot_clim_std = bet_cp_tot_clim.std('month')
bettoskj_cp_tot_clim_std = bettoskj_cp_tot_clim.std('month')
skj_cp_tot_anom_std = skj_cp_tot_anom.std('time')
bet_cp_tot_anom_std = bet_cp_tot_anom.std('time')
bettoskj_cp_tot_anom_std = bettoskj_cp_tot_anom.std('time')
skj_cp_tot_anom_enln_std = skj_cp_tot_anom[onienln!=0].std('time')
bet_cp_tot_anom_enln_std = bet_cp_tot_anom[onienln!=0].std('time')
bettoskj_cp_tot_anom_enln_std = bettoskj_cp_tot_anom[onienln!=0].std('time')
| 0.303422 | 0.765462 |
```
#Importing necessary libraries
import keras
import numpy as np
import pandas as pd
from keras.applications import vgg16, inception_v3, resnet50, mobilenet
from keras import models
from keras import layers
from keras import optimizers
import cv2
from sklearn.metrics import classification_report, confusion_matrix
import matplotlib.pyplot as plt
import os
#Load the ResNet50 model
resnet_model = resnet50.ResNet50(weights=None, include_top=False, input_shape=(64, 64, 3))
# Checking the trainable status of the individual layers
for layer in resnet_model.layers:
print(layer, layer.trainable)
# Adding classifier on top of Convolutional base
# create the model
model = models.Sequential()
# Add the resnet50 convolutional model
model.add(resnet_model)
# Adding new Layers
model.add(layers.Flatten())
model.add(layers.Dense(1024, activation='relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(9, activation='softmax'))
# Showing summary of model
model.summary()
# Fitting the CNN to the images(Image Augmentation, Image Preprocessing)
from keras.preprocessing.image import ImageDataGenerator
train_datagen = ImageDataGenerator(
rescale=1./255,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True)
# Normalizing the test set
test_datagen = ImageDataGenerator(rescale=1./255)
# path to your experimental data
os.chdir('/home/sachin_sharma/Desktop/jpg_data')
# This will create 80:20 split of training and test set
training_set = train_datagen.flow_from_directory(
'TrainingSet',
target_size=(64,64),
batch_size=32,
class_mode='categorical')
# This will create the Test set
test_set = test_datagen.flow_from_directory(
'TestSet',
target_size=(64,64),
batch_size=32,
class_mode='categorical',
shuffle=False)
# Compile the model
model.compile(loss='categorical_crossentropy',
optimizer=optimizers.RMSprop(lr=1e-4),
metrics=['acc'])
# Train the model
history = model.fit_generator(
training_set,
steps_per_epoch=(training_set.samples/32),
epochs=30,
validation_data=test_set,
validation_steps=(test_set.samples/32))
model.save('exp_a_1.1.h5')
# Visualizing the mapping between labels
training_set.class_indices
# Confusion Matrix
Y_pred = model.predict_generator(test_set, test_set.samples//32 +1 )
y_pred = np.argmax(Y_pred, axis=1) # predictions
print('Confusion Matrix')
cm = confusion_matrix(test_set.classes, y_pred)
#print(cm)
# visualizing results in table
def cm2df(cm, labels):
df = pd.DataFrame()
# rows
for i, row_label in enumerate(labels):
rowdata={}
# columns
for j, col_label in enumerate(labels):
rowdata[col_label]=cm[i,j]
df = df.append(pd.DataFrame.from_dict({row_label:rowdata}, orient='index'))
return df[labels]
df = cm2df(cm, ["AnnualCrop", "Buildup", "Forest", "HerbaceousVegetation", "Highway", "Pasture", "PermanentCrop", "River", "SeaLake"])
print(df)
# Classification report
print('Classification Report')
target_names = ['AnnualCrop','Buildup','Forest', 'HerbaceousVegetation', 'Highway', 'Pasture', 'PermanentCrop', 'River', 'SeaLake']
classificn_report = classification_report(test_set.classes, y_pred, target_names=target_names)
print(classificn_report)
# Plotting the Loss and Classification Accuracy
model.metrics_names
print(history.history.keys())
# "Accuracy"
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('Model Accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
# "Loss"
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
```
|
github_jupyter
|
#Importing necessary libraries
import keras
import numpy as np
import pandas as pd
from keras.applications import vgg16, inception_v3, resnet50, mobilenet
from keras import models
from keras import layers
from keras import optimizers
import cv2
from sklearn.metrics import classification_report, confusion_matrix
import matplotlib.pyplot as plt
import os
#Load the ResNet50 model
resnet_model = resnet50.ResNet50(weights=None, include_top=False, input_shape=(64, 64, 3))
# Checking the trainable status of the individual layers
for layer in resnet_model.layers:
print(layer, layer.trainable)
# Adding classifier on top of Convolutional base
# create the model
model = models.Sequential()
# Add the resnet50 convolutional model
model.add(resnet_model)
# Adding new Layers
model.add(layers.Flatten())
model.add(layers.Dense(1024, activation='relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(9, activation='softmax'))
# Showing summary of model
model.summary()
# Fitting the CNN to the images(Image Augmentation, Image Preprocessing)
from keras.preprocessing.image import ImageDataGenerator
train_datagen = ImageDataGenerator(
rescale=1./255,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True)
# Normalizing the test set
test_datagen = ImageDataGenerator(rescale=1./255)
# path to your experimental data
os.chdir('/home/sachin_sharma/Desktop/jpg_data')
# This will create 80:20 split of training and test set
training_set = train_datagen.flow_from_directory(
'TrainingSet',
target_size=(64,64),
batch_size=32,
class_mode='categorical')
# This will create the Test set
test_set = test_datagen.flow_from_directory(
'TestSet',
target_size=(64,64),
batch_size=32,
class_mode='categorical',
shuffle=False)
# Compile the model
model.compile(loss='categorical_crossentropy',
optimizer=optimizers.RMSprop(lr=1e-4),
metrics=['acc'])
# Train the model
history = model.fit_generator(
training_set,
steps_per_epoch=(training_set.samples/32),
epochs=30,
validation_data=test_set,
validation_steps=(test_set.samples/32))
model.save('exp_a_1.1.h5')
# Visualizing the mapping between labels
training_set.class_indices
# Confusion Matrix
Y_pred = model.predict_generator(test_set, test_set.samples//32 +1 )
y_pred = np.argmax(Y_pred, axis=1) # predictions
print('Confusion Matrix')
cm = confusion_matrix(test_set.classes, y_pred)
#print(cm)
# visualizing results in table
def cm2df(cm, labels):
df = pd.DataFrame()
# rows
for i, row_label in enumerate(labels):
rowdata={}
# columns
for j, col_label in enumerate(labels):
rowdata[col_label]=cm[i,j]
df = df.append(pd.DataFrame.from_dict({row_label:rowdata}, orient='index'))
return df[labels]
df = cm2df(cm, ["AnnualCrop", "Buildup", "Forest", "HerbaceousVegetation", "Highway", "Pasture", "PermanentCrop", "River", "SeaLake"])
print(df)
# Classification report
print('Classification Report')
target_names = ['AnnualCrop','Buildup','Forest', 'HerbaceousVegetation', 'Highway', 'Pasture', 'PermanentCrop', 'River', 'SeaLake']
classificn_report = classification_report(test_set.classes, y_pred, target_names=target_names)
print(classificn_report)
# Plotting the Loss and Classification Accuracy
model.metrics_names
print(history.history.keys())
# "Accuracy"
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('Model Accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
# "Loss"
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
| 0.814164 | 0.492615 |
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Finding-Outliers" data-toc-modified-id="Finding-Outliers-1"><span class="toc-item-num">1 </span>Finding Outliers</a></span></li><li><span><a href="#Exercise" data-toc-modified-id="Exercise-2"><span class="toc-item-num">2 </span>Exercise</a></span></li><li><span><a href="#Demo:-2-Dimensional-Analysis" data-toc-modified-id="Demo:-2-Dimensional-Analysis-3"><span class="toc-item-num">3 </span>Demo: 2-Dimensional Analysis</a></span></li><li><span><a href="#Conclusion" data-toc-modified-id="Conclusion-4"><span class="toc-item-num">4 </span>Conclusion</a></span></li></ul></div>
# Finding Outliers
In this exercise, you'll practice looking for outliers. You'll look at the World Bank GDP and population data sets. First, you'll look at the data from a one-dimensional perspective and then a two-dimensional perspective.
Run the code below to import the data sets and prepare the data for analysis. The code:
* reads in the data sets
* reshapes the datasets to a long format
* uses back fill and forward fill to fill in missing values
* merges the gdp and population data together
* shows the first 10 values in the data set
```
import pandas as pd
import numpy as np
# read in the projects data set and do basic wrangling
gdp = pd.read_csv('../data/gdp_data.csv', skiprows=4)
gdp.drop(['Unnamed: 62', 'Country Code', 'Indicator Name', 'Indicator Code'], inplace=True, axis=1)
population = pd.read_csv('../data/population_data.csv', skiprows=4)
population.drop(['Unnamed: 62', 'Country Code', 'Indicator Name', 'Indicator Code'], inplace=True, axis=1)
# Reshape the data sets so that they are in long format
gdp_melt = gdp.melt(id_vars=['Country Name'],
var_name='year',
value_name='gdp')
# Use back fill and forward fill to fill in missing gdp values
gdp_melt['gdp'] = gdp_melt.sort_values('year').groupby('Country Name')['gdp'].fillna(method='ffill').fillna(method='bfill')
population_melt = population.melt(id_vars=['Country Name'],
var_name='year',
value_name='population')
# Use back fill and forward fill to fill in missing population values
population_melt['population'] = population_melt.sort_values('year').groupby('Country Name')['population'].fillna(method='ffill').fillna(method='bfill')
# merge the population and gdp data together into one data frame
df_country = gdp_melt.merge(population_melt, on=('Country Name', 'year'))
# filter data for the year 2016
df_2016 = df_country[df_country['year'] == '2016']
# see what the data looks like
df_2016.head(10)
```
# Exercise
Explore the data set to identify outliers using the Tukey rule. Follow the TODOs.
```
import matplotlib.pyplot as plt
%matplotlib inline
# TODO: Make a boxplot of the population data for the year 2016
df_2016.plot('population', kind='box')
# TODO: Make a boxplot of the gdp data for the year 2016
df_2016.plot('gdp', kind='box')
```
Use the Tukey rule to determine what values of the population data are outliers for the year 2016. The Tukey rule finds outliers in one-dimension. The steps are:
* Find the first quartile (ie .25 quantile)
* Find the third quartile (ie .75 quantile)
* Calculate the inter-quartile range (Q3 - Q1)
* Any value that is greater than Q3 + 1.5 * IQR is an outlier
* Any value that is less than Qe - 1.5 * IQR is an outlier
```
# TODO: Filter the data for the year 2016 and put the results in the population_2016 variable. You only need
# to keep the Country Name and population columns
population_2016 = df_2016[['Country Name','population']]
# TODO: Calculate the first quartile of the population values
# HINT: you can use the pandas quantile method
Q1 = population_2016['population'].quantile(0.25)
# TODO: Calculate the third quartile of the population values
Q3 = population_2016['population'].quantile(0.75)
# TODP: Calculate the interquartile range Q3 - Q1
IQR = Q3 - Q1
# TODO: Calculate the maximum value and minimum values according to the Tukey rule
# max_value is Q3 + 1.5 * IQR while min_value is Q1 - 1.5 * IQR
max_value = Q3 + 1.5 * IQR
min_value = Q1 - 1.5 * IQR
# TODO: filter the population_2016 data for population values that are greater than max_value or less than min_value
population_outliers = population_2016[(population_2016['population'] > max_value) | (population_2016['population'] < min_value)]
population_outliers
```
Many of these aren't countries at all but rather aggregates of various countries. Notice as well that the min_value calculated above was negative. According to the Tukey rule, there are no minimum population outliers in this data set. If you were going to study how population and gdp correlate, you might want to remove these aggregated regions from the data set.
Next, use the Tukey method to do the same analysis for gdp.
```
# TODO: Filter the data for the year 2016 and put the results in the population_2016 variable. You only need
# to keep the Country Name and population columns
gdp_2016 = df_2016[['Country Name','gdp']]
# TODO: Calculate the first quartile of the population values
# HINT: you can use the pandas quantile method
Q1 = gdp_2016['gdp'].quantile(0.25)
# TODO: Calculate the third quartile of the population values
Q3 = gdp_2016['gdp'].quantile(0.75)
# TODP: Calculate the interquartile range Q3 - Q1
IQR = Q3 - Q1
# TODO: Calculate the maximum value and minimum values according to the Tukey rule
# max_value is Q3 + 1.5 * IQR while min_value is Q1 - 1.5 * IQR
max_value = Q3 + 1.5 * IQR
min_value = Q1 - 1.5 * IQR
# TODO: filter the population_2016 data for population values that are greater than max_value or less than min_value
gdp_outliers = gdp_2016[(gdp_2016['gdp'] > max_value) | (gdp_2016['gdp'] < min_value)]
gdp_outliers
```
Clearly many of these outliers are due to regional data getting aggregated together.
Remove these data points and redo the analysis. There's a list provided below of the 'Country Name' values that are not actually countries.
```
# TODO: remove the rows from the data that have Country Name values in the non_countries list
# Store the filter results back into the df_2016 variable
non_countries = ['World',
'High income',
'OECD members',
'Post-demographic dividend',
'IDA & IBRD total',
'Low & middle income',
'Middle income',
'IBRD only',
'East Asia & Pacific',
'Europe & Central Asia',
'North America',
'Upper middle income',
'Late-demographic dividend',
'European Union',
'East Asia & Pacific (excluding high income)',
'East Asia & Pacific (IDA & IBRD countries)',
'Euro area',
'Early-demographic dividend',
'Lower middle income',
'Latin America & Caribbean',
'Latin America & the Caribbean (IDA & IBRD countries)',
'Latin America & Caribbean (excluding high income)',
'Europe & Central Asia (IDA & IBRD countries)',
'Middle East & North Africa',
'Europe & Central Asia (excluding high income)',
'South Asia (IDA & IBRD)',
'South Asia',
'Arab World',
'IDA total',
'Sub-Saharan Africa',
'Sub-Saharan Africa (IDA & IBRD countries)',
'Sub-Saharan Africa (excluding high income)',
'Middle East & North Africa (excluding high income)',
'Middle East & North Africa (IDA & IBRD countries)',
'Central Europe and the Baltics',
'Pre-demographic dividend',
'IDA only',
'Least developed countries: UN classification',
'IDA blend',
'Fragile and conflict affected situations',
'Heavily indebted poor countries (HIPC)',
'Low income',
'Small states',
'Other small states',
'Not classified',
'Caribbean small states',
'Pacific island small states']
# remove non countries from the data
df_2016 = df_2016[~df_2016['Country Name'].isin(non_countries)]
# TODO: Re-rerun the Tukey code with this filtered data to find population outliers
# TODO: Filter the data for the year 2016 and put the results in the population_2016 variable. You only need
# to keep the Country Name and population columns
population_2016 = df_2016[['Country Name','population']]
# TODO: Calculate the first quartile of the population values
# HINT: you can use the pandas quantile method
Q1 = population_2016['population'].quantile(0.25)
# TODO: Calculate the third quartile of the population values
Q3 = population_2016['population'].quantile(0.75)
# TODO: Calculate the interquartile range Q3 - Q1
IQR = Q3 - Q1
# TODO: Calculate the maximum value and minimum values according to the Tukey rule
# max_value is Q3 + 1.5 * IQR while min_value is Q1 - 1.5 * IQR
max_value = Q3 + 1.5 * IQR
min_value = Q1 - 1.5 * IQR
# TODO: filter the population_2016 data for population values that are greater than max_value or less than min_value
population_outliers = population_2016[(population_2016['population'] > max_value) | (population_2016['population'] < min_value)]
population_outliers
# TODO: Filter the data for the year 2016 and put the results in the population_2016 variable. You only need
# to keep the Country Name and population columns
gdp_2016 = df_2016[['Country Name','gdp']]
# TODO: Calculate the first quartile of the population values
# HINT: you can use the pandas quantile method
Q1 = gdp_2016['gdp'].quantile(0.25)
# TODO: Calculate the third quartile of the population values
Q3 = gdp_2016['gdp'].quantile(0.75)
# TODO: Calculate the interquartile range Q3 - Q1
IQR = Q3 - Q1
# TODO: Calculate the maximum value and minimum values according to the Tukey rule
# max_value is Q3 + 1.5 * IQR while min_value is Q1 - 1.5 * IQR
max_value = Q3 + 1.5 * IQR
min_value = Q1 - 1.5 * IQR
# TODO: filter the population_2016 data for population values that are greater than max_value or less than min_value
gdp_outliers = gdp_2016[(gdp_2016['gdp'] > max_value) | (gdp_2016['gdp'] < min_value)]
gdp_outliers
```
Next, write code to determine which countries are in the population_outliers array and in the gdp_outliers array.
```
# TODO: Find country names that are in both the population_outliers and the gdp_outliers
list(set(population_outliers['Country Name']).intersection(gdp_outliers['Country Name']))
```
These countries have both relatively high populations and high GDPs. That might be an indication that although these countries have high values for both gdp and population, they're not true outliers when looking at these values from a two-dimensional perspective.
Now write code to find countries in population_outliers but not in the gdp_outliers.
```
# TODO: Find country names that are in the population outliers list but not the gdp outliers list
# HINT: Python's set() and list() methods should be helpful
list(set(population_outliers['Country Name']) - set(gdp_outliers['Country Name']))
```
These countries are population outliers but not GDP outliers. If looking at outliers from a two-dimensional perspective, there's some indication that these countries might be outliers.
And finally, write code to find countries that are in the gdp_outliers array but not the population_outliers array.
```
# TODO: Find country names that are in the gdp outliers list but not the population outliers list
# HINT: Python's set() and list() methods should be helpful
list(set(gdp_outliers['Country Name']) - set(population_outliers['Country Name']))
```
On the other hand, these countries have high GDP but are not population outliers.
# Demo: 2-Dimensional Analysis
Next, look at the data from a two-dimensional perspective. You don't have to do anything in this section other than run the code cells below. This gives a basic example of how outlier removal affects machine learning algorithms.
The next code cell plots the GDP vs Population data including the country name of each point.
```
# run the code cell below
x = list(df_2016['population'])
y = list(df_2016['gdp'])
text = df_2016['Country Name']
fig, ax = plt.subplots(figsize=(15,10))
ax.scatter(x, y)
plt.title('GDP vs Population')
plt.xlabel('population')
plt.ylabel('GDP')
for i, txt in enumerate(text):
ax.annotate(txt, (x[i],y[i]))
```
The United States, China, and India have such larger values that it's hard to see this data. Let's take those countries out for a moment and look at the data again.
```
# Run the code below to see the results
df_no_large = (df_2016['Country Name'] != 'United States') & (df_2016['Country Name'] != 'India') & (df_2016['Country Name'] != 'China')
x = list(df_2016[df_no_large]['population'])
y = list(df_2016[df_no_large]['gdp'])
text = df_2016[df_no_large]['Country Name']
fig, ax = plt.subplots(figsize=(15,10))
ax.scatter(x, y)
plt.title('GDP vs Population')
plt.xlabel('population')
plt.ylabel('GDP')
for i, txt in enumerate(text):
ax.annotate(txt, (x[i],y[i]))
```
Run the code below to build a simple linear regression model with the population and gdp data for 2016.
```
from sklearn.linear_model import LinearRegression
# fit a linear regression model on the population and gdp data
model = LinearRegression()
model.fit(df_2016['population'].values.reshape(-1, 1), df_2016['gdp'].values.reshape(-1, 1))
# plot the data along with predictions from the linear regression model
inputs = np.linspace(1, 2000000000, num=50)
predictions = model.predict(inputs.reshape(-1,1))
df_2016.plot('population', 'gdp', kind='scatter')
plt.plot(inputs, predictions)
print(model.predict(1000000000))
```
Notice that the code ouputs a GDP value of 6.54e+12 when population equals 1e9. Now run the code below when the United States is taken out of the data set.
```
# Remove the United States to see what happens with the linear regression model
df_2016[df_2016['Country Name'] != 'United States'].plot('population', 'gdp', kind='scatter')
# plt.plot(inputs, predictions)
model.fit(df_2016[df_2016['Country Name'] != 'United States']['population'].values.reshape(-1, 1),
df_2016[df_2016['Country Name'] != 'United States']['gdp'].values.reshape(-1, 1))
inputs = np.linspace(1, 2000000000, num=50)
predictions = model.predict(inputs.reshape(-1,1))
plt.plot(inputs, predictions)
print(model.predict(1000000000))
```
Notice that the code now ouputs a GDP value of 5.26e+12 when population equals 1e9. In other words, removing the United States shifted the linear regression line down.
# Conclusion
Data scientists sometimes have the task of creating an outlier removal model. In this exercise, you've used the Tukey rule. There are other one-dimensional models like eliminating data that is far from the mean. There are also more sophisticated models that take into account multi-dimensional data.
Remember, however, that this is a course on data engineering. As a data engineer, your job will be to remove outliers using code based on whatever model you're given.
If you were using the Tukey rule, for example, you'd calculate Q1, Q3, and IQR on your training data. You'd need to store these results. Then as new data comes in, you'd use these stored values to eliminate any outliers.
|
github_jupyter
|
import pandas as pd
import numpy as np
# read in the projects data set and do basic wrangling
gdp = pd.read_csv('../data/gdp_data.csv', skiprows=4)
gdp.drop(['Unnamed: 62', 'Country Code', 'Indicator Name', 'Indicator Code'], inplace=True, axis=1)
population = pd.read_csv('../data/population_data.csv', skiprows=4)
population.drop(['Unnamed: 62', 'Country Code', 'Indicator Name', 'Indicator Code'], inplace=True, axis=1)
# Reshape the data sets so that they are in long format
gdp_melt = gdp.melt(id_vars=['Country Name'],
var_name='year',
value_name='gdp')
# Use back fill and forward fill to fill in missing gdp values
gdp_melt['gdp'] = gdp_melt.sort_values('year').groupby('Country Name')['gdp'].fillna(method='ffill').fillna(method='bfill')
population_melt = population.melt(id_vars=['Country Name'],
var_name='year',
value_name='population')
# Use back fill and forward fill to fill in missing population values
population_melt['population'] = population_melt.sort_values('year').groupby('Country Name')['population'].fillna(method='ffill').fillna(method='bfill')
# merge the population and gdp data together into one data frame
df_country = gdp_melt.merge(population_melt, on=('Country Name', 'year'))
# filter data for the year 2016
df_2016 = df_country[df_country['year'] == '2016']
# see what the data looks like
df_2016.head(10)
import matplotlib.pyplot as plt
%matplotlib inline
# TODO: Make a boxplot of the population data for the year 2016
df_2016.plot('population', kind='box')
# TODO: Make a boxplot of the gdp data for the year 2016
df_2016.plot('gdp', kind='box')
# TODO: Filter the data for the year 2016 and put the results in the population_2016 variable. You only need
# to keep the Country Name and population columns
population_2016 = df_2016[['Country Name','population']]
# TODO: Calculate the first quartile of the population values
# HINT: you can use the pandas quantile method
Q1 = population_2016['population'].quantile(0.25)
# TODO: Calculate the third quartile of the population values
Q3 = population_2016['population'].quantile(0.75)
# TODP: Calculate the interquartile range Q3 - Q1
IQR = Q3 - Q1
# TODO: Calculate the maximum value and minimum values according to the Tukey rule
# max_value is Q3 + 1.5 * IQR while min_value is Q1 - 1.5 * IQR
max_value = Q3 + 1.5 * IQR
min_value = Q1 - 1.5 * IQR
# TODO: filter the population_2016 data for population values that are greater than max_value or less than min_value
population_outliers = population_2016[(population_2016['population'] > max_value) | (population_2016['population'] < min_value)]
population_outliers
# TODO: Filter the data for the year 2016 and put the results in the population_2016 variable. You only need
# to keep the Country Name and population columns
gdp_2016 = df_2016[['Country Name','gdp']]
# TODO: Calculate the first quartile of the population values
# HINT: you can use the pandas quantile method
Q1 = gdp_2016['gdp'].quantile(0.25)
# TODO: Calculate the third quartile of the population values
Q3 = gdp_2016['gdp'].quantile(0.75)
# TODP: Calculate the interquartile range Q3 - Q1
IQR = Q3 - Q1
# TODO: Calculate the maximum value and minimum values according to the Tukey rule
# max_value is Q3 + 1.5 * IQR while min_value is Q1 - 1.5 * IQR
max_value = Q3 + 1.5 * IQR
min_value = Q1 - 1.5 * IQR
# TODO: filter the population_2016 data for population values that are greater than max_value or less than min_value
gdp_outliers = gdp_2016[(gdp_2016['gdp'] > max_value) | (gdp_2016['gdp'] < min_value)]
gdp_outliers
# TODO: remove the rows from the data that have Country Name values in the non_countries list
# Store the filter results back into the df_2016 variable
non_countries = ['World',
'High income',
'OECD members',
'Post-demographic dividend',
'IDA & IBRD total',
'Low & middle income',
'Middle income',
'IBRD only',
'East Asia & Pacific',
'Europe & Central Asia',
'North America',
'Upper middle income',
'Late-demographic dividend',
'European Union',
'East Asia & Pacific (excluding high income)',
'East Asia & Pacific (IDA & IBRD countries)',
'Euro area',
'Early-demographic dividend',
'Lower middle income',
'Latin America & Caribbean',
'Latin America & the Caribbean (IDA & IBRD countries)',
'Latin America & Caribbean (excluding high income)',
'Europe & Central Asia (IDA & IBRD countries)',
'Middle East & North Africa',
'Europe & Central Asia (excluding high income)',
'South Asia (IDA & IBRD)',
'South Asia',
'Arab World',
'IDA total',
'Sub-Saharan Africa',
'Sub-Saharan Africa (IDA & IBRD countries)',
'Sub-Saharan Africa (excluding high income)',
'Middle East & North Africa (excluding high income)',
'Middle East & North Africa (IDA & IBRD countries)',
'Central Europe and the Baltics',
'Pre-demographic dividend',
'IDA only',
'Least developed countries: UN classification',
'IDA blend',
'Fragile and conflict affected situations',
'Heavily indebted poor countries (HIPC)',
'Low income',
'Small states',
'Other small states',
'Not classified',
'Caribbean small states',
'Pacific island small states']
# remove non countries from the data
df_2016 = df_2016[~df_2016['Country Name'].isin(non_countries)]
# TODO: Re-rerun the Tukey code with this filtered data to find population outliers
# TODO: Filter the data for the year 2016 and put the results in the population_2016 variable. You only need
# to keep the Country Name and population columns
population_2016 = df_2016[['Country Name','population']]
# TODO: Calculate the first quartile of the population values
# HINT: you can use the pandas quantile method
Q1 = population_2016['population'].quantile(0.25)
# TODO: Calculate the third quartile of the population values
Q3 = population_2016['population'].quantile(0.75)
# TODO: Calculate the interquartile range Q3 - Q1
IQR = Q3 - Q1
# TODO: Calculate the maximum value and minimum values according to the Tukey rule
# max_value is Q3 + 1.5 * IQR while min_value is Q1 - 1.5 * IQR
max_value = Q3 + 1.5 * IQR
min_value = Q1 - 1.5 * IQR
# TODO: filter the population_2016 data for population values that are greater than max_value or less than min_value
population_outliers = population_2016[(population_2016['population'] > max_value) | (population_2016['population'] < min_value)]
population_outliers
# TODO: Filter the data for the year 2016 and put the results in the population_2016 variable. You only need
# to keep the Country Name and population columns
gdp_2016 = df_2016[['Country Name','gdp']]
# TODO: Calculate the first quartile of the population values
# HINT: you can use the pandas quantile method
Q1 = gdp_2016['gdp'].quantile(0.25)
# TODO: Calculate the third quartile of the population values
Q3 = gdp_2016['gdp'].quantile(0.75)
# TODO: Calculate the interquartile range Q3 - Q1
IQR = Q3 - Q1
# TODO: Calculate the maximum value and minimum values according to the Tukey rule
# max_value is Q3 + 1.5 * IQR while min_value is Q1 - 1.5 * IQR
max_value = Q3 + 1.5 * IQR
min_value = Q1 - 1.5 * IQR
# TODO: filter the population_2016 data for population values that are greater than max_value or less than min_value
gdp_outliers = gdp_2016[(gdp_2016['gdp'] > max_value) | (gdp_2016['gdp'] < min_value)]
gdp_outliers
# TODO: Find country names that are in both the population_outliers and the gdp_outliers
list(set(population_outliers['Country Name']).intersection(gdp_outliers['Country Name']))
# TODO: Find country names that are in the population outliers list but not the gdp outliers list
# HINT: Python's set() and list() methods should be helpful
list(set(population_outliers['Country Name']) - set(gdp_outliers['Country Name']))
# TODO: Find country names that are in the gdp outliers list but not the population outliers list
# HINT: Python's set() and list() methods should be helpful
list(set(gdp_outliers['Country Name']) - set(population_outliers['Country Name']))
# run the code cell below
x = list(df_2016['population'])
y = list(df_2016['gdp'])
text = df_2016['Country Name']
fig, ax = plt.subplots(figsize=(15,10))
ax.scatter(x, y)
plt.title('GDP vs Population')
plt.xlabel('population')
plt.ylabel('GDP')
for i, txt in enumerate(text):
ax.annotate(txt, (x[i],y[i]))
# Run the code below to see the results
df_no_large = (df_2016['Country Name'] != 'United States') & (df_2016['Country Name'] != 'India') & (df_2016['Country Name'] != 'China')
x = list(df_2016[df_no_large]['population'])
y = list(df_2016[df_no_large]['gdp'])
text = df_2016[df_no_large]['Country Name']
fig, ax = plt.subplots(figsize=(15,10))
ax.scatter(x, y)
plt.title('GDP vs Population')
plt.xlabel('population')
plt.ylabel('GDP')
for i, txt in enumerate(text):
ax.annotate(txt, (x[i],y[i]))
from sklearn.linear_model import LinearRegression
# fit a linear regression model on the population and gdp data
model = LinearRegression()
model.fit(df_2016['population'].values.reshape(-1, 1), df_2016['gdp'].values.reshape(-1, 1))
# plot the data along with predictions from the linear regression model
inputs = np.linspace(1, 2000000000, num=50)
predictions = model.predict(inputs.reshape(-1,1))
df_2016.plot('population', 'gdp', kind='scatter')
plt.plot(inputs, predictions)
print(model.predict(1000000000))
# Remove the United States to see what happens with the linear regression model
df_2016[df_2016['Country Name'] != 'United States'].plot('population', 'gdp', kind='scatter')
# plt.plot(inputs, predictions)
model.fit(df_2016[df_2016['Country Name'] != 'United States']['population'].values.reshape(-1, 1),
df_2016[df_2016['Country Name'] != 'United States']['gdp'].values.reshape(-1, 1))
inputs = np.linspace(1, 2000000000, num=50)
predictions = model.predict(inputs.reshape(-1,1))
plt.plot(inputs, predictions)
print(model.predict(1000000000))
| 0.237841 | 0.988324 |
# Collaborative filtering on Google Analytics data
This notebook demonstrates how to implement a WALS matrix refactorization approach to do collaborative filtering.
```
import os
PROJECT = "cloud-training-demos" # REPLACE WITH YOUR PROJECT ID
BUCKET = "cloud-training-demos-ml" # REPLACE WITH YOUR BUCKET NAME
REGION = "us-central1" # REPLACE WITH YOUR BUCKET REGION e.g. us-central1
# Do not change these
os.environ["PROJECT"] = PROJECT
os.environ["BUCKET"] = BUCKET
os.environ["REGION"] = REGION
os.environ["TFVERSION"] = "1.13"
%%bash
gcloud config set project $PROJECT
gcloud config set compute/region $REGION
import tensorflow as tf
print(tf.__version__)
```
## Create raw dataset
<p>
For collaborative filtering, we don't need to know anything about either the users or the content. Essentially, all we need to know is userId, itemId, and rating that the particular user gave the particular item.
<p>
In this case, we are working with newspaper articles. The company doesn't ask their users to rate the articles. However, we can use the time-spent on the page as a proxy for rating.
<p>
Normally, we would also add a time filter to this ("latest 7 days"), but our dataset is itself limited to a few days.
```
from google.cloud import bigquery
bq = bigquery.Client(project = PROJECT)
sql = """
WITH CTE_visitor_page_content AS (
SELECT
# Schema: https://support.google.com/analytics/answer/3437719?hl=en
# For a completely unique visit-session ID, we combine combination of fullVisitorId and visitNumber:
CONCAT(fullVisitorID,'-',CAST(visitNumber AS STRING)) AS visitorId,
(SELECT MAX(IF(index=10, value, NULL)) FROM UNNEST(hits.customDimensions)) AS latestContentId,
(LEAD(hits.time, 1) OVER (PARTITION BY fullVisitorId ORDER BY hits.time ASC) - hits.time) AS session_duration
FROM
`cloud-training-demos.GA360_test.ga_sessions_sample`,
UNNEST(hits) AS hits
WHERE
# only include hits on pages
hits.type = "PAGE"
GROUP BY
fullVisitorId,
visitNumber,
latestContentId,
hits.time )
-- Aggregate web stats
SELECT
visitorId,
latestContentId as contentId,
SUM(session_duration) AS session_duration
FROM
CTE_visitor_page_content
WHERE
latestContentId IS NOT NULL
GROUP BY
visitorId,
latestContentId
HAVING
session_duration > 0
"""
df = bq.query(sql).to_dataframe()
df.head()
stats = df.describe()
stats
df[["session_duration"]].plot(kind="hist", logy=True, bins=100, figsize=[8,5])
# The rating is the session_duration scaled to be in the range 0-1. This will help with training.
median = stats.loc["50%", "session_duration"]
df["rating"] = 0.3 * df["session_duration"] / median
df.loc[df["rating"] > 1, "rating"] = 1
df[["rating"]].plot(kind="hist", logy=True, bins=100, figsize=[8,5])
del df["session_duration"]
%%bash
rm -rf data
mkdir data
df.to_csv(path_or_buf = "data/collab_raw.csv", index = False, header = False)
!head data/collab_raw.csv
```
## Create dataset for WALS
<p>
The raw dataset (above) won't work for WALS:
<ol>
<li> The userId and itemId have to be 0,1,2 ... so we need to create a mapping from visitorId (in the raw data) to userId and contentId (in the raw data) to itemId.
<li> We will need to save the above mapping to a file because at prediction time, we'll need to know how to map the contentId in the table above to the itemId.
<li> We'll need two files: a "rows" dataset where all the items for a particular user are listed; and a "columns" dataset where all the users for a particular item are listed.
</ol>
<p>
### Mapping
```
import pandas as pd
import numpy as np
def create_mapping(values, filename):
with open(filename, 'w') as ofp:
value_to_id = {value:idx for idx, value in enumerate(values.unique())}
for value, idx in value_to_id.items():
ofp.write("{},{}\n".format(value, idx))
return value_to_id
df = pd.read_csv(filepath_or_buffer = "data/collab_raw.csv",
header = None,
names = ["visitorId", "contentId", "rating"],
dtype = {"visitorId": str, "contentId": str, "rating": np.float})
df.to_csv(path_or_buf = "data/collab_raw.csv", index = False, header = False)
user_mapping = create_mapping(df["visitorId"], "data/users.csv")
item_mapping = create_mapping(df["contentId"], "data/items.csv")
!head -3 data/*.csv
df["userId"] = df["visitorId"].map(user_mapping.get)
df["itemId"] = df["contentId"].map(item_mapping.get)
mapped_df = df[["userId", "itemId", "rating"]]
mapped_df.to_csv(path_or_buf = "data/collab_mapped.csv", index = False, header = False)
mapped_df.head()
```
### Creating rows and columns datasets
```
import pandas as pd
import numpy as np
mapped_df = pd.read_csv(filepath_or_buffer = "data/collab_mapped.csv", header = None, names = ["userId", "itemId", "rating"])
mapped_df.head()
NITEMS = np.max(mapped_df["itemId"]) + 1
NUSERS = np.max(mapped_df["userId"]) + 1
mapped_df["rating"] = np.round(mapped_df["rating"].values, 2)
print("{} items, {} users, {} interactions".format( NITEMS, NUSERS, len(mapped_df) ))
grouped_by_items = mapped_df.groupby("itemId")
iter = 0
for item, grouped in grouped_by_items:
print(item, grouped["userId"].values, grouped["rating"].values)
iter = iter + 1
if iter > 5:
break
import tensorflow as tf
grouped_by_items = mapped_df.groupby("itemId")
with tf.python_io.TFRecordWriter("data/users_for_item") as ofp:
for item, grouped in grouped_by_items:
example = tf.train.Example(features = tf.train.Features(feature = {
"key": tf.train.Feature(int64_list = tf.train.Int64List(value = [item])),
"indices": tf.train.Feature(int64_list = tf.train.Int64List(value = grouped["userId"].values)),
"values": tf.train.Feature(float_list = tf.train.FloatList(value = grouped["rating"].values))
}))
ofp.write(example.SerializeToString())
grouped_by_users = mapped_df.groupby("userId")
with tf.python_io.TFRecordWriter("data/items_for_user") as ofp:
for user, grouped in grouped_by_users:
example = tf.train.Example(features = tf.train.Features(feature = {
"key": tf.train.Feature(int64_list = tf.train.Int64List(value = [user])),
"indices": tf.train.Feature(int64_list = tf.train.Int64List(value = grouped["itemId"].values)),
"values": tf.train.Feature(float_list = tf.train.FloatList(value = grouped["rating"].values))
}))
ofp.write(example.SerializeToString())
!ls -lrt data
```
To summarize, we created the following data files from collab_raw.csv:
<ol>
<li> ```collab_mapped.csv``` is essentially the same data as in ```collab_raw.csv``` except that ```visitorId``` and ```contentId``` which are business-specific have been mapped to ```userId``` and ```itemId``` which are enumerated in 0,1,2,.... The mappings themselves are stored in ```items.csv``` and ```users.csv``` so that they can be used during inference.
<li> ```users_for_item``` contains all the users/ratings for each item in TFExample format
<li> ```items_for_user``` contains all the items/ratings for each user in TFExample format
</ol>
## Train with WALS
Once you have the dataset, do matrix factorization with WALS using the [WALSMatrixFactorization](https://www.tensorflow.org/versions/master/api_docs/python/tf/contrib/factorization/WALSMatrixFactorization) in the contrib directory.
This is an estimator model, so it should be relatively familiar.
<p>
As usual, we write an input_fn to provide the data to the model, and then create the Estimator to do train_and_evaluate.
Because it is in contrib and hasn't moved over to tf.estimator yet, we use tf.contrib.learn.Experiment to handle the training loop.<p>
Make sure to replace <strong># TODO</strong> in below code.
```
import os
import tensorflow as tf
from tensorflow.python.lib.io import file_io
from tensorflow.contrib.factorization import WALSMatrixFactorization
def read_dataset(mode, args):
def decode_example(protos, vocab_size):
# TODO
return
def remap_keys(sparse_tensor):
# Current indices of our SparseTensor that we need to fix
bad_indices = sparse_tensor.indices # shape = (current_batch_size * (number_of_items/users[i] + 1), 2)
# Current values of our SparseTensor that we need to fix
bad_values = sparse_tensor.values # shape = (current_batch_size * (number_of_items/users[i] + 1),)
# Since batch is ordered, the last value for a batch index is the user
# Find where the batch index chages to extract the user rows
# 1 where user, else 0
user_mask = tf.concat(values = [bad_indices[1:,0] - bad_indices[:-1,0], tf.constant(value = [1], dtype = tf.int64)], axis = 0) # shape = (current_batch_size * (number_of_items/users[i] + 1), 2)
# Mask out the user rows from the values
good_values = tf.boolean_mask(tensor = bad_values, mask = tf.equal(x = user_mask, y = 0)) # shape = (current_batch_size * number_of_items/users[i],)
item_indices = tf.boolean_mask(tensor = bad_indices, mask = tf.equal(x = user_mask, y = 0)) # shape = (current_batch_size * number_of_items/users[i],)
user_indices = tf.boolean_mask(tensor = bad_indices, mask = tf.equal(x = user_mask, y = 1))[:, 1] # shape = (current_batch_size,)
good_user_indices = tf.gather(params = user_indices, indices = item_indices[:,0]) # shape = (current_batch_size * number_of_items/users[i],)
# User and item indices are rank 1, need to make rank 1 to concat
good_user_indices_expanded = tf.expand_dims(input = good_user_indices, axis = -1) # shape = (current_batch_size * number_of_items/users[i], 1)
good_item_indices_expanded = tf.expand_dims(input = item_indices[:, 1], axis = -1) # shape = (current_batch_size * number_of_items/users[i], 1)
good_indices = tf.concat(values = [good_user_indices_expanded, good_item_indices_expanded], axis = 1) # shape = (current_batch_size * number_of_items/users[i], 2)
remapped_sparse_tensor = tf.SparseTensor(indices = good_indices, values = good_values, dense_shape = sparse_tensor.dense_shape)
return remapped_sparse_tensor
def parse_tfrecords(filename, vocab_size):
if mode == tf.estimator.ModeKeys.TRAIN:
num_epochs = None # indefinitely
else:
num_epochs = 1 # end-of-input after this
files = tf.gfile.Glob(filename = os.path.join(args["input_path"], filename))
# Create dataset from file list
dataset = tf.data.TFRecordDataset(files)
dataset = dataset.map(map_func = lambda x: decode_example(x, vocab_size))
dataset = dataset.repeat(count = num_epochs)
dataset = dataset.batch(batch_size = args["batch_size"])
dataset = dataset.map(map_func = lambda x: remap_keys(x))
return dataset.make_one_shot_iterator().get_next()
def _input_fn():
features = {
WALSMatrixFactorization.INPUT_ROWS: parse_tfrecords("items_for_user", args["nitems"]),
WALSMatrixFactorization.INPUT_COLS: parse_tfrecords("users_for_item", args["nusers"]),
WALSMatrixFactorization.PROJECT_ROW: tf.constant(True)
}
return features, None
return _input_fn
def input_cols():
return parse_tfrecords("users_for_item", args["nusers"])
return _input_fn#_subset
```
This code is helpful in developing the input function. You don't need it in production.
```
def try_out():
with tf.Session() as sess:
fn = read_dataset(
mode = tf.estimator.ModeKeys.EVAL,
args = {"input_path": "data", "batch_size": 4, "nitems": NITEMS, "nusers": NUSERS})
feats, _ = fn()
print(feats["input_rows"].eval())
print(feats["input_rows"].eval())
try_out()
def find_top_k(user, item_factors, k):
all_items = tf.matmul(a = tf.expand_dims(input = user, axis = 0), b = tf.transpose(a = item_factors))
topk = tf.nn.top_k(input = all_items, k = k)
return tf.cast(x = topk.indices, dtype = tf.int64)
def batch_predict(args):
import numpy as np
with tf.Session() as sess:
estimator = tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"])
# This is how you would get the row factors for out-of-vocab user data
# row_factors = list(estimator.get_projections(input_fn=read_dataset(tf.estimator.ModeKeys.EVAL, args)))
# user_factors = tf.convert_to_tensor(np.array(row_factors))
# But for in-vocab data, the row factors are already in the checkpoint
user_factors = tf.convert_to_tensor(value = estimator.get_row_factors()[0]) # (nusers, nembeds)
# In either case, we have to assume catalog doesn"t change, so col_factors are read in
item_factors = tf.convert_to_tensor(value = estimator.get_col_factors()[0])# (nitems, nembeds)
# For each user, find the top K items
topk = tf.squeeze(input = tf.map_fn(fn = lambda user: find_top_k(user, item_factors, args["topk"]), elems = user_factors, dtype = tf.int64))
with file_io.FileIO(os.path.join(args["output_dir"], "batch_pred.txt"), mode = 'w') as f:
for best_items_for_user in topk.eval():
f.write(",".join(str(x) for x in best_items_for_user) + '\n')
def train_and_evaluate(args):
train_steps = int(0.5 + (1.0 * args["num_epochs"] * args["nusers"]) / args["batch_size"])
steps_in_epoch = int(0.5 + args["nusers"] / args["batch_size"])
print("Will train for {} steps, evaluating once every {} steps".format(train_steps, steps_in_epoch))
def experiment_fn(output_dir):
return tf.contrib.learn.Experiment(
tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"]),
train_input_fn = read_dataset(tf.estimator.ModeKeys.TRAIN, args),
eval_input_fn = read_dataset(tf.estimator.ModeKeys.EVAL, args),
train_steps = train_steps,
eval_steps = 1,
min_eval_frequency = steps_in_epoch
)
from tensorflow.contrib.learn.python.learn import learn_runner
learn_runner.run(experiment_fn = experiment_fn, output_dir = args["output_dir"])
batch_predict(args)
import shutil
shutil.rmtree(path = "wals_trained", ignore_errors=True)
train_and_evaluate({
"output_dir": "wals_trained",
"input_path": "data/",
"num_epochs": 0.05,
"nitems": NITEMS,
"nusers": NUSERS,
"batch_size": 512,
"n_embeds": 10,
"topk": 3
})
!ls wals_trained
!head wals_trained/batch_pred.txt
```
## Run as a Python module
Let's run it as Python module for just a few steps.
```
os.environ["NITEMS"] = str(NITEMS)
os.environ["NUSERS"] = str(NUSERS)
%%bash
rm -rf wals.tar.gz wals_trained
gcloud ai-platform local train \
--module-name=walsmodel.task \
--package-path=${PWD}/walsmodel \
-- \
--output_dir=${PWD}/wals_trained \
--input_path=${PWD}/data \
--num_epochs=0.01 --nitems=${NITEMS} --nusers=${NUSERS} \
--job-dir=./tmp
```
## Run on Cloud
```
%%bash
gsutil -m cp data/* gs://${BUCKET}/wals/data
%%bash
OUTDIR=gs://${BUCKET}/wals/model_trained
JOBNAME=wals_$(date -u +%y%m%d_%H%M%S)
echo $OUTDIR $REGION $JOBNAME
gsutil -m rm -rf $OUTDIR
gcloud ai-platform jobs submit training $JOBNAME \
--region=$REGION \
--module-name=walsmodel.task \
--package-path=${PWD}/walsmodel \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=BASIC_GPU \
--runtime-version=$TFVERSION \
-- \
--output_dir=$OUTDIR \
--input_path=gs://${BUCKET}/wals/data \
--num_epochs=10 --nitems=${NITEMS} --nusers=${NUSERS}
```
This took <b>10 minutes</b> for me.
## Get row and column factors
Once you have a trained WALS model, you can get row and column factors (user and item embeddings) from the checkpoint file. We'll look at how to use these in the section on building a recommendation system using deep neural networks.
```
def get_factors(args):
with tf.Session() as sess:
estimator = tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"])
row_factors = estimator.get_row_factors()[0]
col_factors = estimator.get_col_factors()[0]
return row_factors, col_factors
args = {
"output_dir": "gs://{}/wals/model_trained".format(BUCKET),
"nitems": NITEMS,
"nusers": NUSERS,
"n_embeds": 10
}
user_embeddings, item_embeddings = get_factors(args)
print(user_embeddings[:3])
print(item_embeddings[:3])
```
You can visualize the embedding vectors using dimensional reduction techniques such as PCA.
```
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import PCA
pca = PCA(n_components = 3)
pca.fit(user_embeddings)
user_embeddings_pca = pca.transform(user_embeddings)
fig = plt.figure(figsize = (8,8))
ax = fig.add_subplot(111, projection = "3d")
xs, ys, zs = user_embeddings_pca[::150].T
ax.scatter(xs, ys, zs)
```
<pre>
# Copyright 2018 Google Inc. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
</pre>
|
github_jupyter
|
import os
PROJECT = "cloud-training-demos" # REPLACE WITH YOUR PROJECT ID
BUCKET = "cloud-training-demos-ml" # REPLACE WITH YOUR BUCKET NAME
REGION = "us-central1" # REPLACE WITH YOUR BUCKET REGION e.g. us-central1
# Do not change these
os.environ["PROJECT"] = PROJECT
os.environ["BUCKET"] = BUCKET
os.environ["REGION"] = REGION
os.environ["TFVERSION"] = "1.13"
%%bash
gcloud config set project $PROJECT
gcloud config set compute/region $REGION
import tensorflow as tf
print(tf.__version__)
from google.cloud import bigquery
bq = bigquery.Client(project = PROJECT)
sql = """
WITH CTE_visitor_page_content AS (
SELECT
# Schema: https://support.google.com/analytics/answer/3437719?hl=en
# For a completely unique visit-session ID, we combine combination of fullVisitorId and visitNumber:
CONCAT(fullVisitorID,'-',CAST(visitNumber AS STRING)) AS visitorId,
(SELECT MAX(IF(index=10, value, NULL)) FROM UNNEST(hits.customDimensions)) AS latestContentId,
(LEAD(hits.time, 1) OVER (PARTITION BY fullVisitorId ORDER BY hits.time ASC) - hits.time) AS session_duration
FROM
`cloud-training-demos.GA360_test.ga_sessions_sample`,
UNNEST(hits) AS hits
WHERE
# only include hits on pages
hits.type = "PAGE"
GROUP BY
fullVisitorId,
visitNumber,
latestContentId,
hits.time )
-- Aggregate web stats
SELECT
visitorId,
latestContentId as contentId,
SUM(session_duration) AS session_duration
FROM
CTE_visitor_page_content
WHERE
latestContentId IS NOT NULL
GROUP BY
visitorId,
latestContentId
HAVING
session_duration > 0
"""
df = bq.query(sql).to_dataframe()
df.head()
stats = df.describe()
stats
df[["session_duration"]].plot(kind="hist", logy=True, bins=100, figsize=[8,5])
# The rating is the session_duration scaled to be in the range 0-1. This will help with training.
median = stats.loc["50%", "session_duration"]
df["rating"] = 0.3 * df["session_duration"] / median
df.loc[df["rating"] > 1, "rating"] = 1
df[["rating"]].plot(kind="hist", logy=True, bins=100, figsize=[8,5])
del df["session_duration"]
%%bash
rm -rf data
mkdir data
df.to_csv(path_or_buf = "data/collab_raw.csv", index = False, header = False)
!head data/collab_raw.csv
import pandas as pd
import numpy as np
def create_mapping(values, filename):
with open(filename, 'w') as ofp:
value_to_id = {value:idx for idx, value in enumerate(values.unique())}
for value, idx in value_to_id.items():
ofp.write("{},{}\n".format(value, idx))
return value_to_id
df = pd.read_csv(filepath_or_buffer = "data/collab_raw.csv",
header = None,
names = ["visitorId", "contentId", "rating"],
dtype = {"visitorId": str, "contentId": str, "rating": np.float})
df.to_csv(path_or_buf = "data/collab_raw.csv", index = False, header = False)
user_mapping = create_mapping(df["visitorId"], "data/users.csv")
item_mapping = create_mapping(df["contentId"], "data/items.csv")
!head -3 data/*.csv
df["userId"] = df["visitorId"].map(user_mapping.get)
df["itemId"] = df["contentId"].map(item_mapping.get)
mapped_df = df[["userId", "itemId", "rating"]]
mapped_df.to_csv(path_or_buf = "data/collab_mapped.csv", index = False, header = False)
mapped_df.head()
import pandas as pd
import numpy as np
mapped_df = pd.read_csv(filepath_or_buffer = "data/collab_mapped.csv", header = None, names = ["userId", "itemId", "rating"])
mapped_df.head()
NITEMS = np.max(mapped_df["itemId"]) + 1
NUSERS = np.max(mapped_df["userId"]) + 1
mapped_df["rating"] = np.round(mapped_df["rating"].values, 2)
print("{} items, {} users, {} interactions".format( NITEMS, NUSERS, len(mapped_df) ))
grouped_by_items = mapped_df.groupby("itemId")
iter = 0
for item, grouped in grouped_by_items:
print(item, grouped["userId"].values, grouped["rating"].values)
iter = iter + 1
if iter > 5:
break
import tensorflow as tf
grouped_by_items = mapped_df.groupby("itemId")
with tf.python_io.TFRecordWriter("data/users_for_item") as ofp:
for item, grouped in grouped_by_items:
example = tf.train.Example(features = tf.train.Features(feature = {
"key": tf.train.Feature(int64_list = tf.train.Int64List(value = [item])),
"indices": tf.train.Feature(int64_list = tf.train.Int64List(value = grouped["userId"].values)),
"values": tf.train.Feature(float_list = tf.train.FloatList(value = grouped["rating"].values))
}))
ofp.write(example.SerializeToString())
grouped_by_users = mapped_df.groupby("userId")
with tf.python_io.TFRecordWriter("data/items_for_user") as ofp:
for user, grouped in grouped_by_users:
example = tf.train.Example(features = tf.train.Features(feature = {
"key": tf.train.Feature(int64_list = tf.train.Int64List(value = [user])),
"indices": tf.train.Feature(int64_list = tf.train.Int64List(value = grouped["itemId"].values)),
"values": tf.train.Feature(float_list = tf.train.FloatList(value = grouped["rating"].values))
}))
ofp.write(example.SerializeToString())
!ls -lrt data
import os
import tensorflow as tf
from tensorflow.python.lib.io import file_io
from tensorflow.contrib.factorization import WALSMatrixFactorization
def read_dataset(mode, args):
def decode_example(protos, vocab_size):
# TODO
return
def remap_keys(sparse_tensor):
# Current indices of our SparseTensor that we need to fix
bad_indices = sparse_tensor.indices # shape = (current_batch_size * (number_of_items/users[i] + 1), 2)
# Current values of our SparseTensor that we need to fix
bad_values = sparse_tensor.values # shape = (current_batch_size * (number_of_items/users[i] + 1),)
# Since batch is ordered, the last value for a batch index is the user
# Find where the batch index chages to extract the user rows
# 1 where user, else 0
user_mask = tf.concat(values = [bad_indices[1:,0] - bad_indices[:-1,0], tf.constant(value = [1], dtype = tf.int64)], axis = 0) # shape = (current_batch_size * (number_of_items/users[i] + 1), 2)
# Mask out the user rows from the values
good_values = tf.boolean_mask(tensor = bad_values, mask = tf.equal(x = user_mask, y = 0)) # shape = (current_batch_size * number_of_items/users[i],)
item_indices = tf.boolean_mask(tensor = bad_indices, mask = tf.equal(x = user_mask, y = 0)) # shape = (current_batch_size * number_of_items/users[i],)
user_indices = tf.boolean_mask(tensor = bad_indices, mask = tf.equal(x = user_mask, y = 1))[:, 1] # shape = (current_batch_size,)
good_user_indices = tf.gather(params = user_indices, indices = item_indices[:,0]) # shape = (current_batch_size * number_of_items/users[i],)
# User and item indices are rank 1, need to make rank 1 to concat
good_user_indices_expanded = tf.expand_dims(input = good_user_indices, axis = -1) # shape = (current_batch_size * number_of_items/users[i], 1)
good_item_indices_expanded = tf.expand_dims(input = item_indices[:, 1], axis = -1) # shape = (current_batch_size * number_of_items/users[i], 1)
good_indices = tf.concat(values = [good_user_indices_expanded, good_item_indices_expanded], axis = 1) # shape = (current_batch_size * number_of_items/users[i], 2)
remapped_sparse_tensor = tf.SparseTensor(indices = good_indices, values = good_values, dense_shape = sparse_tensor.dense_shape)
return remapped_sparse_tensor
def parse_tfrecords(filename, vocab_size):
if mode == tf.estimator.ModeKeys.TRAIN:
num_epochs = None # indefinitely
else:
num_epochs = 1 # end-of-input after this
files = tf.gfile.Glob(filename = os.path.join(args["input_path"], filename))
# Create dataset from file list
dataset = tf.data.TFRecordDataset(files)
dataset = dataset.map(map_func = lambda x: decode_example(x, vocab_size))
dataset = dataset.repeat(count = num_epochs)
dataset = dataset.batch(batch_size = args["batch_size"])
dataset = dataset.map(map_func = lambda x: remap_keys(x))
return dataset.make_one_shot_iterator().get_next()
def _input_fn():
features = {
WALSMatrixFactorization.INPUT_ROWS: parse_tfrecords("items_for_user", args["nitems"]),
WALSMatrixFactorization.INPUT_COLS: parse_tfrecords("users_for_item", args["nusers"]),
WALSMatrixFactorization.PROJECT_ROW: tf.constant(True)
}
return features, None
return _input_fn
def input_cols():
return parse_tfrecords("users_for_item", args["nusers"])
return _input_fn#_subset
def try_out():
with tf.Session() as sess:
fn = read_dataset(
mode = tf.estimator.ModeKeys.EVAL,
args = {"input_path": "data", "batch_size": 4, "nitems": NITEMS, "nusers": NUSERS})
feats, _ = fn()
print(feats["input_rows"].eval())
print(feats["input_rows"].eval())
try_out()
def find_top_k(user, item_factors, k):
all_items = tf.matmul(a = tf.expand_dims(input = user, axis = 0), b = tf.transpose(a = item_factors))
topk = tf.nn.top_k(input = all_items, k = k)
return tf.cast(x = topk.indices, dtype = tf.int64)
def batch_predict(args):
import numpy as np
with tf.Session() as sess:
estimator = tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"])
# This is how you would get the row factors for out-of-vocab user data
# row_factors = list(estimator.get_projections(input_fn=read_dataset(tf.estimator.ModeKeys.EVAL, args)))
# user_factors = tf.convert_to_tensor(np.array(row_factors))
# But for in-vocab data, the row factors are already in the checkpoint
user_factors = tf.convert_to_tensor(value = estimator.get_row_factors()[0]) # (nusers, nembeds)
# In either case, we have to assume catalog doesn"t change, so col_factors are read in
item_factors = tf.convert_to_tensor(value = estimator.get_col_factors()[0])# (nitems, nembeds)
# For each user, find the top K items
topk = tf.squeeze(input = tf.map_fn(fn = lambda user: find_top_k(user, item_factors, args["topk"]), elems = user_factors, dtype = tf.int64))
with file_io.FileIO(os.path.join(args["output_dir"], "batch_pred.txt"), mode = 'w') as f:
for best_items_for_user in topk.eval():
f.write(",".join(str(x) for x in best_items_for_user) + '\n')
def train_and_evaluate(args):
train_steps = int(0.5 + (1.0 * args["num_epochs"] * args["nusers"]) / args["batch_size"])
steps_in_epoch = int(0.5 + args["nusers"] / args["batch_size"])
print("Will train for {} steps, evaluating once every {} steps".format(train_steps, steps_in_epoch))
def experiment_fn(output_dir):
return tf.contrib.learn.Experiment(
tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"]),
train_input_fn = read_dataset(tf.estimator.ModeKeys.TRAIN, args),
eval_input_fn = read_dataset(tf.estimator.ModeKeys.EVAL, args),
train_steps = train_steps,
eval_steps = 1,
min_eval_frequency = steps_in_epoch
)
from tensorflow.contrib.learn.python.learn import learn_runner
learn_runner.run(experiment_fn = experiment_fn, output_dir = args["output_dir"])
batch_predict(args)
import shutil
shutil.rmtree(path = "wals_trained", ignore_errors=True)
train_and_evaluate({
"output_dir": "wals_trained",
"input_path": "data/",
"num_epochs": 0.05,
"nitems": NITEMS,
"nusers": NUSERS,
"batch_size": 512,
"n_embeds": 10,
"topk": 3
})
!ls wals_trained
!head wals_trained/batch_pred.txt
os.environ["NITEMS"] = str(NITEMS)
os.environ["NUSERS"] = str(NUSERS)
%%bash
rm -rf wals.tar.gz wals_trained
gcloud ai-platform local train \
--module-name=walsmodel.task \
--package-path=${PWD}/walsmodel \
-- \
--output_dir=${PWD}/wals_trained \
--input_path=${PWD}/data \
--num_epochs=0.01 --nitems=${NITEMS} --nusers=${NUSERS} \
--job-dir=./tmp
%%bash
gsutil -m cp data/* gs://${BUCKET}/wals/data
%%bash
OUTDIR=gs://${BUCKET}/wals/model_trained
JOBNAME=wals_$(date -u +%y%m%d_%H%M%S)
echo $OUTDIR $REGION $JOBNAME
gsutil -m rm -rf $OUTDIR
gcloud ai-platform jobs submit training $JOBNAME \
--region=$REGION \
--module-name=walsmodel.task \
--package-path=${PWD}/walsmodel \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=BASIC_GPU \
--runtime-version=$TFVERSION \
-- \
--output_dir=$OUTDIR \
--input_path=gs://${BUCKET}/wals/data \
--num_epochs=10 --nitems=${NITEMS} --nusers=${NUSERS}
def get_factors(args):
with tf.Session() as sess:
estimator = tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"])
row_factors = estimator.get_row_factors()[0]
col_factors = estimator.get_col_factors()[0]
return row_factors, col_factors
args = {
"output_dir": "gs://{}/wals/model_trained".format(BUCKET),
"nitems": NITEMS,
"nusers": NUSERS,
"n_embeds": 10
}
user_embeddings, item_embeddings = get_factors(args)
print(user_embeddings[:3])
print(item_embeddings[:3])
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import PCA
pca = PCA(n_components = 3)
pca.fit(user_embeddings)
user_embeddings_pca = pca.transform(user_embeddings)
fig = plt.figure(figsize = (8,8))
ax = fig.add_subplot(111, projection = "3d")
xs, ys, zs = user_embeddings_pca[::150].T
ax.scatter(xs, ys, zs)
| 0.35421 | 0.805709 |
```
# Useful for debugging
%load_ext autoreload
%autoreload 2
%pylab --no-import-all inline
%config InlineBackend.figure_format = 'retina'
```
# LCLS Classic model
```
from lcls_live.bmad import LCLSTaoModel
from lcls_live.epics import epics_proxy
import os
# Make sure this exists
assert 'LCLS_CLASSIC_LATTICE' in os.environ
```
# Get snapshot
```
# Cached EPICS pv data
SNAPSHOT = 'data/epics_snapshot_2018-03-06T15:21:15.000000-08:00.json'
epics = epics_proxy(SNAPSHOT, verbose=True)
M = LCLSTaoModel('lcls_classic', epics = epics ,verbose=True, ploton=True)
print(M)
%%tao
place floor beta_compare
set lattice base = model
```
# Archiver restore
```
# Optional.
# For archiver, if off-site
# Open an SSH tunnel in a terminal like:
# ssh -D 8080 <SLAC username>@<SLAC machine>
# And then set:
if False:
os.environ['http_proxy']='socks5h://localhost:8080'
os.environ['HTTPS_PROXY']='socks5h://localhost:8080'
os.environ['ALL_PROXY']='socks5h://localhost:8080'
# Restore from some other time
#M.archiver_restore('2018-11-06T11:22:45.000000-08:00')
M.archiver_restore('2018-03-06T14:21:29.000000-08:00')
```
## Track particles with CSR
```
%%tao
set beam_init beam_track_end = UNDSTART
set csr_param n_bin = 40
snparticle 10000
set bmad_com csr_and_space_charge_on = T
set csr_param ds_track_step = 0.01
set ele BC1BEG:BC1END CSR_METHOD = 1_dim
set ele BC2BEG:BC2END CSR_METHOD = 1_dim
beamon
beamoff
```
# Plot
```
from pmd_beamphysics import ParticleGroup
P = ParticleGroup(data=M.bunch_data('BC2FIN'))
Palive = P.where(P['status'] == 1)
Pdead = P.where(P['status'] != 1)
Palive.plot('delta_t', 'delta_pz', bins=100)
if len(Pdead) >0:
print(Pdead)
```
# Functional usage
```
from lcls_live.bmad.classic.evaluate import run_LCLSTao, evaluate_LCLSTao
settings00 = {
# 'ele:O_BC1:angle_deg':-5.12345,
# 'ele:O_BC2:angle_deg':-2.0,
# 'ele:O_L1:phase_deg':-25.1,
# 'ele:O_L2:phase_deg':-41.4,
# 'ele:O_L3:phase_deg':0.0,
# 'ele:O_L1_fudge:f': 1.0,
# 'ele:O_L2_fudge:f': 1.0,
# 'ele:O_L3_fudge:f': 1.0,
'ele:CE11:x1_limit': 2.5e-3, # Basic 'horn cutting'
'ele:CE11:x2_limit': 4.0e-3,
'csr_param:n_bin':40,
'csr_param:ds_track_step':0.01,
'beam_init:n_particle': 10000,
'beam:beam_saved_at':'CE11, UNDSTART',
'beam:beam_track_end':'UNDSTART',
'bmad_com:csr_and_space_charge_on':True,
'ele:BC1BEG:BC1END:CSR_METHOD': '1_Dim',
'ele:BC2BEG:BC2END:CSR_METHOD': '1_Dim'
}
M = run_LCLSTao(settings=settings00, model_name='lcls_classic', verbose=True)
```
Because Tao runs as a library in global space, you can patch in commands:
```
%%tao
beamoff
set global plot_on = True
place floor zphase
szpz undstart
x-s floor -.055 -0.02
sc
# This will run the model, and return a dict with values from the following expressions
expressions = [
'lat::orbit.x[end]',
'beam::n_particle_loss[end]'
]
res = evaluate_LCLSTao(settings=settings00,
# epics_json='data/epics_snapshot_2018-03-06T11:22:45.000000-08:00.json',
expressions=expressions,
beam_archive_path = '.'
)
res
# Restore something from the archiver
settings00 = {
'csr_param:n_bin':40,
'csr_param:ds_track_step':0.01,
'beam_init:n_particle': 10000,
'beam:beam_saved_at':'CE11, UNDSTART',
'beam:beam_track_end':'UNDSTART',
'bmad_com:csr_and_space_charge_on':True,
'ele:BC1BEG:BC1END:CSR_METHOD': '1_Dim',
'ele:BC2BEG:BC2END:CSR_METHOD': '1_Dim'
}
res2 = evaluate_LCLSTao(settings=settings00,
epics_json='data/epics_snapshot_2018-03-06T11:22:45.000000-08:00.json',
expressions=expressions,
beam_archive_path = '.'
)
res2
```
# Plot
```
from pmd_beamphysics import particle_paths
import h5py
afile = res['beam_archive']
h5 = h5py.File(afile, 'r')
ppaths = particle_paths(h5)
ppaths
P = ParticleGroup(h5[ppaths[-1]])
Palive = P.where(P['status'] == 1)
Pdead = P.where(P['status'] != 1)
Palive.plot('delta_t', 'delta_pz', bins=100)
# These particles were lost (probably due to collimation)
Pdead
# Cleanup
os.remove(res['beam_archive'])
os.remove(res2['beam_archive'])
res2
```
|
github_jupyter
|
# Useful for debugging
%load_ext autoreload
%autoreload 2
%pylab --no-import-all inline
%config InlineBackend.figure_format = 'retina'
from lcls_live.bmad import LCLSTaoModel
from lcls_live.epics import epics_proxy
import os
# Make sure this exists
assert 'LCLS_CLASSIC_LATTICE' in os.environ
# Cached EPICS pv data
SNAPSHOT = 'data/epics_snapshot_2018-03-06T15:21:15.000000-08:00.json'
epics = epics_proxy(SNAPSHOT, verbose=True)
M = LCLSTaoModel('lcls_classic', epics = epics ,verbose=True, ploton=True)
print(M)
%%tao
place floor beta_compare
set lattice base = model
# Optional.
# For archiver, if off-site
# Open an SSH tunnel in a terminal like:
# ssh -D 8080 <SLAC username>@<SLAC machine>
# And then set:
if False:
os.environ['http_proxy']='socks5h://localhost:8080'
os.environ['HTTPS_PROXY']='socks5h://localhost:8080'
os.environ['ALL_PROXY']='socks5h://localhost:8080'
# Restore from some other time
#M.archiver_restore('2018-11-06T11:22:45.000000-08:00')
M.archiver_restore('2018-03-06T14:21:29.000000-08:00')
%%tao
set beam_init beam_track_end = UNDSTART
set csr_param n_bin = 40
snparticle 10000
set bmad_com csr_and_space_charge_on = T
set csr_param ds_track_step = 0.01
set ele BC1BEG:BC1END CSR_METHOD = 1_dim
set ele BC2BEG:BC2END CSR_METHOD = 1_dim
beamon
beamoff
from pmd_beamphysics import ParticleGroup
P = ParticleGroup(data=M.bunch_data('BC2FIN'))
Palive = P.where(P['status'] == 1)
Pdead = P.where(P['status'] != 1)
Palive.plot('delta_t', 'delta_pz', bins=100)
if len(Pdead) >0:
print(Pdead)
from lcls_live.bmad.classic.evaluate import run_LCLSTao, evaluate_LCLSTao
settings00 = {
# 'ele:O_BC1:angle_deg':-5.12345,
# 'ele:O_BC2:angle_deg':-2.0,
# 'ele:O_L1:phase_deg':-25.1,
# 'ele:O_L2:phase_deg':-41.4,
# 'ele:O_L3:phase_deg':0.0,
# 'ele:O_L1_fudge:f': 1.0,
# 'ele:O_L2_fudge:f': 1.0,
# 'ele:O_L3_fudge:f': 1.0,
'ele:CE11:x1_limit': 2.5e-3, # Basic 'horn cutting'
'ele:CE11:x2_limit': 4.0e-3,
'csr_param:n_bin':40,
'csr_param:ds_track_step':0.01,
'beam_init:n_particle': 10000,
'beam:beam_saved_at':'CE11, UNDSTART',
'beam:beam_track_end':'UNDSTART',
'bmad_com:csr_and_space_charge_on':True,
'ele:BC1BEG:BC1END:CSR_METHOD': '1_Dim',
'ele:BC2BEG:BC2END:CSR_METHOD': '1_Dim'
}
M = run_LCLSTao(settings=settings00, model_name='lcls_classic', verbose=True)
%%tao
beamoff
set global plot_on = True
place floor zphase
szpz undstart
x-s floor -.055 -0.02
sc
# This will run the model, and return a dict with values from the following expressions
expressions = [
'lat::orbit.x[end]',
'beam::n_particle_loss[end]'
]
res = evaluate_LCLSTao(settings=settings00,
# epics_json='data/epics_snapshot_2018-03-06T11:22:45.000000-08:00.json',
expressions=expressions,
beam_archive_path = '.'
)
res
# Restore something from the archiver
settings00 = {
'csr_param:n_bin':40,
'csr_param:ds_track_step':0.01,
'beam_init:n_particle': 10000,
'beam:beam_saved_at':'CE11, UNDSTART',
'beam:beam_track_end':'UNDSTART',
'bmad_com:csr_and_space_charge_on':True,
'ele:BC1BEG:BC1END:CSR_METHOD': '1_Dim',
'ele:BC2BEG:BC2END:CSR_METHOD': '1_Dim'
}
res2 = evaluate_LCLSTao(settings=settings00,
epics_json='data/epics_snapshot_2018-03-06T11:22:45.000000-08:00.json',
expressions=expressions,
beam_archive_path = '.'
)
res2
from pmd_beamphysics import particle_paths
import h5py
afile = res['beam_archive']
h5 = h5py.File(afile, 'r')
ppaths = particle_paths(h5)
ppaths
P = ParticleGroup(h5[ppaths[-1]])
Palive = P.where(P['status'] == 1)
Pdead = P.where(P['status'] != 1)
Palive.plot('delta_t', 'delta_pz', bins=100)
# These particles were lost (probably due to collimation)
Pdead
# Cleanup
os.remove(res['beam_archive'])
os.remove(res2['beam_archive'])
res2
| 0.582847 | 0.664346 |
<a href="https://colab.research.google.com/github/lucerogr/algorithmic-complexity/blob/main/TP.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
!git clone https://github.com/lmcanavals/algorithmic_complexity.git
from algorithmic_complexity.aclib import graphstuff as gs
import pandas as pd
import numpy as np
import networkx as nx
import math
url="https://raw.githubusercontent.com/lmcanavals/algorithmic_complexity/main/data/poblaciones.csv"
poblaciones=pd.read_csv(url)
print(poblaciones)
print(len(poblaciones))
poblaciones.head()
nomdepartamentos = poblaciones['DEPARTAMENTO'].unique()
print(len(nomdepartamentos))
nomdepartamentos
departamentos = dict()
for nom in nomdepartamentos:
departamentos[nom] = poblaciones[poblaciones['DEPARTAMENTO'] == nom]
print(nom, len(departamentos[nom]))
nomprovincias = poblaciones['PROVINCIA'].unique()
print(len(nomprovincias))
nomprovincias
provincias = dict()
for nom in nomprovincias:
provincias[nom] = poblaciones[poblaciones['PROVINCIA'] == nom]
print(nom, len(provincias[nom]))
nomprovincia = input("Ingrese la provincia para mostrar sus distritos: ")
nomdistritos = provincias[nomprovincia]['DISTRITO'].unique()
print("Hay ", len(nomdistritos), " distritos ")
print(" ")
nomdistritos
distritos = dict()
for nom in nomdistritos:
distritos[nom] = provincias[nomprovincia][provincias[nomprovincia]['DISTRITO'] == nom]
print(nom, len(distritos[nom]))
def dist(cp1, cp2):
x1, y1 = float(cp1['LATITUD']), float(cp1['LONGITUD'])
x2, y2 = float(cp2['LATITUD']), float(cp2['LONGITUD'])
return math.sqrt((x1 - x2)**2 + (y1 - y2)**2)
nomdistrito = input("Ingrese el DISTRITO para mostrar sus CENTROS POBLADOS: ")
distrito = distritos[nomdistrito]
G = nx.Graph()
col = 'CENTRO POBLADO'
for i, cp1 in distrito.iterrows():
print(cp1[col])
for j, cp2 in distrito.iterrows():
if cp1[col] != cp2[col]:
G.add_edge(cp1[col], cp2[col], weight=dist(cp1, cp2))
print(G.nodes)
list(G.neighbors('NUEVA ESPERANZA'))
def dijkstra(G, s):
unvisited = []
visited = []
total_weight = 0
current_node = s
neighbor = ''
for node in G.nodes:
if node == s:
visited.append(s)
else:
unvisited.append(node)
while unvisited:
for i, neighbor in enumerate(unvisited):
if i == 0:
current_weight = G.edges[s, neighbor]['weight']
current_node = neighbor
elif G.edges[s, neighbor]['weight'] < current_weight:
current_weight = G.edges[s, neighbor]['weight']
current_node = neighbor
total_weight += current_weight
unvisited.remove(current_node)
visited.append(current_node)
total_weight += G.edges[s, current_node]['weight']
visited.append(s)
return visited, total_weight
dijkstra(G, 'EL HUARANGAL')
def path_taken():
dijkstra(G, 'EL HUARANGAL')
shortest_path = []
shortest_weight = 0
for i, node in enumerate(G.nodes):
path, weight = dijkstra(G, node)
#print("")
#print("Ruta", i + 1, "=", path)
#print("Distancia =", weight)
if i == 0:
shortest_weight = weight
shortest_path = path
elif weight < shortest_weight:
shortest_weight = weight
shortest_path = path
print('--------------------------------------')
print("La ruta más corta que visita cada ciudad es:", shortest_path)
print("La distancia de la ruta es:", shortest_weight)
path_taken()
gs.nx2gv(G, weighted=True, params={'size':'20'})
```
|
github_jupyter
|
!git clone https://github.com/lmcanavals/algorithmic_complexity.git
from algorithmic_complexity.aclib import graphstuff as gs
import pandas as pd
import numpy as np
import networkx as nx
import math
url="https://raw.githubusercontent.com/lmcanavals/algorithmic_complexity/main/data/poblaciones.csv"
poblaciones=pd.read_csv(url)
print(poblaciones)
print(len(poblaciones))
poblaciones.head()
nomdepartamentos = poblaciones['DEPARTAMENTO'].unique()
print(len(nomdepartamentos))
nomdepartamentos
departamentos = dict()
for nom in nomdepartamentos:
departamentos[nom] = poblaciones[poblaciones['DEPARTAMENTO'] == nom]
print(nom, len(departamentos[nom]))
nomprovincias = poblaciones['PROVINCIA'].unique()
print(len(nomprovincias))
nomprovincias
provincias = dict()
for nom in nomprovincias:
provincias[nom] = poblaciones[poblaciones['PROVINCIA'] == nom]
print(nom, len(provincias[nom]))
nomprovincia = input("Ingrese la provincia para mostrar sus distritos: ")
nomdistritos = provincias[nomprovincia]['DISTRITO'].unique()
print("Hay ", len(nomdistritos), " distritos ")
print(" ")
nomdistritos
distritos = dict()
for nom in nomdistritos:
distritos[nom] = provincias[nomprovincia][provincias[nomprovincia]['DISTRITO'] == nom]
print(nom, len(distritos[nom]))
def dist(cp1, cp2):
x1, y1 = float(cp1['LATITUD']), float(cp1['LONGITUD'])
x2, y2 = float(cp2['LATITUD']), float(cp2['LONGITUD'])
return math.sqrt((x1 - x2)**2 + (y1 - y2)**2)
nomdistrito = input("Ingrese el DISTRITO para mostrar sus CENTROS POBLADOS: ")
distrito = distritos[nomdistrito]
G = nx.Graph()
col = 'CENTRO POBLADO'
for i, cp1 in distrito.iterrows():
print(cp1[col])
for j, cp2 in distrito.iterrows():
if cp1[col] != cp2[col]:
G.add_edge(cp1[col], cp2[col], weight=dist(cp1, cp2))
print(G.nodes)
list(G.neighbors('NUEVA ESPERANZA'))
def dijkstra(G, s):
unvisited = []
visited = []
total_weight = 0
current_node = s
neighbor = ''
for node in G.nodes:
if node == s:
visited.append(s)
else:
unvisited.append(node)
while unvisited:
for i, neighbor in enumerate(unvisited):
if i == 0:
current_weight = G.edges[s, neighbor]['weight']
current_node = neighbor
elif G.edges[s, neighbor]['weight'] < current_weight:
current_weight = G.edges[s, neighbor]['weight']
current_node = neighbor
total_weight += current_weight
unvisited.remove(current_node)
visited.append(current_node)
total_weight += G.edges[s, current_node]['weight']
visited.append(s)
return visited, total_weight
dijkstra(G, 'EL HUARANGAL')
def path_taken():
dijkstra(G, 'EL HUARANGAL')
shortest_path = []
shortest_weight = 0
for i, node in enumerate(G.nodes):
path, weight = dijkstra(G, node)
#print("")
#print("Ruta", i + 1, "=", path)
#print("Distancia =", weight)
if i == 0:
shortest_weight = weight
shortest_path = path
elif weight < shortest_weight:
shortest_weight = weight
shortest_path = path
print('--------------------------------------')
print("La ruta más corta que visita cada ciudad es:", shortest_path)
print("La distancia de la ruta es:", shortest_weight)
path_taken()
gs.nx2gv(G, weighted=True, params={'size':'20'})
| 0.287868 | 0.886174 |
# Tensor Creation
```
from __future__ import print_function
import torch
import numpy as np
import matplotlib
%matplotlib inline
import matplotlib.pyplot as plt
from datetime import date
date.today()
author = "kyubyong. https://github.com/Kyubyong/pytorch_exercises"
torch.__version__
np.__version__
```
NOTE on notation
_x, _y, _z, ...: NumPy 0-d or 1-d arrays
_X, _Y, _Z, ...: NumPy 2-d or higer dimensional arrays
x, y, z, ...: 0-d or 1-d tensors
X, Y, Z, ...: 2-d or higher dimensional tensors
## From Python list
Q1. Convert a python list `a` into an int32 tensor.
```
a = [[1, 2, 3], [4, 5, 6]]
X = ...
print(X)
```
Q2. Create a float32 tensor of shape (3, 2), filled with 10.
```
X = ...
print(X)
```
## From Numpy Array
Q3. Convert a NumPy array _x into a tensor.
```
_x = np.array([1, 2, 3])
x = ...
print(x)
```
## Ones and zeros
Q4. Create a 3-by-3 2-D tensor with ones on the diagonal and zeros elsewhere.
```
X = ...
print(X)
```
Q5. Create a tensor with shape of (3, 2) filled with 1's.
```
X = ...
print(X)
```
Q6. Create a tensor with shape of (3, 2) filled with 0's.
```
X = ...
print(X)
```
## Numerical ranges
Q7. Create a 1D tensor which looks like 2, 4, 6, 8, ..., 100.
```
x = ...
print(x)
```
Q8. Create a 1D tensor of 50 evenly spaced elements between 3. and 10., inclusive.
```
x = ...
print(x)
```
Q9. Create a 1-D tensor of 50 element spaced evenly on a log scale between 3. and 10.
```
x = ...
_x = x.numpy()
plt.figure()
plt.scatter(range(len(_x)), _x)
plt.show()
```
## Matrix
Q10. Get the diagonal of X.
```
X = torch.Tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]])
y = ...
print(y)
```
Q11. Get the 1th diagonal of X.
```
X = torch.Tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]])
y = ...
print(y)
```
Q12. Get the sum of the elements of the diagonal of X.
```
X = torch.Tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]])
y = ...
print(y)
```
Q13. Return the lower triangular part of X, the other elements are set to 0.
```
X = torch.Tensor([[1,2,3], [4,5,6], [7,8,9]])
Y = ...
print(Y)
```
Q14. Return the upper triangular part of X, the other elements are set to 0.
```
X = torch.Tensor([[1,2,3], [4,5,6], [7,8,9]])
Y = ...
print(Y)
```
## Save and Load
Q15. Save X to `temp.pt`.
```
X = torch.randn(1, 10)
...
```
Q16. Load the `temp.pt` you just saved.
```
X2 = ...
print(X2)
```
Q17. Print X2 such that all elements are displayed with precision=1 (without actually changing the values of X2).
```
...
print(X2)
```
|
github_jupyter
|
from __future__ import print_function
import torch
import numpy as np
import matplotlib
%matplotlib inline
import matplotlib.pyplot as plt
from datetime import date
date.today()
author = "kyubyong. https://github.com/Kyubyong/pytorch_exercises"
torch.__version__
np.__version__
a = [[1, 2, 3], [4, 5, 6]]
X = ...
print(X)
X = ...
print(X)
_x = np.array([1, 2, 3])
x = ...
print(x)
X = ...
print(X)
X = ...
print(X)
X = ...
print(X)
x = ...
print(x)
x = ...
print(x)
x = ...
_x = x.numpy()
plt.figure()
plt.scatter(range(len(_x)), _x)
plt.show()
X = torch.Tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]])
y = ...
print(y)
X = torch.Tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]])
y = ...
print(y)
X = torch.Tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]])
y = ...
print(y)
X = torch.Tensor([[1,2,3], [4,5,6], [7,8,9]])
Y = ...
print(Y)
X = torch.Tensor([[1,2,3], [4,5,6], [7,8,9]])
Y = ...
print(Y)
X = torch.randn(1, 10)
...
X2 = ...
print(X2)
...
print(X2)
| 0.417271 | 0.978875 |
# Deep Learning avec Keras
**L’objectif de cette première partie de travaux pratiques est de prendre en main la librairie `Keras` [https://keras.io/](https://keras.io/) pour utiliser et entraîner des réseaux de neurones profonds.**
## Exercice 0 : Chargement des données
On va travailler avec la base de données image MNIST, constituée d’images de
caractères manuscrits (60000 images en apprentissage, 10000 en test).
Voici un bout de code pour récupérer les données :
```
from keras.datasets import mnist
# the data, shuffled and split between train and test sets
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
print(X_train.shape[0], 'train samples')
print(X_test.shape[0], 'test samples')
```
On va commencer par afficher les 200 premières images de la base d’apprentissage.
- Écrire un script `exo0.py` qui va récupérer les données avec le code précédent
- Compléter `exo0.py` pour permettre l’affichage demandé en utilisant le code suivant :
```
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.figure(figsize=(7.195, 3.841), dpi=100)
for i in range(200):
plt.subplot(10,20,i+1)
plt.imshow(X_train[i,:].reshape([28,28]), cmap='gray')
plt.axis('off')
plt.show()
```
## Question :
Quel est l’espace dans lequel se trouvent les images ? Quel est sa taille ?
```
print(X_train.shape)
print(X_test.shape)
```
## Exercice 1 : Régression logistique
On va d’abord commencer par créer un modèle de classification linéaire populaire, la régression logistique.
### Modèle de prédiction
Ce modèle correspond à un réseau de neurones à une seule couche, qui va projeter le vecteur d’entrée $ \mathbf{x_i} $ pour une image MNIST
(taille $ 28^2=784 $) avec un vecteur de de paramètres $ \mathbf{w_{c}} $ pour chaque classe (plus un biais $ b_c $).
Pour correspondre à la matrice des données de l’exercice précédent, on considère que chaque exemple $ \mathbf{x_i} $ est un vecteur ligne - taille (1,784).
En regroupant l’ensemble des jeux de paramètres $ \mathbf{w_{c}} $ pour les 10 classes dans une matrice $ \mathbf{W} $ (taille $ 784\times 10 $),
et les biais dans un vecteur $ \mathbf{b} $, on obtient un vecteur
$ \mathbf{\hat{s_i}} =\mathbf{x_i} \mathbf{W} + \mathbf{b} $ de taille (1,10).
Une fonction d’activation de type soft-max sur $ \mathbf{\hat{y_i}} = $ `softmax` $ (\mathbf{s_i}) $ permet d’obtenir le vecteur de sortie prédit par le modèle $ \mathbf{\hat{y_i}} $ - de taille (1,10) - qui représente la probabilité *a posteriori*
$ p(\mathbf{\hat{y_i}} | \mathbf{x_i}) $ pour chacune des 10 classes:
<a id='equation-softmax'></a>
$$
p(\hat{y_{c,i}} | \mathbf{x_i}) ) = \frac{e^{\langle \mathbf{x_i} ; \mathbf{w_{c}}\rangle + b_{c}}}{\sum\limits_{c'=1}^{10} e^{\langle \mathbf{x_i} ; \mathbf{w_{c'}}\rangle + b_{c'}}} \tag{1}
$$
Le schéma ci-dessous illustre le modèle de régression logistique avec un réseau de neurones.
<img src="http://cedric.cnam.fr/~thomen/cours/STA211/_images/LR.png" style="height:200px;" align="center">
### Question :
Quel est le nombre de paramètres du modèle ? Justifier le calcul.
Avec `Keras`, les réseaux de neurones avec une structure de chaîne (réseaux « feedforward »), s’utilisent de la manière suivante:
```
# nb de parametres = 784 * 10 + 10
print("Nombre de paramètres = ", 784 * 10 + 10)
from keras.models import Sequential
model = Sequential()
```
On créé ainsi un réseau de neurones vide. On peut alors ajouter des couches avec la fonction `add`.
Par exemple, l’ajout d’une couche de projection linéaire (couche complètement connectée) de taille 10, suivi de l’ajout d’une couche d’activation de type `softmax`, peuvent s’effectuer de la manière suivante:
```
from keras.layers import Dense, Activation
model.add(Dense(10, input_dim=784, name='fc1'))
model.add(Activation('softmax'))
```
On peut ensuite visualiser l’architecture du réseau avec la méthode `summary()` du modèle.
### Question :
- Écrire un script `exo1.py` permettant de créer le réseau de neurone ci-dessus.
- Vérifier le nombre de paramètres du réseau à apprendre dans la méthode `summary()`.
```
model.summary()
```
### Formulation du problème d’apprentissage
> Afin d’entraîner le réseau de neurones, on va comparer, pour chaque exemple d’apprentissage, la sortie prédite $ \mathbf{\hat{y_i}} $ par le réseau
- équation [(1)](#equation-softmax) - pour l’image $ \mathbf{x_i} $, avec la sortie
réelle $ \mathbf{y_i^*} $ issue de la supervision qui correspond à la catégorie de l’image $ \mathbf{x_i} $:
on utilisera en encodage de type « one-hot » pour $ \mathbf{y_i^*} $, *i.e.* :
<a id='equation-one-hot'></a>
$$
y_{c,i}^* =
\begin{cases}
1 & \text{si c correspond à l'indice de la classe de } \mathbf{x_i} \\
0 & \text{sinon}
\end{cases} \tag{2}
$$
On utilisera le code suivant pour générer des labels au format
0-1 encoding - équation [(2)](#equation-one-hot).
```
from keras.utils import np_utils
K=10
# convert class vectors to binary class matrices
Y_train = np_utils.to_categorical(y_train, K)
Y_test = np_utils.to_categorical(y_test, K)
```
Pour mesurer l’erreur de prédiction, on utilisera une fonction de coût de type entropie croisée (« cross-entropy ») entre $ \mathbf{\hat{y_i}} $ et $ \mathbf{y_i^*} $ :
$ \mathcal{L}(\mathbf{\hat{y_i}}, \mathbf{y_i^*}) = -\sum\limits_{c=1}^{10} y_{c,i}^* log(\hat{y}_{c,i}) = - log(\hat{y}_{c^*,i}) $, où $ c^* $ correspond à l’indice de la classe donné par la supervision pour l’image $ \mathbf{x_i} $.
La fonction de coût finale consistera à moyenner l’entropie croisée sur l’ensemble de la base d’apprentissage $ \mathcal{D} $ constituée de $ N=60000 $ images :
<a id='equation-ce'></a>
$$
\mathcal{L}_{\mathbf{W},\mathbf{b}}(\mathcal{D}) = - \frac{1}{N}\sum_{i=1}^{N} log(\hat{y}_{c^*,i}) \tag{3}
$$
### Question :
La fonction de coût de l’Eq. [(3)](#equation-ce) est-elle convexe par rapports aux paramètres $ \mathbf{W} $, $ \mathbf{b} $ du modèle ? Avec un pas de gradient bien choisi, peut-on assurer la convergence vers le minimum global de la solution ?
### Apprentissage du modèle
Afin d’optimiser les paramètres $ \mathbf{W} $ et $ \mathbf{b} $ pour minimiser l’équation [(3)](#equation-ce) pour notre modèle de régression logistique, nous allons utiliser l’algorithme de rétro-propagation de l’erreur du gradient.
Avec `Keras`, la rétro-propagation de l’erreur est implémentée nativement. On va compiler le modèle en lui passant un loss (ici l” entropie croisée), une méthode d’optimisation (ici une descente de gradient stochastique, stochatic gradient descent, sgd),
et une métrique d’évaluation (ici le taux de bonne prédiction des catégories, accuracy) :
```
from keras.optimizers import SGD
learning_rate = 0.5
sgd = SGD(learning_rate)
model.compile(loss='categorical_crossentropy',optimizer=sgd,metrics=['accuracy'])
```
Enfin, l’apprentissage du modèle sur des données d’apprentissage est mis en place avec la méthode `fit` :
```
batch_size = 100
nb_epoch = 10
model.fit(X_train, Y_train,batch_size=batch_size, epochs=nb_epoch,verbose=1)
```
- batch_size correspond au nombre d’exemples utilisé pour estimer le gradient de la fonction de coût.
- epochs est le nombre d’époques (*i.e.* passages sur l’ensemble des exemples de la base d’apprentissage) lors de la descente de gradient.
On peut ensuite évaluer les performances du modèle dur l’ensemble de test avec la fonction `evaluate`
```
scores = model.evaluate(X_test, Y_test, verbose=0)
print("%s: %.2f%%" % (model.metrics_names[0], scores[0]*100))
print("%s: %.2f%%" % (model.metrics_names[1], scores[1]*100))
```
Le premier élément de score renvoie la fonction de coût sur la base de test, le second élément renvoie le taux de bonne détection (accuracy).
- Implémenter l’apprentissage du modèle sur la base de train de la base MNIST.
- **Évaluer les performances du réseau sur la base de test. Vous devez obtenir un score de l’ordre de 92% sur la base de test pour ce modèle de régression logistique.**
### Notes :
Expression d'un modèle de régression logistique ne permet pas d'avoir une frontière de classification non linéaire. Donc accuracy ne peut pas aller jusqu'à 100%.
## Exercice 2 : Perceptron multi-couches (MLP)
L’objectif de ce second exercice est d’étendre le modèle de régression logistique afin de mettre en place des modèles de prédictions plus riches.
En particulier, on va s’intéresser aux **Perceptron multi-couches (Multi-Layer Percpetron, MLP)**. Contrairement à la régression logistique qui se limite à des séparateurs linéaires,
le Perceptron permet l’apprentissage de frontières de décisions non linéaires, et constituent des approximateurs universels de fonctions.
L’objectif de la séance de travaux pratiques est de mettre en place le code pour effectuer des prédictions et entraîner un Perceptron à une couche cachée.
### Modèle de prédiction
L’architecture du perpcetron à une couche cachée est montrée à la figure ci-dessous.
<img src="http://cedric.cnam.fr/~thomen/cours/STA211/_images/MLP.png" style="height:250px;" align="center">
Si on considère les données de la base MNIST, chaque image est représentée par un vecteur de taille $ 28^2=784 $.
Le perceptron va effecteur les différentes étape de transformation pour produire la prédiction finale, *i.e.* la catégorie sémantique de l’image :
- Une étape de projection linéaire, qui va projeter chaque image sur un vecteur de taille $ (1,L) $, *e.g.* $ L=100 $. En considérant chaque exemple $ \mathbf{x_i} $ est un vecteur ligne - taille $ (1,784) $ - la projection linéaire peut être représentée par la matrice $ \mathbf{W^h} $ (taille $ (784, L) $), et le vecteur de biais $ \mathbf{b^h} $ (taille $ (1, L) $) : $ \mathbf{\hat{u_i}} =\mathbf{x_i} \mathbf{W^h} + \mathbf{b^h} $.
> - Une étape de non linéarité, *e.g.* de type sigmoïde : $ \forall j \in \left\lbrace 1; L \right\rbrace ~ h_{i,j} = \frac{1}{1+exp(-u_{i,j})} $
- Une seconde étape de projection linéaire, qui va projeter le vecteur latent de taille $ (1,L) $ sur un vecteur de taille $ (1,K)=10 $ (nombre de classes). Cette opération de projection linéaire sera représentée par la matrice $ \mathbf{W^y} $ (taille $ (L, K) $), et le vecteur de biais $ \mathbf{b^y} $ (taille $ (1, K) $) : $ \mathbf{\hat{v_i}} =\mathbf{h_i} \mathbf{W^y} + \mathbf{b^y} $.
> - Une étape de non linéarité de type soft-max vue la semaine précédente pour la régression logistique : $ \forall j \in \left\lbrace 1; K \right\rbrace ~ y_{i,j} = \frac{exp(v_{i,j})}{\sum\limits_{i=1}^K exp(v_{i,k})} $
### Question :
- On va utiliser 100 neurones dans la couche cachée du nouveau réseau. Quel est maintenant le nombre de paramètres du modèle MLP ? Justifier le calcul.
- Ecrire un script `exo2.py` qui va enrichir le modèle de régression logistique de l’exercice précédent afin de créer le réseau MLP. Vérifier le nombre de paramètres du modèle avec la méthode `summary()`.
- Sur un réseau séquentiel vide, on va ajouter la méthode add pour insérer une couche cachée (de taille 100):
```
model = Sequential()
model.add(Dense(100, input_dim=784, name='fc1'))
```
- La non-linéarité de type sigmoïde sera obtenue de la manière suivante :
```
model.add(Activation('sigmoid'))
```
### Apprentissage du modèle
**Une fois le modèle MLP créé, la façon de l’entraîner va être strictement identique à ce qui a été écrit dans l’exercice 1 précédent.** En effet, on peut calculer l’erreur - entropie croisée décrite à l’équation [(3)](#equation-ce) - pour chaque exemple d’apprentissage à partir de la
sortie prédite $ \mathbf{\hat{y_i}} $ et de la supervision $ \mathbf{y_i^*} $. **L’algorithme de rétro-propagation du gradient de cette erreur permet alors de mettre à jour l’ensemble des paramètres du réseau.**
### Question :
- Compléter le script `exo2.py` afin d’effectuer l’entraînement du réseau MLP. On choisira 50 époques pour l’apprentissage.
- Avec ce modèle MLP à une couche cachée, la fonction de coût de l’Eq. [(3)](#equation-ce) est-elle convexe par rapports aux paramètres du modèle ? Avec un pas de gradient bien choisi, peut-on assurer la convergence vers le minimum global de la solution ?
- Observer la documentation `Keras` pour voir la façon dont les paramètres du modèles sont initialisés dans les différentes couches.
- **Évaluer les performances du réseau sur la base de test. Vous devez obtenir un score de l’ordre de 98% pour ce modèle MLP.**
- On pourra utiliser la méthode suivante pour sauvegarder le modèle appris :
```
from keras.models import model_from_yaml
def saveModel(model, savename):
# serialize model to YAML
model_yaml = model.to_yaml()
with open(savename+".yaml", "w") as yaml_file:
yaml_file.write(model_yaml)
print("Yaml Model ",savename,".yaml saved to disk")
# serialize weights to HDF5
model.save_weights(savename+".h5")
print("Weights ",savename,".h5 saved to disk")
```
### Results
loss: 6.97%
accuracy: 97.88%
## Exercice 3 : Réseau de neurones convolutif
On va maintenant étendre le perceptron de l’exercice précédent pour mettre en place un réseau de neurones convolutif profond, « Convolutionnal Neural Networks », ConvNets.
**Écrire un script ``exo3.py`` pour mettre en place un ConvNet.**
Les réseaux convolutifs manipulent des images multi-dimensionnelles en entrée (tenseurs). On va donc commencer par reformater les données d’entrée afin que chaque exemple soit de taille $ 28 \times 28 \times 1 $.
```
X_train = X_train.reshape(X_train.shape[0], 28, 28, 1)
X_test = X_test.reshape(X_test.shape[0], 28, 28, 1)
input_shape = (28, 28, 1)
```
Par rapport aux réseaux complètement connectés, les réseaux convolutifs utilisent les briques élémentaires suivantes :
1. Des couches de convolution, qui transforment un tenseur d’entrée de taille $ n_x \times n_y \times p $ en un tenseur de sortie $ n_{x'} \times n_{y'} \times n_H $, où $ n_H $ est le nombre de filtres choisi.
Par exemple, une couche de convolution pour traiter les images d’entrée de MNIST peut être créée de la manière suivante :
```
from keras.models import Sequential
from keras.layers import Dense, Flatten
from keras.layers import Conv2D, MaxPooling2D
Conv2D(32,kernel_size=(5, 5),activation='relu',input_shape=(28, 28, 1),padding='valid')
```
- 32 est le nombre de filtres.
- (5, 5) est la taille spatiale de chaque filtre (masque de convolution).
- padding=”valid” correspond ignorer les bords lors du calcul (et donc à diminuer la taille spatiale en sortie de la convolution).
- **N.B. :** on peut directement inclure dans la couche de convolution la non-linéarité en sortie de la convolution, comme illustré ici dans l’exemple avec une fonction d’activation de type `relu`.
1. Des couches d’agrégation spatiale (pooling), afin de permettre une invariance aux translations locales. Voici par exemple la manière de déclarer une couche de max-pooling:
```
pool = MaxPooling2D(pool_size=(2, 2))
```
- (2, 2) est la taille spatiale sur laquelle l’opération d’agrégation est effectuée.
- **N.B. :** par défaut, le pooling est effectué avec un décalage de 2 neurones, dans l’exemple précédent on obtient donc des cartes de sorties avec des tailles spatiales divisées par deux par rapport à la taille d’entrée.
**Compléter le script** `exo3.py` **pour mettre en place un ConvNet à l’architecture suivante, proche du modèle historique LeNet5** [[LBD+89]](#lecun1989backpropagation) **et montré ci-dessous:**
- Une couche de convolution avec 16 filtres de taille $ 5 \times 5 $, suivie d’une non linéarité de type relu puis d’une couche de max pooling de taille $ 2 \times 2 $.
- Une seconde couche de convolution avec 32 filtres de taille $ 5 \times 5 $, suivie d’une non linéarité de type relu puis d’une couche de max pooling de taille $ 2 \times 2 $.
- Comme dans le réseau LeNet, on considérera la sortie du second bloc convolutif comme un vecteur, ce que revient à « mettre à plat » les couches convolutives précédentes (`model.add(Flatten())`).
- Une couche complètement connectée de taille 100, suivie d’une non linéarité de type sigmoïde.
- Une couche complètement connectée de taille 10, suivie d’une non linéarité de type softmax.
<img src="http://cedric.cnam.fr/~thomen/cours/STA211/_images/LeNet5.png" style="height:200px;" align="center">
- **Apprendre le modèle et évaluer les performances du réseau sur la base de test. Vous devez obtenir un score de l’ordre de 99% pour ce modèle ConvNet.**
- Quelle est le temps d’une époque avec ce modèle convolutif ?
- On pourra sauvegarder le modèle appris avec la méthode `saveModel` précédente
**Apprentissage sur GPU**
- Quelle est le temps d’une époque avec ce modèle convolutif ?
- Vous pourrez tester l’apprentissage sur carte graphique du modèle, et comparer le temps d'entraînement
<a id='lecun1989backpropagation'></a>
\[LBD+89\] Yann LeCun, Bernhard Boser, John S Denker, Donnie Henderson, Richard E Howard, Wayne Hubbard, and Lawrence D Jackel. Backpropagation applied to handwritten zip code recognition. *Neural computation*, 1(4):541–551, 1989.
# Travaux pratiques - Deep Learning et Manifold Untangling
**L’objectif de ce TME est d’illustrer la capacité des réseaux de neurones profonds à apprendre des représentations internes capables de résoudre le problème connu sous le nom de « manifold untangling »** en neuroscience, c’est à dire de séparer les exemples des différentes classes dans l’espace de représentation appris.
Pour cela, on va utiliser des outils de visualisation qui vont permettre de représenter chaque donnée (par exemple une image de la base MNIST) par un point dans l’espace 2D. Ces même outils vont permettre de projeter en 2D les représentations internes des réseaux de neurones, ce qui va permettre d’analyser la séparabilité des points et des classes dans l’espace d’entrée et dans les espaces de représentions appris par les modèles.
**On aura besoin des modules suivants qu’on pourra importer en début de script :**
```
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
from scipy.spatial import ConvexHull
from sklearn.mixture import GaussianMixture
from scipy import linalg
from sklearn.neighbors import NearestNeighbors
from sklearn.manifold import TSNE
```
## Exercice 4 : Visualisation avec t-SNE
La méthode *t-Distributed Stochastic Neighbor Embedding* (t-SNE) [[vdMH08]](#tsne08) est une réduction de dimension non linéaire, dont l’objectif est d’assurer que des points proches dans l’espace de départ présentent des positions proches dans l’espace (2D) projeté. Dit autrement, la mesure de distance entre points dans l’espace 2D doit refléter la mesure de distance dans l’espace initial.
On va appliquer la méthode t-SNE sur les données brutes **de la base de test de MNIST** en utilisant la classe `TSNE` du module `sklearn.manifold` : [http://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html](http://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html) .
**Créer un script** `exo1.py` **dont l’objectif va être d’effectuer une réduction de dimension en 2D des données de la base de test de MNIST en utilisant la méthode t-SNE.**
- Créer une instance de type `TSNE`. **N.B :** on choisira 2 composantes et les paramètres suivants : `init='pca'` (réduire la dimension préalablement avec une ACP), `perplexity=30` (lié au nombre de voisins dans le calcul des distances), `verbose=2` (pour l’affichage lors de l’apprentissage).
- Appliquer la transformation pour obtenir les données projetées en 2D (fonction `fit_transform`). **N.B :** essayer tout d’abord avec un sous-ensemble de la base (*e.g.* 1000 exemples) pour tester l’algorithme, l’apprentissage avec l’ensemble de la base de test pouvant être long.
```
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
print(X_train.shape[0], 'train samples')
print(X_test.shape[0], 'test samples')
# Calcul TSNE
X_embedded = TSNE(n_components=2, perplexity=30, init='pca', verbose=2).fit_transform(X_train)
```
### Visualisation et métrique de séparation des classes
On va maintenant compléter le script `exo1.py` précédent afin de visualiser l’ensemble des points projetés en 2D, et de définir des critères pour analyser la séparabilité des classes dans l’espace projeté.
1. **Calcul de l’enveloppe convexe des points projetés pour chacune des classes.**
On utilisera pour cela la classe `ConvexHull` du module `scipy.spatial` [https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.ConvexHull.html](https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.ConvexHull.html). Sur la base MNIST, on pourra donc utiliser le code suivant pour calculer les enveloppes convexes des points pour les 10 classes :
```
def convexHulls(points, labels):
# computing convex hulls for a set of points with asscoiated labels
convex_hulls = []
for i in range(10):
convex_hulls.append(ConvexHull(points[labels==i,:]))
return convex_hulls
```
où `points` (*resp.* `labels`) dans la méthode `convexHulls(points, labels)` correspond aux images projetées dans le plan 2D avec la méthode t-SNE de l’exercice 1 (*resp.* aux labels, *i.e.* classes, des images).
2. **Calcul de l’ellipse de meilleure approximation des points.**
On utilisera pour cela la classe `GaussianMixture` du module `sklearn.mixture` [http://scikit-learn.org/stable/modules/generated/sklearn.mixture.GaussianMixture.html#sklearn.mixture.GaussianMixture](http://scikit-learn.org/stable/modules/generated/sklearn.mixture.GaussianMixture.html#sklearn.mixture.GaussianMixture).
On pourra donc utiliser le code suivant pour calculer les ellipses de meilleure approximation pour les 10 classes :
```
def best_ellipses(points, labels):
# computing best fiiting ellipse for a set of points with asscoiated labels
gaussians = []
for i in range(10):
gaussians.append(GaussianMixture(n_components=1, covariance_type='full',init_params='random').fit(points[labels==i, :]))
return gaussians
```
3. **Calcul du « Neighborhood Hit » (NH)** [[PNML08]](#dblp-journals-tvcg-paulovichnml08).
Pour chaque point, la métrique NH consiste à calculer, pour les k plus proches voisins (`k-nn`) de ce point, le taux de voisins qui sont de la même classe que le point considéré. La métrique NH est ensuite moyennée sur l’ensemble de la base.
Le code suivant permet de calculer la métrique NH, en utilisant la classe `NearestNeighbors` du module `sklearn.neighbors` :
```
def neighboring_hit(points, labels):
k = 6
nbrs = NearestNeighbors(n_neighbors=k+1, algorithm='ball_tree').fit(points)
distances, indices = nbrs.kneighbors(points)
txs = 0.0
txsc = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
nppts = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
for i in range(len(points)):
tx = 0.0
for j in range(1,k+1):
if (labels[indices[i,j]]== labels[i]):
tx += 1
tx /= k
txsc[labels[i]] += tx
nppts[labels[i]] += 1
txs += tx
for i in range(10):
txsc[i] /= nppts[i]
return txs / len(points)
```
## Question :
En quoi les trois métriques ci-dessus sont-elles liées au problème de la séparabilité des classes ? Qu’est-ce qui les distingue ?
**Compléter le script pour calculer les différentes métriques.**
Vous pouvez ensuite utiliser la fonction `visualization` suivante pour afficher les points ainsi que leur labels, et de visualiser les trois métriques précédentes :
```
# Computing convex hulls, best fitting ellipses & NH
def visualization(points2D, labels, convex_hulls, ellipses ,projname, nh):
points2D_c= []
for i in range(10):
points2D_c.append(points2D[labels==i, :])
# Data Visualization
cmap =cm.tab10
plt.figure(figsize=(3.841, 7.195), dpi=100)
plt.set_cmap(cmap)
plt.subplots_adjust(hspace=0.4 )
plt.subplot(311)
plt.scatter(points2D[:,0], points2D[:,1], c=labels, s=3,edgecolors='none', cmap=cmap, alpha=1.0)
plt.colorbar(ticks=range(10))
plt.title("2D "+projname+" - NH="+str(nh*100.0))
vals = [ i/10.0 for i in range(10)]
sp2 = plt.subplot(312)
for i in range(10):
ch = np.append(convex_hulls[i].vertices,convex_hulls[i].vertices[0])
sp2.plot(points2D_c[i][ch, 0], points2D_c[i][ch, 1], '-',label='$%i$'%i, color=cmap(vals[i]))
plt.colorbar(ticks=range(10))
plt.title(projname+" Convex Hulls")
def plot_results(X, Y_, means, covariances, index, title, color):
splot = plt.subplot(3, 1, 3)
for i, (mean, covar) in enumerate(zip(means, covariances)):
v, w = linalg.eigh(covar)
v = 2. * np.sqrt(2.) * np.sqrt(v)
u = w[0] / linalg.norm(w[0])
# as the DP will not use every component it has access to
# unless it needs it, we shouldn't plot the redundant
# components.
if not np.any(Y_ == i):
continue
plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], .8, color=color, alpha = 0.2)
# Plot an ellipse to show the Gaussian component
angle = np.arctan(u[1] / u[0])
angle = 180. * angle / np.pi # convert to degrees
ell = mpl.patches.Ellipse(mean, v[0], v[1], 180. + angle, color=color)
ell.set_clip_box(splot.bbox)
ell.set_alpha(0.6)
splot.add_artist(ell)
plt.title(title)
plt.subplot(313)
for i in range(10):
plot_results(points2D[labels==i, :], ellipses[i].predict(points2D[labels==i, :]), ellipses[i].means_, ellipses[i].covariances_, 0,projname+" fitting ellipses", cmap(vals[i]))
plt.savefig(projname+".png", dpi=100)
plt.show()
# Visualization
```
- Comparer la méthode t-SNE à une Analyse en Composantes Principales (ACP) [[Hot33]](#hotelling1933analysis). On pourra utiliser la classe `PCA` du module `sklearn.decomposition` [http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html](http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html).
- Analyser la distribution des points et des classes : que peut-on en conclure ?
## Exercice 5 : Séparabilité des classes et représentations internes des réseaux de neurones
On va maintenant s’intéresser à visualisation de l’effet de « manifold untangling » permis par les réseaux de neurones.
**Créer un script dont l’objectif va être d’utiliser la méthode t-SNE de l’exercice 2 pour projeter les couches cachés des réseaux de neurones dans un espace de dimension 2, ce qui permettra de visualiser la distribution des représentations internes et des labels.**
- Commencer par charger le Perceptron entraîné avec Keras dans la partie précédente, en utilisant la méthode loadModel(savename) suivante:
```
from keras.models import model_from_yaml
def loadModel(savename):
with open(savename+".yaml", "r") as yaml_file:
model = model_from_yaml(yaml_file.read())
print("Yaml Model ",savename,".yaml loaded ")
model.load_weights(savename+".h5")
print("Weights ",savename,".h5 loaded ")
return model
```
- On pourra vérifier l’architecture du modèle chargé avec la méthode `summary()`.
- On pourra également évaluer les performances du modèle chargé sur la base de test de MNIST pour vérifier son comportement. **N.B :**: il faudra avoir compilé le modèle au préalable.
```
# Chargement du modèle
from keras.utils import np_utils
from keras.optimizers import SGD
```
**On veut maintenant extraire la couche cachée (donc un vecteur de dimension 100) pour chacune des images de la base de test.**
- Pour cela, on va utiliser la méthode `model.pop()` (permettant de supprimer la couche au sommet du modèle) deux fois (on supprime la couche d’activation softmax et la couche complètement connectée). Ensuite on peut appliquer la méthode `model.predict(X_test)` sur l’ensemble des données de test.
- Finalement, on va utiliser la méthode t-SNE mise en place à l’exercice 2 pour visualiser les représentations internes des données.
**En plus du Perceptron précédent, on pourra visualiser les représentations internes apprises par un réseau convolutif de type LeNet précédent.**
**Conclure sur la capacité des réseaux de neurones à résoudre le problème du Manifold Untangling.**
```
# Extraction des représentations latentes et calcul TSNE
```
<a id='hotelling1933analysis'></a>
\[Hot33\] H. Hotelling. *Analysis of a Complex of Statistical Variables Into Principal Components*. Warwick & York, 1933. URL: [https://books.google.fr/books?id=qJfXAAAAMAAJ](https://books.google.fr/books?id=qJfXAAAAMAAJ).
<a id='dblp-journals-tvcg-paulovichnml08'></a>
\[PNML08\] Fernando Vieira Paulovich, Luis Gu
stavo Nonato, Rosane Minghim, and Haim Levkowitz. Least square projection: A fast high-precision multidimensional projection technique and its application to document mapping. *IEEE Trans. Vis. Comput. Graph.*, 14(3):564–575, 2008.
<a id='tsne08'></a>
\[vdMH08\] Laurens van der Maaten and Geoffrey E. Hinton. Visualizing high-dimensional data using t-sne. *Journal of Machine Learning Research*, 9:2579–2605, 2008.
|
github_jupyter
|
from keras.datasets import mnist
# the data, shuffled and split between train and test sets
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
print(X_train.shape[0], 'train samples')
print(X_test.shape[0], 'test samples')
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.figure(figsize=(7.195, 3.841), dpi=100)
for i in range(200):
plt.subplot(10,20,i+1)
plt.imshow(X_train[i,:].reshape([28,28]), cmap='gray')
plt.axis('off')
plt.show()
print(X_train.shape)
print(X_test.shape)
# nb de parametres = 784 * 10 + 10
print("Nombre de paramètres = ", 784 * 10 + 10)
from keras.models import Sequential
model = Sequential()
from keras.layers import Dense, Activation
model.add(Dense(10, input_dim=784, name='fc1'))
model.add(Activation('softmax'))
model.summary()
from keras.utils import np_utils
K=10
# convert class vectors to binary class matrices
Y_train = np_utils.to_categorical(y_train, K)
Y_test = np_utils.to_categorical(y_test, K)
from keras.optimizers import SGD
learning_rate = 0.5
sgd = SGD(learning_rate)
model.compile(loss='categorical_crossentropy',optimizer=sgd,metrics=['accuracy'])
batch_size = 100
nb_epoch = 10
model.fit(X_train, Y_train,batch_size=batch_size, epochs=nb_epoch,verbose=1)
scores = model.evaluate(X_test, Y_test, verbose=0)
print("%s: %.2f%%" % (model.metrics_names[0], scores[0]*100))
print("%s: %.2f%%" % (model.metrics_names[1], scores[1]*100))
model = Sequential()
model.add(Dense(100, input_dim=784, name='fc1'))
model.add(Activation('sigmoid'))
from keras.models import model_from_yaml
def saveModel(model, savename):
# serialize model to YAML
model_yaml = model.to_yaml()
with open(savename+".yaml", "w") as yaml_file:
yaml_file.write(model_yaml)
print("Yaml Model ",savename,".yaml saved to disk")
# serialize weights to HDF5
model.save_weights(savename+".h5")
print("Weights ",savename,".h5 saved to disk")
X_train = X_train.reshape(X_train.shape[0], 28, 28, 1)
X_test = X_test.reshape(X_test.shape[0], 28, 28, 1)
input_shape = (28, 28, 1)
from keras.models import Sequential
from keras.layers import Dense, Flatten
from keras.layers import Conv2D, MaxPooling2D
Conv2D(32,kernel_size=(5, 5),activation='relu',input_shape=(28, 28, 1),padding='valid')
pool = MaxPooling2D(pool_size=(2, 2))
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
from scipy.spatial import ConvexHull
from sklearn.mixture import GaussianMixture
from scipy import linalg
from sklearn.neighbors import NearestNeighbors
from sklearn.manifold import TSNE
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
print(X_train.shape[0], 'train samples')
print(X_test.shape[0], 'test samples')
# Calcul TSNE
X_embedded = TSNE(n_components=2, perplexity=30, init='pca', verbose=2).fit_transform(X_train)
def convexHulls(points, labels):
# computing convex hulls for a set of points with asscoiated labels
convex_hulls = []
for i in range(10):
convex_hulls.append(ConvexHull(points[labels==i,:]))
return convex_hulls
def best_ellipses(points, labels):
# computing best fiiting ellipse for a set of points with asscoiated labels
gaussians = []
for i in range(10):
gaussians.append(GaussianMixture(n_components=1, covariance_type='full',init_params='random').fit(points[labels==i, :]))
return gaussians
def neighboring_hit(points, labels):
k = 6
nbrs = NearestNeighbors(n_neighbors=k+1, algorithm='ball_tree').fit(points)
distances, indices = nbrs.kneighbors(points)
txs = 0.0
txsc = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
nppts = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
for i in range(len(points)):
tx = 0.0
for j in range(1,k+1):
if (labels[indices[i,j]]== labels[i]):
tx += 1
tx /= k
txsc[labels[i]] += tx
nppts[labels[i]] += 1
txs += tx
for i in range(10):
txsc[i] /= nppts[i]
return txs / len(points)
# Computing convex hulls, best fitting ellipses & NH
def visualization(points2D, labels, convex_hulls, ellipses ,projname, nh):
points2D_c= []
for i in range(10):
points2D_c.append(points2D[labels==i, :])
# Data Visualization
cmap =cm.tab10
plt.figure(figsize=(3.841, 7.195), dpi=100)
plt.set_cmap(cmap)
plt.subplots_adjust(hspace=0.4 )
plt.subplot(311)
plt.scatter(points2D[:,0], points2D[:,1], c=labels, s=3,edgecolors='none', cmap=cmap, alpha=1.0)
plt.colorbar(ticks=range(10))
plt.title("2D "+projname+" - NH="+str(nh*100.0))
vals = [ i/10.0 for i in range(10)]
sp2 = plt.subplot(312)
for i in range(10):
ch = np.append(convex_hulls[i].vertices,convex_hulls[i].vertices[0])
sp2.plot(points2D_c[i][ch, 0], points2D_c[i][ch, 1], '-',label='$%i$'%i, color=cmap(vals[i]))
plt.colorbar(ticks=range(10))
plt.title(projname+" Convex Hulls")
def plot_results(X, Y_, means, covariances, index, title, color):
splot = plt.subplot(3, 1, 3)
for i, (mean, covar) in enumerate(zip(means, covariances)):
v, w = linalg.eigh(covar)
v = 2. * np.sqrt(2.) * np.sqrt(v)
u = w[0] / linalg.norm(w[0])
# as the DP will not use every component it has access to
# unless it needs it, we shouldn't plot the redundant
# components.
if not np.any(Y_ == i):
continue
plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], .8, color=color, alpha = 0.2)
# Plot an ellipse to show the Gaussian component
angle = np.arctan(u[1] / u[0])
angle = 180. * angle / np.pi # convert to degrees
ell = mpl.patches.Ellipse(mean, v[0], v[1], 180. + angle, color=color)
ell.set_clip_box(splot.bbox)
ell.set_alpha(0.6)
splot.add_artist(ell)
plt.title(title)
plt.subplot(313)
for i in range(10):
plot_results(points2D[labels==i, :], ellipses[i].predict(points2D[labels==i, :]), ellipses[i].means_, ellipses[i].covariances_, 0,projname+" fitting ellipses", cmap(vals[i]))
plt.savefig(projname+".png", dpi=100)
plt.show()
# Visualization
from keras.models import model_from_yaml
def loadModel(savename):
with open(savename+".yaml", "r") as yaml_file:
model = model_from_yaml(yaml_file.read())
print("Yaml Model ",savename,".yaml loaded ")
model.load_weights(savename+".h5")
print("Weights ",savename,".h5 loaded ")
return model
# Chargement du modèle
from keras.utils import np_utils
from keras.optimizers import SGD
# Extraction des représentations latentes et calcul TSNE
| 0.74055 | 0.977883 |
```
import pandas as pd
import scipy
import numpy as np
import scipy.sparse as sp
import scipy.io as spio
from scipy.stats import pearsonr
import operator
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import matplotlib.colors as colors
import matplotlib as mpl
from matplotlib.text import TextPath
from matplotlib.patches import PathPatch, Rectangle
from matplotlib.font_manager import FontProperties
from matplotlib import gridspec
from matplotlib.ticker import FormatStrFormatter
from sklearn.metrics import roc_auc_score
import seaborn as sns
import matplotlib.collections as collections
import isolearn.io as isoio
from analyze_aparent_designed_mpra_helpers import *
```
<h2>Load collapsed designed MPRA data</h2>
```
#Load designed MPRA data (Collapsed over experiment replicates)
seq_dict = isoio.load('../data/prepared_data/apa_array_data/apa_array_data_master_seq')
print("n = " + str(len(seq_dict['array_df'])))
print('Avg read count (avg over barcodes) = ' + str(np.mean(seq_dict['array_df'].query("n_barcodes >= 2")['mean_total_count'])))
print('Pooled read count (pooled over barcodes) = ' + str(np.mean(seq_dict['array_df'].query("n_barcodes >= 2")['pooled_total_count'])))
#Load variant dataframe
variant_dict = isoio.load('../data/prepared_data/apa_variant_data/apa_variant_data_master_seq')
print("n (variants) = " + str(len(variant_dict['variant_df'])))
#Load predictions
model_name = 'aparent_theano_legacy_30_31_34_pasaligned'
pred_dict = isoio.load('predictions/apa_array_data_legacy/' + model_name + '_predictions_master_seq')
#Join mpra dataframes with prediction table and calculate cut probabilities
seq_df, variant_df = append_predictions(seq_dict['array_df'], seq_dict['pooled_cuts'], variant_dict['variant_df'], variant_dict['pooled_cuts_var'], variant_dict['pooled_cuts_ref'], pred_dict['array_df'], pred_dict['cut_prob'])
```
<h2>Rare Functional Variant Summary analysis</h2>
```
variant_df_filtered = variant_df.query("n_barcodes_var >= 5 and n_barcodes_ref >= 5 and mean_total_count_var >= 200 and mean_total_count_ref >= 200")
#Filter on human variants
included_experiments = ['acmg_apadb', 'acmg_polyadb', 'sensitive_genes', 'clinvar_wt', 'human_variant']
filter_query = ""
for exp_index, included_experiment in enumerate(included_experiments) :
filter_query += "experiment == '" + str(included_experiment) + "'"
if exp_index < len(included_experiments) - 1 :
filter_query += " or "
human_variant_df = variant_df.query(filter_query).copy()
human_variant_df_filtered = variant_df_filtered.query(filter_query).copy()
human_variant_df['delta_logodds_pred'] = human_variant_df['mean_delta_logodds_pred']
human_variant_df_filtered['delta_logodds_pred'] = human_variant_df_filtered['mean_delta_logodds_pred']
var_df = human_variant_df_filtered.query("variant == 'snv' and snv_pos != -1").copy()
mer6_weights_doubledope = np.load('apa_6mer_weights/apa_6mer_v_general3_antimisprime_orig_pasaligned_margin_doubledope_weights.npy')[1:]
mer6_weights_simple = np.load('apa_6mer_weights/apa_6mer_v_general3_antimisprime_orig_pasaligned_margin_simple_weights.npy')[1:]
mer6_weights_tomm5 = np.load('apa_6mer_weights/apa_6mer_v_general3_antimisprime_orig_pasaligned_margin_tomm5_weights.npy')[1:]
mer6_weights_use = (mer6_weights_tomm5[:4096] + mer6_weights_simple[:4096]) / 2.
mer6_weights_pas = mer6_weights_doubledope[4096:2*4096]
mer6_weights_dse = (mer6_weights_tomm5[2*4096:] + mer6_weights_simple[2*4096:]) / 2.
var_df = append_6mer_delta_logodds_scores(var_df, mer6_weights_use, mer6_weights_pas, mer6_weights_dse)
var_df['delta_logodds_pred'] = var_df['mean_delta_logodds_pred']
save_figs = False
p_thresh = 0.00001
print('n variants = ' + str(len(var_df)))
#Filter on significant variants
discrep_index = (var_df['delta_p_val'] < p_thresh)
print('n variants (stat. signi.) = ' + str(len(var_df.loc[discrep_index])))
#Filter on > 0.1 predicted log fold change
discrep_index = discrep_index & (np.abs(var_df['delta_6mer_score']) > 0.11)
discrep_index = discrep_index & (np.abs(var_df['delta_logodds_pred']) > 0.115)
print('n variants (stat. signi. & strong preds) = ' + str(len(var_df.loc[discrep_index])))
#Calculate the number of correctly predicted variants (using APARENT)
discrep_index_correct = discrep_index & (np.sign(var_df['delta_logodds_true']) == np.sign(var_df['delta_logodds_pred']))
print('n variants (stat. signi. & strong preds & correct APARENT) = ' + str(len(var_df.loc[discrep_index_correct])))
#Filter on sign of APARENT prediction not equal to sign of hexamer predictions, APARENT correct
discrep_index = discrep_index & ((np.sign(var_df['delta_logodds_true']) != np.sign(var_df['delta_6mer_score'])) & (np.sign(var_df['delta_logodds_true']) == np.sign(var_df['delta_logodds_pred'])))
print('n variants (stat. signi. & strong preds & disagree) = ' + str(len(var_df.loc[discrep_index])))
#Plot position scatter of variants
discrep_df = var_df.iloc[np.nonzero(discrep_index)[0]].copy()
fig_name = None
if save_figs :
fig_name = 'rare_variants_neural_net_agrees_with_obs'
plot_position_delta_scatter(discrep_df, min_pred_filter=0.0, figsize=(8, 5), fig_name=fig_name, fig_dpi=150, annotate=None)
discrep_index = (var_df['delta_p_val'] < p_thresh)
discrep_index = discrep_index & (np.abs(var_df['delta_6mer_score']) > 0.11)
discrep_index = discrep_index & (np.abs(var_df['delta_logodds_pred']) > 0.115)
#Filter on sign of APARENT prediction not equal to sign of hexamer predictions, hexamer model correct
discrep_index = discrep_index & ((np.sign(var_df['delta_logodds_true']) == np.sign(var_df['delta_6mer_score'])) & (np.sign(var_df['delta_logodds_true']) != np.sign(var_df['delta_logodds_pred'])))
print('n variants (stat. signi. & strong preds & disagree) = ' + str(len(var_df.loc[discrep_index])))
discrep_df = var_df.iloc[np.nonzero(discrep_index)[0]].copy()
#Plot position scatter of variants
fig_name = None
if save_figs :
fig_name = 'rare_variants_6mer_model_agrees_with_obs'
plot_position_delta_scatter(discrep_df, min_pred_filter=0.0, figsize=(8, 5), fig_name=fig_name, fig_dpi=150, annotate=None)
```
|
github_jupyter
|
import pandas as pd
import scipy
import numpy as np
import scipy.sparse as sp
import scipy.io as spio
from scipy.stats import pearsonr
import operator
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import matplotlib.colors as colors
import matplotlib as mpl
from matplotlib.text import TextPath
from matplotlib.patches import PathPatch, Rectangle
from matplotlib.font_manager import FontProperties
from matplotlib import gridspec
from matplotlib.ticker import FormatStrFormatter
from sklearn.metrics import roc_auc_score
import seaborn as sns
import matplotlib.collections as collections
import isolearn.io as isoio
from analyze_aparent_designed_mpra_helpers import *
#Load designed MPRA data (Collapsed over experiment replicates)
seq_dict = isoio.load('../data/prepared_data/apa_array_data/apa_array_data_master_seq')
print("n = " + str(len(seq_dict['array_df'])))
print('Avg read count (avg over barcodes) = ' + str(np.mean(seq_dict['array_df'].query("n_barcodes >= 2")['mean_total_count'])))
print('Pooled read count (pooled over barcodes) = ' + str(np.mean(seq_dict['array_df'].query("n_barcodes >= 2")['pooled_total_count'])))
#Load variant dataframe
variant_dict = isoio.load('../data/prepared_data/apa_variant_data/apa_variant_data_master_seq')
print("n (variants) = " + str(len(variant_dict['variant_df'])))
#Load predictions
model_name = 'aparent_theano_legacy_30_31_34_pasaligned'
pred_dict = isoio.load('predictions/apa_array_data_legacy/' + model_name + '_predictions_master_seq')
#Join mpra dataframes with prediction table and calculate cut probabilities
seq_df, variant_df = append_predictions(seq_dict['array_df'], seq_dict['pooled_cuts'], variant_dict['variant_df'], variant_dict['pooled_cuts_var'], variant_dict['pooled_cuts_ref'], pred_dict['array_df'], pred_dict['cut_prob'])
variant_df_filtered = variant_df.query("n_barcodes_var >= 5 and n_barcodes_ref >= 5 and mean_total_count_var >= 200 and mean_total_count_ref >= 200")
#Filter on human variants
included_experiments = ['acmg_apadb', 'acmg_polyadb', 'sensitive_genes', 'clinvar_wt', 'human_variant']
filter_query = ""
for exp_index, included_experiment in enumerate(included_experiments) :
filter_query += "experiment == '" + str(included_experiment) + "'"
if exp_index < len(included_experiments) - 1 :
filter_query += " or "
human_variant_df = variant_df.query(filter_query).copy()
human_variant_df_filtered = variant_df_filtered.query(filter_query).copy()
human_variant_df['delta_logodds_pred'] = human_variant_df['mean_delta_logodds_pred']
human_variant_df_filtered['delta_logodds_pred'] = human_variant_df_filtered['mean_delta_logodds_pred']
var_df = human_variant_df_filtered.query("variant == 'snv' and snv_pos != -1").copy()
mer6_weights_doubledope = np.load('apa_6mer_weights/apa_6mer_v_general3_antimisprime_orig_pasaligned_margin_doubledope_weights.npy')[1:]
mer6_weights_simple = np.load('apa_6mer_weights/apa_6mer_v_general3_antimisprime_orig_pasaligned_margin_simple_weights.npy')[1:]
mer6_weights_tomm5 = np.load('apa_6mer_weights/apa_6mer_v_general3_antimisprime_orig_pasaligned_margin_tomm5_weights.npy')[1:]
mer6_weights_use = (mer6_weights_tomm5[:4096] + mer6_weights_simple[:4096]) / 2.
mer6_weights_pas = mer6_weights_doubledope[4096:2*4096]
mer6_weights_dse = (mer6_weights_tomm5[2*4096:] + mer6_weights_simple[2*4096:]) / 2.
var_df = append_6mer_delta_logodds_scores(var_df, mer6_weights_use, mer6_weights_pas, mer6_weights_dse)
var_df['delta_logodds_pred'] = var_df['mean_delta_logodds_pred']
save_figs = False
p_thresh = 0.00001
print('n variants = ' + str(len(var_df)))
#Filter on significant variants
discrep_index = (var_df['delta_p_val'] < p_thresh)
print('n variants (stat. signi.) = ' + str(len(var_df.loc[discrep_index])))
#Filter on > 0.1 predicted log fold change
discrep_index = discrep_index & (np.abs(var_df['delta_6mer_score']) > 0.11)
discrep_index = discrep_index & (np.abs(var_df['delta_logodds_pred']) > 0.115)
print('n variants (stat. signi. & strong preds) = ' + str(len(var_df.loc[discrep_index])))
#Calculate the number of correctly predicted variants (using APARENT)
discrep_index_correct = discrep_index & (np.sign(var_df['delta_logodds_true']) == np.sign(var_df['delta_logodds_pred']))
print('n variants (stat. signi. & strong preds & correct APARENT) = ' + str(len(var_df.loc[discrep_index_correct])))
#Filter on sign of APARENT prediction not equal to sign of hexamer predictions, APARENT correct
discrep_index = discrep_index & ((np.sign(var_df['delta_logodds_true']) != np.sign(var_df['delta_6mer_score'])) & (np.sign(var_df['delta_logodds_true']) == np.sign(var_df['delta_logodds_pred'])))
print('n variants (stat. signi. & strong preds & disagree) = ' + str(len(var_df.loc[discrep_index])))
#Plot position scatter of variants
discrep_df = var_df.iloc[np.nonzero(discrep_index)[0]].copy()
fig_name = None
if save_figs :
fig_name = 'rare_variants_neural_net_agrees_with_obs'
plot_position_delta_scatter(discrep_df, min_pred_filter=0.0, figsize=(8, 5), fig_name=fig_name, fig_dpi=150, annotate=None)
discrep_index = (var_df['delta_p_val'] < p_thresh)
discrep_index = discrep_index & (np.abs(var_df['delta_6mer_score']) > 0.11)
discrep_index = discrep_index & (np.abs(var_df['delta_logodds_pred']) > 0.115)
#Filter on sign of APARENT prediction not equal to sign of hexamer predictions, hexamer model correct
discrep_index = discrep_index & ((np.sign(var_df['delta_logodds_true']) == np.sign(var_df['delta_6mer_score'])) & (np.sign(var_df['delta_logodds_true']) != np.sign(var_df['delta_logodds_pred'])))
print('n variants (stat. signi. & strong preds & disagree) = ' + str(len(var_df.loc[discrep_index])))
discrep_df = var_df.iloc[np.nonzero(discrep_index)[0]].copy()
#Plot position scatter of variants
fig_name = None
if save_figs :
fig_name = 'rare_variants_6mer_model_agrees_with_obs'
plot_position_delta_scatter(discrep_df, min_pred_filter=0.0, figsize=(8, 5), fig_name=fig_name, fig_dpi=150, annotate=None)
| 0.467332 | 0.674613 |
<a href="https://colab.research.google.com/github/sokrypton/ColabFold/blob/main/RoseTTAFold.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# RoseTTAFold
-----------------
- <b><font color='green'>21Aug2021: MMseqs2 API has finished upgrade, all should be ready to go! Report any errors.</font></b>
-----------------
**Limitations**
- This notebook disables a few aspects (templates, pytosetta) of the full rosettafold pipeline.
- For best resuls use the [full pipeline](https://github.com/RosettaCommons/RoseTTAFold) or [Robetta webserver](https://robetta.bakerlab.org/)!
- For a typical Google-Colab session, with a `16G-GPU`, the max total length is **700 residues**. Sometimes a `12G-GPU` is assigned, in which case the max length is lower.
For other related notebooks see [ColabFold](https://github.com/sokrypton/ColabFold)
```
#@title ##Install and import libraries
#@markdown This step can take up to ~2 mins
import os
import sys
from IPython.utils import io
from google.colab import files
if not os.path.isdir("RoseTTAFold"):
with io.capture_output() as captured:
# extra functionality
%shell wget -qnc https://raw.githubusercontent.com/sokrypton/ColabFold/main/beta/colabfold.py
# download model
%shell git clone https://github.com/RosettaCommons/RoseTTAFold.git
%shell wget -qnc https://raw.githubusercontent.com/sokrypton/ColabFold/main/beta/RoseTTAFold__network__Refine_module.patch
%shell patch -u RoseTTAFold/network/Refine_module.py -i RoseTTAFold__network__Refine_module.patch
# download model params
%shell wget -qnc https://files.ipd.uw.edu/pub/RoseTTAFold/weights.tar.gz
%shell tar -xf weights.tar.gz
%shell rm weights.tar.gz
# download scwrl4 (for adding sidechains)
# http://dunbrack.fccc.edu/SCWRL3.php
# Thanks Roland Dunbrack!
%shell wget -qnc https://files.ipd.uw.edu/krypton/TrRosetta/scwrl4.zip
%shell unzip -qqo scwrl4.zip
# install libraries
%shell pip install -q dgl-cu111
%shell pip install -q torch-scatter -f https://pytorch-geometric.com/whl/torch-1.9.0+cu111.html
%shell pip install -q torch-sparse -f https://pytorch-geometric.com/whl/torch-1.9.0+cu111.html
%shell pip install -q torch-geometric
%shell pip install -q py3Dmol
with io.capture_output() as captured:
sys.path.append('/content/RoseTTAFold/network')
import predict_e2e
from parsers import parse_a3m
import colabfold as cf
import py3Dmol
import subprocess
import numpy as np
import matplotlib.pyplot as plt
def get_bfactor(pdb_filename):
bfac = []
for line in open(pdb_filename,"r"):
if line[:4] == "ATOM":
bfac.append(float(line[60:66]))
return np.array(bfac)
def set_bfactor(pdb_filename, bfac):
I = open(pdb_filename,"r").readlines()
O = open(pdb_filename,"w")
for line in I:
if line[0:6] == "ATOM ":
seq_id = int(line[22:26].strip()) - 1
O.write(f"{line[:60]}{bfac[seq_id]:6.2f}{line[66:]}")
O.close()
def do_scwrl(inputs, outputs, exe="./scwrl4/Scwrl4"):
subprocess.run([exe,"-i",inputs,"-o",outputs,"-h"],
stdout=subprocess.DEVNULL, stderr=subprocess.DEVNULL)
bfact = get_bfactor(inputs)
set_bfactor(outputs, bfact)
return bfact
#@markdown ##Input Sequence
sequence = "PIAQIHILEGRSDEQKETLIREVSEAISRSLDAPLTSVRVIITEMAKGHFGIGGELASK" #@param {type:"string"}
sequence = sequence.translate(str.maketrans('', '', ' \n\t')).upper()
jobname = "test" #@param {type:"string"}
jobname = jobname+"_"+cf.get_hash(sequence)[:5]
#@title Search against genetic databases
#@markdown ---
msa_method = "mmseqs2" #@param ["mmseqs2","single_sequence","custom_a3m"]
#@markdown - `mmseqs2` - FAST method from [ColabFold](https://github.com/sokrypton/ColabFold)
#@markdown - `single_sequence` - use single sequence input (not recommended, unless a *denovo* design and you dont expect to find any homologous sequences)
#@markdown - `custom_a3m` Upload custom MSA (a3m format)
# tmp directory
prefix = cf.get_hash(sequence)
os.makedirs('tmp', exist_ok=True)
prefix = os.path.join('tmp',prefix)
os.makedirs(jobname, exist_ok=True)
if msa_method == "mmseqs2":
a3m_lines = cf.run_mmseqs2(sequence, prefix, filter=True)
with open(f"{jobname}/msa.a3m","w") as a3m:
a3m.write(a3m_lines)
elif msa_method == "single_sequence":
with open(f"{jobname}/msa.a3m","w") as a3m:
a3m.write(f">{jobname}\n{sequence}\n")
elif msa_method == "custom_a3m":
print("upload custom a3m")
msa_dict = files.upload()
lines = msa_dict[list(msa_dict.keys())[0]].decode().splitlines()
a3m_lines = []
for line in lines:
line = line.replace("\x00","")
if len(line) > 0 and not line.startswith('#'):
a3m_lines.append(line)
with open(f"{jobname}/msa.a3m","w") as a3m:
a3m.write("\n".join(a3m_lines))
msa_all = parse_a3m(f"{jobname}/msa.a3m")
msa_arr = np.unique(msa_all,axis=0)
total_msa_size = len(msa_arr)
if msa_method == "mmseqs2":
print(f'\n{total_msa_size} Sequences Found in Total (after filtering)\n')
else:
print(f'\n{total_msa_size} Sequences Found in Total\n')
if total_msa_size > 1:
plt.figure(figsize=(8,5),dpi=100)
plt.title("Sequence coverage")
seqid = (msa_all[0] == msa_arr).mean(-1)
seqid_sort = seqid.argsort()
non_gaps = (msa_arr != 20).astype(float)
non_gaps[non_gaps == 0] = np.nan
plt.imshow(non_gaps[seqid_sort]*seqid[seqid_sort,None],
interpolation='nearest', aspect='auto',
cmap="rainbow_r", vmin=0, vmax=1, origin='lower',
extent=(0, msa_arr.shape[1], 0, msa_arr.shape[0]))
plt.plot((msa_arr != 20).sum(0), color='black')
plt.xlim(0,msa_arr.shape[1])
plt.ylim(0,msa_arr.shape[0])
plt.colorbar(label="Sequence identity to query",)
plt.xlabel("Positions")
plt.ylabel("Sequences")
plt.savefig(f"{jobname}/msa_coverage.png", bbox_inches = 'tight')
plt.show()
#@title ## Run RoseTTAFold for mainchain and Scrwl4 for sidechain prediction
# load model
if "rosettafold" not in dir():
rosettafold = predict_e2e.Predictor(model_dir="weights")
# make prediction using model
rosettafold.predict(f"{jobname}/msa.a3m",f"{jobname}/pred")
# pack sidechains using Scwrl4
plddt = do_scwrl(f"{jobname}/pred.pdb",f"{jobname}/pred.scwrl.pdb")
print(f"Predicted LDDT: {plddt.mean()}")
plt.figure(figsize=(8,5),dpi=100)
plt.plot(plddt)
plt.xlabel("positions")
plt.ylabel("plddt")
plt.ylim(0,1)
plt.savefig(f"{jobname}/plddt.png", bbox_inches = 'tight')
plt.show()
#@title Display 3D structure {run: "auto"}
color = "lDDT" #@param ["chain", "lDDT", "rainbow"]
show_sidechains = False #@param {type:"boolean"}
show_mainchains = False #@param {type:"boolean"}
cf.show_pdb(f"{jobname}/pred.scwrl.pdb", show_sidechains, show_mainchains, color, chains=1, vmin=0.5, vmax=0.9).show()
if color == "lDDT": cf.plot_plddt_legend().show()
#@title Download prediction
#@markdown Once this cell has been executed, a zip-archive with
#@markdown the obtained prediction will be automatically downloaded
#@markdown to your computer.
# add settings file
settings_path = f"{jobname}/settings.txt"
with open(settings_path, "w") as text_file:
text_file.write(f"method=RoseTTAFold\n")
text_file.write(f"sequence={sequence}\n")
text_file.write(f"msa_method={msa_method}\n")
text_file.write(f"use_templates=False\n")
# --- Download the predictions ---
!zip -q -r {jobname}.zip {jobname}
files.download(f'{jobname}.zip')
```
|
github_jupyter
|
#@title ##Install and import libraries
#@markdown This step can take up to ~2 mins
import os
import sys
from IPython.utils import io
from google.colab import files
if not os.path.isdir("RoseTTAFold"):
with io.capture_output() as captured:
# extra functionality
%shell wget -qnc https://raw.githubusercontent.com/sokrypton/ColabFold/main/beta/colabfold.py
# download model
%shell git clone https://github.com/RosettaCommons/RoseTTAFold.git
%shell wget -qnc https://raw.githubusercontent.com/sokrypton/ColabFold/main/beta/RoseTTAFold__network__Refine_module.patch
%shell patch -u RoseTTAFold/network/Refine_module.py -i RoseTTAFold__network__Refine_module.patch
# download model params
%shell wget -qnc https://files.ipd.uw.edu/pub/RoseTTAFold/weights.tar.gz
%shell tar -xf weights.tar.gz
%shell rm weights.tar.gz
# download scwrl4 (for adding sidechains)
# http://dunbrack.fccc.edu/SCWRL3.php
# Thanks Roland Dunbrack!
%shell wget -qnc https://files.ipd.uw.edu/krypton/TrRosetta/scwrl4.zip
%shell unzip -qqo scwrl4.zip
# install libraries
%shell pip install -q dgl-cu111
%shell pip install -q torch-scatter -f https://pytorch-geometric.com/whl/torch-1.9.0+cu111.html
%shell pip install -q torch-sparse -f https://pytorch-geometric.com/whl/torch-1.9.0+cu111.html
%shell pip install -q torch-geometric
%shell pip install -q py3Dmol
with io.capture_output() as captured:
sys.path.append('/content/RoseTTAFold/network')
import predict_e2e
from parsers import parse_a3m
import colabfold as cf
import py3Dmol
import subprocess
import numpy as np
import matplotlib.pyplot as plt
def get_bfactor(pdb_filename):
bfac = []
for line in open(pdb_filename,"r"):
if line[:4] == "ATOM":
bfac.append(float(line[60:66]))
return np.array(bfac)
def set_bfactor(pdb_filename, bfac):
I = open(pdb_filename,"r").readlines()
O = open(pdb_filename,"w")
for line in I:
if line[0:6] == "ATOM ":
seq_id = int(line[22:26].strip()) - 1
O.write(f"{line[:60]}{bfac[seq_id]:6.2f}{line[66:]}")
O.close()
def do_scwrl(inputs, outputs, exe="./scwrl4/Scwrl4"):
subprocess.run([exe,"-i",inputs,"-o",outputs,"-h"],
stdout=subprocess.DEVNULL, stderr=subprocess.DEVNULL)
bfact = get_bfactor(inputs)
set_bfactor(outputs, bfact)
return bfact
#@markdown ##Input Sequence
sequence = "PIAQIHILEGRSDEQKETLIREVSEAISRSLDAPLTSVRVIITEMAKGHFGIGGELASK" #@param {type:"string"}
sequence = sequence.translate(str.maketrans('', '', ' \n\t')).upper()
jobname = "test" #@param {type:"string"}
jobname = jobname+"_"+cf.get_hash(sequence)[:5]
#@title Search against genetic databases
#@markdown ---
msa_method = "mmseqs2" #@param ["mmseqs2","single_sequence","custom_a3m"]
#@markdown - `mmseqs2` - FAST method from [ColabFold](https://github.com/sokrypton/ColabFold)
#@markdown - `single_sequence` - use single sequence input (not recommended, unless a *denovo* design and you dont expect to find any homologous sequences)
#@markdown - `custom_a3m` Upload custom MSA (a3m format)
# tmp directory
prefix = cf.get_hash(sequence)
os.makedirs('tmp', exist_ok=True)
prefix = os.path.join('tmp',prefix)
os.makedirs(jobname, exist_ok=True)
if msa_method == "mmseqs2":
a3m_lines = cf.run_mmseqs2(sequence, prefix, filter=True)
with open(f"{jobname}/msa.a3m","w") as a3m:
a3m.write(a3m_lines)
elif msa_method == "single_sequence":
with open(f"{jobname}/msa.a3m","w") as a3m:
a3m.write(f">{jobname}\n{sequence}\n")
elif msa_method == "custom_a3m":
print("upload custom a3m")
msa_dict = files.upload()
lines = msa_dict[list(msa_dict.keys())[0]].decode().splitlines()
a3m_lines = []
for line in lines:
line = line.replace("\x00","")
if len(line) > 0 and not line.startswith('#'):
a3m_lines.append(line)
with open(f"{jobname}/msa.a3m","w") as a3m:
a3m.write("\n".join(a3m_lines))
msa_all = parse_a3m(f"{jobname}/msa.a3m")
msa_arr = np.unique(msa_all,axis=0)
total_msa_size = len(msa_arr)
if msa_method == "mmseqs2":
print(f'\n{total_msa_size} Sequences Found in Total (after filtering)\n')
else:
print(f'\n{total_msa_size} Sequences Found in Total\n')
if total_msa_size > 1:
plt.figure(figsize=(8,5),dpi=100)
plt.title("Sequence coverage")
seqid = (msa_all[0] == msa_arr).mean(-1)
seqid_sort = seqid.argsort()
non_gaps = (msa_arr != 20).astype(float)
non_gaps[non_gaps == 0] = np.nan
plt.imshow(non_gaps[seqid_sort]*seqid[seqid_sort,None],
interpolation='nearest', aspect='auto',
cmap="rainbow_r", vmin=0, vmax=1, origin='lower',
extent=(0, msa_arr.shape[1], 0, msa_arr.shape[0]))
plt.plot((msa_arr != 20).sum(0), color='black')
plt.xlim(0,msa_arr.shape[1])
plt.ylim(0,msa_arr.shape[0])
plt.colorbar(label="Sequence identity to query",)
plt.xlabel("Positions")
plt.ylabel("Sequences")
plt.savefig(f"{jobname}/msa_coverage.png", bbox_inches = 'tight')
plt.show()
#@title ## Run RoseTTAFold for mainchain and Scrwl4 for sidechain prediction
# load model
if "rosettafold" not in dir():
rosettafold = predict_e2e.Predictor(model_dir="weights")
# make prediction using model
rosettafold.predict(f"{jobname}/msa.a3m",f"{jobname}/pred")
# pack sidechains using Scwrl4
plddt = do_scwrl(f"{jobname}/pred.pdb",f"{jobname}/pred.scwrl.pdb")
print(f"Predicted LDDT: {plddt.mean()}")
plt.figure(figsize=(8,5),dpi=100)
plt.plot(plddt)
plt.xlabel("positions")
plt.ylabel("plddt")
plt.ylim(0,1)
plt.savefig(f"{jobname}/plddt.png", bbox_inches = 'tight')
plt.show()
#@title Display 3D structure {run: "auto"}
color = "lDDT" #@param ["chain", "lDDT", "rainbow"]
show_sidechains = False #@param {type:"boolean"}
show_mainchains = False #@param {type:"boolean"}
cf.show_pdb(f"{jobname}/pred.scwrl.pdb", show_sidechains, show_mainchains, color, chains=1, vmin=0.5, vmax=0.9).show()
if color == "lDDT": cf.plot_plddt_legend().show()
#@title Download prediction
#@markdown Once this cell has been executed, a zip-archive with
#@markdown the obtained prediction will be automatically downloaded
#@markdown to your computer.
# add settings file
settings_path = f"{jobname}/settings.txt"
with open(settings_path, "w") as text_file:
text_file.write(f"method=RoseTTAFold\n")
text_file.write(f"sequence={sequence}\n")
text_file.write(f"msa_method={msa_method}\n")
text_file.write(f"use_templates=False\n")
# --- Download the predictions ---
!zip -q -r {jobname}.zip {jobname}
files.download(f'{jobname}.zip')
| 0.379838 | 0.722417 |
```
%matplotlib inline
import numpy as np
import scipy as sc
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import sympy as sp
import itertools
sns.set();
def extract(it):
r"""
Extract the values from a iterable of iterables.
The function extracts the values from a iterable of iterables (eg. a list of tuples) to a list
of coordinates. For example,
[(1, 10), (2, 20), (3, 30), (4, 40)] -> [[1, 2, 3, 4], [10, 20, 30, 40]]
If `it` is a list of M tuples each one with N elements, then `extract` returns
a list of N lists each one with M elements.
Parameters
----------
it : iterable
An iterable of iterables.
Returns
------
A list with the lists of first-elements, second-elements and so on.
"""
return list(zip(*it))
```
# Runge-Kutta methods
The Runge-Kutta methods are in fact a family of methods designed to solve an ODE of the form:
$$y' = f(t, y)$$
with initial condition
$$y(t_{0}) = y_{0}$$
In other words, an initial condition problem.
## Two-stage Runge-Kutta methods
The so-called two-stage Runge-Kutta method has equations:
$$y_{k+1} = y_{k} + h\left(1 - \frac{1}{2\lambda}k_{1} + \frac{1}{2\lambda}k_{2}\right)$$
where
$$k_{1} = f(x_{k}, y_{k})$$
and
$$k_{2} = f(x_{k} + \lambda h, y_{k} + \lambda h k_{1})$$
The name "two-stage" comes from the fact that it is actually computed in two stages. First, we have to find $k_{1}$. Then we use that value to compute $k_{2}$.
Depending on the value given to $\lambda$, the method has different names. If $\lambda$ equals $1$, then it is called _improved Euler's method_. If $\lambda$ equals $2/3$, then it is called _Heun's method_.
### Improved Euler's method
By making $\lambda$ equals to $1$ in the general equation of the two-stage Runge-Kutta, we get the improved Euler's method. The equations are the following:
$$y_{k+1} = y_{k} + h\left(\frac{1}{2}k_{1} + \frac{1}{2}k_{2}\right)$$
with
$$k_{1} = f(x_{k}, y_{k})$$
and
$$k_{2} = f(x_{k} + h, y_{k} + hk_{1})$$
### Heun's method
As I said, the Heun's method comes from making $\lambda$ equals to $2/3$ in the general formula of the two-stage Runge-Kutta. The resulting equations are the following:
$$y_{k+1} = y_{k} + h\left(\frac{1}{4}k_{1} + \frac{3}{4}k_{2}\right)$$
where
$$k_{1} = f(x_{k}, y_{k})$$
and
$$k_{2} = f(x_{k} + \frac{2}{3}h, y_{k} + \frac{2}{3}hk_{1})$$
## Four-stage Runge-Kutta methods
### Classical Runge-Kutta method (RK4)
The method often referred as _classical Runge-Kutta method_ or simply _RK4_ is the Runge-Kutta method of 4 stages given by equations below:
$$y_{k+1} = y_{k} + \frac{h}{6}(k_{1} + 2k_{2} + 2k_{3} + k_{4}), n = 0, 1, 2, \dots$$
with
$$k_{1} = f(x_{k}, y_{k})$$
$$k_{2} = f\left(x_{k} + \frac{h}{2}, y_{k} + \frac{h}{2}k_{1}\right)$$
$$k_{3} = f\left(x_{k} + \frac{h}{2}, x_{k} + \frac{h}{2}k_{2}\right)$$
$$k_{4} = f(x_{k} + h, y_{k} + h k_{3})$$
### Variant of the classical Runge-Kutta method
There is a variation of the classical Runge-Kutta method (RK4) method. It is given by the following equations:
$$y_{k+1} = y_{k} + \frac{h}{8}(k_{1} + 3k_{2} + 3k_{3} + k_{4}), n = 0, 1, 2, \dots$$
with
$$k_{1} = f(x_{k}, y_{k})$$
$$k_{2} = f\left(x_{k} + \frac{h}{3}, y_{k} + \frac{h}{3}k_{1}\right)$$
$$k_{3} = f\left(x_{k} + \frac{2h}{3}, x_{k} + \frac{-h}{3}k_{1} + k_{2}\right)$$
$$k_{4} = f(x_{k} + h, y_{k} + hk_{1} - hk_{2} + hk_{3})$$
## General form and more theory
In general, the whole family of Runge-Kutta methods can be written as
$$y_{k+1} = y_{k} + h \sum_{i=1}^{s}b_{i}k_{i}$$
where
$$k_{1} = f(x_{k}, y_{k})$$
$$k_{2} = f(x_{k} + c_{2}h, y_{k} + h(a_{21}k_{1}))$$
$$k_{3} = f(x_{k} + c_{3}h, y_{k} + h(a_{31}k_{1} + a_{32}k_{2}))$$
$$\vdots$$
$$k_{s} = f(x_{k} + c_{s}h, y_{k} + h(a_{s1}k_{1} + a_{s2}k_{2} + \cdots + a_{ss-1}k_{s-1}))$$
A Runge-Kutta method is specified by
$s \doteq$ the number of stages, for $s \geq 1$,
$b_{i} \doteq$ the weights, for $i \in \{1, 2, \cdots, s\}$,
$c_{i} \doteq$ the loadings, for $i \in \{2, 2, \cdots, s\}$,
$a_{ij} \doteq$ the coefficients of $k_{j}$ in equation of $k_{i}$, for $1 \leq j < i \leq s$.
### Butcher tableau
A compact way of summarising these parameters is the Butcher tableau. Its general form is shown below.
|$0$ | | | | | |
|:-------:|---------|---------|---------|-----------|--------|
|$c_{2}$ |$a_{21}$ | | | | |
|$c_{3}$ |$a_{31}$ |$a_{32}$ | | | |
|$\vdots$ |$\vdots$ |$\vdots$ |$\ddots$ | | |
|$c_{s}$ |$a_{s1}$ |$a_{s2}$ |$\cdots$ |$a_{ss-1}$ | |
| |$b_{1}$ |$b_{2}$ |$\cdots$ |$b_{s-1}$ |$b_{s}$ |
### Method's order
A method is said to have order $p$ if the local truncation error is $O(h^{p+1})$. The minimum number of stages, $s$, required for a method to be of order $p$ until order 8 is given by the following table
|$p$ |1 |2 |3 |4 |5 |6 |7 |8 |
|:------:|---|---|---|---|---|---|---|---|
|min $s$ |1 |2 |3 |4 |6 |7 |9 |11 |
### Consistency
The method is said to be consistent if
$$\sum_{j=1}^{i-1}a_{ij} = c_{i}, \text{for } i = 2, \cdots, s$$
In other words, it is consistent if the sum of $a_{ij}$ on the $i$-th row is equal to the respective $c_{i}$.
### Runge-Kutta matrix
The $s$-by-$s$ Runge-Kutta matrix $M_{\mathit{RK}}$ is the lower triangular matrix defined by the coefficients $a_{ij}$ as shown below
$$M_{\mathit{RK}} = \begin{bmatrix}
0 & 0 & \cdots & 0 & 0 \\[0.3em]
a_{21} & 0 & \cdots & 0 & 0 \\[0.3em]
a_{31} & a_{32} & \cdots & 0 & 0 \\[0.3em]
\vdots & \vdots & \ddots & \vdots & \vdots \\[0.3em]
a_{s1} & a_{s2} & \cdots & a_{ss-1} & 0
\end{bmatrix}$$
## Butcher tableau examples
* Euler's method:
$$y_{n+1} = y_{n} + hf(x_{n}, y_{n})$$
|$0$ | |
|:--:|----|
| |$1$ |
* Improved Euler's method:
$$y_{k+1} = y_{k} + h\left(\frac{1}{2}k_{1} + \frac{1}{2}k_{2}\right)$$
$$k_{1} = f(x_{k}, y_{k})$$
$$k_{2} = f(x_{k} + h, y_{k} + hk_{1})$$
|$0$ | | |
|:--:|--------------|--------------|
|$1$ |$1$ | |
| |$\frac{1}{2}$ |$\frac{1}{2}$ |
* Heun's method:
$$y_{k+1} = y_{k} + h\left(\frac{1}{4}k_{1} + \frac{3}{4}k_{2}\right)$$
$$k_{1} = f(x_{k}, y_{k})$$
$$k_{2} = f(x_{k} + \frac{2}{3}h, y_{k} + \frac{2}{3}hk_{1})$$
|$0$ | | |
|:------------:|--------------|--------------|
|$\frac{2}{3}$ |$\frac{2}{3}$ | |
| |$\frac{1}{4}$ |$\frac{3}{4}$ |
* Classical Runge-Kutta (RK4):
$$y_{k+1} = y_{k} + \frac{h}{6}(k_{1} + 2k_{2} + 2k_{3} + k_{4}), n = 0, 1, 2, \dots$$
$$k_{1} = f(x_{k}, y_{k})$$
$$k_{2} = f\left(x_{k} + \frac{h}{2}, y_{k} + \frac{h}{2}k_{1}\right)$$
$$k_{3} = f\left(x_{k} + \frac{h}{2}, y_{k} + \frac{h}{2}k_{2}\right)$$
$$k_{4} = f(x_{k} + h, y_{k} + h k_{3})$$
|$0$ | | | | |
|:------------:|--------------|--------------|--------------|--------------|
|$\frac{1}{2}$ |$\frac{1}{2}$ | | | |
|$\frac{1}{2}$ |$0$ |$\frac{1}{2}$ | | |
|$1$ |$0$ |$0$ |$1$ | |
| |$\frac{1}{6}$ |$\frac{1}{3}$ |$\frac{1}{3}$ |$\frac{1}{6}$ |
* Variant of the classical Runge-Kutta:
$$y_{k+1} = y_{k} + \frac{h}{8}(k_{1} + 3k_{2} + 3k_{3} + k_{4}), n = 0, 1, 2, \dots$$
$$k_{1} = f(x_{k}, y_{k})$$
$$k_{2} = f\left(x_{k} + \frac{h}{3}, y_{k} + \frac{h}{3}k_{1}\right)$$
$$k_{3} = f\left(x_{k} + \frac{2h}{3}, y_{k} - \frac{h}{3}k_{1} + k_{2}\right)$$
$$k_{4} = f(x_{k} + h, y_{k} + hk_{1} - hk_{2} + hk_{3})$$
|$0$ | | | | |
|:------------:|---------------|--------------|--------------|--------------|
|$\frac{1}{3}$ |$\frac{1}{3}$ | | | |
|$\frac{2}{3}$ |$\frac{-1}{3}$ |$1$ | | |
|$1$ |$1$ |$-1$ |$1$ | |
| |$\frac{1}{8}$ |$\frac{3}{8}$ |$\frac{3}{8}$ |$\frac{1}{8}$ |
## Code
### Two-stage Runge-Kutta methods implementation
```
def rk2(x_0, y_0, f, step=0.001, k_max=None, method='improved_euler'):
r"""
Two-stage Runge-Kutta method for solving first-order ODE.
The function computes `k_max` iterations from the initial conditions `x_0` and `y_0` with
steps of size `step`. It yields a total of `k_max` + 1 values. Being h_{k} the step at x_{k},
the recorrent equation is:
y_{k+1} = y_{k} + h_{k} * (1-(1/(2*lambda)) k_{1} + (1/(2*lambda)) k_{2})
where
k_{1} = f(x_{k}, y_{k})
k_{2} = f(x_{k} + lambda * h_{k}, y_{k} + lambda * h_{k} * k_{1})
When `method` is 'improved_euler', `lambda` is set to 1.
When `method` is 'heun', `lambda` is set to 2/3.
Parameters
----------
x_0 : float
The initial value for the independent variable.
y_0 : array_like
1-D array of initial values for the dependente variable evaluated at `x_0`.
f : callable
The function that represents the first derivative of y with respect to x.
It must accept two arguments: the point x at which it will be evaluated and
the value of y at this point.
step : float, optional
The step size between each iteration.
k_max : number
The maximum number of iterations.
method : ["improved_euler", "heun"]
The specific two-stage method to use.
Yields
------
x_k : float
The point at which the function was evaluated in the last iteration.
y_k : float
The value of the function in the last iteration.
Raises
------
TypeError
If the method argument is invalid or not supported.
"""
if k_max is None: counter = itertools.count()
else: counter = range(k_max)
if method == 'improved_euler':
b1, b2 = 1/2.0, 1/2.0
c2 = 1
a21 = 1
elif method == 'heun':
b1, b2 = 1/4.0, 3/4.0
c2 = 2/3.0
a21 = 2/3.0
else:
raise TypeError("The method {} is not valid or supported.".format(method))
x_k = x_0
y_k = y_0
yield (x_k, y_k)
for k in counter:
k1 = f(x_k, y_k)
k2 = f(x_k + c2 * step, y_k + a21 * step * k1)
y_k = y_k + step * (b1 * k1 + b2 * k2)
x_k = x_k + step
yield (x_k, y_k)
```
### Four-stage Runge-Kutta methods implementation
```
def rk4(x_0, y_0, f, step=0.001, k_max=None, method='classical'):
r"""
Four-stage Runge-Kutta methods for solving first-order ODE.
The function computes `k_max` iterations from the initial conditions `x_0` and `y_0` with
steps of size `step`. It yields a total of `k_max` + 1 values. We call h_{k} the step at x_{k}.
Classical Runge-Kutta method (RK4):
y_{k+1} = y_{k} + h/6 * (k_{1} + 2*k_{2} + 2*k_{3} + k_{4})
where
k_{1} = f(x_{k}, y_{k})
k_{2} = f(x_{k} + h_{k}/2, y_{k} + h_{k}/2 * k_{1})
k_{3} = f(x_{k} + h_{k}/2, y_{k} + h_{k}/2 * k_{2})
k_{3} = f(x_{k} + h_{k}, y_{k} + h_{k} * k_{3})
Variant of the classical Runge-Kutta method:
y_{k+1} = y_{k} + h/8 * (k_{1} + 3*k_{2} + 3*k_{3} + k_{4})
where
k_{1} = f(x_{k}, y_{k})
k_{2} = f(x_{k} + h_{k}/3, y_{k} + h_{k}/3 * k_{1})
k_{3} = f(x_{k} + 2*h_{k}/3, y_{k} - h_{k}/3 * k_{1} + h_{k} * k_{2})
k_{3} = f(x_{k} + h_{k}, y_{k} + h_{k} * k_{1} - h_{k} * k_{2} + h_{k} * k_{3})
Parameters
----------
x_0 : float
The initial value for the independent variable.
y_0 : array_like
1-D array of initial values for the dependente variable evaluated at `x_0`.
f : callable
The function that represents the first derivative of y with respect to x.
It must accept two arguments: the point x at which it will be evaluated and
the value of y at this point.
step : float, optional
The step size between each iteration.
k_max : number
The maximum number of iterations.
method : ["classical", "variant"]
The specific four-stage method to use.
Yields
------
x_k : float
The point at which the function was evaluated in the last iteration.
y_k : float
The value of the function in the last iteration.
Raises
------
TypeError
If the method argument is invalid or not supported.
"""
if k_max is None: counter = itertools.count()
else: counter = range(k_max)
if method == 'classical':
b1, b2, b3, b4 = 1/6.0, 1/3.0, 1/3.0, 1/6.0
c2, c3, c4 = 1/2.0, 1/2.0, 1
a21, a31, a32, a41, a42, a43 = 1/2.0, 0, 1/2.0, 0, 0, 1
elif method == 'variant':
b1, b2, b3, b4 = 1/8.0, 3/8.0, 3/8.0, 1/8.0
c2, c3, c4 = 1/3.0, 2/3.0, 1
a21, a31, a32, a41, a42, a43 = 1/3.0, -1/3.0, 1, 1, -1, 1
else:
raise TypeError("The method {} is not valid or supported.".format(method))
x_k = x_0
y_k = y_0
yield (x_k, y_k)
for k in counter:
k1 = f(x_k, y_k)
k2 = f(x_k + c2 * step, y_k + a21 * step * k1)
k3 = f(x_k + c3 * step, y_k + a31 * step * k1 + a32 * step * k2)
k4 = f(x_k + c4 * step, y_k + a41 * step * k1 + a42 * step * k2 + a43 * step * k3)
y_k = y_k + step * (b1 * k1 + b2 * k2 + b3 * k3 + b4 * k4)
x_k = x_k + step
yield (x_k, y_k)
```
## Examples
### Example 1: two-stage Runge-Kutta methods
Consider the following IVP:
$$y' = x^{2} + y^{2}$$
with
$$y(0) = 0$$
We will solve this IVP using the improved Euler's method and the Heun's method.
```
def example1(x_k, y_k):
return x_k**2 + y_k**2
results = rk2(x_0=0.0, y_0=0.0, f=example1, step=0.1, k_max=10, method='improved_euler')
x, y_improved_euler = extract(results)
results = rk2(x_0=0.0, y_0=0.0, f=example1, step=0.1, k_max=10, method='heun')
x, y_heun = extract(results)
df1 = pd.DataFrame({"x": x, "y_improved_euler": y_improved_euler, "y_heun": y_heun})
df1
fig, ax = plt.subplots(figsize=(13, 8))
plt.plot(df1['x'], df1['y_improved_euler'], label='Improved Euler approximation with step 0.1', color='blue')
plt.plot(df1['x'], df1['y_heun'], label='Heun approximation with step 0.1', color='red')
plt.legend(loc='upper left', fancybox=True, framealpha=1, shadow=True, borderpad=1, frameon=True)
ax.set(title="Two-stage Runge-Kutta methods", xlabel="x", ylabel="y");
```
As we can see from the figure above, the solutions are nearly identical (we almost cannot distinguish between them).
### Example 2: four-stage Runge-Kutta methods
Consider the same IVP of example 1:
$$y' = x^{2} + y^{2}$$
with
$$y(0) = 0$$
We will solve this IVP using both the classical Runge-Kutta method (RK4) and its variant.
```
def example2(x_k, y_k):
return x_k**2 + y_k**2
results = rk4(x_0=0.0, y_0=0.0, f=example2, step=0.1, k_max=10, method='classical')
x, y_classical_rk4 = extract(results)
results = rk4(x_0=0.0, y_0=0.0, f=example2, step=0.1, k_max=10, method='variant')
x, y_variant_rk4 = extract(results)
df2 = pd.DataFrame({"x": x,
"y_classical_rk4": y_classical_rk4,
"y_variant_rk4": y_variant_rk4})
df2
fig, ax = plt.subplots(figsize=(13, 8))
plt.plot(df2['x'], df2['y_classical_rk4'],
label='Classical Runge-Kutta approximation with step 0.1', color='blue')
plt.plot(df2['x'], df2['y_variant_rk4'],
label='Variant of the classical Runge-Kutta approximation with step 0.1', color='red')
plt.legend(loc='upper left', fancybox=True, framealpha=1, shadow=True, borderpad=1, frameon=True)
ax.set(title="Four-stage Runge-Kutta methods", xlabel="x", ylabel="y");
```
As we can see from the figure above, the solutions are nearly identical (we almost cannot distinguish between them).
### Example 3
Consider the following IVP:
$$y' = tan(y) + 1$$
with
$$y(0) = 1$$
for $t \in [1, 1.1]$.
We will solve this IVP using Heun's method.
```
def example3(x_k, y_k):
return np.tan(y_k) + 1
results = rk2(x_0=1.0, y_0=1.0, f=example3, step=0.025, k_max=4, method='heun')
x, y_heun = extract(results)
df3 = pd.DataFrame({"x": x, "y_heun": y_heun})
df3
```
### Example 4: Exercise 8 from section 8.6
The following example is actually the exercise 8 from section 8.6 of [Guidi].
Consider the following IVP:
$$y'' + (\exp(y') - 1) + y = -3\cos(t)$$
with
$$y(0) = y'(0) = 0$$
Find an approximation for the solution through the classical Runge-Kutta method for $t \in [0, 50]$ with $h = 0.01$. From the approximation obtained, find an estimative for the oscillation's amplitude for $t \in [43, 50]$ with 4 digits.
As this problem involves a second-order ODE, we must transform the variables so it becomes a system of first-order ODE:
$$u_{1} = y$$
$$u_{2} = y'$$
Since $u_{2}' = y''$, $y'' = f(t, y, y')$ becomes $u_{2}' = g(t, u_{1}, u_{2})$.
The resulting system of first-order ODE is
$$
\begin{cases}
u_{1}' = u_{2} \\
u_{2}' = -3\cos(t) - \exp(u_{2}) + 1 - u_{1}
\end{cases}
$$
```
def example4(t_k, u_k):
return np.array([u_k[1], -3*np.cos(t_k) - np.exp(u_k[1]) + 1 - u_k[0]])
results = rk4(x_0=0.0, y_0=np.array([0.0, 0.0]), f=example4, step=0.01, k_max=5000, method='classical')
t, ys = extract(results)
y_classical, dy_classical = extract(ys)
df4 = pd.DataFrame({"t": t, "y_classical": y_classical, "dy_classical": dy_classical})
t_interval = (df4.t > 43) & (df4.t < 50)
df4_interval = df4.loc[t_interval, ["t", "y_classical"]]
max_y = df4_interval.loc[:, "y_classical"].max()
min_y = df4_interval.loc[:, "y_classical"].min()
print("The amplitude of oscilattion for t in [43, 50] is {0:.3f}.".format(max_y - min_y))
fig, ax = plt.subplots(figsize=(13, 8))
plt.plot(df4['t'], df4['y_classical'],
label="Classical Runge-Kutta approximation with step 0.01", color='blue')
plt.plot(df4_interval['t'], df4_interval['y_classical'],
label="Interval of interest, $t \in [43, 50]$", color='red')
plt.legend(loc='upper right', fancybox=True, framealpha=1, shadow=True, borderpad=1, frameon=True)
ax.set(title=r"Solution of y'' + (exp(y') - 1) + y = -3cos(t)", xlabel="t", ylabel="y");
```
### Question 2
```
def rk4_modified(x_0, y_0, f, step=0.001, k_max=None):
if k_max is None: counter = itertools.count()
else: counter = range(k_max)
b1, b2, b3, b4, b5 = 1/6.0, 0.0, 0.0, 2/3.0, 1/6.0
c2, c3, c4, c5 = 1/3.0, 1/3.0, 1/2.0, 1.0
a21, a31, a32, a41, a42, a43, a51, a52, a53, a54 = 1/3.0, 1/6.0, 1/6.0, 1/8.0, 0.0, 3/8.0, 1/2.0, 0.0, -3/2.0, 2.0
x_k = x_0
y_k = y_0
yield (x_k, y_k)
for k in counter:
k1 = f(x_k, y_k)
k2 = f(x_k + c2 * step, y_k + a21 * step * k1)
k3 = f(x_k + c3 * step, y_k + a31 * step * k1 + a32 * step * k2)
k4 = f(x_k + c4 * step, y_k + a41 * step * k1 + a42 * step * k2 + a43 * step * k3)
k5 = f(x_k + c5 * step, y_k + a51 * step * k1 + a52 * step * k2 + a53 * step * k3 + a54 * step * k4)
y_k = y_k + step * (b1 * k1 + b2 * k2 + b3 * k3 + b4 * k4 + b5 * k5)
x_k = x_k + step
yield (x_k, y_k)
def question2(t, u_k):
return np.array([(4/5.0) * u_k[0] * u_k[1] - (1/4.0) * u_k[0], -(4/5.0) * u_k[0] * u_k[1]])
results = rk4_modified(x_0=0.0, y_0=np.array([0.005, 0.995]), f=question2, step=0.0125, k_max=800)
t, i_s = extract(results)
i, s = extract(i_s)
i, s = np.array(i), np.array(s)
df5 = pd.DataFrame({"t": t, "I": i, "S": s, "R": (1 - (i + s))})
df5 = df5[["t", "I", "S", "R"]]
print("Ratio I(10)/R(10) is {:.2f}.".format(df5["I"].iloc[-1]/df5["R"].iloc[-1]))
fig, ax = plt.subplots(figsize=(13, 8))
plt.plot(df5['t'], df5['I'],
label="$I(t)$: infected", color='blue')
plt.plot(df5['t'], df5['S'],
label="$S(t)$: non-infected", color='green')
plt.plot(df5['t'], df5['R'],
label="$R(t)$: recovered", color='red')
plt.legend(loc='upper right', fancybox=True, framealpha=1, shadow=True, borderpad=1, frameon=True)
ax.set(title=r"Epidemic evolution: Kermack–McKendrick SIR model", xlabel="t", ylabel="y");
```
## References
* Guidi, L., Notas da disciplina Cálculo Numérico. Disponível em [Notas da disciplina Cálculo Numérico](http://www.mat.ufrgs.br/~guidi/grad/MAT01169/calculo_numerico.pdf).
* Heath, M. T., Scientific Computing: An Introductory Survey, 2nd Edition, McGraw Hill, 2002.
* Wikipedia, [Runge-Kutta methods](https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods).
|
github_jupyter
|
%matplotlib inline
import numpy as np
import scipy as sc
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import sympy as sp
import itertools
sns.set();
def extract(it):
r"""
Extract the values from a iterable of iterables.
The function extracts the values from a iterable of iterables (eg. a list of tuples) to a list
of coordinates. For example,
[(1, 10), (2, 20), (3, 30), (4, 40)] -> [[1, 2, 3, 4], [10, 20, 30, 40]]
If `it` is a list of M tuples each one with N elements, then `extract` returns
a list of N lists each one with M elements.
Parameters
----------
it : iterable
An iterable of iterables.
Returns
------
A list with the lists of first-elements, second-elements and so on.
"""
return list(zip(*it))
def rk2(x_0, y_0, f, step=0.001, k_max=None, method='improved_euler'):
r"""
Two-stage Runge-Kutta method for solving first-order ODE.
The function computes `k_max` iterations from the initial conditions `x_0` and `y_0` with
steps of size `step`. It yields a total of `k_max` + 1 values. Being h_{k} the step at x_{k},
the recorrent equation is:
y_{k+1} = y_{k} + h_{k} * (1-(1/(2*lambda)) k_{1} + (1/(2*lambda)) k_{2})
where
k_{1} = f(x_{k}, y_{k})
k_{2} = f(x_{k} + lambda * h_{k}, y_{k} + lambda * h_{k} * k_{1})
When `method` is 'improved_euler', `lambda` is set to 1.
When `method` is 'heun', `lambda` is set to 2/3.
Parameters
----------
x_0 : float
The initial value for the independent variable.
y_0 : array_like
1-D array of initial values for the dependente variable evaluated at `x_0`.
f : callable
The function that represents the first derivative of y with respect to x.
It must accept two arguments: the point x at which it will be evaluated and
the value of y at this point.
step : float, optional
The step size between each iteration.
k_max : number
The maximum number of iterations.
method : ["improved_euler", "heun"]
The specific two-stage method to use.
Yields
------
x_k : float
The point at which the function was evaluated in the last iteration.
y_k : float
The value of the function in the last iteration.
Raises
------
TypeError
If the method argument is invalid or not supported.
"""
if k_max is None: counter = itertools.count()
else: counter = range(k_max)
if method == 'improved_euler':
b1, b2 = 1/2.0, 1/2.0
c2 = 1
a21 = 1
elif method == 'heun':
b1, b2 = 1/4.0, 3/4.0
c2 = 2/3.0
a21 = 2/3.0
else:
raise TypeError("The method {} is not valid or supported.".format(method))
x_k = x_0
y_k = y_0
yield (x_k, y_k)
for k in counter:
k1 = f(x_k, y_k)
k2 = f(x_k + c2 * step, y_k + a21 * step * k1)
y_k = y_k + step * (b1 * k1 + b2 * k2)
x_k = x_k + step
yield (x_k, y_k)
def rk4(x_0, y_0, f, step=0.001, k_max=None, method='classical'):
r"""
Four-stage Runge-Kutta methods for solving first-order ODE.
The function computes `k_max` iterations from the initial conditions `x_0` and `y_0` with
steps of size `step`. It yields a total of `k_max` + 1 values. We call h_{k} the step at x_{k}.
Classical Runge-Kutta method (RK4):
y_{k+1} = y_{k} + h/6 * (k_{1} + 2*k_{2} + 2*k_{3} + k_{4})
where
k_{1} = f(x_{k}, y_{k})
k_{2} = f(x_{k} + h_{k}/2, y_{k} + h_{k}/2 * k_{1})
k_{3} = f(x_{k} + h_{k}/2, y_{k} + h_{k}/2 * k_{2})
k_{3} = f(x_{k} + h_{k}, y_{k} + h_{k} * k_{3})
Variant of the classical Runge-Kutta method:
y_{k+1} = y_{k} + h/8 * (k_{1} + 3*k_{2} + 3*k_{3} + k_{4})
where
k_{1} = f(x_{k}, y_{k})
k_{2} = f(x_{k} + h_{k}/3, y_{k} + h_{k}/3 * k_{1})
k_{3} = f(x_{k} + 2*h_{k}/3, y_{k} - h_{k}/3 * k_{1} + h_{k} * k_{2})
k_{3} = f(x_{k} + h_{k}, y_{k} + h_{k} * k_{1} - h_{k} * k_{2} + h_{k} * k_{3})
Parameters
----------
x_0 : float
The initial value for the independent variable.
y_0 : array_like
1-D array of initial values for the dependente variable evaluated at `x_0`.
f : callable
The function that represents the first derivative of y with respect to x.
It must accept two arguments: the point x at which it will be evaluated and
the value of y at this point.
step : float, optional
The step size between each iteration.
k_max : number
The maximum number of iterations.
method : ["classical", "variant"]
The specific four-stage method to use.
Yields
------
x_k : float
The point at which the function was evaluated in the last iteration.
y_k : float
The value of the function in the last iteration.
Raises
------
TypeError
If the method argument is invalid or not supported.
"""
if k_max is None: counter = itertools.count()
else: counter = range(k_max)
if method == 'classical':
b1, b2, b3, b4 = 1/6.0, 1/3.0, 1/3.0, 1/6.0
c2, c3, c4 = 1/2.0, 1/2.0, 1
a21, a31, a32, a41, a42, a43 = 1/2.0, 0, 1/2.0, 0, 0, 1
elif method == 'variant':
b1, b2, b3, b4 = 1/8.0, 3/8.0, 3/8.0, 1/8.0
c2, c3, c4 = 1/3.0, 2/3.0, 1
a21, a31, a32, a41, a42, a43 = 1/3.0, -1/3.0, 1, 1, -1, 1
else:
raise TypeError("The method {} is not valid or supported.".format(method))
x_k = x_0
y_k = y_0
yield (x_k, y_k)
for k in counter:
k1 = f(x_k, y_k)
k2 = f(x_k + c2 * step, y_k + a21 * step * k1)
k3 = f(x_k + c3 * step, y_k + a31 * step * k1 + a32 * step * k2)
k4 = f(x_k + c4 * step, y_k + a41 * step * k1 + a42 * step * k2 + a43 * step * k3)
y_k = y_k + step * (b1 * k1 + b2 * k2 + b3 * k3 + b4 * k4)
x_k = x_k + step
yield (x_k, y_k)
def example1(x_k, y_k):
return x_k**2 + y_k**2
results = rk2(x_0=0.0, y_0=0.0, f=example1, step=0.1, k_max=10, method='improved_euler')
x, y_improved_euler = extract(results)
results = rk2(x_0=0.0, y_0=0.0, f=example1, step=0.1, k_max=10, method='heun')
x, y_heun = extract(results)
df1 = pd.DataFrame({"x": x, "y_improved_euler": y_improved_euler, "y_heun": y_heun})
df1
fig, ax = plt.subplots(figsize=(13, 8))
plt.plot(df1['x'], df1['y_improved_euler'], label='Improved Euler approximation with step 0.1', color='blue')
plt.plot(df1['x'], df1['y_heun'], label='Heun approximation with step 0.1', color='red')
plt.legend(loc='upper left', fancybox=True, framealpha=1, shadow=True, borderpad=1, frameon=True)
ax.set(title="Two-stage Runge-Kutta methods", xlabel="x", ylabel="y");
def example2(x_k, y_k):
return x_k**2 + y_k**2
results = rk4(x_0=0.0, y_0=0.0, f=example2, step=0.1, k_max=10, method='classical')
x, y_classical_rk4 = extract(results)
results = rk4(x_0=0.0, y_0=0.0, f=example2, step=0.1, k_max=10, method='variant')
x, y_variant_rk4 = extract(results)
df2 = pd.DataFrame({"x": x,
"y_classical_rk4": y_classical_rk4,
"y_variant_rk4": y_variant_rk4})
df2
fig, ax = plt.subplots(figsize=(13, 8))
plt.plot(df2['x'], df2['y_classical_rk4'],
label='Classical Runge-Kutta approximation with step 0.1', color='blue')
plt.plot(df2['x'], df2['y_variant_rk4'],
label='Variant of the classical Runge-Kutta approximation with step 0.1', color='red')
plt.legend(loc='upper left', fancybox=True, framealpha=1, shadow=True, borderpad=1, frameon=True)
ax.set(title="Four-stage Runge-Kutta methods", xlabel="x", ylabel="y");
def example3(x_k, y_k):
return np.tan(y_k) + 1
results = rk2(x_0=1.0, y_0=1.0, f=example3, step=0.025, k_max=4, method='heun')
x, y_heun = extract(results)
df3 = pd.DataFrame({"x": x, "y_heun": y_heun})
df3
def example4(t_k, u_k):
return np.array([u_k[1], -3*np.cos(t_k) - np.exp(u_k[1]) + 1 - u_k[0]])
results = rk4(x_0=0.0, y_0=np.array([0.0, 0.0]), f=example4, step=0.01, k_max=5000, method='classical')
t, ys = extract(results)
y_classical, dy_classical = extract(ys)
df4 = pd.DataFrame({"t": t, "y_classical": y_classical, "dy_classical": dy_classical})
t_interval = (df4.t > 43) & (df4.t < 50)
df4_interval = df4.loc[t_interval, ["t", "y_classical"]]
max_y = df4_interval.loc[:, "y_classical"].max()
min_y = df4_interval.loc[:, "y_classical"].min()
print("The amplitude of oscilattion for t in [43, 50] is {0:.3f}.".format(max_y - min_y))
fig, ax = plt.subplots(figsize=(13, 8))
plt.plot(df4['t'], df4['y_classical'],
label="Classical Runge-Kutta approximation with step 0.01", color='blue')
plt.plot(df4_interval['t'], df4_interval['y_classical'],
label="Interval of interest, $t \in [43, 50]$", color='red')
plt.legend(loc='upper right', fancybox=True, framealpha=1, shadow=True, borderpad=1, frameon=True)
ax.set(title=r"Solution of y'' + (exp(y') - 1) + y = -3cos(t)", xlabel="t", ylabel="y");
def rk4_modified(x_0, y_0, f, step=0.001, k_max=None):
if k_max is None: counter = itertools.count()
else: counter = range(k_max)
b1, b2, b3, b4, b5 = 1/6.0, 0.0, 0.0, 2/3.0, 1/6.0
c2, c3, c4, c5 = 1/3.0, 1/3.0, 1/2.0, 1.0
a21, a31, a32, a41, a42, a43, a51, a52, a53, a54 = 1/3.0, 1/6.0, 1/6.0, 1/8.0, 0.0, 3/8.0, 1/2.0, 0.0, -3/2.0, 2.0
x_k = x_0
y_k = y_0
yield (x_k, y_k)
for k in counter:
k1 = f(x_k, y_k)
k2 = f(x_k + c2 * step, y_k + a21 * step * k1)
k3 = f(x_k + c3 * step, y_k + a31 * step * k1 + a32 * step * k2)
k4 = f(x_k + c4 * step, y_k + a41 * step * k1 + a42 * step * k2 + a43 * step * k3)
k5 = f(x_k + c5 * step, y_k + a51 * step * k1 + a52 * step * k2 + a53 * step * k3 + a54 * step * k4)
y_k = y_k + step * (b1 * k1 + b2 * k2 + b3 * k3 + b4 * k4 + b5 * k5)
x_k = x_k + step
yield (x_k, y_k)
def question2(t, u_k):
return np.array([(4/5.0) * u_k[0] * u_k[1] - (1/4.0) * u_k[0], -(4/5.0) * u_k[0] * u_k[1]])
results = rk4_modified(x_0=0.0, y_0=np.array([0.005, 0.995]), f=question2, step=0.0125, k_max=800)
t, i_s = extract(results)
i, s = extract(i_s)
i, s = np.array(i), np.array(s)
df5 = pd.DataFrame({"t": t, "I": i, "S": s, "R": (1 - (i + s))})
df5 = df5[["t", "I", "S", "R"]]
print("Ratio I(10)/R(10) is {:.2f}.".format(df5["I"].iloc[-1]/df5["R"].iloc[-1]))
fig, ax = plt.subplots(figsize=(13, 8))
plt.plot(df5['t'], df5['I'],
label="$I(t)$: infected", color='blue')
plt.plot(df5['t'], df5['S'],
label="$S(t)$: non-infected", color='green')
plt.plot(df5['t'], df5['R'],
label="$R(t)$: recovered", color='red')
plt.legend(loc='upper right', fancybox=True, framealpha=1, shadow=True, borderpad=1, frameon=True)
ax.set(title=r"Epidemic evolution: Kermack–McKendrick SIR model", xlabel="t", ylabel="y");
| 0.812384 | 0.938181 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.