code
stringlengths 2.5k
6.36M
| kind
stringclasses 2
values | parsed_code
stringlengths 0
404k
| quality_prob
float64 0
0.98
| learning_prob
float64 0.03
1
|
|---|---|---|---|---|
```
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from typing import List, Tuple
text = """When forty winters shall besiege thy brow,
And dig deep trenches in thy beauty's field,
Thy youth's proud livery so gazed on now,
Will be a totter'd weed of small worth held:
Then being asked, where all thy beauty lies,
Where all the treasure of thy lusty days;
To say, within thine own deep sunken eyes,
Were an all-eating shame, and thriftless praise.
How much more praise deserv'd thy beauty's use,
If thou couldst answer 'This fair child of mine
Shall sum my count, and make my old excuse,'
Proving his beauty by succession thine!
This were to be new made when thou art old,
And see thy blood warm when thou feel'st it cold.""".split()
EMBEDDING_DIM = 10
CONTEXT_SIZE = 2
def get_trigrams(text: List[str]) -> List[Tuple]:
"""Get trigrams of our text
Args:
text: strings split by whitespace
Returns:
trigrams: ([ word_i-2, word_i-1 ], target word)
"""
trigrams = []
for i in range(len(text) - 2):
gram = ([text[i], text[i+1]], text[i+2])
trigrams.append(gram)
return trigrams
trigrams = get_trigrams(text)
trigrams[:3]
```
Create vocabulary and do simple tokenization.
```
vocab = set(text)
word_to_ix = {word: i for i, word in enumerate(vocab)}
class NGram(nn.Module):
def __init__(self, vocab_size, embedding_dim, context_size):
super(NGram, self).__init__()
self.embeddings = nn.Embedding(vocab_size, embedding_dim)
self.linear1 = nn.Linear(context_size * embedding_dim, 128)
self.linear2 = nn.Linear(128, vocab_size)
def forward(self, inputs):
embeds = self.embeddings(inputs).view((1, -1))
out = F.relu(self.linear1(embeds))
out = self.linear2(out)
log_probs = F.log_softmax(out, dim=1)
return log_probs
losses = []
loss_function = nn.NLLLoss()
model = NGram(len(vocab), EMBEDDING_DIM, CONTEXT_SIZE)
optimizer = optim.SGD(model.parameters(), lr=0.001)
for epoch in range(10):
total_loss = 0
for context, target in trigrams:
context_idxs = torch.tensor([word_to_ix[w] for w in context], dtype=torch.long)
optimizer.zero_grad()
log_probs = model(context_idxs)
loss = loss_function(log_probs, torch.tensor([word_to_ix[target]], dtype=torch.long))
loss.backward()
optimizer.step()
total_loss += loss.item()
print(f'Train loss: {total_loss:.2f}')
losses.append(total_loss)
```
|
github_jupyter
|
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from typing import List, Tuple
text = """When forty winters shall besiege thy brow,
And dig deep trenches in thy beauty's field,
Thy youth's proud livery so gazed on now,
Will be a totter'd weed of small worth held:
Then being asked, where all thy beauty lies,
Where all the treasure of thy lusty days;
To say, within thine own deep sunken eyes,
Were an all-eating shame, and thriftless praise.
How much more praise deserv'd thy beauty's use,
If thou couldst answer 'This fair child of mine
Shall sum my count, and make my old excuse,'
Proving his beauty by succession thine!
This were to be new made when thou art old,
And see thy blood warm when thou feel'st it cold.""".split()
EMBEDDING_DIM = 10
CONTEXT_SIZE = 2
def get_trigrams(text: List[str]) -> List[Tuple]:
"""Get trigrams of our text
Args:
text: strings split by whitespace
Returns:
trigrams: ([ word_i-2, word_i-1 ], target word)
"""
trigrams = []
for i in range(len(text) - 2):
gram = ([text[i], text[i+1]], text[i+2])
trigrams.append(gram)
return trigrams
trigrams = get_trigrams(text)
trigrams[:3]
vocab = set(text)
word_to_ix = {word: i for i, word in enumerate(vocab)}
class NGram(nn.Module):
def __init__(self, vocab_size, embedding_dim, context_size):
super(NGram, self).__init__()
self.embeddings = nn.Embedding(vocab_size, embedding_dim)
self.linear1 = nn.Linear(context_size * embedding_dim, 128)
self.linear2 = nn.Linear(128, vocab_size)
def forward(self, inputs):
embeds = self.embeddings(inputs).view((1, -1))
out = F.relu(self.linear1(embeds))
out = self.linear2(out)
log_probs = F.log_softmax(out, dim=1)
return log_probs
losses = []
loss_function = nn.NLLLoss()
model = NGram(len(vocab), EMBEDDING_DIM, CONTEXT_SIZE)
optimizer = optim.SGD(model.parameters(), lr=0.001)
for epoch in range(10):
total_loss = 0
for context, target in trigrams:
context_idxs = torch.tensor([word_to_ix[w] for w in context], dtype=torch.long)
optimizer.zero_grad()
log_probs = model(context_idxs)
loss = loss_function(log_probs, torch.tensor([word_to_ix[target]], dtype=torch.long))
loss.backward()
optimizer.step()
total_loss += loss.item()
print(f'Train loss: {total_loss:.2f}')
losses.append(total_loss)
| 0.842669 | 0.688874 |
**`ICUBAM`: ICU Bed Availability Monitoring and analysis in the *Grand Est région* of France during the COVID-19 epidemic.**
https://doi.org/10.1101/2020.05.18.20091264
Python notebook for the sir-like modeling (see Section IV.1 of the main paper).
(i) compute model, fit to the data, and save best parameters found via maximum likelihood
```
import numpy as np
import pandas as pd
import os.path as op
from scipy.optimize import minimize
from collections import namedtuple
import model_icubam as micu
np.random.seed(13)
data_pop = pd.read_csv(op.join('data', 'pop_dep_2020.csv'), delimiter='\t')
#Fig. 17 (left) is realized using first_date = '2020-03-19' and last_date = '2020-04-29'.
#Fig. 11 and Fig. 17 (right) are realized using first_date = '2020-03-19' and last_date = '2020-04-27'.
first_date = '2020-03-19'
last_date = '2020-04-27'
data = pd.read_csv(op.join(micu.data_path, 'all_bedcounts_2020-05-04_11h02.csv'), index_col=0)
data = data.groupby(['date', 'department']).sum().reset_index()
data = data[data.date >= first_date]
data = data[data.date <= last_date]
sites = ['Ardennes', 'Aube', 'Bas-Rhin', 'Haut-Rhin',
'Marne', 'Meurthe-et-Moselle', 'Meuse', 'Moselle', 'Vosges']
n_sites = len(sites)
depname2depid = {'Ardennes':8, 'Aube':10, 'Marne':51, 'Haute-Marne':52,
'Meurthe-et-Moselle':54, 'Meuse':55, 'Moselle':57, 'Bas-Rhin':67,
'Haut-Rhin':68, 'Vosges':88}
micu.make_dir(micu.fig_path)
micu.make_dir(micu.model_path)
# modeling
def compute_llh(data_obs, data_hat):
cobs, xobs = data_obs
chat, xhat = data_hat
llh = -(np.sum(np.power(cobs-chat, 2))
+ np.sum(np.power(xobs-xhat, 2)))
return llh
def evaluate_estimation(fun_model, pop, params_init, data_obs):
n_days = len(data_obs[0])
data_hat = fun_model(pop, params_init, n_days)
return -compute_llh(data_obs, data_hat)
def fit_model(fun_model, data, sites, params_init, bounds):
params_hat = []
llh = []
for dep in sites:
condition = data.department==dep
pop = data_pop[data_pop.dep=='{}'.format(depname2depid[dep])]['pop'].values[0]
n_days = data[condition].date.shape[0]
data_obs = (data[condition]['n_covid_occ'].values,
data[condition]['n_covid_deaths'].values
+data[condition]['n_covid_healed'].values)
optim_fun = lambda x: evaluate_estimation(fun_model, pop, x, data_obs)
optim_results = minimize(fun=optim_fun, x0=params_init, bounds=bounds)
params_hat.append(optim_results.x)
llh.append(-optim_results.fun)
return np.array(params_hat), np.array(llh)
Params = namedtuple('Params', 'n_days_pre alpha_e beta wei wiout wic wcc wcx')
Bounds = namedtuple('Bounds', 'n_days_pre alpha_e beta wei wiout wic wcc wcx')
compute_model = micu.compute_model_seir
n_days_pre_rg = np.arange(0, 25)
llh_n_days_pre = []
params_hat_n_days_pre = []
for n_days_pre in n_days_pre_rg:
params_init = Params(n_days_pre=n_days_pre, alpha_e=1e-5, beta=0.01,
wei=0.1, wiout=0.2, wic=0.1, wcc=0.1, wcx=0.5)
bounds = Bounds(n_days_pre=(n_days_pre, n_days_pre), alpha_e=(0, 1), beta=(0, 1),
wei=(0, 1), wiout=(0, 1), wic=(0, 1), wcc=(0, 1), wcx=(0, 1))
params_hat, llh = fit_model(compute_model, data, sites, params_init, bounds)
llh_n_days_pre.append(llh)
params_hat_n_days_pre.append(params_hat)
llh_n_days_pre = np.array(llh_n_days_pre)
params_hat_n_days_pre = np.array(params_hat_n_days_pre)
params_hat = []
for k, dep in enumerate(sites):
ind_best = np.argmax(llh_n_days_pre[:,k])
params_hat.append(params_hat_n_days_pre[ind_best, k, :])
params_hat = np.array(params_hat)
params_name = list(params_init._asdict().keys())
df_param = pd.DataFrame([dict([(param, params_hat[k,i]) for i, param in enumerate(params_name)] + [('dep',sites[k])])
for k in range(n_sites)])
df_param.to_csv(op.join(micu.model_path, 'params_hat_{}.csv'.format(last_date)))
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import os.path as op
from scipy.optimize import minimize
from collections import namedtuple
import model_icubam as micu
np.random.seed(13)
data_pop = pd.read_csv(op.join('data', 'pop_dep_2020.csv'), delimiter='\t')
#Fig. 17 (left) is realized using first_date = '2020-03-19' and last_date = '2020-04-29'.
#Fig. 11 and Fig. 17 (right) are realized using first_date = '2020-03-19' and last_date = '2020-04-27'.
first_date = '2020-03-19'
last_date = '2020-04-27'
data = pd.read_csv(op.join(micu.data_path, 'all_bedcounts_2020-05-04_11h02.csv'), index_col=0)
data = data.groupby(['date', 'department']).sum().reset_index()
data = data[data.date >= first_date]
data = data[data.date <= last_date]
sites = ['Ardennes', 'Aube', 'Bas-Rhin', 'Haut-Rhin',
'Marne', 'Meurthe-et-Moselle', 'Meuse', 'Moselle', 'Vosges']
n_sites = len(sites)
depname2depid = {'Ardennes':8, 'Aube':10, 'Marne':51, 'Haute-Marne':52,
'Meurthe-et-Moselle':54, 'Meuse':55, 'Moselle':57, 'Bas-Rhin':67,
'Haut-Rhin':68, 'Vosges':88}
micu.make_dir(micu.fig_path)
micu.make_dir(micu.model_path)
# modeling
def compute_llh(data_obs, data_hat):
cobs, xobs = data_obs
chat, xhat = data_hat
llh = -(np.sum(np.power(cobs-chat, 2))
+ np.sum(np.power(xobs-xhat, 2)))
return llh
def evaluate_estimation(fun_model, pop, params_init, data_obs):
n_days = len(data_obs[0])
data_hat = fun_model(pop, params_init, n_days)
return -compute_llh(data_obs, data_hat)
def fit_model(fun_model, data, sites, params_init, bounds):
params_hat = []
llh = []
for dep in sites:
condition = data.department==dep
pop = data_pop[data_pop.dep=='{}'.format(depname2depid[dep])]['pop'].values[0]
n_days = data[condition].date.shape[0]
data_obs = (data[condition]['n_covid_occ'].values,
data[condition]['n_covid_deaths'].values
+data[condition]['n_covid_healed'].values)
optim_fun = lambda x: evaluate_estimation(fun_model, pop, x, data_obs)
optim_results = minimize(fun=optim_fun, x0=params_init, bounds=bounds)
params_hat.append(optim_results.x)
llh.append(-optim_results.fun)
return np.array(params_hat), np.array(llh)
Params = namedtuple('Params', 'n_days_pre alpha_e beta wei wiout wic wcc wcx')
Bounds = namedtuple('Bounds', 'n_days_pre alpha_e beta wei wiout wic wcc wcx')
compute_model = micu.compute_model_seir
n_days_pre_rg = np.arange(0, 25)
llh_n_days_pre = []
params_hat_n_days_pre = []
for n_days_pre in n_days_pre_rg:
params_init = Params(n_days_pre=n_days_pre, alpha_e=1e-5, beta=0.01,
wei=0.1, wiout=0.2, wic=0.1, wcc=0.1, wcx=0.5)
bounds = Bounds(n_days_pre=(n_days_pre, n_days_pre), alpha_e=(0, 1), beta=(0, 1),
wei=(0, 1), wiout=(0, 1), wic=(0, 1), wcc=(0, 1), wcx=(0, 1))
params_hat, llh = fit_model(compute_model, data, sites, params_init, bounds)
llh_n_days_pre.append(llh)
params_hat_n_days_pre.append(params_hat)
llh_n_days_pre = np.array(llh_n_days_pre)
params_hat_n_days_pre = np.array(params_hat_n_days_pre)
params_hat = []
for k, dep in enumerate(sites):
ind_best = np.argmax(llh_n_days_pre[:,k])
params_hat.append(params_hat_n_days_pre[ind_best, k, :])
params_hat = np.array(params_hat)
params_name = list(params_init._asdict().keys())
df_param = pd.DataFrame([dict([(param, params_hat[k,i]) for i, param in enumerate(params_name)] + [('dep',sites[k])])
for k in range(n_sites)])
df_param.to_csv(op.join(micu.model_path, 'params_hat_{}.csv'.format(last_date)))
| 0.370339 | 0.858659 |
<a href="https://colab.research.google.com/github/Machine-Learning-Tokyo/Intro-to-GANs/blob/master/WassersteinGAN/Faces_COND_WDCGAN.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Faces Wasserstein GAN (WGAN)
In this notebook we use the same model in [Wasserstein GAN (WGAN) -- Solutions]() but used to train on a dataset of faces. As a result, our GAN would produce faces of people.
## Donwload dataset
First of all we need a dataset of faces. We're going to use the [CelebA](http://mmlab.ie.cuhk.edu.hk/projects/CelebA.html) dataset, a dataset with over 200k pictures of celebrities.
To download it we're going to use an script that belongs to the [StarGAN](https://github.com/yunjey/stargan) project. StarGAN is an advanced GAN that modifies faces of people. There is no need to understand it for this notebook, but go ahead and have a look if you have curiosity.
So run the following cells to download the dataset. This will take a while.
```
#%%capture
# download CelebA data
!wget https://raw.githubusercontent.com/yunjey/StarGAN/master/download.sh
!bash download.sh celeba
!echo "There are `ls data/celeba/images | wc -l` images"
```
### Imports
```
from keras.models import Model
from keras.layers import Input, Dense, BatchNormalization, Reshape, Flatten
from keras.layers.advanced_activations import LeakyReLU
from keras.datasets import fashion_mnist
from keras.optimizers import Adam, RMSprop
from keras.layers import Conv2D, UpSampling2D, concatenate, Lambda
from keras.initializers import RandomNormal
from keras.utils import to_categorical
import keras.backend as K
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
from PIL import Image
from matplotlib import animation, rc
from IPython.display import Image as ipyImage
from IPython.display import HTML
from os import listdir
```
## Hidden data loader code
To use a dataset we need a data loader. In our previous WGAN notebooks we used a pre-loaded dataset: fashionMNIST. fashionMNIST is a very easy and rather small dataset so images ar provided inside an array that can be indexed to generate batches. On the contrary, CelebA is a very big one, so it's not feasible to keep it in memory inside an arry. What we're going to do is to implement a loader that will reach the image files in disc and generate the batches on the fly.
The code for this data loader is hidden. It's cumbersome and it's not the point of this exercise so you can ignore it.
```
# templates
DATA_DIR = 'data/celeba/'
IMGS_DIR = '{}images/'.format(DATA_DIR)
CSV_FILE = '{}list_attr_celeba.txt'.format(DATA_DIR)
#@title Data loader
import numpy as np
import cv2
import pandas as pd
from itertools import cycle
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
from random import shuffle
import random
def download_celeba(data_dir, imgs_dir):
%rm -r {data_dir}
%mkdir {data_dir}
%cd {data_dir}
!pip install pydrive
from shutil import unpack_archive
# these classes allow you to request the Google drive API
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from oauth2client.client import GoogleCredentials
from googleapiclient.http import MediaIoBaseDownload
from google.colab import auth
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
file_id_dict = {
'imgs.zip': '0B7EVK8r0v71pZjFTYXZWM3FlRnM',
'attributes.txt': '0B7EVK8r0v71pblRyaVFSWGxPY0U'
}
for file_, id_ in file_id_dict.items():
downloaded = drive.CreateFile({'id': id_})
downloaded.GetContentFile(file_)
# %rm -r {imgs_dir}*
unpack_archive('imgs.zip', imgs_dir)
%rm imgs.zip
def get_imgs_lists(df, category):
pos_img_names = df.index[df[category] == 1]
neg_img_names = df.index[df[category] == -1]
return list(pos_img_names), list(neg_img_names)
def preprocess_img(img, img_shape, crop=None):
img = img / 127.5 - 1
if crop is not None:
cropx, cropy = crop
y,x,_ = img.shape
startx = x//2-(cropx//2)
starty = y//2-(cropy//2)
img = img[starty:starty+cropy,startx:startx+cropx,:]
img = cv2.resize(img, img_shape[:2])
return img
def single_core_category_generator(img_paths, img_shape):
imgs = np.zeros((len(img_paths), *img_shape))
for i, img_path in enumerate(img_paths):
img = mpimg.imread(img_path)
imgs[i] = preprocess_img(img, img_shape)
return imgs
def mp_category_generator(imgs_dir, img_names, img_shape, batch_size):
import multiprocessing as mp
cpu_num = min(mp.cpu_count(), batch_size)
def chunks(lst, n):
for i in range(n):
yield lst[i::n]
shuffle(img_names)
img_names = cycle(img_names)
while True:
imgs = np.zeros((batch_size, *img_shape))
batch_paths = [imgs_dir + next(img_names) for _ in range(batch_size)]
batch_paths = chunks(batch_paths, cpu_num)
pool = mp.Pool(processes=cpu_num)
imgs = [pool.apply(single_core_category_generator,
args=(next(batch_paths), img_shape)) for i in range(cpu_num)]
pool.terminate()
imgs = np.concatenate(imgs)
yield imgs
def category_generator(imgs_dir, img_names, img_shape, batch_size, crop=None):
shuffle(img_names)
img_names = cycle(img_names)
while True:
imgs = np.zeros((batch_size, *img_shape))
for i in range(batch_size):
img_path = imgs_dir + next(img_names)
img = mpimg.imread(img_path)
imgs[i] = preprocess_img(img, img_shape, crop=crop)
yield imgs
def get_generators(img_shape, batch_size, category=None, download=True, crop=None):
data_dir = 'data/'
imgs_dir = '{}celeba/images/'.format(data_dir)
if download:
download_celeba(data_dir, imgs_dir)
imgs_dir = imgs_dir
df = pd.read_csv('{}celeba/list_attr_celeba.txt'.format(data_dir), sep=' +', skiprows=[0])
img_names = list(df.index)
if category is None:
gen = category_generator(imgs_dir, img_names, img_shape, batch_size)
return gen
pos_img_names, neg_img_names = get_imgs_lists(df, category)
pos_gen = category_generator(imgs_dir, pos_img_names, img_shape, batch_size, crop=crop)
neg_gen = category_generator(imgs_dir, neg_img_names, img_shape, batch_size, crop=crop)
return pos_gen, neg_gen
```
### Function to build the generator
```
def build_generator(noise_size, img_shape, num_classes):
# block: Conv, Batch norm, Upsampling
k_size = 5, 5
k_init = RandomNormal(0, 0.01)
filters = 1024 #CHANGE
noise = Input((noise_size,))
labels = Input((num_classes,))
model_input = concatenate([noise, labels])
x = Dense(4*4*filters, kernel_initializer=k_init, activation='relu')(model_input)
x = Reshape((4, 4, filters))(x) # 4, 4
x = BatchNormalization()(x)
x = UpSampling2D()(x) # 8, 8
x = Conv2D(filters // 2, k_size, padding='same', kernel_initializer=k_init, activation='relu')(x)
x = BatchNormalization()(x)
x = UpSampling2D()(x) # 16, 16
x = Conv2D(filters // 4, k_size, padding='same', kernel_initializer=k_init, activation='relu')(x)
x = BatchNormalization()(x)
x = UpSampling2D()(x) # 32, 32
#CHANGE
x = Conv2D(filters // 8, k_size, padding='same', kernel_initializer=k_init, activation='relu')(x)
x = BatchNormalization()(x)
x = UpSampling2D()(x) # 64, 64
img = Conv2D(img_shape[-1], k_size, padding='same', kernel_initializer=k_init, activation='tanh')(x)
generator = Model([noise, labels], img)
return generator
```
### Function to build the discriminator
```
def build_discriminator(img_shape, num_classes):
# block: Conv, Batch norm, LeakyRelu
k_size = 5, 5
k_init = RandomNormal(0, 0.01)
filters = 1024 #CHANGE
img = Input(img_shape) # 64, 64, 3
labels = Input((num_classes,)) # 10
n_labels = Reshape((1, 1, -1))(labels) # (batch_size), 1, 1, 10
n_labels = Lambda(lambda x: K.tile(x, [1, img_shape[0], img_shape[1], 1]))(n_labels) # (batch_size), 64, 64, 10
model_input = concatenate([img, n_labels]) # 64, 64, ? (1 + 10)
#CHANGE
x = Conv2D(filters // 8, k_size, strides=(2, 2), padding='same', kernel_initializer=k_init)(model_input)
x = BatchNormalization()(x)
x = LeakyReLU(alpha=0.2)(x) #32, 32
x = Conv2D(filters // 4, k_size, strides=(2, 2), padding='same', kernel_initializer=k_init)(x)#CHANGE, model_input -> x
x = BatchNormalization()(x)
x = LeakyReLU(alpha=0.2)(x) #16, 16
x = Conv2D(filters // 2, k_size, strides=(2, 2), padding='same', kernel_initializer=k_init)(x)
x = BatchNormalization()(x)
x = LeakyReLU(alpha=0.2)(x) # 8, 8
x = Conv2D(filters, k_size, strides=(2, 2), padding='same', kernel_initializer=k_init)(x)
x = BatchNormalization()(x)
x = LeakyReLU(alpha=0.2)(x) # 4, 4
x = Flatten()(x)
validity = Dense(3, activation='linear', kernel_initializer=k_init)(x) #CHANGE
discriminator = Model([img, labels], validity)
return discriminator
```
### Function to compile the models
```
def critic_loss(y_true, y_pred):
return K.mean(y_true * y_pred)
def get_compiled_models(generator, discriminator, noise_size, num_classes):
optimizer = RMSprop(0.0002)
discriminator.compile(optimizer, loss=critic_loss)
discriminator.trainable = False
noise = Input((noise_size,))
labels = Input((num_classes,))
img = generator([noise, labels])
validity = discriminator([img, labels])
combined = Model([noise, labels], validity)
combined.compile(optimizer, loss=critic_loss)
return generator, discriminator, combined
```
### Function to sample and save generated images
```
#FIXME this is old code, unused
def sample_imgs(generator, noise_size, step, plot_img=True, cond=False, num_classes=10):
np.random.seed(0)
r, c = num_classes, 10
if cond:
noise = np.random.normal(0, 1, (c, noise_size))
noise = np.tile(noise, (r, 1))
sampled_labels = np.arange(r).reshape(-1, 1)
sampled_labels = to_categorical(sampled_labels, r)
sampled_labels = np.repeat(sampled_labels, c, axis=0)
imgs = generator.predict([noise, sampled_labels])
else:
noise = np.random.normal(0, 1, (r*c, noise_size))
imgs = generator.predict_on_batch(noise)
imgs = imgs / 2 + 0.5
imgs = np.reshape(imgs, [r, c, imgs.shape[1], imgs.shape[2], -1])
figsize = 1 * c, 1 * r
fig, axs = plt.subplots(r, c, figsize=figsize)
for i in range(r):
for j in range(c):
img = imgs[i, j] if len(imgs.shape) == 4 else imgs[i, j, :, :, 0]
axs[i, j].imshow(img, cmap='gray')
axs[i, j].axis('off')
plt.subplots_adjust(wspace=0.1, hspace=0.1)
fig.savefig(f'/content/images/{step}.png')
if plot_img:
plt.show()
plt.close()
np.random.seed(None)
rows, cols = 4, 7
sampled_labels = np.array([0.0 if i >= rows*cols/2 else 1.0 for i in range(rows*cols)])
def sample_imgs_(generator, g_loss_buffer, noise_size, step):
test_images = generator.predict([test_noise, sampled_labels])
fig = plt.figure(1, figsize=(2*1.2*cols, 1.2*rows))
gs = gridspec.GridSpec(rows, 2*cols)
for j in range(rows*cols):
plt.subplot(gs[j//cols, j%cols])#invert!
plt.imshow(test_images[j-1]/2.0 + 0.5)
axs = plt.gca()
if j >= rows*cols/2:
axs.tick_params(axis=u'both', which=u'both',length=5)
axs.set_xticks([])
axs.set_yticks([])
else:
axs.axis('off')
#plot error here
plt.subplot(gs[:,cols+1:])
plt.plot(g_loss_buffer)
plt.grid(True)
plt.subplots_adjust(wspace=0.1, hspace=0.1)
fig.savefig('/content/images/{}.png'.format(step))
plt.show()
```
### Function to train the models
Select the save step for debugging images
```
SAVE_STEP = 5
def train(models, data_loader, noise_size, img_shape, num_classes, batch_size, steps):
generator, discriminator, combined = models
pos_loader, neg_loader = data_loader
#CHANGE delete fashion mnist
g_loss_buffer = []
for step in range(1, steps + 1):
for i in range(n_critic):
# train discriminator
if (step + i) % 2 == 0:
real_imgs, labels = next(pos_loader), np.ones(batch_size)
else:
real_imgs, labels = next(neg_loader), np.zeros(batch_size)
noise = np.random.normal(0, 1, (batch_size, noise_size))
gen_imgs = generator.predict([noise, labels])
gen_validity = np.ones(batch_size)
real_validity = - np.ones(batch_size)
r_loss = discriminator.train_on_batch([real_imgs, labels], real_validity)
g_loss = discriminator.train_on_batch([gen_imgs, labels], gen_validity)
disc_loss = np.add(r_loss, g_loss) / 2
# clipping
for layer in discriminator.layers:
weights = layer.get_weights()
clipped_weights = [np.clip(w, -c, c) for w in weights]
layer.set_weights(clipped_weights)
# train generator
noise = np.random.normal(0, 1, (batch_size, noise_size))
gen_loss = combined.train_on_batch([noise, labels], -np.ones(batch_size))
g_loss_buffer.append(gen_loss)
#print progress
if step % SAVE_STEP == 0:
print('step: %d, D_loss: %f, G_loss: %f' % (step, disc_loss, gen_loss))
# save_samples
if step % SAVE_STEP == 0:
sample_imgs_(generator, g_loss_buffer, noise_size, step)
# save model
if step % 1000 == 0:
generator.save('faces_g_step{}.h5'.format(step))
```
### Define hyperparameters
```
%rm -r /content/images
%mkdir /content/images
noise_size = 100
img_shape = 64, 64, 3 #CHANGE
num_classes = 1 #CHANGE
batch_size = 32
steps = 100000
c = 0.01
n_critic = 5
#CHANGE
category = 'Male'
data_loader = get_generators(img_shape, batch_size, category, download=False, crop=(150, 150))
test_noise = np.random.normal(size=(rows*cols, noise_size))
```
### Generate the models
```
generator = build_generator(noise_size, img_shape, num_classes)
discriminator = build_discriminator(img_shape, num_classes)
compiled_models = get_compiled_models(generator, discriminator, noise_size, num_classes)
```
### Train the models
```
train(compiled_models, data_loader, noise_size, img_shape, num_classes, batch_size, steps)
```
## Plot resutls
### Display samples
Let's start by checking the images that we have stored.
```
%ls /content/images
```
You can check any image you wish by doing:
```
image_number = SAVE_STEP
ipyImage('/content/images/%d.png' % image_number)
```
### Do an animation
Probably the best way of showing the training process is by doing an animation with all the images. The next cell will do it for you.
```
path = '/content/images/{}.png'
class AnimObject(object):
def __init__(self, images):
print(len(images))
self.fig, self.ax = plt.subplots()
self.ax.set_title("")
self.fig.set_size_inches((20, 10))
self.plot = plt.imshow(images[0])
plt.tight_layout()
self.images = images
def init(self):
self.plot.set_data(self.images[0])
self.ax.grid(False)
return (self.plot,)
def animate(self, i):
self.plot.set_data(self.images[i])
self.ax.grid(False)
self.ax.set_xticks([])
self.ax.set_yticks([])
self.ax.set_title("index {}".format(i))
return (self.plot,)
def get_figures(template, indices):
import os.path
images = []
for index in indices:
if os.path.isfile(template.format(index)):
images.append(Image.open(template.format(index)))
return images
images = get_figures("/content/images/{}.png",
range(0, SAVE_STEP * len(listdir('/content/images')) + 1, SAVE_STEP))
print(images)
animobject = AnimObject(images)
anim = animation.FuncAnimation(
animobject.fig,
animobject.animate,
frames=len(animobject.images),
interval=150,
blit=True)
HTML(anim.to_jshtml())
```
## Download images and generator
This code is to download the trained model to store it locally on your computer. You probably shouldn't bother about it.
```
gen_path = '/content/fashion_cond_w_dcgan_gen.h5'
generator.save(gen_path)
from google.colab import files
files.download(gen_path)
```
|
github_jupyter
|
#%%capture
# download CelebA data
!wget https://raw.githubusercontent.com/yunjey/StarGAN/master/download.sh
!bash download.sh celeba
!echo "There are `ls data/celeba/images | wc -l` images"
from keras.models import Model
from keras.layers import Input, Dense, BatchNormalization, Reshape, Flatten
from keras.layers.advanced_activations import LeakyReLU
from keras.datasets import fashion_mnist
from keras.optimizers import Adam, RMSprop
from keras.layers import Conv2D, UpSampling2D, concatenate, Lambda
from keras.initializers import RandomNormal
from keras.utils import to_categorical
import keras.backend as K
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
from PIL import Image
from matplotlib import animation, rc
from IPython.display import Image as ipyImage
from IPython.display import HTML
from os import listdir
# templates
DATA_DIR = 'data/celeba/'
IMGS_DIR = '{}images/'.format(DATA_DIR)
CSV_FILE = '{}list_attr_celeba.txt'.format(DATA_DIR)
#@title Data loader
import numpy as np
import cv2
import pandas as pd
from itertools import cycle
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
from random import shuffle
import random
def download_celeba(data_dir, imgs_dir):
%rm -r {data_dir}
%mkdir {data_dir}
%cd {data_dir}
!pip install pydrive
from shutil import unpack_archive
# these classes allow you to request the Google drive API
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from oauth2client.client import GoogleCredentials
from googleapiclient.http import MediaIoBaseDownload
from google.colab import auth
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
file_id_dict = {
'imgs.zip': '0B7EVK8r0v71pZjFTYXZWM3FlRnM',
'attributes.txt': '0B7EVK8r0v71pblRyaVFSWGxPY0U'
}
for file_, id_ in file_id_dict.items():
downloaded = drive.CreateFile({'id': id_})
downloaded.GetContentFile(file_)
# %rm -r {imgs_dir}*
unpack_archive('imgs.zip', imgs_dir)
%rm imgs.zip
def get_imgs_lists(df, category):
pos_img_names = df.index[df[category] == 1]
neg_img_names = df.index[df[category] == -1]
return list(pos_img_names), list(neg_img_names)
def preprocess_img(img, img_shape, crop=None):
img = img / 127.5 - 1
if crop is not None:
cropx, cropy = crop
y,x,_ = img.shape
startx = x//2-(cropx//2)
starty = y//2-(cropy//2)
img = img[starty:starty+cropy,startx:startx+cropx,:]
img = cv2.resize(img, img_shape[:2])
return img
def single_core_category_generator(img_paths, img_shape):
imgs = np.zeros((len(img_paths), *img_shape))
for i, img_path in enumerate(img_paths):
img = mpimg.imread(img_path)
imgs[i] = preprocess_img(img, img_shape)
return imgs
def mp_category_generator(imgs_dir, img_names, img_shape, batch_size):
import multiprocessing as mp
cpu_num = min(mp.cpu_count(), batch_size)
def chunks(lst, n):
for i in range(n):
yield lst[i::n]
shuffle(img_names)
img_names = cycle(img_names)
while True:
imgs = np.zeros((batch_size, *img_shape))
batch_paths = [imgs_dir + next(img_names) for _ in range(batch_size)]
batch_paths = chunks(batch_paths, cpu_num)
pool = mp.Pool(processes=cpu_num)
imgs = [pool.apply(single_core_category_generator,
args=(next(batch_paths), img_shape)) for i in range(cpu_num)]
pool.terminate()
imgs = np.concatenate(imgs)
yield imgs
def category_generator(imgs_dir, img_names, img_shape, batch_size, crop=None):
shuffle(img_names)
img_names = cycle(img_names)
while True:
imgs = np.zeros((batch_size, *img_shape))
for i in range(batch_size):
img_path = imgs_dir + next(img_names)
img = mpimg.imread(img_path)
imgs[i] = preprocess_img(img, img_shape, crop=crop)
yield imgs
def get_generators(img_shape, batch_size, category=None, download=True, crop=None):
data_dir = 'data/'
imgs_dir = '{}celeba/images/'.format(data_dir)
if download:
download_celeba(data_dir, imgs_dir)
imgs_dir = imgs_dir
df = pd.read_csv('{}celeba/list_attr_celeba.txt'.format(data_dir), sep=' +', skiprows=[0])
img_names = list(df.index)
if category is None:
gen = category_generator(imgs_dir, img_names, img_shape, batch_size)
return gen
pos_img_names, neg_img_names = get_imgs_lists(df, category)
pos_gen = category_generator(imgs_dir, pos_img_names, img_shape, batch_size, crop=crop)
neg_gen = category_generator(imgs_dir, neg_img_names, img_shape, batch_size, crop=crop)
return pos_gen, neg_gen
def build_generator(noise_size, img_shape, num_classes):
# block: Conv, Batch norm, Upsampling
k_size = 5, 5
k_init = RandomNormal(0, 0.01)
filters = 1024 #CHANGE
noise = Input((noise_size,))
labels = Input((num_classes,))
model_input = concatenate([noise, labels])
x = Dense(4*4*filters, kernel_initializer=k_init, activation='relu')(model_input)
x = Reshape((4, 4, filters))(x) # 4, 4
x = BatchNormalization()(x)
x = UpSampling2D()(x) # 8, 8
x = Conv2D(filters // 2, k_size, padding='same', kernel_initializer=k_init, activation='relu')(x)
x = BatchNormalization()(x)
x = UpSampling2D()(x) # 16, 16
x = Conv2D(filters // 4, k_size, padding='same', kernel_initializer=k_init, activation='relu')(x)
x = BatchNormalization()(x)
x = UpSampling2D()(x) # 32, 32
#CHANGE
x = Conv2D(filters // 8, k_size, padding='same', kernel_initializer=k_init, activation='relu')(x)
x = BatchNormalization()(x)
x = UpSampling2D()(x) # 64, 64
img = Conv2D(img_shape[-1], k_size, padding='same', kernel_initializer=k_init, activation='tanh')(x)
generator = Model([noise, labels], img)
return generator
def build_discriminator(img_shape, num_classes):
# block: Conv, Batch norm, LeakyRelu
k_size = 5, 5
k_init = RandomNormal(0, 0.01)
filters = 1024 #CHANGE
img = Input(img_shape) # 64, 64, 3
labels = Input((num_classes,)) # 10
n_labels = Reshape((1, 1, -1))(labels) # (batch_size), 1, 1, 10
n_labels = Lambda(lambda x: K.tile(x, [1, img_shape[0], img_shape[1], 1]))(n_labels) # (batch_size), 64, 64, 10
model_input = concatenate([img, n_labels]) # 64, 64, ? (1 + 10)
#CHANGE
x = Conv2D(filters // 8, k_size, strides=(2, 2), padding='same', kernel_initializer=k_init)(model_input)
x = BatchNormalization()(x)
x = LeakyReLU(alpha=0.2)(x) #32, 32
x = Conv2D(filters // 4, k_size, strides=(2, 2), padding='same', kernel_initializer=k_init)(x)#CHANGE, model_input -> x
x = BatchNormalization()(x)
x = LeakyReLU(alpha=0.2)(x) #16, 16
x = Conv2D(filters // 2, k_size, strides=(2, 2), padding='same', kernel_initializer=k_init)(x)
x = BatchNormalization()(x)
x = LeakyReLU(alpha=0.2)(x) # 8, 8
x = Conv2D(filters, k_size, strides=(2, 2), padding='same', kernel_initializer=k_init)(x)
x = BatchNormalization()(x)
x = LeakyReLU(alpha=0.2)(x) # 4, 4
x = Flatten()(x)
validity = Dense(3, activation='linear', kernel_initializer=k_init)(x) #CHANGE
discriminator = Model([img, labels], validity)
return discriminator
def critic_loss(y_true, y_pred):
return K.mean(y_true * y_pred)
def get_compiled_models(generator, discriminator, noise_size, num_classes):
optimizer = RMSprop(0.0002)
discriminator.compile(optimizer, loss=critic_loss)
discriminator.trainable = False
noise = Input((noise_size,))
labels = Input((num_classes,))
img = generator([noise, labels])
validity = discriminator([img, labels])
combined = Model([noise, labels], validity)
combined.compile(optimizer, loss=critic_loss)
return generator, discriminator, combined
#FIXME this is old code, unused
def sample_imgs(generator, noise_size, step, plot_img=True, cond=False, num_classes=10):
np.random.seed(0)
r, c = num_classes, 10
if cond:
noise = np.random.normal(0, 1, (c, noise_size))
noise = np.tile(noise, (r, 1))
sampled_labels = np.arange(r).reshape(-1, 1)
sampled_labels = to_categorical(sampled_labels, r)
sampled_labels = np.repeat(sampled_labels, c, axis=0)
imgs = generator.predict([noise, sampled_labels])
else:
noise = np.random.normal(0, 1, (r*c, noise_size))
imgs = generator.predict_on_batch(noise)
imgs = imgs / 2 + 0.5
imgs = np.reshape(imgs, [r, c, imgs.shape[1], imgs.shape[2], -1])
figsize = 1 * c, 1 * r
fig, axs = plt.subplots(r, c, figsize=figsize)
for i in range(r):
for j in range(c):
img = imgs[i, j] if len(imgs.shape) == 4 else imgs[i, j, :, :, 0]
axs[i, j].imshow(img, cmap='gray')
axs[i, j].axis('off')
plt.subplots_adjust(wspace=0.1, hspace=0.1)
fig.savefig(f'/content/images/{step}.png')
if plot_img:
plt.show()
plt.close()
np.random.seed(None)
rows, cols = 4, 7
sampled_labels = np.array([0.0 if i >= rows*cols/2 else 1.0 for i in range(rows*cols)])
def sample_imgs_(generator, g_loss_buffer, noise_size, step):
test_images = generator.predict([test_noise, sampled_labels])
fig = plt.figure(1, figsize=(2*1.2*cols, 1.2*rows))
gs = gridspec.GridSpec(rows, 2*cols)
for j in range(rows*cols):
plt.subplot(gs[j//cols, j%cols])#invert!
plt.imshow(test_images[j-1]/2.0 + 0.5)
axs = plt.gca()
if j >= rows*cols/2:
axs.tick_params(axis=u'both', which=u'both',length=5)
axs.set_xticks([])
axs.set_yticks([])
else:
axs.axis('off')
#plot error here
plt.subplot(gs[:,cols+1:])
plt.plot(g_loss_buffer)
plt.grid(True)
plt.subplots_adjust(wspace=0.1, hspace=0.1)
fig.savefig('/content/images/{}.png'.format(step))
plt.show()
SAVE_STEP = 5
def train(models, data_loader, noise_size, img_shape, num_classes, batch_size, steps):
generator, discriminator, combined = models
pos_loader, neg_loader = data_loader
#CHANGE delete fashion mnist
g_loss_buffer = []
for step in range(1, steps + 1):
for i in range(n_critic):
# train discriminator
if (step + i) % 2 == 0:
real_imgs, labels = next(pos_loader), np.ones(batch_size)
else:
real_imgs, labels = next(neg_loader), np.zeros(batch_size)
noise = np.random.normal(0, 1, (batch_size, noise_size))
gen_imgs = generator.predict([noise, labels])
gen_validity = np.ones(batch_size)
real_validity = - np.ones(batch_size)
r_loss = discriminator.train_on_batch([real_imgs, labels], real_validity)
g_loss = discriminator.train_on_batch([gen_imgs, labels], gen_validity)
disc_loss = np.add(r_loss, g_loss) / 2
# clipping
for layer in discriminator.layers:
weights = layer.get_weights()
clipped_weights = [np.clip(w, -c, c) for w in weights]
layer.set_weights(clipped_weights)
# train generator
noise = np.random.normal(0, 1, (batch_size, noise_size))
gen_loss = combined.train_on_batch([noise, labels], -np.ones(batch_size))
g_loss_buffer.append(gen_loss)
#print progress
if step % SAVE_STEP == 0:
print('step: %d, D_loss: %f, G_loss: %f' % (step, disc_loss, gen_loss))
# save_samples
if step % SAVE_STEP == 0:
sample_imgs_(generator, g_loss_buffer, noise_size, step)
# save model
if step % 1000 == 0:
generator.save('faces_g_step{}.h5'.format(step))
%rm -r /content/images
%mkdir /content/images
noise_size = 100
img_shape = 64, 64, 3 #CHANGE
num_classes = 1 #CHANGE
batch_size = 32
steps = 100000
c = 0.01
n_critic = 5
#CHANGE
category = 'Male'
data_loader = get_generators(img_shape, batch_size, category, download=False, crop=(150, 150))
test_noise = np.random.normal(size=(rows*cols, noise_size))
generator = build_generator(noise_size, img_shape, num_classes)
discriminator = build_discriminator(img_shape, num_classes)
compiled_models = get_compiled_models(generator, discriminator, noise_size, num_classes)
train(compiled_models, data_loader, noise_size, img_shape, num_classes, batch_size, steps)
%ls /content/images
image_number = SAVE_STEP
ipyImage('/content/images/%d.png' % image_number)
path = '/content/images/{}.png'
class AnimObject(object):
def __init__(self, images):
print(len(images))
self.fig, self.ax = plt.subplots()
self.ax.set_title("")
self.fig.set_size_inches((20, 10))
self.plot = plt.imshow(images[0])
plt.tight_layout()
self.images = images
def init(self):
self.plot.set_data(self.images[0])
self.ax.grid(False)
return (self.plot,)
def animate(self, i):
self.plot.set_data(self.images[i])
self.ax.grid(False)
self.ax.set_xticks([])
self.ax.set_yticks([])
self.ax.set_title("index {}".format(i))
return (self.plot,)
def get_figures(template, indices):
import os.path
images = []
for index in indices:
if os.path.isfile(template.format(index)):
images.append(Image.open(template.format(index)))
return images
images = get_figures("/content/images/{}.png",
range(0, SAVE_STEP * len(listdir('/content/images')) + 1, SAVE_STEP))
print(images)
animobject = AnimObject(images)
anim = animation.FuncAnimation(
animobject.fig,
animobject.animate,
frames=len(animobject.images),
interval=150,
blit=True)
HTML(anim.to_jshtml())
gen_path = '/content/fashion_cond_w_dcgan_gen.h5'
generator.save(gen_path)
from google.colab import files
files.download(gen_path)
| 0.654453 | 0.938576 |
Here, we'll generate an object set with some number of classes, each class having
a different underlying distribution of poses. Objects are points living in 2D
and don't interfere with each other.
We'll reconstruct the distribution of these objects from an observed set, and use
that distribution to imagine new environments.
```
%matplotlib inline
%load_ext autoreload
%autoreload 2
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import numpy as np
import scipy as sp
import scipy.stats
import time
import yaml
from pydrake.all import (RigidBodyTree, RigidBody)
# Generate a ton of reasonable object arrangements, or load them from a file
LOAD_PREGENERATED_ARRANGEMENTS = False
SAVE_FILE = "20180621_saved_arrangements.txt"
N_ENVIRONMENTS = 1000
N_CLASSES = 4
np.random.seed(42)
# These environments will spawn objects
# inside 1x1 unit boxes with offset [class_type % 2, class_type / 2].
# (That is, each class spawns inside its own unique box)
def generate_environment():
environment = {}
n_objects = np.random.randint(20)
environment["n_objects"] = n_objects
for k in range(n_objects):
obj_name = "obj_%04d" % k
environment[obj_name] = {}
class_type = np.random.randint(N_CLASSES)
pose = np.random.random(2) + np.array([class_type%2, class_type/2])
environment[obj_name]["pose"] = pose.tolist()
environment[obj_name]["class"] = class_type
return environment
if LOAD_PREGENERATED_ARRANGEMENTS:
with open(SAVE_FILE, "r") as f:
environments = yaml.load(f)
N_ENVIRONMENTS = environments["n_environments"]
print("Loaded %d environments from file %s" % (N_ENVIRONMENTS, SAVE_FILE))
else:
# Generate arrangements
environments = {}
environments["n_environments"] = N_ENVIRONMENTS
for i in range(N_ENVIRONMENTS):
env_name = "env_%04d" % i
environments[env_name] = generate_environment()
with open(SAVE_FILE, "w") as f:
yaml.dump(environments, f)
print("Saved %d environments to file %s" % (N_ENVIRONMENTS, SAVE_FILE))
# Draw a few example scenes
def draw_environment(environment, ax):
pltcolor = plt.cm.rainbow(np.linspace(0, 1, N_CLASSES))
kr = range(environment["n_objects"])
if len(kr) > 0:
poses = np.vstack([environment["obj_%04d" % k]["pose"] for k in kr]).T.reshape([2, len(kr)])
classes = [environment["obj_%04d" % k]["class"] for k in kr]
ax.scatter(poses[0, :], poses[1, :], alpha=0.8,
c=[pltcolor[k] for k in classes], s=40.)
for k in range(N_CLASSES):
offset = np.array([k%2, k/2])
patch = patches.Rectangle(offset, 1., 1., fill=True, color=pltcolor[k],
linestyle='solid', linewidth=2, alpha=0.3)
ax.add_patch(patch)
plt.figure().set_size_inches(12, 12)
plt.title("Selection of environments from original distribution")
N = 5
for i in range(N):
for j in range(N):
plt.subplot(N, N, i*N+j+1)
draw_environment(environments["env_%04d" % (i*N+j)], plt.gca())
plt.grid(True)
plt.xlim(-.5, 2.5)
plt.ylim(-.5, 2.5)
plt.tight_layout()
```
## Fitting distributions to generated scene data
We're ultimately interested in sampling a number of objects $n$, a set of object classes $c_i$, and a set of object poses $p_i$ $\{[c_0, p_0], ..., [c_n, p_n]\}$.
They have joint distribution $p(n, c, p)$, which we factorize $p(n)\Pi_i\left[p(p_i | c_i)p(c_i)\right]$ -- that is, draw the number of objects and class of each object independently, and then draw each object pose independently based on a class-specific distribution.
So the distributions we need to fit are:
- The distribution of object number $p(n)$, which we'll just draw up a histogram
- The distribution of individual object class $p(c_i)$, which we'll also just draw up a histogram
- The distribution of object pose based on class $p(p_i | c_i)$, which we'll fit with KDE
```
# Get statistics for # object occurance rate and classes
object_number_occurances = np.zeros(N_ENVIRONMENTS)
object_class_occurances = np.zeros(N_CLASSES)
for i in range(N_ENVIRONMENTS):
env = environments["env_%04d" % i]
object_number_occurances[i] = env["n_objects"]
for k in range(env["n_objects"]):
object_class_occurances[env["obj_%04d" % k]["class"]] += 1
n_hist, n_hist_bins = np.histogram(object_number_occurances,
bins=range(int(np.ceil(np.max(object_number_occurances)))+2))
n_pdf = n_hist.astype(np.float64)/np.sum(n_hist)
plt.subplot(2, 1, 1)
plt.bar(n_hist_bins[:-1], n_pdf, align="edge")
plt.xlabel("# objects")
plt.ylabel("occurance rate")
plt.subplot(2, 1, 2)
class_pdf = object_class_occurances / np.sum(object_class_occurances)
plt.bar(range(N_CLASSES), class_pdf, align="edge")
plt.xlabel("object class")
plt.ylabel("occurance rate")
plt.tight_layout()
# Build statistics for object poses per each object class
object_poses_per_class = []
# Useful to have for preallocating occurance vectors
max_num_objects_in_any_environment = int(np.max(object_number_occurances))
for class_k in range(N_CLASSES):
# Overallocate, we'll resize when we're done
poses = np.zeros((2, max_num_objects_in_any_environment*N_ENVIRONMENTS))
total_num_objects = 0
for i in range(N_ENVIRONMENTS):
env = environments["env_%04d" % i]
for k in range(env["n_objects"]):
obj = env["obj_%04d" % k]
if obj["class"] == class_k:
poses[:, total_num_objects] = obj["pose"][:]
total_num_objects += 1
object_poses_per_class.append(poses[:, :total_num_objects])
class_kde_fits = []
plt.figure().set_size_inches(12, 12)
plt.title("Distribution over space, per object class")
for class_k in range(N_CLASSES):
print("Computing KDE for class %d" % class_k)
poses = object_poses_per_class[class_k]
kde_fit = sp.stats.gaussian_kde(poses)
class_kde_fits.append(kde_fit)
xmin = -0.5
xmax = 2.5
ymin = -.5
ymax = 2.5
X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]
positions = np.vstack([X.ravel(), Y.ravel()])
Z = np.reshape(kde_fit(positions).T, X.shape)
plt.subplot(2, 2, class_k+1)
plt.title("Class %d" % class_k)
plt.gca().imshow(np.rot90(Z), vmin=0., vmax=1.,
cmap=plt.cm.gist_earth_r,
extent=[xmin, xmax, ymin, ymax])
plt.scatter(poses[0, :], poses[1, :], s=0.1, c=[1., 0., 1.])
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
```
## Sampling new scenes from this data
We can generate new scenes by sampling up the dependency tree:
1) First sample # of objects
2) Then sample a class for every object, independently
3) Given each object's class, sample its location
We can also evaluate the likelihood of each generated sample
to get an idea how "typical" they are, by finding the likelihood
of each object given its generated position and class and combining
them. However, we have to normalize by the maximum possible likelihood
for an object of that class for every object for the comparison between
two sets of objects to make sense.
```
n_cdf = np.cumsum(n_pdf)
class_cdf = np.cumsum(class_pdf)
# Calculate maximum likelihood value for each class
classwise_max_likelihoods = np.zeros(N_CLASSES)
for i in range(N_CLASSES):
# Evaluate the PDF at a bunch of sample points
xmin = -0.5
xmax = 2.5
ymin = -0.5
ymax = 2.5
X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]
positions = np.vstack([X.ravel(), Y.ravel()])
classwise_max_likelihoods[i] = (np.max(class_kde_fits[i](positions)))
print "Classwise max likelihoods: ", classwise_max_likelihoods
plt.figure().set_size_inches(12, 12)
plt.title("Generated environments matching original distribution")
np.random.seed(42)
N = 5
for i in range(N):
for j in range(N):
total_log_likelihood = 0.
n_objects = np.argmax(n_cdf >= np.random.random())
total_log_likelihood += np.log(n_pdf[n_objects])
environment = {"n_objects": n_objects}
lln = 0
for object_k in range(n_objects):
obj_name = "obj_%04d" % object_k
obj_class = np.argmax(class_cdf >= np.random.random())
total_log_likelihood += np.log(class_pdf[obj_class] / np.max(class_pdf))
obj_pose = class_kde_fits[obj_class].resample([1]).T
total_log_likelihood += (class_kde_fits[obj_class].logpdf(obj_pose) -
np.log(classwise_max_likelihoods[obj_class]))
environment[obj_name] = {"pose": obj_pose,
"class": obj_class}
plt.subplot(N, N, i*N+j+1)
draw_environment(environment, plt.gca())
plt.grid(True)
plt.title("LL: %f" % total_log_likelihood)
plt.xlim(-0.5, 2.5)
plt.ylim(-0.5, 2.5)
print "TODO: Log likelihood is still probably wrong... the scaling with N is weird."
plt.tight_layout()
```
As is visible above, this technique generates reasonable looking scenes. It does, however, generate "impossible" scenes (placing objects slightly out of bounds) with some regularity, since the KDE doesn't capture the sharp edge of the feasible set of object poses.
I attempt to calculate log likelihood scores for each arrangement by calculating
$$ p(c, p, n) = p(n) * {\Large \Pi_{i}^{n}} \left[ \dfrac{p(p_i | c_i)}{\max_{\hat{p}}{p(\hat{p} | c_i})} \dfrac{p(c_i)}{\max_{\hat{c}} p(c)} \right] $$
(which includes normalization on a per-object and per-class basis to make comparison between scenes with different N possible). But I'm not convinced this is right, yet...
|
github_jupyter
|
%matplotlib inline
%load_ext autoreload
%autoreload 2
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import numpy as np
import scipy as sp
import scipy.stats
import time
import yaml
from pydrake.all import (RigidBodyTree, RigidBody)
# Generate a ton of reasonable object arrangements, or load them from a file
LOAD_PREGENERATED_ARRANGEMENTS = False
SAVE_FILE = "20180621_saved_arrangements.txt"
N_ENVIRONMENTS = 1000
N_CLASSES = 4
np.random.seed(42)
# These environments will spawn objects
# inside 1x1 unit boxes with offset [class_type % 2, class_type / 2].
# (That is, each class spawns inside its own unique box)
def generate_environment():
environment = {}
n_objects = np.random.randint(20)
environment["n_objects"] = n_objects
for k in range(n_objects):
obj_name = "obj_%04d" % k
environment[obj_name] = {}
class_type = np.random.randint(N_CLASSES)
pose = np.random.random(2) + np.array([class_type%2, class_type/2])
environment[obj_name]["pose"] = pose.tolist()
environment[obj_name]["class"] = class_type
return environment
if LOAD_PREGENERATED_ARRANGEMENTS:
with open(SAVE_FILE, "r") as f:
environments = yaml.load(f)
N_ENVIRONMENTS = environments["n_environments"]
print("Loaded %d environments from file %s" % (N_ENVIRONMENTS, SAVE_FILE))
else:
# Generate arrangements
environments = {}
environments["n_environments"] = N_ENVIRONMENTS
for i in range(N_ENVIRONMENTS):
env_name = "env_%04d" % i
environments[env_name] = generate_environment()
with open(SAVE_FILE, "w") as f:
yaml.dump(environments, f)
print("Saved %d environments to file %s" % (N_ENVIRONMENTS, SAVE_FILE))
# Draw a few example scenes
def draw_environment(environment, ax):
pltcolor = plt.cm.rainbow(np.linspace(0, 1, N_CLASSES))
kr = range(environment["n_objects"])
if len(kr) > 0:
poses = np.vstack([environment["obj_%04d" % k]["pose"] for k in kr]).T.reshape([2, len(kr)])
classes = [environment["obj_%04d" % k]["class"] for k in kr]
ax.scatter(poses[0, :], poses[1, :], alpha=0.8,
c=[pltcolor[k] for k in classes], s=40.)
for k in range(N_CLASSES):
offset = np.array([k%2, k/2])
patch = patches.Rectangle(offset, 1., 1., fill=True, color=pltcolor[k],
linestyle='solid', linewidth=2, alpha=0.3)
ax.add_patch(patch)
plt.figure().set_size_inches(12, 12)
plt.title("Selection of environments from original distribution")
N = 5
for i in range(N):
for j in range(N):
plt.subplot(N, N, i*N+j+1)
draw_environment(environments["env_%04d" % (i*N+j)], plt.gca())
plt.grid(True)
plt.xlim(-.5, 2.5)
plt.ylim(-.5, 2.5)
plt.tight_layout()
# Get statistics for # object occurance rate and classes
object_number_occurances = np.zeros(N_ENVIRONMENTS)
object_class_occurances = np.zeros(N_CLASSES)
for i in range(N_ENVIRONMENTS):
env = environments["env_%04d" % i]
object_number_occurances[i] = env["n_objects"]
for k in range(env["n_objects"]):
object_class_occurances[env["obj_%04d" % k]["class"]] += 1
n_hist, n_hist_bins = np.histogram(object_number_occurances,
bins=range(int(np.ceil(np.max(object_number_occurances)))+2))
n_pdf = n_hist.astype(np.float64)/np.sum(n_hist)
plt.subplot(2, 1, 1)
plt.bar(n_hist_bins[:-1], n_pdf, align="edge")
plt.xlabel("# objects")
plt.ylabel("occurance rate")
plt.subplot(2, 1, 2)
class_pdf = object_class_occurances / np.sum(object_class_occurances)
plt.bar(range(N_CLASSES), class_pdf, align="edge")
plt.xlabel("object class")
plt.ylabel("occurance rate")
plt.tight_layout()
# Build statistics for object poses per each object class
object_poses_per_class = []
# Useful to have for preallocating occurance vectors
max_num_objects_in_any_environment = int(np.max(object_number_occurances))
for class_k in range(N_CLASSES):
# Overallocate, we'll resize when we're done
poses = np.zeros((2, max_num_objects_in_any_environment*N_ENVIRONMENTS))
total_num_objects = 0
for i in range(N_ENVIRONMENTS):
env = environments["env_%04d" % i]
for k in range(env["n_objects"]):
obj = env["obj_%04d" % k]
if obj["class"] == class_k:
poses[:, total_num_objects] = obj["pose"][:]
total_num_objects += 1
object_poses_per_class.append(poses[:, :total_num_objects])
class_kde_fits = []
plt.figure().set_size_inches(12, 12)
plt.title("Distribution over space, per object class")
for class_k in range(N_CLASSES):
print("Computing KDE for class %d" % class_k)
poses = object_poses_per_class[class_k]
kde_fit = sp.stats.gaussian_kde(poses)
class_kde_fits.append(kde_fit)
xmin = -0.5
xmax = 2.5
ymin = -.5
ymax = 2.5
X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]
positions = np.vstack([X.ravel(), Y.ravel()])
Z = np.reshape(kde_fit(positions).T, X.shape)
plt.subplot(2, 2, class_k+1)
plt.title("Class %d" % class_k)
plt.gca().imshow(np.rot90(Z), vmin=0., vmax=1.,
cmap=plt.cm.gist_earth_r,
extent=[xmin, xmax, ymin, ymax])
plt.scatter(poses[0, :], poses[1, :], s=0.1, c=[1., 0., 1.])
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
n_cdf = np.cumsum(n_pdf)
class_cdf = np.cumsum(class_pdf)
# Calculate maximum likelihood value for each class
classwise_max_likelihoods = np.zeros(N_CLASSES)
for i in range(N_CLASSES):
# Evaluate the PDF at a bunch of sample points
xmin = -0.5
xmax = 2.5
ymin = -0.5
ymax = 2.5
X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]
positions = np.vstack([X.ravel(), Y.ravel()])
classwise_max_likelihoods[i] = (np.max(class_kde_fits[i](positions)))
print "Classwise max likelihoods: ", classwise_max_likelihoods
plt.figure().set_size_inches(12, 12)
plt.title("Generated environments matching original distribution")
np.random.seed(42)
N = 5
for i in range(N):
for j in range(N):
total_log_likelihood = 0.
n_objects = np.argmax(n_cdf >= np.random.random())
total_log_likelihood += np.log(n_pdf[n_objects])
environment = {"n_objects": n_objects}
lln = 0
for object_k in range(n_objects):
obj_name = "obj_%04d" % object_k
obj_class = np.argmax(class_cdf >= np.random.random())
total_log_likelihood += np.log(class_pdf[obj_class] / np.max(class_pdf))
obj_pose = class_kde_fits[obj_class].resample([1]).T
total_log_likelihood += (class_kde_fits[obj_class].logpdf(obj_pose) -
np.log(classwise_max_likelihoods[obj_class]))
environment[obj_name] = {"pose": obj_pose,
"class": obj_class}
plt.subplot(N, N, i*N+j+1)
draw_environment(environment, plt.gca())
plt.grid(True)
plt.title("LL: %f" % total_log_likelihood)
plt.xlim(-0.5, 2.5)
plt.ylim(-0.5, 2.5)
print "TODO: Log likelihood is still probably wrong... the scaling with N is weird."
plt.tight_layout()
| 0.468304 | 0.808143 |
# This tutorials walks you through the process of creating new MXNet operators(or layers).
```
# Custom Op
import os
import mxnet as mx
import numpy as np
class Softmax(mx.operator.CustomOp):
def forward(self, is_train, req, in_data, out_data, aux):
x = in_data[0].asnumpy()
y = np.exp(x-x.max(axis=1).reshape((x.shape[0], 1)))
y /= y.sum(axis=1).reshape((x.shape[0], 1))
# At the end, we used CustomOp.assign to assign the resulting array y to out_data[0].
# It handles assignment based on the value of req, which can be ‘write’, ‘add’, or ‘null’.
self.assign(out_data[0], req[0], mx.nd.array(y))
def backard(self, req, out_grad, in_data, out_data, in_grad, aux):
l = in_data[1].asnumpy().ravel().astype(np.int)
y = out_data[0].asnumpy()
y[np.arange(l.shape[0]), l] -= 1.0
self.assign(in_grad[0], req[0], mx.nd.array(y))
# Still need to define its input/output format by subclassing mx.operator.CustomOpProp.
# First, register the new operator with the name ‘softmax’:
@mx.operator.register("softmax")
class SoftmaxProp(mx.operator.CustomOpProp):
def __init__(self):
super(SoftmaxProp, self).__init__(need_top_grad=False)
def list_arguments(self):
return ['data', 'label']
def list_outputs(self):
return ['output']
# provide infer_shape to declare the shape of the output/weight
# and check the consistency of the input shapes
def infer_shape(self, in_shape):
data_shape = in_shape[0]
label_shape = (in_shape[0][0],)
output_shape = in_shape[0]
# The infer_shape function should always return three lists in this order:
# inputs, outputs, and auxiliary states
return [data_shape, label_shape], [output_shape], []
def infer_type(self, in_type):
dtype = in_type[0]
return [dtype, dtype], [dtype], []
# Finally define a create_operator function that will be calle by the back end to create an instance of softmax:
def create_operator(self, ctx, shapes, dtypes):
return Softmax()
# To use the Custom operator:
# define mlp
data = mx.symbol.Variable('data')
fc1 = mx.symbol.FullyConnected(data = data, name='fc1', num_hidden=128)
act1 = mx.symbol.Activation(data = fc1, name='relu1', act_type="relu")
fc2 = mx.symbol.FullyConnected(data = act1, name = 'fc2', num_hidden = 64)
act2 = mx.symbol.Activation(data = fc2, name='relu2', act_type="relu")
fc3 = mx.symbol.FullyConnected(data = act2, name='fc3', num_hidden=10)
#mlp = mx.symbol.Softmax(data = fc3, name = 'softmax')
mlp = mx.symbol.Custom(data=fc3, name='softmax1', op_type='softmax') # op_type 对应前面 register 的 op 名称
import logging
train, val = get_mnist_iterator(batch_size=100, input_shape=(784, ))
logging.basicConfig(level=logging.DEBUG)
# MXNET_CPU_WORKER_NTHREADS must be greater than 1 for custom op to work on CPU
context = mx.cpu()
mod = mx.mod.Module(mlp, context=context)
mod.fit(train_data=train,
eval_data=val,
optimizer='sgd',
optimizer_params={'learning_rate':0.1, 'momentum':0.9, 'wd':0.00001},
num_epoch=10,
batch_end_callback=mx.callback.Speedometer(100, 100)
)
```
|
github_jupyter
|
# Custom Op
import os
import mxnet as mx
import numpy as np
class Softmax(mx.operator.CustomOp):
def forward(self, is_train, req, in_data, out_data, aux):
x = in_data[0].asnumpy()
y = np.exp(x-x.max(axis=1).reshape((x.shape[0], 1)))
y /= y.sum(axis=1).reshape((x.shape[0], 1))
# At the end, we used CustomOp.assign to assign the resulting array y to out_data[0].
# It handles assignment based on the value of req, which can be ‘write’, ‘add’, or ‘null’.
self.assign(out_data[0], req[0], mx.nd.array(y))
def backard(self, req, out_grad, in_data, out_data, in_grad, aux):
l = in_data[1].asnumpy().ravel().astype(np.int)
y = out_data[0].asnumpy()
y[np.arange(l.shape[0]), l] -= 1.0
self.assign(in_grad[0], req[0], mx.nd.array(y))
# Still need to define its input/output format by subclassing mx.operator.CustomOpProp.
# First, register the new operator with the name ‘softmax’:
@mx.operator.register("softmax")
class SoftmaxProp(mx.operator.CustomOpProp):
def __init__(self):
super(SoftmaxProp, self).__init__(need_top_grad=False)
def list_arguments(self):
return ['data', 'label']
def list_outputs(self):
return ['output']
# provide infer_shape to declare the shape of the output/weight
# and check the consistency of the input shapes
def infer_shape(self, in_shape):
data_shape = in_shape[0]
label_shape = (in_shape[0][0],)
output_shape = in_shape[0]
# The infer_shape function should always return three lists in this order:
# inputs, outputs, and auxiliary states
return [data_shape, label_shape], [output_shape], []
def infer_type(self, in_type):
dtype = in_type[0]
return [dtype, dtype], [dtype], []
# Finally define a create_operator function that will be calle by the back end to create an instance of softmax:
def create_operator(self, ctx, shapes, dtypes):
return Softmax()
# To use the Custom operator:
# define mlp
data = mx.symbol.Variable('data')
fc1 = mx.symbol.FullyConnected(data = data, name='fc1', num_hidden=128)
act1 = mx.symbol.Activation(data = fc1, name='relu1', act_type="relu")
fc2 = mx.symbol.FullyConnected(data = act1, name = 'fc2', num_hidden = 64)
act2 = mx.symbol.Activation(data = fc2, name='relu2', act_type="relu")
fc3 = mx.symbol.FullyConnected(data = act2, name='fc3', num_hidden=10)
#mlp = mx.symbol.Softmax(data = fc3, name = 'softmax')
mlp = mx.symbol.Custom(data=fc3, name='softmax1', op_type='softmax') # op_type 对应前面 register 的 op 名称
import logging
train, val = get_mnist_iterator(batch_size=100, input_shape=(784, ))
logging.basicConfig(level=logging.DEBUG)
# MXNET_CPU_WORKER_NTHREADS must be greater than 1 for custom op to work on CPU
context = mx.cpu()
mod = mx.mod.Module(mlp, context=context)
mod.fit(train_data=train,
eval_data=val,
optimizer='sgd',
optimizer_params={'learning_rate':0.1, 'momentum':0.9, 'wd':0.00001},
num_epoch=10,
batch_end_callback=mx.callback.Speedometer(100, 100)
)
| 0.590897 | 0.875999 |
<img src="images/strathsdr_banner.png" align="left">
# Hardware Accelerated Spectrum Analysis on RFSoC
----
<div class="alert alert-box alert-info">
Please use Jupyter Labs http://board_ip_address/lab for this notebook.
</div>
This notebook presents a flexible hardware accelerated Spectrum Analyzer Module for the Zynq UltraScale+ RFSoC. The Spectrum Analyzer Module was developed by the [University of Strathclyde](https://github.com/strath-sdr).
## Table of Contents
* [Introduction](#introduction)
* [Hardware Setup](#hardware-setup)
* [Software Setup](#software-setup)
* [Simple Tone Generation](#simple-tone-generation)
* [The Spectrum Analyzer](#the-spectrum-analyzer)
* [A Simple Example](#a-simple-example)
* [Conclusion](#conclusion)
## References
* [Xilinx, Inc, "USP RF Data Converter: LogiCORE IP Product Guide", PG269, v2.3, June 2020](https://www.xilinx.com/support/documentation/ip_documentation/usp_rf_data_converter/v2_3/pg269-rf-data-converter.pdf)
## Revision History
* **v1.0** | 12/02/2021 | Spectrum analyzer notebook
* **v1.1** | 15/04/2021 | Update spectral resolution and minimum bandwidth with new value
----
## Introduction <a class="anchor" id="introduction"></a>
The Zynq RFSoC contains high frequency samplers known as RF Data Converters (RF DCs). The RF DCs are tightly coupled with the Programmable Logic (PL), creating a high-throughput, low-latency path between the FPGA and analogue world. The Spectrum Analyzer Module employs the RF Analogue-to-Digital Converters (RF ADCs) to receive RF time domain signals. The received data is manipulated using spectral pre-processing techniques in the PL, to prepare it for frequency domain analysis and visualisation in the Processing System (PS).
A significant portion of the design has been implemented in the RFSoC's PL to prevent the PS from applying highly computational arithemtic. [Figure 1](#fig-1) presents a simple diagram illustrating the system overview for one spectrum analyzer channel. There is a Spectrum Analyzer Module for each available RF ADC channel in the design. The Spectrum Analyzers are also interfaced to their very own flexible decimator, allowing different sample rates to be configured for each channel.
<a class="anchor" id="fig-1"></a>
<figure>
<img src='images/spectrum_analyser_overview.png' height='50%' width='50%'/>
<figcaption><b>Figure 1: The RFSoC Spectrum Analyzer system overview.</b></figcaption>
</figure>
### Hardware Setup <a class="anchor" id="hardware-setup"></a>
Your RFSoC2x2 development board can host two Spectrum Analyzer Modules. There are four SMA interfaces on your board that are labelled DAC1, DAC2, ADC1, and ADC2. To setup your board for this demonstration, you can connect each channel in loopback as shown to the left of [Figure 2](#fig-2), or connect an antenna to one of the channels as shown to the right of [Figure 2](#fig-2).
Don't worry if you don't have an antenna. The default loopback configuration will still be very interesting and is connected as follows:
* Channel 0: DAC2 to ADC2
* Channel 1: DAC1 to ADC1
<a class="anchor" id="fig-2"></a>
<figure>
<img src='images/rfsoc2x2_setup.png' height='75%' width='75%'/>
<figcaption><b>Figure 2: RFSoC2x2 development board setup, (left) loopback mode, (right) with an antenna.</b></figcaption>
</figure>
If you have chosen to use an antenna, you should connect channel 1 in loopback mode and connect the antenna to ADC2. The loopback connection will be useful for validating the initalisation of the spectrum analyzer. **Do Not** attach your antenna to any SMA interfaces labelled DAC1 or DAC2.
<div class="alert alert-box alert-danger">
<b>Caution:</b>
In this demonstration, we generate tones using the RFSoC development board. Your device should be setup in loopback mode. You should understand that the RFSoC platform can also transmit RF signals wirelessly. Remember that unlicensed wireless transmission of RF signals may be illegal in your geographical location. Radio signals may also interfere with nearby devices, such as pacemakers and emergency radio equipment. Note that it is also illegal to intercept and decode particular RF signals. If you are unsure, please seek professional support.
</div>
### Software Setup <a class="anchor" id="software-setup"></a>
We're nearly finished setting up the demonstration system. The majority of the libraries used by the spectrum analyzer design are contained inside the RFSoC-SAM software package. We only need to run a few code cells to initialise the software environment.
The primary module for loading the Spectrum Analyzer design is contained inside `rfsoc_sam.overlay`. The class we are interested in using is `Overlay()`. During initialisation the class downloads the Spectrum Analyzer bitstream to the PL and configures the RF DCs and FPGA IP cores contained in our system. This process may take around a minute to complete.
**Run** the code cell below to load the RFSoC-SAM Overlay class.
```
from rfsoc_sam.overlay import Overlay
sam = Overlay()
```
When the RFSoC-SAM Overlay class is initialising, the setup script will also program the LMK and LMX low-jitter clock chips on the RFSoC2x2 to 122.8MHz and 409.6MHz respectively.
Lets now initialise the analyzer, and setup user control.
```
analyzer = sam.spectrum_analyzer()
```
----
## Simple Tone Generation <a class="anchor" id="simple-tone-generation"></a>
A simple amplitude controller is required to generate tones using the RF Digital-to-Analogue Converters (RF DACs). We use tone generation in this demonstration to provide a signal for the user to inspect when using the Spectrum Analyzer Module.
Run the code cell below to reveal a widget, which can be used to control the transmission frequency and amplitude.
```
analyzer.children[2]
```
## The Spectrum Analyzer <a class="anchor" id="the-spectrum-analyzer"></a>
We will now explore the hardware accelerated Spectrum Analyzer Module. It is worthwhile noting the analyzers capabilities below:
* The analyzer is capable of inspecting 1638.4MHz of bandwidth.
* It can achieve a maximum spectral resolution of 0.244140625kHz.
* The bandwidth is adjustable between 1638.4MHz and 1.6MHz.
* The range of inspection is between 0 to 4096MHz using higher order Nyquist techniques.
```
analyzer.children[1]
```
The Spectrum Analyzer Module contains a hardware accelerated FFT core, which can convert the RF sampled signal to the frequency domain using a range of different FFT lengths, $N = 64$ upto $N = 8192$. The frequency domain signal is further manipulated using a custom floating point processor to obtain the representative Power Spectral Density (PSD) or Power Spectrum. Furthermore, a hardware accelerated decibel (dB) converter is also used to condition the frequency domain signal for visual analysis.
Through the loopback connection, you should be able to use the Spectrum Analyzer Module to locate the tone you previously generated using the tone generator. If you have an antenna connected to your board, try and locate signals of interest using the Spectrum Analyzer's control widgets.
### A Simple Example <a class="anchor" id="a-simple-example"></a>
If you would like to enable stimulus for the spectrum analyzer, you can use your mobile phone to create WiFi traffic. Follow the steps below to create an interesting WiFi spectrum to visualise.
* Connect your mobile phone to an access point that uses WiFi.
* Then configure the spectrum analyzer for a centre frequency of 2400MHz and a decimation factor of 16.
* Switch on the spectrum analyzer and spectrogram.
* Use your phone to stream a video, or music. This will create WiFi traffic for inspection.
* Place your phone close to the RF ADC ports of the spectrum analyzer.
You should see a similar output as given in the [Figure 3](#fig-3) below.
<a class="anchor" id="fig-3"></a>
<figure>
<img src='images/wifi_example.jpg' height='50%' width='50%'/>
<figcaption><b>Figure 3: Capturing a WiFi signal using the Spectrum Analyser Module.</b></figcaption>
</figure>
## Conclusion <a class="anchor" id="conclusion"></a>
This notebook has presented a hardware accelerated Spectrum Analyzer Module for the RFSoC2x2 development board.
|
github_jupyter
|
from rfsoc_sam.overlay import Overlay
sam = Overlay()
analyzer = sam.spectrum_analyzer()
analyzer.children[2]
analyzer.children[1]
| 0.357231 | 0.967564 |
# CNN vs MLP
```
import keras
from keras.models import Sequential
from keras.utils import np_utils
from keras.preprocessing.image import ImageDataGenerator
from keras.layers import Dense, Flatten, Dropout, GlobalAveragePooling2D, \
GlobalAveragePooling2D, Input, BatchNormalization
from keras.layers import Conv2D, MaxPooling2D
from keras.datasets import cifar10
import numpy as np
import os
```
### Definitions
```
def read_data_original():
#READ DATA FRAME
(full_x_train, full_y_train), (full_x_test, full_y_test) = cifar10.load_data()
full_x_train = full_x_train.astype('float32')
#z-score
mean = np.mean(full_x_train,axis=(0,1,2,3))
std = np.std(full_x_train,axis=(0,1,2,3))
full_x_train = (full_x_train-mean)/(std+1e-7)
full_x_test = (full_x_test-mean)/(std+1e-7)
return (full_x_train, full_y_train), (full_x_test, full_y_test)
```
### Load data
```
(full_x_train, full_y_train), (full_x_test, full_y_test) = read_data_original()
num_classes = 10
full_y_train = np_utils.to_categorical(full_y_train,num_classes)
full_y_test = np_utils.to_categorical(full_y_test,num_classes)
```
##### Define data generator
```
datagen = ImageDataGenerator(
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=5,
# randomly shift images vertically (fraction of total height)
height_shift_range=5,
channel_shift_range=0.1, # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
validation_split=0.0)
datagen.fit(full_x_train)
```
### Build model
```
model = Sequential()
model.add(Conv2D(100, kernel_size=3, padding="same", activation="relu", input_shape=(32,32,3)))
model.add(Conv2D(100, kernel_size=3, padding="same", activation="relu"))
model.add(BatchNormalization())
model.add(MaxPooling2D())
model.add(Dropout(0.05))
model.add(Conv2D(200, kernel_size=3, padding="same", activation="relu"))
model.add(Conv2D(200, kernel_size=3, padding="same", activation="relu"))
model.add(BatchNormalization())
model.add(MaxPooling2D())
model.add(Dropout(0.05))
model.add(Conv2D(400, kernel_size=3, padding="same", activation="relu"))
model.add(Conv2D(400, kernel_size=3, padding="same", activation="relu"))
model.add(BatchNormalization())
model.add(MaxPooling2D())
model.add(Dropout(0.05))
model.add(Conv2D(800, kernel_size=3, padding="same", activation="relu"))
model.add(Conv2D(800, kernel_size=3, padding="same", activation="relu"))
model.add(BatchNormalization())
model.add(MaxPooling2D())
model.add(GlobalAveragePooling2D())
model.add(Dropout(0.125))
model.add(Dense(2000))
model.add(Dropout(0.25))
model.add(Dense(10, activation="softmax", name="predictions"))
model.summary()
```
#### Training
```
model.compile(loss='categorical_crossentropy',
optimizer=keras.optimizers.SGD(lr=0.01),
metrics=['accuracy'])
batch_size = 200
epochs = 15
callbacks = []
model.fit_generator(datagen.flow(full_x_train, full_y_train, batch_size=batch_size),
steps_per_epoch=len(full_x_train)//batch_size,
validation_data=(full_x_test, full_y_test),
epochs=epochs, verbose=1, workers=20,
callbacks=callbacks)
scores = model.evaluate(full_x_test, full_y_test, batch_size=batch_size, verbose=1)
print(scores)
```
### Dense model
```
model_dense = Sequential()
#model_dense.add(Input(shape=(32,32,3)))
model_dense.add(Flatten(input_shape=(32,32,3)))
model_dense.add(Dropout(0.125))
model_dense.add(Dense(2000))
model_dense.add(Dropout(0.25))
model_dense.add(Dense(10, activation="softmax", name="predictions"))
model_dense.summary()
model_dense.compile(loss='categorical_crossentropy',
optimizer=keras.optimizers.SGD(lr=0.001),
metrics=['accuracy'])
model_dense.fit_generator(datagen.flow(full_x_train, full_y_train, batch_size=batch_size),
steps_per_epoch=len(full_x_train)//batch_size,
validation_data=(full_x_test, full_y_test),
epochs=epochs, verbose=1, workers=20,
callbacks=callbacks)
scores_dense = model_dense.evaluate(full_x_test, full_y_test, batch_size=batch_size, verbose=1)
print(scores_dense)
```
### Conclusions
For images and video processing, advantages of CNN over MLP constitute in:
- ability to extract spacial features (in a "natural" way, with a sliding window)
- shift robustness
- lower complexity (for larger images)
- tranferrability to different image size
|
github_jupyter
|
import keras
from keras.models import Sequential
from keras.utils import np_utils
from keras.preprocessing.image import ImageDataGenerator
from keras.layers import Dense, Flatten, Dropout, GlobalAveragePooling2D, \
GlobalAveragePooling2D, Input, BatchNormalization
from keras.layers import Conv2D, MaxPooling2D
from keras.datasets import cifar10
import numpy as np
import os
def read_data_original():
#READ DATA FRAME
(full_x_train, full_y_train), (full_x_test, full_y_test) = cifar10.load_data()
full_x_train = full_x_train.astype('float32')
#z-score
mean = np.mean(full_x_train,axis=(0,1,2,3))
std = np.std(full_x_train,axis=(0,1,2,3))
full_x_train = (full_x_train-mean)/(std+1e-7)
full_x_test = (full_x_test-mean)/(std+1e-7)
return (full_x_train, full_y_train), (full_x_test, full_y_test)
(full_x_train, full_y_train), (full_x_test, full_y_test) = read_data_original()
num_classes = 10
full_y_train = np_utils.to_categorical(full_y_train,num_classes)
full_y_test = np_utils.to_categorical(full_y_test,num_classes)
datagen = ImageDataGenerator(
zca_epsilon=1e-06, # epsilon for ZCA whitening
rotation_range=0, # randomly rotate images in the range (degrees, 0 to 180)
# randomly shift images horizontally (fraction of total width)
width_shift_range=5,
# randomly shift images vertically (fraction of total height)
height_shift_range=5,
channel_shift_range=0.1, # set range for random channel shifts
# set mode for filling points outside the input boundaries
fill_mode='nearest',
cval=0., # value used for fill_mode = "constant"
horizontal_flip=True, # randomly flip images
validation_split=0.0)
datagen.fit(full_x_train)
model = Sequential()
model.add(Conv2D(100, kernel_size=3, padding="same", activation="relu", input_shape=(32,32,3)))
model.add(Conv2D(100, kernel_size=3, padding="same", activation="relu"))
model.add(BatchNormalization())
model.add(MaxPooling2D())
model.add(Dropout(0.05))
model.add(Conv2D(200, kernel_size=3, padding="same", activation="relu"))
model.add(Conv2D(200, kernel_size=3, padding="same", activation="relu"))
model.add(BatchNormalization())
model.add(MaxPooling2D())
model.add(Dropout(0.05))
model.add(Conv2D(400, kernel_size=3, padding="same", activation="relu"))
model.add(Conv2D(400, kernel_size=3, padding="same", activation="relu"))
model.add(BatchNormalization())
model.add(MaxPooling2D())
model.add(Dropout(0.05))
model.add(Conv2D(800, kernel_size=3, padding="same", activation="relu"))
model.add(Conv2D(800, kernel_size=3, padding="same", activation="relu"))
model.add(BatchNormalization())
model.add(MaxPooling2D())
model.add(GlobalAveragePooling2D())
model.add(Dropout(0.125))
model.add(Dense(2000))
model.add(Dropout(0.25))
model.add(Dense(10, activation="softmax", name="predictions"))
model.summary()
model.compile(loss='categorical_crossentropy',
optimizer=keras.optimizers.SGD(lr=0.01),
metrics=['accuracy'])
batch_size = 200
epochs = 15
callbacks = []
model.fit_generator(datagen.flow(full_x_train, full_y_train, batch_size=batch_size),
steps_per_epoch=len(full_x_train)//batch_size,
validation_data=(full_x_test, full_y_test),
epochs=epochs, verbose=1, workers=20,
callbacks=callbacks)
scores = model.evaluate(full_x_test, full_y_test, batch_size=batch_size, verbose=1)
print(scores)
model_dense = Sequential()
#model_dense.add(Input(shape=(32,32,3)))
model_dense.add(Flatten(input_shape=(32,32,3)))
model_dense.add(Dropout(0.125))
model_dense.add(Dense(2000))
model_dense.add(Dropout(0.25))
model_dense.add(Dense(10, activation="softmax", name="predictions"))
model_dense.summary()
model_dense.compile(loss='categorical_crossentropy',
optimizer=keras.optimizers.SGD(lr=0.001),
metrics=['accuracy'])
model_dense.fit_generator(datagen.flow(full_x_train, full_y_train, batch_size=batch_size),
steps_per_epoch=len(full_x_train)//batch_size,
validation_data=(full_x_test, full_y_test),
epochs=epochs, verbose=1, workers=20,
callbacks=callbacks)
scores_dense = model_dense.evaluate(full_x_test, full_y_test, batch_size=batch_size, verbose=1)
print(scores_dense)
| 0.83772 | 0.85446 |
# Stochastic Gradient Descent
In this section, we are going to introduce the basic principles of stochastic gradient descent.
Next, we use $x=10$ as the initial value and assume $\eta=0.2$. Using gradient descent to iterate $x$ 10 times, we can see that, eventually, the value of $x$ approaches the optimal solution.
## Stochastic Gradient Descent (SGD)
In deep learning, the objective function is usually the average of the loss functions for each example in the training data set. We assume that $f_i(\boldsymbol{x})$ is the loss function of the training data instance with $n$ examples, an index of $i$, and parameter vector of $\boldsymbol{x}$, then we have the objective function
$$f(\boldsymbol{x}) = \frac{1}{n} \sum_{i = 1}^n f_i(\boldsymbol{x}).$$
The gradient of the objective function at $\boldsymbol{x}$ is computed as
$$\nabla f(\boldsymbol{x}) = \frac{1}{n} \sum_{i = 1}^n \nabla f_i(\boldsymbol{x}).$$
If gradient descent is used, the computing cost for each independent variable iteration is $\mathcal{O}(n)$, which grows linearly with $n$. Therefore, when the model training data instance is large, the cost of gradient descent for each iteration will be very high.
Stochastic gradient descent (SGD) reduces computational cost at each iteration. At each iteration of stochastic gradient descent, we uniformly sample an index $i\in{1,\ldots,n}$ for data instances at random, and compute the gradient $\nabla f_i(\boldsymbol{x})$ to update $\boldsymbol{x}$:
$$\boldsymbol{x} \leftarrow \boldsymbol{x} - \eta \nabla f_i(\boldsymbol{x}).$$
Here, $\eta$ is the learning rate. We can see that the computing cost for each iteration drops from $\mathcal{O}(n)$ of the gradient descent to the constant $\mathcal{O}(1)$. We should mention that the stochastic gradient $\nabla f_i(\boldsymbol{x})$ is the unbiased estimate of gradient $\nabla f(\boldsymbol{x})$.
$$\mathbb{E}i \nabla f_i(\boldsymbol{x}) = \frac{1}{n} \sum{i = 1}^n \nabla f_i(\boldsymbol{x}) = \nabla f(\boldsymbol{x}).$$
This means that, on average, the stochastic gradient is a good estimate of the gradient.
Now, we will compare it to gradient descent by adding random noise with a mean of 0 to the gradient to simulate a SGD.
```
%matplotlib inline
import matplotlib.pyplot as plt
import d2l
import numpy as np
def f(x1, x2): return x1 ** 2 + 2 * x2 ** 2 # objective
def gradf(x1, x2): return (2 * x1, 4 * x2) # gradient
def sgd(x1, x2, s1, s2): # simulate noisy gradient
(g1, g2) = gradf(x1, x2) # compute gradient
(g1, g2) = (g1 + np.random.normal(0.1), g2 + np.random.normal(0.1))
return (x1 -eta * g1, x2 -eta * g2, 0, 0) # update variables
def train_2d(trainer):
x1, x2, s1, s2 = -5, -2, 0, 0
results = [(x1, x2)]
for i in range(20):
x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
results.append((x1, x2))
print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))
return results
eta = 0.1
d2l.show_trace_2d(f, train_2d(sgd))
```
As we can see, the iterative trajectory of the independent variable in the SGD is more tortuous than in the gradient descent. This is due to the noise added in the experiment, which reduced the accuracy of the simulated stochastic gradient. In practice, such noise usually comes from individual examples in the training data set.
## Summary
* If we use a more suitable learning rate and update the independent variable in the opposite direction of the gradient, the value of the objective function might be reduced. Gradient descent repeats this update process until a solution that meets the requirements is obtained.
* Problems occur when the learning rate is too small or too large. A suitable learning rate is usually found only after multiple experiments.
* When there are more examples in the training data set, it costs more to compute each iteration for gradient descent, so SGD is preferred in these cases.
## Exercises
* Using a different objective function, observe the iterative trajectory of the independent variable in gradient descent and the SGD.
* In the experiment for gradient descent in two-dimensional space, try to use different learning rates to observe and analyze the experimental phenomena.
|
github_jupyter
|
%matplotlib inline
import matplotlib.pyplot as plt
import d2l
import numpy as np
def f(x1, x2): return x1 ** 2 + 2 * x2 ** 2 # objective
def gradf(x1, x2): return (2 * x1, 4 * x2) # gradient
def sgd(x1, x2, s1, s2): # simulate noisy gradient
(g1, g2) = gradf(x1, x2) # compute gradient
(g1, g2) = (g1 + np.random.normal(0.1), g2 + np.random.normal(0.1))
return (x1 -eta * g1, x2 -eta * g2, 0, 0) # update variables
def train_2d(trainer):
x1, x2, s1, s2 = -5, -2, 0, 0
results = [(x1, x2)]
for i in range(20):
x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
results.append((x1, x2))
print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))
return results
eta = 0.1
d2l.show_trace_2d(f, train_2d(sgd))
| 0.357792 | 0.996146 |
```
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
plt.style.use('fivethirtyeight')
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
df=pd.read_csv("Placement_Data_Full_Class.csv")
df.head()
df.shape
df.info()
df.isnull().sum()
df[df.salary.isnull()==True]['status'].unique()
```
There are 67 Null values in Salaries. The ones not placed falls under this,hece we replace the null values with 0.
```
df.salary.fillna(0,inplace=True)
df.isnull().sum()
df.head()
f,ax=plt.subplots(1,2,figsize=(18,8))
df['status'].value_counts().plot.pie(explode=[0,0.1],autopct='%1.1f%%',ax=ax[0],shadow=True)
ax[0].set_title('Status of placement')
ax[0].set_ylabel('')
sns.countplot('status',data=df,ax=ax[1])
ax[1].set_title('Status of placement')
plt.show()
sns.boxplot(x=df['salary'])
```
Above plot shows one point beyond 800000, this is an outlier as this is not included in the box of other observation i.e no where near the quartiles. Similarly,
```
plt.figure(figsize=(20,10))
i = 1
for x in df.columns:
if df[x].dtypes != 'O':
plt.subplot(2,4,i)
sns.boxplot(df[x])
i+=1
```
We will use Z-score function defined in scipy library to detect the outliers.
# **Labelling**
```
# Label Encode all columns
from sklearn.preprocessing import LabelEncoder
l = LabelEncoder()
cols=['gender','ssc_b','hsc_b','hsc_s','degree_t','workex','specialisation','status']
for i in cols:
df[i] = l.fit_transform(df[i])
df.groupby(['gender','status'])['status'].count()
```
# **Z-score function defined in scipy library to detect the outliers.**
```
z = np.abs(stats.zscore(df))
print(z)
# defining a threshold to identify an outlier.
threshold = 3
print(np.where(z > 3))
print(z[119][14])
```
So, the data point — 119th record on column 'salary' is an outlier and likewise.
```
noutlier_df = df[(z < 3).all(axis=1)]
noutlier_df.shape
df.shape
```
# **Correlation Between The Features.**
```
sns.heatmap(df.corr(),annot=True,cbar= False,linewidths=0.2)
fig=plt.gcf()
fig.set_size_inches(10,8)
plt.show()
```
# **Interpretation**
Now from the above heatmap,we can see that the features are not much correlated. The highest correlation is between status(placement) and ssc_p(Secondary Education percentage- 10th Grade). So we can carry on with all features.
# **MODELS**
```
#train/test split
cols=['ssc_b','hsc_b','hsc_s','specialisation','degree_t']
X = df.drop(cols,axis=1).values
#X = df.drop('status',axis=1).values
y = df['status'].values
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.35, random_state=42)
```
# **NAIVE BAYES**
```
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
y_pred
#Accuracy
from sklearn.metrics import confusion_matrix, accuracy_score
print(confusion_matrix(y_pred,y_test))
print(accuracy_score(y_pred,y_test)*100)
```
# **Decision Tree**
```
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier(random_state=42)
model = GaussianNB()
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
y_pred
#Accuracy
from sklearn.metrics import confusion_matrix, accuracy_score
print(confusion_matrix(y_pred,y_test))
print(accuracy_score(y_pred,y_test)*100)
```
|
github_jupyter
|
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
plt.style.use('fivethirtyeight')
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
df=pd.read_csv("Placement_Data_Full_Class.csv")
df.head()
df.shape
df.info()
df.isnull().sum()
df[df.salary.isnull()==True]['status'].unique()
df.salary.fillna(0,inplace=True)
df.isnull().sum()
df.head()
f,ax=plt.subplots(1,2,figsize=(18,8))
df['status'].value_counts().plot.pie(explode=[0,0.1],autopct='%1.1f%%',ax=ax[0],shadow=True)
ax[0].set_title('Status of placement')
ax[0].set_ylabel('')
sns.countplot('status',data=df,ax=ax[1])
ax[1].set_title('Status of placement')
plt.show()
sns.boxplot(x=df['salary'])
plt.figure(figsize=(20,10))
i = 1
for x in df.columns:
if df[x].dtypes != 'O':
plt.subplot(2,4,i)
sns.boxplot(df[x])
i+=1
# Label Encode all columns
from sklearn.preprocessing import LabelEncoder
l = LabelEncoder()
cols=['gender','ssc_b','hsc_b','hsc_s','degree_t','workex','specialisation','status']
for i in cols:
df[i] = l.fit_transform(df[i])
df.groupby(['gender','status'])['status'].count()
z = np.abs(stats.zscore(df))
print(z)
# defining a threshold to identify an outlier.
threshold = 3
print(np.where(z > 3))
print(z[119][14])
noutlier_df = df[(z < 3).all(axis=1)]
noutlier_df.shape
df.shape
sns.heatmap(df.corr(),annot=True,cbar= False,linewidths=0.2)
fig=plt.gcf()
fig.set_size_inches(10,8)
plt.show()
#train/test split
cols=['ssc_b','hsc_b','hsc_s','specialisation','degree_t']
X = df.drop(cols,axis=1).values
#X = df.drop('status',axis=1).values
y = df['status'].values
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.35, random_state=42)
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
y_pred
#Accuracy
from sklearn.metrics import confusion_matrix, accuracy_score
print(confusion_matrix(y_pred,y_test))
print(accuracy_score(y_pred,y_test)*100)
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier(random_state=42)
model = GaussianNB()
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
y_pred
#Accuracy
from sklearn.metrics import confusion_matrix, accuracy_score
print(confusion_matrix(y_pred,y_test))
print(accuracy_score(y_pred,y_test)*100)
| 0.442877 | 0.797754 |
```
%load_ext autoreload
%autoreload 2
from matplotlib.path import Path
import numpy as np
import argparse
import os, sys
sys.path.append(os.path.dirname(os.getcwd()))
import polygon_primitives.file_writer as fw
import image_processing.camera_processing as cp
import image_processing.utils as utils
from image_processing import polygon_projection
from PIL import Image
import matplotlib.pyplot as plt
%matplotlib inline
```
We first initialize the directories, load the 'pmatrix' file and load the merged polygons.
```
directory = "../data/Drone_Flight/"
out_dir = "../data/Drone_Flight/output/"
facade_file = "../data/Drone_Flight/merged_thermal.txt"
#Load the relevant files, and assign directory paths
image_dir = directory + "Thermal/"
param_dir = directory + "params_thermal/"
p_matrices = np.loadtxt(param_dir + 'pmatrix.txt', usecols=range(1,13))
filenames = np.genfromtxt(param_dir + 'pmatrix.txt', usecols=range(1), dtype=str)
merged_polygons, facade_type_list, file_format = fw.load_merged_polygon_facades(filename=facade_file)
```
We next load the 'offset' file and add a height-adjustment to the polygons, and specify the image that we want to project the facades onto. We then initialize a dictionary for the Cameras. The Camera class stores all information related to the camera, i.e. intrinsic and extrinsic camera parameters.
```
#Load offset and adjust height if necessary for the camera images
offset = np.loadtxt(param_dir + "offset.txt",usecols=range(3))
height_adj = 102.0
offset_adj = np.array([0.0, 0.0, height_adj])
offset = offset + offset_adj
#Create a dictionary mapping the camera filename to a Camera object
camera_dict = polygon_projection.create_camera_dict(param_dir, offset)
#Sets the image file. Note: for thermal images, Pix4D's pmatrix file uses the .tif extension
#So we have to use .tif here, which we change later to load the RJPEG images
image_filename = "DJI_0351.tif"#"DJI_0052.tif"
#Get the camera for the specified image file, and calculate the pmatrix
camera = camera_dict[image_filename]
pmatrix = camera.calc_pmatrix()
#Replace the .tif extension to load the .RJPEG image
image_filename = image_filename.split('.')[0] + '.jpg'
```
Finally, to project the merged polygons onto the image file, we simply load the image and run 'mark_image_file':
```
image = utils.load_image(image_dir + image_filename)
out_image = polygon_projection.mark_image_file(image, merged_polygons, facade_type_list, offset, pmatrix)
#Plotting
plt.imshow(np.asarray(out_image))
plt.show()
```
This can then be saved to an output directory 'out_dir' and filename 'filename', as illustrated below.
```
utils.save_image(out_image, out_dir, image_filename)
```
To crop the image so that only a single facade is visible:
```
cropped_image = polygon_projection.crop_image_outside_building(image, merged_polygons, offset, pmatrix)
#Plotting
plt.imshow(np.asarray(cropped_image))
plt.show()
cropped_image.save('/Users/stouzani/Desktop/Unstructured_ML/Drone/Drone_Data_Capture/Alameda_December_2019/Thermal_preproc/cropped_DJI_0351.png')
cropped_image
im_shape = np.array(image).shape
im_shape
cropped_image = np.array(image)
mask = np.zeros(im_shape[:2], dtype=np.uint8)
mask.shape
for i in range(len(merged_polygons)):
polygon = merged_polygons[i]
projected_facades = polygon_projection.get_projected_facades(polygon, pmatrix, offset=offset)
poly_mask = polygon_projection.get_polygon_mask(im_shape, projected_facades)
mask[np.where(poly_mask)] = 1
plt.figure()
plt.imshow(mask)
np.save('/Users/stouzani/Desktop/Unstructured_ML/Drone/Drone_Data_Capture/Alameda_December_2019/masks_thm/DJI_0351.npy', mask)
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
from matplotlib.path import Path
import numpy as np
import argparse
import os, sys
sys.path.append(os.path.dirname(os.getcwd()))
import polygon_primitives.file_writer as fw
import image_processing.camera_processing as cp
import image_processing.utils as utils
from image_processing import polygon_projection
from PIL import Image
import matplotlib.pyplot as plt
%matplotlib inline
directory = "../data/Drone_Flight/"
out_dir = "../data/Drone_Flight/output/"
facade_file = "../data/Drone_Flight/merged_thermal.txt"
#Load the relevant files, and assign directory paths
image_dir = directory + "Thermal/"
param_dir = directory + "params_thermal/"
p_matrices = np.loadtxt(param_dir + 'pmatrix.txt', usecols=range(1,13))
filenames = np.genfromtxt(param_dir + 'pmatrix.txt', usecols=range(1), dtype=str)
merged_polygons, facade_type_list, file_format = fw.load_merged_polygon_facades(filename=facade_file)
#Load offset and adjust height if necessary for the camera images
offset = np.loadtxt(param_dir + "offset.txt",usecols=range(3))
height_adj = 102.0
offset_adj = np.array([0.0, 0.0, height_adj])
offset = offset + offset_adj
#Create a dictionary mapping the camera filename to a Camera object
camera_dict = polygon_projection.create_camera_dict(param_dir, offset)
#Sets the image file. Note: for thermal images, Pix4D's pmatrix file uses the .tif extension
#So we have to use .tif here, which we change later to load the RJPEG images
image_filename = "DJI_0351.tif"#"DJI_0052.tif"
#Get the camera for the specified image file, and calculate the pmatrix
camera = camera_dict[image_filename]
pmatrix = camera.calc_pmatrix()
#Replace the .tif extension to load the .RJPEG image
image_filename = image_filename.split('.')[0] + '.jpg'
image = utils.load_image(image_dir + image_filename)
out_image = polygon_projection.mark_image_file(image, merged_polygons, facade_type_list, offset, pmatrix)
#Plotting
plt.imshow(np.asarray(out_image))
plt.show()
utils.save_image(out_image, out_dir, image_filename)
cropped_image = polygon_projection.crop_image_outside_building(image, merged_polygons, offset, pmatrix)
#Plotting
plt.imshow(np.asarray(cropped_image))
plt.show()
cropped_image.save('/Users/stouzani/Desktop/Unstructured_ML/Drone/Drone_Data_Capture/Alameda_December_2019/Thermal_preproc/cropped_DJI_0351.png')
cropped_image
im_shape = np.array(image).shape
im_shape
cropped_image = np.array(image)
mask = np.zeros(im_shape[:2], dtype=np.uint8)
mask.shape
for i in range(len(merged_polygons)):
polygon = merged_polygons[i]
projected_facades = polygon_projection.get_projected_facades(polygon, pmatrix, offset=offset)
poly_mask = polygon_projection.get_polygon_mask(im_shape, projected_facades)
mask[np.where(poly_mask)] = 1
plt.figure()
plt.imshow(mask)
np.save('/Users/stouzani/Desktop/Unstructured_ML/Drone/Drone_Data_Capture/Alameda_December_2019/masks_thm/DJI_0351.npy', mask)
| 0.388502 | 0.715275 |
# TFX on KubeFlow Pipelines Example
This notebook should be run inside a KF Pipelines cluster.
### Install TFX and KFP packages
```
!pip3 install tfx==0.13.0 --upgrade
!pip3 install kfp --upgrade
```
### Enable DataFlow API for your GKE cluster
<https://console.developers.google.com/apis/api/dataflow.googleapis.com/overview>
## Get the TFX repo with sample pipeline
```
# Directory and data locations (uses Google Cloud Storage).
import os
_input_bucket = '<your gcs bucket>'
_output_bucket = '<your gcs bucket>'
_pipeline_root = os.path.join(_output_bucket, 'tfx')
# Google Cloud Platform project id to use when deploying this pipeline.
_project_id = '<your project id>'
# copy the trainer code to a storage bucket as the TFX pipeline will need that code file in GCS
from tensorflow import gfile
gfile.Copy('utils/taxi_utils.py', _input_bucket + '/taxi_utils.py')
```
## Configure the TFX pipeline example
Reload this cell by running the load command to get the pipeline configuration file
```
%load tfx/examples/chicago_taxi_pipeline/taxi_pipeline_kubeflow.py
```
Configure:
- Set `_input_bucket` to the GCS directory where you've copied taxi_utils.py. I.e. gs://<my bucket>/<path>/
- Set `_output_bucket` to the GCS directory where you've want the results to be written
- Set GCP project ID (replace my-gcp-project). Note that it should be project ID, not project name.
The dataset in BigQuery has 100M rows, you can change the query parameters in WHERE clause to limit the number of rows used.
```
"""Chicago Taxi example using TFX DSL on Kubeflow."""
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import os
from tfx.components.evaluator.component import Evaluator
from tfx.components.example_gen.big_query_example_gen.component import BigQueryExampleGen
from tfx.components.example_validator.component import ExampleValidator
from tfx.components.model_validator.component import ModelValidator
from tfx.components.pusher.component import Pusher
from tfx.components.schema_gen.component import SchemaGen
from tfx.components.statistics_gen.component import StatisticsGen
from tfx.components.trainer.component import Trainer
from tfx.components.transform.component import Transform
from tfx.orchestration.kubeflow.runner import KubeflowRunner
from tfx.orchestration.pipeline import PipelineDecorator
from tfx.proto import evaluator_pb2
from tfx.proto import pusher_pb2
from tfx.proto import trainer_pb2
# Python module file to inject customized logic into the TFX components. The
# Transform and Trainer both require user-defined functions to run successfully.
# Copy this from the current directory to a GCS bucket and update the location
# below.
_taxi_utils = os.path.join(_input_bucket, 'taxi_utils.py')
# Path which can be listened to by the model server. Pusher will output the
# trained model here.
_serving_model_dir = os.path.join(_output_bucket, 'serving_model/taxi_bigquery')
# Region to use for Dataflow jobs and CMLE training.
# Dataflow: https://cloud.google.com/dataflow/docs/concepts/regional-endpoints
# CMLE: https://cloud.google.com/ml-engine/docs/tensorflow/regions
_gcp_region = 'us-central1'
# A dict which contains the training job parameters to be passed to Google
# Cloud ML Engine. For the full set of parameters supported by Google Cloud ML
# Engine, refer to
# https://cloud.google.com/ml-engine/reference/rest/v1/projects.jobs#Job
_cmle_training_args = {
'pythonModule': None, # Will be populated by TFX
'args': None, # Will be populated by TFX
'region': _gcp_region,
'jobDir': os.path.join(_output_bucket, 'tmp'),
'runtimeVersion': '1.12',
'pythonVersion': '2.7',
'project': _project_id,
}
# A dict which contains the serving job parameters to be passed to Google
# Cloud ML Engine. For the full set of parameters supported by Google Cloud ML
# Engine, refer to
# https://cloud.google.com/ml-engine/reference/rest/v1/projects.models
_cmle_serving_args = {
'model_name': 'chicago_taxi',
'project_id': _project_id,
'runtime_version': '1.12',
}
# The rate at which to sample rows from the Chicago Taxi dataset using BigQuery.
# The full taxi dataset is > 120M record. In the interest of resource
# savings and time, we've set the default for this example to be much smaller.
# Feel free to crank it up and process the full dataset!
_query_sample_rate = 0.001 # Generate a 0.1% random sample.
# TODO(zhitaoli): Remove PipelineDecorator after 0.13.0.
@PipelineDecorator(
pipeline_name='chicago_taxi_pipeline_kubeflow',
log_root='/var/tmp/tfx/logs',
pipeline_root=_pipeline_root,
additional_pipeline_args={
'beam_pipeline_args': [
'--runner=DataflowRunner',
'--experiments=shuffle_mode=auto',
'--project=' + _project_id,
'--temp_location=' + os.path.join(_output_bucket, 'tmp'),
'--region=' + _gcp_region,
],
# Optional args:
# 'tfx_image': custom docker image to use for components. This is needed
# if TFX package is not installed from an RC or released version.
})
def _create_pipeline():
"""Implements the chicago taxi pipeline with TFX."""
query = """
SELECT
pickup_community_area,
fare,
EXTRACT(MONTH FROM trip_start_timestamp) AS trip_start_month,
EXTRACT(HOUR FROM trip_start_timestamp) AS trip_start_hour,
EXTRACT(DAYOFWEEK FROM trip_start_timestamp) AS trip_start_day,
UNIX_SECONDS(trip_start_timestamp) AS trip_start_timestamp,
pickup_latitude,
pickup_longitude,
dropoff_latitude,
dropoff_longitude,
trip_miles,
pickup_census_tract,
dropoff_census_tract,
payment_type,
company,
trip_seconds,
dropoff_community_area,
tips
FROM `bigquery-public-data.chicago_taxi_trips.taxi_trips`
WHERE RAND() < {}""".format(_query_sample_rate)
# Brings data into the pipeline or otherwise joins/converts training data.
example_gen = BigQueryExampleGen(query=query)
# Computes statistics over data for visualization and example validation.
statistics_gen = StatisticsGen(input_data=example_gen.outputs.examples)
# Generates schema based on statistics files.
infer_schema = SchemaGen(stats=statistics_gen.outputs.output)
# Performs anomaly detection based on statistics and data schema.
validate_stats = ExampleValidator(
stats=statistics_gen.outputs.output, schema=infer_schema.outputs.output)
# Performs transformations and feature engineering in training and serving.
transform = Transform(
input_data=example_gen.outputs.examples,
schema=infer_schema.outputs.output,
module_file=_taxi_utils)
# Uses user-provided Python function that implements a model using TF-Learn.
trainer = Trainer(
module_file=_taxi_utils,
transformed_examples=transform.outputs.transformed_examples,
schema=infer_schema.outputs.output,
transform_output=transform.outputs.transform_output,
train_args=trainer_pb2.TrainArgs(num_steps=10000),
eval_args=trainer_pb2.EvalArgs(num_steps=5000),
custom_config={'cmle_training_args': _cmle_training_args})
# Uses TFMA to compute a evaluation statistics over features of a model.
model_analyzer = Evaluator(
examples=example_gen.outputs.examples,
model_exports=trainer.outputs.output,
feature_slicing_spec=evaluator_pb2.FeatureSlicingSpec(specs=[
evaluator_pb2.SingleSlicingSpec(
column_for_slicing=['trip_start_hour'])
]))
# Performs quality validation of a candidate model (compared to a baseline).
model_validator = ModelValidator(
examples=example_gen.outputs.examples, model=trainer.outputs.output)
# Checks whether the model passed the validation steps and pushes the model
# to a file destination if check passed.
pusher = Pusher(
model_export=trainer.outputs.output,
model_blessing=model_validator.outputs.blessing,
custom_config={'cmle_serving_args': _cmle_serving_args},
push_destination=pusher_pb2.PushDestination(
filesystem=pusher_pb2.PushDestination.Filesystem(
base_directory=_serving_model_dir)))
return [
example_gen, statistics_gen, infer_schema, validate_stats, transform,
trainer, model_analyzer, model_validator, pusher
]
pipeline = KubeflowRunner().run(_create_pipeline())
```
## Compile the pipeline and submit a run to the Kubeflow cluster
```
# Get or create a new experiment
import kfp
client = kfp.Client()
experiment_name='TFX Examples'
try:
experiment_id = client.get_experiment(experiment_name=experiment_name).id
except:
experiment_id = client.create_experiment(experiment_name).id
pipeline_filename = 'chicago_taxi_pipeline_kubeflow.tar.gz'
#Submit a pipeline run
run_name = 'Run 1'
run_result = client.run_pipeline(experiment_id, run_name, pipeline_filename, {})
```
### Connect to the ML Metadata Store
```
!pip3 install ml_metadata
from ml_metadata.metadata_store import metadata_store
from ml_metadata.proto import metadata_store_pb2
import os
connection_config = metadata_store_pb2.ConnectionConfig()
connection_config.mysql.host = os.getenv('MYSQL_SERVICE_HOST')
connection_config.mysql.port = int(os.getenv('MYSQL_SERVICE_PORT'))
connection_config.mysql.database = 'mlmetadata'
connection_config.mysql.user = 'root'
store = metadata_store.MetadataStore(connection_config)
# Get all output artifacts
store.get_artifacts()
# Get a specific artifact type
# TFX types
# types = ['ModelExportPath', 'ExamplesPath', 'ModelBlessingPath', 'ModelPushPath', 'TransformPath', 'SchemaPath']
store.get_artifacts_by_type('ExamplesPath')
```
|
github_jupyter
|
!pip3 install tfx==0.13.0 --upgrade
!pip3 install kfp --upgrade
# Directory and data locations (uses Google Cloud Storage).
import os
_input_bucket = '<your gcs bucket>'
_output_bucket = '<your gcs bucket>'
_pipeline_root = os.path.join(_output_bucket, 'tfx')
# Google Cloud Platform project id to use when deploying this pipeline.
_project_id = '<your project id>'
# copy the trainer code to a storage bucket as the TFX pipeline will need that code file in GCS
from tensorflow import gfile
gfile.Copy('utils/taxi_utils.py', _input_bucket + '/taxi_utils.py')
%load tfx/examples/chicago_taxi_pipeline/taxi_pipeline_kubeflow.py
"""Chicago Taxi example using TFX DSL on Kubeflow."""
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import os
from tfx.components.evaluator.component import Evaluator
from tfx.components.example_gen.big_query_example_gen.component import BigQueryExampleGen
from tfx.components.example_validator.component import ExampleValidator
from tfx.components.model_validator.component import ModelValidator
from tfx.components.pusher.component import Pusher
from tfx.components.schema_gen.component import SchemaGen
from tfx.components.statistics_gen.component import StatisticsGen
from tfx.components.trainer.component import Trainer
from tfx.components.transform.component import Transform
from tfx.orchestration.kubeflow.runner import KubeflowRunner
from tfx.orchestration.pipeline import PipelineDecorator
from tfx.proto import evaluator_pb2
from tfx.proto import pusher_pb2
from tfx.proto import trainer_pb2
# Python module file to inject customized logic into the TFX components. The
# Transform and Trainer both require user-defined functions to run successfully.
# Copy this from the current directory to a GCS bucket and update the location
# below.
_taxi_utils = os.path.join(_input_bucket, 'taxi_utils.py')
# Path which can be listened to by the model server. Pusher will output the
# trained model here.
_serving_model_dir = os.path.join(_output_bucket, 'serving_model/taxi_bigquery')
# Region to use for Dataflow jobs and CMLE training.
# Dataflow: https://cloud.google.com/dataflow/docs/concepts/regional-endpoints
# CMLE: https://cloud.google.com/ml-engine/docs/tensorflow/regions
_gcp_region = 'us-central1'
# A dict which contains the training job parameters to be passed to Google
# Cloud ML Engine. For the full set of parameters supported by Google Cloud ML
# Engine, refer to
# https://cloud.google.com/ml-engine/reference/rest/v1/projects.jobs#Job
_cmle_training_args = {
'pythonModule': None, # Will be populated by TFX
'args': None, # Will be populated by TFX
'region': _gcp_region,
'jobDir': os.path.join(_output_bucket, 'tmp'),
'runtimeVersion': '1.12',
'pythonVersion': '2.7',
'project': _project_id,
}
# A dict which contains the serving job parameters to be passed to Google
# Cloud ML Engine. For the full set of parameters supported by Google Cloud ML
# Engine, refer to
# https://cloud.google.com/ml-engine/reference/rest/v1/projects.models
_cmle_serving_args = {
'model_name': 'chicago_taxi',
'project_id': _project_id,
'runtime_version': '1.12',
}
# The rate at which to sample rows from the Chicago Taxi dataset using BigQuery.
# The full taxi dataset is > 120M record. In the interest of resource
# savings and time, we've set the default for this example to be much smaller.
# Feel free to crank it up and process the full dataset!
_query_sample_rate = 0.001 # Generate a 0.1% random sample.
# TODO(zhitaoli): Remove PipelineDecorator after 0.13.0.
@PipelineDecorator(
pipeline_name='chicago_taxi_pipeline_kubeflow',
log_root='/var/tmp/tfx/logs',
pipeline_root=_pipeline_root,
additional_pipeline_args={
'beam_pipeline_args': [
'--runner=DataflowRunner',
'--experiments=shuffle_mode=auto',
'--project=' + _project_id,
'--temp_location=' + os.path.join(_output_bucket, 'tmp'),
'--region=' + _gcp_region,
],
# Optional args:
# 'tfx_image': custom docker image to use for components. This is needed
# if TFX package is not installed from an RC or released version.
})
def _create_pipeline():
"""Implements the chicago taxi pipeline with TFX."""
query = """
SELECT
pickup_community_area,
fare,
EXTRACT(MONTH FROM trip_start_timestamp) AS trip_start_month,
EXTRACT(HOUR FROM trip_start_timestamp) AS trip_start_hour,
EXTRACT(DAYOFWEEK FROM trip_start_timestamp) AS trip_start_day,
UNIX_SECONDS(trip_start_timestamp) AS trip_start_timestamp,
pickup_latitude,
pickup_longitude,
dropoff_latitude,
dropoff_longitude,
trip_miles,
pickup_census_tract,
dropoff_census_tract,
payment_type,
company,
trip_seconds,
dropoff_community_area,
tips
FROM `bigquery-public-data.chicago_taxi_trips.taxi_trips`
WHERE RAND() < {}""".format(_query_sample_rate)
# Brings data into the pipeline or otherwise joins/converts training data.
example_gen = BigQueryExampleGen(query=query)
# Computes statistics over data for visualization and example validation.
statistics_gen = StatisticsGen(input_data=example_gen.outputs.examples)
# Generates schema based on statistics files.
infer_schema = SchemaGen(stats=statistics_gen.outputs.output)
# Performs anomaly detection based on statistics and data schema.
validate_stats = ExampleValidator(
stats=statistics_gen.outputs.output, schema=infer_schema.outputs.output)
# Performs transformations and feature engineering in training and serving.
transform = Transform(
input_data=example_gen.outputs.examples,
schema=infer_schema.outputs.output,
module_file=_taxi_utils)
# Uses user-provided Python function that implements a model using TF-Learn.
trainer = Trainer(
module_file=_taxi_utils,
transformed_examples=transform.outputs.transformed_examples,
schema=infer_schema.outputs.output,
transform_output=transform.outputs.transform_output,
train_args=trainer_pb2.TrainArgs(num_steps=10000),
eval_args=trainer_pb2.EvalArgs(num_steps=5000),
custom_config={'cmle_training_args': _cmle_training_args})
# Uses TFMA to compute a evaluation statistics over features of a model.
model_analyzer = Evaluator(
examples=example_gen.outputs.examples,
model_exports=trainer.outputs.output,
feature_slicing_spec=evaluator_pb2.FeatureSlicingSpec(specs=[
evaluator_pb2.SingleSlicingSpec(
column_for_slicing=['trip_start_hour'])
]))
# Performs quality validation of a candidate model (compared to a baseline).
model_validator = ModelValidator(
examples=example_gen.outputs.examples, model=trainer.outputs.output)
# Checks whether the model passed the validation steps and pushes the model
# to a file destination if check passed.
pusher = Pusher(
model_export=trainer.outputs.output,
model_blessing=model_validator.outputs.blessing,
custom_config={'cmle_serving_args': _cmle_serving_args},
push_destination=pusher_pb2.PushDestination(
filesystem=pusher_pb2.PushDestination.Filesystem(
base_directory=_serving_model_dir)))
return [
example_gen, statistics_gen, infer_schema, validate_stats, transform,
trainer, model_analyzer, model_validator, pusher
]
pipeline = KubeflowRunner().run(_create_pipeline())
# Get or create a new experiment
import kfp
client = kfp.Client()
experiment_name='TFX Examples'
try:
experiment_id = client.get_experiment(experiment_name=experiment_name).id
except:
experiment_id = client.create_experiment(experiment_name).id
pipeline_filename = 'chicago_taxi_pipeline_kubeflow.tar.gz'
#Submit a pipeline run
run_name = 'Run 1'
run_result = client.run_pipeline(experiment_id, run_name, pipeline_filename, {})
!pip3 install ml_metadata
from ml_metadata.metadata_store import metadata_store
from ml_metadata.proto import metadata_store_pb2
import os
connection_config = metadata_store_pb2.ConnectionConfig()
connection_config.mysql.host = os.getenv('MYSQL_SERVICE_HOST')
connection_config.mysql.port = int(os.getenv('MYSQL_SERVICE_PORT'))
connection_config.mysql.database = 'mlmetadata'
connection_config.mysql.user = 'root'
store = metadata_store.MetadataStore(connection_config)
# Get all output artifacts
store.get_artifacts()
# Get a specific artifact type
# TFX types
# types = ['ModelExportPath', 'ExamplesPath', 'ModelBlessingPath', 'ModelPushPath', 'TransformPath', 'SchemaPath']
store.get_artifacts_by_type('ExamplesPath')
| 0.695235 | 0.832849 |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import preprocessing
#initializing pca
from sklearn import decomposition
from feature_selector import FeatureSelector
features_nor_path = 'E:\Analysis-on-GAN\dataset\Dataset_normal.csv'
features_ran_path = 'E:\Analysis-on-GAN\dataset\Dataset_ransom.csv'
# apply supervised feature reduction algorithms on dataset
features_ran_data = pd.read_csv(features_ran_path, header = None)
features_nor_data = pd.read_csv(features_nor_path, header = None)
# delete the first column name row
features_ran_data = features_ran_data[1:]
features_nor_data = features_nor_data[1:]
features_ran_data['label'] = [1]*len(features_ran_data)
features_nor_data['label'] = [0]*len(features_nor_data)
features_ran_data
features_nor_data
features_data = features_ran_data.append(features_nor_data, ignore_index=True)
features_data
features_data.iloc[:,3:-1]
# features = features_data.iloc[1:,3:].values
features_data.to_csv('Dataset.csv', index=False)
features_data.to_csv('Dataset.csv', header=None)
features_data.shape
# create the X, Y matrixes
X, y = features_data.iloc[:,3:-1].values, features_data['label'].values
X.shape
pca = decomposition.PCA()
# the min value in (sample, features)
pca.n_components=333
pcadata = pca.fit_transform(X)
perc_var_explain=pca.explained_variance_/np.sum(pca.explained_variance_)
cumulative_var_explain=np.cumsum(perc_var_explain)
plt.plot(cumulative_var_explain)
plt.grid()
plt.xlabel('n_components')
plt.ylabel('cumulative explained variance')
plt.show()
cummulative_var_explain.shape
pca.components_
# number of components
n_pcs= pca.components_.shape[0]
n_pcs
from collections import Counter
# get the index of the most important feature on EACH component i.e. largest absolute value
# using LIST COMPREHENSION HERE
most_important = [np.abs(pca.components_[i]).argmax() for i in range(n_pcs)]
# most_important_value = [pca.components_[i].max() for i in range(n_pcs)]
# mean_value = np.mean(most_important_value)
# most_important_values = [most_important_value > mean_value]
# most_important_values
initial_feature_names = [x for x in range(3, 122266)]
# get the names
most_important_names = [initial_feature_names[most_important[i]] for i in range(n_pcs)]
# using LIST COMPREHENSION HERE AGAIN
dic = {'PC{}'.format(i+1): most_important_names[i] for i in range(n_pcs)}
# build the dataframe
df = pd.DataFrame(sorted(dic.items()))
df
df[1].value_counts().plot.bar()
Counter(df[1].value_counts()>2)
idx = [x[0] for x in np.where(cumulative_var_explain>=0.99)]
idx
idx = [x[0] for x in np.where(cumulative_var_explain>=0.999)]
idx
idx = [x[0] for x in np.where(cumulative_var_explain>=0.9999)]
idx
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import preprocessing
#initializing pca
from sklearn import decomposition
from feature_selector import FeatureSelector
features_nor_path = 'E:\Analysis-on-GAN\dataset\Dataset_normal.csv'
features_ran_path = 'E:\Analysis-on-GAN\dataset\Dataset_ransom.csv'
# apply supervised feature reduction algorithms on dataset
features_ran_data = pd.read_csv(features_ran_path, header = None)
features_nor_data = pd.read_csv(features_nor_path, header = None)
# delete the first column name row
features_ran_data = features_ran_data[1:]
features_nor_data = features_nor_data[1:]
features_ran_data['label'] = [1]*len(features_ran_data)
features_nor_data['label'] = [0]*len(features_nor_data)
features_ran_data
features_nor_data
features_data = features_ran_data.append(features_nor_data, ignore_index=True)
features_data
features_data.iloc[:,3:-1]
# features = features_data.iloc[1:,3:].values
features_data.to_csv('Dataset.csv', index=False)
features_data.to_csv('Dataset.csv', header=None)
features_data.shape
# create the X, Y matrixes
X, y = features_data.iloc[:,3:-1].values, features_data['label'].values
X.shape
pca = decomposition.PCA()
# the min value in (sample, features)
pca.n_components=333
pcadata = pca.fit_transform(X)
perc_var_explain=pca.explained_variance_/np.sum(pca.explained_variance_)
cumulative_var_explain=np.cumsum(perc_var_explain)
plt.plot(cumulative_var_explain)
plt.grid()
plt.xlabel('n_components')
plt.ylabel('cumulative explained variance')
plt.show()
cummulative_var_explain.shape
pca.components_
# number of components
n_pcs= pca.components_.shape[0]
n_pcs
from collections import Counter
# get the index of the most important feature on EACH component i.e. largest absolute value
# using LIST COMPREHENSION HERE
most_important = [np.abs(pca.components_[i]).argmax() for i in range(n_pcs)]
# most_important_value = [pca.components_[i].max() for i in range(n_pcs)]
# mean_value = np.mean(most_important_value)
# most_important_values = [most_important_value > mean_value]
# most_important_values
initial_feature_names = [x for x in range(3, 122266)]
# get the names
most_important_names = [initial_feature_names[most_important[i]] for i in range(n_pcs)]
# using LIST COMPREHENSION HERE AGAIN
dic = {'PC{}'.format(i+1): most_important_names[i] for i in range(n_pcs)}
# build the dataframe
df = pd.DataFrame(sorted(dic.items()))
df
df[1].value_counts().plot.bar()
Counter(df[1].value_counts()>2)
idx = [x[0] for x in np.where(cumulative_var_explain>=0.99)]
idx
idx = [x[0] for x in np.where(cumulative_var_explain>=0.999)]
idx
idx = [x[0] for x in np.where(cumulative_var_explain>=0.9999)]
idx
| 0.569134 | 0.578091 |
```
import os
import sys
# Add ../src to the list of available Python packages
module_path = os.path.abspath(os.path.join('..', 'src'))
if module_path not in sys.path:
sys.path.insert(0, module_path)
import numpy as np
from sklearn import metrics
import matplotlib.pyplot as plt
from docknet.docknet import Docknet
from docknet.data_generator.cluster_data_generator import ClusterDataGenerator
from docknet.initializer.random_normal_initializer import RandomNormalInitializer
from docknet.optimizer.gradient_descent_optimizer import GradientDescentOptimizer
from docknet.optimizer.adam_optimizer import AdamOptimizer
def scatterplot(axe, X, Y, title, files, rows, index, x0_range, x1_range):
axe.scatter(X[0, :], X[1, :], c=Y[0:], s=2)
aspect = (x0_range[1] - x0_range[0]) / (x1_range[1] - x1_range[0])
axe.set_aspect(aspect)
axe.set_title(title)
axe.set_xlim(x0_range)
axe.set_ylim(x1_range)
axe.set_xlabel('x0')
axe.set_ylabel('x1')
train_size = 2000
test_size = 400
x0_range = (-5., 5.)
x1_range = (-5., 5.)
data_generator = ClusterDataGenerator(x0_range, x1_range)
X_train, Y_train = data_generator.generate_balanced_shuffled_sample(train_size)
X_test, Y_test = data_generator.generate_balanced_shuffled_sample(test_size)
plt.rcParams['figure.figsize'] = [14, 7]
f, axes = plt.subplots(nrows=1, ncols=2)
scatterplot(axes[0], X_train, Y_train, 'Trainset', 1, 2, 1, x0_range, x1_range)
scatterplot(axes[1], X_test, Y_test, 'Testset', 1, 2, 2, x0_range, x1_range)
plt.show()
docknet = Docknet()
docknet.add_input_layer(2)
docknet.add_dense_layer(1, 'sigmoid')
docknet.initializer = RandomNormalInitializer()
docknet.cost_function = 'cross_entropy'
docknet.optimizer = AdamOptimizer()
np.random.seed(1)
epochs = 50
batch_size = round(train_size / 10.)
epoch_errors, iteration_errors = docknet.train(X_train, Y_train, batch_size, max_number_of_epochs=epochs)
plt.subplot(1, 2, 1)
plt.plot(epoch_errors)
plt.xlabel("epoch")
plt.ylabel("loss")
plt.title("Loss evolution")
plt.subplot(1, 2, 2)
plt.plot(iteration_errors)
plt.xlabel("iteration")
plt.ylabel("loss")
plt.title("Loss evolution")
plt.show()
Y_predicted = docknet.predict(X_test)
Y_predicted = np.round(Y_predicted)
correct = Y_predicted == Y_test
wrong = Y_predicted != Y_test
X_correct = X_test[:, correct.reshape(test_size)]
Y_correct = Y_test[correct]
X_wrong = X_test[:, wrong.reshape(test_size)]
Y_wrong = Y_test[wrong]
plt.rcParams['figure.figsize'] = [20, 10]
f, axes = plt.subplots(nrows=1, ncols=3)
scatterplot(axes[0], X_test, Y_test, 'Expected', 1, 3, 1, x0_range, x1_range)
scatterplot(axes[1], X_correct, Y_correct, 'Actual correct', 1, 3, 2, x0_range, x1_range)
scatterplot(axes[2], X_wrong, Y_wrong, 'Actual wrong', 1, 3, 3, x0_range, x1_range)
plt.show()
results = metrics.classification_report(Y_test[0], Y_predicted[0])
print(results)
conf_matrix = metrics.confusion_matrix(Y_test[0], Y_predicted[0])
print(conf_matrix)
```
|
github_jupyter
|
import os
import sys
# Add ../src to the list of available Python packages
module_path = os.path.abspath(os.path.join('..', 'src'))
if module_path not in sys.path:
sys.path.insert(0, module_path)
import numpy as np
from sklearn import metrics
import matplotlib.pyplot as plt
from docknet.docknet import Docknet
from docknet.data_generator.cluster_data_generator import ClusterDataGenerator
from docknet.initializer.random_normal_initializer import RandomNormalInitializer
from docknet.optimizer.gradient_descent_optimizer import GradientDescentOptimizer
from docknet.optimizer.adam_optimizer import AdamOptimizer
def scatterplot(axe, X, Y, title, files, rows, index, x0_range, x1_range):
axe.scatter(X[0, :], X[1, :], c=Y[0:], s=2)
aspect = (x0_range[1] - x0_range[0]) / (x1_range[1] - x1_range[0])
axe.set_aspect(aspect)
axe.set_title(title)
axe.set_xlim(x0_range)
axe.set_ylim(x1_range)
axe.set_xlabel('x0')
axe.set_ylabel('x1')
train_size = 2000
test_size = 400
x0_range = (-5., 5.)
x1_range = (-5., 5.)
data_generator = ClusterDataGenerator(x0_range, x1_range)
X_train, Y_train = data_generator.generate_balanced_shuffled_sample(train_size)
X_test, Y_test = data_generator.generate_balanced_shuffled_sample(test_size)
plt.rcParams['figure.figsize'] = [14, 7]
f, axes = plt.subplots(nrows=1, ncols=2)
scatterplot(axes[0], X_train, Y_train, 'Trainset', 1, 2, 1, x0_range, x1_range)
scatterplot(axes[1], X_test, Y_test, 'Testset', 1, 2, 2, x0_range, x1_range)
plt.show()
docknet = Docknet()
docknet.add_input_layer(2)
docknet.add_dense_layer(1, 'sigmoid')
docknet.initializer = RandomNormalInitializer()
docknet.cost_function = 'cross_entropy'
docknet.optimizer = AdamOptimizer()
np.random.seed(1)
epochs = 50
batch_size = round(train_size / 10.)
epoch_errors, iteration_errors = docknet.train(X_train, Y_train, batch_size, max_number_of_epochs=epochs)
plt.subplot(1, 2, 1)
plt.plot(epoch_errors)
plt.xlabel("epoch")
plt.ylabel("loss")
plt.title("Loss evolution")
plt.subplot(1, 2, 2)
plt.plot(iteration_errors)
plt.xlabel("iteration")
plt.ylabel("loss")
plt.title("Loss evolution")
plt.show()
Y_predicted = docknet.predict(X_test)
Y_predicted = np.round(Y_predicted)
correct = Y_predicted == Y_test
wrong = Y_predicted != Y_test
X_correct = X_test[:, correct.reshape(test_size)]
Y_correct = Y_test[correct]
X_wrong = X_test[:, wrong.reshape(test_size)]
Y_wrong = Y_test[wrong]
plt.rcParams['figure.figsize'] = [20, 10]
f, axes = plt.subplots(nrows=1, ncols=3)
scatterplot(axes[0], X_test, Y_test, 'Expected', 1, 3, 1, x0_range, x1_range)
scatterplot(axes[1], X_correct, Y_correct, 'Actual correct', 1, 3, 2, x0_range, x1_range)
scatterplot(axes[2], X_wrong, Y_wrong, 'Actual wrong', 1, 3, 3, x0_range, x1_range)
plt.show()
results = metrics.classification_report(Y_test[0], Y_predicted[0])
print(results)
conf_matrix = metrics.confusion_matrix(Y_test[0], Y_predicted[0])
print(conf_matrix)
| 0.458349 | 0.564879 |
```
# read depths as int from day1.txt
with open('day1.txt', 'r') as f:
depths = [int(x) for x in f.readlines()]
# To do this, count the number of times a depth measurement increases from the previous measurement. (There is no measurement before the first measurement.) In the example above, the changes are as follows:
# 199 (N/A - no previous measurement)
# 200 (increased)
# 208 (increased)
# 210 (increased)
# 200 (decreased)
# 207 (increased)
# 240 (increased)
# 269 (increased)
# 260 (decreased)
# 263 (increased)
# In this example, there are 7 measurements that are larger than the previous measurement.
# How many measurements are larger than the previous measurement?
def count_larger_depths(depths):
count = 0
for i in range(1, len(depths)):
if depths[i] > depths[i-1]:
count += 1
return count
print(count_larger_depths(depths))
#Instead, consider sums of a three-measurement sliding window. Again considering the above example:
# 199 A
# 200 A B
# 208 A B C
# 210 B C D
# 200 E C D
# 207 E F D
# 240 E F G
# 269 F G H
# 260 G H
# 263 H
# Start by comparing the first and second three-measurement windows. The measurements in the first window are marked A (199, 200, 208); their sum is 199 + 200 + 208 = 607. The second window is marked B (200, 208, 210); its sum is 618. The sum of measurements in the second window is larger than the sum of the first, so this first comparison increased.
# Your goal now is to count the number of times the sum of measurements in this sliding window increases from the previous sum. So, compare A with B, then compare B with C, then C with D, and so on. Stop when there aren't enough measurements left to create a new three-measurement sum.
# In the above example, the sum of each three-measurement window is as follows:
# A: 607 (N/A - no previous sum)
# B: 618 (increased)
# C: 618 (no change)
# D: 617 (decreased)
# E: 647 (increased)
# F: 716 (increased)
# G: 769 (increased)
# H: 792 (increased)
# In this example, there are 5 sums that are larger than the previous sum.
# Consider sums of a three-measurement sliding window. How many sums are larger than the previous sum?
def get_sliding_window_sums(depths):
sums = []
for i in range(3, len(depths)+1):
sums.append(sum(depths[i-3:i]))
return sums
print(count_larger_depths(get_sliding_window_sums(depths)))
def count_larger_sums(depths):
count = 0
for i in range(3, len(depths)):
if sum(depths[i-3:i]) > sum(depths[i-4:i-1]):
count += 1
return count
print(count_larger_sums(depths))
```
|
github_jupyter
|
# read depths as int from day1.txt
with open('day1.txt', 'r') as f:
depths = [int(x) for x in f.readlines()]
# To do this, count the number of times a depth measurement increases from the previous measurement. (There is no measurement before the first measurement.) In the example above, the changes are as follows:
# 199 (N/A - no previous measurement)
# 200 (increased)
# 208 (increased)
# 210 (increased)
# 200 (decreased)
# 207 (increased)
# 240 (increased)
# 269 (increased)
# 260 (decreased)
# 263 (increased)
# In this example, there are 7 measurements that are larger than the previous measurement.
# How many measurements are larger than the previous measurement?
def count_larger_depths(depths):
count = 0
for i in range(1, len(depths)):
if depths[i] > depths[i-1]:
count += 1
return count
print(count_larger_depths(depths))
#Instead, consider sums of a three-measurement sliding window. Again considering the above example:
# 199 A
# 200 A B
# 208 A B C
# 210 B C D
# 200 E C D
# 207 E F D
# 240 E F G
# 269 F G H
# 260 G H
# 263 H
# Start by comparing the first and second three-measurement windows. The measurements in the first window are marked A (199, 200, 208); their sum is 199 + 200 + 208 = 607. The second window is marked B (200, 208, 210); its sum is 618. The sum of measurements in the second window is larger than the sum of the first, so this first comparison increased.
# Your goal now is to count the number of times the sum of measurements in this sliding window increases from the previous sum. So, compare A with B, then compare B with C, then C with D, and so on. Stop when there aren't enough measurements left to create a new three-measurement sum.
# In the above example, the sum of each three-measurement window is as follows:
# A: 607 (N/A - no previous sum)
# B: 618 (increased)
# C: 618 (no change)
# D: 617 (decreased)
# E: 647 (increased)
# F: 716 (increased)
# G: 769 (increased)
# H: 792 (increased)
# In this example, there are 5 sums that are larger than the previous sum.
# Consider sums of a three-measurement sliding window. How many sums are larger than the previous sum?
def get_sliding_window_sums(depths):
sums = []
for i in range(3, len(depths)+1):
sums.append(sum(depths[i-3:i]))
return sums
print(count_larger_depths(get_sliding_window_sums(depths)))
def count_larger_sums(depths):
count = 0
for i in range(3, len(depths)):
if sum(depths[i-3:i]) > sum(depths[i-4:i-1]):
count += 1
return count
print(count_larger_sums(depths))
| 0.556882 | 0.697364 |
# Automatic Vectorization in JAX
[](https://colab.research.google.com/github/google/jax/blob/main/docs/jax-101/03-vectorization.ipynb)
*Authors: Matteo Hessel*
In the previous section we discussed JIT compilation via the `jax.jit` function. This notebook discusses another of JAX's transforms: vectorization via `jax.vmap`.
## Manual Vectorization
Consider the following simple code that computes the convolution of two one-dimensional vectors:
```
import jax
import jax.numpy as jnp
x = jnp.arange(5)
w = jnp.array([2., 3., 4.])
def convolve(x, w):
output = []
for i in range(1, len(x)-1):
output.append(jnp.dot(x[i-1:i+2], w))
return jnp.array(output)
convolve(x, w)
```
Suppose we would like to apply this function to a batch of weights `w` to a batch of vectors `x`.
```
xs = jnp.stack([x, x])
ws = jnp.stack([w, w])
```
The most naive option would be to simply loop over the batch in Python:
```
def manually_batched_convolve(xs, ws):
output = []
for i in range(xs.shape[0]):
output.append(convolve(xs[i], ws[i]))
return jnp.stack(output)
manually_batched_convolve(xs, ws)
```
This produces the correct result, however it is not very efficient.
In order to batch the computation efficiently, you would normally have to rewrite the function manually to ensure it is done in vectorized form. This is not particularly difficult to implement, but does involve changing how the function treats indices, axes, and other parts of the input.
For example, we could manually rewrite `convolve()` to support vectorized computation across the batch dimension as follows:
```
def manually_vectorized_convolve(xs, ws):
output = []
for i in range(1, xs.shape[-1] -1):
output.append(jnp.sum(xs[:, i-1:i+2] * ws, axis=1))
return jnp.stack(output, axis=1)
manually_vectorized_convolve(xs, ws)
```
Such re-implementation is messy and error-prone; fortunately JAX provides another way.
## Automatic Vectorization
In JAX, the `jax.vmap` transformation is designed to generate such a vectorized implementation of a function automatically:
```
auto_batch_convolve = jax.vmap(convolve)
auto_batch_convolve(xs, ws)
```
It does this by tracing the function similarly to `jax.jit`, and automatically adding batch axes at the beginning of each input.
If the batch dimension is not the first, you may use the `in_axes` and `out_axes` arguments to specify the location of the batch dimension in inputs and outputs. These may be an integer if the batch axis is the same for all inputs and outputs, or lists, otherwise.
```
auto_batch_convolve_v2 = jax.vmap(convolve, in_axes=1, out_axes=1)
xst = jnp.transpose(xs)
wst = jnp.transpose(ws)
auto_batch_convolve_v2(xst, wst)
```
`jax.vmap` also supports the case where only one of the arguments is batched: for example, if you would like to convolve to a single set of weights `w` with a batch of vectors `x`; in this case the `in_axes` argument can be set to `None`:
```
batch_convolve_v3 = jax.vmap(convolve, in_axes=[0, None])
batch_convolve_v3(xs, w)
```
## Combining transformations
As with all JAX transformations, `jax.jit` and `jax.vmap` are designed to be composable, which means you can wrap a vmapped function with `jit`, or a JITted function with `vmap`, and everything will work correctly:
```
jitted_batch_convolve = jax.jit(auto_batch_convolve)
jitted_batch_convolve(xs, ws)
```
|
github_jupyter
|
import jax
import jax.numpy as jnp
x = jnp.arange(5)
w = jnp.array([2., 3., 4.])
def convolve(x, w):
output = []
for i in range(1, len(x)-1):
output.append(jnp.dot(x[i-1:i+2], w))
return jnp.array(output)
convolve(x, w)
xs = jnp.stack([x, x])
ws = jnp.stack([w, w])
def manually_batched_convolve(xs, ws):
output = []
for i in range(xs.shape[0]):
output.append(convolve(xs[i], ws[i]))
return jnp.stack(output)
manually_batched_convolve(xs, ws)
def manually_vectorized_convolve(xs, ws):
output = []
for i in range(1, xs.shape[-1] -1):
output.append(jnp.sum(xs[:, i-1:i+2] * ws, axis=1))
return jnp.stack(output, axis=1)
manually_vectorized_convolve(xs, ws)
auto_batch_convolve = jax.vmap(convolve)
auto_batch_convolve(xs, ws)
auto_batch_convolve_v2 = jax.vmap(convolve, in_axes=1, out_axes=1)
xst = jnp.transpose(xs)
wst = jnp.transpose(ws)
auto_batch_convolve_v2(xst, wst)
batch_convolve_v3 = jax.vmap(convolve, in_axes=[0, None])
batch_convolve_v3(xs, w)
jitted_batch_convolve = jax.jit(auto_batch_convolve)
jitted_batch_convolve(xs, ws)
| 0.321247 | 0.991255 |
## 1. Import numpy as np and see the version
** Difficulty Level: L1
** Q. Import numpy as np and print the version number
```
import numpy as np
print(np.__version__)
```
2. How to create a 1D array?
Difficulty Level: L1
Q. Create a 1D array of numbers from 0 to 9
Desired output:
#> array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
```
np.array(range(0,10))
```
3. How to create a boolean array?
Difficulty Level: L1
Q. Create a 3×3 numpy array of all True’s
```
np.array(([1,1,1], [1,1,1], [1,1,1]) , dtype = bool)
```
## 4. How to extract items that satisfy a given condition from 1D array?
Difficulty Level: L1
Q. Extract all odd numbers from arr
arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
```
arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
modulo = np.mod(arr,2)==1
np.extract(modulo, arr)
```
## 5. How to replace items that satisfy a condition with another value in numpy array?
Difficulty Level: L1
Q. Replace all odd numbers in arr with -1
arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
```
arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
np.where(arr % 2 == 1, -1, arr)
```
## How to replace items that satisfy a condition without affecting the original array?
Difficulty Level: L2
Q. Replace all odd numbers in arr with -1 without changing arr
arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
```
# ISO Exercice 5
```
## 7. How to reshape an array?
Difficulty Level: L1
Q. Convert a 1D array to a 2D array with 2 rows
arr = array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
```
arr = np.array(range(0,10))
arr.reshape(2,5)
```
## How to stack two arrays vertically?
Difficulty Level: L2
Q. Stack arrays a and b vertically
a = np.arange(10).reshape(2,-1)
b = np.repeat(1, 10).reshape(2,-1)
```
a = np.arange(10).reshape(2,-1)
b = np.repeat(1, 10).reshape(2,-1)
np.stack((a,b), axis = 0)
```
## 9. How to stack two arrays horizontally?
Difficulty Level: L2
Q. Stack the arrays a and b horizontally.
Desired output : array([[0, 1, 2, 3, 4, 1, 1, 1, 1, 1],
#> [5, 6, 7, 8, 9, 1, 1, 1, 1, 1]])
```
np.hstack((a,b))
```
## 10. How to generate custom sequences in numpy without hardcoding?
Difficulty Level: L2
Q. Create the following pattern without hardcoding. Use only numpy functions and the below input array a.
a = np.array([1,2,3])`
Desired Output : #> array([1, 1, 1, 2, 2, 2, 3, 3, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3])
```
a = np.array([1,2,3])
np.random.choice(a, (1,18))
```
## 11. How to get the common items between two python numpy arrays?
Difficulty Level: L2
Q. Get the common items between a and b
Input:
a = np.array([1,2,3,2,3,4,3,4,5,6])
b = np.array([7,2,10,2,7,4,9,4,9,8])
Desired Output :
array([2, 4])
```
a = np.array([1,2,3,2,3,4,3,4,5,6])
b = np.array([7,2,10,2,7,4,9,4,9,8])
np.intersect1d(a, b)
```
## 12. How to remove from one array those items that exist in another?
Difficulty Level: L2
Q. From array a remove all items present in array b
Input:
a = np.array([1,2,3,4,5])
b = np.array([5,6,7,8,9])
Output :
array([1,2,3,4])
```
a = np.array([1,2,3,4,5])
b = np.array([5,6,7,8,9])
iso = np.intersect1d(a, b)
#Fail
np.setdiff1d(a, b)
```
## 13. How to get the positions where elements of two arrays match?
Difficulty Level: L2
Q. Get the positions where elements of a and b match
Input:
a = np.array([1,2,3,2,3,4,3,4,5,6])
b = np.array([7,2,10,2,7,4,9,4,9,8])
Desired Output:
#> (array([1, 3, 5, 7]),)
```
a = np.array([1,2,3,2,3,4,3,4,5,6])
b = np.array([7,2,10,2,7,4,9,4,9,8])
np.where(a==b)
```
## 14. How to extract all numbers between a given range from a numpy array?
Difficulty Level: L2
Q. Get all items between 5 and 10 from a.
Input:
a = np.array([2, 6, 1, 9, 10, 3, 27])
Desired Output:
(array([6, 9, 10]),)
```
a = np.array([2, 6, 1, 9, 10, 3, 27])
isBetween = np.logical_and(a >= 5, a<= 10)
np.extract(isBetween, a)
```
## 15. How to make a python function that handles scalars to work on numpy arrays?
Difficulty Level: L2
Q. Convert the function maxx that works on two scalars, to work on two arrays.
Input:
def maxx(x, y):
"""Get the maximum of two items"""
if x >= y:
return x
else:
return y
maxx(1, 5)
#> 5
Desired Output:
a = np.array([5, 7, 9, 8, 6, 4, 5])
b = np.array([6, 3, 4, 8, 9, 7, 1])
pair_max(a, b)
#> array([ 6., 7., 9., 8., 9., 7., 5.])
```
#Fail
```
## 16. How to swap two columns in a 2d numpy array?
Difficulty Level: L2
Q. Swap columns 1 and 2 in the array arr.
arr = np.arange(9).reshape(3,3)
```
arr = np.arange(9).reshape(3,3)
arr[:,[0, 1]] = arr[:,[1, 0]]
arr
```
## 17. How to swap two rows in a 2d numpy array?
Difficulty Level: L2
Q. Swap rows 1 and 2 in the array arr:
arr = np.arange(9).reshape(3,3)
```
arr = np.arange(9).reshape(3,3)
arr[[1,0,2],:]
```
## 18. How to reverse the rows of a 2D array?
Difficulty Level: L2
Q. Reverse the rows of a 2D array arr.
Input :
arr = np.arange(9).reshape(3,3)
```
arr = np.arange(9).reshape(3,3)
arr = np.arange(9).reshape(3,3)
np.flip(arr, axis = 1)
```
# 19. How to reverse the columns of a 2D array?
Difficulty Level: L2
Q. Reverse the columns of a 2D array arr.
Input
arr = np.arange(9).reshape(3,3)
```
arr = np.arange(9).reshape(3,3)
np.flip(arr, axis = 0)
```
# 20. How to create a 2D array containing random floats between 5 and 10?
Difficulty Level: L2
Q. Create a 2D array of shape 5x3 to contain random decimal numbers between 5 and 10.
```
np.random.choice(np.array(range(5,11)), (5,3))
```
# 21. How to print only 3 decimal places in python numpy array?
Difficulty Level: L1
Q. Print or show only 3 decimal places of the numpy array rand_arr.
Input : rand_arr = np.random.random((5,3))
```
rand_arr = np.random.random((5,3))
rand_arr.round(decimals = 3)
```
# 22. How to pretty print a numpy array by suppressing the scientific notation (like 1e10)?
Difficulty Level: L1
Q. Pretty print rand_arr by suppressing the scientific notation (like 1e10)
Input :
np.random.seed(100)
rand_arr = np.random.random([3,3])/1e3
rand_arr
```
np.random.seed(100)
rand_arr = np.random.random([3,3])/1e3
#Fail
```
# 23. How to limit the number of items printed in output of numpy array?
Difficulty Level: L1
Q. Limit the number of items printed in python numpy array a to a maximum of 6 elements.
Input:
a = np.arange(15)
Output :
Desired output : array([ 0, 1, 2, ..., 12, 13, 14])
```
a = np.arange(15)
a
np.set_printoptions(threshold = 3)
a
```
# 24. How to print the full numpy array without truncating
Difficulty Level: L1
Q. Print the full numpy array a without truncating.
Input:
np.set_printoptions(threshold=6)
a = np.arange(15)
```
import sys
np.set_printoptions(threshold = sys.maxsize)
a = np.arange(15)
a
```
# 25. How to import a dataset with numbers and texts keeping the text intact in python numpy?
Difficulty Level: L2
Q. Import the iris dataset keeping the text intact.
```
np.genfromtxt('iris.data', delimiter = ',', dtype = object)
```
# 26. How to extract a particular column from 1D array of tuples?
Difficulty Level: L2
Q. Extract the text column species from the 1D iris imported in previous question.
Input:
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_1d = np.genfromtxt(url, delimiter=',', dtype=None)
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_1d = np.genfromtxt(url, delimiter=',', dtype=None)
iris_1d
[print(element[4]) for element in iris_1d]
#fail
#Solution : np.array([row[4] for row in iris_1d])
```
# 27. How to convert a 1d array of tuples to a 2d numpy array?
Difficulty Level: L2
Q. Convert the 1D iris to 2D array iris_2d by omitting the species text field.
Input:
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_1d = np.genfromtxt(url, delimiter=',', dtype=None)
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_1d = np.genfromtxt(url, delimiter=',', dtype=None, usecols = [0,1,2,3])
iris_1d.reshape(2,-1)
iris_1d
```
# 28. How to compute the mean, median, standard deviation of a numpy array?
Difficulty: L1
Q. Find the mean, median, standard deviation of iris's sepallength (1st column)
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
```
iris = np.genfromtxt(url, delimiter=',', dtype='float')
print(np.mean(iris[:,:1]))
print(np.median(iris[:,:1]))
print(np.std(iris[:,:1]))
```
# 29. How to normalize an array so the values range exactly between 0 and 1?
Difficulty: L2
Q. Create a normalized form of iris's sepallength whose values range exactly between 0 and 1 so that the minimum has value 0 and maximum has value 1.
Input:
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
sepallength = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0])
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
sepallength = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0])
#fail
#Solution : Smax, Smin = sepallength.max(), sepallength.min()
#S = (sepallength - Smin)/(Smax - Smin)
```
# 30. How to compute the softmax score?
Difficulty Level: L3
Q. Compute the softmax score of sepallength.
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
sepallength = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0])
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
sepallength = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0])
#fail
#Out of scope
```
# 31. How to find the percentile scores of a numpy array?
Difficulty Level: L1
Q. Find the 5th and 95th percentile of iris's sepallength
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data
sepallength = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0])
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
sepallength = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0])
print(np.percentile(sepallength, 5))
print(np.percentile(sepallength, 95))
```
# 32. How to insert values at random positions in an array?
Difficulty Level: L2
Q. Insert np.nan values at 20 random positions in iris_2d dataset
Input :
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='object')
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='object')
x = 20
while x != 0:
np.insert(arr = iris_2d, obj = np.random.choice(range(1,150)), values = np.nan)
x -= 1
#Fail
#Solution : iris_2d[np.random.randint(150, size=20), np.random.randint(4, size=20)] = np.nan
```
# How to find the position of missing values in numpy array?
Difficulty Level: L2
Q. Find the number and position of missing values in iris_2d's sepallength (1st column)
Input
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float')
iris_2d[np.random.randint(150, size=20), np.random.randint(4, size=20)] = np.nan
#####
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
iris_2d[np.random.randint(150, size=20), np.random.randint(4, size=20)] = np.nan
# number of missing values
isNan = np.isnan(iris_2d[:,0])
isNan.sum()
# number of missing values
np.where(isNan)
```
# 34. How to filter a numpy array based on two or more conditions?
Difficulty Level: L3
Q. Filter the rows of iris_2d that has petallength (3rd column) > 1.5 and sepallength (1st column) < 5.0
Input :
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
```
import numpy as np
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
#iris_2d[2] > 1.5 AND iris_2d[0] < 5.0
#np.where(iris_2d[:, 2] > 1.5)
iris_2d[(iris_2d[:, 0] < 5) & (iris_2d[:, 2] > 1.5)]
```
# 35. How to drop rows that contain a missing value from a numpy array?
Difficulty Level: L3:
Q. Select the rows of iris_2d that does not have any nan value.
Input
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
iris_2d[np.random.randint(150, size=20), np.random.randint(4, size=20)] = np.nan
#Fail
#Solution :
#any_nan_in_row = np.array([~np.any(np.isnan(row)) for row in iris_2d])
#iris_2d[any_nan_in_row][:5]
```
# 36. How to find the correlation between two columns of a numpy array?
Difficulty Level: L2
Q. Find the correlation between SepalLength(1st column) and PetalLength(3rd column) in iris_2d
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris= np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
np.corrcoef(iris[:,0], iris[:,2])
```
# 37. How to find if a given array has any null values?
Difficulty Level: L2
Q. Find out if iris_2d has any missing values.
Input :
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
np.isnan(iris_2d).sum()
#Solution : np.isnan(iris_2d).any()
```
# 38. How to replace all missing values with 0 in a numpy array?
Difficulty Level: L2
Q. Replace all ccurrences of nan with 0 in numpy array
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
iris_2d[np.random.randint(150, size=20), np.random.randint(4, size=20)] = np.nan
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
iris_2d[np.random.randint(150, size=20), np.random.randint(4, size=20)] = np.nan
np.nan_to_num(iris_2d, 0)
```
# 39. How to find the count of unique values in a numpy array?
Difficulty Level: L2
Q. Find the unique values and the count of unique values in iris's species
Input
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
#unique values
np.unique(iris[:,-1], return_counts = True)
```
# 40. How to convert a numeric to a categorical (text) array?
Difficulty Level: L2
Q. Bin the petal length (3rd) column of iris_2d to form a text array, such that if petal length is:
Less than 3 --> 'small'
3-5 --> 'medium'
'>=5 --> 'large'
Input :
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
['small' if value < 3 else 'medium' for value in iris[:,2]]
#Fail
#Solution
#petal_length_bin = np.digitize(iris[:, 2].astype('float'), [0, 3, 5, 10])
#label_map = {1: 'small', 2: 'medium', 3: 'large', 4: np.nan}
#petal_length_cat = [label_map[x] for x in petal_length_bin]
```
# 41. How to create a new column from existing columns of a numpy array?
Difficulty Level: L2
Q. Create a new column for volume in iris_2d, where volume is (pi x petallength x sepal_length^2)/3
Input
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='object')
vol = np.array(((pi*iris_2d[:,2].astype('float')*(iris_2d[:,0].astype('float')**2))/3))
print(np.column_stack((iris_2d, vol)))
vol.shape
```
# 42. How to do probabilistic sampling in numpy?
Difficulty Level: L3
Q. Randomly sample iris's species such that setose is twice the number of versicolor and virginica
Import iris keeping the text column intact
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
```
#Fail
#Hors Scope
```
# 43. How to get the second largest value of an array when grouped by another array?
Difficulty Level: L2
Q. What is the value of second longest petallength of species setosa
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
np.sort(np.unique(iris[:, 1]))[-2]
```
# 44. How to sort a 2D array by a column
Difficulty Level: L2
Q. Sort the iris dataset based on sepallength column.
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
np.argsort(iris, axis = 0)
#Fail
#Solution :
iris[iris[:,0].argsort()]
```
# 45. How to find the most frequent value in a numpy array?
Difficulty Level: L1
Q. Find the most frequent value of petal length (3rd column) in iris dataset.
Input:
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
max_index = np.argmax(np.unique(iris[:,2], return_counts = True)[1])
np.unique(iris[:,2], return_counts = True)[0][max_index]
```
# 46. How to find the position of the first occurrence of a value greater than a given value?
Difficulty Level: L2
Q. Find the position of the first occurrence of a value greater than 1.0 in petalwidth 4th column of iris dataset.
Input:
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
```
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
np.where(iris[:,3].astype('float') > 1)[0][0]
#Better Solution :
#np.argwhere(iris[:, 3].astype(float) > 1.0)[0]
```
# 47. How to replace all values greater than a given value to a given cutoff?
Difficulty Level: L2
Q. From the array a, replace all values greater than 30 to 30 and less than 10 to 10.
Input
np.random.seed(100)
a = np.random.uniform(1,50, 20)
```
np.random.seed(100)
a = np.random.uniform(1,50, 20)
#fail
#Solution :
np.clip(a, a_min=10, a_max=30)
```
# 48. How to get the positions of top n values from a numpy array?
Difficulty Level: L2
Q. Get the positions of top 5 maximum values in a given array a.
np.random.seed(100)
a = np.random.uniform(1,50, 20)
```
np.random.seed(100)
a = np.random.uniform(1,50, 20)
np.argsort(a)[-5:]
```
# 50. How to convert an array of arrays into a flat 1d array?
Difficulty Level: 2
Q. Convert array_of_arrays into a flat linear 1d array.
Input:
arr1 = np.arange(3)
arr2 = np.arange(3,7)
arr3 = np.arange(7,10)
array_of_arrays = np.array([arr1, arr2, arr3])
array_of_arrays
```
arr1 = np.arange(3)
arr2 = np.arange(3,7)
arr3 = np.arange(7,10)
array_of_arrays = np.array([arr1, arr2, arr3], dtype = object)
np.concatenate(array_of_arrays)
```
# 54. How to rank items in an array using numpy?
Difficulty Level: L2
Q. Create the ranks for the given numeric array a.
Input:
np.random.seed(10)
a = np.random.randint(20, size=10)
print(a)
#> [ 9 4 15 0 17 16 17 8 9 0]
```
np.random.seed(10)
a = np.random.randint(20, size=10)
a.argsort()
#fail
#Solution : a.argsort().argsort()
```
# 56. How to find the maximum value in each row of a numpy array 2d?
DifficultyLevel: L2
Q. Compute the maximum for each row in the given array.
```
np.random.seed(100)
a = np.random.randint(1,10, [5,3])
[np.max(row) for row in a]
#Better Solution :
#np.amax(a, axis=1)
```
# 57. How to compute the min-by-max for each row for a numpy array 2d?
DifficultyLevel: L3
Q. Compute the min-by-max for each row for given 2d numpy array.
np.random.seed(100)
a = np.random.randint(1,10, [5,3])
```
np.random.seed(100)
a = np.random.randint(1,10, [5,3])
np.amin(a, axis = 1) / np.amax(a, axis = 1)
#Better Solution
#np.apply_along_axis(lambda x: np.min(x)/np.max(x), arr=a, axis=1)
```
# 58. How to find the duplicate records in a numpy array?
Difficulty Level: L3
Q. Find the duplicate entries (2nd occurrence onwards) in the given numpy array and mark them as True. First time occurrences should be False.
Input
np.random.seed(100)
a = np.random.randint(0, 5, 10)
```
np.random.seed(100)
a = np.random.randint(0, 5, 10)
a
from collections import Counter
[True if Counter(a)[num] > 1 else False for num in a]
#Better Solution
#out = np.full(a.shape[0], True)
#unique_positions = np.unique(a, return_index=True)[1]
#out[unique_positions] = False
```
# 59. How to find the grouped mean in numpy?
Difficulty Level L3
Q. Find the mean of a numeric column grouped by a categorical column in a 2D numpy array
Input :
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
```
url = "C:\\Users\XXX\\Documents\\GitHub\\Python-Exercices\\iris.data"
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
unique_variety = np.unique(iris[:, 4]) #array([b'Iris-setosa', b'Iris-versicolor', b'Iris-virginica'],dtype=object)
for variety in unique_variety:
print(np.mean(iris[:, 0:4], dtype = float, where = iris[:,4] == variety))
#Non fonctionnel
```
60. How to convert a PIL image to numpy array?
Difficulty Level: L3
Q. Import the image from the following URL and convert it to a numpy array.
URL = 'https://upload.wikimedia.org/wikipedia/commons/8/8b/Denali_Mt_McKinley.jpg'
## 61. How to drop all missing values from a numpy array?
Difficulty Level: L2
Q. Drop all nan values from a 1D numpy array
Input:
np.array([1,2,3,np.nan,5,6,7,np.nan])
Desired Output:
array([ 1., 2., 3., 5., 6., 7.])
```
arr = np.array([1,2,3,np.nan,5,6,7,np.nan])
nans = np.where(np.isnan(arr) == True)
np.delete(arr, nans)
```
# 62. How to compute the euclidean distance between two arrays?
Difficulty Level: L3
Q. Compute the euclidean distance between two arrays a and b.
Input:
a = np.array([1,2,3,4,5])
b = np.array([4,5,6,7,8])
```
a = np.array([1,2,3,4,5])
b = np.array([4,5,6,7,8])
np.linalg.norm(a - b)
```
# 64. How to subtract a 1d array from a 2d array, where each item of 1d array subtracts from respective row?
Difficulty Level: L2
Q. Subtract the 1d array b_1d from the 2d array a_2d, such that each item of b_1d subtracts from respective row of a_2d.
a_2d = np.array([[3,3,3],[4,4,4],[5,5,5]])
b_1d = np.array([1,1,1]
```
a_2d = np.array([[3,3,3],[4,4,4],[5,5,5]])
b_1d = np.array([1,2,3])
#Fail
# Solution -> print(a_2d - b_1d[:,None])
```
# 65. How to find the index of n'th repetition of an item in an array
Difficulty Level L2
Q. Find the index of 5th repetition of number 1 in x.
x = np.array([1, 2, 1, 1, 3, 4, 3, 1, 1, 2, 1, 1, 2])
```
x = np.array([1, 2, 1, 1, 3, 4, 3, 1, 1, 2, 1, 1, 2])
np.where(x == 1)[0][5-1]
```
# 66. How to convert numpy's datetime64 object to datetime's datetime object?
Difficulty Level: L2
Q. Convert numpy's datetime64 object to datetime's datetime object
Input:
a numpy datetime64 object
dt64 = np.datetime64('2018-02-25 22:10:10')
```
dt64 = np.datetime64('2018-02-25 22:10:10')
dt64.tolist()
#Better Solution -> dt64.astype(datetime)
```
# 68. How to create a numpy array sequence given only the starting point, length and the step?
Difficulty Level: L2
Q. Create a numpy array of length 10, starting from 5 and has a step of 3 between consecutive numbers
```
np.arange(start = 5, stop = 3*10+5, step = 3)
```
# 69. How to fill in missing dates in an irregular series of numpy dates?
Difficulty Level: L3
Q. Given an array of a non-continuous sequence of dates. Make it a continuous sequence of dates, by filling in the missing dates.
Input
dates = np.arange(np.datetime64('2018-02-01'), np.datetime64('2018-02-25'), 2)
```
dates = np.arange(np.datetime64('2018-02-01'), np.datetime64('2018-02-25'), 2)
#Fail
#Solution :
#filled_in = np.array([np.arange(date, (date+d)) for date, d in zip(dates, np.diff(dates))]).reshape(-1)
#output = np.hstack([filled_in, dates[-1]])
#output
```
|
github_jupyter
|
import numpy as np
print(np.__version__)
np.array(range(0,10))
np.array(([1,1,1], [1,1,1], [1,1,1]) , dtype = bool)
arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
modulo = np.mod(arr,2)==1
np.extract(modulo, arr)
arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
np.where(arr % 2 == 1, -1, arr)
# ISO Exercice 5
arr = np.array(range(0,10))
arr.reshape(2,5)
a = np.arange(10).reshape(2,-1)
b = np.repeat(1, 10).reshape(2,-1)
np.stack((a,b), axis = 0)
np.hstack((a,b))
a = np.array([1,2,3])
np.random.choice(a, (1,18))
a = np.array([1,2,3,2,3,4,3,4,5,6])
b = np.array([7,2,10,2,7,4,9,4,9,8])
np.intersect1d(a, b)
a = np.array([1,2,3,4,5])
b = np.array([5,6,7,8,9])
iso = np.intersect1d(a, b)
#Fail
np.setdiff1d(a, b)
a = np.array([1,2,3,2,3,4,3,4,5,6])
b = np.array([7,2,10,2,7,4,9,4,9,8])
np.where(a==b)
a = np.array([2, 6, 1, 9, 10, 3, 27])
isBetween = np.logical_and(a >= 5, a<= 10)
np.extract(isBetween, a)
#Fail
arr = np.arange(9).reshape(3,3)
arr[:,[0, 1]] = arr[:,[1, 0]]
arr
arr = np.arange(9).reshape(3,3)
arr[[1,0,2],:]
arr = np.arange(9).reshape(3,3)
arr = np.arange(9).reshape(3,3)
np.flip(arr, axis = 1)
arr = np.arange(9).reshape(3,3)
np.flip(arr, axis = 0)
np.random.choice(np.array(range(5,11)), (5,3))
rand_arr = np.random.random((5,3))
rand_arr.round(decimals = 3)
np.random.seed(100)
rand_arr = np.random.random([3,3])/1e3
#Fail
a = np.arange(15)
a
np.set_printoptions(threshold = 3)
a
import sys
np.set_printoptions(threshold = sys.maxsize)
a = np.arange(15)
a
np.genfromtxt('iris.data', delimiter = ',', dtype = object)
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_1d = np.genfromtxt(url, delimiter=',', dtype=None)
iris_1d
[print(element[4]) for element in iris_1d]
#fail
#Solution : np.array([row[4] for row in iris_1d])
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_1d = np.genfromtxt(url, delimiter=',', dtype=None, usecols = [0,1,2,3])
iris_1d.reshape(2,-1)
iris_1d
iris = np.genfromtxt(url, delimiter=',', dtype='float')
print(np.mean(iris[:,:1]))
print(np.median(iris[:,:1]))
print(np.std(iris[:,:1]))
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
sepallength = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0])
#fail
#Solution : Smax, Smin = sepallength.max(), sepallength.min()
#S = (sepallength - Smin)/(Smax - Smin)
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
sepallength = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0])
#fail
#Out of scope
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
sepallength = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0])
print(np.percentile(sepallength, 5))
print(np.percentile(sepallength, 95))
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='object')
x = 20
while x != 0:
np.insert(arr = iris_2d, obj = np.random.choice(range(1,150)), values = np.nan)
x -= 1
#Fail
#Solution : iris_2d[np.random.randint(150, size=20), np.random.randint(4, size=20)] = np.nan
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
iris_2d[np.random.randint(150, size=20), np.random.randint(4, size=20)] = np.nan
# number of missing values
isNan = np.isnan(iris_2d[:,0])
isNan.sum()
# number of missing values
np.where(isNan)
import numpy as np
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
#iris_2d[2] > 1.5 AND iris_2d[0] < 5.0
#np.where(iris_2d[:, 2] > 1.5)
iris_2d[(iris_2d[:, 0] < 5) & (iris_2d[:, 2] > 1.5)]
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
iris_2d[np.random.randint(150, size=20), np.random.randint(4, size=20)] = np.nan
#Fail
#Solution :
#any_nan_in_row = np.array([~np.any(np.isnan(row)) for row in iris_2d])
#iris_2d[any_nan_in_row][:5]
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris= np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
np.corrcoef(iris[:,0], iris[:,2])
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
np.isnan(iris_2d).sum()
#Solution : np.isnan(iris_2d).any()
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[0,1,2,3])
iris_2d[np.random.randint(150, size=20), np.random.randint(4, size=20)] = np.nan
np.nan_to_num(iris_2d, 0)
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
#unique values
np.unique(iris[:,-1], return_counts = True)
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
['small' if value < 3 else 'medium' for value in iris[:,2]]
#Fail
#Solution
#petal_length_bin = np.digitize(iris[:, 2].astype('float'), [0, 3, 5, 10])
#label_map = {1: 'small', 2: 'medium', 3: 'large', 4: np.nan}
#petal_length_cat = [label_map[x] for x in petal_length_bin]
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris_2d = np.genfromtxt(url, delimiter=',', dtype='object')
vol = np.array(((pi*iris_2d[:,2].astype('float')*(iris_2d[:,0].astype('float')**2))/3))
print(np.column_stack((iris_2d, vol)))
vol.shape
#Fail
#Hors Scope
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
np.sort(np.unique(iris[:, 1]))[-2]
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
np.argsort(iris, axis = 0)
#Fail
#Solution :
iris[iris[:,0].argsort()]
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
max_index = np.argmax(np.unique(iris[:,2], return_counts = True)[1])
np.unique(iris[:,2], return_counts = True)[0][max_index]
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
iris = np.genfromtxt(url, delimiter=',', dtype='object')
np.where(iris[:,3].astype('float') > 1)[0][0]
#Better Solution :
#np.argwhere(iris[:, 3].astype(float) > 1.0)[0]
np.random.seed(100)
a = np.random.uniform(1,50, 20)
#fail
#Solution :
np.clip(a, a_min=10, a_max=30)
np.random.seed(100)
a = np.random.uniform(1,50, 20)
np.argsort(a)[-5:]
arr1 = np.arange(3)
arr2 = np.arange(3,7)
arr3 = np.arange(7,10)
array_of_arrays = np.array([arr1, arr2, arr3], dtype = object)
np.concatenate(array_of_arrays)
np.random.seed(10)
a = np.random.randint(20, size=10)
a.argsort()
#fail
#Solution : a.argsort().argsort()
np.random.seed(100)
a = np.random.randint(1,10, [5,3])
[np.max(row) for row in a]
#Better Solution :
#np.amax(a, axis=1)
np.random.seed(100)
a = np.random.randint(1,10, [5,3])
np.amin(a, axis = 1) / np.amax(a, axis = 1)
#Better Solution
#np.apply_along_axis(lambda x: np.min(x)/np.max(x), arr=a, axis=1)
np.random.seed(100)
a = np.random.randint(0, 5, 10)
a
from collections import Counter
[True if Counter(a)[num] > 1 else False for num in a]
#Better Solution
#out = np.full(a.shape[0], True)
#unique_positions = np.unique(a, return_index=True)[1]
#out[unique_positions] = False
url = "C:\\Users\XXX\\Documents\\GitHub\\Python-Exercices\\iris.data"
iris = np.genfromtxt(url, delimiter=',', dtype='object')
names = ('sepallength', 'sepalwidth', 'petallength', 'petalwidth', 'species')
unique_variety = np.unique(iris[:, 4]) #array([b'Iris-setosa', b'Iris-versicolor', b'Iris-virginica'],dtype=object)
for variety in unique_variety:
print(np.mean(iris[:, 0:4], dtype = float, where = iris[:,4] == variety))
#Non fonctionnel
arr = np.array([1,2,3,np.nan,5,6,7,np.nan])
nans = np.where(np.isnan(arr) == True)
np.delete(arr, nans)
a = np.array([1,2,3,4,5])
b = np.array([4,5,6,7,8])
np.linalg.norm(a - b)
a_2d = np.array([[3,3,3],[4,4,4],[5,5,5]])
b_1d = np.array([1,2,3])
#Fail
# Solution -> print(a_2d - b_1d[:,None])
x = np.array([1, 2, 1, 1, 3, 4, 3, 1, 1, 2, 1, 1, 2])
np.where(x == 1)[0][5-1]
dt64 = np.datetime64('2018-02-25 22:10:10')
dt64.tolist()
#Better Solution -> dt64.astype(datetime)
np.arange(start = 5, stop = 3*10+5, step = 3)
dates = np.arange(np.datetime64('2018-02-01'), np.datetime64('2018-02-25'), 2)
#Fail
#Solution :
#filled_in = np.array([np.arange(date, (date+d)) for date, d in zip(dates, np.diff(dates))]).reshape(-1)
#output = np.hstack([filled_in, dates[-1]])
#output
| 0.220678 | 0.985663 |
```
from pathlib import Path
import pandas as pd
import numpy as np
HERE = Path.cwd()
DATA_FOLDER = HERE / "data"
# print(DATA_FOLDER)
roster = pd.read_csv(
DATA_FOLDER / "roster.csv",
converters={"NetID": str.lower, "Email Address": str.lower},
usecols=["Section", "Email Address", "NetID"],
index_col="NetID",
)
#roster.head(10)
hw_exam_grades = pd.read_csv(
DATA_FOLDER / "hw_exam_grades.csv",
converters={"SID": str.lower},
usecols=lambda title: "Submission" not in title,
index_col="SID",
)
hw_exam_grades.head(10)
quiz_grades = pd.DataFrame()
for file_path in DATA_FOLDER.glob("quiz_*_grades.csv"):
quiz_name = " ".join(file_path.stem.title().split("_")[:2])
quiz = pd.read_csv(
file_path,
converters={"Email": str.lower},
index_col=["Email"],
usecols=["Email", "Grade"],
).rename(columns={"Grade": quiz_name})
quiz_grades = pd.concat([quiz_grades, quiz], axis=1)
quiz_grades.head(10)
final_data = pd.merge(
roster,
hw_exam_grades,
left_index=True,
right_index=True,
)
final_data = pd.merge(
final_data, quiz_grades, left_on="Email Address", right_index=True
)
final_data = final_data.fillna(0)
final_data.head(10)
quiz_grades.columns
quiz_grades.index
n_exams = 3
for n in range(1, n_exams + 1):
final_data[f"Exam {n} Score"] = (
final_data[f"Exam {n}"] / final_data[f"Exam {n} - Max Points"]
)
final_data.head()
hw_max_cols = [x for x in final_data.columns if 'Home' in x and 'Max' in x]
hw_cols = [x for x in final_data.columns if 'Home' in x and 'Max' not in x]
# axis=1 specifies that the sum will be done on the rows
hw_score_by_total = final_data[hw_cols].sum(axis=1)/final_data[hw_max_cols].sum(axis=1)
final_data['HW by Total'] = hw_score_by_total
final_data['Homework Score'] = hw_score_by_total
final_data.head()
hw_max_data = final_data[hw_max_cols].set_axis(hw_cols,axis=1)
quiz_scores = final_data.filter(regex=r"^Quiz \d$")
n_quiz = quiz_scores.shape[1]
quiz_max_points = pd.Series(
{'Quiz 1': 11, 'Quiz 2': 15, 'Quiz 3': 17, 'Quiz 4': 14, 'Quiz 5': 12}
)
quiz_score_by_total = quiz_scores.sum(axis=1)/quiz_max_points.sum()
final_data["Quiz Score"] = quiz_score_by_total
quiz_score_by_total
weights = pd.Series(
{
"Exam 1 Score": 0.05,
"Exam 2 Score": 0.1,
"Exam 3 Score": 0.15,
"Quiz Score": 0.30,
"Homework Score": 0.4,
}
)
weights.index
final_data[weights.index]
final_data["Final Score"] = (final_data[weights.index] * weights).sum(axis=1)
final_data.head()
final_data['Ceiling Score'] = np.ceil(final_data['Final Score']*100)
def get_letter_grade(score):
if score>=90:
return 'A'
elif score>=80:
return 'B'
elif score>=70:
return 'C'
elif score>=60:
return 'D'
else:
return 'F'
final_data["Final Grade"] = final_data['Ceiling Score'].map(get_letter_grade)
cols_to_write = ["Last Name", "First Name", "Email Address", "Ceiling Score", "Final Grade"]
final_data[final_data.Section == 1][cols_to_write]
for section, df in final_data.groupby("Section"):
section_file = DATA_FOLDER / f"section_{section}_grades.csv"
df[cols_to_write].sort_values(by=["Last Name", "First Name"]).to_csv(section_file)
grade_counts = final_data['Final Grade'].value_counts().sort_index()
grade_counts.plot.bar()
import scipy.stats
final_data['Final Score'].plot.hist(bins=20, label='Grade Distribution')
```
|
github_jupyter
|
from pathlib import Path
import pandas as pd
import numpy as np
HERE = Path.cwd()
DATA_FOLDER = HERE / "data"
# print(DATA_FOLDER)
roster = pd.read_csv(
DATA_FOLDER / "roster.csv",
converters={"NetID": str.lower, "Email Address": str.lower},
usecols=["Section", "Email Address", "NetID"],
index_col="NetID",
)
#roster.head(10)
hw_exam_grades = pd.read_csv(
DATA_FOLDER / "hw_exam_grades.csv",
converters={"SID": str.lower},
usecols=lambda title: "Submission" not in title,
index_col="SID",
)
hw_exam_grades.head(10)
quiz_grades = pd.DataFrame()
for file_path in DATA_FOLDER.glob("quiz_*_grades.csv"):
quiz_name = " ".join(file_path.stem.title().split("_")[:2])
quiz = pd.read_csv(
file_path,
converters={"Email": str.lower},
index_col=["Email"],
usecols=["Email", "Grade"],
).rename(columns={"Grade": quiz_name})
quiz_grades = pd.concat([quiz_grades, quiz], axis=1)
quiz_grades.head(10)
final_data = pd.merge(
roster,
hw_exam_grades,
left_index=True,
right_index=True,
)
final_data = pd.merge(
final_data, quiz_grades, left_on="Email Address", right_index=True
)
final_data = final_data.fillna(0)
final_data.head(10)
quiz_grades.columns
quiz_grades.index
n_exams = 3
for n in range(1, n_exams + 1):
final_data[f"Exam {n} Score"] = (
final_data[f"Exam {n}"] / final_data[f"Exam {n} - Max Points"]
)
final_data.head()
hw_max_cols = [x for x in final_data.columns if 'Home' in x and 'Max' in x]
hw_cols = [x for x in final_data.columns if 'Home' in x and 'Max' not in x]
# axis=1 specifies that the sum will be done on the rows
hw_score_by_total = final_data[hw_cols].sum(axis=1)/final_data[hw_max_cols].sum(axis=1)
final_data['HW by Total'] = hw_score_by_total
final_data['Homework Score'] = hw_score_by_total
final_data.head()
hw_max_data = final_data[hw_max_cols].set_axis(hw_cols,axis=1)
quiz_scores = final_data.filter(regex=r"^Quiz \d$")
n_quiz = quiz_scores.shape[1]
quiz_max_points = pd.Series(
{'Quiz 1': 11, 'Quiz 2': 15, 'Quiz 3': 17, 'Quiz 4': 14, 'Quiz 5': 12}
)
quiz_score_by_total = quiz_scores.sum(axis=1)/quiz_max_points.sum()
final_data["Quiz Score"] = quiz_score_by_total
quiz_score_by_total
weights = pd.Series(
{
"Exam 1 Score": 0.05,
"Exam 2 Score": 0.1,
"Exam 3 Score": 0.15,
"Quiz Score": 0.30,
"Homework Score": 0.4,
}
)
weights.index
final_data[weights.index]
final_data["Final Score"] = (final_data[weights.index] * weights).sum(axis=1)
final_data.head()
final_data['Ceiling Score'] = np.ceil(final_data['Final Score']*100)
def get_letter_grade(score):
if score>=90:
return 'A'
elif score>=80:
return 'B'
elif score>=70:
return 'C'
elif score>=60:
return 'D'
else:
return 'F'
final_data["Final Grade"] = final_data['Ceiling Score'].map(get_letter_grade)
cols_to_write = ["Last Name", "First Name", "Email Address", "Ceiling Score", "Final Grade"]
final_data[final_data.Section == 1][cols_to_write]
for section, df in final_data.groupby("Section"):
section_file = DATA_FOLDER / f"section_{section}_grades.csv"
df[cols_to_write].sort_values(by=["Last Name", "First Name"]).to_csv(section_file)
grade_counts = final_data['Final Grade'].value_counts().sort_index()
grade_counts.plot.bar()
import scipy.stats
final_data['Final Score'].plot.hist(bins=20, label='Grade Distribution')
| 0.326593 | 0.241735 |
# sympy Laplace Transforms for solving linear ODEs
> I have found that the Laplace transform utility in sympy doesn't do what we need for solving linear ODEs. We've made some needed improvements and included the code in the MATH280 package
- toc: true
In our workflow, we assume sympy as the default, and load the custom-made content from [MATH280 Package](https://github.com/ejbarth/MATH280).
```
from sympy import *
import MATH280
x = Function("x")
t,s = symbols("t s",real=True, nonnegative=true )
```
A famously intense pen-and-paper technique from elementary ODEs class: Laplace Transforms.
Sympy has Laplace capabilities built-in, but with maddening shortcomings.
Let's work with a 2nd order, linear, constant-coefficient, nonhomogeous IVP:
$$ \ddot{x}+3\dot{x}+4x = \sin(2t), \;\;\;\;\;\; x(0)=1, \dot{x}(0)=0$$
```
ode = Eq(x(t).diff(t,2)+3*x(t).diff(t)+4*x(t) , sin(2*t) )
ode
```
## laplace_transform() in sympy
First let's see how the built-in sympy `laplace_transform()` handles that equation:
```
laplace_transform(ode,t,s)
```
Look at that! **'Equality' object has no attribute**. `laplace_transform()` would prefer that we assume the expression we enter is equal to 0:
```
Lx=laplace_transform(x(t).diff(t,2)+3*x(t).diff(t)+4*x(t) - sin(2*t),t,s)
Lx
```
We see the output above is a tuple that includes some conditional statements at the end. To hide that and see just the transform itself, use the option `noconds=True`
```
Lx=laplace_transform(x(t).diff(t,2)+3*x(t).diff(t)+4*x(t) - sin(2*t),t,s,noconds=True)
Lx
```
### Laplace Transform and Derivatives
Notice in that output another hassle: `laplace_transform()` ignores the single most useful property of the Laplace Transform:
$$ {\cal L}\{x'(t)\} = s{\cal L}\{x(t)\} - x(0), \mbox{ and } {\cal L}\{x''(t)\} = s^2{\cal L}\{x(t)\} - sx(0)- x'(0).$$
## laplace() in MATH280
We've reworked that and included an alternative `laplace{}` in the [MATH280 Module](https://github.com/ejbarth/MATH280).
### Solving an equation with Laplace Transforms in four steps:
#### 1. take the transform of everything
```
L = MATH280.laplace(ode,t,s)
L
```
#### 2. plug in the initial conditions
The second step in solving the equation is to plug in the initial conditions:
```
L0=L.subs(x(0),1).subs(Subs(Derivative(x(t), t), t, 0),0)
L0
```
#### 3. solve for the lapace transform of the solution function
The third step is to solve the resulting equation for the symbol ${\cal L}\{x(t)\}$
```
Lx=solve(L0,LaplaceTransform(x(t),t,s))
Lx
```
#### 4. look up the laplace transform to determine the solution
The fourth and final step is to "look up" that complicated expression in the variable $s$ to determine the function of $t$ with that Laplace transform. The built-in sympy funtion `inverse_laplace_transform()` works fine for that, with the slight annoyance that it doesn't align perfectly with the list format of output from `solve()`. So I've included in MATH280 a little wrapper called `laplaceInv()` that extracts the zeroth entry from that list. **I've noticed that this step can run really slowly.**
```
sol = MATH280.laplaceInv(Lx,s,t)
sol
```
Something to notice is that every term as a $\theta(t)$. That's the unit step function: $\theta(t)=1$ if $t\gt 0$ and otherwise zero. Seems to be enforcing the assumption that our solution only makes sense for nonnegative time $t$.
We can plot the solution with sympy plot:
```
plot(sol,(t,0,20))
```
And just in case there was any doubt, we notice that `dsolve()` produces the same solution.
```
dsolve(ode,x(t),ics={x(0):1, x(t).diff(t).subs(t,0):0})
```
## Discontinuous Forcing Functions
We haven't yet explored what I think is *the* reason to consider Laplace Transforms in the first place: discontinuous forcing functions.
### A first-order model with a square wave switch function
Suppose we model a capacitor with an external voltage source that switches on at $t=2$ and off at $t=5$.
The equation, in some idealized units, could be
$$\dot{x} - x = \theta(t-2) - \theta(t-5), \;\;\;\;\; x(0)=0 $$
where $\theta(t-a)$ is the Heaviside unit step function that turns on at $t=a$.
```
capmodel = Eq(x(t).diff(t)+x(t), Heaviside(t-2)-Heaviside(t-5))
capmodel
```
We'll complete the four steps as in the previous example:
```
L=MATH280.laplace(capmodel,t,s)
L
L0=L.subs(x(0),0)
L0
Ls=solve(L0,LaplaceTransform(x(t),t,s))
Ls
capsol=MATH280.laplaceInv(Ls,s,t)
capsol
```
The functional form of the solution looks a little opaque, so lets make a plot of the solution together with the right hand side function:
```
plot(capsol,
Heaviside(t-2)-Heaviside(t-5),
(t,0,15),)
```
### A second-order example with a delta function
Here's an example from the undergraduate ODE textbook by Blanchard, Devaney and Hall:
$$\ddot{x} +2\dot{x}+3x= \delta(t-1)+3\delta(t-4), \;\;\;\;\; x(0)=0, \dot{x}(0)=0$$
```
ode2 = Eq(x(t).diff(t,2)+2*x(t).diff(t)+3*x(t),DiracDelta(t-1)+3*DiracDelta(t-4))
ode2
L=MATH280.laplace(ode2,t,s)
L
Ls=L.subs(x(0),0).subs(Subs(Derivative(x(t), t), t, 0),0)
Ls
Lx=solve(Ls,LaplaceTransform(x(t),t,s))
Lx
sol2 = MATH280.laplaceInv(Lx,s,t)
sol2
plot(sol2,(t,0,20))
```
We can see in the plot above how the impulse at $t=1$ and $t=4$ re-energizes the system.
|
github_jupyter
|
from sympy import *
import MATH280
x = Function("x")
t,s = symbols("t s",real=True, nonnegative=true )
ode = Eq(x(t).diff(t,2)+3*x(t).diff(t)+4*x(t) , sin(2*t) )
ode
laplace_transform(ode,t,s)
Lx=laplace_transform(x(t).diff(t,2)+3*x(t).diff(t)+4*x(t) - sin(2*t),t,s)
Lx
Lx=laplace_transform(x(t).diff(t,2)+3*x(t).diff(t)+4*x(t) - sin(2*t),t,s,noconds=True)
Lx
L = MATH280.laplace(ode,t,s)
L
L0=L.subs(x(0),1).subs(Subs(Derivative(x(t), t), t, 0),0)
L0
Lx=solve(L0,LaplaceTransform(x(t),t,s))
Lx
sol = MATH280.laplaceInv(Lx,s,t)
sol
plot(sol,(t,0,20))
dsolve(ode,x(t),ics={x(0):1, x(t).diff(t).subs(t,0):0})
capmodel = Eq(x(t).diff(t)+x(t), Heaviside(t-2)-Heaviside(t-5))
capmodel
L=MATH280.laplace(capmodel,t,s)
L
L0=L.subs(x(0),0)
L0
Ls=solve(L0,LaplaceTransform(x(t),t,s))
Ls
capsol=MATH280.laplaceInv(Ls,s,t)
capsol
plot(capsol,
Heaviside(t-2)-Heaviside(t-5),
(t,0,15),)
ode2 = Eq(x(t).diff(t,2)+2*x(t).diff(t)+3*x(t),DiracDelta(t-1)+3*DiracDelta(t-4))
ode2
L=MATH280.laplace(ode2,t,s)
L
Ls=L.subs(x(0),0).subs(Subs(Derivative(x(t), t), t, 0),0)
Ls
Lx=solve(Ls,LaplaceTransform(x(t),t,s))
Lx
sol2 = MATH280.laplaceInv(Lx,s,t)
sol2
plot(sol2,(t,0,20))
| 0.294925 | 0.966092 |
```
import numpy as np
import plotly.graph_objs as go
from ipywidgets import widgets
import scipy.stats as spst
lmbda_value=widgets.FloatSlider(
value=0.2,
min=0.01,
max=3,
step=0.01,
description="poisson arrival rate",
disabled=False,
continuous_update=False,
orientation='horizontal',
readout=True,
readout_format='.2f',
)
t=np.linspace(0,6,1000)
lmbda_n=-0.1*t*(t-5)+1
trace1=go.Scatter(x=t,y=lmbda_n,name="Nonhomogeneous Poisson" ,mode="lines")
trace2= go.Scatter(x=[0,6],y=[lmbda_value.value,lmbda_value.value], mode="lines", name="Invalid homogeneous",line=dict(
color="green", dash='dash',width=1))
trace3=go.Scatter(x=t,y=lmbda_n/lmbda_value.value,name="Invalid homogeneous" ,mode="lines",line=dict(
color="green", dash='dash',width=1))
g1 = go.FigureWidget(data=[trace1,trace2],
layout=go.Layout(
title=dict(
text="change homogeneous proposal rate",
),
hovermode=None,
margin={'l': 0, 'r': 0, 't': 0, 'b': 0},width=400, height=300 ),
)
g2 = go.FigureWidget(data=[trace3],
layout=go.Layout(
title=dict(
text="acceptance probability",
),
hovermode=None,
margin={'l': 0, 'r': 0, 't': 0, 'b': 0},width=400, height=300 ),
)
g1.update_layout(barmode='group',
title_x=0.5,
title_y=0.9,
xaxis=dict(range=[-1,7]),
yaxis=dict(range=[0,3]),
legend=dict(
x=0.1,
y=0.9,
traceorder="normal",
font=dict(
family="sans-serif",
size=12,
color="black"
))
)
g2.update_layout(barmode='group',
title_x=0.5,
title_y=0.9,
xaxis=dict(range=[-1,7]),
legend=dict(
x=1.7,
y=0.7,
traceorder="normal",
font=dict(
family="sans-serif",
size=12,
color="black"
))
)
def response1(change):
with g1.batch_update():
g1.data[1].y= [lmbda_value.value,lmbda_value.value]
if lmbda_value.value>= np.max(lmbda_n):
g1.data[1].line.color="red"
g1.data[1].line.dash="solid"
g1.data[1].line.width=5
g1.data[1].name="Valid homogeneous"
else:
g1.data[1].line.color="green"
g1.data[1].line.dash="dash"
g1.data[1].line.width=1
g1.data[1].name="Invalid homogeneous"
with g2.batch_update():
g2.data[0].y= lmbda_n/lmbda_value.value
if lmbda_value.value>= np.max(lmbda_n):
g2.data[0].line.color="red"
g2.data[0].line.dash="solid"
g2.data[0].line.width=5
g2.data[0].name="Valid homogeneous"
else:
g2.data[0].line.color="green"
g2.data[0].line.dash="dash"
g2.data[0].line.width=1
g2.data[0].name="Invalid homogeneous"
lmbda_value.observe(response1,names="value")
widget1=widgets.HBox([g1,g2])
Widget=widgets.VBox([lmbda_value,widget1] )
Widget
lmbda_value=widgets.FloatSlider(
value=10,
min=1,
max=60,
step=1,
description="poisson arrival rate",
disabled=False,
continuous_update=False,
orientation='horizontal',
readout=True,
readout_format='.2f',
)
next_proposal=widgets.Button(
description="next proposal")
clear=widgets.Button(
description="clear")
lmbda_value=widgets.FloatSlider(
value=10,
min=1,
max=60,
step=1,
description="poisson arrival rate",
disabled=False,
continuous_update=False,
orientation='horizontal',
readout=True,
readout_format='.2f',
)
t=np.linspace(0,6,1000)
lmbda_n=-0.1*t*(t-5)+1
accepted=np.array([])
rejected=np.array([])
lmbda_m=np.max(-0.1*t*(t-5)+1)
tr=0
trace1=go.Scatter(x=t,y=lmbda_n/lmbda_m,name="acceptance probability" ,mode="lines",line=dict(
color="green", dash='dash',width=1),hoverinfo='skip')
trace2=go.Scatter(x=[0,6],y=[0,0],name="timeline" ,mode="lines",line=dict(
color="gray", dash='solid',width=20),hoverinfo='skip')
trace3=go.Scatter(x=[],y=[],name="accepted arrivals" ,hoverinfo="text", text="",mode="markers",marker=dict(
color="blue", size=10))
trace4=go.Scatter(x=[],y=[],name="rejected arrivals" ,hoverinfo="text", text="",mode="markers",marker=dict(
color="red", size=10))
g = go.FigureWidget(data=[trace1,trace2,trace3,trace4],
layout=go.Layout(
title=dict(
text="acceptance probability",
),
hovermode=None,
margin={'l': 0, 'r': 0, 't': 0, 'b': 0},width=800, height=300 )
)
g.update_layout(hovermode='x unified',
title_x=0.5,
title_y=0.9,
xaxis=dict(range=[-1,7] ),
yaxis=dict(range=[-0.1,1]),
legend=dict(
x=1.1,
y=0.7,
traceorder="normal",
font=dict(
family="sans-serif",
size=12,
color="black"
))
)
def response1(change):
global tr,accepted, rejected,next_proposal
tr=tr-1/lmbda_m*np.log(np.random.rand())
ar=(-0.1*tr*(tr-5)+1)/lmbda_m
keep=np.random.rand()<ar
if keep==True:
accepted=np.append(accepted,tr)
else:
rejected=np.append(rejected,tr)
a_rate=(-0.1*accepted*(accepted-5)+1)/lmbda_m
r_rate=(-0.1*rejected*(rejected-5)+1)/lmbda_m
if len(a_rate)>0:
a_text=["accepted time: "+str(np.round(accepted[i],3))+ "<br>acceptance_rate: " +str(np.round(a_rate[i],3)) for i in range(len(a_rate))]
else:
a_text=""
if len(r_rate)>0:
r_text=["rejected time: "+str(np.round(rejected[i],3))+ "<br>acceptance_rate: "+str(np.round(r_rate[i],3)) for i in range(len(r_rate))]
else:
r_text=""
if tr>6:
next_proposal.disabled=True
else:
with g.batch_update():
g.data[2].y=np.repeat(0,len(accepted))
g.data[2].x=accepted
g.data[3].y=np.repeat(0,len(rejected))
g.data[3].x=rejected
g.data[2].text=a_text
g.data[3].text=r_text
def response2(change):
global tr,accepted, rejected ,next_proposal
tr=0
accepted=np.array([])
rejected=np.array([])
next_proposal.disabled=False
with g.batch_update():
g.data[2].y=np.repeat(0,len(accepted))
g.data[2].x=accepted
g.data[3].y=np.repeat(0,len(rejected))
g.data[3].x=rejected
next_proposal.on_click(response1)
clear.on_click(response2)
container1 = widgets.HBox([next_proposal,clear])
widget1=widgets.HBox([g ])
Widget=widgets.VBox([container1,widget1] )
Widget
```
|
github_jupyter
|
import numpy as np
import plotly.graph_objs as go
from ipywidgets import widgets
import scipy.stats as spst
lmbda_value=widgets.FloatSlider(
value=0.2,
min=0.01,
max=3,
step=0.01,
description="poisson arrival rate",
disabled=False,
continuous_update=False,
orientation='horizontal',
readout=True,
readout_format='.2f',
)
t=np.linspace(0,6,1000)
lmbda_n=-0.1*t*(t-5)+1
trace1=go.Scatter(x=t,y=lmbda_n,name="Nonhomogeneous Poisson" ,mode="lines")
trace2= go.Scatter(x=[0,6],y=[lmbda_value.value,lmbda_value.value], mode="lines", name="Invalid homogeneous",line=dict(
color="green", dash='dash',width=1))
trace3=go.Scatter(x=t,y=lmbda_n/lmbda_value.value,name="Invalid homogeneous" ,mode="lines",line=dict(
color="green", dash='dash',width=1))
g1 = go.FigureWidget(data=[trace1,trace2],
layout=go.Layout(
title=dict(
text="change homogeneous proposal rate",
),
hovermode=None,
margin={'l': 0, 'r': 0, 't': 0, 'b': 0},width=400, height=300 ),
)
g2 = go.FigureWidget(data=[trace3],
layout=go.Layout(
title=dict(
text="acceptance probability",
),
hovermode=None,
margin={'l': 0, 'r': 0, 't': 0, 'b': 0},width=400, height=300 ),
)
g1.update_layout(barmode='group',
title_x=0.5,
title_y=0.9,
xaxis=dict(range=[-1,7]),
yaxis=dict(range=[0,3]),
legend=dict(
x=0.1,
y=0.9,
traceorder="normal",
font=dict(
family="sans-serif",
size=12,
color="black"
))
)
g2.update_layout(barmode='group',
title_x=0.5,
title_y=0.9,
xaxis=dict(range=[-1,7]),
legend=dict(
x=1.7,
y=0.7,
traceorder="normal",
font=dict(
family="sans-serif",
size=12,
color="black"
))
)
def response1(change):
with g1.batch_update():
g1.data[1].y= [lmbda_value.value,lmbda_value.value]
if lmbda_value.value>= np.max(lmbda_n):
g1.data[1].line.color="red"
g1.data[1].line.dash="solid"
g1.data[1].line.width=5
g1.data[1].name="Valid homogeneous"
else:
g1.data[1].line.color="green"
g1.data[1].line.dash="dash"
g1.data[1].line.width=1
g1.data[1].name="Invalid homogeneous"
with g2.batch_update():
g2.data[0].y= lmbda_n/lmbda_value.value
if lmbda_value.value>= np.max(lmbda_n):
g2.data[0].line.color="red"
g2.data[0].line.dash="solid"
g2.data[0].line.width=5
g2.data[0].name="Valid homogeneous"
else:
g2.data[0].line.color="green"
g2.data[0].line.dash="dash"
g2.data[0].line.width=1
g2.data[0].name="Invalid homogeneous"
lmbda_value.observe(response1,names="value")
widget1=widgets.HBox([g1,g2])
Widget=widgets.VBox([lmbda_value,widget1] )
Widget
lmbda_value=widgets.FloatSlider(
value=10,
min=1,
max=60,
step=1,
description="poisson arrival rate",
disabled=False,
continuous_update=False,
orientation='horizontal',
readout=True,
readout_format='.2f',
)
next_proposal=widgets.Button(
description="next proposal")
clear=widgets.Button(
description="clear")
lmbda_value=widgets.FloatSlider(
value=10,
min=1,
max=60,
step=1,
description="poisson arrival rate",
disabled=False,
continuous_update=False,
orientation='horizontal',
readout=True,
readout_format='.2f',
)
t=np.linspace(0,6,1000)
lmbda_n=-0.1*t*(t-5)+1
accepted=np.array([])
rejected=np.array([])
lmbda_m=np.max(-0.1*t*(t-5)+1)
tr=0
trace1=go.Scatter(x=t,y=lmbda_n/lmbda_m,name="acceptance probability" ,mode="lines",line=dict(
color="green", dash='dash',width=1),hoverinfo='skip')
trace2=go.Scatter(x=[0,6],y=[0,0],name="timeline" ,mode="lines",line=dict(
color="gray", dash='solid',width=20),hoverinfo='skip')
trace3=go.Scatter(x=[],y=[],name="accepted arrivals" ,hoverinfo="text", text="",mode="markers",marker=dict(
color="blue", size=10))
trace4=go.Scatter(x=[],y=[],name="rejected arrivals" ,hoverinfo="text", text="",mode="markers",marker=dict(
color="red", size=10))
g = go.FigureWidget(data=[trace1,trace2,trace3,trace4],
layout=go.Layout(
title=dict(
text="acceptance probability",
),
hovermode=None,
margin={'l': 0, 'r': 0, 't': 0, 'b': 0},width=800, height=300 )
)
g.update_layout(hovermode='x unified',
title_x=0.5,
title_y=0.9,
xaxis=dict(range=[-1,7] ),
yaxis=dict(range=[-0.1,1]),
legend=dict(
x=1.1,
y=0.7,
traceorder="normal",
font=dict(
family="sans-serif",
size=12,
color="black"
))
)
def response1(change):
global tr,accepted, rejected,next_proposal
tr=tr-1/lmbda_m*np.log(np.random.rand())
ar=(-0.1*tr*(tr-5)+1)/lmbda_m
keep=np.random.rand()<ar
if keep==True:
accepted=np.append(accepted,tr)
else:
rejected=np.append(rejected,tr)
a_rate=(-0.1*accepted*(accepted-5)+1)/lmbda_m
r_rate=(-0.1*rejected*(rejected-5)+1)/lmbda_m
if len(a_rate)>0:
a_text=["accepted time: "+str(np.round(accepted[i],3))+ "<br>acceptance_rate: " +str(np.round(a_rate[i],3)) for i in range(len(a_rate))]
else:
a_text=""
if len(r_rate)>0:
r_text=["rejected time: "+str(np.round(rejected[i],3))+ "<br>acceptance_rate: "+str(np.round(r_rate[i],3)) for i in range(len(r_rate))]
else:
r_text=""
if tr>6:
next_proposal.disabled=True
else:
with g.batch_update():
g.data[2].y=np.repeat(0,len(accepted))
g.data[2].x=accepted
g.data[3].y=np.repeat(0,len(rejected))
g.data[3].x=rejected
g.data[2].text=a_text
g.data[3].text=r_text
def response2(change):
global tr,accepted, rejected ,next_proposal
tr=0
accepted=np.array([])
rejected=np.array([])
next_proposal.disabled=False
with g.batch_update():
g.data[2].y=np.repeat(0,len(accepted))
g.data[2].x=accepted
g.data[3].y=np.repeat(0,len(rejected))
g.data[3].x=rejected
next_proposal.on_click(response1)
clear.on_click(response2)
container1 = widgets.HBox([next_proposal,clear])
widget1=widgets.HBox([g ])
Widget=widgets.VBox([container1,widget1] )
Widget
| 0.382372 | 0.232735 |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
import seaborn as sns
sns.set()
df = pd.read_table('SMSSpamCollection', header = None)
df.head()
df[0].value_counts()
df.rename(columns = {0: 'label',
1: 'text'}, inplace=True)
df.head()
classes = df['label']
print(classes.value_counts())
classes.value_counts().plot(kind='bar')
plt.show()
```
# EDA
```
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
df['spam'] = encoder.fit_transform(df['label'])
df.head()
import string
string.punctuation
import nltk
from nltk.corpus import stopwords
from nltk.stem import WordNetLemmatizer
#df['text'][0]
lem = WordNetLemmatizer()
def remove_punc_and_stopwords(text):
punc_rem = [ch.lower() for ch in text if ch not in string.punctuation]
punc_rem = ''.join(punc_rem).split() #will get individual words for each text
stop_rem = [lem.lemmatize(word) for word in punc_rem if word not in set(stopwords.words('english'))]
return stop_rem
#remove_punc_and_stopwords(df['text'][0:2])
df['text'].apply(remove_punc_and_stopwords).head(1)
df.head()
df_ham = df[df['spam'] == 0]
df_spam = df[df['spam'] == 1]
df_ham['text'] = df_ham['text'].apply(remove_punc_and_stopwords)
df_spam['text'] = df_spam['text'].apply(remove_punc_and_stopwords)
df_ham.head()
words_ham = df_ham['text'].to_list()
words_spam = df_spam['text'].to_list()
words_ham[:2]
#type(words_ham)
list_ham_words = []
for sublist in words_ham:
for item in sublist:
list_ham_words.append(item)
list_ham_words[:10]
list_spam_words = []
for sublist in words_spam:
for item in sublist:
list_spam_words.append(item)
list_spam_words[:10]
f_ham = nltk.FreqDist(list_ham_words)
f_spam = nltk.FreqDist(list_spam_words)
#print(type(df_ham['text']))
f_ham.most_common(2)
df_top_30_ham_words = pd.DataFrame(f_ham.most_common(30), columns={'word', 'count'})
df_top_30_spam_words = pd.DataFrame(f_spam.most_common(30), columns={'word', 'count'})
plt.figure(figsize=(15,6))
sns.barplot(x = 'word',
y = 'count',
data = df_top_30_ham_words)
plt.xticks(rotation = 'vertical')
plt.show()
plt.figure(figsize=(15,6))
sns.barplot(x = 'word',
y = 'count',
data = df_top_30_spam_words)
plt.xticks(rotation = 'vertical')
plt.show()
from sklearn.feature_extraction.text import CountVectorizer
text = ["The quick brown fox jumped over the lazy dog."]
# create the transform
vectorizer = CountVectorizer()
# tokenize and build vocab
vectorizer.fit(text)
# summarize
print(vectorizer.vocabulary_)
print(len(vectorizer.vocabulary_))
# encode document
vector = vectorizer.transform(text)
# summarize encoded vector
print(vector.shape)
print(type(vector))
print(vector.toarray())
from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer(analyzer=remove_punc_and_stopwords)
tfidf_data = vectorizer.fit_transform(df['text'])
type(tfidf_data)
tfidf_data.shape
```
# train-test split
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(tfidf_data, df['spam'], random_state = 2, test_size = 0.25)
print(X_train.shape)
print(X_test.shape)
from sklearn.metrics import mean_squared_error, classification_report, confusion_matrix, accuracy_score
```
# Naive Bayes
```
from sklearn.naive_bayes import MultinomialNB
mnb_classifier = MultinomialNB()
mnb_model = mnb_classifier.fit(X_train, y_train)
mnb_ypred = mnb_model.predict(X_test)
mnb_acc = accuracy_score(y_test, mnb_ypred)
mnb_acc
```
# Try Naive Bayes after Scaling with MaxAbsScaler()
# KNN with GridSearchCV
# Classification Pipelines
```
X_train_p, X_test_p, y_train_p, y_test_p = train_test_split(df['text'], df['spam'], random_state = 2, test_size = 0.25)
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.pipeline import Pipeline
pipe = Pipeline([('bow', CountVectorizer(analyzer = remove_punc_and_stopwords)),
('tfidf', TfidfTransformer()),
('mnb_clf', MultinomialNB())])
pipe.fit(X_train_p, y_train_p)
pipe_ypred = pipe.predict(X_test_p)
pipe_acc = accuracy_score(y_test_p, pipe_ypred)
print(pipe_acc)
from sklearn.model_selection import GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
pipe = Pipeline([('tfidf', TfidfVectorizer(analyzer = remove_punc_and_stopwords)),
('knn_clf', KNeighborsClassifier())])
param_grid = {'knn_clf__n_neighbors' : [5, 8, 10, 15]}
model = GridSearchCV(pipe, param_grid=param_grid, cv = 5, n_jobs=-1)
model.fit(X_train_p, y_train_p)
model_ypred = model.predict(X_test_p)
model_acc = accuracy_score(y_test_p, model_ypred)
model_acc
print(model.best_params_)
print(model.best_score_)
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
import seaborn as sns
sns.set()
df = pd.read_table('SMSSpamCollection', header = None)
df.head()
df[0].value_counts()
df.rename(columns = {0: 'label',
1: 'text'}, inplace=True)
df.head()
classes = df['label']
print(classes.value_counts())
classes.value_counts().plot(kind='bar')
plt.show()
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
df['spam'] = encoder.fit_transform(df['label'])
df.head()
import string
string.punctuation
import nltk
from nltk.corpus import stopwords
from nltk.stem import WordNetLemmatizer
#df['text'][0]
lem = WordNetLemmatizer()
def remove_punc_and_stopwords(text):
punc_rem = [ch.lower() for ch in text if ch not in string.punctuation]
punc_rem = ''.join(punc_rem).split() #will get individual words for each text
stop_rem = [lem.lemmatize(word) for word in punc_rem if word not in set(stopwords.words('english'))]
return stop_rem
#remove_punc_and_stopwords(df['text'][0:2])
df['text'].apply(remove_punc_and_stopwords).head(1)
df.head()
df_ham = df[df['spam'] == 0]
df_spam = df[df['spam'] == 1]
df_ham['text'] = df_ham['text'].apply(remove_punc_and_stopwords)
df_spam['text'] = df_spam['text'].apply(remove_punc_and_stopwords)
df_ham.head()
words_ham = df_ham['text'].to_list()
words_spam = df_spam['text'].to_list()
words_ham[:2]
#type(words_ham)
list_ham_words = []
for sublist in words_ham:
for item in sublist:
list_ham_words.append(item)
list_ham_words[:10]
list_spam_words = []
for sublist in words_spam:
for item in sublist:
list_spam_words.append(item)
list_spam_words[:10]
f_ham = nltk.FreqDist(list_ham_words)
f_spam = nltk.FreqDist(list_spam_words)
#print(type(df_ham['text']))
f_ham.most_common(2)
df_top_30_ham_words = pd.DataFrame(f_ham.most_common(30), columns={'word', 'count'})
df_top_30_spam_words = pd.DataFrame(f_spam.most_common(30), columns={'word', 'count'})
plt.figure(figsize=(15,6))
sns.barplot(x = 'word',
y = 'count',
data = df_top_30_ham_words)
plt.xticks(rotation = 'vertical')
plt.show()
plt.figure(figsize=(15,6))
sns.barplot(x = 'word',
y = 'count',
data = df_top_30_spam_words)
plt.xticks(rotation = 'vertical')
plt.show()
from sklearn.feature_extraction.text import CountVectorizer
text = ["The quick brown fox jumped over the lazy dog."]
# create the transform
vectorizer = CountVectorizer()
# tokenize and build vocab
vectorizer.fit(text)
# summarize
print(vectorizer.vocabulary_)
print(len(vectorizer.vocabulary_))
# encode document
vector = vectorizer.transform(text)
# summarize encoded vector
print(vector.shape)
print(type(vector))
print(vector.toarray())
from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer(analyzer=remove_punc_and_stopwords)
tfidf_data = vectorizer.fit_transform(df['text'])
type(tfidf_data)
tfidf_data.shape
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(tfidf_data, df['spam'], random_state = 2, test_size = 0.25)
print(X_train.shape)
print(X_test.shape)
from sklearn.metrics import mean_squared_error, classification_report, confusion_matrix, accuracy_score
from sklearn.naive_bayes import MultinomialNB
mnb_classifier = MultinomialNB()
mnb_model = mnb_classifier.fit(X_train, y_train)
mnb_ypred = mnb_model.predict(X_test)
mnb_acc = accuracy_score(y_test, mnb_ypred)
mnb_acc
X_train_p, X_test_p, y_train_p, y_test_p = train_test_split(df['text'], df['spam'], random_state = 2, test_size = 0.25)
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.pipeline import Pipeline
pipe = Pipeline([('bow', CountVectorizer(analyzer = remove_punc_and_stopwords)),
('tfidf', TfidfTransformer()),
('mnb_clf', MultinomialNB())])
pipe.fit(X_train_p, y_train_p)
pipe_ypred = pipe.predict(X_test_p)
pipe_acc = accuracy_score(y_test_p, pipe_ypred)
print(pipe_acc)
from sklearn.model_selection import GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
pipe = Pipeline([('tfidf', TfidfVectorizer(analyzer = remove_punc_and_stopwords)),
('knn_clf', KNeighborsClassifier())])
param_grid = {'knn_clf__n_neighbors' : [5, 8, 10, 15]}
model = GridSearchCV(pipe, param_grid=param_grid, cv = 5, n_jobs=-1)
model.fit(X_train_p, y_train_p)
model_ypred = model.predict(X_test_p)
model_acc = accuracy_score(y_test_p, model_ypred)
model_acc
print(model.best_params_)
print(model.best_score_)
| 0.386532 | 0.632162 |
# Foundations of Computational Economics
by Fedor Iskhakov, ANU
<img src="_static/img/dag3logo.png" style="width:256px;">
## Representing numbers in a computer
<img src="_static/img/lecture.png" style="width:64px;">
<img src="_static/img/youtube.png" style="width:65px;">
[https://youtu.be/AMFCQXFtamo](https://youtu.be/AMFCQXFtamo)
Description: Binary and hexadecimal numbers. Floating point numbers. Numerical stability and potential issues. Numerical noise.
### Floating point arithmetics
- Because computers only work with 0 and 1 internally, all real numbers
have to be represented in *binary* format
- This leads to many peculiar arithmetics properties of seemingly
simple mathematical expressions
- Understanding how computers work with real numbers is essential for
computational economics
#### Simple example
What is the result of the comparison?
```
a = 0.1
b = 0.1
c = 0.1
a+b+c == 0.3
```
#### So can we now trust the following calculation?
```
interest = 0.04
compounding = 365
investment = 1000
t=10
daily = 1 + interest/compounding
sum = investment*(daily**(compounding*t))
format(sum, '.25f')
```
#### Compare to exact calculation
```
#using floats
interest1 = 0.04
compounding = 365*24
t=100 #years
investment1 = 10e9 #one billion
daily1 = 1 + interest1/compounding
sum1 = investment1*(daily1**(compounding*t))
print('Amount computed using naive computation: %0.20e'%sum1)
#the same using precise decimal representation
from decimal import *
getcontext().prec = 100 #set precision of decimal calculations
interest2 = Decimal(interest1)
daily2 = 1 + interest2/compounding
investment2 = Decimal(investment1)
sum2 = investment2*(daily2**(compounding*t)) #using exact decimals
print('Amount computed using exact computation: %0.20e'%sum2)
diff=sum2-Decimal.from_float(sum1)
print('The difference is: %0.10f'%diff)
```
#### So, what is happening?
- Real numbers are represented with certain precision
- In some cases, the errors may have economic significance
- In order to write robust code suitable for the task at hand we have
to understand what we should expect and why
*Numerical stability* of the code is an important property!
#### Number representation in decimal form
$ r $ — real number
$ b $ — *base* (radix)
$ d_0,d_1,d_2,...,d_k $ — digits (from lowest to highest)
$$
r = d_k \cdot b^k + d_{k-1} \cdot b^{k-1} + \dots + d_2 \cdot b^2 + d_1 \cdot b + d_0
$$
For example for decimals $ b=10 $ (0,1,..,9) we have
$$
7,631 = 7 \cdot 1000 + 6 \cdot 100 + 3 \cdot 10 + 1
$$
$$
19,048 = 1 \cdot 10000 + 9 \cdot 1000 + 0 \cdot 100 + 4 \cdot 10 + 8
$$
#### Number representation in binary form
Now let $ b=2 $, so we only have digits 0 and 1
$$
101011_{binary} = 1 \cdot 2^5 + 0 \cdot 2^4 + 1 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2 + 1 = 43_{10}
$$
$$
25_{10} = 16 + 8 + 1 = 2^4 + 2^3 + 2^0 = 11001_{binary}
$$
Other common bases are 8 and 16 (with digits
$ 0,1,2,\dots,9,a,b,c,d,e,f) $
#### Counting in binary
$ 0_{binary} $ $ \rightarrow $ $ 1_{binary} $
$ \rightarrow $ $ 10_{binary} $ $ \rightarrow $
$ 11_{binary} $ $ \rightarrow $ ??
*Is it possible to count to 1000 using 10 fingers?*
#### How many digits are needed?
- In base-10 we need 1 digit to count up to 9, 2 digits to count up to 99 and so on
- In base-2 we need 1 digit to count up to 1, 2 digits to count up to 11 = $ 3_{10} $ and so on
- In base-16 we need 1 digit to count up to 15, 2 digits to count up to ff = $ 255_{10} $ and so on
**In base-**$ b $ **it takes** $ n $ **digits to count up to up to** $ b^n - 1 $
#### Similar structure for fractions
In base-$ b $ using $ k $ *fractional* digits
$$
1.r = 1 + d_{-1} \cdot b^{-1} + d_{-2} \cdot b^{-2} + \dots + d_{-k} \cdot b^{-k}
$$
$$
1.5627 = \frac{15,627}{10,000} = 1 + 5 \cdot 10^{-1} + 6 \cdot 10^{-2} + 2 \cdot 10^{-3} + 7 \cdot 10^{-4}
$$
Yet, for some numbers there is no finite decimal representation
$$
\frac{4}{3} = 1 + 3 \cdot 10^{-1} + 3 \cdot 10^{-2} + 3 \cdot 10^{-3} + \dots = 1.333\dots
$$
$$
\frac{4}{3} = 1 + \frac{1}{3} = 1 + \frac{10}{3} 10^{-1} = 1 + 3 \cdot 10^{-1} + \frac{1}{3}10^{-1}
$$
$$
= 1.3 + \frac{10}{3} \cdot 10^{-2} = 1.3 + 3 \cdot 10^{-2} + \frac{1}{3}10^{-2}
$$
$$
= 1.33 + \frac{10}{3} \cdot 10^{-3} = 1.33 + 3 \cdot 10^{-3} + \frac{1}{3}10^{-3} = \dots
$$
#### In binary
$$
0.1 =\frac{1}{10} = \frac{16}{10} 2^{-4} = 0.0001_b + \frac{6}{10} 2^{-4} =
$$
$$
0.0001_b + \frac{12}{10} 2^{-5} = 0.00011_b + \frac{2}{10} 2^{-5} =
$$
$$
0.00011_b + \frac{16}{10} 2^{-8} = 0.00011001_b + \frac{6}{10} 2^{-8} = 0.000110011...
$$
Therefore $ 0.1 $ can not be represented in binary exactly!
#### Scientific notation
$$
r = r_0 \cdot b ^ e
$$
$ 0 \le r_0 < b $ — mantissa (coefficient)
$ b $ — base (radix)
$ e $ — exponent
- Useful for writing both big and small numbers
- *Approximate representation when a finite number of digits are used to record the mantissa*
#### Rounding error
Squeezing infinitely many real numbers into a finite number of *bits*
requires an approximate representation
$ p $ — number of digits in the representation for $ r_0 $
$ e $ — exponent between $ e_{min} $ and $ e_{max} $, taking up $ p_e $ bits to encode
$$
r \approx \pm d_0. d_1 d_2 \dots d_p \cdot b^e
$$
The float takes the total of $ 1 + p + p_e $ digits + one bit for the sign
#### Bits in float point representation
<img src="_static/img/bit_map.gif" style="width:700px;">
#### Distribution of representable real numbers
<img src="_static/img/float_map.jpg" style="width:700px;">
#### The main issues to be aware of
1. Rounding errors $ \leftrightarrow $ loss of precision when
numbers are represented in binary form $ \Rightarrow $ can not
compare floats for equality
1. Catastrophic cancellation $ \leftrightarrow $ potential drastic
loss of precision when substracting close real numbers represented by
floats $ \Rightarrow $ innocent formulas may in fact be
numerically unstable
1. Overflow $ \leftrightarrow $ obtaining a real number that is too
large to be represented as float
1. Underflow $ \leftrightarrow $ obtaining a real number that is
indistinguishable from zero
*Look at these cases in the Lab*
### Further learning resources
- Binary arithmetics on paper and in electronic circuit
[https://www.youtube.com/watch?v=wvJc9CZcvBc](https://www.youtube.com/watch?v=wvJc9CZcvBc)
- Counting to 1024 using fingers
[https://www.youtube.com/watch?v=UixU1oRW64Q](https://www.youtube.com/watch?v=UixU1oRW64Q)
- Basic intro into floating-point representation
[https://www.youtube.com/watch?v=PZRI1IfStY0](https://www.youtube.com/watch?v=PZRI1IfStY0)
- “What Every Computer Scientist Should Know About Floating-Point Arithmetics” by David Goldberg (pdf)
[http://www.itu.dk/~sestoft/bachelor/IEEE754_article.pdf](http://www.itu.dk/~sestoft/bachelor/IEEE754_article.pdf)
|
github_jupyter
|
a = 0.1
b = 0.1
c = 0.1
a+b+c == 0.3
interest = 0.04
compounding = 365
investment = 1000
t=10
daily = 1 + interest/compounding
sum = investment*(daily**(compounding*t))
format(sum, '.25f')
#using floats
interest1 = 0.04
compounding = 365*24
t=100 #years
investment1 = 10e9 #one billion
daily1 = 1 + interest1/compounding
sum1 = investment1*(daily1**(compounding*t))
print('Amount computed using naive computation: %0.20e'%sum1)
#the same using precise decimal representation
from decimal import *
getcontext().prec = 100 #set precision of decimal calculations
interest2 = Decimal(interest1)
daily2 = 1 + interest2/compounding
investment2 = Decimal(investment1)
sum2 = investment2*(daily2**(compounding*t)) #using exact decimals
print('Amount computed using exact computation: %0.20e'%sum2)
diff=sum2-Decimal.from_float(sum1)
print('The difference is: %0.10f'%diff)
| 0.306735 | 0.992539 |
Import necessary packages: Numpy, Pandas, matplotlib
```
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
```
Mount your google drive (if you have a google account) or upload files (go on the file icon on the left -> right click). Copy path of zip.train and zip.test and load them as numpy arrays using the following code (insert the path as string).
```
path_to_train = '/content/drive/My Drive/ML_Class_2020/KNN/zip.train'
path_to_test = '/content/drive/My Drive/ML_Class_2020/KNN/zip.test'
training_data = np.array(pd.read_csv(path_to_train, sep=' ', header=None))
test_data = np.array(pd.read_csv(path_to_test, sep =' ',header=None))
X_train, y_train = training_data[:,1:-1], training_data[:,0]
X_test, y_test = test_data[:,1:], test_data[:,0]
# We only want to classify two different digits. You can choose which digits you want to classify youself
X_train = X_train[np.logical_or(y_train == 0, y_train == 1)]
y_train = y_train[np.logical_or(y_train == 0, y_train == 1)]
X_test = X_test[np.logical_or(y_test == 0, y_test == 1)]
y_test = y_test[np.logical_or(y_test == 0, y_test == 1)]
def show_numbers(X):
num_samples = 90
indices = np.random.choice(range(len(X)), num_samples)
print(indices.shape)
sample_digits = X[indices]
fig = plt.figure(figsize=(20, 6))
for i in range(num_samples):
ax = plt.subplot(6, 15, i + 1)
img = 1-sample_digits[i].reshape((16, 16))
plt.imshow(img, cmap='gray')
plt.axis('off')
show_numbers(X_train)
```
Implement Logistic Regression, do gradient descent until training converges (find a good criterion for when that is the case yourself) and test the accuracy on your test data.
```
print(X_train.shape)
matrix = np.arange(2199)
matrix = np.transpose(np.broadcast_to(np.transpose(matrix), (2199,2199))[:256,:])
matrix = matrix*(2*np.ones((2199,256)))
print(matrix.shape, matrix)
#x = np.transpose(np.arange((2199,2199))[:256])*np.ones((2199,256))
#matrix = np.broadcast_to(X_train[:,0], X_train.shape)
print(matrix)
print(np.mean(np.array([[0.5,0.4],[0.4,0.6]]), axis=0))
# Logistic Regression
def sigmoid(X):
return 1/(1 + np.exp(-X))
def sigmoid_prime(X):
return np.exp(-X)/(1+np.exp(-X))**2
def CE(X,Y):
return -Y*np.log(X) - (1 - Y)*np.log(1 - X)
def CE_prime(X,Y):
return (1 - Y)/(1 - X) - Y/X
def MSE(X,Y):
return
class LogisticRegression():
def __init__(self):
# initialize weight, bias and learning rate
self.w = np.random.randn(X_train.shape[1])
self.b = np.random.randn(1)
self.lr = 0.05
def forward(self, X):
# z = X^T w + b
linear_out = np.sum(X*self.w, axis=1) + self.b*np.ones(X.shape[0])
activation = sigmoid(linear_out)
return activation, linear_out, X
def loss(self, activation, target):
return CE(activation, target)
def gradientDescent(self, activation, linear_out, X, Y):
backward = CE_prime(activation, Y)*sigmoid_prime(linear_out)
broadcasted_backward = np.transpose(np.broadcast_to(backward, (X.shape[0],X.shape[0]))[:256])
weight_gradient = np.mean(broadcasted_backward*X, axis=0)
bias_gradient = np.mean(backward*np.ones(X.shape[0]), axis=0)
# apply gradient descent
self.w = self.w - self.lr*weight_gradient
self.b = self.b - self.lr*bias_gradient
def get_label(self, activation):
return np.round(activation)
model = LogisticRegression()
episodes = 100
losses = []
for episode in range(episodes):
output = model.forward(X_train)
activation = output[0]
avg_loss = np.mean(model.loss(activation, y_train), axis=0)
losses.append(avg_loss)
# gradient descent
model.gradientDescent(*output, y_train)
plt.plot(losses)
plt.show()
output_test = model.forward(X_test)
accuracy = np.mean(model.get_label(output_test[0]) == y_test)
print(accuracy)
```
Logistic Regression can be interpreted as a neural network with just a single layer. It uses the Cross Entropy to measure the performance of the layer (i.e. of the "trained" weight **w**). In ML we call this the **Loss function**.
What happens when you take the Means Squared Error (MSE) instead of the Cross Entropy? Does this also work? Implement MSE and try for yourself.
(Optional) Can you think of a way to classify more than one class (in this case 10 classes)? How would you change the way **w** is defined?
|
github_jupyter
|
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
path_to_train = '/content/drive/My Drive/ML_Class_2020/KNN/zip.train'
path_to_test = '/content/drive/My Drive/ML_Class_2020/KNN/zip.test'
training_data = np.array(pd.read_csv(path_to_train, sep=' ', header=None))
test_data = np.array(pd.read_csv(path_to_test, sep =' ',header=None))
X_train, y_train = training_data[:,1:-1], training_data[:,0]
X_test, y_test = test_data[:,1:], test_data[:,0]
# We only want to classify two different digits. You can choose which digits you want to classify youself
X_train = X_train[np.logical_or(y_train == 0, y_train == 1)]
y_train = y_train[np.logical_or(y_train == 0, y_train == 1)]
X_test = X_test[np.logical_or(y_test == 0, y_test == 1)]
y_test = y_test[np.logical_or(y_test == 0, y_test == 1)]
def show_numbers(X):
num_samples = 90
indices = np.random.choice(range(len(X)), num_samples)
print(indices.shape)
sample_digits = X[indices]
fig = plt.figure(figsize=(20, 6))
for i in range(num_samples):
ax = plt.subplot(6, 15, i + 1)
img = 1-sample_digits[i].reshape((16, 16))
plt.imshow(img, cmap='gray')
plt.axis('off')
show_numbers(X_train)
print(X_train.shape)
matrix = np.arange(2199)
matrix = np.transpose(np.broadcast_to(np.transpose(matrix), (2199,2199))[:256,:])
matrix = matrix*(2*np.ones((2199,256)))
print(matrix.shape, matrix)
#x = np.transpose(np.arange((2199,2199))[:256])*np.ones((2199,256))
#matrix = np.broadcast_to(X_train[:,0], X_train.shape)
print(matrix)
print(np.mean(np.array([[0.5,0.4],[0.4,0.6]]), axis=0))
# Logistic Regression
def sigmoid(X):
return 1/(1 + np.exp(-X))
def sigmoid_prime(X):
return np.exp(-X)/(1+np.exp(-X))**2
def CE(X,Y):
return -Y*np.log(X) - (1 - Y)*np.log(1 - X)
def CE_prime(X,Y):
return (1 - Y)/(1 - X) - Y/X
def MSE(X,Y):
return
class LogisticRegression():
def __init__(self):
# initialize weight, bias and learning rate
self.w = np.random.randn(X_train.shape[1])
self.b = np.random.randn(1)
self.lr = 0.05
def forward(self, X):
# z = X^T w + b
linear_out = np.sum(X*self.w, axis=1) + self.b*np.ones(X.shape[0])
activation = sigmoid(linear_out)
return activation, linear_out, X
def loss(self, activation, target):
return CE(activation, target)
def gradientDescent(self, activation, linear_out, X, Y):
backward = CE_prime(activation, Y)*sigmoid_prime(linear_out)
broadcasted_backward = np.transpose(np.broadcast_to(backward, (X.shape[0],X.shape[0]))[:256])
weight_gradient = np.mean(broadcasted_backward*X, axis=0)
bias_gradient = np.mean(backward*np.ones(X.shape[0]), axis=0)
# apply gradient descent
self.w = self.w - self.lr*weight_gradient
self.b = self.b - self.lr*bias_gradient
def get_label(self, activation):
return np.round(activation)
model = LogisticRegression()
episodes = 100
losses = []
for episode in range(episodes):
output = model.forward(X_train)
activation = output[0]
avg_loss = np.mean(model.loss(activation, y_train), axis=0)
losses.append(avg_loss)
# gradient descent
model.gradientDescent(*output, y_train)
plt.plot(losses)
plt.show()
output_test = model.forward(X_test)
accuracy = np.mean(model.get_label(output_test[0]) == y_test)
print(accuracy)
| 0.630799 | 0.930078 |
```
import warnings
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris
```
## 1) 載入資料集
```
iris = load_iris()
df_data = pd.DataFrame(data= np.c_[iris['data'], iris['target']],
columns= ['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm','Species'])
df_data
```
# 2) EDA (Exploratory Data Analysis) 探索式資料分析
主要概念是透過數據統計的方式視覺化資料。做EDA的好處可以從各種面向先了解資料的狀況,以利後續的模型分析。
## 直方圖
```
#直方圖 histograms
df_data.hist(alpha=0.6,layout=(3,3), figsize=(12, 8), bins=10)
plt.tight_layout()
plt.show()
fig, axes = plt.subplots(nrows=1,ncols=4)
fig.set_size_inches(15, 4)
sns.histplot(df_data["SepalLengthCm"][:],ax=axes[0], kde=True)
sns.histplot(df_data["SepalWidthCm"][:],ax=axes[1], kde=True)
sns.histplot(df_data["PetalLengthCm"][:],ax=axes[2], kde=True)
sns.histplot(df_data["PetalWidthCm"][:],ax=axes[3], kde=True)
```
## 核密度估計Kernel Density Estimation(KDE)
```
from pandas.plotting import scatter_matrix
scatter_matrix( df_data,figsize=(10, 10),color='b',diagonal='kde')
sns.pairplot(df_data, hue="Species", height=2, diag_kind="kde")
```
## 關聯分析 (correlation map)
```
df_data[['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm','Species']]
# correlation calculate
corr = df_data[['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm','Species']].corr()
plt.figure(figsize=(8,8))
sns.heatmap(corr, square=True, annot=True, cmap="RdBu_r") #center=0, cmap="YlGnBu"
# correlation calculate
corr = df_data[['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm','Species']].corr()
# 將矩陣型簡化為對角矩陣型
mask = np.triu(np.ones_like(corr, dtype=np.bool))
plt.figure(figsize=(8,8))
sns.heatmap(corr, square=True, annot=True, mask=mask, cmap="RdBu_r") #center=0, cmap="YlGnBu"
```
## 散佈圖
```
sns.lmplot("SepalLengthCm", "SepalWidthCm", hue='Species', data=df_data, fit_reg=False, legend=False)
plt.legend(title='Species', loc='upper right', labels=['Iris-Setosa', 'Iris-Versicolour', 'Iris-Virginica'])
sns.lmplot("PetalLengthCm", "PetalWidthCm", hue='Species', data=df_data, fit_reg=False, legend=False)
plt.legend(title='target', loc='upper left', labels=['Iris-Setosa', 'Iris-Versicolour', 'Iris-Virginica'])
```
## 箱形圖
透過箱形圖可以分析每個特徵的分布狀況以及是否有離群值
```
fig, axes = plt.subplots(nrows=1, ncols=5, figsize=(10,5), sharey=True)
axes[0].boxplot(df_data['SepalLengthCm'],showmeans=True)
axes[0].set_title('SepalLengthCm')
axes[1].boxplot(df_data['SepalWidthCm'],showmeans=True)
axes[1].set_title('SepalWidthCm')
axes[2].boxplot(df_data['PetalLengthCm'],showmeans=True)
axes[2].set_title('PetalLengthCm')
axes[3].boxplot(df_data['PetalWidthCm'],showmeans=True)
axes[3].set_title('PetalWidthCm')
axes[4].boxplot(df_data['Species'],showmeans=True)
axes[4].set_title('Species')
```
|
github_jupyter
|
import warnings
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris
iris = load_iris()
df_data = pd.DataFrame(data= np.c_[iris['data'], iris['target']],
columns= ['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm','Species'])
df_data
#直方圖 histograms
df_data.hist(alpha=0.6,layout=(3,3), figsize=(12, 8), bins=10)
plt.tight_layout()
plt.show()
fig, axes = plt.subplots(nrows=1,ncols=4)
fig.set_size_inches(15, 4)
sns.histplot(df_data["SepalLengthCm"][:],ax=axes[0], kde=True)
sns.histplot(df_data["SepalWidthCm"][:],ax=axes[1], kde=True)
sns.histplot(df_data["PetalLengthCm"][:],ax=axes[2], kde=True)
sns.histplot(df_data["PetalWidthCm"][:],ax=axes[3], kde=True)
from pandas.plotting import scatter_matrix
scatter_matrix( df_data,figsize=(10, 10),color='b',diagonal='kde')
sns.pairplot(df_data, hue="Species", height=2, diag_kind="kde")
df_data[['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm','Species']]
# correlation calculate
corr = df_data[['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm','Species']].corr()
plt.figure(figsize=(8,8))
sns.heatmap(corr, square=True, annot=True, cmap="RdBu_r") #center=0, cmap="YlGnBu"
# correlation calculate
corr = df_data[['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm','Species']].corr()
# 將矩陣型簡化為對角矩陣型
mask = np.triu(np.ones_like(corr, dtype=np.bool))
plt.figure(figsize=(8,8))
sns.heatmap(corr, square=True, annot=True, mask=mask, cmap="RdBu_r") #center=0, cmap="YlGnBu"
sns.lmplot("SepalLengthCm", "SepalWidthCm", hue='Species', data=df_data, fit_reg=False, legend=False)
plt.legend(title='Species', loc='upper right', labels=['Iris-Setosa', 'Iris-Versicolour', 'Iris-Virginica'])
sns.lmplot("PetalLengthCm", "PetalWidthCm", hue='Species', data=df_data, fit_reg=False, legend=False)
plt.legend(title='target', loc='upper left', labels=['Iris-Setosa', 'Iris-Versicolour', 'Iris-Virginica'])
fig, axes = plt.subplots(nrows=1, ncols=5, figsize=(10,5), sharey=True)
axes[0].boxplot(df_data['SepalLengthCm'],showmeans=True)
axes[0].set_title('SepalLengthCm')
axes[1].boxplot(df_data['SepalWidthCm'],showmeans=True)
axes[1].set_title('SepalWidthCm')
axes[2].boxplot(df_data['PetalLengthCm'],showmeans=True)
axes[2].set_title('PetalLengthCm')
axes[3].boxplot(df_data['PetalWidthCm'],showmeans=True)
axes[3].set_title('PetalWidthCm')
axes[4].boxplot(df_data['Species'],showmeans=True)
axes[4].set_title('Species')
| 0.485356 | 0.883488 |
*Ronica Reddick*
&
*Nick Pulito*
*in association with*
*"Those Data Bootcamp Guys"* -- Professors Backus and Coleman
**present**
# **"3 Guys Named Chris"**
# Scene 1: "The Set-Up"
Hollywood hunks come and go, but every so often a star builds a lasting career out of blowing stuff up. Currently, there is no shortage of beef cake on the silver screen with Chris Evans, Chris Hemsworth, and Chris Pratt all regularly starring in blockbuster films. There is no denying the bankability of the Chrises, but which Chris has staying power?
The now defunct *Grantland* podcast had a “market correction” theory they applied to Hollywood actors. The idea is that there’s only room in the market for one A list celebrity of a particular type and that over time the market will choose its favorite.The hosts would compare two Hollywood actors with similar “types” and predict which one would still have a career in 20 years.
Using data from Box Office Mojo we decided to test the market correction theory on the Chrises by comparing the box office numbers of their biggest hits to those of heroes from the days of yore: Tom Cruise, Arnold Schwarzenegger, and Bruce Willis. We were looking for patterns in the box office receipts of the old guard that may shed some light on who which Chris will be on top in 2035, and to see if any of the box office heroes of yesteryear had a little more staying power than the others.
```
#This guided coding excercise requires associated .csv files: CE1.csv, CH1.csv, CP1.csv, Arnold1.csv, Bruce1.csv, and Tom1.csv
#make sure you have these supplemental materials ready to go in your active directory before proceeding
#Let's start coding! We first need to make sure our preliminary packages are in order. We imported the following...
#some may have ended up superfluous, but we figured it was better to cover our bases!
import pandas as pd
import sys
import matplotlib as mpl
import matplotlib.pyplot as plt
import sys
import os
import datetime as dt
import csv
import requests, io
from bs4 import BeautifulSoup
%matplotlib inline
print('\nPython version: ', sys.version)
print('Pandas version: ', pd.__version__)
print('Requests version: ', requests.__version__)
print("Today's date:", dt.date.today())
```
# Scene 2: "The Chris Contenders"
**Methodology**
To dive into which Chris will have staying power in years to come, we looked to authoritative Hollywood Data Source BoxOfficeMojo.com. A bit of simple webscraping gave us film titles broken out by actor, with adjusted box office revenues in tow.
We wanted to aggregate data for our "Three Chrises" and compare it to 3 Hollywood legends who have had variable staying power over the years: Bruce Willis, Tom Cruise, and Arnold Schwarzenegger.
**Digging up data on our leading gentlemen**
Cells that follow show our process for scraping and organizing the data for the Chris contenders.
# **Chris Evans**
“The All American Hero”
Age: 34
Height: 6’
Known for: Captain America ($267,656,500); The Avengers; Fantastic Four
Legit Roles: Snowpiercer
Biggest Hit: Marvel’s The Avengers $659,640,800
```
# data scraped from Box Office Mojo, the authoritative source for Hollywood Box Office Data
# chris evans
url = 'http://www.boxofficemojo.com/people/chart/?view=Actor&id=chrisevans.htm'
evans = pd.read_html(url)
print('Ouput has type', type(evans), 'and length', len(evans))
print('First element has type', type(evans[0]))
#we have a list of dataframes, and the cut of data we want is represented by the below
evans[2]
ce=evans[2]
print("type=", type(ce)," ", "length=", len(ce), "shape=", ce.shape)
print(ce)
ce.to_csv("ce.csv")
#since scraped dataset is small, and had a tricky double index, we decided to export to csv and do a quick cleanup there
#removed indices; cleaned titles; cleaned date
#Clean File saved as CE1.csv
#this is the path for my machine; you'll have to link to the CE1.csv file that you've saved on your machine
path='C:\\Users\\Nick\\Desktop\\Data_Bootcamp\\Final Project\\CE1.csv'
CE = pd.read_csv(path)
print(type(CE), "shape is", CE.shape, "types:", CE.dtypes)
print(CE) #this is going to be much better for us to work with
#this looks good! let's test and make sure the data makes sense with a simple plot:
CE.plot.scatter('Release Year', 'Adjusted Gross')
#we love what we see, let's repeat it for our other leading gentlemen
```
# Chris Hemsworth
“The Heartthrob”
Age: 32
Height: 6’ 3”
Known for: Thor; The Avengers; Snow White and the Huntsman
Legit Roles: Rush
Biggest Hit: Marvel’s The Avengers $659,640,800
Biggest Thor Movie: $212,276,600
```
# same process for our second leading Chris
# chris hemsworth
url = 'http://www.boxofficemojo.com/people/chart/?view=Actor&id=chrishemsworth.htm'
hemsworth = pd.read_html(url)
print('Ouput has type', type(hemsworth), 'and length', len(hemsworth))
print('First element has type', type(hemsworth[0]))
hemsworth[3]
ch=hemsworth[3]
print("type=", type(ch)," ", "length=", len(ch), "shape=", ch.shape)
print(ch)
ch.to_csv("ch.csv")
#since scraped dataset is small, and had a tricky double index, we decided to export to csv and do a quick cleanup there
#Cleaned File saved as CH1.csv
path='C:\\Users\\Nick\\Desktop\\Data_Bootcamp\\Final Project\\CH1.csv'
#again, this is the path on my machine, you'll want to make sure you adjust to wherever you saved down CH1
CH = pd.read_csv(path)
print(type(CH), "shape is", CH.shape, "types:", CH.dtypes)
CH.plot.scatter('Release Year', 'Adjusted Gross')
```
*Our data looks good! The axes are a little strange, but we just want to make sure we have data we can work with!*
# Chris Pratt
“The Everyman”
Age: 36
Height: 6’ 2”
Known for: Guardians of the Galaxy ($353,303,500); Jurassic World (1 + one in pre); Parks & Rec (TV)
Legit Roles: Her, Moneyball
Biggest Role: Jurassic World $678,242,100
```
# Chris number three, coming through!
# chris pratt
url = 'http://www.boxofficemojo.com/people/chart/?view=Actor&id=chrispratt.htm'
pratt = pd.read_html(url)
print('Ouput has type', type(pratt), 'and length', len(pratt))
print('First element has type', type(pratt[0]))
pratt[3]
cp=pratt[3]
print("type=", type(cp)," ", "length=", len(cp), "shape=", cp.shape)
print(cp)
cp.to_csv("cp.csv")
#since scraped dataset is small, and had a tricky double index, we decided to export to csv and do a quick cleanup there
#Cleaned File saved as CP1.csv
path='C:\\Users\\Nick\\Desktop\\Data_Bootcamp\\Final Project\\CP1.csv'
#remember to adjust path to where you've saved the .csv down
CP = pd.read_csv(path)
print(type(CP), "shape is", CP.shape, "types:", CP.dtypes)
CP.plot.scatter('Release Year', 'Adjusted Gross')
```
**Now that we've got that sorted out, let's take a look at all three Chrises together. How do their box office titles stack up with one another over time?**
```
plt.scatter(CE['Release Year'], CE['Adjusted Gross'],
color="purple")
plt.scatter(CH['Release Year'], CH['Adjusted Gross'],
color="red")
plt.scatter(CP['Release Year'], CP['Adjusted Gross'],
color="orange")
plt.title('Chris Film Box Office Share Over Time')
```
In the graph above, we color coded our Chris contingency as follows:
Chris Evans: Purple
Chris Hemsworth: Red
Chris Pratt: Orange
A few things stand out. First, we can see right away that Chris Evans has, to date, had the longest career at the box office, dating back to 2001. Does this maybe suggest some longevity right off the bat? We're not so quick to draw that conclusion, especially since his biggest box office hit is shared with Chris Hemsworth in the Marvel Avengers movie.
Looking back at our raw data, we can also note that Pratt seems to have had the biggest breakout hit with his 2015 with Jurassic World, one of the top grossing films of all time, where he was the sole leading man.
*This data gives us one view, but what other cuts might we want to look at?*
```
fig, ax = plt.subplots(nrows=3, ncols=1, sharex=True, sharey=True)
CE['Adjusted Gross'].head(10).plot(kind="bar",ax=ax[0], color='purple', title="Evans")
CH['Adjusted Gross'].head(10).plot(kind="bar",ax=ax[1], color='red', title="Hemsworth")
CP['Adjusted Gross'].head(10).plot(kind="bar",ax=ax[2], color='orange', title="Pratt")
```
In the above, we take a look at the box office grosses for the top 10 films for each Chris. Here, we start to wonder if maybe Evans has a more consistent box office performance. Of his top 10 filims, 9 are in the $200 million range, a stat unmatched by our other two gentlemen.
*This is an interesting insight, but what does it look like over time?*
```
plt.bar(CE['Release Year'], CE['Adjusted Gross'],
align='center',
color='pink')
plt.title('Chris Evans')
```
Buoyed by franchise films in the last five years, Chris Evans has been a steady player, but hasn't excelled outside the Marvel universe franchises. All his biggest hits are as a member of a franchise / ensemble. Evans's Marvel hits since 2011 have performed well, though non-Marvel titles have largely been blips on the radar.
```
plt.bar(CH['Release Year'], CH['Adjusted Gross'],
align='center',
color='red')
plt.title("Chris Hemsworth")
```
Hemsworth had a *very* rough 2015. He featured prominently in 4 films, only one of which was a box office success (another Marvel Avengers installment). After a breakout 2012, are the tides turning after major flops like In the Heart of the Sea?
```
plt.bar(CP['Release Year'], CP['Adjusted Gross'],
align='center',
color='orange')
plt.title("Chris Pratt")
```
Pratt may have been a slower starter than our other leading gentlemen, but his 2014 breakout Guardians of the Galaxy cemented his status as leading man potential, and 2015's Jurassic World broke tons of box office records. As a non-Marvel film (though a franchise reboot), Jurassic World is unique in that it may be a standalone hit for Pratt, and everyone will be closely watching his box office performance in whatever leading man project he chooses next.
```
plt.bar(CE['Release Year'], CE['Adjusted Gross'],
align='center',
color='purple')
plt.bar(CH['Release Year'], CH['Adjusted Gross'],
align='center',
color='red')
plt.bar(CP['Release Year'], CP['Adjusted Gross'],
align='center',
color='orange')
plt.title('Chris Film Box Office Share Over Time')
```
We love this data cut. Here, we take a comparative look of our Chrises over time. Keeping our colors consistent, Evans is purple, Hemsworth is red, Pratt is orange.
One slight issue; movies where both Hemsworth and Evans were cast (Avengers) -- the graph chooses just one color. Here's a flipped view:
```
plt.bar(CH['Release Year'], CH['Adjusted Gross'],
align='center',
color='red')
plt.bar(CE['Release Year'], CE['Adjusted Gross'],
align='center',
color='purple')
plt.bar(CP['Release Year'], CP['Adjusted Gross'],
align='center',
color='orange')
plt.title('Chris Film Box Office Share Over Time')
```
*Whoa! Where did Hemsworth go?*
What these two cuts show us is that Evans and Hemsworth are both heavily reliant on their Marvel franchise hits, where they are sharing the limelight, whereas Pratt has been more of a solo vehicle, especially in more recent years.
# **Scene 3: The "OGs"**
In order to determine which Chris has staying power we pulled data on Hollywood stars of yore (Bruce Willis, Arnold Schwarzenegger, and Tom Cruise) for comparison. Given the volume of data on the older stars, we isolated the top ten grossing films for each hero.
# Bruce Willis
Heyday: The late 80s to the late 90s
Known for: Die Hard franchise
Biggest Movie: The Sixth Sense $494,028,900
Type: Leading Man/Action Hero Hybrid
```
#Movie scraping and data arranging like we did before
#Bruce Willis
url = 'http://www.boxofficemojo.com/people/chart/?id=brucewillis.htm'
willis = pd.read_html(url)
print('Ouput has type', type(willis), 'and length', len(willis))
print('First element has type', type(willis[0]))
willis[2]
bruce=willis[2]
bruce.to_csv("Bruce.csv") #Converting dataframe into a csv file
#editing and cleaning as needed, resaved as Bruce1.csv
path='/Users/Nick/Desktop/data_bootcamp/Final Project/Bruce1.csv'
BWillis = pd.read_csv(path)
print(type(BWillis), BWillis.shape, BWillis.dtypes)
import matplotlib as mpl
mpl.rcParams.update(mpl.rcParamsDefault)
BWillis.plot.scatter('Release Year', 'Adjusted Gross')
#That's a lot of films! Let's narrow:
BW=BWillis.head(11)
print(BW)
#we'll come back to this later, but let's get our other leading men in the frame!
```
# **Arnold Schwarzenegger**
Heyday: Mid 80s to the mid 90s
Known for: the Terminator franchise
Biggest Movie: Terminator 2: Judgement Day $417,471,700
Type: Beefcake w/comedic chops
```
#here we go again!
#Arnold Schwarzenegger
url = 'http://www.boxofficemojo.com/people/chart/?id=arnoldschwarzenegger.htm'
schwarz = pd.read_html(url)
print('Ouput has type', type(schwarz), 'and length', len(schwarz))
print('First element has type', type(schwarz[0]))
schwarz[2]
arnold=schwarz[2]
print("type=", type(arnold)," ", "length=", len(arnold))
arnold.shape
print(arnold)
arnold.to_csv("Arnold.csv")
path='/Users/Nick/Desktop/data_bootcamp/Final Project/Arnold1.csv'
ASchwarz = pd.read_csv(path)
print(type(ASchwarz), ASchwarz.shape, ASchwarz.dtypes)
print(ASchwarz)
ASchwarz.plot.scatter('Release Year', 'Adjusted Gross')
#let's scale back sample size again
AS=ASchwarz.head(11)
#we'll use this soon
```
# **Tom Cruise**
Heyday: Mid 80’s - early aughts
Known for: Mission Impossible franchise
Biggest Movie: Top Gun $$412,055,200
Type: Cocky leading man
```
#last but not least, our data for Tom Cruise
url = 'http://www.boxofficemojo.com/people/chart/?id=tomcruise.htm'
cruise = pd.read_html(url)
print('Ouput has type', type(cruise), 'and length', len(cruise))
print('First element has type', type(cruise[0]))
cruise[3]
Tom=cruise[3]
Tom.to_csv("Tom.csv")
path='/Users/Nick/Desktop/data_bootcamp/Final Project/Tom1.csv'
TCruise = pd.read_csv(path)
print(type(TCruise), TCruise.shape, TCruise.dtypes)
print(TCruise)
TCruise.plot.scatter('Release Year', 'Adjusted Gross')
#cutting down to the top 10
TC=TCruise.head(11)
```
# Scene 4: "The Final Showdown"
```
#All of the old school action stars in one histogram. Representing share of box office cumulatively over time.
plt.bar(TC['Release Year'],
TC['Adjusted Gross'],
align='center',
color='Blue')
plt.bar(BW['Release Year'],
BW['Adjusted Gross'],
align='center',
color='Green')
plt.bar(AS['Release Year'],
AS['Adjusted Gross'],
align='center',
color='Yellow')
plt.title('"OG" Leading Box Office over Time')
```
LEGEND:
Tom Cruise = Blue
Bruce Willis = Green
Arnold Schwarzenegger = Yellow
```
#As a reminder, here's what we are comparing against:
fig, ax = plt.subplots(nrows=3, ncols=1, sharex=True, sharey=True)
CE['Adjusted Gross'].head(10).plot(kind="bar",ax=ax[0], color='purple', title="Evans")
CH['Adjusted Gross'].head(10).plot(kind="bar",ax=ax[1], color='red', title="Hemsworth")
CP['Adjusted Gross'].head(10).plot(kind="bar",ax=ax[2], color='orange', title="Pratt")
plt.bar(CE['Release Year'], CE['Adjusted Gross'],
align='center',
color='purple')
plt.bar(CH['Release Year'], CH['Adjusted Gross'],
align='center',
color='red')
plt.bar(CP['Release Year'], CP['Adjusted Gross'],
align='center',
color='orange')
plt.title('Chris Film Box Office Share Over Time')
```
LEGEND:
Chris Evans = Purple
Chris Hemsworth = Red
Chris Pratt = Orange
# **Our Findings**
Tom Cruise (blue) has obvious staying power with films raking in over 200 million over two decades. Arnold's biggest films are clustered in a 10 year period. Bruce Willis also had clusters of hits with his biggest successes in the late nineties. If our Chrises want to stay relevant in 2035 they'll need to adopt the "slow and steady wins the race" strategy of Tom Cruise (as long as slow and steady comes with strong receipts).
# The Verdict!
The Winner: Chris Pratt! Looking at the data we predict that Chris Pratt is in the best position to capitalize going forward given his strong hauls in solo vehicles over the past several years. If he can keep his popularity up over the next decade he will be the Chris you take your grandkids to the movies to see. The upward trajectory matches our legends, and we like the trend that we see coupled with soft factors like his "everyman" appeal.
Dark Horse: Chris Evans if he can successfully spin his Marvel success into a solo vehicle for leading roles that aren't franchises.
Throw him a lifesaver: Chris Hemsworth. The once bright Thor star is floundering in solo projects, and may go the downward route of Bruce Willis.
# *The End*
|
github_jupyter
|
#This guided coding excercise requires associated .csv files: CE1.csv, CH1.csv, CP1.csv, Arnold1.csv, Bruce1.csv, and Tom1.csv
#make sure you have these supplemental materials ready to go in your active directory before proceeding
#Let's start coding! We first need to make sure our preliminary packages are in order. We imported the following...
#some may have ended up superfluous, but we figured it was better to cover our bases!
import pandas as pd
import sys
import matplotlib as mpl
import matplotlib.pyplot as plt
import sys
import os
import datetime as dt
import csv
import requests, io
from bs4 import BeautifulSoup
%matplotlib inline
print('\nPython version: ', sys.version)
print('Pandas version: ', pd.__version__)
print('Requests version: ', requests.__version__)
print("Today's date:", dt.date.today())
# data scraped from Box Office Mojo, the authoritative source for Hollywood Box Office Data
# chris evans
url = 'http://www.boxofficemojo.com/people/chart/?view=Actor&id=chrisevans.htm'
evans = pd.read_html(url)
print('Ouput has type', type(evans), 'and length', len(evans))
print('First element has type', type(evans[0]))
#we have a list of dataframes, and the cut of data we want is represented by the below
evans[2]
ce=evans[2]
print("type=", type(ce)," ", "length=", len(ce), "shape=", ce.shape)
print(ce)
ce.to_csv("ce.csv")
#since scraped dataset is small, and had a tricky double index, we decided to export to csv and do a quick cleanup there
#removed indices; cleaned titles; cleaned date
#Clean File saved as CE1.csv
#this is the path for my machine; you'll have to link to the CE1.csv file that you've saved on your machine
path='C:\\Users\\Nick\\Desktop\\Data_Bootcamp\\Final Project\\CE1.csv'
CE = pd.read_csv(path)
print(type(CE), "shape is", CE.shape, "types:", CE.dtypes)
print(CE) #this is going to be much better for us to work with
#this looks good! let's test and make sure the data makes sense with a simple plot:
CE.plot.scatter('Release Year', 'Adjusted Gross')
#we love what we see, let's repeat it for our other leading gentlemen
# same process for our second leading Chris
# chris hemsworth
url = 'http://www.boxofficemojo.com/people/chart/?view=Actor&id=chrishemsworth.htm'
hemsworth = pd.read_html(url)
print('Ouput has type', type(hemsworth), 'and length', len(hemsworth))
print('First element has type', type(hemsworth[0]))
hemsworth[3]
ch=hemsworth[3]
print("type=", type(ch)," ", "length=", len(ch), "shape=", ch.shape)
print(ch)
ch.to_csv("ch.csv")
#since scraped dataset is small, and had a tricky double index, we decided to export to csv and do a quick cleanup there
#Cleaned File saved as CH1.csv
path='C:\\Users\\Nick\\Desktop\\Data_Bootcamp\\Final Project\\CH1.csv'
#again, this is the path on my machine, you'll want to make sure you adjust to wherever you saved down CH1
CH = pd.read_csv(path)
print(type(CH), "shape is", CH.shape, "types:", CH.dtypes)
CH.plot.scatter('Release Year', 'Adjusted Gross')
# Chris number three, coming through!
# chris pratt
url = 'http://www.boxofficemojo.com/people/chart/?view=Actor&id=chrispratt.htm'
pratt = pd.read_html(url)
print('Ouput has type', type(pratt), 'and length', len(pratt))
print('First element has type', type(pratt[0]))
pratt[3]
cp=pratt[3]
print("type=", type(cp)," ", "length=", len(cp), "shape=", cp.shape)
print(cp)
cp.to_csv("cp.csv")
#since scraped dataset is small, and had a tricky double index, we decided to export to csv and do a quick cleanup there
#Cleaned File saved as CP1.csv
path='C:\\Users\\Nick\\Desktop\\Data_Bootcamp\\Final Project\\CP1.csv'
#remember to adjust path to where you've saved the .csv down
CP = pd.read_csv(path)
print(type(CP), "shape is", CP.shape, "types:", CP.dtypes)
CP.plot.scatter('Release Year', 'Adjusted Gross')
plt.scatter(CE['Release Year'], CE['Adjusted Gross'],
color="purple")
plt.scatter(CH['Release Year'], CH['Adjusted Gross'],
color="red")
plt.scatter(CP['Release Year'], CP['Adjusted Gross'],
color="orange")
plt.title('Chris Film Box Office Share Over Time')
fig, ax = plt.subplots(nrows=3, ncols=1, sharex=True, sharey=True)
CE['Adjusted Gross'].head(10).plot(kind="bar",ax=ax[0], color='purple', title="Evans")
CH['Adjusted Gross'].head(10).plot(kind="bar",ax=ax[1], color='red', title="Hemsworth")
CP['Adjusted Gross'].head(10).plot(kind="bar",ax=ax[2], color='orange', title="Pratt")
plt.bar(CE['Release Year'], CE['Adjusted Gross'],
align='center',
color='pink')
plt.title('Chris Evans')
plt.bar(CH['Release Year'], CH['Adjusted Gross'],
align='center',
color='red')
plt.title("Chris Hemsworth")
plt.bar(CP['Release Year'], CP['Adjusted Gross'],
align='center',
color='orange')
plt.title("Chris Pratt")
plt.bar(CE['Release Year'], CE['Adjusted Gross'],
align='center',
color='purple')
plt.bar(CH['Release Year'], CH['Adjusted Gross'],
align='center',
color='red')
plt.bar(CP['Release Year'], CP['Adjusted Gross'],
align='center',
color='orange')
plt.title('Chris Film Box Office Share Over Time')
plt.bar(CH['Release Year'], CH['Adjusted Gross'],
align='center',
color='red')
plt.bar(CE['Release Year'], CE['Adjusted Gross'],
align='center',
color='purple')
plt.bar(CP['Release Year'], CP['Adjusted Gross'],
align='center',
color='orange')
plt.title('Chris Film Box Office Share Over Time')
#Movie scraping and data arranging like we did before
#Bruce Willis
url = 'http://www.boxofficemojo.com/people/chart/?id=brucewillis.htm'
willis = pd.read_html(url)
print('Ouput has type', type(willis), 'and length', len(willis))
print('First element has type', type(willis[0]))
willis[2]
bruce=willis[2]
bruce.to_csv("Bruce.csv") #Converting dataframe into a csv file
#editing and cleaning as needed, resaved as Bruce1.csv
path='/Users/Nick/Desktop/data_bootcamp/Final Project/Bruce1.csv'
BWillis = pd.read_csv(path)
print(type(BWillis), BWillis.shape, BWillis.dtypes)
import matplotlib as mpl
mpl.rcParams.update(mpl.rcParamsDefault)
BWillis.plot.scatter('Release Year', 'Adjusted Gross')
#That's a lot of films! Let's narrow:
BW=BWillis.head(11)
print(BW)
#we'll come back to this later, but let's get our other leading men in the frame!
#here we go again!
#Arnold Schwarzenegger
url = 'http://www.boxofficemojo.com/people/chart/?id=arnoldschwarzenegger.htm'
schwarz = pd.read_html(url)
print('Ouput has type', type(schwarz), 'and length', len(schwarz))
print('First element has type', type(schwarz[0]))
schwarz[2]
arnold=schwarz[2]
print("type=", type(arnold)," ", "length=", len(arnold))
arnold.shape
print(arnold)
arnold.to_csv("Arnold.csv")
path='/Users/Nick/Desktop/data_bootcamp/Final Project/Arnold1.csv'
ASchwarz = pd.read_csv(path)
print(type(ASchwarz), ASchwarz.shape, ASchwarz.dtypes)
print(ASchwarz)
ASchwarz.plot.scatter('Release Year', 'Adjusted Gross')
#let's scale back sample size again
AS=ASchwarz.head(11)
#we'll use this soon
#last but not least, our data for Tom Cruise
url = 'http://www.boxofficemojo.com/people/chart/?id=tomcruise.htm'
cruise = pd.read_html(url)
print('Ouput has type', type(cruise), 'and length', len(cruise))
print('First element has type', type(cruise[0]))
cruise[3]
Tom=cruise[3]
Tom.to_csv("Tom.csv")
path='/Users/Nick/Desktop/data_bootcamp/Final Project/Tom1.csv'
TCruise = pd.read_csv(path)
print(type(TCruise), TCruise.shape, TCruise.dtypes)
print(TCruise)
TCruise.plot.scatter('Release Year', 'Adjusted Gross')
#cutting down to the top 10
TC=TCruise.head(11)
#All of the old school action stars in one histogram. Representing share of box office cumulatively over time.
plt.bar(TC['Release Year'],
TC['Adjusted Gross'],
align='center',
color='Blue')
plt.bar(BW['Release Year'],
BW['Adjusted Gross'],
align='center',
color='Green')
plt.bar(AS['Release Year'],
AS['Adjusted Gross'],
align='center',
color='Yellow')
plt.title('"OG" Leading Box Office over Time')
#As a reminder, here's what we are comparing against:
fig, ax = plt.subplots(nrows=3, ncols=1, sharex=True, sharey=True)
CE['Adjusted Gross'].head(10).plot(kind="bar",ax=ax[0], color='purple', title="Evans")
CH['Adjusted Gross'].head(10).plot(kind="bar",ax=ax[1], color='red', title="Hemsworth")
CP['Adjusted Gross'].head(10).plot(kind="bar",ax=ax[2], color='orange', title="Pratt")
plt.bar(CE['Release Year'], CE['Adjusted Gross'],
align='center',
color='purple')
plt.bar(CH['Release Year'], CH['Adjusted Gross'],
align='center',
color='red')
plt.bar(CP['Release Year'], CP['Adjusted Gross'],
align='center',
color='orange')
plt.title('Chris Film Box Office Share Over Time')
| 0.173253 | 0.875574 |
```
import numpy as np
from numpy import linalg as LA
import functools
from collections import namedtuple, Iterator, Generator
import operator
class Iteration(object):
def __init__(self, low, high):
self.low = low
self.high = high
def __iter__(self):
counter = self.low
while self.high >= counter:
yield counter
counter += 1
it = Iteration(0, 15)
for num in it:
print(num, end=' ')
print()
Iterate1 = namedtuple('Iterate', 'iteration, rnorm, x')
StoppingCriterion = namedtuple('StoppingCriterion', 'predicate, is_exceptional, exception')
maxit_exceeded = StoppingCriterion(predicate=(lambda it: it > 25),
is_exceptional=True,
exception=RuntimeError)
rnorm_above_rtol = StoppingCriterion(predicate=(lambda rnorm: rnorm > 1.0e-8),
is_exceptional=False,
exception=RuntimeError)
criteria = [maxit_exceeded, rnorm_above_rtol]
exit_iteration = False
for criterion in criteria:
exit_iteration = exit_iteration or criterion.predicate(5)
print(exit_iteration)
class LinearIteration(object):
def __init__(self, stepper, iterate, max_it=25):
self.stepper = stepper
self.iterate = iterate
self.max_it = max_it
self.niterations = 0
def __iter__(self):
# We do not start from zero as this might be a restart
counter = self.iterate.iteration
try:
while self.max_it > counter:
x_next = self.stepper(self.iterate.x)
rnorm = LA.norm(x_next - self.iterate.x)
counter +=1
self.niterations += 1
self.iterate = Iterate1(iteration=counter, rnorm=rnorm, x=x_next)
print('{0:d} {1:.3E}'.format(self.iterate.iteration, self.iterate.rnorm))
yield self.iterate
raise RuntimeError('Maximum number of iterations ({0:d}) exceeded without meeting stopping criteria'.format(self.max_it))
except RuntimeError as err:
# clean up/checkpoint actions before dying
print('cleaning up the mess')
raise
finally:
# clean up/checkpoint actions
print('finally!')
def jacobi_step(A, b, x):
D = np.diag(A)
O = A - np.diagflat(D)
return (b - np.einsum('ij,j->i', O, x)) / D
def quadratic_form(A, b, x):
# Compute quadratic form 1/2 xAx + xb
return (0.5 * np.einsum('i,ij,j->', x, A, x) + np.einsum('i,i->', x,b))
dim = 1000
M = np.random.randn(dim, dim)
# Make sure our matrix is SPD
A = 0.5 * (M + M.transpose())
A = A * A.transpose()
A += dim * np.eye(dim)
b = np.random.rand(dim)
x_ref = LA.solve(A, b)
def relative_error_to_reference(x, x_ref):
return LA.norm(x - x_ref) / LA.norm(x_ref)
print('Jacobi algorithm')
#x_jacobi = jacobi(A, b)
stepper = functools.partial(jacobi_step, A, b)
energy = functools.partial(quadratic_form, A, b)
x_0 = np.zeros_like(b)
x_jacobi = Iterate1(iteration=0, x=x_0, rnorm=LA.norm(b - np.einsum('ij,j->i', A, x_0)))
jacobi = LinearIteration(stepper, iterate=x_jacobi)
# First converge to a loose threshold
rtol=1.0e-4
for x_jacobi in jacobi:
if x_jacobi.rnorm < rtol:
break
print(jacobi.niterations)
print('Jacobi relative error to reference {:.5E}\n'.format(
relative_error_to_reference(x_jacobi.x, x_ref)))
# Then take latest iterate and restart
restarted_jacobi = LinearIteration(stepper, iterate=x_jacobi)
rtol=1.0e-7
for x_jacobi in restarted_jacobi:
if x_jacobi.rnorm < rtol:
break
print(restarted_jacobi.niterations)
print('Jacobi relative error to reference {:.5E}\n'.format(
relative_error_to_reference(x_jacobi.x, x_ref)))
# Example from https://www.usenix.org/system/files/login/articles/12_beazley-online.pdf
from contextlib import contextmanager
@contextmanager
def manager():
# Everything before yield is part of _ _enter_ _
print("Entering")
try:
yield "SomeValue"
# Everything beyond the yield is part of _ _exit_ _
except Exception as e:
print("An error occurred: %s" % e)
raise
else:
print("No errors occurred")
with manager() as val:
print("Hello, world")
print(val)
x = int('whatever')
class BoundedRepeater(Iterator):
def __init__(self, value, max_repeats):
self.value = value
self.max_repeats = max_repeats
self.count = 0
def __next__(self):
try:
if self.count >= self.max_repeats:
raise StopIteration('Exceeded maximum number of repeats!!!')
self.count += 1
return self.value
except StopIteration as e:
print(e)
raise
finally:
print('cleaning up, finally!')
repeater = BoundedRepeater('Hello', 3)
# This causes the exception to be raised
#next(repeater)
from typing import Dict, List, Tuple, Callable
class Iterate:
def __init__(self, iteration: int, x: List[float], stats: Dict[str, float]) -> None:
"""
stats is a dictionary containing the statistics (e.g. norm of residual) for the current iterate.
The key, value pair is the name and value of the statistics
"""
self._iteration = iteration
self._x = x
self._stats = stats
def __str__(self) -> str:
"""
This is used for print(iterate), so mostly in debugging and we want full info: iteration number, vector and stats
FIXME we possibly want also print_out to print a line in the final report
"""
message = 'Iteration number {0:2d}'.format(self._iteration)
return '\n'.join()
def compute_stats(self, funcs: Dict[str, Callable[..., float]]) -> None:
"""
Apply `funcs` on `_x` to update `_stats`
FIXME: I think funcs and stats should be both members, so we avoid having them out of sync...
"""
for key, f in funcs:
self._stats[key] = f(self._x)
class Criterion:
def __init__(self, threshold, comparison, exception, message):
self.threshold = threshold
self.comparison = comparison
self.exception = exception
self.message = message.format(self.threshold)
def compare(self, value):
return self.comparison(value, self.threshold)
def throw(self):
raise self.exception(self.message)
maxit_exceeded = Criterion(threshold=25,
comparison=(lambda value, threshold: value > threshold),
exception=RuntimeError,
message='Maximum number of iterations ({0:d}) exceeded')
rnorm_above_rtol = Criterion(threshold=1.0e-10,
comparison=(lambda value, threshold: value < threshold),
exception=RuntimeError,
message='Residual norm below threshold {0:.1E}')
denergy_below_etol = Criterion(threshold=1.0e-3,
comparison=(lambda value, threhold: abs(value) < threshold),
exception=RuntimeError,
message='Energy difference below threshold {0:.1E}')
# This is any on a list of custom predicates
def check_failure(predicates, values):
for i, p in enumerate(predicates):
if p.compare(values[i]):
raise p.throw()
return False
# This is all() on a list of custom predicates
def check_success(predicates, values):
for i, p in enumerate(predicates):
if not p.compare(values[i]):
return False
return True
class IterativeSolver(Iterator):
def __init__(self, stepper, iterate, failures, successes):
self.stepper = stepper
self.iterate = iterate
self.failures = failures
self.successes = successes
self.niterations = 0
# Print iteration header
self._header()
def _header(self):
print(' # It. |r| |dE|')
print('-----------------------------------')
def __next__(self):
# We do not start from zero as this might be a restart
counter = self.iterate.iteration
rnorm = 0.0
denergy = 0.0
try:
failed = check_failure(self.failures, [self.iterate.iteration])
if not failed:
x_next = self.stepper(self.iterate.x)
rnorm = LA.norm(x_next - self.iterate.x)
denergy = energy(x_next) - energy(self.iterate.x)
self.niterations += 1
counter += 1
self.iterate = Iterate(iteration=counter, rnorm=rnorm, x=x_next)
except:
success_messages = '\n'.join(map(lambda x: x.message, self.successes))
print('Success criteria not met within maximum number of iterations')
print(success_messages)
raise
finally:
# clean up/checkpoint actions after each iteration
# Print information on iteration
print(' {0:2d} {1:.3E} {2:.3E}'.format(self.iterate.iteration, self.iterate.rnorm, abs(denergy)))
# Check for success
if check_success(self.successes, [self.iterate.rnorm, denergy]):
success_messages = '\n'.join(map(lambda x: x.message, self.successes))
print(success_messages)
raise StopIteration
x_0 = np.zeros_like(b)
x_jacobi = Iterate(iteration=0, x=x_0, rnorm=LA.norm(b - np.einsum('ij,j->i', A, x_0)))
jacobi2 = IterativeSolver(stepper, x_jacobi, [maxit_exceeded], [rnorm_above_rtol, denergy_below_etol])
# First converge to a loose threshold
for _ in jacobi2:
pass
print('jacobi2.niterations ', jacobi2.niterations)
print('Jacobi relative error to reference {:.5E}\n'.format(relative_error_to_reference(jacobi2.iterate.x, x_ref)))
class Fibonacci(Generator):
def __init__(self):
self.a, self.b = 0, 1
def send(self, ignored_arg):
return_value = self.a
self.a, self.b = self.b, self.a+self.b
return return_value
def throw(self, type=None, value=None, traceback=None):
raise StopIteration
class IterGen(Generator):
def __init__(self, start, stop):
self.start = start
self.stop = stop
self.counter = 0
def send(self, value):
try:
if self.counter > self.stop:
self.throw(RuntimeError, val='Exceeded maximum number of repeats!!!')
return self.counter
except RuntimeError as e:
print(e)
raise
finally:
# Checkpoint, if necessary
# Check early exit convergence criteria and stop
# Update counter
self.counter += 1
print('cleaning up, finally!')
def throw(self, type, val=None, tb=None):
# Throw if no convergence achieved and maximum number of iterations reached
raise type(val)
class IterativeSolver2(Generator):
def __init__(self, stepper, iterate, iteration_stop, early_exit):
self.stepper = stepper
self.iterate = iterate
self.iteration_stop = iteration_stop
self.early_exit = early_exit
self.niterations = 0
# Print iteration header
self._header()
def _header(self):
print(' # It. |r| ')
print('-------------------')
def send(self, value):
# We do not start from zero as this might be a restart
counter = self.iterate.iteration
try:
if self.niterations > self.iteration_stop.threshold:
self.throw(RuntimeError, val=self.iteration_stop.message)
x_next = self.stepper(self.iterate.x)
rnorm = LA.norm(x_next - self.iterate.x)
self.niterations += 1
counter += 1
self.iterate = Iterate(iteration=counter, rnorm=rnorm, x=x_next)
return self.iterate
except RuntimeError as err:
# clean up/checkpoint actions before dying
print(err)
raise
finally:
# clean up/checkpoint actions after each iteration
# Print information on iteration
print(' {0:d} {1:.3E}'.format(self.iterate.iteration, self.iterate.rnorm))
# Check convergence
if self.iterate.rnorm < self.early_exit.threshold:
print(self.early_exit.message)
return self.iterate
def throw(self, type, val=None, tb=None):
# Throw if no convergence achieved and maximum number of iterations reached
raise type(val)
x_0 = np.zeros_like(b)
x_jacobi = Iterate(iteration=0, x=x_0, rnorm=LA.norm(b - np.einsum('ij,j->i', A, x_0)))
jacobi_gen = IterativeSolver2(stepper, x_jacobi, maxit_exceeded, rnorm_above_rtol)
import contextlib
@contextlib.contextmanager
def mylist():
try:
l = [1, 2, 3, 4, 5]
yield l
finally:
print("exit scope")
with mylist() as l:
print(l)
```
|
github_jupyter
|
import numpy as np
from numpy import linalg as LA
import functools
from collections import namedtuple, Iterator, Generator
import operator
class Iteration(object):
def __init__(self, low, high):
self.low = low
self.high = high
def __iter__(self):
counter = self.low
while self.high >= counter:
yield counter
counter += 1
it = Iteration(0, 15)
for num in it:
print(num, end=' ')
print()
Iterate1 = namedtuple('Iterate', 'iteration, rnorm, x')
StoppingCriterion = namedtuple('StoppingCriterion', 'predicate, is_exceptional, exception')
maxit_exceeded = StoppingCriterion(predicate=(lambda it: it > 25),
is_exceptional=True,
exception=RuntimeError)
rnorm_above_rtol = StoppingCriterion(predicate=(lambda rnorm: rnorm > 1.0e-8),
is_exceptional=False,
exception=RuntimeError)
criteria = [maxit_exceeded, rnorm_above_rtol]
exit_iteration = False
for criterion in criteria:
exit_iteration = exit_iteration or criterion.predicate(5)
print(exit_iteration)
class LinearIteration(object):
def __init__(self, stepper, iterate, max_it=25):
self.stepper = stepper
self.iterate = iterate
self.max_it = max_it
self.niterations = 0
def __iter__(self):
# We do not start from zero as this might be a restart
counter = self.iterate.iteration
try:
while self.max_it > counter:
x_next = self.stepper(self.iterate.x)
rnorm = LA.norm(x_next - self.iterate.x)
counter +=1
self.niterations += 1
self.iterate = Iterate1(iteration=counter, rnorm=rnorm, x=x_next)
print('{0:d} {1:.3E}'.format(self.iterate.iteration, self.iterate.rnorm))
yield self.iterate
raise RuntimeError('Maximum number of iterations ({0:d}) exceeded without meeting stopping criteria'.format(self.max_it))
except RuntimeError as err:
# clean up/checkpoint actions before dying
print('cleaning up the mess')
raise
finally:
# clean up/checkpoint actions
print('finally!')
def jacobi_step(A, b, x):
D = np.diag(A)
O = A - np.diagflat(D)
return (b - np.einsum('ij,j->i', O, x)) / D
def quadratic_form(A, b, x):
# Compute quadratic form 1/2 xAx + xb
return (0.5 * np.einsum('i,ij,j->', x, A, x) + np.einsum('i,i->', x,b))
dim = 1000
M = np.random.randn(dim, dim)
# Make sure our matrix is SPD
A = 0.5 * (M + M.transpose())
A = A * A.transpose()
A += dim * np.eye(dim)
b = np.random.rand(dim)
x_ref = LA.solve(A, b)
def relative_error_to_reference(x, x_ref):
return LA.norm(x - x_ref) / LA.norm(x_ref)
print('Jacobi algorithm')
#x_jacobi = jacobi(A, b)
stepper = functools.partial(jacobi_step, A, b)
energy = functools.partial(quadratic_form, A, b)
x_0 = np.zeros_like(b)
x_jacobi = Iterate1(iteration=0, x=x_0, rnorm=LA.norm(b - np.einsum('ij,j->i', A, x_0)))
jacobi = LinearIteration(stepper, iterate=x_jacobi)
# First converge to a loose threshold
rtol=1.0e-4
for x_jacobi in jacobi:
if x_jacobi.rnorm < rtol:
break
print(jacobi.niterations)
print('Jacobi relative error to reference {:.5E}\n'.format(
relative_error_to_reference(x_jacobi.x, x_ref)))
# Then take latest iterate and restart
restarted_jacobi = LinearIteration(stepper, iterate=x_jacobi)
rtol=1.0e-7
for x_jacobi in restarted_jacobi:
if x_jacobi.rnorm < rtol:
break
print(restarted_jacobi.niterations)
print('Jacobi relative error to reference {:.5E}\n'.format(
relative_error_to_reference(x_jacobi.x, x_ref)))
# Example from https://www.usenix.org/system/files/login/articles/12_beazley-online.pdf
from contextlib import contextmanager
@contextmanager
def manager():
# Everything before yield is part of _ _enter_ _
print("Entering")
try:
yield "SomeValue"
# Everything beyond the yield is part of _ _exit_ _
except Exception as e:
print("An error occurred: %s" % e)
raise
else:
print("No errors occurred")
with manager() as val:
print("Hello, world")
print(val)
x = int('whatever')
class BoundedRepeater(Iterator):
def __init__(self, value, max_repeats):
self.value = value
self.max_repeats = max_repeats
self.count = 0
def __next__(self):
try:
if self.count >= self.max_repeats:
raise StopIteration('Exceeded maximum number of repeats!!!')
self.count += 1
return self.value
except StopIteration as e:
print(e)
raise
finally:
print('cleaning up, finally!')
repeater = BoundedRepeater('Hello', 3)
# This causes the exception to be raised
#next(repeater)
from typing import Dict, List, Tuple, Callable
class Iterate:
def __init__(self, iteration: int, x: List[float], stats: Dict[str, float]) -> None:
"""
stats is a dictionary containing the statistics (e.g. norm of residual) for the current iterate.
The key, value pair is the name and value of the statistics
"""
self._iteration = iteration
self._x = x
self._stats = stats
def __str__(self) -> str:
"""
This is used for print(iterate), so mostly in debugging and we want full info: iteration number, vector and stats
FIXME we possibly want also print_out to print a line in the final report
"""
message = 'Iteration number {0:2d}'.format(self._iteration)
return '\n'.join()
def compute_stats(self, funcs: Dict[str, Callable[..., float]]) -> None:
"""
Apply `funcs` on `_x` to update `_stats`
FIXME: I think funcs and stats should be both members, so we avoid having them out of sync...
"""
for key, f in funcs:
self._stats[key] = f(self._x)
class Criterion:
def __init__(self, threshold, comparison, exception, message):
self.threshold = threshold
self.comparison = comparison
self.exception = exception
self.message = message.format(self.threshold)
def compare(self, value):
return self.comparison(value, self.threshold)
def throw(self):
raise self.exception(self.message)
maxit_exceeded = Criterion(threshold=25,
comparison=(lambda value, threshold: value > threshold),
exception=RuntimeError,
message='Maximum number of iterations ({0:d}) exceeded')
rnorm_above_rtol = Criterion(threshold=1.0e-10,
comparison=(lambda value, threshold: value < threshold),
exception=RuntimeError,
message='Residual norm below threshold {0:.1E}')
denergy_below_etol = Criterion(threshold=1.0e-3,
comparison=(lambda value, threhold: abs(value) < threshold),
exception=RuntimeError,
message='Energy difference below threshold {0:.1E}')
# This is any on a list of custom predicates
def check_failure(predicates, values):
for i, p in enumerate(predicates):
if p.compare(values[i]):
raise p.throw()
return False
# This is all() on a list of custom predicates
def check_success(predicates, values):
for i, p in enumerate(predicates):
if not p.compare(values[i]):
return False
return True
class IterativeSolver(Iterator):
def __init__(self, stepper, iterate, failures, successes):
self.stepper = stepper
self.iterate = iterate
self.failures = failures
self.successes = successes
self.niterations = 0
# Print iteration header
self._header()
def _header(self):
print(' # It. |r| |dE|')
print('-----------------------------------')
def __next__(self):
# We do not start from zero as this might be a restart
counter = self.iterate.iteration
rnorm = 0.0
denergy = 0.0
try:
failed = check_failure(self.failures, [self.iterate.iteration])
if not failed:
x_next = self.stepper(self.iterate.x)
rnorm = LA.norm(x_next - self.iterate.x)
denergy = energy(x_next) - energy(self.iterate.x)
self.niterations += 1
counter += 1
self.iterate = Iterate(iteration=counter, rnorm=rnorm, x=x_next)
except:
success_messages = '\n'.join(map(lambda x: x.message, self.successes))
print('Success criteria not met within maximum number of iterations')
print(success_messages)
raise
finally:
# clean up/checkpoint actions after each iteration
# Print information on iteration
print(' {0:2d} {1:.3E} {2:.3E}'.format(self.iterate.iteration, self.iterate.rnorm, abs(denergy)))
# Check for success
if check_success(self.successes, [self.iterate.rnorm, denergy]):
success_messages = '\n'.join(map(lambda x: x.message, self.successes))
print(success_messages)
raise StopIteration
x_0 = np.zeros_like(b)
x_jacobi = Iterate(iteration=0, x=x_0, rnorm=LA.norm(b - np.einsum('ij,j->i', A, x_0)))
jacobi2 = IterativeSolver(stepper, x_jacobi, [maxit_exceeded], [rnorm_above_rtol, denergy_below_etol])
# First converge to a loose threshold
for _ in jacobi2:
pass
print('jacobi2.niterations ', jacobi2.niterations)
print('Jacobi relative error to reference {:.5E}\n'.format(relative_error_to_reference(jacobi2.iterate.x, x_ref)))
class Fibonacci(Generator):
def __init__(self):
self.a, self.b = 0, 1
def send(self, ignored_arg):
return_value = self.a
self.a, self.b = self.b, self.a+self.b
return return_value
def throw(self, type=None, value=None, traceback=None):
raise StopIteration
class IterGen(Generator):
def __init__(self, start, stop):
self.start = start
self.stop = stop
self.counter = 0
def send(self, value):
try:
if self.counter > self.stop:
self.throw(RuntimeError, val='Exceeded maximum number of repeats!!!')
return self.counter
except RuntimeError as e:
print(e)
raise
finally:
# Checkpoint, if necessary
# Check early exit convergence criteria and stop
# Update counter
self.counter += 1
print('cleaning up, finally!')
def throw(self, type, val=None, tb=None):
# Throw if no convergence achieved and maximum number of iterations reached
raise type(val)
class IterativeSolver2(Generator):
def __init__(self, stepper, iterate, iteration_stop, early_exit):
self.stepper = stepper
self.iterate = iterate
self.iteration_stop = iteration_stop
self.early_exit = early_exit
self.niterations = 0
# Print iteration header
self._header()
def _header(self):
print(' # It. |r| ')
print('-------------------')
def send(self, value):
# We do not start from zero as this might be a restart
counter = self.iterate.iteration
try:
if self.niterations > self.iteration_stop.threshold:
self.throw(RuntimeError, val=self.iteration_stop.message)
x_next = self.stepper(self.iterate.x)
rnorm = LA.norm(x_next - self.iterate.x)
self.niterations += 1
counter += 1
self.iterate = Iterate(iteration=counter, rnorm=rnorm, x=x_next)
return self.iterate
except RuntimeError as err:
# clean up/checkpoint actions before dying
print(err)
raise
finally:
# clean up/checkpoint actions after each iteration
# Print information on iteration
print(' {0:d} {1:.3E}'.format(self.iterate.iteration, self.iterate.rnorm))
# Check convergence
if self.iterate.rnorm < self.early_exit.threshold:
print(self.early_exit.message)
return self.iterate
def throw(self, type, val=None, tb=None):
# Throw if no convergence achieved and maximum number of iterations reached
raise type(val)
x_0 = np.zeros_like(b)
x_jacobi = Iterate(iteration=0, x=x_0, rnorm=LA.norm(b - np.einsum('ij,j->i', A, x_0)))
jacobi_gen = IterativeSolver2(stepper, x_jacobi, maxit_exceeded, rnorm_above_rtol)
import contextlib
@contextlib.contextmanager
def mylist():
try:
l = [1, 2, 3, 4, 5]
yield l
finally:
print("exit scope")
with mylist() as l:
print(l)
| 0.684053 | 0.360348 |
```
!pip install eli5
import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import cross_val_score
import eli5
from eli5.sklearn import PermutationImportance
from ast import literal_eval
from tqdm import tqdm_notebook
cd "/content/drive/My Drive/Colab Notebooks/dw_matrix"
df = pd.read_csv("data/men_shoes.csv", low_memory=False)
df.shape
df.values
df.columns
df['brand_cat'] = df['brand'].map(lambda x: str(x).lower()).factorize()[0]
feats1 = ['brand_cat']
x = df[ feats1 ].values
y = df[ 'prices_amountmin' ].values
model = DecisionTreeRegressor(max_depth=5)
scores = cross_val_score(model, x, y, scoring='neg_mean_absolute_error')
np.mean(scores), np.std(scores)
def run_model(feast1, model=DecisionTreeRegressor(max_depth=5)):
x = df[ feats1 ].values
y = df['prices_amountmin'].values
scores = cross_val_score(model, x, y, scoring='neg_mean_absolute_error')
return np.mean(scores), np.std(scores)
run_model(['brand_cat'])
model = RandomForestRegressor(max_depth=5, n_estimators=100, random_state=0)
run_model(['brand_cat'], model)
df.head()
df.features.head().values
test = {'key': 'value'}
test['key']
str(test)
str_dict = '[{"key":"Gender","value":["Men"]},{"key":"Shoe Size","value":["M"]},{"key":"Shoe Category","value":["Men\'s Shoes"]},{"key":"Color","value":["Multicolor"]},{"key":"Manufacturer Part Number","value":["8190-W-NAVY-7.5"]},{"key":"Brand","value":["Josmo"]}]'
literal_eval(str_dict)[0]['key']
literal_eval(str_dict)[0]['value']
literal_eval(str_dict)[0]['value'][0]
def parse_features(x):
output_dict = {}
if str(x) == 'nan': return output_dict
features = literal_eval(x.replace('\\"', '"'))
for item in features:
key = item['key'].lower().strip()
value = item['value'][0].lower().strip()
output_dict[key] = value
return output_dict
df['features_parsed'] = df['features'].map(parse_features)
df['features_parsed'].head().values
[
{'key': 'Gender', 'value': ['Men']},
{'key': 'Shoe Size', 'value': ['M']},
{'key': 'Shoe Category', 'value': ["Men's Shoes"]},
{'key': 'Color', 'value': ['Multicolor']},
{'key': 'Manufacturer Part Number', 'value': ['8190-W-NAVY-7.5']},
{'key': 'Brand', 'value': ['Josmo']}]
{
'Gender': 'Men',
'Shoe Size': 'M',
}
keys = set()
df['features_parsed'].map( lambda x: keys.update(x.keys()))
len(keys)
df.features_parsed.head().values
def get_name_feat(key):
return 'feat_' + key
for key in tqdm_notebook(keys):
df[get_name_feat(key)] = df.features_parsed.map(lambda feats1: feats1[key] if key in feats1 else np.nan)
df.columns
df[ False == df['feat_athlete'].isnull() ].shape[0] / df.shape[0] * 100
df.shape[0]
keys_stat = {}
for key in keys:
keys_stat[key] = df[ False == df[get_name_feat(key)].isnull() ].shape[0] / df.shape[0] * 100
{k:v for k,v in keys_stat.items() if v > 30}
df['feat_brand_cat'] = df['feat_brand'].factorize()[0]
df['feat_color_cat'] = df['feat_color'].factorize()[0]
df['feat_gender_cat'] = df['feat_gender'].factorize()[0]
df['feat_manufacturer part number_cat'] = df['feat_manufacturer part number'].factorize()[0]
df['feat_material_cat'] = df['feat_material'].factorize()[0]
df['feat_sport_cat'] = df['feat_sport'].factorize()[0]
df['feat_style_cat'] = df['feat_style'].factorize()[0]
for key in keys:
df[get_name_feat(key) + '_cat'] = df[get_name_feat(key)].factorize()[0]
df [ df.brand == df.feat_brand ].shape
df [ df.brand != df.feat_brand ].shape
df['brand'] = df['brand'].map(lambda x: str(x).lower())
df [ df.brand != df.feat_brand ][ ['brand', 'feat_brand'] ].head()
df [ df.brand == df.feat_brand ].shape
run_model(['brand_cat'] , model )
feats3 = ['']
feats4 = ['brand_cat', 'feat_brand_cat', 'feat_color_cat', 'feat_gender_cat', 'feat_manufacturer part number_cat', 'feat_material_cat']
model = RandomForestRegressor(max_depth=5, n_estimators=100)
run_model( feats4 , model )
x = df[ feats4 ].values
y = df['prices_amountmin'].values
m = RandomForestRegressor(max_depth=5, n_estimators=100, random_state=0)
m.fit(x, y)
perm = PermutationImportance(m, random_state=1).fit(x, y);
eli5.show_weights(perm, feature_names = feats4)
feats5 = ['brand_cat', 'feat_brand_cat', 'feat_shape_cat', 'feat_gender_cat', 'feat_material_cat', 'feat_style_cat', 'feat_metal type_cat']
model = RandomForestRegressor(max_depth=5, n_estimators=100)
result = run_model(feats5, model)
x = df[ feats5 ].values
y = df['prices_amountmin'].values
m = RandomForestRegressor(max_depth=5, n_estimators=100, random_state=0)
m.fit(x, y)
print(result)
perm = PermutationImportance(m, random_state=1).fit(x, y);
eli5.show_weights(perm, feature_names = feats5)
df['brand'].value_counts(normalize=True)
df[ df['brand'] == 'nike'].features_parsed.head().values
df[ df['brand'] == 'nike'].features_parsed.sample(5).values
!git add matrix_one/day5.ipynb
!git commit -m "1st ML for Men's Shoe Prices - day 5 "
!git config --global user.email "[email protected]"
!git config --global user.name "Lukasz"
!git push -u origin master
```
|
github_jupyter
|
!pip install eli5
import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import cross_val_score
import eli5
from eli5.sklearn import PermutationImportance
from ast import literal_eval
from tqdm import tqdm_notebook
cd "/content/drive/My Drive/Colab Notebooks/dw_matrix"
df = pd.read_csv("data/men_shoes.csv", low_memory=False)
df.shape
df.values
df.columns
df['brand_cat'] = df['brand'].map(lambda x: str(x).lower()).factorize()[0]
feats1 = ['brand_cat']
x = df[ feats1 ].values
y = df[ 'prices_amountmin' ].values
model = DecisionTreeRegressor(max_depth=5)
scores = cross_val_score(model, x, y, scoring='neg_mean_absolute_error')
np.mean(scores), np.std(scores)
def run_model(feast1, model=DecisionTreeRegressor(max_depth=5)):
x = df[ feats1 ].values
y = df['prices_amountmin'].values
scores = cross_val_score(model, x, y, scoring='neg_mean_absolute_error')
return np.mean(scores), np.std(scores)
run_model(['brand_cat'])
model = RandomForestRegressor(max_depth=5, n_estimators=100, random_state=0)
run_model(['brand_cat'], model)
df.head()
df.features.head().values
test = {'key': 'value'}
test['key']
str(test)
str_dict = '[{"key":"Gender","value":["Men"]},{"key":"Shoe Size","value":["M"]},{"key":"Shoe Category","value":["Men\'s Shoes"]},{"key":"Color","value":["Multicolor"]},{"key":"Manufacturer Part Number","value":["8190-W-NAVY-7.5"]},{"key":"Brand","value":["Josmo"]}]'
literal_eval(str_dict)[0]['key']
literal_eval(str_dict)[0]['value']
literal_eval(str_dict)[0]['value'][0]
def parse_features(x):
output_dict = {}
if str(x) == 'nan': return output_dict
features = literal_eval(x.replace('\\"', '"'))
for item in features:
key = item['key'].lower().strip()
value = item['value'][0].lower().strip()
output_dict[key] = value
return output_dict
df['features_parsed'] = df['features'].map(parse_features)
df['features_parsed'].head().values
[
{'key': 'Gender', 'value': ['Men']},
{'key': 'Shoe Size', 'value': ['M']},
{'key': 'Shoe Category', 'value': ["Men's Shoes"]},
{'key': 'Color', 'value': ['Multicolor']},
{'key': 'Manufacturer Part Number', 'value': ['8190-W-NAVY-7.5']},
{'key': 'Brand', 'value': ['Josmo']}]
{
'Gender': 'Men',
'Shoe Size': 'M',
}
keys = set()
df['features_parsed'].map( lambda x: keys.update(x.keys()))
len(keys)
df.features_parsed.head().values
def get_name_feat(key):
return 'feat_' + key
for key in tqdm_notebook(keys):
df[get_name_feat(key)] = df.features_parsed.map(lambda feats1: feats1[key] if key in feats1 else np.nan)
df.columns
df[ False == df['feat_athlete'].isnull() ].shape[0] / df.shape[0] * 100
df.shape[0]
keys_stat = {}
for key in keys:
keys_stat[key] = df[ False == df[get_name_feat(key)].isnull() ].shape[0] / df.shape[0] * 100
{k:v for k,v in keys_stat.items() if v > 30}
df['feat_brand_cat'] = df['feat_brand'].factorize()[0]
df['feat_color_cat'] = df['feat_color'].factorize()[0]
df['feat_gender_cat'] = df['feat_gender'].factorize()[0]
df['feat_manufacturer part number_cat'] = df['feat_manufacturer part number'].factorize()[0]
df['feat_material_cat'] = df['feat_material'].factorize()[0]
df['feat_sport_cat'] = df['feat_sport'].factorize()[0]
df['feat_style_cat'] = df['feat_style'].factorize()[0]
for key in keys:
df[get_name_feat(key) + '_cat'] = df[get_name_feat(key)].factorize()[0]
df [ df.brand == df.feat_brand ].shape
df [ df.brand != df.feat_brand ].shape
df['brand'] = df['brand'].map(lambda x: str(x).lower())
df [ df.brand != df.feat_brand ][ ['brand', 'feat_brand'] ].head()
df [ df.brand == df.feat_brand ].shape
run_model(['brand_cat'] , model )
feats3 = ['']
feats4 = ['brand_cat', 'feat_brand_cat', 'feat_color_cat', 'feat_gender_cat', 'feat_manufacturer part number_cat', 'feat_material_cat']
model = RandomForestRegressor(max_depth=5, n_estimators=100)
run_model( feats4 , model )
x = df[ feats4 ].values
y = df['prices_amountmin'].values
m = RandomForestRegressor(max_depth=5, n_estimators=100, random_state=0)
m.fit(x, y)
perm = PermutationImportance(m, random_state=1).fit(x, y);
eli5.show_weights(perm, feature_names = feats4)
feats5 = ['brand_cat', 'feat_brand_cat', 'feat_shape_cat', 'feat_gender_cat', 'feat_material_cat', 'feat_style_cat', 'feat_metal type_cat']
model = RandomForestRegressor(max_depth=5, n_estimators=100)
result = run_model(feats5, model)
x = df[ feats5 ].values
y = df['prices_amountmin'].values
m = RandomForestRegressor(max_depth=5, n_estimators=100, random_state=0)
m.fit(x, y)
print(result)
perm = PermutationImportance(m, random_state=1).fit(x, y);
eli5.show_weights(perm, feature_names = feats5)
df['brand'].value_counts(normalize=True)
df[ df['brand'] == 'nike'].features_parsed.head().values
df[ df['brand'] == 'nike'].features_parsed.sample(5).values
!git add matrix_one/day5.ipynb
!git commit -m "1st ML for Men's Shoe Prices - day 5 "
!git config --global user.email "[email protected]"
!git config --global user.name "Lukasz"
!git push -u origin master
| 0.460289 | 0.359224 |
```
%matplotlib inline
from ggplot import *
```
### Colors
ggplot comes with a variety of "scales" that allow you to theme your plots and make them easier to interpret. In addition to the deafult color schemes that ggplot provides, there are also several color `scales` which allow you to specify more targeted "palettes" of colors to use in your plots.
#### `scale_color_brewer`
`scale_color_brewer` provides sets of colors that are optimized for displaying data on maps. It comes from Cynthia Brewer's aptly named [Color Brewer](http://colorbrewer2.org/). Lucky for us, these palettes also look great on plots that aren't maps.
```
ggplot(aes(x='carat', y='price', color='clarity'), data=diamonds) +\
geom_point() +\
scale_color_brewer(type='qual')
ggplot(aes(x='carat', y='price', color='clarity'), data=diamonds) + \
geom_point() + \
scale_color_brewer(type='seq')
ggplot(aes(x='carat', y='price', color='clarity'), data=diamonds) + \
geom_point() + \
scale_color_brewer(type='seq', palette=4)
ggplot(aes(x='carat', y='price', color='clarity'), data=diamonds) + \
geom_point() + \
scale_color_brewer(type='div', palette=5)
```
#### `scale_color_gradient`
`scale_color_gradient` allows you to create gradients of colors that can represent a spectrum of values. For instance, if you're displaying temperature data, you might want to have lower values be blue, hotter values be red, and middle values be somewhere in between. `scale_color_gradient` will calculate the colors each point should be--even those in between colors.
```
import pandas as pd
temperature = pd.DataFrame({"celsius": range(-88, 58)})
temperature['farenheit'] = temperature.celsius*1.8 + 32
temperature['kelvin'] = temperature.celsius + 273.15
ggplot(temperature, aes(x='celsius', y='farenheit', color='kelvin')) + \
geom_point() + \
scale_color_gradient(low='blue', high='red')
ggplot(aes(x='x', y='y', color='z'), data=diamonds.head(1000)) +\
geom_point() +\
scale_color_gradient(low='red', high='white')
ggplot(aes(x='x', y='y', color='z'), data=diamonds.head(1000)) +\
geom_point() +\
scale_color_gradient(low='#05D9F6', high='#5011D1')
ggplot(aes(x='x', y='y', color='z'), data=diamonds.head(1000)) +\
geom_point() +\
scale_color_gradient(low='#E1FA72', high='#F46FEE')
```
#### `scale_color_manual`
Want to just specify the colors yourself? No problem, just use `scale_color_manual`. Add it to your plot as a layer and specify the colors you'd like using a list.
```
my_colors = [
"#ff7f50",
"#ff8b61",
"#ff9872",
"#ffa584",
"#ffb296",
"#ffbfa7",
"#ffcbb9",
"#ffd8ca",
"#ffe5dc",
"#fff2ed"
]
ggplot(aes(x='carat', y='price', color='clarity'), data=diamonds) + \
geom_point() + \
scale_color_manual(values=my_colors)
# https://coolors.co/app/69a2b0-659157-a1c084-edb999-e05263
ggplot(aes(x='carat', y='price', color='cut'), data=diamonds) + \
geom_point() + \
scale_color_manual(values=['#69A2B0', '#659157', '#A1C084', '#EDB999', '#E05263'])
```
|
github_jupyter
|
%matplotlib inline
from ggplot import *
ggplot(aes(x='carat', y='price', color='clarity'), data=diamonds) +\
geom_point() +\
scale_color_brewer(type='qual')
ggplot(aes(x='carat', y='price', color='clarity'), data=diamonds) + \
geom_point() + \
scale_color_brewer(type='seq')
ggplot(aes(x='carat', y='price', color='clarity'), data=diamonds) + \
geom_point() + \
scale_color_brewer(type='seq', palette=4)
ggplot(aes(x='carat', y='price', color='clarity'), data=diamonds) + \
geom_point() + \
scale_color_brewer(type='div', palette=5)
import pandas as pd
temperature = pd.DataFrame({"celsius": range(-88, 58)})
temperature['farenheit'] = temperature.celsius*1.8 + 32
temperature['kelvin'] = temperature.celsius + 273.15
ggplot(temperature, aes(x='celsius', y='farenheit', color='kelvin')) + \
geom_point() + \
scale_color_gradient(low='blue', high='red')
ggplot(aes(x='x', y='y', color='z'), data=diamonds.head(1000)) +\
geom_point() +\
scale_color_gradient(low='red', high='white')
ggplot(aes(x='x', y='y', color='z'), data=diamonds.head(1000)) +\
geom_point() +\
scale_color_gradient(low='#05D9F6', high='#5011D1')
ggplot(aes(x='x', y='y', color='z'), data=diamonds.head(1000)) +\
geom_point() +\
scale_color_gradient(low='#E1FA72', high='#F46FEE')
my_colors = [
"#ff7f50",
"#ff8b61",
"#ff9872",
"#ffa584",
"#ffb296",
"#ffbfa7",
"#ffcbb9",
"#ffd8ca",
"#ffe5dc",
"#fff2ed"
]
ggplot(aes(x='carat', y='price', color='clarity'), data=diamonds) + \
geom_point() + \
scale_color_manual(values=my_colors)
# https://coolors.co/app/69a2b0-659157-a1c084-edb999-e05263
ggplot(aes(x='carat', y='price', color='cut'), data=diamonds) + \
geom_point() + \
scale_color_manual(values=['#69A2B0', '#659157', '#A1C084', '#EDB999', '#E05263'])
| 0.569853 | 0.947769 |
# Generate simulated infrastructure telemetry
```
# Install requiered packages if needed (only once)
!pip install pytimeparse
!pip install -i https://test.pypi.org/simple/ v3io-generator --upgrade
!pip install faker
!pip install pyarrow --upgrade
import os
import time
import yaml
import pandas as pd
import datetime
import itertools
# DB Connection
import v3io_frames as v3f
# Data generator
from v3io_generator import metrics_generator, deployment_generator
```
General definitions
```
%env SAVE_TO_KV = True
%env DEPLOYMENT_TABLE = netops_devices
```
## Create Metadata
the following section will create a list of devices which are scattered in multiple datacenters
```
def _create_deployment():
print('creating deployment')
# Create meta-data factory
dep_gen = deployment_generator.deployment_generator()
faker=dep_gen.get_faker()
# Design meta-data
dep_gen.add_level(name='company',number=2,level_type=faker.company)
dep_gen.add_level('data_center',number=2,level_type=faker.street_name)
dep_gen.add_level('device',number=2,level_type=faker.msisdn)
# Create meta-data
deployment_df = dep_gen.generate_deployment()
return deployment_df
def _is_deployment_exist(path):
# Checking shared path for the devices table
return os.path.exists(f'/v3io/bigdata/{path}')
def _get_deployment_from_kv(path):
print(f'Retrieving deployment from {path}')
# Read the devices table from our KV store
deployment_df = client.read(backend='kv', table=path)
# Reset index to column
deployment_df.index.name = 'device'
deployment_df = deployment_df.reset_index()
return deployment_df
def _save_deployment_to_kv(path, df, client=v3f.Client('framesd:8081')):
# Save deployment to our KV store
client.write(backend='kv', table='netops_devices',dfs=df, index_cols=['device'])
def get_or_create_deployment(path, save_to_cloud=False, client=v3f.Client('framesd:8081')):
if _is_deployment_exist(path):
# Get deployment from KV
deployment_df = _get_deployment_from_kv(path)
else:
# Create deployment
deployment_df = _create_deployment()
if save_to_cloud:
_save_deployment_to_kv(path, deployment_df, client)
return deployment_df
# Create our DB client
client = v3f.Client('framesd:8081')
deployment_df = get_or_create_deployment(os.environ['DEPLOYMENT_TABLE'], os.environ['SAVE_TO_KV'])
deployment_df
```
Read from our KV to make sure we have backup
```
# verify the table is written
client.read(backend='kv', table='netops_devices')
```
## Add initial values
```
deployment_df['cpu_utilization'] = 70
deployment_df['latency'] = 0
deployment_df['packet_loss'] = 0
deployment_df['throughput'] = 290
deployment_df.head()
```
## Generate simulated metrics per device
Metrics schema (describe simulated values) is read from `metrics_configuration.yaml`
```
# Load metrics configuration from YAML file
with open('configurations/metrics_configuration.yaml', 'r') as f:
metrics_configuration = yaml.load(f)
# Create metrics generator based on YAML configuration
met_gen = metrics_generator.Generator_df(metrics_configuration, user_hierarchy=deployment_df, initial_timestamp=time.time())
metrics = met_gen.generate_range(start_time=datetime.datetime.now(),
end_time=datetime.datetime.now()+datetime.timedelta(hours=1),
as_df=True,
as_iterator=True)
df = pd.concat(itertools.chain(metrics))
df.head(5)
```
## Save to Iguazio Time-series Database
```
# uncomment the line below if you want to reset the TSDB table
client.delete(backend='tsdb', table='netops_metrics_jupyter')
# create a new table, need to specify estimated sample rate
client.create(backend='tsdb', table='netops_metrics_jupyter', attrs={'rate': '1/m'})
# write the dataframe into the time-seried DB, note the company,data_center,device indexes are automatically converted to search optimized labels
client.write(backend='tsdb', table='netops_metrics_jupyter', dfs=df)
```
## Verify that the data was written
```
client.read(backend='tsdb', query='select avg(cpu_utilization), avg(latency) , avg(packet_loss) , avg(throughput) from netops_metrics_jupyter group by company, data_center, device',
start="now-1d", end='now+1d', multi_index=True, step='5m').head(10)
```
### Save the generated dataset to parquet for future reproducability
```
# craete directory if doesnt exist
!mkdir data
import pyarrow as pa
from pyarrow import parquet as pq
#write the dataframe into a parquet (on iguazio file system)
version = '1.0'
filepath = 'data/netops_metrics.v{}.parquet'.format(version)
pq.write_table(pa.Table.from_pandas(df), filepath)
```
### Reading the data from parquet into the time-series DB
if we want to reproduce the same results we can rebuild the TSDB from the saved parquet file
```
# uncomment the line below if you want to reset the TSDB table
client.delete(backend='tsdb', table='netops_metrics_jupyter')
client.create(backend='tsdb', table='netops_metrics_jupyter', attrs={'rate': '1/m'})
# read the parquet into memory and print the head
pqdf = pq.read_table(filepath).to_pandas()
pqdf.head()
# write the dataframe into the time-seried DB, uncomment the line below
client.write(backend='tsdb', table='netops_metrics_jupyter', dfs=pqdf)
# verify the table is written
client.read(backend='tsdb', query='select avg(cpu_utilization) , avg(latency) , avg(packet_loss) , avg(throughput) from netops_metrics_jupyter group by company, data_center, device',
start="now-1d", end='now+1d', multi_index=True, step='5m').head(10)
```
|
github_jupyter
|
# Install requiered packages if needed (only once)
!pip install pytimeparse
!pip install -i https://test.pypi.org/simple/ v3io-generator --upgrade
!pip install faker
!pip install pyarrow --upgrade
import os
import time
import yaml
import pandas as pd
import datetime
import itertools
# DB Connection
import v3io_frames as v3f
# Data generator
from v3io_generator import metrics_generator, deployment_generator
%env SAVE_TO_KV = True
%env DEPLOYMENT_TABLE = netops_devices
def _create_deployment():
print('creating deployment')
# Create meta-data factory
dep_gen = deployment_generator.deployment_generator()
faker=dep_gen.get_faker()
# Design meta-data
dep_gen.add_level(name='company',number=2,level_type=faker.company)
dep_gen.add_level('data_center',number=2,level_type=faker.street_name)
dep_gen.add_level('device',number=2,level_type=faker.msisdn)
# Create meta-data
deployment_df = dep_gen.generate_deployment()
return deployment_df
def _is_deployment_exist(path):
# Checking shared path for the devices table
return os.path.exists(f'/v3io/bigdata/{path}')
def _get_deployment_from_kv(path):
print(f'Retrieving deployment from {path}')
# Read the devices table from our KV store
deployment_df = client.read(backend='kv', table=path)
# Reset index to column
deployment_df.index.name = 'device'
deployment_df = deployment_df.reset_index()
return deployment_df
def _save_deployment_to_kv(path, df, client=v3f.Client('framesd:8081')):
# Save deployment to our KV store
client.write(backend='kv', table='netops_devices',dfs=df, index_cols=['device'])
def get_or_create_deployment(path, save_to_cloud=False, client=v3f.Client('framesd:8081')):
if _is_deployment_exist(path):
# Get deployment from KV
deployment_df = _get_deployment_from_kv(path)
else:
# Create deployment
deployment_df = _create_deployment()
if save_to_cloud:
_save_deployment_to_kv(path, deployment_df, client)
return deployment_df
# Create our DB client
client = v3f.Client('framesd:8081')
deployment_df = get_or_create_deployment(os.environ['DEPLOYMENT_TABLE'], os.environ['SAVE_TO_KV'])
deployment_df
# verify the table is written
client.read(backend='kv', table='netops_devices')
deployment_df['cpu_utilization'] = 70
deployment_df['latency'] = 0
deployment_df['packet_loss'] = 0
deployment_df['throughput'] = 290
deployment_df.head()
# Load metrics configuration from YAML file
with open('configurations/metrics_configuration.yaml', 'r') as f:
metrics_configuration = yaml.load(f)
# Create metrics generator based on YAML configuration
met_gen = metrics_generator.Generator_df(metrics_configuration, user_hierarchy=deployment_df, initial_timestamp=time.time())
metrics = met_gen.generate_range(start_time=datetime.datetime.now(),
end_time=datetime.datetime.now()+datetime.timedelta(hours=1),
as_df=True,
as_iterator=True)
df = pd.concat(itertools.chain(metrics))
df.head(5)
# uncomment the line below if you want to reset the TSDB table
client.delete(backend='tsdb', table='netops_metrics_jupyter')
# create a new table, need to specify estimated sample rate
client.create(backend='tsdb', table='netops_metrics_jupyter', attrs={'rate': '1/m'})
# write the dataframe into the time-seried DB, note the company,data_center,device indexes are automatically converted to search optimized labels
client.write(backend='tsdb', table='netops_metrics_jupyter', dfs=df)
client.read(backend='tsdb', query='select avg(cpu_utilization), avg(latency) , avg(packet_loss) , avg(throughput) from netops_metrics_jupyter group by company, data_center, device',
start="now-1d", end='now+1d', multi_index=True, step='5m').head(10)
# craete directory if doesnt exist
!mkdir data
import pyarrow as pa
from pyarrow import parquet as pq
#write the dataframe into a parquet (on iguazio file system)
version = '1.0'
filepath = 'data/netops_metrics.v{}.parquet'.format(version)
pq.write_table(pa.Table.from_pandas(df), filepath)
# uncomment the line below if you want to reset the TSDB table
client.delete(backend='tsdb', table='netops_metrics_jupyter')
client.create(backend='tsdb', table='netops_metrics_jupyter', attrs={'rate': '1/m'})
# read the parquet into memory and print the head
pqdf = pq.read_table(filepath).to_pandas()
pqdf.head()
# write the dataframe into the time-seried DB, uncomment the line below
client.write(backend='tsdb', table='netops_metrics_jupyter', dfs=pqdf)
# verify the table is written
client.read(backend='tsdb', query='select avg(cpu_utilization) , avg(latency) , avg(packet_loss) , avg(throughput) from netops_metrics_jupyter group by company, data_center, device',
start="now-1d", end='now+1d', multi_index=True, step='5m').head(10)
| 0.625095 | 0.407157 |
```
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator
def extractMetrics(type, result):
# 对Bug统计情况画图
CodeGen_number = {"Confirmed Bug": result['CodeGen'][1], "Fixed Bug": result['CodeGen'][0]}
CodeGen = CodeGen_number[type]
Implementation_number = {"Confirmed Bug": result['Implementation'][1], "Fixed Bug": result['Implementation'][0]}
Implementation = Implementation_number[type]
Parser_number = {"Confirmed Bug": result['Parser'][1], "Fixed Bug": result['Parser'][0]}
Parser = Parser_number[type]
RegExp_Engine_number = {"Confirmed Bug": result['RegExp Engine'][1], "Fixed Bug": result['RegExp Engine'][0]}
RegExp_Engine = RegExp_Engine_number[type]
Strict_Mode_number = {"Confirmed Bug": result['Strict Mode'][1], "Fixed Bug": result['Strict Mode'][0]}
Strict_Mode = Strict_Mode_number[type]
Optimizer_number = {"Confirmed Bug": result['Optimizer'][1], "Fixed Bug": result['Optimizer'][0]}
Optimizer = Optimizer_number[type]
return [CodeGen, Implementation, Parser, RegExp_Engine, Strict_Mode, Optimizer]
def drawBars(result):
arguments = ["CodeGen", "Implementation", "Parser", "RegExp Engine", "Strict Mode", "Optimizer"]
Confirmed = extractMetrics("Confirmed Bug", result)
Fixed = extractMetrics("Fixed Bug", result)
types = [Confirmed, Fixed]
types_names = ["Confirmed Bug", "Fixed Bug"]
fc = ['k', 'dimgray', 'grey', 'darkgray', 'lightgray', 'gainsboro']
x = list(range(len(Confirmed)))
total_width, n = 2, 6
width = total_width / n
# 设置主次刻度间隔
ymajorLocator = MultipleLocator(20)
yminorLocator = MultipleLocator(10)
# 设置y轴刻度值
plt.yticks([0, 20, 40, 60])
plt.ylim(0, 60)
# 设置主次刻度线
plt.grid(which="major", axis="y", linestyle="-")
plt.grid(which="minor", axis="y", linestyle="--")
# 显示主次刻度
plt.gca().yaxis.set_major_locator(ymajorLocator)
plt.gca().yaxis.set_minor_locator(yminorLocator)
plt.xticks(rotation=10)
plt.xlabel("JS Compontents")
plt.ylabel("Number of Bugs")
# 显示柱状图
for i in range(len(types)):
if i == len(types) - 3:
# zorder越大,表示柱子越靠后,不会被虚线覆盖
plt.bar(x, types[i], width=width, label=types_names[i], tick_label=arguments, fc=fc[i], zorder=2)
else:
plt.bar(x, types[i], width=width, label=types_names[i], tick_label=arguments, fc=fc[i], zorder=2)
for j in range(len(x)):
x[j] = x[j] + width
plt.legend(loc='upper center', fontsize=10, ncol=3)
plt.show()
plt.style.use('ggplot')
if __name__ == "__main__":
result = {'CodeGen': [42, 49], 'Implementation': [41, 45], 'Parser': [13, 15], 'RegExp Engine': [8, 9], 'Strict Mode': [8, 8], 'Optimizer': [3, 3]}
drawBars(result)
```
|
github_jupyter
|
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator
def extractMetrics(type, result):
# 对Bug统计情况画图
CodeGen_number = {"Confirmed Bug": result['CodeGen'][1], "Fixed Bug": result['CodeGen'][0]}
CodeGen = CodeGen_number[type]
Implementation_number = {"Confirmed Bug": result['Implementation'][1], "Fixed Bug": result['Implementation'][0]}
Implementation = Implementation_number[type]
Parser_number = {"Confirmed Bug": result['Parser'][1], "Fixed Bug": result['Parser'][0]}
Parser = Parser_number[type]
RegExp_Engine_number = {"Confirmed Bug": result['RegExp Engine'][1], "Fixed Bug": result['RegExp Engine'][0]}
RegExp_Engine = RegExp_Engine_number[type]
Strict_Mode_number = {"Confirmed Bug": result['Strict Mode'][1], "Fixed Bug": result['Strict Mode'][0]}
Strict_Mode = Strict_Mode_number[type]
Optimizer_number = {"Confirmed Bug": result['Optimizer'][1], "Fixed Bug": result['Optimizer'][0]}
Optimizer = Optimizer_number[type]
return [CodeGen, Implementation, Parser, RegExp_Engine, Strict_Mode, Optimizer]
def drawBars(result):
arguments = ["CodeGen", "Implementation", "Parser", "RegExp Engine", "Strict Mode", "Optimizer"]
Confirmed = extractMetrics("Confirmed Bug", result)
Fixed = extractMetrics("Fixed Bug", result)
types = [Confirmed, Fixed]
types_names = ["Confirmed Bug", "Fixed Bug"]
fc = ['k', 'dimgray', 'grey', 'darkgray', 'lightgray', 'gainsboro']
x = list(range(len(Confirmed)))
total_width, n = 2, 6
width = total_width / n
# 设置主次刻度间隔
ymajorLocator = MultipleLocator(20)
yminorLocator = MultipleLocator(10)
# 设置y轴刻度值
plt.yticks([0, 20, 40, 60])
plt.ylim(0, 60)
# 设置主次刻度线
plt.grid(which="major", axis="y", linestyle="-")
plt.grid(which="minor", axis="y", linestyle="--")
# 显示主次刻度
plt.gca().yaxis.set_major_locator(ymajorLocator)
plt.gca().yaxis.set_minor_locator(yminorLocator)
plt.xticks(rotation=10)
plt.xlabel("JS Compontents")
plt.ylabel("Number of Bugs")
# 显示柱状图
for i in range(len(types)):
if i == len(types) - 3:
# zorder越大,表示柱子越靠后,不会被虚线覆盖
plt.bar(x, types[i], width=width, label=types_names[i], tick_label=arguments, fc=fc[i], zorder=2)
else:
plt.bar(x, types[i], width=width, label=types_names[i], tick_label=arguments, fc=fc[i], zorder=2)
for j in range(len(x)):
x[j] = x[j] + width
plt.legend(loc='upper center', fontsize=10, ncol=3)
plt.show()
plt.style.use('ggplot')
if __name__ == "__main__":
result = {'CodeGen': [42, 49], 'Implementation': [41, 45], 'Parser': [13, 15], 'RegExp Engine': [8, 9], 'Strict Mode': [8, 8], 'Optimizer': [3, 3]}
drawBars(result)
| 0.268845 | 0.649912 |
# Interpretability II: Definitions of Interpretability
## Copyright notice
Parts of this code are adapted from https://open_nsfw.gitlab.io/code.py, (c) 2016 Gabriel Goh and https://github.com/Evolving-AI-Lab/synthesizing/blob/master/act_max.py, (c) 2016 Anh Nguyen, [MIT License](https://github.com/Evolving-AI-Lab/synthesizing/blob/master/LICENSE). This version (c) 2018 Fabian Offert, [MIT License](LICENSE).
## Background
Please see [Offert 2018].
## Docker
This example code is based on Gabriel Goh's [Image Synthesis from Yahoo's open_nsfw](https://open_nsfw.gitlab.io/) project, which is based on the [original implementation](https://github.com/Evolving-AI-Lab/synthesizing) of [Nguyen 2016], which is based on the [Caffe framework](http://caffe.berkeleyvision.org/). While I am working on a Keras implementation of the example code (which also requires the porting of the deep generator network from [Dosovitskiy 2016] and Yahoo's [open_nsfw model](https://github.com/yahoo/open_nsfw)), at this point it only works in Caffe. Hence, to run it, please use the [nsfw-docker container](https://github.com/zentralwerkstatt/AIWG/tree/master/nsfw-docker) provided in this repository, instead of the [keras-docker](https://github.com/zentralwerkstatt/AIWG/tree/master/keras-docker) container. The container is available in a GPU and CPU version. Due to limitations in the [nvidia-docker wrapper](https://github.com/NVIDIA/nvidia-docker), the GPU version only runs on Linux.
## Imports
We import the usual libraries and the Caffe framework.
```
import warnings
warnings.filterwarnings('ignore')
import caffe
import numpy as np
import math, random
import sys, subprocess
from IPython.display import clear_output, Image, display
from scipy.misc import imresize
import scipy.misc, scipy.io
import os
from io import BytesIO
import PIL.Image
```
## Settings
We have to tell Caffe explicitly where to run. Change this according to the nsfw-docker type you are using. We also load the models we will use: a deep generator network based on [Dosovitskiy 2016] trained to optimize "codes" based on the fc6 layer of CaffeNet, and open_nsfw. Note: the model definitions in Caffe are stored in external protocol buffer files called `deploy.prototxt`.
```
# caffe.set_mode_cpu()
caffe.set_mode_gpu()
gp = "../synthesizing/nets/upconv/fc6/"
tp = "../synthesizing/nets/open_nsfw/"
ap = "../synthesizing/act_range/3x/fc6.txt"
generator = caffe.Net(gp + "generator.prototxt", gp + "generator.caffemodel", caffe.TEST)
classifier = caffe.Classifier(tp + "deploy.prototxt", tp + "resnet_50_1by2_nsfw.caffemodel", mean = np.float32([104.0, 117.0, 123.0]), channel_swap = (2,1,0))
```
## Image preprocessing and deprocessing
We are using the same image helper functions as in the ["Deep Dreaming" notebook](2-deepdream.ipynb) and the ["Feature Visualization" notebook](3-features.ipynb), with one exception: in the `deprocess_image` function, we have to switch the final result from BGR to RGB, as open_nsfw is based on a version of ResNet50, which operates in BGR.
```
def deprocess_image(x):
h = x.shape[2]
w = x.shape[3]
n = np.zeros((h, w, 3))
n[:] = x[0].copy().transpose((1,2,0))
x = n
x += 120.
x /= 240.
x *= 255.
x = np.clip(x, 0, 255).astype('uint8') # Clip to visible range
x = x[:,:,::-1] # BGR to RGB
return x
# Simple save function based on scipy
def save_image(img, fname):
pil_img = deprocess_image(np.copy(img))
scipy.misc.imsave(fname, pil_img)
def save_image_numbered(img, nr, folder):
f = '{0:03d}'.format(nr)
p = folder + '/' + f + '.jpg'
save_image(img, p)
def show_image(img, fmt='jpeg'):
img = deprocess_image(np.copy(img))
f = BytesIO()
PIL.Image.fromarray(img).save(f, fmt)
display(Image(data=f.getvalue()))
```
## Additional image preprocessing and deprocessing
As the generator and the classifier operate on differently sized images, we also have to define two functions to crop and pad images.
```
def get_shape(data_shape):
if len(data_shape) == 4:
return (data_shape[2], data_shape[3])
else:
raise Exception("Data shape invalid.")
def crop(classifier, classifier_in, generator, generator_out, image):
data_shape = classifier.blobs[classifier_in].data.shape
image_size = get_shape(data_shape)
output_size = get_shape(generator.blobs[generator_out].data.shape)
topleft = ((output_size[0] - image_size[0])/2, (output_size[1] - image_size[1])/2)
return image.copy()[:,:,topleft[0]:topleft[0]+image_size[0], topleft[1]:topleft[1]+image_size[1]]
def pad(classifier, classifier_in, generator, generator_out, image):
data_shape = classifier.blobs[classifier_in].data.shape
image_size = get_shape(data_shape)
output_size = get_shape(generator.blobs[generator_out].data.shape)
topleft = ((output_size[0] - image_size[0])/2, (output_size[1] - image_size[1])/2)
o = np.zeros(generator.blobs[generator_out].data.shape)
o[:,:,topleft[0]:topleft[0]+image_size[0], topleft[1]:topleft[1]+image_size[1]] = image
return o
```
## Gradient ascent function
Commentary is provided inline.
```
def grad(classifier,
classifier_in,
classifier_out,
generator,
generator_in,
generator_out,
channel,
channel_opt,
code):
# Generator forward pass: generator takes a code and outputs an image
image = generator.forward(feat=code)[generator_out]
# Crop the image so it fits the classifier
image = crop(classifier, classifier_in, generator, generator_out, image)
# Classifier forward pass
actual_acts = classifier.forward(data=image, end=classifier_out)
# Create *optimal* activations for the classifier's output layer (the fake ground truth)
# np.ndarray.flat is just a 1D iterator over an array
# In Caffe, .data is the data for a layer when the graph is running
optimal_acts = np.zeros_like(classifier.blobs[classifier_out].data)
optimal_acts.flat[channel] = channel_opt
# We would like the last layer of the classifier to produce these optimal activations
# In Caffe, .diff is the gradient for a layer when the graph is running
classifier.blobs[classifier_out].diff[:] = optimal_acts
# Classifier backward pass: from these optimal activations, we generate an image
# Basically we backpropagate one layer to far to include the input layer
optimal_image = classifier.backward(start=classifier_out, diffs=[classifier_in])[classifier_in][0] # ?
# Cleanup
classifier.blobs[classifier_out].diff.fill(0.)
# Pad the image so it fits the generator
optimal_image = pad(classifier, classifier_in, generator, generator_out, optimal_image)
# We would like the last layer of the generator to produce this optimal image
generator.blobs[generator_out].diff[...] = optimal_image
# Generator backward pass: from this optimal image, we generate a code
optimized_code = generator.backward(start=generator_out)[generator_in]
# Cleanup
generator.blobs[generator_out].diff.fill(0.)
return optimized_code, image
```
## Hyperparameters
```
max_img = 5
total_iters = 300
alpha = 1.0
NSFW = 1
SFW = 0
FOLDER = '4-nsfw'
```
## Activation maximization with natural image prior
We now run the algorithm, starting with a random "code" which we optimize for `iterations` iterations with the gradient asscent function defined above.
```
# Create output directory if it does not exist yet
if not os.path.exists(FOLDER):
os.makedirs(FOLDER)
for n in range(max_img):
code = np.random.normal(0, 1, generator.blobs['feat'].data.shape)
# Load the activation range
upper_bound = lower_bound = None
# Set up clipping bounds
upper_bound = np.loadtxt(ap, delimiter=' ', usecols=np.arange(0, 4096), unpack=True)
upper_bound = upper_bound.reshape(4096)
# Lower bound of 0 due to ReLU
lower_bound = np.zeros(4096)
for i in range(total_iters):
step_size = (alpha + (1e-10 - alpha) * i) / total_iters
g, image = grad(classifier, 'data', 'prob', generator, 'feat', 'deconv0', SFW, 1., code)
code = code - step_size*g/np.abs(g).mean()
code = np.maximum(code, lower_bound)
code = np.minimum(code, upper_bound)
show_image(image)
save_image_numbered(image, n, FOLDER)
```
## Classification
To prove our hypothesis that open_nsfw was trained on a single ImageNet class used as an approximation of the non-concept of non-pornography, we classify the "SFW" images produced above by a network trained on ImageNet. We do this in Keras, so we have to use [a separate notebook running in a separate Docker container provided here](4-nsfw/classify.ipynb).
## Bibliography
- Dosovitskiy, Alexey, and Thomas Brox. "Generating Images with Perceptual Similarity Metrics Based on Deep Networks." In Advances in Neural Information Processing Systems, 658–66, 2016. http://papers.nips.cc/paper/6157-generating- images-with-perceptual-similarity-metrics-based-on-deep-networks.
- Nguyen, Anh, Alexey Dosovitskiy, Jason Yosinski, Thomas Brox, and Jeff Clune. "Synthesizing the Preferred Inputs for Neurons in Neural Networks via Deep Generator Networks." In Advances in Neural Information Processing Systems,
3387–95, 2016. http://papers.nips.cc/paper/6519-synthesizing-the-preferred- inputs-for-neurons-in-neural-networks-via-deep-generator-networks.
- Offert, Fabian. ""I know it when I see it". Visualization and Intuitive Interpretability". arXiv preprint arXiv:1711.08042, 2017. https://arxiv.org/abs/1711.08042
|
github_jupyter
|
import warnings
warnings.filterwarnings('ignore')
import caffe
import numpy as np
import math, random
import sys, subprocess
from IPython.display import clear_output, Image, display
from scipy.misc import imresize
import scipy.misc, scipy.io
import os
from io import BytesIO
import PIL.Image
# caffe.set_mode_cpu()
caffe.set_mode_gpu()
gp = "../synthesizing/nets/upconv/fc6/"
tp = "../synthesizing/nets/open_nsfw/"
ap = "../synthesizing/act_range/3x/fc6.txt"
generator = caffe.Net(gp + "generator.prototxt", gp + "generator.caffemodel", caffe.TEST)
classifier = caffe.Classifier(tp + "deploy.prototxt", tp + "resnet_50_1by2_nsfw.caffemodel", mean = np.float32([104.0, 117.0, 123.0]), channel_swap = (2,1,0))
def deprocess_image(x):
h = x.shape[2]
w = x.shape[3]
n = np.zeros((h, w, 3))
n[:] = x[0].copy().transpose((1,2,0))
x = n
x += 120.
x /= 240.
x *= 255.
x = np.clip(x, 0, 255).astype('uint8') # Clip to visible range
x = x[:,:,::-1] # BGR to RGB
return x
# Simple save function based on scipy
def save_image(img, fname):
pil_img = deprocess_image(np.copy(img))
scipy.misc.imsave(fname, pil_img)
def save_image_numbered(img, nr, folder):
f = '{0:03d}'.format(nr)
p = folder + '/' + f + '.jpg'
save_image(img, p)
def show_image(img, fmt='jpeg'):
img = deprocess_image(np.copy(img))
f = BytesIO()
PIL.Image.fromarray(img).save(f, fmt)
display(Image(data=f.getvalue()))
def get_shape(data_shape):
if len(data_shape) == 4:
return (data_shape[2], data_shape[3])
else:
raise Exception("Data shape invalid.")
def crop(classifier, classifier_in, generator, generator_out, image):
data_shape = classifier.blobs[classifier_in].data.shape
image_size = get_shape(data_shape)
output_size = get_shape(generator.blobs[generator_out].data.shape)
topleft = ((output_size[0] - image_size[0])/2, (output_size[1] - image_size[1])/2)
return image.copy()[:,:,topleft[0]:topleft[0]+image_size[0], topleft[1]:topleft[1]+image_size[1]]
def pad(classifier, classifier_in, generator, generator_out, image):
data_shape = classifier.blobs[classifier_in].data.shape
image_size = get_shape(data_shape)
output_size = get_shape(generator.blobs[generator_out].data.shape)
topleft = ((output_size[0] - image_size[0])/2, (output_size[1] - image_size[1])/2)
o = np.zeros(generator.blobs[generator_out].data.shape)
o[:,:,topleft[0]:topleft[0]+image_size[0], topleft[1]:topleft[1]+image_size[1]] = image
return o
def grad(classifier,
classifier_in,
classifier_out,
generator,
generator_in,
generator_out,
channel,
channel_opt,
code):
# Generator forward pass: generator takes a code and outputs an image
image = generator.forward(feat=code)[generator_out]
# Crop the image so it fits the classifier
image = crop(classifier, classifier_in, generator, generator_out, image)
# Classifier forward pass
actual_acts = classifier.forward(data=image, end=classifier_out)
# Create *optimal* activations for the classifier's output layer (the fake ground truth)
# np.ndarray.flat is just a 1D iterator over an array
# In Caffe, .data is the data for a layer when the graph is running
optimal_acts = np.zeros_like(classifier.blobs[classifier_out].data)
optimal_acts.flat[channel] = channel_opt
# We would like the last layer of the classifier to produce these optimal activations
# In Caffe, .diff is the gradient for a layer when the graph is running
classifier.blobs[classifier_out].diff[:] = optimal_acts
# Classifier backward pass: from these optimal activations, we generate an image
# Basically we backpropagate one layer to far to include the input layer
optimal_image = classifier.backward(start=classifier_out, diffs=[classifier_in])[classifier_in][0] # ?
# Cleanup
classifier.blobs[classifier_out].diff.fill(0.)
# Pad the image so it fits the generator
optimal_image = pad(classifier, classifier_in, generator, generator_out, optimal_image)
# We would like the last layer of the generator to produce this optimal image
generator.blobs[generator_out].diff[...] = optimal_image
# Generator backward pass: from this optimal image, we generate a code
optimized_code = generator.backward(start=generator_out)[generator_in]
# Cleanup
generator.blobs[generator_out].diff.fill(0.)
return optimized_code, image
max_img = 5
total_iters = 300
alpha = 1.0
NSFW = 1
SFW = 0
FOLDER = '4-nsfw'
# Create output directory if it does not exist yet
if not os.path.exists(FOLDER):
os.makedirs(FOLDER)
for n in range(max_img):
code = np.random.normal(0, 1, generator.blobs['feat'].data.shape)
# Load the activation range
upper_bound = lower_bound = None
# Set up clipping bounds
upper_bound = np.loadtxt(ap, delimiter=' ', usecols=np.arange(0, 4096), unpack=True)
upper_bound = upper_bound.reshape(4096)
# Lower bound of 0 due to ReLU
lower_bound = np.zeros(4096)
for i in range(total_iters):
step_size = (alpha + (1e-10 - alpha) * i) / total_iters
g, image = grad(classifier, 'data', 'prob', generator, 'feat', 'deconv0', SFW, 1., code)
code = code - step_size*g/np.abs(g).mean()
code = np.maximum(code, lower_bound)
code = np.minimum(code, upper_bound)
show_image(image)
save_image_numbered(image, n, FOLDER)
| 0.519278 | 0.954984 |
# Decision Trees
- Context
This database contains 76 attributes, but all published experiments refer to using a subset of 14 of them. In particular, the Cleveland database is the only one that has been used by ML researchers to
this date. The "goal" field refers to the presence of heart disease in the patient. It is integer valued from 0 (no presence) to 1.
- Content
**Attribute Information**
- age
- sex
- chest pain type (4 values)
- resting blood pressure
- serum cholestoral in mg/dl
- fasting blood sugar > 120 mg/dl
- resting electrocardiographic results (values 0,1,2)
- maximum heart rate achieved
- exercise induced angina
- oldpeak = ST depression induced by exercise relative to rest
- the slope of the peak exercise ST segment
- number of major vessels (0-3) colored by flourosopy
- thal: 3 = normal; 6 = fixed defect; 7 = reversable defect
The names and social security numbers of the patients were recently removed from the database, replaced with dummy values.
___
***Things to do***
- Perform the data pre-processing.
- Deal with missing values
- Perform EDA
- Using `StandardScalar` standardize the variables expect the target variable
- Convert the scaled features to a dataframe
- Split into training and testing set
- Fit Decision Tree, Logistic Regression, KNN classifier
- Get Predictions
- For KNN, create a plot `K-value` vs `error` to get the optimal value of K.
- Retrain it with new K.
- Compare accuracies using confusion matrices
- Visualize the Decision Tree using sklearn
***What will be new***
- You will learn the Decision Tree classifier and how it works.
- How to visualize a Decision tree (Scikit learn actually has some built-in visualization capabilities for decision trees, you won't use this often and it requires you to install the pydot library) - Sample code is shared below
***What will be tricky***
- Visualizing the decision tree might be a bit tricky for you because you haven't done anything like this before.
- I have shared a sample code of how to visualize a decision tree, it will help you.
##### Note: Like KNN, Decision Tree also has a Regression model as well. So you can apply this on the linear regression data set and compare the accuracy with other models
```
### Sample code for Decision Tree visualization
from IPython.display import Image
from sklearn.externals.six import StringIO
from sklearn.tree import export_graphviz
import pydot
features = list(df.columns[1:])
features
dot_data = StringIO()
export_graphviz(dtree, out_file=dot_data,feature_names=features,filled=True,rounded=True)
graph = pydot.graph_from_dot_data(dot_data.getvalue())
Image(graph[0].create_png())
# 2nd sample code
dtree = DecisionTreeClassifier()
dtree = dtree.fit(X, y)
data = tree.export_graphviz(dtree, out_file=None, feature_names=features)
graph = pydotplus.graph_from_dot_data(data)
graph.write_png('mydecisiontree.png')
img=pltimg.imread('mydecisiontree.png')
imgplot = plt.imshow(img)
plt.show()
import pandas as pd
df = pd.read_csv('heart.csv')
df.head()
# DF info:
- df.shape : 383 x 14
- no missing values
- all numeric values
```
## Standardize, split into train/ test, save a pandas df
```
# lets standardize the data
from sklearn import preprocessing
from sklearn.preprocessing import StandardScaler
# separate the data from the target attributes
X = df[['age','sex', 'cp', 'trestbps', 'chol', 'fbs' , 'restecg' , 'thalach', 'exang', 'oldpeak', 'slope', 'ca', 'thal']]
y = df['target']
# Get column names first (provided data was organised this way)
names = X.columns
# standardize the data attributes
scaler = preprocessing.StandardScaler()
scaled_df = scaler.fit_transform(X)
# save as pandas datagrame
scaled_df = pd.DataFrame(scaled_df, columns=names)
scaled_df = pd.concat((scaled_df,y),axis=1) # add the column with string values
scaled_df.head()
```
## EDA
```
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(12,12))
mask = np.triu(scaled_df.corr())
sns.heatmap(scaled_df.corr(), vmin=-1, vmax=1, center= 0, cmap= 'coolwarm', linewidths=1, linecolor='white', square=True, mask = mask, cbar=True, cbar_kws={"shrink": .5}, annot=True, fmt='.1g')
features_mean=list(df.columns[0:13])
# split dataframe into two based on diagnosis
df1 = df[df['target'] ==1]
df0 = df[df['target'] ==0]
#Stack the data
plt.rcParams.update({'font.size': 8})
fig, axes = plt.subplots(nrows=3, ncols=5, figsize=(16,10))
axes = axes.ravel()
for idx,ax in enumerate(axes):
ax.figure
binwidth= (max(df[features_mean[idx]]) - min(df[features_mean[idx]]))/50
ax.hist([df1[features_mean[idx]],df0[features_mean[idx]]], bins=np.arange(min(df[features_mean[idx]]), max(df[features_mean[idx]]) + binwidth, binwidth) , alpha=0.5,stacked=True, label=['1','0'],color=['r','g'])
ax.legend(loc='upper right')
ax.set_title(features_mean[idx])
plt.tight_layout()
plt.show()
# Actually, I am interesteed to know whether it is possible just to disclose 13 graphs instead of 15 (5x3 grid)
indicators to look at:
- high cp (> 0)
- high thalach (> 150)
- low exang (0)
- low ddpeak (0)
- high slope (2)
- thal of 2
```
## Machine Learning
```
X = scaled_df[['age','sex', 'cp', 'trestbps', 'chol', 'fbs' , 'restecg' , 'thalach', 'exang', 'oldpeak', 'slope', 'ca', 'thal']]
y = df['target']
from sklearn.model_selection import train_test_split
# Prepare the test / train sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
```
### Logistic Regression
```
from sklearn.linear_model import LogisticRegression
# Logistic Regression
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
y_pred = logreg.predict(X_test)
acc_log = round(logreg.score(X_test, y_test) * 100, 2)
acc_log
from sklearn import model_selection
import warnings
warnings.filterwarnings("ignore")
kfold = model_selection.KFold(n_splits=10, random_state=100)
model_kfold = LogisticRegression()
results_kfold = model_selection.cross_val_score(model_kfold, X_test, y_test, cv=kfold)
print("Accuracy: %.2f%%" % (results_kfold.mean()*100.0))
print(results_kfold)
coeff_df = pd.DataFrame(scaled_df.columns.delete(0))
coeff_df.columns = ['Feature']
coeff_df["Correlation"] = pd.Series(logreg.coef_[0])
coeff_df.sort_values(by='Correlation', ascending=False)
```
### KNN Classifier
```
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
import matplotlib.pyplot as plt
# KNN Classifier
knn = KNeighborsClassifier(n_neighbors = 3)
knn.fit(X_train, y_train)
Y_pred = knn.predict(X_test)
acc_knn = round(knn.score(X_test, y_test) * 100, 2)
acc_knn
error_rate = []
for i in range(1,10):
knn = KNeighborsClassifier(n_neighbors=i)
knn.fit(X_train,y_train)
pred_i = knn.predict(X_test)
error_rate.append(np.mean(pred_i != y_test))
plt.figure(figsize=(10,6))
plt.plot(range(1,10),error_rate,color='blue', linestyle='dashed', marker='o',
markerfacecolor='red', markersize=10)
plt.title('Error Rate vs. K Value')
plt.xlabel('K')
plt.ylabel('Error Rate')
from sklearn.neighbors import KNeighborsClassifier
# KNN Classifier
knn = KNeighborsClassifier(n_neighbors = 9)
knn.fit(X_train, y_train)
Y_pred = knn.predict(X_test)
acc_knn = round(knn.score(X_test, y_test) * 100, 2)
acc_knn
# I do not understand the output:
# - The accuracy is supposed to be better with n = 9 than n =3 according to the graph above
# - however, with an n =3, the accuracy is actually better
```
### Decision Tree
```
from sklearn.tree import DecisionTreeClassifier
classifier = DecisionTreeClassifier()
classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_test)
acc_tree = round(classifier.score(X_train, y_train) * 100, 2)
acc_tree
from sklearn.metrics import accuracy_score
score = accuracy_score(y_test, y_pred)
score
score = classifier.score(X_test, y_test)
score
from sklearn.metrics import classification_report, confusion_matrix
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))
# the decision classifier tree model scores 100
# however, when looking at the confusion matrix above, results look different.
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus
feature_cols = ['age','sex', 'cp', 'trestbps', 'chol', 'fbs' , 'restecg' , 'thalach', 'exang', 'oldpeak', 'slope', 'ca', 'thal']
dot_data = StringIO()
export_graphviz(classifier, out_file=dot_data,
filled=True, rounded=True,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('diabetes.png')
Image(graph.create_png())
```
|
github_jupyter
|
### Sample code for Decision Tree visualization
from IPython.display import Image
from sklearn.externals.six import StringIO
from sklearn.tree import export_graphviz
import pydot
features = list(df.columns[1:])
features
dot_data = StringIO()
export_graphviz(dtree, out_file=dot_data,feature_names=features,filled=True,rounded=True)
graph = pydot.graph_from_dot_data(dot_data.getvalue())
Image(graph[0].create_png())
# 2nd sample code
dtree = DecisionTreeClassifier()
dtree = dtree.fit(X, y)
data = tree.export_graphviz(dtree, out_file=None, feature_names=features)
graph = pydotplus.graph_from_dot_data(data)
graph.write_png('mydecisiontree.png')
img=pltimg.imread('mydecisiontree.png')
imgplot = plt.imshow(img)
plt.show()
import pandas as pd
df = pd.read_csv('heart.csv')
df.head()
# DF info:
- df.shape : 383 x 14
- no missing values
- all numeric values
# lets standardize the data
from sklearn import preprocessing
from sklearn.preprocessing import StandardScaler
# separate the data from the target attributes
X = df[['age','sex', 'cp', 'trestbps', 'chol', 'fbs' , 'restecg' , 'thalach', 'exang', 'oldpeak', 'slope', 'ca', 'thal']]
y = df['target']
# Get column names first (provided data was organised this way)
names = X.columns
# standardize the data attributes
scaler = preprocessing.StandardScaler()
scaled_df = scaler.fit_transform(X)
# save as pandas datagrame
scaled_df = pd.DataFrame(scaled_df, columns=names)
scaled_df = pd.concat((scaled_df,y),axis=1) # add the column with string values
scaled_df.head()
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(12,12))
mask = np.triu(scaled_df.corr())
sns.heatmap(scaled_df.corr(), vmin=-1, vmax=1, center= 0, cmap= 'coolwarm', linewidths=1, linecolor='white', square=True, mask = mask, cbar=True, cbar_kws={"shrink": .5}, annot=True, fmt='.1g')
features_mean=list(df.columns[0:13])
# split dataframe into two based on diagnosis
df1 = df[df['target'] ==1]
df0 = df[df['target'] ==0]
#Stack the data
plt.rcParams.update({'font.size': 8})
fig, axes = plt.subplots(nrows=3, ncols=5, figsize=(16,10))
axes = axes.ravel()
for idx,ax in enumerate(axes):
ax.figure
binwidth= (max(df[features_mean[idx]]) - min(df[features_mean[idx]]))/50
ax.hist([df1[features_mean[idx]],df0[features_mean[idx]]], bins=np.arange(min(df[features_mean[idx]]), max(df[features_mean[idx]]) + binwidth, binwidth) , alpha=0.5,stacked=True, label=['1','0'],color=['r','g'])
ax.legend(loc='upper right')
ax.set_title(features_mean[idx])
plt.tight_layout()
plt.show()
# Actually, I am interesteed to know whether it is possible just to disclose 13 graphs instead of 15 (5x3 grid)
indicators to look at:
- high cp (> 0)
- high thalach (> 150)
- low exang (0)
- low ddpeak (0)
- high slope (2)
- thal of 2
X = scaled_df[['age','sex', 'cp', 'trestbps', 'chol', 'fbs' , 'restecg' , 'thalach', 'exang', 'oldpeak', 'slope', 'ca', 'thal']]
y = df['target']
from sklearn.model_selection import train_test_split
# Prepare the test / train sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
from sklearn.linear_model import LogisticRegression
# Logistic Regression
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
y_pred = logreg.predict(X_test)
acc_log = round(logreg.score(X_test, y_test) * 100, 2)
acc_log
from sklearn import model_selection
import warnings
warnings.filterwarnings("ignore")
kfold = model_selection.KFold(n_splits=10, random_state=100)
model_kfold = LogisticRegression()
results_kfold = model_selection.cross_val_score(model_kfold, X_test, y_test, cv=kfold)
print("Accuracy: %.2f%%" % (results_kfold.mean()*100.0))
print(results_kfold)
coeff_df = pd.DataFrame(scaled_df.columns.delete(0))
coeff_df.columns = ['Feature']
coeff_df["Correlation"] = pd.Series(logreg.coef_[0])
coeff_df.sort_values(by='Correlation', ascending=False)
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
import matplotlib.pyplot as plt
# KNN Classifier
knn = KNeighborsClassifier(n_neighbors = 3)
knn.fit(X_train, y_train)
Y_pred = knn.predict(X_test)
acc_knn = round(knn.score(X_test, y_test) * 100, 2)
acc_knn
error_rate = []
for i in range(1,10):
knn = KNeighborsClassifier(n_neighbors=i)
knn.fit(X_train,y_train)
pred_i = knn.predict(X_test)
error_rate.append(np.mean(pred_i != y_test))
plt.figure(figsize=(10,6))
plt.plot(range(1,10),error_rate,color='blue', linestyle='dashed', marker='o',
markerfacecolor='red', markersize=10)
plt.title('Error Rate vs. K Value')
plt.xlabel('K')
plt.ylabel('Error Rate')
from sklearn.neighbors import KNeighborsClassifier
# KNN Classifier
knn = KNeighborsClassifier(n_neighbors = 9)
knn.fit(X_train, y_train)
Y_pred = knn.predict(X_test)
acc_knn = round(knn.score(X_test, y_test) * 100, 2)
acc_knn
# I do not understand the output:
# - The accuracy is supposed to be better with n = 9 than n =3 according to the graph above
# - however, with an n =3, the accuracy is actually better
from sklearn.tree import DecisionTreeClassifier
classifier = DecisionTreeClassifier()
classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_test)
acc_tree = round(classifier.score(X_train, y_train) * 100, 2)
acc_tree
from sklearn.metrics import accuracy_score
score = accuracy_score(y_test, y_pred)
score
score = classifier.score(X_test, y_test)
score
from sklearn.metrics import classification_report, confusion_matrix
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))
# the decision classifier tree model scores 100
# however, when looking at the confusion matrix above, results look different.
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus
feature_cols = ['age','sex', 'cp', 'trestbps', 'chol', 'fbs' , 'restecg' , 'thalach', 'exang', 'oldpeak', 'slope', 'ca', 'thal']
dot_data = StringIO()
export_graphviz(classifier, out_file=dot_data,
filled=True, rounded=True,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('diabetes.png')
Image(graph.create_png())
| 0.776792 | 0.965803 |
## 飞桨PaddlePaddle X WeChaty AI ChatBot 创意赛
大赛链接: https://aistudio.baidu.com/aistudio/competition/detail/79
PaddleHub是飞桨推出的预训练的深度学习模型的集合(Hub),在计算机视觉和文本方面都可以有非常多的实际应用。
而Chatbot近几年来的商业应用也越来越多,WeChaty就是一个非常好用且支持多种语言多个平台的开源聊天机器人框架SDK,对开发Chatbot非常友好。
### 赛题难点和重点
总的来说,就是一场应用场景的脑洞比赛,把Hub中的模型用到生活场景中。
一开始会有很多想法,但事实上为了保证有一个比较好的模型质量必须先保证想要解决的问题的数据集的数量和质量。由于个人选手比较难找到高质量且专业的数据集,我们决定从现有的模型中选取一个相对成熟的深度学习网络,并尽量不在一开始就尝试fine tune。
第二个一开始比较困难的事情,是因为需要用到AI模型必须就要通过Python。而在python-Wechaty部署上我们遇到了不少麻烦。

尝试了PadLocal的方式对接GateWay,但是由于是foreign IP,微信登陆的QRcode一直无法加载,最后只能选择使用docker + 免费Web协议。底层的对接实现是基于TypeScript语言,故无法直接在python-wechaty中使用该服务。可是Wechaty社区能够直接将其转化成对应的服务让多语言调用,从而实现:底层复用的特性。
整体步骤分为两步:
* 使用Docker启动web协议服务
* 使用python-wechaty连接服务
配置文件就在根目录下: [./wechaty_test.sh](wechaty_test.sh)
跟着[这个网页](https://python-wechaty.readthedocs.io/zh_CN/latest/introduction/use-web-protocol/)也可以轻松配置,只是稍微不同的是用来登陆微信的QR码不会出现在终端,而需要打开终端里出现的地址。
## 方案
出于模型质量和大小的考量,首先我们选择了PaddleHub的OCR模型(服务器端精度更高的版本),想基于WeChaty实现一个图片中文字识别的微信机器人。
换言之就是通过WeChaty将PaddleHub的OCR装到微信里 :)
PaddleHub识别文字算法均采用CRNN(Convolutional Recurrent Neural Network)即卷积递归神经网络。其是DCNN和RNN的组合,专门用于识别图像中的序列式对象。与CTC loss配合使用,进行文字识别,可以直接从文本词级或行级的标注中学习,不需要详细的字符级的标注。该Module支持直接预测。 移动端与服务器端主要在于骨干网络的差异性,移动端采用MobileNetV3,服务器端采用ResNet50_vd。具体介绍可以参考PaddleHub[官方Notebook](https://aistudio.baidu.com/aistudio/projectdetail/507159)。
CRNN的网络结构图:
<div align=center> <img src="https://ai-studio-static-online.cdn.bcebos.com/af68e45eea184b4c966f23ad7d9fd295e07e1fc31cc74134b4bd99ee275bed63"/>
OCR最基础的用法就是用户发送图片给chatbot,接受到图片之后会发送一条识别出来的所有文字消息回复。
简单的例子就是快递单单号,身份证件号码,行程单号码日期,小红书的文字图片,笔记,等等的图片转换为文字(或者不知道怎么念但是需要打的字。。。)
实现基础功能之后,还可以再加上某一个行业的特定用途。通过python函数,或者另一个AI模型继续对识别出来的文字进行加工处理。
## 具体实现
### 第一步 安装包
这里提供aistudio可以运行的版本,在本机上运行的话在终端去掉前面的!就可以了。
```
#需要将PaddleHub和PaddlePaddle统一升级到2.0版本
!pip install paddlehub==2.0.0 -i https://pypi.tuna.tsinghua.edu.cn/simple
!pip install paddlepaddle==2.0.0 -i https://pypi.tuna.tsinghua.edu.cn/simple
#该Module依赖于第三方库shapely、pyclipper,使用该Module之前,请先安装shapely、pyclipper
!pip install shapely -i https://pypi.tuna.tsinghua.edu.cn/simple
!pip install pyclipper -i https://pypi.tuna.tsinghua.edu.cn/simple
```
### 第二步 调用paddlehub 加载OCR预训练模型
这两行代码在test.py中可以看到,**paddlehub将预训练好的模型封装的好处就是可以直接放在实际应用的python代码中**。
这里用移动端模型做例子,实际使用了服务端的模型(在test.py中可见)。
```
import paddlehub as hub
# 加载移动端预训练模型
ocr = hub.Module(name="chinese_ocr_db_crnn_mobile")
# 服务端可以加载大模型,效果更好
# ocr = hub.Module(name="chinese_ocr_db_crnn_server")
```
### 第三步 识别图片
```
import cv2
# 读取测试文件夹test.txt中的照片路径
np_images =[cv2.imread("/home/aistudio/express.jpg")]
results = ocr.recognize_text(
images=np_images, # 图片数据,ndarray.shape 为 [H, W, C],BGR格式;
use_gpu=False, # 是否使用 GPU;若使用GPU,请先设置CUDA_VISIBLE_DEVICES环境变量
output_dir='ocr_result', # 图片的保存路径,默认设为 ocr_result;
visualization=True, # 是否将识别结果保存为图片文件;
box_thresh=0.5, # 检测文本框置信度的阈值;
text_thresh=0.5) # 识别中文文本置信度的阈值;
data = results[0]['data']
save_path = results[0]['save_path']
s = ""
for information in data:
s += information['text']
s += '\n'
print(s)
```
### 第四步 效果展示
在完成第三部分的一键OCR预测之后,由于我们设置了visualization=True,所以我们会自动将识别结果保存为图片文件,并默认保存在ocr_result文件夹中。**刷新即可获取到新生成的ocr_result文件夹。**
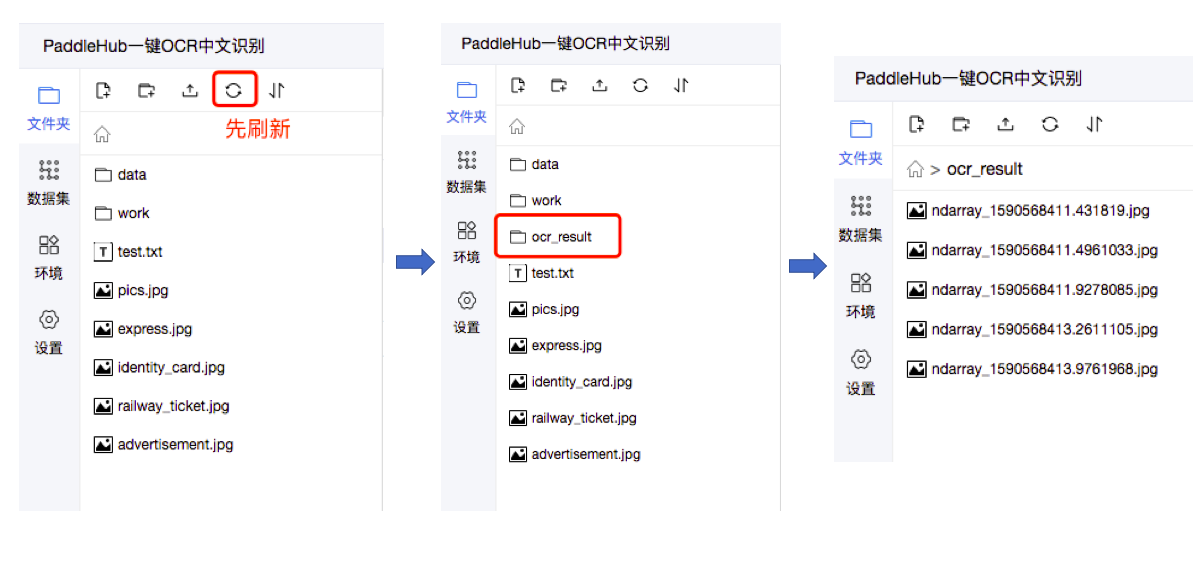
识别前与识别后的结果:
```
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
# 识别前的图片 与 识别后的效果图
test_img_path = ["./express.jpg", "./ocr_result/ndarray_1619654937.8608792.jpg"]
img1 = mpimg.imread(test_img_path[0])
plt.figure(figsize=(10,10))
plt.imshow(img1)
plt.axis('off')
plt.show()
img1 = mpimg.imread(test_img_path[1])
plt.figure(figsize=(10,10))
plt.imshow(img1)
plt.axis('off')
plt.show()
```
接下来的改进方向则是根据某个行业方向加上有意思或者别的量化指标,比如根据食品的营养成分表进行饮食推荐。
### References
* python-WeChaty使用相关参考github repo(有很多python实例在/examples子文件夹中): [https://github.com/wechaty/python-wechaty](https://github.com/wechaty/python-wechaty)
* PaddleHub一键OCR中文识别(超轻量8.1M模型,火爆): [https://aistudio.baidu.com/aistudio/projectdetail/507159](https://aistudio.baidu.com/aistudio/projectdetail/507159)
* 另外对OCR感兴趣的同学可以参加目前的这个比赛:[https://aistudio.baidu.com/aistudio/competition/detail/75](https://aistudio.baidu.com/aistudio/competition/detail/75)
### Roadmap
第一稿(2021/04/29):我们先从实现基础架构开始 :)
请点击[此处](https://ai.baidu.com/docs#/AIStudio_Project_Notebook/a38e5576)查看本环境基本用法. <br>
Please click [here ](https://ai.baidu.com/docs#/AIStudio_Project_Notebook/a38e5576) for more detailed instructions.
|
github_jupyter
|
#需要将PaddleHub和PaddlePaddle统一升级到2.0版本
!pip install paddlehub==2.0.0 -i https://pypi.tuna.tsinghua.edu.cn/simple
!pip install paddlepaddle==2.0.0 -i https://pypi.tuna.tsinghua.edu.cn/simple
#该Module依赖于第三方库shapely、pyclipper,使用该Module之前,请先安装shapely、pyclipper
!pip install shapely -i https://pypi.tuna.tsinghua.edu.cn/simple
!pip install pyclipper -i https://pypi.tuna.tsinghua.edu.cn/simple
import paddlehub as hub
# 加载移动端预训练模型
ocr = hub.Module(name="chinese_ocr_db_crnn_mobile")
# 服务端可以加载大模型,效果更好
# ocr = hub.Module(name="chinese_ocr_db_crnn_server")
import cv2
# 读取测试文件夹test.txt中的照片路径
np_images =[cv2.imread("/home/aistudio/express.jpg")]
results = ocr.recognize_text(
images=np_images, # 图片数据,ndarray.shape 为 [H, W, C],BGR格式;
use_gpu=False, # 是否使用 GPU;若使用GPU,请先设置CUDA_VISIBLE_DEVICES环境变量
output_dir='ocr_result', # 图片的保存路径,默认设为 ocr_result;
visualization=True, # 是否将识别结果保存为图片文件;
box_thresh=0.5, # 检测文本框置信度的阈值;
text_thresh=0.5) # 识别中文文本置信度的阈值;
data = results[0]['data']
save_path = results[0]['save_path']
s = ""
for information in data:
s += information['text']
s += '\n'
print(s)
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
# 识别前的图片 与 识别后的效果图
test_img_path = ["./express.jpg", "./ocr_result/ndarray_1619654937.8608792.jpg"]
img1 = mpimg.imread(test_img_path[0])
plt.figure(figsize=(10,10))
plt.imshow(img1)
plt.axis('off')
plt.show()
img1 = mpimg.imread(test_img_path[1])
plt.figure(figsize=(10,10))
plt.imshow(img1)
plt.axis('off')
plt.show()
| 0.297062 | 0.789173 |
```
%matplotlib inline
```
# Plotting Learning Curves
On the left side the learning curve of a naive Bayes classifier is shown for
the digits dataset. Note that the training score and the cross-validation score
are both not very good at the end. However, the shape of the curve can be found
in more complex datasets very often: the training score is very high at the
beginning and decreases and the cross-validation score is very low at the
beginning and increases. On the right side we see the learning curve of an SVM
with RBF kernel. We can see clearly that the training score is still around
the maximum and the validation score could be increased with more training
samples.
```
# From http://scikit-learn.org/stable/auto_examples/model_selection/plot_learning_curve.html
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
"""
Generate a simple plot of the test and training learning curve.
Parameters
----------
estimator : object type that implements the "fit" and "predict" methods
An object of that type which is cloned for each validation.
title : string
Title for the chart.
X : array-like, shape (n_samples, n_features)
Training vector, where n_samples is the number of samples and
n_features is the number of features.
y : array-like, shape (n_samples) or (n_samples, n_features), optional
Target relative to X for classification or regression;
None for unsupervised learning.
ylim : tuple, shape (ymin, ymax), optional
Defines minimum and maximum yvalues plotted.
cv : int, cross-validation generator or an iterable, optional
Determines the cross-validation splitting strategy.
Possible inputs for cv are:
- None, to use the default 3-fold cross-validation,
- integer, to specify the number of folds.
- An object to be used as a cross-validation generator.
- An iterable yielding train/test splits.
For integer/None inputs, if ``y`` is binary or multiclass,
:class:`StratifiedKFold` used. If the estimator is not a classifier
or if ``y`` is neither binary nor multiclass, :class:`KFold` is used.
Refer :ref:`User Guide <cross_validation>` for the various
cross-validators that can be used here.
n_jobs : integer, optional
Number of jobs to run in parallel (default 1).
"""
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel("Training examples")
plt.ylabel("Score")
train_sizes, train_scores, test_scores = learning_curve(
estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Cross-validation score")
plt.legend(loc="best")
return plt
digits = load_digits()
X, y = digits.data, digits.target
title = "Learning Curves (Naive Bayes)"
# Cross validation with 100 iterations to get smoother mean test and train
# score curves, each time with 20% data randomly selected as a validation set.
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
estimator = GaussianNB()
plot_learning_curve(estimator, title, X, y, ylim=(0.7, 1.01), cv=cv, n_jobs=4)
title = "Learning Curves (SVM, RBF kernel, $\gamma=0.001$)"
# SVC is more expensive so we do a lower number of CV iterations:
cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
estimator = SVC(gamma=0.001)
plot_learning_curve(estimator, title, X, y, (0.7, 1.01), cv=cv, n_jobs=4)
plt.show()
np.linspace(.1, 1.0, 10)
```
|
github_jupyter
|
%matplotlib inline
# From http://scikit-learn.org/stable/auto_examples/model_selection/plot_learning_curve.html
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
"""
Generate a simple plot of the test and training learning curve.
Parameters
----------
estimator : object type that implements the "fit" and "predict" methods
An object of that type which is cloned for each validation.
title : string
Title for the chart.
X : array-like, shape (n_samples, n_features)
Training vector, where n_samples is the number of samples and
n_features is the number of features.
y : array-like, shape (n_samples) or (n_samples, n_features), optional
Target relative to X for classification or regression;
None for unsupervised learning.
ylim : tuple, shape (ymin, ymax), optional
Defines minimum and maximum yvalues plotted.
cv : int, cross-validation generator or an iterable, optional
Determines the cross-validation splitting strategy.
Possible inputs for cv are:
- None, to use the default 3-fold cross-validation,
- integer, to specify the number of folds.
- An object to be used as a cross-validation generator.
- An iterable yielding train/test splits.
For integer/None inputs, if ``y`` is binary or multiclass,
:class:`StratifiedKFold` used. If the estimator is not a classifier
or if ``y`` is neither binary nor multiclass, :class:`KFold` is used.
Refer :ref:`User Guide <cross_validation>` for the various
cross-validators that can be used here.
n_jobs : integer, optional
Number of jobs to run in parallel (default 1).
"""
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel("Training examples")
plt.ylabel("Score")
train_sizes, train_scores, test_scores = learning_curve(
estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Cross-validation score")
plt.legend(loc="best")
return plt
digits = load_digits()
X, y = digits.data, digits.target
title = "Learning Curves (Naive Bayes)"
# Cross validation with 100 iterations to get smoother mean test and train
# score curves, each time with 20% data randomly selected as a validation set.
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
estimator = GaussianNB()
plot_learning_curve(estimator, title, X, y, ylim=(0.7, 1.01), cv=cv, n_jobs=4)
title = "Learning Curves (SVM, RBF kernel, $\gamma=0.001$)"
# SVC is more expensive so we do a lower number of CV iterations:
cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
estimator = SVC(gamma=0.001)
plot_learning_curve(estimator, title, X, y, (0.7, 1.01), cv=cv, n_jobs=4)
plt.show()
np.linspace(.1, 1.0, 10)
| 0.942533 | 0.973968 |
<a href="https://colab.research.google.com/github/the-redlord/Image_denoising-keras/blob/master/ImageDenoising.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# TASK #1: PROJECT OVERVIEW


# TASK #2: IMPORT LIBRARIES AND DATASET
```
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import random
from tensorflow.keras.layers import Conv2D,Conv2DTranspose
# Load dataset
(X_train, y_train),(X_test,y_test) = tf.keras.datasets.fashion_mnist.load_data()
# Visualize a sample image
plt.imshow(X_train[0],cmap='gray')
# check out the shape of the training data
X_train.shape
# check out the shape of the testing data
X_test.shape
y_train.shape
y_test.shape
```
# TASK #3: PERFORM DATA VISUALIZATION
```
# Let's view some images!
i = random.randint(1,60000)
plt.imshow(X_train[i], cmap='gray')
label = y_train[i]
label
# Let's view more images in a grid format
# Define the dimensions of the plot grid
W_grid = 10
L_grid = 10
# fig, axes = plt.subplots(L_grid, W_grid)
# subplot return the figure object and axes object
# we can use the axes object to plot specific figures at various locations
fig, axes = plt.subplots(L_grid, W_grid, figsize = (17,17))
axes = axes.ravel() # flaten the 15 x 15 matrix into 225 array
n_training = len(X_train) # get the length of the training dataset
# Select a random number from 0 to n_training
for i in np.arange(0,W_grid * L_grid):
index = np.random.randint(0,n_training)
axes[i].imshow(X_train[index])
axes[i].set_title(y_train[index], fontsize = 8)
axes[i].axis('off')
```
# TASK #4: PERFORM DATA PREPROCESSING
```
# normalize data
X_train = X_train / 255
X_test = X_test / 255
X_train
# add some noise
noise_factor = 0.3
noise_dataset = []
for img in X_train:
noisy_img = img + noise_factor * np.random.randn(*img.shape)
noisy_img = np.clip(noisy_img,0,1)
noise_dataset.append(noisy_img)
noise_dataset = np.array(noise_dataset)
plt.imshow(noise_dataset[22], cmap='gray')
# add noise to testing dataset
noise_factor = 0.1
noise_test_dataset = []
for img in X_test:
noisy_img = img + noise_factor * np.random.randn(*img.shape)
noisy_img = np.clip(noisy_img,0,1)
noise_test_dataset.append(noisy_img)
noise_test_dataset = np.array(noise_test_dataset)
```
# TASK #5: UNDERSTAND THE THEORY AND INTUITION BEHIND AUTOENCODERS




# TASK #6: BUILD AND TRAIN AUTOENCODER DEEP LEARNING MODEL
```
autoencoder = tf.keras.models.Sequential()
# encoder
autoencoder.add(tf.keras.layers.Input(shape=(28,28,1)))
autoencoder.add(Conv2D(filters=16,kernel_size=(3,3),strides=2,padding='same'))
autoencoder.add(Conv2D(filters=8,kernel_size=(3,3),strides=2,padding='same'))
# image layer
autoencoder.add(Conv2D(filters=8,kernel_size=(3,3),strides=1,padding='same'))
# decoder
autoencoder.add(Conv2DTranspose(filters=16,kernel_size=(3,3),strides=2,padding='same'))
autoencoder.add(Conv2DTranspose(filters=1,kernel_size=(3,3),strides=2,padding='same',activation='sigmoid'))
autoencoder.compile(loss='binary_crossentropy', optimizer=tf.keras.optimizers.Adam(lr=0.001))
autoencoder.summary()
autoencoder.fit(noise_dataset.reshape(-1, 28, 28, 1),
X_train.reshape(-1, 28, 28, 1),
epochs = 10,
batch_size = 200,
validation_data = (noise_test_dataset.reshape(-1, 28, 28, 1), X_test.reshape(-1, 28, 28, 1)))
```
# TASK #7: EVALUATE TRAINED MODEL PERFORMANCE
```
evaluation = autoencoder.evaluate(noise_test_dataset.reshape(-1, 28, 28, 1), X_test.reshape(-1, 28, 28, 1))
print('Test accuracy: {:.3f}'.format(evaluation))
predicted = autoencoder.predict(noise_test_dataset[:10].reshape(-1,28,28,1))
tfig, axes = plt.subplots(nrows=2, ncols=10, sharex=True, sharey=True, figsize=(20,4))
for images, row in zip([noise_test_dataset[:10], predicted], axes):
for img, ax in zip(images, row):
ax.imshow(img.reshape((28, 28)), cmap='Greys_r')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
```
# EXCELLENT WORK!
- 0 = T-shirt/top
- 1 = Trouser
- 2 = Pullover
- 3 = Dress
- 4 = Coat
- 5 = Sandal
- 6 = Shirt
- 7 = Sneaker
- 8 = Bag
- 9 = Ankle boot
|
github_jupyter
|
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import random
from tensorflow.keras.layers import Conv2D,Conv2DTranspose
# Load dataset
(X_train, y_train),(X_test,y_test) = tf.keras.datasets.fashion_mnist.load_data()
# Visualize a sample image
plt.imshow(X_train[0],cmap='gray')
# check out the shape of the training data
X_train.shape
# check out the shape of the testing data
X_test.shape
y_train.shape
y_test.shape
# Let's view some images!
i = random.randint(1,60000)
plt.imshow(X_train[i], cmap='gray')
label = y_train[i]
label
# Let's view more images in a grid format
# Define the dimensions of the plot grid
W_grid = 10
L_grid = 10
# fig, axes = plt.subplots(L_grid, W_grid)
# subplot return the figure object and axes object
# we can use the axes object to plot specific figures at various locations
fig, axes = plt.subplots(L_grid, W_grid, figsize = (17,17))
axes = axes.ravel() # flaten the 15 x 15 matrix into 225 array
n_training = len(X_train) # get the length of the training dataset
# Select a random number from 0 to n_training
for i in np.arange(0,W_grid * L_grid):
index = np.random.randint(0,n_training)
axes[i].imshow(X_train[index])
axes[i].set_title(y_train[index], fontsize = 8)
axes[i].axis('off')
# normalize data
X_train = X_train / 255
X_test = X_test / 255
X_train
# add some noise
noise_factor = 0.3
noise_dataset = []
for img in X_train:
noisy_img = img + noise_factor * np.random.randn(*img.shape)
noisy_img = np.clip(noisy_img,0,1)
noise_dataset.append(noisy_img)
noise_dataset = np.array(noise_dataset)
plt.imshow(noise_dataset[22], cmap='gray')
# add noise to testing dataset
noise_factor = 0.1
noise_test_dataset = []
for img in X_test:
noisy_img = img + noise_factor * np.random.randn(*img.shape)
noisy_img = np.clip(noisy_img,0,1)
noise_test_dataset.append(noisy_img)
noise_test_dataset = np.array(noise_test_dataset)
autoencoder = tf.keras.models.Sequential()
# encoder
autoencoder.add(tf.keras.layers.Input(shape=(28,28,1)))
autoencoder.add(Conv2D(filters=16,kernel_size=(3,3),strides=2,padding='same'))
autoencoder.add(Conv2D(filters=8,kernel_size=(3,3),strides=2,padding='same'))
# image layer
autoencoder.add(Conv2D(filters=8,kernel_size=(3,3),strides=1,padding='same'))
# decoder
autoencoder.add(Conv2DTranspose(filters=16,kernel_size=(3,3),strides=2,padding='same'))
autoencoder.add(Conv2DTranspose(filters=1,kernel_size=(3,3),strides=2,padding='same',activation='sigmoid'))
autoencoder.compile(loss='binary_crossentropy', optimizer=tf.keras.optimizers.Adam(lr=0.001))
autoencoder.summary()
autoencoder.fit(noise_dataset.reshape(-1, 28, 28, 1),
X_train.reshape(-1, 28, 28, 1),
epochs = 10,
batch_size = 200,
validation_data = (noise_test_dataset.reshape(-1, 28, 28, 1), X_test.reshape(-1, 28, 28, 1)))
evaluation = autoencoder.evaluate(noise_test_dataset.reshape(-1, 28, 28, 1), X_test.reshape(-1, 28, 28, 1))
print('Test accuracy: {:.3f}'.format(evaluation))
predicted = autoencoder.predict(noise_test_dataset[:10].reshape(-1,28,28,1))
tfig, axes = plt.subplots(nrows=2, ncols=10, sharex=True, sharey=True, figsize=(20,4))
for images, row in zip([noise_test_dataset[:10], predicted], axes):
for img, ax in zip(images, row):
ax.imshow(img.reshape((28, 28)), cmap='Greys_r')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
| 0.9003 | 0.983455 |
# An Introduction to Set Theory
## Sets and elements
Sets are collections of objects. In math we wrap the set in curly braces and separate elements with commas, here is a set with three numbers $\{1,2,4\}$. We often name sets with a capital letter like $A=\{1,2,4\}$.
Things in the set are called **elements** of the set. The symbol $\in$ means "is an element of the set". So $1 \in \{1,2,4\}$. We put a slash through the symbol if it isn't an element of the set, so $3 \not\in \{1,2,4\}$. Let's see how this works in Python.
```
# Make a set A = {1,2}
A = {1,2}
# The strings are formatted using "f-strings"
print(f"Our set is {A}")
print(f"1 is in A? {1 in A}")
print(f"3 is in A? {3 in A}")
# We can also construct sets from other "iterables" like lists using the set() function
print(set([1,2]))
```
### Set-builder notation
Sometimes we want to specify an infinite set like the even numbers. We might write this as $\{2,4,6,8,...\}$ and most people will understand. **Set-builder notation** writes it as $\{x | x \text{ is an even number}\}$. This is pronounced "the set of x where x is an even number".
We could say $\{x|x \text{ is a solution to } x^3 - 5x^2 - 2x + 10 = 0\}$ if we are having trouble finding the solutions of $x^3 - 5x^2 - 2x + 10 = 0$. The solutions are $\{-\sqrt{2},\sqrt{2},5\}$, so
$$\{-\sqrt{2},\sqrt{2},5\} =\{x|x \text{ is a solution to } x^3 - 5x^2 - 2x + 10 = 0\}$$
But what does it mean for sets to be equal?
## Set equality and subsets
### Equality
Sets are equal when they have the same elements, **order doesn't matter**.
$$\{1,2\} = \{2,1\}$$
Also $\{1,1,2\} = \{1,2\}$, but since duplicate elements are redundant we say that **sets don't have duplicate elements**.
```
print({1,2} == {2,1})
print({1,1,2} == {1,2})
```
### Subsets
$A \subseteq B$ is pronounced "A is a **subset** of B" and it means that everything in A is also in B. For example $\{1,2\} \subseteq \{1,2,3\}$. Sets are considered subsets of themselves so $\{1,2\} \subseteq \{1,2\}$.
$\{1,2,3\} \supseteq \{1,2\}$ is pronounced "$B$ is a **superset** of $A$".
If sets are subsets of eachother, they are equal. More formally, if $A \subseteq B$ and $B \subseteq A$ then $A = B$. Consider why this is true. This technique is commonly used in proofs of set equality.
```
A = {1,2}
B = {1,2,3}
print(f"A is a subset of B? {A.issubset(B)}")
print(f"B is a subset of A? {B.issubset(A)}")
print(f"B is a subset of A? {B.issuperset(A)}")
```
## Venn Diagrams and Set Operations
Let's define some sets before we talk about how to visualize them with **venn diagrams** and combine them with **set operations**.
```
S = {1,2,3,4,5,6,7,8,9,10}
A = {1,3,5,7}
B = {2,3,4,5}
```
### Venn Diagrams
In a Venn Diagram each set is represented by a circle. The set $S$ is represented by a black box, think of it as the universe containing all things.

### Union
$A \cup B$ is "$A$ union $B$". The union of two sets is the set of all elements that are in either set (or in both sets).

```
A.union(B)
```
### Intersection
$A \cap B$ is "$A$ intersect $B$". Elements in the intersection must belong to both sets $A$ and $B$.

```
A.intersection(B)
```
### Difference
$A-B$ is the difference of $A$ and $B$ and is set of all elements that are in $A$ but not in $B$. It can also be written $A \backslash B$.

```
# The complement of set A
A.difference(B)
```
### Complement
$A^C$ is "the complement of $A$". The complement of a set is all elements that are not in the set. This is relative to our "universe" of possible elements $S$.

```
# Python doesn't have a "complement" function on sets. You just take the "universal set" S and subtract A from it.
S.difference(A)
```
## Sample Space and Empty Set
The **sample space** $S$ is the set of all possible elements. In probability there are different outcomes to experiments, and the sample space typically represents all possible outcomes. So when flipping coins the sample space is $\{H,T\}$. There are some identities for the sample space.
$$A \cup S = S$$
$$A \cap S = A$$
```
print(f"{S} == {A.union(S)}")
print(f"{A} == {A.intersection(S)}")
```
## De Morgan's Laws
De Morgan's laws are formulas for the complement of a union or intersection of sets.
$$(A \cap B)^C = A^C \cup B^C \\
(A \cup B)^C = A^C \cap B^C$$
One way of memorizing these formulas is that you bring the complement inside the parentheses to both sets and flip the union or intersection upside down.
Let's see if these laws make any sense. Let $T$ be the set of tennis players and $H$ be the set of hockey players. $(T \cap H)^C$ is the set of people that don't play both tennis and hockey. $T^C \cup H^C$ is people that don't play tennis or they don't play hockey. If I don't play both sports then I either don't play tennis or I don't play hockey, so $(T \cap H)^C \subseteq T^C \cup H^C$. If I don't play tennis or I don't play hockey then it is true that I don't play both sports, so $T^C \cup H^C \subseteq (T \cap H)^C$. This means that the sets are equal, ponder this for some time. A similar argument can be made for the complement of the union. If this is not convincing spend some time with a Venn diagram and see if you can get it to make sense.
## 3 or More Sets
### Associativity
You can take the intersection or union of more than two sets.
$$\{1,2\} \cap \{2,3\} \cap \{3,4\} = \emptyset$$
There are no elements in the intersection of these three sets because no number appears in all three sets, so this is the empty set.
Intersections are associative, meaning it doesn't matter what order you take them in. This is also true of unions.
$$(A \cap B) \cap C= A \cap (B \cap C)$$
$$(A \cup B) \cup C= A \cup (B \cup C)$$
### Distributive Property
If you mix together unions and intersections in an expression it isn't associative.
$$A \cap (B \cup C) \not= (A \cap B) \cup C$$
But the distributive property is true of intersections and unions.
$$A \cap (B \cup C) = (A \cap B) \cup (A \cap C) \\
A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$$
It is easier to remember these distributive formulas by comparing them to the way multiplication distributes over addition. $a(b+c)=ab+ac$. Just pretend that the multiplication is an intersection and the addition is a union.
### Messy Venn Diagrams
You can draw a Venn diagram for three sets with three circles. It gets a little complicated. I wouldn't bother drawing a Venn diagram for 4 sets.


|
github_jupyter
|
# Make a set A = {1,2}
A = {1,2}
# The strings are formatted using "f-strings"
print(f"Our set is {A}")
print(f"1 is in A? {1 in A}")
print(f"3 is in A? {3 in A}")
# We can also construct sets from other "iterables" like lists using the set() function
print(set([1,2]))
print({1,2} == {2,1})
print({1,1,2} == {1,2})
A = {1,2}
B = {1,2,3}
print(f"A is a subset of B? {A.issubset(B)}")
print(f"B is a subset of A? {B.issubset(A)}")
print(f"B is a subset of A? {B.issuperset(A)}")
S = {1,2,3,4,5,6,7,8,9,10}
A = {1,3,5,7}
B = {2,3,4,5}
A.union(B)
A.intersection(B)
# The complement of set A
A.difference(B)
# Python doesn't have a "complement" function on sets. You just take the "universal set" S and subtract A from it.
S.difference(A)
print(f"{S} == {A.union(S)}")
print(f"{A} == {A.intersection(S)}")
| 0.411111 | 0.980949 |
# NumPy = Numerical Python
Numpy is an important package for numerical computing in Python. Most computational packages use numpy multidimensional array as the main structure to store and manipulate data.
Numpy is large topic. In this lecture, **we cover**:
- Fast vectorized array operations for data manipulation, cleaning, subsetting, filtering, transformation, and any other kinds of computation.
- Popular methods on array object like sorting, unique, and set operations
- Efficient descriptive statistic, and summarizing data
- Merging and joining together datasets
- Expressing conditional logic as array expression instead of loops
- Groupd-wise data manipulation (aggregration, transformation, function application)
```
import numpy as np
```
# The Numpy ndarray: A Multidimensional Array Object
## Creating ndarrays
To create an array, use the *array* function. This function accept any sequence-like object and produces a new NumPy array containing the passed data.
```
data1 = [1, 2, 3]
array1 = np.array(data1) # data passed in is a list
array1
data2 = (4, 5, 6)
array2 = np.array(data2) # data passed in is a tuple
array2
type(array2)
```
Obviously, we can create a numpy array directly as follow:
```
array3 = np.array([7, 8, 9])
array3
```
If we passed a nested sequences to the *array* function, a multidimensional array is created
```
data4 = [[1, 2, 3], [4, 5, 6]]
array4 = np.array(data4)
array4
np.array([[1, 2, 3], [4, 5, 6]])
```
We see that *data4* is a list of 2 element where each element is a list of 3 elements. Thus, *array4* is a *2x3* array (or matrix). We can check the number of dimensions of an array and its shape using
```
array4.ndim # array4 has 2 dimension
array4.shape # array 2 rows and 3 columns, the shape is returned in a 2-d tuple
```
### Some useful functions for creating new special arrays
```
# Create array of 0s
np.zeros([2, 3])
# Create array of 1s
np.ones([3, 3])
# Create an array of range
np.arange(10, 100)
# Create an identity matrix
np.eye(4)
```
## Arithmetic with Numpy Arrays
When numerical data are stored in numpy arrays, we can perform batch operations on data (like matrix operations in math) without writing any loops. We call this feature vectorization. Any arithmetic operations between equal-size arrays applies the operation element-wise. For example, we have
```
my_list = [[1, 2, 3], [4, 5, 6]]
```
Then, we want to create a new list where its elements are elements of my_list squared as
```
[[i**2 for i in item ] for item in my_list]
```
Using numpy array and vectorizaton we can do the same but much simpler as
```
array = np.array(my_list)
array
array * array
```
Other arithmetic operations
```
array - array
array ** 3
1 / array
```
We can compare two arrays of the same shape element-wise. The result is a boolean array.
```
array_2 = np.array([[2, 4, 0], [5, 1, 9]])
array_2
array
array_2 > array
```
## Basic Indexing and Slicing
For one dimensional numpy, slicing is similar to Python lists
```
array = np.arange(100)
array
array[0]
array[-2]
array[:3]
array[-3:]
array[2:6]
```
We should notice that array slices are **views** on the original array. This means that the data is not copied, and any modification to the view will be reflected in the source array. For example,
```
array_slice = array[2:6]
array_slice
array_slice[0] = 99
array_slice
array
```
If we want a copy of a slice, we need to do it explicitly as
```
array_slice_copied = array[-3:].copy()
array_slice_copied
array_slice_copied[:] = 99
array_slice_copied
array
```
For higher dimensional array, for example, 2-dimensional arrays, the elements at each indexc are no longer scalars but rather one-dimensional arrays.
```
array_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
array_2d
array_2d[2]
```
We can select an individual element by two ways:
```
# Access recursively the element at row 1, column 1
array_2d[1][1]
# Comma separated list
array_2d[0, 2]
```
### Indexing with slices
```
array_2d
# Return the first row
array_2d[0]
# Return the first two row
array_2d[:2]
# Return the second column
array_2d[:, 2]
# Return the square submatrix at the upper right corner
array_2d[:2, -2:]
```
**Remember again, slice is a view. Modify a slice changes the orginal array.**
```
array_2d
array_2d[:2, :2] = 99
array_2d
```
## Comparison Operators
```
array = np.array([1, 2, 3, 4, 5, 6])
array
array > 3
array >= 3
array == 3
array != 3
```
## Boolean Arrays
```
a = np.array([[2, -7, 1], [-4, 3, 8], [5, 0, -6]])
a
# Which number is positive ?
a > 0
# How many negative number ?
(a < 0).sum()
# Are there any number equal to 0 ?
(a == 0).any()
# Are all value less than 8 ?
(a < 8).all()
```
## Boolean Indexing
```
a = np.array([-2, -1, 0, 1, 2])
# Boolean mask
a > 0
# Pass the boolean mask to index
a[a > 0]
# Create a random 2 dimensional array
b = np.random.randint(1, 10, (3, 3))
b
# Index with a boolean mask
b[b <= 4]
# We can set values of an array with boolean mask
b[b==9] = 0
b
a = np.array([1, 3, 5, 7, 9])
a
np.where(a > 4)
```
## Fancy Indexing
If we want to access elements at non consecutinuous index of a numpy array, we use fancy indexing. For example,
```
a = np.random.randint(0, 9, 10)
a
```
We retrieve elements at even indicies of the above array as
```
a[[0, 2, 5, 6, 8]]
```
Fancy indexing also works with multiple dimensions arrays
```
b = np.arange(9).reshape(3,3)
b
```
To get the elements at specific locations, we pass in two tuples. The first one indicates the row indicies and the second one determines column indicies.
```
# Get elements at the four corners of the array, the indicies of those position are (0, 0); (0, 2); (2, 0); (2, 2)
row_indicies = (0, 0, 1, 2)
column_indicies = (0, 2, 1, 1)
b[row_indicies, column_indicies]
```
We can combine fancy indexing with other indexing methods to get desired elements.
```
# Simple + fancy
b[1, [0, 2]]
# Slicing + fancy
b[[0, 2], -2:]
# Boolean + fancy
b[[True, False, True]][:, [0, 2]]
```
We can create a new array by using fancy indexing
```
b
b[[0, 0, 1, 1, 2, 2]]
```
We can modify data of array using fancy indexing
```
b = np.arange(9).reshape(3, 3)
b
b[[0, 1], [2, 0]] = 99
b
a = np.arange(10)
a
np.where(a > 3)
```
# Universal Function
## Array Arithmetic
```
x = np.arange(5)
print(x)
print(x + 2)
print(x - 2)
print(x * 2)
print(x / 2)
print(x // 2)
print(x ** 2)
print(x % 2)
```
## Absolute value
```
x = np.array([-2, -1, 0, 1, 2])
print(x)
print(np.abs(x))
```
The numpy absolute function can work with complex numbers and return the magnitude of it.
```
x = np.array([-1 + 1j, 2 - 2j, 3 + 4j])
print(x)
print(np.abs(x))
```
## Trigonometric functions
```
x = np.linspace(-2 * np.pi, 2 * np.pi, 5)
x
y = np.sin(x)
y
import numpy as np
import matplotlib.pyplot as plt
plt.style.use("ggplot")
x = np.linspace(-2 * np.pi, 2 * np.pi, 100)
y = np.sin(x)
plt.plot(x, y)
```
## Exponents and logarithms
```
x = np.linspace(-2, 2, 100)
y = np.exp(x)
plt.plot(x, y)
x = np.linspace(0.0001, 2, 1000)
y = np.log(x)
plt.plot(x, y)
```
We can combine those functions to calculate complex math functions
```
x = np.linspace(-5, 5, 1000)
y = (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
plt.plot(x, y)
```
# Aggregations: Sum, Min, Max
## Summing the Values in an Array
Given an array
```
a = np.random.randn(5)
a
```
We can use the sum function of python or use the method of numpy as follow
```
sum(a)
a.sum()
```
It is recommended to use the numpy version, because it is computed much more quickly
```
big_array = np.random.randn(1000000)
%time sum(big_array)
%time big_array.sum()
```
## Min and Max
Again, python has built in mix and max function. However, numpy version is better.
```
a = np.random.randn(5)
a
a.min()
a.max()
```
## Multi dimensional aggregates
When we have two (or more) dimensionals array, we can choose which dimension to perform aggregration.
```
a = np.random.randn(3, 4)
a
print(a.sum()) # sum all of the elements
print(a.sum(axis = 0)) # sum on column
print(a.sum(axis = 1)) # sum on row
print(a.min())
print(a.min(axis = 0)) #column
print(a.min(axis = 1)) #row
print(a.max())
print(a.max(axis = 0))
print(a.max(axis = 1))
```
## Sorting
To return a sorted version of the array without modifying the input, you can use *np.sort*
```
a = np.random.randn(5)
a
np.sort(a)
a
```
To sort the array in-place, calling the *sort* method on the array
```
a = np.random.randn(5)
a
a
```
A related function is *argsort*, which instead returns the indices of the sorted elements:
```
a = np.random.randn(5)
a
np.argsort(a)
a[np.argsort(a)]
np.argmin(a)
a
a.dtype
```
## Sorting along rows or columns
A useful feature of NumPy's sorting algorithms is the ability to sort along specific rows or columns of a multidimensional array using the axis argument. For example:
```
a = np.random.randint(0, 9, (4, 5))
a
np.sort(a, axis=0)
np.sort(a, axis=1)
np.sort(a)
```
# Homework
1. Given a 1D array, negate all elements which are between 3 and 8, in place (not created a new array).
2. Create random vector of size 10 and replace the maximum value by 0
3. How to find common values between two arrays?
4. Reverse a vector (first element becomes last)
5. Create a 3x3 matrix with values ranging from 0 to 8
6. Find indices of non-zero elements from the array [1,2,0,0,4,0]
7. Create a 3x3x3 array with random values
8. Create a random vector of size 30 and find the mean value
9. Create a 2d array with 1 on the border and 0 inside
10. Given an array x of 20 integers in the range (0, 100)
```
x = np.random.randint(0, 100, 20)
x
```
and an random float in the range (0, 20)
```
y = np.random.uniform(0, 20)
y
```
Find the index of x where the value at that index is closest to y.
|
github_jupyter
|
import numpy as np
data1 = [1, 2, 3]
array1 = np.array(data1) # data passed in is a list
array1
data2 = (4, 5, 6)
array2 = np.array(data2) # data passed in is a tuple
array2
type(array2)
array3 = np.array([7, 8, 9])
array3
data4 = [[1, 2, 3], [4, 5, 6]]
array4 = np.array(data4)
array4
np.array([[1, 2, 3], [4, 5, 6]])
array4.ndim # array4 has 2 dimension
array4.shape # array 2 rows and 3 columns, the shape is returned in a 2-d tuple
# Create array of 0s
np.zeros([2, 3])
# Create array of 1s
np.ones([3, 3])
# Create an array of range
np.arange(10, 100)
# Create an identity matrix
np.eye(4)
my_list = [[1, 2, 3], [4, 5, 6]]
[[i**2 for i in item ] for item in my_list]
array = np.array(my_list)
array
array * array
array - array
array ** 3
1 / array
array_2 = np.array([[2, 4, 0], [5, 1, 9]])
array_2
array
array_2 > array
array = np.arange(100)
array
array[0]
array[-2]
array[:3]
array[-3:]
array[2:6]
array_slice = array[2:6]
array_slice
array_slice[0] = 99
array_slice
array
array_slice_copied = array[-3:].copy()
array_slice_copied
array_slice_copied[:] = 99
array_slice_copied
array
array_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
array_2d
array_2d[2]
# Access recursively the element at row 1, column 1
array_2d[1][1]
# Comma separated list
array_2d[0, 2]
array_2d
# Return the first row
array_2d[0]
# Return the first two row
array_2d[:2]
# Return the second column
array_2d[:, 2]
# Return the square submatrix at the upper right corner
array_2d[:2, -2:]
array_2d
array_2d[:2, :2] = 99
array_2d
array = np.array([1, 2, 3, 4, 5, 6])
array
array > 3
array >= 3
array == 3
array != 3
a = np.array([[2, -7, 1], [-4, 3, 8], [5, 0, -6]])
a
# Which number is positive ?
a > 0
# How many negative number ?
(a < 0).sum()
# Are there any number equal to 0 ?
(a == 0).any()
# Are all value less than 8 ?
(a < 8).all()
a = np.array([-2, -1, 0, 1, 2])
# Boolean mask
a > 0
# Pass the boolean mask to index
a[a > 0]
# Create a random 2 dimensional array
b = np.random.randint(1, 10, (3, 3))
b
# Index with a boolean mask
b[b <= 4]
# We can set values of an array with boolean mask
b[b==9] = 0
b
a = np.array([1, 3, 5, 7, 9])
a
np.where(a > 4)
a = np.random.randint(0, 9, 10)
a
a[[0, 2, 5, 6, 8]]
b = np.arange(9).reshape(3,3)
b
# Get elements at the four corners of the array, the indicies of those position are (0, 0); (0, 2); (2, 0); (2, 2)
row_indicies = (0, 0, 1, 2)
column_indicies = (0, 2, 1, 1)
b[row_indicies, column_indicies]
# Simple + fancy
b[1, [0, 2]]
# Slicing + fancy
b[[0, 2], -2:]
# Boolean + fancy
b[[True, False, True]][:, [0, 2]]
b
b[[0, 0, 1, 1, 2, 2]]
b = np.arange(9).reshape(3, 3)
b
b[[0, 1], [2, 0]] = 99
b
a = np.arange(10)
a
np.where(a > 3)
x = np.arange(5)
print(x)
print(x + 2)
print(x - 2)
print(x * 2)
print(x / 2)
print(x // 2)
print(x ** 2)
print(x % 2)
x = np.array([-2, -1, 0, 1, 2])
print(x)
print(np.abs(x))
x = np.array([-1 + 1j, 2 - 2j, 3 + 4j])
print(x)
print(np.abs(x))
x = np.linspace(-2 * np.pi, 2 * np.pi, 5)
x
y = np.sin(x)
y
import numpy as np
import matplotlib.pyplot as plt
plt.style.use("ggplot")
x = np.linspace(-2 * np.pi, 2 * np.pi, 100)
y = np.sin(x)
plt.plot(x, y)
x = np.linspace(-2, 2, 100)
y = np.exp(x)
plt.plot(x, y)
x = np.linspace(0.0001, 2, 1000)
y = np.log(x)
plt.plot(x, y)
x = np.linspace(-5, 5, 1000)
y = (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
plt.plot(x, y)
a = np.random.randn(5)
a
sum(a)
a.sum()
big_array = np.random.randn(1000000)
%time sum(big_array)
%time big_array.sum()
a = np.random.randn(5)
a
a.min()
a.max()
a = np.random.randn(3, 4)
a
print(a.sum()) # sum all of the elements
print(a.sum(axis = 0)) # sum on column
print(a.sum(axis = 1)) # sum on row
print(a.min())
print(a.min(axis = 0)) #column
print(a.min(axis = 1)) #row
print(a.max())
print(a.max(axis = 0))
print(a.max(axis = 1))
a = np.random.randn(5)
a
np.sort(a)
a
a = np.random.randn(5)
a
a
a = np.random.randn(5)
a
np.argsort(a)
a[np.argsort(a)]
np.argmin(a)
a
a.dtype
a = np.random.randint(0, 9, (4, 5))
a
np.sort(a, axis=0)
np.sort(a, axis=1)
np.sort(a)
x = np.random.randint(0, 100, 20)
x
y = np.random.uniform(0, 20)
y
| 0.550366 | 0.994672 |
###### 20 November 2018, by Jeroen van Lidth de Jeude - [NETWORKS](http://networks.imtlucca.it/) - [IMT School for Advanced Studies Lucca](https://www.imtlucca.it/jeroen.vanlidth)
# Exponential Random Graph Null Models for Graph Structures with Modular Hierarchies
For clustered data the null model can be taken to include information on the modular structure. In this notebook we provide code to solve a configuration null model in every block of the block structure of the adjacency matrix. We detail this approach in the paper: [*"Reconstructing Mesoscale Network Structures" - Jeroen van Lidth de Jeude, Riccardo Di Clemente, Guido Caldarelli, Fabio Saracco and Tiziano Squartini (15/05/2018)*](https://arxiv.org/abs/1805.06005)

## Modular structures
Examples of modular structures are core-periphery and bow-tie-like structures. (Below showing the adjacency matrices representing the block structure - darker colors indicate a higher edge density.)

It is these blocks of the adjacency matrices that we will model in this notebook.
## Null models
As detailed in the paper, we use the configuration model and include information for which nodes belong to which partition/block. We provide the code for both the Directed Configuration Model and the Reciprocated Configuration Model.

# Code
This code consists of the usual Directed Configuration Model, Reciprocated Configuration Model, and their block verion alternatives.
For the Block Directed Configuration Model we have to solve the:
- *monopartite* DCM in the diagonal blocks (within clusters/blocks)
- *bipartite* DCM in the off-diagonal blocks (between clusters)
The functions provided are therfore:
- Monopartite:
- system of equations of the monopartite DCM
- numerical solver of the system of equations
- Bipartite
- system of equations of the bipartite DCM
- numerical solver of the system of equations
- Blocks: the function to solve the monopartite diagonal blocks and the bipartite off-diagonal blocks, and combine these into the overall matrix of edge probabilities
#### Potential Issues
Potential known issues in this script are:
- blocks/clusters should be of at least size n=2, otherwise the code will error
- as usual the numerical solving can bring problems. Different solvers can be tried if the standard solver does not converge
```
from numba import jit
import numpy as np
# For the numerical solver
from scipy.optimize import least_squares
```
## Functions
Some of the basic code looks long, but these are mostly tricks to improve the numerical solveing, like for nodes with zero in- or out-degree.
```
@jit
def equations_to_solve_dcm(p, k_out, k_in):
"""DCM equations for numerical solver.
Args:
p: list of independent variables [x y]
adjacency_matrix: numpy.array adjacency matrix to be solved
Returns:
numpy array of observed degree - expected degree
"""
n_nodes = len(k_out)
# print(len(p), len(k_out), len(k_in))
p = np.array(p)
num_x_nonzero_nodes = np.count_nonzero(k_out)
x_nonzero = p[0:num_x_nonzero_nodes]
y_nonzero = p[num_x_nonzero_nodes:len(p)]
x = np.zeros(n_nodes)
x[k_out != 0] = x_nonzero
y = np.zeros(n_nodes)
y[k_in != 0] = y_nonzero
# Expected degrees
k_out_exp = np.zeros(x.shape[0])
k_in_exp = np.zeros(x.shape[0])
for i in np.arange(x.shape[0]):
for j in np.arange(x.shape[0]):
if i != j:
k_out_exp[i] += (x[i] * y[j]) / (1 + x[i] * y[j])
k_in_exp[i] += (x[j] * y[i]) / (1 + x[j] * y[i])
k_out_nonzero = k_out[k_out != 0]
k_in_nonzero = k_in[k_in != 0]
k_out_exp_nonzero = k_out_exp[k_out != 0]
k_in_exp_nonzero = k_in_exp[k_in != 0]
f1 = k_out_nonzero - k_out_exp_nonzero
f2 = k_in_nonzero - k_in_exp_nonzero
return np.concatenate((f1, f2))
def numerically_solve_dcm(adjacency_matrix):
"""Solves the DCM numerically with least squares.
Directed Binary Configuration Model is solved using the
system of equations. The optimization is done using
scipy.optimize.least_squares on the system of equations.
Args:
adjacency_matrix : numpy.array adjacency matrix (binary, square)
Returns:
numpy.array probability matrix with dcm probabilities
"""
n_nodes = len(adjacency_matrix)
# Rough estimate of initial values
k_in = np.sum(adjacency_matrix, 0)
k_out = np.sum(adjacency_matrix, 1)
x_initial_values = k_out / np.sqrt(np.sum(k_out) + 1) # plus one to prevent dividing by zero
y_initial_values = k_in / np.sqrt(np.sum(k_in) + 1)
x_initial_values = x_initial_values[k_out != 0]
y_initial_values = y_initial_values[k_in != 0]
initial_values = np.concatenate((x_initial_values, y_initial_values))
#print(len(adjacency_matrix), len(x_initial_values), len(y_initial_values))
boundslu = tuple([0] * len(initial_values)), tuple([np.inf] * len(initial_values))
x_solved = least_squares(fun=equations_to_solve_dcm,
x0=initial_values,
args=(k_out, k_in,),
bounds=boundslu,
max_nfev=1e2,
ftol=1e-5, xtol=1e-5, gtol=1e-5)
print(x_solved.cost, x_solved.message)
# Numerical solution checks
assert x_solved.cost < 0.1, 'Numerical convergence problem: final cost function evaluation > 1'
# Set extremely small values to zero
# x_solved.x[x_solved.x < 1e-8] = 0
p = x_solved.x
p = np.array(p)
num_x_nonzero_nodes = np.count_nonzero(k_out)
x_nonzero = p[0:num_x_nonzero_nodes]
y_nonzero = p[num_x_nonzero_nodes:len(p)]
x = np.zeros(n_nodes)
x[k_out != 0] = x_nonzero
y = np.zeros(n_nodes)
y[k_in != 0] = y_nonzero
x_array = x
y_array = y
p_adjacency = np.zeros([n_nodes, n_nodes])
for i in np.arange(n_nodes):
for j in np.arange(n_nodes):
if i == j:
continue
p_adjacency[i, j] = x_array[i] * y_array[j] / (1 + x_array[i] * y_array[j])
return p_adjacency
@jit
def equations_to_solve_dcm_bipartite(p, k_r_out, h_c_in, h_c_out, k_r_in):
"""DCM Bipartite equations for numerical solver.
Args:
p: list of independent variables [x y]
m_adjacency_matrix: above diagonal rectangular matrix
n_adjacency_matrix: under diagonal rectangular matrix
Returns:
numpy array of observed degree - expected degree
"""
r = len(k_r_out)
c = len(h_c_in)
p = np.array(p)
num_nonzero_kro = np.count_nonzero(k_r_out)
num_nonzero_hci = np.count_nonzero(h_c_in)
num_nonzero_hco = np.count_nonzero(h_c_out)
num_nonzero_kri = np.count_nonzero(k_r_in)
xrt_nonzero = p[0:num_nonzero_kro]
ycb_nonzero = p[num_nonzero_kro:num_nonzero_kro + num_nonzero_hci]
xcb_nonzero = p[num_nonzero_kro + num_nonzero_hci:num_nonzero_kro + num_nonzero_hci + num_nonzero_hco]
yrt_nonzero = p[num_nonzero_kro + num_nonzero_hci + num_nonzero_hco:len(p)]
xrt = np.zeros(r)
xrt[k_r_out != 0] = xrt_nonzero
ycb = np.zeros(c)
ycb[h_c_in != 0] = ycb_nonzero
xcb = np.zeros(c)
xcb[h_c_out != 0] = xcb_nonzero
yrt = np.zeros(r)
yrt[k_r_in != 0] = yrt_nonzero
# Expected degrees
k_r_out_exp = np.zeros(r)
h_c_in_exp = np.zeros(c)
h_c_out_exp = np.zeros(c)
k_r_in_exp = np.zeros(r)
for r_i in np.arange(r):
for c_i in np.arange(c):
xrt_ycb = (xrt[r_i] * ycb[c_i]) / (1 + xrt[r_i] * ycb[c_i])
k_r_out_exp[r_i] += xrt_ycb
h_c_in_exp[c_i] += xrt_ycb
xcb_yrt = (xcb[c_i] * yrt[r_i]) / (1 + xcb[c_i] * yrt[r_i])
h_c_out_exp[c_i] += xcb_yrt
k_r_in_exp[r_i] += xcb_yrt
k_r_out_nonzero = k_r_out[k_r_out != 0]
h_c_in_nonzero = h_c_in[h_c_in != 0]
h_c_out_nonzero = h_c_out[h_c_out != 0]
k_r_in_nonzero = k_r_in[k_r_in != 0]
k_r_out_exp_nonzero = k_r_out_exp[k_r_out != 0]
h_c_in_exp_nonzero = h_c_in_exp[h_c_in != 0]
h_c_out_exp_nonzero = h_c_out_exp[h_c_out != 0]
k_r_in_exp_nonzero = k_r_in_exp[k_r_in != 0]
f1 = k_r_out_nonzero - k_r_out_exp_nonzero
f2 = h_c_in_nonzero - h_c_in_exp_nonzero
f3 = h_c_out_nonzero - h_c_out_exp_nonzero
f4 = k_r_in_nonzero - k_r_in_exp_nonzero
return np.concatenate((f1, f2, f3, f4))
def numerically_solve_dcm_bipartite_likelihood(m_adjacency_matrix, n_adjacency_matrix):
"""Solves the Bipartite DCM numerically with least squares.
Bipartite Directed Binary Configuration Model is solved using the
system of equations. The optimization is done using
scipy.optimize.least_squares on the system of equations.
Args:
m_adjacency_matrix: numpy.array above diagonal rectangular matrix (binary)
n_adjacency_matrix: numpy.array under diagonal rectangular matrix (binary)
Returns:
loglikelihood of the configuration
"""
def safe_ln(x):
if x <= 0:
return 0
return np.log(x)
# Observed degrees
k_r_out = np.sum(m_adjacency_matrix, 1)
h_c_in = np.sum(m_adjacency_matrix, 0)
h_c_out = np.sum(n_adjacency_matrix, 1)
k_r_in = np.sum(n_adjacency_matrix, 0)
# Rough estimate of initial values
x_initial_values_1 = k_r_out / np.sqrt(np.sum(k_r_out) + 1) # plus one to prevent dividing by zero
y_initial_values_1 = h_c_in / np.sqrt(np.sum(h_c_in) + 1)
x_initial_values_2 = h_c_out / np.sqrt(np.sum(h_c_out) + 1)
y_initial_values_2 = k_r_in / np.sqrt(np.sum(k_r_in) + 1)
x_initial_values_1 = x_initial_values_1[k_r_out != 0]
y_initial_values_1 = y_initial_values_1[h_c_in != 0]
x_initial_values_2 = x_initial_values_2[h_c_out != 0]
y_initial_values_2 = y_initial_values_2[k_r_in != 0]
initial_values = np.concatenate((x_initial_values_1, y_initial_values_1,
x_initial_values_2, y_initial_values_2))
boundslu = tuple([0] * len(initial_values)), tuple([np.inf] * len(initial_values))
x_solved = least_squares(fun=equations_to_solve_dcm_bipartite,
x0=initial_values,
args=(k_r_out, h_c_in, h_c_out, k_r_in,),
bounds=boundslu,
max_nfev=1e4,
ftol=1e-15, xtol=1e-15, gtol=1e-15)
print(x_solved.cost, x_solved.message)
# Numerical solution checks
assert x_solved.cost < 1, 'Numerical convergence problem: final cost function evaluation > 1'
# Set extremely small values to zero for likelihood problems (log(very small number) = large)
# x_solved.x[x_solved.x < 1e-7] = 0
r = len(k_r_out)
c = len(h_c_in)
p = np.array(x_solved.x)
num_nonzero_kro = np.count_nonzero(k_r_out)
num_nonzero_hci = np.count_nonzero(h_c_in)
num_nonzero_hco = np.count_nonzero(h_c_out)
num_nonzero_kri = np.count_nonzero(k_r_in)
xrt_nonzero = p[0:num_nonzero_kro]
ycb_nonzero = p[num_nonzero_kro:num_nonzero_kro + num_nonzero_hci]
xcb_nonzero = p[num_nonzero_kro + num_nonzero_hci:num_nonzero_kro + num_nonzero_hci + num_nonzero_hco]
yrt_nonzero = p[num_nonzero_kro + num_nonzero_hci + num_nonzero_hco:len(p)]
xrt = np.zeros(r)
xrt[k_r_out != 0] = xrt_nonzero
ycb = np.zeros(c)
ycb[h_c_in != 0] = ycb_nonzero
xcb = np.zeros(c)
xcb[h_c_out != 0] = xcb_nonzero
yrt = np.zeros(r)
yrt[k_r_in != 0] = yrt_nonzero
l_r = 0
for r in np.arange(m_adjacency_matrix.shape[0]):
l_r += (k_r_out[r] * safe_ln(xrt[r])) + (k_r_in[r] * safe_ln(yrt[r]))
l_c = 0
for c in np.arange(m_adjacency_matrix.shape[1]):
l_c += (h_c_out[c] * safe_ln(xcb[c])) + (h_c_in[c] * safe_ln(ycb[c]))
l_rc = 0
for r in np.arange(m_adjacency_matrix.shape[0]):
for c in np.arange(m_adjacency_matrix.shape[1]):
l_rc += safe_ln((1 + xrt[r] * ycb[c]) * (1 + xcb[c] * yrt[r]))
likelihood = l_r + l_c - l_rc
#print(m_adjacency_matrix, n_adjacency_matrix)
#print(xrt, ycb, xcb,yrt)
p_m_adj = np.zeros_like(m_adjacency_matrix, dtype=np.float)
for r in np.arange(m_adjacency_matrix.shape[0]):
for c in np.arange(m_adjacency_matrix.shape[1]):
p_m_adj[r,c] = (xrt[r]*ycb[c]) / (1+(xrt[r]*ycb[c]))
p_n_adj = np.zeros_like(n_adjacency_matrix, dtype=np.float)
for c in np.arange(m_adjacency_matrix.shape[1]):
for r in np.arange(m_adjacency_matrix.shape[0]):
p_n_adj[c,r] = (xcb[c]*yrt[r]) / (1+(xcb[c]*yrt[r]))
return p_m_adj, p_n_adj, likelihood
def numerically_solve_block_dcm(adj, partitioning):
"""Solves the Bipartite DCM numerically with least squares for all blocks indicated
with the partitioning vector
Bipartite Directed Binary Configuration Model is solved using the
system of equations. The optimization is done using
scipy.optimize.least_squares on the system of equations.
Args:
adj: numpy.array binary square adjacency matrix
partitioning: numpy.array integer vector of node belonging. e.g. [0,1,0,1],
for nodes 0&2 belonging to cluster one and nodes 1&3 belonging to cluster 2
Returns:
p_adj: numpy.array square matrix of probabilities.
"""
n_nodes = adj.shape[0]
B = len(set(partitioning))
p_adj = np.zeros_like(adj, dtype=np.float)
for i in np.arange(B):
for j in np.arange(B):
if i <= j:
adj_block = adj[np.ix_(np.where(partitioning==i)[0], np.where(partitioning==j)[0])]
if i == j: # Diagonal square block
if np.sum(adj_block) > 0: # Block with links
p_adj_block = numerically_solve_dcm(adj_block)
else: # Block without links
p_adj_block = np.zeros_like(adj_block)
p_adj[np.ix_(np.where(partitioning==i)[0], np.where(partitioning==j)[0])] = p_adj_block.copy()
else: # Off diagonal block
adj_block_lower = adj[np.ix_(np.where(partitioning==j)[0], np.where(partitioning==i)[0])]
if np.sum(adj_block) + np.sum(adj_block_lower) > 0: # Block with links
p_m_adj, p_n_adj, likelihood = numerically_solve_dcm_bipartite_likelihood(adj_block,
adj_block_lower)
else:
p_m_adj = np.zeros_like(adj_block)
p_n_adj = np.zeros_like(adj_block_lower)
p_adj[np.ix_(np.where(partitioning==i)[0], np.where(partitioning==j)[0])] = p_m_adj
p_adj[np.ix_(np.where(partitioning==j)[0], np.where(partitioning==i)[0])] = p_n_adj
return p_adj
```
## Working Example: Clustered Graph with two blocks
In this example we generate a randomly filled adjacency matrix, with different edge-densities in the different blocks of the adjacency: we create a random graph with modular (clustered) structure.
The functions for the null-model solving is:
- `numerically_solve_block_dcm(adjacency_matrix, partitioning)` block model DCM
- `numerically_solve_dcm(adjacency_matrix)` non-block DCM
```
n1 = 10 # Size first cluster
n2 = 8 # Size second cluster
a1 = (np.random.rand(n1,n1) < 0.7) # Generate random matrix blocks
a2 = (np.random.rand(n1,n2) < 0.2) # Low edge-density block
a3 = (np.random.rand(n2,n1) < 0.2)
a4 = (np.random.rand(n2,n2) < 0.7) # High edge-density block
adjacency_matrix = np.bmat([[a1, a2],
[a3, a4]]) # Join blocks
np.fill_diagonal(adjacency_matrix,0) # Prevent self-loops
adjacency_matrix = adjacency_matrix.astype(int) # Force binary links
adjacency_matrix = np.asarray(adjacency_matrix) # Format as np.ndarray instead of np.matrix
partitioning = np.concatenate([np.zeros(n1), np.ones(n2)]) # Cluster information
```
Now we compute the null models and visualise the result: the original matrix, the matrix of edge probabilities as predicted by the normal Directed Configuration Model, and the matix of edge probabilities as predicted by the block version of the DCM
```
# Loading matplotlib library for visualisation
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
```
For the block model, the function should also get the variable indicating the node-specific group information: the partitioning. This should be an array of length of the number of nodes, where all entries indicate to which cluster the node belongs.
```
p_adj = numerically_solve_block_dcm(adjacency_matrix, partitioning) # Solve block null model
p_dcm = numerically_solve_dcm(adjacency_matrix) # Solve the non-block dcm
adjacencies = [adjacency_matrix, p_adj, p_dcm]
titles = ['Original matrix', 'Block-DCM probabilities', 'DCM probabilities (non-block)']
colormap = 'Blues'
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(15,5))
for i, ax in enumerate(axes.flat):
im = ax.imshow(adjacencies[i], vmin=0, vmax=1, cmap = colormap)
ax.set_title(titles[i])
fig.subplots_adjust(right=0.9)
cbar_ax = fig.add_axes([0.95, 0.15, 0.05, 0.7])
fig.colorbar(im, cax=cbar_ax)
cbar_ax.set_title('edge-probability')
plt.show()
```
## A note on model preformances
From a visual inspection of the adjacency matrices, it might seem that the null model encoding the block structure is the better fitting null model (because it visually recreates the block structure). Whether this is the case we answer in our paper ["Reconstructing Mesoscale Network Structures"](https://arxiv.org/abs/1805.06005) . (Short answer: the increase in number of fitting parameters that the encoding of the modular structure brings is not always worth it.)
## Reciprocated constraints null model
We can follow the same procedure, but with a different null model: the Reciprocated Configuration Model. This null model contraints the reciprocated degree sequences (in-degree, out-degree, reciprocated-degree).
```
@jit
def equations_to_solve_rcm(p, k_out, k_in, k_rec):
"""RCM equations for numerical solver.
Args:
p: list of independent variables [x y z]
adjacency_matrix: adjacency matrix to be solved
Returns:
numpy array of observed degree - expected degree
"""
n_nodes = len(k_out)
p = np.array(p)
num_x_nonzero_nodes = np.count_nonzero(k_out)
num_y_nonzero_nodes = np.count_nonzero(k_in)
x_nonzero = p[0:num_x_nonzero_nodes]
y_nonzero = p[num_x_nonzero_nodes:num_x_nonzero_nodes + num_y_nonzero_nodes]
z_nonzero = p[num_x_nonzero_nodes + num_y_nonzero_nodes:len(p)]
# print(len(k_out),len(k_in),len(k_rec),len(x_nonzero),len(y_nonzero),len(z_nonzero))
x = np.zeros(n_nodes)
x[k_out != 0] = x_nonzero
y = np.zeros(n_nodes)
y[k_in != 0] = y_nonzero
z = np.zeros(n_nodes)
z[k_rec != 0] = z_nonzero
# Expected degrees
k_out_exp = np.zeros(x.shape[0])
k_in_exp = np.zeros(x.shape[0])
k_rec_exp = np.zeros(x.shape[0])
for i in np.arange(x.shape[0]):
for j in np.arange(x.shape[0]):
if i != j:
k_out_exp[i] += (x[i] * y[j]) / (1 + x[i] * y[j] + x[j] * y[i] + z[i] * z[j])
k_in_exp[i] += (x[j] * y[i]) / (1 + x[i] * y[j] + x[j] * y[i] + z[i] * z[j])
k_rec_exp[i] += (z[i] * z[j]) / (1 + x[i] * y[j] + x[j] * y[i] + z[i] * z[j])
k_out_nonzero = k_out[k_out != 0]
k_in_nonzero = k_in[k_in != 0]
k_rec_nonzero = k_rec[k_rec != 0]
k_out_exp_nonzero = k_out_exp[k_out != 0]
k_in_exp_nonzero = k_in_exp[k_in != 0]
k_rec_exp_nonzero = k_rec_exp[k_rec != 0]
f1 = k_out_nonzero - k_out_exp_nonzero
f2 = k_in_nonzero - k_in_exp_nonzero
f3 = k_rec_nonzero - k_rec_exp_nonzero
return np.concatenate((f1, f2, f3))
def numerically_solve_rcm(adjacency_matrix):
"""Solves the RCM numerically with least squares.
Reciprocated Binary Configuration Model is solved using the
system of equations. The optimization is done using
scipy.optimize.least_squares on the system of equations.
Args:
adjacency_matrix : numpy.array adjacency matrix (binary, square)
Returns:
numpy.array probability matrices with dcm probabilities:
p_out_edges, p_in_edges, p_reciprocated_edges
"""
n_nodes = len(adjacency_matrix)
# Observed degrees
k_rec = np.zeros(adjacency_matrix.shape[0], dtype=np.int)
k_out = np.zeros(adjacency_matrix.shape[0], dtype=np.int)
k_in = np.zeros(adjacency_matrix.shape[0], dtype=np.int)
for i in np.arange(adjacency_matrix.shape[0]):
for j in np.arange(adjacency_matrix.shape[0]):
if i != j:
k_rec_i = np.min((adjacency_matrix[i, j], adjacency_matrix[j, i]))
k_out[i] += adjacency_matrix[i, j] - k_rec_i
k_in[i] += adjacency_matrix[j, i] - k_rec_i
k_rec[i] += k_rec_i
# Rough estimate of initial values
x_initial_values = k_out / np.sqrt(np.sum(k_out) + 1) # plus one to prevent dividing by zero
y_initial_values = k_in / np.sqrt(np.sum(k_in) + 1)
z_initial_values = k_rec / np.sqrt(np.sum(k_rec) + 1)
x_initial_values = x_initial_values[k_out != 0]
y_initial_values = y_initial_values[k_in != 0]
z_initial_values = z_initial_values[k_rec != 0]
initial_values = np.concatenate((x_initial_values, y_initial_values, z_initial_values))
boundslu = tuple([0] * len(initial_values)), tuple([np.inf] * len(initial_values))
x_solved = least_squares(fun=equations_to_solve_rcm,
x0=initial_values,
args=(k_out, k_in, k_rec,),
bounds=boundslu,
max_nfev=1e4,
ftol=1e-15, xtol=1e-15, gtol=1e-15)
print(x_solved.cost, x_solved.message)
# Numerical solution checks
assert x_solved.cost < 1, 'Numerical convergence problem: final cost function evaluation > 1'
p = np.array(x_solved.x)
num_x_nonzero_nodes = np.count_nonzero(k_out)
num_y_nonzero_nodes = np.count_nonzero(k_in)
x_nonzero = p[0:num_x_nonzero_nodes]
y_nonzero = p[num_x_nonzero_nodes:num_x_nonzero_nodes + num_y_nonzero_nodes]
z_nonzero = p[num_x_nonzero_nodes + num_y_nonzero_nodes:len(p)]
x = np.zeros(n_nodes)
x[k_out != 0] = x_nonzero
y = np.zeros(n_nodes)
y[k_in != 0] = y_nonzero
z = np.zeros(n_nodes)
z[k_rec != 0] = z_nonzero
x_array = x
y_array = y
z_array = z
p_out = np.zeros([n_nodes, n_nodes])
for i in np.arange(n_nodes):
for j in np.arange(n_nodes):
if i == j:
continue
p_out[i, j] = x_array[i] * y_array[j] / (
1 + x_array[i] * y_array[j] + x_array[j] * y_array[i] + z_array[i] * z_array[j])
p_in = np.zeros([n_nodes, n_nodes])
for i in np.arange(n_nodes):
for j in np.arange(n_nodes):
if i == j:
continue
p_in[i, j] = x_array[j] * y_array[i] / (
1 + x_array[i] * y_array[j] + x_array[j] * y_array[i] + z_array[i] * z_array[j])
p_rec = np.zeros([n_nodes, n_nodes])
for i in np.arange(n_nodes):
for j in np.arange(n_nodes):
if i == j:
continue
p_rec[i, j] = z_array[i] * z_array[j] / (
1 + x_array[i] * y_array[j] + x_array[j] * y_array[i] + z_array[i] * z_array[j])
return p_out, p_in, p_rec
@jit
def equations_to_solve_rcm_bipartite(p, k_r_out, k_r_in, k_r_rec, h_c_in, h_c_out, h_c_rec):
"""RCM Bipartite equations for numerical solver.
Args:
p: list of independent variables [x y]
m_adjacency_matrix: above diagonal rectangular matrix
n_adjacency_matrix: under diagonal rectangular matrix
Returns:
numpy array of observed degree - expected degree
"""
r = len(k_r_out)
c = len(h_c_in)
p = np.array(p)
n0_kro = np.count_nonzero(k_r_out)
n0_kri = np.count_nonzero(k_r_in)
n0_krr = np.count_nonzero(k_r_rec)
n0_hci = np.count_nonzero(h_c_in)
n0_hco = np.count_nonzero(h_c_out)
n0_hcr = np.count_nonzero(h_c_rec)
xrt_nonzero = p[0:n0_kro]
ycb_nonzero = p[n0_kro:n0_kro + n0_hci]
zcb_nonzero = p[n0_kro + n0_hci:n0_kro + n0_hci + n0_hcr]
xcb_nonzero = p[n0_kro + n0_hci + n0_hcr:n0_kro + n0_hci + n0_hcr + n0_hco]
yrt_nonzero = p[n0_kro + n0_hci + n0_hcr + n0_hco:n0_kro + n0_hci + n0_hcr + n0_hco + n0_kri]
zrt_nonzero = p[n0_kro + n0_hci + n0_hcr + n0_hco + n0_kri:len(p)]
xrt = np.zeros(r)
xrt[k_r_out != 0] = xrt_nonzero
ycb = np.zeros(c)
ycb[h_c_in != 0] = ycb_nonzero
zcb = np.zeros(c)
zcb[h_c_rec != 0] = zcb_nonzero
xcb = np.zeros(c)
xcb[h_c_out != 0] = xcb_nonzero
yrt = np.zeros(r)
yrt[k_r_in != 0] = yrt_nonzero
zrt = np.zeros(r)
zrt[k_r_rec != 0] = zrt_nonzero
# Expected degrees
k_r_out_exp = np.zeros(r)
k_r_in_exp = np.zeros(r)
k_r_rec_exp = np.zeros(r)
h_c_in_exp = np.zeros(c)
h_c_out_exp = np.zeros(c)
h_c_rec_exp = np.zeros(c)
for r_i in np.arange(r):
for c_i in np.arange(c):
xrt_ycb = xrt[r_i] * ycb[c_i] / (1 + xrt[r_i] * ycb[c_i] + xcb[c_i] * yrt[r_i] + zrt[r_i] * zcb[c_i])
xcb_yrt = xcb[c_i] * yrt[r_i] / (1 + xrt[r_i] * ycb[c_i] + xcb[c_i] * yrt[r_i] + zrt[r_i] * zcb[c_i])
zrt_zcb = zrt[r_i] * zcb[c_i] / (1 + xrt[r_i] * ycb[c_i] + xcb[c_i] * yrt[r_i] + zrt[r_i] * zcb[c_i])
k_r_out_exp[r_i] += xrt_ycb
k_r_in_exp[r_i] += xcb_yrt
k_r_rec_exp[r_i] += zrt_zcb
h_c_in_exp[c_i] += xrt_ycb
h_c_out_exp[c_i] += xcb_yrt
h_c_rec_exp[c_i] += zrt_zcb
k_r_out_nonzero = k_r_out[k_r_out != 0]
k_r_in_nonzero = k_r_in[k_r_in != 0]
k_r_rec_nonzero = k_r_rec[k_r_rec != 0]
h_c_in_nonzero = h_c_in[h_c_in != 0]
h_c_out_nonzero = h_c_out[h_c_out != 0]
h_c_rec_nonzero = h_c_rec[h_c_rec != 0]
k_r_out_exp_nonzero = k_r_out_exp[k_r_out != 0]
k_r_in_exp_nonzero = k_r_in_exp[k_r_in != 0]
k_r_rec_exp_nonzero = k_r_rec_exp[k_r_rec != 0]
h_c_in_exp_nonzero = h_c_in_exp[h_c_in != 0]
h_c_out_exp_nonzero = h_c_out_exp[h_c_out != 0]
h_c_rec_exp_nonzero = h_c_rec_exp[h_c_rec != 0]
f1 = k_r_out_nonzero - k_r_out_exp_nonzero
f2 = h_c_in_nonzero - h_c_in_exp_nonzero
f3 = h_c_out_nonzero - h_c_out_exp_nonzero
f4 = k_r_in_nonzero - k_r_in_exp_nonzero
f5 = k_r_rec_nonzero - k_r_rec_exp_nonzero
f6 = h_c_rec_nonzero - h_c_rec_exp_nonzero
return np.concatenate((f1, f2, f3, f4, f5, f6))
def numerically_solve_rcm_bipartite_likelihood(m_adjacency_matrix, n_adjacency_matrix):
"""Solves the Bipartite RCM numerically with least squares.
Bipartite Reciprocated Binary Configuration Model is solved using the
system of equations. The optimization is done using
scipy.optimize.least_squares on the system of equations.
Args:
m_adjacency_matrix: numpy.array above diagonal rectangular matrix (binary)
n_adjacency_matrix: numpy.array under diagonal rectangular matrix (binary)
Returns:
loglikelihood of the configuration
"""
def safe_ln(x):
if x <= 0:
return 0
return np.log(x)
# Observed 'degrees'
r = m_adjacency_matrix.shape[0]
c = m_adjacency_matrix.shape[1]
k_r_out = np.zeros(r, dtype=np.int)
k_r_in = np.zeros(r, dtype=np.int)
k_r_rec = np.zeros(r, dtype=np.int)
h_c_in = np.zeros(c, dtype=np.int)
h_c_out = np.zeros(c, dtype=np.int)
h_c_rec = np.zeros(c, dtype=np.int)
for r_i in np.arange(r):
for c_i in np.arange(c):
k_r_out[r_i] += m_adjacency_matrix[r_i, c_i] * (1 - n_adjacency_matrix[c_i, r_i])
k_r_in[r_i] += n_adjacency_matrix[c_i, r_i] * (1 - m_adjacency_matrix[r_i, c_i])
k_r_rec[r_i] += m_adjacency_matrix[r_i, c_i] * (n_adjacency_matrix[c_i, r_i])
for c_i in np.arange(c):
for r_i in np.arange(r):
h_c_out[c_i] += n_adjacency_matrix[c_i, r_i] * (1 - m_adjacency_matrix[r_i, c_i])
h_c_in[c_i] += m_adjacency_matrix[r_i, c_i] * (1 - n_adjacency_matrix[c_i, r_i])
h_c_rec[c_i] += m_adjacency_matrix[r_i, c_i] * (n_adjacency_matrix[c_i, r_i])
# Rough estimate of initial values
x_initial_values_1 = k_r_out / np.sqrt(np.sum(k_r_out) + 1) # plus one to prevent dividing by zero
y_initial_values_1 = h_c_in / np.sqrt(np.sum(h_c_in) + 1)
z_initial_values_1 = h_c_rec / np.sqrt(np.sum(h_c_rec) + 1)
x_initial_values_2 = h_c_out / np.sqrt(np.sum(h_c_out) + 1)
y_initial_values_2 = k_r_in / np.sqrt(np.sum(k_r_in) + 1)
z_initial_values_2 = k_r_rec / np.sqrt(np.sum(k_r_rec) + 1)
x_initial_values_1 = x_initial_values_1[k_r_out != 0]
y_initial_values_1 = y_initial_values_1[h_c_in != 0]
z_initial_values_1 = z_initial_values_1[h_c_rec != 0]
x_initial_values_2 = x_initial_values_2[h_c_out != 0]
y_initial_values_2 = y_initial_values_2[k_r_in != 0]
z_initial_values_2 = z_initial_values_2[k_r_rec != 0]
initial_values = np.concatenate((x_initial_values_1, y_initial_values_1,
z_initial_values_1,
x_initial_values_2, y_initial_values_2,
z_initial_values_2))
boundslu = tuple([0] * len(initial_values)), tuple([np.inf] * len(initial_values))
x_solved = least_squares(fun=equations_to_solve_rcm_bipartite,
x0=initial_values,
args=(k_r_out, k_r_in, k_r_rec, h_c_in, h_c_out, h_c_rec,),
bounds=boundslu,
max_nfev=1e4,
ftol=1e-15, xtol=1e-15, gtol=1e-15)
print(x_solved.cost, x_solved.message)
# Numerical solution checks
assert x_solved.cost < 1, 'Numerical convergence problem: final cost function evaluation > 1'
# Set extremely small values to zero for likelihood problems (log(very small number) = large)
# x_solved.x[x_solved.x < 1e-7] = 0
r = len(k_r_out)
c = len(h_c_in)
p = np.array(x_solved.x)
n0_kro = np.count_nonzero(k_r_out)
n0_kri = np.count_nonzero(k_r_in)
n0_krr = np.count_nonzero(k_r_rec)
n0_hci = np.count_nonzero(h_c_in)
n0_hco = np.count_nonzero(h_c_out)
n0_hcr = np.count_nonzero(h_c_rec)
xrt_nonzero = p[0:n0_kro]
ycb_nonzero = p[n0_kro:n0_kro + n0_hci]
zcb_nonzero = p[n0_kro + n0_hci:n0_kro + n0_hci + n0_hcr]
xcb_nonzero = p[n0_kro + n0_hci + n0_hcr:n0_kro + n0_hci + n0_hcr + n0_hco]
yrt_nonzero = p[n0_kro + n0_hci + n0_hcr + n0_hco:n0_kro + n0_hci + n0_hcr + n0_hco + n0_kri]
zrt_nonzero = p[n0_kro + n0_hci + n0_hcr + n0_hco + n0_kri:len(p)]
xrt = np.zeros(r)
xrt[k_r_out != 0] = xrt_nonzero
ycb = np.zeros(c)
ycb[h_c_in != 0] = ycb_nonzero
zcb = np.zeros(c)
zcb[h_c_rec != 0] = zcb_nonzero
xcb = np.zeros(c)
xcb[h_c_out != 0] = xcb_nonzero
yrt = np.zeros(r)
yrt[k_r_in != 0] = yrt_nonzero
zrt = np.zeros(r)
zrt[k_r_rec != 0] = zrt_nonzero
l_r = 0
for r in np.arange(m_adjacency_matrix.shape[0]):
l_r += k_r_out[r] * safe_ln(xrt[r]) + k_r_in[r] * safe_ln(yrt[r]) + k_r_rec[r] * safe_ln(zrt[r])
l_c = 0
for c in np.arange(m_adjacency_matrix.shape[1]):
l_c += h_c_out[c] * safe_ln(xcb[c]) + h_c_in[c] * safe_ln(ycb[c]) + h_c_rec[c] * safe_ln(zcb[c])
l_rc = 0
for r in np.arange(m_adjacency_matrix.shape[0]):
for c in np.arange(m_adjacency_matrix.shape[1]):
l_rc += safe_ln(1 + xrt[r] * ycb[c] + xcb[c] * yrt[r] + zrt[r] * zcb[c])
likelihood = l_r + l_c - l_rc
# Probability matrices
p_out = np.zeros_like(m_adjacency_matrix, dtype=np.float)
for r in np.arange(m_adjacency_matrix.shape[0]):
for c in np.arange(m_adjacency_matrix.shape[1]):
denominator = (1 + xrt[r] * ycb[c] + xcb[c] * yrt[r] + zrt[r] * zcb[c])
p_out[r,c] = (xrt[r] * ycb[c]) / denominator
p_in = np.zeros_like(n_adjacency_matrix, dtype=np.float)
for c in np.arange(m_adjacency_matrix.shape[1]):
for r in np.arange(m_adjacency_matrix.shape[0]):
denominator = (1 + xrt[r] * ycb[c] + xcb[c] * yrt[r] + zrt[r] * zcb[c])
p_in[c,r] = (xcb[c] * yrt[r]) / denominator
p_rec = np.zeros_like(m_adjacency_matrix, dtype=np.float)
for r in np.arange(m_adjacency_matrix.shape[0]):
for c in np.arange(m_adjacency_matrix.shape[1]):
denominator = (1 + xrt[r] * ycb[c] + xcb[c] * yrt[r] + zrt[r] * zcb[c])
p_rec[r,c] = (zrt[r] * zcb[c]) / denominator
p_m = p_out + p_rec
p_n = p_in + np.transpose(p_rec)
return p_m, p_n, likelihood
def numerically_solve_block_rcm(adj, partitioning):
"""Solves the Bipartite RCM numerically with least squares for all blocks indicated
with the partitioning vector
Bipartite Reciprocated Binary Configuration Model is solved using the
system of equations. The optimization is done using
scipy.optimize.least_squares on the system of equations.
Args:
adj: numpy.array binary square adjacency matrix
partitioning: numpy.array integer vector of node belonging. e.g. [0,1,0,1],
for nodes 0&2 belonging to cluster one and nodes 1&3 belonging to cluster 2
Returns:
p_adj: numpy.array square matrix of probabilities.
"""
n_nodes = adj.shape[0]
B = len(set(partitioning))
p_adj = np.zeros_like(adj, dtype=np.float)
for i in np.arange(B):
for j in np.arange(B):
if i <= j:
adj_block = adj[np.ix_(np.where(partitioning==i)[0], np.where(partitioning==j)[0])]
if i == j: # Diagonal square block
if np.sum(adj_block) > 0: # Block with links
p_out, p_in, p_rec = numerically_solve_rcm(adj_block)
p_adj_block = p_out + p_in + p_rec
else: # Block without links
p_adj_block = np.zeros_like(adj_block)
p_adj[np.ix_(np.where(partitioning==i)[0], np.where(partitioning==j)[0])] = p_adj_block.copy()
else: # Off diagonal block
adj_block_lower = adj[np.ix_(np.where(partitioning==j)[0], np.where(partitioning==i)[0])]
if np.sum(adj_block) + np.sum(adj_block_lower) > 0: # Block with links
p_m_adj, p_n_adj, likelihood = numerically_solve_rcm_bipartite_likelihood(adj_block,
adj_block_lower)
else:
p_m_adj = np.zeros_like(adj_block)
p_n_adj = np.zeros_like(adj_block_lower)
p_adj[np.ix_(np.where(partitioning==i)[0], np.where(partitioning==j)[0])] = p_m_adj
p_adj[np.ix_(np.where(partitioning==j)[0], np.where(partitioning==i)[0])] = p_n_adj
return p_adj
```
## Example - block structures
```
n1 = 10 # Size first cluster
n2 = 8 # Size second cluster
a1 = (np.random.rand(n1,n1) < 0.7) # Generate random matrix blocks
a2 = (np.random.rand(n1,n2) < 0.2) # Low edge-density block
a3 = (np.random.rand(n2,n1) < 0.2)
a4 = (np.random.rand(n2,n2) < 0.7) # High edge-density block
adjacency_matrix = np.bmat([[a1, a2],
[a3, a4]]) # Join blocks
np.fill_diagonal(adjacency_matrix,0) # Prevent self-loops
adjacency_matrix = adjacency_matrix.astype(int) # Force binary links
adjacency_matrix = np.asarray(adjacency_matrix) # Format as np.ndarray instead of np.matrix
partitioning = np.concatenate([np.zeros(n1), np.ones(n2)]) # Cluster information
p_block_rcm = numerically_solve_block_rcm(adjacency_matrix, partitioning) # Solve block null model
p_out, p_in, p_rec = numerically_solve_rcm(adjacency_matrix) # Solve the non-block dcm
p_rcm = p_in + p_out + p_rec
adjacencies = [adjacency_matrix, p_block_rcm, p_rcm]
titles = ['Original matrix', 'Block-RCM probabilities', 'RCM probabilities (non-block)']
colormap = 'Blues'
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(15,5))
for i, ax in enumerate(axes.flat):
im = ax.imshow(adjacencies[i], vmin=0, vmax=1, cmap = colormap)
ax.set_title(titles[i])
fig.subplots_adjust(right=0.9)
cbar_ax = fig.add_axes([0.95, 0.15, 0.05, 0.7])
fig.colorbar(im, cax=cbar_ax)
cbar_ax.set_title('edge-probability')
plt.show()
```
### Useful links
This work was done within the [NETWORKS](http://networks.imtlucca.it/) research group at [IMT School for Advanced Studies Lucca](http://www.imtlucca.it/) with [Tiziano Squartini](https://www.imtlucca.it/tiziano.squartini), [Guido Caldarelli](http://www.guidocaldarelli.com/), [Fabio Saracco](https://www.imtlucca.it/fabio.saracco) and [Riccardo Di Clemente](http://www.riccardodiclemente.com/) at UCL .
The Maximum Entropy null models are based on the many works of the collaborators mentioned above, see also [Maximum-Entropy Networks](https://www.springer.com/it/book/9783319694368), [The Statistical Physics of Real-World Networks](https://arxiv.org/abs/1810.05095) and [Analytical maximum-likelihood method to detect patterns in real networks](http://iopscience.iop.org/article/10.1088/1367-2630/13/8/083001/meta).
For more information, please check out our [paper](https://arxiv.org/abs/1805.06005).
|
github_jupyter
|
from numba import jit
import numpy as np
# For the numerical solver
from scipy.optimize import least_squares
@jit
def equations_to_solve_dcm(p, k_out, k_in):
"""DCM equations for numerical solver.
Args:
p: list of independent variables [x y]
adjacency_matrix: numpy.array adjacency matrix to be solved
Returns:
numpy array of observed degree - expected degree
"""
n_nodes = len(k_out)
# print(len(p), len(k_out), len(k_in))
p = np.array(p)
num_x_nonzero_nodes = np.count_nonzero(k_out)
x_nonzero = p[0:num_x_nonzero_nodes]
y_nonzero = p[num_x_nonzero_nodes:len(p)]
x = np.zeros(n_nodes)
x[k_out != 0] = x_nonzero
y = np.zeros(n_nodes)
y[k_in != 0] = y_nonzero
# Expected degrees
k_out_exp = np.zeros(x.shape[0])
k_in_exp = np.zeros(x.shape[0])
for i in np.arange(x.shape[0]):
for j in np.arange(x.shape[0]):
if i != j:
k_out_exp[i] += (x[i] * y[j]) / (1 + x[i] * y[j])
k_in_exp[i] += (x[j] * y[i]) / (1 + x[j] * y[i])
k_out_nonzero = k_out[k_out != 0]
k_in_nonzero = k_in[k_in != 0]
k_out_exp_nonzero = k_out_exp[k_out != 0]
k_in_exp_nonzero = k_in_exp[k_in != 0]
f1 = k_out_nonzero - k_out_exp_nonzero
f2 = k_in_nonzero - k_in_exp_nonzero
return np.concatenate((f1, f2))
def numerically_solve_dcm(adjacency_matrix):
"""Solves the DCM numerically with least squares.
Directed Binary Configuration Model is solved using the
system of equations. The optimization is done using
scipy.optimize.least_squares on the system of equations.
Args:
adjacency_matrix : numpy.array adjacency matrix (binary, square)
Returns:
numpy.array probability matrix with dcm probabilities
"""
n_nodes = len(adjacency_matrix)
# Rough estimate of initial values
k_in = np.sum(adjacency_matrix, 0)
k_out = np.sum(adjacency_matrix, 1)
x_initial_values = k_out / np.sqrt(np.sum(k_out) + 1) # plus one to prevent dividing by zero
y_initial_values = k_in / np.sqrt(np.sum(k_in) + 1)
x_initial_values = x_initial_values[k_out != 0]
y_initial_values = y_initial_values[k_in != 0]
initial_values = np.concatenate((x_initial_values, y_initial_values))
#print(len(adjacency_matrix), len(x_initial_values), len(y_initial_values))
boundslu = tuple([0] * len(initial_values)), tuple([np.inf] * len(initial_values))
x_solved = least_squares(fun=equations_to_solve_dcm,
x0=initial_values,
args=(k_out, k_in,),
bounds=boundslu,
max_nfev=1e2,
ftol=1e-5, xtol=1e-5, gtol=1e-5)
print(x_solved.cost, x_solved.message)
# Numerical solution checks
assert x_solved.cost < 0.1, 'Numerical convergence problem: final cost function evaluation > 1'
# Set extremely small values to zero
# x_solved.x[x_solved.x < 1e-8] = 0
p = x_solved.x
p = np.array(p)
num_x_nonzero_nodes = np.count_nonzero(k_out)
x_nonzero = p[0:num_x_nonzero_nodes]
y_nonzero = p[num_x_nonzero_nodes:len(p)]
x = np.zeros(n_nodes)
x[k_out != 0] = x_nonzero
y = np.zeros(n_nodes)
y[k_in != 0] = y_nonzero
x_array = x
y_array = y
p_adjacency = np.zeros([n_nodes, n_nodes])
for i in np.arange(n_nodes):
for j in np.arange(n_nodes):
if i == j:
continue
p_adjacency[i, j] = x_array[i] * y_array[j] / (1 + x_array[i] * y_array[j])
return p_adjacency
@jit
def equations_to_solve_dcm_bipartite(p, k_r_out, h_c_in, h_c_out, k_r_in):
"""DCM Bipartite equations for numerical solver.
Args:
p: list of independent variables [x y]
m_adjacency_matrix: above diagonal rectangular matrix
n_adjacency_matrix: under diagonal rectangular matrix
Returns:
numpy array of observed degree - expected degree
"""
r = len(k_r_out)
c = len(h_c_in)
p = np.array(p)
num_nonzero_kro = np.count_nonzero(k_r_out)
num_nonzero_hci = np.count_nonzero(h_c_in)
num_nonzero_hco = np.count_nonzero(h_c_out)
num_nonzero_kri = np.count_nonzero(k_r_in)
xrt_nonzero = p[0:num_nonzero_kro]
ycb_nonzero = p[num_nonzero_kro:num_nonzero_kro + num_nonzero_hci]
xcb_nonzero = p[num_nonzero_kro + num_nonzero_hci:num_nonzero_kro + num_nonzero_hci + num_nonzero_hco]
yrt_nonzero = p[num_nonzero_kro + num_nonzero_hci + num_nonzero_hco:len(p)]
xrt = np.zeros(r)
xrt[k_r_out != 0] = xrt_nonzero
ycb = np.zeros(c)
ycb[h_c_in != 0] = ycb_nonzero
xcb = np.zeros(c)
xcb[h_c_out != 0] = xcb_nonzero
yrt = np.zeros(r)
yrt[k_r_in != 0] = yrt_nonzero
# Expected degrees
k_r_out_exp = np.zeros(r)
h_c_in_exp = np.zeros(c)
h_c_out_exp = np.zeros(c)
k_r_in_exp = np.zeros(r)
for r_i in np.arange(r):
for c_i in np.arange(c):
xrt_ycb = (xrt[r_i] * ycb[c_i]) / (1 + xrt[r_i] * ycb[c_i])
k_r_out_exp[r_i] += xrt_ycb
h_c_in_exp[c_i] += xrt_ycb
xcb_yrt = (xcb[c_i] * yrt[r_i]) / (1 + xcb[c_i] * yrt[r_i])
h_c_out_exp[c_i] += xcb_yrt
k_r_in_exp[r_i] += xcb_yrt
k_r_out_nonzero = k_r_out[k_r_out != 0]
h_c_in_nonzero = h_c_in[h_c_in != 0]
h_c_out_nonzero = h_c_out[h_c_out != 0]
k_r_in_nonzero = k_r_in[k_r_in != 0]
k_r_out_exp_nonzero = k_r_out_exp[k_r_out != 0]
h_c_in_exp_nonzero = h_c_in_exp[h_c_in != 0]
h_c_out_exp_nonzero = h_c_out_exp[h_c_out != 0]
k_r_in_exp_nonzero = k_r_in_exp[k_r_in != 0]
f1 = k_r_out_nonzero - k_r_out_exp_nonzero
f2 = h_c_in_nonzero - h_c_in_exp_nonzero
f3 = h_c_out_nonzero - h_c_out_exp_nonzero
f4 = k_r_in_nonzero - k_r_in_exp_nonzero
return np.concatenate((f1, f2, f3, f4))
def numerically_solve_dcm_bipartite_likelihood(m_adjacency_matrix, n_adjacency_matrix):
"""Solves the Bipartite DCM numerically with least squares.
Bipartite Directed Binary Configuration Model is solved using the
system of equations. The optimization is done using
scipy.optimize.least_squares on the system of equations.
Args:
m_adjacency_matrix: numpy.array above diagonal rectangular matrix (binary)
n_adjacency_matrix: numpy.array under diagonal rectangular matrix (binary)
Returns:
loglikelihood of the configuration
"""
def safe_ln(x):
if x <= 0:
return 0
return np.log(x)
# Observed degrees
k_r_out = np.sum(m_adjacency_matrix, 1)
h_c_in = np.sum(m_adjacency_matrix, 0)
h_c_out = np.sum(n_adjacency_matrix, 1)
k_r_in = np.sum(n_adjacency_matrix, 0)
# Rough estimate of initial values
x_initial_values_1 = k_r_out / np.sqrt(np.sum(k_r_out) + 1) # plus one to prevent dividing by zero
y_initial_values_1 = h_c_in / np.sqrt(np.sum(h_c_in) + 1)
x_initial_values_2 = h_c_out / np.sqrt(np.sum(h_c_out) + 1)
y_initial_values_2 = k_r_in / np.sqrt(np.sum(k_r_in) + 1)
x_initial_values_1 = x_initial_values_1[k_r_out != 0]
y_initial_values_1 = y_initial_values_1[h_c_in != 0]
x_initial_values_2 = x_initial_values_2[h_c_out != 0]
y_initial_values_2 = y_initial_values_2[k_r_in != 0]
initial_values = np.concatenate((x_initial_values_1, y_initial_values_1,
x_initial_values_2, y_initial_values_2))
boundslu = tuple([0] * len(initial_values)), tuple([np.inf] * len(initial_values))
x_solved = least_squares(fun=equations_to_solve_dcm_bipartite,
x0=initial_values,
args=(k_r_out, h_c_in, h_c_out, k_r_in,),
bounds=boundslu,
max_nfev=1e4,
ftol=1e-15, xtol=1e-15, gtol=1e-15)
print(x_solved.cost, x_solved.message)
# Numerical solution checks
assert x_solved.cost < 1, 'Numerical convergence problem: final cost function evaluation > 1'
# Set extremely small values to zero for likelihood problems (log(very small number) = large)
# x_solved.x[x_solved.x < 1e-7] = 0
r = len(k_r_out)
c = len(h_c_in)
p = np.array(x_solved.x)
num_nonzero_kro = np.count_nonzero(k_r_out)
num_nonzero_hci = np.count_nonzero(h_c_in)
num_nonzero_hco = np.count_nonzero(h_c_out)
num_nonzero_kri = np.count_nonzero(k_r_in)
xrt_nonzero = p[0:num_nonzero_kro]
ycb_nonzero = p[num_nonzero_kro:num_nonzero_kro + num_nonzero_hci]
xcb_nonzero = p[num_nonzero_kro + num_nonzero_hci:num_nonzero_kro + num_nonzero_hci + num_nonzero_hco]
yrt_nonzero = p[num_nonzero_kro + num_nonzero_hci + num_nonzero_hco:len(p)]
xrt = np.zeros(r)
xrt[k_r_out != 0] = xrt_nonzero
ycb = np.zeros(c)
ycb[h_c_in != 0] = ycb_nonzero
xcb = np.zeros(c)
xcb[h_c_out != 0] = xcb_nonzero
yrt = np.zeros(r)
yrt[k_r_in != 0] = yrt_nonzero
l_r = 0
for r in np.arange(m_adjacency_matrix.shape[0]):
l_r += (k_r_out[r] * safe_ln(xrt[r])) + (k_r_in[r] * safe_ln(yrt[r]))
l_c = 0
for c in np.arange(m_adjacency_matrix.shape[1]):
l_c += (h_c_out[c] * safe_ln(xcb[c])) + (h_c_in[c] * safe_ln(ycb[c]))
l_rc = 0
for r in np.arange(m_adjacency_matrix.shape[0]):
for c in np.arange(m_adjacency_matrix.shape[1]):
l_rc += safe_ln((1 + xrt[r] * ycb[c]) * (1 + xcb[c] * yrt[r]))
likelihood = l_r + l_c - l_rc
#print(m_adjacency_matrix, n_adjacency_matrix)
#print(xrt, ycb, xcb,yrt)
p_m_adj = np.zeros_like(m_adjacency_matrix, dtype=np.float)
for r in np.arange(m_adjacency_matrix.shape[0]):
for c in np.arange(m_adjacency_matrix.shape[1]):
p_m_adj[r,c] = (xrt[r]*ycb[c]) / (1+(xrt[r]*ycb[c]))
p_n_adj = np.zeros_like(n_adjacency_matrix, dtype=np.float)
for c in np.arange(m_adjacency_matrix.shape[1]):
for r in np.arange(m_adjacency_matrix.shape[0]):
p_n_adj[c,r] = (xcb[c]*yrt[r]) / (1+(xcb[c]*yrt[r]))
return p_m_adj, p_n_adj, likelihood
def numerically_solve_block_dcm(adj, partitioning):
"""Solves the Bipartite DCM numerically with least squares for all blocks indicated
with the partitioning vector
Bipartite Directed Binary Configuration Model is solved using the
system of equations. The optimization is done using
scipy.optimize.least_squares on the system of equations.
Args:
adj: numpy.array binary square adjacency matrix
partitioning: numpy.array integer vector of node belonging. e.g. [0,1,0,1],
for nodes 0&2 belonging to cluster one and nodes 1&3 belonging to cluster 2
Returns:
p_adj: numpy.array square matrix of probabilities.
"""
n_nodes = adj.shape[0]
B = len(set(partitioning))
p_adj = np.zeros_like(adj, dtype=np.float)
for i in np.arange(B):
for j in np.arange(B):
if i <= j:
adj_block = adj[np.ix_(np.where(partitioning==i)[0], np.where(partitioning==j)[0])]
if i == j: # Diagonal square block
if np.sum(adj_block) > 0: # Block with links
p_adj_block = numerically_solve_dcm(adj_block)
else: # Block without links
p_adj_block = np.zeros_like(adj_block)
p_adj[np.ix_(np.where(partitioning==i)[0], np.where(partitioning==j)[0])] = p_adj_block.copy()
else: # Off diagonal block
adj_block_lower = adj[np.ix_(np.where(partitioning==j)[0], np.where(partitioning==i)[0])]
if np.sum(adj_block) + np.sum(adj_block_lower) > 0: # Block with links
p_m_adj, p_n_adj, likelihood = numerically_solve_dcm_bipartite_likelihood(adj_block,
adj_block_lower)
else:
p_m_adj = np.zeros_like(adj_block)
p_n_adj = np.zeros_like(adj_block_lower)
p_adj[np.ix_(np.where(partitioning==i)[0], np.where(partitioning==j)[0])] = p_m_adj
p_adj[np.ix_(np.where(partitioning==j)[0], np.where(partitioning==i)[0])] = p_n_adj
return p_adj
n1 = 10 # Size first cluster
n2 = 8 # Size second cluster
a1 = (np.random.rand(n1,n1) < 0.7) # Generate random matrix blocks
a2 = (np.random.rand(n1,n2) < 0.2) # Low edge-density block
a3 = (np.random.rand(n2,n1) < 0.2)
a4 = (np.random.rand(n2,n2) < 0.7) # High edge-density block
adjacency_matrix = np.bmat([[a1, a2],
[a3, a4]]) # Join blocks
np.fill_diagonal(adjacency_matrix,0) # Prevent self-loops
adjacency_matrix = adjacency_matrix.astype(int) # Force binary links
adjacency_matrix = np.asarray(adjacency_matrix) # Format as np.ndarray instead of np.matrix
partitioning = np.concatenate([np.zeros(n1), np.ones(n2)]) # Cluster information
# Loading matplotlib library for visualisation
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
p_adj = numerically_solve_block_dcm(adjacency_matrix, partitioning) # Solve block null model
p_dcm = numerically_solve_dcm(adjacency_matrix) # Solve the non-block dcm
adjacencies = [adjacency_matrix, p_adj, p_dcm]
titles = ['Original matrix', 'Block-DCM probabilities', 'DCM probabilities (non-block)']
colormap = 'Blues'
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(15,5))
for i, ax in enumerate(axes.flat):
im = ax.imshow(adjacencies[i], vmin=0, vmax=1, cmap = colormap)
ax.set_title(titles[i])
fig.subplots_adjust(right=0.9)
cbar_ax = fig.add_axes([0.95, 0.15, 0.05, 0.7])
fig.colorbar(im, cax=cbar_ax)
cbar_ax.set_title('edge-probability')
plt.show()
@jit
def equations_to_solve_rcm(p, k_out, k_in, k_rec):
"""RCM equations for numerical solver.
Args:
p: list of independent variables [x y z]
adjacency_matrix: adjacency matrix to be solved
Returns:
numpy array of observed degree - expected degree
"""
n_nodes = len(k_out)
p = np.array(p)
num_x_nonzero_nodes = np.count_nonzero(k_out)
num_y_nonzero_nodes = np.count_nonzero(k_in)
x_nonzero = p[0:num_x_nonzero_nodes]
y_nonzero = p[num_x_nonzero_nodes:num_x_nonzero_nodes + num_y_nonzero_nodes]
z_nonzero = p[num_x_nonzero_nodes + num_y_nonzero_nodes:len(p)]
# print(len(k_out),len(k_in),len(k_rec),len(x_nonzero),len(y_nonzero),len(z_nonzero))
x = np.zeros(n_nodes)
x[k_out != 0] = x_nonzero
y = np.zeros(n_nodes)
y[k_in != 0] = y_nonzero
z = np.zeros(n_nodes)
z[k_rec != 0] = z_nonzero
# Expected degrees
k_out_exp = np.zeros(x.shape[0])
k_in_exp = np.zeros(x.shape[0])
k_rec_exp = np.zeros(x.shape[0])
for i in np.arange(x.shape[0]):
for j in np.arange(x.shape[0]):
if i != j:
k_out_exp[i] += (x[i] * y[j]) / (1 + x[i] * y[j] + x[j] * y[i] + z[i] * z[j])
k_in_exp[i] += (x[j] * y[i]) / (1 + x[i] * y[j] + x[j] * y[i] + z[i] * z[j])
k_rec_exp[i] += (z[i] * z[j]) / (1 + x[i] * y[j] + x[j] * y[i] + z[i] * z[j])
k_out_nonzero = k_out[k_out != 0]
k_in_nonzero = k_in[k_in != 0]
k_rec_nonzero = k_rec[k_rec != 0]
k_out_exp_nonzero = k_out_exp[k_out != 0]
k_in_exp_nonzero = k_in_exp[k_in != 0]
k_rec_exp_nonzero = k_rec_exp[k_rec != 0]
f1 = k_out_nonzero - k_out_exp_nonzero
f2 = k_in_nonzero - k_in_exp_nonzero
f3 = k_rec_nonzero - k_rec_exp_nonzero
return np.concatenate((f1, f2, f3))
def numerically_solve_rcm(adjacency_matrix):
"""Solves the RCM numerically with least squares.
Reciprocated Binary Configuration Model is solved using the
system of equations. The optimization is done using
scipy.optimize.least_squares on the system of equations.
Args:
adjacency_matrix : numpy.array adjacency matrix (binary, square)
Returns:
numpy.array probability matrices with dcm probabilities:
p_out_edges, p_in_edges, p_reciprocated_edges
"""
n_nodes = len(adjacency_matrix)
# Observed degrees
k_rec = np.zeros(adjacency_matrix.shape[0], dtype=np.int)
k_out = np.zeros(adjacency_matrix.shape[0], dtype=np.int)
k_in = np.zeros(adjacency_matrix.shape[0], dtype=np.int)
for i in np.arange(adjacency_matrix.shape[0]):
for j in np.arange(adjacency_matrix.shape[0]):
if i != j:
k_rec_i = np.min((adjacency_matrix[i, j], adjacency_matrix[j, i]))
k_out[i] += adjacency_matrix[i, j] - k_rec_i
k_in[i] += adjacency_matrix[j, i] - k_rec_i
k_rec[i] += k_rec_i
# Rough estimate of initial values
x_initial_values = k_out / np.sqrt(np.sum(k_out) + 1) # plus one to prevent dividing by zero
y_initial_values = k_in / np.sqrt(np.sum(k_in) + 1)
z_initial_values = k_rec / np.sqrt(np.sum(k_rec) + 1)
x_initial_values = x_initial_values[k_out != 0]
y_initial_values = y_initial_values[k_in != 0]
z_initial_values = z_initial_values[k_rec != 0]
initial_values = np.concatenate((x_initial_values, y_initial_values, z_initial_values))
boundslu = tuple([0] * len(initial_values)), tuple([np.inf] * len(initial_values))
x_solved = least_squares(fun=equations_to_solve_rcm,
x0=initial_values,
args=(k_out, k_in, k_rec,),
bounds=boundslu,
max_nfev=1e4,
ftol=1e-15, xtol=1e-15, gtol=1e-15)
print(x_solved.cost, x_solved.message)
# Numerical solution checks
assert x_solved.cost < 1, 'Numerical convergence problem: final cost function evaluation > 1'
p = np.array(x_solved.x)
num_x_nonzero_nodes = np.count_nonzero(k_out)
num_y_nonzero_nodes = np.count_nonzero(k_in)
x_nonzero = p[0:num_x_nonzero_nodes]
y_nonzero = p[num_x_nonzero_nodes:num_x_nonzero_nodes + num_y_nonzero_nodes]
z_nonzero = p[num_x_nonzero_nodes + num_y_nonzero_nodes:len(p)]
x = np.zeros(n_nodes)
x[k_out != 0] = x_nonzero
y = np.zeros(n_nodes)
y[k_in != 0] = y_nonzero
z = np.zeros(n_nodes)
z[k_rec != 0] = z_nonzero
x_array = x
y_array = y
z_array = z
p_out = np.zeros([n_nodes, n_nodes])
for i in np.arange(n_nodes):
for j in np.arange(n_nodes):
if i == j:
continue
p_out[i, j] = x_array[i] * y_array[j] / (
1 + x_array[i] * y_array[j] + x_array[j] * y_array[i] + z_array[i] * z_array[j])
p_in = np.zeros([n_nodes, n_nodes])
for i in np.arange(n_nodes):
for j in np.arange(n_nodes):
if i == j:
continue
p_in[i, j] = x_array[j] * y_array[i] / (
1 + x_array[i] * y_array[j] + x_array[j] * y_array[i] + z_array[i] * z_array[j])
p_rec = np.zeros([n_nodes, n_nodes])
for i in np.arange(n_nodes):
for j in np.arange(n_nodes):
if i == j:
continue
p_rec[i, j] = z_array[i] * z_array[j] / (
1 + x_array[i] * y_array[j] + x_array[j] * y_array[i] + z_array[i] * z_array[j])
return p_out, p_in, p_rec
@jit
def equations_to_solve_rcm_bipartite(p, k_r_out, k_r_in, k_r_rec, h_c_in, h_c_out, h_c_rec):
"""RCM Bipartite equations for numerical solver.
Args:
p: list of independent variables [x y]
m_adjacency_matrix: above diagonal rectangular matrix
n_adjacency_matrix: under diagonal rectangular matrix
Returns:
numpy array of observed degree - expected degree
"""
r = len(k_r_out)
c = len(h_c_in)
p = np.array(p)
n0_kro = np.count_nonzero(k_r_out)
n0_kri = np.count_nonzero(k_r_in)
n0_krr = np.count_nonzero(k_r_rec)
n0_hci = np.count_nonzero(h_c_in)
n0_hco = np.count_nonzero(h_c_out)
n0_hcr = np.count_nonzero(h_c_rec)
xrt_nonzero = p[0:n0_kro]
ycb_nonzero = p[n0_kro:n0_kro + n0_hci]
zcb_nonzero = p[n0_kro + n0_hci:n0_kro + n0_hci + n0_hcr]
xcb_nonzero = p[n0_kro + n0_hci + n0_hcr:n0_kro + n0_hci + n0_hcr + n0_hco]
yrt_nonzero = p[n0_kro + n0_hci + n0_hcr + n0_hco:n0_kro + n0_hci + n0_hcr + n0_hco + n0_kri]
zrt_nonzero = p[n0_kro + n0_hci + n0_hcr + n0_hco + n0_kri:len(p)]
xrt = np.zeros(r)
xrt[k_r_out != 0] = xrt_nonzero
ycb = np.zeros(c)
ycb[h_c_in != 0] = ycb_nonzero
zcb = np.zeros(c)
zcb[h_c_rec != 0] = zcb_nonzero
xcb = np.zeros(c)
xcb[h_c_out != 0] = xcb_nonzero
yrt = np.zeros(r)
yrt[k_r_in != 0] = yrt_nonzero
zrt = np.zeros(r)
zrt[k_r_rec != 0] = zrt_nonzero
# Expected degrees
k_r_out_exp = np.zeros(r)
k_r_in_exp = np.zeros(r)
k_r_rec_exp = np.zeros(r)
h_c_in_exp = np.zeros(c)
h_c_out_exp = np.zeros(c)
h_c_rec_exp = np.zeros(c)
for r_i in np.arange(r):
for c_i in np.arange(c):
xrt_ycb = xrt[r_i] * ycb[c_i] / (1 + xrt[r_i] * ycb[c_i] + xcb[c_i] * yrt[r_i] + zrt[r_i] * zcb[c_i])
xcb_yrt = xcb[c_i] * yrt[r_i] / (1 + xrt[r_i] * ycb[c_i] + xcb[c_i] * yrt[r_i] + zrt[r_i] * zcb[c_i])
zrt_zcb = zrt[r_i] * zcb[c_i] / (1 + xrt[r_i] * ycb[c_i] + xcb[c_i] * yrt[r_i] + zrt[r_i] * zcb[c_i])
k_r_out_exp[r_i] += xrt_ycb
k_r_in_exp[r_i] += xcb_yrt
k_r_rec_exp[r_i] += zrt_zcb
h_c_in_exp[c_i] += xrt_ycb
h_c_out_exp[c_i] += xcb_yrt
h_c_rec_exp[c_i] += zrt_zcb
k_r_out_nonzero = k_r_out[k_r_out != 0]
k_r_in_nonzero = k_r_in[k_r_in != 0]
k_r_rec_nonzero = k_r_rec[k_r_rec != 0]
h_c_in_nonzero = h_c_in[h_c_in != 0]
h_c_out_nonzero = h_c_out[h_c_out != 0]
h_c_rec_nonzero = h_c_rec[h_c_rec != 0]
k_r_out_exp_nonzero = k_r_out_exp[k_r_out != 0]
k_r_in_exp_nonzero = k_r_in_exp[k_r_in != 0]
k_r_rec_exp_nonzero = k_r_rec_exp[k_r_rec != 0]
h_c_in_exp_nonzero = h_c_in_exp[h_c_in != 0]
h_c_out_exp_nonzero = h_c_out_exp[h_c_out != 0]
h_c_rec_exp_nonzero = h_c_rec_exp[h_c_rec != 0]
f1 = k_r_out_nonzero - k_r_out_exp_nonzero
f2 = h_c_in_nonzero - h_c_in_exp_nonzero
f3 = h_c_out_nonzero - h_c_out_exp_nonzero
f4 = k_r_in_nonzero - k_r_in_exp_nonzero
f5 = k_r_rec_nonzero - k_r_rec_exp_nonzero
f6 = h_c_rec_nonzero - h_c_rec_exp_nonzero
return np.concatenate((f1, f2, f3, f4, f5, f6))
def numerically_solve_rcm_bipartite_likelihood(m_adjacency_matrix, n_adjacency_matrix):
"""Solves the Bipartite RCM numerically with least squares.
Bipartite Reciprocated Binary Configuration Model is solved using the
system of equations. The optimization is done using
scipy.optimize.least_squares on the system of equations.
Args:
m_adjacency_matrix: numpy.array above diagonal rectangular matrix (binary)
n_adjacency_matrix: numpy.array under diagonal rectangular matrix (binary)
Returns:
loglikelihood of the configuration
"""
def safe_ln(x):
if x <= 0:
return 0
return np.log(x)
# Observed 'degrees'
r = m_adjacency_matrix.shape[0]
c = m_adjacency_matrix.shape[1]
k_r_out = np.zeros(r, dtype=np.int)
k_r_in = np.zeros(r, dtype=np.int)
k_r_rec = np.zeros(r, dtype=np.int)
h_c_in = np.zeros(c, dtype=np.int)
h_c_out = np.zeros(c, dtype=np.int)
h_c_rec = np.zeros(c, dtype=np.int)
for r_i in np.arange(r):
for c_i in np.arange(c):
k_r_out[r_i] += m_adjacency_matrix[r_i, c_i] * (1 - n_adjacency_matrix[c_i, r_i])
k_r_in[r_i] += n_adjacency_matrix[c_i, r_i] * (1 - m_adjacency_matrix[r_i, c_i])
k_r_rec[r_i] += m_adjacency_matrix[r_i, c_i] * (n_adjacency_matrix[c_i, r_i])
for c_i in np.arange(c):
for r_i in np.arange(r):
h_c_out[c_i] += n_adjacency_matrix[c_i, r_i] * (1 - m_adjacency_matrix[r_i, c_i])
h_c_in[c_i] += m_adjacency_matrix[r_i, c_i] * (1 - n_adjacency_matrix[c_i, r_i])
h_c_rec[c_i] += m_adjacency_matrix[r_i, c_i] * (n_adjacency_matrix[c_i, r_i])
# Rough estimate of initial values
x_initial_values_1 = k_r_out / np.sqrt(np.sum(k_r_out) + 1) # plus one to prevent dividing by zero
y_initial_values_1 = h_c_in / np.sqrt(np.sum(h_c_in) + 1)
z_initial_values_1 = h_c_rec / np.sqrt(np.sum(h_c_rec) + 1)
x_initial_values_2 = h_c_out / np.sqrt(np.sum(h_c_out) + 1)
y_initial_values_2 = k_r_in / np.sqrt(np.sum(k_r_in) + 1)
z_initial_values_2 = k_r_rec / np.sqrt(np.sum(k_r_rec) + 1)
x_initial_values_1 = x_initial_values_1[k_r_out != 0]
y_initial_values_1 = y_initial_values_1[h_c_in != 0]
z_initial_values_1 = z_initial_values_1[h_c_rec != 0]
x_initial_values_2 = x_initial_values_2[h_c_out != 0]
y_initial_values_2 = y_initial_values_2[k_r_in != 0]
z_initial_values_2 = z_initial_values_2[k_r_rec != 0]
initial_values = np.concatenate((x_initial_values_1, y_initial_values_1,
z_initial_values_1,
x_initial_values_2, y_initial_values_2,
z_initial_values_2))
boundslu = tuple([0] * len(initial_values)), tuple([np.inf] * len(initial_values))
x_solved = least_squares(fun=equations_to_solve_rcm_bipartite,
x0=initial_values,
args=(k_r_out, k_r_in, k_r_rec, h_c_in, h_c_out, h_c_rec,),
bounds=boundslu,
max_nfev=1e4,
ftol=1e-15, xtol=1e-15, gtol=1e-15)
print(x_solved.cost, x_solved.message)
# Numerical solution checks
assert x_solved.cost < 1, 'Numerical convergence problem: final cost function evaluation > 1'
# Set extremely small values to zero for likelihood problems (log(very small number) = large)
# x_solved.x[x_solved.x < 1e-7] = 0
r = len(k_r_out)
c = len(h_c_in)
p = np.array(x_solved.x)
n0_kro = np.count_nonzero(k_r_out)
n0_kri = np.count_nonzero(k_r_in)
n0_krr = np.count_nonzero(k_r_rec)
n0_hci = np.count_nonzero(h_c_in)
n0_hco = np.count_nonzero(h_c_out)
n0_hcr = np.count_nonzero(h_c_rec)
xrt_nonzero = p[0:n0_kro]
ycb_nonzero = p[n0_kro:n0_kro + n0_hci]
zcb_nonzero = p[n0_kro + n0_hci:n0_kro + n0_hci + n0_hcr]
xcb_nonzero = p[n0_kro + n0_hci + n0_hcr:n0_kro + n0_hci + n0_hcr + n0_hco]
yrt_nonzero = p[n0_kro + n0_hci + n0_hcr + n0_hco:n0_kro + n0_hci + n0_hcr + n0_hco + n0_kri]
zrt_nonzero = p[n0_kro + n0_hci + n0_hcr + n0_hco + n0_kri:len(p)]
xrt = np.zeros(r)
xrt[k_r_out != 0] = xrt_nonzero
ycb = np.zeros(c)
ycb[h_c_in != 0] = ycb_nonzero
zcb = np.zeros(c)
zcb[h_c_rec != 0] = zcb_nonzero
xcb = np.zeros(c)
xcb[h_c_out != 0] = xcb_nonzero
yrt = np.zeros(r)
yrt[k_r_in != 0] = yrt_nonzero
zrt = np.zeros(r)
zrt[k_r_rec != 0] = zrt_nonzero
l_r = 0
for r in np.arange(m_adjacency_matrix.shape[0]):
l_r += k_r_out[r] * safe_ln(xrt[r]) + k_r_in[r] * safe_ln(yrt[r]) + k_r_rec[r] * safe_ln(zrt[r])
l_c = 0
for c in np.arange(m_adjacency_matrix.shape[1]):
l_c += h_c_out[c] * safe_ln(xcb[c]) + h_c_in[c] * safe_ln(ycb[c]) + h_c_rec[c] * safe_ln(zcb[c])
l_rc = 0
for r in np.arange(m_adjacency_matrix.shape[0]):
for c in np.arange(m_adjacency_matrix.shape[1]):
l_rc += safe_ln(1 + xrt[r] * ycb[c] + xcb[c] * yrt[r] + zrt[r] * zcb[c])
likelihood = l_r + l_c - l_rc
# Probability matrices
p_out = np.zeros_like(m_adjacency_matrix, dtype=np.float)
for r in np.arange(m_adjacency_matrix.shape[0]):
for c in np.arange(m_adjacency_matrix.shape[1]):
denominator = (1 + xrt[r] * ycb[c] + xcb[c] * yrt[r] + zrt[r] * zcb[c])
p_out[r,c] = (xrt[r] * ycb[c]) / denominator
p_in = np.zeros_like(n_adjacency_matrix, dtype=np.float)
for c in np.arange(m_adjacency_matrix.shape[1]):
for r in np.arange(m_adjacency_matrix.shape[0]):
denominator = (1 + xrt[r] * ycb[c] + xcb[c] * yrt[r] + zrt[r] * zcb[c])
p_in[c,r] = (xcb[c] * yrt[r]) / denominator
p_rec = np.zeros_like(m_adjacency_matrix, dtype=np.float)
for r in np.arange(m_adjacency_matrix.shape[0]):
for c in np.arange(m_adjacency_matrix.shape[1]):
denominator = (1 + xrt[r] * ycb[c] + xcb[c] * yrt[r] + zrt[r] * zcb[c])
p_rec[r,c] = (zrt[r] * zcb[c]) / denominator
p_m = p_out + p_rec
p_n = p_in + np.transpose(p_rec)
return p_m, p_n, likelihood
def numerically_solve_block_rcm(adj, partitioning):
"""Solves the Bipartite RCM numerically with least squares for all blocks indicated
with the partitioning vector
Bipartite Reciprocated Binary Configuration Model is solved using the
system of equations. The optimization is done using
scipy.optimize.least_squares on the system of equations.
Args:
adj: numpy.array binary square adjacency matrix
partitioning: numpy.array integer vector of node belonging. e.g. [0,1,0,1],
for nodes 0&2 belonging to cluster one and nodes 1&3 belonging to cluster 2
Returns:
p_adj: numpy.array square matrix of probabilities.
"""
n_nodes = adj.shape[0]
B = len(set(partitioning))
p_adj = np.zeros_like(adj, dtype=np.float)
for i in np.arange(B):
for j in np.arange(B):
if i <= j:
adj_block = adj[np.ix_(np.where(partitioning==i)[0], np.where(partitioning==j)[0])]
if i == j: # Diagonal square block
if np.sum(adj_block) > 0: # Block with links
p_out, p_in, p_rec = numerically_solve_rcm(adj_block)
p_adj_block = p_out + p_in + p_rec
else: # Block without links
p_adj_block = np.zeros_like(adj_block)
p_adj[np.ix_(np.where(partitioning==i)[0], np.where(partitioning==j)[0])] = p_adj_block.copy()
else: # Off diagonal block
adj_block_lower = adj[np.ix_(np.where(partitioning==j)[0], np.where(partitioning==i)[0])]
if np.sum(adj_block) + np.sum(adj_block_lower) > 0: # Block with links
p_m_adj, p_n_adj, likelihood = numerically_solve_rcm_bipartite_likelihood(adj_block,
adj_block_lower)
else:
p_m_adj = np.zeros_like(adj_block)
p_n_adj = np.zeros_like(adj_block_lower)
p_adj[np.ix_(np.where(partitioning==i)[0], np.where(partitioning==j)[0])] = p_m_adj
p_adj[np.ix_(np.where(partitioning==j)[0], np.where(partitioning==i)[0])] = p_n_adj
return p_adj
n1 = 10 # Size first cluster
n2 = 8 # Size second cluster
a1 = (np.random.rand(n1,n1) < 0.7) # Generate random matrix blocks
a2 = (np.random.rand(n1,n2) < 0.2) # Low edge-density block
a3 = (np.random.rand(n2,n1) < 0.2)
a4 = (np.random.rand(n2,n2) < 0.7) # High edge-density block
adjacency_matrix = np.bmat([[a1, a2],
[a3, a4]]) # Join blocks
np.fill_diagonal(adjacency_matrix,0) # Prevent self-loops
adjacency_matrix = adjacency_matrix.astype(int) # Force binary links
adjacency_matrix = np.asarray(adjacency_matrix) # Format as np.ndarray instead of np.matrix
partitioning = np.concatenate([np.zeros(n1), np.ones(n2)]) # Cluster information
p_block_rcm = numerically_solve_block_rcm(adjacency_matrix, partitioning) # Solve block null model
p_out, p_in, p_rec = numerically_solve_rcm(adjacency_matrix) # Solve the non-block dcm
p_rcm = p_in + p_out + p_rec
adjacencies = [adjacency_matrix, p_block_rcm, p_rcm]
titles = ['Original matrix', 'Block-RCM probabilities', 'RCM probabilities (non-block)']
colormap = 'Blues'
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(15,5))
for i, ax in enumerate(axes.flat):
im = ax.imshow(adjacencies[i], vmin=0, vmax=1, cmap = colormap)
ax.set_title(titles[i])
fig.subplots_adjust(right=0.9)
cbar_ax = fig.add_axes([0.95, 0.15, 0.05, 0.7])
fig.colorbar(im, cax=cbar_ax)
cbar_ax.set_title('edge-probability')
plt.show()
| 0.689933 | 0.956553 |
# Appendix A - Scrape & Build NBA Salary Dataset
The goal of this notebook is to prepare our course with a pre-existing dataset. The data cleaning is done in the course itself; this is meant only to create the dataset.
```
# %pip install requests requests-html matplotlib pandas
import datetime
from decimal import Decimal
import matplotlib.pyplot as plt
import requests
from requests_html import HTML
import pandas as pd
import pathlib
import time
PERFROM_SCRAPE = True
BASE_DIR = pathlib.Path().resolve().parent.parent
COURSES_DIR = BASE_DIR / 'course'
DATASET_PATH = COURSES_DIR / 'datasets'
OUTPUT_PATH = DATASET_PATH / 'nba-historical-salaries.csv'
COURSES_DIR.exists()
```
For this dataset, we use `hoopshype.com`'s record of player salaries.
```
base_url = 'https://hoopshype.com/salaries/players/'
```
`hoopshype.com`'s salary data starts in the 1990-1991 season.
```
year_start = 1990
```
End scraping at last year's season (this year might not be available).
```
year_end = datetime.datetime.now().year - 1
year_end
dfs = []
if PERFROM_SCRAPE:
for year in range(year_start, year_end+1):
# NBA season spans 2 different calendar years
year_range = f"{year}-{year+1}"
# the lookup salary url is based on the above range
url = f"{base_url}{year_range}/"
# print year and url for manual review
print(year, url)
# perform lookup
r = requests.get(url)
# Convert response html text as a parsable object
html = HTML(html=r.text)
# Find the data table containing
table = html.find('table', first=True)
# table_data list holder
table_data = []
# iterate the table element and append all column values in each row
for el in table.element.getchildren():
for tr in el.getchildren():
row_data = []
for col in tr.getchildren():
row_data.append(col.text_content().strip())
table_data.append(row_data)
# create the initial dataframe
init_df = pd.DataFrame(table_data)
# use the first row as the header
new_header = init_df.iloc[0]
# use everything after the first row as our dataset
init_df = init_df[1:]
# update header
init_df.columns = new_header
# attempt to rename columns, if it's avaiable
# otherwise, move to the next year lookup
try:
renamed_cols = {
"Player": 'player',
f"{new_header[2]}": "salary",
f"{new_header[3]}": "adj_salary"
}
init_df = init_df.rename(columns=renamed_cols)
except:
continue
# create
try:
df = init_df.copy()[['player', 'salary', 'adj_salary']]
except:
continue
# update dataset with year values
df['year-start'] = year
df['year-end'] = year + 1
# append this dataset to our group of datasets
dfs.append(df)
# slow down lookups to ensure our scraping doesn't overload
# hoopshype.com
time.sleep(1.2)
```
Convert our list of dataframes (ie season salaries) into our entire dataset via pandas concat.
```
dataset_df = pd.concat(dfs) #[['player', 'year-start', 'year-end', 'salary', 'adj_salary']]
dataset_df.reset_index(drop=True, inplace=True)
dataset_df.shape
```
Store file to our course data
```
dataset_df.to_csv(OUTPUT_PATH, index=False)
```
|
github_jupyter
|
# %pip install requests requests-html matplotlib pandas
import datetime
from decimal import Decimal
import matplotlib.pyplot as plt
import requests
from requests_html import HTML
import pandas as pd
import pathlib
import time
PERFROM_SCRAPE = True
BASE_DIR = pathlib.Path().resolve().parent.parent
COURSES_DIR = BASE_DIR / 'course'
DATASET_PATH = COURSES_DIR / 'datasets'
OUTPUT_PATH = DATASET_PATH / 'nba-historical-salaries.csv'
COURSES_DIR.exists()
base_url = 'https://hoopshype.com/salaries/players/'
year_start = 1990
year_end = datetime.datetime.now().year - 1
year_end
dfs = []
if PERFROM_SCRAPE:
for year in range(year_start, year_end+1):
# NBA season spans 2 different calendar years
year_range = f"{year}-{year+1}"
# the lookup salary url is based on the above range
url = f"{base_url}{year_range}/"
# print year and url for manual review
print(year, url)
# perform lookup
r = requests.get(url)
# Convert response html text as a parsable object
html = HTML(html=r.text)
# Find the data table containing
table = html.find('table', first=True)
# table_data list holder
table_data = []
# iterate the table element and append all column values in each row
for el in table.element.getchildren():
for tr in el.getchildren():
row_data = []
for col in tr.getchildren():
row_data.append(col.text_content().strip())
table_data.append(row_data)
# create the initial dataframe
init_df = pd.DataFrame(table_data)
# use the first row as the header
new_header = init_df.iloc[0]
# use everything after the first row as our dataset
init_df = init_df[1:]
# update header
init_df.columns = new_header
# attempt to rename columns, if it's avaiable
# otherwise, move to the next year lookup
try:
renamed_cols = {
"Player": 'player',
f"{new_header[2]}": "salary",
f"{new_header[3]}": "adj_salary"
}
init_df = init_df.rename(columns=renamed_cols)
except:
continue
# create
try:
df = init_df.copy()[['player', 'salary', 'adj_salary']]
except:
continue
# update dataset with year values
df['year-start'] = year
df['year-end'] = year + 1
# append this dataset to our group of datasets
dfs.append(df)
# slow down lookups to ensure our scraping doesn't overload
# hoopshype.com
time.sleep(1.2)
dataset_df = pd.concat(dfs) #[['player', 'year-start', 'year-end', 'salary', 'adj_salary']]
dataset_df.reset_index(drop=True, inplace=True)
dataset_df.shape
dataset_df.to_csv(OUTPUT_PATH, index=False)
| 0.244273 | 0.871256 |
# Form Recognizer를 사용하여 영수증 분석

Computer Vision의 AI(인공 지능) 분야에서 OCR(광학 인식)은 인쇄된 문서나 필기 문서를 읽는 데 주로 사용됩니다. 종종 텍스트는 추가적인 처리 또는 분석에 사용할 수 있는 형식으로 문서에서 간단히 추출됩니다.
보다 진보된 OCR 시나리오는 양식의 필드가 나타내는 의미를 이해하면서 구매 주문서나 송장 같은 양식에서 정보를 추출하는 것입니다. **Form Recognizer** 서비스는 이러한 종류의 AI 문제를 위해 특별히 설계되었습니다.
## 영수증 보기
이 예에서는 Form Recognizer의 기본 제공 모델을 사용하여 영수증을 분석합니다.
아래의 **셀 실행**(▷) 단추(셀 왼쪽에 있음)를 클릭하여 실행하고 Form Recognizer를 사용하여 분석할 영수증의 예를 확인해 보세요.
```
import matplotlib.pyplot as plt
from PIL import Image
import os
%matplotlib inline
# Load and display a receipt image
fig = plt.figure(figsize=(6, 6))
image_path = os.path.join('data', 'form-receipt', 'receipt.jpg')
img = Image.open(image_path)
plt.axis('off')
plt.imshow(img)
```
## Form Recognizer 리소스 만들기
먼저 Azure 구독에서 Form Recognizer 리소스를 만듭니다.
1. 다른 브라우저 탭에서 Azure Portal(https://portal.azure.com) 을 열고 Microsoft 계정으로 로그인합니다.
2. **+ 리소스 만들기**를 선택하고 *Form Recognizer*를 검색합니다.
3. 서비스 목록에서 **Form Recognizer**를 선택합니다.
4. **Form Recognizer** 블레이드에서 **만들기**를 선택합니다.
5. **만들기** 블레이드에서 다음 세부 정보를 입력하고 **만들기**를 선택합니다.
- **이름**: 서비스의 고유한 이름
- **구독**: 사용자의 Azure 구독
- **지역**: 사용 가능한 영역
- **가격 책정 계층**: F0
- **리소스 그룹**: 이전에 사용한 기존 리소스 그룹
- **아래 알림을 읽고 이해했음을 확인합니다**. 선택됨.
6. 서비스가 생성될 때까지 기다립니다.
7. Azure Portal에서 새로 생성된 Form Recognizer 서비스를 확인합니다. 그리고 **키 및 엔드포인트** 페이지에서 **Key1** 및 **엔드포인트** 값을 복사하고 아래 코드 셀에 붙여 넣어 **YOUR_FORM_KEY** 및 **YOUR_FORM_ENDPOINT**를 대체합니다.
```
form_key = 'YOUR_FORM_KEY'
form_endpoint = 'YOUR_FORM_ENDPOINT'
print('Ready to use form recognizer at {} using key {}'.format(form_endpoint, form_key))
```
## 영수증 분석
이제 Form Recognizer를 사용하여 영수증을 분석할 준비가 되었습니다.
```
import os
from azure.ai.formrecognizer import FormRecognizerClient
from azure.core.credentials import AzureKeyCredential
# Create a client for the form recognizer service
form_recognizer_client = FormRecognizerClient(endpoint=form_endpoint, credential=AzureKeyCredential(form_key))
try:
print("Analyzing receipt...")
# Get the receipt image file
image_path = os.path.join('data', 'form-receipt', 'receipt.jpg')
# Submit the file data to form recognizer
with open(image_path, "rb") as f:
analyze_receipt = form_recognizer_client.begin_recognize_receipts(receipt=f)
# Get the results
receipt_data = analyze_receipt.result()
# Print the extracted data for the first (and only) receipt
receipt = receipt_data[0]
receipt_type = receipt.fields.get("ReceiptType")
if receipt_type:
print("Receipt Type: {}".format(receipt_type.value))
merchant_address = receipt.fields.get("MerchantAddress")
if merchant_address:
print("Merchant Address: {}".format(merchant_address.value))
merchant_phone = receipt.fields.get("MerchantPhoneNumber")
if merchant_phone:
print("Merchant Phone: {}".format(merchant_phone.value))
transaction_date = receipt.fields.get("TransactionDate")
if transaction_date:
print("Transaction Date: {}".format(transaction_date.value))
print("Receipt items:")
items = receipt.fields.get("Items")
if items:
for idx, item in enumerate(receipt.fields.get("Items").value):
print("\tItem #{}".format(idx+1))
item_name = item.value.get("Name")
if item_name:
print("\t - Name: {}".format(item_name.value))
item_total_price = item.value.get("TotalPrice")
if item_total_price:
print("\t - Price: {}".format(item_total_price.value))
subtotal = receipt.fields.get("Subtotal")
if subtotal:
print("Subtotal: {} ".format(subtotal.value))
tax = receipt.fields.get("Tax")
if tax:
print("Tax: {}".format(tax.value))
total = receipt.fields.get("Total")
if total:
print("Total: {}".format(total.value))
except Exception as ex:
print('Error:', ex)
```
Form Recognizer는 양식에 있는 데이터를 해석하여 가맹점 주소 및 전화번호, 거래 날짜 및 시간, 품목명, 소계, 세금, 총액을 올바르게 식별할 수 있습니다.
## 추가 정보
Form Recognizer 서비스에 대한 자세한 내용은 [Form Recognizer 설명서](https://docs.microsoft.com/ko-kr/azure/cognitive-services/form-recognizer/index)를 참조하세요.
|
github_jupyter
|
import matplotlib.pyplot as plt
from PIL import Image
import os
%matplotlib inline
# Load and display a receipt image
fig = plt.figure(figsize=(6, 6))
image_path = os.path.join('data', 'form-receipt', 'receipt.jpg')
img = Image.open(image_path)
plt.axis('off')
plt.imshow(img)
form_key = 'YOUR_FORM_KEY'
form_endpoint = 'YOUR_FORM_ENDPOINT'
print('Ready to use form recognizer at {} using key {}'.format(form_endpoint, form_key))
import os
from azure.ai.formrecognizer import FormRecognizerClient
from azure.core.credentials import AzureKeyCredential
# Create a client for the form recognizer service
form_recognizer_client = FormRecognizerClient(endpoint=form_endpoint, credential=AzureKeyCredential(form_key))
try:
print("Analyzing receipt...")
# Get the receipt image file
image_path = os.path.join('data', 'form-receipt', 'receipt.jpg')
# Submit the file data to form recognizer
with open(image_path, "rb") as f:
analyze_receipt = form_recognizer_client.begin_recognize_receipts(receipt=f)
# Get the results
receipt_data = analyze_receipt.result()
# Print the extracted data for the first (and only) receipt
receipt = receipt_data[0]
receipt_type = receipt.fields.get("ReceiptType")
if receipt_type:
print("Receipt Type: {}".format(receipt_type.value))
merchant_address = receipt.fields.get("MerchantAddress")
if merchant_address:
print("Merchant Address: {}".format(merchant_address.value))
merchant_phone = receipt.fields.get("MerchantPhoneNumber")
if merchant_phone:
print("Merchant Phone: {}".format(merchant_phone.value))
transaction_date = receipt.fields.get("TransactionDate")
if transaction_date:
print("Transaction Date: {}".format(transaction_date.value))
print("Receipt items:")
items = receipt.fields.get("Items")
if items:
for idx, item in enumerate(receipt.fields.get("Items").value):
print("\tItem #{}".format(idx+1))
item_name = item.value.get("Name")
if item_name:
print("\t - Name: {}".format(item_name.value))
item_total_price = item.value.get("TotalPrice")
if item_total_price:
print("\t - Price: {}".format(item_total_price.value))
subtotal = receipt.fields.get("Subtotal")
if subtotal:
print("Subtotal: {} ".format(subtotal.value))
tax = receipt.fields.get("Tax")
if tax:
print("Tax: {}".format(tax.value))
total = receipt.fields.get("Total")
if total:
print("Total: {}".format(total.value))
except Exception as ex:
print('Error:', ex)
| 0.517083 | 0.916671 |
# Random Walks
You start on the first floor of the Empire State Building. To determine your movements, you roll a single regular dice (die?).
One turn consists of the following:
If you roll 1 or 2, you move one floor down. Note that the first floor is the bottom of the building, so you can't go any lower! Instead, if you roll 3, 4, or 5, you move one floor up. Finally, if you roll a 6, you roll again, and whatever the result you move up that number of floors.
What is the likelihood, after 100 turns, that you are at at least the 70th floor? (Let's assume for simplicity that the Empire State Building has at least 600 floors, just in case.) We'll answer this question by simulating the game a very large number of times. To clarity, you want to END UP at at least the 70th floor; it is possible, after all, to reach that level then dip back down below the threshold.
One catch: at each turn, there's a 0.1% chance that you'll slip and fall back to the first floor. Because you're clumsy.
```
import numpy as np
import matplotlib.pyplot as plt
```
Let's start our analysis by considering just a single turn (described above). Suppose you are on the 50th floor. Here's a simulation of what happens on your next turn. For now, we'll ignore the possibility of slipping back down to the first floor.
```
# This ensures reproducibility. Same sequence of random numbers.
np.random.seed(123)
# Starting floor
floor = 50
# Roll the dice
dice = np.random.randint(1,7)
# if/elif/else structure
if dice <= 2:
floor = floor - 1
elif dice <= 5:
floor = floor + 1
else:
floor = floor + np.random.randint(1,7)
# Print out dice value, and the floor you're on after the turn
print(dice)
print(floor)
```
So according to this simulation, you rolled a 6, which means you rolled again. This time you must've gotten 3, so you moved up three floors to the 53rd.
All 100 turns will together comprise a RANDOM WALK. This random walk will take the form of a list. Let's run one simulation of the whole game, 100 turns.
```
# Initialize random_walk list, starting at floor 1
random_walk = [1]
for x in range(100) :
# At each iteration/turn, the starting floor is given by the ending floor at the previous iteration
floor = random_walk[-1]
dice = np.random.randint(1,7)
if dice <= 2:
# Use max to ensure floor can't go below 1
floor = max(1, floor - 1)
elif dice <= 5:
floor = floor + 1
else:
floor = floor + np.random.randint(1,7)
# Append result to list initialized above
random_walk.append(floor)
print(random_walk)
```
In this simulation, you didn't quite make it up to the 70th floor =(. But this is just one simulation, so it doesn't answer our original question.
Before we proceed to simulating the game multiple times, let's visualize the simulation done above.
```
# Using matplotlib.pyplot
plt.plot(random_walk)
plt.xlabel('Number of turns taken')
plt.ylabel('Floor')
plt.show()
```
Since a single random walk was recorded as a list, we'll record multiple random walks as a list of lists.
Let's start by executing 10 random walks, i.e., by playing the game 10 times. Notice the structure of a nested 'for' loop.
```
# Initialize empty list of lists
all_walks = []
# Simulate random walk 10 times
for i in range(10) :
# Code from before
random_walk = [1]
for x in range(100) :
floor = random_walk[-1]
dice = np.random.randint(1,7)
if dice <= 2:
floor = max(1, floor - 1)
elif dice <= 5:
floor = floor + 1
else:
floor = floor + np.random.randint(1,7)
random_walk.append(floor)
# Append random_walk to all_walks
all_walks.append(random_walk)
print(all_walks)
```
So we get a list with 10 sublists, with each sublist representing a random walk. It's not immediately clear which walks end up at floor 70 or higher. Really we only care about the last element of each of these sublists, the floor at which the walk ends.
But for now, let's create a visually appealing plot of these walks. We'll first convert all_walks to a numpy array, then transpose it, then plot.
```
# Convert all_walks to Numpy array called np_aw
np_aw = np.array(all_walks)
# Transpose np_aw: np_aw_t
np_aw_t = np.transpose(np_aw)
# Plot np_aw_t and show
plt.plot(np_aw_t)
plt.xlabel('Number of turns taken')
plt.ylabel('Floor')
plt.show()
```
Now let's code in your clumsiness, increase the number of simulations, and re-plot.
```
# Initialize empty list of lists, as before
all_walks = []
# Simulate random walk 250 times!
for i in range(250) :
random_walk = [1]
for x in range(100) :
floor = random_walk[-1]
dice = np.random.randint(1,7)
if dice <= 2:
floor = max(1, floor - 1)
elif dice <= 5:
floor = floor + 1
else:
floor = floor + np.random.randint(1,7)
# Implement clumsiness
if np.random.rand(1,1) < 0.001 :
floor = 1
random_walk.append(floor)
all_walks.append(random_walk)
np_aw_t = np.transpose(np.array(all_walks))
plt.plot(np_aw_t)
plt.xlabel('Number of turns taken')
plt.ylabel('Floor')
plt.show()
```
```
all_walks = []
# Simulate random walk 1000 times, because why not
for i in range(1000) :
random_walk = [1]
for x in range(100) :
floor = random_walk[-1]
dice = np.random.randint(1,7)
if dice <= 2:
floor = max(1, floor - 1)
elif dice <= 5:
floor = floor + 1
else:
floor = floor + np.random.randint(1,7)
if np.random.rand() <= 0.001 :
floor = 1
random_walk.append(floor)
all_walks.append(random_walk)
np_aw_t = np.transpose(np.array(all_walks))
# Recover endpoints from np_aw_t
ends = np_aw_t[-1]
# Plot histogram of ends
plt.hist(ends, ec="black")
plt.xlabel('ending floor')
plt.ylabel('number of random walks')
plt.show()
```
Now to find the desired probability....
```
# We are interested in the endpoints greater than or equal to 70
win_the_game = ends[ends >= 70]
# More specifically, the number of such outcomes, divided by 1000
len(win_the_game) / 1000
```
Answer: we've got about a 61% chance of ending up at floor 70 or higher!!
What if our goal was to reach the 60th floor? The 50th floor?
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
# This ensures reproducibility. Same sequence of random numbers.
np.random.seed(123)
# Starting floor
floor = 50
# Roll the dice
dice = np.random.randint(1,7)
# if/elif/else structure
if dice <= 2:
floor = floor - 1
elif dice <= 5:
floor = floor + 1
else:
floor = floor + np.random.randint(1,7)
# Print out dice value, and the floor you're on after the turn
print(dice)
print(floor)
# Initialize random_walk list, starting at floor 1
random_walk = [1]
for x in range(100) :
# At each iteration/turn, the starting floor is given by the ending floor at the previous iteration
floor = random_walk[-1]
dice = np.random.randint(1,7)
if dice <= 2:
# Use max to ensure floor can't go below 1
floor = max(1, floor - 1)
elif dice <= 5:
floor = floor + 1
else:
floor = floor + np.random.randint(1,7)
# Append result to list initialized above
random_walk.append(floor)
print(random_walk)
# Using matplotlib.pyplot
plt.plot(random_walk)
plt.xlabel('Number of turns taken')
plt.ylabel('Floor')
plt.show()
# Initialize empty list of lists
all_walks = []
# Simulate random walk 10 times
for i in range(10) :
# Code from before
random_walk = [1]
for x in range(100) :
floor = random_walk[-1]
dice = np.random.randint(1,7)
if dice <= 2:
floor = max(1, floor - 1)
elif dice <= 5:
floor = floor + 1
else:
floor = floor + np.random.randint(1,7)
random_walk.append(floor)
# Append random_walk to all_walks
all_walks.append(random_walk)
print(all_walks)
# Convert all_walks to Numpy array called np_aw
np_aw = np.array(all_walks)
# Transpose np_aw: np_aw_t
np_aw_t = np.transpose(np_aw)
# Plot np_aw_t and show
plt.plot(np_aw_t)
plt.xlabel('Number of turns taken')
plt.ylabel('Floor')
plt.show()
# Initialize empty list of lists, as before
all_walks = []
# Simulate random walk 250 times!
for i in range(250) :
random_walk = [1]
for x in range(100) :
floor = random_walk[-1]
dice = np.random.randint(1,7)
if dice <= 2:
floor = max(1, floor - 1)
elif dice <= 5:
floor = floor + 1
else:
floor = floor + np.random.randint(1,7)
# Implement clumsiness
if np.random.rand(1,1) < 0.001 :
floor = 1
random_walk.append(floor)
all_walks.append(random_walk)
np_aw_t = np.transpose(np.array(all_walks))
plt.plot(np_aw_t)
plt.xlabel('Number of turns taken')
plt.ylabel('Floor')
plt.show()
all_walks = []
# Simulate random walk 1000 times, because why not
for i in range(1000) :
random_walk = [1]
for x in range(100) :
floor = random_walk[-1]
dice = np.random.randint(1,7)
if dice <= 2:
floor = max(1, floor - 1)
elif dice <= 5:
floor = floor + 1
else:
floor = floor + np.random.randint(1,7)
if np.random.rand() <= 0.001 :
floor = 1
random_walk.append(floor)
all_walks.append(random_walk)
np_aw_t = np.transpose(np.array(all_walks))
# Recover endpoints from np_aw_t
ends = np_aw_t[-1]
# Plot histogram of ends
plt.hist(ends, ec="black")
plt.xlabel('ending floor')
plt.ylabel('number of random walks')
plt.show()
# We are interested in the endpoints greater than or equal to 70
win_the_game = ends[ends >= 70]
# More specifically, the number of such outcomes, divided by 1000
len(win_the_game) / 1000
| 0.470737 | 0.916484 |
```
import numpy as np
import matplotlib as mpl
#mpl.use('pdf')
import matplotlib.pyplot as plt
import numpy as np
plt.rc('font', family='serif', serif='Times')
plt.rc('text', usetex=True)
plt.rc('xtick', labelsize=6)
plt.rc('ytick', labelsize=6)
plt.rc('axes', labelsize=6)
#axes.linewidth : 0.5
plt.rc('axes', linewidth=0.5)
#ytick.major.width : 0.5
plt.rc('ytick.major', width=0.5)
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
plt.rc('ytick.minor', visible=True)
#plt.style.use(r"..\..\styles\infocom.mplstyle") # Insert your save location here
# width as measured in inkscape
fig_width = 3.487
#height = width / 1.618 / 2
fig_height = fig_width / 1.3 / 2
cc_folder_list = ["SF_new_results/", "capacity_results/", "BF_new_results/"]
nc_folder_list = ["SF_new_results_NC/", "capacity_resultsNC/", "BF_new_results_NC/"]
cc_folder_list = ["failure20stages-new-rounding-capacity/" + e for e in cc_folder_list]
nc_folder_list = ["failure20stages-new-rounding-capacity/" + e for e in nc_folder_list]
file_list = ["no-reconfig120.csv", "Link-reconfig120.csv", "LimitedReconfig120.csv", "Any-reconfig120.csv"]
print(cc_folder_list)
print(nc_folder_list)
nc_objective_data = np.full((5, 3), 0)
max_stage = 20
selected_stage = 10
for i in range(3):
for j in range(4):
with open(nc_folder_list[i]+file_list[j], "r") as f:
if j != 2:
f1 = f.readlines()
start_line = 0
for line in f1:
if line.find("%Stage") >= 0:
break
else:
start_line = start_line + 1
#print(start_line)
#print(len(f1))
line = f1[selected_stage+start_line]
line = line.split(",")
if j == 0:
nc_objective_data[0, i] = float(line[2])
if j == 1:
nc_objective_data[1, i] = float(line[2])
if j == 3:
nc_objective_data[4, i] = float(line[2])
else:
f1 = f.readlines()
start_line = 0
start_line1 = 0
for line in f1:
if line.find("%Stage") >= 0:
break
else:
start_line = start_line + 1
for index in range(start_line+max_stage+1, len(f1)):
if f1[index].find("%Stage") >= 0:
start_line1 = index
break
else:
start_line1 = start_line1 + 1
line = f1[selected_stage+start_line]
line = line.split(",")
nc_objective_data[2, i] = float(line[2])
#mesh3data[2, index] = int(line[1])
line = f1[selected_stage+start_line1]
line = line.split(",")
nc_objective_data[3, i] = float(line[2])
print(start_line, start_line1)
print(nc_objective_data)
for i in range(3):
print((nc_objective_data[4][i]-nc_objective_data[1][i])/nc_objective_data[4][i])
#nc_objective_data[]
print((nc_objective_data[4]-nc_objective_data[1])/nc_objective_data[1])
(5850 - 5130) / 5130
nc_initial_data = np.full((5, 3), 0)
max_stage = 20
selected_stage = 0
for i in range(3):
for j in range(4):
with open(nc_folder_list[i]+file_list[j], "r") as f:
if j != 2:
f1 = f.readlines()
start_line = 0
for line in f1:
if line.find("%Stage") >= 0:
break
else:
start_line = start_line + 1
#print(start_line)
#print(len(f1))
line = f1[selected_stage+start_line]
line = line.split(",")
if j == 0:
nc_initial_data[0, i] = float(line[2])
if j == 1:
nc_initial_data[1, i] = float(line[2])
if j == 3:
nc_initial_data[4, i] = float(line[2])
else:
f1 = f.readlines()
start_line = 0
start_line1 = 0
for line in f1:
if line.find("%Stage") >= 0:
break
else:
start_line = start_line + 1
for index in range(start_line+max_stage+1, len(f1)):
if f1[index].find("%Stage") >= 0:
start_line1 = index
break
else:
start_line1 = start_line1 + 1
line = f1[selected_stage+start_line]
line = line.split(",")
nc_initial_data[2, i] = float(line[2])
#mesh3data[2, index] = int(line[1])
line = f1[selected_stage+start_line1]
line = line.split(",")
nc_initial_data[3, i] = float(line[2])
print(nc_initial_data)
import numpy as np
N = 3
ind = np.arange(N)
width = 1 / 6
x = [0, '20', '30', '40']
x_tick_label_list = ['20', '30', '40']
fig, (ax1, ax2) = plt.subplots(1, 2)
ax1.grid(lw = 0.25)
ax2.grid(lw = 0.25)
#ax1.bar(x, objective)
#ax1.bar(x, objective[0])
#label_list = ['No-rec', 'Link-rec', 'Lim-rec(5, 0)', 'Lim-rec(5, 2)', 'Any-rec']
label_list = ['Fix-em', 'Link-rem', 'Any-rem(5, 0)', 'Any-rem(5, 2)', 'Any-rem']
patterns = ('//////','\\\\\\','---', 'ooo', 'xxx', '\\', '\\\\','++', '*', 'O', '.')
plt.rcParams['hatch.linewidth'] = 0.25 # previous pdf hatch linewidth
#plt.rcParams['hatch.linewidth'] = 1.0 # previous svg hatch linewidth
#plt.rcParams['hatch.color'] = 'r'
for i in range(5):
ax1.bar(ind + width * (i-2), nc_objective_data[i], width, label=label_list[i],
#alpha=0.7)
hatch=patterns[i], alpha=0.7)
#yerr=error[i], ecolor='black', capsize=1)
ax1.set_xticklabels(x)
ax1.set_ylabel('AWRSL')
ax1.set_xlabel('Percentage of substrate failures (\%)')
#ax1.set_ylabel('Objective value')
#ax1.set_xlabel('Recovery Scenarios')
ax1.xaxis.set_label_coords(0.5,-0.17)
ax1.yaxis.set_label_coords(-0.17,0.5)
#ax1.legend(loc='upper center', bbox_to_anchor=(0.5, 1.05),
# ncol=3, fancybox=True, shadow=True, fontsize='small')
for i in range(5):
ax2.bar(ind + width * (i-2), nc_initial_data[i], width, label=label_list[i],
#alpha=0.7)
hatch=patterns[i], alpha=0.7)
ax2.set_xticklabels(x)
ax2.set_ylabel('AWRSL at stage 0')
ax2.set_xlabel('Percentage of substrate failures (\%)')
ax2.xaxis.set_label_coords(0.5,-0.17)
ax2.yaxis.set_label_coords(-0.17,0.5)
ax1.legend(loc='upper center', bbox_to_anchor=(1.16, 1.26),
ncol=5, prop={'size': 5}, handletextpad=0.2)
fig.set_size_inches(fig_width, fig_height)
mpl.pyplot.subplots_adjust(wspace = 0.3)
#ax1.grid(color='b', ls = '-.', lw = 0.25)
ax1.set_title('(a)', y=-0.45, fontsize=7)
ax2.set_title('(b)', y=-0.45, fontsize=7)
fig.subplots_adjust(left=.10, bottom=.235, right=.97, top=.85)
plt.show()
fig.savefig('test-heuristic-failure-nc-initial.pdf')
```
|
github_jupyter
|
import numpy as np
import matplotlib as mpl
#mpl.use('pdf')
import matplotlib.pyplot as plt
import numpy as np
plt.rc('font', family='serif', serif='Times')
plt.rc('text', usetex=True)
plt.rc('xtick', labelsize=6)
plt.rc('ytick', labelsize=6)
plt.rc('axes', labelsize=6)
#axes.linewidth : 0.5
plt.rc('axes', linewidth=0.5)
#ytick.major.width : 0.5
plt.rc('ytick.major', width=0.5)
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
plt.rc('ytick.minor', visible=True)
#plt.style.use(r"..\..\styles\infocom.mplstyle") # Insert your save location here
# width as measured in inkscape
fig_width = 3.487
#height = width / 1.618 / 2
fig_height = fig_width / 1.3 / 2
cc_folder_list = ["SF_new_results/", "capacity_results/", "BF_new_results/"]
nc_folder_list = ["SF_new_results_NC/", "capacity_resultsNC/", "BF_new_results_NC/"]
cc_folder_list = ["failure20stages-new-rounding-capacity/" + e for e in cc_folder_list]
nc_folder_list = ["failure20stages-new-rounding-capacity/" + e for e in nc_folder_list]
file_list = ["no-reconfig120.csv", "Link-reconfig120.csv", "LimitedReconfig120.csv", "Any-reconfig120.csv"]
print(cc_folder_list)
print(nc_folder_list)
nc_objective_data = np.full((5, 3), 0)
max_stage = 20
selected_stage = 10
for i in range(3):
for j in range(4):
with open(nc_folder_list[i]+file_list[j], "r") as f:
if j != 2:
f1 = f.readlines()
start_line = 0
for line in f1:
if line.find("%Stage") >= 0:
break
else:
start_line = start_line + 1
#print(start_line)
#print(len(f1))
line = f1[selected_stage+start_line]
line = line.split(",")
if j == 0:
nc_objective_data[0, i] = float(line[2])
if j == 1:
nc_objective_data[1, i] = float(line[2])
if j == 3:
nc_objective_data[4, i] = float(line[2])
else:
f1 = f.readlines()
start_line = 0
start_line1 = 0
for line in f1:
if line.find("%Stage") >= 0:
break
else:
start_line = start_line + 1
for index in range(start_line+max_stage+1, len(f1)):
if f1[index].find("%Stage") >= 0:
start_line1 = index
break
else:
start_line1 = start_line1 + 1
line = f1[selected_stage+start_line]
line = line.split(",")
nc_objective_data[2, i] = float(line[2])
#mesh3data[2, index] = int(line[1])
line = f1[selected_stage+start_line1]
line = line.split(",")
nc_objective_data[3, i] = float(line[2])
print(start_line, start_line1)
print(nc_objective_data)
for i in range(3):
print((nc_objective_data[4][i]-nc_objective_data[1][i])/nc_objective_data[4][i])
#nc_objective_data[]
print((nc_objective_data[4]-nc_objective_data[1])/nc_objective_data[1])
(5850 - 5130) / 5130
nc_initial_data = np.full((5, 3), 0)
max_stage = 20
selected_stage = 0
for i in range(3):
for j in range(4):
with open(nc_folder_list[i]+file_list[j], "r") as f:
if j != 2:
f1 = f.readlines()
start_line = 0
for line in f1:
if line.find("%Stage") >= 0:
break
else:
start_line = start_line + 1
#print(start_line)
#print(len(f1))
line = f1[selected_stage+start_line]
line = line.split(",")
if j == 0:
nc_initial_data[0, i] = float(line[2])
if j == 1:
nc_initial_data[1, i] = float(line[2])
if j == 3:
nc_initial_data[4, i] = float(line[2])
else:
f1 = f.readlines()
start_line = 0
start_line1 = 0
for line in f1:
if line.find("%Stage") >= 0:
break
else:
start_line = start_line + 1
for index in range(start_line+max_stage+1, len(f1)):
if f1[index].find("%Stage") >= 0:
start_line1 = index
break
else:
start_line1 = start_line1 + 1
line = f1[selected_stage+start_line]
line = line.split(",")
nc_initial_data[2, i] = float(line[2])
#mesh3data[2, index] = int(line[1])
line = f1[selected_stage+start_line1]
line = line.split(",")
nc_initial_data[3, i] = float(line[2])
print(nc_initial_data)
import numpy as np
N = 3
ind = np.arange(N)
width = 1 / 6
x = [0, '20', '30', '40']
x_tick_label_list = ['20', '30', '40']
fig, (ax1, ax2) = plt.subplots(1, 2)
ax1.grid(lw = 0.25)
ax2.grid(lw = 0.25)
#ax1.bar(x, objective)
#ax1.bar(x, objective[0])
#label_list = ['No-rec', 'Link-rec', 'Lim-rec(5, 0)', 'Lim-rec(5, 2)', 'Any-rec']
label_list = ['Fix-em', 'Link-rem', 'Any-rem(5, 0)', 'Any-rem(5, 2)', 'Any-rem']
patterns = ('//////','\\\\\\','---', 'ooo', 'xxx', '\\', '\\\\','++', '*', 'O', '.')
plt.rcParams['hatch.linewidth'] = 0.25 # previous pdf hatch linewidth
#plt.rcParams['hatch.linewidth'] = 1.0 # previous svg hatch linewidth
#plt.rcParams['hatch.color'] = 'r'
for i in range(5):
ax1.bar(ind + width * (i-2), nc_objective_data[i], width, label=label_list[i],
#alpha=0.7)
hatch=patterns[i], alpha=0.7)
#yerr=error[i], ecolor='black', capsize=1)
ax1.set_xticklabels(x)
ax1.set_ylabel('AWRSL')
ax1.set_xlabel('Percentage of substrate failures (\%)')
#ax1.set_ylabel('Objective value')
#ax1.set_xlabel('Recovery Scenarios')
ax1.xaxis.set_label_coords(0.5,-0.17)
ax1.yaxis.set_label_coords(-0.17,0.5)
#ax1.legend(loc='upper center', bbox_to_anchor=(0.5, 1.05),
# ncol=3, fancybox=True, shadow=True, fontsize='small')
for i in range(5):
ax2.bar(ind + width * (i-2), nc_initial_data[i], width, label=label_list[i],
#alpha=0.7)
hatch=patterns[i], alpha=0.7)
ax2.set_xticklabels(x)
ax2.set_ylabel('AWRSL at stage 0')
ax2.set_xlabel('Percentage of substrate failures (\%)')
ax2.xaxis.set_label_coords(0.5,-0.17)
ax2.yaxis.set_label_coords(-0.17,0.5)
ax1.legend(loc='upper center', bbox_to_anchor=(1.16, 1.26),
ncol=5, prop={'size': 5}, handletextpad=0.2)
fig.set_size_inches(fig_width, fig_height)
mpl.pyplot.subplots_adjust(wspace = 0.3)
#ax1.grid(color='b', ls = '-.', lw = 0.25)
ax1.set_title('(a)', y=-0.45, fontsize=7)
ax2.set_title('(b)', y=-0.45, fontsize=7)
fig.subplots_adjust(left=.10, bottom=.235, right=.97, top=.85)
plt.show()
fig.savefig('test-heuristic-failure-nc-initial.pdf')
| 0.107028 | 0.423935 |
<img src="http://imgur.com/1ZcRyrc.png" style="float: left; margin: 20px; height: 85px">
# Capstone Project
# Steering Angle Prediction
by: Lee Melvin DSI-15
## Notebook 02: Modeling
## Content
- [Import libraries](#Import-libraries)
- [Modeling summary](#Modeling-summary)
- [Model 1](#Model-1)
- [Model 1 camera1](#Model-1-camera1)
- [Model 1 camera2](#Model-1-camera2)
- [Model 1 camera3](#Model-1-camera3)
- [Model 1 camera4](#Model-1-camera4)
- [Model 1 camera5](#Model-1-camera5)
- [Model 1 camera6](#Model-1-camera6)
- [Model 1 camera7](#Model-1-camera7)
- [Model 1 camera8](#Model-1-camera8)
- [Model 1 camera9](#Model-1-camera9)
- [Model 2](#Model-2)
- [Model 2 camera8](#Model-2-camera8)
- [Model 2 camera1](#Model-2-camera1)
- [Model 2 camera9](#Model-2-camera9)
- [Model 2 camera2](#Model-2-camera2)
- [Model 2 camera3](#Model-2-camera3)
- [Model 2 camera4](#Model-2-camera4)
- [Model 2 camera5](#Model-2-camera5)
- [Model 2 camera6](#Model-2-camera6)
- [Model 2 camera7](#Model-2-camera7)
- [Model 3](#Model-3)
- [Model 3 camera8](#Model-3-camera8)
- [Model 3 camera1](#Model-3-camera1)
- [Model 3 camera9](#Model-3-camera9)
- [Model 3 camera2](#Model-3-camera2)
- [Model 3 camera3](#Model-3-camera3)
- [Model 3 camera4](#Model-3-camera4)
- [Model 3 camera5](#Model-3-camera5)
- [Model 3 camera6](#Model-3-camera6)
- [Model 3 camera7](#Model-3-camera7)
## Import libraries
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from numpy import load
from numpy import asarray
from numpy import savez_compressed
from sklearn.model_selection import train_test_split
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.optimizers import Adam
from keras.metrics import RootMeanSquaredError
from keras.models import load_model
from keras.callbacks import *
%matplotlib inline
```
## Modeling summary
Due to the large dataset I'll be using Google Colab for training. 3 Models architecture were use, the first model was a combinational of using [Nvidia's research](https://developer.nvidia.com/blog/deep-learning-self-driving-cars/) and [comma.ai's research](https://github.com/commaai/research). The second model utilises the full architecture of [comma.ai's research](https://github.com/commaai/research). The last model was with a tweak activation layer from comma.ai's `ELU` to `ReLU`.
The model will be trained with 9 different batches of datasets from `camera1` to `camera9`. I started experimenting with the dataset training order for model 2 and 3. They both utilise the following pattern:
- 1st: `camera8`, `day`
- 2nd: `camera1`, `day`
- 3rd: `camera9`, `night`
- 4th: `camera2`, `day`
- 5th: `camera3`, `night`
- 6th: `camera4`, `day`
- 7th: `camera5`, `day`
- 8th: `camera6`, `night`
- 9th: `camera7`, `day`
In hindsight it was foolish to do so as I shouldn't expected the model to have any preference for sequence of data being feed in as the weights will adjust accordingly when new data is fed in. Each individual dataset goes through the following steps:
- `camera{number}_cleaned.npz` is loaded and goes through `camera_processing` function
- `log{number}_cleaned.csv` is loaded and goes through `log_processing` function
- Both the `camera` and `log` files are then goes through `train_split` function
- Using the `train_load` function the `train_test_split` data is loaded
- Model is instantiated and checkpoints are set
- History of model is saved for analysis
- The steps are then repeated for each individual batch of data
- For model 2 and 3 only steps from `train_load` function onwards is used as the dataset has already been split and saved
For subsequent models 2 and 3, I notice from model 1 that majority of the dataset `val_loss` starts to plateau around 30 epochs, hence, I take that as the measurement for subsequent models.
- `Model 1` is trained with `100 epochs` per dataset
- `Model 2` is trained with `30 epochs` per dataset
- `Model 3` is trained with `30 epochs` per dataset
## Model 1
### Model 1 camera1
```
"""
I'll be training using Google Colab, my compressed cleaned data set from notebook 01 are saved into Google drive. Using the
2 lines of code below we are able to mount Google drive to Google Colab's Virtual Machine
from google.colab import drive
drive.mount('/content/drive')
"""
def camera_processing(camera_file, file_name):
# camera file as .npz file
camera = camera_file.f.arr_0
# convert to float type to prevent error
camera = camera.astype('float32')
# regularise the pixel count
camera = camera/255
# reshape the array to include 1 channel
camera = camera.reshape(camera.shape[0], camera.shape[1], camera.shape[2], 1)
# save the file into compressed .npz format again due to RAM management
savez_compressed(f'/content/drive/My Drive/datasets/{file_name}_train', camera)
return print('Done')
def log_processing(log_file, file_name):
# convert steering angle from degree to radian
log_file['steering_avg_radian'] = log_file['steering_avg'] * np.pi / 180
# save the file to .csv again due to RAM management
log_file.to_csv(f'/content/drive/My Drive/datasets/{file_name}_train.csv')
return print('Done')
def train_split(camera_file_name, log_file_name):
# load camera file
X = load(f'/content/drive/My Drive/datasets/{camera_file_name}_train.npz')
X = X.f.arr_0
# load log file
log = pd.read_csv(f'/content/drive/My Drive/datasets/{log_file_name}_train.csv')
# true steering wheel value is converted to an array
y = log['steering_avg_radian']
y = y.to_numpy()
y = y.reshape(y.shape[0], 1)
# train test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=True)
# save them into individual file of .npz format due to RAM management
savez_compressed(f'/content/drive/My Drive/datasets/{camera_file_name}_X_train', X_train)
savez_compressed(f'/content/drive/My Drive/datasets/{camera_file_name}_X_test', X_test)
savez_compressed(f'/content/drive/My Drive/datasets/{camera_file_name}_y_train', y_train)
savez_compressed(f'/content/drive/My Drive/datasets/{camera_file_name}_y_test', y_test)
return print('Done')
def train_load(camera_file_name):
# load the dataset from Google drive to the Virtual Machine Cloud Storage for RAM management
!cp -r "/content/drive/My Drive/datasets/{camera_file_name}_X_train.npz" ./X_train.npz
!cp -r "/content/drive/My Drive/datasets/{camera_file_name}_X_test.npz" ./X_test.npz
!cp -r "/content/drive/My Drive/datasets/{camera_file_name}_y_train.npz" ./y_train.npz
!cp -r "/content/drive/My Drive/datasets/{camera_file_name}_y_test.npz" ./y_test.npz
X_train = load('./X_train.npz')
X_train = X_train.f.arr_0
X_test = load('./X_test.npz')
X_test = X_test.f.arr_0
y_train = load('./y_train.npz')
y_train = y_train.f.arr_0
y_test = load('./y_test.npz')
y_test = y_test.f.arr_0
return X_train, X_test, y_train, y_test
# load camera and log data
camera1 = load('/content/drive/My Drive/datasets/camera1_cleaned.npz')
log1 = pd.read_csv('/content/drive/My Drive/datasets/log1_cleaned.csv')
# goes through processing function
camera_processing(camera1, 'camera1')
# goes through processing function
log_processing(log1, 'log1')
# train_test_split camera2 data
train_split('camera1', 'log1')
# load the data for camera2
X_train, X_test, y_train, y_test = train_load('camera1')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
model = Sequential()
model.add(Conv2D(16, (3, 3), input_shape=(80, 160, 1), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(32, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(300, activation='relu'))
model.add(Dropout(.5))
model.add(Dense(100, activation='relu'))
model.add(Dropout(.25))
model.add(Dense(20, activation='relu'))
model.add(Dense(1))
model.compile(loss='mse', optimizer=Adam(lr=1e-04), metrics=[RootMeanSquaredError()])
from keras.callbacks import *
filepath = "/content/drive/My Drive/epochs/model_1_camera1.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
def model_history(model_name):
# convert the history to pandas dataframe for analysis later
model = pd.DataFrame({'loss': history.history['loss'],
'root_mean_squared_error': history.history['root_mean_squared_error'],
'val_loss': history.history['val_loss'],
'val_root_mean_squared_error': history.history['val_root_mean_squared_error']},
columns = ['loss', 'root_mean_squared_error', 'val_loss', 'val_root_mean_squared_error'])
model.to_csv(f'/content/drive/My Drive/datasets/{model_name}.csv', index=False)
return model
model_1_camera1 = model_history('model_1_camera1')
```
### Model 1 camera2
```
# load model 1 from camera1
model = load_model('/content/drive/My Drive/epochs/model_1_camera1.0095-0.0495.h5')
# load camera and log data
camera2 = load('/content/drive/My Drive/datasets/camera2_cleaned.npz')
log2 = pd.read_csv('/content/drive/My Drive/datasets/log2_cleaned.csv')
# goes through processing function
camera_processing(camera2, 'camera2')
# goes through processing function
log_processing(log2, 'log2')
# train_test_split camera2 data
train_split('camera2', 'log2')
# load the data for camera2
X_train, X_test, y_train, y_test = train_load('camera2')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
# set checkpoints
filepath = "/content/drive/My Drive/epochs/model_1_camera2.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
# save model history for analysis later
model_1_camera2 = model_history('model_1_camera2')
```
### Model 1 camera3
```
model = load_model('/content/drive/My Drive/epochs/model_1_camera2.0082-0.0074.h5')
camera3 = load('/content/drive/My Drive/datasets/camera3_cleaned.npz')
log3 = pd.read_csv('/content/drive/My Drive/datasets/log3_cleaned.csv')
camera_processing(camera3, 'camera3')
log_processing(log3, 'log3')
train_split('camera3', 'log3')
X_train, X_test, y_train, y_test = train_load('camera3')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_1_camera3.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
model_1_camera3 = model_history('model_1_camera3')
```
### Model 1 camera4
```
model = load_model('/content/drive/My Drive/epochs/model_1_camera3.0097-0.0141.h5')
camera4 = load('/content/drive/My Drive/datasets/camera4_cleaned.npz')
log4 = pd.read_csv('/content/drive/My Drive/datasets/log4_cleaned.csv')
camera_processing(camera4, 'camera4')
log_processing(log4, 'log4')
train_split('camera4', 'log4')
X_train, X_test, y_train, y_test = train_load('camera4')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_1_camera4.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
model_1_camera4 = model_history('model_1_camera4')
```
### Model 1 camera5
```
model = load_model('/content/drive/My Drive/epochs/model_1_camera4.0097-0.0368.h5')
camera5 = load('/content/drive/My Drive/datasets/camera5_cleaned.npz')
log5 = pd.read_csv('/content/drive/My Drive/datasets/log5_cleaned.csv')
camera_processing(camera5, 'camera5')
log_processing(log5, 'log5')
train_split('camera5', 'log5')
X_train, X_test, y_train, y_test = train_load('camera5')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_1_camera5.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
model_1_camera5 = model_history('model_1_camera5')
```
### Model 1 camera6
```
model = load_model('/content/drive/My Drive/epochs/model_1_camera5.0099-0.0496.h5')
camera6 = load('/content/drive/My Drive/datasets/camera6_cleaned.npz')
log6 = pd.read_csv('/content/drive/My Drive/datasets/log6_cleaned.csv')
camera_processing(camera6, 'camera6')
log_processing(log6, 'log6')
train_split('camera6', 'log6')
X_train, X_test, y_train, y_test = train_load('camera6')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_1_camera6.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
model_1_camera6 = model_history('model_1_camera6')
```
### Model 1 camera7
```
model = load_model('/content/drive/My Drive/epochs/model_1_camera6.0095-0.0321.h5')
camera7 = load('/content/drive/My Drive/datasets/camera7_cleaned.npz')
log7 = pd.read_csv('/content/drive/My Drive/datasets/log7_cleaned.csv')
camera_processing(camera7, 'camera7')
log_processing(log7, 'log7')
train_split('camera7', 'log7')
X_train, X_test, y_train, y_test = train_load('camera7')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_1_camera7.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
model_1_camera7 = model_history('model_1_camera7')
```
### Model 1 camera8
```
model = load_model('/content/drive/My Drive/epochs/model_1_camera7.0086-0.0160.h5')
camera8 = load('/content/drive/My Drive/datasets/camera8_cleaned.npz')
log8 = pd.read_csv('/content/drive/My Drive/datasets/log8_cleaned.csv')
camera_processing(camera8, 'camera8')
log_processing(log8, 'log8')
train_split('camera8', 'log8')
X_train, X_test, y_train, y_test = train_load('camera8')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_1_camera8.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
model_1_camera8 = model_history('model_1_camera8')
```
### Model 1 camera9
```
model = load_model('/content/drive/My Drive/epochs/model_1_camera8.0088-0.1415.h5')
camera9 = load('/content/drive/My Drive/datasets/camera9_cleaned.npz')
log9 = pd.read_csv('/content/drive/My Drive/datasets/log9_cleaned.csv')
camera_processing(camera9, 'camera9')
log_processing(log9, 'log9')
train_split('camera9', 'log9')
X_train, X_test, y_train, y_test = train_load('camera9')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_1_camera9.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
model_1_camera9 = model_history('model_1_camera9')
```
## Model 2
### Model 2 camera8
```
X_train, X_test, y_train, y_test = train_load('camera8')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
model = Sequential()
model.add(Conv2D(16, (8, 8), strides=(4, 4), activation='elu', padding="same"))
model.add(Conv2D(32, (5, 5), strides=(2, 2), activation='elu', padding="same"))
model.add(Conv2D(64, (5, 5), strides=(2, 2), padding="same"))
model.add(Flatten())
model.add(Dropout(.2))
model.add(Dense(512, activation='elu'))
model.add(Dropout(.5))
model.add(Dense(1))
model.compile(loss='mse', optimizer=Adam(lr=1e-04), metrics=[RootMeanSquaredError()])
filepath = "/content/drive/My Drive/epochs/model_2_1_camera8.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera8 = model_history('model_2_1_camera8')
```
### Model 2 camera1
```
model = load_model('/content/drive/My Drive/epochs/model_2_1_camera8.0004-0.3364.h5')
X_train, X_test, y_train, y_test = train_load('camera1')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_2_camera1.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera1 = model_history('model_2_2_camera1')
```
### Model 2 camera9
```
model = load_model('/content/drive/My Drive/epochs/model_2_2_camera1.0006-0.2219.h5')
X_train, X_test, y_train, y_test = train_load('camera9')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_3_camera9.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera9 = model_history('model_2_3_camera9')
```
### Model 2 camera2
```
model = load_model('/content/drive/My Drive/epochs/model_2_3_camera9.0003-0.0526.h5')
X_train, X_test, y_train, y_test = train_load('camera2')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_4_camera2.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera2 = model_history('model_2_4_camera2')
```
### Model 2 camera3
```
model = load_model('/content/drive/My Drive/epochs/model_2_4_camera2.0004-0.0382.h5')
X_train, X_test, y_train, y_test = train_load('camera3')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_5_camera3.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera3 = model_history('model_2_5_camera3')
```
### Model 2 camera4
```
model = load_model('/content/drive/My Drive/epochs/model_2_5_camera3.0008-0.0464.h5')
X_train, X_test, y_train, y_test = train_load('camera4')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_6_camera4.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera4 = model_history('model_2_6_camera4')
```
### Model 2 camera5
```
model = load_model('/content/drive/My Drive/epochs/model_2_6_camera4.0004-0.1318.h5')
X_train, X_test, y_train, y_test = train_load('camera5')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_7_camera5.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera5 = model_history('model_2_7_camera5')
```
### Model 2 camera6
```
model = load_model('/content/drive/My Drive/epochs/model_2_7_camera5.0008-0.1320.h5')
X_train, X_test, y_train, y_test = train_load('camera6')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_8_camera6.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera6 = model_history('model_2_8_camera6')
```
### Model 2 camera7
```
model = load_model('/content/drive/My Drive/epochs/model_2_8_camera6.0004-0.0703.h5')
X_train, X_test, y_train, y_test = train_load('camera7')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_9_camera7.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera7 = model_history('model_2_9_camera7')
```
## Model 3
### Model 3 camera8
```
X_train, X_test, y_train, y_test = train_load('camera8')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
model = Sequential()
model.add(Conv2D(16, (8, 8), strides=(4, 4), activation='relu', padding="same"))
model.add(Conv2D(32, (5, 5), strides=(2, 2), activation='relu', padding="same"))
model.add(Conv2D(64, (5, 5), strides=(2, 2), padding="same"))
model.add(Flatten())
model.add(Dropout(.2))
model.add(Dense(512, activation='relu'))
model.add(Dropout(.5))
model.add(Dense(1))
model.compile(loss='mse', optimizer=Adam(lr=1e-04), metrics=[RootMeanSquaredError()])
filepath = "/content/drive/My Drive/epochs/model_3_1_camera8.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera8 = model_history('model_3_1_camera8')
```
### Model 3 camera1
```
model = load_model('/content/drive/My Drive/epochs/model_3_1_camera8.0030-0.0674.h5')
X_train, X_test, y_train, y_test = train_load('camera1')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_2_camera1.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera1 = model_history('model_3_2_camera1')
```
### Model 3 camera9
```
model = load_model('/content/drive/My Drive/epochs/model_3_2_camera1.0030-0.0825.h5')
X_train, X_test, y_train, y_test = train_load('camera9')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_3_camera9.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera9 = model_history('model_3_3_camera9')
```
### Model 3 camera2
```
model = load_model('/content/drive/My Drive/epochs/model_3_3_camera9.0030-0.0295.h5')
X_train, X_test, y_train, y_test = train_load('camera2')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_4_camera2.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera2 = model_history('model_3_4_camera2')
```
### Model 3 camera3
```
model = load_model('/content/drive/My Drive/epochs/model_3_4_camera2.0030-0.0163.h5')
X_train, X_test, y_train, y_test = train_load('camera3')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_5_camera3.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera3 = model_history('model_3_5_camera3')
```
### Model 3 camera4
```
model = load_model('/content/drive/My Drive/epochs/model_3_5_camera3.0028-0.0240.h5')
X_train, X_test, y_train, y_test = train_load('camera4')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_6_camera4.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera4 = model_history('model_3_6_camera4')
```
### Model 3 camera5
```
model = load_model('/content/drive/My Drive/epochs/model_3_6_camera4.0030-0.1283.h5')
X_train, X_test, y_train, y_test = train_load('camera5')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_7_camera5.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera5 = model_history('model_3_7_camera5')
```
### Model 3 camera6
```
model = load_model('/content/drive/My Drive/epochs/model_3_7_camera5.0028-0.1441.h5')
X_train, X_test, y_train, y_test = train_load('camera6')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_8_camera6.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera6 = model_history('model_3_8_camera6')
```
### Model 3 camera7
```
model = load_model('/content/drive/My Drive/epochs/model_3_8_camera6.0016-0.0756.h5')
X_train, X_test, y_train, y_test = train_load('camera7')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_9_camera7.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera7 = model_history('model_3_9_camera7')
```
## End of Notebook 02: Modeling proceed to Notebook 03: Model Selection
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from numpy import load
from numpy import asarray
from numpy import savez_compressed
from sklearn.model_selection import train_test_split
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.optimizers import Adam
from keras.metrics import RootMeanSquaredError
from keras.models import load_model
from keras.callbacks import *
%matplotlib inline
"""
I'll be training using Google Colab, my compressed cleaned data set from notebook 01 are saved into Google drive. Using the
2 lines of code below we are able to mount Google drive to Google Colab's Virtual Machine
from google.colab import drive
drive.mount('/content/drive')
"""
def camera_processing(camera_file, file_name):
# camera file as .npz file
camera = camera_file.f.arr_0
# convert to float type to prevent error
camera = camera.astype('float32')
# regularise the pixel count
camera = camera/255
# reshape the array to include 1 channel
camera = camera.reshape(camera.shape[0], camera.shape[1], camera.shape[2], 1)
# save the file into compressed .npz format again due to RAM management
savez_compressed(f'/content/drive/My Drive/datasets/{file_name}_train', camera)
return print('Done')
def log_processing(log_file, file_name):
# convert steering angle from degree to radian
log_file['steering_avg_radian'] = log_file['steering_avg'] * np.pi / 180
# save the file to .csv again due to RAM management
log_file.to_csv(f'/content/drive/My Drive/datasets/{file_name}_train.csv')
return print('Done')
def train_split(camera_file_name, log_file_name):
# load camera file
X = load(f'/content/drive/My Drive/datasets/{camera_file_name}_train.npz')
X = X.f.arr_0
# load log file
log = pd.read_csv(f'/content/drive/My Drive/datasets/{log_file_name}_train.csv')
# true steering wheel value is converted to an array
y = log['steering_avg_radian']
y = y.to_numpy()
y = y.reshape(y.shape[0], 1)
# train test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=True)
# save them into individual file of .npz format due to RAM management
savez_compressed(f'/content/drive/My Drive/datasets/{camera_file_name}_X_train', X_train)
savez_compressed(f'/content/drive/My Drive/datasets/{camera_file_name}_X_test', X_test)
savez_compressed(f'/content/drive/My Drive/datasets/{camera_file_name}_y_train', y_train)
savez_compressed(f'/content/drive/My Drive/datasets/{camera_file_name}_y_test', y_test)
return print('Done')
def train_load(camera_file_name):
# load the dataset from Google drive to the Virtual Machine Cloud Storage for RAM management
!cp -r "/content/drive/My Drive/datasets/{camera_file_name}_X_train.npz" ./X_train.npz
!cp -r "/content/drive/My Drive/datasets/{camera_file_name}_X_test.npz" ./X_test.npz
!cp -r "/content/drive/My Drive/datasets/{camera_file_name}_y_train.npz" ./y_train.npz
!cp -r "/content/drive/My Drive/datasets/{camera_file_name}_y_test.npz" ./y_test.npz
X_train = load('./X_train.npz')
X_train = X_train.f.arr_0
X_test = load('./X_test.npz')
X_test = X_test.f.arr_0
y_train = load('./y_train.npz')
y_train = y_train.f.arr_0
y_test = load('./y_test.npz')
y_test = y_test.f.arr_0
return X_train, X_test, y_train, y_test
# load camera and log data
camera1 = load('/content/drive/My Drive/datasets/camera1_cleaned.npz')
log1 = pd.read_csv('/content/drive/My Drive/datasets/log1_cleaned.csv')
# goes through processing function
camera_processing(camera1, 'camera1')
# goes through processing function
log_processing(log1, 'log1')
# train_test_split camera2 data
train_split('camera1', 'log1')
# load the data for camera2
X_train, X_test, y_train, y_test = train_load('camera1')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
model = Sequential()
model.add(Conv2D(16, (3, 3), input_shape=(80, 160, 1), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(32, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(300, activation='relu'))
model.add(Dropout(.5))
model.add(Dense(100, activation='relu'))
model.add(Dropout(.25))
model.add(Dense(20, activation='relu'))
model.add(Dense(1))
model.compile(loss='mse', optimizer=Adam(lr=1e-04), metrics=[RootMeanSquaredError()])
from keras.callbacks import *
filepath = "/content/drive/My Drive/epochs/model_1_camera1.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
def model_history(model_name):
# convert the history to pandas dataframe for analysis later
model = pd.DataFrame({'loss': history.history['loss'],
'root_mean_squared_error': history.history['root_mean_squared_error'],
'val_loss': history.history['val_loss'],
'val_root_mean_squared_error': history.history['val_root_mean_squared_error']},
columns = ['loss', 'root_mean_squared_error', 'val_loss', 'val_root_mean_squared_error'])
model.to_csv(f'/content/drive/My Drive/datasets/{model_name}.csv', index=False)
return model
model_1_camera1 = model_history('model_1_camera1')
# load model 1 from camera1
model = load_model('/content/drive/My Drive/epochs/model_1_camera1.0095-0.0495.h5')
# load camera and log data
camera2 = load('/content/drive/My Drive/datasets/camera2_cleaned.npz')
log2 = pd.read_csv('/content/drive/My Drive/datasets/log2_cleaned.csv')
# goes through processing function
camera_processing(camera2, 'camera2')
# goes through processing function
log_processing(log2, 'log2')
# train_test_split camera2 data
train_split('camera2', 'log2')
# load the data for camera2
X_train, X_test, y_train, y_test = train_load('camera2')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
# set checkpoints
filepath = "/content/drive/My Drive/epochs/model_1_camera2.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
# save model history for analysis later
model_1_camera2 = model_history('model_1_camera2')
model = load_model('/content/drive/My Drive/epochs/model_1_camera2.0082-0.0074.h5')
camera3 = load('/content/drive/My Drive/datasets/camera3_cleaned.npz')
log3 = pd.read_csv('/content/drive/My Drive/datasets/log3_cleaned.csv')
camera_processing(camera3, 'camera3')
log_processing(log3, 'log3')
train_split('camera3', 'log3')
X_train, X_test, y_train, y_test = train_load('camera3')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_1_camera3.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
model_1_camera3 = model_history('model_1_camera3')
model = load_model('/content/drive/My Drive/epochs/model_1_camera3.0097-0.0141.h5')
camera4 = load('/content/drive/My Drive/datasets/camera4_cleaned.npz')
log4 = pd.read_csv('/content/drive/My Drive/datasets/log4_cleaned.csv')
camera_processing(camera4, 'camera4')
log_processing(log4, 'log4')
train_split('camera4', 'log4')
X_train, X_test, y_train, y_test = train_load('camera4')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_1_camera4.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
model_1_camera4 = model_history('model_1_camera4')
model = load_model('/content/drive/My Drive/epochs/model_1_camera4.0097-0.0368.h5')
camera5 = load('/content/drive/My Drive/datasets/camera5_cleaned.npz')
log5 = pd.read_csv('/content/drive/My Drive/datasets/log5_cleaned.csv')
camera_processing(camera5, 'camera5')
log_processing(log5, 'log5')
train_split('camera5', 'log5')
X_train, X_test, y_train, y_test = train_load('camera5')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_1_camera5.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
model_1_camera5 = model_history('model_1_camera5')
model = load_model('/content/drive/My Drive/epochs/model_1_camera5.0099-0.0496.h5')
camera6 = load('/content/drive/My Drive/datasets/camera6_cleaned.npz')
log6 = pd.read_csv('/content/drive/My Drive/datasets/log6_cleaned.csv')
camera_processing(camera6, 'camera6')
log_processing(log6, 'log6')
train_split('camera6', 'log6')
X_train, X_test, y_train, y_test = train_load('camera6')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_1_camera6.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
model_1_camera6 = model_history('model_1_camera6')
model = load_model('/content/drive/My Drive/epochs/model_1_camera6.0095-0.0321.h5')
camera7 = load('/content/drive/My Drive/datasets/camera7_cleaned.npz')
log7 = pd.read_csv('/content/drive/My Drive/datasets/log7_cleaned.csv')
camera_processing(camera7, 'camera7')
log_processing(log7, 'log7')
train_split('camera7', 'log7')
X_train, X_test, y_train, y_test = train_load('camera7')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_1_camera7.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
model_1_camera7 = model_history('model_1_camera7')
model = load_model('/content/drive/My Drive/epochs/model_1_camera7.0086-0.0160.h5')
camera8 = load('/content/drive/My Drive/datasets/camera8_cleaned.npz')
log8 = pd.read_csv('/content/drive/My Drive/datasets/log8_cleaned.csv')
camera_processing(camera8, 'camera8')
log_processing(log8, 'log8')
train_split('camera8', 'log8')
X_train, X_test, y_train, y_test = train_load('camera8')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_1_camera8.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
model_1_camera8 = model_history('model_1_camera8')
model = load_model('/content/drive/My Drive/epochs/model_1_camera8.0088-0.1415.h5')
camera9 = load('/content/drive/My Drive/datasets/camera9_cleaned.npz')
log9 = pd.read_csv('/content/drive/My Drive/datasets/log9_cleaned.csv')
camera_processing(camera9, 'camera9')
log_processing(log9, 'log9')
train_split('camera9', 'log9')
X_train, X_test, y_train, y_test = train_load('camera9')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_1_camera9.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=100,
verbose=1,
callbacks=callbacks_list)
model_1_camera9 = model_history('model_1_camera9')
X_train, X_test, y_train, y_test = train_load('camera8')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
model = Sequential()
model.add(Conv2D(16, (8, 8), strides=(4, 4), activation='elu', padding="same"))
model.add(Conv2D(32, (5, 5), strides=(2, 2), activation='elu', padding="same"))
model.add(Conv2D(64, (5, 5), strides=(2, 2), padding="same"))
model.add(Flatten())
model.add(Dropout(.2))
model.add(Dense(512, activation='elu'))
model.add(Dropout(.5))
model.add(Dense(1))
model.compile(loss='mse', optimizer=Adam(lr=1e-04), metrics=[RootMeanSquaredError()])
filepath = "/content/drive/My Drive/epochs/model_2_1_camera8.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera8 = model_history('model_2_1_camera8')
model = load_model('/content/drive/My Drive/epochs/model_2_1_camera8.0004-0.3364.h5')
X_train, X_test, y_train, y_test = train_load('camera1')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_2_camera1.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera1 = model_history('model_2_2_camera1')
model = load_model('/content/drive/My Drive/epochs/model_2_2_camera1.0006-0.2219.h5')
X_train, X_test, y_train, y_test = train_load('camera9')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_3_camera9.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera9 = model_history('model_2_3_camera9')
model = load_model('/content/drive/My Drive/epochs/model_2_3_camera9.0003-0.0526.h5')
X_train, X_test, y_train, y_test = train_load('camera2')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_4_camera2.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera2 = model_history('model_2_4_camera2')
model = load_model('/content/drive/My Drive/epochs/model_2_4_camera2.0004-0.0382.h5')
X_train, X_test, y_train, y_test = train_load('camera3')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_5_camera3.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera3 = model_history('model_2_5_camera3')
model = load_model('/content/drive/My Drive/epochs/model_2_5_camera3.0008-0.0464.h5')
X_train, X_test, y_train, y_test = train_load('camera4')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_6_camera4.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera4 = model_history('model_2_6_camera4')
model = load_model('/content/drive/My Drive/epochs/model_2_6_camera4.0004-0.1318.h5')
X_train, X_test, y_train, y_test = train_load('camera5')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_7_camera5.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera5 = model_history('model_2_7_camera5')
model = load_model('/content/drive/My Drive/epochs/model_2_7_camera5.0008-0.1320.h5')
X_train, X_test, y_train, y_test = train_load('camera6')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_8_camera6.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera6 = model_history('model_2_8_camera6')
model = load_model('/content/drive/My Drive/epochs/model_2_8_camera6.0004-0.0703.h5')
X_train, X_test, y_train, y_test = train_load('camera7')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_2_9_camera7.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_2_camera7 = model_history('model_2_9_camera7')
X_train, X_test, y_train, y_test = train_load('camera8')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
model = Sequential()
model.add(Conv2D(16, (8, 8), strides=(4, 4), activation='relu', padding="same"))
model.add(Conv2D(32, (5, 5), strides=(2, 2), activation='relu', padding="same"))
model.add(Conv2D(64, (5, 5), strides=(2, 2), padding="same"))
model.add(Flatten())
model.add(Dropout(.2))
model.add(Dense(512, activation='relu'))
model.add(Dropout(.5))
model.add(Dense(1))
model.compile(loss='mse', optimizer=Adam(lr=1e-04), metrics=[RootMeanSquaredError()])
filepath = "/content/drive/My Drive/epochs/model_3_1_camera8.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera8 = model_history('model_3_1_camera8')
model = load_model('/content/drive/My Drive/epochs/model_3_1_camera8.0030-0.0674.h5')
X_train, X_test, y_train, y_test = train_load('camera1')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_2_camera1.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera1 = model_history('model_3_2_camera1')
model = load_model('/content/drive/My Drive/epochs/model_3_2_camera1.0030-0.0825.h5')
X_train, X_test, y_train, y_test = train_load('camera9')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_3_camera9.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera9 = model_history('model_3_3_camera9')
model = load_model('/content/drive/My Drive/epochs/model_3_3_camera9.0030-0.0295.h5')
X_train, X_test, y_train, y_test = train_load('camera2')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_4_camera2.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera2 = model_history('model_3_4_camera2')
model = load_model('/content/drive/My Drive/epochs/model_3_4_camera2.0030-0.0163.h5')
X_train, X_test, y_train, y_test = train_load('camera3')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_5_camera3.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera3 = model_history('model_3_5_camera3')
model = load_model('/content/drive/My Drive/epochs/model_3_5_camera3.0028-0.0240.h5')
X_train, X_test, y_train, y_test = train_load('camera4')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_6_camera4.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera4 = model_history('model_3_6_camera4')
model = load_model('/content/drive/My Drive/epochs/model_3_6_camera4.0030-0.1283.h5')
X_train, X_test, y_train, y_test = train_load('camera5')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_7_camera5.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera5 = model_history('model_3_7_camera5')
model = load_model('/content/drive/My Drive/epochs/model_3_7_camera5.0028-0.1441.h5')
X_train, X_test, y_train, y_test = train_load('camera6')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_8_camera6.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera6 = model_history('model_3_8_camera6')
model = load_model('/content/drive/My Drive/epochs/model_3_8_camera6.0016-0.0756.h5')
X_train, X_test, y_train, y_test = train_load('camera7')
X_train.shape, X_test.shape, y_train.shape, y_test.shape
filepath = "/content/drive/My Drive/epochs/model_3_9_camera7.{epoch:04d}-{val_loss:.4f}.h5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_best_only=True, mode='min')
callbacks_list = [checkpoint]
history = model.fit(X_train,
y_train,
batch_size=64,
validation_data=(X_test, y_test),
epochs=30,
verbose=1,
callbacks=callbacks_list)
model_3_camera7 = model_history('model_3_9_camera7')
| 0.809502 | 0.940626 |
# MindSpore API概述
`Ascend` `GPU` `CPU` `入门`
[](https://authoring-modelarts-cnnorth4.huaweicloud.com/console/lab?share-url-b64=aHR0cHM6Ly9taW5kc3BvcmUtd2Vic2l0ZS5vYnMuY24tbm9ydGgtNC5teWh1YXdlaWNsb3VkLmNvbS9ub3RlYm9vay9tb2RlbGFydHMvcHJvZ3JhbW1pbmdfZ3VpZGUvbWluZHNwb3JlX2FwaV9zdHJ1Y3R1cmUuaXB5bmI=&imageid=65f636a0-56cf-49df-b941-7d2a07ba8c8c) [](https://obs.dualstack.cn-north-4.myhuaweicloud.com/mindspore-website/notebook/master/programming_guide/zh_cn/mindspore_api_structure.ipynb) [](https://obs.dualstack.cn-north-4.myhuaweicloud.com/mindspore-website/notebook/master/programming_guide/zh_cn/mindspore_api_structure.py) [](https://gitee.com/mindspore/docs/blob/master/docs/mindspore/programming_guide/source_zh_cn/api_structure.ipynb)
## 总体架构
MindSpore是一个全场景深度学习框架,旨在实现易开发、高效执行、全场景覆盖三大目标,其中易开发表现为API友好、调试难度低,高效执行包括计算效率、数据预处理效率和分布式训练效率,全场景则指框架同时支持云、边缘以及端侧场景。
ME(MindExpression)提供了用户级应用软件编程接口(Application Programming Interface,API),用于科学计算以及构建和训练神经网络,并将用户的Python代码转换为数据流图。更多总体架构的相关内容请参见[总体架构](https://www.mindspore.cn/docs/programming_guide/zh-CN/master/architecture.html)。
## 设计理念
MindSpore源于全产业的最佳实践,向数据科学家和算法工程师提供了统一的模型训练、推理和导出等接口,支持端、边、云等不同场景下的灵活部署,推动深度学习和科学计算等领域繁荣发展。
MindSpore目前提供了Python编程范式,用户使用Python原生控制逻辑即可构建复杂的神经网络模型,AI编程变得简单,具体示例请参见[初学入门](https://www.mindspore.cn/tutorials/zh-CN/master/quick_start.html)。
目前主流的深度学习框架的执行模式有两种,分别为静态图模式和动态图模式。静态图模式拥有较高的训练性能,但难以调试。动态图模式相较于静态图模式虽然易于调试,但难以高效执行。MindSpore提供了动态图和静态图统一的编码方式,大大增加了静态图和动态图的可兼容性,用户无需开发多套代码,仅变更一行代码便可切换动态图/静态图模式,例如设置`context.set_context(mode=context.PYNATIVE_MODE)`切换成动态图模式,设置`context.set_context(mode=context.GRAPH_MODE)`即可切换成静态图模式,用户可拥有更轻松的开发调试及性能体验。
神经网络模型通常基于梯度下降算法进行训练,但手动求导过程复杂,结果容易出错。MindSpore的基于源码转换(Source Code Transformation,SCT)的自动微分(Automatic Differentiation)机制采用函数式可微分编程架构,在接口层提供Python编程接口,包括控制流的表达。用户可聚焦于模型算法的数学原生表达,无需手动进行求导,自动微分的样例代码如下所示。
> 本样例适用于GPU和Ascend环境。
```
import mindspore as ms
from mindspore import ops
grad_all = ops.composite.GradOperation()
def func(x):
return x * x * x
def df_func(x):
return grad_all(func)(x)
@ms.ms_function
def df2_func(x):
return grad_all(df_func)(x)
if __name__ == "__main__":
print(df2_func(ms.Tensor(2, ms.float32)))
```
其中,第一步定义了一个函数(计算图),第二步利用MindSpore提供的反向接口进行自动微分,定义了一个一阶导数函数(计算图),第三步定义了一个二阶导数函数(计算图),最后给定输入就能获取第一步定义的函数在指定处的二阶导数,二阶导数求导结果为`12`。
此外,SCT能够将Python代码转换为MindSpore函数中间表达(Intermediate Representation,IR),该函数中间表达构造出能够在不同设备解析和执行的计算图,并且在执行该计算图前,应用了多种软硬件协同优化技术,端、边、云等不同场景下的性能和效率得到针对性的提升。
如何提高数据处理能力以匹配人工智能芯片的算力,是保证人工智能芯片发挥极致性能的关键。MindSpore为用户提供了多种数据处理算子,通过自动数据加速技术实现了高性能的流水线,包括数据加载、数据论证、数据转换等,支持CV/NLP/GNN等全场景的数据处理能力。MindRecord是MindSpore的自研数据格式,具有读写高效、易于分布式处理等优点,用户可将非标准的数据集和常用的数据集转换为MindRecord格式,从而获得更好的性能体验,转换详情请参见[MindSpore数据格式转换](https://www.mindspore.cn/docs/programming_guide/zh-CN/master/dataset_conversion.html)。MindSpore支持加载常用的数据集和多种数据存储格式下的数据集,例如通过`dataset=dataset.Cifar10Dataset("Cifar10Data/")`即可完成CIFAR-10数据集的加载,其中`Cifar10Data/`为数据集本地所在目录,用户也可通过`GeneratorDataset`自定义数据集的加载方式。数据增强是一种基于(有限)数据生成新数据的方法,能够减少网络模型过拟合的现象,从而提高模型的泛化能力。MindSpore除了支持用户自定义数据增强外,还提供了自动数据增强方式,使得数据增强更加灵活,详情请见[自动数据增强](https://www.mindspore.cn/docs/programming_guide/zh-CN/master/auto_augmentation.html)。
深度学习神经网络模型通常含有较多的隐藏层进行特征提取,但特征提取随机化、调试过程不可视限制了深度学习技术的可信和调优。MindSpore支持可视化调试调优(MindInsight),提供训练看板、溯源、性能分析和调试器等功能,帮助用户发现模型训练过程中出现的偏差,轻松进行模型调试和性能调优。例如用户可在初始化网络前,通过`profiler=Profiler()`初始化`Profiler`对象,自动收集训练过程中的算子耗时等信息并记录到文件中,在训练结束后调用`profiler.analyse()`停止收集并生成性能分析结果,以可视化形式供用户查看分析,从而更高效地调试网络性能,更多调试调优相关内容请见[训练过程可视化](https://www.mindspore.cn/mindinsight/docs/zh-CN/master/index.html)。
随着神经网络模型和数据集的规模不断增加,分布式并行训练成为了神经网络训练的常见做法,但分布式并行训练的策略选择和编写十分复杂,这严重制约着深度学习模型的训练效率,阻碍深度学习的发展。MindSpore统一了单机和分布式训练的编码方式,开发者无需编写复杂的分布式策略,在单机代码中添加少量代码即可实现分布式训练,例如设置`context.set_auto_parallel_context(parallel_mode=ParallelMode.AUTO_PARALLEL)`便可自动建立代价模型,为用户选择一种较优的并行模式,提高神经网络训练效率,大大降低了AI开发门槛,使用户能够快速实现模型思路,更多内容请见[分布式并行训练](https://www.mindspore.cn/docs/programming_guide/zh-CN/master/distributed_training.html)。
## 层次结构
MindSpore向用户提供了3个不同层次的API,支撑用户进行网络构建、整图执行、子图执行以及单算子执行,从低到高分别为Low-Level Python API、Medium-Level Python API以及High-Level Python API。

- Low-Level Python API
第一层为低阶API,主要包括张量定义、基础算子、自动微分等模块,用户可使用低阶API轻松实现张量定义和求导计算,例如用户可通过`Tensor`接口自定义张量,使用`ops.composite`模块下的`GradOperation`算子计算函数在指定处的导数。
- Medium-Level Python API
第二层为中阶API,其封装了低阶API,提供网络层、优化器、损失函数等模块,用户可通过中阶API灵活构建神经网络和控制执行流程,快速实现模型算法逻辑,例如用户可调用`Cell`接口构建神经网络模型和计算逻辑,通过使用`loss`模块和`Optimizer`接口为神经网络模型添加损失函数和优化方式,利用`dataset`模块对数据进行处理以供模型的训练和推导使用。
- High-Level Python API
第三层为高阶API,其在中阶API的基础上又提供了训练推理的管理、混合精度训练、调试调优等高级接口,方便用户控制整网的执行流程和实现神经网络的训练推理及调优,例如用户使用Model接口,指定要训练的神经网络模型和相关的训练设置,对神经网络模型进行训练,通过`Profiler`接口调试神经网络性能。
|
github_jupyter
|
import mindspore as ms
from mindspore import ops
grad_all = ops.composite.GradOperation()
def func(x):
return x * x * x
def df_func(x):
return grad_all(func)(x)
@ms.ms_function
def df2_func(x):
return grad_all(df_func)(x)
if __name__ == "__main__":
print(df2_func(ms.Tensor(2, ms.float32)))
| 0.338186 | 0.891528 |
<header style="background-image: url('img/typewriter-801921_640.jpg'); background-size: cover; padding: 50px 0;background-repeat: no-repeat;">
<div style="padding: 10px 25px; background-color: #fff9 !important;">
<h1 style="color: black;text-shadow: #fff 5px 5px 0px; margin-bottom: 2em">Document your project<br/>with Markdown, Sphinx,<br/>and Read the Docs</h1>
</div>
</header>
The talk will loosely follow the structure of the official Sphinx tutorial, using Markdown instead of reStructuredText to be more approachable for contributors. It has an estimate duration of 90-120 minutes.
-1. Creating your Sphinx project (15 minutes)
Tutorial introduction, basic project scaffolding using sphinx-quickstart, explanation of the different files that were created.
-2. MyST vs reStructuredText (5 minutes)
Differences between the two markup languages, current status of the ecosystem, pros and cons.
-3. Write Markdown, build HTML (15 minutes)
First steps writing prose documentation using MyST, a flavor of Markdown compatible with Sphinx that adds roles and directives from reStructuredText. Building of HTML documentation using the Sphinx Makefile.
-4. Customizing Sphinx (5 minutes)
Enabling extensions: sphinx.ext.durations to measure performance, furo to use different HTML themes.
-5. Adding cross references (15 minutes)
Adding cross references to other pages of the documentation, specific targets, and objects outside our own project using intersphinx.
-6. Integrating Jupyter notebooks (10 minutes)
Using Jupyter notebooks as pages for the Sphinx documentation, tips and tricks for interactive widgets.
-7. Documenting code automatically (15 minutes)
Leveraging Sphinx code documentation capabilities. Using autodoc to integrate docs from Python docstrings.
-8. Deploying to Read the Docs (10 minutes)
Creating a project on Read the Docs for automatic deployment of the documentation. Enabling pull request reviews.
# Contents
1. Creating your Sphinx project
2. MyST vs reStructuredText
3. Write Markdown, build HTML
4. Customizing Sphinx
5. Adding cross references
6. Integrating Jupyter notebooks
7. Documenting code automatically
8. Deploying to Read the Docs
# 1. Creating your Sphinx project

> Sphinx is a tool that makes it easy to create intelligent and beautiful documentation
https://www.sphinx-doc.org/
- Sphinx reads **source files** and generates an **output**
- The source files can be reStructuredText, **Markdown**, **Python**, Jupyter notebooks, images, ...
- The **output** can be **HTML**, PDF, _man pages_, EPUB, ...
- Therefore, Sphinx can also be considered a **static site generator** (SSG)!
Some interesting functionalities:
- Multiple different **output formats** ("builders")
- **Cross-references** and automatic hyperlinks for functions, classes, figures, glossary terms, and more
- **Hierarchical structure** using trees of documents, with automatic breadcrumbs
- **Automatic numbering**
- **Code loading capabilities** and syntax highlight
- **Extensible**! https://sphinx-extensions.readthedocs.io/
**Objetive**: Document a tiny Python library, available at https://github.com/readthedocs/tutorial-sphinx-markdown-library (and a submodule of this repository)

# It's demo time!
# Where to go from here
- This tutorial https://github.com/readthedocs/tutorial-sphinx-markdown
- MyST intro https://myst-parser.readthedocs.io/en/latest/sphinx/intro.html
- Sphinx tutorial (in reST) https://www.sphinx-doc.org/en/master/tutorial/
- Read the Docs tutorial https://docs.readthedocs.io/en/stable/tutorial/
💌 <[email protected]>
Thank you!
|
github_jupyter
|
<header style="background-image: url('img/typewriter-801921_640.jpg'); background-size: cover; padding: 50px 0;background-repeat: no-repeat;">
<div style="padding: 10px 25px; background-color: #fff9 !important;">
<h1 style="color: black;text-shadow: #fff 5px 5px 0px; margin-bottom: 2em">Document your project<br/>with Markdown, Sphinx,<br/>and Read the Docs</h1>
</div>
</header>
The talk will loosely follow the structure of the official Sphinx tutorial, using Markdown instead of reStructuredText to be more approachable for contributors. It has an estimate duration of 90-120 minutes.
-1. Creating your Sphinx project (15 minutes)
Tutorial introduction, basic project scaffolding using sphinx-quickstart, explanation of the different files that were created.
-2. MyST vs reStructuredText (5 minutes)
Differences between the two markup languages, current status of the ecosystem, pros and cons.
-3. Write Markdown, build HTML (15 minutes)
First steps writing prose documentation using MyST, a flavor of Markdown compatible with Sphinx that adds roles and directives from reStructuredText. Building of HTML documentation using the Sphinx Makefile.
-4. Customizing Sphinx (5 minutes)
Enabling extensions: sphinx.ext.durations to measure performance, furo to use different HTML themes.
-5. Adding cross references (15 minutes)
Adding cross references to other pages of the documentation, specific targets, and objects outside our own project using intersphinx.
-6. Integrating Jupyter notebooks (10 minutes)
Using Jupyter notebooks as pages for the Sphinx documentation, tips and tricks for interactive widgets.
-7. Documenting code automatically (15 minutes)
Leveraging Sphinx code documentation capabilities. Using autodoc to integrate docs from Python docstrings.
-8. Deploying to Read the Docs (10 minutes)
Creating a project on Read the Docs for automatic deployment of the documentation. Enabling pull request reviews.
# Contents
1. Creating your Sphinx project
2. MyST vs reStructuredText
3. Write Markdown, build HTML
4. Customizing Sphinx
5. Adding cross references
6. Integrating Jupyter notebooks
7. Documenting code automatically
8. Deploying to Read the Docs
# 1. Creating your Sphinx project

> Sphinx is a tool that makes it easy to create intelligent and beautiful documentation
https://www.sphinx-doc.org/
- Sphinx reads **source files** and generates an **output**
- The source files can be reStructuredText, **Markdown**, **Python**, Jupyter notebooks, images, ...
- The **output** can be **HTML**, PDF, _man pages_, EPUB, ...
- Therefore, Sphinx can also be considered a **static site generator** (SSG)!
Some interesting functionalities:
- Multiple different **output formats** ("builders")
- **Cross-references** and automatic hyperlinks for functions, classes, figures, glossary terms, and more
- **Hierarchical structure** using trees of documents, with automatic breadcrumbs
- **Automatic numbering**
- **Code loading capabilities** and syntax highlight
- **Extensible**! https://sphinx-extensions.readthedocs.io/
**Objetive**: Document a tiny Python library, available at https://github.com/readthedocs/tutorial-sphinx-markdown-library (and a submodule of this repository)

# It's demo time!
# Where to go from here
- This tutorial https://github.com/readthedocs/tutorial-sphinx-markdown
- MyST intro https://myst-parser.readthedocs.io/en/latest/sphinx/intro.html
- Sphinx tutorial (in reST) https://www.sphinx-doc.org/en/master/tutorial/
- Read the Docs tutorial https://docs.readthedocs.io/en/stable/tutorial/
💌 <[email protected]>
Thank you!
| 0.728169 | 0.543893 |
## 1. Google Play Store apps and reviews
<p>Mobile apps are everywhere. They are easy to create and can be lucrative. Because of these two factors, more and more apps are being developed. In this notebook, we will do a comprehensive analysis of the Android app market by comparing over ten thousand apps in Google Play across different categories. We'll look for insights in the data to devise strategies to drive growth and retention.</p>
<p><img src="https://assets.datacamp.com/production/project_619/img/google_play_store.png" alt="Google Play logo"></p>
<p>Let's take a look at the data, which consists of two files:</p>
<ul>
<li><code>apps.csv</code>: contains all the details of the applications on Google Play. There are 13 features that describe a given app.</li>
<li><code>user_reviews.csv</code>: contains 100 reviews for each app, <a href="https://www.androidpolice.com/2019/01/21/google-play-stores-redesigned-ratings-and-reviews-section-lets-you-easily-filter-by-star-rating/">most helpful first</a>. The text in each review has been pre-processed and attributed with three new features: Sentiment (Positive, Negative or Neutral), Sentiment Polarity and Sentiment Subjectivity.</li>
</ul>
```
# Read in dataset
import pandas as pd
apps_with_duplicates = pd.read_csv("datasets/apps.csv")
# Drop duplicates
apps = apps_with_duplicates.drop_duplicates()
# Print the total number of apps
print('Total number of apps in the dataset = ', len(apps))
# Have a look at a random sample of 5 rows
n = 5
apps.sample(n)
apps['Price'].unique()
```
## 2. Data cleaning
<p>The three features that we will be working with most frequently henceforth are <code>Installs</code>, <code>Size</code>, and <code>Price</code>. A careful glance of the dataset reveals that some of these columns mandate data cleaning in order to be consumed by code we'll write later. Specifically, the presence of special characters (<code>, $ +</code>) and letters (<code>M k</code>) in the <code>Installs</code>, <code>Size</code>, and <code>Price</code> columns make their conversion to a numerical data type difficult. Let's clean by removing these and converting each column to a numeric type.</p>
```
# List of characters to remove
chars_to_remove = ['+',',','$']
# List of column names to clean
cols_to_clean = ['Installs','Price']
# Loop for each column
for col in cols_to_clean:
# Replace each character with an empty string
for char in chars_to_remove:
apps[col] = apps[col].str.replace(char, '')
# Convert col to numeric
apps[col] = pd.to_numeric(apps[col])
```
## 3. Exploring app categories
<p>With more than 1 billion active users in 190 countries around the world, Google Play continues to be an important distribution platform to build a global audience. For businesses to get their apps in front of users, it's important to make them more quickly and easily discoverable on Google Play. To improve the overall search experience, Google has introduced the concept of grouping apps into categories.</p>
<p>This brings us to the following questions:</p>
<ul>
<li>Which category has the highest share of (active) apps in the market? </li>
<li>Is any specific category dominating the market?</li>
<li>Which categories have the fewest number of apps?</li>
</ul>
<p>We will see that there are <code>33</code> unique app categories present in our dataset. <em>Family</em> and <em>Game</em> apps have the highest market prevalence. Interestingly, <em>Tools</em>, <em>Business</em> and <em>Medical</em> apps are also at the top.</p>
```
import plotly
plotly.offline.init_notebook_mode(connected=True)
import plotly.graph_objs as go
# Print the total number of unique categories
num_categories = len(apps['Category'].unique())
print('Number of categories = ', num_categories)
# Count the number of apps in each 'Category' and sort them in descending order
num_apps_in_category = apps['Category'].value_counts().sort_values(ascending = False)
data = [go.Bar(
x = num_apps_in_category.index, # index = category name
y = num_apps_in_category.values, # value = count
)]
plotly.offline.iplot(data)
```
## 4. Distribution of app ratings
<p>After having witnessed the market share for each category of apps, let's see how all these apps perform on an average. App ratings (on a scale of 1 to 5) impact the discoverability, conversion of apps as well as the company's overall brand image. Ratings are a key performance indicator of an app.</p>
<p>From our research, we found that the average volume of ratings across all app categories is <code>4.17</code>. The histogram plot is skewed to the right indicating that the majority of the apps are highly rated with only a few exceptions in the low-rated apps.</p>
```
# Average rating of apps
avg_app_rating = apps['Rating'].mean()
print('Average app rating = ', avg_app_rating)
# Distribution of apps according to their ratings
data = [go.Histogram(
x = apps['Rating']
)]
# Vertical dashed line to indicate the average app rating
layout = {'shapes': [{
'type' :'line',
'x0': avg_app_rating,
'y0': 0,
'x1': avg_app_rating,
'y1': 1000,
'line': { 'dash': 'dashdot'}
}]
}
plotly.offline.iplot({'data': data, 'layout': layout})
```
## 5. Size and price of an app
<p>Let's now examine app size and app price. For size, if the mobile app is too large, it may be difficult and/or expensive for users to download. Lengthy download times could turn users off before they even experience your mobile app. Plus, each user's device has a finite amount of disk space. For price, some users expect their apps to be free or inexpensive. These problems compound if the developing world is part of your target market; especially due to internet speeds, earning power and exchange rates.</p>
<p>How can we effectively come up with strategies to size and price our app?</p>
<ul>
<li>Does the size of an app affect its rating? </li>
<li>Do users really care about system-heavy apps or do they prefer light-weighted apps? </li>
<li>Does the price of an app affect its rating? </li>
<li>Do users always prefer free apps over paid apps?</li>
</ul>
<p>We find that the majority of top rated apps (rating over 4) range from 2 MB to 20 MB. We also find that the vast majority of apps price themselves under \$10.</p>
```
%matplotlib inline
import seaborn as sns
sns.set_style("darkgrid")
import warnings
warnings.filterwarnings("ignore")
# Plot size vs. rating
plt1 = sns.jointplot(x = apps['Size'], y = apps['Rating'], kind = 'hex')
# Subset out apps whose type is 'Paid'
paid_apps = apps[apps['Type'] == 'Paid']
# Plot price vs. rating
plt2 = sns.jointplot(x = paid_apps['Price'], y = paid_apps['Rating'])
```
## 6. Relation between app category and app price
<p>So now comes the hard part. How are companies and developers supposed to make ends meet? What monetization strategies can companies use to maximize profit? The costs of apps are largely based on features, complexity, and platform.</p>
<p>There are many factors to consider when selecting the right pricing strategy for your mobile app. It is important to consider the willingness of your customer to pay for your app. A wrong price could break the deal before the download even happens. Potential customers could be turned off by what they perceive to be a shocking cost, or they might delete an app they’ve downloaded after receiving too many ads or simply not getting their money's worth.</p>
<p>Different categories demand different price ranges. Some apps that are simple and used daily, like the calculator app, should probably be kept free. However, it would make sense to charge for a highly-specialized medical app that diagnoses diabetic patients. Below, we see that <em>Medical and Family</em> apps are the most expensive. Some medical apps extend even up to \$80! All game apps are reasonably priced below \$20.</p>
```
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
fig.set_size_inches(15, 8)
# Select a few popular app categories
popular_app_cats = apps[apps.Category.isin(['GAME', 'FAMILY', 'PHOTOGRAPHY',
'MEDICAL', 'TOOLS', 'FINANCE',
'LIFESTYLE','BUSINESS'])]
# Examine the price trend by plotting Price vs Category
ax = sns.stripplot(x = popular_app_cats['Price'], y = popular_app_cats['Category'], jitter=True, linewidth=1)
ax.set_title('App pricing trend across categories')
# Apps whose Price is greater than 200
apps_above_200 = popular_app_cats[['Category', 'App', 'Price']][popular_app_cats['Price'] > 200]
apps_above_200
```
## 7. Filter out "junk" apps
<p>It looks like a bunch of the really expensive apps are "junk" apps. That is, apps that don't really have a purpose. Some app developer may create an app called <em>I Am Rich Premium</em> or <em>most expensive app (H)</em> just for a joke or to test their app development skills. Some developers even do this with malicious intent and try to make money by hoping people accidentally click purchase on their app in the store.</p>
<p>Let's filter out these junk apps and re-do our visualization. The distribution of apps under \$20 becomes clearer.</p>
```
# Select apps priced below $100
apps_under_100 = popular_app_cats[popular_app_cats['Price']<=100]
fig, ax = plt.subplots()
fig.set_size_inches(15, 8)
# Examine price vs category with the authentic apps
ax = sns.stripplot(x='Price', y='Category', data=apps_under_100,
jitter=True, linewidth=1)
ax.set_title('App pricing trend across categories after filtering for junk apps')
```
## 8. Popularity of paid apps vs free apps
<p>For apps in the Play Store today, there are five types of pricing strategies: free, freemium, paid, paymium, and subscription. Let's focus on free and paid apps only. Some characteristics of free apps are:</p>
<ul>
<li>Free to download.</li>
<li>Main source of income often comes from advertisements.</li>
<li>Often created by companies that have other products and the app serves as an extension of those products.</li>
<li>Can serve as a tool for customer retention, communication, and customer service.</li>
</ul>
<p>Some characteristics of paid apps are:</p>
<ul>
<li>Users are asked to pay once for the app to download and use it.</li>
<li>The user can't really get a feel for the app before buying it.</li>
</ul>
<p>Are paid apps installed as much as free apps? It turns out that paid apps have a relatively lower number of installs than free apps, though the difference is not as stark as I would have expected!</p>
```
trace0 = go.Box(
# Data for paid apps
y=apps[apps['Type'] == 'Paid']['Installs'],
name = 'Paid'
)
trace1 = go.Box(
# Data for free apps
y=apps[apps['Type'] == 'Free']['Installs'],
name = 'Free'
)
layout = go.Layout(
title = "Number of downloads of paid apps vs. free apps",
yaxis = dict(
type = 'log',
autorange = True
)
)
# Add trace0 and trace1 to a list for plotting
data = [trace0, trace1]
plotly.offline.iplot({'data': data, 'layout': layout})
```
## 9. Sentiment analysis of user reviews
<p>Mining user review data to determine how people feel about your product, brand, or service can be done using a technique called sentiment analysis. User reviews for apps can be analyzed to identify if the mood is positive, negative or neutral about that app. For example, positive words in an app review might include words such as 'amazing', 'friendly', 'good', 'great', and 'love'. Negative words might be words like 'malware', 'hate', 'problem', 'refund', and 'incompetent'.</p>
<p>By plotting sentiment polarity scores of user reviews for paid and free apps, we observe that free apps receive a lot of harsh comments, as indicated by the outliers on the negative y-axis. Reviews for paid apps appear never to be extremely negative. This may indicate something about app quality, i.e., paid apps being of higher quality than free apps on average. The median polarity score for paid apps is a little higher than free apps, thereby syncing with our previous observation.</p>
<p>In this notebook, we analyzed over ten thousand apps from the Google Play Store. We can use our findings to inform our decisions should we ever wish to create an app ourselves.</p>
```
# Load user_reviews.csv
reviews_df = pd.read_csv('datasets/user_reviews.csv')
# Join and merge the two dataframe
merged_df = pd.merge(apps, reviews_df, on = 'App', how = "inner")
# Drop NA values from Sentiment and Translated_Review columns
merged_df = merged_df.dropna(subset=['Sentiment', 'Translated_Review'])
sns.set_style('ticks')
fig, ax = plt.subplots()
fig.set_size_inches(11, 8)
# User review sentiment polarity for paid vs. free apps
ax = sns.boxplot(x = 'Type', y = 'Sentiment_Polarity', data = merged_df)
ax.set_title('Sentiment Polarity Distribution')
```
|
github_jupyter
|
# Read in dataset
import pandas as pd
apps_with_duplicates = pd.read_csv("datasets/apps.csv")
# Drop duplicates
apps = apps_with_duplicates.drop_duplicates()
# Print the total number of apps
print('Total number of apps in the dataset = ', len(apps))
# Have a look at a random sample of 5 rows
n = 5
apps.sample(n)
apps['Price'].unique()
# List of characters to remove
chars_to_remove = ['+',',','$']
# List of column names to clean
cols_to_clean = ['Installs','Price']
# Loop for each column
for col in cols_to_clean:
# Replace each character with an empty string
for char in chars_to_remove:
apps[col] = apps[col].str.replace(char, '')
# Convert col to numeric
apps[col] = pd.to_numeric(apps[col])
import plotly
plotly.offline.init_notebook_mode(connected=True)
import plotly.graph_objs as go
# Print the total number of unique categories
num_categories = len(apps['Category'].unique())
print('Number of categories = ', num_categories)
# Count the number of apps in each 'Category' and sort them in descending order
num_apps_in_category = apps['Category'].value_counts().sort_values(ascending = False)
data = [go.Bar(
x = num_apps_in_category.index, # index = category name
y = num_apps_in_category.values, # value = count
)]
plotly.offline.iplot(data)
# Average rating of apps
avg_app_rating = apps['Rating'].mean()
print('Average app rating = ', avg_app_rating)
# Distribution of apps according to their ratings
data = [go.Histogram(
x = apps['Rating']
)]
# Vertical dashed line to indicate the average app rating
layout = {'shapes': [{
'type' :'line',
'x0': avg_app_rating,
'y0': 0,
'x1': avg_app_rating,
'y1': 1000,
'line': { 'dash': 'dashdot'}
}]
}
plotly.offline.iplot({'data': data, 'layout': layout})
%matplotlib inline
import seaborn as sns
sns.set_style("darkgrid")
import warnings
warnings.filterwarnings("ignore")
# Plot size vs. rating
plt1 = sns.jointplot(x = apps['Size'], y = apps['Rating'], kind = 'hex')
# Subset out apps whose type is 'Paid'
paid_apps = apps[apps['Type'] == 'Paid']
# Plot price vs. rating
plt2 = sns.jointplot(x = paid_apps['Price'], y = paid_apps['Rating'])
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
fig.set_size_inches(15, 8)
# Select a few popular app categories
popular_app_cats = apps[apps.Category.isin(['GAME', 'FAMILY', 'PHOTOGRAPHY',
'MEDICAL', 'TOOLS', 'FINANCE',
'LIFESTYLE','BUSINESS'])]
# Examine the price trend by plotting Price vs Category
ax = sns.stripplot(x = popular_app_cats['Price'], y = popular_app_cats['Category'], jitter=True, linewidth=1)
ax.set_title('App pricing trend across categories')
# Apps whose Price is greater than 200
apps_above_200 = popular_app_cats[['Category', 'App', 'Price']][popular_app_cats['Price'] > 200]
apps_above_200
# Select apps priced below $100
apps_under_100 = popular_app_cats[popular_app_cats['Price']<=100]
fig, ax = plt.subplots()
fig.set_size_inches(15, 8)
# Examine price vs category with the authentic apps
ax = sns.stripplot(x='Price', y='Category', data=apps_under_100,
jitter=True, linewidth=1)
ax.set_title('App pricing trend across categories after filtering for junk apps')
trace0 = go.Box(
# Data for paid apps
y=apps[apps['Type'] == 'Paid']['Installs'],
name = 'Paid'
)
trace1 = go.Box(
# Data for free apps
y=apps[apps['Type'] == 'Free']['Installs'],
name = 'Free'
)
layout = go.Layout(
title = "Number of downloads of paid apps vs. free apps",
yaxis = dict(
type = 'log',
autorange = True
)
)
# Add trace0 and trace1 to a list for plotting
data = [trace0, trace1]
plotly.offline.iplot({'data': data, 'layout': layout})
# Load user_reviews.csv
reviews_df = pd.read_csv('datasets/user_reviews.csv')
# Join and merge the two dataframe
merged_df = pd.merge(apps, reviews_df, on = 'App', how = "inner")
# Drop NA values from Sentiment and Translated_Review columns
merged_df = merged_df.dropna(subset=['Sentiment', 'Translated_Review'])
sns.set_style('ticks')
fig, ax = plt.subplots()
fig.set_size_inches(11, 8)
# User review sentiment polarity for paid vs. free apps
ax = sns.boxplot(x = 'Type', y = 'Sentiment_Polarity', data = merged_df)
ax.set_title('Sentiment Polarity Distribution')
| 0.706697 | 0.982305 |
# Log runs to an experiment
## Types of experiments
There are two types of experiments in MLflow: _notebook_ and _workspace_.
* A notebook experiment is associated with a specific notebook. Databricks creates a notebook experiment by default when a run is started using `mlflow.start_run()` and there is no active experiment.
* Workspace experiments are not associated with any notebook, and any notebook can log a run to these experiments by using the experiment name or the experiment ID when initiating a run.
This notebook creates a Random Forest model on a simple dataset and uses the MLflow Tracking API to log the model and selected model parameters and metrics.
```
# Import the dataset from scikit-learn and create the training and test datasets.
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_diabetes
db = load_diabetes()
X = db.data
y = db.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
```
By default, MLflow runs are logged to the notebook experiment, as illustrated in the following code block.
```
import mlflow
import mlflow.sklearn
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
# In this run, neither the experiment_id nor the experiment_name parameter is provided. MLflow automatically creates a notebook experiment and logs runs to it.
# Access these runs using the Experiment sidebar. Click Experiment at the upper right of this screen.
with mlflow.start_run():
n_estimators = 100
max_depth = 6
max_features = 3
# Create and train model
rf = RandomForestRegressor(n_estimators = n_estimators, max_depth = max_depth, max_features = max_features)
rf.fit(X_train, y_train)
# Make predictions
predictions = rf.predict(X_test)
# Log parameters
mlflow.log_param("num_trees", n_estimators)
mlflow.log_param("maxdepth", max_depth)
mlflow.log_param("max_feat", max_features)
# Log model
mlflow.sklearn.log_model(rf, "random-forest-model")
# Create metrics
mse = mean_squared_error(y_test, predictions)
# Log metrics
mlflow.log_metric("mse", mse)
```
To log MLflow runs to a workspace experiment, use `mlflow.set_experiment()` as illustrated in the following code block. An alternative is to set the experiment_id parameter in `mlflow.start_run()`; for example, `mlflow.start_run(experiment_id=1234567)`.
```
# This run uses mlflow.set_experiment() to specify an experiment in the workspace where runs should be logged.
# If the experiment specified by experiment_name does not exist in the workspace, MLflow creates it.
# Access these runs using the experiment name in the workspace file tree.
experiment_name = "/Shared/diabetes_experiment/"
mlflow.set_experiment(experiment_name)
with mlflow.start_run():
n_estimators = 110
max_depth = 8
max_features = 7
# Create and train model
rf = RandomForestRegressor(n_estimators = n_estimators, max_depth = max_depth, max_features = max_features)
rf.fit(X_train, y_train)
# Make predictions
predictions = rf.predict(X_test)
# Log parameters
mlflow.log_param("num_trees", n_estimators)
mlflow.log_param("maxdepth", max_depth)
mlflow.log_param("max_feat", max_features)
# Log model
mlflow.sklearn.log_model(rf, "random-forest-model")
# Create metrics
mse = mean_squared_error(y_test, predictions)
# Log metrics
mlflow.log_metric("mse", mse)
```
|
github_jupyter
|
# Import the dataset from scikit-learn and create the training and test datasets.
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_diabetes
db = load_diabetes()
X = db.data
y = db.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
import mlflow
import mlflow.sklearn
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
# In this run, neither the experiment_id nor the experiment_name parameter is provided. MLflow automatically creates a notebook experiment and logs runs to it.
# Access these runs using the Experiment sidebar. Click Experiment at the upper right of this screen.
with mlflow.start_run():
n_estimators = 100
max_depth = 6
max_features = 3
# Create and train model
rf = RandomForestRegressor(n_estimators = n_estimators, max_depth = max_depth, max_features = max_features)
rf.fit(X_train, y_train)
# Make predictions
predictions = rf.predict(X_test)
# Log parameters
mlflow.log_param("num_trees", n_estimators)
mlflow.log_param("maxdepth", max_depth)
mlflow.log_param("max_feat", max_features)
# Log model
mlflow.sklearn.log_model(rf, "random-forest-model")
# Create metrics
mse = mean_squared_error(y_test, predictions)
# Log metrics
mlflow.log_metric("mse", mse)
# This run uses mlflow.set_experiment() to specify an experiment in the workspace where runs should be logged.
# If the experiment specified by experiment_name does not exist in the workspace, MLflow creates it.
# Access these runs using the experiment name in the workspace file tree.
experiment_name = "/Shared/diabetes_experiment/"
mlflow.set_experiment(experiment_name)
with mlflow.start_run():
n_estimators = 110
max_depth = 8
max_features = 7
# Create and train model
rf = RandomForestRegressor(n_estimators = n_estimators, max_depth = max_depth, max_features = max_features)
rf.fit(X_train, y_train)
# Make predictions
predictions = rf.predict(X_test)
# Log parameters
mlflow.log_param("num_trees", n_estimators)
mlflow.log_param("maxdepth", max_depth)
mlflow.log_param("max_feat", max_features)
# Log model
mlflow.sklearn.log_model(rf, "random-forest-model")
# Create metrics
mse = mean_squared_error(y_test, predictions)
# Log metrics
mlflow.log_metric("mse", mse)
| 0.839603 | 0.990044 |
# Containers
In Python a container is something that contains something. Containers may be sequences, sets or mappings. Thus a collection is an **abstraction** of **"something"** that:
- May contain **something**
- Sequences are iterable
- Collections have a size
We usually talk about generic container types such as `List[T]`, `Set[T]`, `Tuple[T, ...]`. But we can also imagine taking the abstraction to a higher-order making the left side generic as well, e.g `Something[T]`. What do types of `Something` have in common?
> *A something within a something*
A container is really just some kind of box that you can pull values out of. Can values be pushed out of a container?
## Mapping
A mapping object maps immutable values to arbitrary objects. There is both `Mapping` and `MutableMapping`. The most known mutable mapping is the `dict` type.
## Sequence
A sequence is an iterable container such as `List`, `Tuple`, `str`, ...
## Immutable data types
Immutable data types are important in functional programming. Immutable means that it's not possible to make any changes after the type have been created. Most data structures in Python are mutable such as `List` and `Dict`, but Python also have a few immutable data types:
* Strings
* Tuples
* Iterable
The advantages of immutable data types are:
* Thread-safe. Multiple threads cannot modify or corrupt the state.
* Safe to share and reuse
* Easy to reason about. Reduces the cognitive load
* Easier to debug
Expression extends Python with a couple of more immutable data types:
## FrozenList
A FrozenList is an immutable List type. The implementation is based on the already immutable tuple type but gives it a list feeling and lots of functions and methods to work with it.
```
from expression.collections import FrozenList
xs = FrozenList.of_seq(range(10))
print(xs)
ys = xs.cons(10)
print(ys)
zs = xs.tail()
print(zs)
```
## Map
The Expression Map module is an immutable Dict type. The implementation is based on map type from F# and uses a balanced binary tree implementation.
```
from expression.collections import Map
items = dict(a=10, b=20).items()
xs = Map.of_seq(items)
print(xs)
ys = xs.filter(lambda k, v: v>10)
print(ys)
```
## Functions are Containers
It might not be obvious at first, but functions can also be containers. This is because values might be stored in function closures. That means that a value might be visible in the scope of the function.
> A closure is a poor man's object. An object is a poor man's closure.
In functional programming we often use function arguments to store values instead of objects
```
def hat(item):
def pull():
return item
return pull
small_hat = lambda item: lambda pull: item
pull = hat("rabbit")
pull()
```
## List out of lambda (LOL)
We can even create a fully functional list implementation using only functions:
```
empty_list = None
def prepend(el, lst):
return lambda selector: selector(el, lst)
def head(lst):
return lst(lambda h, t: h)
def tail(lst):
return lst(lambda h, t: t)
def is_empty(lst):
return (lst == empty_list)
a = prepend("a", prepend("b", empty_list))
assert("a" == head(a))
assert("b" == head(tail(a)))
assert(tail(tail(a))==empty_list)
assert(not is_empty(a))
assert(is_empty(empty_list))
print("all tests are green!")
```
## LOL (more compact)
A list can be created using only lambda functions:
```
empty_list = None
prepend = lambda el, lst: lambda selector: selector(el, lst)
head = lambda lst: lst(lambda h, t: h)
tail = lambda lst: lst(lambda h, t: t)
is_empty = lambda lst: lst is empty_list
a = prepend("a", prepend("b", empty_list))
assert("a" == head(a))
assert("b" == head(tail(a)))
assert(tail(tail(a))==empty_list)
assert(not is_empty(a))
assert(is_empty(empty_list))
print("all tests are green!")
```
## Pull vs Push
List, iterables, mappings, strings etc are what we call "pull" collections. This is because we are actively pulling the values out of the collection by calling the `next()` function on the Iterator.
```
iterable = [1, 2, 3]
iterator = iter(iterable) # get iterator
value = next(iterator)
print(value)
value = next(iterator)
print(value)
value = next(iterator)
print(value)
# value = next(iterator)
```
## Push Collections
A push collection is something that pushes values out of the collection. This can be seen as temporal (push) containers vs spatial (pull) collections. This collection is called an Observable and is the dual (or the opposite) of an Iterable.
An `Iterable` have getter for getting an `Iterator` (__iter__)
An `Obserable` have a setter for setting an `Observer` (subscribe)
An `Iterator` have a getter for getting the next value (__next__)
An `Observer` have a setter for setting the next value (on_next, or send)
Summarized:
* Iterable is a getter-getter function
* Observable is a setter-setter function
Let's try to implement an Observable using only functions:
```
import sys
def observer(value):
print(f"got value: {value}")
def infinite():
def subscribe(obv):
for x in range(1000):
obv(x)
return subscribe
def take(count):
def obs(source):
def subscribe(obv):
n = count
def observer(value):
nonlocal n
if n > 0:
obv(value)
n -= 1
source(observer)
return subscribe
return obs
take(10)(infinite())(observer)
def pipe(arg, *fns):
for fn in fns:
arg = fn(arg)
return arg
observable = pipe(
infinite(), # infinite sequence of values
take(10) # take the first 10
)
observable(observer)
```
[RxPY](https://github.com/ReactiveX/RxPY) is an implementation of `Observable` and [aioreactive](https://github.com/dbrattli/aioreactive) project is an implementation of `AsyncObservable`.
|
github_jupyter
|
from expression.collections import FrozenList
xs = FrozenList.of_seq(range(10))
print(xs)
ys = xs.cons(10)
print(ys)
zs = xs.tail()
print(zs)
from expression.collections import Map
items = dict(a=10, b=20).items()
xs = Map.of_seq(items)
print(xs)
ys = xs.filter(lambda k, v: v>10)
print(ys)
def hat(item):
def pull():
return item
return pull
small_hat = lambda item: lambda pull: item
pull = hat("rabbit")
pull()
empty_list = None
def prepend(el, lst):
return lambda selector: selector(el, lst)
def head(lst):
return lst(lambda h, t: h)
def tail(lst):
return lst(lambda h, t: t)
def is_empty(lst):
return (lst == empty_list)
a = prepend("a", prepend("b", empty_list))
assert("a" == head(a))
assert("b" == head(tail(a)))
assert(tail(tail(a))==empty_list)
assert(not is_empty(a))
assert(is_empty(empty_list))
print("all tests are green!")
empty_list = None
prepend = lambda el, lst: lambda selector: selector(el, lst)
head = lambda lst: lst(lambda h, t: h)
tail = lambda lst: lst(lambda h, t: t)
is_empty = lambda lst: lst is empty_list
a = prepend("a", prepend("b", empty_list))
assert("a" == head(a))
assert("b" == head(tail(a)))
assert(tail(tail(a))==empty_list)
assert(not is_empty(a))
assert(is_empty(empty_list))
print("all tests are green!")
iterable = [1, 2, 3]
iterator = iter(iterable) # get iterator
value = next(iterator)
print(value)
value = next(iterator)
print(value)
value = next(iterator)
print(value)
# value = next(iterator)
import sys
def observer(value):
print(f"got value: {value}")
def infinite():
def subscribe(obv):
for x in range(1000):
obv(x)
return subscribe
def take(count):
def obs(source):
def subscribe(obv):
n = count
def observer(value):
nonlocal n
if n > 0:
obv(value)
n -= 1
source(observer)
return subscribe
return obs
take(10)(infinite())(observer)
def pipe(arg, *fns):
for fn in fns:
arg = fn(arg)
return arg
observable = pipe(
infinite(), # infinite sequence of values
take(10) # take the first 10
)
observable(observer)
| 0.558568 | 0.957794 |
<center><h1 style="font-size:3em">Activation functions in DL</h1></center>
```
import numpy as np
import matplotlib.pyplot as plt
# Data which will go through activations
x = np.linspace(-10,10,100)
```
# ReLU
```
def relu(x):
return max(0,x)
def der_relu(x):
if x <= 0 :
return 0
if x > 0 :
return 1
plt.figure(figsize=(12,8))
plt.plot(x, list(map(lambda x: relu(x),x)), label="relu")
plt.plot(x, list(map(lambda x: der_relu(x),x)), label="derivative")
plt.title("ReLU")
plt.legend()
plt.show()
```
# Leaky-ReLU
```
def leaky_relu(x):
return max(0.01*x,x)
def der_leaky_relu(x):
if x < 0 :
return 0.01
if x >= 0 :
return 1
plt.figure(figsize=(12,8))
plt.plot(x, list(map(lambda x: leaky_relu(x),x)), label="leaky-relu")
plt.plot(x, list(map(lambda x: der_leaky_relu(x),x)), label="derivative")
plt.title("Leaky-ReLU")
plt.legend()
plt.show()
```
# ELU
```
def elu(x):
if x > 0 :
return x
else :
return (np.exp(x)-1)
def der_elu(x):
if x > 0 :
return 1
else :
return np.exp(x)
plt.figure(figsize=(12,8))
plt.plot(x, list(map(lambda x: elu(x),x)), label="elu")
plt.plot(x, list(map(lambda x: der_elu(x),x)), label="derivative")
plt.title("ELU")
plt.legend()
plt.show()
```
# Softplus
```
def softplus(x):
return np.log(1+np.exp(x))
def der_softplus(x):
return 1/(1+np.exp(x))*np.exp(x)
plt.figure(figsize=(12,8))
plt.plot(x, list(map(lambda x: softplus(x),x)), label="softplus")
plt.plot(x, list(map(lambda x: der_softplus(x),x)), label="derivative")
plt.title("Softplus")
plt.legend()
plt.show()
```
# Softmax
```
def softmax(x):
return 1/(1+np.exp(-x))
def der_softmax(x):
return 1/(1+np.exp(-x)) * (1-1/(1+np.exp(-x)))
plt.figure(figsize=(12,8))
plt.plot(x, list(map(lambda x: softmax(x),x)), label="softmax")
plt.plot(x, list(map(lambda x: der_softmax(x),x)), label="derivative")
plt.title("Softmax")
plt.legend()
plt.show()
```
# Hyperbolic Tangent
```
def hyperb(x):
return (np.exp(x)-np.exp(-x)) / (np.exp(x) + np.exp(-x))
def der_hyperb(x):
return 1 - ((np.exp(x)-np.exp(-x)) / (np.exp(x) + np.exp(-x)))**2
plt.figure(figsize=(12,8))
plt.plot(x, list(map(lambda x: hyperb(x),x)), label="hyperbolic")
plt.plot(x, list(map(lambda x: der_hyperb(x),x)), label="derivative")
plt.title("Hyperbolic")
plt.legend()
plt.show()
```
# Arctan
```
def arctan(x):
return np.arctan(x)
def der_arctan(x):
return 1 / (1+x**2)
plt.figure(figsize=(12,8))
plt.plot(x, list(map(lambda x: arctan(x),x)), label="arctan")
plt.plot(x, list(map(lambda x: der_arctan(x),x)), label="derivative")
plt.title("Arctan")
plt.legend()
plt.show()
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
# Data which will go through activations
x = np.linspace(-10,10,100)
def relu(x):
return max(0,x)
def der_relu(x):
if x <= 0 :
return 0
if x > 0 :
return 1
plt.figure(figsize=(12,8))
plt.plot(x, list(map(lambda x: relu(x),x)), label="relu")
plt.plot(x, list(map(lambda x: der_relu(x),x)), label="derivative")
plt.title("ReLU")
plt.legend()
plt.show()
def leaky_relu(x):
return max(0.01*x,x)
def der_leaky_relu(x):
if x < 0 :
return 0.01
if x >= 0 :
return 1
plt.figure(figsize=(12,8))
plt.plot(x, list(map(lambda x: leaky_relu(x),x)), label="leaky-relu")
plt.plot(x, list(map(lambda x: der_leaky_relu(x),x)), label="derivative")
plt.title("Leaky-ReLU")
plt.legend()
plt.show()
def elu(x):
if x > 0 :
return x
else :
return (np.exp(x)-1)
def der_elu(x):
if x > 0 :
return 1
else :
return np.exp(x)
plt.figure(figsize=(12,8))
plt.plot(x, list(map(lambda x: elu(x),x)), label="elu")
plt.plot(x, list(map(lambda x: der_elu(x),x)), label="derivative")
plt.title("ELU")
plt.legend()
plt.show()
def softplus(x):
return np.log(1+np.exp(x))
def der_softplus(x):
return 1/(1+np.exp(x))*np.exp(x)
plt.figure(figsize=(12,8))
plt.plot(x, list(map(lambda x: softplus(x),x)), label="softplus")
plt.plot(x, list(map(lambda x: der_softplus(x),x)), label="derivative")
plt.title("Softplus")
plt.legend()
plt.show()
def softmax(x):
return 1/(1+np.exp(-x))
def der_softmax(x):
return 1/(1+np.exp(-x)) * (1-1/(1+np.exp(-x)))
plt.figure(figsize=(12,8))
plt.plot(x, list(map(lambda x: softmax(x),x)), label="softmax")
plt.plot(x, list(map(lambda x: der_softmax(x),x)), label="derivative")
plt.title("Softmax")
plt.legend()
plt.show()
def hyperb(x):
return (np.exp(x)-np.exp(-x)) / (np.exp(x) + np.exp(-x))
def der_hyperb(x):
return 1 - ((np.exp(x)-np.exp(-x)) / (np.exp(x) + np.exp(-x)))**2
plt.figure(figsize=(12,8))
plt.plot(x, list(map(lambda x: hyperb(x),x)), label="hyperbolic")
plt.plot(x, list(map(lambda x: der_hyperb(x),x)), label="derivative")
plt.title("Hyperbolic")
plt.legend()
plt.show()
def arctan(x):
return np.arctan(x)
def der_arctan(x):
return 1 / (1+x**2)
plt.figure(figsize=(12,8))
plt.plot(x, list(map(lambda x: arctan(x),x)), label="arctan")
plt.plot(x, list(map(lambda x: der_arctan(x),x)), label="derivative")
plt.title("Arctan")
plt.legend()
plt.show()
| 0.696887 | 0.987387 |
## Influenza national summary (green and yellow chart)
```
library(ggplot2)
library(reshape2)
data1 <-read.csv("Influenza national summary (green and yellow chart).csv", header=T)
names(data1)<- c("Week", "A","B","PercentPositiveA","PercentPositiveB","TotalTested","PercentPositive")
bar_data <- data1[,c(1,2,3)]
melt_bar <- melt(bar_data, id = c('Week'))
melt_bar <- melt_bar[! is.na(melt_bar$value) ,]
line_data <- data1[,c(1,4,5,7)]
melt_line <- melt(line_data, id = c('Week'))
names(melt_line)
melt_line$variable <- factor(melt_line$variable,levels = c("PercentPositive", "PercentPositiveA", "PercentPositiveB"))
chart1 <- ggplot() +
geom_bar(data = melt_bar, aes(x = factor(Week), y = value, fill = variable), color = 'black', stat = 'identity') +
scale_fill_manual(values = c('yellow', 'darkgreen')) +
xlab('Week') +
ylab('Number of positive specimens') +
geom_line(data = melt_line, aes(x = factor(Week), y = value*400, color = variable, group = variable, linetype = variable)) +
scale_y_continuous(sec.axis = sec_axis(~.*(1/400), name = "Percent Positive", breaks = seq(0,35,5)), breaks = seq(0,14000,2000), limits = c(0,14000)) +
theme(axis.text.x = element_text(angle = 60),
legend.title = element_blank(),
axis.ticks.x = element_blank(),
axis.line.x.top = element_line(size = 1),
axis.line.y = element_line(size=1),
panel.background = element_rect(fill = 'white')) +
#scale_x_date(breaks = melt_bar[seq(1, length(Week), by = 2)]) +scale_x_date(breaks = melt_bar[seq(1, length(Week), by = 2)]) +
scale_color_manual(values = c("black", "orange", "green")) +
#scale_linetype_manual(values = c("solid", "longdashed", "dashed")) +
ggtitle("Influenza Positive Tests Reported to CDC by U.S. Clinical Laboratories, \nNational Summary, 2018-2019 Season")
#scale_x_discrete(limits = melt_bar$Week[seq(1, length(melt_bar$Week), by = 2)])
chart1
```
## Positive tested
```
library(ggplot2)
library(reshape2)
library(plotly)
data2 <- read.csv("Positive tested.csv", header=T)
names(data2) <- c('Week', 'H3N2v', 'A (H1N1)pdm09', 'A (H3N2)', 'A (Unable to sub type)', 'A(Subtyping not performed)', 'B (lineaege not performed)', 'B (Victoria lineage)', 'B (Yamagata lineage)', 'Total tested')
data2 <- data2[, -c(5,10)]
data_melt <- melt(data2, id = c('Week'))
data_melt$variable <- factor(data_melt$variable, levels = c('A(Subtyping not performed)','A (H1N1)pdm09', 'A (H3N2)','H3N2v','B (lineaege not performed)', 'B (Victoria lineage)', 'B (Yamagata lineage)'))
chart2 <- ggplot(data = data_melt) +
xlab('Week') +
ylab('Number of positive specimens') +
ggtitle("Influenza Positive Tests Reported to CDC by U.S. Public Health Laboratories, \nNational Summary, 2018-2019 Season") +
geom_bar(mapping = aes(x = factor(Week), y = value, fill = variable), color = 'black', stat = 'identity') +
theme(axis.text.x = element_text(angle = 60),
legend.title = element_blank(),
axis.ticks.x = element_blank(),
axis.line.x.top = element_line(size = 1),
axis.line.y = element_line(size =1),
panel.background = element_rect(fill = 'white')) +
scale_fill_manual(values = c('#F5F236', '#F29E06', '#FA0C05', '#992BFF', '#005533', '#99FF00', '#66D533'))
#ggplotly(chart2)
chart2
print(data_melt$Week[seq(1,length(data_melt$Week),2)])
#ggplotly(chart2)
```
## Flu heat map of USA (Required)
```
library(ggplot2)
library(usmap)
data3 <- read.csv("StateDatabyWeekforMap_2018-19week40-8.csv", header=T)
colfunc <- colorRampPalette(c("red", "yellow", "green"))
usmapdata <- merge(x=data3, y=statepop, x.by=STATENAME, y.by=full, x.all= TRUE)
usmapdata <- usmapdata[ usmapdata$STATENAME == usmapdata$full & usmapdata$WEEK == 8,]
unique(usmapdata$ACTIVITY.LEVEL)
usmapdata$ACTIVITY.LEVEL <- factor(usmapdata$ACTIVITY.LEVEL, levels = c("Level 10", "Level 9", "Level 8", "Level 7", "Level 6", "Level 5", "Level 4", "Level 1"))
plot_usmap(data = usmapdata, values = "ACTIVITY.LEVEL", lines = "black") +
scale_fill_manual(values = c("#FF0000", "#FF3800" ,"#FF7100" ,"#FFAA00" ,"#FFE200" ,"#E2FF00" ,"#AAFF00", "#71FF00", "#38FF00" ,"#00FF00")) +
theme(legend.position = "right",
legend.title = element_text("ILI Activity Level", face = "bold"),
plot.title = element_text(hjust = 0.5, face="bold")) +
ggtitle("2018-19 Influenza Season Week 8 ending Feb 23, 2019")
```
## Mortality
```
library(ggplot2)
library(stringr)
library(plotly)
chart3_data <- read.csv(file = 'NCHSData08.csv', header = T)
names(chart3_data)
chart3_data = chart3_data[, !(names(chart3_data) %in% c('All.Deaths', 'Pneumonia.Deaths','Influenza.Deaths'))]
names(chart3_data) <- c('Year','Week','P&I','Expected','Threshold')
melt_data <- melt(chart3_data, id = c('Year','Week'))
melt_data <- melt_data[!(melt_data$Year<2014 | melt_data$Year>2018),] #filtering data below 2014 and above 2018
melt_data <- melt_data[!(melt_data$Year==2014 & melt_data$Week<40),] #filering data earlier to week 40 2014
melt_data$MMWR_Week <- factor(as.Date(paste(melt_data$Year, melt_data$Week, 01, sep="-"), "%Y-%U-%u"))
melt_data <- melt_data[,-c(1,2)]
chart3 <- ggplot() +
ggtitle("Pneumonia and Influenza Mortality Surveillance from \nthe National Center for Health Statistics Mortality Surveillance System \nData through the week ending February 16, 2019, as February 28, 2019") +
geom_line(data = melt_data, mapping = aes(x = as.Date(MMWR_Week), y = value, group = variable, color = variable, linetype = variable)) +
scale_color_manual(values = c('red', 'black', 'black')) +
scale_linetype_manual(values = c('solid','dashed','solid')) +
scale_x_date(date_labels = "%Y %U", date_breaks = "10 week") +
scale_y_continuous(limits = c(4,12)) +
xlab('MMWR Week') +
ylab('% All Deaths Due to P & I') +
theme(axis.title = element_text(face = "bold"),
axis.text = element_text(face = "bold"),
axis.text.x = element_text(angle=90),
axis.line.y = element_line(size=0.5),
axis.line.x = element_line(size=0.5),
axis.line.x.top = element_line(size = 0.5),
#axis.ticks.x = element_blank(),
axis.ticks.length = unit(1,'mm'),
legend.title = element_blank() ,
legend.text = element_text(face = "bold",margin = margin(1.5,1.5,1.5,1.5,"mm")), #to add space between legend symbol and name
legend.key = element_rect(fill = "white"), #to make legend symbol background white
panel.background = element_rect(fill = "white", colour = NA)) #to make the chart background white
chart3
```
## Pediatric deaths
```
library(ggplot2)
library(plotly)
library(tidyverse)
##chart4
chart4_data <- read.csv(file = 'INFLUENZA-ASSOCIATED PEDIATRIC MORTALITY.csv', header = T) #skip is used to skip n lines from beginning
#names(chart4_data) <- c("SEASON","WEEK.NUMBER","No. of Deaths","Deaths Reported Previous Week","Deaths Reported Current Week")
#head(chart4_data)
library(tidyverse)
aggregate <- as.data.frame(aggregate(chart4_data$NO..OF.DEATHS, list(chart4_data$SEASON), FUN = sum))
aggregate[,2]
chart4_data <- chart4_data[,-3]
melt_data <- melt(chart4_data, id = c('SEASON','WEEK.NUMBER'))
melt_data$WEEK.NUMBER <- as.Date(paste(melt_data$WEEK.NUMBER, 01, sep="-"), "%Y-%U-%u")
#length(unique(melt_data$WEEK.NUMBER))
#names(melt_data)
chart4 <- ggplot() +
geom_bar(data = melt_data, mapping = aes(x = WEEK.NUMBER, y = value, fill = variable), stat = "identity", color = "black") +
#facet_wrap(~ SEASON, ncol = 2) +
scale_x_date(date_labels = "%Y %U", date_breaks = "6 week") +
scale_y_continuous(limits = c(0,30), breaks = seq(0,30,5)) +
scale_fill_manual(values = c('#008000','#00AAFF')) +
xlab('Week of Death') +
ylab('Number of deaths') +
ggtitle("Number of Influenza-Associated Pediatric Deaths by Week of Death: 2015-2016 season to present") +
theme(axis.title = element_text(face = "bold"),
axis.text = element_text(face = "bold"),
axis.text.x = element_text(angle=90),
axis.line.y = element_line(size=0.5),
#axis.line.x = element_line(size=0.5),
axis.line.x = element_line(size = 0.5),
#axis.ticks.x = element_blank(),
axis.ticks.length = unit(1,'mm'),
legend.title = element_blank() ,
legend.text = element_text(face = "bold",margin = margin(1.5,1.5,1.5,1.5,"mm")), #to add space between legend symbol and name
legend.key = element_rect(fill = "white"), #to make legend symbol background white
legend.position = 'bottom',
panel.background = element_rect(fill = "white", colour = NA),#to make the chart background white
legend.box.background = element_rect(color = 'black', size = 2)) +
annotate("text",x = as.Date('2016 10','%Y %U'), y = 25, label = ('2015-206 \nNumber of Deaths \n Reported = 94')) +
annotate("text",x = as.Date('2017 05','%Y %U'), y = 25, label = ('2016-2017 \nNumber of Deaths \n Reported = 110')) +
annotate("text",x = as.Date('2018 04','%Y %U'), y = 25, label = ('2017-2018 \nNumber of Deaths \n Reported = 185')) +
annotate("text",x = as.Date('2019 06','%Y %U'), y = 25, label = ('2018-2019 \nNumber of Deaths \n Reported = 56'))
chart4
```
## Influenza national summary (green and yellow chart) for 52 Weeks
```
library(ggplot2)
library(reshape2)
data1 <-read.csv("WHO_NREVSS_Clinical_Labs.csv", header=T)
names(data1)<- c("Region Type","Region","Year","Week","TotalTested", "A","B","PercentPositive","PercentPositiveA","PercentPositiveB")
data1$wy <- paste(data1$Year, data1$Week, sep = '-')
#names(data1)
#head(data1$wy)
bar_data <- data1[,c(6,7,11)]
melt_bar <- melt(bar_data, id = c('wy'))
melt_bar <- melt_bar[! is.na(melt_bar$value) ,]
#names(melt_bar)
line_data <- data1[,c(8,9,10,11)]
melt_line <- melt(line_data, id = c('wy'))
#names(melt_line)
melt_line$variable <- factor(melt_line$variable,levels = c("PercentPositive", "PercentPositiveA", "PercentPositiveB"))
chart8 <- ggplot() +
geom_bar(data = melt_bar, aes(x = factor(wy), y = value, fill = variable), color = 'black', stat = 'identity') +
scale_fill_manual(values = c('yellow', 'darkgreen')) +
xlab('Week') +
ylab('Number of positive specimens') +
geom_line(data = melt_line, aes(x = factor(wy), y = value*400, color = variable, group = variable, linetype = variable)) +
scale_y_continuous(sec.axis = sec_axis(~.*(1/400), name = "Percent Positive", breaks = seq(0,35,5)), breaks = seq(0,14000,2000), limits = c(0,14000)) +
theme(legend.title = element_blank(),
axis.ticks.x = element_blank(),
axis.line.x.top = element_line(size = 1),
axis.line.y = element_line(size=1),
axis.text.x = element_text(angle=90),
panel.background = element_rect(fill = 'white')) +
scale_color_manual(values = c("black", "orange", "green")) +
#scale_linetype_manual(values = c("solid", "longdashed", "dashed")) +
ggtitle("Influenza Positive Tests Reported to CDC by U.S. Clinical Laboratories, \nNational Summary, 2018-2019 Season")
chart8
```
## Positive tested 52 Weeks
```
library(ggplot2)
library(reshape2)
library(plotly)
data7 <-read.csv(file ='WHO_NREVSS_Public_Health_Labs.csv', header=T)
names(data7) <- c('Region Type','Region','Year','Week','Total tested','A (H1N1)pdm09','A (H3N2)','A(Subtyping not performed)','B (lineaege not performed)', 'B (Victoria lineage)', 'B (Yamagata lineage)' ,'H3N2v')
data7$yw <- paste(data7$Year,data7$Week,sep='-')
data7 <- data7[, -c(1,2,3,4,5)]
#names(data7)
data_melt <- melt(data7, id = c('yw'))
data_melt$variable <- factor(data_melt$variable, levels = c('A(Subtyping not performed)','A (H1N1)pdm09', 'A (H3N2)','H3N2v','B (lineaege not performed)', 'B (Victoria lineage)', 'B (Yamagata lineage)'))
chart7 <- ggplot(data = data_melt) +
xlab('Week') +
ylab('Number of positive specimens') +
ggtitle("Influenza Positive Tests Reported to CDC by U.S. Public Health Laboratories, \nNational Summary, 2018-2019 Season") +
geom_bar(mapping = aes(x = factor(yw), y = value, fill = variable), color = 'black', stat = 'identity') +
theme(legend.title = element_blank(),
axis.ticks.x = element_blank(),
axis.line.x.top = element_line(size = 1),
axis.text = element_text(angle = 90),
axis.line.y = element_line(size =1),
panel.background = element_rect(fill = 'white')) +
scale_fill_manual(values = c('#F5F236', '#F29E06', '#FA0C05', '#992BFF', '#005533', '#99FF00', '#66D533'))
#ggplotly(chart7)
chart7
```
## Influenza national summary (green and yellow chart) for New York State
```
library(ggplot2)
library(reshape2)
data1 <-read.csv("WHO_NREVSS_Clinical_Labs_NY.csv", header=T)
names(data1)<- c("Region Type","Region","Year","Week","TotalTested", "A","B","PercentPositive","PercentPositiveA","PercentPositiveB")
data1$wy <- paste(data1$Year, data1$Week, sep = '-')
#names(data1)
#head(data1$wy)
bar_data <- data1[,c(6,7,11)]
melt_bar <- melt(bar_data, id = c('wy'))
melt_bar <- melt_bar[! is.na(melt_bar$value) ,]
#names(melt_bar)
line_data <- data1[,c(8,9,10,11)]
melt_line <- melt(line_data, id = c('wy'))
#names(melt_line)
melt_line$variable <- factor(melt_line$variable,levels = c("PercentPositive", "PercentPositiveA", "PercentPositiveB"))
chart8 <- ggplot() +
geom_bar(data = melt_bar, aes(x = factor(wy), y = value, fill = variable), color = 'black', stat = 'identity') +
scale_fill_manual(values = c('yellow', 'darkgreen')) +
xlab('Week') +
ylab('Number of positive specimens') +
geom_line(data = melt_line, aes(x = factor(wy), y = value*400, color = variable, group = variable, linetype = variable)) +
scale_y_continuous(sec.axis = sec_axis(~.*(1/400), name = "Percent Positive", breaks = seq(0,35,5)), breaks = seq(0,14000,2000), limits = c(0,14000)) +
theme(legend.title = element_blank(),
axis.ticks.x = element_blank(),
axis.line.x.top = element_line(size = 1),
axis.line.y = element_line(size=1),
axis.text.x = element_text(angle=90),
panel.background = element_rect(fill = 'white')) +
scale_color_manual(values = c("black", "orange", "green")) +
#scale_linetype_manual(values = c("solid", "longdashed", "dashed")) +
ggtitle("Influenza Positive Tests Reported to CDC by U.S. Clinical Laboratories, \nNational Summary, 2018-2019 Season")
chart8
```
|
github_jupyter
|
library(ggplot2)
library(reshape2)
data1 <-read.csv("Influenza national summary (green and yellow chart).csv", header=T)
names(data1)<- c("Week", "A","B","PercentPositiveA","PercentPositiveB","TotalTested","PercentPositive")
bar_data <- data1[,c(1,2,3)]
melt_bar <- melt(bar_data, id = c('Week'))
melt_bar <- melt_bar[! is.na(melt_bar$value) ,]
line_data <- data1[,c(1,4,5,7)]
melt_line <- melt(line_data, id = c('Week'))
names(melt_line)
melt_line$variable <- factor(melt_line$variable,levels = c("PercentPositive", "PercentPositiveA", "PercentPositiveB"))
chart1 <- ggplot() +
geom_bar(data = melt_bar, aes(x = factor(Week), y = value, fill = variable), color = 'black', stat = 'identity') +
scale_fill_manual(values = c('yellow', 'darkgreen')) +
xlab('Week') +
ylab('Number of positive specimens') +
geom_line(data = melt_line, aes(x = factor(Week), y = value*400, color = variable, group = variable, linetype = variable)) +
scale_y_continuous(sec.axis = sec_axis(~.*(1/400), name = "Percent Positive", breaks = seq(0,35,5)), breaks = seq(0,14000,2000), limits = c(0,14000)) +
theme(axis.text.x = element_text(angle = 60),
legend.title = element_blank(),
axis.ticks.x = element_blank(),
axis.line.x.top = element_line(size = 1),
axis.line.y = element_line(size=1),
panel.background = element_rect(fill = 'white')) +
#scale_x_date(breaks = melt_bar[seq(1, length(Week), by = 2)]) +scale_x_date(breaks = melt_bar[seq(1, length(Week), by = 2)]) +
scale_color_manual(values = c("black", "orange", "green")) +
#scale_linetype_manual(values = c("solid", "longdashed", "dashed")) +
ggtitle("Influenza Positive Tests Reported to CDC by U.S. Clinical Laboratories, \nNational Summary, 2018-2019 Season")
#scale_x_discrete(limits = melt_bar$Week[seq(1, length(melt_bar$Week), by = 2)])
chart1
library(ggplot2)
library(reshape2)
library(plotly)
data2 <- read.csv("Positive tested.csv", header=T)
names(data2) <- c('Week', 'H3N2v', 'A (H1N1)pdm09', 'A (H3N2)', 'A (Unable to sub type)', 'A(Subtyping not performed)', 'B (lineaege not performed)', 'B (Victoria lineage)', 'B (Yamagata lineage)', 'Total tested')
data2 <- data2[, -c(5,10)]
data_melt <- melt(data2, id = c('Week'))
data_melt$variable <- factor(data_melt$variable, levels = c('A(Subtyping not performed)','A (H1N1)pdm09', 'A (H3N2)','H3N2v','B (lineaege not performed)', 'B (Victoria lineage)', 'B (Yamagata lineage)'))
chart2 <- ggplot(data = data_melt) +
xlab('Week') +
ylab('Number of positive specimens') +
ggtitle("Influenza Positive Tests Reported to CDC by U.S. Public Health Laboratories, \nNational Summary, 2018-2019 Season") +
geom_bar(mapping = aes(x = factor(Week), y = value, fill = variable), color = 'black', stat = 'identity') +
theme(axis.text.x = element_text(angle = 60),
legend.title = element_blank(),
axis.ticks.x = element_blank(),
axis.line.x.top = element_line(size = 1),
axis.line.y = element_line(size =1),
panel.background = element_rect(fill = 'white')) +
scale_fill_manual(values = c('#F5F236', '#F29E06', '#FA0C05', '#992BFF', '#005533', '#99FF00', '#66D533'))
#ggplotly(chart2)
chart2
print(data_melt$Week[seq(1,length(data_melt$Week),2)])
#ggplotly(chart2)
library(ggplot2)
library(usmap)
data3 <- read.csv("StateDatabyWeekforMap_2018-19week40-8.csv", header=T)
colfunc <- colorRampPalette(c("red", "yellow", "green"))
usmapdata <- merge(x=data3, y=statepop, x.by=STATENAME, y.by=full, x.all= TRUE)
usmapdata <- usmapdata[ usmapdata$STATENAME == usmapdata$full & usmapdata$WEEK == 8,]
unique(usmapdata$ACTIVITY.LEVEL)
usmapdata$ACTIVITY.LEVEL <- factor(usmapdata$ACTIVITY.LEVEL, levels = c("Level 10", "Level 9", "Level 8", "Level 7", "Level 6", "Level 5", "Level 4", "Level 1"))
plot_usmap(data = usmapdata, values = "ACTIVITY.LEVEL", lines = "black") +
scale_fill_manual(values = c("#FF0000", "#FF3800" ,"#FF7100" ,"#FFAA00" ,"#FFE200" ,"#E2FF00" ,"#AAFF00", "#71FF00", "#38FF00" ,"#00FF00")) +
theme(legend.position = "right",
legend.title = element_text("ILI Activity Level", face = "bold"),
plot.title = element_text(hjust = 0.5, face="bold")) +
ggtitle("2018-19 Influenza Season Week 8 ending Feb 23, 2019")
library(ggplot2)
library(stringr)
library(plotly)
chart3_data <- read.csv(file = 'NCHSData08.csv', header = T)
names(chart3_data)
chart3_data = chart3_data[, !(names(chart3_data) %in% c('All.Deaths', 'Pneumonia.Deaths','Influenza.Deaths'))]
names(chart3_data) <- c('Year','Week','P&I','Expected','Threshold')
melt_data <- melt(chart3_data, id = c('Year','Week'))
melt_data <- melt_data[!(melt_data$Year<2014 | melt_data$Year>2018),] #filtering data below 2014 and above 2018
melt_data <- melt_data[!(melt_data$Year==2014 & melt_data$Week<40),] #filering data earlier to week 40 2014
melt_data$MMWR_Week <- factor(as.Date(paste(melt_data$Year, melt_data$Week, 01, sep="-"), "%Y-%U-%u"))
melt_data <- melt_data[,-c(1,2)]
chart3 <- ggplot() +
ggtitle("Pneumonia and Influenza Mortality Surveillance from \nthe National Center for Health Statistics Mortality Surveillance System \nData through the week ending February 16, 2019, as February 28, 2019") +
geom_line(data = melt_data, mapping = aes(x = as.Date(MMWR_Week), y = value, group = variable, color = variable, linetype = variable)) +
scale_color_manual(values = c('red', 'black', 'black')) +
scale_linetype_manual(values = c('solid','dashed','solid')) +
scale_x_date(date_labels = "%Y %U", date_breaks = "10 week") +
scale_y_continuous(limits = c(4,12)) +
xlab('MMWR Week') +
ylab('% All Deaths Due to P & I') +
theme(axis.title = element_text(face = "bold"),
axis.text = element_text(face = "bold"),
axis.text.x = element_text(angle=90),
axis.line.y = element_line(size=0.5),
axis.line.x = element_line(size=0.5),
axis.line.x.top = element_line(size = 0.5),
#axis.ticks.x = element_blank(),
axis.ticks.length = unit(1,'mm'),
legend.title = element_blank() ,
legend.text = element_text(face = "bold",margin = margin(1.5,1.5,1.5,1.5,"mm")), #to add space between legend symbol and name
legend.key = element_rect(fill = "white"), #to make legend symbol background white
panel.background = element_rect(fill = "white", colour = NA)) #to make the chart background white
chart3
library(ggplot2)
library(plotly)
library(tidyverse)
##chart4
chart4_data <- read.csv(file = 'INFLUENZA-ASSOCIATED PEDIATRIC MORTALITY.csv', header = T) #skip is used to skip n lines from beginning
#names(chart4_data) <- c("SEASON","WEEK.NUMBER","No. of Deaths","Deaths Reported Previous Week","Deaths Reported Current Week")
#head(chart4_data)
library(tidyverse)
aggregate <- as.data.frame(aggregate(chart4_data$NO..OF.DEATHS, list(chart4_data$SEASON), FUN = sum))
aggregate[,2]
chart4_data <- chart4_data[,-3]
melt_data <- melt(chart4_data, id = c('SEASON','WEEK.NUMBER'))
melt_data$WEEK.NUMBER <- as.Date(paste(melt_data$WEEK.NUMBER, 01, sep="-"), "%Y-%U-%u")
#length(unique(melt_data$WEEK.NUMBER))
#names(melt_data)
chart4 <- ggplot() +
geom_bar(data = melt_data, mapping = aes(x = WEEK.NUMBER, y = value, fill = variable), stat = "identity", color = "black") +
#facet_wrap(~ SEASON, ncol = 2) +
scale_x_date(date_labels = "%Y %U", date_breaks = "6 week") +
scale_y_continuous(limits = c(0,30), breaks = seq(0,30,5)) +
scale_fill_manual(values = c('#008000','#00AAFF')) +
xlab('Week of Death') +
ylab('Number of deaths') +
ggtitle("Number of Influenza-Associated Pediatric Deaths by Week of Death: 2015-2016 season to present") +
theme(axis.title = element_text(face = "bold"),
axis.text = element_text(face = "bold"),
axis.text.x = element_text(angle=90),
axis.line.y = element_line(size=0.5),
#axis.line.x = element_line(size=0.5),
axis.line.x = element_line(size = 0.5),
#axis.ticks.x = element_blank(),
axis.ticks.length = unit(1,'mm'),
legend.title = element_blank() ,
legend.text = element_text(face = "bold",margin = margin(1.5,1.5,1.5,1.5,"mm")), #to add space between legend symbol and name
legend.key = element_rect(fill = "white"), #to make legend symbol background white
legend.position = 'bottom',
panel.background = element_rect(fill = "white", colour = NA),#to make the chart background white
legend.box.background = element_rect(color = 'black', size = 2)) +
annotate("text",x = as.Date('2016 10','%Y %U'), y = 25, label = ('2015-206 \nNumber of Deaths \n Reported = 94')) +
annotate("text",x = as.Date('2017 05','%Y %U'), y = 25, label = ('2016-2017 \nNumber of Deaths \n Reported = 110')) +
annotate("text",x = as.Date('2018 04','%Y %U'), y = 25, label = ('2017-2018 \nNumber of Deaths \n Reported = 185')) +
annotate("text",x = as.Date('2019 06','%Y %U'), y = 25, label = ('2018-2019 \nNumber of Deaths \n Reported = 56'))
chart4
library(ggplot2)
library(reshape2)
data1 <-read.csv("WHO_NREVSS_Clinical_Labs.csv", header=T)
names(data1)<- c("Region Type","Region","Year","Week","TotalTested", "A","B","PercentPositive","PercentPositiveA","PercentPositiveB")
data1$wy <- paste(data1$Year, data1$Week, sep = '-')
#names(data1)
#head(data1$wy)
bar_data <- data1[,c(6,7,11)]
melt_bar <- melt(bar_data, id = c('wy'))
melt_bar <- melt_bar[! is.na(melt_bar$value) ,]
#names(melt_bar)
line_data <- data1[,c(8,9,10,11)]
melt_line <- melt(line_data, id = c('wy'))
#names(melt_line)
melt_line$variable <- factor(melt_line$variable,levels = c("PercentPositive", "PercentPositiveA", "PercentPositiveB"))
chart8 <- ggplot() +
geom_bar(data = melt_bar, aes(x = factor(wy), y = value, fill = variable), color = 'black', stat = 'identity') +
scale_fill_manual(values = c('yellow', 'darkgreen')) +
xlab('Week') +
ylab('Number of positive specimens') +
geom_line(data = melt_line, aes(x = factor(wy), y = value*400, color = variable, group = variable, linetype = variable)) +
scale_y_continuous(sec.axis = sec_axis(~.*(1/400), name = "Percent Positive", breaks = seq(0,35,5)), breaks = seq(0,14000,2000), limits = c(0,14000)) +
theme(legend.title = element_blank(),
axis.ticks.x = element_blank(),
axis.line.x.top = element_line(size = 1),
axis.line.y = element_line(size=1),
axis.text.x = element_text(angle=90),
panel.background = element_rect(fill = 'white')) +
scale_color_manual(values = c("black", "orange", "green")) +
#scale_linetype_manual(values = c("solid", "longdashed", "dashed")) +
ggtitle("Influenza Positive Tests Reported to CDC by U.S. Clinical Laboratories, \nNational Summary, 2018-2019 Season")
chart8
library(ggplot2)
library(reshape2)
library(plotly)
data7 <-read.csv(file ='WHO_NREVSS_Public_Health_Labs.csv', header=T)
names(data7) <- c('Region Type','Region','Year','Week','Total tested','A (H1N1)pdm09','A (H3N2)','A(Subtyping not performed)','B (lineaege not performed)', 'B (Victoria lineage)', 'B (Yamagata lineage)' ,'H3N2v')
data7$yw <- paste(data7$Year,data7$Week,sep='-')
data7 <- data7[, -c(1,2,3,4,5)]
#names(data7)
data_melt <- melt(data7, id = c('yw'))
data_melt$variable <- factor(data_melt$variable, levels = c('A(Subtyping not performed)','A (H1N1)pdm09', 'A (H3N2)','H3N2v','B (lineaege not performed)', 'B (Victoria lineage)', 'B (Yamagata lineage)'))
chart7 <- ggplot(data = data_melt) +
xlab('Week') +
ylab('Number of positive specimens') +
ggtitle("Influenza Positive Tests Reported to CDC by U.S. Public Health Laboratories, \nNational Summary, 2018-2019 Season") +
geom_bar(mapping = aes(x = factor(yw), y = value, fill = variable), color = 'black', stat = 'identity') +
theme(legend.title = element_blank(),
axis.ticks.x = element_blank(),
axis.line.x.top = element_line(size = 1),
axis.text = element_text(angle = 90),
axis.line.y = element_line(size =1),
panel.background = element_rect(fill = 'white')) +
scale_fill_manual(values = c('#F5F236', '#F29E06', '#FA0C05', '#992BFF', '#005533', '#99FF00', '#66D533'))
#ggplotly(chart7)
chart7
library(ggplot2)
library(reshape2)
data1 <-read.csv("WHO_NREVSS_Clinical_Labs_NY.csv", header=T)
names(data1)<- c("Region Type","Region","Year","Week","TotalTested", "A","B","PercentPositive","PercentPositiveA","PercentPositiveB")
data1$wy <- paste(data1$Year, data1$Week, sep = '-')
#names(data1)
#head(data1$wy)
bar_data <- data1[,c(6,7,11)]
melt_bar <- melt(bar_data, id = c('wy'))
melt_bar <- melt_bar[! is.na(melt_bar$value) ,]
#names(melt_bar)
line_data <- data1[,c(8,9,10,11)]
melt_line <- melt(line_data, id = c('wy'))
#names(melt_line)
melt_line$variable <- factor(melt_line$variable,levels = c("PercentPositive", "PercentPositiveA", "PercentPositiveB"))
chart8 <- ggplot() +
geom_bar(data = melt_bar, aes(x = factor(wy), y = value, fill = variable), color = 'black', stat = 'identity') +
scale_fill_manual(values = c('yellow', 'darkgreen')) +
xlab('Week') +
ylab('Number of positive specimens') +
geom_line(data = melt_line, aes(x = factor(wy), y = value*400, color = variable, group = variable, linetype = variable)) +
scale_y_continuous(sec.axis = sec_axis(~.*(1/400), name = "Percent Positive", breaks = seq(0,35,5)), breaks = seq(0,14000,2000), limits = c(0,14000)) +
theme(legend.title = element_blank(),
axis.ticks.x = element_blank(),
axis.line.x.top = element_line(size = 1),
axis.line.y = element_line(size=1),
axis.text.x = element_text(angle=90),
panel.background = element_rect(fill = 'white')) +
scale_color_manual(values = c("black", "orange", "green")) +
#scale_linetype_manual(values = c("solid", "longdashed", "dashed")) +
ggtitle("Influenza Positive Tests Reported to CDC by U.S. Clinical Laboratories, \nNational Summary, 2018-2019 Season")
chart8
| 0.509032 | 0.861596 |
```
import numpy as np
import pandas as pd
import warnings
import geopy.distance
import tensorflow as tf
from tensorflow import keras
from sklearn.model_selection import train_test_split
warnings.filterwarnings('ignore')
from sklearn.metrics import mean_squared_error
import math
train_df = pd.read_csv("./data/train.csv")
test_df = pd.read_csv("./data/test.csv")
idx_trn = train_df.date.isin(train_df.date.unique()[:-7])
trn_df = train_df[idx_trn]
val_df = train_df[np.invert(idx_trn)]
```
# Function start
```
def data_prepare(df):
try:
y = df['18~20_ride']
except:
y = None
df['date'] = pd.to_datetime(df['date'])
df['weekday'] = df['date'].dt.weekday
df = pd.get_dummies(df, columns=['weekday'])
df['in_out'] = df['in_out'].map({'시내':0,'시외':1})
coords_jejusi = (33.500770, 126.522761) #제주시의 위도 경도
coords_seoquipo = (33.259429, 126.558217) #서귀포시의 위도 경도
df['dis_jejusi'] = [geopy.distance.vincenty((df['latitude'].iloc[i], df['longitude'].iloc[i]), coords_jejusi).km for i in range(len(df))]
df['dis_seoquipo'] = [geopy.distance.vincenty((df['latitude'].iloc[i], df['longitude'].iloc[i]), coords_seoquipo).km for i in range(len(df))]
return df, y
trn, y_trn = data_prepare(trn_df)
val, y_val = data_prepare(val_df)
te, _ = data_prepare(test_df)
input_var=['in_out','latitude','longitude','6~7_ride', '7~8_ride', '8~9_ride', '9~10_ride',
'10~11_ride', '11~12_ride', '6~7_takeoff', '7~8_takeoff', '8~9_takeoff',
'9~10_takeoff', '10~11_takeoff', '11~12_takeoff','weekday_0', 'weekday_1', 'weekday_2', 'weekday_3', 'weekday_4',
'weekday_5', 'weekday_6', 'dis_jejusi', 'dis_seoquipo']
target=['18~20_ride']
x_trn = trn[input_var]
x_val = val[input_var]
x_te = te[input_var]
keras.backend.clear_session()
inputs = keras.Input(shape=(24,))
x = keras.layers.Dense(128, activation='relu')(inputs)
x = keras.layers.Dense(256, activation='relu')(x)
x = keras.layers.Dense(32, activation='tanh')(x)
outputs = keras.layers.Dense(1, activation='linear')(x)
model = keras.Model(inputs=inputs, outputs=outputs, name='dacon_c13_model')
model.compile(loss='mse' )
model.fit(x=x_trn,
y=y_trn,
batch_size=512,epochs=100,validation_data=(x_val, y_val)
)
# emb_week = keras.layers.Embedding(7, 3)
def esitimate_model(mdl, x_trn, y_trn, x_val, y_val):
trns = mdl.predict(x_trn)
vals = mdl.predict(x_val)
print(math.sqrt(mean_squared_error(y_true=y_trn, y_pred=trns)))
print(math.sqrt(mean_squared_error(y_true=y_val, y_pred=vals)))
from sklearn.ensemble import RandomForestRegressor
rf = ExtraTreesRegressor(max_depth=20, random_state=1991)
import lightgbm as lgb
m = lgb.LGBMRegressor(n_estimators=2000, num_leaves=31)
m.fit(x_trn, y_trn)
esitimate_model(m, x_trn, y_trn, x_val, y_val)
```
# Sumbmission
```
test_df['18~20_ride'] = m.predict(x_te)
test_df[['id','18~20_ride']].to_csv("lgb_base.csv",index=False)
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import warnings
import geopy.distance
import tensorflow as tf
from tensorflow import keras
from sklearn.model_selection import train_test_split
warnings.filterwarnings('ignore')
from sklearn.metrics import mean_squared_error
import math
train_df = pd.read_csv("./data/train.csv")
test_df = pd.read_csv("./data/test.csv")
idx_trn = train_df.date.isin(train_df.date.unique()[:-7])
trn_df = train_df[idx_trn]
val_df = train_df[np.invert(idx_trn)]
def data_prepare(df):
try:
y = df['18~20_ride']
except:
y = None
df['date'] = pd.to_datetime(df['date'])
df['weekday'] = df['date'].dt.weekday
df = pd.get_dummies(df, columns=['weekday'])
df['in_out'] = df['in_out'].map({'시내':0,'시외':1})
coords_jejusi = (33.500770, 126.522761) #제주시의 위도 경도
coords_seoquipo = (33.259429, 126.558217) #서귀포시의 위도 경도
df['dis_jejusi'] = [geopy.distance.vincenty((df['latitude'].iloc[i], df['longitude'].iloc[i]), coords_jejusi).km for i in range(len(df))]
df['dis_seoquipo'] = [geopy.distance.vincenty((df['latitude'].iloc[i], df['longitude'].iloc[i]), coords_seoquipo).km for i in range(len(df))]
return df, y
trn, y_trn = data_prepare(trn_df)
val, y_val = data_prepare(val_df)
te, _ = data_prepare(test_df)
input_var=['in_out','latitude','longitude','6~7_ride', '7~8_ride', '8~9_ride', '9~10_ride',
'10~11_ride', '11~12_ride', '6~7_takeoff', '7~8_takeoff', '8~9_takeoff',
'9~10_takeoff', '10~11_takeoff', '11~12_takeoff','weekday_0', 'weekday_1', 'weekday_2', 'weekday_3', 'weekday_4',
'weekday_5', 'weekday_6', 'dis_jejusi', 'dis_seoquipo']
target=['18~20_ride']
x_trn = trn[input_var]
x_val = val[input_var]
x_te = te[input_var]
keras.backend.clear_session()
inputs = keras.Input(shape=(24,))
x = keras.layers.Dense(128, activation='relu')(inputs)
x = keras.layers.Dense(256, activation='relu')(x)
x = keras.layers.Dense(32, activation='tanh')(x)
outputs = keras.layers.Dense(1, activation='linear')(x)
model = keras.Model(inputs=inputs, outputs=outputs, name='dacon_c13_model')
model.compile(loss='mse' )
model.fit(x=x_trn,
y=y_trn,
batch_size=512,epochs=100,validation_data=(x_val, y_val)
)
# emb_week = keras.layers.Embedding(7, 3)
def esitimate_model(mdl, x_trn, y_trn, x_val, y_val):
trns = mdl.predict(x_trn)
vals = mdl.predict(x_val)
print(math.sqrt(mean_squared_error(y_true=y_trn, y_pred=trns)))
print(math.sqrt(mean_squared_error(y_true=y_val, y_pred=vals)))
from sklearn.ensemble import RandomForestRegressor
rf = ExtraTreesRegressor(max_depth=20, random_state=1991)
import lightgbm as lgb
m = lgb.LGBMRegressor(n_estimators=2000, num_leaves=31)
m.fit(x_trn, y_trn)
esitimate_model(m, x_trn, y_trn, x_val, y_val)
test_df['18~20_ride'] = m.predict(x_te)
test_df[['id','18~20_ride']].to_csv("lgb_base.csv",index=False)
| 0.436622 | 0.605041 |
# Visualizing characteristics of doctorate recipients
The goal of this blog post is to explain the process of creating a dashboard visalization using *streamlit*. This dashboard visualizes data about doctorate recipients including: demographic information, field of study, and postgraduation plans. Data was collected from the National Center for Science and Engineering Statistics (NCSES) and datasets can be found here: https://ncses.nsf.gov/pubs/nsf19301/data. Analyses were performed using the pandas library and visualizations were created using the matplotlib and plotly libraries along with streamlit's widget features.
**View dashboard visualization: https://share.streamlit.io/saahithirao/bios-823-blog/hw4.py**
**View code: https://github.com/saahithirao/bios-823-blog/blob/master/hw4.py** This code can be downloaded to a personal machine and run using >>streamlit run hw4.py
**Doctorate recipients by gender & race from 2008-2017**
This visualization displays an interactive data table of doctorate recipents by gender and race from 2008 to 2017. The user can click on a year on the sidebar to display data for that year and can select to view data by gender or race. Since there was no dataset that contained all of this information, I opted to combine two different datasets: one that contained data on females and on that contained data on males. I extracted the necessary information to create the visualization, as shown below, and merged the two dataframes. Then, using streamlit's widget features, I created a sidebar that allows the user to select a specific year that they want to see data for and/or filter the data by gender and race to explore the data further and make comparisons. Code for this is shown below and linked above.
```
import pandas as pd
df = pd.read_excel("https://ncses.nsf.gov/pubs/nsf19301/assets/data/tables/sed17-sr-tab021.xlsx", header=3)
df = df.rename(columns={'Ethnicity, race, and citizenship status':'Race'})
df_female = (
df.
drop(df[df['Race'].str.contains('citizen')].index.tolist()).
drop(df[df['Race'].str.contains('visa')].index.tolist()).
drop(df[df['Race'].str.contains('Hispanic')].index.tolist()).
drop(df[df['Race'].str.contains('Ethnicity')].index.tolist()).
reset_index().
drop(columns = ['index'])
)
df_female["Gender"] = "Female"
df_female
# Creating widget for selecting data by year and gender (separately)
st.sidebar.header("User Input")
selected_year = st.sidebar.selectbox('Year', list(reversed(range(2008,2017))))
phds = load_data(selected_year)
unique_gender = phds.Gender.unique()
select_gender = st.sidebar.multiselect('Gender', unique_gender, unique_gender)
df_selected = phds[(phds.Gender.isin(select_gender))]
```
**Number of doctorate recipients by gender over time**
This visualization displays an interactive plot illustrating number of doctorate recipients over time and separated by gender. The user can hover over points to view data for that year. This plot shows a similar trend over time for males and females with a slight decrease in number of PhDs in 2010 and a steady increase until 2015. The gap, however, between males and females does not seem to be decreasing over time, which shows that there is still a disparity between receiving a doctorate degree by gender. The code below shows how the plot was created.
```
import plotly.express as px
df_select = df_female[df_female["Race"] == "All doctorate recipients"]
df2 = (df_select.drop(['Gender'], axis=1))
df_long = pd.melt(df2,id_vars=['Race'],var_name='Year', value_name='phds')
df_long['Gender'] = ['Female']*10
df_select_male = df_male[df_male["Race"] == "All doctorate recipients"]
df3 = (df_select_male.drop(['Gender'], axis=1))
df_long2 = pd.melt(df3,id_vars=['Race'],var_name='Year', value_name='phds')
df_long2['Gender'] = ['Male']*10
df_combine_plot = pd.concat([df_long, df_long2], ignore_index=True)
fig = px.line(df_combine_plot,
x='Year', y='phds', color='Gender',
labels = {
"phds": "Number of PhDs"
})
fig.update_traces(mode='markers+lines')
```
**Summary of doctorate recipients across years by gender**
This static data table displays summary statistics of aggregated data across time of doctorate recipients by gender. The table follows from the plot to understand, overall, the trends in receiving a PhD by gender.
```
summary = pd.DataFrame({'Gender': ['Female','Male'],
'Min': [df_long['phds'].min(), df_long2['phds'].min()],
'Mean' : [df_long['phds'].mean(), df_long2['phds'].mean()],
'Median': [df_long['phds'].median(), df_long2['phds'].median()],
'Max': [df_long['phds'].max(), df_long2['phds'].max()]})
```
**Visualizing all doctorate recipients by field of study in 2017**
Now, turning to another aspect of the data, we will look closer at doctorates by field of study. This requires a new dataset. The data was transposed and all doctorate recipient information was extracted. In order to visualize number of doctorates by field of study, I created a simple bar plot. The user can hover over bars to display information specific to that field of study. This plot illustrates which fields awarded more PhDs. The code is shown below and the plot is displayed in the dashboard.
```
dat = pd.read_excel("https://ncses.nsf.gov/pubs/nsf19301/assets/data/tables/sed17-sr-tab054.xlsx", header=3)
dat_all = dat.iloc[[0]]
dat_T = dat_all.T
dat_T = dat_T.rename(columns=dat_T.iloc[0]).reset_index()
dat_T = dat_T.iloc[1:]
dat_T
fig = px.bar(dat_T, x='index', y='All doctorate recipients (number)c',
labels={'All doctorate recipients (number)c':'All Doctorates', 'index':'Field of Study'})
```
**Visualizing field of study by gender in 2017**
In the visualizations above, we saw the breakdown of number of doctorate recipients by gender. Here, we will take a look at doctorate recipients by gender and field of study. This stacked bar plot was created by transposing the data into a wide format and separate bars were created for males and females. The user can hover over the bars to view data of a specific field by gender. This plot illustrates which fields had a smaller female to male ratio or vice versa. The code is shown below and the figure is displayed in the dashboard linked above.
```
# create stacked bar plot by gender
from plotly import graph_objects as go
to_plot = dat[dat['Characteristic'].str.contains('ale')]
plot = to_plot.T
plot2 = (
plot.
rename(columns=plot.iloc[0]).
drop(plot.index[0]).
reset_index().
drop(columns=['Female doctorate recipients (number)', 'Male doctorate recipients (number)'])
)
fig2 = go.Figure(
data=[
go.Bar(
name="Male",
x=plot2["index"],
y=plot2["Male"],
offsetgroup=1,
),
go.Bar(
name="Female",
x=plot2["index"],
y=plot2["Female"],
offsetgroup=1,
base=plot2["Male"],
hovertext= [f'Count: {val}' for val in plot2["Female"]]
)
],
layout=go.Layout(
title="Percent of Doctorate Recipients by Broad Field of Study and Gender",
yaxis_title="Percent"
)
)
```
|
github_jupyter
|
import pandas as pd
df = pd.read_excel("https://ncses.nsf.gov/pubs/nsf19301/assets/data/tables/sed17-sr-tab021.xlsx", header=3)
df = df.rename(columns={'Ethnicity, race, and citizenship status':'Race'})
df_female = (
df.
drop(df[df['Race'].str.contains('citizen')].index.tolist()).
drop(df[df['Race'].str.contains('visa')].index.tolist()).
drop(df[df['Race'].str.contains('Hispanic')].index.tolist()).
drop(df[df['Race'].str.contains('Ethnicity')].index.tolist()).
reset_index().
drop(columns = ['index'])
)
df_female["Gender"] = "Female"
df_female
# Creating widget for selecting data by year and gender (separately)
st.sidebar.header("User Input")
selected_year = st.sidebar.selectbox('Year', list(reversed(range(2008,2017))))
phds = load_data(selected_year)
unique_gender = phds.Gender.unique()
select_gender = st.sidebar.multiselect('Gender', unique_gender, unique_gender)
df_selected = phds[(phds.Gender.isin(select_gender))]
import plotly.express as px
df_select = df_female[df_female["Race"] == "All doctorate recipients"]
df2 = (df_select.drop(['Gender'], axis=1))
df_long = pd.melt(df2,id_vars=['Race'],var_name='Year', value_name='phds')
df_long['Gender'] = ['Female']*10
df_select_male = df_male[df_male["Race"] == "All doctorate recipients"]
df3 = (df_select_male.drop(['Gender'], axis=1))
df_long2 = pd.melt(df3,id_vars=['Race'],var_name='Year', value_name='phds')
df_long2['Gender'] = ['Male']*10
df_combine_plot = pd.concat([df_long, df_long2], ignore_index=True)
fig = px.line(df_combine_plot,
x='Year', y='phds', color='Gender',
labels = {
"phds": "Number of PhDs"
})
fig.update_traces(mode='markers+lines')
summary = pd.DataFrame({'Gender': ['Female','Male'],
'Min': [df_long['phds'].min(), df_long2['phds'].min()],
'Mean' : [df_long['phds'].mean(), df_long2['phds'].mean()],
'Median': [df_long['phds'].median(), df_long2['phds'].median()],
'Max': [df_long['phds'].max(), df_long2['phds'].max()]})
dat = pd.read_excel("https://ncses.nsf.gov/pubs/nsf19301/assets/data/tables/sed17-sr-tab054.xlsx", header=3)
dat_all = dat.iloc[[0]]
dat_T = dat_all.T
dat_T = dat_T.rename(columns=dat_T.iloc[0]).reset_index()
dat_T = dat_T.iloc[1:]
dat_T
fig = px.bar(dat_T, x='index', y='All doctorate recipients (number)c',
labels={'All doctorate recipients (number)c':'All Doctorates', 'index':'Field of Study'})
# create stacked bar plot by gender
from plotly import graph_objects as go
to_plot = dat[dat['Characteristic'].str.contains('ale')]
plot = to_plot.T
plot2 = (
plot.
rename(columns=plot.iloc[0]).
drop(plot.index[0]).
reset_index().
drop(columns=['Female doctorate recipients (number)', 'Male doctorate recipients (number)'])
)
fig2 = go.Figure(
data=[
go.Bar(
name="Male",
x=plot2["index"],
y=plot2["Male"],
offsetgroup=1,
),
go.Bar(
name="Female",
x=plot2["index"],
y=plot2["Female"],
offsetgroup=1,
base=plot2["Male"],
hovertext= [f'Count: {val}' for val in plot2["Female"]]
)
],
layout=go.Layout(
title="Percent of Doctorate Recipients by Broad Field of Study and Gender",
yaxis_title="Percent"
)
)
| 0.498535 | 0.990263 |
# XGBoost による顧客のチャーン予測
_**勾配ブースティング木を使ったモバイル顧客の離脱率予測**_
---
---
## Contents
1. [Background](#Background)
1. [Setup](#Setup)
1. [Data](#Data)
1. [Train](#Train)
1. [Host](#Host)
1. [Evaluate](#Evaluate)
1. [Relative cost of errors](#Relative-cost-of-errors)
1. [Extensions](#Extensions)
---
## Background
_この Notebook は [AWS blog post](https://aws.amazon.com/blogs/ai/predicting-customer-churn-with-amazon-machine-learning/) とそれに付随する SageMaker Examples の和訳です_
顧客を失うことはビジネスでは高く付きます。満足度の低い顧客を早い段階で特定することで、利用継続のインセンティブを与えられる可能性があります。この Notebook は機械学習 (ML) を用いて満足度の低い顧客を自動的に特定する方法 -- 顧客のチャーン予測 (customer churn prediction) とも呼ばれます -- を説明します。ML モデルが完璧な予測をすることはまれなので、この Notebook では ML を利用する経済的な結果を決める際の予測ミスの相対的なコストをどう取り入れるかについても書きます。
ここでは我々にとって身近なチャーン、携帯電話事業者を解約する例を用いることにします (不満ならいつでも見つけられそうです。) もし通信会社が自分が解約しようとしていることを知っているなら、一時的なインセンティブ -- いつでも携帯をアップグレードできるとか、新しい機能が使えるようになるとか -- を与えて契約を継続させるでしょう。インセンティブは通常、失った顧客を再獲得するよりも圧倒的にコスト効率が良いのです。
---
## Setup
_このノートブックの作成およびテストは ml.m4.xlarge ノートブックインスタンスを用いて行われました。_
以下のものを用意して始めましょう:
- トレーニングとモデルデータの置き場所として使う S3 バケットとプレフィックス。ノートブックインスタンス・学習・デプロイ場所と同じリージョンにある必要があります。
- 学習・デプロイ用のコンテナがデータにアクセスするための IAM ロール ARN。これらの作成方法については[ドキュメント](https://docs.aws.amazon.com/ja_jp/IAM/latest/UserGuide/id_roles_create_for-service.html)を参照して下さい。_[注意] もしノートブックインスタンス、学習、デプロイの際に2つ以上のロールが必要な場合、boto regexp を適切な IAM ロール の ARN 文字列で置き換えて下さい。_
```
# Define IAM role
import boto3
import re
import sagemaker
role = sagemaker.get_execution_role()
sess = sagemaker.Session()
bucket = sess.default_bucket()
prefix = 'DEMO-xgboost-churn'
```
次に、必要な Python ライブラリを import します。
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import io
import os
import sys
import time
import json
from IPython.display import display
from time import strftime, gmtime
import sagemaker
from sagemaker.predictor import csv_serializer
```
---
## Data
携帯電話事業者はどの顧客が解約し、誰がサービスを継続利用しているかの履歴データを持っています。この過去の情報を使って ML モデルを学習させることにより、ある事業者の解約率を予測するモデルを構築することができます。モデルを学習させた後、任意の顧客情報 (学習に使った情報と同様のもの) をモデルに入力することによって、顧客が解約しようとしているかを予測することができます。もちろん、モデルが予測を間違えることもあります -- 結局のところ、未来を予測することは一筋縄ではいかないということなのです。しかし、ここではその予測誤差とどう付き合っていくかについても言及します。
今回扱うのは、Daniel T. Larose の [Discovering Knowledge in Data](https://www.amazon.com/dp/0470908742/) という本で述べられている公開データセットです。これは University of California Irvine (UCI) 機械学習レポジトリの著者に帰属します。さて、ダウンロードしてデータセットを見てみましょう:
```
!wget http://dataminingconsultant.com/DKD2e_data_sets.zip
!unzip -o DKD2e_data_sets.zip
churn = pd.read_csv('./Data sets/churn.txt')
pd.set_option('display.max_columns', 500)
churn
```
最近の基準からすると比較的小さなデータセットで、とある US の携帯事業者の顧客データを 3,333 レコードと、それぞれ 21 個の属性で表しています。それぞれの属性は:
- `State`: 顧客が住んでる US の州 (2文字の略号): OH, NJ など
- `Account Length`: このアカウントがアクティブだった日数
- `Area Code`: 顧客の電話番号に対応する3桁の地域コード
- `Phone`: のこりの7桁の電話番号
- `Int’l Plan`: 顧客が国際電話プランに契約しているかどうか: yes/no
- `VMail Plan`: 顧客がボイスメール機能を使っているかどうか: yes/no
- `VMail Message`: (恐らく) 月ごとのボイスメールの平均メッセージ数
- `Day Mins`: 日中に使用された通話時間の合計数
- `Day Calls`: 日中にかけられた電話の回数
- `Day Charge`: 昼間の通話料金
- `Eve Mins, Eve Calls, Eve Charge`: 夕方の通話料金
- `Night Mins`, `Night Calls`, `Night Charge`: 夜間の通話料金
- `Intl Mins`, `Intl Calls`, `Intl Charge`: 国際電話の通話料金
- `CustServ Calls`: カスタマーサービスへの通話数
- `Churn?`: 顧客が解約したかどうか: true/false
最後の属性 `Churn?` はターゲット属性として知られています -- 我々が ML モデルに予測してほしい属性です。ターゲット属性が2値なので、我々のモデルは2値の予測 (2値分類) を行うよう設計します。
それではデータを見てみましょう:
```
# Frequency tables for each categorical feature
for column in churn.select_dtypes(include=['object']).columns:
display(pd.crosstab(index=churn[column], columns='% observations', normalize='columns'))
# Histograms for each numeric features
display(churn.describe())
%matplotlib inline
hist = churn.hist(bins=30, sharey=True, figsize=(10, 10))
```
すぐに以下のことが分かります:
- `State` は一様に分布している。
- `Phone` は実用的でない大量の一意な値を取る。プレフィックスを使うことはできるかもしれないが、どういう割当がされてるか分からないなら使わないほうがよさそう。
- 顧客の 14% だけが解約している。2クラス間のデータ数に不均衡があるものの、それほど極端ではない。
- ほとんどの数値特徴量は驚くほどいい感じに分布していて、釣り鐘型 -- ガウシアン的な分布をしている。`VMail Message` は特筆すべき例外 (そして `Area Code` は非数値型に変換すべき特徴量として現れている)。
```
churn = churn.drop('Phone', axis=1)
churn['Area Code'] = churn['Area Code'].astype(object)
```
次はそれぞれの特徴量とターゲット変数間の関係を見てみましょう。
```
for column in churn.select_dtypes(include=['object']).columns:
if column != 'Churn?':
display(pd.crosstab(index=churn[column], columns=churn['Churn?'], normalize='columns'))
for column in churn.select_dtypes(exclude=['object']).columns:
print(column)
hist = churn[[column, 'Churn?']].hist(by='Churn?', bins=30)
plt.show()
```
面白いことにチャーンは:
- 地理的に均等に分布している
- 国際プランに入っている傾向がある
- ボイスメールには入らない傾向にある
- 日毎の利用時間が二峰性になっている (非解約者に比べて高いか低いかのどちらか)
- 多くの顧客がカスタマーサービスを使っている (多くの問題を経験した顧客が解約しやすい、というのは理解できる)
ように見えます。これに加えて、解約者は `Day Mins` や `Day Charge` のような特徴量について非常に似通った分布をしていることがわかります。通話時間は金額と相関するため特に驚きはないですね。それでは特徴量の関係についてもう少し深く見てみましょう。
```
display(churn.corr())
pd.plotting.scatter_matrix(churn, figsize=(12, 12))
plt.show()
```
いくつかの特徴量は本質的に 100% の相関を持っていることが分かります。これらの特徴量ペアを含め、些細な冗長性やバイアスとして扱われるものもありますが、いくつかの機械学習のアルゴリズムには致命的な問題となる可能性があります。それぞれから高い相関を持つペアを取り除いてみましょう。`Day Mins` から `Day Charge` を、`Night Mins` から `Night Charge` を、`Intl Mins` から `Intl Charge` を除外します:
```
churn = churn.drop(['Day Charge', 'Eve Charge', 'Night Charge', 'Intl Charge'], axis=1)
```
さて、これでデータセットの前処理が終わったので、どのアルゴリズムを使うかを決定しましょう。上で述べたとおり、特定の値が (中間ではなく) 高いか低いかのどちらかにあればチャーンと予測できそうなことが分かっています。これを線形回帰などのアルゴリズムに入れるためには、多項式の (bucketed) 項を作る必要があります。かわりにこの問題を勾配ブースティング木を使ってモデル化することを考えましょう。Amazon SageMaker はマネージドで、分散学習でき、リアルタイム推論エンドポイントをデプロイできる XGBoost コンテナを提供しています。XGBoost は、特徴量とターゲット変数間の非線形な関係を自然に説明し、特徴量間の複雑な関係も記述する勾配ブースティング木 (gradient tree boosting) を用いています [[KDD'16](https://dl.acm.org/citation.cfm?id=2939785)]。
Amazon SageMaker XGBoost は CSV あるいは LibSVM フォーマットどちらのデータでも学習できます。この例では CSV にこだわります。データは
- 予測変数を1列目にもつ
- ヘッダ行をもたない
必要があります。まずはじめにカテゴリ変数を数値に変換しましょう。
```
model_data = pd.get_dummies(churn)
model_data = pd.concat([model_data['Churn?_True.'], model_data.drop(['Churn?_False.', 'Churn?_True.'], axis=1)], axis=1)
```
そして、データを training, validation, test セットに分けましょう。これによりモデルの過学習を防ぐことができ、未知のデータを用いてモデルの精度をテストすることが可能になります。
```
train_data, validation_data, test_data = np.split(model_data.sample(frac=1, random_state=1729), [int(0.7 * len(model_data)), int(0.9 * len(model_data))])
train_data.to_csv('train.csv', header=False, index=False)
validation_data.to_csv('validation.csv', header=False, index=False)
```
これらのファイルを S3 にアップロードします。
```
boto3.Session().resource('s3').Bucket(bucket).Object(os.path.join(prefix, 'train/train.csv')).upload_file('train.csv')
boto3.Session().resource('s3').Bucket(bucket).Object(os.path.join(prefix, 'validation/validation.csv')).upload_file('validation.csv')
```
---
## Train
トレーニングに移ります。まず XGBoost アルゴリズムコンテナの場所を指定する必要があります。
```
from sagemaker.amazon.amazon_estimator import get_image_uri
container = get_image_uri(boto3.Session().region_name, 'xgboost', '0.90-1')
```
次に、今回 CSV ファイルを使ってトレーニングを行うので、S3 に置いたファイルのポインターとして学習用の関数が使う `s3_input` を作ります。
```
s3_input_train = sagemaker.s3_input(s3_data='s3://{}/{}/train'.format(bucket, prefix), content_type='csv')
s3_input_validation = sagemaker.s3_input(s3_data='s3://{}/{}/validation/'.format(bucket, prefix), content_type='csv')
```
ここで、いくつかのパラメータ -- 学習に使うインスタンスの種類・数と XGBoost のハイパーパラメータ -- を指定します。いくつかの重要なパラメータは:
- `max_depth` はアルゴリズム内でそれぞれの木がどれくらい深く作られるかをコントロールします。木が深いほどフィッティングは良くなりますが、計算量が多くなり過学習しやすくもなります。典型的にはモデルのパフォーマンスとトレードオフがあり、多数の浅い木と少数の深い木の間でパラメータを探索する必要があります。
- `subsample` は学習データのサンプリングをコントロールします。これは過学習を防ぎますが、あまり低くしすぎるとデータ不足になります。
- `num_round` はブースティングのラウンド数をコントロールします。これは本質的には前のイテレーションの残差を使って引き続きモデルを学習させます。これも、ラウンドを増やせば学習データに対するフィッティングは良くなりますが、計算量が増えたり過学習する可能性があります。
- `eta` は各ブースティングラウンドのアグレッシブさを決定します。値が大きい方が保守的なブースティングになります。
- `gamma` は木の成長がどれだけアグレッシブかを決めます。大きい値のほうが保守的なモデルを作ります。
詳細は GitHub [page](https://github.com/dmlc/xgboost/blob/master/doc/parameter.rst) を読んで XGBoost のハイパーパラメータを確認して下さい。
```
sess = sagemaker.Session()
xgb = sagemaker.estimator.Estimator(container,
role,
train_instance_count=1,
train_instance_type='ml.m4.xlarge',
output_path='s3://{}/{}/output'.format(bucket, prefix),
sagemaker_session=sess)
xgb.set_hyperparameters(max_depth=5,
eta=0.2,
gamma=4,
min_child_weight=6,
subsample=0.8,
silent=0,
objective='binary:logistic',
num_round=100)
xgb.fit({'train': s3_input_train, 'validation': s3_input_validation})
```
---
## Host
それではモデルを学習させたので、エンドポイントにデプロイしましょう。
```
xgb_predictor = xgb.deploy(initial_instance_count=1,
instance_type='ml.m4.xlarge')
```
### Evaluate
これでエンドポイントが立ち上がったので、http POST リクエストを投げることでリアルタイム推論を非常に簡単に行うことができます。しかしまず、`test_data` の NumPy array をエンドポイントの裏のモデルに渡すために、シリアライザーとデシリアライザーを設定しなければなりません。
```
xgb_predictor.content_type = 'text/csv'
xgb_predictor.serializer = csv_serializer
xgb_predictor.deserializer = None
```
以下の機能を持った簡単な関数を作ります:
1. test データセットをループする
1. ミニバッチに分割する
1. CSV string payload に変換する
1. XGBoost エンドポイントを呼び出してミニバッチに対する予測を行う
1. 予測値を集めてモデルから出力された CSV を NumPy array に変換する
```
def predict(data, rows=500):
split_array = np.array_split(data, int(data.shape[0] / float(rows) + 1))
predictions = ''
for array in split_array:
predictions = ','.join([predictions, xgb_predictor.predict(array).decode('utf-8')])
return np.fromstring(predictions[1:], sep=',')
predictions = predict(test_data.as_matrix()[:, 1:])
```
機械学習モデルのパフォーマンスを比較する多くの方法がありますが、単純に正しい値と予測値を比べてみましょう。この場合、単純に顧客が解約する (`1`) か、しない (`0`) かを予測することで、混同行列が得られます。
```
pd.crosstab(index=test_data.iloc[:, 0], columns=np.round(predictions), rownames=['actual'], colnames=['predictions'])
```
_[注意] アルゴリズムの乱択性により、結果が少し違って見えるかもしれません。_
解約した人 48人のうち、39人を正しく予測することができました (true positive)。間違えて予測された4人はそのまま契約を続けるでしょう (false positive)。そのほか解約しないと予測された9人の顧客は実際に離脱しています (false negative)。
ここで重要な点は `np.round()` 関数が原因で0.5という単純な閾値 (カットオフ値) を設定していることです。`xgboost` からの予測は0から1の間の連続値を取るので、それを元々の2クラスに戻して解釈しています。しかし、離脱する顧客は、解約しようとして企業がより積極的に引き留めようとする顧客よりもコストがかかることが期待されるので、このカットオフを調整する必要があります。これはほとんど確実に false positive を増やしますが、同時にtrue positive も増やし、false negative を減らします。
ざっくりとした直観を得るために、予測結果の連続量を見てみましょう。
```
plt.hist(predictions)
plt.show()
```
モデルから出力された連続値は0と1の間ですが、0.1と0.9の間に十分な値があるため、cutoffを変えれば実際に予測される顧客数が変化するはずです。例えば、
```
pd.crosstab(index=test_data.iloc[:, 0], columns=np.where(predictions > 0.3, 1, 0))
```
カットオフ値を0.5から0.3に変化させることで、もう1人の true positive と 3人の false positive、そして false negative が1人少なくなったことが分かります。数字は全体的に少ないですが、カットオフの変化により顧客の 6-10% に影響を与えています。これは正しい判断なのでしょうか?3人の顧客を繋ぎ止められますが、同時に5人に不要なインセンティブを与えていることになります。最適なカットオフを決めることは実世界に機械学習を応用する上で重要なステップになります。もう少し一般的に議論して、いくつかの仮定のもとでの解を考えましょう。
### Relative cost of errors
どんな2値分類問題も同じような感度のカットオフを生むことはありませんが、これ自体では特に問題とはなりません。結局、もし2クラスのスコアが十分簡単に分離可能なら、問題はそれほど難しくなく、ML ではなく単純なルールで問題を解くことが可能です。
これより重要なのはもし ML モデルで推論させても、モデルが間違って false positive と false negative を割り振るコストがあることです。同じように、true positives と true negatives の正しい推論に付随したコストも見る必要があります。なぜなら、カットオフの選び方はこれらの統計量の4つ全てに関わるからで、各推論に対して4つの出力がどのようなビジネス上の相対コストを生むか考慮する必要があるからです。
#### Assigning costs
今回問題にした携帯事業者の解約におけるコストとは何でしょうか? もちろんコストはビジネス上で取りうる具体的なアクションに依存します。ここでいくつかの仮定を置いてみましょう。
はじめに、true negative のコストを ¥0 (\*) とします。我々のモデルは本質的に、この場合幸せな顧客正しく特定できていることになるので、何もする必要はありません。
次に false negative は一番問題で、離脱しそうな顧客が留まると間違って予測するからです。顧客を失い、放棄所得、広告コスト、管理コスト、店頭コスト、そして恐らく携帯電話ハードウェア補助金を含む、代わりの顧客を獲得するコストを支払う必要があります。
最後に、解約しそうとモデルが予測した顧客については、リテンションのためのインセンティブが仮に一万円だとしましょう。もし事業会社が自分にこういう譲歩をしてきたら、さすがに解約までにもう一回考え直すでしょう。これが true positive と false positive の結果に対するコストです。ここで false posivie (顧客は満足だが誤って離脱と予測) の場合、一万円を _ドブに捨てる_ ことになります。恐らくこの一万円をもっと賢く使うことはできたでしょうが、既存の顧客の支持を高める可能性もあるため、それほど悪い選択ではありません。
\* 以下 \$1 = ¥100 というレートで訳すことにします
#### Finding the optimal cutoff
false negatives が false positives よりも相当コストがかかるのは明らかです。顧客数をもとにエラーを最適化するかわりに、このようなコスト関数を最小化しましょう:
```txt
$500 * FN(C) + $0 * TN(C) + $100 * FP(C) + $100 * TP(C)
```
ここで `FN(C)` は false negative がカットオフ `C` の関数であることを意味し、`TN, FP, TP` についても同様です。上の式の結果を最小化するカットオフ `C` を探す必要があります。
これを行う素直な方法は、複数の考えられるカットオフについてシミュレーションを走らせることです。以下では100通りのカットオフについてforループで計算を行います。
```
cutoffs = np.arange(0.01, 1, 0.01)
costs = []
for c in cutoffs:
costs.append(np.sum(np.sum(np.array([[0, 100], [500, 100]]) *
pd.crosstab(index=test_data.iloc[:, 0],
columns=np.where(predictions > c, 1, 0)))))
costs = np.array(costs)
plt.plot(cutoffs, costs)
plt.show()
print('Cost is minimized near a cutoff of:', cutoffs[np.argmin(costs)], 'for a cost of:', np.min(costs))
```
上の図は、閾値を低くしすぎると全顧客に対してリテンションインセンティブを渡すことになりコストが跳ね上がることを示しています。一方で、閾値を高くしすぎるとあまりに多くの顧客を手放すことになり最終的に同じぐらいコストがかかります。全体のコストはカットオフが 0.46 のときに最小の 84万円 になり、何もしない場合に 200万円 以上失うのよりは圧倒的に良いという結果になります。
---
## Extensions
このノートブックでは顧客が離脱するのを予測するモデルを構築する方法と、true/false positive と false negative により生じるコストを最適化する閾値の決め方について披露しました。これを拡張するにはいくつかの方法が考えられます:
- リテンションインセンティブを受け取る顧客も離脱の可能性がある。インセンティブを受け取っても解約する確率を含めるとリテンションプログラムのROIが向上する。
- 低価格のプランに移行したり課金オプションを無効化する顧客は別の種類のチャーンとしてモデル化できる。
- 顧客行動の発展をモデル化する。もし使用量が落ちてカスタマーサービスへの連絡回数が増えている場合、解約される可能性が高い。顧客情報は行動傾向を取り入れるべきである。
- 実際の学習データと金銭的コストはもっと複雑になり得る。
- それぞれのチャーンに合わせた複数のモデルが必要。
これらの複雑さに関わらず、このノートブックで説明したものと似たような原理は適用できるはずです。
### Optimizing model for prediction using Neo API
SageMaker Neo API を用いれば学習済みのモデルを特定のハードウェア用に最適化することが可能です。`compile_model()` 関数を呼ぶ際に、ターゲットとなるインスタンスファミリー (ここでは C5) とコンパイル済みのモデルを保存する S3 バケットを指定します。
** [重要] もし以下のコマンドが permission error になる場合、ノートブックの上部にスクロールして `get_execution_role()` により返される execution role の値を確認して下さい。このロールには ``output_path`` で指定される S3 バケットへのアクセス権限が必要です。
```
output_path = '/'.join(xgb.output_path.split('/')[:-1])
compiled_model = xgb.compile_model(target_instance_family='ml_c5',
input_shape={'data':[1, 69]},
role=role,
framework='xgboost',
framework_version='0.7',
output_path=output_path)
```
### Creating an inference Endpoint
コンパイル済みのモデルをデプロイすることができます (コンパイルのターゲットと同じインスタンスを指定する必要があります)。この操作により、推論のための SageMaker エンドポイントが作成されます。
``deploy`` 関数の引数はエンドポイントに使われるインスタンス数とタイプを指定することができます。コンパイル時に指定されたインスタンスを選択して下さい (今回は `ml_c5` )。Neo API は Deep Learning Runtime (DLR) と呼ばれる特別なランタイムを使い最適化されたモデルを走らせます。
```
# known issue: need to manually specify endpoint name
compiled_model.name = 'deployed-xgboost-customer-churn'
# There is a known issue where SageMaker SDK locates the incorrect docker image URI for XGBoost
# For now, we manually set Image URI
compiled_model.image = get_image_uri(sess.boto_region_name, 'xgboost-neo', repo_version='latest')
compiled_predictor = compiled_model.deploy(initial_instance_count = 1, instance_type = 'ml.c5.4xlarge')
```
### Making an inference request
コンパイルされたモデルは CSV の入力を受け付けます。
```
compiled_predictor.content_type = 'text/csv'
compiled_predictor.serializer = csv_serializer
compiled_predictor.deserializer = None
def optimized_predict(data, rows=500):
split_array = np.array_split(data, int(data.shape[0] / float(rows) + 1))
predictions = ''
for array in split_array:
predictions = ','.join([predictions, compiled_predictor.predict(array).decode('utf-8')])
return np.fromstring(predictions[1:], sep=',')
# Batch prediction is not supported yet; need to send one data point at a time
dtest = test_data.as_matrix()
predictions = []
for i in range(dtest.shape[0]):
predictions.append(optimized_predict(dtest[i:i+1, 1:]))
predictions = np.array(predictions).squeeze()
predictions
```
### (Optional) Clean-up
このノートブックによって作られたリソースを削除していい場合、以下のセルを実行してください。このコマンドは上で作成したエンドポイントを削除して意図しない請求を防ぐことができます。
(必要であれば、このノートブック自体を走らせているノートブックインスタンスも SageMaker のマネージメントコンソールから停止させて下さい。)
```
sagemaker.Session().delete_endpoint(xgb_predictor.endpoint)
sagemaker.Session().delete_endpoint(compiled_predictor.endpoint)
```
|
github_jupyter
|
# Define IAM role
import boto3
import re
import sagemaker
role = sagemaker.get_execution_role()
sess = sagemaker.Session()
bucket = sess.default_bucket()
prefix = 'DEMO-xgboost-churn'
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import io
import os
import sys
import time
import json
from IPython.display import display
from time import strftime, gmtime
import sagemaker
from sagemaker.predictor import csv_serializer
!wget http://dataminingconsultant.com/DKD2e_data_sets.zip
!unzip -o DKD2e_data_sets.zip
churn = pd.read_csv('./Data sets/churn.txt')
pd.set_option('display.max_columns', 500)
churn
# Frequency tables for each categorical feature
for column in churn.select_dtypes(include=['object']).columns:
display(pd.crosstab(index=churn[column], columns='% observations', normalize='columns'))
# Histograms for each numeric features
display(churn.describe())
%matplotlib inline
hist = churn.hist(bins=30, sharey=True, figsize=(10, 10))
churn = churn.drop('Phone', axis=1)
churn['Area Code'] = churn['Area Code'].astype(object)
for column in churn.select_dtypes(include=['object']).columns:
if column != 'Churn?':
display(pd.crosstab(index=churn[column], columns=churn['Churn?'], normalize='columns'))
for column in churn.select_dtypes(exclude=['object']).columns:
print(column)
hist = churn[[column, 'Churn?']].hist(by='Churn?', bins=30)
plt.show()
display(churn.corr())
pd.plotting.scatter_matrix(churn, figsize=(12, 12))
plt.show()
churn = churn.drop(['Day Charge', 'Eve Charge', 'Night Charge', 'Intl Charge'], axis=1)
model_data = pd.get_dummies(churn)
model_data = pd.concat([model_data['Churn?_True.'], model_data.drop(['Churn?_False.', 'Churn?_True.'], axis=1)], axis=1)
train_data, validation_data, test_data = np.split(model_data.sample(frac=1, random_state=1729), [int(0.7 * len(model_data)), int(0.9 * len(model_data))])
train_data.to_csv('train.csv', header=False, index=False)
validation_data.to_csv('validation.csv', header=False, index=False)
boto3.Session().resource('s3').Bucket(bucket).Object(os.path.join(prefix, 'train/train.csv')).upload_file('train.csv')
boto3.Session().resource('s3').Bucket(bucket).Object(os.path.join(prefix, 'validation/validation.csv')).upload_file('validation.csv')
from sagemaker.amazon.amazon_estimator import get_image_uri
container = get_image_uri(boto3.Session().region_name, 'xgboost', '0.90-1')
s3_input_train = sagemaker.s3_input(s3_data='s3://{}/{}/train'.format(bucket, prefix), content_type='csv')
s3_input_validation = sagemaker.s3_input(s3_data='s3://{}/{}/validation/'.format(bucket, prefix), content_type='csv')
sess = sagemaker.Session()
xgb = sagemaker.estimator.Estimator(container,
role,
train_instance_count=1,
train_instance_type='ml.m4.xlarge',
output_path='s3://{}/{}/output'.format(bucket, prefix),
sagemaker_session=sess)
xgb.set_hyperparameters(max_depth=5,
eta=0.2,
gamma=4,
min_child_weight=6,
subsample=0.8,
silent=0,
objective='binary:logistic',
num_round=100)
xgb.fit({'train': s3_input_train, 'validation': s3_input_validation})
xgb_predictor = xgb.deploy(initial_instance_count=1,
instance_type='ml.m4.xlarge')
xgb_predictor.content_type = 'text/csv'
xgb_predictor.serializer = csv_serializer
xgb_predictor.deserializer = None
def predict(data, rows=500):
split_array = np.array_split(data, int(data.shape[0] / float(rows) + 1))
predictions = ''
for array in split_array:
predictions = ','.join([predictions, xgb_predictor.predict(array).decode('utf-8')])
return np.fromstring(predictions[1:], sep=',')
predictions = predict(test_data.as_matrix()[:, 1:])
pd.crosstab(index=test_data.iloc[:, 0], columns=np.round(predictions), rownames=['actual'], colnames=['predictions'])
plt.hist(predictions)
plt.show()
pd.crosstab(index=test_data.iloc[:, 0], columns=np.where(predictions > 0.3, 1, 0))
$500 * FN(C) + $0 * TN(C) + $100 * FP(C) + $100 * TP(C)
cutoffs = np.arange(0.01, 1, 0.01)
costs = []
for c in cutoffs:
costs.append(np.sum(np.sum(np.array([[0, 100], [500, 100]]) *
pd.crosstab(index=test_data.iloc[:, 0],
columns=np.where(predictions > c, 1, 0)))))
costs = np.array(costs)
plt.plot(cutoffs, costs)
plt.show()
print('Cost is minimized near a cutoff of:', cutoffs[np.argmin(costs)], 'for a cost of:', np.min(costs))
output_path = '/'.join(xgb.output_path.split('/')[:-1])
compiled_model = xgb.compile_model(target_instance_family='ml_c5',
input_shape={'data':[1, 69]},
role=role,
framework='xgboost',
framework_version='0.7',
output_path=output_path)
# known issue: need to manually specify endpoint name
compiled_model.name = 'deployed-xgboost-customer-churn'
# There is a known issue where SageMaker SDK locates the incorrect docker image URI for XGBoost
# For now, we manually set Image URI
compiled_model.image = get_image_uri(sess.boto_region_name, 'xgboost-neo', repo_version='latest')
compiled_predictor = compiled_model.deploy(initial_instance_count = 1, instance_type = 'ml.c5.4xlarge')
compiled_predictor.content_type = 'text/csv'
compiled_predictor.serializer = csv_serializer
compiled_predictor.deserializer = None
def optimized_predict(data, rows=500):
split_array = np.array_split(data, int(data.shape[0] / float(rows) + 1))
predictions = ''
for array in split_array:
predictions = ','.join([predictions, compiled_predictor.predict(array).decode('utf-8')])
return np.fromstring(predictions[1:], sep=',')
# Batch prediction is not supported yet; need to send one data point at a time
dtest = test_data.as_matrix()
predictions = []
for i in range(dtest.shape[0]):
predictions.append(optimized_predict(dtest[i:i+1, 1:]))
predictions = np.array(predictions).squeeze()
predictions
sagemaker.Session().delete_endpoint(xgb_predictor.endpoint)
sagemaker.Session().delete_endpoint(compiled_predictor.endpoint)
| 0.367611 | 0.914176 |
```
import pandas as pd
from textblob import TextBlob
import os
import nltk
import re
from collections import Counter
import matplotlib.pyplot as plt
import string
import preprocessor as p
from nltk.corpus import stopwords
from nltk import word_tokenize
import glob
df_swiggy = pd.DataFrame()
for file_name in glob.glob("swiggy/"+'*.csv'):
df = pd.read_csv(file_name)
df_swiggy = df_swiggy.append(df)
swiggy = '\n'.join(df_swiggy['full_text'])
swiggy = swiggy + '\n'
text_file = open("swiggy.txt", "w")
text_file.write(swiggy)
text_file.close()
df_zomato = pd.DataFrame()
for file_name in glob.glob("zomato/"+'*.csv'):
df = pd.read_csv(file_name)
df_zomato = df_zomato.append(df)
zomato = '\n'.join(df_zomato['full_text'])
zomato = zomato + '\n'
text_file = open("zomato.txt", "w")
text_file.write(zomato)
text_file.close()
#Emoji patterns
emoji_pattern = re.compile("["
u"\U0001F600-\U0001F64F" # emoticons
u"\U0001F300-\U0001F5FF" # symbols & pictographs
u"\U0001F680-\U0001F6FF" # transport & map symbols
u"\U0001F1E0-\U0001F1FF" # flags (iOS)
u"\U00002702-\U000027B0"
u"\U000024C2-\U0001F251"
"]+", flags=re.UNICODE)
#HappyEmoticons
emoticons_happy = set([
':-)', ':)', ';)', ':o)', ':]', ':3', ':c)', ':>', '=]', '8)', '=)', ':}',
':^)', ':-D', ':D', '8-D', '8D', 'x-D', 'xD', 'X-D', 'XD', '=-D', '=D',
'=-3', '=3', ':-))', ":'-)", ":')", ':*', ':^*', '>:P', ':-P', ':P', 'X-P',
'x-p', 'xp', 'XP', ':-p', ':p', '=p', ':-b', ':b', '>:)', '>;)', '>:-)',
'<3'
])
# Sad Emoticons
emoticons_sad = set([
':L', ':-/', '>:/', ':S', '>:[', ':@', ':-(', ':[', ':-||', '=L', ':<',
':-[', ':-<', '=\\', '=/', '>:(', ':(', '>.<', ":'-(", ":'(", ':\\', ':-c',
':c', ':{', '>:\\', ';('
])
#combine sad and happy emoticons
emoticons = emoticons_happy.union(emoticons_sad)
df_swiggy['full_text'].head(20)
#https://towardsdatascience.com/with-the-emergence-of-social-media-high-quality-of-structured-and-unstructured-information-shared-b16103f8bb2e
#https://pypi.org/project/tweet-preprocessor/
import preprocessor as p
def clean_tweets_preprocessing(text) :
#print(text)
# text = BeautifulSoup(text, 'lxml')
# print(text)
# text = re.sub("http[^[:space:]]*", "", text) #remove mentions
# text = re.sub("[^[:alpha:][:space:]]*", "", text) #remove URLs
# text = re.sub("@[^[:space:]]*", "", text)
text = p.clean(text)
print(text)
return text
def clean_tweets(tweet):
stop_words = set(stopwords.words('english'))
stop_words_list = list(stop_words)
stop_words_list.extend(['Humans','May', 'Water', 'may', 'water', 'definitely', 'nice', 'Zomato', 'Order','order','swiggy','food','guy','time'])
#after tweepy preprocessing the colon symbol left remain after #removing mentions
tweet = re.sub(r':', '', tweet)
tweet = re.sub(r'…', '', tweet)
tweet = tweet.lower()
#replace consecutive non-ASCII characters with a space
tweet = re.sub(r'[^\x00-\x7F]+',' ', tweet)
#remove emojis from tweet
tweet = emoji_pattern.sub(r'', tweet)
word_tokens = word_tokenize(tweet)
#filter using NLTK library append it to a string
filtered_tweet = [w for w in word_tokens if not w in stop_words_list]
filtered_tweet = []
#looping through conditions
for w in word_tokens:
#check tokens against stop words , emoticons and punctuations
if w not in stop_words_list and w not in emoticons and w not in string.punctuation:
filtered_tweet.append(w)
return ' '.join(filtered_tweet)
#print(word_tokens)
#print(filtered_sentence)return tweet
df['full_text'] = df['full_text'].apply(lambda x: clean_tweets_preprocessing(x))
df['full_text'] = df['full_text'].apply(lambda x: clean_tweets(x))
text_corpus = '.'.join(df['full_text'])
from wordcloud import WordCloud
cloud = WordCloud(background_color="white").generate(text_corpus)
plt.figure(figsize=(20,20))
plt.imshow(cloud)
plt.axis('off')
plt.show()
#https://medium.com/@yhpf/sentiment-analysis-with-textblob-af2da55ccc9
def sentiment_func(tweet):
try:
return TextBlob(tweet).sentiment
except:
return None
df['tweet_polarity'] = df['full_text'].apply(sentiment_func)
df['Polarity'] = df['tweet_polarity'].apply(lambda x: x[0])
df['Subjectivity'] = df['tweet_polarity'].apply(lambda x: x[1])
df[['full_text','tweet_polarity','Polarity','Subjectivity']].head(50)
#https://towardsdatascience.com/almost-real-time-twitter-sentiment-analysis-with-tweep-vader-f88ed5b93b1c
# most common words in twitter dataset
all_words = []
for line in list(df['full_text']):
words = line.split()
for word in words:
all_words.append(word.lower())# plot word frequency distribution of first few words
plt.figure(figsize=(12,5))
plt.xticks(fontsize=13, rotation=90)
fd = nltk.FreqDist(all_words)
fd.plot(25,cumulative=False)# log-log of all words
word_counts = sorted(Counter(all_words).values(), reverse=True)
plt.figure(figsize=(12,5))
plt.loglog(word_counts, linestyle='-', linewidth=1.5)
plt.ylabel("Freq")
plt.xlabel("Word Rank")
#https://towardsdatascience.com/almost-real-time-twitter-sentiment-analysis-with-tweep-vader-f88ed5b93b1c
#https://towardsdatascience.com/@rickykim78
```{r text.clean}
text.clean = function(text, # x=text_corpus
remove_numbers=TRUE, # whether to drop numbers? Default is TRUE
remove_stopwords=TRUE) # whether to drop stopwords? Default is TRUE
{ text = gsub("@[A-Za-z0-9_]+", '', text) #remove all @mention
text = gsub("https?://[A-Za-z0-9./]+", "", text) #remove links
text = iconv(text, "latin1", "ASCII", sub="") #remove other language characters
text = gsub("[^a-zA-Z\\s]", " ", text) #remove all #, numbers, etc non alphabets
text = gsub(' +', ' ', text) #all double spaces with single
text = gsub("[^[:alnum:]]", " ", text) #remove non alpha numeric
text = tolower(text) # convert to lower case characters
text = stripWhitespace(text) #remove extra white spaces
text = gsub("^\\s+|\\s+$", "", text) #remove extra spaces at beginning and end
english_stopwords = tm::stopwords('english')
#external_stopwords = readLines('stopwords/twitter-stopwords.txt')
#common = unique(c(english_stopwords, external_stopwords)) #combine two lists
#stopwords = unique(gsub("'"," ",common)) #final list
text = removeWords(text,english_stopwords) #remove all stopwords
text = stripWhitespace(text)
#do stemming later
return(text)
}
```
|
github_jupyter
|
import pandas as pd
from textblob import TextBlob
import os
import nltk
import re
from collections import Counter
import matplotlib.pyplot as plt
import string
import preprocessor as p
from nltk.corpus import stopwords
from nltk import word_tokenize
import glob
df_swiggy = pd.DataFrame()
for file_name in glob.glob("swiggy/"+'*.csv'):
df = pd.read_csv(file_name)
df_swiggy = df_swiggy.append(df)
swiggy = '\n'.join(df_swiggy['full_text'])
swiggy = swiggy + '\n'
text_file = open("swiggy.txt", "w")
text_file.write(swiggy)
text_file.close()
df_zomato = pd.DataFrame()
for file_name in glob.glob("zomato/"+'*.csv'):
df = pd.read_csv(file_name)
df_zomato = df_zomato.append(df)
zomato = '\n'.join(df_zomato['full_text'])
zomato = zomato + '\n'
text_file = open("zomato.txt", "w")
text_file.write(zomato)
text_file.close()
#Emoji patterns
emoji_pattern = re.compile("["
u"\U0001F600-\U0001F64F" # emoticons
u"\U0001F300-\U0001F5FF" # symbols & pictographs
u"\U0001F680-\U0001F6FF" # transport & map symbols
u"\U0001F1E0-\U0001F1FF" # flags (iOS)
u"\U00002702-\U000027B0"
u"\U000024C2-\U0001F251"
"]+", flags=re.UNICODE)
#HappyEmoticons
emoticons_happy = set([
':-)', ':)', ';)', ':o)', ':]', ':3', ':c)', ':>', '=]', '8)', '=)', ':}',
':^)', ':-D', ':D', '8-D', '8D', 'x-D', 'xD', 'X-D', 'XD', '=-D', '=D',
'=-3', '=3', ':-))', ":'-)", ":')", ':*', ':^*', '>:P', ':-P', ':P', 'X-P',
'x-p', 'xp', 'XP', ':-p', ':p', '=p', ':-b', ':b', '>:)', '>;)', '>:-)',
'<3'
])
# Sad Emoticons
emoticons_sad = set([
':L', ':-/', '>:/', ':S', '>:[', ':@', ':-(', ':[', ':-||', '=L', ':<',
':-[', ':-<', '=\\', '=/', '>:(', ':(', '>.<', ":'-(", ":'(", ':\\', ':-c',
':c', ':{', '>:\\', ';('
])
#combine sad and happy emoticons
emoticons = emoticons_happy.union(emoticons_sad)
df_swiggy['full_text'].head(20)
#https://towardsdatascience.com/with-the-emergence-of-social-media-high-quality-of-structured-and-unstructured-information-shared-b16103f8bb2e
#https://pypi.org/project/tweet-preprocessor/
import preprocessor as p
def clean_tweets_preprocessing(text) :
#print(text)
# text = BeautifulSoup(text, 'lxml')
# print(text)
# text = re.sub("http[^[:space:]]*", "", text) #remove mentions
# text = re.sub("[^[:alpha:][:space:]]*", "", text) #remove URLs
# text = re.sub("@[^[:space:]]*", "", text)
text = p.clean(text)
print(text)
return text
def clean_tweets(tweet):
stop_words = set(stopwords.words('english'))
stop_words_list = list(stop_words)
stop_words_list.extend(['Humans','May', 'Water', 'may', 'water', 'definitely', 'nice', 'Zomato', 'Order','order','swiggy','food','guy','time'])
#after tweepy preprocessing the colon symbol left remain after #removing mentions
tweet = re.sub(r':', '', tweet)
tweet = re.sub(r'…', '', tweet)
tweet = tweet.lower()
#replace consecutive non-ASCII characters with a space
tweet = re.sub(r'[^\x00-\x7F]+',' ', tweet)
#remove emojis from tweet
tweet = emoji_pattern.sub(r'', tweet)
word_tokens = word_tokenize(tweet)
#filter using NLTK library append it to a string
filtered_tweet = [w for w in word_tokens if not w in stop_words_list]
filtered_tweet = []
#looping through conditions
for w in word_tokens:
#check tokens against stop words , emoticons and punctuations
if w not in stop_words_list and w not in emoticons and w not in string.punctuation:
filtered_tweet.append(w)
return ' '.join(filtered_tweet)
#print(word_tokens)
#print(filtered_sentence)return tweet
df['full_text'] = df['full_text'].apply(lambda x: clean_tweets_preprocessing(x))
df['full_text'] = df['full_text'].apply(lambda x: clean_tweets(x))
text_corpus = '.'.join(df['full_text'])
from wordcloud import WordCloud
cloud = WordCloud(background_color="white").generate(text_corpus)
plt.figure(figsize=(20,20))
plt.imshow(cloud)
plt.axis('off')
plt.show()
#https://medium.com/@yhpf/sentiment-analysis-with-textblob-af2da55ccc9
def sentiment_func(tweet):
try:
return TextBlob(tweet).sentiment
except:
return None
df['tweet_polarity'] = df['full_text'].apply(sentiment_func)
df['Polarity'] = df['tweet_polarity'].apply(lambda x: x[0])
df['Subjectivity'] = df['tweet_polarity'].apply(lambda x: x[1])
df[['full_text','tweet_polarity','Polarity','Subjectivity']].head(50)
#https://towardsdatascience.com/almost-real-time-twitter-sentiment-analysis-with-tweep-vader-f88ed5b93b1c
# most common words in twitter dataset
all_words = []
for line in list(df['full_text']):
words = line.split()
for word in words:
all_words.append(word.lower())# plot word frequency distribution of first few words
plt.figure(figsize=(12,5))
plt.xticks(fontsize=13, rotation=90)
fd = nltk.FreqDist(all_words)
fd.plot(25,cumulative=False)# log-log of all words
word_counts = sorted(Counter(all_words).values(), reverse=True)
plt.figure(figsize=(12,5))
plt.loglog(word_counts, linestyle='-', linewidth=1.5)
plt.ylabel("Freq")
plt.xlabel("Word Rank")
#https://towardsdatascience.com/almost-real-time-twitter-sentiment-analysis-with-tweep-vader-f88ed5b93b1c
#https://towardsdatascience.com/@rickykim78
| 0.327346 | 0.148602 |
# BatchNorm intuitions
```
%matplotlib inline
# %matplotlib notebook
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch import nn
import torch.utils.data as Data
import torch.nn.functional as F
torch.manual_seed(42)
np.random.seed(42)
```
## 1. Impact on activations and results
```
class ExperimentParams():
def __init__(self):
self.num_samples = 2000
self.batch_size = 64
self.lr = 3e-2
self.n_hidden = 8
self.num_epochs = 12
self.num_workers = 4
self.activation = F.tanh
self.bias_init = -0.2
self.device = 'cuda' if torch.cuda.is_available() else 'cpu'
self.data_dir = '/home/docker_user/'
args = ExperimentParams()
# training data
x = np.linspace(-7, 10, args.num_samples)[:, np.newaxis]
noise = np.random.normal(0, 2, x.shape)
y = np.square(x) - 5 + noise
# test data
test_x = np.linspace(-7, 10, 200)[:, np.newaxis]
noise = np.random.normal(0, 2, test_x.shape)
test_y = np.square(test_x) - 5 + noise
train_x, train_y = torch.from_numpy(x).float(), torch.from_numpy(y).float()
test_x, test_y = torch.from_numpy(test_x).float(), torch.from_numpy(test_y).float()
train_dataset = Data.TensorDataset(train_x, train_y)
train_loader = Data.DataLoader(dataset=train_dataset, batch_size=args.batch_size, shuffle=True, num_workers=2,)
# show data
plt.scatter(train_x.numpy(), train_y.numpy(), c='#FF9359', s=50, alpha=0.2, label='train')
plt.legend(loc='upper left')
class Net(nn.Module):
def __init__(self, n_hidden,batch_normalization=False, bias_init= -0.2):
super(Net, self).__init__()
self.n_hidden = n_hidden
self.do_bn = batch_normalization
self.fcs = []
self.bns = []
self.bn_input = nn.BatchNorm1d(1, momentum=0.5)
self.activation = nn.Tanh()
self.bias_init = bias_init
for i in range(self.n_hidden): # build hidden layers and BN layers
input_size = 1 if i == 0 else 10
fc = nn.Linear(input_size, 10)
setattr(self, 'fc%i' % i, fc) # IMPORTANT set layer to the Module
self._set_init(fc) # parameters initialization
self.fcs.append(fc)
if self.do_bn:
bn = nn.BatchNorm1d(10, momentum=0.5)
setattr(self, 'bn%i' % i, bn) # IMPORTANT set layer to the Module
self.bns.append(bn)
self.predict = nn.Linear(10, 1) # output layer
self._set_init(self.predict) # parameters initialization
def _set_init(self, layer):
nn.init.normal_(layer.weight, mean=0., std=.1)
nn.init.constant_(layer.bias, self.bias_init)
def forward(self, x):
pre_activation = [x]
if self.do_bn:
x = self.bn_input(x) # input batch normalization
layer_input = [x]
for i in range(self.n_hidden):
x = self.fcs[i](x)
pre_activation.append(x)
if self.do_bn:
x = self.bns[i](x) # batch normalization
x = self.activation(x)
layer_input.append(x)
out = self.predict(x)
return out, layer_input, pre_activation
nets = [Net(n_hidden=args.n_hidden, batch_normalization=False), Net(n_hidden=args.n_hidden, batch_normalization=True)]
print(*nets) # print net architecture
optimizers = [torch.optim.Adam(net.parameters(), lr=args.lr) for net in nets]
loss_fn = torch.nn.MSELoss()
def plot_histogram(l_in, l_in_bn, pre_ac, pre_ac_bn):
for i, (ax_pa, ax_pa_bn, ax, ax_bn) in enumerate(zip(axs[0, :], axs[1, :], axs[2, :], axs[3, :])):
[a.clear() for a in [ax_pa, ax_pa_bn, ax, ax_bn]]
if i == 0:
p_range = (-7, 10)
the_range = (-7, 10)
else:
p_range = (-4, 4)
the_range = (-1, 1)
ax_pa.set_title('L' + str(i))
ax_pa.hist(pre_ac[i].data.numpy().ravel(), bins=10, range=p_range, color='orange', alpha=0.5);
ax_pa_bn.hist(pre_ac_bn[i].data.numpy().ravel(), bins=10, range=p_range, color='green', alpha=0.5)
ax.hist(l_in[i].data.numpy().ravel(), bins=10, range=the_range, color='orange');
ax_bn.hist(l_in_bn[i].data.numpy().ravel(), bins=10, range=the_range, color='green')
for a in [ax_pa, ax, ax_pa_bn, ax_bn]:
a.set_yticks(())
a.set_xticks(())
ax_pa_bn.set_xticks(p_range)
ax_bn.set_xticks(the_range)
axs[0, 0].set_ylabel('PreAct');
axs[1, 0].set_ylabel('BN PreAct');
axs[2, 0].set_ylabel('Act');
axs[3, 0].set_ylabel('BN Act')
plt.pause(0.01)
# training
losses = [[], []] # record loss for two networks
for epoch in range(args.num_epochs):
print('Epoch: ', epoch)
layer_inputs, pre_acts = [], []
for net, l in zip(nets, losses):
net.eval() # set eval mode to fix moving_mean and moving_var
pred, layer_input, pre_act = net(test_x)
l.append(loss_fn(pred, test_y).item())
layer_inputs.append(layer_input)
pre_acts.append(pre_act)
net.train() # free moving_mean and moving_var
f, axs = plt.subplots(4, args.n_hidden+1, figsize=(10, 5))
plot_histogram(*layer_inputs, *pre_acts) # plot histogram
for step, (b_x, b_y) in enumerate(train_loader):
for net, opt in zip(nets, optimizers): # train for each network
pred, _, _ = net(b_x)
loss = loss_fn(pred, b_y)
opt.zero_grad()
loss.backward()
opt.step() # it will also learns the parameters in Batch Normalization
# plot training loss
plt.figure(2)
plt.plot(losses[0], c='orange', lw=3, label='Original')
plt.plot(losses[1], c='green', lw=3, label='Batch Normalization')
plt.xlabel('step');
plt.ylabel('test loss');
plt.ylim((0, 2000));
plt.legend(loc='best')
# evaluation
# set net to eval mode to freeze the parameters in batch normalization layers
[net.eval() for net in nets] # set eval mode to fix moving_mean and moving_var
preds = [net(test_x)[0] for net in nets]
plt.figure(3)
plt.plot(test_x.data.numpy(), preds[0].data.numpy(), c='orange', lw=4, label='Original')
plt.plot(test_x.data.numpy(), preds[1].data.numpy(), c='green', lw=4, label='Batch Normalization')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='r', s=50, alpha=0.2, label='train')
plt.legend(loc='best')
plt.show()
```
## 2. Dependency on weight initialization
We will generate a toy dataset using `scikit-learn`
```
from sklearn import datasets
x, y = datasets.make_circles(n_samples=args.num_samples, factor=.5, noise=.05)
train_x, train_y = torch.from_numpy(x).float(), torch.from_numpy(y).long()
# test data
test_x, test_y = datasets.make_circles(n_samples=200, factor=.5, noise=.05)
test_x, test_y = torch.from_numpy(test_x).float(), torch.from_numpy(test_y).long()
train_dataset = Data.TensorDataset(train_x, train_y)
train_loader = Data.DataLoader(dataset=train_dataset, batch_size=args.batch_size, shuffle=True, num_workers=2,)
plt.figure(figsize=(10,10))
colors = ['orange', 'green']
for i in range(2):
inds = np.where(y==i)[0]
plt.scatter(x[inds,0], x[inds,1], alpha=0.5, color=colors[i])
plt.legend(['class 0', 'class 1'])
```
This is a script for creating a model on the fly
```
def create_model(with_batchnorm, nc = 32, depth = 16):
modules = []
modules.append(nn.Linear(2, nc))
if with_batchnorm:
modules.append(nn.BatchNorm1d(nc))
modules.append(nn.ReLU())
for d in range(depth):
modules.append(nn.Linear(nc, nc))
if with_batchnorm:
modules.append(nn.BatchNorm1d(nc))
modules.append(nn.ReLU())
modules.append(nn.Linear(nc, 2))
return nn.Sequential(*modules)
stds = [1e-3, 1e-2, 1e-1, 1e0, 1e1]
args.num_epochs = 10
accuracies = [[], []]
losses = [[], []] # record test loss for two networks
for std in stds:
print(f'Initializing nets with std: {std}')
nets = [create_model(with_batchnorm=False), create_model(with_batchnorm=True)]
optimizers = [torch.optim.Adam(net.parameters(), lr=args.lr) for net in nets]
loss_fn = torch.nn.CrossEntropyLoss()
for net in nets:
with torch.no_grad():
for p in net.parameters(): p.normal_(0, std)
net.train()
for epoch in range(args.num_epochs):
for step, (b_x, b_y) in enumerate(train_loader):
for net, opt in zip(nets, optimizers): # train for each network
output = net(b_x)
loss = loss_fn(output, b_y)
opt.zero_grad()
loss.backward()
opt.step() # it will also learns the parameters in Batch Normalization
for net, l, acc in zip(nets, losses, accuracies):
net.eval()
output = net(test_x)
l.append(loss_fn(output, test_y).item())
_,pred = torch.max(output.data,1)
corrects = torch.sum(pred == test_y).float()/test_y.numel()
acc.append(corrects.item())
# plotting
plt.cla()
plt.plot(stds, losses[0], 'orange', lw=3, label='no batchnorm')
plt.plot(stds, losses[1], 'green', lw=3, label='with batchnorm')
plt.legend(loc='upper left');
plt.xlabel('weight std')
plt.ylabel('test loss')
plt.title('Test loss')
plt.grid(True)
plt.pause(0.1)
plt.show()
plt.cla()
plt.plot(stds, accuracies[0], 'orange', lw=3, label='no batchnorm')
plt.plot(stds, accuracies[1], 'green', lw=3, label='with batchnorm')
plt.legend(loc='upper left');
plt.xlabel('weight std')
plt.ylabel('test accuracy')
plt.title('Test accuracy')
plt.grid(True)
plt.pause(0.1)
plt.show()
```
# 3. Exercises
1. Code a similar pipeline from Dropout, with conv layers, comparing variant with and without BatchNorm. What do you notice?
2. Try out larger learning rate values. Plot the decrease in training and test error.
3. Do we need Batch Normalization in every layer? Experiment with it?
|
github_jupyter
|
%matplotlib inline
# %matplotlib notebook
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch import nn
import torch.utils.data as Data
import torch.nn.functional as F
torch.manual_seed(42)
np.random.seed(42)
class ExperimentParams():
def __init__(self):
self.num_samples = 2000
self.batch_size = 64
self.lr = 3e-2
self.n_hidden = 8
self.num_epochs = 12
self.num_workers = 4
self.activation = F.tanh
self.bias_init = -0.2
self.device = 'cuda' if torch.cuda.is_available() else 'cpu'
self.data_dir = '/home/docker_user/'
args = ExperimentParams()
# training data
x = np.linspace(-7, 10, args.num_samples)[:, np.newaxis]
noise = np.random.normal(0, 2, x.shape)
y = np.square(x) - 5 + noise
# test data
test_x = np.linspace(-7, 10, 200)[:, np.newaxis]
noise = np.random.normal(0, 2, test_x.shape)
test_y = np.square(test_x) - 5 + noise
train_x, train_y = torch.from_numpy(x).float(), torch.from_numpy(y).float()
test_x, test_y = torch.from_numpy(test_x).float(), torch.from_numpy(test_y).float()
train_dataset = Data.TensorDataset(train_x, train_y)
train_loader = Data.DataLoader(dataset=train_dataset, batch_size=args.batch_size, shuffle=True, num_workers=2,)
# show data
plt.scatter(train_x.numpy(), train_y.numpy(), c='#FF9359', s=50, alpha=0.2, label='train')
plt.legend(loc='upper left')
class Net(nn.Module):
def __init__(self, n_hidden,batch_normalization=False, bias_init= -0.2):
super(Net, self).__init__()
self.n_hidden = n_hidden
self.do_bn = batch_normalization
self.fcs = []
self.bns = []
self.bn_input = nn.BatchNorm1d(1, momentum=0.5)
self.activation = nn.Tanh()
self.bias_init = bias_init
for i in range(self.n_hidden): # build hidden layers and BN layers
input_size = 1 if i == 0 else 10
fc = nn.Linear(input_size, 10)
setattr(self, 'fc%i' % i, fc) # IMPORTANT set layer to the Module
self._set_init(fc) # parameters initialization
self.fcs.append(fc)
if self.do_bn:
bn = nn.BatchNorm1d(10, momentum=0.5)
setattr(self, 'bn%i' % i, bn) # IMPORTANT set layer to the Module
self.bns.append(bn)
self.predict = nn.Linear(10, 1) # output layer
self._set_init(self.predict) # parameters initialization
def _set_init(self, layer):
nn.init.normal_(layer.weight, mean=0., std=.1)
nn.init.constant_(layer.bias, self.bias_init)
def forward(self, x):
pre_activation = [x]
if self.do_bn:
x = self.bn_input(x) # input batch normalization
layer_input = [x]
for i in range(self.n_hidden):
x = self.fcs[i](x)
pre_activation.append(x)
if self.do_bn:
x = self.bns[i](x) # batch normalization
x = self.activation(x)
layer_input.append(x)
out = self.predict(x)
return out, layer_input, pre_activation
nets = [Net(n_hidden=args.n_hidden, batch_normalization=False), Net(n_hidden=args.n_hidden, batch_normalization=True)]
print(*nets) # print net architecture
optimizers = [torch.optim.Adam(net.parameters(), lr=args.lr) for net in nets]
loss_fn = torch.nn.MSELoss()
def plot_histogram(l_in, l_in_bn, pre_ac, pre_ac_bn):
for i, (ax_pa, ax_pa_bn, ax, ax_bn) in enumerate(zip(axs[0, :], axs[1, :], axs[2, :], axs[3, :])):
[a.clear() for a in [ax_pa, ax_pa_bn, ax, ax_bn]]
if i == 0:
p_range = (-7, 10)
the_range = (-7, 10)
else:
p_range = (-4, 4)
the_range = (-1, 1)
ax_pa.set_title('L' + str(i))
ax_pa.hist(pre_ac[i].data.numpy().ravel(), bins=10, range=p_range, color='orange', alpha=0.5);
ax_pa_bn.hist(pre_ac_bn[i].data.numpy().ravel(), bins=10, range=p_range, color='green', alpha=0.5)
ax.hist(l_in[i].data.numpy().ravel(), bins=10, range=the_range, color='orange');
ax_bn.hist(l_in_bn[i].data.numpy().ravel(), bins=10, range=the_range, color='green')
for a in [ax_pa, ax, ax_pa_bn, ax_bn]:
a.set_yticks(())
a.set_xticks(())
ax_pa_bn.set_xticks(p_range)
ax_bn.set_xticks(the_range)
axs[0, 0].set_ylabel('PreAct');
axs[1, 0].set_ylabel('BN PreAct');
axs[2, 0].set_ylabel('Act');
axs[3, 0].set_ylabel('BN Act')
plt.pause(0.01)
# training
losses = [[], []] # record loss for two networks
for epoch in range(args.num_epochs):
print('Epoch: ', epoch)
layer_inputs, pre_acts = [], []
for net, l in zip(nets, losses):
net.eval() # set eval mode to fix moving_mean and moving_var
pred, layer_input, pre_act = net(test_x)
l.append(loss_fn(pred, test_y).item())
layer_inputs.append(layer_input)
pre_acts.append(pre_act)
net.train() # free moving_mean and moving_var
f, axs = plt.subplots(4, args.n_hidden+1, figsize=(10, 5))
plot_histogram(*layer_inputs, *pre_acts) # plot histogram
for step, (b_x, b_y) in enumerate(train_loader):
for net, opt in zip(nets, optimizers): # train for each network
pred, _, _ = net(b_x)
loss = loss_fn(pred, b_y)
opt.zero_grad()
loss.backward()
opt.step() # it will also learns the parameters in Batch Normalization
# plot training loss
plt.figure(2)
plt.plot(losses[0], c='orange', lw=3, label='Original')
plt.plot(losses[1], c='green', lw=3, label='Batch Normalization')
plt.xlabel('step');
plt.ylabel('test loss');
plt.ylim((0, 2000));
plt.legend(loc='best')
# evaluation
# set net to eval mode to freeze the parameters in batch normalization layers
[net.eval() for net in nets] # set eval mode to fix moving_mean and moving_var
preds = [net(test_x)[0] for net in nets]
plt.figure(3)
plt.plot(test_x.data.numpy(), preds[0].data.numpy(), c='orange', lw=4, label='Original')
plt.plot(test_x.data.numpy(), preds[1].data.numpy(), c='green', lw=4, label='Batch Normalization')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='r', s=50, alpha=0.2, label='train')
plt.legend(loc='best')
plt.show()
from sklearn import datasets
x, y = datasets.make_circles(n_samples=args.num_samples, factor=.5, noise=.05)
train_x, train_y = torch.from_numpy(x).float(), torch.from_numpy(y).long()
# test data
test_x, test_y = datasets.make_circles(n_samples=200, factor=.5, noise=.05)
test_x, test_y = torch.from_numpy(test_x).float(), torch.from_numpy(test_y).long()
train_dataset = Data.TensorDataset(train_x, train_y)
train_loader = Data.DataLoader(dataset=train_dataset, batch_size=args.batch_size, shuffle=True, num_workers=2,)
plt.figure(figsize=(10,10))
colors = ['orange', 'green']
for i in range(2):
inds = np.where(y==i)[0]
plt.scatter(x[inds,0], x[inds,1], alpha=0.5, color=colors[i])
plt.legend(['class 0', 'class 1'])
def create_model(with_batchnorm, nc = 32, depth = 16):
modules = []
modules.append(nn.Linear(2, nc))
if with_batchnorm:
modules.append(nn.BatchNorm1d(nc))
modules.append(nn.ReLU())
for d in range(depth):
modules.append(nn.Linear(nc, nc))
if with_batchnorm:
modules.append(nn.BatchNorm1d(nc))
modules.append(nn.ReLU())
modules.append(nn.Linear(nc, 2))
return nn.Sequential(*modules)
stds = [1e-3, 1e-2, 1e-1, 1e0, 1e1]
args.num_epochs = 10
accuracies = [[], []]
losses = [[], []] # record test loss for two networks
for std in stds:
print(f'Initializing nets with std: {std}')
nets = [create_model(with_batchnorm=False), create_model(with_batchnorm=True)]
optimizers = [torch.optim.Adam(net.parameters(), lr=args.lr) for net in nets]
loss_fn = torch.nn.CrossEntropyLoss()
for net in nets:
with torch.no_grad():
for p in net.parameters(): p.normal_(0, std)
net.train()
for epoch in range(args.num_epochs):
for step, (b_x, b_y) in enumerate(train_loader):
for net, opt in zip(nets, optimizers): # train for each network
output = net(b_x)
loss = loss_fn(output, b_y)
opt.zero_grad()
loss.backward()
opt.step() # it will also learns the parameters in Batch Normalization
for net, l, acc in zip(nets, losses, accuracies):
net.eval()
output = net(test_x)
l.append(loss_fn(output, test_y).item())
_,pred = torch.max(output.data,1)
corrects = torch.sum(pred == test_y).float()/test_y.numel()
acc.append(corrects.item())
# plotting
plt.cla()
plt.plot(stds, losses[0], 'orange', lw=3, label='no batchnorm')
plt.plot(stds, losses[1], 'green', lw=3, label='with batchnorm')
plt.legend(loc='upper left');
plt.xlabel('weight std')
plt.ylabel('test loss')
plt.title('Test loss')
plt.grid(True)
plt.pause(0.1)
plt.show()
plt.cla()
plt.plot(stds, accuracies[0], 'orange', lw=3, label='no batchnorm')
plt.plot(stds, accuracies[1], 'green', lw=3, label='with batchnorm')
plt.legend(loc='upper left');
plt.xlabel('weight std')
plt.ylabel('test accuracy')
plt.title('Test accuracy')
plt.grid(True)
plt.pause(0.1)
plt.show()
| 0.801237 | 0.865679 |
# Maxpooling Layer
In this notebook, we add and visualize the output of a maxpooling layer in a CNN.
A convolutional layer + activation function, followed by a pooling layer, and a linear layer (to create a desired output size) make up the basic layers of a CNN.
<img src='notebook_ims/CNN_all_layers.png' height=50% width=50% />
### Import the image
```
import cv2
import matplotlib.pyplot as plt
%matplotlib inline
# TODO: Feel free to try out your own images here by changing img_path
# to a file path to another image on your computer!
img_path = 'data/udacity_sdc.png'
# load color image
bgr_img = cv2.imread(img_path)
# convert to grayscale
gray_img = cv2.cvtColor(bgr_img, cv2.COLOR_BGR2GRAY)
# normalize, rescale entries to lie in [0,1]
gray_img = gray_img.astype("float32")/255
# plot image
plt.imshow(gray_img, cmap='gray')
plt.show()
```
### Define and visualize the filters
```
import numpy as np
## TODO: Feel free to modify the numbers here, to try out another filter!
filter_vals = np.array([[-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1]])
print('Filter shape: ', filter_vals.shape)
# Defining four different filters,
# all of which are linear combinations of the `filter_vals` defined above
# define four filters
filter_1 = filter_vals
filter_2 = -filter_1
filter_3 = filter_1.T
filter_4 = -filter_3
filters = np.array([filter_1, filter_2, filter_3, filter_4])
# For an example, print out the values of filter 1
print('Filter 1: \n', filter_1)
```
### Define convolutional and pooling layers
You've seen how to define a convolutional layer, next is a:
* Pooling layer
In the next cell, we initialize a convolutional layer so that it contains all the created filters. Then add a maxpooling layer, [documented here](http://pytorch.org/docs/stable/_modules/torch/nn/modules/pooling.html), with a kernel size of (2x2) so you can see that the image resolution has been reduced after this step!
A maxpooling layer reduces the x-y size of an input and only keeps the most *active* pixel values. Below is an example of a 2x2 pooling kernel, with a stride of 2, applied to a small patch of grayscale pixel values; reducing the size of the patch by a factor of 4. Only the maximum pixel values in 2x2 remain in the new, pooled output.
<img src='notebook_ims/maxpooling_ex.png' height=50% width=50% />
```
import torch
import torch.nn as nn
import torch.nn.functional as F
# define a neural network with a convolutional layer with four filters
# AND a pooling layer of size (2, 2)
class Net(nn.Module):
def __init__(self, weight):
super(Net, self).__init__()
# initializes the weights of the convolutional layer to be the weights of the 4 defined filters
k_height, k_width = weight.shape[2:]
# defines the convolutional layer, assumes there are 4 grayscale filters
# torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
self.conv = nn.Conv2d(1, 4, kernel_size=(k_height, k_width), bias=False)
self.conv.weight = torch.nn.Parameter(weight)
# define a pooling layer
self.pool = nn.MaxPool2d(2, 2)
def forward(self, x):
# calculates the output of a convolutional layer
# pre- and post-activation
conv_x = self.conv(x)
activated_x = F.relu(conv_x)
# applies pooling layer
pooled_x = self.pool(activated_x)
# returns all layers
return conv_x, activated_x, pooled_x
# instantiate the model and set the weights
weight = torch.from_numpy(filters).unsqueeze(1).type(torch.FloatTensor)
model = Net(weight)
# print out the layer in the network
print(model)
```
### Visualize the output of each filter
First, we'll define a helper function, `viz_layer` that takes in a specific layer and number of filters (optional argument), and displays the output of that layer once an image has been passed through.
```
# helper function for visualizing the output of a given layer
# default number of filters is 4
def viz_layer(layer, n_filters= 4):
fig = plt.figure(figsize=(20, 20))
for i in range(n_filters):
ax = fig.add_subplot(1, n_filters, i+1)
# grab layer outputs
ax.imshow(np.squeeze(layer[0,i].data.numpy()), cmap='gray')
ax.set_title('Output %s' % str(i+1))
```
Let's look at the output of a convolutional layer after a ReLu activation function is applied.
#### ReLU activation
A ReLU function turns all negative pixel values in 0's (black). See the equation pictured below for input pixel values, `x`.
<img src='notebook_ims/relu_ex.png' height=50% width=50% />
```
# plot original image
plt.imshow(gray_img, cmap='gray')
# visualize all filters
fig = plt.figure(figsize=(12, 6))
fig.subplots_adjust(left=0, right=1.5, bottom=0.8, top=1, hspace=0.05, wspace=0.05)
for i in range(4):
ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[])
ax.imshow(filters[i], cmap='gray')
ax.set_title('Filter %s' % str(i+1))
# convert the image into an input Tensor
gray_img_tensor = torch.from_numpy(gray_img).unsqueeze(0).unsqueeze(1)
# get all the layers
conv_layer, activated_layer, pooled_layer = model(gray_img_tensor)
# visualize the output of the activated conv layer
viz_layer(activated_layer)
```
### Visualize the output of the pooling layer
Then, take a look at the output of a pooling layer. The pooling layer takes as input the feature maps pictured above and reduces the dimensionality of those maps, by some pooling factor, by constructing a new, smaller image of only the maximum (brightest) values in a given kernel area.
Take a look at the values on the x, y axes to see how the image has changed size.
```
# visualize the output of the pooling layer
viz_layer(pooled_layer)
```
|
github_jupyter
|
import cv2
import matplotlib.pyplot as plt
%matplotlib inline
# TODO: Feel free to try out your own images here by changing img_path
# to a file path to another image on your computer!
img_path = 'data/udacity_sdc.png'
# load color image
bgr_img = cv2.imread(img_path)
# convert to grayscale
gray_img = cv2.cvtColor(bgr_img, cv2.COLOR_BGR2GRAY)
# normalize, rescale entries to lie in [0,1]
gray_img = gray_img.astype("float32")/255
# plot image
plt.imshow(gray_img, cmap='gray')
plt.show()
import numpy as np
## TODO: Feel free to modify the numbers here, to try out another filter!
filter_vals = np.array([[-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1]])
print('Filter shape: ', filter_vals.shape)
# Defining four different filters,
# all of which are linear combinations of the `filter_vals` defined above
# define four filters
filter_1 = filter_vals
filter_2 = -filter_1
filter_3 = filter_1.T
filter_4 = -filter_3
filters = np.array([filter_1, filter_2, filter_3, filter_4])
# For an example, print out the values of filter 1
print('Filter 1: \n', filter_1)
import torch
import torch.nn as nn
import torch.nn.functional as F
# define a neural network with a convolutional layer with four filters
# AND a pooling layer of size (2, 2)
class Net(nn.Module):
def __init__(self, weight):
super(Net, self).__init__()
# initializes the weights of the convolutional layer to be the weights of the 4 defined filters
k_height, k_width = weight.shape[2:]
# defines the convolutional layer, assumes there are 4 grayscale filters
# torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
self.conv = nn.Conv2d(1, 4, kernel_size=(k_height, k_width), bias=False)
self.conv.weight = torch.nn.Parameter(weight)
# define a pooling layer
self.pool = nn.MaxPool2d(2, 2)
def forward(self, x):
# calculates the output of a convolutional layer
# pre- and post-activation
conv_x = self.conv(x)
activated_x = F.relu(conv_x)
# applies pooling layer
pooled_x = self.pool(activated_x)
# returns all layers
return conv_x, activated_x, pooled_x
# instantiate the model and set the weights
weight = torch.from_numpy(filters).unsqueeze(1).type(torch.FloatTensor)
model = Net(weight)
# print out the layer in the network
print(model)
# helper function for visualizing the output of a given layer
# default number of filters is 4
def viz_layer(layer, n_filters= 4):
fig = plt.figure(figsize=(20, 20))
for i in range(n_filters):
ax = fig.add_subplot(1, n_filters, i+1)
# grab layer outputs
ax.imshow(np.squeeze(layer[0,i].data.numpy()), cmap='gray')
ax.set_title('Output %s' % str(i+1))
# plot original image
plt.imshow(gray_img, cmap='gray')
# visualize all filters
fig = plt.figure(figsize=(12, 6))
fig.subplots_adjust(left=0, right=1.5, bottom=0.8, top=1, hspace=0.05, wspace=0.05)
for i in range(4):
ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[])
ax.imshow(filters[i], cmap='gray')
ax.set_title('Filter %s' % str(i+1))
# convert the image into an input Tensor
gray_img_tensor = torch.from_numpy(gray_img).unsqueeze(0).unsqueeze(1)
# get all the layers
conv_layer, activated_layer, pooled_layer = model(gray_img_tensor)
# visualize the output of the activated conv layer
viz_layer(activated_layer)
# visualize the output of the pooling layer
viz_layer(pooled_layer)
| 0.685423 | 0.988668 |
```
import tensorflow as tf
import numpy as np
import tensorflow.keras.layers as nn
import os
from riptide.utils.preprocessing.cifarnet_preprocessing import preprocess_image
from matplotlib import pyplot as plt
%matplotlib inline
@tf.custom_gradient
def AlphaClip(x, alpha):
output = tf.clip_by_value(x, 0, alpha)
def grad_fn(dy):
x_grad_mask = tf.cast(tf.logical_and(x >= 0, x <= alpha), tf.float32)
alpha_grad_mask = tf.cast(x >= alpha, tf.float32)
alpha_grad = tf.reduce_sum(dy * alpha_grad_mask)
x_grad = dy * x_grad_mask
return [x_grad, alpha_grad]
return output, grad_fn
@tf.custom_gradient
def AlphaQuantize(x, alpha, bits):
output = tf.round(x * ((2**bits - 1) / alpha)) * (alpha / (2**bits - 1))
def grad_fn(dy):
return [dy, None, None]
return output, grad_fn
class PACT(tf.keras.layers.Layer):
def __init__(self, quantize=False, bits=2.):
super(PACT, self).__init__()
self.quantize = quantize
self.bits = bits
def build(self, input_shape):
self.alpha = self.add_variable(
'alpha', shape=[],
initializer=tf.keras.initializers.Constant([10.], dtype=tf.float32),
#regularizer=tf.keras.regularizers.l2(0.01))
regularizer = tf.keras.regularizers.l2(0.0002))
def call(self, inputs):
outputs = AlphaClip(inputs, self.alpha)
if self.quantize:
with tf.name_scope('QA'):
outputs = AlphaQuantize(outputs, self.alpha, self.bits)
tf.summary.histogram('activation', inputs)
tf.summary.histogram('quantized_activation', outputs)
return outputs
def get_config(self):
return {'quantize': self.quantize, 'bits': self.bits}
def compute_output_shape(self, input_shape):
return input_shape
def get_sawb_coefficients(bits):
bits = int(bits)
assert bits <= 4, "Currently only supports bitwidths up to 4."
coefficient_dict = {1: [0., 1.], 2: [3.19, -2.14], 3: [7.40, -6.66], 4: [11.86, -11.68]}
return coefficient_dict[bits]
@tf.custom_gradient
def SAWBQuantize(x, alpha, bits):
# Clip between -alpha and alpha
clipped = tf.clip_by_value(x, -alpha, alpha)
# Rescale to [0, alpha]
scaled = (clipped + alpha) / 2.
# Quantize.
quantized = tf.round(scaled * ((2**bits - 1) / alpha)) * (alpha / (2**bits - 1))
# Rescale to negative range.
output = (2 * quantized) - alpha
def grad_fn(dy):
return [dy, None, None]
return output, grad_fn
class SAWBConv2D(tf.keras.layers.Conv2D):
def __init__(self, *args, bits=2., **kwargs):
super(SAWBConv2D, self).__init__(*args, **kwargs)
self.bits = float(bits)
self.c1, self.c2 = get_sawb_coefficients(bits)
self.alpha = None
def call(self, inputs):
# Compute proper scale for our weights.
alpha = self.c1 * tf.sqrt(tf.reduce_mean(self.kernel**2)) + self.c2 * tf.reduce_mean(tf.abs(self.kernel))
self.alpha = alpha
# Quantize kernel
with tf.name_scope("QW"):
q_kernel = SAWBQuantize(self.kernel, alpha, self.bits)
tf.summary.histogram("weight", self.kernel)
tf.summary.histogram("quantized_weight", q_kernel)
# Invoke convolution
outputs = self._convolution_op(inputs, q_kernel)
if self.use_bias:
if self.data_format == 'channels_first':
outputs = tf.nn.bias_add(
outputs, self.bias, data_format='NCHW')
else:
outputs = tf.nn.bias_add(
outputs, self.bias, data_format='NHWC')
if self.activation is not None:
outputs = self.activation(outputs)
return outputs
def preprocess(image, label):
image = tf.image.resize_image_with_crop_or_pad(image, 40, 40)
image = tf.random_crop(image, [32, 32, 3])
image = tf.image.random_flip_left_right(image)
return image, label
batch_size = 128
(train_data, train_labels), (test_data, test_labels) = tf.keras.datasets.cifar10.load_data()
train_labels = train_labels.astype(np.int32)
test_labels = test_labels.astype(np.int32)
AUTOTUNE = tf.data.experimental.AUTOTUNE
def train_transform(data, label):
data = preprocess_image(data, 32, 32, is_training=True)
return data, label
def test_transform(data, label):
data = preprocess_image(data, 32, 32, is_training=False)
return data, label
def train_input_fn():
ds = tf.data.Dataset.from_tensor_slices((train_data, train_labels))
ds = ds.prefetch(batch_size)
ds = ds.shuffle(10000)
ds = ds.repeat()
ds = ds.map(train_transform, num_parallel_calls=AUTOTUNE)
ds = ds.batch(batch_size)
ds = ds.prefetch(AUTOTUNE)
return ds
def test_input_fn():
ds = tf.data.Dataset.from_tensor_slices((test_data, test_labels))
ds = ds.map(test_transform, num_parallel_calls=AUTOTUNE)
ds = ds.batch(batch_size)
ds = ds.repeat(1)
return ds
cfg = {
'VGG11': [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'VGG13': [64, 64, 'M', 128, 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'VGG16': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'M', 512, 512, 512, 'M', 512, 512, 512, 'M'],
'VGG19': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 256, 'M', 512, 512, 512, 512, 'M', 512, 512, 512, 512, 'M'],
}
class VGG(tf.keras.models.Model):
def __init__(self, name, *args, **kwargs):
super(VGG, self).__init__(*args, **kwargs)
self.reg = tf.keras.regularizers.l2(0.0002)
self.features = self._make_layers(cfg[name])
self.flatten = nn.Flatten()
self.classifier = nn.Dense(10, activation='softmax', kernel_regularizer=self.reg)
def call(self, inputs, training=True):
features = self.features(inputs, training=training)
features = self.flatten(features)
output = self.classifier(features)
return output
def _make_layers(self, cfg):
layers = [nn.Conv2D(cfg[0], kernel_size=3, padding='same', kernel_regularizer=self.reg), nn.BatchNormalization(), nn.Activation('relu')]#PACT(quantize=True)]
for x in cfg[1:]:
if x == 'M':
layers += [nn.MaxPool2D(pool_size=2, strides=2)]
else:
layers += [nn.Conv2D(x, kernel_size=3, padding='same'),
#SAWBConv2D(x, kernel_size=3, padding='same', kernel_regularizer=self.reg),
nn.BatchNormalization(),
#PACT(quantize=True)]
nn.Activation('relu')]
layers += [nn.GlobalAveragePooling2D()]
return tf.keras.models.Sequential(layers)
tf.compat.v1.summary.image
def model_fn(features, labels, mode):
tf.compat.v1.summary.image('images', features, max_outputs=4)
model = VGG('VGG11')
optimizer = tf.compat.v1.train.AdamOptimizer()
loss_fn = tf.keras.losses.SparseCategoricalCrossentropy()
training = (mode == tf.estimator.ModeKeys.TRAIN)
predictions = model(features, training=training)
reg_losses = model.get_losses_for(None) + model.get_losses_for(features)
total_loss = loss_fn(labels, predictions)
if reg_losses:
total_loss += tf.math.add_n(reg_losses)
accuracy = tf.compat.v1.metrics.accuracy(labels=labels,
predictions=tf.math.argmax(predictions, axis=-1),
name='acc_op')
update_ops = model.get_updates_for(None) + model.get_updates_for(features)
with tf.control_dependencies(update_ops):
train_op = optimizer.minimize(
total_loss,
var_list=model.trainable_variables,
global_step=tf.compat.v1.train.get_or_create_global_step())
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions,
loss=total_loss,
train_op=train_op,
eval_metric_ops={'accuracy':accuracy})
experiment_name = 'vgg_baseline_full5'
model_path = os.path.join('/data', 'jwfromm', 'cifar_models', experiment_name)
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.INFO)
sessconfig = tf.compat.v1.ConfigProto()
sessconfig.gpu_options.allow_growth=True
runconfig = tf.estimator.RunConfig(session_config=sessconfig)
classifier = tf.estimator.Estimator(
model_fn=model_fn, model_dir=model_path, config=runconfig)
NUM_STEPS = np.ceil(len(train_data)/batch_size)
EPOCHS = 200
train_spec = tf.estimator.TrainSpec(
input_fn=train_input_fn, max_steps=NUM_STEPS * EPOCHS)
eval_spec = tf.estimator.EvalSpec(input_fn=test_input_fn)
tf.estimator.train_and_evaluate(classifier, train_spec, eval_spec)
```
|
github_jupyter
|
import tensorflow as tf
import numpy as np
import tensorflow.keras.layers as nn
import os
from riptide.utils.preprocessing.cifarnet_preprocessing import preprocess_image
from matplotlib import pyplot as plt
%matplotlib inline
@tf.custom_gradient
def AlphaClip(x, alpha):
output = tf.clip_by_value(x, 0, alpha)
def grad_fn(dy):
x_grad_mask = tf.cast(tf.logical_and(x >= 0, x <= alpha), tf.float32)
alpha_grad_mask = tf.cast(x >= alpha, tf.float32)
alpha_grad = tf.reduce_sum(dy * alpha_grad_mask)
x_grad = dy * x_grad_mask
return [x_grad, alpha_grad]
return output, grad_fn
@tf.custom_gradient
def AlphaQuantize(x, alpha, bits):
output = tf.round(x * ((2**bits - 1) / alpha)) * (alpha / (2**bits - 1))
def grad_fn(dy):
return [dy, None, None]
return output, grad_fn
class PACT(tf.keras.layers.Layer):
def __init__(self, quantize=False, bits=2.):
super(PACT, self).__init__()
self.quantize = quantize
self.bits = bits
def build(self, input_shape):
self.alpha = self.add_variable(
'alpha', shape=[],
initializer=tf.keras.initializers.Constant([10.], dtype=tf.float32),
#regularizer=tf.keras.regularizers.l2(0.01))
regularizer = tf.keras.regularizers.l2(0.0002))
def call(self, inputs):
outputs = AlphaClip(inputs, self.alpha)
if self.quantize:
with tf.name_scope('QA'):
outputs = AlphaQuantize(outputs, self.alpha, self.bits)
tf.summary.histogram('activation', inputs)
tf.summary.histogram('quantized_activation', outputs)
return outputs
def get_config(self):
return {'quantize': self.quantize, 'bits': self.bits}
def compute_output_shape(self, input_shape):
return input_shape
def get_sawb_coefficients(bits):
bits = int(bits)
assert bits <= 4, "Currently only supports bitwidths up to 4."
coefficient_dict = {1: [0., 1.], 2: [3.19, -2.14], 3: [7.40, -6.66], 4: [11.86, -11.68]}
return coefficient_dict[bits]
@tf.custom_gradient
def SAWBQuantize(x, alpha, bits):
# Clip between -alpha and alpha
clipped = tf.clip_by_value(x, -alpha, alpha)
# Rescale to [0, alpha]
scaled = (clipped + alpha) / 2.
# Quantize.
quantized = tf.round(scaled * ((2**bits - 1) / alpha)) * (alpha / (2**bits - 1))
# Rescale to negative range.
output = (2 * quantized) - alpha
def grad_fn(dy):
return [dy, None, None]
return output, grad_fn
class SAWBConv2D(tf.keras.layers.Conv2D):
def __init__(self, *args, bits=2., **kwargs):
super(SAWBConv2D, self).__init__(*args, **kwargs)
self.bits = float(bits)
self.c1, self.c2 = get_sawb_coefficients(bits)
self.alpha = None
def call(self, inputs):
# Compute proper scale for our weights.
alpha = self.c1 * tf.sqrt(tf.reduce_mean(self.kernel**2)) + self.c2 * tf.reduce_mean(tf.abs(self.kernel))
self.alpha = alpha
# Quantize kernel
with tf.name_scope("QW"):
q_kernel = SAWBQuantize(self.kernel, alpha, self.bits)
tf.summary.histogram("weight", self.kernel)
tf.summary.histogram("quantized_weight", q_kernel)
# Invoke convolution
outputs = self._convolution_op(inputs, q_kernel)
if self.use_bias:
if self.data_format == 'channels_first':
outputs = tf.nn.bias_add(
outputs, self.bias, data_format='NCHW')
else:
outputs = tf.nn.bias_add(
outputs, self.bias, data_format='NHWC')
if self.activation is not None:
outputs = self.activation(outputs)
return outputs
def preprocess(image, label):
image = tf.image.resize_image_with_crop_or_pad(image, 40, 40)
image = tf.random_crop(image, [32, 32, 3])
image = tf.image.random_flip_left_right(image)
return image, label
batch_size = 128
(train_data, train_labels), (test_data, test_labels) = tf.keras.datasets.cifar10.load_data()
train_labels = train_labels.astype(np.int32)
test_labels = test_labels.astype(np.int32)
AUTOTUNE = tf.data.experimental.AUTOTUNE
def train_transform(data, label):
data = preprocess_image(data, 32, 32, is_training=True)
return data, label
def test_transform(data, label):
data = preprocess_image(data, 32, 32, is_training=False)
return data, label
def train_input_fn():
ds = tf.data.Dataset.from_tensor_slices((train_data, train_labels))
ds = ds.prefetch(batch_size)
ds = ds.shuffle(10000)
ds = ds.repeat()
ds = ds.map(train_transform, num_parallel_calls=AUTOTUNE)
ds = ds.batch(batch_size)
ds = ds.prefetch(AUTOTUNE)
return ds
def test_input_fn():
ds = tf.data.Dataset.from_tensor_slices((test_data, test_labels))
ds = ds.map(test_transform, num_parallel_calls=AUTOTUNE)
ds = ds.batch(batch_size)
ds = ds.repeat(1)
return ds
cfg = {
'VGG11': [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'VGG13': [64, 64, 'M', 128, 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'VGG16': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'M', 512, 512, 512, 'M', 512, 512, 512, 'M'],
'VGG19': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 256, 'M', 512, 512, 512, 512, 'M', 512, 512, 512, 512, 'M'],
}
class VGG(tf.keras.models.Model):
def __init__(self, name, *args, **kwargs):
super(VGG, self).__init__(*args, **kwargs)
self.reg = tf.keras.regularizers.l2(0.0002)
self.features = self._make_layers(cfg[name])
self.flatten = nn.Flatten()
self.classifier = nn.Dense(10, activation='softmax', kernel_regularizer=self.reg)
def call(self, inputs, training=True):
features = self.features(inputs, training=training)
features = self.flatten(features)
output = self.classifier(features)
return output
def _make_layers(self, cfg):
layers = [nn.Conv2D(cfg[0], kernel_size=3, padding='same', kernel_regularizer=self.reg), nn.BatchNormalization(), nn.Activation('relu')]#PACT(quantize=True)]
for x in cfg[1:]:
if x == 'M':
layers += [nn.MaxPool2D(pool_size=2, strides=2)]
else:
layers += [nn.Conv2D(x, kernel_size=3, padding='same'),
#SAWBConv2D(x, kernel_size=3, padding='same', kernel_regularizer=self.reg),
nn.BatchNormalization(),
#PACT(quantize=True)]
nn.Activation('relu')]
layers += [nn.GlobalAveragePooling2D()]
return tf.keras.models.Sequential(layers)
tf.compat.v1.summary.image
def model_fn(features, labels, mode):
tf.compat.v1.summary.image('images', features, max_outputs=4)
model = VGG('VGG11')
optimizer = tf.compat.v1.train.AdamOptimizer()
loss_fn = tf.keras.losses.SparseCategoricalCrossentropy()
training = (mode == tf.estimator.ModeKeys.TRAIN)
predictions = model(features, training=training)
reg_losses = model.get_losses_for(None) + model.get_losses_for(features)
total_loss = loss_fn(labels, predictions)
if reg_losses:
total_loss += tf.math.add_n(reg_losses)
accuracy = tf.compat.v1.metrics.accuracy(labels=labels,
predictions=tf.math.argmax(predictions, axis=-1),
name='acc_op')
update_ops = model.get_updates_for(None) + model.get_updates_for(features)
with tf.control_dependencies(update_ops):
train_op = optimizer.minimize(
total_loss,
var_list=model.trainable_variables,
global_step=tf.compat.v1.train.get_or_create_global_step())
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions,
loss=total_loss,
train_op=train_op,
eval_metric_ops={'accuracy':accuracy})
experiment_name = 'vgg_baseline_full5'
model_path = os.path.join('/data', 'jwfromm', 'cifar_models', experiment_name)
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.INFO)
sessconfig = tf.compat.v1.ConfigProto()
sessconfig.gpu_options.allow_growth=True
runconfig = tf.estimator.RunConfig(session_config=sessconfig)
classifier = tf.estimator.Estimator(
model_fn=model_fn, model_dir=model_path, config=runconfig)
NUM_STEPS = np.ceil(len(train_data)/batch_size)
EPOCHS = 200
train_spec = tf.estimator.TrainSpec(
input_fn=train_input_fn, max_steps=NUM_STEPS * EPOCHS)
eval_spec = tf.estimator.EvalSpec(input_fn=test_input_fn)
tf.estimator.train_and_evaluate(classifier, train_spec, eval_spec)
| 0.82559 | 0.606557 |
# Sentiment assessment of verified users
```
import datetime
import os
import re
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from IPython.display import clear_output
DATADIRECTORYALL = "../data/sentiment/ALL-pattern/"
DATADIRECTORYRIVM = "../data/sentiment/rivm-pattern/"
DATADIRECTORYTEXT = "../data/text/"
DATADIRECTORYEMOJI = "../data/sentiment-emoji/"
SENTIMENT = "sentiment"
COUNT = "count"
DATA = "data"
LABEL = "label"
HIGHLIGHT = "highlight"
HIGHLIGHTLABEL = "highlightlabel"
FILEPATTERNALL = "2.*z"
IDSTR = "id_str"
VERIFIED = "verified"
def squeal(text=None):
clear_output(wait=True)
if not text is None: print(text)
def getSentimentPerHourVerified(dataDirectory,filePattern=FILEPATTERNALL):
fileList = sorted(os.listdir(dataDirectory))
sentimentPerHour = {}
for inFileName in fileList:
if re.search(filePattern,inFileName):
squeal(inFileName)
try:
df = pd.read_csv(dataDirectory+inFileName,compression="gzip",header=None,index_col=0)
dfText = pd.read_csv(DATADIRECTORYTEXT+inFileName,compression="gzip",index_col=IDSTR)
dictVerified = {i:df.loc[i] for i in dfText.index if dfText.loc[i][VERIFIED] == 1 and i in df.index}
dfVerified = pd.DataFrame.from_dict(dictVerified).T
except: continue
sentiment = sum(dfVerified[1])/len(dfVerified)
hour = inFileName[0:11]
sentimentPerHour[hour] = { SENTIMENT:sentiment, COUNT:len(dfVerified) }
sentimentPerHour = {key:sentimentPerHour[key] for key in sorted(sentimentPerHour.keys())}
return(sentimentPerHour)
def makeSentimentPerDay(sentimentPerHour):
sentimentPerDay = {}
for hour in sentimentPerHour:
day = re.sub("..$","12",hour)
if not day in sentimentPerDay: sentimentPerDay[day] = {SENTIMENT:0,COUNT:0}
sentimentPerDay[day][SENTIMENT] += sentimentPerHour[hour][SENTIMENT]*sentimentPerHour[hour][COUNT]
sentimentPerDay[day][COUNT] += sentimentPerHour[hour][COUNT]
for day in sentimentPerDay:
sentimentPerDay[day][SENTIMENT] /= sentimentPerDay[day][COUNT]
return(sentimentPerDay)
DATEFORMATHOUR = "%Y%m%d-%H"
DATEFORMATMONTH = "%-d/%-m"
DATEFORMATHRSMINS = "%H:%M"
DEFAULTTITLE = "Sentiment scores of Dutch tweets of verified users"
def visualizeSentiment(dataSources,title=DEFAULTTITLE,dateFormat=DATEFORMATMONTH):
font = {"size":14}
matplotlib.rc("font",**font)
fig,ax = plt.subplots(figsize=(12,6))
ax.xaxis.set_major_formatter(mdates.DateFormatter(dateFormat))
for i in range(0,len(dataSources)):
data = dataSources[i][DATA]
label = dataSources[i][LABEL]
lineData= ax.plot_date([datetime.datetime.strptime(key,DATEFORMATHOUR) for key in data],\
[data[key][SENTIMENT] for key in data],xdate=True,fmt="-",label=label)
if HIGHLIGHT in dataSources[i]:
highlight = dataSources[i][HIGHLIGHT]
highlightlabel = dataSources[i][HIGHLIGHTLABEL]
color = lineData[-1].get_color()
ax.plot_date([datetime.datetime.strptime(key,DATEFORMATHOUR) for key in highlight],
[data[key][SENTIMENT] for key in highlight],\
fmt="o",color=color,label=highlightlabel)
plt.title(title)
plt.legend(framealpha=0.2)
plt.show()
return(ax)
highlight = ["20200301-12","20200309-12",\
"20200312-12","20200315-12","20200317-12","20200319-12","20200323-12","20200331-12","20200407-12",\
"20200415-12","20200421-12","20200429-12","20200506-12","20200513-12","20200519-12","20200527-12"] # ,"20200603-12"]
sentimentPerHour = getSentimentPerHourVerified(DATADIRECTORYALL,filePattern="20200[2-5]")
sentimentPerDay = makeSentimentPerDay(sentimentPerHour)
dummy = visualizeSentiment([{DATA:sentimentPerHour,LABEL:"per hour"},
{DATA:sentimentPerDay,LABEL:"per day",\
HIGHLIGHT:highlight,HIGHLIGHTLABEL:"press conference"}],\
title=DEFAULTTITLE)
pd.DataFrame.from_dict(sentimentPerHour).T.to_csv("sentiment-verified.csv",index_label="date")
```
|
github_jupyter
|
import datetime
import os
import re
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from IPython.display import clear_output
DATADIRECTORYALL = "../data/sentiment/ALL-pattern/"
DATADIRECTORYRIVM = "../data/sentiment/rivm-pattern/"
DATADIRECTORYTEXT = "../data/text/"
DATADIRECTORYEMOJI = "../data/sentiment-emoji/"
SENTIMENT = "sentiment"
COUNT = "count"
DATA = "data"
LABEL = "label"
HIGHLIGHT = "highlight"
HIGHLIGHTLABEL = "highlightlabel"
FILEPATTERNALL = "2.*z"
IDSTR = "id_str"
VERIFIED = "verified"
def squeal(text=None):
clear_output(wait=True)
if not text is None: print(text)
def getSentimentPerHourVerified(dataDirectory,filePattern=FILEPATTERNALL):
fileList = sorted(os.listdir(dataDirectory))
sentimentPerHour = {}
for inFileName in fileList:
if re.search(filePattern,inFileName):
squeal(inFileName)
try:
df = pd.read_csv(dataDirectory+inFileName,compression="gzip",header=None,index_col=0)
dfText = pd.read_csv(DATADIRECTORYTEXT+inFileName,compression="gzip",index_col=IDSTR)
dictVerified = {i:df.loc[i] for i in dfText.index if dfText.loc[i][VERIFIED] == 1 and i in df.index}
dfVerified = pd.DataFrame.from_dict(dictVerified).T
except: continue
sentiment = sum(dfVerified[1])/len(dfVerified)
hour = inFileName[0:11]
sentimentPerHour[hour] = { SENTIMENT:sentiment, COUNT:len(dfVerified) }
sentimentPerHour = {key:sentimentPerHour[key] for key in sorted(sentimentPerHour.keys())}
return(sentimentPerHour)
def makeSentimentPerDay(sentimentPerHour):
sentimentPerDay = {}
for hour in sentimentPerHour:
day = re.sub("..$","12",hour)
if not day in sentimentPerDay: sentimentPerDay[day] = {SENTIMENT:0,COUNT:0}
sentimentPerDay[day][SENTIMENT] += sentimentPerHour[hour][SENTIMENT]*sentimentPerHour[hour][COUNT]
sentimentPerDay[day][COUNT] += sentimentPerHour[hour][COUNT]
for day in sentimentPerDay:
sentimentPerDay[day][SENTIMENT] /= sentimentPerDay[day][COUNT]
return(sentimentPerDay)
DATEFORMATHOUR = "%Y%m%d-%H"
DATEFORMATMONTH = "%-d/%-m"
DATEFORMATHRSMINS = "%H:%M"
DEFAULTTITLE = "Sentiment scores of Dutch tweets of verified users"
def visualizeSentiment(dataSources,title=DEFAULTTITLE,dateFormat=DATEFORMATMONTH):
font = {"size":14}
matplotlib.rc("font",**font)
fig,ax = plt.subplots(figsize=(12,6))
ax.xaxis.set_major_formatter(mdates.DateFormatter(dateFormat))
for i in range(0,len(dataSources)):
data = dataSources[i][DATA]
label = dataSources[i][LABEL]
lineData= ax.plot_date([datetime.datetime.strptime(key,DATEFORMATHOUR) for key in data],\
[data[key][SENTIMENT] for key in data],xdate=True,fmt="-",label=label)
if HIGHLIGHT in dataSources[i]:
highlight = dataSources[i][HIGHLIGHT]
highlightlabel = dataSources[i][HIGHLIGHTLABEL]
color = lineData[-1].get_color()
ax.plot_date([datetime.datetime.strptime(key,DATEFORMATHOUR) for key in highlight],
[data[key][SENTIMENT] for key in highlight],\
fmt="o",color=color,label=highlightlabel)
plt.title(title)
plt.legend(framealpha=0.2)
plt.show()
return(ax)
highlight = ["20200301-12","20200309-12",\
"20200312-12","20200315-12","20200317-12","20200319-12","20200323-12","20200331-12","20200407-12",\
"20200415-12","20200421-12","20200429-12","20200506-12","20200513-12","20200519-12","20200527-12"] # ,"20200603-12"]
sentimentPerHour = getSentimentPerHourVerified(DATADIRECTORYALL,filePattern="20200[2-5]")
sentimentPerDay = makeSentimentPerDay(sentimentPerHour)
dummy = visualizeSentiment([{DATA:sentimentPerHour,LABEL:"per hour"},
{DATA:sentimentPerDay,LABEL:"per day",\
HIGHLIGHT:highlight,HIGHLIGHTLABEL:"press conference"}],\
title=DEFAULTTITLE)
pd.DataFrame.from_dict(sentimentPerHour).T.to_csv("sentiment-verified.csv",index_label="date")
| 0.190837 | 0.416263 |
# Conditional Probabilities
### George Tzanetakis, University of Victoria
In this notebook we explore conditional probabilities
Define a helper random variable class based on the scipy discrete random variable functionality providing both numeric and symbolic RVs
```
%matplotlib inline
import matplotlib.pyplot as plt
from scipy import stats
import numpy as np
class Random_Variable:
def __init__(self, name, values, probability_distribution):
self.name = name
self.values = values
self.probability_distribution = probability_distribution
if all(type(item) is np.int64 for item in values):
self.type = 'numeric'
self.rv = stats.rv_discrete(name = name, values = (values, probability_distribution))
elif all(type(item) is str for item in values):
self.type = 'symbolic'
self.rv = stats.rv_discrete(name = name, values = (np.arange(len(values)), probability_distribution))
self.symbolic_values = values
else:
self.type = 'undefined'
def sample(self,size):
if (self.type =='numeric'):
return self.rv.rvs(size=size)
elif (self.type == 'symbolic'):
numeric_samples = self.rv.rvs(size=size)
mapped_samples = [self.values[x] for x in numeric_samples]
return mapped_samples
# samples to generate
num_samples = 100
## Prior probabilities of a song being jazz or country
values = ['country', 'jazz']
probs = [0.7, 0.3]
genre = Random_Variable('genre',values, probs)
# conditional probabilities of a song having lyrics or not given the genre
values = ['no', 'yes']
probs = [0.9, 0.1]
lyrics_if_jazz = Random_Variable('lyrics_if_jazz', values, probs)
values = ['no', 'yes']
probs = [0.2, 0.8]
lyrics_if_country = Random_Variable('lyrics_if_country', values, probs)
# generating proces first sample prior and then based on outcome
# choose which conditional probability distribution to use
random_lyrics_samples = []
for n in range(num_samples):
random_genre_sample = genre.sample(1)[0]
if (random_genre_sample == 'jazz'):
random_lyrics_sample = (lyrics_if_jazz.sample(1)[0], 'jazz')
else:
random_lyrics_sample = (lyrics_if_country.sample(1)[0], 'country')
random_lyrics_samples.append(random_lyrics_sample)
random_lyrics_samples
# Let's now estimate the conditional probabilities using the generated samples
# First only consider jazz
jazz_samples = [x for x in random_lyrics_samples if x[1] == 'jazz']
# estimate the probability of an event specified
# as a predicated over the possible outcomes
def estimate_event_probability(f, samples):
return len(list(filter(f, samples))) / len(samples)
est_no = len([x for x in jazz_samples if x[0] == 'no']) / len(jazz_samples)
est_yes = len([x for x in jazz_samples if x[0] == 'yes']) / len(jazz_samples)
print(est_no, est_yes)
```
|
github_jupyter
|
%matplotlib inline
import matplotlib.pyplot as plt
from scipy import stats
import numpy as np
class Random_Variable:
def __init__(self, name, values, probability_distribution):
self.name = name
self.values = values
self.probability_distribution = probability_distribution
if all(type(item) is np.int64 for item in values):
self.type = 'numeric'
self.rv = stats.rv_discrete(name = name, values = (values, probability_distribution))
elif all(type(item) is str for item in values):
self.type = 'symbolic'
self.rv = stats.rv_discrete(name = name, values = (np.arange(len(values)), probability_distribution))
self.symbolic_values = values
else:
self.type = 'undefined'
def sample(self,size):
if (self.type =='numeric'):
return self.rv.rvs(size=size)
elif (self.type == 'symbolic'):
numeric_samples = self.rv.rvs(size=size)
mapped_samples = [self.values[x] for x in numeric_samples]
return mapped_samples
# samples to generate
num_samples = 100
## Prior probabilities of a song being jazz or country
values = ['country', 'jazz']
probs = [0.7, 0.3]
genre = Random_Variable('genre',values, probs)
# conditional probabilities of a song having lyrics or not given the genre
values = ['no', 'yes']
probs = [0.9, 0.1]
lyrics_if_jazz = Random_Variable('lyrics_if_jazz', values, probs)
values = ['no', 'yes']
probs = [0.2, 0.8]
lyrics_if_country = Random_Variable('lyrics_if_country', values, probs)
# generating proces first sample prior and then based on outcome
# choose which conditional probability distribution to use
random_lyrics_samples = []
for n in range(num_samples):
random_genre_sample = genre.sample(1)[0]
if (random_genre_sample == 'jazz'):
random_lyrics_sample = (lyrics_if_jazz.sample(1)[0], 'jazz')
else:
random_lyrics_sample = (lyrics_if_country.sample(1)[0], 'country')
random_lyrics_samples.append(random_lyrics_sample)
random_lyrics_samples
# Let's now estimate the conditional probabilities using the generated samples
# First only consider jazz
jazz_samples = [x for x in random_lyrics_samples if x[1] == 'jazz']
# estimate the probability of an event specified
# as a predicated over the possible outcomes
def estimate_event_probability(f, samples):
return len(list(filter(f, samples))) / len(samples)
est_no = len([x for x in jazz_samples if x[0] == 'no']) / len(jazz_samples)
est_yes = len([x for x in jazz_samples if x[0] == 'yes']) / len(jazz_samples)
print(est_no, est_yes)
| 0.487307 | 0.888855 |
# Data Scientist Nanodegree
## Supervised Learning
## Project: Finding Donors for *CharityML*
Welcome to the first project of the Data Scientist Nanodegree! In this notebook, some template code has already been provided for you, and it will be your job to implement the additional functionality necessary to successfully complete this project. Sections that begin with **'Implementation'** in the header indicate that the following block of code will require additional functionality which you must provide. Instructions will be provided for each section and the specifics of the implementation are marked in the code block with a `'TODO'` statement. Please be sure to read the instructions carefully!
In addition to implementing code, there will be questions that you must answer which relate to the project and your implementation. Each section where you will answer a question is preceded by a **'Question X'** header. Carefully read each question and provide thorough answers in the following text boxes that begin with **'Answer:'**. Your project submission will be evaluated based on your answers to each of the questions and the implementation you provide.
>**Note:** Please specify WHICH VERSION OF PYTHON you are using when submitting this notebook. Code and Markdown cells can be executed using the **Shift + Enter** keyboard shortcut. In addition, Markdown cells can be edited by typically double-clicking the cell to enter edit mode.
> **I am using Python 3.0**
## Getting Started
In this project, you will employ several supervised algorithms of your choice to accurately model individuals' income using data collected from the 1994 U.S. Census. You will then choose the best candidate algorithm from preliminary results and further optimize this algorithm to best model the data. Your goal with this implementation is to construct a model that accurately predicts whether an individual makes more than $50,000. This sort of task can arise in a non-profit setting, where organizations survive on donations. Understanding an individual's income can help a non-profit better understand how large of a donation to request, or whether or not they should reach out to begin with. While it can be difficult to determine an individual's general income bracket directly from public sources, we can (as we will see) infer this value from other publically available features.
The dataset for this project originates from the [UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/datasets/Census+Income). The datset was donated by Ron Kohavi and Barry Becker, after being published in the article _"Scaling Up the Accuracy of Naive-Bayes Classifiers: A Decision-Tree Hybrid"_. You can find the article by Ron Kohavi [online](https://www.aaai.org/Papers/KDD/1996/KDD96-033.pdf). The data we investigate here consists of small changes to the original dataset, such as removing the `'fnlwgt'` feature and records with missing or ill-formatted entries.
----
## Exploring the Data
Run the code cell below to load necessary Python libraries and load the census data. Note that the last column from this dataset, `'income'`, will be our target label (whether an individual makes more than, or at most, $50,000 annually). All other columns are features about each individual in the census database.
```
# Import libraries necessary for this project
import numpy as np
import pandas as pd
from time import time
from IPython.display import display # Allows the use of display() for DataFrames
# Import supplementary visualization code visuals.py
import visuals as vs
# Pretty display for notebooks
%matplotlib inline
# Load the Census dataset
data = pd.read_csv("census.csv")
# Success - Display the first record
display(data.head(n=1))
```
### Implementation: Data Exploration
A cursory investigation of the dataset will determine how many individuals fit into either group, and will tell us about the percentage of these individuals making more than \$50,000. In the code cell below, you will need to compute the following:
- The total number of records, `'n_records'`
- The number of individuals making more than \$50,000 annually, `'n_greater_50k'`.
- The number of individuals making at most \$50,000 annually, `'n_at_most_50k'`.
- The percentage of individuals making more than \$50,000 annually, `'greater_percent'`.
** HINT: ** You may need to look at the table above to understand how the `'income'` entries are formatted.
```
# TODO: Total number of records
n_records = len(data)
# TODO: Number of records where individual's income is more than $50,000
n_greater_50k = data['income'].value_counts()['>50K']
# TODO: Number of records where individual's income is at most $50,000
n_at_most_50k = data['income'].value_counts()['<=50K']
# TODO: Percentage of individuals whose income is more than $50,000
greater_percent = data['income'].value_counts(normalize = True)['>50K']*100
# Print the results
print("Total number of records: {}".format(n_records))
print("Individuals making more than $50,000: {}".format(n_greater_50k))
print("Individuals making at most $50,000: {}".format(n_at_most_50k))
print("Percentage of individuals making more than $50,000: {}%".format(greater_percent))
```
** Featureset Exploration **
* **age**: continuous.
* **workclass**: Private, Self-emp-not-inc, Self-emp-inc, Federal-gov, Local-gov, State-gov, Without-pay, Never-worked.
* **education**: Bachelors, Some-college, 11th, HS-grad, Prof-school, Assoc-acdm, Assoc-voc, 9th, 7th-8th, 12th, Masters, 1st-4th, 10th, Doctorate, 5th-6th, Preschool.
* **education-num**: continuous.
* **marital-status**: Married-civ-spouse, Divorced, Never-married, Separated, Widowed, Married-spouse-absent, Married-AF-spouse.
* **occupation**: Tech-support, Craft-repair, Other-service, Sales, Exec-managerial, Prof-specialty, Handlers-cleaners, Machine-op-inspct, Adm-clerical, Farming-fishing, Transport-moving, Priv-house-serv, Protective-serv, Armed-Forces.
* **relationship**: Wife, Own-child, Husband, Not-in-family, Other-relative, Unmarried.
* **race**: Black, White, Asian-Pac-Islander, Amer-Indian-Eskimo, Other.
* **sex**: Female, Male.
* **capital-gain**: continuous.
* **capital-loss**: continuous.
* **hours-per-week**: continuous.
* **native-country**: United-States, Cambodia, England, Puerto-Rico, Canada, Germany, Outlying-US(Guam-USVI-etc), India, Japan, Greece, South, China, Cuba, Iran, Honduras, Philippines, Italy, Poland, Jamaica, Vietnam, Mexico, Portugal, Ireland, France, Dominican-Republic, Laos, Ecuador, Taiwan, Haiti, Columbia, Hungary, Guatemala, Nicaragua, Scotland, Thailand, Yugoslavia, El-Salvador, Trinadad&Tobago, Peru, Hong, Holand-Netherlands.
----
## Preparing the Data
Before data can be used as input for machine learning algorithms, it often must be cleaned, formatted, and restructured — this is typically known as **preprocessing**. Fortunately, for this dataset, there are no invalid or missing entries we must deal with, however, there are some qualities about certain features that must be adjusted. This preprocessing can help tremendously with the outcome and predictive power of nearly all learning algorithms.
### Transforming Skewed Continuous Features
A dataset may sometimes contain at least one feature whose values tend to lie near a single number, but will also have a non-trivial number of vastly larger or smaller values than that single number. Algorithms can be sensitive to such distributions of values and can underperform if the range is not properly normalized. With the census dataset two features fit this description: '`capital-gain'` and `'capital-loss'`.
Run the code cell below to plot a histogram of these two features. Note the range of the values present and how they are distributed.
```
# Split the data into features and target label
income_raw = data['income']
features_raw = data.drop('income', axis = 1)
# Visualize skewed continuous features of original data
vs.distribution(data)
```
For highly-skewed feature distributions such as `'capital-gain'` and `'capital-loss'`, it is common practice to apply a <a href="https://en.wikipedia.org/wiki/Data_transformation_(statistics)">logarithmic transformation</a> on the data so that the very large and very small values do not negatively affect the performance of a learning algorithm. Using a logarithmic transformation significantly reduces the range of values caused by outliers. Care must be taken when applying this transformation however: The logarithm of `0` is undefined, so we must translate the values by a small amount above `0` to apply the the logarithm successfully.
Run the code cell below to perform a transformation on the data and visualize the results. Again, note the range of values and how they are distributed.
```
# Log-transform the skewed features
skewed = ['capital-gain', 'capital-loss']
features_log_transformed = pd.DataFrame(data = features_raw)
features_log_transformed[skewed] = features_raw[skewed].apply(lambda x: np.log(x + 1))
# Visualize the new log distributions
vs.distribution(features_log_transformed, transformed = True)
```
### Normalizing Numerical Features
In addition to performing transformations on features that are highly skewed, it is often good practice to perform some type of scaling on numerical features. Applying a scaling to the data does not change the shape of each feature's distribution (such as `'capital-gain'` or `'capital-loss'` above); however, normalization ensures that each feature is treated equally when applying supervised learners. Note that once scaling is applied, observing the data in its raw form will no longer have the same original meaning, as exampled below.
Run the code cell below to normalize each numerical feature. We will use [`sklearn.preprocessing.MinMaxScaler`](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html) for this.
```
# Import sklearn.preprocessing.StandardScaler
from sklearn.preprocessing import MinMaxScaler
# Initialize a scaler, then apply it to the features
scaler = MinMaxScaler() # default=(0, 1)
numerical = ['age', 'education-num', 'capital-gain', 'capital-loss', 'hours-per-week']
features_log_minmax_transform = pd.DataFrame(data = features_log_transformed)
features_log_minmax_transform[numerical] = scaler.fit_transform(features_log_transformed[numerical])
# Show an example of a record with scaling applied
display(features_log_minmax_transform.head(n = 5))
```
### Implementation: Data Preprocessing
From the table in **Exploring the Data** above, we can see there are several features for each record that are non-numeric. Typically, learning algorithms expect input to be numeric, which requires that non-numeric features (called *categorical variables*) be converted. One popular way to convert categorical variables is by using the **one-hot encoding** scheme. One-hot encoding creates a _"dummy"_ variable for each possible category of each non-numeric feature. For example, assume `someFeature` has three possible entries: `A`, `B`, or `C`. We then encode this feature into `someFeature_A`, `someFeature_B` and `someFeature_C`.
| | someFeature | | someFeature_A | someFeature_B | someFeature_C |
| :-: | :-: | | :-: | :-: | :-: |
| 0 | B | | 0 | 1 | 0 |
| 1 | C | ----> one-hot encode ----> | 0 | 0 | 1 |
| 2 | A | | 1 | 0 | 0 |
Additionally, as with the non-numeric features, we need to convert the non-numeric target label, `'income'` to numerical values for the learning algorithm to work. Since there are only two possible categories for this label ("<=50K" and ">50K"), we can avoid using one-hot encoding and simply encode these two categories as `0` and `1`, respectively. In code cell below, you will need to implement the following:
- Use [`pandas.get_dummies()`](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.get_dummies.html?highlight=get_dummies#pandas.get_dummies) to perform one-hot encoding on the `'features_log_minmax_transform'` data.
- Convert the target label `'income_raw'` to numerical entries.
- Set records with "<=50K" to `0` and records with ">50K" to `1`.
```
# TODO: One-hot encode the 'features_log_minmax_transform' data using pandas.get_dummies()
features_final = pd.get_dummies(features_log_minmax_transform)
# TODO: Encode the 'income_raw' data to numerical values
income = income_raw.replace({'<=50K': 0, '>50K': 1})
# Print the number of features after one-hot encoding
encoded = list(features_final.columns)
print("{} total features after one-hot encoding.".format(len(encoded)))
# Uncomment the following line to see the encoded feature names
print (encoded)
```
### Shuffle and Split Data
Now all _categorical variables_ have been converted into numerical features, and all numerical features have been normalized. As always, we will now split the data (both features and their labels) into training and test sets. 80% of the data will be used for training and 20% for testing.
Run the code cell below to perform this split.
```
# Import train_test_split
from sklearn.model_selection import train_test_split
# Split the 'features' and 'income' data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(features_final,
income,
test_size = 0.2,
random_state = 0)
# Show the results of the split
print("Training set has {} samples.".format(X_train.shape[0]))
print("Testing set has {} samples.".format(X_test.shape[0]))
```
----
## Evaluating Model Performance
In this section, we will investigate four different algorithms, and determine which is best at modeling the data. Three of these algorithms will be supervised learners of your choice, and the fourth algorithm is known as a *naive predictor*.
### Metrics and the Naive Predictor
*CharityML*, equipped with their research, knows individuals that make more than \$50,000 are most likely to donate to their charity. Because of this, *CharityML* is particularly interested in predicting who makes more than \$50,000 accurately. It would seem that using **accuracy** as a metric for evaluating a particular model's performace would be appropriate. Additionally, identifying someone that *does not* make more than \$50,000 as someone who does would be detrimental to *CharityML*, since they are looking to find individuals willing to donate. Therefore, a model's ability to precisely predict those that make more than \$50,000 is *more important* than the model's ability to **recall** those individuals. We can use **F-beta score** as a metric that considers both precision and recall:
$$ F_{\beta} = (1 + \beta^2) \cdot \frac{precision \cdot recall}{\left( \beta^2 \cdot precision \right) + recall} $$
In particular, when $\beta = 0.5$, more emphasis is placed on precision. This is called the **F$_{0.5}$ score** (or F-score for simplicity).
Looking at the distribution of classes (those who make at most $\$ 50,000$, and those who make more), it's clear most individuals do not make more than $\$50,000$. This can greatly affect **accuracy**, since we could simply say *"this person does not make more than \$50,000"* and generally be right, without ever looking at the data! Making such a statement would be called **naive**, since we have not considered any information to substantiate the claim. It is always important to consider the *naive prediction* for your data, to help establish a benchmark for whether a model is performing well. That been said, using that prediction would be pointless: If we predicted all people made less than \$50,000, *CharityML* would identify no one as donors.
#### Note: Recap of accuracy, precision, recall
** Accuracy ** measures how often the classifier makes the correct prediction. It’s the ratio of the number of correct predictions to the total number of predictions (the number of test data points).
** Precision ** tells us what proportion of messages we classified as spam, actually were spam.
It is a ratio of true positives(words classified as spam, and which are actually spam) to all positives(all words classified as spam, irrespective of whether that was the correct classificatio), in other words it is the ratio of
`[True Positives/(True Positives + False Positives)]`
** Recall(sensitivity)** tells us what proportion of messages that actually were spam were classified by us as spam.
It is a ratio of true positives(words classified as spam, and which are actually spam) to all the words that were actually spam, in other words it is the ratio of
`[True Positives/(True Positives + False Negatives)]`
For classification problems that are skewed in their classification distributions like in our case, for example if we had a 100 text messages and only 2 were spam and the rest 98 weren't, accuracy by itself is not a very good metric. We could classify 90 messages as not spam(including the 2 that were spam but we classify them as not spam, hence they would be false negatives) and 10 as spam(all 10 false positives) and still get a reasonably good accuracy score. For such cases, precision and recall come in very handy. These two metrics can be combined to get the F1 score, which is weighted average(harmonic mean) of the precision and recall scores. This score can range from 0 to 1, with 1 being the best possible F1 score(we take the harmonic mean as we are dealing with ratios).
### Question 1 - Naive Predictor Performace
* If we chose a model that always predicted an individual made more than $50,000, what would that model's accuracy and F-score be on this dataset? You must use the code cell below and assign your results to `'accuracy'` and `'fscore'` to be used later.
** Please note ** that the the purpose of generating a naive predictor is simply to show what a base model without any intelligence would look like. In the real world, ideally your base model would be either the results of a previous model or could be based on a research paper upon which you are looking to improve. When there is no benchmark model set, getting a result better than random choice is a place you could start from.
** HINT: **
* When we have a model that always predicts '1' (i.e. the individual makes more than 50k) then our model will have no True Negatives(TN) or False Negatives(FN) as we are not making any negative('0' value) predictions. Therefore our Accuracy in this case becomes the same as our Precision(True Positives/(True Positives + False Positives)) as every prediction that we have made with value '1' that should have '0' becomes a False Positive; therefore our denominator in this case is the total number of records we have in total.
* Our Recall score(True Positives/(True Positives + False Negatives)) in this setting becomes 1 as we have no False Negatives.
```
'''
TP = np.sum(income) # Counting the ones as this is the naive case. Note that 'income' is the 'income_raw' data
encoded to numerical values done in the data preprocessing step.
FP = income.count() - TP # Specific to the naive case
TN = 0 # No predicted negatives in the naive case
FN = 0 # No predicted negatives in the naive case
'''
# TODO: Calculate accuracy, precision and recall
accuracy = (np.sum(income) + 0)/income.count()
recall = np.sum(income)/(np.sum(income) + 0)
precision = np.sum(income)/income.count()
# TODO: Calculate F-score using the formula above for beta = 0.5 and correct values for precision and recall.
fscore = (1+ 0.5**2) * recall * precision /(0.5**2 * precision + recall)
# Print the results
print("Naive Predictor: [Accuracy score: {:.4f}, F-score: {:.4f}]".format(accuracy, fscore))
```
### Supervised Learning Models
**The following are some of the supervised learning models that are currently available in** [`scikit-learn`](http://scikit-learn.org/stable/supervised_learning.html) **that you may choose from:**
- Gaussian Naive Bayes (GaussianNB)
- Decision Trees
- Ensemble Methods (Bagging, AdaBoost, Random Forest, Gradient Boosting)
- K-Nearest Neighbors (KNeighbors)
- Stochastic Gradient Descent Classifier (SGDC)
- Support Vector Machines (SVM)
- Logistic Regression
### Question 2 - Model Application
List three of the supervised learning models above that are appropriate for this problem that you will test on the census data. For each model chosen
- Describe one real-world application in industry where the model can be applied.
- What are the strengths of the model; when does it perform well?
- What are the weaknesses of the model; when does it perform poorly?
- What makes this model a good candidate for the problem, given what you know about the data?
** HINT: **
Structure your answer in the same format as above^, with 4 parts for each of the three models you pick. Please include references with your answer.
**Answer: **
1. Random Forest
- Real-World City Data for Urban Planning in a Visual Semantic Decision Support System. [https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6567884/]
- improve the predictive accuracy and control over-fitting; They provide a reliable feature importance estimate. [https://www.oreilly.com/library/view/hands-on-machine-learning/9781789346411/e17de38e-421e-4577-afc3-efdd4e02a468.xhtml]
- An ensemble model is inherently less interpretable than an individual decision tree. [https://www.oreilly.com/library/view/hands-on-machine-learning/9781789346411/e17de38e-421e-4577-afc3-efdd4e02a468.xhtml]
- The accuracy and the the prediction power on new data is important in this problem.
2. Support Vector Machiens (SVM)
- Face detection – SVMc classify parts of the image as a face and non-face and create a square boundary around the face. (resource: [https://data-flair.training/blogs/applications-of-svm/])
- Effective in high dimensional spaces; Uses a subset of training points in the decision function (called support vectors), so it is also memory efficient. [https://scikit-learn.org/stable/modules/svm.html]
- If the number of features is much greater than the number of samples, avoid over-fitting in choosing Kernel functions and regularization term is crucial. [https://scikit-learn.org/stable/modules/svm.html]
- The dimension of the feature space is very hight.
3. AdaBoost
- Admission of students to a university where either they will be admitted or denied. [https://www.educba.com/adaboost-algorithm/]
- It is fast and simple. It has the flexibility to be combined with any machine learning algorithm. [https://www.educba.com/adaboost-algorithm/]
- It is from empirical evidence and particularly vulnerable to uniform noise. [https://www.educba.com/adaboost-algorithm/]
- It can be combined with decision trees in this problem.
### Implementation - Creating a Training and Predicting Pipeline
To properly evaluate the performance of each model you've chosen, it's important that you create a training and predicting pipeline that allows you to quickly and effectively train models using various sizes of training data and perform predictions on the testing data. Your implementation here will be used in the following section.
In the code block below, you will need to implement the following:
- Import `fbeta_score` and `accuracy_score` from [`sklearn.metrics`](http://scikit-learn.org/stable/modules/classes.html#sklearn-metrics-metrics).
- Fit the learner to the sampled training data and record the training time.
- Perform predictions on the test data `X_test`, and also on the first 300 training points `X_train[:300]`.
- Record the total prediction time.
- Calculate the accuracy score for both the training subset and testing set.
- Calculate the F-score for both the training subset and testing set.
- Make sure that you set the `beta` parameter!
```
# TODO: Import two metrics from sklearn - fbeta_score and accuracy_score
from sklearn.metrics import fbeta_score, accuracy_score
def train_predict(learner, sample_size, X_train, y_train, X_test, y_test):
'''
inputs:
- learner: the learning algorithm to be trained and predicted on
- sample_size: the size of samples (number) to be drawn from training set
- X_train: features training set
- y_train: income training set
- X_test: features testing set
- y_test: income testing set
'''
results = {}
# TODO: Fit the learner to the training data using slicing with 'sample_size' using .fit(training_features[:], training_labels[:])
start = time() # Get start time
learner = learner.fit(X_train[:sample_size], y_train[:sample_size])
end = time() # Get end time
# TODO: Calculate the training time
results['train_time'] = end - start
# TODO: Get the predictions on the test set(X_test),
# then get predictions on the first 300 training samples(X_train) using .predict()
start = time() # Get start time
predictions_test = learner.predict(X_test)
predictions_train = learner.predict(X_train[:300])
end = time() # Get end time
# TODO: Calculate the total prediction time
results['pred_time'] = end - start
# TODO: Compute accuracy on the first 300 training samples which is y_train[:300]
results['acc_train'] = accuracy_score(y_train[:300], predictions_train)
# TODO: Compute accuracy on test set using accuracy_score()
results['acc_test'] = accuracy_score(y_test, predictions_test)
# TODO: Compute F-score on the the first 300 training samples using fbeta_score()
results['f_train'] = fbeta_score(y_train[:300], predictions_train, beta = 0.5)
# TODO: Compute F-score on the test set which is y_test
results['f_test'] = fbeta_score(y_test, predictions_test, beta = 0.5)
# Success
print("{} trained on {} samples.".format(learner.__class__.__name__, sample_size))
# Return the results
return results
```
### Implementation: Initial Model Evaluation
In the code cell, you will need to implement the following:
- Import the three supervised learning models you've discussed in the previous section.
- Initialize the three models and store them in `'clf_A'`, `'clf_B'`, and `'clf_C'`.
- Use a `'random_state'` for each model you use, if provided.
- **Note:** Use the default settings for each model — you will tune one specific model in a later section.
- Calculate the number of records equal to 1%, 10%, and 100% of the training data.
- Store those values in `'samples_1'`, `'samples_10'`, and `'samples_100'` respectively.
**Note:** Depending on which algorithms you chose, the following implementation may take some time to run!
```
# TODO: Import the three supervised learning models from sklearn
from sklearn.svm import SVC
from sklearn.ensemble import AdaBoostClassifier, RandomForestClassifier
# TODO: Initialize the three models
clf_A = RandomForestClassifier(random_state = 0)
clf_B = SVC(random_state = 1)
clf_C = AdaBoostClassifier(random_state = 2)
# TODO: Calculate the number of samples for 1%, 10%, and 100% of the training data
# HINT: samples_100 is the entire training set i.e. len(y_train)
# HINT: samples_10 is 10% of samples_100 (ensure to set the count of the values to be `int` and not `float`)
# HINT: samples_1 is 1% of samples_100 (ensure to set the count of the values to be `int` and not `float`)
samples_100 = len(y_train)
samples_10 = int(0.1*samples_100)
samples_1 = int(0.01*samples_100)
# Collect results on the learners
results = {}
for clf in [clf_A, clf_B, clf_C]:
clf_name = clf.__class__.__name__
results[clf_name] = {}
for i, samples in enumerate([samples_1, samples_10, samples_100]):
results[clf_name][i] = \
train_predict(clf, samples, X_train, y_train, X_test, y_test)
# Run metrics visualization for the three supervised learning models chosen
vs.evaluate(results, accuracy, fscore)
```
----
## Improving Results
In this final section, you will choose from the three supervised learning models the *best* model to use on the student data. You will then perform a grid search optimization for the model over the entire training set (`X_train` and `y_train`) by tuning at least one parameter to improve upon the untuned model's F-score.
### Question 3 - Choosing the Best Model
* Based on the evaluation you performed earlier, in one to two paragraphs, explain to *CharityML* which of the three models you believe to be most appropriate for the task of identifying individuals that make more than \$50,000.
** HINT: **
Look at the graph at the bottom left from the cell above(the visualization created by `vs.evaluate(results, accuracy, fscore)`) and check the F score for the testing set when 100% of the training set is used. Which model has the highest score? Your answer should include discussion of the:
* metrics - F score on the testing when 100% of the training data is used,
* prediction/training time
* the algorithm's suitability for the data.
**Answer: **
The AdaBoostClassifier performs the best among the chosen 3 machine learning models because of the following reasons.
**First**, F-score of AdaBoostClassifier is the highest on the testing when 100% of the training data is used.
**Second**, the prediction an trainning time are shorter than the other two models in all fitting with different sample sizes.
**Third**, AdaBoostClassifier is an ensemble model combined with decision tree classifier as the weak learners. It is good for improving the accuracy and controling the overfitting shown in the RandomForestClassifier.
### Question 4 - Describing the Model in Layman's Terms
* In one to two paragraphs, explain to *CharityML*, in layman's terms, how the final model chosen is supposed to work. Be sure that you are describing the major qualities of the model, such as how the model is trained and how the model makes a prediction. Avoid using advanced mathematical jargon, such as describing equations.
** HINT: **
When explaining your model, if using external resources please include all citations.
**Answer: **
AdaBoostClassifier is chosen to be the final model.
First of all, AdaBoostClassifier is an ensemble model.
It can be seen as a **genius learner** who has knowledge or expertise of several **weak learners**.
These weak leareners will learn the knowledge in the training data sequentially.
The first learner investigates the training data and make prediction on the income of the testing data.
The second learner will be more careful on the misclassified samples by the first learner.
The third learner will investigate the data and be more careful on the misclassifed sampled by the second learner.
Repeat this process until the last weak learner finish the learning.
Then, the genius learner will combine the knowlegde gained by all the weak learners and make prediction on the testing data.
This model achieves high accuracy and F score. In addition, it runs very fast.
### Implementation: Model Tuning
Fine tune the chosen model. Use grid search (`GridSearchCV`) with at least one important parameter tuned with at least 3 different values. You will need to use the entire training set for this. In the code cell below, you will need to implement the following:
- Import [`sklearn.grid_search.GridSearchCV`](http://scikit-learn.org/0.17/modules/generated/sklearn.grid_search.GridSearchCV.html) and [`sklearn.metrics.make_scorer`](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.make_scorer.html).
- Initialize the classifier you've chosen and store it in `clf`.
- Set a `random_state` if one is available to the same state you set before.
- Create a dictionary of parameters you wish to tune for the chosen model.
- Example: `parameters = {'parameter' : [list of values]}`.
- **Note:** Avoid tuning the `max_features` parameter of your learner if that parameter is available!
- Use `make_scorer` to create an `fbeta_score` scoring object (with $\beta = 0.5$).
- Perform grid search on the classifier `clf` using the `'scorer'`, and store it in `grid_obj`.
- Fit the grid search object to the training data (`X_train`, `y_train`), and store it in `grid_fit`.
**Note:** Depending on the algorithm chosen and the parameter list, the following implementation may take some time to run!
```
# TODO: Import 'GridSearchCV', 'make_scorer', and any other necessary libraries
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer
# TODO: Initialize the classifier
clf = AdaBoostClassifier(random_state = 3)
# TODO: Create the parameters list you wish to tune, using a dictionary if needed.
# HINT: parameters = {'parameter_1': [value1, value2], 'parameter_2': [value1, value2]}
parameters = {'n_estimators': list([20,50,100]), 'learning_rate': [0.1, 0.5, 1, 2]}
# TODO: Make an fbeta_score scoring object using make_scorer()
scorer = make_scorer(fbeta_score, beta = 0.5)
# TODO: Perform grid search on the classifier using 'scorer' as the scoring method using GridSearchCV()
grid_obj = GridSearchCV(estimator = clf, scoring = scorer, param_grid = parameters)
# TODO: Fit the grid search object to the training data and find the optimal parameters using fit()
grid_fit = grid_obj.fit(X_train, y_train)
# Get the estimator
best_clf = grid_fit.best_estimator_
# Make predictions using the unoptimized and model
predictions = (clf.fit(X_train, y_train)).predict(X_test)
best_predictions = best_clf.predict(X_test)
# Report the before-and-afterscores
print("Unoptimized model\n------")
print("Accuracy score on testing data: {:.4f}".format(accuracy_score(y_test, predictions)))
print("F-score on testing data: {:.4f}".format(fbeta_score(y_test, predictions, beta = 0.5)))
print("\nOptimized Model\n------")
print("Final accuracy score on the testing data: {:.4f}".format(accuracy_score(y_test, best_predictions)))
print("Final F-score on the testing data: {:.4f}".format(fbeta_score(y_test, best_predictions, beta = 0.5)))
print(best_clf)
```
### Question 5 - Final Model Evaluation
* What is your optimized model's accuracy and F-score on the testing data?
* Are these scores better or worse than the unoptimized model?
* How do the results from your optimized model compare to the naive predictor benchmarks you found earlier in **Question 1**?_
**Note:** Fill in the table below with your results, and then provide discussion in the **Answer** box.
#### Results:
| Metric | Unoptimized Model | Optimized Model |
| :------------: | :---------------: | :-------------: |
| Accuracy Score | 0.8576 | 0.8606 |
| F-score | 0.7246 | 0.7316 |
**Answer: **
- The optimized model's accuracy and F-score on the testing data are 0.8606 and 0.7216, respectively.
- Yes, these scores are better than the unoptimzed model.
- It outperforms the naive predictor very much. Recall that in Question 1, the corresponding scores for Naive Prediction are 0.2478 and 0.2917 respectively.
----
## Feature Importance
An important task when performing supervised learning on a dataset like the census data we study here is determining which features provide the most predictive power. By focusing on the relationship between only a few crucial features and the target label we simplify our understanding of the phenomenon, which is most always a useful thing to do. In the case of this project, that means we wish to identify a small number of features that most strongly predict whether an individual makes at most or more than \$50,000.
Choose a scikit-learn classifier (e.g., adaboost, random forests) that has a `feature_importance_` attribute, which is a function that ranks the importance of features according to the chosen classifier. In the next python cell fit this classifier to training set and use this attribute to determine the top 5 most important features for the census dataset.
### Question 6 - Feature Relevance Observation
When **Exploring the Data**, it was shown there are thirteen available features for each individual on record in the census data. Of these thirteen records, which five features do you believe to be most important for prediction, and in what order would you rank them and why?
**Answer:**
- Five features: occupation > hours-per-week > capital-loss > capital-gain > education_level
- The income of each person has 2 main resources including salary paid and investment in other capital.
- The amount of salary depends on the type of **occupation**, **hours-per-week**.
- The income from investment is indicated in the column **capital-loss* and **capital-gain**.
- In addition, **education_level** may also affect the income.
### Implementation - Extracting Feature Importance
Choose a `scikit-learn` supervised learning algorithm that has a `feature_importance_` attribute availble for it. This attribute is a function that ranks the importance of each feature when making predictions based on the chosen algorithm.
In the code cell below, you will need to implement the following:
- Import a supervised learning model from sklearn if it is different from the three used earlier.
- Train the supervised model on the entire training set.
- Extract the feature importances using `'.feature_importances_'`.
```
# TODO: Import a supervised learning model that has 'feature_importances_'
from sklearn.ensemble import AdaBoostClassifier
# TODO: Train the supervised model on the training set using .fit(X_train, y_train)
model = AdaBoostClassifier(n_estimators = 100, learning_rate = 1.0).fit(X_train, y_train)
# TODO: Extract the feature importances using .feature_importances_
importances = model.feature_importances_
# Plot
vs.feature_plot(importances, X_train, y_train)
```
### Question 7 - Extracting Feature Importance
Observe the visualization created above which displays the five most relevant features for predicting if an individual makes at most or above \$50,000.
* How do these five features compare to the five features you discussed in **Question 6**?
* If you were close to the same answer, how does this visualization confirm your thoughts?
* If you were not close, why do you think these features are more relevant?
**Answer:**
- The five features found are **capital-gain**, **capital-loss**, **age**, **hours-per-week** and **education-num**. Three features of them are the same as my guess in **Question 6**.
- In the figure above, y-axis shows the weight of feature importance of the five most relevant features in x-axis. The declining feature weight confirms their order.
### Feature Selection
How does a model perform if we only use a subset of all the available features in the data? With less features required to train, the expectation is that training and prediction time is much lower — at the cost of performance metrics. From the visualization above, we see that the top five most important features contribute more than half of the importance of **all** features present in the data. This hints that we can attempt to *reduce the feature space* and simplify the information required for the model to learn. The code cell below will use the same optimized model you found earlier, and train it on the same training set *with only the top five important features*.
```
# Import functionality for cloning a model
from sklearn.base import clone
# Reduce the feature space
X_train_reduced = X_train[X_train.columns.values[(np.argsort(importances)[::-1])[:5]]]
X_test_reduced = X_test[X_test.columns.values[(np.argsort(importances)[::-1])[:5]]]
# Train on the "best" model found from grid search earlier
clf = (clone(best_clf)).fit(X_train_reduced, y_train)
# Make new predictions
reduced_predictions = clf.predict(X_test_reduced)
# Report scores from the final model using both versions of data
print("Final Model trained on full data\n------")
print("Accuracy on testing data: {:.4f}".format(accuracy_score(y_test, best_predictions)))
print("F-score on testing data: {:.4f}".format(fbeta_score(y_test, best_predictions, beta = 0.5)))
print("\nFinal Model trained on reduced data\n------")
print("Accuracy on testing data: {:.4f}".format(accuracy_score(y_test, reduced_predictions)))
print("F-score on testing data: {:.4f}".format(fbeta_score(y_test, reduced_predictions, beta = 0.5)))
```
### Question 8 - Effects of Feature Selection
* How does the final model's F-score and accuracy score on the reduced data using only five features compare to those same scores when all features are used?
* If training time was a factor, would you consider using the reduced data as your training set?
```
all_result = train_predict(clone(best_clf), samples_100, X_train, y_train, X_test, y_test)
reduced_result = train_predict(clone(best_clf), samples_100, X_train_reduced, y_train, X_test_reduced, y_test)
print('Train time for model with reduced features and all features are {} and {} respectively'.format( reduced_result['train_time'], all_result['train_time']))
```
**Answer:**
- The final model with reduced data has lower *Accuracy* and *F-score* compared to the model with all features included.
- Yes. The train time for the final model with reduced features and all features has big difference. They are 1.24 and 4.85 respectively.
> **Note**: Once you have completed all of the code implementations and successfully answered each question above, you may finalize your work by exporting the iPython Notebook as an HTML document. You can do this by using the menu above and navigating to
**File -> Download as -> HTML (.html)**. Include the finished document along with this notebook as your submission.
|
github_jupyter
|
# Import libraries necessary for this project
import numpy as np
import pandas as pd
from time import time
from IPython.display import display # Allows the use of display() for DataFrames
# Import supplementary visualization code visuals.py
import visuals as vs
# Pretty display for notebooks
%matplotlib inline
# Load the Census dataset
data = pd.read_csv("census.csv")
# Success - Display the first record
display(data.head(n=1))
# TODO: Total number of records
n_records = len(data)
# TODO: Number of records where individual's income is more than $50,000
n_greater_50k = data['income'].value_counts()['>50K']
# TODO: Number of records where individual's income is at most $50,000
n_at_most_50k = data['income'].value_counts()['<=50K']
# TODO: Percentage of individuals whose income is more than $50,000
greater_percent = data['income'].value_counts(normalize = True)['>50K']*100
# Print the results
print("Total number of records: {}".format(n_records))
print("Individuals making more than $50,000: {}".format(n_greater_50k))
print("Individuals making at most $50,000: {}".format(n_at_most_50k))
print("Percentage of individuals making more than $50,000: {}%".format(greater_percent))
# Split the data into features and target label
income_raw = data['income']
features_raw = data.drop('income', axis = 1)
# Visualize skewed continuous features of original data
vs.distribution(data)
# Log-transform the skewed features
skewed = ['capital-gain', 'capital-loss']
features_log_transformed = pd.DataFrame(data = features_raw)
features_log_transformed[skewed] = features_raw[skewed].apply(lambda x: np.log(x + 1))
# Visualize the new log distributions
vs.distribution(features_log_transformed, transformed = True)
# Import sklearn.preprocessing.StandardScaler
from sklearn.preprocessing import MinMaxScaler
# Initialize a scaler, then apply it to the features
scaler = MinMaxScaler() # default=(0, 1)
numerical = ['age', 'education-num', 'capital-gain', 'capital-loss', 'hours-per-week']
features_log_minmax_transform = pd.DataFrame(data = features_log_transformed)
features_log_minmax_transform[numerical] = scaler.fit_transform(features_log_transformed[numerical])
# Show an example of a record with scaling applied
display(features_log_minmax_transform.head(n = 5))
# TODO: One-hot encode the 'features_log_minmax_transform' data using pandas.get_dummies()
features_final = pd.get_dummies(features_log_minmax_transform)
# TODO: Encode the 'income_raw' data to numerical values
income = income_raw.replace({'<=50K': 0, '>50K': 1})
# Print the number of features after one-hot encoding
encoded = list(features_final.columns)
print("{} total features after one-hot encoding.".format(len(encoded)))
# Uncomment the following line to see the encoded feature names
print (encoded)
# Import train_test_split
from sklearn.model_selection import train_test_split
# Split the 'features' and 'income' data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(features_final,
income,
test_size = 0.2,
random_state = 0)
# Show the results of the split
print("Training set has {} samples.".format(X_train.shape[0]))
print("Testing set has {} samples.".format(X_test.shape[0]))
'''
TP = np.sum(income) # Counting the ones as this is the naive case. Note that 'income' is the 'income_raw' data
encoded to numerical values done in the data preprocessing step.
FP = income.count() - TP # Specific to the naive case
TN = 0 # No predicted negatives in the naive case
FN = 0 # No predicted negatives in the naive case
'''
# TODO: Calculate accuracy, precision and recall
accuracy = (np.sum(income) + 0)/income.count()
recall = np.sum(income)/(np.sum(income) + 0)
precision = np.sum(income)/income.count()
# TODO: Calculate F-score using the formula above for beta = 0.5 and correct values for precision and recall.
fscore = (1+ 0.5**2) * recall * precision /(0.5**2 * precision + recall)
# Print the results
print("Naive Predictor: [Accuracy score: {:.4f}, F-score: {:.4f}]".format(accuracy, fscore))
# TODO: Import two metrics from sklearn - fbeta_score and accuracy_score
from sklearn.metrics import fbeta_score, accuracy_score
def train_predict(learner, sample_size, X_train, y_train, X_test, y_test):
'''
inputs:
- learner: the learning algorithm to be trained and predicted on
- sample_size: the size of samples (number) to be drawn from training set
- X_train: features training set
- y_train: income training set
- X_test: features testing set
- y_test: income testing set
'''
results = {}
# TODO: Fit the learner to the training data using slicing with 'sample_size' using .fit(training_features[:], training_labels[:])
start = time() # Get start time
learner = learner.fit(X_train[:sample_size], y_train[:sample_size])
end = time() # Get end time
# TODO: Calculate the training time
results['train_time'] = end - start
# TODO: Get the predictions on the test set(X_test),
# then get predictions on the first 300 training samples(X_train) using .predict()
start = time() # Get start time
predictions_test = learner.predict(X_test)
predictions_train = learner.predict(X_train[:300])
end = time() # Get end time
# TODO: Calculate the total prediction time
results['pred_time'] = end - start
# TODO: Compute accuracy on the first 300 training samples which is y_train[:300]
results['acc_train'] = accuracy_score(y_train[:300], predictions_train)
# TODO: Compute accuracy on test set using accuracy_score()
results['acc_test'] = accuracy_score(y_test, predictions_test)
# TODO: Compute F-score on the the first 300 training samples using fbeta_score()
results['f_train'] = fbeta_score(y_train[:300], predictions_train, beta = 0.5)
# TODO: Compute F-score on the test set which is y_test
results['f_test'] = fbeta_score(y_test, predictions_test, beta = 0.5)
# Success
print("{} trained on {} samples.".format(learner.__class__.__name__, sample_size))
# Return the results
return results
# TODO: Import the three supervised learning models from sklearn
from sklearn.svm import SVC
from sklearn.ensemble import AdaBoostClassifier, RandomForestClassifier
# TODO: Initialize the three models
clf_A = RandomForestClassifier(random_state = 0)
clf_B = SVC(random_state = 1)
clf_C = AdaBoostClassifier(random_state = 2)
# TODO: Calculate the number of samples for 1%, 10%, and 100% of the training data
# HINT: samples_100 is the entire training set i.e. len(y_train)
# HINT: samples_10 is 10% of samples_100 (ensure to set the count of the values to be `int` and not `float`)
# HINT: samples_1 is 1% of samples_100 (ensure to set the count of the values to be `int` and not `float`)
samples_100 = len(y_train)
samples_10 = int(0.1*samples_100)
samples_1 = int(0.01*samples_100)
# Collect results on the learners
results = {}
for clf in [clf_A, clf_B, clf_C]:
clf_name = clf.__class__.__name__
results[clf_name] = {}
for i, samples in enumerate([samples_1, samples_10, samples_100]):
results[clf_name][i] = \
train_predict(clf, samples, X_train, y_train, X_test, y_test)
# Run metrics visualization for the three supervised learning models chosen
vs.evaluate(results, accuracy, fscore)
# TODO: Import 'GridSearchCV', 'make_scorer', and any other necessary libraries
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer
# TODO: Initialize the classifier
clf = AdaBoostClassifier(random_state = 3)
# TODO: Create the parameters list you wish to tune, using a dictionary if needed.
# HINT: parameters = {'parameter_1': [value1, value2], 'parameter_2': [value1, value2]}
parameters = {'n_estimators': list([20,50,100]), 'learning_rate': [0.1, 0.5, 1, 2]}
# TODO: Make an fbeta_score scoring object using make_scorer()
scorer = make_scorer(fbeta_score, beta = 0.5)
# TODO: Perform grid search on the classifier using 'scorer' as the scoring method using GridSearchCV()
grid_obj = GridSearchCV(estimator = clf, scoring = scorer, param_grid = parameters)
# TODO: Fit the grid search object to the training data and find the optimal parameters using fit()
grid_fit = grid_obj.fit(X_train, y_train)
# Get the estimator
best_clf = grid_fit.best_estimator_
# Make predictions using the unoptimized and model
predictions = (clf.fit(X_train, y_train)).predict(X_test)
best_predictions = best_clf.predict(X_test)
# Report the before-and-afterscores
print("Unoptimized model\n------")
print("Accuracy score on testing data: {:.4f}".format(accuracy_score(y_test, predictions)))
print("F-score on testing data: {:.4f}".format(fbeta_score(y_test, predictions, beta = 0.5)))
print("\nOptimized Model\n------")
print("Final accuracy score on the testing data: {:.4f}".format(accuracy_score(y_test, best_predictions)))
print("Final F-score on the testing data: {:.4f}".format(fbeta_score(y_test, best_predictions, beta = 0.5)))
print(best_clf)
# TODO: Import a supervised learning model that has 'feature_importances_'
from sklearn.ensemble import AdaBoostClassifier
# TODO: Train the supervised model on the training set using .fit(X_train, y_train)
model = AdaBoostClassifier(n_estimators = 100, learning_rate = 1.0).fit(X_train, y_train)
# TODO: Extract the feature importances using .feature_importances_
importances = model.feature_importances_
# Plot
vs.feature_plot(importances, X_train, y_train)
# Import functionality for cloning a model
from sklearn.base import clone
# Reduce the feature space
X_train_reduced = X_train[X_train.columns.values[(np.argsort(importances)[::-1])[:5]]]
X_test_reduced = X_test[X_test.columns.values[(np.argsort(importances)[::-1])[:5]]]
# Train on the "best" model found from grid search earlier
clf = (clone(best_clf)).fit(X_train_reduced, y_train)
# Make new predictions
reduced_predictions = clf.predict(X_test_reduced)
# Report scores from the final model using both versions of data
print("Final Model trained on full data\n------")
print("Accuracy on testing data: {:.4f}".format(accuracy_score(y_test, best_predictions)))
print("F-score on testing data: {:.4f}".format(fbeta_score(y_test, best_predictions, beta = 0.5)))
print("\nFinal Model trained on reduced data\n------")
print("Accuracy on testing data: {:.4f}".format(accuracy_score(y_test, reduced_predictions)))
print("F-score on testing data: {:.4f}".format(fbeta_score(y_test, reduced_predictions, beta = 0.5)))
all_result = train_predict(clone(best_clf), samples_100, X_train, y_train, X_test, y_test)
reduced_result = train_predict(clone(best_clf), samples_100, X_train_reduced, y_train, X_test_reduced, y_test)
print('Train time for model with reduced features and all features are {} and {} respectively'.format( reduced_result['train_time'], all_result['train_time']))
| 0.51879 | 0.988992 |
# Semantic Segmentation Inference using ONNX Runtime
In this example notebook, we describe how to use a pre-trained Semantic Segmentation model for inference using the ONNX Runtime interface.
- The user can choose the model (see section titled *Choosing a Pre-Compiled Model*)
- The models used in this example were trained on either ***City Scapes*** or ***ADE 20K*** datasets because they are widely used dataset developed for training and benchmarking semantic segmentation AI models.
- We perform inference on a few sample images.
- We also describe the input preprocessing and output postprocessing steps, demonstrate how to collect various benchmarking statistics and how to visualize the data.
## Choosing a Pre-Compiled Model
We provide a set of precompiled artifacts to use with this notebook that will appear as a drop-down list once the first code cell is executed.
<img src=docs/images/drop_down.PNG width="400">
## Semantic Segmentation
Semantic Segmentation is a popular computer vision algorithm used in many applications such as Free Space Detection and Lane Detection. The image below shows semantic segmentation results on few sample images.
<img src=docs/images/SEG.PNG width="700">
## ONNX Runtime based Work flow
The diagram below describes the steps for ONNX Runtime based workflow.
Note:
- The user needs to compile models(sub-graph creation and quantization) on a PC to generate model artifacts.
- For this notebook we use pre-compiled models artifacts
- The generated artifacts can then be used to run inference on the target.
- Users can run this notebook as-is, only action required is to select a model.
<img src=docs/images/onnx_work_flow_2.png width="400">
```
import os
import cv2
import numpy as np
import ipywidgets as widgets
from scripts.utils import get_eval_configs
last_artifacts_id = selected_model_id.value if "selected_model_id" in locals() else None
prebuilt_configs, selected_model_id = get_eval_configs('segmentation','onnxrt', num_quant_bits = 8, last_artifacts_id = last_artifacts_id)
display(selected_model_id)
print(f'Selected Model: {selected_model_id.label}')
config = prebuilt_configs[selected_model_id.value]
config['session'].set_param('model_id', selected_model_id.value)
config['session'].start()
```
## Define utility function to preprocess input images
Below, we define a utility function to preprocess images for the model. This function takes a path as input, loads the image and preprocesses the images as required by the model. The steps below are shown as a reference (no user action required):
1. Load image
2. Convert BGR image to RGB
3. Scale image
4. Apply per-channel pixel scaling and mean subtraction
5. Convert RGB Image to BGR.
6. Convert the image to NCHW format
- The input arguments of this utility function is selected automatically by this notebook based on the model selected in the drop-down
```
def preprocess(image_path, size, mean, scale, layout, reverse_channels):
# Step 1
img = cv2.imread(image_path)
# Step 2
img = img[:,:,::-1]
# Step 3
img = cv2.resize(img, (size[1], size[0]), interpolation=cv2.INTER_CUBIC)
# Step 4
img = img.astype('float32')
for mean, scale, ch in zip(mean, scale, range(img.shape[2])):
img[:,:,ch] = ((img.astype('float32')[:,:,ch] - mean) * scale)
# Step 5
if reverse_channels:
img = img[:,:,::-1]
# Step 6
if layout == 'NCHW':
img = np.expand_dims(np.transpose(img, (2,0,1)),axis=0)
else:
img = np.expand_dims(img,axis=0)
return img
```
## Create the model using the stored artifacts
<div class="alert alert-block alert-warning">
<b>Warning:</b> It is recommended to use the ONNX Runtime APIs in the cells below without any modifications.
</div>
```
import onnxruntime as rt
onnx_model_path = config['session'].get_param('model_file')
delegate_options = {}
so = rt.SessionOptions()
delegate_options['artifacts_folder'] = config['session'].get_param('artifacts_folder')
EP_list = ['TIDLExecutionProvider','CPUExecutionProvider']
sess = rt.InferenceSession(onnx_model_path ,providers=EP_list, provider_options=[delegate_options, {}], sess_options=so)
input_details = sess.get_inputs()
output_details = sess.get_outputs()
```
## Run the model for inference
### Preprocessing and Inference
- We perform inference on a set of images from the `/sample-images` directory.
- We use a loop to preprocess the selected images, and provide them as the input to the network.
### Postprocessing and Visualization
- Once the inference results are available, we postpocess the results and visualize the inferred classes for each of the input images.
- Semantic segmentation models return results as a list (i.e. `numpy.ndarray`) with one element to represent the class ID.
- We use the `seg_mask_overlay()` function to postprocess the results.
- Then, in this notebook, we use *matplotlib* to plot the original images and the corresponding results.
```
from scripts.utils import get_preproc_props
# use results from the past inferences
images = [('sample-images/ADE_val_00001801.jpg', 221),
('sample-images/ti_lindau_I00000.jpg', 222)]
size, mean, scale, layout, reverse_channels = get_preproc_props(config)
print(f'Image size: {size}')
import tqdm
import matplotlib.pyplot as plt
from PIL import Image
from scripts.utils import seg_mask_overlay
plt.figure(figsize=(20,10))
for num in tqdm.trange(len(images)):
image_file, grid = images[num]
img = Image.open(image_file).convert('RGB')
ax = plt.subplot(grid)
img_in = preprocess(image_file , size, mean, scale, layout, reverse_channels)
if not input_details[0].type == 'tensor(float)':
img_in = np.uint8(img_in)
res = sess.run(None, {input_details[0].name: img_in})
org_size = img.size
img = seg_mask_overlay(res, img, layout).resize(org_size)
ax.imshow(img)
plt.show()
```
## Plot Inference benchmarking statistics
- During model execution several benchmarking statistics such as timestamps at different checkpoints, DDR bandwidth are collected and stored.
- The `get_TI_benchmark_data()` function can be used to collect these statistics. The statistics are collected as a dictionary of `annotations` and corresponding markers.
- We provide the utility function plot_TI_benchmark_data to visualize these benchmark KPIs.
<div class="alert alert-block alert-info">
<b>Note:</b> The values represented by <i>Inferences Per Second</i> and <i>Inference Time Per Image</i> uses the total time taken by the inference except the time taken for copying inputs and outputs. In a performance oriented system, these operations can be bypassed by writing the data directly into shared memory and performing on-the-fly input / output normalization.
</div>
```
from scripts.utils import plot_TI_performance_data, plot_TI_DDRBW_data, get_benchmark_output
stats = sess.get_TI_benchmark_data()
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(10,5))
plot_TI_performance_data(stats, axis=ax)
plt.show()
tt, st, rb, wb = get_benchmark_output(stats)
print(f'SoC: J721E/DRA829/TDA4VM')
print(f' OPP:')
print(f' Cortex-A72 @2GHZ')
print(f' DSP C7x-MMA @1GHZ')
print(f' DDR @4266 MT/s\n')
print(f'{selected_model_id.label} :')
print(f' Inferences Per Second : {1000.0/tt :7.2f} fps')
print(f' Inference Time Per Image : {tt :7.2f} ms')
print(f' DDR usage Per Image : {rb+ wb : 7.2f} MB')
```
|
github_jupyter
|
import os
import cv2
import numpy as np
import ipywidgets as widgets
from scripts.utils import get_eval_configs
last_artifacts_id = selected_model_id.value if "selected_model_id" in locals() else None
prebuilt_configs, selected_model_id = get_eval_configs('segmentation','onnxrt', num_quant_bits = 8, last_artifacts_id = last_artifacts_id)
display(selected_model_id)
print(f'Selected Model: {selected_model_id.label}')
config = prebuilt_configs[selected_model_id.value]
config['session'].set_param('model_id', selected_model_id.value)
config['session'].start()
def preprocess(image_path, size, mean, scale, layout, reverse_channels):
# Step 1
img = cv2.imread(image_path)
# Step 2
img = img[:,:,::-1]
# Step 3
img = cv2.resize(img, (size[1], size[0]), interpolation=cv2.INTER_CUBIC)
# Step 4
img = img.astype('float32')
for mean, scale, ch in zip(mean, scale, range(img.shape[2])):
img[:,:,ch] = ((img.astype('float32')[:,:,ch] - mean) * scale)
# Step 5
if reverse_channels:
img = img[:,:,::-1]
# Step 6
if layout == 'NCHW':
img = np.expand_dims(np.transpose(img, (2,0,1)),axis=0)
else:
img = np.expand_dims(img,axis=0)
return img
import onnxruntime as rt
onnx_model_path = config['session'].get_param('model_file')
delegate_options = {}
so = rt.SessionOptions()
delegate_options['artifacts_folder'] = config['session'].get_param('artifacts_folder')
EP_list = ['TIDLExecutionProvider','CPUExecutionProvider']
sess = rt.InferenceSession(onnx_model_path ,providers=EP_list, provider_options=[delegate_options, {}], sess_options=so)
input_details = sess.get_inputs()
output_details = sess.get_outputs()
from scripts.utils import get_preproc_props
# use results from the past inferences
images = [('sample-images/ADE_val_00001801.jpg', 221),
('sample-images/ti_lindau_I00000.jpg', 222)]
size, mean, scale, layout, reverse_channels = get_preproc_props(config)
print(f'Image size: {size}')
import tqdm
import matplotlib.pyplot as plt
from PIL import Image
from scripts.utils import seg_mask_overlay
plt.figure(figsize=(20,10))
for num in tqdm.trange(len(images)):
image_file, grid = images[num]
img = Image.open(image_file).convert('RGB')
ax = plt.subplot(grid)
img_in = preprocess(image_file , size, mean, scale, layout, reverse_channels)
if not input_details[0].type == 'tensor(float)':
img_in = np.uint8(img_in)
res = sess.run(None, {input_details[0].name: img_in})
org_size = img.size
img = seg_mask_overlay(res, img, layout).resize(org_size)
ax.imshow(img)
plt.show()
from scripts.utils import plot_TI_performance_data, plot_TI_DDRBW_data, get_benchmark_output
stats = sess.get_TI_benchmark_data()
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(10,5))
plot_TI_performance_data(stats, axis=ax)
plt.show()
tt, st, rb, wb = get_benchmark_output(stats)
print(f'SoC: J721E/DRA829/TDA4VM')
print(f' OPP:')
print(f' Cortex-A72 @2GHZ')
print(f' DSP C7x-MMA @1GHZ')
print(f' DDR @4266 MT/s\n')
print(f'{selected_model_id.label} :')
print(f' Inferences Per Second : {1000.0/tt :7.2f} fps')
print(f' Inference Time Per Image : {tt :7.2f} ms')
print(f' DDR usage Per Image : {rb+ wb : 7.2f} MB')
| 0.377082 | 0.971752 |
```
#please check, by ece
# TODO, ece can you please document all of these functions - like I've done for the scoring functions above
def gaussian_kernel(i, j, sigma):
return np.exp(-np.power((i-j),2)/(2*np.power(sigma,2)))
def gaussian_kernel_estimation(i, j, sigma, N):
#TODO the one with the cumulative density function CDF
pass
def triangle_kernel(i, j, sigma):
absolute = np.absolute(i-j)
return 1 - (absolute/sigma) if(absolute <= sigma) else 0
def cosine_kernel(i, j, sigma):
absolute = np.absolute(i-j)
k = 0.0
if absolute <= sigma:
k = (1 + np.cos((absolute*math.pi)/sigma))/2
return k
def circle_kernel(i, j, sigma):
absolute = np.absolute(i-j)
k = 0.0
if absolute <= sigma:
k = np.sqrt(1 - np.power(absolute/sigma, 2))
return k
def passage_kernel(i, j, sigma):
absolute = np.absolute(i-j)
return 1 if(absolute <= sigma) else 0
#find document lengths (including stop words)
doc_lengths = []
for int_doc_id in range(index.document_base(), index.maximum_document()):
doc_lengths.append(len(index.document(int_doc_id)[1]))
#maximum doc length including stop words
max_length = max(doc_lengths)
#average doc length including stop words
avg_length = sum(doc_lengths)/len(doc_lengths)
print(max_length, avg_length, len(doc_lengths))
#output
#2939 461.63406987976697 164597
import pickle
import collections
import numpy as np
import math
max_doc_length = 2939
sigma = 50
gaussian_pickle = collections.defaultdict(float)
#gaussian_estimation_pickle = collections.defaultdict(float)
triangle_pickle = collections.defaultdict(float)
cosine_pickle = collections.defaultdict(float)
circle_pickle = collections.defaultdict(float)
passage_pickle = collections.defaultdict(float)
#calculate kernel values for positions i,j for all kernels
#store the values in dictionaries, keys being the tuples in the form of (i,j)
#sigma is 50
for i in range(max_doc_length):
if i%100 == 0:
print(i)
for j in range(max_doc_length):
gaussian_pickle[(i,j)] = gaussian_kernel(i,j,sigma)
#gaussian_estimation_pickle = gaussian_estimation_kernel(i,j,sigma, N)
triangle_pickle[(i,j)] = triangle_kernel(i,j,sigma)
cosine_pickle[(i,j)] = cosine_kernel(i,j,sigma)
circle_pickle[(i,j)] = circle_kernel(i,j,sigma)
passage_pickle[(i,j)] = passage_kernel(i,j,sigma)
#pickle the kernel dictionaries
pickle.dump(gaussian_pickle, open("gaussian.p", "wb"))
#pickle.dump(gaussian_estimation_pickle, open("gaussian_estimation.p", "wb"))
pickle.dump(triangle_pickle, open("triangle.p", "wb"))
pickle.dump(cosine_pickle, open("cosine.p", "wb"))
pickle.dump(circle_pickle, open("circle.p", "wb"))
pickle.dump(passage_pickle, open("passage.p", "wb"))
#load back the pickled kernel dictionaries
gaussian = pickle.load( open("gaussian.p", "rb"))
#gaussian_estimation = pickle.load( open("gaussian_estimation.p", "rb"))
triangle = pickle.load( open("triangle.p", "rb"))
cosine = pickle.load( open("cosine.p", "rb"))
circle = pickle.load( open("circle.p", "rb"))
passage = pickle.load( open("passage.p", "rb"))
gaussian[(1234,2156)]
z_gaussian = collections.defaultdict(float)
z_triangle = collections.defaultdict(float)
z_cosine = collections.defaultdict(float)
z_circle = collections.defaultdict(float)
z_passage = collections.defaultdict(float)
for i in range(max_doc_length):
for j in range(max_doc_length):
z_gaussian[i] += gaussian[(i,j)]
z_triangle[i] += triangle[(i,j)]
z_cosine[i] += cosine[(i,j)]
z_circle[i] += circle[(i,j)]
z_passage[i] += passage[(i,j)]
#pickle the Z value dictionaries
pickle.dump(z_gaussian, open("gaussian_z.p", "wb"))
pickle.dump(z_triangle, open("triangle_z.p", "wb"))
pickle.dump(z_cosine, open("cosine_z.p", "wb"))
pickle.dump(z_circle, open("circle_z.p", "wb"))
pickle.dump(z_passage, open("passage_z.p", "wb"))
#load back the pickled z dictionaries
gaussian_z = pickle.load( open("gaussian_z.p", "rb"))
# triangle_z = pickle.load( open("triangle_z.p", "rb"))
# cosine_z = pickle.load( open("cosine_z.p", "rb"))
# circle_z = pickle.load( open("circle_z.p", "rb"))
# passage_z = pickle.load( open("passage_z.p", "rb"))
gaussian_z[2123]
```
|
github_jupyter
|
#please check, by ece
# TODO, ece can you please document all of these functions - like I've done for the scoring functions above
def gaussian_kernel(i, j, sigma):
return np.exp(-np.power((i-j),2)/(2*np.power(sigma,2)))
def gaussian_kernel_estimation(i, j, sigma, N):
#TODO the one with the cumulative density function CDF
pass
def triangle_kernel(i, j, sigma):
absolute = np.absolute(i-j)
return 1 - (absolute/sigma) if(absolute <= sigma) else 0
def cosine_kernel(i, j, sigma):
absolute = np.absolute(i-j)
k = 0.0
if absolute <= sigma:
k = (1 + np.cos((absolute*math.pi)/sigma))/2
return k
def circle_kernel(i, j, sigma):
absolute = np.absolute(i-j)
k = 0.0
if absolute <= sigma:
k = np.sqrt(1 - np.power(absolute/sigma, 2))
return k
def passage_kernel(i, j, sigma):
absolute = np.absolute(i-j)
return 1 if(absolute <= sigma) else 0
#find document lengths (including stop words)
doc_lengths = []
for int_doc_id in range(index.document_base(), index.maximum_document()):
doc_lengths.append(len(index.document(int_doc_id)[1]))
#maximum doc length including stop words
max_length = max(doc_lengths)
#average doc length including stop words
avg_length = sum(doc_lengths)/len(doc_lengths)
print(max_length, avg_length, len(doc_lengths))
#output
#2939 461.63406987976697 164597
import pickle
import collections
import numpy as np
import math
max_doc_length = 2939
sigma = 50
gaussian_pickle = collections.defaultdict(float)
#gaussian_estimation_pickle = collections.defaultdict(float)
triangle_pickle = collections.defaultdict(float)
cosine_pickle = collections.defaultdict(float)
circle_pickle = collections.defaultdict(float)
passage_pickle = collections.defaultdict(float)
#calculate kernel values for positions i,j for all kernels
#store the values in dictionaries, keys being the tuples in the form of (i,j)
#sigma is 50
for i in range(max_doc_length):
if i%100 == 0:
print(i)
for j in range(max_doc_length):
gaussian_pickle[(i,j)] = gaussian_kernel(i,j,sigma)
#gaussian_estimation_pickle = gaussian_estimation_kernel(i,j,sigma, N)
triangle_pickle[(i,j)] = triangle_kernel(i,j,sigma)
cosine_pickle[(i,j)] = cosine_kernel(i,j,sigma)
circle_pickle[(i,j)] = circle_kernel(i,j,sigma)
passage_pickle[(i,j)] = passage_kernel(i,j,sigma)
#pickle the kernel dictionaries
pickle.dump(gaussian_pickle, open("gaussian.p", "wb"))
#pickle.dump(gaussian_estimation_pickle, open("gaussian_estimation.p", "wb"))
pickle.dump(triangle_pickle, open("triangle.p", "wb"))
pickle.dump(cosine_pickle, open("cosine.p", "wb"))
pickle.dump(circle_pickle, open("circle.p", "wb"))
pickle.dump(passage_pickle, open("passage.p", "wb"))
#load back the pickled kernel dictionaries
gaussian = pickle.load( open("gaussian.p", "rb"))
#gaussian_estimation = pickle.load( open("gaussian_estimation.p", "rb"))
triangle = pickle.load( open("triangle.p", "rb"))
cosine = pickle.load( open("cosine.p", "rb"))
circle = pickle.load( open("circle.p", "rb"))
passage = pickle.load( open("passage.p", "rb"))
gaussian[(1234,2156)]
z_gaussian = collections.defaultdict(float)
z_triangle = collections.defaultdict(float)
z_cosine = collections.defaultdict(float)
z_circle = collections.defaultdict(float)
z_passage = collections.defaultdict(float)
for i in range(max_doc_length):
for j in range(max_doc_length):
z_gaussian[i] += gaussian[(i,j)]
z_triangle[i] += triangle[(i,j)]
z_cosine[i] += cosine[(i,j)]
z_circle[i] += circle[(i,j)]
z_passage[i] += passage[(i,j)]
#pickle the Z value dictionaries
pickle.dump(z_gaussian, open("gaussian_z.p", "wb"))
pickle.dump(z_triangle, open("triangle_z.p", "wb"))
pickle.dump(z_cosine, open("cosine_z.p", "wb"))
pickle.dump(z_circle, open("circle_z.p", "wb"))
pickle.dump(z_passage, open("passage_z.p", "wb"))
#load back the pickled z dictionaries
gaussian_z = pickle.load( open("gaussian_z.p", "rb"))
# triangle_z = pickle.load( open("triangle_z.p", "rb"))
# cosine_z = pickle.load( open("cosine_z.p", "rb"))
# circle_z = pickle.load( open("circle_z.p", "rb"))
# passage_z = pickle.load( open("passage_z.p", "rb"))
gaussian_z[2123]
| 0.177063 | 0.383843 |
## week08: Text classification with simple features
```
import heapq
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import StratifiedKFold
%matplotlib inline
```
# Задача классификации текстов
Задача классификации текстов заключается в том, чтобы определить по документу его класс.
В данном случае предлагается рассмотреть в качестве документов - письма, заранее отклассифицированных по 20 темам.
```
all_categories = fetch_20newsgroups().target_names
all_categories
```
Возьмём всего 3 темы, но из одного раздела (документы из близких тем сложнее отличать друг от друга)
```
categories = [
'sci.electronics',
'sci.space',
'sci.med'
]
train_data = fetch_20newsgroups(subset='train',
categories=categories,
remove=('headers', 'footers', 'quotes'))
test_data = fetch_20newsgroups(subset='test',
categories=categories,
remove=('headers', 'footers', 'quotes'))
```
## Векторизация текстов
**Вопрос: как описать текстовые документы пространством признаков?**
**Идея №1**: мешок слов (bag-of-words) - каждый документ или текст выглядит как неупорядоченный набор слов без сведений о связях между ними.
<img src='https://st2.depositphotos.com/2454953/9959/i/450/depositphotos_99593622-stock-photo-holidays-travel-bag-word-cloud.jpg'>
**Идея №2**: создаём вектор "слов", каждая компонента отвечает отдельному слову.
Для векторизации текстов воспользуемся [CountVectorizer](https://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.CountVectorizer.html). Можно всячески варировать извлечение признаков (убирать редкие слова, убирать частые слова, убирать слова общей лексики, брать биграмы и т.д.)
```
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
CountVectorizer()
count_vectorizer = CountVectorizer(min_df=5, ngram_range=(1, 2))
sparse_feature_matrix = count_vectorizer.fit_transform(train_data.data)
sparse_feature_matrix
num_2_words = {
v: k
for k, v in count_vectorizer.vocabulary_.items()
}
```
Слова с наибольшим положительным весом, являются характерными словами темы
```
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, f1_score
from sklearn.metrics.scorer import make_scorer
from sklearn.model_selection import cross_val_score, GridSearchCV
```
Воспользуемся `macro`-average для оценки качества решения в задаче многоклассовой классификации.
```
f_scorer = make_scorer(f1_score, average='macro')
```
Обучим логистическую регрессию для предсказания темы документа
```
algo = LogisticRegression(C=0.00001)
algo.fit(sparse_feature_matrix, train_data.target)
W = algo.coef_.shape[1]
for c in algo.classes_:
topic_words = [
num_2_words[w_num]
for w_num in heapq.nlargest(10, range(W), key=lambda w: algo.coef_[c, w])
]
print(', '.join(topic_words))
```
Сравним качество на обучающей и отложенной выборках.
```
algo.fit(sparse_feature_matrix, train_data.target)
f_scorer(algo, sparse_feature_matrix, train_data.target)
f_scorer(algo, count_vectorizer.transform(test_data.data), test_data.target)
```
Значения f-меры получились очень низкие.
**Вопрос:** в чём причина?
```
plt.hist(algo.coef_[0], bins=500)
plt.xlim([-0.0006, 0.0006])
plt.show()
```
** Какую выбрать метрику для регуляризации? **
```
algo = LogisticRegression(penalty='l1', C=0.1)
arr = cross_val_score(algo, sparse_feature_matrix, train_data.target, cv=5, scoring=f_scorer)
print(arr)
print(np.mean(arr))
algo.fit(sparse_feature_matrix, train_data.target)
f_scorer(algo, sparse_feature_matrix, train_data.target)
f_scorer(algo, count_vectorizer.transform(test_data.data), test_data.target)
```
Подберём оптимальное значение параметра регуляризации
```
def grid_plot(x, y, x_label, title, y_label='f_measure'):
plt.figure(figsize=(12, 6))
plt.grid(True),
plt.plot(x, y, 'go-')
plt.xlabel(x_label)
plt.ylabel(y_label)
plt.title(title)
print(*map(float, np.logspace(-2, 2, 10)))
lr_grid = {
'C': np.logspace(-2, 2, 10),
}
gs = GridSearchCV(LogisticRegression(penalty='l1'), lr_grid, scoring=f_scorer, cv=5, n_jobs=5)
%time gs.fit(sparse_feature_matrix, train_data.target)
print("best_params: {}, best_score: {}".format(gs.best_params_, gs.best_score_))
```
Рассмотрим график:
```
grid_plot(
lr_grid['C'], gs.cv_results_['mean_test_score'], 'C - coefficient of regularization', 'LogReg(penalty=l1)'
)
lr_grid = {
'C': np.linspace(1, 20, 40),
}
gs = GridSearchCV(LogisticRegression(penalty='l1'), lr_grid, scoring=f_scorer, cv=5, n_jobs=5)
%time gs.fit(sparse_feature_matrix, train_data.target)
print("best_params: {}, best_score: {}".format(gs.best_params_, gs.best_score_))
grid_plot(
lr_grid['C'], gs.cv_results_['mean_test_score'], 'C - coefficient of regularization', 'LogReg(penalty=l1)'
)
lr_final = LogisticRegression(penalty='l1', C=10)
%time lr_final.fit(sparse_feature_matrix, train_data.target)
accuracy_score(lr_final.predict(sparse_feature_matrix), train_data.target)
f_scorer(lr_final, sparse_feature_matrix, train_data.target)
accuracy_score(lr_final.predict(count_vectorizer.transform(test_data.data)), test_data.target)
f_scorer(lr_final, count_vectorizer.transform(test_data.data), test_data.target)
```
## Регуляризация вместе с векторизацией признаков
Чтобы не делать векторизацию и обучение раздельно, есть удобный класс Pipeline. Он позволяет объединить в цепочку последовательность действий
```
from sklearn.pipeline import Pipeline
pipeline = Pipeline([
("vectorizer", CountVectorizer(min_df=5, ngram_range=(1, 2))),
("algo", LogisticRegression())
])
pipeline.fit(train_data.data, train_data.target)
f_scorer(pipeline, train_data.data, train_data.target)
f_scorer(pipeline, test_data.data, test_data.target)
```
Значения такие же как мы получали ранее, делая шаги раздельно.
```
from sklearn.pipeline import make_pipeline
```
При кроссвалидации нужно, чтобы CountVectorizer не обучался на тесте (иначе объекты становятся зависимыми). Pipeline позволяет это просто сделать.
```
pipeline = make_pipeline(CountVectorizer(min_df=5, ngram_range=(1, 2)), LogisticRegression())
arr = cross_val_score(pipeline, train_data.data, train_data.target, cv=5, scoring=f_scorer)
print(arr)
print(np.mean(arr))
```
В Pipeline можно добавлять новые шаги препроцессинга данных
```
from sklearn.feature_extraction.text import TfidfTransformer
pipeline = make_pipeline(CountVectorizer(min_df=5, ngram_range=(1, 2)), TfidfTransformer(), LogisticRegression())
arr = cross_val_score(pipeline, train_data.data, train_data.target, cv=5, scoring=f_scorer)
print(arr)
print(np.mean(arr))
pipeline.fit(train_data.data, train_data.target)
accuracy_score(pipeline.predict(train_data.data), train_data.target)
f_scorer(pipeline, train_data.data, train_data.target)
accuracy_score(pipeline.predict(test_data.data), test_data.target)
f_scorer(pipeline, test_data.data, test_data.target)
```
Качество стало немного лучше
# Классификация сообщений чатов
В качестве задания предлагается построить модель классификации текстов, соответствующих сообщениям из чатов по ML, Python и знакомствам.
**Данные** можно взять с <a src="https://www.kaggle.com/c/tfstextclassification">соревнования на Kaggle</a>, проведенное в рамках курса "Диалоговые системы" в Тинькофф. Прямая [ссылка](https://www.dropbox.com/s/8wckwzfy63ajxpm/tfstextclassification.zip?dl=0) на скачивание.
```
import pandas as pd
# data_path = 'data/{}'
df = pd.read_csv('data/train.csv')
```
### Первичный анализ данных
```
print(df.shape)
df.head()
label = 0
print('Label: ', label, '\n'+'='*100+'\n')
print(*df[df['label'] == label].sample(10).text, sep='\n'+'-'*100+'\n\n')
label = 1
print('Label: ', label, '\n'+'='*100+'\n')
print(*df[df['label'] == label].sample(10).text, sep='\n'+'-'*100+'\n\n')
label = 2
print('Label: ', label, '\n'+'='*100+'\n')
print(*df[df['label'] == label].sample(10).text, sep='\n'+'-'*100+'\n\n')
```
### Разделим данные на train/test
```
skf = StratifiedKFold(3, random_state=37)
train_index, test_index = next(skf.split(df.text, df.label))
train_df, test_df = df.iloc[train_index], df.iloc[test_index]
print(train_df.shape, test_df.shape)
train_df.head()
test_df.head()
```
## Baseline
```
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.decomposition import TruncatedSVD
from xgboost.sklearn import XGBClassifier
```
Преобразуем данные
```
X_train = train_df.text
y_train = train_df.label
print(X_train.shape)
X_test = test_df.text
y_test = test_df.label
print(X_test.shape)
```
Подготовим pipeline
```
pipeline = Pipeline([
("vectorizer", CountVectorizer()),
("clf", DecisionTreeClassifier()),
])
```
Обучим классификатор
```
%%time
clf = pipeline
clf.fit(X_train, y_train)
```
Оценим качество
```
print("Train_acc: {:.4f}, train_f-measure: {:.4f}".format(
accuracy_score(clf.predict(X_train), y_train),
f_scorer(clf, X_train, y_train)
))
print("Test_acc: {:.4f}, test_f-measure: {:.4f}".format(
accuracy_score(clf.predict(X_test), y_test),
f_scorer(clf, X_test, y_test)
))
```
### Your turn
Как видим, наша модель переобучилась. Для получения лучших результатов попробуйте воспользоваться более хитрыми и походящими инструментами.
1. Попробуйте поработать с параметрами `CountVectorizer`.
2. Попробуйте воспользоваться TF-IDF для кодирования текстовой информации ([ссылка](https://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.TfidfVectorizer.html)).
3. Попробуйте воспользоваться другими моделями и средствами снижения размерности.
Формальный критерий успешности выполнения данного (опционального) задания:
* Проведен честный эксперимент с апробацией различных методов (>=3)
* Полученный алгоритм не выказывает явных следов переобучения (качество на train и test не различаются более, чем на 0.03 условных попугая)
* Test accuracy >= 0.835, f1-score >= 0.815
|
github_jupyter
|
import heapq
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import StratifiedKFold
%matplotlib inline
all_categories = fetch_20newsgroups().target_names
all_categories
categories = [
'sci.electronics',
'sci.space',
'sci.med'
]
train_data = fetch_20newsgroups(subset='train',
categories=categories,
remove=('headers', 'footers', 'quotes'))
test_data = fetch_20newsgroups(subset='test',
categories=categories,
remove=('headers', 'footers', 'quotes'))
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
CountVectorizer()
count_vectorizer = CountVectorizer(min_df=5, ngram_range=(1, 2))
sparse_feature_matrix = count_vectorizer.fit_transform(train_data.data)
sparse_feature_matrix
num_2_words = {
v: k
for k, v in count_vectorizer.vocabulary_.items()
}
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, f1_score
from sklearn.metrics.scorer import make_scorer
from sklearn.model_selection import cross_val_score, GridSearchCV
f_scorer = make_scorer(f1_score, average='macro')
algo = LogisticRegression(C=0.00001)
algo.fit(sparse_feature_matrix, train_data.target)
W = algo.coef_.shape[1]
for c in algo.classes_:
topic_words = [
num_2_words[w_num]
for w_num in heapq.nlargest(10, range(W), key=lambda w: algo.coef_[c, w])
]
print(', '.join(topic_words))
algo.fit(sparse_feature_matrix, train_data.target)
f_scorer(algo, sparse_feature_matrix, train_data.target)
f_scorer(algo, count_vectorizer.transform(test_data.data), test_data.target)
plt.hist(algo.coef_[0], bins=500)
plt.xlim([-0.0006, 0.0006])
plt.show()
algo = LogisticRegression(penalty='l1', C=0.1)
arr = cross_val_score(algo, sparse_feature_matrix, train_data.target, cv=5, scoring=f_scorer)
print(arr)
print(np.mean(arr))
algo.fit(sparse_feature_matrix, train_data.target)
f_scorer(algo, sparse_feature_matrix, train_data.target)
f_scorer(algo, count_vectorizer.transform(test_data.data), test_data.target)
def grid_plot(x, y, x_label, title, y_label='f_measure'):
plt.figure(figsize=(12, 6))
plt.grid(True),
plt.plot(x, y, 'go-')
plt.xlabel(x_label)
plt.ylabel(y_label)
plt.title(title)
print(*map(float, np.logspace(-2, 2, 10)))
lr_grid = {
'C': np.logspace(-2, 2, 10),
}
gs = GridSearchCV(LogisticRegression(penalty='l1'), lr_grid, scoring=f_scorer, cv=5, n_jobs=5)
%time gs.fit(sparse_feature_matrix, train_data.target)
print("best_params: {}, best_score: {}".format(gs.best_params_, gs.best_score_))
grid_plot(
lr_grid['C'], gs.cv_results_['mean_test_score'], 'C - coefficient of regularization', 'LogReg(penalty=l1)'
)
lr_grid = {
'C': np.linspace(1, 20, 40),
}
gs = GridSearchCV(LogisticRegression(penalty='l1'), lr_grid, scoring=f_scorer, cv=5, n_jobs=5)
%time gs.fit(sparse_feature_matrix, train_data.target)
print("best_params: {}, best_score: {}".format(gs.best_params_, gs.best_score_))
grid_plot(
lr_grid['C'], gs.cv_results_['mean_test_score'], 'C - coefficient of regularization', 'LogReg(penalty=l1)'
)
lr_final = LogisticRegression(penalty='l1', C=10)
%time lr_final.fit(sparse_feature_matrix, train_data.target)
accuracy_score(lr_final.predict(sparse_feature_matrix), train_data.target)
f_scorer(lr_final, sparse_feature_matrix, train_data.target)
accuracy_score(lr_final.predict(count_vectorizer.transform(test_data.data)), test_data.target)
f_scorer(lr_final, count_vectorizer.transform(test_data.data), test_data.target)
from sklearn.pipeline import Pipeline
pipeline = Pipeline([
("vectorizer", CountVectorizer(min_df=5, ngram_range=(1, 2))),
("algo", LogisticRegression())
])
pipeline.fit(train_data.data, train_data.target)
f_scorer(pipeline, train_data.data, train_data.target)
f_scorer(pipeline, test_data.data, test_data.target)
from sklearn.pipeline import make_pipeline
pipeline = make_pipeline(CountVectorizer(min_df=5, ngram_range=(1, 2)), LogisticRegression())
arr = cross_val_score(pipeline, train_data.data, train_data.target, cv=5, scoring=f_scorer)
print(arr)
print(np.mean(arr))
from sklearn.feature_extraction.text import TfidfTransformer
pipeline = make_pipeline(CountVectorizer(min_df=5, ngram_range=(1, 2)), TfidfTransformer(), LogisticRegression())
arr = cross_val_score(pipeline, train_data.data, train_data.target, cv=5, scoring=f_scorer)
print(arr)
print(np.mean(arr))
pipeline.fit(train_data.data, train_data.target)
accuracy_score(pipeline.predict(train_data.data), train_data.target)
f_scorer(pipeline, train_data.data, train_data.target)
accuracy_score(pipeline.predict(test_data.data), test_data.target)
f_scorer(pipeline, test_data.data, test_data.target)
import pandas as pd
# data_path = 'data/{}'
df = pd.read_csv('data/train.csv')
print(df.shape)
df.head()
label = 0
print('Label: ', label, '\n'+'='*100+'\n')
print(*df[df['label'] == label].sample(10).text, sep='\n'+'-'*100+'\n\n')
label = 1
print('Label: ', label, '\n'+'='*100+'\n')
print(*df[df['label'] == label].sample(10).text, sep='\n'+'-'*100+'\n\n')
label = 2
print('Label: ', label, '\n'+'='*100+'\n')
print(*df[df['label'] == label].sample(10).text, sep='\n'+'-'*100+'\n\n')
skf = StratifiedKFold(3, random_state=37)
train_index, test_index = next(skf.split(df.text, df.label))
train_df, test_df = df.iloc[train_index], df.iloc[test_index]
print(train_df.shape, test_df.shape)
train_df.head()
test_df.head()
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.decomposition import TruncatedSVD
from xgboost.sklearn import XGBClassifier
X_train = train_df.text
y_train = train_df.label
print(X_train.shape)
X_test = test_df.text
y_test = test_df.label
print(X_test.shape)
pipeline = Pipeline([
("vectorizer", CountVectorizer()),
("clf", DecisionTreeClassifier()),
])
%%time
clf = pipeline
clf.fit(X_train, y_train)
print("Train_acc: {:.4f}, train_f-measure: {:.4f}".format(
accuracy_score(clf.predict(X_train), y_train),
f_scorer(clf, X_train, y_train)
))
print("Test_acc: {:.4f}, test_f-measure: {:.4f}".format(
accuracy_score(clf.predict(X_test), y_test),
f_scorer(clf, X_test, y_test)
))
| 0.604399 | 0.956309 |
<a id="title_ID"></a>
# JWST calwebb_image2, background unit tests
<span style="color:red"> **Instruments Affected**</span>: NIRCam, NIRISS, NIRSpec, MIRI, FGS
### Table of Contents
<div style="text-align: left">
<br> [Introduction](#intro)
<br> [JWST Unit Tests](#unit)
<br> [Defining Terms](#terms)
<br> [Test Description](#description)
<br> [Data Description](#data_descr)
<br> [Imports](#imports)
<br> [Convenience Functions](#functions)
<br> [Perform Tests](#testing)
<br> [About This Notebook](#about)
<br>
</div>
<a id="intro"></a>
# Introduction
This is the validation notebook that displays the unit tests for the Background step in calwebb_image2. This notebook runs and displays the unit tests that are performed as a part of the normal software continuous integration process. For more information on the pipeline visit the links below.
* Pipeline description: https://jwst-pipeline.readthedocs.io/en/latest/jwst/background/index.html
* Pipeline code: https://github.com/spacetelescope/jwst/tree/master/jwst/
[Top of Page](#title_ID)
<a id="unit"></a>
# JWST Unit Tests
JWST unit tests are located in the "tests" folder for each pipeline step within the [GitHub repository](https://github.com/spacetelescope/jwst/tree/master/jwst/), e.g., ```jwst/background/tests```.
* Unit test README: https://github.com/spacetelescope/jwst#unit-tests
[Top of Page](#title_ID)
<a id="terms"></a>
# Defining Terms
These are terms or acronymns used in this notebook that may not be known a general audience.
* JWST: James Webb Space Telescope
* NIRCam: Near-Infrared Camera
[Top of Page](#title_ID)
<a id="description"></a>
# Test Description
Unit testing is a software testing method by which individual units of source code are tested to determine whether they are working sufficiently well. Unit tests do not require a separate data file; the test creates the necessary test data and parameters as a part of the test code.
[Top of Page](#title_ID)
<a id="data_descr"></a>
# Data Description
Data used for unit tests is created on the fly within the test itself, and is typically an array in the expected format of JWST data with added metadata needed to run through the pipeline.
[Top of Page](#title_ID)
<a id="imports"></a>
# Imports
* tempfile for creating temporary output products
* pytest for unit test functions
* jwst for the JWST Pipeline
* IPython.display for display pytest reports
[Top of Page](#title_ID)
```
import tempfile
import os
import pytest
import jwst
from IPython.display import IFrame
from IPython.core.display import HTML
```
<a id="functions"></a>
# Convenience Functions
Here we define any convenience functions to help with running the unit tests.
[Top of Page](#title_ID)
<a id="testing"></a>
# Perform Tests
Below we run the unit tests for the Background step.
[Top of Page](#title_ID)
```
print("Testing JWST Pipeline {}".format(jwst.__version__))
jwst_dir = os.path.dirname(jwst.__file__)
bkg = os.path.join(jwst_dir, 'background')
associations = os.path.join(jwst_dir, 'associations')
datamodels = os.path.join(jwst_dir, 'datamodels')
stpipe = os.path.join(jwst_dir, 'stpipe')
regtest = os.path.join(jwst_dir, 'regtest')
with tempfile.TemporaryDirectory() as tmpdir:
outdir = os.path.join(tmpdir, 'regtest_report.html')
!pytest {bkg} -v --ignore={associations} --ignore={datamodels} --ignore={stpipe} --ignore={regtest} --html={outdir} --self-contained-html
with open(os.path.join(tmpdir, "regtest_report.html")) as report_file:
html_report = "".join(report_file.readlines())
HTML(html_report)
```
<a id="about"></a>
## About This Notebook
**Author:** Alicia Canipe, Staff Scientist, NIRCam
<br>**Updated On:** 01/07/2021
[Top of Page](#title_ID)
<img style="float: right;" src="./stsci_pri_combo_mark_horizonal_white_bkgd.png" alt="stsci_pri_combo_mark_horizonal_white_bkgd" width="200px"/>
|
github_jupyter
|
import tempfile
import os
import pytest
import jwst
from IPython.display import IFrame
from IPython.core.display import HTML
print("Testing JWST Pipeline {}".format(jwst.__version__))
jwst_dir = os.path.dirname(jwst.__file__)
bkg = os.path.join(jwst_dir, 'background')
associations = os.path.join(jwst_dir, 'associations')
datamodels = os.path.join(jwst_dir, 'datamodels')
stpipe = os.path.join(jwst_dir, 'stpipe')
regtest = os.path.join(jwst_dir, 'regtest')
with tempfile.TemporaryDirectory() as tmpdir:
outdir = os.path.join(tmpdir, 'regtest_report.html')
!pytest {bkg} -v --ignore={associations} --ignore={datamodels} --ignore={stpipe} --ignore={regtest} --html={outdir} --self-contained-html
with open(os.path.join(tmpdir, "regtest_report.html")) as report_file:
html_report = "".join(report_file.readlines())
HTML(html_report)
| 0.103987 | 0.953362 |
<h1 align="center"> Image Denoising using a Deep Convolutional Autoencoder </h1>
<h1 align="center"> <a href="https://github.com/bagheri365/" target="_blank" rel="noopener noreferrer">Alireza Bagheri</a></h1>
<h1>Table of contents</h1>
<ul>
<li><a href="#Data">Data Preparation</a> </li>
<ul>
<li><a href="#load_data">Load Data</a> </li>
<li><a href="#scale_data"> Scale and Reshape the Data </a></li>
<li><a href="#noisy_data"> Add Noise to the Data </a> </li>
</ul>
<li><a href="#Denoising_autencoder"> Denoising Autoencoder </a></li>
<ul>
<li><a href="#encoder"> Build Encoder Model </a></li>
<li><a href="#decoder"> Build Decoder Model </a></li>
<li><a href="#autoencoder"> Train the Autoencoder </a></li>
</ul>
<li><a href="#results"> Results </a></li>
<li><a href="#ref"> Reference </a></li>
</ul>
## Data Preparation <a name="Data"></a>
### Load Data <a name="load_data"></a>
```
from tensorflow.keras.datasets import mnist
(X_train, _), (X_test, _) = mnist.load_data()
print('X_train shape:', X_train.shape)
print('X_test shape:', X_test.shape)
```
### Scale and Reshape the Data <a name="scale_data"></a>
```
# Scale X to range between 0 and 1
X_train = X_train.astype('float32') / 255.
X_test = X_test.astype('float32') / 255.
# Reshape X to (n_samples/batch_size, height, width, n_channels)
X_train = X_train.reshape(-1, 28, 28, 1)
X_test = X_test.reshape(-1, 28, 28, 1)
print('X_train shape:', X_train.shape)
print('X_test shape:', X_test.shape)
```
### Add Noise to the Data <a name="noisy_data"></a>
```
import numpy as np
noise_factor = 0.5
noise = noise_factor * np.random.normal(loc= 0.5, scale= 0.5, size= X_train.shape)
X_train_noisy = X_train + noise
X_train_noisy = np.clip(X_train_noisy, 0., 1.)
noise = noise_factor * np.random.normal(loc= 0.5, scale= 0.5, size= X_test.shape)
X_test_noisy = X_test + noise
X_test_noisy = np.clip(X_test_noisy, 0., 1.)
```
## Denoising Autoencoder <a name="Denoising_autencoder"></a>
### Build Encoder Model <a name="encoder"></a>
```
from tensorflow.keras.layers import Input, Conv2D, MaxPooling2D, UpSampling2D, Activation
from tensorflow.keras.models import Model
import warnings; warnings.filterwarnings('ignore')
input_img = Input(shape=(28,28,1), name='Encoder_input')
# Encoder
Enc = Conv2D(16, (3, 3), padding='same', activation='relu', name='Enc_conv2d_1')(input_img)
Enc = MaxPooling2D(pool_size=(2,2), padding='same', name='Enc_max_pooling2d_1')(Enc)
Enc = Conv2D(8,(3, 3), padding='same', activation='relu', name='Enc_conv2d_2')(Enc)
Enc = MaxPooling2D(pool_size=(2,2), padding='same', name='Enc_max_pooling2d_2')(Enc)
Encoded = Conv2D(1, (3, 3), padding='same', activation='sigmoid', name='Enc_conv2d_3')(Enc)
# Instantiate the Encoder Model
encoder = Model(inputs = input_img, outputs = Encoded)
encoder.summary()
```
### Build Decoder Model <a name="decoder"></a>
```
# Decoder
Dec = Conv2D(8, (3, 3), padding='same', activation='relu', name ='Dec_conv2d_1')(Encoded)
Dec = UpSampling2D((2, 2), name = 'Dec_upsampling2d_1')(Dec)
Dec = Conv2D(16, (3, 3), padding='same', activation='relu', name ='Dec_conv2d_2')(Dec)
Dec = UpSampling2D((2, 2), name = 'Dec_upsampling2d_2')(Dec)
decoded = Conv2D(1,(3, 3), padding='same', activation='sigmoid', name ='Dec_conv2d_3')(Dec)
# Instantiate the Autoencoder Model
autoencoder = Model(inputs = input_img, outputs = decoded)
autoencoder.summary()
```
### Train the Autoencoder <a name="autoencoder"></a>
#### Compile and train the autoencoder
```
# Compile the autoencoder
autoencoder.compile(loss='mse', optimizer='adam')
# Train the autoencoder
history = autoencoder.fit(X_train_noisy, X_train,
epochs = 10,
batch_size = 20,
shuffle = True,
validation_split = 1/6).history
```
#### Plot loss versus epochs
```
import matplotlib.pyplot as plt
%matplotlib inline
tr_loss = history['loss']
val_loss = history['val_loss']
epochs = range(1, len(tr_loss)+1)
fig = plt.figure(figsize=(8, 4))
fig.tight_layout()
plt.plot(epochs, tr_loss,'r')
plt.plot(epochs, val_loss,'b')
plt.title('Model loss')
plt.ylabel('MSE')
plt.xlabel('Epoch')
plt.legend(['Training', 'Validation'], loc='upper right')
plt.show()
```
#### Save the trained model
```
from keras.models import model_from_json
# Save the Encoder
model_json = encoder.to_json()
with open("logs/Encoder_model.json", "w") as json_file:
json_file.write(model_json)
encoder.save_weights("logs/Encoder_weights.h5")
# Save the Autoencoder
model_json = autoencoder.to_json()
with open("logs/Autoencoder_model.json", "w") as json_file:
json_file.write(model_json)
autoencoder.save_weights("logs/Autoencoder_weights.h5")
```
### Results <a name="results"></a>
#### Load the trained model
```
from tensorflow.keras.models import model_from_json
import warnings; warnings.filterwarnings('ignore')
with open('logs/Encoder_model.json', 'r') as f:
Myencoder = model_from_json(f.read())
Myencoder.load_weights("logs/Encoder_weights.h5")
with open('logs/Autoencoder_model.json', 'r') as f:
MyAutoencoder = model_from_json(f.read())
MyAutoencoder.load_weights("logs/Autoencoder_weights.h5")
```
#### Plot denoised images
```
# Pick randomly some images from test set
num_images = 10
random_test_images = np.random.randint(X_test.shape[0], size= num_images)
# Predict the Encoder and the Autoencoder outputs from the noisy test images
encoded_imgs = Myencoder.predict(X_test_noisy)
decoded_imgs = MyAutoencoder.predict(X_test_noisy)
plt.figure(figsize=(20, 10))
fig.tight_layout()
for i, image_idx in enumerate(random_test_images):
# Plot original image
ax = plt.subplot(4, num_images, i + 1)
plt.imshow(X_test[image_idx].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
if i == num_images//2:
ax.set_title('Original Images')
# Plot noised image
ax = plt.subplot(4, num_images, num_images + i + 1)
plt.imshow(X_test_noisy[image_idx].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
if i == num_images//2:
ax.set_title('Noised Images')
# Plot encoded image
ax = plt.subplot(4, num_images, 2*num_images + i + 1)
plt.imshow(encoded_imgs[image_idx].reshape(7, 7))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
if i == num_images//2:
ax.set_title('Encoded Images')
# Plot reconstructed image
ax = plt.subplot(4, num_images, 3*num_images + i + 1)
plt.imshow(decoded_imgs[image_idx].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
if i == num_images//2:
ax.set_title('Denoised Images')
plt.show()
```
### Reference <a name="ref"></a>
https://keras.io/examples/mnist_denoising_autoencoder/
|
github_jupyter
|
from tensorflow.keras.datasets import mnist
(X_train, _), (X_test, _) = mnist.load_data()
print('X_train shape:', X_train.shape)
print('X_test shape:', X_test.shape)
# Scale X to range between 0 and 1
X_train = X_train.astype('float32') / 255.
X_test = X_test.astype('float32') / 255.
# Reshape X to (n_samples/batch_size, height, width, n_channels)
X_train = X_train.reshape(-1, 28, 28, 1)
X_test = X_test.reshape(-1, 28, 28, 1)
print('X_train shape:', X_train.shape)
print('X_test shape:', X_test.shape)
import numpy as np
noise_factor = 0.5
noise = noise_factor * np.random.normal(loc= 0.5, scale= 0.5, size= X_train.shape)
X_train_noisy = X_train + noise
X_train_noisy = np.clip(X_train_noisy, 0., 1.)
noise = noise_factor * np.random.normal(loc= 0.5, scale= 0.5, size= X_test.shape)
X_test_noisy = X_test + noise
X_test_noisy = np.clip(X_test_noisy, 0., 1.)
from tensorflow.keras.layers import Input, Conv2D, MaxPooling2D, UpSampling2D, Activation
from tensorflow.keras.models import Model
import warnings; warnings.filterwarnings('ignore')
input_img = Input(shape=(28,28,1), name='Encoder_input')
# Encoder
Enc = Conv2D(16, (3, 3), padding='same', activation='relu', name='Enc_conv2d_1')(input_img)
Enc = MaxPooling2D(pool_size=(2,2), padding='same', name='Enc_max_pooling2d_1')(Enc)
Enc = Conv2D(8,(3, 3), padding='same', activation='relu', name='Enc_conv2d_2')(Enc)
Enc = MaxPooling2D(pool_size=(2,2), padding='same', name='Enc_max_pooling2d_2')(Enc)
Encoded = Conv2D(1, (3, 3), padding='same', activation='sigmoid', name='Enc_conv2d_3')(Enc)
# Instantiate the Encoder Model
encoder = Model(inputs = input_img, outputs = Encoded)
encoder.summary()
# Decoder
Dec = Conv2D(8, (3, 3), padding='same', activation='relu', name ='Dec_conv2d_1')(Encoded)
Dec = UpSampling2D((2, 2), name = 'Dec_upsampling2d_1')(Dec)
Dec = Conv2D(16, (3, 3), padding='same', activation='relu', name ='Dec_conv2d_2')(Dec)
Dec = UpSampling2D((2, 2), name = 'Dec_upsampling2d_2')(Dec)
decoded = Conv2D(1,(3, 3), padding='same', activation='sigmoid', name ='Dec_conv2d_3')(Dec)
# Instantiate the Autoencoder Model
autoencoder = Model(inputs = input_img, outputs = decoded)
autoencoder.summary()
# Compile the autoencoder
autoencoder.compile(loss='mse', optimizer='adam')
# Train the autoencoder
history = autoencoder.fit(X_train_noisy, X_train,
epochs = 10,
batch_size = 20,
shuffle = True,
validation_split = 1/6).history
import matplotlib.pyplot as plt
%matplotlib inline
tr_loss = history['loss']
val_loss = history['val_loss']
epochs = range(1, len(tr_loss)+1)
fig = plt.figure(figsize=(8, 4))
fig.tight_layout()
plt.plot(epochs, tr_loss,'r')
plt.plot(epochs, val_loss,'b')
plt.title('Model loss')
plt.ylabel('MSE')
plt.xlabel('Epoch')
plt.legend(['Training', 'Validation'], loc='upper right')
plt.show()
from keras.models import model_from_json
# Save the Encoder
model_json = encoder.to_json()
with open("logs/Encoder_model.json", "w") as json_file:
json_file.write(model_json)
encoder.save_weights("logs/Encoder_weights.h5")
# Save the Autoencoder
model_json = autoencoder.to_json()
with open("logs/Autoencoder_model.json", "w") as json_file:
json_file.write(model_json)
autoencoder.save_weights("logs/Autoencoder_weights.h5")
from tensorflow.keras.models import model_from_json
import warnings; warnings.filterwarnings('ignore')
with open('logs/Encoder_model.json', 'r') as f:
Myencoder = model_from_json(f.read())
Myencoder.load_weights("logs/Encoder_weights.h5")
with open('logs/Autoencoder_model.json', 'r') as f:
MyAutoencoder = model_from_json(f.read())
MyAutoencoder.load_weights("logs/Autoencoder_weights.h5")
# Pick randomly some images from test set
num_images = 10
random_test_images = np.random.randint(X_test.shape[0], size= num_images)
# Predict the Encoder and the Autoencoder outputs from the noisy test images
encoded_imgs = Myencoder.predict(X_test_noisy)
decoded_imgs = MyAutoencoder.predict(X_test_noisy)
plt.figure(figsize=(20, 10))
fig.tight_layout()
for i, image_idx in enumerate(random_test_images):
# Plot original image
ax = plt.subplot(4, num_images, i + 1)
plt.imshow(X_test[image_idx].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
if i == num_images//2:
ax.set_title('Original Images')
# Plot noised image
ax = plt.subplot(4, num_images, num_images + i + 1)
plt.imshow(X_test_noisy[image_idx].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
if i == num_images//2:
ax.set_title('Noised Images')
# Plot encoded image
ax = plt.subplot(4, num_images, 2*num_images + i + 1)
plt.imshow(encoded_imgs[image_idx].reshape(7, 7))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
if i == num_images//2:
ax.set_title('Encoded Images')
# Plot reconstructed image
ax = plt.subplot(4, num_images, 3*num_images + i + 1)
plt.imshow(decoded_imgs[image_idx].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
if i == num_images//2:
ax.set_title('Denoised Images')
plt.show()
| 0.903067 | 0.965576 |
<a href="https://colab.research.google.com/github/novoforce/Exploring-Pytorch/blob/master/nlp/3000_NLP_crash.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import nltk
nltk.download()
paragraph = """I have three visions for India. In 3000 years of our history, people from all over
the world have come and invaded us, captured our lands, conquered our minds.
From Alexander onwards, the Greeks, the Turks, the Moguls, the Portuguese, the British,
the French, the Dutch, all of them came and looted us, took over what was ours.
Yet we have not done this to any other nation. We have not conquered anyone.
We have not grabbed their land, their culture,
their history and tried to enforce our way of life on them.
Why? Because we respect the freedom of others.That is why my
first vision is that of freedom. I believe that India got its first vision of
this in 1857, when we started the War of Independence. It is this freedom that
we must protect and nurture and build on. If we are not free, no one will respect us.
My second vision for India’s development. For fifty years we have been a developing nation.
It is time we see ourselves as a developed nation. We are among the top 5 nations of the world
in terms of GDP. We have a 10 percent growth rate in most areas. Our poverty levels are falling.
Our achievements are being globally recognised today. Yet we lack the self-confidence to
see ourselves as a developed nation, self-reliant and self-assured. Isn’t this incorrect?
I have a third vision. India must stand up to the world. Because I believe that unless India
stands up to the world, no one will respect us. Only strength respects strength. We must be
strong not only as a military power but also as an economic power. Both must go hand-in-hand.
My good fortune was to have worked with three great minds. Dr. Vikram Sarabhai of the Dept. of
space, Professor Satish Dhawan, who succeeded him and Dr. Brahm Prakash, father of nuclear material.
I was lucky to have worked with all three of them closely and consider this the great opportunity of my life.
I see four milestones in my career"""
```
# Tokenization
```
#sentence tokenization
sentences = nltk.sent_tokenize(paragraph)
print('Tokenized sentences:> ',sentences)
#word tokenization
words = nltk.word_tokenize(paragraph)
print('Tokenizaed words:> ',words)
```
# Stemming
```
from nltk.stem import PorterStemmer
from nltk.corpus import stopwords
sentences = nltk.sent_tokenize(paragraph)
stemmer = PorterStemmer()
for i in range(len(sentences)):
words = nltk.word_tokenize(sentences[i])
words = [stemmer.stem(word) for word in words if word not in set(stopwords.words('english'))]
sentences[i] = ' '.join(words)
print('Stemmed sentences:> ',sentences)
```
# Lemmentization
```
from nltk.stem import WordNetLemmatizer
sentences = nltk.sent_tokenize(paragraph)
lemmatizer = WordNetLemmatizer()
# Lemmatization
for i in range(len(sentences)):
words = nltk.word_tokenize(sentences[i])
words = [lemmatizer.lemmatize(word) for word in words if word not in set(stopwords.words('english'))]
sentences[i] = ' '.join(words)
print('Lemmentizaed sentences:> ',sentences)
```
# Bag of words
```
import re
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
from nltk.stem import WordNetLemmatizer
ps = PorterStemmer()
wordnet=WordNetLemmatizer()
sentences = nltk.sent_tokenize(paragraph)
corpus = []
for i in range(len(sentences)):
review = re.sub('[^a-zA-Z]', ' ', sentences[i])
review = review.lower()
review = review.split()
review = [ps.stem(word) for word in review if not word in set(stopwords.words('english'))]
review = ' '.join(review)
corpus.append(review)
# Creating the Bag of Words model
from sklearn.feature_extraction.text import CountVectorizer
cv = CountVectorizer(max_features = 1500)
X = cv.fit_transform(corpus).toarray()
X
```
# TF/IDF
```
import re
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
from nltk.stem import WordNetLemmatizer
ps = PorterStemmer()
wordnet=WordNetLemmatizer()
sentences = nltk.sent_tokenize(paragraph)
corpus = []
for i in range(len(sentences)):
review = re.sub('[^a-zA-Z]', ' ', sentences[i])
review = review.lower()
review = review.split()
review = [wordnet.lemmatize(word) for word in review if not word in set(stopwords.words('english'))]
review = ' '.join(review)
corpus.append(review)
# Creating the TF-IDF model
from sklearn.feature_extraction.text import TfidfVectorizer
cv = TfidfVectorizer()
X = cv.fit_transform(corpus).toarray()
```
|
github_jupyter
|
import nltk
nltk.download()
paragraph = """I have three visions for India. In 3000 years of our history, people from all over
the world have come and invaded us, captured our lands, conquered our minds.
From Alexander onwards, the Greeks, the Turks, the Moguls, the Portuguese, the British,
the French, the Dutch, all of them came and looted us, took over what was ours.
Yet we have not done this to any other nation. We have not conquered anyone.
We have not grabbed their land, their culture,
their history and tried to enforce our way of life on them.
Why? Because we respect the freedom of others.That is why my
first vision is that of freedom. I believe that India got its first vision of
this in 1857, when we started the War of Independence. It is this freedom that
we must protect and nurture and build on. If we are not free, no one will respect us.
My second vision for India’s development. For fifty years we have been a developing nation.
It is time we see ourselves as a developed nation. We are among the top 5 nations of the world
in terms of GDP. We have a 10 percent growth rate in most areas. Our poverty levels are falling.
Our achievements are being globally recognised today. Yet we lack the self-confidence to
see ourselves as a developed nation, self-reliant and self-assured. Isn’t this incorrect?
I have a third vision. India must stand up to the world. Because I believe that unless India
stands up to the world, no one will respect us. Only strength respects strength. We must be
strong not only as a military power but also as an economic power. Both must go hand-in-hand.
My good fortune was to have worked with three great minds. Dr. Vikram Sarabhai of the Dept. of
space, Professor Satish Dhawan, who succeeded him and Dr. Brahm Prakash, father of nuclear material.
I was lucky to have worked with all three of them closely and consider this the great opportunity of my life.
I see four milestones in my career"""
#sentence tokenization
sentences = nltk.sent_tokenize(paragraph)
print('Tokenized sentences:> ',sentences)
#word tokenization
words = nltk.word_tokenize(paragraph)
print('Tokenizaed words:> ',words)
from nltk.stem import PorterStemmer
from nltk.corpus import stopwords
sentences = nltk.sent_tokenize(paragraph)
stemmer = PorterStemmer()
for i in range(len(sentences)):
words = nltk.word_tokenize(sentences[i])
words = [stemmer.stem(word) for word in words if word not in set(stopwords.words('english'))]
sentences[i] = ' '.join(words)
print('Stemmed sentences:> ',sentences)
from nltk.stem import WordNetLemmatizer
sentences = nltk.sent_tokenize(paragraph)
lemmatizer = WordNetLemmatizer()
# Lemmatization
for i in range(len(sentences)):
words = nltk.word_tokenize(sentences[i])
words = [lemmatizer.lemmatize(word) for word in words if word not in set(stopwords.words('english'))]
sentences[i] = ' '.join(words)
print('Lemmentizaed sentences:> ',sentences)
import re
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
from nltk.stem import WordNetLemmatizer
ps = PorterStemmer()
wordnet=WordNetLemmatizer()
sentences = nltk.sent_tokenize(paragraph)
corpus = []
for i in range(len(sentences)):
review = re.sub('[^a-zA-Z]', ' ', sentences[i])
review = review.lower()
review = review.split()
review = [ps.stem(word) for word in review if not word in set(stopwords.words('english'))]
review = ' '.join(review)
corpus.append(review)
# Creating the Bag of Words model
from sklearn.feature_extraction.text import CountVectorizer
cv = CountVectorizer(max_features = 1500)
X = cv.fit_transform(corpus).toarray()
X
import re
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
from nltk.stem import WordNetLemmatizer
ps = PorterStemmer()
wordnet=WordNetLemmatizer()
sentences = nltk.sent_tokenize(paragraph)
corpus = []
for i in range(len(sentences)):
review = re.sub('[^a-zA-Z]', ' ', sentences[i])
review = review.lower()
review = review.split()
review = [wordnet.lemmatize(word) for word in review if not word in set(stopwords.words('english'))]
review = ' '.join(review)
corpus.append(review)
# Creating the TF-IDF model
from sklearn.feature_extraction.text import TfidfVectorizer
cv = TfidfVectorizer()
X = cv.fit_transform(corpus).toarray()
| 0.154631 | 0.951997 |
# Running MAGICC in Parallel
The code in this notebook is a work in progress so it is quite verbose. In future prettier wrappers can be written but for now it's helpful to have things in one place.
```
import glob
import logging
import multiprocessing
import os.path
from concurrent.futures import ProcessPoolExecutor
from subprocess import CalledProcessError
import f90nml
import matplotlib.pyplot as plt
import numpy as np
from openscm_runner.adapters.magicc7._parallel_process import _parallel_process
from scmdata import df_append
from _magicc_instances import _MagiccInstances
from tqdm.autonotebook import tqdm
from matplotlib.lines import Line2D
import seaborn as sns
logger = logging.getLogger()
logger.setLevel(logging.INFO)
stderr_info_handler = logging.StreamHandler()
formatter = logging.Formatter("%(name)s - %(levelname)s: %(message)s")
stderr_info_handler.setFormatter(formatter)
logger.addHandler(stderr_info_handler)
```
## Config
```
# how many MAGICC workers to use
NWORKERS = 4
# where should MAGICC copies be made
MAGICC_ROOT_DIR = os.path.expanduser(os.path.join(
""))
MAGICC_ROOT_DIR
data_path = ''
plots_path = ''
# where is the MAGICC executable to copy
os.environ["MAGICC_EXECUTABLE_6"] = os.path.expanduser(os.path.join())
os.environ["MAGICC_EXECUTABLE_6"]
```
## Parallel setup
```
shared_manager = multiprocessing.Manager()
shared_dict = shared_manager.dict()
if not os.path.isdir(MAGICC_ROOT_DIR):
os.makedirs(MAGICC_ROOT_DIR)
def init_magicc_worker(dict_shared_instances, root_dir):
logger.debug("Initialising process %s", multiprocessing.current_process())
logger.debug("Existing instances %s", dict_shared_instances)
def _run_func(magicc, cfg):
try:
scenario = cfg.pop("scenario")
res = magicc.run(**cfg)
res.set_meta(cfg["run_id"], "run_id")
res.set_meta(scenario, "scenario")
return res
except CalledProcessError as e:
# Swallow the exception, but return None
logger.debug("magicc run failed: {} (cfg: {})".format(e.stderr, cfg))
return None
instances = _MagiccInstances(existing_instances=shared_dict)
def _execute_run(cfg, run_func, setup_func):
magicc = instances.get(root_dir=MAGICC_ROOT_DIR, init_callback=setup_func)
return run_func(magicc, cfg)
def make_runs_list(cfgs):
"""
Turn the configs into a list which can be run in parallel.
Assigns ``run_id`` for each run if it's not already there.
"""
out = [
{
"cfg": {**{"run_id": i}, **cfg},
"run_func": _run_func,
"setup_func": _setup_func,
}
for i, cfg in enumerate(cfgs)
]
if not all(["scenario" in c["cfg"] for c in out]):
raise KeyError("Please include a key 'scenario' in each config")
return out
```
## Modify general MAGICC setup
```
def _setup_func(magicc):
logger.info(
"Setting up MAGICC worker in %s", magicc.root_dir,
)
magicc.set_config(
# can set config to be used in all runs here e.g.
# out_forcing=1
# OUT_CARBONCYCLE = 1,
# OUT_FORCING = 1,
RF_TOTAL_CONSTANTAFTERYR = 2500,
RF_TROPOZ_CONSTANTAFTERYR = 2500,
RF_STRATOZ_CONSTANTAFTERYR = 2500,
# FILE_TUNINGMODEL_2 = '', #C4MIP_UVIC
)
magicc.set_years(
# modify start- and endyear
endyear=2500
)
```
## Runs
First we need to get all our configs as a list of dictionaries, like the below.
```
# fetch the 600 probabilistic parameter sets from the MAGICC run directory
rundir=""
rundir_files = os.listdir(rundir)
probabilistic_files = [x for x in rundir_files if "MAGTUNE_DRAWNSET_CDF_RogeljIPCCrepresent_" in x ]
# one could also load the configs from the probabilistic sets using f90nml
# choose scenario
scenarios = [""]
# load probabilistic sets
cfgs = []
for scen in scenarios:
for f in probabilistic_files:
nml = f90nml.read(rundir+f)["nml_allcfgs"]
# add scenario information
nml["file_emissionscenario"]=scen
nml["scenario"]=scen.replace(".SCEN", "")
# append
cfgs.append(nml)
#cfgs = [
# {
# "core_climatesensitivity": cs,
# "rf_cloud_albedo_aer_wm2": rfcloud,
# "file_emissionscenario": scen,
# "scenario": scen.replace(".SCEN", "")
# }
# for cs, rfcloud in zip(
# np.round(np.linspace(2, 6, 50), 2),
# np.round(np.linspace(-0.2, -1.5, 50), 2)
# )
# for scen in ["RCP26.SCEN", "RCP45.SCEN"]
#]
#cfgs[:1]
runs = make_runs_list(cfgs)
#runs[:1]
try:
pool = ProcessPoolExecutor(
max_workers=NWORKERS,
initializer=init_magicc_worker,
initargs=(shared_dict, MAGICC_ROOT_DIR),
)
res_raw = _parallel_process(
func=_execute_run,
configuration=runs,
pool=pool,
config_are_kwargs=True,
front_serial=2,
front_parallel=2,
)
res = df_append([r for r in res_raw if r is not None])
finally:
instances.cleanup()
shared_manager.shutdown()
pool.shutdown()
temp_world = res.filter(variable="Surface Temperature", region = 'World').process_over("run_id", "median").T
rf_world = res.filter(variable="Radiative Forcing", region = 'World').process_over("run_id", "median").T
em_world = res.filter(variable="KYOTOGHGS_GWPEMIS", region = 'World').process_over("run_id", "median").T
temp_world_17 = res.filter(variable="Surface Temperature", region = 'World').process_over("run_id", operation="quantile", q=0.17).T
temp_world_83 = res.filter(variable="Surface Temperature", region = 'World').process_over("run_id", operation="quantile", q=0.83).T
rf_world_17 = res.filter(variable="Radiative Forcing", region = 'World').process_over("run_id", operation="quantile", q=0.17).T
rf_world_83 = res.filter(variable="Radiative Forcing", region = 'World').process_over("run_id", operation="quantile", q=0.83).T
temp_world.to_csv(data_path + 'median_temperatures_csv/' + 'temp_med_NDC5_SCa.csv')
temp_world_17.to_csv(data_path + 'quantile_temperatures_csv/' + 'temp_q17_NDC5_SCa.csv')
temp_world_83.to_csv(data_path + 'quantile_temperatures_csv/' + 'temp_q83_NDC5_SCa.csv')
rf_world.to_csv(data_path + 'median_rf_csv/' + 'rf_med_NDC5_SCa.csv')
rf_world_17.to_csv(data_path + 'quantile_rf_csv/' + 'rf_q17_NDC5_SCa.csv')
rf_world_83.to_csv(data_path + 'quantile_rf_csv/' + 'rf_q83_NDC5_SCa.csv')
em_world.to_csv(data_path + 'em_world.csv')
```
|
github_jupyter
|
import glob
import logging
import multiprocessing
import os.path
from concurrent.futures import ProcessPoolExecutor
from subprocess import CalledProcessError
import f90nml
import matplotlib.pyplot as plt
import numpy as np
from openscm_runner.adapters.magicc7._parallel_process import _parallel_process
from scmdata import df_append
from _magicc_instances import _MagiccInstances
from tqdm.autonotebook import tqdm
from matplotlib.lines import Line2D
import seaborn as sns
logger = logging.getLogger()
logger.setLevel(logging.INFO)
stderr_info_handler = logging.StreamHandler()
formatter = logging.Formatter("%(name)s - %(levelname)s: %(message)s")
stderr_info_handler.setFormatter(formatter)
logger.addHandler(stderr_info_handler)
# how many MAGICC workers to use
NWORKERS = 4
# where should MAGICC copies be made
MAGICC_ROOT_DIR = os.path.expanduser(os.path.join(
""))
MAGICC_ROOT_DIR
data_path = ''
plots_path = ''
# where is the MAGICC executable to copy
os.environ["MAGICC_EXECUTABLE_6"] = os.path.expanduser(os.path.join())
os.environ["MAGICC_EXECUTABLE_6"]
shared_manager = multiprocessing.Manager()
shared_dict = shared_manager.dict()
if not os.path.isdir(MAGICC_ROOT_DIR):
os.makedirs(MAGICC_ROOT_DIR)
def init_magicc_worker(dict_shared_instances, root_dir):
logger.debug("Initialising process %s", multiprocessing.current_process())
logger.debug("Existing instances %s", dict_shared_instances)
def _run_func(magicc, cfg):
try:
scenario = cfg.pop("scenario")
res = magicc.run(**cfg)
res.set_meta(cfg["run_id"], "run_id")
res.set_meta(scenario, "scenario")
return res
except CalledProcessError as e:
# Swallow the exception, but return None
logger.debug("magicc run failed: {} (cfg: {})".format(e.stderr, cfg))
return None
instances = _MagiccInstances(existing_instances=shared_dict)
def _execute_run(cfg, run_func, setup_func):
magicc = instances.get(root_dir=MAGICC_ROOT_DIR, init_callback=setup_func)
return run_func(magicc, cfg)
def make_runs_list(cfgs):
"""
Turn the configs into a list which can be run in parallel.
Assigns ``run_id`` for each run if it's not already there.
"""
out = [
{
"cfg": {**{"run_id": i}, **cfg},
"run_func": _run_func,
"setup_func": _setup_func,
}
for i, cfg in enumerate(cfgs)
]
if not all(["scenario" in c["cfg"] for c in out]):
raise KeyError("Please include a key 'scenario' in each config")
return out
def _setup_func(magicc):
logger.info(
"Setting up MAGICC worker in %s", magicc.root_dir,
)
magicc.set_config(
# can set config to be used in all runs here e.g.
# out_forcing=1
# OUT_CARBONCYCLE = 1,
# OUT_FORCING = 1,
RF_TOTAL_CONSTANTAFTERYR = 2500,
RF_TROPOZ_CONSTANTAFTERYR = 2500,
RF_STRATOZ_CONSTANTAFTERYR = 2500,
# FILE_TUNINGMODEL_2 = '', #C4MIP_UVIC
)
magicc.set_years(
# modify start- and endyear
endyear=2500
)
# fetch the 600 probabilistic parameter sets from the MAGICC run directory
rundir=""
rundir_files = os.listdir(rundir)
probabilistic_files = [x for x in rundir_files if "MAGTUNE_DRAWNSET_CDF_RogeljIPCCrepresent_" in x ]
# one could also load the configs from the probabilistic sets using f90nml
# choose scenario
scenarios = [""]
# load probabilistic sets
cfgs = []
for scen in scenarios:
for f in probabilistic_files:
nml = f90nml.read(rundir+f)["nml_allcfgs"]
# add scenario information
nml["file_emissionscenario"]=scen
nml["scenario"]=scen.replace(".SCEN", "")
# append
cfgs.append(nml)
#cfgs = [
# {
# "core_climatesensitivity": cs,
# "rf_cloud_albedo_aer_wm2": rfcloud,
# "file_emissionscenario": scen,
# "scenario": scen.replace(".SCEN", "")
# }
# for cs, rfcloud in zip(
# np.round(np.linspace(2, 6, 50), 2),
# np.round(np.linspace(-0.2, -1.5, 50), 2)
# )
# for scen in ["RCP26.SCEN", "RCP45.SCEN"]
#]
#cfgs[:1]
runs = make_runs_list(cfgs)
#runs[:1]
try:
pool = ProcessPoolExecutor(
max_workers=NWORKERS,
initializer=init_magicc_worker,
initargs=(shared_dict, MAGICC_ROOT_DIR),
)
res_raw = _parallel_process(
func=_execute_run,
configuration=runs,
pool=pool,
config_are_kwargs=True,
front_serial=2,
front_parallel=2,
)
res = df_append([r for r in res_raw if r is not None])
finally:
instances.cleanup()
shared_manager.shutdown()
pool.shutdown()
temp_world = res.filter(variable="Surface Temperature", region = 'World').process_over("run_id", "median").T
rf_world = res.filter(variable="Radiative Forcing", region = 'World').process_over("run_id", "median").T
em_world = res.filter(variable="KYOTOGHGS_GWPEMIS", region = 'World').process_over("run_id", "median").T
temp_world_17 = res.filter(variable="Surface Temperature", region = 'World').process_over("run_id", operation="quantile", q=0.17).T
temp_world_83 = res.filter(variable="Surface Temperature", region = 'World').process_over("run_id", operation="quantile", q=0.83).T
rf_world_17 = res.filter(variable="Radiative Forcing", region = 'World').process_over("run_id", operation="quantile", q=0.17).T
rf_world_83 = res.filter(variable="Radiative Forcing", region = 'World').process_over("run_id", operation="quantile", q=0.83).T
temp_world.to_csv(data_path + 'median_temperatures_csv/' + 'temp_med_NDC5_SCa.csv')
temp_world_17.to_csv(data_path + 'quantile_temperatures_csv/' + 'temp_q17_NDC5_SCa.csv')
temp_world_83.to_csv(data_path + 'quantile_temperatures_csv/' + 'temp_q83_NDC5_SCa.csv')
rf_world.to_csv(data_path + 'median_rf_csv/' + 'rf_med_NDC5_SCa.csv')
rf_world_17.to_csv(data_path + 'quantile_rf_csv/' + 'rf_q17_NDC5_SCa.csv')
rf_world_83.to_csv(data_path + 'quantile_rf_csv/' + 'rf_q83_NDC5_SCa.csv')
em_world.to_csv(data_path + 'em_world.csv')
| 0.238196 | 0.443781 |
# Ising Model
```
import numpy as np
import pandas as pd
from pystatplottools.pdf_env.loading_figure_mode import loading_figure_mode
fma, plt = loading_figure_mode(develop=True) # develop=False will export the generated figures as pngs into "./data/RectangleData"
plt.style.use('seaborn-dark-palette')
if 'root_dir' not in locals():
# Navigate to simulations/IsingModel directory as simulation root directory
import os
os.chdir("../simulations/IsingModel")
root_dir = os.getcwd()
# To be able to compute custom measures
import sys
sys.path.append("./../../python_scripts")
mcmc_model_dir = "IsingModelMetropolis/"
mcmc_data_dir = root_dir + "/data/" + mcmc_model_dir
mcmc_results_dir = root_dir + "/results/" + mcmc_model_dir
data_dir = root_dir + "/data/" + mcmc_model_dir
results_dir = root_dir + "/results/" + mcmc_model_dir
```
## MCMC Results
### Expectation Values
```
from mcmctools.modes.expectation_value import load_expectation_value_results
expectation_values = load_expectation_value_results(files_dir="IsingModelMetropolis")
expectation_values
```
## Correlation Times
```
from pystatplottools.utils.utils import load_json
# Loaded from different simulation
correlation_times = load_json("./results/IsingModelMetropolis/correlation_time_results.json")
print(correlation_times)
```
## Configurations as Pytorch Dataset
We show how the mcmc configurations can be stored and loaded as a .pt file.
(See also python_scripts/loading_configurations.py and python_scripts/pytorch_data_generation.py)
### Preparation
```
data_generator_args = {
# ConfigDataGenerator Args
"data_type": "target_param",
# Args for ConfigurationLoader
"path": mcmc_data_dir,
"total_number_of_data_per_file": 10000,
"identifier": "expectation_value",
"running_parameter": "beta",
"chunksize": 400 # If no chunksize is given, all data is loaded at once
}
# Prepare in memory dataset
from pystatplottools.pytorch_data_generation.data_generation.datagenerationroutines import prepare_in_memory_dataset
from mcmctools.pytorch.data_generation.datagenerationroutines import data_generator_factory
prepare_in_memory_dataset(
root=data_dir,
batch_size=89,
data_generator_args=data_generator_args,
data_generator_name="BatchConfigDataGenerator",
data_generator_factory=data_generator_factory
)
```
### Generating and Loading the Dataset
```
# Load in memory dataset
from pystatplottools.pytorch_data_generation.data_generation.datagenerationroutines import load_in_memory_dataset
# The dataset is generated and stored as a .pt file in the data_dir/data directory the first time this function is called. Otherwise the .pt is loaded.
data_loader = load_in_memory_dataset(
root=data_dir, batch_size=89, data_generator_factory=data_generator_factory, slices=None, shuffle=True,
num_workers=0, rebuild=False
# sample_data_generator_name="ConfigDataGenerator" # optional: for a generation of new samples
)
# Load training data
for batch_idx, batch in enumerate(data_loader):
data, target = batch
# print(batch_idx, len(data))
```
### Inspection of the Dataset - Sample Visualization
```
from pystatplottools.visualization import sample_visualization
config_dim = (4, 4) # Dimension of the data
ab = (-1, 1) # Data is expected to be in the range (-1, 1)
# Random samples
config, label = data_loader.dataset.get_random_sample()
batch, batch_label = data_loader.dataset.get_random_batch(108)
# Single Sample
sample_visualization.fd_im_single_sample(sample=config, label=label, config_dim=config_dim, ab=ab,
fma=fma, filename="single_sample", directory=results_dir, figsize=(4, 4));
# Batch with labels
sample_visualization.fd_im_batch(batch, batch_labels=batch_label, num_samples=36, dim=(6, 6),
config_dim=config_dim, ab=ab,
fma=fma, filename="batch", directory=results_dir, width=2.3, ratio=1.0, figsize=(12, 12));
# Batch grid
sample_visualization.fd_im_batch_grid(batch, config_dim=config_dim, ab=ab,
fma=fma, filename="batch_grid", directory=results_dir);
```
## Data Evaluation with the pystatplottools Library
We demonstrate possible ways to use the pystatplottools library to evaluate results of a mcmc simulation.
### Preparation
```
# Load all data
from mcmctools.loading.loading import load_data
# skipcols=[] Can be used to load only certain columns of the different files
data, filenames = load_data(files_dir=mcmc_model_dir, running_parameter="beta",
identifier="expectation_value") # , skipcols=["Config"])
from mcmctools.utils.json import load_configs
sim_params, execution_params, running_parameter = load_configs(
files_dir="IsingModelMetropolis", mode="expectation_value", project_base_dir="./")
data
```
### Transform to Balanced Dataset
A trick is applied to obtain a mean value for the magnetization that is approximately zero for all temperatures
without an external field - this trick should of course not be applied if the external field is finite.
```
mean_values = data.groupby("beta")["Mean"].apply(lambda x: x.mean())
percentages = (1 + mean_values) / 2.0
for beta in data.index.unique(level=0):
random_index = None
num_to_be_changed_rows = int(len(data) / len(data.index.unique(level=0)) * (percentages - 0.5).loc[beta])
if num_to_be_changed_rows < 0:
random_index = (data.loc[beta]["Mean"] < 0).sample(abs(num_to_be_changed_rows)).index
elif num_to_be_changed_rows > 0:
random_index = (data.loc[beta]["Mean"] > 0).sample(abs(num_to_be_changed_rows)).index
if random_index is not None:
data.loc[(beta, random_index), ("Config", slice(None))] = data.loc[
(beta, random_index), ("Config", slice(None))].apply(lambda x: -1.0 * x)
data.Mean = data.Config.values.mean(axis=1)
```
### Compute the Energy of the Ising Model from the Samples
```
from mcmctools.modes.expectation_value import compute_measures_over_config
new_measures, data = compute_measures_over_config(data=data, measures=["Energy", "SecondMoment", "AbsMean"], sim_params=sim_params)
data
```
### Alternativ Computation of the Expectation Values
#### General Statistics
```
from pystatplottools.expectation_values.expectation_value import ExpectationValue
ep = ExpectationValue(data=data)
# Computes for the given columns the respective expectation values - The expectation values are computed seperately for each inverse temperature 'beta'
ep.compute_expectation_value(columns=["Mean", "AbsMean", "SecondMoment"],
exp_values=["mean", "max", "min", "secondmoment", "fourthmoment"])
expectation_values = ep.expectation_values
if "Config" in data.columns:
expectation_values = expectation_values.droplevel(level=1, axis=1)
expectation_values
```
#### Visualization
```
fig, axes = fma.newfig(1.4, ratio=0.5, ncols=2, figsize=(12, 5))
betas = expectation_values.index.values.astype(np.float32)
axes[0].plot(betas, expectation_values["Mean"]["mean"], label="Mean")
axes[0].plot(betas, expectation_values["Mean"]["min"], color="C{}".format(1), ls="-.", label="Min")
axes[0].plot(betas, expectation_values["Mean"]["max"], color="C{}".format(1), ls="--", label="Max")
axes[0].plot(betas,
expectation_values["Mean"]["secondmoment"] - expectation_values["Mean"]["mean"].apply(
lambda x: np.power(x, 2.0)
),
color="C{}".format(1), ls=":", label="Variance")
axes[0].legend()
axes[0].set_xlabel("Beta")
axes[0].set_ylabel("Mean")
axes[1].plot(betas, expectation_values["AbsMean"]["mean"], label="AbsMean")
axes[1].plot(betas, expectation_values["AbsMean"]["min"], color="C{}".format(1), ls="-.", label="Min")
axes[1].plot(betas, expectation_values["AbsMean"]["max"], color="C{}".format(1), ls="--", label="Max")
axes[1].plot(betas,
expectation_values["AbsMean"]["secondmoment"] - expectation_values["AbsMean"]["mean"].apply(
lambda x: np.power(x, 2.0)
), color="C{}".format(1), ls=":", label="Variance")
axes[1].legend()
axes[1].set_xlabel("Beta")
axes[1].set_ylabel("AbsMean")
plt.tight_layout()
fma.savefig(results_dir, "expectation_values")
```
#### Specific Heat and Binder Cumulant
```
# Add necessary expectation values to exisiting expectation values
ep.compute_expectation_value(columns=["Mean"], exp_values=["secondmoment", "fourthmoment"])
ep.compute_expectation_value(columns=["Energy"], exp_values=["var"])
expectation_values = ep.expectation_values
if "Config" in data.columns:
expectation_values = expectation_values.droplevel(level=1, axis=1)
n_sites = len(data.iloc[0]["Config"])
binder_cumulant = 1.0 - expectation_values["Mean"]["fourthmoment"] / (
3.0 * expectation_values["Mean"]["secondmoment"].pow(2.0))
specific_heat = np.power(expectation_values.index.values.astype(np.float), 2.0) / n_sites * \
expectation_values["Energy"]["var"]
observables = pd.concat([binder_cumulant, specific_heat], axis=1, keys=["BinderCumulant", "SpecificHeat"])
observables
```
#### Visualization
```
fig, axes = fma.newfig(1.4, ratio=0.5, ncols=2, figsize=(12, 5))
betas = observables.index.values.astype(np.float32)
axes[0].plot(betas, observables["BinderCumulant"])
axes[0].set_xlabel("Beta")
axes[0].set_ylabel("Binder Cumulant")
axes[1].plot(betas, observables["SpecificHeat"])
axes[1].set_xlabel("Beta")
axes[1].set_ylabel("Specific Heat")
plt.tight_layout()
fma.savefig(results_dir, "observables")
```
### Histograms for the Different Inverse Temperatures
```
from pystatplottools.distributions.marginal_distribution import MarginalDistribution
histograms = MarginalDistribution(data=data)
range_min, range_max = histograms.extract_min_max_range_values(columns=["Mean", "AbsMean", "Energy"])
histograms.compute(
axes_indices=["Mean", "AbsMean", "Energy"],
range_min=range_min,
range_max=range_max,
nbins=8,
statistic='probability',
bin_scales='linear'
)
linearized_histograms = histograms.linearize(
order_by_bin=True,
bin_alignment="center"
)
linearized_histograms
```
#### Visualization
```
from pystatplottools.utils.bins_and_alignment import revert_align_bins
betas = data.index.unique(0)
fig, axes = fma.newfig(1.8, nrows=3, ncols=7, ratio=0.5, figsize=(12, 5))
for i, beta in enumerate(list(betas)[::4]):
for j, observable in enumerate(["Mean", "AbsMean", "Energy"]):
binedges = revert_align_bins(
data_range=linearized_histograms.loc[observable]["bin"].values,
bin_alignment="center"
)
width = 0.9 * (binedges[1:] - binedges[:-1])
axes[j][i].bar(
x=linearized_histograms.loc[observable]["bin"].values,
height=linearized_histograms.loc[observable][beta].values,
width=width
)
axes[j][i].set_xlabel(observable)
from pystatplottools.visualization.utils import add_fancy_legend_box
add_fancy_legend_box(ax=axes[j][i], name=float(beta))
for j, observable in enumerate(["Mean", "AbsMean", "Energy"]):
axes[j][0].set_ylabel("P(" + observable + ")")
plt.tight_layout()
fma.savefig(results_dir, "histograms")
```
### Joint Distribution and Contour Plot - Probability of Mean vs. Temperature With Logarithmic Scale
```
from pystatplottools.distributions.joint_distribution import JointDistribution
from pystatplottools.utils.utils import drop_index_level
joint_distribution = JointDistribution(data=drop_index_level(data))
range_min, range_max = joint_distribution.extract_min_max_range_values(["Beta", "Mean"])
joint_distribution.compute(
axes_indices=["Beta", "Mean"],
range_min=[0.05, range_min[1]],
range_max=[0.75, range_max[1]],
nbins=[7, 10],
statistic="probability"
)
# The histograms can be accessed via: joint_distribution.distribution or linearized.
# Transforms joint_distribution into a linear list of mid boundaries for the different bins
# and the respective statistics for the values
linearized_joint_distribution = joint_distribution.linearize(
output_statistics_name="prob",
dataframes_as_columns=False,
bin_alignment="center"
)
linearized_joint_distribution
```
#### Visualization
```
# Contour plot
fig, ax = fma.newfig(1.4, figsize=(10, 7))
from pystatplottools.plotting.contour2D import Contour2D
contour2D = Contour2D(
ax=ax,
data=linearized_joint_distribution.loc["df"],
x="Beta", # possibility to rescale x and y axis or perform other operation for x axis
# like computing a mass difference
y="Mean",
z_index="prob"
)
norm, levs = contour2D.get_log_norm_and_levs(lev_min=0.00001, lev_max=1, lev_num=40)
contour2D.set_ax_labels(x_label="Beta", y_label="Mean")
cf = contour2D.pcolormesh(
norm=norm,
levs=levs,
cmap="PiYG"
)
contour2D.add_colorbar(fig=fig, cf=cf, z_label="Probability")
plt.tight_layout()
fma.savefig(results_dir, "mean_vs_beta")
```
|
github_jupyter
|
import numpy as np
import pandas as pd
from pystatplottools.pdf_env.loading_figure_mode import loading_figure_mode
fma, plt = loading_figure_mode(develop=True) # develop=False will export the generated figures as pngs into "./data/RectangleData"
plt.style.use('seaborn-dark-palette')
if 'root_dir' not in locals():
# Navigate to simulations/IsingModel directory as simulation root directory
import os
os.chdir("../simulations/IsingModel")
root_dir = os.getcwd()
# To be able to compute custom measures
import sys
sys.path.append("./../../python_scripts")
mcmc_model_dir = "IsingModelMetropolis/"
mcmc_data_dir = root_dir + "/data/" + mcmc_model_dir
mcmc_results_dir = root_dir + "/results/" + mcmc_model_dir
data_dir = root_dir + "/data/" + mcmc_model_dir
results_dir = root_dir + "/results/" + mcmc_model_dir
from mcmctools.modes.expectation_value import load_expectation_value_results
expectation_values = load_expectation_value_results(files_dir="IsingModelMetropolis")
expectation_values
from pystatplottools.utils.utils import load_json
# Loaded from different simulation
correlation_times = load_json("./results/IsingModelMetropolis/correlation_time_results.json")
print(correlation_times)
data_generator_args = {
# ConfigDataGenerator Args
"data_type": "target_param",
# Args for ConfigurationLoader
"path": mcmc_data_dir,
"total_number_of_data_per_file": 10000,
"identifier": "expectation_value",
"running_parameter": "beta",
"chunksize": 400 # If no chunksize is given, all data is loaded at once
}
# Prepare in memory dataset
from pystatplottools.pytorch_data_generation.data_generation.datagenerationroutines import prepare_in_memory_dataset
from mcmctools.pytorch.data_generation.datagenerationroutines import data_generator_factory
prepare_in_memory_dataset(
root=data_dir,
batch_size=89,
data_generator_args=data_generator_args,
data_generator_name="BatchConfigDataGenerator",
data_generator_factory=data_generator_factory
)
# Load in memory dataset
from pystatplottools.pytorch_data_generation.data_generation.datagenerationroutines import load_in_memory_dataset
# The dataset is generated and stored as a .pt file in the data_dir/data directory the first time this function is called. Otherwise the .pt is loaded.
data_loader = load_in_memory_dataset(
root=data_dir, batch_size=89, data_generator_factory=data_generator_factory, slices=None, shuffle=True,
num_workers=0, rebuild=False
# sample_data_generator_name="ConfigDataGenerator" # optional: for a generation of new samples
)
# Load training data
for batch_idx, batch in enumerate(data_loader):
data, target = batch
# print(batch_idx, len(data))
from pystatplottools.visualization import sample_visualization
config_dim = (4, 4) # Dimension of the data
ab = (-1, 1) # Data is expected to be in the range (-1, 1)
# Random samples
config, label = data_loader.dataset.get_random_sample()
batch, batch_label = data_loader.dataset.get_random_batch(108)
# Single Sample
sample_visualization.fd_im_single_sample(sample=config, label=label, config_dim=config_dim, ab=ab,
fma=fma, filename="single_sample", directory=results_dir, figsize=(4, 4));
# Batch with labels
sample_visualization.fd_im_batch(batch, batch_labels=batch_label, num_samples=36, dim=(6, 6),
config_dim=config_dim, ab=ab,
fma=fma, filename="batch", directory=results_dir, width=2.3, ratio=1.0, figsize=(12, 12));
# Batch grid
sample_visualization.fd_im_batch_grid(batch, config_dim=config_dim, ab=ab,
fma=fma, filename="batch_grid", directory=results_dir);
# Load all data
from mcmctools.loading.loading import load_data
# skipcols=[] Can be used to load only certain columns of the different files
data, filenames = load_data(files_dir=mcmc_model_dir, running_parameter="beta",
identifier="expectation_value") # , skipcols=["Config"])
from mcmctools.utils.json import load_configs
sim_params, execution_params, running_parameter = load_configs(
files_dir="IsingModelMetropolis", mode="expectation_value", project_base_dir="./")
data
mean_values = data.groupby("beta")["Mean"].apply(lambda x: x.mean())
percentages = (1 + mean_values) / 2.0
for beta in data.index.unique(level=0):
random_index = None
num_to_be_changed_rows = int(len(data) / len(data.index.unique(level=0)) * (percentages - 0.5).loc[beta])
if num_to_be_changed_rows < 0:
random_index = (data.loc[beta]["Mean"] < 0).sample(abs(num_to_be_changed_rows)).index
elif num_to_be_changed_rows > 0:
random_index = (data.loc[beta]["Mean"] > 0).sample(abs(num_to_be_changed_rows)).index
if random_index is not None:
data.loc[(beta, random_index), ("Config", slice(None))] = data.loc[
(beta, random_index), ("Config", slice(None))].apply(lambda x: -1.0 * x)
data.Mean = data.Config.values.mean(axis=1)
from mcmctools.modes.expectation_value import compute_measures_over_config
new_measures, data = compute_measures_over_config(data=data, measures=["Energy", "SecondMoment", "AbsMean"], sim_params=sim_params)
data
from pystatplottools.expectation_values.expectation_value import ExpectationValue
ep = ExpectationValue(data=data)
# Computes for the given columns the respective expectation values - The expectation values are computed seperately for each inverse temperature 'beta'
ep.compute_expectation_value(columns=["Mean", "AbsMean", "SecondMoment"],
exp_values=["mean", "max", "min", "secondmoment", "fourthmoment"])
expectation_values = ep.expectation_values
if "Config" in data.columns:
expectation_values = expectation_values.droplevel(level=1, axis=1)
expectation_values
fig, axes = fma.newfig(1.4, ratio=0.5, ncols=2, figsize=(12, 5))
betas = expectation_values.index.values.astype(np.float32)
axes[0].plot(betas, expectation_values["Mean"]["mean"], label="Mean")
axes[0].plot(betas, expectation_values["Mean"]["min"], color="C{}".format(1), ls="-.", label="Min")
axes[0].plot(betas, expectation_values["Mean"]["max"], color="C{}".format(1), ls="--", label="Max")
axes[0].plot(betas,
expectation_values["Mean"]["secondmoment"] - expectation_values["Mean"]["mean"].apply(
lambda x: np.power(x, 2.0)
),
color="C{}".format(1), ls=":", label="Variance")
axes[0].legend()
axes[0].set_xlabel("Beta")
axes[0].set_ylabel("Mean")
axes[1].plot(betas, expectation_values["AbsMean"]["mean"], label="AbsMean")
axes[1].plot(betas, expectation_values["AbsMean"]["min"], color="C{}".format(1), ls="-.", label="Min")
axes[1].plot(betas, expectation_values["AbsMean"]["max"], color="C{}".format(1), ls="--", label="Max")
axes[1].plot(betas,
expectation_values["AbsMean"]["secondmoment"] - expectation_values["AbsMean"]["mean"].apply(
lambda x: np.power(x, 2.0)
), color="C{}".format(1), ls=":", label="Variance")
axes[1].legend()
axes[1].set_xlabel("Beta")
axes[1].set_ylabel("AbsMean")
plt.tight_layout()
fma.savefig(results_dir, "expectation_values")
# Add necessary expectation values to exisiting expectation values
ep.compute_expectation_value(columns=["Mean"], exp_values=["secondmoment", "fourthmoment"])
ep.compute_expectation_value(columns=["Energy"], exp_values=["var"])
expectation_values = ep.expectation_values
if "Config" in data.columns:
expectation_values = expectation_values.droplevel(level=1, axis=1)
n_sites = len(data.iloc[0]["Config"])
binder_cumulant = 1.0 - expectation_values["Mean"]["fourthmoment"] / (
3.0 * expectation_values["Mean"]["secondmoment"].pow(2.0))
specific_heat = np.power(expectation_values.index.values.astype(np.float), 2.0) / n_sites * \
expectation_values["Energy"]["var"]
observables = pd.concat([binder_cumulant, specific_heat], axis=1, keys=["BinderCumulant", "SpecificHeat"])
observables
fig, axes = fma.newfig(1.4, ratio=0.5, ncols=2, figsize=(12, 5))
betas = observables.index.values.astype(np.float32)
axes[0].plot(betas, observables["BinderCumulant"])
axes[0].set_xlabel("Beta")
axes[0].set_ylabel("Binder Cumulant")
axes[1].plot(betas, observables["SpecificHeat"])
axes[1].set_xlabel("Beta")
axes[1].set_ylabel("Specific Heat")
plt.tight_layout()
fma.savefig(results_dir, "observables")
from pystatplottools.distributions.marginal_distribution import MarginalDistribution
histograms = MarginalDistribution(data=data)
range_min, range_max = histograms.extract_min_max_range_values(columns=["Mean", "AbsMean", "Energy"])
histograms.compute(
axes_indices=["Mean", "AbsMean", "Energy"],
range_min=range_min,
range_max=range_max,
nbins=8,
statistic='probability',
bin_scales='linear'
)
linearized_histograms = histograms.linearize(
order_by_bin=True,
bin_alignment="center"
)
linearized_histograms
from pystatplottools.utils.bins_and_alignment import revert_align_bins
betas = data.index.unique(0)
fig, axes = fma.newfig(1.8, nrows=3, ncols=7, ratio=0.5, figsize=(12, 5))
for i, beta in enumerate(list(betas)[::4]):
for j, observable in enumerate(["Mean", "AbsMean", "Energy"]):
binedges = revert_align_bins(
data_range=linearized_histograms.loc[observable]["bin"].values,
bin_alignment="center"
)
width = 0.9 * (binedges[1:] - binedges[:-1])
axes[j][i].bar(
x=linearized_histograms.loc[observable]["bin"].values,
height=linearized_histograms.loc[observable][beta].values,
width=width
)
axes[j][i].set_xlabel(observable)
from pystatplottools.visualization.utils import add_fancy_legend_box
add_fancy_legend_box(ax=axes[j][i], name=float(beta))
for j, observable in enumerate(["Mean", "AbsMean", "Energy"]):
axes[j][0].set_ylabel("P(" + observable + ")")
plt.tight_layout()
fma.savefig(results_dir, "histograms")
from pystatplottools.distributions.joint_distribution import JointDistribution
from pystatplottools.utils.utils import drop_index_level
joint_distribution = JointDistribution(data=drop_index_level(data))
range_min, range_max = joint_distribution.extract_min_max_range_values(["Beta", "Mean"])
joint_distribution.compute(
axes_indices=["Beta", "Mean"],
range_min=[0.05, range_min[1]],
range_max=[0.75, range_max[1]],
nbins=[7, 10],
statistic="probability"
)
# The histograms can be accessed via: joint_distribution.distribution or linearized.
# Transforms joint_distribution into a linear list of mid boundaries for the different bins
# and the respective statistics for the values
linearized_joint_distribution = joint_distribution.linearize(
output_statistics_name="prob",
dataframes_as_columns=False,
bin_alignment="center"
)
linearized_joint_distribution
# Contour plot
fig, ax = fma.newfig(1.4, figsize=(10, 7))
from pystatplottools.plotting.contour2D import Contour2D
contour2D = Contour2D(
ax=ax,
data=linearized_joint_distribution.loc["df"],
x="Beta", # possibility to rescale x and y axis or perform other operation for x axis
# like computing a mass difference
y="Mean",
z_index="prob"
)
norm, levs = contour2D.get_log_norm_and_levs(lev_min=0.00001, lev_max=1, lev_num=40)
contour2D.set_ax_labels(x_label="Beta", y_label="Mean")
cf = contour2D.pcolormesh(
norm=norm,
levs=levs,
cmap="PiYG"
)
contour2D.add_colorbar(fig=fig, cf=cf, z_label="Probability")
plt.tight_layout()
fma.savefig(results_dir, "mean_vs_beta")
| 0.670393 | 0.788135 |
```
# coding: utf-8
from glob import glob
import os.path as op
import pandas as pd
import numpy as np
from bids.layout import BIDSLayout
out_dir = '/home/data/nbc/Sutherland_HIVCB/EAT-behavioral/'
dset_dir = '/home/data/nbc/Sutherland_HIVCB/dset/'
layout = BIDSLayout(dset_dir)
subjects = layout.get_subjects()
#subjects = subjects[:5]
#subjects.remove('283')
#subjects.remove('397')
#subjects.remove('406')
out_df = pd.DataFrame(
columns=['n_correct_incongruent', 'n_incorrect_incongruent', 'n_incongruent',
'n_correct_repeat', 'n_incorrect_repeat', 'n_repeat',
'n_correct_nogo', 'n_incorrect_go', 'n_incorrect_nogo', 'n_nogo',
'n_correct_go', 'n_incorrect_go', 'n_go', 'n_nogo_aware',
'n_nogo_unaware', 'n_nogo_noresponse',
'mean_pre_correct_rt', 'mean_post_correct_rt',
'mean_aware_stroop_rt', 'mean_aware_repeat_rt',
'mean_unaware_stroop_rt', 'mean_unaware_repeat_rt',
'mean_pre_aware_rt', 'mean_post_aware_rt',
'mean_pre_unaware_rt', 'mean_post_unaware_rt',
'mean_nogo_aware_rt', 'mean_nogo_unaware_rt',
'mean_incorrect_incongruent_rt', 'std_incorrect_incongruent_rt',
'mean_incongruent_rt', 'std_incongruent_rt',
'mean_incorrect_repeat_rt', 'std_incorrect_repeat_rt',
'mean_repeat_rt', 'std_repeat_rt',
'mean_incorrect_nogo_rt', 'std_incorrect_nogo_rt',
'mean_correct_nogo_rt', 'std_correct_nogo_rt',
'mean_correct_go_rt', 'std_correct_go_rt',
'n_aware_repeat', 'n_unaware_repeat', 'n_aware_stroop', 'n_unaware_stroop',
'mean_incorrect_go_rt', 'std_incorrect_go_rt', 'mean_onepost_aware_rt', 'mean_onepost_unaware_rt'],
index=subjects)
for subject in subjects:
files = sorted(glob(op.join(dset_dir, 'sub-'+subject+'/func/sub-*_task-errorawareness*events.tsv')))
if not files:
print('{0} failed'.format(subject))
continue
else:
print('{0} running'.format(subject))
dfs = [pd.read_csv(f, sep='\t') for f in files]
df = pd.concat(dfs)
df['go'] = df['trial_type_2'].str.startswith('go').astype(int)
#df['nogo_error'] = df['trial_type_2'].str.startswith('nogoIncorrect').astype(int)
acc_df1 = df.groupby(['trial_type', 'trial_accuracy']).count()
acc_df2 = df.groupby(['trial_type']).count()
acc_df3 = df.groupby(['trial_type_2', 'trial_accuracy']).count()
acc_df4 = df.groupby(['trial_type_2']).count()
acc_df5 = df.groupby(['trial_type_2']).count()
acc_df6 = df.groupby(['trial_type_3']).count()
rt_df1 = df.groupby(['trial_type', 'trial_accuracy']).mean()
rt_df2 = df.groupby(['trial_type']).mean()
rt_df3 = df.groupby(['trial_type_2', 'trial_accuracy']).mean()
rt_df4 = df.groupby(['trial_type_2']).mean()
rt_df5 = df.groupby(['trial_type', 'trial_accuracy']).std()
rt_df6 = df.groupby(['trial_type']).std()
rt_df7 = df.groupby(['trial_type_2', 'trial_accuracy']).std()
rt_df8 = df.groupby(['trial_type_2']).std()
rt_df9 = df.groupby(['trial_type_2']).mean()
rt_df12 = df.groupby(['trial_type_3']).mean()
df['all_nogoIncorrect'] = df['trial_type_2'].str.startswith('nogoIncorrect')
rt_df10 = df.groupby(['all_nogoIncorrect']).mean()
rt_df11 = df.groupby(['all_nogoIncorrect']).std()
try:
out_df.loc[subject, 'n_correct_incongruent'] = acc_df1.loc[('incongruent', 1), 'onset']
except:
out_df.loc[subject, 'n_correct_incongruent'] = 0
try:
out_df.loc[subject, 'n_incorrect_incongruent'] = acc_df1.loc[('incongruent', 0), 'onset']
out_df.loc[subject, 'mean_incorrect_incongruent_rt'] = rt_df1.loc[('incongruent', 0), 'response_time']
out_df.loc[subject, 'std_incorrect_incongruent_rt'] = rt_df5.loc[('incongruent', 0), 'response_time']
except:
out_df.loc[subject, 'n_correct_incongruent'] = 0
out_df.loc[subject, 'mean_incorrect_incongruent_rt'] = np.NaN
out_df.loc[subject, 'std_incorrect_incongruent_rt'] = np.NaN
try:
out_df.loc[subject, 'n_correct_repeat'] = acc_df1.loc[('repeat', 1), 'onset']
except:
out_df.loc[subject, 'n_correct_repeat'] = 0
try:
out_df.loc[subject, 'n_incorrect_repeat'] = acc_df1.loc[('repeat', 0), 'onset']
out_df.loc[subject, 'mean_incorrect_repeat_rt'] = rt_df1.loc[('repeat', 0), 'response_time']
out_df.loc[subject, 'std_incorrect_repeat_rt'] = rt_df5.loc[('repeat', 0), 'response_time']
except:
out_df.loc[subject, 'n_incorrect_repeat'] = 0
out_df.loc[subject, 'mean_incorrect_repeat_rt'] = np.NaN
out_df.loc[subject, 'std_incorrect_repeat_rt'] = np.NaN
out_df.loc[subject, 'n_correct_nogo'] = df.loc[df['trial_type_2'] == 'nogoCorrect'].shape[0]
out_df.loc[subject, 'n_correct_go'] = df.loc[df['trial_type_2'] == 'goCorrect'].shape[0]
out_df.loc[subject, 'n_incorrect_nogo'] = df.loc[df['trial_type_2'].str.startswith('nogoIncorrect')].shape[0]
out_df.loc[subject, 'n_correct_nogo'] = df.loc[df['trial_type_2'] == 'nogoCorrect'].shape[0]
out_df.loc[subject, 'n_incorrect_go'] = df.loc[df['trial_type_2'] == 'goIncorrect'].shape[0]
out_df.loc[subject, 'n_nogo_aware'] = df.loc[df['trial_type_2'] == 'nogoIncorrectAware'].shape[0]
out_df.loc[subject, 'n_nogo_unaware'] = df.loc[df['trial_type_2'] == 'nogoIncorrectUnaware'].shape[0]
out_df.loc[subject, 'n_nogo_noresponse'] = df.loc[df['trial_type_2'].str.startswith('nogoIncorrectNoResponse')].shape[0]
#out_df.loc[subject, 'n_nogo'] = df.loc[df['trial_type_2'].str.startswith('nogo')].shape[0]
#out_df.loc[subject, 'n_go'] = df.loc[df['trial_type_2'].str.startswith('go')].shape[0]
try:
out_df.loc[subject, 'mean_incorrect_nogo_rt'] = rt_df10.loc[1, 'response_time']
out_df.loc[subject, 'std_incorrect_nogo_rt'] = rt_df11.loc[1, 'response_time']
except:
out_df.loc[subject, 'mean_incorrect_nogo_rt'] = np.NaN
out_df.loc[subject, 'std_incorrect_nogo_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_correct_nogo_rt'] = rt_df9.loc['nogoCorrect', 'response_time']
out_df.loc[subject, 'std_correct_nogo_rt'] = rt_df8.loc['nogoCorrect', 'response_time']
except:
out_df.loc[subject, 'mean_correct_nogo_rt'] = np.NaN
out_df.loc[subject, 'std_correct_nogo_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_correct_go_rt'] = rt_df9.loc['goCorrect', 'response_time']
out_df.loc[subject, 'std_correct_go_rt'] = rt_df8.loc['goCorrect', 'response_time']
except:
out_df.loc[subject, 'mean_correct_go_rt'] = np.NaN
out_df.loc[subject, 'std_correct_go_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_incorrect_go_rt'] = rt_df9.loc['goIncorrect', 'response_time']
out_df.loc[subject, 'std_incorrect_go_rt'] = rt_df8.loc['goIncorrect', 'response_time']
except:
out_df.loc[subject, 'mean_incorrect_go_rt'] = np.NaN
out_df.loc[subject, 'std_incorrect_go_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_nogo_aware_rt'] = rt_df9.loc['nogoIncorrectAware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_aware'] = 0
out_df.loc[subject, 'mean_nogo_aware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_nogo_unaware_rt'] = rt_df9.loc['nogoIncorrectUnaware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_unaware'] = 0
out_df.loc[subject, 'mean_nogo_unaware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_aware_stroop_rt'] = rt_df12.loc['stroopIncorrectAware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_aware'] = 0
out_df.loc[subject, 'mean_aware_stroop_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_aware_repeat_rt'] = rt_df12.loc['repeatIncorrectAware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_aware'] = 0
out_df.loc[subject, 'mean_aware_repeat_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_unaware_stroop_rt'] = rt_df12.loc['stroopIncorrectUnaware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_unaware'] = 0
out_df.loc[subject, 'mean_unaware_stroop_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_unaware_repeat_rt'] = rt_df12.loc['repeatIncorrectUnaware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_unaware'] = 0
out_df.loc[subject, 'mean_unaware_repeat_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_pre_aware_rt'] = rt_df12.loc['preIncorrectAware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_aware'] = 0
out_df.loc[subject, 'mean_pre_aware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_post_aware_rt'] = rt_df12.loc['postIncorrectAware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_aware'] = 0
out_df.loc[subject, 'mean_post_aware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_onepost_aware_rt'] = rt_df12.loc['onepostIncorrectAware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_aware'] = 0
out_df.loc[subject, 'mean_onepost_aware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_pre_unaware_rt'] = rt_df12.loc['preIncorrectUnaware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_unaware'] = 0
out_df.loc[subject, 'mean_pre_unaware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_post_unaware_rt'] = rt_df12.loc['postIncorrectUnaware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_unaware'] = 0
out_df.loc[subject, 'mean_post_unaware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_onepost_unaware_rt'] = rt_df12.loc['onepostIncorrectUnaware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_unaware'] = 0
out_df.loc[subject, 'mean_onepost_unaware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_pre_correct_rt'] = rt_df12.loc['pre-nogoCorrect', 'response_time']
except:
out_df.loc[subject, 'n_nogo_correct'] = 0
out_df.loc[subject, 'mean_pre_correct_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_post_correct_rt'] = rt_df12.loc['post-nogoCorrect', 'response_time']
except:
out_df.loc[subject, 'n_nogo_correct'] = 0
out_df.loc[subject, 'mean_post_correct_rt'] = np.NaN
out_df.loc[subject, 'n_incongruent'] = acc_df2.loc['incongruent', 'onset']
out_df.loc[subject, 'mean_incongruent_rt'] = rt_df2.loc['incongruent', 'response_time']
out_df.loc[subject, 'std_incongruent_rt'] = rt_df6.loc['incongruent', 'response_time']
out_df.loc[subject, 'n_repeat'] = acc_df2.loc['repeat', 'onset']
out_df.loc[subject, 'mean_repeat_rt'] = rt_df2.loc['repeat', 'response_time']
out_df.loc[subject, 'std_repeat_rt'] = rt_df6.loc['repeat', 'response_time']
try:
out_df.loc[subject, 'n_aware_stroop'] = acc_df6.loc['stroopIncorrectAware', 'onset']
except:
out_df.loc[subject, 'n_aware_stroop'] = 0
try:
out_df.loc[subject, 'n_aware_repeat'] = acc_df6.loc['repeatIncorrectAware', 'onset']
except:
out_df.loc[subject, 'n_aware_repeat'] = 0
try:
out_df.loc[subject, 'n_unaware_repeat'] = acc_df6.loc['repeatIncorrectUnaware', 'onset']
except:
out_df.loc[subject, 'n_unaware_repeat'] = 0
try:
out_df.loc[subject, 'n_unaware_stroop'] = acc_df6.loc['stroopIncorrectUnaware', 'onset']
except:
out_df.loc[subject, 'n_unaware_stroop'] = 0
#out_df.loc[subject, 'mean_nogo_rt'] = rt_df4.loc[0, 'response_time']
#out_df.loc[subject, 'std_nogo_rt'] = rt_df8.loc[0, 'response_time']
#out_df.loc[subject, 'mean_go_rt'] = rt_df4.loc[1, 'response_time']
#out_df.loc[subject, 'std_go_rt'] = rt_df8.loc[1, 'response_time']
out_df.to_csv(op.join(out_dir, 'eat_performance.csv'), index_label='subject_id')
```
|
github_jupyter
|
# coding: utf-8
from glob import glob
import os.path as op
import pandas as pd
import numpy as np
from bids.layout import BIDSLayout
out_dir = '/home/data/nbc/Sutherland_HIVCB/EAT-behavioral/'
dset_dir = '/home/data/nbc/Sutherland_HIVCB/dset/'
layout = BIDSLayout(dset_dir)
subjects = layout.get_subjects()
#subjects = subjects[:5]
#subjects.remove('283')
#subjects.remove('397')
#subjects.remove('406')
out_df = pd.DataFrame(
columns=['n_correct_incongruent', 'n_incorrect_incongruent', 'n_incongruent',
'n_correct_repeat', 'n_incorrect_repeat', 'n_repeat',
'n_correct_nogo', 'n_incorrect_go', 'n_incorrect_nogo', 'n_nogo',
'n_correct_go', 'n_incorrect_go', 'n_go', 'n_nogo_aware',
'n_nogo_unaware', 'n_nogo_noresponse',
'mean_pre_correct_rt', 'mean_post_correct_rt',
'mean_aware_stroop_rt', 'mean_aware_repeat_rt',
'mean_unaware_stroop_rt', 'mean_unaware_repeat_rt',
'mean_pre_aware_rt', 'mean_post_aware_rt',
'mean_pre_unaware_rt', 'mean_post_unaware_rt',
'mean_nogo_aware_rt', 'mean_nogo_unaware_rt',
'mean_incorrect_incongruent_rt', 'std_incorrect_incongruent_rt',
'mean_incongruent_rt', 'std_incongruent_rt',
'mean_incorrect_repeat_rt', 'std_incorrect_repeat_rt',
'mean_repeat_rt', 'std_repeat_rt',
'mean_incorrect_nogo_rt', 'std_incorrect_nogo_rt',
'mean_correct_nogo_rt', 'std_correct_nogo_rt',
'mean_correct_go_rt', 'std_correct_go_rt',
'n_aware_repeat', 'n_unaware_repeat', 'n_aware_stroop', 'n_unaware_stroop',
'mean_incorrect_go_rt', 'std_incorrect_go_rt', 'mean_onepost_aware_rt', 'mean_onepost_unaware_rt'],
index=subjects)
for subject in subjects:
files = sorted(glob(op.join(dset_dir, 'sub-'+subject+'/func/sub-*_task-errorawareness*events.tsv')))
if not files:
print('{0} failed'.format(subject))
continue
else:
print('{0} running'.format(subject))
dfs = [pd.read_csv(f, sep='\t') for f in files]
df = pd.concat(dfs)
df['go'] = df['trial_type_2'].str.startswith('go').astype(int)
#df['nogo_error'] = df['trial_type_2'].str.startswith('nogoIncorrect').astype(int)
acc_df1 = df.groupby(['trial_type', 'trial_accuracy']).count()
acc_df2 = df.groupby(['trial_type']).count()
acc_df3 = df.groupby(['trial_type_2', 'trial_accuracy']).count()
acc_df4 = df.groupby(['trial_type_2']).count()
acc_df5 = df.groupby(['trial_type_2']).count()
acc_df6 = df.groupby(['trial_type_3']).count()
rt_df1 = df.groupby(['trial_type', 'trial_accuracy']).mean()
rt_df2 = df.groupby(['trial_type']).mean()
rt_df3 = df.groupby(['trial_type_2', 'trial_accuracy']).mean()
rt_df4 = df.groupby(['trial_type_2']).mean()
rt_df5 = df.groupby(['trial_type', 'trial_accuracy']).std()
rt_df6 = df.groupby(['trial_type']).std()
rt_df7 = df.groupby(['trial_type_2', 'trial_accuracy']).std()
rt_df8 = df.groupby(['trial_type_2']).std()
rt_df9 = df.groupby(['trial_type_2']).mean()
rt_df12 = df.groupby(['trial_type_3']).mean()
df['all_nogoIncorrect'] = df['trial_type_2'].str.startswith('nogoIncorrect')
rt_df10 = df.groupby(['all_nogoIncorrect']).mean()
rt_df11 = df.groupby(['all_nogoIncorrect']).std()
try:
out_df.loc[subject, 'n_correct_incongruent'] = acc_df1.loc[('incongruent', 1), 'onset']
except:
out_df.loc[subject, 'n_correct_incongruent'] = 0
try:
out_df.loc[subject, 'n_incorrect_incongruent'] = acc_df1.loc[('incongruent', 0), 'onset']
out_df.loc[subject, 'mean_incorrect_incongruent_rt'] = rt_df1.loc[('incongruent', 0), 'response_time']
out_df.loc[subject, 'std_incorrect_incongruent_rt'] = rt_df5.loc[('incongruent', 0), 'response_time']
except:
out_df.loc[subject, 'n_correct_incongruent'] = 0
out_df.loc[subject, 'mean_incorrect_incongruent_rt'] = np.NaN
out_df.loc[subject, 'std_incorrect_incongruent_rt'] = np.NaN
try:
out_df.loc[subject, 'n_correct_repeat'] = acc_df1.loc[('repeat', 1), 'onset']
except:
out_df.loc[subject, 'n_correct_repeat'] = 0
try:
out_df.loc[subject, 'n_incorrect_repeat'] = acc_df1.loc[('repeat', 0), 'onset']
out_df.loc[subject, 'mean_incorrect_repeat_rt'] = rt_df1.loc[('repeat', 0), 'response_time']
out_df.loc[subject, 'std_incorrect_repeat_rt'] = rt_df5.loc[('repeat', 0), 'response_time']
except:
out_df.loc[subject, 'n_incorrect_repeat'] = 0
out_df.loc[subject, 'mean_incorrect_repeat_rt'] = np.NaN
out_df.loc[subject, 'std_incorrect_repeat_rt'] = np.NaN
out_df.loc[subject, 'n_correct_nogo'] = df.loc[df['trial_type_2'] == 'nogoCorrect'].shape[0]
out_df.loc[subject, 'n_correct_go'] = df.loc[df['trial_type_2'] == 'goCorrect'].shape[0]
out_df.loc[subject, 'n_incorrect_nogo'] = df.loc[df['trial_type_2'].str.startswith('nogoIncorrect')].shape[0]
out_df.loc[subject, 'n_correct_nogo'] = df.loc[df['trial_type_2'] == 'nogoCorrect'].shape[0]
out_df.loc[subject, 'n_incorrect_go'] = df.loc[df['trial_type_2'] == 'goIncorrect'].shape[0]
out_df.loc[subject, 'n_nogo_aware'] = df.loc[df['trial_type_2'] == 'nogoIncorrectAware'].shape[0]
out_df.loc[subject, 'n_nogo_unaware'] = df.loc[df['trial_type_2'] == 'nogoIncorrectUnaware'].shape[0]
out_df.loc[subject, 'n_nogo_noresponse'] = df.loc[df['trial_type_2'].str.startswith('nogoIncorrectNoResponse')].shape[0]
#out_df.loc[subject, 'n_nogo'] = df.loc[df['trial_type_2'].str.startswith('nogo')].shape[0]
#out_df.loc[subject, 'n_go'] = df.loc[df['trial_type_2'].str.startswith('go')].shape[0]
try:
out_df.loc[subject, 'mean_incorrect_nogo_rt'] = rt_df10.loc[1, 'response_time']
out_df.loc[subject, 'std_incorrect_nogo_rt'] = rt_df11.loc[1, 'response_time']
except:
out_df.loc[subject, 'mean_incorrect_nogo_rt'] = np.NaN
out_df.loc[subject, 'std_incorrect_nogo_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_correct_nogo_rt'] = rt_df9.loc['nogoCorrect', 'response_time']
out_df.loc[subject, 'std_correct_nogo_rt'] = rt_df8.loc['nogoCorrect', 'response_time']
except:
out_df.loc[subject, 'mean_correct_nogo_rt'] = np.NaN
out_df.loc[subject, 'std_correct_nogo_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_correct_go_rt'] = rt_df9.loc['goCorrect', 'response_time']
out_df.loc[subject, 'std_correct_go_rt'] = rt_df8.loc['goCorrect', 'response_time']
except:
out_df.loc[subject, 'mean_correct_go_rt'] = np.NaN
out_df.loc[subject, 'std_correct_go_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_incorrect_go_rt'] = rt_df9.loc['goIncorrect', 'response_time']
out_df.loc[subject, 'std_incorrect_go_rt'] = rt_df8.loc['goIncorrect', 'response_time']
except:
out_df.loc[subject, 'mean_incorrect_go_rt'] = np.NaN
out_df.loc[subject, 'std_incorrect_go_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_nogo_aware_rt'] = rt_df9.loc['nogoIncorrectAware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_aware'] = 0
out_df.loc[subject, 'mean_nogo_aware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_nogo_unaware_rt'] = rt_df9.loc['nogoIncorrectUnaware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_unaware'] = 0
out_df.loc[subject, 'mean_nogo_unaware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_aware_stroop_rt'] = rt_df12.loc['stroopIncorrectAware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_aware'] = 0
out_df.loc[subject, 'mean_aware_stroop_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_aware_repeat_rt'] = rt_df12.loc['repeatIncorrectAware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_aware'] = 0
out_df.loc[subject, 'mean_aware_repeat_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_unaware_stroop_rt'] = rt_df12.loc['stroopIncorrectUnaware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_unaware'] = 0
out_df.loc[subject, 'mean_unaware_stroop_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_unaware_repeat_rt'] = rt_df12.loc['repeatIncorrectUnaware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_unaware'] = 0
out_df.loc[subject, 'mean_unaware_repeat_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_pre_aware_rt'] = rt_df12.loc['preIncorrectAware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_aware'] = 0
out_df.loc[subject, 'mean_pre_aware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_post_aware_rt'] = rt_df12.loc['postIncorrectAware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_aware'] = 0
out_df.loc[subject, 'mean_post_aware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_onepost_aware_rt'] = rt_df12.loc['onepostIncorrectAware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_aware'] = 0
out_df.loc[subject, 'mean_onepost_aware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_pre_unaware_rt'] = rt_df12.loc['preIncorrectUnaware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_unaware'] = 0
out_df.loc[subject, 'mean_pre_unaware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_post_unaware_rt'] = rt_df12.loc['postIncorrectUnaware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_unaware'] = 0
out_df.loc[subject, 'mean_post_unaware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_onepost_unaware_rt'] = rt_df12.loc['onepostIncorrectUnaware', 'response_time']
except:
out_df.loc[subject, 'n_nogo_unaware'] = 0
out_df.loc[subject, 'mean_onepost_unaware_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_pre_correct_rt'] = rt_df12.loc['pre-nogoCorrect', 'response_time']
except:
out_df.loc[subject, 'n_nogo_correct'] = 0
out_df.loc[subject, 'mean_pre_correct_rt'] = np.NaN
try:
out_df.loc[subject, 'mean_post_correct_rt'] = rt_df12.loc['post-nogoCorrect', 'response_time']
except:
out_df.loc[subject, 'n_nogo_correct'] = 0
out_df.loc[subject, 'mean_post_correct_rt'] = np.NaN
out_df.loc[subject, 'n_incongruent'] = acc_df2.loc['incongruent', 'onset']
out_df.loc[subject, 'mean_incongruent_rt'] = rt_df2.loc['incongruent', 'response_time']
out_df.loc[subject, 'std_incongruent_rt'] = rt_df6.loc['incongruent', 'response_time']
out_df.loc[subject, 'n_repeat'] = acc_df2.loc['repeat', 'onset']
out_df.loc[subject, 'mean_repeat_rt'] = rt_df2.loc['repeat', 'response_time']
out_df.loc[subject, 'std_repeat_rt'] = rt_df6.loc['repeat', 'response_time']
try:
out_df.loc[subject, 'n_aware_stroop'] = acc_df6.loc['stroopIncorrectAware', 'onset']
except:
out_df.loc[subject, 'n_aware_stroop'] = 0
try:
out_df.loc[subject, 'n_aware_repeat'] = acc_df6.loc['repeatIncorrectAware', 'onset']
except:
out_df.loc[subject, 'n_aware_repeat'] = 0
try:
out_df.loc[subject, 'n_unaware_repeat'] = acc_df6.loc['repeatIncorrectUnaware', 'onset']
except:
out_df.loc[subject, 'n_unaware_repeat'] = 0
try:
out_df.loc[subject, 'n_unaware_stroop'] = acc_df6.loc['stroopIncorrectUnaware', 'onset']
except:
out_df.loc[subject, 'n_unaware_stroop'] = 0
#out_df.loc[subject, 'mean_nogo_rt'] = rt_df4.loc[0, 'response_time']
#out_df.loc[subject, 'std_nogo_rt'] = rt_df8.loc[0, 'response_time']
#out_df.loc[subject, 'mean_go_rt'] = rt_df4.loc[1, 'response_time']
#out_df.loc[subject, 'std_go_rt'] = rt_df8.loc[1, 'response_time']
out_df.to_csv(op.join(out_dir, 'eat_performance.csv'), index_label='subject_id')
| 0.181626 | 0.124665 |
# Backpropagation by Hand
The API for this MLP network was inspired by sklearn.
Derivations of update rules included but the network itself has a low accuracy for some reason, even with randomized weights, different activation functions etc.
Only the Kullbach-Liebler divergence was attempted, and unfortunately, although the derivations seem accurate (matrix dimensions line up), the gradient is too small to move the weights. It is not known why.
```
import numpy as np
import pickle
import random
""" Import training data and labels """
train_data = np.genfromtxt('./train_data.csv', delimiter=',')
train_labels = np.genfromtxt('./train_labels.csv', delimiter=',')
```
## Activation Functions
We include the following activation functions that can be used with the network.
- Sigmoid $S(x)=\frac{e^{x}}{1+e^{x}}$: a smooth and therefore differentiable alternative to the Signum function.
- Tanh $tanh(x)$: hyperbolic tan, similar to the sigmoid function but steeper around 0.
- ReLU $relu(x)=max\{0, x\}$: a non-linear ramp function
Also, the derivatives of these function are included.
```
""" Activation functions """
def sigmoid(x): # sigmoid activation
""" sigmoid function """
return 1/(np.exp(-x)+1)
def sigmoid_derivative(x):
return sigmoid(x)*(1-sigmoid(x))
def tanh(x): # tanh activation
""" tanh function"""
return np.tanh(x)
def sec2h(x): # derivative of tanh
cosh2x = np.power(np.cosh(x), 2)
return 1/cosh2x
def relu(x):
return np.maximum(0, x)
def relu_derivative(x):
return(np.heaviside(x, 0))
```
## Gradient Calculation Functions
Contains the evaluations of the derivatives necessary to compute the gradient of the weights.
Our network with activation function $\mathcal{F}$ will output the vector $$\vec{y}^{pred}=\mathcal{F}\bigg(\hat{W}^{O}\mathcal{F}\bigg(\hat{W}^{H}\vec{x}\bigg)\bigg)$$
Using a loss function $\mathcal{L}(\vec{y}^{pred}, \vec{y}_{target})$ we want to calculate the gradient with respect to the weights in the layer $i$ $\frac{\partial \mathcal{L}}{\partial \hat{W}^{i}}$ and then adjust the weights in this direction.
Note: matrix calculus identities retrieved from here https://web.stanford.edu/class/cs224n/readings/gradient-notes.pdf
Since $$\vec{y}^{pred}=\mathcal{F}(\vec{u})=\mathcal{F}\bigg(\hat{W}^{O}\vec{O}^{H}\bigg)=\mathcal{F}\bigg(\hat{W}^{O}\mathcal{F}\big(\vec{v}\big)\bigg)=\mathcal{F}\bigg(\hat{W}^{O}\mathcal{F}\bigg(\hat{W}^{H}\vec{x}\bigg)\bigg)$$ we arrive at the following chain rule formulae for the gradients
$$\frac{\partial \mathcal{L}}{\partial \hat{W}^{H}}=\frac{\partial \mathcal{L}}{\partial \vec{O}^H}\frac{\partial \vec{O}^H}{\partial \hat{W}^H}=\bigg(\frac{\partial \mathcal{L}}{\partial \vec{O}^H}\bigg)^T\big(\vec{x}\big)^T=\big(\vec{\delta_1} \hat{\delta_2} \hat{\delta_3}\big)^T\big(\vec{x}\big)^T$$
$$\frac{\partial \mathcal{L}}{\partial \hat{W}^{O}}=\frac{\partial \mathcal{L}}{\partial \vec{O}^O}\frac{\partial \vec{O}^O}{\partial \hat{W}^O}=\bigg(\frac{\partial \mathcal{L}}{\partial \vec{O}^O}\bigg)^T\big(\vec{O}^H\big)^T=\big(\vec{\delta_1} \hat{\delta_2}\big)^T\bigg(\vec{O}^H\bigg)^T$$
where we have introduced
$$\vec{\delta_1}=\frac{\partial \mathcal{L}}{\partial \vec{y}^{pred}}$$
$$\hat{\delta_2}=\frac{\partial \vec{y}^{pred}}{\partial \vec{u}}=diag\bigg(\mathcal{F\prime}\bigg({\hat{W}^O\vec{O}^H}\bigg)\bigg)$$
$$\hat{\delta_3}=\frac{\partial \vec{u}}{\partial \vec{O}^H}=\hat{W}^O$$
## Sigmoid Derivative
Therefore, for a sigmoid function:
$$\hat{\delta_2}=diag\bigg(S\bigg(\hat{W}^O\vec{O}^H\bigg)\big(1-S\bigg(\hat{W}^O\vec{O}^H\bigg)\big)\bigg)$$
## Tanh Derivative
for the tanh function:
$$\hat{\delta_2}=diag\bigg(sech^2\big(\hat{W}^O\vec{O}^H\big)\bigg)$$
To calculate $\vec{\delta_1}$ we need to consider the loss function we are using:
### Kullbach-Liebler Divergence
The Kullbach-Liebler Divergence of two probability distributions $P$ and $Q$ over a sample space $\chi$ is given by $$\mathcal{L}_{KL}\Big( P|| Q \Big)=\sum_{x\in\chi}P(x)\log\bigg(\frac{P(x)}{Q(x)}\bigg)=\sum_{x\in\chi}P(x)\bigg(\log(P(x))-\log(Q(x))\bigg)$$ where $P$ is the reference distribution.
In this case, we will take the one-hot encoded target values as the distribution $P$, and our softmaxed network output as the distribution $Q$.
Using $\sigma$ for the softmax function on $\vec{y}^{pred}$, we have
$$\mathcal{L}_{KL}=\sum_{i} y^{(targ)}_i\bigg(\log\big(y^{(targ)}_i\big)-\log(\vec{\sigma}_i)\bigg)$$
$$\vec{\delta_1}=\frac{\partial \mathcal{L}_{KL}}{\partial \vec{y}^{pred}}=\frac{\partial \mathcal{L}_{KL}}{\partial \sigma}\frac{\partial \sigma}{\partial \vec{y}^{pred}}$$
and the vector derivative of the softmax function is
$$\frac{\partial \vec{\sigma}}{\partial \vec{y}^{pred}}\bigg|_{i,j}=\begin{cases} \frac{\Bigg(\bigg(\sum_k \exp(y^{pred}_k)\bigg)-\exp(y^{pred}_{i})\Bigg)\exp(y^{pred}_{i})}{\bigg(\sum_k \exp(y^{pred}_k)\bigg)^2} &\mbox{if } i=j \\
\frac{-\exp(y^{pred}_{i})\exp(y^{pred}_{j})}{\bigg(\sum_k \exp(y^{pred}_k)\bigg)^2} & \mbox{if } i\neq j \end{cases}$$
## Utility Functions
Some useful functions for processing output.
- Softmax: converts neural network output into a probability distribution
- Softmax-to-one-hot: converts softmaxed data into one hot by setting the highest probability to 1 and the others to 0.
```
""" Utility functions """
def softmax(x_array): # softmax function
""" Softmax function """
return np.exp(x_array)/np.sum(np.exp(x_array))
def softmax_derivative(x_array):
x_exp = np.exp(x_array)
x_sum = np.sum(np.exp(x_array))
diag = lambda ex: (x_sum*ex-(ex**2))/(x_sum**2)
offdiag = lambda ex1, ex2: -(ex1*ex2)/(x_sum**2)
sigma_prime_matrix = np.array([[diag(x1) if i==j
else offdiag(x1, x2)
for j, x2 in enumerate(x_exp)]
for i, x1 in enumerate(x_exp)])
return sigma_prime_matrix
def softmax_to_one_hot(softmax_array): # convert softmax back to one hot
""" Converts softmax vector to one hot encoded array """
output = np.zeros(len(softmax_array), dtype='int')
output[np.argmax(softmax_array)]=1
return output
def train_test_split(inp_data, out_data, frac=0.7, random_seed=420):
""" Shuffles a list of indices and returns split, randomized data """
assert(len(inp_data)==len(out_data))
idxs = np.arange(len(inp_data)) # generate list of indices
random.Random(random_seed).shuffle(idxs) # randomly permute the list
split_idx = round(len(inp_data)*frac) # get the first frac of the indices
X_train, y_train = inp_data[:split_idx], out_data[:split_idx] # split the data
X_test, y_test = inp_data[split_idx:], out_data[split_idx:] # hold the test set
return X_train, y_train, X_test, y_test
```
## Multilayer Perceptron Classes
We define a Node class to provide a neuron API for use by the network.
The node is supplied with an activation function and input dimensions, and has a method for evaluating the function over the inputs, and updating the weights.
```
class Node:
""" Generic Node class """
input_weights = None
activation_function = None
def __init__(self, input_dimension, activation_function):
self.input_weights = np.random.rand(input_dimension)
self.activation_function = activation_function
def fire(self, input_vector):
assert(len(input_vector) == len(self.input_weights))
wTx = np.inner(self.input_weights, input_vector)
return self.activation_function(wTx)
def update_weights(self, new_weights):
assert(new_weights.size == self.input_weights.size)
self.input_weights = new_weights
```
The MLPNetwork class composes nodes into a network and provides an interface for interaction
```
class MLPNetwork:
""" Class that composes Nodes into a NN and provides interface """
num_hidden_nodes = None
activation_function = None
loss_function = None
hidden_layer = None
output_layer = None
hidden_output = None
network_output = None
learning_rate = None
network_created = False
verbose = None
def __init__(self, num_hidden_nodes, activation_function=sigmoid, loss_function='kldiv', verbose=True, learning_rate=0.1):
assert(num_hidden_nodes>0)
self.num_hidden_nodes = num_hidden_nodes
self.activation_function = activation_function
self.loss_function = loss_function
self.learning_rate = learning_rate
self.verbose = verbose
def build_network(self, input_dimension, output_dimension):
""" Builds the network from parameters """
self.input_dimension = input_dimension
self.output_dimension = output_dimension
self.hidden_layer = [Node(self.input_dimension+1, self.activation_function)
for num in range(self.num_hidden_nodes)]
""" Add bias neuron to hidden layer """
self.hidden_layer.append(Node(self.input_dimension+1, self.activation_function))
self.output_layer = [Node(self.num_hidden_nodes+1, self.activation_function)
for num in range(self.output_dimension)]
self.network_created = True
def delete_network(self):
""" Deletes the network """
self.hidden_layer = None
self.output_layer = None
self.network_created = False
def training_epoch(self, X, y_target, point_idx=(None, None)):
if (self.verbose and point_idx!=(None, None)):
this_percentage = round(100*(point_idx[0]/point_idx[1]))
print("[*] Training {0}%".format(this_percentage), end='\r')
y_pred = self.feedforward(X)
self.backpropagate(X, y_pred)
return y_pred
def train(self, X_train, y_train):
if not self.network_created:
self.build_network(X_train.shape[1], y_train.shape[1])
training_set = zip(X_train, y_train)
total = len(X_train)
y_preds = np.array([self.training_epoch(X, y_target, (idx, total))
for idx, (X, y_target) in enumerate(training_set)])
def read_weight_matrices(self):
""" Read the weights from the layer nodes into matrices """
self.hidden_weights = np.array([hidden_node.input_weights
for hidden_node in self.hidden_layer])
self.output_weights = np.array([output_node.input_weights
for output_node in self.output_layer])
def write_weight_matrices(self):
""" Write a new weight matrix back to the nodes """
[self.hidden_layer[idx].update_weights(weight_vector)
for idx, weight_vector in enumerate(self.hidden_weights)]
[self.output_layer[idx].update_weights(weight_vector)
for idx, weight_vector in enumerate(self.output_weights)]
def backpropagate(self, X, y):
self.read_weight_matrices() # grab current weights
if self.loss_function == 'test':
#gradient_hidden =
#gradient_output =
pass
else:
if self.loss_function == 'kldiv':
""" row vector (row vector right multiplies matrix) """
kl_deriv = y/softmax(self.network_output)
sm_deriv = softmax_derivative(self.network_output)
delta_1 = np.matmul(kl_deriv, sm_deriv)
if self.activation_function == relu:
""" matrix """
delta_2 = np.diag(relu_derivative(self.output_weights @ self.hidden_output))
elif self.activation_function == sigmoid:
""" matrix """
delta_2 = np.diag(self.network_output*(1-self.network_output))
elif self.activation_function == tanh:
""" matrix """
delta_2 = np.diag(sec2h(self.output_weights @ self.hidden_output))
""" matrix """
delta_3 = self.output_weights
""" matrix (row vector right multiplies matrix right multiplies matrix right multiplies matrix).T right multiplies (column vector).T """
gradient_hidden = np.outer((delta_1 @ delta_2 @ delta_3).T, np.append(X, 1).T)
""" matrix (row vector right multiplies matrix right multiplies matrix).T right multiplies (column vector).T """
gradient_output = np.outer((delta_1 @ delta_2).T, (self.hidden_output).T)
self.hidden_weights = self.hidden_weights-self.learning_rate*gradient_hidden
self.output_weights = self.output_weights-self.learning_rate*gradient_output
self.write_weight_matrices()
def predict(self, X_test):
output_vector = [self.feedforward(X_t) for X_t in X_test]
y_pred = np.array([softmax_to_one_hot(softmax(output)) for output in output_vector])
return y_pred
def feedforward(self, input_vector):
""" Propagates a single datapoint with bias through the network """
bias = 1
self.hidden_output = np.array([hidden_node.fire(np.append(input_vector,bias)) for hidden_node in self.hidden_layer])
self.network_output = np.array([output_node.fire(self.hidden_output) for output_node in self.output_layer])
return self.network_output
def import_config(self, filename='./mlpconfig'):
config_file = pickle.load(open(filename, 'rb'))
self.hidden_weights = config_file['h_weights']
self.output_weights = config_file['o_weights']
self.num_hidden_nodes = config_file['nhidden']
self.loss_function = config_file['loss']
self.build_network(config_file['idim'], config_file['odim'])
self.write_weight_matrices()
def export_config(self, filename='./mlpconfig'):
cfg_dict = {'h_weights':self.hidden_weights,
'o_weights':self.output_weights,
'nhidden':self.num_hidden_nodes,
'loss':self.loss_function,
'idim':self.input_dimension,
'odim':self.output_dimension}
pickle.dump(cfg_dict, open(filename, 'wb+'))
```
## Usage
Following the sklearn API, a network is initialized with various parameter values.
The training set is loaded and split.
```
mlp_net = MLPNetwork(num_hidden_nodes=100,
activation_function=tanh,
loss_function='kldiv',
verbose=True,
learning_rate=0.1)
X_train, y_train, X_test, y_test = train_test_split(train_data, train_labels)
```
The network is trained via the train method, which takes a training and test set as arguments.
Prediction is done via the predict method and takes X values as an argument.
```
mlp_net.train(X_train, y_train)
y_predictions = mlp_net.predict(X_test)
```
The configuration of the network can be exported with the method below, and imported by replacing export with import.
A filename can be supplied, but there is a default ('./mlpconfig').
```
mlp_net.export_config()
```
The following code simply checks that a model with weights loaded gives the same result as one with training.
```
mlp_net2 = MLPNetwork(num_hidden_nodes=100,
activation_function=tanh,
loss_function='kldiv',
verbose=True,
learning_rate=0.1)
mlp_net2.import_config()
y_predictions2 = mlp_net.predict(X_test)
print(y_predictions.shape==y_predictions2.shape)
```
|
github_jupyter
|
import numpy as np
import pickle
import random
""" Import training data and labels """
train_data = np.genfromtxt('./train_data.csv', delimiter=',')
train_labels = np.genfromtxt('./train_labels.csv', delimiter=',')
""" Activation functions """
def sigmoid(x): # sigmoid activation
""" sigmoid function """
return 1/(np.exp(-x)+1)
def sigmoid_derivative(x):
return sigmoid(x)*(1-sigmoid(x))
def tanh(x): # tanh activation
""" tanh function"""
return np.tanh(x)
def sec2h(x): # derivative of tanh
cosh2x = np.power(np.cosh(x), 2)
return 1/cosh2x
def relu(x):
return np.maximum(0, x)
def relu_derivative(x):
return(np.heaviside(x, 0))
""" Utility functions """
def softmax(x_array): # softmax function
""" Softmax function """
return np.exp(x_array)/np.sum(np.exp(x_array))
def softmax_derivative(x_array):
x_exp = np.exp(x_array)
x_sum = np.sum(np.exp(x_array))
diag = lambda ex: (x_sum*ex-(ex**2))/(x_sum**2)
offdiag = lambda ex1, ex2: -(ex1*ex2)/(x_sum**2)
sigma_prime_matrix = np.array([[diag(x1) if i==j
else offdiag(x1, x2)
for j, x2 in enumerate(x_exp)]
for i, x1 in enumerate(x_exp)])
return sigma_prime_matrix
def softmax_to_one_hot(softmax_array): # convert softmax back to one hot
""" Converts softmax vector to one hot encoded array """
output = np.zeros(len(softmax_array), dtype='int')
output[np.argmax(softmax_array)]=1
return output
def train_test_split(inp_data, out_data, frac=0.7, random_seed=420):
""" Shuffles a list of indices and returns split, randomized data """
assert(len(inp_data)==len(out_data))
idxs = np.arange(len(inp_data)) # generate list of indices
random.Random(random_seed).shuffle(idxs) # randomly permute the list
split_idx = round(len(inp_data)*frac) # get the first frac of the indices
X_train, y_train = inp_data[:split_idx], out_data[:split_idx] # split the data
X_test, y_test = inp_data[split_idx:], out_data[split_idx:] # hold the test set
return X_train, y_train, X_test, y_test
class Node:
""" Generic Node class """
input_weights = None
activation_function = None
def __init__(self, input_dimension, activation_function):
self.input_weights = np.random.rand(input_dimension)
self.activation_function = activation_function
def fire(self, input_vector):
assert(len(input_vector) == len(self.input_weights))
wTx = np.inner(self.input_weights, input_vector)
return self.activation_function(wTx)
def update_weights(self, new_weights):
assert(new_weights.size == self.input_weights.size)
self.input_weights = new_weights
class MLPNetwork:
""" Class that composes Nodes into a NN and provides interface """
num_hidden_nodes = None
activation_function = None
loss_function = None
hidden_layer = None
output_layer = None
hidden_output = None
network_output = None
learning_rate = None
network_created = False
verbose = None
def __init__(self, num_hidden_nodes, activation_function=sigmoid, loss_function='kldiv', verbose=True, learning_rate=0.1):
assert(num_hidden_nodes>0)
self.num_hidden_nodes = num_hidden_nodes
self.activation_function = activation_function
self.loss_function = loss_function
self.learning_rate = learning_rate
self.verbose = verbose
def build_network(self, input_dimension, output_dimension):
""" Builds the network from parameters """
self.input_dimension = input_dimension
self.output_dimension = output_dimension
self.hidden_layer = [Node(self.input_dimension+1, self.activation_function)
for num in range(self.num_hidden_nodes)]
""" Add bias neuron to hidden layer """
self.hidden_layer.append(Node(self.input_dimension+1, self.activation_function))
self.output_layer = [Node(self.num_hidden_nodes+1, self.activation_function)
for num in range(self.output_dimension)]
self.network_created = True
def delete_network(self):
""" Deletes the network """
self.hidden_layer = None
self.output_layer = None
self.network_created = False
def training_epoch(self, X, y_target, point_idx=(None, None)):
if (self.verbose and point_idx!=(None, None)):
this_percentage = round(100*(point_idx[0]/point_idx[1]))
print("[*] Training {0}%".format(this_percentage), end='\r')
y_pred = self.feedforward(X)
self.backpropagate(X, y_pred)
return y_pred
def train(self, X_train, y_train):
if not self.network_created:
self.build_network(X_train.shape[1], y_train.shape[1])
training_set = zip(X_train, y_train)
total = len(X_train)
y_preds = np.array([self.training_epoch(X, y_target, (idx, total))
for idx, (X, y_target) in enumerate(training_set)])
def read_weight_matrices(self):
""" Read the weights from the layer nodes into matrices """
self.hidden_weights = np.array([hidden_node.input_weights
for hidden_node in self.hidden_layer])
self.output_weights = np.array([output_node.input_weights
for output_node in self.output_layer])
def write_weight_matrices(self):
""" Write a new weight matrix back to the nodes """
[self.hidden_layer[idx].update_weights(weight_vector)
for idx, weight_vector in enumerate(self.hidden_weights)]
[self.output_layer[idx].update_weights(weight_vector)
for idx, weight_vector in enumerate(self.output_weights)]
def backpropagate(self, X, y):
self.read_weight_matrices() # grab current weights
if self.loss_function == 'test':
#gradient_hidden =
#gradient_output =
pass
else:
if self.loss_function == 'kldiv':
""" row vector (row vector right multiplies matrix) """
kl_deriv = y/softmax(self.network_output)
sm_deriv = softmax_derivative(self.network_output)
delta_1 = np.matmul(kl_deriv, sm_deriv)
if self.activation_function == relu:
""" matrix """
delta_2 = np.diag(relu_derivative(self.output_weights @ self.hidden_output))
elif self.activation_function == sigmoid:
""" matrix """
delta_2 = np.diag(self.network_output*(1-self.network_output))
elif self.activation_function == tanh:
""" matrix """
delta_2 = np.diag(sec2h(self.output_weights @ self.hidden_output))
""" matrix """
delta_3 = self.output_weights
""" matrix (row vector right multiplies matrix right multiplies matrix right multiplies matrix).T right multiplies (column vector).T """
gradient_hidden = np.outer((delta_1 @ delta_2 @ delta_3).T, np.append(X, 1).T)
""" matrix (row vector right multiplies matrix right multiplies matrix).T right multiplies (column vector).T """
gradient_output = np.outer((delta_1 @ delta_2).T, (self.hidden_output).T)
self.hidden_weights = self.hidden_weights-self.learning_rate*gradient_hidden
self.output_weights = self.output_weights-self.learning_rate*gradient_output
self.write_weight_matrices()
def predict(self, X_test):
output_vector = [self.feedforward(X_t) for X_t in X_test]
y_pred = np.array([softmax_to_one_hot(softmax(output)) for output in output_vector])
return y_pred
def feedforward(self, input_vector):
""" Propagates a single datapoint with bias through the network """
bias = 1
self.hidden_output = np.array([hidden_node.fire(np.append(input_vector,bias)) for hidden_node in self.hidden_layer])
self.network_output = np.array([output_node.fire(self.hidden_output) for output_node in self.output_layer])
return self.network_output
def import_config(self, filename='./mlpconfig'):
config_file = pickle.load(open(filename, 'rb'))
self.hidden_weights = config_file['h_weights']
self.output_weights = config_file['o_weights']
self.num_hidden_nodes = config_file['nhidden']
self.loss_function = config_file['loss']
self.build_network(config_file['idim'], config_file['odim'])
self.write_weight_matrices()
def export_config(self, filename='./mlpconfig'):
cfg_dict = {'h_weights':self.hidden_weights,
'o_weights':self.output_weights,
'nhidden':self.num_hidden_nodes,
'loss':self.loss_function,
'idim':self.input_dimension,
'odim':self.output_dimension}
pickle.dump(cfg_dict, open(filename, 'wb+'))
mlp_net = MLPNetwork(num_hidden_nodes=100,
activation_function=tanh,
loss_function='kldiv',
verbose=True,
learning_rate=0.1)
X_train, y_train, X_test, y_test = train_test_split(train_data, train_labels)
mlp_net.train(X_train, y_train)
y_predictions = mlp_net.predict(X_test)
mlp_net.export_config()
mlp_net2 = MLPNetwork(num_hidden_nodes=100,
activation_function=tanh,
loss_function='kldiv',
verbose=True,
learning_rate=0.1)
mlp_net2.import_config()
y_predictions2 = mlp_net.predict(X_test)
print(y_predictions.shape==y_predictions2.shape)
| 0.533154 | 0.969091 |
# <span style="color:green"> Numerical Simulation Laboratory (NSL) </span>
## <span style="color:blue"> Numerical exercises 5</span>
<span style="color:red">**Nota:** non dimenticare di calcolare il modulo quadro della funzione d'onda!</span>
<span style="color:red">È più comodo lavorare nelle unità di misura dell'atomo di Bohr.</span>
<span style="color:red">**Attenzione**: dopo aver settato accettazione al 50%, non dovrebbero esserci problemi a fare una scelta sensata per la grandezza dei blocchi - basta che ne trovi una affinché i blocchi siano scorrelati tra di loro (e quindi una qualunque scelta di blocco maggiore andrà sicuramente bene).</span>
<span style="color:red">Per vedere se ha finito il Metropolis, prova a plottare una scelta del raggio e vedere dove si va (come scelta sensata iniziale si potrebbe prendere il raggio di Bohr). Sperimenta magari a prendere anche raggi più grandi. Dal grafico del raggio istantaneo si può vedere bene come cambia l'equilibrazione se prendo un raggio troppo grande.</span>
<span style='color:red'> La vera probabilità che devo usare è $$ P = \frac 1 \pi a_0^3 \cdot e^{-2 \frac r {a_0}}$$</span>
In quantum physics a **wave function**, $\Psi$, is a mathematical description of the state of a quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements made on the system can be derived from it.
For now on, let's consider the simple case of a non-relativistic single particle, without spin, in three spatial dimensions. The state of such a particle is completely described by its wave function, $\Psi(\vec{r},t)$, where $\vec{r}$ is position and $t$ is time.
For one spinless particle, if the wave function is interpreted as a probability amplitude, the square modulus of the wave function, $|\Psi(\vec{r},t)|^2$, is interpreted as the probability density that the particle is at $\vec{r}$ at time $t$. Once we have a probability density, we can use Monte Carlo ...
#### Hydrogen atom
The wave functions of the eigenstates of an electron in a Hydrogen atom (this is the only atom for which the Schroedinger equation has been solved exactly) are expressed in terms of spherical harmonics and generalized Laguerre polynomials. It is convenient to use spherical coordinates, and the wave function can be separated into functions of each coordinate:
$$
\Psi_{n,l,m}(r,\theta,\phi)=
\sqrt{\left(\frac{2}{na_0}\right)^3 \frac{(n-l-1)!}{2n[(n+l)!]}}
e^{-r/na_0}\left(\frac{2r}{na_0}\right)^l L_{n-l-1}^{2l+1}\left(\frac{2r}{na_0}\right)
Y_l^m(\theta,\phi)
$$
where $a_0=4\pi\epsilon_0\hbar^2/m_e e^2=0.0529$ nm is the Bohr radius, $L_{n-l-1}^{2l+1}$ are the generalized Laguerre polynomials of degree $n-l-1$, $n=1,2,...$ is the principal quantum number, $l=0,1, ..., n-1$ the azimuthal quantum number, $m=-l, -l+1, ..., l-1, l$ the magnetic quantum number.
For example, the ground state wave function is:
$$
\Psi_{1,0,0}(r,\theta,\phi)=
\frac{a_0^{3/2}}{\sqrt{\pi}} e^{-a_0 r}
$$
whereas one of the three $2p$ excited state is:
$$
\Psi_{2,1,0}(r,\theta,\phi)=
\frac{a_0^{5/2}}{8}\sqrt{\frac{2}{\pi}} r e^{-a_0 r/2} \cos(\theta)
$$
<span style="color:blue">Expectation values for the radius turns out to be exactly:
$$
\left\langle r \right\rangle_{\Psi_{1,0,0}} = \frac{3}{2}a_0
\quad
\left\langle r \right\rangle_{\Psi_{2,1,0}} = 5 a_0
$$
</span>
### Exercise 05.1
Use the Metropolis algorithm to sample $|\Psi_{1,0,0}(x,y,z)|^2$ and $|\Psi_{2,1,0}(x,y,z)|^2$ **in Cartesian coordinates** using an uniform transition probability $T(\vec{x}|\vec{y})$. Use the sampled positions to estimate $\left\langle r \right\rangle_{\Psi_{1,0,0}}$ and $\left\langle r \right\rangle_{\Psi_{2,1,0}}$. As usual, use data blocking and give an estimate of the statistical uncertainties.
<span style="color:red">Show a picture of your estimations of $\left\langle r \right\rangle_{\Psi_{1,0,0}}$ and $\left\langle r \right\rangle_{\Psi_{2,1,0}}$</span> and their uncertainties with a large number of *throws* $M$ (e.g. $M\ge 10^6$) as a function of the number of blocks, $N$</font>.
- Use Bohr radius units, $a_0$ for distances
- Choose the step of the uniform transition probability $T(\vec{x}|\vec{y})$ in order to obtain 50% of acceptance in both cases
- Choose a reasonable starting point in the 3D space and equilibrate your sampling before to start measuring the radius. What do you observe when you start very far from the origin?
- How large should be the number of Monte Carlo Metropolis steps in each block?
- If you use a multivariate normal transition probability $T(\vec{x}|\vec{y})$, i.e. a Gaussian for each coordinate, your result for $\left\langle r \right\rangle_{\Psi_{1,0,0}}$ and $\left\langle r \right\rangle_{\Psi_{2,1,0}}$ is equivalent?
You can use a Python code similar to the following one to observe how the sampled points distribute into the 3D space:
```
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
M=1000
f = np.loadtxt("Ex5/3Dmap.txt")
X=f[:,0]
Y=f[:,1]
Z=f[:,2]
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(X, Y, Z, c=Z, marker='.')
plt.title('2p orbital in H atom')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.view_init(0, 0)
plt.savefig('3dmap.png')
plt.show()
f1 = np.loadtxt('Ex5/data.txt', skiprows=1)
x1 = np.arange(len(f1))
plt.style.use('classic')
plt.errorbar(x1, f1[:,0], yerr=f1[:,1])
plt.title('Average Radius for 1s in H')
plt.xlabel('blocks')
plt.ylabel('<r>')
plt.axhline(1.5, color='red')
plt.show()
f2 = np.loadtxt('Ex5/data2.txt', skiprows=1)
x2 = np.arange(len(f2))
print(f2.shape)
plt.errorbar(x2, f2[:,0], yerr=f2[:,1])
plt.title('Average Radius for 2p in H')
plt.xlabel('blocks')
plt.ylabel('<r>')
plt.axhline(5, color='red')
plt.show()
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
M=1000
f = np.loadtxt("Ex5/3Dmap.txt")
X=f[:,0]
Y=f[:,1]
Z=f[:,2]
print(f.shape)
```
|
github_jupyter
|
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
M=1000
f = np.loadtxt("Ex5/3Dmap.txt")
X=f[:,0]
Y=f[:,1]
Z=f[:,2]
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(X, Y, Z, c=Z, marker='.')
plt.title('2p orbital in H atom')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.view_init(0, 0)
plt.savefig('3dmap.png')
plt.show()
f1 = np.loadtxt('Ex5/data.txt', skiprows=1)
x1 = np.arange(len(f1))
plt.style.use('classic')
plt.errorbar(x1, f1[:,0], yerr=f1[:,1])
plt.title('Average Radius for 1s in H')
plt.xlabel('blocks')
plt.ylabel('<r>')
plt.axhline(1.5, color='red')
plt.show()
f2 = np.loadtxt('Ex5/data2.txt', skiprows=1)
x2 = np.arange(len(f2))
print(f2.shape)
plt.errorbar(x2, f2[:,0], yerr=f2[:,1])
plt.title('Average Radius for 2p in H')
plt.xlabel('blocks')
plt.ylabel('<r>')
plt.axhline(5, color='red')
plt.show()
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
M=1000
f = np.loadtxt("Ex5/3Dmap.txt")
X=f[:,0]
Y=f[:,1]
Z=f[:,2]
print(f.shape)
| 0.374676 | 0.993022 |
# Developing an AI application
Going forward, AI algorithms will be incorporated into more and more everyday applications. For example, you might want to include an image classifier in a smart phone app. To do this, you'd use a deep learning model trained on hundreds of thousands of images as part of the overall application architecture. A large part of software development in the future will be using these types of models as common parts of applications.
In this project, you'll train an image classifier to recognize different species of flowers. You can imagine using something like this in a phone app that tells you the name of the flower your camera is looking at. In practice you'd train this classifier, then export it for use in your application. We'll be using [this dataset](http://www.robots.ox.ac.uk/~vgg/data/flowers/102/index.html) of 102 flower categories, you can see a few examples below.
<img src='assets/Flowers.png' width=500px>
The project is broken down into multiple steps:
* Load and preprocess the image dataset
* Train the image classifier on your dataset
* Use the trained classifier to predict image content
We'll lead you through each part which you'll implement in Python.
When you've completed this project, you'll have an application that can be trained on any set of labeled images. Here your network will be learning about flowers and end up as a command line application. But, what you do with your new skills depends on your imagination and effort in building a dataset. For example, imagine an app where you take a picture of a car, it tells you what the make and model is, then looks up information about it. Go build your own dataset and make something new.
First up is importing the packages you'll need. It's good practice to keep all the imports at the beginning of your code. As you work through this notebook and find you need to import a package, make sure to add the import up here.
Please make sure if you are running this notebook in the workspace that you have chosen GPU rather than CPU mode.
```
# Imports here
import torch
import numpy as np
from torch import nn
from torch import optim
import torch.nn.functional as F
from torchvision import datasets, transforms, models
from PIL import Image
import json
import matplotlib.pyplot as plt
# Code re-used from the previous Udacity section on Transfer Learning
```
## Load the data
Here you'll use `torchvision` to load the data ([documentation](http://pytorch.org/docs/0.3.0/torchvision/index.html)). The data should be included alongside this notebook, otherwise you can [download it here](https://s3.amazonaws.com/content.udacity-data.com/nd089/flower_data.tar.gz). The dataset is split into three parts, training, validation, and testing. For the training, you'll want to apply transformations such as random scaling, cropping, and flipping. This will help the network generalize leading to better performance. You'll also need to make sure the input data is resized to 224x224 pixels as required by the pre-trained networks.
The validation and testing sets are used to measure the model's performance on data it hasn't seen yet. For this you don't want any scaling or rotation transformations, but you'll need to resize then crop the images to the appropriate size.
The pre-trained networks you'll use were trained on the ImageNet dataset where each color channel was normalized separately. For all three sets you'll need to normalize the means and standard deviations of the images to what the network expects. For the means, it's `[0.485, 0.456, 0.406]` and for the standard deviations `[0.229, 0.224, 0.225]`, calculated from the ImageNet images. These values will shift each color channel to be centered at 0 and range from -1 to 1.
```
def load_data(data_dir):
"""Load the training, validation and the test data.
Args:
data_dir: The data sirectory which will host the training, validation, and the test data.
Returns:
dataloaders: A dictionary with PyTorch Dataloaders for training, test, and validation data
"""
train_dir = data_dir + '/train'
valid_dir = data_dir + '/valid'
test_dir = data_dir + '/test'
data_transforms = {
'training' : transforms.Compose([transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])]) ,
'val|test' : transforms.Compose([transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])])
}
# TODO: Load the datasets with ImageFolder
image_datasets = {
'training' : datasets.ImageFolder(train_dir, transform=data_transforms['training']) ,
'validation': datasets.ImageFolder(valid_dir, transform=data_transforms['val|test']) ,
'test' : datasets.ImageFolder(test_dir, transform=data_transforms['val|test'])
}
# TODO: Using the image datasets and the trainforms, define the dataloaders
dataloaders = {
'training' : torch.utils.data.DataLoader(image_datasets['training'], batch_size=64, shuffle=True) ,
'validation' : torch.utils.data.DataLoader(image_datasets['validation'], batch_size=32) ,
'test' : torch.utils.data.DataLoader(image_datasets['test'], batch_size=32)
}
return image_datasets, dataloaders
image_datasets, dataloaders = load_data('flowers')
```
### Label mapping
You'll also need to load in a mapping from category label to category name. You can find this in the file `cat_to_name.json`. It's a JSON object which you can read in with the [`json` module](https://docs.python.org/2/library/json.html). This will give you a dictionary mapping the integer encoded categories to the actual names of the flowers.
```
with open('cat_to_name.json', 'r') as f:
cat_to_name = json.load(f)
```
# Building and training the classifier
Now that the data is ready, it's time to build and train the classifier. As usual, you should use one of the pretrained models from `torchvision.models` to get the image features. Build and train a new feed-forward classifier using those features.
We're going to leave this part up to you. Refer to [the rubric](https://review.udacity.com/#!/rubrics/1663/view) for guidance on successfully completing this section. Things you'll need to do:
* Load a [pre-trained network](http://pytorch.org/docs/master/torchvision/models.html) (If you need a starting point, the VGG networks work great and are straightforward to use)
* Define a new, untrained feed-forward network as a classifier, using ReLU activations and dropout
* Train the classifier layers using backpropagation using the pre-trained network to get the features
* Track the loss and accuracy on the validation set to determine the best hyperparameters
We've left a cell open for you below, but use as many as you need. Our advice is to break the problem up into smaller parts you can run separately. Check that each part is doing what you expect, then move on to the next. You'll likely find that as you work through each part, you'll need to go back and modify your previous code. This is totally normal!
When training make sure you're updating only the weights of the feed-forward network. You should be able to get the validation accuracy above 70% if you build everything right. Make sure to try different hyperparameters (learning rate, units in the classifier, epochs, etc) to find the best model. Save those hyperparameters to use as default values in the next part of the project.
One last important tip if you're using the workspace to run your code: To avoid having your workspace disconnect during the long-running tasks in this notebook, please read in the earlier page in this lesson called Intro to GPU Workspaces about Keeping Your Session Active. You'll want to include code from the workspace_utils.py module.
```
# TODO: Build and train your network
def build_model(arch = 'vgg16', hidden_layers = 4096, is_gpu = True):
"""Build a pretrained model with custom classifier.
Model will have two hidden layers,
and support three kind of architectures.
Args:
arch: Architecture
hidden_layers: Hidden Layer
is_gpu: Boolean flag for the use of GPUs
Returns:
The requisite model with pretrained features, and adjusted classifier
"""
if arch == 'vgg16':
model = models.vgg16(pretrained = True)
input_layer = 25088
elif arch == 'densenet161' :
model = models.densenet161(pretrained = True)
input_layer = 2208
elif arch == 'alexnet':
model = models.alexnet(pretrained = True)
input_layer = 9216
else:
raise ValueError("The arch should be in ['vgg16', ''densenet161', alexnet']")
output_layers = 1002 # No of clases
for param in model.parameters():
param.requires_grad = False
from collections import OrderedDict
classifier = nn.Sequential(OrderedDict([
('fc1', nn.Linear(input_layer, hidden_layers)),
('relu', nn.ReLU()),
('fc2', nn.Linear(hidden_layers, output_layers)),
('output', nn.LogSoftmax(dim=1))
]))
model.classifier = classifier
if is_gpu and torch.cuda.is_available():
model.cuda()
return model
model = build_model()
model
def train_model(model, training_data = dataloaders['training'],
validation_data = dataloaders['validation'],
epochs = 3, learning_rate = .001, is_gpu = True):
"""Train the model
Args:
model: NN Model to be trained
training_data: Trainig data for the model to be trained
validation_data: Validation data for checking error
epochs: no of times the model will go over all the images
learning_rate: learning rate
is_gpu: Boolean flag to indicate if GPU is to be used or not
"""
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.classifier.parameters(), learning_rate)
steps = 0
# change to cuda
if is_gpu and torch.cuda.is_available():
model.to('cuda')
for e in range(epochs):
running_loss = 0
no_of_steps_error = 0
for _, (inputs, labels) in enumerate(training_data ):
no_of_steps_error += 1
steps += 1
if is_gpu and torch.cuda.is_available():
inputs, labels = inputs.to('cuda'), labels.to('cuda')
optimizer.zero_grad()
# Forward and backward passes
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
# Evaluate the validation loss and accuracy
val_loss_running = 0
no_of_val_steps = 0
for _, (inputs_v, labels_v) in enumerate(validation_data):
if is_gpu and torch.cuda.is_available():
inputs_v, labels_v = inputs_v.to('cuda'), labels_v.to('cuda')
optimizer.zero_grad()
output_v = model.forward(inputs_v)
val_loss = criterion(output_v,labels_v)
val_loss_running += val_loss.item()
no_of_val_steps +=1
val_accuracy = check_accuracy(model, validation_data)
print("Epoch: {}/{}... ".format(e+1, epochs),
"Loss: {:.4f}".format(running_loss/no_of_steps_error),
"Validation Loss: {:.4f}".format(val_loss_running/no_of_val_steps),
"Validation Accuracy : {:.2f}%".format(val_accuracy*100))
train_model(model)
```
## Testing your network
It's good practice to test your trained network on test data, images the network has never seen either in training or validation. This will give you a good estimate for the model's performance on completely new images. Run the test images through the network and measure the accuracy, the same way you did validation. You should be able to reach around 70% accuracy on the test set if the model has been trained well.
```
# TODO: Do validation on the test set
def check_accuracy(nn_model, testing_data = dataloaders['test'], is_gpu = True):
"""Prints accuracy for a model for a certain dataset_type
Args:
nn_model: Particular Model
testing_data : The data on which accuracy is to be tested
is_gpu: Boolean flag to indicate if GPU is to be used or not
Returns:
accuracy: Accuracy of the model
"""
correct = 0
total = 0
with torch.no_grad():
for data in testing_data:
images, labels = data
if is_gpu:
images, labels = images.to('cuda'), labels.to('cuda')
outputs = nn_model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
accuracy = correct / total
return accuracy
accuracy = check_accuracy(model)
print("Accuracy: {:.2f}%".format(accuracy*100))
```
## Save the checkpoint
Now that your network is trained, save the model so you can load it later for making predictions. You probably want to save other things such as the mapping of classes to indices which you get from one of the image datasets: `image_datasets['train'].class_to_idx`. You can attach this to the model as an attribute which makes inference easier later on.
```model.class_to_idx = image_datasets['train'].class_to_idx```
Remember that you'll want to completely rebuild the model later so you can use it for inference. Make sure to include any information you need in the checkpoint. If you want to load the model and keep training, you'll want to save the number of epochs as well as the optimizer state, `optimizer.state_dict`. You'll likely want to use this trained model in the next part of the project, so best to save it now.
```
# TODO: Save the checkpoint
def save_checkpoint(model, hidden_layers = 4096, epochs = 3, training_data = image_datasets['training'],
save_dir = 'saved_model.pth'):
model.class_to_idx = training_data.class_to_idx
torch.save({
'hidden_layers':hidden_layers,
'arch': 'vgg16',
'no_of_epochs': epochs,
'optimizer': 'adam',
'class_to_idx':model.class_to_idx,
'state_dict':model.state_dict()},
save_dir)
save_checkpoint(model)
```
## Loading the checkpoint
At this point it's good to write a function that can load a checkpoint and rebuild the model. That way you can come back to this project and keep working on it without having to retrain the network.
```
# TODO: Write a function that loads a checkpoint and rebuilds the model
def load_model(path):
"""Recall the model's characteristics, and then re-build it
Args:
path: Path where model was saved
Returns:
loaded_model: Re-built model
"""
saved_model = torch.load(path)
arch = saved_model['arch']
hidden_layers = saved_model['hidden_layers']
loaded_model = build_model(arch = arch, hidden_layers = hidden_layers)
loaded_model.class_to_idx = saved_model['class_to_idx']
loaded_model.load_state_dict(saved_model['state_dict'])
return loaded_model
loaded_model = load_model('saved_model.pth')
# Checking if load_model is working
accuracy = check_accuracy(loaded_model)
print("Accuracy: {:.2f}%".format(accuracy*100))
```
# Inference for classification
Now you'll write a function to use a trained network for inference. That is, you'll pass an image into the network and predict the class of the flower in the image. Write a function called `predict` that takes an image and a model, then returns the top $K$ most likely classes along with the probabilities. It should look like
```python
probs, classes = predict(image_path, model)
print(probs)
print(classes)
> [ 0.01558163 0.01541934 0.01452626 0.01443549 0.01407339]
> ['70', '3', '45', '62', '55']
```
First you'll need to handle processing the input image such that it can be used in your network.
## Image Preprocessing
You'll want to use `PIL` to load the image ([documentation](https://pillow.readthedocs.io/en/latest/reference/Image.html)). It's best to write a function that preprocesses the image so it can be used as input for the model. This function should process the images in the same manner used for training.
First, resize the images where the shortest side is 256 pixels, keeping the aspect ratio. This can be done with the [`thumbnail`](http://pillow.readthedocs.io/en/3.1.x/reference/Image.html#PIL.Image.Image.thumbnail) or [`resize`](http://pillow.readthedocs.io/en/3.1.x/reference/Image.html#PIL.Image.Image.thumbnail) methods. Then you'll need to crop out the center 224x224 portion of the image.
Color channels of images are typically encoded as integers 0-255, but the model expected floats 0-1. You'll need to convert the values. It's easiest with a Numpy array, which you can get from a PIL image like so `np_image = np.array(pil_image)`.
As before, the network expects the images to be normalized in a specific way. For the means, it's `[0.485, 0.456, 0.406]` and for the standard deviations `[0.229, 0.224, 0.225]`. You'll want to subtract the means from each color channel, then divide by the standard deviation.
And finally, PyTorch expects the color channel to be the first dimension but it's the third dimension in the PIL image and Numpy array. You can reorder dimensions using [`ndarray.transpose`](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.ndarray.transpose.html). The color channel needs to be first and retain the order of the other two dimensions.
```
def process_image(image):
''' Scales, crops, and normalizes a PIL image for a PyTorch model,
returns an Numpy array
'''
img = Image.open(image)
transform = transforms.Compose([transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])])
transformed_img = transform(img)
return transformed_img.numpy()
```
To check your work, the function below converts a PyTorch tensor and displays it in the notebook. If your `process_image` function works, running the output through this function should return the original image (except for the cropped out portions).
```
def imshow(image, ax=None, title=None):
if ax is None:
fig, ax = plt.subplots()
# PyTorch tensors assume the color channel is the first dimension
# but matplotlib assumes is the third dimension
image = image.transpose((1, 2, 0))
# Undo preprocessing
mean = np.array([0.485, 0.456, 0.406])
std = np.array([0.229, 0.224, 0.225])
image = std * image + mean
# Image needs to be clipped between 0 and 1 or it looks like noise when displayed
image = np.clip(image, 0, 1)
ax.imshow(image)
return ax
```
### Using a random image from the test directory to test the various functions being created
```
Image.open("flowers/test/10/image_07090.jpg")
imshow(process_image("flowers/test/10/image_07090.jpg"))
```
## Class Prediction
Once you can get images in the correct format, it's time to write a function for making predictions with your model. A common practice is to predict the top 5 or so (usually called top-$K$) most probable classes. You'll want to calculate the class probabilities then find the $K$ largest values.
To get the top $K$ largest values in a tensor use [`x.topk(k)`](http://pytorch.org/docs/master/torch.html#torch.topk). This method returns both the highest `k` probabilities and the indices of those probabilities corresponding to the classes. You need to convert from these indices to the actual class labels using `class_to_idx` which hopefully you added to the model or from an `ImageFolder` you used to load the data ([see here](#Save-the-checkpoint)). Make sure to invert the dictionary so you get a mapping from index to class as well.
Again, this method should take a path to an image and a model checkpoint, then return the probabilities and classes.
```python
probs, classes = predict(image_path, model)
print(probs)
print(classes)
> [ 0.01558163 0.01541934 0.01452626 0.01443549 0.01407339]
> ['70', '3', '45', '62', '55']
```
```
def predict(image_path, model, topk=5):
''' Predict the class (or classes) of an image using a trained deep learning model.
Args:
image_path:image path
model: model used for inference
topk: No of probabilities and classes to be retreived
'''
image = process_image(image_path)
image = torch.from_numpy(image)
# https://discuss.pytorch.org/t/converting-numpy-array-to-tensor-on-gpu/19423
# Forum used to uncover the 'magical' function unsqueeze
image = image.unsqueeze_(0).float()
image = image.to('cuda')
output = model.forward(image)
probability = F.softmax(output.data,dim=1)
return probability.topk(topk)
```
## Sanity Checking
Now that you can use a trained model for predictions, check to make sure it makes sense. Even if the testing accuracy is high, it's always good to check that there aren't obvious bugs. Use `matplotlib` to plot the probabilities for the top 5 classes as a bar graph, along with the input image. It should look like this:
<img src='assets/inference_example.png' width=300px>
You can convert from the class integer encoding to actual flower names with the `cat_to_name.json` file (should have been loaded earlier in the notebook). To show a PyTorch tensor as an image, use the `imshow` function defined above.
```
def draw_bar_chart(cat_name, prob):
"""Function to draw the bar chart
Source: # https://matplotlib.org/gallery/lines_bars_and_markers/barh.html
Args:
cat_name: A tuple of category names
prob: Numpy data array of probabilities
Returns:
None
"""
plt.rcdefaults()
fig, ax = plt.subplots()
y_pos = np.arange(len(cat_name))
ax.barh(y_pos, prob, align='center',
color='green', ecolor='black')
ax.set_yticks(y_pos)
ax.set_yticklabels(cat_name)
ax.invert_yaxis() # labels read top-to-bottom
ax.set_xlabel('Which flower is this?')
ax.set_title('Probablity')
plt.show()
def sanity_check(model, image_path):
"""Does an inference check for a particular flower image
Args:
model: model to be used for inference
image_path: Image path
Returns:
None
"""
prob, cat = predict(image_path, model)
prob = prob.cpu().numpy()[0]
cat = cat.cpu().numpy()[0]
cat_name = []
for category in cat:
cat_name.append(cat_to_name[str(category)])
cat_name = tuple(cat_name)
imshow(process_image(image_path))
draw_bar_chart(cat_name, prob)
# TODO: Display an image along with the top 5 classes
sanity_check(loaded_model, 'flowers/test/101/image_07983.jpg')
```
|
github_jupyter
|
# Imports here
import torch
import numpy as np
from torch import nn
from torch import optim
import torch.nn.functional as F
from torchvision import datasets, transforms, models
from PIL import Image
import json
import matplotlib.pyplot as plt
# Code re-used from the previous Udacity section on Transfer Learning
def load_data(data_dir):
"""Load the training, validation and the test data.
Args:
data_dir: The data sirectory which will host the training, validation, and the test data.
Returns:
dataloaders: A dictionary with PyTorch Dataloaders for training, test, and validation data
"""
train_dir = data_dir + '/train'
valid_dir = data_dir + '/valid'
test_dir = data_dir + '/test'
data_transforms = {
'training' : transforms.Compose([transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])]) ,
'val|test' : transforms.Compose([transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])])
}
# TODO: Load the datasets with ImageFolder
image_datasets = {
'training' : datasets.ImageFolder(train_dir, transform=data_transforms['training']) ,
'validation': datasets.ImageFolder(valid_dir, transform=data_transforms['val|test']) ,
'test' : datasets.ImageFolder(test_dir, transform=data_transforms['val|test'])
}
# TODO: Using the image datasets and the trainforms, define the dataloaders
dataloaders = {
'training' : torch.utils.data.DataLoader(image_datasets['training'], batch_size=64, shuffle=True) ,
'validation' : torch.utils.data.DataLoader(image_datasets['validation'], batch_size=32) ,
'test' : torch.utils.data.DataLoader(image_datasets['test'], batch_size=32)
}
return image_datasets, dataloaders
image_datasets, dataloaders = load_data('flowers')
with open('cat_to_name.json', 'r') as f:
cat_to_name = json.load(f)
# TODO: Build and train your network
def build_model(arch = 'vgg16', hidden_layers = 4096, is_gpu = True):
"""Build a pretrained model with custom classifier.
Model will have two hidden layers,
and support three kind of architectures.
Args:
arch: Architecture
hidden_layers: Hidden Layer
is_gpu: Boolean flag for the use of GPUs
Returns:
The requisite model with pretrained features, and adjusted classifier
"""
if arch == 'vgg16':
model = models.vgg16(pretrained = True)
input_layer = 25088
elif arch == 'densenet161' :
model = models.densenet161(pretrained = True)
input_layer = 2208
elif arch == 'alexnet':
model = models.alexnet(pretrained = True)
input_layer = 9216
else:
raise ValueError("The arch should be in ['vgg16', ''densenet161', alexnet']")
output_layers = 1002 # No of clases
for param in model.parameters():
param.requires_grad = False
from collections import OrderedDict
classifier = nn.Sequential(OrderedDict([
('fc1', nn.Linear(input_layer, hidden_layers)),
('relu', nn.ReLU()),
('fc2', nn.Linear(hidden_layers, output_layers)),
('output', nn.LogSoftmax(dim=1))
]))
model.classifier = classifier
if is_gpu and torch.cuda.is_available():
model.cuda()
return model
model = build_model()
model
def train_model(model, training_data = dataloaders['training'],
validation_data = dataloaders['validation'],
epochs = 3, learning_rate = .001, is_gpu = True):
"""Train the model
Args:
model: NN Model to be trained
training_data: Trainig data for the model to be trained
validation_data: Validation data for checking error
epochs: no of times the model will go over all the images
learning_rate: learning rate
is_gpu: Boolean flag to indicate if GPU is to be used or not
"""
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.classifier.parameters(), learning_rate)
steps = 0
# change to cuda
if is_gpu and torch.cuda.is_available():
model.to('cuda')
for e in range(epochs):
running_loss = 0
no_of_steps_error = 0
for _, (inputs, labels) in enumerate(training_data ):
no_of_steps_error += 1
steps += 1
if is_gpu and torch.cuda.is_available():
inputs, labels = inputs.to('cuda'), labels.to('cuda')
optimizer.zero_grad()
# Forward and backward passes
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
# Evaluate the validation loss and accuracy
val_loss_running = 0
no_of_val_steps = 0
for _, (inputs_v, labels_v) in enumerate(validation_data):
if is_gpu and torch.cuda.is_available():
inputs_v, labels_v = inputs_v.to('cuda'), labels_v.to('cuda')
optimizer.zero_grad()
output_v = model.forward(inputs_v)
val_loss = criterion(output_v,labels_v)
val_loss_running += val_loss.item()
no_of_val_steps +=1
val_accuracy = check_accuracy(model, validation_data)
print("Epoch: {}/{}... ".format(e+1, epochs),
"Loss: {:.4f}".format(running_loss/no_of_steps_error),
"Validation Loss: {:.4f}".format(val_loss_running/no_of_val_steps),
"Validation Accuracy : {:.2f}%".format(val_accuracy*100))
train_model(model)
# TODO: Do validation on the test set
def check_accuracy(nn_model, testing_data = dataloaders['test'], is_gpu = True):
"""Prints accuracy for a model for a certain dataset_type
Args:
nn_model: Particular Model
testing_data : The data on which accuracy is to be tested
is_gpu: Boolean flag to indicate if GPU is to be used or not
Returns:
accuracy: Accuracy of the model
"""
correct = 0
total = 0
with torch.no_grad():
for data in testing_data:
images, labels = data
if is_gpu:
images, labels = images.to('cuda'), labels.to('cuda')
outputs = nn_model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
accuracy = correct / total
return accuracy
accuracy = check_accuracy(model)
print("Accuracy: {:.2f}%".format(accuracy*100))
Remember that you'll want to completely rebuild the model later so you can use it for inference. Make sure to include any information you need in the checkpoint. If you want to load the model and keep training, you'll want to save the number of epochs as well as the optimizer state, `optimizer.state_dict`. You'll likely want to use this trained model in the next part of the project, so best to save it now.
## Loading the checkpoint
At this point it's good to write a function that can load a checkpoint and rebuild the model. That way you can come back to this project and keep working on it without having to retrain the network.
# Inference for classification
Now you'll write a function to use a trained network for inference. That is, you'll pass an image into the network and predict the class of the flower in the image. Write a function called `predict` that takes an image and a model, then returns the top $K$ most likely classes along with the probabilities. It should look like
First you'll need to handle processing the input image such that it can be used in your network.
## Image Preprocessing
You'll want to use `PIL` to load the image ([documentation](https://pillow.readthedocs.io/en/latest/reference/Image.html)). It's best to write a function that preprocesses the image so it can be used as input for the model. This function should process the images in the same manner used for training.
First, resize the images where the shortest side is 256 pixels, keeping the aspect ratio. This can be done with the [`thumbnail`](http://pillow.readthedocs.io/en/3.1.x/reference/Image.html#PIL.Image.Image.thumbnail) or [`resize`](http://pillow.readthedocs.io/en/3.1.x/reference/Image.html#PIL.Image.Image.thumbnail) methods. Then you'll need to crop out the center 224x224 portion of the image.
Color channels of images are typically encoded as integers 0-255, but the model expected floats 0-1. You'll need to convert the values. It's easiest with a Numpy array, which you can get from a PIL image like so `np_image = np.array(pil_image)`.
As before, the network expects the images to be normalized in a specific way. For the means, it's `[0.485, 0.456, 0.406]` and for the standard deviations `[0.229, 0.224, 0.225]`. You'll want to subtract the means from each color channel, then divide by the standard deviation.
And finally, PyTorch expects the color channel to be the first dimension but it's the third dimension in the PIL image and Numpy array. You can reorder dimensions using [`ndarray.transpose`](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.ndarray.transpose.html). The color channel needs to be first and retain the order of the other two dimensions.
To check your work, the function below converts a PyTorch tensor and displays it in the notebook. If your `process_image` function works, running the output through this function should return the original image (except for the cropped out portions).
### Using a random image from the test directory to test the various functions being created
## Class Prediction
Once you can get images in the correct format, it's time to write a function for making predictions with your model. A common practice is to predict the top 5 or so (usually called top-$K$) most probable classes. You'll want to calculate the class probabilities then find the $K$ largest values.
To get the top $K$ largest values in a tensor use [`x.topk(k)`](http://pytorch.org/docs/master/torch.html#torch.topk). This method returns both the highest `k` probabilities and the indices of those probabilities corresponding to the classes. You need to convert from these indices to the actual class labels using `class_to_idx` which hopefully you added to the model or from an `ImageFolder` you used to load the data ([see here](#Save-the-checkpoint)). Make sure to invert the dictionary so you get a mapping from index to class as well.
Again, this method should take a path to an image and a model checkpoint, then return the probabilities and classes.
## Sanity Checking
Now that you can use a trained model for predictions, check to make sure it makes sense. Even if the testing accuracy is high, it's always good to check that there aren't obvious bugs. Use `matplotlib` to plot the probabilities for the top 5 classes as a bar graph, along with the input image. It should look like this:
<img src='assets/inference_example.png' width=300px>
You can convert from the class integer encoding to actual flower names with the `cat_to_name.json` file (should have been loaded earlier in the notebook). To show a PyTorch tensor as an image, use the `imshow` function defined above.
| 0.766905 | 0.98366 |
# **Phrase Generator Model**
This notebook trains a model using Keras (and TensorFlow Backend) to finish your phrase in the style of author/poet William Shakespeare.
Below we do the following:
1. Setup training environment
2. Load and clean the Shakespeare test samples.
3. Train a word-level, neural network language model.
4. Convert the model to CoreML format.
5. Deliver the model to an app using Skafos
```
# First, let's install the tools and dependencies we need.
!pip install keras skafos coremltools
# Import tools and libraries
import os
import re
import zipfile
import urllib
import skafos
from skafos import models
import numpy as np
from keras.optimizers import RMSprop
from keras.models import Sequential
from keras.layers import Dense, LSTM, Embedding
from keras.preprocessing.text import Tokenizer
from keras.utils import to_categorical
# Check the skafos version
skafos.get_version()
```
## Data Preparation
The training data for this example are samples of text from some pieces authored by William Shakespeare.
The code below does the following:
- Downloads the data from a public S3 bucket provided by Skafos.
- Defines some helper functions to parse the text.
- Tokenizes the text.
- Prepares the training data, building input sequences for the model.
```
# Specify the data set download url
data_path = "Shakespeare.zip"
data_url = "https://s3.amazonaws.com/skafos.example.data/PhraseGenModel/{}".format(data_path)
# Download the dataset
retrieve = urllib.request.urlretrieve(data_url, data_path)
# Unzip
zip_ref = zipfile.ZipFile(data_path, 'r')
zip_ref.extractall()
zip_ref.close()
# Helper functions
# Remove stage direction and comments
def remove_stage_dir(text):
text = re.sub("[\<].*?[\>]", "", text)
text = re.sub("\\s+", " ", text)
return text
# Remove the word "SPEECH" adn the number following after that in the corpus
def remove_SPEECH(text):
text = re.sub("SPEECH \d+", "", text)
text = re.sub("\\s+", " ", text)
return text
# Read in Shakespeare files
in_sentences = []
for filename in os.listdir():
if filename.endswith(".txt"):
text = ''.join(open(filename, encoding = "utf-8-sig", mode="r").readlines())
# Chop up into sentences
split_text = re.split(r' *[\.\?!][\'"\)\]]* *', remove_stage_dir(text))
for chunk in split_text:
in_sentences.append(chunk.strip())
print(in_sentences[0:10])
# Some constants
# Length of extracted text sample
maxlen = 10
# Stride of sampling
step = 2
# This holds our samples sequences
sentences = []
# This holds the next word (as training label)
next_word = []
# Prepare the Tokenizer
tokenizer = Tokenizer()
tokenizer.fit_on_texts(list(in_sentences))
list_tokenized_train = tokenizer.texts_to_sequences(list(in_sentences))
# Get vocabulary size
vocab_size = len(tokenizer.word_index) + 1
print(f'{vocab_size} total unique words in our training data corpus', flush=True)
# Stick the encoded words back together as a long sequence
token_word = []
for line in range (0,len(in_sentences)):
that_sentences = list_tokenized_train[line]
for i in range(0,len(that_sentences)):
token_word.append(that_sentences[i])
# Sample from the sequence
for i in range(0, len(token_word) - maxlen, step):
sentences.append(token_word[i: i + maxlen])
next_word.append(token_word[i + maxlen])
print('Number of sentences:', len(sentences))
# Prepare the training data sequences
x = np.asarray(sentences)
y = to_categorical(next_word, num_classes=vocab_size)
seq_length = x.shape[1]
# Do some garbage collection
del(sentences, in_sentences, next_word, token_word)
```
## Model Training
The phrase generation model takes sequences of tokenized text as input and tries to predict the most likely next word from the vocabulary. You can create phrases by recursively feeding previous predictions, adding a single word at a time to a phrase.. almost like a "digital Shakespeare". The Keras model uses three different layer types in the neural network: Embedding, LSTM, and Dense. Links to relevant documentation are provided in the cell below.
```
# Create the model
model = Sequential()
model.add(Embedding(input_dim=vocab_size, output_dim=256, input_length=seq_length)) # Docs: https://www.tensorflow.org/api_docs/python/tf/keras/layers/Embedding
model.add(LSTM(units=256)) # Docs: https://www.tensorflow.org/api_docs/python/tf/keras/layers/LSTM
model.add(Dense(vocab_size, activation='softmax')) # Docs: https://www.tensorflow.org/api_docs/python/tf/keras/layers/Dense
print(model.summary(), flush=True)
# Compile the model
# Since our predictions are one-hot encoded, use `categorical_crossentropy` as the loss
optimizer = RMSprop(lr=0.01)
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy']) # keep track of accuracy along the way
# Train the model for a few epochs
model.fit(x, y, batch_size=256, epochs=15)
# Pickup training from where you left off last with the following
# Using an initial_epoch of 15 and epochs of 20, the model will begin at epoch 16 and train up until it reaches 20 (from where you last left off)
model.fit(x, y, batch_size=256, initial_epoch=15, epochs=20)
```
## Model Validation
Below we reverse and export the tokenizer so we can lookup a word based on it's index. Then we test out the newly trained model with some sample text.
```
import json
# Invert the tokenizer map so we can lookup a word by it's index
index_word_lookup = dict(map(reversed, tokenizer.word_index.items()))
index_word_lookup_file = 'index_word_lookup.json'
# Save it to a json object
with open(index_word_lookup_file, 'w') as fp:
json.dump(index_word_lookup, fp)
from keras.preprocessing.sequence import pad_sequences
# Function to generate new text based on the input
def generate_text(seed_text, next_words, max_sequence_len, model):
for j in range(next_words):
token_list = pad_sequences(
sequences=tokenizer.texts_to_sequences([seed_text]),
maxlen=max_sequence_len,
padding='pre'
)
predicted = model.predict_classes(token_list, verbose=0)
# Generate the output word
seed_text += " " + index_word_lookup[predicted[0]]
return seed_text
# Test out the language model by passing in some seed text and the number of words
generate_text("You shall go see", 3, maxlen, model)
```
## Deliver your model to an iOS App with Skafos
As a final step to optimize your model for use on mobile devices, we need to convert our model from a Keras object to CoreML format. After conversion, we will use the [Skafos SDK](https://sdk.skafos.ai) to upload it to Skafos!
To execute the following steps, you will need to do the following:
- [Sign-up for a Skafos account](https://dashboard.skafos.ai/sign-up) if you haven't already.
- Navigate to the [account settings page on Skafos](https://dashboard.skafos.ai/settings/account) to get an API token.
```
import coremltools
# Convert the language model to Core ML format
model_name = "PhraseGenModel"
coreml_model_name = model_name + ".mlmodel"
coreml_model = coremltools.converters.keras.convert(
model,
input_names=['tokenizedInputSeq'],
output_names=['tokenProbs']
)
# Add description information (if you want) and save the file
coreml_model.short_description = 'Predicts the most likely next word given a string of text'
coreml_model.input_description['tokenizedInputSeq'] = 'An array of tokenized text'
coreml_model.output_description['tokenProbs'] = 'An array of token probabilities across the entire vocabulary'
coreml_model.save(coreml_model_name)
# Skafos SDK Upload Model Version
# Set your API Token first for repeated use
os.environ["SKAFOS_API_TOKEN"] = "<YOUR-SKAFOS-API-TOKEN>"
# Get a summary of your existing apps and models on Skafos, so you can determine where to deliver this model.
res = skafos.summary()
print(res)
# You can retrieve this info with skafos.summary()
org_name = "<YOUR-SKAFOS-ORG-NAME>" # Example: "mike-gmail-com-467h2"
app_name = "<YOUR-SKAFOS-APP-NAME>" # Example: "PhraseGenerator"
model_name = "<YOUR-SKAFOS-MODEL-NAME>" # Example: "PhraseGenModel"
# Upload model version to Skafos
model_upload_result = models.upload_version(
files = [coreml_model_name, index_word_lookup_file],
description = "Shakespeare model",
org_name = org_name,
app_name = app_name,
model_name = model_name
)
```
|
github_jupyter
|
# First, let's install the tools and dependencies we need.
!pip install keras skafos coremltools
# Import tools and libraries
import os
import re
import zipfile
import urllib
import skafos
from skafos import models
import numpy as np
from keras.optimizers import RMSprop
from keras.models import Sequential
from keras.layers import Dense, LSTM, Embedding
from keras.preprocessing.text import Tokenizer
from keras.utils import to_categorical
# Check the skafos version
skafos.get_version()
# Specify the data set download url
data_path = "Shakespeare.zip"
data_url = "https://s3.amazonaws.com/skafos.example.data/PhraseGenModel/{}".format(data_path)
# Download the dataset
retrieve = urllib.request.urlretrieve(data_url, data_path)
# Unzip
zip_ref = zipfile.ZipFile(data_path, 'r')
zip_ref.extractall()
zip_ref.close()
# Helper functions
# Remove stage direction and comments
def remove_stage_dir(text):
text = re.sub("[\<].*?[\>]", "", text)
text = re.sub("\\s+", " ", text)
return text
# Remove the word "SPEECH" adn the number following after that in the corpus
def remove_SPEECH(text):
text = re.sub("SPEECH \d+", "", text)
text = re.sub("\\s+", " ", text)
return text
# Read in Shakespeare files
in_sentences = []
for filename in os.listdir():
if filename.endswith(".txt"):
text = ''.join(open(filename, encoding = "utf-8-sig", mode="r").readlines())
# Chop up into sentences
split_text = re.split(r' *[\.\?!][\'"\)\]]* *', remove_stage_dir(text))
for chunk in split_text:
in_sentences.append(chunk.strip())
print(in_sentences[0:10])
# Some constants
# Length of extracted text sample
maxlen = 10
# Stride of sampling
step = 2
# This holds our samples sequences
sentences = []
# This holds the next word (as training label)
next_word = []
# Prepare the Tokenizer
tokenizer = Tokenizer()
tokenizer.fit_on_texts(list(in_sentences))
list_tokenized_train = tokenizer.texts_to_sequences(list(in_sentences))
# Get vocabulary size
vocab_size = len(tokenizer.word_index) + 1
print(f'{vocab_size} total unique words in our training data corpus', flush=True)
# Stick the encoded words back together as a long sequence
token_word = []
for line in range (0,len(in_sentences)):
that_sentences = list_tokenized_train[line]
for i in range(0,len(that_sentences)):
token_word.append(that_sentences[i])
# Sample from the sequence
for i in range(0, len(token_word) - maxlen, step):
sentences.append(token_word[i: i + maxlen])
next_word.append(token_word[i + maxlen])
print('Number of sentences:', len(sentences))
# Prepare the training data sequences
x = np.asarray(sentences)
y = to_categorical(next_word, num_classes=vocab_size)
seq_length = x.shape[1]
# Do some garbage collection
del(sentences, in_sentences, next_word, token_word)
# Create the model
model = Sequential()
model.add(Embedding(input_dim=vocab_size, output_dim=256, input_length=seq_length)) # Docs: https://www.tensorflow.org/api_docs/python/tf/keras/layers/Embedding
model.add(LSTM(units=256)) # Docs: https://www.tensorflow.org/api_docs/python/tf/keras/layers/LSTM
model.add(Dense(vocab_size, activation='softmax')) # Docs: https://www.tensorflow.org/api_docs/python/tf/keras/layers/Dense
print(model.summary(), flush=True)
# Compile the model
# Since our predictions are one-hot encoded, use `categorical_crossentropy` as the loss
optimizer = RMSprop(lr=0.01)
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy']) # keep track of accuracy along the way
# Train the model for a few epochs
model.fit(x, y, batch_size=256, epochs=15)
# Pickup training from where you left off last with the following
# Using an initial_epoch of 15 and epochs of 20, the model will begin at epoch 16 and train up until it reaches 20 (from where you last left off)
model.fit(x, y, batch_size=256, initial_epoch=15, epochs=20)
import json
# Invert the tokenizer map so we can lookup a word by it's index
index_word_lookup = dict(map(reversed, tokenizer.word_index.items()))
index_word_lookup_file = 'index_word_lookup.json'
# Save it to a json object
with open(index_word_lookup_file, 'w') as fp:
json.dump(index_word_lookup, fp)
from keras.preprocessing.sequence import pad_sequences
# Function to generate new text based on the input
def generate_text(seed_text, next_words, max_sequence_len, model):
for j in range(next_words):
token_list = pad_sequences(
sequences=tokenizer.texts_to_sequences([seed_text]),
maxlen=max_sequence_len,
padding='pre'
)
predicted = model.predict_classes(token_list, verbose=0)
# Generate the output word
seed_text += " " + index_word_lookup[predicted[0]]
return seed_text
# Test out the language model by passing in some seed text and the number of words
generate_text("You shall go see", 3, maxlen, model)
import coremltools
# Convert the language model to Core ML format
model_name = "PhraseGenModel"
coreml_model_name = model_name + ".mlmodel"
coreml_model = coremltools.converters.keras.convert(
model,
input_names=['tokenizedInputSeq'],
output_names=['tokenProbs']
)
# Add description information (if you want) and save the file
coreml_model.short_description = 'Predicts the most likely next word given a string of text'
coreml_model.input_description['tokenizedInputSeq'] = 'An array of tokenized text'
coreml_model.output_description['tokenProbs'] = 'An array of token probabilities across the entire vocabulary'
coreml_model.save(coreml_model_name)
# Skafos SDK Upload Model Version
# Set your API Token first for repeated use
os.environ["SKAFOS_API_TOKEN"] = "<YOUR-SKAFOS-API-TOKEN>"
# Get a summary of your existing apps and models on Skafos, so you can determine where to deliver this model.
res = skafos.summary()
print(res)
# You can retrieve this info with skafos.summary()
org_name = "<YOUR-SKAFOS-ORG-NAME>" # Example: "mike-gmail-com-467h2"
app_name = "<YOUR-SKAFOS-APP-NAME>" # Example: "PhraseGenerator"
model_name = "<YOUR-SKAFOS-MODEL-NAME>" # Example: "PhraseGenModel"
# Upload model version to Skafos
model_upload_result = models.upload_version(
files = [coreml_model_name, index_word_lookup_file],
description = "Shakespeare model",
org_name = org_name,
app_name = app_name,
model_name = model_name
)
| 0.726814 | 0.894144 |
<h1> Time series prediction using RNNs, with TensorFlow and Cloud ML Engine </h1>
This notebook illustrates:
<ol>
<li> Creating a Recurrent Neural Network in TensorFlow
<li> Creating a Custom Estimator in tf.estimator
<li> Training on Cloud ML Engine
</ol>
<p>
<h3> Simulate some time-series data </h3>
Essentially a set of sinusoids with random amplitudes and frequencies.
```
import tensorflow as tf
print tf.__version__
import numpy as np
import seaborn as sns
import pandas as pd
SEQ_LEN = 10
def create_time_series():
freq = (np.random.random() * 0.5) + 0.1 # 0.1 to 0.6
ampl = np.random.random() + 0.5 # 0.5 to 1.5
x = np.sin(np.arange(0, SEQ_LEN) * freq) * ampl
return x
for i in xrange(0, 5):
sns.tsplot( create_time_series() ); # 5 series
def to_csv(filename, N):
with open(filename, 'w') as ofp:
for lineno in xrange(0, N):
seq = create_time_series()
line = ",".join(map(str, seq))
ofp.write(line + '\n')
to_csv('train.csv', 1000) # 1000 sequences
to_csv('valid.csv', 50)
!head -5 train.csv valid.csv
```
<h2> RNN </h2>
For more info, see:
<ol>
<li> http://colah.github.io/posts/2015-08-Understanding-LSTMs/ for the theory
<li> https://www.tensorflow.org/tutorials/recurrent for explanations
<li> https://github.com/tensorflow/models/tree/master/tutorials/rnn/ptb for sample code
</ol>
Here, we are trying to predict from 9 values of a timeseries, the tenth value.
<p>
<h3> Imports </h3>
Several tensorflow packages and shutil
```
import tensorflow as tf
import shutil
import tensorflow.contrib.metrics as metrics
import tensorflow.contrib.rnn as rnn
```
<h3> Input Fn to read CSV </h3>
Our CSV file structure is quite simple -- a bunch of floating point numbers (note the type of DEFAULTS). We ask for the data to be read BATCH_SIZE sequences at a time. The Estimator API in tf.contrib.learn wants the features returned as a dict. We'll just call this timeseries column 'rawdata'.
<p>
Our CSV file sequences consist of 10 numbers. We'll assume that 9 of them are inputs and we need to predict the last one.
```
DEFAULTS = [[0.0] for x in xrange(0, SEQ_LEN)]
BATCH_SIZE = 20
TIMESERIES_COL = 'rawdata'
# In each sequence, column index 0 to N_INPUTS - 1 are features, and column index N_INPUTS to SEQ_LEN are labels
N_OUTPUTS = 1
N_INPUTS = SEQ_LEN - N_OUTPUTS
```
Reading data using the Estimator API in tf.estimator requires an input_fn. This input_fn needs to return a dict of features and the corresponding labels.
<p>
So, we read the CSV file. The Tensor format here will be a scalar -- entire line. We then decode the CSV. At this point, all_data will contain a list of scalar Tensors. There will be SEQ_LEN of these tensors.
<p>
We split this list of SEQ_LEN tensors into a list of N_INPUTS Tensors and a list of N_OUTPUTS Tensors. We stack them along the first dimension to then get a vector Tensor for each. We then put the inputs into a dict and call it features. The other is the ground truth, so labels.
```
# Read data and convert to needed format
def read_dataset(filename, mode, batch_size = 512):
def _input_fn():
# Provide the ability to decode a CSV
def decode_csv(line):
# all_data is a list of scalar tensors
all_data = tf.decode_csv(line, record_defaults = DEFAULTS)
inputs = all_data[:len(all_data) - N_OUTPUTS] # first N_INPUTS values
labels = all_data[len(all_data) - N_OUTPUTS:] # last N_OUTPUTS values
# Convert each list of rank R tensors to one rank R+1 tensor
inputs = tf.stack(inputs, axis = 0)
labels = tf.stack(labels, axis = 0)
# Convert input R+1 tensor into a feature dictionary of one R+1 tensor
features = {TIMESERIES_COL: inputs}
return features, labels
# Create list of files that match pattern
file_list = tf.gfile.Glob(filename)
# Create dataset from file list
dataset = tf.data.TextLineDataset(file_list).map(decode_csv)
if mode == tf.estimator.ModeKeys.TRAIN:
num_epochs = None # indefinitely
dataset = dataset.shuffle(buffer_size = 10 * batch_size)
else:
num_epochs = 1 # end-of-input after this
dataset = dataset.repeat(num_epochs).batch(batch_size)
iterator = dataset.make_one_shot_iterator()
batch_features, batch_labels = iterator.get_next()
return batch_features, batch_labels
return _input_fn
```
<h3> Define RNN </h3>
A recursive neural network consists of possibly stacked LSTM cells.
<p>
The RNN has one output per input, so it will have 8 output cells. We use only the last output cell, but rather use it directly, we do a matrix multiplication of that cell by a set of weights to get the actual predictions. This allows for a degree of scaling between inputs and predictions if necessary (we don't really need it in this problem).
<p>
Finally, to supply a model function to the Estimator API, you need to return a EstimatorSpec. The rest of the function creates the necessary objects.
```
LSTM_SIZE = 3 # number of hidden layers in each of the LSTM cells
# Create the inference model
def simple_rnn(features, labels, mode):
# 0. Reformat input shape to become a sequence
x = tf.split(features[TIMESERIES_COL], N_INPUTS, 1)
# 1. Configure the RNN
lstm_cell = rnn.BasicLSTMCell(LSTM_SIZE, forget_bias = 1.0)
outputs, _ = rnn.static_rnn(lstm_cell, x, dtype = tf.float32)
# Slice to keep only the last cell of the RNN
outputs = outputs[-1]
# Output is result of linear activation of last layer of RNN
weight = tf.Variable(tf.random_normal([LSTM_SIZE, N_OUTPUTS]))
bias = tf.Variable(tf.random_normal([N_OUTPUTS]))
predictions = tf.matmul(outputs, weight) + bias
# 2. Loss function, training/eval ops
if mode == tf.estimator.ModeKeys.TRAIN or mode == tf.estimator.ModeKeys.EVAL:
loss = tf.losses.mean_squared_error(labels, predictions)
train_op = tf.contrib.layers.optimize_loss(
loss = loss,
global_step = tf.train.get_global_step(),
learning_rate = 0.01,
optimizer = "SGD")
eval_metric_ops = {
"rmse": tf.metrics.root_mean_squared_error(labels, predictions)
}
else:
loss = None
train_op = None
eval_metric_ops = None
# 3. Create predictions
predictions_dict = {"predicted": predictions}
# 4. Create export outputs
export_outputs = {"predict_export_outputs": tf.estimator.export.PredictOutput(outputs = predictions)}
# 5. Return EstimatorSpec
return tf.estimator.EstimatorSpec(
mode = mode,
predictions = predictions_dict,
loss = loss,
train_op = train_op,
eval_metric_ops = eval_metric_ops,
export_outputs = export_outputs)
```
<h3> Estimator </h3>
Distributed training is launched off using an Estimator. The key line here is that we use tf.estimator.Estimator rather than, say tf.estimator.DNNRegressor. This allows us to provide a model_fn, which will be our RNN defined above. Note also that we specify a serving_input_fn -- this is how we parse the input data provided to us at prediction time.
```
# Create functions to read in respective datasets
def get_train():
return read_dataset(filename = 'train.csv', mode = tf.estimator.ModeKeys.TRAIN, batch_size = 512)
def get_valid():
return read_dataset(filename = 'valid.csv', mode = tf.estimator.ModeKeys.EVAL, batch_size = 512)
# Create serving input function
def serving_input_fn():
feature_placeholders = {
TIMESERIES_COL: tf.placeholder(tf.float32, [None, N_INPUTS])
}
features = {
key: tf.expand_dims(tensor, -1)
for key, tensor in feature_placeholders.items()
}
features[TIMESERIES_COL] = tf.squeeze(features[TIMESERIES_COL], axis = [2])
return tf.estimator.export.ServingInputReceiver(features, feature_placeholders)
# Create custom estimator's train and evaluate function
def train_and_evaluate(output_dir):
estimator = tf.estimator.Estimator(model_fn = simple_rnn,
model_dir = output_dir)
train_spec = tf.estimator.TrainSpec(input_fn = get_train(),
max_steps = 1000)
exporter = tf.estimator.LatestExporter('exporter', serving_input_fn)
eval_spec = tf.estimator.EvalSpec(input_fn = get_valid(),
steps = None,
exporters = exporter)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
# Run the model
shutil.rmtree('outputdir', ignore_errors = True) # start fresh each time
train_and_evaluate('outputdir')
```
<h3> Standalone Python module </h3>
To train this on Cloud ML Engine, we take the code in this notebook and make a standalone Python module.
```
%bash
# Run module as-is
echo $PWD
rm -rf outputdir
export PYTHONPATH=${PYTHONPATH}:${PWD}/simplernn
python -m trainer.task \
--train_data_paths="${PWD}/train.csv*" \
--eval_data_paths="${PWD}/valid.csv*" \
--output_dir=${PWD}/outputdir \
--job-dir=./tmp
```
Try out online prediction. This is how the REST API will work after you train on Cloud ML Engine
```
%writefile test.json
{"rawdata": [0,0.214,0.406,0.558,0.655,0.687,0.65,0.549,0.393]}
%bash
MODEL_DIR=$(ls ./outputdir/export/exporter/)
gcloud ml-engine local predict --model-dir=./outputdir/export/exporter/$MODEL_DIR --json-instances=test.json
```
<h3> Cloud ML Engine </h3>
Now to train on Cloud ML Engine.
```
%bash
# Run module on Cloud ML Engine
BUCKET=cloud-training-demos-ml # CHANGE AS NEEDED
OUTDIR=gs://${BUCKET}/simplernn/model_trained
JOBNAME=simplernn_$(date -u +%y%m%d_%H%M%S)
REGION=us-central1
gsutil -m rm -rf $OUTDIR
gcloud ml-engine jobs submit training $JOBNAME \
--region=$REGION \
--module-name=trainer.task \
--package-path=${PWD}/simplernn/trainer \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=BASIC \
--runtime-version=1.4 \
-- \
--train_data_paths="gs://${BUCKET}/train.csv*" \
--eval_data_paths="gs://${BUCKET}/valid.csv*" \
--output_dir=$OUTDIR
```
<h2> Variant: long sequence </h2>
To create short sequences from a very long sequence.
```
import tensorflow as tf
import numpy as np
def breakup(sess, x, lookback_len):
N = sess.run(tf.size(x))
windows = [tf.slice(x, [b], [lookback_len]) for b in xrange(0, N-lookback_len)]
windows = tf.stack(windows)
return windows
x = tf.constant(np.arange(1,11, dtype=np.float32))
with tf.Session() as sess:
print 'input=', x.eval()
seqx = breakup(sess, x, 5)
print 'output=', seqx.eval()
```
## Variant: Keras
You can also invoke a Keras model from within the Estimator framework by creating an estimator from the compiled Keras model:
```
def make_keras_estimator(output_dir):
from tensorflow import keras
model = keras.models.Sequential()
model.add(keras.layers.Dense(32, input_shape=(N_INPUTS,), name=TIMESERIES_INPUT_LAYER))
model.add(keras.layers.Activation('relu'))
model.add(keras.layers.Dense(1))
model.compile(loss = 'mean_squared_error',
optimizer = 'adam',
metrics = ['mae', 'mape']) # mean absolute [percentage] error
return keras.estimator.model_to_estimator(model)
%bash
# Run module as-is
echo $PWD
rm -rf outputdir
export PYTHONPATH=${PYTHONPATH}:${PWD}/simplernn
python -m trainer.task \
--train_data_paths="${PWD}/train.csv*" \
--eval_data_paths="${PWD}/valid.csv*" \
--output_dir=${PWD}/outputdir \
--job-dir=./tmp --keras
```
Copyright 2017 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
|
github_jupyter
|
import tensorflow as tf
print tf.__version__
import numpy as np
import seaborn as sns
import pandas as pd
SEQ_LEN = 10
def create_time_series():
freq = (np.random.random() * 0.5) + 0.1 # 0.1 to 0.6
ampl = np.random.random() + 0.5 # 0.5 to 1.5
x = np.sin(np.arange(0, SEQ_LEN) * freq) * ampl
return x
for i in xrange(0, 5):
sns.tsplot( create_time_series() ); # 5 series
def to_csv(filename, N):
with open(filename, 'w') as ofp:
for lineno in xrange(0, N):
seq = create_time_series()
line = ",".join(map(str, seq))
ofp.write(line + '\n')
to_csv('train.csv', 1000) # 1000 sequences
to_csv('valid.csv', 50)
!head -5 train.csv valid.csv
import tensorflow as tf
import shutil
import tensorflow.contrib.metrics as metrics
import tensorflow.contrib.rnn as rnn
DEFAULTS = [[0.0] for x in xrange(0, SEQ_LEN)]
BATCH_SIZE = 20
TIMESERIES_COL = 'rawdata'
# In each sequence, column index 0 to N_INPUTS - 1 are features, and column index N_INPUTS to SEQ_LEN are labels
N_OUTPUTS = 1
N_INPUTS = SEQ_LEN - N_OUTPUTS
# Read data and convert to needed format
def read_dataset(filename, mode, batch_size = 512):
def _input_fn():
# Provide the ability to decode a CSV
def decode_csv(line):
# all_data is a list of scalar tensors
all_data = tf.decode_csv(line, record_defaults = DEFAULTS)
inputs = all_data[:len(all_data) - N_OUTPUTS] # first N_INPUTS values
labels = all_data[len(all_data) - N_OUTPUTS:] # last N_OUTPUTS values
# Convert each list of rank R tensors to one rank R+1 tensor
inputs = tf.stack(inputs, axis = 0)
labels = tf.stack(labels, axis = 0)
# Convert input R+1 tensor into a feature dictionary of one R+1 tensor
features = {TIMESERIES_COL: inputs}
return features, labels
# Create list of files that match pattern
file_list = tf.gfile.Glob(filename)
# Create dataset from file list
dataset = tf.data.TextLineDataset(file_list).map(decode_csv)
if mode == tf.estimator.ModeKeys.TRAIN:
num_epochs = None # indefinitely
dataset = dataset.shuffle(buffer_size = 10 * batch_size)
else:
num_epochs = 1 # end-of-input after this
dataset = dataset.repeat(num_epochs).batch(batch_size)
iterator = dataset.make_one_shot_iterator()
batch_features, batch_labels = iterator.get_next()
return batch_features, batch_labels
return _input_fn
LSTM_SIZE = 3 # number of hidden layers in each of the LSTM cells
# Create the inference model
def simple_rnn(features, labels, mode):
# 0. Reformat input shape to become a sequence
x = tf.split(features[TIMESERIES_COL], N_INPUTS, 1)
# 1. Configure the RNN
lstm_cell = rnn.BasicLSTMCell(LSTM_SIZE, forget_bias = 1.0)
outputs, _ = rnn.static_rnn(lstm_cell, x, dtype = tf.float32)
# Slice to keep only the last cell of the RNN
outputs = outputs[-1]
# Output is result of linear activation of last layer of RNN
weight = tf.Variable(tf.random_normal([LSTM_SIZE, N_OUTPUTS]))
bias = tf.Variable(tf.random_normal([N_OUTPUTS]))
predictions = tf.matmul(outputs, weight) + bias
# 2. Loss function, training/eval ops
if mode == tf.estimator.ModeKeys.TRAIN or mode == tf.estimator.ModeKeys.EVAL:
loss = tf.losses.mean_squared_error(labels, predictions)
train_op = tf.contrib.layers.optimize_loss(
loss = loss,
global_step = tf.train.get_global_step(),
learning_rate = 0.01,
optimizer = "SGD")
eval_metric_ops = {
"rmse": tf.metrics.root_mean_squared_error(labels, predictions)
}
else:
loss = None
train_op = None
eval_metric_ops = None
# 3. Create predictions
predictions_dict = {"predicted": predictions}
# 4. Create export outputs
export_outputs = {"predict_export_outputs": tf.estimator.export.PredictOutput(outputs = predictions)}
# 5. Return EstimatorSpec
return tf.estimator.EstimatorSpec(
mode = mode,
predictions = predictions_dict,
loss = loss,
train_op = train_op,
eval_metric_ops = eval_metric_ops,
export_outputs = export_outputs)
# Create functions to read in respective datasets
def get_train():
return read_dataset(filename = 'train.csv', mode = tf.estimator.ModeKeys.TRAIN, batch_size = 512)
def get_valid():
return read_dataset(filename = 'valid.csv', mode = tf.estimator.ModeKeys.EVAL, batch_size = 512)
# Create serving input function
def serving_input_fn():
feature_placeholders = {
TIMESERIES_COL: tf.placeholder(tf.float32, [None, N_INPUTS])
}
features = {
key: tf.expand_dims(tensor, -1)
for key, tensor in feature_placeholders.items()
}
features[TIMESERIES_COL] = tf.squeeze(features[TIMESERIES_COL], axis = [2])
return tf.estimator.export.ServingInputReceiver(features, feature_placeholders)
# Create custom estimator's train and evaluate function
def train_and_evaluate(output_dir):
estimator = tf.estimator.Estimator(model_fn = simple_rnn,
model_dir = output_dir)
train_spec = tf.estimator.TrainSpec(input_fn = get_train(),
max_steps = 1000)
exporter = tf.estimator.LatestExporter('exporter', serving_input_fn)
eval_spec = tf.estimator.EvalSpec(input_fn = get_valid(),
steps = None,
exporters = exporter)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
# Run the model
shutil.rmtree('outputdir', ignore_errors = True) # start fresh each time
train_and_evaluate('outputdir')
%bash
# Run module as-is
echo $PWD
rm -rf outputdir
export PYTHONPATH=${PYTHONPATH}:${PWD}/simplernn
python -m trainer.task \
--train_data_paths="${PWD}/train.csv*" \
--eval_data_paths="${PWD}/valid.csv*" \
--output_dir=${PWD}/outputdir \
--job-dir=./tmp
%writefile test.json
{"rawdata": [0,0.214,0.406,0.558,0.655,0.687,0.65,0.549,0.393]}
%bash
MODEL_DIR=$(ls ./outputdir/export/exporter/)
gcloud ml-engine local predict --model-dir=./outputdir/export/exporter/$MODEL_DIR --json-instances=test.json
%bash
# Run module on Cloud ML Engine
BUCKET=cloud-training-demos-ml # CHANGE AS NEEDED
OUTDIR=gs://${BUCKET}/simplernn/model_trained
JOBNAME=simplernn_$(date -u +%y%m%d_%H%M%S)
REGION=us-central1
gsutil -m rm -rf $OUTDIR
gcloud ml-engine jobs submit training $JOBNAME \
--region=$REGION \
--module-name=trainer.task \
--package-path=${PWD}/simplernn/trainer \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=BASIC \
--runtime-version=1.4 \
-- \
--train_data_paths="gs://${BUCKET}/train.csv*" \
--eval_data_paths="gs://${BUCKET}/valid.csv*" \
--output_dir=$OUTDIR
import tensorflow as tf
import numpy as np
def breakup(sess, x, lookback_len):
N = sess.run(tf.size(x))
windows = [tf.slice(x, [b], [lookback_len]) for b in xrange(0, N-lookback_len)]
windows = tf.stack(windows)
return windows
x = tf.constant(np.arange(1,11, dtype=np.float32))
with tf.Session() as sess:
print 'input=', x.eval()
seqx = breakup(sess, x, 5)
print 'output=', seqx.eval()
def make_keras_estimator(output_dir):
from tensorflow import keras
model = keras.models.Sequential()
model.add(keras.layers.Dense(32, input_shape=(N_INPUTS,), name=TIMESERIES_INPUT_LAYER))
model.add(keras.layers.Activation('relu'))
model.add(keras.layers.Dense(1))
model.compile(loss = 'mean_squared_error',
optimizer = 'adam',
metrics = ['mae', 'mape']) # mean absolute [percentage] error
return keras.estimator.model_to_estimator(model)
%bash
# Run module as-is
echo $PWD
rm -rf outputdir
export PYTHONPATH=${PYTHONPATH}:${PWD}/simplernn
python -m trainer.task \
--train_data_paths="${PWD}/train.csv*" \
--eval_data_paths="${PWD}/valid.csv*" \
--output_dir=${PWD}/outputdir \
--job-dir=./tmp --keras
| 0.676299 | 0.966379 |
# Statistics Fundamentals
Statistics is primarily about analyzing data samples, and that starts with udnerstanding the distribution of data in a sample.
## Analyzing Data Distribution
A great deal of statistical analysis is based on the way that data values are distributed within the dataset. In this section, we'll explore some statistics that you can use to tell you about the values in a dataset.
### Measures of Central Tendency
The term *measures of central tendency* sounds a bit grand, but really it's just a fancy way of saying that we're interested in knowing where the middle value in our data is. For example, suppose decide to conduct a study into the comparative salaries of people who graduated from the same school. You might record the results like this:
| Name | Salary |
|----------|-------------|
| Dan | 50,000 |
| Joann | 54,000 |
| Pedro | 50,000 |
| Rosie | 189,000 |
| Ethan | 55,000 |
| Vicky | 40,000 |
| Frederic | 59,000 |
Now, some of the former-students may earn a lot, and others may earn less; but what's the salary in the middle of the range of all salaries?
#### Mean
A common way to define the central value is to use the *mean*, often called the *average*. This is calculated as the sum of the values in the dataset, divided by the number of observations in the dataset. When the dataset consists of the full population, the mean is represented by the Greek symbol ***μ*** (*mu*), and the formula is written like this:
\begin{equation}\mu = \frac{\displaystyle\sum_{i=1}^{N}X_{i}}{N}\end{equation}
More commonly, when working with a sample, the mean is represented by ***x̄*** (*x-bar*), and the formula is written like this (note the lower case letters used to indicate values from a sample):
\begin{equation}\bar{x} = \frac{\displaystyle\sum_{i=1}^{n}x_{i}}{n}\end{equation}
In the case of our list of heights, this can be calculated as:
\begin{equation}\bar{x} = \frac{50000+54000+50000+189000+55000+40000+59000}{7}\end{equation}
Which is **71,000**.
>In technical terminology, ***x̄*** is a *statistic* (an estimate based on a sample of data) and ***μ*** is a *parameter* (a true value based on the entire population). A lot of the time, the parameters for the full population will be impossible (or at the very least, impractical) to measure; so we use statistics obtained from a representative sample to approximate them. In this case, we can use the sample mean of salary for our selection of surveyed students to try to estimate the actual average salary of all students who graduate from our school.
In Python, when working with data in a *pandas.dataframe*, you can use the ***mean*** function, like this:
```
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000]})
print (df['Salary'].mean())
```
So, is **71,000** really the central value? Or put another way, would it be reasonable for a graduate of this school to expect to earn $71,000? After all, that's the average salary of a graduate from this school.
If you look closely at the salaries, you can see that out of the seven former students, six earn less than the mean salary. The data is *skewed* by the fact that Rosie has clearly managed to find a much higher-paid job than her classmates.
#### Median
OK, let's see if we can find another definition for the central value that more closely reflects the expected earning potential of students attending our school. Another measure of central tendancy we can use is the *median*. To calculate the median, we need to sort the values into ascending order and then find the middle-most value. When there are an odd number of observations, you can find the position of the median value using this formula (where *n* is the number of observations):
\begin{equation}\frac{n+1}{2}\end{equation}
Remember that this formula returns the *position* of the median value in the sorted list; not the value itself.
If the number of observations is even, then things are a little (but not much) more complicated. In this case you calculate the median as the average of the two middle-most values, which are found like this:
\begin{equation}\frac{n}{2} \;\;\;\;and \;\;\;\; \frac{n}{2} + 1\end{equation}
So, for our graduate salaries; first lets sort the dataset:
| Salary |
|-------------|
| 40,000 |
| 50,000 |
| 50,000 |
| 54,000 |
| 55,000 |
| 59,000 |
| 189,000 |
There's an odd number of observation (7), so the median value is at position (7 + 1) ÷ 2; in other words, position 4:
| Salary |
|-------------|
| 40,000 |
| 50,000 |
| 50,000 |
|***>54,000*** |
| 55,000 |
| 59,000 |
| 189,000 |
So the median salary is **54,000**.
The *pandas.dataframe* class in Python has a ***median*** function to find the median:
```
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000]})
print (df['Salary'].median())
```
#### Mode
Another related statistic is the *mode*, which indicates the most frequently occurring value. If you think about it, this is potentially a good indicator of how much a student might expect to earn when they graduate from the school; out of all the salaries that are being earned by former students, the mode is earned by more than any other.
Looking at our list of salaries, there are two instances of former students earning **50,000**, but only one instance each for all other salaries:
| Salary |
|-------------|
| 40,000 |
|***>50,000***|
|***>50,000***|
| 54,000 |
| 55,000 |
| 59,000 |
| 189,000 |
The mode is therefore **50,000**.
As you might expect, the *pandas.dataframe* class has a ***mode*** function to return the mode:
```
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000]})
print (df['Salary'].mode())
```
##### Multimodal Data
It's not uncommon for a set of data to have more than one value as the mode. For example, suppose Ethan receives a raise that takes his salary to **59,000**:
| Salary |
|-------------|
| 40,000 |
|***>50,000***|
|***>50,000***|
| 54,000 |
|***>59,000***|
|***>59,000***|
| 189,000 |
Now there are two values with the highest frequency. This dataset is *bimodal*. More generally, when there is more than one mode value, the data is considered *multimodal*.
The *pandas.dataframe.**mode*** function returns all of the modes:
```
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,59000,40000,59000]})
print (df['Salary'].mode())
```
### Distribution and Density
Now we know something about finding the center, we can start to explore how the data is distributed around it. What we're interested in here is understanding the general "shape" of the data distribution so that we can begin to get a feel for what a 'typical' value might be expected to be.
We can start by finding the extremes - the minimum and maximum. In the case of our salary data, the lowest paid graduate from our school is Vicky, with a salary of **40,000**; and the highest-paid graduate is Rosie, with **189,000**.
The *pandas.dataframe* class has ***min*** and ***max*** functions to return these values.
Run the following code to compare the minimum and maximum salaries to the central measures we calculated previously:
```
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000]})
print ('Min: ' + str(df['Salary'].min()))
print ('Mode: ' + str(df['Salary'].mode()[0]))
print ('Median: ' + str(df['Salary'].median()))
print ('Mean: ' + str(df['Salary'].mean()))
print ('Max: ' + str(df['Salary'].max()))
```
We can examine these values, and get a sense for how the data is distributed - for example, we can see that the *mean* is closer to the max than the *median*, and that both are closer to the *min* than to the *max*.
However, it's generally easier to get a sense of the distribution by visualizing the data. Let's start by creating a histogram of the salaries, highlighting the *mean* and *median* salaries (the *min*, *max* are fairly self-evident, and the *mode* is wherever the highest bar is):
```
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000]})
salary = df['Salary']
salary.plot.hist(title='Salary Distribution', color='lightblue', bins=25)
plt.axvline(salary.mean(), color='magenta', linestyle='dashed', linewidth=2)
plt.axvline(salary.median(), color='green', linestyle='dashed', linewidth=2)
plt.show()
```
The <span style="color:magenta">***mean***</span> and <span style="color:green">***median***</span> are shown as dashed lines. Note the following:
- *Salary* is a continuous data value - graduates could potentially earn any value along the scale, even down to a fraction of cent.
- The number of bins in the histogram determines the size of each salary band for which we're counting frequencies. Fewer bins means merging more individual salaries together to be counted as a group.
- The majority of the data is on the left side of the histogram, reflecting the fact that most graduates earn between 40,000 and 55,000
- The mean is a higher value than the median and mode.
- There are gaps in the histogram for salary bands that nobody earns.
The histogram shows the relative frequency of each salary band, based on the number of bins. It also gives us a sense of the *density* of the data for each point on the salary scale. With enough data points, and small enough bins, we could view this density as a line that shows the shape of the data distribution.
Run the following cell to show the density of the salary data as a line on top of the histogram:
```
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000]})
salary = df['Salary']
density = stats.gaussian_kde(salary)
n, x, _ = plt.hist(salary, histtype='step', normed=True, bins=25)
plt.plot(x, density(x)*5)
plt.axvline(salary.mean(), color='magenta', linestyle='dashed', linewidth=2)
plt.axvline(salary.median(), color='green', linestyle='dashed', linewidth=2)
plt.show()
```
Note that the density line takes the form of an asymmetric curve that has a "peak" on the left and a long tail on the right. We describe this sort of data distribution as being *skewed*; that is, the data is not distributed symmetrically but "bunched together" on one side. In this case, the data is bunched together on the left, creating a long tail on the right; and is described as being *right-skewed* because some infrequently occurring high values are pulling the *mean* to the right.
Let's take a look at another set of data. We know how much money our graduates make, but how many hours per week do they need to work to earn their salaries? Here's the data:
| Name | Hours |
|----------|-------|
| Dan | 41 |
| Joann | 40 |
| Pedro | 36 |
| Rosie | 30 |
| Ethan | 35 |
| Vicky | 39 |
| Frederic | 40 |
Run the following code to show the distribution of the hours worked:
```
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Hours':[41,40,36,30,35,39,40]})
hours = df['Hours']
density = stats.gaussian_kde(hours)
n, x, _ = plt.hist(hours, histtype='step', normed=True, bins=25)
plt.plot(x, density(x)*7)
plt.axvline(hours.mean(), color='magenta', linestyle='dashed', linewidth=2)
plt.axvline(hours.median(), color='green', linestyle='dashed', linewidth=2)
plt.show()
```
Once again, the distribution is skewed, but this time it's **left-skewed**. Note that the curve is asymmetric with the <span style="color:magenta">***mean***</span> to the left of the <span style="color:green">***median***</span> and the *mode*; and the average weekly working hours skewed to the lower end.
Once again, Rosie seems to be getting the better of the deal. She earns more than her former classmates for working fewer hours. Maybe a look at the test scores the students achieved on their final grade at school might help explain her success:
| Name | Grade |
|----------|-------|
| Dan | 50 |
| Joann | 50 |
| Pedro | 46 |
| Rosie | 95 |
| Ethan | 50 |
| Vicky | 5 |
| Frederic | 57 |
Let's take a look at the distribution of these grades:
```
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Grade':[50,50,46,95,50,5,57]})
grade = df['Grade']
density = stats.gaussian_kde(grade)
n, x, _ = plt.hist(grade, histtype='step', normed=True, bins=25)
plt.plot(x, density(x)*7.5)
plt.axvline(grade.mean(), color='magenta', linestyle='dashed', linewidth=2)
plt.axvline(grade.median(), color='green', linestyle='dashed', linewidth=2)
plt.show()
```
This time, the distribution is symmetric, forming a "bell-shaped" curve. The <span style="color:magenta">***mean***</span>, <span style="color:green">***median***</span>, and mode are at the same location, and the data tails off evenly on both sides from a central peak.
Statisticians call this a *normal* distribution (or sometimes a *Gaussian* distribution), and it occurs quite commonly in many scenarios due to something called the *Central Limit Theorem*, which reflects the way continuous probability works - more about that later.
#### Skewness and Kurtosis
You can measure *skewness* (in which direction the data is skewed and to what degree) and kurtosis (how "peaked" the data is) to get an idea of the shape of the data distribution. In Python, you can use the ***skew*** and ***kurt*** functions to find this:
```
%matplotlib inline
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import scipy.stats as stats
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,30,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
numcols = ['Salary', 'Hours', 'Grade']
for col in numcols:
print(df[col].name + ' skewness: ' + str(df[col].skew()))
print(df[col].name + ' kurtosis: ' + str(df[col].kurt()))
density = stats.gaussian_kde(df[col])
n, x, _ = plt.hist(df[col], histtype='step', normed=True, bins=25)
plt.plot(x, density(x)*6)
plt.show()
print('\n')
```
Now let's look at the distribution of a real dataset - let's see how the heights of the father's measured in Galton's study of parent and child heights are distributed:
```
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
import statsmodels.api as sm
df = sm.datasets.get_rdataset('GaltonFamilies', package='HistData').data
fathers = df['father']
density = stats.gaussian_kde(fathers)
n, x, _ = plt.hist(fathers, histtype='step', normed=True, bins=50)
plt.plot(x, density(x)*2.5)
plt.axvline(fathers.mean(), color='magenta', linestyle='dashed', linewidth=2)
plt.axvline(fathers.median(), color='green', linestyle='dashed', linewidth=2)
plt.show()
```
As you can see, the father's height measurements are approximately normally distributed - in other words, they form a more or less *normal* distribution that is symmetric around the mean.
### Measures of Variance
We can see from the distribution plots of our data that the values in our dataset can vary quite widely. We can use various measures to quantify this variance.
#### Range
A simple way to quantify the variance in a dataset is to identify the difference between the lowest and highest values. This is called the *range*, and is calculated by subtracting the minimim value from the maximum value.
The following Python code creates a single Pandas dataframe for our school graduate data, and calculates the *range* for each of the numeric features:
```
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,30,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
numcols = ['Salary', 'Hours', 'Grade']
for col in numcols:
print(df[col].name + ' range: ' + str(df[col].max() - df[col].min()))
```
#### Percentiles and Quartiles
The range is easy to calculate, but it's not a particularly useful statistic. For example, a range of 149,000 between the lowest and highest salary does not tell us which value within that range a graduate is most likely to earn - it doesn't tell us nothing about how the salaries are distributed around the mean within that range. The range tells us very little about the comparative position of an individual value within the distribution - for example, Frederic scored 57 in his final grade at school; which is a pretty good score (it's more than all but one of his classmates); but this isn't immediately apparent from a score of 57 and range of 90.
##### Percentiles
A percentile tells us where a given value is ranked in the overall distribution. For example, 25% of the data in a distribution has a value lower than the 25th percentile; 75% of the data has a value lower than the 75th percentile, and so on. Note that half of the data has a value lower than the 50th percentile - so the 50th percentile is also the median!
Let's examine Frederic's grade using this approach. We know he scored 57, but how does he rank compared to his fellow students?
Well, there are seven students in total, and five of them scored less than Frederic; so we can calculate the percentile for Frederic's grade like this:
\begin{equation}\frac{5}{7} \times 100 \approx 71.4\end{equation}
So Frederic's score puts him at the 71.4th percentile in his class.
In Python, you can use the ***percentileofscore*** function in the *scipy.stats* package to calculate the percentile for a given value in a set of values:
```
import pandas as pd
from scipy import stats
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,30,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
print(stats.percentileofscore(df['Grade'], 57, 'strict'))
```
We've used the strict definition of percentile; but sometimes it's calculated as being the percentage of values that are less than *or equal to* the value you're comparing. In this case, the calculation for Frederic's percentile would include his own score:
\begin{equation}\frac{6}{7} \times 100 \approx 85.7\end{equation}
You can calculate this way in Python by using the ***weak*** mode of the ***percentileofscore*** function:
```
import pandas as pd
from scipy import stats
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,30,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
print(stats.percentileofscore(df['Grade'], 57, 'weak'))
```
We've considered the percentile of Frederic's grade, and used it to rank him compared to his fellow students. So what about Dan, Joann, and Ethan? How do they compare to the rest of the class? They scored the same grade (50), so in a sense they share a percentile.
To deal with this *grouped* scenario, we can average the percentage rankings for the matching scores. We treat half of the scores matching the one we're ranking as if they are below it, and half as if they are above it. In this case, there were three matching scores of 50, and for each of these we calculate the percentile as if 1 was below and 1 was above. So the calculation for a percentile for Joann based on scores being less than or equal to 50 is:
\begin{equation}(\frac{4}{7}) \times 100 \approx 57.14\end{equation}
The value of **4** consists of the two scores that are below Joann's score of 50, Joann's own score, and half of the scores that are the same as Joann's (of which there are two, so we count one).
In Python, the ***percentileofscore*** function has a ***rank*** function that calculates grouped percentiles like this:
```
import pandas as pd
from scipy import stats
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,30,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
print(stats.percentileofscore(df['Grade'], 50, 'rank'))
```
##### Quartiles
Rather than using individual percentiles to compare data, we can consider the overall spread of the data by dividing those percentiles into four *quartiles*. The first quartile contains the values from the minimum to the 25th percentile, the second from the 25th percentile to the 50th percentile (which is the median), the third from the 50th percentile to the 75th percentile, and the fourth from the 75th percentile to the maximum.
In Python, you can use the ***quantile*** function of the *pandas.dataframe* class to find the threshold values at the 25th, 50th, and 75th percentiles (*quantile* is a generic term for a ranked position, such as a percentile or quartile).
Run the following code to find the quartile thresholds for the weekly hours worked by our former students:
```
# Quartiles
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,17,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
print(df['Hours'].quantile([0.25, 0.5, 0.75]))
```
Its usually easier to understand how data is distributed across the quartiles by visualizing it. You can use a histogram, but many data scientists use a kind of visualization called a *box plot* (or a *box and whiskers* plot).
Let's create a box plot for the weekly hours:
```
%matplotlib inline
import pandas as pd
from matplotlib import pyplot as plt
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,30,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
# Plot a box-whisker chart
df['Hours'].plot(kind='box', title='Weekly Hours Distribution', figsize=(10,8))
plt.show()
```
The box plot consists of:
- A rectangular *box* that shows where the data between the 25th and 75th percentile (the second and third quartile) lie. This part of the distribution is often referred to as the *interquartile range* - it contains the middle 50 data values.
- *Whiskers* that extend from the box to the bottom of the first quartile and the top of the fourth quartile to show the full range of the data.
- A line in the box that shows that location of the median (the 50th percentile, which is also the threshold between the second and third quartile)
In this case, you can see that the interquartile range is between 35 and 40, with the median nearer the top of that range. The range of the first quartile is from around 30 to 35, and the fourth quartile is from 40 to 41.
#### Outliers
Let's take a look at another box plot - this time showing the distribution of the salaries earned by our former classmates:
```
%matplotlib inline
import pandas as pd
from matplotlib import pyplot as plt
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,30,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
# Plot a box-whisker chart
df['Salary'].plot(kind='box', title='Salary Distribution', figsize=(10,8))
plt.show()
```
So what's going on here?
Well, as we've already noticed, Rosie earns significantly more than her former classmates. So much more in fact, that her salary has been identifed as an *outlier*. An outlier is a value that is so far from the center of the distribution compared to other values that it skews the distribution by affecting the mean. There are all sorts of reasons that you might have outliers in your data, including data entry errors, failures in sensors or data-generating equipment, or genuinely anomalous values.
So what should we do about it?
This really depends on the data, and what you're trying to use it for. In this case, let's assume we're trying to figure out what's a reasonable expectation of salary for a graduate of our school to earn. Ignoring for the moment that we have an extremly small dataset on which to base our judgement, it looks as if Rosie's salary could be either an error (maybe she mis-typed it in the form used to collect data) or a genuine anomaly (maybe she became a professional athelete or some other extremely highly paid job). Either way, it doesn't seem to represent a salary that a typical graduate might earn.
Let's see what the distribution of the data looks like without the outlier:
```
%matplotlib inline
import pandas as pd
from matplotlib import pyplot as plt
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,17,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
# Plot a box-whisker chart
df['Salary'].plot(kind='box', title='Salary Distribution', figsize=(10,8), showfliers=False)
plt.show()
```
Now it looks like there's a more even distribution of salaries. It's still not quite symmetrical, but there's much less overall variance. There's potentially some cause here to disregard Rosie's salary data when we compare the salaries, as it is tending to skew the analysis.
So is that OK? Can we really just ignore a data value we don't like?
Again, it depends on what you're analyzing. Let's take a look at the distribution of final grades:
```
%matplotlib inline
import pandas as pd
from matplotlib import pyplot as plt
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,17,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
# Plot a box-whisker chart
df['Grade'].plot(kind='box', title='Grade Distribution', figsize=(10,8))
plt.show()
```
Once again there are outliers, this time at both ends of the distribution. However, think about what this data represents. If we assume that the grade for the final test is based on a score out of 100, it seems reasonable to expect that some students will score very low (maybe even 0) and some will score very well (maybe even 100); but most will get a score somewhere in the middle. The reason that the low and high scores here look like outliers might just be because we have so few data points. Let's see what happens if we include a few more students in our data:
```
%matplotlib inline
import pandas as pd
from matplotlib import pyplot as plt
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic', 'Jimmie', 'Rhonda', 'Giovanni', 'Francesca', 'Rajab', 'Naiyana', 'Kian', 'Jenny'],
'Grade':[50,50,46,95,50,5,57,42,26,72,78,60,40,17,85]})
# Plot a box-whisker chart
df['Grade'].plot(kind='box', title='Grade Distribution', figsize=(10,8))
plt.show()
```
With more data, there are some more high and low scores; so we no longer consider the isolated cases to be outliers.
The key point to take away here is that you need to really understand the data and what you're trying to do with it, and you need to ensure that you have a reasonable sample size, before determining what to do with outlier values.
#### Variance and Standard Deviation
We've seen how to understand the *spread* of our data distribution using the range, percentiles, and quartiles; and we've seen the effect of outliers on the distribution. Now it's time to look at how to measure the amount of variance in the data.
##### Variance
Variance is measured as the average of the squared difference from the mean. For a full population, it's indicated by a squared Greek letter *sigma* (***σ<sup>2</sup>***) and calculated like this:
\begin{equation}\sigma^{2} = \frac{\displaystyle\sum_{i=1}^{N} (X_{i} -\mu)^{2}}{N}\end{equation}
For a sample, it's indicated as ***s<sup>2</sup>*** calculated like this:
\begin{equation}s^{2} = \frac{\displaystyle\sum_{i=1}^{n} (x_{i} -\bar{x})^{2}}{n-1}\end{equation}
In both cases, we sum the difference between the individual data values and the mean and square the result. Then, for a full population we just divide by the number of data items to get the average. When using a sample, we divide by the total number of items **minus 1** to correct for sample bias.
Let's work this out for our student grades (assuming our data is a sample from the larger student population).
First, we need to calculate the mean grade:
\begin{equation}\bar{x} = \frac{50+50+46+95+50+5+57}{7}\approx 50.43\end{equation}
Then we can plug that into our formula for the variance:
\begin{equation}s^{2} = \frac{(50-50.43)^{2}+(50-50.43)^{2}+(46-50.43)^{2}+(95-50.43)^{2}+(50-50.43)^{2}+(5-50.43)^{2}+(57-50.43)^{2}}{7-1}\end{equation}
So:
\begin{equation}s^{2} = \frac{0.185+0.185+19.625+1986.485+0.185+2063.885+43.165}{6}\end{equation}
Which simplifies to:
\begin{equation}s^{2} = \frac{4113.715}{6}\end{equation}
Giving the result:
\begin{equation}s^{2} \approx 685.619\end{equation}
The higher the variance, the more spread your data is around the mean.
In Python, you can use the ***var*** function of the *pandas.dataframe* class to calculate the variance of a column in a dataframe:
```
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,17,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
print(df['Grade'].var())
```
##### Standard Deviation
To calculate the variance, we squared the difference of each value from the mean. If we hadn't done this, the numerator of our fraction would always end up being zero (because the mean is at the center of our values). However, this means that the variance is not in the same unit of measurement as our data - in our case, since we're calculating the variance for grade points, it's in grade points squared; which is not very helpful.
To get the measure of variance back into the same unit of measurement, we need to find its square root:
\begin{equation}s = \sqrt{685.619} \approx 26.184\end{equation}
So what does this value represent?
It's the *standard deviation* for our grades data. More formally, it's calculated like this for a full population:
\begin{equation}\sigma = \sqrt{\frac{\displaystyle\sum_{i=1}^{N} (X_{i} -\mu)^{2}}{N}}\end{equation}
Or like this for a sample:
\begin{equation}s = \sqrt{\frac{\displaystyle\sum_{i=1}^{n} (x_{i} -\bar{x})^{2}}{n-1}}\end{equation}
Note that in both cases, it's just the square root of the corresponding variance forumla!
In Python, you can calculate it using the ***std*** function:
```
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,17,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
print(df['Grade'].std())
```
#### Standard Deviation in a Normal Distribution
In statistics and data science, we spend a lot of time considering *normal* distributions; because they occur so frequently. The standard deviation has an important relationship to play in a normal distribution.
Run the following cell to show a histogram of a *standard normal* distribution (which is a distribution with a mean of 0 and a standard deviation of 1):
```
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
# Create a random standard normal distribution
df = pd.DataFrame(np.random.randn(100000, 1), columns=['Grade'])
# Plot the distribution as a histogram with a density curve
grade = df['Grade']
density = stats.gaussian_kde(grade)
n, x, _ = plt.hist(grade, color='lightgrey', normed=True, bins=100)
plt.plot(x, density(x))
# Get the mean and standard deviation
s = df['Grade'].std()
m = df['Grade'].mean()
# Annotate 1 stdev
x1 = [m-s, m+s]
y1 = [0.25, 0.25]
plt.plot(x1,y1, color='magenta')
plt.annotate('1s (68.26%)', (x1[1],y1[1]))
# Annotate 2 stdevs
x2 = [m-(s*2), m+(s*2)]
y2 = [0.05, 0.05]
plt.plot(x2,y2, color='green')
plt.annotate('2s (95.45%)', (x2[1],y2[1]))
# Annotate 3 stdevs
x3 = [m-(s*3), m+(s*3)]
y3 = [0.005, 0.005]
plt.plot(x3,y3, color='orange')
plt.annotate('3s (99.73%)', (x3[1],y3[1]))
# Show the location of the mean
plt.axvline(grade.mean(), color='grey', linestyle='dashed', linewidth=1)
plt.show()
```
The horizontal colored lines show the percentage of data within 1, 2, and 3 standard deviations of the mean (plus or minus).
In any normal distribution:
- Approximately 68.26% of values fall within one standard deviation from the mean.
- Approximately 95.45% of values fall within two standard deviations from the mean.
- Approximately 99.73% of values fall within three standard deviations from the mean.
#### Z Score
So in a normal (or close to normal) distribution, standard deviation provides a way to evaluate how far from a mean a given range of values falls, allowing us to compare where a particular value lies within the distribution. For example, suppose Rosie tells you she was the highest scoring student among her friends - that doesn't really help us assess how well she scored. She may have scored only a fraction of a point above the second-highest scoring student. Even if we know she was in the top quartile; if we don't know how the rest of the grades are distributed it's still not clear how well she performed compared to her friends.
However, if she tells you how many standard deviations higher than the mean her score was, this will help you compare her score to that of her classmates.
So how do we know how many standard deviations above or below the mean a particular value is? We call this a *Z Score*, and it's calculated like this for a full population:
\begin{equation}Z = \frac{x - \mu}{\sigma}\end{equation}
or like this for a sample:
\begin{equation}Z = \frac{x - \bar{x}}{s}\end{equation}
So, let's examine Rosie's grade of 95. Now that we know the *mean* grade is 50.43 and the *standard deviation* is 26.184, we can calculate the Z Score for this grade like this:
\begin{equation}Z = \frac{95 - 50.43}{26.184} = 1.702\end{equation}.
So Rosie's grade is 1.702 standard deviations above the mean.
### Summarizing Data Distribution in Python
We've seen how to obtain individual statistics in Python, but you can also use the ***describe*** function to retrieve summary statistics for all numeric columns in a dataframe. These summary statistics include many of the statistics we've examined so far (though it's worth noting that the *median* is not included):
```
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,17,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
print(df.describe())
```
|
github_jupyter
|
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000]})
print (df['Salary'].mean())
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000]})
print (df['Salary'].median())
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000]})
print (df['Salary'].mode())
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,59000,40000,59000]})
print (df['Salary'].mode())
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000]})
print ('Min: ' + str(df['Salary'].min()))
print ('Mode: ' + str(df['Salary'].mode()[0]))
print ('Median: ' + str(df['Salary'].median()))
print ('Mean: ' + str(df['Salary'].mean()))
print ('Max: ' + str(df['Salary'].max()))
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000]})
salary = df['Salary']
salary.plot.hist(title='Salary Distribution', color='lightblue', bins=25)
plt.axvline(salary.mean(), color='magenta', linestyle='dashed', linewidth=2)
plt.axvline(salary.median(), color='green', linestyle='dashed', linewidth=2)
plt.show()
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000]})
salary = df['Salary']
density = stats.gaussian_kde(salary)
n, x, _ = plt.hist(salary, histtype='step', normed=True, bins=25)
plt.plot(x, density(x)*5)
plt.axvline(salary.mean(), color='magenta', linestyle='dashed', linewidth=2)
plt.axvline(salary.median(), color='green', linestyle='dashed', linewidth=2)
plt.show()
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Hours':[41,40,36,30,35,39,40]})
hours = df['Hours']
density = stats.gaussian_kde(hours)
n, x, _ = plt.hist(hours, histtype='step', normed=True, bins=25)
plt.plot(x, density(x)*7)
plt.axvline(hours.mean(), color='magenta', linestyle='dashed', linewidth=2)
plt.axvline(hours.median(), color='green', linestyle='dashed', linewidth=2)
plt.show()
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Grade':[50,50,46,95,50,5,57]})
grade = df['Grade']
density = stats.gaussian_kde(grade)
n, x, _ = plt.hist(grade, histtype='step', normed=True, bins=25)
plt.plot(x, density(x)*7.5)
plt.axvline(grade.mean(), color='magenta', linestyle='dashed', linewidth=2)
plt.axvline(grade.median(), color='green', linestyle='dashed', linewidth=2)
plt.show()
%matplotlib inline
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import scipy.stats as stats
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,30,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
numcols = ['Salary', 'Hours', 'Grade']
for col in numcols:
print(df[col].name + ' skewness: ' + str(df[col].skew()))
print(df[col].name + ' kurtosis: ' + str(df[col].kurt()))
density = stats.gaussian_kde(df[col])
n, x, _ = plt.hist(df[col], histtype='step', normed=True, bins=25)
plt.plot(x, density(x)*6)
plt.show()
print('\n')
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
import statsmodels.api as sm
df = sm.datasets.get_rdataset('GaltonFamilies', package='HistData').data
fathers = df['father']
density = stats.gaussian_kde(fathers)
n, x, _ = plt.hist(fathers, histtype='step', normed=True, bins=50)
plt.plot(x, density(x)*2.5)
plt.axvline(fathers.mean(), color='magenta', linestyle='dashed', linewidth=2)
plt.axvline(fathers.median(), color='green', linestyle='dashed', linewidth=2)
plt.show()
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,30,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
numcols = ['Salary', 'Hours', 'Grade']
for col in numcols:
print(df[col].name + ' range: ' + str(df[col].max() - df[col].min()))
import pandas as pd
from scipy import stats
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,30,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
print(stats.percentileofscore(df['Grade'], 57, 'strict'))
import pandas as pd
from scipy import stats
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,30,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
print(stats.percentileofscore(df['Grade'], 57, 'weak'))
import pandas as pd
from scipy import stats
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,30,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
print(stats.percentileofscore(df['Grade'], 50, 'rank'))
# Quartiles
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,17,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
print(df['Hours'].quantile([0.25, 0.5, 0.75]))
%matplotlib inline
import pandas as pd
from matplotlib import pyplot as plt
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,30,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
# Plot a box-whisker chart
df['Hours'].plot(kind='box', title='Weekly Hours Distribution', figsize=(10,8))
plt.show()
%matplotlib inline
import pandas as pd
from matplotlib import pyplot as plt
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,30,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
# Plot a box-whisker chart
df['Salary'].plot(kind='box', title='Salary Distribution', figsize=(10,8))
plt.show()
%matplotlib inline
import pandas as pd
from matplotlib import pyplot as plt
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,17,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
# Plot a box-whisker chart
df['Salary'].plot(kind='box', title='Salary Distribution', figsize=(10,8), showfliers=False)
plt.show()
%matplotlib inline
import pandas as pd
from matplotlib import pyplot as plt
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,17,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
# Plot a box-whisker chart
df['Grade'].plot(kind='box', title='Grade Distribution', figsize=(10,8))
plt.show()
%matplotlib inline
import pandas as pd
from matplotlib import pyplot as plt
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic', 'Jimmie', 'Rhonda', 'Giovanni', 'Francesca', 'Rajab', 'Naiyana', 'Kian', 'Jenny'],
'Grade':[50,50,46,95,50,5,57,42,26,72,78,60,40,17,85]})
# Plot a box-whisker chart
df['Grade'].plot(kind='box', title='Grade Distribution', figsize=(10,8))
plt.show()
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,17,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
print(df['Grade'].var())
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,17,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
print(df['Grade'].std())
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
# Create a random standard normal distribution
df = pd.DataFrame(np.random.randn(100000, 1), columns=['Grade'])
# Plot the distribution as a histogram with a density curve
grade = df['Grade']
density = stats.gaussian_kde(grade)
n, x, _ = plt.hist(grade, color='lightgrey', normed=True, bins=100)
plt.plot(x, density(x))
# Get the mean and standard deviation
s = df['Grade'].std()
m = df['Grade'].mean()
# Annotate 1 stdev
x1 = [m-s, m+s]
y1 = [0.25, 0.25]
plt.plot(x1,y1, color='magenta')
plt.annotate('1s (68.26%)', (x1[1],y1[1]))
# Annotate 2 stdevs
x2 = [m-(s*2), m+(s*2)]
y2 = [0.05, 0.05]
plt.plot(x2,y2, color='green')
plt.annotate('2s (95.45%)', (x2[1],y2[1]))
# Annotate 3 stdevs
x3 = [m-(s*3), m+(s*3)]
y3 = [0.005, 0.005]
plt.plot(x3,y3, color='orange')
plt.annotate('3s (99.73%)', (x3[1],y3[1]))
# Show the location of the mean
plt.axvline(grade.mean(), color='grey', linestyle='dashed', linewidth=1)
plt.show()
import pandas as pd
df = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic'],
'Salary':[50000,54000,50000,189000,55000,40000,59000],
'Hours':[41,40,36,17,35,39,40],
'Grade':[50,50,46,95,50,5,57]})
print(df.describe())
| 0.30632 | 0.990945 |
```
#dependencies
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import time
import gmaps
#Open CSV file
gun_violence = "gun_violence_data.csv"
gun_violence_pd = pd.read_csv(gun_violence)
# gun_violence_pd.head()
gun_violence_red = gun_violence_pd[["incident_id", "date", "city_or_county", "n_killed", "n_injured",
"participant_age_group", "participant_gender",
"n_guns_involved", "participant_status", "participant_type",
"state_house_district", "state_senate_district"]]
gun_violence_red.head(5)
#Rename The Columns
gun_violence_red = gun_violence_red.rename(columns={"incident_id": "Incident ID",
"date": "Date",
"state": "State",
"city_or_county": "City/County",
"n_killed": "Killed",
"n_injured": "Injured",
"participant_age_group": "Age Group",
"participant_gender": "Gender",
"gun_stolen": "Gun Stolen",
"n_guns_involved": "Number of Guns involved",
"participant_status": "Participant Status",
"participant_type": "Associated with Participant",
"state_house_district": "State House District",
"state_senate_district": "State Senate District"
})
gun_violence_red.head()
# counting for genders:
def countGender(genderStr,ismale=True):
x = genderStr
try:
results = [1 if 'female' in e.lower() else 0 for e in x.split('||')]
females = sum(results)
males = len(results) - females
# print(f'Females: {females} & Males: {males}')
if ismale:
return males
else:
return females
except:
# print(f"Data not available: {x}")
return x
# Female
gun_female = gun_violence_red['Gender'].apply(lambda my_str: countGender(my_str,ismale=False))
# Male
gun_male = gun_violence_red['Gender'].apply(lambda my_str: countGender(my_str))
gun_violence_df = gun_violence_red
gun_violence_df['Female'] = gun_female
gun_violence_df['Male'] = gun_male
gun_violence_df = gun_violence_df.drop(columns=["Gender"])
display(gun_violence_df.head())
def countType(raw_str, str_type):
try:
results = [1 if str_type in e.lower() else 0 for e in raw_str.split('||')]
return sum(results)
except:
return raw_str
#Creating/separating the individual variables for each age group
# Adult
adult_group = gun_violence_df['Age Group'].apply(lambda x: countType(x, 'adult'))
adult_group.head(10)
# Teen
teen_group = gun_violence_df['Age Group'].apply(lambda x: countType(x, 'teen'))
teen_group.head(10)
# Child
child_group = gun_violence_df['Age Group'].apply(lambda x: countType(x, 'child'))
child_group.head(10)
# Killed
gun_kill = gun_violence_pd['participant_status'].apply(lambda x: countType(x, 'killed'))
# Injured
gun_injured = gun_violence_pd['participant_status'].apply(lambda x: countType(x, 'injured'))
# Unharmed
gun_unharmed = gun_violence_pd['participant_status'].apply(lambda x: countType(x, 'unharmed'))
# Arrested
gun_arrested = gun_violence_pd['participant_status'].apply(lambda x: countType(x, 'arrested'))
gun_violence_df["Children (0-11)"] = child_group
gun_violence_df["Teens (12-17)"] = teen_group
gun_violence_df["Adults (18+)"] = adult_group
gun_violence_df["Killed"] = gun_kill
gun_violence_df["Injured"] = gun_injured
gun_violence_df["Unharmed"] = gun_unharmed
gun_violence_df["Arrested"] = gun_arrested
gun_violence_df = gun_violence_df.drop(columns=["Age Group"])
gun_violence_df = gun_violence_df.drop(columns=["Associated with Participant"])
gun_violence_df = gun_violence_df.drop(columns=["Participant Status"])
gun_violence_df.head()
# GUN TYPES
gun_types = pd.DataFrame({"source_string": gun_violence_pd["gun_type"]})
gun_types["source_clean"] = gun_types["source_string"].str.replace('\d+::', ',', regex=True).str.replace('\d+:', ',', regex=True).str.replace('|', '', regex=False).str[1:]
#gun_types.head()
split_by_gun_df = gun_types["source_clean"].str.split(',', expand=True).rename(columns = lambda x: "gun_"+str(x))
#split_by_gun_df.head()
gun_total = split_by_gun_df.apply(pd.value_counts)
gun_total["Total"] = gun_total.sum(axis=1)
most_common_guns = gun_total.sort_values(["Total"], ascending=False)
most_common_guns["Total"]
# PARTISAN DATA
partisan_read = pd.read_csv('partisan_data.csv')
partisan_df = pd.DataFrame(partisan_read)
partisan_df.head()
partisan_df['state'] = ''
partisan_df['congressional_district'] = ''
for row in range (0, len(partisan_df)):
partisan_df['state'][row] = partisan_df['District'][row][0:-2]
partisan_df['congressional_district'][row] = partisan_df['District'][row].split(' ')[-1]
partisan_df.head()
partisan_df['partisan_lean']= partisan_df["PVI"]
#converting "R+" and "D+" into positive (for Republicans) and negative (for Democrats) numbers
for row in range (0, len(partisan_df)):
if partisan_df['PVI'][row][0:2] == "R+":
partisan_df['partisan_lean'][row] = int(partisan_df["PVI"][row][2:])
elif partisan_df['partisan_lean'][row][0:2] == "D+":
partisan_df['partisan_lean'][row] = int("-" + partisan_df['PVI'][row][2:])
else:
partisan_df["PVI"][row] = 0
partisan_df_clean = partisan_df[['state', 'congressional_district', 'partisan_lean']]
partisan_df_clean.head()
pd.to_numeric(partisan_df_clean['congressional_district'], errors='ignore')
partisan_df[partisan_df['congressional_district']=="AL"]['congressional_district']
# Retrieve Google API key from config.py
from config_3 import gkey
target = "all incidents"
params = {"address": target, "key": gkey}
# Build URL using the Google MAps API
base_url = "https://maps.googleapis.com/maps/api/geocode/json"
print("coordinates of incidents")
# Run Request
response = requests.get(base_url, params=params)
print(response.url)
# Extract lat/lng
location_data = pd.DataFrame({"Latitude": gun_violence_pd["latitude"],
"Longitude":gun_violence_pd["longitude"]})
#location_data.head()
location_data_clean = location_data.dropna(how='any')
fig = gmaps.figure()
# Create heat layer
heat_layer = gmaps.heatmap_layer(location_data_clean, dissipating=False, max_intensity=10, point_radius=0.2)
# Add Layer
fig.add_layer(heat_layer)
fig
```
|
github_jupyter
|
#dependencies
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import time
import gmaps
#Open CSV file
gun_violence = "gun_violence_data.csv"
gun_violence_pd = pd.read_csv(gun_violence)
# gun_violence_pd.head()
gun_violence_red = gun_violence_pd[["incident_id", "date", "city_or_county", "n_killed", "n_injured",
"participant_age_group", "participant_gender",
"n_guns_involved", "participant_status", "participant_type",
"state_house_district", "state_senate_district"]]
gun_violence_red.head(5)
#Rename The Columns
gun_violence_red = gun_violence_red.rename(columns={"incident_id": "Incident ID",
"date": "Date",
"state": "State",
"city_or_county": "City/County",
"n_killed": "Killed",
"n_injured": "Injured",
"participant_age_group": "Age Group",
"participant_gender": "Gender",
"gun_stolen": "Gun Stolen",
"n_guns_involved": "Number of Guns involved",
"participant_status": "Participant Status",
"participant_type": "Associated with Participant",
"state_house_district": "State House District",
"state_senate_district": "State Senate District"
})
gun_violence_red.head()
# counting for genders:
def countGender(genderStr,ismale=True):
x = genderStr
try:
results = [1 if 'female' in e.lower() else 0 for e in x.split('||')]
females = sum(results)
males = len(results) - females
# print(f'Females: {females} & Males: {males}')
if ismale:
return males
else:
return females
except:
# print(f"Data not available: {x}")
return x
# Female
gun_female = gun_violence_red['Gender'].apply(lambda my_str: countGender(my_str,ismale=False))
# Male
gun_male = gun_violence_red['Gender'].apply(lambda my_str: countGender(my_str))
gun_violence_df = gun_violence_red
gun_violence_df['Female'] = gun_female
gun_violence_df['Male'] = gun_male
gun_violence_df = gun_violence_df.drop(columns=["Gender"])
display(gun_violence_df.head())
def countType(raw_str, str_type):
try:
results = [1 if str_type in e.lower() else 0 for e in raw_str.split('||')]
return sum(results)
except:
return raw_str
#Creating/separating the individual variables for each age group
# Adult
adult_group = gun_violence_df['Age Group'].apply(lambda x: countType(x, 'adult'))
adult_group.head(10)
# Teen
teen_group = gun_violence_df['Age Group'].apply(lambda x: countType(x, 'teen'))
teen_group.head(10)
# Child
child_group = gun_violence_df['Age Group'].apply(lambda x: countType(x, 'child'))
child_group.head(10)
# Killed
gun_kill = gun_violence_pd['participant_status'].apply(lambda x: countType(x, 'killed'))
# Injured
gun_injured = gun_violence_pd['participant_status'].apply(lambda x: countType(x, 'injured'))
# Unharmed
gun_unharmed = gun_violence_pd['participant_status'].apply(lambda x: countType(x, 'unharmed'))
# Arrested
gun_arrested = gun_violence_pd['participant_status'].apply(lambda x: countType(x, 'arrested'))
gun_violence_df["Children (0-11)"] = child_group
gun_violence_df["Teens (12-17)"] = teen_group
gun_violence_df["Adults (18+)"] = adult_group
gun_violence_df["Killed"] = gun_kill
gun_violence_df["Injured"] = gun_injured
gun_violence_df["Unharmed"] = gun_unharmed
gun_violence_df["Arrested"] = gun_arrested
gun_violence_df = gun_violence_df.drop(columns=["Age Group"])
gun_violence_df = gun_violence_df.drop(columns=["Associated with Participant"])
gun_violence_df = gun_violence_df.drop(columns=["Participant Status"])
gun_violence_df.head()
# GUN TYPES
gun_types = pd.DataFrame({"source_string": gun_violence_pd["gun_type"]})
gun_types["source_clean"] = gun_types["source_string"].str.replace('\d+::', ',', regex=True).str.replace('\d+:', ',', regex=True).str.replace('|', '', regex=False).str[1:]
#gun_types.head()
split_by_gun_df = gun_types["source_clean"].str.split(',', expand=True).rename(columns = lambda x: "gun_"+str(x))
#split_by_gun_df.head()
gun_total = split_by_gun_df.apply(pd.value_counts)
gun_total["Total"] = gun_total.sum(axis=1)
most_common_guns = gun_total.sort_values(["Total"], ascending=False)
most_common_guns["Total"]
# PARTISAN DATA
partisan_read = pd.read_csv('partisan_data.csv')
partisan_df = pd.DataFrame(partisan_read)
partisan_df.head()
partisan_df['state'] = ''
partisan_df['congressional_district'] = ''
for row in range (0, len(partisan_df)):
partisan_df['state'][row] = partisan_df['District'][row][0:-2]
partisan_df['congressional_district'][row] = partisan_df['District'][row].split(' ')[-1]
partisan_df.head()
partisan_df['partisan_lean']= partisan_df["PVI"]
#converting "R+" and "D+" into positive (for Republicans) and negative (for Democrats) numbers
for row in range (0, len(partisan_df)):
if partisan_df['PVI'][row][0:2] == "R+":
partisan_df['partisan_lean'][row] = int(partisan_df["PVI"][row][2:])
elif partisan_df['partisan_lean'][row][0:2] == "D+":
partisan_df['partisan_lean'][row] = int("-" + partisan_df['PVI'][row][2:])
else:
partisan_df["PVI"][row] = 0
partisan_df_clean = partisan_df[['state', 'congressional_district', 'partisan_lean']]
partisan_df_clean.head()
pd.to_numeric(partisan_df_clean['congressional_district'], errors='ignore')
partisan_df[partisan_df['congressional_district']=="AL"]['congressional_district']
# Retrieve Google API key from config.py
from config_3 import gkey
target = "all incidents"
params = {"address": target, "key": gkey}
# Build URL using the Google MAps API
base_url = "https://maps.googleapis.com/maps/api/geocode/json"
print("coordinates of incidents")
# Run Request
response = requests.get(base_url, params=params)
print(response.url)
# Extract lat/lng
location_data = pd.DataFrame({"Latitude": gun_violence_pd["latitude"],
"Longitude":gun_violence_pd["longitude"]})
#location_data.head()
location_data_clean = location_data.dropna(how='any')
fig = gmaps.figure()
# Create heat layer
heat_layer = gmaps.heatmap_layer(location_data_clean, dissipating=False, max_intensity=10, point_radius=0.2)
# Add Layer
fig.add_layer(heat_layer)
fig
| 0.124293 | 0.20951 |
# Obsessed with Boba? Analyzing Bubble Tea Shops in NYC Using the Yelp Fusion API
Exploratory Data Analysis
```
# # imports for Google Colab Sessions
# !apt install gdal-bin python-gdal python3-gdal
# # Install rtree - Geopandas requirment
# !apt install python3-rtree
# # Install Geopandas
# !pip install git+git://github.com/geopandas/geopandas.git
# # Install descartes - Geopandas requirment
# !pip install descartes
import pandas as pd
import numpy as np
import geopandas as gpd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set(color_codes=True)
# google colab path to data
url = 'https://raw.githubusercontent.com/mebauer/boba-nyc/master/teabook/boba-nyc.csv'
df = pd.read_csv(url)
# # local path to data
# df = pd.read_csv('boba-nyc.csv')
df.head()
# preview last five rows
df.tail()
rows, columns = df.shape
print('number of rows: {}\nnumber of columns: {}'.format(rows, columns))
# review concise summary of data
df.info()
# identifiying number of nulls and percentage of total per column
ser1 = df.isnull().sum().sort_values(ascending=False)
ser2 = round((df.isnull().sum().sort_values(ascending=False) / len(df)) * 100, 2)
pd.concat([ser1.rename('null_count'), ser2.rename('null_perc')], axis=1)
# descriptive statistics of numeric columns
df.describe()
# descriptive statistics of string/object columns
df.describe(include=['O']).T
# confirm that unique id is actually unique
print('id is unique: {}'.format(df['id'].is_unique))
df.head()
# identify number of unique bubble tea shop entries
names_counts = df['name'].value_counts().reset_index()
names_counts = names_counts.rename(columns={'index':'name', 'name':'counts'})
print('number of unique bubble tea shops: {}'.format(len(names_counts)))
# save file
name_counts_file_path = '../teaapp/name_counts.csv'
names_counts.to_csv(name_counts_file_path)
# view dataframe
names_counts
df['name'].value_counts().reset_index(drop=False)
names_counts = df['name'].value_counts().reset_index(drop=False)
names_counts = names_counts.rename(columns={'index':'names', 'name':'counts'})
fig, ax = plt.subplots(figsize=(8, 6))
sns.barplot(x='counts',
y="names",
data=names_counts.head(10),
ax=ax)
plt.title('Number of bubble tea shops by business in nyc', fontsize=15)
plt.tight_layout()
review_count_df = df.groupby(by='name')['review_count'].mean().sort_values(ascending=False)
review_count_df = round(review_count_df, 2)
review_count_df = review_count_df.reset_index()
review_count_df.head()
fig, ax = plt.subplots(figsize=(8, 6))
sns.barplot(x="review_count",
y="name",
data=review_count_df.head(20),
ax=ax)
plt.title('Average number of reviews per business in nyc', fontsize=15)
plt.tight_layout()
most_reviewed = df.sort_values(by='review_count', ascending=False).head(20)
most_reviewed.head()
fig, ax = plt.subplots(figsize=(8, 6))
sns.barplot(x="review_count",
y="alias",
data=most_reviewed,
ax=ax)
plt.title('Most reviews per business location in nyc', fontsize=15)
plt.tight_layout()
df['rating'].describe()
fig, ax = plt.subplots(figsize=(8, 6))
sns.countplot(data=df,
x="rating")
plt.title('Count of Yelp ratings per business location in nyc', fontsize=15)
plt.tight_layout()
price_df = df['price'].dropna().value_counts()
price_df = price_df.reset_index()
price_df.columns = ['price', 'counts']
price_df
price_df['price'] = price_df['price'].str.count('\\$')
price_df
fig, ax = plt.subplots(figsize=(8, 6))
sns.barplot(y="counts",
x="price",
data=price_df,
ax=ax)
plt.title('Yelp price level (1 = $) per business location in NYC', fontsize=15)
plt.tight_layout()
url = 'https://data.cityofnewyork.us/api/geospatial/cpf4-rkhq?method=export&format=Shapefile'
neighborhoods = gpd.read_file(url)
neighborhoods.head()
neighborhoods.crs
neighborhoods = neighborhoods.to_crs('EPSG:4326')
neighborhoods.crs
df.head()
gdf = gpd.GeoDataFrame(df, crs=4326,
geometry=gpd.points_from_xy(df.longitude, df.latitude))
gdf.head()
join_df = gpd.sjoin(gdf,
neighborhoods,
op='intersects')
join_df.head()
join_df = join_df.groupby(by=['ntaname', 'shape_area'])['id'].count().sort_values(ascending=False)
join_df = join_df.reset_index()
join_df = join_df.rename(columns={'id':'counts'})
join_df['counts_squaremile'] = join_df['counts'] / (join_df['shape_area'] / 27878400)
join_df.head()
fig, ax = plt.subplots(figsize=(10, 6))
data = join_df.sort_values(by='counts', ascending=False).head(20)
sns.barplot(x="counts",
y="ntaname",
data=data,
ax=ax)
plt.title('Most bubble tea locations per neighborhood in NYC', fontsize=15)
plt.ylabel('neighborhood')
plt.xlabel('count')
plt.tight_layout()
plt.savefig('busineses-per-neighborhood.png', dpi=200)
fig, ax = plt.subplots(figsize=(10, 6))
data = join_df.sort_values(by='counts_squaremile', ascending=False).head(20)
sns.barplot(x="counts_squaremile",
y="ntaname",
data=data,
ax=ax)
plt.suptitle('Most bubble tea locations per square mile by neighborhood in NYC',
fontsize=15,
y=.96, x=.60)
plt.ylabel('neighborhood')
plt.xlabel('count per square mile')
plt.tight_layout()
plt.savefig('busineses-per-neighborhood.png', dpi=200)
```
|
github_jupyter
|
# # imports for Google Colab Sessions
# !apt install gdal-bin python-gdal python3-gdal
# # Install rtree - Geopandas requirment
# !apt install python3-rtree
# # Install Geopandas
# !pip install git+git://github.com/geopandas/geopandas.git
# # Install descartes - Geopandas requirment
# !pip install descartes
import pandas as pd
import numpy as np
import geopandas as gpd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set(color_codes=True)
# google colab path to data
url = 'https://raw.githubusercontent.com/mebauer/boba-nyc/master/teabook/boba-nyc.csv'
df = pd.read_csv(url)
# # local path to data
# df = pd.read_csv('boba-nyc.csv')
df.head()
# preview last five rows
df.tail()
rows, columns = df.shape
print('number of rows: {}\nnumber of columns: {}'.format(rows, columns))
# review concise summary of data
df.info()
# identifiying number of nulls and percentage of total per column
ser1 = df.isnull().sum().sort_values(ascending=False)
ser2 = round((df.isnull().sum().sort_values(ascending=False) / len(df)) * 100, 2)
pd.concat([ser1.rename('null_count'), ser2.rename('null_perc')], axis=1)
# descriptive statistics of numeric columns
df.describe()
# descriptive statistics of string/object columns
df.describe(include=['O']).T
# confirm that unique id is actually unique
print('id is unique: {}'.format(df['id'].is_unique))
df.head()
# identify number of unique bubble tea shop entries
names_counts = df['name'].value_counts().reset_index()
names_counts = names_counts.rename(columns={'index':'name', 'name':'counts'})
print('number of unique bubble tea shops: {}'.format(len(names_counts)))
# save file
name_counts_file_path = '../teaapp/name_counts.csv'
names_counts.to_csv(name_counts_file_path)
# view dataframe
names_counts
df['name'].value_counts().reset_index(drop=False)
names_counts = df['name'].value_counts().reset_index(drop=False)
names_counts = names_counts.rename(columns={'index':'names', 'name':'counts'})
fig, ax = plt.subplots(figsize=(8, 6))
sns.barplot(x='counts',
y="names",
data=names_counts.head(10),
ax=ax)
plt.title('Number of bubble tea shops by business in nyc', fontsize=15)
plt.tight_layout()
review_count_df = df.groupby(by='name')['review_count'].mean().sort_values(ascending=False)
review_count_df = round(review_count_df, 2)
review_count_df = review_count_df.reset_index()
review_count_df.head()
fig, ax = plt.subplots(figsize=(8, 6))
sns.barplot(x="review_count",
y="name",
data=review_count_df.head(20),
ax=ax)
plt.title('Average number of reviews per business in nyc', fontsize=15)
plt.tight_layout()
most_reviewed = df.sort_values(by='review_count', ascending=False).head(20)
most_reviewed.head()
fig, ax = plt.subplots(figsize=(8, 6))
sns.barplot(x="review_count",
y="alias",
data=most_reviewed,
ax=ax)
plt.title('Most reviews per business location in nyc', fontsize=15)
plt.tight_layout()
df['rating'].describe()
fig, ax = plt.subplots(figsize=(8, 6))
sns.countplot(data=df,
x="rating")
plt.title('Count of Yelp ratings per business location in nyc', fontsize=15)
plt.tight_layout()
price_df = df['price'].dropna().value_counts()
price_df = price_df.reset_index()
price_df.columns = ['price', 'counts']
price_df
price_df['price'] = price_df['price'].str.count('\\$')
price_df
fig, ax = plt.subplots(figsize=(8, 6))
sns.barplot(y="counts",
x="price",
data=price_df,
ax=ax)
plt.title('Yelp price level (1 = $) per business location in NYC', fontsize=15)
plt.tight_layout()
url = 'https://data.cityofnewyork.us/api/geospatial/cpf4-rkhq?method=export&format=Shapefile'
neighborhoods = gpd.read_file(url)
neighborhoods.head()
neighborhoods.crs
neighborhoods = neighborhoods.to_crs('EPSG:4326')
neighborhoods.crs
df.head()
gdf = gpd.GeoDataFrame(df, crs=4326,
geometry=gpd.points_from_xy(df.longitude, df.latitude))
gdf.head()
join_df = gpd.sjoin(gdf,
neighborhoods,
op='intersects')
join_df.head()
join_df = join_df.groupby(by=['ntaname', 'shape_area'])['id'].count().sort_values(ascending=False)
join_df = join_df.reset_index()
join_df = join_df.rename(columns={'id':'counts'})
join_df['counts_squaremile'] = join_df['counts'] / (join_df['shape_area'] / 27878400)
join_df.head()
fig, ax = plt.subplots(figsize=(10, 6))
data = join_df.sort_values(by='counts', ascending=False).head(20)
sns.barplot(x="counts",
y="ntaname",
data=data,
ax=ax)
plt.title('Most bubble tea locations per neighborhood in NYC', fontsize=15)
plt.ylabel('neighborhood')
plt.xlabel('count')
plt.tight_layout()
plt.savefig('busineses-per-neighborhood.png', dpi=200)
fig, ax = plt.subplots(figsize=(10, 6))
data = join_df.sort_values(by='counts_squaremile', ascending=False).head(20)
sns.barplot(x="counts_squaremile",
y="ntaname",
data=data,
ax=ax)
plt.suptitle('Most bubble tea locations per square mile by neighborhood in NYC',
fontsize=15,
y=.96, x=.60)
plt.ylabel('neighborhood')
plt.xlabel('count per square mile')
plt.tight_layout()
plt.savefig('busineses-per-neighborhood.png', dpi=200)
| 0.383641 | 0.800926 |
```
from collections import defaultdict
import warnings
import logging
import gffutils
import pybedtools
import pandas as pd
from copy import deepcopy
import re
gencode_v25 = '/home/cmb-06/as/wenzhenl/genomes/hg38/annotation/gencode.v25.annotation.gtf'
gencode_v25_db = '/home/cmb-06/as/wenzhenl/genomes/hg38/annotation/gencode.v25.annotation.gtf.db'
prefix = '/staging/as/wenzhenl/hg38_'
#db = gffutils.create_db(gencode_v25, dbfn=gencode_v25_db, force=True,
# merge_strategy='merge',
# disable_infer_genes=True, disable_infer_transcripts=True)
db = gffutils.FeatureDB(gencode_v25_db, keep_order=True)
all_cds = defaultdict(list)
all_utrs = defaultdict(list)
for cds in db.features_of_type('CDS', order_by='start'):
assert(len(cds['gene_id']) == 1)
all_cds[cds['gene_id'][0]].append(cds)
for utr in db.features_of_type('UTR', order_by='start'):
assert(len(utr['gene_id']) == 1)
all_utrs[utr['gene_id'][0]].append(utr)
all_utr3 = defaultdict(list)
all_utr5 = defaultdict(list)
for gene, gene_cds in all_cds.items():
# find first cds
first_cds = gene_cds[0]
for cds in gene_cds:
if cds.start < first_cds.start:
first_cds = cds
# find last cds
last_cds = gene_cds[-1]
for cds in gene_cds:
if cds.stop > last_cds.stop:
last_cds = cds
if gene in all_utrs:
for orig_utr in all_utrs[gene]:
utr = deepcopy(orig_utr)
strand = utr.strand
if utr.start < first_cds.start:
if utr.stop >= first_cds.start:
utr.stop = first_cds.start - 1
if strand == '+':
all_utr5[gene].append(utr)
else:
all_utr3[gene].append(utr)
elif utr.stop > last_cds.stop:
if utr.start <= last_cds.stop:
utr.start = last_cds.stop + 1
if strand == '+':
all_utr3[gene].append(utr)
else:
all_utr5[gene].append(utr)
def create_bed(region_dict):
bed = ""
for gene, regions in sorted(region_dict.items(), key=lambda x: x[0]):
if regions:
regions = list(db.merge(regions))
regions.sort(key=lambda x: x.start)
for region in regions:
bed += '{}\t{}\t{}\t{}\t{}\t{}\n'.format(region.chrom, region.start-1, region.stop, re.sub('\.\d+', '', gene), '.', region.strand)
return bed
utr3_bed = create_bed(all_utr3)
utr3_bedtool = pybedtools.BedTool(utr3_bed, from_string=True)
utr3_bedtool.remove_invalid().sort().saveas('{}.UTR3.bed'.format(prefix))
utr5_bed = create_bed(all_utr5)
utr5_bedtool = pybedtools.BedTool(utr5_bed, from_string=True)
utr5_bedtool.remove_invalid().sort().saveas('{}.UTR5.bed'.format(prefix))
cds_bed = create_bed(all_cds)
cds_bedtool = pybedtools.BedTool(cds_bed, from_string=True)
cds_bedtool.remove_invalid().sort().saveas('{}.cds.bed'.format(prefix))
```
|
github_jupyter
|
from collections import defaultdict
import warnings
import logging
import gffutils
import pybedtools
import pandas as pd
from copy import deepcopy
import re
gencode_v25 = '/home/cmb-06/as/wenzhenl/genomes/hg38/annotation/gencode.v25.annotation.gtf'
gencode_v25_db = '/home/cmb-06/as/wenzhenl/genomes/hg38/annotation/gencode.v25.annotation.gtf.db'
prefix = '/staging/as/wenzhenl/hg38_'
#db = gffutils.create_db(gencode_v25, dbfn=gencode_v25_db, force=True,
# merge_strategy='merge',
# disable_infer_genes=True, disable_infer_transcripts=True)
db = gffutils.FeatureDB(gencode_v25_db, keep_order=True)
all_cds = defaultdict(list)
all_utrs = defaultdict(list)
for cds in db.features_of_type('CDS', order_by='start'):
assert(len(cds['gene_id']) == 1)
all_cds[cds['gene_id'][0]].append(cds)
for utr in db.features_of_type('UTR', order_by='start'):
assert(len(utr['gene_id']) == 1)
all_utrs[utr['gene_id'][0]].append(utr)
all_utr3 = defaultdict(list)
all_utr5 = defaultdict(list)
for gene, gene_cds in all_cds.items():
# find first cds
first_cds = gene_cds[0]
for cds in gene_cds:
if cds.start < first_cds.start:
first_cds = cds
# find last cds
last_cds = gene_cds[-1]
for cds in gene_cds:
if cds.stop > last_cds.stop:
last_cds = cds
if gene in all_utrs:
for orig_utr in all_utrs[gene]:
utr = deepcopy(orig_utr)
strand = utr.strand
if utr.start < first_cds.start:
if utr.stop >= first_cds.start:
utr.stop = first_cds.start - 1
if strand == '+':
all_utr5[gene].append(utr)
else:
all_utr3[gene].append(utr)
elif utr.stop > last_cds.stop:
if utr.start <= last_cds.stop:
utr.start = last_cds.stop + 1
if strand == '+':
all_utr3[gene].append(utr)
else:
all_utr5[gene].append(utr)
def create_bed(region_dict):
bed = ""
for gene, regions in sorted(region_dict.items(), key=lambda x: x[0]):
if regions:
regions = list(db.merge(regions))
regions.sort(key=lambda x: x.start)
for region in regions:
bed += '{}\t{}\t{}\t{}\t{}\t{}\n'.format(region.chrom, region.start-1, region.stop, re.sub('\.\d+', '', gene), '.', region.strand)
return bed
utr3_bed = create_bed(all_utr3)
utr3_bedtool = pybedtools.BedTool(utr3_bed, from_string=True)
utr3_bedtool.remove_invalid().sort().saveas('{}.UTR3.bed'.format(prefix))
utr5_bed = create_bed(all_utr5)
utr5_bedtool = pybedtools.BedTool(utr5_bed, from_string=True)
utr5_bedtool.remove_invalid().sort().saveas('{}.UTR5.bed'.format(prefix))
cds_bed = create_bed(all_cds)
cds_bedtool = pybedtools.BedTool(cds_bed, from_string=True)
cds_bedtool.remove_invalid().sort().saveas('{}.cds.bed'.format(prefix))
| 0.277277 | 0.136839 |
```
import numpy as np
import cvxpy as cp
import networkx as nx
import matplotlib.pyplot as plt
# Build transportation grah
G = nx.DiGraph()
# Add nodes
G.add_node(0, supply=7)
G.add_node(1, supply=11)
G.add_node(2, supply=18)
G.add_node(3, supply=12)
G.add_node(4, supply=-10)
G.add_node(5, supply=-23)
G.add_node(6, supply=-15)
# Add edges
capacity = 20
G.add_edge(0, 4, weight=5, capacity=capacity)
G.add_edge(0, 5, weight=6, capacity=capacity)
G.add_edge(1, 4, weight=8, capacity=capacity)
G.add_edge(1, 5, weight=4, capacity=capacity)
G.add_edge(1, 6, weight=3, capacity=capacity)
G.add_edge(2, 5, weight=5, capacity=capacity)
G.add_edge(3, 5, weight=3, capacity=capacity)
G.add_edge(3, 6, weight=6, capacity=capacity)
# Note minus sign for convention
# In our formulation:
# -> 1 means arc exits node
# -> -1 means arc enters node
A = -nx.linalg.graphmatrix.incidence_matrix(G, oriented=True)
print("A =\n", A.todense())
# Get weights, capacities, and supply vectors
c = np.array([G[u][v]['weight'] for u,v in G.edges])
u = np.array([G[u][v]['capacity'] for u,v in G.edges])
b = np.array([G.nodes[u]['supply'] for u in G.nodes])
# Solve transportation problem
# Note: you need to install GLPK. It is part of CVXOPT.
# Just run:
# pip install cvxopt
#
# GLPK runs a simple method, which, as you know, returns exactly integral
# solutions at vertices. Other solvers such as ECOS use interior-point methods
# and they return slightly imprecise solutions that are not exactly integral.
x = cp.Variable(len(G.edges))
objective = cp.Minimize(c @ x)
constraints = [A @ x == b, 0 <= x, x <= u]
problem = cp.Problem(objective, constraints)
problem.solve(solver=cp.GLPK)
print("Optimal cost =", problem.objective.value)
# Show solution
# Note: x is integral!
print("x = ", x.value)
fig, ax = plt.subplots(1, 1, figsize=(15, 10))
cmap = plt.cm.Blues
# Positions in 2d plot
layout = {0: np.array([0.0, 4.0]),
1: np.array([0.0, 3.0]),
2: np.array([0.0, 2.0]),
3: np.array([0.0, 1.0]),
4: np.array([1.0, 3.5]),
5: np.array([1.0, 2.5]),
6: np.array([1.0, 1.5]),
}
nx.draw_networkx_nodes(G, layout, node_color='w', edgecolors='k', node_size=2000)
nx.draw_networkx_edges(G, layout, edge_cmap=cmap, edge_color=x.value,
width=2, arrowsize=30, min_target_margin=20)
# Print colormap
sm = plt.cm.ScalarMappable(cmap=cmap,
norm=plt.Normalize(vmin=0, vmax=capacity)
)
cbar = plt.colorbar(sm)
plt.show()
```
|
github_jupyter
|
import numpy as np
import cvxpy as cp
import networkx as nx
import matplotlib.pyplot as plt
# Build transportation grah
G = nx.DiGraph()
# Add nodes
G.add_node(0, supply=7)
G.add_node(1, supply=11)
G.add_node(2, supply=18)
G.add_node(3, supply=12)
G.add_node(4, supply=-10)
G.add_node(5, supply=-23)
G.add_node(6, supply=-15)
# Add edges
capacity = 20
G.add_edge(0, 4, weight=5, capacity=capacity)
G.add_edge(0, 5, weight=6, capacity=capacity)
G.add_edge(1, 4, weight=8, capacity=capacity)
G.add_edge(1, 5, weight=4, capacity=capacity)
G.add_edge(1, 6, weight=3, capacity=capacity)
G.add_edge(2, 5, weight=5, capacity=capacity)
G.add_edge(3, 5, weight=3, capacity=capacity)
G.add_edge(3, 6, weight=6, capacity=capacity)
# Note minus sign for convention
# In our formulation:
# -> 1 means arc exits node
# -> -1 means arc enters node
A = -nx.linalg.graphmatrix.incidence_matrix(G, oriented=True)
print("A =\n", A.todense())
# Get weights, capacities, and supply vectors
c = np.array([G[u][v]['weight'] for u,v in G.edges])
u = np.array([G[u][v]['capacity'] for u,v in G.edges])
b = np.array([G.nodes[u]['supply'] for u in G.nodes])
# Solve transportation problem
# Note: you need to install GLPK. It is part of CVXOPT.
# Just run:
# pip install cvxopt
#
# GLPK runs a simple method, which, as you know, returns exactly integral
# solutions at vertices. Other solvers such as ECOS use interior-point methods
# and they return slightly imprecise solutions that are not exactly integral.
x = cp.Variable(len(G.edges))
objective = cp.Minimize(c @ x)
constraints = [A @ x == b, 0 <= x, x <= u]
problem = cp.Problem(objective, constraints)
problem.solve(solver=cp.GLPK)
print("Optimal cost =", problem.objective.value)
# Show solution
# Note: x is integral!
print("x = ", x.value)
fig, ax = plt.subplots(1, 1, figsize=(15, 10))
cmap = plt.cm.Blues
# Positions in 2d plot
layout = {0: np.array([0.0, 4.0]),
1: np.array([0.0, 3.0]),
2: np.array([0.0, 2.0]),
3: np.array([0.0, 1.0]),
4: np.array([1.0, 3.5]),
5: np.array([1.0, 2.5]),
6: np.array([1.0, 1.5]),
}
nx.draw_networkx_nodes(G, layout, node_color='w', edgecolors='k', node_size=2000)
nx.draw_networkx_edges(G, layout, edge_cmap=cmap, edge_color=x.value,
width=2, arrowsize=30, min_target_margin=20)
# Print colormap
sm = plt.cm.ScalarMappable(cmap=cmap,
norm=plt.Normalize(vmin=0, vmax=capacity)
)
cbar = plt.colorbar(sm)
plt.show()
| 0.623377 | 0.666545 |
<a href="https://colab.research.google.com/github/Rob1Ham/DS-Unit-2-Kaggle-Challenge/blob/master/module1/Rob_Hamilton_assignment_kaggle_challenge_1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Lambda School Data Science, Unit 2: Predictive Modeling
# Kaggle Challenge, Module 1
## Assignment
- [ ] Do train/validate/test split with the Tanzania Waterpumps data.
- [ ] Define a function to wrangle train, validate, and test sets in the same way. Clean outliers and engineer features. (For example, [what other columns have zeros and shouldn't?](https://github.com/Quartz/bad-data-guide#zeros-replace-missing-values) What other columns are duplicates, or nearly duplicates? Can you extract the year from date_recorded? Can you engineer new features, such as the number of years from waterpump construction to waterpump inspection?)
- [ ] Select features. Use a scikit-learn pipeline to encode categoricals, impute missing values, and fit a decision tree classifier.
- [ ] Get your validation accuracy score.
- [ ] Get and plot your feature importances.
- [ ] Submit your predictions to our Kaggle competition. (Go to our Kaggle InClass competition webpage. Use the blue **Submit Predictions** button to upload your CSV file. Or you can use the Kaggle API to submit your predictions.)
- [ ] Commit your notebook to your fork of the GitHub repo.
## Stretch Goals
### Reading
- A Visual Introduction to Machine Learning
- [Part 1: A Decision Tree](http://www.r2d3.us/visual-intro-to-machine-learning-part-1/)
- [Part 2: Bias and Variance](http://www.r2d3.us/visual-intro-to-machine-learning-part-2/)
- [Decision Trees: Advantages & Disadvantages](https://christophm.github.io/interpretable-ml-book/tree.html#advantages-2)
- [How a Russian mathematician constructed a decision tree — by hand — to solve a medical problem](http://fastml.com/how-a-russian-mathematician-constructed-a-decision-tree-by-hand-to-solve-a-medical-problem/)
- [How decision trees work](https://brohrer.github.io/how_decision_trees_work.html)
- [Let’s Write a Decision Tree Classifier from Scratch](https://www.youtube.com/watch?v=LDRbO9a6XPU) — _Don’t worry about understanding the code, just get introduced to the concepts. This 10 minute video has excellent diagrams and explanations._
- [Random Forests for Complete Beginners: The definitive guide to Random Forests and Decision Trees](https://victorzhou.com/blog/intro-to-random-forests/)
### Doing
- [ ] Add your own stretch goal(s) !
- [ ] Try other [scikit-learn imputers](https://scikit-learn.org/stable/modules/impute.html).
- [ ] Try other [scikit-learn scalers](https://scikit-learn.org/stable/modules/preprocessing.html).
- [ ] Make exploratory visualizations and share on Slack.
#### Exploratory visualizations
Visualize the relationships between feature(s) and target. I recommend you do this with your training set, after splitting your data.
For this problem, you may want to create a new column to represent the target as a number, 0 or 1. For example:
```python
train['functional'] = (train['status_group']=='functional').astype(int)
```
You can try [Seaborn "Categorical estimate" plots](https://seaborn.pydata.org/tutorial/categorical.html) for features with reasonably few unique values. (With too many unique values, the plot is unreadable.)
- Categorical features. (If there are too many unique values, you can replace less frequent values with "OTHER.")
- Numeric features. (If there are too many unique values, you can [bin with pandas cut / qcut functions](https://pandas.pydata.org/pandas-docs/stable/getting_started/basics.html?highlight=qcut#discretization-and-quantiling).)
You can try [Seaborn linear model plots](https://seaborn.pydata.org/tutorial/regression.html) with numeric features. For this problem, you may want to use the parameter `logistic=True`
You do _not_ need to use Seaborn, but it's nice because it includes confidence intervals to visualize uncertainty.
#### High-cardinality categoricals
This code from a previous assignment demonstrates how to replace less frequent values with 'OTHER'
```python
# Reduce cardinality for NEIGHBORHOOD feature ...
# Get a list of the top 10 neighborhoods
top10 = train['NEIGHBORHOOD'].value_counts()[:10].index
# At locations where the neighborhood is NOT in the top 10,
# replace the neighborhood with 'OTHER'
train.loc[~train['NEIGHBORHOOD'].isin(top10), 'NEIGHBORHOOD'] = 'OTHER'
test.loc[~test['NEIGHBORHOOD'].isin(top10), 'NEIGHBORHOOD'] = 'OTHER'
```
```
# If you're in Colab...
import os, sys
in_colab = 'google.colab' in sys.modules
if in_colab:
# Install required python packages:
# category_encoders, version >= 2.0
# pandas-profiling, version >= 2.0
# plotly, version >= 4.0
!pip install --upgrade category_encoders pandas-profiling plotly
# Pull files from Github repo
os.chdir('/content')
!git init .
!git remote add origin https://github.com/LambdaSchool/DS-Unit-2-Kaggle-Challenge.git
!git pull origin master
# Change into directory for module
os.chdir('module1')
import pandas as pd
from sklearn.model_selection import train_test_split
train = pd.merge(pd.read_csv('../data/tanzania/train_features.csv'),
pd.read_csv('../data/tanzania/train_labels.csv'))
test = pd.read_csv('../data/tanzania/test_features.csv')
sample_submission = pd.read_csv('../data/tanzania/sample_submission.csv')
train.shape, test.shape
import numpy as np
train , val = train_test_split(train, train_size=0.80, test_size=0.20,
stratify=train['status_group'])
target = 'status_group'
train_features = train.drop(columns=[target,'id'])
numeric_features = train_features.select_dtypes(include='number').columns.tolist()
cardinality = train_features.select_dtypes(exclude='number').nunique()
categorical_features = cardinality[cardinality <=50].index.tolist()
features = numeric_features + categorical_features
X_train = train[features]
y_train = train[target]
X_val = val[features]
y_val = val[target]
X_test = test[features]
import category_encoders as ce
from sklearn.impute import SimpleImputer
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
LogisticRegression(multi_class='auto',solver='lbfgs',n_jobs=-1)
)
pipeline.fit(X_train, y_train)
print('Validation Accuracy',pipeline.score(X_val,y_val))
y_pred = pipeline.predict(X_test)
from sklearn.tree import DecisionTreeClassifier
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
DecisionTreeClassifier()
)
pipeline.fit(X_train, y_train)
print('Validation Accuracy',pipeline.score(X_val,y_val))
y_pred = pipeline.predict(X_test)
#trying to see if min leaf size will help with validation score
for minleaf in range(1,100,10):
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
DecisionTreeClassifier(min_samples_leaf=minleaf)
)
pipeline.fit(X_train, y_train)
print("Number of leafs is "+str(minleaf))
print('Validation Accuracy',pipeline.score(X_val,y_val))
#y_pred = pipeline.predict(X_test)
#scalling down to narrower range, and seeing if standard scaler impacts score
for minleaf in range(1,11):
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
DecisionTreeClassifier(min_samples_leaf=minleaf)
)
pipeline.fit(X_train, y_train)
print("Number of leafs is "+str(minleaf))
print('Validation Accuracy',pipeline.score(X_val,y_val))
#y_pred = pipeline.predict(X_test)
#checkingfixing number of leafs at 8, seeing if changing split threshold helps
for minleaf in range(2,11):
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
DecisionTreeClassifier(min_samples_leaf=8,min_samples_split=minleaf)
)
pipeline.fit(X_train, y_train)
print("Number of leafs to split is "+str(minleaf))
print('Validation Accuracy',pipeline.score(X_val,y_val))
#y_pred = pipeline.predict(X_test)
#it does not have an ability to help forecsat, trying to change max_depth
#checkingfixing number of leafs at 8, seeing if changing split threshold helps
for maxdepth in range(1,100,10):
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
DecisionTreeClassifier(min_samples_leaf=8,max_depth=maxdepth)
)
pipeline.fit(X_train, y_train)
print("Maximum Depth iss "+str(maxdepth))
print('Validation Accuracy',pipeline.score(X_val,y_val))
#y_pred = pipeline.predict(X_test)
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
DecisionTreeClassifier(min_samples_leaf=8,max_depth=31)
)
pipeline.fit(X_train, y_train)
#print("Maximum Depth iss "+str(maxdepth))
print('Validation Accuracy',pipeline.score(X_val,y_val))
y_pred = pipeline.predict(X_test)
#now to pull into the pipeline and look at the coefficients of varliables
%matplotlib inline
import matplotlib.pyplot as plt
encoder = pipeline.named_steps['onehotencoder']
model = pipeline.named_steps['decisiontreeclassifier']
encoded_columns = encoder.transform(X_val).columns
importances = pd.Series(model.feature_importances_, encoded_columns)
plt.figure(figsize=(10,30))
importances.sort_values().plot.barh(color='grey');
y_pred
submission = sample_submission.copy()
submission['status_group'] = y_pred
submission.to_csv('rob-hamilton-submission2.csv', index=False)
from google.colab import files
files.download('rob-hamilton-submission2.csv')
import xgboost as xgb
```
|
github_jupyter
|
train['functional'] = (train['status_group']=='functional').astype(int)
# Reduce cardinality for NEIGHBORHOOD feature ...
# Get a list of the top 10 neighborhoods
top10 = train['NEIGHBORHOOD'].value_counts()[:10].index
# At locations where the neighborhood is NOT in the top 10,
# replace the neighborhood with 'OTHER'
train.loc[~train['NEIGHBORHOOD'].isin(top10), 'NEIGHBORHOOD'] = 'OTHER'
test.loc[~test['NEIGHBORHOOD'].isin(top10), 'NEIGHBORHOOD'] = 'OTHER'
# If you're in Colab...
import os, sys
in_colab = 'google.colab' in sys.modules
if in_colab:
# Install required python packages:
# category_encoders, version >= 2.0
# pandas-profiling, version >= 2.0
# plotly, version >= 4.0
!pip install --upgrade category_encoders pandas-profiling plotly
# Pull files from Github repo
os.chdir('/content')
!git init .
!git remote add origin https://github.com/LambdaSchool/DS-Unit-2-Kaggle-Challenge.git
!git pull origin master
# Change into directory for module
os.chdir('module1')
import pandas as pd
from sklearn.model_selection import train_test_split
train = pd.merge(pd.read_csv('../data/tanzania/train_features.csv'),
pd.read_csv('../data/tanzania/train_labels.csv'))
test = pd.read_csv('../data/tanzania/test_features.csv')
sample_submission = pd.read_csv('../data/tanzania/sample_submission.csv')
train.shape, test.shape
import numpy as np
train , val = train_test_split(train, train_size=0.80, test_size=0.20,
stratify=train['status_group'])
target = 'status_group'
train_features = train.drop(columns=[target,'id'])
numeric_features = train_features.select_dtypes(include='number').columns.tolist()
cardinality = train_features.select_dtypes(exclude='number').nunique()
categorical_features = cardinality[cardinality <=50].index.tolist()
features = numeric_features + categorical_features
X_train = train[features]
y_train = train[target]
X_val = val[features]
y_val = val[target]
X_test = test[features]
import category_encoders as ce
from sklearn.impute import SimpleImputer
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
LogisticRegression(multi_class='auto',solver='lbfgs',n_jobs=-1)
)
pipeline.fit(X_train, y_train)
print('Validation Accuracy',pipeline.score(X_val,y_val))
y_pred = pipeline.predict(X_test)
from sklearn.tree import DecisionTreeClassifier
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
DecisionTreeClassifier()
)
pipeline.fit(X_train, y_train)
print('Validation Accuracy',pipeline.score(X_val,y_val))
y_pred = pipeline.predict(X_test)
#trying to see if min leaf size will help with validation score
for minleaf in range(1,100,10):
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
DecisionTreeClassifier(min_samples_leaf=minleaf)
)
pipeline.fit(X_train, y_train)
print("Number of leafs is "+str(minleaf))
print('Validation Accuracy',pipeline.score(X_val,y_val))
#y_pred = pipeline.predict(X_test)
#scalling down to narrower range, and seeing if standard scaler impacts score
for minleaf in range(1,11):
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
DecisionTreeClassifier(min_samples_leaf=minleaf)
)
pipeline.fit(X_train, y_train)
print("Number of leafs is "+str(minleaf))
print('Validation Accuracy',pipeline.score(X_val,y_val))
#y_pred = pipeline.predict(X_test)
#checkingfixing number of leafs at 8, seeing if changing split threshold helps
for minleaf in range(2,11):
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
DecisionTreeClassifier(min_samples_leaf=8,min_samples_split=minleaf)
)
pipeline.fit(X_train, y_train)
print("Number of leafs to split is "+str(minleaf))
print('Validation Accuracy',pipeline.score(X_val,y_val))
#y_pred = pipeline.predict(X_test)
#it does not have an ability to help forecsat, trying to change max_depth
#checkingfixing number of leafs at 8, seeing if changing split threshold helps
for maxdepth in range(1,100,10):
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
DecisionTreeClassifier(min_samples_leaf=8,max_depth=maxdepth)
)
pipeline.fit(X_train, y_train)
print("Maximum Depth iss "+str(maxdepth))
print('Validation Accuracy',pipeline.score(X_val,y_val))
#y_pred = pipeline.predict(X_test)
pipeline = make_pipeline(
ce.OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
DecisionTreeClassifier(min_samples_leaf=8,max_depth=31)
)
pipeline.fit(X_train, y_train)
#print("Maximum Depth iss "+str(maxdepth))
print('Validation Accuracy',pipeline.score(X_val,y_val))
y_pred = pipeline.predict(X_test)
#now to pull into the pipeline and look at the coefficients of varliables
%matplotlib inline
import matplotlib.pyplot as plt
encoder = pipeline.named_steps['onehotencoder']
model = pipeline.named_steps['decisiontreeclassifier']
encoded_columns = encoder.transform(X_val).columns
importances = pd.Series(model.feature_importances_, encoded_columns)
plt.figure(figsize=(10,30))
importances.sort_values().plot.barh(color='grey');
y_pred
submission = sample_submission.copy()
submission['status_group'] = y_pred
submission.to_csv('rob-hamilton-submission2.csv', index=False)
from google.colab import files
files.download('rob-hamilton-submission2.csv')
import xgboost as xgb
| 0.343782 | 0.984155 |
# Modeling and Simulation in Python
Chapter 11: Rotation
Copyright 2017 Allen Downey
License: [Creative Commons Attribution 4.0 International](https://creativecommons.org/licenses/by/4.0)
```
# If you want the figures to appear in the notebook,
# and you want to interact with them, use
# %matplotlib notebook
# If you want the figures to appear in the notebook,
# and you don't want to interact with them, use
# %matplotlib inline
# If you want the figures to appear in separate windows, use
# %matplotlib qt5
# tempo switch from one to another, you have to select Kernel->Restart
%matplotlib inline
from modsim import *
```
### Rolling paper
We'll start by loading the units we need.
```
radian = UNITS.radian
m = UNITS.meter
s = UNITS.second
```
And creating a `Condition` object with the system parameters
```
condition = Condition(Rmin = 0.02 * m,
Rmax = 0.055 * m,
L = 47 * m,
duration = 130 * s)
```
The following function estimates the parameter `k`, which is the increase in the radius of the roll for each radian of rotation.
```
def estimate_k(condition):
"""Estimates the parameter `k`.
condition: Condition with Rmin, Rmax, and L
returns: k in meters per radian
"""
unpack(condition)
Ravg = (Rmax + Rmin) / 2
Cavg = 2 * pi * Ravg
revs = L / Cavg
rads = 2 * pi * revs
k = (Rmax - Rmin) / rads
return k
```
As usual, `make_system` takes a `Condition` object and returns a `System` object.
```
def make_system(condition):
"""Make a system object.
condition: Condition with Rmin, Rmax, and L
returns: System with init, k, and ts
"""
unpack(condition)
init = State(theta = 0 * radian,
y = 0 * m,
r = Rmin)
k = estimate_k(condition)
ts = linspace(0, duration, 101)
return System(init=init, k=k, ts=ts)
```
Testing `make_system`
```
system = make_system(condition)
system
system.init
```
Now we can write a slope function based on the differential equations
$\omega = \frac{d\theta}{dt} = 10$
$\frac{dy}{dt} = r \frac{d\theta}{dt}$
$\frac{dr}{dt} = k \frac{d\theta}{dt}$
```
def slope_func(state, t, system):
"""Computes the derivatives of the state variables.
state: State object with theta, y, r
t: time
system: System object with r, k
returns: sequence of derivatives
"""
theta, y, r = state
unpack(system)
omega = 10 * radian / s
dydt = r * omega
drdt = k * omega
return omega, dydt, drdt
```
Testing `slope_func`
```
slope_func(system.init, 0*s, system)
```
Now we can run the simulation.
```
run_odeint(system, slope_func)
```
And look at the results.
```
system.results.tail()
```
Extracting one time series per variable (and converting `r` to radians):
```
thetas = system.results.theta
ys = system.results.y
rs = system.results.r * 1000
```
Plotting `theta`
```
plot(thetas, label='theta')
decorate(xlabel='Time (s)',
ylabel='Angle (rad)')
```
Plotting `y`
```
plot(ys, color='green', label='y')
decorate(xlabel='Time (s)',
ylabel='Length (m)')
```
Plotting `r`
```
plot(rs, color='red', label='r')
decorate(xlabel='Time (s)',
ylabel='Radius (mm)')
```
We can also see the relationship between `y` and `r`, which I derive analytically in the book.
```
plot(rs, ys, color='purple')
decorate(xlabel='Radius (mm)',
ylabel='Length (m)',
legend=False)
```
And here's the figure from the book.
```
subplot(3, 1, 1)
plot(thetas, label='theta')
decorate(ylabel='Angle (rad)')
subplot(3, 1, 2)
plot(ys, color='green', label='y')
decorate(ylabel='Length (m)')
subplot(3, 1, 3)
plot(rs, color='red', label='r')
decorate(xlabel='Time(s)',
ylabel='Radius (mm)')
savefig('chap11-fig01.pdf')
```
We can use interpolation to find the time when `y` is 47 meters.
```
T = interp_inverse(ys, kind='cubic')
t_end = T(47)
t_end
```
At that point `r` is 55 mm, which is `Rmax`, as expected.
```
R = interpolate(rs, kind='cubic')
R(t_end)
```
The total amount of rotation is 1253 rad.
```
THETA = interpolate(thetas, kind='cubic')
THETA(t_end)
```
### Unrolling
For unrolling the paper, we need more units:
```
kg = UNITS.kilogram
N = UNITS.newton
```
And a few more parameters in the `Condition` object.
```
condition = Condition(Rmin = 0.02 * m,
Rmax = 0.055 * m,
Mcore = 15e-3 * kg,
Mroll = 215e-3 * kg,
L = 47 * m,
tension = 2e-4 * N,
duration = 180 * s)
```
`make_system` computes `rho_h`, which we'll need to compute moment of inertia, and `k`, which we'll use to compute `r`.
```
def make_system(condition):
"""Make a system object.
condition: Condition with Rmin, Rmax, Mcore, Mroll,
L, tension, and duration
returns: System with init, k, rho_h, Rmin, Rmax,
Mcore, Mroll, ts
"""
unpack(condition)
init = State(theta = 0 * radian,
omega = 0 * radian/s,
y = L)
area = pi * (Rmax**2 - Rmin**2)
rho_h = Mroll / area
k = (Rmax**2 - Rmin**2) / 2 / L / radian
ts = linspace(0, duration, 101)
return System(init=init, k=k, rho_h=rho_h,
Rmin=Rmin, Rmax=Rmax,
Mcore=Mcore, Mroll=Mroll,
ts=ts)
```
Testing `make_system`
```
system = make_system(condition)
system
system.init
```
Here's how we compute `I` as a function of `r`:
```
def moment_of_inertia(r, system):
"""Moment of inertia for a roll of toilet paper.
r: current radius of roll in meters
system: System object with Mcore, rho, Rmin, Rmax
returns: moment of inertia in kg m**2
"""
unpack(system)
Icore = Mcore * Rmin**2
Iroll = pi * rho_h / 2 * (r**4 - Rmin**4)
return Icore + Iroll
```
When `r` is `Rmin`, `I` is small.
```
moment_of_inertia(system.Rmin, system)
```
As `r` increases, so does `I`.
```
moment_of_inertia(system.Rmax, system)
```
Here's the slope function.
```
def slope_func(state, t, system):
"""Computes the derivatives of the state variables.
state: State object with theta, omega, y
t: time
system: System object with Rmin, k, Mcore, rho_h, tension
returns: sequence of derivatives
"""
theta, omega, y = state
unpack(system)
r = sqrt(2*k*y + Rmin**2)
I = moment_of_inertia(r, system)
tau = r * tension
alpha = tau / I
dydt = -r * omega
return omega, alpha, dydt
```
Testing `slope_func`
```
slope_func(system.init, 0*s, system)
```
Now we can run the simulation.
```
run_odeint(system, slope_func)
```
And look at the results.
```
system.results.tail()
```
Extrating the time series
```
thetas = system.results.theta
omegas = system.results.omega
ys = system.results.y
```
Plotting `theta`
```
plot(thetas, label='theta')
decorate(xlabel='Time (s)',
ylabel='Angle (rad)')
```
Plotting `omega`
```
plot(omegas, color='orange', label='omega')
decorate(xlabel='Time (s)',
ylabel='Angular velocity (rad/s)')
```
Plotting `y`
```
plot(ys, color='green', label='y')
decorate(xlabel='Time (s)',
ylabel='Length (m)')
```
Here's the figure from the book.
```
subplot(3, 1, 1)
plot(thetas, label='theta')
decorate(ylabel='Angle (rad)')
subplot(3, 1, 2)
plot(omegas, color='orange', label='omega')
decorate(ylabel='Angular velocity (rad/s)')
subplot(3, 1, 3)
plot(ys, color='green', label='y')
decorate(xlabel='Time(s)',
ylabel='Length (m)')
savefig('chap11-fig02.pdf')
```
### Yo-yo
**Exercise:** Simulate the descent of a yo-yo. How long does it take to reach the end of the string?
I provide a `Condition` object with the system parameters:
* `Rmin` is the radius of the axle. `Rmax` is the radius of the axle plus rolled string.
* `Rout` is the radius of the yo-yo body. `mass` is the total mass of the yo-yo, ignoring the string.
* `L` is the length of the string.
* `g` is the acceleration of gravity.
```
condition = Condition(Rmin = 8e-3 * m,
Rmax = 16e-3 * m,
Rout = 35e-3 * m,
mass = 50e-3 * kg,
L = 1 * m,
g = 9.8 * m / s**2,
duration = 1 * s)
```
Here's a `make_system` function that computes `I` and `k` based on the system parameters.
I estimated `I` by modeling the yo-yo as a solid cylinder with uniform density ([see here](https://en.wikipedia.org/wiki/List_of_moments_of_inertia)). In reality, the distribution of weight in a yo-yo is often designed to achieve desired effects. But we'll keep it simple.
```
def make_system(condition):
"""Make a system object.
condition: Condition with Rmin, Rmax, Rout,
mass, L, g, duration
returns: System with init, k, Rmin, Rmax, mass,
I, g, ts
"""
unpack(condition)
init = State(theta = 0 * radian,
omega = 0 * radian/s,
y = L,
v = 0 * m / s)
I = mass * Rout**2 / 2
k = (Rmax**2 - Rmin**2) / 2 / L / radian
ts = linspace(0, duration, 101)
return System(init=init, k=k,
Rmin=Rmin, Rmax=Rmax,
mass=mass, I=I, g=g,
ts=ts)
```
Testing `make_system`
```
system = make_system(condition)
system
system.init
```
Write a slope function for this system, using these results from the book:
$ r = \sqrt{2 k y + R_{min}^2} $
$ T = m g I / I^* $
$ a = -m g r^2 / I^* $
$ \alpha = m g r / I^* $
where $I^*$ is the augmented moment of inertia, $I + m r^2$.
Hint: If `y` is less than 0, it means you have reached the end of the string, so the equation for `r` is no longer valid. In this case, the simplest thing to do it return the sequence of derivatives `0, 0, 0, 0`
```
# Solution
def slope_func(state, t, system):
"""Computes the derivatives of the state variables.
state: State object with theta, omega, y, v
t: time
system: System object with Rmin, k, I, mass
returns: sequence of derivatives
"""
theta, omega, y, v = state
unpack(system)
if y < 0 * m:
return 0, 0, 0, 0
r = sqrt(2*k*y + Rmin**2)
alpha = mass * g * r / (I + mass * r**2)
a = -r * alpha
return omega, alpha, v, a
```
Test your slope function with the initial conditions.
```
slope_func(system.init, 0*s, system)
```
Then run the simulation.
```
run_odeint(system, slope_func)
```
Check the final conditions. If things have gone according to plan, the final value of `y` should be close to 0.
```
system.results.tail()
```
Plot the results.
```
thetas = system.results.theta
ys = system.results.y
```
`theta` should increase and accelerate.
```
plot(thetas, label='theta')
decorate(xlabel='Time (s)',
ylabel='Angle (rad)')
```
`y` should decrease and accelerate down.
```
plot(ys, color='green', label='y')
decorate(xlabel='Time (s)',
ylabel='Length (m)')
```
|
github_jupyter
|
# If you want the figures to appear in the notebook,
# and you want to interact with them, use
# %matplotlib notebook
# If you want the figures to appear in the notebook,
# and you don't want to interact with them, use
# %matplotlib inline
# If you want the figures to appear in separate windows, use
# %matplotlib qt5
# tempo switch from one to another, you have to select Kernel->Restart
%matplotlib inline
from modsim import *
radian = UNITS.radian
m = UNITS.meter
s = UNITS.second
condition = Condition(Rmin = 0.02 * m,
Rmax = 0.055 * m,
L = 47 * m,
duration = 130 * s)
def estimate_k(condition):
"""Estimates the parameter `k`.
condition: Condition with Rmin, Rmax, and L
returns: k in meters per radian
"""
unpack(condition)
Ravg = (Rmax + Rmin) / 2
Cavg = 2 * pi * Ravg
revs = L / Cavg
rads = 2 * pi * revs
k = (Rmax - Rmin) / rads
return k
def make_system(condition):
"""Make a system object.
condition: Condition with Rmin, Rmax, and L
returns: System with init, k, and ts
"""
unpack(condition)
init = State(theta = 0 * radian,
y = 0 * m,
r = Rmin)
k = estimate_k(condition)
ts = linspace(0, duration, 101)
return System(init=init, k=k, ts=ts)
system = make_system(condition)
system
system.init
def slope_func(state, t, system):
"""Computes the derivatives of the state variables.
state: State object with theta, y, r
t: time
system: System object with r, k
returns: sequence of derivatives
"""
theta, y, r = state
unpack(system)
omega = 10 * radian / s
dydt = r * omega
drdt = k * omega
return omega, dydt, drdt
slope_func(system.init, 0*s, system)
run_odeint(system, slope_func)
system.results.tail()
thetas = system.results.theta
ys = system.results.y
rs = system.results.r * 1000
plot(thetas, label='theta')
decorate(xlabel='Time (s)',
ylabel='Angle (rad)')
plot(ys, color='green', label='y')
decorate(xlabel='Time (s)',
ylabel='Length (m)')
plot(rs, color='red', label='r')
decorate(xlabel='Time (s)',
ylabel='Radius (mm)')
plot(rs, ys, color='purple')
decorate(xlabel='Radius (mm)',
ylabel='Length (m)',
legend=False)
subplot(3, 1, 1)
plot(thetas, label='theta')
decorate(ylabel='Angle (rad)')
subplot(3, 1, 2)
plot(ys, color='green', label='y')
decorate(ylabel='Length (m)')
subplot(3, 1, 3)
plot(rs, color='red', label='r')
decorate(xlabel='Time(s)',
ylabel='Radius (mm)')
savefig('chap11-fig01.pdf')
T = interp_inverse(ys, kind='cubic')
t_end = T(47)
t_end
R = interpolate(rs, kind='cubic')
R(t_end)
THETA = interpolate(thetas, kind='cubic')
THETA(t_end)
kg = UNITS.kilogram
N = UNITS.newton
condition = Condition(Rmin = 0.02 * m,
Rmax = 0.055 * m,
Mcore = 15e-3 * kg,
Mroll = 215e-3 * kg,
L = 47 * m,
tension = 2e-4 * N,
duration = 180 * s)
def make_system(condition):
"""Make a system object.
condition: Condition with Rmin, Rmax, Mcore, Mroll,
L, tension, and duration
returns: System with init, k, rho_h, Rmin, Rmax,
Mcore, Mroll, ts
"""
unpack(condition)
init = State(theta = 0 * radian,
omega = 0 * radian/s,
y = L)
area = pi * (Rmax**2 - Rmin**2)
rho_h = Mroll / area
k = (Rmax**2 - Rmin**2) / 2 / L / radian
ts = linspace(0, duration, 101)
return System(init=init, k=k, rho_h=rho_h,
Rmin=Rmin, Rmax=Rmax,
Mcore=Mcore, Mroll=Mroll,
ts=ts)
system = make_system(condition)
system
system.init
def moment_of_inertia(r, system):
"""Moment of inertia for a roll of toilet paper.
r: current radius of roll in meters
system: System object with Mcore, rho, Rmin, Rmax
returns: moment of inertia in kg m**2
"""
unpack(system)
Icore = Mcore * Rmin**2
Iroll = pi * rho_h / 2 * (r**4 - Rmin**4)
return Icore + Iroll
moment_of_inertia(system.Rmin, system)
moment_of_inertia(system.Rmax, system)
def slope_func(state, t, system):
"""Computes the derivatives of the state variables.
state: State object with theta, omega, y
t: time
system: System object with Rmin, k, Mcore, rho_h, tension
returns: sequence of derivatives
"""
theta, omega, y = state
unpack(system)
r = sqrt(2*k*y + Rmin**2)
I = moment_of_inertia(r, system)
tau = r * tension
alpha = tau / I
dydt = -r * omega
return omega, alpha, dydt
slope_func(system.init, 0*s, system)
run_odeint(system, slope_func)
system.results.tail()
thetas = system.results.theta
omegas = system.results.omega
ys = system.results.y
plot(thetas, label='theta')
decorate(xlabel='Time (s)',
ylabel='Angle (rad)')
plot(omegas, color='orange', label='omega')
decorate(xlabel='Time (s)',
ylabel='Angular velocity (rad/s)')
plot(ys, color='green', label='y')
decorate(xlabel='Time (s)',
ylabel='Length (m)')
subplot(3, 1, 1)
plot(thetas, label='theta')
decorate(ylabel='Angle (rad)')
subplot(3, 1, 2)
plot(omegas, color='orange', label='omega')
decorate(ylabel='Angular velocity (rad/s)')
subplot(3, 1, 3)
plot(ys, color='green', label='y')
decorate(xlabel='Time(s)',
ylabel='Length (m)')
savefig('chap11-fig02.pdf')
condition = Condition(Rmin = 8e-3 * m,
Rmax = 16e-3 * m,
Rout = 35e-3 * m,
mass = 50e-3 * kg,
L = 1 * m,
g = 9.8 * m / s**2,
duration = 1 * s)
def make_system(condition):
"""Make a system object.
condition: Condition with Rmin, Rmax, Rout,
mass, L, g, duration
returns: System with init, k, Rmin, Rmax, mass,
I, g, ts
"""
unpack(condition)
init = State(theta = 0 * radian,
omega = 0 * radian/s,
y = L,
v = 0 * m / s)
I = mass * Rout**2 / 2
k = (Rmax**2 - Rmin**2) / 2 / L / radian
ts = linspace(0, duration, 101)
return System(init=init, k=k,
Rmin=Rmin, Rmax=Rmax,
mass=mass, I=I, g=g,
ts=ts)
system = make_system(condition)
system
system.init
# Solution
def slope_func(state, t, system):
"""Computes the derivatives of the state variables.
state: State object with theta, omega, y, v
t: time
system: System object with Rmin, k, I, mass
returns: sequence of derivatives
"""
theta, omega, y, v = state
unpack(system)
if y < 0 * m:
return 0, 0, 0, 0
r = sqrt(2*k*y + Rmin**2)
alpha = mass * g * r / (I + mass * r**2)
a = -r * alpha
return omega, alpha, v, a
slope_func(system.init, 0*s, system)
run_odeint(system, slope_func)
system.results.tail()
thetas = system.results.theta
ys = system.results.y
plot(thetas, label='theta')
decorate(xlabel='Time (s)',
ylabel='Angle (rad)')
plot(ys, color='green', label='y')
decorate(xlabel='Time (s)',
ylabel='Length (m)')
| 0.78842 | 0.985229 |
# Facial Expression Recognition Project
## Library Installations and Imports
```
!pip install -U -q PyDrive
!apt-get -qq install -y graphviz && pip install -q pydot
!pip install -q keras
from google.colab import files
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from google.colab import auth
from oauth2client.client import GoogleCredentials
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import pydot
import tensorflow as tf
from tensorflow.python.client import device_lib
from keras.models import Sequential
from keras.layers import Conv2D, LocallyConnected2D, MaxPooling2D, Dense
from keras.layers import Activation, Dropout, Flatten
from keras.callbacks import EarlyStopping
from keras.utils import plot_model, to_categorical
from keras import backend as K
```
### Confirm Tensorflow and GPU Support
```
K.tensorflow_backend._get_available_gpus()
device_lib.list_local_devices()
tf.test.gpu_device_name()
```
## Helper Functions
```
def uploadFiles():
uploaded = files.upload()
for fn in uploaded.keys():
print('User uploaded file "{name}" with length {length} bytes'.format(
name=fn, length=len(uploaded[fn])))
filenames = list(uploaded.keys())
for f in filenames:
data = str(uploaded[f], 'utf-8')
file = open(f, 'w')
file.write(data)
file.close()
def pullImage(frame, index: int):
"""
Takes in a pandas data frame object and an index and returns the 48 x 48 pixel
matrix as well as the label for the type of emotion.
"""
img = frame.loc[index]['pixels'].split(' ')
img = np.array([np.int(i) for i in img])
img.resize(48,48)
label = np.uint8(frame.loc[index]['emotion'])
return img, label
def splitImage_Labels(frame):
"""
Takes in a pandas data frame object filled with pixel field and label field
and returns two numpy arrays; one for images and one for labels.
"""
labels = np.empty(len(frame))
images = np.empty((len(frame), 48, 48, 1)) # using channel last notation.
for i in range(len(frame)):
img, lbl = pullImage(frame, i)
img = np.reshape(img, (48,48,1))
images[i], labels[i] = img, lbl
return images.astype(np.uint8), to_categorical(labels, 7).astype(np.uint8)
```
## Import FER2013 Dataset and Other Files
```
# Authenticate and create the PyDrive client.
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
# previous token was 4/AACID65Nxa7BHDHpZA-B8KTFCD_ctqRXJjozgUjW5rirIQVTFwJzE3E
fer2013 = drive.CreateFile({'id':'1Xdlvej7eXaVcfCf3CsQ1LcSFAiNx_63c'})
fer2013.GetContentFile('fer2013file.csv')
```
Save file as a pandas dataframe.
```
df = pd.read_csv('fer2013file.csv')
```
## Parse Data
Each image is a 48 x 48 grayscale photo.
The contents of pixel string are space-separated pixel values in row major order.
Emotional assignment convention:
* 0 = Angry
* 1 = Disgust
* 2 = Fear
* 3 = Happy
* 4 = Sad
* 5 = Surprise
* 6 = Neutral
```
df_Training = df[df.Usage == 'Training']
df_Testing = df[df.Usage == 'PrivateTest'].reset_index(drop = True)
img_train, lbl_train = splitImage_Labels(df_Training)
img_test, lbl_test = splitImage_Labels(df_Testing)
print('Type and Shape of Image Datasets: ' + '\n\tTraining: ' + '\t' +
str(type(img_train[0][0][0][0])) + '\t' + str(img_train.shape) +
'\n\tTesting: ' + '\t' + str(type(img_train[0][0][0][0])) + '\t' +
str(img_test.shape))
print('Type and Shape of Image Datasets: ' + '\n\tTraining: ' + '\t' +
str(type(lbl_train[0][0])) + '\t' + str(lbl_train.shape) +
'\n\tTesting: ' + '\t' + str(type(lbl_train[0][0])) + '\t' +
str(lbl_test.shape))
```
### Save Data to .npy Files
```
#np.save('img_train.npy', img_train)
#np.save('lbl_train.npy', lbl_train)
#np.save('img_test.npy', img_test)
#np.save('lbl_test.npy', img_test)
```
### Verify Image Import
```
plt.imshow(np.reshape(img_train[0], (48,48)))
plt.title('Training Image 1 (with label ' + str(lbl_train[0]) + ')')
plt.imshow(np.reshape(img_test[0], (48,48)))
plt.title('Training Image 1 (with label ' + str(lbl_test[0]) + ')')
```
## Build Convolutional Neural Network Model
```
model = Sequential()
```
### Phase 1
- Locally-Connected Convlutional Filtering Phase.
- The locally-connected layer works similarly to the traditional 2D convolutional layer, except that weights are unshared, that is, a different set of filters is applied at each different patch of the input.
- **Ouput Filters: 32**
- **Kernal Size: 4x4**
- **Stride: 1 (default)**
- **Non-Active Padding**
```
outputFilters = 32
kernelSize = 4
model.add(LocallyConnected2D(outputFilters, kernelSize, padding='valid',
activation='relu', input_shape=img_train[0].shape))
model.summary()
```
### Phase 2
- Convolutional and Max Pooling Phase.
- **Kernal Size: 3x3**
- **Ouput Filters: 32**
- **Stride: 1 (default)**
- **Active Padding**
```
outputFilters = 32
kernelSize = 3
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.summary()
```
### Phase 2
- Convolutional and Max Pooling Phase.
- **Kernal Size: 3x3**
- **Ouput Filters: 64**
- **Stride: 1 (default)**
- **Active Padding**
```
outputFilters = 64
kernelSize = 3
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.summary()
```
### Level 3
- Size of Convolutional Template Filter: 3 x 3 pixels
- Size of Template Stride: 3 pixels (for both horizontal and vertical stride)
- Number of output filters in the convolution: 128
- Padding protocol: Output is same dimensions as original image.
```
outputFilters = 128
kernelSize = 3
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.summary()
```
### Dense Layers
```
layerSize = 64
dropoutRate = 0.5
model.add(Flatten())
model.add(Dense(layerSize, activation='relu'))
model.add(Dropout(dropoutRate))
model.add(Dense(layerSize, activation='relu'))
model.add(Dropout(dropoutRate))
model.add(Dense(7, activation='softmax'))
model.summary()
```
### Show Model Structure
```
plot_model(model, to_file='model.png', show_shapes=True)
from IPython.display import Image
Image(filename='model.png')
```
## Compile, Train, and Evaluate the Model
```
batchSize = 128
trainingEpochs = 50
model.compile(optimizer='adam', loss='categorical_crossentropy',
metrics=['accuracy'])
#early_stopping = EarlyStopping(monitor='val_loss', patience=5, verbose=1)
trainingHistory = model.fit(img_train, lbl_train, batch_size=batchSize,
epochs=trainingEpochs,
validation_split=0.3,
# callbacks=[early_stopping],
shuffle=True,)
trainingAccuracy = trainingHistory.history['acc']
validationAccuracy = trainingHistory.history['val_acc']
print("Done Training: ")
print('Final Training Accuracy: ', trainingAccuracy[-1])
print('Final Validation Accuracy: ', validationAccuracy[-1])
print('Overfit Ratio: ', validationAccuracy[-1]/trainingAccuracy[-1])
metrics = model.evaluate(img_test, lbl_test, batch_size=batchSize, verbose=1)
print('Evaluation Loss: ', metrics[0])
print('Evaluation Accuracy: ', metrics[1])
```
|
github_jupyter
|
!pip install -U -q PyDrive
!apt-get -qq install -y graphviz && pip install -q pydot
!pip install -q keras
from google.colab import files
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from google.colab import auth
from oauth2client.client import GoogleCredentials
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import pydot
import tensorflow as tf
from tensorflow.python.client import device_lib
from keras.models import Sequential
from keras.layers import Conv2D, LocallyConnected2D, MaxPooling2D, Dense
from keras.layers import Activation, Dropout, Flatten
from keras.callbacks import EarlyStopping
from keras.utils import plot_model, to_categorical
from keras import backend as K
K.tensorflow_backend._get_available_gpus()
device_lib.list_local_devices()
tf.test.gpu_device_name()
def uploadFiles():
uploaded = files.upload()
for fn in uploaded.keys():
print('User uploaded file "{name}" with length {length} bytes'.format(
name=fn, length=len(uploaded[fn])))
filenames = list(uploaded.keys())
for f in filenames:
data = str(uploaded[f], 'utf-8')
file = open(f, 'w')
file.write(data)
file.close()
def pullImage(frame, index: int):
"""
Takes in a pandas data frame object and an index and returns the 48 x 48 pixel
matrix as well as the label for the type of emotion.
"""
img = frame.loc[index]['pixels'].split(' ')
img = np.array([np.int(i) for i in img])
img.resize(48,48)
label = np.uint8(frame.loc[index]['emotion'])
return img, label
def splitImage_Labels(frame):
"""
Takes in a pandas data frame object filled with pixel field and label field
and returns two numpy arrays; one for images and one for labels.
"""
labels = np.empty(len(frame))
images = np.empty((len(frame), 48, 48, 1)) # using channel last notation.
for i in range(len(frame)):
img, lbl = pullImage(frame, i)
img = np.reshape(img, (48,48,1))
images[i], labels[i] = img, lbl
return images.astype(np.uint8), to_categorical(labels, 7).astype(np.uint8)
# Authenticate and create the PyDrive client.
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
# previous token was 4/AACID65Nxa7BHDHpZA-B8KTFCD_ctqRXJjozgUjW5rirIQVTFwJzE3E
fer2013 = drive.CreateFile({'id':'1Xdlvej7eXaVcfCf3CsQ1LcSFAiNx_63c'})
fer2013.GetContentFile('fer2013file.csv')
df = pd.read_csv('fer2013file.csv')
df_Training = df[df.Usage == 'Training']
df_Testing = df[df.Usage == 'PrivateTest'].reset_index(drop = True)
img_train, lbl_train = splitImage_Labels(df_Training)
img_test, lbl_test = splitImage_Labels(df_Testing)
print('Type and Shape of Image Datasets: ' + '\n\tTraining: ' + '\t' +
str(type(img_train[0][0][0][0])) + '\t' + str(img_train.shape) +
'\n\tTesting: ' + '\t' + str(type(img_train[0][0][0][0])) + '\t' +
str(img_test.shape))
print('Type and Shape of Image Datasets: ' + '\n\tTraining: ' + '\t' +
str(type(lbl_train[0][0])) + '\t' + str(lbl_train.shape) +
'\n\tTesting: ' + '\t' + str(type(lbl_train[0][0])) + '\t' +
str(lbl_test.shape))
#np.save('img_train.npy', img_train)
#np.save('lbl_train.npy', lbl_train)
#np.save('img_test.npy', img_test)
#np.save('lbl_test.npy', img_test)
plt.imshow(np.reshape(img_train[0], (48,48)))
plt.title('Training Image 1 (with label ' + str(lbl_train[0]) + ')')
plt.imshow(np.reshape(img_test[0], (48,48)))
plt.title('Training Image 1 (with label ' + str(lbl_test[0]) + ')')
model = Sequential()
outputFilters = 32
kernelSize = 4
model.add(LocallyConnected2D(outputFilters, kernelSize, padding='valid',
activation='relu', input_shape=img_train[0].shape))
model.summary()
outputFilters = 32
kernelSize = 3
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.summary()
outputFilters = 64
kernelSize = 3
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.summary()
outputFilters = 128
kernelSize = 3
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(Conv2D(outputFilters, kernelSize, padding='same', activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.summary()
layerSize = 64
dropoutRate = 0.5
model.add(Flatten())
model.add(Dense(layerSize, activation='relu'))
model.add(Dropout(dropoutRate))
model.add(Dense(layerSize, activation='relu'))
model.add(Dropout(dropoutRate))
model.add(Dense(7, activation='softmax'))
model.summary()
plot_model(model, to_file='model.png', show_shapes=True)
from IPython.display import Image
Image(filename='model.png')
batchSize = 128
trainingEpochs = 50
model.compile(optimizer='adam', loss='categorical_crossentropy',
metrics=['accuracy'])
#early_stopping = EarlyStopping(monitor='val_loss', patience=5, verbose=1)
trainingHistory = model.fit(img_train, lbl_train, batch_size=batchSize,
epochs=trainingEpochs,
validation_split=0.3,
# callbacks=[early_stopping],
shuffle=True,)
trainingAccuracy = trainingHistory.history['acc']
validationAccuracy = trainingHistory.history['val_acc']
print("Done Training: ")
print('Final Training Accuracy: ', trainingAccuracy[-1])
print('Final Validation Accuracy: ', validationAccuracy[-1])
print('Overfit Ratio: ', validationAccuracy[-1]/trainingAccuracy[-1])
metrics = model.evaluate(img_test, lbl_test, batch_size=batchSize, verbose=1)
print('Evaluation Loss: ', metrics[0])
print('Evaluation Accuracy: ', metrics[1])
| 0.677687 | 0.78287 |
## Corona progression in The Netherlands
```
import csv
import pandas as pd
import re
DATE = "Date_of_report"
DEAD = "Deceased"
HOSPITALIZED = "Hospital_admission"
INFILENAME = "corona-nl-totals.csv"
INFECTED = "Total_reported"
URL = "https://data.rivm.nl/covid-19/COVID-19_aantallen_gemeente_cumulatief.csv"
def summarizeDate(date):
return(re.sub(r"-","",date.split()[0]))
def readData():
try:
df = pd.read_csv(URL,sep=";")
dfGroups = df.groupby(DATE)
lastDead,lastHospitalized,lastInfected = 0,0,0
data = {}
for date,group in dfGroups:
date = summarizeDate(date)
dead = sum(group[DEAD])
hospitalized = sum(group[HOSPITALIZED])
infected = sum(group[INFECTED])
data[date] = {INFECTED:infected-lastInfected,HOSPITALIZED:hospitalized-lastHospitalized,DEAD:dead-lastDead}
lastDead,lastHospitalized,lastInfected = dead,hospitalized,infected
pd.DataFrame.from_dict(data).to_csv(INFILENAME)
print(f"stored data in file {INFILENAME}")
except:
data = pd.read_csv(INFILENAME,index_col=0).T.to_dict()
print(f"read data from file {INFILENAME}")
return(data)
data = readData()
print(f"updated until {list(data.keys())[-1]} ({list(data.values())[-1][INFECTED]})")
def combine(listIn,maxCount):
listOut = []
for i in range(0,len(listIn)):
total = 0
count = 0
for j in range(i,i-maxCount,-1):
if j >= 0:
total += listIn[j]
count += 1
listOut.append(total/count)
return(listOut)
import datetime
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
DATEPATTERN = "%Y%m%d"
PLOTFILENAME = "corona-nl.png"
WEEKLENGTH = 7
MAXDATE = "99999999"
def visualize(data):
x = [datetime.datetime.strptime(str(date),DATEPATTERN) for date in data if date < MAXDATE]
infected = combine([data[date][INFECTED] for date in data if date < MAXDATE],WEEKLENGTH)
hospitalized = combine([data[date][HOSPITALIZED] for date in data if date < MAXDATE],WEEKLENGTH)
dead = combine([data[date][DEAD] for date in data if date < MAXDATE],WEEKLENGTH)
plt.subplots(figsize=(14,6))
ax = plt.subplot(121)
ax.xaxis.set_major_formatter(mdates.DateFormatter("%-m-%-y"))
plt.plot_date(x,infected,fmt="-",label="new infections")
plt.plot_date(x,hospitalized,fmt="-",label="new hospitalizations")
plt.plot_date(x,dead,fmt="-",label="new deaths")
plt.legend()
plt.title(" COVID-19 numbers for The Netherlands")
ax = plt.subplot(122)
ax.xaxis.set_major_formatter(mdates.DateFormatter("%-m-%-y"))
plt.yscale("log")
plt.plot_date(x,infected,fmt="-",label="new infections")
plt.plot_date(x,hospitalized,fmt="-",label="new hospitalizations")
plt.plot_date(x,dead,fmt="-",label="new deaths")
plt.legend()
plt.title("(moving average over 7 days) ")
plt.savefig(PLOTFILENAME)
plt.show()
return([int(x) for x in infected[-8:]], [int(x) for x in hospitalized[-8:]], [int(x) for x in dead[-8:]])
visualize(data)
```
|
github_jupyter
|
import csv
import pandas as pd
import re
DATE = "Date_of_report"
DEAD = "Deceased"
HOSPITALIZED = "Hospital_admission"
INFILENAME = "corona-nl-totals.csv"
INFECTED = "Total_reported"
URL = "https://data.rivm.nl/covid-19/COVID-19_aantallen_gemeente_cumulatief.csv"
def summarizeDate(date):
return(re.sub(r"-","",date.split()[0]))
def readData():
try:
df = pd.read_csv(URL,sep=";")
dfGroups = df.groupby(DATE)
lastDead,lastHospitalized,lastInfected = 0,0,0
data = {}
for date,group in dfGroups:
date = summarizeDate(date)
dead = sum(group[DEAD])
hospitalized = sum(group[HOSPITALIZED])
infected = sum(group[INFECTED])
data[date] = {INFECTED:infected-lastInfected,HOSPITALIZED:hospitalized-lastHospitalized,DEAD:dead-lastDead}
lastDead,lastHospitalized,lastInfected = dead,hospitalized,infected
pd.DataFrame.from_dict(data).to_csv(INFILENAME)
print(f"stored data in file {INFILENAME}")
except:
data = pd.read_csv(INFILENAME,index_col=0).T.to_dict()
print(f"read data from file {INFILENAME}")
return(data)
data = readData()
print(f"updated until {list(data.keys())[-1]} ({list(data.values())[-1][INFECTED]})")
def combine(listIn,maxCount):
listOut = []
for i in range(0,len(listIn)):
total = 0
count = 0
for j in range(i,i-maxCount,-1):
if j >= 0:
total += listIn[j]
count += 1
listOut.append(total/count)
return(listOut)
import datetime
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
DATEPATTERN = "%Y%m%d"
PLOTFILENAME = "corona-nl.png"
WEEKLENGTH = 7
MAXDATE = "99999999"
def visualize(data):
x = [datetime.datetime.strptime(str(date),DATEPATTERN) for date in data if date < MAXDATE]
infected = combine([data[date][INFECTED] for date in data if date < MAXDATE],WEEKLENGTH)
hospitalized = combine([data[date][HOSPITALIZED] for date in data if date < MAXDATE],WEEKLENGTH)
dead = combine([data[date][DEAD] for date in data if date < MAXDATE],WEEKLENGTH)
plt.subplots(figsize=(14,6))
ax = plt.subplot(121)
ax.xaxis.set_major_formatter(mdates.DateFormatter("%-m-%-y"))
plt.plot_date(x,infected,fmt="-",label="new infections")
plt.plot_date(x,hospitalized,fmt="-",label="new hospitalizations")
plt.plot_date(x,dead,fmt="-",label="new deaths")
plt.legend()
plt.title(" COVID-19 numbers for The Netherlands")
ax = plt.subplot(122)
ax.xaxis.set_major_formatter(mdates.DateFormatter("%-m-%-y"))
plt.yscale("log")
plt.plot_date(x,infected,fmt="-",label="new infections")
plt.plot_date(x,hospitalized,fmt="-",label="new hospitalizations")
plt.plot_date(x,dead,fmt="-",label="new deaths")
plt.legend()
plt.title("(moving average over 7 days) ")
plt.savefig(PLOTFILENAME)
plt.show()
return([int(x) for x in infected[-8:]], [int(x) for x in hospitalized[-8:]], [int(x) for x in dead[-8:]])
visualize(data)
| 0.253769 | 0.484136 |
# Training Neural Networks
The network we built in the previous part isn't so smart, it doesn't know anything about our handwritten digits. Neural networks with non-linear activations work like universal function approximators. There is some function that maps your input to the output. For example, images of handwritten digits to class probabilities. The power of neural networks is that we can train them to approximate this function, and basically any function given enough data and compute time.
<img src="assets/function_approx.png" width=500px>
At first the network is naive, it doesn't know the function mapping the inputs to the outputs. We train the network by showing it examples of real data, then adjusting the network parameters such that it approximates this function.
To find these parameters, we need to know how poorly the network is predicting the real outputs. For this we calculate a **loss function** (also called the cost), a measure of our prediction error. For example, the mean squared loss is often used in regression and binary classification problems
$$
\ell = \frac{1}{2n}\sum_i^n{\left(y_i - \hat{y}_i\right)^2}
$$
where $n$ is the number of training examples, $y_i$ are the true labels, and $\hat{y}_i$ are the predicted labels.
By minimizing this loss with respect to the network parameters, we can find configurations where the loss is at a minimum and the network is able to predict the correct labels with high accuracy. We find this minimum using a process called **gradient descent**. The gradient is the slope of the loss function and points in the direction of fastest change. To get to the minimum in the least amount of time, we then want to follow the gradient (downwards). You can think of this like descending a mountain by following the steepest slope to the base.
<img src='assets/gradient_descent.png' width=350px>
## Backpropagation
For single layer networks, gradient descent is simple to implement. However, it's more complicated for deeper, multilayer neural networks like the one we've built. Complicated enough that it took about 30 years before researchers figured out how to train multilayer networks, although it's straightforward once you learn about it.
This is done through **backpropagation** which is really just an application of the chain rule from calculus. It's easiest to understand if we convert a two layer network into a graph representation.
<img src='assets/w1_backprop_graph.png' width=400px>
In the forward pass through the network, our data and operations go from right to left here. To train the weights with gradient descent, we propagate the gradient of the cost backwards through the network. Mathematically, this is really just calculating the gradient of the loss with respect to the weights using the chain rule.
$$
\frac{\partial \ell}{\partial w_1} = \frac{\partial l_1}{\partial w_1} \frac{\partial s}{\partial l_1} \frac{\partial l_2}{\partial s} \frac{\partial \ell}{\partial l_2}
$$
We update our weights using this gradient with some learning rate $\alpha$.
$$
w^\prime = w - \alpha \frac{\partial \ell}{\partial w}
$$
The learning rate is set such that the weight update steps are small enough that the iterative method settles in a minimum.
The first thing we need to do for training is define our loss function. In PyTorch, you'll usually see this as `criterion`. Here we're using softmax output, so we want to use `criterion = nn.CrossEntropyLoss()` as our loss. Later when training, you use `loss = criterion(output, targets)` to calculate the actual loss.
We also need to define the optimizer we're using, SGD or Adam, or something along those lines. Here I'll just use SGD with `torch.optim.SGD`, passing in the network parameters and the learning rate.
## Autograd
Torch provides a module, `autograd`, for automatically calculating the gradient of tensors. It does this by keeping track of operations performed on tensors. To make sure PyTorch keeps track of operations on a tensor and calculates the gradients, you need to set `requires_grad` on a tensor. You can do this at creation with the `requires_grad` keyword, or at any time with `x.requires_grad_(True)`.
You can turn off gradients for a block of code with the `torch.no_grad()` content:
```python
x = torch.zeros(1, requires_grad=True)
>>> with torch.no_grad():
... y = x * 2
>>> y.requires_grad
False
```
Also, you can turn on or off gradients altogether with `torch.set_grad_enabled(True|False)`.
The gradients are computed with respect to some variable `z` with `z.backward()`. This does a backward pass through the operations that created `z`.
```
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
from collections import OrderedDict
import numpy as np
import time
import torch
from torch import nn
from torch import optim
import torch.nn.functional as F
import helper
x = torch.randn(2,2, requires_grad=True)
print(x)
y = x**2
print(y)
```
Below we can see the operation that created `y`, a power operation `PowBackward0`.
```
## grad_fn shows the function that generated this variable
print(y.grad_fn)
```
The autgrad module keeps track of these operations and knows how to calculate the gradient for each one. In this way, it's able to calculate the gradients for a chain of operations, with respect to any one tensor. Let's reduce the tensor `y` to a scalar value, the mean.
```
z = y.mean()
print(z)
```
You can check the gradients for `x` and `y` but they are empty currently.
```
print(x.grad)
```
To calculate the gradients, you need to run the `.backward` method on a Variable, `z` for example. This will calculate the gradient for `z` with respect to `x`
$$
\frac{\partial z}{\partial x} = \frac{\partial}{\partial x}\left[\frac{1}{n}\sum_i^n x_i^2\right] = \frac{x}{2}
$$
```
z.backward()
print(x.grad)
print(x/2)
```
These gradients calculations are particularly useful for neural networks. For training we need the gradients of the weights with respect to the cost. With PyTorch, we run data forward through the network to calculate the cost, then, go backwards to calculate the gradients with respect to the cost. Once we have the gradients we can make a gradient descent step.
## Get the data and define the network
The same as we saw in part 3, we'll load the MNIST dataset and define our network.
```
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
#transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
transforms.Normalize((0.5,), (0.5,)),
])
# Download and load the training data
trainset = datasets.MNIST('MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
```
I'll build a network with `nn.Sequential` here. Only difference from the last part is I'm not actually using softmax on the output, but instead just using the raw output from the last layer. This is because the output from softmax is a probability distribution. Often, the output will have values really close to zero or really close to one. Due to [inaccuracies with representing numbers as floating points](https://docs.python.org/3/tutorial/floatingpoint.html), computations with a softmax output can lose accuracy and become unstable. To get around this, we'll use the raw output, called the **logits**, to calculate the loss.
```
# Hyperparameters for our network
input_size = 784
hidden_sizes = [128, 64]
output_size = 10
# Build a feed-forward network
# In order to avoid numerical instability of softmax, activation in last layer also ReLU
model = nn.Sequential(OrderedDict([
('fc1', nn.Linear(input_size, hidden_sizes[0])),
('relu1', nn.ReLU()),
('fc2', nn.Linear(hidden_sizes[0], hidden_sizes[1])),
('relu2', nn.ReLU()),
('logits', nn.Linear(hidden_sizes[1], output_size))]))
```
## Training the network!
The first thing we need to do for training is define our loss function. In PyTorch, you'll usually see this as `criterion`. Here we're using softmax output, so we want to use `criterion = nn.CrossEntropyLoss()` as our loss. Later when training, you use `loss = criterion(output, targets)` to calculate the actual loss.
We also need to define the optimizer we're using, SGD or Adam, or something along those lines. Here I'll just use SGD with `torch.optim.SGD`, passing in the network parameters and the learning rate.
```
# criterion: error or loss function: MSE, Cross-Entropy, etc
# optimizer: minimization method for loss function: Stochastic Gradient Descent (SGD)
# we want to optimize all params (weights and biases) -> model.parameters()
# learning rate for optimizer: lr
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
```
First, let's consider just one learning step before looping through all the data. The general process with PyTorch:
* Make a forward pass through the network to get the logits
* Use the logits to calculate the loss
* Perform a backward pass through the network with `loss.backward()` to calculate the gradients
* Take a step with the optimizer to update the weights
Below I'll go through one training step and print out the weights and gradients so you can see how it changes.
```
# Training repeats in for loop these steps
# 1) get next batch and resize it
# 2) clear gradients (because they accumulate) and make forward pass with batch
# 3) compute loss with criterion
# 4) compute gradient of loss function
# 5) perform a step with the optimizer = update weights with learning rate
print('Initial weights - ', model.fc1.weight)
images, labels = next(iter(trainloader))
images.resize_(64, 784)
# Clear the gradients, do this because gradients are accumulated
optimizer.zero_grad()
# Forward pass, then backward pass, then update weights
output = model.forward(images)
loss = criterion(output, labels)
loss.backward()
print('Gradient -', model.fc1.weight.grad)
optimizer.step()
# new weights after step can be visualized
print('Updated weights - ', model.fc1.weight)
```
### Training for real
Now we'll put this algorithm into a loop so we can go through all the images. This is fairly straightforward. We'll loop through the mini-batches in our dataset, pass the data through the network to calculate the losses, get the gradients, then run the optimizer.
```
optimizer = optim.SGD(model.parameters(), lr=0.003)
# Define number of epochs = number of passes through whole training set
epochs = 3
print_every = 40
# one step (weight update) for each batch processed
steps = 0
for e in range(epochs):
running_loss = 0
for images, labels in iter(trainloader):
steps += 1
# Flatten MNIST images into a 784 long vector
images.resize_(images.size()[0], 784)
optimizer.zero_grad()
# Forward and backward passes
output = model.forward(images)
loss = criterion(output, labels)
loss.backward()
optimizer.step()
# loss is a scalar tensor -> unpack its value for comput8ing average
running_loss += loss.item()
if steps % print_every == 0:
# print loss average during last print_every steps
print("Epoch: {}/{}... ".format(e+1, epochs),
"Loss: {:.4f}".format(running_loss/print_every))
running_loss = 0
```
With the network trained, we can check out it's predictions.
```
images, labels = next(iter(trainloader))
img = images[0].view(1, 784)
# Turn off gradients to speed up this part
with torch.no_grad():
logits = model.forward(img)
# Output of the network are logits, need to take softmax for probabilities
ps = F.softmax(logits, dim=1)
helper.view_classify(img.view(1, 28, 28), ps)
```
Now our network is brilliant. It can accurately predict the digits in our images. Next up you'll write the code for training a neural network on a more complex dataset.
|
github_jupyter
|
x = torch.zeros(1, requires_grad=True)
>>> with torch.no_grad():
... y = x * 2
>>> y.requires_grad
False
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
from collections import OrderedDict
import numpy as np
import time
import torch
from torch import nn
from torch import optim
import torch.nn.functional as F
import helper
x = torch.randn(2,2, requires_grad=True)
print(x)
y = x**2
print(y)
## grad_fn shows the function that generated this variable
print(y.grad_fn)
z = y.mean()
print(z)
print(x.grad)
z.backward()
print(x.grad)
print(x/2)
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
#transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
transforms.Normalize((0.5,), (0.5,)),
])
# Download and load the training data
trainset = datasets.MNIST('MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# Hyperparameters for our network
input_size = 784
hidden_sizes = [128, 64]
output_size = 10
# Build a feed-forward network
# In order to avoid numerical instability of softmax, activation in last layer also ReLU
model = nn.Sequential(OrderedDict([
('fc1', nn.Linear(input_size, hidden_sizes[0])),
('relu1', nn.ReLU()),
('fc2', nn.Linear(hidden_sizes[0], hidden_sizes[1])),
('relu2', nn.ReLU()),
('logits', nn.Linear(hidden_sizes[1], output_size))]))
# criterion: error or loss function: MSE, Cross-Entropy, etc
# optimizer: minimization method for loss function: Stochastic Gradient Descent (SGD)
# we want to optimize all params (weights and biases) -> model.parameters()
# learning rate for optimizer: lr
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
# Training repeats in for loop these steps
# 1) get next batch and resize it
# 2) clear gradients (because they accumulate) and make forward pass with batch
# 3) compute loss with criterion
# 4) compute gradient of loss function
# 5) perform a step with the optimizer = update weights with learning rate
print('Initial weights - ', model.fc1.weight)
images, labels = next(iter(trainloader))
images.resize_(64, 784)
# Clear the gradients, do this because gradients are accumulated
optimizer.zero_grad()
# Forward pass, then backward pass, then update weights
output = model.forward(images)
loss = criterion(output, labels)
loss.backward()
print('Gradient -', model.fc1.weight.grad)
optimizer.step()
# new weights after step can be visualized
print('Updated weights - ', model.fc1.weight)
optimizer = optim.SGD(model.parameters(), lr=0.003)
# Define number of epochs = number of passes through whole training set
epochs = 3
print_every = 40
# one step (weight update) for each batch processed
steps = 0
for e in range(epochs):
running_loss = 0
for images, labels in iter(trainloader):
steps += 1
# Flatten MNIST images into a 784 long vector
images.resize_(images.size()[0], 784)
optimizer.zero_grad()
# Forward and backward passes
output = model.forward(images)
loss = criterion(output, labels)
loss.backward()
optimizer.step()
# loss is a scalar tensor -> unpack its value for comput8ing average
running_loss += loss.item()
if steps % print_every == 0:
# print loss average during last print_every steps
print("Epoch: {}/{}... ".format(e+1, epochs),
"Loss: {:.4f}".format(running_loss/print_every))
running_loss = 0
images, labels = next(iter(trainloader))
img = images[0].view(1, 784)
# Turn off gradients to speed up this part
with torch.no_grad():
logits = model.forward(img)
# Output of the network are logits, need to take softmax for probabilities
ps = F.softmax(logits, dim=1)
helper.view_classify(img.view(1, 28, 28), ps)
| 0.916798 | 0.994885 |
```
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2
from scipy.stats import multivariate_normal
np.random.seed(42)
train_data = np.loadtxt('hwk3data\hwk3data\EMGaussian.train')
test_data = np.loadtxt('hwk3data\hwk3data\EMGaussian.test')
data = train_data
n_clusters = 4
n_iter = 50
def covariance(x):
x_mu = np.mean(x,axis=0)
cov = np.zeros((x.shape[1],x.shape[1]))
for i in range(x.shape[0]):
cov += np.outer((x[i,:] - x_mu),(x[i,:] - x_mu))
cov = cov*1.0/x.shape[0]
return cov
def weighted_covariance(x, x_mu, tau):
cov = np.zeros((x.shape[1],x.shape[1]))
for i in range(x.shape[0]):
cov += tau[i]*np.outer((x[i,:] - x_mu),(x[i,:] - x_mu))
cov = cov*1.0/np.sum(tau)
return cov
def plot_ellipse(semimaj=1,semimin=1,phi=0,x_cent=0,y_cent=0,theta_num=1e3,ax=None,plot_kwargs=None,\
fill=False,fill_kwargs=None,data_out=False,cov=None,mass_level=0.68,colour='b',label=''):
# Get Ellipse Properties from cov matrix
if cov is not None:
eig_vec,eig_val,u = np.linalg.svd(cov)
# Make sure 0th eigenvector has positive x-coordinate
if eig_vec[0][0] < 0:
eig_vec[0] *= -1
semimaj = np.sqrt(eig_val[0])
semimin = np.sqrt(eig_val[1])
if mass_level is None:
multiplier = np.sqrt(2.279)
else:
distances = np.linspace(0,20,20001)
chi2_cdf = chi2.cdf(distances,df=2)
multiplier = np.sqrt(distances[np.where(np.abs(chi2_cdf-mass_level)==np.abs(chi2_cdf-mass_level).min())[0][0]])
semimaj *= multiplier
semimin *= multiplier
phi = np.arccos(np.dot(eig_vec[0],np.array([1,0])))
if eig_vec[0][1] < 0 and phi > 0:
phi *= -1
# Generate data for ellipse structure
theta = np.linspace(0,2*np.pi,theta_num)
r = 1 / np.sqrt((np.cos(theta))**2 + (np.sin(theta))**2)
x = r*np.cos(theta)
y = r*np.sin(theta)
data = np.array([x,y])
S = np.array([[semimaj,0],[0,semimin]])
R = np.array([[np.cos(phi),-np.sin(phi)],[np.sin(phi),np.cos(phi)]])
T = np.dot(R,S)
data = np.dot(T,data)
data[0] += x_cent
data[1] += y_cent
# Output data?
if data_out == True:
return data
# Plot!
return_fig = False
if ax is None:
return_fig = True
fig,ax = plt.subplots()
if plot_kwargs is None:
ax.plot(data[0],data[1],color=colour,label=label,linestyle='-')
else:
ax.plot(data[0],data[1],color=colour,label=label,**plot_kwargs)
if fill == True:
ax.fill(data[0],data[1],**fill_kwargs)
if return_fig == True:
return fig
def plot_ellipse_cov(cov, cent, ax, colour='b',label=''):
w,v = np.linalg.eig(cov)
semi_major_axis_len = 2*np.sqrt(4.6*w[0])
semi_minor_axis_len = 2*np.sqrt(4.6*w[1])
theta = np.arctan(v[1,0]/v[0,0])
plot_ellipse(semi_major_axis_len, semi_minor_axis_len, theta, cent[0], cent[1], ax=ax, colour=colour,label=label)
def compute_NLL(data, mu_list, sigma_list, pi_list):
nll = 0
mu_0 = mu_list[0]
mu_1 = mu_list[1]
mu_2 = mu_list[2]
mu_3 = mu_list[3]
sigma_0 = sigma_list[0]
sigma_1 = sigma_list[1]
sigma_2 = sigma_list[2]
sigma_3 = sigma_list[3]
pi_0 = pi_list[0]
pi_1 = pi_list[1]
pi_2 = pi_list[2]
pi_3 = pi_list[3]
for i in range(data.shape[0]):
x = pi_0*multivariate_normal.pdf(data[i,:],mean=mu_0,cov=sigma_0) + pi_1*multivariate_normal.pdf(data[i,:],mean=mu_1,cov=sigma_1) + pi_2*multivariate_normal.pdf(data[i,:],mean=mu_2,cov=sigma_2) + pi_3*multivariate_normal.pdf(data[i,:],mean=mu_3,cov=sigma_3)
nll += np.log(x)
nll /= data.shape[0]
return nll
def compute_k_means_loss(cluster_list, mu_list):
loss = 0
cluster_0 = cluster_list[0]
cluster_1 = cluster_list[1]
cluster_2 = cluster_list[2]
cluster_3 = cluster_list[3]
mu_0 = mu_list[0]
mu_1 = mu_list[1]
mu_2 = mu_list[2]
mu_3 = mu_list[3]
for i in range(cluster_0.shape[0]):
loss += (np.linalg.norm(cluster_0[i,:] - mu_0.reshape(1,-1)))**2
for i in range(cluster_1.shape[0]):
loss += (np.linalg.norm(cluster_1[i,:] - mu_1.reshape(1,-1)))**2
for i in range(cluster_2.shape[0]):
loss += (np.linalg.norm(cluster_2[i,:] - mu_2.reshape(1,-1)))**2
for i in range(cluster_3.shape[0]):
loss += (np.linalg.norm(cluster_3[i,:] - mu_3.reshape(1,-1)))**2
return loss
def k_means(data, n_clusters, n_iter):
init_means_coord = np.zeros((n_clusters, 2))
flag = True
while(flag):
init_means_coord[:,0] = np.random.uniform(np.min(data[:,0]),np.max(data[:,0]),size=(n_clusters))
init_means_coord[:,1] = np.random.uniform(np.min(data[:,1]),np.max(data[:,1]),size=(n_clusters))
labels = np.zeros((data.shape[0],1))
for i in range(labels.shape[0]):
dist = np.linalg.norm(np.tile(data[i,:],(n_clusters,1)) - init_means_coord, axis=1).reshape(-1,1)
dist_argmax = np.argmax(dist, axis=0)
labels[i,0] = dist_argmax[0]
if len(np.unique(labels)) == n_clusters:
flag = False
for iter in range(n_iter):
# E step
for i in range(labels.shape[0]):
dist = np.linalg.norm(np.tile(data[i,:],(n_clusters,1)) - init_means_coord, axis=1).reshape(-1,1)
dist_argmin = np.argmin(dist, axis=0)
labels[i,0] = dist_argmin[0]
try:
assert len(np.unique(labels)) == n_clusters
except:
non_present_labels = np.setdiff1d(np.arange(n_clusters),np.unique(labels)).tolist()
labels_idx = np.random.choice(labels.shape[0],len(non_present_labels))
for i,lbl in enumerate(non_present_labels):
labels[labels_idx[i]] = lbl
assert len(np.unique(labels)) == n_clusters
# M step
for i in range(n_clusters):
init_means_coord[i,:] = np.mean(np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==i]),axis=0)
if np.any(np.isnan(init_means_coord)):
print 'ERROR!!!'
break
return labels
for trial in range(5):
labels = k_means(data, n_clusters, n_iter)
cluster_0 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==0]).reshape(-1,2)
cluster_1 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==1]).reshape(-1,2)
cluster_2 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==2]).reshape(-1,2)
cluster_3 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==3]).reshape(-1,2)
cluster_0_mu = np.mean(cluster_0,axis=0)
cluster_1_mu = np.mean(cluster_1,axis=0)
cluster_2_mu = np.mean(cluster_2,axis=0)
cluster_3_mu = np.mean(cluster_3,axis=0)
cluster_list = [cluster_0, cluster_1, cluster_2, cluster_3]
mu_list = [cluster_0_mu, cluster_1_mu, cluster_2_mu, cluster_3_mu]
k_means_loss = compute_k_means_loss(cluster_list, mu_list)
print 'K-means Trial ID: %d loss = %f' % (trial, k_means_loss)
print 'Cluster 0 co-ordinates:'
print cluster_0_mu
print '\n'
print 'Cluster 1 co-ordinates:'
print cluster_1_mu
print '\n'
print 'Cluster 2 co-ordinates:'
print cluster_2_mu
print '\n'
print 'Cluster 3 co-ordinates:'
print cluster_3_mu
print '\n'
plt.plot(cluster_0[:,0], cluster_0[:,1], '*', c='red',label='cluster 0')
plt.plot(cluster_1[:,0], cluster_1[:,1], '*', c='blue',label='cluster 1')
plt.plot(cluster_2[:,0], cluster_2[:,1], '*', c='orange',label='cluster 2')
plt.plot(cluster_3[:,0], cluster_3[:,1], '*', c='magenta',label='cluster 3')
plt.plot(cluster_0_mu[0],cluster_0_mu[1],'o',c='black',label='cluster centers')
plt.plot(cluster_1_mu[0],cluster_1_mu[1],'o',c='black')
plt.plot(cluster_2_mu[0],cluster_2_mu[1],'o',c='black')
plt.plot(cluster_3_mu[0],cluster_3_mu[1],'o',c='black')
plt.legend()
plt.xlabel('x[0]')
plt.ylabel('x[1]')
plt.title('Cluster assignment for train data (K-means) PART-8(a)')
plt.show()
# PART-B (EM with identity matrix as covariance)
cluster_0_mu = np.mean(cluster_0,axis=0)
cluster_1_mu = np.mean(cluster_1,axis=0)
cluster_2_mu = np.mean(cluster_2,axis=0)
cluster_3_mu = np.mean(cluster_3,axis=0)
cluster_0_sigma_2 = np.mean((np.linalg.norm(cluster_0 - cluster_0_mu.reshape(1,-1),axis=1))**2)/cluster_0_mu.shape[0]
cluster_1_sigma_2 = np.mean((np.linalg.norm(cluster_1 - cluster_1_mu.reshape(1,-1),axis=1))**2)/cluster_1_mu.shape[0]
cluster_2_sigma_2 = np.mean((np.linalg.norm(cluster_2 - cluster_2_mu.reshape(1,-1),axis=1))**2)/cluster_2_mu.shape[0]
cluster_3_sigma_2 = np.mean((np.linalg.norm(cluster_3 - cluster_3_mu.reshape(1,-1),axis=1))**2)/cluster_3_mu.shape[0]
pi_0 = cluster_0.shape[0]*1.0/labels.shape[0]
pi_1 = cluster_1.shape[0]*1.0/labels.shape[0]
pi_2 = cluster_2.shape[0]*1.0/labels.shape[0]
pi_3 = cluster_3.shape[0]*1.0/labels.shape[0]
tau = np.zeros((data.shape[0],n_clusters))
n_iter = 20
for iter in range(n_iter):
# E step
for i in range(tau.shape[0]):
tau[i,0] = pi_0*multivariate_normal.pdf(data[i,:], mean=cluster_0_mu, cov=cluster_0_sigma_2*np.eye(cluster_0_mu.shape[0]))
tau[i,1] = pi_1*multivariate_normal.pdf(data[i,:], mean=cluster_1_mu, cov=cluster_1_sigma_2*np.eye(cluster_1_mu.shape[0]))
tau[i,2] = pi_2*multivariate_normal.pdf(data[i,:], mean=cluster_2_mu, cov=cluster_2_sigma_2*np.eye(cluster_2_mu.shape[0]))
tau[i,3] = pi_3*multivariate_normal.pdf(data[i,:], mean=cluster_3_mu, cov=cluster_3_sigma_2*np.eye(cluster_3_mu.shape[0]))
norm_factor = np.sum(tau[i,:])
tau[i,0] = tau[i,0]/norm_factor
tau[i,1] = tau[i,1]/norm_factor
tau[i,2] = tau[i,2]/norm_factor
tau[i,3] = tau[i,3]/norm_factor
# M step
cluster_0_mu = np.sum(data*tau[:,0].reshape(-1,1),axis=0)/np.sum(tau[:,0])
cluster_1_mu = np.sum(data*tau[:,1].reshape(-1,1),axis=0)/np.sum(tau[:,1])
cluster_2_mu = np.sum(data*tau[:,2].reshape(-1,1),axis=0)/np.sum(tau[:,2])
cluster_3_mu = np.sum(data*tau[:,3].reshape(-1,1),axis=0)/np.sum(tau[:,3])
cluster_0_sigma_2 = np.sum((np.linalg.norm((data - cluster_0_mu.reshape(1,-1)),axis=1)**2)*tau[:,0],axis=0)/(np.sum(tau[:,0])*cluster_0_mu.shape[0])
cluster_1_sigma_2 = np.sum((np.linalg.norm((data - cluster_1_mu.reshape(1,-1)),axis=1)**2)*tau[:,1],axis=0)/(np.sum(tau[:,1])*cluster_1_mu.shape[0])
cluster_2_sigma_2 = np.sum((np.linalg.norm((data - cluster_2_mu.reshape(1,-1)),axis=1)**2)*tau[:,2],axis=0)/(np.sum(tau[:,2])*cluster_2_mu.shape[0])
cluster_3_sigma_2 = np.sum((np.linalg.norm((data - cluster_3_mu.reshape(1,-1)),axis=1)**2)*tau[:,3],axis=0)/(np.sum(tau[:,3])*cluster_3_mu.shape[0])
pi_0 = np.sum(tau[:,0])/data.shape[0]
pi_1 = np.sum(tau[:,1])/data.shape[0]
pi_2 = np.sum(tau[:,2])/data.shape[0]
pi_3 = np.sum(tau[:,3])/data.shape[0]
cluster_0 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==0]).reshape(-1,2)
cluster_1 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==1]).reshape(-1,2)
cluster_2 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==2]).reshape(-1,2)
cluster_3 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==3]).reshape(-1,2)
print 'mean vector for Gaussian ID: 0'
print cluster_0_mu
print 'covariance matrix for Gaussian ID: 0'
print cluster_0_sigma_2*np.eye(cluster_0.shape[1])
print 'mean vector for Gaussian ID: 1'
print cluster_1_mu
print 'covariance matrix for Gaussian ID: 1'
print cluster_1_sigma_2*np.eye(cluster_1.shape[1])
print 'mean vector for Gaussian ID: 2'
print cluster_2_mu
print 'covariance matrix for Gaussian ID: 2'
print cluster_2_sigma_2*np.eye(cluster_2.shape[1])
print 'mean vector for Gaussian ID: 3'
print cluster_3_mu
print 'covariance matrix for Gaussian ID: 3'
print cluster_3_sigma_2*np.eye(cluster_3.shape[1])
plt.figure()
plt.plot(cluster_0[:,0], cluster_0[:,1], '*', c='red',label='Gaussian ID 0')
plt.plot(cluster_1[:,0], cluster_1[:,1], '*', c='blue',label='Gaussian ID 1')
plt.plot(cluster_2[:,0], cluster_2[:,1], '*', c='orange',label='Gaussian ID 2')
plt.plot(cluster_3[:,0], cluster_3[:,1], '*', c='magenta',label='Gaussian ID 3')
plt.plot(cluster_0_mu[0],cluster_0_mu[1],'o',c='black',label='Gaussian centers')
plt.plot(cluster_1_mu[0],cluster_1_mu[1],'o',c='black')
plt.plot(cluster_2_mu[0],cluster_2_mu[1],'o',c='black')
plt.plot(cluster_3_mu[0],cluster_3_mu[1],'o',c='black')
plot_ellipse_cov(cluster_0_sigma_2*np.eye(cluster_0.shape[1]),cluster_0_mu, ax=plt, colour='red',label='Gaussian ID 0 ellipse')
plot_ellipse_cov(cluster_1_sigma_2*np.eye(cluster_1.shape[1]),cluster_1_mu, ax=plt, colour='blue',label='Gaussian ID 1 ellipse')
plot_ellipse_cov(cluster_2_sigma_2*np.eye(cluster_2.shape[1]),cluster_2_mu, ax=plt, colour='orange',label='Gaussian ID 2 ellipse')
plot_ellipse_cov(cluster_3_sigma_2*np.eye(cluster_3.shape[1]),cluster_3_mu, ax=plt, colour='magenta',label='Gaussian ID 3 ellipse')
plt.legend(bbox_to_anchor=(1.1, 1.0))
plt.xlabel('x[0]')
plt.ylabel('x[1]')
plt.title('Representation for train data (Identity cov. matrix), centers, covariance matrices (using ellipse) PART-8(b)')
plt.show()
mu_list = [cluster_0_mu, cluster_1_mu, cluster_2_mu, cluster_3_mu]
sigma_list = [cluster_0_sigma_2*np.eye(cluster_0.shape[1]), cluster_1_sigma_2*np.eye(cluster_1.shape[1]), cluster_2_sigma_2*np.eye(cluster_2.shape[1]), cluster_3_sigma_2*np.eye(cluster_3.shape[1])]
pi_list = [pi_0, pi_1, pi_2, pi_3]
train_avg_NLL = compute_NLL(train_data, mu_list, sigma_list, pi_list)
print 'Normalized log-likelihood for train data identity covariance matrix = %f' % train_avg_NLL
test_avg_NLL = compute_NLL(test_data, mu_list, sigma_list, pi_list)
print 'Normalized log-likelihood for test data identity covariance matrix = %f' % test_avg_NLL
# PART-C (EM with general matrix as covariance)
labels = k_means(data, n_clusters, n_iter)
cluster_0 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==0]).reshape(-1,2)
cluster_1 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==1]).reshape(-1,2)
cluster_2 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==2]).reshape(-1,2)
cluster_3 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==3]).reshape(-1,2)
cluster_0_mu = np.mean(cluster_0,axis=0)
cluster_1_mu = np.mean(cluster_1,axis=0)
cluster_2_mu = np.mean(cluster_2,axis=0)
cluster_3_mu = np.mean(cluster_3,axis=0)
cluster_0_sigma = covariance(cluster_0)
cluster_1_sigma = covariance(cluster_1)
cluster_2_sigma = covariance(cluster_2)
cluster_3_sigma = covariance(cluster_3)
pi_0 = cluster_0.shape[0]*1.0/labels.shape[0]
pi_1 = cluster_1.shape[0]*1.0/labels.shape[0]
pi_2 = cluster_2.shape[0]*1.0/labels.shape[0]
pi_3 = cluster_3.shape[0]*1.0/labels.shape[0]
tau = np.zeros((data.shape[0],n_clusters))
n_iter = 20
for iter in range(n_iter):
# E step
for i in range(tau.shape[0]):
tau[i,0] = pi_0*multivariate_normal.pdf(data[i,:], mean=cluster_0_mu, cov=cluster_0_sigma)
tau[i,1] = pi_1*multivariate_normal.pdf(data[i,:], mean=cluster_1_mu, cov=cluster_1_sigma)
tau[i,2] = pi_2*multivariate_normal.pdf(data[i,:], mean=cluster_2_mu, cov=cluster_2_sigma)
tau[i,3] = pi_3*multivariate_normal.pdf(data[i,:], mean=cluster_3_mu, cov=cluster_3_sigma)
norm_factor = np.sum(tau[i,:])
tau[i,0] = tau[i,0]/norm_factor
tau[i,1] = tau[i,1]/norm_factor
tau[i,2] = tau[i,2]/norm_factor
tau[i,3] = tau[i,3]/norm_factor
# M step
cluster_0_mu = np.sum(data*tau[:,0].reshape(-1,1),axis=0)/np.sum(tau[:,0])
cluster_1_mu = np.sum(data*tau[:,1].reshape(-1,1),axis=0)/np.sum(tau[:,1])
cluster_2_mu = np.sum(data*tau[:,2].reshape(-1,1),axis=0)/np.sum(tau[:,2])
cluster_3_mu = np.sum(data*tau[:,3].reshape(-1,1),axis=0)/np.sum(tau[:,3])
cluster_0_sigma = weighted_covariance(data, cluster_0_mu.reshape(1,-1), tau[:,0])
cluster_1_sigma = weighted_covariance(data, cluster_1_mu.reshape(1,-1), tau[:,1])
cluster_2_sigma = weighted_covariance(data, cluster_2_mu.reshape(1,-1), tau[:,2])
cluster_3_sigma = weighted_covariance(data, cluster_3_mu.reshape(1,-1), tau[:,3])
pi_0 = np.sum(tau[:,0])/data.shape[0]
pi_1 = np.sum(tau[:,1])/data.shape[0]
pi_2 = np.sum(tau[:,2])/data.shape[0]
pi_3 = np.sum(tau[:,3])/data.shape[0]
cluster_0 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==0]).reshape(-1,2)
cluster_1 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==1]).reshape(-1,2)
cluster_2 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==2]).reshape(-1,2)
cluster_3 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==3]).reshape(-1,2)
print 'mean vector for Gaussian ID: 0'
print cluster_0_mu
print 'covariance matrix for Gaussian ID: 0'
print cluster_0_sigma
print 'mean vector for Gaussian ID: 1'
print cluster_1_mu
print 'covariance matrix for Gaussian ID: 1'
print cluster_1_sigma
print 'mean vector for Gaussian ID: 2'
print cluster_2_mu
print 'covariance matrix for Gaussian ID: 2'
print cluster_2_sigma
print 'mean vector for Gaussian ID: 3'
print cluster_3_mu
print 'covariance matrix for Gaussian ID: 3'
print cluster_3_sigma
plt.figure()
plt.plot(cluster_0[:,0], cluster_0[:,1], '*', c='red',label='Gaussian ID 0')
plt.plot(cluster_1[:,0], cluster_1[:,1], '*', c='blue',label='Gaussian ID 1')
plt.plot(cluster_2[:,0], cluster_2[:,1], '*', c='orange',label='Gaussian ID 2')
plt.plot(cluster_3[:,0], cluster_3[:,1], '*', c='magenta',label='Gaussian ID 3')
plt.plot(cluster_0_mu[0],cluster_0_mu[1],'o',c='black',label='Gaussian centers')
plt.plot(cluster_1_mu[0],cluster_1_mu[1],'o',c='black')
plt.plot(cluster_2_mu[0],cluster_2_mu[1],'o',c='black')
plt.plot(cluster_3_mu[0],cluster_3_mu[1],'o',c='black')
plot_ellipse_cov(cluster_0_sigma,cluster_0_mu, ax=plt, colour='red',label='Gaussian ID 0 ellipse')
plot_ellipse_cov(cluster_1_sigma,cluster_1_mu, ax=plt, colour='blue',label='Gaussian ID 1 ellipse')
plot_ellipse_cov(cluster_2_sigma,cluster_2_mu, ax=plt, colour='orange',label='Gaussian ID 2 ellipse')
plot_ellipse_cov(cluster_3_sigma,cluster_3_mu, ax=plt, colour='magenta',label='Gaussian ID 3 ellipse')
plt.legend(bbox_to_anchor=(1.1, 1.0))
plt.xlabel('x[0]')
plt.ylabel('x[1]')
plt.title('Representation for train data (General cov. matrix), centers, covariance matrices (using ellipse) PART-8(c)')
plt.show()
mu_list = [cluster_0_mu, cluster_1_mu, cluster_2_mu, cluster_3_mu]
sigma_list = [cluster_0_sigma, cluster_1_sigma, cluster_2_sigma, cluster_3_sigma]
pi_list = [pi_0, pi_1, pi_2, pi_3]
train_avg_NLL = compute_NLL(train_data, mu_list, sigma_list, pi_list)
print 'Normalized log-likelihood for train data general covariance matrix = %f' % train_avg_NLL
test_avg_NLL = compute_NLL(test_data, mu_list, sigma_list, pi_list)
print 'Normalized log-likelihood for test data general covariance matrix = %f' % test_avg_NLL
```
|
github_jupyter
|
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2
from scipy.stats import multivariate_normal
np.random.seed(42)
train_data = np.loadtxt('hwk3data\hwk3data\EMGaussian.train')
test_data = np.loadtxt('hwk3data\hwk3data\EMGaussian.test')
data = train_data
n_clusters = 4
n_iter = 50
def covariance(x):
x_mu = np.mean(x,axis=0)
cov = np.zeros((x.shape[1],x.shape[1]))
for i in range(x.shape[0]):
cov += np.outer((x[i,:] - x_mu),(x[i,:] - x_mu))
cov = cov*1.0/x.shape[0]
return cov
def weighted_covariance(x, x_mu, tau):
cov = np.zeros((x.shape[1],x.shape[1]))
for i in range(x.shape[0]):
cov += tau[i]*np.outer((x[i,:] - x_mu),(x[i,:] - x_mu))
cov = cov*1.0/np.sum(tau)
return cov
def plot_ellipse(semimaj=1,semimin=1,phi=0,x_cent=0,y_cent=0,theta_num=1e3,ax=None,plot_kwargs=None,\
fill=False,fill_kwargs=None,data_out=False,cov=None,mass_level=0.68,colour='b',label=''):
# Get Ellipse Properties from cov matrix
if cov is not None:
eig_vec,eig_val,u = np.linalg.svd(cov)
# Make sure 0th eigenvector has positive x-coordinate
if eig_vec[0][0] < 0:
eig_vec[0] *= -1
semimaj = np.sqrt(eig_val[0])
semimin = np.sqrt(eig_val[1])
if mass_level is None:
multiplier = np.sqrt(2.279)
else:
distances = np.linspace(0,20,20001)
chi2_cdf = chi2.cdf(distances,df=2)
multiplier = np.sqrt(distances[np.where(np.abs(chi2_cdf-mass_level)==np.abs(chi2_cdf-mass_level).min())[0][0]])
semimaj *= multiplier
semimin *= multiplier
phi = np.arccos(np.dot(eig_vec[0],np.array([1,0])))
if eig_vec[0][1] < 0 and phi > 0:
phi *= -1
# Generate data for ellipse structure
theta = np.linspace(0,2*np.pi,theta_num)
r = 1 / np.sqrt((np.cos(theta))**2 + (np.sin(theta))**2)
x = r*np.cos(theta)
y = r*np.sin(theta)
data = np.array([x,y])
S = np.array([[semimaj,0],[0,semimin]])
R = np.array([[np.cos(phi),-np.sin(phi)],[np.sin(phi),np.cos(phi)]])
T = np.dot(R,S)
data = np.dot(T,data)
data[0] += x_cent
data[1] += y_cent
# Output data?
if data_out == True:
return data
# Plot!
return_fig = False
if ax is None:
return_fig = True
fig,ax = plt.subplots()
if plot_kwargs is None:
ax.plot(data[0],data[1],color=colour,label=label,linestyle='-')
else:
ax.plot(data[0],data[1],color=colour,label=label,**plot_kwargs)
if fill == True:
ax.fill(data[0],data[1],**fill_kwargs)
if return_fig == True:
return fig
def plot_ellipse_cov(cov, cent, ax, colour='b',label=''):
w,v = np.linalg.eig(cov)
semi_major_axis_len = 2*np.sqrt(4.6*w[0])
semi_minor_axis_len = 2*np.sqrt(4.6*w[1])
theta = np.arctan(v[1,0]/v[0,0])
plot_ellipse(semi_major_axis_len, semi_minor_axis_len, theta, cent[0], cent[1], ax=ax, colour=colour,label=label)
def compute_NLL(data, mu_list, sigma_list, pi_list):
nll = 0
mu_0 = mu_list[0]
mu_1 = mu_list[1]
mu_2 = mu_list[2]
mu_3 = mu_list[3]
sigma_0 = sigma_list[0]
sigma_1 = sigma_list[1]
sigma_2 = sigma_list[2]
sigma_3 = sigma_list[3]
pi_0 = pi_list[0]
pi_1 = pi_list[1]
pi_2 = pi_list[2]
pi_3 = pi_list[3]
for i in range(data.shape[0]):
x = pi_0*multivariate_normal.pdf(data[i,:],mean=mu_0,cov=sigma_0) + pi_1*multivariate_normal.pdf(data[i,:],mean=mu_1,cov=sigma_1) + pi_2*multivariate_normal.pdf(data[i,:],mean=mu_2,cov=sigma_2) + pi_3*multivariate_normal.pdf(data[i,:],mean=mu_3,cov=sigma_3)
nll += np.log(x)
nll /= data.shape[0]
return nll
def compute_k_means_loss(cluster_list, mu_list):
loss = 0
cluster_0 = cluster_list[0]
cluster_1 = cluster_list[1]
cluster_2 = cluster_list[2]
cluster_3 = cluster_list[3]
mu_0 = mu_list[0]
mu_1 = mu_list[1]
mu_2 = mu_list[2]
mu_3 = mu_list[3]
for i in range(cluster_0.shape[0]):
loss += (np.linalg.norm(cluster_0[i,:] - mu_0.reshape(1,-1)))**2
for i in range(cluster_1.shape[0]):
loss += (np.linalg.norm(cluster_1[i,:] - mu_1.reshape(1,-1)))**2
for i in range(cluster_2.shape[0]):
loss += (np.linalg.norm(cluster_2[i,:] - mu_2.reshape(1,-1)))**2
for i in range(cluster_3.shape[0]):
loss += (np.linalg.norm(cluster_3[i,:] - mu_3.reshape(1,-1)))**2
return loss
def k_means(data, n_clusters, n_iter):
init_means_coord = np.zeros((n_clusters, 2))
flag = True
while(flag):
init_means_coord[:,0] = np.random.uniform(np.min(data[:,0]),np.max(data[:,0]),size=(n_clusters))
init_means_coord[:,1] = np.random.uniform(np.min(data[:,1]),np.max(data[:,1]),size=(n_clusters))
labels = np.zeros((data.shape[0],1))
for i in range(labels.shape[0]):
dist = np.linalg.norm(np.tile(data[i,:],(n_clusters,1)) - init_means_coord, axis=1).reshape(-1,1)
dist_argmax = np.argmax(dist, axis=0)
labels[i,0] = dist_argmax[0]
if len(np.unique(labels)) == n_clusters:
flag = False
for iter in range(n_iter):
# E step
for i in range(labels.shape[0]):
dist = np.linalg.norm(np.tile(data[i,:],(n_clusters,1)) - init_means_coord, axis=1).reshape(-1,1)
dist_argmin = np.argmin(dist, axis=0)
labels[i,0] = dist_argmin[0]
try:
assert len(np.unique(labels)) == n_clusters
except:
non_present_labels = np.setdiff1d(np.arange(n_clusters),np.unique(labels)).tolist()
labels_idx = np.random.choice(labels.shape[0],len(non_present_labels))
for i,lbl in enumerate(non_present_labels):
labels[labels_idx[i]] = lbl
assert len(np.unique(labels)) == n_clusters
# M step
for i in range(n_clusters):
init_means_coord[i,:] = np.mean(np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==i]),axis=0)
if np.any(np.isnan(init_means_coord)):
print 'ERROR!!!'
break
return labels
for trial in range(5):
labels = k_means(data, n_clusters, n_iter)
cluster_0 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==0]).reshape(-1,2)
cluster_1 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==1]).reshape(-1,2)
cluster_2 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==2]).reshape(-1,2)
cluster_3 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==3]).reshape(-1,2)
cluster_0_mu = np.mean(cluster_0,axis=0)
cluster_1_mu = np.mean(cluster_1,axis=0)
cluster_2_mu = np.mean(cluster_2,axis=0)
cluster_3_mu = np.mean(cluster_3,axis=0)
cluster_list = [cluster_0, cluster_1, cluster_2, cluster_3]
mu_list = [cluster_0_mu, cluster_1_mu, cluster_2_mu, cluster_3_mu]
k_means_loss = compute_k_means_loss(cluster_list, mu_list)
print 'K-means Trial ID: %d loss = %f' % (trial, k_means_loss)
print 'Cluster 0 co-ordinates:'
print cluster_0_mu
print '\n'
print 'Cluster 1 co-ordinates:'
print cluster_1_mu
print '\n'
print 'Cluster 2 co-ordinates:'
print cluster_2_mu
print '\n'
print 'Cluster 3 co-ordinates:'
print cluster_3_mu
print '\n'
plt.plot(cluster_0[:,0], cluster_0[:,1], '*', c='red',label='cluster 0')
plt.plot(cluster_1[:,0], cluster_1[:,1], '*', c='blue',label='cluster 1')
plt.plot(cluster_2[:,0], cluster_2[:,1], '*', c='orange',label='cluster 2')
plt.plot(cluster_3[:,0], cluster_3[:,1], '*', c='magenta',label='cluster 3')
plt.plot(cluster_0_mu[0],cluster_0_mu[1],'o',c='black',label='cluster centers')
plt.plot(cluster_1_mu[0],cluster_1_mu[1],'o',c='black')
plt.plot(cluster_2_mu[0],cluster_2_mu[1],'o',c='black')
plt.plot(cluster_3_mu[0],cluster_3_mu[1],'o',c='black')
plt.legend()
plt.xlabel('x[0]')
plt.ylabel('x[1]')
plt.title('Cluster assignment for train data (K-means) PART-8(a)')
plt.show()
# PART-B (EM with identity matrix as covariance)
cluster_0_mu = np.mean(cluster_0,axis=0)
cluster_1_mu = np.mean(cluster_1,axis=0)
cluster_2_mu = np.mean(cluster_2,axis=0)
cluster_3_mu = np.mean(cluster_3,axis=0)
cluster_0_sigma_2 = np.mean((np.linalg.norm(cluster_0 - cluster_0_mu.reshape(1,-1),axis=1))**2)/cluster_0_mu.shape[0]
cluster_1_sigma_2 = np.mean((np.linalg.norm(cluster_1 - cluster_1_mu.reshape(1,-1),axis=1))**2)/cluster_1_mu.shape[0]
cluster_2_sigma_2 = np.mean((np.linalg.norm(cluster_2 - cluster_2_mu.reshape(1,-1),axis=1))**2)/cluster_2_mu.shape[0]
cluster_3_sigma_2 = np.mean((np.linalg.norm(cluster_3 - cluster_3_mu.reshape(1,-1),axis=1))**2)/cluster_3_mu.shape[0]
pi_0 = cluster_0.shape[0]*1.0/labels.shape[0]
pi_1 = cluster_1.shape[0]*1.0/labels.shape[0]
pi_2 = cluster_2.shape[0]*1.0/labels.shape[0]
pi_3 = cluster_3.shape[0]*1.0/labels.shape[0]
tau = np.zeros((data.shape[0],n_clusters))
n_iter = 20
for iter in range(n_iter):
# E step
for i in range(tau.shape[0]):
tau[i,0] = pi_0*multivariate_normal.pdf(data[i,:], mean=cluster_0_mu, cov=cluster_0_sigma_2*np.eye(cluster_0_mu.shape[0]))
tau[i,1] = pi_1*multivariate_normal.pdf(data[i,:], mean=cluster_1_mu, cov=cluster_1_sigma_2*np.eye(cluster_1_mu.shape[0]))
tau[i,2] = pi_2*multivariate_normal.pdf(data[i,:], mean=cluster_2_mu, cov=cluster_2_sigma_2*np.eye(cluster_2_mu.shape[0]))
tau[i,3] = pi_3*multivariate_normal.pdf(data[i,:], mean=cluster_3_mu, cov=cluster_3_sigma_2*np.eye(cluster_3_mu.shape[0]))
norm_factor = np.sum(tau[i,:])
tau[i,0] = tau[i,0]/norm_factor
tau[i,1] = tau[i,1]/norm_factor
tau[i,2] = tau[i,2]/norm_factor
tau[i,3] = tau[i,3]/norm_factor
# M step
cluster_0_mu = np.sum(data*tau[:,0].reshape(-1,1),axis=0)/np.sum(tau[:,0])
cluster_1_mu = np.sum(data*tau[:,1].reshape(-1,1),axis=0)/np.sum(tau[:,1])
cluster_2_mu = np.sum(data*tau[:,2].reshape(-1,1),axis=0)/np.sum(tau[:,2])
cluster_3_mu = np.sum(data*tau[:,3].reshape(-1,1),axis=0)/np.sum(tau[:,3])
cluster_0_sigma_2 = np.sum((np.linalg.norm((data - cluster_0_mu.reshape(1,-1)),axis=1)**2)*tau[:,0],axis=0)/(np.sum(tau[:,0])*cluster_0_mu.shape[0])
cluster_1_sigma_2 = np.sum((np.linalg.norm((data - cluster_1_mu.reshape(1,-1)),axis=1)**2)*tau[:,1],axis=0)/(np.sum(tau[:,1])*cluster_1_mu.shape[0])
cluster_2_sigma_2 = np.sum((np.linalg.norm((data - cluster_2_mu.reshape(1,-1)),axis=1)**2)*tau[:,2],axis=0)/(np.sum(tau[:,2])*cluster_2_mu.shape[0])
cluster_3_sigma_2 = np.sum((np.linalg.norm((data - cluster_3_mu.reshape(1,-1)),axis=1)**2)*tau[:,3],axis=0)/(np.sum(tau[:,3])*cluster_3_mu.shape[0])
pi_0 = np.sum(tau[:,0])/data.shape[0]
pi_1 = np.sum(tau[:,1])/data.shape[0]
pi_2 = np.sum(tau[:,2])/data.shape[0]
pi_3 = np.sum(tau[:,3])/data.shape[0]
cluster_0 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==0]).reshape(-1,2)
cluster_1 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==1]).reshape(-1,2)
cluster_2 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==2]).reshape(-1,2)
cluster_3 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==3]).reshape(-1,2)
print 'mean vector for Gaussian ID: 0'
print cluster_0_mu
print 'covariance matrix for Gaussian ID: 0'
print cluster_0_sigma_2*np.eye(cluster_0.shape[1])
print 'mean vector for Gaussian ID: 1'
print cluster_1_mu
print 'covariance matrix for Gaussian ID: 1'
print cluster_1_sigma_2*np.eye(cluster_1.shape[1])
print 'mean vector for Gaussian ID: 2'
print cluster_2_mu
print 'covariance matrix for Gaussian ID: 2'
print cluster_2_sigma_2*np.eye(cluster_2.shape[1])
print 'mean vector for Gaussian ID: 3'
print cluster_3_mu
print 'covariance matrix for Gaussian ID: 3'
print cluster_3_sigma_2*np.eye(cluster_3.shape[1])
plt.figure()
plt.plot(cluster_0[:,0], cluster_0[:,1], '*', c='red',label='Gaussian ID 0')
plt.plot(cluster_1[:,0], cluster_1[:,1], '*', c='blue',label='Gaussian ID 1')
plt.plot(cluster_2[:,0], cluster_2[:,1], '*', c='orange',label='Gaussian ID 2')
plt.plot(cluster_3[:,0], cluster_3[:,1], '*', c='magenta',label='Gaussian ID 3')
plt.plot(cluster_0_mu[0],cluster_0_mu[1],'o',c='black',label='Gaussian centers')
plt.plot(cluster_1_mu[0],cluster_1_mu[1],'o',c='black')
plt.plot(cluster_2_mu[0],cluster_2_mu[1],'o',c='black')
plt.plot(cluster_3_mu[0],cluster_3_mu[1],'o',c='black')
plot_ellipse_cov(cluster_0_sigma_2*np.eye(cluster_0.shape[1]),cluster_0_mu, ax=plt, colour='red',label='Gaussian ID 0 ellipse')
plot_ellipse_cov(cluster_1_sigma_2*np.eye(cluster_1.shape[1]),cluster_1_mu, ax=plt, colour='blue',label='Gaussian ID 1 ellipse')
plot_ellipse_cov(cluster_2_sigma_2*np.eye(cluster_2.shape[1]),cluster_2_mu, ax=plt, colour='orange',label='Gaussian ID 2 ellipse')
plot_ellipse_cov(cluster_3_sigma_2*np.eye(cluster_3.shape[1]),cluster_3_mu, ax=plt, colour='magenta',label='Gaussian ID 3 ellipse')
plt.legend(bbox_to_anchor=(1.1, 1.0))
plt.xlabel('x[0]')
plt.ylabel('x[1]')
plt.title('Representation for train data (Identity cov. matrix), centers, covariance matrices (using ellipse) PART-8(b)')
plt.show()
mu_list = [cluster_0_mu, cluster_1_mu, cluster_2_mu, cluster_3_mu]
sigma_list = [cluster_0_sigma_2*np.eye(cluster_0.shape[1]), cluster_1_sigma_2*np.eye(cluster_1.shape[1]), cluster_2_sigma_2*np.eye(cluster_2.shape[1]), cluster_3_sigma_2*np.eye(cluster_3.shape[1])]
pi_list = [pi_0, pi_1, pi_2, pi_3]
train_avg_NLL = compute_NLL(train_data, mu_list, sigma_list, pi_list)
print 'Normalized log-likelihood for train data identity covariance matrix = %f' % train_avg_NLL
test_avg_NLL = compute_NLL(test_data, mu_list, sigma_list, pi_list)
print 'Normalized log-likelihood for test data identity covariance matrix = %f' % test_avg_NLL
# PART-C (EM with general matrix as covariance)
labels = k_means(data, n_clusters, n_iter)
cluster_0 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==0]).reshape(-1,2)
cluster_1 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==1]).reshape(-1,2)
cluster_2 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==2]).reshape(-1,2)
cluster_3 = np.asarray([data[j,:] for j in range(data.shape[0]) if labels[j,0]==3]).reshape(-1,2)
cluster_0_mu = np.mean(cluster_0,axis=0)
cluster_1_mu = np.mean(cluster_1,axis=0)
cluster_2_mu = np.mean(cluster_2,axis=0)
cluster_3_mu = np.mean(cluster_3,axis=0)
cluster_0_sigma = covariance(cluster_0)
cluster_1_sigma = covariance(cluster_1)
cluster_2_sigma = covariance(cluster_2)
cluster_3_sigma = covariance(cluster_3)
pi_0 = cluster_0.shape[0]*1.0/labels.shape[0]
pi_1 = cluster_1.shape[0]*1.0/labels.shape[0]
pi_2 = cluster_2.shape[0]*1.0/labels.shape[0]
pi_3 = cluster_3.shape[0]*1.0/labels.shape[0]
tau = np.zeros((data.shape[0],n_clusters))
n_iter = 20
for iter in range(n_iter):
# E step
for i in range(tau.shape[0]):
tau[i,0] = pi_0*multivariate_normal.pdf(data[i,:], mean=cluster_0_mu, cov=cluster_0_sigma)
tau[i,1] = pi_1*multivariate_normal.pdf(data[i,:], mean=cluster_1_mu, cov=cluster_1_sigma)
tau[i,2] = pi_2*multivariate_normal.pdf(data[i,:], mean=cluster_2_mu, cov=cluster_2_sigma)
tau[i,3] = pi_3*multivariate_normal.pdf(data[i,:], mean=cluster_3_mu, cov=cluster_3_sigma)
norm_factor = np.sum(tau[i,:])
tau[i,0] = tau[i,0]/norm_factor
tau[i,1] = tau[i,1]/norm_factor
tau[i,2] = tau[i,2]/norm_factor
tau[i,3] = tau[i,3]/norm_factor
# M step
cluster_0_mu = np.sum(data*tau[:,0].reshape(-1,1),axis=0)/np.sum(tau[:,0])
cluster_1_mu = np.sum(data*tau[:,1].reshape(-1,1),axis=0)/np.sum(tau[:,1])
cluster_2_mu = np.sum(data*tau[:,2].reshape(-1,1),axis=0)/np.sum(tau[:,2])
cluster_3_mu = np.sum(data*tau[:,3].reshape(-1,1),axis=0)/np.sum(tau[:,3])
cluster_0_sigma = weighted_covariance(data, cluster_0_mu.reshape(1,-1), tau[:,0])
cluster_1_sigma = weighted_covariance(data, cluster_1_mu.reshape(1,-1), tau[:,1])
cluster_2_sigma = weighted_covariance(data, cluster_2_mu.reshape(1,-1), tau[:,2])
cluster_3_sigma = weighted_covariance(data, cluster_3_mu.reshape(1,-1), tau[:,3])
pi_0 = np.sum(tau[:,0])/data.shape[0]
pi_1 = np.sum(tau[:,1])/data.shape[0]
pi_2 = np.sum(tau[:,2])/data.shape[0]
pi_3 = np.sum(tau[:,3])/data.shape[0]
cluster_0 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==0]).reshape(-1,2)
cluster_1 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==1]).reshape(-1,2)
cluster_2 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==2]).reshape(-1,2)
cluster_3 = np.asarray([data[j,:] for j in range(data.shape[0]) if np.argmax(tau[j,:])==3]).reshape(-1,2)
print 'mean vector for Gaussian ID: 0'
print cluster_0_mu
print 'covariance matrix for Gaussian ID: 0'
print cluster_0_sigma
print 'mean vector for Gaussian ID: 1'
print cluster_1_mu
print 'covariance matrix for Gaussian ID: 1'
print cluster_1_sigma
print 'mean vector for Gaussian ID: 2'
print cluster_2_mu
print 'covariance matrix for Gaussian ID: 2'
print cluster_2_sigma
print 'mean vector for Gaussian ID: 3'
print cluster_3_mu
print 'covariance matrix for Gaussian ID: 3'
print cluster_3_sigma
plt.figure()
plt.plot(cluster_0[:,0], cluster_0[:,1], '*', c='red',label='Gaussian ID 0')
plt.plot(cluster_1[:,0], cluster_1[:,1], '*', c='blue',label='Gaussian ID 1')
plt.plot(cluster_2[:,0], cluster_2[:,1], '*', c='orange',label='Gaussian ID 2')
plt.plot(cluster_3[:,0], cluster_3[:,1], '*', c='magenta',label='Gaussian ID 3')
plt.plot(cluster_0_mu[0],cluster_0_mu[1],'o',c='black',label='Gaussian centers')
plt.plot(cluster_1_mu[0],cluster_1_mu[1],'o',c='black')
plt.plot(cluster_2_mu[0],cluster_2_mu[1],'o',c='black')
plt.plot(cluster_3_mu[0],cluster_3_mu[1],'o',c='black')
plot_ellipse_cov(cluster_0_sigma,cluster_0_mu, ax=plt, colour='red',label='Gaussian ID 0 ellipse')
plot_ellipse_cov(cluster_1_sigma,cluster_1_mu, ax=plt, colour='blue',label='Gaussian ID 1 ellipse')
plot_ellipse_cov(cluster_2_sigma,cluster_2_mu, ax=plt, colour='orange',label='Gaussian ID 2 ellipse')
plot_ellipse_cov(cluster_3_sigma,cluster_3_mu, ax=plt, colour='magenta',label='Gaussian ID 3 ellipse')
plt.legend(bbox_to_anchor=(1.1, 1.0))
plt.xlabel('x[0]')
plt.ylabel('x[1]')
plt.title('Representation for train data (General cov. matrix), centers, covariance matrices (using ellipse) PART-8(c)')
plt.show()
mu_list = [cluster_0_mu, cluster_1_mu, cluster_2_mu, cluster_3_mu]
sigma_list = [cluster_0_sigma, cluster_1_sigma, cluster_2_sigma, cluster_3_sigma]
pi_list = [pi_0, pi_1, pi_2, pi_3]
train_avg_NLL = compute_NLL(train_data, mu_list, sigma_list, pi_list)
print 'Normalized log-likelihood for train data general covariance matrix = %f' % train_avg_NLL
test_avg_NLL = compute_NLL(test_data, mu_list, sigma_list, pi_list)
print 'Normalized log-likelihood for test data general covariance matrix = %f' % test_avg_NLL
| 0.567817 | 0.555496 |
```
import tensorflow as tf
print(tf.__version__)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
series = pd.read_csv('database.csv')
time = np.array(range(0,len(series['Date'])))
#time = pd.to_datetime(series['Date'],format = "%m/%d/%Y" )
Magnitude = np.array(np.array(series['Magnitude']))
#print(time)
plt.plot(time,Magnitude)
plt.show()
split_time = 22000
time_train = time[:split_time]
x_train = Magnitude[:split_time]
time_valid = time[split_time:]
x_valid = Magnitude[split_time:]
window_size = 30
batch_size = 32
shuffle_buffer_size = 1000
print(len(series['Date']))
def windowed_dataset(Magnitude, window_size, batch_size, shuffle_buffer):
Magnitude = tf.expand_dims(Magnitude, axis=-1)
ds = tf.data.Dataset.from_tensor_slices(Magnitude)
ds = ds.window(window_size + 1, shift=1, drop_remainder=True)
ds = ds.flat_map(lambda w: w.batch(window_size + 1))
ds = ds.shuffle(shuffle_buffer)
ds = ds.map(lambda w: (w[:-1], w[1:]))
return ds.batch(batch_size).prefetch(1)
def model_forecast(model, Magnitude, window_size):
ds = tf.data.Dataset.from_tensor_slices(Magnitude)
ds = ds.window(window_size, shift=1, drop_remainder=True)
ds = ds.flat_map(lambda w: w.batch(window_size))
ds = ds.batch(60).prefetch(1)
forecast = model.predict(ds)
return forecast
tf.keras.backend.clear_session()
tf.random.set_seed(51)
np.random.seed(51)
train_set = windowed_dataset(x_train, window_size=60, batch_size=100, shuffle_buffer=shuffle_buffer_size)
model = tf.keras.models.Sequential([
tf.keras.layers.Conv1D(filters=60, kernel_size=5,
strides=1, padding="causal",
activation="relu",
input_shape=[None, 1]),
tf.keras.layers.LSTM(60, return_sequences=True),
tf.keras.layers.LSTM(60, return_sequences=True),
tf.keras.layers.Dense(50, activation="relu"),
tf.keras.layers.Dense(25, activation="relu"),
tf.keras.layers.Dense(1),
tf.keras.layers.Lambda(lambda x: x * 400)
])
optimizer = tf.keras.optimizers.SGD(lr=1e-7, momentum=0.9)
model.compile(loss=tf.keras.losses.Huber(),
optimizer=optimizer,
metrics=["mae"])
history = model.fit(train_set,epochs=50)
def plot_series(time, Magnitude , start=0, end=None):
plt.plot(time[start:end], Magnitude[start:end], )
plt.xlabel("Дата")
plt.ylabel("Значение")
plt.title("Валидация")
plt.grid(True)
rnn_forecast = model_forecast(model, Magnitude[...,np.newaxis], window_size)
rnn_forecast = rnn_forecast[split_time - window_size:-1, -1, -0]
print(x_train)
plt.figure(figsize=(10, 6))
plot_series(time_train[110:500], x_valid[110:500])
plot_series(time_train[110:500], rnn_forecast[110:500])
print(rnn_forecast)
print(x_valid)
tf.keras.metrics.mean_absolute_error(x_valid, rnn_forecast).numpy()
plt.plot(history.epoch, history.history["loss"])
plt.show()
print(history.history)
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
mae=history.history['mae']
loss=history.history['loss']
epochs=range(len(loss)) # Get number of epochs
#------------------------------------------------
# Plot MAE and Loss
#------------------------------------------------
plt.plot(epochs, mae, 'r')
plt.plot(epochs, loss, 'b')
plt.title('MAE and Loss')
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend(["MAE", "Loss"])
plt.figure()
epochs_zoom = epochs[20:]
mae_zoom = mae[20:]
loss_zoom = loss[20:]
#------------------------------------------------
# Plot Zoomed MAE and Loss
#------------------------------------------------
plt.plot(epochs_zoom, mae_zoom, 'r')
plt.plot(epochs_zoom, loss_zoom, 'b')
plt.title('MAE and Loss')
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend(["MAE", "Loss"])
plt.figure()
model.summary()
```
|
github_jupyter
|
import tensorflow as tf
print(tf.__version__)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
series = pd.read_csv('database.csv')
time = np.array(range(0,len(series['Date'])))
#time = pd.to_datetime(series['Date'],format = "%m/%d/%Y" )
Magnitude = np.array(np.array(series['Magnitude']))
#print(time)
plt.plot(time,Magnitude)
plt.show()
split_time = 22000
time_train = time[:split_time]
x_train = Magnitude[:split_time]
time_valid = time[split_time:]
x_valid = Magnitude[split_time:]
window_size = 30
batch_size = 32
shuffle_buffer_size = 1000
print(len(series['Date']))
def windowed_dataset(Magnitude, window_size, batch_size, shuffle_buffer):
Magnitude = tf.expand_dims(Magnitude, axis=-1)
ds = tf.data.Dataset.from_tensor_slices(Magnitude)
ds = ds.window(window_size + 1, shift=1, drop_remainder=True)
ds = ds.flat_map(lambda w: w.batch(window_size + 1))
ds = ds.shuffle(shuffle_buffer)
ds = ds.map(lambda w: (w[:-1], w[1:]))
return ds.batch(batch_size).prefetch(1)
def model_forecast(model, Magnitude, window_size):
ds = tf.data.Dataset.from_tensor_slices(Magnitude)
ds = ds.window(window_size, shift=1, drop_remainder=True)
ds = ds.flat_map(lambda w: w.batch(window_size))
ds = ds.batch(60).prefetch(1)
forecast = model.predict(ds)
return forecast
tf.keras.backend.clear_session()
tf.random.set_seed(51)
np.random.seed(51)
train_set = windowed_dataset(x_train, window_size=60, batch_size=100, shuffle_buffer=shuffle_buffer_size)
model = tf.keras.models.Sequential([
tf.keras.layers.Conv1D(filters=60, kernel_size=5,
strides=1, padding="causal",
activation="relu",
input_shape=[None, 1]),
tf.keras.layers.LSTM(60, return_sequences=True),
tf.keras.layers.LSTM(60, return_sequences=True),
tf.keras.layers.Dense(50, activation="relu"),
tf.keras.layers.Dense(25, activation="relu"),
tf.keras.layers.Dense(1),
tf.keras.layers.Lambda(lambda x: x * 400)
])
optimizer = tf.keras.optimizers.SGD(lr=1e-7, momentum=0.9)
model.compile(loss=tf.keras.losses.Huber(),
optimizer=optimizer,
metrics=["mae"])
history = model.fit(train_set,epochs=50)
def plot_series(time, Magnitude , start=0, end=None):
plt.plot(time[start:end], Magnitude[start:end], )
plt.xlabel("Дата")
plt.ylabel("Значение")
plt.title("Валидация")
plt.grid(True)
rnn_forecast = model_forecast(model, Magnitude[...,np.newaxis], window_size)
rnn_forecast = rnn_forecast[split_time - window_size:-1, -1, -0]
print(x_train)
plt.figure(figsize=(10, 6))
plot_series(time_train[110:500], x_valid[110:500])
plot_series(time_train[110:500], rnn_forecast[110:500])
print(rnn_forecast)
print(x_valid)
tf.keras.metrics.mean_absolute_error(x_valid, rnn_forecast).numpy()
plt.plot(history.epoch, history.history["loss"])
plt.show()
print(history.history)
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
mae=history.history['mae']
loss=history.history['loss']
epochs=range(len(loss)) # Get number of epochs
#------------------------------------------------
# Plot MAE and Loss
#------------------------------------------------
plt.plot(epochs, mae, 'r')
plt.plot(epochs, loss, 'b')
plt.title('MAE and Loss')
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend(["MAE", "Loss"])
plt.figure()
epochs_zoom = epochs[20:]
mae_zoom = mae[20:]
loss_zoom = loss[20:]
#------------------------------------------------
# Plot Zoomed MAE and Loss
#------------------------------------------------
plt.plot(epochs_zoom, mae_zoom, 'r')
plt.plot(epochs_zoom, loss_zoom, 'b')
plt.title('MAE and Loss')
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend(["MAE", "Loss"])
plt.figure()
model.summary()
| 0.593374 | 0.394172 |
# Time of day analysis of criminal offenses
In this notebook I perform a simple analysis of the variation of criminal offenses as a function of the time of day, using R. This is an assignment for the online course Practical Predictive Analytics: Models and Methods and its main purpose is to showcase the use of plots to convey information. The data comes from two separate data sets, one corresponding to San Francisco and the other to Seattle. Both cover the period of Summer 2014.
## San Francisco data
I will work first with the San Francisco data and begin by calling the `summary` and `str` functions. Below I have commented the former to reduce the output.
```
sanfran<-read.csv("sanfrancisco_incidents_summer_2014.csv", na.strings = c(""))
# summary(sanfran)
str(sanfran)
```
Notice that the time was read as a factor data type, so I will convert it to a time format and create a new column which stores the hour, truncating the minutes.
```
sanfran$Hour<-strptime(sanfran$Time, "%H") # Converts to time format. Truncates minutes.
# At this moment the time is stored in seconds since a default date.
# Convert to seconds since midnight (remove date information)
sanfran$Hour<-as.numeric(sanfran$Hour- trunc(sanfran$Hour, "days"))
# Convert to whole hours.
sanfran$Hour<-as.integer(floor(sanfran$Hour/3600))
```
Now as a quick exploration, I will determine the most common offenses by counting the total number of each type and ordering them. In order to keep a moderate output, I only show the top 10.
```
offenses<-summary(sanfran$Category)
off_ordering<-order(offenses, decreasing=TRUE)
offenses<-offenses[off_ordering]
print(offenses[1:10])
```
I will study some of the offenses with the largest sample size. In particular I am interested in seeing how they are distributed throughout the day and whether we can classify them based on this.
In order to achieve this I will start by binning the times in 3 hour intervals. Other intervals work, but this is the smallest I found that displays the data clearly. The code can be modified to a different number of bins by changing the variable nhours to the desired value. The intervals are indexed the following way: 0 means 00:00 to 02:59 and so forth.
```
# Bin the hours in intervals of nhours hours (must be a divisor of 24).
nhours<-3
bins<-0:(23/nhours)*nhours
sanfran$Hour.bin<-nhours*floor(sanfran$Hour/nhours)
```
The next step is to find the total number of offences of each kind per time interval.
```
# Create a matrix of offense/Time of day
offenset_t<-tapply(sanfran$Category, list(sanfran$Hour.bin, sanfran$Category), length)
# Replace NAs by 0
for (x in 1:(24/nhours)) {
offenset_t[x, is.na(offenset_t[x,])]<-0
}
# print (offenset_t)
```
I normalized the data in order to compare different types of offense meaningfully. Specifically, for each offense type, I divided all bins by the total number of offenses of that type. This way I obtain a probability distribution that shows, given an offense of a particular type, the probability of that occuring at each time interval.
```
# Normalize: For each offense type, divide the data by the total number of offenses of that type.
for (x in 1:length(offenset_t[1, ]) ) {
total<-sum(offenset_t[ ,x])
offenset_t[ ,x]<-offenset_t[ ,x]/total
}
```
In order to facilitate plotting these distributions, I created two data frames with a small subset of the data.
```
# Arrange into data frame
crime<-data.frame(Number=offenset_t[ ,"ASSAULT"], Hour=bins, Offense=rep("ASSAULT", length(bins)))
crime<-rbind(crime, data.frame(Number=offenset_t[ ,"VEHICLE THEFT"], Hour=bins, Offense=rep("VEHICLE THEFT", length(bins))))
crime<-rbind(crime, data.frame(Number=offenset_t[ ,"LARCENY/THEFT"], Hour=bins, Offense=rep("LARCENY/THEFT", length(bins))))
crime2<-data.frame(Number=offenset_t[ ,"OTHER OFFENSES"], Hour=bins, Offense=rep("OTHER OFFENSES", length(bins)))
crime2<-rbind(crime2, data.frame(Number=offenset_t[ ,"NON-CRIMINAL"], Hour=bins, Offense=rep("NON-CRIMINAL", length(bins))))
crime2<-rbind(crime2, data.frame(Number=offenset_t[ ,"WARRANTS"], Hour=bins, Offense=rep("WARRANTS", length(bins))))
# Create plots using ggplot2
library(ggplot2)
ggplot(crime, aes(x=Hour, y=Number)) + geom_point(aes(color=Offense, shape=Offense), size=2.5) +xlab("Time of day") +ylab("Distribution") +ggtitle("San Francisco")
ggplot(crime2, aes(x=Hour, y=Number)) + geom_point(aes(color=Offense, shape=Offense), size=2.5) +xlab("Time of day") +ylab("Distribution") +ggtitle("San Francisco")
```
In these plots, I show the probability distribution for the 6 most frequent offenses, separated in two groups. The distributions in the two plots are very similar. The offenses tend to occurr much less in the 3-6 AM interval and increase after this point. However, an important difference is that in the first plot the probabilities is roughly peaked in the evening (6-9 PM), while in the second one the peak is in the late afternoon (3-6 PM). Based on this we could roughly classify the first set as "Evening" and the second as "Late afternoon".
# Seattle data
At this point an interesting question we can ask is whether this classification works in Seattle and whether the same types of offenses will receive the same classification. As we will see soon, the Seattle data does not have the same schema, i.e., the information is presented in a different way and the definition of the offenses may not be the same, which makes the task more difficult. However, some conclusions can still be drawn.
I begin by looking at the structure of the Seattle data.
```
seattle<-read.csv("seattle_incidents_summer_2014.csv", na.strings = c(""))
# summary(seattle)
str(seattle)
```
In this set, instead of a single time of the incident we are sometimes given a beginning and ending time, which makes comparing the two data sets difficult. The simple solution I chose was to ignore the latter and assume that the error of using the former is reduced by the use of bins for the time intervals. It is hard to understand the meaning of the ending time because sometimes it is months appart from the beginning time.
An additional, but small complication is that the date and time are combined in the same column, so I had to separate them first.
```
# Extract the times (in one hour bins)
seattle$Hour<- strptime(seattle$Occurred.Date.or.Date.Range.Start, "%m/%d/%Y %I:%M:%S %p") # Converts to time format.
# Convert to seconds since midnight.
seattle$Hour<-as.numeric(seattle$Hour- trunc(seattle$Hour, "days"))
seattle$Hour<-as.integer(floor(seattle$Hour/3600))
```
Again, I order the offenses by frequency. In contrast with the San Francisco data, the data here is divided in sub-categories. For example, each type of theft is listed separately (carprowl, shoplift, and so forth). I show the top 15 offenses to illustrate this.
```
# Order offenses by frequency (decreasing)
offenses<-summary(seattle$Offense.Type)
off_ordering<-order(offenses, decreasing=TRUE)
offenses<-offenses[off_ordering]
print(offenses[1:15])
```
For a better comparison with San Francisco, I will remove the sub-classification for the most common offenses and recalculate the top 10.
```
# For comparison with San Francisco, collapse some of the categories.
seattle$Offense.Type<-as.character(seattle$Offense.Type)
for (x in 1:length(seattle$Offense.Type)) {
if (grepl("VEH-THEFT", seattle$Offense.Type[x])) {
seattle$Category[x]<-"VEH-THEFT"
} else if (grepl("THEFT", seattle$Offense.Type[x])) {
seattle$Category[x]<-"THEFT"
} else if (grepl("ASSLT", seattle$Offense.Type[x])) {
seattle$Category[x]<-"ASSAULT"
} else if (grepl("BURGLARY", seattle$Offense.Type[x])) {
seattle$Category[x]<-"BURGLARY"
} else if (grepl("WARRA", seattle$Offense.Type[x])) {
seattle$Category[x]<-"WARRANT"
} else if (grepl("DISTURBANCE", seattle$Offense.Type[x])) {
seattle$Category[x]<-"DISTURBANCE"
} else if (grepl("PROPERTY DAMAGE", seattle$Offense.Type[x])) {
seattle$Category[x]<-"PROPERTY DAMAGE"
} else {
seattle$Category[x]<-seattle$Offense.Type[x]
}
}
seattle$Category<-as.factor(seattle$Category)
# Order new set of offenses by frequency (decreasing)
offenses<-summary(seattle$Category)
off_ordering<-order(offenses, decreasing=TRUE)
offenses<-offenses[off_ordering]
print(offenses[1:10])
```
The most frequent offenses are not exactly the same as in San Francisco, which may be either because of an actual difference between the cities or because the classification that is being used is not the same. Perhaps even a combination of both.
To proceed, I will again bin the time in intervals of 3 hours, calculate the number of offenses per type, per time interval, normalized the data, and plot the 6 most common offenses. I also included the type "warrant" because it was included in the San Francisco plots and will give us another point of comparison.
```
# Bin the hours in intervals of nhours hours (must be a divisor of 24).
nhours<-3
bins<-0:(23/nhours)*nhours
seattle$Hour.bin<-nhours*floor(seattle$Hour/nhours)
# Create a matrix of offense/Time of day
offenset_t<-tapply(seattle$Category, list(seattle$Hour.bin, seattle$Category), length)
# Replace NAs by 0
for (x in 1:(24/nhours)) {
offenset_t[x, is.na(offenset_t[x,])]<-0
}
# Normalize: For each offense type, divide the data by the total number of offenses of that type.
for (x in 1:length(offenset_t[1, ]) ) {
total<-sum(offenset_t[ ,x])
offenset_t[ ,x]<-offenset_t[ ,x]/total
}
# Arrange into data frame
crime<-data.frame(Number=offenset_t[ ,"ASSAULT"], Hour=bins, Offense=rep("ASSAULT", length(bins)))
crime<-rbind(crime, data.frame(Number=offenset_t[ ,"VEH-THEFT"], Hour=bins, Offense=rep("VEH-THEFT", length(bins))))
crime<-rbind(crime, data.frame(Number=offenset_t[ ,"THEFT"], Hour=bins, Offense=rep("THEFT", length(bins))))
crime<-rbind(crime, data.frame(Number=offenset_t[ ,"PROPERTY DAMAGE"], Hour=bins, Offense=rep("PROPERTY DAMAGE", length(bins))))
crime2<-data.frame(Number=offenset_t[ ,"BURGLARY"], Hour=bins, Offense=rep("BURGLARY", length(bins)))
crime2<-rbind(crime2, data.frame(Number=offenset_t[ ,"DISTURBANCE"], Hour=bins, Offense=rep("DISTURBANCE", length(bins))))
crime2<-rbind(crime2, data.frame(Number=offenset_t[ ,"WARRANT"], Hour=bins, Offense=rep("WARRANT", length(bins))))
# Plot the data
library(ggplot2)
ggplot(crime, aes(x=Hour, y=Number)) + geom_point(aes(color=Offense, shape=Offense), size=2.5) +xlab("Time of day") +ylab("Distribution") +ggtitle("Seattle")
ggplot(crime2, aes(x=Hour, y=Number)) + geom_point(aes(color=Offense, shape=Offense), size=2.5) +xlab("Time of day") +ylab("Distribution") +ggtitle("Seattle")
```
Here I separated the data again into two groups, based on where the distributions are peaked. The "evening" offenses match the case of San Francisco (except for "property damage", which I did not include before). An important difference is that in this dataset the peaks seems to be shifted to the 9PM-12AM block. In other words, some of these offenses seem to occur later in the night than in San Francisco.
In the second plot the only comparison we can make with San Francisco is for warrants. It is easily seen that they are sharply peaked in the 12-3 PM block, instead of in the 3-6 PM block as it was in San Francisco.
# Conclusions
In this notebook I have analyzed the similarities and differences between the time-of-day distributions of the most frequent criminal offenses in San Francisco and Seattle using Summer 2014 data. For each city I qualitatively classified these offenses in two groups, depending whether the distributions were biased toward the evening or the afternoon. Comparing the two cities I highlighted the fact that the evening offenses seem to be biased toward a later time in Seattle. Also, in the specific case of warrants the bias in Seattle is toward an earlier time of day. One important caveat to keep in mind is that the date and time data for Seattle were sometimes presented with a begin-to-end format, in which case the end date was ignored to simplify the analysis.
|
github_jupyter
|
sanfran<-read.csv("sanfrancisco_incidents_summer_2014.csv", na.strings = c(""))
# summary(sanfran)
str(sanfran)
sanfran$Hour<-strptime(sanfran$Time, "%H") # Converts to time format. Truncates minutes.
# At this moment the time is stored in seconds since a default date.
# Convert to seconds since midnight (remove date information)
sanfran$Hour<-as.numeric(sanfran$Hour- trunc(sanfran$Hour, "days"))
# Convert to whole hours.
sanfran$Hour<-as.integer(floor(sanfran$Hour/3600))
offenses<-summary(sanfran$Category)
off_ordering<-order(offenses, decreasing=TRUE)
offenses<-offenses[off_ordering]
print(offenses[1:10])
# Bin the hours in intervals of nhours hours (must be a divisor of 24).
nhours<-3
bins<-0:(23/nhours)*nhours
sanfran$Hour.bin<-nhours*floor(sanfran$Hour/nhours)
# Create a matrix of offense/Time of day
offenset_t<-tapply(sanfran$Category, list(sanfran$Hour.bin, sanfran$Category), length)
# Replace NAs by 0
for (x in 1:(24/nhours)) {
offenset_t[x, is.na(offenset_t[x,])]<-0
}
# print (offenset_t)
# Normalize: For each offense type, divide the data by the total number of offenses of that type.
for (x in 1:length(offenset_t[1, ]) ) {
total<-sum(offenset_t[ ,x])
offenset_t[ ,x]<-offenset_t[ ,x]/total
}
# Arrange into data frame
crime<-data.frame(Number=offenset_t[ ,"ASSAULT"], Hour=bins, Offense=rep("ASSAULT", length(bins)))
crime<-rbind(crime, data.frame(Number=offenset_t[ ,"VEHICLE THEFT"], Hour=bins, Offense=rep("VEHICLE THEFT", length(bins))))
crime<-rbind(crime, data.frame(Number=offenset_t[ ,"LARCENY/THEFT"], Hour=bins, Offense=rep("LARCENY/THEFT", length(bins))))
crime2<-data.frame(Number=offenset_t[ ,"OTHER OFFENSES"], Hour=bins, Offense=rep("OTHER OFFENSES", length(bins)))
crime2<-rbind(crime2, data.frame(Number=offenset_t[ ,"NON-CRIMINAL"], Hour=bins, Offense=rep("NON-CRIMINAL", length(bins))))
crime2<-rbind(crime2, data.frame(Number=offenset_t[ ,"WARRANTS"], Hour=bins, Offense=rep("WARRANTS", length(bins))))
# Create plots using ggplot2
library(ggplot2)
ggplot(crime, aes(x=Hour, y=Number)) + geom_point(aes(color=Offense, shape=Offense), size=2.5) +xlab("Time of day") +ylab("Distribution") +ggtitle("San Francisco")
ggplot(crime2, aes(x=Hour, y=Number)) + geom_point(aes(color=Offense, shape=Offense), size=2.5) +xlab("Time of day") +ylab("Distribution") +ggtitle("San Francisco")
seattle<-read.csv("seattle_incidents_summer_2014.csv", na.strings = c(""))
# summary(seattle)
str(seattle)
# Extract the times (in one hour bins)
seattle$Hour<- strptime(seattle$Occurred.Date.or.Date.Range.Start, "%m/%d/%Y %I:%M:%S %p") # Converts to time format.
# Convert to seconds since midnight.
seattle$Hour<-as.numeric(seattle$Hour- trunc(seattle$Hour, "days"))
seattle$Hour<-as.integer(floor(seattle$Hour/3600))
# Order offenses by frequency (decreasing)
offenses<-summary(seattle$Offense.Type)
off_ordering<-order(offenses, decreasing=TRUE)
offenses<-offenses[off_ordering]
print(offenses[1:15])
# For comparison with San Francisco, collapse some of the categories.
seattle$Offense.Type<-as.character(seattle$Offense.Type)
for (x in 1:length(seattle$Offense.Type)) {
if (grepl("VEH-THEFT", seattle$Offense.Type[x])) {
seattle$Category[x]<-"VEH-THEFT"
} else if (grepl("THEFT", seattle$Offense.Type[x])) {
seattle$Category[x]<-"THEFT"
} else if (grepl("ASSLT", seattle$Offense.Type[x])) {
seattle$Category[x]<-"ASSAULT"
} else if (grepl("BURGLARY", seattle$Offense.Type[x])) {
seattle$Category[x]<-"BURGLARY"
} else if (grepl("WARRA", seattle$Offense.Type[x])) {
seattle$Category[x]<-"WARRANT"
} else if (grepl("DISTURBANCE", seattle$Offense.Type[x])) {
seattle$Category[x]<-"DISTURBANCE"
} else if (grepl("PROPERTY DAMAGE", seattle$Offense.Type[x])) {
seattle$Category[x]<-"PROPERTY DAMAGE"
} else {
seattle$Category[x]<-seattle$Offense.Type[x]
}
}
seattle$Category<-as.factor(seattle$Category)
# Order new set of offenses by frequency (decreasing)
offenses<-summary(seattle$Category)
off_ordering<-order(offenses, decreasing=TRUE)
offenses<-offenses[off_ordering]
print(offenses[1:10])
# Bin the hours in intervals of nhours hours (must be a divisor of 24).
nhours<-3
bins<-0:(23/nhours)*nhours
seattle$Hour.bin<-nhours*floor(seattle$Hour/nhours)
# Create a matrix of offense/Time of day
offenset_t<-tapply(seattle$Category, list(seattle$Hour.bin, seattle$Category), length)
# Replace NAs by 0
for (x in 1:(24/nhours)) {
offenset_t[x, is.na(offenset_t[x,])]<-0
}
# Normalize: For each offense type, divide the data by the total number of offenses of that type.
for (x in 1:length(offenset_t[1, ]) ) {
total<-sum(offenset_t[ ,x])
offenset_t[ ,x]<-offenset_t[ ,x]/total
}
# Arrange into data frame
crime<-data.frame(Number=offenset_t[ ,"ASSAULT"], Hour=bins, Offense=rep("ASSAULT", length(bins)))
crime<-rbind(crime, data.frame(Number=offenset_t[ ,"VEH-THEFT"], Hour=bins, Offense=rep("VEH-THEFT", length(bins))))
crime<-rbind(crime, data.frame(Number=offenset_t[ ,"THEFT"], Hour=bins, Offense=rep("THEFT", length(bins))))
crime<-rbind(crime, data.frame(Number=offenset_t[ ,"PROPERTY DAMAGE"], Hour=bins, Offense=rep("PROPERTY DAMAGE", length(bins))))
crime2<-data.frame(Number=offenset_t[ ,"BURGLARY"], Hour=bins, Offense=rep("BURGLARY", length(bins)))
crime2<-rbind(crime2, data.frame(Number=offenset_t[ ,"DISTURBANCE"], Hour=bins, Offense=rep("DISTURBANCE", length(bins))))
crime2<-rbind(crime2, data.frame(Number=offenset_t[ ,"WARRANT"], Hour=bins, Offense=rep("WARRANT", length(bins))))
# Plot the data
library(ggplot2)
ggplot(crime, aes(x=Hour, y=Number)) + geom_point(aes(color=Offense, shape=Offense), size=2.5) +xlab("Time of day") +ylab("Distribution") +ggtitle("Seattle")
ggplot(crime2, aes(x=Hour, y=Number)) + geom_point(aes(color=Offense, shape=Offense), size=2.5) +xlab("Time of day") +ylab("Distribution") +ggtitle("Seattle")
| 0.35768 | 0.972441 |
# FDT in climate science (fluctuation dissipation theorem)
FDT: The use of fluctuation dissipation theorem can be traced back to Annus mirabilis in 1905. The year that Albert Einstein published 5 legendary paper which changed how we see the world. However, I am not going to talk about "Relativity". Instead, this project will focus on FDT, a theorem was applied to explain Brownian motion (or other fields in Statistical mechanics). FDT has a lot of names in climate science and you might be able to name a few of them, such as (1) linear response function, (2) Jacobian Matrix, (3) Green's function, (4) linear inverse model or (5) Markov train.
Before I jump into the details of FDT, I would like give you a general picture of the physical assumption over different dynamical models (or dynamical systems). All of the dynamical models we use today are based on different physical assumption. For example, when we use a global climate model with cumulus parameterization, we are assuming a quasi-equilibrium state of short-lived cumulus cloud, which nearly strikes balance with large-scale tendency. When we use cloud permitting model, we can use vertical wind shear and static stability to approximate the large eddies in the boundary layer (i.e. boundary layer scheme). In addition, in a large eddy simulation (cloud resolving), we assume the physical processes (i.e. condensation) are relatively fast compared to the lifecycle of cloud and turbulence. Thus, when we predict the "resolved scale systems" (e.g. those can be seen by the grid), the "unresovled scales" are parameterized. A good news is, most of time, these assumptions are quite robust (except some cases going through cross-scale gray zones). This indicates that if we want to forecast the large-scale systems, we don't need to do deterministic forecast for the small-scale systems. Insead, what we need is the statistics of these systems (i.e. parameterization).
Then...what is the assumption of FDT? FDT can ba regarded as a reduced-dimension dynamical model, in which the time series of normal modes are predicted. Typically, these normal modes are red in spectrum (i.e. Gaussian or linear), while high frequency systems (those can't be described by the normal mode) are white in spectrum (i.e. random process). Just like the physical parameterizations mentioned above, these high frequency systems are parameterized in FDT. Thus, what we really care is when the predictable signal (e.g. those normal modes) is greater than the stochastic process (i.e. unpredictable components).
Here, I use a very simple O.D.E as an example.
$
\begin{equation}
\frac{d}{dt}\mathbf x= \mathbf A \mathbf x+\mathbf\epsilon \label{eq:1}\tag{1}
\end{equation}
$
In equation $\ref{eq:1}$, $\mathbf{x}$ is the predictable components (i.e. the time series of normal modes), which has a dimension of $n\times1$ and $\epsilon$ is the sotchastic part (i.e. random white noise) with the same dimension as $\mathbf{x}$. If we drop the unpredictable part, we can have the general solution of $\ref{eq:1}$.
$
\begin{equation}
\mathbf{x}_{\tau}=e^{\mathbf A \tau} \mathbf{x}_{0} \label{eq:2}\tag{2}
\end{equation}
$
In equation $\eqref{eq:2}$, $e^{\mathbf A \tau}$ is so-called "propagator operator", which carries the information of $\mathbf{x}$ from $t=0$ to $t=\tau$ and has a dimension of $n\times n$. If you still remember the high school mathematics, we will find the $e^{\mathbf A \tau}$ matrix is just like the matrix we use for coordinate transform (i.e. Jacobian matrix). For example, you have a vector $(a,b)$ and you want to rotate this vector counter-clockwise for $\theta$ degrees, what does the formulation look like ?
$
\begin{equation}
\begin{bmatrix}
a'\\
b'
\end{bmatrix}=
\begin{bmatrix}
cos(\theta) & -sin(\theta) \\
sin(\theta) & cos(\theta)
\end{bmatrix}
\begin{bmatrix}
a\\
b
\end{bmatrix} \label{eq:3}\tag{3}
\end{equation}
$
$\mathbf{x}_{0}$ is just like the vector $(a,b)$ and $\mathbf{x}_{\tau}$ is similar to vector $(a',b')$. $e^{\mathbf A \tau}$ is the matrix we use for coordinate transform. Similar formulations can be found in a lot of places, such as stastistical test, fourier transform, Laplace transform...etc (I will write another discussion about these analogs).
Apparently, the key is to derive the propagator operator $e^{\mathbf A \tau}$, which enables us to develop this simplified model. I will provide details in the following part.
***
# Developing a simple climate model from observational data
To solve $e^{\mathbf A \tau}$ in $\eqref{eq:2}$ numerically, we can use inverse approach. (of course the forward approach is another option as well, which is computationally less expensive but also characterized by some drawbacks ). The first step to solve $e^{\mathbf A \tau}$ is, we multiply both sides of $\eqref{eq:2}$ by $\mathbf{x}_{0}^T$.
$
\begin{equation}
\mathbf{x}_{\tau}\mathbf{x}_{0}^{T}=e^{\mathbf A \tau} \mathbf{x}_{0} \mathbf{x}_{0}^{T} \label{eq:4} \tag{4}
\end{equation}
$
then we can have
$
\begin{equation}
\mathbf{C}_\tau=e^{\mathbf A \tau} \mathbf{C}_0 \label{eq:5}\tag{5}
\end{equation}
$
where $\mathbf{x}_{\tau}\mathbf{x}_{0}^{T}=\mathbf{C}_\tau$ and $\mathbf{x}_{0} \mathbf{x}_{0}^{T}=\mathbf{C}_0$. $\mathbf{C}_\tau$ and $\mathbf{C}_0$ are covariance matrices of $\mathbf{x}$ between (1)$t=\tau$ and $t=0$ and (2) $t=0$ and $t=0$. Now, we can find all three matrices in $\eqref{eq:5}$ have dimension of $n\times n$. This means we can iverse any matrix in $\eqref{eq:5}$ directly as long as the det is not 0. Luckily, using normal modes ensures that the det of $\mathbf{C}_0$ won't be 0. Thus, multiplying both sides of $\eqref{eq:5}$ by the inversed $\mathbf{C}_0 $, we can ultimately get $e^{\mathbf A \tau}$. Woohoo! (Looks easy right?).
$
\begin{equation}
\mathbf{C}_\tau \mathbf{C}_0^{-1}=e^{\mathbf A \tau} \label{eq:6}\tag{6}
\end{equation}
$
***
# Limitation of Inverse modeling: $\tau$ test
Although the steps of driving $e^{\mathbf A \tau}$ look simple, there is still a very important criteria. Let's go back to the assumption at the very beginning. From $\eqref{eq:1}$ to $\eqref{eq:2}$, we drop $\epsilon$. The reason we can drop this term is that...
$
\begin{equation}
(\frac{d}{dt}\mathbf x)\mathbf x^{T}= \mathbf A \mathbf x\mathbf x^{T}+\mathbf\epsilon \mathbf x^{T}\label{eq:7} \tag{7}
\end{equation}
$
the last term of $\eqref{eq:7}$ is nearlly zero because $\epsilon$ is white in spectrum (you will only get mean 0 (or nearly zero) when you multiply a matrix with a white noise matrix). This indicates that there is no information of $\epsilon$ passed from fomer time step to next time step. On the other hand, everything left (i.e. the predictable part, $\mathbf{x}$) should be red. This assumption gives us the following way to test our data.
Specifically, we can examine if a dataset can be used in FDT by checking the diagonal elements of $\mathbf{C}_\tau \mathbf{C}_0^{-1}$ in $\eqref{eq:6}$. Because if the general solution in $\eqref{eq:4}$ hold for every $\tau$, we will only have one $\mathbf{A}$ matrix regardless of the value of $\tau$, which means...
$
\begin{equation}
tr(\mathbf A)=tr(\mathbf{ln}(\mathbf{C}_\tau \mathbf{C}_0^{-1})/\tau)=const
\label{eq:8}
\tag{8}
\end{equation}
$
If we find $\eqref{eq:8}$ doesn't hold for every $\tau$, we can't apply FDT to a given dataset.
|
github_jupyter
|
# FDT in climate science (fluctuation dissipation theorem)
FDT: The use of fluctuation dissipation theorem can be traced back to Annus mirabilis in 1905. The year that Albert Einstein published 5 legendary paper which changed how we see the world. However, I am not going to talk about "Relativity". Instead, this project will focus on FDT, a theorem was applied to explain Brownian motion (or other fields in Statistical mechanics). FDT has a lot of names in climate science and you might be able to name a few of them, such as (1) linear response function, (2) Jacobian Matrix, (3) Green's function, (4) linear inverse model or (5) Markov train.
Before I jump into the details of FDT, I would like give you a general picture of the physical assumption over different dynamical models (or dynamical systems). All of the dynamical models we use today are based on different physical assumption. For example, when we use a global climate model with cumulus parameterization, we are assuming a quasi-equilibrium state of short-lived cumulus cloud, which nearly strikes balance with large-scale tendency. When we use cloud permitting model, we can use vertical wind shear and static stability to approximate the large eddies in the boundary layer (i.e. boundary layer scheme). In addition, in a large eddy simulation (cloud resolving), we assume the physical processes (i.e. condensation) are relatively fast compared to the lifecycle of cloud and turbulence. Thus, when we predict the "resolved scale systems" (e.g. those can be seen by the grid), the "unresovled scales" are parameterized. A good news is, most of time, these assumptions are quite robust (except some cases going through cross-scale gray zones). This indicates that if we want to forecast the large-scale systems, we don't need to do deterministic forecast for the small-scale systems. Insead, what we need is the statistics of these systems (i.e. parameterization).
Then...what is the assumption of FDT? FDT can ba regarded as a reduced-dimension dynamical model, in which the time series of normal modes are predicted. Typically, these normal modes are red in spectrum (i.e. Gaussian or linear), while high frequency systems (those can't be described by the normal mode) are white in spectrum (i.e. random process). Just like the physical parameterizations mentioned above, these high frequency systems are parameterized in FDT. Thus, what we really care is when the predictable signal (e.g. those normal modes) is greater than the stochastic process (i.e. unpredictable components).
Here, I use a very simple O.D.E as an example.
$
\begin{equation}
\frac{d}{dt}\mathbf x= \mathbf A \mathbf x+\mathbf\epsilon \label{eq:1}\tag{1}
\end{equation}
$
In equation $\ref{eq:1}$, $\mathbf{x}$ is the predictable components (i.e. the time series of normal modes), which has a dimension of $n\times1$ and $\epsilon$ is the sotchastic part (i.e. random white noise) with the same dimension as $\mathbf{x}$. If we drop the unpredictable part, we can have the general solution of $\ref{eq:1}$.
$
\begin{equation}
\mathbf{x}_{\tau}=e^{\mathbf A \tau} \mathbf{x}_{0} \label{eq:2}\tag{2}
\end{equation}
$
In equation $\eqref{eq:2}$, $e^{\mathbf A \tau}$ is so-called "propagator operator", which carries the information of $\mathbf{x}$ from $t=0$ to $t=\tau$ and has a dimension of $n\times n$. If you still remember the high school mathematics, we will find the $e^{\mathbf A \tau}$ matrix is just like the matrix we use for coordinate transform (i.e. Jacobian matrix). For example, you have a vector $(a,b)$ and you want to rotate this vector counter-clockwise for $\theta$ degrees, what does the formulation look like ?
$
\begin{equation}
\begin{bmatrix}
a'\\
b'
\end{bmatrix}=
\begin{bmatrix}
cos(\theta) & -sin(\theta) \\
sin(\theta) & cos(\theta)
\end{bmatrix}
\begin{bmatrix}
a\\
b
\end{bmatrix} \label{eq:3}\tag{3}
\end{equation}
$
$\mathbf{x}_{0}$ is just like the vector $(a,b)$ and $\mathbf{x}_{\tau}$ is similar to vector $(a',b')$. $e^{\mathbf A \tau}$ is the matrix we use for coordinate transform. Similar formulations can be found in a lot of places, such as stastistical test, fourier transform, Laplace transform...etc (I will write another discussion about these analogs).
Apparently, the key is to derive the propagator operator $e^{\mathbf A \tau}$, which enables us to develop this simplified model. I will provide details in the following part.
***
# Developing a simple climate model from observational data
To solve $e^{\mathbf A \tau}$ in $\eqref{eq:2}$ numerically, we can use inverse approach. (of course the forward approach is another option as well, which is computationally less expensive but also characterized by some drawbacks ). The first step to solve $e^{\mathbf A \tau}$ is, we multiply both sides of $\eqref{eq:2}$ by $\mathbf{x}_{0}^T$.
$
\begin{equation}
\mathbf{x}_{\tau}\mathbf{x}_{0}^{T}=e^{\mathbf A \tau} \mathbf{x}_{0} \mathbf{x}_{0}^{T} \label{eq:4} \tag{4}
\end{equation}
$
then we can have
$
\begin{equation}
\mathbf{C}_\tau=e^{\mathbf A \tau} \mathbf{C}_0 \label{eq:5}\tag{5}
\end{equation}
$
where $\mathbf{x}_{\tau}\mathbf{x}_{0}^{T}=\mathbf{C}_\tau$ and $\mathbf{x}_{0} \mathbf{x}_{0}^{T}=\mathbf{C}_0$. $\mathbf{C}_\tau$ and $\mathbf{C}_0$ are covariance matrices of $\mathbf{x}$ between (1)$t=\tau$ and $t=0$ and (2) $t=0$ and $t=0$. Now, we can find all three matrices in $\eqref{eq:5}$ have dimension of $n\times n$. This means we can iverse any matrix in $\eqref{eq:5}$ directly as long as the det is not 0. Luckily, using normal modes ensures that the det of $\mathbf{C}_0$ won't be 0. Thus, multiplying both sides of $\eqref{eq:5}$ by the inversed $\mathbf{C}_0 $, we can ultimately get $e^{\mathbf A \tau}$. Woohoo! (Looks easy right?).
$
\begin{equation}
\mathbf{C}_\tau \mathbf{C}_0^{-1}=e^{\mathbf A \tau} \label{eq:6}\tag{6}
\end{equation}
$
***
# Limitation of Inverse modeling: $\tau$ test
Although the steps of driving $e^{\mathbf A \tau}$ look simple, there is still a very important criteria. Let's go back to the assumption at the very beginning. From $\eqref{eq:1}$ to $\eqref{eq:2}$, we drop $\epsilon$. The reason we can drop this term is that...
$
\begin{equation}
(\frac{d}{dt}\mathbf x)\mathbf x^{T}= \mathbf A \mathbf x\mathbf x^{T}+\mathbf\epsilon \mathbf x^{T}\label{eq:7} \tag{7}
\end{equation}
$
the last term of $\eqref{eq:7}$ is nearlly zero because $\epsilon$ is white in spectrum (you will only get mean 0 (or nearly zero) when you multiply a matrix with a white noise matrix). This indicates that there is no information of $\epsilon$ passed from fomer time step to next time step. On the other hand, everything left (i.e. the predictable part, $\mathbf{x}$) should be red. This assumption gives us the following way to test our data.
Specifically, we can examine if a dataset can be used in FDT by checking the diagonal elements of $\mathbf{C}_\tau \mathbf{C}_0^{-1}$ in $\eqref{eq:6}$. Because if the general solution in $\eqref{eq:4}$ hold for every $\tau$, we will only have one $\mathbf{A}$ matrix regardless of the value of $\tau$, which means...
$
\begin{equation}
tr(\mathbf A)=tr(\mathbf{ln}(\mathbf{C}_\tau \mathbf{C}_0^{-1})/\tau)=const
\label{eq:8}
\tag{8}
\end{equation}
$
If we find $\eqref{eq:8}$ doesn't hold for every $\tau$, we can't apply FDT to a given dataset.
| 0.849971 | 0.971184 |
## Visualize a representation of the spherized LINCS Cell Painting dataset
```
import umap
import pathlib
import numpy as np
import pandas as pd
import plotnine as gg
from pycytominer.cyto_utils import infer_cp_features
np.random.seed(9876)
profile_path = pathlib.Path("profiles")
batches = ["2016_04_01_a549_48hr_batch1", "2017_12_05_Batch2"]
norm_methods = ["whole_plate", "dmso"]
file_filler = "_dmso_spherized_profiles_with_input_normalized_by_"
output_dir = pathlib.Path("figures")
output_dir = {batch: pathlib.Path(output_dir, batch) for batch in batches}
# Identify UMAP embeddings for all spherized profiles
embeddings = {batch: {} for batch in batches}
for batch in batches:
for norm_method in norm_methods:
file = pathlib.Path(profile_path, f"{batch}{file_filler}{norm_method}.csv.gz")
print(f"Now obtaining UMAP embeddings for {file}...")
# Load spherized data
spherized_df = pd.read_csv(file)
# Extract features
cp_features = infer_cp_features(spherized_df)
meta_features = infer_cp_features(spherized_df, metadata=True)
# Fit UMAP
reducer = umap.UMAP(random_state=123)
embedding_df = reducer.fit_transform(spherized_df.loc[:, cp_features])
embedding_df = pd.DataFrame(embedding_df)
embedding_df.columns = ["UMAP_0", "UMAP_1"]
embedding_df = pd.concat(
[
spherized_df.loc[:, meta_features],
embedding_df
],
axis="columns"
)
embedding_df = embedding_df.assign(dmso_label="DMSO")
embedding_df.loc[embedding_df.Metadata_broad_sample != "DMSO", "dmso_label"] = "compound"
embeddings[batch][norm_method] = embedding_df
print("done.\n")
```
### Output a series of visualizations for the spherized profiles
1. Batch 1 - Both normalization methods - UMAP highlighting compound vs. non-compound
2. Batch 1 - Both normalization methods - UMAP highlighting plate
3. Batch 2 - Both normalization methods - UMAP highlighting compound vs. non-compound
4. Batch 2 - Both normalization methods - UMAP highlighting plate
5. Batch 2 - Both normalization methods - UMAP highlighting different cell lines
6. Batch 2 - Both normalization methods - UMAP highlighting different time points
There will be a total of 12 figures, distributed in two pdf files.
```
batch = "2016_04_01_a549_48hr_batch1"
plotlist = []
for norm_method in norm_methods:
for color_type in ["Metadata_broad_sample", "Metadata_Plate"]:
output_file = pathlib.Path(output_dir[batch], f"{batch}_{norm_method}_colorby{color_type}.png")
output_file.parent.mkdir(exist_ok=True)
label = f"Batch 1: Normalized by {norm_method.upper()}\nColored by {color_type}"
embedding_gg = (
gg.ggplot(embeddings[batch][norm_method], gg.aes(x="UMAP_0", y="UMAP_1"))
+ gg.geom_point(gg.aes(color=color_type), size=0.1, alpha=0.2)
+ gg.facet_grid("~dmso_label")
+ gg.ggtitle(label)
+ gg.theme_bw()
+ gg.xlab("UMAP X")
+ gg.ylab("UMAP Y")
+ gg.theme(
legend_position="none",
strip_text=gg.element_text(size=5),
strip_background=gg.element_rect(colour="black", fill="#fdfff4"),
axis_text=gg.element_text(size=6),
axis_title=gg.element_text(size=7),
title=gg.element_text(size=7),
figure_size=(5.5, 3)
)
)
plotlist.append(embedding_gg)
output_file = pathlib.Path(output_dir[batch], f"{batch}_UMAPs.pdf")
output_file.parent.mkdir(exist_ok=True)
gg.save_as_pdf_pages(plotlist, output_file)
batch = "2017_12_05_Batch2"
plotlist = []
for norm_method in norm_methods:
for color_type in [
"Metadata_broad_sample", "Metadata_Plate", "Metadata_cell_line", "Metadata_time_point"
]:
output_file = pathlib.Path(output_dir[batch], f"{batch}_{norm_method}_colorby{color_type}.png")
output_file.parent.mkdir(exist_ok=True)
label = f"Batch 2: Normalized by {norm_method.upper()}\nColored by {color_type}"
embedding_gg = (
gg.ggplot(embeddings[batch][norm_method], gg.aes(x="UMAP_0", y="UMAP_1"))
+ gg.geom_point(gg.aes(color=color_type), size=0.1, alpha=0.2)
+ gg.facet_grid("~dmso_label")
+ gg.ggtitle(label)
+ gg.theme_bw()
+ gg.xlab("UMAP X")
+ gg.ylab("UMAP Y")
+ gg.theme(
legend_position="none",
strip_text=gg.element_text(size=5),
strip_background=gg.element_rect(colour="black", fill="#fdfff4"),
axis_text=gg.element_text(size=6),
axis_title=gg.element_text(size=7),
title=gg.element_text(size=7),
figure_size=(5.5, 3)
)
)
if color_type in ["Metadata_cell_line", "Metadata_time_point"]:
embedding_gg = (
embedding_gg
+ gg.theme(
legend_position="right",
figure_size=(6, 3)
)
)
plotlist.append(embedding_gg)
output_file = pathlib.Path(output_dir[batch], f"{batch}_UMAPs.pdf")
output_file.parent.mkdir(exist_ok=True)
gg.save_as_pdf_pages(plotlist, output_file)
```
|
github_jupyter
|
import umap
import pathlib
import numpy as np
import pandas as pd
import plotnine as gg
from pycytominer.cyto_utils import infer_cp_features
np.random.seed(9876)
profile_path = pathlib.Path("profiles")
batches = ["2016_04_01_a549_48hr_batch1", "2017_12_05_Batch2"]
norm_methods = ["whole_plate", "dmso"]
file_filler = "_dmso_spherized_profiles_with_input_normalized_by_"
output_dir = pathlib.Path("figures")
output_dir = {batch: pathlib.Path(output_dir, batch) for batch in batches}
# Identify UMAP embeddings for all spherized profiles
embeddings = {batch: {} for batch in batches}
for batch in batches:
for norm_method in norm_methods:
file = pathlib.Path(profile_path, f"{batch}{file_filler}{norm_method}.csv.gz")
print(f"Now obtaining UMAP embeddings for {file}...")
# Load spherized data
spherized_df = pd.read_csv(file)
# Extract features
cp_features = infer_cp_features(spherized_df)
meta_features = infer_cp_features(spherized_df, metadata=True)
# Fit UMAP
reducer = umap.UMAP(random_state=123)
embedding_df = reducer.fit_transform(spherized_df.loc[:, cp_features])
embedding_df = pd.DataFrame(embedding_df)
embedding_df.columns = ["UMAP_0", "UMAP_1"]
embedding_df = pd.concat(
[
spherized_df.loc[:, meta_features],
embedding_df
],
axis="columns"
)
embedding_df = embedding_df.assign(dmso_label="DMSO")
embedding_df.loc[embedding_df.Metadata_broad_sample != "DMSO", "dmso_label"] = "compound"
embeddings[batch][norm_method] = embedding_df
print("done.\n")
batch = "2016_04_01_a549_48hr_batch1"
plotlist = []
for norm_method in norm_methods:
for color_type in ["Metadata_broad_sample", "Metadata_Plate"]:
output_file = pathlib.Path(output_dir[batch], f"{batch}_{norm_method}_colorby{color_type}.png")
output_file.parent.mkdir(exist_ok=True)
label = f"Batch 1: Normalized by {norm_method.upper()}\nColored by {color_type}"
embedding_gg = (
gg.ggplot(embeddings[batch][norm_method], gg.aes(x="UMAP_0", y="UMAP_1"))
+ gg.geom_point(gg.aes(color=color_type), size=0.1, alpha=0.2)
+ gg.facet_grid("~dmso_label")
+ gg.ggtitle(label)
+ gg.theme_bw()
+ gg.xlab("UMAP X")
+ gg.ylab("UMAP Y")
+ gg.theme(
legend_position="none",
strip_text=gg.element_text(size=5),
strip_background=gg.element_rect(colour="black", fill="#fdfff4"),
axis_text=gg.element_text(size=6),
axis_title=gg.element_text(size=7),
title=gg.element_text(size=7),
figure_size=(5.5, 3)
)
)
plotlist.append(embedding_gg)
output_file = pathlib.Path(output_dir[batch], f"{batch}_UMAPs.pdf")
output_file.parent.mkdir(exist_ok=True)
gg.save_as_pdf_pages(plotlist, output_file)
batch = "2017_12_05_Batch2"
plotlist = []
for norm_method in norm_methods:
for color_type in [
"Metadata_broad_sample", "Metadata_Plate", "Metadata_cell_line", "Metadata_time_point"
]:
output_file = pathlib.Path(output_dir[batch], f"{batch}_{norm_method}_colorby{color_type}.png")
output_file.parent.mkdir(exist_ok=True)
label = f"Batch 2: Normalized by {norm_method.upper()}\nColored by {color_type}"
embedding_gg = (
gg.ggplot(embeddings[batch][norm_method], gg.aes(x="UMAP_0", y="UMAP_1"))
+ gg.geom_point(gg.aes(color=color_type), size=0.1, alpha=0.2)
+ gg.facet_grid("~dmso_label")
+ gg.ggtitle(label)
+ gg.theme_bw()
+ gg.xlab("UMAP X")
+ gg.ylab("UMAP Y")
+ gg.theme(
legend_position="none",
strip_text=gg.element_text(size=5),
strip_background=gg.element_rect(colour="black", fill="#fdfff4"),
axis_text=gg.element_text(size=6),
axis_title=gg.element_text(size=7),
title=gg.element_text(size=7),
figure_size=(5.5, 3)
)
)
if color_type in ["Metadata_cell_line", "Metadata_time_point"]:
embedding_gg = (
embedding_gg
+ gg.theme(
legend_position="right",
figure_size=(6, 3)
)
)
plotlist.append(embedding_gg)
output_file = pathlib.Path(output_dir[batch], f"{batch}_UMAPs.pdf")
output_file.parent.mkdir(exist_ok=True)
gg.save_as_pdf_pages(plotlist, output_file)
| 0.637257 | 0.666381 |
# Tutorial: Creating and Processing a Dataset for PyTorch
```
from hrtfdata.torch.full import CIPIC, ARI, Listen, BiLi, ITA, HUTUBS, SADIE2, ThreeDThreeA, CHEDAR, Widespread, SONICOM
from hrtfdata.torch import collate_dict_dataset
from torch.utils.data import DataLoader, Dataset
from pathlib import Path
import matplotlib.pyplot as plt
import numpy as np
base_dir = Path('../HRTF Datasets')
```
## Introduction
This tutorial assumes you have completed the tutorial "Using a dataset of planes in PyTorch" (available at `docs/tutorial-plane.ipynb`), so go read that first if you haven't done so already.
As mentioned in the previous tutorial, the purpose of `hrtfdata` is to provide PyTorch [`Datasets`](https://pytorch.org/docs/stable/data.html#torch.utils.data.Dataset) for multiple collections in a unified programming interface. What is not immediately apparent from using the `XPlane` classes, is that you can do more than simply load predefined datasets. The idea behind `hrtfdata` is that you can select any information contained in an HRTF data collection and combine them into a PyTorch dataset with your desired characteristics. It can be helpful to think of the classes in `hrtfdata.torch.full` as `Dataset` _generators_ and the classes in `hrtfdata.pytorch.planar` as predefined configurations of those generators (with added helper functionality like plotting etc.).
The same data collections as for the plane datasets are available for use:
- CIPIC
- ARI
- Listen
- BiLi
- ITA
- HUTUBS
- SADIE II
- 3D3A
- CHEDAR
- Widespread
- SONICOM
Each of them has a corresponding class that can be loaded from `hrtfdata.torch.full`, as is done above.
## The concept of "specifications"
To create a `Dataset`, you need to define its "specification", meaning that you need to tell what information you want to use as `features` and optionally what as `target` labels and/or as `groups`. Each of these specifications takes the form of a Python dictionary with any combination of the following keys:
- collection: a string identifier of the name of the data collection
- subject: an integer giving the identifier of the subject in the collection
- side: a string indicating the side of the head
- hrirs: an array containing the HRIRs for the given positions and side of the head
These four pieces of information are available for every collection. The following keys (and corresponding information) are sometimes available, depending on the collection, and will be discussed in a later tutorial:
- image: an array containing the pixel values of an image associated with a given side of the head
- 3d-model: an array containing a 3D model
- anthropometry: an array containing anthropometric measurements
The values for each of these keys are also Python dictionaries themselves, and allow to pass parameters for each type of info. The first three types `collection`, `subject` and `side` have no parameters, so an empty dictionary `{}` should be passed as value for these keys. The `hrir` type does allow to pass parameters in the form of a dictionary with the following keys:
- domain: the HRIR/HRTF representation (`time`, `magnitude`, `magnitude_db`, `phase` or `complex`, default: `time`)
- side: selecting a side of the head (`left`, `right`, `both`, `both-left`, `both-right`, `None`, default: `None` meaning any side available)
- row_angles: a list of angles in degrees to select from the fundamental coordinate plane (explained later), default: all available
- column_angles: a list of angles in degrees to select from the projection coordinate plane (explained later), default: all available
An example should make this clearer: the three `spec`s used in the creation of `XPlane` datasets roughly correspond to the following.
```
domain = 'magnitude_db'
side = 'left'
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain}}, target_spec={'side': {}}, group_spec={'subject': {}})
```
## Dataset functionality
The resulting dataset has the a large part of the functionality of plane datasets, excluding plotting. So you can get its length, index individual data points as dictionaries and check their keys.
```
isinstance(ds, Dataset), len(ds), ds[0].keys()
```
You can verify that the `target` and `group` value indeed contain the side of the head and the subject id of the data point, as requested.
```
ds[0]['target'], ds[0]['group']
```
As a reminder, the dict format of the data points requires the use of the non-default `collate_dict_dataset` collation function when creating a `torch.util.data.DataLoader` (to convert the dataset into expected `(feature, target)` pairs), but also allows to split the dataset while keeping according to groups.
```
DataLoader(ds, collate_fn=collate_dict_dataset)
```
Moreover, you can get the sample rate of the HRIR and its corresponding HRTF frequencies.
```
ds.hrir_samplerate, ds.hrtf_frequencies
```
The ids of all available subjects and of this particular selection (all by default) can also be obtained using the properties `available_subject_ids` and `subject_ids`. The actual selection can be achieved by passing the argument `subject_ids` to the dataset constructor, just like for plane datasets (including the `first`, `last` and `random` options).
```
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain}}, target_spec={'side': {}}, group_spec={'subject': {}}, subject_ids='random')
ds.available_subject_ids[:10], ds.subject_ids
```
## More specification examples
Only `feature_spec` is obligatory, `target_spec` and/or `group_spec` can be absent, leading to empty values, which is especially useful for situations where no target labels are needed (e.g. GANs).
```
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain}}, subject_ids='first')
ds[0]['target'], ds[0]['group']
```
Multiple elements of information can be given in a `spec`, which will then be combined into one multi-dimensional element, for instance a target label consisting of three parts as below.
```
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {}}, target_spec={'collection': {}, 'subject': {}, 'side': {}}, subject_ids='first')
ds[0]['target']
```
HRIRs do not necessarily need to be used as features they can be used in any spec just like any other type of information.
```
ds = ARI(base_dir / 'ARI', feature_spec={'side': {}}, target_spec={'hrirs': {}}, subject_ids='first')
ds[0]['features'], ds[0]['target'].shape, ds[0]['target'].dtype
```
The dtype of numerical values is `np.float32` by default, but this can be changed by passing a `dtype` argument to the constructor. When requesting an HRTF in the `complex` domain, it is necessary to specify a complex dtype too, otherwise an error will be thrown.
```
try:
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'domain': 'complex'}}, subject_ids='first')
except ValueError as e:
print(e)
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'domain': 'complex'}}, subject_ids='first', dtype=np.complex64)
ds[0]['features'].shape, ds[0]['features'].dtype
```
## Layout of HRIR data
Regardless of where the HRIRs are used, they are always stored as a 3-dimensional array. In order to describe the data layout independently of coordinate system, we need to define two terms. The _fundamental_ plane of a coordinate system is the reference plane onto which each point gets projected. Its angles span a range of 360 degrees. The _orthogonal_ plane of a coordinate system is the plane defined by a point, its projection and the origin. Its angles span a range of 180 degrees. In practice, the fundamental plane will nearly always be the horizontal plane because only the CIPIC collection uses interaural-polar coordinates, all other supported collections use vertical-polar coordinates.
The various spatial positions for which a HRIR measurement is available are organised along the rows and columns of the 3D array. The values of a single HRIR/HRTF (depending on the selected `domain`) for a particular position determined by row and column index are stored in the third dimension. The rows are ordered by increasing angle in the fundamental plane, constrained to the interval [-180, 180) (so vertical angles for CIPIC, azimuths for all the rest). The columns of the array are ordered by increasing angle in the orthogonal plane, constrained to the interval [-90, 90] (so lateral angles for CIPIC, elevations for all the rest).
This means that the spherical positions are stored as a [plate carrée](https://en.wikipedia.org/wiki/Equirectangular_projection) projection. The first and last column are always the positions closest to the poles, regardless of the coordinate system, although the measurements for the poles are not necessarily present (in the collection or just in a particular subselection).
```
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain}}, target_spec={'side': {}}, group_spec={'subject': {}}, subject_ids='first')
ds[0]['features'].shape
```
The actual values of the angles can be read from the `row_angles` and `column_angles` properties.
```
(len(ds.row_angles), len(ds.column_angles)), ds.row_angles, ds.column_angles
```
By default, all positions available in a collection are read, but a selection can be made by adding them to the `spec` as one or more angles. A value of `None` signifies all available, the default.
```
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain, 'row_angles': None, 'column_angles': None}}, subject_ids='first')
ds[0]['features'].shape
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain, 'row_angles': 0, 'column_angles': 0}}, subject_ids='first')
ds[0]['features'].shape, ds.row_angles, ds.column_angles
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain, 'row_angles': np.arange(-180, 180, 20), 'column_angles': (-180, 0)}}, subject_ids='first')
ds[0]['features'].shape, ds.row_angles, ds.column_angles
```
Requesting an angle that is not available in the collection will be silently ignored. So when using the positional values in further processing, it is advised to use the exact angles that are returned by reading the relevant properties instead of using the requested values.
```
requested_column_angles = (0, 3.14)
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain, 'row_angles': 0, 'column_angles': requested_column_angles}}, subject_ids='first')
actual_column_angles = ds.column_angles
ds[0]['features'].shape, ds.row_angles, ds.column_angles
(requested_column_angles == actual_column_angles).all()
```
Only when none of the requested angles are available, an exception will be thrown.
```
try:
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain, 'row_angles': 0, 'column_angles': 3.14}}, subject_ids='first')
except ValueError as e:
print(e)
```
If we think of the row and column angles as forming a matrix of available positions, then this matrix is not necessarily dense. Not every collection has chosen a spatial sampling where every row/column angle combination is measured. Consequently, the 3D array of HRIRs is stored as a [NumPy masked array](https://numpy.org/doc/stable/reference/maskedarray.html), where row/column combinations that have not been measured are masked.
We can visualise the distribution of the spatial positions by plotting the mask of a collection (technically a single, third dimension slice of the mask but all slices are the same since either all samples of a HRIR are present or none). Do note that the masks are displayed by position index, not actual angles, and that the angular sampling is not necessarily regular. Therefore these plots cannot be interpreted as representations of the angular distribution of the measurement positions.
```
collections = (
(CIPIC, base_dir / 'CIPIC'),
(ARI, base_dir / 'ARI'),
(Listen, base_dir / 'Ircam Listen'),
(BiLi, base_dir / 'Ircam BiLi'),
(ITA, base_dir / 'ITA Aachen'),
(HUTUBS, base_dir / 'HUTUBS'),
(SADIE2, base_dir / 'SADIE II'),
(ThreeDThreeA, base_dir / '3D3A'),
(CHEDAR, base_dir / 'CHEDAR'),
(Widespread, base_dir / 'Widespread'),
(SONICOM, base_dir / 'SONICOM'),
)
from math import ceil
fig = plt.figure(figsize=(16, 10))
for idx, (collection, data_dir) in enumerate(collections):
ds = collection(data_dir, feature_spec={'hrirs': {}}, subject_ids='first')
ax = fig.add_subplot(2, ceil(len(collections)/2), idx+1)
ax.set_title(collection.__name__)
ax.matshow(np.ma.getmaskarray(ds[0]['features'][:, :, 0]))
ax.set_aspect(0.5)
```
## Processing HRIRs further
It is possible to process the HRIRs further without needing to modify any internal code. To that end, each dataset constructor accepts a callable as argument `hrir_transform`. The callable itself takes one argument, the 3D array of HRIRs and needs to return the modified array. For instance, suppose that dB conversion of the HRTF magnitudes was not built-in, then it could be added by passing the function below.
```
def db_calc(hrtfs):
return 20*np.log10(np.clip(hrtfs, 3.305e-7, None))
external_db_calc = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'domain': 'magnitude'}}, subject_ids='first', hrir_transform=db_calc)
builtin_db_calc = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'domain': 'magnitude_db'}}, subject_ids='first')
np.allclose(external_db_calc[0]['features'], builtin_db_calc[0]['features'])
```
The returned HRIRs do not necessarily need to have the same shape as the input. For instance, this is done by the `XPlane` classes, which return 2D planes. Internally, the `plane` argument of the constructor is converted into a set of row and column angles, which get read and subsequently stitched together into a single plane to form the output.
|
github_jupyter
|
from hrtfdata.torch.full import CIPIC, ARI, Listen, BiLi, ITA, HUTUBS, SADIE2, ThreeDThreeA, CHEDAR, Widespread, SONICOM
from hrtfdata.torch import collate_dict_dataset
from torch.utils.data import DataLoader, Dataset
from pathlib import Path
import matplotlib.pyplot as plt
import numpy as np
base_dir = Path('../HRTF Datasets')
domain = 'magnitude_db'
side = 'left'
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain}}, target_spec={'side': {}}, group_spec={'subject': {}})
isinstance(ds, Dataset), len(ds), ds[0].keys()
ds[0]['target'], ds[0]['group']
DataLoader(ds, collate_fn=collate_dict_dataset)
ds.hrir_samplerate, ds.hrtf_frequencies
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain}}, target_spec={'side': {}}, group_spec={'subject': {}}, subject_ids='random')
ds.available_subject_ids[:10], ds.subject_ids
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain}}, subject_ids='first')
ds[0]['target'], ds[0]['group']
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {}}, target_spec={'collection': {}, 'subject': {}, 'side': {}}, subject_ids='first')
ds[0]['target']
ds = ARI(base_dir / 'ARI', feature_spec={'side': {}}, target_spec={'hrirs': {}}, subject_ids='first')
ds[0]['features'], ds[0]['target'].shape, ds[0]['target'].dtype
try:
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'domain': 'complex'}}, subject_ids='first')
except ValueError as e:
print(e)
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'domain': 'complex'}}, subject_ids='first', dtype=np.complex64)
ds[0]['features'].shape, ds[0]['features'].dtype
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain}}, target_spec={'side': {}}, group_spec={'subject': {}}, subject_ids='first')
ds[0]['features'].shape
(len(ds.row_angles), len(ds.column_angles)), ds.row_angles, ds.column_angles
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain, 'row_angles': None, 'column_angles': None}}, subject_ids='first')
ds[0]['features'].shape
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain, 'row_angles': 0, 'column_angles': 0}}, subject_ids='first')
ds[0]['features'].shape, ds.row_angles, ds.column_angles
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain, 'row_angles': np.arange(-180, 180, 20), 'column_angles': (-180, 0)}}, subject_ids='first')
ds[0]['features'].shape, ds.row_angles, ds.column_angles
requested_column_angles = (0, 3.14)
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain, 'row_angles': 0, 'column_angles': requested_column_angles}}, subject_ids='first')
actual_column_angles = ds.column_angles
ds[0]['features'].shape, ds.row_angles, ds.column_angles
(requested_column_angles == actual_column_angles).all()
try:
ds = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'side': side, 'domain': domain, 'row_angles': 0, 'column_angles': 3.14}}, subject_ids='first')
except ValueError as e:
print(e)
collections = (
(CIPIC, base_dir / 'CIPIC'),
(ARI, base_dir / 'ARI'),
(Listen, base_dir / 'Ircam Listen'),
(BiLi, base_dir / 'Ircam BiLi'),
(ITA, base_dir / 'ITA Aachen'),
(HUTUBS, base_dir / 'HUTUBS'),
(SADIE2, base_dir / 'SADIE II'),
(ThreeDThreeA, base_dir / '3D3A'),
(CHEDAR, base_dir / 'CHEDAR'),
(Widespread, base_dir / 'Widespread'),
(SONICOM, base_dir / 'SONICOM'),
)
from math import ceil
fig = plt.figure(figsize=(16, 10))
for idx, (collection, data_dir) in enumerate(collections):
ds = collection(data_dir, feature_spec={'hrirs': {}}, subject_ids='first')
ax = fig.add_subplot(2, ceil(len(collections)/2), idx+1)
ax.set_title(collection.__name__)
ax.matshow(np.ma.getmaskarray(ds[0]['features'][:, :, 0]))
ax.set_aspect(0.5)
def db_calc(hrtfs):
return 20*np.log10(np.clip(hrtfs, 3.305e-7, None))
external_db_calc = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'domain': 'magnitude'}}, subject_ids='first', hrir_transform=db_calc)
builtin_db_calc = ARI(base_dir / 'ARI', feature_spec={'hrirs': {'domain': 'magnitude_db'}}, subject_ids='first')
np.allclose(external_db_calc[0]['features'], builtin_db_calc[0]['features'])
| 0.475605 | 0.991041 |
# Select the LCLS-II py3 kernel in the top right
# Import libraries
```
import numpy as np
import matplotlib.pyplot as plt
import psana as ps
```
# Specify experiment and run number. Then generate datasource
```
exp = 'tmolv2918'
run_number = 215
ds = ps.DataSource(exp=exp, run=run_number)
run = next(ds.runs())
```
# Specify the detectors and analyses to conduct shot-by-shot and let the TMOanalysis library handle the rest
```
detectors = {}
# Fast detectors
# detectors['sample']={'pskey':'timing', 'get':lambda det: det}
detectors['evrs'] = {'pskey':'timing', 'get':lambda det: det.raw.eventcodes}
detectors['tmo_atmopal']={'pskey':'tmo_atmopal', 'get':lambda det: det.raw.image}
detectors['vls']={'pskey':'andor', 'get':lambda det: det.raw.value}
detectors['gmd']={'pskey':'gmd', 'get':lambda det: det.raw.energy}
detectors['hsd']={'pskey':'hsd', 'get':lambda det: det.raw.waveforms}
detectors['photonEnergy']={'pskey':'ebeam', 'get':lambda det: det.raw.ebeamPhotonEnergy}
# Important Epics
detectors['vitaraDelay']={'pskey':'las_fs14_target_time', 'get':lambda det: det}
# Analysis is of form {analysisKey: {'function': analysisFunction(), 'detectorKey': 'key', 'analyzeEvery':1}}
# Function element is optional. If not provided, raw data is returned.
analysis = {}
analysis['vitaraDelay'] = {'function':lambda x: x, 'detectorKey':'vitaraDelay'}
analysis['evrs'] = {'detectorKey':'evrs'}
analysis['vls1D'] = {'function': lambda x: x, 'detectorKey':'vls'}
analysis['pulseEnergy'] = {'detectorKey':'gmd'}
analysis['photonEnergy'] = {'detectorKey':'photonEnergy'}
# analysis['wfTime'] = {'function': lambda x: x[0]['times'], 'detectorKey':'hsd'}
resample = lambda x, rebin_factor: x.reshape(-1, rebin_factor).mean(1)
analysis['itof-time'] = {'function': lambda x: resample(x[0]['times'],10), 'detectorKey':'hsd'}
analysis['itof-waveform'] = {'function': lambda x: resample(x[0][0],10), 'detectorKey':'hsd'}
analysis['diode-time'] = {'function': lambda x: x[0]['times'].astype(float)[:5000], 'detectorKey':'hsd'}
analysis['diode-waveform'] = {'function': lambda x: x[9][0].astype(float)[:5000], 'detectorKey':'hsd'}
analysis['atm-proj1'] = {'function': lambda x: np.sum(x[360:500,:],axis=0), 'detectorKey':'tmo_atmopal'}
analysis['atm-proj2'] = {'function': lambda x: np.sum(x[0:240,:],axis=0), 'detectorKey':'tmo_atmopal'}
analysis['atm-proj3'] = {'function': lambda x: np.sum(x[240:360,:],axis=0), 'detectorKey':'tmo_atmopal'}
import data
import loop
data.H5Writer(exp=exp,
runNumber=run_number,
detectors=detectors,
analysisDict=analysis,
outputDir='.',
ncores=1,
nread=300,
loopStyle=lambda itr: loop.timeIt(itr, printEverySec=1))
```
# Load in H5 file for analysis
```
import h5py
data=h5py.File('./run-215.h5','r')
data.keys()
```
# Example plots and analyses
## Histogram of pulse energies
```
pe = np.array( data['pulseEnergy'] ) *1.0e3
plt.hist( pe, bins=20);
plt.xlabel("Pulse energy / uJ");
```
## TOF traces
```
evrs = np.array( data['evrs'] ).astype(int)
itofWaveform = np.array( data['itof-waveform'] )
print(evrs.shape, itofWaveform.shape)
t = np.array( data['itof-time'] )[0,:]
gas_on = evrs[:,70]==1
gas_off = np.logical_not(gas_on)
plt.plot(t, itofWaveform[gas_on,:].mean(0), 'k', label='Jet on');
plt.plot(t, itofWaveform[gas_off,:].mean(0), 'r', alpha=0.5, label='Jet off');
plt.title("ion TOF traces");
plt.legend()
plt.xlabel("ToF / us")
```
# Print detectors available in this (exp, run)
Fast detectors. Make a measurement every shot
```
run.detnames
```
# Print epics detectors available
These are slow detectors. While they write a value for every event, they do not update at 120Hz.
```
def getEpics(run):
epicsNames = []
for key in run.epicsinfo:
epicsNames.append( key[0] )
return epicsNames
getEpics(run)
```
# Test data access for a detector
Use a test evt to see what the detector object returns
Many of the detectors call functions are undocumented. Try typing '<Detector Obj>.' then pressing tab to determine the call function. For example,
```python
gmd.[tab]
gmd.raw.[tab]
gmd.raw.energy
help(gmd.raw.energy)
```
shows you that the xray pulse energy may be read by `gmd.raw.energy(evt0)`
```
evt0=next( run.events() )
gmd = run.Detector('gmd') # xray pulse energy monitor
help(gmd.raw.energy)
gmd.raw.energy(evt0)
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import psana as ps
exp = 'tmolv2918'
run_number = 215
ds = ps.DataSource(exp=exp, run=run_number)
run = next(ds.runs())
detectors = {}
# Fast detectors
# detectors['sample']={'pskey':'timing', 'get':lambda det: det}
detectors['evrs'] = {'pskey':'timing', 'get':lambda det: det.raw.eventcodes}
detectors['tmo_atmopal']={'pskey':'tmo_atmopal', 'get':lambda det: det.raw.image}
detectors['vls']={'pskey':'andor', 'get':lambda det: det.raw.value}
detectors['gmd']={'pskey':'gmd', 'get':lambda det: det.raw.energy}
detectors['hsd']={'pskey':'hsd', 'get':lambda det: det.raw.waveforms}
detectors['photonEnergy']={'pskey':'ebeam', 'get':lambda det: det.raw.ebeamPhotonEnergy}
# Important Epics
detectors['vitaraDelay']={'pskey':'las_fs14_target_time', 'get':lambda det: det}
# Analysis is of form {analysisKey: {'function': analysisFunction(), 'detectorKey': 'key', 'analyzeEvery':1}}
# Function element is optional. If not provided, raw data is returned.
analysis = {}
analysis['vitaraDelay'] = {'function':lambda x: x, 'detectorKey':'vitaraDelay'}
analysis['evrs'] = {'detectorKey':'evrs'}
analysis['vls1D'] = {'function': lambda x: x, 'detectorKey':'vls'}
analysis['pulseEnergy'] = {'detectorKey':'gmd'}
analysis['photonEnergy'] = {'detectorKey':'photonEnergy'}
# analysis['wfTime'] = {'function': lambda x: x[0]['times'], 'detectorKey':'hsd'}
resample = lambda x, rebin_factor: x.reshape(-1, rebin_factor).mean(1)
analysis['itof-time'] = {'function': lambda x: resample(x[0]['times'],10), 'detectorKey':'hsd'}
analysis['itof-waveform'] = {'function': lambda x: resample(x[0][0],10), 'detectorKey':'hsd'}
analysis['diode-time'] = {'function': lambda x: x[0]['times'].astype(float)[:5000], 'detectorKey':'hsd'}
analysis['diode-waveform'] = {'function': lambda x: x[9][0].astype(float)[:5000], 'detectorKey':'hsd'}
analysis['atm-proj1'] = {'function': lambda x: np.sum(x[360:500,:],axis=0), 'detectorKey':'tmo_atmopal'}
analysis['atm-proj2'] = {'function': lambda x: np.sum(x[0:240,:],axis=0), 'detectorKey':'tmo_atmopal'}
analysis['atm-proj3'] = {'function': lambda x: np.sum(x[240:360,:],axis=0), 'detectorKey':'tmo_atmopal'}
import data
import loop
data.H5Writer(exp=exp,
runNumber=run_number,
detectors=detectors,
analysisDict=analysis,
outputDir='.',
ncores=1,
nread=300,
loopStyle=lambda itr: loop.timeIt(itr, printEverySec=1))
import h5py
data=h5py.File('./run-215.h5','r')
data.keys()
pe = np.array( data['pulseEnergy'] ) *1.0e3
plt.hist( pe, bins=20);
plt.xlabel("Pulse energy / uJ");
evrs = np.array( data['evrs'] ).astype(int)
itofWaveform = np.array( data['itof-waveform'] )
print(evrs.shape, itofWaveform.shape)
t = np.array( data['itof-time'] )[0,:]
gas_on = evrs[:,70]==1
gas_off = np.logical_not(gas_on)
plt.plot(t, itofWaveform[gas_on,:].mean(0), 'k', label='Jet on');
plt.plot(t, itofWaveform[gas_off,:].mean(0), 'r', alpha=0.5, label='Jet off');
plt.title("ion TOF traces");
plt.legend()
plt.xlabel("ToF / us")
run.detnames
def getEpics(run):
epicsNames = []
for key in run.epicsinfo:
epicsNames.append( key[0] )
return epicsNames
getEpics(run)
gmd.[tab]
gmd.raw.[tab]
gmd.raw.energy
help(gmd.raw.energy)
evt0=next( run.events() )
gmd = run.Detector('gmd') # xray pulse energy monitor
help(gmd.raw.energy)
gmd.raw.energy(evt0)
| 0.335677 | 0.860486 |
```
import open3d as o3d
import numpy as np
import os
import sys
# monkey patches visualization and provides helpers to load geometries
sys.path.append('..')
import open3d_tutorial as o3dtut
# change to True if you want to interact with the visualization windows
o3dtut.interactive = not "CI" in os.environ
```
# File IO
This tutorial shows how basic data structures are read and written by Open3D.
## Point cloud
The code below reads and writes a point cloud.
```
print("Testing IO for point cloud ...")
pcd = o3d.io.read_point_cloud("../../test_data/fragment.pcd")
print(pcd)
o3d.io.write_point_cloud("copy_of_fragment.pcd", pcd)
```
By default, Open3D tries to infer the file type by the filename extension. The following point cloud file types are supported:
Format | Description
---------|---------------
`xyz` | Each line contains `[x, y, z]`, where `x`, `y`, `z` are the 3D coordinates
`xyzn` | Each line contains `[x, y, z, nx, ny, nz]`, where `nx`, `ny`, `nz` are the normals
`xyzrgb` | Each line contains `[x, y, z, r, g, b]`, where `r`, `g`, `b` are in floats of range `[0, 1]`
`pts` | The first line is an integer representing the number of points. The subsequent lines follow one of these formats: `[x, y, z, i, r, g, b]`, `[x, y, z, r, g, b]`, `[x, y, z, i]` or `[x, y, z]`, where `x`, `y`, `z`, `i` are of type `double` and `r`, `g`, `b` are of type `uint8`
`ply` | See [Polygon File Format](http://paulbourke.net/dataformats/ply), the ply file can contain both point cloud and mesh data
`pcd` | See [Point Cloud Data](http://pointclouds.org/documentation/tutorials/pcd_file_format.html)
It’s also possible to specify the file type explicitly. In this case, the file extension will be ignored.
```
pcd = o3d.io.read_point_cloud("../../test_data/my_points.txt", format='xyz')
```
## Mesh
The code below reads and writes a mesh.
```
print("Testing IO for meshes ...")
mesh = o3d.io.read_triangle_mesh("../../test_data/knot.ply")
print(mesh)
o3d.io.write_triangle_mesh("copy_of_knot.ply", mesh)
```
Compared to the point cloud data structure, a mesh has triangles that define the 3D surface.
By default, Open3D tries to infer the file type by the filename extension. The following mesh file types are supported:
Format | Description
----------------|---------------
`ply` | See [Polygon File Format](http://paulbourke.net/dataformats/ply/), the ply file can contain both point cloud and mesh data
`stl` | See [StereoLithography](http://www.fabbers.com/tech/STL_Format)
`obj` | See [Object Files](http://paulbourke.net/dataformats/obj/)
`off` | See [Object File Format](http://www.geomview.org/docs/html/OFF.html)
`gltf`/`glb` | See [GL Transmission Format](https://github.com/KhronosGroup/glTF/tree/master/specification/2.0)
## Image
The code below reads and writes an image.
```
print("Testing IO for images ...")
img = o3d.io.read_image("../../test_data/Juneau.jpg")
print(img)
o3d.io.write_image("copy_of_Juneau.jpg", img)
```
The size of the image is readily displayed using `print(img)`.
Both `jpg` and `png` image files are supported.
|
github_jupyter
|
import open3d as o3d
import numpy as np
import os
import sys
# monkey patches visualization and provides helpers to load geometries
sys.path.append('..')
import open3d_tutorial as o3dtut
# change to True if you want to interact with the visualization windows
o3dtut.interactive = not "CI" in os.environ
print("Testing IO for point cloud ...")
pcd = o3d.io.read_point_cloud("../../test_data/fragment.pcd")
print(pcd)
o3d.io.write_point_cloud("copy_of_fragment.pcd", pcd)
pcd = o3d.io.read_point_cloud("../../test_data/my_points.txt", format='xyz')
print("Testing IO for meshes ...")
mesh = o3d.io.read_triangle_mesh("../../test_data/knot.ply")
print(mesh)
o3d.io.write_triangle_mesh("copy_of_knot.ply", mesh)
print("Testing IO for images ...")
img = o3d.io.read_image("../../test_data/Juneau.jpg")
print(img)
o3d.io.write_image("copy_of_Juneau.jpg", img)
| 0.132964 | 0.92462 |
<a href="https://colab.research.google.com/github/dev-eajnim/OpenCV-3-Computer-Vision-with-Python-Cookbook/blob/master/convolution_neural_network.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import tensorflow as tf
```
텐서플로 1.7.0 버전에서부터는 샘플 데이터를 다운로드하는 기능이 제외될 예정이라는 경고가 발생합니다. 대신 케라스(Keras)를 사용하여 MNIST 데이터를 다운받습니다.
simple_neural_network 예제에서 MNIST 데이터를 이미 다운 받았으므로 다시 다운 받지 않습니다.
```
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data()
X_train = X_train.astype(np.float32).reshape(-1, 28*28) / 255.0
X_test = X_test.astype(np.float32).reshape(-1, 28*28) / 255.0
y_train = tf.keras.utils.to_categorical(y_train)
y_test = tf.keras.utils.to_categorical(y_test)
y_train = y_train.astype(np.int32)
y_test = y_test.astype(np.int32)
```
배치 데이터를 만들기 위해 파이썬 제너레이터 함수를 정의합니다.
```
def shuffle_batch(X, y, batch_size):
rnd_idx = np.random.permutation(len(X))
n_batches = len(X) // batch_size
for batch_idx in np.array_split(rnd_idx, n_batches):
X_batch, y_batch = X[batch_idx], y[batch_idx]
yield X_batch, y_batch
```
x, y\_ 플레이스홀더를 지정하고 x 를 28x28x1 크기로 차원을 변경합니다.
```
x = tf.placeholder("float", shape=[None, 784])
y_ = tf.placeholder("float", shape=[None, 10])
x_image = tf.reshape(x, [-1,28,28,1])
print("x_image=", x_image)
```
가중치를 표준편차 0.1을 갖는 난수로 초기화하는 함수와 바이어스를 0.1로 초기화하는 함수를 정의합니다.
```
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
```
stride는 1로 하고 패딩은 0으로 하는 콘볼루션 레이어를 만드는 함수와 2x2 맥스 풀링 레이어를 위한 함수를 정의합니다.
```
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
```
첫번째 콘볼루션 레이어를 만들기 위해 가중치와 바이어스 텐서를 만들고 활성화함수는 렐루 함수를 사용했습니다. 그리고 콘볼루션 레이어 뒤에 맥스 풀링 레이어를 추가했습니다.
```
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
```
SAME 패딩이므로 콘볼루션으로는 차원이 변경되지 않고 풀링 단계에서 스트라이드에 따라 차원이 반으로 줄어든다.
```
print(x_image.get_shape())
print(h_conv1.get_shape())
h_pool1.get_shape()
```
두번째 콘볼루션 레이어와 풀링 레이어를 만듭니다. 첫번째 콘볼루션의 필터가 32개라 두번째 콘볼루션의 컬러 채널이 32개가 되는 것과 같은 효과가 있습니다.
```
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
```
SAME 패딩이므로 콘볼루션으로는 차원이 변경되지 않고 풀링 단계에서 스트라이드에 따라 차원이 반으로 줄어든다.
```
print(h_conv2.get_shape())
h_pool2.get_shape()
```
마지막 소프트맥스 레이어에 연결하기 위해 완전연결 레이어를 추가합니다. 이전 콘볼루션의 레이어의 결과 텐서를 다시 1차원 텐서로 변환하여 렐루 활성화 함수에 전달합니다.
```
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
```
드롭아웃되지 않을 확률 값을 저장할 플레이스홀더를 만들고 드롭아웃 레이어를 추가합니다.
```
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
```
마지막으로 소프트맥스 레이어를 추가합니다.
```
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
```
크로스엔트로피와 최적화알고리즘, 평가를 위한 연산을 정의합니다.
```
cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
```
세션을 시작하고 변수를 초기화 합니다.
```
sess = tf.Session()
sess.run(tf.global_variables_initializer())
```
20,000번 반복을 수행합니다.
```
for i in range(20000):
batch = next(shuffle_batch(X_train, y_train, 100))
if i % 1000 == 0:
train_accuracy = sess.run(accuracy, feed_dict={
x:batch[0], y_: batch[1], keep_prob: 1.0})
print("step %d, training accuracy %g"%(i, train_accuracy))
sess.run(train_step, feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
```
최종 정확도를 출력합니다.
```
print("test accuracy %g"% sess.run(
accuracy, feed_dict={x: X_test, y_: y_test, keep_prob: 1.0}))
```
|
github_jupyter
|
import tensorflow as tf
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data()
X_train = X_train.astype(np.float32).reshape(-1, 28*28) / 255.0
X_test = X_test.astype(np.float32).reshape(-1, 28*28) / 255.0
y_train = tf.keras.utils.to_categorical(y_train)
y_test = tf.keras.utils.to_categorical(y_test)
y_train = y_train.astype(np.int32)
y_test = y_test.astype(np.int32)
def shuffle_batch(X, y, batch_size):
rnd_idx = np.random.permutation(len(X))
n_batches = len(X) // batch_size
for batch_idx in np.array_split(rnd_idx, n_batches):
X_batch, y_batch = X[batch_idx], y[batch_idx]
yield X_batch, y_batch
x = tf.placeholder("float", shape=[None, 784])
y_ = tf.placeholder("float", shape=[None, 10])
x_image = tf.reshape(x, [-1,28,28,1])
print("x_image=", x_image)
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
print(x_image.get_shape())
print(h_conv1.get_shape())
h_pool1.get_shape()
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
print(h_conv2.get_shape())
h_pool2.get_shape()
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
sess = tf.Session()
sess.run(tf.global_variables_initializer())
for i in range(20000):
batch = next(shuffle_batch(X_train, y_train, 100))
if i % 1000 == 0:
train_accuracy = sess.run(accuracy, feed_dict={
x:batch[0], y_: batch[1], keep_prob: 1.0})
print("step %d, training accuracy %g"%(i, train_accuracy))
sess.run(train_step, feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
print("test accuracy %g"% sess.run(
accuracy, feed_dict={x: X_test, y_: y_test, keep_prob: 1.0}))
| 0.806396 | 0.987747 |
# Police Bias Algorithm
## Racial Bias Score
```
import pandas as pd
import numpy as np
import math
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.special import ndtr
```
### Dataframe of the features that will be examined in the police department from 2016 to 2019
DataFrame that contains all of our features:
**For the purposes of this algorithm, I inputted dummy data for values in order to test out the algorithm and look at the differences in z scores**
```
nyc = pd.read_csv('../data_clean/nyc.csv')
cities = nyc
cities = cities.loc[: , "city":"other_uof"]
cities
```
### 2019 Population Statistics
#### Population Statistics Breakdown according to US Census
Calculations for the populations
```
black_pop = cities['black_pct'] * cities['total_pop']
white_pop = cities['white_pct'] * cities['total_pop']
latinx_pop = cities['latinx_pct']* cities['total_pop']
asian_pop = cities['asian_pct']* cities['total_pop']
other_pop = cities['other_pct']* cities['total_pop']
```
### Arrest Disparities By Stops and Race
```
#ratio of stops according to racial makeup of city
pct_black_stops_to_pop = cities['black_drive_stops']/black_pop
pct_white_stops_to_pop = cities['white_drive_stops']/white_pop
pct_latinx_stops_to_pop = cities['latinx_drive_stops']/latinx_pop
pct_asian_stops_to_pop = cities['asian_drive_stops']/asian_pop
pct_other_stops_to_pop = cities['other_drive_stops']/other_pop
```
## Logit Scores
### Black to White Racial Bias Score
```
logit_white = np.log(pct_white_stops_to_pop/(1-pct_white_stops_to_pop))
logit_black = np.log(pct_black_stops_to_pop/(1-pct_black_stops_to_pop))
black_logit_score = round((logit_black - logit_white), 3)
#cities['black bias percentages'] = np.exp(black_logit_score)/(1+np.exp(black_logit_score))
```
### Latinx to White Racial Bias Score
```
logit_latinx = np.log(pct_latinx_stops_to_pop/(1-pct_latinx_stops_to_pop))
latinx_logit_score = round((logit_latinx - logit_white), 3)
#cities['latinx bias percentages'] = np.exp(latinx_logit_score)/(1+np.exp(latinx_logit_score))
```
### Asian to White Racial Bias Score
```
logit_asian = np.log(pct_asian_stops_to_pop/(1-pct_asian_stops_to_pop))
asian_logit_score = round((logit_asian - logit_white), 3)
#cities['asian bias percentages'] = np.exp(asian_logit_score)/(1+np.exp(asian_logit_score))
```
### Other racial groups to White Racial Bias Score
```
logit_other = np.log(pct_other_stops_to_pop/(1-pct_other_stops_to_pop))
other_logit_score = round((logit_other - logit_white), 3)
#cities['other bias percentages'] = np.exp(other_logit_score)/(1+np.exp(other_logit_score))
```
## Racial Bias Z Score
### Defining helper functions
Converting z scores to p values (percentages).
```
#convert all standardized scores into percentages
def percent(z_score_array):
return 1- norm.cdf(abs(z_score_array)) #returns p-value
```
Plotting the normal curve with the z score.
```
def plot_normal(z_scores, racial_group):
x_all = np.arange(-10, 10, 0.001)
max_z = max(z_scores)
if max_z >=0:
x_shade = np.arange(max_z, max(x_all),0.001)
else:
x_shade = np.arange(min(x_all), max_z, 0.001)
y = norm.pdf(x_shade,0,1)
fig, ax = plt.subplots(figsize=(6,4))
ax.plot(x_all,norm.pdf(x_all,0,1))
ax.fill_between(x_shade,y,0, alpha=0.3, color='b')
ax.set_xlim([-4,4])
ax.set_xlabel('# of Standard Deviations Outside the Mean')
ax.set_yticklabels([])
ax.set_title('Normal Gaussian Curve - Showing ' + racial_group + ' Racial Bias Z Score')
plt.show()
```
### Calculating Each Z Score
In a perfect, equal world, the racial bias score would be 0. A larger z score indicates that the difference between arrests by race is large. A smaller z score indicates that the difference between arrests according to race is small. A negative z score indicates that more white people than black people are being arrested for stops.
```
black_z_score = (black_logit_score - black_logit_score.mean()) / black_logit_score.std()
black_p_val = percent(black_z_score)
cities['black bias percentages'] = black_p_val
black_z_score, black_p_val
plot_normal(black_z_score, 'African American')
latinx_z_score = (latinx_logit_score - latinx_logit_score.mean()) / latinx_logit_score.std()
latinx_p_val = percent(latinx_z_score)
cities['latinx bias percentages'] = latinx_p_val
plot_normal(latinx_z_score, 'Latinx')
asian_z_score = (asian_logit_score - asian_logit_score.mean()) / asian_logit_score.std()
asian_p_val = percent(asian_z_score)
cities['asian bias percentages'] = asian_p_val
plot_normal(asian_z_score, 'Asian')
other_z_score = (other_logit_score - other_logit_score.mean()) / other_logit_score.std()
other_p_val = percent(other_z_score)
cities['other bias percentages'] = other_p_val
plot_normal(other_z_score, 'Other')
cities['black bias score'] = black_z_score
cities['latinx bias score'] = latinx_z_score
cities['asian bias score'] = asian_z_score
cities['other bias score'] = other_z_score
bias_col = cities.loc[: , "black bias score":"other bias score"]
cities['average racial bias score'] = bias_col.mean(axis=1)
cities['max racial bias score'] = bias_col.max(axis=1) #largest number of standard deviations from 0
bias_percent_col = cities.loc[: , "black bias percentages":"other bias percentages"]
cities['average racial bias percentage'] = bias_percent_col.mean(axis=1)
cities['min racial bias percentage'] = bias_percent_col.min(axis=1) #smallest probability that the observed happens under the null
cities
```
### Confidence Intervals
We use a t test to determine whether the difference in racial bias scores per year are due to chance or statistically significant. To do this, we use an independent sample t test to find the 95% confidence interval.
**df = 10, alpha = 0.05, t_table_score = 1.96**
We compare all scores to 0, since we would presume the racial bias scores were calculated by taking the difference of the logit white score and the logit of other racial groups, so in an equal society, we would expect the bias score to be 0. If the calculated value is less than the cutoff of 2.228, then p > 0.05, which means that the differences in means is not due to chance. As the p-value is greater than the alpha value, we cannot conclude that there is a difference between means.
```
#sum the scores in each column
black_bias_sum = sum(cities['black bias score'])
#calculate the means of each group
black_bias_avg = black_bias_sum/4
#use formula
black_bias = black_bias_avg
def mean_confidence_interval(data):
m = sum(data)/4
z = 1.96
sd = data.std()
rn = 2
return (m, m-((1.96*sd)/rn), m+((1.96*sd)/rn))
black_bias_CI = mean_confidence_interval(cities['black bias percentages'])
print('Average and 95% Confidence Interval for African Americans:', black_bias_CI)
#sum the scores in each column
latinx_bias_sum = sum(cities['latinx bias score'])
#calculate the means of each group
latinx_bias_avg = latinx_bias_sum/4
#use formula
latinx_bias = latinx_bias_avg
latinx_bias_CI = mean_confidence_interval(cities['latinx bias percentages'])
print('Average and 95% Confidence Interval for Latinx:', latinx_bias_CI)
#sum the scores in each column
asian_bias_sum = sum(cities['asian bias score'])
#calculate the means of each group
asian_bias_avg = asian_bias_sum/4
#use formula
asian_bias = asian_bias_avg
asian_bias_CI = mean_confidence_interval(cities['asian bias percentages'])
print('Average and 95% Confidence Interval for Asians:', asian_bias_CI)
#sum the scores in each column
other_bias_sum = sum(cities['other bias score'])
#calculate the means of each group
other_bias_avg = other_bias_sum/4
#use formula
other_bias = other_bias_avg
other_bias_CI = mean_confidence_interval(cities['other bias percentages'])
print('Average and 95% Confidence Interval for Other Racial Groups:', other_bias_CI)
def pval(val):
if val < 0.05:
return 'Statistically Significant'
else:
return 'Likely Due to Chance'
def zval(zscore):
if abs(zscore) < 1.96:
return 'Likely Due to Chance'
else:
return 'Statistically Significant'
x_ticks = ("Black", "Latinx", "Asian", "Other")
x_1 = np.arange(1,5)
y_1 = [i[0] for i in [black_bias_CI, latinx_bias_CI, asian_bias_CI, other_bias_CI]]
err_1 = [i[2]-i[0] for i in [black_bias_CI, latinx_bias_CI, asian_bias_CI, other_bias_CI]]
plt.errorbar(x=x_1, y=y_1, yerr=err_1, color="blue", capsize=3,
linestyle="None",
marker="s", markersize=7, mfc="black", mec="black")
plt.xticks(x_1, x_ticks)
plt.ylabel('Average Racial Bias Score')
plt.xlabel('Racial Group')
plt.title('Average Racial Bias Score with Confidence Intervals')
plt.tight_layout()
plt.show()
```
## P-Values of Calculated Racial Bias Z Scores. Are the differences in racial bias score due to chance?
```
print('Black:' , zval(black_bias),','
, 'Latinx:' , zval(latinx_bias), ','
, 'Asian:' , zval(asian_bias), ','
, 'Other:' , zval(other_bias))
```
## Excessive Force Score According to Race
Binomial ~ (n = number of black people arrested, p = probability of being handled with excessive force if they had been white)
What would the likelihood of excessive force look like if the victims had been white?
```
#white excessive force by arrest
p = np.exp(np.log(cities['white_uof']) - np.log(cities['white_drive_stops']))
#black excessive force by arrest
p_black = np.exp(np.log(cities['black_uof']) - np.log(cities['black_drive_stops']))
p_latinx = np.exp(np.log(cities['latinx_uof']) - np.log(cities['latinx_drive_stops']))
p_asian = np.exp(np.log(cities['asian_uof']) - np.log(cities['asian_drive_stops']))
p_other = np.exp(np.log(cities['other_uof']) - np.log(cities['other_drive_stops']))
```
The excessive force score is caluclated using two binomial distibutions :
<br> 1. Binomial(n= number of black drive stops, p= probability of black uof)
<br> 2. Binomial(n= number of white drive stops, p_black= probability of white uof)
<br> We assume that these two binomial distributions are independent. We then compute the following hypothesis test to see if the difference between these distributions is statistically significant:
<br> H_null: p_black = p_white, H_alt: p_black > p_white
<br> Using the test statistic: Z = (p_black - p_white) / sqrt(p_hat * (1-p_hat) * (1/n_1 + 1/n_2)),
p_hat = (n_1 * p_black + n_2 * p_white)/(n_1 + n_2)
<br> This gives us our excessive force score, and allows us to either fail to reject or reject the null hypothesis based on our selected confidence level to see whether the difference in excessive force between white and non-white people is statistically significant.
The larger the z score is, the less likely it is that the probability of excessive force on white and non-white civilians is the same. This indicates a larger disparity between treatment of white vs non-white civilians. A positive z-score means that the probability of excessive force is higher for non-white civilians than white civilians, since it is the number of standard deviations the probability of non-white versus white is from 0.
### Definining helper functions
```
def plot_normal_ex(z_scores, racial_group):
x_all = np.arange(-10, 10, 0.001)
max_z = max(z_scores)
if max_z >=0:
x_shade = np.arange(max_z, max(x_all),0.001)
else:
x_shade = np.arange(min(x_all), max_z, 0.001)
y = norm.pdf(x_shade,0,1)
fig, ax = plt.subplots(figsize=(6,4))
ax.plot(x_all,norm.pdf(x_all,0,1))
ax.fill_between(x_shade,y,0, alpha=0.3, color='b')
ax.set_xlim([-4,4])
ax.set_xlabel('# of Standard Deviations Outside the Mean')
ax.set_yticklabels([])
ax.set_title('Normal Gaussian Curve - Showing ' + racial_group + ' Excessive Force Score')
plt.show()
```
### Black Excessive Force Score
```
#using a binomial, I find the average and standard deviation
#using a binomial, I find the average and standard deviation
black_mean_by_arrest = cities['white_drive_stops'] * p
black_var_by_arrest = cities['black_drive_stops'] * p * (1 - p)
black_std_by_arrest = np.sqrt(black_var_by_arrest)
black_force_score1 = round((cities['black_uof'] - black_mean_by_arrest) / black_std_by_arrest, 2)
#Binomial(n=number of black drive stops, p=probability of black uof)
black_mean_by_arrest2 = cities['black_drive_stops'] * p_black
black_var_by_arrest2 = cities['black_drive_stops'] * p_black * (1 - p_black)
black_std_by_arrest2 = np.sqrt(black_var_by_arrest2)
black_force_score2 = round((cities['black_uof'] - black_mean_by_arrest2) / black_std_by_arrest2, 2)
#excessive force score is calculated using a hypothesis test - significant difference btw two independent binomial dist.
#z score tells us if the difference between the two binomial distributions is statistically significant
p_hat = (black_mean_by_arrest + black_mean_by_arrest2)/(cities['white_drive_stops']+cities['black_drive_stops'])
black_force_score = (p_black-p)/np.sqrt( p_hat* (1-p_hat)* ( (1/cities['white_drive_stops']) + (1/cities['black_drive_stops']) ) )
black_force_percent = [percent(i) for i in np.array(black_force_score)]
black_force_score
plot_normal_ex(black_force_score, 'African American') # so large it does not show on this acis
```
### Latinx Excessive Force Score
```
latin_mean_by_arrest = cities['white_drive_stops'] * p
latin_var_by_arrest = cities['latinx_drive_stops'] * p * (1 - p)
latin_std_by_arrest = np.sqrt(latin_var_by_arrest)
latin_force_score1 = round((cities['latinx_uof'] - latin_mean_by_arrest) / latin_std_by_arrest, 2)
latin_mean_by_arrest2 = cities['latinx_drive_stops'] * p_latinx
latin_var_by_arrest2 = cities['latinx_drive_stops'] * p_latinx * (1 - p_latinx)
latin_std_by_arrest2 = np.sqrt(latin_var_by_arrest2)
latin_force_score2 = round((cities['latinx_uof'] - latin_mean_by_arrest2) / latin_std_by_arrest2, 2)
#excessive force score is calculated using a hypothesis test - significant difference btw two independent binomial dist.
#z score tells us if the difference between the two binomial distributions is statistically significant
p_hat = (latin_mean_by_arrest + latin_mean_by_arrest2)/(cities['white_drive_stops'] + cities['latinx_drive_stops'])
latinx_force_score =(p_latinx-p)/np.sqrt( p_hat* (1-p_hat)* ( (1/cities['white_drive_stops']) + (1/cities['latinx_drive_stops']) ) )
latinx_force_percent = [percent(i) for i in np.array(latinx_force_score)]
latinx_force_score, latinx_force_percent
plot_normal_ex(latinx_force_score, 'Latinx')
```
### Asian Excessive Force Score
```
asian_mean_by_arrest = cities['asian_drive_stops'] * p
asian_var_by_arrest = cities['asian_drive_stops'] * p * (1 - p)
asian_std_by_arrest = np.sqrt(asian_var_by_arrest)
asian_force_score1 = round((cities['asian_uof'] - asian_mean_by_arrest) / asian_std_by_arrest, 2)
asian_mean_by_arrest2 = cities['asian_drive_stops'] * p_asian
asian_var_by_arrest2 = cities['asian_drive_stops'] * p_asian * (1 - p_asian)
asian_std_by_arrest2 = np.sqrt(asian_var_by_arrest2)
asian_force_score2 = round((cities['asian_uof'] - asian_mean_by_arrest2) / asian_std_by_arrest2, 2)
#excessive force score is calculated using a hypothesis test - significant difference btw two independent binomial dist.
#z score tells us if the difference between the two binomial distributions is statistically significant
p_hat = (asian_mean_by_arrest + asian_mean_by_arrest2)/(cities['white_drive_stops']+cities['asian_drive_stops'])
asian_force_score = (p_asian-p)/np.sqrt( p_hat* (1-p_hat)* ( (1/cities['white_drive_stops']) + (1/cities['asian_drive_stops']) ) )
asian_force_percent = [percent(i) for i in np.array(asian_force_score)]
asian_force_score
plot_normal_ex(asian_force_score, 'Asian')
```
### Other Excessive Force Score
```
other_mean_by_arrest = cities['white_drive_stops'] * p
other_var_by_arrest = cities['other_drive_stops'] * p * (1 - p)
other_std_by_arrest = np.sqrt(other_var_by_arrest)
other_force_score1 = round((cities['other_uof'] - other_mean_by_arrest) / other_std_by_arrest, 2)
other_mean_by_arrest2 = cities['other_drive_stops'] * p_other
other_var_by_arrest2 = cities['other_drive_stops'] * p_other * (1 - p_other)
other_std_by_arrest2 = np.sqrt(other_var_by_arrest2)
other_force_score2 = round((cities['other_uof'] - other_mean_by_arrest2) / other_std_by_arrest2, 2)
#excessive force score is calculated using a hypothesis test - significant difference btw two independent binomial dist.
#z score tells us if the difference between the two binomial distributions is statistically significant
p_hat = (other_mean_by_arrest + other_mean_by_arrest2)/(cities['white_drive_stops']+ cities['other_drive_stops'])
other_force_score = (p_other-p)/np.sqrt( p_hat* (1-p_hat)* ( (1/cities['white_drive_stops']) + (1/cities['other_drive_stops']) ) )
other_force_percent = [percent(i) for i in np.array(other_force_score)]
other_force_percent
plot_normal_ex(other_force_score, 'Other')
```
## Excessive Force Score
```
all = [black_force_score, latinx_force_score, asian_force_score, other_force_score]
avg_excessive_force_score = (sum(all)/len(all))/np.sqrt(4*(.5)**2) # taking the weighted average of all z scores and then normalizing by the variance
avg_force_percent = (sum(black_force_percent) + sum(latinx_force_percent) + sum(asian_force_percent) + sum(other_force_percent))/len(all)
cities['black excessive force score'] = black_force_score
cities['latinx excessive force score'] = latinx_force_score
cities['asian excessive force score'] = asian_force_score
cities['other excessive force score'] = other_force_score
cities['average excessive force score'] = avg_excessive_force_score
cities['black excessive force percent'] = black_force_percent
cities['latinx excessive force percent'] = latinx_force_percent
cities['asian excessive force percent'] = asian_force_percent
cities['other excessive force percent'] = other_force_percent
force_col = cities.loc[: , "black excessive force score":"other excessive force score"]
cities['average excessive force score'] = force_col.mean(axis=1)
cities['max excessive force score'] = force_col.max(axis=1)
force_col_percent = cities.loc[: , "black excessive force percent":"other excessive force percent"]
cities['average force percent'] = force_col_percent.mean(axis=1)
cities['min force percent'] = force_col_percent.min(axis=1)
plot_normal_ex(avg_excessive_force_score, 'Average')
cities
```
## Confidence Intervals
The exceessive force score is calculated using a z-test. This z-score tells us whether the excessive force is statistically significant or not. Using a one-tailed test at the 95% confidence level, we can compare the z-score to z = 2.086. If z > 2.086, we reject the null hypothesis that the difference in binomial distributions is due to chance, else we fail to reject the null hypothesis that the difference is statistically significant.
```
def pval(val):
if val < 0.05:
return 'Statistically Significant'
else:
return 'Likely Due to Chance'
def zval(zscore):
if zscore < 2.086:
return 'Likely Due to Chance'
else:
return 'Statistically Significant'
#sum the scores in each column
black_ex_sum = sum(cities['black excessive force score'])
#calculate the means of each group
black_ex_avg = black_ex_sum/4
#sum the scores in each column
latinx_ex_sum = sum(cities['latinx excessive force score'])
#calculate the means of each group
latinx_ex_avg = latinx_ex_sum/4
#sum the scores in each column
asian_ex_sum = sum(cities['asian excessive force score'])
#calculate the means of each group
asian_ex_avg = asian_ex_sum/4
#sum the scores in each column
other_ex_sum = sum(cities['other excessive force score'])
#calculate the means of each group
other_ex_avg = other_ex_sum/4
#using the average z-score over all years
print('Black:' , zval(black_ex_avg),','
, 'Latinx:' , zval(latinx_ex_avg), ','
, 'Asian:' , zval(asian_ex_avg), ','
, 'Other:' , zval(other_ex_avg))
black_force_CI = mean_confidence_interval(cities['black excessive force score'])
print('Average and 95% Confidence Interval for African Americans:', black_force_CI)
latinx_force_CI = mean_confidence_interval(cities['latinx excessive force score'])
print('Average and 95% Confidence Interval for Latinx:', latinx_force_CI)
latinx_force_CI[2]
asian_force_CI = mean_confidence_interval(cities['asian excessive force score'])
print('Average and 95% Confidence Interval for Asians:', asian_force_CI)
other_force_CI = mean_confidence_interval(cities['other excessive force score'])
print('Average and 95% Confidence Interval for Other Racial Groups:', other_force_CI)
x_ticks = ("Black", "Latinx", "Asian", "Other")
x_1 = np.arange(1,5)
y_1 = [black_ex_avg, latinx_ex_avg, asian_ex_avg, other_ex_avg]
err_1 = [i[2]-i[0] for i in [black_force_CI, latinx_force_CI, asian_force_CI, other_force_CI]]
plt.errorbar(x=x_1, y=y_1, yerr=err_1, color="blue", capsize=3,
linestyle="None",
marker="s", markersize=7, mfc="black", mec="black")
plt.xticks(x_1, x_ticks)
plt.ylabel('Average Excessive Force Score')
plt.xlabel('Racial Group')
plt.title('Average Excessive Force Score with Confidence Intervals')
plt.tight_layout()
plt.show()
```
## Diagnostic Score
Finally, we calculate the diagnostic score. The racial bias score was a z score that represented whether the difference between white and non-white traffic stops was statistically significant. We took the max over all non-white racial groups in a given year to get the max z score. The excessive force score was also a z score that represented whether the difference between the probability of excessive force being used on white vs non white civilians was statistically significant. Again, we took the max over all non-white racial groups to get the max excessive force score for a given year. To calculate the diagnostic score, we first take the average of the p-values of the max racial bias scores and max excessive force scores, because the average of two z-scores alone is not a z-score. We then convert this averaged percentiles to z-scores, to see how many deviations away from 0 the overall racial bias is in a police department.
```
def z_score(p_val):
return norm.ppf(1-p_val)
diagnostic_percentile = (cities['min racial bias percentage'] + cities['min force percent'])/2 #taking the highest racial bias/excessive force score
diagnostic_score = z_score(diagnostic_percentile)
cities['diagnostic score'] = diagnostic_score
cities['diagnostic percentile'] = diagnostic_percentile
cities
cities.to_csv('nyc_bias_score.csv')
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import math
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.special import ndtr
nyc = pd.read_csv('../data_clean/nyc.csv')
cities = nyc
cities = cities.loc[: , "city":"other_uof"]
cities
black_pop = cities['black_pct'] * cities['total_pop']
white_pop = cities['white_pct'] * cities['total_pop']
latinx_pop = cities['latinx_pct']* cities['total_pop']
asian_pop = cities['asian_pct']* cities['total_pop']
other_pop = cities['other_pct']* cities['total_pop']
#ratio of stops according to racial makeup of city
pct_black_stops_to_pop = cities['black_drive_stops']/black_pop
pct_white_stops_to_pop = cities['white_drive_stops']/white_pop
pct_latinx_stops_to_pop = cities['latinx_drive_stops']/latinx_pop
pct_asian_stops_to_pop = cities['asian_drive_stops']/asian_pop
pct_other_stops_to_pop = cities['other_drive_stops']/other_pop
logit_white = np.log(pct_white_stops_to_pop/(1-pct_white_stops_to_pop))
logit_black = np.log(pct_black_stops_to_pop/(1-pct_black_stops_to_pop))
black_logit_score = round((logit_black - logit_white), 3)
#cities['black bias percentages'] = np.exp(black_logit_score)/(1+np.exp(black_logit_score))
logit_latinx = np.log(pct_latinx_stops_to_pop/(1-pct_latinx_stops_to_pop))
latinx_logit_score = round((logit_latinx - logit_white), 3)
#cities['latinx bias percentages'] = np.exp(latinx_logit_score)/(1+np.exp(latinx_logit_score))
logit_asian = np.log(pct_asian_stops_to_pop/(1-pct_asian_stops_to_pop))
asian_logit_score = round((logit_asian - logit_white), 3)
#cities['asian bias percentages'] = np.exp(asian_logit_score)/(1+np.exp(asian_logit_score))
logit_other = np.log(pct_other_stops_to_pop/(1-pct_other_stops_to_pop))
other_logit_score = round((logit_other - logit_white), 3)
#cities['other bias percentages'] = np.exp(other_logit_score)/(1+np.exp(other_logit_score))
#convert all standardized scores into percentages
def percent(z_score_array):
return 1- norm.cdf(abs(z_score_array)) #returns p-value
def plot_normal(z_scores, racial_group):
x_all = np.arange(-10, 10, 0.001)
max_z = max(z_scores)
if max_z >=0:
x_shade = np.arange(max_z, max(x_all),0.001)
else:
x_shade = np.arange(min(x_all), max_z, 0.001)
y = norm.pdf(x_shade,0,1)
fig, ax = plt.subplots(figsize=(6,4))
ax.plot(x_all,norm.pdf(x_all,0,1))
ax.fill_between(x_shade,y,0, alpha=0.3, color='b')
ax.set_xlim([-4,4])
ax.set_xlabel('# of Standard Deviations Outside the Mean')
ax.set_yticklabels([])
ax.set_title('Normal Gaussian Curve - Showing ' + racial_group + ' Racial Bias Z Score')
plt.show()
black_z_score = (black_logit_score - black_logit_score.mean()) / black_logit_score.std()
black_p_val = percent(black_z_score)
cities['black bias percentages'] = black_p_val
black_z_score, black_p_val
plot_normal(black_z_score, 'African American')
latinx_z_score = (latinx_logit_score - latinx_logit_score.mean()) / latinx_logit_score.std()
latinx_p_val = percent(latinx_z_score)
cities['latinx bias percentages'] = latinx_p_val
plot_normal(latinx_z_score, 'Latinx')
asian_z_score = (asian_logit_score - asian_logit_score.mean()) / asian_logit_score.std()
asian_p_val = percent(asian_z_score)
cities['asian bias percentages'] = asian_p_val
plot_normal(asian_z_score, 'Asian')
other_z_score = (other_logit_score - other_logit_score.mean()) / other_logit_score.std()
other_p_val = percent(other_z_score)
cities['other bias percentages'] = other_p_val
plot_normal(other_z_score, 'Other')
cities['black bias score'] = black_z_score
cities['latinx bias score'] = latinx_z_score
cities['asian bias score'] = asian_z_score
cities['other bias score'] = other_z_score
bias_col = cities.loc[: , "black bias score":"other bias score"]
cities['average racial bias score'] = bias_col.mean(axis=1)
cities['max racial bias score'] = bias_col.max(axis=1) #largest number of standard deviations from 0
bias_percent_col = cities.loc[: , "black bias percentages":"other bias percentages"]
cities['average racial bias percentage'] = bias_percent_col.mean(axis=1)
cities['min racial bias percentage'] = bias_percent_col.min(axis=1) #smallest probability that the observed happens under the null
cities
#sum the scores in each column
black_bias_sum = sum(cities['black bias score'])
#calculate the means of each group
black_bias_avg = black_bias_sum/4
#use formula
black_bias = black_bias_avg
def mean_confidence_interval(data):
m = sum(data)/4
z = 1.96
sd = data.std()
rn = 2
return (m, m-((1.96*sd)/rn), m+((1.96*sd)/rn))
black_bias_CI = mean_confidence_interval(cities['black bias percentages'])
print('Average and 95% Confidence Interval for African Americans:', black_bias_CI)
#sum the scores in each column
latinx_bias_sum = sum(cities['latinx bias score'])
#calculate the means of each group
latinx_bias_avg = latinx_bias_sum/4
#use formula
latinx_bias = latinx_bias_avg
latinx_bias_CI = mean_confidence_interval(cities['latinx bias percentages'])
print('Average and 95% Confidence Interval for Latinx:', latinx_bias_CI)
#sum the scores in each column
asian_bias_sum = sum(cities['asian bias score'])
#calculate the means of each group
asian_bias_avg = asian_bias_sum/4
#use formula
asian_bias = asian_bias_avg
asian_bias_CI = mean_confidence_interval(cities['asian bias percentages'])
print('Average and 95% Confidence Interval for Asians:', asian_bias_CI)
#sum the scores in each column
other_bias_sum = sum(cities['other bias score'])
#calculate the means of each group
other_bias_avg = other_bias_sum/4
#use formula
other_bias = other_bias_avg
other_bias_CI = mean_confidence_interval(cities['other bias percentages'])
print('Average and 95% Confidence Interval for Other Racial Groups:', other_bias_CI)
def pval(val):
if val < 0.05:
return 'Statistically Significant'
else:
return 'Likely Due to Chance'
def zval(zscore):
if abs(zscore) < 1.96:
return 'Likely Due to Chance'
else:
return 'Statistically Significant'
x_ticks = ("Black", "Latinx", "Asian", "Other")
x_1 = np.arange(1,5)
y_1 = [i[0] for i in [black_bias_CI, latinx_bias_CI, asian_bias_CI, other_bias_CI]]
err_1 = [i[2]-i[0] for i in [black_bias_CI, latinx_bias_CI, asian_bias_CI, other_bias_CI]]
plt.errorbar(x=x_1, y=y_1, yerr=err_1, color="blue", capsize=3,
linestyle="None",
marker="s", markersize=7, mfc="black", mec="black")
plt.xticks(x_1, x_ticks)
plt.ylabel('Average Racial Bias Score')
plt.xlabel('Racial Group')
plt.title('Average Racial Bias Score with Confidence Intervals')
plt.tight_layout()
plt.show()
print('Black:' , zval(black_bias),','
, 'Latinx:' , zval(latinx_bias), ','
, 'Asian:' , zval(asian_bias), ','
, 'Other:' , zval(other_bias))
#white excessive force by arrest
p = np.exp(np.log(cities['white_uof']) - np.log(cities['white_drive_stops']))
#black excessive force by arrest
p_black = np.exp(np.log(cities['black_uof']) - np.log(cities['black_drive_stops']))
p_latinx = np.exp(np.log(cities['latinx_uof']) - np.log(cities['latinx_drive_stops']))
p_asian = np.exp(np.log(cities['asian_uof']) - np.log(cities['asian_drive_stops']))
p_other = np.exp(np.log(cities['other_uof']) - np.log(cities['other_drive_stops']))
def plot_normal_ex(z_scores, racial_group):
x_all = np.arange(-10, 10, 0.001)
max_z = max(z_scores)
if max_z >=0:
x_shade = np.arange(max_z, max(x_all),0.001)
else:
x_shade = np.arange(min(x_all), max_z, 0.001)
y = norm.pdf(x_shade,0,1)
fig, ax = plt.subplots(figsize=(6,4))
ax.plot(x_all,norm.pdf(x_all,0,1))
ax.fill_between(x_shade,y,0, alpha=0.3, color='b')
ax.set_xlim([-4,4])
ax.set_xlabel('# of Standard Deviations Outside the Mean')
ax.set_yticklabels([])
ax.set_title('Normal Gaussian Curve - Showing ' + racial_group + ' Excessive Force Score')
plt.show()
#using a binomial, I find the average and standard deviation
#using a binomial, I find the average and standard deviation
black_mean_by_arrest = cities['white_drive_stops'] * p
black_var_by_arrest = cities['black_drive_stops'] * p * (1 - p)
black_std_by_arrest = np.sqrt(black_var_by_arrest)
black_force_score1 = round((cities['black_uof'] - black_mean_by_arrest) / black_std_by_arrest, 2)
#Binomial(n=number of black drive stops, p=probability of black uof)
black_mean_by_arrest2 = cities['black_drive_stops'] * p_black
black_var_by_arrest2 = cities['black_drive_stops'] * p_black * (1 - p_black)
black_std_by_arrest2 = np.sqrt(black_var_by_arrest2)
black_force_score2 = round((cities['black_uof'] - black_mean_by_arrest2) / black_std_by_arrest2, 2)
#excessive force score is calculated using a hypothesis test - significant difference btw two independent binomial dist.
#z score tells us if the difference between the two binomial distributions is statistically significant
p_hat = (black_mean_by_arrest + black_mean_by_arrest2)/(cities['white_drive_stops']+cities['black_drive_stops'])
black_force_score = (p_black-p)/np.sqrt( p_hat* (1-p_hat)* ( (1/cities['white_drive_stops']) + (1/cities['black_drive_stops']) ) )
black_force_percent = [percent(i) for i in np.array(black_force_score)]
black_force_score
plot_normal_ex(black_force_score, 'African American') # so large it does not show on this acis
latin_mean_by_arrest = cities['white_drive_stops'] * p
latin_var_by_arrest = cities['latinx_drive_stops'] * p * (1 - p)
latin_std_by_arrest = np.sqrt(latin_var_by_arrest)
latin_force_score1 = round((cities['latinx_uof'] - latin_mean_by_arrest) / latin_std_by_arrest, 2)
latin_mean_by_arrest2 = cities['latinx_drive_stops'] * p_latinx
latin_var_by_arrest2 = cities['latinx_drive_stops'] * p_latinx * (1 - p_latinx)
latin_std_by_arrest2 = np.sqrt(latin_var_by_arrest2)
latin_force_score2 = round((cities['latinx_uof'] - latin_mean_by_arrest2) / latin_std_by_arrest2, 2)
#excessive force score is calculated using a hypothesis test - significant difference btw two independent binomial dist.
#z score tells us if the difference between the two binomial distributions is statistically significant
p_hat = (latin_mean_by_arrest + latin_mean_by_arrest2)/(cities['white_drive_stops'] + cities['latinx_drive_stops'])
latinx_force_score =(p_latinx-p)/np.sqrt( p_hat* (1-p_hat)* ( (1/cities['white_drive_stops']) + (1/cities['latinx_drive_stops']) ) )
latinx_force_percent = [percent(i) for i in np.array(latinx_force_score)]
latinx_force_score, latinx_force_percent
plot_normal_ex(latinx_force_score, 'Latinx')
asian_mean_by_arrest = cities['asian_drive_stops'] * p
asian_var_by_arrest = cities['asian_drive_stops'] * p * (1 - p)
asian_std_by_arrest = np.sqrt(asian_var_by_arrest)
asian_force_score1 = round((cities['asian_uof'] - asian_mean_by_arrest) / asian_std_by_arrest, 2)
asian_mean_by_arrest2 = cities['asian_drive_stops'] * p_asian
asian_var_by_arrest2 = cities['asian_drive_stops'] * p_asian * (1 - p_asian)
asian_std_by_arrest2 = np.sqrt(asian_var_by_arrest2)
asian_force_score2 = round((cities['asian_uof'] - asian_mean_by_arrest2) / asian_std_by_arrest2, 2)
#excessive force score is calculated using a hypothesis test - significant difference btw two independent binomial dist.
#z score tells us if the difference between the two binomial distributions is statistically significant
p_hat = (asian_mean_by_arrest + asian_mean_by_arrest2)/(cities['white_drive_stops']+cities['asian_drive_stops'])
asian_force_score = (p_asian-p)/np.sqrt( p_hat* (1-p_hat)* ( (1/cities['white_drive_stops']) + (1/cities['asian_drive_stops']) ) )
asian_force_percent = [percent(i) for i in np.array(asian_force_score)]
asian_force_score
plot_normal_ex(asian_force_score, 'Asian')
other_mean_by_arrest = cities['white_drive_stops'] * p
other_var_by_arrest = cities['other_drive_stops'] * p * (1 - p)
other_std_by_arrest = np.sqrt(other_var_by_arrest)
other_force_score1 = round((cities['other_uof'] - other_mean_by_arrest) / other_std_by_arrest, 2)
other_mean_by_arrest2 = cities['other_drive_stops'] * p_other
other_var_by_arrest2 = cities['other_drive_stops'] * p_other * (1 - p_other)
other_std_by_arrest2 = np.sqrt(other_var_by_arrest2)
other_force_score2 = round((cities['other_uof'] - other_mean_by_arrest2) / other_std_by_arrest2, 2)
#excessive force score is calculated using a hypothesis test - significant difference btw two independent binomial dist.
#z score tells us if the difference between the two binomial distributions is statistically significant
p_hat = (other_mean_by_arrest + other_mean_by_arrest2)/(cities['white_drive_stops']+ cities['other_drive_stops'])
other_force_score = (p_other-p)/np.sqrt( p_hat* (1-p_hat)* ( (1/cities['white_drive_stops']) + (1/cities['other_drive_stops']) ) )
other_force_percent = [percent(i) for i in np.array(other_force_score)]
other_force_percent
plot_normal_ex(other_force_score, 'Other')
all = [black_force_score, latinx_force_score, asian_force_score, other_force_score]
avg_excessive_force_score = (sum(all)/len(all))/np.sqrt(4*(.5)**2) # taking the weighted average of all z scores and then normalizing by the variance
avg_force_percent = (sum(black_force_percent) + sum(latinx_force_percent) + sum(asian_force_percent) + sum(other_force_percent))/len(all)
cities['black excessive force score'] = black_force_score
cities['latinx excessive force score'] = latinx_force_score
cities['asian excessive force score'] = asian_force_score
cities['other excessive force score'] = other_force_score
cities['average excessive force score'] = avg_excessive_force_score
cities['black excessive force percent'] = black_force_percent
cities['latinx excessive force percent'] = latinx_force_percent
cities['asian excessive force percent'] = asian_force_percent
cities['other excessive force percent'] = other_force_percent
force_col = cities.loc[: , "black excessive force score":"other excessive force score"]
cities['average excessive force score'] = force_col.mean(axis=1)
cities['max excessive force score'] = force_col.max(axis=1)
force_col_percent = cities.loc[: , "black excessive force percent":"other excessive force percent"]
cities['average force percent'] = force_col_percent.mean(axis=1)
cities['min force percent'] = force_col_percent.min(axis=1)
plot_normal_ex(avg_excessive_force_score, 'Average')
cities
def pval(val):
if val < 0.05:
return 'Statistically Significant'
else:
return 'Likely Due to Chance'
def zval(zscore):
if zscore < 2.086:
return 'Likely Due to Chance'
else:
return 'Statistically Significant'
#sum the scores in each column
black_ex_sum = sum(cities['black excessive force score'])
#calculate the means of each group
black_ex_avg = black_ex_sum/4
#sum the scores in each column
latinx_ex_sum = sum(cities['latinx excessive force score'])
#calculate the means of each group
latinx_ex_avg = latinx_ex_sum/4
#sum the scores in each column
asian_ex_sum = sum(cities['asian excessive force score'])
#calculate the means of each group
asian_ex_avg = asian_ex_sum/4
#sum the scores in each column
other_ex_sum = sum(cities['other excessive force score'])
#calculate the means of each group
other_ex_avg = other_ex_sum/4
#using the average z-score over all years
print('Black:' , zval(black_ex_avg),','
, 'Latinx:' , zval(latinx_ex_avg), ','
, 'Asian:' , zval(asian_ex_avg), ','
, 'Other:' , zval(other_ex_avg))
black_force_CI = mean_confidence_interval(cities['black excessive force score'])
print('Average and 95% Confidence Interval for African Americans:', black_force_CI)
latinx_force_CI = mean_confidence_interval(cities['latinx excessive force score'])
print('Average and 95% Confidence Interval for Latinx:', latinx_force_CI)
latinx_force_CI[2]
asian_force_CI = mean_confidence_interval(cities['asian excessive force score'])
print('Average and 95% Confidence Interval for Asians:', asian_force_CI)
other_force_CI = mean_confidence_interval(cities['other excessive force score'])
print('Average and 95% Confidence Interval for Other Racial Groups:', other_force_CI)
x_ticks = ("Black", "Latinx", "Asian", "Other")
x_1 = np.arange(1,5)
y_1 = [black_ex_avg, latinx_ex_avg, asian_ex_avg, other_ex_avg]
err_1 = [i[2]-i[0] for i in [black_force_CI, latinx_force_CI, asian_force_CI, other_force_CI]]
plt.errorbar(x=x_1, y=y_1, yerr=err_1, color="blue", capsize=3,
linestyle="None",
marker="s", markersize=7, mfc="black", mec="black")
plt.xticks(x_1, x_ticks)
plt.ylabel('Average Excessive Force Score')
plt.xlabel('Racial Group')
plt.title('Average Excessive Force Score with Confidence Intervals')
plt.tight_layout()
plt.show()
def z_score(p_val):
return norm.ppf(1-p_val)
diagnostic_percentile = (cities['min racial bias percentage'] + cities['min force percent'])/2 #taking the highest racial bias/excessive force score
diagnostic_score = z_score(diagnostic_percentile)
cities['diagnostic score'] = diagnostic_score
cities['diagnostic percentile'] = diagnostic_percentile
cities
cities.to_csv('nyc_bias_score.csv')
| 0.49292 | 0.882833 |
```
!wget https://www.dropbox.com/s/0pigmmmynbf9xwq/dataset1.zip
!unzip dataset1.zip
dir_data = "/content/dataset1"
dir_seg = dir_data + "/annotations_prepped_train/"
dir_img = dir_data + "/images_prepped_train/"
import glob, os
all_img_paths = glob.glob(os.path.join(dir_img, '*.png'))
all_img_paths[:5]
import glob, os
all_mask_paths = glob.glob(os.path.join(dir_seg, '*.png'))
all_mask_paths[:5]
all_img_paths[0].split('/')[4]
x = []
y = []
count = 0
import cv2
from scipy import ndimage
for i in range(len(all_img_paths)):
img = cv2.imread(all_img_paths[i])
img = cv2.resize(img,(224,224))
mask_path = dir_seg+all_img_paths[i].split('/')[4]
img_mask = ndimage.imread(mask_path)
img_mask = cv2.resize(img_mask,(224,224))
x.append(img)
y.append(img_mask)
if(i%100==0):
print(i)
import numpy as np
np.array(y).shape
np.array(x).shape
x = np.array(x)
y = np.array(y)
y2 = np.where(y==8,1,0)
y2.shape
y.shape
import matplotlib.pyplot as plt
%matplotlib inline
plt.subplot(221)
plt.imshow(x[0])
plt.axis('off')
plt.title('Original image')
plt.grid('off')
plt.subplot(222)
plt.imshow(y2[0])
plt.axis('off')
plt.title('Masked image')
plt.grid('off')
plt.subplot(223)
plt.imshow(x[2])
plt.axis('off')
plt.grid('off')
plt.subplot(224)
plt.imshow(y2[2])
plt.axis('off')
plt.grid('off')
plt.show()
plt.hist(y[0,100:,:50].flatten())
x = np.array(x)
y2 = np.array(y2)
y2 = y2.reshape(y2.shape[0],y2.shape[1],y2.shape[2],1)
print(x.shape, y2.shape)
x = x/255
print(np.max(x))
from keras.applications.vgg16 import VGG16 as PTModel
base_pretrained_model = PTModel(input_shape = (224,224,3), include_top = False, weights = 'imagenet')
base_pretrained_model.trainable = False
base_pretrained_model.summary()
from keras.layers import Input, Conv2D, concatenate, UpSampling2D, BatchNormalization, Activation, Cropping2D, ZeroPadding2D
from keras.layers import Input, merge, Conv2D, MaxPooling2D,UpSampling2D, Dropout, Cropping2D, merge, concatenate
from keras.optimizers import Adam
from keras.callbacks import ModelCheckpoint, LearningRateScheduler
from keras import backend as K
from keras.models import Model
conv1 = Model(inputs=base_pretrained_model.input,outputs=base_pretrained_model.get_layer('block1_conv2').output).output
conv2 = Model(inputs=base_pretrained_model.input,outputs=base_pretrained_model.get_layer('block2_conv2').output).output
conv3 = Model(inputs=base_pretrained_model.input,outputs=base_pretrained_model.get_layer('block3_conv3').output).output
conv4 = Model(inputs=base_pretrained_model.input,outputs=base_pretrained_model.get_layer('block4_conv3').output).output
drop4 = Dropout(0.5)(conv4)
conv5 = Model(inputs=base_pretrained_model.input,outputs=base_pretrained_model.get_layer('block5_conv3').output).output
drop5 = Dropout(0.5)(conv5)
up6 = Conv2D(512, 2, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(UpSampling2D(size =(2,2))(drop5))
merge6 = concatenate([drop4,up6], axis = 3)
conv6 = Conv2D(512, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(merge6)
conv6 = Conv2D(512, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(conv6)
conv6 = BatchNormalization()(conv6)
up7 = Conv2D(256, 2, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(UpSampling2D(size =(2,2))(conv6))
merge7 = concatenate([conv3,up7], axis = 3)
conv7 = Conv2D(256, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(merge7)
conv7 = Conv2D(256, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(conv7)
conv7 = BatchNormalization()(conv7)
up8 = Conv2D(128, 2, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(UpSampling2D(size =(2,2))(conv7))
merge8 = concatenate([conv2,up8],axis = 3)
conv8 = Conv2D(128, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(merge8)
conv8 = Conv2D(128, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(conv8)
conv8 = BatchNormalization()(conv8)
up9 = Conv2D(64, 2, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(UpSampling2D(size =(2,2))(conv8))
merge9 = concatenate([conv1,up9], axis = 3)
conv9 = Conv2D(64, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(merge9)
conv9 = Conv2D(64, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(conv9)
conv9 = Conv2D(64, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(conv9)
conv9 = BatchNormalization()(conv9)
conv10 = Conv2D(1, 1, activation = 'sigmoid')(conv9)
model = Model(input = base_pretrained_model.input, output = conv10)
model.summary()
for layer in model.layers[:18]:
layer.trainable = False
model.compile(optimizer=Adam(1e-3, decay = 1e-6),
loss='binary_crossentropy', metrics = ['accuracy'])
np.max(x)
np.sum(y2)
history = model.fit(x,y2,epochs=15,batch_size=1,validation_split=0.1)
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
acc_values = history_dict['acc']
val_acc_values = history_dict['val_acc']
epochs = range(1, len(val_loss_values) + 1)
plt.subplot(211)
plt.plot(epochs, history.history['loss'], 'ro', label='Training loss')
plt.plot(epochs, val_loss_values, 'b', label='Test loss')
plt.title('Training and test loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.grid('off')
plt.show()
plt.subplot(212)
plt.plot(epochs, history.history['acc'], 'ro', label='Training accuracy')
plt.plot(epochs, val_acc_values, 'b', label='Test accuracy')
plt.title('Training and test accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.gca().set_yticklabels(['{:.0f}%'.format(x*100) for x in plt.gca().get_yticks()])
plt.legend()
plt.grid('off')
plt.show()
y_pred = model.predict(x[-2:].reshape(2,224,224,3))
y_predi = np.argmax(y_pred, axis=3)
y_testi = np.argmax(y2[-2:].reshape(2,224,224,1), axis=3)
#np.mean(y_predi == y_testi)
y_pred.shape
plt.imshow(y_pred[-1,:,:,0])
np.sum(y_testi)
np.mean(y_predi == y_testi)
import tensorflow as tf
from keras.backend.tensorflow_backend import set_session
import keras, sys, time, warnings
from keras.models import *
from keras.layers import *
import pandas as pd
y2.shape
import matplotlib.pyplot as plt
%matplotlib inline
plt.subplot(231)
plt.imshow(x[-1])
plt.axis('off')
plt.title('Original image')
plt.grid('off')
plt.subplot(232)
plt.imshow(y2[-1,:,:,0])
plt.axis('off')
plt.title('Actual mask image')
plt.grid('off')
plt.subplot(233)
plt.imshow(y_pred[-1,:,:,0])
plt.axis('off')
plt.title('Predicted mask image')
plt.grid('off')
plt.subplot(234)
plt.imshow(x[-2])
plt.axis('off')
plt.grid('off')
plt.subplot(235)
plt.imshow(y2[-2,:,:,0])
plt.axis('off')
plt.grid('off')
plt.subplot(236)
plt.imshow(y_pred[-2,:,:,0])
plt.axis('off')
plt.grid('off')
plt.show()
from keras.utils import plot_model
plot_model(model, show_shapes=True, show_layer_names=True, to_file='model.png')
from IPython.display import Image
Image(retina=True, filename='model.png')
```
|
github_jupyter
|
!wget https://www.dropbox.com/s/0pigmmmynbf9xwq/dataset1.zip
!unzip dataset1.zip
dir_data = "/content/dataset1"
dir_seg = dir_data + "/annotations_prepped_train/"
dir_img = dir_data + "/images_prepped_train/"
import glob, os
all_img_paths = glob.glob(os.path.join(dir_img, '*.png'))
all_img_paths[:5]
import glob, os
all_mask_paths = glob.glob(os.path.join(dir_seg, '*.png'))
all_mask_paths[:5]
all_img_paths[0].split('/')[4]
x = []
y = []
count = 0
import cv2
from scipy import ndimage
for i in range(len(all_img_paths)):
img = cv2.imread(all_img_paths[i])
img = cv2.resize(img,(224,224))
mask_path = dir_seg+all_img_paths[i].split('/')[4]
img_mask = ndimage.imread(mask_path)
img_mask = cv2.resize(img_mask,(224,224))
x.append(img)
y.append(img_mask)
if(i%100==0):
print(i)
import numpy as np
np.array(y).shape
np.array(x).shape
x = np.array(x)
y = np.array(y)
y2 = np.where(y==8,1,0)
y2.shape
y.shape
import matplotlib.pyplot as plt
%matplotlib inline
plt.subplot(221)
plt.imshow(x[0])
plt.axis('off')
plt.title('Original image')
plt.grid('off')
plt.subplot(222)
plt.imshow(y2[0])
plt.axis('off')
plt.title('Masked image')
plt.grid('off')
plt.subplot(223)
plt.imshow(x[2])
plt.axis('off')
plt.grid('off')
plt.subplot(224)
plt.imshow(y2[2])
plt.axis('off')
plt.grid('off')
plt.show()
plt.hist(y[0,100:,:50].flatten())
x = np.array(x)
y2 = np.array(y2)
y2 = y2.reshape(y2.shape[0],y2.shape[1],y2.shape[2],1)
print(x.shape, y2.shape)
x = x/255
print(np.max(x))
from keras.applications.vgg16 import VGG16 as PTModel
base_pretrained_model = PTModel(input_shape = (224,224,3), include_top = False, weights = 'imagenet')
base_pretrained_model.trainable = False
base_pretrained_model.summary()
from keras.layers import Input, Conv2D, concatenate, UpSampling2D, BatchNormalization, Activation, Cropping2D, ZeroPadding2D
from keras.layers import Input, merge, Conv2D, MaxPooling2D,UpSampling2D, Dropout, Cropping2D, merge, concatenate
from keras.optimizers import Adam
from keras.callbacks import ModelCheckpoint, LearningRateScheduler
from keras import backend as K
from keras.models import Model
conv1 = Model(inputs=base_pretrained_model.input,outputs=base_pretrained_model.get_layer('block1_conv2').output).output
conv2 = Model(inputs=base_pretrained_model.input,outputs=base_pretrained_model.get_layer('block2_conv2').output).output
conv3 = Model(inputs=base_pretrained_model.input,outputs=base_pretrained_model.get_layer('block3_conv3').output).output
conv4 = Model(inputs=base_pretrained_model.input,outputs=base_pretrained_model.get_layer('block4_conv3').output).output
drop4 = Dropout(0.5)(conv4)
conv5 = Model(inputs=base_pretrained_model.input,outputs=base_pretrained_model.get_layer('block5_conv3').output).output
drop5 = Dropout(0.5)(conv5)
up6 = Conv2D(512, 2, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(UpSampling2D(size =(2,2))(drop5))
merge6 = concatenate([drop4,up6], axis = 3)
conv6 = Conv2D(512, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(merge6)
conv6 = Conv2D(512, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(conv6)
conv6 = BatchNormalization()(conv6)
up7 = Conv2D(256, 2, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(UpSampling2D(size =(2,2))(conv6))
merge7 = concatenate([conv3,up7], axis = 3)
conv7 = Conv2D(256, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(merge7)
conv7 = Conv2D(256, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(conv7)
conv7 = BatchNormalization()(conv7)
up8 = Conv2D(128, 2, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(UpSampling2D(size =(2,2))(conv7))
merge8 = concatenate([conv2,up8],axis = 3)
conv8 = Conv2D(128, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(merge8)
conv8 = Conv2D(128, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(conv8)
conv8 = BatchNormalization()(conv8)
up9 = Conv2D(64, 2, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(UpSampling2D(size =(2,2))(conv8))
merge9 = concatenate([conv1,up9], axis = 3)
conv9 = Conv2D(64, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(merge9)
conv9 = Conv2D(64, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(conv9)
conv9 = Conv2D(64, 3, activation = 'relu', padding = 'same',kernel_initializer = 'he_normal')(conv9)
conv9 = BatchNormalization()(conv9)
conv10 = Conv2D(1, 1, activation = 'sigmoid')(conv9)
model = Model(input = base_pretrained_model.input, output = conv10)
model.summary()
for layer in model.layers[:18]:
layer.trainable = False
model.compile(optimizer=Adam(1e-3, decay = 1e-6),
loss='binary_crossentropy', metrics = ['accuracy'])
np.max(x)
np.sum(y2)
history = model.fit(x,y2,epochs=15,batch_size=1,validation_split=0.1)
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
acc_values = history_dict['acc']
val_acc_values = history_dict['val_acc']
epochs = range(1, len(val_loss_values) + 1)
plt.subplot(211)
plt.plot(epochs, history.history['loss'], 'ro', label='Training loss')
plt.plot(epochs, val_loss_values, 'b', label='Test loss')
plt.title('Training and test loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.grid('off')
plt.show()
plt.subplot(212)
plt.plot(epochs, history.history['acc'], 'ro', label='Training accuracy')
plt.plot(epochs, val_acc_values, 'b', label='Test accuracy')
plt.title('Training and test accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.gca().set_yticklabels(['{:.0f}%'.format(x*100) for x in plt.gca().get_yticks()])
plt.legend()
plt.grid('off')
plt.show()
y_pred = model.predict(x[-2:].reshape(2,224,224,3))
y_predi = np.argmax(y_pred, axis=3)
y_testi = np.argmax(y2[-2:].reshape(2,224,224,1), axis=3)
#np.mean(y_predi == y_testi)
y_pred.shape
plt.imshow(y_pred[-1,:,:,0])
np.sum(y_testi)
np.mean(y_predi == y_testi)
import tensorflow as tf
from keras.backend.tensorflow_backend import set_session
import keras, sys, time, warnings
from keras.models import *
from keras.layers import *
import pandas as pd
y2.shape
import matplotlib.pyplot as plt
%matplotlib inline
plt.subplot(231)
plt.imshow(x[-1])
plt.axis('off')
plt.title('Original image')
plt.grid('off')
plt.subplot(232)
plt.imshow(y2[-1,:,:,0])
plt.axis('off')
plt.title('Actual mask image')
plt.grid('off')
plt.subplot(233)
plt.imshow(y_pred[-1,:,:,0])
plt.axis('off')
plt.title('Predicted mask image')
plt.grid('off')
plt.subplot(234)
plt.imshow(x[-2])
plt.axis('off')
plt.grid('off')
plt.subplot(235)
plt.imshow(y2[-2,:,:,0])
plt.axis('off')
plt.grid('off')
plt.subplot(236)
plt.imshow(y_pred[-2,:,:,0])
plt.axis('off')
plt.grid('off')
plt.show()
from keras.utils import plot_model
plot_model(model, show_shapes=True, show_layer_names=True, to_file='model.png')
from IPython.display import Image
Image(retina=True, filename='model.png')
| 0.583915 | 0.465327 |
# Example Model Servers with Seldon
## Prerequistes
You will need
- [Git clone of Seldon Core](https://github.com/SeldonIO/seldon-core)
- A running Kubernetes cluster with kubectl authenticated
- [seldon-core Python package](https://pypi.org/project/seldon-core/) (```pip install seldon-core>=0.2.6.1```)
- [Helm client](https://helm.sh/)
### Creating a Kubernetes Cluster
Follow the [Kubernetes documentation to create a cluster](https://kubernetes.io/docs/setup/).
Once created ensure ```kubectl``` is authenticated against the running cluster.
## Setup
```
!kubectl create namespace seldon
!kubectl config set-context $(kubectl config current-context) --namespace=seldon
!kubectl create clusterrolebinding kube-system-cluster-admin --clusterrole=cluster-admin --serviceaccount=kube-system:default
```
## Install Helm
```
!kubectl -n kube-system create sa tiller
!kubectl create clusterrolebinding tiller --clusterrole cluster-admin --serviceaccount=kube-system:tiller
!helm init --service-account tiller
!kubectl rollout status deploy/tiller-deploy -n kube-system
```
## Start seldon-core
```
!helm install ../helm-charts/seldon-core-operator --name seldon-core --set usageMetrics.enabled=true --namespace seldon-system
!kubectl rollout status statefulset.apps/seldon-operator-controller-manager -n seldon-system
```
## Setup Ingress
There are gRPC issues with the latest Ambassador, so we rewcommend 0.40.2 until these are fixed.
```
!helm install stable/ambassador --name ambassador --set crds.keep=false
!kubectl rollout status deployment.apps/ambassador
```
### Port Forward to Ambassador
```
kubectl port-forward $(kubectl get pods -n seldon -l app.kubernetes.io/name=ambassador -o jsonpath='{.items[0].metadata.name}') -n seldon 8003:8080
```
## Serve SKlearn Iris Model
```
!pygmentize ../servers/sklearnserver/samples/iris.yaml
!kubectl apply -f ../servers/sklearnserver/samples/iris.yaml
!kubectl rollout status deploy/iris-default-8bb3ef6
from seldon_core.seldon_client import SeldonClient
sc = SeldonClient(deployment_name="sklearn",namespace="seldon")
r = sc.predict(gateway="ambassador",transport="rest",shape=(1,4))
print(r)
!kubectl delete -f ../servers/sklearnserver/samples/iris.yaml
```
## Serve XGBoost Iris Model
```
!pygmentize ../servers/xgboostserver/samples/iris.yaml
!kubectl apply -f ../servers/xgboostserver/samples/iris.yaml
!kubectl rollout status deploy/iris-default-5299e79
from seldon_core.seldon_client import SeldonClient
sc = SeldonClient(deployment_name="xgboost",namespace="seldon")
r = sc.predict(gateway="ambassador",transport="rest",shape=(1,4))
print(r)
!kubectl delete -f ../servers/xgboostserver/samples/iris.yaml
```
## Serve Tensorflow MNIST Model
**Will only work on a GCP Kubernetes Cluster**
```
!pygmentize ../servers/tfserving/samples/mnist_rest.yaml
!kubectl apply -f ../servers/tfserving/samples/mnist_rest.yaml
!kubectl rollout status deploy/mnist-default-d53c803
from seldon_core.seldon_client import SeldonClient
sc = SeldonClient(deployment_name="tfserving",namespace="seldon")
r = sc.predict(gateway="ambassador",transport="rest",shape=(1,784))
print(r)
!kubectl delete -f ../servers/tfserving/samples/mnist_rest.yaml
```
|
github_jupyter
|
!kubectl create namespace seldon
!kubectl config set-context $(kubectl config current-context) --namespace=seldon
!kubectl create clusterrolebinding kube-system-cluster-admin --clusterrole=cluster-admin --serviceaccount=kube-system:default
!kubectl -n kube-system create sa tiller
!kubectl create clusterrolebinding tiller --clusterrole cluster-admin --serviceaccount=kube-system:tiller
!helm init --service-account tiller
!kubectl rollout status deploy/tiller-deploy -n kube-system
!helm install ../helm-charts/seldon-core-operator --name seldon-core --set usageMetrics.enabled=true --namespace seldon-system
!kubectl rollout status statefulset.apps/seldon-operator-controller-manager -n seldon-system
!helm install stable/ambassador --name ambassador --set crds.keep=false
!kubectl rollout status deployment.apps/ambassador
kubectl port-forward $(kubectl get pods -n seldon -l app.kubernetes.io/name=ambassador -o jsonpath='{.items[0].metadata.name}') -n seldon 8003:8080
!pygmentize ../servers/sklearnserver/samples/iris.yaml
!kubectl apply -f ../servers/sklearnserver/samples/iris.yaml
!kubectl rollout status deploy/iris-default-8bb3ef6
from seldon_core.seldon_client import SeldonClient
sc = SeldonClient(deployment_name="sklearn",namespace="seldon")
r = sc.predict(gateway="ambassador",transport="rest",shape=(1,4))
print(r)
!kubectl delete -f ../servers/sklearnserver/samples/iris.yaml
!pygmentize ../servers/xgboostserver/samples/iris.yaml
!kubectl apply -f ../servers/xgboostserver/samples/iris.yaml
!kubectl rollout status deploy/iris-default-5299e79
from seldon_core.seldon_client import SeldonClient
sc = SeldonClient(deployment_name="xgboost",namespace="seldon")
r = sc.predict(gateway="ambassador",transport="rest",shape=(1,4))
print(r)
!kubectl delete -f ../servers/xgboostserver/samples/iris.yaml
!pygmentize ../servers/tfserving/samples/mnist_rest.yaml
!kubectl apply -f ../servers/tfserving/samples/mnist_rest.yaml
!kubectl rollout status deploy/mnist-default-d53c803
from seldon_core.seldon_client import SeldonClient
sc = SeldonClient(deployment_name="tfserving",namespace="seldon")
r = sc.predict(gateway="ambassador",transport="rest",shape=(1,784))
print(r)
!kubectl delete -f ../servers/tfserving/samples/mnist_rest.yaml
| 0.288268 | 0.93835 |
# List and its default Functions
```
a = ["asish","rishabh","ankur"]
print(len(a))
#define a list
my_list = [4,7,0,3]
#get an iterator using iter()
my_iter = iter(my_list)
#iterate through it using next()
#output:4
print(next(my_iter))
#output:7
print(next(my_iter))
#next(obj) is same as obj.__next__()
#output:0
print(my_iter.__next__())
#output:3
print(my_iter.__next__())
#This will raise error,no items left
next(my_iter)
>>> for element in my_list:
print (element)
number = [1,2,3,4,5,6,7,8,9]
largest_number = max(number);
print("The largest number is:", largest_number)
languages = ["Python", "C Programming", "Java"]
largest_string = max(languages);
print("The largest string is:", largest_string)
number = [1,2,3,4,5,6,7,8,9]
smallest_number = min(number);
print("The smallest number is:", smallest_number)
languages = ["Python", "C Programming", "Java"]
smallest_string = min(languages);
print("The smallest string is:", smallest_string)
#How range works in python
#empty range
print(list(range(0)))
#using range(stop)
print(list(range(10)))
#using range(start, stop)
print(list(range(1, 10)))
start=2
stop=14
step=2
print(list(range(start, stop, step)))
```
# Dictionary and its default Functions
```
d= {1: "one", 2: "two"}
d.clear()
print('d =', d)
original = {1: "one", 2: "two"}
new = original.copy()
print('original:', original)
print('new:', new)
person = {'name': 'Asish', 'age':22}
print('Name: ',person.get('name'))
print('Age: ',person.get('age'))
#value is not provided
print('Salary: ',person.get('salary'))
#value is provided
print('Salary: ',person.get('salary',0.0))
#random sales dictionary
sales = { 'apple': 2, 'orange': 3, 'grapes' : 4}
items = sales.items()
print('original items:', items)
#delete an item from dictionary
del[sales['apple']]
print('updated items:',items)
person = {'name': 'Asish', 'age': 22, 'salary':3500.0}
print(person.keys())
empty_dict = {}
print(empty_dict.keys())
#random sales dictionary
sales = { 'apple': 2, 'orange': 3, 'grapes' : 4}
element = sales.pop('apple')
print('The popped element is:',element)
print('The dictionary is:',sales)
person = {'name': 'Asish', 'age': 22, 'salary':3500.0}
#('salary',3500.0)is inserted at the last,so it is removed.
result=person.popitem()
print('Return value =', result)
print('Person =', person)
#inserting a new element pair
person['profession'] = 'Plumber'
#now ('profession', 'plumber')is the lastest element
result=person.popitem()
print('Return value =', result)
print('Person =', person)
person = {'name': 'Asish', 'age':22}
age=person.setdefault('age')
print('Person =', person)
print('Age =', age)
d= {1: "one", 2: "three"}
d1= {2: "two"}
#update the value of key 2
d.update(d1)
print(d)
d1= {3: "three"}
#adds element with key 3
d.update(d1)
print(d)
#random sales dictionary
sales = { 'apple': 2, 'orange': 3, 'grapes' : 4}
print(sales.values())
```
# Sets and its default Functions
```
#set of vowels
vowels = {'a','e', 'i', 'u'}
#adding 'o'
vowels.add('o')
print('vowels are:',vowels)
#adding 'a' again
vowels.add('a')
print('vowels are:',vowels)
#set of vowels
vowels = {'a', 'e', 'i', 'o', 'u'}
print('vowels(before clear):', vowels)
#clearing vowels
vowels.clear()
print('vowels(after clear):', vowels)
numbers = {1,2,3,4}
new_numbers = numbers
new_numbers.add(5)
print('numbers:', numbers)
print('new_numbers:', new_numbers)
A = {'a', 'b', 'c','d'}
B = {'c', 'f', 'g'}
#Equivalent to A-B
print(A.difference(B))
#Equivalent to B-A
print(B.difference(A))
A = {'a', 'b', 'c','d'}
B = {'c', 'f', 'g'}
result = A.difference_update(B)
print('A = ', A)
print('B = ', B)
print('result = ', result)
A = {'a', 'b', 'c','d'}
print('Return value is', A.pop())
print('A = ', A)
#language set
language = {'English', 'French', 'German'}
#removing 'German' from language
language.remove('German')
#updated language set
print('updated language set:', language)
A = {'a', 'c', 'd'}
B = {'c', 'd', 2}
C = {1,2,3}
print('A U B =', A.union(B))
print('B U C =', B.union(C))
print('A U B U C =', A.union(B, C))
print('A.union()=', A.union())
A = {'a', 'b'}
B = {1,2,3}
result = A.update(B)
print('A = ', A)
print('result = ', result)
```
# Tuple and explore default methods
```
#Use of Tuple count()
#Vowels tuple
vowels = ('a', 'e', 'i', 'o', 'i', 'u')
#count element 'i'
count = vowels.count('i')
#print count
print('The count of i is:', count)
#count element 'p'
count = vowels.count('p')
#print count
print('The count of p is:', count)
#Vowels tuple
vowels = ('a', 'e', 'i', 'o', 'i', 'u')
#index of 'e' in vowels
index=vowels.index('e')
print('The index of e:', index)
#element of i is searched
#index of the first 'i' is returned
index = vowels.index('i')
print('The index of i:', index)
```
# String and explore default methods
```
#define string
string = "Python is awesome,isn't it?"
substring = "is"
count = string.count(substring)
#print count
print("The count is:", count)
string = "python is AWesome."
capitalized_string = string.capitalize()
print('Old String: ', string)
print('Capitalized String:', capitalized_string)
# unicode string
string = 'pythön!'
# print string
print('The string is:', string)
# default encoding to utf-8
string_utf = string.encode()
# print result
print('The encoded version is:', string_utf)
string = "Python is awesome"
new_string = string.center(24)
print("Centered String: ", new_string)
s = 'this is good'
print(s.islower())
s = 'th!s is a1so g00d'
print(s.islower())
s = 'this is Not good'
print(s.islower())
```
|
github_jupyter
|
a = ["asish","rishabh","ankur"]
print(len(a))
#define a list
my_list = [4,7,0,3]
#get an iterator using iter()
my_iter = iter(my_list)
#iterate through it using next()
#output:4
print(next(my_iter))
#output:7
print(next(my_iter))
#next(obj) is same as obj.__next__()
#output:0
print(my_iter.__next__())
#output:3
print(my_iter.__next__())
#This will raise error,no items left
next(my_iter)
>>> for element in my_list:
print (element)
number = [1,2,3,4,5,6,7,8,9]
largest_number = max(number);
print("The largest number is:", largest_number)
languages = ["Python", "C Programming", "Java"]
largest_string = max(languages);
print("The largest string is:", largest_string)
number = [1,2,3,4,5,6,7,8,9]
smallest_number = min(number);
print("The smallest number is:", smallest_number)
languages = ["Python", "C Programming", "Java"]
smallest_string = min(languages);
print("The smallest string is:", smallest_string)
#How range works in python
#empty range
print(list(range(0)))
#using range(stop)
print(list(range(10)))
#using range(start, stop)
print(list(range(1, 10)))
start=2
stop=14
step=2
print(list(range(start, stop, step)))
d= {1: "one", 2: "two"}
d.clear()
print('d =', d)
original = {1: "one", 2: "two"}
new = original.copy()
print('original:', original)
print('new:', new)
person = {'name': 'Asish', 'age':22}
print('Name: ',person.get('name'))
print('Age: ',person.get('age'))
#value is not provided
print('Salary: ',person.get('salary'))
#value is provided
print('Salary: ',person.get('salary',0.0))
#random sales dictionary
sales = { 'apple': 2, 'orange': 3, 'grapes' : 4}
items = sales.items()
print('original items:', items)
#delete an item from dictionary
del[sales['apple']]
print('updated items:',items)
person = {'name': 'Asish', 'age': 22, 'salary':3500.0}
print(person.keys())
empty_dict = {}
print(empty_dict.keys())
#random sales dictionary
sales = { 'apple': 2, 'orange': 3, 'grapes' : 4}
element = sales.pop('apple')
print('The popped element is:',element)
print('The dictionary is:',sales)
person = {'name': 'Asish', 'age': 22, 'salary':3500.0}
#('salary',3500.0)is inserted at the last,so it is removed.
result=person.popitem()
print('Return value =', result)
print('Person =', person)
#inserting a new element pair
person['profession'] = 'Plumber'
#now ('profession', 'plumber')is the lastest element
result=person.popitem()
print('Return value =', result)
print('Person =', person)
person = {'name': 'Asish', 'age':22}
age=person.setdefault('age')
print('Person =', person)
print('Age =', age)
d= {1: "one", 2: "three"}
d1= {2: "two"}
#update the value of key 2
d.update(d1)
print(d)
d1= {3: "three"}
#adds element with key 3
d.update(d1)
print(d)
#random sales dictionary
sales = { 'apple': 2, 'orange': 3, 'grapes' : 4}
print(sales.values())
#set of vowels
vowels = {'a','e', 'i', 'u'}
#adding 'o'
vowels.add('o')
print('vowels are:',vowels)
#adding 'a' again
vowels.add('a')
print('vowels are:',vowels)
#set of vowels
vowels = {'a', 'e', 'i', 'o', 'u'}
print('vowels(before clear):', vowels)
#clearing vowels
vowels.clear()
print('vowels(after clear):', vowels)
numbers = {1,2,3,4}
new_numbers = numbers
new_numbers.add(5)
print('numbers:', numbers)
print('new_numbers:', new_numbers)
A = {'a', 'b', 'c','d'}
B = {'c', 'f', 'g'}
#Equivalent to A-B
print(A.difference(B))
#Equivalent to B-A
print(B.difference(A))
A = {'a', 'b', 'c','d'}
B = {'c', 'f', 'g'}
result = A.difference_update(B)
print('A = ', A)
print('B = ', B)
print('result = ', result)
A = {'a', 'b', 'c','d'}
print('Return value is', A.pop())
print('A = ', A)
#language set
language = {'English', 'French', 'German'}
#removing 'German' from language
language.remove('German')
#updated language set
print('updated language set:', language)
A = {'a', 'c', 'd'}
B = {'c', 'd', 2}
C = {1,2,3}
print('A U B =', A.union(B))
print('B U C =', B.union(C))
print('A U B U C =', A.union(B, C))
print('A.union()=', A.union())
A = {'a', 'b'}
B = {1,2,3}
result = A.update(B)
print('A = ', A)
print('result = ', result)
#Use of Tuple count()
#Vowels tuple
vowels = ('a', 'e', 'i', 'o', 'i', 'u')
#count element 'i'
count = vowels.count('i')
#print count
print('The count of i is:', count)
#count element 'p'
count = vowels.count('p')
#print count
print('The count of p is:', count)
#Vowels tuple
vowels = ('a', 'e', 'i', 'o', 'i', 'u')
#index of 'e' in vowels
index=vowels.index('e')
print('The index of e:', index)
#element of i is searched
#index of the first 'i' is returned
index = vowels.index('i')
print('The index of i:', index)
#define string
string = "Python is awesome,isn't it?"
substring = "is"
count = string.count(substring)
#print count
print("The count is:", count)
string = "python is AWesome."
capitalized_string = string.capitalize()
print('Old String: ', string)
print('Capitalized String:', capitalized_string)
# unicode string
string = 'pythön!'
# print string
print('The string is:', string)
# default encoding to utf-8
string_utf = string.encode()
# print result
print('The encoded version is:', string_utf)
string = "Python is awesome"
new_string = string.center(24)
print("Centered String: ", new_string)
s = 'this is good'
print(s.islower())
s = 'th!s is a1so g00d'
print(s.islower())
s = 'this is Not good'
print(s.islower())
| 0.167934 | 0.704332 |
<a href="https://colab.research.google.com/github/kkavyapriyanka/Keyword_verification/blob/main/KeyWordVerification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
!pip install contractions
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import re, string, unicodedata
import nltk
import contractions
import inflect
from nltk import word_tokenize, sent_tokenize
from nltk.corpus import stopwords
from nltk.stem import LancasterStemmer, WordNetLemmatizer
import gensim
from gensim.models import Word2Vec
import matplotlib.pyplot as plt
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from sklearn.naive_bayes import BernoulliNB, MultinomialNB
from sklearn.metrics import accuracy_score, confusion_matrix,f1_score
from sklearn.model_selection import StratifiedKFold,train_test_split,cross_val_score,GridSearchCV,RandomizedSearchCV
nltk.download('all')
from google.colab import drive
drive.mount('/content/drive')
wv = gensim.models.KeyedVectors.load_word2vec_format("/content/drive/MyDrive/Colab Notebooks/GoogleNews-vectors-negative300.bin.gz", binary=True)
wv.init_sims(replace=True)
data=pd.read_csv('/content/drive/MyDrive/Colab Notebooks/keyword_verification.csv')
data.shape
data=data.dropna()
data.shape
data.info()
data.head()
```
#Data Preprocessing
```
data['keyword'].unique()
data['keyword'] = [i.replace('%20', '_') for i in data['keyword']]
data['keyword'].unique()
def replace_contractions(text):
"""Replace contractions in string of text"""
return contractions.fix(text)
def remove_URL(sample):
"""Remove URLs from a sample string"""
return re.sub(r"http\S+", "", sample)
def remove_non_ascii(words):
"""Remove non-ASCII characters from list of tokenized words"""
new_words = []
for word in words:
new_word = unicodedata.normalize('NFKD', word).encode('ascii', 'ignore').decode('utf-8', 'ignore')
new_words.append(new_word)
return new_words
def to_lowercase(words):
"""Convert all characters to lowercase from list of tokenized words"""
new_words = []
for word in words:
new_word = word.lower()
new_words.append(new_word)
return new_words
def remove_punctuation(words):
"""Remove punctuation from list of tokenized words"""
new_words = []
for word in words:
new_word = re.sub(r'[^\w\s]', '', word)
if new_word != '':
new_words.append(new_word)
return new_words
def replace_numbers(words):
"""Replace all interger occurrences in list of tokenized words with textual representation"""
p = inflect.engine()
new_words = []
for word in words:
if word.isdigit():
new_word = p.number_to_words(word)
new_words.append(new_word)
else:
new_words.append(word)
return new_words
def remove_stopwords(words):
"""Remove stop words from list of tokenized words"""
new_words = []
for word in words:
if word not in stopwords.words('english'):
new_words.append(word)
return new_words
def stem_words(words):
"""Stem words in list of tokenized words"""
stemmer = LancasterStemmer()
stems = []
for word in words:
stem = stemmer.stem(word)
stems.append(stem)
return stems
def lemmatize_verbs(words):
"""Lemmatize verbs in list of tokenized words"""
lemmatizer = WordNetLemmatizer()
lemmas = []
for word in words:
lemma = lemmatizer.lemmatize(word, pos='v')
lemmas.append(lemma)
return lemmas
def remove_emoji(string):
emoji_pattern = re.compile("["
u"\U0001F600-\U0001F64F" # emoticons
u"\U0001F300-\U0001F5FF" # symbols & pictographs
u"\U0001F680-\U0001F6FF" # transport & map symbols
u"\U0001F1E0-\U0001F1FF" # flags (iOS)
u"\U00002702-\U000027B0"
u"\U000024C2-\U0001F251"
"]+", flags=re.UNICODE)
return emoji_pattern.sub(r'', string)
def normalize(words):
words = remove_non_ascii(words)
# words = to_lowercase(words)
words = remove_punctuation(words)
words = replace_numbers(words)
words = remove_stopwords(words)
return words
def preprocess(sample):
sample = remove_URL(sample)
sample = replace_contractions(sample)
sample=remove_emoji(sample)
words = nltk.word_tokenize(sample)
text=normalize(words)
return " ".join(text)
words="❤️❤️❤️ he gave us everything. He had a horri"
words = remove_emoji(words)
print(words)
data['clean_text']=data['text'].apply(preprocess)
data['clean_text'].head()
print(data.duplicated().unique())
print(data.duplicated(subset=['clean_text']).unique())
data=data.drop_duplicates(subset=['clean_text'], keep='last')
data.head()
data['corpus']=data['keyword']+' '+data['clean_text']
X = data['corpus']
Y=data['target']
X.shape,Y.shape
```
#TF IDF with Stratified K Fold & Naive Bayes
```
skfold=StratifiedKFold(n_splits=5,shuffle=True)
i=1
score_vals=[]
for trainindex,testindex in skfold.split(X,Y):
# print(X[2966])
xtr,xcv=X.iloc[trainindex],X.iloc[testindex]
ytr,ycv=Y.iloc[trainindex],Y.iloc[testindex]
print(xtr.shape,ytr.shape,xcv.shape,ycv.shape)
tfidf=TfidfVectorizer()
xtr=tfidf.fit_transform(xtr.values)
xcv=tfidf.transform(xcv.values)
nbs=BernoulliNB(alpha=10)
nbs.fit(xtr,ytr)
pred=nbs.predict(xcv)
# score=accuracy_score(ycv,pred)*100
score=f1_score(ycv,pred, average='weighted')
print(f"For {i} fold {score}")
score_vals.append(score)
i+=1
plt.plot([1,2,3,4,5],score_vals)
plt.xlabel("Number of Folds") # Text for X-Axis
plt.ylabel("Score") # Text for Y-Axis
plt.title("F1 Score")
plt.show()
```
#Word2Vec with Stratified K Fold & Naive Bayes
```
def word_averaging(words):
all_words, mean = set(), []
for word in words:
if isinstance(word, np.ndarray):
mean.append(word)
elif word in wv.vocab:
mean.append(wv.syn0norm[wv.vocab[word].index])
all_words.add(wv.vocab[word].index)
if not mean:
# FIXME: remove these examples in pre-processing
return np.zeros(wv.vector_size,)
mean = gensim.matutils.unitvec(np.array(mean).mean(axis=0)).astype(np.float32)
return mean
def word_averaging_list(text_list):
return np.vstack([word_averaging(post) for post in text_list ])
def w2v_tokenize_text(text):
tokens = []
for sent in nltk.sent_tokenize(text, language='english'):
for word in nltk.word_tokenize(sent, language='english'):
if len(word) < 2:
continue
tokens.append(word)
return tokens
skfold=StratifiedKFold(n_splits=5,shuffle=True)
i=1
score_vals=[]
for trainindex,testindex in skfold.split(X,Y):
# print(X[2966])
xtr,xcv=X.iloc[trainindex],X.iloc[testindex]
ytr,ycv=Y.iloc[trainindex],Y.iloc[testindex]
print(xtr.shape,ytr.shape,xcv.shape,ycv.shape,xtr.values[0])
xcv_tokenized = xcv.apply(w2v_tokenize_text)
xtr_tokenized = xtr.apply(w2v_tokenize_text)
Xtr_word_average = word_averaging_list(xtr_tokenized)
Xcv_word_average = word_averaging_list(xcv_tokenized)
params={'alpha':[10,100,20,30,40,50]}
rndm=RandomizedSearchCV(BernoulliNB(),params,cv=3,scoring="f1")
rndm.fit(Xtr_word_average,ytr)
nbs=BernoulliNB(alpha=rndm.best_params_['alpha'])
nbs.fit(Xtr_word_average,ytr)
pred=nbs.predict(Xcv_word_average)
score=f1_score(ycv,pred, average='weighted')
score_vals.append(score)
print(f"For {i} fold {score}")
i+=1
plt.plot([1,2,3,4,5],score_vals)
plt.xlabel("Number of Folds") # Text for X-Axis
plt.ylabel("Score") # Text for Y-Axis
plt.title("F1 Score")
plt.show()
```
#Approach
Data preprocessed using techniques like removing stop words,emojis,unicodes,punctuations etc.
Word2Vec performed well than TFIDF with 81 % F1 Score
As the Data is Imbalance i prefering F1 Score over Accuracy
Class Weights are assigned to ensure model gives preference in lowering the error rate for low class labelled data
Stratified K Fold Cross Validation used to ensure the utilisation of all observations in training and testing
RandomSearchCv is used as hyper parameter tuning technique to find the best optimal paramter value for alpha
```
```
|
github_jupyter
|
!pip install contractions
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import re, string, unicodedata
import nltk
import contractions
import inflect
from nltk import word_tokenize, sent_tokenize
from nltk.corpus import stopwords
from nltk.stem import LancasterStemmer, WordNetLemmatizer
import gensim
from gensim.models import Word2Vec
import matplotlib.pyplot as plt
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from sklearn.naive_bayes import BernoulliNB, MultinomialNB
from sklearn.metrics import accuracy_score, confusion_matrix,f1_score
from sklearn.model_selection import StratifiedKFold,train_test_split,cross_val_score,GridSearchCV,RandomizedSearchCV
nltk.download('all')
from google.colab import drive
drive.mount('/content/drive')
wv = gensim.models.KeyedVectors.load_word2vec_format("/content/drive/MyDrive/Colab Notebooks/GoogleNews-vectors-negative300.bin.gz", binary=True)
wv.init_sims(replace=True)
data=pd.read_csv('/content/drive/MyDrive/Colab Notebooks/keyword_verification.csv')
data.shape
data=data.dropna()
data.shape
data.info()
data.head()
data['keyword'].unique()
data['keyword'] = [i.replace('%20', '_') for i in data['keyword']]
data['keyword'].unique()
def replace_contractions(text):
"""Replace contractions in string of text"""
return contractions.fix(text)
def remove_URL(sample):
"""Remove URLs from a sample string"""
return re.sub(r"http\S+", "", sample)
def remove_non_ascii(words):
"""Remove non-ASCII characters from list of tokenized words"""
new_words = []
for word in words:
new_word = unicodedata.normalize('NFKD', word).encode('ascii', 'ignore').decode('utf-8', 'ignore')
new_words.append(new_word)
return new_words
def to_lowercase(words):
"""Convert all characters to lowercase from list of tokenized words"""
new_words = []
for word in words:
new_word = word.lower()
new_words.append(new_word)
return new_words
def remove_punctuation(words):
"""Remove punctuation from list of tokenized words"""
new_words = []
for word in words:
new_word = re.sub(r'[^\w\s]', '', word)
if new_word != '':
new_words.append(new_word)
return new_words
def replace_numbers(words):
"""Replace all interger occurrences in list of tokenized words with textual representation"""
p = inflect.engine()
new_words = []
for word in words:
if word.isdigit():
new_word = p.number_to_words(word)
new_words.append(new_word)
else:
new_words.append(word)
return new_words
def remove_stopwords(words):
"""Remove stop words from list of tokenized words"""
new_words = []
for word in words:
if word not in stopwords.words('english'):
new_words.append(word)
return new_words
def stem_words(words):
"""Stem words in list of tokenized words"""
stemmer = LancasterStemmer()
stems = []
for word in words:
stem = stemmer.stem(word)
stems.append(stem)
return stems
def lemmatize_verbs(words):
"""Lemmatize verbs in list of tokenized words"""
lemmatizer = WordNetLemmatizer()
lemmas = []
for word in words:
lemma = lemmatizer.lemmatize(word, pos='v')
lemmas.append(lemma)
return lemmas
def remove_emoji(string):
emoji_pattern = re.compile("["
u"\U0001F600-\U0001F64F" # emoticons
u"\U0001F300-\U0001F5FF" # symbols & pictographs
u"\U0001F680-\U0001F6FF" # transport & map symbols
u"\U0001F1E0-\U0001F1FF" # flags (iOS)
u"\U00002702-\U000027B0"
u"\U000024C2-\U0001F251"
"]+", flags=re.UNICODE)
return emoji_pattern.sub(r'', string)
def normalize(words):
words = remove_non_ascii(words)
# words = to_lowercase(words)
words = remove_punctuation(words)
words = replace_numbers(words)
words = remove_stopwords(words)
return words
def preprocess(sample):
sample = remove_URL(sample)
sample = replace_contractions(sample)
sample=remove_emoji(sample)
words = nltk.word_tokenize(sample)
text=normalize(words)
return " ".join(text)
words="❤️❤️❤️ he gave us everything. He had a horri"
words = remove_emoji(words)
print(words)
data['clean_text']=data['text'].apply(preprocess)
data['clean_text'].head()
print(data.duplicated().unique())
print(data.duplicated(subset=['clean_text']).unique())
data=data.drop_duplicates(subset=['clean_text'], keep='last')
data.head()
data['corpus']=data['keyword']+' '+data['clean_text']
X = data['corpus']
Y=data['target']
X.shape,Y.shape
skfold=StratifiedKFold(n_splits=5,shuffle=True)
i=1
score_vals=[]
for trainindex,testindex in skfold.split(X,Y):
# print(X[2966])
xtr,xcv=X.iloc[trainindex],X.iloc[testindex]
ytr,ycv=Y.iloc[trainindex],Y.iloc[testindex]
print(xtr.shape,ytr.shape,xcv.shape,ycv.shape)
tfidf=TfidfVectorizer()
xtr=tfidf.fit_transform(xtr.values)
xcv=tfidf.transform(xcv.values)
nbs=BernoulliNB(alpha=10)
nbs.fit(xtr,ytr)
pred=nbs.predict(xcv)
# score=accuracy_score(ycv,pred)*100
score=f1_score(ycv,pred, average='weighted')
print(f"For {i} fold {score}")
score_vals.append(score)
i+=1
plt.plot([1,2,3,4,5],score_vals)
plt.xlabel("Number of Folds") # Text for X-Axis
plt.ylabel("Score") # Text for Y-Axis
plt.title("F1 Score")
plt.show()
def word_averaging(words):
all_words, mean = set(), []
for word in words:
if isinstance(word, np.ndarray):
mean.append(word)
elif word in wv.vocab:
mean.append(wv.syn0norm[wv.vocab[word].index])
all_words.add(wv.vocab[word].index)
if not mean:
# FIXME: remove these examples in pre-processing
return np.zeros(wv.vector_size,)
mean = gensim.matutils.unitvec(np.array(mean).mean(axis=0)).astype(np.float32)
return mean
def word_averaging_list(text_list):
return np.vstack([word_averaging(post) for post in text_list ])
def w2v_tokenize_text(text):
tokens = []
for sent in nltk.sent_tokenize(text, language='english'):
for word in nltk.word_tokenize(sent, language='english'):
if len(word) < 2:
continue
tokens.append(word)
return tokens
skfold=StratifiedKFold(n_splits=5,shuffle=True)
i=1
score_vals=[]
for trainindex,testindex in skfold.split(X,Y):
# print(X[2966])
xtr,xcv=X.iloc[trainindex],X.iloc[testindex]
ytr,ycv=Y.iloc[trainindex],Y.iloc[testindex]
print(xtr.shape,ytr.shape,xcv.shape,ycv.shape,xtr.values[0])
xcv_tokenized = xcv.apply(w2v_tokenize_text)
xtr_tokenized = xtr.apply(w2v_tokenize_text)
Xtr_word_average = word_averaging_list(xtr_tokenized)
Xcv_word_average = word_averaging_list(xcv_tokenized)
params={'alpha':[10,100,20,30,40,50]}
rndm=RandomizedSearchCV(BernoulliNB(),params,cv=3,scoring="f1")
rndm.fit(Xtr_word_average,ytr)
nbs=BernoulliNB(alpha=rndm.best_params_['alpha'])
nbs.fit(Xtr_word_average,ytr)
pred=nbs.predict(Xcv_word_average)
score=f1_score(ycv,pred, average='weighted')
score_vals.append(score)
print(f"For {i} fold {score}")
i+=1
plt.plot([1,2,3,4,5],score_vals)
plt.xlabel("Number of Folds") # Text for X-Axis
plt.ylabel("Score") # Text for Y-Axis
plt.title("F1 Score")
plt.show()
| 0.321886 | 0.698381 |
### Import
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
pd.set_option('display.max_columns', None)
plt.style.use('ggplot')
```
### Load data
```
df_raw = pd.read_csv('data/companies.csv')
df_raw.head(5)
df_raw.shape
```
### Data cleaning function
```
def data_cleaning(df):
#drop duplicates
df.drop_duplicates(inplace = True)
# Office column (how many offices, nan = 1 office)
df['office'] = df.office.str.split(' ', expand = True)[0]
df['office'].fillna('1', inplace = True)
df['office'] = pd.to_numeric(df.office)
# change column name
df.rename(columns = {'heakth_care_on_site': 'health_care_on_site'}, inplace = True)
# Create category column base on industry column
df['category'] = df['industry']
for index, indus in enumerate(df['category']):
if indus in ['Accounting','Legal']:
df['category'].iloc[index] = 'Accounting & Legal'
elif indus == 'Aerospace & Defense':
df['category'].iloc[index] = 'Aerospace & Defense'
elif indus in ['Food Production','Farm Support Services']:
df['category'].iloc[index] = 'Agriculture & Forestry'
elif indus in ['Sports & Recreation','Museums, Zoos & Amusement Parks','Photography',
'Movie Theaters','Gambling','Performing Arts']:
df['category'].iloc[index] = 'Arts, Entertainment & Recreation'
elif indus == 'Biotech & Pharmaceuticals':
df['category'].iloc[index] = 'Biotech & Pharmaceuticals'
elif indus in ['Consulting','Staffing & Outsourcing',
'Architectural & Engineering Services','Membership Organizations',
'Building & Personnel Services','Security Services','Wholesale',
'Research & Development','Advertising & Marketing','Business Service Centers & Copy Shops']:
df['category'].iloc[index] = 'Business Services'
elif indus == 'Construction' :
df['category'].iloc[index] = 'Construction'
elif indus in ['Health, Beauty, & Fitness','Consumer Product Rental']:
df['category'].iloc[index] = 'Customer Services'
elif indus in ['K-12 Education','Education Training Services','Colleges & Universities','Preschool & Child Care']:
df['category'].iloc[index] = 'Education'
elif indus in ['Investment Banking & Asset Management','Banks & Credit Unions',
'Financial Transaction Processing','Brokerage Services',
'Lending','Financial Analytics & Research','Stock Exchanges']:
df['category'].iloc[index] = 'Finance'
elif indus in ['Federal Agencies','Municipal Governments','State & Regional Agencies']:
df['category'].iloc[index] = 'Goverment'
elif indus == 'Health Care Services & Hospitals' :
df['category'].iloc[index] = 'Health Care Services & Hospitals'
elif indus in ['Internet','Computer Hardware & Software','IT Services',
'Enterprise Software & Network Solutions']:
df['category'].iloc[index] = 'Information Technology'
elif indus in ['Insurance Carriers','Insurance Agencies & Brokerages']:
df['category'].iloc[index] = 'Insurance'
elif indus in ['Miscellaneous Manufacturing','Transportation Equipment Manufacturing',
'Health Care Products Manufacturing','Electrical & Electronic Manufacturing',
'Consumer Products Manufacturing','Food & Beverage Manufacturing',
'Industrial Manufacturing','Chemical Manufacturing','Metal & Mineral Manufacturing']:
df['category'].iloc[index] = 'Manufacturing'
elif indus in ['Motion Picture Production & Distribution','TV Broadcast & Cable Networks',
'Music Production & Distribution','Video Games','News Outlet','Radio','Publishing']:
df['category'].iloc[index] = 'Media'
elif indus in ['Social Assistance','Health Fundraising Organizations',
'Grantmaking Foundations','Religious Organizations']:
df['category'].iloc[index] = 'Non-Profit'
elif indus in ['Oil & Gas Exploration & Production','Energy','Oil & Gas Services','Utilities','Mining']:
df['category'].iloc[index] = 'Oil, Gas, Energy & Utilities'
elif indus == 'Real Estate':
df['category'].iloc[index] = 'Real Estate'
elif indus in ['Fast-Food & Quick-Service Restaurants','Casual Restaurants',
'Catering & Food Service Contractors','Upscale Restaurants']:
df['category'].iloc[index] = 'Restaurants, Bars & Food Services'
elif indus in ['General Merchandise & Superstores','Department, Clothing, & Shoe Stores',
'Home Furniture & Housewares Stores','Home Centers & Hardware Stores',
'Grocery Stores & Supermarkets','Consumer Electronics & Appliances Stores',
'Drug & Health Stores','Food & Beverage Stores','Pet & Pet Supplies Stores',
'Beauty & Personal Accessories Stores','Automotive Parts & Accessories Stores',
'Other Retail Stores','Office Supply Stores','Vehicle Dealers',
'Sporting Goods Stores','Toy & Hobby Stores',
'Commercial Equipment Repair & Maintenance','General Repair & Maintenance',
'Veterinary Services','Auctions & Galleries','Commercial Equipment Rental',
'Media & Entertainment Retail Stores','Gift, Novelty & Souvenir Stores']:
df['category'].iloc[index] = 'Retail'
elif indus in ['Telecommunications Services','Cable, Internet & Telephone Providers',
'Telecommunications Manufacturing']:
df['category'].iloc[index] = 'Telecommunications'
elif indus in ['Logistics & Supply Chain','Express Delivery Services','Transportation Management',
'Rail','Trucking','Bus Transportation Services', 'Truck Rental & Leasing','Gas Stations',
'Convenience Stores & Truck Stops','Shipping']:
df['category'].iloc[index] = 'Transportation & Logistics'
elif indus in ['Hotels, Motels, & Resorts','Airlines','Car Rental','Cruise Ships','Travel Agencies']:
df['category'].iloc[index] = 'Travel & Tourism'
# convert review_counts,salaries_count,jobs_count,interviews_count,benefits_count into numeric
# review counts
df.review_counts[df.review_counts == '--'] = '0'
df.review_counts = (df.review_counts.replace(r'[K,k]+$', '', regex=True).astype(float) * \
df.review_counts.str.extract(r'[\d\.]+([K,k]+)', expand=False)
.fillna(1)
.replace(['K','k'], [10**3,10**3]).astype(int))
# salaries review count
df.salaries_count[df.salaries_count == '--'] = '0'
df.salaries_count = (df.salaries_count.replace(r'[K,k]+$', '', regex=True).astype(float) * \
df.salaries_count.str.extract(r'[\d\.]+([K,k]+)', expand=False)
.fillna(1)
.replace(['K','k'], [10**3,10**3]).astype(int))
#jobs review counts
df.jobs_count[df.jobs_count == '--'] = '0'
df.jobs_count = (df.jobs_count.replace(r'[K,k]+$', '', regex=True).astype(float) * \
df.jobs_count.str.extract(r'[\d\.]+([K,k]+)', expand=False)
.fillna(1)
.replace(['K','k'], [10**3,10**3]).astype(int))
# inteviews review counts
df.interviews_count[df.interviews_count == '--'] = '0'
df.interviews_count = (df.interviews_count.replace(r'[K,k]+$', '', regex=True).astype(float) * \
df.interviews_count.str.extract(r'[\d\.]+([K,k]+)', expand=False)
.fillna(1)
.replace(['K','k'], [10**3,10**3]).astype(int))
# benefits review counts
df.benefits_count[df.benefits_count == '--'] = '0'
df.benefits_count = (df.benefits_count.replace(r'[K,k]+$', '', regex=True).astype(float) * \
df.benefits_count.str.extract(r'[\d\.]+([K,k]+)', expand=False)
.fillna(1)
.replace(['K','k'], [10**3,10**3]).astype(int))
# founded column
df.founded.fillna(round(df.founded.mean(),0), inplace = True)
# company size
# 1 = less 5000 employees
# 2 = 5001 to 10000 employees
# 3 = 10000+ employees
df['size'] = df['size'].map({'10000+ Employees': 3,
'5001 to 10000 Employees':2,
'1001 to 5000 Employees' : 1,
'201 to 500 Employees' : 1,
'501 to 1000 Employees' : 1,
'1 to 50 Employees': 1,
'Unknown' :1})
# delete null values
df.dropna(inplace = True)
#interview_possitive, negative, neutral
df.interview_possitive = pd.to_numeric(df.interview_possitive.str.strip('%'))/100
df.interview_negative = pd.to_numeric(df.interview_negative.str.strip('%'))/100
df.interview_neutral = pd.to_numeric(df.interview_neutral.str.strip('%'))/100
# 1 = 'Unknown / Non-Applicable'
# 2 = 'Less than $100 million (USD)'
# 3 = '$100 to $500 million (USD)'
# 4 = '$500 million to $1 billion (USD)'
# 5 = '$1 to $2 billion (USD)'
# 6 = '$2 to $5 billion (USD)'
# 7 = '$5 to $10 billion (USD)'
# 8 = '$10+ billion (USD)'
df['revenue'] = df['revenue'].map({'$10+ billion (USD)':8,
'$5 to $10 billion (USD)':7,
'$2 to $5 billion (USD)' :6,
'$1 to $2 billion (USD)':5,
'$500 million to $1 billion (USD)':4,
'$100 to $500 million (USD)' :3,
'$50 to $100 million (USD)':2,
'$25 to $50 million (USD)':2,
'$10 to $25 million (USD)':2,
'$5 to $10 million (USD)':2,
'$1 to $5 million (USD)':2,
'Less than $1 million (USD)':2,
'Unknown / Non-Applicable':1})
#company type
df.company_type[df.company_type.str.contains('Public')] = 'Public'
df.company_type[df.company_type.str.contains('Private')] = 'Private'
df['company_type'] = df['company_type'].map({'Public' :'Public',
'Private' :'Private',
'Subsidiary or Business Segment':'Subsidiary or Business Segment',
'College / University':'Education',
'Nonprofit Organization': 'Nonprofit Organization',
'Government': 'Government',
'Hospital':'Hospital',
'School / School District': 'Education',
'Franchise': 'Others',
'Unknown':'Others',
'Self-employed':'Others',
'Contract':'Others'})
# Create state column base on head quarter column
df['state'] = df.head_quarter.apply(lambda head_quarter : head_quarter.split(',')[1])
return df
```
### Call data cleaning fuction
```
df = data_cleaning(df_raw)
```
### Create company rank classification base on rating
```
# Create company rank column
df['company_rank'] = df['rating']
for index, rk in enumerate(df['company_rank']):
if rk >= 4.1:
df['company_rank'].iloc[index] = 2
elif (rk >= 3.9) & (rk < 4.1) :
df['company_rank'].iloc[index] = 1
elif (rk < 3.9):
# bellow 3.9
df['company_rank'].iloc[index] = 0
df['company_rank'] = df['company_rank'].astype(int)
df['company_rank'].value_counts(normalize = True).sort_index()
```
### Check outliers
```
plt.figure(figsize = (12,4) )
plt.title('Rating')
sns.boxplot(x = df['rating'].values, color='r');
```
### Rating Distribution
```
plt.figure(figsize = (10,8) )
plt.title('Rating Distribution')
df['rating'].hist(color = 'b');
plt.figure(figsize = (6,6) )
plt.title("Company's Ranking Distribution")
df['company_rank'].hist(color = 'b');
```
### Base line 36%
```
df['company_rank'].value_counts(normalize= True).sort_index()
```
Class 1 (average class) has the least data
### Explore Data Analysis
```
df.describe().transpose()
```
### Check top 30 Ranking
```
df[['name','rating']].sort_values('rating', ascending= False).head(30)
```
### Company size
```
size_df = pd.DataFrame(df.groupby('size').agg('mean')['company_rank'])
# 1 = less 5000 employees
# 2 = 5001 to 10000 employees
# 3 = 10000+ employees
plt.figure(figsize = (12,6))
sns.barplot(x = 'size', y = 'company_rank', data= size_df.reset_index().sort_values('company_rank'))
plt.xticks([0,1,2],['less 5000 employees','5001 to 10000 employees','10000+ employees'],rotation = 30)
plt.title("Company size vs Company's Ranking", fontsize = 20)
plt.xlabel('Company Size', fontsize = 16)
plt.ylabel("Company's Ranking Average ", fontsize = 16)
;
```
One feature that turned out to be significant is the company size. As you can see, the smaller the company the better the ratings. Companies with less than 5,000 employees have the highest average ranking.
### Company Cotegories
```
category_df = pd.DataFrame(df.groupby('category').agg('mean')['company_rank'])
category_df.sort_values('company_rank')
clrs = ['black' if (x < 1.24) else 'red' for x in category_df['company_rank'].sort_values()]
plt.figure(figsize = (15,6))
sns.barplot(x = 'category', y = 'company_rank', data= category_df.reset_index().sort_values('company_rank'), palette= clrs)
plt.title("Company Categories vs Company's Ranking", fontsize = 20)
plt.xlabel('Company Categories', fontsize = 16)
plt.ylabel("Company's Ranking Average ", fontsize = 16)
plt.xticks(rotation = 80, rotation_mode = 'default', fontsize = 12)
;
```
Biotech & Pharmaceuticals, Non-Profit, Construction, Real Estate, Education are the top 5
```
revenue_df = pd.DataFrame(df.groupby('revenue').agg('mean')['company_rank'])
```
### Company with 100 to 500 million (USD) revenue is the best
```
revenue_df
# 1 = 'Unknown / Non-Applicable'
# 2 = 'Less than $100 million (USD)'
# 3 = '$100 to $500 million (USD)'
# 4 = '$500 million to $1 billion (USD)'
# 5 = '$1 to $2 billion (USD)'
# 6 = '$2 to $5 billion (USD)'
# 7 = '$5 to $10 billion (USD)'
# 8 = '$10+ billion (USD)'
plt.figure(figsize = (15,8))
clrs = ['black' if (x < 1.2) else 'red' for x in revenue_df['company_rank']]
sns.barplot(x = 'revenue', y = 'company_rank', data= revenue_df.reset_index().sort_values('company_rank'),palette = clrs)
plt.xticks(rotation = 45)
plt.title("Company Revenue vs Company's Ranking", fontsize = 20)
plt.xticks([0, 1, 2,3,4,5,6,7], ['Unknown / Non-Applicable','Less than $100 million (USD)','$100 to $500 million (USD)',
'$500 million to $1 billion (USD)','$1 to $2 billion (USD)','$2 to $5 billion (USD)',
'$5 to $10 billion (USD)','$10+ billion (USD)'],rotation=20)
plt.xlabel('Revenue', fontsize = 16)
plt.ylabel("Company's ranking", fontsize = 16)
;
```
### Check all Features and Company's Ranking Correlation
```
df.drop(columns = ['rating','benefits_score']).corr()[['company_rank']].sort_values('company_rank')
# code from global lesson 3.07
plt.figure(figsize=(8, 30))
sns.heatmap(df.drop(columns = ['rating','benefits_score','size','interview_neutral', 'interview_possitive']).corr()[['company_rank']].sort_values('company_rank', ascending= False),
annot=True,
cmap='coolwarm',
vmin=-1,
vmax=1);
```
Information technology companies are ranked seventh. Let's see the top 5 positive and top 5 negative below
### Top 5 Positive Correlation
```
# code from global lesson 3.07
plt.figure(figsize=(6, 8))
sns.heatmap(df.drop(columns = ['rating','benefits_score','size','interview_neutral', 'interview_possitive']).corr()[['company_rank']].sort_values('company_rank', ascending= False).iloc[1:6,],
annot=True,
cmap='coolwarm',
vmin=-0.5,
vmax=0.5)
plt.title('Top 5 Positive Correlation', fontsize = 16)
plt.xticks([0.5],["Company's Ranking"],fontsize = 12)
plt.yticks([0.5,1.5,2.5,3.5,4.5],['Interview Difficulty','Gym Membership','Work from Home','Health Care on Site','Free Lunch or Snacks'],fontsize = 12, rotation=0);
```
Now let’s see if the type of company and its area of business can predict employee satisfaction. As you can see, the results are robust. Companies in the field of education had by far the highest average ranking, followed by real estate, construction, and non-profit organizations.
```
# code from global lesson 3.07
plt.figure(figsize=(6, 8))
sns.heatmap(df.drop(columns = ['rating','benefits_score','size','interview_neutral', 'interview_possitive']).corr()[['company_rank']].sort_values('company_rank').head(5),
annot=True,
cmap='coolwarm',
vmin=-0.5,
vmax=0.5);
plt.title('Top 5 Negative Correlation', fontsize = 16)
plt.xticks([0.5],["Company's Ranking"],fontsize = 12)
plt.yticks([0.5,1.5,2.5,3.5,4.5],['Bereavement Leave','Military Leave','Performance Bonus','Employee Discount','Supplemental Workers \nCompensation'],fontsize = 12);
```
The lowest average rankings went to retail companies, followed by transportation and logistics, and restaurant and bars.
### Top 10 rare benefits
```
df_benefit = df.iloc[:,20:79].mean()
df_benefit1 = pd.DataFrame(df_benefit)
df_benefit1['feature'] = df_benefit1.index
df_benefit1.columns = ['avg','features']
plt.figure(figsize = (12,6))
sns.barplot(x = 'features', y = 'avg', data= df_benefit1.sort_values('avg').head(10))
plt.xticks(rotation = 45)
plt.title('Top 10 Rare Benefits', fontsize = 16);
```
### Top 10 the most popular benefits
```
plt.figure(figsize = (12,6))
sns.barplot(x = 'features', y = 'avg', data= df_benefit1.sort_values('avg', ascending=False).iloc[6:,].head(10))
plt.xticks(rotation = 45)
plt.title('Top 10 the most Popular Benefits', fontsize = 16);
```
### Save the clean data into csv file
```
df.to_csv('data/clean_df.csv', index = False)
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
pd.set_option('display.max_columns', None)
plt.style.use('ggplot')
df_raw = pd.read_csv('data/companies.csv')
df_raw.head(5)
df_raw.shape
def data_cleaning(df):
#drop duplicates
df.drop_duplicates(inplace = True)
# Office column (how many offices, nan = 1 office)
df['office'] = df.office.str.split(' ', expand = True)[0]
df['office'].fillna('1', inplace = True)
df['office'] = pd.to_numeric(df.office)
# change column name
df.rename(columns = {'heakth_care_on_site': 'health_care_on_site'}, inplace = True)
# Create category column base on industry column
df['category'] = df['industry']
for index, indus in enumerate(df['category']):
if indus in ['Accounting','Legal']:
df['category'].iloc[index] = 'Accounting & Legal'
elif indus == 'Aerospace & Defense':
df['category'].iloc[index] = 'Aerospace & Defense'
elif indus in ['Food Production','Farm Support Services']:
df['category'].iloc[index] = 'Agriculture & Forestry'
elif indus in ['Sports & Recreation','Museums, Zoos & Amusement Parks','Photography',
'Movie Theaters','Gambling','Performing Arts']:
df['category'].iloc[index] = 'Arts, Entertainment & Recreation'
elif indus == 'Biotech & Pharmaceuticals':
df['category'].iloc[index] = 'Biotech & Pharmaceuticals'
elif indus in ['Consulting','Staffing & Outsourcing',
'Architectural & Engineering Services','Membership Organizations',
'Building & Personnel Services','Security Services','Wholesale',
'Research & Development','Advertising & Marketing','Business Service Centers & Copy Shops']:
df['category'].iloc[index] = 'Business Services'
elif indus == 'Construction' :
df['category'].iloc[index] = 'Construction'
elif indus in ['Health, Beauty, & Fitness','Consumer Product Rental']:
df['category'].iloc[index] = 'Customer Services'
elif indus in ['K-12 Education','Education Training Services','Colleges & Universities','Preschool & Child Care']:
df['category'].iloc[index] = 'Education'
elif indus in ['Investment Banking & Asset Management','Banks & Credit Unions',
'Financial Transaction Processing','Brokerage Services',
'Lending','Financial Analytics & Research','Stock Exchanges']:
df['category'].iloc[index] = 'Finance'
elif indus in ['Federal Agencies','Municipal Governments','State & Regional Agencies']:
df['category'].iloc[index] = 'Goverment'
elif indus == 'Health Care Services & Hospitals' :
df['category'].iloc[index] = 'Health Care Services & Hospitals'
elif indus in ['Internet','Computer Hardware & Software','IT Services',
'Enterprise Software & Network Solutions']:
df['category'].iloc[index] = 'Information Technology'
elif indus in ['Insurance Carriers','Insurance Agencies & Brokerages']:
df['category'].iloc[index] = 'Insurance'
elif indus in ['Miscellaneous Manufacturing','Transportation Equipment Manufacturing',
'Health Care Products Manufacturing','Electrical & Electronic Manufacturing',
'Consumer Products Manufacturing','Food & Beverage Manufacturing',
'Industrial Manufacturing','Chemical Manufacturing','Metal & Mineral Manufacturing']:
df['category'].iloc[index] = 'Manufacturing'
elif indus in ['Motion Picture Production & Distribution','TV Broadcast & Cable Networks',
'Music Production & Distribution','Video Games','News Outlet','Radio','Publishing']:
df['category'].iloc[index] = 'Media'
elif indus in ['Social Assistance','Health Fundraising Organizations',
'Grantmaking Foundations','Religious Organizations']:
df['category'].iloc[index] = 'Non-Profit'
elif indus in ['Oil & Gas Exploration & Production','Energy','Oil & Gas Services','Utilities','Mining']:
df['category'].iloc[index] = 'Oil, Gas, Energy & Utilities'
elif indus == 'Real Estate':
df['category'].iloc[index] = 'Real Estate'
elif indus in ['Fast-Food & Quick-Service Restaurants','Casual Restaurants',
'Catering & Food Service Contractors','Upscale Restaurants']:
df['category'].iloc[index] = 'Restaurants, Bars & Food Services'
elif indus in ['General Merchandise & Superstores','Department, Clothing, & Shoe Stores',
'Home Furniture & Housewares Stores','Home Centers & Hardware Stores',
'Grocery Stores & Supermarkets','Consumer Electronics & Appliances Stores',
'Drug & Health Stores','Food & Beverage Stores','Pet & Pet Supplies Stores',
'Beauty & Personal Accessories Stores','Automotive Parts & Accessories Stores',
'Other Retail Stores','Office Supply Stores','Vehicle Dealers',
'Sporting Goods Stores','Toy & Hobby Stores',
'Commercial Equipment Repair & Maintenance','General Repair & Maintenance',
'Veterinary Services','Auctions & Galleries','Commercial Equipment Rental',
'Media & Entertainment Retail Stores','Gift, Novelty & Souvenir Stores']:
df['category'].iloc[index] = 'Retail'
elif indus in ['Telecommunications Services','Cable, Internet & Telephone Providers',
'Telecommunications Manufacturing']:
df['category'].iloc[index] = 'Telecommunications'
elif indus in ['Logistics & Supply Chain','Express Delivery Services','Transportation Management',
'Rail','Trucking','Bus Transportation Services', 'Truck Rental & Leasing','Gas Stations',
'Convenience Stores & Truck Stops','Shipping']:
df['category'].iloc[index] = 'Transportation & Logistics'
elif indus in ['Hotels, Motels, & Resorts','Airlines','Car Rental','Cruise Ships','Travel Agencies']:
df['category'].iloc[index] = 'Travel & Tourism'
# convert review_counts,salaries_count,jobs_count,interviews_count,benefits_count into numeric
# review counts
df.review_counts[df.review_counts == '--'] = '0'
df.review_counts = (df.review_counts.replace(r'[K,k]+$', '', regex=True).astype(float) * \
df.review_counts.str.extract(r'[\d\.]+([K,k]+)', expand=False)
.fillna(1)
.replace(['K','k'], [10**3,10**3]).astype(int))
# salaries review count
df.salaries_count[df.salaries_count == '--'] = '0'
df.salaries_count = (df.salaries_count.replace(r'[K,k]+$', '', regex=True).astype(float) * \
df.salaries_count.str.extract(r'[\d\.]+([K,k]+)', expand=False)
.fillna(1)
.replace(['K','k'], [10**3,10**3]).astype(int))
#jobs review counts
df.jobs_count[df.jobs_count == '--'] = '0'
df.jobs_count = (df.jobs_count.replace(r'[K,k]+$', '', regex=True).astype(float) * \
df.jobs_count.str.extract(r'[\d\.]+([K,k]+)', expand=False)
.fillna(1)
.replace(['K','k'], [10**3,10**3]).astype(int))
# inteviews review counts
df.interviews_count[df.interviews_count == '--'] = '0'
df.interviews_count = (df.interviews_count.replace(r'[K,k]+$', '', regex=True).astype(float) * \
df.interviews_count.str.extract(r'[\d\.]+([K,k]+)', expand=False)
.fillna(1)
.replace(['K','k'], [10**3,10**3]).astype(int))
# benefits review counts
df.benefits_count[df.benefits_count == '--'] = '0'
df.benefits_count = (df.benefits_count.replace(r'[K,k]+$', '', regex=True).astype(float) * \
df.benefits_count.str.extract(r'[\d\.]+([K,k]+)', expand=False)
.fillna(1)
.replace(['K','k'], [10**3,10**3]).astype(int))
# founded column
df.founded.fillna(round(df.founded.mean(),0), inplace = True)
# company size
# 1 = less 5000 employees
# 2 = 5001 to 10000 employees
# 3 = 10000+ employees
df['size'] = df['size'].map({'10000+ Employees': 3,
'5001 to 10000 Employees':2,
'1001 to 5000 Employees' : 1,
'201 to 500 Employees' : 1,
'501 to 1000 Employees' : 1,
'1 to 50 Employees': 1,
'Unknown' :1})
# delete null values
df.dropna(inplace = True)
#interview_possitive, negative, neutral
df.interview_possitive = pd.to_numeric(df.interview_possitive.str.strip('%'))/100
df.interview_negative = pd.to_numeric(df.interview_negative.str.strip('%'))/100
df.interview_neutral = pd.to_numeric(df.interview_neutral.str.strip('%'))/100
# 1 = 'Unknown / Non-Applicable'
# 2 = 'Less than $100 million (USD)'
# 3 = '$100 to $500 million (USD)'
# 4 = '$500 million to $1 billion (USD)'
# 5 = '$1 to $2 billion (USD)'
# 6 = '$2 to $5 billion (USD)'
# 7 = '$5 to $10 billion (USD)'
# 8 = '$10+ billion (USD)'
df['revenue'] = df['revenue'].map({'$10+ billion (USD)':8,
'$5 to $10 billion (USD)':7,
'$2 to $5 billion (USD)' :6,
'$1 to $2 billion (USD)':5,
'$500 million to $1 billion (USD)':4,
'$100 to $500 million (USD)' :3,
'$50 to $100 million (USD)':2,
'$25 to $50 million (USD)':2,
'$10 to $25 million (USD)':2,
'$5 to $10 million (USD)':2,
'$1 to $5 million (USD)':2,
'Less than $1 million (USD)':2,
'Unknown / Non-Applicable':1})
#company type
df.company_type[df.company_type.str.contains('Public')] = 'Public'
df.company_type[df.company_type.str.contains('Private')] = 'Private'
df['company_type'] = df['company_type'].map({'Public' :'Public',
'Private' :'Private',
'Subsidiary or Business Segment':'Subsidiary or Business Segment',
'College / University':'Education',
'Nonprofit Organization': 'Nonprofit Organization',
'Government': 'Government',
'Hospital':'Hospital',
'School / School District': 'Education',
'Franchise': 'Others',
'Unknown':'Others',
'Self-employed':'Others',
'Contract':'Others'})
# Create state column base on head quarter column
df['state'] = df.head_quarter.apply(lambda head_quarter : head_quarter.split(',')[1])
return df
df = data_cleaning(df_raw)
# Create company rank column
df['company_rank'] = df['rating']
for index, rk in enumerate(df['company_rank']):
if rk >= 4.1:
df['company_rank'].iloc[index] = 2
elif (rk >= 3.9) & (rk < 4.1) :
df['company_rank'].iloc[index] = 1
elif (rk < 3.9):
# bellow 3.9
df['company_rank'].iloc[index] = 0
df['company_rank'] = df['company_rank'].astype(int)
df['company_rank'].value_counts(normalize = True).sort_index()
plt.figure(figsize = (12,4) )
plt.title('Rating')
sns.boxplot(x = df['rating'].values, color='r');
plt.figure(figsize = (10,8) )
plt.title('Rating Distribution')
df['rating'].hist(color = 'b');
plt.figure(figsize = (6,6) )
plt.title("Company's Ranking Distribution")
df['company_rank'].hist(color = 'b');
df['company_rank'].value_counts(normalize= True).sort_index()
df.describe().transpose()
df[['name','rating']].sort_values('rating', ascending= False).head(30)
size_df = pd.DataFrame(df.groupby('size').agg('mean')['company_rank'])
# 1 = less 5000 employees
# 2 = 5001 to 10000 employees
# 3 = 10000+ employees
plt.figure(figsize = (12,6))
sns.barplot(x = 'size', y = 'company_rank', data= size_df.reset_index().sort_values('company_rank'))
plt.xticks([0,1,2],['less 5000 employees','5001 to 10000 employees','10000+ employees'],rotation = 30)
plt.title("Company size vs Company's Ranking", fontsize = 20)
plt.xlabel('Company Size', fontsize = 16)
plt.ylabel("Company's Ranking Average ", fontsize = 16)
;
category_df = pd.DataFrame(df.groupby('category').agg('mean')['company_rank'])
category_df.sort_values('company_rank')
clrs = ['black' if (x < 1.24) else 'red' for x in category_df['company_rank'].sort_values()]
plt.figure(figsize = (15,6))
sns.barplot(x = 'category', y = 'company_rank', data= category_df.reset_index().sort_values('company_rank'), palette= clrs)
plt.title("Company Categories vs Company's Ranking", fontsize = 20)
plt.xlabel('Company Categories', fontsize = 16)
plt.ylabel("Company's Ranking Average ", fontsize = 16)
plt.xticks(rotation = 80, rotation_mode = 'default', fontsize = 12)
;
revenue_df = pd.DataFrame(df.groupby('revenue').agg('mean')['company_rank'])
revenue_df
# 1 = 'Unknown / Non-Applicable'
# 2 = 'Less than $100 million (USD)'
# 3 = '$100 to $500 million (USD)'
# 4 = '$500 million to $1 billion (USD)'
# 5 = '$1 to $2 billion (USD)'
# 6 = '$2 to $5 billion (USD)'
# 7 = '$5 to $10 billion (USD)'
# 8 = '$10+ billion (USD)'
plt.figure(figsize = (15,8))
clrs = ['black' if (x < 1.2) else 'red' for x in revenue_df['company_rank']]
sns.barplot(x = 'revenue', y = 'company_rank', data= revenue_df.reset_index().sort_values('company_rank'),palette = clrs)
plt.xticks(rotation = 45)
plt.title("Company Revenue vs Company's Ranking", fontsize = 20)
plt.xticks([0, 1, 2,3,4,5,6,7], ['Unknown / Non-Applicable','Less than $100 million (USD)','$100 to $500 million (USD)',
'$500 million to $1 billion (USD)','$1 to $2 billion (USD)','$2 to $5 billion (USD)',
'$5 to $10 billion (USD)','$10+ billion (USD)'],rotation=20)
plt.xlabel('Revenue', fontsize = 16)
plt.ylabel("Company's ranking", fontsize = 16)
;
df.drop(columns = ['rating','benefits_score']).corr()[['company_rank']].sort_values('company_rank')
# code from global lesson 3.07
plt.figure(figsize=(8, 30))
sns.heatmap(df.drop(columns = ['rating','benefits_score','size','interview_neutral', 'interview_possitive']).corr()[['company_rank']].sort_values('company_rank', ascending= False),
annot=True,
cmap='coolwarm',
vmin=-1,
vmax=1);
# code from global lesson 3.07
plt.figure(figsize=(6, 8))
sns.heatmap(df.drop(columns = ['rating','benefits_score','size','interview_neutral', 'interview_possitive']).corr()[['company_rank']].sort_values('company_rank', ascending= False).iloc[1:6,],
annot=True,
cmap='coolwarm',
vmin=-0.5,
vmax=0.5)
plt.title('Top 5 Positive Correlation', fontsize = 16)
plt.xticks([0.5],["Company's Ranking"],fontsize = 12)
plt.yticks([0.5,1.5,2.5,3.5,4.5],['Interview Difficulty','Gym Membership','Work from Home','Health Care on Site','Free Lunch or Snacks'],fontsize = 12, rotation=0);
# code from global lesson 3.07
plt.figure(figsize=(6, 8))
sns.heatmap(df.drop(columns = ['rating','benefits_score','size','interview_neutral', 'interview_possitive']).corr()[['company_rank']].sort_values('company_rank').head(5),
annot=True,
cmap='coolwarm',
vmin=-0.5,
vmax=0.5);
plt.title('Top 5 Negative Correlation', fontsize = 16)
plt.xticks([0.5],["Company's Ranking"],fontsize = 12)
plt.yticks([0.5,1.5,2.5,3.5,4.5],['Bereavement Leave','Military Leave','Performance Bonus','Employee Discount','Supplemental Workers \nCompensation'],fontsize = 12);
df_benefit = df.iloc[:,20:79].mean()
df_benefit1 = pd.DataFrame(df_benefit)
df_benefit1['feature'] = df_benefit1.index
df_benefit1.columns = ['avg','features']
plt.figure(figsize = (12,6))
sns.barplot(x = 'features', y = 'avg', data= df_benefit1.sort_values('avg').head(10))
plt.xticks(rotation = 45)
plt.title('Top 10 Rare Benefits', fontsize = 16);
plt.figure(figsize = (12,6))
sns.barplot(x = 'features', y = 'avg', data= df_benefit1.sort_values('avg', ascending=False).iloc[6:,].head(10))
plt.xticks(rotation = 45)
plt.title('Top 10 the most Popular Benefits', fontsize = 16);
df.to_csv('data/clean_df.csv', index = False)
| 0.154567 | 0.765506 |
# 梯度下降
:label:`sec_gd`
尽管*梯度下降*(gradient descent)很少直接用于深度学习,
但了解它是理解下一节随机梯度下降算法的关键。
例如,由于学习率过大,优化问题可能会发散,这种现象早已在梯度下降中出现。
同样地,*预处理*(preconditioning)是梯度下降中的一种常用技术,
还被沿用到更高级的算法中。
让我们从简单的一维梯度下降开始。
## 一维梯度下降
为什么梯度下降算法可以优化目标函数?
一维中的梯度下降给我们很好的启发。
考虑一类连续可微实值函数$f: \mathbb{R} \rightarrow \mathbb{R}$,
利用泰勒展开,我们可以得到
$$f(x + \epsilon) = f(x) + \epsilon f'(x) + \mathcal{O}(\epsilon^2).$$
:eqlabel:`gd-taylor`
即在一阶近似中,$f(x+\epsilon)$可通过$x$处的函数值$f(x)$和一阶导数$f'(x)$得出。
我们可以假设在负梯度方向上移动的$\epsilon$会减少$f$。
为了简单起见,我们选择固定步长$\eta > 0$,然后取$\epsilon = -\eta f'(x)$。
将其代入泰勒展开式我们可以得到
$$f(x - \eta f'(x)) = f(x) - \eta f'^2(x) + \mathcal{O}(\eta^2 f'^2(x)).$$
:eqlabel:`gd-taylor-2`
如果其导数$f'(x) \neq 0$没有消失,我们就能继续展开,这是因为$\eta f'^2(x)>0$。
此外,我们总是可以令$\eta$小到足以使高阶项变得不相关。
因此,
$$f(x - \eta f'(x)) \lessapprox f(x).$$
这意味着,如果我们使用
$$x \leftarrow x - \eta f'(x)$$
来迭代$x$,函数$f(x)$的值可能会下降。
因此,在梯度下降中,我们首先选择初始值$x$和常数$\eta > 0$,
然后使用它们连续迭代$x$,直到停止条件达成。
例如,当梯度$|f'(x)|$的幅度足够小或迭代次数达到某个值时。
下面我们来展示如何实现梯度下降。为了简单起见,我们选用目标函数$f(x)=x^2$。
尽管我们知道$x=0$时$f(x)$能取得最小值,
但我们仍然使用这个简单的函数来观察$x$的变化。
```
%matplotlib inline
import numpy as np
import torch
from d2l import torch as d2l
def f(x): # 目标函数
return x ** 2
def f_grad(x): # 目标函数的梯度(导数)
return 2 * x
```
接下来,我们使用$x=10$作为初始值,并假设$\eta=0.2$。
使用梯度下降法迭代$x$共10次,我们可以看到,$x$的值最终将接近最优解。
```
def gd(eta, f_grad):
x = 10.0
results = [x]
for i in range(10):
x -= eta * f_grad(x)
results.append(float(x))
print(f'epoch 10, x: {x:f}')
return results
results = gd(0.2, f_grad)
```
对进行$x$优化的过程可以绘制如下。
```
def show_trace(results, f):
n = max(abs(min(results)), abs(max(results)))
f_line = torch.arange(-n, n, 0.01)
d2l.set_figsize()
d2l.plot([f_line, results], [[f(x) for x in f_line], [
f(x) for x in results]], 'x', 'f(x)', fmts=['-', '-o'])
show_trace(results, f)
```
### 学习率
:label:`subsec_gd-learningrate`
*学习率*(learning rate)决定目标函数能否收敛到局部最小值,以及何时收敛到最小值。
学习率$\eta$可由算法设计者设置。
请注意,如果我们使用的学习率太小,将导致$x$的更新非常缓慢,需要更多的迭代。
例如,考虑同一优化问题中$\eta = 0.05$的进度。
如下所示,尽管经过了10个步骤,我们仍然离最优解很远。
```
show_trace(gd(0.05, f_grad), f)
```
相反,如果我们使用过高的学习率,$\left|\eta f'(x)\right|$对于一阶泰勒展开式可能太大。
也就是说, :eqref:`gd-taylor`中的$\mathcal{O}(\eta^2 f'^2(x))$可能变得显著了。
在这种情况下,$x$的迭代不能保证降低$f(x)$的值。
例如,当学习率为$\eta=1.1$时,$x$超出了最优解$x=0$并逐渐发散。
```
show_trace(gd(1.1, f_grad), f)
```
### 局部最小值
为了演示非凸函数的梯度下降,考虑函数$f(x) = x \cdot \cos(cx)$,其中$c$为某常数。
这个函数有无穷多个局部最小值。
根据我们选择的学习率,我们最终可能只会得到许多解的一个。
下面的例子说明了(不切实际的)高学习率如何导致较差的局部最小值。
```
c = torch.tensor(0.15 * np.pi)
def f(x): # 目标函数
return x * torch.cos(c * x)
def f_grad(x): # 目标函数的梯度
return torch.cos(c * x) - c * x * torch.sin(c * x)
show_trace(gd(2, f_grad), f)
```
## 多元梯度下降
现在我们对单变量的情况有了更好的理解,让我们考虑一下$\mathbf{x} = [x_1, x_2, \ldots, x_d]^\top$的情况。
即目标函数$f: \mathbb{R}^d \to \mathbb{R}$将向量映射成标量。
相应地,它的梯度也是多元的:它是一个由$d$个偏导数组成的向量:
$$\nabla f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_d}\bigg]^\top.$$
梯度中的每个偏导数元素$\partial f(\mathbf{x})/\partial x_i$代表了当输入$x_i$时$f$在$\mathbf{x}$处的变化率。
和先前单变量的情况一样,我们可以对多变量函数使用相应的泰勒近似来思考。
具体来说,
$$f(\mathbf{x} + \boldsymbol{\epsilon}) = f(\mathbf{x}) + \mathbf{\boldsymbol{\epsilon}}^\top \nabla f(\mathbf{x}) + \mathcal{O}(\|\boldsymbol{\epsilon}\|^2).$$
:eqlabel:`gd-multi-taylor`
换句话说,在$\boldsymbol{\epsilon}$的二阶项中,
最陡下降的方向由负梯度$-\nabla f(\mathbf{x})$得出。
选择合适的学习率$\eta > 0$来生成典型的梯度下降算法:
$$\mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f(\mathbf{x}).$$
这个算法在实践中的表现如何呢?
我们构造一个目标函数$f(\mathbf{x})=x_1^2+2x_2^2$,
并有二维向量$\mathbf{x} = [x_1, x_2]^\top$作为输入,
标量作为输出。
梯度由$\nabla f(\mathbf{x}) = [2x_1, 4x_2]^\top$给出。
我们将从初始位置$[-5, -2]$通过梯度下降观察$\mathbf{x}$的轨迹。
我们还需要两个辅助函数:
第一个是update函数,并将其应用于初始值20次;
第二个函数会显示$\mathbf{x}$的轨迹。
```
def train_2d(trainer, steps=20, f_grad=None): #@save
"""用定制的训练机优化2D目标函数"""
# s1和s2是稍后将使用的内部状态变量
x1, x2, s1, s2 = -5, -2, 0, 0
results = [(x1, x2)]
for i in range(steps):
if f_grad:
x1, x2, s1, s2 = trainer(x1, x2, s1, s2, f_grad)
else:
x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
results.append((x1, x2))
print(f'epoch {i + 1}, x1: {float(x1):f}, x2: {float(x2):f}')
return results
def show_trace_2d(f, results): #@save
"""显示优化过程中2D变量的轨迹"""
d2l.set_figsize()
d2l.plt.plot(*zip(*results), '-o', color='#ff7f0e')
x1, x2 = torch.meshgrid(torch.arange(-5.5, 1.0, 0.1),
torch.arange(-3.0, 1.0, 0.1))
d2l.plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
d2l.plt.xlabel('x1')
d2l.plt.ylabel('x2')
```
接下来,我们观察学习率$\eta = 0.1$时优化变量$\mathbf{x}$的轨迹。
可以看到,经过20步之后,$\mathbf{x}$的值接近其位于$[0, 0]$的最小值。
虽然进展相当顺利,但相当缓慢。
```
def f_2d(x1, x2): # 目标函数
return x1 ** 2 + 2 * x2 ** 2
def f_2d_grad(x1, x2): # 目标函数的梯度
return (2 * x1, 4 * x2)
def gd_2d(x1, x2, s1, s2, f_grad):
g1, g2 = f_grad(x1, x2)
return (x1 - eta * g1, x2 - eta * g2, 0, 0)
eta = 0.1
show_trace_2d(f_2d, train_2d(gd_2d, f_grad=f_2d_grad))
```
## 自适应方法
正如我们在 :numref:`subsec_gd-learningrate`中所看到的,选择“恰到好处”的学习率$\eta$是很棘手的。
如果我们把它选得太小,就没有什么进展;如果太大,得到的解就会振荡,甚至可能发散。
如果我们可以自动确定$\eta$,或者完全不必选择学习率,会怎么样?
除了考虑目标函数的值和梯度、还考虑它的曲率的二阶方法可以帮我们解决这个问题。
虽然由于计算代价的原因,这些方法不能直接应用于深度学习,但它们为如何设计高级优化算法提供了有用的思维直觉,这些算法可以模拟下面概述的算法的许多理想特性。
### 牛顿法
回顾一些函数$f: \mathbb{R}^d \rightarrow \mathbb{R}$的泰勒展开式,事实上我们可以把它写成
$$f(\mathbf{x} + \boldsymbol{\epsilon}) = f(\mathbf{x}) + \boldsymbol{\epsilon}^\top \nabla f(\mathbf{x}) + \frac{1}{2} \boldsymbol{\epsilon}^\top \nabla^2 f(\mathbf{x}) \boldsymbol{\epsilon} + \mathcal{O}(\|\boldsymbol{\epsilon}\|^3).$$
:eqlabel:`gd-hot-taylor`
为了避免繁琐的符号,我们将$\mathbf{H} \stackrel{\mathrm{def}}{=} \nabla^2 f(\mathbf{x})$定义为$f$的Hessian,是$d \times d$矩阵。
当$d$的值很小且问题很简单时,$\mathbf{H}$很容易计算。
但是对于深度神经网络而言,考虑到$\mathbf{H}$可能非常大,
$\mathcal{O}(d^2)$个条目的存储代价会很高,
此外通过反向传播进行计算可能雪上加霜。
然而,我们姑且先忽略这些考量,看看会得到什么算法。
毕竟,$f$的最小值满足$\nabla f = 0$。
遵循 :numref:`sec_calculus`中的微积分规则,
通过取$\boldsymbol{\epsilon}$对 :eqref:`gd-hot-taylor`的导数,
再忽略不重要的高阶项,我们便得到
$$\nabla f(\mathbf{x}) + \mathbf{H} \boldsymbol{\epsilon} = 0 \text{ and hence }
\boldsymbol{\epsilon} = -\mathbf{H}^{-1} \nabla f(\mathbf{x}).$$
也就是说,作为优化问题的一部分,我们需要将Hessian矩阵$\mathbf{H}$求逆。
举一个简单的例子,对于$f(x) = \frac{1}{2} x^2$,我们有$\nabla f(x) = x$和$\mathbf{H} = 1$。
因此,对于任何$x$,我们可以获得$\epsilon = -x$。
换言之,单单一步就足以完美地收敛,而无须任何调整。
我们在这里比较幸运:泰勒展开式是确切的,因为$f(x+\epsilon)= \frac{1}{2} x^2 + \epsilon x + \frac{1}{2} \epsilon^2$。
让我们看看其他问题。
给定一个凸双曲余弦函数$c$,其中$c$为某些常数,
我们可以看到经过几次迭代后,得到了$x=0$处的全局最小值。
```
c = torch.tensor(0.5)
def f(x): # O目标函数
return torch.cosh(c * x)
def f_grad(x): # 目标函数的梯度
return c * torch.sinh(c * x)
def f_hess(x): # 目标函数的Hessian
return c**2 * torch.cosh(c * x)
def newton(eta=1):
x = 10.0
results = [x]
for i in range(10):
x -= eta * f_grad(x) / f_hess(x)
results.append(float(x))
print('epoch 10, x:', x)
return results
show_trace(newton(), f)
```
现在让我们考虑一个非凸函数,比如$f(x) = x \cos(c x)$,$c$为某些常数。
请注意在牛顿法中,我们最终将除以Hessian。
这意味着如果二阶导数是负的,$f$的值可能会趋于增加。
这是这个算法的致命缺陷!
让我们看看实践中会发生什么。
```
c = torch.tensor(0.15 * np.pi)
def f(x): # 目标函数
return x * torch.cos(c * x)
def f_grad(x): # 目标函数的梯度
return torch.cos(c * x) - c * x * torch.sin(c * x)
def f_hess(x): # 目标函数的Hessian
return - 2 * c * torch.sin(c * x) - x * c**2 * torch.cos(c * x)
show_trace(newton(), f)
```
这发生了惊人的错误。我们怎样才能修正它?
一种方法是用取Hessian的绝对值来修正,另一个策略是重新引入学习率。
这似乎违背了初衷,但不完全是——拥有二阶信息可以使我们在曲率较大时保持谨慎,而在目标函数较平坦时则采用较大的学习率。
让我们看看在学习率稍小的情况下它是如何生效的,比如$\eta = 0.5$。
如我们所见,我们有了一个相当高效的算法。
```
show_trace(newton(0.5), f)
```
### 收敛性分析
在此,我们以三次可微的目标凸函数$f$为例,分析它的牛顿法收敛速度。
假设它们的二阶导数不为零,即$f'' > 0$。
用$x^{(k)}$表示$x$在第$k^\mathrm{th}$次迭代时的值,
令$e^{(k)} \stackrel{\mathrm{def}}{=} x^{(k)} - x^*$表示$k^\mathrm{th}$迭代时与最优性的距离。
通过泰勒展开,我们得到条件$f'(x^*) = 0$可以写成
$$0 = f'(x^{(k)} - e^{(k)}) = f'(x^{(k)}) - e^{(k)} f''(x^{(k)}) + \frac{1}{2} (e^{(k)})^2 f'''(\xi^{(k)}),$$
这对某些$\xi^{(k)} \in [x^{(k)} - e^{(k)}, x^{(k)}]$成立。
将上述展开除以$f''(x^{(k)})$得到
$$e^{(k)} - \frac{f'(x^{(k)})}{f''(x^{(k)})} = \frac{1}{2} (e^{(k)})^2 \frac{f'''(\xi^{(k)})}{f''(x^{(k)})}.$$
回想之前的方程$x^{(k+1)} = x^{(k)} - f'(x^{(k)}) / f''(x^{(k)})$。
插入这个更新方程,取两边的绝对值,我们得到
$$\left|e^{(k+1)}\right| = \frac{1}{2}(e^{(k)})^2 \frac{\left|f'''(\xi^{(k)})\right|}{f''(x^{(k)})}.$$
因此,每当我们处于有界区域$\left|f'''(\xi^{(k)})\right| / (2f''(x^{(k)})) \leq c$,
我们就有一个二次递减误差
$$\left|e^{(k+1)}\right| \leq c (e^{(k)})^2.$$
另一方面,优化研究人员称之为“线性”收敛,而$\left|e^{(k+1)}\right| \leq \alpha \left|e^{(k)}\right|$这样的条件称为“恒定”收敛速度。
请注意,我们无法估计整体收敛的速度,但是一旦我们接近极小值,收敛将变得非常快。
另外,这种分析要求$f$在高阶导数上表现良好,即确保$f$在变化他的值方面没有任何“超常”的特性。
### 预处理
计算和存储完整的Hessian非常昂贵,而改善这个问题的一种方法是“预处理”。
它回避了计算整个Hessian,而只计算“对角线”项,即如下的算法更新:
$$\mathbf{x} \leftarrow \mathbf{x} - \eta \mathrm{diag}(\mathbf{H})^{-1} \nabla f(\mathbf{x}).$$
虽然这不如完整的牛顿法精确,但它仍然比不使用要好得多。
为什么预处理有效呢?
假设一个变量以毫米表示高度,另一个变量以公里表示高度的情况。
假设这两种自然尺度都以米为单位,那么我们的参数化就出现了严重的不匹配。
幸运的是,使用预处理可以消除这种情况。
梯度下降的有效预处理相当于为每个变量选择不同的学习率(矢量$\mathbf{x}$的坐标)。
我们将在后面一节看到,预处理推动了随机梯度下降优化算法的一些创新。
### 梯度下降和线搜索
梯度下降的一个关键问题是我们可能会超过目标或进展不足,
解决这一问题的简单方法是结合使用线搜索和梯度下降。
也就是说,我们使用$\nabla f(\mathbf{x})$给出的方向,
然后进行二分搜索,以确定哪个学习率$\eta$使$f(\mathbf{x} - \eta \nabla f(\mathbf{x}))$取最小值。
有关分析和证明,此算法收敛迅速(请参见 :cite:`Boyd.Vandenberghe.2004`)。
然而,对深度学习而言,这不太可行。
因为线搜索的每一步都需要评估整个数据集上的目标函数,实现它的方式太昂贵了。
## 小结
* 学习率的大小很重要:学习率太大会使模型发散,学习率太小会没有进展。
* 梯度下降会可能陷入局部极小值,而得不到全局最小值。
* 在高维模型中,调整学习率是很复杂的。
* 预处理有助于调节比例。
* 牛顿法在凸问题中一旦开始正常工作,速度就会快得多。
* 对于非凸问题,不要不作任何调整就使用牛顿法。
## 练习
1. 用不同的学习率和目标函数进行梯度下降实验。
1. 在区间$[a, b]$中实现线搜索以最小化凸函数。
1. 你是否需要导数来进行二分搜索,即决定选择$[a, (a+b)/2]$还是$[(a+b)/2, b]$。
1. 算法的收敛速度有多快?
1. 实现该算法,并将其应用于求$\log (\exp(x) + \exp(-2x -3))$的最小值。
1. 设计一个定义在$\mathbb{R}^2$上的目标函数,它的梯度下降非常缓慢。提示:不同坐标的缩放方式不同。
1. 使用预处理实现牛顿方法的轻量级版本:
1. 使用对角Hessian作为预条件。
1. 使用它的绝对值,而不是实际值(可能有符号)。
1. 将此应用于上述问题。
1. 将上述算法应用于多个目标函数(凸或非凸)。如果你把坐标旋转$45$度会怎么样?
[Discussions](https://discuss.d2l.ai/t/3836)
|
github_jupyter
|
%matplotlib inline
import numpy as np
import torch
from d2l import torch as d2l
def f(x): # 目标函数
return x ** 2
def f_grad(x): # 目标函数的梯度(导数)
return 2 * x
def gd(eta, f_grad):
x = 10.0
results = [x]
for i in range(10):
x -= eta * f_grad(x)
results.append(float(x))
print(f'epoch 10, x: {x:f}')
return results
results = gd(0.2, f_grad)
def show_trace(results, f):
n = max(abs(min(results)), abs(max(results)))
f_line = torch.arange(-n, n, 0.01)
d2l.set_figsize()
d2l.plot([f_line, results], [[f(x) for x in f_line], [
f(x) for x in results]], 'x', 'f(x)', fmts=['-', '-o'])
show_trace(results, f)
show_trace(gd(0.05, f_grad), f)
show_trace(gd(1.1, f_grad), f)
c = torch.tensor(0.15 * np.pi)
def f(x): # 目标函数
return x * torch.cos(c * x)
def f_grad(x): # 目标函数的梯度
return torch.cos(c * x) - c * x * torch.sin(c * x)
show_trace(gd(2, f_grad), f)
def train_2d(trainer, steps=20, f_grad=None): #@save
"""用定制的训练机优化2D目标函数"""
# s1和s2是稍后将使用的内部状态变量
x1, x2, s1, s2 = -5, -2, 0, 0
results = [(x1, x2)]
for i in range(steps):
if f_grad:
x1, x2, s1, s2 = trainer(x1, x2, s1, s2, f_grad)
else:
x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
results.append((x1, x2))
print(f'epoch {i + 1}, x1: {float(x1):f}, x2: {float(x2):f}')
return results
def show_trace_2d(f, results): #@save
"""显示优化过程中2D变量的轨迹"""
d2l.set_figsize()
d2l.plt.plot(*zip(*results), '-o', color='#ff7f0e')
x1, x2 = torch.meshgrid(torch.arange(-5.5, 1.0, 0.1),
torch.arange(-3.0, 1.0, 0.1))
d2l.plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
d2l.plt.xlabel('x1')
d2l.plt.ylabel('x2')
def f_2d(x1, x2): # 目标函数
return x1 ** 2 + 2 * x2 ** 2
def f_2d_grad(x1, x2): # 目标函数的梯度
return (2 * x1, 4 * x2)
def gd_2d(x1, x2, s1, s2, f_grad):
g1, g2 = f_grad(x1, x2)
return (x1 - eta * g1, x2 - eta * g2, 0, 0)
eta = 0.1
show_trace_2d(f_2d, train_2d(gd_2d, f_grad=f_2d_grad))
c = torch.tensor(0.5)
def f(x): # O目标函数
return torch.cosh(c * x)
def f_grad(x): # 目标函数的梯度
return c * torch.sinh(c * x)
def f_hess(x): # 目标函数的Hessian
return c**2 * torch.cosh(c * x)
def newton(eta=1):
x = 10.0
results = [x]
for i in range(10):
x -= eta * f_grad(x) / f_hess(x)
results.append(float(x))
print('epoch 10, x:', x)
return results
show_trace(newton(), f)
c = torch.tensor(0.15 * np.pi)
def f(x): # 目标函数
return x * torch.cos(c * x)
def f_grad(x): # 目标函数的梯度
return torch.cos(c * x) - c * x * torch.sin(c * x)
def f_hess(x): # 目标函数的Hessian
return - 2 * c * torch.sin(c * x) - x * c**2 * torch.cos(c * x)
show_trace(newton(), f)
show_trace(newton(0.5), f)
| 0.395951 | 0.98104 |

# Welcome to terrainbento
You have just cloned the `examples_test_and_tutorials` repository for the terrainbento multi-model package. Congratulations!
If you are interested in reading about the details of terrainbento, this package is described in [Barnhart et al. (2019)](https://www.geosci-model-dev.net/12/1267/2019/).
The documentation for the package is provided [here](http://terrainbento.readthedocs.io/en/latest/).
If you are interested in the source code, you can find it [on GitHub](https://github.com/TerrainBento/terrainbento). If there is a feature that terrainbento does not have that you are interested in, if you have a clarification question, or if you find an error, please make an [Issue on GitHub](https://github.com/TerrainBento/terrainbento/issues) so we can improve the package.
This notebook exists to provide a hyperlinked guide to the supporting examples, tests, and tutorials we have created in support of this package.
## Introduction
terrainbento was designed to make it easy to create alternative models to be compared in Earth surface dynamics. The package has 28 model programs and a model base class that makes it possible to make additional models within the same framework.
The simplest model, called Basic, evolves topography using stream power and linear diffusion. It has the following governing equation:
$\frac{\partial \eta}{\partial t} = - KQ^{1/2}S + D\nabla^2 \eta$
where $K$ and $D$ are constants, $Q$ is discharge, $S$ is local slope, and $\eta$ is the topography. Other models modify Basic by adding or changing a process component and changing the governing equation. See the [model Basic documentation](https://terrainbento.readthedocs.io/en/latest/source/terrainbento.derived_models.model_basic.html) for additional information.
## Example usage
There are three additional introductory tutorials.
1) [Introduction terrainbento](example_usage/Introduction_to_terrainbento.ipynb)
2) [Introduction to boundary conditions in terrainbento](example_usage/introduction_to_boundary_conditions.ipynb)
3) [Introduction to output writers in terrainbento](example_usage/introduction_to_output_writers.ipynb).
## Example Coupled Models
This section provides links to five notebooks that show the usage of five example models provided in terrainbento. In each of these notebooks we provide the governing equation(s) for the model, initialize and run the model, make a slope-area plot, save a NetCDF of the final topography, and plot a image of the final topography.
1) [Basic](coupled_process_elements/model_basic_steady_solution.ipynb) the simplest landscape evolution model in the terrainbento package.
2) [BasicVm](coupled_process_elements/model_basic_var_m_steady_solution.ipynb) which permits the drainage area exponent to change
3) [BasicCh](coupled_process_elements/model_basicCh_steady_solution.ipynb) which uses a non-linear hillslope erosion and transport law
4) [BasicVs](coupled_process_elements/model_basicVs_steady_solution.ipynb) which uses variable source area hydrology
5) [BasisRt](coupled_process_elements/model_basicRt_steady_solution.ipynb) which allows for two lithologies with different K values
6) [RealDEM](coupled_process_elements/model_basic_realDEM.ipynb) Run the basic terrainbento model with a real DEM as initial condition.
## Terrainnbento challenge
- [Make your own gif](coupled_process_elements/Challenge.ipynb)
|
github_jupyter
|

# Welcome to terrainbento
You have just cloned the `examples_test_and_tutorials` repository for the terrainbento multi-model package. Congratulations!
If you are interested in reading about the details of terrainbento, this package is described in [Barnhart et al. (2019)](https://www.geosci-model-dev.net/12/1267/2019/).
The documentation for the package is provided [here](http://terrainbento.readthedocs.io/en/latest/).
If you are interested in the source code, you can find it [on GitHub](https://github.com/TerrainBento/terrainbento). If there is a feature that terrainbento does not have that you are interested in, if you have a clarification question, or if you find an error, please make an [Issue on GitHub](https://github.com/TerrainBento/terrainbento/issues) so we can improve the package.
This notebook exists to provide a hyperlinked guide to the supporting examples, tests, and tutorials we have created in support of this package.
## Introduction
terrainbento was designed to make it easy to create alternative models to be compared in Earth surface dynamics. The package has 28 model programs and a model base class that makes it possible to make additional models within the same framework.
The simplest model, called Basic, evolves topography using stream power and linear diffusion. It has the following governing equation:
$\frac{\partial \eta}{\partial t} = - KQ^{1/2}S + D\nabla^2 \eta$
where $K$ and $D$ are constants, $Q$ is discharge, $S$ is local slope, and $\eta$ is the topography. Other models modify Basic by adding or changing a process component and changing the governing equation. See the [model Basic documentation](https://terrainbento.readthedocs.io/en/latest/source/terrainbento.derived_models.model_basic.html) for additional information.
## Example usage
There are three additional introductory tutorials.
1) [Introduction terrainbento](example_usage/Introduction_to_terrainbento.ipynb)
2) [Introduction to boundary conditions in terrainbento](example_usage/introduction_to_boundary_conditions.ipynb)
3) [Introduction to output writers in terrainbento](example_usage/introduction_to_output_writers.ipynb).
## Example Coupled Models
This section provides links to five notebooks that show the usage of five example models provided in terrainbento. In each of these notebooks we provide the governing equation(s) for the model, initialize and run the model, make a slope-area plot, save a NetCDF of the final topography, and plot a image of the final topography.
1) [Basic](coupled_process_elements/model_basic_steady_solution.ipynb) the simplest landscape evolution model in the terrainbento package.
2) [BasicVm](coupled_process_elements/model_basic_var_m_steady_solution.ipynb) which permits the drainage area exponent to change
3) [BasicCh](coupled_process_elements/model_basicCh_steady_solution.ipynb) which uses a non-linear hillslope erosion and transport law
4) [BasicVs](coupled_process_elements/model_basicVs_steady_solution.ipynb) which uses variable source area hydrology
5) [BasisRt](coupled_process_elements/model_basicRt_steady_solution.ipynb) which allows for two lithologies with different K values
6) [RealDEM](coupled_process_elements/model_basic_realDEM.ipynb) Run the basic terrainbento model with a real DEM as initial condition.
## Terrainnbento challenge
- [Make your own gif](coupled_process_elements/Challenge.ipynb)
| 0.817356 | 0.912553 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.