code
stringlengths 2.5k
6.36M
| kind
stringclasses 2
values | parsed_code
stringlengths 0
404k
| quality_prob
float64 0
0.98
| learning_prob
float64 0.03
1
|
|---|---|---|---|---|
<img src='./img/EU-Copernicus-EUM_3Logos.png' alt='Logo EU Copernicus EUMETSAT' align='right' width='40%'></img>
<br>
<a href="./00_index.ipynb"><< Index</a><span style="float:right;"><a href="./11_sentinel3_slstr_frp_Californian_fires.ipynb">11 - Sentinel-3 SLSTR FRP - Californian Fires>></a>
<br>
# Optional: Introduction to Python and Project Jupyter
## Project Jupyter
<div class="alert alert-block alert-success" align="center">
<b><i>"Project Jupyter exists to develop open-source software, open-standards, and services for interactive computing across dozens of programming languages."</i></b>
</div>
<br>
Project Jupyter offers different tools to facilitate interactive computing, either with a web-based application (`Jupyter Notebooks`), an interactive development environment (`JupyterLab`) or via a `JupyterHub` that brings interactive computing to groups of users.
<br>
<center><img src='./img/jupyter_environment.png' alt='Logo Jupyter environment' width='60%'></img></center>
* **Jupyter Notebook** is an open-source web application that allows you to create and share documents that contain live code, equations, visualizations and narrative text.
* **JupyterLab 1.0: Jupyter’s Next-Generation Notebook Interface** <br> JupyterLab is a web-based interactive development environment for Jupyter notebooks, code, and data.
* **JupyterHub** <br>JupyterHub brings the power of notebooks to groups of users. It gives users access to computational environments and resources without burdening the users with installation and maintenance tasks. <br> Users - including students, researchers, and data scientists - can get their work done in their own workspaces on shared resources which can be managed efficiently by system administrators.
<hr>
## Why Jupyter Notebooks?
* Started with Python support, now **support of over 40 programming languages, including Python, R, Julia, ...**
* Notebooks can **easily be shared via GitHub, NBViewer, etc.**
* **Code, data and visualizations are combined in one place**
* A great tool for **teaching**
* **JupyterHub allows you to access an environment ready to code**
## Installation
### Installing Jupyter using Anaconda
Anaconda comes with the Jupyter Notebook installed. You just have to download Anaconda and following the installation instructions. Once installed, the jupyter notebook can be started with:
```
jupyter notebook
```
### Installing Jupyter with pip
Experienced Python users may want to install Jupyter using Python's package manager `pip`.
With `Python3` you do:
```
python3 -m pip install --upgrade pip
python3 -m pip install jupyter
```
In order to run the notebook, you run the same command as with Anaconda at the Terminal :
```
jupyter notebook
```
## Jupyter notebooks UI
* Notebook dashboard
* Create new notebook
* Notebook editor (UI)
* Menu
* Toolbar
* Notebook area and cells
* Cell types
* Code
* Markdown
* Edit (green) vs. Command mode (blue)
<br>
<div style='text-align:center;'>
<figure><img src='./img/notebook_ui.png' width='100%'/>
<figcaption><i>Notebook editor User Interface (UI)</i></figcaption>
</figure>
</div>
## Shortcuts
Get an overview of the shortcuts by hitting `H` or go to `Help/Keyboard shortcuts`
#### Most useful shortcuts
* `Esc` - switch to command mode
* `B` - insert below
* `A` - insert above
* `M` - Change current cell to Markdown
* `Y` - Change current cell to code
* `DD` - Delete cell
* `Enter` - go back to edit mode
* `Esc + F` - Find and replace on your code
* `Shift + Down / Upwards` - Select multiple cells
* `Shift + M` - Merge multiple cells
## Cell magics
Magic commands can make your life a lot easier, as you only have one command instead of an entire function or multiple lines of code.<br>
> Go to an [extensive overview of magic commands]()
### Some of the handy ones
**Overview of available magic commands**
```
%lsmagic
```
**See and set environment variables**
```
%env
```
**Install and list libraries**
```
!pip install numpy
!pip list | grep pandas
```
**Write cell content to a Python file**
```
%%writefile hello_world.py
print('Hello World')
```
**Load a Python file**
```
%pycat hello_world.py
```
**Get the time of cell execution**
```
%%time
tmpList = []
for i in range(100):
tmpList.append(i+i)
print(tmpList)
```
**Show matplotlib plots inline**
```
%matplotlib inline
```
<br>
## Sharing Jupyter Notebooks
### Sharing static Jupyter Notebooks
* [nbviewer](https://nbviewer.jupyter.org/) - A simple way to share Jupyter Notebooks. You can simply paste the GitHub location of your Jupyter notebook there and it is nicely rendered.
* [GitHub](https://github.com/) - GitHub offers an internal rendering of Jupyter Notebooks. There are some limitations and time delays of the proper rendering. Thus, we would suggest to use `nbviewer` to share nicely rendered Jupyter Notebooks.
### Reproducible Jupyter Notebooks
<img src="./img/mybinder_logo.png" align="left" width="30%"></img>
[Binder](https://mybinder.org/) allows you to open notebooks hosted on a Git repo in an executable environment, making the code immediately reproducible by anyone, anywhere.
Binder builds a Docker image of the repo where the notebooks are hosted.
<br>
## Ressources
* [Project Jupyter](https://jupyter.org/)
* [JupyterHub](https://jupyterhub.readthedocs.io/en/stable/)
* [JupyterLab](https://jupyterlab.readthedocs.io/en/stable/)
* [nbviewer](https://nbviewer.jupyter.org/)
* [Binder](https://mybinder.org/)
<br>
<a href="./00_index.ipynb"><< Index</a><span style="float:right;"><a href="./11_sentinel3_slstr_frp_Californian_fires.ipynb">11 - Sentinel-3 SLSTR FRP - Californian Fires>></a>
<hr>
<img src='./img/copernicus_logo.png' alt='Logo EU Copernicus' align='right' width='20%'><br><br><br>
<p style="text-align:right;">This project is licensed under the <a href="./LICENSE">MIT License</a> and is developed under a Copernicus contract.
|
github_jupyter
|
jupyter notebook
python3 -m pip install --upgrade pip
python3 -m pip install jupyter
jupyter notebook
%lsmagic
%env
!pip install numpy
!pip list | grep pandas
%%writefile hello_world.py
print('Hello World')
%pycat hello_world.py
%%time
tmpList = []
for i in range(100):
tmpList.append(i+i)
print(tmpList)
%matplotlib inline
| 0.324556 | 0.939471 |
## AIF module demo
### Import modules
```
import sys
import matplotlib.pyplot as plt
import numpy as np
sys.path.append('..')
%load_ext autoreload
%autoreload 2
```
### Classic Parker AIF
Create a Parker AIF object. This can be used to return arterial plasma Gd concentration for any time points.
```
import aifs
# Create the AIF object
parker_aif = aifs.parker(hct=0.42)
# Plot concentration for specific times
t_parker = np.linspace(0.,100.,1000)
c_ap_parker = parker_aif.c_ap(t_parker)
plt.plot(t_parker, c_ap_parker)
plt.xlabel('time (s)')
plt.ylabel('concentration (mM)')
plt.title('Classic Parker');
```
### Patient-specific AIF
Create an individual AIF object based on a series of time-concentration data points.
The object can then be used to generate concentrations at arbitrary times.
```
# define concentration-time measurements
t_patient = np.array([19.810000,59.430000,99.050000,138.670000,178.290000,217.910000,257.530000,297.150000,336.770000,376.390000,416.010000,455.630000,495.250000,534.870000,574.490000,614.110000,653.730000,693.350000,732.970000,772.590000,812.210000,851.830000,891.450000,931.070000,970.690000,1010.310000,1049.930000,1089.550000,1129.170000,1168.790000,1208.410000,1248.030000])
c_p_patient = np.array([-0.004937,0.002523,0.002364,0.005698,0.264946,0.738344,1.289008,1.826013,1.919158,1.720187,1.636699,1.423867,1.368308,1.263610,1.190378,1.132603,1.056400,1.066964,1.025331,1.015179,0.965908,0.928219,0.919029,0.892000,0.909929,0.865766,0.857195,0.831985,0.823747,0.815591,0.776007,0.783767])
# create AIF object from measurements
patient_aif = aifs.patient_specific(t_patient, c_p_patient)
# get AIF conc at original temporal resolution
c_p_patient_lowres = patient_aif.c_ap(t_patient)
# get (interpolated) AIF conc at higher temporal resolution
t_patient_highres = np.linspace(0., max(t_patient), 200) # required time points
c_p_patient_highres = patient_aif.c_ap(t_patient_highres)
plt.plot(t_patient, c_p_patient, 'o', label='original data')
plt.plot(t_patient, c_p_patient_lowres, 'x', label='low res')
plt.plot(t_patient_highres, c_p_patient_highres, '-', label='high res')
plt.legend()
plt.xlabel('time (s)')
plt.ylabel('concentration (mM)')
plt.title('Individual AIF');
```
### Classic Parker AIF with time delay
```
c_ap_parker_early = parker_aif.c_ap(t_parker+10)
c_ap_parker_late = parker_aif.c_ap(t_parker-10)
plt.plot(t_parker, c_ap_parker,label='unshifted')
plt.plot(t_parker, c_ap_parker_early,label='early')
plt.plot(t_parker, c_ap_parker_late,label='late')
plt.xlabel('time (s)')
plt.ylabel('concentration (mM)')
plt.legend()
plt.title('Classic Parker');
```
### Patient-specific AIF with time delay
```
c_p_patient_highres_early = patient_aif.c_ap(t_patient_highres+100)
c_p_patient_highres_late = patient_aif.c_ap(t_patient_highres-100)
plt.plot(t_patient_highres, c_p_patient_highres, label='unshifted')
plt.plot(t_patient_highres, c_p_patient_highres_early, label='early')
plt.plot(t_patient_highres, c_p_patient_highres_late, label='late')
plt.xlabel('time (s)')
plt.ylabel('concentration (mM)')
plt.legend()
plt.title('Patient-specific AIF');
```
### AIFs using in Manning et al., MRM (2021) and Heye et al., NeuroImage (2016)
```
manning_fast_aif = aifs.manning_fast(hct=0.42, t_start=3*39.62) # fast injection, Manning et al., MRM (2021)
manning_slow_aif = aifs.manning_slow() # slow injection, Manning et al., MRM (2021)
heye_aif = aifs.heye(hct=0.45, t_start=3*39.62) # Heye et al., NeuroImage (2016)
parker_aif = aifs.parker(hct=0.42, t_start=3*39.62)
t = np.arange(0, 1400, 0.1)
# Plot concentration for specific times
plt.figure(0, figsize=(8,8))
plt.plot(t, manning_fast_aif.c_ap(t), label='Manning (fast injection)')
plt.plot(t, manning_slow_aif.c_ap(t), label='Manning (slow injection)')
plt.plot(t, heye_aif.c_ap(t), label='Heye')
plt.plot(t, parker_aif.c_ap(t), '--', label='Parker')
plt.legend()
plt.xlabel('time (s)')
plt.ylabel('concentration (mM)')
```
|
github_jupyter
|
import sys
import matplotlib.pyplot as plt
import numpy as np
sys.path.append('..')
%load_ext autoreload
%autoreload 2
import aifs
# Create the AIF object
parker_aif = aifs.parker(hct=0.42)
# Plot concentration for specific times
t_parker = np.linspace(0.,100.,1000)
c_ap_parker = parker_aif.c_ap(t_parker)
plt.plot(t_parker, c_ap_parker)
plt.xlabel('time (s)')
plt.ylabel('concentration (mM)')
plt.title('Classic Parker');
# define concentration-time measurements
t_patient = np.array([19.810000,59.430000,99.050000,138.670000,178.290000,217.910000,257.530000,297.150000,336.770000,376.390000,416.010000,455.630000,495.250000,534.870000,574.490000,614.110000,653.730000,693.350000,732.970000,772.590000,812.210000,851.830000,891.450000,931.070000,970.690000,1010.310000,1049.930000,1089.550000,1129.170000,1168.790000,1208.410000,1248.030000])
c_p_patient = np.array([-0.004937,0.002523,0.002364,0.005698,0.264946,0.738344,1.289008,1.826013,1.919158,1.720187,1.636699,1.423867,1.368308,1.263610,1.190378,1.132603,1.056400,1.066964,1.025331,1.015179,0.965908,0.928219,0.919029,0.892000,0.909929,0.865766,0.857195,0.831985,0.823747,0.815591,0.776007,0.783767])
# create AIF object from measurements
patient_aif = aifs.patient_specific(t_patient, c_p_patient)
# get AIF conc at original temporal resolution
c_p_patient_lowres = patient_aif.c_ap(t_patient)
# get (interpolated) AIF conc at higher temporal resolution
t_patient_highres = np.linspace(0., max(t_patient), 200) # required time points
c_p_patient_highres = patient_aif.c_ap(t_patient_highres)
plt.plot(t_patient, c_p_patient, 'o', label='original data')
plt.plot(t_patient, c_p_patient_lowres, 'x', label='low res')
plt.plot(t_patient_highres, c_p_patient_highres, '-', label='high res')
plt.legend()
plt.xlabel('time (s)')
plt.ylabel('concentration (mM)')
plt.title('Individual AIF');
c_ap_parker_early = parker_aif.c_ap(t_parker+10)
c_ap_parker_late = parker_aif.c_ap(t_parker-10)
plt.plot(t_parker, c_ap_parker,label='unshifted')
plt.plot(t_parker, c_ap_parker_early,label='early')
plt.plot(t_parker, c_ap_parker_late,label='late')
plt.xlabel('time (s)')
plt.ylabel('concentration (mM)')
plt.legend()
plt.title('Classic Parker');
c_p_patient_highres_early = patient_aif.c_ap(t_patient_highres+100)
c_p_patient_highres_late = patient_aif.c_ap(t_patient_highres-100)
plt.plot(t_patient_highres, c_p_patient_highres, label='unshifted')
plt.plot(t_patient_highres, c_p_patient_highres_early, label='early')
plt.plot(t_patient_highres, c_p_patient_highres_late, label='late')
plt.xlabel('time (s)')
plt.ylabel('concentration (mM)')
plt.legend()
plt.title('Patient-specific AIF');
manning_fast_aif = aifs.manning_fast(hct=0.42, t_start=3*39.62) # fast injection, Manning et al., MRM (2021)
manning_slow_aif = aifs.manning_slow() # slow injection, Manning et al., MRM (2021)
heye_aif = aifs.heye(hct=0.45, t_start=3*39.62) # Heye et al., NeuroImage (2016)
parker_aif = aifs.parker(hct=0.42, t_start=3*39.62)
t = np.arange(0, 1400, 0.1)
# Plot concentration for specific times
plt.figure(0, figsize=(8,8))
plt.plot(t, manning_fast_aif.c_ap(t), label='Manning (fast injection)')
plt.plot(t, manning_slow_aif.c_ap(t), label='Manning (slow injection)')
plt.plot(t, heye_aif.c_ap(t), label='Heye')
plt.plot(t, parker_aif.c_ap(t), '--', label='Parker')
plt.legend()
plt.xlabel('time (s)')
plt.ylabel('concentration (mM)')
| 0.440229 | 0.811527 |
<img style="float: right; height: 80px;" src="../_static/ENGAGE.png">
# 2.3. Figure 3-variation - Net-zero CO2 emissions systems
<a href="https://github.com/iiasa/ENGAGE-netzero-analysis/blob/main/LICENSE">
<img style="float: left; height: 30px; padding: 5px; margin-top: 8px; " src="https://img.shields.io/github/license/iiasa/ENGAGE-netzero-analysis">
</a>
Licensed under the [MIT License](https://github.com/iiasa/ENGAGE-netzero-analysis/blob/main/LICENSE).
This notebook is part of a repository to generate figures and analysis for the manuscript
> Keywan Riahi, Christoph Bertram, Daniel Huppmann, et al. <br />
> Cost and attainability of meeting stringent climate targets without overshoot <br />
> **Nature Climate Change**, 2021 <br />
> doi: [10.1038/s41558-021-01215-2](https://doi.org/10.1038/s41558-021-01215-2)
The scenario data used in this analysis should be cited as
> ENGAGE Global Scenarios (Version 2.0) <br />
> doi: [10.5281/zenodo.5553976](https://doi.org/10.5281/zenodo.5553976)
The data can be accessed and downloaded via the **ENGAGE Scenario Explorer** at [https://data.ece.iiasa.ac.at/engage](https://data.ece.iiasa.ac.at/engage).<br />
*Please refer to the [license](https://data.ece.iiasa.ac.at/engage/#/license)
of the scenario ensemble before redistributing this data or adapted material.*
The source code of this notebook is available on GitHub
at [https://github.com/iiasa/ENGAGE-netzero-analysis](https://github.com/iiasa/ENGAGE-netzero-analysis).<br />
A rendered version can be seen at [https://data.ece.iiasa.ac.at/engage-netzero-analysis](https://data.ece.iiasa.ac.at/engage-netzero-analysis).
```
from pathlib import Path
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import pyam
from utils import get_netzero_data
```
## Import the scenario snapshot used for this analysis and the plotting configuration
```
data_folder = Path("../data/")
output_folder = Path("output")
output_format = "png"
plot_args = dict(facecolor="white", dpi=300)
rc = pyam.run_control()
rc.update("plotting_config.yaml")
df = pyam.IamDataFrame(data_folder / "ENGAGE_fig3.xlsx")
```
All figures in this notebook use the same scenario.
```
scenario = "EN_NPi2020_1000"
```
Apply renaming for nicer plots.
```
df.rename(model=rc['rename_mapping']['model'], inplace=True)
df.rename(region=rc['rename_mapping']['region'], inplace=True)
```
The REMIND model does not reach net-zero CO2 emissions before the end of the century in the selected scenario
used in these figures.
It is therefore excluded from this notebook.
```
df = (
df.filter(scenario=scenario)
.filter(model="REMIND*", keep=False)
.convert_unit("Mt CO2/yr", "Gt CO2/yr")
)
```
## Prepare CO2 emissions data
Aggregate two categories of "Other" emissions to show as one category.
```
components = [f"Emissions|CO2|{i}" for i in ["Other", "Energy|Demand|Other"]]
df_other = df.aggregate(variable="Emissions|CO2|Other", components=components)
df = df.filter(variable=components, keep=False).append(df_other)
sectors_mapping = {
"AFOLU": "AFOLU",
"Energy|Demand": "Energy Demand",
"Energy|Demand|Industry": "Industry",
"Energy|Demand|Transportation": "Transportation",
"Energy|Demand|Residential and Commercial": "Buildings",
"Energy|Supply": "Energy Supply",
"Industrial Processes": "Industrial Processes",
"Other": "Other"
}
# explode short dictionary-keys to full variable string
for key in list(sectors_mapping):
sectors_mapping[f"Emissions|CO2|{key}"] = sectors_mapping.pop(key)
df.rename(variable=sectors_mapping, inplace=True)
sectors = list(sectors_mapping.values())
```
## Development of emissions by sector & regions in one illustrative model
This section generates Figure 1.1-15 in the Supplementary Information.
```
model='MESSAGEix-GLOBIOM'
df_sector = (
df.filter(variable=sectors)
.filter(region='World', keep=False)
.filter(variable='Energy Demand', keep=False) # show disaggregation of demand sectors
)
_df_sector = df_sector.filter(model=model)
fig, ax = plt.subplots(1, len(_df_sector.region), figsize=(12, 4), sharey=True)
for i, r in enumerate(_df_sector.region):
(
_df_sector.filter(region=r)
.plot.stack(ax=ax[i], total=dict(lw=3, color='black'), title=None, legend=False)
)
ax[i].set_xlabel(None)
ax[i].set_ylabel(None)
ax[i].set_title(r)
plt.tight_layout()
ax[0].set_ylabel("Gt CO2")
ax[i].legend(loc=1)
plt.tight_layout()
fig.savefig(output_folder / f"fig3_annex_sectoral_regional_illustrative.{output_format}", **plot_args)
```
## Emissions by sectors & regions in the year of net-zero
This section generates Figure 1.1-16 in the Supplementary Information.
```
lst = []
df_sector.filter(region="Other", keep=False, inplace=True)
df_netzero = get_netzero_data(df_sector, "netzero|CO2", default_year=2100)
fig, ax = plt.subplots(1, len(df_sector.region), figsize=(12, 4), sharey=True)
for i, r in enumerate(df_sector.region):
df_netzero.filter(region=r).plot.bar(ax=ax[i], x="model", stacked=True, legend=False)
ax[i].axhline(0, color="black", linewidth=0.5)
ax[i].set_title(r)
ax[i].set_xlabel(None)
ax[i].set_ylim(-6, 6)
^
plt.tight_layout()
fig.savefig(output_folder / f"fig3_annex_sectoral_regional_netzero.{output_format}", **plot_args)
```
|
github_jupyter
|
from pathlib import Path
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import pyam
from utils import get_netzero_data
data_folder = Path("../data/")
output_folder = Path("output")
output_format = "png"
plot_args = dict(facecolor="white", dpi=300)
rc = pyam.run_control()
rc.update("plotting_config.yaml")
df = pyam.IamDataFrame(data_folder / "ENGAGE_fig3.xlsx")
scenario = "EN_NPi2020_1000"
df.rename(model=rc['rename_mapping']['model'], inplace=True)
df.rename(region=rc['rename_mapping']['region'], inplace=True)
df = (
df.filter(scenario=scenario)
.filter(model="REMIND*", keep=False)
.convert_unit("Mt CO2/yr", "Gt CO2/yr")
)
components = [f"Emissions|CO2|{i}" for i in ["Other", "Energy|Demand|Other"]]
df_other = df.aggregate(variable="Emissions|CO2|Other", components=components)
df = df.filter(variable=components, keep=False).append(df_other)
sectors_mapping = {
"AFOLU": "AFOLU",
"Energy|Demand": "Energy Demand",
"Energy|Demand|Industry": "Industry",
"Energy|Demand|Transportation": "Transportation",
"Energy|Demand|Residential and Commercial": "Buildings",
"Energy|Supply": "Energy Supply",
"Industrial Processes": "Industrial Processes",
"Other": "Other"
}
# explode short dictionary-keys to full variable string
for key in list(sectors_mapping):
sectors_mapping[f"Emissions|CO2|{key}"] = sectors_mapping.pop(key)
df.rename(variable=sectors_mapping, inplace=True)
sectors = list(sectors_mapping.values())
model='MESSAGEix-GLOBIOM'
df_sector = (
df.filter(variable=sectors)
.filter(region='World', keep=False)
.filter(variable='Energy Demand', keep=False) # show disaggregation of demand sectors
)
_df_sector = df_sector.filter(model=model)
fig, ax = plt.subplots(1, len(_df_sector.region), figsize=(12, 4), sharey=True)
for i, r in enumerate(_df_sector.region):
(
_df_sector.filter(region=r)
.plot.stack(ax=ax[i], total=dict(lw=3, color='black'), title=None, legend=False)
)
ax[i].set_xlabel(None)
ax[i].set_ylabel(None)
ax[i].set_title(r)
plt.tight_layout()
ax[0].set_ylabel("Gt CO2")
ax[i].legend(loc=1)
plt.tight_layout()
fig.savefig(output_folder / f"fig3_annex_sectoral_regional_illustrative.{output_format}", **plot_args)
lst = []
df_sector.filter(region="Other", keep=False, inplace=True)
df_netzero = get_netzero_data(df_sector, "netzero|CO2", default_year=2100)
fig, ax = plt.subplots(1, len(df_sector.region), figsize=(12, 4), sharey=True)
for i, r in enumerate(df_sector.region):
df_netzero.filter(region=r).plot.bar(ax=ax[i], x="model", stacked=True, legend=False)
ax[i].axhline(0, color="black", linewidth=0.5)
ax[i].set_title(r)
ax[i].set_xlabel(None)
ax[i].set_ylim(-6, 6)
^
plt.tight_layout()
fig.savefig(output_folder / f"fig3_annex_sectoral_regional_netzero.{output_format}", **plot_args)
| 0.445047 | 0.941547 |
# Session 2 - Training a Network w/ Tensorflow
<p class="lead">
Assignment: Teach a Deep Neural Network to Paint
</p>
<p class="lead">
Parag K. Mital<br />
<a href="https://www.kadenze.com/courses/creative-applications-of-deep-learning-with-tensorflow/info">Creative Applications of Deep Learning w/ Tensorflow</a><br />
<a href="https://www.kadenze.com/partners/kadenze-academy">Kadenze Academy</a><br />
<a href="https://twitter.com/hashtag/CADL">#CADL</a>
</p>
This work is licensed under a <a rel="license" href="http://creativecommons.org/licenses/by-nc-sa/4.0/">Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License</a>.
# Learning Goals
* Learn how to create a Neural Network
* Learn to use a neural network to paint an image
* Apply creative thinking to the inputs, outputs, and definition of a network
# Outline
<!-- MarkdownTOC autolink=true autoanchor=true bracket=round -->
- [Assignment Synopsis](#assignment-synopsis)
- [Part One - Fully Connected Network](#part-one---fully-connected-network)
- [Instructions](#instructions)
- [Code](#code)
- [Variable Scopes](#variable-scopes)
- [Part Two - Image Painting Network](#part-two---image-painting-network)
- [Instructions](#instructions-1)
- [Preparing the Data](#preparing-the-data)
- [Cost Function](#cost-function)
- [Explore](#explore)
- [A Note on Crossvalidation](#a-note-on-crossvalidation)
- [Part Three - Learning More than One Image](#part-three---learning-more-than-one-image)
- [Instructions](#instructions-2)
- [Code](#code-1)
- [Part Four - Open Exploration \(Extra Credit\)](#part-four---open-exploration-extra-credit)
- [Assignment Submission](#assignment-submission)
<!-- /MarkdownTOC -->
This next section will just make sure you have the right version of python and the libraries that we'll be using. Don't change the code here but make sure you "run" it (use "shift+enter")!
```
# First check the Python version
import sys
if sys.version_info < (3,4):
print('You are running an older version of Python!\n\n' \
'You should consider updating to Python 3.4.0 or ' \
'higher as the libraries built for this course ' \
'have only been tested in Python 3.4 and higher.\n')
print('Try installing the Python 3.5 version of anaconda '
'and then restart `jupyter notebook`:\n' \
'https://www.continuum.io/downloads\n\n')
# Now get necessary libraries
try:
import os
import numpy as np
import matplotlib.pyplot as plt
from skimage.transform import resize
from skimage import data
from scipy.misc import imresize
except ImportError:
print('You are missing some packages! ' \
'We will try installing them before continuing!')
!pip install "numpy>=1.11.0" "matplotlib>=1.5.1" "scikit-image>=0.11.3" "scikit-learn>=0.17" "scipy>=0.17.0"
import os
import numpy as np
import matplotlib.pyplot as plt
from skimage.transform import resize
from skimage import data
from scipy.misc import imresize
print('Done!')
# Import Tensorflow
try:
import tensorflow as tf
except ImportError:
print("You do not have tensorflow installed!")
print("Follow the instructions on the following link")
print("to install tensorflow before continuing:")
print("")
print("https://github.com/pkmital/CADL#installation-preliminaries")
# This cell includes the provided libraries from the zip file
# and a library for displaying images from ipython, which
# we will use to display the gif
try:
from libs import utils, gif
import IPython.display as ipyd
except ImportError:
print("Make sure you have started notebook in the same directory" +
" as the provided zip file which includes the 'libs' folder" +
" and the file 'utils.py' inside of it. You will NOT be able"
" to complete this assignment unless you restart jupyter"
" notebook inside the directory created by extracting"
" the zip file or cloning the github repo.")
# We'll tell matplotlib to inline any drawn figures like so:
%matplotlib inline
plt.style.use('ggplot')
# Bit of formatting because I don't like the default inline code style:
from IPython.core.display import HTML
HTML("""<style> .rendered_html code {
padding: 2px 4px;
color: #c7254e;
background-color: #f9f2f4;
border-radius: 4px;
} </style>""")
```
<a name="assignment-synopsis"></a>
# Assignment Synopsis
In this assignment, we're going to create our first neural network capable of taking any two continuous values as inputs. Those two values will go through a series of multiplications, additions, and nonlinearities, coming out of the network as 3 outputs. Remember from the last homework, we used convolution to filter an image so that the representations in the image were accentuated. We're not going to be using convolution w/ Neural Networks until the next session, but we're effectively doing the same thing here: using multiplications to accentuate the representations in our data, in order to minimize whatever our cost function is. To find out what those multiplications need to be, we're going to use Gradient Descent and Backpropagation, which will take our cost, and find the appropriate updates to all the parameters in our network to best optimize the cost. In the next session, we'll explore much bigger networks and convolution. This "toy" network is really to help us get up and running with neural networks, and aid our exploration of the different components that make up a neural network. You will be expected to explore manipulations of the neural networks in this notebook as much as possible to help aid your understanding of how they effect the final result.
We're going to build our first neural network to understand what color "to paint" given a location in an image, or the row, col of the image. So in goes a row/col, and out goes a R/G/B. In the next lesson, we'll learn what this network is really doing is performing regression. For now, we'll focus on the creative applications of such a network to help us get a better understanding of the different components that make up the neural network. You'll be asked to explore many of the different components of a neural network, including changing the inputs/outputs (i.e. the dataset), the number of layers, their activation functions, the cost functions, learning rate, and batch size. You'll also explore a modification to this same network which takes a 3rd input: an index for an image. This will let us try to learn multiple images at once, though with limited success.
We'll now dive right into creating deep neural networks, and I'm going to show you the math along the way. Don't worry if a lot of it doesn't make sense, and it really takes a bit of practice before it starts to come together.
<a name="part-one---fully-connected-network"></a>
# Part One - Fully Connected Network
<a name="instructions"></a>
## Instructions
Create the operations necessary for connecting an input to a network, defined by a `tf.Placeholder`, to a series of fully connected, or linear, layers, using the formula:
$$\textbf{H} = \phi(\textbf{X}\textbf{W} + \textbf{b})$$
where $\textbf{H}$ is an output layer representing the "hidden" activations of a network, $\phi$ represents some nonlinearity, $\textbf{X}$ represents an input to that layer, $\textbf{W}$ is that layer's weight matrix, and $\textbf{b}$ is that layer's bias.
If you're thinking, what is going on? Where did all that math come from? Don't be afraid of it. Once you learn how to "speak" the symbolic representation of the equation, it starts to get easier. And once we put it into practice with some code, it should start to feel like there is some association with what is written in the equation, and what we've written in code. Practice trying to say the equation in a meaningful way: "The output of a hidden layer is equal to some input multiplied by another matrix, adding some bias, and applying a non-linearity". Or perhaps: "The hidden layer is equal to a nonlinearity applied to an input multiplied by a matrix and adding some bias". Explore your own interpretations of the equation, or ways of describing it, and it starts to become much, much easier to apply the equation.
The first thing that happens in this equation is the input matrix $\textbf{X}$ is multiplied by another matrix, $\textbf{W}$. This is the most complicated part of the equation. It's performing matrix multiplication, as we've seen from last session, and is effectively scaling and rotating our input. The bias $\textbf{b}$ allows for a global shift in the resulting values. Finally, the nonlinearity of $\phi$ allows the input space to be nonlinearly warped, allowing it to express a lot more interesting distributions of data. Have a look below at some common nonlinearities. If you're unfamiliar with looking at graphs like this, it is common to read the horizontal axis as X, as the input, and the vertical axis as Y, as the output.
```
xs = np.linspace(-6, 6, 100)
plt.plot(xs, np.maximum(xs, 0), label='relu')
plt.plot(xs, 1 / (1 + np.exp(-xs)), label='sigmoid')
plt.plot(xs, np.tanh(xs), label='tanh')
plt.xlabel('Input')
plt.xlim([-6, 6])
plt.ylabel('Output')
plt.ylim([-1.5, 1.5])
plt.title('Common Activation Functions/Nonlinearities')
plt.legend(loc='lower right')
```
Remember, having series of linear followed by nonlinear operations is what makes neural networks expressive. By stacking a lot of "linear" + "nonlinear" operations in a series, we can create a deep neural network! Have a look at the output ranges of the above nonlinearity when considering which nonlinearity seems most appropriate. For instance, the `relu` is always above 0, but does not saturate at any value above 0, meaning it can be anything above 0. That's unlike the `sigmoid` which does saturate at both 0 and 1, meaning its values for a single output neuron will always be between 0 and 1. Similarly, the `tanh` saturates at -1 and 1.
Choosing between these is often a matter of trial and error. Though you can make some insights depending on your normalization scheme. For instance, if your output is expected to be in the range of 0 to 1, you may not want to use a `tanh` function, which ranges from -1 to 1, but likely would want to use a `sigmoid`. Keep the ranges of these activation functions in mind when designing your network, especially the final output layer of your network.
<a name="code"></a>
## Code
In this section, we're going to work out how to represent a fully connected neural network with code. First, create a 2D `tf.placeholder` called $\textbf{X}$ with `None` for the batch size and 2 features. Make its `dtype` `tf.float32`. Recall that we use the dimension of `None` for the batch size dimension to say that this dimension can be any number. Here is the docstring for the `tf.placeholder` function, have a look at what args it takes:
Help on function placeholder in module `tensorflow.python.ops.array_ops`:
```python
placeholder(dtype, shape=None, name=None)
```
Inserts a placeholder for a tensor that will be always fed.
**Important**: This tensor will produce an error if evaluated. Its value must
be fed using the `feed_dict` optional argument to `Session.run()`,
`Tensor.eval()`, or `Operation.run()`.
For example:
```python
x = tf.placeholder(tf.float32, shape=(1024, 1024))
y = tf.matmul(x, x)
with tf.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed.
rand_array = np.random.rand(1024, 1024)
print(sess.run(y, feed_dict={x: rand_array})) # Will succeed.
```
Args:
dtype: The type of elements in the tensor to be fed.
shape: The shape of the tensor to be fed (optional). If the shape is not
specified, you can feed a tensor of any shape.
name: A name for the operation (optional).
Returns:
A `Tensor` that may be used as a handle for feeding a value, but not
evaluated directly.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
# Create a placeholder with None x 2 dimensions of dtype tf.float32, and name it "X":
X = ...
```
Now multiply the tensor using a new variable, $\textbf{W}$, which has 2 rows and 20 columns, so that when it is left mutiplied by $\textbf{X}$, the output of the multiplication is None x 20, giving you 20 output neurons. Recall that the `tf.matmul` function takes two arguments, the left hand ($\textbf{W}$) and right hand side ($\textbf{X}$) of a matrix multiplication.
To create $\textbf{W}$, you will use `tf.get_variable` to create a matrix which is `2 x 20` in dimension. Look up the docstrings of functions `tf.get_variable` and `tf.random_normal_initializer` to get familiar with these functions. There are many options we will ignore for now. Just be sure to set the `name`, `shape` (this is the one that has to be [2, 20]), `dtype` (i.e. tf.float32), and `initializer` (the `tf.random_normal_intializer` you should create) when creating your $\textbf{W}$ variable with `tf.get_variable(...)`.
For the random normal initializer, often the mean is set to 0, and the standard deviation is set based on the number of neurons. But that really depends on the input and outputs of your network, how you've "normalized" your dataset, what your nonlinearity/activation function is, and what your expected range of inputs/outputs are. Don't worry about the values for the initializer for now, as this part will take a bit more experimentation to understand better!
This part is to encourage you to learn how to look up the documentation on Tensorflow, ideally using `tf.get_variable?` in the notebook. If you are really stuck, just scroll down a bit and I've shown you how to use it.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
W = tf.get_variable(...
h = tf.matmul(...
```
And add to this result another new variable, $\textbf{b}$, which has [20] dimensions. These values will be added to every output neuron after the multiplication above. Instead of the `tf.random_normal_initializer` that you used for creating $\textbf{W}$, now use the `tf.constant_initializer`. Often for bias, you'll set the constant bias initialization to 0 or 1.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
b = tf.get_variable(...
h = tf.nn.bias_add(...
```
So far we have done:
$$\textbf{X}\textbf{W} + \textbf{b}$$
Finally, apply a nonlinear activation to this output, such as `tf.nn.relu`, to complete the equation:
$$\textbf{H} = \phi(\textbf{X}\textbf{W} + \textbf{b})$$
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
h = ...
```
Now that we've done all of this work, let's stick it inside a function. I've already done this for you and placed it inside the `utils` module under the function name `linear`. We've already imported the `utils` module so we can call it like so, `utils.linear(...)`. The docstring is copied below, and the code itself. Note that this function is slightly different to the one in the lecture. It does not require you to specify `n_input`, and the input `scope` is called `name`. It also has a few more extras in there including automatically converting a 4-d input tensor to a 2-d tensor so that you can fully connect the layer with a matrix multiply (don't worry about what this means if it doesn't make sense!).
```python
utils.linear??
```
```python
def linear(x, n_output, name=None, activation=None, reuse=None):
"""Fully connected layer
Parameters
----------
x : tf.Tensor
Input tensor to connect
n_output : int
Number of output neurons
name : None, optional
Scope to apply
Returns
-------
op : tf.Tensor
Output of fully connected layer.
"""
if len(x.get_shape()) != 2:
x = flatten(x, reuse=reuse)
n_input = x.get_shape().as_list()[1]
with tf.variable_scope(name or "fc", reuse=reuse):
W = tf.get_variable(
name='W',
shape=[n_input, n_output],
dtype=tf.float32,
initializer=tf.contrib.layers.xavier_initializer())
b = tf.get_variable(
name='b',
shape=[n_output],
dtype=tf.float32,
initializer=tf.constant_initializer(0.0))
h = tf.nn.bias_add(
name='h',
value=tf.matmul(x, W),
bias=b)
if activation:
h = activation(h)
return h, W
```
<a name="variable-scopes"></a>
## Variable Scopes
Note that since we are using `variable_scope` and explicitly telling the scope which name we would like, if there is *already* a variable created with the same name, then Tensorflow will raise an exception! If this happens, you should consider one of three possible solutions:
1. If this happens while you are interactively editing a graph, you may need to reset the current graph:
```python
tf.reset_default_graph()
```
You should really only have to use this if you are in an interactive console! If you are creating Python scripts to run via command line, you should really be using solution 3 listed below, and be explicit with your graph contexts!
2. If this happens and you were not expecting any name conflicts, then perhaps you had a typo and created another layer with the same name! That's a good reason to keep useful names for everything in your graph!
3. More likely, you should be using context managers when creating your graphs and running sessions. This works like so:
```python
g = tf.Graph()
with tf.Session(graph=g) as sess:
Y_pred, W = linear(X, 2, 3, activation=tf.nn.relu)
```
or:
```python
g = tf.Graph()
with tf.Session(graph=g) as sess, g.as_default():
Y_pred, W = linear(X, 2, 3, activation=tf.nn.relu)
```
You can now write the same process as the above steps by simply calling:
```
h, W = utils.linear(
x=X, n_output=20, name='linear', activation=tf.nn.relu)
```
<a name="part-two---image-painting-network"></a>
# Part Two - Image Painting Network
<a name="instructions-1"></a>
## Instructions
Follow along the steps below, first setting up input and output data of the network, $\textbf{X}$ and $\textbf{Y}$. Then work through building the neural network which will try to compress the information in $\textbf{X}$ through a series of linear and non-linear functions so that whatever it is given as input, it minimized the error of its prediction, $\hat{\textbf{Y}}$, and the true output $\textbf{Y}$ through its training process. You'll also create an animated GIF of the training which you'll need to submit for the homework!
Through this, we'll explore our first creative application: painting an image. This network is just meant to demonstrate how easily networks can be scaled to more complicated tasks without much modification. It is also meant to get you thinking about neural networks as building blocks that can be reconfigured, replaced, reorganized, and get you thinking about how the inputs and outputs can be anything you can imagine.
<a name="preparing-the-data"></a>
## Preparing the Data
We'll follow an example that Andrej Karpathy has done in his online demonstration of "image inpainting". What we're going to do is teach the network to go from the location on an image frame to a particular color. So given any position in an image, the network will need to learn what color to paint. Let's first get an image that we'll try to teach a neural network to paint.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
# First load an image
img = ...
# Be careful with the size of your image.
# Try a fairly small image to begin with,
# then come back here and try larger sizes.
img = imresize(img, (100, 100))
plt.figure(figsize=(5, 5))
plt.imshow(img)
# Make sure you save this image as "reference.png"
# and include it in your zipped submission file
# so we can tell what image you are trying to paint!
plt.imsave(fname='reference.png', arr=img)
```
In the lecture, I showed how to aggregate the pixel locations and their colors using a loop over every pixel position. I put that code into a function `split_image` below. Feel free to experiment with other features for `xs` or `ys`.
```
def split_image(img):
# We'll first collect all the positions in the image in our list, xs
xs = []
# And the corresponding colors for each of these positions
ys = []
# Now loop over the image
for row_i in range(img.shape[0]):
for col_i in range(img.shape[1]):
# And store the inputs
xs.append([row_i, col_i])
# And outputs that the network needs to learn to predict
ys.append(img[row_i, col_i])
# we'll convert our lists to arrays
xs = np.array(xs)
ys = np.array(ys)
return xs, ys
```
Let's use this function to create the inputs (xs) and outputs (ys) to our network as the pixel locations (xs) and their colors (ys):
```
xs, ys = split_image(img)
# and print the shapes
xs.shape, ys.shape
```
Also remember, we should normalize our input values!
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
# Normalize the input (xs) using its mean and standard deviation
xs = ...
# Just to make sure you have normalized it correctly:
print(np.min(xs), np.max(xs))
assert(np.min(xs) > -3.0 and np.max(xs) < 3.0)
```
Similarly for the output:
```
print(np.min(ys), np.max(ys))
```
We'll normalize the output using a simpler normalization method, since we know the values range from 0-255:
```
ys = ys / 255.0
print(np.min(ys), np.max(ys))
```
Scaling the image values like this has the advantage that it is still interpretable as an image, unlike if we have negative values.
What we're going to do is use regression to predict the value of a pixel given its (row, col) position. So the input to our network is `X = (row, col)` value. And the output of the network is `Y = (r, g, b)`.
We can get our original image back by reshaping the colors back into the original image shape. This works because the `ys` are still in order:
```
plt.imshow(ys.reshape(img.shape))
```
But when we give inputs of (row, col) to our network, it won't know what order they are, because we will randomize them. So it will have to *learn* what color value should be output for any given (row, col).
Create 2 placeholders of `dtype` `tf.float32`: one for the input of the network, a `None x 2` dimension placeholder called $\textbf{X}$, and another for the true output of the network, a `None x 3` dimension placeholder called $\textbf{Y}$.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
# Let's reset the graph:
tf.reset_default_graph()
# Create a placeholder of None x 2 dimensions and dtype tf.float32
# This will be the input to the network which takes the row/col
X = tf.placeholder(...
# Create the placeholder, Y, with 3 output dimensions instead of 2.
# This will be the output of the network, the R, G, B values.
Y = tf.placeholder(...
```
Now create a deep neural network that takes your network input $\textbf{X}$ of 2 neurons, multiplies it by a linear and non-linear transformation which makes its shape [None, 20], meaning it will have 20 output neurons. Then repeat the same process again to give you 20 neurons again, and then again and again until you've done 6 layers of 20 neurons. Then finally one last layer which will output 3 neurons, your predicted output, which I've been denoting mathematically as $\hat{\textbf{Y}}$, for a total of 6 hidden layers, or 8 layers total including the input and output layers. Mathematically, we'll be creating a deep neural network that looks just like the previous fully connected layer we've created, but with a few more connections. So recall the first layer's connection is:
\begin{align}
\textbf{H}_1=\phi(\textbf{X}\textbf{W}_1 + \textbf{b}_1) \\
\end{align}
So the next layer will take that output, and connect it up again:
\begin{align}
\textbf{H}_2=\phi(\textbf{H}_1\textbf{W}_2 + \textbf{b}_2) \\
\end{align}
And same for every other layer:
\begin{align}
\textbf{H}_3=\phi(\textbf{H}_2\textbf{W}_3 + \textbf{b}_3) \\
\textbf{H}_4=\phi(\textbf{H}_3\textbf{W}_4 + \textbf{b}_4) \\
\textbf{H}_5=\phi(\textbf{H}_4\textbf{W}_5 + \textbf{b}_5) \\
\textbf{H}_6=\phi(\textbf{H}_5\textbf{W}_6 + \textbf{b}_6) \\
\end{align}
Including the very last layer, which will be the prediction of the network:
\begin{align}
\hat{\textbf{Y}}=\phi(\textbf{H}_6\textbf{W}_7 + \textbf{b}_7)
\end{align}
Remember if you run into issues with variable scopes/names, that you cannot recreate a variable with the same name! Revisit the section on <a href='#Variable-Scopes'>Variable Scopes</a> if you get stuck with name issues.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
# We'll create 6 hidden layers. Let's create a variable
# to say how many neurons we want for each of the layers
# (try 20 to begin with, then explore other values)
n_neurons = ...
# Create the first linear + nonlinear layer which will
# take the 2 input neurons and fully connects it to 20 neurons.
# Use the `utils.linear` function to do this just like before,
# but also remember to give names for each layer, such as
# "1", "2", ... "5", or "layer1", "layer2", ... "layer6".
h1, W1 = ...
# Create another one:
h2, W2 = ...
# and four more (or replace all of this with a loop if you can!):
h3, W3 = ...
h4, W4 = ...
h5, W5 = ...
h6, W6 = ...
# Now, make one last layer to make sure your network has 3 outputs:
Y_pred, W7 = utils.linear(h6, 3, activation=None, name='pred')
assert(X.get_shape().as_list() == [None, 2])
assert(Y_pred.get_shape().as_list() == [None, 3])
assert(Y.get_shape().as_list() == [None, 3])
```
<a name="cost-function"></a>
## Cost Function
Now we're going to work on creating a `cost` function. The cost should represent how much `error` there is in the network, and provide the optimizer this value to help it train the network's parameters using gradient descent and backpropagation.
Let's say our error is `E`, then the cost will be:
$$cost(\textbf{Y}, \hat{\textbf{Y}}) = \frac{1}{\text{B}} \displaystyle\sum\limits_{b=0}^{\text{B}} \textbf{E}_b
$$
where the error is measured as, e.g.:
$$\textbf{E} = \displaystyle\sum\limits_{c=0}^{\text{C}} (\textbf{Y}_{c} - \hat{\textbf{Y}}_{c})^2$$
Don't worry if this scares you. This is mathematically expressing the same concept as: "the cost of an actual $\textbf{Y}$, and a predicted $\hat{\textbf{Y}}$ is equal to the mean across batches, of which there are $\text{B}$ total batches, of the sum of distances across $\text{C}$ color channels of every predicted output and true output". Basically, we're trying to see on average, or at least within a single minibatches average, how wrong was our prediction? We create a measure of error for every output feature by squaring the predicted output and the actual output it should have, i.e. the actual color value it should have output for a given input pixel position. By squaring it, we penalize large distances, but not so much small distances.
Consider how the square function (i.e., $f(x) = x^2$) changes for a given error. If our color values range between 0-255, then a typical amount of error would be between $0$ and $128^2$. For example if my prediction was (120, 50, 167), and the color should have been (0, 100, 120), then the error for the Red channel is (120 - 0) or 120. And the Green channel is (50 - 100) or -50, and for the Blue channel, (167 - 120) = 47. When I square this result, I get: (120)^2, (-50)^2, and (47)^2. I then add all of these and that is my error, $\textbf{E}$, for this one observation. But I will have a few observations per minibatch. So I add all the error in my batch together, then divide by the number of observations in the batch, essentially finding the mean error of my batch.
Let's try to see what the square in our measure of error is doing graphically.
```
error = np.linspace(0.0, 128.0**2, 100)
loss = error**2.0
plt.plot(error, loss)
plt.xlabel('error')
plt.ylabel('loss')
```
This is known as the $l_2$ (pronounced el-two) loss. It doesn't penalize small errors as much as it does large errors. This is easier to see when we compare it with another common loss, the $l_1$ (el-one) loss. It is linear in error, by taking the absolute value of the error. We'll compare the $l_1$ loss with normalized values from $0$ to $1$. So instead of having $0$ to $255$ for our RGB values, we'd have $0$ to $1$, simply by dividing our color values by $255.0$.
```
error = np.linspace(0.0, 1.0, 100)
plt.plot(error, error**2, label='l_2 loss')
plt.plot(error, np.abs(error), label='l_1 loss')
plt.xlabel('error')
plt.ylabel('loss')
plt.legend(loc='lower right')
```
So unlike the $l_2$ loss, the $l_1$ loss is really quickly upset if there is *any* error at all: as soon as error moves away from $0.0$, to $0.1$, the $l_1$ loss is $0.1$. But the $l_2$ loss is $0.1^2 = 0.01$. Having a stronger penalty on smaller errors often leads to what the literature calls "sparse" solutions, since it favors activations that try to explain as much of the data as possible, rather than a lot of activations that do a sort of good job, but when put together, do a great job of explaining the data. Don't worry about what this means if you are more unfamiliar with Machine Learning. There is a lot of literature surrounding each of these loss functions that we won't have time to get into, but look them up if they interest you.
During the lecture, we've seen how to create a cost function using Tensorflow. To create a $l_2$ loss function, you can for instance use tensorflow's `tf.squared_difference` or for an $l_1$ loss function, `tf.abs`. You'll need to refer to the `Y` and `Y_pred` variables only, and your resulting cost should be a single value. Try creating the $l_1$ loss to begin with, and come back here after you have trained your network, to compare the performance with a $l_2$ loss.
The equation for computing cost I mentioned above is more succintly written as, for $l_2$ norm:
$$cost(\textbf{Y}, \hat{\textbf{Y}}) = \frac{1}{\text{B}} \displaystyle\sum\limits_{b=0}^{\text{B}} \displaystyle\sum\limits_{c=0}^{\text{C}} (\textbf{Y}_{c} - \hat{\textbf{Y}}_{c})^2$$
For $l_1$ norm, we'd have:
$$cost(\textbf{Y}, \hat{\textbf{Y}}) = \frac{1}{\text{B}} \displaystyle\sum\limits_{b=0}^{\text{B}} \displaystyle\sum\limits_{c=0}^{\text{C}} \text{abs}(\textbf{Y}_{c} - \hat{\textbf{Y}}_{c})$$
Remember, to understand this equation, try to say it out loud: the $cost$ given two variables, $\textbf{Y}$, the actual output we want the network to have, and $\hat{\textbf{Y}}$ the predicted output from the network, is equal to the mean across $\text{B}$ batches, of the sum of $\textbf{C}$ color channels distance between the actual and predicted outputs. If you're still unsure, refer to the lecture where I've computed this, or scroll down a bit to where I've included the answer.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
# first compute the error, the inner part of the summation.
# This should be the l1-norm or l2-norm of the distance
# between each color channel.
error = ...
assert(error.get_shape().as_list() == [None, 3])
```
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
# Now sum the error for each feature in Y.
# If Y is [Batch, Features], the sum should be [Batch]:
sum_error = ...
assert(sum_error.get_shape().as_list() == [None])
```
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
# Finally, compute the cost, as the mean error of the batch.
# This should be a single value.
cost = ...
assert(cost.get_shape().as_list() == [])
```
We now need an `optimizer` which will take our `cost` and a `learning_rate`, which says how far along the gradient to move. This optimizer calculates all the gradients in our network with respect to the `cost` variable and updates all of the weights in our network using backpropagation. We'll then create mini-batches of our training data and run the `optimizer` using a `session`.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
# Refer to the help for the function
optimizer = tf.train....minimize(cost)
# Create parameters for the number of iterations to run for (< 100)
n_iterations = ...
# And how much data is in each minibatch (< 500)
batch_size = ...
# Then create a session
sess = tf.Session()
```
We'll now train our network! The code below should do this for you if you've setup everything else properly. Please read through this and make sure you understand each step! Note that this can take a VERY LONG time depending on the size of your image (make it < 100 x 100 pixels), the number of neurons per layer (e.g. < 30), the number of layers (e.g. < 8), and number of iterations (< 1000). Welcome to Deep Learning :)
```
# Initialize all your variables and run the operation with your session
sess.run(tf.initialize_all_variables())
# Optimize over a few iterations, each time following the gradient
# a little at a time
imgs = []
costs = []
gif_step = n_iterations // 10
step_i = 0
for it_i in range(n_iterations):
# Get a random sampling of the dataset
idxs = np.random.permutation(range(len(xs)))
# The number of batches we have to iterate over
n_batches = len(idxs) // batch_size
# Now iterate over our stochastic minibatches:
for batch_i in range(n_batches):
# Get just minibatch amount of data
idxs_i = idxs[batch_i * batch_size: (batch_i + 1) * batch_size]
# And optimize, also returning the cost so we can monitor
# how our optimization is doing.
training_cost = sess.run(
[cost, optimizer],
feed_dict={X: xs[idxs_i], Y: ys[idxs_i]})[0]
# Also, every 20 iterations, we'll draw the prediction of our
# input xs, which should try to recreate our image!
if (it_i + 1) % gif_step == 0:
costs.append(training_cost / n_batches)
ys_pred = Y_pred.eval(feed_dict={X: xs}, session=sess)
img = np.clip(ys_pred.reshape(img.shape), 0, 1)
imgs.append(img)
# Plot the cost over time
fig, ax = plt.subplots(1, 2)
ax[0].plot(costs)
ax[0].set_xlabel('Iteration')
ax[0].set_ylabel('Cost')
ax[1].imshow(img)
fig.suptitle('Iteration {}'.format(it_i))
plt.show()
# Save the images as a GIF
_ = gif.build_gif(imgs, saveto='single.gif', show_gif=False)
```
Let's now display the GIF we've just created:
```
ipyd.Image(url='single.gif?{}'.format(np.random.rand()),
height=500, width=500)
```
<a name="explore"></a>
## Explore
Go back over the previous cells and exploring changing different parameters of the network. I would suggest first trying to change the `learning_rate` parameter to different values and see how the cost curve changes. What do you notice? Try exponents of $10$, e.g. $10^1$, $10^2$, $10^3$... and so on. Also try changing the `batch_size`: $50, 100, 200, 500, ...$ How does it effect how the cost changes over time?
Be sure to explore other manipulations of the network, such as changing the loss function to $l_2$ or $l_1$. How does it change the resulting learning? Also try changing the activation functions, the number of layers/neurons, different optimizers, and anything else that you may think of, and try to get a basic understanding on this toy problem of how it effects the network's training. Also try comparing creating a fairly shallow/wide net (e.g. 1-2 layers with many neurons, e.g. > 100), versus a deep/narrow net (e.g. 6-20 layers with fewer neurons, e.g. < 20). What do you notice?
<a name="a-note-on-crossvalidation"></a>
## A Note on Crossvalidation
The cost curve plotted above is only showing the cost for our "training" dataset. Ideally, we should split our dataset into what are called "train", "validation", and "test" sets. This is done by taking random subsets of the entire dataset. For instance, we partition our dataset by saying we'll only use 80% of it for training, 10% for validation, and the last 10% for testing. Then when training as above, you would only use the 80% of the data you had partitioned, and then monitor accuracy on both the data you have used to train, but also that new 10% of unseen validation data. This gives you a sense of how "general" your network is. If it is performing just as well on that 10% of data, then you know it is doing a good job. Finally, once you are done training, you would test one last time on your "test" dataset. Ideally, you'd do this a number of times, so that every part of the dataset had a chance to be the test set. This would also give you a measure of the variance of the accuracy on the final test. If it changes a lot, you know something is wrong. If it remains fairly stable, then you know that it is a good representation of the model's accuracy on unseen data.
We didn't get a chance to cover this in class, as it is less useful for exploring creative applications, though it is very useful to know and to use in practice, as it avoids overfitting/overgeneralizing your network to all of the data. Feel free to explore how to do this on the application above!
<a name="part-three---learning-more-than-one-image"></a>
# Part Three - Learning More than One Image
<a name="instructions-2"></a>
## Instructions
We're now going to make use of our Dataset from Session 1 and apply what we've just learned to try and paint every single image in our dataset. How would you guess is the best way to approach this? We could for instance feed in every possible image by having multiple row, col -> r, g, b values. So for any given row, col, we'd have 100 possible r, g, b values. This likely won't work very well as there are many possible values a pixel could take, not just one. What if we also tell the network *which* image's row and column we wanted painted? We're going to try and see how that does.
You can execute all of the cells below unchanged to see how this works with the first 100 images of the celeb dataset. But you should replace the images with your own dataset, and vary the parameters of the network to get the best results!
I've placed the same code for running the previous algorithm into two functions, `build_model` and `train`. You can directly call the function `train` with a 4-d image shaped as N x H x W x C, and it will collect all of the points of every image and try to predict the output colors of those pixels, just like before. The only difference now is that you are able to try this with a few images at a time. There are a few ways we could have tried to handle multiple images. The way I've shown in the `train` function is to include an additional input neuron for *which* image it is. So as well as receiving the row and column, the network will also receive as input which image it is as a number. This should help the network to better distinguish the patterns it uses, as it has knowledge that helps it separates its process based on which image is fed as input.
```
def build_model(xs, ys, n_neurons, n_layers, activation_fn,
final_activation_fn, cost_type):
xs = np.asarray(xs)
ys = np.asarray(ys)
if xs.ndim != 2:
raise ValueError(
'xs should be a n_observates x n_features, ' +
'or a 2-dimensional array.')
if ys.ndim != 2:
raise ValueError(
'ys should be a n_observates x n_features, ' +
'or a 2-dimensional array.')
n_xs = xs.shape[1]
n_ys = ys.shape[1]
X = tf.placeholder(name='X', shape=[None, n_xs],
dtype=tf.float32)
Y = tf.placeholder(name='Y', shape=[None, n_ys],
dtype=tf.float32)
current_input = X
for layer_i in range(n_layers):
current_input = utils.linear(
current_input, n_neurons,
activation=activation_fn,
name='layer{}'.format(layer_i))[0]
Y_pred = utils.linear(
current_input, n_ys,
activation=final_activation_fn,
name='pred')[0]
if cost_type == 'l1_norm':
cost = tf.reduce_mean(tf.reduce_sum(
tf.abs(Y - Y_pred), 1))
elif cost_type == 'l2_norm':
cost = tf.reduce_mean(tf.reduce_sum(
tf.squared_difference(Y, Y_pred), 1))
else:
raise ValueError(
'Unknown cost_type: {}. '.format(
cost_type) + 'Use only "l1_norm" or "l2_norm"')
return {'X': X, 'Y': Y, 'Y_pred': Y_pred, 'cost': cost}
def train(imgs,
learning_rate=0.0001,
batch_size=200,
n_iterations=10,
gif_step=2,
n_neurons=30,
n_layers=10,
activation_fn=tf.nn.relu,
final_activation_fn=tf.nn.tanh,
cost_type='l2_norm'):
N, H, W, C = imgs.shape
all_xs, all_ys = [], []
for img_i, img in enumerate(imgs):
xs, ys = split_image(img)
all_xs.append(np.c_[xs, np.repeat(img_i, [xs.shape[0]])])
all_ys.append(ys)
xs = np.array(all_xs).reshape(-1, 3)
xs = (xs - np.mean(xs, 0)) / np.std(xs, 0)
ys = np.array(all_ys).reshape(-1, 3)
ys = ys / 127.5 - 1
g = tf.Graph()
with tf.Session(graph=g) as sess:
model = build_model(xs, ys, n_neurons, n_layers,
activation_fn, final_activation_fn,
cost_type)
optimizer = tf.train.AdamOptimizer(
learning_rate=learning_rate).minimize(model['cost'])
sess.run(tf.initialize_all_variables())
gifs = []
costs = []
step_i = 0
for it_i in range(n_iterations):
# Get a random sampling of the dataset
idxs = np.random.permutation(range(len(xs)))
# The number of batches we have to iterate over
n_batches = len(idxs) // batch_size
training_cost = 0
# Now iterate over our stochastic minibatches:
for batch_i in range(n_batches):
# Get just minibatch amount of data
idxs_i = idxs[batch_i * batch_size:
(batch_i + 1) * batch_size]
# And optimize, also returning the cost so we can monitor
# how our optimization is doing.
cost = sess.run(
[model['cost'], optimizer],
feed_dict={model['X']: xs[idxs_i],
model['Y']: ys[idxs_i]})[0]
training_cost += cost
print('iteration {}/{}: cost {}'.format(
it_i + 1, n_iterations, training_cost / n_batches))
# Also, every 20 iterations, we'll draw the prediction of our
# input xs, which should try to recreate our image!
if (it_i + 1) % gif_step == 0:
costs.append(training_cost / n_batches)
ys_pred = model['Y_pred'].eval(
feed_dict={model['X']: xs}, session=sess)
img = ys_pred.reshape(imgs.shape)
gifs.append(img)
return gifs
```
<a name="code-1"></a>
## Code
Below, I've shown code for loading the first 100 celeb files. Run through the next few cells to see how this works with the celeb dataset, and then come back here and replace the `imgs` variable with your own set of images. For instance, you can try your entire sorted dataset from Session 1 as an N x H x W x C array. Explore!
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
celeb_imgs = utils.get_celeb_imgs()
plt.figure(figsize=(10, 10))
plt.imshow(utils.montage(celeb_imgs).astype(np.uint8))
# It doesn't have to be 100 images, explore!
imgs = np.array(celeb_imgs).copy()
```
Explore changing the parameters of the `train` function and your own dataset of images. Note, you do not have to use the dataset from the last assignment! Explore different numbers of images, whatever you prefer.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
# Change the parameters of the train function and
# explore changing the dataset
gifs = train(imgs=imgs)
```
Now we'll create a gif out of the training process. Be sure to call this 'multiple.gif' for your homework submission:
```
montage_gifs = [np.clip(utils.montage(
(m * 127.5) + 127.5), 0, 255).astype(np.uint8)
for m in gifs]
_ = gif.build_gif(montage_gifs, saveto='multiple.gif')
```
And show it in the notebook
```
ipyd.Image(url='multiple.gif?{}'.format(np.random.rand()),
height=500, width=500)
```
What we're seeing is the training process over time. We feed in our `xs`, which consist of the pixel values of each of our 100 images, it goes through the neural network, and out come predicted color values for every possible input value. We visualize it above as a gif by seeing how at each iteration the network has predicted the entire space of the inputs. We can visualize just the last iteration as a "latent" space, going from the first image (the top left image in the montage), to the last image, (the bottom right image).
```
final = gifs[-1]
final_gif = [np.clip(((m * 127.5) + 127.5), 0, 255).astype(np.uint8) for m in final]
gif.build_gif(final_gif, saveto='final.gif')
ipyd.Image(url='final.gif?{}'.format(np.random.rand()),
height=200, width=200)
```
<a name="part-four---open-exploration-extra-credit"></a>
# Part Four - Open Exploration (Extra Credit)
I now what you to explore what other possible manipulations of the network and/or dataset you could imagine. Perhaps a process that does the reverse, tries to guess where a given color should be painted? What if it was only taught a certain palette, and had to reason about other colors, how it would interpret those colors? Or what if you fed it pixel locations that weren't part of the training set, or outside the frame of what it was trained on? Or what happens with different activation functions, number of layers, increasing number of neurons or lesser number of neurons? I leave any of these as an open exploration for you.
Try exploring this process with your own ideas, materials, and networks, and submit something you've created as a gif! To aid exploration, be sure to scale the image down quite a bit or it will require a much larger machine, and much more time to train. Then whenever you think you may be happy with the process you've created, try scaling up the resolution and leave the training to happen over a few hours/overnight to produce something truly stunning!
Make sure to name the result of your gif: "explore.gif", and be sure to include it in your zip file.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
```
# Train a network to produce something, storing every few
# iterations in the variable gifs, then export the training
# over time as a gif.
...
gif.build_gif(montage_gifs, saveto='explore.gif')
ipyd.Image(url='explore.gif?{}'.format(np.random.rand()),
height=500, width=500)
```
<a name="assignment-submission"></a>
# Assignment Submission
After you've completed the notebook, create a zip file of the current directory using the code below. This code will make sure you have included this completed ipython notebook and the following files named exactly as:
<pre>
session-2/
session-2.ipynb
single.gif
multiple.gif
final.gif
explore.gif*
libs/
utils.py
* = optional/extra-credit
</pre>
You'll then submit this zip file for your second assignment on Kadenze for "Assignment 2: Teach a Deep Neural Network to Paint"! If you have any questions, remember to reach out on the forums and connect with your peers or with me.
To get assessed, you'll need to be a premium student! This will allow you to build an online portfolio of all of your work and receive grades. If you aren't already enrolled as a student, register now at http://www.kadenze.com/ and join the [#CADL](https://twitter.com/hashtag/CADL) community to see what your peers are doing! https://www.kadenze.com/courses/creative-applications-of-deep-learning-with-tensorflow/info
Also, if you share any of the GIFs on Facebook/Twitter/Instagram/etc..., be sure to use the #CADL hashtag so that other students can find your work!
```
utils.build_submission('session-2.zip',
('reference.png',
'single.gif',
'multiple.gif',
'final.gif',
'session-2.ipynb'),
('explore.gif'))
```
|
github_jupyter
|
# First check the Python version
import sys
if sys.version_info < (3,4):
print('You are running an older version of Python!\n\n' \
'You should consider updating to Python 3.4.0 or ' \
'higher as the libraries built for this course ' \
'have only been tested in Python 3.4 and higher.\n')
print('Try installing the Python 3.5 version of anaconda '
'and then restart `jupyter notebook`:\n' \
'https://www.continuum.io/downloads\n\n')
# Now get necessary libraries
try:
import os
import numpy as np
import matplotlib.pyplot as plt
from skimage.transform import resize
from skimage import data
from scipy.misc import imresize
except ImportError:
print('You are missing some packages! ' \
'We will try installing them before continuing!')
!pip install "numpy>=1.11.0" "matplotlib>=1.5.1" "scikit-image>=0.11.3" "scikit-learn>=0.17" "scipy>=0.17.0"
import os
import numpy as np
import matplotlib.pyplot as plt
from skimage.transform import resize
from skimage import data
from scipy.misc import imresize
print('Done!')
# Import Tensorflow
try:
import tensorflow as tf
except ImportError:
print("You do not have tensorflow installed!")
print("Follow the instructions on the following link")
print("to install tensorflow before continuing:")
print("")
print("https://github.com/pkmital/CADL#installation-preliminaries")
# This cell includes the provided libraries from the zip file
# and a library for displaying images from ipython, which
# we will use to display the gif
try:
from libs import utils, gif
import IPython.display as ipyd
except ImportError:
print("Make sure you have started notebook in the same directory" +
" as the provided zip file which includes the 'libs' folder" +
" and the file 'utils.py' inside of it. You will NOT be able"
" to complete this assignment unless you restart jupyter"
" notebook inside the directory created by extracting"
" the zip file or cloning the github repo.")
# We'll tell matplotlib to inline any drawn figures like so:
%matplotlib inline
plt.style.use('ggplot')
# Bit of formatting because I don't like the default inline code style:
from IPython.core.display import HTML
HTML("""<style> .rendered_html code {
padding: 2px 4px;
color: #c7254e;
background-color: #f9f2f4;
border-radius: 4px;
} </style>""")
xs = np.linspace(-6, 6, 100)
plt.plot(xs, np.maximum(xs, 0), label='relu')
plt.plot(xs, 1 / (1 + np.exp(-xs)), label='sigmoid')
plt.plot(xs, np.tanh(xs), label='tanh')
plt.xlabel('Input')
plt.xlim([-6, 6])
plt.ylabel('Output')
plt.ylim([-1.5, 1.5])
plt.title('Common Activation Functions/Nonlinearities')
plt.legend(loc='lower right')
placeholder(dtype, shape=None, name=None)
x = tf.placeholder(tf.float32, shape=(1024, 1024))
y = tf.matmul(x, x)
with tf.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed.
rand_array = np.random.rand(1024, 1024)
print(sess.run(y, feed_dict={x: rand_array})) # Will succeed.
# Create a placeholder with None x 2 dimensions of dtype tf.float32, and name it "X":
X = ...
W = tf.get_variable(...
h = tf.matmul(...
b = tf.get_variable(...
h = tf.nn.bias_add(...
h = ...
utils.linear??
def linear(x, n_output, name=None, activation=None, reuse=None):
"""Fully connected layer
Parameters
----------
x : tf.Tensor
Input tensor to connect
n_output : int
Number of output neurons
name : None, optional
Scope to apply
Returns
-------
op : tf.Tensor
Output of fully connected layer.
"""
if len(x.get_shape()) != 2:
x = flatten(x, reuse=reuse)
n_input = x.get_shape().as_list()[1]
with tf.variable_scope(name or "fc", reuse=reuse):
W = tf.get_variable(
name='W',
shape=[n_input, n_output],
dtype=tf.float32,
initializer=tf.contrib.layers.xavier_initializer())
b = tf.get_variable(
name='b',
shape=[n_output],
dtype=tf.float32,
initializer=tf.constant_initializer(0.0))
h = tf.nn.bias_add(
name='h',
value=tf.matmul(x, W),
bias=b)
if activation:
h = activation(h)
return h, W
tf.reset_default_graph()
g = tf.Graph()
with tf.Session(graph=g) as sess:
Y_pred, W = linear(X, 2, 3, activation=tf.nn.relu)
```
or:
```python
g = tf.Graph()
with tf.Session(graph=g) as sess, g.as_default():
Y_pred, W = linear(X, 2, 3, activation=tf.nn.relu)
```
You can now write the same process as the above steps by simply calling:
<a name="part-two---image-painting-network"></a>
# Part Two - Image Painting Network
<a name="instructions-1"></a>
## Instructions
Follow along the steps below, first setting up input and output data of the network, $\textbf{X}$ and $\textbf{Y}$. Then work through building the neural network which will try to compress the information in $\textbf{X}$ through a series of linear and non-linear functions so that whatever it is given as input, it minimized the error of its prediction, $\hat{\textbf{Y}}$, and the true output $\textbf{Y}$ through its training process. You'll also create an animated GIF of the training which you'll need to submit for the homework!
Through this, we'll explore our first creative application: painting an image. This network is just meant to demonstrate how easily networks can be scaled to more complicated tasks without much modification. It is also meant to get you thinking about neural networks as building blocks that can be reconfigured, replaced, reorganized, and get you thinking about how the inputs and outputs can be anything you can imagine.
<a name="preparing-the-data"></a>
## Preparing the Data
We'll follow an example that Andrej Karpathy has done in his online demonstration of "image inpainting". What we're going to do is teach the network to go from the location on an image frame to a particular color. So given any position in an image, the network will need to learn what color to paint. Let's first get an image that we'll try to teach a neural network to paint.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
In the lecture, I showed how to aggregate the pixel locations and their colors using a loop over every pixel position. I put that code into a function `split_image` below. Feel free to experiment with other features for `xs` or `ys`.
Let's use this function to create the inputs (xs) and outputs (ys) to our network as the pixel locations (xs) and their colors (ys):
Also remember, we should normalize our input values!
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
Similarly for the output:
We'll normalize the output using a simpler normalization method, since we know the values range from 0-255:
Scaling the image values like this has the advantage that it is still interpretable as an image, unlike if we have negative values.
What we're going to do is use regression to predict the value of a pixel given its (row, col) position. So the input to our network is `X = (row, col)` value. And the output of the network is `Y = (r, g, b)`.
We can get our original image back by reshaping the colors back into the original image shape. This works because the `ys` are still in order:
But when we give inputs of (row, col) to our network, it won't know what order they are, because we will randomize them. So it will have to *learn* what color value should be output for any given (row, col).
Create 2 placeholders of `dtype` `tf.float32`: one for the input of the network, a `None x 2` dimension placeholder called $\textbf{X}$, and another for the true output of the network, a `None x 3` dimension placeholder called $\textbf{Y}$.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
Now create a deep neural network that takes your network input $\textbf{X}$ of 2 neurons, multiplies it by a linear and non-linear transformation which makes its shape [None, 20], meaning it will have 20 output neurons. Then repeat the same process again to give you 20 neurons again, and then again and again until you've done 6 layers of 20 neurons. Then finally one last layer which will output 3 neurons, your predicted output, which I've been denoting mathematically as $\hat{\textbf{Y}}$, for a total of 6 hidden layers, or 8 layers total including the input and output layers. Mathematically, we'll be creating a deep neural network that looks just like the previous fully connected layer we've created, but with a few more connections. So recall the first layer's connection is:
\begin{align}
\textbf{H}_1=\phi(\textbf{X}\textbf{W}_1 + \textbf{b}_1) \\
\end{align}
So the next layer will take that output, and connect it up again:
\begin{align}
\textbf{H}_2=\phi(\textbf{H}_1\textbf{W}_2 + \textbf{b}_2) \\
\end{align}
And same for every other layer:
\begin{align}
\textbf{H}_3=\phi(\textbf{H}_2\textbf{W}_3 + \textbf{b}_3) \\
\textbf{H}_4=\phi(\textbf{H}_3\textbf{W}_4 + \textbf{b}_4) \\
\textbf{H}_5=\phi(\textbf{H}_4\textbf{W}_5 + \textbf{b}_5) \\
\textbf{H}_6=\phi(\textbf{H}_5\textbf{W}_6 + \textbf{b}_6) \\
\end{align}
Including the very last layer, which will be the prediction of the network:
\begin{align}
\hat{\textbf{Y}}=\phi(\textbf{H}_6\textbf{W}_7 + \textbf{b}_7)
\end{align}
Remember if you run into issues with variable scopes/names, that you cannot recreate a variable with the same name! Revisit the section on <a href='#Variable-Scopes'>Variable Scopes</a> if you get stuck with name issues.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
<a name="cost-function"></a>
## Cost Function
Now we're going to work on creating a `cost` function. The cost should represent how much `error` there is in the network, and provide the optimizer this value to help it train the network's parameters using gradient descent and backpropagation.
Let's say our error is `E`, then the cost will be:
$$cost(\textbf{Y}, \hat{\textbf{Y}}) = \frac{1}{\text{B}} \displaystyle\sum\limits_{b=0}^{\text{B}} \textbf{E}_b
$$
where the error is measured as, e.g.:
$$\textbf{E} = \displaystyle\sum\limits_{c=0}^{\text{C}} (\textbf{Y}_{c} - \hat{\textbf{Y}}_{c})^2$$
Don't worry if this scares you. This is mathematically expressing the same concept as: "the cost of an actual $\textbf{Y}$, and a predicted $\hat{\textbf{Y}}$ is equal to the mean across batches, of which there are $\text{B}$ total batches, of the sum of distances across $\text{C}$ color channels of every predicted output and true output". Basically, we're trying to see on average, or at least within a single minibatches average, how wrong was our prediction? We create a measure of error for every output feature by squaring the predicted output and the actual output it should have, i.e. the actual color value it should have output for a given input pixel position. By squaring it, we penalize large distances, but not so much small distances.
Consider how the square function (i.e., $f(x) = x^2$) changes for a given error. If our color values range between 0-255, then a typical amount of error would be between $0$ and $128^2$. For example if my prediction was (120, 50, 167), and the color should have been (0, 100, 120), then the error for the Red channel is (120 - 0) or 120. And the Green channel is (50 - 100) or -50, and for the Blue channel, (167 - 120) = 47. When I square this result, I get: (120)^2, (-50)^2, and (47)^2. I then add all of these and that is my error, $\textbf{E}$, for this one observation. But I will have a few observations per minibatch. So I add all the error in my batch together, then divide by the number of observations in the batch, essentially finding the mean error of my batch.
Let's try to see what the square in our measure of error is doing graphically.
This is known as the $l_2$ (pronounced el-two) loss. It doesn't penalize small errors as much as it does large errors. This is easier to see when we compare it with another common loss, the $l_1$ (el-one) loss. It is linear in error, by taking the absolute value of the error. We'll compare the $l_1$ loss with normalized values from $0$ to $1$. So instead of having $0$ to $255$ for our RGB values, we'd have $0$ to $1$, simply by dividing our color values by $255.0$.
So unlike the $l_2$ loss, the $l_1$ loss is really quickly upset if there is *any* error at all: as soon as error moves away from $0.0$, to $0.1$, the $l_1$ loss is $0.1$. But the $l_2$ loss is $0.1^2 = 0.01$. Having a stronger penalty on smaller errors often leads to what the literature calls "sparse" solutions, since it favors activations that try to explain as much of the data as possible, rather than a lot of activations that do a sort of good job, but when put together, do a great job of explaining the data. Don't worry about what this means if you are more unfamiliar with Machine Learning. There is a lot of literature surrounding each of these loss functions that we won't have time to get into, but look them up if they interest you.
During the lecture, we've seen how to create a cost function using Tensorflow. To create a $l_2$ loss function, you can for instance use tensorflow's `tf.squared_difference` or for an $l_1$ loss function, `tf.abs`. You'll need to refer to the `Y` and `Y_pred` variables only, and your resulting cost should be a single value. Try creating the $l_1$ loss to begin with, and come back here after you have trained your network, to compare the performance with a $l_2$ loss.
The equation for computing cost I mentioned above is more succintly written as, for $l_2$ norm:
$$cost(\textbf{Y}, \hat{\textbf{Y}}) = \frac{1}{\text{B}} \displaystyle\sum\limits_{b=0}^{\text{B}} \displaystyle\sum\limits_{c=0}^{\text{C}} (\textbf{Y}_{c} - \hat{\textbf{Y}}_{c})^2$$
For $l_1$ norm, we'd have:
$$cost(\textbf{Y}, \hat{\textbf{Y}}) = \frac{1}{\text{B}} \displaystyle\sum\limits_{b=0}^{\text{B}} \displaystyle\sum\limits_{c=0}^{\text{C}} \text{abs}(\textbf{Y}_{c} - \hat{\textbf{Y}}_{c})$$
Remember, to understand this equation, try to say it out loud: the $cost$ given two variables, $\textbf{Y}$, the actual output we want the network to have, and $\hat{\textbf{Y}}$ the predicted output from the network, is equal to the mean across $\text{B}$ batches, of the sum of $\textbf{C}$ color channels distance between the actual and predicted outputs. If you're still unsure, refer to the lecture where I've computed this, or scroll down a bit to where I've included the answer.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
We now need an `optimizer` which will take our `cost` and a `learning_rate`, which says how far along the gradient to move. This optimizer calculates all the gradients in our network with respect to the `cost` variable and updates all of the weights in our network using backpropagation. We'll then create mini-batches of our training data and run the `optimizer` using a `session`.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
We'll now train our network! The code below should do this for you if you've setup everything else properly. Please read through this and make sure you understand each step! Note that this can take a VERY LONG time depending on the size of your image (make it < 100 x 100 pixels), the number of neurons per layer (e.g. < 30), the number of layers (e.g. < 8), and number of iterations (< 1000). Welcome to Deep Learning :)
Let's now display the GIF we've just created:
<a name="explore"></a>
## Explore
Go back over the previous cells and exploring changing different parameters of the network. I would suggest first trying to change the `learning_rate` parameter to different values and see how the cost curve changes. What do you notice? Try exponents of $10$, e.g. $10^1$, $10^2$, $10^3$... and so on. Also try changing the `batch_size`: $50, 100, 200, 500, ...$ How does it effect how the cost changes over time?
Be sure to explore other manipulations of the network, such as changing the loss function to $l_2$ or $l_1$. How does it change the resulting learning? Also try changing the activation functions, the number of layers/neurons, different optimizers, and anything else that you may think of, and try to get a basic understanding on this toy problem of how it effects the network's training. Also try comparing creating a fairly shallow/wide net (e.g. 1-2 layers with many neurons, e.g. > 100), versus a deep/narrow net (e.g. 6-20 layers with fewer neurons, e.g. < 20). What do you notice?
<a name="a-note-on-crossvalidation"></a>
## A Note on Crossvalidation
The cost curve plotted above is only showing the cost for our "training" dataset. Ideally, we should split our dataset into what are called "train", "validation", and "test" sets. This is done by taking random subsets of the entire dataset. For instance, we partition our dataset by saying we'll only use 80% of it for training, 10% for validation, and the last 10% for testing. Then when training as above, you would only use the 80% of the data you had partitioned, and then monitor accuracy on both the data you have used to train, but also that new 10% of unseen validation data. This gives you a sense of how "general" your network is. If it is performing just as well on that 10% of data, then you know it is doing a good job. Finally, once you are done training, you would test one last time on your "test" dataset. Ideally, you'd do this a number of times, so that every part of the dataset had a chance to be the test set. This would also give you a measure of the variance of the accuracy on the final test. If it changes a lot, you know something is wrong. If it remains fairly stable, then you know that it is a good representation of the model's accuracy on unseen data.
We didn't get a chance to cover this in class, as it is less useful for exploring creative applications, though it is very useful to know and to use in practice, as it avoids overfitting/overgeneralizing your network to all of the data. Feel free to explore how to do this on the application above!
<a name="part-three---learning-more-than-one-image"></a>
# Part Three - Learning More than One Image
<a name="instructions-2"></a>
## Instructions
We're now going to make use of our Dataset from Session 1 and apply what we've just learned to try and paint every single image in our dataset. How would you guess is the best way to approach this? We could for instance feed in every possible image by having multiple row, col -> r, g, b values. So for any given row, col, we'd have 100 possible r, g, b values. This likely won't work very well as there are many possible values a pixel could take, not just one. What if we also tell the network *which* image's row and column we wanted painted? We're going to try and see how that does.
You can execute all of the cells below unchanged to see how this works with the first 100 images of the celeb dataset. But you should replace the images with your own dataset, and vary the parameters of the network to get the best results!
I've placed the same code for running the previous algorithm into two functions, `build_model` and `train`. You can directly call the function `train` with a 4-d image shaped as N x H x W x C, and it will collect all of the points of every image and try to predict the output colors of those pixels, just like before. The only difference now is that you are able to try this with a few images at a time. There are a few ways we could have tried to handle multiple images. The way I've shown in the `train` function is to include an additional input neuron for *which* image it is. So as well as receiving the row and column, the network will also receive as input which image it is as a number. This should help the network to better distinguish the patterns it uses, as it has knowledge that helps it separates its process based on which image is fed as input.
<a name="code-1"></a>
## Code
Below, I've shown code for loading the first 100 celeb files. Run through the next few cells to see how this works with the celeb dataset, and then come back here and replace the `imgs` variable with your own set of images. For instance, you can try your entire sorted dataset from Session 1 as an N x H x W x C array. Explore!
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
Explore changing the parameters of the `train` function and your own dataset of images. Note, you do not have to use the dataset from the last assignment! Explore different numbers of images, whatever you prefer.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
Now we'll create a gif out of the training process. Be sure to call this 'multiple.gif' for your homework submission:
And show it in the notebook
What we're seeing is the training process over time. We feed in our `xs`, which consist of the pixel values of each of our 100 images, it goes through the neural network, and out come predicted color values for every possible input value. We visualize it above as a gif by seeing how at each iteration the network has predicted the entire space of the inputs. We can visualize just the last iteration as a "latent" space, going from the first image (the top left image in the montage), to the last image, (the bottom right image).
<a name="part-four---open-exploration-extra-credit"></a>
# Part Four - Open Exploration (Extra Credit)
I now what you to explore what other possible manipulations of the network and/or dataset you could imagine. Perhaps a process that does the reverse, tries to guess where a given color should be painted? What if it was only taught a certain palette, and had to reason about other colors, how it would interpret those colors? Or what if you fed it pixel locations that weren't part of the training set, or outside the frame of what it was trained on? Or what happens with different activation functions, number of layers, increasing number of neurons or lesser number of neurons? I leave any of these as an open exploration for you.
Try exploring this process with your own ideas, materials, and networks, and submit something you've created as a gif! To aid exploration, be sure to scale the image down quite a bit or it will require a much larger machine, and much more time to train. Then whenever you think you may be happy with the process you've created, try scaling up the resolution and leave the training to happen over a few hours/overnight to produce something truly stunning!
Make sure to name the result of your gif: "explore.gif", and be sure to include it in your zip file.
<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
<a name="assignment-submission"></a>
# Assignment Submission
After you've completed the notebook, create a zip file of the current directory using the code below. This code will make sure you have included this completed ipython notebook and the following files named exactly as:
<pre>
session-2/
session-2.ipynb
single.gif
multiple.gif
final.gif
explore.gif*
libs/
utils.py
* = optional/extra-credit
</pre>
You'll then submit this zip file for your second assignment on Kadenze for "Assignment 2: Teach a Deep Neural Network to Paint"! If you have any questions, remember to reach out on the forums and connect with your peers or with me.
To get assessed, you'll need to be a premium student! This will allow you to build an online portfolio of all of your work and receive grades. If you aren't already enrolled as a student, register now at http://www.kadenze.com/ and join the [#CADL](https://twitter.com/hashtag/CADL) community to see what your peers are doing! https://www.kadenze.com/courses/creative-applications-of-deep-learning-with-tensorflow/info
Also, if you share any of the GIFs on Facebook/Twitter/Instagram/etc..., be sure to use the #CADL hashtag so that other students can find your work!
| 0.585338 | 0.954647 |
Integration by parts is another technique for simplifying integrands. As we saw in previous posts, each differentiation rule has a corresponding integration rule. In the case of integration by parts, the corresponding differentiation rule is the Product Rule. The technique of integration by parts allows us to simplify integrands of the form:
$$ \int f(x) g(x) dx $$
Examples of this form include:
$$ \int x \cos{x} \space dx, \qquad \int e^x \cos{x} \space dx, \qquad \int x^2 e^x \space dx $$
As integration by parts is the product rule applied to integrals, it helps to state the Product Rule again. The Product Rule is defined as:
$$ \frac{d}{dx} \big[ f(x)g(x) \big] = f^{\prime}(x) g(x) + f(x) g^{\prime}(x) $$
When we apply the product rule to indefinite integrals, we can restate the rule as:
$$ \int \frac{d}{dx} \big[f(x)g(x)\big] \space dx = \int \big[f^{\prime} g(x) + f(x) g^{\prime}(x) \big] \space dx $$
Then, rearranging so we get $f(x)g^{\prime}(x) \space dx$ on the left side of the equation:
$$ \int f(x)g^{\prime}(x) \space dx = \int \frac{d}{dx} \big[f(x)g(x)\big] \space dx - \int f^{\prime}(x)g(x) \space dx $$
Which gives us the integration by parts formula! The formula is typically written in differential form:
$$ \int u \space dv = uv - \int v \space du $$
## Examples
The following examples walkthrough several problems that can be solved using integration by parts. We also employ the wonderful [SymPy](https://www.sympy.org/en/index.html) package for symbolic computation to confirm our answers. To use SymPy later to verify our answers, we load the modules we will require and initialize several variables for use with the SymPy library.
```
from sympy import symbols, limit, diff, sin, cos, log, tan, sqrt, init_printing, plot, integrate
from mpmath import ln, e, pi, cosh, sinh
init_printing()
x = symbols('x')
y = symbols('y')
```
Example 1: Evaluate the integrand $ \int x \sin{\frac{x}{2}} \space dx $
Recalling the differential form of the integration by parts formula, $ \int u \space dv = uv - \int v \space du $, we set $u = x$ and $dv = \sin{\frac{x}{2}}$
Solving for the derivative of $u$, we arrive at $du = 1 \space dx = dx$. Next, we find the antiderivative of $dv$. To find this antiderivative, we employ the Substitution Rule.
$$ u = \frac{1}{2}x, \qquad du = {1}{2} \space dx, \qquad \frac{du}{dx} = 2 $$
$$ y = \sin{u}, \qquad dy = -\cos{u} \space du, \qquad \frac{dy}{du} = -\cos{u} $$
Therefore, $v = -2 \cos{\frac{x}{2}}$
Entering these into the integration by parts formula:
$$ -2x\cos{\frac{x}{2}} - (-2)\int \cos{\frac{x}{2}} $$
Then, solving for the integrand $\int \cos{\frac{x}{2}}$, we employ the Substitution Rule again as before to arrive at $2\sin{\frac{x}{2}}$ (the steps in solving this integrand are the same as before when we solved for $\int \sin{\frac{x}{2}}$). Thus, the integral is evaluated as:
$$ -2x\cos{\frac{x}{2}} + 4\sin{\frac{x}{2}} + C $$
Using SymPy's [`integrate`](https://docs.sympy.org/latest/modules/integrals/integrals.html), we can verify our answer is correct (SymPy does not include the constant of integration $C$).
```
integrate(x * sin(x / 2), x)
```
Example 2: Evaluate $\int t^2 \cos{t} \space dt$
We start by setting $u = t^2$ and $dv = \cos{t}$. The derivative of $t^2$ is $2t$, thus $du = 2t \space dt$, or $\frac{du}{dt} = 2t$. Integrating $dv = \cos{t}$ gives us $v = \sin{t} \space du$. Entering these into the integration by parts formula:
$$ t^2 \sin{t} - 2\int t \sin{t} $$
Therefore, we must do another round of integration by parts to solve $\int t \sin{t}$.
$$ u = t, \qquad du = dt $$
$$ dv = \sin{t}, \qquad v = -\cos{t} \space du $$
Putting these together into the integration by parts formula with the above:
$$ t^2 \sin{t} - 2 \big(-t \cos{t} + \int \cos{t} \space dt \big) $$
Which gives us the solution:
$$ t^2 \sin{t} + 2t \cos{t} - 2 \sin{t} + C$$
As before, we can verify that our answer is correct by leveraging SymPy.
```
t = symbols('t')
integrate(t ** 2 * cos(t), t)
```
Example 3: $\int x e^x \space dx$
Here, we set $u = x$ and $dv = e^x$. Therefore, $du = dx$ and $v = e^x \space dx$. Putting these together in the integration by parts formula:
$$ xe^x - \int e^x $$
As the integral of $e^x$ is just $e^x$, our answer is:
$$ xe^x - e^x + C $$
We can again verify our answer is accurate using SymPy.
```
integrate(x * e ** x, x)
```
## References
[Hass, J. and Weir, M. (n.d.). Thomas' calculus. 13th ed.](https://amzn.to/2SuuPOz)
[Stewart, J. (2007). Essential calculus: Early transcendentals. Belmont, CA: Thomson Higher Education.](https://amzn.to/38dnRV0)
|
github_jupyter
|
from sympy import symbols, limit, diff, sin, cos, log, tan, sqrt, init_printing, plot, integrate
from mpmath import ln, e, pi, cosh, sinh
init_printing()
x = symbols('x')
y = symbols('y')
integrate(x * sin(x / 2), x)
t = symbols('t')
integrate(t ** 2 * cos(t), t)
integrate(x * e ** x, x)
| 0.639286 | 0.994396 |
# Translate `dzn` to `smt2` for OptiMathSAT
### Check Versions of Tools
```
import os
import subprocess
my_env = os.environ.copy()
output = subprocess.check_output(f'''/home/{my_env['USER']}/optimathsat/bin/optimathsat -version''',
shell=True, universal_newlines=True)
output
output = subprocess.check_output(f'''/home/{my_env['USER']}/minizinc/build/minizinc --version''',
shell=True, universal_newlines=True)
output
```
First generate the FlatZinc files using the MiniZinc tool. Make sure that a `smt2` folder is located inside `./minizinc/share/minizinc/`. Else, to enable OptiMathSAT's support for global constraints download the [smt2.tar.gz](http://optimathsat.disi.unitn.it/data/smt2.tar.gz) package and unpack it there using
```zsh
tar xf smt2.tar.gz $MINIZINC_PATH/share/minizinc/
```
If next output shows a list of `.mzn` files, then this dependency is satified.
```
output = subprocess.check_output(f'''ls -la /home/{my_env['USER']}/minizinc/share/minizinc/smt2/''',
shell=True, universal_newlines=True)
print(output)
```
## Transform `dzn` to `fzn` Using a Model `mzn`
Then transform the desired `.dzn` files to `.fzn` using a `Mz.mzn` MiniZinc model.
First list all `dzn` files contained in the `dzn_path` that should get processed.
```
import os
dzn_files = []
dzn_path = f'''/home/{my_env['USER']}/data/dzn/'''
for filename in os.listdir(dzn_path):
if filename.endswith(".dzn"):
dzn_files.append(filename)
len(dzn_files)
```
#### Model $Mz_1$
```
import sys
fzn_path = f'''/home/{my_env['USER']}/data/fzn/smt2/Mz1-noAbs/'''
minizinc_base_cmd = f'''/home/{my_env['USER']}/minizinc/build/minizinc \
-Werror \
--compile --solver org.minizinc.mzn-fzn \
--search-dir /home/{my_env['USER']}/minizinc/share/minizinc/smt2/ \
/home/{my_env['USER']}/models/mzn/Mz1-noAbs.mzn '''
translate_count = 0
for dzn in dzn_files:
translate_count += 1
minizinc_transform_cmd = minizinc_base_cmd + dzn_path + dzn \
+ ' --output-to-file ' + fzn_path + dzn.replace('.', '-') + '.fzn'
print(f'''\r({translate_count}/{len(dzn_files)}) Translating {dzn_path + dzn} to {fzn_path + dzn.replace('.', '-')}.fzn''', end='')
sys.stdout.flush()
subprocess.check_output(minizinc_transform_cmd, shell=True,
universal_newlines=True)
```
#### Model $Mz_2$
```
import sys
fzn_path = f'''/home/{my_env['USER']}/data/fzn/smt2/Mz2-noAbs/'''
minizinc_base_cmd = f'''/home/{my_env['USER']}/minizinc/build/minizinc \
-Werror \
--compile --solver org.minizinc.mzn-fzn \
--search-dir /home/{my_env['USER']}/minizinc/share/minizinc/smt2/ \
/home/{my_env['USER']}/models/mzn/Mz2-noAbs.mzn '''
translate_count = 0
for dzn in dzn_files:
translate_count += 1
minizinc_transform_cmd = minizinc_base_cmd + dzn_path + dzn \
+ ' --output-to-file ' + fzn_path + dzn.replace('.', '-') + '.fzn'
print(f'''\r({translate_count}/{len(dzn_files)}) Translating {dzn_path + dzn} to {fzn_path + dzn.replace('.', '-')}.fzn''', end='')
sys.stdout.flush()
subprocess.check_output(minizinc_transform_cmd, shell=True,
universal_newlines=True)
```
## Translate `fzn` to `smt2`
The generated `.fzn` files can be used to generate a `.smt2` files using the `fzn2smt2.py` script from this [project](https://github.com/PatrickTrentin88/fzn2omt).
**NOTE**: Files `R001` (no cables) and `R002` (one one-sided cable) throw an error while translating.
#### $Mz_1$
```
import os
fzn_files = []
fzn_path = f'''/home/{my_env['USER']}/data/fzn/smt2/Mz1-noAbs/'''
for filename in os.listdir(fzn_path):
if filename.endswith(".fzn"):
fzn_files.append(filename)
len(fzn_files)
smt2_path = f'''/home/{my_env['USER']}/data/smt2/optimathsat/Mz1-noAbs/'''
fzn2smt2_base_cmd = f'''/home/{my_env['USER']}/fzn2omt/bin/fzn2optimathsat.py '''
translate_count = 0
my_env = os.environ.copy()
my_env['PATH'] = f'''/home/{my_env['USER']}/optimathsat/bin/:{my_env['PATH']}'''
for fzn in fzn_files:
translate_count += 1
fzn2smt2_transform_cmd = fzn2smt2_base_cmd + fzn_path + fzn \
+ ' --smt2 ' + smt2_path + fzn.replace('.', '-') + '.smt2'
print(f'''\r({translate_count}/{len(fzn_files)}) Translating {fzn_path + fzn} to {smt2_path + fzn.replace('.', '-')}.smt2''', end='')
try:
output = subprocess.check_output(fzn2smt2_transform_cmd, shell=True, env=my_env,
universal_newlines=True, stderr=subprocess.STDOUT)
except Exception as e:
output = str(e.output)
print(f'''\r{output}''', end='')
sys.stdout.flush()
```
#### $Mz_2$
```
import os
fzn_files = []
fzn_path = f'''/home/{my_env['USER']}/data/fzn/smt2/Mz2-noAbs/'''
for filename in os.listdir(fzn_path):
if filename.endswith(".fzn"):
fzn_files.append(filename)
len(fzn_files)
smt2_path = f'''/home/{my_env['USER']}/data/smt2/optimathsat/Mz2-noAbs/'''
fzn2smt2_base_cmd = f'''/home/{my_env['USER']}/fzn2omt/bin/fzn2optimathsat.py '''
translate_count = 0
my_env = os.environ.copy()
my_env['PATH'] = f'''/home/{my_env['USER']}/optimathsat/bin/:{my_env['PATH']}'''
for fzn in fzn_files:
translate_count += 1
fzn2smt2_transform_cmd = fzn2smt2_base_cmd + fzn_path + fzn \
+ ' --smt2 ' + smt2_path + fzn.replace('.', '-') + '.smt2'
print(f'''\r({translate_count}/{len(fzn_files)}) Translating {fzn_path + fzn} to {smt2_path + fzn.replace('.', '-')}.smt2''', end='')
try:
output = subprocess.check_output(fzn2smt2_transform_cmd, shell=True, env=my_env,
universal_newlines=True, stderr=subprocess.STDOUT)
except Exception as e:
output = str(e.output)
print(f'''\r{output}''', end='')
sys.stdout.flush()
```
## Test Generated `smt2` Files Using `OptiMathSAT`
This shoud generate the `smt2` file without any error. If this was the case then `OptiMathSAT` can be called on a file by running
```zsh
optimathsat output/A004-dzn-smt2-fzn.smt2
```
yielding something similar to
```zsh
sat
(objectives
(obj 88)
)
(error "model generation not enabled")
unsupported
```
#### Test with `smt2` from $Mz_1$
```
try:
result = subprocess.check_output(
f'''/home/{my_env['USER']}/optimathsat/bin/optimathsat \
/home/{my_env['USER']}/data/smt2/optimathsat/Mz1-noAbs/A004-dzn-fzn.smt2''',
shell=True, universal_newlines=True)
except Exception as e:
result = str(e.output)
print(result)
```
#### Test with `smt2` from $Mz_2$
```
result = subprocess.check_output(
f'''/home/{my_env['USER']}/optimathsat/bin/optimathsat \
/home/{my_env['USER']}/data/smt2/optimathsat/Mz2-noAbs/A004-dzn-fzn.smt2''',
shell=True, universal_newlines=True)
print(result)
```
### Adjust `smt2` Files According to Chapter 5.2 in Paper
Contrary to the `z3` version we're dropping the settings and the optimization function for OptiMathSAT `smt2` files, as those are set by the [OMT Python Timeout Wrapper](https://github.com/kw90/omt_python_timeout_wrapper).
- Add lower and upper bounds for the decision variable `pfc`
- Add number of cavities as comments for later solution extraction (workaround)
```
import os
import re
def adjust_smt2_file(smt2_path: str, file: str, write_path: str):
with open(smt2_path+'/'+file, 'r+') as myfile:
data = "".join(line for line in myfile)
filename = os.path.splitext(file)[0]
newFile = open(os.path.join(write_path, filename +'.smt2'),"w+")
newFile.write(data)
newFile.close()
openFile = open(os.path.join(write_path, filename +'.smt2'))
data = openFile.readlines()
additionalLines = data[-6:]
data = data[:-6]
openFile.close()
newFile = open(os.path.join(write_path, filename +'.smt2'),"w+")
newFile.writelines([item for item in data])
newFile.close()
with open(os.path.join(write_path, filename +'.smt2'),"r") as myfile:
data = "".join(line for line in myfile)
newFile = open(os.path.join(write_path, filename +'.smt2'),"w+")
matches = re.findall(r'\(define-fun .\d\d \(\) Int (\d+)\)', data)
try:
cavity_count = int(matches[0])
newFile.write(f''';; k={cavity_count}\n''')
newFile.write(f''';; Extract pfc from\n''')
for i in range(0,cavity_count):
newFile.write(f''';; X_INTRODUCED_{str(i)}_\n''')
newFile.write(data)
for i in range(1,cavity_count+1):
lb = f'''(define-fun lbound{str(i)} () Bool (> X_INTRODUCED_{str(i-1)}_ 0))\n'''
ub = f'''(define-fun ubound{str(i)} () Bool (<= X_INTRODUCED_{str(i-1)}_ {str(cavity_count)}))\n'''
assertLb = f'''(assert lbound{str(i)})\n'''
assertUb = f'''(assert ubound{str(i)})\n'''
newFile.write(lb)
newFile.write(ub)
newFile.write(assertLb)
newFile.write(assertUb)
except:
print(f'''\nCheck {filename} for completeness - data missing?''')
newFile.close()
```
#### $Mz_1$
```
import os
smt2_files = []
smt2_path = f'''/home/{my_env['USER']}/data/smt2/optimathsat/Mz1-noAbs'''
for filename in os.listdir(smt2_path):
if filename.endswith(".smt2"):
smt2_files.append(filename)
len(smt2_files)
fix_count = 0
for smt2 in smt2_files:
fix_count += 1
print(f'''\r{fix_count}/{len(smt2_files)} Fixing file {smt2}''', end='')
adjust_smt2_file(smt2_path=smt2_path, file=smt2, write_path=f'''{smt2_path}''')
sys.stdout.flush()
```
#### $Mz_2$
```
import os
smt2_files = []
smt2_path = f'''/home/{my_env['USER']}/data/smt2/optimathsat/Mz2-noAbs'''
for filename in os.listdir(smt2_path):
if filename.endswith(".smt2"):
smt2_files.append(filename)
len(smt2_files)
fix_count = 0
for smt2 in smt2_files:
fix_count += 1
print(f'''\r{fix_count}/{len(smt2_files)} Fixing file {smt2}''', end='')
adjust_smt2_file(smt2_path=smt2_path, file=smt2, write_path=f'''{smt2_path}''')
sys.stdout.flush()
```
|
github_jupyter
|
import os
import subprocess
my_env = os.environ.copy()
output = subprocess.check_output(f'''/home/{my_env['USER']}/optimathsat/bin/optimathsat -version''',
shell=True, universal_newlines=True)
output
output = subprocess.check_output(f'''/home/{my_env['USER']}/minizinc/build/minizinc --version''',
shell=True, universal_newlines=True)
output
tar xf smt2.tar.gz $MINIZINC_PATH/share/minizinc/
output = subprocess.check_output(f'''ls -la /home/{my_env['USER']}/minizinc/share/minizinc/smt2/''',
shell=True, universal_newlines=True)
print(output)
import os
dzn_files = []
dzn_path = f'''/home/{my_env['USER']}/data/dzn/'''
for filename in os.listdir(dzn_path):
if filename.endswith(".dzn"):
dzn_files.append(filename)
len(dzn_files)
import sys
fzn_path = f'''/home/{my_env['USER']}/data/fzn/smt2/Mz1-noAbs/'''
minizinc_base_cmd = f'''/home/{my_env['USER']}/minizinc/build/minizinc \
-Werror \
--compile --solver org.minizinc.mzn-fzn \
--search-dir /home/{my_env['USER']}/minizinc/share/minizinc/smt2/ \
/home/{my_env['USER']}/models/mzn/Mz1-noAbs.mzn '''
translate_count = 0
for dzn in dzn_files:
translate_count += 1
minizinc_transform_cmd = minizinc_base_cmd + dzn_path + dzn \
+ ' --output-to-file ' + fzn_path + dzn.replace('.', '-') + '.fzn'
print(f'''\r({translate_count}/{len(dzn_files)}) Translating {dzn_path + dzn} to {fzn_path + dzn.replace('.', '-')}.fzn''', end='')
sys.stdout.flush()
subprocess.check_output(minizinc_transform_cmd, shell=True,
universal_newlines=True)
import sys
fzn_path = f'''/home/{my_env['USER']}/data/fzn/smt2/Mz2-noAbs/'''
minizinc_base_cmd = f'''/home/{my_env['USER']}/minizinc/build/minizinc \
-Werror \
--compile --solver org.minizinc.mzn-fzn \
--search-dir /home/{my_env['USER']}/minizinc/share/minizinc/smt2/ \
/home/{my_env['USER']}/models/mzn/Mz2-noAbs.mzn '''
translate_count = 0
for dzn in dzn_files:
translate_count += 1
minizinc_transform_cmd = minizinc_base_cmd + dzn_path + dzn \
+ ' --output-to-file ' + fzn_path + dzn.replace('.', '-') + '.fzn'
print(f'''\r({translate_count}/{len(dzn_files)}) Translating {dzn_path + dzn} to {fzn_path + dzn.replace('.', '-')}.fzn''', end='')
sys.stdout.flush()
subprocess.check_output(minizinc_transform_cmd, shell=True,
universal_newlines=True)
import os
fzn_files = []
fzn_path = f'''/home/{my_env['USER']}/data/fzn/smt2/Mz1-noAbs/'''
for filename in os.listdir(fzn_path):
if filename.endswith(".fzn"):
fzn_files.append(filename)
len(fzn_files)
smt2_path = f'''/home/{my_env['USER']}/data/smt2/optimathsat/Mz1-noAbs/'''
fzn2smt2_base_cmd = f'''/home/{my_env['USER']}/fzn2omt/bin/fzn2optimathsat.py '''
translate_count = 0
my_env = os.environ.copy()
my_env['PATH'] = f'''/home/{my_env['USER']}/optimathsat/bin/:{my_env['PATH']}'''
for fzn in fzn_files:
translate_count += 1
fzn2smt2_transform_cmd = fzn2smt2_base_cmd + fzn_path + fzn \
+ ' --smt2 ' + smt2_path + fzn.replace('.', '-') + '.smt2'
print(f'''\r({translate_count}/{len(fzn_files)}) Translating {fzn_path + fzn} to {smt2_path + fzn.replace('.', '-')}.smt2''', end='')
try:
output = subprocess.check_output(fzn2smt2_transform_cmd, shell=True, env=my_env,
universal_newlines=True, stderr=subprocess.STDOUT)
except Exception as e:
output = str(e.output)
print(f'''\r{output}''', end='')
sys.stdout.flush()
import os
fzn_files = []
fzn_path = f'''/home/{my_env['USER']}/data/fzn/smt2/Mz2-noAbs/'''
for filename in os.listdir(fzn_path):
if filename.endswith(".fzn"):
fzn_files.append(filename)
len(fzn_files)
smt2_path = f'''/home/{my_env['USER']}/data/smt2/optimathsat/Mz2-noAbs/'''
fzn2smt2_base_cmd = f'''/home/{my_env['USER']}/fzn2omt/bin/fzn2optimathsat.py '''
translate_count = 0
my_env = os.environ.copy()
my_env['PATH'] = f'''/home/{my_env['USER']}/optimathsat/bin/:{my_env['PATH']}'''
for fzn in fzn_files:
translate_count += 1
fzn2smt2_transform_cmd = fzn2smt2_base_cmd + fzn_path + fzn \
+ ' --smt2 ' + smt2_path + fzn.replace('.', '-') + '.smt2'
print(f'''\r({translate_count}/{len(fzn_files)}) Translating {fzn_path + fzn} to {smt2_path + fzn.replace('.', '-')}.smt2''', end='')
try:
output = subprocess.check_output(fzn2smt2_transform_cmd, shell=True, env=my_env,
universal_newlines=True, stderr=subprocess.STDOUT)
except Exception as e:
output = str(e.output)
print(f'''\r{output}''', end='')
sys.stdout.flush()
optimathsat output/A004-dzn-smt2-fzn.smt2
#### Test with `smt2` from $Mz_1$
#### Test with `smt2` from $Mz_2$
### Adjust `smt2` Files According to Chapter 5.2 in Paper
Contrary to the `z3` version we're dropping the settings and the optimization function for OptiMathSAT `smt2` files, as those are set by the [OMT Python Timeout Wrapper](https://github.com/kw90/omt_python_timeout_wrapper).
- Add lower and upper bounds for the decision variable `pfc`
- Add number of cavities as comments for later solution extraction (workaround)
#### $Mz_1$
#### $Mz_2$
| 0.197135 | 0.586612 |
A friend of mine claimed on Facebook:
> It was recently suggested that the NBA finals were rigged, perhaps to increase television ratings. So I did a simple analysis - suppose each game is a coin flip and each team has a 50% chance of winning each game. What is the expected distribution for the lengths the finals will go and how does it compare with reality?
> A simple calculation reveals P(4) = 8/64, P(5) = 16/64, P(6) = 20/64 and P(7) = 20/64.
> How does this compare with history? Out of 67 series n(4) = 8, n(5) = 16, n(6) = 24 and n(7) = 19 so pretty damn close to the shitty coin flip model.
> TL:DR - a simple statistical model suggests the nba finals are not rigged
3 things:
1. I know nothing about basketball.
2. I don't think that anybody's rigging games.
3. Let's examine this claim closer.
```
%matplotlib inline
# Standard imports.
import numpy as np
import pylab
import scipy
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# Resize plots.
pylab.rcParams['figure.figsize'] = 8, 4
# Simulate 1000 series
game_lengths = []
for i in range(10000):
wins_a = 0
wins_b = 0
for j in range(7):
winning_team = np.random.rand() > .5
if winning_team:
wins_b += 1
else:
wins_a += 1
if wins_a >= 4 or wins_b >= 4:
break
game_lengths.append(j + 1)
continue
game_lengths = np.array(game_lengths)
plt.hist(game_lengths)
_ = plt.title('Game lengths under null hypothesis')
plt.xlabel('Game lengths')
print game_lengths.mean()
```
Indeed, the coin flip model predicts that the distribution of game weights will have a lot of bulk around 6 and 7 games. What about historical games?
```
game_lengths_historical = np.hstack(([4] * 8, [5] * 16, [6] * 24, [7] * 19))
plt.hist(game_lengths_historical)
_ = plt.title('Historical game lengths')
print game_lengths_historical.mean()
```
In fact, the historical game distribution indicates that the playoffs are slightly shorter than expected by chance. Does that mean that historical games haven't been rigged? Well, for one thing, you have to think about might cause game lengths to be shorter: blowouts. If one team is way better than the other, you would expect the series to be shorter than 7. In fact, the simulation with p = .5 represents the most extreme scenario, where every final is between two teams of exactly equal ability.
That is almost certainly never the case; consider the Boston Celtics winning streak of the 60's - they must have been much stronger than any other team! We can estimate the (implied) probability of winning from sports betting data. Sports betters have every incentive to produce calibrated predictions, because it directly impacts their bottom line.
I looked at the moneylines from 2004 - 2015:
http://www.oddsshark.com/nba/nba-finals-historical-series-odds-list
```
dfs = pd.read_html('http://www.oddsshark.com/nba/nba-finals-historical-series-odds-list')
df = dfs[0]
df.columns = pd.Index(['year', 'west', 'west_moneyline', 'east', 'east_moneyline'])
df
```
I had a quick read through of:
http://www.bettingexpert.com/how-to/convert-odds
To transform these values into odds. Let's see what we get:
```
def moneyline_to_odds(val):
if val < 0:
return -val / (-val + 100.0)
else:
return 100 / (val + 100.0)
mean_odds = (df.west_moneyline.map(moneyline_to_odds) -
df.east_moneyline.map(moneyline_to_odds)
+ 1) / 2.0
plt.hist(mean_odds, np.arange(21) / 20.0)
plt.title('Implied west conference winning odds')
```
This is clearly not a delta distribution around 0.5 - there are favorites and underdogs. Let's fit this function to a beta distribution by eyeballing (the distribution has no particular signifiance here - it's just a convenience.
```
# Remove the West conference bias by flipping the sign of the odds at random.
alphas = np.zeros(25)
for n in range(25):
flip_bits = np.random.rand(mean_odds.size) > .5
mean_odds_shuffled = mean_odds * flip_bits + (1 - flip_bits) * (1 - mean_odds)
alpha, beta, _, _ = scipy.stats.beta.fit(mean_odds_shuffled)
# Symmetrize the result to have a mean of .5
alphas[n] = ((alpha + beta)/2)
alpha = np.array(alphas).mean()
plt.hist(mean_odds_shuffled, np.arange(21) / 20.0)
x = np.arange(101) / 100.0
y = scipy.stats.beta.pdf(x, 1 + alpha, 1 + alpha) * 1.0
plt.plot(x, y, 'r-')
plt.legend(['observations', 'Fitted distribution'])
plt.title('Implied winning odds (east/west randomized)')
```
The fitted distribution is pretty broad -- but that's a distribution for the whole series of 6 games. If your win percentage for the whole series is 60%, what is it for a single game? Let's find out:
```
game_win_percentages = np.arange(.5, 1, .01)
series_win_percentages = np.zeros_like(game_win_percentages)
Nsims = 4000
for k, frac in enumerate(game_win_percentages):
wins = 0
for i in range(Nsims):
wins_a = 0
wins_b = 0
for j in range(7):
winning_team = np.random.rand() > frac
if winning_team:
wins_b += 1
else:
wins_a += 1
if wins_a == 4 or wins_b == 4:
break
wins += (wins_a == 4) * 1
series_win_percentages[k] = wins / float(Nsims)
def logit(p):
return np.log(p / (1 - p))
def logistic(x):
"""Returns the logistic of the numeric argument to the function."""
return 1 / (1 + np.exp(-x))
plt.plot(game_win_percentages, series_win_percentages)
# Fit a logistic function by eye balling.
plt.plot(game_win_percentages, logistic(2.3*logit(game_win_percentages)))
plt.xlabel('game win percentage')
plt.ylabel('series win percentage')
plt.legend(['empirical', 'curve fit'])
```
We see that a series amplifies the signal as to which team is best or not - if a team has 70% odds of winning per game, that means they have a 90% chance of winning the series! Let's run a simulation to see the distribution of game lengths under this more subtle model.
```
def inverse_map(y):
x = logistic(1 / 2.3 * logit(y))
return x
assert np.allclose(inverse_map(logistic(2.3*logit(game_win_percentages))),
game_win_percentages)
plt.hist(np.random.beta(alpha + 1, alpha + 1, 1000))
# Simulate 1000 series
game_lengths = []
for i in range(10000):
# Pick a per series win percentage
series_win_percentage = np.random.beta(alpha + 1, alpha + 1)
# Transform to a per-game win percentage
game_win_percentage = inverse_map(series_win_percentage)
wins_a = 0
wins_b = 0
for j in range(7):
winning_team = np.random.rand() > game_win_percentage
if winning_team:
wins_b += 1
else:
wins_a += 1
if wins_a >= 4 or wins_b >= 4:
break
game_lengths.append(j + 1)
continue
game_lengths = np.array(game_lengths)
plt.hist(game_lengths)
_ = plt.title('Game lengths under (more sophisticated) null hypothesis')
plt.xlabel('Game length')
game_lengths.mean()
```
There is some movement towards shorter series in this simulation - series are shorter than observed in reality by about one game per 6 years. This is significant, however:
```
m = game_lengths_historical.mean()
ci = game_lengths_historical.std() / np.sqrt(float(game_lengths_historical.size))
print "Simulated series length is %.2f" % game_lengths.mean()
print "95%% CI for observed series length is [%.2f, %.2f]" % (m - 1.96*ci, m + 1.96*ci)
```
That's not significant. Although 5.66 is on the low side of the distribution, decreasing the size of these error bars and declaring significance - and foul play! - would take decades!
There's other processes that might contribute to increasing the series length - the most likely of which is the home effect. To see this, recall that for the first 4 games, two games are played at one team's stadium, and 2 others are played at the other teams stadium. If you have two teams which are exactly even, but which win 70% of home games, it's more likely that you'll end up 2-2 at the end of the 4 games than without a home team advantage:
```
plt.subplot(121)
plt.hist(np.random.binomial(4, 0.5, size = (10000)), np.arange(6) - .5)
plt.title('Games won by team A\nno home team advantage')
plt.ylim([0, 4500])
plt.subplot(122)
plt.hist(np.random.binomial(2, 0.7, size = (10000)) +
np.random.binomial(2, 0.3, size = (10000)), np.arange(6) - .5)
plt.title('Games won by team A\nwith home team advantage')
plt.ylim([0, 4500])
```
[70% is much higher than the home team advantage we see these days](http://espn.go.com/nba/story/_/id/12241619/home-court-advantage-decline), but it will nevertheless make series longer. In any case, it would decades, with these methods, to measure any sort of foul play creating longer series; this is a job for investigative reporter, not a statistician!
|
github_jupyter
|
%matplotlib inline
# Standard imports.
import numpy as np
import pylab
import scipy
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# Resize plots.
pylab.rcParams['figure.figsize'] = 8, 4
# Simulate 1000 series
game_lengths = []
for i in range(10000):
wins_a = 0
wins_b = 0
for j in range(7):
winning_team = np.random.rand() > .5
if winning_team:
wins_b += 1
else:
wins_a += 1
if wins_a >= 4 or wins_b >= 4:
break
game_lengths.append(j + 1)
continue
game_lengths = np.array(game_lengths)
plt.hist(game_lengths)
_ = plt.title('Game lengths under null hypothesis')
plt.xlabel('Game lengths')
print game_lengths.mean()
game_lengths_historical = np.hstack(([4] * 8, [5] * 16, [6] * 24, [7] * 19))
plt.hist(game_lengths_historical)
_ = plt.title('Historical game lengths')
print game_lengths_historical.mean()
dfs = pd.read_html('http://www.oddsshark.com/nba/nba-finals-historical-series-odds-list')
df = dfs[0]
df.columns = pd.Index(['year', 'west', 'west_moneyline', 'east', 'east_moneyline'])
df
def moneyline_to_odds(val):
if val < 0:
return -val / (-val + 100.0)
else:
return 100 / (val + 100.0)
mean_odds = (df.west_moneyline.map(moneyline_to_odds) -
df.east_moneyline.map(moneyline_to_odds)
+ 1) / 2.0
plt.hist(mean_odds, np.arange(21) / 20.0)
plt.title('Implied west conference winning odds')
# Remove the West conference bias by flipping the sign of the odds at random.
alphas = np.zeros(25)
for n in range(25):
flip_bits = np.random.rand(mean_odds.size) > .5
mean_odds_shuffled = mean_odds * flip_bits + (1 - flip_bits) * (1 - mean_odds)
alpha, beta, _, _ = scipy.stats.beta.fit(mean_odds_shuffled)
# Symmetrize the result to have a mean of .5
alphas[n] = ((alpha + beta)/2)
alpha = np.array(alphas).mean()
plt.hist(mean_odds_shuffled, np.arange(21) / 20.0)
x = np.arange(101) / 100.0
y = scipy.stats.beta.pdf(x, 1 + alpha, 1 + alpha) * 1.0
plt.plot(x, y, 'r-')
plt.legend(['observations', 'Fitted distribution'])
plt.title('Implied winning odds (east/west randomized)')
game_win_percentages = np.arange(.5, 1, .01)
series_win_percentages = np.zeros_like(game_win_percentages)
Nsims = 4000
for k, frac in enumerate(game_win_percentages):
wins = 0
for i in range(Nsims):
wins_a = 0
wins_b = 0
for j in range(7):
winning_team = np.random.rand() > frac
if winning_team:
wins_b += 1
else:
wins_a += 1
if wins_a == 4 or wins_b == 4:
break
wins += (wins_a == 4) * 1
series_win_percentages[k] = wins / float(Nsims)
def logit(p):
return np.log(p / (1 - p))
def logistic(x):
"""Returns the logistic of the numeric argument to the function."""
return 1 / (1 + np.exp(-x))
plt.plot(game_win_percentages, series_win_percentages)
# Fit a logistic function by eye balling.
plt.plot(game_win_percentages, logistic(2.3*logit(game_win_percentages)))
plt.xlabel('game win percentage')
plt.ylabel('series win percentage')
plt.legend(['empirical', 'curve fit'])
def inverse_map(y):
x = logistic(1 / 2.3 * logit(y))
return x
assert np.allclose(inverse_map(logistic(2.3*logit(game_win_percentages))),
game_win_percentages)
plt.hist(np.random.beta(alpha + 1, alpha + 1, 1000))
# Simulate 1000 series
game_lengths = []
for i in range(10000):
# Pick a per series win percentage
series_win_percentage = np.random.beta(alpha + 1, alpha + 1)
# Transform to a per-game win percentage
game_win_percentage = inverse_map(series_win_percentage)
wins_a = 0
wins_b = 0
for j in range(7):
winning_team = np.random.rand() > game_win_percentage
if winning_team:
wins_b += 1
else:
wins_a += 1
if wins_a >= 4 or wins_b >= 4:
break
game_lengths.append(j + 1)
continue
game_lengths = np.array(game_lengths)
plt.hist(game_lengths)
_ = plt.title('Game lengths under (more sophisticated) null hypothesis')
plt.xlabel('Game length')
game_lengths.mean()
m = game_lengths_historical.mean()
ci = game_lengths_historical.std() / np.sqrt(float(game_lengths_historical.size))
print "Simulated series length is %.2f" % game_lengths.mean()
print "95%% CI for observed series length is [%.2f, %.2f]" % (m - 1.96*ci, m + 1.96*ci)
plt.subplot(121)
plt.hist(np.random.binomial(4, 0.5, size = (10000)), np.arange(6) - .5)
plt.title('Games won by team A\nno home team advantage')
plt.ylim([0, 4500])
plt.subplot(122)
plt.hist(np.random.binomial(2, 0.7, size = (10000)) +
np.random.binomial(2, 0.3, size = (10000)), np.arange(6) - .5)
plt.title('Games won by team A\nwith home team advantage')
plt.ylim([0, 4500])
| 0.66061 | 0.972623 |
```
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import seaborn as sns
tf.__version__
```
# Attention in practice
## Transformers - scaled dot product self-attention
<br><br>
$$\Large Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$$
<br><br>
where:
* $Q$ is a **query** matrix $\in \mathbb{R}^{L_Q \times D}$
<br><br>
* $K$ is a **key** matrix $\in \mathbb{R}^{L_K \times D}$
<br><br>
* $D$ is the embedding dimensionality
<br><br>
Let's stop here for a while and contemplate this sub-equation:
<br><br>
$$\Large W_A = softmax(QK^T)$$
where $W_A \in \mathbb{R}^{L_Q \times L_K}$
<br><br><br><br>
Now, let's add the $V$ matrix:
<br><br>
$$\Large Attention(Q, K, V) = softmax(QK^T)V$$
<br><br>
* $V$ is a **value** matrix $\in \mathbb{R}^{L_K \times D}$
...and is in fact pretty often the same matrix as $K$
<br><br>
Let's try to make sense out of this:
<br><br>
<img src='content/att_2.jpg' width=700>
<br><br>
You can also think about attention as a **soft dictionary** object:
<br><br>
<img src="https://cdn-ak.f.st-hatena.com/images/fotolife/e/ey_nosukeru/20190622/20190622045649.png" width=600>
<br><br>
<br><br>
<br><br>
<br><br>
We're still missing one element. Let's get back to the full formula:
$$\Large Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$$
<br><br>
* $\sqrt{d_k}$ is the embedding dimensinality.
<br><br>
<br><br>
"*We suspect that for large values of $d_k$, the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients.*"
Vaswani et al., 2017
<br><br>
<br><br>
### Going multihead
<br><br>
<img src='content/multi.jpg' width=400>
<br><br>
$$\Large Multihead(Q, K, V) = Concat(h_i, ..., h_m)W^O$$
<br><br>
where:
$$\Large h_i = Attention(QW^Q_i, KW^K_i, VW^V_i)$$
<br><br>
<img src="https://jalammar.github.io/images/t/transformer_multi-headed_self-attention-recap.png" width=700>
<p style="text-align: center; font-size: 10px">Source: <a herf="https://jalammar.github.io">https://jalammar.github.io</a></p>
## Transformer encoder with MHA from scratch
The code in this notebook is heavily based on Trung Tran's implementation and blog post that can be found here:
https://trungtran.io/2019/04/29/create-the-transformer-with-tensorflow-2-0/
A full transformer model consists of an **encoder** and a **decoder**:
<img src="https://www.researchgate.net/publication/323904682/figure/fig1/AS:606458626465792@1521602412057/The-Transformer-model-architecture_W640.jpg" width=350>
<br><br>
Today, we're going to focus on the **encoder** part only:
<img src="https://www.researchgate.net/publication/334288604/figure/fig1/AS:778232232148992@1562556431066/The-Transformer-encoder-structure_W640.jpg" width=200>
### Positional embeddings
<br><br>
$$ \Large PE_{pos, 2i} = sin(\frac{pos}{10000^{2i/d}})$$
<br><br>
$$ \Large PE_{pos, 2i+1} = cos(\frac{pos}{10000^{2i/d}})$$
```
def positional_embedding(pos, model_size):
pos_emb = np.zeros((1, model_size))
for i in range(model_size):
if i % 2 == 0:
pos_emb[:, i] = np.sin(pos / 10000 ** (i / model_size))
else:
pos_emb[:, i] = np.cos(pos / 10000 ** ((i - 1) / model_size))
return pos_emb
max_len = 1024
MODEL_SIZE = 128
pes = []
for i in range(max_len):
pes.append(positional_embedding(i, MODEL_SIZE))
pes = np.concatenate(pes, axis=0)
pes = tf.constant(pes, dtype=tf.float32)
plt.figure(figsize=(15, 6))
sns.heatmap(pes.numpy().T)
plt.xlabel('Position')
plt.ylabel('Dimension')
plt.show()
```
### Multihead attention
```
class MultiHeadAttention(tf.keras.Model):
def __init__(self, model_size, h):
"""
model_size: internal embedding dimensionality
h: # of heads
"""
super(MultiHeadAttention, self).__init__()
self.query_size = model_size // h
self.key_size = model_size // h
self.value_size = model_size // h
self.h = h
self.wq = [tf.keras.layers.Dense(self.query_size) for _ in range(h)]
self.wk = [tf.keras.layers.Dense(self.key_size) for _ in range(h)]
self.wv = [tf.keras.layers.Dense(self.value_size) for _ in range(h)]
self.wo = tf.keras.layers.Dense(model_size)
def call(self, query, value):
# query has shape (batch, query_len, model_size)
# value has shape (batch, value_len, model_size)
heads = []
for i in range(self.h):
score = tf.matmul(self.wq[i](query), self.wk[i](value), transpose_b=True)
# Here we scale the score as described in the paper
score /= tf.math.sqrt(tf.dtypes.cast(self.key_size, tf.float32))
# score has shape (batch, query_len, value_len)
alignment = tf.nn.softmax(score, axis=2)
# alignment has shape (batch, query_len, value_len)
head = tf.matmul(alignment, self.wv[i](value))
# head has shape (batch, decoder_len, value_size)
heads.append(head)
# Concatenate all the attention heads
# so that the last dimension summed up to model_size
heads = tf.concat(heads, axis=2)
heads = self.wo(heads)
# heads has shape (batch, query_len, model_size)
return heads
mha = MultiHeadAttention(model_size=8, h=4)
k = np.array(
[
[
[1, 2, 3, 4, 1, 2, 3, 7],
np.random.randn(8)
]
]
)
att = mha(k, k)
print(k.shape, att.shape)
att
```
### Encoder
```
class Encoder(tf.keras.Model):
def __init__(self, vocab_size, model_size, num_layers, h):
super(Encoder, self).__init__()
self.model_size = model_size
self.num_layers = num_layers
self.h = h
# One Embedding layer
self.embedding = tf.keras.layers.Embedding(vocab_size, model_size)
# num_layers Multi-Head Attention and Normalization layers
self.attention = [MultiHeadAttention(model_size, h) for _ in range(num_layers)]
self.attention_norm = [tf.keras.layers.BatchNormalization() for _ in range(num_layers)]
# num_layers FFN and Normalization layers
self.dense_1 = [tf.keras.layers.Dense(model_size * 4, activation='relu') for _ in range(num_layers)]
self.dense_2 = [tf.keras.layers.Dense(model_size) for _ in range(num_layers)]
self.ffn_norm = [tf.keras.layers.BatchNormalization() for _ in range(num_layers)]
def call(self, sequence):
sub_in = []
for i in range(sequence.shape[1]):
# Compute the embedded vector
embed = self.embedding(tf.expand_dims(sequence[:, i], axis=1))
# Add positional encoding to the embedded vector
sub_in.append(embed + pes[i, :])
# Concatenate the result so that the shape is (batch_size, length, model_size)
sub_in = tf.concat(sub_in, axis=1)
# We will have num_layers of (Attention + FFN)
for i in range(self.num_layers):
sub_out = []
# Iterate along the sequence length
for j in range(sub_in.shape[1]):
# Compute the context vector towards the whole sequence
attention = self.attention[i](
tf.expand_dims(sub_in[:, j, :], axis=1), sub_in)
sub_out.append(attention)
# Concatenate the result to have shape (batch_size, length, model_size)
sub_out = tf.concat(sub_out, axis=1)
# Residual connection
sub_out = sub_in + sub_out
# Normalize the output
sub_out = self.attention_norm[i](sub_out)
# The FFN input is the output of the Multi-Head Attention
ffn_in = sub_out
ffn_out = self.dense_2[i](self.dense_1[i](ffn_in))
# Add the residual connection
ffn_out = ffn_in + ffn_out
# Normalize the output
ffn_out = self.ffn_norm[i](ffn_out)
# Assign the FFN output to the next layer's Multi-Head Attention input
sub_in = ffn_out
# Return the result when done
return ffn_out
```
|
github_jupyter
|
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import seaborn as sns
tf.__version__
def positional_embedding(pos, model_size):
pos_emb = np.zeros((1, model_size))
for i in range(model_size):
if i % 2 == 0:
pos_emb[:, i] = np.sin(pos / 10000 ** (i / model_size))
else:
pos_emb[:, i] = np.cos(pos / 10000 ** ((i - 1) / model_size))
return pos_emb
max_len = 1024
MODEL_SIZE = 128
pes = []
for i in range(max_len):
pes.append(positional_embedding(i, MODEL_SIZE))
pes = np.concatenate(pes, axis=0)
pes = tf.constant(pes, dtype=tf.float32)
plt.figure(figsize=(15, 6))
sns.heatmap(pes.numpy().T)
plt.xlabel('Position')
plt.ylabel('Dimension')
plt.show()
class MultiHeadAttention(tf.keras.Model):
def __init__(self, model_size, h):
"""
model_size: internal embedding dimensionality
h: # of heads
"""
super(MultiHeadAttention, self).__init__()
self.query_size = model_size // h
self.key_size = model_size // h
self.value_size = model_size // h
self.h = h
self.wq = [tf.keras.layers.Dense(self.query_size) for _ in range(h)]
self.wk = [tf.keras.layers.Dense(self.key_size) for _ in range(h)]
self.wv = [tf.keras.layers.Dense(self.value_size) for _ in range(h)]
self.wo = tf.keras.layers.Dense(model_size)
def call(self, query, value):
# query has shape (batch, query_len, model_size)
# value has shape (batch, value_len, model_size)
heads = []
for i in range(self.h):
score = tf.matmul(self.wq[i](query), self.wk[i](value), transpose_b=True)
# Here we scale the score as described in the paper
score /= tf.math.sqrt(tf.dtypes.cast(self.key_size, tf.float32))
# score has shape (batch, query_len, value_len)
alignment = tf.nn.softmax(score, axis=2)
# alignment has shape (batch, query_len, value_len)
head = tf.matmul(alignment, self.wv[i](value))
# head has shape (batch, decoder_len, value_size)
heads.append(head)
# Concatenate all the attention heads
# so that the last dimension summed up to model_size
heads = tf.concat(heads, axis=2)
heads = self.wo(heads)
# heads has shape (batch, query_len, model_size)
return heads
mha = MultiHeadAttention(model_size=8, h=4)
k = np.array(
[
[
[1, 2, 3, 4, 1, 2, 3, 7],
np.random.randn(8)
]
]
)
att = mha(k, k)
print(k.shape, att.shape)
att
class Encoder(tf.keras.Model):
def __init__(self, vocab_size, model_size, num_layers, h):
super(Encoder, self).__init__()
self.model_size = model_size
self.num_layers = num_layers
self.h = h
# One Embedding layer
self.embedding = tf.keras.layers.Embedding(vocab_size, model_size)
# num_layers Multi-Head Attention and Normalization layers
self.attention = [MultiHeadAttention(model_size, h) for _ in range(num_layers)]
self.attention_norm = [tf.keras.layers.BatchNormalization() for _ in range(num_layers)]
# num_layers FFN and Normalization layers
self.dense_1 = [tf.keras.layers.Dense(model_size * 4, activation='relu') for _ in range(num_layers)]
self.dense_2 = [tf.keras.layers.Dense(model_size) for _ in range(num_layers)]
self.ffn_norm = [tf.keras.layers.BatchNormalization() for _ in range(num_layers)]
def call(self, sequence):
sub_in = []
for i in range(sequence.shape[1]):
# Compute the embedded vector
embed = self.embedding(tf.expand_dims(sequence[:, i], axis=1))
# Add positional encoding to the embedded vector
sub_in.append(embed + pes[i, :])
# Concatenate the result so that the shape is (batch_size, length, model_size)
sub_in = tf.concat(sub_in, axis=1)
# We will have num_layers of (Attention + FFN)
for i in range(self.num_layers):
sub_out = []
# Iterate along the sequence length
for j in range(sub_in.shape[1]):
# Compute the context vector towards the whole sequence
attention = self.attention[i](
tf.expand_dims(sub_in[:, j, :], axis=1), sub_in)
sub_out.append(attention)
# Concatenate the result to have shape (batch_size, length, model_size)
sub_out = tf.concat(sub_out, axis=1)
# Residual connection
sub_out = sub_in + sub_out
# Normalize the output
sub_out = self.attention_norm[i](sub_out)
# The FFN input is the output of the Multi-Head Attention
ffn_in = sub_out
ffn_out = self.dense_2[i](self.dense_1[i](ffn_in))
# Add the residual connection
ffn_out = ffn_in + ffn_out
# Normalize the output
ffn_out = self.ffn_norm[i](ffn_out)
# Assign the FFN output to the next layer's Multi-Head Attention input
sub_in = ffn_out
# Return the result when done
return ffn_out
| 0.758779 | 0.925836 |
# "Prezzi e rendimenti con Pandas"
> "Integrare direttamente in un post un notebook di Jupyter"
- toc: false
- branch: master
- badges: true
- comments: true
- categories: [jupyter, pandas, finanza]
- image: images/2021-06-23-prezzi-e-rendimenti-con-pandas.png
- hide: false
[fastpages](https://fastpages.fast.ai/), la piattaforma sulla quale è costruito questo blog, permette di integrare direttamente dei *notebook* di `Jupyter` nei *post*. Per provare questa funzionalità, costruiamo un breve *notebook* su come gestire prezzi e rendimenti delle azioni con `Pandas`, in alternativa a Excel. In questo modo, potremo osservare in azione alcuni degli strumenti che ho descritto in un mio [post](https://marcobonifacio.github.io/blog/python/finanza/2021/05/05/python-per-la-finanza.html) precedente.
```
#collapse
import pandas as pd
import altair as alt
import yfinance as yf
```
Scarichiamo da Yahoo! Finance i prezzi di quattro azioni statunitensi, identificate attraverso i loro *ticker*: **Apple** (AAPL), **Microsoft** (MSFT), **McDonald's** (MCD) e **Coca-Cola** (KO). Due azioni della *new economy* e due della *old*, come si diceva qualche anno fa.
```
#collapse
tickers = 'AAPL MSFT MCD KO'
data = yf.download(tickers=tickers, period='2y')
```
A questo punto, eliminiamo dal database che abbiamo costruito i prezzi *open*, *high*, *low* e il volume negoziato per tenerci solo i prezzi di chiusura, rettificati dei dividendi eventualmente distribuiti e delle *corporate action*. Vediamo le prime righe del *database* dei prezzi.
```
#collapse
prices = data.xs('Adj Close', axis=1, level=0)
prices.tail()
```
Possiamo fare un primo grafico dell'andamento dei prezzi delle quattro azioni negli ultimi due anni, utilizzando `Altair`, una libreria che permette di produrre grafici interattivi.
```
#collapse
alt.Chart(
prices.reset_index().melt(
'Date',
var_name='Stock',
value_name='Price'
)
).mark_line().encode(
x='Date:T',
y='Price:Q',
color='Stock:N',
tooltip=['Stock', 'Price']
).properties(
title='Andamento prezzi negli ultimi due anni'
).interactive()
```
Per avere la possibilità di confrontare i quattro grafici, ribasiamo i dati facendo partire gli andamenti da quota 100.
```
#collapse
rebased_prices = prices.div(prices.iloc[0, :]).mul(100)
alt.Chart(
rebased_prices.reset_index().melt(
'Date',
var_name='Stock',
value_name='Price'
)
).mark_line().encode(
x='Date:T',
y='Price:Q',
color='Stock:N',
tooltip=['Stock', 'Price']
).properties(
title='Andamento prezzi ribasati negli ultimi due anni'
).interactive()
```
Passiamo ora ai rendimenti e calcoliamo i rendimenti mensili delle quattro azioni.
```
#collapse
monthly_returns = prices.resample('M').last().pct_change()
```
Possiamo fare un grafico a barre dei rendimenti appena calcolati, divisi per mese.
```
#collapse
alt.Chart(
monthly_returns.reset_index().melt(
'Date',
var_name='Stock',
value_name='Return'
)
).mark_bar().encode(
y='Stock:N',
x='Return:Q',
color='Stock:N',
row='Date:T',
tooltip=['Stock', 'Return']
).properties(
title='Rendimenti percentuali per mese'
).interactive()
```
Oppure lo stesso grafico raggruppato per titolo, dove notiamo come **Apple** sia stato il titolo più volatile negli ultimi due anni, ma **Coca-Cola** e **McDonald's** abbiano avuto i maggiori *drawdown*.
```
#collapse
alt.Chart(
monthly_returns.reset_index().melt(
'Date',
var_name='Stock',
value_name='Return'
)
).mark_bar().encode(
x='Date:T',
y='Return:Q',
color='Stock:N',
row='Stock:N',
tooltip=['Stock', 'Return']
).properties(
title='Rendimenti percentuali per mese'
).interactive()
```
Ci fermiamo qui con questo post di prova, che mostra le potenzialità di analisi esplorativa di Pandas, in grado in poche righe di codice di scaricare, elaborare e visualizzare serie storiche di dati con grande facilità.
|
github_jupyter
|
#collapse
import pandas as pd
import altair as alt
import yfinance as yf
#collapse
tickers = 'AAPL MSFT MCD KO'
data = yf.download(tickers=tickers, period='2y')
#collapse
prices = data.xs('Adj Close', axis=1, level=0)
prices.tail()
#collapse
alt.Chart(
prices.reset_index().melt(
'Date',
var_name='Stock',
value_name='Price'
)
).mark_line().encode(
x='Date:T',
y='Price:Q',
color='Stock:N',
tooltip=['Stock', 'Price']
).properties(
title='Andamento prezzi negli ultimi due anni'
).interactive()
#collapse
rebased_prices = prices.div(prices.iloc[0, :]).mul(100)
alt.Chart(
rebased_prices.reset_index().melt(
'Date',
var_name='Stock',
value_name='Price'
)
).mark_line().encode(
x='Date:T',
y='Price:Q',
color='Stock:N',
tooltip=['Stock', 'Price']
).properties(
title='Andamento prezzi ribasati negli ultimi due anni'
).interactive()
#collapse
monthly_returns = prices.resample('M').last().pct_change()
#collapse
alt.Chart(
monthly_returns.reset_index().melt(
'Date',
var_name='Stock',
value_name='Return'
)
).mark_bar().encode(
y='Stock:N',
x='Return:Q',
color='Stock:N',
row='Date:T',
tooltip=['Stock', 'Return']
).properties(
title='Rendimenti percentuali per mese'
).interactive()
#collapse
alt.Chart(
monthly_returns.reset_index().melt(
'Date',
var_name='Stock',
value_name='Return'
)
).mark_bar().encode(
x='Date:T',
y='Return:Q',
color='Stock:N',
row='Stock:N',
tooltip=['Stock', 'Return']
).properties(
title='Rendimenti percentuali per mese'
).interactive()
| 0.338842 | 0.805173 |
# Data Curation - Investigation of Wikipedia Traffic
In this notebook, we will construct and analyze a dataset of monthly traffic on English Wikipedia from January 1 2008 through August 30 2021.
```
import json
import requests
import pandas as pd
from functools import reduce
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import numpy as np
```
## Data Acquisition
In this portion, we will utilize the Wikimedia Foundations REST API in order to extract view count data of wikipedia across multiple access site types (desktop, app-web, app-mobile).
```
# Set endpoints without parameters
endpoint_legacy = 'https://wikimedia.org/api/rest_v1/metrics/legacy/pagecounts/aggregate/{project}/{access-site}/{granularity}/{start}/{end}'
endpoint_pageviews = 'https://wikimedia.org/api/rest_v1/metrics/pageviews/aggregate/{project}/{access}/{agent}/{granularity}/{start}/{end}'
# Set header with personal github account, email
headers = {
'User-Agent': 'https://github.com/TrevorNims',
'From': '[email protected]'
}
# Define helper functions to specify parameters for each of the two types of endpoints.
# Each function allows for a single parameter to specify the type of access-site.
def set_legacy_access_site(access_site):
params = {"project" : "en.wikipedia.org",
"access-site" : access_site,
"granularity" : "monthly",
"start" : "2008010100",
"end" : "2021090100"
}
return params
def set_pageviews_access_site(access_site):
params = {"project" : "en.wikipedia.org",
"access" : access_site,
# filter out web crawlers
"agent" : "user",
"granularity" : "monthly",
"start" : "2008010100",
"end" : '2021090100'
}
return params
# Define function that calls wikimedia api, takes an unformatted endpoint string and
# an endpoint parameter dictionary as parameters and returns the response of the api
# call
def api_call(endpoint, parameters):
call = requests.get(endpoint.format(**parameters), headers=headers)
response = call.json()
return response
# Set parameters for the two types of access-sites for the legacy endpoint
legacy_desktop_params = set_legacy_access_site('desktop-site')
legacy_mobile_params = set_legacy_access_site('mobile-site')
# Set parameters for the three types of access-sites for the pageviews endpoint
pageviews_desktop_params = set_pageviews_access_site('desktop')
pageviews_mobile_web_params = set_pageviews_access_site('mobile-web')
pageviews_mobile_app_params = set_pageviews_access_site('mobile-app')
# Create lists of the endpoint parameters, their respective unformatted endpoints,
# and their json filenames
all_params = [legacy_desktop_params, legacy_mobile_params, pageviews_desktop_params,
pageviews_mobile_web_params, pageviews_mobile_app_params]
all_endpoints = [endpoint_legacy, endpoint_legacy, endpoint_pageviews,
endpoint_pageviews, endpoint_pageviews]
all_filenames = ['pagecounts_desktop-site_200801-202108.json', 'pagecounts_mobile-site_200801-202108.json',
'pageviews_desktop_200801-202108.json', 'pageviews_mobile-web_200801-202108.json',
'pageviews_mobile-app_200801-202108.json']
# Make an api call for each endpoint parameter dictionary and save the
# results in a json file with the matching filename.
for endpoint, params, filename in zip(all_endpoints, all_params, all_filenames):
data = api_call(endpoint, params)
# remove singular json parent wrapper provided by api
data = data['items']
with open('data/' + filename, 'w') as json_file:
json.dump(data, json_file)
```
## Data Processing
We have now saved a dataset for each type of access-site (5 in all) in the json format, and can continue with data cleaning. This will consist of aggregating the .json files produced earlier into a single pandas dataframe that contains view counts over time for each of the access sites.
```
# Create column name list for distinction between view counts
count_column_name_list = ['pagecount_desktop_views', 'pagecount_mobile_views', 'pageview_desktop_views',
'pageview_mobile-web_views', 'pageview_mobile-app_views']
# Instantiate list to hold each individual dataframe prior to merge
df_merge_list = []
for i, filename in enumerate(all_filenames):
# Read in data into a pandas dataframe, ensuring that pandas
# does not try to auto-convert the timestamp (will result in incorrect dates)
df = pd.read_json('data/' + filename, convert_dates=False)
# Specify whether the view count column is labeled 'count' or 'views', this depends
# on the ordering of 'all_filenames'
keyword = 'count'
if i > 1:
keyword = 'views'
# re-arrange timestamp to match desired format
years = df['timestamp'].apply(lambda x: str(x)[0:4])
months = df['timestamp'].apply(lambda x: str(x)[4:6])
df['year'] = years
df['month'] = months
df = df[['year', 'month', keyword]]
# re-label view count column
column_name = count_column_name_list[i]
df = df.rename(columns={keyword : column_name})
df_merge_list.append(df)
# Merge all dataframes in 'df_merge_list', filling NaN values with 0
df_merged = reduce(lambda left,right: pd.merge(left, right, how='outer'), df_merge_list).fillna(0)
# Manipulate 'df_merged' to calculate derived columns, combine pageview app view counts into single column
df_merged['pagecount_all_views'] = df_merged['pagecount_desktop_views'] + df_merged['pagecount_mobile_views']
df_merged['pageview_mobile_views'] = df_merged['pageview_mobile-web_views'] + df_merged['pageview_mobile-app_views']
df_merged = df_merged.drop(columns=['pageview_mobile-web_views', 'pageview_mobile-app_views'], axis = 1)
df_merged['pageview_all_views'] = df_merged['pageview_desktop_views'] + df_merged['pageview_mobile_views']
# Save dataframe to csv file
df_merged.to_csv('data/en-wikipedia_traffic_200801-202108.csv')
```
## Data Analysis
Now we will create a graph of the data to visually analyze traffic trends, aggregating the view count data into three columns: Mobile Traffic, Desktop Traffic, and All Traffic.
```
# Create new column 'date' as a datetime representation of 'year' and 'month' columns
df_merged['date'] = df_merged['month'] + '-' + df_merged['year']
df_merged['date'] = pd.to_datetime(df_merged['date'], format='%m-%Y')
# Create list of columns that will be created for the final visualization
traffic_display_names = ['Mobile Traffic', 'Desktop Traffic', 'All Traffic']
# Create the final columns
df_merged[traffic_display_names[0]] = df_merged['pagecount_mobile_views'] + df_merged['pageview_mobile_views']
df_merged[traffic_display_names[1]] = df_merged['pagecount_desktop_views'] + df_merged['pageview_desktop_views']
df_merged[traffic_display_names[2]] = df_merged['Desktop Traffic'] + df_merged['Mobile Traffic']
# Replace zero values with NaN to prevent them from being plotted
df_merged.replace(0, np.NaN, inplace=True)
# Create plot, save figure
fig, ax = plt.subplots(figsize=(16, 10))
colors = ['b', 'r', 'k']
for i, col_name in enumerate(traffic_display_names):
ax.plot(df_merged['date'], df_merged[col_name], color=colors[i])
ax.set(xlabel="Date", ylabel='Number of Views',
title='Wikipedia Traffic by Month\n 2008-2021')
ax.legend(traffic_display_names)
# Format the x axis to show years only
ax.xaxis.set_major_locator(mdates.YearLocator())
ax.xaxis.set_major_formatter(mdates.DateFormatter("%Y"))
plt.savefig('visualizations/Wikipedia_Traffic_By_Month.png', facecolor ='w', edgecolor ='w')
plt.show()
```
As can be seen above, traffic was originally confined solely to desktop views. However, in late 2014, mobile access was initiated, with a huge spike in traffic seen soon after its advent.
|
github_jupyter
|
import json
import requests
import pandas as pd
from functools import reduce
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import numpy as np
# Set endpoints without parameters
endpoint_legacy = 'https://wikimedia.org/api/rest_v1/metrics/legacy/pagecounts/aggregate/{project}/{access-site}/{granularity}/{start}/{end}'
endpoint_pageviews = 'https://wikimedia.org/api/rest_v1/metrics/pageviews/aggregate/{project}/{access}/{agent}/{granularity}/{start}/{end}'
# Set header with personal github account, email
headers = {
'User-Agent': 'https://github.com/TrevorNims',
'From': '[email protected]'
}
# Define helper functions to specify parameters for each of the two types of endpoints.
# Each function allows for a single parameter to specify the type of access-site.
def set_legacy_access_site(access_site):
params = {"project" : "en.wikipedia.org",
"access-site" : access_site,
"granularity" : "monthly",
"start" : "2008010100",
"end" : "2021090100"
}
return params
def set_pageviews_access_site(access_site):
params = {"project" : "en.wikipedia.org",
"access" : access_site,
# filter out web crawlers
"agent" : "user",
"granularity" : "monthly",
"start" : "2008010100",
"end" : '2021090100'
}
return params
# Define function that calls wikimedia api, takes an unformatted endpoint string and
# an endpoint parameter dictionary as parameters and returns the response of the api
# call
def api_call(endpoint, parameters):
call = requests.get(endpoint.format(**parameters), headers=headers)
response = call.json()
return response
# Set parameters for the two types of access-sites for the legacy endpoint
legacy_desktop_params = set_legacy_access_site('desktop-site')
legacy_mobile_params = set_legacy_access_site('mobile-site')
# Set parameters for the three types of access-sites for the pageviews endpoint
pageviews_desktop_params = set_pageviews_access_site('desktop')
pageviews_mobile_web_params = set_pageviews_access_site('mobile-web')
pageviews_mobile_app_params = set_pageviews_access_site('mobile-app')
# Create lists of the endpoint parameters, their respective unformatted endpoints,
# and their json filenames
all_params = [legacy_desktop_params, legacy_mobile_params, pageviews_desktop_params,
pageviews_mobile_web_params, pageviews_mobile_app_params]
all_endpoints = [endpoint_legacy, endpoint_legacy, endpoint_pageviews,
endpoint_pageviews, endpoint_pageviews]
all_filenames = ['pagecounts_desktop-site_200801-202108.json', 'pagecounts_mobile-site_200801-202108.json',
'pageviews_desktop_200801-202108.json', 'pageviews_mobile-web_200801-202108.json',
'pageviews_mobile-app_200801-202108.json']
# Make an api call for each endpoint parameter dictionary and save the
# results in a json file with the matching filename.
for endpoint, params, filename in zip(all_endpoints, all_params, all_filenames):
data = api_call(endpoint, params)
# remove singular json parent wrapper provided by api
data = data['items']
with open('data/' + filename, 'w') as json_file:
json.dump(data, json_file)
# Create column name list for distinction between view counts
count_column_name_list = ['pagecount_desktop_views', 'pagecount_mobile_views', 'pageview_desktop_views',
'pageview_mobile-web_views', 'pageview_mobile-app_views']
# Instantiate list to hold each individual dataframe prior to merge
df_merge_list = []
for i, filename in enumerate(all_filenames):
# Read in data into a pandas dataframe, ensuring that pandas
# does not try to auto-convert the timestamp (will result in incorrect dates)
df = pd.read_json('data/' + filename, convert_dates=False)
# Specify whether the view count column is labeled 'count' or 'views', this depends
# on the ordering of 'all_filenames'
keyword = 'count'
if i > 1:
keyword = 'views'
# re-arrange timestamp to match desired format
years = df['timestamp'].apply(lambda x: str(x)[0:4])
months = df['timestamp'].apply(lambda x: str(x)[4:6])
df['year'] = years
df['month'] = months
df = df[['year', 'month', keyword]]
# re-label view count column
column_name = count_column_name_list[i]
df = df.rename(columns={keyword : column_name})
df_merge_list.append(df)
# Merge all dataframes in 'df_merge_list', filling NaN values with 0
df_merged = reduce(lambda left,right: pd.merge(left, right, how='outer'), df_merge_list).fillna(0)
# Manipulate 'df_merged' to calculate derived columns, combine pageview app view counts into single column
df_merged['pagecount_all_views'] = df_merged['pagecount_desktop_views'] + df_merged['pagecount_mobile_views']
df_merged['pageview_mobile_views'] = df_merged['pageview_mobile-web_views'] + df_merged['pageview_mobile-app_views']
df_merged = df_merged.drop(columns=['pageview_mobile-web_views', 'pageview_mobile-app_views'], axis = 1)
df_merged['pageview_all_views'] = df_merged['pageview_desktop_views'] + df_merged['pageview_mobile_views']
# Save dataframe to csv file
df_merged.to_csv('data/en-wikipedia_traffic_200801-202108.csv')
# Create new column 'date' as a datetime representation of 'year' and 'month' columns
df_merged['date'] = df_merged['month'] + '-' + df_merged['year']
df_merged['date'] = pd.to_datetime(df_merged['date'], format='%m-%Y')
# Create list of columns that will be created for the final visualization
traffic_display_names = ['Mobile Traffic', 'Desktop Traffic', 'All Traffic']
# Create the final columns
df_merged[traffic_display_names[0]] = df_merged['pagecount_mobile_views'] + df_merged['pageview_mobile_views']
df_merged[traffic_display_names[1]] = df_merged['pagecount_desktop_views'] + df_merged['pageview_desktop_views']
df_merged[traffic_display_names[2]] = df_merged['Desktop Traffic'] + df_merged['Mobile Traffic']
# Replace zero values with NaN to prevent them from being plotted
df_merged.replace(0, np.NaN, inplace=True)
# Create plot, save figure
fig, ax = plt.subplots(figsize=(16, 10))
colors = ['b', 'r', 'k']
for i, col_name in enumerate(traffic_display_names):
ax.plot(df_merged['date'], df_merged[col_name], color=colors[i])
ax.set(xlabel="Date", ylabel='Number of Views',
title='Wikipedia Traffic by Month\n 2008-2021')
ax.legend(traffic_display_names)
# Format the x axis to show years only
ax.xaxis.set_major_locator(mdates.YearLocator())
ax.xaxis.set_major_formatter(mdates.DateFormatter("%Y"))
plt.savefig('visualizations/Wikipedia_Traffic_By_Month.png', facecolor ='w', edgecolor ='w')
plt.show()
| 0.575349 | 0.839931 |
# Laboratorio 8
```
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import plot_confusion_matrix
%matplotlib inline
digits_X, digits_y = datasets.load_digits(return_X_y=True, as_frame=True)
digits = pd.concat([digits_X, digits_y], axis=1)
digits.head()
```
## Ejercicio 1
(1 pto.)
Utilizando todos los datos, ajusta un modelo de regresión logística a los datos de dígitos. No agregues intercepto y define un máximo de iteraciones de 400.
Obtén el _score_ y explica el tan buen resultado.
```
logistic = LogisticRegression(fit_intercept= False , max_iter = 400)
logistic.fit(digits_X, digits_y)
print(f"El score del modelo de regresión logística es {logistic.score(digits_X, digits_y)}")
```
__Respuesta:__ El score devuelve la precisión media entre las etiquetas y los datos de prueba. Como en este ejercicio se esta utilizando los dato de prueba iguales a los valores de la etiqueta, entonces es de esperar que tengamos un resultado muy bueno.
## Ejercicio 2
(1 pto.)
Utilizando todos los datos, ¿Cuál es la mejor elección del parámetro $k$ al ajustar un modelo kNN a los datos de dígitos? Utiliza valores $k=2, ..., 10$.
```
for k in range(2,11):
neigh = KNeighborsClassifier(n_neighbors=k)
neigh.fit(digits_X, digits_y)
print(f"El score del modelo de kNN con k={k} es {neigh.score(digits_X, digits_y)}")
```
__Respuesta:__ La mejor elección del parámetro __k__ es 3.
## Ejercicio 3
(1 pto.)
Grafica la matriz de confusión normalizada por predicción de ambos modelos (regresión logística y kNN con la mejor elección de $k$).
¿Qué conclusión puedes sacar?
Hint: Revisa el argumento `normalize` de la matriz de confusión.
```
plot_confusion_matrix(logistic, digits_X, digits_y, normalize = 'pred');
best_knn = KNeighborsClassifier(n_neighbors=3)
best_knn.fit(digits_X, digits_y)
plot_confusion_matrix(best_knn, digits_X, digits_y, normalize = 'pred');
```
__Respuesta:__ Podemos concluir que el modelo de regreción lineal nos entrega una mejor predicción que el modelo de kNN. En este ejemplo pudimos ver que mientras que el modelo de regreción lineal acerto en todos los valores, el modelo de kNN fallo levemente en la predicción de los números 1, 3, 4, 6, 8, 9.
## Ejercicio 4
(1 pto.)
Escoge algún registro donde kNN se haya equivocado, _plotea_ la imagen y comenta las razones por las que el algoritmo se pudo haber equivocado.
```
i_test = 29
```
El valor real del registro seleccionado es
```
i = 9
neigh.predict(digits_X.iloc[[i_test], :])
```
Mentras que la predicción dada por kNN es
```
neigh.predict_proba(digits_X.iloc[[i_test], :])
```
A continuación la imagen
```
plt.imshow(digits_X.loc[[i], :].to_numpy().reshape(8, 8), cmap=plt.cm.gray_r, interpolation='nearest');
```
__Respuesta:__ El algoritmo se pudo haber equivocado porque la maquina pudo haber considerado que los pixeles del centro de la imagen, al estar mas cargado (negro) vendrían siendo parte de la linea central curva del 3.
|
github_jupyter
|
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import plot_confusion_matrix
%matplotlib inline
digits_X, digits_y = datasets.load_digits(return_X_y=True, as_frame=True)
digits = pd.concat([digits_X, digits_y], axis=1)
digits.head()
logistic = LogisticRegression(fit_intercept= False , max_iter = 400)
logistic.fit(digits_X, digits_y)
print(f"El score del modelo de regresión logística es {logistic.score(digits_X, digits_y)}")
for k in range(2,11):
neigh = KNeighborsClassifier(n_neighbors=k)
neigh.fit(digits_X, digits_y)
print(f"El score del modelo de kNN con k={k} es {neigh.score(digits_X, digits_y)}")
plot_confusion_matrix(logistic, digits_X, digits_y, normalize = 'pred');
best_knn = KNeighborsClassifier(n_neighbors=3)
best_knn.fit(digits_X, digits_y)
plot_confusion_matrix(best_knn, digits_X, digits_y, normalize = 'pred');
i_test = 29
i = 9
neigh.predict(digits_X.iloc[[i_test], :])
neigh.predict_proba(digits_X.iloc[[i_test], :])
plt.imshow(digits_X.loc[[i], :].to_numpy().reshape(8, 8), cmap=plt.cm.gray_r, interpolation='nearest');
| 0.738386 | 0.956756 |
## CASE STUDY - Deploying a recommender
We have seen the movie lens data on a toy dataset now lets try something a little bigger. You have some
choices.
* [MovieLens Downloads](https://grouplens.org/datasets/movielens/latest/)
If your resources are limited (your working on a computer with limited amount of memory)
> continue to use the sample_movielens_ranting.csv
If you have a computer with at least 8GB of RAM
> download the ml-latest-small.zip
If you have the computational resources (access to Spark cluster or high-memory machine)
> download the ml-latest.zip
The two important pages for documentation are below.
* [Spark MLlib collaborative filtering docs](https://spark.apache.org/docs/latest/ml-collaborative-filtering.html)
* [Spark ALS docs](https://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.recommendation.ALS)
```
import os
import shutil
import pandas as pd
import numpy as np
import pyspark as ps
from pyspark.ml import Pipeline
from pyspark.ml.evaluation import RegressionEvaluator
from pyspark.ml.recommendation import ALS
from pyspark.sql import Row
from pyspark.sql.types import DoubleType
## ensure the spark context is available
spark = (ps.sql.SparkSession.builder
.appName("sandbox")
.getOrCreate()
)
sc = spark.sparkContext
print(spark.version)
```
### Ensure the data are downloaded and specify the file paths here
```
data_dir = os.path.join(".", "data")
ratings_file = os.path.join(data_dir, "ratings.csv")
movies_file = os.path.join(data_dir, "movies.csv")
# Load the data
ratings = spark.read.csv(ratings_file, header=True, inferSchema=True)
movies = spark.read.csv(movies_file, header=True, inferSchema=True)
ratings.show(n=4)
movies.show(n=4)
```
## QUESTION 1
Explore the movie lens data a little and summarize it
```
## (summarize the data)
## rename columns
ratings = ratings.withColumnRenamed("movieID", "movie_id")
ratings = ratings.withColumnRenamed("userID", "user_id")
ratings.describe().show()
print("Unique users {}".format(ratings.select("user_id").distinct().count()))
print("Unique movies {}".format(ratings.select("movie_id").distinct().count()))
print('Movies with Rating > 2: {}'.format(ratings.filter('rating > 2').select('movie_id').distinct().count()))
print('Movies with Rating > 3: {}'.format(ratings.filter('rating > 3').select('movie_id').distinct().count()))
print('Movies with Rating > 4: {}'.format(ratings.filter('rating > 4').select('movie_id').distinct().count()))
```
## QUESTION 2
Find the ten most popular movies---that is the then movies with the highest average rating
>Hint: you may want to subset the movie matrix to only consider movies with a minimum number of ratings
```
## Group movies
movies_counts = ratings.groupBy("movie_id").count()
movies_rating = ratings.groupBy("movie_id").avg("rating")
movies_rating_and_count = movies_counts.join(movies_rating, "movie_id")
## Consider movies with more than 100 views
threshold = 100
top_movies = movies_rating_and_count.filter("count > 100").orderBy("avg(rating)", ascending=False)
## Add the movie titles to data frame
movies = movies.withColumnRenamed("movieID", "movie_id")
top_movies = top_movies.join(movies, "movie_id")
top_movies.toPandas().head(10)
```
## QUESTION 3
Compare at least 5 different values for the ``regParam``
Use the `` ALS.trainImplicit()`` and compare it to the ``.fit()`` method. See the [Spark ALS docs](https://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.recommendation.ALS)
for example usage.
```
## split the data set to train and test set
(train, test) = ratings.randomSplit([0.8, 0.2])
## Create a function to train the model
def train_model(reg_param, implicit_prefs=False):
als = ALS(maxIter=5, regParam=reg_param, userCol="user_id", itemCol="movie_id", ratingCol="rating", coldStartStrategy="drop", implicitPrefs=implicit_prefs)
model = als.fit(train)
predictions = model.transform(test)
evaluator = RegressionEvaluator(metricName="rmse", labelCol="rating", predictionCol="prediction")
rmse = evaluator.evaluate(predictions)
print("regParam={}, RMSE={}".format(reg_param, np.round(rmse,2)))
for reg_param in [0.01, 0.05, 0.1, 0.15, 0.25]:
train_model(reg_param)
```
## QUESTION 4
With your best `regParam` try using the `implicitPrefs` flag.
```
train_model(reg_param=0.1, implicit_prefs=True)
```
## QUESTION 5
Use model persistence to save your finalized model
```
## re-train using the whole data set
print("...training")
als = ALS(maxIter=5, regParam=0.1, userCol="user_id", itemCol="movie_id", ratingCol="rating", coldStartStrategy="drop")
model = als.fit(ratings)
## save the model for furture use
save_dir = "./models/saved-recommender"
if os.path.isdir(save_dir):
print("...overwritting saved model")
shutil.rmtree(save_dir)
## save the top-ten movies
print("...saving top-movies")
top_movies.toPandas().head(10).to_csv("./data/top-movies.csv", index=False)
## save model
model.save(save_dir)
print("done.")
```
## QUESTION 6
Use ``spark-submit`` to load the model and demonstrate that you can load the model and interface with it.
```
from pyspark.ml.recommendation import ALSModel
from_saved_model = ALSModel.load(save_dir)
test = spark.createDataFrame([(1, 5), (1, 10), (2, 1)], ["user_id", "movie_id"])
predictions = sorted(model.transform(test).collect(), key=lambda r: r[0])
print(predictions)
%%writefile ./scripts/case-study-spark-submit.sh
#!/bin/bash
${SPARK_HOME}/bin/spark-submit \
--master local[4] \
--executor-memory 1G \
--driver-memory 1G \
$@
!chmod 711 ./scripts/case-study-spark-submit.sh
! ./scripts/case-study-spark-submit.sh ./scripts/recommender-submit.py
```
|
github_jupyter
|
import os
import shutil
import pandas as pd
import numpy as np
import pyspark as ps
from pyspark.ml import Pipeline
from pyspark.ml.evaluation import RegressionEvaluator
from pyspark.ml.recommendation import ALS
from pyspark.sql import Row
from pyspark.sql.types import DoubleType
## ensure the spark context is available
spark = (ps.sql.SparkSession.builder
.appName("sandbox")
.getOrCreate()
)
sc = spark.sparkContext
print(spark.version)
data_dir = os.path.join(".", "data")
ratings_file = os.path.join(data_dir, "ratings.csv")
movies_file = os.path.join(data_dir, "movies.csv")
# Load the data
ratings = spark.read.csv(ratings_file, header=True, inferSchema=True)
movies = spark.read.csv(movies_file, header=True, inferSchema=True)
ratings.show(n=4)
movies.show(n=4)
## (summarize the data)
## rename columns
ratings = ratings.withColumnRenamed("movieID", "movie_id")
ratings = ratings.withColumnRenamed("userID", "user_id")
ratings.describe().show()
print("Unique users {}".format(ratings.select("user_id").distinct().count()))
print("Unique movies {}".format(ratings.select("movie_id").distinct().count()))
print('Movies with Rating > 2: {}'.format(ratings.filter('rating > 2').select('movie_id').distinct().count()))
print('Movies with Rating > 3: {}'.format(ratings.filter('rating > 3').select('movie_id').distinct().count()))
print('Movies with Rating > 4: {}'.format(ratings.filter('rating > 4').select('movie_id').distinct().count()))
## Group movies
movies_counts = ratings.groupBy("movie_id").count()
movies_rating = ratings.groupBy("movie_id").avg("rating")
movies_rating_and_count = movies_counts.join(movies_rating, "movie_id")
## Consider movies with more than 100 views
threshold = 100
top_movies = movies_rating_and_count.filter("count > 100").orderBy("avg(rating)", ascending=False)
## Add the movie titles to data frame
movies = movies.withColumnRenamed("movieID", "movie_id")
top_movies = top_movies.join(movies, "movie_id")
top_movies.toPandas().head(10)
## split the data set to train and test set
(train, test) = ratings.randomSplit([0.8, 0.2])
## Create a function to train the model
def train_model(reg_param, implicit_prefs=False):
als = ALS(maxIter=5, regParam=reg_param, userCol="user_id", itemCol="movie_id", ratingCol="rating", coldStartStrategy="drop", implicitPrefs=implicit_prefs)
model = als.fit(train)
predictions = model.transform(test)
evaluator = RegressionEvaluator(metricName="rmse", labelCol="rating", predictionCol="prediction")
rmse = evaluator.evaluate(predictions)
print("regParam={}, RMSE={}".format(reg_param, np.round(rmse,2)))
for reg_param in [0.01, 0.05, 0.1, 0.15, 0.25]:
train_model(reg_param)
train_model(reg_param=0.1, implicit_prefs=True)
## re-train using the whole data set
print("...training")
als = ALS(maxIter=5, regParam=0.1, userCol="user_id", itemCol="movie_id", ratingCol="rating", coldStartStrategy="drop")
model = als.fit(ratings)
## save the model for furture use
save_dir = "./models/saved-recommender"
if os.path.isdir(save_dir):
print("...overwritting saved model")
shutil.rmtree(save_dir)
## save the top-ten movies
print("...saving top-movies")
top_movies.toPandas().head(10).to_csv("./data/top-movies.csv", index=False)
## save model
model.save(save_dir)
print("done.")
from pyspark.ml.recommendation import ALSModel
from_saved_model = ALSModel.load(save_dir)
test = spark.createDataFrame([(1, 5), (1, 10), (2, 1)], ["user_id", "movie_id"])
predictions = sorted(model.transform(test).collect(), key=lambda r: r[0])
print(predictions)
%%writefile ./scripts/case-study-spark-submit.sh
#!/bin/bash
${SPARK_HOME}/bin/spark-submit \
--master local[4] \
--executor-memory 1G \
--driver-memory 1G \
$@
!chmod 711 ./scripts/case-study-spark-submit.sh
! ./scripts/case-study-spark-submit.sh ./scripts/recommender-submit.py
| 0.492188 | 0.888662 |
```
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
df=pd.read_csv('WA_Fn-UseC_-Marketing-Customer-Value-Analysis.csv')
df.shape
df.head(3)
df.columns
df.groupby('Gender').count()
df.groupby(['Response','Gender']).count()
ax = df.groupby('Response').count()['Customer'].plot(
kind='bar',
color='orchid',
grid=True,
figsize=(10, 5),
title='Marketing Engagement'
)
ax.set_xlabel("Response ")
ax.set_ylabel("Count")
#df.groupby('Response').count()['Customer'] Here "Customer can be replaced with any other column name"
ax = df.groupby('Response').count()['Customer'].plot(kind='pie',autopct='%.1f%%')
print(ax)
by_offer_type_df = df.loc[df['Response'] == 'Yes', # count only engaged customers
].groupby([
'Renew Offer Type'
# engaged customers grouped by renewal offer type
]).count()['Customer'] / df.groupby('Renew Offer Type').count()['Customer']
by_offer_type_df
odf=(df.loc[df['Response']=="Yes"].groupby(['Renew Offer Type']).count()['Customer']/df.groupby('Renew Offer Type').count()['Customer'])*100
odf.plot(kind='bar',title="TITLE",color="pink")
odf.plot(kind='line',color='black',grid=True)
df.head()
ax=df.groupby(["Renew Offer Type","Vehicle Class"]).count()['Customer']/df.groupby('Renew Offer Type').count()['Customer']
ax=ax.unstack().fillna(0)
ax.plot(kind='bar')
ax.set_ylabel('Engagement Rate (%)')
df.groupby('Sales Channel').count()["Customer"]
by_sales_channel_df = df.loc[df['Response'] == 'Yes'].groupby(['Sales Channel']).count()['Customer']/df.groupby('Sales Channel').count()['Customer']
by_sales_channel_df
df[["Coverage","Gender"]].head(6)
bins=[0,25,50,75,100]
df.groupby('Months Since Policy Inception')["Customer"].count().plot(color="grey")
by_months_since_inception_df = df.loc[
df['Response'] == 'Yes'
].groupby(
by='Months Since Policy Inception'
)['Response'].count() / df.groupby(
by='Months Since Policy Inception'
)['Response'].count() * 100.0
by_months_since_inception_df.plot()
#df.groupby(by='Months Since Policy Inception')['Response'].count()
df.loc[df['Response'] == 'Yes'].groupby(by='Months Since Policy Inception')['Response'].count().plot.scatter()
df.loc[
(df['CLV Segment'] == 'Low') & (df['Policy Age Segment'] == 'Low')
].plot.scatter(
color='green',
grid=True,
figsize=(10, 7)
)
df.groupby('Response')['Months Since Policy Inception'].count().plot(kind='scatter')
#df.loc[df['Response'] == 'Yes'].groupby(by='Months Since Policy Inception')['Response'].count()
df['Customer Lifetime Value'].describe()
df['Policy Age Segment'] = df['Months Since Policy Inception'].apply(
lambda x: 'High' if x > df['Months Since Policy Inception'].median() else 'Low'
)
df
df['CLV Segment'] = df['Customer Lifetime Value'].apply(lambda x: 'High' if x > df['Customer Lifetime Value'].median() else 'Low')
df['CLV Segment']
df
ax = df.loc[(df['CLV Segment'] == 'High') & (df['Policy Age Segment'] == 'High')].plot.scatter(x='Months Since Policy Inception',y='Customer Lifetime Value',logy=True,color='red',figsize=(20,12))
df.loc[(df['CLV Segment'] == 'Low') & (df['Policy Age Segment'] == 'High')].plot.scatter(ax=ax,x='Months Since Policy Inception',y='Customer Lifetime Value',logy=True,color='blue')
df.loc[(df['CLV Segment'] == 'High') & (df['Policy Age Segment'] == 'Low')].plot.scatter(ax=ax,x='Months Since Policy Inception',y='Customer Lifetime Value',logy=True,color='orange')
df.loc[(df['CLV Segment'] == 'Low') & (df['Policy Age Segment'] == 'High')].plot.scatter(x='Months Since Policy Inception',y='Customer Lifetime Value',logy=True,color='blue')
```
|
github_jupyter
|
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
df=pd.read_csv('WA_Fn-UseC_-Marketing-Customer-Value-Analysis.csv')
df.shape
df.head(3)
df.columns
df.groupby('Gender').count()
df.groupby(['Response','Gender']).count()
ax = df.groupby('Response').count()['Customer'].plot(
kind='bar',
color='orchid',
grid=True,
figsize=(10, 5),
title='Marketing Engagement'
)
ax.set_xlabel("Response ")
ax.set_ylabel("Count")
#df.groupby('Response').count()['Customer'] Here "Customer can be replaced with any other column name"
ax = df.groupby('Response').count()['Customer'].plot(kind='pie',autopct='%.1f%%')
print(ax)
by_offer_type_df = df.loc[df['Response'] == 'Yes', # count only engaged customers
].groupby([
'Renew Offer Type'
# engaged customers grouped by renewal offer type
]).count()['Customer'] / df.groupby('Renew Offer Type').count()['Customer']
by_offer_type_df
odf=(df.loc[df['Response']=="Yes"].groupby(['Renew Offer Type']).count()['Customer']/df.groupby('Renew Offer Type').count()['Customer'])*100
odf.plot(kind='bar',title="TITLE",color="pink")
odf.plot(kind='line',color='black',grid=True)
df.head()
ax=df.groupby(["Renew Offer Type","Vehicle Class"]).count()['Customer']/df.groupby('Renew Offer Type').count()['Customer']
ax=ax.unstack().fillna(0)
ax.plot(kind='bar')
ax.set_ylabel('Engagement Rate (%)')
df.groupby('Sales Channel').count()["Customer"]
by_sales_channel_df = df.loc[df['Response'] == 'Yes'].groupby(['Sales Channel']).count()['Customer']/df.groupby('Sales Channel').count()['Customer']
by_sales_channel_df
df[["Coverage","Gender"]].head(6)
bins=[0,25,50,75,100]
df.groupby('Months Since Policy Inception')["Customer"].count().plot(color="grey")
by_months_since_inception_df = df.loc[
df['Response'] == 'Yes'
].groupby(
by='Months Since Policy Inception'
)['Response'].count() / df.groupby(
by='Months Since Policy Inception'
)['Response'].count() * 100.0
by_months_since_inception_df.plot()
#df.groupby(by='Months Since Policy Inception')['Response'].count()
df.loc[df['Response'] == 'Yes'].groupby(by='Months Since Policy Inception')['Response'].count().plot.scatter()
df.loc[
(df['CLV Segment'] == 'Low') & (df['Policy Age Segment'] == 'Low')
].plot.scatter(
color='green',
grid=True,
figsize=(10, 7)
)
df.groupby('Response')['Months Since Policy Inception'].count().plot(kind='scatter')
#df.loc[df['Response'] == 'Yes'].groupby(by='Months Since Policy Inception')['Response'].count()
df['Customer Lifetime Value'].describe()
df['Policy Age Segment'] = df['Months Since Policy Inception'].apply(
lambda x: 'High' if x > df['Months Since Policy Inception'].median() else 'Low'
)
df
df['CLV Segment'] = df['Customer Lifetime Value'].apply(lambda x: 'High' if x > df['Customer Lifetime Value'].median() else 'Low')
df['CLV Segment']
df
ax = df.loc[(df['CLV Segment'] == 'High') & (df['Policy Age Segment'] == 'High')].plot.scatter(x='Months Since Policy Inception',y='Customer Lifetime Value',logy=True,color='red',figsize=(20,12))
df.loc[(df['CLV Segment'] == 'Low') & (df['Policy Age Segment'] == 'High')].plot.scatter(ax=ax,x='Months Since Policy Inception',y='Customer Lifetime Value',logy=True,color='blue')
df.loc[(df['CLV Segment'] == 'High') & (df['Policy Age Segment'] == 'Low')].plot.scatter(ax=ax,x='Months Since Policy Inception',y='Customer Lifetime Value',logy=True,color='orange')
df.loc[(df['CLV Segment'] == 'Low') & (df['Policy Age Segment'] == 'High')].plot.scatter(x='Months Since Policy Inception',y='Customer Lifetime Value',logy=True,color='blue')
| 0.427516 | 0.255901 |
# Recurrent Neural Network
This notebook was created by Camille-Amaury JUGE, in order to better understand Self Organizing Maps (SOM) principles and how they work.
(it follows the exercices proposed by Hadelin de Ponteves on Udemy : https://www.udemy.com/course/le-deep-learning-de-a-a-z/)
## Imports
```
import numpy as np
import pandas as pd
from minisom import MiniSom
import matplotlib.pyplot as plt
from pylab import rcParams, bone, pcolor, colorbar, plot, show
rcParams['figure.figsize'] = 16, 10
# scikit learn
from sklearn.preprocessing import MinMaxScaler, StandardScaler
# keras
import keras
from keras.layers import Dense
from keras.models import Sequential
```
## preprocessing
The dataset represents customers of a bank and if they've been approved to possess a credit card. We want to isolate fraudsters from normal customers. This will serve as an indicator for manual processing.
The dataset has been anonymised, then we don't have clear variables names and individuals name.
```
df = pd.read_csv("Credit_card_Applications.csv")
df.head()
df.describe().transpose().round(2)
df.dtypes
```
The dataset represents 690 anonym customers, since the amount of data is really low, we will try to group those customers by proximity using SOMs. We expect to have a suspicious group.
Since Fraud is a behavior which acts differently than normality, we expect fraudsters neurons to be apart from the generality. Then we will use a distance called "MID".
Firstly, we are going to separate the classes column (validated or refused) from the rest.
```
X = df.iloc[:,:-1].values
Y = df.iloc[:,-1].values
```
Since it's a non-supervised model, our Y doesn't represent the Label but will help us in interpretation.
Then, we are going to scale our variable.
```
scaler = MinMaxScaler()
X = scaler.fit_transform(X)
```
## Model
### SOMs
we will :
* create a 10 \* 10 SOM.
* Instanciate the weight randomly.
```
_map_size = (10,10)
_iteration = 100
model_som = MiniSom(x=_map_size[0], y=_map_size[1], input_len=X.shape[1])
model_som.random_weights_init(X)
model_som.train_random(X, num_iteration=_iteration)
```
### Visualization
```
bone()
pcolor(model_som.distance_map().T)
colorbar()
markers = ["o", "s"]
colors = ["r", "g"]
for i, x in enumerate(X):
# get the winner neurons of the line (x)
winner = model_som.winner(x)
plot(winner[0] + 0.5, winner[1] + 0.5, markers[Y[i]],
markeredgecolor = colors[Y[i]],
markerfacecolor = "None",
markersize=20,
markeredgewidth=2)
show()
```
We will get the coordinates of White winners (supposed fraudsters) neurons here :
* (1,4)
* (2,2)
* (2,8)
* (3,8)
```
mappings = model_som.win_map(X)
fraudsters = np.concatenate((mappings[(1,4)], mappings[(2,2)],
mappings[(3,8)], mappings[(3,8)]),
axis = 0)
fraudsters = pd.DataFrame(scaler.inverse_transform(fraudsters))
fraudsters.iloc[:, 0] = fraudsters.iloc[:, 0].astype(int)
fraudsters.head(5)
print("{} fraudsters detected".format(fraudsters.shape[0]))
```
Then we have the supposed fraudsters.
Now, we can go further. We want to evaluate a scoring method that will give the probability of a customer to be a fraudster or not. For that purpose, we will use an ANN.
```
X_ann = df.iloc[:, 1:]
Y_ann = np.zeros(X_ann.shape[0])
for i in range(X_ann.shape[0]):
for j in range(fraudsters.shape[0]):
if df.iloc[i, 0] == fraudsters.iloc[j,0]:
Y_ann[i] = 1
break
scaler_ann = StandardScaler()
X_ann = scaler_ann.fit_transform(X_ann)
def model():
model = Sequential()
model.add(Dense(units=10, kernel_initializer="uniform", activation="relu",
input_dim=15))
model.add(Dense(units=1, kernel_initializer="uniform", activation="sigmoid"))
model.compile(optimizer="adam", loss="binary_crossentropy",
metrics=["accuracy"])
return model
model = model()
model.fit(X_ann, Y_ann, epochs = 10)
y_pred = model.predict(X_ann)
```
since we had a little amount of data, we use the training set as the test set (else we would proceed as always with separate dataset).
```
y_pred = np.concatenate((df.iloc[:,0:1], y_pred), axis=1)
y_pred
y_pred = pd.DataFrame(y_pred[y_pred[:,1].argsort()])
y_pred.head(-5)
```
|
github_jupyter
|
import numpy as np
import pandas as pd
from minisom import MiniSom
import matplotlib.pyplot as plt
from pylab import rcParams, bone, pcolor, colorbar, plot, show
rcParams['figure.figsize'] = 16, 10
# scikit learn
from sklearn.preprocessing import MinMaxScaler, StandardScaler
# keras
import keras
from keras.layers import Dense
from keras.models import Sequential
df = pd.read_csv("Credit_card_Applications.csv")
df.head()
df.describe().transpose().round(2)
df.dtypes
X = df.iloc[:,:-1].values
Y = df.iloc[:,-1].values
scaler = MinMaxScaler()
X = scaler.fit_transform(X)
_map_size = (10,10)
_iteration = 100
model_som = MiniSom(x=_map_size[0], y=_map_size[1], input_len=X.shape[1])
model_som.random_weights_init(X)
model_som.train_random(X, num_iteration=_iteration)
bone()
pcolor(model_som.distance_map().T)
colorbar()
markers = ["o", "s"]
colors = ["r", "g"]
for i, x in enumerate(X):
# get the winner neurons of the line (x)
winner = model_som.winner(x)
plot(winner[0] + 0.5, winner[1] + 0.5, markers[Y[i]],
markeredgecolor = colors[Y[i]],
markerfacecolor = "None",
markersize=20,
markeredgewidth=2)
show()
mappings = model_som.win_map(X)
fraudsters = np.concatenate((mappings[(1,4)], mappings[(2,2)],
mappings[(3,8)], mappings[(3,8)]),
axis = 0)
fraudsters = pd.DataFrame(scaler.inverse_transform(fraudsters))
fraudsters.iloc[:, 0] = fraudsters.iloc[:, 0].astype(int)
fraudsters.head(5)
print("{} fraudsters detected".format(fraudsters.shape[0]))
X_ann = df.iloc[:, 1:]
Y_ann = np.zeros(X_ann.shape[0])
for i in range(X_ann.shape[0]):
for j in range(fraudsters.shape[0]):
if df.iloc[i, 0] == fraudsters.iloc[j,0]:
Y_ann[i] = 1
break
scaler_ann = StandardScaler()
X_ann = scaler_ann.fit_transform(X_ann)
def model():
model = Sequential()
model.add(Dense(units=10, kernel_initializer="uniform", activation="relu",
input_dim=15))
model.add(Dense(units=1, kernel_initializer="uniform", activation="sigmoid"))
model.compile(optimizer="adam", loss="binary_crossentropy",
metrics=["accuracy"])
return model
model = model()
model.fit(X_ann, Y_ann, epochs = 10)
y_pred = model.predict(X_ann)
y_pred = np.concatenate((df.iloc[:,0:1], y_pred), axis=1)
y_pred
y_pred = pd.DataFrame(y_pred[y_pred[:,1].argsort()])
y_pred.head(-5)
| 0.652574 | 0.978467 |
### Reloading Modules
Reloading modules is something you may find yourself wanting to do if you modify the code for a module while your program is running.
Although you technically can do so, and I'll show you two ways of doing it, it's not recommended. Let me show you how to do it first, and then the pitfalls with both methods.
The safest is just to make your code changes, and restart your app.
Even if you are trying to monkey patch (change at run-time) a code module and you want everyone who uses that module to "see" the change, they very well may not, depending on how they are accessing your module.
As usual, working with external modules in Jupyter is not the easiest thing in the world, so I'm just going to create simple modules right from inside the notebook. You can just create files in the same folder as your notebook/main app instead.
```
import os
def create_module_file(module_name, **kwargs):
'''Create a module file named <module_name>.py.
Module has a single function (print_values) that will print
out the supplied (stringified) kwargs.
'''
module_file_name = f'{module_name}.py'
module_rel_file_path = module_file_name
module_abs_file_path = os.path.abspath(module_rel_file_path)
with open(module_abs_file_path, 'w') as f:
f.write(f'# {module_name}.py\n\n')
f.write(f"print('running {module_file_name}...')\n\n")
f.write(f'def print_values():\n')
for key, value in kwargs.items():
f.write(f"\tprint('{str(key)}', '{str(value)}')\n")
create_module_file('test', k1=10, k2='python')
```
This should have resulted in the creation of a file named `test.py` in your notebook/project directory that should look like this:
`# test.py`
`print('running test.py...')`
``def print_values():
print('k1', '10')
print('k2', 'python')
``
Now let's go ahead and import it using a plain `import`:
```
import test
test
```
And we can now call the `print_values` function:
```
test.print_values()
```
Now suppose, we modify the module by adding an extra key:
```
create_module_file('test', k1=10, k2='python', k3='cheese')
test.print_values()
```
Nope, nothing changed...
Maybe we can just re-import it?? You shoudl know the answer to that one...
```
import test
test.print_values()
id(test)
```
The module object is the same one we initially loaded - our namespace and `sys.modules` still points to that old one. Somehow we have to force Python to *reload* the module.
At this point, I hope you're thinking "let's just remove it from `sys.modules`, this way Python will not see it in the cache and rerun the import.
That's a good idea - let's try that.
```
import sys
del sys.modules['test']
import test
test.print_values()
```
and, in fact, the `id` has also changed:
```
id(test)
```
That worked!
But here's the problem with that approach.
Suppose some other module in your program has already loaded that module using
`import test`.
What is in their namespace? A variable (symbol) called `test` that points to which object? The one that was first loaded, not the second one we just put back into the `sys.modules` dict.
In other words, they have no idea the module changed and they'll just keep using the old object at the original memory address.
Fortunately, `importlib` has a way to reload the contents of the module object without affecting the memory address.
That is already much better.
Let's try it:
```
id(test)
test.print_values()
create_module_file('test', k1=10, k2='python',
k3='cheese', k4='parrots')
import importlib
importlib.reload(test)
```
As we can see the module was executed...
what about the `id`?
```
id(test)
```
Stayed the same...
So now, let's call that function:
```
test.print_values()
```
As you can see, we have the correct output. And we did not have to reimport the module, which means any other module that had imported the old object, now is going to automatically be using the new "version" of the same object (same memory address)
So, all's well that ends well...
Not quite. :-)
Consider this example instead, were we use a `from` style import:
```
create_module_file('test2', k1='python')
from test2 import print_values
print_values()
```
Works great.
What's the `id` of `print_values`?
```
id(print_values)
```
Now let's modify `test2.py`:
```
create_module_file('test2', k1='python', k2='cheese')
```
And reload it using `importlib.reload`:
```
importlib.reload(test2)
```
Ok, so we don't have `test2` in our namespace... Easy enough, let's import it directly (or get it out of `sys.modules`):
```
import test2
test2.print_values()
id(test2.print_values)
id(print_values)
```
Now let's try the reload:
```
importlib.reload(test2)
```
OK, the module was re-imported...
Now let's run the `print_values` function:
```
test2.print_values()
```
But remember how we actually imported `print_values` from `test2`?
```
print_values()
```
Ouch - that's not right!
Let's look at the `id`s of those two functions, and compare them to what we had before we ran the reload:
```
id(test2.print_values)
id(print_values)
```
As you can see the `test2.print_values` function is a new object, but `print_values` **still** points to the old function that exists in the first "version" of `test2`.
And that is why reloading is just not safe.
If someone using your module binds directly to an attribute in your module, either via how they import:
`from test2 import print_values`
or even by doing something like this:
`pv = test2.print_values`
their binding is now set to a specific memory address.
When you reload the module, the object `test2` has ben mutated, and the `print_values` function is now a new object, but any bindings to the "old" version of the function remain.
So, in general, stay away from reloading modules dynamically.
|
github_jupyter
|
import os
def create_module_file(module_name, **kwargs):
'''Create a module file named <module_name>.py.
Module has a single function (print_values) that will print
out the supplied (stringified) kwargs.
'''
module_file_name = f'{module_name}.py'
module_rel_file_path = module_file_name
module_abs_file_path = os.path.abspath(module_rel_file_path)
with open(module_abs_file_path, 'w') as f:
f.write(f'# {module_name}.py\n\n')
f.write(f"print('running {module_file_name}...')\n\n")
f.write(f'def print_values():\n')
for key, value in kwargs.items():
f.write(f"\tprint('{str(key)}', '{str(value)}')\n")
create_module_file('test', k1=10, k2='python')
import test
test
test.print_values()
create_module_file('test', k1=10, k2='python', k3='cheese')
test.print_values()
import test
test.print_values()
id(test)
import sys
del sys.modules['test']
import test
test.print_values()
id(test)
id(test)
test.print_values()
create_module_file('test', k1=10, k2='python',
k3='cheese', k4='parrots')
import importlib
importlib.reload(test)
id(test)
test.print_values()
create_module_file('test2', k1='python')
from test2 import print_values
print_values()
id(print_values)
create_module_file('test2', k1='python', k2='cheese')
importlib.reload(test2)
import test2
test2.print_values()
id(test2.print_values)
id(print_values)
importlib.reload(test2)
test2.print_values()
print_values()
id(test2.print_values)
id(print_values)
| 0.16248 | 0.850655 |
<img src="images/usm.jpg" width="480" height="240" align="left"/>
# MAT281 - Laboratorio N°06
## Objetivos de la clase
* Reforzar los conceptos básicos del E.D.A..
## Contenidos
* [Problema 01](#p1)
## Problema 01
<img src="./images/logo_iris.jpg" width="360" height="360" align="center"/>
El **Iris dataset** es un conjunto de datos que contine una muestras de tres especies de Iris (Iris setosa, Iris virginica e Iris versicolor). Se midió cuatro rasgos de cada muestra: el largo y ancho del sépalo y pétalo, en centímetros.
Lo primero es cargar el conjunto de datos y ver las primeras filas que lo componen:
```
# librerias
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
pd.set_option('display.max_columns', 500) # Ver más columnas de los dataframes
# Ver gráficos de matplotlib en jupyter notebook/lab
%matplotlib inline
# cargar datos
df = pd.read_csv(os.path.join("data","iris_contaminados.csv"))
df.columns = ['sepalLength',
'sepalWidth',
'petalLength',
'petalWidth',
'species']
df.head()
```
### Bases del experimento
Lo primero es identificar las variables que influyen en el estudio y la naturaleza de esta.
* **species**:
* Descripción: Nombre de la especie de Iris.
* Tipo de dato: *string*
* Limitantes: solo existen tres tipos (setosa, virginia y versicolor).
* **sepalLength**:
* Descripción: largo del sépalo.
* Tipo de dato: *integer*.
* Limitantes: los valores se encuentran entre 4.0 y 7.0 cm.
* **sepalWidth**:
* Descripción: ancho del sépalo.
* Tipo de dato: *integer*.
* Limitantes: los valores se encuentran entre 2.0 y 4.5 cm.
* **petalLength**:
* Descripción: largo del pétalo.
* Tipo de dato: *integer*.
* Limitantes: los valores se encuentran entre 1.0 y 7.0 cm.
* **petalWidth**:
* Descripción: ancho del pépalo.
* Tipo de dato: *integer*.
* Limitantes: los valores se encuentran entre 0.1 y 2.5 cm.
Su objetivo es realizar un correcto **E.D.A.**, para esto debe seguir las siguientes intrucciones:
1. Realizar un conteo de elementos de la columna **species** y corregir según su criterio. Reemplace por "default" los valores nan..
```
print("hay")
print(len(df.species)-1)
print("elementos en la columna species")
#Todo a minuscula y sin espacios"
df['species'] = df['species'].str.lower().str.strip()
#Se cambian los valores nan por default"
df.loc[df['species'].isnull(),'species'] = 'default'
```
2. Realizar un gráfico de box-plot sobre el largo y ancho de los petalos y sépalos. Reemplace por **0** los valores nan.
```
df.columns=df.columns.str.lower().str.strip()
df.loc[df['sepallength']=='null','sepallength']= 0
df.loc[df['sepalwidth']=='null','sepalwidth']= 0
df.loc[df['petallength']=='null','petallength']= 0
df.loc[df['petalwidth']=='null','petalwidth']= 0
sns.boxplot(data=df)
```
3. Anteriormente se define un rango de valores válidos para los valores del largo y ancho de los petalos y sépalos. Agregue una columna denominada **label** que identifique cuál de estos valores esta fuera del rango de valores válidos.
```
#VALORES VALIDOS
lista=[]
i=0
while i<=(len(df)-1):
if df['sepallength'][i]>=4.0 and df['sepallength'][i]<=7.0:
if df['sepalwidth'][i]>=2.0 and df['sepalwidth'][i]<=4.5:
if df['petallength'][i]>=1.0 and df['petallength'][i]<=7.0:
if df['petalwidth'][i]>=0.1 and df['petalwidth'][i]<=2.5:
lista.append('validar')
i+=1
else:
lista.append('invalidar')
i+=1
else:
lista.append('invalidar')
i+=1
else:
lista.append('invalidar')
i+=1
else:
lista.append('invalidar')
i+=1
df.insert(5,'label',lista)
```
4. Realice un gráfico de *sepalLength* vs *petalLength* y otro de *sepalWidth* vs *petalWidth* categorizados por la etiqueta **label**. Concluya sus resultados.
```
sns.lineplot(
x='sepallength',
y='petallength',
hue='label',
data=df,
ci = None,
)
sns.lineplot(
x='sepalwidth',
y='petalwidth',
hue='label',
data=df,
ci = None,
)
```
5. Filtre los datos válidos y realice un gráfico de *sepalLength* vs *petalLength* categorizados por la etiqueta **species**.
```
#Se filtran las tres columnas
mask_sepallength_inf = df['sepallength']>=4.0
mask_sepallength_sup = df['sepallength']<=7.0
mask_sepallength= mask_sepallength_inf & mask_sepallength_sup
mask_sepalwidth_inf = df['sepalwidth']>=2.0
mask_sepalwidth_sup = df['sepalwidth']<=4.5
mask_sepalwidth= mask_sepalwidth_inf & mask_sepalwidth_sup
mask_petallength_inf = df['petallength']>=1.0
mask_petallength_sup = df['petallength']<=7.0
mask_petallength= mask_petallength_inf & mask_petallength_sup
mask_petalwidth_inf = df['petalwidth']>=0.1
mask_petalwidth_sup = df['petalwidth']<=2.5
mask_petalwidth= mask_petalwidth_inf & mask_petalwidth_sup
mask_species=df['species']!='default'
df_filtrado= df[mask_sepallength & mask_sepalwidth & mask_petallength & mask_petalwidth & mask_species]
sns.lineplot(
x='sepallength',
y='petallength',
hue='species',
data=df_filtrado,
ci = None,
)
```
|
github_jupyter
|
# librerias
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
pd.set_option('display.max_columns', 500) # Ver más columnas de los dataframes
# Ver gráficos de matplotlib en jupyter notebook/lab
%matplotlib inline
# cargar datos
df = pd.read_csv(os.path.join("data","iris_contaminados.csv"))
df.columns = ['sepalLength',
'sepalWidth',
'petalLength',
'petalWidth',
'species']
df.head()
print("hay")
print(len(df.species)-1)
print("elementos en la columna species")
#Todo a minuscula y sin espacios"
df['species'] = df['species'].str.lower().str.strip()
#Se cambian los valores nan por default"
df.loc[df['species'].isnull(),'species'] = 'default'
df.columns=df.columns.str.lower().str.strip()
df.loc[df['sepallength']=='null','sepallength']= 0
df.loc[df['sepalwidth']=='null','sepalwidth']= 0
df.loc[df['petallength']=='null','petallength']= 0
df.loc[df['petalwidth']=='null','petalwidth']= 0
sns.boxplot(data=df)
#VALORES VALIDOS
lista=[]
i=0
while i<=(len(df)-1):
if df['sepallength'][i]>=4.0 and df['sepallength'][i]<=7.0:
if df['sepalwidth'][i]>=2.0 and df['sepalwidth'][i]<=4.5:
if df['petallength'][i]>=1.0 and df['petallength'][i]<=7.0:
if df['petalwidth'][i]>=0.1 and df['petalwidth'][i]<=2.5:
lista.append('validar')
i+=1
else:
lista.append('invalidar')
i+=1
else:
lista.append('invalidar')
i+=1
else:
lista.append('invalidar')
i+=1
else:
lista.append('invalidar')
i+=1
df.insert(5,'label',lista)
sns.lineplot(
x='sepallength',
y='petallength',
hue='label',
data=df,
ci = None,
)
sns.lineplot(
x='sepalwidth',
y='petalwidth',
hue='label',
data=df,
ci = None,
)
#Se filtran las tres columnas
mask_sepallength_inf = df['sepallength']>=4.0
mask_sepallength_sup = df['sepallength']<=7.0
mask_sepallength= mask_sepallength_inf & mask_sepallength_sup
mask_sepalwidth_inf = df['sepalwidth']>=2.0
mask_sepalwidth_sup = df['sepalwidth']<=4.5
mask_sepalwidth= mask_sepalwidth_inf & mask_sepalwidth_sup
mask_petallength_inf = df['petallength']>=1.0
mask_petallength_sup = df['petallength']<=7.0
mask_petallength= mask_petallength_inf & mask_petallength_sup
mask_petalwidth_inf = df['petalwidth']>=0.1
mask_petalwidth_sup = df['petalwidth']<=2.5
mask_petalwidth= mask_petalwidth_inf & mask_petalwidth_sup
mask_species=df['species']!='default'
df_filtrado= df[mask_sepallength & mask_sepalwidth & mask_petallength & mask_petalwidth & mask_species]
sns.lineplot(
x='sepallength',
y='petallength',
hue='species',
data=df_filtrado,
ci = None,
)
| 0.095244 | 0.886125 |
# <font color='blue'>Data Science Academy - Python Fundamentos - Capítulo 7</font>
## Download: http://github.com/dsacademybr
```
# Versão da Linguagem Python
from platform import python_version
print('Versão da Linguagem Python Usada Neste Jupyter Notebook:', python_version())
```
## Missão 2: Implementar o Algoritmo de Ordenação "Selection sort".
## Nível de Dificuldade: Alto
## Premissas
* As duplicatas são permitidas?
* Sim
* Podemos assumir que a entrada é válida?
* Não
* Podemos supor que isso se encaixa na memória?
* Sim
## Teste Cases
* None -> Exception
* [] -> []
* One element -> [element]
* Two or more elements
## Algoritmo
Animação do Wikipedia:

Podemos fazer isso de forma recursiva ou iterativa. Iterativamente será mais eficiente, pois não requer sobrecarga de espaço extra com as chamadas recursivas.
* Para cada elemento
* Verifique cada elemento à direita para encontrar o min
* Se min < elemento atual, swap
## Solução
```
class SelectionSort(object):
def sort(self, data):
if data is None:
raise TypeError('Dados não podem ser None')
if len(data) < 2:
return data
for i in range(len(data) - 1):
min_index = i
for j in range(i + 1, len(data)):
if data[j] < data[min_index]:
min_index = j
if data[min_index] < data[i]:
data[i], data[min_index] = data[min_index], data[i]
return data
def sort_iterative_alt(self, data):
if data is None:
raise TypeError('Dados não podem ser None')
if len(data) < 2:
return data
for i in range(len(data) - 1):
self._swap(data, i, self._find_min_index(data, i))
return data
def sort_recursive(self, data):
if data is None:
raise TypeError('Dados não podem ser None')
if len(data) < 2:
return data
return self._sort_recursive(data, start=0)
def _sort_recursive(self, data, start):
if data is None:
return
if start < len(data) - 1:
swap(data, start, self._find_min_index(data, start))
self._sort_recursive(data, start + 1)
return data
def _find_min_index(self, data, start):
min_index = start
for i in range(start + 1, len(data)):
if data[i] < data[min_index]:
min_index = i
return min_index
def _swap(self, data, i, j):
if i != j:
data[i], data[j] = data[j], data[i]
return data
```
## Teste da Solução
```
%%writefile missao4.py
from nose.tools import assert_equal, assert_raises
class TestSelectionSort(object):
def test_selection_sort(self, func):
print('None input')
assert_raises(TypeError, func, None)
print('Input vazio')
assert_equal(func([]), [])
print('Um elemento')
assert_equal(func([5]), [5])
print('Dois ou mais elementos')
data = [5, 1, 7, 2, 6, -3, 5, 7, -10]
assert_equal(func(data), sorted(data))
print('Sua solução foi executada com sucesso! Parabéns!')
def main():
test = TestSelectionSort()
try:
selection_sort = SelectionSort()
test.test_selection_sort(selection_sort.sort)
except NameError:
pass
if __name__ == '__main__':
main()
%run -i missao4.py
```
## Fim
### Obrigado - Data Science Academy - <a href="http://facebook.com/dsacademybr">facebook.com/dsacademybr</a>
|
github_jupyter
|
# Versão da Linguagem Python
from platform import python_version
print('Versão da Linguagem Python Usada Neste Jupyter Notebook:', python_version())
class SelectionSort(object):
def sort(self, data):
if data is None:
raise TypeError('Dados não podem ser None')
if len(data) < 2:
return data
for i in range(len(data) - 1):
min_index = i
for j in range(i + 1, len(data)):
if data[j] < data[min_index]:
min_index = j
if data[min_index] < data[i]:
data[i], data[min_index] = data[min_index], data[i]
return data
def sort_iterative_alt(self, data):
if data is None:
raise TypeError('Dados não podem ser None')
if len(data) < 2:
return data
for i in range(len(data) - 1):
self._swap(data, i, self._find_min_index(data, i))
return data
def sort_recursive(self, data):
if data is None:
raise TypeError('Dados não podem ser None')
if len(data) < 2:
return data
return self._sort_recursive(data, start=0)
def _sort_recursive(self, data, start):
if data is None:
return
if start < len(data) - 1:
swap(data, start, self._find_min_index(data, start))
self._sort_recursive(data, start + 1)
return data
def _find_min_index(self, data, start):
min_index = start
for i in range(start + 1, len(data)):
if data[i] < data[min_index]:
min_index = i
return min_index
def _swap(self, data, i, j):
if i != j:
data[i], data[j] = data[j], data[i]
return data
%%writefile missao4.py
from nose.tools import assert_equal, assert_raises
class TestSelectionSort(object):
def test_selection_sort(self, func):
print('None input')
assert_raises(TypeError, func, None)
print('Input vazio')
assert_equal(func([]), [])
print('Um elemento')
assert_equal(func([5]), [5])
print('Dois ou mais elementos')
data = [5, 1, 7, 2, 6, -3, 5, 7, -10]
assert_equal(func(data), sorted(data))
print('Sua solução foi executada com sucesso! Parabéns!')
def main():
test = TestSelectionSort()
try:
selection_sort = SelectionSort()
test.test_selection_sort(selection_sort.sort)
except NameError:
pass
if __name__ == '__main__':
main()
%run -i missao4.py
| 0.297572 | 0.920397 |
####Ridge and Lasso Regression Implementation
#### Regularization
Regularization is an important concept that is used to avoid overfitting of the data, especially when the trained and test data are much varying.
Regularization is implemented by adding a “penalty” term to the best fit derived from the trained data, to achieve a lesser variance with the tested data and also restricts the influence of predictor variables over the output variable by compressing their coefficients.
In regularization, what we do is normally reduce the magnitude of the coefficients. We can reduce the magnitude of the coefficients by using different types of regression techniques which uses regularization to overcome this problem.
#### LASSO
The LASSO (Least Absolute Shrinkage and Selection Operator) involves penalizing the absolute size of the regression coefficients.
By penalizing or constraining the sum of the absolute values of the estimates you make some of your coefficients zero. The larger the penalty applied, the further estimates are shrunk towards zero. This is convenient when we want some automatic feature/variable selection, or when dealing with highly correlated predictors, where standard regression will usually have regression coefficients that are too large. This method performs L2 regularization
Mathematical equation of Lasso Regression
Residual Sum of Squares + λ * (Sum of the absolute value of the magnitude of coefficients)
#### Ridge
Ridge regression was developed as a possible solution to the imprecision of least square estimators when linear regression models have some multicollinear (highly correlated) independent variables—by creating a ridge regression estimator (RR). This provides a more precise ridge parameters estimate, as its variance and mean square estimator are often smaller than the least square estimators previously derived.
This method performs L2 regularization.
The cost function for ridge regression:
Min(||Y – X(theta)||^2 + λ||theta||^2)
Lambda is the penalty term. λ given here is denoted by an alpha parameter in the ridge function. So, by changing the values of alpha, we are controlling the penalty term. The higher the values of alpha, the bigger is the penalty and therefore the magnitude of coefficients is reduced.
It shrinks the parameters. Therefore, it is used to prevent multicollinearity
It reduces the model complexity by coefficient shrinkage
```
import pandas as pd
import numpy as np
import seaborn as sns
df = pd.read_csv("https://raw.githubusercontent.com/Dixit01/100daysofML/main/Lasso_%26_Ridge_regression/auto-detail.csv")
df
df.info()
df['horsepower'].unique()
```
We have horsepower and car name column as object.
we will convert horsepower object column to numeric snd will drop car name.
```
df=df.drop('car name',axis=1)
df=df.replace('?',np.nan)
df=df.apply(lambda x: x.fillna(x.median()),axis=0)
df
df['horsepower'] = pd.to_numeric(df['horsepower'])
df.info()
# seperating target and prediction column
#mpg is the target column
X = df.drop('mpg', axis=1)
Y = df[['mpg']]
```
```
import matplotlib.pyplot as plt
for i in (X.columns):
plt.figure()
sns.histplot(X[i])
sns.histplot(Y['mpg'])
```
##### Scaling and train test split
```
from sklearn import preprocessing
X_scaled = preprocessing.scale(X)
X_scaled = pd.DataFrame(X_scaled, columns=X.columns)
Y_scaled = preprocessing.scale(Y)
Y_scaled = pd.DataFrame(Y_scaled, columns=Y.columns)
X_scaled
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X_scaled, Y_scaled, test_size=0.30, random_state=1)
```
#### Linear Regression
```
from sklearn.linear_model import LinearRegression
regression_model = LinearRegression()
regression_model.fit(X_train, Y_train)
for i, col_name in enumerate(X_train.columns):
print("The coefficient for {} is {}".format(col_name, regression_model.coef_[0][i]))
print('\n')
print("The intercept for our model is {}".format(regression_model.intercept_))
```
#### Regularized Ridge Model
```
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=0.3) #coefficients are prevented to become too big by this alpha value
ridge.fit(X_train,Y_train)
for i,col in enumerate(X_train.columns):
print ("Ridge model coefficients for {} is {}:".format(col,ridge.coef_[0][i]))
```
##### Regularized LASSO Model
```
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=0.1)
lasso.fit(X_train,Y_train)
for i,col in enumerate(X_train):
print ("Lasso model coefficients for {} is {}:".format(col,lasso.coef_[i]))
```
Comparing the scores
```
print(regression_model.score(X_train, Y_train))
print(regression_model.score(X_test, Y_test))
print(ridge.score(X_train, Y_train))
print(ridge.score(X_test, Y_test))
print(lasso.score(X_train, Y_train))
print(lasso.score(X_test, Y_test))
```
linear and ridge models accuracy are almost same because both coefficients values are similar while the performance of lasso slightly gone down but used only 5 dimensions while other two used 8 dimensions. This model is feasible compared to other two because dimensions are reduced.
_____
|
github_jupyter
|
import pandas as pd
import numpy as np
import seaborn as sns
df = pd.read_csv("https://raw.githubusercontent.com/Dixit01/100daysofML/main/Lasso_%26_Ridge_regression/auto-detail.csv")
df
df.info()
df['horsepower'].unique()
df=df.drop('car name',axis=1)
df=df.replace('?',np.nan)
df=df.apply(lambda x: x.fillna(x.median()),axis=0)
df
df['horsepower'] = pd.to_numeric(df['horsepower'])
df.info()
# seperating target and prediction column
#mpg is the target column
X = df.drop('mpg', axis=1)
Y = df[['mpg']]
import matplotlib.pyplot as plt
for i in (X.columns):
plt.figure()
sns.histplot(X[i])
sns.histplot(Y['mpg'])
from sklearn import preprocessing
X_scaled = preprocessing.scale(X)
X_scaled = pd.DataFrame(X_scaled, columns=X.columns)
Y_scaled = preprocessing.scale(Y)
Y_scaled = pd.DataFrame(Y_scaled, columns=Y.columns)
X_scaled
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X_scaled, Y_scaled, test_size=0.30, random_state=1)
from sklearn.linear_model import LinearRegression
regression_model = LinearRegression()
regression_model.fit(X_train, Y_train)
for i, col_name in enumerate(X_train.columns):
print("The coefficient for {} is {}".format(col_name, regression_model.coef_[0][i]))
print('\n')
print("The intercept for our model is {}".format(regression_model.intercept_))
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=0.3) #coefficients are prevented to become too big by this alpha value
ridge.fit(X_train,Y_train)
for i,col in enumerate(X_train.columns):
print ("Ridge model coefficients for {} is {}:".format(col,ridge.coef_[0][i]))
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=0.1)
lasso.fit(X_train,Y_train)
for i,col in enumerate(X_train):
print ("Lasso model coefficients for {} is {}:".format(col,lasso.coef_[i]))
print(regression_model.score(X_train, Y_train))
print(regression_model.score(X_test, Y_test))
print(ridge.score(X_train, Y_train))
print(ridge.score(X_test, Y_test))
print(lasso.score(X_train, Y_train))
print(lasso.score(X_test, Y_test))
| 0.455925 | 0.989171 |
# Multi-Layer Networks
Now that we have tried our hand at some single-layer nets, let's see how they _stack up_ compared to multi-layer nets.
We will be exploring the basic concepts of learning non-linear functions using the classic XOR problem, and then explore the basics of "deep learning" technology on this problem as well. After that, we will see if a multi-layer approach can perform better than single-layer approach on some data sets that we have seen before. In particular, we will try to explore the wider vs. deeper issue, and see if ReLU really helps.
For now, let's look into the XOR problem, and see what insights we can gain when comparing single- and multi-layer network approaches.
```
# NN-Tools
import numpy as np
import keras
# Visualization
from IPython.display import SVG
from IPython.display import display
from keras.utils.vis_utils import model_to_dot
# Printing
from sympy import *
init_printing(use_latex=True)
# Plotting
import matplotlib.pyplot as plt
%matplotlib inline
```
Let's create the XOR data set. As we mentioned in class, _avoiding zeros_ in the **input** patterns is a good general approach for stable learning behavior.
```
# XOR data set
X = np.array([[-1,-1],[-1,1],[1,-1],[1,1]])
display(Matrix(X))
Y = np.array([0,1,1,0])
display(Matrix(Y))
```
We are performing a classification task since there are **two discrete targets**, so using **binary cross-entropy** error at the output layer makes sense. Also, binary cross-entropy suggest the **sigmoid** activation function for the **output** unit since it is comparing only two classes. Given that the hyperbolic tangent (tanh) activation function is a decent choice for two-layer networks, let's create a network with a hidden layer consisting of units which use this activation function. Also, we will keep it rather small: just two units.
```
# Multi-layer net with tanh hidden layer
model = keras.models.Sequential()
model.add(keras.layers.Dense(2,input_dim=2,activation='tanh'))
model.add(keras.layers.Dense(1,activation='sigmoid'))
model.compile(loss='binary_crossentropy',optimizer='adam')
print(model.summary())
```
Since the input vectors are of length 2, and the hidden layer is of size 2, there will be a 2x2=4 element weight matrix connecting the input layer to the hidden layer. Also, each hidden unit will have a bias weight (6 weights total so far). The hidden to output layer weight matrix will be 2x1=2, and the output unit has its own bias weight as well (total of 9, altogether).
```
for i in model.get_weights():
display(Matrix(i))
```
You can see that for tanh units, the bias weight is initialized to zero. We know that zero-element weights can be problematic in some cases, but remember that the bias is **always** used and therefore has access to the full delta for the units. They will only differentiate when required by the task at-hand.
If we want a graph-like representation of our network, we can use some functions from `keras.utils.viz_utils` and the `SVD()` function from `IPython.display` to create such a representation:
```
SVG(model_to_dot(model).create(prog='dot', format='svg'))
```
Not so interesting really for this simple network, but will be more informative for more complex models that we make later in the semester.
Before we get to training, let's see if we can set up a visualization tool that will help us understand how the network is behaving. Simple examples can be very insightful since they can often be investigated more thoroughly than a more complex example, given that the simple example contains the interesting elements that we are looking for.
First, we will create a **meshgrid** of data points (i.e. feature vectors) which _cover_ the space of input vectors for the XOR task thoroughly. This isn't easy to do in a high-dimensional space, since the space requirements grow exponentially with the dimensionality of the input vectors. However, just two dimensions can be visualized and covered with a reasonable number of points.
The `linspace()` function will be used again to create a set of points, now ranging from -2 to 2 (20 distinct values in that range). Next, we use the `meshgrid()` function to create all possible combinations of those values (20x20=400 points!). The `xgrid` and `ygrid` data structures are each 20x20 matrices, where each point we want to visualize will be a combination of corresponding values from each matrix: $\left[ xgrid_{ij}, ygrid_{ij} \right]$ for all i,j. However, this means we need to flatten each of those matrices and combine their corresponding elements into these 2-dimensional vectors. We use a combination of `ravel()` (to perform the flattening) and `vstack()` (to perform the concatenation). The result will actually be the transpose of the final data matrix that we want, so don't forget the `T` at the end.
Now, we will plot all of those data points in green just to show the grid we have made. However, we will also then plot the XOR input vectors (X) colored by their corresponding class labels (0,1), and also a little larger to make them stand out. In this case, red is zero, and blue is one.
```
# Sample plot of classification space
xpoints = np.linspace(-2,2,20)
ypoints = np.linspace(-2,2,20)
xgrid, ygrid = np.meshgrid(xpoints,ypoints)
positions = np.vstack([xgrid.ravel(),ygrid.ravel()]).T
# Green grid points where we will evaluate the network
# outputs.
plt.plot(positions[:,0],positions[:,1],'go')
# Color the zero-expected outputs red
plt.plot(X[[0,3],0],X[[0,3],1],'ro',markersize=10)
# Color the one-expected outputs blue
plt.plot(X[[1,2],0],X[[1,2],1],'bo',markersize=10)
plt.show()
```
Now, let's use this data to visualize how the XOR network behaves. That is, we can use the visualization to examine the current decision boundary that the network is using. You may ask, how could there be a boundary before training? Well, we initialize the weights in the network randomly, so while probably not very useful, the boundary is already there.
For this operation, we need to use the `predict_classes()` function from the model. This is similar to "testing" the neural network, but instead of calculating a loss or accuracy value, we prefer to just see what class label (`predictions`) was assigned to each input vector. We provide all of the grid `positions` calculated above and each one gets assigned to a class of 0 or 1. We can then separate the data into two sets: those input vectors classified as a zero and those input vectors classified as a one. We perform a slice using a boolean operator this time, and then select the matching rows from the `positions` matrix and create two non-overlapping matrices of vectors: `zeros` and `ones`.
Now, rather than coloring them green, we can color them according to the class label that the network _predicted_ for each vector in the grid. By making the XOR vectors a little larger on the plot, it's easy to separate them from the others in the grid as well.
```
# Let's color those points by the classification labels...
predictions = model.predict_classes(positions)[:,0]
zeros = positions[predictions==0,:]
ones = positions[predictions==1,:]
# Color predictions by class
plt.plot(zeros[:,0],zeros[:,1],'ro')
plt.plot(ones[:,0],ones[:,1],'bo')
# Color the zero-expected outputs red
plt.plot(X[[0,3],0],X[[0,3],1],'ro',markersize=10)
# Color the one-expected outputs blue
plt.plot(X[[1,2],0],X[[1,2],1],'bo',markersize=10)
plt.show()
```
The grid point covering let's us visualize the decision boundary determined by the network, since the grid points will change from red to blue or vice-versa.
As you can see, the network starts with a suboptimal decision boundary for the task (as expected). Now, let's see if the network can learn to solve the problem.
```
# Train it!
history = model.fit(X, Y,
batch_size=1,
epochs=1000,
verbose=0)
# summarize history for loss
plt.plot(history.history['loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train'], loc='upper left')
plt.show()
```
Now that we have trained the network for a little while, let's see what the network has learned. We can perform the same steps as above, but using predictions from the network _after training_.
```
# Let's color those points by the classification labels...
predictions = model.predict_classes(positions)[:,0]
zeros = positions[predictions==0,:]
ones = positions[predictions==1,:]
# Color predictions by class
plt.plot(zeros[:,0],zeros[:,1],'ro')
plt.plot(ones[:,0],ones[:,1],'bo')
# Color the zero-expected outputs red
plt.plot(X[[0,3],0],X[[0,3],1],'ro',markersize=10)
# Color the one-expected outputs blue
plt.plot(X[[1,2],0],X[[1,2],1],'bo',markersize=10)
plt.show()
```
So, the tanh hidden units were able to provide good boundaries that the output unit could use to decipher the class structure in the data, even in a non-linear manner. If you reinitialized the network weights, you might find that the learned boundary is not always the same. Some problems can be solved in different ways, and therefore different networks may utilize different ways of partitioning the feature space to solve them even if being trained on _the same data_.
## Enter the ReLU
Let's try to see what happens if we utilize our new activation function, ReLU, which we now know has some nice properties for solving complex problems using deeper networks.
The same approach will be used here as was used above, so we will only replace the tanh function with the ReLU activation function. Remember that it has been suggested in the deep learning literature, that initializing the bias on ReLU units to a small positive value for the bias. We will use that technique here to demonstrate how this might work, but it _may not always be a good idea_. Keep that in mind during the exercises below...
```
# Multi-layer net with ReLU hidden layer
model = keras.models.Sequential()
model.add(keras.layers.Dense(2,input_dim=2,activation='relu',
bias_initializer=keras.initializers.Constant(0.1)))
model.add(keras.layers.Dense(1,activation='sigmoid'))
model.compile(loss='binary_crossentropy',optimizer='adam')
print(model.summary())
for i in model.get_weights():
display(Matrix(i))
```
Let's see how this net stacks up to the tanh net using our visualization method above. Remember, we are still _pre-training_ here for this network.
```
# Let's color those points by the classification labels...
predictions = model.predict_classes(positions)[:,0]
zeros = positions[predictions==0,:]
ones = positions[predictions==1,:]
# Color predictions by class
plt.plot(zeros[:,0],zeros[:,1],'ro')
plt.plot(ones[:,0],ones[:,1],'bo')
# Color the zero-expected outputs red
plt.plot(X[[0,3],0],X[[0,3],1],'ro',markersize=10)
# Color the one-expected outputs blue
plt.plot(X[[1,2],0],X[[1,2],1],'bo',markersize=10)
plt.show()
```
Sometimes, we will see a boundary, but with other weights we may not. Let's see if some training pushes that boundary into the visible space of input vectors...
```
# Train it!
history = model.fit(X, Y,
batch_size=1,
epochs=1000,
verbose=0)
# summarize history for loss
plt.plot(history.history['loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train'], loc='upper left')
plt.show()
# Let's color those points by the classification labels...
predictions = model.predict_classes(positions)[:,0]
zeros = positions[predictions==0,:]
ones = positions[predictions==1,:]
# Color predictions by class
plt.plot(zeros[:,0],zeros[:,1],'ro')
plt.plot(ones[:,0],ones[:,1],'bo')
# Color the zero-expected outputs red
plt.plot(X[[0,3],0],X[[0,3],1],'ro',markersize=10)
# Color the one-expected outputs blue
plt.plot(X[[1,2],0],X[[1,2],1],'bo',markersize=10)
plt.show()
```
Well, that's not very promising is it? Is ReLU that useful after-all? What might be the problem here?
We've seen how to train a multilayer network using both tanh and ReLU at least, even if the results are not very spectacular. However, you should have some intuition about how this problem might be rectified using some hints on the slides and what we have talked about in class...
## Classifying MNIST
The MNIST data set consists of 60,000 images of handwritten digits for training and 10,000 images of handwritten digits for testing. We looked at this data in our last homework assignment some, but now we will try to train up a network for classifying these images.
First, let's load the data and prepare it for presentation to a network.
```
from keras.datasets import mnist
# Digits are zero through nine, so 10 classes
num_classes = 10
# input image dimensions
img_rows, img_cols = 28, 28
# the data, shuffled and split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(x_train.shape[0], img_rows * img_cols)
x_test = x_test.reshape(x_test.shape[0], img_rows * img_cols)
# Data normalization (0-255 is encoded as 0-1 instead)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255.0
x_test /= 255.0
# Convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
# Shape information
print('x_train shape:', x_train.shape)
print('y_train shape:', y_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
```
You can see that we have flattened each image (28x28 pixels) into a 728-element vector using the `reshape()` function. The intensity values in the original data are in the range 0-255, but we divide them all by 255 in order to scale the intensity between 0 and 1. This just keeps us from starting at extreme values in the weight space (where tanh and sigmoid get stuck easily). Finally, we convert the integer class labels (originally just 0,1,2,...,9) into the categorical representation that we need for `categorical cross-entropy`.
OK, so we need to train a network to recognize these digits. We will fully utilize the training/validation data alone when tuning parameters, and run a final accuracy check on the _test_ data which was _never seen_ during the training process. Let's see what a single-layer network can do to start with...
```
model = keras.models.Sequential()
# Linear
model.add(keras.layers.Dense(num_classes, activation='softmax',input_shape=[x_train.shape[1]]))
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adam(),
metrics=['accuracy'])
model.summary()
# Train it!
history = model.fit(x_train, y_train,
batch_size=128,
epochs=30,
verbose=1,
validation_split = 0.2)
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
plt.figure()
# summarize history for accuracy
plt.subplot(211)
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
# summarize history for loss
plt.subplot(212)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.tight_layout()
plt.show()
```
Excellent! Let's take one more look at that accuracy...
```
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
```
Just a single layer network is capable of performing above 92% accuracy on examples that it has never even seen during training. So, the gauntlet has been thown: can a deeper net do better? It will take some modifications to the architecture (tuning the *inductive bias*) in order to get there...
|
github_jupyter
|
# NN-Tools
import numpy as np
import keras
# Visualization
from IPython.display import SVG
from IPython.display import display
from keras.utils.vis_utils import model_to_dot
# Printing
from sympy import *
init_printing(use_latex=True)
# Plotting
import matplotlib.pyplot as plt
%matplotlib inline
# XOR data set
X = np.array([[-1,-1],[-1,1],[1,-1],[1,1]])
display(Matrix(X))
Y = np.array([0,1,1,0])
display(Matrix(Y))
# Multi-layer net with tanh hidden layer
model = keras.models.Sequential()
model.add(keras.layers.Dense(2,input_dim=2,activation='tanh'))
model.add(keras.layers.Dense(1,activation='sigmoid'))
model.compile(loss='binary_crossentropy',optimizer='adam')
print(model.summary())
for i in model.get_weights():
display(Matrix(i))
SVG(model_to_dot(model).create(prog='dot', format='svg'))
# Sample plot of classification space
xpoints = np.linspace(-2,2,20)
ypoints = np.linspace(-2,2,20)
xgrid, ygrid = np.meshgrid(xpoints,ypoints)
positions = np.vstack([xgrid.ravel(),ygrid.ravel()]).T
# Green grid points where we will evaluate the network
# outputs.
plt.plot(positions[:,0],positions[:,1],'go')
# Color the zero-expected outputs red
plt.plot(X[[0,3],0],X[[0,3],1],'ro',markersize=10)
# Color the one-expected outputs blue
plt.plot(X[[1,2],0],X[[1,2],1],'bo',markersize=10)
plt.show()
# Let's color those points by the classification labels...
predictions = model.predict_classes(positions)[:,0]
zeros = positions[predictions==0,:]
ones = positions[predictions==1,:]
# Color predictions by class
plt.plot(zeros[:,0],zeros[:,1],'ro')
plt.plot(ones[:,0],ones[:,1],'bo')
# Color the zero-expected outputs red
plt.plot(X[[0,3],0],X[[0,3],1],'ro',markersize=10)
# Color the one-expected outputs blue
plt.plot(X[[1,2],0],X[[1,2],1],'bo',markersize=10)
plt.show()
# Train it!
history = model.fit(X, Y,
batch_size=1,
epochs=1000,
verbose=0)
# summarize history for loss
plt.plot(history.history['loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train'], loc='upper left')
plt.show()
# Let's color those points by the classification labels...
predictions = model.predict_classes(positions)[:,0]
zeros = positions[predictions==0,:]
ones = positions[predictions==1,:]
# Color predictions by class
plt.plot(zeros[:,0],zeros[:,1],'ro')
plt.plot(ones[:,0],ones[:,1],'bo')
# Color the zero-expected outputs red
plt.plot(X[[0,3],0],X[[0,3],1],'ro',markersize=10)
# Color the one-expected outputs blue
plt.plot(X[[1,2],0],X[[1,2],1],'bo',markersize=10)
plt.show()
# Multi-layer net with ReLU hidden layer
model = keras.models.Sequential()
model.add(keras.layers.Dense(2,input_dim=2,activation='relu',
bias_initializer=keras.initializers.Constant(0.1)))
model.add(keras.layers.Dense(1,activation='sigmoid'))
model.compile(loss='binary_crossentropy',optimizer='adam')
print(model.summary())
for i in model.get_weights():
display(Matrix(i))
# Let's color those points by the classification labels...
predictions = model.predict_classes(positions)[:,0]
zeros = positions[predictions==0,:]
ones = positions[predictions==1,:]
# Color predictions by class
plt.plot(zeros[:,0],zeros[:,1],'ro')
plt.plot(ones[:,0],ones[:,1],'bo')
# Color the zero-expected outputs red
plt.plot(X[[0,3],0],X[[0,3],1],'ro',markersize=10)
# Color the one-expected outputs blue
plt.plot(X[[1,2],0],X[[1,2],1],'bo',markersize=10)
plt.show()
# Train it!
history = model.fit(X, Y,
batch_size=1,
epochs=1000,
verbose=0)
# summarize history for loss
plt.plot(history.history['loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train'], loc='upper left')
plt.show()
# Let's color those points by the classification labels...
predictions = model.predict_classes(positions)[:,0]
zeros = positions[predictions==0,:]
ones = positions[predictions==1,:]
# Color predictions by class
plt.plot(zeros[:,0],zeros[:,1],'ro')
plt.plot(ones[:,0],ones[:,1],'bo')
# Color the zero-expected outputs red
plt.plot(X[[0,3],0],X[[0,3],1],'ro',markersize=10)
# Color the one-expected outputs blue
plt.plot(X[[1,2],0],X[[1,2],1],'bo',markersize=10)
plt.show()
from keras.datasets import mnist
# Digits are zero through nine, so 10 classes
num_classes = 10
# input image dimensions
img_rows, img_cols = 28, 28
# the data, shuffled and split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(x_train.shape[0], img_rows * img_cols)
x_test = x_test.reshape(x_test.shape[0], img_rows * img_cols)
# Data normalization (0-255 is encoded as 0-1 instead)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255.0
x_test /= 255.0
# Convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
# Shape information
print('x_train shape:', x_train.shape)
print('y_train shape:', y_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
model = keras.models.Sequential()
# Linear
model.add(keras.layers.Dense(num_classes, activation='softmax',input_shape=[x_train.shape[1]]))
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adam(),
metrics=['accuracy'])
model.summary()
# Train it!
history = model.fit(x_train, y_train,
batch_size=128,
epochs=30,
verbose=1,
validation_split = 0.2)
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
plt.figure()
# summarize history for accuracy
plt.subplot(211)
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
# summarize history for loss
plt.subplot(212)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.tight_layout()
plt.show()
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
| 0.83622 | 0.993487 |
<p style="align: center;"><img align=center src="https://s8.hostingkartinok.com/uploads/images/2018/08/308b49fcfbc619d629fe4604bceb67ac.jpg" style="height:450px;" width=500/></p>
<h3 style="text-align: center;"><b>Школа глубокого обучения ФПМИ МФТИ</b></h3>
<h3 style="text-align: center;"><b>Продвинутый поток. Весна 2021</b></h3>
<h1 style="text-align: center;"><b>Домашнее задание. Библиотека sklearn и классификация с помощью KNN</b></h1>
На основе [курса по Машинному Обучению ФИВТ МФТИ](https://github.com/ml-mipt/ml-mipt) и [Открытого курса по Машинному Обучению](https://habr.com/ru/company/ods/blog/322626/).
---
<h2 style="text-align: center;"><b>K Nearest Neighbors (KNN)</b></h2>
Метод ближайших соседей (k Nearest Neighbors, или kNN) — очень популярный метод классификации, также иногда используемый в задачах регрессии. Это один из самых понятных подходов к классификации. На уровне интуиции суть метода такова: посмотри на соседей; какие преобладают --- таков и ты. Формально основой метода является гипотеза компактности: если метрика расстояния между примерами введена достаточно удачно, то схожие примеры гораздо чаще лежат в одном классе, чем в разных.
<img src='https://hsto.org/web/68d/a45/6f0/68da456f00f8434e87628dbe7e3f54a7.png' width=600>
Для классификации каждого из объектов тестовой выборки необходимо последовательно выполнить следующие операции:
* Вычислить расстояние до каждого из объектов обучающей выборки
* Отобрать объектов обучающей выборки, расстояние до которых минимально
* Класс классифицируемого объекта — это класс, наиболее часто встречающийся среди $k$ ближайших соседей
Будем работать с подвыборкой из [данных о типе лесного покрытия из репозитория UCI](http://archive.ics.uci.edu/ml/datasets/Covertype). Доступно 7 различных классов. Каждый объект описывается 54 признаками, 40 из которых являются бинарными. Описание данных доступно по ссылке.
### Обработка данных
```
import pandas as pd
import numpy as np
```
Сcылка на датасет (лежит в папке): https://drive.google.com/drive/folders/16TSz1P-oTF8iXSQ1xrt0r_VO35xKmUes?usp=sharing
```
all_data = pd.read_csv('forest_dataset.csv')
all_data.head()
pd.shape
all_data.describe()
unique_labels, frequency = np.unique(all_data[all_data.columns[-1]], return_counts=True)
print(frequency)
all_data.shape
```
Выделим значения метки класса в переменную `labels`, признаковые описания --- в переменную `feature_matrix`. Так как данные числовые и не имеют пропусков, переведем их в `numpy`-формат с помощью метода `.values`.
```
all_data[all_data.columns[-1]].values
labels = all_data[all_data.columns[-1]].values
feature_matrix = all_data[all_data.columns[:-1]].values
all_data.groupby('54').max()
```
### Пара слов о sklearn
**[sklearn](https://scikit-learn.org/stable/index.html)** -- удобная библиотека для знакомства с машинным обучением. В ней реализованны большинство стандартных алгоритмов для построения моделей и работ с выборками. У неё есть подробная документация на английском, с которой вам придётся поработать.
`sklearn` предпологает, что ваши выборки имеют вид пар $(X, y)$, где $X$ -- матрица признаков, $y$ -- вектор истинных значений целевой переменной, или просто $X$, если целевые переменные неизвестны.
Познакомимся со вспомогательной функцией
[train_test_split](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html).
С её помощью можно разбить выборку на обучающую и тестовую части.
```
from sklearn.model_selection import train_test_split
```
Вернёмся к датасету. Сейчас будем работать со всеми 7 типами покрытия (данные уже находятся в переменных `feature_matrix` и `labels`, если Вы их не переопределили). Разделим выборку на обучающую и тестовую с помощью метода `train_test_split`.
```
train_feature_matrix, test_feature_matrix, train_labels, test_labels = train_test_split(
feature_matrix, labels, test_size=0.2, random_state=42)
feature_matrix.shape
train_feature_matrix.shape
labels.shape
test_labels.shape
```
Параметр `test_size` контролирует, какая часть выборки будет тестовой. Более подробно о нём можно прочитать в [документации](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html).
Основные объекты `sklearn` -- так называемые `estimators`, что можно перевести как *оценщики*, но не стоит, так как по сути это *модели*. Они делятся на **классификаторы** и **регрессоры**.
В качестве примера модели можно привести классификаторы
[метод ближайших соседей](https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html) и
[логистическую регрессию](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html). Что такое логистическая регрессия и как она работает сейчас не важно.
У всех моделей в `sklearn` обязательно должно быть хотя бы 2 метода (подробнее о методах и классах в python будет в следующих занятиях) -- `fit` и `predict`.
Метод `fit(X, y)` отвечает за обучение модели и принимает на вход обучающую выборку в виде *матрицы признаков* $X$ и *вектора ответов* $y$.
У обученной после `fit` модели теперь можно вызывать метод `predict(X)`, который вернёт предсказания этой модели на всех объектах из матрицы $X$ в виде вектора.
Вызывать `fit` у одной и той же модели можно несколько раз, каждый раз она будет обучаться заново на переданном наборе данных.
Ещё у моделей есть *гиперпараметры*, которые обычно задаются при создании модели.
Рассмотрим всё это на примере логистической регрессии.
```
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import LinearRegression
clf = LinearRegression()
clf.fit(train_feature_matrix, train_labels)
clf.predict(test_feature_matrix)
# создание модели с указанием гиперпараметра C
clf = LogisticRegression(C=1)
# обучение модели
clf.fit(train_feature_matrix, train_labels)
# предсказание на тестовой выборке
y_pred = clf.predict(test_feature_matrix)
y_pred[1000]
```
Теперь хотелось бы измерить качество нашей модели. Для этого можно использовать метод `score(X, y)`, который посчитает какую-то функцию ошибки на выборке $X, y$, но какую конкретно уже зависит от модели. Также можно использовать одну из функций модуля `metrics`, например [accuracy_score](https://scikit-learn.org/stable/modules/generated/sklearn.metrics.accuracy_score.html), которая, как понятно из названия, вычислит нам точность предсказаний.
```
from sklearn.metrics import accuracy_score
print(f"accuracy score: {accuracy_score(test_labels, y_pred)}")
```
Наконец, последним, о чём хотелось бы упомянуть, будет перебор гиперпараметров по сетке. Так как у моделей есть много гиперпараметров, которые можно изменять, и от этих гиперпараметров существенно зависит качество модели, хотелось бы найти наилучшие в этом смысле параметры. Самый простой способ это сделать -- просто перебрать все возможные варианты в разумных пределах.
Сделать это можно с помощью класса [GridSearchCV](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html), который осуществляет поиск (search) по сетке (grid) и вычисляет качество модели с помощью кросс-валидации (CV).
У логистической регрессии, например, можно поменять параметры `C` и `penalty`. Сделаем это. Учтите, что поиск может занять долгое время. Смысл параметров смотрите в документации.
```
from sklearn.model_selection import GridSearchCV
# заново создадим модель, указав солвер
clf = LogisticRegression(solver='saga')
# опишем сетку, по которой будем искать
param_grid = {
'C': np.arange(1, 5), # также можно указать обычный массив, [1, 2, 3, 4]
'penalty': ['l1', 'l2'],
}
# создадим объект GridSearchCV
search = GridSearchCV(clf, param_grid, n_jobs=-1, cv=5, refit=True, scoring='accuracy')
# запустим поиск
search.fit(feature_matrix, labels)
# выведем наилучшие параметры
print(search.best_params_)
```
В данном случае, поиск перебирает все возможные пары значений C и penalty из заданных множеств.
```
accuracy_score(labels, search.best_estimator_.predict(feature_matrix))
```
Заметьте, что мы передаём в GridSearchCV всю выборку, а не только её обучающую часть. Это можно делать, так как поиск всё равно использует кроссвалидацию. Однако порой от выборки всё-же отделяют *валидационную* часть, так как гиперпараметры в процессе поиска могли переобучиться под выборку.
В заданиях вам предстоит повторить это для метода ближайших соседей.
### Обучение модели
Качество классификации/регрессии методом ближайших соседей зависит от нескольких параметров:
* число соседей `n_neighbors`
* метрика расстояния между объектами `metric`
* веса соседей (соседи тестового примера могут входить с разными весами, например, чем дальше пример, тем с меньшим коэффициентом учитывается его "голос") `weights`
Обучите на датасете `KNeighborsClassifier` из `sklearn`.
```
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
clf = KNeighborsClassifier()
clf.fit(train_feature_matrix, train_labels)
predicted_labels = clf.predict(test_feature_matrix)
accuracy_score(predicted_labels, test_labels)
```
### Вопрос 1:
* Какое качество у вас получилось?
Ответ: 0.7365
Подберём параметры нашей модели
* Переберите по сетке от `1` до `10` параметр числа соседей
* Также вы попробуйте использоввать различные метрики: `['manhattan', 'euclidean']`
* Попробуйте использовать различные стратегии вычисления весов: `[‘uniform’, ‘distance’]`
```
from sklearn.model_selection import GridSearchCV
params = {
"n_neighbors": np.arange(1, 11),
"metric": ['manhattan', 'euclidean'],
"weights": ['uniform', 'distance'],
}
clf_grid = GridSearchCV(clf, params, cv=5, scoring='accuracy', n_jobs=-1)
clf_grid.fit(train_feature_matrix, train_labels)
```
Выведем лучшие параметры
```
print(f"Best parameters: {clf_grid.best_params_}")
```
### Вопрос 2:
* Какую metric следует использовать?
Ответ: manhattan
### Вопрос 3:
* Сколько n_neighbors следует использовать?
Ответ: 4
### Вопрос 4:
* Какой тип weights следует использовать?
Ответ: distance
Используя найденное оптимальное число соседей, вычислите вероятности принадлежности к классам для тестовой выборки (`.predict_proba`).
```
optimal_clf = KNeighborsClassifier(n_neighbors=4)
optimal_clf.fit(train_feature_matrix, train_labels)
pred_prob = optimal_clf.predict_proba(test_feature_matrix)
pred_prob[1]
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
unique, freq = np.unique(test_labels, return_counts=True)
freq = list(map(lambda x: x / len(test_labels),freq))
pred_freq = pred_prob.mean(axis=0)
plt.figure(figsize=(10, 8))
plt.bar(range(1, 8), pred_freq, width=0.4, align="edge", label='prediction', color="red")
plt.bar(range(1, 8), freq, width=-0.4, align="edge", label='real')
plt.ylim(0, 0.54)
plt.set_y
plt.legend()
plt.show()
print(round(pred_freq[2], 2))
```
### Вопрос 5:
* Какая прогнозируемая вероятность pred_freq класса под номером 3 (до 2 знаков после запятой)?
Ответ: 0.05
# Делаем pipeline
```
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
pipe = make_pipeline(
StandardScaler(),
KNeighborsClassifier(**clf_grid.best_params_),
)
pipe.fit(train_feature_matrix, train_labels)
prediction_with_scale = pipe.predict(test_feature_matrix)
print(accuracy_score(prediction_with_scale, test_labels))
```
|
github_jupyter
|
import pandas as pd
import numpy as np
all_data = pd.read_csv('forest_dataset.csv')
all_data.head()
pd.shape
all_data.describe()
unique_labels, frequency = np.unique(all_data[all_data.columns[-1]], return_counts=True)
print(frequency)
all_data.shape
all_data[all_data.columns[-1]].values
labels = all_data[all_data.columns[-1]].values
feature_matrix = all_data[all_data.columns[:-1]].values
all_data.groupby('54').max()
from sklearn.model_selection import train_test_split
train_feature_matrix, test_feature_matrix, train_labels, test_labels = train_test_split(
feature_matrix, labels, test_size=0.2, random_state=42)
feature_matrix.shape
train_feature_matrix.shape
labels.shape
test_labels.shape
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import LinearRegression
clf = LinearRegression()
clf.fit(train_feature_matrix, train_labels)
clf.predict(test_feature_matrix)
# создание модели с указанием гиперпараметра C
clf = LogisticRegression(C=1)
# обучение модели
clf.fit(train_feature_matrix, train_labels)
# предсказание на тестовой выборке
y_pred = clf.predict(test_feature_matrix)
y_pred[1000]
from sklearn.metrics import accuracy_score
print(f"accuracy score: {accuracy_score(test_labels, y_pred)}")
from sklearn.model_selection import GridSearchCV
# заново создадим модель, указав солвер
clf = LogisticRegression(solver='saga')
# опишем сетку, по которой будем искать
param_grid = {
'C': np.arange(1, 5), # также можно указать обычный массив, [1, 2, 3, 4]
'penalty': ['l1', 'l2'],
}
# создадим объект GridSearchCV
search = GridSearchCV(clf, param_grid, n_jobs=-1, cv=5, refit=True, scoring='accuracy')
# запустим поиск
search.fit(feature_matrix, labels)
# выведем наилучшие параметры
print(search.best_params_)
accuracy_score(labels, search.best_estimator_.predict(feature_matrix))
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
clf = KNeighborsClassifier()
clf.fit(train_feature_matrix, train_labels)
predicted_labels = clf.predict(test_feature_matrix)
accuracy_score(predicted_labels, test_labels)
from sklearn.model_selection import GridSearchCV
params = {
"n_neighbors": np.arange(1, 11),
"metric": ['manhattan', 'euclidean'],
"weights": ['uniform', 'distance'],
}
clf_grid = GridSearchCV(clf, params, cv=5, scoring='accuracy', n_jobs=-1)
clf_grid.fit(train_feature_matrix, train_labels)
print(f"Best parameters: {clf_grid.best_params_}")
optimal_clf = KNeighborsClassifier(n_neighbors=4)
optimal_clf.fit(train_feature_matrix, train_labels)
pred_prob = optimal_clf.predict_proba(test_feature_matrix)
pred_prob[1]
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
unique, freq = np.unique(test_labels, return_counts=True)
freq = list(map(lambda x: x / len(test_labels),freq))
pred_freq = pred_prob.mean(axis=0)
plt.figure(figsize=(10, 8))
plt.bar(range(1, 8), pred_freq, width=0.4, align="edge", label='prediction', color="red")
plt.bar(range(1, 8), freq, width=-0.4, align="edge", label='real')
plt.ylim(0, 0.54)
plt.set_y
plt.legend()
plt.show()
print(round(pred_freq[2], 2))
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
pipe = make_pipeline(
StandardScaler(),
KNeighborsClassifier(**clf_grid.best_params_),
)
pipe.fit(train_feature_matrix, train_labels)
prediction_with_scale = pipe.predict(test_feature_matrix)
print(accuracy_score(prediction_with_scale, test_labels))
| 0.517571 | 0.98355 |
# Snail and well
A snail falls at the bottom of a 125 cm well. Each day the snail rises 30 cm. But at night, while sleeping, slides 20 cm because the walls are wet. How many days does it take to escape from the well?
TIP: http://puzzles.nigelcoldwell.co.uk/sixtytwo.htm
## Solución
```
# Assign problem data to variables with representative names
# well height, daily advance, night retreat, accumulated distance
well_height = 125
daily_advance = 30
night_retreat = 20
accumulated_distance = 0
# Assign 0 to the variable that represents the solution
days = 0
# Write the code that solves the problem
#print("Snail is in the well.")
accumulated_distance += (daily_advance-night_retreat)
days += 1
#print(accumulated_distance)
#print(days)
while accumulated_distance < well_height:
#print("Snail is still in the well.")
if well_height - accumulated_distance > daily_advance:
accumulated_distance += (daily_advance-night_retreat)
days += 1
print("Accumulated distance minus night retreat =", accumulated_distance)
#print(days)
else:
accumulated_distance += (daily_advance)
days += 1
print("Accumulated distance with no need of night retreat =", accumulated_distance)
#print(days)
#print("The snail escaped !")
# Print the result with print('Days =', days)
print('Days =', days)
```
## Goals
1. Treatment of variables
2. Use of loop **while**
3. Use of conditional **if-else**
4. Print in console
## Bonus
The distance traveled by the snail is now defined by a list.
```
advance_cm = [30, 21, 33, 77, 44, 45, 23, 45, 12, 34, 55]
```
How long does it take to raise the well?
What is its maximum displacement in one day? And its minimum?
What is its average speed during the day?
What is the standard deviation of its displacement during the day?
```
# Assign problem data to variables with representative names
advance_cm = [30, 21, 33, 77, 44, 45, 23, 45, 12, 34, 55]
# well height, daily advance, night retreat, accumulated distance
well_height = 125
night_retreat = 20
daily_advance = 0
accumulated_distance = 0
# Assign 0 to the variable that represents the solution
days = 0
# Write the code that solves the problem
# Here night retreat is not considered as included in the distance travelled list. It is therefore substracted from daily advances.
for i in advance_cm:
if accumulated_distance <= well_height :
accumulated_distance += i
accumulated_distance -= night_retreat
print("Accumulated distance minus night retreat =", accumulated_distance)
days += 1
else:
break
# Print the result with print('Days =', days)
print('Days =', days)
# What is its maximum displacement in a day? And its minimum?
print("Maximum displacement in a day =", max(advance_cm))
print("Minimum displacement in a day =", min(advance_cm))
# What is its average progress?
print("Average progress =", '{:05.2f}'.format(sum(advance_cm)/len(advance_cm)))
# What is the standard deviation of its displacement during the day?
mean = sum(advance_cm)/len(advance_cm)
sum_sq = 0
for i in advance_cm:
sum_sq += (i-mean)**2
std = (sum_sq/(len(advance_cm)-1))**(0.5)
print("Standard deviation of its displacement =", '{:06.3f}'.format(std))
```
|
github_jupyter
|
# Assign problem data to variables with representative names
# well height, daily advance, night retreat, accumulated distance
well_height = 125
daily_advance = 30
night_retreat = 20
accumulated_distance = 0
# Assign 0 to the variable that represents the solution
days = 0
# Write the code that solves the problem
#print("Snail is in the well.")
accumulated_distance += (daily_advance-night_retreat)
days += 1
#print(accumulated_distance)
#print(days)
while accumulated_distance < well_height:
#print("Snail is still in the well.")
if well_height - accumulated_distance > daily_advance:
accumulated_distance += (daily_advance-night_retreat)
days += 1
print("Accumulated distance minus night retreat =", accumulated_distance)
#print(days)
else:
accumulated_distance += (daily_advance)
days += 1
print("Accumulated distance with no need of night retreat =", accumulated_distance)
#print(days)
#print("The snail escaped !")
# Print the result with print('Days =', days)
print('Days =', days)
advance_cm = [30, 21, 33, 77, 44, 45, 23, 45, 12, 34, 55]
# Assign problem data to variables with representative names
advance_cm = [30, 21, 33, 77, 44, 45, 23, 45, 12, 34, 55]
# well height, daily advance, night retreat, accumulated distance
well_height = 125
night_retreat = 20
daily_advance = 0
accumulated_distance = 0
# Assign 0 to the variable that represents the solution
days = 0
# Write the code that solves the problem
# Here night retreat is not considered as included in the distance travelled list. It is therefore substracted from daily advances.
for i in advance_cm:
if accumulated_distance <= well_height :
accumulated_distance += i
accumulated_distance -= night_retreat
print("Accumulated distance minus night retreat =", accumulated_distance)
days += 1
else:
break
# Print the result with print('Days =', days)
print('Days =', days)
# What is its maximum displacement in a day? And its minimum?
print("Maximum displacement in a day =", max(advance_cm))
print("Minimum displacement in a day =", min(advance_cm))
# What is its average progress?
print("Average progress =", '{:05.2f}'.format(sum(advance_cm)/len(advance_cm)))
# What is the standard deviation of its displacement during the day?
mean = sum(advance_cm)/len(advance_cm)
sum_sq = 0
for i in advance_cm:
sum_sq += (i-mean)**2
std = (sum_sq/(len(advance_cm)-1))**(0.5)
print("Standard deviation of its displacement =", '{:06.3f}'.format(std))
| 0.325521 | 0.934932 |
```
import tensorflow as tf
from tensorflow.keras import datasets, layers, models
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import roc_curve
print("Num GPUs Available: ", len(tf.config.experimental.list_physical_devices('GPU')))
from google.colab import drive
drive.mount('/content/drive')
inFile = 'full'
images = np.load('drive/My Drive/' + inFile + '_images.npy', mmap_mode='r')
labels = np.load('drive/My Drive/' + inFile + '_labels.npy', mmap_mode='r')
```
#DROPOUT
```
# Model 12
#dropout on last hidden layer and on every convolutional layer
from keras.layers import Dropout
X_train, X_test, y_train, y_test = train_test_split(images, labels, test_size=0.2)
model = models.Sequential()
model.add(layers.Conv2D(filters=512, kernel_size=(3, 3), strides=2, activation='relu', input_shape=(512, 512, 1)))
model.add(layers.Dropout(0.5, name="dropout_1")) #<------ Dropout layer (0.5)
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(filters=2*512, kernel_size=(3, 3), strides=1, activation='relu'))
model.add(layers.Dropout(0.5, name="dropout_2")) #<------ Dropout layer (0.5)
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(4*512, (3, 3), activation='relu'))
model.add(layers.Dropout(0.5, name="dropout_3")) #<------ Dropout layer (0.5)
model.add(layers.GlobalAveragePooling2D())
model.add(layers.Dropout(0.5, name="dropout_out")) #<------ Dropout layer (0.5)
model.add(layers.Dense(1, activation='sigmoid'))
print(model.summary())
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),
metrics=['accuracy', tf.keras.metrics.AUC()]) #'FalseNegatives', 'FalsePositives'])
history = model.fit(X_train, y_train, epochs=100,batch_size=5,
validation_data=(X_test, y_test))
```
```
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()
test_loss, test_acc, test_acc = model.evaluate(X_test, y_test, verbose=2)
print(test_acc)
y_pred = model.predict(X_test).ravel()
fpr, tpr, threshold = roc_curve(y_test, y_pred)
plt.plot([0,1], [0,1], 'k--')
plt.plot(fpr, tpr)
plt.show()
```
#L2(0.1) REGULARIZATION ON JUST CONVOLUTIONAL LAYERS
```
# Model 13
from keras.layers import Dropout
from keras import regularizers
from keras.regularizers import l2
X_train, X_test, y_train, y_test = train_test_split(images, labels, test_size=0.2)
model = models.Sequential()
model.add(layers.Conv2D(filters=512, kernel_size=(3, 3), strides=2, activation='relu', input_shape=(512, 512, 1), kernel_regularizer=l2(0.01), bias_regularizer=l2(0.01)))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(filters=2*512, kernel_size=(3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.01), bias_regularizer=l2(0.01)))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(4*512, (3, 3), activation='relu', kernel_regularizer=l2(0.01), bias_regularizer=l2(0.01)))
model.add(layers.GlobalAveragePooling2D())
model.add(layers.Dense(1, activation='sigmoid'))
print(model.summary())
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),
metrics=['accuracy', tf.keras.metrics.AUC()]) #'FalseNegatives', 'FalsePositives'])
history = model.fit(X_train, y_train, epochs=100,batch_size=5,
validation_data=(X_test, y_test))
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()
test_loss, test_acc, test_acc = model.evaluate(X_test, y_test, verbose=2)
print(test_acc)
y_pred = model.predict(X_test).ravel()
fpr, tpr, threshold = roc_curve(y_test, y_pred)
plt.plot([0,1], [0,1], 'k--')
plt.plot(fpr, tpr)
plt.show()
```
#L2 Regularization in only the last convolutional layer, 0.01
```
# Model 14
from keras.layers import Dropout
from keras import regularizers
from keras.regularizers import l2
X_train, X_test, y_train, y_test = train_test_split(images, labels, test_size=0.2)
model = models.Sequential()
model.add(layers.Conv2D(filters=512, kernel_size=(3, 3), strides=2, activation='relu', input_shape=(512, 512, 1)))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(filters=2*512, kernel_size=(3, 3), strides=1, activation='relu'))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(4*512, (3, 3), activation='relu', kernel_regularizer=l2(0.01), bias_regularizer=l2(0.01)))
model.add(layers.GlobalAveragePooling2D())
model.add(layers.Dense(1, activation='sigmoid'))
print(model.summary())
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),
metrics=['accuracy', tf.keras.metrics.AUC()]) #'FalseNegatives', 'FalsePositives'])
history = model.fit(X_train, y_train, epochs=100,batch_size=5,
validation_data=(X_test, y_test))
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()
test_loss, test_acc, test_acc = model.evaluate(X_test, y_test, verbose=2)
print(test_acc)
y_pred = model.predict(X_test).ravel()
fpr, tpr, threshold = roc_curve(y_test, y_pred)
plt.plot([0,1], [0,1], 'k--')
plt.plot(fpr, tpr)
plt.show()
```
L1 Regularization in the Last Convolutional layer, 0.00001
```
# Model 15
from keras.layers import Dropout
from keras import regularizers
from keras.regularizers import l2,l1
X_train, X_test, y_train, y_test = train_test_split(images, labels, test_size=0.2)
model = models.Sequential()
model.add(layers.Conv2D(filters=512, kernel_size=(3, 3), strides=2, activation='relu', input_shape=(512, 512, 1)))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(filters=2*512, kernel_size=(3, 3), strides=1, activation='relu'))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(4*512, (3, 3), activation='relu', kernel_regularizer=l1(0.00001)))
model.add(layers.GlobalAveragePooling2D())
model.add(layers.Dense(1, activation='sigmoid'))
print(model.summary())
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),
metrics=['accuracy', tf.keras.metrics.AUC()]) #'FalseNegatives', 'FalsePositives'])
history = model.fit(X_train, y_train, epochs=100,batch_size=5,
validation_data=(X_test, y_test))
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()
test_loss, test_acc, test_acc = model.evaluate(X_test, y_test, verbose=2)
print(test_acc)
y_pred = model.predict(X_test).ravel()
fpr, tpr, threshold = roc_curve(y_test, y_pred)
plt.plot([0,1], [0,1], 'k--')
plt.plot(fpr, tpr)
plt.show()
```
L1 REGULARIZATION ON JOE'S 4 C 3 L CNNN, ON FINAL CONVOLUTIONAL LAYER AND FINAL DENSE LAYER
```
from keras.layers import Dropout
from keras import regularizers
from keras.regularizers import l2,l1
X_train, X_test, y_train, y_test = train_test_split(images, labels, test_size=0.2)
model = models.Sequential()
model.add(layers.Conv2D(filters=512, kernel_size=(3, 3), strides=2, activation='relu', input_shape=(512, 512, 1)))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(filters=2*512, kernel_size=(3, 3), strides=2, activation='relu'))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(4*512, (3, 3), activation='relu', kernel_regularizer=l1(0.00001)))
model.add(layers.GlobalMaxPooling2D())
model.add(layers.Dense(1000, activation='relu'))
model.add(layers.Dense(300, activation='relu'))
model.add(layers.Dense(100, activation='relu', kernel_regularizer=l1(0.00001)))
model.add(layers.Dense(1, activation='sigmoid'))
print(model.summary())
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),
metrics=['accuracy', tf.keras.metrics.AUC()]) #'FalseNegatives', 'FalsePositives'])
history = model.fit(X_train, y_train, epochs=100,batch_size=5,
validation_data=(X_test, y_test))
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()
test_loss, test_acc, test_acc = model.evaluate(X_test, y_test, verbose=2)
print(test_acc)
y_pred = model.predict(X_test).ravel()
fpr, tpr, threshold = roc_curve(y_test, y_pred)
plt.plot([0,1], [0,1], 'k--')
plt.plot(fpr, tpr)
plt.show()
```
L1 ON ALL LAYERS, 0.000001
```
from keras.layers import Dropout
from keras import regularizers
from keras.regularizers import l2,l1
reg = 0.000001
X_train, X_test, y_train, y_test = train_test_split(images, labels, test_size=0.2)
model = models.Sequential()
model.add(layers.Conv2D(filters=512, kernel_size=(3, 3), strides=2, activation='relu', input_shape=(512, 512, 1), kernel_regularizer=l1(reg)))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(filters=2*512, kernel_size=(3, 3), strides=2, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(4*512, (3, 3), activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.GlobalMaxPooling2D())
model.add(layers.Dense(1000, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dense(300, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dense(100, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dense(1, activation='sigmoid'))
print(model.summary())
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),
metrics=['accuracy', tf.keras.metrics.AUC()]) #'FalseNegatives', 'FalsePositives'])
history = model.fit(X_train, y_train, epochs=100,batch_size=5,
validation_data=(X_test, y_test))
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()
test_loss, test_acc, test_acc = model.evaluate(X_test, y_test, verbose=2)
print(test_acc)
y_pred = model.predict(X_test).ravel()
fpr, tpr, threshold = roc_curve(y_test, y_pred)
plt.plot([0,1], [0,1], 'k--')
plt.plot(fpr, tpr)
plt.show()
from keras.layers import Dropout
from keras import regularizers
from keras.regularizers import l2,l1
reg = 0.0000005
drop = 0.25
X_train, X_test, y_train, y_test = train_test_split(images, labels, test_size=0.2)
model = models.Sequential()
model.add(layers.Conv2D(filters=512, kernel_size=(3, 3), strides=2, activation='relu', input_shape=(512, 512, 1), kernel_regularizer=l1(reg)))
model.add(layers.Dropout(drop, name="dropout_1")) #<------ Dropout layer
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(filters=2*512, kernel_size=(3, 3), strides=2, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dropout(drop, name="dropout_2")) #<------ Dropout layer
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(4*512, (3, 3), activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dropout(drop, name="dropout_3")) #<------ Dropout layer
model.add(layers.GlobalMaxPooling2D())
model.add(layers.Dense(1000, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dropout(drop, name="dropout_4")) #<------ Dropout layer
model.add(layers.Dense(300, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dropout(drop, name="dropout_5")) #<------ Dropout layer
model.add(layers.Dense(100, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dropout(drop, name="dropout_6")) #<------ Dropout layer
model.add(layers.Dense(1, activation='sigmoid'))
print(model.summary())
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),
metrics=['accuracy', tf.keras.metrics.AUC()]) #'FalseNegatives', 'FalsePositives'])
history = model.fit(X_train, y_train, epochs=100,batch_size=5,
validation_data=(X_test, y_test))
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()
test_loss, test_acc, test_acc = model.evaluate(X_test, y_test, verbose=2)
print(test_acc)
y_pred = model.predict(X_test).ravel()
fpr, tpr, threshold = roc_curve(y_test, y_pred)
plt.plot([0,1], [0,1], 'k--')
plt.plot(fpr, tpr)
plt.show()
```
L1 AND DROPOUT,
|
github_jupyter
|
import tensorflow as tf
from tensorflow.keras import datasets, layers, models
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import roc_curve
print("Num GPUs Available: ", len(tf.config.experimental.list_physical_devices('GPU')))
from google.colab import drive
drive.mount('/content/drive')
inFile = 'full'
images = np.load('drive/My Drive/' + inFile + '_images.npy', mmap_mode='r')
labels = np.load('drive/My Drive/' + inFile + '_labels.npy', mmap_mode='r')
# Model 12
#dropout on last hidden layer and on every convolutional layer
from keras.layers import Dropout
X_train, X_test, y_train, y_test = train_test_split(images, labels, test_size=0.2)
model = models.Sequential()
model.add(layers.Conv2D(filters=512, kernel_size=(3, 3), strides=2, activation='relu', input_shape=(512, 512, 1)))
model.add(layers.Dropout(0.5, name="dropout_1")) #<------ Dropout layer (0.5)
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(filters=2*512, kernel_size=(3, 3), strides=1, activation='relu'))
model.add(layers.Dropout(0.5, name="dropout_2")) #<------ Dropout layer (0.5)
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(4*512, (3, 3), activation='relu'))
model.add(layers.Dropout(0.5, name="dropout_3")) #<------ Dropout layer (0.5)
model.add(layers.GlobalAveragePooling2D())
model.add(layers.Dropout(0.5, name="dropout_out")) #<------ Dropout layer (0.5)
model.add(layers.Dense(1, activation='sigmoid'))
print(model.summary())
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),
metrics=['accuracy', tf.keras.metrics.AUC()]) #'FalseNegatives', 'FalsePositives'])
history = model.fit(X_train, y_train, epochs=100,batch_size=5,
validation_data=(X_test, y_test))
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()
test_loss, test_acc, test_acc = model.evaluate(X_test, y_test, verbose=2)
print(test_acc)
y_pred = model.predict(X_test).ravel()
fpr, tpr, threshold = roc_curve(y_test, y_pred)
plt.plot([0,1], [0,1], 'k--')
plt.plot(fpr, tpr)
plt.show()
# Model 13
from keras.layers import Dropout
from keras import regularizers
from keras.regularizers import l2
X_train, X_test, y_train, y_test = train_test_split(images, labels, test_size=0.2)
model = models.Sequential()
model.add(layers.Conv2D(filters=512, kernel_size=(3, 3), strides=2, activation='relu', input_shape=(512, 512, 1), kernel_regularizer=l2(0.01), bias_regularizer=l2(0.01)))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(filters=2*512, kernel_size=(3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.01), bias_regularizer=l2(0.01)))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(4*512, (3, 3), activation='relu', kernel_regularizer=l2(0.01), bias_regularizer=l2(0.01)))
model.add(layers.GlobalAveragePooling2D())
model.add(layers.Dense(1, activation='sigmoid'))
print(model.summary())
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),
metrics=['accuracy', tf.keras.metrics.AUC()]) #'FalseNegatives', 'FalsePositives'])
history = model.fit(X_train, y_train, epochs=100,batch_size=5,
validation_data=(X_test, y_test))
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()
test_loss, test_acc, test_acc = model.evaluate(X_test, y_test, verbose=2)
print(test_acc)
y_pred = model.predict(X_test).ravel()
fpr, tpr, threshold = roc_curve(y_test, y_pred)
plt.plot([0,1], [0,1], 'k--')
plt.plot(fpr, tpr)
plt.show()
# Model 14
from keras.layers import Dropout
from keras import regularizers
from keras.regularizers import l2
X_train, X_test, y_train, y_test = train_test_split(images, labels, test_size=0.2)
model = models.Sequential()
model.add(layers.Conv2D(filters=512, kernel_size=(3, 3), strides=2, activation='relu', input_shape=(512, 512, 1)))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(filters=2*512, kernel_size=(3, 3), strides=1, activation='relu'))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(4*512, (3, 3), activation='relu', kernel_regularizer=l2(0.01), bias_regularizer=l2(0.01)))
model.add(layers.GlobalAveragePooling2D())
model.add(layers.Dense(1, activation='sigmoid'))
print(model.summary())
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),
metrics=['accuracy', tf.keras.metrics.AUC()]) #'FalseNegatives', 'FalsePositives'])
history = model.fit(X_train, y_train, epochs=100,batch_size=5,
validation_data=(X_test, y_test))
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()
test_loss, test_acc, test_acc = model.evaluate(X_test, y_test, verbose=2)
print(test_acc)
y_pred = model.predict(X_test).ravel()
fpr, tpr, threshold = roc_curve(y_test, y_pred)
plt.plot([0,1], [0,1], 'k--')
plt.plot(fpr, tpr)
plt.show()
# Model 15
from keras.layers import Dropout
from keras import regularizers
from keras.regularizers import l2,l1
X_train, X_test, y_train, y_test = train_test_split(images, labels, test_size=0.2)
model = models.Sequential()
model.add(layers.Conv2D(filters=512, kernel_size=(3, 3), strides=2, activation='relu', input_shape=(512, 512, 1)))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(filters=2*512, kernel_size=(3, 3), strides=1, activation='relu'))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(4*512, (3, 3), activation='relu', kernel_regularizer=l1(0.00001)))
model.add(layers.GlobalAveragePooling2D())
model.add(layers.Dense(1, activation='sigmoid'))
print(model.summary())
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),
metrics=['accuracy', tf.keras.metrics.AUC()]) #'FalseNegatives', 'FalsePositives'])
history = model.fit(X_train, y_train, epochs=100,batch_size=5,
validation_data=(X_test, y_test))
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()
test_loss, test_acc, test_acc = model.evaluate(X_test, y_test, verbose=2)
print(test_acc)
y_pred = model.predict(X_test).ravel()
fpr, tpr, threshold = roc_curve(y_test, y_pred)
plt.plot([0,1], [0,1], 'k--')
plt.plot(fpr, tpr)
plt.show()
from keras.layers import Dropout
from keras import regularizers
from keras.regularizers import l2,l1
X_train, X_test, y_train, y_test = train_test_split(images, labels, test_size=0.2)
model = models.Sequential()
model.add(layers.Conv2D(filters=512, kernel_size=(3, 3), strides=2, activation='relu', input_shape=(512, 512, 1)))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(filters=2*512, kernel_size=(3, 3), strides=2, activation='relu'))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(4*512, (3, 3), activation='relu', kernel_regularizer=l1(0.00001)))
model.add(layers.GlobalMaxPooling2D())
model.add(layers.Dense(1000, activation='relu'))
model.add(layers.Dense(300, activation='relu'))
model.add(layers.Dense(100, activation='relu', kernel_regularizer=l1(0.00001)))
model.add(layers.Dense(1, activation='sigmoid'))
print(model.summary())
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),
metrics=['accuracy', tf.keras.metrics.AUC()]) #'FalseNegatives', 'FalsePositives'])
history = model.fit(X_train, y_train, epochs=100,batch_size=5,
validation_data=(X_test, y_test))
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()
test_loss, test_acc, test_acc = model.evaluate(X_test, y_test, verbose=2)
print(test_acc)
y_pred = model.predict(X_test).ravel()
fpr, tpr, threshold = roc_curve(y_test, y_pred)
plt.plot([0,1], [0,1], 'k--')
plt.plot(fpr, tpr)
plt.show()
from keras.layers import Dropout
from keras import regularizers
from keras.regularizers import l2,l1
reg = 0.000001
X_train, X_test, y_train, y_test = train_test_split(images, labels, test_size=0.2)
model = models.Sequential()
model.add(layers.Conv2D(filters=512, kernel_size=(3, 3), strides=2, activation='relu', input_shape=(512, 512, 1), kernel_regularizer=l1(reg)))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(filters=2*512, kernel_size=(3, 3), strides=2, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(4*512, (3, 3), activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.GlobalMaxPooling2D())
model.add(layers.Dense(1000, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dense(300, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dense(100, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dense(1, activation='sigmoid'))
print(model.summary())
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),
metrics=['accuracy', tf.keras.metrics.AUC()]) #'FalseNegatives', 'FalsePositives'])
history = model.fit(X_train, y_train, epochs=100,batch_size=5,
validation_data=(X_test, y_test))
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()
test_loss, test_acc, test_acc = model.evaluate(X_test, y_test, verbose=2)
print(test_acc)
y_pred = model.predict(X_test).ravel()
fpr, tpr, threshold = roc_curve(y_test, y_pred)
plt.plot([0,1], [0,1], 'k--')
plt.plot(fpr, tpr)
plt.show()
from keras.layers import Dropout
from keras import regularizers
from keras.regularizers import l2,l1
reg = 0.0000005
drop = 0.25
X_train, X_test, y_train, y_test = train_test_split(images, labels, test_size=0.2)
model = models.Sequential()
model.add(layers.Conv2D(filters=512, kernel_size=(3, 3), strides=2, activation='relu', input_shape=(512, 512, 1), kernel_regularizer=l1(reg)))
model.add(layers.Dropout(drop, name="dropout_1")) #<------ Dropout layer
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(filters=2*512, kernel_size=(3, 3), strides=2, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dropout(drop, name="dropout_2")) #<------ Dropout layer
model.add(layers.MaxPooling2D((3, 3)))
model.add(layers.Conv2D(4*512, (3, 3), activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dropout(drop, name="dropout_3")) #<------ Dropout layer
model.add(layers.GlobalMaxPooling2D())
model.add(layers.Dense(1000, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dropout(drop, name="dropout_4")) #<------ Dropout layer
model.add(layers.Dense(300, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dropout(drop, name="dropout_5")) #<------ Dropout layer
model.add(layers.Dense(100, activation='relu', kernel_regularizer=l1(reg)))
model.add(layers.Dropout(drop, name="dropout_6")) #<------ Dropout layer
model.add(layers.Dense(1, activation='sigmoid'))
print(model.summary())
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=False),
metrics=['accuracy', tf.keras.metrics.AUC()]) #'FalseNegatives', 'FalsePositives'])
history = model.fit(X_train, y_train, epochs=100,batch_size=5,
validation_data=(X_test, y_test))
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()
test_loss, test_acc, test_acc = model.evaluate(X_test, y_test, verbose=2)
print(test_acc)
y_pred = model.predict(X_test).ravel()
fpr, tpr, threshold = roc_curve(y_test, y_pred)
plt.plot([0,1], [0,1], 'k--')
plt.plot(fpr, tpr)
plt.show()
| 0.819099 | 0.842766 |
```
%matplotlib inline
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import azureml
from azureml.core import Workspace, Run
# check core SDK version number
print("Azure ML SDK Version: ", azureml.core.VERSION)
```
<h2>Connect to workspace</h2>
```
# load workspace configuration from the config.json file in the current folder.
ws = Workspace.from_config()
print(ws.name, ws.location, ws.resource_group, ws.location, sep = '\t')
```
<h2>Create experiment</h2>
```
experiment_name = 'sklearn-mnist'
from azureml.core import Experiment
exp = Experiment(workspace=ws, name=experiment_name)
```
<h2>Explore data</h2>
```
import os
import urllib.request
os.makedirs('./data', exist_ok = True)
urllib.request.urlretrieve('http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz', filename='./data/train-images.gz')
urllib.request.urlretrieve('http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz', filename='./data/train-labels.gz')
urllib.request.urlretrieve('http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz', filename='./data/test-images.gz')
urllib.request.urlretrieve('http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz', filename='./data/test-labels.gz')
```
<h3>Display some sample images</h3>
```
# make sure utils.py is in the same directory as this code
from utils import load_data
# note we also shrink the intensity values (X) from 0-255 to 0-1. This helps the model converge faster.
X_train = load_data('./data/train-images.gz', False) / 255.0
y_train = load_data('./data/train-labels.gz', True).reshape(-1)
X_test = load_data('./data/test-images.gz', False) / 255.0
y_test = load_data('./data/test-labels.gz', True).reshape(-1)
# now let's show some randomly chosen images from the traininng set.
count = 0
sample_size = 30
plt.figure(figsize = (16, 6))
for i in np.random.permutation(X_train.shape[0])[:sample_size]:
count = count + 1
plt.subplot(1, sample_size, count)
plt.axhline('')
plt.axvline('')
plt.text(x=10, y=-10, s=y_train[i], fontsize=18)
plt.imshow(X_train[i].reshape(28, 28), cmap=plt.cm.Greys)
plt.show()
```
<h2>Train a model locally</h2>
```
User-managed environment
from azureml.core.runconfig import RunConfiguration
# Editing a run configuration property on-fly.
run_config_user_managed = RunConfiguration()
run_config_user_managed.environment.python.user_managed_dependencies = True
# You can choose a specific Python environment by pointing to a Python path
#run_config.environment.python.interpreter_path = '/home/ninghai/miniconda3/envs/sdk2/bin/python'
%%time
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression()
clf.fit(X_train, y_train)
y_hat = clf.predict(X_test)
print(np.average(y_hat == y_test))
print(run.get_metrics())
```
<h2>Register model</h2>
```
print(run.get_file_names())
# register model
model = run.register_model(model_name='sklearn_mnist', model_path='outputs/sklearn_mnist_model.pkl')
print(model.name, model.id, model.version, sep = '\t')
```
<h2>Clean up resources</h2>
```
# optionally, delete the Azure Managed Compute cluster
compute_target.delete()
```
|
github_jupyter
|
%matplotlib inline
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import azureml
from azureml.core import Workspace, Run
# check core SDK version number
print("Azure ML SDK Version: ", azureml.core.VERSION)
# load workspace configuration from the config.json file in the current folder.
ws = Workspace.from_config()
print(ws.name, ws.location, ws.resource_group, ws.location, sep = '\t')
experiment_name = 'sklearn-mnist'
from azureml.core import Experiment
exp = Experiment(workspace=ws, name=experiment_name)
import os
import urllib.request
os.makedirs('./data', exist_ok = True)
urllib.request.urlretrieve('http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz', filename='./data/train-images.gz')
urllib.request.urlretrieve('http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz', filename='./data/train-labels.gz')
urllib.request.urlretrieve('http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz', filename='./data/test-images.gz')
urllib.request.urlretrieve('http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz', filename='./data/test-labels.gz')
# make sure utils.py is in the same directory as this code
from utils import load_data
# note we also shrink the intensity values (X) from 0-255 to 0-1. This helps the model converge faster.
X_train = load_data('./data/train-images.gz', False) / 255.0
y_train = load_data('./data/train-labels.gz', True).reshape(-1)
X_test = load_data('./data/test-images.gz', False) / 255.0
y_test = load_data('./data/test-labels.gz', True).reshape(-1)
# now let's show some randomly chosen images from the traininng set.
count = 0
sample_size = 30
plt.figure(figsize = (16, 6))
for i in np.random.permutation(X_train.shape[0])[:sample_size]:
count = count + 1
plt.subplot(1, sample_size, count)
plt.axhline('')
plt.axvline('')
plt.text(x=10, y=-10, s=y_train[i], fontsize=18)
plt.imshow(X_train[i].reshape(28, 28), cmap=plt.cm.Greys)
plt.show()
User-managed environment
from azureml.core.runconfig import RunConfiguration
# Editing a run configuration property on-fly.
run_config_user_managed = RunConfiguration()
run_config_user_managed.environment.python.user_managed_dependencies = True
# You can choose a specific Python environment by pointing to a Python path
#run_config.environment.python.interpreter_path = '/home/ninghai/miniconda3/envs/sdk2/bin/python'
%%time
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression()
clf.fit(X_train, y_train)
y_hat = clf.predict(X_test)
print(np.average(y_hat == y_test))
print(run.get_metrics())
print(run.get_file_names())
# register model
model = run.register_model(model_name='sklearn_mnist', model_path='outputs/sklearn_mnist_model.pkl')
print(model.name, model.id, model.version, sep = '\t')
# optionally, delete the Azure Managed Compute cluster
compute_target.delete()
| 0.38168 | 0.784154 |
### Global Scrum Gathering Austing 2019
___A DEMO of calculating Story Points with Machine Learning___
<br/><br/><br/><br/>
```
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.neighbors import KNeighborsClassifier
```
<br/><br/>
### Let's read the DATA from the CSV file
<br/><br/>
```
df = pd.read_csv("team_sp_details.csv")
df
```
<br/><br/><br/>
### Prepare the Data to be fed into Machine Learning Algorithm
<br/><br/><br/>
```
features= np.zeros((19,4))
column_num = 0
rows = 0
for values in df.iloc[0:19,0:1].values:
features[rows][column_num] = values
rows += 1
column_num = 1
rows = 0
for values in df.iloc[0:19,1:2].values:
features[rows][column_num] = values
rows += 1
column_num = 2
rows = 0
for values in df.iloc[0:19,2:3].values:
if values == 'A':
values = 0
elif values == 'B':
values = 1
elif values == 'C':
values = 2
else:
values = -1
features[rows][column_num] = values
rows += 1
column_num = 3
rows = 0
for values in df.iloc[0:19,3:4].values:
if values == 'Local':
values = 0
elif values == 'Remote':
values = 1
else:
values = -1
features[rows][column_num] = values
rows += 1
#features
test_labels = df.iloc[0:19,0:4].as_matrix()
#test_labels
#features = df.iloc[0:19,0:2].values
labels = df.iloc[0:19,4].values
type(labels)
features, labels
labels.dtype, features.dtype
```
<br/><br/><br/><br/>
### Apply the data in Machine Learning Algorithm
<br/><br/>
___In here we'll be using K Nearest Neighbour M.L. Algorithm___
<br/><br/>
<br/><br/>
___Train the M.L. Algorithm with the available DATA___
<br/><br/>
```
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(features, labels)
```
<br/><br/><br/><br/>
___Now the training is done and My Machine Learning Model is READY TO MAKE PREDICTIONS___
<br/><br/><br/><br/>
___INPUT___
- Team Strength
- Leaves
- Component
- Local Or Remote
<br/><br/><br/><br/>
```
Team_strength = 7
Leaves = 1.5
Component = 2
LocalOrRemote = 1
query = np.array([Team_strength, Leaves, Component, LocalOrRemote])
```
<br/><br/>
___Let's see what our M.L. Algorithm Predicts for the given Data___
<br/><br/>
```
knn.predict([query])
```
<br/><br/><br/><br/><br/><br/><br/><br/><br/><br/>
<br/><br/><br/><br/><br/><br/>
<br/><br/><br/><br/>
### Algorithm Selection
___Machine Learning is all about Data Engineering and Algorithm Selection___
<br/><br/><br/><br/>
___For the above data, we can use another form of Supervised Learning Model called "Regression"___
<br/><br/>
___Difference => It will provide contineous values rather than the values provided with the Training Data___
<br/><br/><br/><br/>
```
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(features, labels)
```
<br/><br/><br/><br/>
___Let's query the same data using the new M.L. model which was trainind with same Data Set___
<br/><br/><br/><br/>
```
Team_strength = 7
Leaves = 1.5
Component = 2
LocalOrRemote = 1
query = np.array([Team_strength, Leaves, Component, LocalOrRemote])
lr.predict([query])
```
|
github_jupyter
|
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.neighbors import KNeighborsClassifier
df = pd.read_csv("team_sp_details.csv")
df
features= np.zeros((19,4))
column_num = 0
rows = 0
for values in df.iloc[0:19,0:1].values:
features[rows][column_num] = values
rows += 1
column_num = 1
rows = 0
for values in df.iloc[0:19,1:2].values:
features[rows][column_num] = values
rows += 1
column_num = 2
rows = 0
for values in df.iloc[0:19,2:3].values:
if values == 'A':
values = 0
elif values == 'B':
values = 1
elif values == 'C':
values = 2
else:
values = -1
features[rows][column_num] = values
rows += 1
column_num = 3
rows = 0
for values in df.iloc[0:19,3:4].values:
if values == 'Local':
values = 0
elif values == 'Remote':
values = 1
else:
values = -1
features[rows][column_num] = values
rows += 1
#features
test_labels = df.iloc[0:19,0:4].as_matrix()
#test_labels
#features = df.iloc[0:19,0:2].values
labels = df.iloc[0:19,4].values
type(labels)
features, labels
labels.dtype, features.dtype
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(features, labels)
Team_strength = 7
Leaves = 1.5
Component = 2
LocalOrRemote = 1
query = np.array([Team_strength, Leaves, Component, LocalOrRemote])
knn.predict([query])
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(features, labels)
Team_strength = 7
Leaves = 1.5
Component = 2
LocalOrRemote = 1
query = np.array([Team_strength, Leaves, Component, LocalOrRemote])
lr.predict([query])
| 0.330147 | 0.962848 |
<table>
<tr align=left><td><img align=left src="https://i.creativecommons.org/l/by/4.0/88x31.png">
<td>Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved MIT license. (c) Kyle T. Mandli</td>
</table>
```
from __future__ import print_function
%matplotlib inline
import numpy
import matplotlib.pyplot as plt
```
# Numerical Methods for Initial Value Problems
We now turn towards time dependent PDEs. Before moving to the full PDEs we will explore numerical methods for systems of ODEs that are initial value problems of the general form
$$
\frac{\text{d} \vec{u}}{\text{d}t} = \vec{f}(t, \vec{u}) \quad \vec{u}(0) = \vec{u}_0
$$
where
- $\vec{u}(t)$ is the state vector
- $\vec{f}(t, \vec{u})$ is a vector-valued function that controls the growth of $\vec{u}$ with time
- $\vec{u}(0)$ is the initial condition at time $t = 0$
Note that the right hand side function $f$ could in actuality be the discretization in space of a PDE, i.e. a system of equations.
#### Examples: Simple radioactive decay
$\vec{u} = [c]$
$$\frac{\text{d} c}{\text{d}t} = -\lambda c \quad c(0) = c_0$$
which has solutions of the form $c(t) = c_0 e^{-\lambda t}$
```
t = numpy.linspace(0.0, 1.6e3, 100)
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, 1.0 * numpy.exp(-decay_constant * t))
axes.set_title("Radioactive Decay with $t_{1/2} = 1600$ years")
axes.set_xlabel('t (years)')
axes.set_ylabel('$c$')
axes.set_ylim((0.5,1.0))
plt.show()
```
#### Examples: Complex radioactive decay (or chemical system).
Chain of decays from one species to another.
$$\begin{aligned}
\frac{\text{d} c_1}{\text{d}t} &= -\lambda_1 c_1 \\
\frac{\text{d} c_2}{\text{d}t} &= \lambda_1 c_1 - \lambda_2 c_2 \\
\frac{\text{d} c_2}{\text{d}t} &= \lambda_2 c_3 - \lambda_3 c_3
\end{aligned}$$
$$\frac{\text{d} \vec{u}}{\text{d}t} = \frac{\text{d}}{\text{d}t}\begin{bmatrix} c_1 \\ c_2 \\ c_3 \end{bmatrix} =
\begin{bmatrix}
-\lambda_1 & 0 & 0 \\
\lambda_1 & -\lambda_2 & 0 \\
0 & \lambda_2 & -\lambda_3
\end{bmatrix} \begin{bmatrix} c_1 \\ c_2 \\ c_3 \end{bmatrix}$$
$$\frac{\text{d} \vec{u}}{\text{d}t} = A \vec{u}$$
For systems of equations like this the general solution to the ODE is the matrix exponential:
$$\vec{u}(t) = \vec{u}_0 e^{A t}$$
#### Examples: Van der Pol Oscillator
$$y'' - \mu (1 - y^2) y' + y = 0~~~~~\text{with}~~~~ y(0) = y_0, ~~~y'(0) = v_0$$
$$\vec{u} = \begin{bmatrix} y \\ y' \end{bmatrix} = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix}$$
$$\frac{\text{d}}{\text{d}t} \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} = \begin{bmatrix} u_2 \\ \mu (1 - u_1^2) u_2 - u_1 \end{bmatrix} = \vec{f}(t, \vec{u})$$
```
import scipy.integrate as integrate
def f(t, u, mu=5):
return numpy.array([u[1], mu * (1.0 - u[0]**2) * u[1] - u[0]])
t = numpy.linspace(0.0, 100, 1000)
u = numpy.empty((2, t.shape[0]))
u[:, 0] = [0.1, 0.0]
integrator = integrate.ode(f)
integrator.set_integrator("dopri5")
integrator.set_initial_value(u[:, 0])
for (n, t_n) in enumerate(t[1:]):
integrator.integrate(t_n)
if not integrator.successful():
break
u[:, n + 1] = integrator.y
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, u[0,:])
axes.set_title("Solution to Van der Pol Oscillator")
axes.set_xlabel("t")
axes.set_ylabel("y(t)")
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(u[0,:], u[1, :])
axes.set_title("Phase Diagram for Van der Pol Oscillator")
axes.set_xlabel("y(t)")
axes.set_ylabel("y'(t)")
plt.show()
```
#### Examples: Heat Equation
Let's try to construct a system of ODEs that represents the heat equation
$$
u_t = u_{xx}.
$$
If we discretize the right hand side with second order, centered differences with $m$ points we would have
$$
\frac{\text{d}}{\text{d} t} U_i(t) = \frac{U_{i+1}(t) - 2 U_i(t) + U_{i-1}(t)}{\Delta x^2}
$$
where we now have $m$ unknown, time dependent functions to solve for. This approach to discretizing a PDE is sometimes called a method-of-lines approach.
## Existence and Uniqueness of Solutions
One important step before diving into the numerical methods for IVP ODE problems is to understand what the behavior of the solutions are, whether they exist, and if they might be unique.
### Linear Systems
For linear ODEs we have the generic system
$$
u'(t) = A(t) u + g(t)
$$
where $A$ is time-dependent matrix and $g$ a vector. Note that linear systems always have a unique solution
If $g(t) = 0$ for all $t$ we say the ODE is *homogeneous* and the matrix $A$ is time independent (then implying that it is also *autonomous*) then the solution to this ODE is
$$
u(t) = u(t_0) e^{A(t - t_0)}.
$$
In the case where $g(t) \neq 0$ for all $t$ the ODE is *inhomogeneous* we can use Duhamel's principle which tells us
$$
u(t) = u(t_0) e^{A(t-t_0)} + \int^t_{t_0} e^{A(t - \tau)} g(\tau) d\tau.
$$
We can think of the operator $e^{A(t-\tau)}$ as the solution operator for the homogeneous ODE which can map the solution at time $\tau$ to the solution at time $t$ giving this form of the solution a Green's function type property.
### Non-linear Existance and Uniqueness
#### Lipschitz Continuity
Generalizing uniqueness to non-linear ODEs requires a special type of continuity called *Lipschitz continuity*. Consider the ODE
$$
u'(t) = f(u,t), \quad \quad \quad u(t_0) = u_0,
$$
we will require a certain amount of smoothness in the right hand side function $f(u,t)$.
We say that $f$ is Lipshitz continuous in $u$ over some domain
$$
\Omega = \{(u,t) : |u - u_0| \leq a, t_0 \leq t \leq t_1 \}
$$
if there exists a constant $L > 0$ such that
$$
|f(u,t) - f(u^\ast, t)| \leq L |u - u^\ast| \quad \quad \forall (u,t) ~\text{and}~ (u^\ast,t) \in \Omega.
$$
If $f(u,t)$ is differentiable with respect to $u$ in $\Omega$, i.e. the Jacobian $f_u = \partial f / \partial u$ exists, and is bounded then we can say
$$
L = \max_{(u,t) \in \Omega} |f_u(u,t)|.
$$
We can use this bound since
$$
f(u,t) = f(u^\ast, t) + f_u(v,t)(u-u^\ast)
$$
for some $v$ chosen to be in-between $u$ and $u^\ast$ which is effectively the Taylor series error bound and implies smoothness of $f$.
With Lipshitz continuity of $f$ we can guarantee a unique solution the IVP at least to time $T = \min(t_1, t_0 + a/S)$ where
$$
S = \max_{(u,t)\in\Omega} |f(u,t)|.
$$
This value $S$ is the modulus of the maximum slope that the solution $u(t)$ can obtain in $\Omega$ and guarantees that we remain in $\Omega$.
#### Example
Consider $u'(t) = (u(t))^2, u(0) = u_0 > 0$. If we define our domain of interest as above we can compute the Lipshitz constant as
$$
L = \max_{(u,t) \in \Omega} | 2 u | = 2 (u_0 + a)
$$
where we have used the restriction from $\Omega$ that $|u - u_0| \leq a$.
Similarly we can compute $S$ to find
$$
S = \max_{(u,t)\in\Omega} |f(u,t)| = (u_0 + a)^2
$$
so that we can guarantee a unique solution up until $T = a / (u_0 + a)^2$. Given that we can choose $a$ we can simply choose a value that maximized $T$, in this case $a = u_0$ does this and we conclude that we have a unique solution up until $T = 1 / 4 u_0$.
Since we also know the exact solution to the ODE above,
$$
u(t) = \frac{1}{1/u_0 - t},
$$
we can see that $|u(t)| < \infty$ as long as $t \neq 1/u_0$. Note that once we reach the pole in the denominator there is no longer a solution possible for the IVP past this point.
#### Example
Consider the IVP
$$
u' = \sqrt{u} \quad \quad u(0) = 0.
$$
Where is this $f$ Lipshitz continuous?
Computing the derivative we find
$$
f_u = \frac{1}{2\sqrt{u}}
$$
which goes to infinity as $u \rightarrow 0$. We can therefore not guarantee a unique solution near the given initial condition. In fact we know this as the ODE has two solutions
$$
u(t) = 0 \quad \text{and} \quad u(t) = \frac{1}{4} t^2.
$$
### Systems of Equations
A similar notion for Lipschitz continuity exists in a particular norm $||\cdot||$ if there is a constant $L$ such that
$$
||f(u,t) - f(u^\ast,t)|| \leq L ||u - u^\ast||
$$
for all $(u,t)$ and $(u^\ast,t)$ in the domain $\Omega = \{(u,t) : ||u-u_0|| \leq a, t_0 \leq t \leq t_1 \}$. Note that if the function $f$ is Lipschitz continuous in one norm it is continuous in any norm.
## Basic Stepping Schemes
Looking back at our work on numerical differentiation why not approximate the derivative as a finite difference:
$$
\frac{u(t + \Delta t) - u(t)}{\Delta t} = f(t, u)
$$
We still need to decide how to evaluate the $f(t, u)$ term however.
Lets look at this from a perspective of quadrature, take the integral of both sides:
$$\begin{aligned}
\int^{t + \Delta t}_t \frac{\text{d} u}{\text{d}\tilde{t}} d\tilde{t} &= \int^{t + \Delta t}_t f(t, u) d\tilde{t} \\ ~ \\
u(t + \Delta t) - u(t) &= \Delta t ~f(t, u(t)) \\ ~ \\
\frac{u(t + \Delta t) - u(t)}{\Delta t} &= f(t, u(t))
\end{aligned}$$
where we have used a left-sided quadrature rule for the integral on the right.
Introducing some notation to simplify things
$$
t_0 = 0 \quad \quad t_1 = t_0 + \Delta t \quad \quad t_n = t_{n-1} + \Delta t = n \Delta t + t_0
$$
$$
U^0 = u(t_0) \quad \quad U^1 = u(t_1) \quad \quad U^n = u(t_n)
$$
we can rewrite our scheme as
$$
\frac{U^{n+1} - U^n}{\Delta t} = f(t_n, U^n)
$$
or
$$
U^{n+1} = U^n + \Delta t f(t_n, U^n)
$$
which is known as the *forward Euler method*. In essence we are approximating the derivative with the value of the function at the point we are at $t_n$.
```
t = numpy.linspace(0.0, 1.6e3, 100)
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, c_0 * numpy.exp(-decay_constant * t), label="True Solution")
# Plot Euler step
dt = 1e3
u_np = c_0 + dt * (-decay_constant * c_0)
axes.plot((0.0, dt), (c_0, u_np), 'k')
axes.plot((dt, dt), (u_np, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, 0.0), (c_0, u_np), 'k--')
axes.plot((0.0, dt), (u_np, u_np), 'k--')
axes.text(400, u_np - 0.05, '$\Delta t$', fontsize=16)
axes.set_title("Radioactive Decay with $t_{1/2} = 1600$ years")
axes.set_xlabel('t (years)')
axes.set_ylabel('$c$')
axes.set_xlim(-1e2, 1.6e3)
axes.set_ylim((0.5,1.0))
plt.show()
```
Note where we expect error due to the approximation and how it manifests in the example below.
```
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
f = lambda t, u: -decay_constant * u
t_exact = numpy.linspace(0.0, 1.6e3, 100)
u_exact = c_0 * numpy.exp(-decay_constant * t_exact)
# Implement Euler
t = numpy.linspace(0.0, 1.6e3, 10)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
U[0] = c_0
for (n, t_n) in enumerate(t[:-1]):
U[n + 1] = U[n] + delta_t * f(t_n, U[n])
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, U, 'or', label="Euler")
axes.plot(t_exact, u_exact, 'k--', label="True Solution")
axes.set_title("Forward Euler")
axes.set_xlabel("t (years)")
axes.set_xlabel("$c(t)$")
axes.set_ylim((0.4,1.1))
axes.legend()
plt.show()
```
A similar method can be derived if we consider instead using the second order accurate central difference:
$$\frac{U^{n+1} - U^{n-1}}{2\Delta t} = f(t_{n}, U^{n})$$
this method is known as the leap-frog method. Note that the way we have written this method requires a previous function evaluation and technically is a "multi-step" method although we do not actually use the current evaluation.
```
t = numpy.linspace(0.0, 1.6e3, 100)
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, c_0 * numpy.exp(-decay_constant * t), label="True Solution")
# Plot Leap-Frog step
dt = 1e3
u_np = c_0 + dt * (-decay_constant * c_0 * numpy.exp(-decay_constant * dt / 2.0))
axes.plot((0.0, dt), (c_0, u_np), 'k')
axes.plot((dt, dt), (u_np, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, 0.0), (c_0, u_np), 'k--')
axes.plot((0.0, dt), (u_np, u_np), 'k--')
axes.text(400, u_np - 0.05, '$\Delta t$', fontsize=16)
axes.set_title("Radioactive Decay with $t_{1/2} = 1600$ years")
axes.set_xlabel('t (years)')
axes.set_ylabel('$c$')
axes.set_xlim(-1e2, 1.6e3)
axes.set_ylim((0.5,1.0))
plt.show()
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
f = lambda t, u: -decay_constant * u
t_exact = numpy.linspace(0.0, 1.6e3, 100)
u_exact = c_0 * numpy.exp(-decay_constant * t_exact)
# Implement leap-frog
t = numpy.linspace(0.0, 1.6e3, 10)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
U[0] = c_0
# First evaluation use Euler to get us going
U[1] = U[0] + delta_t * f(t[0], U[0])
for n in range(1, t.shape[0] - 1):
U[n + 1] = U[n - 1] + 2.0 * delta_t * f(t[n], U[n])
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, U, 'or', label="Leap-Frog")
axes.plot(t_exact, u_exact, 'k--', label="True Solution")
axes.set_title("Leap-Frog")
axes.set_xlabel("t (years)")
axes.set_xlabel("$c(t)$")
axes.set_ylim((0.4,1.1))
axes.legend()
plt.show()
```
Similar to forward Euler is the *backward Euler* method which evaluates the function $f$ at the updated time (right hand quadrature rule) so that
$$
U^{n+1} = U^n + \Delta t f(t_{n+1}, U^{n+1}).
$$
Schemes where the function $f$ is evaluated at the unknown time are called *implicit methods*.
```
t = numpy.linspace(0.0, 1.6e3, 100)
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, c_0 * numpy.exp(-decay_constant * t), label="True Solution")
# Plot Euler step
dt = 1e3
u_np = c_0 + dt * (-decay_constant * c_0 * numpy.exp(-decay_constant * dt))
axes.plot((0.0, dt), (c_0, u_np), 'k')
axes.plot((dt, dt), (u_np, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, 0.0), (c_0, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, dt), (c_0 * numpy.exp(-decay_constant * dt), c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.text(400, u_np - 0.05, '$\Delta t$', fontsize=16)
axes.set_title("Radioactive Decay with $t_{1/2} = 1600$ years")
axes.set_xlabel('t (years)')
axes.set_ylabel('$c$')
axes.set_xlim(-1e2, 1.6e3)
axes.set_ylim((0.5,1.0))
plt.show()
```
Write code that implements the backward Euler method
$$
U^{n+1} = U^n + \Delta t f(t_{n+1}, U^{n+1}).
$$
Note in the following what bias the error tends to have and relate this back to the approximation.
```
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
f = lambda t, u: -decay_constant * u
t_exact = numpy.linspace(0.0, 1.6e3, 100)
u_exact = c_0 * numpy.exp(-decay_constant * t_exact)
# Implement backwards Euler
t = numpy.linspace(0.0, 1.6e3, 10)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
U[0] = c_0
for n in range(0, t.shape[0] - 1):
U[n + 1] = U[n] / (1.0 + decay_constant * delta_t)
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, U, 'or', label="Backwards Euler")
axes.plot(t_exact, u_exact, 'k--', label="True Solution")
axes.set_title("Backwards Euler")
axes.set_xlabel("t (years)")
axes.set_xlabel("$c(t)$")
axes.set_ylim((0.4,1.1))
axes.legend()
plt.show()
```
A modification on the Euler methods involves using the approximated midpoint to evaluate $f(t, u)$ called the midpoint method. The scheme is
$$
\frac{U^{n+1} - U^{n}}{\Delta t} = f\left(\frac{U^n + U^{n+1}}{2} \right).
$$
This is the simplest example of a *symplectic integrator* which has special properties for integrating Hamiltonian systems.
```
t = numpy.linspace(0.0, 1.6e3, 100)
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, c_0 * numpy.exp(-decay_constant * t), label="True Solution")
# Plot Midpoint step
dt = 1e3
u_np = c_0 * (1.0 - decay_constant * dt / 2.0) / (1.0 + decay_constant * dt / 2.0)
axes.plot((0.0, dt), (c_0, u_np), 'k')
axes.plot((dt, dt), (u_np, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, 0.0), (c_0, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, dt), (c_0 * numpy.exp(-decay_constant * dt), c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.text(400, u_np - 0.05, '$\Delta t$', fontsize=16)
axes.set_title("Radioactive Decay with $t_{1/2} = 1600$ years")
axes.set_xlabel('t (years)')
axes.set_ylabel('$c$')
axes.set_xlim(-1e2, 1.6e3)
axes.set_ylim((0.5,1.0))
plt.show()
```
Implement the midpoint method
$$
\frac{U^{n+1} - U^{n}}{\Delta t} = f\left(\frac{U^n + U^{n+1}}{2} \right).
$$
```
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
f = lambda t, u: -decay_constant * u
t_exact = numpy.linspace(0.0, 1.6e3, 100)
u_exact = c_0 * numpy.exp(-decay_constant * t_exact)
# Implement midpoint
t = numpy.linspace(0.0, 1.6e3, 10)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
U[0] = c_0
integration_constant = (1.0 - decay_constant * delta_t / 2.0) / (1.0 + decay_constant * delta_t / 2.0)
for n in range(0, t.shape[0] - 1):
U[n + 1] = U[n] * integration_constant
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, U, 'or', label="Midpoint Method")
axes.plot(t_exact, u_exact, 'k--', label="True Solution")
axes.set_title("Midpoint Method")
axes.set_xlabel("t (years)")
axes.set_xlabel("$c(t)$")
axes.set_ylim((0.4,1.1))
axes.legend()
plt.show()
```
Another simple implicit method is based on integration using the trapezoidal method. The scheme is
$$
\frac{U^{n+1} - U^{n}}{\Delta t} = \frac{1}{2} (f(U^n) + f(U^{n+1}))
$$
```
t = numpy.linspace(0.0, 1.6e3, 100)
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, c_0 * numpy.exp(-decay_constant * t), label="True Solution")
# Plot Trapezoidal step
dt = 1e3
u_np = c_0 * (1.0 - decay_constant * dt / 2.0) / (1.0 + decay_constant * dt / 2.0)
axes.plot((0.0, dt), (c_0, u_np), 'k')
axes.plot((dt, dt), (u_np, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, 0.0), (c_0, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, dt), (c_0 * numpy.exp(-decay_constant * dt), c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.text(400, u_np - 0.05, '$\Delta t$', fontsize=16)
axes.set_title("Radioactive Decay with $t_{1/2} = 1600$ years")
axes.set_xlabel('t (years)')
axes.set_ylabel('$c$')
axes.set_xlim(-1e2, 1.6e3)
axes.set_ylim((0.5,1.0))
plt.show()
```
Again implement the trapezoidal method
$$
\frac{U^{n+1} - U^{n}}{\Delta t} = \frac{1}{2} (f(U^n) + f(U^{n+1}))
$$
What is this method equivalent to and why? Is this generally true?
```
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
t_exact = numpy.linspace(0.0, 1.6e3, 100)
u_exact = c_0 * numpy.exp(-decay_constant * t_exact)
# Implement trapezoidal method
t = numpy.linspace(0.0, 1.6e3, 10)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
U[0] = c_0
integration_constant = (1.0 - decay_constant * delta_t / 2.0) / (1.0 + decay_constant * delta_t / 2.0)
for n in range(t.shape[0] - 1):
U[n + 1] = U[n] * integration_constant
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, U, 'or', label="Trapezoidal")
axes.plot(t_exact, u_exact, 'k--', label="True Solution")
axes.set_title("Trapezoidal")
axes.set_xlabel("t (years)")
axes.set_xlabel("$c(t)$")
axes.set_ylim((0.4,1.1))
axes.legend()
plt.show()
```
## Error Analysis
### Truncation Errors
We can define truncation errors the same as we did before where we insert the true solution of the ODE into the difference equation and use Taylor series expansions. It is important that at this juncture we use the form of the difference that models the derivative directly as otherwise we will find something different.
Define the finite difference approximation to the derivative as $D(U^{n+1}, U^n, U^{n-1}, \ldots)$ and write the schemes above as
$$
D(U^{n+1}, U^n, U^{n-1}, \ldots) = F(t^{n+1}, t^n, t^{n-1}, \ldots, U^{n+1}, U^n, U^{n-1}, \ldots)
$$
where $F(\cdot)$ now has some relation to evaluations of the function $f(t, u)$. Then the local truncation error can be defined as
$$
\tau^n = D(u(t^{n+1}), u(t^n), u(t^{n-1}), \ldots) - F(t^{n+1}, t^n, t^{n-1}, \ldots, u(t^{n+1}), u(t^n), u(t^{n-1}), \ldots)
$$
Similarly if we know
$$
\lim_{\Delta t \rightarrow 0} \tau^n = 0
$$
then the discretized equation is considered consistent.
Order of accuracy is also defined the same way as before. If
$$
|| \tau || \leq C \Delta t^p
$$
uniformly on $t \in [0, T]$ then the discretization is $p$th order accurate. Note that a method is consistent if $p > 0$.
### Error Analysis of Forward Euler
We can analyze the error and convergence order of forward Euler by considering the Taylor series centered at $t_n$:
$$
u(t) = u(t_n) + (t - t_n) u'(t_n) + \frac{u''(t_n)}{2} (t - t_n)^2 + \mathcal{O}((t-t_n)^3)
$$
Try to compute the LTE for forward Euler's method.
Evaluating this series at $t_{n+1}$ gives
$$\begin{aligned}
u(t_{n+1}) &= u(t_n) + (t_{n+1} - t_n) u'(t_n) + \frac{u''(t_n)}{2} (t_{n+1} - t_n)^2 + \mathcal{O}((t_{n+1}-t_n)^3)\\
&=u(t_n) + \Delta t f(t_n, u(t_n)) + \frac{u''(t_n)}{2} \Delta t^2 + \mathcal{O}(\Delta t^3)
\end{aligned}$$
From the definition of truncation error we can use our Taylor series expression and find the truncation error to be
$$\begin{aligned}
\tau^n &= \frac{u(t_{n+1}) - u(t_n)}{\Delta t} - f(t_n, u(t_n)) \\
&= \frac{1}{\Delta t} \left [u(t_n) + \Delta t ~ f(t_n, u(t_n)) + \frac{u''(t_n)}{2} \Delta t^2 + \mathcal{O}(\Delta t^3) - u(t_n) - \Delta t ~ f(t_n, u(t_n)) \right ]\\
&= \frac{1}{\Delta t} \left [ \frac{u''(t_n)}{2} \Delta t^2 + \mathcal{O}(\Delta t^3) \right ] \\
&= \frac{u''(t_n)}{2} \Delta t + \mathcal{O}(\Delta t^2)
\end{aligned}$$
This implies that forwar Euler is first order accurate and therefore consistent.
### Error Analysis of Leap-Frog Method
To easily analyze this method we will expand the Taylor series from before to another order and evaluate at both the needed positions:
$$
u(t) = u(t_n) + (t - t_n) u'(t_n) + (t - t_n)^2 \frac{u''(t_n)}{2} + (t - t_n)^3 \frac{u'''(t_n)}{6} + \mathcal{O}((t-t_n)^4)
$$
leading to
$$\begin{aligned}
u(t_{n+1}) &= u(t_n) + \Delta t f_n + \Delta t^2 \frac{u''(t_n)}{2} + \Delta t^3 \frac{u'''(t_n)}{6} + \mathcal{O}(\Delta t^4)\\
u(t_{n-1}) &= u(t_n) - \Delta t f_n + \Delta t^2 \frac{u''(t_n)}{2} - \Delta t^3 \frac{u'''(t_n)}{6} + \mathcal{O}(\Delta t^4)
\end{aligned}$$
See if you can compute the LTE in this case.
Plugging this into our definition of the truncation error along with the leap-frog method definition leads to
$$\begin{aligned}
\tau^n &= \frac{u(t_{n+1}) - u(t_{n-1})}{2 \Delta t} - f(t_n, u(t_n)) \\
&=\frac{1}{\Delta t} \left[\frac{1}{2}\left( u(t_n) + \Delta t f_n + \Delta t^2 \frac{u''(t_n)}{2} + \Delta t^3 \frac{u'''(t_n)}{6} + \mathcal{O}(\Delta t^4)\right) \right . \\
&\quad \quad\left . - \frac{1}{2} \left ( u(t_n) - \Delta t f_n + \Delta t^2 \frac{u''(t_n)}{2} - \Delta t^3 \frac{u'''(t_n)}{6} + \mathcal{O}(\Delta t^4)\right ) - \Delta t~ f(t_n, u(t_n)) \right ] \\
&= \frac{1}{\Delta t} \left [\Delta t^3 \frac{u'''(t_n)}{6} + \mathcal{O}(\Delta t^5)\right ] \\
&= \Delta t^2 \frac{u'''(t_n)}{6} + \mathcal{O}(\Delta t^4)
\end{aligned}$$
Therefore the method is second order accurate and is consistent.
```
# Compare accuracy between Euler and Leap-Frog
f = lambda t, u: -u
u_exact = lambda t: numpy.exp(-t)
u_0 = 1.0
t_f = 10.0
num_steps = [2**n for n in range(4,10)]
delta_t = numpy.empty(len(num_steps))
error = numpy.empty((5, len(num_steps)))
for (i, N) in enumerate(num_steps):
t = numpy.linspace(0, t_f, N)
delta_t[i] = t[1] - t[0]
# Note that in the cases below we can instantiate this array now
# rather than every time as none of the implicit methods require
# the space to store the future solution
U = numpy.empty(t.shape)
# Compute ForwardEuler solution
U[0] = u_0
for n in range(t.shape[0] - 1):
U[n+1] = U[n] + delta_t[i] * f(t[n], U[n])
error[0, i] = numpy.linalg.norm(delta_t[i] * (U - u_exact(t)), ord=1)
# Compute Leap-Frog
U[0] = u_0
U[1] = U[0] + delta_t[i] * f(t[0], U[0])
for n in range(1, t.shape[0] - 1):
U[n+1] = U[n-1] + 2.0 * delta_t[i] * f(t[n], U[n])
error[1, i] = numpy.linalg.norm(delta_t[i] * (U - u_exact(t)), ord=1)
# Compute Backward Euler
U[0] = u_0
for n in range(0, t.shape[0] - 1):
U[n + 1] = U[n] / (1.0 + delta_t[i])
error[2, i] = numpy.linalg.norm(delta_t[i] * (U - u_exact(t)), ord=1)
# Compute mid-pointU[0] = c_0
U[0] = u_0
integration_constant = (1.0 - delta_t[i] / 2.0) / (1.0 + delta_t[i] / 2.0)
for n in range(0, t.shape[0] - 1):
U[n + 1] = U[n] * integration_constant
error[3, i] = numpy.linalg.norm(delta_t[i] * (U - u_exact(t)), ord=1)
# Compute trapezoidal
U[0] = u_0
integration_constant = (1.0 - delta_t[i] / 2.0) / (1.0 + delta_t[i] / 2.0)
for n in range(t.shape[0] - 1):
U[n + 1] = U[n] * integration_constant
error[4, i] = numpy.linalg.norm(delta_t[i] * (U - u_exact(t)), ord=1)
# Plot error vs. delta_t
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
order_C = lambda delta_x, error, order: numpy.exp(numpy.log(error) - order * numpy.log(delta_x))
style = ['bo', 'go', 'ro', 'cs', 'yo']
label = ['Forward Euler', "Leap-Frog", "Backward Euler", "Mid-Point", "Trapezoidal"]
order = [1, 2, 1, 2, 2]
for k in range(5):
axes.loglog(delta_t, error[k, :], style[k], label=label[k])
axes.loglog(delta_t, order_C(delta_t[2], error[k, 2], order[k]) * delta_t**order[k], 'k--')
# axes.legend(loc=2)
axes.set_title("Comparison of Errors")
axes.set_xlabel("$\Delta t$")
axes.set_ylabel("$|U(t_f) - u(t_f)|$")
plt.show()
```
### One-Step Errors
There is another definition of local truncation error sometimes used in ODE numerical methods called the *one-step error* which is slightly different than our local truncation error definition. Our definition uses the direct discretization of the derivatives to find the LTE where as this alternative bases the error on a form that looks like it is updating the previous value.
As an example consider the leap-frog method, the LTE we found before was based on
$$
\frac{U_{n+1} - U_{n-1}}{2 \Delta t} = f(U_n)
$$
leading us to a second order LTE.
For the one-step error we consider instead
$$
U_{n+1} = U_{n-1} + 2 \Delta t f(U_n)
$$
which leads to the one-step error $\mathcal{O}(\Delta t^3)$ instead!
$$\begin{aligned}
\mathcal{L}^n &= u(t_{n+1}) - u(t_{n-1}) - 2 \Delta t f(u(t_n)) \\
&= \frac{1}{3} \Delta t^3 u'''(t_n) + \mathcal{O}(\Delta t^5) \\
&= 2 ~\Delta t ~\tau^n.
\end{aligned}$$
This one-step error is suggestively named to indicate that perhaps this is the error for one time step where as the global error may be higher. To remain consistent with our previous discussion of convergences we will continue to use our previous definition of the LTE. We will show that with the appropriate definition of stability and a $p$ order LTE we can expect a $p$th order global error. In general for a $p+1$th order one-step error the global error will be $p$th order.
## Taylor Series Methods
A **Taylor series method** can be derived by direct substitution of the right-hand-side function $f(t, u)$ and it's appropriate derivatives into the Taylor series expansion for $u(t_{n+1})$. For a $p$th order method we would look at the Taylor series up to that order and replace all the derivatives of $u$ with derivatives of $f$ instead.
For the general case we have
$$\begin{aligned}
u(t_{n+1}) = u(t_n) + \Delta t u'(t_n) + \frac{\Delta t^2}{2} u''(t_n) + \frac{\Delta t^3}{6} u'''(t_n) + \cdots + \frac{\Delta t^p}{p!} u^{(p)}(t_n)
\end{aligned}$$
which contains derivatives of $u$ up to $p$th order. We then replace these derivatives with the appropriate derivative of $f$ which will always be one less than the derivative of $u$ (due to the original ODE)
$$
u^{(p)}(t_n) = f^{(p-1)}(t_n, u(t_n))
$$
leading to the method
$$
u(t_{n+1}) = u(t_n) + \Delta t f(t_n, u(t_n)) + \frac{\Delta t^2}{2} f'(t_n, u(t_n)) + \frac{\Delta t^3}{6} f''(t_n, u(t_n)) + \cdots + \frac{\Delta t^p}{p!} f^{(p-1)}(t_n, u(t_n)).
$$
The drawback to these methods is that we have to derive a new one each time we have a new $f$ and we also need $p-1$ derivatives of $f$.
### 2nd Order Taylor Series Method
We want terms up to second order so we need to take the derivative of $u' = f(t, u)$ once to find $u'' = f'(t, u)$. See if you can derive the method.
\begin{align*}
u(t_{n+1}) &= u(t_n) + \Delta t u'(t_n) + \frac{\Delta t^2}{2} u''(t_n) \\
&=u(t_n) + \Delta t f(t_n, u(t_n)) + \frac{\Delta t^2}{2} f'(t_n, u(t_n)) \quad \text{or} \\
U^{n+1} &= U^n + \Delta t f(t_n, U^n) + \frac{\Delta t^2}{2} f'(t_n, U^n).
\end{align*}
## Runge-Kutta Methods
One way to derive higher-order ODE solvers is by computing intermediate stages. These are not *multi-step* methods as they still only require information from the current time step but they raise the order of accuracy by adding *stages*. These types of methods are called **Runge-Kutta** methods.
### Example: Two-stage Runge-Kutta Methods
The basic idea behind the simplest of the Runge-Kutta methods is to approximate the solution at $t_n + \Delta t / 2$ via Euler's method and use this in the function evaluation for the final update.
$$\begin{aligned}
U^* &= U^n + \frac{1}{2} \Delta t f(U^n) \\
U^{n+1} &= U^n + \Delta t f(U^*) = U^n + \Delta t f(U^n + \frac{1}{2} \Delta t f(U^n))
\end{aligned}$$
The truncation error can be computed similarly to how we did so before but we do need to figure out how to compute the derivative inside of the function. Note that due to
$$
f(u(t_n)) = u'(t_n)
$$
that differentiating this leads to
$$
f'(u(t_n)) u'(t_n) = u''(t_n)
$$
leading to
$$\begin{aligned}
f\left(u(t_n) + \frac{1}{2} \Delta t f(u(t_n)) \right ) &= f\left(u(t_n) +\frac{1}{2} \Delta t u'(t_n) \right ) \\
&= f(u(t_n)) + \frac{1}{2} \Delta t u'(t_n) f'(u(t_n)) + \frac{1}{8} \Delta t^2 (u'(t_n))^2 f''(u(t_n)) + \mathcal{O}(\Delta t^3) \\
&=u'(t_n) + \frac{1}{2} \Delta t u''(t_n) + \mathcal{O}(\Delta t^2)
\end{aligned}$$
Going back to the truncation error we have
$$\begin{aligned}
\tau^n &= \frac{1}{\Delta t} \left[u(t_n) + \Delta t f\left(u(t_n) + \frac{1}{2} \Delta t f(u(t_n))\right) - \left(u(t_n) + \Delta t f(t_n, u(t_n)) + \frac{u''(t_n)}{2} \Delta t^2 + \mathcal{O}(\Delta t^3) \right ) \right] \\
&=\frac{1}{\Delta t} \left[\Delta t u'(t_n) + \frac{1}{2} \Delta t^2 u''(t_n) + \mathcal{O}(\Delta t^3) - \Delta t u'(t_n) - \frac{u''(t_n)}{2} \Delta t^2 + \mathcal{O}(\Delta t^3) \right] \\
&= \mathcal{O}(\Delta t^2)
\end{aligned}$$
so this method is second order accurate.
### Example: 4-stage Runge-Kutta Method
$\begin{aligned}
Y_1 &= U^n \\
Y_2 &= U^n + \frac{1}{2} \Delta t f(Y_1, t_n) \\
Y_3 &= U^n + \frac{1}{2} \Delta t f(Y_2, t_n + \Delta t / 2) \\
Y_4 &= U^n + \Delta t f(Y_3, t_n + \Delta t / 2) \\
U^{n+1} &= U^n + \frac{\Delta t}{6} \left [f(Y_1, t_n) + 2 f(Y_2, t_n + \Delta t / 2) + 2 f(Y_3, t_n + \Delta t/2) + f(Y_4, t_n + \Delta t) \right ]
\end{aligned}$
```
# Implement and compare the two-stage and 4-stage Runge-Kutta methods
f = lambda t, u: -u
t_exact = numpy.linspace(0.0, 10.0, 100)
u_exact = numpy.exp(-t_exact)
N = 10
t = numpy.linspace(0, 10.0, N)
delta_t = t[1] - t[0]
# RK 2
U_2 = numpy.empty(t.shape)
U_2[0] = 1.0
for (n, t_n) in enumerate(t[1:]):
U_2[n+1] = U_2[n] + 0.5 * delta_t * f(t_n, U_2[n])
U_2[n+1] = U_2[n] + delta_t * f(t_n + 0.5 * delta_t, U_2[n+1])
# RK4
U_4 = numpy.empty(t.shape)
U_4[0] = 1.0
for (n, t_n) in enumerate(t[1:]):
y_1 = U_4[n]
y_2 = U_4[n] + 0.5 * delta_t * f(t_n, y_1)
y_3 = U_4[n] + 0.5 * delta_t * f(t_n + 0.5 * delta_t, y_2)
y_4 = U_4[n] + delta_t * f(t_n + 0.5 * delta_t, y_3)
U_4[n+1] = U_4[n] + delta_t / 6.0 * (f(t_n, y_1) + 2.0 * f(t_n + 0.5 * delta_t, y_2) + 2.0 * f(t_n + 0.5 * delta_t, y_3) + f(t_n + delta_t, y_4))
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t_exact, u_exact, 'k', label="True")
axes.plot(t, U_2, 'ro', label="2-Stage")
axes.plot(t, U_4, 'bo', label="4-Stage")
axes.legend(loc=1)
plt.show()
# Compare accuracy between Euler and RK
f = lambda t, u: -u
u_exact = lambda t: numpy.exp(-t)
t_f = 10.0
num_steps = [2**n for n in range(5,12)]
delta_t = numpy.empty(len(num_steps))
error_euler = numpy.empty(len(num_steps))
error_2 = numpy.empty(len(num_steps))
error_4 = numpy.empty(len(num_steps))
for (i, N) in enumerate(num_steps):
t = numpy.linspace(0, t_f, N)
delta_t[i] = t[1] - t[0]
# Compute Euler solution
U_euler = numpy.empty(t.shape)
U_euler[0] = 1.0
for (n, t_n) in enumerate(t[1:]):
U_euler[n+1] = U_euler[n] + delta_t[i] * f(t_n, U_euler[n])
# Compute 2 and 4-stage
U_2 = numpy.empty(t.shape)
U_4 = numpy.empty(t.shape)
U_2[0] = 1.0
U_4[0] = 1.0
for (n, t_n) in enumerate(t[1:]):
U_2[n+1] = U_2[n] + 0.5 * delta_t[i] * f(t_n, U_2[n])
U_2[n+1] = U_2[n] + delta_t[i] * f(t_n, U_2[n+1])
y_1 = U_4[n]
y_2 = U_4[n] + 0.5 * delta_t[i] * f(t_n, y_1)
y_3 = U_4[n] + 0.5 * delta_t[i] * f(t_n + 0.5 * delta_t[i], y_2)
y_4 = U_4[n] + delta_t[i] * f(t_n + 0.5 * delta_t[i], y_3)
U_4[n+1] = U_4[n] + delta_t[i] / 6.0 * (f(t_n, y_1) + 2.0 * f(t_n + 0.5 * delta_t[i], y_2) + 2.0 * f(t_n + 0.5 * delta_t[i], y_3) + f(t_n + delta_t[i], y_4))
# Compute error for each
error_euler[i] = numpy.abs(U_euler[-1] - u_exact(t_f)) / numpy.abs(u_exact(t_f))
error_2[i] = numpy.abs(U_2[-1] - u_exact(t_f)) / numpy.abs(u_exact(t_f))
error_4[i] = numpy.abs(U_4[-1] - u_exact(t_f)) / numpy.abs(u_exact(t_f))
# Plot error vs. delta_t
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.loglog(delta_t, error_euler, 'bo', label='Forward Euler')
axes.loglog(delta_t, error_2, 'ro', label='2-stage')
axes.loglog(delta_t, error_4, 'go', label="4-stage")
order_C = lambda delta_x, error, order: numpy.exp(numpy.log(error) - order * numpy.log(delta_x))
axes.loglog(delta_t, order_C(delta_t[1], error_euler[1], 1.0) * delta_t**1.0, '--b')
axes.loglog(delta_t, order_C(delta_t[1], error_2[1], 2.0) * delta_t**2.0, '--r')
axes.loglog(delta_t, order_C(delta_t[1], error_4[1], 4.0) * delta_t**4.0, '--g')
axes.legend(loc=4)
axes.set_title("Comparison of Errors")
axes.set_xlabel("$\Delta t$")
axes.set_ylabel("$|U(t_f) - u(t_f)|$")
plt.show()
```
## Linear Multi-Step Methods
Multi-step methods (as introduced via the leap-frog method) are ODE methods that require multiple time step evaluations to work. Some of the advanatages of using a multi-step method rather than one-step method included
- Taylor series methods require differentiating the given equation which can be cumbersome and difficult to impelent
- One-step methods at higher order often require the evaluation of the function $f$ many times
Disadvantages
- Methods are not self-starting, i.e. they require other methods to find the initial values
- The time step $\Delta t$ in one-step methods can be changed at any time while multi-step methods this is much more complex
### General Linear Multi-Step Methods
All linear multi-step methods can be written as the linear combination of past, present and future solutions:
$$
\sum^r_{j=0} \alpha_j U^{n+j} = \Delta t \sum^r_{j=0} \beta_j f(U^{n+j}, t_{n+j})
$$
If $\beta_r = 0$ then the method is explicit (only requires previous time steps). Note that the coefficients are not unique as we can multiply both sides by a constant. In practice a normalization of $\alpha_r = 1$ is used.
#### Example: Adams Methods
$$
U^{n+r} = U^{n+r-1} + \Delta t \sum^r_{j=0} \beta_j f(U^{n+j})
$$
All these methods have $\alpha_r = 1$, $\alpha_{r-1} = -1$ and $\alpha_j=0$ for $j < r - 1$ leaving the method to be specified by how the evaluations of $f$ is done determining the $\beta_j$.
### Adams-Bashforth Methods
The **Adams-Bashforth** methods are explicit solvers that maximize the order of accuracy given a number of steps $r$. This is accomplished by looking at the Taylor series and picking the coefficients $\beta_j$ to elliminate as many terms in the Taylor series as possible.
$$\begin{aligned}
\text{1-step:} & & U_{n+1} &= U_n +\Delta t f(U_n) \\
\text{2-step:} & & U_{n+2} &= U_{n+1} + \frac{\Delta t}{2} (-f(U_n) + 3 f(U_{n+1})) \\
\text{3-step:} & & U_{n+3} &= U_{n+2} + \frac{\Delta t}{12} (5 f(U_n) - 16 f(U_{n+1}) + 23 f(U_{n+2})) \\
\text{4-step:} & & U_{n+4} &= U_{n+3} + \frac{\Delta t}{24} (-9 f(U_n) + 37 f(U_{n+1}) -59 f(U_{n+2}) + 55 f(U_{n+3}))
\end{aligned}$$
```
# Use 2-step Adams-Bashforth to compute solution
f = lambda t, u: -u
t_exact = numpy.linspace(0.0, 10.0, 100)
u_exact = numpy.exp(-t_exact)
N = 50
t = numpy.linspace(0, 10.0, N)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
# Use RK-2 to start the method
U[0] = 1.0
U[1] = U[0] + 0.5 * delta_t * f(t[0], U[0])
U[1] = U[0] + delta_t * f(t[0], U[1])
for n in range(0,len(t)-2):
U[n+2] = U[n + 1] + delta_t / 2.0 * (-f(t[n], U[n]) + 3.0 * f(t[n+1], U[n+1]))
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t_exact, u_exact, 'k', label="True")
axes.plot(t, U, 'ro', label="2-step A-B")
axes.set_title("Adams-Bashforth Method")
axes.set_xlabel("t")
axes.set_xlabel("u(t)")
axes.legend(loc=1)
plt.show()
```
### Adams-Moulton Methods
The **Adams-Moulton** methods are the implicit versions of the Adams-Bashforth methods. Since this gives one additional parameter to use $\beta_r$ these methods are generally one order of accuracy greater than their counterparts.
$$\begin{aligned}
\text{1-step:} & & U_{n+1} &= U_n + \frac{\Delta t}{2} (f(U_n) + f(U_{n+1})) \\
\text{2-step:} & & U_{n+2} &= U_{n+1} + \frac{\Delta t}{12} (-f(U_n) + 8f(U_{n+1}) + 5f(U_{n+2})) \\
\text{3-step:} & & U_{n+3} &= U_{n+2} + \frac{\Delta t}{24} (f(U_n) - 5f(U_{n+1}) + 19f(U_{n+2}) + 9f(U_{n+3})) \\
\text{4-step:} & & U_{n+4} &= U_{n+3} + \frac{\Delta t}{720}(-19 f(U_n) + 106 f(U_{n+1}) -264 f(U_{n+2}) + 646 f(U_{n+3}) + 251 f(U_{n+4}))
\end{aligned}$$
```
# Use 2-step Adams-Moulton to compute solution
# u' = - decay u
decay_constant = 1.0
f = lambda t, u: -decay_constant * u
t_exact = numpy.linspace(0.0, 10.0, 100)
u_exact = numpy.exp(-t_exact)
N = 20
t = numpy.linspace(0, 10.0, N)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
U[0] = 1.0
U[1] = U[0] + 0.5 * delta_t * f(t[0], U[0])
U[1] = U[0] + delta_t * f(t[0], U[1])
integration_constant = 1.0 / (1.0 + 5.0 * decay_constant * delta_t / 12.0)
for n in range(t.shape[0] - 2):
U[n+2] = (U[n+1] + decay_constant * delta_t / 12.0 * (U[n] - 8.0 * U[n+1])) * integration_constant
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t_exact, u_exact, 'k', label="True")
axes.plot(t, U, 'ro', label="2-step A-M")
axes.set_title("Adams-Moulton Method")
axes.set_xlabel("t")
axes.set_xlabel("u(t)")
axes.legend(loc=1)
plt.show()
```
### Truncation Error for Multi-Step Methods
We can again find the truncation error in general for linear multi-step methods:
$$\begin{aligned}
\tau^n &= \frac{1}{\Delta t} \left [\sum^r_{j=0} \alpha_j u(t_{n+j}) - \Delta t \sum^r_{j=0} \beta_j f(t_{n+j}, u(t_{n+j})) \right ]
\end{aligned}$$
Using the general expansion and evalution of the Taylor series about $t_n$ we have
$$\begin{aligned}
u(t_{n+j}) &= u(t_n) + j \Delta t u'(t_n) + \frac{1}{2} (j \Delta t)^2 u''(t_n) + \mathcal{O}(\Delta t^3) \\
u'(t_{n+j}) &= u'(t_n) + j \Delta t u''(t_n) + \frac{1}{2} (j \Delta t)^2 u'''(t_n) + \mathcal{O}(\Delta t^3)
\end{aligned}$$
leading to
$$\begin{aligned}
\tau^n &= \frac{1}{\Delta t}\left( \sum^r_{j=0} \alpha_j\right) u(t_{n}) + \left(\sum^r_{j=0} (j\alpha_j - \beta_j)\right) u'(t_n) + \Delta t \left(\sum^r_{j=0} \left (\frac{1}{2}j^2 \alpha_j - j \beta_j \right) \right) u''(t_n) \\
&\quad \quad + \cdots + \Delta t^{q - 1} \left (\frac{1}{q!} \left(j^q \alpha_j - \frac{1}{(q-1)!} j^{q-1} \beta_j \right) \right) u^{(q)}(t_n) + \cdots
\end{aligned}$$
The method is *consistent* if the first two terms of the expansion vanish, i.e.
$$
\sum^r_{j=0} \alpha_j = 0
$$
and
$$
\sum^r_{j=0} j \alpha_j = \sum^r_{j=0} \beta_j.
$$
```
# Compare accuracy between RK-2, AB-2 and AM-2
f = lambda t, u: -u
u_exact = lambda t: numpy.exp(-t)
t_f = 10.0
num_steps = [2**n for n in range(4,10)]
delta_t = numpy.empty(len(num_steps))
error_rk = numpy.empty(len(num_steps))
error_ab = numpy.empty(len(num_steps))
error_am = numpy.empty(len(num_steps))
for (i, N) in enumerate(num_steps):
t = numpy.linspace(0, t_f, N)
delta_t[i] = t[1] - t[0]
# Compute RK2
U_rk = numpy.empty(t.shape)
U_rk[0] = 1.0
for n in range(t.shape[0]-1):
U_rk[n+1] = U_rk[n] + 0.5 * delta_t[i] * f(t[n], U_rk[n])
U_rk[n+1] = U_rk[n] + delta_t[i] * f(t[n], U_rk[n+1])
# Compute Adams-Bashforth 2-stage
U_ab = numpy.empty(t.shape)
U_ab[:2] = U_rk[:2]
for n in range(t.shape[0] - 2):
U_ab[n+2] = U_ab[n + 1] + delta_t[i] / 2.0 * (-f(t[n], U_ab[n]) + 3.0 * f(t[n+1], U_ab[n+1]))
# Compute Adama-Moulton 2-stage
U_am = numpy.empty(t.shape)
U_am[:2] = U_rk[:2]
decay_constant = 1.0
integration_constant = 1.0 / (1.0 + 5.0 * decay_constant * delta_t[i] / 12.0)
for n in range(t.shape[0] - 2):
U_am[n+2] = (U_am[n+1] + decay_constant * delta_t[i] / 12.0 * (U_am[n] - 8.0 * U_am[n+1])) * integration_constant
# Compute error for each
error_rk[i] = numpy.linalg.norm(delta_t[i] * (U_rk - u_exact(t)), ord=1)
error_ab[i] = numpy.linalg.norm(delta_t[i] * (U_ab - u_exact(t)), ord=1)
error_am[i] = numpy.linalg.norm(delta_t[i] * (U_am - u_exact(t)), ord=1)
# Plot error vs. delta_t
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.loglog(delta_t, error_rk, 'bo', label='RK-2')
axes.loglog(delta_t, error_ab, 'ro', label='AB-2')
axes.loglog(delta_t, error_am, 'go', label="AM-2")
order_C = lambda delta_x, error, order: numpy.exp(numpy.log(error) - order * numpy.log(delta_x))
axes.loglog(delta_t, order_C(delta_t[1], error_rk[1], 2.0) * delta_t**2.0, '--r')
axes.loglog(delta_t, order_C(delta_t[1], error_ab[1], 2.0) * delta_t**2.0, '--r')
axes.loglog(delta_t, order_C(delta_t[1], error_am[1], 3.0) * delta_t**3.0, '--g')
axes.legend(loc=4)
axes.set_title("Comparison of Errors")
axes.set_xlabel("$\Delta t$")
axes.set_ylabel("$|U(t) - u(t)|$")
plt.show()
```
### Predictor-Corrector Methods
One way to simplify the Adams-Moulton methods so that implicit evaluations are not needed is by estimating the required implicit function evaluations with an explicit method. These are often called **predictor-corrector** methods as the explicit method provides a *prediction* of what the solution might be and the not explicit *corrector* step works to make that estimate more accurate.
#### Example: One-Step Adams-Bashforth-Moulton
Use the One-step Adams-Bashforth method to predict the value of $U^{n+1}$ and then use the Adams-Moulton method to correct that value:
$\hat{U}^{n+1} = U^n + \Delta t f(U^n)$
$U^{n+1} = U^n + \frac{1}{2} \Delta t (f(U^n) + f(\hat{U}^{n+1})$
This method is second order accurate.
```
# One-step Adams-Bashforth-Moulton
f = lambda t, u: -u
t_exact = numpy.linspace(0.0, 10.0, 100)
u_exact = numpy.exp(-t_exact)
N = 100
t = numpy.linspace(0, 10.0, N)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
U[0] = 1.0
for n in range(t.shape[0] - 1):
U[n+1] = U[n] + delta_t * f(t[n], U[n])
U[n+1] = U[n] + 0.5 * delta_t * (f(t[n], U[n]) + f(t[n+1], U[n+1]))
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t_exact, u_exact, 'k', label="True")
axes.plot(t, U, 'ro', label="2-step A-B")
axes.set_title("Adams-Bashforth-Moulton P/C Method")
axes.set_xlabel("t")
axes.set_xlabel("u(t)")
axes.legend(loc=1)
plt.show()
# Compare accuracy between RK-2, AB-2 and AM-2
f = lambda t, u: -u
u_exact = lambda t: numpy.exp(-t)
t_f = 10.0
num_steps = [2**n for n in range(4,10)]
delta_t = numpy.empty(len(num_steps))
error_ab = numpy.empty(len(num_steps))
error_am = numpy.empty(len(num_steps))
error_pc = numpy.empty(len(num_steps))
for (i, N) in enumerate(num_steps):
t = numpy.linspace(0, t_f, N)
delta_t[i] = t[1] - t[0]
# RK-2 bootstrap for AB and AM
U_rk = numpy.empty(2)
U_rk[0] = 1.0
U_rk[1] = U_rk[0] + 0.5 * delta_t[i] * f(t[0], U_rk[0])
U_rk[1] = U_rk[0] + delta_t[i] * f(t[0], U_rk[1])
# Compute Adams-Bashforth 2-stage
U_ab = numpy.empty(t.shape)
U_ab[:2] = U_rk[:2]
for n in range(t.shape[0] - 2):
U_ab[n+2] = U_ab[n + 1] + delta_t[i] / 2.0 * (-f(t[n], U_ab[n]) + 3.0 * f(t[n+1], U_ab[n+1]))
# Compute Adams-Moulton 2-stage
U_am = numpy.empty(t.shape)
U_am[:2] = U_ab[:2]
decay_constant = 1.0
integration_constant = 1.0 / (1.0 + 5.0 * decay_constant * delta_t[i] / 12.0)
for n in range(t.shape[0] - 2):
U_am[n+2] = (U_am[n+1] + decay_constant * delta_t[i] / 12.0 * (U_am[n] - 8.0 * U_am[n+1])) * integration_constant
# Compute Adams-Bashforth-Moulton
U_pc = numpy.empty(t.shape)
U_pc[0] = 1.0
for n in range(t.shape[0] - 1):
U_pc[n+1] = U_pc[n] + delta_t[i] * f(t[n], U_pc[n])
U_pc[n+1] = U_pc[n] + 0.5 * delta_t[i] * (f(t[n], U_pc[n]) + f(t[n+1], U_pc[n+1]))
# Compute error for each
error_ab[i] = numpy.linalg.norm(delta_t[i] * (U_ab - u_exact(t)), ord=1)
error_am[i] = numpy.linalg.norm(delta_t[i] * (U_am - u_exact(t)), ord=1)
error_pc[i] = numpy.linalg.norm(delta_t[i] * (U_pc - u_exact(t)), ord=1)
# Plot error vs. delta_t
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.loglog(delta_t, error_pc, 'bo', label='PC')
axes.loglog(delta_t, error_ab, 'ro', label='AB-2')
axes.loglog(delta_t, error_am, 'go', label="AM-2")
order_C = lambda delta_x, error, order: numpy.exp(numpy.log(error) - order * numpy.log(delta_x))
axes.loglog(delta_t, order_C(delta_t[1], error_pc[1], 2.0) * delta_t**2.0, '--b')
axes.loglog(delta_t, order_C(delta_t[1], error_ab[1], 2.0) * delta_t**2.0, '--r')
axes.loglog(delta_t, order_C(delta_t[1], error_am[1], 3.0) * delta_t**3.0, '--g')
axes.legend(loc=4)
axes.set_title("Comparison of Errors")
axes.set_xlabel("$\Delta t$")
axes.set_ylabel("$|U(t) - u(t)|$")
plt.show()
```
|
github_jupyter
|
from __future__ import print_function
%matplotlib inline
import numpy
import matplotlib.pyplot as plt
t = numpy.linspace(0.0, 1.6e3, 100)
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, 1.0 * numpy.exp(-decay_constant * t))
axes.set_title("Radioactive Decay with $t_{1/2} = 1600$ years")
axes.set_xlabel('t (years)')
axes.set_ylabel('$c$')
axes.set_ylim((0.5,1.0))
plt.show()
import scipy.integrate as integrate
def f(t, u, mu=5):
return numpy.array([u[1], mu * (1.0 - u[0]**2) * u[1] - u[0]])
t = numpy.linspace(0.0, 100, 1000)
u = numpy.empty((2, t.shape[0]))
u[:, 0] = [0.1, 0.0]
integrator = integrate.ode(f)
integrator.set_integrator("dopri5")
integrator.set_initial_value(u[:, 0])
for (n, t_n) in enumerate(t[1:]):
integrator.integrate(t_n)
if not integrator.successful():
break
u[:, n + 1] = integrator.y
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, u[0,:])
axes.set_title("Solution to Van der Pol Oscillator")
axes.set_xlabel("t")
axes.set_ylabel("y(t)")
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(u[0,:], u[1, :])
axes.set_title("Phase Diagram for Van der Pol Oscillator")
axes.set_xlabel("y(t)")
axes.set_ylabel("y'(t)")
plt.show()
t = numpy.linspace(0.0, 1.6e3, 100)
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, c_0 * numpy.exp(-decay_constant * t), label="True Solution")
# Plot Euler step
dt = 1e3
u_np = c_0 + dt * (-decay_constant * c_0)
axes.plot((0.0, dt), (c_0, u_np), 'k')
axes.plot((dt, dt), (u_np, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, 0.0), (c_0, u_np), 'k--')
axes.plot((0.0, dt), (u_np, u_np), 'k--')
axes.text(400, u_np - 0.05, '$\Delta t$', fontsize=16)
axes.set_title("Radioactive Decay with $t_{1/2} = 1600$ years")
axes.set_xlabel('t (years)')
axes.set_ylabel('$c$')
axes.set_xlim(-1e2, 1.6e3)
axes.set_ylim((0.5,1.0))
plt.show()
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
f = lambda t, u: -decay_constant * u
t_exact = numpy.linspace(0.0, 1.6e3, 100)
u_exact = c_0 * numpy.exp(-decay_constant * t_exact)
# Implement Euler
t = numpy.linspace(0.0, 1.6e3, 10)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
U[0] = c_0
for (n, t_n) in enumerate(t[:-1]):
U[n + 1] = U[n] + delta_t * f(t_n, U[n])
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, U, 'or', label="Euler")
axes.plot(t_exact, u_exact, 'k--', label="True Solution")
axes.set_title("Forward Euler")
axes.set_xlabel("t (years)")
axes.set_xlabel("$c(t)$")
axes.set_ylim((0.4,1.1))
axes.legend()
plt.show()
t = numpy.linspace(0.0, 1.6e3, 100)
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, c_0 * numpy.exp(-decay_constant * t), label="True Solution")
# Plot Leap-Frog step
dt = 1e3
u_np = c_0 + dt * (-decay_constant * c_0 * numpy.exp(-decay_constant * dt / 2.0))
axes.plot((0.0, dt), (c_0, u_np), 'k')
axes.plot((dt, dt), (u_np, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, 0.0), (c_0, u_np), 'k--')
axes.plot((0.0, dt), (u_np, u_np), 'k--')
axes.text(400, u_np - 0.05, '$\Delta t$', fontsize=16)
axes.set_title("Radioactive Decay with $t_{1/2} = 1600$ years")
axes.set_xlabel('t (years)')
axes.set_ylabel('$c$')
axes.set_xlim(-1e2, 1.6e3)
axes.set_ylim((0.5,1.0))
plt.show()
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
f = lambda t, u: -decay_constant * u
t_exact = numpy.linspace(0.0, 1.6e3, 100)
u_exact = c_0 * numpy.exp(-decay_constant * t_exact)
# Implement leap-frog
t = numpy.linspace(0.0, 1.6e3, 10)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
U[0] = c_0
# First evaluation use Euler to get us going
U[1] = U[0] + delta_t * f(t[0], U[0])
for n in range(1, t.shape[0] - 1):
U[n + 1] = U[n - 1] + 2.0 * delta_t * f(t[n], U[n])
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, U, 'or', label="Leap-Frog")
axes.plot(t_exact, u_exact, 'k--', label="True Solution")
axes.set_title("Leap-Frog")
axes.set_xlabel("t (years)")
axes.set_xlabel("$c(t)$")
axes.set_ylim((0.4,1.1))
axes.legend()
plt.show()
t = numpy.linspace(0.0, 1.6e3, 100)
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, c_0 * numpy.exp(-decay_constant * t), label="True Solution")
# Plot Euler step
dt = 1e3
u_np = c_0 + dt * (-decay_constant * c_0 * numpy.exp(-decay_constant * dt))
axes.plot((0.0, dt), (c_0, u_np), 'k')
axes.plot((dt, dt), (u_np, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, 0.0), (c_0, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, dt), (c_0 * numpy.exp(-decay_constant * dt), c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.text(400, u_np - 0.05, '$\Delta t$', fontsize=16)
axes.set_title("Radioactive Decay with $t_{1/2} = 1600$ years")
axes.set_xlabel('t (years)')
axes.set_ylabel('$c$')
axes.set_xlim(-1e2, 1.6e3)
axes.set_ylim((0.5,1.0))
plt.show()
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
f = lambda t, u: -decay_constant * u
t_exact = numpy.linspace(0.0, 1.6e3, 100)
u_exact = c_0 * numpy.exp(-decay_constant * t_exact)
# Implement backwards Euler
t = numpy.linspace(0.0, 1.6e3, 10)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
U[0] = c_0
for n in range(0, t.shape[0] - 1):
U[n + 1] = U[n] / (1.0 + decay_constant * delta_t)
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, U, 'or', label="Backwards Euler")
axes.plot(t_exact, u_exact, 'k--', label="True Solution")
axes.set_title("Backwards Euler")
axes.set_xlabel("t (years)")
axes.set_xlabel("$c(t)$")
axes.set_ylim((0.4,1.1))
axes.legend()
plt.show()
t = numpy.linspace(0.0, 1.6e3, 100)
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, c_0 * numpy.exp(-decay_constant * t), label="True Solution")
# Plot Midpoint step
dt = 1e3
u_np = c_0 * (1.0 - decay_constant * dt / 2.0) / (1.0 + decay_constant * dt / 2.0)
axes.plot((0.0, dt), (c_0, u_np), 'k')
axes.plot((dt, dt), (u_np, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, 0.0), (c_0, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, dt), (c_0 * numpy.exp(-decay_constant * dt), c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.text(400, u_np - 0.05, '$\Delta t$', fontsize=16)
axes.set_title("Radioactive Decay with $t_{1/2} = 1600$ years")
axes.set_xlabel('t (years)')
axes.set_ylabel('$c$')
axes.set_xlim(-1e2, 1.6e3)
axes.set_ylim((0.5,1.0))
plt.show()
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
f = lambda t, u: -decay_constant * u
t_exact = numpy.linspace(0.0, 1.6e3, 100)
u_exact = c_0 * numpy.exp(-decay_constant * t_exact)
# Implement midpoint
t = numpy.linspace(0.0, 1.6e3, 10)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
U[0] = c_0
integration_constant = (1.0 - decay_constant * delta_t / 2.0) / (1.0 + decay_constant * delta_t / 2.0)
for n in range(0, t.shape[0] - 1):
U[n + 1] = U[n] * integration_constant
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, U, 'or', label="Midpoint Method")
axes.plot(t_exact, u_exact, 'k--', label="True Solution")
axes.set_title("Midpoint Method")
axes.set_xlabel("t (years)")
axes.set_xlabel("$c(t)$")
axes.set_ylim((0.4,1.1))
axes.legend()
plt.show()
t = numpy.linspace(0.0, 1.6e3, 100)
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, c_0 * numpy.exp(-decay_constant * t), label="True Solution")
# Plot Trapezoidal step
dt = 1e3
u_np = c_0 * (1.0 - decay_constant * dt / 2.0) / (1.0 + decay_constant * dt / 2.0)
axes.plot((0.0, dt), (c_0, u_np), 'k')
axes.plot((dt, dt), (u_np, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, 0.0), (c_0, c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.plot((0.0, dt), (c_0 * numpy.exp(-decay_constant * dt), c_0 * numpy.exp(-decay_constant * dt)), 'k--')
axes.text(400, u_np - 0.05, '$\Delta t$', fontsize=16)
axes.set_title("Radioactive Decay with $t_{1/2} = 1600$ years")
axes.set_xlabel('t (years)')
axes.set_ylabel('$c$')
axes.set_xlim(-1e2, 1.6e3)
axes.set_ylim((0.5,1.0))
plt.show()
c_0 = 1.0
decay_constant = numpy.log(2.0) / 1600.0
t_exact = numpy.linspace(0.0, 1.6e3, 100)
u_exact = c_0 * numpy.exp(-decay_constant * t_exact)
# Implement trapezoidal method
t = numpy.linspace(0.0, 1.6e3, 10)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
U[0] = c_0
integration_constant = (1.0 - decay_constant * delta_t / 2.0) / (1.0 + decay_constant * delta_t / 2.0)
for n in range(t.shape[0] - 1):
U[n + 1] = U[n] * integration_constant
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t, U, 'or', label="Trapezoidal")
axes.plot(t_exact, u_exact, 'k--', label="True Solution")
axes.set_title("Trapezoidal")
axes.set_xlabel("t (years)")
axes.set_xlabel("$c(t)$")
axes.set_ylim((0.4,1.1))
axes.legend()
plt.show()
# Compare accuracy between Euler and Leap-Frog
f = lambda t, u: -u
u_exact = lambda t: numpy.exp(-t)
u_0 = 1.0
t_f = 10.0
num_steps = [2**n for n in range(4,10)]
delta_t = numpy.empty(len(num_steps))
error = numpy.empty((5, len(num_steps)))
for (i, N) in enumerate(num_steps):
t = numpy.linspace(0, t_f, N)
delta_t[i] = t[1] - t[0]
# Note that in the cases below we can instantiate this array now
# rather than every time as none of the implicit methods require
# the space to store the future solution
U = numpy.empty(t.shape)
# Compute ForwardEuler solution
U[0] = u_0
for n in range(t.shape[0] - 1):
U[n+1] = U[n] + delta_t[i] * f(t[n], U[n])
error[0, i] = numpy.linalg.norm(delta_t[i] * (U - u_exact(t)), ord=1)
# Compute Leap-Frog
U[0] = u_0
U[1] = U[0] + delta_t[i] * f(t[0], U[0])
for n in range(1, t.shape[0] - 1):
U[n+1] = U[n-1] + 2.0 * delta_t[i] * f(t[n], U[n])
error[1, i] = numpy.linalg.norm(delta_t[i] * (U - u_exact(t)), ord=1)
# Compute Backward Euler
U[0] = u_0
for n in range(0, t.shape[0] - 1):
U[n + 1] = U[n] / (1.0 + delta_t[i])
error[2, i] = numpy.linalg.norm(delta_t[i] * (U - u_exact(t)), ord=1)
# Compute mid-pointU[0] = c_0
U[0] = u_0
integration_constant = (1.0 - delta_t[i] / 2.0) / (1.0 + delta_t[i] / 2.0)
for n in range(0, t.shape[0] - 1):
U[n + 1] = U[n] * integration_constant
error[3, i] = numpy.linalg.norm(delta_t[i] * (U - u_exact(t)), ord=1)
# Compute trapezoidal
U[0] = u_0
integration_constant = (1.0 - delta_t[i] / 2.0) / (1.0 + delta_t[i] / 2.0)
for n in range(t.shape[0] - 1):
U[n + 1] = U[n] * integration_constant
error[4, i] = numpy.linalg.norm(delta_t[i] * (U - u_exact(t)), ord=1)
# Plot error vs. delta_t
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
order_C = lambda delta_x, error, order: numpy.exp(numpy.log(error) - order * numpy.log(delta_x))
style = ['bo', 'go', 'ro', 'cs', 'yo']
label = ['Forward Euler', "Leap-Frog", "Backward Euler", "Mid-Point", "Trapezoidal"]
order = [1, 2, 1, 2, 2]
for k in range(5):
axes.loglog(delta_t, error[k, :], style[k], label=label[k])
axes.loglog(delta_t, order_C(delta_t[2], error[k, 2], order[k]) * delta_t**order[k], 'k--')
# axes.legend(loc=2)
axes.set_title("Comparison of Errors")
axes.set_xlabel("$\Delta t$")
axes.set_ylabel("$|U(t_f) - u(t_f)|$")
plt.show()
# Implement and compare the two-stage and 4-stage Runge-Kutta methods
f = lambda t, u: -u
t_exact = numpy.linspace(0.0, 10.0, 100)
u_exact = numpy.exp(-t_exact)
N = 10
t = numpy.linspace(0, 10.0, N)
delta_t = t[1] - t[0]
# RK 2
U_2 = numpy.empty(t.shape)
U_2[0] = 1.0
for (n, t_n) in enumerate(t[1:]):
U_2[n+1] = U_2[n] + 0.5 * delta_t * f(t_n, U_2[n])
U_2[n+1] = U_2[n] + delta_t * f(t_n + 0.5 * delta_t, U_2[n+1])
# RK4
U_4 = numpy.empty(t.shape)
U_4[0] = 1.0
for (n, t_n) in enumerate(t[1:]):
y_1 = U_4[n]
y_2 = U_4[n] + 0.5 * delta_t * f(t_n, y_1)
y_3 = U_4[n] + 0.5 * delta_t * f(t_n + 0.5 * delta_t, y_2)
y_4 = U_4[n] + delta_t * f(t_n + 0.5 * delta_t, y_3)
U_4[n+1] = U_4[n] + delta_t / 6.0 * (f(t_n, y_1) + 2.0 * f(t_n + 0.5 * delta_t, y_2) + 2.0 * f(t_n + 0.5 * delta_t, y_3) + f(t_n + delta_t, y_4))
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t_exact, u_exact, 'k', label="True")
axes.plot(t, U_2, 'ro', label="2-Stage")
axes.plot(t, U_4, 'bo', label="4-Stage")
axes.legend(loc=1)
plt.show()
# Compare accuracy between Euler and RK
f = lambda t, u: -u
u_exact = lambda t: numpy.exp(-t)
t_f = 10.0
num_steps = [2**n for n in range(5,12)]
delta_t = numpy.empty(len(num_steps))
error_euler = numpy.empty(len(num_steps))
error_2 = numpy.empty(len(num_steps))
error_4 = numpy.empty(len(num_steps))
for (i, N) in enumerate(num_steps):
t = numpy.linspace(0, t_f, N)
delta_t[i] = t[1] - t[0]
# Compute Euler solution
U_euler = numpy.empty(t.shape)
U_euler[0] = 1.0
for (n, t_n) in enumerate(t[1:]):
U_euler[n+1] = U_euler[n] + delta_t[i] * f(t_n, U_euler[n])
# Compute 2 and 4-stage
U_2 = numpy.empty(t.shape)
U_4 = numpy.empty(t.shape)
U_2[0] = 1.0
U_4[0] = 1.0
for (n, t_n) in enumerate(t[1:]):
U_2[n+1] = U_2[n] + 0.5 * delta_t[i] * f(t_n, U_2[n])
U_2[n+1] = U_2[n] + delta_t[i] * f(t_n, U_2[n+1])
y_1 = U_4[n]
y_2 = U_4[n] + 0.5 * delta_t[i] * f(t_n, y_1)
y_3 = U_4[n] + 0.5 * delta_t[i] * f(t_n + 0.5 * delta_t[i], y_2)
y_4 = U_4[n] + delta_t[i] * f(t_n + 0.5 * delta_t[i], y_3)
U_4[n+1] = U_4[n] + delta_t[i] / 6.0 * (f(t_n, y_1) + 2.0 * f(t_n + 0.5 * delta_t[i], y_2) + 2.0 * f(t_n + 0.5 * delta_t[i], y_3) + f(t_n + delta_t[i], y_4))
# Compute error for each
error_euler[i] = numpy.abs(U_euler[-1] - u_exact(t_f)) / numpy.abs(u_exact(t_f))
error_2[i] = numpy.abs(U_2[-1] - u_exact(t_f)) / numpy.abs(u_exact(t_f))
error_4[i] = numpy.abs(U_4[-1] - u_exact(t_f)) / numpy.abs(u_exact(t_f))
# Plot error vs. delta_t
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.loglog(delta_t, error_euler, 'bo', label='Forward Euler')
axes.loglog(delta_t, error_2, 'ro', label='2-stage')
axes.loglog(delta_t, error_4, 'go', label="4-stage")
order_C = lambda delta_x, error, order: numpy.exp(numpy.log(error) - order * numpy.log(delta_x))
axes.loglog(delta_t, order_C(delta_t[1], error_euler[1], 1.0) * delta_t**1.0, '--b')
axes.loglog(delta_t, order_C(delta_t[1], error_2[1], 2.0) * delta_t**2.0, '--r')
axes.loglog(delta_t, order_C(delta_t[1], error_4[1], 4.0) * delta_t**4.0, '--g')
axes.legend(loc=4)
axes.set_title("Comparison of Errors")
axes.set_xlabel("$\Delta t$")
axes.set_ylabel("$|U(t_f) - u(t_f)|$")
plt.show()
# Use 2-step Adams-Bashforth to compute solution
f = lambda t, u: -u
t_exact = numpy.linspace(0.0, 10.0, 100)
u_exact = numpy.exp(-t_exact)
N = 50
t = numpy.linspace(0, 10.0, N)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
# Use RK-2 to start the method
U[0] = 1.0
U[1] = U[0] + 0.5 * delta_t * f(t[0], U[0])
U[1] = U[0] + delta_t * f(t[0], U[1])
for n in range(0,len(t)-2):
U[n+2] = U[n + 1] + delta_t / 2.0 * (-f(t[n], U[n]) + 3.0 * f(t[n+1], U[n+1]))
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t_exact, u_exact, 'k', label="True")
axes.plot(t, U, 'ro', label="2-step A-B")
axes.set_title("Adams-Bashforth Method")
axes.set_xlabel("t")
axes.set_xlabel("u(t)")
axes.legend(loc=1)
plt.show()
# Use 2-step Adams-Moulton to compute solution
# u' = - decay u
decay_constant = 1.0
f = lambda t, u: -decay_constant * u
t_exact = numpy.linspace(0.0, 10.0, 100)
u_exact = numpy.exp(-t_exact)
N = 20
t = numpy.linspace(0, 10.0, N)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
U[0] = 1.0
U[1] = U[0] + 0.5 * delta_t * f(t[0], U[0])
U[1] = U[0] + delta_t * f(t[0], U[1])
integration_constant = 1.0 / (1.0 + 5.0 * decay_constant * delta_t / 12.0)
for n in range(t.shape[0] - 2):
U[n+2] = (U[n+1] + decay_constant * delta_t / 12.0 * (U[n] - 8.0 * U[n+1])) * integration_constant
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t_exact, u_exact, 'k', label="True")
axes.plot(t, U, 'ro', label="2-step A-M")
axes.set_title("Adams-Moulton Method")
axes.set_xlabel("t")
axes.set_xlabel("u(t)")
axes.legend(loc=1)
plt.show()
# Compare accuracy between RK-2, AB-2 and AM-2
f = lambda t, u: -u
u_exact = lambda t: numpy.exp(-t)
t_f = 10.0
num_steps = [2**n for n in range(4,10)]
delta_t = numpy.empty(len(num_steps))
error_rk = numpy.empty(len(num_steps))
error_ab = numpy.empty(len(num_steps))
error_am = numpy.empty(len(num_steps))
for (i, N) in enumerate(num_steps):
t = numpy.linspace(0, t_f, N)
delta_t[i] = t[1] - t[0]
# Compute RK2
U_rk = numpy.empty(t.shape)
U_rk[0] = 1.0
for n in range(t.shape[0]-1):
U_rk[n+1] = U_rk[n] + 0.5 * delta_t[i] * f(t[n], U_rk[n])
U_rk[n+1] = U_rk[n] + delta_t[i] * f(t[n], U_rk[n+1])
# Compute Adams-Bashforth 2-stage
U_ab = numpy.empty(t.shape)
U_ab[:2] = U_rk[:2]
for n in range(t.shape[0] - 2):
U_ab[n+2] = U_ab[n + 1] + delta_t[i] / 2.0 * (-f(t[n], U_ab[n]) + 3.0 * f(t[n+1], U_ab[n+1]))
# Compute Adama-Moulton 2-stage
U_am = numpy.empty(t.shape)
U_am[:2] = U_rk[:2]
decay_constant = 1.0
integration_constant = 1.0 / (1.0 + 5.0 * decay_constant * delta_t[i] / 12.0)
for n in range(t.shape[0] - 2):
U_am[n+2] = (U_am[n+1] + decay_constant * delta_t[i] / 12.0 * (U_am[n] - 8.0 * U_am[n+1])) * integration_constant
# Compute error for each
error_rk[i] = numpy.linalg.norm(delta_t[i] * (U_rk - u_exact(t)), ord=1)
error_ab[i] = numpy.linalg.norm(delta_t[i] * (U_ab - u_exact(t)), ord=1)
error_am[i] = numpy.linalg.norm(delta_t[i] * (U_am - u_exact(t)), ord=1)
# Plot error vs. delta_t
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.loglog(delta_t, error_rk, 'bo', label='RK-2')
axes.loglog(delta_t, error_ab, 'ro', label='AB-2')
axes.loglog(delta_t, error_am, 'go', label="AM-2")
order_C = lambda delta_x, error, order: numpy.exp(numpy.log(error) - order * numpy.log(delta_x))
axes.loglog(delta_t, order_C(delta_t[1], error_rk[1], 2.0) * delta_t**2.0, '--r')
axes.loglog(delta_t, order_C(delta_t[1], error_ab[1], 2.0) * delta_t**2.0, '--r')
axes.loglog(delta_t, order_C(delta_t[1], error_am[1], 3.0) * delta_t**3.0, '--g')
axes.legend(loc=4)
axes.set_title("Comparison of Errors")
axes.set_xlabel("$\Delta t$")
axes.set_ylabel("$|U(t) - u(t)|$")
plt.show()
# One-step Adams-Bashforth-Moulton
f = lambda t, u: -u
t_exact = numpy.linspace(0.0, 10.0, 100)
u_exact = numpy.exp(-t_exact)
N = 100
t = numpy.linspace(0, 10.0, N)
delta_t = t[1] - t[0]
U = numpy.empty(t.shape)
U[0] = 1.0
for n in range(t.shape[0] - 1):
U[n+1] = U[n] + delta_t * f(t[n], U[n])
U[n+1] = U[n] + 0.5 * delta_t * (f(t[n], U[n]) + f(t[n+1], U[n+1]))
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(t_exact, u_exact, 'k', label="True")
axes.plot(t, U, 'ro', label="2-step A-B")
axes.set_title("Adams-Bashforth-Moulton P/C Method")
axes.set_xlabel("t")
axes.set_xlabel("u(t)")
axes.legend(loc=1)
plt.show()
# Compare accuracy between RK-2, AB-2 and AM-2
f = lambda t, u: -u
u_exact = lambda t: numpy.exp(-t)
t_f = 10.0
num_steps = [2**n for n in range(4,10)]
delta_t = numpy.empty(len(num_steps))
error_ab = numpy.empty(len(num_steps))
error_am = numpy.empty(len(num_steps))
error_pc = numpy.empty(len(num_steps))
for (i, N) in enumerate(num_steps):
t = numpy.linspace(0, t_f, N)
delta_t[i] = t[1] - t[0]
# RK-2 bootstrap for AB and AM
U_rk = numpy.empty(2)
U_rk[0] = 1.0
U_rk[1] = U_rk[0] + 0.5 * delta_t[i] * f(t[0], U_rk[0])
U_rk[1] = U_rk[0] + delta_t[i] * f(t[0], U_rk[1])
# Compute Adams-Bashforth 2-stage
U_ab = numpy.empty(t.shape)
U_ab[:2] = U_rk[:2]
for n in range(t.shape[0] - 2):
U_ab[n+2] = U_ab[n + 1] + delta_t[i] / 2.0 * (-f(t[n], U_ab[n]) + 3.0 * f(t[n+1], U_ab[n+1]))
# Compute Adams-Moulton 2-stage
U_am = numpy.empty(t.shape)
U_am[:2] = U_ab[:2]
decay_constant = 1.0
integration_constant = 1.0 / (1.0 + 5.0 * decay_constant * delta_t[i] / 12.0)
for n in range(t.shape[0] - 2):
U_am[n+2] = (U_am[n+1] + decay_constant * delta_t[i] / 12.0 * (U_am[n] - 8.0 * U_am[n+1])) * integration_constant
# Compute Adams-Bashforth-Moulton
U_pc = numpy.empty(t.shape)
U_pc[0] = 1.0
for n in range(t.shape[0] - 1):
U_pc[n+1] = U_pc[n] + delta_t[i] * f(t[n], U_pc[n])
U_pc[n+1] = U_pc[n] + 0.5 * delta_t[i] * (f(t[n], U_pc[n]) + f(t[n+1], U_pc[n+1]))
# Compute error for each
error_ab[i] = numpy.linalg.norm(delta_t[i] * (U_ab - u_exact(t)), ord=1)
error_am[i] = numpy.linalg.norm(delta_t[i] * (U_am - u_exact(t)), ord=1)
error_pc[i] = numpy.linalg.norm(delta_t[i] * (U_pc - u_exact(t)), ord=1)
# Plot error vs. delta_t
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.loglog(delta_t, error_pc, 'bo', label='PC')
axes.loglog(delta_t, error_ab, 'ro', label='AB-2')
axes.loglog(delta_t, error_am, 'go', label="AM-2")
order_C = lambda delta_x, error, order: numpy.exp(numpy.log(error) - order * numpy.log(delta_x))
axes.loglog(delta_t, order_C(delta_t[1], error_pc[1], 2.0) * delta_t**2.0, '--b')
axes.loglog(delta_t, order_C(delta_t[1], error_ab[1], 2.0) * delta_t**2.0, '--r')
axes.loglog(delta_t, order_C(delta_t[1], error_am[1], 3.0) * delta_t**3.0, '--g')
axes.legend(loc=4)
axes.set_title("Comparison of Errors")
axes.set_xlabel("$\Delta t$")
axes.set_ylabel("$|U(t) - u(t)|$")
plt.show()
| 0.74826 | 0.987735 |
<!--BOOK_INFORMATION-->
<img align="left" style="width:80px;height:98px;padding-right:20px;" src="https://raw.githubusercontent.com/joe-papa/pytorch-book/main/files/pytorch-book-cover.jpg">
This notebook contains an excerpt from the [PyTorch Pocket Reference](http://pytorchbook.com) book by [Joe Papa](http://joepapa.ai); content is available [on GitHub](https://github.com/joe-papa/pytorch-book).
[](https://colab.research.google.com/github/joe-papa/pytorch-book/blob/main/03_Deep_Learning_Development_with_PyTorch.ipynb)
# Chapter 3 - Deep Learning Development with PyTorch
```
import torch
import torchvision
print(torch.__version__)
# out: 1.7.0+cu101
print(torchvision.__version__)
# out: 0.8.1+cu101
```
## Data Loading
```
from torchvision.datasets import CIFAR10
train_data = CIFAR10(root="./train/",
train=True,
download=True)
# Use tab complete to view attributes and methods
print(train_data)
# out:
# Dataset CIFAR10
# Number of datapoints: 50000
# Root location: ./train/
# Split: Train
print(len(train_data))
# out: 50000
print(train_data.data.shape) # ndarray
# out: (50000, 32, 32, 3)
print(train_data.targets) # list
# out: [6, 9, ..., 1, 1]
print(train_data.classes)
# out: ['airplane', 'automobile', 'bird',
# 'cat', 'deer', 'dog', 'frog',
# 'horse', 'ship', 'truck']
print(train_data.class_to_idx)
# out:
# {'airplane': 0, 'automobile': 1, 'bird': 2,
# 'cat': 3, 'deer': 4, 'dog': 5, 'frog': 6,
# 'horse': 7, 'ship': 8, 'truck': 9}
print(type(train_data[0]))
# out: <class 'tuple'>
print(len(train_data[0]))
# out: 2
data, label = train_data[0]
print(type(data))
# out: <class 'PIL.Image.Image'>
print(data)
# out:
# <PIL.Image.Image image mode=RGB
# size=32x32 at 0x7FA61D6F1748>
import matplotlib.pyplot as plt
plt.imshow(data)
print(type(label))
# out: <class 'int'>
print(label)
# out: 6
print(train_data.classes[label])
# out: frog
test_data = CIFAR10(root="./test/",
train=False,
download=True)
print(test_data)
# out:
# Dataset CIFAR10
# Number of datapoints: 10000
# Root location: ./test/
# Split: Test
print(len(test_data))
# out: 10000
print(test_data.data.shape) # ndarray
# out: (10000, 32, 32, 3)
```
## Data Transforms
```
from torchvision import transforms
train_transforms = transforms.Compose([
transforms.RandomCrop(32, padding=4),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize(
(0.4914, 0.4822, 0.4465),
(0.2023, 0.1994, 0.2010))])
train_data = CIFAR10(root="./train/",
train=True,
download=True,
transform=train_transforms)
print(train_data)
# out:
# Dataset CIFAR10
# Number of datapoints: 50000
# Root location: ./train/
# Split: Train
# StandardTransform
# Transform: Compose(
# RandomCrop(size=(32, 32),
# padding=4)
# RandomHorizontalFlip(p=0.5)
# ToTensor()
# Normalize(
# mean=(0.4914, 0.4822, 0.4465),
# std=(0.2023, 0.1994, 0.201))
# )
print(train_data.transforms)
# out:
# StandardTransform
# Transform: Compose(
# RandomCrop(size=(32, 32),
# padding=4)
# RandomHorizontalFlip(p=0.5)
# ToTensor()
# Normalize(
# mean=(0.4914, 0.4822, 0.4465),
# std=(0.2023, 0.1994, 0.201))
# )
data, label = train_data[0]
print(type(data))
# out: <class 'torch.Tensor'>
print(data.size())
# out: torch.Size([3, 32, 32])
print(data)
# out:
# tensor([[[-0.1416, ..., -2.4291],
# [-0.0060, ..., -2.4291],
# [-0.7426, ..., -2.4291],
# ...,
# [ 0.5100, ..., -2.2214],
# [-2.2214, ..., -2.2214],
# [-2.2214, ..., -2.2214]]])
plt.imshow(data.permute(1, 2, 0))
test_transforms = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(
(0.4914, 0.4822, 0.4465),
(0.2023, 0.1994, 0.2010))])
test_data = torchvision.datasets.CIFAR10(
root="./test/",
train=False,
transform=test_transforms)
print(test_data)
# out:
# Dataset CIFAR10
# Number of datapoints: 10000
# Root location: ./test/
# Split: Test
# StandardTransform
# Transform: Compose(
# ToTensor()
# Normalize(
# mean=(0.4914, 0.4822, 0.4465),
# std=(0.2023, 0.1994, 0.201)))
```
## Data Batching
```
trainloader = torch.utils.data.DataLoader(
train_data,
batch_size=16,
shuffle=True)
data_batch, labels_batch = next(iter(trainloader))
print(data_batch.size())
# out: torch.Size([16, 3, 32, 32])
print(labels_batch.size())
# out: torch.Size([16])
testloader = torch.utils.data.DataLoader(
test_data,
batch_size=16,
shuffle=False)
```
## Model Design
### Using Existing & Pre-trained models
```
from torchvision import models
vgg16 = models.vgg16(pretrained=True)
print(vgg16.classifier)
# out:
# Sequential(
# (0): Linear(in_features=25088,
# out_features=4096, bias=True)
# (1): ReLU(inplace=True)
# (2): Dropout(p=0.5, inplace=False)
# (3): Linear(in_features=4096,
# out_features=4096, bias=True)
# (4): ReLU(inplace=True)
# (5): Dropout(p=0.5, inplace=False)
# (6): Linear(in_features=4096,
# out_features=1000, bias=True)
# )
waveglow = torch.hub.load(
'nvidia/DeepLearningExamples:torchhub',
'nvidia_waveglow')
torch.hub.list('nvidia/DeepLearningExamples:torchhub')
# out:
# ['checkpoint_from_distributed',
# 'nvidia_ncf',
# 'nvidia_ssd',
# 'nvidia_ssd_processing_utils',
# 'nvidia_tacotron2',
# 'nvidia_waveglow',
# 'unwrap_distributed']
```
## The PyTorch NN Module (torch.nn)
```
import torch.nn as nn
import torch.nn.functional as F
class SimpleNet(nn.Module):
def __init__(self):
super(SimpleNet, self).__init__()
self.fc1 = nn.Linear(2048, 256)
self.fc2 = nn.Linear(256, 64)
self.fc3 = nn.Linear(64,2)
def forward(self, x):
x = x.view(-1, 2048)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.softmax(self.fc3(x),dim=1)
return x
simplenet = SimpleNet()
print(simplenet)
# out:
# SimpleNet(
# (fc1): Linear(in_features=2048,
# out_features=256, bias=True)
# (fc2): Linear(in_features=256,
# out_features=64, bias=True)
# (fc3): Linear(in_features=64,
# out_features=2, bias=True)
# )
input = torch.rand(2048)
output = simplenet(input)
```
## Training
```
from torch import nn
import torch.nn.functional as F
class LeNet5(nn.Module):
def __init__(self):
super(LeNet5, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5) # <1>
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = x.view(-1, int(x.nelement() / x.shape[0]))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
device = "cuda" if torch.cuda.is_available() else "cpu"
model = LeNet5().to(device=device)
```
### Fundamental Training Loop
```
from torch import optim
from torch import nn
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), # <1>
lr=0.001,
momentum=0.9)
N_EPOCHS = 10
for epoch in range(N_EPOCHS): # <1>
epoch_loss = 0.0
for inputs, labels in trainloader:
inputs = inputs.to(device) # <2>
labels = labels.to(device)
optimizer.zero_grad() # <3>
outputs = model(inputs) # <4>
loss = criterion(outputs, labels) # <5>
loss.backward() # <6>
optimizer.step() # <7>
epoch_loss += loss.item() # <8>
print("Epoch: {} Loss: {}".format(epoch,
epoch_loss/len(trainloader)))
# out: (results will vary and make take minutes)
# Epoch: 0 Loss: 1.8982970092773437
# Epoch: 1 Loss: 1.6062103009033204
# Epoch: 2 Loss: 1.484384165763855
# Epoch: 3 Loss: 1.3944422281837463
# Epoch: 4 Loss: 1.334191104450226
# Epoch: 5 Loss: 1.2834235876464843
# Epoch: 6 Loss: 1.2407222446250916
# Epoch: 7 Loss: 1.2081411465930938
# Epoch: 8 Loss: 1.1832368299865723
# Epoch: 9 Loss: 1.1534993273162841
```
Code Annotations:
<1> Our training loop
<2> Need to move inputs and labels to GPU is avail.
<3> Zero out gradients before each backprop or they'll accumulate
<4> Forward pass
<5> Compute loss
<6> Backpropagation, compute gradients
<7> Adjust parameters based on gradients
<8> accumulate batch loss so we can average over epoch
## Validation & Testing
### Splitting Training Dataset into Training & Validation Datasets
```
from torch.utils.data import random_split
train_set, val_set = random_split(
train_data,
[40000, 10000])
trainloader = torch.utils.data.DataLoader(
train_set,
batch_size=16,
shuffle=True)
valloader = torch.utils.data.DataLoader(
val_set,
batch_size=16,
shuffle=True)
print(len(trainloader))
# out: 2500
print(len(valloader))
# out: 625
```
### Training Loop with Validation
```
from torch import optim
from torch import nn
model = LeNet5().to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(),
lr=0.001,
momentum=0.9)
N_EPOCHS = 10
for epoch in range(N_EPOCHS):
# Training
train_loss = 0.0
model.train() # <1>
for inputs, labels in trainloader:
inputs = inputs.to(device)
labels = labels.to(device)
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
train_loss += loss.item()
# Validation
val_loss = 0.0
model.eval() # <2>
for inputs, labels in valloader:
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
loss = criterion(outputs, labels)
val_loss += loss.item()
print("Epoch: {} Train Loss: {} Val Loss: {}".format(
epoch,
train_loss/len(trainloader),
val_loss/len(valloader)))
# out: (results may vary and take a few minutes)
# Epoch: 0 Train Loss: 1.9876076080799103 Val Loss: 1.7407869798660278
# Epoch: 1 Train Loss: 1.6497538920879364 Val Loss: 1.5870195521354675
# Epoch: 2 Train Loss: 1.5117236899614335 Val Loss: 1.4355393668174743
# Epoch: 3 Train Loss: 1.408525426363945 Val Loss: 1.3614536597251892
# Epoch: 4 Train Loss: 1.3395055189609528 Val Loss: 1.2934591544151306
# Epoch: 5 Train Loss: 1.290560259628296 Val Loss: 1.245048282814026
# Epoch: 6 Train Loss: 1.2592685657382012 Val Loss: 1.2859896109580993
# Epoch: 7 Train Loss: 1.235161985707283 Val Loss: 1.2538409409046174
# Epoch: 8 Train Loss: 1.2070518508672714 Val Loss: 1.2157000193595886
# Epoch: 9 Train Loss: 1.189215132522583 Val Loss: 1.1833322570323943
```
### Testing Loop
```
num_correct = 0.0
for x_test_batch, y_test_batch in testloader:
model.eval()
y_test_batch = y_test_batch.to(device)
x_test_batch = x_test_batch.to(device)
y_pred_batch = model(x_test_batch)
_, predicted = torch.max(y_pred_batch, 1)
num_correct += (predicted == y_test_batch).float().sum()
accuracy = num_correct/(len(testloader)*testloader.batch_size)
print(len(testloader), testloader.batch_size)
# out: 625 16
print("Test Accuracy: {}".format(accuracy))
# out: Test Accuracy: 0.6322000026702881
```
## Model Deployment
### Saving Models
```
torch.save(model.state_dict(), "./lenet5_model.pt")
model = LeNet5().to(device)
model.load_state_dict(torch.load("./lenet5_model.pt"))
```
### Deploy to PyTorch Hub
```
dependencies = ['torch']
from torchvision.models.vgg import vgg16
dependencies = ['torch']
from torchvision.models.vgg import vgg16 as _vgg16
# vgg16 is the name of entrypoint
def vgg16(pretrained=False, **kwargs):
""" # This docstring shows up in hub.help()
VGG16 model
pretrained (bool): kwargs, load pretrained
weights into the model
"""
# Call the model, load pretrained weights
model = _vgg16(pretrained=pretrained, **kwargs)
return model
```
|
github_jupyter
|
import torch
import torchvision
print(torch.__version__)
# out: 1.7.0+cu101
print(torchvision.__version__)
# out: 0.8.1+cu101
from torchvision.datasets import CIFAR10
train_data = CIFAR10(root="./train/",
train=True,
download=True)
# Use tab complete to view attributes and methods
print(train_data)
# out:
# Dataset CIFAR10
# Number of datapoints: 50000
# Root location: ./train/
# Split: Train
print(len(train_data))
# out: 50000
print(train_data.data.shape) # ndarray
# out: (50000, 32, 32, 3)
print(train_data.targets) # list
# out: [6, 9, ..., 1, 1]
print(train_data.classes)
# out: ['airplane', 'automobile', 'bird',
# 'cat', 'deer', 'dog', 'frog',
# 'horse', 'ship', 'truck']
print(train_data.class_to_idx)
# out:
# {'airplane': 0, 'automobile': 1, 'bird': 2,
# 'cat': 3, 'deer': 4, 'dog': 5, 'frog': 6,
# 'horse': 7, 'ship': 8, 'truck': 9}
print(type(train_data[0]))
# out: <class 'tuple'>
print(len(train_data[0]))
# out: 2
data, label = train_data[0]
print(type(data))
# out: <class 'PIL.Image.Image'>
print(data)
# out:
# <PIL.Image.Image image mode=RGB
# size=32x32 at 0x7FA61D6F1748>
import matplotlib.pyplot as plt
plt.imshow(data)
print(type(label))
# out: <class 'int'>
print(label)
# out: 6
print(train_data.classes[label])
# out: frog
test_data = CIFAR10(root="./test/",
train=False,
download=True)
print(test_data)
# out:
# Dataset CIFAR10
# Number of datapoints: 10000
# Root location: ./test/
# Split: Test
print(len(test_data))
# out: 10000
print(test_data.data.shape) # ndarray
# out: (10000, 32, 32, 3)
from torchvision import transforms
train_transforms = transforms.Compose([
transforms.RandomCrop(32, padding=4),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize(
(0.4914, 0.4822, 0.4465),
(0.2023, 0.1994, 0.2010))])
train_data = CIFAR10(root="./train/",
train=True,
download=True,
transform=train_transforms)
print(train_data)
# out:
# Dataset CIFAR10
# Number of datapoints: 50000
# Root location: ./train/
# Split: Train
# StandardTransform
# Transform: Compose(
# RandomCrop(size=(32, 32),
# padding=4)
# RandomHorizontalFlip(p=0.5)
# ToTensor()
# Normalize(
# mean=(0.4914, 0.4822, 0.4465),
# std=(0.2023, 0.1994, 0.201))
# )
print(train_data.transforms)
# out:
# StandardTransform
# Transform: Compose(
# RandomCrop(size=(32, 32),
# padding=4)
# RandomHorizontalFlip(p=0.5)
# ToTensor()
# Normalize(
# mean=(0.4914, 0.4822, 0.4465),
# std=(0.2023, 0.1994, 0.201))
# )
data, label = train_data[0]
print(type(data))
# out: <class 'torch.Tensor'>
print(data.size())
# out: torch.Size([3, 32, 32])
print(data)
# out:
# tensor([[[-0.1416, ..., -2.4291],
# [-0.0060, ..., -2.4291],
# [-0.7426, ..., -2.4291],
# ...,
# [ 0.5100, ..., -2.2214],
# [-2.2214, ..., -2.2214],
# [-2.2214, ..., -2.2214]]])
plt.imshow(data.permute(1, 2, 0))
test_transforms = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(
(0.4914, 0.4822, 0.4465),
(0.2023, 0.1994, 0.2010))])
test_data = torchvision.datasets.CIFAR10(
root="./test/",
train=False,
transform=test_transforms)
print(test_data)
# out:
# Dataset CIFAR10
# Number of datapoints: 10000
# Root location: ./test/
# Split: Test
# StandardTransform
# Transform: Compose(
# ToTensor()
# Normalize(
# mean=(0.4914, 0.4822, 0.4465),
# std=(0.2023, 0.1994, 0.201)))
trainloader = torch.utils.data.DataLoader(
train_data,
batch_size=16,
shuffle=True)
data_batch, labels_batch = next(iter(trainloader))
print(data_batch.size())
# out: torch.Size([16, 3, 32, 32])
print(labels_batch.size())
# out: torch.Size([16])
testloader = torch.utils.data.DataLoader(
test_data,
batch_size=16,
shuffle=False)
from torchvision import models
vgg16 = models.vgg16(pretrained=True)
print(vgg16.classifier)
# out:
# Sequential(
# (0): Linear(in_features=25088,
# out_features=4096, bias=True)
# (1): ReLU(inplace=True)
# (2): Dropout(p=0.5, inplace=False)
# (3): Linear(in_features=4096,
# out_features=4096, bias=True)
# (4): ReLU(inplace=True)
# (5): Dropout(p=0.5, inplace=False)
# (6): Linear(in_features=4096,
# out_features=1000, bias=True)
# )
waveglow = torch.hub.load(
'nvidia/DeepLearningExamples:torchhub',
'nvidia_waveglow')
torch.hub.list('nvidia/DeepLearningExamples:torchhub')
# out:
# ['checkpoint_from_distributed',
# 'nvidia_ncf',
# 'nvidia_ssd',
# 'nvidia_ssd_processing_utils',
# 'nvidia_tacotron2',
# 'nvidia_waveglow',
# 'unwrap_distributed']
import torch.nn as nn
import torch.nn.functional as F
class SimpleNet(nn.Module):
def __init__(self):
super(SimpleNet, self).__init__()
self.fc1 = nn.Linear(2048, 256)
self.fc2 = nn.Linear(256, 64)
self.fc3 = nn.Linear(64,2)
def forward(self, x):
x = x.view(-1, 2048)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.softmax(self.fc3(x),dim=1)
return x
simplenet = SimpleNet()
print(simplenet)
# out:
# SimpleNet(
# (fc1): Linear(in_features=2048,
# out_features=256, bias=True)
# (fc2): Linear(in_features=256,
# out_features=64, bias=True)
# (fc3): Linear(in_features=64,
# out_features=2, bias=True)
# )
input = torch.rand(2048)
output = simplenet(input)
from torch import nn
import torch.nn.functional as F
class LeNet5(nn.Module):
def __init__(self):
super(LeNet5, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5) # <1>
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = x.view(-1, int(x.nelement() / x.shape[0]))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
device = "cuda" if torch.cuda.is_available() else "cpu"
model = LeNet5().to(device=device)
from torch import optim
from torch import nn
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), # <1>
lr=0.001,
momentum=0.9)
N_EPOCHS = 10
for epoch in range(N_EPOCHS): # <1>
epoch_loss = 0.0
for inputs, labels in trainloader:
inputs = inputs.to(device) # <2>
labels = labels.to(device)
optimizer.zero_grad() # <3>
outputs = model(inputs) # <4>
loss = criterion(outputs, labels) # <5>
loss.backward() # <6>
optimizer.step() # <7>
epoch_loss += loss.item() # <8>
print("Epoch: {} Loss: {}".format(epoch,
epoch_loss/len(trainloader)))
# out: (results will vary and make take minutes)
# Epoch: 0 Loss: 1.8982970092773437
# Epoch: 1 Loss: 1.6062103009033204
# Epoch: 2 Loss: 1.484384165763855
# Epoch: 3 Loss: 1.3944422281837463
# Epoch: 4 Loss: 1.334191104450226
# Epoch: 5 Loss: 1.2834235876464843
# Epoch: 6 Loss: 1.2407222446250916
# Epoch: 7 Loss: 1.2081411465930938
# Epoch: 8 Loss: 1.1832368299865723
# Epoch: 9 Loss: 1.1534993273162841
from torch.utils.data import random_split
train_set, val_set = random_split(
train_data,
[40000, 10000])
trainloader = torch.utils.data.DataLoader(
train_set,
batch_size=16,
shuffle=True)
valloader = torch.utils.data.DataLoader(
val_set,
batch_size=16,
shuffle=True)
print(len(trainloader))
# out: 2500
print(len(valloader))
# out: 625
from torch import optim
from torch import nn
model = LeNet5().to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(),
lr=0.001,
momentum=0.9)
N_EPOCHS = 10
for epoch in range(N_EPOCHS):
# Training
train_loss = 0.0
model.train() # <1>
for inputs, labels in trainloader:
inputs = inputs.to(device)
labels = labels.to(device)
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
train_loss += loss.item()
# Validation
val_loss = 0.0
model.eval() # <2>
for inputs, labels in valloader:
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
loss = criterion(outputs, labels)
val_loss += loss.item()
print("Epoch: {} Train Loss: {} Val Loss: {}".format(
epoch,
train_loss/len(trainloader),
val_loss/len(valloader)))
# out: (results may vary and take a few minutes)
# Epoch: 0 Train Loss: 1.9876076080799103 Val Loss: 1.7407869798660278
# Epoch: 1 Train Loss: 1.6497538920879364 Val Loss: 1.5870195521354675
# Epoch: 2 Train Loss: 1.5117236899614335 Val Loss: 1.4355393668174743
# Epoch: 3 Train Loss: 1.408525426363945 Val Loss: 1.3614536597251892
# Epoch: 4 Train Loss: 1.3395055189609528 Val Loss: 1.2934591544151306
# Epoch: 5 Train Loss: 1.290560259628296 Val Loss: 1.245048282814026
# Epoch: 6 Train Loss: 1.2592685657382012 Val Loss: 1.2859896109580993
# Epoch: 7 Train Loss: 1.235161985707283 Val Loss: 1.2538409409046174
# Epoch: 8 Train Loss: 1.2070518508672714 Val Loss: 1.2157000193595886
# Epoch: 9 Train Loss: 1.189215132522583 Val Loss: 1.1833322570323943
num_correct = 0.0
for x_test_batch, y_test_batch in testloader:
model.eval()
y_test_batch = y_test_batch.to(device)
x_test_batch = x_test_batch.to(device)
y_pred_batch = model(x_test_batch)
_, predicted = torch.max(y_pred_batch, 1)
num_correct += (predicted == y_test_batch).float().sum()
accuracy = num_correct/(len(testloader)*testloader.batch_size)
print(len(testloader), testloader.batch_size)
# out: 625 16
print("Test Accuracy: {}".format(accuracy))
# out: Test Accuracy: 0.6322000026702881
torch.save(model.state_dict(), "./lenet5_model.pt")
model = LeNet5().to(device)
model.load_state_dict(torch.load("./lenet5_model.pt"))
dependencies = ['torch']
from torchvision.models.vgg import vgg16
dependencies = ['torch']
from torchvision.models.vgg import vgg16 as _vgg16
# vgg16 is the name of entrypoint
def vgg16(pretrained=False, **kwargs):
""" # This docstring shows up in hub.help()
VGG16 model
pretrained (bool): kwargs, load pretrained
weights into the model
"""
# Call the model, load pretrained weights
model = _vgg16(pretrained=pretrained, **kwargs)
return model
| 0.681303 | 0.908982 |
```
import subprocess
import pandas as pd
import os
import sys
import pprint
import local_models.local_models
import logging
import ml_battery.log
from Todd_eeg_utils import *
import rpy2
import numpy as np
import rpy2.robjects.numpy2ri
from rpy2.robjects.packages import importr
import matplotlib.pyplot as plt
logger = logging.getLogger(__name__)
data_dir = "/home/brown/disk2/eeg/Phasespace/Phasespace/data/eeg-text"
transformed_data_dir = "/home/brown/disk2/eeg/transformed_data"
data_info = pd.read_csv(os.path.join(data_dir, "fileinformation.csv"), skiprows=1).iloc[:,2:]
data_info
data_info.shape
how_many_epis = len([which for which in range(data_info.shape[0]) if data_info.iloc[which,4]>0])
how_many_epis
short_classification_data_dir = os.path.join(data_dir, "shortened_classification_data")
os.makedirs(short_classification_data_dir, exist_ok=1)
subsample_rate=5
gpr_subsample_rate=10
timelog = local_models.local_models.loggin.TimeLogger(
logger=logger,
how_often=1, total=how_many_epis,
tag="getting_filtered_data")
for i in range(data_info.shape[0]):
data_file = data_info.iloc[i,0]
data_epipoint = data_info.iloc[i,4]
data_len = data_info.iloc[i,1]
if data_len > data_epipoint > 0:
with timelog:
shortened_data_onset_file = os.path.join(short_classification_data_dir, "{}_onset.dat".format(data_file))
shortened_data_negative_file = os.path.join(short_classification_data_dir, "{}_negative.dat".format(data_file))
if not os.path.isfile(shortened_data_onset_file):
data, data_offset = get_filtered_data(data_file, data_dir)
data_epipoint = int((data_epipoint - data_offset)/subsample_rate)
subsampled_dat = data[::subsample_rate]
HZ = int(SIGNAL_HZ/subsample_rate)
bandwidth = 2*HZ
l = HZ*SECONDS_OF_SIGNAL
n = 2*bandwidth-1
ictal_rng = (max(0,data_epipoint-l), min(subsampled_dat.shape[0], data_epipoint+l))
negative_ictal_rng = (max(0, int(data_epipoint/2)-l), min(subsampled_dat.shape[0], int(data_epipoint/2)+l))
subsample_ictal_rng = (np.array(ictal_rng)/gpr_subsample_rate).astype(int)
subsample_negative_ictal_rng = (np.array(negative_ictal_rng)/gpr_subsample_rate).astype(int)
lm_kernel = local_models.local_models.TriCubeKernel(bandwidth=bandwidth)
index_X = np.arange(subsampled_dat.shape[0]*1.).reshape(-1,1)
index = local_models.local_models.ConstantDistanceSortedIndex(index_X.flatten())
exemplar_rng = (HZ*4,HZ*4+n)
exemplar_X = index_X[slice(*exemplar_rng)]
exemplar_y = subsampled_dat[slice(*exemplar_rng)]
ictal_X = index_X[slice(*ictal_rng)]
ictal_X_gpr_subsampled = index_X[ictal_rng[0] : ictal_rng[1] : gpr_subsample_rate]
exemplar_X_gpr_subsampled = index_X[exemplar_rng[0] : exemplar_rng[1] : gpr_subsample_rate]
negative_ictal_X = index_X[slice(*negative_ictal_rng)]
negative_ictal_X_gpr_subsampled = index_X[negative_ictal_rng[0] : negative_ictal_rng[1] : gpr_subsample_rate]
np.savetxt(shortened_data_onset_file, subsampled_dat[slice(*ictal_rng)])
np.savetxt(shortened_data_negative_file, subsampled_dat[slice(*negative_ictal_rng)])
positive_samples = []
negative_samples = []
for i in range(data_info.shape[0]):
data_file = data_info.iloc[i,0]
data_epipoint = data_info.iloc[i,4]
data_len = data_info.iloc[i,1]
if data_len > data_epipoint > 0:
shortened_data_onset_file = os.path.join(short_classification_data_dir, "{}_onset.dat".format(data_file))
shortened_data_negative_file = os.path.join(short_classification_data_dir, "{}_negative.dat".format(data_file))
positive_samples.append(np.loadtxt(shortened_data_onset_file))
negative_samples.append(np.loadtxt(shortened_data_negative_file))
positive_samples = np.stack(positive_samples)
negative_samples = np.stack(negative_samples)
positive_samples.shape, negative_samples.shape
np.random.seed(0)
indices = list(range(39))
np.random.shuffle(indices)
indices
train_set = indices[:20]
test_set = indices[20:]
positive_train = positive_samples[train_set]
negative_train = negative_samples[train_set]
positive_test = positive_samples[test_set]
negative_test = negative_samples[test_set]
train = np.concatenate((positive_train, negative_train))
test = np.concatenate((positive_test, negative_test))
train_labels = np.concatenate((np.ones(positive_train.shape[0]), np.zeros(negative_train.shape[0])))
test_labels = np.concatenate((np.ones(positive_test.shape[0]), np.zeros(negative_test.shape[0])))
train.shape
positive_samples.shape
rpy2.robjects.numpy2ri.activate()
# Set up our R namespaces
R = rpy2.robjects.r
DTW = importr('dtw')
gc.collect()
R('gc()')
cdists = np.empty((test.shape[0], train.shape[0]))
cdists.shape
timelog = local_models.local_models.loggin.TimeLogger(
logger=logger,
how_often=1, total=len(train_set)*len(test_set)*4,
tag="dtw_matrix")
import gc
# Calculate the alignment vector and corresponding distance
for test_i in range(cdists.shape[0]):
for train_i in range(cdists.shape[1]):
with timelog:
alignment = R.dtw(test[test_i], train[train_i], keep_internals=False, distance_only=True)
dist = alignment.rx('distance')[0][0]
print(dist)
cdists[test_i, train_i] = dist
gc.collect()
R('gc()')
gc.collect()
import sklearn.metrics
cdists_file = os.path.join(short_classification_data_dir, "dtw_cdists.dat")
if "cdists" in globals() and not os.path.exists(cdists_file):
np.savetxt(cdists_file, cdists)
else:
cdists = np.loadtxt(cdists_file)
np.argmin(cdists, axis=1).shape
sum(np.argmin(cdists, axis=1)[:19] == 10) + sum(np.argmin(cdists, axis=1)[:19] == 20)
sum(np.argmin(cdists, axis=1)[19:] == 10) + sum(np.argmin(cdists, axis=1)[19:] == 20)
cm = sklearn.metrics.confusion_matrix(test_labels, train_labels[np.argmin(cdists, axis=1)])
print(cm)
pd.DataFrame(np.round(cdists/10**6,0))
np.argmin(cdists, axis=1)
cols = [0,5,10,20,22,25,26,32,37]
pd.DataFrame(np.round(cdists[:,cols]/10**6,0),columns=cols)
pd.DataFrame(cm, index=[["true"]*2,["-","+"]], columns=[["pred"]*2, ["-", "+"]])
acc = np.sum(np.diag(cm))/np.sum(cm)
prec = cm[1,1]/np.sum(cm[:,1])
rec = cm[1,1]/np.sum(cm[1])
acc,prec,rec
```
|
github_jupyter
|
import subprocess
import pandas as pd
import os
import sys
import pprint
import local_models.local_models
import logging
import ml_battery.log
from Todd_eeg_utils import *
import rpy2
import numpy as np
import rpy2.robjects.numpy2ri
from rpy2.robjects.packages import importr
import matplotlib.pyplot as plt
logger = logging.getLogger(__name__)
data_dir = "/home/brown/disk2/eeg/Phasespace/Phasespace/data/eeg-text"
transformed_data_dir = "/home/brown/disk2/eeg/transformed_data"
data_info = pd.read_csv(os.path.join(data_dir, "fileinformation.csv"), skiprows=1).iloc[:,2:]
data_info
data_info.shape
how_many_epis = len([which for which in range(data_info.shape[0]) if data_info.iloc[which,4]>0])
how_many_epis
short_classification_data_dir = os.path.join(data_dir, "shortened_classification_data")
os.makedirs(short_classification_data_dir, exist_ok=1)
subsample_rate=5
gpr_subsample_rate=10
timelog = local_models.local_models.loggin.TimeLogger(
logger=logger,
how_often=1, total=how_many_epis,
tag="getting_filtered_data")
for i in range(data_info.shape[0]):
data_file = data_info.iloc[i,0]
data_epipoint = data_info.iloc[i,4]
data_len = data_info.iloc[i,1]
if data_len > data_epipoint > 0:
with timelog:
shortened_data_onset_file = os.path.join(short_classification_data_dir, "{}_onset.dat".format(data_file))
shortened_data_negative_file = os.path.join(short_classification_data_dir, "{}_negative.dat".format(data_file))
if not os.path.isfile(shortened_data_onset_file):
data, data_offset = get_filtered_data(data_file, data_dir)
data_epipoint = int((data_epipoint - data_offset)/subsample_rate)
subsampled_dat = data[::subsample_rate]
HZ = int(SIGNAL_HZ/subsample_rate)
bandwidth = 2*HZ
l = HZ*SECONDS_OF_SIGNAL
n = 2*bandwidth-1
ictal_rng = (max(0,data_epipoint-l), min(subsampled_dat.shape[0], data_epipoint+l))
negative_ictal_rng = (max(0, int(data_epipoint/2)-l), min(subsampled_dat.shape[0], int(data_epipoint/2)+l))
subsample_ictal_rng = (np.array(ictal_rng)/gpr_subsample_rate).astype(int)
subsample_negative_ictal_rng = (np.array(negative_ictal_rng)/gpr_subsample_rate).astype(int)
lm_kernel = local_models.local_models.TriCubeKernel(bandwidth=bandwidth)
index_X = np.arange(subsampled_dat.shape[0]*1.).reshape(-1,1)
index = local_models.local_models.ConstantDistanceSortedIndex(index_X.flatten())
exemplar_rng = (HZ*4,HZ*4+n)
exemplar_X = index_X[slice(*exemplar_rng)]
exemplar_y = subsampled_dat[slice(*exemplar_rng)]
ictal_X = index_X[slice(*ictal_rng)]
ictal_X_gpr_subsampled = index_X[ictal_rng[0] : ictal_rng[1] : gpr_subsample_rate]
exemplar_X_gpr_subsampled = index_X[exemplar_rng[0] : exemplar_rng[1] : gpr_subsample_rate]
negative_ictal_X = index_X[slice(*negative_ictal_rng)]
negative_ictal_X_gpr_subsampled = index_X[negative_ictal_rng[0] : negative_ictal_rng[1] : gpr_subsample_rate]
np.savetxt(shortened_data_onset_file, subsampled_dat[slice(*ictal_rng)])
np.savetxt(shortened_data_negative_file, subsampled_dat[slice(*negative_ictal_rng)])
positive_samples = []
negative_samples = []
for i in range(data_info.shape[0]):
data_file = data_info.iloc[i,0]
data_epipoint = data_info.iloc[i,4]
data_len = data_info.iloc[i,1]
if data_len > data_epipoint > 0:
shortened_data_onset_file = os.path.join(short_classification_data_dir, "{}_onset.dat".format(data_file))
shortened_data_negative_file = os.path.join(short_classification_data_dir, "{}_negative.dat".format(data_file))
positive_samples.append(np.loadtxt(shortened_data_onset_file))
negative_samples.append(np.loadtxt(shortened_data_negative_file))
positive_samples = np.stack(positive_samples)
negative_samples = np.stack(negative_samples)
positive_samples.shape, negative_samples.shape
np.random.seed(0)
indices = list(range(39))
np.random.shuffle(indices)
indices
train_set = indices[:20]
test_set = indices[20:]
positive_train = positive_samples[train_set]
negative_train = negative_samples[train_set]
positive_test = positive_samples[test_set]
negative_test = negative_samples[test_set]
train = np.concatenate((positive_train, negative_train))
test = np.concatenate((positive_test, negative_test))
train_labels = np.concatenate((np.ones(positive_train.shape[0]), np.zeros(negative_train.shape[0])))
test_labels = np.concatenate((np.ones(positive_test.shape[0]), np.zeros(negative_test.shape[0])))
train.shape
positive_samples.shape
rpy2.robjects.numpy2ri.activate()
# Set up our R namespaces
R = rpy2.robjects.r
DTW = importr('dtw')
gc.collect()
R('gc()')
cdists = np.empty((test.shape[0], train.shape[0]))
cdists.shape
timelog = local_models.local_models.loggin.TimeLogger(
logger=logger,
how_often=1, total=len(train_set)*len(test_set)*4,
tag="dtw_matrix")
import gc
# Calculate the alignment vector and corresponding distance
for test_i in range(cdists.shape[0]):
for train_i in range(cdists.shape[1]):
with timelog:
alignment = R.dtw(test[test_i], train[train_i], keep_internals=False, distance_only=True)
dist = alignment.rx('distance')[0][0]
print(dist)
cdists[test_i, train_i] = dist
gc.collect()
R('gc()')
gc.collect()
import sklearn.metrics
cdists_file = os.path.join(short_classification_data_dir, "dtw_cdists.dat")
if "cdists" in globals() and not os.path.exists(cdists_file):
np.savetxt(cdists_file, cdists)
else:
cdists = np.loadtxt(cdists_file)
np.argmin(cdists, axis=1).shape
sum(np.argmin(cdists, axis=1)[:19] == 10) + sum(np.argmin(cdists, axis=1)[:19] == 20)
sum(np.argmin(cdists, axis=1)[19:] == 10) + sum(np.argmin(cdists, axis=1)[19:] == 20)
cm = sklearn.metrics.confusion_matrix(test_labels, train_labels[np.argmin(cdists, axis=1)])
print(cm)
pd.DataFrame(np.round(cdists/10**6,0))
np.argmin(cdists, axis=1)
cols = [0,5,10,20,22,25,26,32,37]
pd.DataFrame(np.round(cdists[:,cols]/10**6,0),columns=cols)
pd.DataFrame(cm, index=[["true"]*2,["-","+"]], columns=[["pred"]*2, ["-", "+"]])
acc = np.sum(np.diag(cm))/np.sum(cm)
prec = cm[1,1]/np.sum(cm[:,1])
rec = cm[1,1]/np.sum(cm[1])
acc,prec,rec
| 0.250454 | 0.308464 |
Думаю, вы уже познакомились со стандартными функциями в numpy для вычисления станадртных оценок (среднего, медианы и проч), однако в анализе реальных данных вы, как правило, будете работать с целым датасетом.
В этом разделе мы познакомимся с вычислением описательных статистик для целого датасета.
Большинство из них вычиляются одной командой (методом) describe
С вычислением корреляцонной матрицы мы уже сталкивались во 2 модуле, но освежим и ее
И отдельное внимание уделим вычислению условных и безусловных пропорций.
В датасете framingham.csv представлены данные, которые группа ученых из Фрамингема (США) использовала для выявления риска заболевания ишемической болезнью сердца в течение 10 лет.
Демографические данные:
sex (male): пол, мужчина (1) или женщина (0)
age: возраст
education: уровень образования (0-4: школа-колледж)
Поведенческие данные:
currentSmoker: курильщик (1) или нет (0)
cigsPerDay: количество выкуриваемых сигарет в день (шт.)
Медицинская история:
BPMeds: принимает ли пациент препараты для регулировки артериального давления (0 - нет, 1 - да)
prevalentStroke: случался ли у пациента сердечный приступ (0 - нет, 1 - да)
prevalentHyp: страдает ли пациент гипертонией (0 - нет, 1 - да)
diabetes: страдает ли пациент диабетом (0 - нет, 1 - да)
Физическое состояние:
totChol: уровень холестерина
sysBP: систолическое (верхнее) артериальное давление
diaBP: диастолическое (нижнее) артериальное давление
BMI: индекс массы тела - масса (кг) / рост^2 (в метрах)
heartRate: пульс
glucose: уровень глюкозы
Целевая переменная (на которую авторы строили регрессию):
TenYearCHD: риск заболевания ишемической болезнью сердца в течение 10 лет
Импорт библиотек:
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sn
import matplotlib.mlab as mlab
%matplotlib inline
```
Импорт датасета:
```
df = pd.read_csv('framingham.csv')
```
Шапка датасета:
```
df.head()
```
Размер датасета:
```
df.shape
```
Названия столбцов датасета понадобятся нам, чтобы обращаться к отдельным признакам пациентов:
```
df.columns
```
Поиск missing values:
```
df.isnull().sum()
```
Видим, что у 105 пациентов нет данных об образовании, у 388 - об уровне глюкозы. Недостающие данные могут стать причиной некорректных значений оценок, и от них лучше избавиться.
Количество строк, в которых есть missing values
```
count=0
for i in df.isnull().sum(axis=1):
if i>0:
count=count+1
print('Общее количество строк с пропущенными значениями: ', count)
```
Итого у нас 582 строки, в которых не хватает каких-нибудь данных
Найдем соотношение строк с недостающими данными и общего кол-ва строк
Если их будет относительно немного, то выгоднее избавиться от неполных строк, а если много, то надо посмотреть, в каких столбцах больше всего не хватает данных - возможно, выгоднее будет избавляться от них.
```
count/df.shape[0]
```
Т.к. соотношение мало (13%), можем отбросить строки с отсутствующими данными):
```
df.dropna(axis=0,inplace=True)
```
Размеры датасета после удаления missing values:
```
df.shape
```
Получение описательных статистик при помощи фунции describe:
```
df.describe()
```
Данные полученные из describe:
mean - среднее значение
std - стандартное (среднеквадратичное) отклонение.
min - минимальное значение
max - максимальное значение
25% - нижняя квартиль (медиана меньшей/левой половины выборки)
50% - медиана
75% - верхняя квартиль (медиана большей/правой половины выборки)
Далее строим тепловую карту корреляционной матрицы при помощи функции heatmap и саму корреляционную матрицу. Чем насыщеннее цвет, тем сильнее корреляция.
```
sn.heatmap(df.corr())
```
Можем увидеть сильную корреляцию между диастолическим и систолическим давлением. Корреляции целевой переменной со всеми признаками невелики. Это значит, что линейная связь между ними очень слабая
```
df.corr()
```
Со средним, стандартным отклонением, медианой и корреляцией все ясно.
Давайте выясним, как вычислять выборочные пропорции в датасете
как вычислить долю мужчин в выборке?
Длинный способ: посчитаем количество всех мужчин в выборке при помощи метода value_counts() и поделим его на общее количество пациентов
```
m=df['male'].value_counts() # счетчик разных значений в dataframe
print("Общее количество мужчин и женщин\n", m)
print("Общее количество мужчин:", m[1])
p_male=m[1]/df.shape[0] # считаем пропорцию мужчин среди всех пациентов
print("Доля мужчин среди всех пациентов:", p_male)
```
Короткий способ: задать в методе value_counts() специальный параметр, который будет вычислиять не абсолютные частоты (количества), а относительные (пропорции)
```
df['male'].value_counts(normalize = True ) # параметр normalize = True позволяет считать сразу пропорцию вместо количества
```
С абсолютными пропорциями тоже ясно. Как насчет условных?
Как вычислить долю курильщиков среди мужчин и среди женщин:
```
male_groups=df.groupby('male') # groupgy разбивает датасет на группы по признаку пола
```
Внутри каждой группы можем взять счетчик value_counts() для признака currentSmoker
пол 0 - женщина, пол 1 - мужчина.
```
male_groups['currentSmoker'].value_counts() # можем отдельно вычислить количество курильщиков среди мужчин и среди женщин
```
Итак: курит 808 женщин и 981 мужчин
Теперь вычислим пропорции курильщиков внутри каждого пола.
Вы можете убедиться, что это именно условные пропорции, поделив количество курящих мужчин на общее количество мужчин и сравнив результаты, или если заметите, что вероятности внутри каждой группы пола дают в сумме 1
```
ms=male_groups['currentSmoker'].value_counts(normalize = True)
print('Доли курильщиков среди мужчин и среди женщин\n',ms)
print('Доля курильщиков среди мужчин:',ms[1,1])
```
Как вычислить среднее значение пульса у курящих и не курящих:
```
smok_groups=df.groupby('currentSmoker')
smok_groups['heartRate'].mean()
```
Как вычислить долю пациентов группы риска среди курящих и не курящих:
```
srisk=smok_groups['TenYearCHD'].value_counts(normalize = True)
print('Доли группы риска среди курильщиков и не курильщиков\n',srisk)
print('Доля группы риска среди курильщиков:',srisk[1,1])
```
Трюк по вычислению частот для переменных-индикаторов (значения 1 и 0): сумма значений равна количеству единиц в выборке, а значит, среднее равно доле единиц, то есть частоте:
```
smok_groups['TenYearCHD'].mean()
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sn
import matplotlib.mlab as mlab
%matplotlib inline
df = pd.read_csv('framingham.csv')
df.head()
df.shape
df.columns
df.isnull().sum()
count=0
for i in df.isnull().sum(axis=1):
if i>0:
count=count+1
print('Общее количество строк с пропущенными значениями: ', count)
count/df.shape[0]
df.dropna(axis=0,inplace=True)
df.shape
df.describe()
sn.heatmap(df.corr())
df.corr()
m=df['male'].value_counts() # счетчик разных значений в dataframe
print("Общее количество мужчин и женщин\n", m)
print("Общее количество мужчин:", m[1])
p_male=m[1]/df.shape[0] # считаем пропорцию мужчин среди всех пациентов
print("Доля мужчин среди всех пациентов:", p_male)
df['male'].value_counts(normalize = True ) # параметр normalize = True позволяет считать сразу пропорцию вместо количества
male_groups=df.groupby('male') # groupgy разбивает датасет на группы по признаку пола
male_groups['currentSmoker'].value_counts() # можем отдельно вычислить количество курильщиков среди мужчин и среди женщин
ms=male_groups['currentSmoker'].value_counts(normalize = True)
print('Доли курильщиков среди мужчин и среди женщин\n',ms)
print('Доля курильщиков среди мужчин:',ms[1,1])
smok_groups=df.groupby('currentSmoker')
smok_groups['heartRate'].mean()
srisk=smok_groups['TenYearCHD'].value_counts(normalize = True)
print('Доли группы риска среди курильщиков и не курильщиков\n',srisk)
print('Доля группы риска среди курильщиков:',srisk[1,1])
smok_groups['TenYearCHD'].mean()
| 0.097122 | 0.975507 |
```
import torch
import torch.nn as nn
import numpy as np
import json
import matplotlib.pyplot as plt
%matplotlib inline
from input_pipeline import get_datasets
from network import Network
# https://github.com/DmitryUlyanov/Multicore-TSNE
from MulticoreTSNE import MulticoreTSNE as TSNE
```
# Get validation data
```
svhn, mnist = get_datasets(is_training=False)
```
# Load feature extractor
```
embedder = Network(image_size=(32, 32), embedding_dim=64).cuda()
classifier = nn.Linear(64, 10).cuda()
model = nn.Sequential(embedder, classifier)
model.load_state_dict(torch.load('models/svhn_source'))
model.eval()
model = model[0] # only embedding
```
# Extract features
```
def predict(dataset):
X, y = [], []
for image, label in dataset:
x = model(image.unsqueeze(0).cuda())
X.append(x.detach().cpu().numpy())
y.append(label)
X = np.concatenate(X, axis=0)
y = np.stack(y)
return X, y
X_svhn, y_svhn = predict(svhn)
X_mnist, y_mnist = predict(mnist)
```
# Plot tsne
```
tsne = TSNE(perplexity=200.0, n_jobs=12)
P = tsne.fit_transform(np.concatenate([X_svhn, X_mnist], axis=0))
P_svhn = P[:len(X_svhn)]
P_mnist = P[len(X_svhn):]
plt.figure(figsize=(15, 8))
plt.scatter(P_svhn[:, 0], P_svhn[:, 1], c=y_svhn, cmap='tab10', marker='.', label='svhn')
plt.scatter(P_mnist[:, 0], P_mnist[:, 1], marker='s', c='w', edgecolors='k', label='mnist', alpha=0.3)
plt.title('source is svhn, target is mnist')
plt.legend();
```
# Plot loss curves
```
with open('logs/mnist_source.json', 'r') as f:
logs = json.load(f)
fig, axes = plt.subplots(1, 3, sharex=True, figsize=(15, 5), dpi=100)
axes = axes.flatten()
plt.suptitle('source is MNIST, target is SVHN', fontsize='x-large', y=1.05)
axes[0].plot(logs['step'], logs['classification_loss'], label='train logloss', c='r')
axes[0].plot(logs['val_step'], logs['svhn_logloss'], label='svhn val logloss', marker='o', c='k')
axes[0].plot(logs['val_step'], logs['mnist_logloss'], label='mnist val logloss', marker='o', c='c')
axes[0].legend()
axes[0].set_title('classification losses');
axes[1].plot(logs['step'], logs['walker_loss'], label='walker loss')
axes[1].plot(logs['step'], logs['visit_loss'], label='visit loss')
axes[1].legend()
axes[1].set_title('domain adaptation losses');
axes[2].plot(logs['val_step'], logs['svhn_accuracy'], label='svhn val', c='k')
axes[2].plot(logs['val_step'], logs['mnist_accuracy'], label='mnist val', c='c')
axes[2].legend()
axes[2].set_title('accuracy')
fig.tight_layout();
```
|
github_jupyter
|
import torch
import torch.nn as nn
import numpy as np
import json
import matplotlib.pyplot as plt
%matplotlib inline
from input_pipeline import get_datasets
from network import Network
# https://github.com/DmitryUlyanov/Multicore-TSNE
from MulticoreTSNE import MulticoreTSNE as TSNE
svhn, mnist = get_datasets(is_training=False)
embedder = Network(image_size=(32, 32), embedding_dim=64).cuda()
classifier = nn.Linear(64, 10).cuda()
model = nn.Sequential(embedder, classifier)
model.load_state_dict(torch.load('models/svhn_source'))
model.eval()
model = model[0] # only embedding
def predict(dataset):
X, y = [], []
for image, label in dataset:
x = model(image.unsqueeze(0).cuda())
X.append(x.detach().cpu().numpy())
y.append(label)
X = np.concatenate(X, axis=0)
y = np.stack(y)
return X, y
X_svhn, y_svhn = predict(svhn)
X_mnist, y_mnist = predict(mnist)
tsne = TSNE(perplexity=200.0, n_jobs=12)
P = tsne.fit_transform(np.concatenate([X_svhn, X_mnist], axis=0))
P_svhn = P[:len(X_svhn)]
P_mnist = P[len(X_svhn):]
plt.figure(figsize=(15, 8))
plt.scatter(P_svhn[:, 0], P_svhn[:, 1], c=y_svhn, cmap='tab10', marker='.', label='svhn')
plt.scatter(P_mnist[:, 0], P_mnist[:, 1], marker='s', c='w', edgecolors='k', label='mnist', alpha=0.3)
plt.title('source is svhn, target is mnist')
plt.legend();
with open('logs/mnist_source.json', 'r') as f:
logs = json.load(f)
fig, axes = plt.subplots(1, 3, sharex=True, figsize=(15, 5), dpi=100)
axes = axes.flatten()
plt.suptitle('source is MNIST, target is SVHN', fontsize='x-large', y=1.05)
axes[0].plot(logs['step'], logs['classification_loss'], label='train logloss', c='r')
axes[0].plot(logs['val_step'], logs['svhn_logloss'], label='svhn val logloss', marker='o', c='k')
axes[0].plot(logs['val_step'], logs['mnist_logloss'], label='mnist val logloss', marker='o', c='c')
axes[0].legend()
axes[0].set_title('classification losses');
axes[1].plot(logs['step'], logs['walker_loss'], label='walker loss')
axes[1].plot(logs['step'], logs['visit_loss'], label='visit loss')
axes[1].legend()
axes[1].set_title('domain adaptation losses');
axes[2].plot(logs['val_step'], logs['svhn_accuracy'], label='svhn val', c='k')
axes[2].plot(logs['val_step'], logs['mnist_accuracy'], label='mnist val', c='c')
axes[2].legend()
axes[2].set_title('accuracy')
fig.tight_layout();
| 0.858422 | 0.886813 |
# Tools for visualizing data
This notebook is a "tour" of just a few of the data visualization capabilities available to you in Python. It focuses on two packages: [Bokeh](https://blog.modeanalytics.com/python-data-visualization-libraries/) for creating _interactive_ plots and _[Seaborn]_ for creating "static" (or non-interactive) plots. The former is really where the ability to develop _programmatic_ visualizations, that is, code that generates graphics, really shines. But the latter is important in printed materials and reports. So, both techniques should be a core part of your toolbox.
With that, let's get started!
> **Note 1.** Since visualizations are not amenable to autograding, this notebook is more of a demo of what you can do. It doesn't require you to write any code on your own. However, we strongly encourage you to spend some time experimenting with the basic methods here and generate some variations on your own. Once you start, you'll find it's more than a little fun!
>
> **Note 2.** Though designed for R programs, Hadley Wickham has an [excellent description of many of the principles in this notebook](http://r4ds.had.co.nz/data-visualisation.html).
## Part 0: Downloading some data to visualize
For the demos in this notebook, we'll need the Iris dataset. The following code cell downloads it for you.
```
import requests
import os
import hashlib
import io
def download(file, url_suffix=None, checksum=None):
if url_suffix is None:
url_suffix = file
if not os.path.exists(file):
url = 'https://cse6040.gatech.edu/datasets/{}'.format(url_suffix)
print("Downloading: {} ...".format(url))
r = requests.get(url)
with open(file, 'w', encoding=r.encoding) as f:
f.write(r.text)
if checksum is not None:
with io.open(file, 'r', encoding='utf-8', errors='replace') as f:
body = f.read()
body_checksum = hashlib.md5(body.encode('utf-8')).hexdigest()
assert body_checksum == checksum, \
"Downloaded file '{}' has incorrect checksum: '{}' instead of '{}'".format(file, body_checksum, checksum)
print("'{}' is ready!".format(file))
datasets = {'iris.csv': ('tidy', 'd1175c032e1042bec7f974c91e4a65ae'),
'tips.csv': ('seaborn-data', 'ee24adf668f8946d4b00d3e28e470c82'),
'anscombe.csv': ('seaborn-data', '2c824795f5d51593ca7d660986aefb87'),
'titanic.csv': ('seaborn-data', '56f29cc0b807cb970a914ed075227f94')
}
for filename, (category, checksum) in datasets.items():
download(filename, url_suffix='{}/{}'.format(category, filename), checksum=checksum)
print("\n(All data appears to be ready.)")
```
# Part 1: Bokeh and the Grammar of Graphics ("lite")
Let's start with some methods for creating an interactive visualization in Python and Jupyter, based on the [Bokeh](https://bokeh.pydata.org/en/latest/) package. It generates JavaScript-based visualizations, which you can then run in a web browser, without you having to know or write any JS yourself. The web-friendly aspect of Bokeh makes it an especially good package for creating interactive visualizations in a Jupyter notebook, since it's also browser-based.
The design and use of Bokeh is based on Leland Wilkinson's Grammar of Graphics (GoG).
> If you've encountered GoG ideas before, it was probably when using the best known implementation of GoG, namely, Hadley Wickham's R package, [ggplot2](http://ggplot2.org/).
## Setup
Here are the modules we'll need for this notebook:
```
from IPython.display import display, Markdown
import pandas as pd
import bokeh
```
Bokeh is designed to output HTML, which you can then embed in any website. To embed Bokeh output into a Jupyter notebook, we need to do the following:
```
from bokeh.io import output_notebook
from bokeh.io import show
output_notebook ()
```
## Philosophy: Grammar of Graphics
[The Grammar of Graphics](http://www.springer.com.prx.library.gatech.edu/us/book/9780387245447) is an idea of Leland Wilkinson. Its basic idea is that the way most people think about visualizing data is ad hoc and unsystematic, whereas there exists in fact a "formal language" for describing visual displays.
The reason why this idea is important and powerful in the context of our course is that it makes visualization more systematic, thereby making it easier to create those visualizations through code.
The high-level concept is simple:
1. Start with a (tidy) data set.
2. Transform it into a new (tidy) data set.
3. Map variables to geometric objects (e.g., bars, points, lines) or other aesthetic "flourishes" (e.g., color).
4. Rescale or transform the visual coordinate system.
5. Render and enjoy!
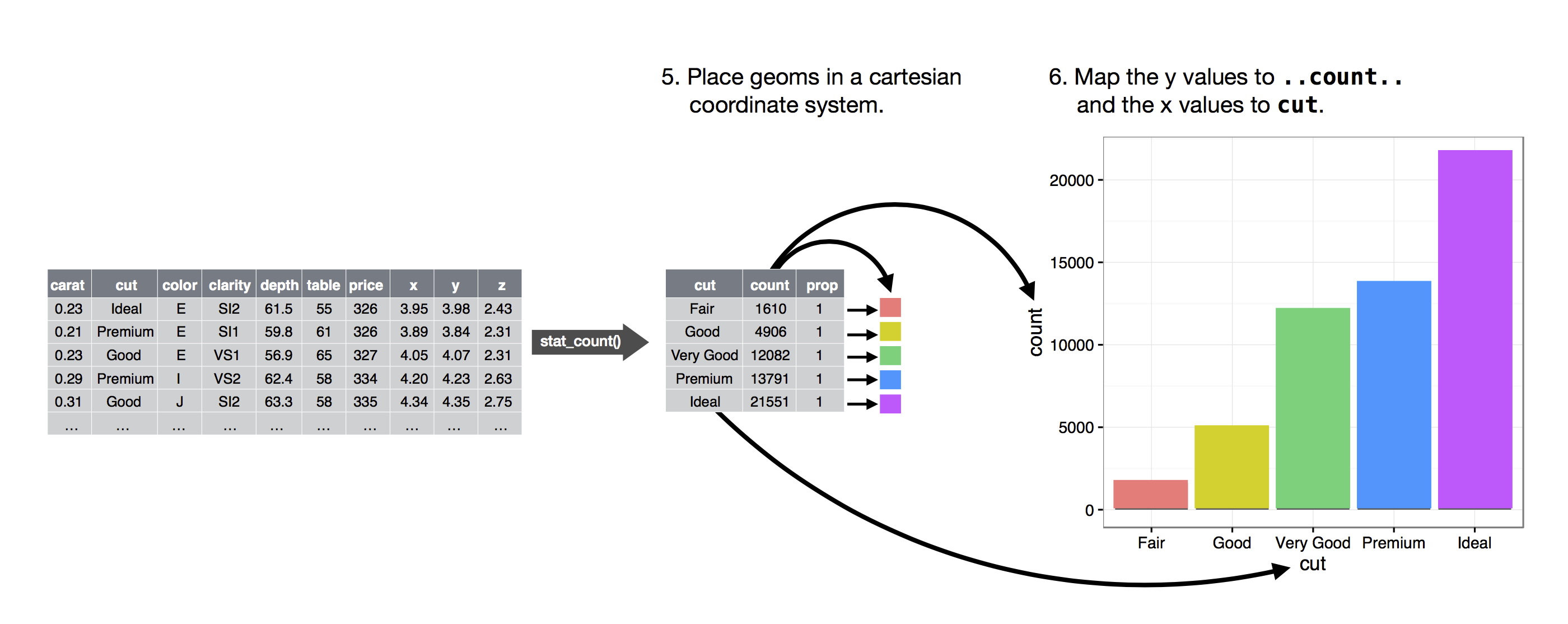
> This image is "liberated" from: http://r4ds.had.co.nz/data-visualisation.html
## HoloViews
Before seeing Bokeh directly, let's start with an easier way to take advantage of Bokeh, which is through a higher-level interface known as [HoloViews](http://holoviews.org/). HoloViews provides a simplified interface suitable for "canned" charts.
To see it in action, let's load the Iris data set and study relationships among its variables, such as petal length vs. petal width.
The cells below demonstrate histograms, simple scatter plots, and box plots. However, there is a much larger gallery of options: http://holoviews.org/reference/index.html
```
flora = pd.read_csv ('iris.csv')
display (flora.head ())
from bokeh.io import show
import holoviews as hv
import numpy as np
hv.extension('bokeh')
```
### 1. Histogram
* The Histogram(f, e) can takes two arguments, frequencies and edges (bin boundaries).
* These can easily be created using numpy's histogram function as illustrated below.
* The plot is interactive and comes with a bunch of tools. You can customize these tools as well; for your many options, see http://bokeh.pydata.org/en/latest/docs/user_guide/tools.html.
> You may see some warnings appear in a pink-shaded box. You can ignore these. They are caused by some slightly older version of the Bokeh library that is running on Vocareum.
```
frequencies, edges = np.histogram(flora['petal width'], bins = 5)
hv.Histogram(frequencies, edges, label = 'Histogram')
```
A user can interact with the chart above using the tools shown on the right-hand side. Indeed, you can select or customize these tools! You'll see an example below.
### 2. ScatterPlot
```
hv.Scatter(flora[['petal width','sepal length']],label = 'Scatter plot')
```
### 3. BoxPlot
```
hv.BoxWhisker(flora['sepal length'], label = "Box whiskers plot")
```
## Mid-level charts: the Plotting interface
Beyond the canned methods above, Bokeh provides a "mid-level" interface that more directly exposes the grammar of graphics methodology for constructing visual displays.
The basic procedure is
* Create a blank canvas by calling `bokeh.plotting.figure`
* Add glyphs, which are geometric shapes.
> For a full list of glyphs, refer to the methods of `bokeh.plotting.figure`: http://bokeh.pydata.org/en/latest/docs/reference/plotting.html
```
from bokeh.plotting import figure
# Create a canvas with a specific set of tools for the user:
TOOLS = 'pan,box_zoom,wheel_zoom,lasso_select,save,reset,help'
p = figure(width=500, height=500, tools=TOOLS)
print(p)
# Add one or more glyphs
p.triangle(x=flora['petal width'], y=flora['petal length'])
show(p)
```
**Using data from Pandas.** Here is another way to do the same thing, but using a Pandas data frame as input.
```
from bokeh.models import ColumnDataSource
data=ColumnDataSource(flora)
p=figure()
p.triangle(source=data, x='petal width', y='petal length')
show(p)
```
**Color maps.** Let's make a map that assigns each unique species its own color. Incidentally, there are many choices of colors! http://bokeh.pydata.org/en/latest/docs/reference/palettes.html
```
# Determine the unique species
unique_species = flora['species'].unique()
print(unique_species)
# Map each species with a unique color
from bokeh.palettes import brewer
color_map = dict(zip(unique_species, brewer['Dark2'][len(unique_species)]))
print(color_map)
# Create data sources for each species
data_sources = {}
for s in unique_species:
data_sources[s] = ColumnDataSource(flora[flora['species']==s])
```
Now we can more programmatically generate the same plot as above, but use a unique color for each species.
```
p = figure()
for s in unique_species:
p.triangle(source=data_sources[s], x='petal width', y='petal length', color=color_map[s])
show(p)
```
That's just a quick tour of what you can do with Bokeh. We will incorporate it into some of our future labs. At this point, we'd encourage you to experiment with the code cells above and try generating your own variations!
# Part 2: Static visualizations using Seaborn
Parts of this lab are taken from publicly available Seaborn tutorials.
http://seaborn.pydata.org/tutorial/distributions.html
They were adapted for use in this notebook by [Shang-Tse Chen at Georgia Tech](https://www.cc.gatech.edu/~schen351).
```
import seaborn as sns
# The following Jupyter "magic" command forces plots to appear inline
# within the notebook.
%matplotlib inline
```
When dealing with a set of data, often the first thing we want to do is get a sense for how the variables are distributed. Here, we will look at some of the tools in seborn for examining univariate and bivariate distributions.
### Plotting univariate distributions
distplot() function will draw a histogram and fit a kernel density estimate
```
import numpy as np
x = np.random.normal(size=100)
sns.distplot(x)
```
## Plotting bivariate distributions
The easiest way to visualize a bivariate distribution in seaborn is to use the jointplot() function, which creates a multi-panel figure that shows both the bivariate (or joint) relationship between two variables along with the univariate (or marginal) distribution of each on separate axes.
```
mean, cov = [0, 1], [(1, .5), (.5, 1)]
data = np.random.multivariate_normal(mean, cov, 200)
df = pd.DataFrame(data, columns=["x", "y"])
```
**Basic scatter plots.** The most familiar way to visualize a bivariate distribution is a scatterplot, where each observation is shown with point at the x and y values. You can draw a scatterplot with the matplotlib plt.scatter function, and it is also the default kind of plot shown by the jointplot() function:
```
sns.jointplot(x="x", y="y", data=df)
```
**Hexbin plots.** The bivariate analogue of a histogram is known as a “hexbin” plot, because it shows the counts of observations that fall within hexagonal bins. This plot works best with relatively large datasets. It’s availible through the matplotlib plt.hexbin function and as a style in jointplot()
```
sns.jointplot(x="x", y="y", data=df, kind="hex")
```
**Kernel density estimation.** It is also posible to use the kernel density estimation procedure described above to visualize a bivariate distribution. In seaborn, this kind of plot is shown with a contour plot and is available as a style in jointplot()
```
sns.jointplot(x="x", y="y", data=df, kind="kde")
```
## Visualizing pairwise relationships in a dataset
To plot multiple pairwise bivariate distributions in a dataset, you can use the pairplot() function. This creates a matrix of axes and shows the relationship for each pair of columns in a DataFrame. by default, it also draws the univariate distribution of each variable on the diagonal Axes:
```
sns.pairplot(flora)
# We can add colors to different species
sns.pairplot(flora, hue="species")
```
### Visualizing linear relationships
```
tips = pd.read_csv("tips.csv")
tips.head()
```
We can use the function `regplot` to show the linear relationship between total_bill and tip.
It also shows the 95% confidence interval.
```
sns.regplot(x="total_bill", y="tip", data=tips)
```
### Visualizing higher order relationships
```
anscombe = pd.read_csv("anscombe.csv")
sns.regplot(x="x", y="y", data=anscombe[anscombe["dataset"] == "II"])
```
The plot clearly shows that this is not a good model.
Let's try to fit a polynomial regression model with degree 2.
```
sns.regplot(x="x", y="y", data=anscombe[anscombe["dataset"] == "II"], order=2)
```
**Strip plots.** This is similar to scatter plot but used when one variable is categorical.
```
sns.stripplot(x="day", y="total_bill", data=tips)
```
**Box plots.**
```
sns.boxplot(x="day", y="total_bill", hue="time", data=tips)
```
**Bar plots.**
```
titanic = pd.read_csv("titanic.csv")
sns.barplot(x="sex", y="survived", hue="class", data=titanic)
```
**Fin!** That ends this tour of basic plotting functionality available to you in Python. It only scratches the surface of what is possible. We'll explore more advanced features in future labs, but in the meantime, we encourage you to play with the code in this notebook and try to generate your own visualizations of datasets you care about!
Although this notebook did not require you to write any code, go ahead and "submit" it for grading. You'll effectively get "free points" for doing so: the code cell below gives it to you.
```
# Test cell: `freebie_test`
assert True
```
|
github_jupyter
|
import requests
import os
import hashlib
import io
def download(file, url_suffix=None, checksum=None):
if url_suffix is None:
url_suffix = file
if not os.path.exists(file):
url = 'https://cse6040.gatech.edu/datasets/{}'.format(url_suffix)
print("Downloading: {} ...".format(url))
r = requests.get(url)
with open(file, 'w', encoding=r.encoding) as f:
f.write(r.text)
if checksum is not None:
with io.open(file, 'r', encoding='utf-8', errors='replace') as f:
body = f.read()
body_checksum = hashlib.md5(body.encode('utf-8')).hexdigest()
assert body_checksum == checksum, \
"Downloaded file '{}' has incorrect checksum: '{}' instead of '{}'".format(file, body_checksum, checksum)
print("'{}' is ready!".format(file))
datasets = {'iris.csv': ('tidy', 'd1175c032e1042bec7f974c91e4a65ae'),
'tips.csv': ('seaborn-data', 'ee24adf668f8946d4b00d3e28e470c82'),
'anscombe.csv': ('seaborn-data', '2c824795f5d51593ca7d660986aefb87'),
'titanic.csv': ('seaborn-data', '56f29cc0b807cb970a914ed075227f94')
}
for filename, (category, checksum) in datasets.items():
download(filename, url_suffix='{}/{}'.format(category, filename), checksum=checksum)
print("\n(All data appears to be ready.)")
from IPython.display import display, Markdown
import pandas as pd
import bokeh
from bokeh.io import output_notebook
from bokeh.io import show
output_notebook ()
flora = pd.read_csv ('iris.csv')
display (flora.head ())
from bokeh.io import show
import holoviews as hv
import numpy as np
hv.extension('bokeh')
frequencies, edges = np.histogram(flora['petal width'], bins = 5)
hv.Histogram(frequencies, edges, label = 'Histogram')
hv.Scatter(flora[['petal width','sepal length']],label = 'Scatter plot')
hv.BoxWhisker(flora['sepal length'], label = "Box whiskers plot")
from bokeh.plotting import figure
# Create a canvas with a specific set of tools for the user:
TOOLS = 'pan,box_zoom,wheel_zoom,lasso_select,save,reset,help'
p = figure(width=500, height=500, tools=TOOLS)
print(p)
# Add one or more glyphs
p.triangle(x=flora['petal width'], y=flora['petal length'])
show(p)
from bokeh.models import ColumnDataSource
data=ColumnDataSource(flora)
p=figure()
p.triangle(source=data, x='petal width', y='petal length')
show(p)
# Determine the unique species
unique_species = flora['species'].unique()
print(unique_species)
# Map each species with a unique color
from bokeh.palettes import brewer
color_map = dict(zip(unique_species, brewer['Dark2'][len(unique_species)]))
print(color_map)
# Create data sources for each species
data_sources = {}
for s in unique_species:
data_sources[s] = ColumnDataSource(flora[flora['species']==s])
p = figure()
for s in unique_species:
p.triangle(source=data_sources[s], x='petal width', y='petal length', color=color_map[s])
show(p)
import seaborn as sns
# The following Jupyter "magic" command forces plots to appear inline
# within the notebook.
%matplotlib inline
import numpy as np
x = np.random.normal(size=100)
sns.distplot(x)
mean, cov = [0, 1], [(1, .5), (.5, 1)]
data = np.random.multivariate_normal(mean, cov, 200)
df = pd.DataFrame(data, columns=["x", "y"])
sns.jointplot(x="x", y="y", data=df)
sns.jointplot(x="x", y="y", data=df, kind="hex")
sns.jointplot(x="x", y="y", data=df, kind="kde")
sns.pairplot(flora)
# We can add colors to different species
sns.pairplot(flora, hue="species")
tips = pd.read_csv("tips.csv")
tips.head()
sns.regplot(x="total_bill", y="tip", data=tips)
anscombe = pd.read_csv("anscombe.csv")
sns.regplot(x="x", y="y", data=anscombe[anscombe["dataset"] == "II"])
sns.regplot(x="x", y="y", data=anscombe[anscombe["dataset"] == "II"], order=2)
sns.stripplot(x="day", y="total_bill", data=tips)
sns.boxplot(x="day", y="total_bill", hue="time", data=tips)
titanic = pd.read_csv("titanic.csv")
sns.barplot(x="sex", y="survived", hue="class", data=titanic)
# Test cell: `freebie_test`
assert True
| 0.46393 | 0.928668 |
# Titanic Case Study
<img align="right" width="300" src="https://upload.wikimedia.org/wikipedia/it/5/53/TitanicFilm.jpg">
The sinking of the Titanic is one of the most infamous shipwrecks in history. On April 15, 1912, during her maiden voyage, the Titanic sank after colliding with an iceberg, killing 1502 out of 2224 passengers and crew. This sensational tragedy shocked the international community and led to better safety regulations for ships.
One of the reasons that the shipwreck led to such loss of life was that there were not enough lifeboats for the passengers and crew. Although there was some element of luck involved in surviving the sinking, some groups of people were more likely to survive than others, such as women, children, and the upper-class.
In this notebook, we will try to figure out if we are able to predict people who survive or not by using ***classification*** in python.
The **Titanic** dataset became famous after that ***Kaggle*** launched the competition to discover label the passengers as survived or not by exploiting some available features ([link](https://www.kaggle.com/c/titanic)).
### Library import
```
%matplotlib inline
import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt
```
### KDD Process
1. Dataset load and features semantics
1. Data Cleaning (handle missing values, remove useless variables)
1. Feature Engineering
1. Classification Preprocessing (feature reshaping, train/test partitioning)
1. Parameter Tuning
1. Perform Classification
1. Analyze the classification results
1. Analyze the classification performance
1. Can we improve the performance using another classifier?
```
df = pd.read_csv("data/titanic.csv", skipinitialspace=True, sep=',')
df.head()
df.info()
```
Each record is described by 12 variables:
* The ``Survived`` variable is our outcome or dependent variable. It is a binary nominal datatype of 1 for survived and 0 for did not survive. All other variables are potential predictor or independent variables. It's important to note, more predictor variables do not make a better model, but the right variables.
* The ``PassengerID`` and ``Ticket`` variables are assumed to be random unique identifiers, that have no impact on the outcome variable. Thus, they will be excluded from analysis.
* The ``Pclass`` variable is an ordinal datatype for the ticket class, a proxy for socio-economic status (SES), representing 1 = upper class, 2 = middle class, and 3 = lower class.
* The ``Name`` variable is a nominal datatype. It could be used in feature engineering to derive the gender from title, family size from surname, and SES from titles like doctor or master. Since these variables already exist, we'll make use of it to see if title, like master, makes a difference.
* The ``Sex`` and ``Embarked`` variables are a nominal datatype. They will be converted to dummy variables for mathematical calculations.
* The ``Age`` and ``Fare`` variable are continuous quantitative datatypes.
* The ``SibSp`` represents number of related siblings/spouse aboard and ``Parch`` represents number of related parents/children aboard. Both are discrete quantitative datatypes. This can be used for feature engineering to create a family size and is alone variable.
* The ``Cabin`` variable is a nominal datatype that can be used in feature engineering for approximate position on ship when the incident occurred and SES from deck levels. However, since there are many null values, it does not add value and thus is excluded from analysis.
```
df.describe(include='all')
```
### Data cleaning
```
df.isnull().sum()
df['Embarked'] = df['Embarked'].fillna(df['Embarked'].mode()[0])
#df['Age'] = df['Age'].fillna(df['Age'].median(), inplace=True)
df['Age'] = df['Age'].groupby([df['Sex'], df['Pclass']]).apply(lambda x: x.fillna(x.median()))
```
Remove useless variables
```
column2drop = ['PassengerId', 'Name', 'Cabin']
df.drop(column2drop, axis=1, inplace=True)
df.head()
```
### Feature Engineering
```
df.boxplot(['Fare'], by='Pclass', showfliers=True)
plt.show()
```
From a carefull data analysis emerges that the Fare is cumulative with respect to various Tickets with the same identifier. Consequently we proceed in correcting the Fare of each passenger by dividing it with the number of Tickets with the same identifier.
```
dfnt = df[['Pclass', 'Ticket']].groupby(['Ticket']).count().reset_index()
dfnt['NumTickets'] = dfnt['Pclass']
dfnt.drop(['Pclass'], axis=1, inplace=True)
dfnt.head()
df = df.join(dfnt.set_index('Ticket'), on='Ticket')
df.head()
df['Fare'] = df['Fare']/df['NumTickets']
```
It is also important to consider the number of people a passenger is travelling with.
```
df['FamilySize'] = df['SibSp'] + df['Parch'] + 1
```
And if he/she is traveling alone or not
```
df['IsAlone'] = 1 # initialize to yes/1 is alone
df['IsAlone'].loc[df['FamilySize'] > 1] = 0 # update to no/0 if family size is greater than 1
```
The features NumTickets and Ticket helped in correcting Fare and we do not need theme any more.
The features SibSp and Parch are redundant with respect to FamilySize.
```
column2drop = ['SibSp', 'Parch', 'NumTickets', 'Ticket']
df.drop(column2drop, axis=1, inplace=True)
df.head()
```
----
### Classification Preprocessing
Feature Reshaping
```
from sklearn.preprocessing import LabelEncoder
label_encoders = dict()
column2encode = ['Sex', 'Embarked']
for col in column2encode:
le = LabelEncoder()
df[col] = le.fit_transform(df[col])
label_encoders[col] = le
df.head()
```
Train/Test partitioning
```
from sklearn.model_selection import train_test_split
attributes = [col for col in df.columns if col != 'Survived']
X = df[attributes].values
y = df['Survived']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)
```
### Parameter Tuning
```
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import RandomizedSearchCV
def report(results, n_top=3):
for i in range(1, n_top + 1):
candidates = np.flatnonzero(results['rank_test_score'] == i)
for candidate in candidates:
print("Model with rank: {0}".format(i))
print("Mean validation score: {0:.3f} (std: {1:.3f})".format(
results['mean_test_score'][candidate],
results['std_test_score'][candidate]))
print("Parameters: {0}".format(results['params'][candidate]))
print("")
param_list = {'max_depth': [None] + list(np.arange(2, 20)),
'min_samples_split': [2, 5, 10, 20, 30, 50, 100],
'min_samples_leaf': [1, 5, 10, 20, 30, 50, 100],
}
clf = DecisionTreeClassifier(criterion='gini', max_depth=None, min_samples_split=2, min_samples_leaf=1)
random_search = RandomizedSearchCV(clf, param_distributions=param_list, n_iter=100)
random_search.fit(X, y)
report(random_search.cv_results_, n_top=3)
```
### Perform Clustering
```
clf = DecisionTreeClassifier(criterion='gini', max_depth=6, min_samples_split=2, min_samples_leaf=5)
clf = clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
y_pred_tr = clf.predict(X_train)
```
### Analyze the classification results
Features Importance
```
for col, imp in zip(attributes, clf.feature_importances_):
print(col, imp)
```
Visualize the decision tree
```
import pydotplus
from sklearn import tree
from IPython.display import Image
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=attributes,
class_names=['Survived' if x == 1 else 'Not Survived' for x in clf.classes_],
filled=True, rounded=True,
special_characters=True,
max_depth=3)
graph = pydotplus.graph_from_dot_data(dot_data)
Image(graph.create_png())
```
### Analyze the classification performance
```
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score, f1_score, classification_report
from sklearn.metrics import roc_curve, auc, roc_auc_score
```
Evaluate the performance
```
print('Train Accuracy %s' % accuracy_score(y_train, y_pred_tr))
print('Train F1-score %s' % f1_score(y_train, y_pred_tr, average=None))
print()
print('Test Accuracy %s' % accuracy_score(y_test, y_pred))
print('Test F1-score %s' % f1_score(y_test, y_pred, average=None))
print(classification_report(y_test, y_pred))
confusion_matrix(y_test, y_pred)
fpr, tpr, _ = roc_curve(y_test, y_pred)
roc_auc = auc(fpr, tpr)
print(roc_auc)
roc_auc = roc_auc_score(y_test, y_pred, average=None)
roc_auc
plt.figure(figsize=(8, 5))
plt.plot(fpr, tpr, label='ROC curve (area = %0.2f)' % (roc_auc))
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate', fontsize=20)
plt.ylabel('True Positive Rate', fontsize=20)
plt.tick_params(axis='both', which='major', labelsize=22)
plt.legend(loc="lower right", fontsize=14, frameon=False)
plt.show()
```
Cross Validation
```
from sklearn.model_selection import cross_val_score
scores = cross_val_score(clf, X, y, cv=10)
print('Accuracy: %0.4f (+/- %0.2f)' % (scores.mean(), scores.std() * 2))
scores = cross_val_score(clf, X, y, cv=10, scoring='f1_macro')
print('F1-score: %0.4f (+/- %0.2f)' % (scores.mean(), scores.std() * 2))
```
### Can we improve the performance using another classifier?
```
from sklearn.ensemble import RandomForestClassifier
param_list = {'max_depth': [None] + list(np.arange(2, 20)),
'min_samples_split': [2, 5, 10, 20, 30, 50, 100],
'min_samples_leaf': [1, 5, 10, 20, 30, 50, 100],
}
clf = RandomForestClassifier(n_estimators=100, criterion='gini', max_depth=None,
min_samples_split=2, min_samples_leaf=1, class_weight=None)
random_search = RandomizedSearchCV(clf, param_distributions=param_list, n_iter=100)
random_search.fit(X, y)
report(random_search.cv_results_, n_top=3)
clf = random_search.best_estimator_
y_pred = clf.predict(X_test)
y_pred_tr = clf.predict(X_train)
print('Train Accuracy %s' % accuracy_score(y_train, y_pred_tr))
print('Train F1-score %s' % f1_score(y_train, y_pred_tr, average=None))
print()
print('Test Accuracy %s' % accuracy_score(y_test, y_pred))
print('Test F1-score %s' % f1_score(y_test, y_pred, average=None))
print(classification_report(y_test, y_pred))
confusion_matrix(y_test, y_pred)
fpr, tpr, _ = roc_curve(y_test, y_pred)
roc_auc = auc(fpr, tpr)
print(roc_auc)
roc_auc = roc_auc_score(y_test, y_pred, average=None)
roc_auc
plt.figure(figsize=(8, 5))
plt.plot(fpr, tpr, label='ROC curve (area = %0.2f)' % (roc_auc))
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate', fontsize=20)
plt.ylabel('True Positive Rate', fontsize=20)
plt.tick_params(axis='both', which='major', labelsize=22)
plt.legend(loc="lower right", fontsize=14, frameon=False)
plt.show()
```
|
github_jupyter
|
%matplotlib inline
import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt
df = pd.read_csv("data/titanic.csv", skipinitialspace=True, sep=',')
df.head()
df.info()
df.describe(include='all')
df.isnull().sum()
df['Embarked'] = df['Embarked'].fillna(df['Embarked'].mode()[0])
#df['Age'] = df['Age'].fillna(df['Age'].median(), inplace=True)
df['Age'] = df['Age'].groupby([df['Sex'], df['Pclass']]).apply(lambda x: x.fillna(x.median()))
column2drop = ['PassengerId', 'Name', 'Cabin']
df.drop(column2drop, axis=1, inplace=True)
df.head()
df.boxplot(['Fare'], by='Pclass', showfliers=True)
plt.show()
dfnt = df[['Pclass', 'Ticket']].groupby(['Ticket']).count().reset_index()
dfnt['NumTickets'] = dfnt['Pclass']
dfnt.drop(['Pclass'], axis=1, inplace=True)
dfnt.head()
df = df.join(dfnt.set_index('Ticket'), on='Ticket')
df.head()
df['Fare'] = df['Fare']/df['NumTickets']
df['FamilySize'] = df['SibSp'] + df['Parch'] + 1
df['IsAlone'] = 1 # initialize to yes/1 is alone
df['IsAlone'].loc[df['FamilySize'] > 1] = 0 # update to no/0 if family size is greater than 1
column2drop = ['SibSp', 'Parch', 'NumTickets', 'Ticket']
df.drop(column2drop, axis=1, inplace=True)
df.head()
from sklearn.preprocessing import LabelEncoder
label_encoders = dict()
column2encode = ['Sex', 'Embarked']
for col in column2encode:
le = LabelEncoder()
df[col] = le.fit_transform(df[col])
label_encoders[col] = le
df.head()
from sklearn.model_selection import train_test_split
attributes = [col for col in df.columns if col != 'Survived']
X = df[attributes].values
y = df['Survived']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import RandomizedSearchCV
def report(results, n_top=3):
for i in range(1, n_top + 1):
candidates = np.flatnonzero(results['rank_test_score'] == i)
for candidate in candidates:
print("Model with rank: {0}".format(i))
print("Mean validation score: {0:.3f} (std: {1:.3f})".format(
results['mean_test_score'][candidate],
results['std_test_score'][candidate]))
print("Parameters: {0}".format(results['params'][candidate]))
print("")
param_list = {'max_depth': [None] + list(np.arange(2, 20)),
'min_samples_split': [2, 5, 10, 20, 30, 50, 100],
'min_samples_leaf': [1, 5, 10, 20, 30, 50, 100],
}
clf = DecisionTreeClassifier(criterion='gini', max_depth=None, min_samples_split=2, min_samples_leaf=1)
random_search = RandomizedSearchCV(clf, param_distributions=param_list, n_iter=100)
random_search.fit(X, y)
report(random_search.cv_results_, n_top=3)
clf = DecisionTreeClassifier(criterion='gini', max_depth=6, min_samples_split=2, min_samples_leaf=5)
clf = clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
y_pred_tr = clf.predict(X_train)
for col, imp in zip(attributes, clf.feature_importances_):
print(col, imp)
import pydotplus
from sklearn import tree
from IPython.display import Image
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=attributes,
class_names=['Survived' if x == 1 else 'Not Survived' for x in clf.classes_],
filled=True, rounded=True,
special_characters=True,
max_depth=3)
graph = pydotplus.graph_from_dot_data(dot_data)
Image(graph.create_png())
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score, f1_score, classification_report
from sklearn.metrics import roc_curve, auc, roc_auc_score
print('Train Accuracy %s' % accuracy_score(y_train, y_pred_tr))
print('Train F1-score %s' % f1_score(y_train, y_pred_tr, average=None))
print()
print('Test Accuracy %s' % accuracy_score(y_test, y_pred))
print('Test F1-score %s' % f1_score(y_test, y_pred, average=None))
print(classification_report(y_test, y_pred))
confusion_matrix(y_test, y_pred)
fpr, tpr, _ = roc_curve(y_test, y_pred)
roc_auc = auc(fpr, tpr)
print(roc_auc)
roc_auc = roc_auc_score(y_test, y_pred, average=None)
roc_auc
plt.figure(figsize=(8, 5))
plt.plot(fpr, tpr, label='ROC curve (area = %0.2f)' % (roc_auc))
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate', fontsize=20)
plt.ylabel('True Positive Rate', fontsize=20)
plt.tick_params(axis='both', which='major', labelsize=22)
plt.legend(loc="lower right", fontsize=14, frameon=False)
plt.show()
from sklearn.model_selection import cross_val_score
scores = cross_val_score(clf, X, y, cv=10)
print('Accuracy: %0.4f (+/- %0.2f)' % (scores.mean(), scores.std() * 2))
scores = cross_val_score(clf, X, y, cv=10, scoring='f1_macro')
print('F1-score: %0.4f (+/- %0.2f)' % (scores.mean(), scores.std() * 2))
from sklearn.ensemble import RandomForestClassifier
param_list = {'max_depth': [None] + list(np.arange(2, 20)),
'min_samples_split': [2, 5, 10, 20, 30, 50, 100],
'min_samples_leaf': [1, 5, 10, 20, 30, 50, 100],
}
clf = RandomForestClassifier(n_estimators=100, criterion='gini', max_depth=None,
min_samples_split=2, min_samples_leaf=1, class_weight=None)
random_search = RandomizedSearchCV(clf, param_distributions=param_list, n_iter=100)
random_search.fit(X, y)
report(random_search.cv_results_, n_top=3)
clf = random_search.best_estimator_
y_pred = clf.predict(X_test)
y_pred_tr = clf.predict(X_train)
print('Train Accuracy %s' % accuracy_score(y_train, y_pred_tr))
print('Train F1-score %s' % f1_score(y_train, y_pred_tr, average=None))
print()
print('Test Accuracy %s' % accuracy_score(y_test, y_pred))
print('Test F1-score %s' % f1_score(y_test, y_pred, average=None))
print(classification_report(y_test, y_pred))
confusion_matrix(y_test, y_pred)
fpr, tpr, _ = roc_curve(y_test, y_pred)
roc_auc = auc(fpr, tpr)
print(roc_auc)
roc_auc = roc_auc_score(y_test, y_pred, average=None)
roc_auc
plt.figure(figsize=(8, 5))
plt.plot(fpr, tpr, label='ROC curve (area = %0.2f)' % (roc_auc))
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate', fontsize=20)
plt.ylabel('True Positive Rate', fontsize=20)
plt.tick_params(axis='both', which='major', labelsize=22)
plt.legend(loc="lower right", fontsize=14, frameon=False)
plt.show()
| 0.520496 | 0.986726 |
# Esma 3016
## Edgar Acuna
### Agosto 2019
### Lab 3: Organizacion y presentacion de datos cuantitativos continuos.
#### Usaremos el modulo numpy, el modulo pandas, que se usa para hacer analisis estadistico basico y el modulo matplotlib que se usa para hacer la tabla de frecuencias y las graficas.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
#Leyendo datos de la internet, las columnas tienen nombres
datos=pd.read_csv("http://academic.uprm.edu/eacuna/clase97.txt",sep=" ")
#Viendo las seis primera fila de la tabla de datos
datos.head()
#Este en un primer intento de hacer la tabla de frecuencias
#para datos agrupados usando numpy solamente
#Este comando encuentra las frecuencias absolutas
#y los puntos del corte en forma automatica usando numpy
conteo, cortes=np.histogram(datos['gpa'])
#Aqui se muestran las frecuencias absolutas de los intervalos y los puntos de cortes respectivos
conteo, cortes
```
#### Comentario: Demasiados intervalos,10, para tan solo 28 datos en lo que sigue vamos a construir una tabla de frecuencias con 5 intervalos
```
#Los puntos de cortes de los 5 intervalos son entrados manualmente
#la amplitud que se ha usado es (Mayor-menor)/5=.34 redondeado a .35
cortesf=[2.15,2.5,2.85,3.2,3.55,3.9]
conteof, cortesf=np.histogram(datos['gpa'],bins=cortesf)
#estas son las frecuencias absolutas
conteof
#estos son los puntos de cortes
cortesf
#Calculo de las frecuencias absolutas usando pandas
a1=pd.cut(datos['gpa'],cortesf,right=False)
t1=pd.value_counts(a1,sort=False)
t1=pd.DataFrame(t1)
t1
#determinado automaticamente el ancho de cada uno de los 5 intervalos
m=min(datos['gpa'])
M=max(datos['gpa'])
ancho=(M-m)/5
gpa1=np.array(datos['gpa'])
cortes1=np.linspace(m,M,num=6)
cortes1
#construyendo la tabla de frecuencias usando la funcion crosstab de pandas
a, b=pd.cut(gpa1,bins=cortes1,include_lowest=True, right=True, retbins=True)
tablag=pd.crosstab(a,columns='counts')
tablag
# Hallando las frecuencias relativas porcentuales y las acumuladas
tablag['frec.relat.porc']=tablag*100/tablag.sum()
tablag['frec.acum']=tablag.counts.cumsum()
tablag['frec.relat.porc.acum']=tablag['frec.acum']*100/tablag['counts'].sum()
tablag.round(3)
#Haciendo una funcion que haga la tabla completa de distribucion de frecuencias para datos agrupados
def tablafreqag(datos,str,k):
"""
:param datos: Es el nombre de la base de datos
:param str: Es el nombre de la variable a usar de la base de datos.
:param k: Numero de intervalos
"""
import pandas as pd
m=min(datos[str])
M=max(datos[str])
ancho=(M-m)/k
var1=np.array(datos[str])
cortes1=np.linspace(m,M,num=k+1)
a, b=pd.cut(var1,bins=cortes1,include_lowest=True, right=True, retbins=True)
tablag=pd.crosstab(a,columns='counts')
tablag['frec.relat.porc']=tablag*100/tablag.sum()
tablag['frec.acum']=tablag.counts.cumsum()
tablag['frec.relat.porc.acum']=tablag['frec.acum']*100/tablag['counts'].sum()
tablag.round(3)
return tablag;
tablafreqag(datos,'gpa',5)
# Pidiendo ayuda acerca de la funcion hist
help(plt.hist)
plt.hist(datos['gpa'],bins=6)
plt.hist(datos['gpa'],bins=cortesf)
plt.title('Histograma de GPA ')
xl=cortesf
yl=conteof
for a,b in zip(xl,yl):
plt.text(a+.17,b,str(b))
```
El histograma tiene menor cantidad de datos en el lado izquierdo que en el lado derecho entonces es ASIMETRICO a la izquierda. La muestra no es buena para sacar conclsuiones
```
plt.style.use('ggplot')
with plt.style.context('ggplot'):
# plot command goes here
plt.hist(datos['gpa'],bins=5)
plt.show()
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
#Leyendo datos de la internet, las columnas tienen nombres
datos=pd.read_csv("http://academic.uprm.edu/eacuna/clase97.txt",sep=" ")
#Viendo las seis primera fila de la tabla de datos
datos.head()
#Este en un primer intento de hacer la tabla de frecuencias
#para datos agrupados usando numpy solamente
#Este comando encuentra las frecuencias absolutas
#y los puntos del corte en forma automatica usando numpy
conteo, cortes=np.histogram(datos['gpa'])
#Aqui se muestran las frecuencias absolutas de los intervalos y los puntos de cortes respectivos
conteo, cortes
#Los puntos de cortes de los 5 intervalos son entrados manualmente
#la amplitud que se ha usado es (Mayor-menor)/5=.34 redondeado a .35
cortesf=[2.15,2.5,2.85,3.2,3.55,3.9]
conteof, cortesf=np.histogram(datos['gpa'],bins=cortesf)
#estas son las frecuencias absolutas
conteof
#estos son los puntos de cortes
cortesf
#Calculo de las frecuencias absolutas usando pandas
a1=pd.cut(datos['gpa'],cortesf,right=False)
t1=pd.value_counts(a1,sort=False)
t1=pd.DataFrame(t1)
t1
#determinado automaticamente el ancho de cada uno de los 5 intervalos
m=min(datos['gpa'])
M=max(datos['gpa'])
ancho=(M-m)/5
gpa1=np.array(datos['gpa'])
cortes1=np.linspace(m,M,num=6)
cortes1
#construyendo la tabla de frecuencias usando la funcion crosstab de pandas
a, b=pd.cut(gpa1,bins=cortes1,include_lowest=True, right=True, retbins=True)
tablag=pd.crosstab(a,columns='counts')
tablag
# Hallando las frecuencias relativas porcentuales y las acumuladas
tablag['frec.relat.porc']=tablag*100/tablag.sum()
tablag['frec.acum']=tablag.counts.cumsum()
tablag['frec.relat.porc.acum']=tablag['frec.acum']*100/tablag['counts'].sum()
tablag.round(3)
#Haciendo una funcion que haga la tabla completa de distribucion de frecuencias para datos agrupados
def tablafreqag(datos,str,k):
"""
:param datos: Es el nombre de la base de datos
:param str: Es el nombre de la variable a usar de la base de datos.
:param k: Numero de intervalos
"""
import pandas as pd
m=min(datos[str])
M=max(datos[str])
ancho=(M-m)/k
var1=np.array(datos[str])
cortes1=np.linspace(m,M,num=k+1)
a, b=pd.cut(var1,bins=cortes1,include_lowest=True, right=True, retbins=True)
tablag=pd.crosstab(a,columns='counts')
tablag['frec.relat.porc']=tablag*100/tablag.sum()
tablag['frec.acum']=tablag.counts.cumsum()
tablag['frec.relat.porc.acum']=tablag['frec.acum']*100/tablag['counts'].sum()
tablag.round(3)
return tablag;
tablafreqag(datos,'gpa',5)
# Pidiendo ayuda acerca de la funcion hist
help(plt.hist)
plt.hist(datos['gpa'],bins=6)
plt.hist(datos['gpa'],bins=cortesf)
plt.title('Histograma de GPA ')
xl=cortesf
yl=conteof
for a,b in zip(xl,yl):
plt.text(a+.17,b,str(b))
plt.style.use('ggplot')
with plt.style.context('ggplot'):
# plot command goes here
plt.hist(datos['gpa'],bins=5)
plt.show()
| 0.385028 | 0.796649 |
```
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
# Decision stump used as weak classifier
class DecisionStump():
def __init__(self):
self.polarity = 1
self.feature_idx = None
self.threshold = None
self.alpha = None
def predict(self, X):
n_samples = X.shape[0]
X_column = X[:, self.feature_idx]
predictions = np.ones(n_samples)
if self.polarity == 1:
predictions[X_column < self.threshold] = -1
else:
predictions[X_column > self.threshold] = -1
return predictions
class Adaboost():
def __init__(self, n_clf=5):
self.n_clf = n_clf
def fit(self, X, y):
n_samples, n_features = X.shape
# Initialize weights to 1/N
w = np.full(n_samples, (1 / n_samples))
self.clfs = []
# Iterate through classifiers
for _ in range(self.n_clf):
clf = DecisionStump()
min_error = float('inf')
# greedy search to find best threshold and feature
for feature_i in range(n_features):
X_column = X[:, feature_i]
thresholds = np.unique(X_column)
for threshold in thresholds:
# predict with polarity 1
p = 1
predictions = np.ones(n_samples)
predictions[X_column < threshold] = -1
# Error = sum of weights of misclassified samples
misclassified = w[y != predictions]
error = sum(misclassified)
if error > 0.5:
error = 1 - error
p = -1
# store the best configuration
if error < min_error:
clf.polarity = p
clf.threshold = threshold
clf.feature_idx = feature_i
min_error = error
# calculate alpha
EPS = 1e-10
clf.alpha = 0.5 * np.log((1.0 - min_error + EPS) / (min_error + EPS))
# calculate predictions and update weights
predictions = clf.predict(X)
w *= np.exp(-clf.alpha * y * predictions)
# Normalize to one
w /= np.sum(w)
# Save classifier
self.clfs.append(clf)
def predict(self, X):
clf_preds = [clf.alpha * clf.predict(X) for clf in self.clfs]
y_pred = np.sum(clf_preds, axis=0)
y_pred = np.sign(y_pred)
return y_pred
def accuracy(y_true, y_pred):
accuracy = np.sum(y_true == y_pred) / len(y_true)
return accuracy
data = datasets.load_breast_cancer()
X = data.data
y = data.target
y[y == 0] = -1
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=5)
# Adaboost classification with 5 weak classifiers
clf = Adaboost(n_clf=5)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
acc = accuracy(y_test, y_pred)
print ("Accuracy:", acc)
```
|
github_jupyter
|
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
# Decision stump used as weak classifier
class DecisionStump():
def __init__(self):
self.polarity = 1
self.feature_idx = None
self.threshold = None
self.alpha = None
def predict(self, X):
n_samples = X.shape[0]
X_column = X[:, self.feature_idx]
predictions = np.ones(n_samples)
if self.polarity == 1:
predictions[X_column < self.threshold] = -1
else:
predictions[X_column > self.threshold] = -1
return predictions
class Adaboost():
def __init__(self, n_clf=5):
self.n_clf = n_clf
def fit(self, X, y):
n_samples, n_features = X.shape
# Initialize weights to 1/N
w = np.full(n_samples, (1 / n_samples))
self.clfs = []
# Iterate through classifiers
for _ in range(self.n_clf):
clf = DecisionStump()
min_error = float('inf')
# greedy search to find best threshold and feature
for feature_i in range(n_features):
X_column = X[:, feature_i]
thresholds = np.unique(X_column)
for threshold in thresholds:
# predict with polarity 1
p = 1
predictions = np.ones(n_samples)
predictions[X_column < threshold] = -1
# Error = sum of weights of misclassified samples
misclassified = w[y != predictions]
error = sum(misclassified)
if error > 0.5:
error = 1 - error
p = -1
# store the best configuration
if error < min_error:
clf.polarity = p
clf.threshold = threshold
clf.feature_idx = feature_i
min_error = error
# calculate alpha
EPS = 1e-10
clf.alpha = 0.5 * np.log((1.0 - min_error + EPS) / (min_error + EPS))
# calculate predictions and update weights
predictions = clf.predict(X)
w *= np.exp(-clf.alpha * y * predictions)
# Normalize to one
w /= np.sum(w)
# Save classifier
self.clfs.append(clf)
def predict(self, X):
clf_preds = [clf.alpha * clf.predict(X) for clf in self.clfs]
y_pred = np.sum(clf_preds, axis=0)
y_pred = np.sign(y_pred)
return y_pred
def accuracy(y_true, y_pred):
accuracy = np.sum(y_true == y_pred) / len(y_true)
return accuracy
data = datasets.load_breast_cancer()
X = data.data
y = data.target
y[y == 0] = -1
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=5)
# Adaboost classification with 5 weak classifiers
clf = Adaboost(n_clf=5)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
acc = accuracy(y_test, y_pred)
print ("Accuracy:", acc)
| 0.798423 | 0.560794 |
<a href="https://colab.research.google.com/github/priyanshgupta1998/Natural-language-processing-NLP-/blob/master/NLTK_NLP.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
```
#Stemming and Lemmatization with Python NLTK
This is a demonstration of stemming and lemmatization for the 17 languages supported by the NLTK 2.0.4 stem package.
Stemming is a process of removing and replacing word suffixes to arrive at a common root form of the word.
For stemming English words with NLTK, you can choose between the **PorterStemmer** or the **LancasterStemmer**.
The Porter Stemming Algorithm is the oldest stemming algorithm supported in NLTK.
The Lancaster Stemming Algorithm is much newer and can be more aggressive than the Porter stemming algorithm.
The WordNet Lemmatizer uses the WordNet Database to lookup lemmas. Lemmas differ from stems in that a lemma is a canonical form of the word, while a stem may not be a real word.
##Non-English Stemmers
Stemming for Portuguese is available in NLTK with the **RSLPStemmer** and also with the **SnowballStemmer**. Arabic stemming is supported with the **ISRIStemmer**.
Snowball is actually a language for creating stemmers. The NLTK Snowball stemmer currently supports the following languages:
Danish
Dutch
English
Finnish
French
German
Hungarian
Italian
Norwegian
Porter
Portuguese
Romanian
Russian
Spanish
Swedish
```
from nltk import wordpunct_tokenize
wordpunct_tokenize("That's thirty minutes away. I'll be there in ten.")
import nltk
nltk.download('stopwords')
from nltk.corpus import stopwords
print(len(stopwords.fileids()))
print(stopwords.fileids())
text = '''
There's a passage I got memorized. Ezekiel 25:17. "The path of the righteous man is beset on all sides\
by the inequities of the selfish and the tyranny of evil men. Blessed is he who, in the name of charity\
and good will, shepherds the weak through the valley of the darkness, for he is truly his brother's keeper\
and the finder of lost children. And I will strike down upon thee with great vengeance and furious anger\
those who attempt to poison and destroy My brothers. And you will know I am the Lord when I lay My vengeance\
upon you." Now... I been sayin' that shit for years. And if you ever heard it, that meant your ass. You'd\
be dead right now. I never gave much thought to what it meant. I just thought it was a cold-blooded thing\
to say to a motherfucker before I popped a cap in his ass. But I saw some shit this mornin' made me think\
twice. See, now I'm thinking: maybe it means you're the evil man. And I'm the righteous man. And Mr.\
9mm here... he's the shepherd protecting my righteous ass in the valley of darkness. Or it could mean\
you're the righteous man and I'm the shepherd and it's the world that's evil and selfish. And I'd like\
that. But that shit ain't the truth. The truth is you're the weak. And I'm the tyranny of evil men.\
But I'm tryin', Ringo. I'm tryin' real hard to be the shepherd.
'''
languages_ratios = {}
tokens = wordpunct_tokenize(text)
words = [word.lower() for word in tokens]
print(words)
for language in stopwords.fileids():
stopwords_set = set(stopwords.words(language))
print(stopwords_set)
for language in stopwords.fileids():
stopwords_set = set(stopwords.words(language))
words_set = set(words)
common_elements = words_set.intersection(stopwords_set)
languages_ratios[language] = len(common_elements) # language "score"
print(languages_ratios)
most_rated_language = max(languages_ratios, key=languages_ratios.get)
most_rated_language
```
#N-GRAMS
`an n-gram is a contiguous sequence of n items from a given sample of text or speech.`
` N-Gram-Based text categorization is useful also for identifying the topic of the text and not just language.`
`The items can be phonemes, syllables, letters, words or base pairs according to the application. The n-grams typically are collected from a text or speech corpus.`
`N-grams of texts are extensively used in text mining and natural language processing tasks.when computing the n-grams you typically move one word forward (although you can move X words forward in more advanced scenarios)`
` N-gram models is used to estimate the probability of the last word of an N-gram given the previous words, and also to assign probabilities to entire sequences. we can use n-gram models to derive a probability of the sentence.`
To perform N-Gram-Based Text Categorization we need to compute N-grams (with N=1 to 5) for each word - and apostrophes.
bi-grams: _T, TE, EX, XT, T_
tri-grams: _TE, TEX, EXT, XT_, T_ _
quad-grams: _TEX, TEXT, EXT_, XT_ _, T_ _ _
```
from nltk.tokenize import RegexpTokenizer
tokenizer = RegexpTokenizer("[a-zA-Z'`éèî]+")
print(tokenizer.tokenize("Le temps est un grand maître, dit-on, le malheur est qu'il tue ses élèves."))
from nltk.util import ngrams
generated_ngrams = ngrams('TEXT', 4, pad_left=True, pad_right=True)
print(list(generated_ngrams))
from nltk.util import ngrams
generated_ngrams = ngrams('TEXT', 4, pad_left=True, pad_right=True , left_pad_symbol=' ')
print(list(generated_ngrams))
generated_ngrams = ngrams('TEXT', 4, pad_left=True, pad_right=True, left_pad_symbol=' ', right_pad_symbol=' ')
k = list(generated_ngrams)
print(k)
print(k[4])
''.join(k[4])
from functools import partial
from nltk import ngrams
x = 'TEXT'
print(len(list(ngrams(x, 2))) , list(ngrams(x, 2)))
padded_ngrams = partial(ngrams, pad_left=True, pad_right=True, left_pad_symbol='_', right_pad_symbol='_')
print(list(padded_ngrams(x, 2)))
print(len(list(padded_ngrams(x, 2))))
print(len(list(padded_ngrams(x, 3))))
print(len(list(padded_ngrams(x, 4))))
print(len(list(padded_ngrams(x, 5))))
import numpy as np
from nltk.util import ngrams as ng
from nltk import ngrams as ngr
print(ngr)
print(ng)
# ngrams_statistics = {}
# for ngram in ngrams:
# if not ngrams_statistics.has_key(ngram):
# ngrams_statistics.update({ngram:1})
# else:
# ngram_occurrences = ngrams_statistics[ngram]
# ngrams_statistics.update({ngram:ngram_occurrences+1})
```
|
github_jupyter
|
```
#Stemming and Lemmatization with Python NLTK
This is a demonstration of stemming and lemmatization for the 17 languages supported by the NLTK 2.0.4 stem package.
Stemming is a process of removing and replacing word suffixes to arrive at a common root form of the word.
For stemming English words with NLTK, you can choose between the **PorterStemmer** or the **LancasterStemmer**.
The Porter Stemming Algorithm is the oldest stemming algorithm supported in NLTK.
The Lancaster Stemming Algorithm is much newer and can be more aggressive than the Porter stemming algorithm.
The WordNet Lemmatizer uses the WordNet Database to lookup lemmas. Lemmas differ from stems in that a lemma is a canonical form of the word, while a stem may not be a real word.
##Non-English Stemmers
Stemming for Portuguese is available in NLTK with the **RSLPStemmer** and also with the **SnowballStemmer**. Arabic stemming is supported with the **ISRIStemmer**.
Snowball is actually a language for creating stemmers. The NLTK Snowball stemmer currently supports the following languages:
Danish
Dutch
English
Finnish
French
German
Hungarian
Italian
Norwegian
Porter
Portuguese
Romanian
Russian
Spanish
Swedish
#N-GRAMS
`an n-gram is a contiguous sequence of n items from a given sample of text or speech.`
` N-Gram-Based text categorization is useful also for identifying the topic of the text and not just language.`
`The items can be phonemes, syllables, letters, words or base pairs according to the application. The n-grams typically are collected from a text or speech corpus.`
`N-grams of texts are extensively used in text mining and natural language processing tasks.when computing the n-grams you typically move one word forward (although you can move X words forward in more advanced scenarios)`
` N-gram models is used to estimate the probability of the last word of an N-gram given the previous words, and also to assign probabilities to entire sequences. we can use n-gram models to derive a probability of the sentence.`
To perform N-Gram-Based Text Categorization we need to compute N-grams (with N=1 to 5) for each word - and apostrophes.
bi-grams: _T, TE, EX, XT, T_
tri-grams: _TE, TEX, EXT, XT_, T_ _
quad-grams: _TEX, TEXT, EXT_, XT_ _, T_ _ _
| 0.850608 | 0.917672 |
# Sklearn
## sklearn.tree
документация: http://scikit-learn.org/stable/modules/classes.html#module-sklearn.tree
примеры: http://scikit-learn.org/stable/modules/classes.html#module-sklearn.tree
```
from matplotlib.colors import ListedColormap
from sklearn import cross_validation, datasets, metrics, tree
import numpy as np
%pylab inline
```
### Генерация данных
```
classification_problem = datasets.make_classification(n_features = 2, n_informative = 2,
n_classes = 3, n_redundant=0,
n_clusters_per_class=1, random_state=3)
colors = ListedColormap(['red', 'blue', 'yellow'])
light_colors = ListedColormap(['lightcoral', 'lightblue', 'lightyellow'])
pylab.figure(figsize=(8,6))
pylab.scatter(map(lambda x: x[0], classification_problem[0]), map(lambda x: x[1], classification_problem[0]),
c=classification_problem[1], cmap=colors, s=100)
train_data, test_data, train_labels, test_labels = cross_validation.train_test_split(classification_problem[0],
classification_problem[1],
test_size = 0.3,
random_state = 1)
```
### Модель DecisionTreeClassifier
```
clf = tree.DecisionTreeClassifier(random_state=1)
clf.fit(train_data, train_labels)
predictions = clf.predict(test_data)
metrics.accuracy_score(test_labels, predictions)
predictions
```
### Разделяющая поверхность
```
def get_meshgrid(data, step=.05, border=.5,):
x_min, x_max = data[:, 0].min() - border, data[:, 0].max() + border
y_min, y_max = data[:, 1].min() - border, data[:, 1].max() + border
return np.meshgrid(np.arange(x_min, x_max, step), np.arange(y_min, y_max, step))
def plot_decision_surface(estimator, train_data, train_labels, test_data, test_labels,
colors = colors, light_colors = light_colors):
#fit model
estimator.fit(train_data, train_labels)
#set figure size
pyplot.figure(figsize = (16, 6))
#plot decision surface on the train data
pyplot.subplot(1,2,1)
xx, yy = get_meshgrid(train_data)
mesh_predictions = np.array(estimator.predict(np.c_[xx.ravel(), yy.ravel()])).reshape(xx.shape)
pyplot.pcolormesh(xx, yy, mesh_predictions, cmap = light_colors)
pyplot.scatter(train_data[:, 0], train_data[:, 1], c = train_labels, s = 100, cmap = colors)
pyplot.title('Train data, accuracy={:.2f}'.format(metrics.accuracy_score(train_labels, estimator.predict(train_data))))
#plot decision surface on the test data
pyplot.subplot(1,2,2)
pyplot.pcolormesh(xx, yy, mesh_predictions, cmap = light_colors)
pyplot.scatter(test_data[:, 0], test_data[:, 1], c = test_labels, s = 100, cmap = colors)
pyplot.title('Test data, accuracy={:.2f}'.format(metrics.accuracy_score(test_labels, estimator.predict(test_data))))
estimator = tree.DecisionTreeClassifier(random_state = 1, max_depth = 1)
plot_decision_surface(estimator, train_data, train_labels, test_data, test_labels)
plot_decision_surface(tree.DecisionTreeClassifier(random_state = 1, max_depth = 2),
train_data, train_labels, test_data, test_labels)
plot_decision_surface(tree.DecisionTreeClassifier(random_state = 1, max_depth = 3),
train_data, train_labels, test_data, test_labels)
plot_decision_surface(tree.DecisionTreeClassifier(random_state = 1),
train_data, train_labels, test_data, test_labels)
plot_decision_surface(tree.DecisionTreeClassifier(random_state = 1, min_samples_leaf = 3),
train_data, train_labels, test_data, test_labels)
```
|
github_jupyter
|
from matplotlib.colors import ListedColormap
from sklearn import cross_validation, datasets, metrics, tree
import numpy as np
%pylab inline
classification_problem = datasets.make_classification(n_features = 2, n_informative = 2,
n_classes = 3, n_redundant=0,
n_clusters_per_class=1, random_state=3)
colors = ListedColormap(['red', 'blue', 'yellow'])
light_colors = ListedColormap(['lightcoral', 'lightblue', 'lightyellow'])
pylab.figure(figsize=(8,6))
pylab.scatter(map(lambda x: x[0], classification_problem[0]), map(lambda x: x[1], classification_problem[0]),
c=classification_problem[1], cmap=colors, s=100)
train_data, test_data, train_labels, test_labels = cross_validation.train_test_split(classification_problem[0],
classification_problem[1],
test_size = 0.3,
random_state = 1)
clf = tree.DecisionTreeClassifier(random_state=1)
clf.fit(train_data, train_labels)
predictions = clf.predict(test_data)
metrics.accuracy_score(test_labels, predictions)
predictions
def get_meshgrid(data, step=.05, border=.5,):
x_min, x_max = data[:, 0].min() - border, data[:, 0].max() + border
y_min, y_max = data[:, 1].min() - border, data[:, 1].max() + border
return np.meshgrid(np.arange(x_min, x_max, step), np.arange(y_min, y_max, step))
def plot_decision_surface(estimator, train_data, train_labels, test_data, test_labels,
colors = colors, light_colors = light_colors):
#fit model
estimator.fit(train_data, train_labels)
#set figure size
pyplot.figure(figsize = (16, 6))
#plot decision surface on the train data
pyplot.subplot(1,2,1)
xx, yy = get_meshgrid(train_data)
mesh_predictions = np.array(estimator.predict(np.c_[xx.ravel(), yy.ravel()])).reshape(xx.shape)
pyplot.pcolormesh(xx, yy, mesh_predictions, cmap = light_colors)
pyplot.scatter(train_data[:, 0], train_data[:, 1], c = train_labels, s = 100, cmap = colors)
pyplot.title('Train data, accuracy={:.2f}'.format(metrics.accuracy_score(train_labels, estimator.predict(train_data))))
#plot decision surface on the test data
pyplot.subplot(1,2,2)
pyplot.pcolormesh(xx, yy, mesh_predictions, cmap = light_colors)
pyplot.scatter(test_data[:, 0], test_data[:, 1], c = test_labels, s = 100, cmap = colors)
pyplot.title('Test data, accuracy={:.2f}'.format(metrics.accuracy_score(test_labels, estimator.predict(test_data))))
estimator = tree.DecisionTreeClassifier(random_state = 1, max_depth = 1)
plot_decision_surface(estimator, train_data, train_labels, test_data, test_labels)
plot_decision_surface(tree.DecisionTreeClassifier(random_state = 1, max_depth = 2),
train_data, train_labels, test_data, test_labels)
plot_decision_surface(tree.DecisionTreeClassifier(random_state = 1, max_depth = 3),
train_data, train_labels, test_data, test_labels)
plot_decision_surface(tree.DecisionTreeClassifier(random_state = 1),
train_data, train_labels, test_data, test_labels)
plot_decision_surface(tree.DecisionTreeClassifier(random_state = 1, min_samples_leaf = 3),
train_data, train_labels, test_data, test_labels)
| 0.847983 | 0.932207 |
```
import numpy as np
questions1 = np.array([("At a party do you", "interact with many, including strangers", "interact with a few, known to you"),
("At parties do you", "Stay late, with increasing energy", "Leave early, with decreasing energy"),
("In your social groups do you", "Keep abreast of others happenings", "Get behind on the news"),
("Are you usually rather", "Quick to agree to a time", "Reluctant to agree to a time"),
("In company do you", "Start conversations", "Wait to be approached"),
("Does new interaction with others", "Stimulate and energize you", "Tax your reserves"),
("Do you prefer", "Many friends with brief contact", "A few friends with longer contact"),
("Do you", "Speak easily and at length with strangers", "Find little to say to strangers"),
("When the phone rings do you", "Quickly get to it first", "Hope someone else will answer"),
("At networking functions you are", "Easy to approach", "A little reserved")],dtype=str)
questions2 = np.array([("Are you more", "Realistic", "Philosophically inclined "),
("Are you a more", "Sensible person", "Reflective person "),
("Are you usually more interested in", "Specifics", "Concepts "),
("Facts", "Speak for themselves", "Usually require interpretation "),
("Traditional common sense is", "Usually trustworthy", "often misleading "),
("Are you more frequently", "A practical sort of person", "An abstract sort of person "),
("Are you more drawn to", "Substantial information", "Credible assumptions "),
("Are you usually more interested in the", "Particular instance", "General case "),
("Do you prize more in yourself a", "Good sense of reality", "Good imagination "),
("Do you have more fun with", "Hands-on experience", "Blue-sky fantasy "),
("Are you usually more", "Fair minded", "Kind hearted"),
("Is it more natural to be", "Fair to others", "Nice to others"),
("Are you more naturally", "Impartial", "Compassionate"),
("Are you inclined to be more", "Cool headed", "Warm hearted"),
("Are you usually more", "Tough minded", "Tender hearted"),
("Which is more satisfying", "To discuss an issue throughly", "To arrive at agreement on an issue"),
("Are you more comfortable when you are", "Objective", "Personal"),
("Are you typically more a person of", "Clear reason", "Strong feeling"),
("In judging are you usually more", "Neutral", "Charitable"),
("Are you usually more", "Unbiased", "compassionate")],dtype=str)
questions3 = np.array([("Do you tend to be more", "Dispassionate", "Sympathetic"),
("In first approaching others are you more", "Impersonal and detached", "Personal and engaging"),
("In judging are you more likely to be", "Impersonal", "Sentimental"),
("Would you rather be", "More just than merciful", "More merciful than just"),
("Are you usually more", "Tough minded", "Tender hearted"),
("Which rules you more", "Your head", "Your heart"),
("Do you value in yourself more that you are", "Unwavering", "Devoted"),
("Are you inclined more to be", "Fair-minded", "Sympathetic"),
("Are you convinced by?", "Evidence", "Someone you trust"),
("Are you typically more", "Just than lenient", "Lenient than just")],dtype=str)
questions4 = np.array([("Do you prefer to work", "To deadlines", "Just whenever"),
("Are you usually more", "Punctual", "Leisurely"),
("Do you usually", "Settle things", "Keep options open"),
("Are you more comfortable", "Setting a schedule", "Putting things off"),
("Are you more prone to keep things", "well organized", "Open-ended"),
("Are you more comfortable with work", "Contracted", "Done on a casual basis"),
("Are you more comfortable with", "Final statements", "Tentative statements"),
("Is it preferable mostly to", "Make sure things are arranged", "Just let things happen"),
("Do you prefer?", "Getting something done", "Having the option to go back"),
("Is it more like you to", "Make snap judgements", "Delay making judgements")],dtype=str)
questions5 = np.array([("Do you tend to choose", "Rather carefully", "Somewhat impulsively"),
("Does it bother you more having things", "Incomplete", "Completed"),
("Are you usually rather", "Quick to agree to a time", "Reluctant to agree to a time"),
("Are you more comfortable with", "Written agreements", "Handshake agreements"),
("Do you put more value on the", "Definite", "Variable"),
("Do you prefer things to be", "Neat and orderly", "Optional"),
("Are you more comfortable", "After a decision", "Before a decision"),
("Is it your way more to", "Get things settled", "Put off settlement"),
("Do you prefer to?", "Set things up perfectly", "Allow things to come together"),
("Do you tend to be more", "Deliberate than spontaneous", "Spontaneous than deliberate")],dtype=str)
def test(questions):
total_count = []
for idx, question in enumerate(questions):
total_count.append(ask(question))
if total_count.count(1) > total_count.count(2):
return 1
else:
return 2
def ask(question):
type_count1 = 0
type_count2 = 0
answer = input(f" {question[0]}: \n 1. {question[1]}\n 2. {question[2]}\n")
if answer == '1':
return 1
if answer == '2':
return 2
else:
print("Make sure your input is 1 or 2")
ask(question)
def main():
EorI = test(questions1)
EorI = 'E' if EorI == 1 else 'I'
SorN = test(questions2)
SorN = 'S' if SorN == 1 else 'N'
TorF = test(np.concatenate((questions3, questions4), axis=0))
TorF = 'T' if TorF == 1 else 'F'
JorP = test(questions5)
JorP = 'J' if JorP == 1 else 'P'
print(f"Your character is : ",EorI+SorN+TorF+JorP)
return 0
main()
```
|
github_jupyter
|
import numpy as np
questions1 = np.array([("At a party do you", "interact with many, including strangers", "interact with a few, known to you"),
("At parties do you", "Stay late, with increasing energy", "Leave early, with decreasing energy"),
("In your social groups do you", "Keep abreast of others happenings", "Get behind on the news"),
("Are you usually rather", "Quick to agree to a time", "Reluctant to agree to a time"),
("In company do you", "Start conversations", "Wait to be approached"),
("Does new interaction with others", "Stimulate and energize you", "Tax your reserves"),
("Do you prefer", "Many friends with brief contact", "A few friends with longer contact"),
("Do you", "Speak easily and at length with strangers", "Find little to say to strangers"),
("When the phone rings do you", "Quickly get to it first", "Hope someone else will answer"),
("At networking functions you are", "Easy to approach", "A little reserved")],dtype=str)
questions2 = np.array([("Are you more", "Realistic", "Philosophically inclined "),
("Are you a more", "Sensible person", "Reflective person "),
("Are you usually more interested in", "Specifics", "Concepts "),
("Facts", "Speak for themselves", "Usually require interpretation "),
("Traditional common sense is", "Usually trustworthy", "often misleading "),
("Are you more frequently", "A practical sort of person", "An abstract sort of person "),
("Are you more drawn to", "Substantial information", "Credible assumptions "),
("Are you usually more interested in the", "Particular instance", "General case "),
("Do you prize more in yourself a", "Good sense of reality", "Good imagination "),
("Do you have more fun with", "Hands-on experience", "Blue-sky fantasy "),
("Are you usually more", "Fair minded", "Kind hearted"),
("Is it more natural to be", "Fair to others", "Nice to others"),
("Are you more naturally", "Impartial", "Compassionate"),
("Are you inclined to be more", "Cool headed", "Warm hearted"),
("Are you usually more", "Tough minded", "Tender hearted"),
("Which is more satisfying", "To discuss an issue throughly", "To arrive at agreement on an issue"),
("Are you more comfortable when you are", "Objective", "Personal"),
("Are you typically more a person of", "Clear reason", "Strong feeling"),
("In judging are you usually more", "Neutral", "Charitable"),
("Are you usually more", "Unbiased", "compassionate")],dtype=str)
questions3 = np.array([("Do you tend to be more", "Dispassionate", "Sympathetic"),
("In first approaching others are you more", "Impersonal and detached", "Personal and engaging"),
("In judging are you more likely to be", "Impersonal", "Sentimental"),
("Would you rather be", "More just than merciful", "More merciful than just"),
("Are you usually more", "Tough minded", "Tender hearted"),
("Which rules you more", "Your head", "Your heart"),
("Do you value in yourself more that you are", "Unwavering", "Devoted"),
("Are you inclined more to be", "Fair-minded", "Sympathetic"),
("Are you convinced by?", "Evidence", "Someone you trust"),
("Are you typically more", "Just than lenient", "Lenient than just")],dtype=str)
questions4 = np.array([("Do you prefer to work", "To deadlines", "Just whenever"),
("Are you usually more", "Punctual", "Leisurely"),
("Do you usually", "Settle things", "Keep options open"),
("Are you more comfortable", "Setting a schedule", "Putting things off"),
("Are you more prone to keep things", "well organized", "Open-ended"),
("Are you more comfortable with work", "Contracted", "Done on a casual basis"),
("Are you more comfortable with", "Final statements", "Tentative statements"),
("Is it preferable mostly to", "Make sure things are arranged", "Just let things happen"),
("Do you prefer?", "Getting something done", "Having the option to go back"),
("Is it more like you to", "Make snap judgements", "Delay making judgements")],dtype=str)
questions5 = np.array([("Do you tend to choose", "Rather carefully", "Somewhat impulsively"),
("Does it bother you more having things", "Incomplete", "Completed"),
("Are you usually rather", "Quick to agree to a time", "Reluctant to agree to a time"),
("Are you more comfortable with", "Written agreements", "Handshake agreements"),
("Do you put more value on the", "Definite", "Variable"),
("Do you prefer things to be", "Neat and orderly", "Optional"),
("Are you more comfortable", "After a decision", "Before a decision"),
("Is it your way more to", "Get things settled", "Put off settlement"),
("Do you prefer to?", "Set things up perfectly", "Allow things to come together"),
("Do you tend to be more", "Deliberate than spontaneous", "Spontaneous than deliberate")],dtype=str)
def test(questions):
total_count = []
for idx, question in enumerate(questions):
total_count.append(ask(question))
if total_count.count(1) > total_count.count(2):
return 1
else:
return 2
def ask(question):
type_count1 = 0
type_count2 = 0
answer = input(f" {question[0]}: \n 1. {question[1]}\n 2. {question[2]}\n")
if answer == '1':
return 1
if answer == '2':
return 2
else:
print("Make sure your input is 1 or 2")
ask(question)
def main():
EorI = test(questions1)
EorI = 'E' if EorI == 1 else 'I'
SorN = test(questions2)
SorN = 'S' if SorN == 1 else 'N'
TorF = test(np.concatenate((questions3, questions4), axis=0))
TorF = 'T' if TorF == 1 else 'F'
JorP = test(questions5)
JorP = 'J' if JorP == 1 else 'P'
print(f"Your character is : ",EorI+SorN+TorF+JorP)
return 0
main()
| 0.253399 | 0.760651 |
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sqlalchemy import create_engine
# Uncomment these lines and change directories to write to hdf instead
# dbname = '/Users/rbiswas/data/LSST/OpSimData/kraken_1042_sqlite.db'#enigma_1189_sqlite.db'
# engine = create_engine('sqlite:///' + dbname)
# Summary = pd.read_sql_table('Summary', engine, index_col='obsHistID')
# Summary.to_hdf('/Users/rbiswas/data/LSST/OpSimData/kraken_1042.hdf', 'table')
df = pd.read_hdf('/Users/rbiswas/data/LSST/OpSimData/kraken_1042.hdf', 'table')
df = df.query('fieldID==1427 and propID == 152')
print(df.expMJD.min())
print((df.expMJD.max() + df.expMJD.min()) / 2.)
df.propID.hist()
import OpSimSummary.summarize_opsim as so
ds = so.SummaryOpsim(summarydf=df)
(df.expMJD.max() + df.expMJD.min()) / 2.
```
If I forget dithers and just look at how many observations per field:
- Look at the number of unique nights with different bands: For the full survey this number of visits is 1680, see figure in Input 13
- For half of the survey, the same quantity is 824, see figure 1nput 14
- For a year the number is ~150. See figure on input 15
```
full_survey = ds.cadence_plot(fieldID=1427, mjd_center=61404, mjd_range=[-1825, 1825],
observedOnly=False, colorbar=True);
plt.close()
full_survey[0]
half_survey = ds.cadence_plot(fieldID=1427, mjd_center=61404, mjd_range=[-1825, 1],
observedOnly=False, colorbar=True);
second_year = ds.cadence_plot(fieldID=1427, mjd_center=60200, mjd_range=[-150, 150],
observedOnly=False, colorbar=True);
secondYearObs = ds.cadence_plot(fieldID=1427, mjd_center=60300, mjd_range=[-0, 30], observedOnly=False)
plt.close()
secondYearObs[0]
```
## List of obsHistIDs with unique nights
#### Proposal :
1. We want to select all the unique night and band combinations in the 10 years of Kraken. As we have seen above this is 1680 visits.
2. We will give the phosim instance catalogs and seds for running phosim on the cluster, and we should run these in order of expMJD or night. If we run out of compute time at a 1000, then we will have a little more than half of the survey
3. When we get more (phoSim) simulation time, we can finish the 10 years. If we have more time than than, I suggest we **fill in other observations in the 2nd year** as shown in the above figure around 60300. This is another 500 observations. After than we can fill in the rest of the second year and then other years. The priority for the the second year (and could have been elsewhere) is because I can make sure that there a few supernovae that are at high redshift and 'visible' at that time. I need to know this ahead of time, and that is why I putting this out now.
```
df['obsID'] = df.index.values
uniqueObs = df.groupby(['night', 'filter'])
aa = uniqueObs['airmass'].agg({'myInds': lambda x: x.idxmin()}).myInds.astype(int).values
ourOpSim = df.ix[aa]
```
#### How much does it help our airmass distribution by choosing the lowest airmass of the available ones
```
axs = df.hist(by='filter', column='airmass', histtype='step', lw=2, alpha=1, color='k', normed=True);
axs = df.ix[aa].hist(by='filter', column='airmass', histtype='step', lw=2, alpha=1, color='r', ax=axs, normed=True)
df.obsID.unique().size, df.obsID.size
ourOpSim.head()
```
Our culled opsim that we shall try out first is now 'ourOpSim' . We can write this our to a csv file, or a database. We can also view the list of obsHistIDs
```
ourOpSim.obsID.values
ourOpSim.obsID.to_csv('FirstSet_obsHistIDs.csv')
ourOpSim.to_csv('SelectedKrakenVisits.csv')
xx = ourOpSim.groupby(['night', 'filter']).aggregate('count')
assert(all(xx.max() == 1))
```
# Scratch
### Find the obsHistIDs corresponding to the lowest airmass of visits
```
dff = uniqueObs['airmass'].agg({'myInds': lambda x: x.idxmin()})
aa = dff.myInds.astype(int).values
aa.sort()
l = []
for key in keys:
l.append(uniqueObs.get_group(key).airmass.idxmin())
```
|
github_jupyter
|
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sqlalchemy import create_engine
# Uncomment these lines and change directories to write to hdf instead
# dbname = '/Users/rbiswas/data/LSST/OpSimData/kraken_1042_sqlite.db'#enigma_1189_sqlite.db'
# engine = create_engine('sqlite:///' + dbname)
# Summary = pd.read_sql_table('Summary', engine, index_col='obsHistID')
# Summary.to_hdf('/Users/rbiswas/data/LSST/OpSimData/kraken_1042.hdf', 'table')
df = pd.read_hdf('/Users/rbiswas/data/LSST/OpSimData/kraken_1042.hdf', 'table')
df = df.query('fieldID==1427 and propID == 152')
print(df.expMJD.min())
print((df.expMJD.max() + df.expMJD.min()) / 2.)
df.propID.hist()
import OpSimSummary.summarize_opsim as so
ds = so.SummaryOpsim(summarydf=df)
(df.expMJD.max() + df.expMJD.min()) / 2.
full_survey = ds.cadence_plot(fieldID=1427, mjd_center=61404, mjd_range=[-1825, 1825],
observedOnly=False, colorbar=True);
plt.close()
full_survey[0]
half_survey = ds.cadence_plot(fieldID=1427, mjd_center=61404, mjd_range=[-1825, 1],
observedOnly=False, colorbar=True);
second_year = ds.cadence_plot(fieldID=1427, mjd_center=60200, mjd_range=[-150, 150],
observedOnly=False, colorbar=True);
secondYearObs = ds.cadence_plot(fieldID=1427, mjd_center=60300, mjd_range=[-0, 30], observedOnly=False)
plt.close()
secondYearObs[0]
df['obsID'] = df.index.values
uniqueObs = df.groupby(['night', 'filter'])
aa = uniqueObs['airmass'].agg({'myInds': lambda x: x.idxmin()}).myInds.astype(int).values
ourOpSim = df.ix[aa]
axs = df.hist(by='filter', column='airmass', histtype='step', lw=2, alpha=1, color='k', normed=True);
axs = df.ix[aa].hist(by='filter', column='airmass', histtype='step', lw=2, alpha=1, color='r', ax=axs, normed=True)
df.obsID.unique().size, df.obsID.size
ourOpSim.head()
ourOpSim.obsID.values
ourOpSim.obsID.to_csv('FirstSet_obsHistIDs.csv')
ourOpSim.to_csv('SelectedKrakenVisits.csv')
xx = ourOpSim.groupby(['night', 'filter']).aggregate('count')
assert(all(xx.max() == 1))
dff = uniqueObs['airmass'].agg({'myInds': lambda x: x.idxmin()})
aa = dff.myInds.astype(int).values
aa.sort()
l = []
for key in keys:
l.append(uniqueObs.get_group(key).airmass.idxmin())
| 0.518302 | 0.741042 |
_Author:_ Eric Bruning, Texas Tech University, 11 June 2021
## The joy of the always-transformable 3D earth-centered, earth-fixed coordinate
The basic principle we'll exploit here is that geodetic latitude, longitude, and altitude are a proper 3D coordinate basis referenced with repsect to an ellipsoid. Those coordinates can be mapped, with no approximations, forward and backward to any other 3D coordinate basis, including a cartesian system located at the center of the earth, and which rotates with the earth.
## Setup
```
import numpy as np
import pyproj as proj4
def centers_to_edges(x):
xedge=np.zeros(x.shape[0]+1)
xedge[1:-1] = (x[:-1] + x[1:])/2.0
dx = np.mean(np.abs(xedge[2:-1] - xedge[1:-2]))
xedge[0] = xedge[1] - dx
xedge[-1] = xedge[-2] + dx
return xedge
def get_proj(ctr_lon, ctr_lat):
# Define a WGS84 earth (just to show doing so for an arbitrary globe)
earth_major, earth_minor = 6378137.0, 6356752.3142
hou_ctr_lat, hou_ctr_lon = ctr_lat, ctr_lon
# x, y = np.meshgrid(x,y)
stereo = proj4.crs.CRS(proj='stere', a=earth_major, b=earth_minor,
lat_0=hou_ctr_lat, lon_0=hou_ctr_lon)
lla = proj4.crs.CRS(proj='latlong', a=earth_major, b=earth_minor)
ecef = proj4.crs.CRS(proj='geocent', a=earth_major, b=earth_minor)
return lla, ecef, stereo
def get_grid_ctr_edge(dlat=0.1, dlon=0.1, dalt=1000.0, ctr_lon=0.0, ctr_lat=0):
hou_ctr_lat, hou_ctr_lon = ctr_lat, ctr_lon
nlon, nlat = 50, 50
nalt = 50
lon = dlon*(np.arange(nlon, dtype='float') - nlon/2) + dlon/2
lat = dlat*(np.arange(nlat, dtype='float') - nlat/2) + dlat/2
alt = dalt*(np.arange(nalt, dtype='float') - nalt/2) + dalt/2
lon += hou_lon
lat += hou_lat
alt += hou_alt - alt.min()
lon_edge = centers_to_edges(lon)
lat_edge = centers_to_edges(lat)
alt_edge = centers_to_edges(alt)
return lon, lat, alt, lon_edge, lat_edge, alt_edge
```
Set up coordinate systems and transformers between each
```
hou_lat, hou_lon, hou_alt = 29.4719, -95.0792, 0.0
lla, ecef, stereo = get_proj(hou_lon, hou_lat)
lon, lat, alt, lon_edge, lat_edge, alt_edge = get_grid_ctr_edge(ctr_lon=hou_lon, ctr_lat=hou_lat)
lla_to_ecef = proj4.Transformer.from_crs(lla, ecef)
```
Where is our center location in earth-centered, earth-fixed cartesian coordinates? _ECEF X, Y, and Z have nothing to do with east, north, and up_. Rather, their unit vectors point from the earth center toward z=north pole, x=(0°N,0°E) and y=(0°N, 90°E), the right handed vector with x and z. See the [WGS84 implementation manual, Appendix B.](https://www.icao.int/safety/pbn/Documentation/EUROCONTROL/Eurocontrol%20WGS%2084%20Implementation%20Manual.pdf)
It'll be a big number in kilometers, in each vector component, and absolute distance from Earth's center should be close to 6370 km.
```
Xctr_ecef, Yctr_ecef, Zctr_ecef = lla_to_ecef.transform(hou_lon, hou_lat, hou_alt)
print(Xctr_ecef/1000, Yctr_ecef/1000, Zctr_ecef/1000)
def distance_3d(x,y,z):
""" Given x, y, and z distances from (0,0,0), find the total distance along a ray from the origin"""
return(np.sqrt(x*x + y*y +z*z))
hou_distance_from_earth_center = distance_3d(Xctr_ecef/1000, Yctr_ecef/1000, Zctr_ecef/1000)
print(hou_distance_from_earth_center)
```
Next we'll create a 3D mesh of lat, lon, alt that corresponds to regular geodetic coordinates. These arrays are redundant along two of their axes, of course - that's what it means to be "regular."
We will use the grid edges (formally, the node positions where the grid box boundaries intersect) instead of the grid cell centers, since we want to think of a mesh that (in this case) wraps around the earth elliposid, with some distortion of the shape of those cell interiors. Specifically, the great circle distance along the elliposid along lontitude changes substantially with latitude. There is also a subtle expansion of the cells in altitude, in a sort of conical expansion.
```
lon_edge_3d, lat_edge_3d, alt_edge_3d, = np.meshgrid(lon_edge, lat_edge, alt_edge, indexing='ij')
lon_3d, lat_3d, alt_3d, = np.meshgrid(lon, lat, alt, indexing='ij')
print(lon_edge_3d[:,0,0])
print(lat_edge_3d[0,:,0])
print(alt_edge_3d[0,0,:])
zi_at_ground = 0 # actually the edge 0.5 dz below the ellipsoid (500 m for 1 km spacing).
zi_top = -1 # actually the edge 0.5 dz below the ellipsoid (500 m for 1 km spacing).
yi_north_edge = -1
yi_south_edge = 0
xi_east_edge = -1
xi_west_edge = 0
```
The indexing order above corresponds to variation along lon, lat, alt, or east, north, and up. These are x, y, z in the local reference frame tangent to the ground as they are commonly used in meteorology.
Now, we convert to ECEF coordinates. These will be ordinary distances in meters.
```
Xecef_edge_3d, Yecef_edge_3d, Zecef_edge_3d = lla_to_ecef.transform(lon_edge_3d, lat_edge_3d, alt_edge_3d)
print(Xecef_edge_3d[:,0,0])
print(Yecef_edge_3d[0,:,0])
print(Zecef_edge_3d[0,0,:])
```
## Tests
Since our grid was regular in latitude, longitude and altitude, we should observe
1. a difference in the east-west spacing as we move north-south
2. not much difference in north-south spacing as we move east-west (only that due to the ellipsoid's oblateness)
3. larger spacing at higher altitudes
4. No difference in altitude spacing regardless of position
The distances along the edges use all three ECEF coordinates, since they do not vary regularly with lon,lat,alt.
We are going to calculate grid spacings as though the earth is locally flat over the 0.1 deg spacing of our grid. Strictly speaking, the edges of our grid boxes make a chord with the earth's curvature.
1. Here is where we expect the largest difference: it's about 500 m for a 0.1 deg spacing in lat and lon across a 5 deg span.
```
# Calculate all E-W spacings. We move east, along a line of latitude, and calculate for all longitudes and altitudes
left_edges = slice(None, -1)
right_edges = slice(1, None)
ew_spacing_X = (Xecef_edge_3d[right_edges, :, :] - Xecef_edge_3d[left_edges, :, :])
ew_spacing_Y = (Yecef_edge_3d[right_edges, :, :] - Yecef_edge_3d[left_edges, :, :])
ew_spacing_Z = (Zecef_edge_3d[right_edges, :, :] - Zecef_edge_3d[left_edges, :, :])
ew_distances = distance_3d(ew_spacing_X, ew_spacing_Y, ew_spacing_Z)
print("Difference in east-west spacing as we move north-south, along west edge")
print(ew_distances[xi_west_edge, yi_north_edge, zi_at_ground])
print(ew_distances[xi_west_edge, yi_south_edge, zi_at_ground])
print("Difference in east-west spacing as we move north-south, along east edge")
print(ew_distances[xi_east_edge, yi_north_edge, zi_at_ground])
print(ew_distances[xi_east_edge, yi_south_edge, zi_at_ground])
print("There is a change in east-west distance due to the narrowing of lines of longitude toward the poles.")
print("The pairs are identifical no matter their longitudintal position, as it should be geometrically")
```
2. Here is the difference due to oblateness: about 10 m for a 0.1 deg lat lon spacing across a 5 deg span.
```
# Calculate all N-S spacings. We move north, along a line of longitude, and calculate for all longitudes and altitudes
# This is indexing like a[1:] - a[:-1]
left_edges = slice(None, -1)
right_edges = slice(1, None)
ns_spacing_X = (Xecef_edge_3d[:, right_edges, :] - Xecef_edge_3d[:, left_edges, :])
ns_spacing_Y = (Yecef_edge_3d[:, right_edges, :] - Yecef_edge_3d[:, left_edges, :])
ns_spacing_Z = (Zecef_edge_3d[:, right_edges, :] - Zecef_edge_3d[:, left_edges, :])
ns_distances = distance_3d(ns_spacing_X, ns_spacing_Y, ns_spacing_Z)
print("Difference in north-south spacing as we move east-west, along south edge")
print(ns_distances[xi_east_edge, yi_south_edge, zi_at_ground])
print(ns_distances[xi_west_edge, yi_south_edge, zi_at_ground])
print("Difference in north-south spacing as we move east-west, along north edge")
print(ns_distances[xi_east_edge, yi_north_edge, zi_at_ground])
print(ns_distances[xi_west_edge, yi_north_edge, zi_at_ground])
print("The north-south spacing is not identical along the northern and southern edges, since the earth is oblate.")
print("There is no difference in in the north-south spacing along each edge, as expected from geometry.")
```
3. Here is the difference in east west and north south spacing as a function of altitude. There's about a 70 m increase in e-w spacing (at this latitude) at the top of the column, and a 100 m increase in n-s spacing, for a 50 km depth (troposphere and stratosphere).
```
# Calculate all N-S spacings. We move north, along a line of longitude, and calculate for all longitudes and altitudes
# This is indexing like a[1:] - a[:-1]
print("Spacing at ground and top in east-west direction, northwest corner")
print(ew_distances[xi_west_edge, yi_north_edge, zi_at_ground])
print(ew_distances[xi_west_edge, yi_north_edge, zi_top])
print("Spacing at ground and top in east-west direction, southwest corner")
print(ew_distances[xi_west_edge, yi_south_edge, zi_at_ground])
print(ew_distances[xi_west_edge, yi_south_edge, zi_top])
print("Spacing at ground and top in north-south direction, northwest corner")
print(ns_distances[xi_west_edge, yi_north_edge, zi_at_ground])
print(ns_distances[xi_west_edge, yi_north_edge, zi_top])
print("Spacing at ground and top in north-south direction, southwest corner")
print(ns_distances[xi_west_edge, yi_south_edge, zi_at_ground])
print(ns_distances[xi_west_edge, yi_south_edge, zi_top])
```
4. Here is the difference in vertical spacing as a function of horizontal position. No difference.
```
# Calculate all N-S spacings. We move north, along a line of longitude, and calculate for all longitudes and altitudes
# This is indexing like a[1:] - a[:-1]
left_edges = slice(None, -1)
right_edges = slice(1, None)
ud_spacing_X = (Xecef_edge_3d[:, :, right_edges] - Xecef_edge_3d[:, :, left_edges])
ud_spacing_Y = (Yecef_edge_3d[:, :, right_edges] - Yecef_edge_3d[:, :, left_edges])
ud_spacing_Z = (Zecef_edge_3d[:, :, right_edges] - Zecef_edge_3d[:, :, left_edges])
ud_distances = distance_3d(ud_spacing_X, ud_spacing_Y, ud_spacing_Z)
print("Difference in vertical spacing as we move up, southeast corner")
print(ud_distances[xi_east_edge, yi_south_edge, zi_at_ground])
print(ud_distances[xi_east_edge, yi_south_edge, zi_top])
print("Difference in vertical spacing as we move up, northeast corner")
print(ud_distances[xi_east_edge, yi_north_edge, zi_at_ground])
print(ud_distances[xi_east_edge, yi_north_edge, zi_top])
print("Difference in vertical spacing as we move up, northwest corner")
print(ud_distances[xi_west_edge, yi_north_edge, zi_at_ground])
print(ud_distances[xi_west_edge, yi_north_edge, zi_top])
print("Difference in vertical spacing as we move up, southwest corner")
print(ud_distances[xi_west_edge, yi_south_edge, zi_at_ground])
print(ud_distances[xi_west_edge, yi_south_edge, zi_top])
print("There is no difference in the vertical spacing, as it should be given the definition of our grid.")
```
## Summary
For a regular latitude, longitude grid, at the latitude of Houston:
- The largest difference is in the east-west spacing with north-south position, about 500 m / 10000 m
- The difference due to oblateness in n-s spacing with n-s position is 50x smaller, about 10 m / 10000 m
- The difference in spacing as a function of altitude is in between the above, and surprisingly large: 100 m / 10000 m
- Altitude spacing remains constant.
It is also a hypothesis that the rate of change of these spacings with position on the earth's surface (in the limit of small dx, dy) are related to the proj4 map factors.
The calculations above are easily adjusted to try other locations and grid spacings.
**Extension to map projections and model grid coordinates**
One could also compare the distances calculate in the exercise above to the stereographic x, y coordinate distances. Note we already defined the necessary stereographic coordinate system …
The same process as above could be done to convert a (for example) stereographic model grid to ECEF, from which the exact volumes could be calculated. Define a new proj4.Transformer.from_crs(stereo, lla), convert a meshgrid of 2D model x, y coords to (lat, lon), and replicate the 2D lat lon over the number of sigma coordinates to get 3D lon, lat grids. The 3D alt grid can be calcualted from the height information of each model sigma level at each model grid point. Then convert to ECEF!
## Bonus: grid volumes
These are the exact volumes in m$^3$ of our 3D mesh.
While the volumes are not cubes, they are (I think) guaranteed to be convex since the faces are all planar and the postions are monotonic. So we can use the convex hull. We also try an approximate calculation using the simple spacings.
For a 0.1 deg grid that's about 10 km horizonal, and with 1 km vertical spacing we should have volumes of about 10x10x1=100 km$^3$
```
import numpy as np
from scipy.spatial import ConvexHull
# Need an Mx8x3 array for M grid boxes with 8 corners.
# WSB, ESB,
# ENB, WNB,
# WST, EST,
# ENT, WNT (east west north south bottom top)
# S,W,B are :-1
# N,E,T are 1:
x_corners = [Xecef_edge_3d[:-1,:-1,:-1], Xecef_edge_3d[ 1:,:-1,:-1],
Xecef_edge_3d[ 1:, 1:,:-1], Xecef_edge_3d[:-1, 1:,:-1],
Xecef_edge_3d[:-1,:-1, 1:], Xecef_edge_3d[ 1:,:-1, 1:],
Xecef_edge_3d[ 1:, 1:, 1:], Xecef_edge_3d[:-1, 1:, 1:],]
y_corners = [Yecef_edge_3d[:-1,:-1,:-1], Yecef_edge_3d[ 1:,:-1,:-1],
Yecef_edge_3d[ 1:, 1:,:-1], Yecef_edge_3d[:-1, 1:,:-1],
Yecef_edge_3d[:-1,:-1, 1:], Yecef_edge_3d[ 1:,:-1, 1:],
Yecef_edge_3d[ 1:, 1:, 1:], Yecef_edge_3d[:-1, 1:, 1:],]
z_corners = [Zecef_edge_3d[:-1,:-1,:-1], Zecef_edge_3d[ 1:,:-1,:-1],
Zecef_edge_3d[ 1:, 1:,:-1], Zecef_edge_3d[:-1, 1:,:-1],
Zecef_edge_3d[:-1,:-1, 1:], Zecef_edge_3d[ 1:,:-1, 1:],
Zecef_edge_3d[ 1:, 1:, 1:], Zecef_edge_3d[:-1, 1:, 1:],]
# Get an Mx8 array
x_corner_points = np.vstack([a.flatten() for a in x_corners])
y_corner_points = np.vstack([a.flatten() for a in y_corners])
z_corner_points = np.vstack([a.flatten() for a in z_corners])
point_stack = np.asarray((x_corner_points,y_corner_points,z_corner_points)).T
volumes = np.fromiter((ConvexHull(polygon).volume for polygon in point_stack),
dtype=float, count=point_stack.shape[0])
volumes.shape=lon_3d.shape
print("Convex hull min, max volumes")
print(volumes.min()/(1e3**3))
print(volumes.max()/(1e3**3))
# Approximate version. Shapes are (50,51,51) (51,50,51) (51,51,50) to start.
# There are actually four E-W distances at the S, N, bottom, and top edges of each box,
# and so on.
ew_mean = (ew_distances[:,1:,1:]+ew_distances[:,1:,:-1]+ew_distances[:,:-1,1:]+ew_distances[:,:-1,:-1])/4
ns_mean = (ns_distances[1:,:,1:]+ns_distances[1:,:,:-1]+ns_distances[:-1,:,1:]+ns_distances[:-1,:,:-1])/4
ud_mean = (ud_distances[1:,1:,:]+ud_distances[1:,:-1,:]+ud_distances[:-1,1:,:]+ud_distances[:-1,:-1,:])/4
volumes_approx = ew_mean * ns_mean * ud_mean
print("Approximate min, max volumes")
print(volumes_approx.min()/(1e3**3))
print(volumes_approx.max()/(1e3**3))
```
It turns out the approximate volume calculation is quite good, without all the expense of the convex hull calculation!
## Regularizing lat-lon
Practically speaking, datasets might contain angles that are 0 to 360 longitude or various other departures from -180 to 180. No doubt we'd even find a -720 to -360 somewhere in the wild…
```
weird_lons = np.arange(-360, 360, 30)
weird_lats = np.zeros_like(weird_lons)
```
Proj won't regularize it for us with an identity transformation:
```
lla_to_lla = proj4.Transformer.from_crs(lla, lla)
print(lla_to_lla.transform(weird_lons, weird_lats))
```
But we do get that behavior if we're willing to bear a computational penalty of a round-trip through ECEF:
```
ecef_to_lla = proj4.Transformer.from_crs(ecef, lla)
print(ecef_to_lla.transform(*lla_to_ecef.transform(weird_lons, weird_lats)))
```
This solution gives us a predictably-bounded set of coordinates, to which we could predictably apply other logic for shifting the data with respect to a center longitude of interest.
|
github_jupyter
|
import numpy as np
import pyproj as proj4
def centers_to_edges(x):
xedge=np.zeros(x.shape[0]+1)
xedge[1:-1] = (x[:-1] + x[1:])/2.0
dx = np.mean(np.abs(xedge[2:-1] - xedge[1:-2]))
xedge[0] = xedge[1] - dx
xedge[-1] = xedge[-2] + dx
return xedge
def get_proj(ctr_lon, ctr_lat):
# Define a WGS84 earth (just to show doing so for an arbitrary globe)
earth_major, earth_minor = 6378137.0, 6356752.3142
hou_ctr_lat, hou_ctr_lon = ctr_lat, ctr_lon
# x, y = np.meshgrid(x,y)
stereo = proj4.crs.CRS(proj='stere', a=earth_major, b=earth_minor,
lat_0=hou_ctr_lat, lon_0=hou_ctr_lon)
lla = proj4.crs.CRS(proj='latlong', a=earth_major, b=earth_minor)
ecef = proj4.crs.CRS(proj='geocent', a=earth_major, b=earth_minor)
return lla, ecef, stereo
def get_grid_ctr_edge(dlat=0.1, dlon=0.1, dalt=1000.0, ctr_lon=0.0, ctr_lat=0):
hou_ctr_lat, hou_ctr_lon = ctr_lat, ctr_lon
nlon, nlat = 50, 50
nalt = 50
lon = dlon*(np.arange(nlon, dtype='float') - nlon/2) + dlon/2
lat = dlat*(np.arange(nlat, dtype='float') - nlat/2) + dlat/2
alt = dalt*(np.arange(nalt, dtype='float') - nalt/2) + dalt/2
lon += hou_lon
lat += hou_lat
alt += hou_alt - alt.min()
lon_edge = centers_to_edges(lon)
lat_edge = centers_to_edges(lat)
alt_edge = centers_to_edges(alt)
return lon, lat, alt, lon_edge, lat_edge, alt_edge
hou_lat, hou_lon, hou_alt = 29.4719, -95.0792, 0.0
lla, ecef, stereo = get_proj(hou_lon, hou_lat)
lon, lat, alt, lon_edge, lat_edge, alt_edge = get_grid_ctr_edge(ctr_lon=hou_lon, ctr_lat=hou_lat)
lla_to_ecef = proj4.Transformer.from_crs(lla, ecef)
Xctr_ecef, Yctr_ecef, Zctr_ecef = lla_to_ecef.transform(hou_lon, hou_lat, hou_alt)
print(Xctr_ecef/1000, Yctr_ecef/1000, Zctr_ecef/1000)
def distance_3d(x,y,z):
""" Given x, y, and z distances from (0,0,0), find the total distance along a ray from the origin"""
return(np.sqrt(x*x + y*y +z*z))
hou_distance_from_earth_center = distance_3d(Xctr_ecef/1000, Yctr_ecef/1000, Zctr_ecef/1000)
print(hou_distance_from_earth_center)
lon_edge_3d, lat_edge_3d, alt_edge_3d, = np.meshgrid(lon_edge, lat_edge, alt_edge, indexing='ij')
lon_3d, lat_3d, alt_3d, = np.meshgrid(lon, lat, alt, indexing='ij')
print(lon_edge_3d[:,0,0])
print(lat_edge_3d[0,:,0])
print(alt_edge_3d[0,0,:])
zi_at_ground = 0 # actually the edge 0.5 dz below the ellipsoid (500 m for 1 km spacing).
zi_top = -1 # actually the edge 0.5 dz below the ellipsoid (500 m for 1 km spacing).
yi_north_edge = -1
yi_south_edge = 0
xi_east_edge = -1
xi_west_edge = 0
Xecef_edge_3d, Yecef_edge_3d, Zecef_edge_3d = lla_to_ecef.transform(lon_edge_3d, lat_edge_3d, alt_edge_3d)
print(Xecef_edge_3d[:,0,0])
print(Yecef_edge_3d[0,:,0])
print(Zecef_edge_3d[0,0,:])
# Calculate all E-W spacings. We move east, along a line of latitude, and calculate for all longitudes and altitudes
left_edges = slice(None, -1)
right_edges = slice(1, None)
ew_spacing_X = (Xecef_edge_3d[right_edges, :, :] - Xecef_edge_3d[left_edges, :, :])
ew_spacing_Y = (Yecef_edge_3d[right_edges, :, :] - Yecef_edge_3d[left_edges, :, :])
ew_spacing_Z = (Zecef_edge_3d[right_edges, :, :] - Zecef_edge_3d[left_edges, :, :])
ew_distances = distance_3d(ew_spacing_X, ew_spacing_Y, ew_spacing_Z)
print("Difference in east-west spacing as we move north-south, along west edge")
print(ew_distances[xi_west_edge, yi_north_edge, zi_at_ground])
print(ew_distances[xi_west_edge, yi_south_edge, zi_at_ground])
print("Difference in east-west spacing as we move north-south, along east edge")
print(ew_distances[xi_east_edge, yi_north_edge, zi_at_ground])
print(ew_distances[xi_east_edge, yi_south_edge, zi_at_ground])
print("There is a change in east-west distance due to the narrowing of lines of longitude toward the poles.")
print("The pairs are identifical no matter their longitudintal position, as it should be geometrically")
# Calculate all N-S spacings. We move north, along a line of longitude, and calculate for all longitudes and altitudes
# This is indexing like a[1:] - a[:-1]
left_edges = slice(None, -1)
right_edges = slice(1, None)
ns_spacing_X = (Xecef_edge_3d[:, right_edges, :] - Xecef_edge_3d[:, left_edges, :])
ns_spacing_Y = (Yecef_edge_3d[:, right_edges, :] - Yecef_edge_3d[:, left_edges, :])
ns_spacing_Z = (Zecef_edge_3d[:, right_edges, :] - Zecef_edge_3d[:, left_edges, :])
ns_distances = distance_3d(ns_spacing_X, ns_spacing_Y, ns_spacing_Z)
print("Difference in north-south spacing as we move east-west, along south edge")
print(ns_distances[xi_east_edge, yi_south_edge, zi_at_ground])
print(ns_distances[xi_west_edge, yi_south_edge, zi_at_ground])
print("Difference in north-south spacing as we move east-west, along north edge")
print(ns_distances[xi_east_edge, yi_north_edge, zi_at_ground])
print(ns_distances[xi_west_edge, yi_north_edge, zi_at_ground])
print("The north-south spacing is not identical along the northern and southern edges, since the earth is oblate.")
print("There is no difference in in the north-south spacing along each edge, as expected from geometry.")
# Calculate all N-S spacings. We move north, along a line of longitude, and calculate for all longitudes and altitudes
# This is indexing like a[1:] - a[:-1]
print("Spacing at ground and top in east-west direction, northwest corner")
print(ew_distances[xi_west_edge, yi_north_edge, zi_at_ground])
print(ew_distances[xi_west_edge, yi_north_edge, zi_top])
print("Spacing at ground and top in east-west direction, southwest corner")
print(ew_distances[xi_west_edge, yi_south_edge, zi_at_ground])
print(ew_distances[xi_west_edge, yi_south_edge, zi_top])
print("Spacing at ground and top in north-south direction, northwest corner")
print(ns_distances[xi_west_edge, yi_north_edge, zi_at_ground])
print(ns_distances[xi_west_edge, yi_north_edge, zi_top])
print("Spacing at ground and top in north-south direction, southwest corner")
print(ns_distances[xi_west_edge, yi_south_edge, zi_at_ground])
print(ns_distances[xi_west_edge, yi_south_edge, zi_top])
# Calculate all N-S spacings. We move north, along a line of longitude, and calculate for all longitudes and altitudes
# This is indexing like a[1:] - a[:-1]
left_edges = slice(None, -1)
right_edges = slice(1, None)
ud_spacing_X = (Xecef_edge_3d[:, :, right_edges] - Xecef_edge_3d[:, :, left_edges])
ud_spacing_Y = (Yecef_edge_3d[:, :, right_edges] - Yecef_edge_3d[:, :, left_edges])
ud_spacing_Z = (Zecef_edge_3d[:, :, right_edges] - Zecef_edge_3d[:, :, left_edges])
ud_distances = distance_3d(ud_spacing_X, ud_spacing_Y, ud_spacing_Z)
print("Difference in vertical spacing as we move up, southeast corner")
print(ud_distances[xi_east_edge, yi_south_edge, zi_at_ground])
print(ud_distances[xi_east_edge, yi_south_edge, zi_top])
print("Difference in vertical spacing as we move up, northeast corner")
print(ud_distances[xi_east_edge, yi_north_edge, zi_at_ground])
print(ud_distances[xi_east_edge, yi_north_edge, zi_top])
print("Difference in vertical spacing as we move up, northwest corner")
print(ud_distances[xi_west_edge, yi_north_edge, zi_at_ground])
print(ud_distances[xi_west_edge, yi_north_edge, zi_top])
print("Difference in vertical spacing as we move up, southwest corner")
print(ud_distances[xi_west_edge, yi_south_edge, zi_at_ground])
print(ud_distances[xi_west_edge, yi_south_edge, zi_top])
print("There is no difference in the vertical spacing, as it should be given the definition of our grid.")
import numpy as np
from scipy.spatial import ConvexHull
# Need an Mx8x3 array for M grid boxes with 8 corners.
# WSB, ESB,
# ENB, WNB,
# WST, EST,
# ENT, WNT (east west north south bottom top)
# S,W,B are :-1
# N,E,T are 1:
x_corners = [Xecef_edge_3d[:-1,:-1,:-1], Xecef_edge_3d[ 1:,:-1,:-1],
Xecef_edge_3d[ 1:, 1:,:-1], Xecef_edge_3d[:-1, 1:,:-1],
Xecef_edge_3d[:-1,:-1, 1:], Xecef_edge_3d[ 1:,:-1, 1:],
Xecef_edge_3d[ 1:, 1:, 1:], Xecef_edge_3d[:-1, 1:, 1:],]
y_corners = [Yecef_edge_3d[:-1,:-1,:-1], Yecef_edge_3d[ 1:,:-1,:-1],
Yecef_edge_3d[ 1:, 1:,:-1], Yecef_edge_3d[:-1, 1:,:-1],
Yecef_edge_3d[:-1,:-1, 1:], Yecef_edge_3d[ 1:,:-1, 1:],
Yecef_edge_3d[ 1:, 1:, 1:], Yecef_edge_3d[:-1, 1:, 1:],]
z_corners = [Zecef_edge_3d[:-1,:-1,:-1], Zecef_edge_3d[ 1:,:-1,:-1],
Zecef_edge_3d[ 1:, 1:,:-1], Zecef_edge_3d[:-1, 1:,:-1],
Zecef_edge_3d[:-1,:-1, 1:], Zecef_edge_3d[ 1:,:-1, 1:],
Zecef_edge_3d[ 1:, 1:, 1:], Zecef_edge_3d[:-1, 1:, 1:],]
# Get an Mx8 array
x_corner_points = np.vstack([a.flatten() for a in x_corners])
y_corner_points = np.vstack([a.flatten() for a in y_corners])
z_corner_points = np.vstack([a.flatten() for a in z_corners])
point_stack = np.asarray((x_corner_points,y_corner_points,z_corner_points)).T
volumes = np.fromiter((ConvexHull(polygon).volume for polygon in point_stack),
dtype=float, count=point_stack.shape[0])
volumes.shape=lon_3d.shape
print("Convex hull min, max volumes")
print(volumes.min()/(1e3**3))
print(volumes.max()/(1e3**3))
# Approximate version. Shapes are (50,51,51) (51,50,51) (51,51,50) to start.
# There are actually four E-W distances at the S, N, bottom, and top edges of each box,
# and so on.
ew_mean = (ew_distances[:,1:,1:]+ew_distances[:,1:,:-1]+ew_distances[:,:-1,1:]+ew_distances[:,:-1,:-1])/4
ns_mean = (ns_distances[1:,:,1:]+ns_distances[1:,:,:-1]+ns_distances[:-1,:,1:]+ns_distances[:-1,:,:-1])/4
ud_mean = (ud_distances[1:,1:,:]+ud_distances[1:,:-1,:]+ud_distances[:-1,1:,:]+ud_distances[:-1,:-1,:])/4
volumes_approx = ew_mean * ns_mean * ud_mean
print("Approximate min, max volumes")
print(volumes_approx.min()/(1e3**3))
print(volumes_approx.max()/(1e3**3))
weird_lons = np.arange(-360, 360, 30)
weird_lats = np.zeros_like(weird_lons)
lla_to_lla = proj4.Transformer.from_crs(lla, lla)
print(lla_to_lla.transform(weird_lons, weird_lats))
ecef_to_lla = proj4.Transformer.from_crs(ecef, lla)
print(ecef_to_lla.transform(*lla_to_ecef.transform(weird_lons, weird_lats)))
| 0.610221 | 0.927692 |
# <center>Phase 2 - Publication<center>
```
# General imports.
import sqlite3
import pandas as pd
from matplotlib_venn import venn2, venn3
import scipy.stats as scs
import textwrap
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from itertools import combinations
import os
from matplotlib.colors import ListedColormap
from matplotlib import ticker
from scipy.stats import ttest_ind
import math
from timeit import default_timer as timer
# Imports from neighbor directories.
import sys
sys.path.append("..")
from src.utilities import field_registry as fieldreg
# IPython magics for this notebook.
%matplotlib inline
# Use latex font for matplotlib
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
# Switches
SAVE_OUTPUT = False
# Data Globals
FR = fieldreg.FieldRegistry()
TOTAL_USERS = 0
REMAINING_USERS = 0
TOTAL_DOGS = 0
REMAINING_DOGS = 0
PREVALENCE = lambda x: (x / REMAINING_DOGS) * 100
CATEGORY_MATRIX = pd.DataFrame()
# Database Globals
USER_TABLE = 'users'
DOG_TABLE = 'dogs'
BIAS_FILTER = '''
USING (record_id)
WHERE question_reason_for_part_3 = 0
OR (question_reason_for_part_3 = 1 AND q01_main != 1)'''
CON = sqlite3.connect('../data/processed/processed.db')
def createStringDataFrame(table, fields, labels, filtered=True):
query = 'SELECT ' + fields + ' FROM ' + table
if filtered:
table2 = USER_TABLE if table == DOG_TABLE else DOG_TABLE
query += ' JOIN ' + table2 + ' ' + BIAS_FILTER
df = pd.read_sql_query(query, CON)
df.columns = labels
return df
def convertToNumeric(df):
df = df.apply(pd.to_numeric, errors='coerce')
return df
def createNumericDataFrame(table, fields, labels, filtered=True):
df = createStringDataFrame(table, fields, labels, filtered)
return convertToNumeric(df)
def replaceFields(df, column, replacement_dict):
df[column].replace(replacement_dict, inplace=True)
def getValueCountAndPrevalence(df, field):
s = df[field].value_counts()
p = s.apply(PREVALENCE).round().astype(int)
rv = pd.concat([s, p], axis=1)
rv.columns = ['frequency', 'prevalence']
return rv
def createCategoryMatrix():
fields = []
labels = []
counter = 1
for cat, subdict in FR.labels.items():
for key, value in subdict.items():
if counter == 11:
counter += 1;
fields.append('q02_main_{}'.format(counter))
labels.append(key[0])
break
counter += 1
fields = ', '.join(fields)
df = createNumericDataFrame(DOG_TABLE, fields, labels, filtered=True)
cols = []
pvalue = {}
for col in df:
cols.append(col)
pvalue[col] = {}
pairs = list(combinations(df.columns, 2))
for pair in pairs:
contingency = pd.crosstab(df[pair[0]], df[pair[1]])
c, p, dof, expected = scs.chi2_contingency(contingency, correction=False)
pvalue[pair[0]][pair[1]] = p
pvalue[pair[1]][pair[0]] = p
df = pd.DataFrame(pvalue).sort_index(ascending=True)
return df
def createQuestionMatrix():
fields = ''
for cat, sublist in FR.fields.items():
for field in sublist:
fields += '{}, '.format(field)
fields = fields[:-2]
labels = []
for cat, subdict in FR.labels.items():
for key, value in subdict.items():
labels.append(key)
df = createNumericDataFrame(DOG_TABLE, fields, labels, filtered=True)
cols = []
pvalue = {}
for col in df:
cols.append(col)
pvalue[col] = {}
pairs = list(combinations(df.columns, 2))
for pair in pairs:
contingency = pd.crosstab(df[pair[0]], df[pair[1]])
c, p, dof, expected = scs.chi2_contingency(contingency, correction=False)
pvalue[pair[0]][pair[1]] = p
pvalue[pair[1]][pair[0]] = p
df = pd.DataFrame(pvalue).sort_index(ascending=True)
return df
def createCorrelationMatrix():
fields = []
labels = []
counter = 1
for cat, subdict in FR.labels.items():
for key, value in subdict.items():
if counter == 11:
counter += 1;
fields.append('q02_main_{}'.format(counter))
labels.append(key[0])
break
counter += 1
fields = ', '.join(fields)
df = createNumericDataFrame(DOG_TABLE, fields, labels, filtered=True)
return df.corr()
def createOddsRatioMatrix():
fields = []
labels = []
counter = 1
for cat, subdict in FR.labels.items():
for key, value in subdict.items():
if counter == 11:
counter += 1;
fields.append('q02_main_{}'.format(counter))
labels.append(key[0])
break
counter += 1
fields = ', '.join(fields)
df = createNumericDataFrame(DOG_TABLE, fields, labels, filtered=True)
cols = []
pvalue = {}
for col in df:
cols.append(col)
pvalue[col] = {}
pairs = list(combinations(df.columns, 2))
for pair in pairs:
contingency = pd.crosstab(df[pair[0]], df[pair[1]])
c, p, dof, expected = scs.chi2_contingency(contingency, correction=False)
pvalue[pair[0]][pair[1]] = getOddsRatio(contingency)
pvalue[pair[1]][pair[0]] = getOddsRatio(contingency)
df = pd.DataFrame(pvalue).sort_index(ascending=True)
return df
def displayOddsRatio(df):
odds, ci_low, ci_high, tot = getOddsRatioAndConfidenceInterval(df)
print('OR = %.2f, 95%% CI: %.2f-%.2f, n = %d'
%(round(odds, 2), round(ci_low, 2), round(ci_high, 2), tot))
def getOddsRatio(df):
return (df[1][1]/df[1][0])/(df[0][1]/df[0][0])
def getOddsRatioAndConfidenceInterval(df):
odds = getOddsRatio(df)
nl_or = math.log(odds)
se_nl_or = math.sqrt((1/df[0][0])+(1/df[0][1])+(1/df[1][0])+(1/df[1][1]))
ci_low = math.exp(nl_or - (1.96 * se_nl_or))
ci_high = math.exp(nl_or + (1.96 * se_nl_or))
tot = df[0][0] + df[0][1] + df[1][0] + df[1][1]
return odds, ci_low, ci_high, tot
def get_significance_category(p):
if np.isnan(p):
return p
elif p > 10**(-3):
return -1
elif p <= 10**(-3) and p > 10**(-6):
return 0
else:
return 1
def displaySeriesMedian(s, units=""):
print('MD = %.2f %s (SD = %.2f, min = %.2f, max = %.2f, n = %d)'
%(round(s.median(), 2), units, round(s.std(), 2), round(s.min(), 2), round(s.max(), 2), s.count()))
def displaySeriesMean(s, units=""):
print('M = %.2f %s (SD = %.2f, min = %.2f, max = %.2f, n = %d)'
%(round(s.mean(), 2), units, round(s.std(), 2), round(s.min(), 2), round(s.max(), 2), s.count()))
def convert_to_binary_response(x, y=1):
x = float(x)
if x < y:
return 0
return 1
def exportTable(data, title):
if not SAVE_OUTPUT:
return
file_ = os.path.join('..', 'reports', 'tables', title) + '.tex'
with open(file_, 'w') as tf:
tf.write(r'\documentclass[varwidth=\maxdimen]{standalone}\usepackage{booktabs}\begin{document}')
tf.write(df.to_latex())
tf.write(r'\end{document}')
def exportFigure(figure, title):
if not SAVE_OUTPUT:
return
file_ = os.path.join('..', 'reports', 'figures', title) + '.pdf'
figure.tight_layout()
figure.savefig(file_, format='pdf')
```
## <center>Demographics</center>
### Number of participants:
```
df = createNumericDataFrame(USER_TABLE, 'COUNT(*)', ['count'], filtered=False)
# Assign value to global.
TOTAL_USERS = df['count'][0]
print('N = %d owners [unadjusted]' %TOTAL_USERS)
```
### Number of participating dogs:
```
df = createNumericDataFrame(DOG_TABLE, 'COUNT(*)', ['count'], filtered=False)
# Assign value to global.
TOTAL_DOGS = df['count'][0]
print('N = %d dogs [unadjusted]' %TOTAL_DOGS)
```
### Suspicion of behavior problems as one of multiple motivating factors:
```
fields = ('question_reason_for_part_1, question_reason_for_part_2, '
'question_reason_for_part_3, question_reason_for_part_4, '
'question_reason_for_part_5')
labels = ['love for dogs', 'you help shelter animals', 'suspicion of behavior problems',
'work with animals', 'other']
df = createNumericDataFrame(USER_TABLE, fields, labels, filtered=False)
df = df[df[labels[2]] == 1]
df['sum'] = df.sum(axis=1)
s = df.sum(0, skipna=False)
print('n = %d owners (%d%%) [unadjusted]' %(s.iloc[2], round((s.iloc[2]/TOTAL_USERS)*100, 0)))
```
### Suspicion of behavior problems as the sole motivating factor:
```
fields = ('question_reason_for_part_1, question_reason_for_part_2, '
'question_reason_for_part_3, question_reason_for_part_4, '
'question_reason_for_part_5')
labels = ['love for dogs', 'you help shelter animals', 'suspicion of behavior problems',
'work with animals', 'other']
df = createNumericDataFrame(USER_TABLE, fields, labels, filtered=False)
df = df[df[labels[2]] == 1]
df['sum'] = df.sum(axis=1)
df = df[df['sum'] == 1]
s = df.sum(0, skipna=False)
print('n = %d owners (%d%%) [unadjusted]' %(s.iloc[2], round((s.iloc[2]/TOTAL_USERS)*100, 0)))
```
### Adjusting sample for bias:
```
fields = 'q02_score'
labels = ['Score']
df_adjusted_dogs = createNumericDataFrame(DOG_TABLE, fields, labels)
REMAINING_DOGS = len(df_adjusted_dogs.index)
df_adjusted_users = createNumericDataFrame(USER_TABLE, 'COUNT(DISTINCT email)', ['count'])
REMAINING_USERS = df_adjusted_users['count'][0]
# Display the count results.
print('Adjusted study population:')
print('N = %d owners (adjusted)' %REMAINING_USERS)
print('N = %d dogs (adjusted)' %REMAINING_DOGS)
```
### Dogs per household:
```
fields = 'record_id'
labels = ['record index']
df = createStringDataFrame(DOG_TABLE, fields, labels)
record_dict = {}
for index, row in df.iterrows():
key = row.iloc[0]
if not key in record_dict:
record_dict[key] = 1
else:
record_dict[key] += 1
s = pd.Series(record_dict, name='dogs')
displaySeriesMedian(s, 'dogs')
```
### Age at date of response
```
fields = 'dog_age_today_months'
labels = ['age (months)']
df = createNumericDataFrame(DOG_TABLE, fields, labels)
displaySeriesMedian(df[labels[0]], 'months')
```
### Gender and neutered status:
```
fields = 'dog_sex, dog_spayed'
labels = ['Gender', 'Neutered']
df = createStringDataFrame(DOG_TABLE, fields, labels)
replacements = {'':'No response', '1':'Male', '2':'Female'}
replaceFields(df, labels[0], replacements)
replacements = {'':'No response', '0':'No', '1':'Yes', '2':"I don't know"}
replaceFields(df, labels[1], replacements)
df = pd.crosstab(df[labels[0]], df[labels[1]], margins=True)
print("males: n = %d (%d%%), neutered: n = %d (%d%%), intact: n = %d (%d%%)"
%(df.loc['Male', 'All'], round((df.loc['Male', 'All']/df.loc['All', 'All'])*100, 0),
df.loc['Male', 'Yes'], round((df.loc['Male', 'Yes']/df.loc['Male', 'All'])*100, 0),
df.loc['Male', 'No'], round((df.loc['Male', 'No']/df.loc['Male', 'All'])*100, 0)))
print("females: n = %d (%d%%), neutered: n = %d (%d%%), intact: n = %d (%d%%)"
%(df.loc['Female', 'All'], round((df.loc['Female', 'All']/df.loc['All', 'All'])*100, 0),
df.loc['Female', 'Yes'], round((df.loc['Female', 'Yes']/df.loc['Female', 'All'])*100, 0),
df.loc['Female', 'No'], round((df.loc['Female', 'No']/df.loc['Female', 'All'])*100, 0)))
```
## <center>Prevalence of Behavior Problems</center>
### Number of dogs with behavior problems and overall prevalence:
```
fields = 'q02_score'
labels = ['Score']
df_adjusted_dogs = createNumericDataFrame(DOG_TABLE, fields, labels)
cnt_total_dogs_w_problems_adjusted = len(
df_adjusted_dogs[df_adjusted_dogs[labels[0]] != 0].index)
print('Dogs with behavior problems: n = %d dogs' %(cnt_total_dogs_w_problems_adjusted))
# Calculate the adjusted prevalence.
prevalence_adjusted = PREVALENCE(cnt_total_dogs_w_problems_adjusted)
print('Overall prevalence: %d%% (%d/%d dogs)'
%(round(prevalence_adjusted, 0), cnt_total_dogs_w_problems_adjusted, REMAINING_DOGS))
```
### Prevalence of behavior problem categories (Table 1):
```
start = timer()
fields = []
labels = []
for counter, category in enumerate(FR.categories, 1):
if counter > 10:
counter += 1;
fields.append('q02_main_{}'.format(counter))
labels.append(category)
fields = ', '.join(fields)
original_df = createNumericDataFrame(DOG_TABLE, fields, labels, filtered=True)
original_sums = original_df.sum()
display(original_sums.apply(PREVALENCE).round().astype(int))
def get_bootstrap_samples(data, count=10):
master_df = pd.DataFrame()
for i in range(count):
sample_df = data.sample(len(data.index), replace=True)
sums = sample_df.sum().apply(PREVALENCE).round().astype(int)
master_df = master_df.append(sums, ignore_index=True)
return master_df
master_df = get_bootstrap_samples(original_df, count=10000)
alpha = 0.95
lower = (1-alpha)/2
upper = alpha+lower
for name, values in master_df.iteritems():
print(name + ':')
values = values.sort_values(ascending=True)
values = values.reset_index(drop=True)
print(values[int(lower * len(values))])
print(values[int(upper * len(values))])
# Calculate the prevalence of each behavior problem.
#prevalences = sums.apply(PREVALENCE).round().astype(int)
end = timer()
print('\ntime:')
print(end - start)
```
### Prevalence of behavior problem category subtypes (Table 2):
```
sums = pd.Series()
for i in range(0, 12):
all_fields = FR.fields[FR.categories[i]].copy()
all_labels = list(FR.labels[FR.categories[i]].values()).copy()
df = createNumericDataFrame(DOG_TABLE, ', '.join(all_fields), all_labels, filtered=True)
if sums.empty:
sums = df.sum().sort_values(ascending=False)
else:
sums = sums.append(df.sum().sort_values(ascending=False))
# Calculate the prevalence of each behavior problem.
prevalences = sums.apply(PREVALENCE).round().astype(int)
# Create a table.
df = pd.DataFrame(index=sums.index, data={'Frequency':sums.values,
'Prevalence (%)': prevalences.values.round(2)})
df.columns.name = 'Behavior problem'
display(df.head())
print("Note: Only showing dataframe head to conserve notebook space")
exportTable(df, 'table_2')
```
## <center>Owner-directed Aggression</center>
### Owner-directed aggression and maleness:
```
fields = 'q03_main_1, dog_sex'
labels = ['owner-directed', 'gender']
df = createStringDataFrame(DOG_TABLE, fields, labels)
df = df[df[labels[1]] != '']
df = df.apply(pd.to_numeric)
def gender_to_binary_response(x):
x = int(x)
if x != 1:
return 0
return 1
df[labels[0]] = df[labels[0]].apply(
lambda x: convert_to_binary_response(x))
df[labels[1]] = df[labels[1]].apply(
lambda x: gender_to_binary_response(x))
# Execute a chi-squared test of independence.
contingency = pd.crosstab(df[labels[0]], df[labels[1]], margins=False)
print('Chi-squared Test of Independence for %s and %s:' %(labels[0], labels[1]))
c, p, dof, expected = scs.chi2_contingency(contingency, correction=False)
print('chi2 = %f, p = %.2E, dof = %d' %(c, p, dof))
displayOddsRatio(contingency)
```
## Example
```
start = timer()
data = pd.Series([30, 37, 36, 43, 42, 43, 43, 46, 41, 42])
display(data.mean())
x = np.array([])
for i in range(100):
if not i:
x = np.array(data.sample(len(data.index), replace=True).values)
else:
x = np.vstack([x, np.array(data.sample(len(data.index), replace=True).values)])
df = pd.DataFrame(x).transpose()
def agg_ci(data, confidence=0.95):
stats = data.agg(['mean']).transpose()
return stats
df = agg_ci(df)
df['diff'] = df.apply(lambda x: x['mean'] - 40.3, axis=1)
df = df.sort_values(by=['diff'])
alpha = 0.95
lower = (1-alpha)/2
upper = alpha+lower
print(df.iloc[int(lower * len(df.index))])
print(df.iloc[int(upper * len(df.index))])
display(df.hist())
end = timer()
print(end - start)
```
|
github_jupyter
|
# General imports.
import sqlite3
import pandas as pd
from matplotlib_venn import venn2, venn3
import scipy.stats as scs
import textwrap
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from itertools import combinations
import os
from matplotlib.colors import ListedColormap
from matplotlib import ticker
from scipy.stats import ttest_ind
import math
from timeit import default_timer as timer
# Imports from neighbor directories.
import sys
sys.path.append("..")
from src.utilities import field_registry as fieldreg
# IPython magics for this notebook.
%matplotlib inline
# Use latex font for matplotlib
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
# Switches
SAVE_OUTPUT = False
# Data Globals
FR = fieldreg.FieldRegistry()
TOTAL_USERS = 0
REMAINING_USERS = 0
TOTAL_DOGS = 0
REMAINING_DOGS = 0
PREVALENCE = lambda x: (x / REMAINING_DOGS) * 100
CATEGORY_MATRIX = pd.DataFrame()
# Database Globals
USER_TABLE = 'users'
DOG_TABLE = 'dogs'
BIAS_FILTER = '''
USING (record_id)
WHERE question_reason_for_part_3 = 0
OR (question_reason_for_part_3 = 1 AND q01_main != 1)'''
CON = sqlite3.connect('../data/processed/processed.db')
def createStringDataFrame(table, fields, labels, filtered=True):
query = 'SELECT ' + fields + ' FROM ' + table
if filtered:
table2 = USER_TABLE if table == DOG_TABLE else DOG_TABLE
query += ' JOIN ' + table2 + ' ' + BIAS_FILTER
df = pd.read_sql_query(query, CON)
df.columns = labels
return df
def convertToNumeric(df):
df = df.apply(pd.to_numeric, errors='coerce')
return df
def createNumericDataFrame(table, fields, labels, filtered=True):
df = createStringDataFrame(table, fields, labels, filtered)
return convertToNumeric(df)
def replaceFields(df, column, replacement_dict):
df[column].replace(replacement_dict, inplace=True)
def getValueCountAndPrevalence(df, field):
s = df[field].value_counts()
p = s.apply(PREVALENCE).round().astype(int)
rv = pd.concat([s, p], axis=1)
rv.columns = ['frequency', 'prevalence']
return rv
def createCategoryMatrix():
fields = []
labels = []
counter = 1
for cat, subdict in FR.labels.items():
for key, value in subdict.items():
if counter == 11:
counter += 1;
fields.append('q02_main_{}'.format(counter))
labels.append(key[0])
break
counter += 1
fields = ', '.join(fields)
df = createNumericDataFrame(DOG_TABLE, fields, labels, filtered=True)
cols = []
pvalue = {}
for col in df:
cols.append(col)
pvalue[col] = {}
pairs = list(combinations(df.columns, 2))
for pair in pairs:
contingency = pd.crosstab(df[pair[0]], df[pair[1]])
c, p, dof, expected = scs.chi2_contingency(contingency, correction=False)
pvalue[pair[0]][pair[1]] = p
pvalue[pair[1]][pair[0]] = p
df = pd.DataFrame(pvalue).sort_index(ascending=True)
return df
def createQuestionMatrix():
fields = ''
for cat, sublist in FR.fields.items():
for field in sublist:
fields += '{}, '.format(field)
fields = fields[:-2]
labels = []
for cat, subdict in FR.labels.items():
for key, value in subdict.items():
labels.append(key)
df = createNumericDataFrame(DOG_TABLE, fields, labels, filtered=True)
cols = []
pvalue = {}
for col in df:
cols.append(col)
pvalue[col] = {}
pairs = list(combinations(df.columns, 2))
for pair in pairs:
contingency = pd.crosstab(df[pair[0]], df[pair[1]])
c, p, dof, expected = scs.chi2_contingency(contingency, correction=False)
pvalue[pair[0]][pair[1]] = p
pvalue[pair[1]][pair[0]] = p
df = pd.DataFrame(pvalue).sort_index(ascending=True)
return df
def createCorrelationMatrix():
fields = []
labels = []
counter = 1
for cat, subdict in FR.labels.items():
for key, value in subdict.items():
if counter == 11:
counter += 1;
fields.append('q02_main_{}'.format(counter))
labels.append(key[0])
break
counter += 1
fields = ', '.join(fields)
df = createNumericDataFrame(DOG_TABLE, fields, labels, filtered=True)
return df.corr()
def createOddsRatioMatrix():
fields = []
labels = []
counter = 1
for cat, subdict in FR.labels.items():
for key, value in subdict.items():
if counter == 11:
counter += 1;
fields.append('q02_main_{}'.format(counter))
labels.append(key[0])
break
counter += 1
fields = ', '.join(fields)
df = createNumericDataFrame(DOG_TABLE, fields, labels, filtered=True)
cols = []
pvalue = {}
for col in df:
cols.append(col)
pvalue[col] = {}
pairs = list(combinations(df.columns, 2))
for pair in pairs:
contingency = pd.crosstab(df[pair[0]], df[pair[1]])
c, p, dof, expected = scs.chi2_contingency(contingency, correction=False)
pvalue[pair[0]][pair[1]] = getOddsRatio(contingency)
pvalue[pair[1]][pair[0]] = getOddsRatio(contingency)
df = pd.DataFrame(pvalue).sort_index(ascending=True)
return df
def displayOddsRatio(df):
odds, ci_low, ci_high, tot = getOddsRatioAndConfidenceInterval(df)
print('OR = %.2f, 95%% CI: %.2f-%.2f, n = %d'
%(round(odds, 2), round(ci_low, 2), round(ci_high, 2), tot))
def getOddsRatio(df):
return (df[1][1]/df[1][0])/(df[0][1]/df[0][0])
def getOddsRatioAndConfidenceInterval(df):
odds = getOddsRatio(df)
nl_or = math.log(odds)
se_nl_or = math.sqrt((1/df[0][0])+(1/df[0][1])+(1/df[1][0])+(1/df[1][1]))
ci_low = math.exp(nl_or - (1.96 * se_nl_or))
ci_high = math.exp(nl_or + (1.96 * se_nl_or))
tot = df[0][0] + df[0][1] + df[1][0] + df[1][1]
return odds, ci_low, ci_high, tot
def get_significance_category(p):
if np.isnan(p):
return p
elif p > 10**(-3):
return -1
elif p <= 10**(-3) and p > 10**(-6):
return 0
else:
return 1
def displaySeriesMedian(s, units=""):
print('MD = %.2f %s (SD = %.2f, min = %.2f, max = %.2f, n = %d)'
%(round(s.median(), 2), units, round(s.std(), 2), round(s.min(), 2), round(s.max(), 2), s.count()))
def displaySeriesMean(s, units=""):
print('M = %.2f %s (SD = %.2f, min = %.2f, max = %.2f, n = %d)'
%(round(s.mean(), 2), units, round(s.std(), 2), round(s.min(), 2), round(s.max(), 2), s.count()))
def convert_to_binary_response(x, y=1):
x = float(x)
if x < y:
return 0
return 1
def exportTable(data, title):
if not SAVE_OUTPUT:
return
file_ = os.path.join('..', 'reports', 'tables', title) + '.tex'
with open(file_, 'w') as tf:
tf.write(r'\documentclass[varwidth=\maxdimen]{standalone}\usepackage{booktabs}\begin{document}')
tf.write(df.to_latex())
tf.write(r'\end{document}')
def exportFigure(figure, title):
if not SAVE_OUTPUT:
return
file_ = os.path.join('..', 'reports', 'figures', title) + '.pdf'
figure.tight_layout()
figure.savefig(file_, format='pdf')
df = createNumericDataFrame(USER_TABLE, 'COUNT(*)', ['count'], filtered=False)
# Assign value to global.
TOTAL_USERS = df['count'][0]
print('N = %d owners [unadjusted]' %TOTAL_USERS)
df = createNumericDataFrame(DOG_TABLE, 'COUNT(*)', ['count'], filtered=False)
# Assign value to global.
TOTAL_DOGS = df['count'][0]
print('N = %d dogs [unadjusted]' %TOTAL_DOGS)
fields = ('question_reason_for_part_1, question_reason_for_part_2, '
'question_reason_for_part_3, question_reason_for_part_4, '
'question_reason_for_part_5')
labels = ['love for dogs', 'you help shelter animals', 'suspicion of behavior problems',
'work with animals', 'other']
df = createNumericDataFrame(USER_TABLE, fields, labels, filtered=False)
df = df[df[labels[2]] == 1]
df['sum'] = df.sum(axis=1)
s = df.sum(0, skipna=False)
print('n = %d owners (%d%%) [unadjusted]' %(s.iloc[2], round((s.iloc[2]/TOTAL_USERS)*100, 0)))
fields = ('question_reason_for_part_1, question_reason_for_part_2, '
'question_reason_for_part_3, question_reason_for_part_4, '
'question_reason_for_part_5')
labels = ['love for dogs', 'you help shelter animals', 'suspicion of behavior problems',
'work with animals', 'other']
df = createNumericDataFrame(USER_TABLE, fields, labels, filtered=False)
df = df[df[labels[2]] == 1]
df['sum'] = df.sum(axis=1)
df = df[df['sum'] == 1]
s = df.sum(0, skipna=False)
print('n = %d owners (%d%%) [unadjusted]' %(s.iloc[2], round((s.iloc[2]/TOTAL_USERS)*100, 0)))
fields = 'q02_score'
labels = ['Score']
df_adjusted_dogs = createNumericDataFrame(DOG_TABLE, fields, labels)
REMAINING_DOGS = len(df_adjusted_dogs.index)
df_adjusted_users = createNumericDataFrame(USER_TABLE, 'COUNT(DISTINCT email)', ['count'])
REMAINING_USERS = df_adjusted_users['count'][0]
# Display the count results.
print('Adjusted study population:')
print('N = %d owners (adjusted)' %REMAINING_USERS)
print('N = %d dogs (adjusted)' %REMAINING_DOGS)
fields = 'record_id'
labels = ['record index']
df = createStringDataFrame(DOG_TABLE, fields, labels)
record_dict = {}
for index, row in df.iterrows():
key = row.iloc[0]
if not key in record_dict:
record_dict[key] = 1
else:
record_dict[key] += 1
s = pd.Series(record_dict, name='dogs')
displaySeriesMedian(s, 'dogs')
fields = 'dog_age_today_months'
labels = ['age (months)']
df = createNumericDataFrame(DOG_TABLE, fields, labels)
displaySeriesMedian(df[labels[0]], 'months')
fields = 'dog_sex, dog_spayed'
labels = ['Gender', 'Neutered']
df = createStringDataFrame(DOG_TABLE, fields, labels)
replacements = {'':'No response', '1':'Male', '2':'Female'}
replaceFields(df, labels[0], replacements)
replacements = {'':'No response', '0':'No', '1':'Yes', '2':"I don't know"}
replaceFields(df, labels[1], replacements)
df = pd.crosstab(df[labels[0]], df[labels[1]], margins=True)
print("males: n = %d (%d%%), neutered: n = %d (%d%%), intact: n = %d (%d%%)"
%(df.loc['Male', 'All'], round((df.loc['Male', 'All']/df.loc['All', 'All'])*100, 0),
df.loc['Male', 'Yes'], round((df.loc['Male', 'Yes']/df.loc['Male', 'All'])*100, 0),
df.loc['Male', 'No'], round((df.loc['Male', 'No']/df.loc['Male', 'All'])*100, 0)))
print("females: n = %d (%d%%), neutered: n = %d (%d%%), intact: n = %d (%d%%)"
%(df.loc['Female', 'All'], round((df.loc['Female', 'All']/df.loc['All', 'All'])*100, 0),
df.loc['Female', 'Yes'], round((df.loc['Female', 'Yes']/df.loc['Female', 'All'])*100, 0),
df.loc['Female', 'No'], round((df.loc['Female', 'No']/df.loc['Female', 'All'])*100, 0)))
fields = 'q02_score'
labels = ['Score']
df_adjusted_dogs = createNumericDataFrame(DOG_TABLE, fields, labels)
cnt_total_dogs_w_problems_adjusted = len(
df_adjusted_dogs[df_adjusted_dogs[labels[0]] != 0].index)
print('Dogs with behavior problems: n = %d dogs' %(cnt_total_dogs_w_problems_adjusted))
# Calculate the adjusted prevalence.
prevalence_adjusted = PREVALENCE(cnt_total_dogs_w_problems_adjusted)
print('Overall prevalence: %d%% (%d/%d dogs)'
%(round(prevalence_adjusted, 0), cnt_total_dogs_w_problems_adjusted, REMAINING_DOGS))
start = timer()
fields = []
labels = []
for counter, category in enumerate(FR.categories, 1):
if counter > 10:
counter += 1;
fields.append('q02_main_{}'.format(counter))
labels.append(category)
fields = ', '.join(fields)
original_df = createNumericDataFrame(DOG_TABLE, fields, labels, filtered=True)
original_sums = original_df.sum()
display(original_sums.apply(PREVALENCE).round().astype(int))
def get_bootstrap_samples(data, count=10):
master_df = pd.DataFrame()
for i in range(count):
sample_df = data.sample(len(data.index), replace=True)
sums = sample_df.sum().apply(PREVALENCE).round().astype(int)
master_df = master_df.append(sums, ignore_index=True)
return master_df
master_df = get_bootstrap_samples(original_df, count=10000)
alpha = 0.95
lower = (1-alpha)/2
upper = alpha+lower
for name, values in master_df.iteritems():
print(name + ':')
values = values.sort_values(ascending=True)
values = values.reset_index(drop=True)
print(values[int(lower * len(values))])
print(values[int(upper * len(values))])
# Calculate the prevalence of each behavior problem.
#prevalences = sums.apply(PREVALENCE).round().astype(int)
end = timer()
print('\ntime:')
print(end - start)
sums = pd.Series()
for i in range(0, 12):
all_fields = FR.fields[FR.categories[i]].copy()
all_labels = list(FR.labels[FR.categories[i]].values()).copy()
df = createNumericDataFrame(DOG_TABLE, ', '.join(all_fields), all_labels, filtered=True)
if sums.empty:
sums = df.sum().sort_values(ascending=False)
else:
sums = sums.append(df.sum().sort_values(ascending=False))
# Calculate the prevalence of each behavior problem.
prevalences = sums.apply(PREVALENCE).round().astype(int)
# Create a table.
df = pd.DataFrame(index=sums.index, data={'Frequency':sums.values,
'Prevalence (%)': prevalences.values.round(2)})
df.columns.name = 'Behavior problem'
display(df.head())
print("Note: Only showing dataframe head to conserve notebook space")
exportTable(df, 'table_2')
fields = 'q03_main_1, dog_sex'
labels = ['owner-directed', 'gender']
df = createStringDataFrame(DOG_TABLE, fields, labels)
df = df[df[labels[1]] != '']
df = df.apply(pd.to_numeric)
def gender_to_binary_response(x):
x = int(x)
if x != 1:
return 0
return 1
df[labels[0]] = df[labels[0]].apply(
lambda x: convert_to_binary_response(x))
df[labels[1]] = df[labels[1]].apply(
lambda x: gender_to_binary_response(x))
# Execute a chi-squared test of independence.
contingency = pd.crosstab(df[labels[0]], df[labels[1]], margins=False)
print('Chi-squared Test of Independence for %s and %s:' %(labels[0], labels[1]))
c, p, dof, expected = scs.chi2_contingency(contingency, correction=False)
print('chi2 = %f, p = %.2E, dof = %d' %(c, p, dof))
displayOddsRatio(contingency)
start = timer()
data = pd.Series([30, 37, 36, 43, 42, 43, 43, 46, 41, 42])
display(data.mean())
x = np.array([])
for i in range(100):
if not i:
x = np.array(data.sample(len(data.index), replace=True).values)
else:
x = np.vstack([x, np.array(data.sample(len(data.index), replace=True).values)])
df = pd.DataFrame(x).transpose()
def agg_ci(data, confidence=0.95):
stats = data.agg(['mean']).transpose()
return stats
df = agg_ci(df)
df['diff'] = df.apply(lambda x: x['mean'] - 40.3, axis=1)
df = df.sort_values(by=['diff'])
alpha = 0.95
lower = (1-alpha)/2
upper = alpha+lower
print(df.iloc[int(lower * len(df.index))])
print(df.iloc[int(upper * len(df.index))])
display(df.hist())
end = timer()
print(end - start)
| 0.31732 | 0.754124 |
# Model with dit dah sequence recognition - 36 characters - element order prediction
Builds on `RNN-Morse-chars-single-ddp06` with element order encoding, In `RNN-Morse-chars-single-ddp06` particularly when applyijng minmax on the raw predictions we noticed that it was not good at all at sorting the dits and dahs (everything went to the dah senses) but was good at predicting the element (dit or dah) relative position (order). Here we exploit this feature exclusively. The length of dits and dahs is roughly respected and the element (the "on" keying) is reinforced from the noisy original signal.
Uses 5 element Morse encoding thus the 36 character alphabet.
Training material will be generated as random Morse strings rather than actual characters to maintain enough diversity
## Create string
Each character in the alphabet should happen a large enough number of times. As a rule of thumb we will take some multiple of the number of characters in the alphabet. If the multiplier is large enough the probability of each character appearance will be even over the alphabet.
Seems to get better results looking at the gated graphs but procedural decision has to be tuned.
```
import MorseGen
morse_gen = MorseGen.Morse()
alphabet = morse_gen.alphabet36
print(132/len(alphabet))
morse_cwss = MorseGen.get_morse_eles(nchars=132*5, nwords=27*5, max_elt=5)
print(alphabet)
print(len(morse_cwss), morse_cwss[0])
```
## Generate dataframe and extract envelope
```
Fs = 8000
decim = 128
samples_per_dit = morse_gen.nb_samples_per_dit(Fs, 13)
n_prev = int((samples_per_dit/128)*12*2) + 1
print(f'Samples per dit at {Fs} Hz is {samples_per_dit}. Decimation is {samples_per_dit/decim:.2f}. Look back is {n_prev}.')
label_df = morse_gen.encode_df_decim_ord_morse(morse_cwss, samples_per_dit, decim, 5)
env = label_df['env'].to_numpy()
print(type(env), len(env))
import numpy as np
def get_new_data(morse_gen, SNR_dB=-23, nchars=132, nwords=27, morse_cwss=None, max_elt=5):
decim = 128
if not morse_cwss:
morse_cwss = MorseGen.get_morse_eles(nchars=nchars, nwords=nwords, max_elt=max_elt)
print(len(morse_cwss), morse_cwss[0])
Fs = 8000
samples_per_dit = morse_gen.nb_samples_per_dit(Fs, 13)
#n_prev = int((samples_per_dit/decim)*19) + 1 # number of samples to look back is slightly more than a "O" a word space (3*4+7=19)
#n_prev = int((samples_per_dit/decim)*23) + 1 # (4*4+7=23)
n_prev = int((samples_per_dit/decim)*27) + 1 # number of samples to look back is slightly more than a "0" a word space (5*4+7=27)
print(f'Samples per dit at {Fs} Hz is {samples_per_dit}. Decimation is {samples_per_dit/decim:.2f}. Look back is {n_prev}.')
label_df = morse_gen.encode_df_decim_ord_morse(morse_cwss, samples_per_dit, decim, max_elt)
# extract the envelope
envelope = label_df['env'].to_numpy()
# remove the envelope
label_df.drop(columns=['env'], inplace=True)
SNR_linear = 10.0**(SNR_dB/10.0)
SNR_linear *= 256 # Apply original FFT
print(f'Resulting SNR for original {SNR_dB} dB is {(10.0 * np.log10(SNR_linear)):.2f} dB')
t = np.linspace(0, len(envelope)-1, len(envelope))
power = np.sum(envelope**2)/len(envelope)
noise_power = power/SNR_linear
noise = np.sqrt(noise_power)*np.random.normal(0, 1, len(envelope))
# noise = butter_lowpass_filter(raw_noise, 0.9, 3) # Noise is also filtered in the original setup from audio. This empirically simulates it
signal = (envelope + noise)**2
signal[signal > 1.0] = 1.0 # a bit crap ...
return envelope, signal, label_df, n_prev
```
Try it...
```
import matplotlib.pyplot as plt
max_ele = morse_gen.max_ele(alphabet)
envelope, signal, label_df, n_prev = get_new_data(morse_gen, SNR_dB=-17, morse_cwss=morse_cwss, max_elt=max_ele)
# Show
print(n_prev)
print(type(signal), signal.shape)
print(type(label_df), label_df.shape)
x0 = 0
x1 = 1500
plt.figure(figsize=(50,4))
plt.plot(signal[x0:x1]*0.7, label="sig")
plt.plot(envelope[x0:x1]*0.9, label='env')
plt.plot(label_df[x0:x1].ele*0.9 + 1.0, label='ele')
plt.plot(label_df[x0:x1].chr*0.9 + 1.0, label='chr', color="orange")
plt.plot(label_df[x0:x1].wrd*0.9 + 1.0, label='wrd')
for i in range(max_ele):
plt.plot(label_df[x0:x1][f'e{i}']*0.9 + 2.0 + i, label=f'e{i}')
plt.title("signal and labels")
plt.legend(loc=2)
plt.grid()
```
## Create data loader
### Define dataset
```
import torch
class MorsekeyingDataset(torch.utils.data.Dataset):
def __init__(self, morse_gen, device, SNR_dB=-23, nchars=132, nwords=27, morse_cwss=None, max_elt=5):
self.max_ele = max_elt
self.envelope, self.signal, self.label_df0, self.seq_len = get_new_data(morse_gen, SNR_dB=SNR_dB, morse_cwss=morse_cwss, max_elt=max_elt)
self.label_df = self.label_df0
self.X = torch.FloatTensor(self.signal).to(device)
self.y = torch.FloatTensor(self.label_df.values).to(device)
def __len__(self):
return self.X.__len__() - self.seq_len
def __getitem__(self, index):
return (self.X[index:index+self.seq_len], self.y[index+self.seq_len])
def get_envelope(self):
return self.envelope
def get_signal(self):
return self.signal
def get_X(self):
return self.X
def get_labels(self):
return self.label_df
def get_labels0(self):
return self.label_df0
def get_seq_len(self):
return self.seq_len()
def max_ele(self):
return self.max_ele
```
### Define keying data loader
```
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
train_chr_dataset = MorsekeyingDataset(morse_gen, device, -20, 132*5, 27*5, morse_cwss, max_ele)
train_chr_loader = torch.utils.data.DataLoader(train_chr_dataset, batch_size=1, shuffle=False) # Batch size must be 1
signal = train_chr_dataset.get_signal()
envelope = train_chr_dataset.get_envelope()
label_df = train_chr_dataset.get_labels()
label_df0 = train_chr_dataset.get_labels0()
print(type(signal), signal.shape)
print(type(label_df), label_df.shape)
x0 = 0
x1 = 1500
plt.figure(figsize=(50,4))
plt.plot(signal[x0:x1]*0.8, label="sig", color="cornflowerblue")
plt.plot(envelope[x0:x1]*0.9, label='env', color="orange")
plt.plot(label_df[x0:x1].ele*0.9 + 1.0, label='ele', color="orange")
plt.plot(label_df[x0:x1].chr*0.9 + 1.0, label='chr', color="green")
plt.plot(label_df[x0:x1].wrd*0.9 + 1.0, label='wrd', color="red")
for i in range(max_ele):
label_key = f'e{i}'
plt.plot(label_df[x0:x1][label_key]*0.9 + 2.0, label=label_key)
plt.title("keying - signal and labels")
plt.legend(loc=2)
plt.grid()
```
## Create model classes
```
import torch
import torch.nn as nn
class MorseLSTM(nn.Module):
"""
Initial implementation
"""
def __init__(self, device, input_size=1, hidden_layer_size=8, output_size=6):
super().__init__()
self.device = device # This is the only way to get things work properly with device
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_layer_size)
self.linear = nn.Linear(hidden_layer_size, output_size)
self.hidden_cell = (torch.zeros(1, 1, self.hidden_layer_size).to(self.device),
torch.zeros(1, 1, self.hidden_layer_size).to(self.device))
def forward(self, input_seq):
lstm_out, self.hidden_cell = self.lstm(input_seq.view(len(input_seq), 1, -1), self.hidden_cell)
predictions = self.linear(lstm_out.view(len(input_seq), -1))
return predictions[-1]
def zero_hidden_cell(self):
self.hidden_cell = (
torch.zeros(1, 1, self.hidden_layer_size).to(device),
torch.zeros(1, 1, self.hidden_layer_size).to(device)
)
class MorseBatchedLSTM(nn.Module):
"""
Initial implementation
"""
def __init__(self, device, input_size=1, hidden_layer_size=8, output_size=6):
super().__init__()
self.device = device # This is the only way to get things work properly with device
self.input_size = input_size
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_layer_size)
self.linear = nn.Linear(hidden_layer_size, output_size)
self.hidden_cell = (torch.zeros(1, 1, self.hidden_layer_size).to(self.device),
torch.zeros(1, 1, self.hidden_layer_size).to(self.device))
def _minmax(self, x):
x -= x.min(0)[0]
x /= x.max(0)[0]
def _hardmax(self, x):
x /= x.sum()
def _sqmax(self, x):
x = x**2
x /= x.sum()
def forward(self, input_seq):
#print(len(input_seq), input_seq.shape, input_seq.view(-1, 1, 1).shape)
lstm_out, self.hidden_cell = self.lstm(input_seq.view(-1, 1, self.input_size), self.hidden_cell)
predictions = self.linear(lstm_out.view(len(input_seq), -1))
self._minmax(predictions[-1])
return predictions[-1]
def zero_hidden_cell(self):
self.hidden_cell = (
torch.zeros(1, 1, self.hidden_layer_size).to(device),
torch.zeros(1, 1, self.hidden_layer_size).to(device)
)
class MorseBatchedMultiLSTM(nn.Module):
"""
Initial implementation
"""
def __init__(self, device, input_size=1, hidden_layer1_size=6, output1_size=6, hidden_layer2_size=12, output_size=14):
super().__init__()
self.device = device # This is the only way to get things work properly with device
self.input_size = input_size
self.hidden_layer1_size = hidden_layer1_size
self.output1_size = output1_size
self.hidden_layer2_size = hidden_layer2_size
self.output_size = output_size
self.lstm1 = nn.LSTM(input_size=input_size, hidden_size=hidden_layer1_size)
self.linear1 = nn.Linear(hidden_layer1_size, output1_size)
self.hidden1_cell = (torch.zeros(1, 1, self.hidden_layer1_size).to(self.device),
torch.zeros(1, 1, self.hidden_layer1_size).to(self.device))
self.lstm2 = nn.LSTM(input_size=output1_size, hidden_size=hidden_layer2_size)
self.linear2 = nn.Linear(hidden_layer2_size, output_size)
self.hidden2_cell = (torch.zeros(1, 1, self.hidden_layer2_size).to(self.device),
torch.zeros(1, 1, self.hidden_layer2_size).to(self.device))
def _minmax(self, x):
x -= x.min(0)[0]
x /= x.max(0)[0]
def _hardmax(self, x):
x /= x.sum()
def _sqmax(self, x):
x = x**2
x /= x.sum()
def forward(self, input_seq):
#print(len(input_seq), input_seq.shape, input_seq.view(-1, 1, 1).shape)
lstm1_out, self.hidden1_cell = self.lstm1(input_seq.view(-1, 1, self.input_size), self.hidden1_cell)
pred1 = self.linear1(lstm1_out.view(len(input_seq), -1))
lstm2_out, self.hidden2_cell = self.lstm2(pred1.view(-1, 1, self.output1_size), self.hidden2_cell)
predictions = self.linear2(lstm2_out.view(len(pred1), -1))
self._minmax(predictions[-1])
return predictions[-1]
def zero_hidden_cell(self):
self.hidden1_cell = (
torch.zeros(1, 1, self.hidden_layer1_size).to(device),
torch.zeros(1, 1, self.hidden_layer1_size).to(device)
)
self.hidden2_cell = (
torch.zeros(1, 1, self.hidden_layer2_size).to(device),
torch.zeros(1, 1, self.hidden_layer2_size).to(device)
)
class MorseLSTM2(nn.Module):
"""
LSTM stack
"""
def __init__(self, device, input_size=1, hidden_layer_size=8, output_size=6, dropout=0.2):
super().__init__()
self.device = device # This is the only way to get things work properly with device
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size, hidden_layer_size, num_layers=2, dropout=dropout)
self.linear = nn.Linear(hidden_layer_size, output_size)
self.hidden_cell = (torch.zeros(2, 1, self.hidden_layer_size).to(self.device),
torch.zeros(2, 1, self.hidden_layer_size).to(self.device))
def forward(self, input_seq):
lstm_out, self.hidden_cell = self.lstm(input_seq.view(len(input_seq), 1, -1), self.hidden_cell)
predictions = self.linear(lstm_out.view(len(input_seq), -1))
return predictions[-1]
def zero_hidden_cell(self):
self.hidden_cell = (
torch.zeros(2, 1, self.hidden_layer_size).to(device),
torch.zeros(2, 1, self.hidden_layer_size).to(device)
)
class MorseNoHLSTM(nn.Module):
"""
Do not keep hidden cell
"""
def __init__(self, device, input_size=1, hidden_layer_size=8, output_size=6):
super().__init__()
self.device = device # This is the only way to get things work properly with device
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size, hidden_layer_size)
self.linear = nn.Linear(hidden_layer_size, output_size)
def forward(self, input_seq):
h0 = torch.zeros(1, 1, self.hidden_layer_size).to(self.device)
c0 = torch.zeros(1, 1, self.hidden_layer_size).to(self.device)
lstm_out, _ = self.lstm(input_seq.view(len(input_seq), 1, -1), (h0, c0))
predictions = self.linear(lstm_out.view(len(input_seq), -1))
return predictions[-1]
class MorseBiLSTM(nn.Module):
"""
Attempt Bidirectional LSTM: does not work
"""
def __init__(self, device, input_size=1, hidden_size=12, num_layers=1, num_classes=6):
super(MorseEnvBiLSTM, self).__init__()
self.device = device # This is the only way to get things work properly with device
self.hidden_size = hidden_size
self.num_layers = num_layers
self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True, bidirectional=True)
self.fc = nn.Linear(hidden_size*2, num_classes) # 2 for bidirection
def forward(self, x):
# Set initial states
h0 = torch.zeros(self.num_layers*2, x.size(0), self.hidden_size).to(device) # 2 for bidirection
c0 = torch.zeros(self.num_layers*2, x.size(0), self.hidden_size).to(device)
# Forward propagate LSTM
out, _ = self.lstm(x.view(len(x), 1, -1), (h0, c0)) # out: tensor of shape (batch_size, seq_length, hidden_size*2)
# Decode the hidden state of the last time step
out = self.fc(out[:, -1, :])
return out[-1]
```
Create the keying model instance and print the details
```
#morse_chr_model = MorseBatchedMultiLSTM(device, hidden_layer1_size=12, output1_size=4, hidden_layer2_size=15, output_size=max_ele+3).to(device) # This is the only way to get things work properly with device
morse_chr_model = MorseBatchedLSTM(device, hidden_layer_size=50, output_size=max_ele+3).to(device)
morse_chr_loss_function = nn.MSELoss()
morse_chr_optimizer = torch.optim.Adam(morse_chr_model.parameters(), lr=0.002)
morse_chr_milestones = [4, 9]
morse_chr_scheduler = torch.optim.lr_scheduler.MultiStepLR(morse_chr_optimizer, milestones=morse_chr_milestones, gamma=0.5)
print(morse_chr_model)
print(morse_chr_model.device)
# Input and hidden tensors are not at the same device, found input tensor at cuda:0 and hidden tensor at cpu
for m in morse_chr_model.parameters():
print(m.shape, m.device)
X_t = torch.rand(n_prev)
X_t = X_t.cuda()
print("Input shape", X_t.shape, X_t.view(-1, 1, 1).shape)
print(X_t)
morse_chr_model(X_t)
import torchinfo
torchinfo.summary(morse_chr_model)
```
## Train model
```
it = iter(train_chr_loader)
X, y = next(it)
print(X.reshape(n_prev,1).shape, X[0].shape, y[0].shape)
print(X[0], y[0])
X, y = next(it)
print(X[0], y[0])
%%time
from tqdm.notebook import tqdm
print(morse_chr_scheduler.last_epoch)
epochs = 4
morse_chr_model.train()
for i in range(epochs):
train_losses = []
loop = tqdm(enumerate(train_chr_loader), total=len(train_chr_loader), leave=True)
for j, train in loop:
X_train = train[0][0]
y_train = train[1][0]
morse_chr_optimizer.zero_grad()
if morse_chr_model.__class__.__name__ in ["MorseLSTM", "MorseLSTM2", "MorseBatchedLSTM", "MorseBatchedLSTM2", "MorseBatchedMultiLSTM"]:
morse_chr_model.zero_hidden_cell() # this model needs to reset the hidden cell
y_pred = morse_chr_model(X_train)
single_loss = morse_chr_loss_function(y_pred, y_train)
single_loss.backward()
morse_chr_optimizer.step()
train_losses.append(single_loss.item())
# update progress bar
if j % 1000 == 0:
loop.set_description(f"Epoch [{i+1}/{epochs}]")
loop.set_postfix(loss=np.mean(train_losses))
morse_chr_scheduler.step()
print(f'final: {i+1:3} epochs loss: {np.mean(train_losses):6.4f}')
save_model = True
if save_model:
torch.save(morse_chr_model.state_dict(), 'models/morse_ord36_model')
else:
morse_chr_model.load_state_dict(torch.load('models/morse_ord36_model', map_location=device))
```
<pre><code>
MorseBatchedLSTM(
(lstm): LSTM(1, 50)
(linear): Linear(in_features=50, out_features=8, bias=True)
)
final: 16 epochs loss: 0.0418
CPU times: user 35min 41s, sys: 39.3 s, total: 36min 20s
Wall time: 36min 10s
126 IFU DE F4EXB = R TNX RPT ES INFO ALEX = RIG IS FTD/1200 GW 10_W ANT IS 3AGI = WX IS SUNNY ES WARM 32C = HW AR F5SFU DE F4EXD K
final: 4 epochs loss: 0.0402
CPU times: user 8min 57s, sys: 9.29 s, total: 9min 7s
Wall time: 9min 4s
126 IFU DE F4EXB = R TNX RPT ES INFO ALE4 =RIG IS FTDXJ20_ PWR 100V ANT IS YAGI X WX IS SUNNY ES WARM 32C = HW AR R5SFU DE F4EXB K /// take 1 ///
126 IFU BE F4EKD = R TTX RPT ES ITFO ALEV XRIG IS FTDX1200 PWR 100V ANT ES YAGI = WX IS SUNNY EH PARM 32C = HW AR G5SFU DE U4EXB K /// take 2 ///
final: 4 epochs loss: 0.0381 /// in fact it could be good to divide LR again by 2 at 20th epoch ///
CPU times: user 8min 55s, sys: 9.62 s, total: 9min 4s
Wall time: 9min 2s
127 IFU DE F4EXB = R TNX RPT ES INFO ALE4 = RIG IS FTDX1200 PWR 100V ANT IS YAGI X WX IS SUNNY ES WARM 32C = HW AR R5SFU DE F4EXB K
127 IFU TE F4EXD X R TTX RWT ES ITUÖ ALEV K NIM SI FTDX1200 PWR 100V ANT ES YAGI = WX IS IUNNY EH PARM 32C = HW AR G5SFU DE U4EXB K
final: 4 epochs loss: 0.0351
CPU times: user 8min 59s, sys: 9.74 s, total: 9min 9s
Wall time: 9min 6s
126 IFU DE F4EXB = R TNX RPT ES INFO ALE4 = RIG IS FTDX1200 PWR 100V ANT IS YAGI X WX IS SUNNY E GARM 32C = HW AR F5SFU DE F4EXB K
126 SFU NE F4EKB X R TTX RPT ES ITFO TLE4 = NIG SS FTDX1200 PWR 100V ANT ES YAGI X MX ES SUNNY E ÖARM Ü2C = HW AR F5SFU BE A4EXB K
final: 4 epochs loss: 0.0355
CPU times: user 9min 2s, sys: 10.1 s, total: 9min 12s
Wall time: 9min 10s
126 IFU DE F4EXB = R TNX RPT ES INFO ALEU = RIG IS FTDX12__ PWR 100V ANT IS YAGI X WX IS SUNNY E GARM V2C = HW AR F5SFU DE F4EXB K
126 IRU DE F4EXD X R TTX RPT ES INRO ALEW = GIM SS FTDX1200 PWR 100V ANT AS YAGI = MX IS IUNNY E ÖARM Ü2C = HW AR R5SFU DE U4EXB K
</code></pre>
```
%%time
p_char_train = torch.empty(1,max_ele+3).to(device)
morse_chr_model.eval()
loop = tqdm(enumerate(train_chr_loader), total=len(train_chr_loader))
for j, train in loop:
with torch.no_grad():
X_chr = train[0][0]
pred_val = morse_chr_model(X_chr)
p_char_train = torch.cat([p_char_train, pred_val.reshape(1,max_ele+3)])
p_char_train = p_char_train[1:] # Remove garbge
print(p_char_train.shape) # t -> chars(t)
```
### Post process
- Move to CPU to ger chars(time)
- Transpose to get times(char)
```
p_char_train_c = p_char_train.cpu() # t -> chars(t) on CPU
p_char_train_t = torch.transpose(p_char_train_c, 0, 1).cpu() # c -> times(c) on CPU
print(p_char_train_c.shape, p_char_train_t.shape)
X_train_chr = train_chr_dataset.X.cpu()
label_df_chr = train_chr_dataset.get_labels()
env_chr = train_chr_dataset.get_envelope()
l_alpha = label_df_chr[n_prev:].reset_index(drop=True)
plt.figure(figsize=(50,6))
plt.plot(l_alpha[x0:x1]["chr"]*3, label="ychr", alpha=0.2, color="black")
plt.plot(X_train_chr[x0+n_prev:x1+n_prev]*0.8, label='sig')
plt.plot(env_chr[x0+n_prev:x1+n_prev]*0.9, label='env')
plt.plot(p_char_train_t[0][x0:x1]*0.9 + 1.0, label='e', color="orange")
plt.plot(p_char_train_t[1][x0:x1]*0.9 + 1.0, label='c', color="green")
plt.plot(p_char_train_t[2][x0:x1]*0.9 + 1.0, label='w', color="red")
color_list = ["green", "red", "orange", "purple", "cornflowerblue"]
for i in range(max_ele):
plt.plot(p_char_train_t[i+3][x0:x1]*0.9 + 2.0, label=f'e{i}', color=color_list[i])
plt.title("predictions")
plt.legend(loc=2)
plt.grid()
```
## Test
### Test dataset and data loader
```
teststr = "F5SFU DE F4EXB = R TNX RPT ES INFO ALEX = RIG IS FTDX1200 PWR 100W ANT IS YAGI = WX IS SUNNY ES WARM 32C = HW AR F5SFU DE F4EXB KN"
test_cwss = morse_gen.cws_to_cwss(teststr)
test_chr_dataset = MorsekeyingDataset(morse_gen, device, -17, 132*5, 27*5, test_cwss, max_ele)
test_chr_loader = torch.utils.data.DataLoader(test_chr_dataset, batch_size=1, shuffle=False) # Batch size must be 1
```
### Run the model
```
p_chr_test = torch.empty(1,max_ele+3).to(device)
morse_chr_model.eval()
loop = tqdm(enumerate(test_chr_loader), total=len(test_chr_loader))
for j, test in loop:
with torch.no_grad():
X_test = test[0]
pred_val = morse_chr_model(X_test[0])
p_chr_test = torch.cat([p_chr_test, pred_val.reshape(1,max_ele+3)])
# drop first garbage sample
p_chr_test = p_chr_test[1:]
print(p_chr_test.shape)
p_chr_test_c = p_chr_test.cpu() # t -> chars(t) on CPU
p_chr_test_t = torch.transpose(p_chr_test_c, 0, 1).cpu() # c -> times(c) on CPU
print(p_chr_test_c.shape, p_chr_test_t.shape)
```
### Show results
```
X_test_chr = test_chr_dataset.X.cpu()
label_df_t = test_chr_dataset.get_labels()
env_test = test_chr_dataset.get_envelope()
l_alpha_t = label_df_t[n_prev:].reset_index(drop=True)
```
#### Raw results
```
plt.figure(figsize=(100,4))
plt.plot(l_alpha_t[:]["chr"]*4, label="ychr", alpha=0.2, color="black")
plt.plot(X_test_chr[n_prev:]*0.8, label='sig')
plt.plot(env_test[n_prev:]*0.9, label='env')
plt.plot(p_chr_test_t[0]*0.9 + 1.0, label='e', color="purple")
plt.plot(p_chr_test_t[1]*0.9 + 2.0, label='c', color="green")
plt.plot(p_chr_test_t[2]*0.9 + 2.0, label='w', color="red")
color_list = ["green", "red", "orange", "purple", "cornflowerblue"]
for i in range(max_ele):
plt_a = plt.plot(p_chr_test_t[i+3]*0.9 + 3.0, label=f'e{i}', color=color_list[i])
plt.title("predictions")
plt.legend(loc=2)
plt.grid()
plt.savefig('img/predicted.png')
```
### Integration by moving average
Implemented with convolution with a square window
```
p_chr_test_tn = p_chr_test_t.numpy()
ele_len = round(samples_per_dit / 256)
win = np.ones(ele_len)/ele_len
p_chr_test_tlp = np.apply_along_axis(lambda m: np.convolve(m, win, mode='full'), axis=1, arr=p_chr_test_tn)
plt.figure(figsize=(100,4))
plt.plot(l_alpha_t[:]["chr"]*4, label="ychr", alpha=0.2, color="black")
plt.plot(X_test_chr[n_prev:]*0.9, label='sig')
plt.plot(env_test[n_prev:]*0.9, label='env')
plt.plot(p_chr_test_tlp[0]*0.9 + 1.0, label='e', color="purple")
plt.plot(p_chr_test_tlp[1]*0.9 + 2.0, label='c', color="green")
plt.plot(p_chr_test_tlp[2]*0.9 + 2.0, label='w', color="red")
color_list = ["green", "red", "orange", "purple", "cornflowerblue"]
for i in range(max_ele):
plt.plot(p_chr_test_tlp[i+3,:]*0.9 + 3.0, label=f'e{i}', color=color_list[i])
plt.title("predictions")
plt.legend(loc=2)
plt.grid()
plt.savefig('img/predicted_lp.png')
```
### Apply threshold
```
p_chr_test_tn = p_chr_test_t.numpy()
ele_len = round(samples_per_dit / 256)
win = np.ones(ele_len)/ele_len
p_chr_test_tlp = np.apply_along_axis(lambda m: np.convolve(m, win, mode='full'), axis=1, arr=p_chr_test_tn)
for i in range(max_ele+3):
p_chr_test_tlp[i][p_chr_test_tlp[i] < 0.5] = 0
plt.figure(figsize=(100,4))
plt.plot(l_alpha_t[:]["chr"]*4, label="ychr", alpha=0.2, color="black")
plt.plot(X_test_chr[n_prev:]*0.9, label='sig')
plt.plot(env_test[n_prev:]*0.9, label='env')
plt.plot(p_chr_test_tlp[0]*0.9 + 1.0, label='e', color="purple")
plt.plot(p_chr_test_tlp[1]*0.9 + 2.0, label='c', color="green")
plt.plot(p_chr_test_tlp[2]*0.9 + 2.0, label='w', color="red")
color_list = ["green", "red", "orange", "purple", "cornflowerblue"]
for i in range(max_ele):
plt.plot(p_chr_test_tlp[i+3,:]*0.9 + 3.0, label=f'e{i}', color=color_list[i])
plt.title("predictions")
plt.legend(loc=2)
plt.grid()
plt.savefig('img/predicted_lpthr.png')
```
## Procedural decision making
### take 1
Hard limits with hard values
```
class MorseDecoderPos:
def __init__(self, alphabet, dit_len, npos, thr):
self.nb_alpha = len(alphabet)
self.alphabet = alphabet
self.dit_len = dit_len
self.npos = npos
self.thr = thr
self.res = ""
self.morsestr = ""
self.pprev = 0
self.wsep = False
self.csep = False
self.lcounts = [0 for x in range(3+self.npos)]
self.morse_gen = MorseGen.Morse()
self.revmorsecode = self.morse_gen.revmorsecode
self.dit_l = 0.3
self.dit_h = 1.2
self.dah_l = 1.5
print(self.dit_l*dit_len, self.dit_h*dit_len, self.dah_l*dit_len)
def new_samples(self, samples):
for i, s in enumerate(samples): # e, c, w, [pos]
if s >= self.thr:
self.lcounts[i] += 1
else:
if i == 1:
self.lcounts[1] = 0
self.csep = False
if i == 2:
self.lcounts[2] = 0
self.wsep = False
if i == 1 and self.lcounts[1] > 1.2*self.dit_len and not self.csep: # character separator
morsestr = ""
for ip in range(3,3+self.npos):
if self.lcounts[ip] >= self.dit_l*self.dit_len and self.lcounts[ip] < self.dit_h*self.dit_len: # dit
morsestr += "."
elif self.lcounts[ip] > self.dah_l*self.dit_len: # dah
morsestr += "-"
char = self.revmorsecode.get(morsestr, '_')
self.res += char
#print(self.lcounts[3:], morsestr, char)
self.csep = True
self.lcounts[3:] = self.npos*[0]
if i == 2 and self.lcounts[2] > 2.5*self.dit_len and not self.wsep: # word separator
self.res += " "
#print("w")
self.wsep = True
dit_len = round(samples_per_dit / decim)
chr_len = round(samples_per_dit*2 / decim)
wrd_len = round(samples_per_dit*4 / decim)
print(dit_len)
decoder = MorseDecoderPos(alphabet, dit_len, max_ele, 0.9)
#p_chr_test_clp = torch.transpose(p_chr_test_tlp, 0, 1)
p_chr_test_clp = p_chr_test_tlp.transpose()
for s in p_chr_test_clp:
decoder.new_samples(s) # e, c, w, [pos]
print(len(decoder.res), decoder.res)
```
### take 2
Hard limits with soft values
```
class MorseDecoderPos:
def __init__(self, alphabet, dit_len, npos, thr):
self.nb_alpha = len(alphabet)
self.alphabet = alphabet
self.dit_len = dit_len
self.npos = npos
self.thr = thr
self.res = ""
self.morsestr = ""
self.pprev = 0
self.wsep = False
self.csep = False
self.scounts = [0 for x in range(3)] # separators
self.ecounts = [0 for x in range(self.npos)] # Morse elements
self.morse_gen = MorseGen.Morse()
self.revmorsecode = self.morse_gen.revmorsecode
self.dit_l = 0.3
self.dit_h = 1.2
self.dah_l = 1.5
print(self.dit_l*dit_len, self.dit_h*dit_len, self.dah_l*dit_len)
def new_samples(self, samples):
for i, s in enumerate(samples): # e, c, w, [pos]
if s >= self.thr:
if i < 3:
self.scounts[i] += 1
else:
if i == 1:
self.scounts[1] = 0
self.csep = False
if i == 2:
self.scounts[2] = 0
self.wsep = False
if i >= 3:
self.ecounts[i-3] += s
if i == 1 and self.scounts[1] > 1.2*self.dit_len and not self.csep: # character separator
morsestr = ""
for ip in range(self.npos):
if self.ecounts[ip] >= self.dit_l*self.dit_len and self.ecounts[ip] < self.dit_h*self.dit_len: # dit
morsestr += "."
elif self.ecounts[ip] > self.dah_l*self.dit_len: # dah
morsestr += "-"
char = self.revmorsecode.get(morsestr, '_')
self.res += char
#print(self.ecounts, morsestr, char)
self.csep = True
self.ecounts = self.npos*[0]
if i == 2 and self.scounts[2] > 2.5*self.dit_len and not self.wsep: # word separator
self.res += " "
#print("w")
self.wsep = True
dit_len = round(samples_per_dit / decim)
chr_len = round(samples_per_dit*2 / decim)
wrd_len = round(samples_per_dit*4 / decim)
print(dit_len)
decoder = MorseDecoderPos(alphabet, dit_len, max_ele, 0.9)
#p_chr_test_clp = torch.transpose(p_chr_test_tlp, 0, 1)
p_chr_test_clp = p_chr_test_tlp.transpose()
for s in p_chr_test_clp:
decoder.new_samples(s) # e, c, w, [pos]
print(len(decoder.res), decoder.res)
```
|
github_jupyter
|
import MorseGen
morse_gen = MorseGen.Morse()
alphabet = morse_gen.alphabet36
print(132/len(alphabet))
morse_cwss = MorseGen.get_morse_eles(nchars=132*5, nwords=27*5, max_elt=5)
print(alphabet)
print(len(morse_cwss), morse_cwss[0])
Fs = 8000
decim = 128
samples_per_dit = morse_gen.nb_samples_per_dit(Fs, 13)
n_prev = int((samples_per_dit/128)*12*2) + 1
print(f'Samples per dit at {Fs} Hz is {samples_per_dit}. Decimation is {samples_per_dit/decim:.2f}. Look back is {n_prev}.')
label_df = morse_gen.encode_df_decim_ord_morse(morse_cwss, samples_per_dit, decim, 5)
env = label_df['env'].to_numpy()
print(type(env), len(env))
import numpy as np
def get_new_data(morse_gen, SNR_dB=-23, nchars=132, nwords=27, morse_cwss=None, max_elt=5):
decim = 128
if not morse_cwss:
morse_cwss = MorseGen.get_morse_eles(nchars=nchars, nwords=nwords, max_elt=max_elt)
print(len(morse_cwss), morse_cwss[0])
Fs = 8000
samples_per_dit = morse_gen.nb_samples_per_dit(Fs, 13)
#n_prev = int((samples_per_dit/decim)*19) + 1 # number of samples to look back is slightly more than a "O" a word space (3*4+7=19)
#n_prev = int((samples_per_dit/decim)*23) + 1 # (4*4+7=23)
n_prev = int((samples_per_dit/decim)*27) + 1 # number of samples to look back is slightly more than a "0" a word space (5*4+7=27)
print(f'Samples per dit at {Fs} Hz is {samples_per_dit}. Decimation is {samples_per_dit/decim:.2f}. Look back is {n_prev}.')
label_df = morse_gen.encode_df_decim_ord_morse(morse_cwss, samples_per_dit, decim, max_elt)
# extract the envelope
envelope = label_df['env'].to_numpy()
# remove the envelope
label_df.drop(columns=['env'], inplace=True)
SNR_linear = 10.0**(SNR_dB/10.0)
SNR_linear *= 256 # Apply original FFT
print(f'Resulting SNR for original {SNR_dB} dB is {(10.0 * np.log10(SNR_linear)):.2f} dB')
t = np.linspace(0, len(envelope)-1, len(envelope))
power = np.sum(envelope**2)/len(envelope)
noise_power = power/SNR_linear
noise = np.sqrt(noise_power)*np.random.normal(0, 1, len(envelope))
# noise = butter_lowpass_filter(raw_noise, 0.9, 3) # Noise is also filtered in the original setup from audio. This empirically simulates it
signal = (envelope + noise)**2
signal[signal > 1.0] = 1.0 # a bit crap ...
return envelope, signal, label_df, n_prev
import matplotlib.pyplot as plt
max_ele = morse_gen.max_ele(alphabet)
envelope, signal, label_df, n_prev = get_new_data(morse_gen, SNR_dB=-17, morse_cwss=morse_cwss, max_elt=max_ele)
# Show
print(n_prev)
print(type(signal), signal.shape)
print(type(label_df), label_df.shape)
x0 = 0
x1 = 1500
plt.figure(figsize=(50,4))
plt.plot(signal[x0:x1]*0.7, label="sig")
plt.plot(envelope[x0:x1]*0.9, label='env')
plt.plot(label_df[x0:x1].ele*0.9 + 1.0, label='ele')
plt.plot(label_df[x0:x1].chr*0.9 + 1.0, label='chr', color="orange")
plt.plot(label_df[x0:x1].wrd*0.9 + 1.0, label='wrd')
for i in range(max_ele):
plt.plot(label_df[x0:x1][f'e{i}']*0.9 + 2.0 + i, label=f'e{i}')
plt.title("signal and labels")
plt.legend(loc=2)
plt.grid()
import torch
class MorsekeyingDataset(torch.utils.data.Dataset):
def __init__(self, morse_gen, device, SNR_dB=-23, nchars=132, nwords=27, morse_cwss=None, max_elt=5):
self.max_ele = max_elt
self.envelope, self.signal, self.label_df0, self.seq_len = get_new_data(morse_gen, SNR_dB=SNR_dB, morse_cwss=morse_cwss, max_elt=max_elt)
self.label_df = self.label_df0
self.X = torch.FloatTensor(self.signal).to(device)
self.y = torch.FloatTensor(self.label_df.values).to(device)
def __len__(self):
return self.X.__len__() - self.seq_len
def __getitem__(self, index):
return (self.X[index:index+self.seq_len], self.y[index+self.seq_len])
def get_envelope(self):
return self.envelope
def get_signal(self):
return self.signal
def get_X(self):
return self.X
def get_labels(self):
return self.label_df
def get_labels0(self):
return self.label_df0
def get_seq_len(self):
return self.seq_len()
def max_ele(self):
return self.max_ele
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
train_chr_dataset = MorsekeyingDataset(morse_gen, device, -20, 132*5, 27*5, morse_cwss, max_ele)
train_chr_loader = torch.utils.data.DataLoader(train_chr_dataset, batch_size=1, shuffle=False) # Batch size must be 1
signal = train_chr_dataset.get_signal()
envelope = train_chr_dataset.get_envelope()
label_df = train_chr_dataset.get_labels()
label_df0 = train_chr_dataset.get_labels0()
print(type(signal), signal.shape)
print(type(label_df), label_df.shape)
x0 = 0
x1 = 1500
plt.figure(figsize=(50,4))
plt.plot(signal[x0:x1]*0.8, label="sig", color="cornflowerblue")
plt.plot(envelope[x0:x1]*0.9, label='env', color="orange")
plt.plot(label_df[x0:x1].ele*0.9 + 1.0, label='ele', color="orange")
plt.plot(label_df[x0:x1].chr*0.9 + 1.0, label='chr', color="green")
plt.plot(label_df[x0:x1].wrd*0.9 + 1.0, label='wrd', color="red")
for i in range(max_ele):
label_key = f'e{i}'
plt.plot(label_df[x0:x1][label_key]*0.9 + 2.0, label=label_key)
plt.title("keying - signal and labels")
plt.legend(loc=2)
plt.grid()
import torch
import torch.nn as nn
class MorseLSTM(nn.Module):
"""
Initial implementation
"""
def __init__(self, device, input_size=1, hidden_layer_size=8, output_size=6):
super().__init__()
self.device = device # This is the only way to get things work properly with device
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_layer_size)
self.linear = nn.Linear(hidden_layer_size, output_size)
self.hidden_cell = (torch.zeros(1, 1, self.hidden_layer_size).to(self.device),
torch.zeros(1, 1, self.hidden_layer_size).to(self.device))
def forward(self, input_seq):
lstm_out, self.hidden_cell = self.lstm(input_seq.view(len(input_seq), 1, -1), self.hidden_cell)
predictions = self.linear(lstm_out.view(len(input_seq), -1))
return predictions[-1]
def zero_hidden_cell(self):
self.hidden_cell = (
torch.zeros(1, 1, self.hidden_layer_size).to(device),
torch.zeros(1, 1, self.hidden_layer_size).to(device)
)
class MorseBatchedLSTM(nn.Module):
"""
Initial implementation
"""
def __init__(self, device, input_size=1, hidden_layer_size=8, output_size=6):
super().__init__()
self.device = device # This is the only way to get things work properly with device
self.input_size = input_size
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_layer_size)
self.linear = nn.Linear(hidden_layer_size, output_size)
self.hidden_cell = (torch.zeros(1, 1, self.hidden_layer_size).to(self.device),
torch.zeros(1, 1, self.hidden_layer_size).to(self.device))
def _minmax(self, x):
x -= x.min(0)[0]
x /= x.max(0)[0]
def _hardmax(self, x):
x /= x.sum()
def _sqmax(self, x):
x = x**2
x /= x.sum()
def forward(self, input_seq):
#print(len(input_seq), input_seq.shape, input_seq.view(-1, 1, 1).shape)
lstm_out, self.hidden_cell = self.lstm(input_seq.view(-1, 1, self.input_size), self.hidden_cell)
predictions = self.linear(lstm_out.view(len(input_seq), -1))
self._minmax(predictions[-1])
return predictions[-1]
def zero_hidden_cell(self):
self.hidden_cell = (
torch.zeros(1, 1, self.hidden_layer_size).to(device),
torch.zeros(1, 1, self.hidden_layer_size).to(device)
)
class MorseBatchedMultiLSTM(nn.Module):
"""
Initial implementation
"""
def __init__(self, device, input_size=1, hidden_layer1_size=6, output1_size=6, hidden_layer2_size=12, output_size=14):
super().__init__()
self.device = device # This is the only way to get things work properly with device
self.input_size = input_size
self.hidden_layer1_size = hidden_layer1_size
self.output1_size = output1_size
self.hidden_layer2_size = hidden_layer2_size
self.output_size = output_size
self.lstm1 = nn.LSTM(input_size=input_size, hidden_size=hidden_layer1_size)
self.linear1 = nn.Linear(hidden_layer1_size, output1_size)
self.hidden1_cell = (torch.zeros(1, 1, self.hidden_layer1_size).to(self.device),
torch.zeros(1, 1, self.hidden_layer1_size).to(self.device))
self.lstm2 = nn.LSTM(input_size=output1_size, hidden_size=hidden_layer2_size)
self.linear2 = nn.Linear(hidden_layer2_size, output_size)
self.hidden2_cell = (torch.zeros(1, 1, self.hidden_layer2_size).to(self.device),
torch.zeros(1, 1, self.hidden_layer2_size).to(self.device))
def _minmax(self, x):
x -= x.min(0)[0]
x /= x.max(0)[0]
def _hardmax(self, x):
x /= x.sum()
def _sqmax(self, x):
x = x**2
x /= x.sum()
def forward(self, input_seq):
#print(len(input_seq), input_seq.shape, input_seq.view(-1, 1, 1).shape)
lstm1_out, self.hidden1_cell = self.lstm1(input_seq.view(-1, 1, self.input_size), self.hidden1_cell)
pred1 = self.linear1(lstm1_out.view(len(input_seq), -1))
lstm2_out, self.hidden2_cell = self.lstm2(pred1.view(-1, 1, self.output1_size), self.hidden2_cell)
predictions = self.linear2(lstm2_out.view(len(pred1), -1))
self._minmax(predictions[-1])
return predictions[-1]
def zero_hidden_cell(self):
self.hidden1_cell = (
torch.zeros(1, 1, self.hidden_layer1_size).to(device),
torch.zeros(1, 1, self.hidden_layer1_size).to(device)
)
self.hidden2_cell = (
torch.zeros(1, 1, self.hidden_layer2_size).to(device),
torch.zeros(1, 1, self.hidden_layer2_size).to(device)
)
class MorseLSTM2(nn.Module):
"""
LSTM stack
"""
def __init__(self, device, input_size=1, hidden_layer_size=8, output_size=6, dropout=0.2):
super().__init__()
self.device = device # This is the only way to get things work properly with device
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size, hidden_layer_size, num_layers=2, dropout=dropout)
self.linear = nn.Linear(hidden_layer_size, output_size)
self.hidden_cell = (torch.zeros(2, 1, self.hidden_layer_size).to(self.device),
torch.zeros(2, 1, self.hidden_layer_size).to(self.device))
def forward(self, input_seq):
lstm_out, self.hidden_cell = self.lstm(input_seq.view(len(input_seq), 1, -1), self.hidden_cell)
predictions = self.linear(lstm_out.view(len(input_seq), -1))
return predictions[-1]
def zero_hidden_cell(self):
self.hidden_cell = (
torch.zeros(2, 1, self.hidden_layer_size).to(device),
torch.zeros(2, 1, self.hidden_layer_size).to(device)
)
class MorseNoHLSTM(nn.Module):
"""
Do not keep hidden cell
"""
def __init__(self, device, input_size=1, hidden_layer_size=8, output_size=6):
super().__init__()
self.device = device # This is the only way to get things work properly with device
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size, hidden_layer_size)
self.linear = nn.Linear(hidden_layer_size, output_size)
def forward(self, input_seq):
h0 = torch.zeros(1, 1, self.hidden_layer_size).to(self.device)
c0 = torch.zeros(1, 1, self.hidden_layer_size).to(self.device)
lstm_out, _ = self.lstm(input_seq.view(len(input_seq), 1, -1), (h0, c0))
predictions = self.linear(lstm_out.view(len(input_seq), -1))
return predictions[-1]
class MorseBiLSTM(nn.Module):
"""
Attempt Bidirectional LSTM: does not work
"""
def __init__(self, device, input_size=1, hidden_size=12, num_layers=1, num_classes=6):
super(MorseEnvBiLSTM, self).__init__()
self.device = device # This is the only way to get things work properly with device
self.hidden_size = hidden_size
self.num_layers = num_layers
self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True, bidirectional=True)
self.fc = nn.Linear(hidden_size*2, num_classes) # 2 for bidirection
def forward(self, x):
# Set initial states
h0 = torch.zeros(self.num_layers*2, x.size(0), self.hidden_size).to(device) # 2 for bidirection
c0 = torch.zeros(self.num_layers*2, x.size(0), self.hidden_size).to(device)
# Forward propagate LSTM
out, _ = self.lstm(x.view(len(x), 1, -1), (h0, c0)) # out: tensor of shape (batch_size, seq_length, hidden_size*2)
# Decode the hidden state of the last time step
out = self.fc(out[:, -1, :])
return out[-1]
#morse_chr_model = MorseBatchedMultiLSTM(device, hidden_layer1_size=12, output1_size=4, hidden_layer2_size=15, output_size=max_ele+3).to(device) # This is the only way to get things work properly with device
morse_chr_model = MorseBatchedLSTM(device, hidden_layer_size=50, output_size=max_ele+3).to(device)
morse_chr_loss_function = nn.MSELoss()
morse_chr_optimizer = torch.optim.Adam(morse_chr_model.parameters(), lr=0.002)
morse_chr_milestones = [4, 9]
morse_chr_scheduler = torch.optim.lr_scheduler.MultiStepLR(morse_chr_optimizer, milestones=morse_chr_milestones, gamma=0.5)
print(morse_chr_model)
print(morse_chr_model.device)
# Input and hidden tensors are not at the same device, found input tensor at cuda:0 and hidden tensor at cpu
for m in morse_chr_model.parameters():
print(m.shape, m.device)
X_t = torch.rand(n_prev)
X_t = X_t.cuda()
print("Input shape", X_t.shape, X_t.view(-1, 1, 1).shape)
print(X_t)
morse_chr_model(X_t)
import torchinfo
torchinfo.summary(morse_chr_model)
it = iter(train_chr_loader)
X, y = next(it)
print(X.reshape(n_prev,1).shape, X[0].shape, y[0].shape)
print(X[0], y[0])
X, y = next(it)
print(X[0], y[0])
%%time
from tqdm.notebook import tqdm
print(morse_chr_scheduler.last_epoch)
epochs = 4
morse_chr_model.train()
for i in range(epochs):
train_losses = []
loop = tqdm(enumerate(train_chr_loader), total=len(train_chr_loader), leave=True)
for j, train in loop:
X_train = train[0][0]
y_train = train[1][0]
morse_chr_optimizer.zero_grad()
if morse_chr_model.__class__.__name__ in ["MorseLSTM", "MorseLSTM2", "MorseBatchedLSTM", "MorseBatchedLSTM2", "MorseBatchedMultiLSTM"]:
morse_chr_model.zero_hidden_cell() # this model needs to reset the hidden cell
y_pred = morse_chr_model(X_train)
single_loss = morse_chr_loss_function(y_pred, y_train)
single_loss.backward()
morse_chr_optimizer.step()
train_losses.append(single_loss.item())
# update progress bar
if j % 1000 == 0:
loop.set_description(f"Epoch [{i+1}/{epochs}]")
loop.set_postfix(loss=np.mean(train_losses))
morse_chr_scheduler.step()
print(f'final: {i+1:3} epochs loss: {np.mean(train_losses):6.4f}')
save_model = True
if save_model:
torch.save(morse_chr_model.state_dict(), 'models/morse_ord36_model')
else:
morse_chr_model.load_state_dict(torch.load('models/morse_ord36_model', map_location=device))
%%time
p_char_train = torch.empty(1,max_ele+3).to(device)
morse_chr_model.eval()
loop = tqdm(enumerate(train_chr_loader), total=len(train_chr_loader))
for j, train in loop:
with torch.no_grad():
X_chr = train[0][0]
pred_val = morse_chr_model(X_chr)
p_char_train = torch.cat([p_char_train, pred_val.reshape(1,max_ele+3)])
p_char_train = p_char_train[1:] # Remove garbge
print(p_char_train.shape) # t -> chars(t)
p_char_train_c = p_char_train.cpu() # t -> chars(t) on CPU
p_char_train_t = torch.transpose(p_char_train_c, 0, 1).cpu() # c -> times(c) on CPU
print(p_char_train_c.shape, p_char_train_t.shape)
X_train_chr = train_chr_dataset.X.cpu()
label_df_chr = train_chr_dataset.get_labels()
env_chr = train_chr_dataset.get_envelope()
l_alpha = label_df_chr[n_prev:].reset_index(drop=True)
plt.figure(figsize=(50,6))
plt.plot(l_alpha[x0:x1]["chr"]*3, label="ychr", alpha=0.2, color="black")
plt.plot(X_train_chr[x0+n_prev:x1+n_prev]*0.8, label='sig')
plt.plot(env_chr[x0+n_prev:x1+n_prev]*0.9, label='env')
plt.plot(p_char_train_t[0][x0:x1]*0.9 + 1.0, label='e', color="orange")
plt.plot(p_char_train_t[1][x0:x1]*0.9 + 1.0, label='c', color="green")
plt.plot(p_char_train_t[2][x0:x1]*0.9 + 1.0, label='w', color="red")
color_list = ["green", "red", "orange", "purple", "cornflowerblue"]
for i in range(max_ele):
plt.plot(p_char_train_t[i+3][x0:x1]*0.9 + 2.0, label=f'e{i}', color=color_list[i])
plt.title("predictions")
plt.legend(loc=2)
plt.grid()
teststr = "F5SFU DE F4EXB = R TNX RPT ES INFO ALEX = RIG IS FTDX1200 PWR 100W ANT IS YAGI = WX IS SUNNY ES WARM 32C = HW AR F5SFU DE F4EXB KN"
test_cwss = morse_gen.cws_to_cwss(teststr)
test_chr_dataset = MorsekeyingDataset(morse_gen, device, -17, 132*5, 27*5, test_cwss, max_ele)
test_chr_loader = torch.utils.data.DataLoader(test_chr_dataset, batch_size=1, shuffle=False) # Batch size must be 1
p_chr_test = torch.empty(1,max_ele+3).to(device)
morse_chr_model.eval()
loop = tqdm(enumerate(test_chr_loader), total=len(test_chr_loader))
for j, test in loop:
with torch.no_grad():
X_test = test[0]
pred_val = morse_chr_model(X_test[0])
p_chr_test = torch.cat([p_chr_test, pred_val.reshape(1,max_ele+3)])
# drop first garbage sample
p_chr_test = p_chr_test[1:]
print(p_chr_test.shape)
p_chr_test_c = p_chr_test.cpu() # t -> chars(t) on CPU
p_chr_test_t = torch.transpose(p_chr_test_c, 0, 1).cpu() # c -> times(c) on CPU
print(p_chr_test_c.shape, p_chr_test_t.shape)
X_test_chr = test_chr_dataset.X.cpu()
label_df_t = test_chr_dataset.get_labels()
env_test = test_chr_dataset.get_envelope()
l_alpha_t = label_df_t[n_prev:].reset_index(drop=True)
plt.figure(figsize=(100,4))
plt.plot(l_alpha_t[:]["chr"]*4, label="ychr", alpha=0.2, color="black")
plt.plot(X_test_chr[n_prev:]*0.8, label='sig')
plt.plot(env_test[n_prev:]*0.9, label='env')
plt.plot(p_chr_test_t[0]*0.9 + 1.0, label='e', color="purple")
plt.plot(p_chr_test_t[1]*0.9 + 2.0, label='c', color="green")
plt.plot(p_chr_test_t[2]*0.9 + 2.0, label='w', color="red")
color_list = ["green", "red", "orange", "purple", "cornflowerblue"]
for i in range(max_ele):
plt_a = plt.plot(p_chr_test_t[i+3]*0.9 + 3.0, label=f'e{i}', color=color_list[i])
plt.title("predictions")
plt.legend(loc=2)
plt.grid()
plt.savefig('img/predicted.png')
p_chr_test_tn = p_chr_test_t.numpy()
ele_len = round(samples_per_dit / 256)
win = np.ones(ele_len)/ele_len
p_chr_test_tlp = np.apply_along_axis(lambda m: np.convolve(m, win, mode='full'), axis=1, arr=p_chr_test_tn)
plt.figure(figsize=(100,4))
plt.plot(l_alpha_t[:]["chr"]*4, label="ychr", alpha=0.2, color="black")
plt.plot(X_test_chr[n_prev:]*0.9, label='sig')
plt.plot(env_test[n_prev:]*0.9, label='env')
plt.plot(p_chr_test_tlp[0]*0.9 + 1.0, label='e', color="purple")
plt.plot(p_chr_test_tlp[1]*0.9 + 2.0, label='c', color="green")
plt.plot(p_chr_test_tlp[2]*0.9 + 2.0, label='w', color="red")
color_list = ["green", "red", "orange", "purple", "cornflowerblue"]
for i in range(max_ele):
plt.plot(p_chr_test_tlp[i+3,:]*0.9 + 3.0, label=f'e{i}', color=color_list[i])
plt.title("predictions")
plt.legend(loc=2)
plt.grid()
plt.savefig('img/predicted_lp.png')
p_chr_test_tn = p_chr_test_t.numpy()
ele_len = round(samples_per_dit / 256)
win = np.ones(ele_len)/ele_len
p_chr_test_tlp = np.apply_along_axis(lambda m: np.convolve(m, win, mode='full'), axis=1, arr=p_chr_test_tn)
for i in range(max_ele+3):
p_chr_test_tlp[i][p_chr_test_tlp[i] < 0.5] = 0
plt.figure(figsize=(100,4))
plt.plot(l_alpha_t[:]["chr"]*4, label="ychr", alpha=0.2, color="black")
plt.plot(X_test_chr[n_prev:]*0.9, label='sig')
plt.plot(env_test[n_prev:]*0.9, label='env')
plt.plot(p_chr_test_tlp[0]*0.9 + 1.0, label='e', color="purple")
plt.plot(p_chr_test_tlp[1]*0.9 + 2.0, label='c', color="green")
plt.plot(p_chr_test_tlp[2]*0.9 + 2.0, label='w', color="red")
color_list = ["green", "red", "orange", "purple", "cornflowerblue"]
for i in range(max_ele):
plt.plot(p_chr_test_tlp[i+3,:]*0.9 + 3.0, label=f'e{i}', color=color_list[i])
plt.title("predictions")
plt.legend(loc=2)
plt.grid()
plt.savefig('img/predicted_lpthr.png')
class MorseDecoderPos:
def __init__(self, alphabet, dit_len, npos, thr):
self.nb_alpha = len(alphabet)
self.alphabet = alphabet
self.dit_len = dit_len
self.npos = npos
self.thr = thr
self.res = ""
self.morsestr = ""
self.pprev = 0
self.wsep = False
self.csep = False
self.lcounts = [0 for x in range(3+self.npos)]
self.morse_gen = MorseGen.Morse()
self.revmorsecode = self.morse_gen.revmorsecode
self.dit_l = 0.3
self.dit_h = 1.2
self.dah_l = 1.5
print(self.dit_l*dit_len, self.dit_h*dit_len, self.dah_l*dit_len)
def new_samples(self, samples):
for i, s in enumerate(samples): # e, c, w, [pos]
if s >= self.thr:
self.lcounts[i] += 1
else:
if i == 1:
self.lcounts[1] = 0
self.csep = False
if i == 2:
self.lcounts[2] = 0
self.wsep = False
if i == 1 and self.lcounts[1] > 1.2*self.dit_len and not self.csep: # character separator
morsestr = ""
for ip in range(3,3+self.npos):
if self.lcounts[ip] >= self.dit_l*self.dit_len and self.lcounts[ip] < self.dit_h*self.dit_len: # dit
morsestr += "."
elif self.lcounts[ip] > self.dah_l*self.dit_len: # dah
morsestr += "-"
char = self.revmorsecode.get(morsestr, '_')
self.res += char
#print(self.lcounts[3:], morsestr, char)
self.csep = True
self.lcounts[3:] = self.npos*[0]
if i == 2 and self.lcounts[2] > 2.5*self.dit_len and not self.wsep: # word separator
self.res += " "
#print("w")
self.wsep = True
dit_len = round(samples_per_dit / decim)
chr_len = round(samples_per_dit*2 / decim)
wrd_len = round(samples_per_dit*4 / decim)
print(dit_len)
decoder = MorseDecoderPos(alphabet, dit_len, max_ele, 0.9)
#p_chr_test_clp = torch.transpose(p_chr_test_tlp, 0, 1)
p_chr_test_clp = p_chr_test_tlp.transpose()
for s in p_chr_test_clp:
decoder.new_samples(s) # e, c, w, [pos]
print(len(decoder.res), decoder.res)
class MorseDecoderPos:
def __init__(self, alphabet, dit_len, npos, thr):
self.nb_alpha = len(alphabet)
self.alphabet = alphabet
self.dit_len = dit_len
self.npos = npos
self.thr = thr
self.res = ""
self.morsestr = ""
self.pprev = 0
self.wsep = False
self.csep = False
self.scounts = [0 for x in range(3)] # separators
self.ecounts = [0 for x in range(self.npos)] # Morse elements
self.morse_gen = MorseGen.Morse()
self.revmorsecode = self.morse_gen.revmorsecode
self.dit_l = 0.3
self.dit_h = 1.2
self.dah_l = 1.5
print(self.dit_l*dit_len, self.dit_h*dit_len, self.dah_l*dit_len)
def new_samples(self, samples):
for i, s in enumerate(samples): # e, c, w, [pos]
if s >= self.thr:
if i < 3:
self.scounts[i] += 1
else:
if i == 1:
self.scounts[1] = 0
self.csep = False
if i == 2:
self.scounts[2] = 0
self.wsep = False
if i >= 3:
self.ecounts[i-3] += s
if i == 1 and self.scounts[1] > 1.2*self.dit_len and not self.csep: # character separator
morsestr = ""
for ip in range(self.npos):
if self.ecounts[ip] >= self.dit_l*self.dit_len and self.ecounts[ip] < self.dit_h*self.dit_len: # dit
morsestr += "."
elif self.ecounts[ip] > self.dah_l*self.dit_len: # dah
morsestr += "-"
char = self.revmorsecode.get(morsestr, '_')
self.res += char
#print(self.ecounts, morsestr, char)
self.csep = True
self.ecounts = self.npos*[0]
if i == 2 and self.scounts[2] > 2.5*self.dit_len and not self.wsep: # word separator
self.res += " "
#print("w")
self.wsep = True
dit_len = round(samples_per_dit / decim)
chr_len = round(samples_per_dit*2 / decim)
wrd_len = round(samples_per_dit*4 / decim)
print(dit_len)
decoder = MorseDecoderPos(alphabet, dit_len, max_ele, 0.9)
#p_chr_test_clp = torch.transpose(p_chr_test_tlp, 0, 1)
p_chr_test_clp = p_chr_test_tlp.transpose()
for s in p_chr_test_clp:
decoder.new_samples(s) # e, c, w, [pos]
print(len(decoder.res), decoder.res)
| 0.542136 | 0.89382 |
<div style="width:900px;background:#F9EECF;border:1px solid black;text-align:left;padding:20px;">
<span style="color:purple;font-size:13pt"><b>Data Dictionary</span></b>
</div>
<div style="width:900px;float:left;padding:20px;align:left;">
Descriptors:
<br><br>
<style type="text/css">
.tg {border-collapse:collapse;border-spacing:0;}
.tg td{font-family:Arial, sans-serif;font-size:14px;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg th{font-family:Arial, sans-serif;font-size:14px;font-weight:normal;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg .tg-2lp6{font-weight:bold;background-color:#bbdaff;vertical-align:top}
.tg .tg-amwm{font-weight:bold;text-align:center;vertical-align:top}
.tg .tg-36xf{font-weight:bold;background-color:#bbdaff}
.tg .tg-yw4l{vertical-align:top}
.tg .tg-yw42{vertical-align:top;color:blue}
</style>
<table class="tg">
<tr>
<th class="tg-36xf">Feature Name</th>
<th class="tg-2lp6">Description</th>
<th class="tg-2lp6">Metrics</th>
</tr>
<tr>
<td class="tg-yw4l">RecordID</td>
<td class="tg-yw4l">A unique integer for each ICU stay </td>
<td class="tg-yw4l">Integer</td>
</tr>
<tr>
<td class="tg-yw4l">Age</td>
<td class="tg-yw4l">Age</td>
<td class="tg-yw4l">(years)</td>
</tr>
<tr>
<td class="tg-yw4l">Height</td>
<td class="tg-yw4l">Height</td>
<td class="tg-yw4l">(cm)</td>
</tr>
<tr>
<td class="tg-yw4l">ICUtype</td>
<td class="tg-yw4l">ICU Type</td>
<td class="tg-yw4l">(1: Coronary Care Unit, 2: Cardiac Surgery Recovery Unit, <br>3: Medical ICU, or 4: Surgical ICU)</td>
</tr>
<tr>
<td class="tg-yw4l">Gender</td>
<td class="tg-yw4l">Gender</td>
<td class="tg-yw4l">(0: female, or 1: male)</td>
</tr>
</table>
<br><br>
These 37 variables may be observed once, more than once, or not at all in some cases:
<br><br>
<table class="tg">
<tr>
<th class="tg-36xf">Feature Name</th>
<th class="tg-2lp6">Description</th>
<th class="tg-2lp6">Metrics</th>
</tr>
<tr>
<td class="tg-yw4l">Albumin</td>
<td class="tg-yw4l">Albumin </td>
<td class="tg-yw4l">(g/dL)</td>
</tr>
<tr>
<td class="tg-yw4l">ALP</td>
<td class="tg-yw4l">Alkaline phosphatase</td>
<td class="tg-yw4l">(IU/L)</td>
</tr>
<tr>
<td class="tg-yw4l">ALT</td>
<td class="tg-yw4l">Alanine transaminase</td>
<td class="tg-yw4l">(IU/L)</td>
</tr>
<tr>
<td class="tg-yw4l">AST</td>
<td class="tg-yw4l">Aspartate transaminase</td>
<td class="tg-yw4l">(IU/L)</td>
</tr>
<tr>
<td class="tg-yw4l">Bilirubin</td>
<td class="tg-yw4l">Bilirubin</td>
<td class="tg-yw4l">(mg/dL)</td>
</tr>
<tr>
<td class="tg-yw4l">BUN</td>
<td class="tg-yw4l">Blood urea nitrogen</td>
<td class="tg-yw4l">(mg/dL)</td>
</tr>
<tr>
<td class="tg-yw4l">Cholesterol</td>
<td class="tg-yw4l">Cholesterol</td>
<td class="tg-yw4l">(mg/dL)</td>
</tr>
<tr>
<td class="tg-yw4l">Creatinine</td>
<td class="tg-yw4l">Serum creatinine</td>
<td class="tg-yw4l">(mg/dL)</td>
</tr>
<tr>
<td class="tg-yw4l">DiasABP <td class="tg-yw4l">Invasive diastolic arterial blood pressure <td class="tg-yw4l">(mmHg)</tr>
<tr><td class="tg-yw4l">FiO2 <td class="tg-yw4l">Fractional inspired O2 <td class="tg-yw4l">(0-1)</tr>
<tr><td class="tg-yw4l">GCS <td class="tg-yw4l">Glasgow Coma Score <td class="tg-yw4l">(3-15)</tr>
<tr><td class="tg-yw4l">Glucose <td class="tg-yw4l">Serum glucose <td class="tg-yw4l">(mg/dL)</tr>
<tr><td class="tg-yw4l">HCO3 <td class="tg-yw4l">Serum bicarbonate <td class="tg-yw4l">(mmol/L)</tr>
<tr><td class="tg-yw4l">HCT <td class="tg-yw4l">Hematocrit <td class="tg-yw4l">(%)</tr>
<tr><td class="tg-yw4l">HR <td class="tg-yw4l">Heart rate <td class="tg-yw4l">(bpm)</tr>
<tr><td class="tg-yw4l">K <td class="tg-yw4l">Serum potassium <td class="tg-yw4l">(mEq/L)</tr>
<tr><td class="tg-yw4l">Lactate <td class="tg-yw4l">Lactate<td class="tg-yw4l">(mmol/L)</tr>
<tr><td class="tg-yw4l">Mg <td class="tg-yw4l">Serum magnesium <td class="tg-yw4l">(mmol/L)</tr>
<tr><td class="tg-yw4l">MAP <td class="tg-yw4l">Invasive mean arterial blood pressure <td class="tg-yw4l">(mmHg)</tr>
<tr><td class="tg-yw4l">MechVent <td class="tg-yw4l">Mechanical ventilation respiration <td class="tg-yw4l">(0:false, or 1:true)</tr>
<tr><td class="tg-yw4l">Na <td class="tg-yw4l">Serum sodium <td class="tg-yw4l">(mEq/L)</tr>
<tr><td class="tg-yw4l">NIDiasABP <td class="tg-yw4l">Non-invasive diastolic arterial blood pressure <td class="tg-yw4l">(mmHg)</tr>
<tr><td class="tg-yw4l">NIMAP <td class="tg-yw4l">Non-invasive mean arterial blood pressure <td class="tg-yw4l">(mmHg)</tr>
<tr><td class="tg-yw4l">NISysABP <td class="tg-yw4l">Non-invasive systolic arterial blood pressure <td class="tg-yw4l">(mmHg)</tr>
<tr><td class="tg-yw4l">PaCO2 <td class="tg-yw4l">partial pressure of arterial CO2 <td class="tg-yw4l">(mmHg)</tr>
<tr><td class="tg-yw4l">PaO2 <td class="tg-yw4l">Partial pressure of arterial O2 <td class="tg-yw4l">(mmHg)</tr>
<tr><td class="tg-yw4l">pH <td class="tg-yw4l">Arterial pH <td class="tg-yw4l">(0-14)</tr>
<tr><td class="tg-yw4l">Platelets <td class="tg-yw4l">Platelets<td class="tg-yw4l">(cells/nL)</tr>
<tr><td class="tg-yw4l">RespRate <td class="tg-yw4l">Respiration rate <td class="tg-yw4l">(bpm)</tr>
<tr><td class="tg-yw4l">SaO2 <td class="tg-yw4l">O2 saturation in hemoglobin <td class="tg-yw4l">(%)</tr>
<tr><td class="tg-yw4l">SysABP <td class="tg-yw4l">Invasive systolic arterial blood pressure <td class="tg-yw4l">(mmHg)</tr>
<tr><td class="tg-yw4l">Temp <td class="tg-yw4l">Temperature <td class="tg-yw4l">(°C)</tr>
<tr><td class="tg-yw4l">TropI <td class="tg-yw4l">Troponin-I <td class="tg-yw4l">(μg/L)</tr>
<tr><td class="tg-yw4l">TropT <td class="tg-yw4l">Troponin-T <td class="tg-yw4l">(μg/L)</tr>
<tr><td class="tg-yw4l">Urine <td class="tg-yw4l">Urine output <td class="tg-yw4l">(mL)</tr>
<tr><td class="tg-yw4l">WBC <td class="tg-yw4l">White blood cell count <td class="tg-yw4l">(cells/nL)</tr>
<tr><td class="tg-yw4l">Weight <td class="tg-yw4l">Weight<td class="tg-yw4l">(kg)</tr></table>
<br><br>
Outcomes-Related Descriptors:
<table class="tg">
<tr>
<th class="tg-36xf">Outcomes</th>
<th class="tg-2lp6">Description</th>
<th class="tg-2lp6">Metrics</th>
</tr>
<tr>
<td class="tg-yw4l">SAPS-I score</td>
<td class="tg-yw4l">(Le Gall et al., 1984) </td>
<td class="tg-yw4l">between 0 to 163</td>
</tr>
<tr>
<td class="tg-yw4l">SOFA score</td>
<td class="tg-yw4l">(Ferreira et al., 2001) </td>
<td class="tg-yw4l">between 0 to 4</td>
</tr>
<tr>
<td class="tg-yw4l">Length of stay</td>
<td class="tg-yw4l">Length of stay </td>
<td class="tg-yw4l">(days)</td>
</tr>
<tr>
<td class="tg-yw4l">Survival</td>
<td class="tg-yw4l">Survival</td>
<td class="tg-yw4l">(days)</td>
</tr>
<tr>
<td class="tg-yw42"><b>In-hospital death</b></td>
<td class="tg-yw42"><b>Target Variable</b></td>
<td class="tg-yw42"><b>(0: survivor, or 1: died in-hospital)</b></td>
</tr>
<div style="width:900px;background:#F9EECF;border:1px solid black;text-align:left;padding:20px;">
<span style="color:purple;font-size:13pt"><b>Import Packages</span></b>
</div>
```
# Import packages
import pandas as pd
import numpy as np
import seaborn as sns
from sklearn.preprocessing import RobustScaler, OneHotEncoder
from sklearn.pipeline import FeatureUnion
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.model_selection import GridSearchCV
from statsmodels.stats.outliers_influence import variance_inflation_factor
pd.set_option('display.max_columns', 200)
pd.set_option('display.max_rows',200)
sns.set_style('whitegrid')
sns.set(rc={"figure.figsize": (15, 8)})
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
# Simple cleaning on csv file
X = pd.read_csv('mortality_filled_median.csv')
X.set_index('recordid',inplace=True)
X.columns
X.drop('Unnamed: 0',axis=1,inplace=True)
y = X['in-hospital_death']
X = X.drop('in-hospital_death',axis=1) # identify predictors
# Train test split
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=2,stratify=y)
# Using SMOTEEN + Weighted Logistic Loss
from imblearn.combine import SMOTEENN
from imblearn.over_sampling import SMOTE
smoteenn = SMOTEENN(random_state=2,smote=SMOTE(ratio={1:1100},random_state=2))
X_train_res, y_train_res = smoteenn.fit_sample(X_train, y_train)
y_train_res.sum()/ len(y_train_res) # Percentage of samples in the minority class
```
<div style="width:900px;background:#F9EECF;border:1px solid black;text-align:left;padding:20px;">
<p><b>SMOTEENN + Weighted Logistic Loss</b>
<br> Random Forest
</div>
```
from sklearn.ensemble import RandomForestClassifier
rfc_params = {
'n_estimators':[20,25,30,35,40,45],
'max_depth':[None,2,4],
'max_features':[None,'log2','sqrt',2,3],
'min_samples_split':[2,3,4,5]
}
rfc_gs = GridSearchCV(RandomForestClassifier(random_state=6,class_weight='balanced'), \
rfc_params, cv=5, verbose=1,n_jobs=-1)
rfc_gs.fit(X_train_res, y_train_res)
rfc_best = rfc_gs.best_estimator_
print rfc_gs.best_params_
print rfc_gs.best_score_
from sklearn.metrics import classification_report
y_pred = rfc_best.predict(X_test)
print classification_report(y_test,y_pred)
rfc = RandomForestClassifier(random_state=6,class_weight='balanced',max_features = 3, min_samples_split= 3,
n_estimators= 20, max_depth= None)
rfc.fit(X_train_res, y_train_res)
y_pred = rfc.predict(X_test)
print classification_report(y_test,y_pred)
```
|
github_jupyter
|
# Import packages
import pandas as pd
import numpy as np
import seaborn as sns
from sklearn.preprocessing import RobustScaler, OneHotEncoder
from sklearn.pipeline import FeatureUnion
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.model_selection import GridSearchCV
from statsmodels.stats.outliers_influence import variance_inflation_factor
pd.set_option('display.max_columns', 200)
pd.set_option('display.max_rows',200)
sns.set_style('whitegrid')
sns.set(rc={"figure.figsize": (15, 8)})
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
# Simple cleaning on csv file
X = pd.read_csv('mortality_filled_median.csv')
X.set_index('recordid',inplace=True)
X.columns
X.drop('Unnamed: 0',axis=1,inplace=True)
y = X['in-hospital_death']
X = X.drop('in-hospital_death',axis=1) # identify predictors
# Train test split
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=2,stratify=y)
# Using SMOTEEN + Weighted Logistic Loss
from imblearn.combine import SMOTEENN
from imblearn.over_sampling import SMOTE
smoteenn = SMOTEENN(random_state=2,smote=SMOTE(ratio={1:1100},random_state=2))
X_train_res, y_train_res = smoteenn.fit_sample(X_train, y_train)
y_train_res.sum()/ len(y_train_res) # Percentage of samples in the minority class
from sklearn.ensemble import RandomForestClassifier
rfc_params = {
'n_estimators':[20,25,30,35,40,45],
'max_depth':[None,2,4],
'max_features':[None,'log2','sqrt',2,3],
'min_samples_split':[2,3,4,5]
}
rfc_gs = GridSearchCV(RandomForestClassifier(random_state=6,class_weight='balanced'), \
rfc_params, cv=5, verbose=1,n_jobs=-1)
rfc_gs.fit(X_train_res, y_train_res)
rfc_best = rfc_gs.best_estimator_
print rfc_gs.best_params_
print rfc_gs.best_score_
from sklearn.metrics import classification_report
y_pred = rfc_best.predict(X_test)
print classification_report(y_test,y_pred)
rfc = RandomForestClassifier(random_state=6,class_weight='balanced',max_features = 3, min_samples_split= 3,
n_estimators= 20, max_depth= None)
rfc.fit(X_train_res, y_train_res)
y_pred = rfc.predict(X_test)
print classification_report(y_test,y_pred)
| 0.745584 | 0.224204 |
```
### Running in Google Colab? You'll want to uncomment and run these cell once each time you start this notebook.
"""
!wget https://raw.githubusercontent.com/psheehan/CIERA-HS-Program/master/BonusProblems/Module2/type1a_sne.csv
"""
```
# The Expansion of the Universe
In the early 20th Century, astronomers made a surprising discovery about the Universe that we're going to explore here. Astronomer's were keenly interested in measuring the distances to "spiral nebulae" to understand whether they were a part of our galaxy, or extra-galactic (they would turn out to be extra-galaxies - separate galaxies on their own!), and at the same time were able to measure how fast those galaxies were moving towards or away from us.
Let's recreate the now famous work of Edwin Hubble, who plotted the distances and velocities of those galaxies against eachother. In this directory there is a file called "type1a_sne.csv" that has the measured distances (in units of mega-parsecs) and velocities (in km s$^{-1}$) for a number of galaxies. Load those data in to two lists:
Now, make a plot with distance on the x-axis any velocity on the y-axis. Make sure to include nice axes labels! In this dataset, a negative velocity means that the galaxy is moving towards us, and a positive velocity mean that the galaxy is moving away from us. What do you notice?
This is what Hubble discovered back in 1929 - all galaxies, regardless of where you look (outside of a few particularly close ones), are moving away from us. What this means is that our Universe is expanding!
Let's calculate how quickly the Universe is expanding from this data. The way we are going to do that is by drawing a line that fits through all of the data points. The value of the slope of that line is the "Hubble Constant". First, we need to create the x and y values for the line:
```
# Create an array with x values to draw the line at.
x = # FILL IN CODE
# Define a function that takes two arguments, the slope and an x value, and returns
# the y value for the line y = m * x.
# Finally, apply the function you created to your x values to create an array of y values at
# those x values.
y = # FILL IN CODE
```
Now, let's re-make your plot of galaxy distances versus galaxy velocities from above. Then, also plot the line you created above on it. Does the line go through the data? If not, adjust the value of the slope until it does:
Let's record the value of the slope that makes the line fit through the data. This is your Hubble Constant:
```
H0 =
```
What are the units of the Hubble Constant? You might notice that they are (distance)/(time)/(distance), or to simplify, 1/time, or a rate. What this means, then, is that $1/H_0$ has units of (time), i.e. it's a measurement of how *old* the Universe is and is called the Hubble Time. Calculate the age of the Universe using your Hubble Constant:
```
# Pay attention to units!
```
The Hubble Time is an estimate of the age of a Universe that _has no matter in it_. We know that this isn't the case because we are sitting here today. For a Universe with matter in it, the gravity from that matter tends to counter the expansion of the Universe and slow it down. A more detailed calculation shows that for a Universe with the exact right amount of matter such that the Universe ends up coasting at a constant speed, the age of the Universe is more accurately calculated as $2/(3\,H_0)$:
<img src="expanding_universe.png">
Use that formula to calculate a more accurate age of the Universe from your Hubble Constant:
This is one of a few different ways to calculate the age of the Universe, and our current best measurement from the Planck satellite is 13.8 billion years, and their Hubble constant is about 68 km/s/Mpc. How do your numbers compare?
If you numbers are different, you aren't alone! It turns out one of the interesting problems in astronomy today is that different ways of measuring the Hubble Constant get slightly different answers.
<img src="freedman.png">
Although the differences are small, they are also significant. Why are they different? One comes from distances to galaxies, in the same way that you calculated the Hubble Constant here. The other comes from density fluctuations in the early universe when it was only 380,000 years old (cool!). Maybe there's some physics we don't understand creating the discrepancy. Or, maybe we are systematically measuring something incorrectly and we just don't know. Stay tuned!
|
github_jupyter
|
### Running in Google Colab? You'll want to uncomment and run these cell once each time you start this notebook.
"""
!wget https://raw.githubusercontent.com/psheehan/CIERA-HS-Program/master/BonusProblems/Module2/type1a_sne.csv
"""
# Create an array with x values to draw the line at.
x = # FILL IN CODE
# Define a function that takes two arguments, the slope and an x value, and returns
# the y value for the line y = m * x.
# Finally, apply the function you created to your x values to create an array of y values at
# those x values.
y = # FILL IN CODE
H0 =
# Pay attention to units!
| 0.831622 | 0.988939 |
```
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import sklearn
import pandas as pd
import os
import sys
import time
import tensorflow as tf
from tensorflow import keras
print(tf.__version__)
print(sys.version_info)
for module in mpl, np, pd, sklearn, tf, keras:
print(module.__name__, module.__version__)
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing()
from sklearn.model_selection import train_test_split
x_train_all, x_test, y_train_all, y_test = train_test_split(
housing.data, housing.target, random_state = 7)
x_train, x_valid, y_train, y_valid = train_test_split(
x_train_all, y_train_all, random_state = 11)
print(x_train.shape, y_train.shape)
print(x_valid.shape, y_valid.shape)
print(x_test.shape, y_test.shape)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
x_train_scaled = scaler.fit_transform(x_train)
x_valid_scaled = scaler.transform(x_valid)
x_test_scaled = scaler.transform(x_test)
output_dir = "generate_csv"
if not os.path.exists(output_dir):
os.mkdir(output_dir)
def save_to_csv(output_dir, data, name_prefix,
header=None, n_parts=10):
path_format = os.path.join(output_dir, "{}_{:02d}.csv")
filenames = []
for file_idx, row_indices in enumerate(
np.array_split(np.arange(len(data)), n_parts)):
part_csv = path_format.format(name_prefix, file_idx)
filenames.append(part_csv)
with open(part_csv, "wt", encoding="utf-8") as f:
if header is not None:
f.write(header + "\n")
for row_index in row_indices:
f.write(",".join(
[repr(col) for col in data[row_index]]))
f.write('\n')
return filenames
train_data = np.c_[x_train_scaled, y_train]
valid_data = np.c_[x_valid_scaled, y_valid]
test_data = np.c_[x_test_scaled, y_test]
header_cols = housing.feature_names + ["MidianHouseValue"]
header_str = ",".join(header_cols)
train_filenames = save_to_csv(output_dir, train_data, "train",
header_str, n_parts=20)
valid_filenames = save_to_csv(output_dir, valid_data, "valid",
header_str, n_parts=10)
test_filenames = save_to_csv(output_dir, test_data, "test",
header_str, n_parts=10)
import pprint
print("train filenames:")
pprint.pprint(train_filenames)
print("valid filenames:")
pprint.pprint(valid_filenames)
print("test filenames:")
pprint.pprint(test_filenames)
# 1. filename -> dataset
# 2. read file -> dataset -> datasets -> merge
# 3. parse csv
filename_dataset = tf.data.Dataset.list_files(train_filenames)
for filename in filename_dataset:
print(filename)
n_readers = 5
dataset = filename_dataset.interleave(
lambda filename: tf.data.TextLineDataset(filename).skip(1),
cycle_length = n_readers
)
for line in dataset.take(15):
print(line.numpy())
# tf.io.decode_csv(str, record_defaults)
sample_str = '1,2,3,4,5'
record_defaults = [
tf.constant(0, dtype=tf.int32),
0,
np.nan,
"hello",
tf.constant([])
]
parsed_fields = tf.io.decode_csv(sample_str, record_defaults)
print(parsed_fields)
try:
parsed_fields = tf.io.decode_csv(',,,,', record_defaults)
except tf.errors.InvalidArgumentError as ex:
print(ex)
try:
parsed_fields = tf.io.decode_csv('1,2,3,4,5,6,7', record_defaults)
except tf.errors.InvalidArgumentError as ex:
print(ex)
def parse_csv_line(line, n_fields = 9):
defs = [tf.constant(np.nan)] * n_fields
parsed_fields = tf.io.decode_csv(line, record_defaults=defs)
x = tf.stack(parsed_fields[0:-1])
y = tf.stack(parsed_fields[-1:])
return x, y
parse_csv_line(b'-0.9868720801669367,0.832863080552588,-0.18684708416901633,-0.14888949288707784,-0.4532302419670616,-0.11504995754593579,1.6730974284189664,-0.7465496877362412,1.138',
n_fields=9)
# 1. filename -> dataset
# 2. read file -> dataset -> datasets -> merge
# 3. parse csv
def csv_reader_dataset(filenames, n_readers=5,
batch_size=32, n_parse_threads=5,
shuffle_buffer_size=10000):
dataset = tf.data.Dataset.list_files(filenames)
dataset = dataset.repeat()
dataset = dataset.interleave(
lambda filename: tf.data.TextLineDataset(filename).skip(1),
cycle_length = n_readers
)
dataset.shuffle(shuffle_buffer_size)
dataset = dataset.map(parse_csv_line,
num_parallel_calls=n_parse_threads)
dataset = dataset.batch(batch_size)
return dataset
train_set = csv_reader_dataset(train_filenames, batch_size=3)
for x_batch, y_batch in train_set.take(2):
print("x:")
pprint.pprint(x_batch)
print("y:")
pprint.pprint(y_batch)
batch_size = 32
train_set = csv_reader_dataset(train_filenames,
batch_size = batch_size)
valid_set = csv_reader_dataset(valid_filenames,
batch_size = batch_size)
test_set = csv_reader_dataset(test_filenames,
batch_size = batch_size)
model = keras.models.Sequential([
keras.layers.Dense(30, activation='relu',
input_shape=[8]),
keras.layers.Dense(1),
])
model.compile(loss="mean_squared_error", optimizer="sgd")
callbacks = [keras.callbacks.EarlyStopping(
patience=5, min_delta=1e-2)]
history = model.fit(train_set,
validation_data = valid_set,
steps_per_epoch = 11160 // batch_size,
validation_steps = 3870 // batch_size,
epochs = 100,
callbacks = callbacks)
model.evaluate(test_set, steps = 5160 // batch_size)
```
|
github_jupyter
|
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import sklearn
import pandas as pd
import os
import sys
import time
import tensorflow as tf
from tensorflow import keras
print(tf.__version__)
print(sys.version_info)
for module in mpl, np, pd, sklearn, tf, keras:
print(module.__name__, module.__version__)
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing()
from sklearn.model_selection import train_test_split
x_train_all, x_test, y_train_all, y_test = train_test_split(
housing.data, housing.target, random_state = 7)
x_train, x_valid, y_train, y_valid = train_test_split(
x_train_all, y_train_all, random_state = 11)
print(x_train.shape, y_train.shape)
print(x_valid.shape, y_valid.shape)
print(x_test.shape, y_test.shape)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
x_train_scaled = scaler.fit_transform(x_train)
x_valid_scaled = scaler.transform(x_valid)
x_test_scaled = scaler.transform(x_test)
output_dir = "generate_csv"
if not os.path.exists(output_dir):
os.mkdir(output_dir)
def save_to_csv(output_dir, data, name_prefix,
header=None, n_parts=10):
path_format = os.path.join(output_dir, "{}_{:02d}.csv")
filenames = []
for file_idx, row_indices in enumerate(
np.array_split(np.arange(len(data)), n_parts)):
part_csv = path_format.format(name_prefix, file_idx)
filenames.append(part_csv)
with open(part_csv, "wt", encoding="utf-8") as f:
if header is not None:
f.write(header + "\n")
for row_index in row_indices:
f.write(",".join(
[repr(col) for col in data[row_index]]))
f.write('\n')
return filenames
train_data = np.c_[x_train_scaled, y_train]
valid_data = np.c_[x_valid_scaled, y_valid]
test_data = np.c_[x_test_scaled, y_test]
header_cols = housing.feature_names + ["MidianHouseValue"]
header_str = ",".join(header_cols)
train_filenames = save_to_csv(output_dir, train_data, "train",
header_str, n_parts=20)
valid_filenames = save_to_csv(output_dir, valid_data, "valid",
header_str, n_parts=10)
test_filenames = save_to_csv(output_dir, test_data, "test",
header_str, n_parts=10)
import pprint
print("train filenames:")
pprint.pprint(train_filenames)
print("valid filenames:")
pprint.pprint(valid_filenames)
print("test filenames:")
pprint.pprint(test_filenames)
# 1. filename -> dataset
# 2. read file -> dataset -> datasets -> merge
# 3. parse csv
filename_dataset = tf.data.Dataset.list_files(train_filenames)
for filename in filename_dataset:
print(filename)
n_readers = 5
dataset = filename_dataset.interleave(
lambda filename: tf.data.TextLineDataset(filename).skip(1),
cycle_length = n_readers
)
for line in dataset.take(15):
print(line.numpy())
# tf.io.decode_csv(str, record_defaults)
sample_str = '1,2,3,4,5'
record_defaults = [
tf.constant(0, dtype=tf.int32),
0,
np.nan,
"hello",
tf.constant([])
]
parsed_fields = tf.io.decode_csv(sample_str, record_defaults)
print(parsed_fields)
try:
parsed_fields = tf.io.decode_csv(',,,,', record_defaults)
except tf.errors.InvalidArgumentError as ex:
print(ex)
try:
parsed_fields = tf.io.decode_csv('1,2,3,4,5,6,7', record_defaults)
except tf.errors.InvalidArgumentError as ex:
print(ex)
def parse_csv_line(line, n_fields = 9):
defs = [tf.constant(np.nan)] * n_fields
parsed_fields = tf.io.decode_csv(line, record_defaults=defs)
x = tf.stack(parsed_fields[0:-1])
y = tf.stack(parsed_fields[-1:])
return x, y
parse_csv_line(b'-0.9868720801669367,0.832863080552588,-0.18684708416901633,-0.14888949288707784,-0.4532302419670616,-0.11504995754593579,1.6730974284189664,-0.7465496877362412,1.138',
n_fields=9)
# 1. filename -> dataset
# 2. read file -> dataset -> datasets -> merge
# 3. parse csv
def csv_reader_dataset(filenames, n_readers=5,
batch_size=32, n_parse_threads=5,
shuffle_buffer_size=10000):
dataset = tf.data.Dataset.list_files(filenames)
dataset = dataset.repeat()
dataset = dataset.interleave(
lambda filename: tf.data.TextLineDataset(filename).skip(1),
cycle_length = n_readers
)
dataset.shuffle(shuffle_buffer_size)
dataset = dataset.map(parse_csv_line,
num_parallel_calls=n_parse_threads)
dataset = dataset.batch(batch_size)
return dataset
train_set = csv_reader_dataset(train_filenames, batch_size=3)
for x_batch, y_batch in train_set.take(2):
print("x:")
pprint.pprint(x_batch)
print("y:")
pprint.pprint(y_batch)
batch_size = 32
train_set = csv_reader_dataset(train_filenames,
batch_size = batch_size)
valid_set = csv_reader_dataset(valid_filenames,
batch_size = batch_size)
test_set = csv_reader_dataset(test_filenames,
batch_size = batch_size)
model = keras.models.Sequential([
keras.layers.Dense(30, activation='relu',
input_shape=[8]),
keras.layers.Dense(1),
])
model.compile(loss="mean_squared_error", optimizer="sgd")
callbacks = [keras.callbacks.EarlyStopping(
patience=5, min_delta=1e-2)]
history = model.fit(train_set,
validation_data = valid_set,
steps_per_epoch = 11160 // batch_size,
validation_steps = 3870 // batch_size,
epochs = 100,
callbacks = callbacks)
model.evaluate(test_set, steps = 5160 // batch_size)
| 0.438304 | 0.397324 |
---
## <span style="color:orange"> Inside account B (centralized feature store)</span>
---
<div style="text-align: justify">This notebook must be run within account B. Using this notebook, you will be setting up a centralized feature store in this account. First, you will create a feature group that will be store a collection of customer centric features. Then, you will populate some features into this newly created feature group. The features will be written to both the Online and Offline stores of the centralized feature store.
Later, you will see, 1/ how to read features from the Online store and 2/ how to read features from the Offline store via an Athena query to create a training set for your data science work.</div>
**IMPORTANT:** This notebook must run be run BEFORE you execute notebook [account-a.ipynb](./account-a.ipynb)
### Imports
```
import sagemaker
import logging
import pandas
import boto3
import json
import time
```
#### Setup logging
```
logger = logging.getLogger('sagemaker')
logger.setLevel(logging.INFO)
logger.addHandler(logging.StreamHandler())
logger.info(f'[Using Boto3 version: {boto3.__version__}]')
```
### Essentials
The Offline store S3 location can be a S3 bucket or a S3 prefix.
```
OFFLINE_STORE_BUCKET = '<YOUR OFFLINE STORE S3 BUCKET NAME>' # e.g., sagemaker-offline-store
OFFLINE_STORE_PREFIX = '<PREFIX WITHIN OFFLINE STORE BUCKET>' # this is optional, e.g., project-x
OFFLINE_STORE_LOCATION = f's3://{OFFLINE_STORE_BUCKET}/{OFFLINE_STORE_PREFIX}'
ACCOUNT_ID = boto3.client('sts').get_caller_identity().get('Account')
REGION = boto3.Session().region_name
FEATURE_GROUP_NAME = '<YOUR FEATURE GROUP NAME>' # e.g., customers
role_arn = sagemaker.get_execution_role()
sagemaker_client = boto3.client('sagemaker')
sagemaker_featurestore_runtime_client = boto3.client(service_name='sagemaker-featurestore-runtime')
s3_client = boto3.client(service_name='s3')
athena_client = boto3.client(service_name='athena')
offline_config = {'OfflineStoreConfig': {'S3StorageConfig': {'S3Uri': OFFLINE_STORE_LOCATION }}}
# offline_config = {} # uncomment and use this line if needed to write ONLY to the Online feature store
```
### Load schema
```
def load_schema(schema):
feature_definitions = []
for col in schema['features']:
feature = {'FeatureName': col['name']}
if col['type'] == 'double':
feature['FeatureType'] = 'Fractional'
elif col['type'] == 'bigint':
feature['FeatureType'] = 'Integral'
else:
feature['FeatureType'] = 'String'
feature_definitions.append(feature)
return feature_definitions, schema['record_identifier_feature_name'], schema['event_time_feature_name']
schema = json.loads(open('./schema/customers.json').read())
feature_definitions, record_identifier_feature_name, event_time_feature_name = load_schema(schema)
feature_definitions
```
### Create a feature group
Uncomment and run the cell below if the feature group already exists or during re-runs.
```
# sagemaker_client.delete_feature_group(FeatureGroupName=FEATURE_GROUP_NAME)
sagemaker_client.create_feature_group(FeatureGroupName=FEATURE_GROUP_NAME,
RecordIdentifierFeatureName=record_identifier_feature_name,
EventTimeFeatureName=event_time_feature_name,
FeatureDefinitions=feature_definitions,
Description=schema['description'],
Tags=schema['tags'],
OnlineStoreConfig={'EnableOnlineStore': True},
RoleArn=role_arn,
**offline_config)
sagemaker_client.describe_feature_group(FeatureGroupName=FEATURE_GROUP_NAME)
```
### Populate features to the feature group
```
customers_df = pandas.read_csv('./data/customers.csv', header=None)
customers_df
records = []
for _, row in customers_df.iterrows():
cid, name, age, marital_status, sex, city, state = row
record = []
record.append({'ValueAsString': str(cid), 'FeatureName': 'cid'})
record.append({'ValueAsString': name, 'FeatureName': 'name'})
record.append({'ValueAsString': str(age), 'FeatureName': 'age'})
record.append({'ValueAsString': marital_status, 'FeatureName': 'marital_status'})
record.append({'ValueAsString': sex, 'FeatureName': 'sex'})
record.append({'ValueAsString': city, 'FeatureName': 'city'})
record.append({'ValueAsString': state, 'FeatureName': 'state'})
event_time_feature = {'ValueAsString': str(int(round(time.time()))), 'FeatureName': 'created_at'}
record.append(event_time_feature)
records.append(record)
```
#### Write features to the feature store
```
for record in records:
response = sagemaker_featurestore_runtime_client.put_record(FeatureGroupName=FEATURE_GROUP_NAME,
Record=record)
print(response['ResponseMetadata']['HTTPStatusCode'])
```
#### Verify if you can retrieve features from your feature group using record identifier
Here, you are reading features from the Online store.
```
response = sagemaker_featurestore_runtime_client.get_record(FeatureGroupName=FEATURE_GROUP_NAME,
RecordIdentifierValueAsString='1002')
response
```
### Get records from the Offline store (S3 bucket)
Now let us wait for the data to appear in the Offline store (S3 bucket) before moving forward to creating a dataset. This will take approximately take <= 5 minutes.
```
feature_group_s3_prefix = f'{OFFLINE_STORE_PREFIX}/{ACCOUNT_ID}/sagemaker/{REGION}/offline-store/{FEATURE_GROUP_NAME}/data'
feature_group_s3_prefix
offline_store_contents = None
while offline_store_contents is None:
objects = s3_client.list_objects(Bucket=OFFLINE_STORE_BUCKET, Prefix=feature_group_s3_prefix)
if 'Contents' in objects and len(objects['Contents']) > 1:
logger.info('[Features are available in Offline Store!]')
offline_store_contents = objects['Contents']
else:
logger.info('[Waiting for data in Offline Store...]')
time.sleep(60)
```
### Use Athena to query features from the Offline store and create a training set
```
feature_group = sagemaker_client.describe_feature_group(FeatureGroupName=FEATURE_GROUP_NAME)
glue_table_name = feature_group['OfflineStoreConfig']['DataCatalogConfig']['TableName']
query_string = f'SELECT * FROM "{glue_table_name}"'
query_string
```
#### Run Athena query and save results
You can save the results of the Athena query to a folder within the Offline store S3 bucket or any other bucket. Here, we are storing the query results to a prefix within the Offline store s3 bucket.
```
response = athena_client.start_query_execution(
QueryString=query_string,
QueryExecutionContext={
'Database': 'sagemaker_featurestore',
'Catalog': 'AwsDataCatalog'
},
ResultConfiguration={
'OutputLocation': f's3://{OFFLINE_STORE_BUCKET}/query_results/{FEATURE_GROUP_NAME}',
}
)
query_results = athena_client.get_query_results(QueryExecutionId=response['QueryExecutionId'],
MaxResults=100)
training_set_csv_s3_key = None
for s3_object in s3_client.list_objects(Bucket=OFFLINE_STORE_BUCKET)['Contents']:
key = s3_object['Key']
if key.startswith(f'query_results/{FEATURE_GROUP_NAME}') and key.endswith('csv'):
training_set_csv_s3_key = key
training_set_s3_path = f's3://{OFFLINE_STORE_BUCKET}/{training_set_csv_s3_key}'
training_set_s3_path
training_set = pandas.read_csv(training_set_s3_path)
training_set
```
|
github_jupyter
|
import sagemaker
import logging
import pandas
import boto3
import json
import time
logger = logging.getLogger('sagemaker')
logger.setLevel(logging.INFO)
logger.addHandler(logging.StreamHandler())
logger.info(f'[Using Boto3 version: {boto3.__version__}]')
OFFLINE_STORE_BUCKET = '<YOUR OFFLINE STORE S3 BUCKET NAME>' # e.g., sagemaker-offline-store
OFFLINE_STORE_PREFIX = '<PREFIX WITHIN OFFLINE STORE BUCKET>' # this is optional, e.g., project-x
OFFLINE_STORE_LOCATION = f's3://{OFFLINE_STORE_BUCKET}/{OFFLINE_STORE_PREFIX}'
ACCOUNT_ID = boto3.client('sts').get_caller_identity().get('Account')
REGION = boto3.Session().region_name
FEATURE_GROUP_NAME = '<YOUR FEATURE GROUP NAME>' # e.g., customers
role_arn = sagemaker.get_execution_role()
sagemaker_client = boto3.client('sagemaker')
sagemaker_featurestore_runtime_client = boto3.client(service_name='sagemaker-featurestore-runtime')
s3_client = boto3.client(service_name='s3')
athena_client = boto3.client(service_name='athena')
offline_config = {'OfflineStoreConfig': {'S3StorageConfig': {'S3Uri': OFFLINE_STORE_LOCATION }}}
# offline_config = {} # uncomment and use this line if needed to write ONLY to the Online feature store
def load_schema(schema):
feature_definitions = []
for col in schema['features']:
feature = {'FeatureName': col['name']}
if col['type'] == 'double':
feature['FeatureType'] = 'Fractional'
elif col['type'] == 'bigint':
feature['FeatureType'] = 'Integral'
else:
feature['FeatureType'] = 'String'
feature_definitions.append(feature)
return feature_definitions, schema['record_identifier_feature_name'], schema['event_time_feature_name']
schema = json.loads(open('./schema/customers.json').read())
feature_definitions, record_identifier_feature_name, event_time_feature_name = load_schema(schema)
feature_definitions
# sagemaker_client.delete_feature_group(FeatureGroupName=FEATURE_GROUP_NAME)
sagemaker_client.create_feature_group(FeatureGroupName=FEATURE_GROUP_NAME,
RecordIdentifierFeatureName=record_identifier_feature_name,
EventTimeFeatureName=event_time_feature_name,
FeatureDefinitions=feature_definitions,
Description=schema['description'],
Tags=schema['tags'],
OnlineStoreConfig={'EnableOnlineStore': True},
RoleArn=role_arn,
**offline_config)
sagemaker_client.describe_feature_group(FeatureGroupName=FEATURE_GROUP_NAME)
customers_df = pandas.read_csv('./data/customers.csv', header=None)
customers_df
records = []
for _, row in customers_df.iterrows():
cid, name, age, marital_status, sex, city, state = row
record = []
record.append({'ValueAsString': str(cid), 'FeatureName': 'cid'})
record.append({'ValueAsString': name, 'FeatureName': 'name'})
record.append({'ValueAsString': str(age), 'FeatureName': 'age'})
record.append({'ValueAsString': marital_status, 'FeatureName': 'marital_status'})
record.append({'ValueAsString': sex, 'FeatureName': 'sex'})
record.append({'ValueAsString': city, 'FeatureName': 'city'})
record.append({'ValueAsString': state, 'FeatureName': 'state'})
event_time_feature = {'ValueAsString': str(int(round(time.time()))), 'FeatureName': 'created_at'}
record.append(event_time_feature)
records.append(record)
for record in records:
response = sagemaker_featurestore_runtime_client.put_record(FeatureGroupName=FEATURE_GROUP_NAME,
Record=record)
print(response['ResponseMetadata']['HTTPStatusCode'])
response = sagemaker_featurestore_runtime_client.get_record(FeatureGroupName=FEATURE_GROUP_NAME,
RecordIdentifierValueAsString='1002')
response
feature_group_s3_prefix = f'{OFFLINE_STORE_PREFIX}/{ACCOUNT_ID}/sagemaker/{REGION}/offline-store/{FEATURE_GROUP_NAME}/data'
feature_group_s3_prefix
offline_store_contents = None
while offline_store_contents is None:
objects = s3_client.list_objects(Bucket=OFFLINE_STORE_BUCKET, Prefix=feature_group_s3_prefix)
if 'Contents' in objects and len(objects['Contents']) > 1:
logger.info('[Features are available in Offline Store!]')
offline_store_contents = objects['Contents']
else:
logger.info('[Waiting for data in Offline Store...]')
time.sleep(60)
feature_group = sagemaker_client.describe_feature_group(FeatureGroupName=FEATURE_GROUP_NAME)
glue_table_name = feature_group['OfflineStoreConfig']['DataCatalogConfig']['TableName']
query_string = f'SELECT * FROM "{glue_table_name}"'
query_string
response = athena_client.start_query_execution(
QueryString=query_string,
QueryExecutionContext={
'Database': 'sagemaker_featurestore',
'Catalog': 'AwsDataCatalog'
},
ResultConfiguration={
'OutputLocation': f's3://{OFFLINE_STORE_BUCKET}/query_results/{FEATURE_GROUP_NAME}',
}
)
query_results = athena_client.get_query_results(QueryExecutionId=response['QueryExecutionId'],
MaxResults=100)
training_set_csv_s3_key = None
for s3_object in s3_client.list_objects(Bucket=OFFLINE_STORE_BUCKET)['Contents']:
key = s3_object['Key']
if key.startswith(f'query_results/{FEATURE_GROUP_NAME}') and key.endswith('csv'):
training_set_csv_s3_key = key
training_set_s3_path = f's3://{OFFLINE_STORE_BUCKET}/{training_set_csv_s3_key}'
training_set_s3_path
training_set = pandas.read_csv(training_set_s3_path)
training_set
| 0.108366 | 0.773259 |
<img src="images/dask_horizontal.svg" align="right" width="30%">
# Table of Contents
* [Arrays](#Arrays)
* [Blocked Algorithms](#Blocked-Algorithms)
* [Exercise: Compute the mean using a blocked algorithm](#Exercise:--Compute-the-mean-using-a-blocked-algorithm)
* [Exercise: Compute the mean](#Exercise:--Compute-the-mean)
* [Example](#Example)
* [Exercise: Meteorological data](#Exercise:--Meteorological-data)
* [Exercise: Subsample and store](#Exercise:--Subsample-and-store)
* [Example: Lennard-Jones potential](#Example:-Lennard-Jones-potential)
* [Dask version](#Dask-version)
* [Profiling](#Profiling)
```
# be sure to shut down other kernels running distributed clients
from dask.distributed import Client
client = Client(processes=False)
```
# Arrays
<img src="images/array.png" width="25%" align="right">
Dask array provides a parallel, larger-than-memory, n-dimensional array using blocked algorithms. Simply put: distributed Numpy.
* **Parallel**: Uses all of the cores on your computer
* **Larger-than-memory**: Lets you work on datasets that are larger than your available memory by breaking up your array into many small pieces, operating on those pieces in an order that minimizes the memory footprint of your computation, and effectively streaming data from disk.
* **Blocked Algorithms**: Perform large computations by performing many smaller computations
**Related Documentation**
* http://dask.readthedocs.io/en/latest/array.html
* http://dask.readthedocs.io/en/latest/array-api.html
## Blocked Algorithms
A *blocked algorithm* executes on a large dataset by breaking it up into many small blocks.
For example, consider taking the sum of a billion numbers. We might instead break up the array into 1,000 chunks, each of size 1,000,000, take the sum of each chunk, and then take the sum of the intermediate sums.
We achieve the intended result (one sum on one billion numbers) by performing many smaller results (one thousand sums on one million numbers each, followed by another sum of a thousand numbers.)
We do exactly this with Python and NumPy in the following example:
**Create random dataset**
```
# create data if it doesn't already exist
from prep import random_array
random_array()
# Load data with h5py
# this gives the load prescription, but does no real work.
import h5py
import os
f = h5py.File(os.path.join('data', 'random.hdf5'), mode='r')
dset = f['/x']
```
**Compute sum using blocked algorithm**
Here we compute the sum of this large array on disk by
1. Computing the sum of each 1,000,000 sized chunk of the array
2. Computing the sum of the 1,000 intermediate sums
Note that we are fetching every partial result from the cluster and summing them here, in the notebook kernel.
```
# Compute sum of large array, one million numbers at a time
sums = []
for i in range(0, 1000000000, 1000000):
chunk = dset[i: i + 1000000] # pull out numpy array
sums.append(chunk.sum())
total = sum(sums)
print(total)
```
### Exercise: Compute the mean using a blocked algorithm
Now that we've seen the simple example above try doing a slightly more complicated problem, compute the mean of the array. You can do this by changing the code above with the following alterations:
1. Compute the sum of each block
2. Compute the length of each block
3. Compute the sum of the 1,000 intermediate sums and the sum of the 1,000 intermediate lengths and divide one by the other
This approach is overkill for our case but does nicely generalize if we don't know the size of the array or individual blocks beforehand.
```
# Compute the mean of the array
%load solutions/Array-01.py
```
`dask.array` contains these algorithms
--------------------------------------------
Dask.array is a NumPy-like library that does these kinds of tricks to operate on large datasets that don't fit into memory. It extends beyond the linear problems discussed above to full N-Dimensional algorithms and a decent subset of the NumPy interface.
**Create `dask.array` object**
You can create a `dask.array` `Array` object with the `da.from_array` function. This function accepts
1. `data`: Any object that supports NumPy slicing, like `dset`
2. `chunks`: A chunk size to tell us how to block up our array, like `(1000000,)`
```
import dask.array as da
x = da.from_array(dset, chunks=(1000000,))
```
** Manipulate `dask.array` object as you would a numpy array**
Now that we have an `Array` we perform standard numpy-style computations like arithmetic, mathematics, slicing, reductions, etc..
The interface is familiar, but the actual work is different. dask_array.sum() does not do the same thing as numpy_array.sum().
**What's the difference?**
`dask_array.sum()` builds an expression of the computation. It does not do the computation yet. `numpy_array.sum()` computes the sum immediately.
*Why the difference?*
Dask arrays are split into chunks. Each chunk must have computations run on that chunk explicitly. If the desired answer comes from a small slice of the entire dataset, running the computation over all data would be wasteful of CPU and memory.
```
result = x.sum()
result
```
**Compute result**
Dask.array objects are lazily evaluated. Operations like `.sum` build up a graph of blocked tasks to execute.
We ask for the final result with a call to `.compute()`. This triggers the actual computation.
```
result.compute()
```
### Exercise: Compute the mean
And the variance, std, etc.. This should be a trivial change to the example above.
Look at what other operations you can do with the Jupyter notebook's tab-completion.
Does this match your result from before?
Performance and Parallelism
-------------------------------
<img src="images/fail-case.gif" width="40%" align="right">
In our first examples we used `for` loops to walk through the array one block at a time. For simple operations like `sum` this is optimal. However for complex operations we may want to traverse through the array differently. In particular we may want the following:
1. Use multiple cores in parallel
2. Chain operations on a single blocks before moving on to the next one
Dask.array translates your array operations into a graph of inter-related tasks with data dependencies between them. Dask then executes this graph in parallel with multiple threads. We'll discuss more about this in the next section.
### Example
1. Construct a 20000x20000 array of normally distributed random values broken up into 1000x1000 sized chunks
2. Take the mean along one axis
3. Take every 100th element
```
import numpy as np
import dask.array as da
x = da.random.normal(10, 0.1, size=(20000, 20000), # 400 million element array
chunks=(1000, 1000)) # Cut into 1000x1000 sized chunks
y = x.mean(axis=0)[::100] # Perform NumPy-style operations
x.nbytes / 1e9 # Gigabytes of the input processed lazily
%%time
y.compute() # Time to compute the result
```
Performance comparision
---------------------------
The following experiment was performed on a heavy personal laptop. Your performance may vary. If you attempt the NumPy version then please ensure that you have more than 4GB of main memory.
**NumPy: 19s, Needs gigabytes of memory**
```python
import numpy as np
%%time
x = np.random.normal(10, 0.1, size=(20000, 20000))
y = x.mean(axis=0)[::100]
y
CPU times: user 19.6 s, sys: 160 ms, total: 19.8 s
Wall time: 19.7 s
```
**Dask Array: 4s, Needs megabytes of memory**
```python
import dask.array as da
%%time
x = da.random.normal(10, 0.1, size=(20000, 20000), chunks=(1000, 1000))
y = x.mean(axis=0)[::100]
y.compute()
CPU times: user 29.4 s, sys: 1.07 s, total: 30.5 s
Wall time: 4.01 s
```
**Discussion**
Notice that the Dask array computation ran in 4 seconds, but used 29.4 seconds of user CPU time. The numpy computation ran in 19.7 seconds and used 19.6 seconds of user CPU time.
Dask finished faster, but used more total CPU time because Dask was able to transparently parallelize the computation because of the chunk size.
*Questions*
* What happens if the dask chunks=(20000,20000)?
* Will the computation run in 4 seconds?
* How much memory will be used?
* What happens if the dask chunks=(25,25)?
* What happens to CPU and memory?
### Exercise: Meteorological data
There is 2GB of somewhat artifical weather data in HDF5 files in `data/weather-big/*.hdf5`. We'll use the `h5py` library to interact with this data and `dask.array` to compute on it.
Our goal is to visualize the average temperature on the surface of the Earth for this month. This will require a mean over all of this data. We'll do this in the following steps
1. Create `h5py.Dataset` objects for each of the days of data on disk (`dsets`)
2. Wrap these with `da.from_array` calls
3. Stack these datasets along time with a call to `da.stack`
4. Compute the mean along the newly stacked time axis with the `.mean()` method
5. Visualize the result with `matplotlib.pyplot.imshow`
```
from prep import create_weather # Prep data if it doesn't exist
create_weather()
import h5py
from glob import glob
import os
filenames = sorted(glob(os.path.join('data', 'weather-big', '*.hdf5')))
dsets = [h5py.File(filename, mode='r')['/t2m'] for filename in filenames]
dsets[0]
dsets[0][:5, :5] # Slicing into h5py.Dataset object gives a numpy array
%matplotlib inline
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(16, 8))
plt.imshow(dsets[0][::4, ::4], cmap='RdBu_r')
```
**Integrate with `dask.array`**
Make a list of `dask.array` objects out of your list of `h5py.Dataset` objects using the `da.from_array` function with a chunk size of `(500, 500)`.
**Stack this list of `dask.array` objects into a single `dask.array` object with `da.stack`**
Stack these along the first axis so that the shape of the resulting array is `(31, 5760, 11520)`.
**Plot the mean of this array along the time (`0th`) axis**
```
fig = plt.figure(figsize=(16, 8))
plt.imshow(..., cmap='RdBu_r')
```
**Plot the difference of the first day from the mean**
** Solution**
```
%load solutions/Array-02.py
```
### Exercise: Subsample and store
In the above exercise the result of our computation is small, so we can call `compute` safely. Sometimes our result is still too large to fit into memory and we want to save it to disk. In these cases you can use one of the following two functions
1. `da.store`: Store dask.array into any object that supports numpy setitem syntax, e.g.
f = h5py.File('myfile.hdf5')
output = f.create_dataset(shape=..., dtype=...)
da.store(my_dask_array, output)
2. `da.to_hdf5`: A specialized function that creates and stores a `dask.array` object into an `HDF5` file.
da.to_hdf5('data/myfile.hdf5', '/output', my_dask_array)
The task in this exercise is to use numpy step slicing to subsample the full dataset by a factor of two in both the latitude and longitude direction and then store this result to disk using one of the functions listed above.
As a reminder, Python slicing takes three elements
start:stop:step
>>> L = [1, 2, 3, 4, 5, 6, 7]
>>> L[::3]
[1, 4, 7]
```
%load solutions/Array-03.py
```
## Example: Lennard-Jones potential
The [Lennard-Jones](https://en.wikipedia.org/wiki/Lennard-Jones_potential) is used in partical simuluations in physics, chemistry and engineering. It is highly parallelizable.
First, we'll run and profile the Numpy version on 7,000 particles.
```
import numpy as np
# make a random collection of particles
def make_cluster(natoms, radius=40, seed=1981):
np.random.seed(seed)
cluster = np.random.normal(0, radius, (natoms,3))-0.5
return cluster
def lj(r2):
sr6 = (1./r2)**3
pot = 4.*(sr6*sr6 - sr6)
return pot
# build the matrix of distances
def distances(cluster):
diff = cluster[:, np.newaxis, :] - cluster[np.newaxis, :, :]
mat = (diff*diff).sum(-1)
return mat
# the lj function is evaluated over the upper traingle
# after removing distances near zero
def potential(cluster):
d2 = distances(cluster)
dtri = np.triu(d2)
energy = lj(dtri[dtri > 1e-6]).sum()
return energy
cluster = make_cluster(int(7e3), radius=500)
%time potential(cluster)
```
Notice that the most time consuming function is `distances`.
```
%load_ext snakeviz
%snakeviz potential(cluster)
```
### Dask version
Here's the Dask version. Only the `potential` function needs to be rewritten to best utilize Dask.
Note that `da.nansum` has been used over the full $NxN$ distance matrix to improve parallel efficiency.
```
import dask.array as da
# compute the potential on the entire
# matrix of distances and ignore division by zero
def potential_dask(cluster):
d2 = distances(cluster)
energy = da.nansum(lj(d2))/2.
return energy
```
Let's convert the NumPy array to a Dask array. Since the entire NumPy array fits in memory it is more computationally efficient to chunk the array by number of CPU cores.
```
from os import cpu_count
dcluster = da.from_array(cluster, chunks=cluster.shape[0]//cpu_count())
```
This step should scale quite well with number of cores. The warnings are complaining about dividing by zero, which is why we used `da.nansum` in `potential_dask`.
```
e = potential_dask(dcluster)
%time e.compute()
```
The distributed [dashboard](http://127.0.0.1:8787/tasks) shows the execution of the tasks, allowing a visualization of which is taking the most time.
Limitations
-----------
Dask.array does not implement the entire numpy interface. Users expecting this
will be disappointed. Notably dask.array has the following failings:
1. Dask does not implement all of ``np.linalg``. This has been done by a
number of excellent BLAS/LAPACK implementations and is the focus of
numerous ongoing academic research projects.
2. Dask.array does not support any operation where the resulting shape
depends on the values of the array. In order to form the Dask graph we
must be able to infer the shape of the array before actually executing the
operation. This precludes operations like indexing one Dask array with
another or operations like ``np.where``.
3. Dask.array does not attempt operations like ``sort`` which are notoriously
difficult to do in parallel and are of somewhat diminished value on very
large data (you rarely actually need a full sort).
Often we include parallel-friendly alternatives like ``topk``.
4. Dask development is driven by immediate need, and so many lesser used
functions, like ``np.full_like`` have not been implemented purely out of
laziness. These would make excellent community contributions.
|
github_jupyter
|
# be sure to shut down other kernels running distributed clients
from dask.distributed import Client
client = Client(processes=False)
# create data if it doesn't already exist
from prep import random_array
random_array()
# Load data with h5py
# this gives the load prescription, but does no real work.
import h5py
import os
f = h5py.File(os.path.join('data', 'random.hdf5'), mode='r')
dset = f['/x']
# Compute sum of large array, one million numbers at a time
sums = []
for i in range(0, 1000000000, 1000000):
chunk = dset[i: i + 1000000] # pull out numpy array
sums.append(chunk.sum())
total = sum(sums)
print(total)
# Compute the mean of the array
%load solutions/Array-01.py
import dask.array as da
x = da.from_array(dset, chunks=(1000000,))
result = x.sum()
result
result.compute()
import numpy as np
import dask.array as da
x = da.random.normal(10, 0.1, size=(20000, 20000), # 400 million element array
chunks=(1000, 1000)) # Cut into 1000x1000 sized chunks
y = x.mean(axis=0)[::100] # Perform NumPy-style operations
x.nbytes / 1e9 # Gigabytes of the input processed lazily
%%time
y.compute() # Time to compute the result
import numpy as np
%%time
x = np.random.normal(10, 0.1, size=(20000, 20000))
y = x.mean(axis=0)[::100]
y
CPU times: user 19.6 s, sys: 160 ms, total: 19.8 s
Wall time: 19.7 s
import dask.array as da
%%time
x = da.random.normal(10, 0.1, size=(20000, 20000), chunks=(1000, 1000))
y = x.mean(axis=0)[::100]
y.compute()
CPU times: user 29.4 s, sys: 1.07 s, total: 30.5 s
Wall time: 4.01 s
from prep import create_weather # Prep data if it doesn't exist
create_weather()
import h5py
from glob import glob
import os
filenames = sorted(glob(os.path.join('data', 'weather-big', '*.hdf5')))
dsets = [h5py.File(filename, mode='r')['/t2m'] for filename in filenames]
dsets[0]
dsets[0][:5, :5] # Slicing into h5py.Dataset object gives a numpy array
%matplotlib inline
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(16, 8))
plt.imshow(dsets[0][::4, ::4], cmap='RdBu_r')
fig = plt.figure(figsize=(16, 8))
plt.imshow(..., cmap='RdBu_r')
%load solutions/Array-02.py
%load solutions/Array-03.py
import numpy as np
# make a random collection of particles
def make_cluster(natoms, radius=40, seed=1981):
np.random.seed(seed)
cluster = np.random.normal(0, radius, (natoms,3))-0.5
return cluster
def lj(r2):
sr6 = (1./r2)**3
pot = 4.*(sr6*sr6 - sr6)
return pot
# build the matrix of distances
def distances(cluster):
diff = cluster[:, np.newaxis, :] - cluster[np.newaxis, :, :]
mat = (diff*diff).sum(-1)
return mat
# the lj function is evaluated over the upper traingle
# after removing distances near zero
def potential(cluster):
d2 = distances(cluster)
dtri = np.triu(d2)
energy = lj(dtri[dtri > 1e-6]).sum()
return energy
cluster = make_cluster(int(7e3), radius=500)
%time potential(cluster)
%load_ext snakeviz
%snakeviz potential(cluster)
import dask.array as da
# compute the potential on the entire
# matrix of distances and ignore division by zero
def potential_dask(cluster):
d2 = distances(cluster)
energy = da.nansum(lj(d2))/2.
return energy
from os import cpu_count
dcluster = da.from_array(cluster, chunks=cluster.shape[0]//cpu_count())
e = potential_dask(dcluster)
%time e.compute()
| 0.482185 | 0.989034 |
## Saving Files with NumPy
### 1. Run the following cells:
```
import numpy as np
np.set_printoptions(suppress = True, linewidth = 150)
lending_co_saving = np.genfromtxt("Lending-Company-Saving.csv",
delimiter = ',',
dtype = np.str)
print(lending_co_saving)
lending_co_total_price = np.genfromtxt("Lending-Company-Total-Price.csv",
delimiter = ',',
dtype = np.str)
print(lending_co_total_price)
```
### 2. Store the data from <i> lending_co_saving_1 </i> and <i> lending_co_saving_2 </i> in separate .npy files.
You can use the names "Saving-Exercise-1" and "Saving-Exercise-2".
```
np.save("Saving-Exercise-1", lending_co_saving)
np.save("Saving-Exercise-2", lending_co_total_price)
```
### 3. Now load the two .npy files we just created and display their contents
```
array_npy_1 = np.load("Saving-Exercise-1.npy")
print(array_npy_1)
array_npy_2 = np.load("Saving-Exercise-2.npy")
print(array_npy_2)
```
### 4. These look identical to the arrays we stored with np.save(), so let's use the np.array_equal() function to compare them.
A) array_npy_1 and lending_co_saving
B) array_npy_2 amd lending_co_total_price
```
np.array_equal(array_npy_1 ,lending_co_saving)
np.array_equal(array_npy_2, lending_co_total_price,)
```
### 5. Create an .npz file with both <i> lending_co_savig </i> and <i> lending_co_total_price </i>, and load it back into Python.
```
np.savez("Saving-Exercise-3", lending_co_saving, lending_co_total_price)
array_npz = np.load("Saving-Exercise-3.npz")
```
### 6. Use the <i> files </i> attribute to examine the different .npy files in the .npz, and then display them on the screen.
```
array_npz.files
array_npz['arr_0']
array_npz['arr_1']
```
### 7. Assign more appropriate names for the .npy files in the .npz, load it and check the <i> files </i> attribute once again.
```
np.savez("Saving-Exercise-3", saving = lending_co_saving, total_price = lending_co_total_price)
array_npz = np.load("Saving-Exercise-3.npz")
array_npz.files
```
### 8. Display the two arrays from the .npz.
```
print(array_npz['saving'])
print(array_npz['total_price'])
```
### 9. Save the <i> lending_co_saving </i> array using the <i> np.savetxt() </i>. Specify the following:
A) Set the file extension to .csv
B) Set the format to strings ("%s")
C) Set the delimiter t0 ','
```
np.savetxt("Saving-Exercise-4.csv",
lending_co_saving,
fmt = "%s",
delimiter = ','
)
```
### 10. Re-import the dataset, display it on the screen and compare it to <i> lending_co_saving</i>.
```
array_csv = np.genfromtxt("Saving-Exercise-4.csv", delimiter = ',', dtype = np.str)
print(array_csv)
np.array_equal(array_csv, lending_co_saving)
```
|
github_jupyter
|
import numpy as np
np.set_printoptions(suppress = True, linewidth = 150)
lending_co_saving = np.genfromtxt("Lending-Company-Saving.csv",
delimiter = ',',
dtype = np.str)
print(lending_co_saving)
lending_co_total_price = np.genfromtxt("Lending-Company-Total-Price.csv",
delimiter = ',',
dtype = np.str)
print(lending_co_total_price)
np.save("Saving-Exercise-1", lending_co_saving)
np.save("Saving-Exercise-2", lending_co_total_price)
array_npy_1 = np.load("Saving-Exercise-1.npy")
print(array_npy_1)
array_npy_2 = np.load("Saving-Exercise-2.npy")
print(array_npy_2)
np.array_equal(array_npy_1 ,lending_co_saving)
np.array_equal(array_npy_2, lending_co_total_price,)
np.savez("Saving-Exercise-3", lending_co_saving, lending_co_total_price)
array_npz = np.load("Saving-Exercise-3.npz")
array_npz.files
array_npz['arr_0']
array_npz['arr_1']
np.savez("Saving-Exercise-3", saving = lending_co_saving, total_price = lending_co_total_price)
array_npz = np.load("Saving-Exercise-3.npz")
array_npz.files
print(array_npz['saving'])
print(array_npz['total_price'])
np.savetxt("Saving-Exercise-4.csv",
lending_co_saving,
fmt = "%s",
delimiter = ','
)
array_csv = np.genfromtxt("Saving-Exercise-4.csv", delimiter = ',', dtype = np.str)
print(array_csv)
np.array_equal(array_csv, lending_co_saving)
| 0.153644 | 0.851274 |
# Sampling the VAE
By [Allison Parrish](http://www.decontextualize.com/)
I wrote a little helper class to make it easier to sample strings from the VAE model—in particular, models trained with tokens from `bpemb`. This notebook takes you through the functionality, using the included `poetry_500k_sample` model.
```
%load_ext autoreload
%autoreload 2
import argparse, importlib
import torch
from vaesampler import BPEmbVaeSampler
```
First, load the configuration and assign the parameters to a `Namespace` object. Then, create the `BPEmbVaeSampler` object with the same `bpemb` parameters used to train the model and the path to the pre-trained model.
```
config_file = "config.config_poetry_500k_sample"
params = argparse.Namespace(**importlib.import_module(config_file).params)
bpvs = BPEmbVaeSampler(lang='en', vs=10000, dim=100,
decode_from="./models/poetry_500k_sample/2019-08-09T08:27:43.289493-011.pt",
params=params)
```
## Decoding
The main thing you'll want to do is decode strings from a latent variable `z`. This variable has a Gaussian distribution (or at least it *should*—that's the whole point of a VAE, right?). There are three methods for decoding strings from `z`:
* `.sample()` samples the (softmax) distribution of the output with the given temperature at each step;
* `.greedy()` always picks the most likely next token;
* `.beam()` expands multiple "branches" of the output and returns the most likely branch
(These methods use the underlying implementations in the `LSTMDecoder` class.)
Below you'll find some examples of each. First, `.sample()` with a temperature of 1.0. (Increase the temperature for more unlikely output; it approximates `.greedy()` as the temperature approaches 0.)
```
with torch.no_grad():
print("\n".join(bpvs.sample(torch.randn(14, 32), temperature=1.0)))
```
Greedy decoding (usually boring):
```
with torch.no_grad():
print("\n".join(bpvs.greedy(torch.randn(14, 32))))
```
Beam search (a good compromise, but slow):
```
with torch.no_grad():
print("\n".join(bpvs.beam(torch.randn(14, 32), 4)))
```
## Homotopies (linear interpolation)
Using the VAE, you can explore linear interpolations between two lines of poetry. The code in the cell below picks two points at random in the latent space and decodes at evenly-spaced points between the two:
```
with torch.no_grad():
x = torch.randn(1, 32)
y = torch.randn(1, 32)
steps = 10
for i in range(steps + 1):
z = (x * (i/steps)) + (y * 1-(i/steps))
#print(bpvs.sample(z, 0.2)[0])
#print(bpvs.greedy(z)[0])
print(bpvs.beam(z, 3)[0])
```
Using this same logic, you can produce variations on a line of poetry by adding a bit of random noise to the vector:
```
with torch.no_grad():
x = torch.randn(1, 32)
steps = 14
for i in range(steps + 1):
z = x + (torch.randn(1, 32)*0.1)
print(bpvs.sample(z, 0.35)[0])
#print(bpvs.greedy(z)[0])
#print(bpvs.beam(z, 4)[0])
```
## Reconstructions
You can ask the model to produce the latent vector for any given input. (Using `BPEmb` helps ensure that arbitrary inputs won't contain out-of-vocabulary tokens.)
The `.z()` method returns a sample from the latent Gaussian, while `.mu()` returns the mean. You can then pass this to `.sample()`, `.beam()`, or `.greedy()` to produce a string. The model's reconstructions aren't very accurate, but you can usually see some hint of the original string's meaning or structure in the output.
```
strs = ["This is just to say",
"I have eaten the plums",
"That were in the icebox"]
bpvs.sample(bpvs.z(strs), 0.5)
bpvs.beam(bpvs.mu(strs), 2)
bpvs.greedy(bpvs.mu(strs))
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
import argparse, importlib
import torch
from vaesampler import BPEmbVaeSampler
config_file = "config.config_poetry_500k_sample"
params = argparse.Namespace(**importlib.import_module(config_file).params)
bpvs = BPEmbVaeSampler(lang='en', vs=10000, dim=100,
decode_from="./models/poetry_500k_sample/2019-08-09T08:27:43.289493-011.pt",
params=params)
with torch.no_grad():
print("\n".join(bpvs.sample(torch.randn(14, 32), temperature=1.0)))
with torch.no_grad():
print("\n".join(bpvs.greedy(torch.randn(14, 32))))
with torch.no_grad():
print("\n".join(bpvs.beam(torch.randn(14, 32), 4)))
with torch.no_grad():
x = torch.randn(1, 32)
y = torch.randn(1, 32)
steps = 10
for i in range(steps + 1):
z = (x * (i/steps)) + (y * 1-(i/steps))
#print(bpvs.sample(z, 0.2)[0])
#print(bpvs.greedy(z)[0])
print(bpvs.beam(z, 3)[0])
with torch.no_grad():
x = torch.randn(1, 32)
steps = 14
for i in range(steps + 1):
z = x + (torch.randn(1, 32)*0.1)
print(bpvs.sample(z, 0.35)[0])
#print(bpvs.greedy(z)[0])
#print(bpvs.beam(z, 4)[0])
strs = ["This is just to say",
"I have eaten the plums",
"That were in the icebox"]
bpvs.sample(bpvs.z(strs), 0.5)
bpvs.beam(bpvs.mu(strs), 2)
bpvs.greedy(bpvs.mu(strs))
| 0.225076 | 0.991522 |
<a href="https://colab.research.google.com/github/daniil-lyakhov/QArithmetic/blob/master/translation_transformer.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Setup
```
!pip install -U spacy -q
!python -m spacy download en_core_web_sm
!python -m spacy download ru_core_news_sm
import numpy as np
import pandas as pd
%matplotlib inline
```
# Full dataset loading
ParaCrawl Rus-Eng dataset was choosen for experiments, link:
https://lindat.mff.cuni.cz/repository/xmlui/handle/11372/LRT-2610
```
!wget "https://lindat.mff.cuni.cz/repository/xmlui/bitstream/handle/11372/LRT-2610/paracrawl-release1.en-ru.zipporah0-dedup-clean.tgz?sequence=9&isAllowed=y" -O out.tgz
!tar -xvf out.tgz
lines_eng = open('paracrawl-release1.en-ru.zipporah0-dedup-clean.en', 'r').readlines()
lines_rus = open('paracrawl-release1.en-ru.zipporah0-dedup-clean.ru', 'r').readlines()
lines_rus[:10]
lines_eng[:10]
len(lines_eng)
```
# EDA
Check elements length
```
def get_statistics(lines_rus, lines_eng):
lenghts = {}
for data, key in [(lines_rus, 'rus'), (lines_eng, 'eng')]:
lenghts[key] = np.array([len(sent) for sent in data], dtype=int)
def collect_statistics(arr):
res = {}
res['mean'] = arr.mean()
res['argmin'] = np.argmin(arr)
res['argmax'] = np.argmax(arr)
res['min'] = arr.min()
res['max'] = arr.max()
return res
stat_rus = collect_statistics(lenghts['rus'])
stat_eng = collect_statistics(lenghts['eng'])
ratious = lenghts['rus'] / lenghts['eng']
stat_ratious = collect_statistics(ratious)
def get_pair(idx):
return lines_eng[idx], lines_rus[idx]
smallest = get_pair(stat_eng['argmin'])
longest = get_pair(stat_eng['argmax'])
smallest_ratio = get_pair(stat_ratious['argmin'])
biggest_ratio = get_pair(stat_ratious['argmax'])
len_stat_srt = f'Lenght statistics:\nRus:{stat_rus}\nEng{stat_eng}\nRus / Eng {stat_ratious}'
extreems_ex_str = f'Pairs\nSmallest: {smallest}\n'\
f'Longest: {longest}\n'\
f'Smallest ratio: {smallest_ratio}\n'\
f'Biggest ratio: {biggest_ratio}'
counts = f'Counts of pairs: {len(lines_rus)}'
descr = len_stat_srt + '\n' + extreems_ex_str + '\n' + counts
retval = {}
retval['rus'] = stat_rus
retval['eng'] = stat_eng
retval['ratious'] = ratious
retval['len'] = lenghts
return descr, retval
stats_init = get_statistics(lines_rus, lines_eng)
print(stats_init[0])
from collections import Counter
import matplotlib.pyplot as plt
def plot_len_hist(stat):
plt.hist(stat[1]['len']['eng'], 40, facecolor='g')#[x[0] for x in distr['eng']], 40, facecolor='g')
plt.xlabel('Length of sentence, charecters')
plt.ylabel('Amount of senteces with such length')
plt.show()
plot_len_hist(stats_init)
def plot_counts_boxplot(stats):
l = stats[1]['len']
plt.boxplot(l['eng'])
#plt.boxplot(l['rus'])
plt.ylabel("Length of Eng sentence")
plt.show()
plot_counts_boxplot(stats_init)
```
### Harsh filtering
Remove elements with links
```
stop_chrt = ['http', 'url', 'www', 'html']
junk_elems = [(idx, sent) for lines in [lines_eng, lines_rus]
for idx, sent in enumerate(lines)
if any(sw in sent for sw in stop_chrt)]
junk_elems[:20], len(junk_elems)
filtered_lines = {}
junk_idxs = set([x[0] for x in junk_elems])
for data, key in [(lines_rus, 'rus'), (lines_eng, 'eng')]:
filtered_lines[key] = [sent for idx, sent in enumerate(data) if idx not in junk_idxs]
stats_hard_filtered = get_statistics(filtered_lines['rus'], filtered_lines['eng'])
print(stats_hard_filtered[0])
plot_counts_boxplot(stats_hard_filtered)
# Clean RAM
lines_eng = lines_rus = None
```
### Filter too long and too small *phrases* and bad ratio
```
l = stats_hard_filtered[1]['len']
min_q = np.quantile(l['eng'], 0.35)
max_q = np.quantile(l['eng'], 0.65)
print(f'min_q {min_q}, max_q {max_q}')
min_ratio = 1 / 2
max_ratio = 2
ratious = stats_hard_filtered[1]['ratious']
bad_ratio_idxs = np.where((ratious < min_ratio) |
(ratious > max_ratio))[0]
print(f'Pairs with bad ratio: {len(bad_ratio_idxs)}')
def get_pair(idx):
return filtered_lines['eng'][idx], filtered_lines['rus'][idx]
np.random.seed(42)
print('Pairs with bad ratio examples:')
for idx in np.random.choice(bad_ratio_idxs, 10):
print(get_pair(idx))
good_ri = set(range(len(ratious))) - set(bad_ratio_idxs)
ratious[list(good_ri)].max()
for key in ['eng', 'rus']:
filtered_lines[key] = [sent for idx, sent in enumerate(filtered_lines[key]) if idx in good_ri]
print(f'{len(bad_ratio_idxs)} elements was removed')
outlayers_idxs = {idx for lang in ['rus', 'eng']
for idx, data in enumerate(filtered_lines[lang])
if len(data) < min_q or len(data) > max_q}
#outlayers_idxs.union(set(bad_ratio_idxs))
filtered_lines_filter_q = {}
for key, data in filtered_lines.items():
filtered_lines_filter_q[key] = [sent for idx, sent in enumerate(data)
if idx not in outlayers_idxs]
print(f'{len(outlayers_idxs)} elements was removed')
stat_filtered_q = get_statistics(filtered_lines_filter_q['rus'],
filtered_lines_filter_q['eng'])
print(stat_filtered_q[0])
plot_counts_boxplot(stat_filtered_q)
```
GT: ('Top of performance 85 %\n', 'Максимальная яйценоскость 85 %\n'), interesting!
Looks like non translated outlayer appears in dataset, let's filter em
```
russian_alph = 'абвгдеёжзийклмнопрстуфхцчшщъыьэюя'
eng_alph = 'abcdefghigklmnopqrstuvwxyz'
any_russian_ch = lambda x: any(rus_ch in x for rus_ch in russian_alph)
any_eng_ch = lambda x: any(eng_ch in x for eng_ch in eng_alph)
non_translated_idxs = {idx for idx, data in enumerate(filtered_lines_filter_q['rus'])
if not any_russian_ch(data)}
language_mixed = {idx for idx, data in enumerate(filtered_lines_filter_q['eng'])
if any_russian_ch(data)}.union({
idx for idx, data in enumerate(filtered_lines_filter_q['rus'])
if any_eng_ch(data)
})
outlayers = non_translated_idxs.union(language_mixed)
print(f'{len(outlayers)} non translated pairs was found')
def get_pair(idx):
return filtered_lines_filter_q['eng'][idx], filtered_lines_filter_q['rus'][idx]
np.random.seed(42)
print('Not translated pairs example')
for idx in np.random.choice(list(non_translated_idxs), 10):
print(get_pair(idx))
filtered_final = {}
for key, data in filtered_lines_filter_q.items():
filtered_final[key] = [sent for idx, sent in enumerate(data)
if idx not in outlayers]
print(f'{len(outlayers)} elements was removed')
stat_filtered_final = get_statistics(filtered_final['rus'],
filtered_final['eng'])
print(stat_filtered_final[0])
plot_counts_boxplot(stat_filtered_final)
plot_len_hist(stat_filtered_final)
```
Let's try to remove all pairs contains digits
```
digits_in_sent = {idx for lang in ['rus', 'eng']
for idx, data in enumerate(filtered_final[lang])
if any(char.isdigit() for char in data)}
print(f'Count of pairs with digits: {len(digits_in_sent)}')
filtered_small = {}
for key, data in filtered_final.items():
filtered_small[key] = [sent for idx, sent in enumerate(data)
if idx not in digits_in_sent]
print(f'{len(digits_in_sent)} elements was removed')
stat_filtered_small = get_statistics(filtered_small['rus'],
filtered_small['eng'])
print(stat_filtered_small[0])
plot_counts_boxplot(stat_filtered_small)
plot_len_hist(stat_filtered_small)
```
# Part where you can save/load filtered dataset
```
file_path = 'filtered_transl.csv'
# Write filtered data
with open(file_path, "w", newline='', encoding="utf-8") as out:
out.write(pd.DataFrame(data=filtered_small).to_csv(index=False))
#@title Choose load or process filtered data
load_data = True #@param {type:"boolean"}
if not load_data:
lines_eng, lines_rus = filtered_lines_filter_q['eng'], filtered_lines_filter_q['rus']
else:
# Load filtered data
df = pd.read_csv(file_path, index_col=False)
lines_eng, lines_rus = list(df['eng']), list(df['rus'])
df
# Just to check everything is loaded ok
lines_eng[:5], lines_rus[:5]
# Take only N elements from dataset
N = 100000
lines_eng, lines_rus = lines_eng[:N], lines_rus[:N]
```
# Models
```
from torchtext.data.utils import get_tokenizer
from torchtext.vocab import build_vocab_from_iterator
from typing import Iterable, List
SRC_LANGUAGE = 'eng'
TGT_LANGUAGE = 'rus'
# Place-holders
token_transform = {}
vocab_transform = {}
# Create source and target language tokenizer. Make sure to install the dependencies.
token_transform[SRC_LANGUAGE] = get_tokenizer('spacy', language='ru_core_news_sm')
token_transform[TGT_LANGUAGE] = get_tokenizer('spacy', language='en_core_web_sm')
# helper function to yield list of tokens
def yield_tokens(data_iter: Iterable, language: str) -> List[str]:
for data_sample in data_iter:
yield token_transform[language](data_sample)
# Define special symbols and indices
UNK_IDX, PAD_IDX, BOS_IDX, EOS_IDX = 0, 1, 2, 3
# Make sure the tokens are in order of their indices to properly insert them in vocab
special_symbols = ['<unk>', '<pad>', '<bos>', '<eos>']
for train_iter, ln in [(lines_eng, 'eng'), (lines_rus, 'rus')]:
# Create torchtext's Vocab object
vocab_transform[ln] = build_vocab_from_iterator(yield_tokens(train_iter, ln),
min_freq=1,
specials=special_symbols,
special_first=True)
# Set UNK_IDX as the default index. This index is returned when the token is not found.
# If not set, it throws RuntimeError when the queried token is not found in the Vocabulary.
for ln in [SRC_LANGUAGE, TGT_LANGUAGE]:
vocab_transform[ln].set_default_index(UNK_IDX)
```
## Seq2Seq Network using LSTM
```
class EncoderRNN(nn.Module):
def __init__(self, input_size, hidden_size):
super(EncoderRNN, self).__init__()
self.hidden_size = hidden_size
self.embedding = nn.Embedding(input_size, hidden_size)
self.gru = nn.GRU(hidden_size, hidden_size)
def forward(self, input, hidden):
embedded = self.embedding(input).view(1, 1, -1)
output = embedded
output, hidden = self.gru(output, hidden)
return output, hidden
def initHidden(self):
return torch.zeros(1, 1, self.hidden_size, device=device)
class AttnDecoderRNN(nn.Module):
def __init__(self, hidden_size, output_size, dropout_p=0.1, max_length=MAX_LENGTH):
super(AttnDecoderRNN, self).__init__()
self.hidden_size = hidden_size
self.output_size = output_size
self.dropout_p = dropout_p
self.max_length = max_length
self.embedding = nn.Embedding(self.output_size, self.hidden_size)
self.attn = nn.Linear(self.hidden_size * 2, self.max_length)
self.attn_combine = nn.Linear(self.hidden_size * 2, self.hidden_size)
self.dropout = nn.Dropout(self.dropout_p)
self.gru = nn.GRU(self.hidden_size, self.hidden_size)
self.out = nn.Linear(self.hidden_size, self.output_size)
def forward(self, input, hidden, encoder_outputs):
embedded = self.embedding(input).view(1, 1, -1)
embedded = self.dropout(embedded)
attn_weights = F.softmax(
self.attn(torch.cat((embedded[0], hidden[0]), 1)), dim=1)
attn_applied = torch.bmm(attn_weights.unsqueeze(0),
encoder_outputs.unsqueeze(0))
output = torch.cat((embedded[0], attn_applied[0]), 1)
output = self.attn_combine(output).unsqueeze(0)
output = F.relu(output)
output, hidden = self.gru(output, hidden)
output = F.log_softmax(self.out(output[0]), dim=1)
return output, hidden, attn_weights
def initHidden(self):
return torch.zeros(1, 1, self.hidden_size, device=device)
def indexesFromSentence(lang, sentence):
return [lang.word2index[word] for word in sentence.split(' ')]
def tensorFromSentence(lang, sentence):
indexes = indexesFromSentence(lang, sentence)
indexes.append(EOS_token)
return torch.tensor(indexes, dtype=torch.long, device=device).view(-1, 1)
def tensorsFromPair(pair):
input_tensor = tensorFromSentence(input_lang, pair[0])
target_tensor = tensorFromSentence(output_lang, pair[1])
return (input_tensor, target_tensor)
teacher_forcing_ratio = 0.5
def train(input_tensor, target_tensor, encoder, decoder, encoder_optimizer, decoder_optimizer, criterion, max_length=MAX_LENGTH):
encoder_hidden = encoder.initHidden()
encoder_optimizer.zero_grad()
decoder_optimizer.zero_grad()
input_length = input_tensor.size(0)
target_length = target_tensor.size(0)
encoder_outputs = torch.zeros(max_length, encoder.hidden_size, device=device)
loss = 0
for ei in range(input_length):
encoder_output, encoder_hidden = encoder(
input_tensor[ei], encoder_hidden)
encoder_outputs[ei] = encoder_output[0, 0]
decoder_input = torch.tensor([[SOS_token]], device=device)
decoder_hidden = encoder_hidden
use_teacher_forcing = True if random.random() < teacher_forcing_ratio else False
if use_teacher_forcing:
# Teacher forcing: Feed the target as the next input
for di in range(target_length):
decoder_output, decoder_hidden, decoder_attention = decoder(
decoder_input, decoder_hidden, encoder_outputs)
loss += criterion(decoder_output, target_tensor[di])
decoder_input = target_tensor[di] # Teacher forcing
else:
# Without teacher forcing: use its own predictions as the next input
for di in range(target_length):
decoder_output, decoder_hidden, decoder_attention = decoder(
decoder_input, decoder_hidden, encoder_outputs)
topv, topi = decoder_output.topk(1)
decoder_input = topi.squeeze().detach() # detach from history as input
loss += criterion(decoder_output, target_tensor[di])
if decoder_input.item() == EOS_token:
break
loss.backward()
encoder_optimizer.step()
decoder_optimizer.step()
return loss.item() / target_length
import time
import math
def asMinutes(s):
m = math.floor(s / 60)
s -= m * 60
return '%dm %ds' % (m, s)
def timeSince(since, percent):
now = time.time()
s = now - since
es = s / (percent)
rs = es - s
return '%s (- %s)' % (asMinutes(s), asMinutes(rs))
```
Seq2Seq Network using Transformer
---------------------------------
Transformer is a Seq2Seq model introduced in `“Attention is all you
need” <https://papers.nips.cc/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf>`__
paper for solving machine translation tasks.
Below, we will create a Seq2Seq network that uses Transformer. The network
consists of three parts. First part is the embedding layer. This layer converts tensor of input indices
into corresponding tensor of input embeddings. These embedding are further augmented with positional
encodings to provide position information of input tokens to the model. The second part is the
actual `Transformer <https://pytorch.org/docs/stable/generated/torch.nn.Transformer.html>`__ model.
Finally, the output of Transformer model is passed through linear layer
that give un-normalized probabilities for each token in the target language.
```
from torch import Tensor
import torch
import torch.nn as nn
from torch.nn import Transformer
import math
DEVICE = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# helper Module that adds positional encoding to the token embedding to introduce a notion of word order.
class PositionalEncoding(nn.Module):
def __init__(self,
emb_size: int,
dropout: float,
maxlen: int = 5000):
super(PositionalEncoding, self).__init__()
den = torch.exp(- torch.arange(0, emb_size, 2)* math.log(10000) / emb_size)
pos = torch.arange(0, maxlen).reshape(maxlen, 1)
pos_embedding = torch.zeros((maxlen, emb_size))
pos_embedding[:, 0::2] = torch.sin(pos * den)
pos_embedding[:, 1::2] = torch.cos(pos * den)
pos_embedding = pos_embedding.unsqueeze(-2)
self.dropout = nn.Dropout(dropout)
self.register_buffer('pos_embedding', pos_embedding)
def forward(self, token_embedding: Tensor):
return self.dropout(token_embedding + self.pos_embedding[:token_embedding.size(0), :])
# helper Module to convert tensor of input indices into corresponding tensor of token embeddings
class TokenEmbedding(nn.Module):
def __init__(self, vocab_size: int, emb_size):
super(TokenEmbedding, self).__init__()
self.embedding = nn.Embedding(vocab_size, emb_size)
self.emb_size = emb_size
def forward(self, tokens: Tensor):
return self.embedding(tokens.long()) * math.sqrt(self.emb_size)
# Seq2Seq Network
class Seq2SeqTransformer(nn.Module):
def __init__(self,
num_encoder_layers: int,
num_decoder_layers: int,
emb_size: int,
nhead: int,
src_vocab_size: int,
tgt_vocab_size: int,
dim_feedforward: int = 512,
dropout: float = 0.1):
super(Seq2SeqTransformer, self).__init__()
self.transformer = Transformer(d_model=emb_size,
nhead=nhead,
num_encoder_layers=num_encoder_layers,
num_decoder_layers=num_decoder_layers,
dim_feedforward=dim_feedforward,
dropout=dropout)
self.generator = nn.Linear(emb_size, tgt_vocab_size)
self.src_tok_emb = TokenEmbedding(src_vocab_size, emb_size)
self.tgt_tok_emb = TokenEmbedding(tgt_vocab_size, emb_size)
self.positional_encoding = PositionalEncoding(
emb_size, dropout=dropout)
def forward(self,
src: Tensor,
trg: Tensor,
src_mask: Tensor,
tgt_mask: Tensor,
src_padding_mask: Tensor,
tgt_padding_mask: Tensor,
memory_key_padding_mask: Tensor):
src_emb = self.positional_encoding(self.src_tok_emb(src))
tgt_emb = self.positional_encoding(self.tgt_tok_emb(trg))
outs = self.transformer(src_emb, tgt_emb, src_mask, tgt_mask, None,
src_padding_mask, tgt_padding_mask, memory_key_padding_mask)
return self.generator(outs)
def encode(self, src: Tensor, src_mask: Tensor):
return self.transformer.encoder(self.positional_encoding(
self.src_tok_emb(src)), src_mask)
def decode(self, tgt: Tensor, memory: Tensor, tgt_mask: Tensor):
return self.transformer.decoder(self.positional_encoding(
self.tgt_tok_emb(tgt)), memory,
tgt_mask)
```
During training, we need a subsequent word mask that will prevent model to look into
the future words when making predictions. We will also need masks to hide
source and target padding tokens. Below, let's define a function that will take care of both.
```
def generate_square_subsequent_mask(sz):
mask = (torch.triu(torch.ones((sz, sz), device=DEVICE)) == 1).transpose(0, 1)
mask = mask.float().masked_fill(mask == 0, float('-inf')).masked_fill(mask == 1, float(0.0))
return mask
def create_mask(src, tgt):
src_seq_len = src.shape[0]
tgt_seq_len = tgt.shape[0]
tgt_mask = generate_square_subsequent_mask(tgt_seq_len)
src_mask = torch.zeros((src_seq_len, src_seq_len),device=DEVICE).type(torch.bool)
src_padding_mask = (src == PAD_IDX).transpose(0, 1)
tgt_padding_mask = (tgt == PAD_IDX).transpose(0, 1)
return src_mask, tgt_mask, src_padding_mask, tgt_padding_mask
```
Let's now define the parameters of our model and instantiate the same. Below, we also
define our loss function which is the cross-entropy loss and the optmizer used for training.
```
from torch.optim.lr_scheduler import ExponentialLR
torch.manual_seed(0)
SRC_VOCAB_SIZE = len(vocab_transform[SRC_LANGUAGE])
TGT_VOCAB_SIZE = len(vocab_transform[TGT_LANGUAGE])
EMB_SIZE = 512
NHEAD = 8
FFN_HID_DIM = 512
BATCH_SIZE = 64
NUM_ENCODER_LAYERS = 3
NUM_DECODER_LAYERS = 3
transformer = Seq2SeqTransformer(NUM_ENCODER_LAYERS, NUM_DECODER_LAYERS, EMB_SIZE,
NHEAD, SRC_VOCAB_SIZE, TGT_VOCAB_SIZE, FFN_HID_DIM)
for p in transformer.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
transformer = transformer.to(DEVICE)
loss_fn = torch.nn.CrossEntropyLoss(ignore_index=PAD_IDX)
optimizer = torch.optim.Adam(transformer.parameters(), lr=0.0001, betas=(0.9, 0.98), eps=1e-7)
scheduler = ExponentialLR(optimizer, gamma=0.99)
```
Collation
---------
As seen in the ``Data Sourcing and Processing`` section, our data iterator yields a pair of raw strings.
We need to convert these string pairs into the batched tensors that can be processed by our ``Seq2Seq`` network
defined previously. Below we define our collate function that convert batch of raw strings into batch tensors that
can be fed directly into our model.
```
from torch.nn.utils.rnn import pad_sequence
# helper function to club together sequential operations
def sequential_transforms(*transforms):
def func(txt_input):
for transform in transforms:
txt_input = transform(txt_input)
return txt_input
return func
# function to add BOS/EOS and create tensor for input sequence indices
def tensor_transform(token_ids: List[int]):
return torch.cat((torch.tensor([BOS_IDX]),
torch.tensor(token_ids),
torch.tensor([EOS_IDX])))
# src and tgt language text transforms to convert raw strings into tensors indices
text_transform = {}
for ln in [SRC_LANGUAGE, TGT_LANGUAGE]:
text_transform[ln] = sequential_transforms(token_transform[ln], #Tokenization
vocab_transform[ln], #Numericalization
tensor_transform) # Add BOS/EOS and create tensor
# function to collate data samples into batch tesors
def collate_fn(batch):
src_batch, tgt_batch = [], []
for src_sample, tgt_sample in batch:
src_batch.append(text_transform[SRC_LANGUAGE](src_sample.rstrip("\n")))
tgt_batch.append(text_transform[TGT_LANGUAGE](tgt_sample.rstrip("\n")))
src_batch = pad_sequence(src_batch, padding_value=PAD_IDX)
tgt_batch = pad_sequence(tgt_batch, padding_value=PAD_IDX)
return src_batch, tgt_batch
```
Let's define training and evaluation loop that will be called for each
epoch.
Define iterators
```
N_train = int(N * 0.9)
complete_ds = list(zip(lines_eng, lines_rus))
train_iter = complete_ds[:N_train]
test_iter = complete_ds[N_train:]
N_train
from torch.utils.data import DataLoader
from tqdm import tqdm
def train_epoch(model, optimizer):
model.train()
losses = 0
train_dataloader = DataLoader(train_iter, batch_size=BATCH_SIZE, collate_fn=collate_fn)
with tqdm(train_dataloader) as t:
for src, tgt in t:
src = src.to(DEVICE)
tgt = tgt.to(DEVICE)
tgt_input = tgt[:-1, :]
src_mask, tgt_mask, src_padding_mask, tgt_padding_mask = create_mask(src, tgt_input)
logits = model(src, tgt_input, src_mask, tgt_mask,src_padding_mask, tgt_padding_mask, src_padding_mask)
optimizer.zero_grad()
tgt_out = tgt[1:, :]
loss = loss_fn(logits.reshape(-1, logits.shape[-1]), tgt_out.reshape(-1))
loss.backward()
optimizer.step()
losses += loss.item()
t.set_description(f'Loss: {loss.item()}')
return losses / len(train_dataloader)
def evaluate(model):
model.eval()
losses = 0
val_dataloader = DataLoader(test_iter, batch_size=BATCH_SIZE,
collate_fn=collate_fn)
for src, tgt in val_dataloader:
src = src.to(DEVICE)
tgt = tgt.to(DEVICE)
tgt_input = tgt[:-1, :]
src_mask, tgt_mask, src_padding_mask, tgt_padding_mask = create_mask(src, tgt_input)
logits = model(src, tgt_input, src_mask, tgt_mask,src_padding_mask, tgt_padding_mask, src_padding_mask)
tgt_out = tgt[1:, :]
loss = loss_fn(logits.reshape(-1, logits.shape[-1]), tgt_out.reshape(-1))
losses += loss.item()
return losses / len(val_dataloader)
```
Now we have all the ingredients to train our model. Let's do it!
```
import torch
from timeit import default_timer as timer
from torch.utils.tensorboard import SummaryWriter
NUM_EPOCHS = 18
sw = SummaryWriter()
for epoch in range(1, NUM_EPOCHS+1):
start_time = timer()
train_loss = train_epoch(transformer, optimizer)
end_time = timer()
val_loss = evaluate(transformer)
print((f"Epoch: {epoch}, Train loss: {train_loss:.3f}, Val loss: {val_loss:.3f}, "f"Epoch time = {(end_time - start_time):.3f}s"))
sw.add_scalar('Loss/train', train_loss)
sw.add_scalar('Loss/val', val_loss)
scheduler.step()
# Save last ckpt
PATH = 'transformer.ckpt'
torch.save(transformer.state_dict(), PATH)
# function to generate output sequence using greedy algorithm
def greedy_decode(model, src, src_mask, max_len, start_symbol):
src = src.to(DEVICE)
src_mask = src_mask.to(DEVICE)
memory = model.encode(src, src_mask)
ys = torch.ones(1, 1).fill_(start_symbol).type(torch.long).to(DEVICE)
for i in range(max_len-1):
memory = memory.to(DEVICE)
tgt_mask = (generate_square_subsequent_mask(ys.size(0))
.type(torch.bool)).to(DEVICE)
out = model.decode(ys, memory, tgt_mask)
out = out.transpose(0, 1)
prob = model.generator(out[:, -1])
_, next_word = torch.max(prob, dim=1)
next_word = next_word.item()
ys = torch.cat([ys,
torch.ones(1, 1).type_as(src.data).fill_(next_word)], dim=0)
if next_word == EOS_IDX:
break
return ys
# actual function to translate input sentence into target language
def translate(model: torch.nn.Module, src_sentence: str):
model.eval()
src = text_transform[SRC_LANGUAGE](src_sentence).view(-1, 1)
num_tokens = src.shape[0]
src_mask = (torch.zeros(num_tokens, num_tokens)).type(torch.bool)
tgt_tokens = greedy_decode(
model, src, src_mask, max_len=num_tokens + 5, start_symbol=BOS_IDX).flatten()
return " ".join(vocab_transform[TGT_LANGUAGE].lookup_tokens(list(tgt_tokens.cpu().numpy()))).replace("<bos>", "").replace("<eos>", "")
print(translate(transformer, "I love you"))
print(translate(transformer, "This is success"))
print(translate(transformer, 'Where is a bathroom'))
print(translate(transformer, 'Sad teddy bear'))
print(translate(transformer, 'I hate you'))
print(translate(transformer, 'How can I pay for this?'))
print(translate(transformer, 'Do you want to play a game with me?'))
print(translate(transformer, 'How can you really?'))
```
References
----------
1. Attention is all you need paper.
https://papers.nips.cc/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf
2. The annotated transformer. https://nlp.seas.harvard.edu/2018/04/03/attention.html#positional-encoding
|
github_jupyter
|
!pip install -U spacy -q
!python -m spacy download en_core_web_sm
!python -m spacy download ru_core_news_sm
import numpy as np
import pandas as pd
%matplotlib inline
!wget "https://lindat.mff.cuni.cz/repository/xmlui/bitstream/handle/11372/LRT-2610/paracrawl-release1.en-ru.zipporah0-dedup-clean.tgz?sequence=9&isAllowed=y" -O out.tgz
!tar -xvf out.tgz
lines_eng = open('paracrawl-release1.en-ru.zipporah0-dedup-clean.en', 'r').readlines()
lines_rus = open('paracrawl-release1.en-ru.zipporah0-dedup-clean.ru', 'r').readlines()
lines_rus[:10]
lines_eng[:10]
len(lines_eng)
def get_statistics(lines_rus, lines_eng):
lenghts = {}
for data, key in [(lines_rus, 'rus'), (lines_eng, 'eng')]:
lenghts[key] = np.array([len(sent) for sent in data], dtype=int)
def collect_statistics(arr):
res = {}
res['mean'] = arr.mean()
res['argmin'] = np.argmin(arr)
res['argmax'] = np.argmax(arr)
res['min'] = arr.min()
res['max'] = arr.max()
return res
stat_rus = collect_statistics(lenghts['rus'])
stat_eng = collect_statistics(lenghts['eng'])
ratious = lenghts['rus'] / lenghts['eng']
stat_ratious = collect_statistics(ratious)
def get_pair(idx):
return lines_eng[idx], lines_rus[idx]
smallest = get_pair(stat_eng['argmin'])
longest = get_pair(stat_eng['argmax'])
smallest_ratio = get_pair(stat_ratious['argmin'])
biggest_ratio = get_pair(stat_ratious['argmax'])
len_stat_srt = f'Lenght statistics:\nRus:{stat_rus}\nEng{stat_eng}\nRus / Eng {stat_ratious}'
extreems_ex_str = f'Pairs\nSmallest: {smallest}\n'\
f'Longest: {longest}\n'\
f'Smallest ratio: {smallest_ratio}\n'\
f'Biggest ratio: {biggest_ratio}'
counts = f'Counts of pairs: {len(lines_rus)}'
descr = len_stat_srt + '\n' + extreems_ex_str + '\n' + counts
retval = {}
retval['rus'] = stat_rus
retval['eng'] = stat_eng
retval['ratious'] = ratious
retval['len'] = lenghts
return descr, retval
stats_init = get_statistics(lines_rus, lines_eng)
print(stats_init[0])
from collections import Counter
import matplotlib.pyplot as plt
def plot_len_hist(stat):
plt.hist(stat[1]['len']['eng'], 40, facecolor='g')#[x[0] for x in distr['eng']], 40, facecolor='g')
plt.xlabel('Length of sentence, charecters')
plt.ylabel('Amount of senteces with such length')
plt.show()
plot_len_hist(stats_init)
def plot_counts_boxplot(stats):
l = stats[1]['len']
plt.boxplot(l['eng'])
#plt.boxplot(l['rus'])
plt.ylabel("Length of Eng sentence")
plt.show()
plot_counts_boxplot(stats_init)
stop_chrt = ['http', 'url', 'www', 'html']
junk_elems = [(idx, sent) for lines in [lines_eng, lines_rus]
for idx, sent in enumerate(lines)
if any(sw in sent for sw in stop_chrt)]
junk_elems[:20], len(junk_elems)
filtered_lines = {}
junk_idxs = set([x[0] for x in junk_elems])
for data, key in [(lines_rus, 'rus'), (lines_eng, 'eng')]:
filtered_lines[key] = [sent for idx, sent in enumerate(data) if idx not in junk_idxs]
stats_hard_filtered = get_statistics(filtered_lines['rus'], filtered_lines['eng'])
print(stats_hard_filtered[0])
plot_counts_boxplot(stats_hard_filtered)
# Clean RAM
lines_eng = lines_rus = None
l = stats_hard_filtered[1]['len']
min_q = np.quantile(l['eng'], 0.35)
max_q = np.quantile(l['eng'], 0.65)
print(f'min_q {min_q}, max_q {max_q}')
min_ratio = 1 / 2
max_ratio = 2
ratious = stats_hard_filtered[1]['ratious']
bad_ratio_idxs = np.where((ratious < min_ratio) |
(ratious > max_ratio))[0]
print(f'Pairs with bad ratio: {len(bad_ratio_idxs)}')
def get_pair(idx):
return filtered_lines['eng'][idx], filtered_lines['rus'][idx]
np.random.seed(42)
print('Pairs with bad ratio examples:')
for idx in np.random.choice(bad_ratio_idxs, 10):
print(get_pair(idx))
good_ri = set(range(len(ratious))) - set(bad_ratio_idxs)
ratious[list(good_ri)].max()
for key in ['eng', 'rus']:
filtered_lines[key] = [sent for idx, sent in enumerate(filtered_lines[key]) if idx in good_ri]
print(f'{len(bad_ratio_idxs)} elements was removed')
outlayers_idxs = {idx for lang in ['rus', 'eng']
for idx, data in enumerate(filtered_lines[lang])
if len(data) < min_q or len(data) > max_q}
#outlayers_idxs.union(set(bad_ratio_idxs))
filtered_lines_filter_q = {}
for key, data in filtered_lines.items():
filtered_lines_filter_q[key] = [sent for idx, sent in enumerate(data)
if idx not in outlayers_idxs]
print(f'{len(outlayers_idxs)} elements was removed')
stat_filtered_q = get_statistics(filtered_lines_filter_q['rus'],
filtered_lines_filter_q['eng'])
print(stat_filtered_q[0])
plot_counts_boxplot(stat_filtered_q)
russian_alph = 'абвгдеёжзийклмнопрстуфхцчшщъыьэюя'
eng_alph = 'abcdefghigklmnopqrstuvwxyz'
any_russian_ch = lambda x: any(rus_ch in x for rus_ch in russian_alph)
any_eng_ch = lambda x: any(eng_ch in x for eng_ch in eng_alph)
non_translated_idxs = {idx for idx, data in enumerate(filtered_lines_filter_q['rus'])
if not any_russian_ch(data)}
language_mixed = {idx for idx, data in enumerate(filtered_lines_filter_q['eng'])
if any_russian_ch(data)}.union({
idx for idx, data in enumerate(filtered_lines_filter_q['rus'])
if any_eng_ch(data)
})
outlayers = non_translated_idxs.union(language_mixed)
print(f'{len(outlayers)} non translated pairs was found')
def get_pair(idx):
return filtered_lines_filter_q['eng'][idx], filtered_lines_filter_q['rus'][idx]
np.random.seed(42)
print('Not translated pairs example')
for idx in np.random.choice(list(non_translated_idxs), 10):
print(get_pair(idx))
filtered_final = {}
for key, data in filtered_lines_filter_q.items():
filtered_final[key] = [sent for idx, sent in enumerate(data)
if idx not in outlayers]
print(f'{len(outlayers)} elements was removed')
stat_filtered_final = get_statistics(filtered_final['rus'],
filtered_final['eng'])
print(stat_filtered_final[0])
plot_counts_boxplot(stat_filtered_final)
plot_len_hist(stat_filtered_final)
digits_in_sent = {idx for lang in ['rus', 'eng']
for idx, data in enumerate(filtered_final[lang])
if any(char.isdigit() for char in data)}
print(f'Count of pairs with digits: {len(digits_in_sent)}')
filtered_small = {}
for key, data in filtered_final.items():
filtered_small[key] = [sent for idx, sent in enumerate(data)
if idx not in digits_in_sent]
print(f'{len(digits_in_sent)} elements was removed')
stat_filtered_small = get_statistics(filtered_small['rus'],
filtered_small['eng'])
print(stat_filtered_small[0])
plot_counts_boxplot(stat_filtered_small)
plot_len_hist(stat_filtered_small)
file_path = 'filtered_transl.csv'
# Write filtered data
with open(file_path, "w", newline='', encoding="utf-8") as out:
out.write(pd.DataFrame(data=filtered_small).to_csv(index=False))
#@title Choose load or process filtered data
load_data = True #@param {type:"boolean"}
if not load_data:
lines_eng, lines_rus = filtered_lines_filter_q['eng'], filtered_lines_filter_q['rus']
else:
# Load filtered data
df = pd.read_csv(file_path, index_col=False)
lines_eng, lines_rus = list(df['eng']), list(df['rus'])
df
# Just to check everything is loaded ok
lines_eng[:5], lines_rus[:5]
# Take only N elements from dataset
N = 100000
lines_eng, lines_rus = lines_eng[:N], lines_rus[:N]
from torchtext.data.utils import get_tokenizer
from torchtext.vocab import build_vocab_from_iterator
from typing import Iterable, List
SRC_LANGUAGE = 'eng'
TGT_LANGUAGE = 'rus'
# Place-holders
token_transform = {}
vocab_transform = {}
# Create source and target language tokenizer. Make sure to install the dependencies.
token_transform[SRC_LANGUAGE] = get_tokenizer('spacy', language='ru_core_news_sm')
token_transform[TGT_LANGUAGE] = get_tokenizer('spacy', language='en_core_web_sm')
# helper function to yield list of tokens
def yield_tokens(data_iter: Iterable, language: str) -> List[str]:
for data_sample in data_iter:
yield token_transform[language](data_sample)
# Define special symbols and indices
UNK_IDX, PAD_IDX, BOS_IDX, EOS_IDX = 0, 1, 2, 3
# Make sure the tokens are in order of their indices to properly insert them in vocab
special_symbols = ['<unk>', '<pad>', '<bos>', '<eos>']
for train_iter, ln in [(lines_eng, 'eng'), (lines_rus, 'rus')]:
# Create torchtext's Vocab object
vocab_transform[ln] = build_vocab_from_iterator(yield_tokens(train_iter, ln),
min_freq=1,
specials=special_symbols,
special_first=True)
# Set UNK_IDX as the default index. This index is returned when the token is not found.
# If not set, it throws RuntimeError when the queried token is not found in the Vocabulary.
for ln in [SRC_LANGUAGE, TGT_LANGUAGE]:
vocab_transform[ln].set_default_index(UNK_IDX)
class EncoderRNN(nn.Module):
def __init__(self, input_size, hidden_size):
super(EncoderRNN, self).__init__()
self.hidden_size = hidden_size
self.embedding = nn.Embedding(input_size, hidden_size)
self.gru = nn.GRU(hidden_size, hidden_size)
def forward(self, input, hidden):
embedded = self.embedding(input).view(1, 1, -1)
output = embedded
output, hidden = self.gru(output, hidden)
return output, hidden
def initHidden(self):
return torch.zeros(1, 1, self.hidden_size, device=device)
class AttnDecoderRNN(nn.Module):
def __init__(self, hidden_size, output_size, dropout_p=0.1, max_length=MAX_LENGTH):
super(AttnDecoderRNN, self).__init__()
self.hidden_size = hidden_size
self.output_size = output_size
self.dropout_p = dropout_p
self.max_length = max_length
self.embedding = nn.Embedding(self.output_size, self.hidden_size)
self.attn = nn.Linear(self.hidden_size * 2, self.max_length)
self.attn_combine = nn.Linear(self.hidden_size * 2, self.hidden_size)
self.dropout = nn.Dropout(self.dropout_p)
self.gru = nn.GRU(self.hidden_size, self.hidden_size)
self.out = nn.Linear(self.hidden_size, self.output_size)
def forward(self, input, hidden, encoder_outputs):
embedded = self.embedding(input).view(1, 1, -1)
embedded = self.dropout(embedded)
attn_weights = F.softmax(
self.attn(torch.cat((embedded[0], hidden[0]), 1)), dim=1)
attn_applied = torch.bmm(attn_weights.unsqueeze(0),
encoder_outputs.unsqueeze(0))
output = torch.cat((embedded[0], attn_applied[0]), 1)
output = self.attn_combine(output).unsqueeze(0)
output = F.relu(output)
output, hidden = self.gru(output, hidden)
output = F.log_softmax(self.out(output[0]), dim=1)
return output, hidden, attn_weights
def initHidden(self):
return torch.zeros(1, 1, self.hidden_size, device=device)
def indexesFromSentence(lang, sentence):
return [lang.word2index[word] for word in sentence.split(' ')]
def tensorFromSentence(lang, sentence):
indexes = indexesFromSentence(lang, sentence)
indexes.append(EOS_token)
return torch.tensor(indexes, dtype=torch.long, device=device).view(-1, 1)
def tensorsFromPair(pair):
input_tensor = tensorFromSentence(input_lang, pair[0])
target_tensor = tensorFromSentence(output_lang, pair[1])
return (input_tensor, target_tensor)
teacher_forcing_ratio = 0.5
def train(input_tensor, target_tensor, encoder, decoder, encoder_optimizer, decoder_optimizer, criterion, max_length=MAX_LENGTH):
encoder_hidden = encoder.initHidden()
encoder_optimizer.zero_grad()
decoder_optimizer.zero_grad()
input_length = input_tensor.size(0)
target_length = target_tensor.size(0)
encoder_outputs = torch.zeros(max_length, encoder.hidden_size, device=device)
loss = 0
for ei in range(input_length):
encoder_output, encoder_hidden = encoder(
input_tensor[ei], encoder_hidden)
encoder_outputs[ei] = encoder_output[0, 0]
decoder_input = torch.tensor([[SOS_token]], device=device)
decoder_hidden = encoder_hidden
use_teacher_forcing = True if random.random() < teacher_forcing_ratio else False
if use_teacher_forcing:
# Teacher forcing: Feed the target as the next input
for di in range(target_length):
decoder_output, decoder_hidden, decoder_attention = decoder(
decoder_input, decoder_hidden, encoder_outputs)
loss += criterion(decoder_output, target_tensor[di])
decoder_input = target_tensor[di] # Teacher forcing
else:
# Without teacher forcing: use its own predictions as the next input
for di in range(target_length):
decoder_output, decoder_hidden, decoder_attention = decoder(
decoder_input, decoder_hidden, encoder_outputs)
topv, topi = decoder_output.topk(1)
decoder_input = topi.squeeze().detach() # detach from history as input
loss += criterion(decoder_output, target_tensor[di])
if decoder_input.item() == EOS_token:
break
loss.backward()
encoder_optimizer.step()
decoder_optimizer.step()
return loss.item() / target_length
import time
import math
def asMinutes(s):
m = math.floor(s / 60)
s -= m * 60
return '%dm %ds' % (m, s)
def timeSince(since, percent):
now = time.time()
s = now - since
es = s / (percent)
rs = es - s
return '%s (- %s)' % (asMinutes(s), asMinutes(rs))
from torch import Tensor
import torch
import torch.nn as nn
from torch.nn import Transformer
import math
DEVICE = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# helper Module that adds positional encoding to the token embedding to introduce a notion of word order.
class PositionalEncoding(nn.Module):
def __init__(self,
emb_size: int,
dropout: float,
maxlen: int = 5000):
super(PositionalEncoding, self).__init__()
den = torch.exp(- torch.arange(0, emb_size, 2)* math.log(10000) / emb_size)
pos = torch.arange(0, maxlen).reshape(maxlen, 1)
pos_embedding = torch.zeros((maxlen, emb_size))
pos_embedding[:, 0::2] = torch.sin(pos * den)
pos_embedding[:, 1::2] = torch.cos(pos * den)
pos_embedding = pos_embedding.unsqueeze(-2)
self.dropout = nn.Dropout(dropout)
self.register_buffer('pos_embedding', pos_embedding)
def forward(self, token_embedding: Tensor):
return self.dropout(token_embedding + self.pos_embedding[:token_embedding.size(0), :])
# helper Module to convert tensor of input indices into corresponding tensor of token embeddings
class TokenEmbedding(nn.Module):
def __init__(self, vocab_size: int, emb_size):
super(TokenEmbedding, self).__init__()
self.embedding = nn.Embedding(vocab_size, emb_size)
self.emb_size = emb_size
def forward(self, tokens: Tensor):
return self.embedding(tokens.long()) * math.sqrt(self.emb_size)
# Seq2Seq Network
class Seq2SeqTransformer(nn.Module):
def __init__(self,
num_encoder_layers: int,
num_decoder_layers: int,
emb_size: int,
nhead: int,
src_vocab_size: int,
tgt_vocab_size: int,
dim_feedforward: int = 512,
dropout: float = 0.1):
super(Seq2SeqTransformer, self).__init__()
self.transformer = Transformer(d_model=emb_size,
nhead=nhead,
num_encoder_layers=num_encoder_layers,
num_decoder_layers=num_decoder_layers,
dim_feedforward=dim_feedforward,
dropout=dropout)
self.generator = nn.Linear(emb_size, tgt_vocab_size)
self.src_tok_emb = TokenEmbedding(src_vocab_size, emb_size)
self.tgt_tok_emb = TokenEmbedding(tgt_vocab_size, emb_size)
self.positional_encoding = PositionalEncoding(
emb_size, dropout=dropout)
def forward(self,
src: Tensor,
trg: Tensor,
src_mask: Tensor,
tgt_mask: Tensor,
src_padding_mask: Tensor,
tgt_padding_mask: Tensor,
memory_key_padding_mask: Tensor):
src_emb = self.positional_encoding(self.src_tok_emb(src))
tgt_emb = self.positional_encoding(self.tgt_tok_emb(trg))
outs = self.transformer(src_emb, tgt_emb, src_mask, tgt_mask, None,
src_padding_mask, tgt_padding_mask, memory_key_padding_mask)
return self.generator(outs)
def encode(self, src: Tensor, src_mask: Tensor):
return self.transformer.encoder(self.positional_encoding(
self.src_tok_emb(src)), src_mask)
def decode(self, tgt: Tensor, memory: Tensor, tgt_mask: Tensor):
return self.transformer.decoder(self.positional_encoding(
self.tgt_tok_emb(tgt)), memory,
tgt_mask)
def generate_square_subsequent_mask(sz):
mask = (torch.triu(torch.ones((sz, sz), device=DEVICE)) == 1).transpose(0, 1)
mask = mask.float().masked_fill(mask == 0, float('-inf')).masked_fill(mask == 1, float(0.0))
return mask
def create_mask(src, tgt):
src_seq_len = src.shape[0]
tgt_seq_len = tgt.shape[0]
tgt_mask = generate_square_subsequent_mask(tgt_seq_len)
src_mask = torch.zeros((src_seq_len, src_seq_len),device=DEVICE).type(torch.bool)
src_padding_mask = (src == PAD_IDX).transpose(0, 1)
tgt_padding_mask = (tgt == PAD_IDX).transpose(0, 1)
return src_mask, tgt_mask, src_padding_mask, tgt_padding_mask
from torch.optim.lr_scheduler import ExponentialLR
torch.manual_seed(0)
SRC_VOCAB_SIZE = len(vocab_transform[SRC_LANGUAGE])
TGT_VOCAB_SIZE = len(vocab_transform[TGT_LANGUAGE])
EMB_SIZE = 512
NHEAD = 8
FFN_HID_DIM = 512
BATCH_SIZE = 64
NUM_ENCODER_LAYERS = 3
NUM_DECODER_LAYERS = 3
transformer = Seq2SeqTransformer(NUM_ENCODER_LAYERS, NUM_DECODER_LAYERS, EMB_SIZE,
NHEAD, SRC_VOCAB_SIZE, TGT_VOCAB_SIZE, FFN_HID_DIM)
for p in transformer.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
transformer = transformer.to(DEVICE)
loss_fn = torch.nn.CrossEntropyLoss(ignore_index=PAD_IDX)
optimizer = torch.optim.Adam(transformer.parameters(), lr=0.0001, betas=(0.9, 0.98), eps=1e-7)
scheduler = ExponentialLR(optimizer, gamma=0.99)
from torch.nn.utils.rnn import pad_sequence
# helper function to club together sequential operations
def sequential_transforms(*transforms):
def func(txt_input):
for transform in transforms:
txt_input = transform(txt_input)
return txt_input
return func
# function to add BOS/EOS and create tensor for input sequence indices
def tensor_transform(token_ids: List[int]):
return torch.cat((torch.tensor([BOS_IDX]),
torch.tensor(token_ids),
torch.tensor([EOS_IDX])))
# src and tgt language text transforms to convert raw strings into tensors indices
text_transform = {}
for ln in [SRC_LANGUAGE, TGT_LANGUAGE]:
text_transform[ln] = sequential_transforms(token_transform[ln], #Tokenization
vocab_transform[ln], #Numericalization
tensor_transform) # Add BOS/EOS and create tensor
# function to collate data samples into batch tesors
def collate_fn(batch):
src_batch, tgt_batch = [], []
for src_sample, tgt_sample in batch:
src_batch.append(text_transform[SRC_LANGUAGE](src_sample.rstrip("\n")))
tgt_batch.append(text_transform[TGT_LANGUAGE](tgt_sample.rstrip("\n")))
src_batch = pad_sequence(src_batch, padding_value=PAD_IDX)
tgt_batch = pad_sequence(tgt_batch, padding_value=PAD_IDX)
return src_batch, tgt_batch
N_train = int(N * 0.9)
complete_ds = list(zip(lines_eng, lines_rus))
train_iter = complete_ds[:N_train]
test_iter = complete_ds[N_train:]
N_train
from torch.utils.data import DataLoader
from tqdm import tqdm
def train_epoch(model, optimizer):
model.train()
losses = 0
train_dataloader = DataLoader(train_iter, batch_size=BATCH_SIZE, collate_fn=collate_fn)
with tqdm(train_dataloader) as t:
for src, tgt in t:
src = src.to(DEVICE)
tgt = tgt.to(DEVICE)
tgt_input = tgt[:-1, :]
src_mask, tgt_mask, src_padding_mask, tgt_padding_mask = create_mask(src, tgt_input)
logits = model(src, tgt_input, src_mask, tgt_mask,src_padding_mask, tgt_padding_mask, src_padding_mask)
optimizer.zero_grad()
tgt_out = tgt[1:, :]
loss = loss_fn(logits.reshape(-1, logits.shape[-1]), tgt_out.reshape(-1))
loss.backward()
optimizer.step()
losses += loss.item()
t.set_description(f'Loss: {loss.item()}')
return losses / len(train_dataloader)
def evaluate(model):
model.eval()
losses = 0
val_dataloader = DataLoader(test_iter, batch_size=BATCH_SIZE,
collate_fn=collate_fn)
for src, tgt in val_dataloader:
src = src.to(DEVICE)
tgt = tgt.to(DEVICE)
tgt_input = tgt[:-1, :]
src_mask, tgt_mask, src_padding_mask, tgt_padding_mask = create_mask(src, tgt_input)
logits = model(src, tgt_input, src_mask, tgt_mask,src_padding_mask, tgt_padding_mask, src_padding_mask)
tgt_out = tgt[1:, :]
loss = loss_fn(logits.reshape(-1, logits.shape[-1]), tgt_out.reshape(-1))
losses += loss.item()
return losses / len(val_dataloader)
import torch
from timeit import default_timer as timer
from torch.utils.tensorboard import SummaryWriter
NUM_EPOCHS = 18
sw = SummaryWriter()
for epoch in range(1, NUM_EPOCHS+1):
start_time = timer()
train_loss = train_epoch(transformer, optimizer)
end_time = timer()
val_loss = evaluate(transformer)
print((f"Epoch: {epoch}, Train loss: {train_loss:.3f}, Val loss: {val_loss:.3f}, "f"Epoch time = {(end_time - start_time):.3f}s"))
sw.add_scalar('Loss/train', train_loss)
sw.add_scalar('Loss/val', val_loss)
scheduler.step()
# Save last ckpt
PATH = 'transformer.ckpt'
torch.save(transformer.state_dict(), PATH)
# function to generate output sequence using greedy algorithm
def greedy_decode(model, src, src_mask, max_len, start_symbol):
src = src.to(DEVICE)
src_mask = src_mask.to(DEVICE)
memory = model.encode(src, src_mask)
ys = torch.ones(1, 1).fill_(start_symbol).type(torch.long).to(DEVICE)
for i in range(max_len-1):
memory = memory.to(DEVICE)
tgt_mask = (generate_square_subsequent_mask(ys.size(0))
.type(torch.bool)).to(DEVICE)
out = model.decode(ys, memory, tgt_mask)
out = out.transpose(0, 1)
prob = model.generator(out[:, -1])
_, next_word = torch.max(prob, dim=1)
next_word = next_word.item()
ys = torch.cat([ys,
torch.ones(1, 1).type_as(src.data).fill_(next_word)], dim=0)
if next_word == EOS_IDX:
break
return ys
# actual function to translate input sentence into target language
def translate(model: torch.nn.Module, src_sentence: str):
model.eval()
src = text_transform[SRC_LANGUAGE](src_sentence).view(-1, 1)
num_tokens = src.shape[0]
src_mask = (torch.zeros(num_tokens, num_tokens)).type(torch.bool)
tgt_tokens = greedy_decode(
model, src, src_mask, max_len=num_tokens + 5, start_symbol=BOS_IDX).flatten()
return " ".join(vocab_transform[TGT_LANGUAGE].lookup_tokens(list(tgt_tokens.cpu().numpy()))).replace("<bos>", "").replace("<eos>", "")
print(translate(transformer, "I love you"))
print(translate(transformer, "This is success"))
print(translate(transformer, 'Where is a bathroom'))
print(translate(transformer, 'Sad teddy bear'))
print(translate(transformer, 'I hate you'))
print(translate(transformer, 'How can I pay for this?'))
print(translate(transformer, 'Do you want to play a game with me?'))
print(translate(transformer, 'How can you really?'))
| 0.330471 | 0.810066 |
# An introduction to solving biological problems with Python
## Day 1 - Session 1: Variables
- [Printing values](#Printing-values)
- [Exercises 1.1.1](#Exercises-1.1.1)
- [Using variables](#Using-variables)
- [Exercises 1.1.2](#Exercises-1.1.2)
## Printing values
The first bit of python syntax we're going to learn is the <tt>print</tt> statement. This command lets us print messages to the user, and also to see what Python thinks is the value of some expression (very useful when debugging your programs).
We will go into details later on, but for now just note that to print some text you have to enclose it in "quotation marks".
We will go into detail on the arithmetic operations supported in python shortly, but you can try exploring python's calculating abilities.
```
print("Hello from python!")
print(34)
print(2 + 3)
```
You can print multiple expressions you need to seperate them with commas. Python will insert a space between each element, and a newline at the end of the message (though you can suppress this behaviour by leaving a trailing comma at the end of the command).
```
print("The answer:", 42)
```
To start the Python interpreter, open a terminal window, type the command `python3`, then enter Python commands after the prompt `>>>` and press `Enter` when you're done.
<center><img src="img/python_shell.png"></center>
Python will run the code you typed, and might display some output on the line below, before leaving you with another prompt which looks like `>>>`.
If you want to exit the interactive interpreter you can type the command `quit()` or type `Ctrl-D`.
## Exercises 1.1.1
1. In Jupyter, insert a new cell below this one to print your name. Execute the code by pressing `run cell` from the menu bar or use your keyboard `Ctrl-Enter`.
2. Do now the same using the interpreter
## Using variables
In the <tt>print</tt> commands above we have directly operated on values such as text strings and numbers. When programming we will typically want to deal with rather more complex expressions where it is useful to be able to assign a name to an expression, especially if we are trying to deal with multiple values at the same time.
We can give a name to a value using _variables_, the name is apt because the values stored in a variable can _vary_. Unlike some other languages, the type of value assigned to a variable can also change (this is one of the reasons why python is known as a _dynamic_ language).
A variable can be assigned to a simple value...
```
x = 3
print(x)
```
... or the outcome of a more complex expression.
```
x = 2 + 2
print(x)
```
A variable can be called whatever you like (as long as it starts with a character, it does not contain space and is meaningful) and you assign a value to a variable with the **`=` operator**. Note that this is different to mathematical equality (which we will come to later...)
You can <tt>print</tt> a variable to see what python thinks its current value is.
```
serine = "TCA"
print(serine, "codes for serine")
serine = "TCG"
print("as does", serine)
```
In the interactive interpreter you don't have to <tt>print</tt> everything, if you type a variable name (or just a value), the interpreter will automatically print out what python thinks the value is. Note though that this is not the case if your code is in a file.
```
3 + 4
x = 5
3 * x
```
Variables can be used on the right hand side of an assignment as well, in which case they will be evaluated before the value is assigned to the variable on the left hand side.
```
x = 5
y = x * 3
print(y)
```
or just `y` in the interpreter and in Jupyter notebook
```
y
```
You can use the current value of a variable itself in an assignment
```
y = y + 1
y
```
In fact this is such a common idiom that there are special operators that will do this implicitly (more on these later)
```
y += 1
y
```
## Exercises 1.1.2
In the interpreter:
1. Create a variable and assign it the string value of your first name, assign your age to another variable (you are free to lie!), print out a message saying how old you are
2. Use the addition operator to add 10 to your age and print out a message saying how old you will be in 10 years time
## Next session
Go to our next notebook: [python_basic_1_2](python_basic_1_2.ipynb)
|
github_jupyter
|
print("Hello from python!")
print(34)
print(2 + 3)
print("The answer:", 42)
x = 3
print(x)
x = 2 + 2
print(x)
serine = "TCA"
print(serine, "codes for serine")
serine = "TCG"
print("as does", serine)
3 + 4
x = 5
3 * x
x = 5
y = x * 3
print(y)
y
y = y + 1
y
y += 1
y
| 0.123656 | 0.987616 |
# Exponential Modeling of COVID-19 Confirmed Cases
This is not a good model for long or even medium-term predictions, it is able to fit initial outbreaks quite well. Logistic modeling is more sophisticated and accurate.
### Defining our parameters and loading the data
Here am looking at the confirmed and fatal cases for Italy through March 17.
```
ESTIMATE_DAYS = 3
data_key = 'IT'
date_limit = '2020-03-17'
import pandas as pd
import seaborn as sns
sns.set()
df = pd.read_csv(f'https://storage.googleapis.com/covid19-open-data/v2/{data_key}/main.csv').set_index('date')
def get_outbreak_mask(data: pd.DataFrame, threshold: int = 10):
''' Returns a mask for > N confirmed cases '''
return data['total_confirmed'] > threshold
cols = ['total_confirmed', 'total_deceased']
# Get data only for the columns we care about
df = df[cols]
# Get data only for the selected dates
df = df[df.index <= date_limit]
# Get data only after the outbreak begun
df = df[get_outbreak_mask(df)]
```
### Plotting the data
Let's take a first look at the data. A visual inspection will typically give us a lot of information.
```
df.plot(kind='bar', figsize=(16, 8));
```
### Modeling the data
The data appears to follow an exponential curve.
```
from scipy import optimize
def exponential_function(x: float, a: float, b: float, c: float):
''' a * (b ^ x) + c '''
return a * (b ** x) + c
X, y = list(range(len(df))), df['total_confirmed'].tolist()
params, _ = optimize.curve_fit(exponential_function, X, y)
print('Estimated function: {0:.3f} * ({1:.3f} ^ X) + {2:.3f}'.format(*params))
confirmed = df[['total_confirmed']].rename(columns={'total_confirmed': 'Ground Truth'})
ax = confirmed.plot(kind='bar', figsize=(16, 8))
estimate = [exponential_function(x, *params) for x in X]
ax.plot(df.index, estimate, color='red', label='Estimate')
ax.legend();
```
### Validating the model
That curve looks like a very good fit! Even though proper epidemiology models are fundamentally different (because diseases can't grow exponentially indefinitely), the exponential model should be good for short term predictions.
```
params_validate, _ = optimize.curve_fit(exponential_function, X[:-ESTIMATE_DAYS], y[:-ESTIMATE_DAYS])
# Project zero for all values except for the last ESTIMATE_DAYS
projected = [0] * len(X[:-ESTIMATE_DAYS]) + [exponential_function(x, *params_validate) for x in X[-ESTIMATE_DAYS:]]
projected = pd.Series(projected, index=df.index, name='Projected')
confirmed = pd.DataFrame({'Ground Truth': df['total_confirmed'], 'Projected': projected})
ax = confirmed.plot(kind='bar', figsize=(16, 8))
estimate = [exponential_function(x, *params_validate) for x in X]
ax.plot(df.index, estimate, color='red', label='Estimate')
ax.legend();
```
### Projecting future data
It looks like my exponential model slightly overestimates the confirmed cases. That's a good sign! It means that the disease is slowing down a bit. The numbers are close enough that a 3-day projection is probably an accurate enough estimate.
```
import datetime
# Append N new days to our indices
date_format = '%Y-%m-%d'
date_range = [datetime.datetime.strptime(date, date_format) for date in df.index]
for _ in range(ESTIMATE_DAYS): date_range.append(date_range[-1] + datetime.timedelta(days=1))
date_range = [datetime.datetime.strftime(date, date_format) for date in date_range]
# Perform projection with the previously estimated parameters
projected = [0] * len(X) + [exponential_function(x, *params) for x in range(len(X), len(X) + ESTIMATE_DAYS)]
projected = pd.Series(projected, index=date_range, name='Projected')
df_ = pd.DataFrame({'Confirmed': df['total_confirmed'], 'Projected': projected})
ax = df_.plot(kind='bar', figsize=(16, 8))
estimate = [exponential_function(x, *params) for x in range(len(date_range))]
ax.plot(date_range, estimate, color='red', label='Estimate')
ax.legend();
```
|
github_jupyter
|
ESTIMATE_DAYS = 3
data_key = 'IT'
date_limit = '2020-03-17'
import pandas as pd
import seaborn as sns
sns.set()
df = pd.read_csv(f'https://storage.googleapis.com/covid19-open-data/v2/{data_key}/main.csv').set_index('date')
def get_outbreak_mask(data: pd.DataFrame, threshold: int = 10):
''' Returns a mask for > N confirmed cases '''
return data['total_confirmed'] > threshold
cols = ['total_confirmed', 'total_deceased']
# Get data only for the columns we care about
df = df[cols]
# Get data only for the selected dates
df = df[df.index <= date_limit]
# Get data only after the outbreak begun
df = df[get_outbreak_mask(df)]
df.plot(kind='bar', figsize=(16, 8));
from scipy import optimize
def exponential_function(x: float, a: float, b: float, c: float):
''' a * (b ^ x) + c '''
return a * (b ** x) + c
X, y = list(range(len(df))), df['total_confirmed'].tolist()
params, _ = optimize.curve_fit(exponential_function, X, y)
print('Estimated function: {0:.3f} * ({1:.3f} ^ X) + {2:.3f}'.format(*params))
confirmed = df[['total_confirmed']].rename(columns={'total_confirmed': 'Ground Truth'})
ax = confirmed.plot(kind='bar', figsize=(16, 8))
estimate = [exponential_function(x, *params) for x in X]
ax.plot(df.index, estimate, color='red', label='Estimate')
ax.legend();
params_validate, _ = optimize.curve_fit(exponential_function, X[:-ESTIMATE_DAYS], y[:-ESTIMATE_DAYS])
# Project zero for all values except for the last ESTIMATE_DAYS
projected = [0] * len(X[:-ESTIMATE_DAYS]) + [exponential_function(x, *params_validate) for x in X[-ESTIMATE_DAYS:]]
projected = pd.Series(projected, index=df.index, name='Projected')
confirmed = pd.DataFrame({'Ground Truth': df['total_confirmed'], 'Projected': projected})
ax = confirmed.plot(kind='bar', figsize=(16, 8))
estimate = [exponential_function(x, *params_validate) for x in X]
ax.plot(df.index, estimate, color='red', label='Estimate')
ax.legend();
import datetime
# Append N new days to our indices
date_format = '%Y-%m-%d'
date_range = [datetime.datetime.strptime(date, date_format) for date in df.index]
for _ in range(ESTIMATE_DAYS): date_range.append(date_range[-1] + datetime.timedelta(days=1))
date_range = [datetime.datetime.strftime(date, date_format) for date in date_range]
# Perform projection with the previously estimated parameters
projected = [0] * len(X) + [exponential_function(x, *params) for x in range(len(X), len(X) + ESTIMATE_DAYS)]
projected = pd.Series(projected, index=date_range, name='Projected')
df_ = pd.DataFrame({'Confirmed': df['total_confirmed'], 'Projected': projected})
ax = df_.plot(kind='bar', figsize=(16, 8))
estimate = [exponential_function(x, *params) for x in range(len(date_range))]
ax.plot(date_range, estimate, color='red', label='Estimate')
ax.legend();
| 0.773131 | 0.940243 |
Get coordinates for error ellipses, based on coordinates
x-error, y-error (1 sigma) and error correllation, and scaling
factor (defaults to 95% confidence).
```
%matplotlib inline
import numpy as np
import math
import matplotlib.pyplot as plt
import matplotlib as mpl
```
Calculate major and minor axes and inclination of ellipse.
returns x_size, y_size, theta.
```
def calc_ellipse_params(x_err, y_err, rho, scale=2.4477):
xy_err = rho * x_err * y_err
covmat = np.matrix([[x_err**2,xy_err],
[xy_err, y_err**2]])
eig = np.linalg.eigvals(covmat)
theta = 1/2 * math.atan((2*xy_err)/(x_err**2-y_err**2))
x_size = eig[0]**0.5 * scale
y_size = eig[1]**0.5 * scale
if x_err >= y_err:
theta = -theta
return (x_size, y_size, theta)
def ellipse_formula(x,y,a,b,theta):
x_t = lambda t: x + a*math.cos(t)*math.cos(theta) - b*math.sin(t)*math.sin(theta)
y_t = lambda t: y + b*math.sin(t)*math.cos(theta) - a*math.cos(t)*math.sin(theta)
return lambda t:[x_t(t), y_t(t)]
def ellipse(x,y,a,b,theta, num_pts=200):
form = ellipse_formula(x,y,a,b,theta)
return np.array([form(t) for t in np.linspace(0,2*math.pi, num=num_pts)][:-1])
```
Ellipse formula generator, similar to error ellipse, but returns a function taking an angle
(positive rotation direction) in degrees and returns the edge coordinate in that direction.
```
def error_ellipse_formula(x, y, x_err, y_err, rho, scale=2.4477):
x_size, y_size, theta = calc_ellipse_params(x_err, y_err, rho, scale)
return ellipse_formula(x,y,x_size,y_size,theta)
```
Takes data coordinates, 1 sigma errors, error correllation factor, scale
(95% conf default (2.4477), and number of edge points).
returns a coordinate matrix for for the error ellipse edges for each datapoint,
in data coordinates.
This can be used for creating matplotlib patches.
```
def error_ellipse(x, y, x_err, y_err, rho, scale=2.4477, num_points = 200):
x_size, y_size, theta = calc_ellipse_params(x_err, y_err, rho, scale)
return ellipse(x,y,x_size,y_size,theta,num_points)
```
Example of plotting a data set:
```
fig, ax = plt.subplots(dpi=150)
rng = np.random.RandomState(1129412)
for i in range(1,10):
x, y = i/10 + (rng.rand()-0.5)/10, i/10+(rng.rand()-0.5)/10
x_err, y_err = 0.01+rng.rand()/50, 0.01+rng.rand()/50
rho = 0.7*rng.rand() + 0.2
e_coords = error_ellipse(x, y, x_err, y_err, rho)
e = mpl.patches.Polygon(e_coords, fc='none', ec='k', lw=0.5, joinstyle='round')
ax.add_patch(e)
ax.set_aspect('equal')
plt.savefig('output_12_0.png');
```
In order to evaluate a regression fit, we calculate the 'best fit' distance, defined as the shortest distance from an analysis point, in relation to the error ellipse size. This corresponds to the distance between the ellipse center and the first point on the line the ellipse touches under scaling.
```
fig, ax = plt.subplots(dpi=150)
pts = [
#x, y, x_err, y_err, rho, scale
[0.5, 0.3, 0.04, 0.06, 0.5, 0.5],
[0.5, 0.3, 0.04, 0.06, 0.5, 1.8],
[0.5, 0.3, 0.04, 0.06, 0.5, 3.6],
[0.5, 0.3, 0.04, 0.06, 0.5, 6],
]
for pt in pts:
e_coords = error_ellipse(*pt)
e = mpl.patches.Polygon(e_coords, joinstyle='round', ls=':', fc='none', ec='C3', lw=1)
ax.add_patch(e)
ax.plot([0.1,0.9], [0.2, 0.7]);
ax.annotate('', xy=(0.5,0.3), xytext=(0.59,0.51), xycoords='data', arrowprops={'arrowstyle': '|-|'})
ax.annotate('Best fit\ndistance', xy=(0.56,0.3), xycoords='data', fontsize=12)
ax.annotate('Regression line', xy=(0.17,0.3), c='k', xycoords='data', rotation =31, fontsize=12);
ax.set_aspect('equal')
plt.savefig('output_14_0.png');
def get_bestfitdist(x, y, x_err, y_err, rho, fit):
shift_vec = np.matrix([[0,fit.y0]])
l0 = np.matrix([[1,fit.alpha]])
coords = np.array([[x,y]]) - shift_vec
a, b, theta = calc_ellipse_params(
x_err, y_err, rho)
ellipse_form = ellipse_formula(
x,y,a,b,theta)
scale_mx_1 = np.matrix([[1,0],[0,b/a]])
scale_mx_2 = np.matrix([[1,0],[0,a/b]])
rot_mx = lambda t: np.matrix([[np.cos(t), - np.sin(t)],
[np.sin(t), np.cos(t)]])
c_pp = (coords@ rot_mx(theta) @scale_mx_1).T
l0_pp = (l0@ rot_mx(theta) @scale_mx_1).T
l0_alpha = l0_pp[1,0]/l0_pp[0,0]
n_pp = np.matrix([[-l0_pp[1,0],l0_pp[0,0]]]).T
n_alpha = n_pp[1,0]/n_pp[0,0]
n_0 = c_pp[1,0] - c_pp[0,0]*n_alpha
x_intercept = n_0 / (l0_alpha-n_alpha)
c_adj_pp = np.matrix([[x_intercept,l0_alpha*x_intercept]])
n = ((n_pp.T * scale_mx_2) * rot_mx(-theta)) + shift_vec
n = n/np.linalg.norm(n)
c = ((c_pp.T * scale_mx_2) * rot_mx(-theta)) + shift_vec
c_adj = ((c_adj_pp * scale_mx_2) * rot_mx(-theta)) + shift_vec
theta_n = np.arccos(n[0,0])
ell_coords = ellipse_form(theta_n)
dir_95_conf = np.linalg.norm(np.array(c)[0]- np.array(ell_coords))
misfit = np.linalg.norm(c-c_adj) * (1 if c[0,0] >= c_adj[0,0] else -1)
return (c_adj, misfit, n, theta_n, dir_95_conf)
```
|
github_jupyter
|
%matplotlib inline
import numpy as np
import math
import matplotlib.pyplot as plt
import matplotlib as mpl
def calc_ellipse_params(x_err, y_err, rho, scale=2.4477):
xy_err = rho * x_err * y_err
covmat = np.matrix([[x_err**2,xy_err],
[xy_err, y_err**2]])
eig = np.linalg.eigvals(covmat)
theta = 1/2 * math.atan((2*xy_err)/(x_err**2-y_err**2))
x_size = eig[0]**0.5 * scale
y_size = eig[1]**0.5 * scale
if x_err >= y_err:
theta = -theta
return (x_size, y_size, theta)
def ellipse_formula(x,y,a,b,theta):
x_t = lambda t: x + a*math.cos(t)*math.cos(theta) - b*math.sin(t)*math.sin(theta)
y_t = lambda t: y + b*math.sin(t)*math.cos(theta) - a*math.cos(t)*math.sin(theta)
return lambda t:[x_t(t), y_t(t)]
def ellipse(x,y,a,b,theta, num_pts=200):
form = ellipse_formula(x,y,a,b,theta)
return np.array([form(t) for t in np.linspace(0,2*math.pi, num=num_pts)][:-1])
def error_ellipse_formula(x, y, x_err, y_err, rho, scale=2.4477):
x_size, y_size, theta = calc_ellipse_params(x_err, y_err, rho, scale)
return ellipse_formula(x,y,x_size,y_size,theta)
def error_ellipse(x, y, x_err, y_err, rho, scale=2.4477, num_points = 200):
x_size, y_size, theta = calc_ellipse_params(x_err, y_err, rho, scale)
return ellipse(x,y,x_size,y_size,theta,num_points)
fig, ax = plt.subplots(dpi=150)
rng = np.random.RandomState(1129412)
for i in range(1,10):
x, y = i/10 + (rng.rand()-0.5)/10, i/10+(rng.rand()-0.5)/10
x_err, y_err = 0.01+rng.rand()/50, 0.01+rng.rand()/50
rho = 0.7*rng.rand() + 0.2
e_coords = error_ellipse(x, y, x_err, y_err, rho)
e = mpl.patches.Polygon(e_coords, fc='none', ec='k', lw=0.5, joinstyle='round')
ax.add_patch(e)
ax.set_aspect('equal')
plt.savefig('output_12_0.png');
fig, ax = plt.subplots(dpi=150)
pts = [
#x, y, x_err, y_err, rho, scale
[0.5, 0.3, 0.04, 0.06, 0.5, 0.5],
[0.5, 0.3, 0.04, 0.06, 0.5, 1.8],
[0.5, 0.3, 0.04, 0.06, 0.5, 3.6],
[0.5, 0.3, 0.04, 0.06, 0.5, 6],
]
for pt in pts:
e_coords = error_ellipse(*pt)
e = mpl.patches.Polygon(e_coords, joinstyle='round', ls=':', fc='none', ec='C3', lw=1)
ax.add_patch(e)
ax.plot([0.1,0.9], [0.2, 0.7]);
ax.annotate('', xy=(0.5,0.3), xytext=(0.59,0.51), xycoords='data', arrowprops={'arrowstyle': '|-|'})
ax.annotate('Best fit\ndistance', xy=(0.56,0.3), xycoords='data', fontsize=12)
ax.annotate('Regression line', xy=(0.17,0.3), c='k', xycoords='data', rotation =31, fontsize=12);
ax.set_aspect('equal')
plt.savefig('output_14_0.png');
def get_bestfitdist(x, y, x_err, y_err, rho, fit):
shift_vec = np.matrix([[0,fit.y0]])
l0 = np.matrix([[1,fit.alpha]])
coords = np.array([[x,y]]) - shift_vec
a, b, theta = calc_ellipse_params(
x_err, y_err, rho)
ellipse_form = ellipse_formula(
x,y,a,b,theta)
scale_mx_1 = np.matrix([[1,0],[0,b/a]])
scale_mx_2 = np.matrix([[1,0],[0,a/b]])
rot_mx = lambda t: np.matrix([[np.cos(t), - np.sin(t)],
[np.sin(t), np.cos(t)]])
c_pp = (coords@ rot_mx(theta) @scale_mx_1).T
l0_pp = (l0@ rot_mx(theta) @scale_mx_1).T
l0_alpha = l0_pp[1,0]/l0_pp[0,0]
n_pp = np.matrix([[-l0_pp[1,0],l0_pp[0,0]]]).T
n_alpha = n_pp[1,0]/n_pp[0,0]
n_0 = c_pp[1,0] - c_pp[0,0]*n_alpha
x_intercept = n_0 / (l0_alpha-n_alpha)
c_adj_pp = np.matrix([[x_intercept,l0_alpha*x_intercept]])
n = ((n_pp.T * scale_mx_2) * rot_mx(-theta)) + shift_vec
n = n/np.linalg.norm(n)
c = ((c_pp.T * scale_mx_2) * rot_mx(-theta)) + shift_vec
c_adj = ((c_adj_pp * scale_mx_2) * rot_mx(-theta)) + shift_vec
theta_n = np.arccos(n[0,0])
ell_coords = ellipse_form(theta_n)
dir_95_conf = np.linalg.norm(np.array(c)[0]- np.array(ell_coords))
misfit = np.linalg.norm(c-c_adj) * (1 if c[0,0] >= c_adj[0,0] else -1)
return (c_adj, misfit, n, theta_n, dir_95_conf)
| 0.439026 | 0.941975 |
# Output Examples
This notebook is designed to provide examples of different types of outputs that can be used to test the JupyterLab frontend and other Jupyter frontends.
```
from IPython.display import display
from IPython.display import HTML, Image, Latex, Math, Markdown, SVG
```
## Text
Plain text:
```
text = """Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nullam urna
libero, dictum a egestas non, placerat vel neque. In imperdiet iaculis fermentum.
Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia
Curae; Cras augue tortor, tristique vitae varius nec, dictum eu lectus. Pellentesque
id eleifend eros. In non odio in lorem iaculis sollicitudin. In faucibus ante ut
arcu fringilla interdum. Maecenas elit nulla, imperdiet nec blandit et, consequat
ut elit."""
print(text)
```
Text as output:
```
text
```
Standard error:
```
import sys; print('this is stderr', file=sys.stderr)
```
## HTML
```
div = HTML('<div style="width:100px;height:100px;background:grey;" />')
div
for i in range(3):
print(10**10)
display(div)
```
## Markdown
```
md = Markdown("""
### Subtitle
This is some *markdown* text with math $F=ma$.
""")
md
display(md)
```
## LaTeX
Examples LaTeX in a markdown cell:
\begin{align}
\nabla \times \vec{\mathbf{B}} -\, \frac1c\, \frac{\partial\vec{\mathbf{E}}}{\partial t} & = \frac{4\pi}{c}\vec{\mathbf{j}} \\ \nabla \cdot \vec{\mathbf{E}} & = 4 \pi \rho \\
\nabla \times \vec{\mathbf{E}}\, +\, \frac1c\, \frac{\partial\vec{\mathbf{B}}}{\partial t} & = \vec{\mathbf{0}} \\
\nabla \cdot \vec{\mathbf{B}} & = 0
\end{align}
```
math = Latex("$F=ma$")
math
maxwells = Latex(r"""
\begin{align}
\nabla \times \vec{\mathbf{B}} -\, \frac1c\, \frac{\partial\vec{\mathbf{E}}}{\partial t} & = \frac{4\pi}{c}\vec{\mathbf{j}} \\ \nabla \cdot \vec{\mathbf{E}} & = 4 \pi \rho \\
\nabla \times \vec{\mathbf{E}}\, +\, \frac1c\, \frac{\partial\vec{\mathbf{B}}}{\partial t} & = \vec{\mathbf{0}} \\
\nabla \cdot \vec{\mathbf{B}} & = 0
\end{align}
""")
maxwells
```
## Image
```
img = Image("https://apod.nasa.gov/apod/image/1707/GreatWallMilkyWay_Yu_1686.jpg")
img
```
Set the image metadata:
```
img2 = Image(
"https://apod.nasa.gov/apod/image/1707/GreatWallMilkyWay_Yu_1686.jpg",
width=100,
height=200
)
img2
```
## SVG
```
svg_source = """
<svg width="400" height="110">
<rect width="300" height="100" style="fill:#E0E0E0;" />
</svg>
"""
svg = SVG(svg_source)
svg
for i in range(3):
print(10**10)
display(svg)
```
|
github_jupyter
|
from IPython.display import display
from IPython.display import HTML, Image, Latex, Math, Markdown, SVG
text = """Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nullam urna
libero, dictum a egestas non, placerat vel neque. In imperdiet iaculis fermentum.
Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia
Curae; Cras augue tortor, tristique vitae varius nec, dictum eu lectus. Pellentesque
id eleifend eros. In non odio in lorem iaculis sollicitudin. In faucibus ante ut
arcu fringilla interdum. Maecenas elit nulla, imperdiet nec blandit et, consequat
ut elit."""
print(text)
text
import sys; print('this is stderr', file=sys.stderr)
div = HTML('<div style="width:100px;height:100px;background:grey;" />')
div
for i in range(3):
print(10**10)
display(div)
md = Markdown("""
### Subtitle
This is some *markdown* text with math $F=ma$.
""")
md
display(md)
math = Latex("$F=ma$")
math
maxwells = Latex(r"""
\begin{align}
\nabla \times \vec{\mathbf{B}} -\, \frac1c\, \frac{\partial\vec{\mathbf{E}}}{\partial t} & = \frac{4\pi}{c}\vec{\mathbf{j}} \\ \nabla \cdot \vec{\mathbf{E}} & = 4 \pi \rho \\
\nabla \times \vec{\mathbf{E}}\, +\, \frac1c\, \frac{\partial\vec{\mathbf{B}}}{\partial t} & = \vec{\mathbf{0}} \\
\nabla \cdot \vec{\mathbf{B}} & = 0
\end{align}
""")
maxwells
img = Image("https://apod.nasa.gov/apod/image/1707/GreatWallMilkyWay_Yu_1686.jpg")
img
img2 = Image(
"https://apod.nasa.gov/apod/image/1707/GreatWallMilkyWay_Yu_1686.jpg",
width=100,
height=200
)
img2
svg_source = """
<svg width="400" height="110">
<rect width="300" height="100" style="fill:#E0E0E0;" />
</svg>
"""
svg = SVG(svg_source)
svg
for i in range(3):
print(10**10)
display(svg)
| 0.323487 | 0.929824 |
### Generate examples for DRS Passport revisions
```
from fasp.search import DiscoverySearchClient, Gen3ManifestClient
from fasp.loc import DRSMetaResolver
from fasp.runner import FASPRunner
faspRunner = FASPRunner(program='GTEX_TCGA_Federated_Analysis.ipynb')
runNote = 'GTEX and TCGA via FASPRunner'
```
Add comments
```
import json
# TCGA Query - CRDC
searchClient = DiscoverySearchClient('https://ga4gh-search-adapter-presto-public.prod.dnastack.com/')
queries = ["""
SELECT 'crdc:'||file_id drs_id
FROM search_cloud.cshcodeathon.gdc_rel24_filedata_active
where data_format = 'BAM'
and project_disease_type = 'Breast Invasive Carcinoma'
limit 3""",
"""
SELECT file_id drs_id
FROM search_cloud.cshcodeathon.gdc_rel24_filedata_active
where data_format = 'BAM'
and project_disease_type = 'Breast Invasive Carcinoma'
limit 3"""]
def getSeln(query):
res = searchClient.runQuery(query)
seln = []
for r in res:
seln.append(r[0])
#print(json.dumps(res[0:3][0], indent=4))
selection = {"selection":seln}
print(json.dumps(selection, indent=4))
for q in queries:
getSeln(q)
query = '''select 'crdc:'||drs_id
from search_cloud.cshcodeathon.gecco_gen3_drs_index i
join dbgap_demo.scr_gecco_susceptibility.sample_multi sa on sa.sample_id = i.sample_id
join dbgap_demo.scr_gecco_susceptibility.subject_phenotypes_multi su on su.dbgap_subject_id = sa.dbgap_subject_id
where age between 50 and 55
and affection_status = 'Case'
and file_type = 'cram' limit 3'''
getSeln(query)
query = '''select 'sradrs:'||sra_drs_id, sex, age
from search_cloud.cshcodeathon.gecco_sra_drs_index i
join dbgap_demo.scr_gecco_susceptibility.sample_multi sa on sa.sample_id = i.sample_id
join dbgap_demo.scr_gecco_susceptibility.subject_phenotypes_multi su on su.dbgap_subject_id = sa.dbgap_subject_id
where age between 50 and 55
and affection_status = 'Case'
and file_type = 'cram' limit 10'''
getSeln(query)
elixirQuery = "SELECT 'egadrs:'||fileid, filename FROM dbgap_demo.scr_ega.scr_egapancreatic_sample_multi p join dbgap_demo.scr_ega.scr_egapancreatic_files f on f.sample_primary_id = p.sample_primary_id where phenotype = 'pancreatic adenocarcinoma' limit 3"
getSeln(elixirQuery)
```
A Search and WES client are then set up to work with the Anvil data
The Search client here is a placeholder to search a local file. That file contains file ids downloaded as a manifest from the Gen3 Anvil portal. That list of files in that manifest had already been filtered to relevant samples. The anv: DRS prefix was added in an edited version of the file.
#Todo check what access_ids DRSMetaresolver is using for each run
```
from fasp.workflow import sbcgcWESClient
searchClient = Gen3ManifestClient('../fasp/data/gtex/gtex-cram-manifest_wCuries.json')
# drsClient No need to reset this. DRS Metasolver will pick the right client
#wesClient = sbWESClient(settings['SevenBridgesInstance'], settings['SevenBridgesProject'],
#'~/.keys/sbcgc_key.json')
wesClient = sbcgcWESClient(settings['SevenBridgesProject'])
faspRunner.configure(searchClient, drsClient, wesClient)
runList2 = faspRunner.runQuery(3, runNote)
```
|
github_jupyter
|
from fasp.search import DiscoverySearchClient, Gen3ManifestClient
from fasp.loc import DRSMetaResolver
from fasp.runner import FASPRunner
faspRunner = FASPRunner(program='GTEX_TCGA_Federated_Analysis.ipynb')
runNote = 'GTEX and TCGA via FASPRunner'
import json
# TCGA Query - CRDC
searchClient = DiscoverySearchClient('https://ga4gh-search-adapter-presto-public.prod.dnastack.com/')
queries = ["""
SELECT 'crdc:'||file_id drs_id
FROM search_cloud.cshcodeathon.gdc_rel24_filedata_active
where data_format = 'BAM'
and project_disease_type = 'Breast Invasive Carcinoma'
limit 3""",
"""
SELECT file_id drs_id
FROM search_cloud.cshcodeathon.gdc_rel24_filedata_active
where data_format = 'BAM'
and project_disease_type = 'Breast Invasive Carcinoma'
limit 3"""]
def getSeln(query):
res = searchClient.runQuery(query)
seln = []
for r in res:
seln.append(r[0])
#print(json.dumps(res[0:3][0], indent=4))
selection = {"selection":seln}
print(json.dumps(selection, indent=4))
for q in queries:
getSeln(q)
query = '''select 'crdc:'||drs_id
from search_cloud.cshcodeathon.gecco_gen3_drs_index i
join dbgap_demo.scr_gecco_susceptibility.sample_multi sa on sa.sample_id = i.sample_id
join dbgap_demo.scr_gecco_susceptibility.subject_phenotypes_multi su on su.dbgap_subject_id = sa.dbgap_subject_id
where age between 50 and 55
and affection_status = 'Case'
and file_type = 'cram' limit 3'''
getSeln(query)
query = '''select 'sradrs:'||sra_drs_id, sex, age
from search_cloud.cshcodeathon.gecco_sra_drs_index i
join dbgap_demo.scr_gecco_susceptibility.sample_multi sa on sa.sample_id = i.sample_id
join dbgap_demo.scr_gecco_susceptibility.subject_phenotypes_multi su on su.dbgap_subject_id = sa.dbgap_subject_id
where age between 50 and 55
and affection_status = 'Case'
and file_type = 'cram' limit 10'''
getSeln(query)
elixirQuery = "SELECT 'egadrs:'||fileid, filename FROM dbgap_demo.scr_ega.scr_egapancreatic_sample_multi p join dbgap_demo.scr_ega.scr_egapancreatic_files f on f.sample_primary_id = p.sample_primary_id where phenotype = 'pancreatic adenocarcinoma' limit 3"
getSeln(elixirQuery)
from fasp.workflow import sbcgcWESClient
searchClient = Gen3ManifestClient('../fasp/data/gtex/gtex-cram-manifest_wCuries.json')
# drsClient No need to reset this. DRS Metasolver will pick the right client
#wesClient = sbWESClient(settings['SevenBridgesInstance'], settings['SevenBridgesProject'],
#'~/.keys/sbcgc_key.json')
wesClient = sbcgcWESClient(settings['SevenBridgesProject'])
faspRunner.configure(searchClient, drsClient, wesClient)
runList2 = faspRunner.runQuery(3, runNote)
| 0.193642 | 0.44059 |
```
import pandas as pd
from sqlalchemy import create_engine
db="sqlite:///top2020.db"
engine = create_engine(db,echo=False)
df_entries = pd.read_sql_table('entries',engine)
df_albums = pd.read_sql_table('albums',engine,index_col='id')
df_users = pd.read_sql_table('users',engine,index_col='id')
df_genres = pd.read_sql_table('genres',engine,index_col='id')
def build_entries():
entries = pd.merge(df_entries, df_albums, left_on='album_id', right_on='id')
entries = pd.merge(entries, df_genres, left_on='genre_id', right_on='id')
return entries
entries = build_entries()
entries.head()
def format_entries(entries):
map = {
'id':'entry_id',
'user_id':'user_id',
'album_id':'album_id',
'name_y':'album',
'genre_id':'genre_id',
'name':'genre',
'position':'position',
'score':'score'
}
drop_cols = (x for x in entries.columns if x not in map.keys())
entries.drop(drop_cols, axis=1, inplace=True)
entries.rename(map, axis=1, inplace=True)
entries.set_index('entry_id', drop=False, inplace=True)
return entries
entries = format_entries(entries)
entries.head()
def build_album_results(entries):
aggfunc = {
'position': ['mean','min','max'],
'score': ['count','sum','mean','max','min']
}
album_stats = pd.pivot_table(entries, index = ['genre_id','genre','album_id','album'], values = ['score','position'], aggfunc=aggfunc)
album_ranking = album_stats.rank(method='dense',ascending=False)[('score','sum')]
album_genre_ranking = album_stats.groupby('genre_id').rank(method='dense',ascending=False)[('score','sum')]
album_results = pd.merge(album_stats, album_ranking, left_index=True, right_index=True)
album_results = pd.merge(album_results, album_genre_ranking, left_index=True, right_index=True)
album_results.reset_index(inplace=True)
return album_results
album_results = build_album_results(entries)
album_results.head()
def format_album_results(album_results):
album_results.columns = album_results.columns.map('|'.join).str.strip('|')
map = {
'score_y|sum':'rank',
'album_id':'album_id',
'album':'album',
'score|sum':'genre_rank',
'genre_id':'genre_id',
'genre':'genre',
'score_x|count':'nb_votes',
'score_x|sum':'total_score',
'score_x|mean':'mean_score',
'score_x|max':'highest_score',
'score_x|min':'lowest_score',
'position|mean':'mean_position',
'position|min':'highest_position',
'position|max':'lowest_position'
}
album_results = album_results.reindex(columns=map.keys())
drop_cols = (x for x in album_results.columns if x not in map.keys())
album_results.drop(drop_cols, axis=1, inplace=True)
album_results.rename(map, axis=1, inplace=True)
album_results.set_index('album_id', inplace=True, drop=True)
album_results.sort_values('rank', inplace=True)
return album_results
album_results = format_album_results(album_results)
album_results.head()
def extend_entries(entries, album_results):
album_keepcols = [
'album_id',
'total_score'
]
album_dropcols = (x for x in album_results.columns if x not in album_keepcols)
album_scores = album_results.drop(album_dropcols, axis=1)
full_entries = pd.merge(entries, album_scores, on='album_id')
full_entries = pd.merge(full_entries, df_users, left_on='user_id', right_on='id')
full_entries.set_index('entry_id', inplace=True)
cols = [
'user_id',
'name',
'album_id',
'album',
'genre_id',
'genre',
'top_size',
'position',
'score',
'total_score'
]
full_entries = full_entries.reindex(columns=cols)
return full_entries
full_entries = extend_entries(entries, album_results)
full_entries.head()
def compute_entry_stats(df):
df['pop_score'] = df['score'] * df['total_score'] / 1000
# idea for a future implementation
# df['pop_score'] = df['score'] * ( df['total_score'] - df['total_score'].quantile(q=0.666) ) / 1000
df['edgyness'] = df['top_size'] / df['pop_score']
df.sort_values('entry_id', inplace=True)
full_entries = compute_entry_stats(full_entries)
full_entries.head()
def compute_user_stats(full_entries):
user_genres = pd.pivot_table(full_entries, index=['name'], columns=['genre'], values=['score'], aggfunc=['sum'])
aggfunc = {
'pop_score': 'sum',
'edgyness': 'mean'
}
user_edgyness = pd.pivot_table(full_entries, index = ['name'], values=['pop_score','edgyness'], aggfunc=aggfunc)
user_edgyness.sort_values(('edgyness'), ascending=False, inplace=True)
return user_genres,user_edgyness
user_genres, user_edgyness = compute_user_stats(full_entries)
user_edgyness.head(20)
user_genres.head(20)
def compute_genre_stats(df):
genre_stats = pd.pivot_table(df, index=['genre'], values=['nb_votes','total_score'], aggfunc=['sum'])
genre_stats.sort_values(('sum','nb_votes'), ascending=False, inplace=True)
genre_stats['weight'] = genre_stats[('sum','total_score')] * 100.0 / genre_stats[('sum','total_score')].sum()
return genre_stats
genre_stats = compute_genre_stats(album_results)
genre_stats.head(20)
```
|
github_jupyter
|
import pandas as pd
from sqlalchemy import create_engine
db="sqlite:///top2020.db"
engine = create_engine(db,echo=False)
df_entries = pd.read_sql_table('entries',engine)
df_albums = pd.read_sql_table('albums',engine,index_col='id')
df_users = pd.read_sql_table('users',engine,index_col='id')
df_genres = pd.read_sql_table('genres',engine,index_col='id')
def build_entries():
entries = pd.merge(df_entries, df_albums, left_on='album_id', right_on='id')
entries = pd.merge(entries, df_genres, left_on='genre_id', right_on='id')
return entries
entries = build_entries()
entries.head()
def format_entries(entries):
map = {
'id':'entry_id',
'user_id':'user_id',
'album_id':'album_id',
'name_y':'album',
'genre_id':'genre_id',
'name':'genre',
'position':'position',
'score':'score'
}
drop_cols = (x for x in entries.columns if x not in map.keys())
entries.drop(drop_cols, axis=1, inplace=True)
entries.rename(map, axis=1, inplace=True)
entries.set_index('entry_id', drop=False, inplace=True)
return entries
entries = format_entries(entries)
entries.head()
def build_album_results(entries):
aggfunc = {
'position': ['mean','min','max'],
'score': ['count','sum','mean','max','min']
}
album_stats = pd.pivot_table(entries, index = ['genre_id','genre','album_id','album'], values = ['score','position'], aggfunc=aggfunc)
album_ranking = album_stats.rank(method='dense',ascending=False)[('score','sum')]
album_genre_ranking = album_stats.groupby('genre_id').rank(method='dense',ascending=False)[('score','sum')]
album_results = pd.merge(album_stats, album_ranking, left_index=True, right_index=True)
album_results = pd.merge(album_results, album_genre_ranking, left_index=True, right_index=True)
album_results.reset_index(inplace=True)
return album_results
album_results = build_album_results(entries)
album_results.head()
def format_album_results(album_results):
album_results.columns = album_results.columns.map('|'.join).str.strip('|')
map = {
'score_y|sum':'rank',
'album_id':'album_id',
'album':'album',
'score|sum':'genre_rank',
'genre_id':'genre_id',
'genre':'genre',
'score_x|count':'nb_votes',
'score_x|sum':'total_score',
'score_x|mean':'mean_score',
'score_x|max':'highest_score',
'score_x|min':'lowest_score',
'position|mean':'mean_position',
'position|min':'highest_position',
'position|max':'lowest_position'
}
album_results = album_results.reindex(columns=map.keys())
drop_cols = (x for x in album_results.columns if x not in map.keys())
album_results.drop(drop_cols, axis=1, inplace=True)
album_results.rename(map, axis=1, inplace=True)
album_results.set_index('album_id', inplace=True, drop=True)
album_results.sort_values('rank', inplace=True)
return album_results
album_results = format_album_results(album_results)
album_results.head()
def extend_entries(entries, album_results):
album_keepcols = [
'album_id',
'total_score'
]
album_dropcols = (x for x in album_results.columns if x not in album_keepcols)
album_scores = album_results.drop(album_dropcols, axis=1)
full_entries = pd.merge(entries, album_scores, on='album_id')
full_entries = pd.merge(full_entries, df_users, left_on='user_id', right_on='id')
full_entries.set_index('entry_id', inplace=True)
cols = [
'user_id',
'name',
'album_id',
'album',
'genre_id',
'genre',
'top_size',
'position',
'score',
'total_score'
]
full_entries = full_entries.reindex(columns=cols)
return full_entries
full_entries = extend_entries(entries, album_results)
full_entries.head()
def compute_entry_stats(df):
df['pop_score'] = df['score'] * df['total_score'] / 1000
# idea for a future implementation
# df['pop_score'] = df['score'] * ( df['total_score'] - df['total_score'].quantile(q=0.666) ) / 1000
df['edgyness'] = df['top_size'] / df['pop_score']
df.sort_values('entry_id', inplace=True)
full_entries = compute_entry_stats(full_entries)
full_entries.head()
def compute_user_stats(full_entries):
user_genres = pd.pivot_table(full_entries, index=['name'], columns=['genre'], values=['score'], aggfunc=['sum'])
aggfunc = {
'pop_score': 'sum',
'edgyness': 'mean'
}
user_edgyness = pd.pivot_table(full_entries, index = ['name'], values=['pop_score','edgyness'], aggfunc=aggfunc)
user_edgyness.sort_values(('edgyness'), ascending=False, inplace=True)
return user_genres,user_edgyness
user_genres, user_edgyness = compute_user_stats(full_entries)
user_edgyness.head(20)
user_genres.head(20)
def compute_genre_stats(df):
genre_stats = pd.pivot_table(df, index=['genre'], values=['nb_votes','total_score'], aggfunc=['sum'])
genre_stats.sort_values(('sum','nb_votes'), ascending=False, inplace=True)
genre_stats['weight'] = genre_stats[('sum','total_score')] * 100.0 / genre_stats[('sum','total_score')].sum()
return genre_stats
genre_stats = compute_genre_stats(album_results)
genre_stats.head(20)
| 0.519765 | 0.194291 |
Figures for Estuarine Exchange Paper
```
from salishsea_tools import nc_tools, viz_tools
from cmocean import cm
import matplotlib.pyplot as plt
from mpl_toolkits.basemap import Basemap
from matplotlib.patches import Rectangle
import netCDF4 as nc
from scipy.io import loadmat
import numpy as np
import xarray as xr
%matplotlib inline
```
## Map ##
copied heavily from http://nbviewer.jupyter.org/urls/bitbucket.org/salishsea/analysis-ben/raw/tip/notebooks/Maps.ipynb
```
plt.rcParams['font.size'] = 14
def plot_annotations(ax, m, annotations, zorder=None):
"""
"""
# Plot Locations
for annotation_label, annotation in annotations.items():
ax.text(*annotation['text'], annotation_label, transform=ax.transAxes,
fontsize=annotation['font']+1, rotation=annotation['rotate'], zorder=zorder)
if annotation['marker'] is not None:
x, y = m(*annotation['marker'])
ax.plot(x, y, 'ko', markersize=8, markerfacecolor=annotation['color'], zorder=zorder)
if annotation['arrow'] is not None:
ax.arrow(*annotation['arrow'], head_width=0.01, fc='k', transform=ax.transAxes, zorder=zorder)
def plot_basemap(ax, w_map, lons=None, lats=None, offset=[None, None], zorder=[0, 1, 2]):
"""
"""
# Define map window
lon_0 = (w_map[1] - w_map[0]) / 2 + w_map[0]
lat_0 = (w_map[3] - w_map[2]) / 2 + w_map[2]
# Make projection
m = Basemap(projection='lcc', resolution='h',
lon_0=lon_0, lat_0=lat_0,
llcrnrlon=w_map[0], urcrnrlon=w_map[1],
llcrnrlat=w_map[2], urcrnrlat=w_map[3], ax=ax)
# Default lon/lat intervals
if lons is None:
lons = np.floor([w_map[0], w_map[1] + 1])
if lats is None:
lats = np.floor([w_map[2], w_map[3] + 1])
# Add features and labels
m.drawcoastlines(zorder=zorder[1])
m.fillcontinents(color='Burlywood', zorder=zorder[0])
m.drawmeridians(np.arange(*lons), labels=[0, 0, 1, 0], color='dimgray', yoffset=offset[1], zorder=zorder[2])
m.drawparallels(np.arange(*lats), labels=[0, 1, 0, 0], color='dimgray', xoffset=offset[0], zorder=zorder[2])
return m
def plot_thalweg(ax, T_lon, T_lat):
lines = np.loadtxt('/home/sallen/MEOPAR/Tools/bathymetry/thalweg_working.txt', delimiter=" ", unpack=False)
lines = lines.astype(int)
thalweg_lon = T_lon[lines[:,0],lines[:,1]]
thalweg_lat = T_lat[lines[:,0],lines[:,1]]
ax.plot(thalweg_lon, thalweg_lat, 'r')
# Victoria_sill_j = 178-1;
# Victoria_sill_i = np.arange(235,302+1)-1
# vs_lon = T_lon[Victoria_sill_i, Victoria_sill_j]
# vs_lat = T_lat[Victoria_sill_i, Victoria_sill_j]
# ax.plot(vs_lon, vs_lat, 'b')
# ax.plot(thalweg_lon[1480], thalweg_lat[1480], 'r*')
# ax.plot(thalweg_lon[1539], thalweg_lat[1539], 'ro')
def plot_map(ax, cst, bounds, grid, grid_old, T, w_map = [-127, -121, 46.5, 51.5]):
"""Plot Strait of Georgia study area on Basemap object
"""
# Plot Basemap
m = plot_basemap(ax, w_map, offset=[-30000, -15000], zorder=[0, 1, 7])
# Plot Fraser River
for bound in bounds:
i_old = 0
for i in np.argwhere(np.isnan(cst['ncst'][bound[0]:bound[1], 1]))[:, 0]:
x, y = m(cst['ncst'][bound[0]:bound[1], 0][i_old:i],
cst['ncst'][bound[0]:bound[1], 1][i_old:i])
ax.plot(x, y, 'k-')
i_old = i + 1
# Convert lon/lat to x, y
x, y = m(grid['nav_lon'].values, grid['nav_lat'].values)
# Overlay model domain
C = ax.contourf(x, y, T['vosaline'].isel(time_counter=23, deptht=0), range(21, 34), cmap='BrBG_r', extend='both', zorder=2)
ax.contourf(x, y, grid['Bathymetry'], [-0.01, 0.01], colors='dimgray', zorder=3)
ax.contourf(x, y, grid_old['Bathymetry'], [-0.01, 0.01], colors='lightgray', zorder=3)
ax.contour( x, y, grid_old['Bathymetry'], [0], colors='Black', zorder=4)
# Colorbar
fig.subplots_adjust(bottom=0.15)
cax = fig.add_axes([0.15, 0.1, 0.73, 0.01])
cbar = fig.colorbar(C, cax=cax, orientation='horizontal', label='Salinity [g/kg]')
cbar.set_label(label='Salinity [g/kg]', size=14)
cbar.ax.set_yticklabels(cbar.ax.get_yticklabels(), size=14)
#cbar.set_ticks(range(0, 550, 50))
# Box around model domain
ax.plot(x[ :, 0], y[ :, 0], 'k-', zorder=6)
ax.plot(x[ :, -1], y[ :, -1], 'k-', zorder=6)
ax.plot(x[ 0, :], y[ 0, :], 'k-', zorder=6)
ax.plot(x[-1, :], y[-1, :], 'k-', zorder=6)
# Define Significant Landmarks and Locations
annotations = {
'Pacific\nOcean' : {'text': [0.10, 0.250], 'font': 14, 'rotate': 0, 'color': 'r', 'marker': None, 'arrow': None},
'British\nColumbia' : {'text': [0.65, 0.850], 'font': 14, 'rotate': 0, 'color': 'r', 'marker': None, 'arrow': None},
'Washington\nState' : {'text': [0.70, 0.030], 'font': 14, 'rotate': 0, 'color': 'r', 'marker': None, 'arrow': None},
# 'Strait of Georgia' : {'text': [0.50, 0.575], 'font': 13, 'rotate': -40, 'color': 'r', 'marker': None, 'arrow': None},
# 'Juan de Fuca Strait': {'text': [0.36, 0.400], 'font': 13, 'rotate': -21, 'color': 'r', 'marker': None, 'arrow': None},
'Fraser River' : {'text': [0.80, 0.530], 'font': 13, 'rotate': 15, 'color': 'r', 'marker': None, 'arrow': None},
'Puget\nSound' : {'text': [0.60, 0.120], 'font': 13, 'rotate': 0, 'color': 'r', 'marker': None, 'arrow': None},
'Vancouver' : {'text': [0.68, 0.550], 'font': 12, 'rotate': 0, 'color': 'r', 'marker': [-123.10, 49.25], 'arrow': None},
'Victoria' : {'text': [0.53, 0.380], 'font': 12, 'rotate': 0, 'color': 'r', 'marker': [-123.37, 48.43], 'arrow': None},
'Seattle' : {'text': [0.81, 0.230], 'font': 12, 'rotate': 0, 'color': 'r', 'marker': [-122.33, 47.61], 'arrow': None},
}
# Timestamp
ax.text(0.02, 0.01, '3 September 2017 2330 UTC', transform=ax.transAxes)
# Plot Annotations
plot_annotations(ax, m, annotations, zorder=7)
# Plot Thalweg
# plot_thalweg(ax, x, y)
# Load NEMO grid
grid_NEMO = xr.open_dataset(
'/home/sallen/MEOPAR/sea_initial/bathymetry_201803b.nc', mask_and_scale=False)
grid_OLD = xr.open_dataset(
'/home/sallen/MEOPAR/grid/bathymetry_201702.nc', mask_and_scale=False)
#T_NEMO = xr.open_dataset('/data/sallen/results/MEOPAR/new_waves/part2_06apr17/SalishSea_1h_20170406_20170505_grid_T_20170415-20170415.nc')
T_NEMO = xr.open_dataset('/results2/SalishSea/nowcast-green.201806/03sep17/SalishSea_1h_20170903_20170903_grid_T.nc')
# Load Fraser coastline
PNWrivers = loadmat('/ocean/rich/more/mmapbase/bcgeo/PNWrivers.mat')
# Define Fraser coastline regions
bounds = [[0, 26000], [61500, 77000], [107500, 114000], [200000, 203000], [326000, 327000]]
# Make figure window
fig, ax = plt.subplots(1, 1, figsize=(10, 13))
# Plot Model Domain (using new bathy)
#plot_map(ax, PNWrivers, bounds, grid_NEMO, grid_OLD, T_NEMO)
# Plot Model Domain using only base bathymetry
plot_map(ax, PNWrivers, bounds, grid_OLD, grid_OLD, T_NEMO)
plt.savefig('allen_map_19aug19.png')
plt.savefig('allen_map_19aug19.pdf')
# Define Fraser coastline regions
bounds = [[0, 26000], [61500, 77000], [107500, 114000], [200000, 203000], [326000, 327000]]
# Make figure window
fig, ax = plt.subplots(1, 1, figsize=(10, 13))
# Plot Model Domain
plot_map(ax, PNWrivers, bounds, grid_NEMO, grid_NEMO, T_NEMO, w_map = [-124, -122, 48, 49.2])
fig, ax = plt.subplots(1, 1)
x=1;y=1
plot_mudflats(ax, x, y)
```
|
github_jupyter
|
from salishsea_tools import nc_tools, viz_tools
from cmocean import cm
import matplotlib.pyplot as plt
from mpl_toolkits.basemap import Basemap
from matplotlib.patches import Rectangle
import netCDF4 as nc
from scipy.io import loadmat
import numpy as np
import xarray as xr
%matplotlib inline
plt.rcParams['font.size'] = 14
def plot_annotations(ax, m, annotations, zorder=None):
"""
"""
# Plot Locations
for annotation_label, annotation in annotations.items():
ax.text(*annotation['text'], annotation_label, transform=ax.transAxes,
fontsize=annotation['font']+1, rotation=annotation['rotate'], zorder=zorder)
if annotation['marker'] is not None:
x, y = m(*annotation['marker'])
ax.plot(x, y, 'ko', markersize=8, markerfacecolor=annotation['color'], zorder=zorder)
if annotation['arrow'] is not None:
ax.arrow(*annotation['arrow'], head_width=0.01, fc='k', transform=ax.transAxes, zorder=zorder)
def plot_basemap(ax, w_map, lons=None, lats=None, offset=[None, None], zorder=[0, 1, 2]):
"""
"""
# Define map window
lon_0 = (w_map[1] - w_map[0]) / 2 + w_map[0]
lat_0 = (w_map[3] - w_map[2]) / 2 + w_map[2]
# Make projection
m = Basemap(projection='lcc', resolution='h',
lon_0=lon_0, lat_0=lat_0,
llcrnrlon=w_map[0], urcrnrlon=w_map[1],
llcrnrlat=w_map[2], urcrnrlat=w_map[3], ax=ax)
# Default lon/lat intervals
if lons is None:
lons = np.floor([w_map[0], w_map[1] + 1])
if lats is None:
lats = np.floor([w_map[2], w_map[3] + 1])
# Add features and labels
m.drawcoastlines(zorder=zorder[1])
m.fillcontinents(color='Burlywood', zorder=zorder[0])
m.drawmeridians(np.arange(*lons), labels=[0, 0, 1, 0], color='dimgray', yoffset=offset[1], zorder=zorder[2])
m.drawparallels(np.arange(*lats), labels=[0, 1, 0, 0], color='dimgray', xoffset=offset[0], zorder=zorder[2])
return m
def plot_thalweg(ax, T_lon, T_lat):
lines = np.loadtxt('/home/sallen/MEOPAR/Tools/bathymetry/thalweg_working.txt', delimiter=" ", unpack=False)
lines = lines.astype(int)
thalweg_lon = T_lon[lines[:,0],lines[:,1]]
thalweg_lat = T_lat[lines[:,0],lines[:,1]]
ax.plot(thalweg_lon, thalweg_lat, 'r')
# Victoria_sill_j = 178-1;
# Victoria_sill_i = np.arange(235,302+1)-1
# vs_lon = T_lon[Victoria_sill_i, Victoria_sill_j]
# vs_lat = T_lat[Victoria_sill_i, Victoria_sill_j]
# ax.plot(vs_lon, vs_lat, 'b')
# ax.plot(thalweg_lon[1480], thalweg_lat[1480], 'r*')
# ax.plot(thalweg_lon[1539], thalweg_lat[1539], 'ro')
def plot_map(ax, cst, bounds, grid, grid_old, T, w_map = [-127, -121, 46.5, 51.5]):
"""Plot Strait of Georgia study area on Basemap object
"""
# Plot Basemap
m = plot_basemap(ax, w_map, offset=[-30000, -15000], zorder=[0, 1, 7])
# Plot Fraser River
for bound in bounds:
i_old = 0
for i in np.argwhere(np.isnan(cst['ncst'][bound[0]:bound[1], 1]))[:, 0]:
x, y = m(cst['ncst'][bound[0]:bound[1], 0][i_old:i],
cst['ncst'][bound[0]:bound[1], 1][i_old:i])
ax.plot(x, y, 'k-')
i_old = i + 1
# Convert lon/lat to x, y
x, y = m(grid['nav_lon'].values, grid['nav_lat'].values)
# Overlay model domain
C = ax.contourf(x, y, T['vosaline'].isel(time_counter=23, deptht=0), range(21, 34), cmap='BrBG_r', extend='both', zorder=2)
ax.contourf(x, y, grid['Bathymetry'], [-0.01, 0.01], colors='dimgray', zorder=3)
ax.contourf(x, y, grid_old['Bathymetry'], [-0.01, 0.01], colors='lightgray', zorder=3)
ax.contour( x, y, grid_old['Bathymetry'], [0], colors='Black', zorder=4)
# Colorbar
fig.subplots_adjust(bottom=0.15)
cax = fig.add_axes([0.15, 0.1, 0.73, 0.01])
cbar = fig.colorbar(C, cax=cax, orientation='horizontal', label='Salinity [g/kg]')
cbar.set_label(label='Salinity [g/kg]', size=14)
cbar.ax.set_yticklabels(cbar.ax.get_yticklabels(), size=14)
#cbar.set_ticks(range(0, 550, 50))
# Box around model domain
ax.plot(x[ :, 0], y[ :, 0], 'k-', zorder=6)
ax.plot(x[ :, -1], y[ :, -1], 'k-', zorder=6)
ax.plot(x[ 0, :], y[ 0, :], 'k-', zorder=6)
ax.plot(x[-1, :], y[-1, :], 'k-', zorder=6)
# Define Significant Landmarks and Locations
annotations = {
'Pacific\nOcean' : {'text': [0.10, 0.250], 'font': 14, 'rotate': 0, 'color': 'r', 'marker': None, 'arrow': None},
'British\nColumbia' : {'text': [0.65, 0.850], 'font': 14, 'rotate': 0, 'color': 'r', 'marker': None, 'arrow': None},
'Washington\nState' : {'text': [0.70, 0.030], 'font': 14, 'rotate': 0, 'color': 'r', 'marker': None, 'arrow': None},
# 'Strait of Georgia' : {'text': [0.50, 0.575], 'font': 13, 'rotate': -40, 'color': 'r', 'marker': None, 'arrow': None},
# 'Juan de Fuca Strait': {'text': [0.36, 0.400], 'font': 13, 'rotate': -21, 'color': 'r', 'marker': None, 'arrow': None},
'Fraser River' : {'text': [0.80, 0.530], 'font': 13, 'rotate': 15, 'color': 'r', 'marker': None, 'arrow': None},
'Puget\nSound' : {'text': [0.60, 0.120], 'font': 13, 'rotate': 0, 'color': 'r', 'marker': None, 'arrow': None},
'Vancouver' : {'text': [0.68, 0.550], 'font': 12, 'rotate': 0, 'color': 'r', 'marker': [-123.10, 49.25], 'arrow': None},
'Victoria' : {'text': [0.53, 0.380], 'font': 12, 'rotate': 0, 'color': 'r', 'marker': [-123.37, 48.43], 'arrow': None},
'Seattle' : {'text': [0.81, 0.230], 'font': 12, 'rotate': 0, 'color': 'r', 'marker': [-122.33, 47.61], 'arrow': None},
}
# Timestamp
ax.text(0.02, 0.01, '3 September 2017 2330 UTC', transform=ax.transAxes)
# Plot Annotations
plot_annotations(ax, m, annotations, zorder=7)
# Plot Thalweg
# plot_thalweg(ax, x, y)
# Load NEMO grid
grid_NEMO = xr.open_dataset(
'/home/sallen/MEOPAR/sea_initial/bathymetry_201803b.nc', mask_and_scale=False)
grid_OLD = xr.open_dataset(
'/home/sallen/MEOPAR/grid/bathymetry_201702.nc', mask_and_scale=False)
#T_NEMO = xr.open_dataset('/data/sallen/results/MEOPAR/new_waves/part2_06apr17/SalishSea_1h_20170406_20170505_grid_T_20170415-20170415.nc')
T_NEMO = xr.open_dataset('/results2/SalishSea/nowcast-green.201806/03sep17/SalishSea_1h_20170903_20170903_grid_T.nc')
# Load Fraser coastline
PNWrivers = loadmat('/ocean/rich/more/mmapbase/bcgeo/PNWrivers.mat')
# Define Fraser coastline regions
bounds = [[0, 26000], [61500, 77000], [107500, 114000], [200000, 203000], [326000, 327000]]
# Make figure window
fig, ax = plt.subplots(1, 1, figsize=(10, 13))
# Plot Model Domain (using new bathy)
#plot_map(ax, PNWrivers, bounds, grid_NEMO, grid_OLD, T_NEMO)
# Plot Model Domain using only base bathymetry
plot_map(ax, PNWrivers, bounds, grid_OLD, grid_OLD, T_NEMO)
plt.savefig('allen_map_19aug19.png')
plt.savefig('allen_map_19aug19.pdf')
# Define Fraser coastline regions
bounds = [[0, 26000], [61500, 77000], [107500, 114000], [200000, 203000], [326000, 327000]]
# Make figure window
fig, ax = plt.subplots(1, 1, figsize=(10, 13))
# Plot Model Domain
plot_map(ax, PNWrivers, bounds, grid_NEMO, grid_NEMO, T_NEMO, w_map = [-124, -122, 48, 49.2])
fig, ax = plt.subplots(1, 1)
x=1;y=1
plot_mudflats(ax, x, y)
| 0.726814 | 0.783243 |
# Metadata
```
Course: DS5001
Module: 098 Lab
Topic: Gibbs Sampler
Author: R.C. Alvarado
Purpose: We develop an LDA topic modeler using collapsed Gibbs sample as described by [Griffiths and Steyvers (2004)].
```
## Setup
```
import pandas as pd
import numpy as np
from tqdm import tqdm
import re
from nltk.corpus import stopwords
```
## Functions
### Convert Corpus
We convert the list of token lists (DOC) into TOKEN and VOCAB tables.
```
class Corpus():
def __init__(self, doclist):
self.docs = doclist
# Create DOC table from F1 doclist
self.DOC = pd.DataFrame(doclist, columns=['doc_str'])
self.DOC.index.name = 'doc_id'
self.DOC
# Convert docs into tokens
stop_words = set(stopwords.words('english'))
tokens = []
for i, doc in enumerate(doclist):
for j, token in enumerate(doc.split()):
term_str = re.sub(r'[\W_]+', '', token).lower()
if term_str not in stop_words:
tokens.append((i, j, term_str))
self.TOKEN = pd.DataFrame(tokens, columns=['doc_id','token_num','term_str'])\
.set_index(['doc_id','token_num'])
# Extract vocabulary
self.VOCAB = self.TOKEN.term_str.value_counts().to_frame('n')
self.VOCAB.index.name = 'term_str'
```
### Gibbs Sampler
We sample each document and word combination in the BOW table. In each case,
we are looking for two values:
* the topic with which a word has been most frequently labeled
* the topic with which the document has the most labeled words
We combine these values in order to align the label of the current word with the rest of the data.\
If a the topic is highly associated with both the word and the document, then that topic will get a high value.
Note that all that is going on here is a sorting operation -- the random assignment does not predict anything.\
Instead, we are just gathering words under topics and topics under documents.
**From Darling 2011:**
<hr />
<div style="float:left;">
<img src="images/gibbs-algo-text.png" width="650px" />
<img src="images/gibbs-algo.png" width="650px" />
</div>
```
class GibbsSampler():
n_topics:int = 10
n_iters:int = 100
a:float = 1.
b:float = .1
# See Griffiths and Steyvers 2004
# a = 1 # 50 / n_topics
# b = .1 # 200 / W
def __init__(self, corpus:Corpus):
self.corpus = corpus
self.N = len(corpus.TOKEN)
self.W = len(corpus.VOCAB)
def _estimate_z(self, row):
# Get row elements
d = row.name[0] # Current document
z = row.topic_id # Current assigned topic
w = row.term_str # Current term
# Zero out the current topic assignment
# We want current state of everything else
row[z] = 0
# Number of words assigned to each topic k in the document -- C(w|d,k)
n_dk = self.Z.loc[d, self.zcols].sum()
# Number of times word w is assigned to each topic -- C(w|k)
n_kw = self.Z.loc[self.Z.term_str == w, self.zcols].sum()
# Number of times any word is assigned to each topic -- C(W|k)
n_k = self.Z[self.zcols].sum()
# Generate probalities
# Note formula involves a LOCAL and a GLOBAL measure, kinda like TF-IDF
pz = (n_dk + self.a) * ((n_kw + self.b) / (n_k + self.b * self.W))
# Sample to get new z
z2 = pz.sample().index[0]
# Update the token assignment (redundantly)
row[z2] = 1
row.topic_id = z2
def generate_model(self):
# Create topics table
self.zcols = range(self.n_topics)
self.topics = pd.DataFrame(index=self.zcols)
# Randomly assign topics to toknes
self.corpus.TOKEN['topic_id'] = self.topics.sample(self.N, replace=True).index
# Create one-hot-encoding topic columns for easier computation
self.Z = pd.concat([self.corpus.TOKEN, pd.get_dummies(self.corpus.TOKEN.topic_id)], axis=1)
# Iterate
for x in tqdm(range(self.n_iters)):
self.Z.apply(self._estimate_z, 1)
# Create topic model tables
self.topics['n_tokens'] = self.Z.value_counts('topic_id')
self.theta = self.Z.value_counts(['doc_id','topic_id']).unstack(fill_value=0)
self.phi = self.Z.value_counts(['term_str','topic_id']).unstack(fill_value=0)
self.theta = (self.theta.T / self.theta.T.sum()).T
# Get top words for each topic
self.topics['top_terms'] = self.topics\
.apply(lambda x: self.phi.loc[self.phi[x.name] > 0, x.name]\
.sort_values(ascending=False)\
.head().index.to_list(), 1)
```
## Demo 1
We use a toy example to see if the method works.\
Because our codd is not vert efficient, we just
### Data
A small F1 corpus.
```
raw_docs = """
I ate a banana and a spinach smoothie for breakfast.
I like to eat broccoli and bananas.
Chinchillas and kittens are cute.
My sister adopted a kitten yesterday.
Look at this cute hamster munching on a piece of broccoli.
""".split("\n")[1:-1]
```
### Process
```
pd.options.mode.chained_assignment = None
corpus1 = Corpus(raw_docs)
model1 = GibbsSampler(corpus1)
model1.n_topics = 2
model1.n_iters = 1000
model1.generate_model()
model1.topics
```
## Demo 2
### Data
```
some_documents = [
["Hadoop", "Big Data", "HBase", "Java", "Spark", "Storm", "Cassandra"],
["NoSQL", "MongoDB", "Cassandra", "HBase", "Postgres"],
["Python", "scikit-learn", "scipy", "numpy", "statsmodels", "pandas"],
["R", "Python", "statistics", "regression", "probability"],
["machine learning", "regression", "decision trees", "libsvm"],
["Python", "R", "Java", "C++", "Haskell", "programming languages"],
["statistics", "probability", "mathematics", "theory"],
["machine learning", "scikit-learn", "Mahout", "neural networks"],
["neural networks", "deep learning", "Big Data", "artificial intelligence"],
["Hadoop", "Java", "MapReduce", "Big Data"],
["statistics", "R", "statsmodels"],
["C++", "deep learning", "artificial intelligence", "probability"],
["pandas", "R", "Python"],
["databases", "HBase", "Postgres", "MySQL", "MongoDB"],
["libsvm", "regression", "support vector machines"]
]
raw_docs2 = [' '.join(item) for item in some_documents]
```
### Process
```
corpus2 = Corpus(raw_docs2)
model2 = GibbsSampler(corpus2)
model2.n_topics = 10
model2.n_iters = 200
model2.generate_model()
model2.topics
corpus2.DOC.join(model2.theta).style.background_gradient(cmap='GnBu', high=.5, axis=1)
model2.topics.sort_values('n_tokens', ascending=False).style.bar()
```
|
github_jupyter
|
Course: DS5001
Module: 098 Lab
Topic: Gibbs Sampler
Author: R.C. Alvarado
Purpose: We develop an LDA topic modeler using collapsed Gibbs sample as described by [Griffiths and Steyvers (2004)].
import pandas as pd
import numpy as np
from tqdm import tqdm
import re
from nltk.corpus import stopwords
class Corpus():
def __init__(self, doclist):
self.docs = doclist
# Create DOC table from F1 doclist
self.DOC = pd.DataFrame(doclist, columns=['doc_str'])
self.DOC.index.name = 'doc_id'
self.DOC
# Convert docs into tokens
stop_words = set(stopwords.words('english'))
tokens = []
for i, doc in enumerate(doclist):
for j, token in enumerate(doc.split()):
term_str = re.sub(r'[\W_]+', '', token).lower()
if term_str not in stop_words:
tokens.append((i, j, term_str))
self.TOKEN = pd.DataFrame(tokens, columns=['doc_id','token_num','term_str'])\
.set_index(['doc_id','token_num'])
# Extract vocabulary
self.VOCAB = self.TOKEN.term_str.value_counts().to_frame('n')
self.VOCAB.index.name = 'term_str'
class GibbsSampler():
n_topics:int = 10
n_iters:int = 100
a:float = 1.
b:float = .1
# See Griffiths and Steyvers 2004
# a = 1 # 50 / n_topics
# b = .1 # 200 / W
def __init__(self, corpus:Corpus):
self.corpus = corpus
self.N = len(corpus.TOKEN)
self.W = len(corpus.VOCAB)
def _estimate_z(self, row):
# Get row elements
d = row.name[0] # Current document
z = row.topic_id # Current assigned topic
w = row.term_str # Current term
# Zero out the current topic assignment
# We want current state of everything else
row[z] = 0
# Number of words assigned to each topic k in the document -- C(w|d,k)
n_dk = self.Z.loc[d, self.zcols].sum()
# Number of times word w is assigned to each topic -- C(w|k)
n_kw = self.Z.loc[self.Z.term_str == w, self.zcols].sum()
# Number of times any word is assigned to each topic -- C(W|k)
n_k = self.Z[self.zcols].sum()
# Generate probalities
# Note formula involves a LOCAL and a GLOBAL measure, kinda like TF-IDF
pz = (n_dk + self.a) * ((n_kw + self.b) / (n_k + self.b * self.W))
# Sample to get new z
z2 = pz.sample().index[0]
# Update the token assignment (redundantly)
row[z2] = 1
row.topic_id = z2
def generate_model(self):
# Create topics table
self.zcols = range(self.n_topics)
self.topics = pd.DataFrame(index=self.zcols)
# Randomly assign topics to toknes
self.corpus.TOKEN['topic_id'] = self.topics.sample(self.N, replace=True).index
# Create one-hot-encoding topic columns for easier computation
self.Z = pd.concat([self.corpus.TOKEN, pd.get_dummies(self.corpus.TOKEN.topic_id)], axis=1)
# Iterate
for x in tqdm(range(self.n_iters)):
self.Z.apply(self._estimate_z, 1)
# Create topic model tables
self.topics['n_tokens'] = self.Z.value_counts('topic_id')
self.theta = self.Z.value_counts(['doc_id','topic_id']).unstack(fill_value=0)
self.phi = self.Z.value_counts(['term_str','topic_id']).unstack(fill_value=0)
self.theta = (self.theta.T / self.theta.T.sum()).T
# Get top words for each topic
self.topics['top_terms'] = self.topics\
.apply(lambda x: self.phi.loc[self.phi[x.name] > 0, x.name]\
.sort_values(ascending=False)\
.head().index.to_list(), 1)
raw_docs = """
I ate a banana and a spinach smoothie for breakfast.
I like to eat broccoli and bananas.
Chinchillas and kittens are cute.
My sister adopted a kitten yesterday.
Look at this cute hamster munching on a piece of broccoli.
""".split("\n")[1:-1]
pd.options.mode.chained_assignment = None
corpus1 = Corpus(raw_docs)
model1 = GibbsSampler(corpus1)
model1.n_topics = 2
model1.n_iters = 1000
model1.generate_model()
model1.topics
some_documents = [
["Hadoop", "Big Data", "HBase", "Java", "Spark", "Storm", "Cassandra"],
["NoSQL", "MongoDB", "Cassandra", "HBase", "Postgres"],
["Python", "scikit-learn", "scipy", "numpy", "statsmodels", "pandas"],
["R", "Python", "statistics", "regression", "probability"],
["machine learning", "regression", "decision trees", "libsvm"],
["Python", "R", "Java", "C++", "Haskell", "programming languages"],
["statistics", "probability", "mathematics", "theory"],
["machine learning", "scikit-learn", "Mahout", "neural networks"],
["neural networks", "deep learning", "Big Data", "artificial intelligence"],
["Hadoop", "Java", "MapReduce", "Big Data"],
["statistics", "R", "statsmodels"],
["C++", "deep learning", "artificial intelligence", "probability"],
["pandas", "R", "Python"],
["databases", "HBase", "Postgres", "MySQL", "MongoDB"],
["libsvm", "regression", "support vector machines"]
]
raw_docs2 = [' '.join(item) for item in some_documents]
corpus2 = Corpus(raw_docs2)
model2 = GibbsSampler(corpus2)
model2.n_topics = 10
model2.n_iters = 200
model2.generate_model()
model2.topics
corpus2.DOC.join(model2.theta).style.background_gradient(cmap='GnBu', high=.5, axis=1)
model2.topics.sort_values('n_tokens', ascending=False).style.bar()
| 0.639173 | 0.856272 |
# Dudas y preguntas frecuentes
### Las ventanas no muestran las imágenes
Hace falta `cv.waitKey(ms)` para [refrescar el interfaz](https://docs.opencv.org/4.1.0/d7/dfc/group__highgui.html#ga5628525ad33f52eab17feebcfba38bd7) de opencv. Esto se hace automáticamente dentro del bucle de captura de autoStream(). En cualquier otro caso es necesario llamar a esta función para que se refresquen la ventanas aunque no necesitemos la tecla pulsada.
### Un módulo no tiene las funciones que debería tener
Si un archivo del directorio de trabajo tiene el mismo nombre que un módulo del sistema (por ejemplo "numpy.py", "dlib.py", etc.), un import de ese módulo producirá un error: Python cargará el archivo local en lugar del módulo y no encontrará sus funciones. Simplemente hay que tener cuidado con los nombres de archivo de nuestro código fuente para que no coincidan con ningún módulo.
### Ejercicio COLOR
Se trata de crear una aplicación parecida a la que se muestra en el siguiente pantallazo: La ventana superior es la imagen en vivo de la webcam (o la fuente de video deseada). Cuando se marca un ROI con el ratón se muestran los histogramas (normalizados) de los 3 canales por separado. Y si se pulsa una cierta tecla se guarda el recuadro como un modelo más y se muestra en la ventana "models" de abajo a la izquierda. En este caso vemos que se han guardado ya tres modelos. En todo momento (siempre que haya algún modelo guardado) se comparan los histogramas del ROI actual con los de todos los modelos. Las distancias se muestran arriba a la izquierda. La menor, 0.32, nos indica que el segundo modelo es el más parecido, y se muestra en la ventana "detected". Si la menor distancia es muy grande se puede rechazar la decisión y y mostrar un recuadro negro.
La comparación entre histogramas puede hacerse de muchas formas. Una muy sencilla es la suma de diferencias absolutas en cada canal y quedarnos el máximo de los tres canales.
Los modelos serán en general rectángulos de tamaños diferentes, y que tampoco tienen por qué coincidir con el tamaño del ROI que queremos clasificar. Esto implica que los histogramas deben normalizarse.
La ventana de models puede construirse con unas miniaturas reescaladas a una misma altura predeterminada y ancho proporcional al original, o simplemente a un cuadrado fijo.

### Ejercicio SIFT
Algunas recomendaciones:
Los objetos deben tener "detalles" para que aparezcan dentro suficientes puntos de interés. Hay objetos muy uniformes que producen muy pocos puntos, o salen casi todos por los bordes o el exterior, y entonces no son muy apropiados para este método. Por ejemplo una libreta con tapas negras, o un teléfono móvil, una botella de cristal sin etiqueta, etc. no funcionan bien.
Pulsando una tecla se pueden ir guardando modelos sobre la marcha, pero es conveniente leerlos de una carpeta para agilizar el uso del programa.
Hay que calcular una sola vez los keypoints y descriptores de los modelos. En el bucle de captura solo deben calcularse los de la imagen actual.
Para reducir el tiempo de cálculo se puede trabajar con imágenes me menor resolución (eg. 400x300) y limitar el número de keypoints en las comparaciones (parámetro nfeatures).
Usando autoStream() lo normal es que se produzca un retardo en las imágenes, por lo que es preferible usar la captura con hilo mediante la utilidad Camera de umucv.
Sí a pesar de todo el proceso va muy lento, se puede efectuar la extracción de keypoints y la comparación con los modelos solo cuando detectemos que la imagen está bastante quieta o cuando pulsemos una tecla.
Si los modelos tienen diferente número de keypoints la comparación debe hacerse teniendo en cuenta el porcentaje de coincidencias, no el valor absoluto.
Se puede rechazar la decisión cuando el porcentaje ganador sea pequeño, cuando el segundo mejor sea parecido al primero, o cuando haya pocas coincidencias en la imagen, entre otras situaciones que dependen de la aplicación.
Cuando no se detecta ningún keypoint los descriptores no se devuelven como un array de dimension 0x128, sino como un valor `None`. Hay que tener cuidado con esto para que no se produzcan errores en tiempo de ejecución. Esto puede ocurrir cuando la cámara apunta hacia la mesa, o está muy desenfocada.
Aquí hay un [vídeo de ejemplo](https://robot.inf.um.es/material/va/sift-demo.mp4) de lo que se puede conseguir sin muchas complicaciones. Se muestra en pequeño el modelo ganador, su porcentaje, y la diferencia con el segundo mejor. Observa que los objetos se reconocen aunque no se vean enteros en la imagen, con diferentes tamaños, con cualquier rotación en el plano de imagen, y con cierta inclinación de perspectiva. Hay también cierta resistencia al desenfoque y a reflejos. (Aunque no se ven en esta breve secuencia, pueden producirse clasificaciones erróneas cuando la escena tiene muchos puntos y no hay ningún modelo conocido.)
El algoritmo SIFT está en el repositorio "non-free" de opencv. Si vuestra distribución no lo incluye podéis utilizar el método AKAZE, que funciona igual de bien o mejor. Solo hay que cambiar una línea:
# sift = cv.xfeatures2d.SIFT_create( ..parámetros.. )
sift = cv.AKAZE_create() # tiene otros parámetros pero la configuración por omisión funciona bastante bien.
### Ejercicio VROT
Inicialmente vamos a estudiar solo los giros en los ángulos "[pan][pan]" (izquierda-derecha) y "[tilt][tilt]" (arriba-abajo).
[pan]:https://en.wikipedia.org/wiki/Panning_(camera)
[tilt]: https://en.wikipedia.org/wiki/Tilt_(camera)
En este ejercicio lo más sencillo es partir de code/lk_tracks.py y reducir la longitud de los tracks para que sus longitudes se aproximen más al movimiento instantáneo. El siguiente pantallazo muestra el efecto de un giro de la cámara hacia la izquiera y ligeramente hacia abajo. Como la escena es estática, el movimiento de todos los puntos es bastante regular. (No es exactamente igual de largo porque sabemos que la relación de ángulos y pixels lleva una arcotangente, pero si el FOV no es muy grande las diferencias no son importantes).
En naranja dibujamos el vector medio de todos esos desplazamientos. Lo dibujamos desde el centro de la imagen, ampliado para que vea mejor y en dirección opuesta (la del giro de la cámara).
Con esto tenemos el desplazamiento de la cámara en los últimos $n$ frames (la longitud de los tracks), que podemos pasar a pixels/frame. Con los parámetros de la cámara obtenidos en el ejercicio FOV podemos convertirlo a grados/frame. Y con el período de muestreo, que podemos medir con time.time() o deducirlo de los fps de captura, podemos pasarlo a grados/segundo.

Opcionalmente, además de la velocidad de giro, puedes mostrar en pantalla el ángulo total de rotación acumulado en cada eje, para comprobar a ojo que el valor es aproximadamente correcto cuando giras la cámara un ángulo conocido de p. ej. 90 grados.
En este ejercicio no buscamos mucha precisión. Lo importante es obtener el orden de magnitud correcto de las medidas.
|
github_jupyter
|
# Dudas y preguntas frecuentes
### Las ventanas no muestran las imágenes
Hace falta `cv.waitKey(ms)` para [refrescar el interfaz](https://docs.opencv.org/4.1.0/d7/dfc/group__highgui.html#ga5628525ad33f52eab17feebcfba38bd7) de opencv. Esto se hace automáticamente dentro del bucle de captura de autoStream(). En cualquier otro caso es necesario llamar a esta función para que se refresquen la ventanas aunque no necesitemos la tecla pulsada.
### Un módulo no tiene las funciones que debería tener
Si un archivo del directorio de trabajo tiene el mismo nombre que un módulo del sistema (por ejemplo "numpy.py", "dlib.py", etc.), un import de ese módulo producirá un error: Python cargará el archivo local en lugar del módulo y no encontrará sus funciones. Simplemente hay que tener cuidado con los nombres de archivo de nuestro código fuente para que no coincidan con ningún módulo.
### Ejercicio COLOR
Se trata de crear una aplicación parecida a la que se muestra en el siguiente pantallazo: La ventana superior es la imagen en vivo de la webcam (o la fuente de video deseada). Cuando se marca un ROI con el ratón se muestran los histogramas (normalizados) de los 3 canales por separado. Y si se pulsa una cierta tecla se guarda el recuadro como un modelo más y se muestra en la ventana "models" de abajo a la izquierda. En este caso vemos que se han guardado ya tres modelos. En todo momento (siempre que haya algún modelo guardado) se comparan los histogramas del ROI actual con los de todos los modelos. Las distancias se muestran arriba a la izquierda. La menor, 0.32, nos indica que el segundo modelo es el más parecido, y se muestra en la ventana "detected". Si la menor distancia es muy grande se puede rechazar la decisión y y mostrar un recuadro negro.
La comparación entre histogramas puede hacerse de muchas formas. Una muy sencilla es la suma de diferencias absolutas en cada canal y quedarnos el máximo de los tres canales.
Los modelos serán en general rectángulos de tamaños diferentes, y que tampoco tienen por qué coincidir con el tamaño del ROI que queremos clasificar. Esto implica que los histogramas deben normalizarse.
La ventana de models puede construirse con unas miniaturas reescaladas a una misma altura predeterminada y ancho proporcional al original, o simplemente a un cuadrado fijo.

### Ejercicio SIFT
Algunas recomendaciones:
Los objetos deben tener "detalles" para que aparezcan dentro suficientes puntos de interés. Hay objetos muy uniformes que producen muy pocos puntos, o salen casi todos por los bordes o el exterior, y entonces no son muy apropiados para este método. Por ejemplo una libreta con tapas negras, o un teléfono móvil, una botella de cristal sin etiqueta, etc. no funcionan bien.
Pulsando una tecla se pueden ir guardando modelos sobre la marcha, pero es conveniente leerlos de una carpeta para agilizar el uso del programa.
Hay que calcular una sola vez los keypoints y descriptores de los modelos. En el bucle de captura solo deben calcularse los de la imagen actual.
Para reducir el tiempo de cálculo se puede trabajar con imágenes me menor resolución (eg. 400x300) y limitar el número de keypoints en las comparaciones (parámetro nfeatures).
Usando autoStream() lo normal es que se produzca un retardo en las imágenes, por lo que es preferible usar la captura con hilo mediante la utilidad Camera de umucv.
Sí a pesar de todo el proceso va muy lento, se puede efectuar la extracción de keypoints y la comparación con los modelos solo cuando detectemos que la imagen está bastante quieta o cuando pulsemos una tecla.
Si los modelos tienen diferente número de keypoints la comparación debe hacerse teniendo en cuenta el porcentaje de coincidencias, no el valor absoluto.
Se puede rechazar la decisión cuando el porcentaje ganador sea pequeño, cuando el segundo mejor sea parecido al primero, o cuando haya pocas coincidencias en la imagen, entre otras situaciones que dependen de la aplicación.
Cuando no se detecta ningún keypoint los descriptores no se devuelven como un array de dimension 0x128, sino como un valor `None`. Hay que tener cuidado con esto para que no se produzcan errores en tiempo de ejecución. Esto puede ocurrir cuando la cámara apunta hacia la mesa, o está muy desenfocada.
Aquí hay un [vídeo de ejemplo](https://robot.inf.um.es/material/va/sift-demo.mp4) de lo que se puede conseguir sin muchas complicaciones. Se muestra en pequeño el modelo ganador, su porcentaje, y la diferencia con el segundo mejor. Observa que los objetos se reconocen aunque no se vean enteros en la imagen, con diferentes tamaños, con cualquier rotación en el plano de imagen, y con cierta inclinación de perspectiva. Hay también cierta resistencia al desenfoque y a reflejos. (Aunque no se ven en esta breve secuencia, pueden producirse clasificaciones erróneas cuando la escena tiene muchos puntos y no hay ningún modelo conocido.)
El algoritmo SIFT está en el repositorio "non-free" de opencv. Si vuestra distribución no lo incluye podéis utilizar el método AKAZE, que funciona igual de bien o mejor. Solo hay que cambiar una línea:
# sift = cv.xfeatures2d.SIFT_create( ..parámetros.. )
sift = cv.AKAZE_create() # tiene otros parámetros pero la configuración por omisión funciona bastante bien.
### Ejercicio VROT
Inicialmente vamos a estudiar solo los giros en los ángulos "[pan][pan]" (izquierda-derecha) y "[tilt][tilt]" (arriba-abajo).
[pan]:https://en.wikipedia.org/wiki/Panning_(camera)
[tilt]: https://en.wikipedia.org/wiki/Tilt_(camera)
En este ejercicio lo más sencillo es partir de code/lk_tracks.py y reducir la longitud de los tracks para que sus longitudes se aproximen más al movimiento instantáneo. El siguiente pantallazo muestra el efecto de un giro de la cámara hacia la izquiera y ligeramente hacia abajo. Como la escena es estática, el movimiento de todos los puntos es bastante regular. (No es exactamente igual de largo porque sabemos que la relación de ángulos y pixels lleva una arcotangente, pero si el FOV no es muy grande las diferencias no son importantes).
En naranja dibujamos el vector medio de todos esos desplazamientos. Lo dibujamos desde el centro de la imagen, ampliado para que vea mejor y en dirección opuesta (la del giro de la cámara).
Con esto tenemos el desplazamiento de la cámara en los últimos $n$ frames (la longitud de los tracks), que podemos pasar a pixels/frame. Con los parámetros de la cámara obtenidos en el ejercicio FOV podemos convertirlo a grados/frame. Y con el período de muestreo, que podemos medir con time.time() o deducirlo de los fps de captura, podemos pasarlo a grados/segundo.

Opcionalmente, además de la velocidad de giro, puedes mostrar en pantalla el ángulo total de rotación acumulado en cada eje, para comprobar a ojo que el valor es aproximadamente correcto cuando giras la cámara un ángulo conocido de p. ej. 90 grados.
En este ejercicio no buscamos mucha precisión. Lo importante es obtener el orden de magnitud correcto de las medidas.
| 0.553264 | 0.834542 |
# Collision Avoidance - Live Demo
In this notebook we'll use the model we trained to detect whether the robot is ``free`` or ``blocked`` to enable a collision avoidance behavior on the robot.
## Load the trained model
We'll assumed that you've already downloaded the ``best_model.pth`` to your workstation as instructed in the training notebook. Now, you should upload this model into this notebook's
directory by using the Jupyter Lab upload tool. Once that's finished there should be a file named ``best_model.pth`` in this notebook's directory.
> Please make sure the file has uploaded fully before calling the next cell
Execute the code below to initialize the PyTorch model. This should look very familiar from the training notebook.
```
import torch
import torchvision
model = torchvision.models.alexnet(pretrained=False)
model.classifier[6] = torch.nn.Linear(model.classifier[6].in_features, 2)
```
Next, load the trained weights from the ``best_model.pth`` file that you uploaded
```
model.load_state_dict(torch.load('best_model.pth'))
```
Currently, the model weights are located on the CPU memory execute the code below to transfer to the GPU device.
```
device = torch.device('cuda')
model = model.to(device)
```
### Create the preprocessing function
We have now loaded our model, but there's a slight issue. The format that we trained our model doesn't *exactly* match the format of the camera. To do that,
we need to do some *preprocessing*. This involves the following steps
1. Convert from BGR to RGB
2. Convert from HWC layout to CHW layout
3. Normalize using same parameters as we did during training (our camera provides values in [0, 255] range and training loaded images in [0, 1] range so we need to scale by 255.0
4. Transfer the data from CPU memory to GPU memory
5. Add a batch dimension
```
import cv2
import numpy as np
mean = 255.0 * np.array([0.485, 0.456, 0.406])
stdev = 255.0 * np.array([0.229, 0.224, 0.225])
normalize = torchvision.transforms.Normalize(mean, stdev)
def preprocess(camera_value):
global device, normalize
x = camera_value
x = cv2.cvtColor(x, cv2.COLOR_BGR2RGB)
x = x.transpose((2, 0, 1))
x = torch.from_numpy(x).float()
x = normalize(x)
x = x.to(device)
x = x[None, ...]
return x
```
Great! We've now defined our pre-processing function which can convert images from the camera format to the neural network input format.
Now, let's start and display our camera. You should be pretty familiar with this by now. We'll also create a slider that will display the
probability that the robot is blocked. We'll also display a slider that allows us to control the robot's base speed.
```
import traitlets
from IPython.display import display
import ipywidgets.widgets as widgets
from jetbot import Camera, bgr8_to_jpeg
camera = Camera.instance(width=224, height=224)
image = widgets.Image(format='jpeg', width=224, height=224)
blocked_slider = widgets.FloatSlider(description='blocked', min=0.0, max=1.0, orientation='vertical')
speed_slider = widgets.FloatSlider(description='speed', min=0.0, max=0.5, value=0.0, step=0.01, orientation='horizontal')
camera_link = traitlets.dlink((camera, 'value'), (image, 'value'), transform=bgr8_to_jpeg)
display(widgets.VBox([widgets.HBox([image, blocked_slider]), speed_slider]))
```
We'll also create our robot instance which we'll need to drive the motors.
```
from jetbot import Robot
robot = Robot()
```
Next, we'll create a function that will get called whenever the camera's value changes. This function will do the following steps
1. Pre-process the camera image
2. Execute the neural network
3. While the neural network output indicates we're blocked, we'll turn left, otherwise we go forward.
```
import torch.nn.functional as F
import time
def update(change):
global blocked_slider, robot
x = change['new']
x = preprocess(x)
y = model(x)
# we apply the `softmax` function to normalize the output vector so it sums to 1 (which makes it a probability distribution)
y = F.softmax(y, dim=1)
prob_blocked = float(y.flatten()[0])
blocked_slider.value = prob_blocked
if prob_blocked < 0.9:
robot.forward(speed_slider.value)
else:
robot.left(speed_slider.value)
time.sleep(0.001)
update({'new': camera.value}) # we call the function once to initialize
```
Cool! We've created our neural network execution function, but now we need to attach it to the camera for processing.
We accomplish that with the ``observe`` function.
> WARNING: This code may move the robot!! Adjust the speed slider we defined earlier to control the base robot speed. Some kits can move fast, so start slow, and gradually increase the value.
```
camera.observe(update, names='value') # this attaches the 'update' function to the 'value' traitlet of our camera
```
Awesome! If your robot is plugged in it should now be generating new commands with each new camera frame. Perhaps start by placing your robot on the ground and seeing what it does when it reaches an obstacle.
If you want to stop this behavior, you can unattach this callback by executing the code below.
```
import time
camera.unobserve(update, names='value')
time.sleep(0.1) # add a small sleep to make sure frames have finished processing
robot.stop()
```
Perhaps you want the robot to run without streaming video to the browser. You can unlink the camera as below.
```
camera_link.unlink() # don't stream to browser (will still run camera)
```
To continue streaming call the following.
```
camera_link.link() # stream to browser (wont run camera)
```
Again, let's close the camera conneciton properly so that we can use the camera in other notebooks.
```
camera.stop()
```
### Conclusion
That's it for this live demo! Hopefully you had some fun and your robot avoided collisions intelligently!
If your robot wasn't avoiding collisions very well, try to spot where it fails. The beauty is that we can collect more data for these failure scenarios
and the robot should get even better :)
|
github_jupyter
|
import torch
import torchvision
model = torchvision.models.alexnet(pretrained=False)
model.classifier[6] = torch.nn.Linear(model.classifier[6].in_features, 2)
model.load_state_dict(torch.load('best_model.pth'))
device = torch.device('cuda')
model = model.to(device)
import cv2
import numpy as np
mean = 255.0 * np.array([0.485, 0.456, 0.406])
stdev = 255.0 * np.array([0.229, 0.224, 0.225])
normalize = torchvision.transforms.Normalize(mean, stdev)
def preprocess(camera_value):
global device, normalize
x = camera_value
x = cv2.cvtColor(x, cv2.COLOR_BGR2RGB)
x = x.transpose((2, 0, 1))
x = torch.from_numpy(x).float()
x = normalize(x)
x = x.to(device)
x = x[None, ...]
return x
import traitlets
from IPython.display import display
import ipywidgets.widgets as widgets
from jetbot import Camera, bgr8_to_jpeg
camera = Camera.instance(width=224, height=224)
image = widgets.Image(format='jpeg', width=224, height=224)
blocked_slider = widgets.FloatSlider(description='blocked', min=0.0, max=1.0, orientation='vertical')
speed_slider = widgets.FloatSlider(description='speed', min=0.0, max=0.5, value=0.0, step=0.01, orientation='horizontal')
camera_link = traitlets.dlink((camera, 'value'), (image, 'value'), transform=bgr8_to_jpeg)
display(widgets.VBox([widgets.HBox([image, blocked_slider]), speed_slider]))
from jetbot import Robot
robot = Robot()
import torch.nn.functional as F
import time
def update(change):
global blocked_slider, robot
x = change['new']
x = preprocess(x)
y = model(x)
# we apply the `softmax` function to normalize the output vector so it sums to 1 (which makes it a probability distribution)
y = F.softmax(y, dim=1)
prob_blocked = float(y.flatten()[0])
blocked_slider.value = prob_blocked
if prob_blocked < 0.9:
robot.forward(speed_slider.value)
else:
robot.left(speed_slider.value)
time.sleep(0.001)
update({'new': camera.value}) # we call the function once to initialize
camera.observe(update, names='value') # this attaches the 'update' function to the 'value' traitlet of our camera
import time
camera.unobserve(update, names='value')
time.sleep(0.1) # add a small sleep to make sure frames have finished processing
robot.stop()
camera_link.unlink() # don't stream to browser (will still run camera)
camera_link.link() # stream to browser (wont run camera)
camera.stop()
| 0.706798 | 0.981788 |
```
! pip install pyspark[sql]
```
# Quickstart: DataFrame
This is a short introduction and quickstart for the PySpark DataFrame API. PySpark DataFrames are lazily evaluated. They are implemented on top of [RDD](https://spark.apache.org/docs/latest/rdd-programming-guide.html#overview)s. When Spark [transforms](https://spark.apache.org/docs/latest/rdd-programming-guide.html#transformations) data, it does not immediately compute the transformation but plans how to compute later. When [actions](https://spark.apache.org/docs/latest/rdd-programming-guide.html#actions) such as `collect()` are explicitly called, the computation starts.
This notebook shows the basic usages of the DataFrame, geared mainly for new users. You can run the latest version of these examples by yourself in 'Live Notebook: DataFrame' at [the quickstart page](https://spark.apache.org/docs/latest/api/python/getting_started/index.html).
There is also other useful information in Apache Spark documentation site, see the latest version of [Spark SQL and DataFrames](https://spark.apache.org/docs/latest/sql-programming-guide.html), [RDD Programming Guide](https://spark.apache.org/docs/latest/rdd-programming-guide.html), [Structured Streaming Programming Guide](https://spark.apache.org/docs/latest/structured-streaming-programming-guide.html), [Spark Streaming Programming Guide](https://spark.apache.org/docs/latest/streaming-programming-guide.html) and [Machine Learning Library (MLlib) Guide](https://spark.apache.org/docs/latest/ml-guide.html).
PySpark applications start with initializing `SparkSession` which is the entry point of PySpark as below. In case of running it in PySpark shell via <code>pyspark</code> executable, the shell automatically creates the session in the variable <code>spark</code> for users.
```
from pyspark.sql import SparkSession
spark = SparkSession.builder.getOrCreate()
```
## DataFrame Creation
A PySpark DataFrame can be created via `pyspark.sql.SparkSession.createDataFrame` typically by passing a list of lists, tuples, dictionaries and `pyspark.sql.Row`s, a [pandas DataFrame](https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.html) and an RDD consisting of such a list.
`pyspark.sql.SparkSession.createDataFrame` takes the `schema` argument to specify the schema of the DataFrame. When it is omitted, PySpark infers the corresponding schema by taking a sample from the data.
Firstly, you can create a PySpark DataFrame from a list of rows
```
from datetime import datetime, date
import pandas as pd
from pyspark.sql import Row
df = spark.createDataFrame([
Row(a=1, b=2., c='string1', d=date(2000, 1, 1), e=datetime(2000, 1, 1, 12, 0)),
Row(a=2, b=3., c='string2', d=date(2000, 2, 1), e=datetime(2000, 1, 2, 12, 0)),
Row(a=4, b=5., c='string3', d=date(2000, 3, 1), e=datetime(2000, 1, 3, 12, 0))
])
df
```
Create a PySpark DataFrame with an explicit schema.
```
df = spark.createDataFrame([
(1, 2., 'string1', date(2000, 1, 1), datetime(2000, 1, 1, 12, 0)),
(2, 3., 'string2', date(2000, 2, 1), datetime(2000, 1, 2, 12, 0)),
(3, 4., 'string3', date(2000, 3, 1), datetime(2000, 1, 3, 12, 0))
], schema='a long, b double, c string, d date, e timestamp')
df
```
Create a PySpark DataFrame from a pandas DataFrame
```
pandas_df = pd.DataFrame({
'a': [1, 2, 3],
'b': [2., 3., 4.],
'c': ['string1', 'string2', 'string3'],
'd': [date(2000, 1, 1), date(2000, 2, 1), date(2000, 3, 1)],
'e': [datetime(2000, 1, 1, 12, 0), datetime(2000, 1, 2, 12, 0), datetime(2000, 1, 3, 12, 0)]
})
df = spark.createDataFrame(pandas_df)
df
```
Create a PySpark DataFrame from an RDD consisting of a list of tuples.
```
rdd = spark.sparkContext.parallelize([
(1, 2., 'string1', date(2000, 1, 1), datetime(2000, 1, 1, 12, 0)),
(2, 3., 'string2', date(2000, 2, 1), datetime(2000, 1, 2, 12, 0)),
(3, 4., 'string3', date(2000, 3, 1), datetime(2000, 1, 3, 12, 0))
])
df = spark.createDataFrame(rdd, schema=['a', 'b', 'c', 'd', 'e'])
df
```
The DataFrames created above all have the same results and schema.
```
# All DataFrames above result same.
df.show()
df.printSchema()
```
## Viewing Data
The top rows of a DataFrame can be displayed using `DataFrame.show()`.
```
df.show(1)
```
Alternatively, you can enable `spark.sql.repl.eagerEval.enabled` configuration for the eager evaluation of PySpark DataFrame in notebooks such as Jupyter. The number of rows to show can be controlled via `spark.sql.repl.eagerEval.maxNumRows` configuration.
```
spark.conf.set('spark.sql.repl.eagerEval.enabled', True)
df
```
The rows can also be shown vertically. This is useful when rows are too long to show horizontally.
```
df.show(1, vertical=True)
```
You can see the DataFrame's schema and column names as follows:
```
df.columns
df.printSchema()
```
Show the summary of the DataFrame
```
df.select("a", "b", "c").describe().show()
```
`DataFrame.collect()` collects the distributed data to the driver side as the local data in Python. Note that this can throw an out-of-memory error when the dataset is too large to fit in the driver side because it collects all the data from executors to the driver side.
```
df.collect()
```
In order to avoid throwing an out-of-memory exception, use `DataFrame.take()` or `DataFrame.tail()`.
```
df.take(1)
```
PySpark DataFrame also provides the conversion back to a [pandas DataFrame](https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.html) to leverage pandas API. Note that `toPandas` also collects all data into the driver side that can easily cause an out-of-memory-error when the data is too large to fit into the driver side.
```
df.toPandas()
```
## Selecting and Accessing Data
PySpark DataFrame is lazily evaluated and simply selecting a column does not trigger the computation but it returns a `Column` instance.
```
df.a
```
In fact, most of column-wise operations return `Column`s.
```
from pyspark.sql import Column
from pyspark.sql.functions import upper
type(df.c) == type(upper(df.c)) == type(df.c.isNull())
```
These `Column`s can be used to select the columns from a DataFrame. For example, `DataFrame.select()` takes the `Column` instances that returns another DataFrame.
```
df.select(df.c).show()
```
Assign new `Column` instance.
```
df.withColumn('upper_c', upper(df.c)).show()
```
To select a subset of rows, use `DataFrame.filter()`.
```
df.filter(df.a == 1).show()
```
## Applying a Function
PySpark supports various UDFs and APIs to allow users to execute Python native functions. See also the latest [Pandas UDFs](https://spark.apache.org/docs/latest/sql-pyspark-pandas-with-arrow.html#pandas-udfs-aka-vectorized-udfs) and [Pandas Function APIs](https://spark.apache.org/docs/latest/sql-pyspark-pandas-with-arrow.html#pandas-function-apis). For instance, the example below allows users to directly use the APIs in [a pandas Series](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.Series.html) within Python native function.
```
import pandas
from pyspark.sql.functions import pandas_udf
@pandas_udf('long')
def pandas_plus_one(series: pd.Series) -> pd.Series:
# Simply plus one by using pandas Series.
return series + 1
df.select(pandas_plus_one(df.a)).show()
```
Another example is `DataFrame.mapInPandas` which allows users directly use the APIs in a [pandas DataFrame](https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.html) without any restrictions such as the result length.
```
def pandas_filter_func(iterator):
for pandas_df in iterator:
yield pandas_df[pandas_df.a == 1]
df.mapInPandas(pandas_filter_func, schema=df.schema).show()
```
## Grouping Data
PySpark DataFrame also provides a way of handling grouped data by using the common approach, split-apply-combine strategy.
It groups the data by a certain condition applies a function to each group and then combines them back to the DataFrame.
```
df = spark.createDataFrame([
['red', 'banana', 1, 10], ['blue', 'banana', 2, 20], ['red', 'carrot', 3, 30],
['blue', 'grape', 4, 40], ['red', 'carrot', 5, 50], ['black', 'carrot', 6, 60],
['red', 'banana', 7, 70], ['red', 'grape', 8, 80]], schema=['color', 'fruit', 'v1', 'v2'])
df.show()
```
Grouping and then applying the `avg()` function to the resulting groups.
```
df.groupby('color').avg().show()
```
You can also apply a Python native function against each group by using pandas API.
```
def plus_mean(pandas_df):
return pandas_df.assign(v1=pandas_df.v1 - pandas_df.v1.mean())
df.groupby('color').applyInPandas(plus_mean, schema=df.schema).show()
```
Co-grouping and applying a function.
```
df1 = spark.createDataFrame(
[(20000101, 1, 1.0), (20000101, 2, 2.0), (20000102, 1, 3.0), (20000102, 2, 4.0)],
('time', 'id', 'v1'))
df2 = spark.createDataFrame(
[(20000101, 1, 'x'), (20000101, 2, 'y')],
('time', 'id', 'v2'))
def asof_join(l, r):
return pd.merge_asof(l, r, on='time', by='id')
df1.groupby('id').cogroup(df2.groupby('id')).applyInPandas(
asof_join, schema='time int, id int, v1 double, v2 string').show()
```
## Getting Data in/out
CSV is straightforward and easy to use. Parquet and ORC are efficient and compact file formats to read and write faster.
There are many other data sources available in PySpark such as JDBC, text, binaryFile, Avro, etc. See also the latest [Spark SQL, DataFrames and Datasets Guide](https://spark.apache.org/docs/latest/sql-programming-guide.html) in Apache Spark documentation.
### CSV
```
df.write.csv('foo.csv', header=True)
spark.read.csv('foo.csv', header=True).show()
```
### Parquet
```
df.write.parquet('bar.parquet')
spark.read.parquet('bar.parquet').show()
```
### ORC
```
df.write.orc('zoo.orc')
spark.read.orc('zoo.orc').show()
```
## Working with SQL
DataFrame and Spark SQL share the same execution engine so they can be interchangeably used seamlessly. For example, you can register the DataFrame as a table and run a SQL easily as below:
```
df.createOrReplaceTempView("tableA")
spark.sql("SELECT count(*) from tableA").show()
```
In addition, UDFs can be registered and invoked in SQL out of the box:
```
@pandas_udf("integer")
def add_one(s: pd.Series) -> pd.Series:
return s + 1
spark.udf.register("add_one", add_one)
spark.sql("SELECT add_one(v1) FROM tableA").show()
```
These SQL expressions can directly be mixed and used as PySpark columns.
```
from pyspark.sql.functions import expr
df.selectExpr('add_one(v1)').show()
df.select(expr('count(*)') > 0).show()
```
|
github_jupyter
|
! pip install pyspark[sql]
from pyspark.sql import SparkSession
spark = SparkSession.builder.getOrCreate()
from datetime import datetime, date
import pandas as pd
from pyspark.sql import Row
df = spark.createDataFrame([
Row(a=1, b=2., c='string1', d=date(2000, 1, 1), e=datetime(2000, 1, 1, 12, 0)),
Row(a=2, b=3., c='string2', d=date(2000, 2, 1), e=datetime(2000, 1, 2, 12, 0)),
Row(a=4, b=5., c='string3', d=date(2000, 3, 1), e=datetime(2000, 1, 3, 12, 0))
])
df
df = spark.createDataFrame([
(1, 2., 'string1', date(2000, 1, 1), datetime(2000, 1, 1, 12, 0)),
(2, 3., 'string2', date(2000, 2, 1), datetime(2000, 1, 2, 12, 0)),
(3, 4., 'string3', date(2000, 3, 1), datetime(2000, 1, 3, 12, 0))
], schema='a long, b double, c string, d date, e timestamp')
df
pandas_df = pd.DataFrame({
'a': [1, 2, 3],
'b': [2., 3., 4.],
'c': ['string1', 'string2', 'string3'],
'd': [date(2000, 1, 1), date(2000, 2, 1), date(2000, 3, 1)],
'e': [datetime(2000, 1, 1, 12, 0), datetime(2000, 1, 2, 12, 0), datetime(2000, 1, 3, 12, 0)]
})
df = spark.createDataFrame(pandas_df)
df
rdd = spark.sparkContext.parallelize([
(1, 2., 'string1', date(2000, 1, 1), datetime(2000, 1, 1, 12, 0)),
(2, 3., 'string2', date(2000, 2, 1), datetime(2000, 1, 2, 12, 0)),
(3, 4., 'string3', date(2000, 3, 1), datetime(2000, 1, 3, 12, 0))
])
df = spark.createDataFrame(rdd, schema=['a', 'b', 'c', 'd', 'e'])
df
# All DataFrames above result same.
df.show()
df.printSchema()
df.show(1)
spark.conf.set('spark.sql.repl.eagerEval.enabled', True)
df
df.show(1, vertical=True)
df.columns
df.printSchema()
df.select("a", "b", "c").describe().show()
df.collect()
df.take(1)
df.toPandas()
df.a
from pyspark.sql import Column
from pyspark.sql.functions import upper
type(df.c) == type(upper(df.c)) == type(df.c.isNull())
df.select(df.c).show()
df.withColumn('upper_c', upper(df.c)).show()
df.filter(df.a == 1).show()
import pandas
from pyspark.sql.functions import pandas_udf
@pandas_udf('long')
def pandas_plus_one(series: pd.Series) -> pd.Series:
# Simply plus one by using pandas Series.
return series + 1
df.select(pandas_plus_one(df.a)).show()
def pandas_filter_func(iterator):
for pandas_df in iterator:
yield pandas_df[pandas_df.a == 1]
df.mapInPandas(pandas_filter_func, schema=df.schema).show()
df = spark.createDataFrame([
['red', 'banana', 1, 10], ['blue', 'banana', 2, 20], ['red', 'carrot', 3, 30],
['blue', 'grape', 4, 40], ['red', 'carrot', 5, 50], ['black', 'carrot', 6, 60],
['red', 'banana', 7, 70], ['red', 'grape', 8, 80]], schema=['color', 'fruit', 'v1', 'v2'])
df.show()
df.groupby('color').avg().show()
def plus_mean(pandas_df):
return pandas_df.assign(v1=pandas_df.v1 - pandas_df.v1.mean())
df.groupby('color').applyInPandas(plus_mean, schema=df.schema).show()
df1 = spark.createDataFrame(
[(20000101, 1, 1.0), (20000101, 2, 2.0), (20000102, 1, 3.0), (20000102, 2, 4.0)],
('time', 'id', 'v1'))
df2 = spark.createDataFrame(
[(20000101, 1, 'x'), (20000101, 2, 'y')],
('time', 'id', 'v2'))
def asof_join(l, r):
return pd.merge_asof(l, r, on='time', by='id')
df1.groupby('id').cogroup(df2.groupby('id')).applyInPandas(
asof_join, schema='time int, id int, v1 double, v2 string').show()
df.write.csv('foo.csv', header=True)
spark.read.csv('foo.csv', header=True).show()
df.write.parquet('bar.parquet')
spark.read.parquet('bar.parquet').show()
df.write.orc('zoo.orc')
spark.read.orc('zoo.orc').show()
df.createOrReplaceTempView("tableA")
spark.sql("SELECT count(*) from tableA").show()
@pandas_udf("integer")
def add_one(s: pd.Series) -> pd.Series:
return s + 1
spark.udf.register("add_one", add_one)
spark.sql("SELECT add_one(v1) FROM tableA").show()
from pyspark.sql.functions import expr
df.selectExpr('add_one(v1)').show()
df.select(expr('count(*)') > 0).show()
| 0.61057 | 0.993568 |
# BigQuery command-line tool
The BigQuery command-line tool is installed as part of the [Cloud SDK](https://cloud-dot-devsite.googleplex.com/sdk/docs/) and can be used to interact with BigQuery. When you use CLI commands in a notebook, the command must be prepended with a `!`.
## View available commands
To view the available commands for the BigQuery command-line tool, use the `help` command.
```
!bq help
```
## Create a new dataset
A dataset is contained within a specific [project](https://cloud.google.com/bigquery/docs/projects). Datasets are top-level containers that are used to organize and control access to your [tables](https://cloud.google.com/bigquery/docs/tables) and [views](https://cloud.google.com/bigquery/docs/views). A table or view must belong to a dataset. You need to create at least one dataset before [loading data into BigQuery](https://cloud.google.com/bigquery/loading-data-into-bigquery).
First, name your new dataset:
```
dataset_id = "your_new_dataset"
```
The following command creates a new dataset in the US using the ID defined above.
NOTE: In the examples in this notebook, the `dataset_id` variable is referenced in the commands using both `{}` and `$`. To avoid creating and using variables, replace these interpolated variables with literal values and remove the `{}` and `$` characters.
```
!bq --location=US mk --dataset $dataset_id
```
The response should look like the following:
```
Dataset 'your-project-id:your_new_dataset' successfully created.
```
## List datasets
The following command lists all datasets in your default project.
```
!bq ls
```
The response should look like the following:
```
datasetId
------------------------------
your_new_dataset
```
## Load data from a local file to a table
The following example demonstrates how to load a local CSV file into a new or existing table. See [SourceFormat](https://googleapis.github.io/google-cloud-python/latest/bigquery/generated/google.cloud.bigquery.job.SourceFormat.html#google.cloud.bigquery.job.SourceFormat) in the Python client library documentation for a list of available source formats. For more information, see [Loading Data into BigQuery from a local data source](https://cloud.google.com/bigquery/docs/loading-data-local) in the BigQuery documentation.
```
!bq \
--location=US \
load \
--autodetect \
--skip_leading_rows=1 \
--source_format=CSV \
{dataset_id}.us_states_local_file \
'resources/us-states.csv'
```
## Load data from Cloud Storage to a table
The following example demonstrates how to load a local CSV file into a new table. See [SourceFormat](https://googleapis.github.io/google-cloud-python/latest/bigquery/generated/google.cloud.bigquery.job.SourceFormat.html#google.cloud.bigquery.job.SourceFormat) in the Python client library documentation for a list of available source formats. For more information, see [Introduction to loading data from Cloud Storage](https://cloud.google.com/bigquery/docs/loading-data-cloud-storage) in the BigQuery documentation.
```
!bq \
--location=US \
load \
--autodetect \
--skip_leading_rows=1 \
--source_format=CSV \
{dataset_id}.us_states_gcs \
'gs://cloud-samples-data/bigquery/us-states/us-states.csv'
```
## Run a query
The BigQuery command-line tool has a `query` command for running queries, but it is recommended to use the [magic command](./BigQuery%20Query%20Magic.ipynb) for this purpose.
## Cleaning Up
The following code deletes the dataset created for this tutorial, including all tables in the dataset.
```
!bq rm -r -f --dataset $dataset_id
```
|
github_jupyter
|
!bq help
dataset_id = "your_new_dataset"
!bq --location=US mk --dataset $dataset_id
Dataset 'your-project-id:your_new_dataset' successfully created.
!bq ls
datasetId
------------------------------
your_new_dataset
!bq \
--location=US \
load \
--autodetect \
--skip_leading_rows=1 \
--source_format=CSV \
{dataset_id}.us_states_local_file \
'resources/us-states.csv'
!bq \
--location=US \
load \
--autodetect \
--skip_leading_rows=1 \
--source_format=CSV \
{dataset_id}.us_states_gcs \
'gs://cloud-samples-data/bigquery/us-states/us-states.csv'
!bq rm -r -f --dataset $dataset_id
| 0.196518 | 0.979472 |
```
%%capture
%%bash
. /opt/conda/bin/activat
conda install -c bioconda freebayes=1.3.1
%%bash
#freebayes -G 10 -F 0.3 -f p_ctg_cns_H1.fa reads_H1.bam > var_H1.vcf &
#freebayes -G 10 -F 0.3 -f p_ctg_cns_H2.fa reads_H2.bam > var_H2.vcf &
%%bash
# this takes about one hours to run
freebayes-parallel <(fasta_generate_regions.py p_ctg_cns_H1.fa.fai 500000) 8 \
-G 10 -F 0.3 -f p_ctg_cns_H1.fa reads_H1.bam > var_H1_2.vcf &
freebayes-parallel <(fasta_generate_regions.py p_ctg_cns_H2.fa.fai 500000) 8 \
-G 10 -F 0.3 -f p_ctg_cns_H2.fa reads_H2.bam > var_H2_2.vcf &
%%bash
bgzip var_H1_2.vcf
bgzip var_H2_2.vcf
%%bash
tabix -p vcf var_H1_2.vcf.gz
tabix -p vcf var_H2_2.vcf.gz
import gzip
f = gzip.open("var_H1_2.vcf.gz")
v_pos = []
for row in f:
if row[0] == ord(b'#'):
continue
row = row.strip().split()
if row[0] != b'000000F':
continue
if len(row[3]) != len(row[4]):
continue
position = int(row[1])
v_pos.append(position)
f = gzip.open("reads_H1.var.vcf.gz")
for row in f:
if row[0] == ord(b'#'):
continue
row = row.strip().split()
if row[0] != b'000000F':
continue
position = int(row[1])
k, v = row[-2:]
k = k.split(b':')
v = v.split(b':')
d = dict(zip(k,v))
AD = [int(_) for _ in d[b'AD'].split(b',')]
if min(AD)/sum(AD) < 0.25:
continue
pos = int(row[1])
v_pos.append(position)
v_pos.sort()
SNP_cluster=[]
cluster_d = 10000
for position in v_pos:
if len(SNP_cluster) == 0 or position - SNP_cluster[-1][-1] > cluster_d:
SNP_cluster.append([position])
else:
SNP_cluster[-1].append(position)
for c in SNP_cluster:
#print("H1", len(c), '000000F:{}-{}'.format(min(c)-50, max(c)+50), max(c)-min(c)+100)
print('000000F\t{}\t{}'.format(min(c)-50, max(c)+50))
for c in SNP_cluster:
print((min(c)-50, max(c)+50))
f = gzip.open("var_H2_2.vcf.gz")
v_pos = []
for row in f:
if row[0] == ord(b'#'):
continue
row = row.strip().split()
if row[0] != b'000000F':
continue
if len(row[3]) != len(row[4]):
continue
position = int(row[1])
v_pos.append(position)
f = gzip.open("reads_H2.var.vcf.gz")
for row in f:
if row[0] == ord(b'#'):
continue
row = row.strip().split()
if row[0] != b'000000F':
continue
position = int(row[1])
k, v = row[-2:]
k = k.split(b':')
v = v.split(b':')
d = dict(zip(k,v))
AD = [int(_) for _ in d[b'AD'].split(b',')]
if min(AD)/sum(AD) < 0.25:
continue
pos = int(row[1])
v_pos.append(position)
v_pos.sort()
SNP_cluster=[]
cluster_d = 10000
for position in v_pos:
if len(SNP_cluster) == 0 or position - SNP_cluster[-1][-1] > cluster_d:
SNP_cluster.append([position])
else:
SNP_cluster[-1].append(position)
for c in SNP_cluster:
#print("H2", len(c), '000000F:{}-{}'.format(min(c)-50, max(c)+50), max(c)-min(c)+100)
print('000000F\t{}\t{}'.format(min(c)-50, max(c)+50))
for c in SNP_cluster:
print((min(c)-50, max(c)+50))
```
|
github_jupyter
|
%%capture
%%bash
. /opt/conda/bin/activat
conda install -c bioconda freebayes=1.3.1
%%bash
#freebayes -G 10 -F 0.3 -f p_ctg_cns_H1.fa reads_H1.bam > var_H1.vcf &
#freebayes -G 10 -F 0.3 -f p_ctg_cns_H2.fa reads_H2.bam > var_H2.vcf &
%%bash
# this takes about one hours to run
freebayes-parallel <(fasta_generate_regions.py p_ctg_cns_H1.fa.fai 500000) 8 \
-G 10 -F 0.3 -f p_ctg_cns_H1.fa reads_H1.bam > var_H1_2.vcf &
freebayes-parallel <(fasta_generate_regions.py p_ctg_cns_H2.fa.fai 500000) 8 \
-G 10 -F 0.3 -f p_ctg_cns_H2.fa reads_H2.bam > var_H2_2.vcf &
%%bash
bgzip var_H1_2.vcf
bgzip var_H2_2.vcf
%%bash
tabix -p vcf var_H1_2.vcf.gz
tabix -p vcf var_H2_2.vcf.gz
import gzip
f = gzip.open("var_H1_2.vcf.gz")
v_pos = []
for row in f:
if row[0] == ord(b'#'):
continue
row = row.strip().split()
if row[0] != b'000000F':
continue
if len(row[3]) != len(row[4]):
continue
position = int(row[1])
v_pos.append(position)
f = gzip.open("reads_H1.var.vcf.gz")
for row in f:
if row[0] == ord(b'#'):
continue
row = row.strip().split()
if row[0] != b'000000F':
continue
position = int(row[1])
k, v = row[-2:]
k = k.split(b':')
v = v.split(b':')
d = dict(zip(k,v))
AD = [int(_) for _ in d[b'AD'].split(b',')]
if min(AD)/sum(AD) < 0.25:
continue
pos = int(row[1])
v_pos.append(position)
v_pos.sort()
SNP_cluster=[]
cluster_d = 10000
for position in v_pos:
if len(SNP_cluster) == 0 or position - SNP_cluster[-1][-1] > cluster_d:
SNP_cluster.append([position])
else:
SNP_cluster[-1].append(position)
for c in SNP_cluster:
#print("H1", len(c), '000000F:{}-{}'.format(min(c)-50, max(c)+50), max(c)-min(c)+100)
print('000000F\t{}\t{}'.format(min(c)-50, max(c)+50))
for c in SNP_cluster:
print((min(c)-50, max(c)+50))
f = gzip.open("var_H2_2.vcf.gz")
v_pos = []
for row in f:
if row[0] == ord(b'#'):
continue
row = row.strip().split()
if row[0] != b'000000F':
continue
if len(row[3]) != len(row[4]):
continue
position = int(row[1])
v_pos.append(position)
f = gzip.open("reads_H2.var.vcf.gz")
for row in f:
if row[0] == ord(b'#'):
continue
row = row.strip().split()
if row[0] != b'000000F':
continue
position = int(row[1])
k, v = row[-2:]
k = k.split(b':')
v = v.split(b':')
d = dict(zip(k,v))
AD = [int(_) for _ in d[b'AD'].split(b',')]
if min(AD)/sum(AD) < 0.25:
continue
pos = int(row[1])
v_pos.append(position)
v_pos.sort()
SNP_cluster=[]
cluster_d = 10000
for position in v_pos:
if len(SNP_cluster) == 0 or position - SNP_cluster[-1][-1] > cluster_d:
SNP_cluster.append([position])
else:
SNP_cluster[-1].append(position)
for c in SNP_cluster:
#print("H2", len(c), '000000F:{}-{}'.format(min(c)-50, max(c)+50), max(c)-min(c)+100)
print('000000F\t{}\t{}'.format(min(c)-50, max(c)+50))
for c in SNP_cluster:
print((min(c)-50, max(c)+50))
| 0.040683 | 0.350157 |
# The Debugging Book
## Sitemap
While the chapters of this book can be read one after the other, there are many possible paths through the book. In this graph, an arrow _A_ → _B_ means that chapter _A_ is a prerequisite for chapter _B_. You can pick arbitrary paths in this graph to get to the topics that interest you most:
```
# ignore
from IPython.display import SVG
# ignore
SVG(filename='PICS/Sitemap.svg')
```
## [Table of Contents](index.ipynb)
### <a href="01_Intro.ipynb" title="Part I: Whetting Your Appetite (01_Intro) In this part, we introduce the topics of the book.">Part I: Whetting Your Appetite</a>
* <a href="Tours.ipynb" title="Tours through the Book (Tours) ">Tours through the Book</a>
* <a href="Intro_Debugging.ipynb" title="Introduction to Debugging (Intro_Debugging) In this book, we want to explore debugging - the art and science of fixing bugs in computer software. In particular, we want to explore techniques that automatically answer questions like: Where is the bug? When does it occur? And how can we repair it? But before we start automating the debugging process, we first need to understand what this process is.">Introduction to Debugging</a>
### <a href="02_Observing.ipynb" title="Part II: Observing Executions (02_Observing) In this part, we show how to observe executions – by tracing, by interactively debugging, and more.">Part II: Observing Executions</a>
* <a href="Tracer.ipynb" title="Tracing Executions (Tracer) In this chapter, we show how to observe program state during an execution – a prerequisite for logging and interactive debugging. Thanks to the power of Python, we can do this in a few lines of code.">Tracing Executions</a>
* <a href="Debugger.ipynb" title="How Debuggers Work (Debugger) Interactive debuggers are tools that allow you to selectively observe the program state during an execution. In this chapter, you will learn how such debuggers work – by building your own debugger.">How Debuggers Work</a>
* <a href="Assertions.ipynb" title="Asserting Expectations (Assertions) In the previous chapters on tracing and interactive debugging, we have seen how to observe executions. By checking our observations against our expectations, we can find out when and how the program state is faulty. So far, we have assumed that this check would be done by humans – that is, us. However, having this check done by a computer, for instance as part of the execution, is infinitely more rigorous and efficient. In this chapter, we introduce techniques to specify our expectations and to check them at runtime, enabling us to detect faults right as they occur.">Asserting Expectations</a>
### <a href="03_Dependencies.ipynb" title="Part III: Flows and Dependencies (03_Dependencies) In this part, we show how to follow where specific (faulty) values come from, and why they came to be.">Part III: Flows and Dependencies</a>
* <a href="Slicer.ipynb" title="Tracking Failure Origins (Slicer) The question of "Where does this value come from?" is fundamental for debugging. Which earlier variables could possibly have influenced the current erroneous state? And how did their values come to be?">Tracking Failure Origins</a>
### <a href="04_Reducing.ipynb" title="Part IV: Reducing Failure Causes (04_Reducing) In this part, we show how to narrow down failures by systematic experimentation.">Part IV: Reducing Failure Causes</a>
* <a href="DeltaDebugger.ipynb" title="Reducing Failure-Inducing Inputs (DeltaDebugger) A standard problem in debugging is this: Your program fails after processing some large input. Only a part of this input, however, is responsible for the failure. Reducing the input to a failure-inducing minimum not only eases debugging – it also helps in understanding why and when the program fails. In this chapter, we present techniques that automatically reduce and simplify failure-inducing inputs to a minimum, notably the popular Delta Debugging technique.">Reducing Failure-Inducing Inputs</a>
* <a href="ChangeDebugger.ipynb" title="Isolating Failure-Inducing Changes (ChangeDebugger) "Yesterday, my program worked. Today, it does not. Why?" In debugging, as elsewhere in software development, code keeps on changing. Thus, it can happen that a piece of code that yesterday was working perfectly, today no longer runs – because we (or others) have made some changes to it that cause it to fail. The good news is that for debugging, we can actually exploit this version history to narrow down the changes that caused the failure – be it by us or by others.">Isolating Failure-Inducing Changes</a>
### <a href="05_Abstracting.ipynb" title="Part V: Abstracting Failures (05_Abstracting) In this part, we show how to determine abstract failure conditions.">Part V: Abstracting Failures</a>
* <a href="StatisticalDebugger.ipynb" title="Statistical Debugging (StatisticalDebugger) In this chapter, we introduce statistical debugging – the idea that specific events during execution could be statistically correlated with failures. We start with coverage of individual lines and then proceed towards further execution features.">Statistical Debugging</a>
* <a href="DynamicInvariants.ipynb" title="Mining Function Specifications (DynamicInvariants) In the chapter on assertions, we have seen how important it is to check whether the result is as expected. In this chapter, we introduce a technique that allows us to mine function specifications from a set of given executions, resulting in abstract and formal descriptions of what the function expects and what it delivers.">Mining Function Specifications</a>
* <a href="DDSetDebugger.ipynb" title="Generalizing Failure Circumstances (DDSetDebugger) One central question in debugging is: Does this bug occur in other situations, too? In this chapter, we present a technique that is set to generalize the circumstances under which a failure occurs. The DDSET algorithm takes a failure-inducing input, breaks it into individual elements. For each element, it tries to find whether it can be replaced by others in the same category, and if so, it generalizes the concrete element to the very category. The result is a pattern that characterizes the failure condition: "The failure occurs for all inputs of the form (<expr> * <expr>).">Generalizing Failure Circumstances</a>
* <a href="PerformanceDebugger.ipynb" title="Debugging Performance Issues (PerformanceDebugger) Most chapters of this book deal with functional issues – that is, issues related to the functionality (or its absence) of the code in question. However, debugging can also involve nonfunctional issues, however – performance, usability, reliability, and more. In this chapter, we give a short introduction on how to debug such nonfunctional issues, notably performance issues.">Debugging Performance Issues</a>
### <a href="06_Repairing.ipynb" title="Part VI: Automatic Repair (06_Repairing) In this part, we show how to automatically repair code.">Part VI: Automatic Repair</a>
* <a href="Repairer.ipynb" title="Repairing Code Automatically (Repairer) So far, we have discussed how to track failures and how to locate defects in code. Let us now discuss how to repair defects – that is, to correct the code such that the failure no longer occurs. We will discuss how to repair code automatically – by systematically searching through possible fixes and evolving the most promising candidates.">Repairing Code Automatically</a>
### <a href="07_In_the_Large.ipynb" title="Part VII: Debugging in the Large (07_In_the_Large) In this part, we show how to track failures, changes, and fixes.">Part VII: Debugging in the Large</a>
* <a href="Tracking.ipynb" title="Tracking Bugs (Tracking) So far, we have assumed that failures would be discovered and fixed by a single programmer during development. But what if the user who discovers a bug is different from the developer who eventually fixes it? In this case, users have to report bugs, and one needs to ensure that reported bugs are systematically tracked. This is the job of dedicated bug tracking systems, which we will discuss (and demo) in this chapter.">Tracking Bugs</a>
* <a href="ChangeCounter.ipynb" title="Where the Bugs are (ChangeCounter) Every time a bug is fixed, developers leave a trace – in the version database when they commit the fix, or in the bug database when they close the bug. In this chapter, we learn how to mine these repositories for past changes and bugs, and how to map them to individual modules and functions, highlighting those project components that have seen most changes and fixes over time.">Where the Bugs are</a>
### <a href="99_Appendices.ipynb" title="Appendices (99_Appendices) This part holds notebooks and modules that support other notebooks.">Appendices</a>
* <a href="ExpectError.ipynb" title="Error Handling (ExpectError) The code in this notebook helps with handling errors. Normally, an error in notebook code causes the execution of the code to stop; while an infinite loop in notebook code causes the notebook to run without end. This notebook provides two classes to help address these concerns.">Error Handling</a>
* <a href="Timer.ipynb" title="Timer (Timer) The code in this notebook helps with measuring time.">Timer</a>
* <a href="Timeout.ipynb" title="Timeout (Timeout) The code in this notebook helps in interrupting execution after a given time.">Timeout</a>
* <a href="ClassDiagram.ipynb" title="Class Diagrams (ClassDiagram) This is a simple viewer for class diagrams. Customized towards the book.">Class Diagrams</a>
* <a href="StackInspector.ipynb" title="Inspecting Call Stacks (StackInspector) In this book, for many purposes, we need to lookup a function's location, source code, or simply definition. The class StackInspector provides a number of convenience methods for this purpose.">Inspecting Call Stacks</a>
|
github_jupyter
|
# ignore
from IPython.display import SVG
# ignore
SVG(filename='PICS/Sitemap.svg')
| 0.240061 | 0.949576 |
# Resolução dos Exercícios - Versão PC
# Resolução dos Exercícios - Lista II
### 1. Crie um dicionário com 5 entradas e suas respectivas chaves e valores. Faça:
* a) Imprima todas as chaves do dicionário.
* b) Imprima todas os valores do dicionário.
* c) Imprima todas os itens do dicionário.
* d) Imprima o 2º item do dicicionário.
* e) Imprima o dicionário completo.
* f) Percorra o dicionário, imprimindo para cada entrada o modelo "(chave) tem como valor (valor)".
```
# Criando uma dict
studDict = {'joia1':'corrente',
'joia2':'pulseira',
'joia3':'anel',
'joia4':'brinco'}
# a) Imprima todas as chaves do dicionário.
studDict.keys()
# b) Imprima todas os valores do dicionário.
studDict.values()
# c) Imprima todas os itens do dicionário.
studDict.items()
# d) Imprima o 2º item do dicicionário.
studDict['joia2']
# e) Imprima o dicionário completo.
studDict
# f) Percorra o dicionário, imprimindo para
# cada entrada o modelo "(chave) tem como valor (valor)".
for k in studDict.keys():
print('chave: ' + str(k) + ' Valor: ' + str(studDict[k]))
```
### 2. Crie um arquivo e:
* a) Escreva nele os números de 1 a 10.
* b) Depois de escrito, imprima na tela todos os números do arquivo.
* c) Escreva no arquivo os números de 11 a 20, substituindo os números
que estavam antes no arquivo.
* d) Escreva no arquivo os números de 21 a 30, adicionando os números
no final do arquivo (sem apagar o que já estavam lá).
* e) Imprima na tela todos os números do arquivo novamente (de 11 a
30).
* f) Imprima na tela todos os números do arquivo novamente, mas agora
linha por linha.
```
# Criando e abrindo o arquivo
exerc2_arq = open('exerc2.txt','w')
# a) Escreva nele os números de 1 a 10.
exerc2_arq.write('1, 2, 3, 4, 5, 6, 7, 8, 9, 10')
# b) Depois de escrito, imprima na tela todos os números do arquivo.
exerc2_arq = open('exerc2.txt','r')
reading = exerc2_arq.read()
print(reading)
# c) Escreva no arquivo os números de 11 a 20,
# substituindo os números que estavam antes no arquivo.
exerc2_arq = open('exerc2.txt','w')
exerc2_arq.write('11, 12, 13, 14, 15, 16, 17, 18, 19, 20, '+ '\n')
exerc2_arq = open('exerc2.txt','r')
reading = exerc2_arq.read()
print(reading)
# d) Escreva no arquivo os números de 21 a 30,
# adicionando os números no final do arquivo (sem apagar o que já estavam lá).
exerc2_arq = open('exerc2.txt','a')
exerc2_arq.write('21, 22, 23, 24, 25, 26, 27, 28, 29, 30')
exerc2_arq.close()
# e) Imprima na tela todos os números do arquivo novamente (de 11 a 30).
exerc2_arq = open('exerc2.txt','r')
reading = exerc2_arq.read()
exerc2_arq.close()
print(reading)
# f) Imprima na tela todos os números do arquivo
# novamente, mas agora linha por linha.
exerc2_arq = open('exerc2.txt','r')
print(exerc2_arq.readlines())
```
### 3. Crie uma variável com a string “ instituto de ciências matemáticas e de computação” e faça:
* a) Concatene (adicione) uma outra string chamada “usp”.
* b) Concatene (adicione) uma outra informação: 2021.
* c) Verifique o tamanho da nova string (com as informações adicionadas
das questões a e b), com referência a caracteres e espaços.
* d) Transforme a string inteiramente em maiúsculo.
* e) Transforme a string inteiramente em minúsculo.
* f) Retire o espaço que está no início da string e imprima a string.
* g) Substitua todas as letras ‘a’ por ‘x’.
* h) Separe a string em palavras únicas.
* i) Verifique quantas palavras existem na string.
* j) Separe a string por meio da palavra “de”.
* k) Verifique agora quantas palavras/frases foram formadas quando
houve a separação pela palavra “de”.
* l) Junte as palavras que foram separadas (pode usar a separação
resultante da questão h ou j).
* m) Junte as palavras que foram separadas, mas agora separadas por uma
barra invertida, não por espaços (pode usar a separação resultante da
questão h ou j).
```
# Criando variável
var_usp = ' instituto de ciências matemáticas e de computação'
var_usp
# a) Concatene (adicione) uma outra string chamada “usp”.
var_usp = var_usp + ' usp'
var_usp
# b) Concatene (adicione) uma outra informação: 2021.
var_usp = var_usp + ' 2021'
var_usp
# c) Verifique o tamanho da nova string (com as informações
# adicionadas das questões a) e b), com referência a caracteres e espaços.
print(len(var_usp))
# d) Transforme a string inteiramente em maiúsculo.
var_usp.upper()
# e) Transforme a string inteiramente em minúsculo.
var_usp.lower()
# f) Retire o espaço que está no início da string e imprima a string.
var_usp = var_usp.strip()
var_usp
# g) Substitua todas as letras ‘a’ por ‘x’.
var_usp.replace('a','x')
# h) Separe a string em palavras únicas.
var_usp1 = var_usp.split()
var_usp1
# i) Verifique quantas palavras existem na string.
print(len(var_usp1))
# j) Separe a string por meio da palavra “de”.
var_usp = 'de'.join(var_usp)
var_usp2 = var_usp.split()
var_usp2
# k) Verifique agora quantas palavras/frases foram formadas
# quando houve a separação pela palavra “de”.
print(len(var_usp))
# l) Junte as palavras que foram separadas (pode usar a
# separação resultante da questão h) ou j).
var_usp = ' '.join(var_usp1)
var_usp
# m) Junte as palavras que foram separadas, mas agora separadas
# por uma barra invertida, não por espaços (pode usar a separação
# resultante da questão h) ou j).
var_usp = "\\".join(var_usp1)
var_usp
```
### 4. Crie uma lista com números de 0 a 9 (em qualquer ordem) e faça:
* a) Tokenize o corpus inteiro (palavras, números e pontuações).
* b) Verifique a quantidade de tokens do corpus.
* c) Tokenize o corpus apenas por suas palavras.
* d) Verifique a quantidade de palavras do corpus.
* e) Verifique a frequência de palavras no corpus.
* f) Verifique quais são as 5, 10 e 15 palavras mais frequentes do corpus.
* g) Extraia as stopwords do NLTK (não do corpus ainda).
* h) Verifique a frequência dos tokens sem stopwords do corpus.
* i) Extraia todos os bigramas do corpus.
* j) Extraia todos os trigramas do corpus.
* k) Extraia todos os 4-gramas do corpus.
* l) Retorne as entidades nomeadas do corpus, usando os bigramas e
trigramas.
* m) Escolha 3 palavras do seu corpus e faça o stemming delas.
* n) Separe uma sentença do seu corpus e retorne todas as classes
gramaticais das palavras da sentença. Analise se o etiquetador
acertou todas as classes gramaticais.
* o) Retorne as classes gramaticais de todas as palavras do seu corpus.
* p) Retorne as entidades nomeadas do seu corpus, usando a técnica de
chunking.
```
# Criando a lista
list01 = [0,1,2,3,4,5,6,7,8,9]
list01
# a) Tokenize o corpus inteiro (palavras, números e pontuações).
# b) Verifique a quantidade de tokens do corpus.
# c) Tokenize o corpus apenas por suas palavras.
# d) Verifique a quantidade de palavras do corpus.
# e) Verifique a frequência de palavras no corpus.
# f) Verifique quais são as 5, 10 e 15 palavras mais frequentes do corpus.
# g) Extraia as stopwords do NLTK (não do corpus ainda).
# h) Verifique a frequência dos tokens sem stopwords do corpus.
# i) Extraia todos os bigramas do corpus.
# j) Extraia todos os trigramas do corpus.
# k) Extraia todos os 4-gramas do corpus.
# l) Retorne as entidades nomeadas do corpus, usando os bigramas e trigramas.
# m) Escolha 3 palavras do seu corpus e faça o stemming delas.
''' n) Separe uma sentença do seu corpus e retorne
todas as classes gramaticais das palavras da sentença.
Analise se o etiquetador acertou todas as classes gramaticais. '''
# o) Retorne as classes gramaticais de todas as palavras do seu corpus.
# p) Retorne as entidades nomeadas do seu corpus, usando a técnica de chunking.
```
### Exercícios de fixação presentes nos slides da aula que se encontram no Drive do curso:
* Parte I (slides 26 a 29).
* Parte II (slide 33).
#### Exercícios - Parte I
```
# Abrindo arquivo txt do corpus no disco local e salvando em uma variável
text_qbdata = open('textos/qbdata.txt','r')
reading_qbdata = text_qbdata.read()
text_qbdata.close()
reading_qbdata
```
##### 1. Dado o arquivo qbdata.txt, retorne o rating de cada QB na forma “nome do QB teve valor XX.X’ e escreva em um arquivo novo.
##### 2. Pensando em uma agenda, construa um dicionário com informações do contato sendo: CPF, nome, telefone e user no Twitter.
##### Ao final, imprima todos os contatos da seguinte forma:
* CPF: nome, telefone (user)
#### Exercícios - Parte II
##### Faça uma análise descritiva completa do nosso corpus de teste, utilizando as funções do NLTK.
> Exemplos de atributos:
* Quantidade de tokens.
* Quantidade de sentenças / média do tamanho das
sentenças.
* Quantidade de substantivos, adjetivos, advérbios...
* Quantidade de palavras com o mesmo radical.
* Quantidade de símbolos de pontuação.
* Palavras mais frequentes do corpus.
|
github_jupyter
|
# Criando uma dict
studDict = {'joia1':'corrente',
'joia2':'pulseira',
'joia3':'anel',
'joia4':'brinco'}
# a) Imprima todas as chaves do dicionário.
studDict.keys()
# b) Imprima todas os valores do dicionário.
studDict.values()
# c) Imprima todas os itens do dicionário.
studDict.items()
# d) Imprima o 2º item do dicicionário.
studDict['joia2']
# e) Imprima o dicionário completo.
studDict
# f) Percorra o dicionário, imprimindo para
# cada entrada o modelo "(chave) tem como valor (valor)".
for k in studDict.keys():
print('chave: ' + str(k) + ' Valor: ' + str(studDict[k]))
# Criando e abrindo o arquivo
exerc2_arq = open('exerc2.txt','w')
# a) Escreva nele os números de 1 a 10.
exerc2_arq.write('1, 2, 3, 4, 5, 6, 7, 8, 9, 10')
# b) Depois de escrito, imprima na tela todos os números do arquivo.
exerc2_arq = open('exerc2.txt','r')
reading = exerc2_arq.read()
print(reading)
# c) Escreva no arquivo os números de 11 a 20,
# substituindo os números que estavam antes no arquivo.
exerc2_arq = open('exerc2.txt','w')
exerc2_arq.write('11, 12, 13, 14, 15, 16, 17, 18, 19, 20, '+ '\n')
exerc2_arq = open('exerc2.txt','r')
reading = exerc2_arq.read()
print(reading)
# d) Escreva no arquivo os números de 21 a 30,
# adicionando os números no final do arquivo (sem apagar o que já estavam lá).
exerc2_arq = open('exerc2.txt','a')
exerc2_arq.write('21, 22, 23, 24, 25, 26, 27, 28, 29, 30')
exerc2_arq.close()
# e) Imprima na tela todos os números do arquivo novamente (de 11 a 30).
exerc2_arq = open('exerc2.txt','r')
reading = exerc2_arq.read()
exerc2_arq.close()
print(reading)
# f) Imprima na tela todos os números do arquivo
# novamente, mas agora linha por linha.
exerc2_arq = open('exerc2.txt','r')
print(exerc2_arq.readlines())
# Criando variável
var_usp = ' instituto de ciências matemáticas e de computação'
var_usp
# a) Concatene (adicione) uma outra string chamada “usp”.
var_usp = var_usp + ' usp'
var_usp
# b) Concatene (adicione) uma outra informação: 2021.
var_usp = var_usp + ' 2021'
var_usp
# c) Verifique o tamanho da nova string (com as informações
# adicionadas das questões a) e b), com referência a caracteres e espaços.
print(len(var_usp))
# d) Transforme a string inteiramente em maiúsculo.
var_usp.upper()
# e) Transforme a string inteiramente em minúsculo.
var_usp.lower()
# f) Retire o espaço que está no início da string e imprima a string.
var_usp = var_usp.strip()
var_usp
# g) Substitua todas as letras ‘a’ por ‘x’.
var_usp.replace('a','x')
# h) Separe a string em palavras únicas.
var_usp1 = var_usp.split()
var_usp1
# i) Verifique quantas palavras existem na string.
print(len(var_usp1))
# j) Separe a string por meio da palavra “de”.
var_usp = 'de'.join(var_usp)
var_usp2 = var_usp.split()
var_usp2
# k) Verifique agora quantas palavras/frases foram formadas
# quando houve a separação pela palavra “de”.
print(len(var_usp))
# l) Junte as palavras que foram separadas (pode usar a
# separação resultante da questão h) ou j).
var_usp = ' '.join(var_usp1)
var_usp
# m) Junte as palavras que foram separadas, mas agora separadas
# por uma barra invertida, não por espaços (pode usar a separação
# resultante da questão h) ou j).
var_usp = "\\".join(var_usp1)
var_usp
# Criando a lista
list01 = [0,1,2,3,4,5,6,7,8,9]
list01
# a) Tokenize o corpus inteiro (palavras, números e pontuações).
# b) Verifique a quantidade de tokens do corpus.
# c) Tokenize o corpus apenas por suas palavras.
# d) Verifique a quantidade de palavras do corpus.
# e) Verifique a frequência de palavras no corpus.
# f) Verifique quais são as 5, 10 e 15 palavras mais frequentes do corpus.
# g) Extraia as stopwords do NLTK (não do corpus ainda).
# h) Verifique a frequência dos tokens sem stopwords do corpus.
# i) Extraia todos os bigramas do corpus.
# j) Extraia todos os trigramas do corpus.
# k) Extraia todos os 4-gramas do corpus.
# l) Retorne as entidades nomeadas do corpus, usando os bigramas e trigramas.
# m) Escolha 3 palavras do seu corpus e faça o stemming delas.
''' n) Separe uma sentença do seu corpus e retorne
todas as classes gramaticais das palavras da sentença.
Analise se o etiquetador acertou todas as classes gramaticais. '''
# o) Retorne as classes gramaticais de todas as palavras do seu corpus.
# p) Retorne as entidades nomeadas do seu corpus, usando a técnica de chunking.
# Abrindo arquivo txt do corpus no disco local e salvando em uma variável
text_qbdata = open('textos/qbdata.txt','r')
reading_qbdata = text_qbdata.read()
text_qbdata.close()
reading_qbdata
| 0.160858 | 0.835316 |
# Implementation of a Devito viscoacoustic equations
## This tutorial is contributed by SENAI CIMATEC (2020)
This tutorial is based on:
<br>**Linear inversion in layered viscoacoustic media using a time‐domain method** (1994)
<br>Joakim O. Blanch and William W. Symes
<br>SEG Technical Program Expanded Abstracts
<br>https://doi.org/10.1190/1.1822695
<br>**True-amplitude prestack depth migration** (2007)
<br>Feng Deng and George A. McMechan
<br>GEOPHYSICS Technical Papers
<br>https://doi.org/10.1190/1.2714334
<br>**Attenuation compensation for least-squares reverse time migration using the viscoacoustic-wave equation** (2014)
<br>Gaurav Dutta and Gerard T. Schuster
<br>GEOPHYSICS Technical Papers
<br>https://doi.org/10.1190/geo2013-0414.1
<br>**Multiscale viscoacoustic waveform inversion with the second generation wavelet transform and adaptive time–space domain finite-difference method** (2014)
<br>Zhiming Ren, Yang Liu,and Qunshan Zhang
<br>Geophysical Journal International, Volume 197, Issue 2, 1 May 2014, Pages 948–974
<br>https://doi.org/10.1093/gji/ggu024
<br>**Viscoacoustic prestack reverse time migration based on the optimal time-space domain high-order finite-difference method** (2014)
<br>Yan Zhao, Yang Liu, and Zhi-Ming Ren
<br>Appl. Geophys. 11, 50–62.
<br>https://doi.org/10.1007/s11770-014-0414-8
<br>**A stable and efficient approach of Q reverse time migration** (2018)
<br>Yan Zhao, Ningbo Mao, and Zhiming Ren
<br>GEOPHYSICS Technical Papers
<br>https://doi.org/10.1190/geo2018-0022.1
## Introduction
The conversion of mechanical energy to heat, occurs during the propagation of seismic waves on the subsurface, due to the viscosity of the rocks. The presence of oil and gas in these rocks causes seismic attenuations. Thus, associated effects, such as dispersion and dissipation, can significantly affect the amplitudes, as well as the phase of the seismic pulse. However, in the seismic exploration, the subsurface has still been considered as an ideal elastic/acoustic medium, that is, disregarding its mitigating effect. In practice, the propagation of seismic waves on the subsurface is in many ways different from propagation in an ideal solid.
For example, some subsurface rocks have anisotropic properties, are heterogeneous, porous and so on. The acoustic/elastic wave equation is not sensitive enough to describe propagation in these more complicated mediums. Generally, the viscosity of materials in the subsurface causes energy dissipation and consequently a decrease in amplitude, in addition to modifying the frequency content of the waves. This phenomenon of energy dissipation of the wave is called seismic absorption or attenuation.
The goal of this tutorial is to perform a seismic modeling taking into account the viscosity of the medium, so that it is possible to more accurately simulate the seismic data and consequently build images with better resolution in the processing of this data, in addition to extracting more detailed information on rocky materials through seismic inversion.
This tutorial follow three main viscoacoustic approaches in time-space domain:
- Blanch and Symes (1995) / Dutta and Schuster (2014)
- Ren et al. (2014)
- Deng and McMechan (2007)
<h1><center>Table of symbols</center></h1>
| Symbol | Description
| :--- | :---
|$f$ |Frequency |
|$f_o$ |Reference frequency |
|$\omega$ |Angular frenquency |
|$\omega_0$ |Angular Reference Frequency |
|$v$ |Velocity model |
|$v_0$ |Reference velocity at $\omega_0$ |
|$\kappa$ |Bulk modulus |
|$g$ |Absorption coefficient |
|$\tau$ |Relaxation time |
|$\tau_\sigma$ |Stress relaxation parameter |
|$\tau_\epsilon$ |Strain relaxation parameter |
|$Q$ |Quality factor |
|$\eta$ |Viscosity |
|$\rho$ |Density |
|$\nabla$ |Nabla operator |
|$P({\bf x},t)$ |Pressure field |
|$r({\bf x},t)$ |Memory variable |
|${\bf v}({\bf x},t)$ |Particle velocity |
|$S({\bf x}_s,t)$ |Source |
# Seismic modelling with Devito
Before start with the viscoacoustic approaches we will describe a setup of seismic modelling with Devito in a simple 2D case. We will create a physical model of our domain and define a single source and an according set of receivers to model for the forward model. But first, we initialize some basic utilities.
```
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
from devito import *
from examples.seismic.source import RickerSource, WaveletSource, TimeAxis
from examples.seismic import ModelViscoacoustic, plot_image, setup_geometry, plot_velocity
nx = 300
nz = 300
# Define a physical size
shape = (nx, nz)
spacing = (20., 20.)
origin = (0., 0.)
nlayers = 3
nbl = 50
space_order = 8
dtype = np.float32
# Model physical parameters:
vp = np.zeros(shape)
qp = np.zeros(shape)
rho = np.zeros(shape)
# Define a velocity profile. The velocity is in km/s
vp_top = 1.5
vp_bottom = 3.5
# Define a velocity profile in km/s
v = np.empty(shape, dtype=dtype)
v[:] = vp_top # Top velocity (background)
vp_i = np.linspace(vp_top, vp_bottom, nlayers)
for i in range(1, nlayers):
v[..., i*int(shape[-1] / nlayers):] = vp_i[i] # Bottom velocity
qp[:] = 3.516*((v[:]*1000.)**2.2)*10**(-6) # Li's empirical formula
rho[:] = 0.31*(v[:]*1000.)**0.25 # Gardner's relation
#NBVAL_IGNORE_OUTPUT
model = ModelViscoacoustic(space_order=space_order, vp=v, qp=qp, b=1/rho,
origin=origin, shape=shape, spacing=spacing,
nbl=nbl)
#NBVAL_IGNORE_OUTPUT
aspect_ratio = model.shape[0]/model.shape[1]
plt_options_model = {'cmap': 'jet', 'extent': [model.origin[0], model.origin[0] + model.domain_size[0],
model.origin[1] + model.domain_size[1], model.origin[1]]}
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(15, 5))
slices = [slice(model.nbl, -model.nbl), slice(model.nbl, -model.nbl)]
img1 = ax[0].imshow(np.transpose(model.vp.data[slices]), vmin=1.5, vmax=3.5, **plt_options_model)
fig.colorbar(img1, ax=ax[0])
ax[0].set_title(r"V (km/s)", fontsize=20)
ax[0].set_xlabel('X (m)', fontsize=20)
ax[0].set_ylabel('Depth (m)', fontsize=20)
ax[0].set_aspect('auto')
img2 = ax[1].imshow(np.transpose(qp), vmin=15, vmax=220, **plt_options_model)
fig.colorbar(img2, ax=ax[1])
ax[1].set_title("Q", fontsize=20)
ax[1].set_xlabel('X (m)', fontsize=20)
ax[1].set_ylabel('Depth (m)', fontsize=20)
ax[1].set_aspect('auto')
img3 = ax[2].imshow(np.transpose(rho), vmin=1.9, vmax=2.4, **plt_options_model)
fig.colorbar(img3, ax=ax[2])
ax[2].set_title(r"Density $\rho$ (g/cm^3)", fontsize=20)
ax[2].set_xlabel('X (m)', fontsize=20)
ax[2].set_ylabel('Depth (m)', fontsize=20)
ax[2].set_aspect('auto')
plt.tight_layout()
f0 = 0.005 # peak/dominant frequency
b = model.b
rho = 1./b
# velocity model
vp = model.vp
t_s = (sp.sqrt(1.+1./model.qp**2)-1./model.qp)/f0
t_ep = 1./(f0**2*t_s)
tt = (t_ep/t_s) - 1.
s = model.grid.stepping_dim.spacing
damp = model.damp
# Time step in ms and time range:
t0, tn = 0., 2000.
dt = model.critical_dt
time_range = TimeAxis(start=t0, stop=tn, step=dt)
from examples.seismic import Receiver
def src_rec(p, model):
src = RickerSource(name='src', grid=model.grid, f0=f0, time_range=time_range)
src.coordinates.data[0, :] = np.array(model.domain_size) * .5
src.coordinates.data[0, -1] = 8.
# Create symbol for receivers
rec = Receiver(name='rec', grid=model.grid, npoint=shape[0], time_range=time_range)
# Prescribe even spacing for receivers along the x-axis
rec.coordinates.data[:, 0] = np.linspace(0, model.domain_size[0], num=shape[0])
rec.coordinates.data[:, 1] = 8.
src_term = src.inject(field=p.forward, expr=(s*src))
rec_term = rec.interpolate(expr=p)
return src_term + rec_term, src, rec
```
Auxiliary functions for plotting data:
```
def plot_receiver(rec):
rec_plot = rec.resample(num=1001)
scale_for_plot = np.diag(np.linspace(1.0, 2.5, 1001)**2.0)
# Pressure (txx + tzz) data at sea surface
extent = [rec_plot.coordinates.data[0, 0], rec_plot.coordinates.data[-1, 0], 1e-3*tn, t0]
aspect = rec_plot.coordinates.data[-1, 0]/(1e-3*tn)/.5
plt.figure(figsize=(10, 10))
plt.imshow(np.dot(scale_for_plot, rec_plot.data), vmin=-.01, vmax=.01, cmap="seismic",
interpolation='lanczos', extent=extent, aspect=aspect)
plt.ylabel("Time (s)", fontsize=20)
plt.xlabel("Receiver position (m)", fontsize=20)
def plot_v_and_p(model, v, p):
slices = [slice(model.nbl, -model.nbl), slice(model.nbl, -model.nbl)]
scale = .5*1e-3
plt_options_model = {'extent': [model.origin[0] , model.origin[0] + model.domain_size[0],
model.origin[1] + model.domain_size[1], model.origin[1]]}
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(15, 7))
ax[0].imshow(np.transpose(v[0].data[0][slices]), vmin=-scale, vmax=scale, cmap="RdGy", **plt_options_model)
ax[0].imshow(np.transpose(model.vp.data[slices]), vmin=1.5, vmax=3.5, cmap="jet", alpha=.5, **plt_options_model)
ax[0].set_aspect('auto')
ax[0].set_xlabel('X (m)', fontsize=20)
ax[0].set_ylabel('Depth (m)', fontsize=20)
ax[0].set_title(r"$v_{x}$", fontsize=20)
ax[1].imshow(np.transpose(v[1].data[0][slices]), vmin=-scale, vmax=scale, cmap="RdGy", **plt_options_model)
ax[1].imshow(np.transpose(model.vp.data[slices]), vmin=1.5, vmax=3.5, cmap="jet", alpha=.5, **plt_options_model)
ax[1].set_aspect('auto')
ax[1].set_xlabel('X (m)', fontsize=20)
ax[1].set_title(r"$v_{z}$", fontsize=20)
ax[2].imshow(np.transpose(p.data[0][slices]), vmin=-scale, vmax=scale, cmap="RdGy", **plt_options_model)
ax[2].imshow(np.transpose(model.vp.data[slices]), vmin=1.5, vmax=3.5, cmap="jet", alpha=.5, **plt_options_model)
ax[2].set_aspect('auto')
ax[2].set_xlabel('X (m)', fontsize=20)
ax[2].set_title(r"$P$", fontsize=20)
```
## Blanch and Symes (1995) / Dutta and Schuster (2014)
The equations of motion for a viscoacoustic medium can be written as:
\begin{equation}
\left\{
\begin{array}{lcl}
\frac{\partial P}{\partial t} + \kappa (\tau + 1)(\nabla \cdot {\bf v}) + r = S({\bf x}_{s}, t) \\
\frac{\partial {\bf v}}{\partial t} + \frac{1}{\rho}\nabla{P} = 0 \\
\frac{\partial r}{\partial t} + \frac{1}{\tau_{\sigma}} [r + \tau \kappa (\nabla \cdot {\bf v})] = 0.
\end{array}
\right.
\label{first-order-dutta}
\end{equation}
Where $\tau = \tau_{\epsilon}/\tau_{\sigma} -1$ represents the magnitude of $Q$. $\tau_{\epsilon}$ and $\tau_{\sigma}$ are, respectively, the stress and strain relaxation parameters, given by:
\begin{equation}
\tau_\sigma = \frac{\sqrt{Q^2+1}-1}{2 \pi f_0 Q}
\end{equation}
and
\begin{equation}
\tau_\epsilon= \frac{\sqrt{Q^2+1}+1}{2\pi f_0 Q}
\end{equation}
```
# Stencil created from Blanch and Symes (1995) / Dutta and Schuster (2014)
def blanch_symes(model, p, r, v):
# Bulk modulus
bm = rho * (vp * vp)
# Define PDE to v
pde_v = v - s * b * grad(p)
u_v = Eq(v.forward, damp * pde_v)
# Define PDE to r
pde_r = r - s * (1. / t_s) * r - s * (1. / t_s) * tt * bm * div(v.forward)
u_r = Eq(r.forward, damp * pde_r)
# Define PDE to p
pde_p = p - s * bm * (tt + 1.) * div(v.forward) - s * r.forward
u_p = Eq(p.forward, damp * pde_p)
return [u_v, u_r, u_p]
# Seismic Modelling from Blanch and Symes (1995) / Dutta and Schuster (2014) viscoacoustic wave equation.
def modelling_blanch_symes(model):
# Create symbols for particle velocity, pressure field, memory variable, source and receivers
v = VectorTimeFunction(name="v", grid=model.grid, time_order=1, space_order=space_order)
p = TimeFunction(name="p", grid=model.grid, time_order=1, space_order=space_order,
staggered=NODE)
r = TimeFunction(name="r", grid=model.grid, time_order=1, space_order=space_order,
staggered=NODE)
# define the source injection and create interpolation expression for receivers
src_rec_expr, src, rec = src_rec(p, model)
eqn = blanch_symes(model, p, r, v)
op = Operator(eqn + src_rec_expr, subs=model.spacing_map)
op(time=time_range.num-1, dt=dt, src=src, rec=rec)
return rec, v, p
#NBVAL_IGNORE_OUTPUT
rec, v, p = modelling_blanch_symes(model)
#NBVAL_IGNORE_OUTPUT
plot_receiver(rec)
assert np.isclose(np.linalg.norm(rec.data), 16, rtol=10)
#NBVAL_IGNORE_OUTPUT
plot_v_and_p(model, v, p)
assert np.isclose(norm(v[0]), 1.87797, atol=1e-3, rtol=0)
```
## Ren et al. (2014)
The viscoacoustic wave equation in time domain is written as:
\begin{equation}
\frac{\partial^{2}P}{\partial{t^2}} - v^{2}\nabla^{2}{P} - \eta\nabla^{2}\left(\frac{\partial P}{\partial t}\right) = S({\bf x}_{s}, t),
\end{equation}
where $\eta = \frac{v^2}{\omega_{0}Q}$ represents the viscosity of medium.
Considering the variable density $\rho$, the equation can be rewritten as:
\begin{equation}
\frac{\partial^{2}P}{\partial{t^2}} - \kappa \nabla \cdot \frac{1}{\rho} \nabla{P} - \eta \rho \nabla \cdot \frac{1}{\rho} \nabla \left(\frac{\partial{P}}{\partial{t}}\right) = S({\bf x}_{s}, t).
\end{equation}
The equation can be written using a first order formulation, given by:
\begin{equation}
\left\{
\begin{array}{ll}
\frac{\partial P}{\partial t} + \kappa \nabla \cdot {\bf v} - \eta \rho \nabla \cdot \frac{1}{\rho} \nabla{P} = S({\bf x}_{s}, t) \\
\frac{\partial {\bf v}}{\partial t} + \frac{1}{\rho} \nabla{P} = 0
\end{array}
\right.
\end{equation}
```
# Stencil created from Ren et al. (2014) viscoacoustic wave equation.
def ren(model, p, v):
# Angular frequency
w = 2. * np.pi * f0
# Define PDE to v
pde_v = v - s * b * grad(p)
u_v = Eq(v.forward, damp * pde_v)
# Define PDE to p
pde_p = p - s * vp * vp * rho * div(v.forward) + s * \
((vp * vp * rho) / (w * model.qp)) * div(b * grad(p, shift=.5), shift=-.5)
u_p = Eq(p.forward, damp * pde_p)
return [u_v, u_p]
# Seismic Modelling from Ren et al. (2014) viscoacoustic wave equation.
def modelling_ren(model):
# Create symbols for particle velocity, pressure field, source and receivers
v = VectorTimeFunction(name="v", grid=model.grid, time_order=1, space_order=space_order)
p = TimeFunction(name="p", grid=model.grid, time_order=1, space_order=space_order,
staggered=NODE)
# define the source injection and create interpolation expression for receivers
src_rec_expr, src, rec = src_rec(p, model)
eqn = ren(model, p, v)
op = Operator(eqn + src_rec_expr, subs=model.spacing_map)
op(time=time_range.num-1, dt=dt, src=src, rec=rec)
return rec, v, p
#NBVAL_IGNORE_OUTPUT
rec, v, p = modelling_ren(model)
#NBVAL_IGNORE_OUTPUT
plot_receiver(rec)
assert np.isclose(np.linalg.norm(rec.data), 15, rtol=10)
#NBVAL_IGNORE_OUTPUT
plot_v_and_p(model, v, p)
assert np.isclose(norm(v[0]), 1.0639238, atol=1e-3, rtol=0)
```
## Deng and McMechan (2007)
The viscoacoustic wave equation for the propagating pressure $P$ in the time-space domain:
\begin{equation}
\frac{1}{v^2}\frac{\partial^{2}P}{\partial{t^2}} - \nabla^{2}P + \frac{g}{v}\frac{\partial P}{\partial{t}} = S({\bf x}_{s}, t),
\label{eq-deng}
\end{equation}
where $g$ is the absorption coefficient, given by:
\begin{equation}
g = \frac{2\pi f_{0}}{vQ},
\end{equation}
The equation can be written using a first order formulation, given by:
\begin{equation}
\left\{
\begin{array}{lcl}
\frac{\partial P}{\partial t} + \kappa (\nabla \cdot {\bf v}) + \frac{2\pi f_{0}}{Q}P= S({\bf x}_{s}, t) \\
\frac{\partial {\bf v}}{\partial t} + \frac{1}{\rho}\nabla{P} = 0 \\
\end{array}
\right.
\end{equation}
```
# Stencil created from Deng and McMechan (2007) viscoacoustic wave equation.
def deng_mcmechan(model, p, v):
# Angular frequency
w = 2. * np.pi * f0
# Define PDE to v
pde_v = v - s * b * grad(p)
u_v = Eq(v.forward, damp * pde_v)
# Define PDE to p
pde_p = p - s * vp * vp * rho * div(v.forward) - s * (w / model.qp) * p
u_p = Eq(p.forward, damp * pde_p)
return [u_v, u_p]
# Seismic Modelling from Deng and McMechan (2007) viscoacoustic wave equation.
def modelling_deng_mcmechan(model):
# Create symbols for particle velocity, pressure field, source and receivers
v = VectorTimeFunction(name="v", grid=model.grid, time_order=1, space_order=space_order)
p = TimeFunction(name="p", grid=model.grid, time_order=1, space_order=space_order,
staggered=NODE)
# define the source injection and create interpolation expression for receivers
src_rec_expr, src, rec = src_rec(p, model)
eqn = deng_mcmechan(model, p, v)
op = Operator(eqn + src_rec_expr, subs=model.spacing_map)
op(time=time_range.num-1, dt=dt, src=src, rec=rec)
return rec, v, p
#NBVAL_IGNORE_OUTPUT
rec, v, p = modelling_deng_mcmechan(model)
#NBVAL_IGNORE_OUTPUT
plot_receiver(rec)
assert np.isclose(np.linalg.norm(rec.data), 16, rtol=10)
#NBVAL_IGNORE_OUTPUT
plot_v_and_p(model, v, p)
assert np.isclose(norm(v[0]), 1.1323929, atol=1e-3, rtol=0)
```
# More references
[1] https://academic.oup.com/gji/article/197/2/948/616510
[2] https://link.springer.com/article/10.1007/s11770-014-0414-8
[3] https://janth.home.xs4all.nl/Software/fdelmodcManual.pdf
|
github_jupyter
|
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
from devito import *
from examples.seismic.source import RickerSource, WaveletSource, TimeAxis
from examples.seismic import ModelViscoacoustic, plot_image, setup_geometry, plot_velocity
nx = 300
nz = 300
# Define a physical size
shape = (nx, nz)
spacing = (20., 20.)
origin = (0., 0.)
nlayers = 3
nbl = 50
space_order = 8
dtype = np.float32
# Model physical parameters:
vp = np.zeros(shape)
qp = np.zeros(shape)
rho = np.zeros(shape)
# Define a velocity profile. The velocity is in km/s
vp_top = 1.5
vp_bottom = 3.5
# Define a velocity profile in km/s
v = np.empty(shape, dtype=dtype)
v[:] = vp_top # Top velocity (background)
vp_i = np.linspace(vp_top, vp_bottom, nlayers)
for i in range(1, nlayers):
v[..., i*int(shape[-1] / nlayers):] = vp_i[i] # Bottom velocity
qp[:] = 3.516*((v[:]*1000.)**2.2)*10**(-6) # Li's empirical formula
rho[:] = 0.31*(v[:]*1000.)**0.25 # Gardner's relation
#NBVAL_IGNORE_OUTPUT
model = ModelViscoacoustic(space_order=space_order, vp=v, qp=qp, b=1/rho,
origin=origin, shape=shape, spacing=spacing,
nbl=nbl)
#NBVAL_IGNORE_OUTPUT
aspect_ratio = model.shape[0]/model.shape[1]
plt_options_model = {'cmap': 'jet', 'extent': [model.origin[0], model.origin[0] + model.domain_size[0],
model.origin[1] + model.domain_size[1], model.origin[1]]}
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(15, 5))
slices = [slice(model.nbl, -model.nbl), slice(model.nbl, -model.nbl)]
img1 = ax[0].imshow(np.transpose(model.vp.data[slices]), vmin=1.5, vmax=3.5, **plt_options_model)
fig.colorbar(img1, ax=ax[0])
ax[0].set_title(r"V (km/s)", fontsize=20)
ax[0].set_xlabel('X (m)', fontsize=20)
ax[0].set_ylabel('Depth (m)', fontsize=20)
ax[0].set_aspect('auto')
img2 = ax[1].imshow(np.transpose(qp), vmin=15, vmax=220, **plt_options_model)
fig.colorbar(img2, ax=ax[1])
ax[1].set_title("Q", fontsize=20)
ax[1].set_xlabel('X (m)', fontsize=20)
ax[1].set_ylabel('Depth (m)', fontsize=20)
ax[1].set_aspect('auto')
img3 = ax[2].imshow(np.transpose(rho), vmin=1.9, vmax=2.4, **plt_options_model)
fig.colorbar(img3, ax=ax[2])
ax[2].set_title(r"Density $\rho$ (g/cm^3)", fontsize=20)
ax[2].set_xlabel('X (m)', fontsize=20)
ax[2].set_ylabel('Depth (m)', fontsize=20)
ax[2].set_aspect('auto')
plt.tight_layout()
f0 = 0.005 # peak/dominant frequency
b = model.b
rho = 1./b
# velocity model
vp = model.vp
t_s = (sp.sqrt(1.+1./model.qp**2)-1./model.qp)/f0
t_ep = 1./(f0**2*t_s)
tt = (t_ep/t_s) - 1.
s = model.grid.stepping_dim.spacing
damp = model.damp
# Time step in ms and time range:
t0, tn = 0., 2000.
dt = model.critical_dt
time_range = TimeAxis(start=t0, stop=tn, step=dt)
from examples.seismic import Receiver
def src_rec(p, model):
src = RickerSource(name='src', grid=model.grid, f0=f0, time_range=time_range)
src.coordinates.data[0, :] = np.array(model.domain_size) * .5
src.coordinates.data[0, -1] = 8.
# Create symbol for receivers
rec = Receiver(name='rec', grid=model.grid, npoint=shape[0], time_range=time_range)
# Prescribe even spacing for receivers along the x-axis
rec.coordinates.data[:, 0] = np.linspace(0, model.domain_size[0], num=shape[0])
rec.coordinates.data[:, 1] = 8.
src_term = src.inject(field=p.forward, expr=(s*src))
rec_term = rec.interpolate(expr=p)
return src_term + rec_term, src, rec
def plot_receiver(rec):
rec_plot = rec.resample(num=1001)
scale_for_plot = np.diag(np.linspace(1.0, 2.5, 1001)**2.0)
# Pressure (txx + tzz) data at sea surface
extent = [rec_plot.coordinates.data[0, 0], rec_plot.coordinates.data[-1, 0], 1e-3*tn, t0]
aspect = rec_plot.coordinates.data[-1, 0]/(1e-3*tn)/.5
plt.figure(figsize=(10, 10))
plt.imshow(np.dot(scale_for_plot, rec_plot.data), vmin=-.01, vmax=.01, cmap="seismic",
interpolation='lanczos', extent=extent, aspect=aspect)
plt.ylabel("Time (s)", fontsize=20)
plt.xlabel("Receiver position (m)", fontsize=20)
def plot_v_and_p(model, v, p):
slices = [slice(model.nbl, -model.nbl), slice(model.nbl, -model.nbl)]
scale = .5*1e-3
plt_options_model = {'extent': [model.origin[0] , model.origin[0] + model.domain_size[0],
model.origin[1] + model.domain_size[1], model.origin[1]]}
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(15, 7))
ax[0].imshow(np.transpose(v[0].data[0][slices]), vmin=-scale, vmax=scale, cmap="RdGy", **plt_options_model)
ax[0].imshow(np.transpose(model.vp.data[slices]), vmin=1.5, vmax=3.5, cmap="jet", alpha=.5, **plt_options_model)
ax[0].set_aspect('auto')
ax[0].set_xlabel('X (m)', fontsize=20)
ax[0].set_ylabel('Depth (m)', fontsize=20)
ax[0].set_title(r"$v_{x}$", fontsize=20)
ax[1].imshow(np.transpose(v[1].data[0][slices]), vmin=-scale, vmax=scale, cmap="RdGy", **plt_options_model)
ax[1].imshow(np.transpose(model.vp.data[slices]), vmin=1.5, vmax=3.5, cmap="jet", alpha=.5, **plt_options_model)
ax[1].set_aspect('auto')
ax[1].set_xlabel('X (m)', fontsize=20)
ax[1].set_title(r"$v_{z}$", fontsize=20)
ax[2].imshow(np.transpose(p.data[0][slices]), vmin=-scale, vmax=scale, cmap="RdGy", **plt_options_model)
ax[2].imshow(np.transpose(model.vp.data[slices]), vmin=1.5, vmax=3.5, cmap="jet", alpha=.5, **plt_options_model)
ax[2].set_aspect('auto')
ax[2].set_xlabel('X (m)', fontsize=20)
ax[2].set_title(r"$P$", fontsize=20)
# Stencil created from Blanch and Symes (1995) / Dutta and Schuster (2014)
def blanch_symes(model, p, r, v):
# Bulk modulus
bm = rho * (vp * vp)
# Define PDE to v
pde_v = v - s * b * grad(p)
u_v = Eq(v.forward, damp * pde_v)
# Define PDE to r
pde_r = r - s * (1. / t_s) * r - s * (1. / t_s) * tt * bm * div(v.forward)
u_r = Eq(r.forward, damp * pde_r)
# Define PDE to p
pde_p = p - s * bm * (tt + 1.) * div(v.forward) - s * r.forward
u_p = Eq(p.forward, damp * pde_p)
return [u_v, u_r, u_p]
# Seismic Modelling from Blanch and Symes (1995) / Dutta and Schuster (2014) viscoacoustic wave equation.
def modelling_blanch_symes(model):
# Create symbols for particle velocity, pressure field, memory variable, source and receivers
v = VectorTimeFunction(name="v", grid=model.grid, time_order=1, space_order=space_order)
p = TimeFunction(name="p", grid=model.grid, time_order=1, space_order=space_order,
staggered=NODE)
r = TimeFunction(name="r", grid=model.grid, time_order=1, space_order=space_order,
staggered=NODE)
# define the source injection and create interpolation expression for receivers
src_rec_expr, src, rec = src_rec(p, model)
eqn = blanch_symes(model, p, r, v)
op = Operator(eqn + src_rec_expr, subs=model.spacing_map)
op(time=time_range.num-1, dt=dt, src=src, rec=rec)
return rec, v, p
#NBVAL_IGNORE_OUTPUT
rec, v, p = modelling_blanch_symes(model)
#NBVAL_IGNORE_OUTPUT
plot_receiver(rec)
assert np.isclose(np.linalg.norm(rec.data), 16, rtol=10)
#NBVAL_IGNORE_OUTPUT
plot_v_and_p(model, v, p)
assert np.isclose(norm(v[0]), 1.87797, atol=1e-3, rtol=0)
# Stencil created from Ren et al. (2014) viscoacoustic wave equation.
def ren(model, p, v):
# Angular frequency
w = 2. * np.pi * f0
# Define PDE to v
pde_v = v - s * b * grad(p)
u_v = Eq(v.forward, damp * pde_v)
# Define PDE to p
pde_p = p - s * vp * vp * rho * div(v.forward) + s * \
((vp * vp * rho) / (w * model.qp)) * div(b * grad(p, shift=.5), shift=-.5)
u_p = Eq(p.forward, damp * pde_p)
return [u_v, u_p]
# Seismic Modelling from Ren et al. (2014) viscoacoustic wave equation.
def modelling_ren(model):
# Create symbols for particle velocity, pressure field, source and receivers
v = VectorTimeFunction(name="v", grid=model.grid, time_order=1, space_order=space_order)
p = TimeFunction(name="p", grid=model.grid, time_order=1, space_order=space_order,
staggered=NODE)
# define the source injection and create interpolation expression for receivers
src_rec_expr, src, rec = src_rec(p, model)
eqn = ren(model, p, v)
op = Operator(eqn + src_rec_expr, subs=model.spacing_map)
op(time=time_range.num-1, dt=dt, src=src, rec=rec)
return rec, v, p
#NBVAL_IGNORE_OUTPUT
rec, v, p = modelling_ren(model)
#NBVAL_IGNORE_OUTPUT
plot_receiver(rec)
assert np.isclose(np.linalg.norm(rec.data), 15, rtol=10)
#NBVAL_IGNORE_OUTPUT
plot_v_and_p(model, v, p)
assert np.isclose(norm(v[0]), 1.0639238, atol=1e-3, rtol=0)
# Stencil created from Deng and McMechan (2007) viscoacoustic wave equation.
def deng_mcmechan(model, p, v):
# Angular frequency
w = 2. * np.pi * f0
# Define PDE to v
pde_v = v - s * b * grad(p)
u_v = Eq(v.forward, damp * pde_v)
# Define PDE to p
pde_p = p - s * vp * vp * rho * div(v.forward) - s * (w / model.qp) * p
u_p = Eq(p.forward, damp * pde_p)
return [u_v, u_p]
# Seismic Modelling from Deng and McMechan (2007) viscoacoustic wave equation.
def modelling_deng_mcmechan(model):
# Create symbols for particle velocity, pressure field, source and receivers
v = VectorTimeFunction(name="v", grid=model.grid, time_order=1, space_order=space_order)
p = TimeFunction(name="p", grid=model.grid, time_order=1, space_order=space_order,
staggered=NODE)
# define the source injection and create interpolation expression for receivers
src_rec_expr, src, rec = src_rec(p, model)
eqn = deng_mcmechan(model, p, v)
op = Operator(eqn + src_rec_expr, subs=model.spacing_map)
op(time=time_range.num-1, dt=dt, src=src, rec=rec)
return rec, v, p
#NBVAL_IGNORE_OUTPUT
rec, v, p = modelling_deng_mcmechan(model)
#NBVAL_IGNORE_OUTPUT
plot_receiver(rec)
assert np.isclose(np.linalg.norm(rec.data), 16, rtol=10)
#NBVAL_IGNORE_OUTPUT
plot_v_and_p(model, v, p)
assert np.isclose(norm(v[0]), 1.1323929, atol=1e-3, rtol=0)
| 0.761538 | 0.900879 |
# Pore size distribution
Often, pore size distributions are a very important part of adsorbent characterisation. The pyGAPS framework includes several common classical methods which are applicable to mesoporous or microporous materials. A DFT-fitting method is also provided together with an internal N2/carbon applicable DFT kernel. The user can also specify their own DFT kernel.
A complete aplicability guide and info on each function parameters can be found in the [manual](../manual/characterisation.rst).
First, make sure the data is imported.
```
%run import.ipynb
```
## Mesoporous pore size distribution
Let's start by analysing the mesoporous size distribution of some of our nitrogen physisorption samples.
The MCM-41 sample should have a very well defined, singular pore size in the mesopore range, with the pores as open-ended cylinders. We can use a common method, relying on a description of the adsorbate in the pores based on the Kelvin equation and the thickness of the adsorbed layer. These methods are derivatives of the BJH (Barrett, Joyner and Halenda) method.
```
isotherm = next(i for i in isotherms_n2_77k if i.material=='MCM-41')
print(isotherm.material)
result_dict = pygaps.psd_mesoporous(
isotherm,
pore_geometry='cylinder',
verbose=True)
```
The distribution is what we expected, a single narrow peak. Since we asked for extra verbosity, the function has generated a graph which we can display with `plt.show()`. The graph automaticaly sets a minimum limit of 1.5 angstrom, where the Kelvin equation methods break down.
The result dictionary returned contains the x and y points of the graph.
Depending on the sample, the distribution can be a well defined or broad, single or multimodal, or, in the case of adsorbents without mesoporoes, not relevant at all. For example, using the Takeda 5A carbon, and specifying a slit pore geometry:
```
isotherm = next(i for i in isotherms_n2_77k if i.material=='Takeda 5A')
print(isotherm.material)
result_dict_meso = pygaps.psd_mesoporous(
isotherm,
psd_model='pygaps-DH',
pore_geometry='slit',
verbose=True)
```
Now let's break down the available settings with the mesoporous PSD function.
- A `psd_model` parameter to select specific implementations of the methods, such as the original BJH method or the DH method.
- A `pore_geometry` parameter can be used to specify the known pore geometry of the pore. The Kelvin equation parameters change appropriately.
- Classical models are commonly applied on the desorption branch of the isotherm. This is also the default in this code, although the user can specify the adsorption branch to be used with the `branch` parameter.
- The function used for evaluating the layer thickness can be specified by the `thickness_model` parameter. Either a named internal model ('Halsey', 'Harkins/Jura', etc.) or a cusom user function which takes pressure as an argument is accepted.
- If the user wants to use a custom function for the Kelvin model, they can do so through the `kelvin_model` parameters. This must be a name of an internal model ('Kelvin', 'Kelvin-KJS', etc.) or a custom function.
Below we use the adsorption branch and the Halsey thickness curve to look at the MCM-41 pores. We use the Kruck-Jaroniec-Sayari correction of the Kelvin model.
```
isotherm = next(i for i in isotherms_n2_77k if i.material=='MCM-41')
print(isotherm.material)
result_dict = pygaps.psd_mesoporous(
isotherm,
psd_model='DH',
pore_geometry='cylinder',
branch='ads',
thickness_model='Halsey',
kelvin_model='Kelvin-KJS',
verbose=True)
```
<div class="alert alert-info">
**Note:** If the user wants to customise the standard plots which are displayed, they are available for use in the `pygaps.graphing.calcgraph` module
</div>
## Microporous pore size distribution
For microporous samples, we can use the `psd_microporous` function. The available model is an implementation of the Horvath-Kawazoe (HK) method.
The HK model uses a list of parameters which describe the interaction between the adsorbate and the adsorbent. These should be selected on a *per case* basis by using the `adsorbate_model` and `adsorbent_model` keywords. If they are not specified, the function assumes a carbon model for the sample surface and takes the required adsorbate properties (*magnetic susceptibility, polarizability, molecular diameter, surface density, liquid density and molar mass*) from the specific internal adsorbate. The pore geometry is also assumed to be *slit-like*.
Let's look at using the function on the carbon sample:
```
isotherm = next(i for i in isotherms_n2_77k if i.material=='Takeda 5A')
print(isotherm.material)
result_dict_micro = pygaps.psd_microporous(
isotherm,
psd_model='HK',
verbose=True)
```
We see that we could have a peak around 0.7 nm, but could use more adsorption data at low pressure for better resolution. It should be noted that the model breaks down with pores bigger than around 3 nm.
The framework comes with other models for the surface, like as the Saito-Foley derived oxide-ion model. Below is an attempt to use the HK method with these parameters for the UiO-66 sample and some user-specified parameters for the adsorbate interaction. We should not expect the results to be very accurate, due to the different surface properties and heterogeneity of the MOF.
```
adsorbate_params = {
'molecular_diameter': 0.3,
'polarizability': 1.76e-3,
'magnetic_susceptibility': 3.6e-8,
'surface_density': 6.71e+18,
'liquid_density': 0.806,
'adsorbate_molar_mass': 28.0134
}
isotherm = next(i for i in isotherms_n2_77k if i.material=='UiO-66(Zr)')
print(isotherm.material)
result_dict = pygaps.psd_microporous(
isotherm,
psd_model='HK',
adsorbent_model='AlSiOxideIon',
adsorbate_model=adsorbate_params,
verbose=True)
```
A bimodal pore size distribution is seen, with peaks at around 0.7 and 0.8 nanometers. UiO-66 does indeed have two cages, a tetrahedral cage and an octahedral one, with the sizes of 0.8 and 1.1 nm respectively.
## DFT pore size distribution
The DFT method is the most powerful method for pore size distribution calculations. It requires a *DFT kernel*, or a collection of previously simulated adsorption isotherms which cover the entire pore range which we want to investigate. The calculation of the DFT kernel is currently *not* in the scope of this framework.
The user can specify their own kernel, in a CSV format, which will be used for the isotherm fitting on the `psd_dft` function. Alternatively, a common DFT kernel is included with the framework, which is
simulated with nitrogen on a carbon material and slit-like pores in the range of 0.4-10 nanometres.
Let's run the fitting of this internal kernel on the carbon sample:
```
isotherm = next(i for i in isotherms_n2_77k if i.material=='Takeda 5A')
result_dict_dft = pygaps.psd_dft(
isotherm,
kernel='DFT-N2-77K-carbon-slit',
verbose=True)
```
The output is automatically smoothed using a b-spline method. Further (or less) smoothing can be specified by the `bspline_order` parameter. The higher the order, more smoothing is applied. Specify "0" to return the data *as-fitted*.
```
isotherm = next(i for i in isotherms_n2_77k if i.material=='Takeda 5A')
result_dict_dft = pygaps.psd_dft(
isotherm,
bspline_order=5,
verbose=True)
```
## Comparing all the PSD methods
For comparison purposes, we will compare the pore size distributions obtained through all the methods above. The sample on which all methods are applicable is the Takeda carbon.
We will first plot the data using the existing function plot, then use the graph returned to plot the remaining results.
```
from pygaps.graphing.calcgraph import psd_plot
ax = psd_plot(result_dict_dft['pore_widths'], result_dict_dft['pore_distribution'],
method='comparison', labeldiff='DFT', labelcum=None, left=0.4, right=8)
ax.plot(result_dict_micro['pore_widths'], result_dict_micro['pore_distribution'], label='microporous')
ax.plot(result_dict_meso['pore_widths'], result_dict_meso['pore_distribution'], label='mesoporous')
ax.legend(loc='best')
plt.show()
```
|
github_jupyter
|
%run import.ipynb
isotherm = next(i for i in isotherms_n2_77k if i.material=='MCM-41')
print(isotherm.material)
result_dict = pygaps.psd_mesoporous(
isotherm,
pore_geometry='cylinder',
verbose=True)
isotherm = next(i for i in isotherms_n2_77k if i.material=='Takeda 5A')
print(isotherm.material)
result_dict_meso = pygaps.psd_mesoporous(
isotherm,
psd_model='pygaps-DH',
pore_geometry='slit',
verbose=True)
isotherm = next(i for i in isotherms_n2_77k if i.material=='MCM-41')
print(isotherm.material)
result_dict = pygaps.psd_mesoporous(
isotherm,
psd_model='DH',
pore_geometry='cylinder',
branch='ads',
thickness_model='Halsey',
kelvin_model='Kelvin-KJS',
verbose=True)
isotherm = next(i for i in isotherms_n2_77k if i.material=='Takeda 5A')
print(isotherm.material)
result_dict_micro = pygaps.psd_microporous(
isotherm,
psd_model='HK',
verbose=True)
adsorbate_params = {
'molecular_diameter': 0.3,
'polarizability': 1.76e-3,
'magnetic_susceptibility': 3.6e-8,
'surface_density': 6.71e+18,
'liquid_density': 0.806,
'adsorbate_molar_mass': 28.0134
}
isotherm = next(i for i in isotherms_n2_77k if i.material=='UiO-66(Zr)')
print(isotherm.material)
result_dict = pygaps.psd_microporous(
isotherm,
psd_model='HK',
adsorbent_model='AlSiOxideIon',
adsorbate_model=adsorbate_params,
verbose=True)
isotherm = next(i for i in isotherms_n2_77k if i.material=='Takeda 5A')
result_dict_dft = pygaps.psd_dft(
isotherm,
kernel='DFT-N2-77K-carbon-slit',
verbose=True)
isotherm = next(i for i in isotherms_n2_77k if i.material=='Takeda 5A')
result_dict_dft = pygaps.psd_dft(
isotherm,
bspline_order=5,
verbose=True)
from pygaps.graphing.calcgraph import psd_plot
ax = psd_plot(result_dict_dft['pore_widths'], result_dict_dft['pore_distribution'],
method='comparison', labeldiff='DFT', labelcum=None, left=0.4, right=8)
ax.plot(result_dict_micro['pore_widths'], result_dict_micro['pore_distribution'], label='microporous')
ax.plot(result_dict_meso['pore_widths'], result_dict_meso['pore_distribution'], label='mesoporous')
ax.legend(loc='best')
plt.show()
| 0.301773 | 0.991204 |
<a href="https://colab.research.google.com/github/alexisakov/RTPI/blob/master/Hard_numbers_Case_study_1_Label_classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Case 1. Product label classification: 'The Dumpling'
Import Yandex MyStem for lemmatizatio + requests for talking to API + scikit-learn which will do most of the work.
```
!wget http://download.cdn.yandex.net/mystem/mystem-3.0-linux3.1-64bit.tar.gz
!tar -xvf mystem-3.0-linux3.1-64bit.tar.gz
!cp mystem /root/.local/bin/mystem
pip install pymystem3
from pymystem3 import Mystem
import requests
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.feature_extraction.text import CountVectorizer,TfidfVectorizer
m = Mystem()
```
Set up connection to the Hard Numbers API - you will need your API Key - reach us to get one: https://t.me/xiskv.
```
base_url='http://rtpiapi.hrdn.io/'
token = 'YOUR API KEY GOES HERE'
request_headers = {'Authorization': f'Bearer {token}',
'Content-Type': 'application/json',
'Range-Unit': 'items'
}
```
Here we get all the text label data:
```
request_url = base_url + 'rtpi_product_name'
response = requests.get(request_url, headers = request_headers).json()
```
Overall there is about 153k labels
```
len(response)
response[0]
```
Now let's make a call to both text lable table rtpi_product_name and the general dictionary of traked products rtpi_price_page so that we get those text labels that we have already matched with the Rosstat's codebook:
```
request_url = base_url + 'rtpi_product_name?select=*,rtpi_price_page(rosstat_id)&(rosstat_id.rosstat_id.not.is.null)'
responseXY = requests.get(request_url, headers = request_headers).json()
responseXY = [x for x in responseXY if (x['rtpi_price_page']['rosstat_id'])]
len(responseXY)
```
For reference here is the Rosstat's current codebook: https://rosstat.gov.ru/storage/mediabank/j3LP7dsR/nabor_2020.xlsx
Okay, here is a bit of flattenting of our list of dicts - just to keep things tidy:
```
[x.update(x['rtpi_price_page']) for x in responseXY];
[x.pop('rtpi_price_page',None) for x in responseXY];
```
Now, let's use Y.MyStem to standardize/lemmatize product labels:
```
[x.update({'product_name': ''.join(m.lemmatize(x['product_name'])).rstrip()}) for x in responseXY];
[x.update({'product_name': ''.join(m.lemmatize(x['product_name'])).rstrip()}) for x in response];
responseXY[0]
```
Okay - now the most interesting part - let's fit the logistic regression to the text data - this will allow us to use machine learning to automate labelling - whoa!
```
xydf = pd.DataFrame(responseXY)
xydf.head()
```
To keep things simple I choose to fit the model to classify just one type of product - dumplings, which have Rosstat's code of '106':
```
targetProductCode = 106
Y = xydf['rosstat_id'].apply(lambda x: 1 if x == targetProductCode else 0)
```
There is this number of dumplings which we have manually labeled at this point:
```
Y.sum()
```
Now vectorize our text labels:
```
tfidf_vectorizer=TfidfVectorizer(use_idf=True, max_df=0.95)
tfidf_vectorizer.fit_transform(xydf['product_name'].values)
X = tfidf_vectorizer.transform(xydf['product_name'].values)
```
Fit the linear regression:
```
scikit_log_reg = LogisticRegression(verbose=1, solver='liblinear',random_state=0, C=5, penalty='l2',max_iter=1000)
model=scikit_log_reg.fit(X,Y)
```
Extract class probabilities and get k observations with maximum probability of being a dumpling:
```
probs = model.predict_proba(X)
k = 20
best_n = np.argsort(probs, axis=0)
xydf['product_name'].values[best_n[-k:,1]]
```
Good enough!
Now it is time to realy test our approach - and see how does it perform out of sample.
First, we filter the whole sample so that no training data slips into it:
```
trainid = [y['web_price_id'] for y in responseXY]
test = [x for x in response if x['web_price_id'] not in trainid]
testdf = pd.DataFrame(test)
```
Do the same routine: vectorize labels - evaluate probabilities - get top k observations with highets probabilities of being a dumpling:
```
testX = tfidf_vectorizer.transform(testdf['product_name'].values)
testprobs = model.predict_proba(testX)
test_best_n = np.argsort(testprobs, axis=0)
testdf['product_name'].values[test_best_n[-k:,1]]
```
Again - seems decent - and that's it for our toy example of product labelling.
```
```
|
github_jupyter
|
!wget http://download.cdn.yandex.net/mystem/mystem-3.0-linux3.1-64bit.tar.gz
!tar -xvf mystem-3.0-linux3.1-64bit.tar.gz
!cp mystem /root/.local/bin/mystem
pip install pymystem3
from pymystem3 import Mystem
import requests
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.feature_extraction.text import CountVectorizer,TfidfVectorizer
m = Mystem()
base_url='http://rtpiapi.hrdn.io/'
token = 'YOUR API KEY GOES HERE'
request_headers = {'Authorization': f'Bearer {token}',
'Content-Type': 'application/json',
'Range-Unit': 'items'
}
request_url = base_url + 'rtpi_product_name'
response = requests.get(request_url, headers = request_headers).json()
len(response)
response[0]
request_url = base_url + 'rtpi_product_name?select=*,rtpi_price_page(rosstat_id)&(rosstat_id.rosstat_id.not.is.null)'
responseXY = requests.get(request_url, headers = request_headers).json()
responseXY = [x for x in responseXY if (x['rtpi_price_page']['rosstat_id'])]
len(responseXY)
[x.update(x['rtpi_price_page']) for x in responseXY];
[x.pop('rtpi_price_page',None) for x in responseXY];
[x.update({'product_name': ''.join(m.lemmatize(x['product_name'])).rstrip()}) for x in responseXY];
[x.update({'product_name': ''.join(m.lemmatize(x['product_name'])).rstrip()}) for x in response];
responseXY[0]
xydf = pd.DataFrame(responseXY)
xydf.head()
targetProductCode = 106
Y = xydf['rosstat_id'].apply(lambda x: 1 if x == targetProductCode else 0)
Y.sum()
tfidf_vectorizer=TfidfVectorizer(use_idf=True, max_df=0.95)
tfidf_vectorizer.fit_transform(xydf['product_name'].values)
X = tfidf_vectorizer.transform(xydf['product_name'].values)
scikit_log_reg = LogisticRegression(verbose=1, solver='liblinear',random_state=0, C=5, penalty='l2',max_iter=1000)
model=scikit_log_reg.fit(X,Y)
probs = model.predict_proba(X)
k = 20
best_n = np.argsort(probs, axis=0)
xydf['product_name'].values[best_n[-k:,1]]
trainid = [y['web_price_id'] for y in responseXY]
test = [x for x in response if x['web_price_id'] not in trainid]
testdf = pd.DataFrame(test)
testX = tfidf_vectorizer.transform(testdf['product_name'].values)
testprobs = model.predict_proba(testX)
test_best_n = np.argsort(testprobs, axis=0)
testdf['product_name'].values[test_best_n[-k:,1]]
| 0.458591 | 0.903294 |
# TESS 2015 - Introduction to Solar Data Analysis in Python
<img src="https://raw.github.com/sunpy/sunpy-logo/master/generated/sunpy_logo_compact_192x239.png">
# SunPy!
## Author: Steven Christe
Email: [email protected]
Through tutorials and presentations we will demonstrate how free and open-source Python and SunPy library can be used to analyze solar data. Depending on interest, dinner may be ordered after the main presentation (roughly an hour) and a hands-on help session will take place for the remainder of the evening. Installing the following software is recommended but not required: Anaconda Python and SunPy.
Schedule: 19:00 to 22:00
+ 18:00-18:15 pm: Organization (chatroom, organize dinner)?
+ 18:15-19:00 pm: Intro to SunPy (presentation)
+ 19:00-19:15 pm: Break
+ 19:15-20:15: Dinner & Installation Workshop
+ 20:15-22:00: SunPy Workshop
## What is SunPy?
### A community-developed, free and open-source solar data analysis environment for Python.
+ website: [http://www.sunpy.org](http://www.sunpy.org)<br>
+ documentation: [http://docs.sunpy.org](http://docs.sunpy.org)<br>
+ code (version control!): [https://github.com/sunpy/sunpy](https://github.com/sunpy/sunpy)
+ Mailing list: https://groups.google.com/forum/#!forum/sunpy**
+ IRC: #sunpy on freenode.net [web client](https://kiwiirc.com/client/irc.freenode.net/#SunPy)
SunPy is built upon foundational libraries which enable scientific computing in Python which includes
+ [NumPy](http://numpy.org)
+ [SciPy](http://scipy.org)
+ [matplotlib](http://matplotlib.org)
+ [AstroPy](http://astropy.org)
<p>Supported observations
<ul>Images
<li>SDO AIA and HMI</li>
<li>SOHO EIT, LASCO, MDI</li>
<li>STEREO EUVI and COR</li>
<li>TRACE</li>
<li>Yohkoh SXT</li>
<li>RHESSI mapcubes (beta)</li>
<li>PROBA2 SWAP</li>
<li>IRIS Slit-Jaw (beta)</li>
</ul>
<ul>Time Series
<li>GOES XRS</li>
<li>PROBA2 LYRA</li>
<li>Fermi GBM</li>
<li>SDO EVE</li>
<li>RHESSI Summary Lightcurves</li>
<li>Nobeyama Radioheliograph LightCurve</li>
<li>NOAA Solar Cycle monthly indices</li>
<li>NOAA Solar Cycle Prediction</li>
</ul>
<ul>Spectra
<li>Callisto</li>
<li>STEREO SWAVES</li>
</ul>
<p>Supported data retrieval services
<ul>
<li>Virtual Solar Observatory (VSO)</li>
<li>JSOC</li>
<li>Heliophysics Events Knowledgebase (HEK)</li>
<li>Helio</li>
<li>Helioviewer</li>
</ul>
</p>
<p>Supported file formats include
<ul>
<li>FITS (read/write)</li>
<li>Comma-separated files, text files (read/write)</li>
<li>ANA (read/write)</li>
<li>JPG2 (read/write)</li>
</ul>
</p>
# What is this webby notebooky magic?!
## ipython notebook (now known as jupyter)
similar to matlab, mathematica, maple
Some setup...
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
%matplotlib inline
matplotlib.rc('savefig', dpi=120)
import warnings
warnings.simplefilter("ignore", Warning)
from matplotlib import dates
import sunpy
sunpy.system_info()
```
SunPy version (stable) 0.5
# Let's study a flare!
## Searching for events in the HEK
```
from sunpy.net import hek
client = hek.HEKClient()
tstart, tend = '2014/01/01 00:00:00', '2014/01/02 00:00:00'
result = client.query(hek.attrs.Time(tstart, tend),
hek.attrs.EventType('FL'),
hek.attrs.FRM.Name=='SSW Latest Events')
len(result)
result[0]
for res in result:
print(res.get('fl_goescls'))
result = client.query(hek.attrs.Time(tstart, tend),
hek.attrs.EventType('FL'),
hek.attrs.FRM.Name=='SSW Latest Events',
hek.attrs.FL.GOESCls>'M')
len(result)
result
```
We can find out when this event occured
```
result[0].get('event_peaktime')
```
and where it occurred
```
result[0].get('hpc_coord')
```
# Lightcurves!
## Let's look at the GOES curve for this event.
First some time manipulation!
```
from sunpy.time import TimeRange, parse_time
from datetime import timedelta
tmax = parse_time(result[0].get('event_peaktime'))
tmax
tr = TimeRange(tmax - timedelta(minutes=30), tmax + timedelta(minutes=30))
tr
from sunpy.lightcurve import GOESLightCurve
goes = GOESLightCurve.create(tr)
goes.peek()
```
The data is stored in a standard place
```
goes.data
```
This is a pandas dataframe! Provides lots of additional functionality. For example
```
print('The max flux is {flux:2.5f} at {time}'.format(flux=goes.data['xrsb'].max(), time=goes.data['xrsb'].idxmax()))
```
Compares well to the official max from the HEK
```
str(tmax)
goes.peek()
plt.axhline(goes.data['xrsb'].max())
plt.axvline(goes.data['xrsb'].idxmax())
```
Meta data is also stored in a standard place
```
goes.meta
```
This is a dictionary like the hek results so...
```
goes.meta.get('COMMENT')
goes.data.resample('10s', how='mean')
```
# Solar Images in SunPy
SunPy has a `Map` type that supports 2D images, it makes it simple to read data in from any filetype supported in `sunpy.io` which is currently FITS, JPEG2000 and ANA files. You can also create maps from any `(data, metadata)` pair.
Let's download an AIA image of this flare from the vso
```
from sunpy.net import vso
client=vso.VSOClient()
```
Then do a search.
```
recs = client.query(vso.attrs.Time(tr), vso.attrs.Instrument('AIA'))
```
It works, now lets see how many results we have!
```
recs.num_records()
```
That's way too many!
So that is every image that SDO/AIA had on that day. Let us reduce that amount.
To do this, we will limit the time search for a specify a wavelength.
```
recs = client.query(vso.attrs.Time('2014/01/01 18:52:08', '2014/01/01 18:52:15'),
vso.attrs.Instrument('AIA'),
vso.attrs.Wave(171,171))
recs.num_records()
recs.show()
```
Let's also grab another wavelength for later.
```
recs = client.query(vso.attrs.Time('2014/01/01 18:52:08', '2014/01/01 18:52:15'),
vso.attrs.Instrument('AIA'),
vso.attrs.Wave(94,171))
recs.num_records()
```
Let's download this data!
```
f = client.get(recs, methods = ('URL-FILE_Rice')).wait()
f
```
For SunPy the top level name-space is kept clean. Importing SunPy does not give you access to much. You need to import specific names. SciPy is the same.
So, the place to start here is with the core SunPy data object. It is called Map.
```
from sunpy.map import Map
aia = Map(f[1])
aia
```
Maps contain both the image data and the metadata associated with the image, this metadata currently does not deviate much from the standard FITS WCS keywords, but presented in a instrument-independent manner.
```
aia.peek()
```
# SunPy Maps!
Maps are the same for each file, **regardless of source**. It does not matter if the source is SDO or SOHO, for example.
The most used attributes are as follows (some of them will look similar to NumPy's Array):
```
aia.data
```
The data (stored in a numpy array)
```
type(aia.data)
aia.mean(),aia.max(),aia.min()
```
Because it is just a numpy array you have access to all of those function
The standard deviation
```
aia.data.std()
aia.data.shape
```
The original metadata (stored in a dictionary)
```
aia.meta
aia.meta.keys()
aia.meta.get('rsun_obs')
```
We also provide quick access to some key metadata values as object variables (these are shortcuts)
```
print(aia.date, aia.coordinate_system, aia.detector, aia.dsun)
```
Maps also provide some nice map specific functions such as submaps. Let's zoom in on the flare location which was given to us by the HEK.
```
result[0].get('hpc_coord')
point = [665.04, -233.4096]
dx = 50
dy = 50
xrange = [point[0] - dx, point[0] + dx]
yrange = [point[1] - dy, point[1] + dy]
aia.submap(xrange,yrange).peek()
plt.plot(point[0], point[1], '+')
plt.xlim(xrange)
plt.ylim(yrange)
```
The default image scale is definitely not right. Let's fix that so we can see the flare region better.
```
smap = aia.submap(xrange,yrange)
import matplotlib.colors as colors
norm = colors.Normalize(0, 3000)
smap.plot(norm=norm)
plt.plot(point[0], point[1], '+')
smap.draw_grid(grid_spacing=1)
plt.colorbar()
```
## Composite Maps
Let's plot the two channels we downloaded from AIA together! Composite map is the way to do this. Let's check out the other map we got.
```
aia131 = Map(f[0])
aia131
smap131 = aia131.submap(xrange, yrange)
smap131.peek()
norm = colors.Normalize(0, 4000)
smap131.plot(norm=norm)
plt.colorbar()
smap171 = smap
compmap = Map(smap171, smap131, composite=True)
levels = np.arange(0,100,5)
print(levels)
compmap.set_levels(1, levels, percent=True)
compmap.set_mpl_color_normalizer(0, norm)
compmap.set_colors(1, plt.cm.Reds)
compmap.plot(norm=norm)
plt.show()
```
Some other topics...
## Solar Constants
```
from sunpy.sun import constants as solar_constants
solar_constants.mass
print(solar_constants.mass)
(solar_constants.mass/solar_constants.volume).cgs
solar_constants.volume + solar_constants.density
```
Not all constants have a short-cut assigned to them (as above). The rest of the constants are stored in a dictionary. The following code grabs the dictionary and gets all of the keys.:
```
solar_constants.physical_constants.keys()
type(solar_constants.mass)
```
These are astropy constants which are a subclass of Quantities (numbers with units) which are a great idea.
```
from astropy import units as u
u.keV
u.keV.decompose()
```
This has been a simple overview of AstroPy units. IF you want to read more, see http://astropy.readthedocs.org/en/latest/units/.
## More References
+ [Python for Data Analysis](http://shop.oreilly.com/product/0636920023784.do) by Wes McKinney is great
+ [Lectures on scientific computing with Python](http://jrjohansson.github.io) Great lectures on scientific computing in Python
## Consider [contributing](http://sunpy.org/contribute/) to SunPy!
+ Provide feedback on the [mailing list](https://groups.google.com/forum/#!forum/sunpy)
+ Report [bugs](https://github.com/sunpy/sunpy/issues)
+ Provide Code (see our [developer guide](http://sunpy.readthedocs.org/en/stable/dev.html))
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
%matplotlib inline
matplotlib.rc('savefig', dpi=120)
import warnings
warnings.simplefilter("ignore", Warning)
from matplotlib import dates
import sunpy
sunpy.system_info()
from sunpy.net import hek
client = hek.HEKClient()
tstart, tend = '2014/01/01 00:00:00', '2014/01/02 00:00:00'
result = client.query(hek.attrs.Time(tstart, tend),
hek.attrs.EventType('FL'),
hek.attrs.FRM.Name=='SSW Latest Events')
len(result)
result[0]
for res in result:
print(res.get('fl_goescls'))
result = client.query(hek.attrs.Time(tstart, tend),
hek.attrs.EventType('FL'),
hek.attrs.FRM.Name=='SSW Latest Events',
hek.attrs.FL.GOESCls>'M')
len(result)
result
result[0].get('event_peaktime')
result[0].get('hpc_coord')
from sunpy.time import TimeRange, parse_time
from datetime import timedelta
tmax = parse_time(result[0].get('event_peaktime'))
tmax
tr = TimeRange(tmax - timedelta(minutes=30), tmax + timedelta(minutes=30))
tr
from sunpy.lightcurve import GOESLightCurve
goes = GOESLightCurve.create(tr)
goes.peek()
goes.data
print('The max flux is {flux:2.5f} at {time}'.format(flux=goes.data['xrsb'].max(), time=goes.data['xrsb'].idxmax()))
str(tmax)
goes.peek()
plt.axhline(goes.data['xrsb'].max())
plt.axvline(goes.data['xrsb'].idxmax())
goes.meta
goes.meta.get('COMMENT')
goes.data.resample('10s', how='mean')
from sunpy.net import vso
client=vso.VSOClient()
recs = client.query(vso.attrs.Time(tr), vso.attrs.Instrument('AIA'))
recs.num_records()
recs = client.query(vso.attrs.Time('2014/01/01 18:52:08', '2014/01/01 18:52:15'),
vso.attrs.Instrument('AIA'),
vso.attrs.Wave(171,171))
recs.num_records()
recs.show()
recs = client.query(vso.attrs.Time('2014/01/01 18:52:08', '2014/01/01 18:52:15'),
vso.attrs.Instrument('AIA'),
vso.attrs.Wave(94,171))
recs.num_records()
f = client.get(recs, methods = ('URL-FILE_Rice')).wait()
f
from sunpy.map import Map
aia = Map(f[1])
aia
aia.peek()
aia.data
type(aia.data)
aia.mean(),aia.max(),aia.min()
aia.data.std()
aia.data.shape
aia.meta
aia.meta.keys()
aia.meta.get('rsun_obs')
print(aia.date, aia.coordinate_system, aia.detector, aia.dsun)
result[0].get('hpc_coord')
point = [665.04, -233.4096]
dx = 50
dy = 50
xrange = [point[0] - dx, point[0] + dx]
yrange = [point[1] - dy, point[1] + dy]
aia.submap(xrange,yrange).peek()
plt.plot(point[0], point[1], '+')
plt.xlim(xrange)
plt.ylim(yrange)
smap = aia.submap(xrange,yrange)
import matplotlib.colors as colors
norm = colors.Normalize(0, 3000)
smap.plot(norm=norm)
plt.plot(point[0], point[1], '+')
smap.draw_grid(grid_spacing=1)
plt.colorbar()
aia131 = Map(f[0])
aia131
smap131 = aia131.submap(xrange, yrange)
smap131.peek()
norm = colors.Normalize(0, 4000)
smap131.plot(norm=norm)
plt.colorbar()
smap171 = smap
compmap = Map(smap171, smap131, composite=True)
levels = np.arange(0,100,5)
print(levels)
compmap.set_levels(1, levels, percent=True)
compmap.set_mpl_color_normalizer(0, norm)
compmap.set_colors(1, plt.cm.Reds)
compmap.plot(norm=norm)
plt.show()
from sunpy.sun import constants as solar_constants
solar_constants.mass
print(solar_constants.mass)
(solar_constants.mass/solar_constants.volume).cgs
solar_constants.volume + solar_constants.density
solar_constants.physical_constants.keys()
type(solar_constants.mass)
from astropy import units as u
u.keV
u.keV.decompose()
| 0.47317 | 0.947478 |
## basic knowledge
* Represents computations as graphs.
* Executes graphs in the context of Sessions.
* Represents data as tensors.
* Maintains state with Variables.
* Uses feeds and fetches to get data into and out of arbitrary operations.
```
import tensorflow as tf
import numpy as np
import pandas as pd
import matplotlib
%matplotlib inline
```
### build graph
* So we should build the graph first
To build the graph start with ops that do not need any input and then pass their output to other ops that do
computation
```
# the ops add the default graph by default
matrix1 = tf.constant([[2.,3.]])
matrix2 = tf.constant([[2.,3.],[2.,3.]])
product = tf.matmul(matrix1,matrix2)
```
### launching graph
* To launch a graph ,create a session object.Without arguments session launch the default graph.
```
sess = tf.Session()
result = sess.run(product)
print(result)
sess.close()
```
### Interactive usage
* use it so that can avoids having to keep a variable holding the session
* use eval() for tensor and use run() for ops
```
sess = tf.InteractiveSession()
x = tf.Variable([1.,2.])
a = tf.constant([3.,4.])
# must initilize the variable
x.initializer.run()
# sub a from x
sub = tf.sub(a,x)
sub.eval()
sess.close()
```
### Variables
* Variables maintain state across executions of the graph.
```
# reset the graph
tf.reset_default_graph()
# counter
state = tf.Variable(0,name="counter")
# constant
one = tf.constant(1)
# new state
new_state = tf.add(state,one)
# assign new_state to state
# note that assign return the ref of state
update = tf.assign(state,new_state)
# init ops
init = tf.initialize_all_variables()
with tf.Session() as sess:
# initialize variable
sess.run(init)
# print the initial state
print(sess.run(state))
# update three times
for _ in range(3):
print(sess.run(update))
```
* you can also get multiple tensors just by pass in the array of tensors
### feeds
* feeds temporarily replaces the output of the op with the tensor value.The common case is that load the data to
train
```
tf.reset_default_graph()
input1 = tf.placeholder(tf.float32,shape=[None,2])
input2 = tf.placeholder(tf.float32,shape=[2,1])
output = tf.matmul(input1,input2)
with tf.Session() as sess:
res = sess.run([output],feed_dict={input1:[[4.,5.]],input2:[[3.],[5.]]})
print(res)
```
### Others
* do some experiments
```
with tf.Session() as sess:
logits = tf.Variable([[0.2,0.3,0.5],[0.3,0.3,0.4]],name='logits')
labels = [0,1]
init = tf.initialize_all_variables()
sess.run(init)
correct_number = tf.nn.in_top_k(logits,labels,1)
true = tf.reduce_sum(tf.cast(correct_number,tf.int32))
cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits,labels,
name='xentropy')
# print(true)
print(sess.run(true))
print(sess.run(cross_entropy))
```
|
github_jupyter
|
import tensorflow as tf
import numpy as np
import pandas as pd
import matplotlib
%matplotlib inline
# the ops add the default graph by default
matrix1 = tf.constant([[2.,3.]])
matrix2 = tf.constant([[2.,3.],[2.,3.]])
product = tf.matmul(matrix1,matrix2)
sess = tf.Session()
result = sess.run(product)
print(result)
sess.close()
sess = tf.InteractiveSession()
x = tf.Variable([1.,2.])
a = tf.constant([3.,4.])
# must initilize the variable
x.initializer.run()
# sub a from x
sub = tf.sub(a,x)
sub.eval()
sess.close()
# reset the graph
tf.reset_default_graph()
# counter
state = tf.Variable(0,name="counter")
# constant
one = tf.constant(1)
# new state
new_state = tf.add(state,one)
# assign new_state to state
# note that assign return the ref of state
update = tf.assign(state,new_state)
# init ops
init = tf.initialize_all_variables()
with tf.Session() as sess:
# initialize variable
sess.run(init)
# print the initial state
print(sess.run(state))
# update three times
for _ in range(3):
print(sess.run(update))
tf.reset_default_graph()
input1 = tf.placeholder(tf.float32,shape=[None,2])
input2 = tf.placeholder(tf.float32,shape=[2,1])
output = tf.matmul(input1,input2)
with tf.Session() as sess:
res = sess.run([output],feed_dict={input1:[[4.,5.]],input2:[[3.],[5.]]})
print(res)
with tf.Session() as sess:
logits = tf.Variable([[0.2,0.3,0.5],[0.3,0.3,0.4]],name='logits')
labels = [0,1]
init = tf.initialize_all_variables()
sess.run(init)
correct_number = tf.nn.in_top_k(logits,labels,1)
true = tf.reduce_sum(tf.cast(correct_number,tf.int32))
cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits,labels,
name='xentropy')
# print(true)
print(sess.run(true))
print(sess.run(cross_entropy))
| 0.397821 | 0.941385 |
```
%matplotlib inline
import librosa, librosa.display, numpy, matplotlib.pyplot as plt, IPython.display as ipd
plt.style.use('seaborn-muted')
plt.rcParams['figure.figsize'] = (14, 5)
plt.rcParams['axes.grid'] = True
plt.rcParams['axes.spines.left'] = False
plt.rcParams['axes.spines.right'] = False
plt.rcParams['axes.spines.bottom'] = False
plt.rcParams['axes.spines.top'] = False
plt.rcParams['axes.xmargin'] = 0
plt.rcParams['axes.ymargin'] = 0
plt.rcParams['image.cmap'] = 'gray'
plt.rcParams['image.interpolation'] = None
```
[← Back to Index](index.html)
# MIDI Note to Frequency Conversion Table
- **note**: note name
- **midi-ET**: MIDI number, equal temperament
- **Hertz-ET**: frequency in Hertz, equal temperament
- **midi-PT**: MIDI number, Pythagorean tuning
- **Hertz-PT**: frequency in Hertz, Pythagorean tuning
```
note_pt = dict()
# Sharps
note_pt['A4'] = 440.0
for octave in range(0, 10):
note_pt['A{}'.format(octave)] = 440.0*2**(octave-4)
note_pt['E1'] = 1.5*note_pt['A0']
for octave in range(0, 10):
note_pt['E{}'.format(octave)] = note_pt['E1']*2**(octave-1)
note_pt['B0'] = 1.5*note_pt['E0']
for octave in range(0, 10):
note_pt['B{}'.format(octave)] = note_pt['B0']*2**(octave-0)
note_pt['F#1'] = 1.5*note_pt['B0']
for octave in range(0, 10):
note_pt['F#{}'.format(octave)] = note_pt['F#1']*2**(octave-1)
note_pt['C#1'] = 1.5*note_pt['F#0']
for octave in range(0, 10):
note_pt['C#{}'.format(octave)] = note_pt['C#1']*2**(octave-1)
note_pt['G#0'] = 1.5*note_pt['C#0']
for octave in range(0, 10):
note_pt['G#{}'.format(octave)] = note_pt['G#0']*2**(octave-0)
note_pt['D#1'] = 1.5*note_pt['G#0']
for octave in range(0, 10):
note_pt['D#{}'.format(octave)] = note_pt['D#1']*2**(octave-1)
note_pt['A#0'] = 1.5*note_pt['D#0']
for octave in range(0, 10):
note_pt['A#{}'.format(octave)] = note_pt['A#0']*2**(octave-0)
note_pt['E#1'] = 1.5*note_pt['A#0']
for octave in range(0, 10):
note_pt['E#{}'.format(octave)] = note_pt['E#1']*2**(octave-1)
note_pt['B#0'] = 1.5*note_pt['E#0']
for octave in range(0, 10):
note_pt['B#{}'.format(octave)] = note_pt['B#0']*2**(octave-0)
# Flats
note_pt['D0'] = 2/3*note_pt['A0']
for octave in range(0, 10):
note_pt['D{}'.format(octave)] = note_pt['D0']*2**octave
note_pt['G0'] = 2/3*note_pt['D1']
for octave in range(0, 10):
note_pt['G{}'.format(octave)] = note_pt['G0']*2**octave
note_pt['C0'] = 2/3*note_pt['G0']
for octave in range(0, 10):
note_pt['C{}'.format(octave)] = note_pt['C0']*2**octave
note_pt['F0'] = 2/3*note_pt['C1']
for octave in range(0, 10):
note_pt['F{}'.format(octave)] = note_pt['F0']*2**octave
note_pt['Bb0'] = 2/3*note_pt['F1']
for octave in range(0, 10):
note_pt['Bb{}'.format(octave)] = note_pt['Bb0']*2**octave
note_pt['Eb0'] = 2/3*note_pt['Bb0']
for octave in range(0, 10):
note_pt['Eb{}'.format(octave)] = note_pt['Eb0']*2**octave
note_pt['Ab0'] = 2/3*note_pt['Eb1']
for octave in range(0, 10):
note_pt['Ab{}'.format(octave)] = note_pt['Ab0']*2**octave
note_pt['Db0'] = 2/3*note_pt['Ab0']
for octave in range(0, 10):
note_pt['Db{}'.format(octave)] = note_pt['Db0']*2**octave
note_pt['Gb0'] = 2/3*note_pt['Db1']
for octave in range(0, 10):
note_pt['Gb{}'.format(octave)] = note_pt['Gb0']*2**octave
note_pt['Cb0'] = 2/3*note_pt['Gb0']
for octave in range(0, 10):
note_pt['Cb{}'.format(octave)] = note_pt['Cb0']*2**octave
note_pt['Fb0'] = 2/3*note_pt['Cb1']
for octave in range(0, 10):
note_pt['Fb{}'.format(octave)] = note_pt['Fb0']*2**octave
sorted_notes = sorted(note_pt.items(), key=lambda x:x[1])
markdown = """|note|midi-ET|Hertz-ET|midi-PT|Hertz-PT|\n"""
markdown += """|----|----|-----|----|----|-----|\n"""
for note, f_pt in sorted_notes:
midi_et = librosa.note_to_midi(note)
f_et = librosa.midi_to_hz(midi_et)
midi_pt = librosa.hz_to_midi(f_pt)
if note.startswith('A') and midi_et % 12 == 9:
ipd.display_markdown(markdown, raw=True)
markdown = """|note|midi-ET|Hertz-ET|midi-PT|Hertz-PT|\n"""
markdown += """|----|----|-----|----|----|-----|\n"""
markdown += """|{}|{}|{:.5g}|{:.3f}|{:.5g}|\n""".format(
note, midi_et, f_et, midi_pt, f_pt
)
ipd.display_markdown(markdown, raw=True)
```
[← Back to Index](index.html)
|
github_jupyter
|
%matplotlib inline
import librosa, librosa.display, numpy, matplotlib.pyplot as plt, IPython.display as ipd
plt.style.use('seaborn-muted')
plt.rcParams['figure.figsize'] = (14, 5)
plt.rcParams['axes.grid'] = True
plt.rcParams['axes.spines.left'] = False
plt.rcParams['axes.spines.right'] = False
plt.rcParams['axes.spines.bottom'] = False
plt.rcParams['axes.spines.top'] = False
plt.rcParams['axes.xmargin'] = 0
plt.rcParams['axes.ymargin'] = 0
plt.rcParams['image.cmap'] = 'gray'
plt.rcParams['image.interpolation'] = None
note_pt = dict()
# Sharps
note_pt['A4'] = 440.0
for octave in range(0, 10):
note_pt['A{}'.format(octave)] = 440.0*2**(octave-4)
note_pt['E1'] = 1.5*note_pt['A0']
for octave in range(0, 10):
note_pt['E{}'.format(octave)] = note_pt['E1']*2**(octave-1)
note_pt['B0'] = 1.5*note_pt['E0']
for octave in range(0, 10):
note_pt['B{}'.format(octave)] = note_pt['B0']*2**(octave-0)
note_pt['F#1'] = 1.5*note_pt['B0']
for octave in range(0, 10):
note_pt['F#{}'.format(octave)] = note_pt['F#1']*2**(octave-1)
note_pt['C#1'] = 1.5*note_pt['F#0']
for octave in range(0, 10):
note_pt['C#{}'.format(octave)] = note_pt['C#1']*2**(octave-1)
note_pt['G#0'] = 1.5*note_pt['C#0']
for octave in range(0, 10):
note_pt['G#{}'.format(octave)] = note_pt['G#0']*2**(octave-0)
note_pt['D#1'] = 1.5*note_pt['G#0']
for octave in range(0, 10):
note_pt['D#{}'.format(octave)] = note_pt['D#1']*2**(octave-1)
note_pt['A#0'] = 1.5*note_pt['D#0']
for octave in range(0, 10):
note_pt['A#{}'.format(octave)] = note_pt['A#0']*2**(octave-0)
note_pt['E#1'] = 1.5*note_pt['A#0']
for octave in range(0, 10):
note_pt['E#{}'.format(octave)] = note_pt['E#1']*2**(octave-1)
note_pt['B#0'] = 1.5*note_pt['E#0']
for octave in range(0, 10):
note_pt['B#{}'.format(octave)] = note_pt['B#0']*2**(octave-0)
# Flats
note_pt['D0'] = 2/3*note_pt['A0']
for octave in range(0, 10):
note_pt['D{}'.format(octave)] = note_pt['D0']*2**octave
note_pt['G0'] = 2/3*note_pt['D1']
for octave in range(0, 10):
note_pt['G{}'.format(octave)] = note_pt['G0']*2**octave
note_pt['C0'] = 2/3*note_pt['G0']
for octave in range(0, 10):
note_pt['C{}'.format(octave)] = note_pt['C0']*2**octave
note_pt['F0'] = 2/3*note_pt['C1']
for octave in range(0, 10):
note_pt['F{}'.format(octave)] = note_pt['F0']*2**octave
note_pt['Bb0'] = 2/3*note_pt['F1']
for octave in range(0, 10):
note_pt['Bb{}'.format(octave)] = note_pt['Bb0']*2**octave
note_pt['Eb0'] = 2/3*note_pt['Bb0']
for octave in range(0, 10):
note_pt['Eb{}'.format(octave)] = note_pt['Eb0']*2**octave
note_pt['Ab0'] = 2/3*note_pt['Eb1']
for octave in range(0, 10):
note_pt['Ab{}'.format(octave)] = note_pt['Ab0']*2**octave
note_pt['Db0'] = 2/3*note_pt['Ab0']
for octave in range(0, 10):
note_pt['Db{}'.format(octave)] = note_pt['Db0']*2**octave
note_pt['Gb0'] = 2/3*note_pt['Db1']
for octave in range(0, 10):
note_pt['Gb{}'.format(octave)] = note_pt['Gb0']*2**octave
note_pt['Cb0'] = 2/3*note_pt['Gb0']
for octave in range(0, 10):
note_pt['Cb{}'.format(octave)] = note_pt['Cb0']*2**octave
note_pt['Fb0'] = 2/3*note_pt['Cb1']
for octave in range(0, 10):
note_pt['Fb{}'.format(octave)] = note_pt['Fb0']*2**octave
sorted_notes = sorted(note_pt.items(), key=lambda x:x[1])
markdown = """|note|midi-ET|Hertz-ET|midi-PT|Hertz-PT|\n"""
markdown += """|----|----|-----|----|----|-----|\n"""
for note, f_pt in sorted_notes:
midi_et = librosa.note_to_midi(note)
f_et = librosa.midi_to_hz(midi_et)
midi_pt = librosa.hz_to_midi(f_pt)
if note.startswith('A') and midi_et % 12 == 9:
ipd.display_markdown(markdown, raw=True)
markdown = """|note|midi-ET|Hertz-ET|midi-PT|Hertz-PT|\n"""
markdown += """|----|----|-----|----|----|-----|\n"""
markdown += """|{}|{}|{:.5g}|{:.3f}|{:.5g}|\n""".format(
note, midi_et, f_et, midi_pt, f_pt
)
ipd.display_markdown(markdown, raw=True)
| 0.257298 | 0.657662 |
## Create RxNorm -> CUI lookup with UMLS API
First, acquire a [UMLS license](https://www.nlm.nih.gov/databases/umls.html#license_request) if you don't already have one.
Then, replace `'MY-SECRET-KEY'` in the cell below with your UMLS API key.
Then we can initialize embeddings for the RxNorm codes in the annotations, using existing CUI embeddings.
```
import time
from umls_api_auth import Authentication
import requests as rq
from collections import defaultdict
from tqdm import tqdm
rxns = set([line.strip()[3:] for line in open('vocab.txt') if line.startswith('RX_')])
auth = Authentication('MY-SECRET-KEY')
tgt = auth.gettgt()
URI = "https://uts-ws.nlm.nih.gov/rest"
rxn2cuis = defaultdict(set)
for med in tqdm(rxns):
route = f'/content/current/source/RXNORM/{med}/atoms'
query = {'ticket': auth.getst(tgt)}
res = rq.get(URI+route, params=query)
if res.status_code == 200:
cuis = [result['concept'].split('/')[-1] for result in res.json()['result']]
rxn2cuis[med].update(cuis)
# rate limit to 20 requests/sec
time.sleep(0.05)
with open('data/rxn2cuis.txt', 'w') as of:
for rxn, cuis in rxn2cuis.items():
for cui in cuis:
of.write(','.join([rxn, cui]) + '\n')
```
## Initialize problem and target embeddings
Section 3.2 "Initialization and pre-processing"
```
%run init_embed.py embeddings/claims_codes_hs_300.txt w2v 300
```
## Table 2: held-out triplets, Choi et al embeddings
Section 4.1 "Held-out triplets"
```
%run train.py embeddings/clinicalml.txt\
vocab.txt \
data/train_rand.csv \
--patience 10\
--max_epochs 100\
--criterion mr\
--px_codes data/intersect_pxs.txt\
--rxn_codes data/intersect_rxns.txt\
--loinc_codes data/intersect_loincs.txt\
--use_negs\
--lr 1e-4\
--split_type triplets\
--run_test
```
Compare the above to line 4 "Choi et al (2016)" of Table 2 in the paper.
## Table 3: held-out problems, Choi et al embeddings
Section 4.2 "Held-out problems"
```
%run train.py embeddings/clinicalml.txt\
vocab.txt \
data/train_probs.csv \
--patience 10\
--max_epochs 100\
--criterion mr\
--px_codes data/intersect_pxs.txt\
--rxn_codes data/intersect_rxns.txt\
--loinc_codes data/intersect_loincs.txt\
--use_negs\
--lr 1e-4\
--run_test
```
Compare the above results (under "METRICS") to line 4 "Choi et al (2016)" of Table 3 in the paper.
## Table 5: Examples
This will not give identical results, as the table in the paper is derived from a model that uses the site-specific data features.
```
# Paste the result directory (after "THIS RUN'S RESULT DIR IS: " above) into
s = open('results/distmult_clinicalml_Jul_31_16:25:33/html_examples.txt').read().split('\n')
from IPython.display import HTML
s = '\n'.join(s)
h = HTML(s); h
```
## Table 3 (cont): Ontology baselines
```
%run compute_ndfrt_baseline.py
```
Compare the above results (MRR and H@5) to line 1 "Ontology baselines" of Table 3 in the paper: columns "Medications MRR" and "Medications H@5"
Before running the below, edit the line in `compute_cpt_baseline.py` that has `'MY-SECRET-KEY'` to instead use your UMLS API key.
```
%run compute_cpt_baseline.py
```
Compare the above results (MRR and H@5) to line 1 "Ontology baselines" of Table 3 in the paper: columns "Procedures MRR" and "Procedures H@5"
|
github_jupyter
|
import time
from umls_api_auth import Authentication
import requests as rq
from collections import defaultdict
from tqdm import tqdm
rxns = set([line.strip()[3:] for line in open('vocab.txt') if line.startswith('RX_')])
auth = Authentication('MY-SECRET-KEY')
tgt = auth.gettgt()
URI = "https://uts-ws.nlm.nih.gov/rest"
rxn2cuis = defaultdict(set)
for med in tqdm(rxns):
route = f'/content/current/source/RXNORM/{med}/atoms'
query = {'ticket': auth.getst(tgt)}
res = rq.get(URI+route, params=query)
if res.status_code == 200:
cuis = [result['concept'].split('/')[-1] for result in res.json()['result']]
rxn2cuis[med].update(cuis)
# rate limit to 20 requests/sec
time.sleep(0.05)
with open('data/rxn2cuis.txt', 'w') as of:
for rxn, cuis in rxn2cuis.items():
for cui in cuis:
of.write(','.join([rxn, cui]) + '\n')
%run init_embed.py embeddings/claims_codes_hs_300.txt w2v 300
%run train.py embeddings/clinicalml.txt\
vocab.txt \
data/train_rand.csv \
--patience 10\
--max_epochs 100\
--criterion mr\
--px_codes data/intersect_pxs.txt\
--rxn_codes data/intersect_rxns.txt\
--loinc_codes data/intersect_loincs.txt\
--use_negs\
--lr 1e-4\
--split_type triplets\
--run_test
%run train.py embeddings/clinicalml.txt\
vocab.txt \
data/train_probs.csv \
--patience 10\
--max_epochs 100\
--criterion mr\
--px_codes data/intersect_pxs.txt\
--rxn_codes data/intersect_rxns.txt\
--loinc_codes data/intersect_loincs.txt\
--use_negs\
--lr 1e-4\
--run_test
# Paste the result directory (after "THIS RUN'S RESULT DIR IS: " above) into
s = open('results/distmult_clinicalml_Jul_31_16:25:33/html_examples.txt').read().split('\n')
from IPython.display import HTML
s = '\n'.join(s)
h = HTML(s); h
%run compute_ndfrt_baseline.py
%run compute_cpt_baseline.py
| 0.342681 | 0.794305 |
```
import requests
from bs4 import BeautifulSoup
import tqdm.notebook as tq
import pickle
import pandas as pd
import numpy as np
def get_pages(page_url):
headers = {
'User-Agent':'Mozilla/5.0 (Macintosh; Intel Mac OS X 10_15_7) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/91.0.4472.164 Safari/537.36'
}
response = requests.get(url=page_url,headers=headers)
page_soup = BeautifulSoup(response.text,'lxml')
return page_soup
auth = requests.auth.HTTPBasicAuth('bCnE1U61Wqixgs2wy28POg','vEY7k3_j7o3PZZvP-tEt6DnhWr1x5A')
data = {'grant_type': 'password',
'username': 'Delta_Wang11',
'password': 'delta113420'
}
headers = {'User-Agent':'Mozilla/5.0 (Macintosh; Intel Mac OS X 10_15_7) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/93.0.4577.82 Safari/537.36'}
res = requests.post('https://www.reddit.com/api/v1/access_token',
auth=auth, data=data, headers=headers)
TOKEN = res.json()['access_token']
headers = {**headers, **{'Authorization':f"bearer {TOKEN}"}}
requests.get('https://oauth.reddit.com/api/v1/me',headers=headers)
res = requests.get("https://oauth.reddit.com/user/gleophas",headers=headers)
df = pd.read_csv('../data/author/ARS_neg_author.csv')
team = ['ARS','MNC','MNU','LIV','CHE','TOT']
stype = ['pos','neg']
Karma = []
for t in team:
for s in stype:
Karma = []
df = pd.read_csv(f'../data/author/{t}_{s}_author.csv')
for a in tq.tqdm(df.author):
print(a)
url = f'https://www.reddit.com/user/{a}'
soup = get_pages(url)
k = soup.find('span',class_='_1hNyZSklmcC7R_IfCUcXmZ')
if k is None:
Karma.append(-1)
else:
Karma.append(int(k.text.replace(",","")))
df['Karma'] = Karma
df.to_csv(f'../data/author/Karma/{t}_{s}_author_Karma.csv',index=False)
soup.find('span',class_='_1hNyZSklmcC7R_IfCUcXmZ').text
df0 = pd.DataFrame()
for t in team:
for s in stype:
Karma = []
df = pd.read_csv(f'../data/author/{t}_{s}_author.csv')
df0 = pd.concat([df0,df])
df0
df0['KarmaPerComment'] = df0['Karma']/df0['all_comments']
dfs = df0.loc[df0.Karma!=-1].sort_values(by='Karma',ascending=False).iloc[1:]
dfs = dfs.loc[dfs.all_comments!=0]
import matplotlib.pyplot as plt
plt.figure(figsize = (12,9))
plt.scatter(dfs['sentiment_score'],dfs['Karma'])
plt.grid(axis='y', alpha=0.75)
plt.ylabel('Num of comments')
plt.xlabel('Date')
plt.show()
teams = ['MNU']
stypes = ['neg']
for t in teams:
for s in stypes:
print(t)
dfa = pd.read_csv(f'../data/author/Karma/{t}_{s}_author_Karma.csv')
dfc = pd.read_csv(f'../data/comments/author_bg/{t}_{s}_author_bg.csv',lineterminator='\n')
dfcg = dfc.groupby('author')['id'].count()
dfa = dfa.set_index('author')
a_c = []
for a in dfa.index:
if a in dfcg.index:
a_c.append(dfcg[a])
else:
a_c.append(0)
dfa['all_comments'] = a_c
dfa = dfa.reset_index()
dfa.to_csv(f'../data/author/{t}_{s}_author.csv',index=False)
dfa = pd.read_csv('../data/author/Karma/ARS_neg_author_Karma.csv')
dfc = pd.read_csv('../data/comments/author_bg/ARS_neg_author_bg.csv')
dfcg = dfc.groupby('author')['id'].count()
dfa = dfa.set_index('author')
dfa['all_comments'] = np.zeros(dfa.shape[0])
a_c = []
for a in dfa.index:
if a in dfcg.index:
a_c.append(dfcg[a])
else:
a_c.append(0)
dfa['all_comments'] = a_c
dfa
```
|
github_jupyter
|
import requests
from bs4 import BeautifulSoup
import tqdm.notebook as tq
import pickle
import pandas as pd
import numpy as np
def get_pages(page_url):
headers = {
'User-Agent':'Mozilla/5.0 (Macintosh; Intel Mac OS X 10_15_7) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/91.0.4472.164 Safari/537.36'
}
response = requests.get(url=page_url,headers=headers)
page_soup = BeautifulSoup(response.text,'lxml')
return page_soup
auth = requests.auth.HTTPBasicAuth('bCnE1U61Wqixgs2wy28POg','vEY7k3_j7o3PZZvP-tEt6DnhWr1x5A')
data = {'grant_type': 'password',
'username': 'Delta_Wang11',
'password': 'delta113420'
}
headers = {'User-Agent':'Mozilla/5.0 (Macintosh; Intel Mac OS X 10_15_7) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/93.0.4577.82 Safari/537.36'}
res = requests.post('https://www.reddit.com/api/v1/access_token',
auth=auth, data=data, headers=headers)
TOKEN = res.json()['access_token']
headers = {**headers, **{'Authorization':f"bearer {TOKEN}"}}
requests.get('https://oauth.reddit.com/api/v1/me',headers=headers)
res = requests.get("https://oauth.reddit.com/user/gleophas",headers=headers)
df = pd.read_csv('../data/author/ARS_neg_author.csv')
team = ['ARS','MNC','MNU','LIV','CHE','TOT']
stype = ['pos','neg']
Karma = []
for t in team:
for s in stype:
Karma = []
df = pd.read_csv(f'../data/author/{t}_{s}_author.csv')
for a in tq.tqdm(df.author):
print(a)
url = f'https://www.reddit.com/user/{a}'
soup = get_pages(url)
k = soup.find('span',class_='_1hNyZSklmcC7R_IfCUcXmZ')
if k is None:
Karma.append(-1)
else:
Karma.append(int(k.text.replace(",","")))
df['Karma'] = Karma
df.to_csv(f'../data/author/Karma/{t}_{s}_author_Karma.csv',index=False)
soup.find('span',class_='_1hNyZSklmcC7R_IfCUcXmZ').text
df0 = pd.DataFrame()
for t in team:
for s in stype:
Karma = []
df = pd.read_csv(f'../data/author/{t}_{s}_author.csv')
df0 = pd.concat([df0,df])
df0
df0['KarmaPerComment'] = df0['Karma']/df0['all_comments']
dfs = df0.loc[df0.Karma!=-1].sort_values(by='Karma',ascending=False).iloc[1:]
dfs = dfs.loc[dfs.all_comments!=0]
import matplotlib.pyplot as plt
plt.figure(figsize = (12,9))
plt.scatter(dfs['sentiment_score'],dfs['Karma'])
plt.grid(axis='y', alpha=0.75)
plt.ylabel('Num of comments')
plt.xlabel('Date')
plt.show()
teams = ['MNU']
stypes = ['neg']
for t in teams:
for s in stypes:
print(t)
dfa = pd.read_csv(f'../data/author/Karma/{t}_{s}_author_Karma.csv')
dfc = pd.read_csv(f'../data/comments/author_bg/{t}_{s}_author_bg.csv',lineterminator='\n')
dfcg = dfc.groupby('author')['id'].count()
dfa = dfa.set_index('author')
a_c = []
for a in dfa.index:
if a in dfcg.index:
a_c.append(dfcg[a])
else:
a_c.append(0)
dfa['all_comments'] = a_c
dfa = dfa.reset_index()
dfa.to_csv(f'../data/author/{t}_{s}_author.csv',index=False)
dfa = pd.read_csv('../data/author/Karma/ARS_neg_author_Karma.csv')
dfc = pd.read_csv('../data/comments/author_bg/ARS_neg_author_bg.csv')
dfcg = dfc.groupby('author')['id'].count()
dfa = dfa.set_index('author')
dfa['all_comments'] = np.zeros(dfa.shape[0])
a_c = []
for a in dfa.index:
if a in dfcg.index:
a_c.append(dfcg[a])
else:
a_c.append(0)
dfa['all_comments'] = a_c
dfa
| 0.133274 | 0.106644 |
# Statistics from Stock Data
In this lab we will load stock data into a Pandas Dataframe and calculate some statistics on it. We will be working with stock data from Google, Apple, and Amazon. All the stock data was downloaded from yahoo finance in CSV format. In your workspace you should have a file named GOOG.csv containing the Google stock data, a file named AAPL.csv containing the Apple stock data, and a file named AMZN.csv containing the Amazon stock data. (You can see the workspace folder by clicking on the Jupyter logo in the upper left corner of the workspace.) All the files contain 7 columns of data:
**Date Open High Low Close Adj_Close Volume**
We will start by reading in any of the above CSV files into a DataFrame and see what the data looks like.
```
# We import pandas into Python
import pandas as pd
# We read in a stock data data file into a data frame and see what it looks like
df = pd.read_csv('./GOOG.csv')
# We display the first 5 rows of the DataFrame
df.head()
```
We clearly see that the Dataframe is has automatically labeled the row indices using integers and has labeled the columns of the DataFrame using the names of the columns in the CSV files.
# To Do
You will now load the stock data from Google, Apple, and Amazon into separte DataFrames. However, for each stock data you will only be interested in loading the `Date` and `Adj Close` columns into the Dataframe. In addtion, you want to use the `Date` column as your row index. Finally, you want the DataFrame to recognize the dates as actual dates (year/month/day) and not as strings. For each stock, you can accomplish all theses things in just one line of code by using the appropiate keywords in the `pd.read_csv()` function. Here are a few hints:
* Use the `index_col` keyword to indicate which column you want to use as an index. For example `index_col = ['Open']`
* Set the `parse_dates` keyword equal to `True` to convert the Dates into real dates of the form year/month/day
* Use the `usecols` keyword to select which columns you want to load into the DataFrame. For example `usecols = ['Open', 'High']`
Fill in the code below:
```
# We load the Google stock data into a DataFrame
google_stock = pd.read_csv('./GOOG.csv',parse_dates=True,index_col=['Date'],usecols=['Date','Adj Close'])
# We load the Apple stock data into a DataFrame
apple_stock = pd.read_csv('./AAPL.csv',parse_dates=True,index_col=['Date'],usecols=['Date','Adj Close'])
# We load the Amazon stock data into a DataFrame
amazon_stock = pd.read_csv('./AMZN.csv',parse_dates=True,index_col=['Date'],usecols=['Date','Adj Close'])
```
You can check that you have loaded the data correctly by displaying the head of the DataFrames.
```
# We display the google_stock DataFrame
google_stock.head()
google_stock.columns
```
You will now join the three DataFrames above to create a single new DataFrame that contains all the `Adj Close` for all the stocks. Let's start by creating an empty DataFrame that has as row indices calendar days between `2000-01-01` and `2016-12-31`. We will use the `pd.date_range()` function to create the calendar dates first and then we will create a DataFrame that uses those dates as row indices:
```
# We create calendar dates between '2000-01-01' and '2016-12-31'
dates = pd.date_range('2000-01-01', '2016-12-31')
# We create and empty DataFrame that uses the above dates as indices
all_stocks = pd.DataFrame(index = dates, columns=["Date"])
all_stocks.head()
#all_stocks =all_stocks.rename(columns={" ":'Date'})
#all_stocks.head()
```
# To Do
You will now join the the individual DataFrames, `google_stock`, `apple_stock`, and `amazon_stock`, to the `all_stocks` DataFrame. However, before you do this, it is necessary that you change the name of the columns in each of the three dataframes. This is because the column labels in the `all_stocks` dataframe must be unique. Since all the columns in the individual dataframes have the same name, `Adj Close`, we must change them to the stock name before joining them. In the space below change the column label `Adj Close` of each individual dataframe to the name of the corresponding stock. You can do this by using the `pd.DataFrame.rename()` function.
```
# Change the Adj Close column label to Google
google_stock = google_stock.rename(columns={'Adj Close': 'google_stock'})
# Change the Adj Close column label to Apple
apple_stock = apple_stock.rename(columns={'Adj Close': 'apple_stock'})
# Change the Adj Close column label to Amazon
amazon_stock = amazon_stock.rename(columns={'Adj Close': 'amazon_stock'})
```
You can check that the column labels have been changed correctly by displaying the datadrames
```
apple_stock.head()
# We display the google_stock DataFrame
google_stock.head()
amazon_stock.head()
```
Now that we have unique column labels, we can join the individual DataFrames to the `all_stocks` DataFrame. For this we will use the `dataframe.join()` function. The function `dataframe1.join(dataframe2)` joins `dataframe1` with `dataframe2`. We will join each dataframe one by one to the `all_stocks` dataframe. Fill in the code below to join the dataframes, the first join has been made for you:
```
all_stocks.head()
# We join the Google stock to all_stocks
all_stocks = all_stocks.join(google_stock)
# We join the Apple stock to all_stocks
all_stocks = all_stocks.join(apple_stock)
# We join the Amazon stock to all_stocks
all_stocks =all_stocks.join(amazon_stock)
```
You can check that the dataframes have been joined correctly by displaying the `all_stocks` dataframe
```
# We display the google_stock DataFrame
all_stocks.head()
all_stocks.drop(columns="Date",inplace=True)
all_stocks.head()
```
# To Do
Before we proceed to get some statistics on the stock data, let's first check that we don't have any *NaN* values. In the space below check if there are any *NaN* values in the `all_stocks` dataframe. If there are any, remove any rows that have *NaN* values:
```
# Check if there are any NaN values in the all_stocks dataframe and hoe many are they
all_stocks.isnull().sum()
# Remove any rows that contain NaN values
all_stocks.dropna(axis=0).head()
# Remove any rows that contain NaN values
all_stocks.dropna(axis=0).tail()
```
Now that you have eliminated any *NaN* values we can now calculate some basic statistics on the stock prices. Fill in the code below
```
# Print the average stock price for each stock i.e (mean)
print('mean:\n ',all_stocks.mean(axis=0))
print()
# Print the median stock price for each stock
print('median:\n ', all_stocks.median())
print()
# Print the standard deviation of the stock price for each stock
print('std:\n ', all_stocks.std())
print()
# Print the correlation between stocks
print('corr:\n', all_stocks.corr())
```
We will now look at how we can compute some rolling statistics, also known as moving statistics. We can calculate for example the rolling mean (moving average) of the Google stock price by using the Pandas `dataframe.rolling().mean()` method. The `dataframe.rolling(N).mean()` calculates the rolling mean over an `N`-day window. In other words, we can take a look at the average stock price every `N` days using the above method. Fill in the code below to calculate the average stock price every 150 days for Google stock
```
# We compute the rolling mean using a 3-Day window for stock
rollingMeanAmazon = all_stocks['amazon_stock'].rolling(3).mean()
print(rollingMeanAmazon.head())
print()
# We compute the rolling mean using a 3-Day window for stock
rollingMeanApple = all_stocks['apple_stock'].rolling(3).mean()
print(rollingMeanApple.head())
print()
# We compute the rolling mean using a 3-Day window for stock
rollingMeanGoogle = all_stocks['google_stock'].rolling(3).mean()
print(rollingMeanGoogle.head())
```
We can also visualize the rolling mean by plotting the data in our dataframe. In the following lessons you will learn how to use **Matplotlib** to visualize data. For now I will just import matplotlib and plot the Google stock data on top of the rolling mean. You can play around by changing the rolling mean window and see how the plot changes.
```
# this allows plots to be rendered in the notebook
%matplotlib inline
# We import matplotlib into Python
import matplotlib.pyplot as plt
# We plot the Google stock data
plt.plot(all_stocks['google_stock'])
# We plot the rolling mean ontop of our Google stock data
plt.plot(rollingMeanGoogle)
plt.legend(['Google Stock Price', 'Rolling Mean For Google'])
plt.show()
# this allows plots to be rendered in the notebook
%matplotlib inline
# We import matplotlib into Python
import matplotlib.pyplot as plt
# We plot the Apple stock data
plt.plot(all_stocks['apple_stock'])
# We plot the rolling mean ontop of our Apple stock data
plt.plot(rollingMeanApple)
plt.legend(['Apple Stock Price', 'Rolling Mean For Apple'])
plt.show()
# this allows plots to be rendered in the notebook
%matplotlib inline
# We import matplotlib into Python
import matplotlib.pyplot as plt
# We plot the Amazon stock data
plt.plot(all_stocks['amazon_stock'])
# We plot the rolling mean ontop of our Amazon stock data
plt.plot(rollingMeanAmazon)
plt.legend(['Amazon Stock Price', 'Rolling Mean For Amazon'])
plt.show()
# We compute the rolling mean using a 6-Day window for stock
rollingMeanAmazonOne = all_stocks['amazon_stock'].rolling(6).mean()
print(rollingMeanAmazonOne.head())
print()
# We compute the rolling mean using a 6-Day window for stock
rollingMeanAppleOne = all_stocks['apple_stock'].rolling(6).mean()
print(rollingMeanAppleOne.head())
print()
# We compute the rolling mean using a 6-Day window for stock
rollingMeanGoogleOne = all_stocks['google_stock'].rolling(6).mean()
print(rollingMeanGoogleOne.head())
# this allows plots to be rendered in the notebook
%matplotlib inline
# We import matplotlib into Python
import matplotlib.pyplot as plt
# We plot the Google stock data
plt.plot(all_stocks['google_stock'])
# We plot the rolling mean ontop of our Google stock data
plt.plot(rollingMeanGoogleOne)
plt.legend(['Google Stock Price', 'Rolling Mean For Google'])
plt.show()
# this allows plots to be rendered in the notebook
%matplotlib inline
# We import matplotlib into Python
import matplotlib.pyplot as plt
# We plot the Apple stock data
plt.plot(all_stocks['apple_stock'])
# We plot the rolling mean ontop of our Apple stock data
plt.plot(rollingMeanAppleOne)
plt.legend(['Apple Stock Price', 'Rolling Mean For Apple'])
plt.show()
# this allows plots to be rendered in the notebook
%matplotlib inline
# We import matplotlib into Python
import matplotlib.pyplot as plt
# We plot the Amazon stock data
plt.plot(all_stocks['amazon_stock'])
# We plot the rolling mean ontop of our Amazon stock data
plt.plot(rollingMeanAmazonOne)
plt.legend(['Amazon Stock Price', 'Rolling Mean For Amazon'])
plt.show()
```
# Thank YOU
|
github_jupyter
|
# We import pandas into Python
import pandas as pd
# We read in a stock data data file into a data frame and see what it looks like
df = pd.read_csv('./GOOG.csv')
# We display the first 5 rows of the DataFrame
df.head()
# We load the Google stock data into a DataFrame
google_stock = pd.read_csv('./GOOG.csv',parse_dates=True,index_col=['Date'],usecols=['Date','Adj Close'])
# We load the Apple stock data into a DataFrame
apple_stock = pd.read_csv('./AAPL.csv',parse_dates=True,index_col=['Date'],usecols=['Date','Adj Close'])
# We load the Amazon stock data into a DataFrame
amazon_stock = pd.read_csv('./AMZN.csv',parse_dates=True,index_col=['Date'],usecols=['Date','Adj Close'])
# We display the google_stock DataFrame
google_stock.head()
google_stock.columns
# We create calendar dates between '2000-01-01' and '2016-12-31'
dates = pd.date_range('2000-01-01', '2016-12-31')
# We create and empty DataFrame that uses the above dates as indices
all_stocks = pd.DataFrame(index = dates, columns=["Date"])
all_stocks.head()
#all_stocks =all_stocks.rename(columns={" ":'Date'})
#all_stocks.head()
# Change the Adj Close column label to Google
google_stock = google_stock.rename(columns={'Adj Close': 'google_stock'})
# Change the Adj Close column label to Apple
apple_stock = apple_stock.rename(columns={'Adj Close': 'apple_stock'})
# Change the Adj Close column label to Amazon
amazon_stock = amazon_stock.rename(columns={'Adj Close': 'amazon_stock'})
apple_stock.head()
# We display the google_stock DataFrame
google_stock.head()
amazon_stock.head()
all_stocks.head()
# We join the Google stock to all_stocks
all_stocks = all_stocks.join(google_stock)
# We join the Apple stock to all_stocks
all_stocks = all_stocks.join(apple_stock)
# We join the Amazon stock to all_stocks
all_stocks =all_stocks.join(amazon_stock)
# We display the google_stock DataFrame
all_stocks.head()
all_stocks.drop(columns="Date",inplace=True)
all_stocks.head()
# Check if there are any NaN values in the all_stocks dataframe and hoe many are they
all_stocks.isnull().sum()
# Remove any rows that contain NaN values
all_stocks.dropna(axis=0).head()
# Remove any rows that contain NaN values
all_stocks.dropna(axis=0).tail()
# Print the average stock price for each stock i.e (mean)
print('mean:\n ',all_stocks.mean(axis=0))
print()
# Print the median stock price for each stock
print('median:\n ', all_stocks.median())
print()
# Print the standard deviation of the stock price for each stock
print('std:\n ', all_stocks.std())
print()
# Print the correlation between stocks
print('corr:\n', all_stocks.corr())
# We compute the rolling mean using a 3-Day window for stock
rollingMeanAmazon = all_stocks['amazon_stock'].rolling(3).mean()
print(rollingMeanAmazon.head())
print()
# We compute the rolling mean using a 3-Day window for stock
rollingMeanApple = all_stocks['apple_stock'].rolling(3).mean()
print(rollingMeanApple.head())
print()
# We compute the rolling mean using a 3-Day window for stock
rollingMeanGoogle = all_stocks['google_stock'].rolling(3).mean()
print(rollingMeanGoogle.head())
# this allows plots to be rendered in the notebook
%matplotlib inline
# We import matplotlib into Python
import matplotlib.pyplot as plt
# We plot the Google stock data
plt.plot(all_stocks['google_stock'])
# We plot the rolling mean ontop of our Google stock data
plt.plot(rollingMeanGoogle)
plt.legend(['Google Stock Price', 'Rolling Mean For Google'])
plt.show()
# this allows plots to be rendered in the notebook
%matplotlib inline
# We import matplotlib into Python
import matplotlib.pyplot as plt
# We plot the Apple stock data
plt.plot(all_stocks['apple_stock'])
# We plot the rolling mean ontop of our Apple stock data
plt.plot(rollingMeanApple)
plt.legend(['Apple Stock Price', 'Rolling Mean For Apple'])
plt.show()
# this allows plots to be rendered in the notebook
%matplotlib inline
# We import matplotlib into Python
import matplotlib.pyplot as plt
# We plot the Amazon stock data
plt.plot(all_stocks['amazon_stock'])
# We plot the rolling mean ontop of our Amazon stock data
plt.plot(rollingMeanAmazon)
plt.legend(['Amazon Stock Price', 'Rolling Mean For Amazon'])
plt.show()
# We compute the rolling mean using a 6-Day window for stock
rollingMeanAmazonOne = all_stocks['amazon_stock'].rolling(6).mean()
print(rollingMeanAmazonOne.head())
print()
# We compute the rolling mean using a 6-Day window for stock
rollingMeanAppleOne = all_stocks['apple_stock'].rolling(6).mean()
print(rollingMeanAppleOne.head())
print()
# We compute the rolling mean using a 6-Day window for stock
rollingMeanGoogleOne = all_stocks['google_stock'].rolling(6).mean()
print(rollingMeanGoogleOne.head())
# this allows plots to be rendered in the notebook
%matplotlib inline
# We import matplotlib into Python
import matplotlib.pyplot as plt
# We plot the Google stock data
plt.plot(all_stocks['google_stock'])
# We plot the rolling mean ontop of our Google stock data
plt.plot(rollingMeanGoogleOne)
plt.legend(['Google Stock Price', 'Rolling Mean For Google'])
plt.show()
# this allows plots to be rendered in the notebook
%matplotlib inline
# We import matplotlib into Python
import matplotlib.pyplot as plt
# We plot the Apple stock data
plt.plot(all_stocks['apple_stock'])
# We plot the rolling mean ontop of our Apple stock data
plt.plot(rollingMeanAppleOne)
plt.legend(['Apple Stock Price', 'Rolling Mean For Apple'])
plt.show()
# this allows plots to be rendered in the notebook
%matplotlib inline
# We import matplotlib into Python
import matplotlib.pyplot as plt
# We plot the Amazon stock data
plt.plot(all_stocks['amazon_stock'])
# We plot the rolling mean ontop of our Amazon stock data
plt.plot(rollingMeanAmazonOne)
plt.legend(['Amazon Stock Price', 'Rolling Mean For Amazon'])
plt.show()
| 0.641984 | 0.99083 |
# 14. Построение решения с использованием суперпозиции для переменного дебита
Материалы курсов "Исследования скважин и пластов" и "Гидродинамические исследования скважин" в РГУ нефти и газа имени И.М.Губкина.
Версия 0.4 от 24.11.2021
Хабибуллин Ринат 2021 г.
---
[Открыть на google colab](https://colab.research.google.com/github/khabibullinra/welltest_examples/blob/master/jupyter/14_superposition_variable_rate.ipynb)
# Содержание
* [14.1 Расчет кривой восстановления давления ](#14.1)
* [14.2 Случай для произвольной истории дебитов (ступенчатое изменение дебита)](#14.2)
* [14.3 Случай для произвольной истории дебитов (линейное изменение дебита)](#14.3)
```
# для того, чтобы скрипты гладко работали на https://colab.research.google.com/ пропишем
# установку библиотеки welltest
# библиотека welltest загружает определения функций для безразмерных переменных
# а также грузит anaflow которая обеспечивает работу с обратным преобразованием Лапласа
!pip install welltest
# импортируем библиотки, которые могут пригодиться для проведения расчетов
import numpy as np
import matplotlib.pyplot as plt
from anaflow import get_lap_inv
from scipy.special import kn, iv, expi
from welltest.functions import *
# Решение линейного стока уравнения фильтрации
def pd_ei(td, rd=1):
"""
Решение линейного стока уравнения фильтрации
rd - безразмерное расстояние
td - безразмерное время
"""
# при расчете убедимся, что td=0 не повлияет на расчет, даже если td массив и нулевой только один элемент
td = np.array(td, dtype = float)
return np.multiply(-0.5,
expi(np.divide(-rd**2 / 4 ,
td,
out=np.zeros_like(td), where=td!=0)),
out=np.zeros_like(td), where=td!=0)
```
# 14.1 Расчет кривой восстановления давления <a class="anchor" id="14.1"></a>
Один из самых простых примеров применения суперпозиции. Предполагаем, что добывающая скважина в однородном изотропном пласте запускается в момент времени `t=0` и работает `t_p_hr` часов, после чего останавливается. После остановки скважины забойное давление растет - и мы получим кривую восстановления давления.
Пусть решение задачи запуска скважины (падения давления) будет $P_D(t_D, r_D)$. Тогда решение для изменения давления при запуске и последующей остановки скважины можно представить в виде
$$P_{bu.D}(t_D, t_{prod.D}, r_D) = P_D(t_D) - P_D(t_D-t_{prod.D}, r_D) \cdot \mathcal{H}(t_D-t_{prod.D}) \tag{14.1}$$
где
* $t_D$ - безразмерное время после запуска скважины,
* $t_{prod.D}$ - безразмерное время работы скважины после запуска
* $\mathcal{H}$ - ступенчатая [функция Хевисайда](https://ru.wikipedia.org/wiki/%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D0%A5%D0%B5%D0%B2%D0%B8%D1%81%D0%B0%D0%B9%D0%B4%D0%B0) (в некоторых книгах обозначается как $\theta$)
* $P_D(t_D, r_D)$ - безразмерное давление - решение задачи запуска скважины (падения давления)
* $P_{bu.D}(t_D, t_{prod.D}, r_D)$ - безразмерное давление- решение задачи запуска скважины и последующей остановки скважины
Для проведения векторных расчетов в python удобно выражение с использованием функции Хевисайда
$$ \mathcal{H} = \begin{cases}0 & x < 0\\1 & x = 0\\1 & x > 0\end{cases}$$
Применение функции Хевисайда позволяет избежать в расчетных функциях применение условных операторов в явном виде для отдельных элементов входных массивов. Это потенциально ускоряет расчет.
```
x = np.arange(-2,2,0.01)
y = np.heaviside(x, 1)
plt.rcParams["figure.figsize"] = (8,3)
plt.plot(x,y)
plt.title('Функция Хевисайда $\mathcal{H}$ ')
plt.show()
def pd_build_up(td, td_p):
"""
расчет давления для запуска и последующей остановки скважины
td - время после запуска
td_p - время безразмерное - которое скважина работала до остановки
"""
# применение функции Хевисайда здесь делает расчет корректным
# для входных векторов td
return pd_ei(td) - np.heaviside(td-td_p,1) * pd_ei(td-td_p)
t_arr = np.logspace(-10, 2, 1000)
t_prod_hr = 24
k = 10 # проницаемость
q = 30 # дебит
# переведем размерный массив времени в безразмерные величины
td_arr = td_from_t(t_arr, k_mD=k)
td_prod = td_from_t(t_prod_hr, k_mD=k)
print('время работы скважины {:.2f} часа, что соответсвует безразмерному времени {:.2f}'.format(t_prod_hr, td_prod))
# для заданного массива безразмерных времен рассчитаем безразмерные давления
pd_arr = pd_build_up(td_arr, td_prod)
plt.rcParams["figure.figsize"] = (8,3)
plt.plot(td_arr, pd_arr)
plt.xlabel('td')
plt.ylabel('pd')
plt.title('Решение в безразмерных координатах')
plt.show()
# переведем безразмерные координаты в размерные
p_arr = p_from_pd_atma(pd_arr, k_mD=k, q_sm3day=q)
plt.rcParams["figure.figsize"] = (8,3)
plt.plot(t_arr, p_arr)
plt.xlabel('t, hr')
plt.ylabel('p, atma')
plt.title('Решение в размерных координатах')
plt.show()
```
Нарисуем распределение давления в пласте при запуске и остановке скважины.
Начнем с запуска скважины - нарисуем график изменения давления в пласте для разных моментов времени
```
r_arr = np.logspace(1, 3, 100)
t_arr = np.logspace(-1, 2, 10)
t_arr[0] = 0
t_prod = 100
tv, rv = np.meshgrid(td_from_t(t_arr),rd_from_r(r_arr))
pd_arr =pd_ei(tv, rd=rv)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize = [12,5])
fig.suptitle('Изменение давления в пласте при запуске скважины')
ax1.plot(r_arr, p_from_pd_atma(pd_arr))
ax1.set_label(t_arr)
ax1.set_xlabel('r, m')
ax1.set_ylabel('$p_{wf}, atma$')
ax2.plot(r_arr,p_from_pd_atma(pd_arr))
ax2.set_xscale('log')
ax2.set_xlabel('r, m')
ax2.set_ylabel('$p_{wf}, atma$')
plt.show()
```
Дальше нарисуем графики изменения давления в пласте для различных моментов времени после остановки скважины
```
pd_arr_bu =pd_ei(tv + td_from_t(t_prod), rd=rv) - pd_ei(tv, rd=rv)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize = [12,5])
fig.suptitle('Изменение давления в пласте при запуске скважины')
ax1.plot(r_arr, p_from_pd_atma(pd_arr_bu))
ax1.set_label(t_arr)
ax1.set_xlabel('r, m')
ax1.set_ylabel('$p_{wf}, atma$')
ax2.plot(r_arr,p_from_pd_atma(pd_arr_bu))
ax2.set_xscale('log')
ax2.set_xlabel('r, m')
ax2.set_ylabel('$p_{wf}, atma$')
plt.show()
```
Ну и нарисуем все вместе, чтобы посмотреть что получится
```
fig, (ax1, ax2) = plt.subplots(1, 2, figsize = [12,5])
fig.suptitle('Изменение давления в пласте при запуске скважины')
ax1.plot(r_arr,p_from_pd_atma(pd_arr))
ax1.plot(r_arr,p_from_pd_atma(pd_arr_bu))
ax1.set_label(t_arr)
ax1.set_xlabel('r, m')
ax1.set_ylabel('$p_{wf}, atma$')
ax2.plot(r_arr,p_from_pd_atma(pd_arr))
ax2.plot(r_arr,p_from_pd_atma(pd_arr_bu))
ax2.set_xscale('log')
ax2.set_xlabel('r, m')
ax2.set_ylabel('$p_{wf}, atma$')
plt.show()
```
# 14.2 Случай для произвольной истории дебитов (ступенчатое изменение дебита) <a class="anchor" id="14.2"></a>
```
# создадим историю изменения дебитов
t_history = np.array([ 0., 2., 24. ], dtype=np.float64)
q_history = np.array([10., 5., 0.], dtype=np.float64)
# массивы должны быть одной и той же длины
```
Для расчета изменения давления при переменном дебите введем произвольное референсное значение дебита q_{ref} (например первое не нулевое значение дебита при запуске скважины). Используем это значение для определения безразмерного давления.
$$ p_D = \frac{kh}{ 18.41 q_{ref} B \mu} \left( p_i - p \right) $$
и безразмерного дебита
$$q_D = \frac{q}{q_{ref}}$$
Тогда, используя принцип суперпозиции, можем выписать выражение для изменения давления на скважине и вокруг нее для произвольного момента времени
$$P_{mr.D}(t_D, r_D) = \sum_i \left[ q_{D(i)}-q_{D(i-1)} \right] \cdot p_D\left(t_D-t_{D(i)}, r_D\right)\cdot \mathcal{H}(t_D-t_{D(i)}) \tag{14.2} $$
где
* $i$ - индекс значения дебита в таблице изменения дебитов
* $q_{D(i)}$ - безразмерный дебит с номером $i$, который стартует в момент времени $t_i$. Для первого момента времени $i$ дебит следующий перед ним считается равным нулю
* $t_{D(i)}$ - безразмерный момент времени - включения дебита с номером $i$
* $t_{D}$ - безразмерный момент времени для которого проводится расчет
* $\mathcal{H}$ - ступенчатая [функция Хевисайда](https://ru.wikipedia.org/wiki/%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D0%A5%D0%B5%D0%B2%D0%B8%D1%81%D0%B0%D0%B9%D0%B4%D0%B0#:~:text=%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F%20%D0%A5%D0%B5%D0%B2%D0%B8%D1%81%D0%B0%D0%B9%D0%B4%D0%B0%20%D1%88%D0%B8%D1%80%D0%BE%D0%BA%D0%BE%20%D0%B8%D1%81%D0%BF%D0%BE%D0%BB%D1%8C%D0%B7%D1%83%D0%B5%D1%82%D1%81%D1%8F%20%D0%B2,%D0%B4%D0%BB%D1%8F%20%D0%B7%D0%B0%D0%BF%D0%B8%D1%81%D0%B8%20%D1%8D%D0%BC%D0%BF%D0%B8%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B9%20%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D0%B8%20%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F.)
* $p_D\left(t\right)$ - зависимость безразмерного давление от времени - решение задачи запуска скважины с постоянным единичным дебитом
* $P_{mr.D} $ - безразмерное давление $P_{mr.D}(t_D, r_D)$ учитывающее историю изменения дебитов скважины
```
def pd_superposition(td, td_hist, qd_hist):
"""
расчет безразмерного давления для последовательности безразмерных дебитов
td - время расчета после запуска, безразмерное
td_hist - массив времен изменения режимов работы скважин, безразмерное
qd_hist - массив дебитов установленных после изменения режима работы, безразмерное
"""
# принудительно добавим нули во входные массивы, чтобы учесть запуск скважины
qdh = np.hstack([0, qd_hist])
tdh = np.hstack([0, td_hist])
# построим дебиты виртуальных скважин - разности реальных дебитов при переключении
delta_qd = np.hstack([0, np.diff(qdh)])
# референсный безразмерный дебит это 1
# векторная магия - время может быть вектором и переключения дебитов тоже вектор
# надо организовать сумму по временам, каждая из котороых сумма по переключениям
# делаем при помощи расчета meshgrid и поиска накопленных сумм
qd_v, td_v =np.meshgrid(delta_qd, td)
# используем куммулятивную сумму numpy для того что суммировать результаты
dpd = np.cumsum(qd_v * pd_ei((td_v - tdh)) * np.heaviside((td_v - tdh), 1),1 )
# последний столбец - полная сумма, которая нужна в качестве результата
return dpd[:,-1]
def q_superposition(t, t_hist, q_hist):
"""
расчет давления для запуска и последующей остановки скважины
t_hr - время после запуска в часах
t_hist_hr - массив времен изменения режимов работы скважин
q_hist_sm3day - массив дебитов установленных после изменения режима работы
"""
def interpolate_constant(x, xp, yp):
indices = np.searchsorted(xp, x, side='right')
y = np.concatenate(([0], yp))
return y[indices]
q=[]
for ti in t:
q.append(interpolate_constant(ti, t_hist, q_hist))
return q
td_arr = np.linspace(1e-3, 9e4, 1000)
td_history = np.array([ 0., 2e4, 5e4 ], dtype=np.float64)
qd_history = np.array([10., 5., 0.], dtype=np.float64)
plt.rcParams["figure.figsize"] = (12,5)
fig, (ax1, ax2) = plt.subplots(2,1)
ax1.plot(td_arr, q_superposition(td_arr, td_history, qd_history))
ax2.plot(td_arr, pd_superposition(td_arr, td_history, qd_history), color='red')
ax2.set_xlabel('td')
ax1.set_ylabel('qd')
ax2.set_ylabel('pd')
plt.show()
def p_superposition_atma(t_hr, t_hist_hr, q_hist_sm3day):
"""
расчет давления для запуска и последующей остановки скважины
t_hr - время после запуска в часах
t_hist_hr - массив времен изменения режимов работы скважин
q_hist_sm3day - массив дебитов установленных после изменения режима работы
"""
q_ref=10.
return p_from_pd_atma(pd_superposition(td_from_t(t_hr),
td_from_t(t_hist_hr),
q_hist_sm3day / q_ref),
q_sm3day=q_ref)
t_arr = np.arange(1e-3, 50, 1e-2)
plt.rcParams["figure.figsize"] = (12,5)
fig, (ax1, ax2) = plt.subplots(2,1)
ax1.plot(t_arr, q_superposition(t_arr, t_history, q_history))
ax2.plot(t_arr, p_superposition_atma(t_arr, t_history, q_history), color='red')
ax2.set_xlabel('t, hr')
ax1.set_ylabel('q, m3/day')
ax2.set_ylabel('p, atma')
plt.show()
t_history = np.array([0, 2, 10, 24, 24.1,24.2,24.3,24.4,24.5 ])
q_history = np.array([10, 11, 12, 11, 10, 9, 8, 7, 6])
plt.rcParams["figure.figsize"] = (12,5)
fig, (ax1, ax2) = plt.subplots(2,1)
ax1.plot(t_arr, q_superposition(t_arr, t_history, q_history))
ax2.plot(t_arr, p_superposition_atma(t_arr, t_history, q_history), color='red')
ax2.set_xlabel('t, hr')
ax1.set_ylabel('q, m3/day')
ax2.set_ylabel('p, atma')
plt.show()
```
# 14.3 Случай для произвольной истории дебитов (линейное изменение дебита) <a class="anchor" id="14.3"></a>
Для линейно меняющегося дебита во времени (как и для любой другой зависимости) надо решение проинтегрировать по времени (надо бы подробнее расписать - сделать это позже, например как у Щелкачева в основах нестационарной фильтрации на стр 321).
Для линейной зависимости дебита от времени
$$Q_D = dQ_D \cdot t_D $$
можно получить выражение
$$p_D(r_D,t_D, dQ_D) =-\frac{dQ_D t_D }{2} \left[ \left( 1+ \frac{r_D^2}{4 t_D} \right) Ei \left(- \dfrac{r_D^2}{4t_D} \right) + e^{-\dfrac{r_D^2}{4t_D}} \right] \tag{14.3}$$
где $dQ_D$ - скорость изменения дебита.
Для таблично заданных дебитов и времен можно оценить
$$dQ_{D(i)} = \dfrac{Q_{D(i)}-Q_{D(i-1)}}{t_{D(i)} - t_{D(i-1)} } \tag{14.4}$$
Cравните формулу (14.3) с формулой (9.68) в книге Щелкачева "Основы неустановившейся фильтрации"
Тогда, используя принцип суперпозиции, можем выписать выражение для изменения давления на скважине и вокруг нее для произвольного момента времени
$$P_{mr.D}(t_D, r_D) = \sum_i p_D\left(t_D-t_{D(i)}, r_D, dQ_{D(i+1)} - dQ_{D(i)}\right)\cdot \mathcal{H}(t_D-t_{D(i)}) \tag{14.5} $$
где
* $i$ - индекс значения дебита в таблице изменения дебитов
* $dQ_{D(i)}$ - изменение безразмерного дебита относительно безразмерного времени (14.4)
* $t_{D(i)}$ - безразмерный момент времени - включения дебита с номером $i$
* $t_{D}$ - безразмерный момент времени для которого проводится расчет
* $\mathcal{H}$ - ступенчатая [функция Хевисайда](https://ru.wikipedia.org/wiki/%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D0%A5%D0%B5%D0%B2%D0%B8%D1%81%D0%B0%D0%B9%D0%B4%D0%B0#:~:text=%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F%20%D0%A5%D0%B5%D0%B2%D0%B8%D1%81%D0%B0%D0%B9%D0%B4%D0%B0%20%D1%88%D0%B8%D1%80%D0%BE%D0%BA%D0%BE%20%D0%B8%D1%81%D0%BF%D0%BE%D0%BB%D1%8C%D0%B7%D1%83%D0%B5%D1%82%D1%81%D1%8F%20%D0%B2,%D0%B4%D0%BB%D1%8F%20%D0%B7%D0%B0%D0%BF%D0%B8%D1%81%D0%B8%20%D1%8D%D0%BC%D0%BF%D0%B8%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B9%20%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D0%B8%20%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F.)
* $p_D\left(t\right)$ - зависимость безразмерного давление от времени - решение задачи запуска скважины с постоянным единичным дебитом
* $P_{mr.D} $ - безразмерное давление $P_{mr.D}(t_D, r_D)$ учитывающее историю изменения дебитов скважины
следует обратить внимание, при суперпозиции скорость изменения дебита вычисляется как $dQ_{D(i+1)} - dQ_{D(i)}$. при реализации расчета необходимо предусмотреть, чтобы для первого и последнего шага расчет прошел корректно. Для этого можно, например, добавить к массивам дебитов и времени дополнительный значения в начале и в конце массивов соответствующие постоянным значениям дебита.
Также надо учитывать, что в приведенном выражении массивы должны начинаться со значений $Q_D=0$
```
import sympy as sp
x = sp.symbols('x')
rd, td = sp.symbols('r_d t_d')
# запишем решение в символьном виде
e = sp.expint(1, rd **2 / 4 / td)
e
# проинтегрируем решение по времени
sp.integrate(e, td)
# Решение линейного стока уравнения фильтрации
def pd_lin_ei(td, rd=1, dqd_dtd=1):
"""
Решение линейного стока уравнения фильтрации
rd - безразмерное расстояние
td - безразмерное время
"""
# при расчете убедимся, что td=0 не повлияет на расчет,
# даже если td массив и нулевой только один элемент
td = np.array(td, dtype = float)
pd = (1 + rd**2/4/td) * (-expi(-rd**2 / 4 /td)) - np.exp(-rd**2 / 4 /td)
return dqd_dtd * td * pd / 2
def pd_superposition_lin(td, td_hist, qd_hist):
"""
расчет безразмерного давления для последовательности безразмерных дебитов
td - время расчета после запуска, безразмерное
td_hist - массив времен изменения режимов работы скважин, безразмерное
qd_hist - массив дебитов установленных после изменения режима работы, безразмерное
"""
# принудительно добавим нули во входные массивы, чтобы учесть запуск скважины
qdh = np.hstack([qd_hist])
tdh = np.hstack([td_hist])
# построим дебиты виртуальных скважин - разности реальных дебитов при переключении
delta_qd = np.hstack([np.diff(qdh),0])
delta_td = np.hstack([np.diff(tdh),1])
dq_dt = delta_qd / delta_td
dq_dt = np.diff(np.hstack([0, delta_qd / delta_td]))
# референсный безразмерный дебит это 1
# векторная магия - время может быть вектором и переключения дебитов тоже вектор
# надо организовать сумму по временам, каждая из котороых сумма по переключениям
# делаем при помощи расчета meshgrid и поиска накопленных сумм
qd_v, td_v =np.meshgrid(delta_qd, td)
dpd = np.cumsum(pd_lin_ei((td_v - tdh), dqd_dtd=dq_dt) * np.heaviside((td_v - tdh), 1),1 )
return dpd[:,-1]
def p_superposition_lin_atma(t_hr, t_hist_hr, q_hist_sm3day):
"""
расчет давления для запуска и последующей остановки скважины
t_hr - время после запуска в часах
t_hist_hr - массив времен изменения режимов работы скважин
q_hist_sm3day - массив дебитов установленных после изменения режима работы
"""
q_ref=10
return p_from_pd_atma(pd_superposition_lin(td_from_t(t_hr),
td_from_t(t_hist_hr),
q_hist_sm3day / q_ref),
q_sm3day=q_ref)
```
построим графики для безразмерных времен
```
td_arr = np.linspace(1e-3, 2000, 2000)
td_history = np.array([0., 1, 50, 100, 300, 500 ], dtype=np.float64)
qd_history = np.array([0., 3, 1.4, 1.0, 1.01, 1], dtype=np.float64)
plt.rcParams["figure.figsize"] = (12,8)
fig, (ax1, ax2) = plt.subplots(2,1)
ax1.plot(td_arr, q_superposition(td_arr, td_history, qd_history))
ax1.plot(td_arr, np.interp(td_arr, td_history, qd_history))
ax2.plot(td_arr, pd_superposition_lin(td_arr, td_history, qd_history), color='red')
ax2.plot(td_arr, pd_superposition(td_arr, td_history, qd_history), color='blue')
ax2.set_xlabel('td')
ax1.set_ylabel('qd')
ax2.set_ylabel('pd')
plt.show()
t_history = np.array([0, .02, 10, 24, 24.1,24.2,24.3,24.4,24.5 ])
q_history = np.array([0, 11, 12, 12, 10, 9, 8, 7, 6])
plt.rcParams["figure.figsize"] = (12,5)
fig, (ax1, ax2) = plt.subplots(2,1)
ax1.plot(t_arr, q_superposition(t_arr, t_history, q_history))
ax1.plot(t_arr, np.interp(t_arr, t_history, q_history))
ax2.plot(t_arr, p_superposition_atma(t_arr, t_history, q_history), color='red')
ax2.plot(t_arr, p_superposition_lin_atma(t_arr, t_history, q_history), color='green')
ax2.set_xlabel('t, hr')
ax1.set_ylabel('q, m3/day')
ax2.set_ylabel('p, atma')
plt.show()
t_history = np.array([0, .02, 10, 24, 24.1,24.2,24.3,24.4,24.5 ])
q_history = np.array([0, 11, 12, 12, 10, 9, 8, 7, 6])
plt.rcParams["figure.figsize"] = (12,5)
fig, (ax1, ax2) = plt.subplots(2,1)
ax1.plot(t_arr, q_superposition(t_arr, t_history, q_history))
ax1.plot(t_arr, np.interp(t_arr, t_history, q_history))
ax2.plot(t_arr, p_superposition_atma(t_arr, t_history, q_history), color='red')
ax2.plot(t_arr, p_superposition_lin_atma(t_arr, t_history, q_history), color='green')
ax2.set_xlabel('t, hr')
ax1.set_ylabel('q, m3/day')
ax2.set_ylabel('p, atma')
ax1.set_xlim([23.9,24.6])
ax2.set_xlim([23.9,24.6])
plt.show()
```
|
github_jupyter
|
# для того, чтобы скрипты гладко работали на https://colab.research.google.com/ пропишем
# установку библиотеки welltest
# библиотека welltest загружает определения функций для безразмерных переменных
# а также грузит anaflow которая обеспечивает работу с обратным преобразованием Лапласа
!pip install welltest
# импортируем библиотки, которые могут пригодиться для проведения расчетов
import numpy as np
import matplotlib.pyplot as plt
from anaflow import get_lap_inv
from scipy.special import kn, iv, expi
from welltest.functions import *
# Решение линейного стока уравнения фильтрации
def pd_ei(td, rd=1):
"""
Решение линейного стока уравнения фильтрации
rd - безразмерное расстояние
td - безразмерное время
"""
# при расчете убедимся, что td=0 не повлияет на расчет, даже если td массив и нулевой только один элемент
td = np.array(td, dtype = float)
return np.multiply(-0.5,
expi(np.divide(-rd**2 / 4 ,
td,
out=np.zeros_like(td), where=td!=0)),
out=np.zeros_like(td), where=td!=0)
x = np.arange(-2,2,0.01)
y = np.heaviside(x, 1)
plt.rcParams["figure.figsize"] = (8,3)
plt.plot(x,y)
plt.title('Функция Хевисайда $\mathcal{H}$ ')
plt.show()
def pd_build_up(td, td_p):
"""
расчет давления для запуска и последующей остановки скважины
td - время после запуска
td_p - время безразмерное - которое скважина работала до остановки
"""
# применение функции Хевисайда здесь делает расчет корректным
# для входных векторов td
return pd_ei(td) - np.heaviside(td-td_p,1) * pd_ei(td-td_p)
t_arr = np.logspace(-10, 2, 1000)
t_prod_hr = 24
k = 10 # проницаемость
q = 30 # дебит
# переведем размерный массив времени в безразмерные величины
td_arr = td_from_t(t_arr, k_mD=k)
td_prod = td_from_t(t_prod_hr, k_mD=k)
print('время работы скважины {:.2f} часа, что соответсвует безразмерному времени {:.2f}'.format(t_prod_hr, td_prod))
# для заданного массива безразмерных времен рассчитаем безразмерные давления
pd_arr = pd_build_up(td_arr, td_prod)
plt.rcParams["figure.figsize"] = (8,3)
plt.plot(td_arr, pd_arr)
plt.xlabel('td')
plt.ylabel('pd')
plt.title('Решение в безразмерных координатах')
plt.show()
# переведем безразмерные координаты в размерные
p_arr = p_from_pd_atma(pd_arr, k_mD=k, q_sm3day=q)
plt.rcParams["figure.figsize"] = (8,3)
plt.plot(t_arr, p_arr)
plt.xlabel('t, hr')
plt.ylabel('p, atma')
plt.title('Решение в размерных координатах')
plt.show()
r_arr = np.logspace(1, 3, 100)
t_arr = np.logspace(-1, 2, 10)
t_arr[0] = 0
t_prod = 100
tv, rv = np.meshgrid(td_from_t(t_arr),rd_from_r(r_arr))
pd_arr =pd_ei(tv, rd=rv)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize = [12,5])
fig.suptitle('Изменение давления в пласте при запуске скважины')
ax1.plot(r_arr, p_from_pd_atma(pd_arr))
ax1.set_label(t_arr)
ax1.set_xlabel('r, m')
ax1.set_ylabel('$p_{wf}, atma$')
ax2.plot(r_arr,p_from_pd_atma(pd_arr))
ax2.set_xscale('log')
ax2.set_xlabel('r, m')
ax2.set_ylabel('$p_{wf}, atma$')
plt.show()
pd_arr_bu =pd_ei(tv + td_from_t(t_prod), rd=rv) - pd_ei(tv, rd=rv)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize = [12,5])
fig.suptitle('Изменение давления в пласте при запуске скважины')
ax1.plot(r_arr, p_from_pd_atma(pd_arr_bu))
ax1.set_label(t_arr)
ax1.set_xlabel('r, m')
ax1.set_ylabel('$p_{wf}, atma$')
ax2.plot(r_arr,p_from_pd_atma(pd_arr_bu))
ax2.set_xscale('log')
ax2.set_xlabel('r, m')
ax2.set_ylabel('$p_{wf}, atma$')
plt.show()
fig, (ax1, ax2) = plt.subplots(1, 2, figsize = [12,5])
fig.suptitle('Изменение давления в пласте при запуске скважины')
ax1.plot(r_arr,p_from_pd_atma(pd_arr))
ax1.plot(r_arr,p_from_pd_atma(pd_arr_bu))
ax1.set_label(t_arr)
ax1.set_xlabel('r, m')
ax1.set_ylabel('$p_{wf}, atma$')
ax2.plot(r_arr,p_from_pd_atma(pd_arr))
ax2.plot(r_arr,p_from_pd_atma(pd_arr_bu))
ax2.set_xscale('log')
ax2.set_xlabel('r, m')
ax2.set_ylabel('$p_{wf}, atma$')
plt.show()
# создадим историю изменения дебитов
t_history = np.array([ 0., 2., 24. ], dtype=np.float64)
q_history = np.array([10., 5., 0.], dtype=np.float64)
# массивы должны быть одной и той же длины
def pd_superposition(td, td_hist, qd_hist):
"""
расчет безразмерного давления для последовательности безразмерных дебитов
td - время расчета после запуска, безразмерное
td_hist - массив времен изменения режимов работы скважин, безразмерное
qd_hist - массив дебитов установленных после изменения режима работы, безразмерное
"""
# принудительно добавим нули во входные массивы, чтобы учесть запуск скважины
qdh = np.hstack([0, qd_hist])
tdh = np.hstack([0, td_hist])
# построим дебиты виртуальных скважин - разности реальных дебитов при переключении
delta_qd = np.hstack([0, np.diff(qdh)])
# референсный безразмерный дебит это 1
# векторная магия - время может быть вектором и переключения дебитов тоже вектор
# надо организовать сумму по временам, каждая из котороых сумма по переключениям
# делаем при помощи расчета meshgrid и поиска накопленных сумм
qd_v, td_v =np.meshgrid(delta_qd, td)
# используем куммулятивную сумму numpy для того что суммировать результаты
dpd = np.cumsum(qd_v * pd_ei((td_v - tdh)) * np.heaviside((td_v - tdh), 1),1 )
# последний столбец - полная сумма, которая нужна в качестве результата
return dpd[:,-1]
def q_superposition(t, t_hist, q_hist):
"""
расчет давления для запуска и последующей остановки скважины
t_hr - время после запуска в часах
t_hist_hr - массив времен изменения режимов работы скважин
q_hist_sm3day - массив дебитов установленных после изменения режима работы
"""
def interpolate_constant(x, xp, yp):
indices = np.searchsorted(xp, x, side='right')
y = np.concatenate(([0], yp))
return y[indices]
q=[]
for ti in t:
q.append(interpolate_constant(ti, t_hist, q_hist))
return q
td_arr = np.linspace(1e-3, 9e4, 1000)
td_history = np.array([ 0., 2e4, 5e4 ], dtype=np.float64)
qd_history = np.array([10., 5., 0.], dtype=np.float64)
plt.rcParams["figure.figsize"] = (12,5)
fig, (ax1, ax2) = plt.subplots(2,1)
ax1.plot(td_arr, q_superposition(td_arr, td_history, qd_history))
ax2.plot(td_arr, pd_superposition(td_arr, td_history, qd_history), color='red')
ax2.set_xlabel('td')
ax1.set_ylabel('qd')
ax2.set_ylabel('pd')
plt.show()
def p_superposition_atma(t_hr, t_hist_hr, q_hist_sm3day):
"""
расчет давления для запуска и последующей остановки скважины
t_hr - время после запуска в часах
t_hist_hr - массив времен изменения режимов работы скважин
q_hist_sm3day - массив дебитов установленных после изменения режима работы
"""
q_ref=10.
return p_from_pd_atma(pd_superposition(td_from_t(t_hr),
td_from_t(t_hist_hr),
q_hist_sm3day / q_ref),
q_sm3day=q_ref)
t_arr = np.arange(1e-3, 50, 1e-2)
plt.rcParams["figure.figsize"] = (12,5)
fig, (ax1, ax2) = plt.subplots(2,1)
ax1.plot(t_arr, q_superposition(t_arr, t_history, q_history))
ax2.plot(t_arr, p_superposition_atma(t_arr, t_history, q_history), color='red')
ax2.set_xlabel('t, hr')
ax1.set_ylabel('q, m3/day')
ax2.set_ylabel('p, atma')
plt.show()
t_history = np.array([0, 2, 10, 24, 24.1,24.2,24.3,24.4,24.5 ])
q_history = np.array([10, 11, 12, 11, 10, 9, 8, 7, 6])
plt.rcParams["figure.figsize"] = (12,5)
fig, (ax1, ax2) = plt.subplots(2,1)
ax1.plot(t_arr, q_superposition(t_arr, t_history, q_history))
ax2.plot(t_arr, p_superposition_atma(t_arr, t_history, q_history), color='red')
ax2.set_xlabel('t, hr')
ax1.set_ylabel('q, m3/day')
ax2.set_ylabel('p, atma')
plt.show()
import sympy as sp
x = sp.symbols('x')
rd, td = sp.symbols('r_d t_d')
# запишем решение в символьном виде
e = sp.expint(1, rd **2 / 4 / td)
e
# проинтегрируем решение по времени
sp.integrate(e, td)
# Решение линейного стока уравнения фильтрации
def pd_lin_ei(td, rd=1, dqd_dtd=1):
"""
Решение линейного стока уравнения фильтрации
rd - безразмерное расстояние
td - безразмерное время
"""
# при расчете убедимся, что td=0 не повлияет на расчет,
# даже если td массив и нулевой только один элемент
td = np.array(td, dtype = float)
pd = (1 + rd**2/4/td) * (-expi(-rd**2 / 4 /td)) - np.exp(-rd**2 / 4 /td)
return dqd_dtd * td * pd / 2
def pd_superposition_lin(td, td_hist, qd_hist):
"""
расчет безразмерного давления для последовательности безразмерных дебитов
td - время расчета после запуска, безразмерное
td_hist - массив времен изменения режимов работы скважин, безразмерное
qd_hist - массив дебитов установленных после изменения режима работы, безразмерное
"""
# принудительно добавим нули во входные массивы, чтобы учесть запуск скважины
qdh = np.hstack([qd_hist])
tdh = np.hstack([td_hist])
# построим дебиты виртуальных скважин - разности реальных дебитов при переключении
delta_qd = np.hstack([np.diff(qdh),0])
delta_td = np.hstack([np.diff(tdh),1])
dq_dt = delta_qd / delta_td
dq_dt = np.diff(np.hstack([0, delta_qd / delta_td]))
# референсный безразмерный дебит это 1
# векторная магия - время может быть вектором и переключения дебитов тоже вектор
# надо организовать сумму по временам, каждая из котороых сумма по переключениям
# делаем при помощи расчета meshgrid и поиска накопленных сумм
qd_v, td_v =np.meshgrid(delta_qd, td)
dpd = np.cumsum(pd_lin_ei((td_v - tdh), dqd_dtd=dq_dt) * np.heaviside((td_v - tdh), 1),1 )
return dpd[:,-1]
def p_superposition_lin_atma(t_hr, t_hist_hr, q_hist_sm3day):
"""
расчет давления для запуска и последующей остановки скважины
t_hr - время после запуска в часах
t_hist_hr - массив времен изменения режимов работы скважин
q_hist_sm3day - массив дебитов установленных после изменения режима работы
"""
q_ref=10
return p_from_pd_atma(pd_superposition_lin(td_from_t(t_hr),
td_from_t(t_hist_hr),
q_hist_sm3day / q_ref),
q_sm3day=q_ref)
td_arr = np.linspace(1e-3, 2000, 2000)
td_history = np.array([0., 1, 50, 100, 300, 500 ], dtype=np.float64)
qd_history = np.array([0., 3, 1.4, 1.0, 1.01, 1], dtype=np.float64)
plt.rcParams["figure.figsize"] = (12,8)
fig, (ax1, ax2) = plt.subplots(2,1)
ax1.plot(td_arr, q_superposition(td_arr, td_history, qd_history))
ax1.plot(td_arr, np.interp(td_arr, td_history, qd_history))
ax2.plot(td_arr, pd_superposition_lin(td_arr, td_history, qd_history), color='red')
ax2.plot(td_arr, pd_superposition(td_arr, td_history, qd_history), color='blue')
ax2.set_xlabel('td')
ax1.set_ylabel('qd')
ax2.set_ylabel('pd')
plt.show()
t_history = np.array([0, .02, 10, 24, 24.1,24.2,24.3,24.4,24.5 ])
q_history = np.array([0, 11, 12, 12, 10, 9, 8, 7, 6])
plt.rcParams["figure.figsize"] = (12,5)
fig, (ax1, ax2) = plt.subplots(2,1)
ax1.plot(t_arr, q_superposition(t_arr, t_history, q_history))
ax1.plot(t_arr, np.interp(t_arr, t_history, q_history))
ax2.plot(t_arr, p_superposition_atma(t_arr, t_history, q_history), color='red')
ax2.plot(t_arr, p_superposition_lin_atma(t_arr, t_history, q_history), color='green')
ax2.set_xlabel('t, hr')
ax1.set_ylabel('q, m3/day')
ax2.set_ylabel('p, atma')
plt.show()
t_history = np.array([0, .02, 10, 24, 24.1,24.2,24.3,24.4,24.5 ])
q_history = np.array([0, 11, 12, 12, 10, 9, 8, 7, 6])
plt.rcParams["figure.figsize"] = (12,5)
fig, (ax1, ax2) = plt.subplots(2,1)
ax1.plot(t_arr, q_superposition(t_arr, t_history, q_history))
ax1.plot(t_arr, np.interp(t_arr, t_history, q_history))
ax2.plot(t_arr, p_superposition_atma(t_arr, t_history, q_history), color='red')
ax2.plot(t_arr, p_superposition_lin_atma(t_arr, t_history, q_history), color='green')
ax2.set_xlabel('t, hr')
ax1.set_ylabel('q, m3/day')
ax2.set_ylabel('p, atma')
ax1.set_xlim([23.9,24.6])
ax2.set_xlim([23.9,24.6])
plt.show()
| 0.226441 | 0.932207 |
```
%load_ext autoreload
%autoreload 2
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from pathlib import Path
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
from tqdm import tqdm_notebook
from fastai.conv_learner import ConvLearner
from fastai.dataset import ImageClassifierData, get_cv_idxs
from fastai.transforms import tfms_from_model
%matplotlib inline
```
# Lesson 4 - Adding Dropout to spreadsheet CNN
```
PATH = Path('./data/mnist')
PATH.mkdir(exist_ok=True)
```
## Dataset
```
!kaggle competitions download -c digit-recognizer --path={PATH}
df = pd.read_csv(PATH/'train.csv')
```
### Load a single image
```
img_pixels = df.loc[7, [c for c in df.columns if c.startswith('pixel')]]
img_arr = np.array([int(i) for i in img_pixels])
img_arr = img_arr.reshape((28, 28))
img_arr_float = img_arr / 255.
plt.imshow(img_arr_float, cmap='gray')
plt.show()
img_arr_float = img_arr_float.reshape(1, 28, 28)
img_tensor = torch.from_numpy(img_arr_float)
img_tensor = img_tensor.unsqueeze(0).cpu().float()
```
### Exploring new model
I'll start by improving the model by adding 2 things:
1. Much more output channels in CNN, from 2 to 32 in the first layer and 2 to 64 in the second layer.
2. An extra fully-connected layer on the end.
Let's make sure the outputs are as we expect:
```
conv1 = nn.Conv2d(in_channels=1, out_channels=32, kernel_size=3, padding=1)
conv2 = nn.Conv2d(in_channels=32, out_channels=64, kernel_size=3, padding=1)
output = conv1(Variable(img_tensor))
output.shape
```
Note how I've added 1 pixel of padding on both sides of the output.
This means that the conv will return the same size image output, which is slightly easier to deal with. We then know that the Maxpool will return the size by half:
```
output = F.max_pool2d(output, 2)
output.shape
```
We are also adding Dropout. Let's explore what Dropout with 100% probability will look like.
First, let's see the output image:
```
output[0]
```
Let's now create Dropout with 100% prob:
```
dropout = nn.Dropout(p=1)
dropout_output = dropout(output)
dropout_output[0]
```
Notice how all the activations are 0? What about 0.5?
```
dropout = nn.Dropout(p=0.5)
dropout_output = dropout(output)
dropout_output[0]
```
Now, 50% of the activations are dropped out.
```
class SimpleCNN(nn.Module):
def __init__(self, in_channels=1, p=0.5):
super(SimpleCNN, self).__init__()
self.conv1 = nn.Conv2d(
in_channels=in_channels, out_channels=32, kernel_size=3, padding=1)
self.conv2 = nn.Conv2d(
in_channels=32, out_channels=64, kernel_size=3, padding=1)
self.conv2_dropout = nn.Dropout(p=p)
self.fc1 = nn.Linear(in_features=64 * 7 * 7, out_features=1024)
self.fc1_dropout = nn.Dropout(p=p)
self.fc2 = nn.Linear(in_features=1024, out_features=10)
def forward(self, img_batch):
conv1_output = self.conv1(img_batch)
conv1_relu_output = F.relu(conv1_output)
maxpool1_output = F.max_pool2d(conv1_relu_output, kernel_size=2)
conv2_output = self.conv2(maxpool1_output)
relu2_output = F.relu(conv2_output)
maxpool2_output = F.max_pool2d(relu2_output, kernel_size=2)
dropout2_output = self.conv2_dropout(maxpool2_output)
flattened_output = dropout2_output.view(img_batch.size(0), -1)
fc1_output = self.fc1(flattened_output)
fc1_relu_output = F.relu(fc1_output)
fc1_dropout_output = self.fc1_dropout(fc1_relu_output)
fc2_output = self.fc2(fc1_dropout_output)
return F.log_softmax(fc2_output, dim=1)
```
## Train with Fast.ai ConvLearner (no dropout)
I can then create a ImageClassifierData object as usual, use the `from_model_data` constructor to create a `ConvLearner` from my custom model.
```
train_df = pd.read_csv(PATH/'train_prepared.csv')
val_idx = get_cv_idxs(len(train_df))
```
Let's start with a CNN that drops activations with a probability of 0% (ie no Dropout).
```
cnn = SimpleCNN(in_channels=3, p=0.)
cnn
data = ImageClassifierData.from_csv(
PATH, 'train', PATH/'train_prepared.csv', tfms=tfms_from_model(cnn, 28), val_idxs=val_idx, suffix='.jpg')
conv_learner = ConvLearner.from_model_data(cnn, data)
conv_learner.lr_find()
conv_learner.sched.plot()
conv_learner.fit(0.05, 10)
epoch_num = list(range(conv_learner.sched.epoch))
plt.plot(epoch_num, conv_learner.sched.val_losses, label='Validation loss')
plt.plot(
epoch_num,
[conv_learner.sched.losses[i-1] for i in conv_learner.sched.epochs],
label='Training loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend(loc='upper right')
plt.show()
```
### Train with Dropout
Let's add a bit of dropout. Set it initially to 0.4 and see if we can train a bit longer before we start to overfit.
```
cnn = SimpleCNN(in_channels=3, p=0.5)
cnn
conv_learner = ConvLearner.from_model_data(cnn, data)
conv_learner.lr_find()
conv_learner.sched.plot()
conv_learner.fit(0.01, 10)
epoch_num = list(range(conv_learner.sched.epoch))
plt.plot(epoch_num, conv_learner.sched.val_losses, label='Validation loss')
plt.plot(
epoch_num,
[conv_learner.sched.losses[i-1] for i in conv_learner.sched.epochs],
label='Training loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend(loc='upper right')
plt.show()
```
### Evalute on the test set
```
test_df = pd.read_csv(PATH/'test.csv')
img_1 = test_df.loc[6, [c for c in df.columns if c.startswith('pixel')]]
img_arr = np.array(img_1)
img_arr = img_arr.reshape((28, 28))
img_float = np.array(img_arr) * (1/255)
img_float = np.stack((img_float,) * 3, axis=-1)
img_float = img_float.transpose((2, 0, 1))
img_tensor = torch.from_numpy(img_float)
img_tensor = img_tensor.unsqueeze(0).cpu().float()
preds = torch.exp(conv_learner.model(Variable(img_tensor)))
plt.imshow(img_arr, cmap='gray')
preds
np.argmax(torch.exp(preds.data).numpy())
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from pathlib import Path
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
from tqdm import tqdm_notebook
from fastai.conv_learner import ConvLearner
from fastai.dataset import ImageClassifierData, get_cv_idxs
from fastai.transforms import tfms_from_model
%matplotlib inline
PATH = Path('./data/mnist')
PATH.mkdir(exist_ok=True)
!kaggle competitions download -c digit-recognizer --path={PATH}
df = pd.read_csv(PATH/'train.csv')
img_pixels = df.loc[7, [c for c in df.columns if c.startswith('pixel')]]
img_arr = np.array([int(i) for i in img_pixels])
img_arr = img_arr.reshape((28, 28))
img_arr_float = img_arr / 255.
plt.imshow(img_arr_float, cmap='gray')
plt.show()
img_arr_float = img_arr_float.reshape(1, 28, 28)
img_tensor = torch.from_numpy(img_arr_float)
img_tensor = img_tensor.unsqueeze(0).cpu().float()
conv1 = nn.Conv2d(in_channels=1, out_channels=32, kernel_size=3, padding=1)
conv2 = nn.Conv2d(in_channels=32, out_channels=64, kernel_size=3, padding=1)
output = conv1(Variable(img_tensor))
output.shape
output = F.max_pool2d(output, 2)
output.shape
output[0]
dropout = nn.Dropout(p=1)
dropout_output = dropout(output)
dropout_output[0]
dropout = nn.Dropout(p=0.5)
dropout_output = dropout(output)
dropout_output[0]
class SimpleCNN(nn.Module):
def __init__(self, in_channels=1, p=0.5):
super(SimpleCNN, self).__init__()
self.conv1 = nn.Conv2d(
in_channels=in_channels, out_channels=32, kernel_size=3, padding=1)
self.conv2 = nn.Conv2d(
in_channels=32, out_channels=64, kernel_size=3, padding=1)
self.conv2_dropout = nn.Dropout(p=p)
self.fc1 = nn.Linear(in_features=64 * 7 * 7, out_features=1024)
self.fc1_dropout = nn.Dropout(p=p)
self.fc2 = nn.Linear(in_features=1024, out_features=10)
def forward(self, img_batch):
conv1_output = self.conv1(img_batch)
conv1_relu_output = F.relu(conv1_output)
maxpool1_output = F.max_pool2d(conv1_relu_output, kernel_size=2)
conv2_output = self.conv2(maxpool1_output)
relu2_output = F.relu(conv2_output)
maxpool2_output = F.max_pool2d(relu2_output, kernel_size=2)
dropout2_output = self.conv2_dropout(maxpool2_output)
flattened_output = dropout2_output.view(img_batch.size(0), -1)
fc1_output = self.fc1(flattened_output)
fc1_relu_output = F.relu(fc1_output)
fc1_dropout_output = self.fc1_dropout(fc1_relu_output)
fc2_output = self.fc2(fc1_dropout_output)
return F.log_softmax(fc2_output, dim=1)
train_df = pd.read_csv(PATH/'train_prepared.csv')
val_idx = get_cv_idxs(len(train_df))
cnn = SimpleCNN(in_channels=3, p=0.)
cnn
data = ImageClassifierData.from_csv(
PATH, 'train', PATH/'train_prepared.csv', tfms=tfms_from_model(cnn, 28), val_idxs=val_idx, suffix='.jpg')
conv_learner = ConvLearner.from_model_data(cnn, data)
conv_learner.lr_find()
conv_learner.sched.plot()
conv_learner.fit(0.05, 10)
epoch_num = list(range(conv_learner.sched.epoch))
plt.plot(epoch_num, conv_learner.sched.val_losses, label='Validation loss')
plt.plot(
epoch_num,
[conv_learner.sched.losses[i-1] for i in conv_learner.sched.epochs],
label='Training loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend(loc='upper right')
plt.show()
cnn = SimpleCNN(in_channels=3, p=0.5)
cnn
conv_learner = ConvLearner.from_model_data(cnn, data)
conv_learner.lr_find()
conv_learner.sched.plot()
conv_learner.fit(0.01, 10)
epoch_num = list(range(conv_learner.sched.epoch))
plt.plot(epoch_num, conv_learner.sched.val_losses, label='Validation loss')
plt.plot(
epoch_num,
[conv_learner.sched.losses[i-1] for i in conv_learner.sched.epochs],
label='Training loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend(loc='upper right')
plt.show()
test_df = pd.read_csv(PATH/'test.csv')
img_1 = test_df.loc[6, [c for c in df.columns if c.startswith('pixel')]]
img_arr = np.array(img_1)
img_arr = img_arr.reshape((28, 28))
img_float = np.array(img_arr) * (1/255)
img_float = np.stack((img_float,) * 3, axis=-1)
img_float = img_float.transpose((2, 0, 1))
img_tensor = torch.from_numpy(img_float)
img_tensor = img_tensor.unsqueeze(0).cpu().float()
preds = torch.exp(conv_learner.model(Variable(img_tensor)))
plt.imshow(img_arr, cmap='gray')
preds
np.argmax(torch.exp(preds.data).numpy())
| 0.840488 | 0.833866 |
```
import numpy as np
import matplotlib.pyplot as plt
from tqdm.notebook import tqdm, trange
import seaborn as sns
import random
class CFG:
height = 6
width = 9
start = [2, 0]
goal = [0, 8]
action_Up = [-1, 0]
action_Down = [1, 0]
action_Left = [0, -1]
action_Right = [0, 1]
actions = [action_Up, action_Down, action_Left, action_Right]
alpha = 0.1
epsilon = 0.1
episode = 50
n_run = 50
n_plans = [0, 5, 10, 15, 25, 35, 50]
garma = 0.95
otc = [(1, 2), (2, 2), (3, 2), (4, 5), (0, 7), (1, 7), (2, 7)]
def go(curX, curY, action):
[tmpX, tmpY] = CFG.actions[action]
nextX = max(0, min(curX + tmpX, CFG.height - 1))
nextY = max(0, min(curY + tmpY, CFG.width - 1))
if ((nextX, nextY) in otc):
(nextX, nextY) = (curX, curY)
return (nextX, nextY)
def step(curX, curY, action):
(nextX, nextY) = go(curX, curY, action)
if ([nextX, nextY] == CFG.goal):
return ([nextX, nextY], 1, True)
# if ([nextX, nextY] == [curX, curY]):
# return([nextX, nextY], -1, False)
return ([nextX, nextY], 0, False)
def dyna_Q(n_plan, n_run = CFG.n_run, episode = CFG.episode):
res = np.zeros((episode))
for r in trange(n_run, desc = f'n = {n_plan}'):
# Q = np.random.random((CFG.height, CFG.width, 4))
Q = np.zeros(((CFG.height, CFG.width, 4)))
model = {}
tmp = []
for ep in range(episode):
time = 0
[curX, curY] = CFG.start
while(True):
if (np.random.random()<CFG.epsilon):
action = np.random.choice(np.arange(4))
else:
set_actions = Q[curX, curY,:] == np.max(Q[curX, curY, :])
actions = []
for i in range(4):
if (set_actions[i] == 1):
actions.append(i)
action = np.random.choice(actions)
(Nstate, reward, done) = step(curX, curY, action)
[nextX, nextY] = Nstate
# print(ep, (curX, curY), action, (nextX, nextY))
Q[curX, curY, action] += CFG.alpha * (reward + CFG.garma * np.max(Q[nextX, nextY, :]) - Q[curX, curY, action])
model[((curX, curY), action)] = ((nextX, nextY), reward)
for _ in range(n_plan):
idx = np.random.choice(range(len(model.keys())))
((tmpX, tmpY), tmp_action) = list(model.keys())[idx]
((tmp_NX, tmp_NY), tmp_reward) = model[((tmpX, tmpY), tmp_action)]
Q[tmpX, tmpY, tmp_action] += CFG.alpha * (tmp_reward + CFG.garma * np.max(Q[tmp_NX, tmp_NY, :]) - Q[tmpX, tmpY, tmp_action])
time += 1
if (done):
tmp.append(time)
break
(curX, curY) = (nextX, nextY)
# print(Q)
res += tmp
return res/n_run
for n_plan in CFG.n_plans:
plt.plot(dyna_Q(n_plan), label = f'n = {n_plan}')
plt.legend()
plt.ylim([0, 50])
plt.savefig('figure_8_5.png')
plt.show()
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
from tqdm.notebook import tqdm, trange
import seaborn as sns
import random
class CFG:
height = 6
width = 9
start = [2, 0]
goal = [0, 8]
action_Up = [-1, 0]
action_Down = [1, 0]
action_Left = [0, -1]
action_Right = [0, 1]
actions = [action_Up, action_Down, action_Left, action_Right]
alpha = 0.1
epsilon = 0.1
episode = 50
n_run = 50
n_plans = [0, 5, 10, 15, 25, 35, 50]
garma = 0.95
otc = [(1, 2), (2, 2), (3, 2), (4, 5), (0, 7), (1, 7), (2, 7)]
def go(curX, curY, action):
[tmpX, tmpY] = CFG.actions[action]
nextX = max(0, min(curX + tmpX, CFG.height - 1))
nextY = max(0, min(curY + tmpY, CFG.width - 1))
if ((nextX, nextY) in otc):
(nextX, nextY) = (curX, curY)
return (nextX, nextY)
def step(curX, curY, action):
(nextX, nextY) = go(curX, curY, action)
if ([nextX, nextY] == CFG.goal):
return ([nextX, nextY], 1, True)
# if ([nextX, nextY] == [curX, curY]):
# return([nextX, nextY], -1, False)
return ([nextX, nextY], 0, False)
def dyna_Q(n_plan, n_run = CFG.n_run, episode = CFG.episode):
res = np.zeros((episode))
for r in trange(n_run, desc = f'n = {n_plan}'):
# Q = np.random.random((CFG.height, CFG.width, 4))
Q = np.zeros(((CFG.height, CFG.width, 4)))
model = {}
tmp = []
for ep in range(episode):
time = 0
[curX, curY] = CFG.start
while(True):
if (np.random.random()<CFG.epsilon):
action = np.random.choice(np.arange(4))
else:
set_actions = Q[curX, curY,:] == np.max(Q[curX, curY, :])
actions = []
for i in range(4):
if (set_actions[i] == 1):
actions.append(i)
action = np.random.choice(actions)
(Nstate, reward, done) = step(curX, curY, action)
[nextX, nextY] = Nstate
# print(ep, (curX, curY), action, (nextX, nextY))
Q[curX, curY, action] += CFG.alpha * (reward + CFG.garma * np.max(Q[nextX, nextY, :]) - Q[curX, curY, action])
model[((curX, curY), action)] = ((nextX, nextY), reward)
for _ in range(n_plan):
idx = np.random.choice(range(len(model.keys())))
((tmpX, tmpY), tmp_action) = list(model.keys())[idx]
((tmp_NX, tmp_NY), tmp_reward) = model[((tmpX, tmpY), tmp_action)]
Q[tmpX, tmpY, tmp_action] += CFG.alpha * (tmp_reward + CFG.garma * np.max(Q[tmp_NX, tmp_NY, :]) - Q[tmpX, tmpY, tmp_action])
time += 1
if (done):
tmp.append(time)
break
(curX, curY) = (nextX, nextY)
# print(Q)
res += tmp
return res/n_run
for n_plan in CFG.n_plans:
plt.plot(dyna_Q(n_plan), label = f'n = {n_plan}')
plt.legend()
plt.ylim([0, 50])
plt.savefig('figure_8_5.png')
plt.show()
| 0.134066 | 0.461623 |
# **LINKED LIST**
A linked list is a linear collection of nodes, where each node contains a data value and a reference to the next node in the list.

**Advantages over arrays**
1) Dynamic size
2) Ease of insertion/deletion
**Drawbacks:**
1) Random access is not allowed. We have to access elements sequentially starting from the first node. So we cannot do binary search with linked lists efficiently with its default implementation.
2) Extra memory space for a pointer is required with each element of the list.
3) Not cache friendly. Since array elements are contiguous locations, there is locality of reference which is not there in case of linked lists.
```
#we will discuss how to implement linked lists in python.
#let's get started !!
# let's create Node class:
class Node:
def __init__(self, data=None,next=None):
self.data = data
self.next = next
# let's create Linked list
class LinkedList:
#Function to initialize head
def __init__(self):
self.head = None
def printll(self):
itr =self.head
liststr =" "
while (itr):
liststr += str(itr.data)+' --> ' if itr.next else str(itr.data)
itr = itr.next
print(liststr)
def insertion_at_beginning(self,newdata):
newnode=Node(newdata)
newnode.next=self.head
self.head=newnode
def insertion_at_end(self,newdata):
if self.head is None:
self.head =Node(newdata,None)
return
else:
itr = self.head
while itr.next:
itr =itr.next
itr.next = Node(newdata,None)
def insertion_at(self,index,newdata):
if self.head is None:
self.head =Node(newdata,None)
return
else:
count=0
itr = self.head
while itr:
if count == index-1:
temp = Node(newdata,itr.next)
itr.next=temp
break
itr=itr.next
count=count+1
def insertion_after(self,key,newdata):
if self.head is None:
self.head =Node(newdata,None)
return
else:
count=0
itr = self.head
while itr:
if itr.data == key:
temp=Node(newdata,itr.next)
itr.next =temp
break
itr=itr.next
count=count+1
def remove_beginning(self):
self.head = self.head.next
return
def remove_at(self,index):
if index == 0:
self.remove_beginning()
else:
itr = self.head
count =0
while itr:
if count == index-1:
itr.next = itr.next.next
break
itr = itr.next
count += 1
def length(self):
itr =self.head
count=0
while (itr):
count += 1
itr = itr.next
return count
def remove_end(self):
if self.head is None:
print("EMPTY LINKED LIST")
else:
itr= self.head
count=0
while itr:
if count == (self.length()-2):
itr.next=itr.next.next
count+=1
itr=itr.next
def insert_list(self,list2):
for L in list2:
self.insertion_at_end(L)
if __name__ == '__main__':
list1 = LinkedList()
list1.head = Node("MON")
e2 = Node("TUE")
e3 = Node("WED")
list1.head.next=e2
e2.next=e3
list1.insertion_at_beginning(5)
list1.insertion_at_end(78)
list1.insertion_at(2,788)
list1.insertion_after('MON',14)
list1.remove_beginning()
list1.remove_at(2)
l=list1.length()
print(l)
list1.remove_end()
list1.insert_list([10,20,30,40,50])
list1.printll()
```
|
github_jupyter
|
#we will discuss how to implement linked lists in python.
#let's get started !!
# let's create Node class:
class Node:
def __init__(self, data=None,next=None):
self.data = data
self.next = next
# let's create Linked list
class LinkedList:
#Function to initialize head
def __init__(self):
self.head = None
def printll(self):
itr =self.head
liststr =" "
while (itr):
liststr += str(itr.data)+' --> ' if itr.next else str(itr.data)
itr = itr.next
print(liststr)
def insertion_at_beginning(self,newdata):
newnode=Node(newdata)
newnode.next=self.head
self.head=newnode
def insertion_at_end(self,newdata):
if self.head is None:
self.head =Node(newdata,None)
return
else:
itr = self.head
while itr.next:
itr =itr.next
itr.next = Node(newdata,None)
def insertion_at(self,index,newdata):
if self.head is None:
self.head =Node(newdata,None)
return
else:
count=0
itr = self.head
while itr:
if count == index-1:
temp = Node(newdata,itr.next)
itr.next=temp
break
itr=itr.next
count=count+1
def insertion_after(self,key,newdata):
if self.head is None:
self.head =Node(newdata,None)
return
else:
count=0
itr = self.head
while itr:
if itr.data == key:
temp=Node(newdata,itr.next)
itr.next =temp
break
itr=itr.next
count=count+1
def remove_beginning(self):
self.head = self.head.next
return
def remove_at(self,index):
if index == 0:
self.remove_beginning()
else:
itr = self.head
count =0
while itr:
if count == index-1:
itr.next = itr.next.next
break
itr = itr.next
count += 1
def length(self):
itr =self.head
count=0
while (itr):
count += 1
itr = itr.next
return count
def remove_end(self):
if self.head is None:
print("EMPTY LINKED LIST")
else:
itr= self.head
count=0
while itr:
if count == (self.length()-2):
itr.next=itr.next.next
count+=1
itr=itr.next
def insert_list(self,list2):
for L in list2:
self.insertion_at_end(L)
if __name__ == '__main__':
list1 = LinkedList()
list1.head = Node("MON")
e2 = Node("TUE")
e3 = Node("WED")
list1.head.next=e2
e2.next=e3
list1.insertion_at_beginning(5)
list1.insertion_at_end(78)
list1.insertion_at(2,788)
list1.insertion_after('MON',14)
list1.remove_beginning()
list1.remove_at(2)
l=list1.length()
print(l)
list1.remove_end()
list1.insert_list([10,20,30,40,50])
list1.printll()
| 0.222785 | 0.234253 |
```
# Neural Bayes-MIM
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import torchvision.datasets as datasets
import torch.utils.data as utils
from torch.nn import Parameter
import torch.autograd as autograd
from torch.autograd import Variable
import math
import os
import torch.utils.data as data
import torch.nn as nn
import torch.nn.init as init
import torchvision.transforms as transforms
import torchvision
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['grid.color'] = 'k'
matplotlib.rcParams['grid.linestyle'] = ':'
matplotlib.rcParams['grid.linewidth'] = 0.5
from matplotlib import pyplot
from argparse import Namespace
import pickle as pkl
import tqdm
from tqdm import tnrange, tqdm_notebook
torch.manual_seed(0)
NUM_WORKERS = 0
use_cuda=False
os.environ['CUDA_VISIBLE_DEVICES'] = '0'
class MLPNet(nn.Module):
def __init__(self, dim_inp=None, dim_out=None, bn=True):
super(MLPNet, self).__init__()
self.dim_inp = dim_inp
relu = nn.ReLU()
self.fc1 = nn.Linear(dim_inp, 500)
self.bn1=nn.BatchNorm1d(500) if bn else nn.Sequential()
self.fc2 = nn.Linear(500, 500)
self.bn2=nn.BatchNorm1d(500) if bn else nn.Sequential()
self.fc3 = nn.Linear(500, dim_out)
self.bn3= nn.BatchNorm1d(dim_out) if bn else nn.Sequential() #
def forward(self, x, all=False):
hid={}
x = x.view(-1, self.dim_inp)
x = self.fc1(x)
hid['0'] = x
x = F.relu(self.bn1(x))
x=self.fc2(x)
hid['1'] = x
x = F.relu(self.bn2(x))
x=self.fc3(x)
hid['2'] = x
x = F.relu(self.bn3(x))
if all:
return hid
return x
def get_noise(x):
sz = x.size()
x = x.view(x.size(0), -1)
mn = x.mean(dim=0, keepdim=True)
x = x-mn
eps = torch.randint(0,2, (x.size(0), x.size(0))).cuda(). type('torch.cuda.FloatTensor')
noise = torch.mm(x.t(), eps).t()
norm = torch.norm(noise, dim=1, keepdim=True)
assert not np.any(norm.detach().cpu().numpy()==0), '0 norm {}'.format(torch.min(norm))
noise = noise/norm
return noise.view(sz)
def plot_w(w, n1 = 10,n2=10, save=False):
fig, axes = plt.subplots(n1,n2)
# use global min / max to ensure all weights are shown on the same scale
vmin, vmax = w.min(), w.max()
for coef, ax in zip(w, axes.ravel()):
ax.matshow(coef.reshape(28, 28), cmap=plt.cm.gray, vmin=.5 * vmin,
vmax=.5 * vmax)
ax.set_xticks(())
ax.set_yticks(())
if save:
plt.savefig('plots/mnist_filters.jpg')
else:
plt.show()
# get dataset
def get_dataset(BS):
trans = ([ transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
trans = transforms.Compose(trans)
train_set = torchvision.datasets.MNIST(root='datasets/', train=True, transform=trans, download=True)
trainloader = torch.utils.data.DataLoader(train_set, batch_size=BS, shuffle=True,
num_workers=NUM_WORKERS, pin_memory=True)
test_set = torchvision.datasets.MNIST(root='datasets/', train=False, transform=trans)
testloader = torch.utils.data.DataLoader(test_set, batch_size=BS, shuffle=False, num_workers=NUM_WORKERS)
nb_classes = 10
dim_inp=28*28
return trainloader, testloader, nb_classes, dim_inp
def get_loss(Lx,config=None):
EPSILON=1e-7
CE, gp=0,0
assert isinstance(Lx, dict)
loss = 0
N=0
for key in Lx.keys():
N+=1
Lx_ = Lx[key]
Lx_ = nn.Softmax(dim=1)(Lx_)
ELx = torch.mean(Lx_, dim=0,keepdim=True)#
# CE_ = (ELx* torch.log(ELx.detach()) ).sum(dim=1).mean() # Neural Bayes-MIM-v1
CE_ = - ( ((1./ELx.size(1))*torch.log(ELx) + (1.-1./ELx.size(1))*torch.log(1.-ELx))).sum(1).mean() # v2
CE += CE_
loss += -(Lx_* torch.log(Lx_.detach()+EPSILON) ).sum(dim=1).mean() + (1.+ config.alpha)* CE_
return loss/N, CE/N
def train(config):
flag=0
global trainloader, optimizer, model
model.train()
total_loss, total_grad_pen = 0, 0
loss2=0
tot_iters = len(trainloader)
for batch_idx in (range(tot_iters)):
optimizer.zero_grad()
inputs, targets = next(iter(trainloader))
inputs, targets = inputs.cuda(), targets.cuda()
inputs = inputs.view(inputs.size(0), -1)
b_x0 = Variable(inputs)
noise = np.random.randn()* get_noise(b_x0)
b_x = b_x0 + 0.1*noise
Lx0 = (model(b_x0, config.all))
Lx = (model(b_x, config.all))
loss, _=get_loss(Lx0, config)
L = loss
if math.isnan(L.item()):
flag=1
print('NaN encountered, exiting training.')
break
exit()
hbj
L.backward()
total_loss += loss.item()
beta = config.beta
grad_penalty=0
if config.beta>0:
Lx0 = (model(b_x0))
Lx = (model(b_x))
grad_penalty = ( ((Lx-Lx0)**2).sum(dim=1)/((b_x-b_x0)**2).sum(dim=1) ).mean()
(config.beta* grad_penalty).backward()
total_grad_pen += grad_penalty.item()
optimizer.step()
optimizer.zero_grad()
return total_loss/(batch_idx+1), total_grad_pen/(batch_idx+1),flag
config=Namespace()
config.epsilon=1e-7
config.LEARNING_RATE = 0.001
config.WD = 0.0000
config.EPOCHS = 50
config.dim_inp, config.dim_out = 784, 100
config.beta = 4
config.alpha =4
config.all=True
config.bn=True
trainloader, testloader, nb_classes, dim_inp = get_dataset(BS=500)
model = MLPNet(dim_inp = config.dim_inp, dim_out=config.dim_out, bn=config.bn).cuda()
params = list(model.parameters())
optimizer = torch.optim.Adam(params, lr=config.LEARNING_RATE, weight_decay=config.WD)
loss_list, grad_loss_list = [], []
epoch=0
while epoch<config.EPOCHS:
epoch+=1
loss, grad_loss,flag = train(config)
loss_list.append(loss)
grad_loss_list.append(grad_loss)
print('Epoch {}/{} | loss {:.3f} | grad_loss {:.3f}'.format(epoch, config.EPOCHS, loss, grad_loss))
if flag==1:
break
model_=model
for m in model_.modules():
if isinstance(m, nn.Linear):
w = m.weight
break
w = w.data.cpu().numpy()
print(w.shape)
plot_w(w, n1 = 10,n2=10, save=False)
```
|
github_jupyter
|
# Neural Bayes-MIM
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import torchvision.datasets as datasets
import torch.utils.data as utils
from torch.nn import Parameter
import torch.autograd as autograd
from torch.autograd import Variable
import math
import os
import torch.utils.data as data
import torch.nn as nn
import torch.nn.init as init
import torchvision.transforms as transforms
import torchvision
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['grid.color'] = 'k'
matplotlib.rcParams['grid.linestyle'] = ':'
matplotlib.rcParams['grid.linewidth'] = 0.5
from matplotlib import pyplot
from argparse import Namespace
import pickle as pkl
import tqdm
from tqdm import tnrange, tqdm_notebook
torch.manual_seed(0)
NUM_WORKERS = 0
use_cuda=False
os.environ['CUDA_VISIBLE_DEVICES'] = '0'
class MLPNet(nn.Module):
def __init__(self, dim_inp=None, dim_out=None, bn=True):
super(MLPNet, self).__init__()
self.dim_inp = dim_inp
relu = nn.ReLU()
self.fc1 = nn.Linear(dim_inp, 500)
self.bn1=nn.BatchNorm1d(500) if bn else nn.Sequential()
self.fc2 = nn.Linear(500, 500)
self.bn2=nn.BatchNorm1d(500) if bn else nn.Sequential()
self.fc3 = nn.Linear(500, dim_out)
self.bn3= nn.BatchNorm1d(dim_out) if bn else nn.Sequential() #
def forward(self, x, all=False):
hid={}
x = x.view(-1, self.dim_inp)
x = self.fc1(x)
hid['0'] = x
x = F.relu(self.bn1(x))
x=self.fc2(x)
hid['1'] = x
x = F.relu(self.bn2(x))
x=self.fc3(x)
hid['2'] = x
x = F.relu(self.bn3(x))
if all:
return hid
return x
def get_noise(x):
sz = x.size()
x = x.view(x.size(0), -1)
mn = x.mean(dim=0, keepdim=True)
x = x-mn
eps = torch.randint(0,2, (x.size(0), x.size(0))).cuda(). type('torch.cuda.FloatTensor')
noise = torch.mm(x.t(), eps).t()
norm = torch.norm(noise, dim=1, keepdim=True)
assert not np.any(norm.detach().cpu().numpy()==0), '0 norm {}'.format(torch.min(norm))
noise = noise/norm
return noise.view(sz)
def plot_w(w, n1 = 10,n2=10, save=False):
fig, axes = plt.subplots(n1,n2)
# use global min / max to ensure all weights are shown on the same scale
vmin, vmax = w.min(), w.max()
for coef, ax in zip(w, axes.ravel()):
ax.matshow(coef.reshape(28, 28), cmap=plt.cm.gray, vmin=.5 * vmin,
vmax=.5 * vmax)
ax.set_xticks(())
ax.set_yticks(())
if save:
plt.savefig('plots/mnist_filters.jpg')
else:
plt.show()
# get dataset
def get_dataset(BS):
trans = ([ transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
trans = transforms.Compose(trans)
train_set = torchvision.datasets.MNIST(root='datasets/', train=True, transform=trans, download=True)
trainloader = torch.utils.data.DataLoader(train_set, batch_size=BS, shuffle=True,
num_workers=NUM_WORKERS, pin_memory=True)
test_set = torchvision.datasets.MNIST(root='datasets/', train=False, transform=trans)
testloader = torch.utils.data.DataLoader(test_set, batch_size=BS, shuffle=False, num_workers=NUM_WORKERS)
nb_classes = 10
dim_inp=28*28
return trainloader, testloader, nb_classes, dim_inp
def get_loss(Lx,config=None):
EPSILON=1e-7
CE, gp=0,0
assert isinstance(Lx, dict)
loss = 0
N=0
for key in Lx.keys():
N+=1
Lx_ = Lx[key]
Lx_ = nn.Softmax(dim=1)(Lx_)
ELx = torch.mean(Lx_, dim=0,keepdim=True)#
# CE_ = (ELx* torch.log(ELx.detach()) ).sum(dim=1).mean() # Neural Bayes-MIM-v1
CE_ = - ( ((1./ELx.size(1))*torch.log(ELx) + (1.-1./ELx.size(1))*torch.log(1.-ELx))).sum(1).mean() # v2
CE += CE_
loss += -(Lx_* torch.log(Lx_.detach()+EPSILON) ).sum(dim=1).mean() + (1.+ config.alpha)* CE_
return loss/N, CE/N
def train(config):
flag=0
global trainloader, optimizer, model
model.train()
total_loss, total_grad_pen = 0, 0
loss2=0
tot_iters = len(trainloader)
for batch_idx in (range(tot_iters)):
optimizer.zero_grad()
inputs, targets = next(iter(trainloader))
inputs, targets = inputs.cuda(), targets.cuda()
inputs = inputs.view(inputs.size(0), -1)
b_x0 = Variable(inputs)
noise = np.random.randn()* get_noise(b_x0)
b_x = b_x0 + 0.1*noise
Lx0 = (model(b_x0, config.all))
Lx = (model(b_x, config.all))
loss, _=get_loss(Lx0, config)
L = loss
if math.isnan(L.item()):
flag=1
print('NaN encountered, exiting training.')
break
exit()
hbj
L.backward()
total_loss += loss.item()
beta = config.beta
grad_penalty=0
if config.beta>0:
Lx0 = (model(b_x0))
Lx = (model(b_x))
grad_penalty = ( ((Lx-Lx0)**2).sum(dim=1)/((b_x-b_x0)**2).sum(dim=1) ).mean()
(config.beta* grad_penalty).backward()
total_grad_pen += grad_penalty.item()
optimizer.step()
optimizer.zero_grad()
return total_loss/(batch_idx+1), total_grad_pen/(batch_idx+1),flag
config=Namespace()
config.epsilon=1e-7
config.LEARNING_RATE = 0.001
config.WD = 0.0000
config.EPOCHS = 50
config.dim_inp, config.dim_out = 784, 100
config.beta = 4
config.alpha =4
config.all=True
config.bn=True
trainloader, testloader, nb_classes, dim_inp = get_dataset(BS=500)
model = MLPNet(dim_inp = config.dim_inp, dim_out=config.dim_out, bn=config.bn).cuda()
params = list(model.parameters())
optimizer = torch.optim.Adam(params, lr=config.LEARNING_RATE, weight_decay=config.WD)
loss_list, grad_loss_list = [], []
epoch=0
while epoch<config.EPOCHS:
epoch+=1
loss, grad_loss,flag = train(config)
loss_list.append(loss)
grad_loss_list.append(grad_loss)
print('Epoch {}/{} | loss {:.3f} | grad_loss {:.3f}'.format(epoch, config.EPOCHS, loss, grad_loss))
if flag==1:
break
model_=model
for m in model_.modules():
if isinstance(m, nn.Linear):
w = m.weight
break
w = w.data.cpu().numpy()
print(w.shape)
plot_w(w, n1 = 10,n2=10, save=False)
| 0.813572 | 0.586345 |
# Data and Setup
For this project, our primary dataset will be a dataframe that contains **19095 cities** in the U.S. with a list of variables that characterize certain features for each city. These variables/features include:
* City's Name
* City's State
* City's County
* Latitude Coordinate
* Longitude Coordinate
* Population
* Density
* If Incorporated (if a city is a legitimate city or township)
* If Military (if a town is technically a fort or military base)
* If Capital of State or Nation
* Timezone
* Ranking (1-3, descending in importance with unknown/unstated criteria; more on this later)
* Number of Zip Codes in City
Outside of this dataset, we collected satellite images of each U.S. capital from NASA's Earth API to observe changes over time. NASA pre-processes these images so effects like the time of day are minimized. The API is tricky to work with however, since it provides only so many images throughout a year, and only so many of those images contain traces of land, given that clouds tend to fill most of them.
# Objectives
Now that we have our dataset, we would like to ask the following questions about it:
* Are there meaningful correlations between variables in the *us_cities* dataset?
* Why or why not?
* How do these correlations change when looking at subsets of *us_cities*, such as *capitals*?
* What could be the metric for the *ranking* variable?
* Through satellite image analysis, are there any meaningful correlations with the *capitals* subset?
* Could someone implement a very basic model in this manner and yield accurate predictions for population or density?
* If not, what could be some causes? If so, could this method be broadened to non-capital cities?
```
import os, cv2, requests, base64, imageio
from PIL import Image
from io import BytesIO
from IPython.display import display
from sklearn import tree, linear_model, metrics # linear_model.LinearRegression() for OLS
from sklearn.metrics import homogeneity_score, v_measure_score
from sklearn.preprocessing import scale
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
import statsmodels.formula.api as sm # used statsmodels.formula.api.ols() for OLS
import seaborn as sn
import pandas as pd
import scipy as sc
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
us_cities = pd.read_csv("us_cities_v2.csv")
us_cities['timezone'] = [_[8:] for _ in us_cities['timezone'].values]
capitals = us_cities.loc[us_cities['capital']]
capitals = capitals.reset_index(drop=True)
for _ in ['military', 'incorporated', 'capital']:
us_cities[_] = pd.DataFrame(1*us_cities[_])
incorp = us_cities.loc[us_cities['incorporated']==1]
incorp = incorp.reset_index(drop=True)
display(us_cities)
demo1 = Image.open('_DEMO_Salt_Lake_City_2017_05_01.png')
print('Salt Lake City, 2017 05 01:')
display(demo1.resize([256,256]))
demo2 = Image.open('_DEMO_Salt_Lake_City_2020_05_01.png')
print('Salt Lake City, 2020 05 01:')
display(demo2.resize([256,256]))
```
Images are stored at a lower resolution than stored above, to reduce net file size and processing time.
**Satellite image retrieval code; it takes appoximately forty minutes to cycle through enough semi-clean images (don't worry, it can't bite now)**
```
dates = ['2016-05-01', '2019-05-01']
site = "https://api.nasa.gov/planetary/earth/imagery?"
key = "fooTh1s1saFakeKeyForDEmoPurp0s3sfoo"
def fetch_sat_imgs(dates):
counter = 0
for date in dates:
for i, city in capitals.iterrows():
date_ = date
# Query API for capital image
url = site + "lon=" + str(city['long']) + "&lat=" + str(city['lat']) + \
"&dim=.1&date=" + date + "&api_key=" + api_key
response = requests.get(url)
print("Ok?",response.ok,'i =',i)
if response.ok:
img = Image.open(BytesIO(response.content))
cloudy = is_cloudy(img)
print(cloudy)
attempts = 0
while cloudy and attempts <= 4:
#NOTE - Selects nearest date
date = next_mo(date)
url = site + "lon=" + str(city['long']) + "&lat=" + str(city['lat']) + \
"&dim=.1&date=" + date + "&api_key=" + key1
response = requests.get(url)
img = Image.open(BytesIO(response.content))
cloudy = is_cloudy(img)
attempts += 1
if response.ok:
img = img.resize((32,32))
name = '_' + city['city'].replace(' ','_') + '_' + date.replace('-','_') + '.png'
#saves images to folder with noramalized name
#img.save(name)
date = date_
counter += 1
if attempts > 4:
print(city['city'], date)
date = date_
def next_mo(date):
mo = '0' + str(int(date[5:7]) + 1)
if len(mo) > 2:
mo = mo[1:]
date = date[:5] + mo + date[7:]
return date
def is_cloudy(img):
#Takes Image object, returns bool if it meets 'cloudy' criteria
k = 75 #Threshold coeff.
hist = img.histogram()
Rm = np.mean(hist[:256])
Gm = np.mean(hist[256:512])
Bm = np.mean(hist[512:])
W = [hist[255], hist[511], hist[-1]]
if W[0] > k*Rm or W[1] > k*Gm or W[2] > k*Bm:
return True
else:
return False
```
# Exploratory Analysis
```
print('Description of U.S. Cities Dataset:')
display(us_cities.describe())
print('Mapped Out:')
fig1, (ax1, ax2) = plt.subplots(1, 2, figsize=(20, 6))
ax1.scatter(us_cities['long'], us_cities['lat'], c='#808080')
sn.scatterplot(data=capitals, x='long', y='lat', ax=ax1, hue='population', size='population')
ax2.scatter(us_cities['long'], us_cities['lat'], c='#808080')
sn.scatterplot(data=capitals, x='long', y='lat', ax=ax2, hue='population', size='population')
#sn.color_palette("viridis", as_cmap=True)
ax1.set_xlim([-180, -50])
ax2.set_xlim([-125, -65])
ax2.set_ylim(22, 52)
ax1.set_xlabel('Latitude'); ax1.set_ylabel('Longitude');
ax2.set_xlabel('Latitude'); ax2.set_ylabel('Longitude');
ax1.title.set_text('U.S. Cities and Capitals')
ax2.title.set_text('U.S. Cities and Capitals (Magnified)')
plt.show()
```
**INTERPRETATION:** The description of the full dataset shows us that the minimum population of a 'city' is one person. The mean population of a city falls somewhere above the third quartile, and 67% of our cities are incorporated.
```
#All capitals and military bases are incorporated
labels = ['Incorporated', 'Not Incorporated', 'Military']
sizes = us_cities[['incorporated','military']].value_counts()
sizes = sizes.to_frame()
sizes.plot.pie(labels=labels, subplots=True, autopct='%1.1f%%', figsize=(10, 7))
_ = plt.title('Classifications of U.S. Cities')
corr = us_cities.corr()
c_corr = capitals.corr()
i_corr = incorp.corr()
fig2, (ax1, ax2) = plt.subplots(1, 2, sharex=True, sharey=True, figsize=(20, 6))
heatmap = ax1.pcolor(corr, vmin=-1, vmax=1)
heatmap = ax2.pcolor(c_corr, vmin=-1, vmax=1)
plt.colorbar(heatmap)
ax1.title.set_text('U.S. Cities Correlation Coefficients')
ax2.title.set_text('U.S. Capitals Correlation Coefficients')
labels=list(corr.index)
ticks = list(range(len(labels)))
_ = plt.xticks(ticks=ticks, labels=labels, size='small', stretch=150)
_ = plt.yticks(ticks=ticks, labels=labels, size='small')
plt.show()
print('Correlation Matrix, All U.S. Cities:')
display(corr)
print('Correlation Matrix, All U.S. Capitals:')
display(c_corr)
```
**INTERPRETATION:** From the outset, we see that the variables correlating most with *population* are (number of) *zips*, *ranking*, *capital*, and *density*. *Ranking* correlates most with *density*, *zips*, *population*, and *capital*. The correlation between population and number of ZIP codes makes sense, intuitively and seems to be a redundancy for the most part.
The correlation matrix for the *capitals* subset, most notably, has missing rows and columns which indicates that there is no variation for those variables. In other words, all U.S. capitals are incorporated and none of them are military bases or forts (luckily this is of little surprise).
```
print("'ranking' Value Counts, for Military Bases:")
query = us_cities.loc[us_cities['military']==1]
display(pd.DataFrame(query['ranking'].value_counts()))
print("'ranking' Value Counts, for Capitals:")
display(pd.DataFrame(capitals['ranking'].value_counts()))
print("'ranking' Value Counts, for All Cities:")
display(pd.DataFrame(us_cities['ranking'].value_counts()))
query = us_cities.loc[us_cities['ranking']==1]
display(query.head(10))
```
**INTERPRETATION:** It appears then, that the best quantitive indicators for *ranking* are *population* and *density*. This likely shows that *ranking* prioritizes cities by historical and cultural influence, which otherwise falls outside of the scope of our datasets. Capitals tend to rank higher, it seems, because they are more likely to have higher populations, densities and some form of cultural significance--Philadelphia and Boston, for example, qualify in each of these cases.
Let's try reducing our data into a set of incorporated cities and see if a narrower set will improve correlations:
```
print('Changes in Correlation, Incorporated Cities Only:')
display(pd.DataFrame(corr - i_corr))
print('Number of cities within subset:', len(incorp), '\n')
mask = incorp['population'] > 2500
i_funnel = incorp.loc[mask]
print('Changes in Correlation, Incorporated Cities with Populations > 2500:')
display(corr - i_funnel.corr())
print('Number of cities within subset:', len(i_funnel))
```
**INTERPRETATION:** The reductions in size for each dataset are relatively costly, with rather small changes in correlation. This assessment, however, excludes categorical variables such as *state*, *county*, and *timezone*.
Next up, let's see if there are any noticeable trends for the subset of military bases:
```
m_corr = us_cities.loc[us_cities['military']==1].corr()
print('Correlation Matrix, Military Bases:')
display(m_corr)
```
**INTERPRETATION:** When it comes to military bases, the number of ZIP codes and ranking lose a fair bit of correlation with population. On the other hand, density and latitude coordinates improve, likely due to less variance.
```
capitals['timezone'].value_counts()
```
# Predicting Populations via Linear Regression
Now that we have identified the most important correlations in the dataset, during the explorational analysis, what combination yields the best linear regression?
```
cities_ols = sm.ols(formula="population ~ zips + capital", data=us_cities).fit() #R^2=0.713, best F-stat
# cities_ols = sm.ols(formula="population ~ zips + capital + density", data=us_cities).fit() #R^2=0.714
# cities_ols = sm.ols(formula="population ~ zips", data=us_cities).fit() #R^2=0.706
print('Population ~ zips + capital:')
display(cities_ols.summary())
```
# Classification with Categorical Variables: Decision Trees
The best correlations we have for predicting a city's population are number of ZIPs, density, ranking, and if it is a capital. With a multi-linear regression, we have found a relatively effective model that relies primarily on the number of ZIPs. However, until this point, we have not explored the relationships the dataset has with respect to categorical variables *state*, *timezone*, or *county*.
Decision trees can be effective classifiers when it comes to predicting categorical variables. To use the other, string-type categorical variables, we will have to represent each string value as a unique integer. With this classification method, we want to identify which combinations of variables are best for accurately predicting (a) the state that a city is in and (b) the county a city is in for a specific state. For the second case, we will use California as the study since it should offer a larger sample size with training and testing. State and county lines have important effects on a city's population, density, and even socio-political factors that might play into *ranking*. Using classification, we can see which variables correlate with those state/county lines.
```
fig3 = sn.scatterplot(data=us_cities, x='long', y='lat', hue='state',legend=False)
plt.xlabel('Latitude')
plt.ylabel('Longitude')
_ = plt.xlim([-180, -60])
_ = plt.title('U.S. Cities By State')
plt.show()
mask = us_cities['state_id'] == 'CA'
CA = us_cities.loc[mask].sample(frac=1)
sn.scatterplot(data=CA, x='long', y='lat', hue='county', legend=False)
plt.xlabel('Latitude')
plt.ylabel('Longitude')
_ = plt.title('California Cities By County')
plt.show()
as_num = lambda string : {_:i for i,_ in enumerate(us_cities[string].unique())}
# State Prediction Accuracy (0.5 test split):
# timezone -> [0.303,0.309]
# ranking -> [0.08,0.08]
# [lat,long] -> [1.0,0.97]
# [timezone,ranking] -> [0.305,0.311]
# ['lat','timezone','density'] -> [1.0,0.587]
features = ['lat','long']
X = us_cities[features]
# X['timezone'] = X['timezone'].map(as_num('timezone'))
# X['county'] = X['county'].map(as_num('county'))
X = X.values
y = us_cities['state'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=53, test_size=0.5)
decisionTree = tree.DecisionTreeClassifier()
decisionTree = decisionTree.fit(X_train, y_train)
print("Predicting a City's State:")
y_pred_t = decisionTree.predict(X_train)
print('Accuracy on training data= ', metrics.accuracy_score(y_true = y_train, y_pred = y_pred_t))
y_pred = decisionTree.predict(X_test)
print('Accuracy on test data= ', metrics.accuracy_score(y_true = y_test, y_pred = y_pred))
print('Decision Tree: State with Latitude and Longitude')
_ = tree.plot_tree(decisionTree)
_ = plt.figure(figsize=(20,20))
plt.show()
```
**INTERPRETATION:** It makes plenty of intuitive sense for latitude and longitude to be the best predictors of a given city's state. Interestingly, however, the *timezone* variable can act as a quasi-longitude coordinate, just more discretized. So, using the latitude and timezone of a city can yield about 99.4% and 55.3% accuracy for the training and test data respectively.
```
features = ['county','timezone']
X = us_cities[features]
X['timezone'] = X['timezone'].map(as_num('timezone'))
X['county'] = X['county'].map(as_num('county'))
X = X.values
y = us_cities['state'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=53, test_size=0.5)
decisionTree = tree.DecisionTreeClassifier()
decisionTree = decisionTree.fit(X_train, y_train)
print("Predicting a City's State with Timezone and County:")
y_pred_t = decisionTree.predict(X_train)
print('Accuracy on training data= ', metrics.accuracy_score(y_true = y_train, y_pred = y_pred_t))
y_pred = decisionTree.predict(X_test)
print('Accuracy on test data= ', metrics.accuracy_score(y_true = y_test, y_pred = y_pred))
```
Timezone and county, being geographic/spacial variables, also do relatively well to predict a city's state. Other combinations of variables, however don't seem to compete with the two models shown. **Let's double check this with California.** Perhaps a subset will have more options than using spatial variables.
```
as_num = lambda string : {_:i for i,_ in enumerate(CA[string].unique())}
features = ['lat','long']
X = CA[features]
# X['county'] = X['county'].map(as_num('county'))
X = X.values
y = CA['county'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=53, test_size=0.5)
decisionTree = tree.DecisionTreeClassifier()
decisionTree = decisionTree.fit(X_train, y_train)
print("Predicting a City's State with Timezone and County:")
y_pred_t = decisionTree.predict(X_train)
print('Accuracy on training data= ', metrics.accuracy_score(y_true = y_train, y_pred = y_pred_t))
y_pred = decisionTree.predict(X_test)
print('Accuracy on test data= ', metrics.accuracy_score(y_true = y_test, y_pred = y_pred),'\n')
print('Decision Tree: Counties with Latitude and Longitude')
_ = tree.plot_tree(decisionTree)
_ = plt.figure(figsize=(20,20))
plt.show()
features = ['population','incorporated','lat']
X = CA[features]
# X['county'] = X['county'].map(as_num('county'))
X = X.values
y = CA['county'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=53, test_size=0.5)
decisionTree = tree.DecisionTreeClassifier()
decisionTree = decisionTree.fit(X_train, y_train)
print("Predicting a City's State with Population, 'incorporated' and Latitude:")
y_pred_t = decisionTree.predict(X_train)
print('Accuracy on training data= ', metrics.accuracy_score(y_true = y_train, y_pred = y_pred_t))
y_pred = decisionTree.predict(X_test)
print('Accuracy on test data= ', metrics.accuracy_score(y_true = y_test, y_pred = y_pred))
```
**INTERPRETATION:** Here, we see a similar effectivity for classifying a California city's county, but there is a noticeable dip in accuracy. Perhaps there is a higher likelihood for overlap in coordinates. We also see that all the other variables produce ~0% accuracies on their training sets without some spatial coordinate.
# Image Processing
```
#TODO - Process the RGB hists and intensities with a function, going through
import sys
import skimage
import skimage.io
import skimage.viewer
from skimage import data
from skimage.viewer import ImageViewer
from matplotlib import pyplot as plt
import re
import seaborn as sns
img_list = os.listdir('images/')[1:]
for img_name in img_list:
img = Image.open('images/'+img_name)
#iterate through list and attach read image to capitals dataframe
image = skimage.io.imread('images/'+img_name)
img_list
colors_hist = pd.read_csv("color_histograms.csv")
colors_hist.describe()
bef = colors_hist['bef_hist'].values
aft = colors_hist['aft_hist'].values
sn.pairplot(colors_hist)
# plt.hist(data = colors_hist, x = 'num_var')
df_col = ['city', 'bef', 'aft']
df = pd.DataFrame(columns = df_col)
hist_list = []
i = 0
for img_name in img_list[:6]:
img = Image.open('images/'+img_name)
#iterate through list and attach read image to capitals dataframe
image = skimage.io.imread('images/'+img_name)
colors = ("r", "g", "b")
channel_ids = (0, 1, 2)
# create the histogram plot, with three lines, one for
# each color
plt.xlim([0, 256])
for channel_id, c in zip(channel_ids, colors):
histogram, bin_edges = np.histogram(
image[:, :, channel_id], bins=256, range=(0, 256)
)
plt.plot(bin_edges[0:-1], histogram, color=c)
i+=1
plt.title(img_name)
plt.xlabel("Color value")
plt.ylabel("Pixels")
plt.show()
```
Interpretation: As we can see from the rendered examples, there is a significant change in image color density over time. While through our model and analysis we can not make a direct coorelation between the two values there is a significant change occuring in both. Color density can also be affected by weather and atmospheric conditions. So any correlations would also have to be validated as not simply being a byproduct of another determining factor.
# Peer Feedback
|
github_jupyter
|
import os, cv2, requests, base64, imageio
from PIL import Image
from io import BytesIO
from IPython.display import display
from sklearn import tree, linear_model, metrics # linear_model.LinearRegression() for OLS
from sklearn.metrics import homogeneity_score, v_measure_score
from sklearn.preprocessing import scale
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
import statsmodels.formula.api as sm # used statsmodels.formula.api.ols() for OLS
import seaborn as sn
import pandas as pd
import scipy as sc
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
us_cities = pd.read_csv("us_cities_v2.csv")
us_cities['timezone'] = [_[8:] for _ in us_cities['timezone'].values]
capitals = us_cities.loc[us_cities['capital']]
capitals = capitals.reset_index(drop=True)
for _ in ['military', 'incorporated', 'capital']:
us_cities[_] = pd.DataFrame(1*us_cities[_])
incorp = us_cities.loc[us_cities['incorporated']==1]
incorp = incorp.reset_index(drop=True)
display(us_cities)
demo1 = Image.open('_DEMO_Salt_Lake_City_2017_05_01.png')
print('Salt Lake City, 2017 05 01:')
display(demo1.resize([256,256]))
demo2 = Image.open('_DEMO_Salt_Lake_City_2020_05_01.png')
print('Salt Lake City, 2020 05 01:')
display(demo2.resize([256,256]))
dates = ['2016-05-01', '2019-05-01']
site = "https://api.nasa.gov/planetary/earth/imagery?"
key = "fooTh1s1saFakeKeyForDEmoPurp0s3sfoo"
def fetch_sat_imgs(dates):
counter = 0
for date in dates:
for i, city in capitals.iterrows():
date_ = date
# Query API for capital image
url = site + "lon=" + str(city['long']) + "&lat=" + str(city['lat']) + \
"&dim=.1&date=" + date + "&api_key=" + api_key
response = requests.get(url)
print("Ok?",response.ok,'i =',i)
if response.ok:
img = Image.open(BytesIO(response.content))
cloudy = is_cloudy(img)
print(cloudy)
attempts = 0
while cloudy and attempts <= 4:
#NOTE - Selects nearest date
date = next_mo(date)
url = site + "lon=" + str(city['long']) + "&lat=" + str(city['lat']) + \
"&dim=.1&date=" + date + "&api_key=" + key1
response = requests.get(url)
img = Image.open(BytesIO(response.content))
cloudy = is_cloudy(img)
attempts += 1
if response.ok:
img = img.resize((32,32))
name = '_' + city['city'].replace(' ','_') + '_' + date.replace('-','_') + '.png'
#saves images to folder with noramalized name
#img.save(name)
date = date_
counter += 1
if attempts > 4:
print(city['city'], date)
date = date_
def next_mo(date):
mo = '0' + str(int(date[5:7]) + 1)
if len(mo) > 2:
mo = mo[1:]
date = date[:5] + mo + date[7:]
return date
def is_cloudy(img):
#Takes Image object, returns bool if it meets 'cloudy' criteria
k = 75 #Threshold coeff.
hist = img.histogram()
Rm = np.mean(hist[:256])
Gm = np.mean(hist[256:512])
Bm = np.mean(hist[512:])
W = [hist[255], hist[511], hist[-1]]
if W[0] > k*Rm or W[1] > k*Gm or W[2] > k*Bm:
return True
else:
return False
print('Description of U.S. Cities Dataset:')
display(us_cities.describe())
print('Mapped Out:')
fig1, (ax1, ax2) = plt.subplots(1, 2, figsize=(20, 6))
ax1.scatter(us_cities['long'], us_cities['lat'], c='#808080')
sn.scatterplot(data=capitals, x='long', y='lat', ax=ax1, hue='population', size='population')
ax2.scatter(us_cities['long'], us_cities['lat'], c='#808080')
sn.scatterplot(data=capitals, x='long', y='lat', ax=ax2, hue='population', size='population')
#sn.color_palette("viridis", as_cmap=True)
ax1.set_xlim([-180, -50])
ax2.set_xlim([-125, -65])
ax2.set_ylim(22, 52)
ax1.set_xlabel('Latitude'); ax1.set_ylabel('Longitude');
ax2.set_xlabel('Latitude'); ax2.set_ylabel('Longitude');
ax1.title.set_text('U.S. Cities and Capitals')
ax2.title.set_text('U.S. Cities and Capitals (Magnified)')
plt.show()
#All capitals and military bases are incorporated
labels = ['Incorporated', 'Not Incorporated', 'Military']
sizes = us_cities[['incorporated','military']].value_counts()
sizes = sizes.to_frame()
sizes.plot.pie(labels=labels, subplots=True, autopct='%1.1f%%', figsize=(10, 7))
_ = plt.title('Classifications of U.S. Cities')
corr = us_cities.corr()
c_corr = capitals.corr()
i_corr = incorp.corr()
fig2, (ax1, ax2) = plt.subplots(1, 2, sharex=True, sharey=True, figsize=(20, 6))
heatmap = ax1.pcolor(corr, vmin=-1, vmax=1)
heatmap = ax2.pcolor(c_corr, vmin=-1, vmax=1)
plt.colorbar(heatmap)
ax1.title.set_text('U.S. Cities Correlation Coefficients')
ax2.title.set_text('U.S. Capitals Correlation Coefficients')
labels=list(corr.index)
ticks = list(range(len(labels)))
_ = plt.xticks(ticks=ticks, labels=labels, size='small', stretch=150)
_ = plt.yticks(ticks=ticks, labels=labels, size='small')
plt.show()
print('Correlation Matrix, All U.S. Cities:')
display(corr)
print('Correlation Matrix, All U.S. Capitals:')
display(c_corr)
print("'ranking' Value Counts, for Military Bases:")
query = us_cities.loc[us_cities['military']==1]
display(pd.DataFrame(query['ranking'].value_counts()))
print("'ranking' Value Counts, for Capitals:")
display(pd.DataFrame(capitals['ranking'].value_counts()))
print("'ranking' Value Counts, for All Cities:")
display(pd.DataFrame(us_cities['ranking'].value_counts()))
query = us_cities.loc[us_cities['ranking']==1]
display(query.head(10))
print('Changes in Correlation, Incorporated Cities Only:')
display(pd.DataFrame(corr - i_corr))
print('Number of cities within subset:', len(incorp), '\n')
mask = incorp['population'] > 2500
i_funnel = incorp.loc[mask]
print('Changes in Correlation, Incorporated Cities with Populations > 2500:')
display(corr - i_funnel.corr())
print('Number of cities within subset:', len(i_funnel))
m_corr = us_cities.loc[us_cities['military']==1].corr()
print('Correlation Matrix, Military Bases:')
display(m_corr)
capitals['timezone'].value_counts()
cities_ols = sm.ols(formula="population ~ zips + capital", data=us_cities).fit() #R^2=0.713, best F-stat
# cities_ols = sm.ols(formula="population ~ zips + capital + density", data=us_cities).fit() #R^2=0.714
# cities_ols = sm.ols(formula="population ~ zips", data=us_cities).fit() #R^2=0.706
print('Population ~ zips + capital:')
display(cities_ols.summary())
fig3 = sn.scatterplot(data=us_cities, x='long', y='lat', hue='state',legend=False)
plt.xlabel('Latitude')
plt.ylabel('Longitude')
_ = plt.xlim([-180, -60])
_ = plt.title('U.S. Cities By State')
plt.show()
mask = us_cities['state_id'] == 'CA'
CA = us_cities.loc[mask].sample(frac=1)
sn.scatterplot(data=CA, x='long', y='lat', hue='county', legend=False)
plt.xlabel('Latitude')
plt.ylabel('Longitude')
_ = plt.title('California Cities By County')
plt.show()
as_num = lambda string : {_:i for i,_ in enumerate(us_cities[string].unique())}
# State Prediction Accuracy (0.5 test split):
# timezone -> [0.303,0.309]
# ranking -> [0.08,0.08]
# [lat,long] -> [1.0,0.97]
# [timezone,ranking] -> [0.305,0.311]
# ['lat','timezone','density'] -> [1.0,0.587]
features = ['lat','long']
X = us_cities[features]
# X['timezone'] = X['timezone'].map(as_num('timezone'))
# X['county'] = X['county'].map(as_num('county'))
X = X.values
y = us_cities['state'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=53, test_size=0.5)
decisionTree = tree.DecisionTreeClassifier()
decisionTree = decisionTree.fit(X_train, y_train)
print("Predicting a City's State:")
y_pred_t = decisionTree.predict(X_train)
print('Accuracy on training data= ', metrics.accuracy_score(y_true = y_train, y_pred = y_pred_t))
y_pred = decisionTree.predict(X_test)
print('Accuracy on test data= ', metrics.accuracy_score(y_true = y_test, y_pred = y_pred))
print('Decision Tree: State with Latitude and Longitude')
_ = tree.plot_tree(decisionTree)
_ = plt.figure(figsize=(20,20))
plt.show()
features = ['county','timezone']
X = us_cities[features]
X['timezone'] = X['timezone'].map(as_num('timezone'))
X['county'] = X['county'].map(as_num('county'))
X = X.values
y = us_cities['state'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=53, test_size=0.5)
decisionTree = tree.DecisionTreeClassifier()
decisionTree = decisionTree.fit(X_train, y_train)
print("Predicting a City's State with Timezone and County:")
y_pred_t = decisionTree.predict(X_train)
print('Accuracy on training data= ', metrics.accuracy_score(y_true = y_train, y_pred = y_pred_t))
y_pred = decisionTree.predict(X_test)
print('Accuracy on test data= ', metrics.accuracy_score(y_true = y_test, y_pred = y_pred))
as_num = lambda string : {_:i for i,_ in enumerate(CA[string].unique())}
features = ['lat','long']
X = CA[features]
# X['county'] = X['county'].map(as_num('county'))
X = X.values
y = CA['county'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=53, test_size=0.5)
decisionTree = tree.DecisionTreeClassifier()
decisionTree = decisionTree.fit(X_train, y_train)
print("Predicting a City's State with Timezone and County:")
y_pred_t = decisionTree.predict(X_train)
print('Accuracy on training data= ', metrics.accuracy_score(y_true = y_train, y_pred = y_pred_t))
y_pred = decisionTree.predict(X_test)
print('Accuracy on test data= ', metrics.accuracy_score(y_true = y_test, y_pred = y_pred),'\n')
print('Decision Tree: Counties with Latitude and Longitude')
_ = tree.plot_tree(decisionTree)
_ = plt.figure(figsize=(20,20))
plt.show()
features = ['population','incorporated','lat']
X = CA[features]
# X['county'] = X['county'].map(as_num('county'))
X = X.values
y = CA['county'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=53, test_size=0.5)
decisionTree = tree.DecisionTreeClassifier()
decisionTree = decisionTree.fit(X_train, y_train)
print("Predicting a City's State with Population, 'incorporated' and Latitude:")
y_pred_t = decisionTree.predict(X_train)
print('Accuracy on training data= ', metrics.accuracy_score(y_true = y_train, y_pred = y_pred_t))
y_pred = decisionTree.predict(X_test)
print('Accuracy on test data= ', metrics.accuracy_score(y_true = y_test, y_pred = y_pred))
#TODO - Process the RGB hists and intensities with a function, going through
import sys
import skimage
import skimage.io
import skimage.viewer
from skimage import data
from skimage.viewer import ImageViewer
from matplotlib import pyplot as plt
import re
import seaborn as sns
img_list = os.listdir('images/')[1:]
for img_name in img_list:
img = Image.open('images/'+img_name)
#iterate through list and attach read image to capitals dataframe
image = skimage.io.imread('images/'+img_name)
img_list
colors_hist = pd.read_csv("color_histograms.csv")
colors_hist.describe()
bef = colors_hist['bef_hist'].values
aft = colors_hist['aft_hist'].values
sn.pairplot(colors_hist)
# plt.hist(data = colors_hist, x = 'num_var')
df_col = ['city', 'bef', 'aft']
df = pd.DataFrame(columns = df_col)
hist_list = []
i = 0
for img_name in img_list[:6]:
img = Image.open('images/'+img_name)
#iterate through list and attach read image to capitals dataframe
image = skimage.io.imread('images/'+img_name)
colors = ("r", "g", "b")
channel_ids = (0, 1, 2)
# create the histogram plot, with three lines, one for
# each color
plt.xlim([0, 256])
for channel_id, c in zip(channel_ids, colors):
histogram, bin_edges = np.histogram(
image[:, :, channel_id], bins=256, range=(0, 256)
)
plt.plot(bin_edges[0:-1], histogram, color=c)
i+=1
plt.title(img_name)
plt.xlabel("Color value")
plt.ylabel("Pixels")
plt.show()
| 0.374905 | 0.873323 |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
pd.set_option('display.max_colwidth', None)
import nltk
nltk.download('stopwords')
nltk.download('wordnet')
nltk.download('averaged_perceptron_tagger')
from nltk.tokenize import word_tokenize
from nltk.stem import WordNetLemmatizer
from collections import Counter
from nltk.corpus import stopwords
from nltk.corpus import wordnet
import warnings
warnings.simplefilter(action='ignore')
from tqdm.notebook import tqdm
import pickle
import re
# x = 'Got questions about the COVID-19 #vaccine? Join us tomorrow as we chat with Dr. Haider-Shah about everything you ne… https://t.co/H93qLxlMyW'
x = 'hhh'
```
lists and helper functions
```
mostcommon = ['vaccine', 'get', 'covid', 'make', 'today', '19', 'vaccinate', 'antivaxx', 'anti', 'first', 'time', 'people',
'vaccination', 'receive', 'thank', 'dose', 'week', '2', '1', 'help', 'day', 'one', 'staff', 'home', 'take', 'health', 'safety',
'new', 'interest', 'see', 'theorist', 'u', 'efficacy', 'raise', 'conflict', 'query', 'work', 'youconspiracy', 'shot',
'community', 'second', 'continue', 'go', 'say', 'care', 'resident', 'prediction', 'need', '2nd', 'every', 'safe', 'year',
'good', 'administer', 'know', 'state', 'protect', 'give', 'worker', 'dr', 'visit', 'share', 'family', '11', 'million',
'team', 'part', 'impact', 'come', 'important', 'nothing', 'watch', 'keep', 'across', 'kentucky', 'many', 'much', '000',
'thanks', '37', '6', '22', 'question', 'waste', 'great', 'change', 'life', 'plus', 'footcouple', 'notdrop', 'like', 'want',
'use', 'love', 'well', 'old', 'moment', 'last', 'look', 'roll']
contractions_dict = { "ain't": "are not ","'s":" is ","aren't": "are not",
"can't": "cannot","can't've": "cannot have",
"'cause": "because","could've": "could have","couldn't": "could not",
"couldn't've": "could not have", "didn't": "did not","doesn't": "does not",
"don't": "do not","hadn't": "had not","hadn't've": "had not have",
"hasn't": "has not","haven't": "have not","he'd": "he would",
"he'd've": "he would have","he'll": "he will", "he'll've": "he will have",
"how'd": "how did","how'd'y": "how do you","how'll": "how will",
"I'd": "I would", "I'd've": "I would have","I'll": "I will",
"I'll've": "I will have","I'm": "I am","I've": "I have", "isn't": "is not",
"it'd": "it would","it'd've": "it would have","it'll": "it will",
"it'll've": "it will have", "let's": "let us","ma'am": "madam",
"mayn't": "may not","might've": "might have","mightn't": "might not",
"mightn't've": "might not have","must've": "must have","mustn't": "must not",
"mustn't've": "must not have", "needn't": "need not",
"needn't've": "need not have","o'clock": "of the clock","oughtn't": "ought not",
"oughtn't've": "ought not have","shan't": "shall not","sha'n't": "shall not",
"shan't've": "shall not have","she'd": "she would","she'd've": "she would have",
"she'll": "she will", "she'll've": "she will have","should've": "should have",
"shouldn't": "should not", "shouldn't've": "should not have","so've": "so have",
"that'd": "that would","that'd've": "that would have", "there'd": "there would",
"there'd've": "there would have", "they'd": "they would",
"they'd've": "they would have","they'll": "they will",
"they'll've": "they will have", "they're": "they are","they've": "they have",
"to've": "to have","wasn't": "was not","we'd": "we would",
"we'd've": "we would have","we'll": "we will","we'll've": "we will have",
"we're": "we are","we've": "we have", "weren't": "were not","what'll": "what will",
"what'll've": "what will have","what're": "what are", "what've": "what have",
"when've": "when have","where'd": "where did", "where've": "where have",
"who'll": "who will","who'll've": "who will have","who've": "who have",
"why've": "why have","will've": "will have","won't": "will not",
"won't've": "will not have", "would've": "would have","wouldn't": "would not",
"wouldn't've": "would not have","y'all": "you all", "y'all'd": "you all would",
"y'all'd've": "you all would have","y'all're": "you all are",
"y'all've": "you all have", "you'd": "you would","you'd've": "you would have",
"you'll": "you will","you'll've": "you will have", "you're": "you are",
"you've": "you have"}
contractions_re=re.compile('(%s)' % '|'.join(contractions_dict.keys()))
def expand_contractions(text,contractions_dict=contractions_dict):
def replace(match):
return contractions_dict[match.group(0)]
return contractions_re.sub(replace, text)
def get_wordnet_pos(tag):
if tag.startswith('J'):
return wordnet.ADJ
elif tag.startswith('V'):
return wordnet.VERB
elif tag.startswith('N'):
return wordnet.NOUN
elif tag.startswith('R'):
return wordnet.ADV
else:
return wordnet.NOUN
def most_common_token(token, mostcommon=mostcommon):
new_token=[]
for word in token:
if word in mostcommon:
new_token.append(word)
return new_token
stop_words = set(stopwords.words('english'))
wnl = WordNetLemmatizer()
```
PP
```
def preprocess_input(user_input, stop_wrds=stop_words, wl=wnl):
x = user_input
for_df = {'text':[x], 'user_followers':[2207], 'favorites':[0], 'retweets':[0], 'is_retweet':[1]}
df = pd.DataFrame(for_df)
df.text = df.text.str.lower()
df.text = df.text.apply(lambda x:re.sub('@[^\s]+','',x))
df.text = df.text.apply(lambda x:re.sub(r'\B#\S+','',x))
df.text = df.text.apply(lambda x:re.sub(r"http\S+", "", x))
df.text = df.text.apply(lambda x:' '.join(re.findall(r'\w+', x)))
df.text = df.text.apply(lambda x:re.sub(r'\s+[a-zA-Z]\s+', '', x))
df.text = df.text.apply(lambda x:re.sub(r'\s+', ' ', x, flags=re.I))
df['text']=df['text'].apply(lambda x:expand_contractions(x))
df['tokenized'] = df['text'].apply(word_tokenize)
df['tokenized'] = df['tokenized'].apply(lambda x: [word for word in x if word not in stop_words])
df['pos_tags'] = df['tokenized'].apply(nltk.tag.pos_tag)
df['tokenized'] = df['pos_tags'].apply(lambda x: [(word, get_wordnet_pos(pos_tag)) for (word, pos_tag) in x])
df['tokenized'] = df['tokenized'].apply(lambda x: [wnl.lemmatize(word, tag) for word, tag in x])
df['n_words'] = df['text'].apply(lambda x: len(x.split()))
df['tokenized_common'] = df['tokenized'].apply(lambda x: most_common_token(x))
for word in mostcommon:
df[word]=0
for word in df.tokenized_common:
df[word] = 1
to_drop = ['text', 'tokenized', 'pos_tags', 'tokenized_common']
df = df.drop(to_drop, axis=1)
return df
df = preprocess_input(x)
df
filename = "xgboost.sav"
with open(filename, 'rb') as f:
model = pickle.load(f)
preds = model.predict_proba(df)
result = np.asarray([np.argmax(line) for line in preds])
result[0]
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
pd.set_option('display.max_colwidth', None)
import nltk
nltk.download('stopwords')
nltk.download('wordnet')
nltk.download('averaged_perceptron_tagger')
from nltk.tokenize import word_tokenize
from nltk.stem import WordNetLemmatizer
from collections import Counter
from nltk.corpus import stopwords
from nltk.corpus import wordnet
import warnings
warnings.simplefilter(action='ignore')
from tqdm.notebook import tqdm
import pickle
import re
# x = 'Got questions about the COVID-19 #vaccine? Join us tomorrow as we chat with Dr. Haider-Shah about everything you ne… https://t.co/H93qLxlMyW'
x = 'hhh'
mostcommon = ['vaccine', 'get', 'covid', 'make', 'today', '19', 'vaccinate', 'antivaxx', 'anti', 'first', 'time', 'people',
'vaccination', 'receive', 'thank', 'dose', 'week', '2', '1', 'help', 'day', 'one', 'staff', 'home', 'take', 'health', 'safety',
'new', 'interest', 'see', 'theorist', 'u', 'efficacy', 'raise', 'conflict', 'query', 'work', 'youconspiracy', 'shot',
'community', 'second', 'continue', 'go', 'say', 'care', 'resident', 'prediction', 'need', '2nd', 'every', 'safe', 'year',
'good', 'administer', 'know', 'state', 'protect', 'give', 'worker', 'dr', 'visit', 'share', 'family', '11', 'million',
'team', 'part', 'impact', 'come', 'important', 'nothing', 'watch', 'keep', 'across', 'kentucky', 'many', 'much', '000',
'thanks', '37', '6', '22', 'question', 'waste', 'great', 'change', 'life', 'plus', 'footcouple', 'notdrop', 'like', 'want',
'use', 'love', 'well', 'old', 'moment', 'last', 'look', 'roll']
contractions_dict = { "ain't": "are not ","'s":" is ","aren't": "are not",
"can't": "cannot","can't've": "cannot have",
"'cause": "because","could've": "could have","couldn't": "could not",
"couldn't've": "could not have", "didn't": "did not","doesn't": "does not",
"don't": "do not","hadn't": "had not","hadn't've": "had not have",
"hasn't": "has not","haven't": "have not","he'd": "he would",
"he'd've": "he would have","he'll": "he will", "he'll've": "he will have",
"how'd": "how did","how'd'y": "how do you","how'll": "how will",
"I'd": "I would", "I'd've": "I would have","I'll": "I will",
"I'll've": "I will have","I'm": "I am","I've": "I have", "isn't": "is not",
"it'd": "it would","it'd've": "it would have","it'll": "it will",
"it'll've": "it will have", "let's": "let us","ma'am": "madam",
"mayn't": "may not","might've": "might have","mightn't": "might not",
"mightn't've": "might not have","must've": "must have","mustn't": "must not",
"mustn't've": "must not have", "needn't": "need not",
"needn't've": "need not have","o'clock": "of the clock","oughtn't": "ought not",
"oughtn't've": "ought not have","shan't": "shall not","sha'n't": "shall not",
"shan't've": "shall not have","she'd": "she would","she'd've": "she would have",
"she'll": "she will", "she'll've": "she will have","should've": "should have",
"shouldn't": "should not", "shouldn't've": "should not have","so've": "so have",
"that'd": "that would","that'd've": "that would have", "there'd": "there would",
"there'd've": "there would have", "they'd": "they would",
"they'd've": "they would have","they'll": "they will",
"they'll've": "they will have", "they're": "they are","they've": "they have",
"to've": "to have","wasn't": "was not","we'd": "we would",
"we'd've": "we would have","we'll": "we will","we'll've": "we will have",
"we're": "we are","we've": "we have", "weren't": "were not","what'll": "what will",
"what'll've": "what will have","what're": "what are", "what've": "what have",
"when've": "when have","where'd": "where did", "where've": "where have",
"who'll": "who will","who'll've": "who will have","who've": "who have",
"why've": "why have","will've": "will have","won't": "will not",
"won't've": "will not have", "would've": "would have","wouldn't": "would not",
"wouldn't've": "would not have","y'all": "you all", "y'all'd": "you all would",
"y'all'd've": "you all would have","y'all're": "you all are",
"y'all've": "you all have", "you'd": "you would","you'd've": "you would have",
"you'll": "you will","you'll've": "you will have", "you're": "you are",
"you've": "you have"}
contractions_re=re.compile('(%s)' % '|'.join(contractions_dict.keys()))
def expand_contractions(text,contractions_dict=contractions_dict):
def replace(match):
return contractions_dict[match.group(0)]
return contractions_re.sub(replace, text)
def get_wordnet_pos(tag):
if tag.startswith('J'):
return wordnet.ADJ
elif tag.startswith('V'):
return wordnet.VERB
elif tag.startswith('N'):
return wordnet.NOUN
elif tag.startswith('R'):
return wordnet.ADV
else:
return wordnet.NOUN
def most_common_token(token, mostcommon=mostcommon):
new_token=[]
for word in token:
if word in mostcommon:
new_token.append(word)
return new_token
stop_words = set(stopwords.words('english'))
wnl = WordNetLemmatizer()
def preprocess_input(user_input, stop_wrds=stop_words, wl=wnl):
x = user_input
for_df = {'text':[x], 'user_followers':[2207], 'favorites':[0], 'retweets':[0], 'is_retweet':[1]}
df = pd.DataFrame(for_df)
df.text = df.text.str.lower()
df.text = df.text.apply(lambda x:re.sub('@[^\s]+','',x))
df.text = df.text.apply(lambda x:re.sub(r'\B#\S+','',x))
df.text = df.text.apply(lambda x:re.sub(r"http\S+", "", x))
df.text = df.text.apply(lambda x:' '.join(re.findall(r'\w+', x)))
df.text = df.text.apply(lambda x:re.sub(r'\s+[a-zA-Z]\s+', '', x))
df.text = df.text.apply(lambda x:re.sub(r'\s+', ' ', x, flags=re.I))
df['text']=df['text'].apply(lambda x:expand_contractions(x))
df['tokenized'] = df['text'].apply(word_tokenize)
df['tokenized'] = df['tokenized'].apply(lambda x: [word for word in x if word not in stop_words])
df['pos_tags'] = df['tokenized'].apply(nltk.tag.pos_tag)
df['tokenized'] = df['pos_tags'].apply(lambda x: [(word, get_wordnet_pos(pos_tag)) for (word, pos_tag) in x])
df['tokenized'] = df['tokenized'].apply(lambda x: [wnl.lemmatize(word, tag) for word, tag in x])
df['n_words'] = df['text'].apply(lambda x: len(x.split()))
df['tokenized_common'] = df['tokenized'].apply(lambda x: most_common_token(x))
for word in mostcommon:
df[word]=0
for word in df.tokenized_common:
df[word] = 1
to_drop = ['text', 'tokenized', 'pos_tags', 'tokenized_common']
df = df.drop(to_drop, axis=1)
return df
df = preprocess_input(x)
df
filename = "xgboost.sav"
with open(filename, 'rb') as f:
model = pickle.load(f)
preds = model.predict_proba(df)
result = np.asarray([np.argmax(line) for line in preds])
result[0]
| 0.272025 | 0.48377 |
```
from google.colab import files
data_to_load = files.upload()
import io
import pandas as pd
import pickle
import matplotlib.pyplot as plt
import os
def scores_calc(rouge,metric,scores):
outer_list=[]
for topic in scores:
inner_list=[]
for article in topic:
f1_tmp=article[rouge][metric]
inner_list.append(f1_tmp)
outer_list.append(inner_list)
return outer_list
def average_rouge(itr):
metric_common=[]
for i in range(5):
temp=sum(itr[i])/len(itr[i])
metric_common.append(temp)
return metric_common
def calculate_mean_score_plots():
"""
Input scores from Rouge
Returns:
Mean of Precision and for Rouge-1, Rouge-2 and Rouge-L
Mean of Recall for Rouge-1, Rouge-2 and Rouge-L
Mean of F-1 Score for Rouge-1, Rouge-2 and Rouge-L
"""
with open('/content/list_scores.pkl','rb') as f:
scores=pickle.load(f)
#Rouge-1
f1_r1=scores_calc('rouge-1','f',scores)
p_r1=scores_calc('rouge-1','p',scores)
r_r1=scores_calc('rouge-1','r',scores)
#Rouge-2
f1_r2=scores_calc('rouge-2','f',scores)
p_r2=scores_calc('rouge-2','p',scores)
r_r2=scores_calc('rouge-2','r',scores)
#Rouge-L
f1_rL=scores_calc('rouge-l','f',scores)
p_rL=scores_calc('rouge-l','p',scores)
r_rL=scores_calc('rouge-l','r',scores)
"""
Appending the mean for all the topics in single list.
"""
#Rouge-1
f_r1_avg_all_topics=average_rouge(f1_r1)
p_r1_avg_all_topics=average_rouge(p_r1)
r_r1_avg_all_topics=average_rouge(r_r1)
#Rouge-2
f_r2_avg_all_topics=average_rouge(f1_r2)
p_r2_avg_all_topics=average_rouge(p_r2)
r_r2_avg_all_topics=average_rouge(r_r2)
#Rouge-L
f_rL_avg_all_topics=average_rouge(f1_rL)
p_rL_avg_all_topics=average_rouge(p_rL)
r_rL_avg_all_topics=average_rouge(r_rL)
"""
Creating dataframe
"""
rouge_list=['Rouge 1', 'Rouge 2', 'Rouge L']
f_score=pd.DataFrame([f_r1_avg_all_topics,f_r2_avg_all_topics,f_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
f_score.index = rouge_list
print(f_score)
p_score=pd.DataFrame([p_r1_avg_all_topics,p_r2_avg_all_topics,p_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
p_score.index = rouge_list
print(p_score)
r_score=pd.DataFrame([r_r1_avg_all_topics,r_r2_avg_all_topics,r_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
r_score.index = rouge_list
print(r_score)
"""
Generating plots for f-score, p-score and r-score with metric Rouge-1, Rouge-2 and Rouge-L for all of the topics.
"""
fig1,axs=plt.subplots(1,3,figsize=(12,4))
score_type=zip([f_score,p_score,r_score],["F","R","P"])
for metric,metric_str in score_type:
# plt.close()
if metric_str=="F":
axs[0].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[0].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[0].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[0].legend()
axs[0].title.set_text('F-Score')
axs[0].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
# axs[0].xtick_params(labelrotation=90)
# axs[1].set_xticks([0,1,2,3,4])
# axs[1].set_xticklabels(["Business","Entertainment","Politics","Sports","Tech"])
if metric_str=="P":
axs[1].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[1].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[1].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[1].legend()
axs[1].title.set_text('P-Score')
axs[1].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
if metric_str=="R":
axs[2].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[2].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[2].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[2].legend()
axs[2].title.set_text('R-Score')
axs[2].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
# title=metric_str+"-Score for Rouge-1, Rouge-2 and Rouge-L"
# plt.tight_layout(rect=[0, 0, 1, 0.95])
# filename=metric_str+"_score.png"
# fig1.savefig(os.path.join("Plots/",filename))
calculate_mean_score_plots()
from google.colab import files
data_to_load = files.upload()
def scores_calc(rouge,metric,scores):
outer_list=[]
for topic in scores:
inner_list=[]
for article in topic:
f1_tmp=article[rouge][metric]
inner_list.append(f1_tmp)
outer_list.append(inner_list)
return outer_list
def average_rouge(itr):
metric_common=[]
for i in range(5):
temp=sum(itr[i])/len(itr[i])
metric_common.append(temp)
return metric_common
def calculate_mean_score_plots():
"""
Input scores from Rouge
Returns:
Mean of Precision and for Rouge-1, Rouge-2 and Rouge-L
Mean of Recall for Rouge-1, Rouge-2 and Rouge-L
Mean of F-1 Score for Rouge-1, Rouge-2 and Rouge-L
"""
with open('/content/list_scores (1).pkl','rb') as f:
scores=pickle.load(f)
#Rouge-1
f1_r1=scores_calc('rouge-1','f',scores)
p_r1=scores_calc('rouge-1','p',scores)
r_r1=scores_calc('rouge-1','r',scores)
#Rouge-2
f1_r2=scores_calc('rouge-2','f',scores)
p_r2=scores_calc('rouge-2','p',scores)
r_r2=scores_calc('rouge-2','r',scores)
#Rouge-L
f1_rL=scores_calc('rouge-l','f',scores)
p_rL=scores_calc('rouge-l','p',scores)
r_rL=scores_calc('rouge-l','r',scores)
"""
Appending the mean for all the topics in single list.
"""
#Rouge-1
f_r1_avg_all_topics=average_rouge(f1_r1)
p_r1_avg_all_topics=average_rouge(p_r1)
r_r1_avg_all_topics=average_rouge(r_r1)
#Rouge-2
f_r2_avg_all_topics=average_rouge(f1_r2)
p_r2_avg_all_topics=average_rouge(p_r2)
r_r2_avg_all_topics=average_rouge(r_r2)
#Rouge-L
f_rL_avg_all_topics=average_rouge(f1_rL)
p_rL_avg_all_topics=average_rouge(p_rL)
r_rL_avg_all_topics=average_rouge(r_rL)
"""
Creating dataframe
"""
rouge_list=['Rouge 1', 'Rouge 2', 'Rouge L']
f_score=pd.DataFrame([f_r1_avg_all_topics,f_r2_avg_all_topics,f_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
f_score.index = rouge_list
print(f_score)
p_score=pd.DataFrame([p_r1_avg_all_topics,p_r2_avg_all_topics,p_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
p_score.index = rouge_list
print(p_score)
r_score=pd.DataFrame([r_r1_avg_all_topics,r_r2_avg_all_topics,r_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
r_score.index = rouge_list
print(r_score)
"""
Generating plots for f-score, p-score and r-score with metric Rouge-1, Rouge-2 and Rouge-L for all of the topics.
"""
fig1,axs=plt.subplots(1,3,figsize=(12,4))
score_type=zip([f_score,p_score,r_score],["F","R","P"]) # because flipped inputs in the get scores of rouge . fliiped inputs
for metric,metric_str in score_type:
# plt.close()
if metric_str=="F":
axs[0].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[0].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[0].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[0].legend()
axs[0].title.set_text('F-Score')
axs[0].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
# axs[0].xtick_params(labelrotation=90)
# axs[1].set_xticks([0,1,2,3,4])
# axs[1].set_xticklabels(["Business","Entertainment","Politics","Sports","Tech"])
if metric_str=="P":
axs[1].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[1].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[1].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[1].legend()
axs[1].title.set_text('P-Score')
axs[1].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
if metric_str=="R":
axs[2].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[2].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[2].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[2].legend()
axs[2].title.set_text('R-Score')
axs[2].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
# title=metric_str+"-Score for Rouge-1, Rouge-2 and Rouge-L"
# plt.tight_layout(rect=[0, 0, 1, 0.95])
# filename=metric_str+"_score.png"
# fig1.savefig(os.path.join("Plots/",filename))
calculate_mean_score_plots()
from google.colab import files
data_to_load = files.upload()
def scores_calc(rouge,metric,scores):
outer_list=[]
for topic in scores:
inner_list=[]
for article in topic:
f1_tmp=article[rouge][metric]
inner_list.append(f1_tmp)
outer_list.append(inner_list)
return outer_list
def average_rouge(itr):
metric_common=[]
for i in range(5):
temp=sum(itr[i])/len(itr[i])
metric_common.append(temp)
return metric_common
def calculate_mean_score_plots():
"""
Input scores from Rouge
Returns:
Mean of Precision and for Rouge-1, Rouge-2 and Rouge-L
Mean of Recall for Rouge-1, Rouge-2 and Rouge-L
Mean of F-1 Score for Rouge-1, Rouge-2 and Rouge-L
"""
with open('/content/list_scores_textrank (1).pkl','rb') as f:
scores=pickle.load(f)
#Rouge-1
f1_r1=scores_calc('rouge-1','f',scores)
p_r1=scores_calc('rouge-1','p',scores)
r_r1=scores_calc('rouge-1','r',scores)
#Rouge-2
f1_r2=scores_calc('rouge-2','f',scores)
p_r2=scores_calc('rouge-2','p',scores)
r_r2=scores_calc('rouge-2','r',scores)
#Rouge-L
f1_rL=scores_calc('rouge-l','f',scores)
p_rL=scores_calc('rouge-l','p',scores)
r_rL=scores_calc('rouge-l','r',scores)
"""
Appending the mean for all the topics in single list.
"""
#Rouge-1
f_r1_avg_all_topics=average_rouge(f1_r1)
p_r1_avg_all_topics=average_rouge(p_r1)
r_r1_avg_all_topics=average_rouge(r_r1)
#Rouge-2
f_r2_avg_all_topics=average_rouge(f1_r2)
p_r2_avg_all_topics=average_rouge(p_r2)
r_r2_avg_all_topics=average_rouge(r_r2)
#Rouge-L
f_rL_avg_all_topics=average_rouge(f1_rL)
p_rL_avg_all_topics=average_rouge(p_rL)
r_rL_avg_all_topics=average_rouge(r_rL)
"""
Creating dataframe
"""
rouge_list=['Rouge 1', 'Rouge 2', 'Rouge L']
f_score=pd.DataFrame([f_r1_avg_all_topics,f_r2_avg_all_topics,f_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
f_score.index = rouge_list
print(f_score)
p_score=pd.DataFrame([p_r1_avg_all_topics,p_r2_avg_all_topics,p_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
p_score.index = rouge_list
print(p_score)
r_score=pd.DataFrame([r_r1_avg_all_topics,r_r2_avg_all_topics,r_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
r_score.index = rouge_list
print(r_score)
"""
Generating plots for f-score, p-score and r-score with metric Rouge-1, Rouge-2 and Rouge-L for all of the topics.
"""
fig1,axs=plt.subplots(1,3,figsize=(12,4))
score_type=zip([f_score,p_score,r_score],["F","R","P"])
for metric,metric_str in score_type:
# plt.close()
if metric_str=="F":
axs[0].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[0].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[0].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[0].legend()
axs[0].title.set_text('F-Score')
axs[0].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
# axs[0].xtick_params(labelrotation=90)
# axs[1].set_xticks([0,1,2,3,4])
# axs[1].set_xticklabels(["Business","Entertainment","Politics","Sports","Tech"])
if metric_str=="P":
axs[1].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[1].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[1].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[1].legend()
axs[1].title.set_text('P-Score')
axs[1].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
if metric_str=="R":
axs[2].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[2].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[2].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[2].legend()
axs[2].title.set_text('R-Score')
axs[2].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
# title=metric_str+"-Score for Rouge-1, Rouge-2 and Rouge-L"
# plt.tight_layout(rect=[0, 0, 1, 0.95])
# filename=metric_str+"_score.png"
# fig1.savefig(os.path.join("Plots/",filename))
0.58+0.61
calculate_mean_score_plots()
{'rouge-1': {'f': 0.3578947333401663, 'p': 0.23129251700680273, 'r': 0.7906976744186046},
'rouge-2': {'f': 0.28723403908329564, 'p': 0.18493150684931506, 'r': 0.6428571428571429},
'rouge-l': {'f': 0.4295301973532724, 'p': 0.2962962962962963, 'r': 0.7804878048780488}}
ensemble_prec=ensemble_prec.empty
ensemble_prec
```
precision for rouge 1 2 and l
```
ensemble=pd.DataFrame({'Business':0.79,'Entertainment':0.78,'politics':0.77,'Sports':0.76,'Tech':0.77},index=[0])
ensemble=pd.concat([ensemble,pd.DataFrame({'Business':0.640,'Entertainment':0.65,'politics':0.65,'Sports':0.65,'Tech':0.64},index=[1])],axis=0)
ensemble=pd.concat([ensemble,pd.DataFrame({'Business':0.78,'Entertainment':0.75,'politics':0.77,'Sports':0.77,'Tech':0.76},index=[2])],axis=0)
ensemble=ensemble.reset_index(drop=True)
ensemble
import matplotlib.pyplot as plt
import pandas as pd
plt.plot(ensemble.iloc[0,:])
plt.plot(ensemble.iloc[1,:])
plt.plot(ensemble.iloc[2,:])
plt.legend(['Rouge-1','Rouge-2','Rouge-L'])
plt.title('Precision Rouge for Ensembe')
plt.xlabel('Topic')
plt.ylabel('Precision')
```
## lstm
```
df=pd.DataFrame({'F-Score': [0.729,0.664,0.704], 'P-Score': [0.74,0.68,0.72], 'R-Score': [0.72,0.65,0.69]})
df.index=['T5 Transformer','LSTM (GloVe)','LSTM (FastText)']
df
import plotly.graph_objects as graph
import matplotlib.pyplot as plt
stances=['T5 Transformer','LSTM (GloVe)','LSTM (FastText)']
# plt.figure(figsize=(,6))
fig = graph.Figure(data=[
graph.Bar(name='F-Score', x=stances, y=[0.729,0.664,0.704]),
graph.Bar(name='P-Score', x=stances, y= [0.74,0.68,0.72]),
graph.Bar(name='R-Score', x=stances, y=[0.72,0.65,0.69])],
layout = graph.Layout(
plot_bgcolor='rgba(0,0,0,0)',
legend=dict(
orientation="h",
yanchor="bottom",
y=1.02,
xanchor="right",
x=1,
),
annotations=[
dict(
x=0,
y=0.75,
xref='paper',
yref='paper',
text='',
showarrow=False
)]))
fig.update_xaxes(showgrid=True, gridwidth=2, gridcolor='Gray')
fig.update_yaxes(showgrid=True, gridwidth=2, gridcolor='Gray')
# fig.show()
# Change the bar mode
fig.update_layout(barmode='group')
fig.update_layout(
autosize=True,
width=450,
height=400)
fig.show()
from textblob import TextBlob
TextBlob("full bodied coffee").sentiment # real
TextBlob("bodied coffee").sentiment #t5
TextBlob("great bodied UNK").sentiment # lstm
TextBlob("great bodied coffee").sentiment # lstm fasttext
TextBlob("Best GF pasta on the market!").sentiment # real
TextBlob("gluten free pasta").sentiment # t5
TextBlob("best UNK pasta ever").sentiment # lstm glove
TextBlob("best gluten pasta ever").sentiment # lstm fasttext
```
|Gold Summary | Real | T5 | LSTM(GloVe) | LSTM(FastText) |
|----|--|--|--|--|
|full bodied coffee|0.35|0|0.7|0.8|
|Best GF pasta on the market!|1.0|0.4|1.0|1.0
```
plt.plot([0.47,0.78,0.54])
plt.legend(['Rouge-1','Rouge-2','Rouge-L'])
plt.title('Precision Rouge for Ensembe')
plt.xlabel('Topic')
plt.ylabel('Precision')
import matplotlib.pyplot as plt
x = ['T5 Transformer', 'LSTM (GloVe)', 'LSTM (FastText)']
# x=[0.47,0.78,0.54]
# create an index for each tick position
xi = range(len(x))
# y = [0,10,20,30,40,50,60,70,80,90,100]
# plt.ylim(0.8,1.4)
# plot the index for the x-values
plt.plot([47,78,54], marker='o', linestyle='--', color='b')
plt.xlabel('Abstractive Summarizer')
plt.ylabel('Percentage Change')
plt.xticks(xi, x)
# plt.yticks(range(len([0,10,20,30,40,50,60,70,80,90,100])),[0,10,20,30,40,50,60,70,80,90,100])
plt.title('Average Polarity Change')
# plt.legend()
plt.show()
```
wikipedia
```
# Wikipedia scraper
import bs4 as bs
import urllib.request
import re
import nltk
import logging
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
from gensim.summarization import summarize
from gensim.summarization import keywords
url_topull = input('Enter the Wikipedia URL to pull - ')
scraped_data = urllib.request.urlopen(url_topull)
article = scraped_data.read()
parsed_article = bs.BeautifulSoup(article,'lxml')
paragraphs = parsed_article.find_all('p')
article_text = ""
for p in paragraphs:
article_text += p.text
print("Data pull done")
print("==================================SUMMARY===================================")
print (summarize(article_text,ratio=0.02))
print("==================================KEYWORDS===================================")
print (keywords(article_text,ratio=0.02))
```
The name "coronavirus" is derived from Latin corona, meaning "crown" or "wreath", itself a borrowing from Greek κορώνη korṓnē, "garland, wreath".[11][12] The name was coined by June Almeida and David Tyrrell who first observed and studied human coronaviruses.[13] The word was first used in print in 1968 by an informal group of virologists in the journal Nature to designate the new family of viruses.[10] The name refers to the characteristic appearance of virions (the infective form of the virus) by electron microscopy, which have a fringe of large, bulbous surface projections creating an image reminiscent of the solar corona or halo.[10][13] This morphology is created by the viral spike peplomers, which are proteins on the surface of the virus.[14]
```
```
|
github_jupyter
|
from google.colab import files
data_to_load = files.upload()
import io
import pandas as pd
import pickle
import matplotlib.pyplot as plt
import os
def scores_calc(rouge,metric,scores):
outer_list=[]
for topic in scores:
inner_list=[]
for article in topic:
f1_tmp=article[rouge][metric]
inner_list.append(f1_tmp)
outer_list.append(inner_list)
return outer_list
def average_rouge(itr):
metric_common=[]
for i in range(5):
temp=sum(itr[i])/len(itr[i])
metric_common.append(temp)
return metric_common
def calculate_mean_score_plots():
"""
Input scores from Rouge
Returns:
Mean of Precision and for Rouge-1, Rouge-2 and Rouge-L
Mean of Recall for Rouge-1, Rouge-2 and Rouge-L
Mean of F-1 Score for Rouge-1, Rouge-2 and Rouge-L
"""
with open('/content/list_scores.pkl','rb') as f:
scores=pickle.load(f)
#Rouge-1
f1_r1=scores_calc('rouge-1','f',scores)
p_r1=scores_calc('rouge-1','p',scores)
r_r1=scores_calc('rouge-1','r',scores)
#Rouge-2
f1_r2=scores_calc('rouge-2','f',scores)
p_r2=scores_calc('rouge-2','p',scores)
r_r2=scores_calc('rouge-2','r',scores)
#Rouge-L
f1_rL=scores_calc('rouge-l','f',scores)
p_rL=scores_calc('rouge-l','p',scores)
r_rL=scores_calc('rouge-l','r',scores)
"""
Appending the mean for all the topics in single list.
"""
#Rouge-1
f_r1_avg_all_topics=average_rouge(f1_r1)
p_r1_avg_all_topics=average_rouge(p_r1)
r_r1_avg_all_topics=average_rouge(r_r1)
#Rouge-2
f_r2_avg_all_topics=average_rouge(f1_r2)
p_r2_avg_all_topics=average_rouge(p_r2)
r_r2_avg_all_topics=average_rouge(r_r2)
#Rouge-L
f_rL_avg_all_topics=average_rouge(f1_rL)
p_rL_avg_all_topics=average_rouge(p_rL)
r_rL_avg_all_topics=average_rouge(r_rL)
"""
Creating dataframe
"""
rouge_list=['Rouge 1', 'Rouge 2', 'Rouge L']
f_score=pd.DataFrame([f_r1_avg_all_topics,f_r2_avg_all_topics,f_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
f_score.index = rouge_list
print(f_score)
p_score=pd.DataFrame([p_r1_avg_all_topics,p_r2_avg_all_topics,p_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
p_score.index = rouge_list
print(p_score)
r_score=pd.DataFrame([r_r1_avg_all_topics,r_r2_avg_all_topics,r_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
r_score.index = rouge_list
print(r_score)
"""
Generating plots for f-score, p-score and r-score with metric Rouge-1, Rouge-2 and Rouge-L for all of the topics.
"""
fig1,axs=plt.subplots(1,3,figsize=(12,4))
score_type=zip([f_score,p_score,r_score],["F","R","P"])
for metric,metric_str in score_type:
# plt.close()
if metric_str=="F":
axs[0].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[0].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[0].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[0].legend()
axs[0].title.set_text('F-Score')
axs[0].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
# axs[0].xtick_params(labelrotation=90)
# axs[1].set_xticks([0,1,2,3,4])
# axs[1].set_xticklabels(["Business","Entertainment","Politics","Sports","Tech"])
if metric_str=="P":
axs[1].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[1].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[1].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[1].legend()
axs[1].title.set_text('P-Score')
axs[1].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
if metric_str=="R":
axs[2].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[2].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[2].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[2].legend()
axs[2].title.set_text('R-Score')
axs[2].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
# title=metric_str+"-Score for Rouge-1, Rouge-2 and Rouge-L"
# plt.tight_layout(rect=[0, 0, 1, 0.95])
# filename=metric_str+"_score.png"
# fig1.savefig(os.path.join("Plots/",filename))
calculate_mean_score_plots()
from google.colab import files
data_to_load = files.upload()
def scores_calc(rouge,metric,scores):
outer_list=[]
for topic in scores:
inner_list=[]
for article in topic:
f1_tmp=article[rouge][metric]
inner_list.append(f1_tmp)
outer_list.append(inner_list)
return outer_list
def average_rouge(itr):
metric_common=[]
for i in range(5):
temp=sum(itr[i])/len(itr[i])
metric_common.append(temp)
return metric_common
def calculate_mean_score_plots():
"""
Input scores from Rouge
Returns:
Mean of Precision and for Rouge-1, Rouge-2 and Rouge-L
Mean of Recall for Rouge-1, Rouge-2 and Rouge-L
Mean of F-1 Score for Rouge-1, Rouge-2 and Rouge-L
"""
with open('/content/list_scores (1).pkl','rb') as f:
scores=pickle.load(f)
#Rouge-1
f1_r1=scores_calc('rouge-1','f',scores)
p_r1=scores_calc('rouge-1','p',scores)
r_r1=scores_calc('rouge-1','r',scores)
#Rouge-2
f1_r2=scores_calc('rouge-2','f',scores)
p_r2=scores_calc('rouge-2','p',scores)
r_r2=scores_calc('rouge-2','r',scores)
#Rouge-L
f1_rL=scores_calc('rouge-l','f',scores)
p_rL=scores_calc('rouge-l','p',scores)
r_rL=scores_calc('rouge-l','r',scores)
"""
Appending the mean for all the topics in single list.
"""
#Rouge-1
f_r1_avg_all_topics=average_rouge(f1_r1)
p_r1_avg_all_topics=average_rouge(p_r1)
r_r1_avg_all_topics=average_rouge(r_r1)
#Rouge-2
f_r2_avg_all_topics=average_rouge(f1_r2)
p_r2_avg_all_topics=average_rouge(p_r2)
r_r2_avg_all_topics=average_rouge(r_r2)
#Rouge-L
f_rL_avg_all_topics=average_rouge(f1_rL)
p_rL_avg_all_topics=average_rouge(p_rL)
r_rL_avg_all_topics=average_rouge(r_rL)
"""
Creating dataframe
"""
rouge_list=['Rouge 1', 'Rouge 2', 'Rouge L']
f_score=pd.DataFrame([f_r1_avg_all_topics,f_r2_avg_all_topics,f_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
f_score.index = rouge_list
print(f_score)
p_score=pd.DataFrame([p_r1_avg_all_topics,p_r2_avg_all_topics,p_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
p_score.index = rouge_list
print(p_score)
r_score=pd.DataFrame([r_r1_avg_all_topics,r_r2_avg_all_topics,r_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
r_score.index = rouge_list
print(r_score)
"""
Generating plots for f-score, p-score and r-score with metric Rouge-1, Rouge-2 and Rouge-L for all of the topics.
"""
fig1,axs=plt.subplots(1,3,figsize=(12,4))
score_type=zip([f_score,p_score,r_score],["F","R","P"]) # because flipped inputs in the get scores of rouge . fliiped inputs
for metric,metric_str in score_type:
# plt.close()
if metric_str=="F":
axs[0].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[0].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[0].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[0].legend()
axs[0].title.set_text('F-Score')
axs[0].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
# axs[0].xtick_params(labelrotation=90)
# axs[1].set_xticks([0,1,2,3,4])
# axs[1].set_xticklabels(["Business","Entertainment","Politics","Sports","Tech"])
if metric_str=="P":
axs[1].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[1].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[1].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[1].legend()
axs[1].title.set_text('P-Score')
axs[1].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
if metric_str=="R":
axs[2].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[2].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[2].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[2].legend()
axs[2].title.set_text('R-Score')
axs[2].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
# title=metric_str+"-Score for Rouge-1, Rouge-2 and Rouge-L"
# plt.tight_layout(rect=[0, 0, 1, 0.95])
# filename=metric_str+"_score.png"
# fig1.savefig(os.path.join("Plots/",filename))
calculate_mean_score_plots()
from google.colab import files
data_to_load = files.upload()
def scores_calc(rouge,metric,scores):
outer_list=[]
for topic in scores:
inner_list=[]
for article in topic:
f1_tmp=article[rouge][metric]
inner_list.append(f1_tmp)
outer_list.append(inner_list)
return outer_list
def average_rouge(itr):
metric_common=[]
for i in range(5):
temp=sum(itr[i])/len(itr[i])
metric_common.append(temp)
return metric_common
def calculate_mean_score_plots():
"""
Input scores from Rouge
Returns:
Mean of Precision and for Rouge-1, Rouge-2 and Rouge-L
Mean of Recall for Rouge-1, Rouge-2 and Rouge-L
Mean of F-1 Score for Rouge-1, Rouge-2 and Rouge-L
"""
with open('/content/list_scores_textrank (1).pkl','rb') as f:
scores=pickle.load(f)
#Rouge-1
f1_r1=scores_calc('rouge-1','f',scores)
p_r1=scores_calc('rouge-1','p',scores)
r_r1=scores_calc('rouge-1','r',scores)
#Rouge-2
f1_r2=scores_calc('rouge-2','f',scores)
p_r2=scores_calc('rouge-2','p',scores)
r_r2=scores_calc('rouge-2','r',scores)
#Rouge-L
f1_rL=scores_calc('rouge-l','f',scores)
p_rL=scores_calc('rouge-l','p',scores)
r_rL=scores_calc('rouge-l','r',scores)
"""
Appending the mean for all the topics in single list.
"""
#Rouge-1
f_r1_avg_all_topics=average_rouge(f1_r1)
p_r1_avg_all_topics=average_rouge(p_r1)
r_r1_avg_all_topics=average_rouge(r_r1)
#Rouge-2
f_r2_avg_all_topics=average_rouge(f1_r2)
p_r2_avg_all_topics=average_rouge(p_r2)
r_r2_avg_all_topics=average_rouge(r_r2)
#Rouge-L
f_rL_avg_all_topics=average_rouge(f1_rL)
p_rL_avg_all_topics=average_rouge(p_rL)
r_rL_avg_all_topics=average_rouge(r_rL)
"""
Creating dataframe
"""
rouge_list=['Rouge 1', 'Rouge 2', 'Rouge L']
f_score=pd.DataFrame([f_r1_avg_all_topics,f_r2_avg_all_topics,f_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
f_score.index = rouge_list
print(f_score)
p_score=pd.DataFrame([p_r1_avg_all_topics,p_r2_avg_all_topics,p_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
p_score.index = rouge_list
print(p_score)
r_score=pd.DataFrame([r_r1_avg_all_topics,r_r2_avg_all_topics,r_rL_avg_all_topics],columns=['Business',\
'Entertainment','Politics','Sport','Tech'])
r_score.index = rouge_list
print(r_score)
"""
Generating plots for f-score, p-score and r-score with metric Rouge-1, Rouge-2 and Rouge-L for all of the topics.
"""
fig1,axs=plt.subplots(1,3,figsize=(12,4))
score_type=zip([f_score,p_score,r_score],["F","R","P"])
for metric,metric_str in score_type:
# plt.close()
if metric_str=="F":
axs[0].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[0].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[0].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[0].legend()
axs[0].title.set_text('F-Score')
axs[0].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
# axs[0].xtick_params(labelrotation=90)
# axs[1].set_xticks([0,1,2,3,4])
# axs[1].set_xticklabels(["Business","Entertainment","Politics","Sports","Tech"])
if metric_str=="P":
axs[1].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[1].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[1].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[1].legend()
axs[1].title.set_text('P-Score')
axs[1].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
if metric_str=="R":
axs[2].plot([0,1,2,3,4],metric.iloc[0,:],'b',label='Rouge-1')
axs[2].plot([0,1,2,3,4],metric.iloc[1,:],'r',label='Rouge-2')
axs[2].plot([0,1,2,3,4],metric.iloc[2,:],'g',label='Rouge-L')
axs[2].legend()
axs[2].title.set_text('R-Score')
axs[2].set_xticklabels(["ss","Business","Entertainment","Politics","Sports","Tech"])
for ax in fig1.axes:
plt.sca(ax)
plt.xticks(rotation=25)
# title=metric_str+"-Score for Rouge-1, Rouge-2 and Rouge-L"
# plt.tight_layout(rect=[0, 0, 1, 0.95])
# filename=metric_str+"_score.png"
# fig1.savefig(os.path.join("Plots/",filename))
0.58+0.61
calculate_mean_score_plots()
{'rouge-1': {'f': 0.3578947333401663, 'p': 0.23129251700680273, 'r': 0.7906976744186046},
'rouge-2': {'f': 0.28723403908329564, 'p': 0.18493150684931506, 'r': 0.6428571428571429},
'rouge-l': {'f': 0.4295301973532724, 'p': 0.2962962962962963, 'r': 0.7804878048780488}}
ensemble_prec=ensemble_prec.empty
ensemble_prec
ensemble=pd.DataFrame({'Business':0.79,'Entertainment':0.78,'politics':0.77,'Sports':0.76,'Tech':0.77},index=[0])
ensemble=pd.concat([ensemble,pd.DataFrame({'Business':0.640,'Entertainment':0.65,'politics':0.65,'Sports':0.65,'Tech':0.64},index=[1])],axis=0)
ensemble=pd.concat([ensemble,pd.DataFrame({'Business':0.78,'Entertainment':0.75,'politics':0.77,'Sports':0.77,'Tech':0.76},index=[2])],axis=0)
ensemble=ensemble.reset_index(drop=True)
ensemble
import matplotlib.pyplot as plt
import pandas as pd
plt.plot(ensemble.iloc[0,:])
plt.plot(ensemble.iloc[1,:])
plt.plot(ensemble.iloc[2,:])
plt.legend(['Rouge-1','Rouge-2','Rouge-L'])
plt.title('Precision Rouge for Ensembe')
plt.xlabel('Topic')
plt.ylabel('Precision')
df=pd.DataFrame({'F-Score': [0.729,0.664,0.704], 'P-Score': [0.74,0.68,0.72], 'R-Score': [0.72,0.65,0.69]})
df.index=['T5 Transformer','LSTM (GloVe)','LSTM (FastText)']
df
import plotly.graph_objects as graph
import matplotlib.pyplot as plt
stances=['T5 Transformer','LSTM (GloVe)','LSTM (FastText)']
# plt.figure(figsize=(,6))
fig = graph.Figure(data=[
graph.Bar(name='F-Score', x=stances, y=[0.729,0.664,0.704]),
graph.Bar(name='P-Score', x=stances, y= [0.74,0.68,0.72]),
graph.Bar(name='R-Score', x=stances, y=[0.72,0.65,0.69])],
layout = graph.Layout(
plot_bgcolor='rgba(0,0,0,0)',
legend=dict(
orientation="h",
yanchor="bottom",
y=1.02,
xanchor="right",
x=1,
),
annotations=[
dict(
x=0,
y=0.75,
xref='paper',
yref='paper',
text='',
showarrow=False
)]))
fig.update_xaxes(showgrid=True, gridwidth=2, gridcolor='Gray')
fig.update_yaxes(showgrid=True, gridwidth=2, gridcolor='Gray')
# fig.show()
# Change the bar mode
fig.update_layout(barmode='group')
fig.update_layout(
autosize=True,
width=450,
height=400)
fig.show()
from textblob import TextBlob
TextBlob("full bodied coffee").sentiment # real
TextBlob("bodied coffee").sentiment #t5
TextBlob("great bodied UNK").sentiment # lstm
TextBlob("great bodied coffee").sentiment # lstm fasttext
TextBlob("Best GF pasta on the market!").sentiment # real
TextBlob("gluten free pasta").sentiment # t5
TextBlob("best UNK pasta ever").sentiment # lstm glove
TextBlob("best gluten pasta ever").sentiment # lstm fasttext
plt.plot([0.47,0.78,0.54])
plt.legend(['Rouge-1','Rouge-2','Rouge-L'])
plt.title('Precision Rouge for Ensembe')
plt.xlabel('Topic')
plt.ylabel('Precision')
import matplotlib.pyplot as plt
x = ['T5 Transformer', 'LSTM (GloVe)', 'LSTM (FastText)']
# x=[0.47,0.78,0.54]
# create an index for each tick position
xi = range(len(x))
# y = [0,10,20,30,40,50,60,70,80,90,100]
# plt.ylim(0.8,1.4)
# plot the index for the x-values
plt.plot([47,78,54], marker='o', linestyle='--', color='b')
plt.xlabel('Abstractive Summarizer')
plt.ylabel('Percentage Change')
plt.xticks(xi, x)
# plt.yticks(range(len([0,10,20,30,40,50,60,70,80,90,100])),[0,10,20,30,40,50,60,70,80,90,100])
plt.title('Average Polarity Change')
# plt.legend()
plt.show()
# Wikipedia scraper
import bs4 as bs
import urllib.request
import re
import nltk
import logging
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
from gensim.summarization import summarize
from gensim.summarization import keywords
url_topull = input('Enter the Wikipedia URL to pull - ')
scraped_data = urllib.request.urlopen(url_topull)
article = scraped_data.read()
parsed_article = bs.BeautifulSoup(article,'lxml')
paragraphs = parsed_article.find_all('p')
article_text = ""
for p in paragraphs:
article_text += p.text
print("Data pull done")
print("==================================SUMMARY===================================")
print (summarize(article_text,ratio=0.02))
print("==================================KEYWORDS===================================")
print (keywords(article_text,ratio=0.02))
| 0.39036 | 0.351617 |
# Publications markdown generator for academicpages
Takes a set of bibtex of publications and converts them for use with [academicpages.github.io](academicpages.github.io). This is an interactive Jupyter notebook ([see more info here](http://jupyter-notebook-beginner-guide.readthedocs.io/en/latest/what_is_jupyter.html)).
The core python code is also in `pubsFromBibs.py`.
Run either from the `markdown_generator` folder after replacing updating the publist dictionary with:
* bib file names
* specific venue keys based on your bib file preferences
* any specific pre-text for specific files
* Collection Name (future feature)
TODO: Make this work with other databases of citations,
TODO: Merge this with the existing TSV parsing solution
```
from pybtex.database.input import bibtex
import pybtex.database.input.bibtex
from time import strptime
import string
import html
import os
import re
#todo: incorporate different collection types rather than a catch all publications, requires other changes to template
publist = {
"proceeding": {
"file" : "proceedings.bib",
"venuekey": "booktitle",
"venue-pretext": "In the proceedings of ",
"collection" : {"name":"publications",
"permalink":"/publication/"}
},
"journal":{
"file": "pubs.bib",
"venuekey" : "journal",
"venue-pretext" : "",
"collection" : {"name":"publications",
"permalink":"/publication/"}
}
}
html_escape_table = {
"&": "&",
'"': """,
"'": "'"
}
def html_escape(text):
"""Produce entities within text."""
return "".join(html_escape_table.get(c,c) for c in text)
for pubsource in publist:
parser = bibtex.Parser()
bibdata = parser.parse_file(publist[pubsource]["file"])
#loop through the individual references in a given bibtex file
for bib_id in bibdata.entries:
#reset default date
pub_year = "1900"
pub_month = "01"
pub_day = "01"
b = bibdata.entries[bib_id].fields
try:
pub_year = f'{b["year"]}'
#todo: this hack for month and day needs some cleanup
if "month" in b.keys():
if(len(b["month"])<3):
pub_month = "0"+b["month"]
pub_month = pub_month[-2:]
elif(b["month"] not in range(12)):
tmnth = strptime(b["month"][:3],'%b').tm_mon
pub_month = "{:02d}".format(tmnth)
else:
pub_month = str(b["month"])
if "day" in b.keys():
pub_day = str(b["day"])
pub_date = pub_year+"-"+pub_month+"-"+pub_day
#strip out {} as needed (some bibtex entries that maintain formatting)
clean_title = b["title"].replace("{", "").replace("}","").replace("\\","").replace(" ","-")
url_slug = re.sub("\\[.*\\]|[^a-zA-Z0-9_-]", "", clean_title)
url_slug = url_slug.replace("--","-")
md_filename = (str(pub_date) + "-" + url_slug + ".md").replace("--","-")
html_filename = (str(pub_date) + "-" + url_slug).replace("--","-")
#Build Citation from text
citation = ""
#citation authors - todo - add highlighting for primary author?
for author in bibdata.entries[bib_id].persons["author"]:
citation = citation+" "+author.first_names[0]+" "+author.last_names[0]+", "
#citation title
citation = citation + "\"" + html_escape(b["title"].replace("{", "").replace("}","").replace("\\","")) + ".\""
#add venue logic depending on citation type
venue = publist[pubsource]["venue-pretext"]+b[publist[pubsource]["venuekey"]].replace("{", "").replace("}","").replace("\\","")
citation = citation + " " + html_escape(venue)
citation = citation + ", " + pub_year + "."
## YAML variables
md = "---\ntitle: \"" + html_escape(b["title"].replace("{", "").replace("}","").replace("\\","")) + '"\n'
md += """collection: """ + publist[pubsource]["collection"]["name"]
md += """\npermalink: """ + publist[pubsource]["collection"]["permalink"] + html_filename
note = False
if "note" in b.keys():
if len(str(b["note"])) > 5:
md += "\nexcerpt: '" + html_escape(b["note"]) + "'"
note = True
md += "\ndate: " + str(pub_date)
md += "\nvenue: '" + html_escape(venue) + "'"
url = False
if "url" in b.keys():
if len(str(b["url"])) > 5:
md += "\npaperurl: '" + b["url"] + "'"
url = True
md += "\ncitation: '" + html_escape(citation) + "'"
md += "\n---"
## Markdown description for individual page
if note:
md += "\n" + html_escape(b["note"]) + "\n"
if url:
md += "\n[Access paper here](" + b["url"] + "){:target=\"_blank\"}\n"
else:
md += "\nUse [Google Scholar](https://scholar.google.com/scholar?q="+html.escape(clean_title.replace("-","+"))+"){:target=\"_blank\"} for full citation"
md_filename = os.path.basename(md_filename)
with open("../_publications/" + md_filename, 'w') as f:
f.write(md)
print(f'SUCESSFULLY PARSED {bib_id}: \"', b["title"][:60],"..."*(len(b['title'])>60),"\"")
# field may not exist for a reference
except KeyError as e:
print(f'WARNING Missing Expected Field {e} from entry {bib_id}: \"', b["title"][:30],"..."*(len(b['title'])>30),"\"")
continue
```
|
github_jupyter
|
from pybtex.database.input import bibtex
import pybtex.database.input.bibtex
from time import strptime
import string
import html
import os
import re
#todo: incorporate different collection types rather than a catch all publications, requires other changes to template
publist = {
"proceeding": {
"file" : "proceedings.bib",
"venuekey": "booktitle",
"venue-pretext": "In the proceedings of ",
"collection" : {"name":"publications",
"permalink":"/publication/"}
},
"journal":{
"file": "pubs.bib",
"venuekey" : "journal",
"venue-pretext" : "",
"collection" : {"name":"publications",
"permalink":"/publication/"}
}
}
html_escape_table = {
"&": "&",
'"': """,
"'": "'"
}
def html_escape(text):
"""Produce entities within text."""
return "".join(html_escape_table.get(c,c) for c in text)
for pubsource in publist:
parser = bibtex.Parser()
bibdata = parser.parse_file(publist[pubsource]["file"])
#loop through the individual references in a given bibtex file
for bib_id in bibdata.entries:
#reset default date
pub_year = "1900"
pub_month = "01"
pub_day = "01"
b = bibdata.entries[bib_id].fields
try:
pub_year = f'{b["year"]}'
#todo: this hack for month and day needs some cleanup
if "month" in b.keys():
if(len(b["month"])<3):
pub_month = "0"+b["month"]
pub_month = pub_month[-2:]
elif(b["month"] not in range(12)):
tmnth = strptime(b["month"][:3],'%b').tm_mon
pub_month = "{:02d}".format(tmnth)
else:
pub_month = str(b["month"])
if "day" in b.keys():
pub_day = str(b["day"])
pub_date = pub_year+"-"+pub_month+"-"+pub_day
#strip out {} as needed (some bibtex entries that maintain formatting)
clean_title = b["title"].replace("{", "").replace("}","").replace("\\","").replace(" ","-")
url_slug = re.sub("\\[.*\\]|[^a-zA-Z0-9_-]", "", clean_title)
url_slug = url_slug.replace("--","-")
md_filename = (str(pub_date) + "-" + url_slug + ".md").replace("--","-")
html_filename = (str(pub_date) + "-" + url_slug).replace("--","-")
#Build Citation from text
citation = ""
#citation authors - todo - add highlighting for primary author?
for author in bibdata.entries[bib_id].persons["author"]:
citation = citation+" "+author.first_names[0]+" "+author.last_names[0]+", "
#citation title
citation = citation + "\"" + html_escape(b["title"].replace("{", "").replace("}","").replace("\\","")) + ".\""
#add venue logic depending on citation type
venue = publist[pubsource]["venue-pretext"]+b[publist[pubsource]["venuekey"]].replace("{", "").replace("}","").replace("\\","")
citation = citation + " " + html_escape(venue)
citation = citation + ", " + pub_year + "."
## YAML variables
md = "---\ntitle: \"" + html_escape(b["title"].replace("{", "").replace("}","").replace("\\","")) + '"\n'
md += """collection: """ + publist[pubsource]["collection"]["name"]
md += """\npermalink: """ + publist[pubsource]["collection"]["permalink"] + html_filename
note = False
if "note" in b.keys():
if len(str(b["note"])) > 5:
md += "\nexcerpt: '" + html_escape(b["note"]) + "'"
note = True
md += "\ndate: " + str(pub_date)
md += "\nvenue: '" + html_escape(venue) + "'"
url = False
if "url" in b.keys():
if len(str(b["url"])) > 5:
md += "\npaperurl: '" + b["url"] + "'"
url = True
md += "\ncitation: '" + html_escape(citation) + "'"
md += "\n---"
## Markdown description for individual page
if note:
md += "\n" + html_escape(b["note"]) + "\n"
if url:
md += "\n[Access paper here](" + b["url"] + "){:target=\"_blank\"}\n"
else:
md += "\nUse [Google Scholar](https://scholar.google.com/scholar?q="+html.escape(clean_title.replace("-","+"))+"){:target=\"_blank\"} for full citation"
md_filename = os.path.basename(md_filename)
with open("../_publications/" + md_filename, 'w') as f:
f.write(md)
print(f'SUCESSFULLY PARSED {bib_id}: \"', b["title"][:60],"..."*(len(b['title'])>60),"\"")
# field may not exist for a reference
except KeyError as e:
print(f'WARNING Missing Expected Field {e} from entry {bib_id}: \"', b["title"][:30],"..."*(len(b['title'])>30),"\"")
continue
| 0.18462 | 0.373447 |
# Data Analytics - Preprocessing
# Pair 1 - BAJAJ-AUTO and HEROMOTOCO
---
# 1. Importing required modules
```
import os
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import coint
```
---
# 2. Get the dataset from pairs data
```
pair_df = pd.read_csv("../../Storage/pairs_data/HEROMOTOCO-BAJAJ-AUTO-0.csv")
pair_df.head()
pair_df.describe()
```
---
# 3. Calculation of correlation and co-integration
## 3.1. Calculation of correlation between the 2 stocks' closing prices
```
corr_df = pair_df[["HEROMOTOCO_Close", "BAJAJ-AUTO_Close"]]
corr_df.head()
corr = corr_df.corr()
corr.style.background_gradient()
```
- We can see that the closing prices of the 2 stocks are highly correlated
## 3.2. Calculation of p-value to see if the stocks are co-integrated
```
score, pvalue, _ = coint(pair_df["HEROMOTOCO_Close"], pair_df["BAJAJ-AUTO_Close"])
pvalue
```
- We also find that with a p-value < 0.05, the correlation is statistically significant
## 3.3. Visualization of the pair
```
pair_price_plt = pair_df.plot(x='Date', y=['HEROMOTOCO_Close', 'BAJAJ-AUTO_Close'], figsize=(30,15))
pair_price_plt.set_xlabel("Date")
pair_price_plt.set_ylabel("Price")
```
- We can see that even visually, the stocks are moving in tandem
- This further confirms the validity of the stock pair
---
# 4. Understanding the Spread between the stock pair
## 4.1. Visualizing the spread between the stock pair
```
pair_spread_mean = pair_df['Spread'].mean()
spread_std = pair_df['Spread'].std()
pair_spread_plt = pair_df.plot(x='Date', y=['Spread'], figsize=(30,15))
pair_spread_plt.axhline(pair_spread_mean, c='black')
pair_spread_plt.axhline(pair_spread_mean + spread_std, c='red', ls = "--")
pair_spread_plt.axhline(pair_spread_mean - spread_std, c='red', ls = "--")
pair_spread_plt.set_ylabel("Price")
```
__In the graph above:__
- The blue line is the spread
- The Black line is mean price
- The Red dotted lines represent 1 and 2 standard deviations above and below the mean respectively
## 4.2. Visualizing the zscore of spread between the stock pairs
```
pair_zscore_plt = pair_df.plot(x='Date', y='zscore', figsize=(30,15))
pair_zscore_plt.axhline(0, c='black')
pair_zscore_plt.axhline(1, c='red', ls = "--")
pair_zscore_plt.axhline(-1, c='red', ls = "--")
pair_spread_plt.set_ylabel("zscore")
```
__In the graph above:__
- The blue line is the zscore of the spread
- The Black line is at 0
- The Red dotted lines represent 1 and -1 respectively
---
# 5. Generating orders on the pair
## 5.1. Function definition and parameters for orders generation
```
# long positions
# short positions
# flat positions
# Get out of a position
def generate_orders(prices):
orders = []
position = "FLAT"
# Keep track of last price
# prev_price = None
for price in prices:
# Get out of a LONG position
if position == "LONG" and (price == 0 or price > 0):
orders.append("GET_OUT_OF_POSITION")
position = "FLAT"
# Get out of a SHORT position
elif position == "SHORT" and (price == 0 or price < 0):
orders.append("GET_OUT_OF_POSITION")
position = "FLAT"
# Get into a long position
elif price < -1.5:
position = "LONG"
orders.append("LONG")
# Get into a long position
elif price > 1.5:
position = "SHORT"
orders.append("SHORT")
# Default if no other order is placed
else:
orders.append("FLAT")
return orders
```
## 5.2. Making a copy of the dataframe to add orders
```
pair_orders_df = pair_df.copy()
pair_orders_df.head()
```
## 5.3. Generating orders on the pair
```
pair_orders_df["Orders"] = generate_orders(pair_df["zscore"])
pair_orders_df.head()
```
__In the orders above__:
- *LONG* - denotes that a LONG position be taken on HEROMOTOCO and simultaneously a SHORT position be taken on BAJAJ-AUTO on the closing price of that date.
- *SHORT* - denotes that a SHORT position be taken on HEROMOTOCO and simultaneously a LONG position be taken on BAJAJ-AUTO on the closing price of that date.
- *FLAT* - denotes no order to be placed on that day.
- *GET_OUT_OF_POSTION* - denotes to cash in on all previous orders on that date and have no out standing LONG or SHORT positions as of that date.
## 5.4 Display all orders which are not *FLAT*
```
pair_orders_df[pair_orders_df['Orders'] != "FLAT"]
```
## 5.5. Visualize the orders placed
```
# Plotting the zscore of the Spread of 20 day Simple Moving Average
orders_plt = pair_orders_df.plot(x='Date', y='zscore', figsize=(30,15))
# Plotting the lines at mean, 1 and 2 std. dev.
orders_plt.axhline(0, c='black')
orders_plt.axhline(1, c='red', ls = "--")
orders_plt.axhline(-1, c='red', ls = "--")
# Extracting orders
Orders = pair_orders_df['Orders']
# Plot vertical lines where orders are placed
for order in range(len(Orders)):
if Orders[order] != "FLAT":
# GREEN line for a long position
if Orders[order] == "LONG":
orders_plt.axvline(x=order, c = "green")
# RED line for a short position
elif Orders[order] == "SHORT":
orders_plt.axvline(x=order, c = "red")
# BLACK line for getting out of all positions at that point
else:
orders_plt.axvline(x=order, c = "black")
```
__In the figure above:__
- __Blue line__ - zscore of the Spread
- __Black horizontal line__ at 0 - Mean
- __Red dotted horizontal lines__ - at +1 and -1 standard deviations
- __Green vertical line__ - represents long position taken on that day
- __Red vertical line__ - represents short position taken on that day
- __Black vertical line__ - represents getting out of all open positions till that point
## 5.6 Put the orders into a csv
```
pair_orders_df = pair_orders_df.set_index('Date')
pair_orders_df.to_csv('Pair1_orders.csv')
```
|
github_jupyter
|
import os
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import coint
pair_df = pd.read_csv("../../Storage/pairs_data/HEROMOTOCO-BAJAJ-AUTO-0.csv")
pair_df.head()
pair_df.describe()
corr_df = pair_df[["HEROMOTOCO_Close", "BAJAJ-AUTO_Close"]]
corr_df.head()
corr = corr_df.corr()
corr.style.background_gradient()
score, pvalue, _ = coint(pair_df["HEROMOTOCO_Close"], pair_df["BAJAJ-AUTO_Close"])
pvalue
pair_price_plt = pair_df.plot(x='Date', y=['HEROMOTOCO_Close', 'BAJAJ-AUTO_Close'], figsize=(30,15))
pair_price_plt.set_xlabel("Date")
pair_price_plt.set_ylabel("Price")
pair_spread_mean = pair_df['Spread'].mean()
spread_std = pair_df['Spread'].std()
pair_spread_plt = pair_df.plot(x='Date', y=['Spread'], figsize=(30,15))
pair_spread_plt.axhline(pair_spread_mean, c='black')
pair_spread_plt.axhline(pair_spread_mean + spread_std, c='red', ls = "--")
pair_spread_plt.axhline(pair_spread_mean - spread_std, c='red', ls = "--")
pair_spread_plt.set_ylabel("Price")
pair_zscore_plt = pair_df.plot(x='Date', y='zscore', figsize=(30,15))
pair_zscore_plt.axhline(0, c='black')
pair_zscore_plt.axhline(1, c='red', ls = "--")
pair_zscore_plt.axhline(-1, c='red', ls = "--")
pair_spread_plt.set_ylabel("zscore")
# long positions
# short positions
# flat positions
# Get out of a position
def generate_orders(prices):
orders = []
position = "FLAT"
# Keep track of last price
# prev_price = None
for price in prices:
# Get out of a LONG position
if position == "LONG" and (price == 0 or price > 0):
orders.append("GET_OUT_OF_POSITION")
position = "FLAT"
# Get out of a SHORT position
elif position == "SHORT" and (price == 0 or price < 0):
orders.append("GET_OUT_OF_POSITION")
position = "FLAT"
# Get into a long position
elif price < -1.5:
position = "LONG"
orders.append("LONG")
# Get into a long position
elif price > 1.5:
position = "SHORT"
orders.append("SHORT")
# Default if no other order is placed
else:
orders.append("FLAT")
return orders
pair_orders_df = pair_df.copy()
pair_orders_df.head()
pair_orders_df["Orders"] = generate_orders(pair_df["zscore"])
pair_orders_df.head()
pair_orders_df[pair_orders_df['Orders'] != "FLAT"]
# Plotting the zscore of the Spread of 20 day Simple Moving Average
orders_plt = pair_orders_df.plot(x='Date', y='zscore', figsize=(30,15))
# Plotting the lines at mean, 1 and 2 std. dev.
orders_plt.axhline(0, c='black')
orders_plt.axhline(1, c='red', ls = "--")
orders_plt.axhline(-1, c='red', ls = "--")
# Extracting orders
Orders = pair_orders_df['Orders']
# Plot vertical lines where orders are placed
for order in range(len(Orders)):
if Orders[order] != "FLAT":
# GREEN line for a long position
if Orders[order] == "LONG":
orders_plt.axvline(x=order, c = "green")
# RED line for a short position
elif Orders[order] == "SHORT":
orders_plt.axvline(x=order, c = "red")
# BLACK line for getting out of all positions at that point
else:
orders_plt.axvline(x=order, c = "black")
pair_orders_df = pair_orders_df.set_index('Date')
pair_orders_df.to_csv('Pair1_orders.csv')
| 0.495117 | 0.950273 |
# ML-Agents Use SideChannels
<img src="https://raw.githubusercontent.com/Unity-Technologies/ml-agents/release_18_docs/docs/images/3dball_big.png" align="middle" width="435"/>
## Setup
```
#@title Install Rendering Dependencies { display-mode: "form" }
#@markdown (You only need to run this code when using Colab's hosted runtime)
import os
from IPython.display import HTML, display
def progress(value, max=100):
return HTML("""
<progress
value='{value}'
max='{max}',
style='width: 100%'
>
{value}
</progress>
""".format(value=value, max=max))
pro_bar = display(progress(0, 100), display_id=True)
try:
import google.colab
INSTALL_XVFB = True
except ImportError:
INSTALL_XVFB = 'COLAB_ALWAYS_INSTALL_XVFB' in os.environ
if INSTALL_XVFB:
with open('frame-buffer', 'w') as writefile:
writefile.write("""#taken from https://gist.github.com/jterrace/2911875
XVFB=/usr/bin/Xvfb
XVFBARGS=":1 -screen 0 1024x768x24 -ac +extension GLX +render -noreset"
PIDFILE=./frame-buffer.pid
case "$1" in
start)
echo -n "Starting virtual X frame buffer: Xvfb"
/sbin/start-stop-daemon --start --quiet --pidfile $PIDFILE --make-pidfile --background --exec $XVFB -- $XVFBARGS
echo "."
;;
stop)
echo -n "Stopping virtual X frame buffer: Xvfb"
/sbin/start-stop-daemon --stop --quiet --pidfile $PIDFILE
rm $PIDFILE
echo "."
;;
restart)
$0 stop
$0 start
;;
*)
echo "Usage: /etc/init.d/xvfb {start|stop|restart}"
exit 1
esac
exit 0
""")
pro_bar.update(progress(5, 100))
!apt-get install daemon >/dev/null 2>&1
pro_bar.update(progress(10, 100))
!apt-get install wget >/dev/null 2>&1
pro_bar.update(progress(20, 100))
!wget http://security.ubuntu.com/ubuntu/pool/main/libx/libxfont/libxfont1_1.5.1-1ubuntu0.16.04.4_amd64.deb >/dev/null 2>&1
pro_bar.update(progress(30, 100))
!wget --output-document xvfb.deb http://security.ubuntu.com/ubuntu/pool/universe/x/xorg-server/xvfb_1.18.4-0ubuntu0.12_amd64.deb >/dev/null 2>&1
pro_bar.update(progress(40, 100))
!dpkg -i libxfont1_1.5.1-1ubuntu0.16.04.4_amd64.deb >/dev/null 2>&1
pro_bar.update(progress(50, 100))
!dpkg -i xvfb.deb >/dev/null 2>&1
pro_bar.update(progress(70, 100))
!rm libxfont1_1.5.1-1ubuntu0.16.04.4_amd64.deb
pro_bar.update(progress(80, 100))
!rm xvfb.deb
pro_bar.update(progress(90, 100))
!bash frame-buffer start
os.environ["DISPLAY"] = ":1"
pro_bar.update(progress(100, 100))
```
### Installing ml-agents
```
try:
import mlagents
print("ml-agents already installed")
except ImportError:
!python -m pip install -q mlagents==0.27.0
print("Installed ml-agents")
```
## Side Channel
SideChannels are objects that can be passed to the constructor of a UnityEnvironment or the `make()` method of a registry entry to send non Reinforcement Learning related data.
More information available [here](https://github.com/Unity-Technologies/ml-agents/blob/release_18_docs/docs/Python-API.md#communicating-additional-information-with-the-environment)
### Engine Configuration SideChannel
The [Engine Configuration Side Channel](https://github.com/Unity-Technologies/ml-agents/blob/release_18_docs/docs/Python-API.md#engineconfigurationchannel) is used to configure how the Unity Engine should run.
We will use the GridWorld environment to demonstrate how to use the EngineConfigurationChannel.
```
# -----------------
# This code is used to close an env that might not have been closed before
try:
env.close()
except:
pass
# -----------------
from mlagents_envs.registry import default_registry
env_id = "GridWorld"
# Import the EngineConfigurationChannel class
from mlagents_envs.side_channel.engine_configuration_channel import EngineConfigurationChannel
# Create the side channel
engine_config_channel = EngineConfigurationChannel()
# Pass the side channel to the make method
# Note, the make method takes a LIST of SideChannel as input
env = default_registry[env_id].make(side_channels = [engine_config_channel])
# Configure the Unity Engine
engine_config_channel.set_configuration_parameters(target_frame_rate = 30)
env.reset()
# ...
# Perform experiment on environment
# ...
env.close()
```
### Environment Parameters Channel
The [Environment Parameters Side Channel](https://github.com/Unity-Technologies/ml-agents/blob/release_18_docs/docs/Python-API.md#environmentparameters) is used to modify environment parameters during the simulation.
We will use the GridWorld environment to demonstrate how to use the EngineConfigurationChannel.
```
import matplotlib.pyplot as plt
%matplotlib inline
# -----------------
# This code is used to close an env that might not have been closed before
try:
env.close()
except:
pass
# -----------------
from mlagents_envs.registry import default_registry
env_id = "GridWorld"
# Import the EngineConfigurationChannel class
from mlagents_envs.side_channel.environment_parameters_channel import EnvironmentParametersChannel
# Create the side channel
env_parameters = EnvironmentParametersChannel()
# Pass the side channel to the make method
# Note, the make method takes a LIST of SideChannel as input
env = default_registry[env_id].make(side_channels = [env_parameters])
env.reset()
behavior_name = list(env.behavior_specs)[0]
print("Observation without changing the environment parameters")
decision_steps, terminal_steps = env.get_steps(behavior_name)
plt.imshow(decision_steps.obs[0][0,:,:,:])
plt.show()
print("Increasing the dimensions of the grid from 5 to 7")
env_parameters.set_float_parameter("gridSize", 7)
print("Increasing the number of X from 1 to 5")
env_parameters.set_float_parameter("numObstacles", 5)
# Any change to a SideChannel will only be effective after a step or reset
# In the GridWorld Environment, the grid's dimensions can only change at reset
env.reset()
decision_steps, terminal_steps = env.get_steps(behavior_name)
plt.imshow(decision_steps.obs[0][0,:,:,:])
plt.show()
env.close()
```
### Creating your own Side Channels
You can send various kinds of data between a Unity Environment and Python but you will need to [create your own implementation of a Side Channel](https://github.com/Unity-Technologies/ml-agents/blob/release_18_docs/docs/Custom-SideChannels.md#custom-side-channels) for advanced use cases.
|
github_jupyter
|
#@title Install Rendering Dependencies { display-mode: "form" }
#@markdown (You only need to run this code when using Colab's hosted runtime)
import os
from IPython.display import HTML, display
def progress(value, max=100):
return HTML("""
<progress
value='{value}'
max='{max}',
style='width: 100%'
>
{value}
</progress>
""".format(value=value, max=max))
pro_bar = display(progress(0, 100), display_id=True)
try:
import google.colab
INSTALL_XVFB = True
except ImportError:
INSTALL_XVFB = 'COLAB_ALWAYS_INSTALL_XVFB' in os.environ
if INSTALL_XVFB:
with open('frame-buffer', 'w') as writefile:
writefile.write("""#taken from https://gist.github.com/jterrace/2911875
XVFB=/usr/bin/Xvfb
XVFBARGS=":1 -screen 0 1024x768x24 -ac +extension GLX +render -noreset"
PIDFILE=./frame-buffer.pid
case "$1" in
start)
echo -n "Starting virtual X frame buffer: Xvfb"
/sbin/start-stop-daemon --start --quiet --pidfile $PIDFILE --make-pidfile --background --exec $XVFB -- $XVFBARGS
echo "."
;;
stop)
echo -n "Stopping virtual X frame buffer: Xvfb"
/sbin/start-stop-daemon --stop --quiet --pidfile $PIDFILE
rm $PIDFILE
echo "."
;;
restart)
$0 stop
$0 start
;;
*)
echo "Usage: /etc/init.d/xvfb {start|stop|restart}"
exit 1
esac
exit 0
""")
pro_bar.update(progress(5, 100))
!apt-get install daemon >/dev/null 2>&1
pro_bar.update(progress(10, 100))
!apt-get install wget >/dev/null 2>&1
pro_bar.update(progress(20, 100))
!wget http://security.ubuntu.com/ubuntu/pool/main/libx/libxfont/libxfont1_1.5.1-1ubuntu0.16.04.4_amd64.deb >/dev/null 2>&1
pro_bar.update(progress(30, 100))
!wget --output-document xvfb.deb http://security.ubuntu.com/ubuntu/pool/universe/x/xorg-server/xvfb_1.18.4-0ubuntu0.12_amd64.deb >/dev/null 2>&1
pro_bar.update(progress(40, 100))
!dpkg -i libxfont1_1.5.1-1ubuntu0.16.04.4_amd64.deb >/dev/null 2>&1
pro_bar.update(progress(50, 100))
!dpkg -i xvfb.deb >/dev/null 2>&1
pro_bar.update(progress(70, 100))
!rm libxfont1_1.5.1-1ubuntu0.16.04.4_amd64.deb
pro_bar.update(progress(80, 100))
!rm xvfb.deb
pro_bar.update(progress(90, 100))
!bash frame-buffer start
os.environ["DISPLAY"] = ":1"
pro_bar.update(progress(100, 100))
try:
import mlagents
print("ml-agents already installed")
except ImportError:
!python -m pip install -q mlagents==0.27.0
print("Installed ml-agents")
# -----------------
# This code is used to close an env that might not have been closed before
try:
env.close()
except:
pass
# -----------------
from mlagents_envs.registry import default_registry
env_id = "GridWorld"
# Import the EngineConfigurationChannel class
from mlagents_envs.side_channel.engine_configuration_channel import EngineConfigurationChannel
# Create the side channel
engine_config_channel = EngineConfigurationChannel()
# Pass the side channel to the make method
# Note, the make method takes a LIST of SideChannel as input
env = default_registry[env_id].make(side_channels = [engine_config_channel])
# Configure the Unity Engine
engine_config_channel.set_configuration_parameters(target_frame_rate = 30)
env.reset()
# ...
# Perform experiment on environment
# ...
env.close()
import matplotlib.pyplot as plt
%matplotlib inline
# -----------------
# This code is used to close an env that might not have been closed before
try:
env.close()
except:
pass
# -----------------
from mlagents_envs.registry import default_registry
env_id = "GridWorld"
# Import the EngineConfigurationChannel class
from mlagents_envs.side_channel.environment_parameters_channel import EnvironmentParametersChannel
# Create the side channel
env_parameters = EnvironmentParametersChannel()
# Pass the side channel to the make method
# Note, the make method takes a LIST of SideChannel as input
env = default_registry[env_id].make(side_channels = [env_parameters])
env.reset()
behavior_name = list(env.behavior_specs)[0]
print("Observation without changing the environment parameters")
decision_steps, terminal_steps = env.get_steps(behavior_name)
plt.imshow(decision_steps.obs[0][0,:,:,:])
plt.show()
print("Increasing the dimensions of the grid from 5 to 7")
env_parameters.set_float_parameter("gridSize", 7)
print("Increasing the number of X from 1 to 5")
env_parameters.set_float_parameter("numObstacles", 5)
# Any change to a SideChannel will only be effective after a step or reset
# In the GridWorld Environment, the grid's dimensions can only change at reset
env.reset()
decision_steps, terminal_steps = env.get_steps(behavior_name)
plt.imshow(decision_steps.obs[0][0,:,:,:])
plt.show()
env.close()
| 0.376279 | 0.558628 |
# L03.2 Interactive plots with Bokeh
In order for this lecture to be standalone, we will use the dataset by the [Gapminder foundation](https://www.gapminder.org/). This dataset is very rich and allows us to demonstrate a rich demonstration of Bokeh's capabilities.
## Basic plot
```
from bokeh.plotting import figure
from bokeh.io import output_file, show
import numpy as np
output_file("basic_bokeh.html")
x = np.linspace(-np.pi, np.pi, 256)
y = np.cos(x)
p = figure()
p.line(x, y)
show(p)
```
Running this code creates a html file and opens it in your browser.
```
output_file("basic_bokeh_pretty.html")
golden = 1.618
dpi = 75
h = int(2.5*dpi); w = int(h*golden)
p = figure(plot_width=w, plot_height=h)
p.line(x, y, line_width=2)
p.xaxis.axis_label = "x"
p.yaxis.axis_label = "cos(x)"
p.xgrid.grid_line_color = None
p.ygrid.grid_line_color = None
p.xaxis.minor_tick_line_color = None
p.yaxis.minor_tick_line_color = None
show(p)
```
## Interactive dataset plots
```
import pandas as pd
df = pd.read_csv("gapminder.csv")
df.info()
df['country'].unique() # Display unique entries in row 'country'
df.head(10) # display first 10 entries
```
Looking at the head of the dataframe tells us that we have information on life expectancies, population, and GDP for each country every 5 years. This should allow us to produce some interesting plots!
## Bokeh
### Line charts
We already used line charts in the basic plotting example. Let's check out how life expectancy has been doing over the years in Europe.
```
is_europe = df['continent'] == "Europe"
europe = df[is_europe]
europe.head()
from bokeh.plotting import figure
from bokeh.io import show, reset_output, output_notebook
from bokeh.models import Legend, LegendItem
reset_output()
output_notebook()
# Bokeh does not automatically cycle through colours
from bokeh.palettes import Category20_20 as palette
import itertools
colors = itertools.cycle(palette)
output_notebook()
countries = europe['country'].unique()
# Create a blank figure with labels
fig = figure(plot_width = 600, plot_height = 800,
title = 'Gapminder data',
x_axis_label = 'year', y_axis_label = 'life_expectancy')
# Creating traces by looping over countries
legend_items = []
for country in countries:
is_country = europe['country'] == country
r = fig.line(europe[is_country]['year'],
europe[is_country]['lifeExp'],
line_width=2,
color=next(colors),
alpha=1.0,
muted_alpha=0.0)
legend_items.append((country, [r]))
legend = Legend(items=legend_items, location=(20, 20))
legend.click_policy = "mute"
fig.add_layout(legend, "right")
show(fig)
colors = itertools.cycle(palette)
scandinavians = ['Norway', 'Sweden', 'Denmark']
is_scandinavia = europe['country'].isin(scandinavians)
scandinavia = europe[is_scandinavia]
fig = figure(plot_width = 600, plot_height = 600,
title = 'Gapminder data',
x_axis_label = 'year', y_axis_label = 'life_expectancy')
legend_items = []
for country in scandinavians:
color = next(colors)
is_country = europe['country'] == country
r = fig.line(europe[is_country]['year'],
europe[is_country]['lifeExp'],
line_width=2,
color=color, alpha=1.0,
muted_color=color, muted_alpha=0.2)
legend_items.append((country, [r]))
legend = Legend(items=legend_items, location=(20, 440))
legend.click_policy = "mute"
fig.add_layout(legend, "right")
show(fig)
```
### Bar charts
To illustrate bar charts we'll look at the GDP in Scandinavia over the years.
```
from bokeh.models import ColumnDataSource, FactorRange
from bokeh.palettes import Category20_20 as palette
from bokeh.transform import factor_cmap
years = [str(year) for year in list(europe['year'].unique())]
data = scandinavia[['country', 'year', 'gdpPercap']]
data = scandinavia.to_dict(orient='list')
x = [(year, country) for country in scandinavians for year in years]
data['x'] = x
fig = figure(x_range=FactorRange(*x), plot_height=250, title="Gapminder data",
toolbar_location=None, tools="")
fig.vbar(x='x', top='gdpPercap', width=0.8, source=data,
fill_color=factor_cmap('x', palette=palette, factors=scandinavians, start=1, end=2))
fig.xaxis.major_label_orientation = 1
show(fig)
```
### Bubble plots
To illustrate scatter plots we'll look at life expectancy vs. income per country, where we'll scale the bubble by population size. This is the most well known graphic by Gapminder.
```
from ipywidgets import interact, widgets
from bokeh.io import curdoc, output_notebook, push_notebook
from bokeh.layouts import layout
from bokeh.models import (Button, CategoricalColorMapper, ColumnDataSource,
HoverTool, Label, SingleIntervalTicker, Slider,)
from bokeh.palettes import Spectral6
from bokeh.plotting import figure
output_notebook()
years = df['year'].unique()
plot = figure(x_range=(0, 40000), y_range=(25, 90), title='Gapminder Data', plot_height=300)
plot.xaxis.ticker = SingleIntervalTicker(interval=5000)
plot.xaxis.axis_label = "GDP per capita"
plot.yaxis.ticker = SingleIntervalTicker(interval=20)
plot.yaxis.axis_label = "Life expectancy"
label = Label(x=1.1, y=23, text=str(years[0]), text_font_size='93px', text_color='#eeeeee')
plot.add_layout(label)
is_year = df['year'] == years[0]
source = ColumnDataSource(data=df[is_year])
color_mapper = CategoricalColorMapper(palette=Spectral6, factors=df['continent'].unique())
plot.circle(
x='gdpPercap',
y='lifeExp',
size=10,
source=source,
fill_color={'field': 'continent', 'transform': color_mapper},
fill_alpha=0.8,
line_color='#7c7e71',
line_width=0.5,
line_alpha=0.5,
legend_group='continent',
)
plot.add_tools(HoverTool(tooltips="@country", show_arrow=False, point_policy='follow_mouse'))
def slider_update(year):
label.text = str(year)
is_year = df['year'] == year
source.data = df[is_year]
push_notebook()
show(plot, notebook_handle=True)
interact(slider_update, year=widgets.IntSlider(min=years[0], max=years[-1], step=5, value=years[0]))
```
|
github_jupyter
|
from bokeh.plotting import figure
from bokeh.io import output_file, show
import numpy as np
output_file("basic_bokeh.html")
x = np.linspace(-np.pi, np.pi, 256)
y = np.cos(x)
p = figure()
p.line(x, y)
show(p)
output_file("basic_bokeh_pretty.html")
golden = 1.618
dpi = 75
h = int(2.5*dpi); w = int(h*golden)
p = figure(plot_width=w, plot_height=h)
p.line(x, y, line_width=2)
p.xaxis.axis_label = "x"
p.yaxis.axis_label = "cos(x)"
p.xgrid.grid_line_color = None
p.ygrid.grid_line_color = None
p.xaxis.minor_tick_line_color = None
p.yaxis.minor_tick_line_color = None
show(p)
import pandas as pd
df = pd.read_csv("gapminder.csv")
df.info()
df['country'].unique() # Display unique entries in row 'country'
df.head(10) # display first 10 entries
is_europe = df['continent'] == "Europe"
europe = df[is_europe]
europe.head()
from bokeh.plotting import figure
from bokeh.io import show, reset_output, output_notebook
from bokeh.models import Legend, LegendItem
reset_output()
output_notebook()
# Bokeh does not automatically cycle through colours
from bokeh.palettes import Category20_20 as palette
import itertools
colors = itertools.cycle(palette)
output_notebook()
countries = europe['country'].unique()
# Create a blank figure with labels
fig = figure(plot_width = 600, plot_height = 800,
title = 'Gapminder data',
x_axis_label = 'year', y_axis_label = 'life_expectancy')
# Creating traces by looping over countries
legend_items = []
for country in countries:
is_country = europe['country'] == country
r = fig.line(europe[is_country]['year'],
europe[is_country]['lifeExp'],
line_width=2,
color=next(colors),
alpha=1.0,
muted_alpha=0.0)
legend_items.append((country, [r]))
legend = Legend(items=legend_items, location=(20, 20))
legend.click_policy = "mute"
fig.add_layout(legend, "right")
show(fig)
colors = itertools.cycle(palette)
scandinavians = ['Norway', 'Sweden', 'Denmark']
is_scandinavia = europe['country'].isin(scandinavians)
scandinavia = europe[is_scandinavia]
fig = figure(plot_width = 600, plot_height = 600,
title = 'Gapminder data',
x_axis_label = 'year', y_axis_label = 'life_expectancy')
legend_items = []
for country in scandinavians:
color = next(colors)
is_country = europe['country'] == country
r = fig.line(europe[is_country]['year'],
europe[is_country]['lifeExp'],
line_width=2,
color=color, alpha=1.0,
muted_color=color, muted_alpha=0.2)
legend_items.append((country, [r]))
legend = Legend(items=legend_items, location=(20, 440))
legend.click_policy = "mute"
fig.add_layout(legend, "right")
show(fig)
from bokeh.models import ColumnDataSource, FactorRange
from bokeh.palettes import Category20_20 as palette
from bokeh.transform import factor_cmap
years = [str(year) for year in list(europe['year'].unique())]
data = scandinavia[['country', 'year', 'gdpPercap']]
data = scandinavia.to_dict(orient='list')
x = [(year, country) for country in scandinavians for year in years]
data['x'] = x
fig = figure(x_range=FactorRange(*x), plot_height=250, title="Gapminder data",
toolbar_location=None, tools="")
fig.vbar(x='x', top='gdpPercap', width=0.8, source=data,
fill_color=factor_cmap('x', palette=palette, factors=scandinavians, start=1, end=2))
fig.xaxis.major_label_orientation = 1
show(fig)
from ipywidgets import interact, widgets
from bokeh.io import curdoc, output_notebook, push_notebook
from bokeh.layouts import layout
from bokeh.models import (Button, CategoricalColorMapper, ColumnDataSource,
HoverTool, Label, SingleIntervalTicker, Slider,)
from bokeh.palettes import Spectral6
from bokeh.plotting import figure
output_notebook()
years = df['year'].unique()
plot = figure(x_range=(0, 40000), y_range=(25, 90), title='Gapminder Data', plot_height=300)
plot.xaxis.ticker = SingleIntervalTicker(interval=5000)
plot.xaxis.axis_label = "GDP per capita"
plot.yaxis.ticker = SingleIntervalTicker(interval=20)
plot.yaxis.axis_label = "Life expectancy"
label = Label(x=1.1, y=23, text=str(years[0]), text_font_size='93px', text_color='#eeeeee')
plot.add_layout(label)
is_year = df['year'] == years[0]
source = ColumnDataSource(data=df[is_year])
color_mapper = CategoricalColorMapper(palette=Spectral6, factors=df['continent'].unique())
plot.circle(
x='gdpPercap',
y='lifeExp',
size=10,
source=source,
fill_color={'field': 'continent', 'transform': color_mapper},
fill_alpha=0.8,
line_color='#7c7e71',
line_width=0.5,
line_alpha=0.5,
legend_group='continent',
)
plot.add_tools(HoverTool(tooltips="@country", show_arrow=False, point_policy='follow_mouse'))
def slider_update(year):
label.text = str(year)
is_year = df['year'] == year
source.data = df[is_year]
push_notebook()
show(plot, notebook_handle=True)
interact(slider_update, year=widgets.IntSlider(min=years[0], max=years[-1], step=5, value=years[0]))
| 0.617513 | 0.946646 |
```
import math
import tensorflow as tf
import numpy as np
from keras.datasets import cifar10 #50k training images, 10k Testing images and 10 classes
import matplotlib.pyplot as plt
from tensorflow.python.framework import ops
train,test = cifar10.load_data()
X_train_orig,Y_train_orig = train
X_test_orig,Y_test_orig = test
Y_train_orig
def convert_to_one_hot(Y,num_classes):
OHY = []
for i in Y:
OH = [0]*num_classes
OH[i[0]] = 1
OHY.append(OH)
return np.array(OHY)
X_train = X_train_orig/255.
X_test = X_test_orig/255.
Y_train = convert_to_one_hot(Y_train_orig, 10)
Y_test = convert_to_one_hot(Y_test_orig, 10)
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
conv_layers = {}
plt.imshow(X_train[0]) #CLASS 6 ie FROG
def create_placeholders(n_H0, n_W0, n_C0, n_y):
X = tf.placeholder(tf.float32, [None, n_H0, n_W0, n_C0])
Y = tf.placeholder(tf.float32, [None, n_y])
return X, Y
X, Y = create_placeholders(32, 32, 3, 10)
print ("X = " + str(X))
print ("Y = " + str(Y))
def initialize_parameters():
tf.set_random_seed(1)
#W1 and W2 are filters where list given is [filter height, width, in_channels, out_channels]
W1 = tf.get_variable("W1", [3, 3, 3, 32], initializer=tf.contrib.layers.xavier_initializer(seed=0))
W2 = tf.get_variable("W2", [3, 3, 32, 64], initializer=tf.contrib.layers.xavier_initializer(seed=0))
parameters = {"W1": W1,
"W2": W2}
return parameters
tf.reset_default_graph()
with tf.Session() as sess_test:
parameters = initialize_parameters()
init = tf.global_variables_initializer()
sess_test.run(init)
print("W1 = " + str(parameters["W1"].eval()[1,1,1]))
print("W2 = " + str(parameters["W2"].eval()[1,1,1]))
def forward_propagation(X, parameters):
# Retrieve the parameters from the dictionary "parameters"
W1 = parameters['W1']
W2 = parameters['W2']
# CONV2D: stride of 1, padding 'SAME'
Z1 = tf.nn.conv2d(X,W1,strides=[1, 1 ,1 ,1],padding='SAME')
# RELU
A1 = tf.nn.relu(Z1)
# MAXPOOL: window 4x4, sride 4, padding 'SAME'
P1 = tf.nn.max_pool(A1,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
# CONV2D: filters W2, stride 1, padding 'SAME'
Z2 = tf.nn.conv2d(P1,W2,strides=[1,1,1,1],padding='SAME')
# RELU
A2 = tf.nn.relu(Z2)
# MAXPOOL: window 2x2, stride 2, padding 'SAME'
P2 = tf.nn.max_pool(A2,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
# FLATTEN
P2 = tf.contrib.layers.flatten(P2)
# FULLY-CONNECTED without non-linear activation function (not not call softmax).
# 10 neurons in output layer. Hint: one of the arguments should be "activation_fn=None"
Z3 = tf.contrib.layers.fully_connected(P2,10, activation_fn=None)
return Z3
tf.reset_default_graph()
with tf.Session() as sess:
np.random.seed(1)
X, Y = create_placeholders(32, 32, 3, 10)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
init = tf.global_variables_initializer()
sess.run(init)
a = sess.run(Z3, {X: np.random.randn(2,32,32,3), Y: np.random.randn(2,10)})
print("Z3 = " + str(a))
def compute_cost(Z3, Y):
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=Z3, labels=Y))
return cost
tf.reset_default_graph()
with tf.Session() as sess:
np.random.seed(1)
X, Y = create_placeholders(32, 32, 3, 10)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
cost = compute_cost(Z3, Y)
init = tf.global_variables_initializer()
sess.run(init)
a = sess.run(cost, {X: np.random.randn(4,32,32,3), Y: np.random.randn(4,10)})
print("cost = " + str(a))
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
"""
Creates a list of random minibatches from (X, Y)
Arguments:
X -- input data, of shape (input size, number of examples) (m, Hi, Wi, Ci)
Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples) (m, n_y)
mini_batch_size - size of the mini-batches, integer
seed -- this is only for the purpose of grading, so that you're "random minibatches are the same as ours.
Returns:
mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
"""
m = X.shape[0] # number of training examples
mini_batches = []
np.random.seed(seed)
# Step 1: Shuffle (X, Y)
permutation = list(np.random.permutation(m))
shuffled_X = X[permutation,:,:,:]
shuffled_Y = Y[permutation,:]
# Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
for k in range(0, num_complete_minibatches):
mini_batch_X = shuffled_X[k * mini_batch_size : k * mini_batch_size + mini_batch_size,:,:,:]
mini_batch_Y = shuffled_Y[k * mini_batch_size : k * mini_batch_size + mini_batch_size,:]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
# Handling the end case (last mini-batch < mini_batch_size)
if m % mini_batch_size != 0:
mini_batch_X = shuffled_X[num_complete_minibatches * mini_batch_size : m,:,:,:]
mini_batch_Y = shuffled_Y[num_complete_minibatches * mini_batch_size : m,:]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
return mini_batches
def model(X_train, Y_train, X_test, Y_test, learning_rate=0.009,
num_epochs=50, minibatch_size=64, print_cost=True):
ops.reset_default_graph() # to be able to rerun the model without overwriting tf variables
tf.set_random_seed(1) # to keep results consistent (tensorflow seed)
seed = 3 # to keep results consistent (numpy seed)
(m, n_H0, n_W0, n_C0) = X_train.shape
n_y = Y_train.shape[1]
costs = [] # To keep track of the cost
# Create Placeholders of the correct shape
X, Y = create_placeholders(n_H0, n_W0, n_C0, n_y)
# Initialize parameters
parameters = initialize_parameters()
# Forward propagation: Build the forward propagation in the tensorflow graph
Z3 = forward_propagation(X, parameters)
# Cost function: Add cost function to tensorflow graph
cost = compute_cost(Z3, Y)
# Backpropagation: Define the tensorflow optimizer. Use an AdamOptimizer that minimizes the cost.
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
# Initialize all the variables globally
init = tf.global_variables_initializer()
# Start the session to compute the tensorflow graph
with tf.Session() as sess:
# Run the initialization
sess.run(init)
# Do the training loop
for epoch in range(num_epochs):
minibatch_cost = 0.
num_minibatches = int(m / minibatch_size) # number of minibatches of size minibatch_size in the train set
seed = seed + 1
minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)
for minibatch in minibatches:
# Select a minibatch
(minibatch_X, minibatch_Y) = minibatch
# Run the session to execute the optimizer and the cost, the feedict should contain a minibatch for (X,Y).
_ , temp_cost = sess.run([optimizer, cost], feed_dict={X:minibatch_X, Y:minibatch_Y})
minibatch_cost += temp_cost / num_minibatches
# Print the cost every epoch
if print_cost == True and epoch % 10 == 0:
print ("Cost after epoch %i: %f" % (epoch, minibatch_cost))
if print_cost == True and epoch % 1 == 0:
costs.append(minibatch_cost)
# plot the cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
try:
# Calculate the correct predictions
predict_op = tf.argmax(Z3, 1)
correct_prediction = tf.equal(predict_op, tf.argmax(Y, 1))
# Calculate accuracy on the test set
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print(accuracy)
#train_accuracy = accuracy.eval({X: X_train, Y: Y_train})
test_accuracy = accuracy.eval({X: X_test, Y: Y_test})
#print("Train Accuracy:", train_accuracy)
print("Test Accuracy:", test_accuracy)
except:
print('Memory Full, cannot process accuracy')
test_accuracy = None
return test_accuracy,parameters
test_accuracy,parameters = model(X_train, Y_train, X_test, Y_test)
#INCREASE NUMBER OF EPOCHS FOR BETTER TEST ACCURACY
```
|
github_jupyter
|
import math
import tensorflow as tf
import numpy as np
from keras.datasets import cifar10 #50k training images, 10k Testing images and 10 classes
import matplotlib.pyplot as plt
from tensorflow.python.framework import ops
train,test = cifar10.load_data()
X_train_orig,Y_train_orig = train
X_test_orig,Y_test_orig = test
Y_train_orig
def convert_to_one_hot(Y,num_classes):
OHY = []
for i in Y:
OH = [0]*num_classes
OH[i[0]] = 1
OHY.append(OH)
return np.array(OHY)
X_train = X_train_orig/255.
X_test = X_test_orig/255.
Y_train = convert_to_one_hot(Y_train_orig, 10)
Y_test = convert_to_one_hot(Y_test_orig, 10)
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
conv_layers = {}
plt.imshow(X_train[0]) #CLASS 6 ie FROG
def create_placeholders(n_H0, n_W0, n_C0, n_y):
X = tf.placeholder(tf.float32, [None, n_H0, n_W0, n_C0])
Y = tf.placeholder(tf.float32, [None, n_y])
return X, Y
X, Y = create_placeholders(32, 32, 3, 10)
print ("X = " + str(X))
print ("Y = " + str(Y))
def initialize_parameters():
tf.set_random_seed(1)
#W1 and W2 are filters where list given is [filter height, width, in_channels, out_channels]
W1 = tf.get_variable("W1", [3, 3, 3, 32], initializer=tf.contrib.layers.xavier_initializer(seed=0))
W2 = tf.get_variable("W2", [3, 3, 32, 64], initializer=tf.contrib.layers.xavier_initializer(seed=0))
parameters = {"W1": W1,
"W2": W2}
return parameters
tf.reset_default_graph()
with tf.Session() as sess_test:
parameters = initialize_parameters()
init = tf.global_variables_initializer()
sess_test.run(init)
print("W1 = " + str(parameters["W1"].eval()[1,1,1]))
print("W2 = " + str(parameters["W2"].eval()[1,1,1]))
def forward_propagation(X, parameters):
# Retrieve the parameters from the dictionary "parameters"
W1 = parameters['W1']
W2 = parameters['W2']
# CONV2D: stride of 1, padding 'SAME'
Z1 = tf.nn.conv2d(X,W1,strides=[1, 1 ,1 ,1],padding='SAME')
# RELU
A1 = tf.nn.relu(Z1)
# MAXPOOL: window 4x4, sride 4, padding 'SAME'
P1 = tf.nn.max_pool(A1,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
# CONV2D: filters W2, stride 1, padding 'SAME'
Z2 = tf.nn.conv2d(P1,W2,strides=[1,1,1,1],padding='SAME')
# RELU
A2 = tf.nn.relu(Z2)
# MAXPOOL: window 2x2, stride 2, padding 'SAME'
P2 = tf.nn.max_pool(A2,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
# FLATTEN
P2 = tf.contrib.layers.flatten(P2)
# FULLY-CONNECTED without non-linear activation function (not not call softmax).
# 10 neurons in output layer. Hint: one of the arguments should be "activation_fn=None"
Z3 = tf.contrib.layers.fully_connected(P2,10, activation_fn=None)
return Z3
tf.reset_default_graph()
with tf.Session() as sess:
np.random.seed(1)
X, Y = create_placeholders(32, 32, 3, 10)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
init = tf.global_variables_initializer()
sess.run(init)
a = sess.run(Z3, {X: np.random.randn(2,32,32,3), Y: np.random.randn(2,10)})
print("Z3 = " + str(a))
def compute_cost(Z3, Y):
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=Z3, labels=Y))
return cost
tf.reset_default_graph()
with tf.Session() as sess:
np.random.seed(1)
X, Y = create_placeholders(32, 32, 3, 10)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
cost = compute_cost(Z3, Y)
init = tf.global_variables_initializer()
sess.run(init)
a = sess.run(cost, {X: np.random.randn(4,32,32,3), Y: np.random.randn(4,10)})
print("cost = " + str(a))
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
"""
Creates a list of random minibatches from (X, Y)
Arguments:
X -- input data, of shape (input size, number of examples) (m, Hi, Wi, Ci)
Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples) (m, n_y)
mini_batch_size - size of the mini-batches, integer
seed -- this is only for the purpose of grading, so that you're "random minibatches are the same as ours.
Returns:
mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
"""
m = X.shape[0] # number of training examples
mini_batches = []
np.random.seed(seed)
# Step 1: Shuffle (X, Y)
permutation = list(np.random.permutation(m))
shuffled_X = X[permutation,:,:,:]
shuffled_Y = Y[permutation,:]
# Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
for k in range(0, num_complete_minibatches):
mini_batch_X = shuffled_X[k * mini_batch_size : k * mini_batch_size + mini_batch_size,:,:,:]
mini_batch_Y = shuffled_Y[k * mini_batch_size : k * mini_batch_size + mini_batch_size,:]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
# Handling the end case (last mini-batch < mini_batch_size)
if m % mini_batch_size != 0:
mini_batch_X = shuffled_X[num_complete_minibatches * mini_batch_size : m,:,:,:]
mini_batch_Y = shuffled_Y[num_complete_minibatches * mini_batch_size : m,:]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
return mini_batches
def model(X_train, Y_train, X_test, Y_test, learning_rate=0.009,
num_epochs=50, minibatch_size=64, print_cost=True):
ops.reset_default_graph() # to be able to rerun the model without overwriting tf variables
tf.set_random_seed(1) # to keep results consistent (tensorflow seed)
seed = 3 # to keep results consistent (numpy seed)
(m, n_H0, n_W0, n_C0) = X_train.shape
n_y = Y_train.shape[1]
costs = [] # To keep track of the cost
# Create Placeholders of the correct shape
X, Y = create_placeholders(n_H0, n_W0, n_C0, n_y)
# Initialize parameters
parameters = initialize_parameters()
# Forward propagation: Build the forward propagation in the tensorflow graph
Z3 = forward_propagation(X, parameters)
# Cost function: Add cost function to tensorflow graph
cost = compute_cost(Z3, Y)
# Backpropagation: Define the tensorflow optimizer. Use an AdamOptimizer that minimizes the cost.
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
# Initialize all the variables globally
init = tf.global_variables_initializer()
# Start the session to compute the tensorflow graph
with tf.Session() as sess:
# Run the initialization
sess.run(init)
# Do the training loop
for epoch in range(num_epochs):
minibatch_cost = 0.
num_minibatches = int(m / minibatch_size) # number of minibatches of size minibatch_size in the train set
seed = seed + 1
minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)
for minibatch in minibatches:
# Select a minibatch
(minibatch_X, minibatch_Y) = minibatch
# Run the session to execute the optimizer and the cost, the feedict should contain a minibatch for (X,Y).
_ , temp_cost = sess.run([optimizer, cost], feed_dict={X:minibatch_X, Y:minibatch_Y})
minibatch_cost += temp_cost / num_minibatches
# Print the cost every epoch
if print_cost == True and epoch % 10 == 0:
print ("Cost after epoch %i: %f" % (epoch, minibatch_cost))
if print_cost == True and epoch % 1 == 0:
costs.append(minibatch_cost)
# plot the cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
try:
# Calculate the correct predictions
predict_op = tf.argmax(Z3, 1)
correct_prediction = tf.equal(predict_op, tf.argmax(Y, 1))
# Calculate accuracy on the test set
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print(accuracy)
#train_accuracy = accuracy.eval({X: X_train, Y: Y_train})
test_accuracy = accuracy.eval({X: X_test, Y: Y_test})
#print("Train Accuracy:", train_accuracy)
print("Test Accuracy:", test_accuracy)
except:
print('Memory Full, cannot process accuracy')
test_accuracy = None
return test_accuracy,parameters
test_accuracy,parameters = model(X_train, Y_train, X_test, Y_test)
#INCREASE NUMBER OF EPOCHS FOR BETTER TEST ACCURACY
| 0.716913 | 0.630201 |
```
import numpy as np
import os
from random import shuffle
import re
from bokeh.models import ColumnDataSource, LabelSet
from bokeh.plotting import figure, show, output_file
from bokeh.io import output_notebook
output_notebook()
```
## Downloading dataset
```
import urllib.request
import zipfile
import lxml.etree
# Download the dataset if it's not already there: this may take a minute as it is 75MB
if not os.path.isfile('ted_en-20160408.zip'):
urllib.request.urlretrieve("https://wit3.fbk.eu/get.php?path=XML_releases/xml/ted_en-20160408.zip&filename=ted_en-20160408.zip", filename="ted_en-20160408.zip")
```
# Loading Data
```
# For now, we're only interested in the subtitle text, so let's extract that from the XML:
with zipfile.ZipFile('ted_en-20160408.zip', 'r') as z:
doc1 = lxml.etree.parse(z.open('ted_en-20160408.xml', 'r'))
doc2 = lxml.etree.parse(z.open('ted_en-20160408.xml', 'r'))
input_text = '\n\nGG\n\n'.join(doc1.xpath('//content/text()'))
input_label= '\n'.join(doc2.xpath('//keywords/text()'))
del doc1
del doc2
```
# Pre Processing
```
input_text_noparens = re.sub(r'\([^)]*\)', '', input_text)
sentences_strings_ted = []
keywords_list=[]
clean_input=[]
'''
The following loop seperates each talk into a string and stores it in an array.
'''
for input_para in input_text_noparens.split('\n\nGG\n\n'):
clean_input.append(input_para)
sentences_strings_ted = []
'''
Cleaning the data
'''
for line in clean_input:
m = re.sub(r'^(?:(?P<precolon>[^:]{,20}):)?(?P<postcolon>.*)$',"", line) #Removing names
m=m.replace("'",'') #Removing semi-colons
tokens = re.sub(r"[^a-z0-9]+", " ", m.lower()) #Removing non-alphanumeric characters
sentences_strings_ted.append(tokens.split()) #Tokenizing the input using spaces i.e splitting sentences into words.
'''
Creating labels as follows:
1) If the talk is based on Technology- 100 in binary i.e 4
2) If the talk is based on Technology and Design- 101 in binary i.e 5
'''
for keyword_list in input_label.split('\n'):
temp=[]
outP=[]
countT=0
countE=0
countD=0
for word in keyword_list.split(', '):
if word in ['technology','entertainment','design']:
temp.append(word)
if (len(temp)!=0):
if 'technology' in temp:
countT=1
if 'entertainment' in temp:
countE=1
if 'design' in temp:
countD=1
outStr=str(countT)+str(countE)+str(countD)
label=int(outStr,2)
keywords_list.append(label)
input_list=list(zip(sentences_strings_ted,keywords_list)) #Joining each input with respective label
'''
Splitting dataset for training,testing and validation
'''
training_input=input_list[:1585]
validation_input=input_list[1585:1836]
test_input=input_list[1836:]
```
# Creating Text Embedding
```
from gensim.models import Word2Vec
'''
Creating Text Embedding:
1) Text embedding is the process of representing a word as a vector.
2) This vector can be passed into a neural network as input.
3) I am using Word2Vec to do this task for me. Basically, it will represent each of the words in the input as a vector.
More on Word2Vec:
https://iksinc.wordpress.com/tag/continuous-bag-of-words-cbow/
'''
model_ted = Word2Vec(sentences_strings_ted, min_count=10)# ...
print(len(model_ted.wv.vocab))
'''
To see how well our text embedding has worked.
Printing the most similar words for every word.
'''
model_ted.most_similar("man")
model_ted.most_similar("computer")
curSum=np.zeros((1,100))
print (curSum)
'''
This function will accept an array of words (An entire TED talk) as input. It will find the vector representations of
every word and sum them up. It will divide the final vector by number of words and return it.
This is called Bag of Means method. It is very simple but is very effective at representing
phrases or sentences of different lengths using a vector of fixed length.
'''
def convert_to_vec(input_array):
global model_ted
curSum=np.zeros((1,100))
for word in input_array:
curSum=np.add(curSum,model_ted.wv[word])
curSum=(1.0/(len(input_array)))*curSum
return (curSum)
#print (convert_to_vec(['machine','computer']))
```
# Dataset Class
```
import torch
import torch.nn as nn
from torch.autograd import Variable
from torch.utils.data import Dataset, DataLoader
'''
This is the dataset class for TED_Dataset.
Those unfamiliar with writing a dataset for PyTorch may refer to this excellent tutorial:
http://pytorch.org/tutorials/beginner/data_loading_tutorial.html
'''
class TED_Dataset(Dataset):
training_input=[]
validation_input=[]
test_input=[]
def __init__(self,training_input,validation_input,test_input,train,validate,test):
self.training_input=training_input
self.validation_input=validation_input
self.test_input=test_input
self.train=train
self.validate=validate
self.test=test
def __len__(self):
if self.train==True:
return 1585
elif self.validate==True:
return 250
elif self.test==True:
return 240
def __getitem__(self,idx):
global training_input
global validation_input
global test_input
if self.train==True:
item=training_input[idx]
elif self.validate==True:
item=validation_input[idx]
elif self.test==True:
item=test_input[idx]
global model_ted
curSum=np.zeros((1,100))
input_array=item[0]
label=item[1]
for word in input_array:
if word not in model_ted.wv.vocab:
continue
curSum=np.add(curSum,model_ted.wv[word])
if (len(input_array)!=0):
curSum=(1.0/(len(input_array)))*curSum
else:
#print ("HERE")
curSum=np.zeros((1,100))
sample={'input':curSum,'label':label}
return (sample)
```
# Initialize Dataset
```
#Initializing Datasets
train_dataset=TED_Dataset(train=True,test=False,validate=False,training_input=training_input,validation_input=validation_input,test_input=test_input)
test_dataset=TED_Dataset(train=False,test=True,validate=False,training_input=training_input,validation_input=validation_input,test_input=test_input)
validate_dataset=TED_Dataset(train=False,test=False,validate=True,training_input=training_input,validation_input=validation_input,test_input=test_input)
```
# Making Dataset Iterable
```
#Fixing basic parameters to work with
batch_size = 50
n_iters = 15000
num_epochs = n_iters / (len(train_dataset) / batch_size)
num_epochs = int(num_epochs)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
```
# Neural Network Model
```
'''
The network is defined in the class below.
It is a single-layered feedforward neural network using Tanh as activation function.
'''
class FeedforwardNeuralNetModel(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(FeedforwardNeuralNetModel, self).__init__()
# Linear function 1
self.fc1 = nn.Linear(input_dim, hidden_dim)
# Non-linearity 1
self.tanh1 = nn.Tanh ()
# Linear function 2 (readout): 100 --> 8
self.fc2 = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
# Linear function 1
out = self.fc1(x)
# Non-linearity 1
out = self.tanh1(out)
# Linear function 2
out = self.fc2(out)
return out
```
# Instantiate Model Class
```
input_dim = 100
hidden_dim = 100
output_dim = 8
model = FeedforwardNeuralNetModel(input_dim, hidden_dim, output_dim)
```
# Instantiate Loss Class
```
criterion = nn.CrossEntropyLoss()
```
# Instantiate Optimizer Class
```
learning_rate = 0.1
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
```
# Training Model
```
iter = 0
for epoch in range(num_epochs):
for i,datapoint in enumerate(train_loader):
input_ar=datapoint['input']
labels=datapoint['label']
input_ar = Variable(input_ar.view(-1, 100))
labels = Variable(labels)
input_ar=input_ar.float()
#print (input_ar)
#print (labels)
# Clear gradients w.r.t. parameters
optimizer.zero_grad()
# Forward pass to get output/logits
#print (iter)
outputs = model(input_ar)
# Calculate Loss: softmax --> cross entropy loss
loss = criterion(outputs, labels)
# Getting gradients w.r.t. parameters
loss.backward()
# Updating parameters
optimizer.step()
iter += 1
'''
Testing is done after every 500 training iterations
'''
if iter % 500 == 0:
# Calculate Accuracy
correct = 0
total = 0
# Iterate through test dataset
for ind,test_data in enumerate(test_loader):
test_in=test_data['input']
test_labels=test_data['label']
test_in = Variable(test_in.view(-1, 100))
test_in=test_in.float()
# Forward pass only to get logits/output
outputs = model(test_in)
# Get predictions from the maximum value
_, predicted = torch.max(outputs.data, 1)
# Total number of labels
total += test_labels.size(0)
# Total correct predictions
correct += (predicted.cpu() == test_labels.cpu()).sum()
accuracy = 100 * correct / total
# Print Loss
print('Iteration: {}. Loss: {}. Accuracy: {}'.format(iter, loss.data[0], accuracy))
```
|
github_jupyter
|
import numpy as np
import os
from random import shuffle
import re
from bokeh.models import ColumnDataSource, LabelSet
from bokeh.plotting import figure, show, output_file
from bokeh.io import output_notebook
output_notebook()
import urllib.request
import zipfile
import lxml.etree
# Download the dataset if it's not already there: this may take a minute as it is 75MB
if not os.path.isfile('ted_en-20160408.zip'):
urllib.request.urlretrieve("https://wit3.fbk.eu/get.php?path=XML_releases/xml/ted_en-20160408.zip&filename=ted_en-20160408.zip", filename="ted_en-20160408.zip")
# For now, we're only interested in the subtitle text, so let's extract that from the XML:
with zipfile.ZipFile('ted_en-20160408.zip', 'r') as z:
doc1 = lxml.etree.parse(z.open('ted_en-20160408.xml', 'r'))
doc2 = lxml.etree.parse(z.open('ted_en-20160408.xml', 'r'))
input_text = '\n\nGG\n\n'.join(doc1.xpath('//content/text()'))
input_label= '\n'.join(doc2.xpath('//keywords/text()'))
del doc1
del doc2
input_text_noparens = re.sub(r'\([^)]*\)', '', input_text)
sentences_strings_ted = []
keywords_list=[]
clean_input=[]
'''
The following loop seperates each talk into a string and stores it in an array.
'''
for input_para in input_text_noparens.split('\n\nGG\n\n'):
clean_input.append(input_para)
sentences_strings_ted = []
'''
Cleaning the data
'''
for line in clean_input:
m = re.sub(r'^(?:(?P<precolon>[^:]{,20}):)?(?P<postcolon>.*)$',"", line) #Removing names
m=m.replace("'",'') #Removing semi-colons
tokens = re.sub(r"[^a-z0-9]+", " ", m.lower()) #Removing non-alphanumeric characters
sentences_strings_ted.append(tokens.split()) #Tokenizing the input using spaces i.e splitting sentences into words.
'''
Creating labels as follows:
1) If the talk is based on Technology- 100 in binary i.e 4
2) If the talk is based on Technology and Design- 101 in binary i.e 5
'''
for keyword_list in input_label.split('\n'):
temp=[]
outP=[]
countT=0
countE=0
countD=0
for word in keyword_list.split(', '):
if word in ['technology','entertainment','design']:
temp.append(word)
if (len(temp)!=0):
if 'technology' in temp:
countT=1
if 'entertainment' in temp:
countE=1
if 'design' in temp:
countD=1
outStr=str(countT)+str(countE)+str(countD)
label=int(outStr,2)
keywords_list.append(label)
input_list=list(zip(sentences_strings_ted,keywords_list)) #Joining each input with respective label
'''
Splitting dataset for training,testing and validation
'''
training_input=input_list[:1585]
validation_input=input_list[1585:1836]
test_input=input_list[1836:]
from gensim.models import Word2Vec
'''
Creating Text Embedding:
1) Text embedding is the process of representing a word as a vector.
2) This vector can be passed into a neural network as input.
3) I am using Word2Vec to do this task for me. Basically, it will represent each of the words in the input as a vector.
More on Word2Vec:
https://iksinc.wordpress.com/tag/continuous-bag-of-words-cbow/
'''
model_ted = Word2Vec(sentences_strings_ted, min_count=10)# ...
print(len(model_ted.wv.vocab))
'''
To see how well our text embedding has worked.
Printing the most similar words for every word.
'''
model_ted.most_similar("man")
model_ted.most_similar("computer")
curSum=np.zeros((1,100))
print (curSum)
'''
This function will accept an array of words (An entire TED talk) as input. It will find the vector representations of
every word and sum them up. It will divide the final vector by number of words and return it.
This is called Bag of Means method. It is very simple but is very effective at representing
phrases or sentences of different lengths using a vector of fixed length.
'''
def convert_to_vec(input_array):
global model_ted
curSum=np.zeros((1,100))
for word in input_array:
curSum=np.add(curSum,model_ted.wv[word])
curSum=(1.0/(len(input_array)))*curSum
return (curSum)
#print (convert_to_vec(['machine','computer']))
import torch
import torch.nn as nn
from torch.autograd import Variable
from torch.utils.data import Dataset, DataLoader
'''
This is the dataset class for TED_Dataset.
Those unfamiliar with writing a dataset for PyTorch may refer to this excellent tutorial:
http://pytorch.org/tutorials/beginner/data_loading_tutorial.html
'''
class TED_Dataset(Dataset):
training_input=[]
validation_input=[]
test_input=[]
def __init__(self,training_input,validation_input,test_input,train,validate,test):
self.training_input=training_input
self.validation_input=validation_input
self.test_input=test_input
self.train=train
self.validate=validate
self.test=test
def __len__(self):
if self.train==True:
return 1585
elif self.validate==True:
return 250
elif self.test==True:
return 240
def __getitem__(self,idx):
global training_input
global validation_input
global test_input
if self.train==True:
item=training_input[idx]
elif self.validate==True:
item=validation_input[idx]
elif self.test==True:
item=test_input[idx]
global model_ted
curSum=np.zeros((1,100))
input_array=item[0]
label=item[1]
for word in input_array:
if word not in model_ted.wv.vocab:
continue
curSum=np.add(curSum,model_ted.wv[word])
if (len(input_array)!=0):
curSum=(1.0/(len(input_array)))*curSum
else:
#print ("HERE")
curSum=np.zeros((1,100))
sample={'input':curSum,'label':label}
return (sample)
#Initializing Datasets
train_dataset=TED_Dataset(train=True,test=False,validate=False,training_input=training_input,validation_input=validation_input,test_input=test_input)
test_dataset=TED_Dataset(train=False,test=True,validate=False,training_input=training_input,validation_input=validation_input,test_input=test_input)
validate_dataset=TED_Dataset(train=False,test=False,validate=True,training_input=training_input,validation_input=validation_input,test_input=test_input)
#Fixing basic parameters to work with
batch_size = 50
n_iters = 15000
num_epochs = n_iters / (len(train_dataset) / batch_size)
num_epochs = int(num_epochs)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
'''
The network is defined in the class below.
It is a single-layered feedforward neural network using Tanh as activation function.
'''
class FeedforwardNeuralNetModel(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(FeedforwardNeuralNetModel, self).__init__()
# Linear function 1
self.fc1 = nn.Linear(input_dim, hidden_dim)
# Non-linearity 1
self.tanh1 = nn.Tanh ()
# Linear function 2 (readout): 100 --> 8
self.fc2 = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
# Linear function 1
out = self.fc1(x)
# Non-linearity 1
out = self.tanh1(out)
# Linear function 2
out = self.fc2(out)
return out
input_dim = 100
hidden_dim = 100
output_dim = 8
model = FeedforwardNeuralNetModel(input_dim, hidden_dim, output_dim)
criterion = nn.CrossEntropyLoss()
learning_rate = 0.1
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
iter = 0
for epoch in range(num_epochs):
for i,datapoint in enumerate(train_loader):
input_ar=datapoint['input']
labels=datapoint['label']
input_ar = Variable(input_ar.view(-1, 100))
labels = Variable(labels)
input_ar=input_ar.float()
#print (input_ar)
#print (labels)
# Clear gradients w.r.t. parameters
optimizer.zero_grad()
# Forward pass to get output/logits
#print (iter)
outputs = model(input_ar)
# Calculate Loss: softmax --> cross entropy loss
loss = criterion(outputs, labels)
# Getting gradients w.r.t. parameters
loss.backward()
# Updating parameters
optimizer.step()
iter += 1
'''
Testing is done after every 500 training iterations
'''
if iter % 500 == 0:
# Calculate Accuracy
correct = 0
total = 0
# Iterate through test dataset
for ind,test_data in enumerate(test_loader):
test_in=test_data['input']
test_labels=test_data['label']
test_in = Variable(test_in.view(-1, 100))
test_in=test_in.float()
# Forward pass only to get logits/output
outputs = model(test_in)
# Get predictions from the maximum value
_, predicted = torch.max(outputs.data, 1)
# Total number of labels
total += test_labels.size(0)
# Total correct predictions
correct += (predicted.cpu() == test_labels.cpu()).sum()
accuracy = 100 * correct / total
# Print Loss
print('Iteration: {}. Loss: {}. Accuracy: {}'.format(iter, loss.data[0], accuracy))
| 0.323166 | 0.70784 |
# Exercises 04 - Lists
## 1. Second Element
Complete the function below according to its docstring.
*HINT*: Python starts counting at 0.
```
def select_second(L):
"""Return the second element of the given list.
If the list has no second element, return None.
"""
pass
```
## 2. Captain of the Worst Team
You are analyzing sports teams. Members of each team are stored in a list. The **Coach** is the first name in the list, the **Captain** is the second name in the list, and other players are listed after that.
These lists are stored in another list, which starts with the best team and proceeds through the list to the worst team last. Complete the function below to select the **captain** of the worst team.
```
def losing_team_captain(teams):
"""Given a list of teams, where each team is a list of names, return the 2nd player (captain)
from the last listed team
"""
pass
```
## 3. Purple Shell item
The next iteration of Mario Kart will feature an extra-infuriating new item, the ***Purple Shell***. When used, it warps the last place racer into first place and the first place racer into last place. Complete the function below to implement the Purple Shell's effect.
```
def purple_shell(racers):
"""Given a list of racers, set the first place racer (at the front of the list) to last
place and vice versa.
>>> r = ["Mario", "Bowser", "Luigi"]
>>> purple_shell(r)
>>> r
["Luigi", "Bowser", "Mario"]
"""
pass
```
## 4. Guess the Length!
What are the lengths of the following lists? Fill in the variable `lengths` with your predictions. (Try to make a prediction for each list *without* just calling `len()` on it.)
```
a = [1, 2, 3]
b = [1, [2, 3]]
c = []
d = [1, 2, 3][1:]
# Put your predictions in the list below. Lengths should contain 4 numbers, the
# first being the length of a, the second being the length of b and so on.
lengths = []
```
## 5. Fashionably Late <span title="A bit spicy" style="color: darkgreen ">🌶️</span>
We're using lists to record people who attended our party and what order they arrived in. For example, the following list represents a party with 7 guests, in which Adela showed up first and Ford was the last to arrive:
party_attendees = ['Adela', 'Fleda', 'Owen', 'May', 'Mona', 'Gilbert', 'Ford']
A guest is considered **'fashionably late'** if they arrived after at least half of the party's guests. However, they must not be the very last guest (that's taking it too far). In the above example, Mona and Gilbert are the only guests who were fashionably late.
Complete the function below which takes a list of party attendees as well as a person, and tells us whether that person is fashionably late.
```
def fashionably_late(arrivals, name):
"""Given an ordered list of arrivals to the party and a name, return whether the guest with that
name was fashionably late.
"""
pass
```
# Keep Going 💪
|
github_jupyter
|
def select_second(L):
"""Return the second element of the given list.
If the list has no second element, return None.
"""
pass
def losing_team_captain(teams):
"""Given a list of teams, where each team is a list of names, return the 2nd player (captain)
from the last listed team
"""
pass
def purple_shell(racers):
"""Given a list of racers, set the first place racer (at the front of the list) to last
place and vice versa.
>>> r = ["Mario", "Bowser", "Luigi"]
>>> purple_shell(r)
>>> r
["Luigi", "Bowser", "Mario"]
"""
pass
a = [1, 2, 3]
b = [1, [2, 3]]
c = []
d = [1, 2, 3][1:]
# Put your predictions in the list below. Lengths should contain 4 numbers, the
# first being the length of a, the second being the length of b and so on.
lengths = []
def fashionably_late(arrivals, name):
"""Given an ordered list of arrivals to the party and a name, return whether the guest with that
name was fashionably late.
"""
pass
| 0.695028 | 0.981221 |
# **Image Captioning**
Source: [https://github.com/d-insight/code-bank.git](https://github.com/d-insight/code-bank.git)
License: [MIT License](https://opensource.org/licenses/MIT). See open source [license](LICENSE) in the Code Bank repository.
-------------
## Overview
Given an image like the example below, our goal is to generate a caption such as "a surfer riding on a wave".
<img src="https://upload.wikimedia.org/wikipedia/commons/d/db/Surfing_in_Hawaii.jpg" width="500" height="500" align="center"/>
Image source: https://upload.wikimedia.org/wikipedia/commons/d/db/Surfing_in_Hawaii.jpg
To accomplish this, we'll use an attention-based model, which also enables us to see what parts of the image the model focuses on as it generates a caption. For the image above, here is an overlay of which parts of the image the model associates with which predicted word.
<img src="https://www.tensorflow.org/images/imcap_prediction.png" width="800" height="800" align="center"/>
For this illustration, we are using the [Microsoft COCO](http://cocodataset.org/#home) dataset, a large-scale image dataset for object recognition, image segmentation, and captioning. The entire training data is 13GB big and requires a GPU for efficient model training. We have run the code of the original tutorial on a GPU-powered Google Colab notebook in advance so that we can now import the pre-trained model (see below) and make inferences.
We only include code that's required to make inferences on new images; not the code to train the model from scratch. For the complete code please see the original Google tutorial linked below.
Portions of this page are reproduced from work created and shared by Google and used according to terms described in the [Creative Commons 4.0 Attribution License](https://creativecommons.org/licenses/by/4.0/). For the original tutorial visit: https://www.tensorflow.org/tutorials/text/image_captioning
-------------
## **Part 0**: Setup
### Import packages
```
# Import all packages
import tensorflow as tf
# We'll generate plots of attention in order to see which parts of an image
# our model focuses on during captioning
import matplotlib.pyplot as plt
# Scikit-learn includes many helpful utilities
from sklearn.model_selection import train_test_split
from sklearn.utils import shuffle
import re
import os
import time
import json
import pickle
import numpy as np
from glob import glob
from PIL import Image
from tqdm import tqdm
```
### Constants
```
PATH = 'data/coco-data/'
```
### Support functions
```
def load_image(image_path):
"""
Load and resize image
Args:
image_path (str): path to the image
Returns:
img: TensorFlow image preprocessed for use with the InceptionV3 model
image_path: path to the image
"""
img = tf.io.read_file(image_path)
img = tf.image.decode_jpeg(img, channels=3)
img = tf.image.resize(img, (299, 299))
img = tf.keras.applications.inception_v3.preprocess_input(img)
return img, image_path
# Attention implementation
class BahdanauAttention(tf.keras.Model):
def __init__(self, units):
super(BahdanauAttention, self).__init__()
self.W1 = tf.keras.layers.Dense(units)
self.W2 = tf.keras.layers.Dense(units)
self.V = tf.keras.layers.Dense(1)
def call(self, features, hidden):
# features(CNN_encoder output) shape == (batch_size, 64, embedding_dim)
# hidden shape == (batch_size, hidden_size)
# hidden_with_time_axis shape == (batch_size, 1, hidden_size)
hidden_with_time_axis = tf.expand_dims(hidden, 1)
# score shape == (batch_size, 64, hidden_size)
score = tf.nn.tanh(self.W1(features) + self.W2(hidden_with_time_axis))
# attention_weights shape == (batch_size, 64, 1)
# you get 1 at the last axis because you are applying score to self.V
attention_weights = tf.nn.softmax(self.V(score), axis=1)
# context_vector shape after sum == (batch_size, hidden_size)
context_vector = attention_weights * features
context_vector = tf.reduce_sum(context_vector, axis=1)
return context_vector, attention_weights
class CNN_Encoder(tf.keras.Model):
# Since we have already extracted the features and dumped it using pickle
# This encoder passes those features through a Fully connected layer
def __init__(self, embedding_dim):
super(CNN_Encoder, self).__init__()
# shape after fc == (batch_size, 64, embedding_dim)
self.fc = tf.keras.layers.Dense(embedding_dim)
def call(self, x):
x = self.fc(x)
x = tf.nn.relu(x)
return x
class RNN_Decoder(tf.keras.Model):
def __init__(self, embedding_dim, units, vocab_size):
super(RNN_Decoder, self).__init__()
self.units = units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
self.fc1 = tf.keras.layers.Dense(self.units)
self.fc2 = tf.keras.layers.Dense(vocab_size)
self.attention = BahdanauAttention(self.units)
def call(self, x, features, hidden):
# defining attention as a separate model
context_vector, attention_weights = self.attention(features, hidden)
# x shape after passing through embedding == (batch_size, 1, embedding_dim)
x = self.embedding(x)
# x shape after concatenation == (batch_size, 1, embedding_dim + hidden_size)
x = tf.concat([tf.expand_dims(context_vector, 1), x], axis=-1)
# passing the concatenated vector to the GRU
output, state = self.gru(x)
# shape == (batch_size, max_length, hidden_size)
x = self.fc1(output)
# x shape == (batch_size * max_length, hidden_size)
x = tf.reshape(x, (-1, x.shape[2]))
# output shape == (batch_size * max_length, vocab)
x = self.fc2(x)
return x, state, attention_weights
def reset_state(self, batch_size):
return tf.zeros((batch_size, self.units))
def loss_function(real, pred):
"""
Loss function
Args:
real: ground truth values
pred: predicted values
Returns: function to reduce loss function in tensorflow
"""
mask = tf.math.logical_not(tf.math.equal(real, 0))
loss_ = loss_object(real, pred)
mask = tf.cast(mask, dtype=loss_.dtype)
loss_ *= mask
return tf.reduce_mean(loss_)
@tf.function
def train_step(img_tensor, target):
"""
Runs one training step
Note that the decorator will compile the function into the tensorflow graph for faster execution on GPUs and TPUs
Args:
img_tensor: input image data
targ: target
Returns: loss for batch, total loss
"""
loss = 0
# initializing the hidden state for each batch
# because the captions are not related from image to image
hidden = decoder.reset_state(batch_size=target.shape[0])
dec_input = tf.expand_dims([tokenizer.word_index['<start>']] * target.shape[0], 1)
with tf.GradientTape() as tape:
features = encoder(img_tensor)
for i in range(1, target.shape[1]):
# passing the features through the decoder
predictions, hidden, _ = decoder(dec_input, features, hidden)
loss += loss_function(target[:, i], predictions)
# using teacher forcing
dec_input = tf.expand_dims(target[:, i], 1)
total_loss = (loss / int(target.shape[1]))
trainable_variables = encoder.trainable_variables + decoder.trainable_variables
gradients = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(gradients, trainable_variables))
return loss, total_loss
def evaluate(image):
"""
Predict caption and construct attention plot
Args:
image: image to evaluate
Returns:
result: predicted caption
attention_plot
"""
attention_plot = np.zeros((max_length, attention_features_shape))
hidden = decoder.reset_state(batch_size=1)
temp_input = tf.expand_dims(load_image(image)[0], 0)
img_tensor_val = image_features_extract_model(temp_input)
img_tensor_val = tf.reshape(img_tensor_val, (img_tensor_val.shape[0], -1, img_tensor_val.shape[3]))
features = encoder(img_tensor_val)
dec_input = tf.expand_dims([tokenizer.word_index['<start>']], 0)
result = []
for i in range(max_length):
predictions, hidden, attention_weights = decoder(dec_input, features, hidden)
attention_plot[i] = tf.reshape(attention_weights, (-1, )).numpy()
predicted_id = tf.random.categorical(predictions, 1)[0][0].numpy()
result.append(tokenizer.index_word[predicted_id])
if tokenizer.index_word[predicted_id] == '<end>':
return result, attention_plot
dec_input = tf.expand_dims([predicted_id], 0)
attention_plot = attention_plot[:len(result), :]
return result, attention_plot
def plot_attention(image, result, attention_plot):
"""
Construct the attention plot
Args:
image: input image
result (str): predicted caption
attention_plot: data for attention plot
"""
temp_image = np.array(Image.open(image))
fig = plt.figure(figsize=(14, 14))
len_result = len(result)
for l in range(len_result):
temp_att = np.resize(attention_plot[l], (8, 8))
ax = fig.add_subplot(len_result//2, len_result//2, l+1)
ax.set_title(result[l])
img = ax.imshow(temp_image)
ax.imshow(temp_att, cmap='gray', alpha=0.6, extent=img.get_extent())
plt.tight_layout()
plt.show()
```
## **Part 1**: Load & pre-process data
We'll use the [MS-COCO dataset](http://cocodataset.org/#home) to train our model. The dataset contains over 82,000 images, each of which has at least 5 different caption annotations. The code below loads a sample of 100 images that we have downloaded to save space.
To speed up training for this tutorial, we'll use a subset of 30,000 captions and their corresponding images to train our model. Choosing to use more data would result in improved captioning quality.
```
# Read the json file
annotation_file = 'data/coco-data/captions_train2014.json'
with open(annotation_file, 'r') as f:
annotations = json.load(f)
# Store captions and image names in vectors
all_captions = []
all_img_name_vector = []
for annot in annotations['annotations']:
caption = '<start> ' + annot['caption'] + ' <end>'
image_id = annot['image_id']
full_coco_image_path = PATH + 'COCO_train2014_' + '%012d.jpg' % (image_id)
all_img_name_vector.append(full_coco_image_path)
all_captions.append(caption)
# Shuffle captions and image_names together
# Set a random state
train_captions, img_name_vector = shuffle(all_captions,
all_img_name_vector,
random_state=1)
# Select the first 30000 captions
num_examples = 30000
train_captions = train_captions[:num_examples]
img_name_vector = img_name_vector[:num_examples]
len(train_captions), len(all_captions)
```
## **Part 2**: Set up InceptionV3 model, cache data, and preprocess captions
* First, we'll use InceptionV3 (which is pretrained on Imagenet) to classify each image. We'll extract features from the last convolutional layer. InceptionV3 requires the following pre-processing:
* Resizing the image to 299px by 299px
* [Preprocess the images](https://cloud.google.com/tpu/docs/inception-v3-advanced#preprocessing_stage) using the [preprocess_input](https://www.tensorflow.org/api_docs/python/tf/keras/applications/inception_v3/preprocess_input) method to normalize the image so that it contains pixels in the range of -1 to 1, which matches the format of the images used to train InceptionV3.
* We'll limit the vocabulary size to the top 5,000 words (to save memory). We'll replace all other words with the token "UNK" (unknown).
* We then create word-to-index and index-to-word mappings.
```
# Set up model
image_model = tf.keras.applications.InceptionV3(include_top=False, weights='imagenet')
new_input = image_model.input
hidden_layer = image_model.layers[-1].output
image_features_extract_model = tf.keras.Model(new_input, hidden_layer)
# Choose the top 5000 words from the vocabulary
top_k = 5000
tokenizer = tf.keras.preprocessing.text.Tokenizer(num_words=top_k,
oov_token="<unk>",
filters='!"#$%&()*+.,-/:;=?@[\]^_`{|}~ ')
tokenizer.fit_on_texts(all_captions)
train_seqs = tokenizer.texts_to_sequences(all_captions)
# Create index for padding tag
tokenizer.word_index['<pad>'] = 0
tokenizer.index_word[0] = '<pad>'
```
## **Part 3**: Model: Attention, a CNN Encoder (for image data), and an RNN Decoder (for text data)
Fun fact: the decoder below is identical to the one in the illustration for Neural Machine Translation with Attention for French-to-English translation.
The model architecture is inspired by the [Show, Attend and Tell](https://arxiv.org/pdf/1502.03044.pdf) paper.
* In this example, we extract the features from the lower convolutional layer of InceptionV3 giving us a vector of shape (8, 8, 2048).
* We squash that to a shape of (64, 2048).
* This vector is then passed through the CNN Encoder (which consists of a single Fully connected layer).
* The RNN (here GRU cell) attends over the image to predict the next word.
```
# Feel free to change these parameters according to your system's configuration
BATCH_SIZE = 64
BUFFER_SIZE = 1000
embedding_dim = 256
units = 512
vocab_size = top_k + 1
num_steps = 0.8*len(train_captions) // BATCH_SIZE
# Shape of the vector extracted from InceptionV3 is (64, 2048)
# These two variables represent that vector shape
features_shape = 2048
attention_features_shape = 64
max_length = 49
# Instantiate encoder and decoder
encoder = CNN_Encoder(embedding_dim)
decoder = RNN_Decoder(embedding_dim, units, vocab_size)
# Define the optimizer and loss function
optimizer = tf.keras.optimizers.Adam()
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True, reduction='none')
# Save model checkpoints
checkpoint_path = './data/coco_training_checkpoints'
ckpt = tf.train.Checkpoint(encoder=encoder,
decoder=decoder,
optimizer = optimizer)
ckpt_manager = tf.train.CheckpointManager(ckpt, checkpoint_path, max_to_keep=5)
start_epoch = 0
```
## **Part 4**: Evaluate model
We have pre-trained the model on 30,000 images on a Google Cloud GPU. It took approximately 2.5 hours on a single NVIDIA P100 GPU, which costs around $5,000.
```
# Download pre-trained model checkpoints from Google Cloud storage
# CHECKPOINT LOCATIONS ON GOOGLE MOVED!
!wget -N 'https://storage.googleapis.com/dsfm/coco_training_checkpoints/checkpoint' --directory-prefix='data/coco_training_checkpoints'
!wget -N 'https://storage.googleapis.com/dsfm/coco_training_checkpoints/ckpt-1.data-00000-of-00002' --directory-prefix='data/coco_training_checkpoints'
!wget -N 'https://storage.googleapis.com/dsfm/coco_training_checkpoints/ckpt-1.data-00001-of-00002' --directory-prefix='data/coco_training_checkpoints'
!wget -N 'https://storage.googleapis.com/dsfm/coco_training_checkpoints/ckpt-1.index' --directory-prefix='data/coco_training_checkpoints'
!wget -N 'https://storage.googleapis.com/dsfm/coco_training_checkpoints/tokenizer.pickle' --directory-prefix='data/coco_training_checkpoints'
# Load latest checkpoint
if ckpt_manager.latest_checkpoint:
start_epoch = int(ckpt_manager.latest_checkpoint.split('-')[-1])
# restoring the latest checkpoint in checkpoint_path
ckpt.restore(ckpt_manager.latest_checkpoint)
# Overwrite tokenizer to match pre-trained model
with open('data/coco_training_checkpoints/tokenizer.pickle', 'rb') as handle:
tokenizer = pickle.load(handle)
```
### Your own image
Test the pre-trained model with an image of your choice. There are two things we have to change:
- the image URL
- the image path name, defining the file name on your machine (e.g. image0 below)
A note of caution: we have substantially reduced the training size in the interest of time, so the captions we see might not make a lot of sense. Furthermore, re-run individual image evaluations to get slightly different results, due to the probabilistic nature of the model implemented.
```
# Example of a surfer on a wave
image_url = 'https://tensorflow.org/images/surf.jpg'
image_extension = image_url[-4:]
image_path = tf.keras.utils.get_file('image0'+image_extension, origin=image_url)
result, attention_plot = evaluate(image_path)
print ('Prediction Caption:', ' '.join(result))
plot_attention(image_path, result, attention_plot)
# opening the image
Image.open(image_path)
# Another example
image_url = 'https://upload.wikimedia.org/wikipedia/commons/4/4b/Wdomenada2003b.jpg'
image_extension = image_url[-4:]
image_path = tf.keras.utils.get_file('image1' + image_extension, origin = image_url)
result, attention_plot = evaluate(image_path)
print ('Prediction Caption:', ' '.join(result))
plot_attention(image_path, result, attention_plot)
# opening the image
Image.open(image_path)
```
|
github_jupyter
|
# Import all packages
import tensorflow as tf
# We'll generate plots of attention in order to see which parts of an image
# our model focuses on during captioning
import matplotlib.pyplot as plt
# Scikit-learn includes many helpful utilities
from sklearn.model_selection import train_test_split
from sklearn.utils import shuffle
import re
import os
import time
import json
import pickle
import numpy as np
from glob import glob
from PIL import Image
from tqdm import tqdm
PATH = 'data/coco-data/'
def load_image(image_path):
"""
Load and resize image
Args:
image_path (str): path to the image
Returns:
img: TensorFlow image preprocessed for use with the InceptionV3 model
image_path: path to the image
"""
img = tf.io.read_file(image_path)
img = tf.image.decode_jpeg(img, channels=3)
img = tf.image.resize(img, (299, 299))
img = tf.keras.applications.inception_v3.preprocess_input(img)
return img, image_path
# Attention implementation
class BahdanauAttention(tf.keras.Model):
def __init__(self, units):
super(BahdanauAttention, self).__init__()
self.W1 = tf.keras.layers.Dense(units)
self.W2 = tf.keras.layers.Dense(units)
self.V = tf.keras.layers.Dense(1)
def call(self, features, hidden):
# features(CNN_encoder output) shape == (batch_size, 64, embedding_dim)
# hidden shape == (batch_size, hidden_size)
# hidden_with_time_axis shape == (batch_size, 1, hidden_size)
hidden_with_time_axis = tf.expand_dims(hidden, 1)
# score shape == (batch_size, 64, hidden_size)
score = tf.nn.tanh(self.W1(features) + self.W2(hidden_with_time_axis))
# attention_weights shape == (batch_size, 64, 1)
# you get 1 at the last axis because you are applying score to self.V
attention_weights = tf.nn.softmax(self.V(score), axis=1)
# context_vector shape after sum == (batch_size, hidden_size)
context_vector = attention_weights * features
context_vector = tf.reduce_sum(context_vector, axis=1)
return context_vector, attention_weights
class CNN_Encoder(tf.keras.Model):
# Since we have already extracted the features and dumped it using pickle
# This encoder passes those features through a Fully connected layer
def __init__(self, embedding_dim):
super(CNN_Encoder, self).__init__()
# shape after fc == (batch_size, 64, embedding_dim)
self.fc = tf.keras.layers.Dense(embedding_dim)
def call(self, x):
x = self.fc(x)
x = tf.nn.relu(x)
return x
class RNN_Decoder(tf.keras.Model):
def __init__(self, embedding_dim, units, vocab_size):
super(RNN_Decoder, self).__init__()
self.units = units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
self.fc1 = tf.keras.layers.Dense(self.units)
self.fc2 = tf.keras.layers.Dense(vocab_size)
self.attention = BahdanauAttention(self.units)
def call(self, x, features, hidden):
# defining attention as a separate model
context_vector, attention_weights = self.attention(features, hidden)
# x shape after passing through embedding == (batch_size, 1, embedding_dim)
x = self.embedding(x)
# x shape after concatenation == (batch_size, 1, embedding_dim + hidden_size)
x = tf.concat([tf.expand_dims(context_vector, 1), x], axis=-1)
# passing the concatenated vector to the GRU
output, state = self.gru(x)
# shape == (batch_size, max_length, hidden_size)
x = self.fc1(output)
# x shape == (batch_size * max_length, hidden_size)
x = tf.reshape(x, (-1, x.shape[2]))
# output shape == (batch_size * max_length, vocab)
x = self.fc2(x)
return x, state, attention_weights
def reset_state(self, batch_size):
return tf.zeros((batch_size, self.units))
def loss_function(real, pred):
"""
Loss function
Args:
real: ground truth values
pred: predicted values
Returns: function to reduce loss function in tensorflow
"""
mask = tf.math.logical_not(tf.math.equal(real, 0))
loss_ = loss_object(real, pred)
mask = tf.cast(mask, dtype=loss_.dtype)
loss_ *= mask
return tf.reduce_mean(loss_)
@tf.function
def train_step(img_tensor, target):
"""
Runs one training step
Note that the decorator will compile the function into the tensorflow graph for faster execution on GPUs and TPUs
Args:
img_tensor: input image data
targ: target
Returns: loss for batch, total loss
"""
loss = 0
# initializing the hidden state for each batch
# because the captions are not related from image to image
hidden = decoder.reset_state(batch_size=target.shape[0])
dec_input = tf.expand_dims([tokenizer.word_index['<start>']] * target.shape[0], 1)
with tf.GradientTape() as tape:
features = encoder(img_tensor)
for i in range(1, target.shape[1]):
# passing the features through the decoder
predictions, hidden, _ = decoder(dec_input, features, hidden)
loss += loss_function(target[:, i], predictions)
# using teacher forcing
dec_input = tf.expand_dims(target[:, i], 1)
total_loss = (loss / int(target.shape[1]))
trainable_variables = encoder.trainable_variables + decoder.trainable_variables
gradients = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(gradients, trainable_variables))
return loss, total_loss
def evaluate(image):
"""
Predict caption and construct attention plot
Args:
image: image to evaluate
Returns:
result: predicted caption
attention_plot
"""
attention_plot = np.zeros((max_length, attention_features_shape))
hidden = decoder.reset_state(batch_size=1)
temp_input = tf.expand_dims(load_image(image)[0], 0)
img_tensor_val = image_features_extract_model(temp_input)
img_tensor_val = tf.reshape(img_tensor_val, (img_tensor_val.shape[0], -1, img_tensor_val.shape[3]))
features = encoder(img_tensor_val)
dec_input = tf.expand_dims([tokenizer.word_index['<start>']], 0)
result = []
for i in range(max_length):
predictions, hidden, attention_weights = decoder(dec_input, features, hidden)
attention_plot[i] = tf.reshape(attention_weights, (-1, )).numpy()
predicted_id = tf.random.categorical(predictions, 1)[0][0].numpy()
result.append(tokenizer.index_word[predicted_id])
if tokenizer.index_word[predicted_id] == '<end>':
return result, attention_plot
dec_input = tf.expand_dims([predicted_id], 0)
attention_plot = attention_plot[:len(result), :]
return result, attention_plot
def plot_attention(image, result, attention_plot):
"""
Construct the attention plot
Args:
image: input image
result (str): predicted caption
attention_plot: data for attention plot
"""
temp_image = np.array(Image.open(image))
fig = plt.figure(figsize=(14, 14))
len_result = len(result)
for l in range(len_result):
temp_att = np.resize(attention_plot[l], (8, 8))
ax = fig.add_subplot(len_result//2, len_result//2, l+1)
ax.set_title(result[l])
img = ax.imshow(temp_image)
ax.imshow(temp_att, cmap='gray', alpha=0.6, extent=img.get_extent())
plt.tight_layout()
plt.show()
# Read the json file
annotation_file = 'data/coco-data/captions_train2014.json'
with open(annotation_file, 'r') as f:
annotations = json.load(f)
# Store captions and image names in vectors
all_captions = []
all_img_name_vector = []
for annot in annotations['annotations']:
caption = '<start> ' + annot['caption'] + ' <end>'
image_id = annot['image_id']
full_coco_image_path = PATH + 'COCO_train2014_' + '%012d.jpg' % (image_id)
all_img_name_vector.append(full_coco_image_path)
all_captions.append(caption)
# Shuffle captions and image_names together
# Set a random state
train_captions, img_name_vector = shuffle(all_captions,
all_img_name_vector,
random_state=1)
# Select the first 30000 captions
num_examples = 30000
train_captions = train_captions[:num_examples]
img_name_vector = img_name_vector[:num_examples]
len(train_captions), len(all_captions)
# Set up model
image_model = tf.keras.applications.InceptionV3(include_top=False, weights='imagenet')
new_input = image_model.input
hidden_layer = image_model.layers[-1].output
image_features_extract_model = tf.keras.Model(new_input, hidden_layer)
# Choose the top 5000 words from the vocabulary
top_k = 5000
tokenizer = tf.keras.preprocessing.text.Tokenizer(num_words=top_k,
oov_token="<unk>",
filters='!"#$%&()*+.,-/:;=?@[\]^_`{|}~ ')
tokenizer.fit_on_texts(all_captions)
train_seqs = tokenizer.texts_to_sequences(all_captions)
# Create index for padding tag
tokenizer.word_index['<pad>'] = 0
tokenizer.index_word[0] = '<pad>'
# Feel free to change these parameters according to your system's configuration
BATCH_SIZE = 64
BUFFER_SIZE = 1000
embedding_dim = 256
units = 512
vocab_size = top_k + 1
num_steps = 0.8*len(train_captions) // BATCH_SIZE
# Shape of the vector extracted from InceptionV3 is (64, 2048)
# These two variables represent that vector shape
features_shape = 2048
attention_features_shape = 64
max_length = 49
# Instantiate encoder and decoder
encoder = CNN_Encoder(embedding_dim)
decoder = RNN_Decoder(embedding_dim, units, vocab_size)
# Define the optimizer and loss function
optimizer = tf.keras.optimizers.Adam()
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True, reduction='none')
# Save model checkpoints
checkpoint_path = './data/coco_training_checkpoints'
ckpt = tf.train.Checkpoint(encoder=encoder,
decoder=decoder,
optimizer = optimizer)
ckpt_manager = tf.train.CheckpointManager(ckpt, checkpoint_path, max_to_keep=5)
start_epoch = 0
# Download pre-trained model checkpoints from Google Cloud storage
# CHECKPOINT LOCATIONS ON GOOGLE MOVED!
!wget -N 'https://storage.googleapis.com/dsfm/coco_training_checkpoints/checkpoint' --directory-prefix='data/coco_training_checkpoints'
!wget -N 'https://storage.googleapis.com/dsfm/coco_training_checkpoints/ckpt-1.data-00000-of-00002' --directory-prefix='data/coco_training_checkpoints'
!wget -N 'https://storage.googleapis.com/dsfm/coco_training_checkpoints/ckpt-1.data-00001-of-00002' --directory-prefix='data/coco_training_checkpoints'
!wget -N 'https://storage.googleapis.com/dsfm/coco_training_checkpoints/ckpt-1.index' --directory-prefix='data/coco_training_checkpoints'
!wget -N 'https://storage.googleapis.com/dsfm/coco_training_checkpoints/tokenizer.pickle' --directory-prefix='data/coco_training_checkpoints'
# Load latest checkpoint
if ckpt_manager.latest_checkpoint:
start_epoch = int(ckpt_manager.latest_checkpoint.split('-')[-1])
# restoring the latest checkpoint in checkpoint_path
ckpt.restore(ckpt_manager.latest_checkpoint)
# Overwrite tokenizer to match pre-trained model
with open('data/coco_training_checkpoints/tokenizer.pickle', 'rb') as handle:
tokenizer = pickle.load(handle)
# Example of a surfer on a wave
image_url = 'https://tensorflow.org/images/surf.jpg'
image_extension = image_url[-4:]
image_path = tf.keras.utils.get_file('image0'+image_extension, origin=image_url)
result, attention_plot = evaluate(image_path)
print ('Prediction Caption:', ' '.join(result))
plot_attention(image_path, result, attention_plot)
# opening the image
Image.open(image_path)
# Another example
image_url = 'https://upload.wikimedia.org/wikipedia/commons/4/4b/Wdomenada2003b.jpg'
image_extension = image_url[-4:]
image_path = tf.keras.utils.get_file('image1' + image_extension, origin = image_url)
result, attention_plot = evaluate(image_path)
print ('Prediction Caption:', ' '.join(result))
plot_attention(image_path, result, attention_plot)
# opening the image
Image.open(image_path)
| 0.904248 | 0.989996 |
# One class SVM classification for an imbalanced data set
Date created: Oct 10, 2016
Last modified: Oct 18, 2016
Tags: one-class SVM, Random Forest variable importance, imbalanced data set, anomaly detection, feature selection, semiconductor manufacturing data
About: for an imbalanced semicondutor manufacturing dataset, find explanatory variables with predictive power and build a classifier to detect failures
The [SECOM dataset](http://archive.ics.uci.edu/ml/datasets/SECOM) in the [UCI Machine Learning Repository](http://archive.ics.uci.edu/ml) is semicondutor manufacturing data. There are 1567 records, 590 anonymized features and 104 fails. This makes it an imbalanced with a 14:1 ratio of pass to fails. The process yield has a simple pass/fail response (encoded -1/1).
<h4>Objective</h4>
If the overall objective is to streamline the manufacturing process two things are needed: (i) a good classifier and (ii) feature selection. A streamlined feature set can not only lead to better prediction accuracy and data understanding but also optimize manufacturing resources.
For this exercise, we will look at:
- the use of a one-class SVM for an imbalanced data set
- reducing the number of features to improve classifier performance
<h4>Methodology</h4>
The [Variable Importance](http://www.statistik.uni-dortmund.de/useR-2008/slides/Strobl+Zeileis.pdf) is a byproduct of the random forest classifier construction. We will rank the features in order of importance and the first <i>x</i> ranked features will be used for the classifier.
We will then use the one-class SVM (OCSVM) method to classify the data. In the OCSVM, a decision boundary is learned using only the majority class. The minority class data are outliers in this setup.
<h4>Preprocessing</h4>
The data represents measurements from a large number of processes or sensors; many of the records are missing -- 50-60% of an entire column in 4% of the cases. In addition some measurements are identical/constant and so not useful for prediction. We will remove those columns with high missing count or constant values.<br>
For the random forest classifier, we will impute the remainaing missing values with the median for the column.
For the OCSVM, we will additionally scale the data. We will use the <i>sklearn preprocessing</i> module for both imputing and scaling.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.preprocessing import Imputer
from sklearn.preprocessing import StandardScaler
from sklearn.cross_validation import train_test_split as tts
from sklearn.grid_search import ParameterGrid
from sklearn.ensemble import RandomForestClassifier
from sklearn import svm
import warnings
warnings.filterwarnings("ignore")
from __future__ import division
url = "http://archive.ics.uci.edu/ml/machine-learning-databases/secom/secom.data"
secom = pd.read_table(url, header=None, delim_whitespace=True)
url = "http://archive.ics.uci.edu/ml/machine-learning-databases/secom/secom_labels.data"
y = pd.read_table(url, header=None, usecols=[0], squeeze=True, delim_whitespace=True)
print 'The dataset has {} observations/rows and {} variables/columns.'\
.format(secom.shape[0], secom.shape[1])
print 'The majority class has {} observations, minority class {}.'\
.format(y[y == -1].size, y[y == 1].size)
print 'The dataset is imbalanced. \
The ratio of majority class to minority class is {}:1.'\
.format(int(y[y == -1].size/y[y == 1].size))
```
<h3> Preprocessing </h3>
We will process the missing values first, dropping columns which have a large number of missing values and imputing values for those that have only a few missing values. We will use <i>pandas</i> for this.
```
# what if all the columns/rows with missing values were removed
nmv = secom.dropna(axis=1)
print 'No. of columns after removing columns with missing data: {}'\
.format(nmv.shape[1])
nmv = secom.dropna(axis=0)
print 'No. of rows after removing rows with missing data: {}'\
.format(nmv.shape[0])
# num of missing entries per column
m = map(lambda x: sum(secom[x].isnull()), xrange(secom.shape[1]))
# distribution of columns with missing entries
plt.hist(m, color='turquoise')
plt.title("Distribution of missing values")
plt.xlabel("No. of missing values in a column")
plt.ylabel("Columns")
plt.show()
m_700thresh = filter(lambda i: (m[i] > 700), xrange(secom.shape[1]))
print 'The number of columns with more than 700 missing values: {}'\
.format(len(m_700thresh))
m_200thresh = filter(lambda i: (m[i] > 200), xrange(secom.shape[1]))
print 'The number of columns with more than 200 missing values: {}'\
.format(len(m_200thresh))
# remove columns with more than 200 missing entries
secom_drop_200thresh = secom.dropna(subset=[m_200thresh], axis=1)
print 'No. of columns after dropping columns with more than 200 missing entries: {}'\
.format(secom_drop_200thresh.shape[1])
# remove columns where every entry is identical (the std. dev = 0)
dropthese = [x for x in secom_drop_200thresh.columns.values \
if secom_drop_200thresh[x].std() == 0]
print 'There are {} columns which have identical values recorded. \
We will drop these.' .format(len(dropthese))
secom_drop_200thresh.drop(dropthese, axis=1, inplace=True)
print 'The data set now has {} columns.'\
.format(secom_drop_200thresh.shape[1])
# checking whether there is a mix of categorical variables
print 'The number of categorical variables is: {}'\
.format(sum((secom_drop_200thresh.dtypes == 'categorical')*1))
secom_drop_200thresh.head(2)
# imputing missing values for the random forest
imp = Imputer(missing_values='NaN', strategy='median', axis=0)
secom_imp = pd.DataFrame(imp.fit_transform(secom_drop_200thresh))
```
<h3> Random Forest Variable Importance</h3>
In addition to prediction the Random Forest can also be used to assess variable importance. In the <i>sklearn</i> [RandomForestClassifier](http://scikit-learn.org/stable/modules/ensemble.html#forest) package this is computed from the total decrease in node impurity when a predictor is split. There are issues with this computation (there is a bias towards variables with more categories and correlated variables are arbitrarily selected) but we can ignore these since we will be using many variables for the OCSVM classifier. A bigger concern is the imbalance in the data set as this might affect the variable importance ranking.<br>
The SECOM matrix at this point has 409 variables. We will use the Random Forest to rank the variables in terms of their importance.
```
rf = RandomForestClassifier(n_estimators=100, random_state=7)
rf.fit(secom_imp, y)
# displaying features and their rank
importance = rf.feature_importances_
ranked_indices = np.argsort(importance)[::-1]
print "Feature Rank:"
for i in range(15):
print "{0:3d} column {1:3d} {2:6.4f}"\
.format(i+1, ranked_indices[i], importance[ranked_indices[i]])
print "\n"
for i in xrange(len(importance)-5,len(importance)):
print "{0:3d} column {1:3d} {2:6.4f}"\
.format(i+1, ranked_indices[i], importance[ranked_indices[i]])
navg = 0
for i in range(len(importance)):
if importance[ranked_indices[i]] > np.average(rf.feature_importances_):
navg = navg+1
print 'The number of features better than average is: {}'.format(navg)
# plot of importance vs the number of features
plt.figure(figsize=(8,6))
plt.plot(range(len(importance)), importance[ranked_indices[:]])
plt.axvline(15, color='magenta', linestyle='dashdot', label='n=15')
plt.axvline(40, color='orange', linestyle='dashed', label='n=40')
plt.axvline(65, color='turquoise', linestyle='dashdot', label='n=65')
plt.axvline(100, color='red', linestyle='dotted', label='n=100')
plt.text(15, 0.002, 'n=15', rotation='vertical')
plt.text(40, 0.008, 'n=40', rotation='vertical')
plt.text(65, 0.011, 'n=65', rotation='vertical')
plt.text(100, 0.014, 'n=100', rotation='vertical')
plt.title('Importance vs feature rank')
plt.xlabel('feature rank')
plt.ylabel('importance')
plt.show()
```
From this plot, we see points of inflection around the 15, 40, 65 and 100 mark. We will use these to generate 4-5 sets of features to test out on the one-class SVM. The 50 percentile mark is at 148 so these are reduced feature sets, much smaller than the 409 features we had after cleaning the data. In some of the literature <a href="#ref1">[1]</a> associated with this data set, 40 features were used in the analysis. This was determined by correlation.
<h3> One-class SVM (OCSVM) </h3>
The OCSVM proposed by Schölkopf et al. <a href="#ref2">[2]</a>, <a href="#ref3">[3]</a> can be used to detect negative examples in imbalanced data sets. In the OCSVM, training examples from the majority class are mapped to a feature space circumscribed by a hypersphere; a soft-margin decision boundary is minimized and all points outside are considered outliers.
<h4>Preprocessing</h4>
The data is first divided into a majority class train and test set and the minority class test-only set.
The OCSVM is sensitive to feature scale so the first step is to center and normalize the data. The train and test sets are scaled separately using the mean and variance computed from the training data. This is done to estimate the ability of the model to generalize.
<h4>Parameter Tuning</h4>
The main parameters are the choice of the <i>kernel</i>, <i>nu</i> and <i>gamma</i>. Some preliminary evaluation showed that the linear and polynomial kernels give poor results. This leaves the <i>rbf</i> kernel for further experimentation.
The hyper-parameters for OCSVM with the <i>rbf</i> kernel are nu ($\nu$) and gamma ($\gamma$).<br>
<ul>
<li> <b>nu:</b> the upper bound for the fraction of margin errors (outliers here) allowed in the data and the lower bound for support vectors relative to the total training examples. It has a range of (0,1). The OCSVM nu can be likened to the SVM parameter <i>C</i> in that both are attached to the penalty term of their respective objective functions.
<ol>
<li>Small nu is associated with a smaller margin and higher variance
<li>Large nu is associated with lower misclassification penalty and low model complexity
</ol>
<li> <b>gamma:</b> This is a regularization parameter which for the <i>rbf</i> kernel is equal to $\frac{1}{2\sigma^2}$. It defines the influence of a single training point on points nearby.
<ol>
<li> Low values of gamma (large $\sigma$) imply that training points on or near the decision boundary have high influence. This tends to smoothen the decision boundary (as there are many points exerting an influence) and is related to higher bias.
<li> High values of gamma (small $\sigma$) imply that points on the decision boundary exert less influence. This leads to a more flexible curvy decision boundary that is associated with higher variance.
</ol>
</ul>
```
# function for preprocessing, classification, parameter grid search
def ocsvm_classify(nfeatures, param_grid, printflag=0, printheader=0):
# selecting features and generating a data set
X_ocsvm = secom_imp.loc[y == -1,ranked_indices[:nfeatures]]
X_outlier = secom_imp.loc[y == 1,ranked_indices[:nfeatures]]
if printflag:
print "The majority/minority classes have {}/{} observations. \n"\
.format(X_ocsvm.shape[0], X_outlier.shape[0])
# By convention the majority class has a +1 label
# and the train and test set belong to the majority class.
# This is not to be confused with the secom dataset where
# the majority class has a -1 label
y_ocsvm = np.ones(len(X_ocsvm))
X_train, X_test, y_train, y_test = tts(
X_ocsvm, y_ocsvm, test_size=0.3, random_state=5)
# scaling the split data. The test/outlier data uses scaling parameters
# computed from the training data
standard_scaler = StandardScaler()
X_train_scaled = standard_scaler.fit_transform(X_train)
X_test_scaled = standard_scaler.transform(X_test)
X_outlier_scaled = standard_scaler.transform(X_outlier)
# classify for each set of parameters in the grid
for i in range(len(list(ParameterGrid(param_grid)) )):
nu = ParameterGrid(param_grid)[i]['nu']
gamma = ParameterGrid(param_grid)[i]['gamma']
clf = svm.OneClassSVM(nu=nu, kernel='rbf', gamma=gamma)
clf.fit(X_train_scaled)
y_pred_train = clf.predict(X_train_scaled)
y_pred_test = clf.predict(X_test_scaled)
y_pred_outlier = clf.predict(X_outlier_scaled)
# calculating error
n_error_train = y_pred_train[y_pred_train == -1].size
n_error_test = y_pred_test[y_pred_test == -1].size
n_error_outlier = y_pred_outlier[y_pred_outlier == 1].size
# printing results
if i == 0:
if printheader:
print "nfeatures\tnu\tgamma\t train error\t test error\t outlier error"
print "{0:3d}\t\t{1:3.2f}\t{2:3.2f}\t {3:3d}({4:4.2f}%)\t {5:3d}({6:4.2f}%)\t{7:3d}({8:4.2f}%)"\
.format(nfeatures, nu, gamma, \
n_error_train, round(n_error_train/len(y_train) *100, 2),\
n_error_test, round(n_error_test/len(y_test) *100, 2),\
n_error_outlier, round(n_error_outlier/len(X_outlier) *100, 2))
else:
print "\t\t{0:3.2f}\t{1:3.2f}\t {2:3d}({3:4.2f}%) \t {4:3d}({5:4.2f}%)\t{6:3d}({7:4.2f}%)"\
.format(nu, gamma, \
n_error_train, round(n_error_train/len(y_train) *100, 2),\
n_error_test, round(n_error_test/len(y_test) *100, 2),\
n_error_outlier, round(n_error_outlier/len(X_outlier) *100, 2))
# running a second pass on the tuning matrix (after a coarse first pass)
param_grid = {'nu': [0.03,0.04,0.05], 'gamma': [0.07, 0.08, 0.09, 0.10, 0.15, 0.20]}
ocsvm_classify(40, param_grid, printflag=1, printheader=1)
print "\n"
param_grid = {'nu': [0.1,0.2], 'gamma': [0.04, 0.05, 0.06]}
ocsvm_classify(60, param_grid)
param_grid = {'nu': [0.1], 'gamma': [0.04, 0.05]}
ocsvm_classify(65, param_grid)
param_grid = {'nu': [0.04,0.05], 'gamma': [0.03, 0.04]}
ocsvm_classify(100, param_grid)
print "\n"
param_grid = {'nu': [0.02,0.03, 0.04], 'gamma': [0.10, 0.15, 0.18, 0.20]}
ocsvm_classify(15, param_grid)
```
<h3>Observations</h3>
As gamma increases:
* the outlier classification improves
* the test error also improves
* the train error is not significantly affected
As nu increases:
* the outlier and test error do not change
* the training error changes slightly increasing in some cases, decreasing in others
As n, the number of variables, increases:
* n = 15, train error is much smaller than the outlier error
* n = 40 - 65: this seems to be the most tunable regime. The best results were obtained when the test error and outlier error were in the low 30% range when n=60 and 65.
* n = 100: This is also in the tunable range.
<h3>Discussion</h3>
This parameter grid search was carried out on a single split of the data (rather than cross-validation) but there is an indication the models have high bias since the train error and test error are both high and also because you can reduce the outlier error by increasing the variance via gamma.
The best<sup>**</sup> results were obtained when the test error and outlier error were in the low 30% range for n=40 - 65.
| nfeatures | nu | gamma | train error | test error |outlier error |
|:----------: |:------------:|:-----:|:----------: |:----------:|:----------: |
|40 |0.03 | 0.09 | 169(16.50%) | 148(33.71%) | 32(30.77%)|
|60 |0.10 | 0.05 | 183(17.87%) | 133(30.30%) | 34(32.69%)|
|65 |0.10 | 0.05 |162(15.82%) | 154(35.08%) | 29(27.88%) |
This however is still too high. The OCSVM on this data set also appears to be difficult to tune so rather than find the optimal hyperparameters through cross-validation we will look at other classification methods.
<sup>**</sup>Depending on which point in the production flow the data was recorded, one may wish to optimize for False Positives or False Negatives. If you optimize for detecting False Positives early in the production flow, you will save resources for a device that will be dead in the backend. At the end of the line, detecting false negatives is more important since the chip, which increases in value with each process step, is most valuable at this stage.
<h3> References and Further Reading </h3>
<a name="ref1"></a>[1] [M McCann Y Li L Maguire and A Johnston. "Causality Challenge: Benchmarking relevant signal components for effective monitoring and process control." J. Mach. Learn. Res. Proc. NIPS 2008 workshop on causality](http://www.jmlr.org/proceedings/papers/v6/mccann10a/mccann10a.pdf).
<a name="ref2"></a>[2] [Schölkopf, Bernhard, et al. "Support Vector Method for Novelty Detection." NIPS. Vol. 12. 1999.](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.675.575&rep=rep1&type=pdf)
<a name="ref2"></a>[3] [B. Schölkopf, A. Smola, R. Williamson, and P. L. Bartlett. New support vector algorithms. Neural Computation, 12, 2000, 1207-1245.](http://sci2s.ugr.es/keel/pdf/algorithm/articulo/NewSVM.pdf)
[4] [Statnikov, Alexander, et al. "A Gentle Introduction to Support Vector Machines in Biomedicine."](https://www.stat.auckland.ac.nz/~lee/760/SVM%20tutorial.pdf)
[5] [SVM Parameters](http://www.svms.org/parameters/)
<div style="background-color: #FAAC58; margin-left: 0px; margin-right: 20px; padding-bottom: 8px; padding-left: 8px; padding-right: 8px; padding-top: 8px;">
Author: Meena Mani <br>
email: [email protected] <br>
twitter: @meena_uvaca <br>
</div>
|
github_jupyter
|
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.preprocessing import Imputer
from sklearn.preprocessing import StandardScaler
from sklearn.cross_validation import train_test_split as tts
from sklearn.grid_search import ParameterGrid
from sklearn.ensemble import RandomForestClassifier
from sklearn import svm
import warnings
warnings.filterwarnings("ignore")
from __future__ import division
url = "http://archive.ics.uci.edu/ml/machine-learning-databases/secom/secom.data"
secom = pd.read_table(url, header=None, delim_whitespace=True)
url = "http://archive.ics.uci.edu/ml/machine-learning-databases/secom/secom_labels.data"
y = pd.read_table(url, header=None, usecols=[0], squeeze=True, delim_whitespace=True)
print 'The dataset has {} observations/rows and {} variables/columns.'\
.format(secom.shape[0], secom.shape[1])
print 'The majority class has {} observations, minority class {}.'\
.format(y[y == -1].size, y[y == 1].size)
print 'The dataset is imbalanced. \
The ratio of majority class to minority class is {}:1.'\
.format(int(y[y == -1].size/y[y == 1].size))
# what if all the columns/rows with missing values were removed
nmv = secom.dropna(axis=1)
print 'No. of columns after removing columns with missing data: {}'\
.format(nmv.shape[1])
nmv = secom.dropna(axis=0)
print 'No. of rows after removing rows with missing data: {}'\
.format(nmv.shape[0])
# num of missing entries per column
m = map(lambda x: sum(secom[x].isnull()), xrange(secom.shape[1]))
# distribution of columns with missing entries
plt.hist(m, color='turquoise')
plt.title("Distribution of missing values")
plt.xlabel("No. of missing values in a column")
plt.ylabel("Columns")
plt.show()
m_700thresh = filter(lambda i: (m[i] > 700), xrange(secom.shape[1]))
print 'The number of columns with more than 700 missing values: {}'\
.format(len(m_700thresh))
m_200thresh = filter(lambda i: (m[i] > 200), xrange(secom.shape[1]))
print 'The number of columns with more than 200 missing values: {}'\
.format(len(m_200thresh))
# remove columns with more than 200 missing entries
secom_drop_200thresh = secom.dropna(subset=[m_200thresh], axis=1)
print 'No. of columns after dropping columns with more than 200 missing entries: {}'\
.format(secom_drop_200thresh.shape[1])
# remove columns where every entry is identical (the std. dev = 0)
dropthese = [x for x in secom_drop_200thresh.columns.values \
if secom_drop_200thresh[x].std() == 0]
print 'There are {} columns which have identical values recorded. \
We will drop these.' .format(len(dropthese))
secom_drop_200thresh.drop(dropthese, axis=1, inplace=True)
print 'The data set now has {} columns.'\
.format(secom_drop_200thresh.shape[1])
# checking whether there is a mix of categorical variables
print 'The number of categorical variables is: {}'\
.format(sum((secom_drop_200thresh.dtypes == 'categorical')*1))
secom_drop_200thresh.head(2)
# imputing missing values for the random forest
imp = Imputer(missing_values='NaN', strategy='median', axis=0)
secom_imp = pd.DataFrame(imp.fit_transform(secom_drop_200thresh))
rf = RandomForestClassifier(n_estimators=100, random_state=7)
rf.fit(secom_imp, y)
# displaying features and their rank
importance = rf.feature_importances_
ranked_indices = np.argsort(importance)[::-1]
print "Feature Rank:"
for i in range(15):
print "{0:3d} column {1:3d} {2:6.4f}"\
.format(i+1, ranked_indices[i], importance[ranked_indices[i]])
print "\n"
for i in xrange(len(importance)-5,len(importance)):
print "{0:3d} column {1:3d} {2:6.4f}"\
.format(i+1, ranked_indices[i], importance[ranked_indices[i]])
navg = 0
for i in range(len(importance)):
if importance[ranked_indices[i]] > np.average(rf.feature_importances_):
navg = navg+1
print 'The number of features better than average is: {}'.format(navg)
# plot of importance vs the number of features
plt.figure(figsize=(8,6))
plt.plot(range(len(importance)), importance[ranked_indices[:]])
plt.axvline(15, color='magenta', linestyle='dashdot', label='n=15')
plt.axvline(40, color='orange', linestyle='dashed', label='n=40')
plt.axvline(65, color='turquoise', linestyle='dashdot', label='n=65')
plt.axvline(100, color='red', linestyle='dotted', label='n=100')
plt.text(15, 0.002, 'n=15', rotation='vertical')
plt.text(40, 0.008, 'n=40', rotation='vertical')
plt.text(65, 0.011, 'n=65', rotation='vertical')
plt.text(100, 0.014, 'n=100', rotation='vertical')
plt.title('Importance vs feature rank')
plt.xlabel('feature rank')
plt.ylabel('importance')
plt.show()
# function for preprocessing, classification, parameter grid search
def ocsvm_classify(nfeatures, param_grid, printflag=0, printheader=0):
# selecting features and generating a data set
X_ocsvm = secom_imp.loc[y == -1,ranked_indices[:nfeatures]]
X_outlier = secom_imp.loc[y == 1,ranked_indices[:nfeatures]]
if printflag:
print "The majority/minority classes have {}/{} observations. \n"\
.format(X_ocsvm.shape[0], X_outlier.shape[0])
# By convention the majority class has a +1 label
# and the train and test set belong to the majority class.
# This is not to be confused with the secom dataset where
# the majority class has a -1 label
y_ocsvm = np.ones(len(X_ocsvm))
X_train, X_test, y_train, y_test = tts(
X_ocsvm, y_ocsvm, test_size=0.3, random_state=5)
# scaling the split data. The test/outlier data uses scaling parameters
# computed from the training data
standard_scaler = StandardScaler()
X_train_scaled = standard_scaler.fit_transform(X_train)
X_test_scaled = standard_scaler.transform(X_test)
X_outlier_scaled = standard_scaler.transform(X_outlier)
# classify for each set of parameters in the grid
for i in range(len(list(ParameterGrid(param_grid)) )):
nu = ParameterGrid(param_grid)[i]['nu']
gamma = ParameterGrid(param_grid)[i]['gamma']
clf = svm.OneClassSVM(nu=nu, kernel='rbf', gamma=gamma)
clf.fit(X_train_scaled)
y_pred_train = clf.predict(X_train_scaled)
y_pred_test = clf.predict(X_test_scaled)
y_pred_outlier = clf.predict(X_outlier_scaled)
# calculating error
n_error_train = y_pred_train[y_pred_train == -1].size
n_error_test = y_pred_test[y_pred_test == -1].size
n_error_outlier = y_pred_outlier[y_pred_outlier == 1].size
# printing results
if i == 0:
if printheader:
print "nfeatures\tnu\tgamma\t train error\t test error\t outlier error"
print "{0:3d}\t\t{1:3.2f}\t{2:3.2f}\t {3:3d}({4:4.2f}%)\t {5:3d}({6:4.2f}%)\t{7:3d}({8:4.2f}%)"\
.format(nfeatures, nu, gamma, \
n_error_train, round(n_error_train/len(y_train) *100, 2),\
n_error_test, round(n_error_test/len(y_test) *100, 2),\
n_error_outlier, round(n_error_outlier/len(X_outlier) *100, 2))
else:
print "\t\t{0:3.2f}\t{1:3.2f}\t {2:3d}({3:4.2f}%) \t {4:3d}({5:4.2f}%)\t{6:3d}({7:4.2f}%)"\
.format(nu, gamma, \
n_error_train, round(n_error_train/len(y_train) *100, 2),\
n_error_test, round(n_error_test/len(y_test) *100, 2),\
n_error_outlier, round(n_error_outlier/len(X_outlier) *100, 2))
# running a second pass on the tuning matrix (after a coarse first pass)
param_grid = {'nu': [0.03,0.04,0.05], 'gamma': [0.07, 0.08, 0.09, 0.10, 0.15, 0.20]}
ocsvm_classify(40, param_grid, printflag=1, printheader=1)
print "\n"
param_grid = {'nu': [0.1,0.2], 'gamma': [0.04, 0.05, 0.06]}
ocsvm_classify(60, param_grid)
param_grid = {'nu': [0.1], 'gamma': [0.04, 0.05]}
ocsvm_classify(65, param_grid)
param_grid = {'nu': [0.04,0.05], 'gamma': [0.03, 0.04]}
ocsvm_classify(100, param_grid)
print "\n"
param_grid = {'nu': [0.02,0.03, 0.04], 'gamma': [0.10, 0.15, 0.18, 0.20]}
ocsvm_classify(15, param_grid)
| 0.649245 | 0.986533 |
```
import pandas as pd
import numpy as np
from sqlalchemy import create_engine
from datetime import datetime, date
from ast import literal_eval
import warnings
warnings.filterwarnings('ignore')
engine = create_engine("sqlite:///data/kickstarter.db")
df = pd.read_sql('SELECT * FROM data;', engine)
print(df.shape)
df.head()
df.columns
# get rid of the "column-headers rows"
df = df[df.created_at != "created_at"]
df.shape
df = df.drop(columns=['creator', 'country_displayable_name', 'currency_symbol', 'currency_trailing_code', 'current_currency',
'disable_communication','friends', 'is_backing', 'is_starrable', 'is_starred',
'permissions', 'photo', 'profile', 'source_url', 'urls'])
df.info()
# first looking at the ratio of successful and failed here
df.state.value_counts()
df['state'] = df.state.astype(str)
# Only interested in success/fail champaigns
df = df[(df.state == "successful") | (df.state == "failed")]
df.shape
# Converting datetime objects
df['created_at'] = df['created_at'].astype(int)
df['created_at'] = pd.to_datetime(df['created_at'],unit='s')
df['deadline'] = df['deadline'].astype(int)
df['deadline'] = pd.to_datetime(df['deadline'], unit='s')
df['launched_at'] = df['launched_at'].astype(int)
df['launched_at'] = pd.to_datetime(df['launched_at'],unit='s')
df['state_changed_at'] = df['state_changed_at'].astype(int)
df['state_changed_at'] = pd.to_datetime(df['state_changed_at'],unit='s')
# df['duration'] = df.deadline - df.launched_at
# check for duplicates
df.id.value_counts()
df[df.id == '2028673237']
df.drop_duplicates(subset=['id', 'state'], inplace=True)
df.shape
# Categories - Main category and sub_category
c = df.category.apply(literal_eval)
main_category = []
for i, d in enumerate(c):
try:
main_category.append(d['parent_name'])
except:
main_category.append(np.nan)
df['main_category'] = main_category
df.main_category.value_counts()
sub_category = []
for i, name in enumerate(d['name'] for d in c):
sub_category.append(name)
df['sub_category'] = sub_category
df.sub_category.value_counts()
# Country - needs to condense the list
df.country.value_counts()
dic = {"DK": "OTHER", "NZ": "OTHER", "SG": "OTHER", "CH": "OTHER", "BE": "OTHER", "IE": "OTHER",
"JP": "OTHER", "AT": "OTHER", "NO": "OTHER", "LU": "OTHER", "PL": "OTHER", "GR": "OTHER",
"SI": "OTHER"}
df = df.replace({"country": dic})
df.country.value_counts()
# Currency - needs to convert all goal values to USD
df.currency.value_counts()
df['goal'] = df.goal.astype(float)
df['fx_rate'] = df.fx_rate.astype(float)
df['goal_usd'] = df.goal * df.fx_rate
df.head()
df.usd_type.value_counts()
# checking for NaN
df.isna().sum()
# fill main_category NaN with sub_category
df[df.main_category.isna()]['sub_category'].value_counts()
df.main_category.fillna(df.sub_category, inplace=True)
df.isna().sum()
kickstarter = df[['id', 'goal_usd', 'country', 'created_at', 'deadline', 'launched_at', 'state_changed_at',
'spotlight','staff_pick', 'main_category', 'sub_category', 'blurb', 'state']]
kickstarter.head()
kickstarter.to_csv("./data/kickstarter.csv", index= False)
```
|
github_jupyter
|
import pandas as pd
import numpy as np
from sqlalchemy import create_engine
from datetime import datetime, date
from ast import literal_eval
import warnings
warnings.filterwarnings('ignore')
engine = create_engine("sqlite:///data/kickstarter.db")
df = pd.read_sql('SELECT * FROM data;', engine)
print(df.shape)
df.head()
df.columns
# get rid of the "column-headers rows"
df = df[df.created_at != "created_at"]
df.shape
df = df.drop(columns=['creator', 'country_displayable_name', 'currency_symbol', 'currency_trailing_code', 'current_currency',
'disable_communication','friends', 'is_backing', 'is_starrable', 'is_starred',
'permissions', 'photo', 'profile', 'source_url', 'urls'])
df.info()
# first looking at the ratio of successful and failed here
df.state.value_counts()
df['state'] = df.state.astype(str)
# Only interested in success/fail champaigns
df = df[(df.state == "successful") | (df.state == "failed")]
df.shape
# Converting datetime objects
df['created_at'] = df['created_at'].astype(int)
df['created_at'] = pd.to_datetime(df['created_at'],unit='s')
df['deadline'] = df['deadline'].astype(int)
df['deadline'] = pd.to_datetime(df['deadline'], unit='s')
df['launched_at'] = df['launched_at'].astype(int)
df['launched_at'] = pd.to_datetime(df['launched_at'],unit='s')
df['state_changed_at'] = df['state_changed_at'].astype(int)
df['state_changed_at'] = pd.to_datetime(df['state_changed_at'],unit='s')
# df['duration'] = df.deadline - df.launched_at
# check for duplicates
df.id.value_counts()
df[df.id == '2028673237']
df.drop_duplicates(subset=['id', 'state'], inplace=True)
df.shape
# Categories - Main category and sub_category
c = df.category.apply(literal_eval)
main_category = []
for i, d in enumerate(c):
try:
main_category.append(d['parent_name'])
except:
main_category.append(np.nan)
df['main_category'] = main_category
df.main_category.value_counts()
sub_category = []
for i, name in enumerate(d['name'] for d in c):
sub_category.append(name)
df['sub_category'] = sub_category
df.sub_category.value_counts()
# Country - needs to condense the list
df.country.value_counts()
dic = {"DK": "OTHER", "NZ": "OTHER", "SG": "OTHER", "CH": "OTHER", "BE": "OTHER", "IE": "OTHER",
"JP": "OTHER", "AT": "OTHER", "NO": "OTHER", "LU": "OTHER", "PL": "OTHER", "GR": "OTHER",
"SI": "OTHER"}
df = df.replace({"country": dic})
df.country.value_counts()
# Currency - needs to convert all goal values to USD
df.currency.value_counts()
df['goal'] = df.goal.astype(float)
df['fx_rate'] = df.fx_rate.astype(float)
df['goal_usd'] = df.goal * df.fx_rate
df.head()
df.usd_type.value_counts()
# checking for NaN
df.isna().sum()
# fill main_category NaN with sub_category
df[df.main_category.isna()]['sub_category'].value_counts()
df.main_category.fillna(df.sub_category, inplace=True)
df.isna().sum()
kickstarter = df[['id', 'goal_usd', 'country', 'created_at', 'deadline', 'launched_at', 'state_changed_at',
'spotlight','staff_pick', 'main_category', 'sub_category', 'blurb', 'state']]
kickstarter.head()
kickstarter.to_csv("./data/kickstarter.csv", index= False)
| 0.316264 | 0.223949 |
## CNN - Example
```
import os
import zipfile
import matplotlib.pyplot as plt
import tensorflow as tf
# using wget
!wget --no-check-certificate \
https://storage.googleapis.com/laurencemoroney-blog.appspot.com/horse-or-human.zip \
-O /tmp/horse-or-human.zip
!wget --no-check-certificate \
https://storage.googleapis.com/laurencemoroney-blog.appspot.com/validation-horse-or-human.zip \
-O /tmp/validation-horse-or-human.zip
```
### Load Dataset
```
# using python code
URL = "https://storage.googleapis.com/laurencemoroney-blog.appspot.com/horse-or-human.zip"
# filename = "c:\\Sandbox\\GitHub\\TF_786\\horse-or-human.zip" # windows
filename = "/content/horse-or-human.zip" # unix
zip_file = tf.keras.utils.get_file(origin=URL,
fname=filename,
extract=True)
URL = "https://storage.googleapis.com/laurencemoroney-blog.appspot.com/validation-horse-or-human.zip"
# filename = "c:\\Sandbox\\GitHub\\TF_786\\validation-horse-or-human.zip" # windows
filename = "/content/validation-horse-or-human.zip" # unix
zip_file = tf.keras.utils.get_file(origin=URL,
fname=filename,
extract=True)
```
### Folders
```
filepath = '/content/'
local_zip = filepath + 'horse-or-human.zip'
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall(filepath + 'horse-or-human')
local_zip = filepath + 'validation-horse-or-human.zip'
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall(filepath + 'validation-horse-or-human')
zip_ref.close()
# Directory with our training horse pictures
train_horse_dir = os.path.join(filepath + 'horse-or-human/horses')
# Directory with our training human pictures
train_human_dir = os.path.join(filepath + 'horse-or-human/humans')
# Directory with our training horse pictures
validation_horse_dir = os.path.join(filepath + 'validation-horse-or-human/horses')
# Directory with our training human pictures
validation_human_dir = os.path.join(filepath + 'validation-horse-or-human/humans')
```
### Model # 1
```
model = tf.keras.models.Sequential([
# Note the input shape is the desired size of the image 300x300 with 3 bytes color
# This is the first convolution
tf.keras.layers.Conv2D(16, (3,3), activation='relu', input_shape=(300, 300, 3)),
tf.keras.layers.MaxPooling2D(2, 2),
# The second convolution
tf.keras.layers.Conv2D(32, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# The third convolution
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# The fourth convolution
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# The fifth convolution
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# Flatten the results to feed into a DNN
tf.keras.layers.Flatten(),
# 512 neuron hidden layer
tf.keras.layers.Dense(512, activation='relu'),
# Only 1 output neuron. It will contain a value from 0-1 where 0 for 1 class ('horses') and 1 for the other ('humans')
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.summary()
from tensorflow.keras.optimizers import RMSprop
model.compile(loss='binary_crossentropy',
optimizer=RMSprop(lr=1e-4),
metrics=['accuracy'])
```
### Data Augmentation
```
from tensorflow.keras.preprocessing.image import ImageDataGenerator
# All images will be rescaled by 1./255
train_datagen = ImageDataGenerator(
rescale=1./255,
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
# test data is only normalize.
validation_datagen = ImageDataGenerator(rescale=1/255)
# Flow training images in batches of 128 using train_datagen generator
train_generator = train_datagen.flow_from_directory(
filepath + 'horse-or-human/', # This is the source directory for training images
target_size=(300, 300), # All images will be resized to 150x150
batch_size=128,
# Since we use binary_crossentropy loss, we need binary labels
class_mode='binary')
# Flow training images in batches of 128 using train_datagen generator
validation_generator = validation_datagen.flow_from_directory(
filepath + 'validation-horse-or-human/', # This is the source directory for training images
target_size=(300, 300), # All images will be resized to 150x150
batch_size=32,
# Since we use binary_crossentropy loss, we need binary labels
class_mode='binary')
epochs = 100
history = model.fit_generator(
train_generator,
steps_per_epoch=8, # ? n/batch
epochs=epochs,
verbose=1,
validation_data = validation_generator,
validation_steps=8)
```
#### Evaluation
```
pd.DataFrame(model.history.history).head()
pd.DataFrame(model.history.history).plot()
losses = pd.DataFrame(model.history.history)
losses[['loss','val_loss']].plot()
losses[['accuracy','val_accuracy']].plot()
from sklearn.metrics import classification_report,confusion_matrix
y_prediction = model.predict(x_test).argmax(axis=1)
print(classification_report(y_test,y_prediction))
print(confusion_matrix(y_test,y_prediction))
plt.figure(figsize=(10,6))
sns.heatmap(confusion_matrix(y_test,y_prediction),annot=True)
```
#### Predictions go wrong!
```
# Show some misclassified examples
misclassified_idx = np.where(y_prediction != y_test)[0]
i = np.random.choice(misclassified_idx)
plt.imshow(x_test[i], cmap='gray')
plt.title("True label: %s Predicted: %s" % (labels[y_test[i]], labels[y_prediction[i]]));
def plot_graphs(history, string):
plt.plot(history.history[string])
plt.plot(history.history['val_'+string])
plt.xlabel("Epochs")
plt.ylabel(string)
plt.legend([string, 'val_'+string])
plt.show()
plot_graphs(history, "accuracy")
plot_graphs(history, "loss")
```
|
github_jupyter
|
import os
import zipfile
import matplotlib.pyplot as plt
import tensorflow as tf
# using wget
!wget --no-check-certificate \
https://storage.googleapis.com/laurencemoroney-blog.appspot.com/horse-or-human.zip \
-O /tmp/horse-or-human.zip
!wget --no-check-certificate \
https://storage.googleapis.com/laurencemoroney-blog.appspot.com/validation-horse-or-human.zip \
-O /tmp/validation-horse-or-human.zip
# using python code
URL = "https://storage.googleapis.com/laurencemoroney-blog.appspot.com/horse-or-human.zip"
# filename = "c:\\Sandbox\\GitHub\\TF_786\\horse-or-human.zip" # windows
filename = "/content/horse-or-human.zip" # unix
zip_file = tf.keras.utils.get_file(origin=URL,
fname=filename,
extract=True)
URL = "https://storage.googleapis.com/laurencemoroney-blog.appspot.com/validation-horse-or-human.zip"
# filename = "c:\\Sandbox\\GitHub\\TF_786\\validation-horse-or-human.zip" # windows
filename = "/content/validation-horse-or-human.zip" # unix
zip_file = tf.keras.utils.get_file(origin=URL,
fname=filename,
extract=True)
filepath = '/content/'
local_zip = filepath + 'horse-or-human.zip'
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall(filepath + 'horse-or-human')
local_zip = filepath + 'validation-horse-or-human.zip'
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall(filepath + 'validation-horse-or-human')
zip_ref.close()
# Directory with our training horse pictures
train_horse_dir = os.path.join(filepath + 'horse-or-human/horses')
# Directory with our training human pictures
train_human_dir = os.path.join(filepath + 'horse-or-human/humans')
# Directory with our training horse pictures
validation_horse_dir = os.path.join(filepath + 'validation-horse-or-human/horses')
# Directory with our training human pictures
validation_human_dir = os.path.join(filepath + 'validation-horse-or-human/humans')
model = tf.keras.models.Sequential([
# Note the input shape is the desired size of the image 300x300 with 3 bytes color
# This is the first convolution
tf.keras.layers.Conv2D(16, (3,3), activation='relu', input_shape=(300, 300, 3)),
tf.keras.layers.MaxPooling2D(2, 2),
# The second convolution
tf.keras.layers.Conv2D(32, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# The third convolution
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# The fourth convolution
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# The fifth convolution
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
# Flatten the results to feed into a DNN
tf.keras.layers.Flatten(),
# 512 neuron hidden layer
tf.keras.layers.Dense(512, activation='relu'),
# Only 1 output neuron. It will contain a value from 0-1 where 0 for 1 class ('horses') and 1 for the other ('humans')
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.summary()
from tensorflow.keras.optimizers import RMSprop
model.compile(loss='binary_crossentropy',
optimizer=RMSprop(lr=1e-4),
metrics=['accuracy'])
from tensorflow.keras.preprocessing.image import ImageDataGenerator
# All images will be rescaled by 1./255
train_datagen = ImageDataGenerator(
rescale=1./255,
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
# test data is only normalize.
validation_datagen = ImageDataGenerator(rescale=1/255)
# Flow training images in batches of 128 using train_datagen generator
train_generator = train_datagen.flow_from_directory(
filepath + 'horse-or-human/', # This is the source directory for training images
target_size=(300, 300), # All images will be resized to 150x150
batch_size=128,
# Since we use binary_crossentropy loss, we need binary labels
class_mode='binary')
# Flow training images in batches of 128 using train_datagen generator
validation_generator = validation_datagen.flow_from_directory(
filepath + 'validation-horse-or-human/', # This is the source directory for training images
target_size=(300, 300), # All images will be resized to 150x150
batch_size=32,
# Since we use binary_crossentropy loss, we need binary labels
class_mode='binary')
epochs = 100
history = model.fit_generator(
train_generator,
steps_per_epoch=8, # ? n/batch
epochs=epochs,
verbose=1,
validation_data = validation_generator,
validation_steps=8)
pd.DataFrame(model.history.history).head()
pd.DataFrame(model.history.history).plot()
losses = pd.DataFrame(model.history.history)
losses[['loss','val_loss']].plot()
losses[['accuracy','val_accuracy']].plot()
from sklearn.metrics import classification_report,confusion_matrix
y_prediction = model.predict(x_test).argmax(axis=1)
print(classification_report(y_test,y_prediction))
print(confusion_matrix(y_test,y_prediction))
plt.figure(figsize=(10,6))
sns.heatmap(confusion_matrix(y_test,y_prediction),annot=True)
# Show some misclassified examples
misclassified_idx = np.where(y_prediction != y_test)[0]
i = np.random.choice(misclassified_idx)
plt.imshow(x_test[i], cmap='gray')
plt.title("True label: %s Predicted: %s" % (labels[y_test[i]], labels[y_prediction[i]]));
def plot_graphs(history, string):
plt.plot(history.history[string])
plt.plot(history.history['val_'+string])
plt.xlabel("Epochs")
plt.ylabel(string)
plt.legend([string, 'val_'+string])
plt.show()
plot_graphs(history, "accuracy")
plot_graphs(history, "loss")
| 0.657318 | 0.90101 |
This is the first file in my attempt to create a tic-tac-toe five in a row game and have the computer play it.
TODO:
* Create data stucture that containsa game
* Plot a grid on which the game can be played
* Create the ability to play moves
## Drawing the Board
```
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
```
## Elements of a board:
1. Its size
1. The lines
1. The shaded squares
1. A lack of axes and such
```
width = 11 #[squares]. width of grid. Should be odd
height = 11 #[squares] height of grid. should be odd
gridcolor = 'black'
try:
assert width%2==1 and height%2==1
except:
display("The inputs for width and height must be odd integers")
fig, ax = plt.subplots()
# Control size of figure
ax.set_xlim(-width/2, width/2)
ax.set_ylim(-height/2, height/2)
ax.set_aspect(1)
## Hide original Axes and labels
for side in['top','right','left','bottom']:
ax.spines[side].set_visible(False)
ax.tick_params(axis='both',
which='both',
bottom=False,
top=False,
labelbottom=False,
labelleft=False,
left=False,
right=False)
## Drawing the grid lines
for x in np.arange(-width/2,width/2+1):
ax.axvline(x, color = gridcolor)
for y in np.arange(-height/2,height/2+1):
ax.axhline(y, color = gridcolor)
## Drawing the grid squares
for x in np.arange(-width/2, width/2):
for y in np.arange(-height/2, height/2):
if (np.abs(x+0.5)+np.abs(y+0.5))%2==1:
rect = plt.Rectangle((x,y),1,1, alpha=0.2, color = 'black')
ax.add_artist(rect)
## Draw axes for reference
ax.axhline(0,color = gridcolor)
ax.axvline(0,color= gridcolor)
## Draw a number in the specified square
x,y = (2,3)
x_1dcomp = -0.3
y_1dcomp = -0.2
# Draw a one-digit number
ax.text(x+x_1dcomp,y+y_1dcomp, '4', color = 'black', size=14)
# Draw a two-digit number
x,y = -3,-2
x_2dcomp = -0.4
y_2dcomp = -0.3
ax.text(x+x_2dcomp,y+y_2dcomp, '47', color = 'black', size=14,alpha=1)
# Draw a red two-digit number
x,y = 3,-4
x_2dcomp = -0.45
y_2dcomp = -0.3
ax.text(x+x_2dcomp,y+y_2dcomp, '47', color = 'red', size=14,alpha=1)
```
## Storing a game's data
A game is simply a series of moves, and each move consists of:
1. The location of the move
1. The number played
1. The color of the player for any particular move.
Though the color of each move alternates, and the number played can be calculated from the previous, we will not put such limitations on the game data itself, allowing us to generate arbitrary game situations.
Mostly out of a love of DataFrames, that is what I will use to store game data.
```
class game():
df_template = pd.DataFrame({'marker':[],
'x_loc':[],
'y_loc':[],
'player':[]})
def __init__(self):
self.df = self.df_template.copy(deep=True)
def manual_move(self,mark, x_loc, y_loc, player):
new_row= self.df_template.copy(deep=True)
new_row.marker = [int(mark)]
new_row.x_loc = [int(x_loc)]
new_row.y_loc = [int(y_loc)]
new_row.player = [player]
print(new_row)
self.df = pd.concat([self.df,new_row])
g = game()
g.df
g.manual_move(1,0,0,'black')
g.df
df = game.df_template.copy(deep=True)
df
```
|
github_jupyter
|
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
width = 11 #[squares]. width of grid. Should be odd
height = 11 #[squares] height of grid. should be odd
gridcolor = 'black'
try:
assert width%2==1 and height%2==1
except:
display("The inputs for width and height must be odd integers")
fig, ax = plt.subplots()
# Control size of figure
ax.set_xlim(-width/2, width/2)
ax.set_ylim(-height/2, height/2)
ax.set_aspect(1)
## Hide original Axes and labels
for side in['top','right','left','bottom']:
ax.spines[side].set_visible(False)
ax.tick_params(axis='both',
which='both',
bottom=False,
top=False,
labelbottom=False,
labelleft=False,
left=False,
right=False)
## Drawing the grid lines
for x in np.arange(-width/2,width/2+1):
ax.axvline(x, color = gridcolor)
for y in np.arange(-height/2,height/2+1):
ax.axhline(y, color = gridcolor)
## Drawing the grid squares
for x in np.arange(-width/2, width/2):
for y in np.arange(-height/2, height/2):
if (np.abs(x+0.5)+np.abs(y+0.5))%2==1:
rect = plt.Rectangle((x,y),1,1, alpha=0.2, color = 'black')
ax.add_artist(rect)
## Draw axes for reference
ax.axhline(0,color = gridcolor)
ax.axvline(0,color= gridcolor)
## Draw a number in the specified square
x,y = (2,3)
x_1dcomp = -0.3
y_1dcomp = -0.2
# Draw a one-digit number
ax.text(x+x_1dcomp,y+y_1dcomp, '4', color = 'black', size=14)
# Draw a two-digit number
x,y = -3,-2
x_2dcomp = -0.4
y_2dcomp = -0.3
ax.text(x+x_2dcomp,y+y_2dcomp, '47', color = 'black', size=14,alpha=1)
# Draw a red two-digit number
x,y = 3,-4
x_2dcomp = -0.45
y_2dcomp = -0.3
ax.text(x+x_2dcomp,y+y_2dcomp, '47', color = 'red', size=14,alpha=1)
class game():
df_template = pd.DataFrame({'marker':[],
'x_loc':[],
'y_loc':[],
'player':[]})
def __init__(self):
self.df = self.df_template.copy(deep=True)
def manual_move(self,mark, x_loc, y_loc, player):
new_row= self.df_template.copy(deep=True)
new_row.marker = [int(mark)]
new_row.x_loc = [int(x_loc)]
new_row.y_loc = [int(y_loc)]
new_row.player = [player]
print(new_row)
self.df = pd.concat([self.df,new_row])
g = game()
g.df
g.manual_move(1,0,0,'black')
g.df
df = game.df_template.copy(deep=True)
df
| 0.442155 | 0.974337 |
```
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from keras import initializers
import keras.backend as K
import numpy as np
from tensorflow.keras.layers import *
from keras.regularizers import l2#正则化
#准备训练数据
import pandas as pd
import numpy as np
# normal = pd.read_excel(r'data.xlsx',sheetname=0)
normal_all = pd.read_excel(r'F:\张老师课题学习内容\code\数据集\试验数据(包括压力脉动和振动)\2013.9.12-未发生缠绕前\2013-9-12压力脉动\20130912-1450rmin\8-Q=210.xlsx')
chanrao_all = pd.read_excel(r'F:\张老师课题学习内容\code\数据集\试验数据(包括压力脉动和振动)\2013.9.17-发生缠绕后\压力脉动\9-17下午压力脉动1450rmin\8-2-Q=210.xlsx')
normal=normal_all[["通道10"]]
chanrao=chanrao_all[["通道10"]]
#水泵的两种故障类型信号normal正常,chanrao故障
normal=normal.values.reshape(-1, 800)#(120000,1)-(150, 800)150条长度为800
chanrao=chanrao.values.reshape(-1, 800)
print(normal_all.shape,chanrao_all.shape)
print(normal.shape,chanrao.shape)
import numpy as np
def yuchuli(data,label):#(7:1)(616:88)
#打乱数据顺序
np.random.shuffle(data)
train = data[0:120,:]
test = data[120:150,:]
label_train = np.array([label for i in range(0,120)])
label_test =np.array([label for i in range(0,30)])
return train,test ,label_train ,label_test
def stackkk(a,b,c,d,e,f,g,h):
aa = np.vstack((a, e))
bb = np.vstack((b, f))
cc = np.hstack((c, g))
dd = np.hstack((d, h))
return aa,bb,cc,dd
x_tra0,x_tes0,y_tra0,y_tes0 = yuchuli(normal,0)
x_tra1,x_tes1,y_tra1,y_tes1 = yuchuli(chanrao,1)
tr1,te1,yr1,ye1=stackkk(x_tra0,x_tes0,y_tra0,y_tes0 ,x_tra1,x_tes1,y_tra1,y_tes1)
x_train=tr1
x_test=te1
y_train = yr1
y_test = ye1
#打乱数据
state = np.random.get_state()
np.random.shuffle(x_train)
np.random.set_state(state)
np.random.shuffle(y_train)
state = np.random.get_state()
np.random.shuffle(x_test)
np.random.set_state(state)
np.random.shuffle(y_test)
#对训练集和测试集标准化
def ZscoreNormalization(x):
"""Z-score normaliaztion"""
x = (x - np.mean(x)) / np.std(x)
return x
x_train=ZscoreNormalization(x_train)
x_test=ZscoreNormalization(x_test)
#转化为二维矩阵
x_train = x_train.reshape(-1,800,1,1)
x_test = x_test.reshape(-1,800,1,1)
print(x_train.shape,x_test.shape)
print(y_train.shape,y_test.shape)
def to_one_hot(labels,dimension=2):
results = np.zeros((len(labels),dimension))
for i,label in enumerate(labels):
results[i,label] = 1
return results
one_hot_train_labels = to_one_hot(y_train)
one_hot_test_labels = to_one_hot(y_test)
print(x_train.shape,x_test.shape)
#定义挤压函数
def squash(vectors, axis=-1):
"""
对向量的非线性激活函数
## vectors: some vectors to be squashed, N-dim tensor
## axis: the axis to squash
:return: a Tensor with same shape as input vectors
"""
s_squared_norm = K.sum(K.square(vectors), axis, keepdims=True)
scale = s_squared_norm / (1 + s_squared_norm) / K.sqrt(s_squared_norm + K.epsilon())
return scale * vectors
class Length(layers.Layer):
"""
计算向量的长度。它用于计算与margin_loss中的y_true具有相同形状的张量
Compute the length of vectors. This is used to compute a Tensor that has the same shape with y_true in margin_loss
inputs: shape=[dim_1, ..., dim_{n-1}, dim_n]
output: shape=[dim_1, ..., dim_{n-1}]
"""
def call(self, inputs, **kwargs):
return K.sqrt(K.sum(K.square(inputs), -1))
def compute_output_shape(self, input_shape):
return input_shape[:-1]
def get_config(self):
config = super(Length, self).get_config()
return config
#定义预胶囊层
def PrimaryCap(inputs, dim_capsule, n_channels, kernel_size, strides, padding):
"""
进行普通二维卷积 `n_channels` 次, 然后将所有的胶囊重叠起来
:param inputs: 4D tensor, shape=[None, width, height, channels]
:param dim_capsule: the dim of the output vector of capsule
:param n_channels: the number of types of capsules
:return: output tensor, shape=[None, num_capsule, dim_capsule]
"""
output = layers.Conv2D(filters=dim_capsule*n_channels, kernel_size=kernel_size, strides=strides,
padding=padding,name='primarycap_conv2d')(inputs)
outputs = layers.Reshape(target_shape=[-1, dim_capsule], name='primarycap_reshape')(output)
return layers.Lambda(squash, name='primarycap_squash')(outputs)
class DenseCapsule(layers.Layer):
"""
胶囊层. 输入输出都为向量.
## num_capsule: 本层包含的胶囊数量
## dim_capsule: 输出的每一个胶囊向量的维度
## routings: routing 算法的迭代次数
"""
def __init__(self, num_capsule, dim_capsule, routings=3, kernel_initializer='glorot_uniform',**kwargs):
super(DenseCapsule, self).__init__(**kwargs)
self.num_capsule = num_capsule
self.dim_capsule = dim_capsule
self.routings = routings
self.kernel_initializer = kernel_initializer
def build(self, input_shape):
assert len(input_shape) >= 3, '输入的 Tensor 的形状[None, input_num_capsule, input_dim_capsule]'#(None,1152,8)
self.input_num_capsule = input_shape[1]
self.input_dim_capsule = input_shape[2]
#转换矩阵
self.W = self.add_weight(shape=[self.num_capsule, self.input_num_capsule,
self.dim_capsule, self.input_dim_capsule],
initializer=self.kernel_initializer,name='W')
self.built = True
def call(self, inputs, training=None):
# inputs.shape=[None, input_num_capsuie, input_dim_capsule]
# inputs_expand.shape=[None, 1, input_num_capsule, input_dim_capsule]
inputs_expand = K.expand_dims(inputs, 1)
# 运算优化:将inputs_expand重复num_capsule 次,用于快速和W相乘
# inputs_tiled.shape=[None, num_capsule, input_num_capsule, input_dim_capsule]
inputs_tiled = K.tile(inputs_expand, [1, self.num_capsule, 1, 1])
# 将inputs_tiled的batch中的每一条数据,计算inputs+W
# x.shape = [num_capsule, input_num_capsule, input_dim_capsule]
# W.shape = [num_capsule, input_num_capsule, dim_capsule, input_dim_capsule]
# 将x和W的前两个维度看作'batch'维度,向量和矩阵相乘:
# [input_dim_capsule] x [dim_capsule, input_dim_capsule]^T -> [dim_capsule].
# inputs_hat.shape = [None, num_capsule, input_num_capsule, dim_capsutel
inputs_hat = K.map_fn(lambda x: K.batch_dot(x, self.W, [2, 3]),elems=inputs_tiled)
# Begin: Routing算法
# 将系数b初始化为0.
# b.shape = [None, self.num_capsule, self, input_num_capsule].
b = tf.zeros(shape=[K.shape(inputs_hat)[0], self.num_capsule, self.input_num_capsule])
assert self.routings > 0, 'The routings should be > 0.'
for i in range(self.routings):
# c.shape=[None, num_capsule, input_num_capsule]
C = tf.nn.softmax(b ,axis=1)
# c.shape = [None, num_capsule, input_num_capsule]
# inputs_hat.shape = [None, num_capsule, input_num_capsule, dim_capsule]
# 将c与inputs_hat的前两个维度看作'batch'维度,向量和矩阵相乘:
# [input_num_capsule] x [input_num_capsule, dim_capsule] -> [dim_capsule],
# outputs.shape= [None, num_capsule, dim_capsule]
outputs = squash(K. batch_dot(C, inputs_hat, [2, 2])) # [None, 10, 16]
if i < self.routings - 1:
# outputs.shape = [None, num_capsule, dim_capsule]
# inputs_hat.shape = [None, num_capsule, input_num_capsule, dim_capsule]
# 将outputs和inρuts_hat的前两个维度看作‘batch’ 维度,向量和矩阵相乘:
# [dim_capsule] x [imput_num_capsule, dim_capsule]^T -> [input_num_capsule]
# b.shape = [batch_size. num_capsule, input_nom_capsule]
# b += K.batch_dot(outputs, inputs_hat, [2, 3]) to this b += tf.matmul(self.W, x)
b += K.batch_dot(outputs, inputs_hat, [2, 3])
# End: Routing 算法
return outputs
def compute_output_shape(self, input_shape):
return tuple([None, self.num_capsule, self.dim_capsule])
def get_config(self):
config = {
'num_capsule': self.num_capsule,
'dim_capsule': self.dim_capsule,
'routings': self.routings
}
base_config = super(DenseCapsule, self).get_config()
return dict(list(base_config.items()) + list(config.items()))
from tensorflow import keras
from keras.regularizers import l2#正则化
x = layers.Input(shape=[800,1, 1])
#普通卷积层
conv1 = layers.Conv2D(filters=16, kernel_size=(150, 1),activation='relu',padding='valid',name='conv1')(x)
#池化层
POOL1 = MaxPooling2D((2,1))(conv1)
#普通卷积层
conv2 = layers.Conv2D(filters=32, kernel_size=(2, 1),activation='relu',padding='valid',name='conv2')(POOL1)
#池化层
POOL2 = MaxPooling2D((2,1))(conv2)
#Dropout层
Dropout=layers.Dropout(0.1)(POOL2)
# Layer 3: 使用“squash”激活的Conv2D层, 然后重塑 [None, num_capsule, dim_vector]
primarycaps = PrimaryCap(Dropout, dim_capsule=8, n_channels=12, kernel_size=(4, 1), strides=2, padding='valid')
# Layer 4: 数字胶囊层,动态路由算法在这里工作。
digitcaps = DenseCapsule(num_capsule=2, dim_capsule=16, routings=3, name='digit_caps')(primarycaps)
# Layer 5:这是一个辅助层,用它的长度代替每个胶囊。只是为了符合标签的形状。
out_caps = Length(name='out_caps')(digitcaps)
model = keras.Model(x, out_caps)
model.summary()
#定义优化
model.compile(metrics=['accuracy'],
optimizer='adam',
loss=lambda y_true,y_pred: y_true*K.relu(0.9-y_pred)**2 + 0.25*(1-y_true)*K.relu(y_pred-0.1)**2
)
import time
time_begin = time.time()
history = model.fit(x_train,one_hot_train_labels,
validation_split=0.1,
epochs=50,batch_size=10,
shuffle=True)
time_end = time.time()
time = time_end - time_begin
print('time:', time)
score = model.evaluate(x_test,one_hot_test_labels, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
#绘制acc-loss曲线
import matplotlib.pyplot as plt
plt.plot(history.history['loss'],color='r')
plt.plot(history.history['val_loss'],color='g')
plt.plot(history.history['accuracy'],color='b')
plt.plot(history.history['val_accuracy'],color='k')
plt.title('model loss and acc')
plt.ylabel('Accuracy')
plt.xlabel('epoch')
plt.legend(['train_loss', 'test_loss','train_acc', 'test_acc'], loc='upper left')
# plt.legend(['train_loss','train_acc'], loc='upper left')
#plt.savefig('1.png')
plt.show()
import matplotlib.pyplot as plt
plt.plot(history.history['loss'],color='r')
plt.plot(history.history['accuracy'],color='b')
plt.title('model loss and sccuracy ')
plt.ylabel('loss/sccuracy')
plt.xlabel('epoch')
plt.legend(['train_loss', 'train_sccuracy'], loc='upper left')
plt.show()
```
|
github_jupyter
|
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from keras import initializers
import keras.backend as K
import numpy as np
from tensorflow.keras.layers import *
from keras.regularizers import l2#正则化
#准备训练数据
import pandas as pd
import numpy as np
# normal = pd.read_excel(r'data.xlsx',sheetname=0)
normal_all = pd.read_excel(r'F:\张老师课题学习内容\code\数据集\试验数据(包括压力脉动和振动)\2013.9.12-未发生缠绕前\2013-9-12压力脉动\20130912-1450rmin\8-Q=210.xlsx')
chanrao_all = pd.read_excel(r'F:\张老师课题学习内容\code\数据集\试验数据(包括压力脉动和振动)\2013.9.17-发生缠绕后\压力脉动\9-17下午压力脉动1450rmin\8-2-Q=210.xlsx')
normal=normal_all[["通道10"]]
chanrao=chanrao_all[["通道10"]]
#水泵的两种故障类型信号normal正常,chanrao故障
normal=normal.values.reshape(-1, 800)#(120000,1)-(150, 800)150条长度为800
chanrao=chanrao.values.reshape(-1, 800)
print(normal_all.shape,chanrao_all.shape)
print(normal.shape,chanrao.shape)
import numpy as np
def yuchuli(data,label):#(7:1)(616:88)
#打乱数据顺序
np.random.shuffle(data)
train = data[0:120,:]
test = data[120:150,:]
label_train = np.array([label for i in range(0,120)])
label_test =np.array([label for i in range(0,30)])
return train,test ,label_train ,label_test
def stackkk(a,b,c,d,e,f,g,h):
aa = np.vstack((a, e))
bb = np.vstack((b, f))
cc = np.hstack((c, g))
dd = np.hstack((d, h))
return aa,bb,cc,dd
x_tra0,x_tes0,y_tra0,y_tes0 = yuchuli(normal,0)
x_tra1,x_tes1,y_tra1,y_tes1 = yuchuli(chanrao,1)
tr1,te1,yr1,ye1=stackkk(x_tra0,x_tes0,y_tra0,y_tes0 ,x_tra1,x_tes1,y_tra1,y_tes1)
x_train=tr1
x_test=te1
y_train = yr1
y_test = ye1
#打乱数据
state = np.random.get_state()
np.random.shuffle(x_train)
np.random.set_state(state)
np.random.shuffle(y_train)
state = np.random.get_state()
np.random.shuffle(x_test)
np.random.set_state(state)
np.random.shuffle(y_test)
#对训练集和测试集标准化
def ZscoreNormalization(x):
"""Z-score normaliaztion"""
x = (x - np.mean(x)) / np.std(x)
return x
x_train=ZscoreNormalization(x_train)
x_test=ZscoreNormalization(x_test)
#转化为二维矩阵
x_train = x_train.reshape(-1,800,1,1)
x_test = x_test.reshape(-1,800,1,1)
print(x_train.shape,x_test.shape)
print(y_train.shape,y_test.shape)
def to_one_hot(labels,dimension=2):
results = np.zeros((len(labels),dimension))
for i,label in enumerate(labels):
results[i,label] = 1
return results
one_hot_train_labels = to_one_hot(y_train)
one_hot_test_labels = to_one_hot(y_test)
print(x_train.shape,x_test.shape)
#定义挤压函数
def squash(vectors, axis=-1):
"""
对向量的非线性激活函数
## vectors: some vectors to be squashed, N-dim tensor
## axis: the axis to squash
:return: a Tensor with same shape as input vectors
"""
s_squared_norm = K.sum(K.square(vectors), axis, keepdims=True)
scale = s_squared_norm / (1 + s_squared_norm) / K.sqrt(s_squared_norm + K.epsilon())
return scale * vectors
class Length(layers.Layer):
"""
计算向量的长度。它用于计算与margin_loss中的y_true具有相同形状的张量
Compute the length of vectors. This is used to compute a Tensor that has the same shape with y_true in margin_loss
inputs: shape=[dim_1, ..., dim_{n-1}, dim_n]
output: shape=[dim_1, ..., dim_{n-1}]
"""
def call(self, inputs, **kwargs):
return K.sqrt(K.sum(K.square(inputs), -1))
def compute_output_shape(self, input_shape):
return input_shape[:-1]
def get_config(self):
config = super(Length, self).get_config()
return config
#定义预胶囊层
def PrimaryCap(inputs, dim_capsule, n_channels, kernel_size, strides, padding):
"""
进行普通二维卷积 `n_channels` 次, 然后将所有的胶囊重叠起来
:param inputs: 4D tensor, shape=[None, width, height, channels]
:param dim_capsule: the dim of the output vector of capsule
:param n_channels: the number of types of capsules
:return: output tensor, shape=[None, num_capsule, dim_capsule]
"""
output = layers.Conv2D(filters=dim_capsule*n_channels, kernel_size=kernel_size, strides=strides,
padding=padding,name='primarycap_conv2d')(inputs)
outputs = layers.Reshape(target_shape=[-1, dim_capsule], name='primarycap_reshape')(output)
return layers.Lambda(squash, name='primarycap_squash')(outputs)
class DenseCapsule(layers.Layer):
"""
胶囊层. 输入输出都为向量.
## num_capsule: 本层包含的胶囊数量
## dim_capsule: 输出的每一个胶囊向量的维度
## routings: routing 算法的迭代次数
"""
def __init__(self, num_capsule, dim_capsule, routings=3, kernel_initializer='glorot_uniform',**kwargs):
super(DenseCapsule, self).__init__(**kwargs)
self.num_capsule = num_capsule
self.dim_capsule = dim_capsule
self.routings = routings
self.kernel_initializer = kernel_initializer
def build(self, input_shape):
assert len(input_shape) >= 3, '输入的 Tensor 的形状[None, input_num_capsule, input_dim_capsule]'#(None,1152,8)
self.input_num_capsule = input_shape[1]
self.input_dim_capsule = input_shape[2]
#转换矩阵
self.W = self.add_weight(shape=[self.num_capsule, self.input_num_capsule,
self.dim_capsule, self.input_dim_capsule],
initializer=self.kernel_initializer,name='W')
self.built = True
def call(self, inputs, training=None):
# inputs.shape=[None, input_num_capsuie, input_dim_capsule]
# inputs_expand.shape=[None, 1, input_num_capsule, input_dim_capsule]
inputs_expand = K.expand_dims(inputs, 1)
# 运算优化:将inputs_expand重复num_capsule 次,用于快速和W相乘
# inputs_tiled.shape=[None, num_capsule, input_num_capsule, input_dim_capsule]
inputs_tiled = K.tile(inputs_expand, [1, self.num_capsule, 1, 1])
# 将inputs_tiled的batch中的每一条数据,计算inputs+W
# x.shape = [num_capsule, input_num_capsule, input_dim_capsule]
# W.shape = [num_capsule, input_num_capsule, dim_capsule, input_dim_capsule]
# 将x和W的前两个维度看作'batch'维度,向量和矩阵相乘:
# [input_dim_capsule] x [dim_capsule, input_dim_capsule]^T -> [dim_capsule].
# inputs_hat.shape = [None, num_capsule, input_num_capsule, dim_capsutel
inputs_hat = K.map_fn(lambda x: K.batch_dot(x, self.W, [2, 3]),elems=inputs_tiled)
# Begin: Routing算法
# 将系数b初始化为0.
# b.shape = [None, self.num_capsule, self, input_num_capsule].
b = tf.zeros(shape=[K.shape(inputs_hat)[0], self.num_capsule, self.input_num_capsule])
assert self.routings > 0, 'The routings should be > 0.'
for i in range(self.routings):
# c.shape=[None, num_capsule, input_num_capsule]
C = tf.nn.softmax(b ,axis=1)
# c.shape = [None, num_capsule, input_num_capsule]
# inputs_hat.shape = [None, num_capsule, input_num_capsule, dim_capsule]
# 将c与inputs_hat的前两个维度看作'batch'维度,向量和矩阵相乘:
# [input_num_capsule] x [input_num_capsule, dim_capsule] -> [dim_capsule],
# outputs.shape= [None, num_capsule, dim_capsule]
outputs = squash(K. batch_dot(C, inputs_hat, [2, 2])) # [None, 10, 16]
if i < self.routings - 1:
# outputs.shape = [None, num_capsule, dim_capsule]
# inputs_hat.shape = [None, num_capsule, input_num_capsule, dim_capsule]
# 将outputs和inρuts_hat的前两个维度看作‘batch’ 维度,向量和矩阵相乘:
# [dim_capsule] x [imput_num_capsule, dim_capsule]^T -> [input_num_capsule]
# b.shape = [batch_size. num_capsule, input_nom_capsule]
# b += K.batch_dot(outputs, inputs_hat, [2, 3]) to this b += tf.matmul(self.W, x)
b += K.batch_dot(outputs, inputs_hat, [2, 3])
# End: Routing 算法
return outputs
def compute_output_shape(self, input_shape):
return tuple([None, self.num_capsule, self.dim_capsule])
def get_config(self):
config = {
'num_capsule': self.num_capsule,
'dim_capsule': self.dim_capsule,
'routings': self.routings
}
base_config = super(DenseCapsule, self).get_config()
return dict(list(base_config.items()) + list(config.items()))
from tensorflow import keras
from keras.regularizers import l2#正则化
x = layers.Input(shape=[800,1, 1])
#普通卷积层
conv1 = layers.Conv2D(filters=16, kernel_size=(150, 1),activation='relu',padding='valid',name='conv1')(x)
#池化层
POOL1 = MaxPooling2D((2,1))(conv1)
#普通卷积层
conv2 = layers.Conv2D(filters=32, kernel_size=(2, 1),activation='relu',padding='valid',name='conv2')(POOL1)
#池化层
POOL2 = MaxPooling2D((2,1))(conv2)
#Dropout层
Dropout=layers.Dropout(0.1)(POOL2)
# Layer 3: 使用“squash”激活的Conv2D层, 然后重塑 [None, num_capsule, dim_vector]
primarycaps = PrimaryCap(Dropout, dim_capsule=8, n_channels=12, kernel_size=(4, 1), strides=2, padding='valid')
# Layer 4: 数字胶囊层,动态路由算法在这里工作。
digitcaps = DenseCapsule(num_capsule=2, dim_capsule=16, routings=3, name='digit_caps')(primarycaps)
# Layer 5:这是一个辅助层,用它的长度代替每个胶囊。只是为了符合标签的形状。
out_caps = Length(name='out_caps')(digitcaps)
model = keras.Model(x, out_caps)
model.summary()
#定义优化
model.compile(metrics=['accuracy'],
optimizer='adam',
loss=lambda y_true,y_pred: y_true*K.relu(0.9-y_pred)**2 + 0.25*(1-y_true)*K.relu(y_pred-0.1)**2
)
import time
time_begin = time.time()
history = model.fit(x_train,one_hot_train_labels,
validation_split=0.1,
epochs=50,batch_size=10,
shuffle=True)
time_end = time.time()
time = time_end - time_begin
print('time:', time)
score = model.evaluate(x_test,one_hot_test_labels, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
#绘制acc-loss曲线
import matplotlib.pyplot as plt
plt.plot(history.history['loss'],color='r')
plt.plot(history.history['val_loss'],color='g')
plt.plot(history.history['accuracy'],color='b')
plt.plot(history.history['val_accuracy'],color='k')
plt.title('model loss and acc')
plt.ylabel('Accuracy')
plt.xlabel('epoch')
plt.legend(['train_loss', 'test_loss','train_acc', 'test_acc'], loc='upper left')
# plt.legend(['train_loss','train_acc'], loc='upper left')
#plt.savefig('1.png')
plt.show()
import matplotlib.pyplot as plt
plt.plot(history.history['loss'],color='r')
plt.plot(history.history['accuracy'],color='b')
plt.title('model loss and sccuracy ')
plt.ylabel('loss/sccuracy')
plt.xlabel('epoch')
plt.legend(['train_loss', 'train_sccuracy'], loc='upper left')
plt.show()
| 0.691081 | 0.483466 |
```
GPU_device_id = str(3)
model_id_save_as = 'daepretrain-full-final'
architecture_id = 'final-models/learningcurve-dnn-full-final-features'
model_class_id = 'DAE'
training_dataset_id = '../dataset_generation/hyperparametersearch_dataset_200keV_full_log10time_1000.npy'
difficulty_setting = 'full'
earlystop_patience = 50
num_epochs = 2000
import matplotlib.pyplot as plt
import os
os.environ["CUDA_DEVICE_ORDER"] = "PCI_BUS_ID" # see issue #152
os.environ["CUDA_VISIBLE_DEVICES"] = GPU_device_id
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import FunctionTransformer, LabelBinarizer
from sklearn.model_selection import StratifiedKFold, StratifiedShuffleSplit
import tensorflow as tf
import pickle
import numpy as np
import pandas as pd
from random import choice
from numpy.random import seed
seed(5)
from tensorflow import set_random_seed
set_random_seed(5)
```
#### Import model, training function
```
from annsa.model_classes import build_dae_model, compile_model, mean_normalized_kl_divergence
from annsa.load_dataset import load_easy, load_full, dataset_to_spectrakeys
from annsa.load_pretrained_network import load_features
```
## Training Data Construction
```
training_dataset = np.load(training_dataset_id, allow_pickle=True)
training_source_spectra, training_background_spectra, training_keys = dataset_to_spectrakeys(training_dataset,
sampled=False,
separate_background=True)
```
## Load Model
```
model_features = load_features(architecture_id)
model_features.loss = tf.keras.losses.mean_squared_error
model_features.optimizer = tf.keras.optimizers.Adam
model_features.learning_rate = model_features.learining_rate
model_features.input_dim = 1024
dae_features = model_features.to_dae_model_features()
dae_features.metrics = ['mse']
```
## Train network
# Scale input data
```
training_input = np.random.poisson(training_source_spectra+training_background_spectra)
training_output = training_source_spectra
training_input = dae_features.scaler.transform(training_input)
training_output = dae_features.scaler.transform(training_output)
earlystop_callback = tf.keras.callbacks.EarlyStopping(
monitor='val_mse',
patience=earlystop_patience,
mode='min',
restore_best_weights=True)
csv_logger = tf.keras.callbacks.CSVLogger('./final-models-keras/'+model_id_save_as+'.log')
mlb=LabelBinarizer()
model = compile_model(
build_dae_model,
dae_features)
output = model.fit(
x=training_input,
y=training_output,
batch_size=model_features.batch_size,
validation_split=0.1,
epochs=500,
verbose=1,
shuffle=True,
callbacks=[earlystop_callback, ],
)
model.save('./final-models-keras/'+model_id_save_as+'.hdf5')
```
|
github_jupyter
|
GPU_device_id = str(3)
model_id_save_as = 'daepretrain-full-final'
architecture_id = 'final-models/learningcurve-dnn-full-final-features'
model_class_id = 'DAE'
training_dataset_id = '../dataset_generation/hyperparametersearch_dataset_200keV_full_log10time_1000.npy'
difficulty_setting = 'full'
earlystop_patience = 50
num_epochs = 2000
import matplotlib.pyplot as plt
import os
os.environ["CUDA_DEVICE_ORDER"] = "PCI_BUS_ID" # see issue #152
os.environ["CUDA_VISIBLE_DEVICES"] = GPU_device_id
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import FunctionTransformer, LabelBinarizer
from sklearn.model_selection import StratifiedKFold, StratifiedShuffleSplit
import tensorflow as tf
import pickle
import numpy as np
import pandas as pd
from random import choice
from numpy.random import seed
seed(5)
from tensorflow import set_random_seed
set_random_seed(5)
from annsa.model_classes import build_dae_model, compile_model, mean_normalized_kl_divergence
from annsa.load_dataset import load_easy, load_full, dataset_to_spectrakeys
from annsa.load_pretrained_network import load_features
training_dataset = np.load(training_dataset_id, allow_pickle=True)
training_source_spectra, training_background_spectra, training_keys = dataset_to_spectrakeys(training_dataset,
sampled=False,
separate_background=True)
model_features = load_features(architecture_id)
model_features.loss = tf.keras.losses.mean_squared_error
model_features.optimizer = tf.keras.optimizers.Adam
model_features.learning_rate = model_features.learining_rate
model_features.input_dim = 1024
dae_features = model_features.to_dae_model_features()
dae_features.metrics = ['mse']
training_input = np.random.poisson(training_source_spectra+training_background_spectra)
training_output = training_source_spectra
training_input = dae_features.scaler.transform(training_input)
training_output = dae_features.scaler.transform(training_output)
earlystop_callback = tf.keras.callbacks.EarlyStopping(
monitor='val_mse',
patience=earlystop_patience,
mode='min',
restore_best_weights=True)
csv_logger = tf.keras.callbacks.CSVLogger('./final-models-keras/'+model_id_save_as+'.log')
mlb=LabelBinarizer()
model = compile_model(
build_dae_model,
dae_features)
output = model.fit(
x=training_input,
y=training_output,
batch_size=model_features.batch_size,
validation_split=0.1,
epochs=500,
verbose=1,
shuffle=True,
callbacks=[earlystop_callback, ],
)
model.save('./final-models-keras/'+model_id_save_as+'.hdf5')
| 0.479504 | 0.452475 |
# Tutorial
This notebook is based on the tutorial of the official web-site https://docs.atoti.io/latest/tutorial/tutorial.html.
It requires to install the atoti package by following the instructions below.
The visualization part of the tutorial is not addressed in this lab session.
## Pre-requisite
### Install atoti
```
! pip install atoti
!pip list|grep atoti
```
### Retrieve tutorial data
```
! wget https://nuage.lip6.fr/s/G9jCFZsMw9TAEbm/download/data.tar -O /home/data.tar
! tar xvf /home/data.tar
! head -n 5 data/sales.csv
! head -n 5 data/products.csv
! head -n 5 data/shops.csv
```
###create/restore a session
```
import pandas as pd
import atoti as tt
session = tt.create_session()
```
### data loading
```
sales_table = session.read_csv("data/sales.csv", keys=["Date", "Shop", "Product"])
sales_table.head()
products_table = session.read_csv("data/products.csv", keys=["Product"])
products_table.head()
shops_table = session.read_csv("data/shops.csv", keys=["Shop ID"])
shops_table.head()
```
## Cube creation
https://docs.atoti.io/latest/lib/atoti.session.html#atoti.session.Session.create_cube
```
session.closed
cube = session.create_cube(sales_table,
mode='auto')
cube
cube.schema
l, m, h = cube.levels, cube.measures, cube.hierarchies
h
l
m
```
#### creating dimension hierarchies
##### dates
```
cube.create_date_hierarchy("Date parts", column=sales_table["Date"])
del h['Date']
h
```
##### product categories
we need to join the fact table with the dimension tables
```
sales_table.join(products_table, mapping={"Product": "Product"})
cube.schema
cube.hierarchies
h["Product"] = [l["Category"], l["Sub category"], l["Product"]]
del h["Category"]
del h["Sub category"]
cube.hierarchies
```
##### shop location
```
sales_table.join(shops_table, mapping={"Shop": "Shop ID"})
cube.schema
h
h["Geography"] = [
shops_table["Country"],
shops_table["State or region"],
shops_table["City"],
]
del h["Country"]
del h["State or region"]
del h["City"]
h
```
### cleaning measures
```
m
del m['Date_auto_d.MEAN']
del m['Date_auto_d.SUM']
del m['Date_auto_M.MEAN']
del m['Date_auto_M.SUM']
del m['Date_auto_y.MEAN']
del m['Date_auto_y.SUM']
m
```
### introducing new measures
```
m["Max price"] = tt.agg.max(sales_table["Unit price"])
m
```
## Querying
https://docs.atoti.io/latest/lib/atoti.cube.html#atoti.cube.Cube.query
### returning measures
```
cube.query(m["contributors.COUNT"])
cube.query(m["Quantity.SUM"])
cube.query(m["Unit price.MEAN"])
cube.query(m["Max price"])
```
### slicing: projecting on specific dimensions
```
cube.query(m["contributors.COUNT"],
levels=[l['Country']],
include_totals=True
)
cube.query(m["contributors.COUNT"],
levels=[l['State or region']],
include_totals=True
)
cube.query(m["contributors.COUNT"],
levels=[l['Country'], l['Month']],
include_totals=True
)
cube.query(m["Max price"],
include_totals=True,
levels=[l["Category"]])
```
TODO: suggest releavant queries by chosing other combinations of dimensions and other measures
### dicing: selecting specific dimension members
```
cube.query(m['contributors.COUNT'],
levels=[l['City']],
condition=l["Country"] == "France",
include_totals=True)
cube.query(m['contributors.COUNT'],
levels=[l['City'], l['Year']],
condition=(
(l["Year"] == "2021") & (l["Country"] == "France")
)
)
```
Is it possible to produce any specific aggregation for a specific month?
How?
```
cube.query(m["contributors.COUNT"],
levels=[l['Month']],
include_totals=True
)
```
likewise, is it possible to produce any aggregation for a specific city?
```
h["Geography"]
del h["Geography"]
h["Geography"] = [
# shops_table["Country"],
# shops_table["State or region"],
shops_table["City"],
]
h["Geography"]
cube.query(m["contributors.COUNT"],
levels=[l['City']],
condition= (l["City"] == "Paris"),
include_totals=True
)
```
|
github_jupyter
|
! pip install atoti
!pip list|grep atoti
! wget https://nuage.lip6.fr/s/G9jCFZsMw9TAEbm/download/data.tar -O /home/data.tar
! tar xvf /home/data.tar
! head -n 5 data/sales.csv
! head -n 5 data/products.csv
! head -n 5 data/shops.csv
import pandas as pd
import atoti as tt
session = tt.create_session()
sales_table = session.read_csv("data/sales.csv", keys=["Date", "Shop", "Product"])
sales_table.head()
products_table = session.read_csv("data/products.csv", keys=["Product"])
products_table.head()
shops_table = session.read_csv("data/shops.csv", keys=["Shop ID"])
shops_table.head()
session.closed
cube = session.create_cube(sales_table,
mode='auto')
cube
cube.schema
l, m, h = cube.levels, cube.measures, cube.hierarchies
h
l
m
cube.create_date_hierarchy("Date parts", column=sales_table["Date"])
del h['Date']
h
sales_table.join(products_table, mapping={"Product": "Product"})
cube.schema
cube.hierarchies
h["Product"] = [l["Category"], l["Sub category"], l["Product"]]
del h["Category"]
del h["Sub category"]
cube.hierarchies
sales_table.join(shops_table, mapping={"Shop": "Shop ID"})
cube.schema
h
h["Geography"] = [
shops_table["Country"],
shops_table["State or region"],
shops_table["City"],
]
del h["Country"]
del h["State or region"]
del h["City"]
h
m
del m['Date_auto_d.MEAN']
del m['Date_auto_d.SUM']
del m['Date_auto_M.MEAN']
del m['Date_auto_M.SUM']
del m['Date_auto_y.MEAN']
del m['Date_auto_y.SUM']
m
m["Max price"] = tt.agg.max(sales_table["Unit price"])
m
cube.query(m["contributors.COUNT"])
cube.query(m["Quantity.SUM"])
cube.query(m["Unit price.MEAN"])
cube.query(m["Max price"])
cube.query(m["contributors.COUNT"],
levels=[l['Country']],
include_totals=True
)
cube.query(m["contributors.COUNT"],
levels=[l['State or region']],
include_totals=True
)
cube.query(m["contributors.COUNT"],
levels=[l['Country'], l['Month']],
include_totals=True
)
cube.query(m["Max price"],
include_totals=True,
levels=[l["Category"]])
cube.query(m['contributors.COUNT'],
levels=[l['City']],
condition=l["Country"] == "France",
include_totals=True)
cube.query(m['contributors.COUNT'],
levels=[l['City'], l['Year']],
condition=(
(l["Year"] == "2021") & (l["Country"] == "France")
)
)
cube.query(m["contributors.COUNT"],
levels=[l['Month']],
include_totals=True
)
h["Geography"]
del h["Geography"]
h["Geography"] = [
# shops_table["Country"],
# shops_table["State or region"],
shops_table["City"],
]
h["Geography"]
cube.query(m["contributors.COUNT"],
levels=[l['City']],
condition= (l["City"] == "Paris"),
include_totals=True
)
| 0.308398 | 0.913984 |
```
import warnings
warnings.filterwarnings('ignore')
from datascience import *
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('fivethirtyeight')
```
# COVID-19 Maps
In this report we introduce maps! Some data has geospatial features such as latitude and longitude, giving us the opportunity to understand how instances of our data are spread across different locations.
<img src="longitude-and-latitude.png">
## The Data Science Life Cycle - Table of Contents
<a href='#section 0'>Background Knowledge: Spread of Disease</a>
<a href='#subsection 1a'>Formulating a question or problem</a>
<a href='#subsection 1b'>Acquiring and preparing data</a>
<a href='#subsection 1c'>Conducting exploratory data analysis</a>
<a href='#subsection 1d'>Using prediction and inference to draw conclusions</a>
<br><br>
## Background<a id='section 0'></a>
In March 2020, our lives were turned upside down as the COVID-19 virus spread throughout the United States. The Centers for Disease Control (CDC) collects data to help health scientists better understand how disease spreads.
Making comparisons between counties and states can us understand how rapidly a virus spreads, the impact of restrictions on public gatherings on the spread of a virus, and measure the changes in fatality as the medical profession learns how to treat the virus and as people get vaccinated.
A helpful tool in making sense of COVID-19 are maps, usually used to display dot maps that represent total cases, total deaths, total vaccines administered, and more. John's Hopkin's [COVID-19 Map](https://coronavirus.jhu.edu/map.html) provides a great example.
## Formulating a question or problem <a id='subsection 1a'></a>
It is important to ask questions that will be informative and that will avoid misleading results. There are many different questions we could ask about COVID-19, for example, many researchers use data to predict the outcomes based on intervention techniques such as social distancing.
<div class="alert alert-info">
<b>Question:</b> Take some time to formulate questions you have about this pandemic and the data you would need to answer the questions.
</div>
**Your questions:**
**Data you would need:**
**Article:**
## Acquiring and preparing data <a id='subsection 1b'></a>
You will be looking at data from the COVID-19 Data Repository at Johns Hopkins University. You can find the raw data [here](https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_time_series).
You will be investigating the total/cumulative number of cases, new cases, and fatalities on a month-to-month basis for counties accross the US, from March 2020 to May 2021.
The following table, `covid_data`, contains the data collected for each month from March 2020 through May 2021 for every county in the United States.
```
covid_data = Table().read_table("covid_data/covid_timeseries.csv")
```
Here are some of the important fields in our data set that you will focus on:
|Variable Name | Description |
|:---|:---|
|Admin2 | County name |
|Province_State | State name |
|Latitude | Measurement of location north or south of the equator |
|Longitude | Measurement of location east or west of the prime meridian |
|month| Reporting month represented as the last day of the month, e.g., 3.31.20 |
|total_cases | Cumulative number of COVID cases |
|month_cases| New cases reported in the month |
|total_fatalities | Cumulative number of fatal COVID cases |
|month_fatalities| New fatal cases reported in the month |
|Population | Population in the county |
Let's take a look at the data.
```
# Run this cell show the first ten rows of the data
covid_data.show(10)
```
We are primarily interested in the COVID cases in the United States, so let's select the rows that correspond to the United States. The column <b>iso3</b> will help us select the rows.
Find the United States' country code [here](https://unstats.un.org/unsd/tradekb/knowledgebase/country-code).
```
covid_us = covid_data.where('iso3', are.equal_to("..."))
#KEY
covid_us = covid_data.where('iso3', are.equal_to("USA"))
covid_us.show(10)
```
For our purposes, we will not be using the columns: "iso3", "Country_Region", "Combined_Key".
We will keep the column FIPS because it uniquely identifies a county. For example, Montana and Wyoming both have a county called "Big Horn".
```
cols_to_drop = make_array("...", "...", "...")
covid_us = covid_us.drop(cols_to_drop)
#KEY
cols_to_drop = make_array("iso3", "Country_Region", "Combined_Key")
covid_us = covid_us.drop(cols_to_drop)
covid_us.show(10)
```
Let's give the remaining columns simpler, more meaningful names.
```
old_names = make_array('Admin2', 'Province_State', 'month', "Lat", "Long_", "cases", "cases_new", "fatalities", "fatalities_new")
new_names = make_array('County', 'State', 'Date', "Latitude", "Longitude", "Total_Cases", "New_Cases", "Total_Fatalities", "New_Fatalities")
covid_us = covid_us.relabel(old_names, new_names)
covid_us.show(10)
```
One additional change we will execute is to format the date in our dataset. This will allow us to plot specific columns in our data such as New_Cases or New_Fatalities, and allow us to see how these change throughout time. Simply run the cell below, which correctly formats the date in our dataset.
```
# Converting date into datetime object
covid_us_pd = covid_us.to_df()
date = pd.to_datetime(covid_us_pd.Date, format='%m/%y')
covid_us['Date'] = date.dt.strftime('%m/%Y')
covid_us.show(10)
```
### Cases per 100,000 people
There is more than one way to measure the severity of the pandemic. Rather than looking at pure counts, we may want to adjust it according to how many people are in the county. For example, a county with 6,000 people, half of whom are sick, would have 3,000 infected people. Compared to Los Angeles county, this is not alot of cases. However, it is a lot if we think about it in terms of percentages. For this reason, we also want to compare the rates. We could calculate the percentage of cases in the population:
$$100 * cases/population$$
The percentage represents the average number of cases per 100 people. When percentages are small, we often use rates per 10,000 or 100,000 people, i.e.,
$$100000 * cases/population$$
Let's calculate this statistic for our entire dataset by adding a new column entitled cases_per_100k.
As a first step, we drop the counties that don't have a value for population. If you want, you can dig deeper and see which counties these are. It's just a hand full.
```
covid_us = covid_us.where("...", are.not_equal_to(0))
#KEY
covid_us = covid_us.where('Population', are.not_equal_to(0))
```
<div class="alert alert-info">
<b>Question:</b> Add a column called "Cases_Per100k" that has the number of cases in a county divided by the population of the county.
</div>
```
#What columns should be in the numerator or the denominator
cases_per100k_array = 100000 * covid_us.column('...') / covid_us.column('...')
#Create a new column called CASES_PER100K in our new table
covid_us = covid_us.with_columns('...', cases_per100k_array)
#KEY
#What columns should be in the numerator or the denominator
cases_per100k_array = 100000 * covid_us.column('Total_Cases') / covid_us.column('Population')
#Create a new column called CASES_PER100K in our new table
covid_us = covid_us.with_columns('Cases_Per100k', cases_per100k_array)
covid_us.show(10)
```
<div class="alert alert-info">
<b>Question:</b> Add a column called "New_Cases_Per100k" that has the new number of cases in a county divided by the population of the county.
</div>
```
#What columns should be in the numerator or the denominator
new_cases_per100k_array = 100000 * covid_us.column('...') / covid_us.column('...')
#Create a new column called CASES_PER100K in our new table
covid_us = covid_us.with_columns('...', cases_per100k_array)
#KEY
#What columns should be in the numerator or the denominator
new_cases_per100k_array = 100000 * covid_us.column('New_Cases') / covid_us.column('Population')
#Create a new column called CASES_PER100K in our new table
covid_us = covid_us.with_columns('New_Cases_Per100k', new_cases_per100k_array)
covid_us.show(10)
```
## Conducting exploratory data analysis <a id='subsection 1c'></a>
Often when we begin our explorations, we first narrow down the data to explore. For example, we might choose a particular month to examine, or a particular state, or both. To get us started, let's narrow our exploartions to the first month, March 2020.
```
march_2020 = covid_us.where("Date", are.equal_to("03/2020"))
march_2020.show(10)
```
We will be using <b>dot maps</b> and <b>size maps</b> as a visualization tool to help us understand what the data is telling us.
### Dot map
Dot maps are a simple map with a dot at each (latidude, longitude) pair from our data.
The next cell creates a function called <b>dot_map</b> which we will use to create a dot map.
```
def dot_map(tbl):
"""Create a map with dots to represent a unique location.
Parameters:
tbl (datascience.Table): The Table containing the data needed to plot our map. Note the table
must have a "Latitude" and "Longitude" column for this function to work.
Returns:
(datascience.Map): A map with a dot at each unique (lat, long) pair.
"""
reduced = tbl.select("Latitude", "Longitude")
return Circle.map_table(reduced, area=10, fill_opacity=1)
```
<div class="alert alert-danger" role="alert">
<b>Example:</b> Let's start with a dot map that displays all of our counties. To do so, we can pass in our table <code>march_2020</code> as an argument to <b>dot_map</b>.
</div>
```
dot_map(march_2020)
```
<div class="alert alert-info">
<b>Question:</b> What inference can we draw from this map? Take a look at the spread of counties.
</div>
*Insert answer here*
<div class="alert alert-info">
<b>Question:</b> Assign <code>more_than_100</code> to a table with all counties with more than 100 total cases in March 2020. Pass it in as an argument to <b>dot_map</b>.
</div>
```
more_than_100 = march_2020.where("...", are.above(...))
#KEY
more_than_100 = march_2020.where("Total_Cases", are.above(100))
dot_map(more_than_100)
```
<div class="alert alert-info">
<b>Question:</b> How does the map of counties with more than 100 cases in March 2020 compare to our original size map of all counties in March 2020? What inference can we draw from their differences?
</div>
*Insert answer here*
<div class="alert alert-info">
<b>Question:</b> Assign <code>more_than_per100k</code> to a table with all counties with more than 100 cases per 100k in March 2020. Pass it in as an argument to <b>dot_map</b>.
</div>
```
#KEY
more_than_per100k = march_2020.where("Cases_Per100k", are.above(100))
dot_map(more_than_per100k)
```
<div class="alert alert-info">
<b>Question:</b> How does the map of counties with more than 100 cases per 100k in March 2020 compare to our our previous and original size maps? What inference can we draw from their differences?
</div>
*Insert answer here*
### Size map
Size maps are detail-oriented maps, using color and size data to add more visual information to our map.
The next cell creates a function called <b>size_map</b> which we will use to create a size map.
```
def size_map(tbl):
"""Plots a geographical map where each dot represents a coordinate pair, scaled by a given column.
Parameters:
tbl: The input Table containing the following arguments, in order:
Col 0: latitude
Col 1: longitude
Col 2: type of location
Col 3: color (MUST be labeled "colors")
Col 4: area (MUST be labeled "areas")
Returns:
(datascience.Map): A map with a dot at each (lat, long),
colored according to Col 3,area as in Col 4.
"""
return Circle.map_table(tbl, fill_opacity=0.7)
```
Compared to our function <b>dot_map</b>, this requires a table of a specific format for the table:
| Latitude | Longitude | type | colors | areas
|:---|:---|:---|:---|:---
|...|...|...|...|...
The next two cells create functions <b>get_colors_from_column</b> and <b>get_areas_from_column</b> which will help us create Col 3: colors and Col 4: areas!
Don't worry about the code. We'll explain how to use them in the example.
```
# Col 4: size
def get_areas_from_column(tbl, label):
"""Gets the array values corresponding to the column label in the input table."""
areas = tbl.column(label)
areas[areas == 0] = np.nan
return areas
# Col 3: color
def get_colors_from_column(tbl, col, include_outliers=False):
"""Assigns each row of the input table to a color based on the value of its percentage column."""
vmin = min(tbl.column(col))
vmax = max(tbl.column(col))
if include_outliers:
outlier_min_bound = vmin
outlier_max_bound = vmax
else:
q1 = np.percentile(tbl.column(col), 25)
q3 = np.percentile(tbl.column(col), 75)
IQR = q3 - q1
outlier_min_bound = max(vmin, q1 - 1.5 * IQR)
outlier_max_bound = min(vmax, q3 + 1.5 * IQR)
colorbar_scale = list(np.linspace(outlier_min_bound, outlier_max_bound, 10))
scale_colors = ['#006100', '#3c8000', '#6ba100', '#a3c400', '#dfeb00', '#ffea00', '#ffbb00', '#ff9100', '#ff6200', '#ff2200']
def assign_color(colors, cutoffs, datapoint):
"""Assigns a color to the input percent based on the data's distribution."""
for i, cutoff in enumerate(cutoffs):
if cutoff >= datapoint:
return colors[i - 1] if i > 0 else colors[0]
return colors[-1]
colors = [""] * tbl.num_rows
for i, datapoint in enumerate(tbl.column(col)):
colors[i] = assign_color(scale_colors, colorbar_scale, datapoint)
return colors
```
<div class="alert alert-danger" role="alert">
<b>Example:</b> Let's start with a size map that displays cases per 100k using the same table <code>march_2020</code>. To do so, we will:
<ol>
<li>Pass in our table and column data we wish to work with as our arguments to the function <b>get_colors_from_column</b>. It will return an array with strings that represent colors in hexadecimal format. Larger values will result in green-yellow-orange-red shades in the map.</li>
<li>Pass in our table and column data we wish to work with as our arguments to the function <b>get_areas_from_columns</b>. It will return an array just like .column does. Larger values will result in larger circles by area in the map.
<li>Create a new table selecting "Latitude" and "Longitude", then adding in the columns "type", "colors", and "areas".
</ol>
</div>
```
# Step 1: Use function get_colors_from_column
example_colors = get_colors_from_column(march_2020, "Cases_Per100k")
# Step 2: Use function get_areas_from_column
example_areas = get_areas_from_column(march_2020, "Cases_Per100k")
# Step 3: Create a new table with columns "Latitude", "Longitude", "type", "colors", and "areas"
size_per100k = march_2020.select("Latitude", "Longitude").with_columns("type", "Cases_Per100k",
"colors", example_colors,
"areas", example_areas)
size_map(size_per100k)
```
Explore the map! Pan and zoom as you see fit.
<div class="alert alert-info">
<b>Question:</b> Compare this first size map to the last dot map. What stands out?
</div>
*Insert answere here*
<b>During the holiday season, new cases were reaching all-time highs for numerous reasons, including travel, gatherings, events, and more.
<div class="alert alert-info">
<b>Question:</b> Why would January 2021 be a critical month to visualize? Additionally, what is an important consideration to this discussion? Hint: travel
</div>
*Insert answer here*
<div class="alert alert-info">
<b>Question:</b> Create a size map that displays new cases per 100k using a new table <code>jan_2021</code>.
</div>
```
#KEY
jan_2021 = covid_us.where("Date", are.equal_to("01/2021"))
jan_2021.show(10)
#KEY
q1_colors = get_colors_from_column(jan_2021, "New_Cases_Per100k")
q1_areas = get_areas_from_column(jan_2021, "New_Cases_Per100k") * 0.5 # Reduce area size by 50%
q1_size_per100k = jan_2021.select("Latitude", "Longitude").with_columns("type", "New_Cases_Per100k",
"colors", q1_colors,
"areas", q1_areas)
size_map(q1_size_per100k)
```
<i>Note: The area sizes for all dots are reduced by 50%</i>
<div class="alert alert-info">
<b>Question:</b> What stands out from this map?
</div>
*Insert answer here*
<b> Our data ends at May 2021, so let's take a look at a size map that displays total cases per 100k during that month.</b>
<div class="alert alert-info">
<b>Question:</b> Create a size map that displays cases per 100k using a new table <code>may_2021</code>.
</div>
```
#KEY
may_2021 = covid_us.where("Date", are.equal_to("05/2021"))
may_2021.show(10)
#KEY
q3_colors = get_colors_from_column(may_2021, "Cases_Per100k")
q3_areas = get_areas_from_column(may_2021, "Cases_Per100k") * 0.10 # Reduce area size by 90%
q3_size_per100k = may_2021.select("Latitude", "Longitude").with_columns("type", "Cases_Per100k",
"colors", q3_colors,
"areas", q3_areas)
size_map(q3_size_per100k)
```
<i>Note: The area sizes for all dots are reduced by 90%</i>
<div class="alert alert-info">
<b>Question:</b> What's the difference between the size map using the table <code>march_2020</code> compared to <code>may_2021</code>? What do the differences tell you? Zoom in and focus on counties you are familiar with. Does this match with your recent knowledge on COVID-19 cases?
</div>
*Insert answer here*
## Using prediction and inference to draw conclusions <a id='subsection 1d'></a>
<div class="alert alert-info">
<b>Question:</b> After seeing these map visualizations, tell us something interesting about this data. What detail were you able to uncover?
</div>
*Insert answer here*
<div class="alert alert-info">
<b>Question:</b> What should we consider when looking at this data through maps? What's important to get an accurate read of COVID-19 cases in each county and date?
</div>
*Insert answer here*
Testing, vaccinations, events, mask mandates, etc.
<div class="alert alert-success" role="alert">
<h2 class="alert-heading">Well done!</h2>
<p>In this report you used real-world data from the COVID-19 Data Repository at Johns Hopkins University to draw maps that give you more insight on the progression of COVID-19 cases across United States counties.
<hr>
<p> Notebook created for Berkeley Unboxing Data Science 2021
<p> Adapted from Project 2: COVID-19 by Carlos Ortiz with the support of Ani Adhikari, Deb Nolan, and Will Furtado
</div>
|
github_jupyter
|
import warnings
warnings.filterwarnings('ignore')
from datascience import *
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('fivethirtyeight')
covid_data = Table().read_table("covid_data/covid_timeseries.csv")
# Run this cell show the first ten rows of the data
covid_data.show(10)
covid_us = covid_data.where('iso3', are.equal_to("..."))
#KEY
covid_us = covid_data.where('iso3', are.equal_to("USA"))
covid_us.show(10)
cols_to_drop = make_array("...", "...", "...")
covid_us = covid_us.drop(cols_to_drop)
#KEY
cols_to_drop = make_array("iso3", "Country_Region", "Combined_Key")
covid_us = covid_us.drop(cols_to_drop)
covid_us.show(10)
old_names = make_array('Admin2', 'Province_State', 'month', "Lat", "Long_", "cases", "cases_new", "fatalities", "fatalities_new")
new_names = make_array('County', 'State', 'Date', "Latitude", "Longitude", "Total_Cases", "New_Cases", "Total_Fatalities", "New_Fatalities")
covid_us = covid_us.relabel(old_names, new_names)
covid_us.show(10)
# Converting date into datetime object
covid_us_pd = covid_us.to_df()
date = pd.to_datetime(covid_us_pd.Date, format='%m/%y')
covid_us['Date'] = date.dt.strftime('%m/%Y')
covid_us.show(10)
covid_us = covid_us.where("...", are.not_equal_to(0))
#KEY
covid_us = covid_us.where('Population', are.not_equal_to(0))
#What columns should be in the numerator or the denominator
cases_per100k_array = 100000 * covid_us.column('...') / covid_us.column('...')
#Create a new column called CASES_PER100K in our new table
covid_us = covid_us.with_columns('...', cases_per100k_array)
#KEY
#What columns should be in the numerator or the denominator
cases_per100k_array = 100000 * covid_us.column('Total_Cases') / covid_us.column('Population')
#Create a new column called CASES_PER100K in our new table
covid_us = covid_us.with_columns('Cases_Per100k', cases_per100k_array)
covid_us.show(10)
#What columns should be in the numerator or the denominator
new_cases_per100k_array = 100000 * covid_us.column('...') / covid_us.column('...')
#Create a new column called CASES_PER100K in our new table
covid_us = covid_us.with_columns('...', cases_per100k_array)
#KEY
#What columns should be in the numerator or the denominator
new_cases_per100k_array = 100000 * covid_us.column('New_Cases') / covid_us.column('Population')
#Create a new column called CASES_PER100K in our new table
covid_us = covid_us.with_columns('New_Cases_Per100k', new_cases_per100k_array)
covid_us.show(10)
march_2020 = covid_us.where("Date", are.equal_to("03/2020"))
march_2020.show(10)
def dot_map(tbl):
"""Create a map with dots to represent a unique location.
Parameters:
tbl (datascience.Table): The Table containing the data needed to plot our map. Note the table
must have a "Latitude" and "Longitude" column for this function to work.
Returns:
(datascience.Map): A map with a dot at each unique (lat, long) pair.
"""
reduced = tbl.select("Latitude", "Longitude")
return Circle.map_table(reduced, area=10, fill_opacity=1)
dot_map(march_2020)
more_than_100 = march_2020.where("...", are.above(...))
#KEY
more_than_100 = march_2020.where("Total_Cases", are.above(100))
dot_map(more_than_100)
#KEY
more_than_per100k = march_2020.where("Cases_Per100k", are.above(100))
dot_map(more_than_per100k)
def size_map(tbl):
"""Plots a geographical map where each dot represents a coordinate pair, scaled by a given column.
Parameters:
tbl: The input Table containing the following arguments, in order:
Col 0: latitude
Col 1: longitude
Col 2: type of location
Col 3: color (MUST be labeled "colors")
Col 4: area (MUST be labeled "areas")
Returns:
(datascience.Map): A map with a dot at each (lat, long),
colored according to Col 3,area as in Col 4.
"""
return Circle.map_table(tbl, fill_opacity=0.7)
# Col 4: size
def get_areas_from_column(tbl, label):
"""Gets the array values corresponding to the column label in the input table."""
areas = tbl.column(label)
areas[areas == 0] = np.nan
return areas
# Col 3: color
def get_colors_from_column(tbl, col, include_outliers=False):
"""Assigns each row of the input table to a color based on the value of its percentage column."""
vmin = min(tbl.column(col))
vmax = max(tbl.column(col))
if include_outliers:
outlier_min_bound = vmin
outlier_max_bound = vmax
else:
q1 = np.percentile(tbl.column(col), 25)
q3 = np.percentile(tbl.column(col), 75)
IQR = q3 - q1
outlier_min_bound = max(vmin, q1 - 1.5 * IQR)
outlier_max_bound = min(vmax, q3 + 1.5 * IQR)
colorbar_scale = list(np.linspace(outlier_min_bound, outlier_max_bound, 10))
scale_colors = ['#006100', '#3c8000', '#6ba100', '#a3c400', '#dfeb00', '#ffea00', '#ffbb00', '#ff9100', '#ff6200', '#ff2200']
def assign_color(colors, cutoffs, datapoint):
"""Assigns a color to the input percent based on the data's distribution."""
for i, cutoff in enumerate(cutoffs):
if cutoff >= datapoint:
return colors[i - 1] if i > 0 else colors[0]
return colors[-1]
colors = [""] * tbl.num_rows
for i, datapoint in enumerate(tbl.column(col)):
colors[i] = assign_color(scale_colors, colorbar_scale, datapoint)
return colors
# Step 1: Use function get_colors_from_column
example_colors = get_colors_from_column(march_2020, "Cases_Per100k")
# Step 2: Use function get_areas_from_column
example_areas = get_areas_from_column(march_2020, "Cases_Per100k")
# Step 3: Create a new table with columns "Latitude", "Longitude", "type", "colors", and "areas"
size_per100k = march_2020.select("Latitude", "Longitude").with_columns("type", "Cases_Per100k",
"colors", example_colors,
"areas", example_areas)
size_map(size_per100k)
#KEY
jan_2021 = covid_us.where("Date", are.equal_to("01/2021"))
jan_2021.show(10)
#KEY
q1_colors = get_colors_from_column(jan_2021, "New_Cases_Per100k")
q1_areas = get_areas_from_column(jan_2021, "New_Cases_Per100k") * 0.5 # Reduce area size by 50%
q1_size_per100k = jan_2021.select("Latitude", "Longitude").with_columns("type", "New_Cases_Per100k",
"colors", q1_colors,
"areas", q1_areas)
size_map(q1_size_per100k)
#KEY
may_2021 = covid_us.where("Date", are.equal_to("05/2021"))
may_2021.show(10)
#KEY
q3_colors = get_colors_from_column(may_2021, "Cases_Per100k")
q3_areas = get_areas_from_column(may_2021, "Cases_Per100k") * 0.10 # Reduce area size by 90%
q3_size_per100k = may_2021.select("Latitude", "Longitude").with_columns("type", "Cases_Per100k",
"colors", q3_colors,
"areas", q3_areas)
size_map(q3_size_per100k)
| 0.71123 | 0.951953 |
<img src="../../images/qiskit-heading.gif" alt="Note: In order for images to show up in this jupyter notebook you need to select File => Trusted Notebook" width="500 px" align="left">
# Introducing the Qiskit Transpiler
## Introduction
In this notebook we introduce the Qiskit transpiler and walk through some examples of circuit transformations using **transpiler passes**.
The transpiler is Qiskit's circuit rewriting framework. We do not call it a "compiler" on purpose, since we use compiler in the context of a larger translation from high level applications (potentially many circuits, with classical control flow between them) down to the level of machine pulses. The transpiler, in contrast, is responsible only for circuit-level analysis and transformations.
Circuits are a fundamental and universal model of computation on quantum computers. In the Noisy Intermediate-Scale Quantum (NISQ) regime, we are always limited by the scarcity of quantum resources. The transpiler is a tool that helps us reduce the number of gates and qubits, in order to increase the fidelity of executions.
Circuit optimization is a difficult task (in general QMA-complete). To make it approachable, we break it down. Each transpiler pass is thus responsible for doing one small, well-defined task. Through this "separation of responsibilities", we are able to chain together different passes to achieve an aggressive optimization goal.
Which passes are chained together and in which order has a major effect on the final outcome. This pipeline is determined by a **pass manager**, which schedules the passes and also allows passes to communicate with each other by providing a shared space.
## Transpiler API
There are two main ways to use the transpiler:
1. Use the ``transpile()`` function, and specify some desired transpilation options, like ``basis_gates``, ``coupling_map``, ``initial_layout`` of qubits, or ``optimization_level``.
2. Create your own custom pass manager.
```
from qiskit.compiler import transpile
from qiskit.transpiler import PassManager
```
Let's start by a very simple transpilation task. Suppose we have a single toffoli gate which we want to unroll to a more fundamental basis.
```
from qiskit import QuantumRegister, QuantumCircuit
q = QuantumRegister(3, 'q')
circ = QuantumCircuit(q)
circ.ccx(q[0], q[1], q[2])
circ.draw()
```
### *transpile( ) function*
This function is a convenience function, allowing the user to quickly transpile a circuit with minimal effort. Refer to the function documentation for more info.
```
new_circ = transpile(circ, basis_gates=['u1', 'u3', 'u2', 'cx'])
new_circ.draw(output='mpl')
```
### *PassManager object*
This let's you specify exactly which passes you want.
```
from qiskit.transpiler.passes import Unroller
pass_ = Unroller(['u1', 'u2', 'u3', 'cx'])
pm = PassManager(pass_)
new_circ = pm.run(circ)
new_circ.draw(output='mpl')
```
All of Qiskit's transpiler passes are accessible from ``qiskit.transpiler.passes``.
```
from qiskit.transpiler import passes
[pass_ for pass_ in dir(passes) if pass_[0].isupper()]
```
## Different Variants of the Same Pass
There can be passes that do the same job, but in different ways. For example the ``TrivialLayout``, ``DenseLayout`` and ``NoiseAdaptiveLayout`` all choose a layout (binding of virtual qubits to physical qubits), but using different algorithms and objectives. Similarly, the ``BasicSwap``, ``LookaheadSwap`` and ``StochasticSwap`` all insert swaps to make the circuit compatible with the coupling map. The modularity of the transpiler allows plug-and-play replacements for each pass.
Below, we show the swapper passes all applied to the same circuit, to transform it to match a linear chain topology. You can see differences in performance, where the StochasticSwap is clearly the best. However this can vary depending on the input circuit.
```
from qiskit.transpiler import CouplingMap, Layout
from qiskit.transpiler.passes import BasicSwap, LookaheadSwap, StochasticSwap
coupling = [[0, 1], [1, 2], [2, 3], [3, 4], [4, 5], [5, 6]]
qr = QuantumRegister(7, 'q')
circuit = QuantumCircuit(qr)
circuit.h(qr[3])
circuit.cx(qr[0], qr[6])
circuit.cx(qr[6], qr[0])
circuit.cx(qr[0], qr[1])
circuit.cx(qr[3], qr[1])
circuit.cx(qr[3], qr[0])
coupling_map = CouplingMap(couplinglist=coupling)
layout = Layout({qr[i]: i for i in range(coupling_map.size())})
bs = BasicSwap(coupling_map=coupling_map, initial_layout=layout)
pass_manager = PassManager(bs)
basic_circ = pass_manager.run(circuit)
ls = LookaheadSwap(coupling_map=coupling_map, initial_layout=layout)
pass_manager = PassManager(ls)
lookahead_circ = pass_manager.run(circuit)
ss = StochasticSwap(coupling_map=coupling_map, initial_layout=layout)
pass_manager = PassManager(ss)
stochastic_circ = pass_manager.run(circuit)
circuit.draw(output='mpl')
basic_circ.draw(output='mpl')
lookahead_circ.draw(output='mpl')
stochastic_circ.draw(output='mpl')
```
## Preset Pass Managers
Qiskit comes with several pre-defined pass managers, corresponding to various levels of optimization achieved through different pipelines of passes. Currently ``optimization_level`` 0 through 3 are supported, with higher being more optimized at the expense of more time. Choosing a good pass manager may take trial and error, as it depends heavily on the circuit being transpiled and the backend being targeted.
Here we illustrate the different levels by looking at a state synthesis circuit. We initialize 4 qubits to an arbitrary state, and then try to optimize the circuit that achieves this.
- ``optimization_level=0``: just maps the circuit to the backend, with no explicit optimization (except whatever optimizations the mapper does).
- ``optimization_level=1``: maps the circuit, but also does light-weight optimizations by collapsing adjacent gates.
- ``optimization_level=2``: medium-weight optimization, including a noise-adaptive layout and a gate-cancellation procedure based on gate commutation relationships.
- ``optimization_level=3``: heavy-weight optimization, which in addition to previous steps, does resynthesis of 2-qubit blocks of gates in the circuit.
```
import math
from qiskit.test.mock import FakeTokyo
qr = QuantumRegister(10)
qc = QuantumCircuit(qr)
backend = FakeTokyo() # mimicks the tokyo device in terms of coupling map and basis gates
backend.properties = {} # remove fake properties
random_state = [
1 / math.sqrt(4) * complex(0, 1),
1 / math.sqrt(8) * complex(1, 0),
0,
0,
0,
0,
0,
0,
1 / math.sqrt(8) * complex(1, 0),
1 / math.sqrt(8) * complex(0, 1),
0,
0,
0,
0,
1 / math.sqrt(4) * complex(1, 0),
1 / math.sqrt(8) * complex(1, 0)]
qc.initialize(random_state, qr[0:4])
qc.draw(output='mpl')
```
Now map this to the 20-qubit Tokyo device, with different optimization levels:
```
optimized_0 = transpile(qc, backend=backend, seed_transpiler=11, optimization_level=0)
print('gates = ', optimized_0.count_ops())
print('depth = ', optimized_0.depth())
optimized_1 = transpile(qc, backend=backend, seed_transpiler=11, optimization_level=1)
print('gates = ', optimized_1.count_ops())
print('depth = ', optimized_1.depth())
optimized_2 = transpile(qc, backend=backend, seed_transpiler=11, optimization_level=2)
print('gates = ', optimized_2.count_ops())
print('depth = ', optimized_2.depth())
optimized_3 = transpile(qc, backend=backend, seed_transpiler=11, optimization_level=3)
print('gates = ', optimized_3.count_ops())
print('depth = ', optimized_3.depth())
```
You can see that the circuit gets progressively better (both in terms of depth and the number of expensive cx gates).
|
github_jupyter
|
from qiskit.compiler import transpile
from qiskit.transpiler import PassManager
from qiskit import QuantumRegister, QuantumCircuit
q = QuantumRegister(3, 'q')
circ = QuantumCircuit(q)
circ.ccx(q[0], q[1], q[2])
circ.draw()
new_circ = transpile(circ, basis_gates=['u1', 'u3', 'u2', 'cx'])
new_circ.draw(output='mpl')
from qiskit.transpiler.passes import Unroller
pass_ = Unroller(['u1', 'u2', 'u3', 'cx'])
pm = PassManager(pass_)
new_circ = pm.run(circ)
new_circ.draw(output='mpl')
from qiskit.transpiler import passes
[pass_ for pass_ in dir(passes) if pass_[0].isupper()]
from qiskit.transpiler import CouplingMap, Layout
from qiskit.transpiler.passes import BasicSwap, LookaheadSwap, StochasticSwap
coupling = [[0, 1], [1, 2], [2, 3], [3, 4], [4, 5], [5, 6]]
qr = QuantumRegister(7, 'q')
circuit = QuantumCircuit(qr)
circuit.h(qr[3])
circuit.cx(qr[0], qr[6])
circuit.cx(qr[6], qr[0])
circuit.cx(qr[0], qr[1])
circuit.cx(qr[3], qr[1])
circuit.cx(qr[3], qr[0])
coupling_map = CouplingMap(couplinglist=coupling)
layout = Layout({qr[i]: i for i in range(coupling_map.size())})
bs = BasicSwap(coupling_map=coupling_map, initial_layout=layout)
pass_manager = PassManager(bs)
basic_circ = pass_manager.run(circuit)
ls = LookaheadSwap(coupling_map=coupling_map, initial_layout=layout)
pass_manager = PassManager(ls)
lookahead_circ = pass_manager.run(circuit)
ss = StochasticSwap(coupling_map=coupling_map, initial_layout=layout)
pass_manager = PassManager(ss)
stochastic_circ = pass_manager.run(circuit)
circuit.draw(output='mpl')
basic_circ.draw(output='mpl')
lookahead_circ.draw(output='mpl')
stochastic_circ.draw(output='mpl')
import math
from qiskit.test.mock import FakeTokyo
qr = QuantumRegister(10)
qc = QuantumCircuit(qr)
backend = FakeTokyo() # mimicks the tokyo device in terms of coupling map and basis gates
backend.properties = {} # remove fake properties
random_state = [
1 / math.sqrt(4) * complex(0, 1),
1 / math.sqrt(8) * complex(1, 0),
0,
0,
0,
0,
0,
0,
1 / math.sqrt(8) * complex(1, 0),
1 / math.sqrt(8) * complex(0, 1),
0,
0,
0,
0,
1 / math.sqrt(4) * complex(1, 0),
1 / math.sqrt(8) * complex(1, 0)]
qc.initialize(random_state, qr[0:4])
qc.draw(output='mpl')
optimized_0 = transpile(qc, backend=backend, seed_transpiler=11, optimization_level=0)
print('gates = ', optimized_0.count_ops())
print('depth = ', optimized_0.depth())
optimized_1 = transpile(qc, backend=backend, seed_transpiler=11, optimization_level=1)
print('gates = ', optimized_1.count_ops())
print('depth = ', optimized_1.depth())
optimized_2 = transpile(qc, backend=backend, seed_transpiler=11, optimization_level=2)
print('gates = ', optimized_2.count_ops())
print('depth = ', optimized_2.depth())
optimized_3 = transpile(qc, backend=backend, seed_transpiler=11, optimization_level=3)
print('gates = ', optimized_3.count_ops())
print('depth = ', optimized_3.depth())
| 0.682679 | 0.993076 |
# Momentum
:label:`chapter_momentum`
In :numref:`chapter_gd`, we
mentioned that the gradient of the objective function's independent variable
represents the direction of the objective function's fastest descend at the
current position of the independent variable. Therefore, gradient descent is
also called steepest descent. In each iteration, the gradient descends according
to the current position of the independent variable while updating the latter
along the current position of the gradient. However, this can lead to problems
if the iterative direction of the independent variable relies exclusively on the
current position of the independent variable.
## Exercises with Gradient Descent
Now, we will consider an objective function $f(\boldsymbol{x})=0.1x_1^2+2x_2^2$,
whose input and output are a two-dimensional vector $\boldsymbol{x} =
[x_1, x_2]$ and a scalar, respectively. In contrast to :numref:`chapter_gd`,
here, the coefficient $x_1^2$ is reduced from $1$ to $0.1$. We are going to
implement gradient descent based on this objective function, and demonstrate the
iterative trajectory of the independent variable using the learning rate $0.4$.
```
%matplotlib inline
import d2l
from mxnet import nd
eta = 0.4
def f_2d(x1, x2):
return 0.1 * x1 ** 2 + 2 * x2 ** 2
def gd_2d(x1, x2, s1, s2):
return (x1 - eta * 0.2 * x1, x2 - eta * 4 * x2, 0, 0)
d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))
```
As we can see, at the same position, the slope of the objective function has a larger absolute value in the vertical direction ($x_2$ axis direction) than in the horizontal direction ($x_1$ axis direction). Therefore, given the learning rate, using gradient descent for interaction will cause the independent variable to move more in the vertical direction than in the horizontal one. So we need a small learning rate to prevent the independent variable from overshooting the optimal solution for the objective function in the vertical direction. However, it will cause the independent variable to move slower toward the optimal solution in the horizontal direction.
Now, we try to make the learning rate slightly larger, so the independent variable will continuously overshoot the optimal solution in the vertical direction and gradually diverge.
```
eta = 0.6
d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))
```
## The Momentum Method
The momentum method was proposed to solve the gradient descent problem described
above. Since mini-batch stochastic gradient descent is more general than
gradient descent, the subsequent discussion in this chapter will continue to use
the definition for mini-batch stochastic gradient descent $\mathbf{g}_t$ at
time step $t$ given in :numref:`chapter_minibatch_sgd`. We set the independent
variable at time step $t$ to $\mathbf{x}_t$ and the learning rate to
$\eta_t$. At time step $0$, momentum creates the velocity variable
$\mathbf{v}_0$ and initializes its elements to zero. At time step $t>0$,
momentum modifies the steps of each iteration as follows:
$$
\begin{aligned}
\mathbf{v}_t &\leftarrow \gamma \mathbf{v}_{t-1} + \eta_t \mathbf{g}_t, \\
\mathbf{x}_t &\leftarrow \mathbf{x}_{t-1} - \mathbf{v}_t,
\end{aligned}
$$
Here, the momentum hyperparameter $\gamma$ satisfies $0 \leq \gamma < 1$. When $\gamma=0$, momentum is equivalent to a mini-batch SGD.
Before explaining the mathematical principles behind the momentum method, we should take a look at the iterative trajectory of the gradient descent after using momentum in the experiment.
```
def momentum_2d(x1, x2, v1, v2):
v1 = gamma * v1 + eta * 0.2 * x1
v2 = gamma * v2 + eta * 4 * x2
return x1 - v1, x2 - v2, v1, v2
eta, gamma = 0.4, 0.5
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))
```
As we can see, when using a smaller learning rate ($\eta=0.4$) and momentum hyperparameter ($\gamma=0.5$), momentum moves more smoothly in the vertical direction and approaches the optimal solution faster in the horizontal direction. Now, when we use a larger learning rate ($\eta=0.6$), the independent variable will no longer diverge.
```
eta = 0.6
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))
```
### Expanding the velocity variable $\mathbf v_t$
To understand the momentum method, we can expand the velocity variable over time:
$$
\begin{aligned}
\mathbf{v}_t &= \eta_t \mathbf{g}_t + \gamma \mathbf{v}_{t-1}, \\
&= \eta_t \mathbf{g}_t + \gamma \eta_{t-1} \mathbf{g}_{t-1} + \gamma\mathbf{v}_{t-1}, \\
&\ldots\\
&= \eta_t \mathbf{g}_t + \gamma \eta_{t-1} \mathbf{g}_{t-1} + \ldots + \gamma^{t-1}\eta_1\mathbf g_1. \\
\end{aligned}
$$
As we can see that $\mathbf v_t$ is a weighted sum over all past gradients multiplied by the according learning rate, which is the weight update in normal gradient descent. We just call it the scaled gradient. The weights deceases exponentially with the speed controlled by $\gamma$.
The following code block shows the weights for the past 40 time steps under various $\gamma$s.
```
gammas = [0.95, 0.9, 0.6, 0]
d2l.set_figsize((3.5, 2.5))
for gamma in gammas:
x = nd.arange(40).asnumpy()
d2l.plt.plot(x, gamma ** x, label='gamma = %.2f'%gamma)
d2l.plt.xlabel('time')
d2l.plt.legend();
```
A small $\gamma$ will let the velocity variable focus on more recent scaled gradients. While a large value will have the velocity variable to include more past scaled gradients. Compared to the plain gradient descent, momentum will make the weight updates be more consistent over time. It might smooth the training progress if $\mathbf x$ enters the region that the gradient vary, or walk out region that is too flat.
Also note that $\frac{1}{1-\gamma} = 1 + \gamma + \gamma^2 + \cdots$. So all scaled gradients are similar to each other, e.g. $\eta_t\mathbf g_t\approx \eta\mathbf g$ for all $t$s, then the momentum changes the weight updates from $\eta\mathbf g$ in normal gradient descent into $\frac{\eta}{1-\gamma} \mathbf g$.
## Implementation from Scratch
Compared with mini-batch SGD, the momentum method needs to maintain a velocity variable of the same shape for each independent variable and a momentum hyperparameter is added to the hyperparameter category. In the implementation, we use the state variable `states` to represent the velocity variable in a more general sense.
```
def init_momentum_states(feature_dim):
v_w = nd.zeros((feature_dim, 1))
v_b = nd.zeros(1)
return (v_w, v_b)
def sgd_momentum(params, states, hyperparams):
for p, v in zip(params, states):
v[:] = hyperparams['momentum'] * v + hyperparams['lr'] * p.grad
p[:] -= v
```
When we set the momentum hyperparameter `momentum` to 0.5, it can be treated as a mini-batch SGD: the mini-batch gradient here is the weighted average of twice the mini-batch gradient of the last two time steps.
```
def train_momentum(lr, momentum, num_epochs=2):
d2l.train_ch10(sgd_momentum, init_momentum_states(feature_dim),
{'lr': lr, 'momentum': momentum}, data_iter,
feature_dim, num_epochs)
data_iter, feature_dim = d2l.get_data_ch10(batch_size=10)
train_momentum(0.02, 0.5)
```
When we increase the momentum hyperparameter `momentum` to 0.9, it can still be treated as a mini-batch SGD: the mini-batch gradient here will be the weighted average of ten times the mini-batch gradient of the last 10 time steps. Now we keep the learning rate at 0.02.
```
train_momentum(0.02, 0.9)
```
We can see that the value change of the objective function is not smooth enough at later stages of iteration. Intuitively, ten times the mini-batch gradient is five times larger than two times the mini-batch gradient, so we can try to reduce the learning rate to 1/5 of its original value. Now, the value change of the objective function becomes smoother after its period of decline.
```
train_momentum(0.004, 0.9)
```
## Concise Implementation
In Gluon, we only need to use `momentum` to define the momentum hyperparameter in the `Trainer` instance to implement momentum.
```
d2l.train_gluon_ch10('sgd', {'learning_rate': 0.004, 'momentum': 0.9},
data_iter)
```
## Summary
* The momentum method uses the EWMA concept. It takes the weighted average of past time steps, with weights that decay exponentially by the time step.
* Momentum makes independent variable updates for adjacent time steps more consistent in direction.
## Exercises
* Use other combinations of momentum hyperparameters and learning rates and observe and analyze the different experimental results.
## Scan the QR Code to [Discuss](https://discuss.mxnet.io/t/2374)

|
github_jupyter
|
%matplotlib inline
import d2l
from mxnet import nd
eta = 0.4
def f_2d(x1, x2):
return 0.1 * x1 ** 2 + 2 * x2 ** 2
def gd_2d(x1, x2, s1, s2):
return (x1 - eta * 0.2 * x1, x2 - eta * 4 * x2, 0, 0)
d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))
eta = 0.6
d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))
def momentum_2d(x1, x2, v1, v2):
v1 = gamma * v1 + eta * 0.2 * x1
v2 = gamma * v2 + eta * 4 * x2
return x1 - v1, x2 - v2, v1, v2
eta, gamma = 0.4, 0.5
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))
eta = 0.6
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))
gammas = [0.95, 0.9, 0.6, 0]
d2l.set_figsize((3.5, 2.5))
for gamma in gammas:
x = nd.arange(40).asnumpy()
d2l.plt.plot(x, gamma ** x, label='gamma = %.2f'%gamma)
d2l.plt.xlabel('time')
d2l.plt.legend();
def init_momentum_states(feature_dim):
v_w = nd.zeros((feature_dim, 1))
v_b = nd.zeros(1)
return (v_w, v_b)
def sgd_momentum(params, states, hyperparams):
for p, v in zip(params, states):
v[:] = hyperparams['momentum'] * v + hyperparams['lr'] * p.grad
p[:] -= v
def train_momentum(lr, momentum, num_epochs=2):
d2l.train_ch10(sgd_momentum, init_momentum_states(feature_dim),
{'lr': lr, 'momentum': momentum}, data_iter,
feature_dim, num_epochs)
data_iter, feature_dim = d2l.get_data_ch10(batch_size=10)
train_momentum(0.02, 0.5)
train_momentum(0.02, 0.9)
train_momentum(0.004, 0.9)
d2l.train_gluon_ch10('sgd', {'learning_rate': 0.004, 'momentum': 0.9},
data_iter)
| 0.577257 | 0.994413 |
## Machine Learning - dMRI Kernel
```
# Import modules
import pandas as pd
import numpy as np
import pyreadr
import tqdm
import os
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import ElasticNet
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn import metrics
import matplotlib.pyplot as plt
from math import sqrt
# Data Fetching function
def getData(data):
return pyreadr.read_r(data)[None]
# Get data
batch_df = getData("Preprocessed/Batch_dMRI.rds")
dMRI_df = getData("Preprocessed/Kernel_dMRI.rds")
ocd_df = getData("OCD.rds")
# Preview data
batch_df.head()
dMRI_df.head()
ocd_df.head()
# Run training model
train_coef = []
train_intercept = []
cum_model_coef = []
cum_model_intercept = []
cum_res = []
# Test data Creation
sample_ids_valid = list(batch_df.loc[batch_df['Valid']==1]['SampleID'])
dMRI_np_valid = dMRI_df.loc[dMRI_df['SampleID'].isin(sample_ids_valid)].to_numpy()[:,1:]
ocd_np_valid = np.concatenate(ocd_df.loc[ocd_df['SampleID'].isin(sample_ids_valid)].to_numpy()[:,1:])
for i in range(1,94):
sample_ids = list(batch_df.loc[batch_df['Train_'+str(i)]==1]['SampleID'])
dMRI_np = dMRI_df.loc[dMRI_df['SampleID'].isin(sample_ids)].to_numpy()[:,1:]
ocd_np = np.concatenate(ocd_df.loc[ocd_df['SampleID'].isin(sample_ids)].to_numpy()[:,1:])
ocd_np[ocd_np==2]=1
ocd_np = ocd_np.astype('int')
model = LogisticRegression(penalty='elasticnet', solver='saga', l1_ratio=0.9, max_iter=7000).fit(dMRI_np,ocd_np)
train_coef.append(model.coef_)
train_intercept.append(model.intercept_)
train_coef_1 = np.concatenate(train_coef)
train_intercept_1 = np.concatenate(train_intercept)
#Finding accuracy on each step
cum_model_coef = np.mean(train_coef_1, axis=0)
cum_model_intercept = np.mean(train_intercept_1)
train_y_prob=[]
for j in range(len(dMRI_np_valid)):
train_y_prob.append(1/(1+np.exp(-(np.dot(dMRI_np_valid[j],cum_model_coef)+cum_model_intercept))))
train_y_pred=np.array(train_y_prob)
train_y_pred[train_y_pred>0.5]=1
train_y_pred[train_y_pred<=0.5]=0
train_y_pred = train_y_pred.astype('int64')
ocd_np_valid = ocd_np_valid.astype('int64')
acc_score = accuracy_score(ocd_np_valid,train_y_pred)
tn, fp, fn, tp = confusion_matrix(ocd_np_valid,train_y_pred).ravel()
cum_res.append([acc_score,tn,fp,fn,tp])
print("model", i," processed")
#print(train_coef)
#print(train_intercept)
print(cum_res)
# Plot
plt.figure(figsize=(9,5), tight_layout=True)
plt.ylim(0.4,0.9)
plt.plot([x[0] for x in cum_res])
plt.axhline(0.5, linestyle='--', color='r')
plt.savefig('Preprocessed/KAC_dMRI.svg', bbox_inches='tight')
# Baseline
baseline = np.array([0 for _ in range(len(train_y_prob))])
# ROC Curve
baseline_fpr,baseline_tpr,_ = metrics.roc_curve(ocd_np_valid,baseline)
predicted_fpr,predicted_tpr,_ = metrics.roc_curve(ocd_np_valid,train_y_prob)
plt.figure(figsize=(9,5), tight_layout=True)
plt.plot(baseline_fpr, baseline_tpr, linestyle='--', label='Baseline')
plt.plot(predicted_fpr, predicted_tpr, marker='.', label='Elastic Net')
plt.text(0.7, 0.2, 'AUC = 0.5688', fontsize=18)
plt.savefig('Preprocessed/ROC_dMRI.svg', bbox_inches='tight')
#AUC Curve
print("AUC: ", metrics.auc(predicted_fpr,predicted_tpr))
#Precision Recall Curve
predicted_precision, predicted_recall, _ = metrics.precision_recall_curve(ocd_np_valid, train_y_prob)
baseline_pr=len(ocd_np_valid[ocd_np_valid==1])/len(ocd_np_valid)
plt.figure(figsize=(9,5), tight_layout=True)
plt.plot([0, 1], [baseline_pr, baseline_pr], linestyle='--', label='Baseline')
plt.plot(predicted_precision, predicted_recall, marker='.', label='Elastic Net')
plt.text(0.0, 0.55, 'F1 = 0.2647', fontsize=18)
plt.savefig('Preprocessed/PRC_dMRI.svg', bbox_inches='tight')
# F1-Score
print("F1 Score: ", metrics.f1_score(ocd_np_valid, train_y_pred))
# Confusion matrix calculations
TN, FP, FN, TP = confusion_matrix(ocd_np_valid,train_y_pred).ravel()
print(confusion_matrix(ocd_np_valid,train_y_pred))
P = TP + FN
N = FP + TN
PP = TP + FP
PN = FN + TN
print("Population =", P+N)
print("Prevalence =", P/(P+N))
CK = (2*((TP * TN) - (TN * FP)))/(((TP + FP) * (FP + TN)) + ((TP + FN) * (FN+TN)))
ACC = (TP + TN) / (P + N)
PPV = TP / PP
FOR = FN / PN
FDR = FP / PP
NPV = TN / PN
TPR = TP / P
FPR = FP / N
FNR = FN / P
TNR = TN / N
LRp = TPR / FPR
LRn = FNR / TNR
MK = PPV + NPV - 1
BM = TPR + TNR - 1
PT = (sqrt(TPR+FPR) - FPR) / (TPR - FPR)
DOR = LRp/LRn
BA = (TPR + TNR) / 2
FS = (2*PPV * TPR) / (PPV + TPR)
FM = sqrt(PPV * TPR)
MCC = sqrt(TPR*TNR*PPV*NPV) - sqrt(FPR*FNR*FDR*FOR)
TS = TP / (TP + FN + FP)
print(CK)
print(ACC)
print(PPV)
print(FOR)
print(FDR)
print(NPV)
print(TPR)
print(FPR)
print(TNR)
print(FNR)
print(LRp)
print(LRn)
print(MK)
print(BM)
print(PT)
print(DOR)
print(BA)
print(FS)
print(FM)
print(MCC)
print(TS)
# Save data
with open('Preprocessed/Coef_dMRI.npy', 'wb') as f:
np.save(f, train_coef)
with open('Preprocessed/Inter_dMRI.npy', 'wb') as f:
np.save(f, train_intercept)
```
|
github_jupyter
|
# Import modules
import pandas as pd
import numpy as np
import pyreadr
import tqdm
import os
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import ElasticNet
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn import metrics
import matplotlib.pyplot as plt
from math import sqrt
# Data Fetching function
def getData(data):
return pyreadr.read_r(data)[None]
# Get data
batch_df = getData("Preprocessed/Batch_dMRI.rds")
dMRI_df = getData("Preprocessed/Kernel_dMRI.rds")
ocd_df = getData("OCD.rds")
# Preview data
batch_df.head()
dMRI_df.head()
ocd_df.head()
# Run training model
train_coef = []
train_intercept = []
cum_model_coef = []
cum_model_intercept = []
cum_res = []
# Test data Creation
sample_ids_valid = list(batch_df.loc[batch_df['Valid']==1]['SampleID'])
dMRI_np_valid = dMRI_df.loc[dMRI_df['SampleID'].isin(sample_ids_valid)].to_numpy()[:,1:]
ocd_np_valid = np.concatenate(ocd_df.loc[ocd_df['SampleID'].isin(sample_ids_valid)].to_numpy()[:,1:])
for i in range(1,94):
sample_ids = list(batch_df.loc[batch_df['Train_'+str(i)]==1]['SampleID'])
dMRI_np = dMRI_df.loc[dMRI_df['SampleID'].isin(sample_ids)].to_numpy()[:,1:]
ocd_np = np.concatenate(ocd_df.loc[ocd_df['SampleID'].isin(sample_ids)].to_numpy()[:,1:])
ocd_np[ocd_np==2]=1
ocd_np = ocd_np.astype('int')
model = LogisticRegression(penalty='elasticnet', solver='saga', l1_ratio=0.9, max_iter=7000).fit(dMRI_np,ocd_np)
train_coef.append(model.coef_)
train_intercept.append(model.intercept_)
train_coef_1 = np.concatenate(train_coef)
train_intercept_1 = np.concatenate(train_intercept)
#Finding accuracy on each step
cum_model_coef = np.mean(train_coef_1, axis=0)
cum_model_intercept = np.mean(train_intercept_1)
train_y_prob=[]
for j in range(len(dMRI_np_valid)):
train_y_prob.append(1/(1+np.exp(-(np.dot(dMRI_np_valid[j],cum_model_coef)+cum_model_intercept))))
train_y_pred=np.array(train_y_prob)
train_y_pred[train_y_pred>0.5]=1
train_y_pred[train_y_pred<=0.5]=0
train_y_pred = train_y_pred.astype('int64')
ocd_np_valid = ocd_np_valid.astype('int64')
acc_score = accuracy_score(ocd_np_valid,train_y_pred)
tn, fp, fn, tp = confusion_matrix(ocd_np_valid,train_y_pred).ravel()
cum_res.append([acc_score,tn,fp,fn,tp])
print("model", i," processed")
#print(train_coef)
#print(train_intercept)
print(cum_res)
# Plot
plt.figure(figsize=(9,5), tight_layout=True)
plt.ylim(0.4,0.9)
plt.plot([x[0] for x in cum_res])
plt.axhline(0.5, linestyle='--', color='r')
plt.savefig('Preprocessed/KAC_dMRI.svg', bbox_inches='tight')
# Baseline
baseline = np.array([0 for _ in range(len(train_y_prob))])
# ROC Curve
baseline_fpr,baseline_tpr,_ = metrics.roc_curve(ocd_np_valid,baseline)
predicted_fpr,predicted_tpr,_ = metrics.roc_curve(ocd_np_valid,train_y_prob)
plt.figure(figsize=(9,5), tight_layout=True)
plt.plot(baseline_fpr, baseline_tpr, linestyle='--', label='Baseline')
plt.plot(predicted_fpr, predicted_tpr, marker='.', label='Elastic Net')
plt.text(0.7, 0.2, 'AUC = 0.5688', fontsize=18)
plt.savefig('Preprocessed/ROC_dMRI.svg', bbox_inches='tight')
#AUC Curve
print("AUC: ", metrics.auc(predicted_fpr,predicted_tpr))
#Precision Recall Curve
predicted_precision, predicted_recall, _ = metrics.precision_recall_curve(ocd_np_valid, train_y_prob)
baseline_pr=len(ocd_np_valid[ocd_np_valid==1])/len(ocd_np_valid)
plt.figure(figsize=(9,5), tight_layout=True)
plt.plot([0, 1], [baseline_pr, baseline_pr], linestyle='--', label='Baseline')
plt.plot(predicted_precision, predicted_recall, marker='.', label='Elastic Net')
plt.text(0.0, 0.55, 'F1 = 0.2647', fontsize=18)
plt.savefig('Preprocessed/PRC_dMRI.svg', bbox_inches='tight')
# F1-Score
print("F1 Score: ", metrics.f1_score(ocd_np_valid, train_y_pred))
# Confusion matrix calculations
TN, FP, FN, TP = confusion_matrix(ocd_np_valid,train_y_pred).ravel()
print(confusion_matrix(ocd_np_valid,train_y_pred))
P = TP + FN
N = FP + TN
PP = TP + FP
PN = FN + TN
print("Population =", P+N)
print("Prevalence =", P/(P+N))
CK = (2*((TP * TN) - (TN * FP)))/(((TP + FP) * (FP + TN)) + ((TP + FN) * (FN+TN)))
ACC = (TP + TN) / (P + N)
PPV = TP / PP
FOR = FN / PN
FDR = FP / PP
NPV = TN / PN
TPR = TP / P
FPR = FP / N
FNR = FN / P
TNR = TN / N
LRp = TPR / FPR
LRn = FNR / TNR
MK = PPV + NPV - 1
BM = TPR + TNR - 1
PT = (sqrt(TPR+FPR) - FPR) / (TPR - FPR)
DOR = LRp/LRn
BA = (TPR + TNR) / 2
FS = (2*PPV * TPR) / (PPV + TPR)
FM = sqrt(PPV * TPR)
MCC = sqrt(TPR*TNR*PPV*NPV) - sqrt(FPR*FNR*FDR*FOR)
TS = TP / (TP + FN + FP)
print(CK)
print(ACC)
print(PPV)
print(FOR)
print(FDR)
print(NPV)
print(TPR)
print(FPR)
print(TNR)
print(FNR)
print(LRp)
print(LRn)
print(MK)
print(BM)
print(PT)
print(DOR)
print(BA)
print(FS)
print(FM)
print(MCC)
print(TS)
# Save data
with open('Preprocessed/Coef_dMRI.npy', 'wb') as f:
np.save(f, train_coef)
with open('Preprocessed/Inter_dMRI.npy', 'wb') as f:
np.save(f, train_intercept)
| 0.459561 | 0.604399 |
```
# HIDDEN
import matplotlib
#matplotlib.use('Agg')
path_data = '../../../data/'
from datascience import *
%matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import math
import scipy.stats as stats
plt.style.use('fivethirtyeight')
```
### Implementing the Classifier ###
We are now ready to impelment a $k$-nearest neighbor classifier based on multiple attributes. We have used only two attributes so far, for ease of visualization. But usually predictions will be based on many attributes. Here is an example that shows how multiple attributes can be better than pairs.
### Banknote authentication
This time we'll look at predicting whether a banknote (e.g., a \$20 bill) is counterfeit or legitimate. Researchers have put together a data set for us, based on photographs of many individual banknotes: some counterfeit, some legitimate. They computed a few numbers from each image, using techniques that we won't worry about for this course. So, for each banknote, we know a few numbers that were computed from a photograph of it as well as its class (whether it is counterfeit or not). Let's load it into a table and take a look.
```
banknotes = Table.read_table(path_data + 'banknote.csv')
banknotes
```
Let's look at whether the first two numbers tell us anything about whether the banknote is counterfeit or not. Here's a scatterplot:
```
color_table = Table().with_columns(
'Class', make_array(1, 0),
'Color', make_array('darkblue', 'gold')
)
banknotes = banknotes.join('Class', color_table)
banknotes.scatter('WaveletVar', 'WaveletCurt', colors='Color')
```
Pretty interesting! Those two measurements do seem helpful for predicting whether the banknote is counterfeit or not. However, in this example you can now see that there is some overlap between the blue cluster and the gold cluster. This indicates that there will be some images where it's hard to tell whether the banknote is legitimate based on just these two numbers. Still, you could use a $k$-nearest neighbor classifier to predict the legitimacy of a banknote.
Take a minute and think it through: Suppose we used $k=11$ (say). What parts of the plot would the classifier get right, and what parts would it make errors on? What would the decision boundary look like?
The patterns that show up in the data can get pretty wild. For instance, here's what we'd get if used a different pair of measurements from the images:
```
banknotes.scatter('WaveletSkew', 'Entropy', colors='Color')
```
There does seem to be a pattern, but it's a pretty complex one. Nonetheless, the $k$-nearest neighbors classifier can still be used and will effectively "discover" patterns out of this. This illustrates how powerful machine learning can be: it can effectively take advantage of even patterns that we would not have anticipated, or that we would have thought to "program into" the computer.
### Multiple attributes
So far I've been assuming that we have exactly 2 attributes that we can use to help us make our prediction. What if we have more than 2? For instance, what if we have 3 attributes?
Here's the cool part: you can use the same ideas for this case, too. All you have to do is make a 3-dimensional scatterplot, instead of a 2-dimensional plot. You can still use the $k$-nearest neighbors classifier, but now computing distances in 3 dimensions instead of just 2. It just works. Very cool!
In fact, there's nothing special about 2 or 3. If you have 4 attributes, you can use the $k$-nearest neighbors classifier in 4 dimensions. 5 attributes? Work in 5-dimensional space. And no need to stop there! This all works for arbitrarily many attributes; you just work in a very high dimensional space. It gets wicked-impossible to visualize, but that's OK. The computer algorithm generalizes very nicely: all you need is the ability to compute the distance, and that's not hard. Mind-blowing stuff!
For instance, let's see what happens if we try to predict whether a banknote is counterfeit or not using 3 of the measurements, instead of just 2. Here's what you get:
```
ax = plt.figure(figsize=(8,8)).add_subplot(111, projection='3d')
ax.scatter(banknotes.column('WaveletSkew'),
banknotes.column('WaveletVar'),
banknotes.column('WaveletCurt'),
c=banknotes.column('Color'));
```
Awesome! With just 2 attributes, there was some overlap between the two clusters (which means that the classifier was bound to make some mistakes for pointers in the overlap). But when we use these 3 attributes, the two clusters have almost no overlap. In other words, a classifier that uses these 3 attributes will be more accurate than one that only uses the 2 attributes.
This is a general phenomenom in classification. Each attribute can potentially give you new information, so more attributes sometimes helps you build a better classifier. Of course, the cost is that now we have to gather more information to measure the value of each attribute, but this cost may be well worth it if it significantly improves the accuracy of our classifier.
To sum up: you now know how to use $k$-nearest neighbor classification to predict the answer to a yes/no question, based on the values of some attributes, assuming you have a training set with examples where the correct prediction is known. The general roadmap is this:
1. identify some attributes that you think might help you predict the answer to the question.
2. Gather a training set of examples where you know the values of the attributes as well as the correct prediction.
3. To make predictions in the future, measure the value of the attributes and then use $k$-nearest neighbor classification to predict the answer to the question.
### Distance in Multiple Dimensions ###
We know how to compute distance in 2-dimensional space. If we have a point at coordinates $(x_0,y_0)$ and another at $(x_1,y_1)$, the distance between them is
$$D = \sqrt{(x_0-x_1)^2 + (y_0-y_1)^2}.$$
In 3-dimensional space, the points are $(x_0, y_0, z_0)$ and $(x_1, y_1, z_1)$, and the formula for the distance between them is
$$
D = \sqrt{(x_0-x_1)^2 + (y_0-y_1)^2 + (z_0-z_1)^2}
$$
In $n$-dimensional space, things are a bit harder to visualize, but I think you can see how the formula generalized: we sum up the squares of the differences between each individual coordinate, and then take the square root of that.
In the last section, we defined the function `distance` which returned the distance between two points. We used it in two-dimensions, but the great news is that the function doesn't care how many dimensions there are! It just subtracts the two arrays of coordinates (no matter how long the arrays are), squares the differences and adds up, and then takes the square root. To work in multiple dimensions, we don't have to change the code at all.
```
def distance(point1, point2):
"""Returns the distance between point1 and point2
where each argument is an array
consisting of the coordinates of the point"""
return np.sqrt(np.sum((point1 - point2)**2))
```
Let's use this on a [new dataset](https://archive.ics.uci.edu/ml/datasets/Wine). The table `wine` contains the chemical composition of 178 different Italian wines. The classes are the grape species, called cultivars. There are three classes but let's just see whether we can tell Class 1 apart from the other two.
```
wine = Table.read_table(path_data + 'wine.csv')
# For converting Class to binary
def is_one(x):
if x == 1:
return 1
else:
return 0
wine = wine.with_column('Class', wine.apply(is_one, 0))
wine
```
The first two wines are both in Class 1. To find the distance between them, we first need a table of just the attributes:
```
wine_attributes = wine.drop('Class')
distance(np.array(wine_attributes.row(0)), np.array(wine_attributes.row(1)))
```
The last wine in the table is of Class 0. Its distance from the first wine is:
```
distance(np.array(wine_attributes.row(0)), np.array(wine_attributes.row(177)))
```
That's quite a bit bigger! Let's do some visualization to see if Class 1 really looks different from Class 0.
```
wine_with_colors = wine.join('Class', color_table)
wine_with_colors.scatter('Flavanoids', 'Alcohol', colors='Color')
```
The blue points (Class 1) are almost entirely separate from the gold ones. That is one indication of why the distance between two Class 1 wines would be smaller than the distance between wines of two different classes. We can see a similar phenomenon with a different pair of attributes too:
```
wine_with_colors.scatter('Alcalinity of Ash', 'Ash', colors='Color')
```
But for some pairs the picture is more murky.
```
wine_with_colors.scatter('Magnesium', 'Total Phenols', colors='Color')
```
Let's see if we can implement a classifier based on all of the attributes. After that, we'll see how accurate it is.
### A Plan for the Implementation ###
It's time to write some code to implement the classifier. The input is a `point` that we want to classify. The classifier works by finding the $k$ nearest neighbors of `point` from the training set. So, our approach will go like this:
1. Find the closest $k$ neighbors of `point`, i.e., the $k$ wines from the training set that are most similar to `point`.
2. Look at the classes of those $k$ neighbors, and take the majority vote to find the most-common class of wine. Use that as our predicted class for `point`.
So that will guide the structure of our Python code.
```
def closest(training, p, k):
...
def majority(topkclasses):
...
def classify(training, p, k):
kclosest = closest(training, p, k)
kclosest.classes = kclosest.select('Class')
return majority(kclosest)
```
### Implementation Step 1 ###
To implement the first step for the kidney disease data, we had to compute the distance from each patient in the training set to `point`, sort them by distance, and take the $k$ closest patients in the training set.
That's what we did in the previous section with the point corresponding to Alice. Let's generalize that code. We'll redefine `distance` here, just for convenience.
```
def distance(point1, point2):
"""Returns the distance between point1 and point2
where each argument is an array
consisting of the coordinates of the point"""
return np.sqrt(np.sum((point1 - point2)**2))
def all_distances(training, new_point):
"""Returns an array of distances
between each point in the training set
and the new point (which is a row of attributes)"""
attributes = training.drop('Class')
def distance_from_point(row):
return distance(np.array(new_point), np.array(row))
return attributes.apply(distance_from_point)
def table_with_distances(training, new_point):
"""Augments the training table
with a column of distances from new_point"""
return training.with_column('Distance', all_distances(training, new_point))
def closest(training, new_point, k):
"""Returns a table of the k rows of the augmented table
corresponding to the k smallest distances"""
with_dists = table_with_distances(training, new_point)
sorted_by_distance = with_dists.sort('Distance')
topk = sorted_by_distance.take(np.arange(k))
return topk
```
Let's see how this works on our `wine` data. We'll just take the first wine and find its five nearest neighbors among all the wines. Remember that since this wine is part of the dataset, it is its own nearest neighbor. So we should expect to see it at the top of the list, followed by four others.
First let's extract its attributes:
```
special_wine = wine.drop('Class').row(0)
```
And now let's find its 5 nearest neighbors.
```
closest(wine, special_wine, 5)
```
Bingo! The first row is the nearest neighbor, which is itself – there's a 0 in the `Distance` column as expected. All five nearest neighbors are of Class 1, which is consistent with our earlier observation that Class 1 wines appear to be clumped together in some dimensions.
### Implementation Steps 2 and 3 ###
Next we need to take a "majority vote" of the nearest neighbors and assign our point the same class as the majority.
```
def majority(topkclasses):
ones = topkclasses.where('Class', are.equal_to(1)).num_rows
zeros = topkclasses.where('Class', are.equal_to(0)).num_rows
if ones > zeros:
return 1
else:
return 0
def classify(training, new_point, k):
closestk = closest(training, new_point, k)
topkclasses = closestk.select('Class')
return majority(topkclasses)
classify(wine, special_wine, 5)
```
If we change `special_wine` to be the last one in the dataset, is our classifier able to tell that it's in Class 0?
```
special_wine = wine.drop('Class').row(177)
classify(wine, special_wine, 5)
```
Yes! The classifier gets this one right too.
But we don't yet know how it does with all the other wines, and in any case we know that testing on wines that are already part of the training set might be over-optimistic. In the final section of this chapter, we will separate the wines into a training and test set and then measure the accuracy of our classifier on the test set.
|
github_jupyter
|
# HIDDEN
import matplotlib
#matplotlib.use('Agg')
path_data = '../../../data/'
from datascience import *
%matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import math
import scipy.stats as stats
plt.style.use('fivethirtyeight')
banknotes = Table.read_table(path_data + 'banknote.csv')
banknotes
color_table = Table().with_columns(
'Class', make_array(1, 0),
'Color', make_array('darkblue', 'gold')
)
banknotes = banknotes.join('Class', color_table)
banknotes.scatter('WaveletVar', 'WaveletCurt', colors='Color')
banknotes.scatter('WaveletSkew', 'Entropy', colors='Color')
ax = plt.figure(figsize=(8,8)).add_subplot(111, projection='3d')
ax.scatter(banknotes.column('WaveletSkew'),
banknotes.column('WaveletVar'),
banknotes.column('WaveletCurt'),
c=banknotes.column('Color'));
def distance(point1, point2):
"""Returns the distance between point1 and point2
where each argument is an array
consisting of the coordinates of the point"""
return np.sqrt(np.sum((point1 - point2)**2))
wine = Table.read_table(path_data + 'wine.csv')
# For converting Class to binary
def is_one(x):
if x == 1:
return 1
else:
return 0
wine = wine.with_column('Class', wine.apply(is_one, 0))
wine
wine_attributes = wine.drop('Class')
distance(np.array(wine_attributes.row(0)), np.array(wine_attributes.row(1)))
distance(np.array(wine_attributes.row(0)), np.array(wine_attributes.row(177)))
wine_with_colors = wine.join('Class', color_table)
wine_with_colors.scatter('Flavanoids', 'Alcohol', colors='Color')
wine_with_colors.scatter('Alcalinity of Ash', 'Ash', colors='Color')
wine_with_colors.scatter('Magnesium', 'Total Phenols', colors='Color')
def closest(training, p, k):
...
def majority(topkclasses):
...
def classify(training, p, k):
kclosest = closest(training, p, k)
kclosest.classes = kclosest.select('Class')
return majority(kclosest)
def distance(point1, point2):
"""Returns the distance between point1 and point2
where each argument is an array
consisting of the coordinates of the point"""
return np.sqrt(np.sum((point1 - point2)**2))
def all_distances(training, new_point):
"""Returns an array of distances
between each point in the training set
and the new point (which is a row of attributes)"""
attributes = training.drop('Class')
def distance_from_point(row):
return distance(np.array(new_point), np.array(row))
return attributes.apply(distance_from_point)
def table_with_distances(training, new_point):
"""Augments the training table
with a column of distances from new_point"""
return training.with_column('Distance', all_distances(training, new_point))
def closest(training, new_point, k):
"""Returns a table of the k rows of the augmented table
corresponding to the k smallest distances"""
with_dists = table_with_distances(training, new_point)
sorted_by_distance = with_dists.sort('Distance')
topk = sorted_by_distance.take(np.arange(k))
return topk
special_wine = wine.drop('Class').row(0)
closest(wine, special_wine, 5)
def majority(topkclasses):
ones = topkclasses.where('Class', are.equal_to(1)).num_rows
zeros = topkclasses.where('Class', are.equal_to(0)).num_rows
if ones > zeros:
return 1
else:
return 0
def classify(training, new_point, k):
closestk = closest(training, new_point, k)
topkclasses = closestk.select('Class')
return majority(topkclasses)
classify(wine, special_wine, 5)
special_wine = wine.drop('Class').row(177)
classify(wine, special_wine, 5)
| 0.659844 | 0.957078 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.