Split (1)

train · 959k rows

text stringlengths 2.5k 6.39M	kind stringclasses 3 values
# 3장. 사이킷런을 타고 떠나는 머신 러닝 분류 모델 투어 아래 링크를 통해 이 노트북을 주피터 노트북 뷰어(nbviewer.jupyter.org)로 보거나 구글 코랩(colab.research.google.com)에서 실행할 수 있습니다. <table class="tfo-notebook-buttons" align="left"> <td> <a target="_blank" href="https://nbviewer.jupyter.org/github/rickiepark/python-machine-learning-book-2nd-edition/blob/master/code/ch03/ch03.ipynb"><img src="https://jupyter.org/assets/main-logo.svg" width="28" />주피터 노트북 뷰어로 보기</a> </td> <td> <a target="_blank" href="https://colab.research.google.com/github/rickiepark/python-machine-learning-book-2nd-edition/blob/master/code/ch03/ch03.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />구글 코랩(Colab)에서 실행하기</a> </td> </table> `watermark`는 주피터 노트북에 사용하는 파이썬 패키지를 출력하기 위한 유틸리티입니다. `watermark` 패키지를 설치하려면 다음 셀의 주석을 제거한 뒤 실행하세요. ``` #!pip install watermark %load_ext watermark %watermark -u -d -p numpy,pandas,matplotlib,sklearn ``` # 사이킷런 첫걸음 사이킷런에서 붓꽃 데이터셋을 적재합니다. 세 번째 열은 꽃잎의 길이이고 네 번째 열은 꽃잎의 너비입니다. 클래스는 이미 정수 레이블로 변환되어 있습니다. 0=Iris-Setosa, 1=Iris-Versicolor, 2=Iris-Virginica 입니다. ``` from sklearn import datasets import numpy as np iris = datasets.load_iris() X = iris.data[:, [2, 3]] y = iris.target print('클래스 레이블:', np.unique(y)) ``` 70%는 훈련 데이터 30%는 테스트 데이터로 분할합니다: ``` from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.3, random_state=1, stratify=y) print('y의 레이블 카운트:', np.bincount(y)) print('y_train의 레이블 카운트:', np.bincount(y_train)) print('y_test의 레이블 카운트:', np.bincount(y_test)) ``` 특성을 표준화합니다: ``` from sklearn.preprocessing import StandardScaler sc = StandardScaler() sc.fit(X_train) X_train_std = sc.transform(X_train) X_test_std = sc.transform(X_test) ``` ## 사이킷런으로 퍼셉트론 훈련하기 2장의 `plot_decision_region` 함수를 다시 사용하겠습니다: ``` from sklearn.linear_model import Perceptron ppn = Perceptron(max_iter=40, eta0=0.1, tol=1e-3, random_state=1) ppn.fit(X_train_std, y_train) y_pred = ppn.predict(X_test_std) print('잘못 분류된 샘플 개수: %d' % (y_test != y_pred).sum()) from sklearn.metrics import accuracy_score print('정확도: %.2f' % accuracy_score(y_test, y_pred)) print('정확도: %.2f' % ppn.score(X_test_std, y_test)) from matplotlib.colors import ListedColormap import matplotlib.pyplot as plt def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02): # 마커와 컬러맵을 설정합니다. markers = ('s', 'x', 'o', '^', 'v') colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan') cmap = ListedColormap(colors[:len(np.unique(y))]) # 결정 경계를 그립니다. x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1 x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1 xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution)) Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T) Z = Z.reshape(xx1.shape) plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=cmap) plt.xlim(xx1.min(), xx1.max()) plt.ylim(xx2.min(), xx2.max()) for idx, cl in enumerate(np.unique(y)): plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=colors[idx], marker=markers[idx], label=cl, edgecolor='black') # 테스트 샘플을 부각하여 그립니다. if test_idx: X_test, y_test = X[test_idx, :], y[test_idx] plt.scatter(X_test[:, 0], X_test[:, 1], c='', edgecolor='black', alpha=1.0, linewidth=1, marker='o', s=100, label='test set') ``` 표준화된 훈련 데이터를 사용하여 퍼셉트론 모델을 훈련합니다: ``` X_combined_std = np.vstack((X_train_std, X_test_std)) y_combined = np.hstack((y_train, y_test)) plot_decision_regions(X=X_combined_std, y=y_combined, classifier=ppn, test_idx=range(105, 150)) plt.xlabel('petal length [standardized]') plt.ylabel('petal width [standardized]') plt.legend(loc='upper left') plt.tight_layout() plt.show() ``` # 로지스틱 회귀를 사용한 클래스 확률 모델링 ### 로지스틱 회귀의 이해와 조건부 확률 ``` import matplotlib.pyplot as plt import numpy as np def sigmoid(z): return 1.0 / (1.0 + np.exp(-z)) z = np.arange(-7, 7, 0.1) phi_z = sigmoid(z) plt.plot(z, phi_z) plt.axvline(0.0, color='k') plt.ylim(-0.1, 1.1) plt.xlabel('z') plt.ylabel('$\phi (z)$') # y 축의 눈금과 격자선 plt.yticks([0.0, 0.5, 1.0]) ax = plt.gca() ax.yaxis.grid(True) plt.tight_layout() plt.show() ``` ### 로지스틱 비용 함수의 가중치 학습하기 ``` def cost_1(z): return - np.log(sigmoid(z)) def cost_0(z): return - np.log(1 - sigmoid(z)) z = np.arange(-10, 10, 0.1) phi_z = sigmoid(z) c1 = [cost_1(x) for x in z] plt.plot(phi_z, c1, label='J(w) if y=1') c0 = [cost_0(x) for x in z] plt.plot(phi_z, c0, linestyle='--', label='J(w) if y=0') plt.ylim(0.0, 5.1) plt.xlim([0, 1]) plt.xlabel('$\phi$(z)') plt.ylabel('J(w)') plt.legend(loc='best') plt.tight_layout() plt.show() class LogisticRegressionGD(object): """경사 하강법을 사용한 로지스틱 회귀 분류기 매개변수 ------------ eta : float 학습률 (0.0과 1.0 사이) n_iter : int 훈련 데이터셋 반복 횟수 random_state : int 가중치 무작위 초기화를 위한 난수 생성기 시드 속성 ----------- w_ : 1d-array 학습된 가중치 cost_ : list 에포크마다 누적된 로지스틱 비용 함수 값 """ def __init__(self, eta=0.05, n_iter=100, random_state=1): self.eta = eta self.n_iter = n_iter self.random_state = random_state def fit(self, X, y): """훈련 데이터 학습 매개변수 ---------- X : {array-like}, shape = [n_samples, n_features] n_samples 개의 샘플과 n_features 개의 특성으로 이루어진 훈련 데이터 y : array-like, shape = [n_samples] 타깃값 반환값 ------- self : object """ rgen = np.random.RandomState(self.random_state) self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1]) self.cost_ = [] for i in range(self.n_iter): net_input = self.net_input(X) output = self.activation(net_input) errors = (y - output) self.w_[1:] += self.eta * X.T.dot(errors) self.w_[0] += self.eta * errors.sum() # 오차 제곱합 대신 로지스틱 비용을 계산합니다. cost = -y.dot(np.log(output)) - ((1 - y).dot(np.log(1 - output))) self.cost_.append(cost) return self def net_input(self, X): """최종 입력 계산""" return np.dot(X, self.w_[1:]) + self.w_[0] def activation(self, z): """로지스틱 시그모이드 활성화 계산""" return 1. / (1. + np.exp(-np.clip(z, -250, 250))) def predict(self, X): """단위 계단 함수를 사용하여 클래스 레이블을 반환합니다""" return np.where(self.net_input(X) >= 0.0, 1, 0) # 다음과 동일합니다. # return np.where(self.activation(self.net_input(X)) >= 0.5, 1, 0) X_train_01_subset = X_train[(y_train == 0) \| (y_train == 1)] y_train_01_subset = y_train[(y_train == 0) \| (y_train == 1)] lrgd = LogisticRegressionGD(eta=0.05, n_iter=1000, random_state=1) lrgd.fit(X_train_01_subset, y_train_01_subset) plot_decision_regions(X=X_train_01_subset, y=y_train_01_subset, classifier=lrgd) plt.xlabel('petal length [standardized]') plt.ylabel('petal width [standardized]') plt.legend(loc='upper left') plt.tight_layout() plt.show() ``` ### 사이킷런을 사용해 로지스틱 회귀 모델 훈련하기 ``` from sklearn.linear_model import LogisticRegression lr = LogisticRegression(solver='liblinear', multi_class='auto', C=100.0, random_state=1) lr.fit(X_train_std, y_train) plot_decision_regions(X_combined_std, y_combined, classifier=lr, test_idx=range(105, 150)) plt.xlabel('petal length [standardized]') plt.ylabel('petal width [standardized]') plt.legend(loc='upper left') plt.tight_layout() plt.show() lr.predict_proba(X_test_std[:3, :]) lr.predict_proba(X_test_std[:3, :]).sum(axis=1) lr.predict_proba(X_test_std[:3, :]).argmax(axis=1) lr.predict(X_test_std[:3, :]) lr.predict(X_test_std[0, :].reshape(1, -1)) ``` ### 규제를 사용해 과대적합 피하기 ``` weights, params = [], [] for c in np.arange(-5, 5): lr = LogisticRegression(solver='liblinear', multi_class='auto', C=10.c, random_state=1) lr.fit(X_train_std, y_train) weights.append(lr.coef_[1]) params.append(10.c) weights = np.array(weights) plt.plot(params, weights[:, 0], label='petal length') plt.plot(params, weights[:, 1], linestyle='--', label='petal width') plt.ylabel('weight coefficient') plt.xlabel('C') plt.legend(loc='upper left') plt.xscale('log') plt.show() ``` # 서포트 벡터 머신을 사용한 최대 마진 분류 ``` from sklearn.svm import SVC svm = SVC(kernel='linear', C=1.0, random_state=1) svm.fit(X_train_std, y_train) plot_decision_regions(X_combined_std, y_combined, classifier=svm, test_idx=range(105, 150)) plt.scatter(svm.dual_coef_[0, :], svm.dual_coef_[1, :]) plt.xlabel('petal length [standardized]') plt.ylabel('petal width [standardized]') plt.legend(loc='upper left') plt.tight_layout() plt.show() svm.coef_ svm.dual_coef_, svm.dual_coef_.shape ``` ## 사이킷런의 다른 구현 ``` from sklearn.linear_model import SGDClassifier ppn = SGDClassifier(loss='perceptron') lr = SGDClassifier(loss='log') svm = SGDClassifier(loss='hinge') ``` # 커널 SVM을 사용하여 비선형 문제 풀기 ``` import matplotlib.pyplot as plt import numpy as np np.random.seed(1) X_xor = np.random.randn(200, 2) y_xor = np.logical_xor(X_xor[:, 0] > 0, X_xor[:, 1] > 0) y_xor = np.where(y_xor, 1, -1) plt.scatter(X_xor[y_xor == 1, 0], X_xor[y_xor == 1, 1], c='b', marker='x', label='1') plt.scatter(X_xor[y_xor == -1, 0], X_xor[y_xor == -1, 1], c='r', marker='s', label='-1') plt.xlim([-3, 3]) plt.ylim([-3, 3]) plt.legend(loc='best') plt.tight_layout() plt.show() ``` ## 커널 기법을 사용해 고차원 공간에서 분할 초평면 찾기 ``` svm = SVC(kernel='rbf', random_state=1, gamma=0.10, C=10.0) svm.fit(X_xor, y_xor) plot_decision_regions(X_xor, y_xor, classifier=svm) plt.legend(loc='upper left') plt.tight_layout() plt.show() svm = SVC(kernel='rbf', random_state=1, gamma=0.2, C=1.0) svm.fit(X_train_std, y_train) plot_decision_regions(X_combined_std, y_combined, classifier=svm, test_idx=range(105, 150)) plt.scatter(svm.dual_coef_[0,:], svm.dual_coef_[1,:]) plt.xlabel('petal length [standardized]') plt.ylabel('petal width [standardized]') plt.legend(loc='upper left') plt.tight_layout() plt.show() svm = SVC(kernel='rbf', random_state=1, gamma=100.0, C=1.0) svm.fit(X_train_std, y_train) plot_decision_regions(X_combined_std, y_combined, classifier=svm, test_idx=range(105, 150)) plt.xlabel('petal length [standardized]') plt.ylabel('petal width [standardized]') plt.legend(loc='upper left') plt.tight_layout() plt.show() ``` # 결정 트리 학습 ## 정보 이득 최대화-자원을 최대로 활용하기 ``` import matplotlib.pyplot as plt import numpy as np def gini(p): return p * (1 - p) + (1 - p) * (1 - (1 - p)) def entropy(p): return - p * np.log2(p) - (1 - p) * np.log2((1 - p)) def error(p): return 1 - np.max([p, 1 - p]) x = np.arange(0.0, 1.0, 0.01) ent = [entropy(p) if p != 0 else None for p in x] sc_ent = [e * 0.5 if e else None for e in ent] err = [error(i) for i in x] fig = plt.figure() ax = plt.subplot(111) for i, lab, ls, c, in zip([ent, sc_ent, gini(x), err], ['Entropy', 'Entropy (scaled)', 'Gini Impurity', 'Misclassification Error'], ['-', '-', '--', '-.'], ['black', 'lightgray', 'red', 'green', 'cyan']): line = ax.plot(x, i, label=lab, linestyle=ls, lw=2, color=c) ax.legend(loc='upper center', bbox_to_anchor=(0.5, 1.15), ncol=5, fancybox=True, shadow=False) ax.axhline(y=0.5, linewidth=1, color='k', linestyle='--') ax.axhline(y=1.0, linewidth=1, color='k', linestyle='--') plt.ylim([0, 1.1]) plt.xlabel('p(i=1)') plt.ylabel('Impurity Index') plt.show() ``` ## 결정 트리 만들기 ``` from sklearn.tree import DecisionTreeClassifier tree = DecisionTreeClassifier(criterion='gini', max_depth=4, random_state=1) tree.fit(X_train, y_train) X_combined = np.vstack((X_train, X_test)) y_combined = np.hstack((y_train, y_test)) plot_decision_regions(X_combined, y_combined, classifier=tree, test_idx=range(105, 150)) plt.xlabel('petal length [cm]') plt.ylabel('petal width [cm]') plt.legend(loc='upper left') plt.tight_layout() plt.show() from pydotplus import graph_from_dot_data from sklearn.tree import export_graphviz dot_data = export_graphviz(tree, filled=True, rounded=True, class_names=['Setosa', 'Versicolor', 'Virginica'], feature_names=['petal length', 'petal width'], out_file=None) graph = graph_from_dot_data(dot_data) graph.write_png('tree.png') ``` ![붓꽃 데이터셋의 결정 트리](data/tree.png "붓꽃 데이터셋의 결정 트리") ## 랜덤 포레스트로 여러 개의 결정 트리 연결하기 ``` from sklearn.ensemble import RandomForestClassifier forest = RandomForestClassifier(criterion='gini', n_estimators=25, random_state=1, n_jobs=2) forest.fit(X_train, y_train) plot_decision_regions(X_combined, y_combined, classifier=forest, test_idx=range(105, 150)) plt.xlabel('petal length [cm]') plt.ylabel('petal width [cm]') plt.legend(loc='upper left') plt.tight_layout() plt.show() ``` # K-최근접 이웃: 게으른 학습 알고리즘 ``` from sklearn.neighbors import KNeighborsClassifier knn = KNeighborsClassifier(n_neighbors=5, p=2, metric='minkowski') knn.fit(X_train_std, y_train) plot_decision_regions(X_combined_std, y_combined, classifier=knn, test_idx=range(105, 150)) plt.xlabel('petal length [standardized]') plt.ylabel('petal width [standardized]') plt.legend(loc='upper left') plt.tight_layout() plt.show() ```	github_jupyter
## Importing Necessary Libraries and Functions The first thing we need to do is import the necessary functions and libraries that we will be working with throughout the topic. We should also go ahead and upload all the of the necessary data sets here instead of loading them as we go. We will be using energy production data from PJM Interconnection. They are a regional transmission organization that coordinates the movement of wholesale electricity in parts of the United States. Specifically, we will be focused on a region of Pennsylvania. We will also be using temperature data collected from the National Oceanic and Atmospheric Assocation (NOAA). ``` !conda update -n base -c defaults conda !conda install pandas -y !conda install numpy -y !conda install matplotlib -y !conda install statsmodels -y !pip install scipy import pandas as pd import numpy as np import matplotlib.pyplot as plt import statsmodels.api as sm from statsmodels.graphics import tsaplots from statsmodels.graphics import tsaplots from statsmodels.tsa.arima_model import ARMA from statsmodels.tsa.arima_model import ARIMA from statsmodels.tsa.statespace.sarimax import SARIMAX from statsmodels.tsa.holtwinters import SimpleExpSmoothing, Holt, ExponentialSmoothing ``` Notice how we added an additional pieces above from the ```statsmodels``` module. We need to build time series models in this milestone and so we will need the above pieces to do so. We will be building exponential smoothing models as well as ARIMA models. This milestone builds off the previous ones so we should complete the following steps to the first milestone again to have our data prepped and ready to go. We should also rebuild our last model from milestone 3 since that is our foundational model! ## Preparing the Energy and Temperature Data## First we need to load our weather and energy data sets for cleaning. Let's use the pandas library and the ```read.csv``` function to do this. ``` # Loading the Needed Data Sets weather = pd.read_csv('.../hr_temp_20170201-20200131_subset.csv') energy = pd.read_csv('.../hrl_load_metered - 20170201-20200131.csv') ``` It is always good practice to take a look at the first few observations of the data set to make sure that everything looks like how we expected it to when we read in our CSV file. Let's use the ```head``` function for this. ``` weather.head() ``` Perfect! We have temperature as well as time. There are some other pieces of information like the station number, source of the reading and reading type, but we don't need those. Let's take a look at the first few observations of the energy data as well! ``` energy.head() ``` Great! Again, we have the important information of time as well as megawatt (MW) readings per hour. Again, there are some other varibales that we won't end up using in this data set as well. Let's get rid of the variables we don't need and combine the variables that we do need into one pandas data frame. Dictionaries are an easy way of doing this. Here, we are pulling the MW column from the energy data set as well as the temperature and date columns from the weather data set. These data sets already line up on time which makes this much easier. ``` d = {'MW': energy['mw'], 'Temp': weather['HourlyDryBulbTemperature'], 'Date': weather['DATE']} ``` Now let's create our pandas data frame. ``` df = pd.DataFrame(d) ``` One of the problems when loading a data set you want to run time series analysis on is the type of object Python sees for the "date" variable. Let's look at the pandas data frame data types for each of our variables. ``` print(df.dtypes) ``` Here we can see that the Date variable is a general object and not a "date" according to Python. We can change that with the pandas function ```to_datetime``` as we have below. ``` df['Date'] = pd.to_datetime(df['Date']) print(df.dtypes) ``` Good! Now that we have a ```datetime64``` object in our data set we can easily create other forms of date variables. The hour of day, day of week, month of year, and possibly even the year itself might all impact the energy usage. Let's extract these variables from our date object so that we can use them in our analysis. Pandas has some wonderful functionality to do this with the ```hour```, ```day```, ```dayofweek```, ```month```, and ```year``` functions. Then let's inspect the first few observations to make sure things look correct. ``` df['hour'] = pd.DatetimeIndex(pd.to_datetime(df['Date'])).hour df['day'] = pd.DatetimeIndex(pd.to_datetime(df['Date'])).day df['weekday'] = df['Date'].dt.dayofweek df['month'] = pd.DatetimeIndex(pd.to_datetime(df['Date'])).month df['year'] = pd.DatetimeIndex(pd.to_datetime(df['Date'])).year df.head() ``` Everything looks good in the first few observations above. If you still aren't convinced you could pull different pieces of the data frame to make sure that other observations are structured correctly. Now we should set this Python date object as the index of our data set. This will make it easier for plotting as well as forecasting later. We can use the ```set_index``` function for this. ``` df = df.set_index('Date') ``` Good! Now that we have our data structured as we would like, we can start the cleaning of the data. First, let's check if there are any missing values in the temperature column. The ```is.null``` function will help us here. ``` sum(df['Temp'].isnull()) ``` Looks like there are 37 missing values in our temperature data. We shoudl impute those. However, we don't just want to put the average temperature in these spots as the overall average across three years probably isn't a good guess for any one hour. The temperature of the hours on either side of the missing observation would be more helpful. Let's do a linear interpolation across missing values to help with this. This will essentially draw a straight line between the two known points to fill in the missing values. We can use the ```interpolate(method='linear')``` function for this. ``` df['Temp'] = df['Temp'].interpolate(method='linear') ``` Now let's see if we have any more missing temperature values. ``` sum(df['Temp'].isnull()) ``` No more! Time to check if the energy data has any missing values. ``` sum(df['MW'].isnull()) ``` No missing values there either! Perfect. Now it is time to split the data into two pieces - training and testing. The training data set is the data set we will be building our model on, while the testing data set is what we will be reporting results on since the model wouldn't have seen it ahead of time. Using the date index we can easily do this in our data frame. ``` #Training and Validation Split # train = pd.DataFrame(df['2017-01-01':'2019-12-31']) test = pd.DataFrame(df['2020-01-01':'2020-01-31']) ``` Now let's look at the first few observations for our training data set. ``` train.head() ``` Everything looks good there! Now let's do the same for our testing data set. ``` test.head() ``` Excellent! We now have our data cleaned and split. By combining and cleaning the data sets, we will make the exploration of these data sets as well as the modeling of these data sets much easier for the upcoming sections! ## Building Naive Energy Model Now that we have recreated the pieces of milestone 1 that clean and split our data we can start the modeling phase of milestone 3. First, let's review some of the findings we have from the first two milestones: - Energy usage changes depending on month / season - Energy usage changes depending on day of week - Energy usage changes depending on hour of day - Energy usage changes depending on outside temperature - The relationship between temperature and energy usage appears quadratic in nature Looking at this last bullet point, we need to create a quadratic variable on temperature as temperature in the model by itself won't be enough to model energy usage. It is always good practice to standardize (mean of 0 and standard deviation of 1) any variable you are going to raise to a higher power in a regression to help prevent multicollinearity problems. We can standardize the variable Temp by using the ```mean``` and ```std``` functions. ``` train['Temp_Norm'] = (train['Temp']-train['Temp'].mean())/train['Temp'].std() ``` Now that temperature is standardized (or normalized) we can just multiply it by itself to get our quadratic term. ``` train['Temp_Norm2'] = train['Temp_Norm']*2 ``` Let's do a brief look at the first few observations in our training data set to make sure that things worked as expected. ``` train.head() results = sm.OLS.from_formula('MW ~ Temp_NormC(hour) + Temp_Norm2C(hour) + Temp_NormC(month) + Temp_Norm2C(month) + C(weekday)C(hour)', data=train).fit() print(results.summary()) ``` All of those terms appeared significant too! Excellent. Now we have our naive energy model. It takes into account the hour of day, day of week, month of year, and the complicated relationship with temperature. Time to see how good our predictions are. One evaluation of model performance is the mean absolute percentage error (MAPE). This evaluates on average how far off are our predictions in terms of percentages. We need to get our predictions from our training data set. The ```fittedvalues``` function will do that for us. Then we can calculate the MAPE ourselves. ``` train['fitted'] = results.fittedvalues train['APE'] = abs((train['MW']-train['fitted'])/train['MW'])100 print("Training Naive Model MAPE is: ", train['APE'].mean()) ``` On average, our model incorrectly predicted energy usage by a little over 3.5%! That gives us a good baseline to compare our future models with. ``` test['Temp_Norm'] = (test['Temp']-test['Temp'].mean())/test['Temp'].std() test['Temp_Norm2'] = test['Temp_Norm']2 ``` Let's forecast out our model by scoring the test data set with the linear regression we built. Remember, we don't want to build a model on the test data set, just run the observations through the equation we got from the training model. These are our January 2020 predictions! The ```predict``` function will help us with this. We need to specify which data set we are predicting as you see with the ```predict(test)``` below. Let's look at the first few observations from this prediction! ``` test['pred'] = results.predict(test) test.head() ``` Good! Now let's plot our predictions for the test data set against the actual values. ``` test['MW'].plot(color = 'blue', figsize=(9,7)) plt.ylabel('MW Hours') plt.xlabel('Date') test['pred'].plot(color = 'green', linestyle = 'dashed', figsize=(9,7)) plt.legend(loc="best"); plt.show() ``` Those look like rather good predictions! Let's see what the MAPE is on these. ``` test['APE'] = abs((test['MW']-test['pred'])/test['MW'])100 print("Naive Model MAPE is: ", test['APE'].mean()) ``` Great! Remember, the MAPE is probably going to be higher because our model hasn't seen this data before. This is a great way to truly evaluate how well your model will do when deployed in a real world setting since you won't know energy data before you predict it. Looks like our model is only off by 4.4% on average. The foundation is laid in this step. Model building can be complicated and sometimes it is hard to know when to stop. The best plan is to build a foundational model that you can try to build upon and/or outperform with later editions of your model. Without a good baseline, you won't know how good your final model is. These seasonal effects of hours of day, days of week, months of year as well as the temperature effects build a great first attempt at forecasting future energy usage. This is a great initial model if your boss needs a check-in to see your progress. This model gets you a long way there since you have incorporated temperature's complicated relationship. In the next milestones you get to build on this great foundation to really show your boss what you can do! ## Dynamic Time Series Model Now that we have recreated the important pieces of milestones 1 and 3, we can move on to milestone 4's objectives. We have a great foundational, naive energy model. This model accounts for the energy's relationship with hour of day, day of week, month of year, and the complicated relationship with temperature. However, previous values of energy usage probably play some impact on the prediction of current energy usage. This is the basis for time series modeling! First, we need to get the residuals from the naive energy model. We will use these residuals as inputs to our dynamic time series model. We can use the ```resid``` function to do this. ``` train['resid'] = results.resid ``` Just like with our original energy data, let's plot the residuals from our model to see what we have. ``` ax1 = train['resid'].plot(color = 'blue', figsize=(9,7)) ax1.set_ylabel('Residuals') ax1.set_xlabel('Date') plt.show() ``` Looks like we still see the seasonal effects that we had in our original data. Summer months seem to have bigger residuals (model errors) than the rest of the year. Let's zoom in on a specific week from December to see what our residuals look like. ``` ax1 = train['2019-12-01':'2019-12-07']['resid'].plot(color = 'blue', figsize=(9,7)) ax1.set_ylabel('Residuals') ax1.set_xlabel('Date') plt.show() ``` It appears that we still have some daily effects as well. Different hours of the day we do worse at predicting energy than other hours. Let's see if time series models can help us correct this! ### Exponential Smoothing Models #### Winters Seasonal Exponential Smoothing Model Exponential smoothing models can be used to predict a variety of different types of data. There are different models depending on whether our data is trending and/or contains a seasonal effect as well. The Winters exponential smoothing model accounts for seasonal effects while the Holt exponential smoothing model accounts for trend. Since our residuals don't trend, but still have a seasonal effect we should use the Winter's Seasonal Exponential Smoothing Model. Let's try to forecast our energy residuals with this model! The ```ExponentialSmoothing``` function will help us with this. Remember that we don't want a trend. Also, since our data is hourly and appears we have a daily effect, we set the seasonal periods to 24. You can play around with either an additive (```seasonal='add'```) or multiplicative (```seasonal='mult'```) effect. Use the resources provided with the milestone if you are interested in learning the difference between those! ``` mod_tes = ExponentialSmoothing(train['resid'], trend=None, seasonal='add', seasonal_periods=24) res_tes = mod_tes.fit() print(res_tes.summary()) ``` We can then use the ```forecast``` functions to forecast out the month of January which is 744 observations. Careful though. These forecasts are the residuals. ``` forecast = pd.DataFrame(res_tes.forecast(744)) forecast.index = test.index.copy() ax1 = forecast.plot(color = 'blue', figsize=(9,7)) ax1.set_ylabel('Forecast') ax1.set_xlabel('Date') plt.show() ``` Let's go ahead and save these model fitted values (from the training data) and forecasts (the test data) to our respective data frames. That way we can evaluate them best. ``` train['fitted_resid'] = res_tes.fittedvalues test['pred_resid'] = forecast ``` Our energy forecast isn't the residual forecast. It is the combination the forecast from the naive model and the new exponential smoothing model on the residuals. Add these two forecasts together to get your new dynamic energy model forecasts for each the training and test data sets. ``` train['fitted_ESM'] = train['fitted'] + train['fitted_resid'] test['pred_ESM'] = test['pred'] + test['pred_resid'] ``` Now let's view our forecast just like we did with the naive model! ``` test['MW'].plot(color = 'blue', figsize=(9,7)) plt.ylabel('MW Hours') plt.xlabel('Date') test['pred_ESM'].plot(color = 'green', linestyle = 'dashed', figsize=(9,7)) plt.legend(loc="best"); plt.show() ``` Just like with the naive model, let's calculate the MAPE for our new dynamic energy model using exponential smoothing. First let's do this on the training data. ``` train['APE_ESM'] = abs((train['MW']-train['fitted_ESM'])/train['MW'])100 print("Training Naive + ESM Model MAPE is: ", train['APE_ESM'].mean()) ``` Wow! Our naive model had a training data set of about 3.5%, but this is down to nearly 1.5%! Our model seems to have improved. Let's check the test data set though and calculate a MAPE there. ``` test['APE_ESM'] = abs((test['MW']-test['pred_ESM'])/test['MW'])100 print("Naive + ESM Model MAPE is: ", test['APE_ESM'].mean()) ``` So we didn't see as much improvement in the test data set, but we still have some promise here based on the training data set improvement. Exponential smoothing models aren't the only time series models we could use. Instead of using ESM's we could try another class of time series model - the ARIMA model. ### ARIMA Model #### Model Selection There are many techniques to building ARIMA models. Classical approaches involve looking at correlation functions. More modern approaches use computer algorithms to build grids of models and compare. The nuances of these approaches are discussed in the resources provided. A brief outline is given here. Looking at the correlation patterns of the data across time can reveal the best underlying model for the data. There are two correlation functions that we need to look at to get the full picture: 1. Autocorrelation Function (ACF) 2. Partial Autocorrelation Function (PACF) Let's look at the ACF of our data with the ```plot_acf``` function. ``` fig = tsaplots.plot_acf(train['resid'].diff(24)[25:], lags = 72) plt.show() ``` From this plot we can see an exponentially decreasing pattern. This signals some potential for autoregressive (AR) terms in our model. We also see a random spike at 24. This signals a potential moving average (MA) term as well. Now let's look at the PACF of the residuals with the ```plot_pacf``` function. ``` fig = tsaplots.plot_pacf(train['resid'].diff(24)[25:], lags = 72) plt.show() ``` We have a couple of spikes early on in this plot followed by a lot of nothing. Definitely an AR patterns with 2 as its order (p = 2 in ARIMA terminology). We also see an exponentially decreasing set of spikes every 24 hours. This coincides with the single spike at 24 from the ACF plot. Definitely a moving average (MA) term at that seasonal period (in ARIMA terminology this is Q = 1). We also know that our data still has some seasonal effects every 24 hours so we should take a seasonal difference to account for this. ``` mod = SARIMAX(train['resid'], order=(2,0,0), seasonal_order=(0,1,1,24)) res = mod.fit() print(res.summary()) ``` Let's take a look at the results that we just got. It appears based on the p-values above that all of our terms are significant which is great. Let's forecast out the next 744 hours (our test data set) to see what it looks like. Again, we can use the ```forecast``` function to do this. Remember though, this is only a forecast of our residuals! ``` forecast = pd.DataFrame(res.forecast(744)) forecast.index = test.index.copy() ax1 = forecast.plot(color = 'blue', figsize=(9,7)) ax1.set_ylabel('Forecast') ax1.set_xlabel('Date') plt.show() ``` Just with the ESM model, let's go ahead and save the predicted values and forecasts to our respective data frames. This will make it easier to see how well we did. ``` train['fitted_resid2'] = res.predict() test['pred_resid2'] = forecast ``` Now, let's add these ARIMA forecasts of our residuals to the previous forecasts we developed from our naive energy model to form our dynamic energy model using ARIMA techniques. ``` train['fitted_ARIMA'] = train['fitted'] + train['fitted_resid2'] test['pred_ARIMA'] = test['pred'] + test['pred_resid2'] ``` Let's plot this forecast to see how well we did in the test data set. ``` test['MW'].plot(color = 'blue', figsize=(9,7)) plt.ylabel('MW Hours') plt.xlabel('Date') test['pred_ARIMA'].plot(color = 'green', linestyle = 'dashed', figsize=(9,7)) plt.legend(loc="best"); plt.show() ``` It is visually a little hard to determine how well we did in comparison to the other models that we have developed. Let's calculate the MAPE for both our training and testing data sets. ``` train['APE_ARIMA'] = abs((train['MW']-train['fitted_ARIMA'])/train['MW'])100 print("Training Naive + ARIMA Model MAPE is: ", train['APE_ARIMA'].mean()) ``` Wow! Our naive model had a training data set of about 3.5%, and ESM dynamic model had a MAPE of 1.5%, but this is down to nearly 1.4%! Our model seems to have improved. Let's check the test data set though and calculate a MAPE there. ``` test['APE_ARIMA'] = abs((test['MW']-test['pred_ARIMA'])/test['MW'])100 print("Naive + ARIMA Model MAPE is: ", test['APE_ARIMA'].mean()) ``` Again, we didn't see as much improvement in the test data set, but we still have some promise here based on the training data set improvement. Feel free to play around with other seasonal ARIMA models to see if you can improve the forecasts! These techniques are memory intensive and time consuming however. Just be prepared for this as you build models. If you are running this in a colab environment, you might need to restart the kernel at each model build because of the memory and time consumption. Local installations might not have this problem. One potential improvement to modeling in time series is to ensemble (or average) multiple models' forecasts to make a better forecast. It doesn't always work, but always worth trying since it is rather easy. First, let's take the average of our two residual forecasts and add that to our naive model instead of just picking either the ESM or the ARIMA. ``` train['fitted_Ensemble'] = train['fitted'] + 0.5train['fitted_resid'] + 0.5train['fitted_resid2'] test['pred_Ensemble'] = test['pred'] + 0.5test['pred_resid'] + 0.5test['pred_resid2'] ``` Now let's check the MAPE of both the training and testing data sets. ``` train['APE_Ensemble'] = abs((train['MW']-train['fitted_Ensemble'])/train['MW'])100 print("Training Naive + Ensemble Model MAPE is: ", train['APE_Ensemble'].mean()) test['APE_Ensemble'] = abs((test['MW']-test['pred_Ensemble'])/test['MW'])100 print("Naive + Ensemble Model MAPE is: ", test['APE_Ensemble'].mean()) ``` Looks like the ensemble didn't do too much to improve our forecasts. If that is the case, it might not be the analytical techniques as much as the variables that go into them. That is what we will be covering in the next milestone! So many times forecasters will stop at simple regression techniques or only use time series approaches in isolation. The benefit can really be felt by merging the two together as you will do in this milestone. Gaining the benefit of the external variable relationships as well as the correlations across time can greater improve your forecasts and reduce your prediction errors. Now you can really display your analytical talent for your boss. If they were impressed with your last model, then this one should really help drive home the impact you are making in helping them getting more accurate forecasts to improve their business decisions! #### OPTIONAL Additional Code in ARIMA Python has some built in functions to try and select ARIMA models automatically. Unfortunately, they use grid search techniques to build many different ARIMA models which as mentioned earlier can be both time and memory intensive. For this reason, we are not going over this function in this course. However, feel free to play around with the code below and investigate more on your own! ``` #!pip install scipy #!pip install pmdarima #from pmdarima import auto_arima #mod_auto = auto_arima(train['resid'], start_p=0, start_q=0, max_p=3, max_q=3, #start_P=2, start_Q=0, max_P=2, max_Q=0, m=24, #seaonal=True, trace=True, d=0, D=1, error_action='warn', #stepwise=True) ```	github_jupyter
``` import numpy as np import json import re from collections import defaultdict import spacy import matplotlib.pyplot as plt %matplotlib inline annotation_file = '../vqa-dataset/Annotations/mscoco_%s_annotations.json' annotation_sets = ['train2014', 'val2014'] question_file = '../vqa-dataset/Questions/OpenEnded_mscoco_%s_questions.json' question_sets = ['train2014', 'val2014', 'test-dev2015', 'test2015'] vocab_file = './vocabulary_vqa.txt' answer_file = './answers_vqa.txt' glove_mat_file = './vocabulary_vqa_glove.npy' num_answers = 3000 answer_counts = defaultdict(lambda: 0) for image_set in annotation_sets: with open(annotation_file % image_set) as f: annotations = json.load(f)["annotations"] for ann in annotations: for answer in ann["answers"]: # if answer["answer_confidence"] != "yes": # continue word = answer["answer"] if re.search(r"[^\w\s]", word): continue answer_counts[word] += 1 top_answers = sorted(answer_counts, key=answer_counts.get, reverse=True) print('total answer num: %d, keeping top %d' % (len(top_answers), num_answers)) # add a <unk> symbol to represent the unseen answers. assert('<unk>' not in top_answers) answer_list = ['<unk>'] + top_answers[:num_answers] vocab_set = set() SENTENCE_SPLIT_REGEX = re.compile(r'(\W+)') question_length = [] for image_set in question_sets: with open(question_file % image_set) as f: questions = json.load(f)['questions'] set_question_length = [None]*len(questions) for n_q, q in enumerate(questions): words = SENTENCE_SPLIT_REGEX.split(q['question'].lower()) words = [w.strip() for w in words if len(w.strip()) > 0] vocab_set.update(words) set_question_length[n_q] = len(words) question_length += set_question_length # although we've collected all words in the dataset, # still add a <unk> for future-proof vocab_set.add('<unk>') print('total word num: %d, keeping all' % len(vocab_set)) vocab_list = list(vocab_set) vocab_list.sort() with open(vocab_file, 'w') as f: f.writelines([w+'\n' for w in vocab_list]) with open(answer_file, 'w') as f: f.writelines([w+'\n' for w in answer_list]) # Collect glove vectors for the words glove_dim = 300 glove_mat = np.zeros((len(vocab_list), glove_dim), np.float32) nlp = spacy.load('en', vectors='en_glove_cc_300_1m_vectors') for n, w in enumerate(vocab_list): glove_mat[n] = nlp(w).vector np.save(glove_mat_file, glove_mat) _ = plt.hist(question_length, bins=20) print('maximum question length:', np.max(question_length)) ```	github_jupyter
``` %matplotlib inline ``` # Spectral clustering for image segmentation In this example, an image with connected circles is generated and spectral clustering is used to separate the circles. In these settings, the `spectral_clustering` approach solves the problem know as 'normalized graph cuts': the image is seen as a graph of connected voxels, and the spectral clustering algorithm amounts to choosing graph cuts defining regions while minimizing the ratio of the gradient along the cut, and the volume of the region. As the algorithm tries to balance the volume (ie balance the region sizes), if we take circles with different sizes, the segmentation fails. In addition, as there is no useful information in the intensity of the image, or its gradient, we choose to perform the spectral clustering on a graph that is only weakly informed by the gradient. This is close to performing a Voronoi partition of the graph. In addition, we use the mask of the objects to restrict the graph to the outline of the objects. In this example, we are interested in separating the objects one from the other, and not from the background. ``` print(__doc__) # Authors: Emmanuelle Gouillart <[email protected]> # Gael Varoquaux <[email protected]> # License: BSD 3 clause import numpy as np import matplotlib.pyplot as plt from sklearn.feature_extraction import image from sklearn.cluster import spectral_clustering l = 100 x, y = np.indices((l, l)) center1 = (28, 24) center2 = (40, 50) center3 = (67, 58) center4 = (24, 70) radius1, radius2, radius3, radius4 = 16, 14, 15, 14 circle1 = (x - center1[0]) 2 + (y - center1[1]) 2 < radius1 2 circle2 = (x - center2[0]) 2 + (y - center2[1]) 2 < radius2 2 circle3 = (x - center3[0]) 2 + (y - center3[1]) 2 < radius3 2 circle4 = (x - center4[0]) 2 + (y - center4[1]) 2 < radius4 2 # ############################################################################# # 4 circles img = circle1 + circle2 + circle3 + circle4 # We use a mask that limits to the foreground: the problem that we are # interested in here is not separating the objects from the background, # but separating them one from the other. mask = img.astype(bool) img = img.astype(float) img += 1 + 0.2 * np.random.randn(img.shape) # Convert the image into a graph with the value of the gradient on the # edges. graph = image.img_to_graph(img, mask=mask) # Take a decreasing function of the gradient: we take it weakly # dependent from the gradient the segmentation is close to a voronoi graph.data = np.exp(-graph.data / graph.data.std()) # Force the solver to be arpack, since amg is numerically # unstable on this example labels = spectral_clustering(graph, n_clusters=4, eigen_solver='arpack') label_im = -np.ones(mask.shape) label_im[mask] = labels plt.matshow(img) plt.matshow(label_im) # ############################################################################# # 2 circles img = circle1 + circle2 mask = img.astype(bool) img = img.astype(float) img += 1 + 0.2 np.random.randn(*img.shape) graph = image.img_to_graph(img, mask=mask) graph.data = np.exp(-graph.data / graph.data.std()) labels = spectral_clustering(graph, n_clusters=2, eigen_solver='arpack') label_im = -np.ones(mask.shape) label_im[mask] = labels plt.matshow(img) plt.matshow(label_im) plt.show() ```	github_jupyter
<center> <img src="img/scikit-learn-logo.png" width="40%" /> <br /> <h1>Robust and calibrated estimators with Scikit-Learn</h1> <br /><br /> Gilles Louppe (<a href="https://twitter.com/glouppe">@glouppe</a>) <br /><br /> New York University </center> ``` # Global imports and settings # Matplotlib %matplotlib inline from matplotlib import pyplot as plt plt.rcParams["figure.figsize"] = (8, 8) plt.rcParams["figure.max_open_warning"] = -1 # Print options import numpy as np np.set_printoptions(precision=3) # Slideshow from notebook.services.config import ConfigManager cm = ConfigManager() cm.update('livereveal', {'width': 1440, 'height': 768, 'scroll': True, 'theme': 'simple'}) # Silence warnings import warnings warnings.simplefilter(action="ignore", category=FutureWarning) warnings.simplefilter(action="ignore", category=UserWarning) warnings.simplefilter(action="ignore", category=RuntimeWarning) # Utils from robustness import plot_surface from robustness import plot_outlier_detector %%javascript Reveal.addEventListener("slidechanged", function(event){ window.location.hash = "header"; }); ``` # Motivation _In theory,_ - Samples $x$ are drawn from a distribution $P$; - As data increases, convergence towards the optimal model is guaranteed. _In practice,_ - A few samples may be distant from other samples: - either because they correspond to rare observations, - or because they are due to experimental errors; - Because data is finite, outliers might strongly affect the resulting model. _Today's goal:_ build models that are robust to outliers! # Outline * Motivation * Novelty and anomaly detection * Ensembling for robustness * From least squares to least absolute deviances * Calibration # Novelty and anomaly detection _Novelty detection:_ - Training data is not polluted by outliers, and we are interested in detecting anomalies in new observations. _Outlier detection:_ - Training data contains outliers, and we need to fit the central mode of the training data, ignoring the deviant observations. ## API ``` # Unsupervised learning estimator.fit(X_train) # no "y_train" # Detecting novelty or outliers y_pred = estimator.predict(X_test) # inliers == 1, outliers == -1 y_score = estimator.decision_function(X_test) # outliers == highest scores # Generate data from sklearn.datasets import make_blobs inliers, _ = make_blobs(n_samples=200, centers=2, random_state=1) outliers = np.random.rand(50, 2) outliers = np.min(inliers, axis=0) + (np.max(inliers, axis=0) - np.min(inliers, axis=0)) * outliers X = np.vstack((inliers, outliers)) ground_truth = np.ones(len(X), dtype=np.int) ground_truth[-len(outliers):] = 0 from sklearn.svm import OneClassSVM from sklearn.covariance import EllipticEnvelope from sklearn.ensemble import IsolationForest # Unsupervised learning estimator = OneClassSVM(nu=0.4, kernel="rbf", gamma=0.1) # clf = EllipticEnvelope(contamination=.1) # clf = IsolationForest(max_samples=100) estimator.fit(X) plot_outlier_detector(estimator, X, ground_truth) ``` # Ensembling for robustness ## Bias-variance decomposition __Theorem.__ For the _squared error loss_, the bias-variance decomposition of the expected generalization error at $X=\mathbf{x}$ is $$ \mathbb{E}_{\cal L} \{ Err(\varphi_{\cal L}(\mathbf{x})) \} = \text{noise}(\mathbf{x}) + \text{bias}^2(\mathbf{x}) + \text{var}(\mathbf{x}) $$ <center> <img src="img/bv.png" width="50%" /> </center> ## Variance and robustness - Low variance implies robustness to outliers - High variance implies sensitivity to data pecularities ## Ensembling reduces variance __Theorem.__ For the _squared error loss_, the bias-variance decomposition of the expected generalization error at $X=x$ of an ensemble of $M$ randomized models $\varphi_{{\cal L},\theta_m}$ is $$ \mathbb{E}_{\cal L} \{ Err(\psi_{{\cal L},\theta_1,\dots,\theta_M}(\mathbf{x})) \} = \text{noise}(\mathbf{x}) + \text{bias}^2(\mathbf{x}) + \text{var}(\mathbf{x}) $$ where \begin{align} \text{noise}(\mathbf{x}) &= Err(\varphi_B(\mathbf{x})), \\ \text{bias}^2(\mathbf{x}) &= (\varphi_B(\mathbf{x}) - \mathbb{E}_{{\cal L},\theta} \{ \varphi_{{\cal L},\theta}(\mathbf{x}) \} )^2, \\ \text{var}(\mathbf{x}) &= \rho(\mathbf{x}) \sigma^2_{{\cal L},\theta}(\mathbf{x}) + \frac{1 - \rho(\mathbf{x})}{M} \sigma^2_{{\cal L},\theta}(\mathbf{x}). \end{align} ``` # Load data from sklearn.datasets import load_iris iris = load_iris() X = iris.data[:, [0, 1]] y = iris.target from sklearn.tree import DecisionTreeClassifier clf = DecisionTreeClassifier().fit(X, y) plot_surface(clf, X, y) from sklearn.ensemble import RandomForestClassifier clf = RandomForestClassifier(n_estimators=100).fit(X, y) plot_surface(clf, X, y) ``` # From least squares to least absolute deviances ## Robust learning - Most methods minimize the mean squared error $\frac{1}{N} \sum_i (y_i - \varphi(x_i))^2$ - By definition, squaring residuals gives emphasis to large residuals. - Outliers are thus very likely to have a significant effect. - A robust alternative is to minimize instead the mean absolute deviation $\frac{1}{N} \sum_i \|y_i - \varphi(x_i)\|$ - Large residuals are therefore given much less emphasis. ``` # Generate data from sklearn.datasets import make_regression n_outliers = 3 X, y, coef = make_regression(n_samples=100, n_features=1, n_informative=1, noise=10, coef=True, random_state=0) np.random.seed(1) X[-n_outliers:] = 1 + 0.25 * np.random.normal(size=(n_outliers, 1)) y[-n_outliers:] = -100 + 10 * np.random.normal(size=n_outliers) plt.scatter(X[:-n_outliers], y[:-n_outliers], color="b") plt.scatter(X[-n_outliers:], y[-n_outliers:], color="r") plt.xlim(-3, 3) plt.ylim(-150, 120) plt.show() # Fit with least squares vs. least absolute deviances from sklearn.ensemble import GradientBoostingRegressor clf_ls = GradientBoostingRegressor(loss="ls") clf_lad = GradientBoostingRegressor(loss="lad") clf_ls.fit(X, y) clf_lad.fit(X, y) # Plot X_test = np.linspace(-5, 5).reshape(-1, 1) plt.scatter(X[:-n_outliers], y[:-n_outliers], color="b") plt.scatter(X[-n_outliers:], y[-n_outliers:], color="r") plt.plot(X_test, clf_ls.predict(X_test), "g", label="Least squares") plt.plot(X_test, clf_lad.predict(X_test), "y", label="Lead absolute deviances") plt.xlim(-3, 3) plt.ylim(-150, 120) plt.legend() plt.show() ``` ## Robust scaling - Standardization of a dataset is a common requirement for many machine learning estimators. - Typically this is done by removing the mean and scaling to unit variance. - For similar reasons as before, outliers can influence the sample mean / variance in a negative way. - In such cases, the median and the interquartile range often give better results. ``` # Generate data from sklearn.datasets import make_blobs from sklearn.model_selection import train_test_split X, y = make_blobs(n_samples=100, centers=[(0, 0), (-1, 0)], random_state=0) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0) X_train[0, 0] = -1000 # a fairly large outlier # Scale data from sklearn.preprocessing import StandardScaler from sklearn.preprocessing import RobustScaler standard_scaler = StandardScaler() Xtr_s = standard_scaler.fit_transform(X_train) Xte_s = standard_scaler.transform(X_test) robust_scaler = RobustScaler() Xtr_r = robust_scaler.fit_transform(X_train) Xte_r = robust_scaler.transform(X_test) # Plot data fig, ax = plt.subplots(1, 3, figsize=(12, 4)) ax[0].scatter(X_train[:, 0], X_train[:, 1], color=np.where(y_train == 0, 'r', 'b')) ax[1].scatter(Xtr_s[:, 0], Xtr_s[:, 1], color=np.where(y_train == 0, 'r', 'b')) ax[2].scatter(Xtr_r[:, 0], Xtr_r[:, 1], color=np.where(y_train == 0, 'r', 'b')) ax[0].set_title("Unscaled data") ax[1].set_title("After standard scaling (zoomed in)") ax[2].set_title("After robust scaling (zoomed in)") # for the scaled data, we zoom in to the data center (outlier can't be seen!) for a in ax[1:]: a.set_xlim(-3, 3) a.set_ylim(-3, 3) plt.show() # Classify using kNN from sklearn.neighbors import KNeighborsClassifier knn = KNeighborsClassifier() knn.fit(Xtr_s, y_train) acc_s = knn.score(Xte_s, y_test) print("Test set accuracy using standard scaler: %.3f" % acc_s) knn.fit(Xtr_r, y_train) acc_r = knn.score(Xte_r, y_test) print("Test set accuracy using robust scaler: %.3f" % acc_r) ``` # Calibration - In classification, you often want to predict not only the class label, but also the associated probability. - However, not all classifiers provide well-calibrated probabilities. - Thus, a separate calibration of predicted probabilities is often desirable as a postprocessing ``` from sklearn.datasets import make_blobs from sklearn.model_selection import train_test_split # Generate 3 blobs with 2 classes where the second blob contains # half positive samples and half negative samples. Probability in this # blob is therefore 0.5. X, y = make_blobs(n_samples=10000, n_features=2, cluster_std=1.0, centers=[(-5, -5), (0, 0), (5, 5)], shuffle=False) y[:len(X) // 2] = 0 y[len(X) // 2:] = 1 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=42) # Plot for this_y, color in zip([0, 1], ["r", "b"]): this_X = X_train[y_train == this_y] plt.scatter(this_X[:, 0], this_X[:, 1], c=color, alpha=0.2, label="Class %s" % this_y) plt.legend(loc="best") plt.title("Data") plt.show() from sklearn.naive_bayes import GaussianNB from sklearn.calibration import CalibratedClassifierCV # Without calibration clf = GaussianNB() clf.fit(X_train, y_train) # GaussianNB itself does not support sample-weights prob_pos_clf = clf.predict_proba(X_test)[:, 1] # With isotonic calibration clf_isotonic = CalibratedClassifierCV(clf, cv=2, method='isotonic') clf_isotonic.fit(X_train, y_train) prob_pos_isotonic = clf_isotonic.predict_proba(X_test)[:, 1] # Plot order = np.lexsort((prob_pos_clf, )) plt.plot(prob_pos_clf[order], 'r', label='No calibration') plt.plot(prob_pos_isotonic[order], 'b', label='Isotonic calibration') plt.plot(np.linspace(0, y_test.size, 51)[1::2], y_test[order].reshape(25, -1).mean(1), 'k--', label=r'Empirical') plt.xlabel("Instances sorted according to predicted probability " "(uncalibrated GNB)") plt.ylabel("P(y=1)") plt.legend(loc="upper left") plt.title("Gaussian naive Bayes probabilities") plt.ylim([-0.05, 1.05]) plt.show() ``` # Summary For robust and calibrated estimators: - remove outliers before training; - reduce variance by ensembling estimators; - drive your analysis with loss functions that are robust to outliers; - avoid the squared error loss! - calibrate the output of your classifier if probabilities are important for your problem. ``` questions? ```	github_jupyter
``` import importlib import pathlib import os import sys from datetime import datetime, timedelta import pandas as pd module_path = os.path.abspath(os.path.join('../..')) if module_path not in sys.path: sys.path.append(module_path) datetime.now() ticker="GME" report_name=f"{ticker}_{datetime.now().strftime('%Y%m%d_%H%M%S')}_due_diligence" base_path=os.path.abspath(os.path.join('.')) report_cache_dir = pathlib.Path(base_path, "notebooks", "reports", report_name) if not os.path.isdir(report_cache_dir): print(f"Reports data directory not found. Creating {report_cache_dir}") os.mkdir(report_cache_dir) else: print(f"Found reports directory {report_cache_dir}") print(os.listdir(report_cache_dir)) from gamestonk_terminal.technical_analysis import trendline_api as trend from gamestonk_terminal.due_diligence import finviz_api as finviz df_stock_cache = pathlib.Path(report_cache_dir, f"{ticker}_stock_data.pkl") if os.path.isfile(df_stock_cache): print(f"Found a cache file. Loading {df_stock_cache}") df_stock = pd.read_pickle(df_stock_cache) else: print("Cache file not found. Getting data") df_stock = trend.load_ticker(ticker, (datetime.now() - timedelta(days=180)).strftime("%Y-%m-%d")) df_stock = trend.find_trendline(df_stock, "OC_High", "high") df_stock = trend.find_trendline(df_stock, "OC_Low", "how") print("Savind cache file") df_stock.to_pickle(df_stock_cache) print(os.listdir(report_cache_dir)) import mplfinance as mpf mc = mpf.make_marketcolors(up='green',down='red', edge='black', wick='black', volume='in', ohlc='i') s = mpf.make_mpf_style(marketcolors=mc, gridstyle=":", y_on_right=True) ap0 = [] if "OC_High_trend" in df_stock.columns: ap0.append( mpf.make_addplot(df_stock["OC_High_trend"], color="g"), ) if "OC_Low_trend" in df_stock.columns: ap0.append( mpf.make_addplot(df_stock["OC_Low_trend"], color="b"), ) mpf.plot(df_stock,type='candle',mav=(20,50,200),volume=True, addplot=ap0, xrotation=0, style=s, figratio=(10,7), figscale=2.00, update_width_config=dict(candle_linewidth=1.0,candle_width=0.8, volume_linewidth=1.0)) df_fa = finviz.analyst_df(ticker) df_fa from gamestonk_terminal.fundamental_analysis import market_watch_api as mw mw.prepare_df_financials(ticker, "income") mw.prepare_df_financials(ticker, "income", quarter=True) mw.prepare_df_financials(ticker, "balance") mw.prepare_df_financials(ticker, "cashflow") ```	github_jupyter
# Segmented deformable mirrors We will use segmented deformable mirrors and simulate the PSFs that result from segment pistons and tilts. We will compare this functionality against Poppy, another optical propagation package. First we'll import all packages. ``` import os import numpy as np import matplotlib.pyplot as plt import astropy.units as u import hcipy import poppy # Parameters for the pupil function pupil_diameter = 0.019725 # m gap_size = 90e-6 # m num_rings = 3 segment_flat_to_flat = (pupil_diameter - (2 * num_rings + 1) * gap_size) / (2 * num_rings + 1) focal_length = 1 # m # Parameters for the simulation num_pix = 1024 wavelength = 638e-9 num_airy = 20 sampling = 4 norm = False ``` ## Instantiate the segmented mirrors ### HCIPy SM: `hsm` We need to generate a pupil grid for the aperture, and a focal grid and propagator for the focal plane images after the DM. ``` # HCIPy grids and propagator pupil_grid = hcipy.make_pupil_grid(dims=num_pix, diameter=pupil_diameter) focal_grid = hcipy.make_focal_grid(sampling, num_airy, pupil_diameter=pupil_diameter, reference_wavelength=wavelength, focal_length=focal_length) focal_grid = focal_grid.shifted(focal_grid.delta / 2) prop = hcipy.FraunhoferPropagator(pupil_grid, focal_grid, focal_length) ``` We generate a segmented aperture for the segmented mirror. For convenience, we'll use the HiCAT pupil without spiders. We'll use supersampling to better resolve the segment gaps. ``` aper, segments = hcipy.make_hexagonal_segmented_aperture(num_rings, segment_flat_to_flat, gap_size, starting_ring=1, return_segments=True) aper = hcipy.evaluate_supersampled(aper, pupil_grid, 1) segments = hcipy.evaluate_supersampled(segments, pupil_grid, 1) plt.title('HCIPy aperture') hcipy.imshow_field(aper, cmap='gray') ``` Now we make the segmented mirror. In order to be able to apply the SM to a plane, that plane needs to be a `Wavefront`, which combines a `Field` - here the aperture - with a wavelength, here `wavelength`. In this example here, since the SM doesn't have any extra effects on the pupil since it's still completely flat, we don't actually have to apply the SM, although of course we could. ``` # Instantiate the segmented mirror hsm = hcipy.SegmentedDeformableMirror(segments) # Make a pupil plane wavefront from aperture wf = hcipy.Wavefront(aper, wavelength) # Apply SM if you want to wf = hsm(wf) plt.figure(figsize=(8, 8)) plt.title('Wavefront intensity at HCIPy SM') hcipy.imshow_field(wf.intensity, cmap='gray') plt.colorbar() plt.show() ``` ### Poppy SM: `psm` We'll do the same for Poppy. ``` psm = poppy.dms.HexSegmentedDeformableMirror(name='Poppy SM', rings=3, flattoflat=segment_flat_to_flatu.m, gap=gap_sizeu.m, center=False) # Display the transmission and phase of the poppy sm plt.figure(figsize=(8, 8)) psm.display(what='amplitude') ``` ## Create reference images ### HCIPy reference image We need to apply the SM to the wavefront in the pupil plane and then propagate it to the image plane. ``` # Apply SM to pupil plane wf wf_sm = hsm(wf) # Propagate from SM to image plane im_ref_hc = prop(wf_sm) # Display intensity and phase in image plane plt.figure(figsize=(8, 8)) plt.suptitle('Image plane after HCIPy SM') # Get normalization factor for HCIPy reference image norm_hc = np.max(im_ref_hc.intensity) hcipy.imshow_psf(im_ref_hc, normalization='peak') ``` ### Poppy reference image For the Poppy propagation, we need to make an optical system of which we then calculate the PSF. We match HCIPy's image scale with Poppy. ``` # Make an optical system with the Poppy SM and a detector psm.flatten() pxscle = np.degrees(wavelength / pupil_diameter) * 3600 / sampling fovarc = pxscle * 160 osys = poppy.OpticalSystem() osys.add_pupil(psm) osys.add_detector(pixelscale=pxscle, fov_arcsec=fovarc, oversample=1) # Calculate the PSF psf = osys.calc_psf(wavelength) plt.figure(figsize=(8, 8)) poppy.display_psf(psf, vmin=1e-9, vmax=0.1) # Get the PSF as an array im_ref_pop = psf[0].data print('Poppy PSF shape: {}'.format(im_ref_pop.shape)) # Get normalization from Poppy reference image norm_pop = np.max(im_ref_pop) ``` ### Both reference images side-by-side ``` plt.figure(figsize=(15,6)) plt.subplot(1, 2, 1) hcipy.imshow_field(np.log10(im_ref_hc.intensity / norm_hc), vmin=-10, cmap='inferno') plt.title('HCIPy reference PSF') plt.colorbar() plt.subplot(1, 2, 2) plt.imshow(np.log10(im_ref_pop / norm_pop), origin='lower', vmin=-10, cmap='inferno') plt.title('Poppy reference PSF') plt.colorbar() ref_dif = im_ref_pop / norm_pop - im_ref_hc.intensity.shaped / norm_hc lims = np.max(np.abs(ref_dif)) plt.figure(figsize=(15, 6)) plt.suptitle(f'Maximum relative error: {lims:0.2g} relative to the peak intensity') plt.subplot(1, 2, 1) plt.imshow(ref_dif, origin='lower', vmin=-lims, vmax=lims, cmap='RdBu') plt.title('Full image') plt.colorbar() plt.subplot(1, 2, 2) plt.imshow(ref_dif[60:100,60:100], origin='lower', vmin=-lims, vmax=lims, cmap='RdBu') plt.title('Zoomed in') plt.colorbar() ``` ## Applying aberrations ``` # Define function from rad of phase to m OPD def aber_to_opd(aber_rad, wavelength): aber_m = aber_rad * wavelength / (2 * np.pi) return aber_m aber_rad = 4.0 print('Aberration: {} rad'.format(aber_rad)) print('Aberration: {} m'.format(aber_to_opd(aber_rad, wavelength))) # Poppy and HCIPy have a different way of indexing segments # Figure out which index to poke on which mirror poppy_index_to_hcipy_index = [] for n in range(1, num_rings + 1): base = list(range(3 * (n - 1) * n + 1, 3 * n * (n + 1) + 1)) poppy_index_to_hcipy_index.extend(base[2 * n::-1]) poppy_index_to_hcipy_index.extend(base[:2 * n:-1]) poppy_index_to_hcipy_index = {j: i for i, j in enumerate(poppy_index_to_hcipy_index) if j is not None} hcipy_index_to_poppy_index = {j: i for i, j in poppy_index_to_hcipy_index.items()} # Flatten both SMs just to be sure hsm.flatten() psm.flatten() # Poking segment 35 and 25 for i in [35, 25]: hsm.set_segment_actuators(i, aber_to_opd(aber_rad, wavelength) / 2, 0, 0) psm.set_actuator(hcipy_index_to_poppy_index[i], aber_to_opd(aber_rad, wavelength) * u.m, 0, 0) # Display both segmented mirrors in OPD # HCIPy plt.figure(figsize=(8,8)) plt.title('OPD for HCIPy SM') hcipy.imshow_field(hsm.surface * 2, mask=aper, cmap='RdBu_r', vmin=-5e-7, vmax=5e-7) plt.colorbar() plt.show() # Poppy plt.figure(figsize=(8,8)) psm.display(what='opd') plt.show() ``` ### Show focal plane images ``` ### HCIPy # Apply SM to pupil plane wf wf_fp_pistoned = hsm(wf) # Propagate from SM to image plane im_pistoned_hc = prop(wf_fp_pistoned) ### Poppy # Calculate the PSF psf = osys.calc_psf(wavelength) # Get the PSF as an array im_pistoned_pop = psf[0].data ### Display intensity of both cases image plane plt.figure(figsize=(15, 6)) plt.suptitle('Image plane after SM for $\phi$ = ' + str(aber_rad) + ' rad') plt.subplot(1, 2, 1) hcipy.imshow_field(np.log10(im_pistoned_hc.intensity / norm_hc), cmap='inferno', vmin=-9) plt.title('HCIPy pistoned pair') plt.colorbar() plt.subplot(1, 2, 2) plt.imshow(np.log10(im_pistoned_pop / norm_pop), origin='lower', cmap='inferno', vmin=-9) plt.title('Poppy pistoned pair') plt.colorbar() ``` ## A mix of piston, tip and tilt (PTT) ``` aber_rad_tt = 200e-6 aber_rad_p = 1.8 opd_piston = aber_to_opd(aber_rad_p, wavelength) ### Put aberrations on both SMs # Flatten both SMs hsm.flatten() psm.flatten() ## PISTON for i in [19, 28, 23, 16]: hsm.set_segment_actuators(i, opd_piston / 2, 0, 0) psm.set_actuator(hcipy_index_to_poppy_index[i], opd_piston * u.m, 0, 0) for i in [3, 35, 30, 8]: hsm.set_segment_actuators(i, -0.5 * opd_piston / 2, 0, 0) psm.set_actuator(hcipy_index_to_poppy_index[i], -0.5 * opd_piston * u.m, 0, 0) for i in [14, 18, 1, 32, 12]: hsm.set_segment_actuators(i, 0.3 * opd_piston / 2, 0, 0) psm.set_actuator(hcipy_index_to_poppy_index[i], 0.3 * opd_piston * u.m, 0, 0) ## TIP and TILT for i in [2, 5, 11, 15, 22]: hsm.set_segment_actuators(i, 0, aber_rad_tt / 2, 0.3 * aber_rad_tt / 2) psm.set_actuator(hcipy_index_to_poppy_index[i], 0, aber_rad_tt, 0.3 * aber_rad_tt) for i in [4, 6, 26]: hsm.set_segment_actuators(i, 0, -aber_rad_tt / 2, 0) psm.set_actuator(hcipy_index_to_poppy_index[i], 0, -aber_rad_tt, 0) for i in [34, 31, 7]: hsm.set_segment_actuators(i, 0, 0, 1.3 * aber_rad_tt / 2) psm.set_actuator(hcipy_index_to_poppy_index[i], 0, 0, 1.3 * aber_rad_tt) # Display both segmented mirrors in OPD # HCIPy plt.figure(figsize=(8,8)) plt.title('OPD for HCIPy SM') hcipy.imshow_field(hsm.surface * 2, mask=aper, cmap='RdBu_r', vmin=-5e-7, vmax=5e-7) plt.colorbar() plt.show() # Poppy plt.figure(figsize=(8,8)) psm.display(what='opd') plt.show() ### Propagate to image plane ## HCIPy # Propagate from pupil plane through SM to image plane im_pistoned_hc = prop(hsm(wf)).intensity ## Poppy # Calculate the PSF psf = osys.calc_psf(wavelength) # Get the PSF as an array im_pistoned_pop = psf[0].data ### Display intensity of both cases image plane plt.figure(figsize=(18, 9)) plt.suptitle('Image plane after SM forrandom arangement') plt.subplot(1, 2, 1) hcipy.imshow_field(np.log10(im_pistoned_hc / norm_hc), cmap='inferno', vmin=-9) plt.title('HCIPy random arangement') plt.colorbar() plt.subplot(1, 2, 2) plt.imshow(np.log10(im_pistoned_pop / norm_pop), origin='lower', cmap='inferno', vmin=-9) plt.title('Poppy tipped arangement') plt.colorbar() plt.show() ```	github_jupyter
``` import pandas as pd import numpy as np import matplotlib.pyplot as plt df = pd.read_csv('austin_weather.csv') df.head() df.info() ``` <h2>Visualisasi Scatter Plot Perbandingan Kuantitatif</h2> Pada tugas kali ini kita akan mengamati nilai DewPointAvg (F) dengan mengamati nilai HumidityAvg (%), TempAvg (F), dan WindAvg (MPG) Perhatikan bahwa data kita tidaklah siap untuk di analisis, salah satunya tipe data dari DewPointAvg (F), HumidityAvg (%), dan WindAvg (MPG) adalah object, padahalnya data nya ber isi numeric. maka : - Ubahlah tipe data tersebut menjadi tipe data float Step2 : - Kalian tidak akan dengan mudah mengubah tipe data tersebut karena column tersebut mempunyai nilai '-' yang dimana tidak bisa di ubah ke bentuk float, maka replace lah terlebih dahulu data yang bernilai '-' dengan nilai NaN, gunakan method .replace(). baca dokumentasi https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.replace.html - Isi nilai nan dengan nilai sebelumnya di row tersebut. gunakan method .fillna() dengan argument method bernilai 'ffill', baca dokumentasi https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.fillna.html - Sekarang ubah tipe datanya dengan float, gunakan method .astype(), baca dokumentasi https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.astype.html Setelah ini sebagian data siap untuk di jadikan bahan analisis. maka : Buahlah visualisasi perbandingan kuantitatif scatter plot, sehingga menghasilkan gambar seperti dibawah : ket : - colormap adalah 'coolwarm' - berikat warna terhadap setiap data poin dengan nilai dari column TempAvgF - berikan size terhadap setiap data poin dengan nilai dari column WindAvgMPH, kalikan dengan 20 agar size terlihat lebih besar Berikan pendapat dari insight yang bisa di dapat dari visualisasi perbandingan kuantitatif ini!!! ![image.png](attachment:image.png) ``` # DewPointAvgF # HumidityAvgPercent # TempAvgF # WindAvgMPH df['DewPointAvgF'] = df['DewPointAvgF'].replace({'-':None}) df['HumidityAvgPercent'] = df['HumidityAvgPercent'].replace({'-':None}) df['WindAvgMPH'] = df['WindAvgMPH'].replace({'-':None}) df[df['DewPointAvgF'].isnull()] df[df['HumidityAvgPercent'].isnull()] df[df['WindAvgMPH'].isnull()] df['DewPointAvgF'] = df['DewPointAvgF'].fillna(method='ffill') df['HumidityAvgPercent'] = df['HumidityAvgPercent'].fillna(method='ffill') df['WindAvgMPH'] = df['WindAvgMPH'].fillna(method='ffill') df[df['DewPointAvgF'].isnull()] df[df['HumidityAvgPercent'].isnull()] df[df['WindAvgMPH'].isnull()] df['DewPointAvgF'] = df['DewPointAvgF'].astype(float) df['HumidityAvgPercent'] = df['HumidityAvgPercent'].astype(float) df['WindAvgMPH'] = df['WindAvgMPH'].astype(float) df['TempAvgF'] = df['TempAvgF'].astype(float) df fig, ax = plt.subplots(figsize=(14,7)) D = df['DewPointAvgF'] H = df['HumidityAvgPercent'] W = df['WindAvgMPH'] T = df['TempAvgF'] axmap = ax.scatter(H, D, c=T, cmap='coolwarm', sizes=W*20) ax.set_xlabel('Humidity Avg %') ax.set_ylabel('Dew Point Avg (F)') ax.set_title('Austin Weather') fig.colorbar(axmap) plt.show() ``` Insight yang menurut saya didapat yaitu kita dapat melihat data austin weather dengan data humidity dan dew point, semakin rendah nilainya maka semakin berwarna biru dan semakin tinggi nilainya maka lebih berwarna merah.	github_jupyter
# Convolutional Neural Networks: Step by Step Welcome to Course 4's first assignment! In this assignment, you will implement convolutional (CONV) and pooling (POOL) layers in numpy, including both forward propagation and (optionally) backward propagation. Notation: - Superscript $[l]$ denotes an object of the $l^{th}$ layer. - Example: $a^{[4]}$ is the $4^{th}$ layer activation. $W^{[5]}$ and $b^{[5]}$ are the $5^{th}$ layer parameters. - Superscript $(i)$ denotes an object from the $i^{th}$ example. - Example: $x^{(i)}$ is the $i^{th}$ training example input. - Lowerscript $i$ denotes the $i^{th}$ entry of a vector. - Example: $a^{[l]}_i$ denotes the $i^{th}$ entry of the activations in layer $l$, assuming this is a fully connected (FC) layer. - $n_H$, $n_W$ and $n_C$ denote respectively the height, width and number of channels of a given layer. If you want to reference a specific layer $l$, you can also write $n_H^{[l]}$, $n_W^{[l]}$, $n_C^{[l]}$. - $n_{H_{prev}}$, $n_{W_{prev}}$ and $n_{C_{prev}}$ denote respectively the height, width and number of channels of the previous layer. If referencing a specific layer $l$, this could also be denoted $n_H^{[l-1]}$, $n_W^{[l-1]}$, $n_C^{[l-1]}$. We assume that you are already familiar with `numpy` and/or have completed the previous courses of the specialization. Let's get started! ## 1 - Packages Let's first import all the packages that you will need during this assignment. - [numpy](www.numpy.org) is the fundamental package for scientific computing with Python. - [matplotlib](http://matplotlib.org) is a library to plot graphs in Python. - np.random.seed(1) is used to keep all the random function calls consistent. It will help us grade your work. ``` import numpy as np import h5py import matplotlib.pyplot as plt %matplotlib inline plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots plt.rcParams['image.interpolation'] = 'nearest' plt.rcParams['image.cmap'] = 'gray' %load_ext autoreload %autoreload 2 np.random.seed(1) ``` ## 2 - Outline of the Assignment You will be implementing the building blocks of a convolutional neural network! Each function you will implement will have detailed instructions that will walk you through the steps needed: - Convolution functions, including: - Zero Padding - Convolve window - Convolution forward - Convolution backward (optional) - Pooling functions, including: - Pooling forward - Create mask - Distribute value - Pooling backward (optional) This notebook will ask you to implement these functions from scratch in `numpy`. In the next notebook, you will use the TensorFlow equivalents of these functions to build the following model: <img src="images/model.png" style="width:800px;height:300px;"> Note that for every forward function, there is its corresponding backward equivalent. Hence, at every step of your forward module you will store some parameters in a cache. These parameters are used to compute gradients during backpropagation. ## 3 - Convolutional Neural Networks Although programming frameworks make convolutions easy to use, they remain one of the hardest concepts to understand in Deep Learning. A convolution layer transforms an input volume into an output volume of different size, as shown below. <img src="images/conv_nn.png" style="width:350px;height:200px;"> In this part, you will build every step of the convolution layer. You will first implement two helper functions: one for zero padding and the other for computing the convolution function itself. ### 3.1 - Zero-Padding Zero-padding adds zeros around the border of an image: <img src="images/PAD.png" style="width:600px;height:400px;"> <caption><center> <u> <font color='purple'> Figure 1 </u><font color='purple'> : Zero-Padding<br> Image (3 channels, RGB) with a padding of 2. </center></caption> The main benefits of padding are the following: - It allows you to use a CONV layer without necessarily shrinking the height and width of the volumes. This is important for building deeper networks, since otherwise the height/width would shrink as you go to deeper layers. An important special case is the "same" convolution, in which the height/width is exactly preserved after one layer. - It helps us keep more of the information at the border of an image. Without padding, very few values at the next layer would be affected by pixels as the edges of an image. Exercise: Implement the following function, which pads all the images of a batch of examples X with zeros. [Use np.pad](https://docs.scipy.org/doc/numpy/reference/generated/numpy.pad.html). Note if you want to pad the array "a" of shape $(5,5,5,5,5)$ with `pad = 1` for the 2nd dimension, `pad = 3` for the 4th dimension and `pad = 0` for the rest, you would do: ```python a = np.pad(a, ((0,0), (1,1), (0,0), (3,3), (0,0)), 'constant', constant_values = (..,..)) ``` ``` # GRADED FUNCTION: zero_pad def zero_pad(X, pad): """ Pad with zeros all images of the dataset X. The padding is applied to the height and width of an image, as illustrated in Figure 1. Argument: X -- python numpy array of shape (m, n_H, n_W, n_C) representing a batch of m images pad -- integer, amount of padding around each image on vertical and horizontal dimensions Returns: X_pad -- padded image of shape (m, n_H + 2pad, n_W + 2pad, n_C) """ ### START CODE HERE ### (≈ 1 line) X_pad = np.pad(X, ((0,0),(pad,pad),(pad,pad),(0,0)),'constant',constant_values=(0,0)) ### END CODE HERE ### return X_pad np.random.seed(1) x = np.random.randn(4, 3, 3, 2) x_pad = zero_pad(x, 2) print ("x.shape =", x.shape) print ("x_pad.shape =", x_pad.shape) print ("x[1,1] =", x[1,1]) print ("x_pad[1,1] =", x_pad[1,1]) fig, axarr = plt.subplots(1, 2) axarr[0].set_title('x') axarr[0].imshow(x[0,:,:,0]) axarr[1].set_title('x_pad') axarr[1].imshow(x_pad[0,:,:,0]) ``` Expected Output: <table> <tr> <td> x.shape: </td> <td> (4, 3, 3, 2) </td> </tr> <tr> <td> x_pad.shape: </td> <td> (4, 7, 7, 2) </td> </tr> <tr> <td> x[1,1]: </td> <td> [[ 0.90085595 -0.68372786] [-0.12289023 -0.93576943] [-0.26788808 0.53035547]] </td> </tr> <tr> <td> x_pad[1,1]: </td> <td> [[ 0. 0.] [ 0. 0.] [ 0. 0.] [ 0. 0.] [ 0. 0.] [ 0. 0.] [ 0. 0.]] </td> </tr> </table> ### 3.2 - Single step of convolution In this part, implement a single step of convolution, in which you apply the filter to a single position of the input. This will be used to build a convolutional unit, which: - Takes an input volume - Applies a filter at every position of the input - Outputs another volume (usually of different size) <img src="images/Convolution_schematic.gif" style="width:500px;height:300px;"> <caption><center> <u> <font color='purple'> Figure 2 </u><font color='purple'> : Convolution operation<br> with a filter of 2x2 and a stride of 1 (stride = amount you move the window each time you slide) </center></caption> In a computer vision application, each value in the matrix on the left corresponds to a single pixel value, and we convolve a 3x3 filter with the image by multiplying its values element-wise with the original matrix, then summing them up and adding a bias. In this first step of the exercise, you will implement a single step of convolution, corresponding to applying a filter to just one of the positions to get a single real-valued output. Later in this notebook, you'll apply this function to multiple positions of the input to implement the full convolutional operation. Exercise: Implement conv_single_step(). [Hint](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.sum.html). ``` # GRADED FUNCTION: conv_single_step def conv_single_step(a_slice_prev, W, b): """ Apply one filter defined by parameters W on a single slice (a_slice_prev) of the output activation of the previous layer. Arguments: a_slice_prev -- slice of input data of shape (f, f, n_C_prev) W -- Weight parameters contained in a window - matrix of shape (f, f, n_C_prev) b -- Bias parameters contained in a window - matrix of shape (1, 1, 1) Returns: Z -- a scalar value, result of convolving the sliding window (W, b) on a slice x of the input data """ ### START CODE HERE ### (≈ 2 lines of code) # Element-wise product between a_slice and W. Do not add the bias yet. s = np.multiply(a_slice_prev , W) # Sum over all entries of the volume s. Z = np.sum(s) # Add bias b to Z. Cast b to a float() so that Z results in a scalar value. Z = Z + float(b) ### END CODE HERE ### return Z np.random.seed(1) a_slice_prev = np.random.randn(4, 4, 3) W = np.random.randn(4, 4, 3) b = np.random.randn(1, 1, 1) Z = conv_single_step(a_slice_prev, W, b) print("Z =", Z) ``` Expected Output: <table> <tr> <td> Z </td> <td> -6.99908945068 </td> </tr> </table> ### 3.3 - Convolutional Neural Networks - Forward pass In the forward pass, you will take many filters and convolve them on the input. Each 'convolution' gives you a 2D matrix output. You will then stack these outputs to get a 3D volume: <center> <video width="620" height="440" src="images/conv_kiank.mp4" type="video/mp4" controls> </video> </center> Exercise: Implement the function below to convolve the filters W on an input activation A_prev. This function takes as input A_prev, the activations output by the previous layer (for a batch of m inputs), F filters/weights denoted by W, and a bias vector denoted by b, where each filter has its own (single) bias. Finally you also have access to the hyperparameters dictionary which contains the stride and the padding. Hint: 1. To select a 2x2 slice at the upper left corner of a matrix "a_prev" (shape (5,5,3)), you would do: ```python a_slice_prev = a_prev[0:2,0:2,:] ``` This will be useful when you will define `a_slice_prev` below, using the `start/end` indexes you will define. 2. To define a_slice you will need to first define its corners `vert_start`, `vert_end`, `horiz_start` and `horiz_end`. This figure may be helpful for you to find how each of the corner can be defined using h, w, f and s in the code below. <img src="images/vert_horiz_kiank.png" style="width:400px;height:300px;"> <caption><center> <u> <font color='purple'> Figure 3 </u><font color='purple'> : Definition of a slice using vertical and horizontal start/end (with a 2x2 filter) <br> This figure shows only a single channel. </center></caption> Reminder: The formulas relating the output shape of the convolution to the input shape is: $$ n_H = \lfloor \frac{n_{H_{prev}} - f + 2 \times pad}{stride} \rfloor +1 $$ $$ n_W = \lfloor \frac{n_{W_{prev}} - f + 2 \times pad}{stride} \rfloor +1 $$ $$ n_C = \text{number of filters used in the convolution}$$ For this exercise, we won't worry about vectorization, and will just implement everything with for-loops. ``` # GRADED FUNCTION: conv_forward def conv_forward(A_prev, W, b, hparameters): """ Implements the forward propagation for a convolution function Arguments: A_prev -- output activations of the previous layer, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev) W -- Weights, numpy array of shape (f, f, n_C_prev, n_C) b -- Biases, numpy array of shape (1, 1, 1, n_C) hparameters -- python dictionary containing "stride" and "pad" Returns: Z -- conv output, numpy array of shape (m, n_H, n_W, n_C) cache -- cache of values needed for the conv_backward() function """ ### START CODE HERE ### # Retrieve dimensions from A_prev's shape (≈1 line) (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape # Retrieve dimensions from W's shape (≈1 line) (f, f, n_C_prev, n_C) = W.shape # Retrieve information from "hparameters" (≈2 lines) stride = hparameters["stride"] pad = hparameters["pad"] # Compute the dimensions of the CONV output volume using the formula given above. Hint: use int() to floor. (≈2 lines) n_H = int((n_H_prev -f + 2pad)/(stride))+1 n_W = int((n_W_prev -f + 2pad)/(stride) )+1 # Initialize the output volume Z with zeros. (≈1 line) Z = np.zeros((m,n_H,n_W,n_C)) # Create A_prev_pad by padding A_prev A_prev_pad = zero_pad(A_prev, pad) for i in range(m): # loop over the batch of training examples a_prev_pad = A_prev_pad[i,] # Select ith training example's padded activation for h in range(n_H): # loop over vertical axis of the output volume for w in range(n_W): # loop over horizontal axis of the output volume for c in range(n_C): # loop over channels (= #filters) of the output volume # Find the corners of the current "slice" (≈4 lines) vert_start = h * stride vert_end = vert_start + f horiz_start = w * stride horiz_end = horiz_start + f # Use the corners to define the (3D) slice of a_prev_pad (See Hint above the cell). (≈1 line) a_slice_prev = a_prev_pad[vert_start:vert_end,horiz_start:horiz_end,:] # Convolve the (3D) slice with the correct filter W and bias b, to get back one output neuron. (≈1 line) Z[i, h, w, c] = conv_single_step(a_slice_prev,W[:,:,:,c], b[:,:,:,c]) ### END CODE HERE ### # Making sure your output shape is correct assert(Z.shape == (m, n_H, n_W, n_C)) # Save information in "cache" for the backprop cache = (A_prev, W, b, hparameters) return Z, cache np.random.seed(1) A_prev = np.random.randn(10,4,4,3) W = np.random.randn(2,2,3,8) b = np.random.randn(1,1,1,8) hparameters = {"pad" : 2, "stride": 2} Z, cache_conv = conv_forward(A_prev, W, b, hparameters) print("Z's mean =", np.mean(Z)) print("Z[3,2,1] =", Z[3,2,1]) print("cache_conv[0][1][2][3] =", cache_conv[0][1][2][3]) ``` Expected Output: <table> <tr> <td> Z's mean </td> <td> 0.0489952035289 </td> </tr> <tr> <td> Z[3,2,1] </td> <td> [-0.61490741 -6.7439236 -2.55153897 1.75698377 3.56208902 0.53036437 5.18531798 8.75898442] </td> </tr> <tr> <td> cache_conv[0][1][2][3] </td> <td> [-0.20075807 0.18656139 0.41005165] </td> </tr> </table> Finally, CONV layer should also contain an activation, in which case we would add the following line of code: ```python # Convolve the window to get back one output neuron Z[i, h, w, c] = ... # Apply activation A[i, h, w, c] = activation(Z[i, h, w, c]) ``` You don't need to do it here. ## 4 - Pooling layer The pooling (POOL) layer reduces the height and width of the input. It helps reduce computation, as well as helps make feature detectors more invariant to its position in the input. The two types of pooling layers are: - Max-pooling layer: slides an ($f, f$) window over the input and stores the max value of the window in the output. - Average-pooling layer: slides an ($f, f$) window over the input and stores the average value of the window in the output. <table> <td> <img src="images/max_pool1.png" style="width:500px;height:300px;"> <td> <td> <img src="images/a_pool.png" style="width:500px;height:300px;"> <td> </table> These pooling layers have no parameters for backpropagation to train. However, they have hyperparameters such as the window size $f$. This specifies the height and width of the fxf window you would compute a max or average over. ### 4.1 - Forward Pooling Now, you are going to implement MAX-POOL and AVG-POOL, in the same function. Exercise: Implement the forward pass of the pooling layer. Follow the hints in the comments below. Reminder: As there's no padding, the formulas binding the output shape of the pooling to the input shape is: $$ n_H = \lfloor \frac{n_{H_{prev}} - f}{stride} \rfloor +1 $$ $$ n_W = \lfloor \frac{n_{W_{prev}} - f}{stride} \rfloor +1 $$ $$ n_C = n_{C_{prev}}$$ ``` # GRADED FUNCTION: pool_forward def pool_forward(A_prev, hparameters, mode = "max"): """ Implements the forward pass of the pooling layer Arguments: A_prev -- Input data, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev) hparameters -- python dictionary containing "f" and "stride" mode -- the pooling mode you would like to use, defined as a string ("max" or "average") Returns: A -- output of the pool layer, a numpy array of shape (m, n_H, n_W, n_C) cache -- cache used in the backward pass of the pooling layer, contains the input and hparameters """ # Retrieve dimensions from the input shape (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape # Retrieve hyperparameters from "hparameters" f = hparameters["f"] stride = hparameters["stride"] # Define the dimensions of the output n_H = int(1 + (n_H_prev - f) / stride) n_W = int(1 + (n_W_prev - f) / stride) n_C = n_C_prev # Initialize output matrix A A = np.zeros((m, n_H, n_W, n_C)) ### START CODE HERE ### for i in range(m): # loop over the training examples for h in range(n_H): # loop on the vertical axis of the output volume for w in range(n_W): # loop on the horizontal axis of the output volume for c in range (n_C): # loop over the channels of the output volume # Find the corners of the current "slice" (≈4 lines) vert_start = h * stride vert_end = vert_start + f horiz_start = w * stride horiz_end = horiz_start + f # Use the corners to define the current slice on the ith training example of A_prev, channel c. (≈1 line) a_prev_slice = A_prev[i,vert_start:vert_end,horiz_start:horiz_end,c] # Compute the pooling operation on the slice. Use an if statment to differentiate the modes. Use np.max/np.mean. if mode == "max": A[i, h, w, c] = np.max(a_prev_slice) elif mode == "average": A[i, h, w, c] = np.mean(a_prev_slice) ### END CODE HERE ### # Store the input and hparameters in "cache" for pool_backward() cache = (A_prev, hparameters) # Making sure your output shape is correct assert(A.shape == (m, n_H, n_W, n_C)) return A, cache np.random.seed(1) A_prev = np.random.randn(2, 4, 4, 3) hparameters = {"stride" : 2, "f": 3} A, cache = pool_forward(A_prev, hparameters) print("mode = max") print("A =", A) print() A, cache = pool_forward(A_prev, hparameters, mode = "average") print("mode = average") print("A =", A) ``` Expected Output: <table> <tr> <td> A = </td> <td> [[[[ 1.74481176 0.86540763 1.13376944]]] [[[ 1.13162939 1.51981682 2.18557541]]]] </td> </tr> <tr> <td> A = </td> <td> [[[[ 0.02105773 -0.20328806 -0.40389855]]] [[[-0.22154621 0.51716526 0.48155844]]]] </td> </tr> </table> Congratulations! You have now implemented the forward passes of all the layers of a convolutional network. The remainer of this notebook is optional, and will not be graded. ## 5 - Backpropagation in convolutional neural networks (OPTIONAL / UNGRADED) In modern deep learning frameworks, you only have to implement the forward pass, and the framework takes care of the backward pass, so most deep learning engineers don't need to bother with the details of the backward pass. The backward pass for convolutional networks is complicated. If you wish however, you can work through this optional portion of the notebook to get a sense of what backprop in a convolutional network looks like. When in an earlier course you implemented a simple (fully connected) neural network, you used backpropagation to compute the derivatives with respect to the cost to update the parameters. Similarly, in convolutional neural networks you can to calculate the derivatives with respect to the cost in order to update the parameters. The backprop equations are not trivial and we did not derive them in lecture, but we briefly presented them below. ### 5.1 - Convolutional layer backward pass Let's start by implementing the backward pass for a CONV layer. #### 5.1.1 - Computing dA: This is the formula for computing $dA$ with respect to the cost for a certain filter $W_c$ and a given training example: $$ dA += \sum _{h=0} ^{n_H} \sum_{w=0} ^{n_W} W_c \times dZ_{hw} \tag{1}$$ Where $W_c$ is a filter and $dZ_{hw}$ is a scalar corresponding to the gradient of the cost with respect to the output of the conv layer Z at the hth row and wth column (corresponding to the dot product taken at the ith stride left and jth stride down). Note that at each time, we multiply the the same filter $W_c$ by a different dZ when updating dA. We do so mainly because when computing the forward propagation, each filter is dotted and summed by a different a_slice. Therefore when computing the backprop for dA, we are just adding the gradients of all the a_slices. In code, inside the appropriate for-loops, this formula translates into: ```python da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c] * dZ[i, h, w, c] ``` #### 5.1.2 - Computing dW: This is the formula for computing $dW_c$ ($dW_c$ is the derivative of one filter) with respect to the loss: $$ dW_c += \sum _{h=0} ^{n_H} \sum_{w=0} ^ {n_W} a_{slice} \times dZ_{hw} \tag{2}$$ Where $a_{slice}$ corresponds to the slice which was used to generate the acitivation $Z_{ij}$. Hence, this ends up giving us the gradient for $W$ with respect to that slice. Since it is the same $W$, we will just add up all such gradients to get $dW$. In code, inside the appropriate for-loops, this formula translates into: ```python dW[:,:,:,c] += a_slice * dZ[i, h, w, c] ``` #### 5.1.3 - Computing db: This is the formula for computing $db$ with respect to the cost for a certain filter $W_c$: $$ db = \sum_h \sum_w dZ_{hw} \tag{3}$$ As you have previously seen in basic neural networks, db is computed by summing $dZ$. In this case, you are just summing over all the gradients of the conv output (Z) with respect to the cost. In code, inside the appropriate for-loops, this formula translates into: ```python db[:,:,:,c] += dZ[i, h, w, c] ``` Exercise: Implement the `conv_backward` function below. You should sum over all the training examples, filters, heights, and widths. You should then compute the derivatives using formulas 1, 2 and 3 above. ``` def conv_backward(dZ, cache): """ Implement the backward propagation for a convolution function Arguments: dZ -- gradient of the cost with respect to the output of the conv layer (Z), numpy array of shape (m, n_H, n_W, n_C) cache -- cache of values needed for the conv_backward(), output of conv_forward() Returns: dA_prev -- gradient of the cost with respect to the input of the conv layer (A_prev), numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev) dW -- gradient of the cost with respect to the weights of the conv layer (W) numpy array of shape (f, f, n_C_prev, n_C) db -- gradient of the cost with respect to the biases of the conv layer (b) numpy array of shape (1, 1, 1, n_C) """ ### START CODE HERE ### # Retrieve information from "cache" (A_prev, W, b, hparameters) = cache # Retrieve dimensions from A_prev's shape (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape # Retrieve dimensions from W's shape (f, f, n_C_prev, n_C) = W.shape # Retrieve information from "hparameters" stride = hparameters['stride'] pad = hparameters['pad'] # Retrieve dimensions from dZ's shape (m, n_H, n_W, n_C) = dZ.shape # Initialize dA_prev, dW, db with the correct shapes dA_prev = np.zeros((A_prev.shape)) dW = np.zeros((W.shape)) db = np.zeros((1,1,1,n_C)) # Pad A_prev and dA_prev A_prev_pad = zero_pad(A_prev,pad) dA_prev_pad = zero_pad(dA_prev,pad) for i in range(m): # loop over the training examples # select ith training example from A_prev_pad and dA_prev_pad a_prev_pad = A_prev_pad[i] da_prev_pad = dA_prev_pad[i] for h in range(n_H): # loop over vertical axis of the output volume for w in range(n_W): # loop over horizontal axis of the output volume for c in range(n_C): # loop over the channels of the output volume # Find the corners of the current "slice" vert_start = h * stride vert_end = vert_start + f horiz_start = w * stride horiz_end = horiz_start + f # Use the corners to define the slice from a_prev_pad a_slice = a_prev_pad[vert_start:vert_end,horiz_start:horiz_end,:] # Update gradients for the window and the filter's parameters using the code formulas given above da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c] * dZ[i, h, w, c] dW[:,:,:,c] += a_slice * dZ[i, h, w, c] db[:,:,:,c] += dZ[i, h, w, c] # Set the ith training example's dA_prev to the unpaded da_prev_pad (Hint: use X[pad:-pad, pad:-pad, :]) dA_prev[i, :, :, :] = da_prev_pad[pad:-pad, pad:-pad, :] ### END CODE HERE ### # Making sure your output shape is correct assert(dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev)) return dA_prev, dW, db np.random.seed(1) dA, dW, db = conv_backward(Z, cache_conv) print("dA_mean =", np.mean(dA)) print("dW_mean =", np.mean(dW)) print("db_mean =", np.mean(db)) ``` Expected Output: <table> <tr> <td> dA_mean </td> <td> 1.45243777754 </td> </tr> <tr> <td> dW_mean </td> <td> 1.72699145831 </td> </tr> <tr> <td> db_mean </td> <td> 7.83923256462 </td> </tr> </table> ## 5.2 Pooling layer - backward pass Next, let's implement the backward pass for the pooling layer, starting with the MAX-POOL layer. Even though a pooling layer has no parameters for backprop to update, you still need to backpropagation the gradient through the pooling layer in order to compute gradients for layers that came before the pooling layer. ### 5.2.1 Max pooling - backward pass Before jumping into the backpropagation of the pooling layer, you are going to build a helper function called `create_mask_from_window()` which does the following: $$ X = \begin{bmatrix} 1 && 3 \\ 4 && 2 \end{bmatrix} \quad \rightarrow \quad M =\begin{bmatrix} 0 && 0 \\ 1 && 0 \end{bmatrix}\tag{4}$$ As you can see, this function creates a "mask" matrix which keeps track of where the maximum of the matrix is. True (1) indicates the position of the maximum in X, the other entries are False (0). You'll see later that the backward pass for average pooling will be similar to this but using a different mask. Exercise: Implement `create_mask_from_window()`. This function will be helpful for pooling backward. Hints: - [np.max()]() may be helpful. It computes the maximum of an array. - If you have a matrix X and a scalar x: `A = (X == x)` will return a matrix A of the same size as X such that: ``` A[i,j] = True if X[i,j] = x A[i,j] = False if X[i,j] != x ``` - Here, you don't need to consider cases where there are several maxima in a matrix. ``` def create_mask_from_window(x): """ Creates a mask from an input matrix x, to identify the max entry of x. Arguments: x -- Array of shape (f, f) Returns: mask -- Array of the same shape as window, contains a True at the position corresponding to the max entry of x. """ ### START CODE HERE ### (≈1 line) mask = (x == np.max(x)) ### END CODE HERE ### return mask np.random.seed(1) x = np.random.randn(2,3) mask = create_mask_from_window(x) print('x = ', x) print("mask = ", mask) ``` Expected Output: <table> <tr> <td> x = </td> <td> [[ 1.62434536 -0.61175641 -0.52817175] <br> [-1.07296862 0.86540763 -2.3015387 ]] </td> </tr> <tr> <td> mask = </td> <td> [[ True False False] <br> [False False False]] </td> </tr> </table> Why do we keep track of the position of the max? It's because this is the input value that ultimately influenced the output, and therefore the cost. Backprop is computing gradients with respect to the cost, so anything that influences the ultimate cost should have a non-zero gradient. So, backprop will "propagate" the gradient back to this particular input value that had influenced the cost. ### 5.2.2 - Average pooling - backward pass In max pooling, for each input window, all the "influence" on the output came from a single input value--the max. In average pooling, every element of the input window has equal influence on the output. So to implement backprop, you will now implement a helper function that reflects this. For example if we did average pooling in the forward pass using a 2x2 filter, then the mask you'll use for the backward pass will look like: $$ dZ = 1 \quad \rightarrow \quad dZ =\begin{bmatrix} 1/4 && 1/4 \\ 1/4 && 1/4 \end{bmatrix}\tag{5}$$ This implies that each position in the $dZ$ matrix contributes equally to output because in the forward pass, we took an average. Exercise: Implement the function below to equally distribute a value dz through a matrix of dimension shape. [Hint](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.ones.html) ``` def distribute_value(dz, shape): """ Distributes the input value in the matrix of dimension shape Arguments: dz -- input scalar shape -- the shape (n_H, n_W) of the output matrix for which we want to distribute the value of dz Returns: a -- Array of size (n_H, n_W) for which we distributed the value of dz """ ### START CODE HERE ### # Retrieve dimensions from shape (≈1 line) (n_H, n_W) = shape # Compute the value to distribute on the matrix (≈1 line) average = (dz)/(n_H * n_W) # Create a matrix where every entry is the "average" value (≈1 line) a = np.ones(shape)* average ### END CODE HERE ### return a a = distribute_value(2, (2,2)) print('distributed value =', a) ``` Expected Output: <table> <tr> <td> distributed_value = </td> <td> [[ 0.5 0.5] <br\> [ 0.5 0.5]] </td> </tr> </table> ### 5.2.3 Putting it together: Pooling backward You now have everything you need to compute backward propagation on a pooling layer. Exercise: Implement the `pool_backward` function in both modes (`"max"` and `"average"`). You will once again use 4 for-loops (iterating over training examples, height, width, and channels). You should use an `if/elif` statement to see if the mode is equal to `'max'` or `'average'`. If it is equal to 'average' you should use the `distribute_value()` function you implemented above to create a matrix of the same shape as `a_slice`. Otherwise, the mode is equal to '`max`', and you will create a mask with `create_mask_from_window()` and multiply it by the corresponding value of dZ. ``` def pool_backward(dA, cache, mode = "max"): """ Implements the backward pass of the pooling layer Arguments: dA -- gradient of cost with respect to the output of the pooling layer, same shape as A cache -- cache output from the forward pass of the pooling layer, contains the layer's input and hparameters mode -- the pooling mode you would like to use, defined as a string ("max" or "average") Returns: dA_prev -- gradient of cost with respect to the input of the pooling layer, same shape as A_prev """ ### START CODE HERE ### # Retrieve information from cache (≈1 line) (A_prev, hparameters) = cache # Retrieve hyperparameters from "hparameters" (≈2 lines) stride = hparameters['stride'] f = hparameters['f'] # Retrieve dimensions from A_prev's shape and dA's shape (≈2 lines) m, n_H_prev, n_W_prev, n_C_prev = A_prev.shape m, n_H, n_W, n_C = dA.shape # Initialize dA_prev with zeros (≈1 line) dA_prev = np.zeros((A_prev.shape)) for i in range(m): # loop over the training examples # select training example from A_prev (≈1 line) a_prev = A_prev[i] for h in range(n_H): # loop on the vertical axis for w in range(n_W): # loop on the horizontal axis for c in range(n_C): # loop over the channels (depth) # Find the corners of the current "slice" (≈4 lines) vert_start = h * stride vert_end = vert_start + f horiz_start = w * stride horiz_end = horiz_start + f # Compute the backward propagation in both modes. if mode == "max": # Use the corners and "c" to define the current slice from a_prev (≈1 line) a_prev_slice = a_prev[vert_start:vert_end,horiz_start:horiz_end,c] # Create the mask from a_prev_slice (≈1 line) mask = create_mask_from_window(a_prev_slice) # Set dA_prev to be dA_prev + (the mask multiplied by the correct entry of dA) (≈1 line) dA_prev[i, vert_start: vert_end, horiz_start: horiz_end, c] += mask * dA[i,h,w,c] elif mode == "average": # Get the value a from dA (≈1 line) da = dA[i,h,w,c] # Define the shape of the filter as fxf (≈1 line) shape = (f,f) # Distribute it to get the correct slice of dA_prev. i.e. Add the distributed value of da. (≈1 line) dA_prev[i, vert_start: vert_end, horiz_start: horiz_end, c] += distribute_value(da, shape) ### END CODE ### # Making sure your output shape is correct assert(dA_prev.shape == A_prev.shape) return dA_prev np.random.seed(1) A_prev = np.random.randn(5, 5, 3, 2) hparameters = {"stride" : 1, "f": 2} A, cache = pool_forward(A_prev, hparameters) dA = np.random.randn(5, 4, 2, 2) dA_prev = pool_backward(dA, cache, mode = "max") print("mode = max") print('mean of dA = ', np.mean(dA)) print('dA_prev[1,1] = ', dA_prev[1,1]) print() dA_prev = pool_backward(dA, cache, mode = "average") print("mode = average") print('mean of dA = ', np.mean(dA)) print('dA_prev[1,1] = ', dA_prev[1,1]) ``` Expected Output: mode = max: <table> <tr> <td> mean of dA = </td> <td> 0.145713902729 </td> </tr> <tr> <td> dA_prev[1,1] = </td> <td> [[ 0. 0. ] <br> [ 5.05844394 -1.68282702] <br> [ 0. 0. ]] </td> </tr> </table> mode = average <table> <tr> <td> mean of dA = </td> <td> 0.145713902729 </td> </tr> <tr> <td> dA_prev[1,1] = </td> <td> [[ 0.08485462 0.2787552 ] <br> [ 1.26461098 -0.25749373] <br> [ 1.17975636 -0.53624893]] </td> </tr> </table> ### Congratulations ! Congratulation on completing this assignment. You now understand how convolutional neural networks work. You have implemented all the building blocks of a neural network. In the next assignment you will implement a ConvNet using TensorFlow.	github_jupyter
# Mapboxgl Python Library for location data visualizaiton https://github.com/mapbox/mapboxgl-jupyter ### Requirements These examples require the installation of the following python modules ``` pip install mapboxgl pip install pandas ``` ``` import pandas as pd import os from mapboxgl.utils import * from mapboxgl.viz import * # Load data from sample csv data_url = 'https://raw.githubusercontent.com/mapbox/mapboxgl-jupyter/master/examples/points.csv' df = pd.read_csv(data_url).round(3) df.head(5) df.head(5) ``` ## Set your Mapbox access token. Set a `MAPBOX_ACCESS_TOKEN` environment variable or copy/paste your token If you do not have a Mapbox access token, sign up for an account at https://www.mapbox.com/ If you already have an account, you can grab your token at https://www.mapbox.com/account/ ``` # Must be a public token, starting with `pk` token = 'pk.eyJ1IjoiY3BzYXJhc29uIiwiYSI6ImNqZjl5dXdrMTE5ajQzM216ZXVyN2pqNmsifQ.2ntB_K2-ar1Y0RUzB1Me5w' print(token) ``` ## Create a visualization from a Pandas dataframe ``` # Create a geojson file export from the current dataframe test = df_to_geojson(df, filename='points1.geojson', properties=['Avg Medicare Payments', 'Avg Covered Charges', 'date'], lat='lat', lon='lon', precision=3) # Generate data breaks using numpy quantiles and color stops from colorBrewer measure = 'Avg Medicare Payments' #color_breaks = [round(df[measure].quantile(q=x0.1), 2) for x in range(1,9)] #color_stops = create_color_stops(color_breaks, colors='YlGnBu') color_breaks = [0,10,100,1000,10000] color_stops = create_color_stops(color_breaks, colors='YlGnBu') # Create the viz from the dataframe viz = CircleViz(test, access_token=token, height='300px', center = (-95, 40), zoom = 3, ) ``` ## Add labels to the viz ``` CircleViz?? viz.label_property = "Avg Medicare Payments" viz.show() ``` ## Change viz data property and color scale ``` # Generate a new data domain breaks and a new color palette from colorBrewer2 measure = 'Avg Covered Charges' color_breaks = [round(df[measure].quantile(q=x0.1), 1) for x in range(1,9)] color_stops = create_color_stops(color_breaks, colors='YlOrRd') # Show the viz viz.color_property='Avg Covered Charges' viz.color_stops=color_stops viz.show() ``` ### Change the viz map style ``` viz.style_url='mapbox://styles/mapbox/dark-v9?optimize=true' viz.show() ``` ## Create a graduated cricle viz based on two data properties ``` # Generate data breaks and color stops from colorBrewer measure_color = 'Avg Covered Charges' color_breaks = [round(df[measure_color].quantile(q=x0.1), 2) for x in range(1,9)] color_stops = create_color_stops(color_breaks, colors='Spectral') # Generate radius breaks from data domain and circle-radius range measure_radius = 'Avg Medicare Payments' radius_breaks = [round(df[measure_radius].quantile(q=x0.1), 2) for x in range(1,9)] radius_stops = create_radius_stops(radius_breaks, 0.5, 10) # Create the viz viz2 = GraduatedCircleViz('points1.geojson', access_token=token, color_property = "Avg Covered Charges", color_stops = color_stops, radius_property = "Avg Medicare Payments", radius_stops = radius_stops, center = (-95, 40), zoom = 3, opacity=0.75, below_layer = 'waterway-label') viz2.show() ``` ## Create a heatmap viz ``` #Create a heatmap measure = 'Avg Medicare Payments' heatmap_color_stops = create_color_stops([0.01,0.25,0.5,0.75,1], colors='RdPu') heatmap_radius_stops = [[0,1], [15, 40]] #increase radius with zoom color_breaks = [round(df[measure].quantile(q=x*0.1), 2) for x in range(1,9)] color_stops = create_color_stops(color_breaks, colors='Spectral') heatmap_weight_stops = create_weight_stops(color_breaks) #Create a heatmap viz3 = HeatmapViz('points1.geojson', access_token=token, weight_property = "Avg Medicare Payments", weight_stops = heatmap_weight_stops, color_stops = heatmap_color_stops, radius_stops = heatmap_radius_stops, opacity = 0.9, center = (-95, 40), zoom = 3, below_layer='waterway-label' ) viz3.show() ``` ## Create a clustered circle map ``` #Create a clustered circle map color_stops = create_color_stops([1,10,50,100], colors='BrBG') viz4 = ClusteredCircleViz('points1.geojson', access_token=token, color_stops = color_stops, radius_stops = [[1,5], [10, 10], [50, 15], [100, 20]], cluster_maxzoom = 10, cluster_radius = 30, opacity = 0.9, center = (-95, 40), zoom = 3 ) viz4.show() ``` # Save our viz to an HTML file for distribution ### Note Viz export contains a reference to the data in this visualization. Serve data from the same directory as the HTML file to vis your visualization. ``` with open('viz4.html', 'w') as f: f.write(viz4.create_html()) ``` ### Run exported HTML example Python2: `python -m SimpleHTTPServer 8080` Python3: `python3 -m http.server 8080` Now navigate your browser to `http://localhost:8080/viz4.html` to see the viz	github_jupyter
# ARC Tools ## Coordinates conversions Below, `xyz` and `zmat` refer to Cartesian and internal coordinates, respectively ``` from arc.species.converter import (zmat_to_xyz, xyz_to_str, zmat_from_xyz, zmat_to_str, xyz_to_xyz_file_format, xyz_file_format_to_xyz, check_xyz_dict, check_zmat_dict, zmat_to_str, str_to_zmat) from arc.species.species import ARCSpecies from arc.species.zmat import consolidate_zmat import pprint path = '/home/alongd/Code/runs/T3/35/iteration_0/ARC/calcs/Species/C2H4_0/freq_a6950/output.out' xyz1 = xyz_to_str(path) pprint.pprint(zmat_from_xyz(xyz1)) ``` ##### xyz str to ARC's xyz dict: Note: `xyz_str` could also be a path to a file from which the coordinates will be parsed ``` xyz_str = """O 1.53830201 0.86423425 0.07482439 C 0.94923576 -0.20847619 -0.03881977 C -0.56154542 -0.31516675 -0.05011465 O -1.18981166 0.93489731 0.17603211 H 1.49712659 -1.15833718 -0.15458647 H -0.87737433 -0.70077243 -1.02287491 H -0.87053611 -1.01071746 0.73427128 H -0.48610273 1.61361259 0.11915705""" xyz_dict = check_xyz_dict(xyz_str) pprint.pprint(xyz_dict) ``` ##### ARC's xyz dict to xyz str: ``` xyz_dict = {'symbols': ('S', 'O', 'O', 'N', 'C', 'H', 'H', 'H', 'H', 'H'), 'isotopes': (32, 16, 16, 14, 12, 1, 1, 1, 1, 1), 'coords': ((-0.06618943, -0.12360663, -0.07631983), (-0.79539707, 0.86755487, 1.02675668), (-0.68919931, 0.25421823, -1.34830853), (0.01546439, -1.54297548, 0.44580391), (1.59721519, 0.47861334, 0.00711), (1.94428095, 0.40772394, 1.03719428), (2.20318015, -0.14715186, -0.64755729), (1.59252246, 1.5117895, -0.33908352), (-0.8785689, -2.02453514, 0.38494433), (-1.34135876, 1.49608206, 0.53295071))} xyz_str = xyz_to_str(check_xyz_dict(xyz_dict)) print(xyz_str) ``` ##### xyz (dict or str) to XYZ file format: ``` xyz = """O 1.53830201 0.86423425 0.07482439 C 0.94923576 -0.20847619 -0.03881977 C -0.56154542 -0.31516675 -0.05011465 O -1.18981166 0.93489731 0.17603211 H 1.49712659 -1.15833718 -0.15458647 H -0.87737433 -0.70077243 -1.02287491 H -0.87053611 -1.01071746 0.73427128 H -0.48610273 1.61361259 0.11915705""" xyz_file = xyz_to_xyz_file_format(check_xyz_dict(xyz)) print(xyz_file) ``` ##### XYZ file format to ARC's xyz dict: ``` xyz_file = """7 S 1.02558264 -0.04344404 -0.07343859 O -0.25448248 1.10710477 0.18359696 N -1.30762173 0.15796567 -0.10489290 C -0.49011438 -1.03704380 0.15365747 H -0.64869950 -1.85796321 -0.54773423 H -0.60359153 -1.37304859 1.18613964 H -1.43009127 0.23517346 -1.11797908""" xyz_dict = xyz_file_format_to_xyz(xyz_file) pprint.pprint(xyz_dict) ``` ##### xyz to zmat (non-consolidated): ``` xyz = """C 0.00000000 0.00000000 0.00000000 H 0.63003260 0.63003260 0.63003260 H -0.63003260 -0.63003260 0.63003260 H -0.63003260 0.63003260 -0.63003260 H 0.63003260 -0.63003260 -0.63003260""" zmat = zmat_from_xyz(xyz, mol=ARCSpecies(label='to_zmat', xyz=xyz).mol, consolidate=False) pprint.pprint(zmat) ``` ##### xyz to zmat (consolidated): ``` xyz = """C 0.00000000 0.00000000 0.00000000 H 0.63003260 0.63003260 0.63003260 H -0.63003260 -0.63003260 0.63003260 H -0.63003260 0.63003260 -0.63003260 H 0.63003260 -0.63003260 -0.63003260""" zmat = zmat_from_xyz(xyz, mol=ARCSpecies(label='to_zmat', xyz=xyz).mol, consolidate=True) pprint.pprint(zmat) ``` ##### zmat to xyz: ``` zmat = {'symbols': ('N', 'C', 'X', 'C', 'C', 'C', 'C', 'C', 'C', 'C', 'X', 'C', 'H', 'H', 'H', 'H', 'X', 'H'), 'coords': ((None, None, None), ('R_1_0', None, None), ('RX_2\|10\|16_1\|9\|11', 'AX_2\|3\|10\|11\|16\|17_1\|1\|9\|9\|11\|11_0\|2\|7\|10\|7\|16', None), ('R_3_1', 'AX_2\|3\|10\|11\|16\|17_1\|1\|9\|9\|11\|11_0\|2\|7\|10\|7\|16', 'DX_3\|11\|17_1\|9\|11_2\|10\|16_0\|7\|7'), ('R_4_3', 'A_4_3_1', 'D_4_3_1_0'), ('R_5_3', 'A_5_3_4', 'D_5\|9_3\|7_4\|8_1\|6'), ('R_6_4', 'A_6_4_3', 'D_6_4_3_5'), ('R_7_5', 'A_7_5_3', 'D_7\|8_5\|6_3\|4_4\|3'), ('R_8_6', 'A_8_6_4', 'D_7\|8_5\|6_3\|4_4\|3'), ('R_9_7', 'A_9_7_8', 'D_5\|9_3\|7_4\|8_1\|6'), ('RX_2\|10\|16_1\|9\|11', 'AX_2\|3\|10\|11\|16\|17_1\|1\|9\|9\|11\|11_0\|2\|7\|10\|7\|16', 'DX_10_9_7_8'), ('R_11_9', 'AX_2\|3\|10\|11\|16\|17_1\|1\|9\|9\|11\|11_0\|2\|7\|10\|7\|16', 'DX_3\|11\|17_1\|9\|11_2\|10\|16_0\|7\|7'), ('R_12_8', 'A_12_8_6', 'D_12\|13\|14_8\|6\|4_6\|8\|6_4\|7\|8'), ('R_13_6', 'A_13_6_8', 'D_12\|13\|14_8\|6\|4_6\|8\|6_4\|7\|8'), ('R_14\|15_4\|5', 'A_14_4_6', 'D_12\|13\|14_8\|6\|4_6\|8\|6_4\|7\|8'), ('R_14\|15_4\|5', 'A_15_5_7', 'D_15_5_7_9'), ('RX_2\|10\|16_1\|9\|11', 'AX_2\|3\|10\|11\|16\|17_1\|1\|9\|9\|11\|11_0\|2\|7\|10\|7\|16', 'DX_16_11_7_9'), ('R_17_11', 'AX_2\|3\|10\|11\|16\|17_1\|1\|9\|9\|11\|11_0\|2\|7\|10\|7\|16', 'DX_3\|11\|17_1\|9\|11_2\|10\|16_0\|7\|7')), 'vars': {'R_1_0': 1.160587988259717, 'R_3_1': 1.4334034806467013, 'R_4_3': 1.399627009160122, 'A_4_3_1': 120.07019183443934, 'D_4_3_1_0': 359.9937872737281, 'R_5_3': 1.399473903784766, 'A_5_3_4': 119.881331942158, 'R_6_4': 1.3958533508611464, 'A_6_4_3': 120.08126334426318, 'D_6_4_3_5': 359.9999896133953, 'R_7_5': 1.3971923740671386, 'A_7_5_3': 119.9563068700548, 'R_8_6': 1.3959594593665048, 'A_8_6_4': 119.9482566876851, 'R_9_7': 1.4305023206087322, 'A_9_7_8': 120.02391642181419, 'DX_10_9_7_8': 179.99687489419622, 'R_11_9': 1.2007843136670773, 'R_12_8': 1.0880999543508234, 'A_12_8_6': 119.53324505705585, 'R_13_6': 1.0875755415362989, 'A_13_6_8': 119.9515345136673, 'A_14_4_6': 119.41761055861897, 'A_15_5_7': 119.8756160539422, 'DX_16_11_7_9': 179.99364917335183, 'R_17_11': 1.0653051483625748, 'RX_2\|10\|16_1\|9\|11': 1.0, 'R_14\|15_4\|5': 1.088721623781535, 'AX_2\|3\|10\|11\|16\|17_1\|1\|9\|9\|11\|11_0\|2\|7\|10\|7\|16': 90.0, 'DX_3\|11\|17_1\|9\|11_2\|10\|16_0\|7\|7': 180.0, 'D_12\|13\|14_8\|6\|4_6\|8\|6_4\|7\|8': 180.00000001419417, 'D_5\|9_3\|7_4\|8_1\|6': 180.0000026484778, 'D_15_5_7_9': 7.778248095798993e-06, 'D_7\|8_5\|6_3\|4_4\|3': 6.434770254282058e-06}, 'map': {0: 5, 1: 4, 2: 'X', 3: 3, 4: 2, 5: 6, 6: 1, 7: 7, 8: 0, 9: 8, 10: 'X', 11: 9, 12: 10, 13: 11, 14: 12, 15: 13, 16: 'X', 17: 14}} xyz_dict = zmat_to_xyz(check_zmat_dict(zmat)) pprint.pprint(xyz_dict) ``` ##### consolidated a zmat: ``` zmat = {'symbols': ('C', 'H', 'H', 'H', 'H'), 'coords': ((None, None, None), ('R_0_1', None, None), ('R_0_2', 'A_0_1_2', None), ('R_0_3', 'A_0_1_3', 'D_0_1_2_3'), ('R_0_4', 'A_0_1_4', 'D_0_1_2_4')), 'vars': {'A_0_1_2': 35.26438764560717, 'A_0_1_3': 35.26438764560717, 'A_0_1_4': 35.26438764560717, 'D_0_1_2_3': 324.73561031724535, 'D_0_1_2_4': 35.26438968275465, 'R_0_1': 1.0912484581271156, 'R_0_2': 1.0912484581271156, 'R_0_3': 1.0912484581271156, 'R_0_4': 1.0912484581271156}, 'map': {0: 0, 1: 1, 2: 2, 3: 3, 4: 4}} zmat = consolidate_zmat(zmat) pprint.pprint(zmat) ``` ##### zmat dict to ESS-specific zmat string: ``` zmat = {'symbols': ('C', 'C', 'C', 'C', 'X', 'C', 'C', 'C', 'H', 'H', 'H', 'H', 'H', 'H', 'H', 'H'), 'coords': ((None, None, None), ('R_1\|7_0\|6', None, None), ('R_2\|6_1\|5', 'A_2\|7_1\|6_0\|5', None), ('R_3\|5_2\|3', 'A_3\|6_2\|5_1\|3', 'D_3\|7_2\|6_1\|5_0\|3'), ('RX_4_3', 'AX_4\|5_3\|3_2\|4', 'DX_4_3_2_1'), ('R_3\|5_2\|3', 'AX_4\|5_3\|3_2\|4', 'DX_5_3_4_2'), ('R_2\|6_1\|5', 'A_3\|6_2\|5_1\|3', 'D_6_5_3_1'), ('R_1\|7_0\|6', 'A_2\|7_1\|6_0\|5', 'D_3\|7_2\|6_1\|5_0\|3'), ('R_8\|11\|12\|15_0\|2\|5\|7', 'A_8\|15_0\|7_1\|6', 'D_8_0_1_7'), ('R_9\|14_0\|7', 'A_9\|14_0\|7_1\|6', 'D_9_0_1_8'), ('R_10\|13_1\|6', 'A_10\|13_1\|6_0\|7', 'D_10\|14_1\|7_0\|6_9\|13'), ('R_8\|11\|12\|15_0\|2\|5\|7', 'A_11\|12_2\|5_1\|6', 'D_11\|12_2\|5_1\|6_0\|7'), ('R_8\|11\|12\|15_0\|2\|5\|7', 'A_11\|12_2\|5_1\|6', 'D_11\|12_2\|5_1\|6_0\|7'), ('R_10\|13_1\|6', 'A_10\|13_1\|6_0\|7', 'D_13_6_7_12'), ('R_9\|14_0\|7', 'A_9\|14_0\|7_1\|6', 'D_10\|14_1\|7_0\|6_9\|13'), ('R_8\|11\|12\|15_0\|2\|5\|7', 'A_8\|15_0\|7_1\|6', 'D_15_7_6_14')), 'vars': {'RX_4_3': 1.0, 'DX_4_3_2_1': 219.28799421779138, 'DX_5_3_4_2': 180.0, 'D_6_5_3_1': 78.69721089515058, 'D_8_0_1_7': 303.5079357762497, 'D_9_0_1_8': 179.99747417664557, 'D_13_6_7_12': 180.0829054665434, 'D_15_7_6_14': 180.00215607227028, 'R_1\|7_0\|6': 1.3381887062084776, 'R_2\|6_1\|5': 1.4407904325150618, 'R_3\|5_2\|3': 1.3006576158575789, 'R_8\|11\|12\|15_0\|2\|5\|7': 1.0853633184695155, 'R_9\|14_0\|7': 1.0856141082269883, 'R_10\|13_1\|6': 1.0886528591087101, 'A_2\|7_1\|6_0\|5': 123.19585370239227, 'A_3\|6_2\|5_1\|3': 121.52258708303276, 'AX_4\|5_3\|3_2\|4': 90.0, 'A_8\|15_0\|7_1\|6': 122.24044548570495, 'A_9\|14_0\|7_1\|6': 120.41807743308047, 'A_10\|13_1\|6_0\|7': 119.30818147722846, 'A_11\|12_2\|5_1\|6': 119.14551997750254, 'D_3\|7_2\|6_1\|5_0\|3': 180.11338840380205, 'D_10\|14_1\|7_0\|6_9\|13': 0.011830716823514614, 'D_11\|12_2\|5_1\|6_0\|7': 359.8632362707074}, 'map': {0: 0, 1: 1, 2: 2, 3: 3, 4: 'X15', 5: 4, 6: 5, 7: 6, 8: 7, 9: 8, 10: 9, 11: 10, 12: 11, 13: 12, 14: 13, 15: 14}} # allowed formats are: 'gaussian', 'qchem', 'molpro', 'orca', or 'psi4' zmat_str = zmat_to_str(zmat, zmat_format='gaussian', consolidate=True) print(zmat_str) ```	github_jupyter
# Course Outline * Step 0: 載入套件並下載語料 * Step 1: 將語料讀進來 * Step 2: Contingency table 和 keyness 計算公式 * Step 3: 計算詞頻 * Step 4: 計算 keyness * Step 5: 找出 PTT 兩板的 keywords * Step 6: 視覺化 # Step 0: 載入套件並下載語料 ``` import re # 待會會使用 regular expression import math # 用來計算 log import pandas as pd # 用來製作表格 import matplotlib # python 的繪圖套件 import matplotlib.pyplot as plt # 用來畫圖表 from matplotlib.font_manager import FontProperties # 用來顯示中文字型 from wordcloud import WordCloud # 製作文字雲 from google.colab import files # 將輸出結果匯出 # 用來下載 Google Drive 上的文件 # Colab 已內建此指令 !pip install gdown # 下載語料 (語料已經過斷詞處理) !gdown --id "1q3DAwlRaK9mApM_rtdSlfAvhLRotMAQH" -O "WomenTalk_2020_seg.txt" # 2020 年 WomenTalk 板 !gdown --id "1PG_b7CBB6QLELEDBiRmAT9q9DlLNxksV" -O "Gossiping_2020_seg.txt" # 2020 年 Gossiping 板 # 如果你想試試不同年份的資料 !gdown --id "1mbtnbe_vjVbq87VEZY-z7T6QgZ3gpjJ9" -O "Gossiping_2015_seg.txt" # 2015 年 Gossiping 板 !gdown --id "1QvmzgrelbcfKWCFra7Yegq7FoWqGVfyL" -O "Gossiping_2010_seg.txt" # 2010 年 Gossiping 板 !gdown --id "1GJycMF7q7tMPf5j4aM-7DAGfIIDH_w0t" -O "Gossiping_2005_seg.txt" # 2005 年 Gossiping 板 !gdown --id "1FL3bvOmkeqDrgMBWGfoVtxBqvX9R_ebW" -O "WomenTalk_2015_seg.txt" # 2015 年 WomenTalk 板 !gdown --id "16-XHG9ceyVVWPZ1NSeCyDMoJn0J84L8e" -O "WomenTalk_2010_seg.txt" # 2010 年 WomenTalk 板 !gdown --id "1MfxuFa9wFjVkknpeXUY19rZbh7jrp64J" -O "WomenTalk_2005_seg.txt" # 2005 年 WomenTalk 板 ``` # Step 1: 將語料讀進來 ``` # 我們將 2020 年 Gossiping 板當作 target corpus with open('/content/Gossiping_2020_seg.txt') as f: tgt_content = f.read().strip() # 將 2020 年 WomenTalk 板當作 reference corpus with open('/content/WomenTalk_2020_seg.txt') as f: ref_content = f.read().strip() # 已斷詞的語料是用空白分隔每個詞，所以我們現在要把它們拆開 tgt_corpus = re.split('\s+', tgt_content) ref_corpus = re.split('\s+', ref_content) ``` # Step 2: Contingency table 和 keyness 計算公式 ## 2.1 Contingency Table * 這是我們接下來計算 keyness 會使用的 contingency table \| \| word \| other word \| total \| \|------------\|------------\|-----------------\|----------\| \| tgt_corpus \| a \| b \| (a+b) \| \| ref_corpus \| c \| d \| (c+d) \| \| total \| (a+c) \| (b+d) \| (a+b+c+d)\| * 有了 contingency table，就可以知道計算 keyness 所需要的 observed value 和 expected value O11 = a O12 = b O21 = c O22 = d E11 = ((a+b) * (a+c))/(a+b+c+d) E12 = ((a+b) * (b+d))/(a+b+c+d) E21 = ((c+d) * (a+c))/(a+b+c+d) E22 = ((c+d) * (b+d))/(a+b+c+d) ## 2.2 Keyness 計算公式 * chi-square $$\chi^2 = \sum_{i=1}^n \frac {(O_i - E_i)^2}{E_i}$$ * log-likelihood $$G^2 = 2 \sum_{i=1}^n O_i \times ln \frac{O_i}{E_i}$$ # Step 3: 計算詞頻首先，讓我們定義一個函式。透過這個函式，我們可以取得一些之後計算需要的數值。 ``` # make frequency list def count_freq(corpus): word_freq = {} other_word_freq = {} corpus_size = len(corpus) # count word_freq for word in corpus: if word not in word_freq: word_freq[word] = 1 else: word_freq[word] += 1 # count other_word_freq for key, value in word_freq.items(): other_word_freq[key] = corpus_size - value return word_freq, other_word_freq, corpus_size ``` ## 3.1 練習 ``` ## TODO: 請找出 target corpus 的 corpus size count_freq(tgt_corpus)[2] ## TODO: 請找出 "減肥" 一詞在 target corpus 中出現了幾次 count_freq(tgt_corpus)[0].get('減肥', 0) ## TODO: 請找出 "河蟹" 一詞在 reference corpus 中出現了幾次 count_freq(ref_corpus)[0].get('河蟹', 0) ``` 利用這個函式，我們就可以知道 contingency table 中各欄位的值。 ``` tgt_freq = count_freq(tgt_corpus)[0] tgt_other_freq = count_freq(tgt_corpus)[1] tgt_size = count_freq(tgt_corpus)[2] ref_freq = count_freq(ref_corpus)[0] ref_other_freq = count_freq(ref_corpus)[1] ref_size = count_freq(ref_corpus)[2] ``` # Step 4: 計算 keyness 現在，我們要定義第二個函式，幫助我們計算 keyness。 ``` tgt_corpus_words = set(tgt_corpus) ref_corpus_words = set(ref_corpus) def get_keyness(word): # 處理不在 2 個 corpus 中的詞 if word not in tgt_corpus_words and word not in ref_corpus_words: print(f"{word} not found in both corpora") return {} # 計算 Observed values O11 = tgt_freq.get(word, 0.000001) # 為避免數值中有 0 所造成的 error，我們將其換成一個趨近於 0 的數 O12 = tgt_other_freq.get(word, tgt_size) O21 = ref_freq.get(word, 0.000001) O22 = ref_other_freq.get(word, ref_size) word_total = O11 + O21 otherword_total = O12 + O22 total_size = tgt_size + ref_size ## 計算 Expected values E11 = word_total * tgt_size / total_size E12 = otherword_total * tgt_size / total_size E21 = word_total * ref_size / total_size E22 = otherword_total * ref_size / total_size ## 計算 chi-square value chi2 = (O11 - E11)2/E11 + (O12 - E12)2/E12 + (O21 - E21)2/E21 + (O22 - E22)2/E22 ## 計算 log-likelihood value G2 = 2(O11math.log(O11/E11) + O21math.log(O21/E21) + O12math.log(O12/E12) + O22math.log(O22/E22)) # 紀錄該詞偏好在哪一個 corpus 中出現 preference = 'tgt_corpus' if O11>E11 else 'ref_corpus' result = {'word': word, 'pref': preference, 'chi2': chi2, 'G2': G2} return result ``` ## 4.1 練習 ``` ## TODO: 請找出 "台灣" 的 keyness (以 log-likelihood 計算) get_keyness('台灣')['G2'] ## TODO: 請找出 "喜歡" 偏好在哪一個 corpus 出現 get_keyness('喜歡')['pref'] ## TODO: 搜尋 "最好是啦"，會發生什麼事? get_keyness('最好是啦') ``` 接著，我們將兩個 corpus 都丟進去算 keyness。 ``` all_words = set(tgt_corpus + ref_corpus) keyness = [] for word in all_words: keyness.append(get_keyness(word)) ``` 現在我們已經知道兩個 corpus 中所有字的 keyness 了！ # Step 5: 找出 PTT 兩板的 keywords 為了知道前十名的 keywords，我們要定義最後一個函式。 ``` def get_topn(data=None, pref='tgt_corpus', sort_by='G2', n=10): out = [] for w in data: if w['pref'] == pref: out.append(w) return sorted(out, key=lambda x:x[sort_by], reverse=True)[:n] # 由大到小排序 ``` 這個函式預設將取回 target corpus 中前十名的 keywords。排序預設的 measure 是 log-likelihood 值。 ## 5.1 練習 ``` ## TODO: 找出 Gossiping 板的前十名 keywords，以 log-likelihood 值排序 get_topn(keyness) ## TODO: 找出 WomenTalk 板的前十名 keywords，以 log-likelihood 值排序 get_topn(keyness, pref = 'ref_corpus') ## TODO: 找出 Gossiping 板的前五名 keywords，以 chi-square 值排序 get_topn(keyness, sort_by = 'chi2', n = 5) ## TODO: 找出 WomenTalk 板的前五名 keywords，以 chi-square 值排序 get_topn(keyness, pref = 'ref_corpus', sort_by = 'chi2', n = 5) ``` # Step 6. 視覺化 ``` # 讓 Colab 後續繪圖時顯示繁體中文 # 下載台北思源黑體 !wget -O taipei_sans_tc_beta.ttf https://drive.google.com/uc?id=1eGAsTN1HBpJAkeVM57_C7ccp7hbgSz3_&export=download # 新增字體 matplotlib.font_manager.fontManager.addfont('taipei_sans_tc_beta.ttf') # 將 font-family 設為台北思源黑體 matplotlib.rc('font', family = 'Taipei Sans TC Beta') ``` ## 6.1 表格以 Gossiping 板前十名 keywords 為例 (以 log-likelihood 值排序)，將 `list` 型態的結果轉成 `DataFrame`。 ``` tgt_G2_top10 = get_topn(keyness) tgt_G2_top10_df = pd.DataFrame(tgt_G2_top10) tgt_G2_top10_df # 將 pdDataFrame 轉成表格圖表後輸出檔案 from pandas.plotting import table figure, axes = plt.subplots(figsize=(15, 5)) # 設定背景大小 axes.xaxis.set_visible(False) # 隱藏 x 座標 axes.yaxis.set_visible(False) # 隱藏 y 座標 axes.set_frame_on(False) # 隱藏格線 table = table(axes, tgt_G2_top10_df, # 製作表格圖表 loc='upper right', colWidths=[0.18]len(tgt_G2_top10_df.columns)) table.auto_set_font_size(False) # 將字體大小改為手動 table.set_fontsize(12) # 設定字體大小 table.scale(1.2, 1.2) # 設定表格大小 # 儲存後匯出檔案 plt.savefig('tgt_G2_top10_df.png') #files.download("tgt_G2_top10_df.png") ``` ### 6.1.1 練習 ``` ## TODO: 將 WomenTalk 板前十名 keywords (以 log-likelihood 值排序) 的結果轉成 DataFrame ref_G2_top10 = get_topn(keyness, pref = 'ref_corpus') ref_G2_top10_df = pd.DataFrame(ref_G2_top10) ref_G2_top10_df ``` ###【討論問題】 * Gossiping 板的 keywords 跟 WomenTalk 板有什麼不一樣？造成兩板用詞差異可能的因素有那些？ * 用 chi-square 和 log-likelihood 所算出的 keyword 結果相似嗎？ ## 6.2 長條圖讓我們進一步把資料呈現成長條圖。 ``` # 以 Gossiping 板前十名 keywords 為例 (以 log-likelihood 值排序) tgt_G2_top10_df.plot.bar(x = 'word', y = 'G2') plt.title('八卦板前十大關鍵詞', fontsize=24) # 標題名稱 plt.xlabel('關鍵詞', fontsize=18) # X軸名稱 plt.ylabel('G2', fontsize=18) # Y軸名稱 # 儲存後匯出檔案 plt.savefig('tgt_G2_top10_bar.png') plt.show() #files.download("tgt_G2_top10_bar.png") ``` ### 6.2.1 練習 ``` # 畫出 WomenTalk 板前十名 keywords (以 log-likelihood 值排序) 的長條圖 ref_G2_top10_df.plot.bar(x = 'word', y = 'G2') plt.title('女板前十大關鍵詞', fontsize=24) # 標題名稱 plt.xlabel('關鍵詞', fontsize=18) # X軸名稱 plt.ylabel('G2', fontsize=18) # Y軸名稱 # 儲存後匯出檔案 plt.savefig('ref_G2_top10_bar.png') plt.show() #files.download("ref_G2_top10_bar.png") ``` ## 6.3 文字雲除了長條圖，我們也可以把資料畫成文字雲。 ``` # 先將八卦板的 keyness 轉成 dictionary tgt_dict = {i['word']: i['G2'] for i in keyness if i['pref'] == 'tgt_corpus'} # 製作八卦板關鍵詞文字雲 wordcloud = WordCloud(font_path = 'taipei_sans_tc_beta.ttf') wordcloud.generate_from_frequencies(frequencies = tgt_dict) plt.figure() plt.imshow(wordcloud) plt.axis('off') # 儲存後匯出檔案 plt.savefig('tgt_G2_wordcloud.png') plt.show() #files.download("tgt_G2_wordcloud.png") ``` ### 6.3.1 練習 ``` # 先將女板的 keyness 轉成 dictionary ref_dict = {i['word']: i['G2'] for i in keyness if i['pref'] == 'ref_corpus'} # 製作女板關鍵詞文字雲 wordcloud = WordCloud(font_path = 'taipei_sans_tc_beta.ttf') wordcloud.generate_from_frequencies(frequencies = ref_dict) plt.figure() plt.imshow(wordcloud) plt.axis('off') # 儲存後匯出檔案 plt.savefig('ref_G2_wordcloud.png') plt.show() #files.download("ref_G2_wordcloud.png") ```	github_jupyter
The most common analytical task is to take a bunch of numbers in dataset and summarise it with fewer numbers, preferably a single number. Enter the 'average', sum all the numbers and divide by the count of the numbers. In mathematical terms this is known as the 'arithmetic mean', and doesn't always summarise a dataset correctly. This post looks into the other types of ways that we can summarise a dataset. > The proper term for this method of summarising is determining the central tendency of the dataset. ## Generate The Data First step is to generate a dataset to summarise, to do this we use the `random` package from the standard library. Using matplotlib we can plot our 'number line'. ``` import random import typing random.seed(42) dataset: typing.List = [] for _ in range(50): dataset.append(random.randint(1,100)) print(dataset) import matplotlib.pyplot as plt def plot_1d_data(arr:typing.List, val:float, kwargs): constant_list = [val for _ in range(len(arr))] plt.plot(arr, constant_list, 'x', kwargs) plot_1d_data(dataset,5) ``` ## Median The median is the middle number of the sorted list, in the quite literal sense. For example the median of 1,2,3,4,5 is 3; as is the same for 3,2,4,1,5. The median can be more descriptive of the dataset over the arithmetic mean whenever there are significant outliers in the data that skew the arithmetic mean. > If there is an even amount of numbers in the data, the median becomes the arithmetic mean of the two middle numbers. For example, the median for 1,2,3,4,5,6 is 3.5 (3+4/2). ### When to use Use the median whenever there is a large spread of numbers across the domain ``` import statistics print(f"Median: {statistics.median(dataset)}") plot_1d_data(dataset,5) plt.plot(statistics.median(dataset),5,'x',color='red',markersize=50) plt.annotate('Median',(statistics.median(dataset),5),(statistics.median(dataset),5.1),arrowprops={'width':0.1}) ``` ## Mode The mode of a dataset is the number the appears most in the dataset. It is to be noted that this is the least used method of demonstrating central tendency. ### When to use Mode is best used with nominal data, meaning if the data you are trying to summarise has no quantitative metrics behind it, then mode would be useful. Eg, if you are looking through textual data, finding the most used word is a significant way of summarising the data. ``` import statistics print(f"Mode: {statistics.mode(dataset)}") plot_1d_data(dataset,5) plt.plot(statistics.mode(dataset),5,'x',color='red',markersize=50) plt.annotate('Mode',(statistics.mode(dataset),5),(statistics.mode(dataset),5.1),arrowprops={'width':0.1}) ``` ## Arithmetic Mean This is the most used way of representing central tendency. It is done by summing all the points in the dataset, and then dividing by the number of points (to scale back into the original domain). This is the best way of representing central tendency if the data does not containing outliers that will skew the outcome (which can be overcome by normalisation). ### When to use If the dataset is normally distributed, this is the ideal measure. ``` def arithmetic_mean(dataset: typing.List): return sum(dataset) / len(dataset) print(f"Arithmetic Mean: {arithmetic_mean(dataset)}") plot_1d_data(dataset,5) plt.plot(arithmetic_mean(dataset),5,'x',color='red',markersize=50) plt.annotate('Arithmetic Mean',(arithmetic_mean(dataset),5),(arithmetic_mean(dataset),5.1),arrowprops={'width':0.1}) ``` ## Geometric Mean The geometric mean is calculated by multiplying all numbers in a set, and then calculating the `nth` root of the multiplied figure, when n is the count of numbers. Since this using the `multiplicative` nature of the dataset to find a figure to summarise by, rather than an `additive` figure of the arithmetic mean, thus making it more suitable for datasets with a multiplicative relationship. > We calculate the nth root by raising to the power of the reciprocal. ### When to use If the dataset has a multiplicative nature (eg, growth in population, interest rates, etc), then geometric mean will be a more suitable way of summarising the dataset. The geometric mean is also useful when trying to summarise data with differenting scales or units as the geometric mean is technically unitless. ``` def multiply_list(dataset:typing.List) : # Multiply elements one by one result = 1 for x in dataset: result = result * x return result def geometric_mean(dataset:typing.List): if 0 in dataset: dataset = [x + 1 for x in dataset] return multiply_list(dataset)**(1/len(dataset)) print(f"Geometric Mean: {geometric_mean(dataset)}") plot_1d_data(dataset,5) plt.plot(geometric_mean(dataset),5,'x',color='red',markersize=50) plt.annotate('Geometric Mean',(geometric_mean(dataset),5),(geometric_mean(dataset),5.1),arrowprops={'width':0.1}) ``` ## Harmonic Mean Harmonic mean is calculated by: - taking the reciprocal of all the numbers in the set - calculating the arithmetic mean of this reciprocal set - taking the reciprocal of the calculated mean ### When to use The harmonic mean is very useful when trying to summarise datasets that are in rates or ratios. For example if you were trying to determine the average rate of travel over a trip with many legs. ``` def reciprocal_list(dataset:typing.List): reciprocal_list = [] for x in dataset: reciprocal_list.append(1/x) return reciprocal_list def harmonic_mean(dataset:typing.List): return 1/arithmetic_mean(reciprocal_list(dataset)) print(f"Harmonic Mean: {harmonic_mean(dataset)}") plot_1d_data(dataset,5) plt.plot(harmonic_mean(dataset),5,'x',color='red',markersize=50) plt.annotate('Harmonic Mean',(harmonic_mean(dataset),5),(harmonic_mean(dataset),5.1),arrowprops={'width':0.1}) print(f"Mode: {statistics.mode(dataset)}") print(f"Median: {statistics.median(dataset)}") print(f"Arithmetic Mean: {arithmetic_mean(dataset)}") print(f"Geometric Mean: {geometric_mean(dataset)}") print(f"Harmonic Mean: {harmonic_mean(dataset)}") ``` > Thank you to Andrew Goodwin over on Twitter: <https://twitter.com/ndrewg/status/1296773835585236997> for suggesting some extremely interesting further reading on [Anscombe's Quartet](https://en.m.wikipedia.org/wiki/Anscombe%27s_quartet) and [The Datasaurus Dozen](https://www.autodeskresearch.com/publications/samestats), which are examples of why summary statistics matter of exactly the meaning of this post!	github_jupyter
``` import tensorflow as tf import numpy as np import matplotlib.pyplot as plt import seaborn as sns import pandas as pd from sklearn.preprocessing import MinMaxScaler import model from datetime import datetime from datetime import timedelta sns.set() df = pd.read_csv('/home/husein/space/Stock-Prediction-Comparison/dataset/GOOG-year.csv') date_ori = pd.to_datetime(df.iloc[:, 0]).tolist() df.head() minmax = MinMaxScaler().fit(df.iloc[:, 1:].astype('float32')) df_log = minmax.transform(df.iloc[:, 1:].astype('float32')) df_log = pd.DataFrame(df_log) df_log.head() num_layers = 1 size_layer = 128 timestamp = 5 epoch = 500 dropout_rate = 0.7 future_day = 50 class Model: def __init__(self, learning_rate, num_layers, size, size_layer, output_size, seq_len, forget_bias = 0.1): def lstm_cell(size_layer): return tf.nn.rnn_cell.LSTMCell(size_layer, state_is_tuple = False) def global_pooling(x, func): batch_size = tf.shape(self.X)[0] num_units = x.get_shape().as_list()[-1] x = func(x, x.get_shape().as_list()[1], 1) x = tf.reshape(x, [batch_size, num_units]) return x rnn_cells = tf.nn.rnn_cell.MultiRNNCell([lstm_cell(size_layer) for _ in range(num_layers)], state_is_tuple = False) self.X = tf.placeholder(tf.float32, (None, None, size)) self.Y = tf.placeholder(tf.float32, (None, output_size)) drop = tf.contrib.rnn.DropoutWrapper(rnn_cells, output_keep_prob = forget_bias) self.hidden_layer = tf.placeholder(tf.float32, (None, num_layers * 2 * size_layer)) self.outputs, self.last_state = tf.nn.dynamic_rnn(drop, self.X, initial_state = self.hidden_layer, dtype = tf.float32) self.outputs = self.outputs[:,:,0] x = self.X masks = tf.sign(self.outputs) batch_size = tf.shape(self.X)[0] align = tf.matmul(self.X, tf.transpose(self.X, [0,2,1])) paddings = tf.fill(tf.shape(align), float('-inf')) k_masks = tf.tile(tf.expand_dims(masks, 1), [1, seq_len, 1]) align = tf.where(tf.equal(k_masks, 0), paddings, align) align = tf.nn.tanh(align) q_masks = tf.to_float(masks) q_masks = tf.tile(tf.expand_dims(q_masks, -1), [1, 1, seq_len]) align = q_masks x = tf.matmul(align, x) g_max = global_pooling(x, tf.layers.max_pooling1d) g_avg = global_pooling(x, tf.layers.average_pooling1d) x = tf.concat([g_max, g_avg], -1) rnn_W = tf.Variable(tf.random_normal((seq_len, output_size))) rnn_B = tf.Variable(tf.random_normal([output_size])) self.logits = tf.matmul(self.outputs, rnn_W) + rnn_B self.cost = tf.reduce_mean(tf.square(self.Y - self.logits)) self.optimizer = tf.train.AdamOptimizer(learning_rate).minimize(self.cost) tf.reset_default_graph() modelnn = Model(0.01, num_layers, df_log.shape[1], size_layer, df_log.shape[1], timestamp, dropout_rate) sess = tf.InteractiveSession() sess.run(tf.global_variables_initializer()) for i in range(epoch): init_value = np.zeros((1, num_layers 2 * size_layer)) total_loss = 0 for k in range(0, (df_log.shape[0] // timestamp) * timestamp, timestamp): batch_x = np.expand_dims(df_log.iloc[k: k + timestamp, :].values, axis = 0) batch_y = df_log.iloc[k + 1: k + timestamp + 1, :].values last_state, _, loss = sess.run([modelnn.last_state, modelnn.optimizer, modelnn.cost], feed_dict={modelnn.X: batch_x, modelnn.Y: batch_y, modelnn.hidden_layer: init_value}) loss = np.mean(loss) init_value = last_state total_loss += loss total_loss /= (df_log.shape[0] // timestamp) if (i + 1) % 100 == 0: print('epoch:', i + 1, 'avg loss:', total_loss) output_predict = np.zeros((df_log.shape[0] + future_day, df_log.shape[1])) output_predict[0, :] = df_log.iloc[0, :] upper_b = (df_log.shape[0] // timestamp) * timestamp init_value = np.zeros((1, num_layers * 2 * size_layer)) for k in range(0, (df_log.shape[0] // timestamp) * timestamp, timestamp): try: out_logits, last_state = sess.run([modelnn.logits, modelnn.last_state], feed_dict = {modelnn.X:np.expand_dims(df_log.iloc[k: k + timestamp, :], axis = 0), modelnn.hidden_layer: init_value}) output_predict[k + 1: k + timestamp + 1, :] = out_logits except: out_logits, last_state = sess.run([modelnn.logits, modelnn.last_state], feed_dict = {modelnn.X:np.expand_dims(df_log.iloc[-timestamp:, :], axis = 0), modelnn.hidden_layer: init_value}) output_predict[df_log.shape[0]-timestamp:df_log.shape[0],:] = out_logits init_value = last_state df_log.loc[df_log.shape[0]] = out_logits[-1, :] date_ori.append(date_ori[-1]+timedelta(days=1)) for i in range(future_day - 1): out_logits, last_state = sess.run([modelnn.logits, modelnn.last_state], feed_dict = {modelnn.X:np.expand_dims(df_log.iloc[-timestamp:, :], axis = 0), modelnn.hidden_layer: init_value}) init_value = last_state output_predict[df_log.shape[0], :] = out_logits[-1, :] df_log.loc[df_log.shape[0]] = out_logits[-1, :] date_ori.append(date_ori[-1]+timedelta(days=1)) df_log = minmax.inverse_transform(output_predict) date_ori=pd.Series(date_ori).dt.strftime(date_format='%Y-%m-%d').tolist() current_palette = sns.color_palette("Paired", 12) fig = plt.figure(figsize = (15,10)) ax = plt.subplot(111) x_range_original = np.arange(df.shape[0]) x_range_future = np.arange(df_log.shape[0]) ax.plot(x_range_original, df.iloc[:, 1], label = 'true Open', color = current_palette[0]) ax.plot(x_range_future, df_log[:, 0], label = 'predict Open', color = current_palette[1]) ax.plot(x_range_original, df.iloc[:, 2], label = 'true High', color = current_palette[2]) ax.plot(x_range_future, df_log[:, 1], label = 'predict High', color = current_palette[3]) ax.plot(x_range_original, df.iloc[:, 3], label = 'true Low', color = current_palette[4]) ax.plot(x_range_future, df_log[:, 2], label = 'predict Low', color = current_palette[5]) ax.plot(x_range_original, df.iloc[:, 4], label = 'true Close', color = current_palette[6]) ax.plot(x_range_future, df_log[:, 3], label = 'predict Close', color = current_palette[7]) ax.plot(x_range_original, df.iloc[:, 5], label = 'true Adj Close', color = current_palette[8]) ax.plot(x_range_future, df_log[:, 4], label = 'predict Adj Close', color = current_palette[9]) box = ax.get_position() ax.set_position([box.x0, box.y0 + box.height * 0.1, box.width, box.height * 0.9]) ax.legend(loc = 'upper center', bbox_to_anchor= (0.5, -0.05), fancybox = True, shadow = True, ncol = 5) plt.title('overlap stock market') plt.xticks(x_range_future[::30], date_ori[::30]) plt.show() fig = plt.figure(figsize = (20,8)) plt.subplot(1, 2, 1) plt.plot(x_range_original, df.iloc[:, 1], label = 'true Open', color = current_palette[0]) plt.plot(x_range_original, df.iloc[:, 2], label = 'true High', color = current_palette[2]) plt.plot(x_range_original, df.iloc[:, 3], label = 'true Low', color = current_palette[4]) plt.plot(x_range_original, df.iloc[:, 4], label = 'true Close', color = current_palette[6]) plt.plot(x_range_original, df.iloc[:, 5], label = 'true Adj Close', color = current_palette[8]) plt.xticks(x_range_original[::60], df.iloc[:, 0].tolist()[::60]) plt.legend() plt.title('true market') plt.subplot(1, 2, 2) plt.plot(x_range_future, df_log[:, 0], label = 'predict Open', color = current_palette[1]) plt.plot(x_range_future, df_log[:, 1], label = 'predict High', color = current_palette[3]) plt.plot(x_range_future, df_log[:, 2], label = 'predict Low', color = current_palette[5]) plt.plot(x_range_future, df_log[:, 3], label = 'predict Close', color = current_palette[7]) plt.plot(x_range_future, df_log[:, 4], label = 'predict Adj Close', color = current_palette[9]) plt.xticks(x_range_future[::60], date_ori[::60]) plt.legend() plt.title('predict market') plt.show() fig = plt.figure(figsize = (15,10)) ax = plt.subplot(111) ax.plot(x_range_original, df.iloc[:, -1], label = 'true Volume') ax.plot(x_range_future, df_log[:, -1], label = 'predict Volume') box = ax.get_position() ax.set_position([box.x0, box.y0 + box.height * 0.1, box.width, box.height * 0.9]) ax.legend(loc = 'upper center', bbox_to_anchor= (0.5, -0.05), fancybox = True, shadow = True, ncol = 5) plt.xticks(x_range_future[::30], date_ori[::30]) plt.title('overlap market volume') plt.show() fig = plt.figure(figsize = (20,8)) plt.subplot(1, 2, 1) plt.plot(x_range_original, df.iloc[:, -1], label = 'true Volume') plt.xticks(x_range_original[::60], df.iloc[:, 0].tolist()[::60]) plt.legend() plt.title('true market volume') plt.subplot(1, 2, 2) plt.plot(x_range_future, df_log[:, -1], label = 'predict Volume') plt.xticks(x_range_future[::60], date_ori[::60]) plt.legend() plt.title('predict market volume') plt.show() ```	github_jupyter
``` import pandas as pd import geopandas as gpd import matplotlib.pyplot as plt import numpy as np from shapely.geometry import Point from sklearn.neighbors import KNeighborsRegressor import rasterio as rst from rasterstats import zonal_stats %matplotlib inline path = r"[CHANGE THIS PATH]\Wales\\" data = pd.read_csv(path + "final_data.csv", index_col = 0) ``` # Convert to GeoDataFrame ``` geo_data = gpd.GeoDataFrame(data = data, crs = {'init':'epsg:27700'}, geometry = data.apply(lambda geom: Point(geom['oseast1m'],geom['osnrth1m']),axis=1)) geo_data.head() f, (ax1, ax2, ax3) = plt.subplots(1,3, figsize = (16,6), sharex = True, sharey = True) geo_data[geo_data['Year'] == 2016].plot(column = 'loneills', scheme = 'quantiles', cmap = 'Reds', marker = '.', ax = ax1); geo_data[geo_data['Year'] == 2017].plot(column = 'loneills', scheme = 'quantiles', cmap = 'Reds', marker = '.', ax = ax2); geo_data[geo_data['Year'] == 2018].plot(column = 'loneills', scheme = 'quantiles', cmap = 'Reds', marker = '.', ax = ax3); ``` ## k-nearest neighbour interpolation Non-parametric interpolation of loneliness based on local set of _k_ nearest neighbours for each cell in our evaluation grid. Effectively becomes an inverse distance weighted (idw) interpolation when weights are set to be distance based. ``` def idw_model(k, p): def _inv_distance_index(weights, index=p): return (test==0).astype(int) if np.any(weights == 0) else 1. / weights*index return KNeighborsRegressor(k, weights=_inv_distance_index) def grid(xmin, xmax, ymin, ymax, cellsize): # Set x and y ranges to accommodate cellsize xmin = (xmin // cellsize) cellsize xmax = -(-xmax // cellsize) * cellsize # ceiling division ymin = (ymin // cellsize) * cellsize ymax = -(-ymax // cellsize) * cellsize # Make meshgrid x = np.linspace(xmin,xmax,(xmax-xmin)/cellsize) y = np.linspace(ymin,ymax,(ymax-ymin)/cellsize) return np.meshgrid(x,y) def reshape_grid(xx,yy): return np.append(xx.ravel()[:,np.newaxis],yy.ravel()[:,np.newaxis],1) def reshape_image(z, xx): return np.flip(z.reshape(np.shape(xx)),0) def idw_surface(locations, values, xmin, xmax, ymin, ymax, cellsize, k=5, p=2): # Make and fit the idw model idw = idw_model(k,p).fit(locations, values) # Make the grid to estimate over xx, yy = grid(xmin, xmax, ymin, ymax, cellsize) # reshape the grid for estimation xy = reshape_grid(xx,yy) # Predict the grid values z = idw.predict(xy) # reshape to image array z = reshape_image(z, xx) return z ``` ## 2016 data ``` # Get point locations and values from data points = geo_data[geo_data['Year'] == 2016][['oseast1m','osnrth1m']].values vals = geo_data[geo_data['Year'] == 2016]['loneills'].values surface2016 = idw_surface(points, vals, 90000,656000,10000,654000,250,7,2) # Look at surface f, ax = plt.subplots(figsize = (8,10)) ax.imshow(surface2016, cmap='Reds') ax.set_aspect('equal') ``` ## 2017 Data ``` # Get point locations and values from data points = geo_data[geo_data['Year'] == 2017][['oseast1m','osnrth1m']].values vals = geo_data[geo_data['Year'] == 2017]['loneills'].values surface2017 = idw_surface(points, vals, 90000,656000,10000,654000,250,7,2) # Look at surface f, ax = plt.subplots(figsize = (8,10)) ax.imshow(surface2017, cmap='Reds') ax.set_aspect('equal') ``` ## 2018 Data Get minimum and maximum bounds from the data. Round these down (in case of the 'min's) and up (in case of the 'max's) to get the values for `idw_surface()` ``` print("xmin = ", geo_data['oseast1m'].min(), "\n\r", "xmax = ", geo_data['oseast1m'].max(), "\n\r", "ymin = ", geo_data['osnrth1m'].min(), "\n\r", "ymax = ", geo_data['osnrth1m'].max()) xmin = 175000 xmax = 357000 ymin = 167000 ymax = 393000 # Get point locations and values from data points = geo_data[geo_data['Year'] == 2018][['oseast1m','osnrth1m']].values vals = geo_data[geo_data['Year'] == 2018]['loneills'].values surface2018 = idw_surface(points, vals, xmin,xmax,ymin,ymax,250,7,2) # Look at surface f, ax = plt.subplots(figsize = (8,10)) ax.imshow(surface2018, cmap='Reds') ax.set_aspect('equal') ``` # Extract Values to MSOAs Get 2011 MSOAs from the Open Geography Portal: http://geoportal.statistics.gov.uk/ ``` # Get MSOAs which we use to aggregate the loneills variable. #filestring = './Data/MSOAs/Middle_Layer_Super_Output_Areas_December_2011_Full_Clipped_Boundaries_in_England_and_Wales.shp' filestring = r'[CHANGE THIS PATH]\Data\Boundaries\England and Wales\Middle_Layer_Super_Output_Areas_December_2011_Super_Generalised_Clipped_Boundaries_in_England_and_Wales.shp' msoas = gpd.read_file(filestring) msoas.to_crs({'init':'epsg:27700'}) # keep the Wales MSOAs msoas = msoas[msoas['msoa11cd'].str[:1] == 'W'].copy() # Get GB countries data to use for representation #gb = gpd.read_file('./Data/GB/Countries_December_2017_Generalised_Clipped_Boundaries_in_UK_WGS84.shp') #gb = gb.to_crs({'init':'epsg:27700'}) # get England #eng = gb[gb['ctry17nm'] == 'England'].copy() # Make affine transform for raster trans = rst.Affine.from_gdal(xmin-125,250,0,ymax+125,0,-250) # NB This process is slooow - write bespoke method? # 2016 #msoa_zones = zonal_stats(msoas['geometry'], surface2016, affine = trans, stats = 'mean', nodata = np.nan) #msoas['loneills_2016'] = list(map(lambda x: x['mean'] , msoa_zones)) # 2017 #msoa_zones = zonal_stats(msoas['geometry'], surface2017, affine = trans, stats = 'mean', nodata = np.nan) #msoas['loneills_2017'] = list(map(lambda x: x['mean'] , msoa_zones)) # 2018 msoa_zones = zonal_stats(msoas['geometry'], surface2018, affine = trans, stats = 'mean', nodata = np.nan) msoas['loneills_2018'] = list(map(lambda x: x['mean'] , msoa_zones)) # Check out the distributions of loneills by MSOA f, [ax1, ax2, ax3] = plt.subplots(1,3, figsize=(14,5), sharex = True, sharey=True) #ax1.hist(msoas['loneills_2016'], bins = 30) #ax2.hist(msoas['loneills_2017'], bins = 30) ax3.hist(msoas['loneills_2018'], bins = 30) ax1.set_title("2016") ax2.set_title("2017") ax3.set_title("2018"); bins = [-10, -5, -3, -2, -1, 1, 2, 3, 5, 10, 22] labels = ['#01665e','#35978f', '#80cdc1','#c7eae5','#f5f5f5','#f6e8c3','#dfc27d','#bf812d','#8c510a','#543005'] #msoas['loneills_2016_class'] = pd.cut(msoas['loneills_2016'], bins, labels = labels) #msoas['loneills_2017_class'] = pd.cut(msoas['loneills_2017'], bins, labels = labels) msoas['loneills_2018_class'] = pd.cut(msoas['loneills_2018'], bins, labels = labels) msoas['loneills_2018_class'] = msoas.loneills_2018_class.astype(str) # convert categorical to string f, (ax1, ax2, ax3) = plt.subplots(1,3,figsize = (16,10)) #msoas.plot(color = msoas['loneills_2016_class'], ax=ax1) #msoas.plot(color = msoas['loneills_2017_class'], ax=ax2) msoas.plot(color = msoas['loneills_2018_class'], ax=ax3) #gb.plot(edgecolor = 'k', linewidth = 0.5, facecolor='none', ax=ax1) #gb.plot(edgecolor = 'k', linewidth = 0.5, facecolor='none', ax=ax2) #gb.plot(edgecolor = 'k', linewidth = 0.5, facecolor='none', ax=ax3) # restrict to England #ax1.set_xlim([82672,656000]) #ax1.set_ylim([5342,658000]) #ax2.set_xlim([82672,656000]) #ax2.set_ylim([5342,658000]) #ax3.set_xlim([82672,656000]) #ax3.set_ylim([5342,658000]) # Make a legend # make bespoke legend from matplotlib.patches import Patch handles = [] ranges = ["-10, -5","-5, -3","-3, -2","-2, -1","-1, 1","1, 2","3, 3","3, 5","5, 10","10, 22"] for color, label in zip(labels,ranges): handles.append(Patch(facecolor = color, label = label)) ax1.legend(handles = handles, loc = 2); # Save out msoa data as shapefile and geojson msoas.to_file(path + "msoa_loneliness.shp", driver = 'ESRI Shapefile') # msoas.to_file(path + "msoa_loneliness.geojson", driver = 'GeoJSON') # save out msoa data as csv msoas.to_csv(path + "msoa_loneliness.csv") ```	github_jupyter
``` import json import os import tqdm import pandas as pd ``` ## I. convert emails text (both training and testing) into appropriate jsonl file format ### 6088 entries in training set ( 2000+ machine generated, the rest are human-written) #### 4000+ are from email corpus, 2000+ are from gtp-2 generated and the ENRON Email Dataset ###### kaggle datasets download -d nitishabharathi/email-spam-dataset ``` PATH = '/Users/jessicademacbook/DSCI-550-Assignment-2/data/Grover_input_output/8_GPT-2_Generated_Text_for_Grover/' folders = [f for f in os.listdir(PATH) if not f.startswith('.')] #read all machine txt in each folders, label all machine generated content lis=[] for folder in folders: for i in os.listdir(f'{PATH}{folder}'): f=open(f'{PATH}{folder}/{i}','r') text=f.read() text_dic={"article":text,"label":"machine","split":"train"} lis.append(text_dic) #read all human json in email corpus, label all content as human path='/Users/jessicademacbook/DSCI-550-Assignment-1/data/separated by email/' for i in os.listdir(path): if i.endswith('.json'): f=open(f'{path}{i}','r') text=json.load(f) try: content=text["X-TIKA:content"] if pd.isna(content): pass else: content_dic={"article":content,"label":"human","split":"train"} lis.append(content_dic) except KeyError: pass with open('/Users/jessicademacbook/DSCI-550-Assignment-2/data/Grover_input_output/fake_emails.csv', "r") as f: result=pd.read_csv(f) spam=result['Label']==1 for i in result[spam]['Body']: if pd.isna(i): pass else: dic={"article":i,"label":"machine","split":"train"} lis.append(dic) print('The training set has ', len(lis),'emails in total.') #write to a jsonl file with all human and machine generated email content with open('/Users/jessicademacbook/DSCI-550-Assignment-2/data/Grover_input_output/input_emails.jsonl','w') as outfile: for entry in lis: json.dump(entry, outfile) outfile.write('\n') #check the written jsonl file has correct labels with open('/Users/jessicademacbook/DSCI-550-Assignment-2/data/Grover_input_output/input_emails.jsonl', "r") as f: test=[] for l in f: item = json.loads(l) if pd.isna(item['article']): pass else: test.append(item['article']) print('Are all content are NA-free?', all(test)) ``` ### Collect 800 email text, labeled as test, write to jsonl file for discrimination ``` #get generated text for grover test new_path = '/Users/jessicademacbook/DSCI-550-Assignment-2/data/additional-features-v2/new/4_GPT-2_Generated_Text/' folders = [f for f in os.listdir(new_path) if not f.startswith('.')] test_lis=[] for folder in folders: for i in os.listdir(f'{new_path}{folder}'): f=open(f'{new_path}{folder}/{i}','r') text=f.read() text_dic={"article":text,"split":"test","label":"machine"} test_lis.append(text_dic) print('The file for discrimination has', len(test_lis),'emails in it.') #write to jsonl file with open('/Users/jessicademacbook/DSCI-550-Assignment-2/data/Grover_input_output/test_input.jsonl','w') as f: for entry in test_lis: json.dump(entry, f) f.write('\n') ``` ## II. Grover Training-this part is done in Google Colab, and the corresponding notebook is called Grover_training in the same folder as this one see Grover_training.ipynb ## III. Interpreting Grover training result ``` import numpy as np ``` #### The grover model returns a list of data pair showing the probability of the label being corrected. I labeled all the test input as machine, and the accuracy turns out to be 1, meaning that all 800 emails are identified as machine generated. ``` path='/Users/jessicademacbook/DSCI-550-Assignment-2/data/Grover_input_output/final_outputs_test-probs.npy' data_array = np.load(path) print('The first 20 pairs look like', data_array[0:20]) a=0 for i in data_array: if i[0]>0.95: a=a+1 print(a,"of 800 emails have probability of being machine generated higher than 0.95.") print("All emails are identified as machine generated.") import pandas as pd df = pd.read_csv('../../data/additional-features-v2/new/assignment2.tsv', sep='\t', index_col=0) df['grover results'] = pd.Series(['Machine' for _ in range(800)]) df.to_csv('../../data/additional-features-v2/new/assignment2.tsv', sep='\t') ```	github_jupyter
# Overview This Jupyter Notebook takes in data from a Google Sheet that contains line change details and their associated high level categories and outputs a JSON file for the MyBus tool. The output file is used by the MyBus tool's results page and contains the Line-level changes that are displayed there. Run all cells to generate: `lines-changes.json` ``` import pandas as pd # GOOGLE_SHEET_URL = 'https://docs.google.com/spreadsheets/d/e/2PACX-1vQq0095iOV4dn5McH5IgL4tfjBGLRpCS4XIw-TsZKXubWLyycCfbmnyWdDJRr73ctUMjv32DvKmvVbj/pub?output=csv' # GOOGLE_SHEET_URL = 'https://docs.google.com/spreadsheets/d/e/2PACX-1vQKADb-wnackdlDZwEF0mTpLPh7MpkI4YQV5gv1TYOzltjiGAXcj35GTb4ftP7yKN8mH74MWLPkSUlq/pub?output=csv' GOOGLE_SHEET_URL = 'https://docs.google.com/spreadsheets/d/e/2PACX-1vSENm-oLTxuzcQUX_0tZ9X0Q2_HIudg1hi5p0MMauqWoHCuomsxb6H6AhqOkaeBY-X1ZKBTbFAzDKUM/pub?output=csv' DATA_INPUT_PATH = '../data/input' DATA_OUTPUT_PATH = '../data/' line_changes = pd.read_csv(GOOGLE_SHEET_URL, usecols={'Line Number', 'Line Label', 'Line Description', 'Route changes','Other changes','Schedule Changes','Stop Cancellations', 'Lines Merged', 'Line Discontinued','Details', 'Service', 'Route', 'Schedule', 'Current Schedule URL'}) line_changes.columns = ["line-number","line-label","line-description",'route-changes','other-changes','schedule-changes','stop-cancellations',"lines-merged","line-discontinued","details","card-1","card-2","card-3","current-schedule-url"] line_changes = line_changes.fillna('') line_changes.head() # import shutil import os #define the folders to look through folders = os.listdir("../files/schedules") #set an array for the file types pdfs_list = [] #create a list of file types for root, dirs, files in os.walk("../files/schedules"): for filename in files: lines = filename.replace(" ","").split("_TT")[0].split("-") for line in lines: this_schedule = {} this_schedule['line-number'] = line.lstrip("0") this_schedule['schedule-url'] = "./files/schedules/"+filename pdfs_list.append(this_schedule) # print(line) # print(pdfs_list) schedule_df = pd.DataFrame(pdfs_list) schedule_df.tail(10) schedule_df['line-number'] = schedule_df['line-number'].astype(int) line_changes['line-number'] = line_changes['line-number'].astype(int) merged_lines = line_changes.merge(schedule_df, on=['line-number'],how='outer').fillna('') merged_lines merged_lines.to_json(DATA_OUTPUT_PATH + 'line-changes.json', orient='records') # As of 8/16/21 - total should be 125 lines. print(str(len(merged_lines)) + ' lines') ```	github_jupyter
# Region Based Data Analysis The following notebook will go through prediction analysis for region based Multiple Particle Tracking (MPT) using OGD severity datasets for non-treated (NT) hippocampus, ganglia, thalamus, cortex, and striatum. ## Table of Contents [1. Load Data](#1.-load-data)<br /> [2. Analysis](#2.-analysis)<br /> [3. Modelling](#modelling)<br /> [4. Evaluate Results](#evaluate-results)<br /> --- ## 1. Load Data Loading feature dataset from OGD folders: There are 15 total videos from each age group. ``` # libraries used import boto3 import diff_classifier.aws as aws import pandas as pd import seaborn as sn import numpy as np import matplotlib.pyplot as pl from os import listdir, getcwd, chdir from os.path import isfile, join import os from matplotlib import colors as plt_colors from sklearn.ensemble import RandomForestClassifier from sklearn.model_selection import train_test_split from sklearn import metrics from sklearn.metrics import classification_report from sklearn.metrics import confusion_matrix from sklearn import preprocessing import xgboost as xgb # from xgboost import cv import shap workbookDir = getcwd() print('Current Notebook Dir: ' + workbookDir) chdir(workbookDir) # Go to current workbook Dir chdir('..') # Go up one print(f'Using current directory for loading data: {getcwd()}') workbookDir = getcwd() !pwd dataset_path = workbookDir + '/region_feature_folder/' filelist = [f for f in listdir(dataset_path) if isfile(join(dataset_path, f)) and 'feat' in f and 'ganglia' not in f and 'hippocampus' not in f and 'thalamus' not in f] filelist fstats_tot = None video_num = 0 for filename in filelist: # try: fstats = pd.read_csv(dataset_path + filename, encoding = "ISO-8859-1", index_col='Unnamed: 0') print('{} size: {}'.format(filename, fstats.shape)) if 'cortex' in filename: fstats['region'] = pd.Series(fstats.shape[0]['cortex'], index=fstats.index) elif 'striatum' in filename: fstats['region'] = pd.Series(fstats.shape[0]['striatum'], index=fstats.index) elif 'ganglia' in filename: fstats['region'] = pd.Series(fstats.shape[0]['ganglia'], index=fstats.index) elif 'thalamus' in filename: fstats['region'] = pd.Series(fstats.shape[0]['thalamus'], index=fstats.index) elif 'hippocampus' in filename: fstats['region'] = pd.Series(fstats.shape[0]['hippocampus'], index=fstats.index) else: print('Error, no target') fstats['Video Number'] = pd.Series(fstats.shape[0][video_num], index=fstats.index) if fstats_tot is None: fstats_tot = fstats else: fstats_tot = fstats_tot.append(fstats, ignore_index=True) video_num += 1 # except Exception: # print('Skipped!: {}'.format(filename)) ``` ## 2. Analysis The following columns are present within the downloaded datasets: ``` fstats_tot.columns ``` Many of these features are not useful for prediction or have data which may negatively impact classification. The following features and the target feature are defined in the following cell. We also remove any datapoints that are empty or infinite: ``` fstats_tot features = [ 'alpha', # Fitted anomalous diffusion alpha exponenet 'D_fit', # Fitted anomalous diffusion coefficient 'kurtosis', # Kurtosis of track 'asymmetry1', # Asymmetry of trajecory (0 for circular symmetric, 1 for linear) 'asymmetry2', # Ratio of the smaller to larger principal radius of gyration 'asymmetry3', # An asymmetric feature that accnts for non-cylindrically symmetric pt distributions 'AR', # Aspect ratio of long and short side of trajectory's minimum bounding rectangle 'elongation', # Est. of amount of extension of trajectory from centroid 'boundedness', # How much a particle with Deff is restricted by a circular confinement of radius r 'fractal_dim', # Measure of how complicated a self similar figure is 'trappedness', # Probability that a particle with Deff is trapped in a region 'efficiency', # Ratio of squared net displacement to the sum of squared step lengths 'straightness', # Ratio of net displacement to the sum of squared step lengths 'MSD_ratio', # MSD ratio of the track 'frames', # Number of frames the track spans 'Deff1', # Effective diffusion coefficient at 0.33 s 'Deff2', # Effective diffusion coefficient at 3.3 s # 'angle_mean', # Mean turning angle which is counterclockwise angle from one frame point to another # 'angle_mag_mean', # Magnitude of the turning angle mean # 'angle_var', # Variance of the turning angle # 'dist_tot', # Total distance of the trajectory # 'dist_net', # Net distance from first point to last point # 'progression', # Ratio of the net distance traveled and the total distance 'Mean alpha', 'Mean D_fit', 'Mean kurtosis', 'Mean asymmetry1', 'Mean asymmetry2', 'Mean asymmetry3', 'Mean AR', 'Mean elongation', 'Mean boundedness', 'Mean fractal_dim', 'Mean trappedness', 'Mean efficiency', 'Mean straightness', 'Mean MSD_ratio', 'Mean Deff1', 'Mean Deff2', ] target = 'region' # prediction target (y) ecm = fstats_tot[features + [target] + ['X'] + ['Y']] ecm = ecm[~ecm.isin([np.nan, np.inf, -np.inf]).any(1)] # Removing nan and inf data points # Showing a piece of our data: ecm[target].unique() ``` Before prediction, it is required to balance data. As shown, The current dataset is highly imbalance with most datapoints belonging to P21 and P35 categories. The dataset is reduced using random sampling of each target category. ``` #--------------NOT-ADDED----------------------------- def balance_data(df, target, *kwargs): if 'random_state' not in kwargs: random_state = 1 else: random_state = kwargs['random_state'] if isinstance(target, list): target = target[0] df_target = [] bal_df = [] for name in df[target].unique(): df_target.append((name, df[df[target] == name])) print(f"Ratio before data balance ({':'.join([str(i[0]) for i in df_target])}) = {':'.join([str(len(i[1])) for i in df_target])}") for i in range(len(df_target)): ratio = min([len(i[1]) for i in df_target])/len(df_target[i][1]) bal_df.append(df_target[i][1].sample(frac=ratio, random_state=random_state)) print(f"Ratio after balance ({':'.join([str(i[0]) for i in df_target])}) = {':'.join([str(len(i)) for i in bal_df])}") return pd.concat(bal_df) bal_ecm = balance_data(ecm, target, random_state=1) # ecm_14 = ecm[ecm[target] == 14] # ecm_21 = ecm[ecm[target] == 21] # ecm_28 = ecm[ecm[target] == 28] # ecm_35 = ecm[ecm[target] == 35] # print(f"Ratio before data balance (P14:P21:P28:P35) = {len(ecm_14)}:{len(ecm_21)}:{len(ecm_28)}:{len(ecm_35)}") # ecm_list = [ecm_14, ecm_21, ecm_28, ecm_35] # for i in range(len(ecm_list)): # ratio = min([len(i) for i in ecm_list])/len(ecm_list[i]) # ecm_list[i] = ecm_list[i].sample(frac=ratio, random_state=1) # print(f"Ratio after balance (P14:P21:P28:P35) = {len(ecm_list[0])}:{len(ecm_list[1])}:{len(ecm_list[2])}:{len(ecm_list[3])}") # bal_ecm = pd.concat(ecm_list) ``` ## 3. Modelling The model used for this study is an extreme gradient boosting (XGBoost) decision tree which is a boosted decision tree. This model was used due to its past results within competitions and research. Due to the use of statistical surroundings in our feature analysis, binning is required in order to avoid data leakage between training/testing. The followingcode will implement binning and a checkerboard implementation to select certain bins for the training dataset. ``` # Using checkerboard binning for data split: def checkerboard(size): rows = int(size/2) checks = list(range(0, sizesize, size+1)) for i in range(1, rows): ssize = size - 2i for j in range(0, ssize): checks.append(2i + (size+1)j) for i in range(1, rows): ssize = size - 2i for j in range(0, ssize): checks.append(sizesize - 1 - (2i + (size+1)j)) checks.sort() return checks # Old method # bins = list(range(0, 2048+1, 256)) # bal_ecm['binx'] = pd.cut(bal_ecm.X, bins, labels=[0, 1, 2, 3, 4, 5, 6, 7], include_lowest=True) # bal_ecm['biny'] = pd.cut(bal_ecm.Y, bins, labels=[0, 1, 2, 3, 4, 5, 6, 7], include_lowest=True) # bal_ecm['bins'] = 8bal_ecm['binx'].astype(np.int8) + bal_ecm['biny'].astype(np.int8) # bal_ecm = bal_ecm[np.isfinite(bal_ecm['bins'])] # bal_ecm['bins'] = bal_ecm['bins'].astype(int) # cols = bal_ecm.columns.tolist() # cols = cols[-3:] + cols[:-3] # bal_ecm = bal_ecm[cols] # def bin_data(data, ): # pass resolution = 128 assert not 2048%resolution and resolution >= 128, "resolution needs to be a factor of 2048 and > 128" bins = list(range(0, 2048+1, resolution)) bin_labels = [int(i/resolution) for i in bins][:-1] bal_ecm['binx'] = pd.cut(bal_ecm.X, bins, labels=bin_labels, include_lowest=True) bal_ecm['biny'] = pd.cut(bal_ecm.Y, bins, labels=bin_labels, include_lowest=True) bal_ecm['bins'] = (len(bins)-1)bal_ecm['binx'].astype(np.int32) + bal_ecm['biny'].astype(np.int32) bal_ecm = bal_ecm[np.isfinite(bal_ecm['bins'])] bal_ecm['bins'] = bal_ecm['bins'].astype(int) # cols = bal_ecm.columns.tolist() # cols = cols[-3:] + cols[:-3] # bal_ecm = bal_ecm[cols] # Checkerboard method # seed = 1234 # np.random.seed(seed) # test_val_split = 0.5 # le = preprocessing.LabelEncoder() # bal_ecm['encoded_target'] = le.fit_transform(bal_ecm[target]) # X_train = bal_ecm[~bal_ecm.bins.isin(checkerboard((len(bins)-1)))].reset_index() # X_test_val = bal_ecm[bal_ecm.bins.isin(checkerboard((len(bins)-1)))].reset_index() # y_train = X_train['encoded_target'] # X_val, X_test = train_test_split(X_test_val, test_size=test_val_split, random_state=seed) # y_test = X_test['encoded_target'] # y_val = X_val['encoded_target'] # dtrain = xgb.DMatrix(X_train[features], label=y_train) # dtest = xgb.DMatrix(X_test[features], label=y_test) # dval = xgb.DMatrix(X_val[features], label=y_val) # Regular split seed = 1234 np.random.seed(seed) train_split = 0.8 test_split = 0.5 le = preprocessing.LabelEncoder() bal_ecm['encoded_target'] = le.fit_transform(bal_ecm[target]) training_bins = np.random.choice(bal_ecm.bins.unique(), int(len(bal_ecm.bins.unique())train_split), replace=False) X_train = bal_ecm[bal_ecm.bins.isin(training_bins)] X_test_val = bal_ecm[~bal_ecm.bins.isin(training_bins)] X_val, X_test = train_test_split(X_test_val, test_size=test_split, random_state=seed) y_train = X_train['encoded_target'] y_test = X_test['encoded_target'] y_val = X_val['encoded_target'] dtrain = xgb.DMatrix(X_train[features], label=y_train) dtest = xgb.DMatrix(X_test[features], label=y_test) dval = xgb.DMatrix(X_val[features], label=y_val) #Check lengths of datasets: def get_lengths(df, X_train, X_test, X_val=None): print(f'Tot before split: {len(df)}') print(f'Training: {len(X_train)} ({len(X_train)/len(bal_ecm):.3f}%)') print(f'Testing: {len(X_test)} ({len(X_test)/len(bal_ecm):.3f}%)') try: print(f'Evaluation: {len(X_val)} ({len(X_val)/len(bal_ecm):.3f}%)') except: pass get_lengths(bal_ecm, X_train, X_test, X_val) from xgboost.libpath import find_lib_path import ctypes lib_path = find_lib_path() lib = ctypes.cdll.LoadLibrary(lib_path[0]) ``` Model parameters are based on the best possible XGBoost parameters to minimize logloss error. ``` # Init_params for binary logistic classification init_param = {'max_depth': 3, 'eta': 0.005, 'min_child_weight': 0, 'verbosity': 0, 'objective': 'binary:logistic', 'silent': 'True', 'gamma': 5, 'subsample': 0.15, 'colsample_bytree': 0.8, 'eval_metric': 'logloss'} # from xgboost import XGBClassifier from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score # model = XGBClassifier() # model.predict(X_test[features]) features from xgboost.training import CVPack from xgboost import callback from xgboost.core import CallbackEnv from xgboost.core import EarlyStopException def cv(params, X_train, y_train, features=None, num_boost_round=20, nfold=3, stratified=False, folds=None, metrics=(), obj=None, feval=None, maximize=False, early_stopping_rounds=None, fpreproc=None, as_pandas=True, verbose_eval=None, show_stdv=True, seed=0, callbacks=None, shuffle=True): # pylint: disable = invalid-name """Cross-validation with given parameters. Parameters ---------- params : dict Booster params. dtrain : DMatrix Data to be trained. num_boost_round : int Number of boosting iterations. nfold : int Number of folds in CV. stratified : bool Perform stratified sampling. folds : a KFold or StratifiedKFold instance or list of fold indices Sklearn KFolds or StratifiedKFolds object. Alternatively may explicitly pass sample indices for each fold. For ``n`` folds, folds should be a length ``n`` list of tuples. Each tuple is ``(in,out)`` where ``in`` is a list of indices to be used as the training samples for the ``n`` th fold and ``out`` is a list of indices to be used as the testing samples for the ``n`` th fold. metrics : string or list of strings Evaluation metrics to be watched in CV. obj : function Custom objective function. feval : function Custom evaluation function. maximize : bool Whether to maximize feval. early_stopping_rounds: int Activates early stopping. Cross-Validation metric (average of validation metric computed over CV folds) needs to improve at least once in every early_stopping_rounds round(s) to continue training. The last entry in the evaluation history will represent the best iteration. If there's more than one metric in the eval_metric parameter given in params, the last metric will be used for early stopping. fpreproc : function Preprocessing function that takes (dtrain, dtest, param) and returns transformed versions of those. as_pandas : bool, default True Return pd.DataFrame when pandas is installed. If False or pandas is not installed, return np.ndarray verbose_eval : bool, int, or None, default None Whether to display the progress. If None, progress will be displayed when np.ndarray is returned. If True, progress will be displayed at boosting stage. If an integer is given, progress will be displayed at every given `verbose_eval` boosting stage. show_stdv : bool, default True Whether to display the standard deviation in progress. Results are not affected, and always contains std. seed : int Seed used to generate the folds (passed to numpy.random.seed). callbacks : list of callback functions List of callback functions that are applied at end of each iteration. It is possible to use predefined callbacks by using :ref:`Callback API <callback_api>`. Example: .. code-block:: python [xgb.callback.reset_learning_rate(custom_rates)] shuffle : bool Shuffle data before creating folds. Returns ------- evaluation history : list(string) """ if stratified is True and not SKLEARN_INSTALLED: raise XGBoostError('sklearn needs to be installed in order to use stratified cv') if isinstance(metrics, str): metrics = [metrics] if not features: features = X_train.columns if isinstance(params, list): _metrics = [x[1] for x in params if x[0] == 'eval_metric'] params = dict(params) if 'eval_metric' in params: params['eval_metric'] = _metrics else: params = dict((k, v) for k, v in params.items()) if (not metrics) and 'eval_metric' in params: if isinstance(params['eval_metric'], list): metrics = params['eval_metric'] else: metrics = [params['eval_metric']] params.pop("eval_metric", None) results = {} # create folds in data cvfolds, wt_list = mknfold(X_train, y_train, nfold, params, metrics, features) # setup callbacks callbacks = [] if callbacks is None else callbacks if early_stopping_rounds is not None: callbacks.append(callback.early_stop(early_stopping_rounds, maximize=maximize, verbose=False)) if isinstance(verbose_eval, bool) and verbose_eval: callbacks.append(callback.print_evaluation(show_stdv=show_stdv)) elif isinstance(verbose_eval, int): callbacks.append(callback.print_evaluation(verbose_eval, show_stdv=show_stdv)) callbacks_before_iter = [ cb for cb in callbacks if cb.__dict__.get('before_iteration', False)] callbacks_after_iter = [ cb for cb in callbacks if not cb.__dict__.get('before_iteration', False)] for i in range(num_boost_round): for cb in callbacks_before_iter: cb(CallbackEnv(model=None, cvfolds=cvfolds, iteration=i, begin_iteration=0, end_iteration=num_boost_round, rank=0, evaluation_result_list=None)) for fold in cvfolds: fold.update(i, obj) res = aggcv([f.eval(i, feval) for f in cvfolds], wt_list) for key, mean, std in res: if key + '-mean' not in results: results[key + '-mean'] = [] if key + '-std' not in results: results[key + '-std'] = [] results[key + '-mean'].append(mean) results[key + '-std'].append(std) try: for cb in callbacks_after_iter: cb(CallbackEnv(model=None, cvfolds=cvfolds, iteration=i, begin_iteration=0, end_iteration=num_boost_round, rank=0, evaluation_result_list=res)) except EarlyStopException as e: for k in results: results[k] = results[k][:(e.best_iteration + 1)] break if as_pandas: try: import pandas as pd results = pd.DataFrame.from_dict(results) except ImportError: pass return results def bin_fold(X_train, nfold): bin_list = [X_train[X_train['bins'] == i_bin].index.to_numpy() for i_bin in X_train.bins.unique()] bin_list = sorted(bin_list, key=len) i = 0 while(len(bin_list) > nfold): if (i >= len(bin_list)-1): i = 0 bin_list[i] = np.concatenate([bin_list[i], bin_list.pop()]) i += 1 wt_list = [len(i)/sum(len(s) for s in bin_list) for i in bin_list] return bin_list, wt_list def mknfold(X_train, y_train, nfold, param, evals=(), features=None): if not features: features = X_train.columns dall = xgb.DMatrix(X_train[features], label=y_train) out_idset, wt_list = bin_fold(X_train, nfold) in_idset = [np.concatenate([out_idset[i] for i in range(nfold) if k != i]) for k in range(nfold)] evals = list(evals) ret = [] for k in range(nfold): # perform the slicing using the indexes determined by the above methods x_train_snip = X_train.loc[in_idset[k]][features] y_train_snip = X_train.loc[in_idset[k]]['encoded_target'] x_test_snip = X_train.loc[out_idset[k]][features] y_test_snip = X_train.loc[out_idset[k]]['encoded_target'] dtrain = xgb.DMatrix(x_train_snip, label=y_train_snip) dtest = xgb.DMatrix(x_test_snip, label=y_test_snip) tparam = param plst = list(tparam.items()) + [('eval_metric', itm) for itm in evals] ret.append(CVPack(dtrain, dtest, plst)) return ret, wt_list from xgboost.core import STRING_TYPES def aggcv(rlist, wt_list): # pylint: disable=invalid-name """ Aggregate cross-validation results. If verbose_eval is true, progress is displayed in every call. If verbose_eval is an integer, progress will only be displayed every `verbose_eval` trees, tracked via trial. """ cvmap = {} idx = rlist[0].split()[0] for line in rlist: arr = line.split() assert idx == arr[0] for metric_idx, it in enumerate(arr[1:]): if not isinstance(it, STRING_TYPES): it = it.decode() k, v = it.split(':') if (metric_idx, k) not in cvmap: cvmap[(metric_idx, k)] = [] cvmap[(metric_idx, k)].append(float(v)) msg = idx results = [] for (metric_idx, k), v in sorted(cvmap.items(), key=lambda x: x[0][0]): v = np.array(v) if not isinstance(msg, STRING_TYPES): msg = msg.decode() mean = np.average(v, weights=wt_list) std = np.average((v-mean)*2, weights=wt_list) results.extend([(k, mean, std)]) return results cv(init_param, X_train, y_train, features, num_boost_round=10, nfold=5, early_stopping_rounds=3, metrics={'logloss', 'error'}) from scipy.stats import skewnorm a=10 data = [round(i, 3) for i in skewnorm.rvs(a, size=10, random_state=seed)0.3] data seed = 1234 np.random.seed(seed) import operator import numpy as np def xgb_paramsearch(X_train, y_train, features, init_params, nfold=5, num_boost_round=2000, early_stopping_rounds=3, metrics=None, kwargs): params = {init_params} if 'use_gpu' in kwargs and kwargs['use_gpu']: # GPU integration will cut cv time in ~half: params.update({'gpu_id' : 0, 'tree_method': 'gpu_hist', 'predictor': 'gpu_predictor'}) if 'metrics' not in kwargs: metrics = {params['eval_metric']} else: metrics.add(params['eval_metric']) if params['eval_metric'] in ['map', 'auc', 'aucpr']: eval_f = operator.gt else: eval_f = operator.lt if 'early_break' not in kwargs: early_break = 5 else: early_break = kwargs['early_break'] if 'thresh' not in kwargs: thresh = 0.01 else: thresh = kwargs['thresh'] if 'seed' not in kwargs: seed = 1111 else: seed = kwargs['seed'] best_param = params best_model = cv(params, X_train, y_train, features, nfold=nfold, num_boost_round=num_boost_round, early_stopping_rounds=early_stopping_rounds, metrics=metrics) best_eval = best_model[f"test-{params['eval_metric']}-mean"].min() best_boost_rounds = best_model[f"test-{params['eval_metric']}-mean"].idxmin() def _gs_helper(var1n, var2n, best_model, best_param, best_eval, best_boost_rounds): local_param = {best_param} for var1, var2 in gs_params: print(f"Using CV with {var1n}={{{var1}}}, {var2n}={{{var2}}}") local_param[var1n] = var1 local_param[var2n] = var2 cv_model = cv(local_param, X_train, y_train, features, nfold=nfold, num_boost_round= num_boost_round, early_stopping_rounds=early_stopping_rounds, metrics=metrics) cv_eval = cv_model[f"test-{local_param['eval_metric']}-mean"].min() boost_rounds = cv_model[f"test-{local_param['eval_metric']}-mean"].idxmin() if(eval_f(cv_eval, best_eval)): best_model = cv_model best_param[var1n] = var1 best_param[var2n] = var2 best_eval = cv_eval best_boost_rounds = boost_rounds print(f"New best param found: " f"{local_param['eval_metric']} = {{{best_eval}}}, " f"boost_rounds = {{{best_boost_rounds}}}") return best_model, best_param, best_eval, best_boost_rounds while(early_break >= 0): np.random.seed(seed) best_eval_init = best_eval gs_params = { (subsample, colsample) for subsample in np.random.choice([i/10. for i in range(5,11)], 3) for colsample in np.random.choice([i/10. for i in range(5,11)], 3) } best_model, best_param, best_eval, best_boost_rounds = _gs_helper('subsample', 'colsample_bytree', best_model, best_param, best_eval, best_boost_rounds) gs_params = { (max_depth, min_child_weight) for max_depth in [10] + list(np.random.randint(1, 10, 3)) for min_child_weight in [0, 10] + list(np.random.randint(0, 10, 3)) } best_model, best_param, best_eval, best_boost_rounds = _gs_helper('max_depth', 'min_child_weight', best_model, best_param, best_eval, best_boost_rounds) gs_params = { (eta, gamma) for eta in np.random.choice([.005, .01, .05, .1, .2, .3], 3) for gamma in [0] + list(np.random.choice([0.01, 0.001, 0.2, 0.5, 1.0, 2.0, 3.0, 5.0, 10.0], 3)) } best_model, best_param, best_eval, best_boost_rounds = _gs_helper('eta', 'gamma', best_model, best_param, best_eval, best_boost_rounds) if (abs(best_eval_init - best_eval) < thresh): early_break-=1 seed+=1 return best_model, best_param, best_eval, best_boost_rounds best_model, best_param, best_eval, best_boost_rounds = xgb_paramsearch(X_train, y_train, features, init_params=init_param, nfold=5, num_boost_round=2000, early_stopping_rounds=3, metrics={'logloss', 'error'}, use_gpu='True') param['alpha'] = 50 cv_model[f"test-merror-mean"].min() best_param * only use PEG (try to find 100nm) * maybe look at different features (poor distributions) heterogenious in different ways different features are responsible to accuracies * think about to present code/results! evals = [(dtrain, 'train'), (dval, 'eval')] num_round = best_boost_rounds bst = xgb.train(best_param, dtrain, num_round, evals, early_stopping_rounds=3, ) ###### label = dtest.get_label() ypred1 = bst.predict(dtest) # by default, we predict using all the trees alpha = 0.62 pred = [0 if i < alpha else 1 for i in ypred1] print("Accuracy:",metrics.accuracy_score(y_test, pred)) from datetime import date import json bst.save_model(f'model_xgboost_region_based_cortex_striatum_80_20_split_{str(date.today())}') with open(f'config_xgboost_region_based_cortex_striatum_80_20_split_{str(date.today())}', 'w', encoding='utf-8') as f: json.dump(bst.save_config(), f, ensure_ascii=False, indent=4) from datetime import date import json bst.load_model(f'model_xgboost_P14_P21_P28_P32_50-50-split_2020-07-18') with open(f'config_xgboost_P14_P21_P28_P32_50-50-split_2020-07-18', 'r', encoding='utf-8') as f: config = f.read() config = json.loads(config) setting = bst.load_config(config) ypred1 = bst.predict(dtest) # by default, we predict using all the trees pred = [0 if i < alpha else 1 for i in ypred1] print("Accuracy:",metrics.accuracy_score(y_test, pred)) model_bytearray = bst.save_raw()[4:] def myfun(self=None): return model_bytearray bst.save_raw = myfun # import ctypes # def c_array(ctype, values): # """Convert a python string to c array.""" # if (isinstance(values, np.ndarray) # and values.dtype.itemsize == ctypes.sizeof(ctype)): # return (ctype * len(values)).from_buffer_copy(values) # return (ctype * len(values))(values) # mats = c_array(ctypes.c_void_p, [dtrain.handle]) # tst = X_test[features + [target]] # tst['tst'] = y_test results = X_test[features] results['predicted'] = pred results['actual'] = y_test ``` ## 4. Evaluate Results ``` print('0 == {}'.format(le.inverse_transform([0]))) print('1 == {}'.format(le.inverse_transform([1]))) class_names = ['cortex', 'striatum'] class_results = classification_report(y_test, pred, digits=4, target_names = class_names) print(str(class_results)) confusion_matrix(y_test, pred) pl.figure(figsize=(12,10)) cm_array = confusion_matrix(y_test, pred) df_cm = pd.DataFrame(cm_array, index = class_names, columns = class_names) sn.set(font_scale=1.4) # for label size ax = sn.heatmap(df_cm, annot=True, annot_kws={"size": 16}, cmap="YlGnBu") ax.set(xlabel='Actual', ylabel='Predicted') pl.show() explainer = shap.TreeExplainer(bst) shap_values = explainer.shap_values(X_test[features]) %matplotlib inline colors = ['#999999', '#7995e9'] class_inds = np.argsort([-np.abs(shap_values[i]).mean() for i in range(len(shap_values))]) cmap = plt_colors.ListedColormap(np.array(colors)[class_inds]) # sn.reset_orig() # Reset matplot lib to no longer use seaborn shap.summary_plot(shap_values, X_test[features], class_names=np.array(class_names), title='Total SHAP Values', plot_type='bar', color='#999999') pl.ioff() %matplotlib inline #------SHAP-FILE-------------- import random def get_cmap(shap_values): class_inds = np.argsort([-np.abs(shap_values[i]).mean() for i in range(len(shap_values))]) cmap = plt_colors.ListedColormap(np.array(colors)[class_inds]) return cmap def plot_dependency(feature_name, shap_values, X_df, fig_dim, color, figsize=None, y_range=None, alpha=None): if len(list(color)) is not 1: color = get_cmap(shap_values) colors = enumerate(color) fig, axs = pl.subplots(fig_dim, figsize=figsize) # ax = axs.ravel() cnt = 0 if (fig_dim == (1, 1)): if figsize is not None: axs[x][y].set_ylim(figsize) shap.dependence_plot(feature_name, shap_values, X_df, interaction_index=None, color=next(colors)[1], ax=axs) else: for x in range(fig_dim[0]): for y in range(fig_dim[1]): if figsize is not None: axs[x][y].set_ylim(figsize) shap.dependence_plot(feature_name, shap_values, X_df, interaction_index=None, color=next(colors)[1], ax=axs[x][y]) cnt+=1 plot_dependency("Mean Deff1", shap_values, X_test[features], (1,1), ['#999999']) plot_dependency("Mean fractal_dim", shap_values, X_test[features], (1,1), ['#999999']) plot_dependency("Mean kurtosis", shap_values, X_test[features], (1,1), ['#999999']) plot_dependency("straightness", shap_values, X_test[features], (1,1), ['#999999']) plot_dependency("Mean alpha", shap_values, X_test[features], (1,1), ['#999999']) shap.summary_plot(shap_values, X_test[features], max_display=5, class_names = class_names, title = 'SHAP Value cortex') from modules import anim_plot_changed from importlib import reload reload(anim_plot_changed) _ = anim_plot_changed.rotate_3d(results, [top_feat[0], top_feat[1], top_feat[2]]) _ = anim_plot_changed.rotate_3d(results, [top_feat[0], top_feat[2], top_feat[3]]) _ = anim_plot_changed.rotate_3d(results, [top_feat[1], top_feat[2], top_feat[3]]) from modules import anim_plot_changed from importlib import reload reload(anim_plot_changed) _ = anim_plot_changed.rotate_3d(results, [top_feat[0], top_feat[1], top_feat[2]], anim_param={'frames':np.arange(0,720,1)}, save_param={'filename':'This_is_a_test.gif','fps':50}) from matplotlib import animation from matplotlib.animation import PillowWriter from sklearn import model print(model.feature_importances_) # Feature search (new) -------not in file--------: import operator from sklearn.metrics import accuracy_score def feature_thresholding_helper(X_train, X_test, X_val, new_feat): dtrain = xgb.DMatrix(X_train[new_feat], label=y_train) dtest = xgb.DMatrix(X_test[new_feat], label=y_test) dval = xgb.DMatrix(X_val[new_feat], label=y_val) return dtrain, dtest, dval def feature_thresholding(X_train, y_train, X_test, y_test, X_val, y_val, params, features, nfold=5, num_boost_round=2000, early_stopping_rounds=3, metrics={'mlogloss', 'merror'}, thresh=np.arange(0,.1,.002)): best_thresh = -1 if params['eval_metric'] in ['map', 'auc', 'aucpr']: best_eval = -np.inf eval_f = operator.gt else: best_eval = np.inf eval_f = operator.lt best_eval = -np.inf eval_f = operator.gt for t in thresh: print(f"Using thresh = {t} ",end = '\| ') new_feat = list(np.array(features)[np.array(model.feature_importances_ > t)]) # cv_model = cv(params, # X_train, # y_train, # features=new_feat, # nfold=nfold, # num_boost_round=num_boost_round, # early_stopping_rounds=early_stopping_rounds, # metrics=metrics) # cv_eval = cv_model[f"test-{'merror'}-mean"].min() # print(f"Eval = {cv_eval} ", end = '\| ') # if eval_f(cv_eval, best_eval): # best_thresh = t # best_eval = cv_eval dtrain, dtest, dval = feature_thresholding_helper(X_train, X_test, X_val, new_feat) evals = [(dtrain, 'train'), (dval, 'eval')] bst2 = xgb.train(best_param, dtrain, 1500, evals, early_stopping_rounds=3, verbose_eval=False) ###### label = dtest.get_label() ypred1 = bst2.predict(dtest) # by default, we predict using all the trees pred2 = [np.where(x == np.max(x))[0][0] for x in ypred1] cv_eval = accuracy_score(y_test, pred2) if eval_f(cv_eval, best_eval): best_thresh = t best_eval = cv_eval print(f"Best eval = {best_eval}, Best threshold = {best_thresh}") print(f"Features used:\n{np.array(features)[np.array(model.feature_importances_ > best_thresh)]}") return list(np.array(features)[np.array(model.feature_importances_ > best_thresh)]) new_feat = feature_thresholding(X_train, y_train, X_test, y_test, X_val, y_val, best_param, features) new_feat = list(np.array(features)[np.array(model.feature_importances_ > best_thresh)]) cv_model = cv(best_param, X_train, y_train, features=new_feat, nfold=5, num_boost_round=best_boost_rounds, early_stopping_rounds=3, metrics={'mlogloss', 'merror'}) cv_model dtrain = xgb.DMatrix(X_train[new_feat], label=y_train) dtest = xgb.DMatrix(X_test[new_feat], label=y_test) dval = xgb.DMatrix(X_val[new_feat], label=y_val) evals = [(dtrain, 'train'), (dval, 'eval')] num_round = best_boost_rounds bst = xgb.train(best_param, dtrain, num_round, evals, early_stopping_rounds=3, ) ###### label = dtest.get_label() ypred1 = bst.predict(dtest) # by default, we predict using all the trees pred = [np.where(x == np.max(x))[0][0] for x in ypred1] # print('0 == {}'.format(le.inverse_transform([0]))) # print('1 == {}'.format(le.inverse_transform([1]))) # print('2 == {}'.format(le.inverse_transform([2]))) # print('3 == {}'.format(le.inverse_transform([3]))) class_names = ['P14', 'P21', 'P28', 'P35'] class_results = classification_report(y_test, pred, digits=4, target_names = ['P14', 'P21', 'P28', 'P35']) print(str(class_results)) # Running CV with newly thresholded features; using new seed of 123 to get different unique GS hyperparams best_model2, best_param2, best_eval2, best_boost_rounds2 = xgb_paramsearch(X_train, y_train, new_feat, init_params=best_param, nfold=5, num_boost_round=2000, early_stopping_rounds=3, metrics={'mlogloss', 'merror'}, use_gpu='True', seed=123) seed = 1234 np.random.seed(seed) train_split = 0.7 test_split = 0.5 le = preprocessing.LabelEncoder() bal_ecm['encoded_target'] = le.fit_transform(bal_ecm[target]) training_bins = np.random.choice(bal_ecm.bins.unique(), int(len(bal_ecm.bins.unique())train_split), replace=False) X_train = bal_ecm[bal_ecm.bins.isin(training_bins)] X_test_val = bal_ecm[~bal_ecm.bins.isin(training_bins)] X_val, X_test = train_test_split(X_test_val, test_size=test_split, random_state=seed) y_train = X_train['encoded_target'] y_test = X_test['encoded_target'] y_val = X_val['encoded_target'] dtrain = xgb.DMatrix(X_train[new_feat], label=y_train) dtest = xgb.DMatrix(X_test[new_feat], label=y_test) dval = xgb.DMatrix(X_val[new_feat], label=y_val) best_param2={'max_depth': 5, 'eta': 0.005, 'min_child_weight': 10, 'verbosity': 0, 'objective': 'multi:softprob', 'num_class': 4, 'silent': 'True', 'gamma': 5, 'subsample': 0.6, 'colsample_bytree': 0.5, 'eval_metric': 'mlogloss', 'gpu_id': 0, 'tree_method': 'gpu_hist', 'predictor': 'gpu_predictor'} evals = [(dtrain, 'train'), (dval, 'eval')] num_round = best_boost_rounds bst2 = xgb.train(best_param, dtrain, num_round, evals, early_stopping_rounds=3, ) ###### label = dtest.get_label() ypred1 = bst2.predict(dtest) # by default, we predict using all the trees pred2 = [np.where(x == np.max(x))[0][0] for x in ypred1] print("Accuracy:",metrics.accuracy_score(y_test, pred2)) class_names = ['P14', 'P21', 'P28', 'P35'] class_results = classification_report(y_test, pred2, digits=4, target_names = ['P14', 'P21', 'P28', 'P35']) print(str(class_results)) # param2 = {'max_depth': 2, # 'eta': 0.005, # 'min_child_weight': 0, # 'verbosity': 0, # 'objective': 'multi:softprob', # 'num_class': 4, # 'silent': 'True', # 'gamma': 5, # 'subsample': 0.25, # 'colsample_bytree': 0.3, # 'colsample_bynode':.5, # 'reg_alpha': 0} from sklearn.metrics import accuracy_score model_final = XGBClassifier(param2) new_feat = np.array(features)[np.array(model.feature_importances_ > t)] eval_set = [(X_train[new_feat], y_train), (X_test[new_feat], y_test)] model_final.fit(X_train[new_feat], y_train, verbose=False, eval_set=eval_set, eval_metric=["merror", 'mlogloss']) y_pred_f = model_final.predict(X_test[new_feat]) accuracy = accuracy_score(y_test, y_pred_f) print("Accuracy: %.2f%%" % (accuracy 100.0)) results = model_final.evals_result() epochs = len(results['validation_0']['merror']) x_axis = range(0, epochs) fig, ax = pl.subplots(figsize=(12,12)) ax.plot(x_axis, results['validation_0']['mlogloss'], label='Train') ax.plot(x_axis, results['validation_1']['mlogloss'], label='Test') ax.legend() pl.ylabel('Log Loss') pl.title('XGBoost Log Loss') pl.show() sorted(dict_importance, key=dict_importance.get, reverse=True)[:5] new_feat = np.array(features)[np.array(model.feature_importances_ > best_thresh)] model2.fit(X_train[new_feat], y_train, verbose=False, eval_set=[(X_val[new_feat],y_val)], eval_metric='mlogloss') pred3 = model2.predict(X_test[new_feat]) acc = metrics.accuracy_score(y_test, pred3) print("Accuracy:",metrics.accuracy_score(y_test, pred3)) ```	github_jupyter
# Lab 3: Tables Welcome to lab 3! This week, we'll learn about tables, which let us work with multiple arrays of data about the same things. Tables are described in [Chapter 6](https://www.inferentialthinking.com/chapters/06/Tables) of the text. First, set up the tests and imports by running the cell below. ``` import numpy as np from datascience import * # These lines load the tests. from client.api.notebook import Notebook ok = Notebook('lab03.ok') _ = ok.auth(inline=True) ``` ## 1. Introduction For a collection of things in the world, an array is useful for describing a single attribute of each thing. For example, among the collection of US States, an array could describe the land area of each state. Tables extend this idea by describing multiple attributes for each element of a collection. In most data science applications, we have data about many entities, but we also have several kinds of data about each entity. For example, in the cell below we have two arrays. The first one contains the world population in each year by the US Census Bureau, and the second contains the years themselves (in order, so the first elements in the population and the years arrays correspond). ``` population_amounts = Table.read_table("world_population.csv").column("Population") years = np.arange(1950, 2015+1) print("Population column:", population_amounts) print("Years column:", years) ``` Suppose we want to answer this question: > When did the world population cross 6 billion? You could technically answer this question just from staring at the arrays, but it's a bit convoluted, since you would have to count the position where the population first crossed 6 billion, then find the corresponding element in the years array. In cases like these, it might be easier to put the data into a `Table`, a 2-dimensional type of dataset. The expression below: - creates an empty table using the expression `Table()`, - adds two columns by calling `with_columns` with four arguments, - assigns the result to the name `population`, and finally - evaluates `population` so that we can see the table. The strings `"Year"` and `"Population"` are column labels that we have chosen. The names `population_amounts` and `years` were assigned above to two arrays of the same length. The function `with_columns` (you can find the documentation [here](http://data8.org/datascience/tables.html)) takes in alternating strings (to represent column labels) and arrays (representing the data in those columns), which are all separated by commas. ``` population = Table().with_columns( "Population", population_amounts, "Year", years ) population ``` Now the data are all together in a single table! It's much easier to parse this data,if you need to know what the population was in 1959, for example, you can tell from a single glance. We'll revisit this table later. ## 2. Creating Tables Question 2.1. In the cell below, we've created 2 arrays. Using the steps above, create a table called `top_10_movies` that has two columns called "Rating" and "Name", which hold `top_10_movie_ratings` and `top_10_movie_names` respectively. ``` top_10_movie_ratings = make_array(9.2, 9.2, 9., 8.9, 8.9, 8.9, 8.9, 8.9, 8.9, 8.8) top_10_movie_names = make_array( 'The Shawshank Redemption (1994)', 'The Godfather (1972)', 'The Godfather: Part II (1974)', 'Pulp Fiction (1994)', "Schindler's List (1993)", 'The Lord of the Rings: The Return of the King (2003)', '12 Angry Men (1957)', 'The Dark Knight (2008)', 'Il buono, il brutto, il cattivo (1966)', 'The Lord of the Rings: The Fellowship of the Ring (2001)') top_10_movies = Table().with_columns("Rating", "Name") # We've put this next line here so your table will get printed out when you # run this cell. top_10_movies _ = ok.grade('q2_1') ``` #### Loading a table from a file In most cases, we aren't going to go through the trouble of typing in all the data manually. Instead, we can use our `Table` functions. `Table.read_table` takes one argument, a path to a data file (a string) and returns a table. There are many formats for data files, but CSV ("comma-separated values") is the most common. Below is an example on how to use ``Table.read_table``. The file ``imdb_2015.csv`` contains a table of information about the 250 highest-rated movies on IMDb in 2015. The following code loads it as a table called ``imdb2015``. ``` imdb2015 = Table().read_table("data/imdb_2015.csv") imdb2015 ``` Notice the part about "... (240 rows omitted)." This table is big enough that only a few of its rows are displayed, but the others are still there. 10 are shown, so there are 250 movies total. Where did `imdb_2015.csv` come from? Take a look at [the data folder in the lab](./data). You should see a file called `imdb_2015.csv`. Open up the `imdb_2015.csv` file in that folder and look at the format. What do you notice? The `.csv` filename ending says that this file is in the [CSV (comma-separated value) format](http://edoceo.com/utilitas/csv-file-format). Now do the following exercise accoding to the example above. Question 2.2. The file `imdb_2019.csv` contains a table of information about the 250 highest-rated movies on IMDb. Load it as a table called `imdb2019`. ``` imdb2019 = ... imdb2019 _ = ok.grade('q2_2') ``` ## 3. Using lists A list is another Python sequence type, similar to an array. It's different than an array because the values it contains can all have different types. A single list can contain `int` values, `float` values, and strings. Elements in a list can even be other lists. A list is created by giving a name to the list of values enclosed in square brackets and separated by commas. For example, `values_with_different_types = ['data', 8, ['lab', 3]]` Lists can be useful when working with tables because they can describe the contents of one row in a table, which often corresponds to a sequence of values with different types. A list of lists can be used to describe multiple rows. Each column in a table is a collection of values with the same type (an array). If you create a table column from a list, it will automatically be converted to an array. A row, on the other hand, mixes types. Next, let's use lists to store your favorite pokemons in a table! ``` # Run this cell to recreate the table my_pokemons = Table().with_columns( 'Index', make_array(7, 39, 60), 'Name', make_array('squirtle', 'jigglypuff', 'poliwag') ) my_pokemons ``` Question 3.1. Create a list that describes a new fourth row of this table. The details can be whatever you want, but the list must contain two values: the index of the pokemon in the Pokedex (an `int` value) and the name of the pokemon (a string). How about the "pikachu"? Its index is 25. Or select your favourite pokemons [here](https://pokemondb.net/pokedex/all)! ``` new_pokemon = ... new_pokemon _ = ok.grade('q3_1') ``` Question 3.2. Now let's assemble your team for [pokemon battles](https://bulbapedia.bulbagarden.net/wiki/Pok%C3%A9mon_battle)! Complete the cell below to create a table of six pokemons (`six_pokemons`). For this purpose, first create a table `four_pokemons` that includes `new_pokemon` list as the fourth row to table `my_pokemons`. Then create a table `six_pokemons` from `four_pokemons` by including `other_pokemons` list as later rows. _Hint_: You can use `with_row` to create a new table with one extra row by passing a list of values and `with_rows` to create a table with multiple extra rows by passing a list of lists of values. ``` # Use the method .with_row(...) to create a new table that includes new_pokemon four_pokemons = ... # Use the method .with_rows(...) to create a table that # includes four_pokemons followed by other_pokemons other_pokemons = [[94, 'gengar'], [130, 'gyarados']] six_pokemons = ... six_pokemons _ = ok.grade('q3_2') ``` ## 4. Analyzing datasets With just a few table methods, we can answer some interesting questions about the IMDb2015 dataset. If we want just the ratings of the movies, we can get an array that contains the data in that column: ``` imdb2015.column("Rating") ``` The value of that expression is an array, exactly the same kind of thing you'd get if you typed in `make_array(8.4, 8.3, 8.3, [etc])`. Question 4.1. Find the rating of the highest-rated movie in the dataset in 2015. Hint: Think back to the functions you've learned about for working with arrays of numbers. Ask for help if you can't remember one that's useful for this. ``` highest_rating = ... highest_rating _ = ok.grade('q4_1') ``` That's not very useful, though. You'd probably want to know the name of the movie whose rating you found! To do that, we can sort the entire table by rating, which ensures that the ratings and titles will stay together. ``` imdb2015.sort("Rating") ``` Well, that actually doesn't help much, either -- we sorted the movies from lowest -> highest ratings. To look at the highest-rated movies, sort in reverse order: ``` imdb2015.sort("Rating", descending=True) ``` (The `descending=True` bit is called an optional argument. It has a default value of `False`, so when you explicitly tell the function `descending=True`, then the function will sort in descending order.) So there are actually 2 highest-rated movies in the dataset: The Shawshank Redemption and The Godfather. Some details about sort: 1. The first argument to `sort` is the name of a column to sort by. 2. If the column has strings in it, `sort` will sort alphabetically; if the column has numbers, it will sort numerically. 3. The value of `imdb2015.sort("Rating")` is a copy of `imdb2015`; the `imdb2015` table doesn't get modified. For example, if we called `imdb2015.sort("Rating")`, then running `imdb2015` by itself would still return the unsorted table. 4. Rows always stick together when a table is sorted. It wouldn't make sense to sort just one column and leave the other columns alone. For example, in this case, if we sorted just the "Rating" column, the movies would all end up with the wrong ratings. Question 4.2. Create a version of `imdb2015` that's sorted chronologically, with the earliest movies first. Call it `imdb2015_by_year`. ``` imdb2015_by_year = ... imdb2015_by_year _ = ok.grade('q4_2') ``` Question 4.3. What's the title of the earliest movie in the dataset in 2015? You could just look this up from the output of the previous cell. Instead, write Python code to find out. Hint: Starting with `imdb2015_by_year`, extract the Title column to get an array, then use `item` to get its first item. ``` earliest_movie_title = ... earliest_movie_title _ = ok.grade('q4_3') ``` Question 4.4. What's the title of the earliest movie in the dataset in 2019? Write python code to find out. Store the name of the movie in `earliest_movie_title_2019`. ``` # Replace the ellipsis with your code below. ... earliest_movie_title_2019 = ... earliest_movie_title_2019 _ = ok.grade('q4_4') ``` Optional Question Let's compare the 10 most highly rated movies in `imdb2015` and `imdb2019`. What's added and what's removed? Also, one movie's name is updated; can you spot it? Write your code in the cell below, and replace the ellipsis with your answers in the cell below the next cell. ``` # Write your code here ... ``` ... ## 5. Finding pieces of a dataset Suppose you're interested in movies from the 1940s. Sorting the table by year doesn't help you, because the 1940s are in the middle of the dataset. Instead, we use the table method `where`. ``` forties = imdb2015.where('Decade', are.equal_to(1940)) forties ``` Ignore the syntax for the moment. Instead, try to read that line like this: > Assign the name `forties` to a table whose rows are the rows in the `imdb2015` table `where` the `'Decade'`s `are` `equal` `to` `1940`. Question 5.1. Compute the average rating of movies from the 1940s in `imdb2015`. Hint: The function `np.average` computes the average of an array of numbers. ``` average_rating_in_forties = np.average(forties.column('Rating')) average_rating_in_forties imdb2015.column('Rating').mean() _ = ok.grade('q5_1') ``` Now let's dive into the details a bit more. `where` takes 2 arguments: 1. The name of a column. `where` finds rows where that column's values meet some criterion. 2. Something that describes the criterion that the column needs to meet, called a predicate. To create our predicate, we called the function `are.equal_to` with the value we wanted, 1940. We'll see other predicates soon. `where` returns a table that's a copy of the original table, but with only the rows that meet the given predicate. Question 5.2. Create a table called `ninety_nine` containing the movies that came out in the year 1999 in `imdb2015`. Use `where`. ``` ninety_nine = ... ninety_nine _ = ok.grade('q5_2') ``` So far we've only been finding where a column is exactly equal to a certain value. However, there are many other predicates. Here are a few: \|Predicate\|Example\|Result\| \|-\|-\|-\| \|`are.equal_to`\|`are.equal_to(50)`\|Find rows with values equal to 50\| \|`are.not_equal_to`\|`are.not_equal_to(50)`\|Find rows with values not equal to 50\| \|`are.above`\|`are.above(50)`\|Find rows with values above (and not equal to) 50\| \|`are.above_or_equal_to`\|`are.above_or_equal_to(50)`\|Find rows with values above 50 or equal to 50\| \|`are.below`\|`are.below(50)`\|Find rows with values below 50\| \|`are.between`\|`are.between(2, 10)`\|Find rows with values above or equal to 2 and below 10\| Question 5.3. Using `where` and one of the predicates from the table above, find all the movies with a rating higher than 8.5 in `imdb2015`. Put their data in a table called `really_highly_rated`. Note: `TableName.labels` will return a list of the names of all the columns in a Table. ``` really_highly_rated = ... really_highly_rated _ = ok.grade('q5_3') ``` Question 5.4. Find the average rating for movies released in the 20th century and the average rating for movies released in the 21st century for the movies in `imdb2015`. Hint: Think of the steps you need to do (take the average, find the ratings, find movies released in 20th/21st centuries), and try to put them in an order that makes sense. Confused about the definition of a century? For example, 18th century includes 1700 up to 1799, but not 1800. ``` average_20th_century_rating = ... average_21st_century_rating = ... print("Average 20th century rating:", average_20th_century_rating) print("Average 21st century rating:", average_21st_century_rating) _ = ok.grade('q5_4') ``` The property `num_rows` tells you how many rows are in a table. (A "property" is just a method that doesn't need to be called by adding parentheses.) ``` num_movies_in_dataset = imdb2015.num_rows num_movies_in_dataset ``` Question 5.5. Use `num_rows` (and arithmetic) to find the proportion of movies in `imdb2015` that were released in the 20th century, and the proportion from the 21st century. Hint: The proportion of movies released in the 20th century is the number of movies released in the 20th century, divided by the total number of movies. ``` proportion_in_20th_century = ... proportion_in_21st_century = ... print("Proportion in 20th century:", proportion_in_20th_century) print("Proportion in 21st century:", proportion_in_21st_century) _ = ok.grade('q5_5') ``` Question 5.6. Here's a challenge: Find the number of movies that came out in even years in `imdb2015`. Hint 1: The operator `%` computes the remainder when dividing by a number. So `5 % 2` is 1 and `6 % 2` is 0. A number is even if the remainder is 0 when you divide by 2. Hint 2: `%` can be used on arrays, operating elementwise like `+` or ``. So `make_array(5, 6, 7) % 2` is `array([1, 0, 1])`. Hint 3:* Create a column called "Year Remainder" that's the remainder when each movie's release year is divided by 2. Make a copy of `imdb2015` that includes that column. Then use `where` to find rows where that new column is equal to 0. Then use `num_rows` to count the number of such rows. ``` num_even_year_movies = ... num_even_year_movies _ = ok.grade('q5_6') ``` Question 5.7. Check out the `population` table from the introduction to this lab. Compute the year when the world population first went above 6 billion. ``` year_population_crossed_6_billion = ... year_population_crossed_6_billion _ = ok.grade('q5_7') ``` ## 6. Miscellanea There are a few more table methods you'll need to fill out your toolbox. The first 3 have to do with manipulating the columns in a table. The table `farmers_markets.csv` contains data on farmers' markets in the United States. Each row represents one such market. Question 6.1. Load the dataset into a table. Call it `farmers_markets`. ``` farmers_markets = Table().read_table("farmers_markets.csv") farmers_markets _ = ok.grade('q6_1') ``` You'll notice that it has a large number of columns in it! ### `num_columns` Question 6.2. The table property `num_columns` (example call: `tbl.num_columns`) produces the number of columns in a table. Use it to find the number of columns in our farmers' markets dataset. ``` num_farmers_markets_columns = ... print("The table has", num_farmers_markets_columns, "columns in it!") _ = ok.grade('q6_2') ``` Most of the columns are about particular products -- whether the market sells tofu, pet food, etc. If we're not interested in that stuff, it just makes the table difficult to read. This comes up more than you might think. ### `select` In such situations, we can use the table method `select` to pare down the columns of a table. It takes any number of arguments. Each should be the name or index of a column in the table. It returns a new table with only those columns in it. For example, the value of `imdb2015.select("Year", "Decade")` is a table with only the years and decades of each movie in `imdb2015`. Question 6.3. Use `select` to create a table with only the name, city, state, latitude ('y'), and longitude ('x') of each market. Call that new table `farmers_markets_locations`. ``` farmers_markets_locations = ... farmers_markets_locations _ = ok.grade('q6_3') ``` ### `select` is not `column`! The method `select` is definitely not the same as the method `column`. `farmers_markets.column('y')` is an array of the latitudes of all the markets. `farmers_markets.select('y')` is a table that happens to contain only 1 column, the latitudes of all the markets. Question 6.4. Below, we tried using the function `np.average` to find the average latitude ('y') and average longitude ('x') of the farmers' markets in the table, but we screwed something up. Run the cell to see the (somewhat inscrutable) error message that results from calling `np.average` on a table. Then, fix our code. ``` average_latitude = np.average(farmers_markets.select('y')) average_longitude = np.average(farmers_markets.select('x')) print("The average of US farmers' markets' coordinates is located at (", average_latitude, ",", average_longitude, ")") _ = ok.grade('q6_4') ``` ### `drop` `drop` serves the same purpose as `select`, but it takes away the columns you list instead of the ones you don't list, leaving all the rest of the columns. Question 6.5. Suppose you just didn't want the "FMID" or "updateTime" columns in `farmers_markets`. Create a table that's a copy of `farmers_markets` but doesn't include those columns. Call that table `farmers_markets_without_fmid`. ``` farmers_markets_without_fmid = ... farmers_markets_without_fmid _ = ok.grade('q6_5') ``` #### `take` Let's find the 5 northernmost farmers' markets in the US. You already know how to sort by latitude ('y'), but we haven't seen how to get the first 5 rows of a table. That's what `take` is for. The table method `take` takes as its argument an array of numbers. Each number should be the index of a row in the table. It returns a new table with only those rows. Most often you'll want to use `take` in conjunction with `np.arange` to take the first few rows of a table. Question 6.6. Make a table of the 5 northernmost farmers' markets in `farmers_markets_locations`. Call it `northern_markets`. (It should include the same columns as `farmers_markets_locations`. ``` northern_markets = ... northern_markets _ = ok.grade('q6_6') ``` Question 6.7. Make a table of the farmers' markets in Santa Barbara, California. (It should include the same columns as `farmers_markets_locations`.) ``` sb_markets = ... sb_markets _ = ok.grade('q6_7') ``` Recognize any of them? ## 7. Summary For your reference, here's a table of all the functions and methods we saw in this lab. \|Name\|Example\|Purpose\| \|-\|-\|-\| \|`Table`\|`Table()`\|Create an empty table, usually to extend with data\| \|`Table.read_table`\|`Table.read_table("my_data.csv")`\|Create a table from a data file\| \|`with_columns`\|`tbl = Table().with_columns("N", np.arange(5), "2N", np.arange(0, 10, 2))`\|Create a copy of a table with more columns\| \|`column`\|`tbl.column("N")`\|Create an array containing the elements of a column\| \|`sort`\|`tbl.sort("N")`\|Create a copy of a table sorted by the values in a column\| \|`where`\|`tbl.where("N", are.above(2))`\|Create a copy of a table with only the rows that match some predicate\| \|`num_rows`\|`tbl.num_rows`\|Compute the number of rows in a table\| \|`num_columns`\|`tbl.num_columns`\|Compute the number of columns in a table\| \|`select`\|`tbl.select("N")`\|Create a copy of a table with only some of the columns\| \|`drop`\|`tbl.drop("2N")`\|Create a copy of a table without some of the columns\| \|`take`\|`tbl.take(np.arange(0, 6, 2))`\|Create a copy of the table with only the rows whose indices are in the given array\| <br/> Alright! You're finished with lab 3! Be sure to... - run all the tests (the next cell has a shortcut for that), - Save and Checkpoint from the `File` menu, - run the last cell to submit your work, ``` # For your convenience, you can run this cell to run all the tests at once! import os _ = [ok.grade(q[:-3]) for q in os.listdir("tests") if q.startswith('q')] _ = ok.submit() ```	github_jupyter
``` %matplotlib inline import arviz as az import matplotlib.pyplot as plt import numpy as np import pandas as pd import pymc as pm import scipy as sp import seaborn as sns sns.set(context='notebook', font_scale=1.2, rc={'figure.figsize': (12, 5)}) plt.style.use(['seaborn-colorblind', 'seaborn-darkgrid']) RANDOM_SEED = 8927 np.random.seed(286) # Helper function def stdz(series: pd.Series): """Standardize the given pandas Series""" return (series - series.mean())/series.std() ``` ### 12E1. Which of the following priors will produce more shrinkage in the estimates? - $\alpha_{TANK} \sim Normal(0, 1)$ - $\alpha_{TANK} \sim Normal(0, 2)$ The first option will produce more shrinkage, because the prior is more concentrated: the standard deviation is smaller, so the density piles up more mass around zero and will pull extreme values closer to zero. ### 12E2. Make the following model into a multilevel model: $y_{i} \sim Binomial(1, p_{i})$ $logit(p_{i}) = \alpha_{GROUP[i]} + \beta x_{i}$ $\alpha_{GROUP} \sim Normal(0, 10)$ $\beta \sim Normal(0, 1)$ All that is really required to convert the model to a multilevel model is to take the prior for the vector of intercepts, $\alpha_{GROUP}$, and make it adaptive. This means we define parameters for its mean and standard deviation. Then we assign these two new parameters their own priors, hyperpriors. This is what it looks like: $y_{i} \sim Binomial(1, p_{i})$ $logit(p_{i}) = \alpha_{GROUP[i]} + \beta x_{i}$ $\alpha_{GROUP} \sim Normal(\mu_{\alpha}, \sigma_{\alpha})$ $\beta \sim Normal(0, 1)$ $\mu_{\alpha} \sim Normal(0, 10)$ $\sigma_{\alpha} \sim HalfCauchy(1)$ The exact hyperpriors you assign don’t matter here. Since this problem has no data context, it isn’t really possible to say what sensible priors would be. Note also that an exponential prior on $\sigma_{\alpha}$ is just as sensible, absent context, as the half-Cauchy prior. ### 12E3. Make the following model into a multilevel model: $y_{i} \sim Normal(\mu_{i}, \sigma)$ $\mu_{i} = \alpha_{GROUP[i]} + \beta x_{i}$ $\alpha_{GROUP} \sim Normal(0, 10)$ $\beta \sim Normal(0, 1)$ $\sigma \sim HalfCauchy(2)$ This is very similar to the previous problem. The only trick here is to notice that there is already a standard deviation parameter, σ. But that standard deviation is for the residuals, at the top level. We’ll need yet another standard deviation for the varying intercepts: $y_{i} \sim Normal(\mu_{i}, \sigma)$ $\mu_{i} = \alpha_{GROUP[i]} + \beta x_{i}$ $\alpha_{GROUP} \sim Normal(\mu_{\alpha}, \sigma_{\alpha})$ $\beta \sim Normal(0, 1)$ $\sigma \sim HalfCauchy(2)$ $\mu_{\alpha} \sim Normal(0, 10)$ $\sigma_{\alpha} \sim HalfCauchy(1)$ ### 12E4. Write an example mathematical model formula for a Poisson regression with varying intercepts You can just copy the answer from problem 12E2 and swap out the binomial likelihood for a Poisson, taking care to change the link function from logit to log: $y_{i} \sim Poisson(\lambda_{i})$ $log(\lambda_{i}) = \alpha_{GROUP[i]} + \beta x_{i}$ $\alpha_{GROUP} \sim Normal(\mu_{\alpha}, \sigma_{\alpha})$ $\beta \sim Normal(0, 1)$ $\mu_{\alpha} \sim Normal(0, 10)$ $\sigma_{\alpha} \sim HalfCauchy(1)$ Under the hood, all multilevel models are alike. It doesn’t matter which likelihood function rests at the top. Take care, however, to reconsider priors. The scale of the data and parameters is likely quite different for a Poisson model. Absent any particular context in this problem, you can’t recommend better priors. But in real work, it’s good to think about reasonable values and provide regularizing priors on the relevant scale. ### 12E5. Write an example mathematical model formula for a Poisson regression with two different kinds of varying intercepts - a cross-classified model The cross-classified model adds another varying intercept type. This is no harder than duplicating the original varying intercepts structure. But you have to take care now not to over-parameterize the model by having a hyperprior mean for both intercept types. You can do this by just assigning one of the adaptive priors a mean of zero. Suppose for example that the second cluster type is day: $y_{i} \sim Poisson(\lambda_{i})$ $log(\lambda_{i}) = \alpha_{GROUP[i]} + \alpha_{DAY[i]} + \beta x_{i}$ $\alpha_{GROUP} \sim Normal(\mu_{\alpha}, \sigma_{GROUP})$ $\alpha_{DAY} \sim Normal(0, \sigma_{DAY})$ $\beta \sim Normal(0, 1)$ $\mu_{\alpha} \sim Normal(0, 10)$ $\sigma_{GROUP}, \sigma_{DAY} \sim HalfCauchy(1)$ Or you can just pull the mean intercept out of both priors and put it in the linear model: $y_{i} \sim Poisson(\lambda_{i})$ $log(\lambda_{i}) = \alpha + \alpha_{GROUP[i]} + \alpha_{DAY[i]} + \beta x_{i}$ $\alpha \sim Normal(0, 10)$ $\alpha_{GROUP} \sim Normal(0, \sigma_{GROUP})$ $\alpha_{DAY} \sim Normal(0, \sigma_{DAY})$ $\beta \sim Normal(0, 1)$ $\sigma_{GROUP}, \sigma_{DAY} \sim HalfCauchy(1)$ These are exactly the same model. Although as you’ll see later in Chapter 13, these different forms might be more or less efficient in sampling. ### 12M1. Revisit the Reed frog survival data, reedfrogs.csv, and add the $predation$ and $size$ treatment variables to the varying intercepts model. Consider models with either main effect alone, both main effects, as well as a model including both and their interaction. Instead of focusing on inferences about these two predictor variables, focus on the inferred variation across tanks. Explain why it changes as it does across models. ``` frogs = pd.read_csv('../Data/reedfrogs.csv', sep=",") # Switch predictors to dummies frogs["size"] = pd.Categorical(frogs["size"]).reorder_categories(["small", "big"]).codes frogs["pred"] = pd.Categorical(frogs["pred"]).codes # make the tank cluster variable tank = np.arange(frogs.shape[0]) print(frogs.shape) frogs.head(8) frogs.describe() pred = frogs["pred"].values size = frogs["size"].values n_samples, tuning = 1000, 2000 with pm.Model() as m_itcpt: a = pm.Normal('a', 0., 10.) sigma_tank = pm.HalfCauchy('sigma_tank', 1.) a_tank = pm.Normal('a_tank', a, sigma_tank, shape=frogs.shape[0]) p = pm.math.invlogit(a_tank[tank]) surv = pm.Binomial('surv', n=frogs.density, p=p, observed=frogs.surv) trace_itcpt = pm.sample(n_samples, tune=tuning, cores=2) with pm.Model() as m_p: a = pm.Normal('a', 0., 10.) sigma_tank = pm.HalfCauchy('sigma_tank', 1.) a_tank = pm.Normal('a_tank', a, sigma_tank, shape=frogs.shape[0]) bp = pm.Normal('bp', 0., 1.) p = pm.math.invlogit(a_tank[tank] + bppred) surv = pm.Binomial('surv', n=frogs.density, p=p, observed=frogs.surv) trace_p = pm.sample(n_samples, tune=tuning, cores=2) with pm.Model() as m_s: a = pm.Normal('a', 0., 10.) sigma_tank = pm.HalfCauchy('sigma_tank', 1.) a_tank = pm.Normal('a_tank', a, sigma_tank, shape=frogs.shape[0]) bs = pm.Normal('bs', 0., 1.) p = pm.math.invlogit(a_tank[tank] + bssize) surv = pm.Binomial('surv', n=frogs.density, p=p, observed=frogs.surv) trace_s = pm.sample(n_samples, tune=tuning, cores=2) with pm.Model() as m_p_s: a = pm.Normal('a', 0., 10.) sigma_tank = pm.HalfCauchy('sigma_tank', 1.) a_tank = pm.Normal('a_tank', a, sigma_tank, shape=frogs.shape[0]) bp = pm.Normal('bp', 0., 1.) bs = pm.Normal('bs', 0., 1.) p = pm.math.invlogit(a_tank[tank] + bppred + bssize) surv = pm.Binomial('surv', n=frogs.density, p=p, observed=frogs.surv) trace_p_s = pm.sample(n_samples, tune=tuning, cores=2) with pm.Model() as m_p_s_ps: a = pm.Normal('a', 0., 10.) sigma_tank = pm.HalfCauchy('sigma_tank', 1.) a_tank = pm.Normal('a_tank', a, sigma_tank, shape=frogs.shape[0]) bp = pm.Normal('bp', 0., 1.) bs = pm.Normal('bs', 0., 1.) bps = pm.Normal('bps', 0., 1.) p = pm.math.invlogit(a_tank[tank] + bppred + bssize + bpspredsize) surv = pm.Binomial('surv', n=frogs.density, p=p, observed=frogs.surv) trace_p_s_ps = pm.sample(n_samples, tune=tuning, cores=2) ``` Now we’d like to inspect how the estimated variation across tanks changes from model to model. This means comparing posterior distributions for $\sigma_{tank}$ across the models: ``` az.plot_forest([trace_itcpt, trace_p, trace_s, trace_p_s, trace_p_s_ps], model_names=["m_itcpt", "m_p", "m_s", "m_p_s", "m_p_s_ps"], var_names=["sigma_tank"], credible_interval=.89, figsize=(9,4), combined=True); ``` Note that adding a predictor always decreased the posterior mean variation across tanks. Why? Because the predictors are, well, predicting variation. This leaves less variation for the varying intercepts to mop up. In theory, if we had in the form of predictor variables all of the relevant information that determined the survival outcomes, there would be zero variation across tanks. You might also notice that the $size$ treatment variable reduces the variation much less than does $predation$. The predictor $size$, in these models, doesn’t help prediction very much, so accounting for it has minimal impact on the estimated variation across tanks. ### 12M2. Compare the models you fit just above, using WAIC. Can you reconcile the differences in WAIC with the posterior distributions of the models? ``` az.compare({"m_itcpt": trace_itcpt, "m_p": trace_p, "m_s": trace_s, "m_p_s": trace_p_s, "m_p_s_ps": trace_p_s_ps}, method="pseudo-BMA") ``` The models are extremely close, but m_s seems to be the last one, suggesting that $size$ accounts for very little. Can we see this in the coefficients? ``` def get_coefs(est_summary: pd.DataFrame) -> dict: mean_est = est_summary["mean"].to_dict() coefs = {} coefs['sigma_tank'] = mean_est.get('sigma_tank', np.nan) coefs['bp'] = mean_est.get('bp', np.nan) coefs['bs'] = mean_est.get('bs', np.nan) coefs['bps'] = mean_est.get('bps', np.nan) return coefs pd.DataFrame.from_dict({"m_itcpt": get_coefs(az.summary(trace_itcpt, credible_interval=0.89)), "m_p": get_coefs(az.summary(trace_p, credible_interval=0.89)), "m_s": get_coefs(az.summary(trace_s, credible_interval=0.89)), "m_p_s": get_coefs(az.summary(trace_p_s, credible_interval=0.89)), "m_p_s_ps": get_coefs(az.summary(trace_p_s_ps, credible_interval=0.89))}) ``` The posterior means for $b_{s}$ are smaller in absolute value than those for $b_{p}$. This is consistent with the WAIC comparison. In fact, the standard deviations on these coefficients are big enough that the $b_{s}$ posterior distributions overlap zero quite a bit. Consider for example the model m_s: ``` az.summary(trace_s, var_names=["a", "bs", "sigma_tank"], credible_interval=0.89) ``` But before you conclude that tadpole size doesn’t matter, remember that other models, perhaps including additional predictors, might find new life for $size$. Inference is always conditional on the model. ### 12M3. Re-estimate the basic Reed frog varying intercept model, but now using a Cauchy distribution in place of the Gaussian distribution for the varying intercepts. That is, fit this model: $s_{i} \sim Binomial(n_{i}, p_{i})$ $logit(p_{i}) = \alpha_{TANK[i]}$ $\alpha_{TANK} \sim Cauchy(\alpha, \sigma)$ $\alpha \sim Normal(0, 1)$ $\sigma \sim HalfCauchy(1)$ Compare the posterior means of the intercepts, $\alpha_{TANK}$, to the posterior means produced in the chapter, using the customary Gaussian prior. Can you explain the pattern of differences? ``` with pm.Model() as m_itcpt_cauch: a = pm.Normal('a', 0., 1.) sigma_tank = pm.HalfCauchy('sigma_tank', 1.) a_tank = pm.Cauchy('a_tank', a, sigma_tank, shape=frogs.shape[0]) p = pm.math.invlogit(a_tank[tank]) surv = pm.Binomial('surv', n=frogs.density, p=p, observed=frogs.surv) trace_itcpt_cauch = pm.sample(3000, tune=3000, cores=2, nuts_kwargs={"target_accept": .99}) ``` You might have some trouble sampling efficiently from this posterior, on account of the long tails of the Cauchy. This results in the intercepts a_tank being poorly identifed. You saw a simple example of this problem in Chapter 8, when you met MCMC and learned about diagnosing bad chains. To help the sampler explore the space more efficiently, we've increase the target_accept ratio to 0.99. This topic will come up in more detail in Chapter 13. In any event, be sure to check the chains carefully and sample more if you need to. The problem asked you to compare the posterior means of the a_tank parameters. Plotting the posterior means will be a lot more meaningful than just looking at the values: ``` post_itcpt = pm.trace_to_dataframe(trace_itcpt) a_tank_m = post_itcpt.drop(["a", "sigma_tank"], axis=1).mean() post_itcpt_cauch = pm.trace_to_dataframe(trace_itcpt_cauch) a_tank_mC = post_itcpt_cauch.drop(["a", "sigma_tank"], axis=1).mean() plt.figure(figsize=(10,5)) plt.scatter(x=a_tank_m, y=a_tank_mC) plt.plot([a_tank_m.min()-0.5, a_tank_m.max()+0.5], [a_tank_m.min()-0.5, a_tank_m.max()+0.5], "k--") plt.xlabel("under Gaussian prior") plt.ylabel("under Cauchy prior") plt.title("Posterior mean of each tank's intercept"); ``` The dashed line shows the values for which the intercepts are equal in the two models. You can see that for the majority of tank intercepts, the Cauchy model actually produces posterior means that are essentially the same as those from the Gaussian model. But the large intercepts, under the Gaussian prior, are very much more extreme under the Cauchy prior. For those tanks on the righthand side of the plot, all of the tadpoles survived. So using only the data from each tank alone, the log-odds of survival are infinite. The adaptive prior applies pooling that shrinks those log-odds inwards from infinity, thankfully. But the Gaussian prior causes more shrinkage of the extreme values than the Cauchy prior does. That is what accounts for those 5 extreme points on the right of the plot above. ### 12M4. Fit the following cross-classified multilevel model to the chimpanzees data: $L_{i} \sim Binomial(1, p_{i})$ $logit(p_{i}) = \alpha_{ACTOR[i]} + \alpha_{BLOCK[i]} + (\beta_{P} + \beta_{PC} C_{i}) P_{i}$ $\alpha_{ACTOR} \sim Normal(\alpha, \sigma_{ACTOR})$ $\alpha_{BLOCK} \sim Normal(\gamma, \sigma_{BLOCK})$ $\alpha, \gamma, \beta_{P}, \beta_{PC} \sim Normal(0, 10)$ $\sigma_{ACTOR}, \sigma_{BLOCK} \sim HalfCauchy(1)$ Compare the posterior distribution to that produced by the similar cross-classified model from the chapter. Also compare the number of effective samples. Can you explain the differences? ``` chimp = pd.read_csv('../Data/chimpanzees.csv', sep=";") # we change "actor" and "block" to zero-index chimp.actor = (chimp.actor - 1).astype(int) chimp.block = (chimp.block - 1).astype(int) Nactor = len(chimp.actor.unique()) Nblock = len(chimp.block.unique()) chimp.head() with pm.Model() as m_chapter: sigma_actor = pm.HalfCauchy('sigma_actor', 1.) sigma_block = pm.HalfCauchy('sigma_block', 1.) a_actor = pm.Normal('a_actor', 0., sigma_actor, shape=Nactor) a_block = pm.Normal('a_block', 0., sigma_block, shape=Nblock) a = pm.Normal('a', 0., 10.) bp = pm.Normal('bp', 0., 10.) bpc = pm.Normal('bpc', 0., 10.) p = pm.math.invlogit(a + a_actor[chimp.actor.values] + a_block[chimp.block.values] + (bp + bpc * chimp.condition) * chimp.prosoc_left) pulled_left = pm.Binomial('pulled_left', 1, p, observed=chimp.pulled_left) trace_chapter= pm.sample(1000, tune=3000, cores=2) with pm.Model() as m_exerc: alpha = pm.Normal("alpha", 0., 10.) gamma = pm.Normal("gamma", 0., 10.) sigma_actor = pm.HalfCauchy('sigma_actor', 1.) sigma_block = pm.HalfCauchy('sigma_block', 1.) a_actor = pm.Normal('a_actor', alpha, sigma_actor, shape=Nactor) a_block = pm.Normal('a_block', gamma, sigma_block, shape=Nblock) bp = pm.Normal('bp', 0., 10.) bpc = pm.Normal('bpc', 0., 10.) p = pm.math.invlogit(a_actor[chimp.actor.values] + a_block[chimp.block.values] + (bp + bpc * chimp.condition) * chimp.prosoc_left) pulled_left = pm.Binomial('pulled_left', 1, p, observed=chimp.pulled_left) trace_exerc= pm.sample(1000, tune=3000, cores=2) ``` This is much like the model in the chapter, just with the two varying intercept means inside the two priors, instead of one mean outside both priors (inside the linear model). Since there are two parameters for the means, one inside each adaptive prior, this model is over-parameterized: an infinite number of different values of $\alpha$ and $\gamma$ will produce the same sum $\alpha + \gamma$. In other words, the $\gamma$ parameter is redundant. This will produce a poorly-identified posterior. It’s best to avoid specifying a model like this. As a matter of fact, you probably noticed the second model took a lot more time to sample than the first one (about 10x more time), which is usually a sign of a poorly parametrized model. Remember the folk theorem of statistical computing: "When you have computational problems, often there’s a problem with your model". Now let's look at each model's parameters: ``` az.summary(trace_chapter, var_names=["a", "bp", "bpc", "sigma_actor", "sigma_block"], credible_interval=0.89) az.summary(trace_exerc, var_names=["alpha", "gamma", "bp", "bpc", "sigma_actor", "sigma_block"], credible_interval=0.89) ``` Look at these awful effective sample sizes (ess) and R-hat values for trace_exerc! In a nutshell, the new model (m_exerc) samples quite poorly. This is what happens when you over-parameterize the intercept. Notice however that the inferences about the slopes are practically identical. So even though the over-parameterized model is inefficient, it has identified the slope parameters. ### 12H1. In 1980, a typical Bengali woman could have 5 or more children in her lifetime. By the year 2000, a typical Bengali woman had only 2 or 3 children. You're going to look at a historical set of data, when contraception was widely available but many families chose not to use it. These data reside in bangladesh.csv and come from the 1988 Bangladesh Fertility Survey. Each row is one of 1934 women. There are six variables, but you can focus on three of them for this practice problem: - $district$: ID number of administrative district each woman resided in - $use.contraception$: An indicator (0/1) of whether the woman was using contraception - $urban$: An indicator (0/1) of whether the woman lived in a city, as opposed to living in a rural area The first thing to do is ensure that the cluster variable, $district$, is a contiguous set of integers. Recall that these values will be index values inside the model. If there are gaps, you’ll have parameters for which there is no data to inform them. Worse, the model probably won’t run. Let's look at the unique values of the $district$ variable: ``` d = pd.read_csv('../Data/bangladesh.csv', sep=";") d.head() d.describe() d.district.unique() ``` District 54 is absent. So $district$ isn’t yet a good index variable, because it’s not contiguous. This is easy to fix. Just make a new variable that is contiguous: ``` d["district_id"], _ = pd.factorize(d.district, sort=True) district_id = d.district_id.values Ndistricts = len(d.district_id.unique()) d.district_id.unique() ``` Now there are 60 values, contiguous integers 0 to 59. Now, focus on predicting $use.contraception$, clustered by district ID. Fit both (1) a traditional fixed-effects model that uses an index variable for district and (2) a multilevel model with varying intercepts for district. Plot the predicted proportions of women in each district using contraception, for both the fixed-effects model and the varying-effects model. That is, make a plot in which district_id is on the horizontal axis and expected proportion using contraception is on the vertical. Make one plot for each model, or layer them on the same plot, as you prefer. How do the models disagree? Can you explain the pattern of disagreement? In particular, can you explain the most extreme cases of disagreement, both why they happen, where they do and why the models reach different inferences? ``` with pm.Model() as m_fixed: a_district = pm.Normal('a_district', 0., 10., shape=Ndistricts) p = pm.math.invlogit(a_district[district_id]) used = pm.Bernoulli('used', p=p, observed=d["use.contraception"]) trace_fixed = pm.sample(1000, tune=2000, cores=2) with pm.Model() as m_varying: a = pm.Normal('a', 0., 10.) sigma_district = pm.Exponential('sigma_district', 1.) a_district = pm.Normal('a_district', 0., sigma_district, shape=Ndistricts) p = pm.math.invlogit(a + a_district[district_id]) used = pm.Bernoulli('used', p=p, observed=d["use.contraception"]) trace_varying = pm.sample(1000, tune=2000, cores=2) ``` Sampling was smooth and quick, so the traces should be ok. We can confirm by plotting them: ``` az.plot_trace(trace_fixed, compact=True); az.plot_trace(trace_varying, compact=True); ``` The chains are indeed fine. These models have a lot of parameters, so the summary dataframe we are used to is not really convenient here. Let's use forest plots instead: ``` fig, axes = az.plot_forest([trace_fixed, trace_varying], model_names=["Fixed", "Varying"], credible_interval=0.89, combined=True, figsize=(8,35)) axes[0].grid(); ``` We can already see that some estimates are particularly uncertain in some districts, but only for the fixed-effects model. Chances are these districts are extreme compared to the others, and/or the sample sizes are very small. This would be a case where the varying-effects model's estimates would be better and less volatile in those districts, because it is pooling information - information flows across districts thanks to the higher level common distribution of districts. ``` post_fixed = pm.trace_to_dataframe(trace_fixed) p_mean_fixed = sp.special.expit(post_fixed.mean()) post_varying = pm.trace_to_dataframe(trace_varying) # add a_district to a (because they are offsets of the global intercept), then convert to probabilities with logistic p_mean_varying = sp.special.expit(post_varying.drop(["a", "sigma_district"], axis=1).add(post_varying["a"], axis="index").mean()) global_a = sp.special.expit(post_varying["a"].mean()) plt.figure(figsize=(11,5)) plt.hlines(d["use.contraception"].mean(), -1, Ndistricts, linestyles="dotted", label="Empirical global mean", alpha=.6, lw=2) plt.hlines(global_a, -1, Ndistricts, linestyles="dashed", label="Estimated global mean", alpha=.6, lw=2) plt.plot(np.arange(Ndistricts), p_mean_fixed, "o", ms=6, alpha=.8, label="Fixed-effects estimates") plt.plot(np.arange(Ndistricts), p_mean_varying, "o", fillstyle="none", ms=6, markeredgewidth=1.5, alpha=.8, label="Varying-effects estimates") plt.xlabel("District") plt.ylabel("Probability contraception") plt.legend(ncol=2); ``` The blue points are the fixed-effects estimates, and the open green ones are the varying effects. The dotted line is the observed average proportion of women using contraception, in the entire sample. The dashed line is the average proportion of women using contraception, in the entire sample, as estimated by the varying effects model. Notice first that the green points are always closer to the dashed line, as was the case with the tadpole example in lecture. This results from shrinkage, which results from pooling information. There are cases with rather extreme disagreements, though. The most obvious is district 2, which has a fixed (blue) estimate of 1 but a varying (green) estimate of only 0.44. There are also two districts (10 and 48) for which the fixed estimates are zero, but the varying estimates are 0.18 and 0.30. If you go back to the forest plot above, these are exactly the three districts whose fixed-effects parameters were both far from zero and very uncertain. So what’s going on here? As we suspected, these districts presented extreme results: either all sampled women used contraception or none did. As a result, the fixed-effects estimates were silly. The varying-effects model was able to produce more rational estimates, because it pooled information from other districts. But note that the intensity of pooling was different for these three extreme districts. As we intuited too, depending upon how many women were sampled in each district, there was more or less shrinkage (pooling) towards the grand mean. So for example in the case of district 2, there were only 2 women in the sample, and so there is a lot of distance between the blue and green points. In contrast, district 10 had 21 women in the sample, and so while pooling pulls the estimate off of zero to 0.18, it doesn’t pull it nearly as far as district 2. Another way to think of this phenomenon is to view the same estimates arranged by number of women in the sampled district, on the horizontal axis. Then on the vertical we can plot the distance (absolute value of the difference) between the fixed and varying estimates. Here’s what that looks like: ``` nbr_women = d.groupby("district_id").count()["woman"] abs_dist = (p_mean_fixed - p_mean_varying).abs() plt.figure(figsize=(11,5)) plt.plot(nbr_women, abs_dist, 'o', fillstyle="none", ms=7, markeredgewidth=2, alpha=.6) plt.xlabel("Number of women sampled") plt.ylabel("Shrinkage by district"); ``` You can think of the vertical axis as being the amount of shrinkage. The districts with fewer women sampled show a lot more shrinkage, because there is less information in them. As a result, they are expected to overfit more, and so they are shrunk more towards the overall mean. ### 12H2. Return to the Trolley data from Chapter 11. Define and fit a varying intercepts model for these data. By this I mean to add an intercept parameter for the individuals to the linear model. Cluster the varying intercepts on individual participants, as indicated by the unique values in the id variable. Include $action$, $intention$, and $contact$ as before. Compare the varying intercepts model and a model that ignores individuals, using both WAIC/LOO and posterior predictions. What is the impact of individual variation in these data? This will be adressed in a later pull request, as there is currently an issue with PyMC's OrderedLogistic implementation ### 12H3. The Trolley data are also clustered by $story$, which indicates a unique narrative for each vignette. Define and fit a cross-classified varying intercepts model with both $id$ and $story$. Use the same ordinary terms as in the previous problem. Compare this model to the previous models. What do you infer about the impact of different stories on responses? This will be adressed in a later pull request, as there is currently an issue with PyMC's OrderedLogistic implementation ``` import platform import sys import IPython import matplotlib import scipy print(f"This notebook was created on a computer {platform.machine()}, using: " f"\nPython {sys.version[:5]}\nIPython {IPython.__version__}\nPyMC {pm.__version__}\nArviz {az.__version__}\nNumPy {np.__version__}" f"\nPandas {pd.__version__}\nSciPy {scipy.__version__}\nMatplotlib {matplotlib.__version__}\n") ```	github_jupyter
##### Copyright 2018 The TensorFlow Authors. ``` #@title Licensed under the Apache License, Version 2.0 (the "License"); # you may not use this file except in compliance with the License. # You may obtain a copy of the License at # # https://www.apache.org/licenses/LICENSE-2.0 # # Unless required by applicable law or agreed to in writing, software # distributed under the License is distributed on an "AS IS" BASIS, # WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. # See the License for the specific language governing permissions and # limitations under the License. ``` # Unicode 文字列 <table class="tfo-notebook-buttons" align="left"> <td> <a target="_blank" href="https://www.tensorflow.org/tutorials/load_data/unicode"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a> </td> <td> <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/ja/tutorials/load_data/unicode.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a> </td> <td> <a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/ja/tutorials/load_data/unicode.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a> </td> <td> <a href="https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/ja/tutorials/load_data/unicode.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a> </td> </table> Note: これらのドキュメントは私たちTensorFlowコミュニティが翻訳したものです。コミュニティによる翻訳はベストエフォートであるため、この翻訳が正確であることや[英語の公式ドキュメント](https://www.tensorflow.org/?hl=en)の最新の状態を反映したものであることを保証することはできません。この翻訳の品質を向上させるためのご意見をお持ちの方は、GitHubリポジトリ[tensorflow/docs](https://github.com/tensorflow/docs)にプルリクエストをお送りください。コミュニティによる翻訳やレビューに参加していただける方は、 [[email protected] メーリングリスト](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-ja)にご連絡ください。 ## はじめに自然言語モデルは、しばしば異なる文字セットを使った異なる言語を扱います。 Unicodeは、ほぼすべての言語で文字表示に使われている標準的なエンコードの仕組みです。各文字は、`0` から`0x10FFFF`までの一意の整数の [コードポイント（符号位置）](https://ja.wikipedia.org/wiki/%E7%AC%A6%E5%8F%B7%E7%82%B9) を使ってエンコードされます。1つの Unicode文字列は、ゼロ個以上のコードポイントのシーケンスです。このチュートリアルでは、TensorFlow での Unicode文字列の表現方法と、どうやって Unicode で標準的な文字列操作と同様の操作を行うかについて示します。また、スクリプト検出にもとづいて Unicode 文字列をトークンに分解します。 ``` import tensorflow as tf ``` ## `tf.string` データ型標準的な TensorFlow の`tf.string`型は、バイト列のテンソルを作ります。また、Unicode文字列はデフォルトでは utf-8 でエンコードされます。 ``` tf.constant(u"Thanks 😊") ``` バイト列が最小限の単位として扱われるため、`tf.string` 型のテンソルは可変長のバイト文字列を保持できます。また、文字列長はテンソルの次元には含まれません。 ``` tf.constant([u"You're", u"welcome!"]).shape ``` 注 : Pythonを使って文字列を構成するとき、v2.x系とv3.x系では Unicode の扱いが異なります。v2.x系では、Unicode文字列は上記のようにプレフィックス "u" で明示します。v3.x系では、デフォルトで Unicode としてエンコードされます。 ## Unicode 表現 TensorFlow での Unicode文字列表現は、2つの標準的な方法があります: * `string` スカラー — コードポイントのシーケンスは既知の [文字符合化方式](https://ja.wikipedia.org/wiki/%E6%96%87%E5%AD%97%E7%AC%A6%E5%8F%B7%E5%8C%96%E6%96%B9%E5%BC%8F) でエンコードされる * `int32` ベクトル — 各文字には単一のコードポイントが入るたとえば、以下3つはすべて Unicode文字列 `"语言処理 "`（中国語で「言語処理」を意味します）を表します。 ``` # Unicode文字列。UTF-8にエンコードされた文字列スカラーとして表される text_utf8 = tf.constant(u"语言处理") text_utf8 # Unicode文字列。UTF-16-BEにエンコードされた文字列スカラーとして表される text_utf16be = tf.constant(u"语言处理".encode("UTF-16-BE")) text_utf16be # Unicode文字列。Unicodeコードポイントのベクトルとして表される text_chars = tf.constant([ord(char) for char in u"语言处理"]) text_chars ``` ### Unicode 表現間の変換 TensorFlowでは、これらの異なる Unicode 表現間で変換する方法を用意しています。 * `tf.strings.unicode_decode`：エンコードされた文字列スカラーを、コードポイントのベクトルに変換します。 * `tf.strings.unicode_encode`：コードポイントのベクトルを、エンコードされた文字列スカラーに変換します。 * `tf.strings.unicode_transcode`：エンコードされた文字列スカラーを、別の文字コードに再エンコードします。 ``` tf.strings.unicode_decode(text_utf8, input_encoding='UTF-8') tf.strings.unicode_encode(text_chars, output_encoding='UTF-8') tf.strings.unicode_transcode(text_utf8, input_encoding='UTF8', output_encoding='UTF-16-BE') ``` ### バッチの次元複数の文字列をデコードする場合、各文字列の文字数が等しくない場合があります。返される結果は[`tf.RaggedTensor`](../../guide/ragged_tensor.ipynb)であり、最も内側の次元の長さは各文字列の文字数によって異なります。: ``` # Unicode文字列のバッチ。それぞれが、UTF8にエンコードされた文字列として表される batch_utf8 = [s.encode('UTF-8') for s in [u'hÃllo', u'What is the weather tomorrow', u'Göödnight', u'😊']] batch_chars_ragged = tf.strings.unicode_decode(batch_utf8, input_encoding='UTF-8') for sentence_chars in batch_chars_ragged.to_list(): print(sentence_chars) ``` この `tf.RaggedTensor` を直接使用することも、`tf.RaggedTensor.to_tensor` メソッドを使ってパディングを追加した密な `tf.Tensor` に変換するか、あるいは `tf.RaggedTensor.to_sparse` メソッドを使って `tf.SparseTensor` に変換することもできます。 ``` batch_chars_padded = batch_chars_ragged.to_tensor(default_value=-1) print(batch_chars_padded.numpy()) batch_chars_sparse = batch_chars_ragged.to_sparse() ``` 同じ長さの複数の文字列をエンコードする場合、`tf.Tensor` を入力値として使用できます。 ``` tf.strings.unicode_encode([[99, 97, 116], [100, 111, 103], [ 99, 111, 119]], output_encoding='UTF-8') ``` 可変長の複数の文字列をエンコードする場合、`tf.RaggedTensor` を入力値として使用する必要があります。 ``` tf.strings.unicode_encode(batch_chars_ragged, output_encoding='UTF-8') ``` パディングされた、あるいはスパースな複数の文字列を含むテンソルがある場合は、`unicode_encode` を呼び出す前に `tf.RaggedTensor` に変換します。 ``` tf.strings.unicode_encode( tf.RaggedTensor.from_sparse(batch_chars_sparse), output_encoding='UTF-8') tf.strings.unicode_encode( tf.RaggedTensor.from_tensor(batch_chars_padded, padding=-1), output_encoding='UTF-8') ``` ## Unicode 操作 ### 文字列長 `tf.strings.length` は、文字列長をどう計算するかを示す `unit` パラメーターが使えます。`unit` のデフォルトは `"BYTE"` ですが、`"UTF8_CHAR"` や `"UTF16_CHAR"` など他の値に設定して、エンコードされた `string` 文字列のUnicodeコードポイントの数を決めることができます。 ``` # 最後の絵文字は、UTF8で4バイトを占めることに注意する thanks = u'Thanks 😊'.encode('UTF-8') num_bytes = tf.strings.length(thanks).numpy() num_chars = tf.strings.length(thanks, unit='UTF8_CHAR').numpy() print('{} bytes; {} UTF-8 characters'.format(num_bytes, num_chars)) ``` ### 部分文字列同様に、 `tf.strings.substr` では " `unit`" パラメーターを使い、かつ "`pos`" および "`len`" パラメーターを指定することで、オフセットの種類を決めることができます。 ``` # デフォルト: unit='BYTE'. len=1 の場合、1バイトを返す tf.strings.substr(thanks, pos=7, len=1).numpy() # unit = 'UTF8_CHAR' を指定すると、単一の文字（この場合は4バイト）が返される print(tf.strings.substr(thanks, pos=7, len=1, unit='UTF8_CHAR').numpy()) ``` ### Unicode文字列を分割する `tf.strings.unicode_split` は、Unicode文字列を個々の文字に分割します。 ``` tf.strings.unicode_split(thanks, 'UTF-8').numpy() ``` ### 文字のバイトオフセット `tf.strings.unicode_decode` によって生成された文字テンソルを元の文字列に戻すには、各文字の開始位置のオフセットを知ることが役立ちます。`tf.strings.unicode_decode_with_offsets`メソッドは `unicode_decode` に似ていますが、各文字の開始オフセットを含む2番目のテンソルを返す点が異なります。 ``` codepoints, offsets = tf.strings.unicode_decode_with_offsets(u"🎈🎉🎊", 'UTF-8') for (codepoint, offset) in zip(codepoints.numpy(), offsets.numpy()): print("At byte offset {}: codepoint {}".format(offset, codepoint)) ``` ## Unicode スクリプト各Unicodeコードポイントは、[スクリプト](https://en.wikipedia.org/wiki/Script_%28Unicode%29) として知られる単一のコードポイント集合に属しています。文字スクリプトは、その文字がどの言語なのかを判断するのに役立ちます。たとえば、「Б」がキリル文字であることがわかれば、その文字を含むテキストはロシア語やウクライナ語などのスラブ言語である可能性が高いことがわかります。 TensorFlowは、あるコードポイントがどのスクリプトかを返す `tf.strings.unicode_script` を提供しています。戻り値のスクリプトコードは、[International Components for Unicode](http://site.icu-project.org/home) (ICU) の [`UScriptCode`](http://icu-project.org/apiref/icu4c/uscript_8h.html) に対応する `int32` 値になります。 ``` uscript = tf.strings.unicode_script([33464, 1041]) # ['芸', 'Б'] print(uscript.numpy()) # [17, 8] == [USCRIPT_HAN, USCRIPT_CYRILLIC] ``` `tf.strings.unicode_script` は、多次元のコードポイントの `tf.Tensors` や ` tf.RaggedTensor` にも適用できます。: ``` print(tf.strings.unicode_script(batch_chars_ragged)) ``` ## 例：シンプルなセグメンテーションセグメンテーションは、テキストを単語のような粒度に分割するタスクです。これは、スペース文字を使用して単語を区切れる場合には簡単に行えますが、一部の言語（中国語や日本語など）はスペースを使いませんし、また、一部の言語（ドイツ語など）には、意味を解析するために分ける必要がある、単語を結合した長い複合語があります。Webテキストでは、「NY株価」（ニューヨーク株価）のように、異なる言語とスクリプトがしばしば混在しています。単語の境界を推定してスクリプトを変更することにより、（MLモデルを実装せずに）非常に大まかなセグメンテーションを実行できます。これは、上記の「NY株価」の例のような文字列に対して機能します。さまざまな言語のスペース文字はすべて、実際のテキストとは異なる特別なスクリプトコードである USCRIPT_COMMON として分類されるため、スペースを使用するほとんどの言語でも機能します。 ``` # dtype: string; shape: [num_sentences] # # 処理する文章。この行を編集して、さまざまな入力を試してみてください！ sentence_texts = [u'Hello, world.', u'世界こんにちは'] ``` 最初に、文章を文字ごとのコードポイントにデコードし、それから各文字のスクリプトコード（識別子）を調べます。 ``` # dtype: int32; shape: [num_sentences, (num_chars_per_sentence)] # # sentence_char_codepoint[i, j] は、i番目の文のn番目の文字のコードポイント sentence_char_codepoint = tf.strings.unicode_decode(sentence_texts, 'UTF-8') print(sentence_char_codepoint) # dtype: int32; shape: [num_sentences, (num_chars_per_sentence)] # # sentence_char_scripts[i, j] は、i番目の文のn番目の文字のスクリプトコード sentence_char_script = tf.strings.unicode_script(sentence_char_codepoint) print(sentence_char_script) ``` 次に、これらのスクリプトコードを使って、単語の境界を追加すべき場所を決めます。前の文字とスクリプトコードが異なるそれぞれの文字の先頭に、単語の境界を追加します。: ``` # dtype: bool; shape: [num_sentences, (num_chars_per_sentence)] # # sentence_char_starts_word[i, j] は、i番目の文のn番目の文字が単語の始まりである場合にTrue sentence_char_starts_word = tf.concat( [tf.fill([sentence_char_script.nrows(), 1], True), tf.not_equal(sentence_char_script[:, 1:], sentence_char_script[:, :-1])], axis=1) # dtype: int64; shape: [num_words] # # word_starts[i] は、i番目の単語の始まりである文字のインデックス # （すべての文がフラット化された文字リスト） word_starts = tf.squeeze(tf.where(sentence_char_starts_word.values), axis=1) print(word_starts) ``` そして、これらの目印（開始オフセット）を使って、各単語ごとの文字リストを含む `RaggedTensor` を作成します。: ``` # dtype: int32; shape: [num_words, (num_chars_per_word)] # # word_char_codepoint[i, j] は、i番目の単語のn番目の文字のコードポイント word_char_codepoint = tf.RaggedTensor.from_row_starts( values=sentence_char_codepoint.values, row_starts=word_starts) print(word_char_codepoint) ``` 最後に、`RaggedTensor` をコードポイント単位でセグメント化して、文章に戻します。: ``` # dtype: int64; shape: [num_sentences] # # sentence_num_words[i] は、i番目の文の単語数 sentence_num_words = tf.reduce_sum( tf.cast(sentence_char_starts_word, tf.int64), axis=1) # dtype: int32; shape: [num_sentences, (num_words_per_sentence), (num_chars_per_word)] # # sentence_word_char_codepoint[i, j, k] は、i番目の文のn番目の単語のk番目の文字のコードポイント sentence_word_char_codepoint = tf.RaggedTensor.from_row_lengths( values=word_char_codepoint, row_lengths=sentence_num_words) print(sentence_word_char_codepoint) ``` 最終的な結果を見やすくするために、UTF-8文字列にエンコードします。: ``` tf.strings.unicode_encode(sentence_word_char_codepoint, 'UTF-8').to_list() ```	github_jupyter
``` import warnings warnings.filterwarnings('ignore') %matplotlib notebook import pandas as pd import numpy as np from util import * from sklearn.model_selection import train_test_split from sklearn import metrics from skater.core.global_interpretation.interpretable_models.brlc import BRLC from skater.core.global_interpretation.interpretable_models.bigdatabrlc import BigDataBRLC # Read the datasets df = pd.read_csv('LoanStats3a.csv', skiprows=1) df = df[df.loan_status.isin(['Fully Paid','Charged Off'])] #remove columns that are entirely null for column in df.columns: if df[column].isnull().mean() >= .99: df = df.drop(column, 1) #remove columns with constant values for column in df.columns: if df[column].unique().shape[0] == 1: df = df.drop(column, 1) ``` ### The Data ``` print("The data has {0} rows and {1} fields".format(*df.shape)) df.head(1).T # Quick Summary df.describe() df['int_rate'] = df['int_rate'].apply(process_int_rate) df['term'] = df['term'].apply(process_term) df['emp_length'] = df['emp_length'].apply(process_emp_length) df['revol_util'] = df['revol_util'].apply(process_revol_util) df['pub_rec_bankruptcies'] = df['pub_rec_bankruptcies'].fillna(0) df.head(2).T %matplotlib inline df.loan_status.value_counts().plot(kind='bar') ``` ### DTI also a factor ``` def_by_dti = df.set_index('dti').groupby(by=(lambda x: round_to_nearest(x, 5), 'loan_status'))['loan_amnt'].count().unstack() def_by_dti = (def_by_dti['Charged Off'] / def_by_dti.sum(axis=1)) ax = def_by_dti.plot(kind = 'bar') ``` ### Small business loans are much riskier ``` def_rates_by_categorical(df, 'purpose', with_variance=True) ``` ### (Light) Feature Engineering ``` df_ = df.copy() domain_columns = ['loan_amnt', 'term', 'annual_inc', 'installment_over_income', 'has_employer_info', 'is_employed', 'dti', 'inq_last_6mths', 'delinq_2yrs', 'open_acc', 'int_rate', 'revol_util', 'pub_rec_bankruptcies', 'revol_bal', 'requested_minus_funded', 'debt_to_income' ] #features to engineer df_['requested_minus_funded'] = df_['loan_amnt'] - df_['funded_amnt'] df_['has_employer_info'] = df_['emp_title'].isnull() df_['installment_over_income'] = df_['installment'] / df_['annual_inc'] df_['is_employed'] = df_['emp_length'].isnull() df_['debt_to_income'] = (df_['revol_bal'] + df_['funded_amnt']) / df['annual_inc'] #dummy section dummy_columns = ['home_ownership'] #'grade', 'addr_state' for column in dummy_columns: dummies = pd.get_dummies(df_[column], prefix="{}_is".format(column)) columns_to_add = dummies.columns.values[:-1] dummies = dummies[columns_to_add] df_ = df_.join(dummies) domain_columns.extend(columns_to_add) df_["emp_title"] = df_["emp_title"].fillna("None") df_['target'] = df_['loan_status'].apply(lambda x: 0 if x == 'Charged Off' else 1) domain_columns = list(set(domain_columns)) from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler scaler = StandardScaler() X = scaler.fit_transform(df_[domain_columns].values) X_df = pd.DataFrame(X) # input_data = df_[domain_columns] # input_data.head(2) # input_data["has_employer_info"] = input_data["has_employer_info"].astype('category') # input_data["has_employer_info_Encoded"] = input_data["has_employer_info"].cat.codes # input_data["is_employed"] = input_data["is_employed"].astype('category') # input_data["is_employed_Encoded"] = input_data["is_employed"].cat.codes # input_data = input_data.drop(['has_employer_info', 'is_employed'], axis=1) # # # Remove NaN values # input_data_clean = input_data.dropna() # input_data_clean = input_data_clean[["is_employed_Encoded", "has_employer_info_Encoded"]] # print(input_data_clean.dtypes) # input_data_clean.head(2) # Default test split-size = 0.25 y = df_['target'] Xtrain, Xtest, ytrain, ytest = train_test_split(X_df, y) # split # Target Labels: 1:positive 0:negative np.unique(ytrain) print(len(Xtrain)) print(type(Xtrain)) print(type(ytrain)) Xtrain.head() sbrl_big = BigDataBRLC(sub_sample_percentage=0.1, min_rule_len=1, max_rule_len=3, iterations=10000, n_chains=3, surrogate_estimator="SVM", drop_features=True) n_x, n_y = sbrl_big.subsample(Xtrain, ytrain, pos_label=1) print(len(n_x)) # Create an instance of the estimator from timeit import default_timer as timer from datetime import timedelta start = timer() # Train a model, by default discretizer is enabled. So, you wish to exclude features then exclude them using # the undiscretize_feature_list parameter model = sbrl_big.fit(n_x, n_y, bin_labels='default') elapsed = (timer() - start) print(timedelta(seconds=round(elapsed))) # Features considered sbrl_big.feature_names sbrl_big.print_model() sbrl_big.save_model("model1.pkl") # quick look at the test set Xtest[0:3] # Discretize the testing set similar to train set new_X_test = sbrl_big.discretizer(Xtest, n_x.columns, labels_for_bin='default') #ytest = n_y new_X_test.head(2) print(new_X_test.shape[0]) print(len(ytest)) new_X_train = sbrl_big.discretizer(Xtrain, n_x.columns, labels_for_bin='default') print(new_X_train.shape[0]) print(len(ytrain)) ``` ### Computing performance metrics for BRLC for train and test ``` results_train_sbrl = sbrl_big.predict_proba(new_X_train) fpr_sbrl, tpr_sbrl, thresholds_sbrl = metrics.roc_curve(ytrain, results_train_sbrl[1], pos_label=1) roc_auc_sbrl = metrics.auc(fpr_sbrl, tpr_sbrl) print("AUC-ROC using SBRL(Train): {}".format(roc_auc_sbrl)) print("Accuracy(Train): {}".format(metrics.accuracy_score(ytrain, sbrl_big.predict(new_X_train)[1]))) print("-----------------------------------------------------------------\n") results_test_sbrl = sbrl_big.predict_proba(new_X_test) fpr_sbrl, tpr_sbrl, thresholds_sbrl = metrics.roc_curve(ytest ,results_test_sbrl[1], pos_label=1) roc_auc_sbrl = metrics.auc(fpr_sbrl, tpr_sbrl) print("AUC-ROC using SBRL(Test): {}".format(roc_auc_sbrl)) print("Accuracy(Test): {}".format(metrics.accuracy_score(ytest, sbrl_big.predict(new_X_test)[1]))) ``` ### Evaluating performance of a black box classifier ``` from sklearn.svm import LinearSVC from sklearn.calibration import CalibratedClassifierCV svm = LinearSVC(random_state=0) est = CalibratedClassifierCV(svm) est.fit(Xtrain, ytrain) results_train_svm = pd.DataFrame(est.predict_proba(Xtrain))[1] results_test_svm = pd.DataFrame(est.predict_proba(Xtest))[1] fpr_svm, tpr_svm, thresholds_svm = metrics.roc_curve(ytrain, results_train_svm, pos_label=1) roc_auc_svm = metrics.auc(fpr_svm, tpr_svm) print("AUC-ROC using SVM(Train): {}".format(roc_auc_svm)) print("Accuracy(Test): {}".format(est.score(Xtrain, ytrain))) print("-----------------------------------------------------------------\n") fpr_svm, tpr_svm, thresholds_svm = metrics.roc_curve(ytest, results_test_svm, pos_label=1) roc_auc_svm = metrics.auc(fpr_svm, tpr_svm) print("AUC-ROC using SVM(Test): {}".format(roc_auc_svm)) print("Accuracy(Test): {}".format(est.score(Xtest, ytest))) ```	github_jupyter
``` # This Python 3 environment comes with many helpful analytics libraries installed # It is defined by the kaggle/python Docker image: https://github.com/kaggle/docker-python # For example, here's several helpful packages to load import numpy as np # linear algebra import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv) # Input data files are available in the read-only "../input/" directory # For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory import os for dirname, _, filenames in os.walk('/kaggle/input'): for filename in filenames: print(os.path.join(dirname, filename)) # You can write up to 5GB to the current directory (/kaggle/working/) that gets preserved as output when you create a version using "Save & Run All" # You can also write temporary files to /kaggle/temp/, but they won't be saved outside of the current session import sklearn import matplotlib.pyplot as plt %matplotlib inline import pandas from sklearn.model_selection import train_test_split import numpy Tweet= pd.read_csv("/kaggle/input/twitter-airline-sentiment/Tweets.csv") Tweet.head() import re import nltk from nltk.corpus import stopwords # 数据清洗 def tweet_to_words(raw_tweet): letters_only = re.sub("[^a-zA-Z]", " ",raw_tweet) words = letters_only.lower().split() stops = set(stopwords.words("english")) meaningful_words = [w for w in words if not w in stops] return( " ".join( meaningful_words )) def clean_tweet_length(raw_tweet): letters_only = re.sub("[^a-zA-Z]", " ",raw_tweet) words = letters_only.lower().split() stops = set(stopwords.words("english")) meaningful_words = [w for w in words if not w in stops] return(len(meaningful_words)) # 将标签转换成数字 Tweet['sentiment']=Tweet['airline_sentiment'].apply(lambda x: 0 if x=='negative' else 1) Tweet.fillna('-1', inplace=True) #用的小数据集 Tweet['clean_tweet'] = Tweet[['negativereason', 'name', 'text']].apply(lambda x: ' '.join(x), axis=1) Tweet['clean_tweet']=Tweet['clean_tweet'].apply(lambda x: tweet_to_words(x)) Tweet['Tweet_length']=Tweet['text'].apply(lambda x: clean_tweet_length(x)) Tweet.head() train,test = train_test_split(Tweet,test_size=0.2,random_state=42) # 转换成list，方便特征提取 train_clean_tweet=[] for tweet in train['clean_tweet']: train_clean_tweet.append(tweet) test_clean_tweet=[] for tweet in test['clean_tweet']: test_clean_tweet.append(tweet) from sklearn.feature_extraction.text import CountVectorizer v = CountVectorizer(analyzer = "word") train_features= v.fit_transform(train_clean_tweet) test_features=v.transform(test_clean_tweet) from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier from sklearn.svm import SVC, LinearSVC, NuSVC from sklearn.tree import DecisionTreeClassifier from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier, GradientBoostingClassifier from sklearn.naive_bayes import GaussianNB from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis from sklearn.metrics import accuracy_score from xgboost import XGBClassifier from sklearn.metrics import accuracy_score from sklearn.neural_network import MLPClassifier from sklearn.ensemble import GradientBoostingClassifier from sklearn.discriminant_analysis import LinearDiscriminantAnalysis import matplotlib.pyplot as plt from itertools import cycle from sklearn import svm, datasets from sklearn.metrics import roc_curve, auc from sklearn.model_selection import train_test_split from sklearn.preprocessing import label_binarize from sklearn.multiclass import OneVsRestClassifier from scipy import interp from sklearn.metrics import roc_auc_score from sklearn.metrics import classification_report Classifiers = [ LogisticRegression(C=0.000000001,solver='liblinear',max_iter=200), KNeighborsClassifier(3), SVC(kernel="rbf", C=0.025, probability=True), DecisionTreeClassifier(), RandomForestClassifier(n_estimators=200), AdaBoostClassifier(), GaussianNB(), XGBClassifier(), MLPClassifier(solver='sgd', alpha=1e-5, hidden_layer_sizes=(5, 2), random_state=1, max_iter=500), GradientBoostingClassifier(random_state=0) ]#gpu不能一次性加载这么多模型兵训练 dense_features=train_features.toarray() dense_test= test_features.toarray() Accuracy=[] Model=[] for classifier in Classifiers: try: fit = classifier.fit(train_features,train['sentiment']) pred = fit.predict(test_features) except Exception: fit = classifier.fit(dense_features,train['sentiment']) pred = fit.predict(dense_test) predictions = [round(value) for value in pred] accuracy = accuracy_score(test['sentiment'],predictions) print(classification_report(test.sentiment, predictions, labels=[0,2,4])) Accuracy.append(accuracy) Model.append(classifier.__class__.__name__) print('Accuracy of '+classifier.__class__.__name__+ ' is: '+str(accuracy)) ```	github_jupyter
# ResNet-101 on CIFAR-10 ### Imports ``` import numpy as np import torch import torch.nn as nn import torch.nn.functional as F from torchvision import datasets from torchvision import transforms from torch.utils.data import DataLoader if torch.cuda.is_available(): torch.backends.cudnn.deterministic = True ``` ### Settings and Dataset ``` # Device device = torch.device("cuda" if torch.cuda.is_available() else "cpu") # Hyperparameters random_seed = 1 learning_rate = 0.001 num_epochs = 10 batch_size = 128 torch.manual_seed(random_seed) # Architecture num_features = 784 num_classes = 10 # Data train_dataset = datasets.CIFAR10(root='data', train=True, transform=transforms.ToTensor(), download=True) test_dataset = datasets.CIFAR10(root='data', train=False, transform=transforms.ToTensor()) train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True) test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False) # Checking the dataset for images, labels in train_loader: print('Image batch dimensions:', images.shape) print('Image label dimensions:', labels.shape) break ``` ### Model ``` def conv3x3(in_planes, out_planes, stride=1): """3x3 convolution with padding""" return nn.Conv2d(in_planes, out_planes, kernel_size=3, stride=stride, padding=1, bias=False) class Bottleneck(nn.Module): expansion = 4 def __init__(self, inplanes, planes, stride=1, downsample=None): super(Bottleneck, self).__init__() self.conv1 = nn.Conv2d(inplanes, planes, kernel_size=1, bias=False) self.bn1 = nn.BatchNorm2d(planes) self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=stride, padding=1, bias=False) self.bn2 = nn.BatchNorm2d(planes) self.conv3 = nn.Conv2d(planes, planes * 4, kernel_size=1, bias=False) self.bn3 = nn.BatchNorm2d(planes * 4) self.relu = nn.ReLU(inplace=True) self.downsample = downsample self.stride = stride def forward(self, x): residual = x out = self.conv1(x) out = self.bn1(out) out = self.relu(out) out = self.conv2(out) out = self.bn2(out) out = self.relu(out) out = self.conv3(out) out = self.bn3(out) if self.downsample is not None: residual = self.downsample(x) out += residual out = self.relu(out) return out class ResNet(nn.Module): def __init__(self, block, layers, num_classes, grayscale): self.inplanes = 64 if grayscale: in_dim = 1 else: in_dim = 3 super(ResNet, self).__init__() self.conv1 = nn.Conv2d(in_dim, 64, kernel_size=7, stride=2, padding=3, bias=False) self.bn1 = nn.BatchNorm2d(64) self.relu = nn.ReLU(inplace=True) self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1) self.layer1 = self._make_layer(block, 64, layers[0]) self.layer2 = self._make_layer(block, 128, layers[1], stride=2) self.layer3 = self._make_layer(block, 256, layers[2], stride=2) self.layer4 = self._make_layer(block, 512, layers[3], stride=2) self.avgpool = nn.AvgPool2d(7, stride=1, padding=2) self.fc = nn.Linear(2048, num_classes) for m in self.modules(): if isinstance(m, nn.Conv2d): n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels m.weight.data.normal_(0, (2. / n)*.5) elif isinstance(m, nn.BatchNorm2d): m.weight.data.fill_(1) m.bias.data.zero_() def _make_layer(self, block, planes, blocks, stride=1): downsample = None if stride != 1 or self.inplanes != planes block.expansion: downsample = nn.Sequential( nn.Conv2d(self.inplanes, planes * block.expansion, kernel_size=1, stride=stride, bias=False), nn.BatchNorm2d(planes * block.expansion)) layers = [] layers.append(block(self.inplanes, planes, stride, downsample)) self.inplanes = planes * block.expansion for i in range(1, blocks): layers.append(block(self.inplanes, planes)) return nn.Sequential(layers) def forward(self, x): x = self.conv1(x) x = self.bn1(x) x = self.relu(x) x = self.maxpool(x) x = self.layer1(x) x = self.layer2(x) x = self.layer3(x) x = self.layer4(x) x = x.view(x.size(0), -1) logits = self.fc(x) probas = F.softmax(logits, dim=1) return logits, probas def ResNet101(num_classes): model = ResNet(block=Bottleneck, layers=[3, 4, 23, 3], num_classes=num_classes, grayscale=False) return model model = ResNet101(num_classes) model.to(device) optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate) ``` ### Training ``` def compute_accuracy(model, data_loader): correct_pred, num_examples = 0, 0 for i, (features, targets) in enumerate(data_loader): features = features.to(device) targets = targets.to(device) logits, probas = model(features) _, predicted_labels = torch.max(probas, 1) num_examples += targets.size(0) correct_pred += (predicted_labels == targets).sum() return correct_pred.float()/num_examples 100 for epoch in range(num_epochs): model.train() for batch_idx, (features, targets) in enumerate(train_loader): features = features.to(device) targets = targets.to(device) # Forward and Backprop logits, probas = model(features) cost = F.cross_entropy(logits, targets) optimizer.zero_grad() cost.backward() # update model paramets optimizer.step() # Logging if not batch_idx % 50: print ('Epoch: %03d/%03d \| Batch %04d/%04d \| Cost: %.4f' %(epoch+1, num_epochs, batch_idx, len(train_loader), cost)) model.eval() with torch.set_grad_enabled(False): print('Epoch: %03d/%03d \| Train: %.3f%% ' %( epoch+1, num_epochs, compute_accuracy(model, train_loader))) ``` ### Evaluation ``` with torch.set_grad_enabled(False): print('Test accuracy: %.2f%%' % (compute_accuracy(model, test_loader))) ```	github_jupyter
``` import sys sys.path.append("..") # Adds higher directory to python modules path. from pathlib import Path import glob import numpy as np import tensorflow as tf import pickle import matplotlib.pyplot as plt import random import pickle import os import config import data import random from natsort import natsorted import lfp import gym arm = 'UR5' TEST_DATASET = "UR5_slow_gripper_test" print('Using local setup') WORKING_PATH = Path().absolute().parent print(f'Working path: {WORKING_PATH}') os.chdir(WORKING_PATH) STORAGE_PATH = WORKING_PATH print(f'Storage path: {STORAGE_PATH}') TRAIN_DATA_PATHS = [STORAGE_PATH/'data'/x for x in ["pybullet/UR5" , "pybullet/UR5_high_transition" ,"pybullet/UR5_slow_gripper"]] TEST_DATA_PATH = STORAGE_PATH/'data'/TEST_DATASET import roboticsPlayroomPybullet env = gym.make('UR5PlayAbsRPY1Obj-v0') env.render('human') _ = env.reset() env.render('playback') env.instance.calc_state()['observation'][0:7] env.step(np.array([ -1.91859640e-02, 1.93180365e-01, 0.2, 0.0, 0.0, 0.0, -7.02553025e-06])) plt.figure(figsize = (20,20)) plt.imshow(env.instance.calc_state()['img'][:,:,:]) ``` # Replays the teleop data - This little loop of code replays the teleop data, and optionally saves the images to create an image dataset - Every 30 steps it resets state, because minor errors in the physics compound ``` TRAIN_DATA_PATHS for DIR in TRAIN_DATA_PATHS: DIR = str(DIR) # DIR = str(TRAIN_DATA_PATHS[0]) # glob/natsorted prefer strings obs_act_path = DIR+'/obs_act_etc/' o, a, ag = [], [], [] for demo in natsorted(os.listdir(obs_act_path)): traj = np.load(obs_act_path+demo+'/data.npz') print(demo, len(traj['obs'])) o.append(traj['obs']), a.append(traj['acts']), ag.append(traj['achieved_goals']) print('________________________', len(np.vstack(o))) o, a, ag = np.vstack(o), np.vstack(a), np.vstack(ag) import time jp = traj['joint_poses'] ag = traj['achieved_goals'] for i in range(0, len(jp)): time.sleep(0.02) env.instance.reset_arm_joints(env.instance.arm, jp[i,:]) env.instance.reset_object_pos(ag[]) o.shape env.reset(o[0,:]) d = a for i in range(0, d.shape[1]): plt.hist(d[:,i], bins=1000) #plt.xlim(-0.2,0.2) plt.show() d = a - o[:, :7] for i in range(0, d.shape[1]): plt.hist(d[:,i], bins=1000) plt.xlim(-0.2,0.2) plt.show() d = d[1:] - d[:-1] d = o[150000:150020] f = a[150000:150020] for i in range(0, d.shape[1]): plt.plot(np.linspace(0,len(d),len(d)), d[:,i]) plt.plot(np.linspace(0,len(d),len(d)), f[:,i]) plt.show() import scipy.misc from IPython.display import display, clear_output keys = ['obs', 'acts', 'achieved_goals', 'joint_poses', 'target_poses', 'acts_quat', 'acts_rpy_rel', 'velocities', 'obs_quat'] # for DIR in TRAIN_DATA_PATHS: DIR = str(DIR) # glob/natsorted prefer strings obs_act_path = DIR+'/obs_act_etc/' for demo in natsorted(os.listdir(obs_act_path)): print(demo) start_points = natsorted(glob.glob(DIR+'/states_and_ims/'+str(demo)+'/env_states/.bullet')) traj = np.load(obs_act_path+demo+'/data.npz') d = {k:traj[k] for k in keys} acts = d['acts'] set_len = len(acts) start = 0 end= min(start+30, set_len) print(DIR+'/states_and_ims/'+str(demo)+'/ims') try: os.makedirs(DIR+'/states_and_ims/'+str(demo)+'/ims') except: pass for start_point in start_points: env.p.restoreState(fileName=start_point) env.instance.updateToggles() # need to do it when restoring, colors not carried over for i in range(start, end): o,r,_,_ = env.step(acts[i]) start += 30 end = min(start+30, set_len) import scipy.misc from IPython.display import display, clear_output keys = ['obs', 'acts', 'achieved_goals', 'joint_poses', 'target_poses', 'acts_quat', 'acts_rpy_rel', 'velocities', 'obs_quat', 'gripper_proprioception'] # for DIR in TRAIN_DATA_PATHS: obs_act_path = DIR/'obs_act_etc/' obs_act_path2 = DIR + 'obs_act_etc2/' for demo in natsorted(os.listdir(obs_act_path)): print(demo) start_points = natsorted(glob.glob(DIR+'/states_and_ims/'+str(demo)+'/env_states/.bullet')) traj = np.load(obs_act_path+demo+'/data.npz') d = {k:traj[k] for k in keys} acts = d['acts'] set_len = len(acts) start = 0 end= min(start+30, set_len) print(DIR+'/states_and_ims/'+str(demo)+'/ims') try: os.makedirs(DIR+'/states_and_ims/'+str(demo)+'/ims') except: pass for start_point in start_points: env.p.restoreState(fileName=start_point) env.panda.updateToggles() # need to do it when restoring, colors not carried over for i in range(start, end): #scipy.misc.imsave(DIR+'/states_and_ims/'+str(demo)+'/ims/'+str(i)+'.jpg', o['img']) o,r,_,_ = env.step(acts[i]) # clear_output(wait=True) # fig = plt.imshow(scipy.misc.imread(DIR+'/states_and_ims/'+str(demo)+'/ims/'+str(i)+'.jpg')) # plt.show() #time.sleep(0.05) start += 30 end = min(start+30, set_len) # try: # os.makedirs(obs_act_path2+demo) # except: # pass # np.savez(obs_act_path2+demo+'/data', obs=d['obs'], acts=d['acts'], achieved_goals=d['achieved_goals'], # joint_poses=d['joint_poses'],target_poses=d['target_poses'], acts_quat=d['acts_quat'], # acts_rpy_rel=d['acts_rpy_rel'], velocities = d['velocities'], # obs_quat=d['obs_quat'], gripper_proprioception=d['gripper_proprioception']) env.p.restoreState(fileName=path) vid_path = 'output/videos/trajectory.mp4' with imageio.get_writer(vid_path, mode='I') as writer: for i in range(start, start+WINDOW_SIZE): o ,r, d, _ = env.step(actions[i,:]) writer.append_data(o['img']) clear_output(wait=True) fig = plt.imshow(o['img']) plt.show() keys = ['obs', 'acts', 'achieved_goals', 'joint_poses', 'target_poses', 'acts_quat', 'acts_rpy_rel', 'velocities', 'obs_quat', 'gripper_proprioception'] for DIR in [TRAIN_DATA_PATHS[1]]: obs_act_path = os.path.join(DIR, 'obs_act_etc/') for demo in natsorted(os.listdir(obs_act_path)): if int(demo)>18: print(demo) start_points = natsorted(glob.glob(str(DIR/'states_and_ims'/str(demo)/'env_states/.bullet'))) traj = np.load(obs_act_path+demo+'/data.npz') d = {k:traj[k] for k in keys} acts = d['acts'] set_len = len(acts) start = 0 end= min(start+30, set_len) gripper_proprioception = [] for start_point in start_points: env.p.restoreState(fileName=start_point) for i in range(start, end): o,r,_,_ = env.step(acts[i]) #print(d['gripper_proprioception'][i]) time.sleep(0.015) start += 30 end = min(start+30, set_len) #dataset, cnt = data.create_single_dataset(dataset_path) def load_data(path, keys): dataset = {k:[] for k in keys+['sequence_index','sequence_id']} obs_act_path = os.path.join(path, 'obs_act_etc/') for demo in natsorted(os.listdir(obs_act_path)): print(demo) traj = np.load(obs_act_path+demo+'/data.npz') for k in keys: d = traj[k] if len(d.shape) < 2: d = np.expand_dims(d, axis = 1) # was N, should be N,1 dataset[k].append(d.astype(np.float32)) timesteps = len(traj['obs']) dataset['sequence_index'].append(np.arange(timesteps, dtype=np.int32).reshape(-1, 1)) dataset['sequence_id'].append(np.full(timesteps, fill_value=int(demo), dtype=np.int32).reshape(-1, 1)) # convert to numpy for k in keys+['sequence_index','sequence_id']: dataset[k] = np.vstack(dataset[k]) return dataset keys = ['obs', 'acts', 'achieved_goals', 'joint_poses', 'target_poses', 'acts_rpy', 'acts_rpy_rel', 'velocities', 'obs_rpy', 'obs_rpy_inc_obj', 'gripper_proprioception'] dataset = load_data(UR5, keys) #transition_dataset = load_data(UR5_25, keys) import tensorflow_probability as tfp tfd = tfp.distributions tfb = tfp.bijectors tfpl = tfp.layers scaling = np.array([256.0/4, 256.0/2]).astype(np.float32) def logistic_mixture(inputs, quantized = True): weightings, mu, scale = inputs print(mu.shape, scaling.shape, scale.shape, weightings.shape) mu = munp.expand_dims(scaling,1) print(mu) dist = tfd.Logistic(loc=mu, scale=scale) if quantized: dist = tfd.QuantizedDistribution( distribution=tfd.TransformedDistribution( distribution=dist, bijector=tfb.Shift(shift=-0.5)), low=-128., high=128. ) mixture_dist = tfd.MixtureSameFamily( mixture_distribution=tfd.Categorical(logits=weightings), components_distribution=dist, validate_args=True ) print(mixture_dist) if quantized: quantized_scale = 1/scaling mixture_dist = tfd.TransformedDistribution( distribution=mixture_dist, bijector=tfb.Scale(scale=quantized_scale) ) return mixture_dist mu = np.array([[[-1.5, 0.4, 0.4],[-0.2, 0.3, 0.3]]]).astype(np.float32) std = np.array([[[1.0,1.0,1],[1.0,1.0,1]]]).astype(np.float32) weights = np.array([[[1,1,1],[1,1,1]]]).astype(np.float32) m = logistic_mixture((weights,mu,std)) #m = logistic_mixture(([1], [0.06], [1])) m.sample() samples = np.array([m.sample().numpy() for i in range(0,100)]) samples.shape samples[:,0] plt.hist(np.array(samples[:,:,0]), bins=100) plt.plot(np.linspace(-0.5, 0.5, 100),m.log_prob(np.linspace(-0.5, 0.5, 100))) # Coverage analysis np.set_printoptions(suppress=True) ag = dataset['achieved_goals'] t_ag = transition_dataset['achieved_goals'] def see_diff(ag): diff_ag = abs(np.sum(ag[1:]-ag[:-1],axis = -1)) print(sum(diff_ag == 0)) plt.plot(diff_ag) see_diff(ag[:150000]) see_diff(t_ag[:150000]) mins = np.min(dataset['achieved_goals'], axis = 0) maxes = np.max(dataset['achieved_goals'], axis = 0) bins = np.linspace(mins,maxes+0.01, 11) idx = 0 qs = [] for idx in range(0,ag.shape[1]): quantiles = np.digitize(dataset['achieved_goals'][:,idx], bins[:,idx]) qs.append(quantiles) qs = np.array(qs).T qs.shape np.unique(qs, axis=0).shape[0] from tqdm import tqdm step2 = [] count2 = [] for i in tqdm(np.linspace(1, len(qs), 10)): i = int(i) step2.append(i) count2.append(np.unique(qs[:i], axis=0).shape[0]) import matplotlib.pyplot as plt #plt.plot(step, count) plt.plot(step2, count2) import matplotlib.pyplot as plt plt.plot(step, count) d[''] print(obs_act_path2+demo) try: os.makedirs(obs_act_path2+demo) except: pass np.savez(obs_act_path2+demo+'/data', obs=d['obs'], acts=d['acts'], achieved_goals=d['achieved_goals'], joint_poses=d['joint_poses'],target_poses=d['target_poses'], acts_rpy=d['acts_rpy'], acts_rpy_rel=d['acts_rpy_rel'], velocities = d['velocities'], obs_rpy=d['obs_rpy'], gripper_proprioception=d['gripper_proprioception']) d['obs'] np.load(obs_act_path2+demo+'/data.npz', allow_pickle=True)['obs'] os.make_dirs(obs_act_path2) env.step(acts[i]) print(start_points) rpy_obs = 'obs_rpy' #'rpy_obs' def load_data(path, keys): dataset = {k:[] for k in keys+['sequence_index','sequence_id']} obs_act_path = os.path.join(path, 'obs_act_etc/') for demo in natsorted(os.listdir(obs_act_path)): print(demo) traj = np.load(obs_act_path+demo+'/data.npz') for k in keys: dataset[k].append(traj[k].astype(np.float32)) timesteps = len(traj['obs']) dataset['sequence_index'].append(np.arange(timesteps, dtype=np.int32).reshape(-1, 1)) dataset['sequence_id'].append(np.full(timesteps, fill_value=int(demo), dtype=np.int32).reshape(-1, 1)) # convert to numpy for k in keys+['sequence_index','sequence_id']: dataset[k] = np.vstack(dataset[k]) return dataset keys = ['obs', 'acts', 'achieved_goals', 'joint_poses', 'target_poses', 'acts_rpy', 'acts_rpy_rel', 'velocities', 'obs_rpy'] dataset = load_data(PYBULLET_DATA_DIR, keys) obs_act_path = os.path.join(path, 'obs_act_etc/') starts = [] idxs = [] fs = [] for f in natsorted(os.listdir(obs_act_path)): potential_start_points = glob.glob(TEST_DIR+'/states_and_ims/'+str(f)+'/env_states/.bullet') potential_start_idxs = [int(x.replace('.bullet','').replace(f"{TEST_DIR}/states_and_ims/{str(f)}/env_states/", "")) for x in potential_start_points] folder = [f]len(potential_start_idxs) [starts.append(x) for x in potential_start_points], [idxs.append(x) for x in potential_start_idxs], [fs.append(x) for x in folder] descriptions = { 1: 'lift up', 2: 'take down', 3: 'door left', 4: 'door right', 5: 'drawer in', 6: 'drawer out', 7: 'pick place', 8: 'press button', 9: 'dial on', 10: 'dial off', 11: 'rotate block left', 12: 'rotate block right', 13: 'stand up block', 14: 'knock down block', 15: 'block in cupboard right', 16: 'block in cupboard left', 17: 'block in drawer', 18: 'block out of drawer', 19: 'block out of cupboard right', 20: 'block out of cupboard left', } trajectory_labels = {} done = [] import time for i in range(0,len(starts)): if starts[i] not in done: data = np.load(TEST_DIR+'obs_act_etc/'+str(fs[i])+'/data.npz') traj_len = 40#random.randint(40,50) end = min(len(data['acts'])-1,idxs[i]+traj_len ) acts = data['acts_rpy'][idxs[i]:end] value = "r" while value == "r": env.p.restoreState(fileName=starts[i]) for a in range(0, len(acts)): env.step(acts[a]) time.sleep(0.01) value = input("Label:") if value == 's': break elif value == 'r': pass else: trajectory_labels[starts[i]] = descriptions[int(value)] done.append(starts[i]) np.savez("trajectory_labels", trajectory_labels=trajectory_labels, done=done) len(starts) for k,v in trajectory_labels.items(): if v == 'knock': trajectory_labels[k] = 'knock down block' starts[i] left = np.load(TEST_DIR+'left_right.npz')['left'] right = np.load(TEST_DIR+'left_right.npz')['right'] left_complete = [] right_complete = [] for pth in left: f = pth.split('/')[7] i = pth.split('/')[9].replace('.bullet', '') data = np.load(TEST_DIR+'obs_act_etc/'+f+'/data.npz') o = data['obs'][int(i):int(i)+40] a = data['acts_rpy'][int(i):int(i)+40] pth = pth.replace('/content/drive/My Drive/Robotic Learning/UR5_25Hz_test_suite/', TEST_DIR) left_complete.append((pth, o, a)) for pth in right: f = pth.split('/')[7] i = pth.split('/')[9].replace('.bullet', '') data = np.load(TEST_DIR+'obs_act_etc/'+f+'/data.npz') o = data['obs'][int(i):int(i)+40] a = data['acts_rpy'][int(i):int(i)+40] pth = pth.replace('/content/drive/My Drive/Robotic Learning/UR5_25Hz_test_suite/', TEST_DIR) right_complete.append((pth, o, a)) for i in range(0,50): pth, obs, acts = left_complete[np.random.choice(len(left_complete))] env.p.restoreState(fileName=pth) for a in range(0, len(acts)): env.step(acts[a]) time.sleep(0.001) for i in range(0,50): pth, obs, acts = right_complete[np.random.choice(len(right_complete))] env.p.restoreState(fileName=pth) for a in range(0, len(acts)): env.step(acts[a]) time.sleep(0.001) obs_left = np.array([x[1] for x in left_complete]) obs_right = np.array([x[1] for x in right_complete]) import seaborn as sns fig, axs = plt.subplots(ncols=4, nrows=5,figsize=(20, 20),) for x in range(0, obs_left.shape[2]): shape = obs_left.shape sns.distplot(np.reshape(obs_left[:], [shape[0] * shape[1], shape[2]])[:,x], hist=True, kde=True, bins=int(180/5), color = 'darkblue', hist_kws={'edgecolor':'black'}, kde_kws={'linewidth': 4}, ax=axs[mapping[x][0], mapping[x][1]]) shape = obs_right.shape sns.distplot(np.reshape(obs_right[:], [shape[0] * shape[1], shape[2]])[:,x], hist=True, kde=True, bins=int(180/5), color = 'orange', hist_kws={'edgecolor':'orange'}, kde_kws={'linewidth': 4}, ax=axs[mapping[x][0], mapping[x][1]]) plt.show() acts_left = np.array([x[2] for x in left_complete]) acts_right = np.array([x[2] for x in right_complete]) import seaborn as sns fig, axs = plt.subplots(ncols=4, nrows=2,figsize=(20, 20),) for x in range(0, acts_left.shape[2]): shape = acts_left.shape sns.distplot(np.reshape(acts_left[:], [shape[0] * shape[1], shape[2]])[:,x], hist=True, kde=True, bins=int(180/5), color = 'darkblue', hist_kws={'edgecolor':'black'}, kde_kws={'linewidth': 4}, ax=axs[mapping[x][0], mapping[x][1]]) shape = acts_right.shape sns.distplot(np.reshape(acts_right[:], [shape[0] * shape[1], shape[2]])[:,x], hist=True, kde=True, bins=int(180/5), color = 'orange', hist_kws={'edgecolor':'orange'}, kde_kws={'linewidth': 4}, ax=axs[mapping[x][0], mapping[x][1]]) plt.show() mapping = [] for i in range(0,5): for j in range(0,4): mapping.append([i,j]) mapping obs_left.shape[2]-1 arm_pos = [0.29, -0.01, 0.51] b= [0.25, 0.11, 0.02] realsense_y= translation[2] - bb[0] realsense_x = translation[1] - bb[1] realsense_z = translation[0] - bb[2] # Testing camera transforms camera_coord = (20,20) plt.scatter(camera_coord[0], 480-camera_coord[1], s=40) plt.xlim(0,480) plt.ylim(0,480) import math def gripper_frame_to_robot_frame(x,y, angle): y=-y X = xmath.cos(angle) - ymath.sin(angle) Y = xmath.sin(angle) + ymath.cos(angle) return X, Y current_angle = 0.22 gripper_frame_to_robot_frame(0.02,-0.02, math.pi/2) path = os.getcwd()+ '/sapien_simulator/config/ur5e.srdf' # '/ocrtoc_task/urdf/ur5e.urdf' p.loadURDF(path) height = os.path.exists(path) # Testing that diversity does increase with more training data t_it = iter(train_dataset) mins = np.min(dataset['obs_rpy'], axis = 0) maxes = np.max(dataset['obs_rpy'], axis = 0) shape = dataset['obs_rpy'].shape[1] bins = np.linspace(mins,maxes+0.01, 11) def get_quantisation(ags, bins): qs = [] for idx in range(0 , shape): quantiles = np.digitize(ags[:, idx], bins[:,idx]) qs.append(quantiles) return np.array(qs).T batch = t_it.next() o = tf.reshape(batch['obs'][:,:,:], (-1, OBS_DIM)) coverage = get_quantisation(o, bins) shapes = [] for i in range(0,10): batch = t_it.next() o = tf.reshape(batch['obs'][:,:,:], (-1, OBS_DIM)) c = get_quantisation(o, bins) coverage = np.unique(np.concatenate([coverage, c], 0), axis = 0) shapes.append(coverage.shape[0]) np.unique(get_quantisation(dataset['obs_rpy'], bins), axis = 0).shape plt.plot([120215]*11) plt.plot(old) plt.plot(shapes) plt.plot(one) plt.title("Unique states observed in batches with shuffle size N") plt.legend(['Unique values', 40, 10, 1]) ```	github_jupyter
# Optimization of CNN - TPE In this notebook, we will optimize the hyperparameters of a CNN using the define-by-run model from Optuna. ``` # For reproducible results. # See: # https://keras.io/getting_started/faq/#how-can-i-obtain-reproducible-results-using-keras-during-development import os os.environ['PYTHONHASHSEED'] = '0' import numpy as np import tensorflow as tf import random as python_random # The below is necessary for starting Numpy generated random numbers # in a well-defined initial state. np.random.seed(123) # The below is necessary for starting core Python generated random numbers # in a well-defined state. python_random.seed(123) # The below set_seed() will make random number generation # in the TensorFlow backend have a well-defined initial state. # For further details, see: # https://www.tensorflow.org/api_docs/python/tf/random/set_seed tf.random.set_seed(1234) import itertools from functools import partial import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from sklearn.model_selection import train_test_split from sklearn.metrics import confusion_matrix from keras.utils.np_utils import to_categorical from keras.models import Sequential, load_model from keras.layers import Dense, Flatten, Conv2D, MaxPool2D from keras.optimizers import Adam, RMSprop import optuna ``` # Data Preparation The dataset contains information about images, each image is a hand-written digit. The aim is to have the computer predict which digit was written by the person, automatically, by "looking" at the image. Each image is 28 pixels in height and 28 pixels in width (28 x 28), making a total of 784 pixels. Each pixel value is an integer between 0 and 255, indicating the darkness in a gray-scale of that pixel. The data is stored in a dataframe where each each pixel is a column (so it is flattened and not in the 28 x 28 format). The data set the has 785 columns. The first column, called "label", is the digit that was drawn by the user. The rest of the columns contain the pixel-values of the associated image. ``` # Load the data data = pd.read_csv("../mnist.csv") # first column is the target, the rest of the columns # are the pixels of the image # each row is 1 image data.head() # split dataset into a train and test set X_train, X_test, y_train, y_test = train_test_split( data.drop(['label'], axis=1), # the images data['label'], # the target test_size = 0.1, random_state=0) X_train.shape, X_test.shape # number of images for each digit g = sns.countplot(x=y_train) plt.xlabel('Digits') plt.ylabel('Number of images') ``` There are roughly the same amount of images for each of the 10 digits. ## Image re-scaling We re-scale data for the CNN, between 0 and 1. ``` # Re-scale the data # 255 is the maximum value a pixel can take X_train = X_train / 255 X_test = X_test / 255 ``` ## Reshape The images were stored in a pandas dataframe as 1-D vectors of 784 values. For a CNN with Keras, we need tensors with the following dimensions: width x height x channel. Thus, we reshape all data to 28 x 2 8 x 1, 3-D matrices. The 3rd dimension corresponds to the channel. RGB images have 3 channels. MNIST images are in gray-scale, thus they have only one channel in the 3rd dimension. ``` # Reshape image in 3 dimensions: # height: 28px X width: 28px X channel: 1 X_train = X_train.values.reshape(-1,28,28,1) X_test = X_test.values.reshape(-1,28,28,1) ``` ## Target encoding ``` # the target is 1 variable with the 9 different digits # as values y_train.unique() # For Keras, we need to create 10 dummy variables, # one for each digit # Encode labels to one hot vectors (ex : digit 2 -> [0,0,1,0,0,0,0,0,0,0]) y_train = to_categorical(y_train, num_classes = 10) y_test = to_categorical(y_test, num_classes = 10) # the new target y_train ``` Let's print some example images. ``` # Some image examples g = plt.imshow(X_train[0][:,:,0]) # Some image examples g = plt.imshow(X_train[10][:,:,0]) ``` # Define-by-Run design We create the CNN and add the sampling space for the hyperparameters as we go. This is the Desing-by-run concept. ``` # we will save the model with this name path_best_model = 'cnn_model_2.h5' # starting point for the optimization best_accuracy = 0 # function to create the CNN def objective(trial): # Start construction of a Keras Sequential model. model = Sequential() # Convolutional layers. # We add the different number of conv layers in the following loop: num_conv_layers = trial.suggest_int('num_conv_layers', 1, 3) for i in range(num_conv_layers): # Note, with this configuration, we sample different filters, kernels # stride etc, for each convolutional layer that we add model.add(Conv2D( filters=trial.suggest_categorical('filters_{}'.format(i), [16, 32, 64]), kernel_size=trial.suggest_categorical('kernel_size{}'.format(i), [3, 5]), strides=trial.suggest_categorical('strides{}'.format(i), [1, 2]), activation=trial.suggest_categorical( 'activation{}'.format(i), ['relu', 'tanh']), padding='same', )) # we could also optimize these parameters if we wanted: model.add(MaxPool2D(pool_size=2, strides=2)) # Flatten the 4-rank output of the convolutional layers # to 2-rank that can be input to a fully-connected Dense layer. model.add(Flatten()) # Add fully-connected Dense layers. # The number of layers is a hyper-parameter we want to optimize. # We add the different number of layers in the following loop: num_dense_layers = trial.suggest_int('num_dense_layers', 1, 3) for i in range(num_dense_layers): # Add the dense fully-connected layer to the model. # This has two hyper-parameters we want to optimize: # The number of nodes (neurons) and the activation function. model.add(Dense( units=trial.suggest_int('units{}'.format(i), 5, 512), activation=trial.suggest_categorical( 'activation{}'.format(i), ['relu', 'tanh']), )) # Last fully-connected dense layer with softmax-activation # for use in classification. model.add(Dense(10, activation='softmax')) # Use the Adam method for training the network. optimizer_name = trial.suggest_categorical( 'optimizer_name', ['Adam', 'RMSprop']) if optimizer_name == 'Adam': optimizer = Adam(lr=trial.suggest_float('learning_rate', 1e-6, 1e-2)) else: optimizer = RMSprop( lr=trial.suggest_float('learning_rate', 1e-6, 1e-2), momentum=trial.suggest_float('momentum', 0.1, 0.9), ) # In Keras we need to compile the model so it can be trained. model.compile(optimizer=optimizer, loss='categorical_crossentropy', metrics=['accuracy']) # train the model # we use 3 epochs to be able to run the notebook in a "reasonable" # time. If we increase the epochs, we will have better performance # this could be another parameter to optimize in fact. history = model.fit( x=X_train, y=y_train, epochs=3, batch_size=128, validation_split=0.1, ) # Get the classification accuracy on the validation-set # after the last training-epoch. accuracy = history.history['val_accuracy'][-1] # Save the model if it improves on the best-found performance. # We use the global keyword so we update the variable outside # of this function. global best_accuracy # If the classification accuracy of the saved model is improved ... if accuracy > best_accuracy: # Save the new model to harddisk. # Training CNNs is costly, so we want to avoid having to re-train # the network with the best found parameters. We save it instead # as we search for the best hyperparam space. model.save(path_best_model) # Update the classification accuracy. best_accuracy = accuracy # Delete the Keras model with these hyper-parameters from memory. del model # Remember that Scikit-optimize always minimizes the objective # function, so we need to negate the accuracy (because we want # the maximum accuracy) return accuracy # we need this to store the search # we will use it in the following notebook study_name = "cnn_study_2" # unique identifier of the study. storage_name = "sqlite:///{}.db".format(study_name) study = optuna.create_study( direction='maximize', study_name=study_name, storage=storage_name, load_if_exists=True, ) study.optimize(objective, n_trials=30) ``` # Analyze results ``` study.best_params study.best_value results = study.trials_dataframe() results['value'].sort_values().reset_index(drop=True).plot() plt.title('Convergence plot') plt.xlabel('Iteration') plt.ylabel('Accuracy') results.head() ``` # Evaluate the model ``` # load best model model = load_model(path_best_model) model.summary() # make predictions in test set result = model.evaluate(x=X_test, y=y_test) # print evaluation metrics for name, value in zip(model.metrics_names, result): print(name, value) ``` ## Confusion matrix ``` # Predict the values from the validation dataset y_pred = model.predict(X_test) # Convert predictions classes to one hot vectors y_pred_classes = np.argmax(y_pred, axis = 1) # Convert validation observations to one hot vectors y_true = np.argmax(y_test, axis = 1) # compute the confusion matrix cm = confusion_matrix(y_true, y_pred_classes) cm # let's make it more colourful classes = 10 plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues) plt.title('Confusion matrix') plt.colorbar() tick_marks = np.arange(classes) plt.xticks(tick_marks, range(classes), rotation=45) plt.yticks(tick_marks, range(classes)) for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])): plt.text(j, i, cm[i, j], horizontalalignment="center", color="white" if cm[i, j] > 100 else "black", ) plt.tight_layout() plt.ylabel('True label') plt.xlabel('Predicted label') ``` Here we can see that our CNN performs very well on all digits.	github_jupyter
# QCoDeS Example with Tektronix Keithley 7510 Multimeter In this example we will show how to use a few basic functions of the Keithley 7510 DMM. We attached the 1k Ohm resistor to the front terminals, with no source current or voltage. For more detail about the 7510 DMM, please see the User's Manual: https://www.tek.com/digital-multimeter/high-resolution-digital-multimeters-manual/model-dmm7510-75-digit-graphical-sam-0, or Reference Manual: https://www.tek.com/digital-multimeter/high-resolution-digital-multimeters-manual-9 ``` from qcodes.instrument_drivers.tektronix.keithley_7510 import Keithley7510 dmm = Keithley7510("dmm_7510", 'USB0::0x05E6::0x7510::04450363::INSTR') ``` # To reset the system to default settings: ``` dmm.reset() ``` # To perform measurement with different sense functions: When first turned on, the default sense function is for DC voltage ``` dmm.sense.function() ``` to perform the measurement: ``` dmm.sense.voltage() ``` There'll be an error if try to call other functions, such as current: ``` try: dmm.sense.current() except AttributeError as err: print(err) ``` To switch between functions, do the following: ``` dmm.sense.function('current') dmm.sense.function() dmm.sense.current() ``` And of course, once the sense function is changed to 'current', the user can't make voltage measurement ``` try: dmm.sense.voltage() except AttributeError as err: print(err) ``` The available functions in the driver now are 'voltage', 'current', 'Avoltage', 'Acurrent', 'resistance', and 'Fresistance', where 'A' means 'AC', and 'F' means 'Four-wire' ``` try: dmm.sense.function('ac current') except ValueError as err: print(err) ``` # To set measurement range (positive full-scale measure range): By default, the auto range is on ``` dmm.sense.auto_range() ``` We can change it to 'off' as following ``` dmm.sense.auto_range(0) dmm.sense.auto_range() ``` Note: this auto range setting is for the sense function at this moment, which is 'current' ``` dmm.sense.function() ``` If switch to another function, the auto range is still on, by default ``` dmm.sense.function('voltage') dmm.sense.function() dmm.sense.auto_range() ``` to change the range, use the following ``` dmm.sense.range(10) dmm.sense.range() ``` This will also automatically turn off the auto range: ``` dmm.sense.auto_range() ``` the allowed range (upper limit) value is a set of discrete numbers, for example, 100mV, 1V, 10V, 100V, 100V. If a value other than those allowed values is input, the system will just use the "closest" one: ``` dmm.sense.range(150) dmm.sense.range() dmm.sense.range(105) dmm.sense.range() ``` The driver will not give any error messages for the example above, but if the value is too large or too small, there'll be an error message: ``` try: dmm.sense.range(0.0001) except ValueError as err: print(err) ``` # To set the NPLC (Number of Power Line Cycles) value for measurements: By default, the NPLC is 1 for each sense function ``` dmm.sense.nplc() ``` To set the NPLC value: ``` dmm.sense.nplc(.1) dmm.sense.nplc() ``` Same as the 'range' variable, each sense function has its own NPLC value: ``` dmm.sense.function('resistance') dmm.sense.function() dmm.sense.nplc() ``` # To set the delay: By default, the auto delay is enabled. According to the guide, "When this is enabled, a delay is added after a range or function change to allow the instrument to settle." But it's unclear how much the delay is. ``` dmm.sense.auto_delay() ``` To turn off the auto delay: ``` dmm.sense.auto_delay(0) dmm.sense.auto_delay() ``` To turn the auto delay back on: ``` dmm.sense.auto_delay(1) dmm.sense.auto_delay() ``` There is also an "user_delay", but it is designed for rigger model, please see the user guide for detail. To set the user delay time: First to set a user number to relate the delay time with: (default user number is empty, so an user number has to be set before setting the delay time) ``` dmm.sense.user_number(1) dmm.sense.user_number() ``` By default, the user delay is 0s: ``` dmm.sense.user_delay() ``` Then to set the user delay as following: ``` dmm.sense.user_delay(0.1) dmm.sense.user_delay() ``` The user delay is tied to user number: ``` dmm.sense.user_number(2) dmm.sense.user_number() dmm.sense.user_delay() ``` For the record, the auto delay here is still on: ``` dmm.sense.auto_delay() ``` # To set auto zero (automatic updates to the internal reference measurements): By default, the auto zero is on ``` dmm.sense.auto_zero() ``` To turn off auto zero: ``` dmm.sense.auto_zero(0) dmm.sense.auto_zero() ``` The auto zero setting is also tied to each function, not universal: ``` dmm.sense.function('current') dmm.sense.function() dmm.sense.auto_zero() ``` There is way to ask the system to do auto zero once: ``` dmm.sense.auto_zero_once() ``` See P487 of the Reference Manual for how to use auto zero ONCE. Note: it's not funtion-dependent. # To set averaging filter for measurements, including average count, and filter type: By default, averaging is off: ``` dmm.sense.average() ``` To turn it on: ``` dmm.sense.average(1) dmm.sense.average() ``` Default average count value is 10, remember to turn average on, or it will not work: ``` dmm.sense.average_count() ``` To change the average count: ``` dmm.sense.average_count(23) dmm.sense.average_count() ``` The range for average count is 1 to 100: ``` try: dmm.sense.average_count(200) except ValueError as err: print(err) ``` There are two average types, repeating (default) or moving filter: ``` dmm.sense.average_type() ``` To make changes: ``` dmm.sense.average_type('MOV') dmm.sense.average_type() ```	github_jupyter
# Applying Customizations ``` import pandas as pd import numpy as np import holoviews as hv from holoviews import opts hv.extension('bokeh', 'matplotlib') ``` As introduced in the [Customization](../getting_started/2-Customization.ipynb) section of the 'Getting Started' guide, HoloViews maintains a strict separation between your content (your data and declarations about your data) and its presentation (the details of how this data is represented visually). This separation is achieved by maintaining sets of keyword values ("options") that specify how elements are to appear, stored outside of the element itself. Option keywords can be specified for individual element instances, for all elements of a particular type, or for arbitrary user-defined sets of elements that you give a certain ``group`` and ``label`` (see [Annotating Data](../user_guide/01-Annotating_Data.ipynb)). The options system controls how individual plots appear, but other important settings are made more globally using the "output" system, which controls HoloViews plotting and rendering code (see the [Plots and Renderers](Plots_and_Renderers.ipynb) user guide). In this guide we will show how to customize the visual styling with the options and output systems, focusing on the mechanisms rather than the specific choices available (which are covered in other guides such as [Style Mapping](04-Style_Mapping.ipynb)). ## Core concepts This section offers an overview of some core concepts for customizing visual representation, focusing on how HoloViews keeps content and presentation separate. To start, we will revisit the simple introductory example in the [Customization](../getting_started/2-Customization.ipynb) getting-started guide (which might be helpful to review first). ``` spike_train = pd.read_csv('../assets/spike_train.csv.gz') curve = hv.Curve(spike_train, 'milliseconds', 'Hertz') spikes = hv.Spikes(spike_train, 'milliseconds', []) ``` And now we display the ``curve`` and a ``spikes`` elements together in a layout as we did in the getting-started guide: ``` curve = hv.Curve( spike_train, 'milliseconds', 'Hertz') spikes = hv.Spikes(spike_train, 'milliseconds', []) layout = curve + spikes layout.opts( opts.Curve( height=200, width=900, xaxis=None, line_width=1.50, color='red', tools=['hover']), opts.Spikes(height=150, width=900, yaxis=None, line_width=0.25, color='grey')).cols(1) ``` This example illustrates a number of key concepts, as described below. ### Content versus presentation In the getting-started guide [Introduction](../getting_started/1-Introduction.ipynb), we saw that we can print the string representation of HoloViews objects such as `layout`: ``` print(layout) ``` In the [Customization](../getting_started/2-Customization.ipynb) getting-started guide, the `.opts.info()` method was introduced that lets you see the options associated with (though not stored on) the objects: ``` layout.opts.info() ``` If you inspect all the state of the `Layout`, `Curve`, or `Spikes` objects you will not find any of these keywords, because they are stored in an entirely separate data structure. HoloViews assigns a unique ID per HoloViews object that lets arbitrarily specific customization be associated with that object if needed, while also making it simple to define options that apply to entire classes of objects by type (or group and label if defined). The HoloViews element is thus always a thin wrapper around your data, without any visual styling information or plotting state, even though it seems like the object includes the styling information. This separation between content and presentation is by design, so that you can work with your data and with its presentation entirely independently. If you wish to clear the options that have been associated with an object `obj`, you can call `obj.opts.clear()`. ## Option builders The [Customization](../getting_started/2-Customization.ipynb) getting-started guide also introduces the notion of option builders. One of the option builders in the visualization shown above is: ``` opts.Curve( height=200, width=900, xaxis=None, line_width=1.50, color='red', tools=['hover']) ``` An option builder takes a collection of keywords and returns an `Options` object that stores these keywords together. Why should you use option builders and how are they different from a vanilla dictionary? 1. The option builder specifies which type of HoloViews object the options are for, which is important because each type accepts different options. 2. Knowing the type, the options builder does validation against that type for the currently loaded plotting extensions. Try introducing a typo into one of the keywords above; you should get a helpful error message. Separately, try renaming `line_width` to `linewidth`, and you'll get a different message because the latter is a valid matplotlib keyword. 3. The option builder allows tab-completion in the notebook. This is useful for discovering available keywords for that type of object, which helps prevent mistakes and makes it quicker to specify a set of keywords. In the cell above, the specified options are applicable to `Curve` elements, and different validation and tab completion will be available for other types. The returned `Options` object is different from a dictionary in the following ways: 1. An optional spec is recorded, where this specification is normally just the element name. Above this is simply 'Curve'. Later, in section [Using `group` and `label`](#Using-group-and-label), we will see how this can also specify the `group` and `label`. 2. The keywords are alphanumerically sorted, making it easier to compare `Options` objects. ## Inlining options When customizing a single element, the use of an option builder is not mandatory. If you have a small number of keywords that are common (e.g `color`, `cmap`, `title`, `width`, `height`) it can be clearer to inline them into the `.opts` method call if tab-completion and validation isn't required: ``` np.random.seed(42) array = np.random.random((10,10)) im1 = hv.Image(array).opts(opts.Image(cmap='Reds')) # Using an option builder im2 = hv.Image(array).opts(cmap='Blues') # Without an option builder im1 + im2 ``` You cannot inline keywords for composite objects such as `Layout` or `Overlay` objects. For instance, the `layout` object is: ``` print(layout) ``` To customize this layout, you need to use an option builder to associate your keywords with either the `Curve` or the `Spikes` object, or else you would have had to apply the options to the individual elements before you built the composite object. To illustrate setting by type, note that in the first example, both the `Curve` and the `Spikes` have different `height` values provided. You can also target options by the `group` and `label` as described in section on [using `group` and `label`](#Using-group-and-label). ## Session-specific options One other common need is to set some options for a Python session, whether using Jupyter notebook or not. For this you can set the default options that will apply to all objects created subsequently: ``` opts.defaults( opts.HeatMap(cmap='Summer', colorbar=True, toolbar='above')) ``` The `opt.defaults` method has now set the style used for all `HeatMap` elements used in this session: ``` data = [(chr(65+i), chr(97+j), ij) for i in range(5) for j in range(5) if i!=j] heatmap = hv.HeatMap(data).sort() heatmap ``` ## Discovering options Using tab completion in the option builders is one convenient and easy way of discovering the available options for an element. Another approach is to use `hv.help`. For instance, if you run `hv.help(hv.Curve)` you will see a list of the 'style' and 'plot' options applicable to `Curve`. The distinction between these two types of options can often be ignored for most purposes, but the interested reader is encouraged to read more about them in more detail [below](#Split-into-style,-plot-and-norm-options). For the purposes of discovering the available options, the keywords listed under the 'Style Options' section of the help output is worth noting. These keywords are specific to the active plotting extension and are part of the API for that plotting library. For instance, running `hv.help(hv.Curve)` in the cell below would give you the keywords in the Bokeh documentation that you can reference for customizing the appearance of `Curve` objects. ## Maximizing readability There are many ways to specify options in your code using the above tools, but for creating readable, maintainable code, we recommend making the separation of content and presentation explicit. Someone reading your code can then understand your visualizations in two steps 1) what your data is* in terms of the applicable elements and containers 2) how this data is to be presented visually. The following guide details the approach we have used through out the examples and guides on holoviews.org. We have found that following these rules makes code involving holoviews easier to read and more consistent. The core principle is as follows: *avoid mixing declarations of data, elements and containers with details of their visual appearance. ### Two contrasting examples One of the best ways to do this is to declare all your elements, compose them and then apply all the necessary styling with the `.opts` method before the visualization is rendered to disk or to the screen. For instance, the example from the getting-started guide could have been written sub-optimally as follows: Sub-optimal* ```python curve = hv.Curve( spike_train, 'milliseconds', 'Hertz').opts( height=200, width=900, xaxis=None, line_width=1.50, color='red', tools=['hover']) spikes = hv.Spikes(spike_train, 'milliseconds', vdims=[]).opts( height=150, width=900, yaxis=None, line_width=0.25, color='grey') (curve + spikes).cols(1) ``` Code like that is very difficult to read because it mixes declarations of the data and its dimensions with details about how to present it. The recommended version declares the `Layout`, then separately applies all the options together where it's clear that they are just hints for the visualization: *Recommended* ```python curve = hv.Curve( spike_train, 'milliseconds', 'Hertz') spikes = hv.Spikes(spike_train, 'milliseconds', []) layout = curve + spikes layout.opts( opts.Curve( height=200, width=900, xaxis=None, line_width=1.50, color='red', tools=['hover']), opts.Spikes(height=150, width=900, yaxis=None, line_width=0.25, color='grey')).cols(1) ``` By grouping the options in this way and applying them at the end, you can see the definition of `layout` without being distracted by visual concerns declared later. Conversely, you can modify the visual appearance of `layout` easily without needing to know exactly how it was defined. The [coding style guide](#Coding-style-guide) section below offers additional advice for keeping things readable and consistent. ### When to use multiple`.opts` calls The above coding style applies in many case, but sometimes you have multiple elements of the same type that you need to distinguish visually. For instance, you may have a set of curves where using the `dim` or `Cycle` objects (described in the [Style Mapping](04-Style_Mapping.ipynb) user guide) is not appropriate and you want to customize the appearance of each curve individually. Alternatively, you may be generating elements in a list comprehension for use in `NdOverlay` and have a specific style to apply to each one. In these situations, it is often appropriate to use the inline style of `.opts` locally. In these instances, it is often best to give the individually styled objects a suitable named handle as illustrated by the [legend example](../gallery/demos/bokeh/legend_example.ipynb) of the gallery. ### General advice As HoloViews is highly compositional by design, you can always build long expressions mixing the data and element declarations, the composition of these elements, and their customization. Even though such expressions can be terse they can also be difficult to read. The simplest way to avoid long expressions is to keep some level of separation between these stages: 1. declaration of the data 2. declaration of the elements, including `.opts` to distinguish between elements of the same type if necessary 3. composition with `+` and `` into layouts and overlays, and 4. customization of the composite object, either with a final call to the `.opts` method, or by declaring such settings as the default for your entire session as described [above](#Session-specific-options). When stages are simple enough, it can be appropriate to combine them. For instance, if the declaration of the data is simple enough, you can fold in the declaration of the element. In general, any expression involving three or more of these stages will benefit from being broken up into several steps. These general principles will help you write more readable code. Maximizing readability will always require some level of judgement, but you can maximize consistency by consulting the [coding style guide](#Coding-style-guide) section for more tips. # Customizing display output The options system controls most of the customizations you might want to do, but there are a few settings that are controlled at a more general level that cuts across all HoloViews object types: the active plotting extension (e.g. Bokeh or Matplotlib), the output display format (PNG, SVG, etc.), the output figure size, and other similar options. The `hv.output` utility allows you to modify these more global settings, either for all subsequent objects or for one particular object: `hv.output(*kwargs)`: Customize how the output appears for the rest of the notebook session. `hv.output(obj, kwargs)`: Temporarily affect the display of an object `obj` using the keyword `kwargs`. The `hv.output` utility only has an effect in contexts where HoloViews objects can be automatically displayed, which currently is limited to the Jupyter Notebook (in either its classic or JupyterLab variants). In any other Python context, using `hv.output` has no effect, as there is no automatically displayed output; see the [hv.save() and hv.render()](Plots_and_Renderers.ipynb#Saving-and-rendering) utilities for explicitly creating output in those other contexts. To start with `hv.output`, let us define a `Path` object: ``` lin = np.linspace(0, np.pi2, 200) def lissajous(t, a, b, delta): return (np.sin(a t + delta), np.sin(b * t), t) path = hv.Path([lissajous(lin, 3, 5, np.pi/2)]) path.opts(opts.Path(color='purple', line_width=3, line_dash='dotted')) ``` Now, to illustrate, let's use `hv.output` to switch our plotting extension to matplotlib: ``` hv.output(backend='matplotlib', fig='svg') ``` We can now display our `path` object with some option customization: ``` path.opts(opts.Path(linewidth=2, color='red', linestyle='dotted')) ``` Our plot is now rendered with Matplotlib, in SVG format (try right-clicking the image in the web browser and saving it to disk to confirm). Note that the `opts.Path` option builder now tab completes Matplotlib keywords because we activated the Matplotlib plotting extension beforehand. Specifically, `linewidth` and `linestyle` don't exist in Bokeh, where the corresponding options are called `line_width` and `line_dash` instead. You can see the custom output options that are currently active using `hv.output.info()`: ``` hv.output.info() ``` The info method will always show which backend is active as well as any other custom settings you have specified. These settings apply to the subsequent display of all objects unless you customize the output display settings for a single object. To illustrate how settings are kept separate, let us switch back to Bokeh in this notebook session: ``` hv.output(backend='bokeh') hv.output.info() ``` With Bokeh active, we can now declare options on `path` that we want to apply only to matplotlib: ``` path = path.opts( opts.Path(linewidth=3, color='blue', backend='matplotlib')) path ``` Now we can supply `path` to `hv.output` to customize how it is displayed, while activating matplotlib to generate that display. In the next cell, we render our path at 50% size as an SVG using matplotlib. ``` hv.output(path, backend='matplotlib', fig='svg', size=50) ``` Passing `hv.output` an object will apply the specified settings only for the subsequent display. If you were to view `path` now in the usual way, you would see that it is still being displayed with Bokeh with purple dotted lines. One thing to note is that when we set the options with `backend='matplotlib'`, the active plotting extension was Bokeh. This means that `opts.Path` will tab complete bokeh keywords, and not the matplotlib ones that were specified. In practice you will want to set the backend appropriately before building your options settings, to ensure that you get the most appropriate tab completion. ### Available `hv.output` settings You can see the available settings using `help(hv.output)`. For reference, here are the most commonly used ones: * backend: The backend used by HoloViews. If the necessary libraries are installed this can be `'bokeh'`, `'matplotlib'` or `'plotly'`. * fig : The static figure format. The most common options are `'svg'` and `'png'`. * holomap: The display type for holomaps. With matplotlib and the necessary support libraries, this may be `'gif'` or `'mp4'`. The JavaScript `'scrubber'` widgets as well as the regular `'widgets'` are always supported. * fps: The frames per second used for animations. This setting is used for GIF output and by the scrubber widget. * size: The percentage size of displayed output. Useful for making all display larger or smaller. * dpi: The rendered dpi of the figure. This setting affects raster output such as PNG images. In `help(hv.output)` you will see a few other, less common settings. The `filename` setting particular is not recommended and will be deprecated in favor of `hv.save` in future. ## Coding style guide Using `hv.output` plus option builders with the `.opts` method and `opts.default` covers the functionality required for most HoloViews code written by users. In addition to these recommended tools, HoloViews supports [Notebook Magics](Notebook_Magics.ipynb) (not recommended because they are Jupyter-specific) and literal (nested dictionary) formats useful for developers, as detailed in the [Extending HoloViews](#Extending-HoloViews) section. This section offers further recommendations for how users can structure their code. These are generally tips based on the important principles described in the [maximizing readability](#Maximizing-readability) section that are often helpful but optional. * Use as few `.opts` calls as necessary to style the object the way you want. * You can inline keywords without an option builder if you only have a few common keywords. For instance, `hv.Image(...).opts(cmap='Reds')` is clearer to read than `hv.Image(...).opts(opts.Image(cmap='Reds'))`. * Conversely, you should use an option builder if you have more than four keywords. * When you have multiple option builders, it is often clearest to list them on separate lines with a single intentation in both `.opts` and `opts.defaults`: Not recommended ``` layout.opts(opts.VLine(color='white'), opts.Image(cmap='Reds'), opts.Layout(width=500), opts.Curve(color='blue')) ``` Recommended ``` layout.opts( opts.Curve(color='blue'), opts.Image(cmap='Reds'), opts.Layout(width=500), opts.VLine(color='white')) ``` * The latter is recommended for another reason: if possible, list your element option builders in alphabetical order, before your container option builders in alphabetical order. * Keep the expression before the `.opts` method simple so that the overall expression is readable. * Don't mix `hv.output` and use of the `.opts` method in the same expression. ## What is `.options`? If you tab complete a HoloViews object, you'll notice there is an `.options` method as well as a `.opts` method. So what is the difference? The `.options` method was introduced in HoloViews 1.10 and was the first time HoloViews allowed users to ignore the distinction between 'style', 'plot' and 'norm' options described in the next section. It is largely equivalent to the `.opts` method except that it applies the options on a returned clone of the object. In other words, you have `clone = obj.options(*kwargs)` where `obj` is unaffected by the keywords supplied while `clone` will be customized. Both `.opts` and `.options` support an explicit `clone` keyword, so: `obj.opts(kwargs, clone=True)` is equivalent to `obj.options(kwargs)`, and conversely * `obj.options(kwargs, clone=False)` is equivalent to `obj.opts(kwargs)` For this reason, users only ever need to use `.opts` and occasionally supply `clone=True` if required. The only other difference between these methods is that `.opts` supports the full literal specification that allows splitting into [style, plot and norm options](#Split-into-style,-plot-and-norm-options) (for developers) whereas `.options` does not. ## When should I use `clone=True`? The 'Persistent styles' section of the [customization](../getting_started/2-Customization.ipynb) user guide shows how HoloViews remembers options set for an object (per plotting extension). For instance, we never customized the `spikes` object defined at the start of the notebook but we did customize it when it was part of a `Layout` called `layout`. Examining this `spikes` object, we see the options were applied to the underlying object, not just a copy of it in the layout: ``` spikes ``` This is because `clone=False` by default in the `.opts` method. To illustrate `clone=True`, let's view some purple spikes without affecting the original `spikes` object: ``` purple_spikes = spikes.opts(color='purple', clone=True) purple_spikes ``` Now if you were to look at `spikes` again, you would see it is still looks like the grey version above and only `purple_spikes` is purple. This means that `clone=True` is useful when you want to keep different styles for some HoloViews object (by making styled clones of it) instead of overwriting the options each time you call `.opts`. ## Extending HoloViews In addition to the formats described above for use by users, additional option formats are supported that are less user friendly for data exploration but may be more convenient for library authors building on HoloViews. The first of these is the `Option` list syntax which is typically most useful outside of notebooks, a literal syntax that avoids the need to import `opts`, and then finally a literal syntax that keeps style and plot options separate. ### `Option` list syntax If you find yourself using `obj.opts(options)` where `options` is a list of `Option` objects, use `obj.opts(options)` instead as list input is also supported: ``` options = [ opts.Curve( height=200, width=900, xaxis=None, line_width=1.50, color='grey', tools=['hover']), opts.Spikes(height=150, width=900, yaxis=None, line_width=0.25, color='orange')] layout.opts(options).cols(1) ``` This approach is often best in regular Python code where you are dynamically building up a list of options to apply. Using the option builders early also allows for early validation before use in the `.opts` method. ### Literal syntax This syntax has the advantage of being a pure Python literal but it is harder to work with directly (due to nested dictionaries), is less readable, lacks tab completion support and lacks validation at the point where the keywords are defined: ``` layout.opts( {'Curve': dict(height=200, width=900, xaxis=None, line_width=2, color='blue', tools=['hover']), 'Spikes': dict(height=150, width=900, yaxis=None, line_width=0.25, color='green')}).cols(1) ``` The utility of this format is you don't need to import `opts` and it is easier to dynamically add or remove keywords using Python or if you are storing options in a text file like YAML or JSON and only later applying them in Python code. This format should be avoided when trying to maximize readability or make the available keyword options easy to explore. ### Using `group` and `label` The notion of an element `group` and `label` was introduced in [Annotating Data](./01-Annotating_Data.ipynb). This type of metadata is helpful for organizing large collections of elements with shared styling, such as automatically generated objects from some external software (e.g. a simulator). If you have a large set of elements with semantically meaningful `group` and `label` parameters set, you can use this information to appropriately customize large numbers of visualizations at once. To illustrate, here are four overlaid curves where three have the `group` of 'Sinusoid' and one of these also has the label 'Squared': ``` xs = np.linspace(-np.pi,np.pi,100) curve = hv.Curve((xs, xs/3)) group_curve1 = hv.Curve((xs, np.sin(xs)), group='Sinusoid') group_curve2 = hv.Curve((xs, np.sin(xs+np.pi/4)), group='Sinusoid') label_curve = hv.Curve((xs, np.sin(xs)2), group='Sinusoid', label='Squared') curves = curve group_curve1 * group_curve2 * label_curve curves ``` We can now use the `.opts` method to make all curves blue unless they are in the 'Sinusoid' group in which case they are red. Additionally, if a curve in the 'Sinusoid' group also has the label 'Squared', we can make sure that curve is green with a custom interpolation option: ``` curves.opts( opts.Curve(color='blue'), opts.Curve('Sinusoid', color='red'), opts.Curve('Sinusoid.Squared', interpolation='steps-mid', color='green')) ``` By using `opts.defaults` instead of the `.opts` method, we can use this type of customization to apply options to many elements, including elements that haven't even been created yet. For instance, if we run: ``` opts.defaults(opts.Area('Error', alpha=0.5, color='grey')) ``` Then any `Area` element with a `group` of 'Error' will then be displayed as a semi-transparent grey: ``` X = np.linspace(0,2,10) hv.Area((X, np.random.rand(10), -np.random.rand(10)), vdims=['y', 'y2'], group='Error') ``` ## Split into `style`, `plot` and `norm` options In `HoloViews`, an element such as `Curve` actually has three semantic distinct categories of options: `style`, `plot`, and `norm` options. Normally, a user doesn't need to worry about the distinction if they spend most of their time working with a single plotting extension. When trying to build a system that consistently needs to generate visualizations across different plotting libraries, it can be useful to make this distinction explicit: ##### ``style`` options: ``style`` options are passed directly to the underlying rendering backend that actually draws the plots, allowing you to control the details of how it behaves. Each backend has its own options (e.g. the [``bokeh``](Bokeh_Backend) or plotly backends). For whichever backend has been selected, HoloViews can tell you which options are supported, but you will need to read the corresponding documentation (e.g. [matplotlib](http://matplotlib.org/contents.html), [bokeh](http://bokeh.pydata.org)) for the details of their use. For listing available options, see the ``hv.help`` as described in the [Discovering options](#Discovering-options) section. HoloViews has been designed to be easily extensible to additional backends in the future and each backend would have its own set of style options. ##### ``plot`` options: Each of the various HoloViews plotting classes declares various [Parameters](http://param.pyviz.org) that control how HoloViews builds the visualization for that type of object, such as plot sizes and labels. HoloViews uses these options internally; they are not simply passed to the underlying backend. HoloViews documents these options fully in its online help and in the [Reference Manual](http://holoviews.org/Reference_Manual). These options may vary for different backends in some cases, depending on the support available both in that library and in the HoloViews interface to it, but we try to keep any options that are meaningful for a variety of backends the same for all of them. For listing available options, see the output of ``hv.help``. ##### ``norm`` options: ``norm`` options are a special type of plot option that are applied orthogonally to the above two types, to control normalization. Normalization refers to adjusting the properties of one plot relative to those of another. For instance, two images normalized together would appear with relative brightness levels, with the brightest image using the full range black to white, while the other image is scaled proportionally. Two images normalized independently would both cover the full range from black to white. Similarly, two axis ranges normalized together are effectively linked and will expand to fit the largest range of either axis, while those normalized separately would cover different ranges. For listing available options, see the output of ``hv.help``. You can preserve the semantic distinction between these types of option in an augmented form of the [Literal syntax](#Literal-syntax) as follows: ``` full_literal_spec = { 'Curve': {'style':dict(color='orange')}, 'Curve.Sinusoid': {'style':dict(color='grey')}, 'Curve.Sinusoid.Squared': {'style':dict(color='black'), 'plot':dict(interpolation='steps-mid')}} curves.opts(full_literal_spec) ``` This specification is what HoloViews uses internally, but it is awkward for people to use and is not ever recommended for normal users. That said, it does offer the maximal amount of flexibility and power for integration with other software. For instance, a simulator that can output visualization using either Bokeh or Matplotlib via HoloViews could use this format. By keeping the 'plot' and 'style' options separate, the 'plot' options could be set regardless of the plotting library while the 'style' options would be conditional on the backend. ## Onwards This section of the user guide has described how you can discover and set customization options in HoloViews. Using `hv.help` and the option builders, you should be able to find the options available for any given object you want to display. What hasn't been explored are some of the facilities HoloViews offers to map the dimensions of your data to style options. This important topic is explored in the next user guide [Style Mapping](04-Style_Mapping.ipynb), where you will learn of the `dim` object as well as about the `Cycle` and `Palette` objects.	github_jupyter
# Reading outputs from E+ ``` # some initial set up # if you have not installed epp, and only downloaded it # you will need the following lines import sys # pathnameto_eppy = 'c:/eppy' pathnameto_eppy = '../' sys.path.append(pathnameto_eppy) ``` ## Using titletable() to get at the tables So far we have been making changes to the IDF input file. How about looking at the outputs. Energyplus makes nice htmlout files that look like this. ``` import ex_inits #no need to know this code, it just shows the image below for_images = ex_inits for_images.display_png(for_images.html_snippet1) #display the image below ``` If you look at the clipping of the html file above, you see tables with data in them. Eppy has functions that let you access of these tables and get the data from any of it's cells. Let us say you want to find the "Net Site Energy". This is in table "Site and Source Energy". The number you want is in the third row, second column and it's value is "47694.47" Let us use eppy to extract this number ``` from eppy.results import readhtml # the eppy module with functions to read the html fname = "../eppy/resources/outputfiles/V_7_2/5ZoneCAVtoVAVWarmestTempFlowTable_ABUPS.html" # the html file you want to read filehandle = open(fname, 'r').read() htables = readhtml.titletable(filehandle) # reads the tables with their titles ``` If you open the python file readhtml.py and look at the function titletable, you can see the function documentation. It says the following ``` """return a list of [(title, table), .....] title = previous item with a <b> tag table = rows -> [[cell1, cell2, ..], [cell1, cell2, ..], ..]""" ``` The documentation says that it returns a list. Let us take a look inside this list. Let us look at the first item in the list. ``` firstitem = htables[0] print(firstitem) ``` Ughh !!! that is ugly. Hard to see what it is. Let us use a python module to print it pretty ``` import pprint pp = pprint.PrettyPrinter() pp.pprint(firstitem) ``` Nice. that is a little clearer ``` firstitem_title = firstitem[0] pp.pprint(firstitem_title) firstitem_table = firstitem[1] pp.pprint(firstitem_table) ``` How do we get to value of "Net Site Energy". We know it is in the third row, second column of the table. Easy. ``` thirdrow = firstitem_table[2] # we start counting with 0. So 0, 1, 2 is third row print(thirdrow) thirdrow_secondcolumn = thirdrow[1] thirdrow_secondcolumn ``` the text from the html table is in unicode. That is why you see that weird 'u' letter. Let us convert it to a floating point number ``` net_site_energy = float(thirdrow_secondcolumn) net_site_energy ``` Let us have a little fun with the tables. Get the titles of all the tables ``` alltitles = [htable[0] for htable in htables] alltitles ``` Now let us grab the tables with the titles "Building Area" and "Site to Source Energy Conversion Factors" twotables = [htable for htable in htables if htable[0] in ["Building Area", "Site to Source Energy Conversion Factors"]] twotables Let us leave readtables for now. It gives us the basic functionality to read any of the tables in the html output file. ## Fast HTML table file read The function`readhtml.titletable()` will be slow with extremeley large files. If you are dealing with a very large file use the following functions ``` from eppy.results import fasthtml fname = "../eppy/resources/outputfiles/V_7_2/5ZoneCAVtoVAVWarmestTempFlowTable_ABUPS.html" # the html file you want to read filehandle = open(fname, 'r') # get a file handle to the html file firsttable = fasthtml.tablebyindex(filehandle, 0) pp.pprint(firstitem) filehandle = open(fname, 'r') # get a file handle to the html file namedtable = fasthtml.tablebyname(filehandle, "Site and Source Energy") pp.pprint(namedtable) ``` - You can read only one table at a time - You need to open the file each time you call the function. The function will close the file. ## Using lines_table() to get at the tables We have been using titletable() to get at the tables. There is a constraint using function titletable(). Titletable() assumes that there is a unique title (in HTML bold) just above the table. It is assumed that this title will adequetly describe the table. This is true in most cases and titletable() is perfectly good to use. Unfortuntely there are some tables that do not follow this rule. The snippet below shows one of them. ``` import ex_inits #no need to know this code, it just shows the image below for_images = ex_inits for_images.display_png(for_images.html_snippet2) # display the image below ``` Notice that the HTML snippet shows a table with three lines above it. The first two lines have information that describe the table. We need to look at both those lines to understand what the table contains. So we need a different function that will capture all those lines before the table. The funtion lines_table() described below will do this. ``` from eppy.results import readhtml # the eppy module with functions to read the html fname = "../eppy/resources/outputfiles/V_8_1/ASHRAE30pct.PI.Final11_OfficeMedium_STD2010_Chicago-baseTable.html" # the html file you want to read filehandle = open(fname, 'r').read() # get a file handle to the html file ltables = readhtml.lines_table(filehandle) # reads the tables with their titles ``` The html snippet shown above is the last table in HTML file we just opened. We have used lines_table() to read the tables into the variable ltables. We can get to the last table by ltable[-1]. Let us print it and see what we have. ``` import pprint pp = pprint.PrettyPrinter() pp.pprint(ltables[-1]) ``` We can see that ltables has captured all the lines before the table. Let us make our code more explicit to see this ``` last_ltable = ltables[-1] lines_before_table = last_ltable[0] table_itself = last_ltable[-1] pp.pprint(lines_before_table) ``` We found this table the easy way this time, because we knew it was the last one. How do we find it if we don't know where it is in the file ? Python comes to our rescue :-) Let assume that we want to find the table that has the following two lines before it. - Report: FANGER DURING COOLING AND ADAPTIVE COMFORT - For: PERIMETER_MID_ZN_4 ``` line1 = 'Report: FANGER DURING COOLING AND ADAPTIVE COMFORT' line2 = 'For: PERIMETER_MID_ZN_4' # # check if those two lines are before the table line1 in lines_before_table and line2 in lines_before_table # find all the tables where those two lines are before the table [ltable for ltable in ltables if line1 in ltable[0] and line2 in ltable[0]] ``` That worked ! What if you want to find the words "FANGER" and "PERIMETER_MID_ZN_4" before the table. The following code will do it. ``` # sample code to illustrate what we are going to do last_ltable = ltables[-1] lines_before_table = last_ltable[0] table_itself = last_ltable[-1] # join lines_before_table into a paragraph of text justtext = '\n'.join(lines_before_table) print(justtext) "FANGER" in justtext and "PERIMETER_MID_ZN_4" in justtext # Let us combine the this trick to find the table [ltable for ltable in ltables if "FANGER" in '\n'.join(ltable[0]) and "PERIMETER_MID_ZN_4" in '\n'.join(ltable[0])] ``` ## Extracting data from the tables The tables in the HTML page in general have text in the top header row. The first vertical row has text. The remaining cells have numbers. We can identify the numbers we need by looking at the labelin the top row and the label in the first column. Let us construct a simple example and explore this. ``` # ignore the following three lines. I am using them to construct the table below from IPython.display import HTML atablestring = '<TABLE cellpadding="4" style="border: 1px solid #000000; border-collapse: collapse;" border="1">\n <TR>\n <TD> </TD>\n <TD>a b</TD>\n <TD>b c</TD>\n <TD>c d</TD>\n </TR>\n <TR>\n <TD>x y</TD>\n <TD>1</TD>\n <TD>2</TD>\n <TD>3</TD>\n </TR>\n <TR>\n <TD>y z</TD>\n <TD>4</TD>\n <TD>5</TD>\n <TD>6</TD>\n </TR>\n <TR>\n <TD>z z</TD>\n <TD>7</TD>\n <TD>8</TD>\n <TD>9</TD>\n </TR>\n</TABLE>' HTML(atablestring) ``` This table is actually in the follwoing form: ``` atable = [["", "a b", "b c", "c d"], ["x y", 1, 2, 3 ], ["y z", 4, 5, 6 ], ["z z", 7, 8, 9 ],] ``` We can see the labels in the table. So we an look at row "x y" and column "c d". The value there is 3 right now we can get to it by saying atable[1][3] ``` print(atable[1][3]) ``` readhtml has some functions that will let us address the values by the labels. We use a structure from python called named tuples to do this. The only limitation is that the labels have to be letters or digits. Named tuples does not allow spaces in the labels. We could replace the space with an underscore ' _ '. So "a b" will become "a_b". So we can look for row "x_y" and column "c_d". Let us try this out. ``` from eppy.results import readhtml h_table = readhtml.named_grid_h(atable) print(h_table.x_y.c_d) ``` We can still get to the value by index ``` print(h_table[0][2]) ``` Note that we used atable[1][3], but here we used h_table[0][2]. That is because h_table does not count the rows and columns where the labels are. We can also do the following: ``` print(h_table.x_y[2]) # or print(h_table[0].c_d) ``` Wow … that is pretty cool. What if we want to just check what the labels are ? ``` print(h_table._fields) ``` That gives us the horizontal lables. How about the vertical labels ? ``` h_table.x_y._fields ``` There you go !!! How about if I want to use the labels differently ? Say I want to refer to the row first and then to the column. That woul be saying table.c_d.x_y. We can do that by using a different function ``` v_table = readhtml.named_grid_v(atable) print(v_table.c_d.x_y) ``` And we can do the following ``` print(v_table[2][0]) print(v_table.c_d[0]) print(v_table[2].x_y) ``` Let us try to get the numbers in the first column and then get their sum ``` v_table.a_b ``` Look like we got the right column. But not in the right format. We really need a list of numbers ``` [cell for cell in v_table.a_b] ``` That looks like waht we wanted. Now let us get the sum ``` values_in_first_column = [cell for cell in v_table.a_b] print(values_in_first_column) print(sum(values_in_first_column)) # sum is a builtin function that will sum a list ``` To get the first row we use the variable h_table ``` values_in_first_row = [cell for cell in h_table.x_y] print(values_in_first_row) print(sum(values_in_first_row)) ``` ## Fast HTML table file read To read the html table files you would usually use the functions described in [Reading outputs from E+](./Outputs_Tutorial.html). For instance you would use the functions as shown below. ``` from eppy.results import readhtml # the eppy module with functions to read the html import pprint pp = pprint.PrettyPrinter() fname = "../eppy/resources/outputfiles/V_7_2/5ZoneCAVtoVAVWarmestTempFlowTable_ABUPS.html" # the html file you want to read html_doc = open(fname, 'r').read() htables = readhtml.titletable(html_doc) # reads the tables with their titles firstitem = htables[0] pp.pprint(firstitem) ``` `titletable` reads all the tables in the HTML file. With large E+ models, this file can be extremeely large and `titletable` will load all the tables into memory. This can take several minutes. If you are trying to get one table or one value from a table, waiting several minutes for you reseult can be exessive. If you know which table you are looking for, there is a faster way of doing this. We used index=0 in the above example to get the first table. If you know the index of the file you are looking for, you can use a faster function to get the table as shown below ``` from eppy.results import fasthtml fname = "../eppy/resources/outputfiles/V_7_2/5ZoneCAVtoVAVWarmestTempFlowTable_ABUPS.html" # the html file you want to read filehandle = open(fname, 'r') # get a file handle to the html file firsttable = fasthtml.tablebyindex(filehandle, 0) pp.pprint(firstitem) ``` You can also get the table if you know the title of the table. This is the bold text just before the table in the HTML file. The title of our table is Site and Source Energy. The function `tablebyname` will get us the table. ``` filehandle = open(fname, 'r') # get a file handle to the html file namedtable = fasthtml.tablebyname(filehandle, "Site and Source Energy") pp.pprint(namedtable) ``` Couple of things to note here: - We have to open the file again using `filehandle = open(fname, 'r')` - This is because both `tablebyname` and `tablebyindex` will close the file once they are done - Some tables do not have a bold title just before the table. `tablebyname` will not work for those functions	github_jupyter
# Applying the Expected Context Framework to the Switchboard Corpus ### Using `DualContextWrapper` This notebook demonstrates how our implementation of the Expected Context Framework can be applied to the Switchboard dataset. See [this dissertation](https://tisjune.github.io/research/dissertation) for more details about the framework, and more comments on the below analyses. This notebook will show how to apply `DualContextWrapper`, a wrapper transformer that keeps track of two instances of `ExpectedContextModelTransformer`. For a version of this demo that initializes two separate instances of `ExpectedContextModelTransformer` instead, and that more explicitly demonstrates that functionality, see [this notebook](https://github.com/CornellNLP/Cornell-Conversational-Analysis-Toolkit/blob/ecf/convokit/expected_context_framework/demos/switchboard_exploration_demo.ipynb). ``` import warnings warnings.filterwarnings('ignore') import pandas as pd import numpy as np import math import os ``` ## 1. Loading and preprocessing the dataset For this demo, we'll use the Switchboard corpus---a collection of telephone conversations which have been annotated with various dialog acts. More information on the dataset, as it exists in ConvoKit format, can be found [here](https://convokit.cornell.edu/documentation/switchboard.html); the original data is described [here](https://web.stanford.edu/~jurafsky/ws97/CL-dialog.pdf). We will actually use a preprocessed version of the Switchboard corpus, which we can access below. Since Switchboard consists of transcribed telephone conversations, there are many disfluencies and backchannels, that make utterances messier, and that make it hard to identify what counts as an actual turn. In the version of the corpus we consider, for the purpose of demonstration, we remove the disfluencies and backchannels (acknowledging that we're discarding important parts of the conversations). ``` from convokit import Corpus from convokit import download # OPTION 1: DOWNLOAD CORPUS # UNCOMMENT THESE LINES TO DOWNLOAD CORPUS # DATA_DIR = '<YOUR DIRECTORY>' # SW_CORPUS_PATH = download('switchboard-processed-corpus', data_dir=DATA_DIR) # OPTION 2: READ PREVIOUSLY-DOWNLOADED CORPUS FROM DISK # UNCOMMENT THIS LINE AND REPLACE WITH THE DIRECTORY WHERE THE TENNIS-CORPUS IS LOCATED # SW_CORPUS_PATH = '<YOUR DIRECTORY>' sw_corpus = Corpus(SW_CORPUS_PATH) sw_corpus.print_summary_stats() utt_eg_id = '3496-79' ``` as input, we use a preprocessed version of the utterance that only contains alphabetical words, found in the `alpha_text` metadata field. ``` sw_corpus.get_utterance(utt_eg_id).meta['alpha_text'] ``` In order to avoid capturing topic-specific information, we restrict our analyses to a vocabulary of unigrams that occurs across many topics, and across many conversations: ``` from collections import defaultdict topic_counts = defaultdict(set) for ut in sw_corpus.iter_utterances(): topic = sw_corpus.get_conversation(ut.conversation_id).meta['topic'] for x in set(ut.meta['alpha_text'].lower().split()): topic_counts[x].add(topic) topic_counts = {x: len(y) for x, y in topic_counts.items()} word_convo_counts = defaultdict(set) for ut in sw_corpus.iter_utterances(): for x in set(ut.meta['alpha_text'].lower().split()): word_convo_counts[x].add(ut.conversation_id) word_convo_counts = {x: len(y) for x, y in word_convo_counts.items()} min_topic_words = set(x for x,y in topic_counts.items() if y >= 33) min_convo_words = set(x for x,y in word_convo_counts.items() if y >= 200) vocab = sorted(min_topic_words.intersection(min_convo_words)) len(vocab) from convokit.expected_context_framework import ColNormedTfidfTransformer, DualContextWrapper ``` ## 2. Applying the Expected Context Framework To apply the Expected Context Framework, we start by converting the input utterance text to an input vector representation. Here, we represent utterances in a term-document matrix that's _normalized by columns_ (empirically, we found that this ensures that the representations derived by the framework aren't skewed by the relative frequency of utterances). We use `ColNormedTfidfTransformer` transformer to do this: ``` tfidf_obj = ColNormedTfidfTransformer(input_field='alpha_text', output_field='col_normed_tfidf', binary=True, vocabulary=vocab) _ = tfidf_obj.fit(sw_corpus) _ = tfidf_obj.transform(sw_corpus) ``` We now use the Expected Context Framework. In short, the framework derives vector representations, and other characterizations, of terms and utterances that are based on their _expected conversational context_---i.e., the replies we expect will follow a term or utterance, or the preceding utterances that we expect the term/utterance will reply to. We are going to derive characterizations based both on the _forwards_ context, i.e., the expected replies, and the _backwards_ context, i.e., the expected predecessors. We'll apply the framework in each direction, and then compare the characterizations that result. To take care of both interlocked models, we use the `DualContextWrapper` transformer, which will keep track of two `ExpectedContextModelTransformer`s: one that relates utterances to predecessors (`reply_to`), and that outputs utterance-level attributes with the prefix `bk`; the other that relates utterances to replies (`next_id`) and outputs utterance-level attributes with the prefix `fw`. These parameters are specified via the `context_fields` and `output_prefixes` arguments. Other arguments passed: * `vect_field` and `context_vect_field` respectively denote the input vector representations of utterances and context utterances that `ec_fw` will work with. Here, we'll use the same tf-idf representations that we just computed above. * `n_svd_dims` denotes the dimensionality of the vector representations that `ec_fw` will output. This is something that you can play around with---for this dataset, we found that more dimensions resulted in messier output, and a coarser, lower-dimensional representation was slightly more interpretable. (Technical note: technically, `ec_fw` produces vector representations of dimension `n_svd_dims`-1, since by default, it removes the first latent dimension, which we find tends to strongly reflect term frequency.) * `n_clusters` denotes the number of utterance types that `ec_fw` will infer, given the representations it computes. Note that this is an interpretative step: looking at clusters of utterances helps us get a sense of what information the representations are capturing; this value does not actually impact the representations and other characterizations we derive. * `random_state` and `cluster_random_state` are fixed for this demo, so we produce deterministic output. ``` dual_context_model = DualContextWrapper(context_fields=['reply_to','next_id'], output_prefixes=['bk','fw'], vect_field='col_normed_tfidf', context_vect_field='col_normed_tfidf', n_svd_dims=15, n_clusters=2, random_state=1000, cluster_random_state=1000) ``` We'll fit the transformer on the subset of utterances and replies that have at least 5 unigrams from our vocabulary. ``` dual_context_model.fit(sw_corpus,selector=lambda x: x.meta.get('col_normed_tfidf__n_feats',0)>=5, context_selector=lambda x: x.meta.get('col_normed_tfidf__n_feats',0)>= 5) ``` ### Interpreting derived representations Before applying the two transformers, `ec_fw` and `ec_bk` to transform the corpus, we can examine the representations and characterizations it's derived over the training data (note that in this case, the training data is also the corpus that we analyze, but this needn't be the case in general---see [this demo](https://github.com/CornellNLP/Cornell-Conversational-Analysis-Toolkit/blob/master/convokit/expected_context_framework/demos/wiki_awry_demo.ipynb) for an example). First, to interpret the representations derived by each model, we can inspect the clusters of representations that we've inferred, for both the forwards and backwards direction. We can access the forwards and backwards models as elements of the `ec_models` attribute. The following function calls print out representative terms and utterances, as well as context terms and utterances, per cluster (next two cells; note that the output is quite long). ``` dual_context_model.ec_models[0].print_clusters(corpus=sw_corpus) dual_context_model.ec_models[1].print_clusters(corpus=sw_corpus) ``` demo continues below We can see that in each case, two clusters emerge that roughly correspond to utterances recounting personal experiences, and those providing commentary, generally not about personal matters. We'll label them as such, noting that there's a roughly 50-50 split with slightly more "personal" utterances than "commentary" ones: ``` dual_context_model.ec_models[0].set_cluster_names(['personal', 'commentary']) dual_context_model.ec_models[1].set_cluster_names(['commentary', 'personal']) ``` ### Interpreting derived characterizations The transformer also computes some term-level statistics, which we can return as a Pandas dataframe: * forwards and backwards ranges (`fw_range` and `bk_range` respectively): we roughly interpret these as modeling the strengths of our forwards expectations of the replies that a term tends to get, or the backwards expectations of the predecessors that the term tends to follow. * shift: this statistic corresponds to the distance between the backwards and forwards representations for each term; we interpret it as the extent to which a term shifts the focus of a conversation. * orientation (`orn`): this statistic compares the relative magnitude of forwards and backwards ranges. In a [counseling conversation setting](https://www.cs.cornell.edu/~cristian/Orientation_files/orientation-forwards-backwards.pdf) we interpreted orientation as a measure of the relative extent to which an interlocutor aims to advance the conversation forwards with a term, versus address existing content. ``` term_df = dual_context_model.get_term_df() term_df.head() k=10 print('low orientation') display(term_df.sort_values('orn').head(k)[['orn']]) print('high orientation') display(term_df.sort_values('orn').tail(k)[['orn']]) print('\nlow shift') display(term_df.sort_values('shift').head(k)[['shift']]) print('high shift') display(term_df.sort_values('shift').tail(k)[['shift']]) ``` ### Deriving utterance-level representations We now use the transformer to derive utterance-level characterizations, by transforming the corpus with it. Again, we focus on utterances that are sufficiently long: ``` _ = dual_context_model.transform(sw_corpus, selector=lambda x: x.meta.get('col_normed_tfidf__n_feats',0)>=5) ``` The `transform` function does the following. First, it (or rather, its constituent `ExpectedContextModelTransformer`s) derives vector representations of utterances, stored as `fw_repr` and `bk_repr`: ``` sw_corpus.vectors ``` Next, it derives ranges of utterances, stored in the metadata as `fw_range` and `bk_range`: ``` eg_ut = sw_corpus.get_utterance(utt_eg_id) print('Forwards range:', eg_ut.meta['fw_range']) print('Backwards range:', eg_ut.meta['bk_range']) ``` It also assigns utterances to inferred types: ``` print('Forwards cluster:', eg_ut.meta['fw_clustering.cluster']) print('Backwards cluster:', eg_ut.meta['bk_clustering.cluster']) ``` And computes orientations and shifts: ``` print('shift:', eg_ut.meta['shift']) print('orientation:', eg_ut.meta['orn']) ``` ## 3. Analysis: correspondence to discourse act labels We explore the relation between the characterizations we've derived, and the various annotations that the utterances are labeled with (for more information on the annotation scheme, see the [manual here](https://web.stanford.edu/~jurafsky/ws97/manual.august1.html)). See [this dissertation](https://tisjune.github.io/research/dissertation) for further explanation of the analyses and findings below. A high-level comment is that this is a tough dataset for the framework to work with, given the relative lack of structure---something future work could think more carefully about. To facilitate the analysis, we extract relevant utterance attributes into a Pandas dataframe: ``` df = sw_corpus.get_attribute_table('utterance', ['bk_clustering.cluster', 'fw_clustering.cluster', 'orn', 'shift', 'tags']) df = df[df['bk_clustering.cluster'].notnull()] ``` We will stick to examining the 9 most common tags in the data: ``` tag_subset = ['aa', 'b', 'ba', 'h', 'ny', 'qw', 'qy', 'sd', 'sv'] for tag in tag_subset: df['has_' + tag] = df.tags.apply(lambda x: tag in x.split()) ``` To start, we explore how the forwards and backwards vector representations correspond to these labels. To do this, we will compute log-odds ratios between the inferred utterance clusters and these labels: ``` def compute_log_odds(col, bool_col, val_subset=None): if val_subset is not None: col_vals = val_subset else: col_vals = col.unique() log_odds_entries = [] for val in col_vals: val_true = sum((col == val) & bool_col) val_false = sum((col == val) & ~bool_col) nval_true = sum((col != val) & bool_col) nval_false = sum((col != val) & ~bool_col) log_odds_entries.append({'val': val, 'log_odds': np.log((val_true/val_false)/(nval_true/nval_false))}) return log_odds_entries bk_log_odds = [] for tag in tag_subset: entry = compute_log_odds(df['bk_clustering.cluster'],df['has_' + tag], ['commentary'])[0] entry['tag'] = tag bk_log_odds.append(entry) bk_log_odds_df = pd.DataFrame(bk_log_odds).set_index('tag').sort_values('log_odds')[['log_odds']] fw_log_odds = [] for tag in tag_subset: entry = compute_log_odds(df['fw_clustering.cluster'],df['has_' + tag], ['commentary'])[0] entry['tag'] = tag fw_log_odds.append(entry) fw_log_odds_df = pd.DataFrame(fw_log_odds).set_index('tag').sort_values('log_odds')[['log_odds']] print('forwards types vs labels') display(fw_log_odds_df.T) print('--------------------------') print('backwards types vs labels') display(bk_log_odds_df.T) ``` Tags further towards the right of the above tables (more positive log-odds) are those that co-occur more with the `commentary` than the `personal` utterance type. We briefly note that both forwards and backwards representations seem to draw a distinction between `sv` (opinion statements) and `sd` (non-opinion statements). Next, we explore how the orientation and shift statistics relate to these labels. To do this, we compare statistics for utterances with a particular label, to statistics for utterances without that label. ``` from scipy import stats def cohend(d1, d2): n1, n2 = len(d1), len(d2) s1, s2 = np.var(d1, ddof=1), np.var(d2, ddof=1) s = np.sqrt(((n1 - 1) * s1 + (n2 - 1) * s2) / (n1 + n2 - 2)) u1, u2 = np.mean(d1), np.mean(d2) return (u1 - u2) / s def get_pstars(p): if p < 0.001: return '*' elif p < 0.01: return '' elif p < 0.05: return '' else: return '' stat_col = 'orn' entries = [] for tag in tag_subset: has = df[df['has_' + tag]][stat_col] hasnt = df[~df['has_' + tag]][stat_col] entry = {'tag': tag, 'pval': stats.mannwhitneyu(has, hasnt)[1], 'cd': cohend(has, hasnt)} entry['ps'] = get_pstars(entry['pval'] len(tag_subset)) entries.append(entry) orn_stat_df = pd.DataFrame(entries).set_index('tag').sort_values('cd') orn_stat_df = orn_stat_df[np.abs(orn_stat_df.cd) >= .1] stat_col = 'shift' entries = [] for tag in tag_subset: has = df[df['has_' + tag]][stat_col] hasnt = df[~df['has_' + tag]][stat_col] entry = {'tag': tag, 'pval': stats.mannwhitneyu(has, hasnt)[1], 'cd': cohend(has, hasnt)} entry['ps'] = get_pstars(entry['pval'] * len(tag_subset)) entries.append(entry) shift_stat_df = pd.DataFrame(entries).set_index('tag').sort_values('cd') shift_stat_df = shift_stat_df[np.abs(shift_stat_df.cd) >= .1] ``` (We'll only show labels for which there's a sufficiently large difference, in cohen's delta, between utterances with and without the label) ``` print('orientation vs labels') display(orn_stat_df.T) print('--------------------------') print('shift vs labels') display(shift_stat_df.T) ``` We note that utterances containing questions (`qw`, `qy`) have higher shifts than utterances which do not. If you're familiar with the DAMSL designations for forwards and backwards looking communicative functions, the output for orientation might look a little puzzling/informative that our view of what counts as forwards/backwards is different from the view espoused by the annotation scheme. We discuss this further in [this dissertation](https://tisjune.github.io/research/dissertation). ## 4. Model persistence Finally, we briefly demonstrate how the model can be saved and loaded for later use ``` DUAL_MODEL_PATH = os.path.join(SW_CORPUS_PATH, 'dual_model') dual_context_model.dump(DUAL_MODEL_PATH) ``` We dump latent context representations, clustering information, and various input parameters, for each constituent `ExpectedContextModelTransformer`, in separate directories under `DUAL_MODEL_PATH`: ``` ls $DUAL_MODEL_PATH ``` To load the learned model, we start by initializing a new model: ``` dual_model_new = DualContextWrapper(context_fields=['reply_to','next_id'], output_prefixes=['bk_new','fw_new'], vect_field='col_normed_tfidf', context_vect_field='col_normed_tfidf', wrapper_output_prefix='new', n_svd_dims=15, n_clusters=2, random_state=1000, cluster_random_state=1000) dual_model_new.load(DUAL_MODEL_PATH, model_dirs=['bk','fw']) ``` We see that using the re-loaded model to transform the corpus results in the same representations and characterizations as the original one: ``` _ = dual_model_new.transform(sw_corpus, selector=lambda x: x.meta.get('col_normed_tfidf__n_feats',0)>=5) sw_corpus.vectors np.allclose(sw_corpus.get_vectors('bk_new_repr'), sw_corpus.get_vectors('bk_repr')) np.allclose(sw_corpus.get_vectors('fw_new_repr'), sw_corpus.get_vectors('fw_repr')) for ut in sw_corpus.iter_utterances(selector=lambda x: x.meta.get('col_normed_tfidf__n_feats',0)>=5): assert ut.meta['orn'] == ut.meta['new_orn'] assert ut.meta['shift'] == ut.meta['new_shift'] ``` ## 5. Pipeline usage We also implement a pipeline that handles the following: * processes text (via a pipeline supplied by the user) * transforms text to input representation (via `ColNormedTfidfTransformer`) * derives framework output (via `DualContextWrapper`) ``` from convokit.expected_context_framework import DualContextPipeline # see `demo_text_pipelines.py` in this demo's directory for details # in short, this pipeline will either output the `alpha_text` metadata field # of an utterance, or write the utterance's `text` attribute into the `alpha_text` # metadata field from demo_text_pipelines import switchboard_text_pipeline ``` We initialize the pipeline with the following arguments: * `text_field` specifies which utterance metadata field to use as text input * `text_pipe` specifies the pipeline used to compute the contents of `text_field` * `tfidf_params` specifies the parameters to be passed into the underlying `ColNormedTfidfTransformer` object * `min_terms` specifies the minimum number of terms in the vocabulary that an utterance must contain for it to be considered in fitting and transforming the underlying `DualContextWrapper` object (see the `selector` argument passed into `dual_context_model.fit` above) All other arguments are inherited from `DualContextWrapper`. ``` pipe_obj = DualContextPipeline(context_fields=['reply_to','next_id'], output_prefixes=['bk','fw'], text_field='alpha_text', text_pipe=switchboard_text_pipeline(), tfidf_params={'binary': True, 'vocabulary': vocab}, min_terms=5, n_svd_dims=15, n_clusters=2, random_state=1000, cluster_random_state=1000) # note this might output a warning that `col_normed_tfidf` already exists; # that's okay: the pipeline is just recomputing this matrix pipe_obj.fit(sw_corpus) ``` Note that the pipeline enables us to transform ad-hoc string input: ``` eg_ut_new = pipe_obj.transform_utterance('How old were you when you left ?') # note these attributes have the exact same values as those of eg_ut, computed above print('shift:', eg_ut_new.meta['shift']) print('orientation:', eg_ut_new.meta['orn']) ```	github_jupyter
``` #python packages pd import numpy as np import matplotlib.pyplot as plt #machine learning packages import tensorflow as tf import keras from keras.models import Sequential from keras.layers import Dense, Embedding, LSTM, SpatialDropout1D, Bidirectional, Dropout from keras.layers import CuDNNLSTM from keras.utils.np_utils import to_categorical # from keras.callbacks import EarlyStopping from keras.layers import Dropout from sklearn.model_selection import train_test_split import importlib #custom python scripts import generator import utilis # Check that you are running GPU's utilis.GPU_checker() utilis.aws_setup() %%time # generators importlib.reload(generator) training_generator = generator.Keras_DataGenerator( dataset='train', w_hyp=False) validation_generator = generator.Keras_DataGenerator(dataset='valid', w_hyp= False) #Constants # ARE YOU LOADINNG MODE? VOCAB_SIZE = 1254 INPUT_LENGTH = 1000 EMBEDDING_DIM = 256 # # model def build_model(vocab_size, embedding_dim, input_length): model = Sequential() model.add(Embedding(vocab_size, embedding_dim, input_length=input_length)) model.add(SpatialDropout1D(0.4)) model.add(Bidirectional(CuDNNLSTM(128))) model.add(Dropout(0.4)) model.add(Dense(256, activation='relu')) model.add(Dropout(0.4)) model.add(Dense(41, activation='softmax')) return model model = build_model(VOCAB_SIZE, EMBEDDING_DIM, INPUT_LENGTH) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # print(model.summary()) ## WARNING IF YOU CONTAIN MULTIPLE CORE GPUS # NOTE unclear if these causes a speed up # @TANCREDI, I HAVE TREID THIS ON JUST GOALS AND DOES NOT SEEM TO CAUSE A SPEED UP MAY #CAUSE A SPEED UP IF WE USE HYPOTHESIS # unclea rif this seepd # from keras.utils import multi_gpu_model # model_GPU = multi_gpu_model(model, gpus= 4) # model_GPU.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) ## ARE YOU LOADING A MODEL IF YES RUN TEH FOLLOWING LINES # from keras.models import model_from_json # json_file = open('model.json', 'r') # loaded_model_json = json_file.read() # json_file.close() # loaded_model = model_from_json(loaded_model_json) # # load weights into new model # loaded_model.load_weights("model.h5") # print("Loaded model from disk") # # REMEMEBER TO COMPILE # loaded_model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) #overwriting model # model = loaded_model print(model.summary()) %%time n_epochs = 6 history = model.fit_generator(generator=training_generator, # validation_data=validation_generator, verbose=1, use_multiprocessing= False, epochs=n_epochs) # FOR SAVING MODEL model_json = model.to_json() with open("model.json", "w") as json_file: json_file.write(model_json) # serialize weights to HDF5 model.save_weights("model.h5") print("Saved model to disk") #WARNING_DECIDE_HOW_TO_NAME_LOG #descriptionofmodel_personwhostartsrun #e.g. LSTM_128encoder_etc_tanc LOSS_FILE_NAME = "SIMPLE_LSTM_SMALL_TANK" #WARNING NUMBER 2 - CURRENTLY EVERYTIME YOU RERUN THE CELLS BELOW THE FILES WITH THOSE NAMES GET WRITTEN OVER # save history - WARNING FILE NAME utilis.history_saver_bad(history, LOSS_FILE_NAME) # read numpy array # history_toplot = np.genfromtxt("training_logs/"+ LOSS_FILE_NAME +".csv") # plt.plot(history_toplot) # plt.title('Loss history') # plt.show() %%time n_epochs = 1 history = loaded_model.fit_generator(generator=training_generator, validation_data=validation_generator, verbose=1, use_multiprocessing= False, epochs=n_epochs) ```	github_jupyter
# Underfitting and Overfitting demo using KNN ``` import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline data = pd.read_csv('data_knn_classification_cleaned_titanic.csv') data.head() x = data.drop(['Survived'], axis=1) y = data['Survived'] #Scaling the data from sklearn.preprocessing import StandardScaler ss = StandardScaler() x = ss.fit_transform(x) #split the data from sklearn.model_selection import train_test_split train_x, test_x, train_y, test_y = train_test_split(x, y, random_state=96, stratify=y) ``` # implementing KNN ``` #imporing KNN classifier and f1 score from sklearn.neighbors import KNeighborsClassifier as KNN from sklearn.metrics import f1_score #creating an instance of KNN clf = KNN(n_neighbors = 12) clf.fit(train_x, train_y) train_predict = clf.predict(train_x) k1 = f1_score(train_predict, train_y) print("training: ",k1) test_predict = clf.predict(test_x) k = f1_score(test_predict, test_y) print("testing: ",k) def f1score(k): train_f1 = [] test_f1 = [] for i in k: clf = KNN(n_neighbors = i) clf.fit(train_x, train_y) train_predict = clf.predict(train_x) k1 = f1_score(train_predict, train_y) train_f1.append(k1) test_predict = clf.predict(test_x) k = f1_score(test_predict, test_y) test_f1.append(k) return train_f1, test_f1 k = range(1,50) train_f1, test_f1 = f1score(k) train_f1, test_f1 score = pd.DataFrame({'train score': train_f1, 'test_score':test_f1}, index = k) score #visulaising plt.plot(k, test_f1, color ='red', label ='test') plt.plot(k, train_f1, color ='green', label ='train') plt.xlabel('K Neighbors') plt.ylabel('F1 score') plt.title('f1 curve') plt.ylim(0,4,1) plt.legend() #split the data from sklearn.model_selection import train_test_split train_x, test_x, train_y, test_y = train_test_split(x, y, random_state=42, stratify=y) k = range(1,50) train_f1, test_f1 = f1score(k) #visulaising plt.plot(k, test_f1, color ='red', label ='test') plt.plot(k, train_f1, color ='green', label ='train') plt.xlabel('K Neighbors') plt.ylabel('F1 score') plt.title('f1 curve') #plt.ylim(0,4,1) plt.legend() ''' here the value of k is decided by using both train and test data , instead of (testset) that we can use validation set types: 1. Hold-out validation as we directly divide the data into praprotions, there might be a case where the validation set is biased to only one class (which mean validation set might have data of only one class, these results in set have no idea about the other class) in this we have different distributions 2. Stratified hold out in this we have equal distributions in the hold out scenario we need good amount of data to maintain, so we need to train with lot data. if the dataset is small? and we want to bulid the complex relations out of them? ''' ``` # Bias Variance Tradeoff ``` ''' if variance is high then bias is low if bias is high then variance is low error high bias high variance optimally in btw fit underfit overfit bestfit k range 21<k k<11 12<k<21 complexity low high optimum Generalization error : defines the optimum model btw high bias and high varaince High variance refers to overfitting whereas high bias refers to underfitting and we do not want both of these scenarios. So, the best model is said to have low bias and low variance. ''' ```	github_jupyter
# [ATM 623: Climate Modeling](../index.ipynb) [Brian E. J. Rose](http://www.atmos.albany.edu/facstaff/brose/index.html), University at Albany # Lecture 17: Ice albedo feedback in the EBM ### About these notes: This document uses the interactive [`IPython notebook`](http://ipython.org/notebook.html) format (now also called [`Jupyter`](https://jupyter.org)). The notes can be accessed in several different ways: - The interactive notebooks are hosted on `github` at https://github.com/brian-rose/ClimateModeling_courseware - The latest versions can be viewed as static web pages [rendered on nbviewer](http://nbviewer.ipython.org/github/brian-rose/ClimateModeling_courseware/blob/master/index.ipynb) - A complete snapshot of the notes as of May 2015 (end of spring semester) are [available on Brian's website](http://www.atmos.albany.edu/facstaff/brose/classes/ATM623_Spring2015/Notes/index.html). Many of these notes make use of the `climlab` package, available at https://github.com/brian-rose/climlab ## Contents 1. [Interactive snow and ice line in the EBM](#section1) 2. [Polar-amplified warming in the EBM](#section2) 3. [Effects of diffusivity in the annual mean EBM with albedo feedback](#section3) 4. [Diffusive response to a point source of energy](#section4) ____________ <a id='section1'></a> ## 1. Interactive snow and ice line in the EBM ____________ ### The annual mean EBM the equation is $$ C(\phi) \frac{\partial T_s}{\partial t} = (1-\alpha) ~ Q - \left( A + B~T_s \right) + \frac{D}{\cos⁡\phi } \frac{\partial }{\partial \phi} \left( \cos⁡\phi ~ \frac{\partial T_s}{\partial \phi} \right) $$ ### Temperature-dependent ice line Let the surface albedo be larger wherever the temperature is below some threshold $T_f$: $$ \alpha\left(\phi, T(\phi) \right) = \left\{\begin{array}{ccc} \alpha_0 + \alpha_2 P_2(\sin\phi) & ~ & T(\phi) > T_f \\ a_i & ~ & T(\phi) \le T_f \\ \end{array} \right. $$ ``` %matplotlib inline import numpy as np import matplotlib.pyplot as plt import climlab # for convenience, set up a dictionary with our reference parameters param = {'A':210, 'B':2, 'a0':0.3, 'a2':0.078, 'ai':0.62, 'Tf':-10.} model1 = climlab.EBM_annual( num_lat=180, D=0.55, *param ) print model1 ``` Because we provided a parameter `ai` for the icy albedo, our model now contains several sub-processes contained within the process called `albedo`. Together these implement the step-function formula above. The process called `iceline` simply looks for grid cells with temperature below $T_f$. ``` print model1.param def ebm_plot( model, figsize=(8,12), show=True ): '''This function makes a plot of the current state of the model, including temperature, energy budget, and heat transport.''' templimits = -30,35 radlimits = -340, 340 htlimits = -7,7 latlimits = -90,90 lat_ticks = np.arange(-90,90,30) fig = plt.figure(figsize=figsize) ax1 = fig.add_subplot(3,1,1) ax1.plot(model.lat, model.Ts) ax1.set_xlim(latlimits) ax1.set_ylim(templimits) ax1.set_ylabel('Temperature (deg C)') ax1.set_xticks( lat_ticks ) ax1.grid() ax2 = fig.add_subplot(3,1,2) ax2.plot(model.lat, model.diagnostics['ASR'], 'k--', label='SW' ) ax2.plot(model.lat, -model.diagnostics['OLR'], 'r--', label='LW' ) ax2.plot(model.lat, model.diagnostics['net_radiation'], 'c-', label='net rad' ) ax2.plot(model.lat, model.heat_transport_convergence(), 'g--', label='dyn' ) ax2.plot(model.lat, model.diagnostics['net_radiation'].squeeze() + model.heat_transport_convergence(), 'b-', label='total' ) ax2.set_xlim(latlimits) ax2.set_ylim(radlimits) ax2.set_ylabel('Energy budget (W m$^{-2}$)') ax2.set_xticks( lat_ticks ) ax2.grid() ax2.legend() ax3 = fig.add_subplot(3,1,3) ax3.plot(model.lat_bounds, model.heat_transport() ) ax3.set_xlim(latlimits) ax3.set_ylim(htlimits) ax3.set_ylabel('Heat transport (PW)') ax3.set_xlabel('Latitude') ax3.set_xticks( lat_ticks ) ax3.grid() return fig model1.integrate_years(5) f = ebm_plot(model1) model1.diagnostics['icelat'] ``` ____________ <a id='section2'></a> ## 2. Polar-amplified warming in the EBM ____________ ### Add a small radiative forcing The equivalent of doubling CO2 in this model is something like $$ A \rightarrow A - \delta A $$ where $\delta A = 4$ W m$^{-2}$. ``` deltaA = 4. model2 = climlab.process_like(model1) model2.subprocess['LW'].A = param['A'] - deltaA model2.integrate_years(5, verbose=False) plt.plot(model1.lat, model1.Ts) plt.plot(model2.lat, model2.Ts) ``` The warming is polar-amplified: more warming at the poles than elsewhere. Why? Also, the current ice line is now: ``` model2.diagnostics['icelat'] ``` There is no ice left! Let's do some more greenhouse warming: ``` model3 = climlab.process_like(model1) model3.subprocess['LW'].A = param['A'] - 2deltaA model3.integrate_years(5, verbose=False) plt.plot(model1.lat, model1.Ts) plt.plot(model2.lat, model2.Ts) plt.plot(model3.lat, model3.Ts) plt.xlim(-90, 90) plt.grid() ``` In the ice-free regime, there is no polar-amplified warming. A uniform radiative forcing produces a uniform warming. ____________ <a id='section3'></a> ## 3. Effects of diffusivity in the annual mean EBM with albedo feedback ____________ ### In-class investigation: We will repeat the exercise from Lecture 14, but this time with albedo feedback included in our model. - Solve the annual-mean EBM (integrate out to equilibrium) over a range of different diffusivity parameters. - Make three plots: - Global-mean temperature as a function of $D$ - Equator-to-pole temperature difference $\Delta T$ as a function of $D$ - Poleward heat transport across 35 degrees $\mathcal{H}_{max}$ as a function of $D$ - Choose a value of $D$ that gives a reasonable approximation to observations: - $\Delta T \approx 45$ ºC Use these parameter values: ``` param = {'A':210, 'B':2, 'a0':0.3, 'a2':0.078, 'ai':0.62, 'Tf':-10.} print param ``` ### One possible way to do this: ``` Darray = np.arange(0., 2.05, 0.05) model_list = [] Tmean_list = [] deltaT_list = [] Hmax_list = [] for D in Darray: ebm = climlab.EBM_annual(num_lat=360, D=D, param ) #ebm.subprocess['insolation'].s2 = -0.473 ebm.integrate_years(5., verbose=False) Tmean = ebm.global_mean_temperature() deltaT = np.max(ebm.Ts) - np.min(ebm.Ts) HT = ebm.heat_transport() #Hmax = np.max(np.abs(HT)) ind = np.where(ebm.lat_bounds==35.5)[0] Hmax = HT[ind] model_list.append(ebm) Tmean_list.append(Tmean) deltaT_list.append(deltaT) Hmax_list.append(Hmax) color1 = 'b' color2 = 'r' fig = plt.figure(figsize=(8,6)) ax1 = fig.add_subplot(111) ax1.plot(Darray, deltaT_list, color=color1, label='$\Delta T$') ax1.plot(Darray, Tmean_list, '--', color=color1, label='$\overline{T}$') ax1.set_xlabel('D (W m$^{-2}$ K$^{-1}$)', fontsize=14) ax1.set_xticks(np.arange(Darray[0], Darray[-1], 0.2)) ax1.set_ylabel('Temperature ($^\circ$C)', fontsize=14, color=color1) for tl in ax1.get_yticklabels(): tl.set_color(color1) ax1.legend(loc='center right') ax2 = ax1.twinx() ax2.plot(Darray, Hmax_list, color=color2) ax2.set_ylabel('Poleward heat transport across 35.5$^\circ$ (PW)', fontsize=14, color=color2) for tl in ax2.get_yticklabels(): tl.set_color(color2) ax1.set_title('Effect of diffusivity on EBM with albedo feedback', fontsize=16) ax1.grid() ``` ____________ <a id='section4'></a> ## 4. Diffusive response to a point source of energy ____________ Let's add a point heat source to the EBM and see what sets the spatial structure of the response. We will add a heat source at about 45º latitude. First, we will calculate the response in a model without albedo feedback. ``` param_noalb = {'A': 210, 'B': 2, 'D': 0.55, 'Tf': -10.0, 'a0': 0.3, 'a2': 0.078} m1 = climlab.EBM_annual(num_lat=180, param_noalb) print m1 m1.integrate_years(5.) m2 = climlab.process_like(m1) point_source = climlab.process.energy_budget.ExternalEnergySource(state=m2.state) ind = np.where(m2.lat == 45.5) point_source.heating_rate['Ts'][ind] = 100. m2.add_subprocess('point source', point_source) print m2 m2.integrate_years(5.) plt.plot(m2.lat, m2.Ts - m1.Ts) plt.xlim(-90,90) plt.grid() ``` The warming effects of our point source are felt at all latitudes but the effects decay away from the heat source. Some analysis will show that the length scale of the warming is proportional to $$ \sqrt{\frac{D}{B}} $$ so increases with the diffusivity. Now repeat this calculate with ice albedo feedback ``` m3 = climlab.EBM_annual(num_lat=180, param) m3.integrate_years(5.) m4 = climlab.process_like(m3) point_source = climlab.process.energy_budget.ExternalEnergySource(state=m4.state) point_source.heating_rate['Ts'][ind] = 100. m4.add_subprocess('point source', point_source) m4.integrate_years(5.) plt.plot(m4.lat, m4.Ts - m3.Ts) plt.xlim(-90,90) plt.grid() ``` Now the maximum warming does not coincide with the heat source at 45º! Our heat source has led to melting of snow and ice, which induces an additional heat source in the high northern latitudes. Heat transport communicates the external warming to the ice cap, and also commuicates the increased shortwave absorption due to ice melt globally!** <div class="alert alert-success"> [Back to ATM 623 notebook home](../index.ipynb) </div> ____________ ## Credits The author of this notebook is [Brian E. J. Rose](http://www.atmos.albany.edu/facstaff/brose/index.html), University at Albany. It was developed in support of [ATM 623: Climate Modeling](http://www.atmos.albany.edu/facstaff/brose/classes/ATM623_Spring2015/), a graduate-level course in the [Department of Atmospheric and Envionmental Sciences](http://www.albany.edu/atmos/index.php), offered in Spring 2015. ____________ ____________ ## Version information ____________ ``` %install_ext http://raw.github.com/jrjohansson/version_information/master/version_information.py %load_ext version_information %version_information numpy, climlab ```	github_jupyter
# Neural networks with PyTorch Next I'll show you how to build a neural network with PyTorch. ``` # Import things like usual %matplotlib inline %config InlineBackend.figure_format = 'retina' import numpy as np import torch import helper import matplotlib.pyplot as plt from torchvision import datasets, transforms ``` First up, we need to get our dataset. This is provided through the `torchvision` package. The code below will download the MNIST dataset, then create training and test datasets for us. Don't worry too much about the details here, you'll learn more about this later. ``` # Define a transform to normalize the data transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)), ]) # Download and load the training data trainset = datasets.MNIST('MNIST_data/', download=True, train=True, transform=transform) trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True) # Download and load the test data testset = datasets.MNIST('MNIST_data/', download=True, train=False, transform=transform) testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True) dataiter = iter(trainloader) images, labels = dataiter.next() ``` We have the training data loaded into `trainloader` and we make that an iterator with `iter(trainloader)`. We'd use this to loop through the dataset for training, but here I'm just grabbing the first batch so we can check out the data. We can see below that `images` is just a tensor with size (64, 1, 28, 28). So, 64 images per batch, 1 color channel, and 28x28 images. ``` plt.imshow(images[1].numpy().squeeze(), cmap='Greys_r'); ``` ## Building networks with PyTorch Here I'll use PyTorch to build a simple feedfoward network to classify the MNIST images. That is, the network will receive a digit image as input and predict the digit in the image. <img src="assets/mlp_mnist.png" width=600px> To build a neural network with PyTorch, you use the `torch.nn` module. The network itself is a class inheriting from `torch.nn.Module`. You define each of the operations separately, like `nn.Linear(784, 128)` for a fully connected linear layer with 784 inputs and 128 units. The class needs to include a `forward` method that implements the forward pass through the network. In this method, you pass some input tensor `x` through each of the operations you defined earlier. The `torch.nn` module also has functional equivalents for things like ReLUs in `torch.nn.functional`. This module is usually imported as `F`. Then to use a ReLU activation on some layer (which is just a tensor), you'd do `F.relu(x)`. Below are a few different commonly used activation functions. <img src="assets/activation.png" width=700px> So, for this network, I'll build it with three fully connected layers, then a softmax output for predicting classes. The softmax function is similar to the sigmoid in that it squashes inputs between 0 and 1, but it's also normalized so that all the values sum to one like a proper probability distribution. ``` from torch import nn from torch import optim import torch.nn.functional as F class Network(nn.Module): def __init__(self): super().__init__() # Defining the layers, 128, 64, 10 units each self.fc1 = nn.Linear(784, 128) self.fc2 = nn.Linear(128, 64) # Output layer, 10 units - one for each digit self.fc3 = nn.Linear(64, 10) def forward(self, x): ''' Forward pass through the network, returns the output logits ''' x = self.fc1(x) x = F.relu(x) x = self.fc2(x) x = F.relu(x) x = self.fc3(x) x = F.softmax(x, dim=1) return x model = Network() model ``` ### Initializing weights and biases The weights and such are automatically initialized for you, but it's possible to customize how they are initialized. The weights and biases are tensors attached to the layer you defined, you can get them with `model.fc1.weight` for instance. ``` print(model.fc1.weight) print(model.fc1.bias) ``` For custom initialization, we want to modify these tensors in place. These are actually autograd Variables, so we need to get back the actual tensors with `model.fc1.weight.data`. Once we have the tensors, we can fill them with zeros (for biases) or random normal values. ``` # Set biases to all zeros model.fc1.bias.data.fill_(0) # sample from random normal with standard dev = 0.01 model.fc1.weight.data.normal_(std=0.01) ``` ### Forward pass Now that we have a network, let's see what happens when we pass in an image. This is called the forward pass. We're going to convert the image data into a tensor, then pass it through the operations defined by the network architecture. ``` # Grab some data dataiter = iter(trainloader) images, labels = dataiter.next() # Resize images into a 1D vector, new shape is (batch size, color channels, image pixels) images.resize_(64, 1, 784) # or images.resize_(images.shape[0], 1, 784) to not automatically get batch size # Forward pass through the network img_idx = 0 ps = model.forward(images[img_idx,:]) img = images[img_idx] helper.view_classify(img.view(1, 28, 28), ps) ``` As you can see above, our network has basically no idea what this digit is. It's because we haven't trained it yet, all the weights are random! PyTorch provides a convenient way to build networks like this where a tensor is passed sequentially through operations, `nn.Sequential` ([documentation](https://pytorch.org/docs/master/nn.html#torch.nn.Sequential)). Using this to build the equivalent network: ``` # Hyperparameters for our network input_size = 784 hidden_sizes = [128, 64] output_size = 10 # Build a feed-forward network model = nn.Sequential(nn.Linear(input_size, hidden_sizes[0]), nn.ReLU(), nn.Linear(hidden_sizes[0], hidden_sizes[1]), nn.ReLU(), nn.Linear(hidden_sizes[1], output_size), nn.Softmax(dim=1)) print(model) # Forward pass through the network and display output images, labels = next(iter(trainloader)) images.resize_(images.shape[0], 1, 784) ps = model.forward(images[0,:]) helper.view_classify(images[0].view(1, 28, 28), ps) ``` You can also pass in an `OrderedDict` to name the individual layers and operations. Note that a dictionary keys must be unique, so _each operation must have a different name_. ``` from collections import OrderedDict model = nn.Sequential(OrderedDict([ ('fc1', nn.Linear(input_size, hidden_sizes[0])), ('relu1', nn.ReLU()), ('fc2', nn.Linear(hidden_sizes[0], hidden_sizes[1])), ('relu2', nn.ReLU()), ('output', nn.Linear(hidden_sizes[1], output_size)), ('softmax', nn.Softmax(dim=1))])) model ``` Now it's your turn to build a simple network, use any method I've covered so far. In the next notebook, you'll learn how to train a network so it can make good predictions. >Exercise: Build a network to classify the MNIST images with _three_ hidden layers. Use 400 units in the first hidden layer, 200 units in the second layer, and 100 units in the third layer. Each hidden layer should have a ReLU activation function, and use softmax on the output layer. ``` ## TODO: Your network here ## Run this cell with your model to make sure it works ## # Forward pass through the network and display output images, labels = next(iter(trainloader)) images.resize_(images.shape[0], 1, 784) ps = model.forward(images[0,:]) helper.view_classify(images[0].view(1, 28, 28), ps) ```	github_jupyter
# Example: CanvasXpress boxplot Chart No. 11 This example page demonstrates how to, using the Python package, create a chart that matches the CanvasXpress online example located at: https://www.canvasxpress.org/examples/boxplot-11.html This example is generated using the reproducible JSON obtained from the above page and the `canvasxpress.util.generator.generate_canvasxpress_code_from_json_file()` function. Everything required for the chart to render is included in the code below. Simply run the code block. ``` from canvasxpress.canvas import CanvasXpress from canvasxpress.js.collection import CXEvents from canvasxpress.render.jupyter import CXNoteBook cx = CanvasXpress( render_to="boxplot11", data={ "y": { "smps": [ "Var1", "Var2", "Var3", "Var4", "Var5", "Var6", "Var7", "Var8", "Var9", "Var10", "Var11", "Var12", "Var13", "Var14", "Var15", "Var16", "Var17", "Var18", "Var19", "Var20", "Var21", "Var22", "Var23", "Var24", "Var25", "Var26", "Var27", "Var28", "Var29", "Var30", "Var31", "Var32", "Var33", "Var34", "Var35", "Var36", "Var37", "Var38", "Var39", "Var40", "Var41", "Var42", "Var43", "Var44", "Var45", "Var46", "Var47", "Var48", "Var49", "Var50", "Var51", "Var52", "Var53", "Var54", "Var55", "Var56", "Var57", "Var58", "Var59", "Var60" ], "data": [ [ 4.2, 11.5, 7.3, 5.8, 6.4, 10, 11.2, 11.2, 5.2, 7, 16.5, 16.5, 15.2, 17.3, 22.5, 17.3, 13.6, 14.5, 18.8, 15.5, 23.6, 18.5, 33.9, 25.5, 26.4, 32.5, 26.7, 21.5, 23.3, 29.5, 15.2, 21.5, 17.6, 9.7, 14.5, 10, 8.2, 9.4, 16.5, 9.7, 19.7, 23.3, 23.6, 26.4, 20, 25.2, 25.8, 21.2, 14.5, 27.3, 25.5, 26.4, 22.4, 24.5, 24.8, 30.9, 26.4, 27.3, 29.4, 23 ] ], "vars": [ "len" ] }, "x": { "supp": [ "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "VC", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ", "OJ" ], "order": [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ], "dose": [ 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ] } }, config={ "axisAlgorithm": "rPretty", "axisTickScaleFontFactor": 1.8, "axisTitleFontStyle": "bold", "axisTitleScaleFontFactor": 1.8, "colorBy": "dose", "graphOrientation": "vertical", "graphType": "Boxplot", "groupingFactors": [ "dose" ], "legendScaleFontFactor": 1.8, "showLegend": True, "smpLabelRotate": 90, "smpLabelScaleFontFactor": 1.8, "smpTitle": "dose", "smpTitleFontStyle": "bold", "smpTitleScaleFontFactor": 1.8, "stringSampleFactors": [ "dose" ], "theme": "CanvasXpress", "title": "The Effect of Vitamin C on Tooth Growth in Guinea Pigs", "xAxis2Show": False, "xAxisMinorTicks": False, "xAxisTitle": "len" }, width=613, height=613, events=CXEvents(), after_render=[ [ "switchNumericToString", [ "dose", True ] ] ], other_init_params={ "version": 35, "events": False, "info": False, "afterRenderInit": False, "noValidate": True } ) display = CXNoteBook(cx) display.render(output_file="boxplot_11.html") ```	github_jupyter
# Partial Dependence Plot ## Summary Partial dependence plots visualize the dependence between the response and a set of target features (usually one or two), marginalizing over all the other features. For a perturbation-based interpretability method, it is relatively quick. PDP assumes independence between the features, and can be misleading interpretability-wise when this is not met (e.g. when the model has many high order interactions). ## How it Works The PDP module for `scikit-learn` {cite}`pedregosa2011scikit` provides a succinct description of the algorithm [here](https://scikit-learn.org/stable/modules/partial_dependence.html). Christoph Molnar's "Interpretable Machine Learning" e-book {cite}`molnar2020interpretable` has an excellent overview on partial dependence that can be found [here](https://christophm.github.io/interpretable-ml-book/pdp.html). The conceiving paper "Greedy Function Approximation: A Gradient Boosting Machine" {cite}`friedman2001greedy` provides a good motivation and definition. ## Code Example The following code will train a blackbox pipeline for the breast cancer dataset. Aftewards it will interpret the pipeline and its decisions with Partial Dependence Plots. The visualizations provided will be for global explanations. ``` from interpret import set_visualize_provider from interpret.provider import InlineProvider set_visualize_provider(InlineProvider()) from sklearn.datasets import load_breast_cancer from sklearn.model_selection import train_test_split from sklearn.ensemble import RandomForestClassifier from sklearn.decomposition import PCA from sklearn.pipeline import Pipeline from interpret import show from interpret.blackbox import PartialDependence seed = 1 X, y = load_breast_cancer(return_X_y=True, as_frame=True) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=seed) pca = PCA() rf = RandomForestClassifier(n_estimators=100, n_jobs=-1) blackbox_model = Pipeline([('pca', pca), ('rf', rf)]) blackbox_model.fit(X_train, y_train) pdp = PartialDependence(predict_fn=blackbox_model.predict_proba, data=X_train) pdp_global = pdp.explain_global() show(pdp_global) ``` ## Further Resources - [Paper link to conceiving paper](https://projecteuclid.org/download/pdf_1/euclid.aos/1013203451) - [scikit-learn on their PDP module](https://scikit-learn.org/stable/modules/partial_dependence.html) ## Bibliography ```{bibliography} references.bib :style: unsrt :filter: docname in docnames ``` ## API ### PartialDependence ```{eval-rst} .. autoclass:: interpret.blackbox.PartialDependence :members: :inherited-members: ```	github_jupyter
# A - Using TorchText with Your Own Datasets In this series we have used the IMDb dataset included as a dataset in TorchText. TorchText has many canonical datasets included for classification, language modelling, sequence tagging, etc. However, frequently you'll be wanting to use your own datasets. Luckily, TorchText has functions to help you to this. Recall in the series, we: - defined the `Field`s - loaded the dataset - created the splits As a reminder, the code is shown below: ```python TEXT = data.Field() LABEL = data.LabelField() train_data, test_data = datasets.IMDB.splits(TEXT, LABEL) train_data, valid_data = train_data.split() ``` There are three data formats TorchText can read: `json`, `tsv` (tab separated values) and`csv` (comma separated values). In my opinion, the best formatting for TorchText is `json`, which I'll explain later on. ## Reading JSON Starting with `json`, your data must be in the `json lines` format, i.e. it must be something like: ``` {"name": "John", "location": "United Kingdom", "age": 42, "quote": ["i", "love", "the", "united kingdom"]} {"name": "Mary", "location": "United States", "age": 36, "quote": ["i", "want", "more", "telescopes"]} ``` That is, each line is a `json` object. See `data/train.json` for an example. We then define the fields: ``` from torchtext.legacy import data from torchtext.legacy import datasets NAME = data.Field() SAYING = data.Field() PLACE = data.Field() ``` Next, we must tell TorchText which fields apply to which elements of the `json` object. For `json` data, we must create a dictionary where: - the key matches the key of the `json` object - the value is a tuple where: - the first element becomes the batch object's attribute name - the second element is the name of the `Field` What do we mean when we say "becomes the batch object's attribute name"? Recall in the previous exercises where we accessed the `TEXT` and `LABEL` fields in the train/evaluation loop by using `batch.text` and `batch.label`, this is because TorchText sets the batch object to have a `text` and `label` attribute, each being a tensor containing either the text or the label. A few notes: * The order of the keys in the `fields` dictionary does not matter, as long as its keys match the `json` data keys. - The `Field` name does not have to match the key in the `json` object, e.g. we use `PLACE` for the `"location"` field. - When dealing with `json` data, not all of the keys have to be used, e.g. we did not use the `"age"` field. - Also, if the values of `json` field are a string then the `Fields` tokenization is applied (default is to split the string on spaces), however if the values are a list then no tokenization is applied. Usually it is a good idea for the data to already be tokenized into a list, this saves time as you don't have to wait for TorchText to do it. - The value of the `json` fields do not have to be the same type. Some examples can have their `"quote"` as a string, and some as a list. The tokenization will only get applied to the ones with their `"quote"` as a string. - If you are using a `json` field, every single example must have an instance of that field, e.g. in this example all examples must have a name, location and quote. However, as we are not using the age field, it does not matter if an example does not have it. ``` fields = {'name': ('n', NAME), 'location': ('p', PLACE), 'quote': ('s', SAYING)} ``` Now, in a training loop we can iterate over the data iterator and access the name via `batch.n`, the location via `batch.p`, and the quote via `batch.s`. We then create our datasets (`train_data` and `test_data`) with the `TabularDataset.splits` function. The `path` argument specifices the top level folder common among both datasets, and the `train` and `test` arguments specify the filename of each dataset, e.g. here the train dataset is located at `data/train.json`. We tell the function we are using `json` data, and pass in our `fields` dictionary defined previously. ``` train_data, test_data = data.TabularDataset.splits( path = 'data', train = 'train.json', test = 'test.json', format = 'json', fields = fields ) ``` If you already had a validation dataset, the location of this can be passed as the `validation` argument. ``` train_data, valid_data, test_data = data.TabularDataset.splits( path = 'data', train = 'train.json', validation = 'valid.json', test = 'test.json', format = 'json', fields = fields ) ``` We can then view an example to make sure it has worked correctly. Notice how the field names (`n`, `p` and `s`) match up with what was defined in the `fields` dictionary. Also notice how the word `"United Kingdom"` in `p` has been split by the tokenization, whereas the `"united kingdom"` in `s` has not. This is due to what was mentioned previously, where TorchText assumes that any `json` fields that are lists are already tokenized and no further tokenization is applied. ``` print(vars(train_data[0])) ``` We can now use `train_data`, `test_data` and `valid_data` to build a vocabulary and create iterators, as in the other notebooks. We can access all attributes by using `batch.n`, `batch.p` and `batch.s` for the names, places and sayings, respectively. ## Reading CSV/TSV `csv` and `tsv` are very similar, except csv has elements separated by commas and tsv by tabs. Using the same example above, our `tsv` data will be in the form of: ``` name location age quote John United Kingdom 42 i love the united kingdom Mary United States 36 i want more telescopes ``` That is, on each row the elements are separated by tabs and we have one example per row. The first row is usually a header (i.e. the name of each of the columns), but your data could have no header. You cannot have lists within `tsv` or `csv` data. The way the fields are defined is a bit different to `json`. We now use a list of tuples, where each element is also a tuple. The first element of these inner tuples will become the batch object's attribute name, second element is the `Field` name. Unlike the `json` data, the tuples have to be in the same order that they are within the `tsv` data. Due to this, when skipping a column of data a tuple of `None`s needs to be used, if not then our `SAYING` field will be applied to the `age` column of the `tsv` data and the `quote` column will not be used. However, if you only wanted to use the `name` and `age` column, you could just use two tuples as they are the first two columns. We change our `TabularDataset` to read the correct `.tsv` files, and change the `format` argument to `'tsv'`. If your data has a header, which ours does, it must be skipped by passing `skip_header = True`. If not, TorchText will think the header is an example. By default, `skip_header` will be `False`. ``` fields = [('n', NAME), ('p', PLACE), (None, None), ('s', SAYING)] train_data, valid_data, test_data = data.TabularDataset.splits( path = 'data', train = 'train.tsv', validation = 'valid.tsv', test = 'test.tsv', format = 'tsv', fields = fields, skip_header = True ) print(vars(train_data[0])) ``` Finally, we'll cover `csv` files. This is pretty much the exact same as the `tsv` files, expect with the `format` argument set to `'csv'`. ``` fields = [('n', NAME), ('p', PLACE), (None, None), ('s', SAYING)] train_data, valid_data, test_data = data.TabularDataset.splits( path = 'data', train = 'train.csv', validation = 'valid.csv', test = 'test.csv', format = 'csv', fields = fields, skip_header = True ) print(vars(train_data[0])) ``` ## Why JSON over CSV/TSV? 1. Your `csv` or `tsv` data cannot be stored lists. This means data cannot be already be tokenized, thus everytime you run your Python script that reads this data via TorchText, it has to be tokenized. Using advanced tokenizers, such as the `spaCy` tokenizer, takes a non-negligible amount of time. Thus, it is better to tokenize your datasets and store them in the `json lines` format. 2. If tabs appear in your `tsv` data, or commas appear in your `csv` data, TorchText will think they are delimiters between columns. This will cause your data to be parsed incorrectly. Worst of all TorchText will not alert you to this as it cannot tell the difference between a tab/comma in a field and a tab/comma as a delimiter. As `json` data is essentially a dictionary, you access the data within the fields via its key, so do not have to worry about "surprise" delimiters. ## Iterators Using any of the above datasets, we can then build the vocab and create the iterators. ``` NAME.build_vocab(train_data) SAYING.build_vocab(train_data) PLACE.build_vocab(train_data) ``` Then, we can create the iterators after defining our batch size and device. By default, the train data is shuffled each epoch, but the validation/test data is sorted. However, TorchText doesn't know what to use to sort our data and it would throw an error if we don't tell it. There are two ways to handle this, you can either tell the iterator not to sort the validation/test data by passing `sort = False`, or you can tell it how to sort the data by passing a `sort_key`. A sort key is a function that returns a key on which to sort the data on. For example, `lambda x: x.s` will sort the examples by their `s` attribute, i.e their quote. Ideally, you want to use a sort key as the `BucketIterator` will then be able to sort your examples and then minimize the amount of padding within each batch. We can then iterate over our iterator to get batches of data. Note how by default TorchText has the batch dimension second. ``` import torch device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') BATCH_SIZE = 1 train_iterator, valid_iterator, test_iterator = data.BucketIterator.splits( (train_data, valid_data, test_data), sort = False, #don't sort test/validation data batch_size=BATCH_SIZE, device=device) train_iterator, valid_iterator, test_iterator = data.BucketIterator.splits( (train_data, valid_data, test_data), sort_key = lambda x: x.s, #sort by s attribute (quote) batch_size=BATCH_SIZE, device=device) print('Train:') for batch in train_iterator: print(batch) print('Valid:') for batch in valid_iterator: print(batch) print('Test:') for batch in test_iterator: print(batch) ```	github_jupyter
## Data Analysis ``` import numpy as np import pandas as pd import seaborn as sns import matplotlib.pyplot as plt %matplotlib inline np.random.seed(1) # load data df = pd.read_csv('../input_data/heartdisease_data.csv',sep= ',') df[0:10] ``` The data contains 13 features:<br/> 0) age: Age (years) --> discrete <br/> 1) sex: Sex (1: male, 0: female) --> categorical <br/> 2) cp: Chest pain type (1: typical angina, 2: atypical angina, 3: non-anginal pain, 4: asymptomatic) --> categorical <br/> 3) trestbps: Resting blood pressure (mm Hg on admission to the hospital) --> continuous <br/> 4) chol: Cholesterol measurement (mg/dl) --> continuous <br/> 5) fbs: Fasting blood sugar (0: <120 mg/dl, 1: > 120 mg/dl) --> categorical <br/> 6) restecg: Resting electrocardiographic measurement (0: normal, 1: having ST-T wave abnormality, 2: showing probable or definite left ventricular hypertrophy by Estes' criteria) --> categorical <br/> 7) thalach: Maximum heart rate achieved --> continuous<br/> 8) exang: Exercise induced angina (1: yes; 0: no) --> categorical <br/> 9) oldpeak: ST depression induced by exercise relative to rest ('ST' relates to positions on the ECG plot) --> continuous<br/> 10) slope: The slope of the peak exercise ST segment (1: upsloping, 2: flat, 3: downsloping) --> categorical<br/> 11) ca: The number of major vessels (0-3) --> categorical <br/> 12) thal: Thalassemia (a type of blood disorder) (3: normal; 6: fixed defect; 7: reversable defect) --> categorical <br/> and 1 target: Heart disease (0: no, 1: yes) <br/> ``` # select features and target: df = np.array(df).astype(float) # features: X = df[:,:-1] l,n = X.shape print(l,n) # target: y = df[:,-1] ``` ### Features ``` """ plt.figure(figsize=(11,6)) features = s[0,:8] for j in range(2): for i in range(4): ii = j*4 + i plt.subplot2grid((2,4),(j,i)) bins = np.linspace(min(X[:,ii]), max(X[:,ii]),10, endpoint=False) plt.hist(X[:,ii],bins,histtype='bar',rwidth=0.8,normed=True) plt.title('%s'%features[ii]) plt.tight_layout(h_pad=1, w_pad=1.5) """ ``` ### Target ``` plt.figure(figsize=(4,3)) plt.bar(0,sum(y==0)/float(l),width=0.8,color='blue',label='non disease') plt.bar(1,sum(y==1)/float(l),width=0.8,color='red',label='disease') plt.xlabel('0: non disease, 1: disease') plt.title('target') ``` ### 0) Age ``` ct = pd.crosstab(X[:,0], y) ct.plot.bar(stacked=True,figsize=(12,3)) plt.xlabel('age') ``` ### 1) Sex ``` ct = pd.crosstab(X[:,1], y) ct.plot.bar(stacked=True,figsize=(4,3)) plt.xlabel('0: female, 1: male') ``` ### 2) Chest pain type ``` ct = pd.crosstab(X[:,2], y) ct.plot.bar(stacked=True,figsize=(8,3)) plt.xlabel('Chest pain type') ``` ### 3) Resting blood pressure ``` #ct = pd.crosstab(X[:,3], y) #ct.plot.histo(stacked=True,figsize=(10,3)) #plt.xlabel('Resting blood pressure') ``` ### 5) Fasting blood sugar ``` pd.crosstab(X[:,5], y).plot.bar(stacked=True,figsize=(4,3)) plt.xlabel('0: <120 mg/dl, 1: > 120 mg/dl') ```	github_jupyter
# Single Qubit Gates In the previous section we looked at all the possible states a qubit could be in. We saw that qubits could be represented by 2D vectors, and that their states are limited to the form: $$ \|q\rangle = \cos{(\tfrac{\theta}{2})}\|0\rangle + e^{i\phi}\sin{\tfrac{\theta}{2}}\|1\rangle $$ Where $\theta$ and $\phi$ are real numbers. In this section we will cover _gates,_ the operations that change a qubit between these states. Due to the number of gates and the similarities between them, this chapter is at risk of becoming a list. To counter this, we have included a few digressions to introduce important ideas at appropriate places throughout the chapter. In _The Atoms of Computation_ we came across some gates and used them to perform a classical computation. An important feature of quantum circuits is that, between initialising the qubits and measuring them, the operations (gates) are _always_ reversible! These reversible gates can be represented as matrices, and as rotations around the Bloch sphere. ``` from qiskit import * from math import pi from qiskit.visualization import plot_bloch_multivector ``` ## 1. The Pauli Gates <a id="pauli"></a> You should be familiar with the Pauli matrices from the linear algebra section. If any of the maths here is new to you, you should use the linear algebra section to bring yourself up to speed. We will see here that the Pauli matrices can represent some very commonly used quantum gates. ### 1.1 The X-Gate <a id="xgate"></a> The X-gate is represented by the Pauli-X matrix: $$ X = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} = \|0\rangle\langle1\| + \|1\rangle\langle0\| $$ To see the effect a gate has on a qubit, we simply multiply the qubit’s statevector by the gate. We can see that the X-gate switches the amplitudes of the states $\|0\rangle$ and $\|1\rangle$: $$ X\|0\rangle = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \|1\rangle$$ <!-- ::: q-block.reminder --> ## Reminders <details> <summary>Multiplying Vectors by Matrices</summary> Matrix multiplication is a generalisation of the inner product we saw in the last chapter. In the specific case of multiplying a vector by a matrix (as seen above), we always get a vector back: $$ M\|v\rangle = \begin{bmatrix}a & b \\ c & d \end{bmatrix}\begin{bmatrix}v_0 \\ v_1 \end{bmatrix} = \begin{bmatrix}a\cdot v_0 + b \cdot v_1 \\ c \cdot v_0 + d \cdot v_1 \end{bmatrix} $$ In quantum computing, we can write our matrices in terms of basis vectors: $$X = \|0\rangle\langle1\| + \|1\rangle\langle0\|$$ This can sometimes be clearer than using a box matrix as we can see what different multiplications will result in: $$ \begin{aligned} X\|1\rangle & = (\|0\rangle\langle1\| + \|1\rangle\langle0\|)\|1\rangle \\ & = \|0\rangle\langle1\|1\rangle + \|1\rangle\langle0\|1\rangle \\ & = \|0\rangle \times 1 + \|1\rangle \times 0 \\ & = \|0\rangle \end{aligned} $$ In fact, when we see a ket and a bra multiplied like this: $$ \|a\rangle\langle b\| $$ this is called the _outer product_, which follows the rule: $$ \|a\rangle\langle b\| = \begin{bmatrix} a_0 b_0 & a_0 b_1 & \dots & a_0 b_n\\ a_1 b_0 & \ddots & & \vdots \\ \vdots & & \ddots & \vdots \\ a_n b_0 & \dots & \dots & a_n b_n \\ \end{bmatrix} $$ We can see this does indeed result in the X-matrix as seen above: $$ \|0\rangle\langle1\| + \|1\rangle\langle0\| = \begin{bmatrix}0 & 1 \\ 0 & 0 \end{bmatrix} + \begin{bmatrix}0 & 0 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix}0 & 1 \\ 1 & 0 \end{bmatrix} = X $$ </details> <!-- ::: --> In Qiskit, we can create a short circuit to verify this: ``` # Let's do an X-gate on a \|0> qubit qc = QuantumCircuit(1) qc.x(0) qc.draw() ``` Let's see the result of the above circuit. Note: Here we use <code>plot_bloch_multivector()</code> which takes a qubit's statevector instead of the Bloch vector. ``` # Let's see the result backend = Aer.get_backend('statevector_simulator') out = execute(qc,backend).result().get_statevector() plot_bloch_multivector(out) ``` We can indeed see the state of the qubit is $\|1\rangle$ as expected. We can think of this as a rotation by $\pi$ radians around the x-axis of the Bloch sphere. The X-gate is also often called a NOT-gate, referring to its classical analogue. ### 1.2 The Y & Z-gates <a id="ynzgatez"></a> Similarly to the X-gate, the Y & Z Pauli matrices also act as the Y & Z-gates in our quantum circuits: $$ Y = \begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix} \quad\quad\quad\quad Z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} $$ $$ Y = -i\|0\rangle\langle1\| + i\|1\rangle\langle0\| \quad\quad Z = \|0\rangle\langle0\| - \|1\rangle\langle1\| $$ And, unsurprisingly, they also respectively perform rotations by [[$\pi$\|$2\pi$\|$\frac{\pi}{2}$]] around the y and z-axis of the Bloch sphere. Below is a widget that displays a qubit’s state on the Bloch sphere, pressing one of the buttons will perform the gate on the qubit: ``` # Run the code in this cell to see the widget from qiskit_textbook.widgets import gate_demo gate_demo(gates='pauli') ``` In Qiskit, we can apply the Y and Z-gates to our circuit using: ``` qc.y(0) # Do Y-gate on qubit 0 qc.z(0) # Do Z-gate on qubit 0 qc.draw() ``` ## 2. Digression: The X, Y & Z-Bases <a id="xyzbases"></a> <!-- ::: q-block.reminder --> ## Reminders <details> <summary>Eigenvectors of Matrices</summary> We have seen that multiplying a vector by a matrix results in a vector: $$ M\|v\rangle = \|v'\rangle \leftarrow \text{new vector} $$ If we chose the right vectors and matrices, we can find a case in which this matrix multiplication is the same as doing a multiplication by a scalar: $$ M\|v\rangle = \lambda\|v\rangle $$ (Above, $M$ is a matrix, and $\lambda$ is a scalar). For a matrix $M$, any vector that has this property is called an <i>eigenvector</i> of $M$. For example, the eigenvectors of the Z-matrix are the states $\|0\rangle$ and $\|1\rangle$: $$ \begin{aligned} Z\|0\rangle & = \|0\rangle \\ Z\|1\rangle & = -\|1\rangle \end{aligned} $$ Since we use vectors to describe the state of our qubits, we often call these vectors <i>eigenstates</i> in this context. Eigenvectors are very important in quantum computing, and it is important you have a solid grasp of them. </details> <!-- ::: --> You may also notice that the Z-gate appears to have no effect on our qubit when it is in either of these two states. This is because the states $\|0\rangle$ and $\|1\rangle$ are the two _eigenstates_ of the Z-gate. In fact, the _computational basis_ (the basis formed by the states $\|0\rangle$ and $\|1\rangle$) is often called the Z-basis. This is not the only basis we can use, a popular basis is the X-basis, formed by the eigenstates of the X-gate. We call these two vectors $\|+\rangle$ and $\|-\rangle$: $$ \|+\rangle = \tfrac{1}{\sqrt{2}}(\|0\rangle + \|1\rangle) = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 1 \end{bmatrix}$$ $$ \|-\rangle = \tfrac{1}{\sqrt{2}}(\|0\rangle - \|1\rangle) = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ -1 \end{bmatrix} $$ Another less commonly used basis is that formed by the eigenstates of the Y-gate. These are called: $$ \|\circlearrowleft\rangle, \quad \|\circlearrowright\rangle$$ We leave it as an exercise to calculate these. There are in fact an infinite number of bases; to form one, we simply need two orthogonal vectors. ### Quick Exercises 1. Verify that $\|+\rangle$ and $\|-\rangle$ are in fact eigenstates of the X-gate. 2. What eigenvalues do they have? 3. Why would we not see these eigenvalues appear on the Bloch sphere? 4. Find the eigenstates of the Y-gate, and their co-ordinates on the Bloch sphere. Using only the Pauli-gates it is impossible to move our initialised qubit to any state other than $\|0\rangle$ or $\|1\rangle$, i.e. we cannot achieve superposition. This means we can see no behaviour different to that of a classical bit. To create more interesting states we will need more gates! ## 3. The Hadamard Gate <a id="hgate"></a> The Hadamard gate (H-gate) is a fundamental quantum gate. It allows us to move away from the poles of the Bloch sphere and create a superposition of $\|0\rangle$ and $\|1\rangle$. It has the matrix: $$ H = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} $$ We can see that this performs the transformations below: $$ H\|0\rangle = \|+\rangle $$ $$ H\|1\rangle = \|-\rangle $$ This can be thought of as a rotation around the Bloch vector `[1,0,1]` (the line between the x & z-axis), or as transforming the state of the qubit between the X and Z bases. You can play around with these gates using the widget below: ``` # Run the code in this cell to see the widget from qiskit_textbook.widgets import gate_demo gate_demo(gates='pauli+h') ``` ### Quick Exercise 1. Write the H-gate as the outer products of vectors $\|0\rangle$, $\|1\rangle$, $\|+\rangle$ and $\|-\rangle$. 2. Show that applying the sequence of gates: HZH, to any qubit state is equivalent to applying an X-gate. 3. Find a combination of X, Z and H-gates that is equivalent to a Y-gate (ignoring global phase). ## 4. Digression: Measuring in Different Bases <a id="measuring"></a> We have seen that the Z-axis is not intrinsically special, and that there are infinitely many other bases. Similarly with measurement, we don’t always have to measure in the computational basis (the Z-basis), we can measure our qubits in any basis. As an example, let’s try measuring in the X-basis. We can calculate the probability of measuring either $\|+\rangle$ or $\|-\rangle$: $$ p(\|+\rangle) = \|\langle+\|q\rangle\|^2, \quad p(\|-\rangle) = \|\langle-\|q\rangle\|^2 $$ And after measurement, we are guaranteed to have a qubit in one of these two states. Since Qiskit only allows measuring in the Z-basis, we must create our own using Hadamard gates: ``` # Create the X-measurement function: def x_measurement(qc,qubit,cbit): """Measure 'qubit' in the X-basis, and store the result in 'cbit'""" qc.h(qubit) qc.measure(qubit, cbit) qc.h(qubit) return qc initial_state = [0,1] # Initialise our qubit and measure it qc = QuantumCircuit(1,1) qc.initialize(initial_state, 0) x_measurement(qc, 0, 0) # measure qubit 0 to classical bit 0 qc.draw() ``` In the quick exercises above, we saw you could create an X-gate by sandwiching our Z-gate between two H-gates: $$ X = HZH $$ Starting in the Z-basis, the H-gate switches our qubit to the X-basis, the Z-gate performs a NOT in the X-basis, and the final H-gate returns our qubit to the Z-basis. <img src="images/bloch_HZH.svg"> We can verify this always behaves like an X-gate by multiplying the matrices: $$ HZH = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \tfrac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} =X $$ Following the same logic, we have created an X-measurement by sandwiching our Z-measurement between two H-gates. <img src="images/x-measurement.svg"> Let’s now see the results: ``` backend = Aer.get_backend('statevector_simulator') # Tell Qiskit how to simulate our circuit out_state = execute(qc,backend).result().get_statevector() # Do the simulation, returning the state vector plot_bloch_multivector(out_state) # Display the output state vector ``` We initialised our qubit in the state $\|1\rangle$, but we can see that, after the measurement, we have collapsed our qubit to the states $\|+\rangle$ or $\|-\rangle$. If you run the cell again, you will see different results, but the final state of the qubit will always be $\|+\rangle$ or $\|-\rangle$. ### Quick Exercises 1. If we initialise our qubit in the state $\|+\rangle$, what is the probability of measuring it in state $\|-\rangle$? 2. Use Qiskit to display the probability of measuring a $\|0\rangle$ qubit in the states $\|+\rangle$ and $\|-\rangle$ (Hint: you might want to use <code>.get_counts()</code> and <code>plot_histogram()</code>). 3. Try to create a function that measures in the Y-basis. Measuring in different bases allows us to see Heisenberg’s famous uncertainty principle in action. Having certainty of measuring a state in the Z-basis removes all certainty of measuring a specific state in the X-basis, and vice versa. A common misconception is that the uncertainty is due to the limits in our equipment, but here we can see the uncertainty is actually part of the nature of the qubit. For example, if we put our qubit in the state $\|0\rangle$, our measurement in the Z-basis is certain to be $\|0\rangle$, but our measurement in the X-basis is completely random! Similarly, if we put our qubit in the state $\|-\rangle$, our measurement in the X-basis is certain to be $\|-\rangle$, but now any measurement in the Z-basis will be completely random. More generally: _Whatever state our quantum system is in, there is always a measurement that has a deterministic outcome._ The introduction of the H-gate has allowed us to explore some interesting phenomena, but we are still very limited in our quantum operations. Let us now introduce a new type of gate: ## The R<sub>&straightphi;</sub>-gate The $R_\phi$-gate is _parametrised,_ that is, it needs a number ($\phi$) to tell it exactly what to do. The $R_\phi$-gate performs a rotation of $\phi$ around the Z-axis direction (and as such is sometimes also known as the $R_z$-gate). It has the matrix: $$ R_\phi = \begin{bmatrix} 1 & 0 \\ 0 & e^{i\phi} \end{bmatrix} $$ Where $\phi$ is a real number. You can use the widget below to play around with the $R_\phi$-gate, specify $\phi$ using the slider: ``` # Run the code in this cell to see the widget from qiskit_textbook.widgets import gate_demo gate_demo(gates='pauli+h+rz') ``` In Qiskit, we specify an $R_\phi$-gate using `rz(phi, qubit)`: ``` qc = QuantumCircuit(1) qc.rz(pi/4, 0) qc.draw() ``` You may notice that the Z-gate is a special case of the $R_\phi$-gate, with $\phi = \pi$. In fact there are three more commonly referenced gates we will mention in this chapter, all of which are special cases of the $R_\phi$-gate: ## 6. The I, S and T-gates <a id="istgates"></a> ### 6.1 The I-gate <a id="igate"></a> First comes the I-gate (aka ‘Id-gate’ or ‘Identity gate’). This is simply a gate that does nothing. Its matrix is the identity matrix: $$ I = \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix} $$ Applying the identity gate anywhere in your circuit should have no effect on the qubit state, so it’s interesting this is even considered a gate. There are two main reasons behind this, one is that it is often used in calculations, for example: proving the X-gate is its own inverse: $$ I = XX $$ The second, is that it is often useful when considering real hardware to specify a ‘do-nothing’ or ‘none’ operation. #### Quick Exercise 1. What are the eigenstates of the I-gate? ### 6.2 The S-gates <a id="sgate"></a> The next gate to mention is the S-gate (sometimes known as the $\sqrt{Z}$-gate), this is an $R_\phi$-gate with $\phi = \pi/2$. It does a quarter-turn around the Bloch sphere. It is important to note that unlike every gate introduced in this chapter so far, the S-gate is not its own inverse! As a result, you will often see the $S^\dagger$-gate, (also “S-dagger”, “Sdg” or $\sqrt{Z}^\dagger$-gate). The $S^\dagger$-gate is clearly an $R_\phi$-gate with $\phi = -\pi/2$: $$ S = \begin{bmatrix} 1 & 0 \\ 0 & e^{\frac{i\pi}{2}} \end{bmatrix}, \quad S^\dagger = \begin{bmatrix} 1 & 0 \\ 0 & e^{-\frac{i\pi}{2}} \end{bmatrix}$$ The name "$\sqrt{Z}$-gate" is due to the fact that two successively applied S-gates has the same effect as one Z-gate: $$ SS\|q\rangle = Z\|q\rangle $$ This notation is common throughout quantum computing. To add an S-gate in Qiskit: ``` qc = QuantumCircuit(1) qc.s(0) # Apply S-gate to qubit 0 qc.sdg(0) # Apply Sdg-gate to qubit 0 qc.draw() ``` ### 6.3 The T-gate <a id="tgate"></a> The T-gate is a very commonly used gate, it is an $R_\phi$-gate with $\phi = \pi/4$: $$ T = \begin{bmatrix} 1 & 0 \\ 0 & e^{\frac{i\pi}{4}} \end{bmatrix}, \quad T^\dagger = \begin{bmatrix} 1 & 0 \\ 0 & e^{-\frac{i\pi}{4}} \end{bmatrix}$$ As with the S-gate, the T-gate is sometimes also known as the $\sqrt[4]{Z}$-gate. In Qiskit: ``` qc = QuantumCircuit(1) qc.t(0) # Apply T-gate to qubit 0 qc.tdg(0) # Apply Tdg-gate to qubit 0 qc.draw() ``` You can use the widget below to play around with all the gates introduced in this chapter so far: ``` # Run the code in this cell to see the widget from qiskit_textbook.widgets import gate_demo gate_demo() ``` ## 7. General U-gates <a id="generalU3"></a> As we saw earlier, the I, Z, S & T-gates were all special cases of the more general $R_\phi$-gate. In the same way, the $U_3$-gate is the most general of all single-qubit quantum gates. It is a parametrised gate of the form: $$ U_3(\theta, \phi, \lambda) = \begin{bmatrix} \cos(\theta/2) & -e^{i\lambda}\sin(\theta/2) \\ e^{i\phi}\sin(\theta/2) & e^{i\lambda+i\phi}\cos(\theta/2) \end{bmatrix} $$ Every gate in this chapter could be specified as $U_3(\theta,\phi,\lambda)$, but it is unusual to see this in a circuit diagram, possibly due to the difficulty in reading this. Qiskit provides $U_2$ and $U_1$-gates, which are specific cases of the $U_3$ gate in which $\theta = \tfrac{\pi}{2}$, and $\theta = \phi = 0$ respectively. You will notice that the $U_1$-gate is equivalent to the $R_\phi$-gate. $$ \begin{aligned} U_3(\tfrac{\pi}{2}, \phi, \lambda) = U_2 = \tfrac{1}{\sqrt{2}}\begin{bmatrix} 1 & -e^{i\lambda} \\ e^{i\phi} & e^{i\lambda+i\phi} \end{bmatrix} & \quad & U_3(0, 0, \lambda) = U_1 = \begin{bmatrix} 1 & 0 \\ 0 & e^{i\lambda}\\ \end{bmatrix} \end{aligned} $$ Before running on real IBM quantum hardware, all single-qubit operations are compiled down to $U_1$ , $U_2$ and $U_3$ . For this reason they are sometimes called the _physical gates_. It should be obvious from this that there are an infinite number of possible gates, and that this also includes $R_x$ and $R_y$-gates, although they are not mentioned here. It must also be noted that there is nothing special about the Z-basis, except that it has been selected as the standard computational basis. That is why we have names for the S and T-gates, but not their X and Y equivalents (e.g. $\sqrt{X}$ and $\sqrt[4]{Y}$). ``` import qiskit qiskit.__qiskit_version__ ```	github_jupyter
``` from __future__ import absolute_import import sys import os try: from dotenv import find_dotenv, load_dotenv except: pass import argparse try: sys.path.append(os.path.join(os.path.dirname(__file__), '../src')) except: sys.path.append(os.path.join(os.getcwd(), '../src')) import pandas as pd import numpy as np import torch import torch.nn as nn from torchcontrib.optim import SWA from torch.optim import Adam, SGD from torch.optim.lr_scheduler import CosineAnnealingLR, ReduceLROnPlateau, CyclicLR, \ CosineAnnealingWarmRestarts from consNLP.data import load_data, data_utils, fetch_dataset from consNLP.models import transformer_models, activations, layers, losses, scorers from consNLP.visualization import visualize from consNLP.trainer.trainer import BasicTrainer, PLTrainer, test_pl_trainer from consNLP.trainer.trainer_utils import set_seed, _has_apex, _torch_lightning_available, _has_wandb, _torch_gpu_available, _num_gpus, _torch_tpu_available from consNLP.preprocessing.custom_tokenizer import BERTweetTokenizer if _has_apex: #from torch.cuda import amp from apex import amp if _torch_tpu_available: import torch_xla import torch_xla.core.xla_model as xm import torch_xla.distributed.xla_multiprocessing as xmp if _has_wandb: import wandb try: load_dotenv(find_dotenv()) wandb.login(key=os.environ['WANDB_API_KEY']) except: _has_wandb = False if _torch_lightning_available: import pytorch_lightning as pl from pytorch_lightning import Trainer, seed_everything from pytorch_lightning.loggers import WandbLogger from pytorch_lightning.metrics.metric import NumpyMetric from pytorch_lightning.callbacks import ModelCheckpoint, EarlyStopping, Callback import tokenizers from transformers import AutoModel, AutoTokenizer, AdamW, get_linear_schedule_with_warmup, AutoConfig load_dotenv(find_dotenv()) fetch_dataset(project_dir='../',download_from_kaggle=True,\ kaggle_dataset='lakshmi25npathi/imdb-dataset-of-50k-movie-reviews') parser = argparse.ArgumentParser(prog='Torch trainer function',conflict_handler='resolve') parser.add_argument('--train_data', type=str, default='../data/raw/IMDB Dataset.csv', required=False, help='train data') parser.add_argument('--val_data', type=str, default='', required=False, help='validation data') parser.add_argument('--test_data', type=str, default=None, required=False, help='test data') parser.add_argument('--task_type', type=str, default='binary_sequence_classification', required=False, help='type of task') parser.add_argument('--transformer_model_pretrained_path', type=str, default='roberta-base', required=False, help='transformer model pretrained path or huggingface model name') parser.add_argument('--transformer_config_path', type=str, default='roberta-base', required=False, help='transformer config file path or huggingface model name') parser.add_argument('--transformer_tokenizer_path', type=str, default='roberta-base', required=False, help='transformer tokenizer file path or huggingface model name') parser.add_argument('--bpe_vocab_path', type=str, default='', required=False, help='bytepairencoding vocab file path') parser.add_argument('--bpe_merges_path', type=str, default='', required=False, help='bytepairencoding merges file path') parser.add_argument('--berttweettokenizer_path', type=str, default='', required=False, help='BERTweet tokenizer path') parser.add_argument('--max_text_len', type=int, default=100, required=False, help='maximum length of text') parser.add_argument('--epochs', type=int, default=5, required=False, help='number of epochs') parser.add_argument('--lr', type=float, default=.00003, required=False, help='learning rate') parser.add_argument('--loss_function', type=str, default='bcelogit', required=False, help='loss function') parser.add_argument('--metric', type=str, default='f1', required=False, help='scorer metric') parser.add_argument('--use_lightning_trainer', type=bool, default=False, required=False, help='if lightning trainer needs to be used') parser.add_argument('--use_torch_trainer', type=bool, default=True, required=False, help='if custom torch trainer needs to be used') parser.add_argument('--use_apex', type=bool, default=False, required=False, help='if apex needs to be used') parser.add_argument('--use_gpu', type=bool, default=False, required=False, help='GPU mode') parser.add_argument('--use_TPU', type=bool, default=False, required=False, help='TPU mode') parser.add_argument('--num_gpus', type=int, default=0, required=False, help='Number of GPUs') parser.add_argument('--num_tpus', type=int, default=0, required=False, help='Number of TPUs') parser.add_argument('--train_batch_size', type=int, default=16, required=False, help='train batch size') parser.add_argument('--eval_batch_size', type=int, default=16, required=False, help='eval batch size') parser.add_argument('--model_save_path', type=str, default='../models/sentiment_classification/', required=False, help='seed') parser.add_argument('--wandb_logging', type=bool, default=False, required=False, help='wandb logging needed') parser.add_argument('--seed', type=int, default=42, required=False, help='seed') args, _ = parser.parse_known_args() print ("Wandb Logging: {}, GPU: {}, Pytorch Lightning: {}, TPU: {}, Apex: {}".format(\ _has_wandb and args.wandb_logging, _torch_gpu_available,\ _torch_lightning_available and args.use_lightning_trainer, _torch_tpu_available, _has_apex)) reshape = False final_activation = None convert_output = None if args.task_type == 'binary_sequence_classification': if args.metric != 'roc_auc_score': convert_output = 'round' if args.loss_function == 'bcelogit': final_activation = 'sigmoid' elif args.task_type == 'multiclass_sequence_classification': convert_output = 'max' elif args.task_type == 'binary_token_classification': reshape = True if args.metric != 'roc_auc_score': convert_output = 'round' if args.loss_function == 'bcelogit': final_activation = 'sigmoid' elif args.task_type == 'multiclass_token_classification': reshape = True convert_output = 'max' df = load_data.load_pandas_df(args.train_data,sep=',') df = df.iloc[:1000] df.head(5) model_save_dir = args.model_save_path try: os.makedirs(model_save_dir) except OSError: pass df.sentiment, label2idx = data_utils.convert_categorical_label_to_int(df.sentiment, \ save_path=os.path.join(model_save_dir,'label2idx.pkl')) df.head(5) from sklearn.model_selection import KFold kf = KFold(5) for train_index, val_index in kf.split(df.review, df.sentiment): break train_df = df.iloc[train_index].reset_index(drop=True) val_df = df.iloc[val_index].reset_index(drop=True) train_df.shape, val_df.shape if args.berttweettokenizer_path: tokenizer = BERTweetTokenizer(args.berttweettokenizer_path) else: tokenizer = AutoTokenizer.from_pretrained(args.transformer_model_pretrained_path) if not args.berttweettokenizer_path: try: bpetokenizer = tokenizers.ByteLevelBPETokenizer(args.bpe_vocab_path, \ args.bpe_merges_path) except: bpetokenizer = None else: bpetokenizer = None train_dataset = data_utils.TransformerDataset(train_df.review, bpetokenizer=bpetokenizer, tokenizer=tokenizer, MAX_LEN=args.max_text_len, \ target_label=train_df.sentiment, sequence_target=False, target_text=None, conditional_label=None, conditional_all_labels=None) val_dataset = data_utils.TransformerDataset(val_df.review, bpetokenizer=bpetokenizer, tokenizer=tokenizer, MAX_LEN=args.max_text_len, \ target_label=val_df.sentiment, sequence_target=False, target_text=None, conditional_label=None, conditional_all_labels=None) config = AutoConfig.from_pretrained(args.transformer_config_path, output_hidden_states=True, output_attentions=True) basemodel = AutoModel.from_pretrained(args.transformer_model_pretrained_path,config=config) model = transformer_models.TransformerWithCLS(basemodel) if _torch_tpu_available and args.use_TPU: train_sampler = torch.utils.data.distributed.DistributedSampler( train_dataset, num_replicas=xm.xrt_world_size(), rank=xm.get_ordinal(), shuffle=True ) val_sampler = torch.utils.data.distributed.DistributedSampler( val_dataset, num_replicas=xm.xrt_world_size(), rank=xm.get_ordinal(), shuffle=False ) if _torch_tpu_available and args.use_TPU: train_data_loader = torch.utils.data.DataLoader( train_dataset, batch_size=args.train_batch_size, sampler=train_sampler, drop_last=True,num_workers=2) val_data_loader = torch.utils.data.DataLoader( val_dataset, batch_size=args.eval_batch_size, sampler=val_sampler, drop_last=False,num_workers=1) else: train_data_loader = torch.utils.data.DataLoader( train_dataset, batch_size=args.train_batch_size) val_data_loader = torch.utils.data.DataLoader( val_dataset, batch_size=args.eval_batch_size) ``` ### Run with Pytorch Trainer ``` if args.use_torch_trainer: device = torch.device("cuda" if _torch_gpu_available and args.use_gpu else "cpu") if _torch_tpu_available and args.use_TPU: device=xm.xla_device() print ("Device: {}".format(device)) if args.use_TPU and _torch_tpu_available and args.num_tpus > 1: train_data_loader = torch_xla.distributed.parallel_loader.ParallelLoader(train_data_loader, [device]) train_data_loader = train_data_loader.per_device_loader(device) trainer = BasicTrainer(model, train_data_loader, val_data_loader, device, args.transformer_model_pretrained_path, \ final_activation=final_activation, \ test_data_loader=val_data_loader) param_optimizer = list(trainer.model.named_parameters()) no_decay = ["bias", "LayerNorm.bias", "LayerNorm.weight"] optimizer_parameters = [ { "params": [ p for n, p in param_optimizer if not any(nd in n for nd in no_decay) ], "weight_decay": 0.001, }, { "params": [ p for n, p in param_optimizer if any(nd in n for nd in no_decay) ], "weight_decay": 0.0, }, ] num_train_steps = int(len(train_data_loader) * args.epochs) if _torch_tpu_available and args.use_TPU: optimizer = AdamW(optimizer_parameters, lr=args.lrxm.xrt_world_size()) else: optimizer = AdamW(optimizer_parameters, lr=args.lr) if args.use_apex and _has_apex: model, optimizer = amp.initialize(model, optimizer, opt_level="O1") scheduler = get_linear_schedule_with_warmup(optimizer, num_warmup_steps=0, num_training_steps=num_train_steps) loss = losses.get_loss(args.loss_function) scorer = scorers.SKMetric(args.metric, convert=convert_output, reshape=reshape) def _mp_fn(rank, flags, trainer, epochs, lr, metric, loss_function, optimizer, scheduler, model_save_path, num_gpus, num_tpus, \ max_grad_norm, early_stopping_rounds, snapshot_ensemble, is_amp, use_wandb, seed): torch.set_default_tensor_type('torch.FloatTensor') a = trainer.train(epochs, lr, metric, loss_function, optimizer, scheduler, model_save_path, num_gpus, num_tpus, \ max_grad_norm, early_stopping_rounds, snapshot_ensemble, is_amp, use_wandb, seed) FLAGS = {} if _torch_tpu_available and args.use_TPU: xmp.spawn(_mp_fn, args=(FLAGS, trainer, args.epochs, args.lr, scorer, loss, optimizer, scheduler, args.model_save_path, args.num_gpus, args.num_tpus, \ 1, 3, False, args.use_apex, False, args.seed), nprocs=8, start_method='fork') else: use_wandb = _has_wandb and args.wandb_logging trainer.train(args.epochs, args.lr, scorer, loss, optimizer, scheduler, args.model_save_path, args.num_gpus, args.num_tpus, \ max_grad_norm=1, early_stopping_rounds=3, snapshot_ensemble=False, is_amp=args.use_apex, use_wandb=use_wandb, seed=args.seed) elif args.use_lightning_trainer and _torch_lightning_available: from pytorch_lightning import Trainer, seed_everything seed_everything(args.seed) loss = losses.get_loss(args.loss_function) scorer = scorers.PLMetric(args.metric, convert=convert_output, reshape=reshape) log_args = {'description': args.transformer_model_pretrained_path, 'loss': loss.__class__.__name__, 'epochs': args.epochs, 'learning_rate': args.lr} if _has_wandb and not _torch_tpu_available and args.wandb_logging: wandb.init(project="Project",config=log_args) wandb_logger = WandbLogger() checkpoint_callback = ModelCheckpoint( filepath=args.model_save_path, save_top_k=1, verbose=True, monitor='val_loss', mode='min' ) earlystop = EarlyStopping( monitor='val_loss', patience=3, verbose=False, mode='min' ) if args.use_gpu and _torch_gpu_available: print ("using GPU") if args.wandb_logging: if _has_apex: trainer = Trainer(gpus=args.num_gpus, max_epochs=args.epochs, logger=wandb_logger, precision=16, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: trainer = Trainer(gpus=args.num_gpus, max_epochs=args.epochs, logger=wandb_logger, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: if _has_apex: trainer = Trainer(gpus=args.num_gpus, max_epochs=args.epochs, precision=16, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: trainer = Trainer(gpus=args.num_gpus, max_epochs=args.epochs, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) elif args.use_TPU and _torch_tpu_available: print ("using TPU") if _has_apex: trainer = Trainer(num_tpu_cores=args.num_tpus, max_epochs=args.epochs, precision=16, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: trainer = Trainer(num_tpu_cores=args.num_tpus, max_epochs=args.epochs, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: print ("using CPU") if args.wandb_logging: if _has_apex: trainer = Trainer(max_epochs=args.epochs, logger=wandb_logger, precision=16, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: trainer = Trainer(max_epochs=args.epochs, logger=wandb_logger, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: if _has_apex: trainer = Trainer(max_epochs=args.epochs, precision=16, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: trainer = Trainer(max_epochs=args.epochs, checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) num_train_steps = int(len(train_data_loader) args.epochs) pltrainer = PLTrainer(num_train_steps, model, scorer, loss, args.lr, \ final_activation=final_activation, seed=42) #try: # print ("Loaded model from previous checkpoint") # pltrainer = PLTrainer.load_from_checkpoint(args.model_save_path) #except: # pass trainer.fit(pltrainer, train_data_loader, val_data_loader) test_output1 = trainer.test_output ``` ### Run with Pytorch Lightning Trainer ``` parser = argparse.ArgumentParser(prog='Torch trainer function',conflict_handler='resolve') parser.add_argument('--train_data', type=str, default='../data/raw/IMDB Dataset.csv', required=False, help='train data') parser.add_argument('--val_data', type=str, default='', required=False, help='validation data') parser.add_argument('--test_data', type=str, default=None, required=False, help='test data') parser.add_argument('--transformer_model_pretrained_path', type=str, default='roberta-base', required=False, help='transformer model pretrained path or huggingface model name') parser.add_argument('--transformer_config_path', type=str, default='roberta-base', required=False, help='transformer config file path or huggingface model name') parser.add_argument('--transformer_tokenizer_path', type=str, default='roberta-base', required=False, help='transformer tokenizer file path or huggingface model name') parser.add_argument('--bpe_vocab_path', type=str, default='', required=False, help='bytepairencoding vocab file path') parser.add_argument('--bpe_merges_path', type=str, default='', required=False, help='bytepairencoding merges file path') parser.add_argument('--berttweettokenizer_path', type=str, default='', required=False, help='BERTweet tokenizer path') parser.add_argument('--max_text_len', type=int, default=100, required=False, help='maximum length of text') parser.add_argument('--epochs', type=int, default=5, required=False, help='number of epochs') parser.add_argument('--lr', type=float, default=.00003, required=False, help='learning rate') parser.add_argument('--loss_function', type=str, default='bcelogit', required=False, help='loss function') parser.add_argument('--metric', type=str, default='f1', required=False, help='scorer metric') parser.add_argument('--use_lightning_trainer', type=bool, default=True, required=False, help='if lightning trainer needs to be used') parser.add_argument('--use_torch_trainer', type=bool, default=False, required=False, help='if custom torch trainer needs to be used') parser.add_argument('--use_apex', type=bool, default=False, required=False, help='if apex needs to be used') parser.add_argument('--use_gpu', type=bool, default=False, required=False, help='GPU mode') parser.add_argument('--use_TPU', type=bool, default=False, required=False, help='TPU mode') parser.add_argument('--num_gpus', type=int, default=0, required=False, help='Number of GPUs') parser.add_argument('--num_tpus', type=int, default=0, required=False, help='Number of TPUs') parser.add_argument('--train_batch_size', type=int, default=16, required=False, help='train batch size') parser.add_argument('--eval_batch_size', type=int, default=16, required=False, help='eval batch size') parser.add_argument('--model_save_path', type=str, default='../models/sentiment_classification/', required=False, help='seed') parser.add_argument('--wandb_logging', type=bool, default=False, required=False, help='wandb logging needed') parser.add_argument('--seed', type=int, default=42, required=False, help='seed') args, _ = parser.parse_known_args() print ("Wandb Logging: {}, GPU: {}, Pytorch Lightning: {}, TPU: {}, Apex: {}".format(\ _has_wandb and args.wandb_logging, _torch_gpu_available,\ _torch_lightning_available and args.use_lightning_trainer, _torch_tpu_available, _has_apex)) if args.use_torch_trainer: device = torch.device("cuda" if _torch_gpu_available and args.use_gpu else "cpu") if _torch_tpu_available and args.use_TPU: device=xm.xla_device() print ("Device: {}".format(device)) if args.use_TPU and _torch_tpu_available and args.num_tpus > 1: train_data_loader = torch_xla.distributed.parallel_loader.ParallelLoader(train_data_loader, [device]) train_data_loader = train_data_loader.per_device_loader(device) trainer = BasicTrainer(model, train_data_loader, val_data_loader, device, args.transformer_model_pretrained_path, \ final_activation=final_activation, \ test_data_loader=val_data_loader) param_optimizer = list(trainer.model.named_parameters()) no_decay = ["bias", "LayerNorm.bias", "LayerNorm.weight"] optimizer_parameters = [ { "params": [ p for n, p in param_optimizer if not any(nd in n for nd in no_decay) ], "weight_decay": 0.001, }, { "params": [ p for n, p in param_optimizer if any(nd in n for nd in no_decay) ], "weight_decay": 0.0, }, ] num_train_steps = int(len(train_data_loader) * args.epochs) if _torch_tpu_available and args.use_TPU: optimizer = AdamW(optimizer_parameters, lr=args.lrxm.xrt_world_size()) else: optimizer = AdamW(optimizer_parameters, lr=args.lr) if args.use_apex and _has_apex: model, optimizer = amp.initialize(model, optimizer, opt_level="O1") scheduler = get_linear_schedule_with_warmup(optimizer, num_warmup_steps=0, num_training_steps=num_train_steps) loss = losses.get_loss(args.loss_function) scorer = scorers.SKMetric(args.metric, convert=convert_output, reshape=reshape) def _mp_fn(rank, flags, trainer, epochs, lr, metric, loss_function, optimizer, scheduler, model_save_path, num_gpus, num_tpus, \ max_grad_norm, early_stopping_rounds, snapshot_ensemble, is_amp, use_wandb, seed): torch.set_default_tensor_type('torch.FloatTensor') a = trainer.train(epochs, lr, metric, loss_function, optimizer, scheduler, model_save_path, num_gpus, num_tpus, \ max_grad_norm, early_stopping_rounds, snapshot_ensemble, is_amp, use_wandb, seed) FLAGS = {} if _torch_tpu_available and args.use_TPU: xmp.spawn(_mp_fn, args=(FLAGS, trainer, args.epochs, args.lr, scorer, loss, optimizer, scheduler, args.model_save_path, args.num_gpus, args.num_tpus, \ 1, 3, False, args.use_apex, False, args.seed), nprocs=8, start_method='fork') else: use_wandb = _has_wandb and args.wandb_logging trainer.train(args.epochs, args.lr, scorer, loss, optimizer, scheduler, args.model_save_path, args.num_gpus, args.num_tpus, \ max_grad_norm=1, early_stopping_rounds=3, snapshot_ensemble=False, is_amp=args.use_apex, use_wandb=use_wandb, seed=args.seed) elif args.use_lightning_trainer and _torch_lightning_available: from pytorch_lightning import Trainer, seed_everything seed_everything(args.seed) loss = losses.get_loss(args.loss_function) scorer = scorers.PLMetric(args.metric, convert=convert_output, reshape=reshape) log_args = {'description': args.transformer_model_pretrained_path, 'loss': loss.__class__.__name__, 'epochs': args.epochs, 'learning_rate': args.lr} if _has_wandb and not _torch_tpu_available and args.wandb_logging: wandb.init(project="Project",config=log_args) wandb_logger = WandbLogger() checkpoint_callback = ModelCheckpoint( filepath=args.model_save_path, save_top_k=1, verbose=True, monitor='val_loss', mode='min' ) earlystop = EarlyStopping( monitor='val_loss', patience=3, verbose=False, mode='min' ) if args.use_gpu and _torch_gpu_available: print ("using GPU") if args.wandb_logging: if _has_apex: trainer = Trainer(gpus=args.num_gpus, max_epochs=args.epochs, logger=wandb_logger, precision=16, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: trainer = Trainer(gpus=args.num_gpus, max_epochs=args.epochs, logger=wandb_logger, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: if _has_apex: trainer = Trainer(gpus=args.num_gpus, max_epochs=args.epochs, precision=16, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: trainer = Trainer(gpus=args.num_gpus, max_epochs=args.epochs, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) elif args.use_TPU and _torch_tpu_available: print ("using TPU") if _has_apex: trainer = Trainer(num_tpu_cores=args.num_tpus, max_epochs=args.epochs, precision=16, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: trainer = Trainer(num_tpu_cores=args.num_tpus, max_epochs=args.epochs, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: print ("using CPU") if args.wandb_logging: if _has_apex: trainer = Trainer(max_epochs=args.epochs, logger=wandb_logger, precision=16, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: trainer = Trainer(max_epochs=args.epochs, logger=wandb_logger, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: if _has_apex: trainer = Trainer(max_epochs=args.epochs, precision=16, \ checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) else: trainer = Trainer(max_epochs=args.epochs, checkpoint_callback=checkpoint_callback, callbacks=[earlystop]) num_train_steps = int(len(train_data_loader) args.epochs) pltrainer = PLTrainer(num_train_steps, model, scorer, loss, args.lr, \ final_activation=final_activation, seed=42) #try: # print ("Loaded model from previous checkpoint") # pltrainer = PLTrainer.load_from_checkpoint(args.model_save_path) #except: # pass trainer.fit(pltrainer, train_data_loader, val_data_loader) from tqdm import tqdm test_output2 = [] for val_batch in tqdm(val_data_loader): out = torch.sigmoid(pltrainer(val_batch)).detach().cpu().numpy() test_output2.extend(out[:,0].tolist()) #test_output2 = np.concatenate(test_output2) test_output1 = np.array(test_output1)[:,0] test_output2 = np.array(test_output2) np.corrcoef(test_output1,test_output2) ```	github_jupyter
# Amazon SageMaker Experiment Trials for Distirbuted Training of Mask-RCNN This notebook is a step-by-step tutorial on Amazon SageMaker Experiment Trials for distributed tranining of [Mask R-CNN](https://arxiv.org/abs/1703.06870) implemented in [TensorFlow](https://www.tensorflow.org/) framework. Concretely, we will describe the steps for SagerMaker Experiment Trials for training [TensorPack Faster-RCNN/Mask-RCNN](https://github.com/tensorpack/tensorpack/tree/master/examples/FasterRCNN) and [AWS Samples Mask R-CNN](https://github.com/aws-samples/mask-rcnn-tensorflow) in [Amazon SageMaker](https://aws.amazon.com/sagemaker/) using [Amazon S3](https://aws.amazon.com/s3/) as data source. The outline of steps is as follows: 1. Stage COCO 2017 dataset in [Amazon S3](https://aws.amazon.com/s3/) 2. Build SageMaker training image and push it to [Amazon ECR](https://aws.amazon.com/ecr/) 3. Configure data input channels 4. Configure hyper-prarameters 5. Define training metrics 6. Define training job 7. Define SageMaker Experiment Trials to start the training jobs Before we get started, let us initialize two python variables ```aws_region``` and ```s3_bucket``` that we will use throughout the notebook: ``` aws_region = # aws-region-code e.g. us-east-1 s3_bucket = # your-s3-bucket-name ``` ## Stage COCO 2017 dataset in Amazon S3 We use [COCO 2017 dataset](http://cocodataset.org/#home) for training. We download COCO 2017 training and validation dataset to this notebook instance, extract the files from the dataset archives, and upload the extracted files to your Amazon [S3 bucket](https://docs.aws.amazon.com/en_pv/AmazonS3/latest/gsg/CreatingABucket.html) with the prefix ```mask-rcnn/sagemaker/input/train```. The ```prepare-s3-bucket.sh``` script executes this step. ``` !cat ./prepare-s3-bucket.sh ``` Using your Amazon S3 bucket as argument, run the cell below. If you have already uploaded COCO 2017 dataset to your Amazon S3 bucket in this AWS region, you may skip this step. The expected time to execute this step is 20 minutes. ``` %%time !./prepare-s3-bucket.sh {s3_bucket} ``` ## Build and push SageMaker training images For this step, the [IAM Role](https://docs.aws.amazon.com/IAM/latest/UserGuide/id_roles.html) attached to this notebook instance needs full access to Amazon ECR service. If you created this notebook instance using the ```./stack-sm.sh``` script in this repository, the IAM Role attached to this notebook instance is already setup with full access to ECR service. Below, we have a choice of two different implementations: 1. [TensorPack Faster-RCNN/Mask-RCNN](https://github.com/tensorpack/tensorpack/tree/master/examples/FasterRCNN) implementation supports a maximum per-GPU batch size of 1, and does not support mixed precision. It can be used with mainstream TensorFlow releases. 2. [AWS Samples Mask R-CNN](https://github.com/aws-samples/mask-rcnn-tensorflow) is an optimized implementation that supports a maximum batch size of 4 and supports mixed precision. This implementation uses custom TensorFlow ops. The required custom TensorFlow ops are available in [AWS Deep Learning Container](https://github.com/aws/deep-learning-containers/blob/master/available_images.md) images in ```tensorflow-training``` repository with image tag ```1.15.2-gpu-py36-cu100-ubuntu18.04```, or later. It is recommended that you build and push both SageMaker training images and use either image for training later. ### TensorPack Faster-RCNN/Mask-RCNN Use ```./container/build_tools/build_and_push.sh``` script to build and push the TensorPack Faster-RCNN/Mask-RCNN training image to Amazon ECR. ``` !cat ./container/build_tools/build_and_push.sh ``` Using your AWS region as argument, run the cell below. ``` %%time ! ./container/build_tools/build_and_push.sh {aws_region} ``` Set ```tensorpack_image``` below to Amazon ECR URI of the image you pushed above. ``` tensorpack_image = # mask-rcnn-tensorpack-sagemaker ECR URI ``` ### AWS Samples Mask R-CNN Use ```./container-optimized/build_tools/build_and_push.sh``` script to build and push the AWS Samples Mask R-CNN training image to Amazon ECR. ``` !cat ./container-optimized/build_tools/build_and_push.sh ``` Using your AWS region as argument, run the cell below. ``` %%time ! ./container-optimized/build_tools/build_and_push.sh {aws_region} ``` Set ```aws_samples_image``` below to Amazon ECR URI of the image you pushed above. ``` aws_samples_image = # mask-rcnn-tensorflow-sagemaker ECR URI ``` ## SageMaker Initialization First we upgrade SageMaker to 2.3.0 API. If your notebook is already using latest Sagemaker 2.x API, you may skip the next cell. ``` ! pip install --upgrade pip ! pip install sagemaker==2.3.0 ``` We have staged the data and we have built and pushed the training docker image to Amazon ECR. Now we are ready to start using Amazon SageMaker. ``` %%time import os import time import boto3 import sagemaker from sagemaker import get_execution_role from sagemaker.estimator import Estimator role = get_execution_role() # provide a pre-existing role ARN as an alternative to creating a new role print(f'SageMaker Execution Role:{role}') client = boto3.client('sts') account = client.get_caller_identity()['Account'] print(f'AWS account:{account}') session = boto3.session.Session() region = session.region_name print(f'AWS region:{region}') ``` Next, we set ```training_image``` to the Amazon ECR image URI you saved in a previous step. ``` training_image = # set to tensorpack_image or aws_samples_image print(f'Training image: {training_image}') ``` ## Define SageMaker Data Channels Next, we define the train data channel using EFS file-system. To do so, we need to specify the EFS file-system id, which is shown in the output of the command below. ``` !df -kh \| grep 'fs-' \| sed 's/$fs-[0-9a-z]$./\1/' ``` Set the EFS ```file_system_id``` below to the ouput of the command shown above. In the cell below, we define the `train` data input channel. ``` from sagemaker.inputs import FileSystemInput # Specify EFS ile system id. file_system_id = # 'fs-xxxxxxxx' print(f"EFS file-system-id: {file_system_id}") # Specify directory path for input data on the file system. # You need to provide normalized and absolute path below. file_system_directory_path = '/mask-rcnn/sagemaker/input/train' print(f'EFS file-system data input path: {file_system_directory_path}') # Specify the access mode of the mount of the directory associated with the file system. # Directory must be mounted 'ro'(read-only). file_system_access_mode = 'ro' # Specify your file system type file_system_type = 'EFS' train = FileSystemInput(file_system_id=file_system_id, file_system_type=file_system_type, directory_path=file_system_directory_path, file_system_access_mode=file_system_access_mode) ``` Next, we define the model output location in S3 bucket. ``` prefix = "mask-rcnn/sagemaker" #prefix in your bucket s3_output_location = f's3://{s3_bucket}/{prefix}/output' print(f'S3 model output location: {s3_output_location}') ``` ## Configure Hyper-parameters Next, we define the hyper-parameters. Note, some hyper-parameters are different between the two implementations. The batch size per GPU in TensorPack Faster-RCNN/Mask-RCNN is fixed at 1, but is configurable in AWS Samples Mask-RCNN. The learning rate schedule is specified in units of steps in TensorPack Faster-RCNN/Mask-RCNN, but in epochs in AWS Samples Mask-RCNN. The detault learning rate schedule values shown below correspond to training for a total of 24 epochs, at 120,000 images per epoch. <table align='left'> <caption>TensorPack Faster-RCNN/Mask-RCNN Hyper-parameters</caption> <tr> <th style="text-align:center">Hyper-parameter</th> <th style="text-align:center">Description</th> <th style="text-align:center">Default</th> </tr> <tr> <td style="text-align:center">mode_fpn</td> <td style="text-align:left">Flag to indicate use of Feature Pyramid Network (FPN) in the Mask R-CNN model backbone</td> <td style="text-align:center">"True"</td> </tr> <tr> <td style="text-align:center">mode_mask</td> <td style="text-align:left">A value of "False" means Faster-RCNN model, "True" means Mask R-CNN moodel</td> <td style="text-align:center">"True"</td> </tr> <tr> <td style="text-align:center">eval_period</td> <td style="text-align:left">Number of epochs period for evaluation during training</td> <td style="text-align:center">1</td> </tr> <tr> <td style="text-align:center">lr_schedule</td> <td style="text-align:left">Learning rate schedule in training steps</td> <td style="text-align:center">'[240000, 320000, 360000]'</td> </tr> <tr> <td style="text-align:center">batch_norm</td> <td style="text-align:left">Batch normalization option ('FreezeBN', 'SyncBN', 'GN', 'None') </td> <td style="text-align:center">'FreezeBN'</td> </tr> <tr> <td style="text-align:center">images_per_epoch</td> <td style="text-align:left">Images per epoch </td> <td style="text-align:center">120000</td> </tr> <tr> <td style="text-align:center">data_train</td> <td style="text-align:left">Training data under data directory</td> <td style="text-align:center">'coco_train2017'</td> </tr> <tr> <td style="text-align:center">data_val</td> <td style="text-align:left">Validation data under data directory</td> <td style="text-align:center">'coco_val2017'</td> </tr> <tr> <td style="text-align:center">resnet_arch</td> <td style="text-align:left">Must be 'resnet50' or 'resnet101'</td> <td style="text-align:center">'resnet50'</td> </tr> <tr> <td style="text-align:center">backbone_weights</td> <td style="text-align:left">ResNet backbone weights</td> <td style="text-align:center">'ImageNet-R50-AlignPadding.npz'</td> </tr> <tr> <td style="text-align:center">load_model</td> <td style="text-align:left">Pre-trained model to load</td> <td style="text-align:center"></td> </tr> <tr> <td style="text-align:center">config:</td> <td style="text-align:left">Any hyperparamter prefixed with <b>config:</b> is set as a model config parameter</td> <td style="text-align:center"></td> </tr> </table> <table align='left'> <caption>AWS Samples Mask-RCNN Hyper-parameters</caption> <tr> <th style="text-align:center">Hyper-parameter</th> <th style="text-align:center">Description</th> <th style="text-align:center">Default</th> </tr> <tr> <td style="text-align:center">mode_fpn</td> <td style="text-align:left">Flag to indicate use of Feature Pyramid Network (FPN) in the Mask R-CNN model backbone</td> <td style="text-align:center">"True"</td> </tr> <tr> <td style="text-align:center">mode_mask</td> <td style="text-align:left">A value of "False" means Faster-RCNN model, "True" means Mask R-CNN moodel</td> <td style="text-align:center">"True"</td> </tr> <tr> <td style="text-align:center">eval_period</td> <td style="text-align:left">Number of epochs period for evaluation during training</td> <td style="text-align:center">1</td> </tr> <tr> <td style="text-align:center">lr_epoch_schedule</td> <td style="text-align:left">Learning rate schedule in epochs</td> <td style="text-align:center">'[(16, 0.1), (20, 0.01), (24, None)]'</td> </tr> <tr> <td style="text-align:center">batch_size_per_gpu</td> <td style="text-align:left">Batch size per gpu ( Minimum 1, Maximum 4)</td> <td style="text-align:center">4</td> </tr> <tr> <td style="text-align:center">batch_norm</td> <td style="text-align:left">Batch normalization option ('FreezeBN', 'SyncBN', 'GN', 'None') </td> <td style="text-align:center">'FreezeBN'</td> </tr> <tr> <td style="text-align:center">images_per_epoch</td> <td style="text-align:left">Images per epoch </td> <td style="text-align:center">120000</td> </tr> <tr> <td style="text-align:center">data_train</td> <td style="text-align:left">Training data under data directory</td> <td style="text-align:center">'train2017'</td> </tr> <tr> <td style="text-align:center">data_val</td> <td style="text-align:left">Validation data under data directory</td> <td style="text-align:center">'val2017'</td> </tr> <tr> <td style="text-align:center">resnet_arch</td> <td style="text-align:left">Must be 'resnet50' or 'resnet101'</td> <td style="text-align:center">'resnet50'</td> </tr> <tr> <td style="text-align:center">backbone_weights</td> <td style="text-align:left">ResNet backbone weights</td> <td style="text-align:center">'ImageNet-R50-AlignPadding.npz'</td> </tr> <tr> <td style="text-align:center">load_model</td> <td style="text-align:left">Pre-trained model to load</td> <td style="text-align:center"></td> </tr> <tr> <td style="text-align:center">config:</td> <td style="text-align:left">Any hyperparamter prefixed with <b>config:</b> is set as a model config parameter</td> <td style="text-align:center"></td> </tr> </table> ``` hyperparameters = { "mode_fpn": "True", "mode_mask": "True", "eval_period": 1, "batch_norm": "FreezeBN" } ``` ## Define Training Metrics Next, we define the regular expressions that SageMaker uses to extract algorithm metrics from training logs and send them to [AWS CloudWatch metrics](https://docs.aws.amazon.com/en_pv/AmazonCloudWatch/latest/monitoring/working_with_metrics.html). These algorithm metrics are visualized in SageMaker console. ``` metric_definitions=[ { "Name": "fastrcnn_losses/box_loss", "Regex": ".fastrcnn_losses/box_loss:\\s(\\S+)." }, { "Name": "fastrcnn_losses/label_loss", "Regex": ".fastrcnn_losses/label_loss:\\s(\\S+)." }, { "Name": "fastrcnn_losses/label_metrics/accuracy", "Regex": ".fastrcnn_losses/label_metrics/accuracy:\\s(\\S+)." }, { "Name": "fastrcnn_losses/label_metrics/false_negative", "Regex": ".fastrcnn_losses/label_metrics/false_negative:\\s(\\S+)." }, { "Name": "fastrcnn_losses/label_metrics/fg_accuracy", "Regex": ".fastrcnn_losses/label_metrics/fg_accuracy:\\s(\\S+)." }, { "Name": "fastrcnn_losses/num_fg_label", "Regex": ".fastrcnn_losses/num_fg_label:\\s(\\S+)." }, { "Name": "maskrcnn_loss/accuracy", "Regex": ".maskrcnn_loss/accuracy:\\s(\\S+)." }, { "Name": "maskrcnn_loss/fg_pixel_ratio", "Regex": ".maskrcnn_loss/fg_pixel_ratio:\\s(\\S+)." }, { "Name": "maskrcnn_loss/maskrcnn_loss", "Regex": ".maskrcnn_loss/maskrcnn_loss:\\s(\\S+)." }, { "Name": "maskrcnn_loss/pos_accuracy", "Regex": ".maskrcnn_loss/pos_accuracy:\\s(\\S+)." }, { "Name": "mAP(bbox)/IoU=0.5", "Regex": ".mAP\$bbox\$/IoU=0\\.5:\\s(\\S+)." }, { "Name": "mAP(bbox)/IoU=0.5:0.95", "Regex": ".mAP\$bbox\$/IoU=0\\.5:0\\.95:\\s(\\S+)." }, { "Name": "mAP(bbox)/IoU=0.75", "Regex": ".mAP\$bbox\$/IoU=0\\.75:\\s(\\S+)." }, { "Name": "mAP(bbox)/large", "Regex": ".mAP\$bbox\$/large:\\s(\\S+)." }, { "Name": "mAP(bbox)/medium", "Regex": ".mAP\$bbox\$/medium:\\s(\\S+)." }, { "Name": "mAP(bbox)/small", "Regex": ".mAP\$bbox\$/small:\\s(\\S+)." }, { "Name": "mAP(segm)/IoU=0.5", "Regex": ".mAP\$segm\$/IoU=0\\.5:\\s(\\S+)." }, { "Name": "mAP(segm)/IoU=0.5:0.95", "Regex": ".mAP\$segm\$/IoU=0\\.5:0\\.95:\\s(\\S+)." }, { "Name": "mAP(segm)/IoU=0.75", "Regex": ".mAP\$segm\$/IoU=0\\.75:\\s(\\S+)." }, { "Name": "mAP(segm)/large", "Regex": ".mAP\$segm\$/large:\\s(\\S+)." }, { "Name": "mAP(segm)/medium", "Regex": ".mAP\$segm\$/medium:\\s(\\S+)." }, { "Name": "mAP(segm)/small", "Regex": ".mAP\$segm\$/small:\\s(\\S+)." } ] ``` ## Define SageMaker Experiment To define SageMaker Experiment, we first install `sagemaker-experiments` package. ``` ! pip install sagemaker-experiments==0.1.20 ``` Next, we import the SageMaker Experiment modules. ``` from smexperiments.experiment import Experiment from smexperiments.trial import Trial from smexperiments.trial_component import TrialComponent from smexperiments.tracker import Tracker import time ``` Next, we define a `Tracker` for tracking input data used in the SageMaker Trials in this Experiment. Specify the S3 URL of your dataset in the `value` below and change the name of the dataset if you are using a different dataset. ``` sm = session.client('sagemaker') with Tracker.create(display_name="Preprocessing", sagemaker_boto_client=sm) as tracker: # we can log the s3 uri to the dataset used for training tracker.log_input(name="coco-2017-dataset", media_type="s3/uri", value= f's3://{s3_bucket}/{prefix}/input/train' # specify S3 URL to your dataset ) ``` Next, we create a SageMaker Experiment. ``` mrcnn_experiment = Experiment.create( experiment_name=f"mask-rcnn-experiment-{int(time.time())}", description="Mask R-CNN experiment", sagemaker_boto_client=sm) print(mrcnn_experiment) ``` We run the training job in your private VPC, so we need to set the ```subnets``` and ```security_group_ids``` prior to running the cell below. You may specify multiple subnet ids in the ```subnets``` list. The subnets included in the ```sunbets``` list must be part of the output of ```./stack-sm.sh``` CloudFormation stack script used to create this notebook instance. Specify only one security group id in ```security_group_ids``` list. The security group id must be part of the output of ```./stack-sm.sh``` script. ``` security_group_ids = # ['sg-xxxxxxxx'] subnets = # ['subnet-xxxxxxx', 'subnet-xxxxxxx', 'subnet-xxxxxxx'] sagemaker_session = sagemaker.session.Session(boto_session=session) ``` Next, we use SageMaker [Estimator](https://sagemaker.readthedocs.io/en/stable/estimators.html) API to define a SageMaker Training Job for each SageMaker Trial we need to run within the SageMaker Experiment. We recommned using 8 GPUs, so we set ```train_instance_count=1``` and ```train_instance_type='ml.p3.16xlarge'```, because there are 8 Tesla V100 GPUs per ```ml.p3.16xlarge``` instance. We recommend using 100 GB [Amazon EBS](https://aws.amazon.com/ebs/) storage volume with each training instance, so we set ```train_volume_size = 100```. We want to replicate training data to each training instance, so we set ```input_mode= 'File'```. Next, we will iterate through the Trial parameters and start two trials, one for ResNet architecture `resnet50`, and a second Trial for `resnet101`. ``` trial_params = [ ('resnet50', 'ImageNet-R50-AlignPadding.npz'), ('resnet101', 'ImageNet-R101-AlignPadding.npz')] for resnet_arch, backbone_weights in trial_params: hyperparameters['resnet_arch'] = resnet_arch hyperparameters['backbone_weights'] = backbone_weights trial_name = f"mask-rcnn-{resnet_arch}-{int(time.time())}" mrcnn_trial = Trial.create( trial_name=trial_name, experiment_name=mrcnn_experiment.experiment_name, sagemaker_boto_client=sm, ) # associate the proprocessing trial component with the current trial mrcnn_trial.add_trial_component(tracker.trial_component) print(mrcnn_trial) mask_rcnn_estimator = Estimator(image_uri=training_image, role=role, instance_count=4, instance_type='ml.p3.16xlarge', volume_size = 100, max_run = 400000, input_mode= 'File', output_path=s3_output_location, sagemaker_session=sagemaker_session, hyperparameters = hyperparameters, metric_definitions = metric_definitions, subnets=subnets, security_group_ids=security_group_ids) # Specify directory path for log output on the EFS file system. # You need to provide normalized and absolute path below. # For example, '/mask-rcnn/sagemaker/output/log' # Log output directory must not exist file_system_directory_path = f'/mask-rcnn/sagemaker/output/{mrcnn_trial.trial_name}' print(f"EFS log directory:{file_system_directory_path}") # Create the log output directory. # EFS file-system is mounted on '$HOME/efs' mount point for this notebook. home_dir=os.environ['HOME'] local_efs_path = os.path.join(home_dir,'efs', file_system_directory_path[1:]) print(f"Creating log directory on EFS: {local_efs_path}") assert not os.path.isdir(local_efs_path) ! sudo mkdir -p -m a=rw {local_efs_path} assert os.path.isdir(local_efs_path) # Specify the access mode of the mount of the directory associated with the file system. # Directory must be mounted 'rw'(read-write). file_system_access_mode = 'rw' log = FileSystemInput(file_system_id=file_system_id, file_system_type=file_system_type, directory_path=file_system_directory_path, file_system_access_mode=file_system_access_mode) data_channels = {'train': train, 'log': log} mask_rcnn_estimator.fit(inputs=data_channels, job_name=mrcnn_trial.trial_name, logs=True, experiment_config={"TrialName": mrcnn_trial.trial_name, "TrialComponentDisplayName": "Training"}, wait=False) # sleep in between starting two trials time.sleep(2) search_expression = { "Filters":[ { "Name": "DisplayName", "Operator": "Equals", "Value": "Training", }, { "Name": "metrics.maskrcnn_loss/accuracy.max", "Operator": "LessThan", "Value": "1", } ], } from sagemaker.analytics import ExperimentAnalytics trial_component_analytics = ExperimentAnalytics( sagemaker_session=sagemaker_session, experiment_name=mrcnn_experiment.experiment_name, search_expression=search_expression, sort_by="metrics.maskrcnn_loss/accuracy.max", sort_order="Descending", parameter_names=['resnet_arch'] ) analytic_table = trial_component_analytics.dataframe() for col in analytic_table.columns: print(col) bbox_map=analytic_table[['resnet_arch', 'mAP(bbox)/small - Max', 'mAP(bbox)/medium - Max', 'mAP(bbox)/large - Max']] bbox_map segm_map=analytic_table[['resnet_arch', 'mAP(segm)/small - Max', 'mAP(segm)/medium - Max', 'mAP(segm)/large - Max']] segm_map ```	github_jupyter
# Training on Multiple GPUs :label:`sec_multi_gpu` So far we discussed how to train models efficiently on CPUs and GPUs. We even showed how deep learning frameworks allow one to parallelize computation and communication automatically between them in :numref:`sec_auto_para`. We also showed in :numref:`sec_use_gpu` how to list all the available GPUs on a computer using the `nvidia-smi` command. What we did not discuss is how to actually parallelize deep learning training. Instead, we implied in passing that one would somehow split the data across multiple devices and make it work. The present section fills in the details and shows how to train a network in parallel when starting from scratch. Details on how to take advantage of functionality in high-level APIs is relegated to :numref:`sec_multi_gpu_concise`. We assume that you are familiar with minibatch stochastic gradient descent algorithms such as the ones described in :numref:`sec_minibatch_sgd`. ## Splitting the Problem Let us start with a simple computer vision problem and a slightly archaic network, e.g., with multiple layers of convolutions, pooling, and possibly a few fully-connected layers in the end. That is, let us start with a network that looks quite similar to LeNet :cite:`LeCun.Bottou.Bengio.ea.1998` or AlexNet :cite:`Krizhevsky.Sutskever.Hinton.2012`. Given multiple GPUs (2 if it is a desktop server, 4 on an AWS g4dn.12xlarge instance, 8 on a p3.16xlarge, or 16 on a p2.16xlarge), we want to partition training in a manner as to achieve good speedup while simultaneously benefitting from simple and reproducible design choices. Multiple GPUs, after all, increase both memory and computation ability. In a nutshell, we have the following choices, given a minibatch of training data that we want to classify. First, we could partition the network across multiple GPUs. That is, each GPU takes as input the data flowing into a particular layer, processes data across a number of subsequent layers and then sends the data to the next GPU. This allows us to process data with larger networks when compared with what a single GPU could handle. Besides, memory footprint per GPU can be well controlled (it is a fraction of the total network footprint). However, the interface between layers (and thus GPUs) requires tight synchronization. This can be tricky, in particular if the computational workloads are not properly matched between layers. The problem is exacerbated for large numbers of GPUs. The interface between layers also requires large amounts of data transfer, such as activations and gradients. This may overwhelm the bandwidth of the GPU buses. Moreover, compute-intensive, yet sequential operations are nontrivial to partition. See e.g., :cite:`Mirhoseini.Pham.Le.ea.2017` for a best effort in this regard. It remains a difficult problem and it is unclear whether it is possible to achieve good (linear) scaling on nontrivial problems. We do not recommend it unless there is excellent framework or operating system support for chaining together multiple GPUs. Second, we could split the work layerwise. For instance, rather than computing 64 channels on a single GPU we could split up the problem across 4 GPUs, each of which generates data for 16 channels. Likewise, for a fully-connected layer we could split the number of output units. :numref:`fig_alexnet_original` (taken from :cite:`Krizhevsky.Sutskever.Hinton.2012`) illustrates this design, where this strategy was used to deal with GPUs that had a very small memory footprint (2 GB at the time). This allows for good scaling in terms of computation, provided that the number of channels (or units) is not too small. Besides, multiple GPUs can process increasingly larger networks since the available memory scales linearly. ![Model parallelism in the original AlexNet design due to limited GPU memory.](../img/alexnet-original.svg) :label:`fig_alexnet_original` However, we need a very large number of synchronization or barrier operations since each layer depends on the results from all the other layers. Moreover, the amount of data that needs to be transferred is potentially even larger than when distributing layers across GPUs. Thus, we do not recommend this approach due to its bandwidth cost and complexity. Last, we could partition data across multiple GPUs. This way all GPUs perform the same type of work, albeit on different observations. Gradients are aggregated across GPUs after each minibatch of training data. This is the simplest approach and it can be applied in any situation. We only need to synchronize after each minibatch. That said, it is highly desirable to start exchanging gradients parameters already while others are still being computed. Moreover, larger numbers of GPUs lead to larger minibatch sizes, thus increasing training efficiency. However, adding more GPUs does not allow us to train larger models. ![Parallelization on multiple GPUs. From left to right: original problem, network partitioning, layerwise partitioning, data parallelism.](../img/splitting.svg) :label:`fig_splitting` A comparison of different ways of parallelization on multiple GPUs is depicted in :numref:`fig_splitting`. By and large, data parallelism is the most convenient way to proceed, provided that we have access to GPUs with sufficiently large memory. See also :cite:`Li.Andersen.Park.ea.2014` for a detailed description of partitioning for distributed training. GPU memory used to be a problem in the early days of deep learning. By now this issue has been resolved for all but the most unusual cases. We focus on data parallelism in what follows. ## Data Parallelism Assume that there are $k$ GPUs on a machine. Given the model to be trained, each GPU will maintain a complete set of model parameters independently though parameter values across the GPUs are identical and synchronized. As an example, :numref:`fig_data_parallel` illustrates training with data parallelism when $k=2$. ![Calculation of minibatch stochastic gradient descent using data parallelism on two GPUs.](../img/data-parallel.svg) :label:`fig_data_parallel` In general, the training proceeds as follows: * In any iteration of training, given a random minibatch, we split the examples in the batch into $k$ portions and distribute them evenly across the GPUs. * Each GPU calculates loss and gradient of the model parameters based on the minibatch subset it was assigned. * The local gradients of each of the $k$ GPUs are aggregated to obtain the current minibatch stochastic gradient. * The aggregate gradient is re-distributed to each GPU. * Each GPU uses this minibatch stochastic gradient to update the complete set of model parameters that it maintains. Note that in practice we increase the minibatch size $k$-fold when training on $k$ GPUs such that each GPU has the same amount of work to do as if we were training on a single GPU only. On a 16-GPU server this can increase the minibatch size considerably and we may have to increase the learning rate accordingly. Also note that batch normalization in :numref:`sec_batch_norm` needs to be adjusted, e.g., by keeping a separate batch normalization coefficient per GPU. In what follows we will use a toy network to illustrate multi-GPU training. ``` %matplotlib inline import torch from torch import nn from torch.nn import functional as F from d2l import torch as d2l ``` ## [A Toy Network] We use LeNet as introduced in :numref:`sec_lenet` (with slight modifications). We define it from scratch to illustrate parameter exchange and synchronization in detail. ``` # Initialize model parameters scale = 0.01 W1 = torch.randn(size=(20, 1, 3, 3)) * scale b1 = torch.zeros(20) W2 = torch.randn(size=(50, 20, 5, 5)) * scale b2 = torch.zeros(50) W3 = torch.randn(size=(800, 128)) * scale b3 = torch.zeros(128) W4 = torch.randn(size=(128, 10)) * scale b4 = torch.zeros(10) params = [W1, b1, W2, b2, W3, b3, W4, b4] # Define the model def lenet(X, params): h1_conv = F.conv2d(input=X, weight=params[0], bias=params[1]) h1_activation = F.relu(h1_conv) h1 = F.avg_pool2d(input=h1_activation, kernel_size=(2, 2), stride=(2, 2)) h2_conv = F.conv2d(input=h1, weight=params[2], bias=params[3]) h2_activation = F.relu(h2_conv) h2 = F.avg_pool2d(input=h2_activation, kernel_size=(2, 2), stride=(2, 2)) h2 = h2.reshape(h2.shape[0], -1) h3_linear = torch.mm(h2, params[4]) + params[5] h3 = F.relu(h3_linear) y_hat = torch.mm(h3, params[6]) + params[7] return y_hat # Cross-entropy loss function loss = nn.CrossEntropyLoss(reduction='none') ``` ## Data Synchronization For efficient multi-GPU training we need two basic operations. First we need to have the ability to [distribute a list of parameters to multiple devices] and to attach gradients (`get_params`). Without parameters it is impossible to evaluate the network on a GPU. Second, we need the ability to sum parameters across multiple devices, i.e., we need an `allreduce` function. ``` def get_params(params, device): new_params = [p.to(device) for p in params] for p in new_params: p.requires_grad_() return new_params ``` Let us try it out by copying the model parameters to one GPU. ``` new_params = get_params(params, d2l.try_gpu(0)) print('b1 weight:', new_params[1]) print('b1 grad:', new_params[1].grad) ``` Since we did not perform any computation yet, the gradient with regard to the bias parameter is still zero. Now let us assume that we have a vector distributed across multiple GPUs. The following [`allreduce` function adds up all vectors and broadcasts the result back to all GPUs]. Note that for this to work we need to copy the data to the device accumulating the results. ``` def allreduce(data): for i in range(1, len(data)): data[0][:] += data[i].to(data[0].device) for i in range(1, len(data)): data[i][:] = data[0].to(data[i].device) ``` Let us test this by creating vectors with different values on different devices and aggregate them. ``` data = [torch.ones((1, 2), device=d2l.try_gpu(i)) * (i + 1) for i in range(2)] print('before allreduce:\n', data[0], '\n', data[1]) allreduce(data) print('after allreduce:\n', data[0], '\n', data[1]) ``` ## Distributing Data We need a simple utility function to [distribute a minibatch evenly across multiple GPUs]. For instance, on two GPUs we would like to have half of the data to be copied to either of the GPUs. Since it is more convenient and more concise, we use the built-in function from the deep learning framework to try it out on a $4 \times 5$ matrix. ``` data = torch.arange(20).reshape(4, 5) devices = [torch.device('cuda:0'), torch.device('cuda:1')] split = nn.parallel.scatter(data, devices) print('input :', data) print('load into', devices) print('output:', split) ``` For later reuse we define a `split_batch` function that splits both data and labels. ``` #@save def split_batch(X, y, devices): """Split `X` and `y` into multiple devices.""" assert X.shape[0] == y.shape[0] return (nn.parallel.scatter(X, devices), nn.parallel.scatter(y, devices)) ``` ## Training Now we can implement [multi-GPU training on a single minibatch]. Its implementation is primarily based on the data parallelism approach described in this section. We will use the auxiliary functions we just discussed, `allreduce` and `split_and_load`, to synchronize the data among multiple GPUs. Note that we do not need to write any specific code to achieve parallelism. Since the computational graph does not have any dependencies across devices within a minibatch, it is executed in parallel automatically. ``` def train_batch(X, y, device_params, devices, lr): X_shards, y_shards = split_batch(X, y, devices) # Loss is calculated separately on each GPU ls = [loss(lenet(X_shard, device_W), y_shard).sum() for X_shard, y_shard, device_W in zip( X_shards, y_shards, device_params)] for l in ls: # Backpropagation is performed separately on each GPU l.backward() # Sum all gradients from each GPU and broadcast them to all GPUs with torch.no_grad(): for i in range(len(device_params[0])): allreduce([device_params[c][i].grad for c in range(len(devices))]) # The model parameters are updated separately on each GPU for param in device_params: d2l.sgd(param, lr, X.shape[0]) # Here, we use a full-size batch ``` Now, we can define [the training function]. It is slightly different from the ones used in the previous chapters: we need to allocate the GPUs and copy all the model parameters to all the devices. Obviously each batch is processed using the `train_batch` function to deal with multiple GPUs. For convenience (and conciseness of code) we compute the accuracy on a single GPU, though this is inefficient since the other GPUs are idle. ``` def train(num_gpus, batch_size, lr): train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size) devices = [d2l.try_gpu(i) for i in range(num_gpus)] # Copy model parameters to `num_gpus` GPUs device_params = [get_params(params, d) for d in devices] num_epochs = 10 animator = d2l.Animator('epoch', 'test acc', xlim=[1, num_epochs]) timer = d2l.Timer() for epoch in range(num_epochs): timer.start() for X, y in train_iter: # Perform multi-GPU training for a single minibatch train_batch(X, y, device_params, devices, lr) torch.cuda.synchronize() timer.stop() # Evaluate the model on GPU 0 animator.add(epoch + 1, (d2l.evaluate_accuracy_gpu( lambda x: lenet(x, device_params[0]), test_iter, devices[0]),)) print(f'test acc: {animator.Y[0][-1]:.2f}, {timer.avg():.1f} sec/epoch ' f'on {str(devices)}') ``` Let us see how well this works [on a single GPU]. We first use a batch size of 256 and a learning rate of 0.2. ``` train(num_gpus=1, batch_size=256, lr=0.2) ``` By keeping the batch size and learning rate unchanged and [increasing the number of GPUs to 2], we can see that the test accuracy roughly stays the same compared with the previous experiment. In terms of the optimization algorithms, they are identical. Unfortunately there is no meaningful speedup to be gained here: the model is simply too small; moreover we only have a small dataset, where our slightly unsophisticated approach to implementing multi-GPU training suffered from significant Python overhead. We will encounter more complex models and more sophisticated ways of parallelization going forward. Let us see what happens nonetheless for Fashion-MNIST. ``` train(num_gpus=2, batch_size=256, lr=0.2) ``` ## Summary * There are multiple ways to split deep network training over multiple GPUs. We could split them between layers, across layers, or across data. The former two require tightly choreographed data transfers. Data parallelism is the simplest strategy. * Data parallel training is straightforward. However, it increases the effective minibatch size to be efficient. * In data parallelism, data are split across multiple GPUs, where each GPU executes its own forward and backward operation and subsequently gradients are aggregated and results are broadcast back to the GPUs. * We may use slightly increased learning rates for larger minibatches. ## Exercises 1. When training on $k$ GPUs, change the minibatch size from $b$ to $k \cdot b$, i.e., scale it up by the number of GPUs. 1. Compare accuracy for different learning rates. How does it scale with the number of GPUs? 1. Implement a more efficient `allreduce` function that aggregates different parameters on different GPUs? Why is it more efficient? 1. Implement multi-GPU test accuracy computation. [Discussions](https://discuss.d2l.ai/t/1669)	github_jupyter
``` # Copyright 2021 Google LLC # # Licensed under the Apache License, Version 2.0 (the "License"); # you may not use this file except in compliance with the License. # You may obtain a copy of the License at # # https://www.apache.org/licenses/LICENSE-2.0 # # Unless required by applicable law or agreed to in writing, software # distributed under the License is distributed on an "AS IS" BASIS, # WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. # See the License for the specific language governing permissions and # limitations under the License. ``` # Vertex SDK: AutoML training image classification model for batch prediction <table align="left"> <td> <a href="https://colab.research.google.com/github/GoogleCloudPlatform/vertex-ai-samples/blob/master/notebooks/community/sdk/sdk_automl_image_classification_batch.ipynb"> <img src="https://cloud.google.com/ml-engine/images/colab-logo-32px.png" alt="Colab logo"> Run in Colab </a> </td> <td> <a href="https://github.com/GoogleCloudPlatform/vertex-ai-samples/blob/master/notebooks/community/sdk/sdk_automl_image_classification_batch.ipynb"> <img src="https://cloud.google.com/ml-engine/images/github-logo-32px.png" alt="GitHub logo"> View on GitHub </a> </td> </table> <br/><br/><br/> ## Overview This tutorial demonstrates how to use the Vertex SDK to create image classification models and do batch prediction using Google Cloud's [AutoML](https://cloud.google.com/vertex-ai/docs/start/automl-users). ### Dataset The dataset used for this tutorial is the [Flowers dataset](https://www.tensorflow.org/datasets/catalog/tf_flowers) from [TensorFlow Datasets](https://www.tensorflow.org/datasets/catalog/overview). The version of the dataset you will use in this tutorial is stored in a public Cloud Storage bucket. The trained model predicts the type of flower an image is from a class of five flowers: daisy, dandelion, rose, sunflower, or tulip. ### Objective In this tutorial, you create an AutoML image classification model from a Python script, and then do a batch prediction using the Vertex SDK. You can alternatively create and deploy models using the `gcloud` command-line tool or online using the Google Cloud Console. The steps performed include: - Create a Vertex `Dataset` resource. - Train the model. - View the model evaluation. - Make a batch prediction. There is one key difference between using batch prediction and using online prediction: * Prediction Service: Does an on-demand prediction for the entire set of instances (i.e., one or more data items) and returns the results in real-time. * Batch Prediction Service: Does a queued (batch) prediction for the entire set of instances in the background and stores the results in a Cloud Storage bucket when ready. ### Costs This tutorial uses billable components of Google Cloud (GCP): * Vertex AI * Cloud Storage Learn about [Vertex AI pricing](https://cloud.google.com/vertex-ai/pricing) and [Cloud Storage pricing](https://cloud.google.com/storage/pricing), and use the [Pricing Calculator](https://cloud.google.com/products/calculator/) to generate a cost estimate based on your projected usage. ## Installation Install the latest version of Vertex SDK. ``` import sys import os # Google Cloud Notebook if os.path.exists("/opt/deeplearning/metadata/env_version"): USER_FLAG = '--user' else: USER_FLAG = '' ! pip3 install --upgrade google-cloud-aiplatform $USER_FLAG ``` Install the latest GA version of google-cloud-storage library as well. ``` ! pip3 install -U google-cloud-storage $USER_FLAG ``` ### Restart the kernel Once you've installed the Vertex SDK and Google cloud-storage, you need to restart the notebook kernel so it can find the packages. ``` if not os.getenv("IS_TESTING"): # Automatically restart kernel after installs import IPython app = IPython.Application.instance() app.kernel.do_shutdown(True) ``` ## Before you begin ### GPU runtime Make sure you're running this notebook in a GPU runtime if you have that option. In Colab, select Runtime > Change Runtime Type > GPU ### Set up your Google Cloud project The following steps are required, regardless of your notebook environment. 1. [Select or create a Google Cloud project](https://console.cloud.google.com/cloud-resource-manager). When you first create an account, you get a $300 free credit towards your compute/storage costs. 2. [Make sure that billing is enabled for your project.](https://cloud.google.com/billing/docs/how-to/modify-project) 3. [Enable the Vertex APIs and Compute Engine APIs.](https://console.cloud.google.com/flows/enableapi?apiid=ml.googleapis.com,compute_component) 4. [The Google Cloud SDK](https://cloud.google.com/sdk) is already installed in Google Cloud Notebook. 5. Enter your project ID in the cell below. Then run the cell to make sure the Cloud SDK uses the right project for all the commands in this notebook. Note: Jupyter runs lines prefixed with `!` as shell commands, and it interpolates Python variables prefixed with `$` into these commands. ``` PROJECT_ID = "[your-project-id]" #@param {type:"string"} if PROJECT_ID == "" or PROJECT_ID is None or PROJECT_ID == "[your-project-id]": # Get your GCP project id from gcloud shell_output = !gcloud config list --format 'value(core.project)' 2>/dev/null PROJECT_ID = shell_output[0] print("Project ID:", PROJECT_ID) ! gcloud config set project $PROJECT_ID ``` #### Region You can also change the `REGION` variable, which is used for operations throughout the rest of this notebook. Below are regions supported for Vertex. We recommend that you choose the region closest to you. - Americas: `us-central1` - Europe: `europe-west4` - Asia Pacific: `asia-east1` You may not use a multi-regional bucket for training with Vertex. Not all regions provide support for all Vertex services. For the latest support per region, see the [Vertex locations documentation](https://cloud.google.com/ai-platform-unified/docs/general/locations) ``` REGION = 'us-central1' #@param {type: "string"} ``` #### Timestamp If you are in a live tutorial session, you might be using a shared test account or project. To avoid name collisions between users on resources created, you create a timestamp for each instance session, and append onto the name of resources which will be created in this tutorial. ``` from datetime import datetime TIMESTAMP = datetime.now().strftime("%Y%m%d%H%M%S") ``` ### Authenticate your Google Cloud account If you are using Google Cloud Notebook, your environment is already authenticated. Skip this step. If you are using Colab, run the cell below and follow the instructions when prompted to authenticate your account via oAuth. Otherwise, follow these steps: In the Cloud Console, go to the [Create service account key](https://console.cloud.google.com/apis/credentials/serviceaccountkey) page. Click Create service account. In the Service account name field, enter a name, and click Create. In the Grant this service account access to project section, click the Role drop-down list. Type "Vertex" into the filter box, and select Vertex Administrator. Type "Storage Object Admin" into the filter box, and select Storage Object Admin. Click Create. A JSON file that contains your key downloads to your local environment. Enter the path to your service account key as the GOOGLE_APPLICATION_CREDENTIALS variable in the cell below and run the cell. ``` # If you are running this notebook in Colab, run this cell and follow the # instructions to authenticate your GCP account. This provides access to your # Cloud Storage bucket and lets you submit training jobs and prediction # requests. # If on Google Cloud Notebook, then don't execute this code if not os.path.exists("/opt/deeplearning/metadata/env_version"): if "google.colab" in sys.modules: from google.colab import auth as google_auth google_auth.authenticate_user() # If you are running this notebook locally, replace the string below with the # path to your service account key and run this cell to authenticate your GCP # account. elif not os.getenv("IS_TESTING"): %env GOOGLE_APPLICATION_CREDENTIALS '' ``` ### Create a Cloud Storage bucket The following steps are required, regardless of your notebook environment. When you initialize the Vertex SDK for Python, you specify a Cloud Storage staging bucket. The staging bucket is where all the data associated with your dataset and model resources are retained across sessions. Set the name of your Cloud Storage bucket below. Bucket names must be globally unique across all Google Cloud projects, including those outside of your organization. ``` BUCKET_NAME = "gs://[your-bucket-name]" #@param {type:"string"} if BUCKET_NAME == "" or BUCKET_NAME is None or BUCKET_NAME == "gs://[your-bucket-name]": BUCKET_NAME = "gs://" + PROJECT_ID + "aip-" + TIMESTAMP ``` Only if your bucket doesn't already exist: Run the following cell to create your Cloud Storage bucket. ``` ! gsutil mb -l $REGION $BUCKET_NAME ``` Finally, validate access to your Cloud Storage bucket by examining its contents: ``` ! gsutil ls -al $BUCKET_NAME ``` ### Set up variables Next, set up some variables used throughout the tutorial. ### Import libraries and define constants ``` import google.cloud.aiplatform as aip ``` ## Initialize Vertex SDK Initialize the Vertex SDK for your project and corresponding bucket. ``` aip.init(project=PROJECT_ID, staging_bucket=BUCKET_NAME) ``` # Tutorial Now you are ready to start creating your own AutoML image classification model. ## Create a Dataset Resource First, you create an image Dataset resource for the Flowers dataset. ### Data preparation The Vertex `Dataset` resource for images has some requirements for your data: - Images must be stored in a Cloud Storage bucket. - Each image file must be in an image format (PNG, JPEG, BMP, ...). - There must be an index file stored in your Cloud Storage bucket that contains the path and label for each image. - The index file must be either CSV or JSONL. #### CSV For image classification, the CSV index file has the requirements: - No heading. - First column is the Cloud Storage path to the image. - Second column is the label. #### Location of Cloud Storage training data. Now set the variable `IMPORT_FILE` to the location of the CSV index file in Cloud Storage. ``` IMPORT_FILE = 'gs://cloud-samples-data/vision/automl_classification/flowers/all_data_v2.csv' ``` #### Quick peek at your data You will use a version of the Flowers dataset that is stored in a public Cloud Storage bucket, using a CSV index file. Start by doing a quick peek at the data. You count the number of examples by counting the number of rows in the CSV index file (`wc -l`) and then peek at the first few rows. ``` if 'IMPORT_FILES' in globals(): FILE = IMPORT_FILES[0] else: FILE = IMPORT_FILE count = ! gsutil cat $FILE \| wc -l print("Number of Examples", int(count[0])) print("First 10 rows") ! gsutil cat $FILE \| head ``` ### Create the Dataset Next, create the `Dataset` resource using the `create()` method for the `ImageDataset` class, which takes the following parameters: - `display_name`: The human readable name for the `Dataset` resource. - `gcs_source`: A list of one or more dataset index file to import the data items into the `Dataset` resource. - `import_schema_uri`: The data labeling schema for the data items. This operation may take several minutes. ``` dataset = aip.ImageDataset.create( display_name="Flowers" + "_" + TIMESTAMP, gcs_source=[IMPORT_FILE], import_schema_uri=aip.schema.dataset.ioformat.image.single_label_classification, ) print(dataset.resource_name) ``` ## Train the model Now train an AutoML image classification model using your Vertex `Dataset` resource. To train the model, do the following steps: 1. Create an Vertex training pipeline for the `Dataset` resource. 2. Execute the pipeline to start the training. ### Create and run training pipeline To train an AutoML image classification model, you perform two steps: 1) create a training pipeline, and 2) run the pipeline. #### Create training pipeline An AutoML training pipeline is created with the `AutoMLImageTrainingJob` class, with the following parameters: - `display_name`: The human readable name for the `TrainingJob` resource. - `prediction_type`: The type task to train the model for. - `classification`: An image classification model. - `object_detection`: An image object detection model. - `multi_label`: If a classification task, whether single (`False`) or multi-labeled (`True`). - `model_type`: The type of model for deployment. - `CLOUD`: Deployment on Google Cloud - `CLOUD_HIGH_ACCURACY_1`: Optimized for accuracy over latency for deployment on Google Cloud. - `CLOUD_LOW_LATENCY_`: Optimized for latency over accuracy for deployment on Google Cloud. - `MOBILE_TF_VERSATILE_1`: Deployment on an edge device. - `MOBILE_TF_HIGH_ACCURACY_1`:Optimized for accuracy over latency for deployment on an edge device. - `MOBILE_TF_LOW_LATENCY_1`: Optimized for latency over accuracy for deployment on an edge device. - `base_model`: (optional) Transfer learning from existing `Model` resource -- supported for image classification only. The instantiated object is the DAG for the training job. ``` dag = aip.AutoMLImageTrainingJob( display_name="flowers_" + TIMESTAMP, prediction_type="classification", multi_label=False, model_type="CLOUD", base_model=None, ) ``` #### Run the training pipeline Next, you run the DAG to start the training job by invoking the method `run()`, with the following parameters: - `dataset`: The `Dataset` resource to train the model. - `model_display_name`: The human readable name for the trained model. - `training_fraction_split`: The percentage of the dataset to use for training. - `validation_fraction_split`: The percentage of the dataset to use for validation. - `test_fraction_split`: The percentage of the dataset to use for test (holdout data). - `budget_milli_node_hours`: (optional) Maximum training time specified in unit of millihours (1000 = hour). - `disable_early_stopping`: If `True`, training maybe completed before using the entire budget if the service believes it cannot further improve on the model objective measurements. The `run` method when completed returns the `Model` resource. The execution of the training pipeline will take upto 20 minutes. ``` model = dag.run( dataset=dataset, model_display_name="flowers_" + TIMESTAMP, training_fraction_split=0.8, validation_fraction_split=0.1, test_fraction_split=0.1, budget_milli_node_hours=8000, disable_early_stopping=False ) ``` ## Model deployment for batch prediction Now deploy the trained Vertex `Model` resource you created for batch prediction. This differs from deploying a `Model` resource for online prediction. For online prediction, you: 1. Create an `Endpoint` resource for deploying the `Model` resource to. 2. Deploy the `Model` resource to the `Endpoint` resource. 3. Make online prediction requests to the `Endpoint` resource. For batch-prediction, you: 1. Create a batch prediction job. 2. The job service will provision resources for the batch prediction request. 3. The results of the batch prediction request are returned to the caller. 4. The job service will unprovision the resoures for the batch prediction request. ## Make a batch prediction request Now do a batch prediction to your deployed model. ### Get test item(s) Now do a batch prediction to your Vertex model. You will use arbitrary examples out of the dataset as a test items. Don't be concerned that the examples were likely used in training the model -- we just want to demonstrate how to make a prediction. ``` test_items = !gsutil cat $IMPORT_FILE \| head -n2 if len(str(test_items[0]).split(',')) == 3: _, test_item_1, test_label_1 = str(test_items[0]).split(',') _, test_item_2, test_label_2 = str(test_items[1]).split(',') else: test_item_1, test_label_1 = str(test_items[0]).split(',') test_item_2, test_label_2 = str(test_items[1]).split(',') print(test_item_1, test_label_1) print(test_item_2, test_label_2) ``` ### Copy test item(s) For the batch prediction, you will copy the test items over to your Cloud Storage bucket. ``` file_1 = test_item_1.split('/')[-1] file_2 = test_item_2.split('/')[-1] ! gsutil cp $test_item_1 $BUCKET_NAME/$file_1 ! gsutil cp $test_item_2 $BUCKET_NAME/$file_2 test_item_1 = BUCKET_NAME + "/" + file_1 test_item_2 = BUCKET_NAME + "/" + file_2 ``` ### Make the batch input file Now make a batch input file, which you will store in your local Cloud Storage bucket. The batch input file can be either CSV or JSONL. You will use JSONL in this tutorial. For JSONL file, you make one dictionary entry per line for each data item (instance). The dictionary contains the key/value pairs: - `content`: The Cloud Storage path to the image. - `mime_type`: The content type. In our example, it is an `jpeg` file. For example: {'content': '[your-bucket]/file1.jpg', 'mime_type': 'jpeg'} ``` import tensorflow as tf import json gcs_input_uri = BUCKET_NAME + '/test.jsonl' with tf.io.gfile.GFile(gcs_input_uri, 'w') as f: data = {"content": test_item_1, "mime_type": "image/jpeg"} f.write(json.dumps(data) + '\n') data = {"content": test_item_2, "mime_type": "image/jpeg"} f.write(json.dumps(data) + '\n') print(gcs_input_uri) ! gsutil cat $gcs_input_uri ``` ### Make the batch prediction request Now that your `Model` resource is trained, you can make a batch prediction by invoking the `batch_request()` method, with the following parameters: - `job_display_name`: The human readable name for the batch prediction job. - `gcs_source`: A list of one or more batch request input files. - `gcs_destination_prefix`: The Cloud Storage location for storing the batch prediction resuls. - `sync`: If set to `True`, the call will block while waiting for the asynchronous batch job to complete. ``` batch_predict_job = model.batch_predict( job_display_name="$(DATASET_ALIAS)_" + TIMESTAMP, gcs_source=gcs_input_uri, gcs_destination_prefix=BUCKET_NAME, sync=False ) print(batch_predict_job) ``` ### Wait for completion of batch prediction job Next, wait for the batch job to complete. ``` batch_predict_job.wait() ``` ### Get the predictions Next, get the results from the completed batch prediction job. The results are written to the Cloud Storage output bucket you specified in the batch prediction request. You call the method `iter_outputs()` to get a list of each Cloud Storage file generated with the results. Each file contains one or more prediction requests in a JSON format: - `content`: The prediction request. - `prediction`: The prediction response. - `ids`: The internal assigned unique identifiers for each prediction request. - `displayNames`: The class names for each class label. - `confidences`: The predicted confidence, between 0 and 1, per class label. ``` bp_iter_outputs = batch_predict_job.iter_outputs() prediction_results = list() for blob in bp_iter_outputs: if blob.name.split("/")[-1].startswith("prediction"): prediction_results.append(blob.name) tags = list() for prediction_result in prediction_results: gfile_name = f"gs://{bp_iter_outputs.bucket.name}/{prediction_result}" with tf.io.gfile.GFile(name=gfile_name, mode="r") as gfile: for line in gfile.readlines(): line = json.loads(line) print(line) break ``` # Cleaning up To clean up all GCP resources used in this project, you can [delete the GCP project](https://cloud.google.com/resource-manager/docs/creating-managing-projects#shutting_down_projects) you used for the tutorial. Otherwise, you can delete the individual resources you created in this tutorial: - Dataset - Pipeline - Model - Endpoint - Batch Job - Custom Job - Hyperparameter Tuning Job - Cloud Storage Bucket ``` delete_dataset = True delete_pipeline = True delete_model = True delete_endpoint = True delete_batchjob = True delete_customjob = True delete_hptjob = True delete_bucket = True # Delete the dataset using the Vertex dataset object try: if delete_dataset and 'dataset' in globals(): dataset.delete() except Exception as e: print(e) # Delete the model using the Vertex model object try: if delete_model and 'model' in globals(): model.delete() except Exception as e: print(e) # Delete the endpoint using the Vertex endpoint object try: if delete_endpoint and 'model' in globals(): endpoint.delete() except Exception as e: print(e) # Delete the batch prediction job using the Vertex batch prediction object try: if delete_batchjob and 'model' in globals(): batch_predict_job.delete() except Exception as e: print(e) if delete_bucket and 'BUCKET_NAME' in globals(): ! gsutil rm -r $BUCKET_NAME ```	github_jupyter
<a href="https://qworld.net" target="_blank" align="left"><img src="../qworld/images/header.jpg" align="left"></a> $ \newcommand{\bra}[1]{\langle #1\|} $ $ \newcommand{\ket}[1]{\|#1\rangle} $ $ \newcommand{\braket}[2]{\langle #1\|#2\rangle} $ $ \newcommand{\dot}[2]{ #1 \cdot #2} $ $ \newcommand{\biginner}[2]{\left\langle #1,#2\right\rangle} $ $ \newcommand{\mymatrix}[2]{\left( \begin{array}{#1} #2\end{array} \right)} $ $ \newcommand{\myvector}[1]{\mymatrix{c}{#1}} $ $ \newcommand{\myrvector}[1]{\mymatrix{r}{#1}} $ $ \newcommand{\mypar}[1]{\left( #1 \right)} $ $ \newcommand{\mybigpar}[1]{ \Big( #1 \Big)} $ $ \newcommand{\sqrttwo}{\frac{1}{\sqrt{2}}} $ $ \newcommand{\dsqrttwo}{\dfrac{1}{\sqrt{2}}} $ $ \newcommand{\onehalf}{\frac{1}{2}} $ $ \newcommand{\donehalf}{\dfrac{1}{2}} $ $ \newcommand{\hadamard}{ \mymatrix{rr}{ \sqrttwo & \sqrttwo \\ \sqrttwo & -\sqrttwo }} $ $ \newcommand{\vzero}{\myvector{1\\0}} $ $ \newcommand{\vone}{\myvector{0\\1}} $ $ \newcommand{\stateplus}{\myvector{ \sqrttwo \\ \sqrttwo } } $ $ \newcommand{\stateminus}{ \myrvector{ \sqrttwo \\ -\sqrttwo } } $ $ \newcommand{\myarray}[2]{ \begin{array}{#1}#2\end{array}} $ $ \newcommand{\X}{ \mymatrix{cc}{0 & 1 \\ 1 & 0} } $ $ \newcommand{\I}{ \mymatrix{rr}{1 & 0 \\ 0 & 1} } $ $ \newcommand{\Z}{ \mymatrix{rr}{1 & 0 \\ 0 & -1} } $ $ \newcommand{\Htwo}{ \mymatrix{rrrr}{ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} } } $ $ \newcommand{\CNOT}{ \mymatrix{cccc}{1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0} } $ $ \newcommand{\norm}[1]{ \left\lVert #1 \right\rVert } $ $ \newcommand{\pstate}[1]{ \lceil \mspace{-1mu} #1 \mspace{-1.5mu} \rfloor } $ $ \newcommand{\greenbit}[1] {\mathbf{{\color{green}#1}}} $ $ \newcommand{\bluebit}[1] {\mathbf{{\color{blue}#1}}} $ $ \newcommand{\redbit}[1] {\mathbf{{\color{red}#1}}} $ $ \newcommand{\brownbit}[1] {\mathbf{{\color{brown}#1}}} $ $ \newcommand{\blackbit}[1] {\mathbf{{\color{black}#1}}} $ <font style="font-size:28px;" align="left"><b>Two Probabilistic Bits </b></font> <br> _prepared by Abuzer Yakaryilmaz_ <br><br> [<img src="../qworld/images/watch_lecture.jpg" align="left">](https://youtu.be/ulbd-1c71sk) <br><br><br> Suppose that we have two probabilistic bits, and our probabilistic states respectively are $ \myvector{0.2 \\ 0.8} \mbox{ and } \myvector{0.6 \\ 0.4 }. $ If we combine both bits as a single system, then what is the state of the combined system? In total, we have four different states. We can name them as follows: <ul> <li>00: both bits are in states 0</li> <li>01: the first bit is in state 0 and the second bit is in state 1</li> <li>10: the first bit is in state 1 and the second bit is in state 0</li> <li>11: both bits are in states 1</li> </ul> <h3> Task 1 </h3> <b>Discussion and analysis:</b> What are the probabilities of being in states $ 00 $, $ 01 $, $ 10 $, and $11$? How can we represent these probabilities as a column vector? <h3> Representation for states 0 and 1</h3> The vector representation of state 0 is $ \myvector{1 \\ 0} $. Similarly, the vector representation of state 1 is $ \myvector{0 \\ 1} $. We use $ \pstate{0} $ to represent $ \myvector{1 \\ 0} $ and $ \pstate{1} $ to represent $ \myvector{0 \\ 1} $. Then, the probabilistic state $ \myvector{0.2 \\ 0.8} $ is also represented as $ 0.2 \pstate{0} + 0.8 \pstate{1} $. Similarly, the probabilistic state $ \myvector{0.6 \\ 0.4} $ is also represented as $ 0.6 \pstate{0} + 0.4 \pstate{1} $. <h3> Composite systems </h3> When two systems are composed, then their states are tensored to calculate the state of composite system. The probabilistic state of the first bit is $ \myvector{0.2 \\ 0.8} = 0.2 \pstate{0} + 0.8 \pstate{1} $. The probabilistic state of the second bit is $ \myvector{0.6 \\ 0.4} = 0.6 \pstate{0} + 0.4 \pstate{1} $. Then, the probabilistic state of the composite system is $ \big( 0.2 \pstate{0} + 0.8 \pstate{1} \big) \otimes \big( 0.6 \pstate{0} + 0.4 \pstate{1} \big) $. <h3> Task 2 </h3> Find the probabilistic state of the composite system. <i> Rule 1: Tensor product distributes over addition in the same way as the distribution of multiplication over addition. Rule 2: $ \big( 0.3 \pstate{1} \big) \otimes \big( 0.7 \pstate{0} \big) = (0.3 \cdot 0.7) \big( \pstate{1} \otimes \pstate{0} \big) = 0.21 \pstate{10} $. </i> <a href="CS24_Two_Probabilistic_Bits_Solutions.ipynb#task2">click for our solution</a> <h3> Task 3</h3> Find the probabilistic state of the composite system by calculating this tensor product $ \myvector{0.2 \\ 0.8} \otimes \myvector{0.6 \\ 0.4 } $. <a href="CS24_Two_Probabilistic_Bits_Solutions.ipynb#task3">click for our solution</a> <h3> Task 4</h3> Find the vector representations of $ \pstate{00} $, $ \pstate{01} $, $\pstate{10}$, and $ \pstate{11} $. <i>The vector representation of $ \pstate{ab} $ is $ \pstate{a} \otimes \pstate{b} $ for $ a,b \in \{0,1\} $.</i> <a href="CS24_Two_Probabilistic_Bits_Solutions.ipynb#task4">click for our solution</a> --- <h3> Extra: Task 5 </h3> Suppose that we have three bits. Find the vector representations of $ \pstate{abc} $ for each $ a,b,c \in \{0,1\} $. <h3> Extra: Task 6 </h3> <i>This task is challenging.</i> Suppose that we have four bits. Number 9 is represented as $ 1001 $ in binary. Verify that the vector representation of $ \pstate{1001} $ is the zero vector except its $10$th entry, which is 1. Number 7 is represented as $ 0111 $ in binary. Verify that the vector representation of $ \pstate{0111} $ is the zero vector except its $8$th entry, which is 1. Generalize this idea for any number between 0 and 15. Generalize this idea for any number of bits.	github_jupyter
# Introduction to the Quantum Bit ### Where we'll explore: * Quantum Superposition * Quantum Entanglement * Running experiments on a laptop-hosted simulator * Running experiments on a real quantum computer ### Brandon Warren ### SDE, Zonar Systems github.com/brandonwarren/intro-to-qubit contains this Jupyter notebook and installation tips. ``` import py_cas_slides as slides # real 6-qubit quantum computer, incl interface electronics slides.system() # import QISkit, define function to set backend that will execute our circuits HISTO_SIZE = (9,4) # width, height in inches CIRCUIT_SIZE = 1.0 # scale (e.g. 0.5 is half-size) from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute from qiskit import BasicAer as Aer from qiskit.tools.visualization import plot_histogram from qiskit import __qiskit_version__ print(__qiskit_version__) def set_backend(use_simulator: bool, n_qubits: int, preferred_backend: str=''): if use_simulator: backend = Aer.get_backend('qasm_simulator') else: from qiskit import IBMQ provider = IBMQ.load_account() if preferred_backend: # use backend specified by caller backend = provider.get_backend(preferred_backend) print(f"Using {backend.name()}") else: # use least-busy backend that has enough qubits from qiskit.providers.ibmq import least_busy large_enough_devices = provider.backends(filters=lambda x: x.configuration().n_qubits >= n_qubits and not x.configuration().simulator) backend = least_busy(large_enough_devices) print(f"The best backend is {backend.name()}") return backend def add_missing_keys(counts): # we want all keys present in counts, even if they are zero value for key in ['00', '01', '10', '11']: if key not in counts: counts[key] = 0 # use simulator for now backend = set_backend(use_simulator=True, n_qubits=2) # write code to build this quantum circuit # logic flows left to right # quantum bits begin in ground state (zero) # measurement copies result to classical bit slides.simple_2qubits() # simplest possible 2-qubit circuit # 1. Build simplest possible 2-qubit quantum circuit and draw it q_reg = QuantumRegister(2, 'q') # the 2 qubits we'll be using c_reg = ClassicalRegister(2, 'c') # clasical bits to hold results of measurements circuit = QuantumCircuit(q_reg, c_reg) # begin circuit - just 2 qubits and 2 classical bits # measure while still in ground state circuit.measure(q_reg, c_reg) # measure qubits, place results in classical bits # circuit is now complete circuit.draw(output='mpl', scale=CIRCUIT_SIZE) # run it 1000 times on simulator result = execute(circuit, backend=backend, shots=1000).result() counts = result.get_counts(circuit) print(counts) add_missing_keys(counts) print(counts) plot_histogram(counts, figsize=HISTO_SIZE) # 2. Apply X gate (NOT gate) to high qubit (q1) q_reg = QuantumRegister(2, 'q') c_reg = ClassicalRegister(2, 'c') circuit = QuantumCircuit(q_reg, c_reg) ###### apply X gate to high qubit ###### circuit.x(q_reg[1]) circuit.measure(q_reg, c_reg) circuit.draw(output='mpl', scale=CIRCUIT_SIZE) # run it 1000 times on simulator result = execute(circuit, backend=backend, shots=1000).result() counts = result.get_counts(circuit) print(counts) add_missing_keys(counts) plot_histogram(counts, figsize=HISTO_SIZE) # We've seen the two simplest quantum circuits possible. # Let's take it up a notch and place each qubit into a quantum superposition. # ? slides.super_def() # Like you flip a coin - while it is spinning it is H and T. # When you catch it, it is H or T. # BUT: it is as if it was that way all along. # What's the difference between that, and a coin under a # piece of paper that is revealed? slides.feynman_quote() slides.double_slit() # (2) # Like the photon that is in 2 places at once, the qubit can # be in 2 states at once, and become 0 or 1 when it is measured. # Let's place our 2 qubits in superposion and measure them. # The act of measurement collapses the superposition, # resulting in 1 of the 2 possible values. # H - Hadamard will turn our 0 into a superposition of 0 and 1. # It rotates the state of the qubit. # (coin over table analogy) # 3. Apply H gate to both qubits q_reg = QuantumRegister(2, 'q') c_reg = ClassicalRegister(2, 'c') circuit = QuantumCircuit(q_reg, c_reg) ###### apply H gate to both qubits ###### circuit.h(q_reg[0]) circuit.h(q_reg[1]) circuit.measure(q_reg, c_reg) circuit.draw(output='mpl', scale=CIRCUIT_SIZE) # histo - 2 bits x 2 possibilities = 4 combinations of equal probability result = execute(circuit, backend=backend, shots=1000).result() counts = result.get_counts(circuit) print(counts) add_missing_keys(counts) plot_histogram(counts, figsize=HISTO_SIZE) # TRUE random numbers! (when run on real device) # Special case of superposition, entanglement, revealed by EPR expmt slides.mermin_quote() # Before we get to that, i'd like to set the stage by intro # 2 concepts: locality and hidden variables. # The principle of locality says that for one thing to affect # another, they have to be in the same location, or need some # kind of field or signal connecting the two, with # the fastest possible propagation speed being that of light. # This even applies to gravity, which prop at the speed of light. # [We are 8 light-minutes from the Sun, so if the Sun all of a # sudden vanished somehow, we would still orbit for another 8 min.] # # Even though Einstein helped launch the new field of QM, he never # really liked it. In particular, he couln't accept the randomness. slides.einstein_dice() slides.bohr_response() # (3) slides.epr_nyt() # (4) slides.einstein_vs_bohr() # [Describe entanglement using coins odd,even] # 4. Entanglement - even-parity q_reg = QuantumRegister(2, 'q') c_reg = ClassicalRegister(2, 'c') circuit = QuantumCircuit(q_reg, c_reg) ###### place q[0] in superposition ###### circuit.h(q_reg[0]) ###### CNOT gate - control=q[0] target=q[1] - places into even-parity Bell state # Target is inverted if control is true circuit.cx(q_reg[0], q_reg[1]) circuit.measure(q_reg, c_reg) circuit.draw(output='mpl', scale=CIRCUIT_SIZE) result = execute(circuit, backend=backend, shots=1000).result() counts = result.get_counts(circuit) print(counts) add_missing_keys(counts) plot_histogram(counts, figsize=HISTO_SIZE) # 5. Entanglement - odd-parity q_reg = QuantumRegister(2, 'q') c_reg = ClassicalRegister(2, 'c') circuit = QuantumCircuit(q_reg, c_reg) ###### place q[0] in superposition ###### circuit.h(q_reg[0]) ###### CNOT gate - control=q[0] target=q[1] - places into even-parity Bell state # Target is inverted if control is true circuit.cx(q_reg[0], q_reg[1]) # a 0/1 superposition is converted to a 1/0 superposition # i.e. rotates state 180 degrees # creates odd-parity entanglement circuit.x(q_reg[0]) circuit.measure(q_reg, c_reg) circuit.draw(output='mpl', scale=CIRCUIT_SIZE) result = execute(circuit, backend=backend, shots=1000).result() counts = result.get_counts(circuit) print(counts) add_missing_keys(counts) plot_histogram(counts, figsize=HISTO_SIZE) # (5) slides.Bell_CHSH_inequality() # Let's run the Bell expmt on a real device. # This will not be a simulation! # backend = set_backend(use_simulator=False, n_qubits=2) # 1st avail is RISKY backend = set_backend(use_simulator=False, n_qubits=2, preferred_backend='ibmq_ourense') # [quickly: draw circuits, execute, then go over code and circuits] # 6. Bell experiment import numpy as np # Define the Quantum and Classical Registers q = QuantumRegister(2, 'q') c = ClassicalRegister(2, 'c') # create Bell state bell = QuantumCircuit(q, c) bell.h(q[0]) # place q[0] in superposition bell.cx(q[0], q[1]) # CNOT gate - control=q[0] target=q[1] - places into even-parity Bell state # setup measurement circuits # ZZ not used for Bell inequality, but interesting for real device (i.e. not perfect) meas_zz = QuantumCircuit(q, c) meas_zz.barrier() meas_zz.measure(q, c) # ZW: A=Z=0° B=W=45° meas_zw = QuantumCircuit(q, c) meas_zw.barrier() meas_zw.s(q[1]) meas_zw.h(q[1]) meas_zw.t(q[1]) meas_zw.h(q[1]) meas_zw.measure(q, c) # ZV: A=Z=0° B=V=-45° meas_zv = QuantumCircuit(q, c) meas_zv.barrier() meas_zv.s(q[1]) meas_zv.h(q[1]) meas_zv.tdg(q[1]) meas_zv.h(q[1]) meas_zv.measure(q, c) # XW: A=X=90° B=W=45° meas_xw = QuantumCircuit(q, c) meas_xw.barrier() meas_xw.h(q[0]) meas_xw.s(q[1]) meas_xw.h(q[1]) meas_xw.t(q[1]) meas_xw.h(q[1]) meas_xw.measure(q, c) # XV: A=X=90° B=V=-45° - instead of being 45° diff, # they are 90°+45°=135° = 180°-45°, # which is why the correlation is negative and we negate it # before adding the the rest of the correlations. meas_xv = QuantumCircuit(q, c) meas_xv.barrier() meas_xv.h(q[0]) meas_xv.s(q[1]) meas_xv.h(q[1]) meas_xv.tdg(q[1]) meas_xv.h(q[1]) meas_xv.measure(q, c) # build circuits circuits = [] labels = [] ab_labels = [] circuits.append(bell + meas_zz) labels.append('ZZ') ab_labels.append("") # not used circuits.append(bell + meas_zw) labels.append('ZW') ab_labels.append("<AB>") circuits.append(bell + meas_zv) labels.append('ZV') ab_labels.append("<AB'>") circuits.append(bell + meas_xw) labels.append('XW') ab_labels.append("<A'B>") circuits.append(bell + meas_xv) labels.append('XV') ab_labels.append("<A'B'>") print("Circuit to measure ZZ (A=Z=0° B=Z=0°) - NOT part of Bell expmt") circuits[0].draw(output='mpl', scale=CIRCUIT_SIZE) print("Circuit to measure ZW (A=Z=0° B=W=45°)") print("The gates to the right of the vertical bar rotate the measurement axis.") circuits[1].draw(output='mpl', scale=CIRCUIT_SIZE) print("Circuit to measure ZV (A=Z=0° B=V=-45°)") circuits[2].draw(output='mpl', scale=CIRCUIT_SIZE) print("Circuit to measure XW (A=X=90° B=W=45°)") circuits[3].draw(output='mpl', scale=CIRCUIT_SIZE) print("Circuit to meas XV (A=X=90° B=V=-45°) (negative correlation)") circuits[4].draw(output='mpl', scale=CIRCUIT_SIZE) # execute, then review while waiting from datetime import datetime, timezone import time # execute circuits shots = 1024 job = execute(circuits, backend=backend, shots=shots) print('after call execute()') if backend.name() != 'qasm_simulator': try: info = None max_tries = 3 while max_tries>0 and not info: time.sleep(1) # need to wait a little bit before calling queue_info() info = job.queue_info() print(f'queue_info: {info}') max_tries -= 1 now_utc = datetime.now(timezone.utc) print(f'\njob status: {info._status} as of {now_utc.strftime("%H:%M:%S")} UTC') print(f'position: {info.position}') print(f'estimated start time: {info.estimated_start_time.strftime("%H:%M:%S")}') print(f'estimated complete time: {info.estimated_complete_time.strftime("%H:%M:%S")}') wait_time = info.estimated_complete_time - now_utc wait_min, wait_sec = divmod(wait_time.seconds, 60) print(f'estimated wait time is {wait_min} minutes {wait_sec} seconds') except Exception as err: print(f'error getting job info: {err}') result = job.result() # blocks until complete print(f'job complete as of {datetime.now(timezone.utc).strftime("%H:%M:%S")} UTC') # gather data counts = [] for i, label in enumerate(labels): circuit = circuits[i] data = result.get_counts(circuit) counts.append(data) # show counts of Bell state measured in Z-axis print('\n', labels[0], counts[0], '\n') # show histogram of Bell state measured in Z-axis # real devices are not yet perfect. due to noise. add_missing_keys(counts[0]) plot_histogram(counts[0], figsize=HISTO_SIZE) # tabular output print(' (+) (+) (-) (-)') print(' P(00) P(11) P(01) P(10) correlation') C = 0.0 for i in range(1, len(labels)): AB = 0.0 print(f'{labels[i]} ', end ='') N = 0 for out in ('00', '11', '01', '10'): P = counts[i][out]/float(shots) N += counts[i][out] if out in ('00', '11'): AB += P else: AB -= P print(f'{P:.3f} ', end='') if N != shots: print(f'ERROR: N={N} shots={shots}') print(f'{AB:6.3f} {ab_labels[i]}') if labels[i] == 'XV': # the negative correlation - make it positive before summing it C -= AB else: C += AB print(f"\nC = <AB> + <AB'> + <A'B> - <A'B'>") print(f' = <ZW> + <ZV> + <XW> - <XV>') print(f' = {C:.2f}\n') if C <= 2.0: print("Einstein: 1 Quantum theory: 0") else: print("Einstein: 0 Quantum theory: 1") ``` ## Superposition and entanglement main points * Superposition is demonstrated by the double-slit experiment, which suggests that a photon can be in two positions at once, because the interference pattern only forms if two photons interfere with each other, and it forms even if we send one photon at a time. * Hidden variable theories seek to provide determinism to quantum physics. * The principle of locality states that an influence of one particle on another cannot propagate faster than the speed of light. * Entanglement cannot be explained by local hidden variable theories. ## Summary * Two of the strangest concepts in quantum physics, superposition and entanglement, are used in quantum computing, and are waiting to be explored by you. * You can run simple experiments on your laptop, and when you're ready, run them on a real quantum computer, over the cloud, for free. * IBM's qiskit.org contains software, tutorials, and an active Slack community. * My Github repo includes this presentation, tips on installing IBM's Qiskit on your laptop, and links for varying levels of explanations of superpositions and entanglements: github.com/brandonwarren/intro-to-qubit	github_jupyter
1. Split into train and test data 2. Train model on train data normally 3. Take test data and duplicate into test prime 4. Drop first visit from test prime data 5. Get predicted delta from test prime data. Compare to delta from test data. We know the difference (epsilon) because we dropped actual visits. What percent of time is test delta < test prime delta? 6. Restrict it only to patients with lot of visits. Is this better? ``` %matplotlib inline import matplotlib.pyplot as plt import numpy as np import pickle def clean_plot(): ax = plt.subplot(111) ax.spines["top"].set_visible(False) ax.spines["bottom"].set_visible(False) ax.spines["right"].set_visible(False) ax.spines["left"].set_visible(False) ax.get_xaxis().tick_bottom() ax.get_yaxis().tick_left() plt.grid() import matplotlib.pylab as pylab params = {'legend.fontsize': 'x-large', # 'figure.figsize': (10,6), 'axes.labelsize': 'x-large', 'axes.titlesize':'x-large', 'xtick.labelsize':'x-large', 'ytick.labelsize':'x-large'} pylab.rcParams.update(params) import sys import torch sys.path.append('../data') from load import chf from data_utils import parse_data from synthetic_data import load_piecewise_synthetic_data sys.path.append('../model') from models import Sublign from run_experiments import get_hyperparameters def make_test_prime(test_data_dict_raw, drop_first_T=1.): # drop first year test_data_dict = copy.deepcopy(test_data_dict_raw) eps_lst = list() X = test_data_dict['obs_t_collect'] Y = test_data_dict['Y_collect'] M = test_data_dict['mask_collect'] N_patients = X.shape[0] N_visits = X.shape[1] for i in range(N_patients): eps_i = X[i,1,0] - X[i,0,0] first_visit = X[i,1,0] # move all visits down (essentially destroying the first visit) for j in range(N_visits-gap): X[i,j,0] = X[i,j+gap,0] - first_visit Y[i,j,:] = Y[i,j+gap,:] M[i,j,:] = M[i,j+gap,:] for g in range(1,gap+1): X[i,N_visits-g,0] = int(-1000) Y[i,N_visits-g,:] = int(-1000) M[i,N_visits-g,:] = 0. eps_lst.append(eps_i) return test_data_dict, eps_lst data = chf() max_visits = 38 shuffle = True num_output_dims = data.shape[1] - 4 data_loader, collect_dict, unique_pid = parse_data(data.values, max_visits=max_visits) train_data_loader, train_data_dict, test_data_loader, test_data_dict, test_pid, unique_pid = parse_data(data.values, max_visits=max_visits, test_per=0.2, shuffle=shuffle) # model = Sublign(10, 20, 50, dim_biomarkers=num_output_dims, sigmoid=True, reg_type='l1', auto_delta=True, # max_delta=5, learn_time=True, device=torch.device('cuda')) # # model.fit(data_loader, data_loader, args.epochs, 0.01, verbose=args.verbose,fname='runs/chf.pt',eval_freq=25) # fname='../model/chf_good.pt' # model.load_state_dict(torch.load(fname,map_location=torch.device('cuda'))) test_p_data_dict, eps_lst = make_test_prime(test_data_dict, gap=1) # test_deltas = model.get_deltas(test_data_dict).detach().numpy() # test_p_deltas = model.get_deltas(test_p_data_dict).detach().numpy() print(num_output_dims) # def make_test_prime(test_data_dict_raw, drop_first_T=1.): drop_first_T = 0.5 # drop first year test_data_dict_new = copy.deepcopy(test_data_dict) eps_lst = list() X = test_data_dict_new['obs_t_collect'] Y = test_data_dict_new['Y_collect'] M = test_data_dict_new['mask_collect'] N_patients = X.shape[0] N_visits = X.shape[1] remove_idx = list() X[X == -1000] = np.nan for i in range(N_patients): N_visits_under_thresh = (X[i] < 0.5).sum() gap = N_visits_under_thresh first_valid_visit = X[i,N_visits_under_thresh,0] eps_i = X[i,N_visits_under_thresh,0] for j in range(N_visits-N_visits_under_thresh): X[i,j,0] = X[i,j+gap,0] - first_valid_visit Y[i,j,:] = Y[i,j+gap,:] M[i,j,:] = M[i,j+gap,:] for g in range(1,N_visits_under_thresh+1): X[i,N_visits-g,0] = np.nan Y[i,N_visits-g,:] = np.nan M[i,N_visits-g,:] = 0. if np.isnan(X[i]).all(): remove_idx.append(i) else: eps_lst.append(eps_i) keep_idx = [i for i in range(N_patients) if i not in remove_idx] X = X[keep_idx] Y = Y[keep_idx] M = M[keep_idx] print('Removed %d entries' % len(remove_idx)) X[np.isnan(X)] = -1000 # eps_lst.append(eps_i) # return test_data_dict_new, eps_lst eps_lst X[0] first_valid_visit test_data_dict_new = copy.deepcopy(test_data_dict) X = test_data_dict_new['obs_t_collect'] Y = test_data_dict_new['Y_collect'] M = test_data_dict_new['mask_collect'] X[X == -1000] = np.nan i = 1 N_visits_under_thresh = (X[i] < 0.5).sum() # for j in range(N_visits-N_visits_under_thresh): # X[i,j,0] = X[i,j+gap,0] - first_visit # Y[i,j,:] = Y[i,j+gap,:] # M[i,j,:] = M[i,j+gap,:] # for g in range(1,N_visits_under_thresh+1): # X[i,N_visits-g,0] = np.nan # Y[i,N_visits-g,:] = np.nan # M[i,N_visits-g,:] = 0. # if np.isnan(X[i]).all(): # print('yes') # remove_idx.append(i) (X[1] < 0.5).sum() N_visits_under_thresh N_visits_under_thresh len(remove_idx) X[X == -1000] = np.nan for i in range(10): print(X[i].flatten()) remove_idx X[0][:10] plt.hist(X.flatten()) X.max() Y[1][:10] test_data_dict_new[''] f = open('chf_experiment_results.pk', 'rb') results = pickle.load(f) test_deltas = results['test_deltas'] test_p_deltas = results['test_p_deltas'] eps_lst = results['eps_lst'] test_data_dict = results['test_data_dict'] f.close() test_data_dict['obs_t_collect'][0].shape # get num of visits per patient num_visits_patient_lst = list() for i in test_data_dict['obs_t_collect']: num_visits = (i!=-1000).sum() num_visits_patient_lst.append(num_visits) num_visits_patient_lst = np.array(num_visits_patient_lst) freq_visit_idx = np.where(num_visits_patient_lst > 10)[0] test_p_deltas[freq_visit_idx] test_deltas[freq_visit_idx] np.mean(np.array(test_p_deltas - test_deltas) > 0) test_p_deltas[:20] clean_plot() plt.plot(eps_lst, test_p_deltas - test_deltas, '.') plt.xlabel('Actual eps') plt.ylabel('Estimated eps') # plt.savefig('') import copy def make_test_prime(test_data_dict_raw, gap=1): test_data_dict = copy.deepcopy(test_data_dict_raw) eps_lst = list() X = test_data_dict['obs_t_collect'] Y = test_data_dict['Y_collect'] M = test_data_dict['mask_collect'] N_patients = X.shape[0] N_visits = X.shape[1] for i in range(N_patients): eps_i = X[i,1,0] - X[i,0,0] first_visit = X[i,1,0] # move all visits down (essentially destroying the first visit) for j in range(N_visits-gap): X[i,j,0] = X[i,j+gap,0] - first_visit Y[i,j,:] = Y[i,j+gap,:] M[i,j,:] = M[i,j+gap,:] for g in range(1,gap+1): X[i,N_visits-g,0] = int(-1000) Y[i,N_visits-g,:] = int(-1000) M[i,N_visits-g,:] = 0. eps_lst.append(eps_i) return test_data_dict, eps_lst t_prime_dict, eps_lst = make_test_prime(test_data_dict) t_prime_dict['Y_collect'][1,:,0] test_data_dict['Y_collect'][1,:,0] ``` ## Plot successful model ``` import argparse import numpy as np import pickle import sys import torch import copy from scipy.stats import pearsonr import matplotlib.pyplot as plt from run_experiments import get_hyperparameters from models import Sublign sys.path.append('../data') from data_utils import parse_data from load import load_data_format sys.path.append('../evaluation') from eval_utils import swap_metrics train_data_dict['Y_collect'].shape train_data_dict['t_collect'].shape new_Y = np.zeros((600,101,3)) val_idx_dict = {'%.1f' % j: i for i,j in enumerate(np.linspace(0,10,101))} train_data_dict['obs_t_collect'].max() rounded_t = np.round(train_data_dict['t_collect'],1) N, M, _ = rounded_t.shape for i in range(N): for j in range(M): val = rounded_t[i,j,0] # try: idx = val_idx_dict['%.1f' % val] for k in range(3): new_Y[i,idx,k] = train_data_dict['Y_collect'][i,j,k] # except: # print(val) new_Y.shape (new_Y == 0).sum() / (6001013) # save the files for comparing against SPARTan baseline for i in range(3): a = new_Y[:,:,i] np.savetxt("data1_dim%d.csv" % i, a, deliREDACTEDer=",") true_labels = train_data_dict['s_collect'][:,0] guess_labels = np.ones(600) adjusted_rand_score(true_labels,guess_labels) from sklearn.metrics import adjusted_rand_score # a.shape data_format_num = 1 # C, d_s, d_h, d_rnn, reg_type, lr = get_hyperparameters(data_format_num) anneal, b_vae, C, d_s, d_h, d_rnn, reg_type, lr = get_hyperparameters(data_format_num) C data = load_data_format(data_format_num, 0, cache=True) train_data_loader, train_data_dict, _, _, test_data_loader, test_data_dict, valid_pid, test_pid, unique_pid = parse_data(data.values, max_visits=4, test_per=0.2, valid_per=0.2, shuffle=False) model = Sublign(d_s, d_h, d_rnn, dim_biomarkers=3, sigmoid=True, reg_type='l1', auto_delta=False, max_delta=0, learn_time=False, beta=0.00) model.fit(train_data_loader, test_data_loader, 800, lr, fname='runs/data%d_chf_experiment.pt' % (data_format_num), eval_freq=25) z = model.get_mu(train_data_dict['obs_t_collect'], train_data_dict['Y_collect']) # fname='runs/data%d_chf_experiment.pt' % (data_format_num) # model.load_state_dict(torch.load(fname)) nolign_results = model.score(train_data_dict, test_data_dict) print('ARI: %.3f' % nolign_results['ari']) print(anneal, b_vae, C, d_s, d_h, d_rnn, reg_type, lr) data_format_num = 1 # C, d_s, d_h, d_rnn, reg_type, lr = get_hyperparameters(data_format_num) anneal, b_vae, C, d_s, d_h, d_rnn, reg_type, lr = get_hyperparameters(data_format_num) model = Sublign(d_s, d_h, d_rnn, dim_biomarkers=3, sigmoid=True, reg_type='l1', auto_delta=True, max_delta=5, learn_time=True, beta=0.01) model.fit(train_data_loader, test_data_loader, 800, lr, fname='runs/data%d.pt' % (data_format_num), eval_freq=25) z = model.get_mu(train_data_dict['obs_t_collect'], train_data_dict['Y_collect']) # fname='runs/data%d_chf_experiment.pt' % (data_format_num) # model.load_state_dict(torch.load(fname)) results = model.score(train_data_dict, test_data_dict) print('ARI: %.3f' % results['ari']) # model = Sublign(d_s, d_h, d_rnn, dim_biomarkers=3, sigmoid=True, reg_type='l1', auto_delta=True, max_delta=5, learn_time=True, b_vae=0.) # model.fit(train_data_loader, test_data_loader, 800, lr, fname='runs/data%d_chf_experiment.pt' % (data_format_num), eval_freq=25) # z = model.get_mu(train_data_dict['obs_t_collect'], train_data_dict['Y_collect']) # # fname='runs/data%d_chf_experiment.pt' % (data_format_num) # # model.load_state_dict(torch.load(fname)) # results = model.score(train_data_dict, test_data_dict) # print('ARI: %.3f' % results['ari']) # Visualize latent space (change configs above) X = test_data_dict['obs_t_collect'] Y = test_data_dict['Y_collect'] M = test_data_dict['mask_collect'] test_z, _ = model.get_mu(X,Y) test_z = test_z.detach().numpy() test_subtypes = test_data_dict['s_collect'] from sklearn.manifold import TSNE z_tSNE = TSNE(n_components=2).fit_transform(test_z) test_s0_idx = np.where(test_subtypes==0)[0] test_s1_idx = np.where(test_subtypes==1)[0] clean_plot() plt.plot(z_tSNE[test_s0_idx,0],z_tSNE[test_s0_idx,1],'.') plt.plot(z_tSNE[test_s1_idx,0],z_tSNE[test_s1_idx,1],'.') # plt.title('\nNELBO (down): %.3f, ARI (up): %.3f\n Config: %s\nColors = true subtypes' % # (nelbo, ari, configs)) plt.show() def sigmoid_f(x, beta0, beta1): result = 1. / (1+np.exp(-(beta0 + beta1x))) return result true_betas = [[[-4, 1], [-1,1.], [-8,8] ], [ [-1,1.], [-8,8], [-25, 3.5] ]] # xs = np.linspace(0,10,100) for dim_i in range(3): xs = np.linspace(0,10,100) plt.figure() clean_plot() plt.grid(True) ys = [sigmoid_f(xs_i, true_betas[0][dim_i][0], true_betas[0][dim_i][1]) for xs_i in xs] plt.plot(xs,ys, ':', color='gray', linewidth=5, label='True function') ys = [sigmoid_f(xs_i, true_betas[1][dim_i][0], true_betas[1][dim_i][1]) for xs_i in xs] plt.plot(xs,ys, ':', color='gray', linewidth=5) for subtype_j in range(2): xs = np.linspace(0,10,100) ys = [sigmoid_f(xs_i, nolign_results['cent_lst'][subtype_j,dim_i,0], nolign_results['cent_lst'][subtype_j,dim_i,1]) for xs_i in xs] if subtype_j == 0: plt.plot(xs,ys,linewidth=4, label='SubNoLign subtype', linestyle='-.', color='tab:green') else: plt.plot(xs,ys,linewidth=4, linestyle='--', color='tab:green') ys = [sigmoid_f(xs_i, results['cent_lst'][subtype_j,dim_i,0], results['cent_lst'][subtype_j,dim_i,1]) for xs_i in xs] if subtype_j == 0: plt.plot(xs,ys,linewidth=4, label='SubLign subtype', linestyle='-', color='tab:purple') else: plt.plot(xs,ys,linewidth=4, linestyle='-', color='tab:purple') plt.xlabel('Disease stage') plt.ylabel('Biomarker') plt.legend() plt.savefig('subnolign_data1_subtypes_dim%d.pdf' % dim_i, bbox_inches='tight') # # number dimensions # fig, axs = plt.subplots(1,3, figsize=(8,4)) # for dim_i in range(3): # ax = axs[dim_i] # # number subtypes # for subtype_j in range(2): # xs = np.linspace(0,10,100) # ys = [sigmoid_f(xs_i, model1_results['cent_lst'][subtype_j,dim_i,0], # model1_results['cent_lst'][subtype_j,dim_i,1]) for xs_i in xs] # ax.plot(xs,ys) # ys = [sigmoid_f(xs_i, true_betas[0][dim_i][0], true_betas[0][dim_i][1]) for xs_i in xs] # ax.plot(xs,ys, color='gray') # ys = [sigmoid_f(xs_i, true_betas[1][dim_i][0], true_betas[1][dim_i][1]) for xs_i in xs] # ax.plot(xs,ys, color='gray') # fig.suptitle('True data generating function (gray), learned models (orange, blue)') # plt.savefig('learned_models.pdf',bbox_inches='tight') ``` ## Plot CHF Delta distributions ``` data = pickle.load(open('../clinical_runs/chf_v3_1000.pk', 'rb')) clean_plot() plt.hist(data['deltas'], bins=20) plt.xlabel('Inferred Alignment $\delta_i$ Value') plt.ylabel('Number Heart Failure Patients') plt.savefig('Delta_dist_chf.pdf', bbox_inches='tight') ``` ## Make piecewise data to measure model misspecification ``` from scipy import interpolate x = np.arange(0, 2np.pi+np.pi/4, 2np.pi/8) y = np.sin(x) tck = interpolate.splrep(x, y, s=0) xnew = np.arange(0, 2np.pi, np.pi/50) ynew = interpolate.splev(xnew, tck, der=0) xvals = np.array([9.3578453 , 4.9814664 , 7.86530539, 8.91318433, 2.00779188])[sort_idx] yvals = np.array([0.35722491, 0.12512101, 0.20054626, 0.38183604, 0.58836923])[sort_idx] tck = interpolate.splrep(xvals, yvals, s=0) y N_subtypes,D,N_pts,_ = subtype_points.shape fig, axes = plt.subplots(ncols=3,nrows=1) for d, ax in enumerate(axes.flat): # ax.set_xlim(0,10) # ax.set_ylim(0,1) for k in range(N_subtypes): xs = subtype_points[k,d,:,0] ys = subtype_points[k,d,:,1] sort_idx = np.argsort(xs) ax.plot(xs[sort_idx],ys[sort_idx]) plt.show() # for d in range(D): %%time N_epochs = 800 N_trials = 5 use_sigmoid = True sublign_results = { 'ari':[], 'pear': [], 'swaps': [] } subnolign_results = {'ari': []} for trial in range(N_trials): data_format_num = 1 # C, d_s, d_h, d_rnn, reg_type, lr = get_hyperparameters(data_format_num) anneal, b_vae, C, d_s, d_h, d_rnn, reg_type, lr = get_hyperparameters(data_format_num) # C # data = load_data_format(data_format_num, 0, cache=True) use_sigmoid = False data, subtype_points = load_piecewise_synthetic_data(subtypes=2, increasing=use_sigmoid, D=3, N=2000,M=4, noise=0.25, N_pts=5) train_data_loader, train_data_dict, _, _, test_data_loader, test_data_dict, valid_pid, test_pid, unique_pid = parse_data(data.values, max_visits=4, test_per=0.2, valid_per=0.2, shuffle=False) model = Sublign(d_s, d_h, d_rnn, dim_biomarkers=3, sigmoid=use_sigmoid, reg_type='l1', auto_delta=False, max_delta=5, learn_time=True, beta=1.) model.fit(train_data_loader, test_data_loader, N_epochs, lr, fname='runs/data%d_spline.pt' % (data_format_num), eval_freq=25) # z = model.get_mu(train_data_dict['obs_t_collect'], train_data_dict['Y_collect']) # fname='runs/data%d_chf_experiment.pt' % (data_format_num) # model.load_state_dict(torch.load(fname)) results = model.score(train_data_dict, test_data_dict) print('Sublign results: ARI: %.3f; Pear: %.3f; Swaps: %.3f' % (results['ari'],results['pear'],results['swaps'])) sublign_results['ari'].append(results['ari']) sublign_results['pear'].append(results['pear']) sublign_results['swaps'].append(results['swaps']) model = Sublign(d_s, d_h, d_rnn, dim_biomarkers=3, sigmoid=use_sigmoid, reg_type='l1', auto_delta=False, max_delta=0, learn_time=False, beta=1.) model.fit(train_data_loader, test_data_loader, N_epochs, lr, fname='runs/data%d_spline.pt' % (data_format_num), eval_freq=25) nolign_results = model.score(train_data_dict, test_data_dict) print('SubNoLign results: ARI: %.3f' % (nolign_results['ari'])) subnolign_results['ari'].append(nolign_results['ari']) data_str = 'Increasing' if use_sigmoid else 'Any' print('SubLign-%s & %.2f $\\pm$ %.2f & %.2f $\\pm$ %.2f & %.2f $\\pm$ %.2f \\\\' % ( data_str, np.mean(sublign_results['ari']), np.std(sublign_results['ari']), np.mean(sublign_results['pear']), np.std(sublign_results['pear']), np.mean(sublign_results['swaps']), np.std(sublign_results['swaps']) )) print('SubNoLign-%s & %.2f $\\pm$ %.2f & -- & -- \\\\' % ( data_str, np.mean(sublign_results['ari']), np.std(sublign_results['ari']), )) results = model.score(train_data_dict, test_data_dict) print('Sublign results: ARI: %.3f; Pear: %.3f; Swaps: %.3f' % (results['ari'],results['pear'],results['swaps'])) ```	github_jupyter
``` import numpy as np import pandas as pd import xarray as xr import zarr import math import glob import pickle import statistics import scipy.stats as stats from sklearn.neighbors import KernelDensity import dask import seaborn as sns import matplotlib.pyplot as plt import cartopy.crs as ccrs def get_files(): models = glob.glob("/terra/data/cmip5/global/historical/") avail={} for model in models: zg = glob.glob(str(model)+"/r1i1p1/day/2deg/zg") try: test = zg[0] avail[model.split('/')[-1]] = zg except: pass return avail files = get_files() files['NOAA'] = glob.glob("/home/pmarsh/NOAA_2deg/NOAA_zg/.nc") files['ERA5'] = glob.glob("/home/pmarsh/NOAA_2deg/ERA5_zg/.nc") files.pop('MIROC-ESM') def contourise(x): x = x.fillna(0) x = x.where((x>=limit)) x = x/x return x results={} for model in files.keys(): print(model) x = xr.open_mfdataset(files[model]) if model == 'NOAA': x = x.rename({'hgt':'zg'}) x = x.rename({'level':'plev'}) x = x.sel(plev=850) x = x.sel(time=slice('1950','2005')) elif model == 'ERA5': x = x.rename({'level':'plev'}) x = x.sel(plev=850) x = x.sel(time=slice('1979','2005')) else: x = x.sel(plev=85000) x = x.sel(time=slice('1950','2005')) x = x.load() x = x.sel(lat=slice(-60,0)) x = x[['zg']] x = x.assign_coords(lon=(((x.lon + 180) % 360) - 180)) with dask.config.set(**{'array.slicing.split_large_chunks': True}): x = x.sortby(x.lon) x = x.sel(lon=slice(-50,20)) x = x.resample(time="QS-DEC").mean(dim="time",skipna=True) x = x.load() limit = np.nanquantile(x.zg.values,0.9) results[model]={} for seas in ['DJF','MAM','JJA','SON']: mean_seas = x.where(x.time.dt.season==str(seas)).dropna(dim='time') mean_seas = contourise(mean_seas).zg.fillna(0).mean(dim='time') results[model][seas] = mean_seas.fillna(0) x.close() pickle.dump(results, open( "../HIGH_OUT/SASH_track_2D.p", "wb" ) ) weights = np.cos(np.deg2rad(results['NOAA']['DJF'].lat)) #area weighted #mean absolute error calc scores=[] for index in results: MAE={} for season in ['DJF','MAM','JJA','SON']: ref = results['NOAA'][season] x = results[index][season] MAE[season] = (np.abs(ref - x)).weighted(weights).sum(('lat','lon')) scores.append([index,np.mean(MAE['DJF'].values + MAE['MAM'].values + MAE['JJA'].values + MAE['SON'].values)]) resultsdf = pd.DataFrame(np.array(scores),columns=['model','score']) resultsdf = resultsdf.sort_values('score').set_index('model')['score'] pickle.dump( resultsdf, open( "../HIGH_OUT/scores_2D.p", "wb" ) ) resultsdf.to_csv("../HIGH_OUT/scores_2D.csv") ```	github_jupyter
<a href="https://colab.research.google.com/github/gordicaleksa/get-started-with-JAX/blob/main/Tutorial_3_JAX_Neural_Network_from_Scratch_Colab.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a> # MLP training on MNIST ``` import numpy as np import jax.numpy as jnp from jax.scipy.special import logsumexp import jax from jax import jit, vmap, pmap, grad, value_and_grad from torchvision.datasets import MNIST from torch.utils.data import DataLoader seed = 0 mnist_img_size = (28, 28) def init_MLP(layer_widths, parent_key, scale=0.01): params = [] keys = jax.random.split(parent_key, num=len(layer_widths)-1) for in_width, out_width, key in zip(layer_widths[:-1], layer_widths[1:], keys): weight_key, bias_key = jax.random.split(key) params.append([ scalejax.random.normal(weight_key, shape=(out_width, in_width)), scalejax.random.normal(bias_key, shape=(out_width,)) ] ) return params # test key = jax.random.PRNGKey(seed) MLP_params = init_MLP([784, 512, 256, 10], key) print(jax.tree_map(lambda x: x.shape, MLP_params)) def MLP_predict(params, x): hidden_layers = params[:-1] activation = x for w, b in hidden_layers: activation = jax.nn.relu(jnp.dot(w, activation) + b) w_last, b_last = params[-1] logits = jnp.dot(w_last, activation) + b_last # log(exp(o1)) - log(sum(exp(o1), exp(o2), ..., exp(o10))) # log( exp(o1) / sum(...) ) return logits - logsumexp(logits) # tests # test single example dummy_img_flat = np.random.randn(np.prod(mnist_img_size)) print(dummy_img_flat.shape) prediction = MLP_predict(MLP_params, dummy_img_flat) print(prediction.shape) # test batched function batched_MLP_predict = vmap(MLP_predict, in_axes=(None, 0)) dummy_imgs_flat = np.random.randn(16, np.prod(mnist_img_size)) print(dummy_imgs_flat.shape) predictions = batched_MLP_predict(MLP_params, dummy_imgs_flat) print(predictions.shape) def custom_transform(x): return np.ravel(np.array(x, dtype=np.float32)) def custom_collate_fn(batch): transposed_data = list(zip(batch)) labels = np.array(transposed_data[1]) imgs = np.stack(transposed_data[0]) return imgs, labels batch_size = 128 train_dataset = MNIST(root='train_mnist', train=True, download=True, transform=custom_transform) test_dataset = MNIST(root='test_mnist', train=False, download=True, transform=custom_transform) train_loader = DataLoader(train_dataset, batch_size, shuffle=True, collate_fn=custom_collate_fn, drop_last=True) test_loader = DataLoader(test_dataset, batch_size, shuffle=False, collate_fn=custom_collate_fn, drop_last=True) # test batch_data = next(iter(train_loader)) imgs = batch_data[0] lbls = batch_data[1] print(imgs.shape, imgs[0].dtype, lbls.shape, lbls[0].dtype) # optimization - loading the whole dataset into memory train_images = jnp.array(train_dataset.data).reshape(len(train_dataset), -1) train_lbls = jnp.array(train_dataset.targets) test_images = jnp.array(test_dataset.data).reshape(len(test_dataset), -1) test_lbls = jnp.array(test_dataset.targets) num_epochs = 5 def loss_fn(params, imgs, gt_lbls): predictions = batched_MLP_predict(params, imgs) return -jnp.mean(predictions gt_lbls) def accuracy(params, dataset_imgs, dataset_lbls): pred_classes = jnp.argmax(batched_MLP_predict(params, dataset_imgs), axis=1) return jnp.mean(dataset_lbls == pred_classes) @jit def update(params, imgs, gt_lbls, lr=0.01): loss, grads = value_and_grad(loss_fn)(params, imgs, gt_lbls) return loss, jax.tree_multimap(lambda p, g: p - lr*g, params, grads) # Create a MLP MLP_params = init_MLP([np.prod(mnist_img_size), 512, 256, len(MNIST.classes)], key) for epoch in range(num_epochs): for cnt, (imgs, lbls) in enumerate(train_loader): gt_labels = jax.nn.one_hot(lbls, len(MNIST.classes)) loss, MLP_params = update(MLP_params, imgs, gt_labels) if cnt % 50 == 0: print(loss) print(f'Epoch {epoch}, train acc = {accuracy(MLP_params, train_images, train_lbls)} test acc = {accuracy(MLP_params, test_images, test_lbls)}') imgs, lbls = next(iter(test_loader)) img = imgs[0].reshape(mnist_img_size) gt_lbl = lbls[0] print(img.shape) import matplotlib.pyplot as plt pred = jnp.argmax(MLP_predict(MLP_params, np.ravel(img))) print('pred', pred) print('gt', gt_lbl) plt.imshow(img); plt.show() ``` # Visualizations ``` w = MLP_params[0][0] print(w.shape) w_single = w[500, :].reshape(mnist_img_size) print(w_single.shape) plt.imshow(w_single); plt.show() # todo: visualize embeddings using t-SNE from sklearn.manifold import TSNE def fetch_activations(params, x): hidden_layers = params[:-1] activation = x for w, b in hidden_layers: activation = jax.nn.relu(jnp.dot(w, activation) + b) return activation batched_fetch_activations = vmap(fetch_activations, in_axes=(None, 0)) imgs, lbls = next(iter(test_loader)) batch_activations = batched_fetch_activations(MLP_params, imgs) print(batch_activations.shape) # (128, 2) t_sne_embeddings = TSNE(n_components=2, perplexity=30,).fit_transform(batch_activations) cora_label_to_color_map = {0: "red", 1: "blue", 2: "green", 3: "orange", 4: "yellow", 5: "pink", 6: "gray"} for class_id in range(10): plt.scatter(t_sne_embeddings[lbls == class_id, 0], t_sne_embeddings[lbls == class_id, 1], s=20, color=cora_label_to_color_map[class_id]) plt.show() # todo: dead neurons def fetch_activations2(params, x): hidden_layers = params[:-1] collector = [] activation = x for w, b in hidden_layers: activation = jax.nn.relu(jnp.dot(w, activation) + b) collector.append(activation) return collector batched_fetch_activations2 = vmap(fetch_activations2, in_axes=(None, 0)) imgs, lbls = next(iter(test_loader)) MLP_params2 = init_MLP([np.prod(mnist_img_size), 512, 256, len(MNIST.classes)], key) batch_activations = batched_fetch_activations2(MLP_params2, imgs) print(batch_activations[1].shape) # (128, 512/256) dead_neurons = [np.ones(act.shape[1:]) for act in batch_activations] for layer_id, activations in enumerate(batch_activations): dead_neurons[layer_id] = np.logical_and(dead_neurons[layer_id], (activations == 0).all(axis=0)) for layers in dead_neurons: print(np.sum(layers)) ``` # Parallelization ``` ```	github_jupyter
# Plots One of the most amazing feature of hist is it's powerful plotting family. Here you can see how to plot Hist. ``` from hist import Hist import hist h = Hist( hist.axis.Regular(50, -5, 5, name="S", label="s [units]", flow=False), hist.axis.Regular(50, -5, 5, name="W", label="w [units]", flow=False), ) import numpy as np s_data = np.random.normal(size=100_000) + np.ones(100_000) w_data = np.random.normal(size=100_000) # normal fill h.fill(s_data, w_data) ``` ## Via Matplotlib hist allows you to plot via [Matplotlib](https://matplotlib.org/) like this: ``` import matplotlib.pyplot as plt fig, ax = plt.subplots(figsize=(8, 5)) w, x, y = h.to_numpy() mesh = ax.pcolormesh(x, y, w.T, cmap="RdYlBu") ax.set_xlabel("s") ax.set_ylabel("w") fig.colorbar(mesh) plt.show() ``` ## Via Mplhep [mplhep](https://github.com/scikit-hep/mplhep) is an important visualization tools in Scikit-Hep ecosystem. hist has integrate with mplhep and you can also plot using it. If you want more info about mplhep please visit the official repo to see it. ``` import mplhep fig, axs = plt.subplots(1, 2, figsize=(9, 4)) mplhep.histplot(h.project("S"), ax=axs[0]) mplhep.hist2dplot(h, ax=axs[1]) plt.show() ``` ## Via Plot Hist has plotting methods for 1-D and 2-D histograms, `.plot1d()` and `.plot2d()` respectively. It also provides `.plot()` for plotting according to the its dimension. Moreover, to show the projection of each axis, you can use `.plot2d_full()`. If you have a Hist with higher dimension, you can use `.project()` to extract two dimensions to see it with our plotting suite. Our plotting methods are all based on Matplotlib, so you can pass Matplotlib's `ax` into it, and hist will draw on it. We will create it for you if you do not pass them in. ``` # plot1d fig, ax = plt.subplots(figsize=(6, 4)) h.project("S").plot1d(ax=ax, ls="--", color="teal", lw=3) plt.show() # plot2d fig, ax = plt.subplots(figsize=(6, 6)) h.plot2d(ax=ax, cmap="plasma") plt.show() # plot2d_full plt.figure(figsize=(8, 8)) h.plot2d_full( main_cmap="coolwarm", top_ls="--", top_color="orange", top_lw=2, side_ls=":", side_lw=2, side_color="steelblue", ) plt.show() # auto-plot fig, axs = plt.subplots(1, 2, figsize=(9, 4), gridspec_kw={"width_ratios": [5, 4]}) h.project("W").plot(ax=axs[0], color="darkviolet", lw=2, ls="-.") h.project("W", "S").plot(ax=axs[1], cmap="cividis") plt.show() ``` ## Via Plot Pull Pull plots are commonly used in HEP studies, and we provide a method for them with `.plot_pull()`, which accepts a `Callable` object, like the below `pdf` function, which is then fit to the histogram and the fit and pulls are shown on the plot. As Normal distributions are the generally desired function to fit the histogram data, the `str` aliases `"normal"`, `"gauss"`, and `"gaus"` are supported as well. ``` def pdf(x, a=1 / np.sqrt(2 * np.pi), x0=0, sigma=1, offset=0): return a * np.exp(-((x - x0) ** 2) / (2 * sigma ** 2)) + offset np.random.seed(0) hist_1 = hist.Hist( hist.axis.Regular( 50, -5, 5, name="X", label="x [units]", underflow=False, overflow=False ) ).fill(np.random.normal(size=1000)) fig = plt.figure(figsize=(10, 8)) main_ax_artists, sublot_ax_arists = hist_1.plot_pull( "normal", eb_ecolor="steelblue", eb_mfc="steelblue", eb_mec="steelblue", eb_fmt="o", eb_ms=6, eb_capsize=1, eb_capthick=2, eb_alpha=0.8, fp_c="hotpink", fp_ls="-", fp_lw=2, fp_alpha=0.8, bar_fc="royalblue", pp_num=3, pp_fc="royalblue", pp_alpha=0.618, pp_ec=None, ub_alpha=0.2, ) ``` ## Via Plot Ratio You can also make an arbitrary ratio plot using the `.plot_ratio` API: ``` hist_2 = hist.Hist( hist.axis.Regular( 50, -5, 5, name="X", label="x [units]", underflow=False, overflow=False ) ).fill(np.random.normal(size=1700)) fig = plt.figure(figsize=(10, 8)) main_ax_artists, sublot_ax_arists = hist_1.plot_ratio( hist_2, rp_ylabel=r"Ratio", rp_num_label="hist1", rp_denom_label="hist2", rp_uncert_draw_type="bar", # line or bar ) ``` Ratios between the histogram and a callable, or `str` alias, are supported as well ``` fig = plt.figure(figsize=(10, 8)) main_ax_artists, sublot_ax_arists = hist_1.plot_ratio(pdf) ``` Using the `.plot_ratio` API you can also make efficiency plots (where the numerator is a strict subset of the denominator) ``` hist_3 = hist_2.copy() * 0.7 hist_2.fill(np.random.uniform(-5, 5, 600)) hist_3.fill(np.random.uniform(-5, 5, 200)) fig = plt.figure(figsize=(10, 8)) main_ax_artists, sublot_ax_arists = hist_3.plot_ratio( hist_2, rp_num_label="hist3", rp_denom_label="hist2", rp_uncert_draw_type="line", rp_uncertainty_type="efficiency", ) ```	github_jupyter
# Hands-on Federated Learning: Image Classification In their recent (and exteremly thorough!) review of the federated learning literature [Kairouz, et al (2019)](https://arxiv.org/pdf/1912.04977.pdf) define federated learning as a machine learning setting where multiple entities (clients) collaborate in solving a machine learning problem, under the coordination of a central server or service provider. Each client’s raw data is stored locally and not exchanged or transferred; instead, focused updates intended for immediate aggregation are used to achieve the learning objective. In this tutorial we will use a federated version of the classic MNIST dataset to introduce the Federated Learning (FL) API layer of TensorFlow Federated (TFF), [`tff.learning`](https://www.tensorflow.org/federated/api_docs/python/tff/learning) - a set of high-level interfaces that can be used to perform common types of federated learning tasks, such as federated training, against user-supplied models implemented in TensorFlow or Keras. # Preliminaries ``` import collections import os import typing import matplotlib.pyplot as plt import numpy as np import tensorflow as tf import tensorflow.keras as keras import tensorflow_federated as tff # required to run TFF inside Jupyter notebooks import nest_asyncio nest_asyncio.apply() tff.federated_computation(lambda: 'Hello, World!')() ``` # Preparing the data In the IID setting the local data on each "client" is assumed to be a representative sample of the global data distribution. This is typically the case by construction when performing data parallel training of deep learning models across multiple CPU/GPU "clients". The non-IID case is significantly more complicated as there are many ways in which data can be non-IID and different degress of "non-IIDness". Consider a supervised task with features $X$ and labels $y$. A statistical model of federated learning involves two levels of sampling: 1. Sampling a client $i$ from the distribution over available clients $Q$ 2. Sampling an example $(X,y)$ from that client’s local data distribution $P_i(X,y)$. Non-IID data in federated learning typically refers to differences between $P_i$ and $P_j$ for different clients $i$ and $j$. However, it is worth remembering that both the distribution of available clients, $Q$, and the distribution of local data for client $i$, $P_i$, may change over time which introduces another dimension of “non-IIDness”. Finally, if the local data on a client's device is insufficiently randomized, perhaps ordered by time, then independence is violated locally as well. In order to facilitate experimentation TFF includes federated versions of several popular datasets that exhibit different forms and degrees of non-IIDness. ``` # What datasets are available? tff.simulation.datasets. ``` This tutorial uses a version of MNIST that contains a version of the original NIST dataset that has been re-processed using [LEAF](https://leaf.cmu.edu/) so that the data is keyed by the original writer of the digits. The federated MNIST dataset displays a particular type of non-IIDness: feature distribution skew (covariate shift). Whith feature distribution skew the marginal distributions $P_i(X)$ vary across clients, even though $P(y\|X)$ is shared. In the federated MNIST dataset users are writing the same numbers but each user has a different writing style characterized but different stroke width, slant, etc. ``` tff.simulation.datasets.emnist.load_data? emnist_train, emnist_test = (tff.simulation .datasets .emnist .load_data(only_digits=True, cache_dir="../data")) NUMBER_CLIENTS = len(emnist_train.client_ids) NUMBER_CLIENTS def sample_client_ids(client_ids: typing.List[str], sample_size: typing.Union[float, int], random_state: np.random.RandomState) -> typing.List[str]: """Randomly selects a subset of clients ids.""" number_clients = len(client_ids) error_msg = "'client_ids' must be non-emtpy." assert number_clients > 0, error_msg if isinstance(sample_size, float): error_msg = "Sample size must be between 0 and 1." assert 0 <= sample_size <= 1, error_msg size = int(sample_size * number_clients) elif isinstance(sample_size, int): error_msg = f"Sample size must be between 0 and {number_clients}." assert 0 <= sample_size <= number_clients, error_msg size = sample_size else: error_msg = "Type of 'sample_size' must be 'float' or 'int'." raise TypeError(error_msg) random_idxs = random_state.randint(number_clients, size=size) return [client_ids[i] for i in random_idxs] # these are what the client ids look like _random_state = np.random.RandomState(42) sample_client_ids(emnist_train.client_ids, 10, _random_state) def create_tf_datasets(source: tff.simulation.ClientData, client_ids: typing.Union[None, typing.List[str]]) -> typing.Dict[str, tf.data.Dataset]: """Create tf.data.Dataset instances for clients using their client_id.""" if client_ids is None: client_ids = source.client_ids datasets = {client_id: source.create_tf_dataset_for_client(client_id) for client_id in client_ids} return datasets def sample_client_datasets(source: tff.simulation.ClientData, sample_size: typing.Union[float, int], random_state: np.random.RandomState) -> typing.Dict[str, tf.data.Dataset]: """Randomly selects a subset of client datasets.""" client_ids = sample_client_ids(source.client_ids, sample_size, random_state) client_datasets = create_tf_datasets(source, client_ids) return client_datasets _random_state = np.random.RandomState() client_datasets = sample_client_datasets(emnist_train, sample_size=1, random_state=_random_state) (client_id, client_dataset), _ = client_datasets.items() fig, axes = plt.subplots(1, 5, figsize=(12,6), sharex=True, sharey=True) for i, example in enumerate(client_dataset.take(5)): axes[i].imshow(example["pixels"].numpy(), cmap="gray") axes[i].set_title(example["label"].numpy()) _ = fig.suptitle(x= 0.5, y=0.75, t=f"Training examples for a client {client_id}", fontsize=15) ``` ## Data preprocessing Since each client dataset is already a [`tf.data.Dataset`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset), preprocessing can be accomplished using Dataset transformations. Another option would be to use preprocessing operations from [`sklearn.preprocessing`](https://scikit-learn.org/stable/modules/preprocessing.html). Preprocessing consists of the following steps: 1. `map` a function that flattens the 28 x 28 images into 784-element tensors 2. `map` a function that rename the features from pixels and label to X and y for use with Keras 3. `shuffle` the individual examples 4. `batch` the into training batches We also throw in a `repeat` over the data set to run several epochs on each client device before sending parameters to the server for averaging. ``` AUTOTUNE = (tf.data .experimental .AUTOTUNE) SHUFFLE_BUFFER_SIZE = 1000 NUMBER_TRAINING_EPOCHS = 5 # number of local updates! TRAINING_BATCH_SIZE = 32 TESTING_BATCH_SIZE = 32 NUMBER_FEATURES = 28 28 NUMBER_TARGETS = 10 def _reshape(training_batch): """Extracts and reshapes data from a training sample """ pixels = training_batch["pixels"] label = training_batch["label"] X = tf.reshape(pixels, shape=[-1]) # flattens 2D pixels to 1D y = tf.reshape(label, shape=[1]) return X, y def create_training_dataset(client_dataset: tf.data.Dataset) -> tf.data.Dataset: """Create a training dataset for a client from a raw client dataset.""" training_dataset = (client_dataset.map(_reshape, num_parallel_calls=AUTOTUNE) .shuffle(SHUFFLE_BUFFER_SIZE, seed=None, reshuffle_each_iteration=True) .repeat(NUMBER_TRAINING_EPOCHS) .batch(TRAINING_BATCH_SIZE) .prefetch(buffer_size=AUTOTUNE)) return training_dataset def create_testing_dataset(client_dataset: tf.data.Dataset) -> tf.data.Dataset: """Create a testing dataset for a client from a raw client dataset.""" testing_dataset = (client_dataset.map(_reshape, num_parallel_calls=AUTOTUNE) .batch(TESTING_BATCH_SIZE)) return testing_dataset ``` ## How to choose the clients included in each training round In a typical federated training scenario there will be a very large population of user devices however only a fraction of these devices are likely to be available for training at a given point in time. For example, if the client devices are mobile phones then they might only participate in training when plugged into a power source, off a metered network, and otherwise idle. In a simulated environment, where all data is locally available, an approach is to simply sample a random subset of the clients to be involved in each round of training so that the subset of clients involved will vary from round to round. ### How many clients to include in each round? Updating and averaging a larger number of client models per training round yields better convergence and in a simulated training environment probably makes sense to include as many clients as is computationally feasible. However in real-world training scenario while averaging a larger number of clients improve convergence, it also makes training vulnerable to slowdown due to unpredictable tail delays in computation/communication at/with the clients. ``` def create_federated_data(training_source: tff.simulation.ClientData, testing_source: tff.simulation.ClientData, sample_size: typing.Union[float, int], random_state: np.random.RandomState) -> typing.Dict[str, typing.Tuple[tf.data.Dataset, tf.data.Dataset]]: # sample clients ids from the training dataset client_ids = sample_client_ids(training_source.client_ids, sample_size, random_state) federated_data = {} for client_id in client_ids: # create training dataset for the client _tf_dataset = training_source.create_tf_dataset_for_client(client_id) training_dataset = create_training_dataset(_tf_dataset) # create the testing dataset for the client _tf_dataset = testing_source.create_tf_dataset_for_client(client_id) testing_dataset = create_testing_dataset(_tf_dataset) federated_data[client_id] = (training_dataset, testing_dataset) return federated_data _random_state = np.random.RandomState(42) federated_data = create_federated_data(emnist_train, emnist_test, sample_size=0.01, random_state=_random_state) # keys are client ids, values are (training_dataset, testing_dataset) pairs len(federated_data) ``` # Creating a model with Keras If you are using Keras, you likely already have code that constructs a Keras model. Since the model will need to be replicated on each of the client devices we wrap the model in a no-argument Python function, a representation of which, will eventually be invoked on each client to create the model on that client. ``` def create_keras_model_fn() -> keras.Model: model_fn = keras.models.Sequential([ keras.layers.Input(shape=(NUMBER_FEATURES,)), keras.layers.Dense(units=NUMBER_TARGETS), keras.layers.Softmax(), ]) return model_fn ``` In order to use any model with TFF, it needs to be wrapped in an instance of the [`tff.learning.Model`](https://www.tensorflow.org/federated/api_docs/python/tff/learning/Model) interface, which exposes methods to stamp the model's forward pass, metadata properties, etc, and also introduces additional elements such as ways to control the process of computing federated metrics. Once you have a Keras model like the one we've just defined above, you can have TFF wrap it for you by invoking [`tff.learning.from_keras_model`](https://www.tensorflow.org/federated/api_docs/python/tff/learning/from_keras_model), passing the model and a sample data batch as arguments, as shown below. ``` tff.learning.from_keras_model? def create_tff_model_fn() -> tff.learning.Model: keras_model = create_keras_model_fn() dummy_batch = (tf.constant(0.0, shape=(TRAINING_BATCH_SIZE, NUMBER_FEATURES), dtype=tf.float32), tf.constant(0, shape=(TRAINING_BATCH_SIZE, 1), dtype=tf.int32)) loss_fn = (keras.losses .SparseCategoricalCrossentropy()) metrics = [ keras.metrics.SparseCategoricalAccuracy() ] tff_model_fn = (tff.learning .from_keras_model(keras_model, dummy_batch, loss_fn, None, metrics)) return tff_model_fn ``` Again, since our model will need to be replicated on each of the client devices we wrap the model in a no-argument Python function, a representation of which, will eventually be invoked on each client to create the model on that client. # Training the model on federated data Now that we have a model wrapped as `tff.learning.Model` for use with TFF, we can let TFF construct a Federated Averaging algorithm by invoking the helper function `tff.learning.build_federated_averaging_process` as follows. Keep in mind that the argument needs to be a constructor (such as `create_tff_model_fn` above), not an already-constructed instance, so that the construction of your model can happen in a context controlled by TFF. One critical note on the Federated Averaging algorithm below, there are 2 optimizers: a 1. `client_optimizer_fn` which is only used to compute local model updates on each client. 2. `server_optimizer_fn` applies the averaged update to the global model on the server. N.B. the choice of optimizer and learning rate may need to be different than those you would use to train the model on a standard i.i.d. dataset. Start with stochastic gradient descent with a smaller (than normal) learning rate. ``` tff.learning.build_federated_averaging_process? CLIENT_LEARNING_RATE = 1e-2 SERVER_LEARNING_RATE = 1e0 def create_client_optimizer(learning_rate: float = CLIENT_LEARNING_RATE, momentum: float = 0.0, nesterov: bool = False) -> keras.optimizers.Optimizer: client_optimizer = (keras.optimizers .SGD(learning_rate, momentum, nesterov)) return client_optimizer def create_server_optimizer(learning_rate: float = SERVER_LEARNING_RATE, momentum: float = 0.0, nesterov: bool = False) -> keras.optimizers.Optimizer: server_optimizer = (keras.optimizers .SGD(learning_rate, momentum, nesterov)) return server_optimizer federated_averaging_process = (tff.learning .build_federated_averaging_process(create_tff_model_fn, create_client_optimizer, create_server_optimizer, client_weight_fn=None, stateful_delta_aggregate_fn=None, stateful_model_broadcast_fn=None)) ``` What just happened? TFF has constructed a pair of federated computations (i.e., programs in TFF's internal glue language) and packaged them into a [`tff.utils.IterativeProcess`](https://www.tensorflow.org/federated/api_docs/python/tff/utils/IterativeProcess) in which these computations are available as a pair of properties `initialize` and `next`. It is a goal of TFF to define computations in a way that they could be executed in real federated learning settings, but currently only local execution simulation runtime is implemented. To execute a computation in a simulator, you simply invoke it like a Python function. This default interpreted environment is not designed for high performance, but it will suffice for this tutorial. ## `initialize` A function that takes no arguments and returns the state of the federated averaging process on the server. This function is only called to initialize a federated averaging process after it has been created. ``` # () -> SERVER_STATE print(federated_averaging_process.initialize.type_signature) state = federated_averaging_process.initialize() ``` ## `next` A function that takes current server state and federated data as arguments and returns the updated server state as well as any training metrics. Calling `next` performs a single round of federated averaging consisting of the following steps. 1. pushing the server state (including the model parameters) to the clients 2. on-device training on their local data 3. collecting and averaging model updates 4. producing a new updated model at the server. ``` # extract the training datasets from the federated data federated_training_data = [training_dataset for _, (training_dataset, _) in federated_data.items()] # SERVER_STATE, FEDERATED_DATA -> SERVER_STATE, TRAINING_METRICS state, metrics = federated_averaging_process.next(state, federated_training_data) print(f"round: 0, metrics: {metrics}") ``` Let's run a few more rounds on the same training data (which will over-fit to a particular set of clients but will converge faster). ``` number_training_rounds = 15 for n in range(1, number_training_rounds): state, metrics = federated_averaging_process.next(state, federated_training_data) print(f"round:{n}, metrics:{metrics}") ``` # First attempt at simulating federated averaging A proper federated averaging simulation would randomly sample new clients for each training round, allow for evaluation of training progress on training and testing data, and log training and testing metrics to TensorBoard for reference. Here we define a function that randomly sample new clients prior to each training round and logs training metrics TensorBoard. We defer handling testing data until we discuss federated evaluation towards the end of the tutorial. ``` def simulate_federated_averaging(federated_averaging_process: tff.utils.IterativeProcess, training_source: tff.simulation.ClientData, testing_source: tff.simulation.ClientData, sample_size: typing.Union[float, int], random_state: np.random.RandomState, number_rounds: int, initial_state: None = None, tensorboard_logging_dir: str = None): state = federated_averaging_process.initialize() if initial_state is None else initial_state if tensorboard_logging_dir is not None: if not os.path.isdir(tensorboard_logging_dir): os.makedirs(tensorboard_logging_dir) summary_writer = (tf.summary .create_file_writer(tensorboard_logging_dir)) with summary_writer.as_default(): for n in range(number_rounds): federated_data = create_federated_data(training_source, testing_source, sample_size, random_state) anonymized_training_data = [dataset for _, (dataset, _) in federated_data.items()] state, metrics = federated_averaging_process.next(state, anonymized_training_data) print(f"Round: {n}, Training metrics: {metrics}") for name, value in metrics._asdict().items(): tf.summary.scalar(name, value, step=n) else: for n in range(number_rounds): federated_data = create_federated_data(training_source, testing_source, sample_size, random_state) anonymized_training_data = [dataset for _, (dataset, _) in federated_data.items()] state, metrics = federated_averaging_process.next(state, anonymized_training_data) print(f"Round: {n}, Training metrics: {metrics}") return state, metrics federated_averaging_process = (tff.learning .build_federated_averaging_process(create_tff_model_fn, create_client_optimizer, create_server_optimizer, client_weight_fn=None, stateful_delta_aggregate_fn=None, stateful_model_broadcast_fn=None)) _random_state = np.random.RandomState(42) _tensorboard_logging_dir = "../results/logs/tensorboard" updated_state, current_metrics = simulate_federated_averaging(federated_averaging_process, training_source=emnist_train, testing_source=emnist_test, sample_size=0.01, random_state=_random_state, number_rounds=5, tensorboard_logging_dir=_tensorboard_logging_dir) updated_state current_metrics ``` # Customizing the model implementation Keras is the recommended high-level model API for TensorFlow and you should be using Keras models and creating TFF models using [`tff.learning.from_keras_model`](https://www.tensorflow.org/federated/api_docs/python/tff/learning/from_keras_model) whenever possible. However, [`tff.learning`](https://www.tensorflow.org/federated/api_docs/python/tff/learning) provides a lower-level model interface, [`tff.learning.Model`](https://www.tensorflow.org/federated/api_docs/python/tff/learning/Model), that exposes the minimal functionality necessary for using a model for federated learning. Directly implementing this interface (possibly still using building blocks from [`keras`](https://www.tensorflow.org/guide/keras)) allows for maximum customization without modifying the internals of the federated learning algorithms. Now we are going to repeat the above from scratch! ## Defining model variables We start by defining a new Python class that inherits from `tff.learning.Model`. In the class constructor (i.e., the `__init__` method) we will initialize all relevant variables using TF primatives as well as define the our "input spec" which defines the shape and types of the tensors that will hold input data. ``` class MNISTModel(tff.learning.Model): def __init__(self): # initialize some trainable variables self._weights = tf.Variable( initial_value=lambda: tf.zeros(dtype=tf.float32, shape=(NUMBER_FEATURES, NUMBER_TARGETS)), name="weights", trainable=True ) self._bias = tf.Variable( initial_value=lambda: tf.zeros(dtype=tf.float32, shape=(NUMBER_TARGETS,)), name="bias", trainable=True ) # initialize some variables used in computing metrics self._number_examples = tf.Variable(0.0, name='number_examples', trainable=False) self._total_loss = tf.Variable(0.0, name='total_loss', trainable=False) self._number_true_positives = tf.Variable(0.0, name='number_true_positives', trainable=False) # define the input spec self._input_spec = collections.OrderedDict([ ('X', tf.TensorSpec([None, NUMBER_FEATURES], tf.float32)), ('y', tf.TensorSpec([None, 1], tf.int32)) ]) @property def input_spec(self): return self._input_spec @property def local_variables(self): return [self._number_examples, self._total_loss, self._number_true_positives] @property def non_trainable_variables(self): return [] @property def trainable_variables(self): return [self._weights, self._bias] ``` ## Defining the forward pass With the variables for model parameters and cumulative statistics in place we can now define the `forward_pass` method that computes loss, makes predictions, and updates the cumulative statistics for a single batch of input data. ``` class MNISTModel(tff.learning.Model): def __init__(self): # initialize some trainable variables self._weights = tf.Variable( initial_value=lambda: tf.zeros(dtype=tf.float32, shape=(NUMBER_FEATURES, NUMBER_TARGETS)), name="weights", trainable=True ) self._bias = tf.Variable( initial_value=lambda: tf.zeros(dtype=tf.float32, shape=(NUMBER_TARGETS,)), name="bias", trainable=True ) # initialize some variables used in computing metrics self._number_examples = tf.Variable(0.0, name='number_examples', trainable=False) self._total_loss = tf.Variable(0.0, name='total_loss', trainable=False) self._number_true_positives = tf.Variable(0.0, name='number_true_positives', trainable=False) # define the input spec self._input_spec = collections.OrderedDict([ ('X', tf.TensorSpec([None, NUMBER_FEATURES], tf.float32)), ('y', tf.TensorSpec([None, 1], tf.int32)) ]) @property def input_spec(self): return self._input_spec @property def local_variables(self): return [self._number_examples, self._total_loss, self._number_true_positives] @property def non_trainable_variables(self): return [] @property def trainable_variables(self): return [self._weights, self._bias] @tf.function def _count_true_positives(self, y_true, y_pred): return tf.reduce_sum(tf.cast(tf.equal(y_true, y_pred), tf.float32)) @tf.function def _linear_transformation(self, batch): X = batch['X'] W, b = self.trainable_variables Z = tf.matmul(X, W) + b return Z @tf.function def _loss_fn(self, y_true, probabilities): return -tf.reduce_mean(tf.reduce_sum(tf.one_hot(y_true, NUMBER_TARGETS) * tf.math.log(probabilities), axis=1)) @tf.function def _model_fn(self, batch): Z = self._linear_transformation(batch) probabilities = tf.nn.softmax(Z) return probabilities @tf.function def forward_pass(self, batch, training=True): probabilities = self._model_fn(batch) y_pred = tf.argmax(probabilities, axis=1, output_type=tf.int32) y_true = tf.reshape(batch['y'], shape=[-1]) # compute local variables loss = self._loss_fn(y_true, probabilities) true_positives = self._count_true_positives(y_true, y_pred) number_examples = tf.size(y_true, out_type=tf.float32) # update local variables self._total_loss.assign_add(loss) self._number_true_positives.assign_add(true_positives) self._number_examples.assign_add(number_examples) batch_output = tff.learning.BatchOutput( loss=loss, predictions=y_pred, num_examples=tf.cast(number_examples, tf.int32) ) return batch_output ``` ## Defining the local metrics Next, we define a method `report_local_outputs` that returns a set of local metrics. These are the values, in addition to model updates (which are handled automatically), that are eligible to be aggregated to the server in a federated learning or evaluation process. Finally, we need to determine how to aggregate the local metrics emitted by each device by defining `federated_output_computation`. This is the only part of the code that isn't written in TensorFlow - it's a federated computation expressed in TFF. ``` class MNISTModel(tff.learning.Model): def __init__(self): # initialize some trainable variables self._weights = tf.Variable( initial_value=lambda: tf.zeros(dtype=tf.float32, shape=(NUMBER_FEATURES, NUMBER_TARGETS)), name="weights", trainable=True ) self._bias = tf.Variable( initial_value=lambda: tf.zeros(dtype=tf.float32, shape=(NUMBER_TARGETS,)), name="bias", trainable=True ) # initialize some variables used in computing metrics self._number_examples = tf.Variable(0.0, name='number_examples', trainable=False) self._total_loss = tf.Variable(0.0, name='total_loss', trainable=False) self._number_true_positives = tf.Variable(0.0, name='number_true_positives', trainable=False) # define the input spec self._input_spec = collections.OrderedDict([ ('X', tf.TensorSpec([None, NUMBER_FEATURES], tf.float32)), ('y', tf.TensorSpec([None, 1], tf.int32)) ]) @property def federated_output_computation(self): return self._aggregate_metrics_across_clients @property def input_spec(self): return self._input_spec @property def local_variables(self): return [self._number_examples, self._total_loss, self._number_true_positives] @property def non_trainable_variables(self): return [] @property def trainable_variables(self): return [self._weights, self._bias] @tff.federated_computation def _aggregate_metrics_across_clients(metrics): aggregated_metrics = { 'number_examples': tff.federated_sum(metrics.number_examples), 'average_loss': tff.federated_mean(metrics.average_loss, metrics.number_examples), 'accuracy': tff.federated_mean(metrics.accuracy, metrics.number_examples) } return aggregated_metrics @tf.function def _count_true_positives(self, y_true, y_pred): return tf.reduce_sum(tf.cast(tf.equal(y_true, y_pred), tf.float32)) @tf.function def _linear_transformation(self, batch): X = batch['X'] W, b = self.trainable_variables Z = tf.matmul(X, W) + b return Z @tf.function def _loss_fn(self, y_true, probabilities): return -tf.reduce_mean(tf.reduce_sum(tf.one_hot(y_true, NUMBER_TARGETS) * tf.math.log(probabilities), axis=1)) @tf.function def _model_fn(self, batch): Z = self._linear_transformation(batch) probabilities = tf.nn.softmax(Z) return probabilities @tf.function def forward_pass(self, batch, training=True): probabilities = self._model_fn(batch) y_pred = tf.argmax(probabilities, axis=1, output_type=tf.int32) y_true = tf.reshape(batch['y'], shape=[-1]) # compute local variables loss = self._loss_fn(y_true, probabilities) true_positives = self._count_true_positives(y_true, y_pred) number_examples = tf.cast(tf.size(y_true), tf.float32) # update local variables self._total_loss.assign_add(loss) self._number_true_positives.assign_add(true_positives) self._number_examples.assign_add(number_examples) batch_output = tff.learning.BatchOutput( loss=loss, predictions=y_pred, num_examples=tf.cast(number_examples, tf.int32) ) return batch_output @tf.function def report_local_outputs(self): local_metrics = collections.OrderedDict([ ('number_examples', self._number_examples), ('average_loss', self._total_loss / self._number_examples), ('accuracy', self._number_true_positives / self._number_examples) ]) return local_metrics ``` Here are a few points worth highlighting: * All state that your model will use must be captured as TensorFlow variables, as TFF does not use Python at runtime (remember your code should be written such that it can be deployed to mobile devices). * Your model should describe what form of data it accepts (input_spec), as in general, TFF is a strongly-typed environment and wants to determine type signatures for all components. Declaring the format of your model's input is an essential part of it. * Although technically not required, we recommend wrapping all TensorFlow logic (forward pass, metric calculations, etc.) as tf.functions, as this helps ensure the TensorFlow can be serialized, and removes the need for explicit control dependencies. The above is sufficient for evaluation and algorithms like Federated SGD. However, for Federated Averaging, we need to specify how the model should train locally on each batch. ``` class MNISTrainableModel(MNISTModel, tff.learning.TrainableModel): def __init__(self, optimizer): super().__init__() self._optimizer = optimizer @tf.function def train_on_batch(self, batch): with tf.GradientTape() as tape: output = self.forward_pass(batch) gradients = tape.gradient(output.loss, self.trainable_variables) self._optimizer.apply_gradients(zip(tf.nest.flatten(gradients), tf.nest.flatten(self.trainable_variables))) return output ``` # Simulating federated training with the new model With all the above in place, the remainder of the process looks like what we've seen already - just replace the model constructor with the constructor of our new model class, and use the two federated computations in the iterative process you created to cycle through training rounds. ``` def create_custom_tff_model_fn(): optimizer = keras.optimizers.SGD(learning_rate=0.02) return MNISTrainableModel(optimizer) federated_averaging_process = (tff.learning .build_federated_averaging_process(create_custom_tff_model_fn)) _random_state = np.random.RandomState(42) updated_state, current_metrics = simulate_federated_averaging(federated_averaging_process, training_source=emnist_train, testing_source=emnist_test, sample_size=0.01, random_state=_random_state, number_rounds=10) updated_state current_metrics ``` # Evaluation All of our experiments so far presented only federated training metrics - the average metrics over all batches of data trained across all clients in the round. Should we be concerened about overfitting? Yes! In federated averaging algorithms there are two different ways to over-fit. 1. Overfitting the shared model (especially if we use the same set of clients on each round). 2. Over-ftting local models on the clients. ## Federated evaluation To perform evaluation on federated data, you can construct another federated computation designed for just this purpose, using the [`tff.learning.build_federated_evaluation`](https://www.tensorflow.org/federated/api_docs/python/tff/learning/build_federated_evaluation) function, and passing in your model constructor as an argument. Note that evaluation doesn't perform gradient descent and there's no need to construct optimizers. ``` tff.learning.build_federated_evaluation? federated_evaluation = (tff.learning .build_federated_evaluation(create_custom_tff_model_fn)) # function type signature: SERVER_MODEL, FEDERATED_DATA -> METRICS print(federate_evaluation.type_signature) ``` The `federated_evaluation` function is similar to `tff.utils.IterativeProcess.next` but with two important differences. 1. Function does not return the server state; since evaluation doesn't modify the model or any other aspect of state - you can think of it as stateless. 2. Function only needs the model and doesn't require any other part of server state that might be associated with training, such as optimizer variables. ``` training_metrics = federated_evaluation(updated_state.model, federated_training_data) training_metrics ``` Note the numbers may look marginally better than what was reported by the last round of training. By convention, the training metrics reported by the iterative training process generally reflect the performance of the model at the beginning of the training round, so the evaluation metrics will always be one step ahead. ## Evaluating on client data not used in training Since we are training a shared model for digit classication we might also want to evaluate the performance of the model on client test datasets where the corresponding training dataset was not used in training. ``` _random_state = np.random.RandomState(42) client_datasets = sample_client_datasets(emnist_test, sample_size=0.01, random_state=_random_state) federated_testing_data = [create_testing_dataset(client_dataset) for _, client_dataset in client_datasets.items()] testing_metrics = federated_evaluation(updated_state.model, federated_testing_data) testing_metrics ``` # Adding evaluation to our federated averaging simulation ``` def simulate_federated_averaging(federated_averaging_process: tff.utils.IterativeProcess, federated_evaluation, training_source: tff.simulation.ClientData, testing_source: tff.simulation.ClientData, sample_size: typing.Union[float, int], random_state: np.random.RandomState, number_rounds: int, tensorboard_logging_dir: str = None): state = federated_averaging_process.initialize() if tensorboard_logging_dir is not None: if not os.path.isdir(tensorboard_logging_dir): os.makedirs(tensorboard_logging_dir) summary_writer = (tf.summary .create_file_writer(tensorboard_logging_dir)) with summary_writer.as_default(): for n in range(number_rounds): federated_data = create_federated_data(training_source, testing_source, sample_size, random_state) # extract the training and testing datasets anonymized_training_data = [] anonymized_testing_data = [] for training_dataset, testing_dataset in federated_data.values(): anonymized_training_data.append(training_dataset) anonymized_testing_data.append(testing_dataset) state, _ = federated_averaging_process.next(state, anonymized_training_data) training_metrics = federated_evaluation(state.model, anonymized_training_data) testing_metrics = federated_evaluation(state.model, anonymized_testing_data) print(f"Round: {n}, Training metrics: {training_metrics}, Testing metrics: {testing_metrics}") # tensorboard logging for name, value in training_metrics._asdict().items(): tf.summary.scalar(name, value, step=n) for name, value in testing_metrics._asdict().items(): tf.summary.scalar(name, value, step=n) else: for n in range(number_rounds): federated_data = create_federated_data(training_source, testing_source, sample_size, random_state) # extract the training and testing datasets anonymized_training_data = [] anonymized_testing_data = [] for training_dataset, testing_dataset in federated_data.values(): anonymized_training_data.append(training_dataset) anonymized_testing_data.append(testing_dataset) state, _ = federated_averaging_process.next(state, anonymized_training_data) training_metrics = federated_evaluation(state.model, anonymized_training_data) testing_metrics = federated_evaluation(state.model, anonymized_testing_data) print(f"Round: {n}, Training metrics: {training_metrics}, Testing metrics: {testing_metrics}") return state, (training_metrics, testing_metrics) federated_averaging_process = (tff.learning .build_federated_averaging_process(create_tff_model_fn, create_client_optimizer, create_server_optimizer, client_weight_fn=None, stateful_delta_aggregate_fn=None, stateful_model_broadcast_fn=None)) federated_evaluation = (tff.learning .build_federated_evaluation(create_tff_model_fn)) _random_state = np.random.RandomState(42) updated_state, current_metrics = simulate_federated_averaging(federated_averaging_process, federated_evaluation, training_source=emnist_train, testing_source=emnist_test, sample_size=0.01, random_state=_random_state, number_rounds=15) ``` # Wrapping up ## Interesting resources [PySyft](https://github.com/OpenMined/PySyft) is a Python library for secure and private Deep Learning created by [OpenMined](https://www.openmined.org/). PySyft decouples private data from model training, using [Federated Learning](https://ai.googleblog.com/2017/04/federated-learning-collaborative.html), [Differential Privacy](https://en.wikipedia.org/wiki/Differential_privacy), and [Multi-Party Computation (MPC)](https://en.wikipedia.org/wiki/Secure_multi-party_computation) within the main Deep Learning frameworks like PyTorch and TensorFlow.	github_jupyter
``` import pandas as pd from unidecode import unidecode import nltk from nltk.corpus import stopwords from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.feature_extraction.text import CountVectorizer nltk.download('stopwords') df = pd.read_csv('../base/review.csv',encoding='latin-1') df.head() import string from nltk.stem.snowball import SnowballStemmer import swifter import nltk stemmer = SnowballStemmer("english") stop = set(stopwords.words('english')) def lower(texto): return texto.lower() def normalize(texto): return unidecode(texto) def remove_ponctuation(texto): for punc in string.punctuation: texto = texto.replace(punc," ") return texto def remove_stopwords(texto): ret = [] for palavra in texto.split(): if palavra not in stop: ret.append(palavra) return ' '.join(ret) def stem(texto): ret = [] for palavra in texto.split(): ret.append(stemmer.stem(palavra)) return ' '.join(ret) def remove_number(texto): result = ''.join([i for i in texto if not i.isdigit()]) return result def pipeline(texto): texto = normalize(texto) texto = lower(texto) texto = remove_ponctuation(texto) texto = remove_stopwords(texto) texto = remove_number(texto) texto = stem(texto) return texto df['SentimentText'].apply(lower).head() remove_ponctuation("é, ué!") len(df) df['preproc'] = df['SentimentText'].swifter.apply(pipeline) # vectorizer = CountVectorizer() # X = vectorizer.fit_transform(df['preproc']) # len(vectorizer.get_feature_names()) vectorizer_tfidf = TfidfVectorizer() X = vectorizer_tfidf.fit_transform(df['preproc']) len(vectorizer_tfidf.get_feature_names()) y = df['Sentiment'] from sklearn.linear_model import LogisticRegression from sklearn.model_selection import cross_val_score import numpy as np clf = LogisticRegression(solver='liblinear') np.mean(cross_val_score(clf,X, y, cv=10,scoring='balanced_accuracy')) from sklearn.naive_bayes import MultinomialNB clf = MultinomialNB() np.mean(cross_val_score(clf,X, y, cv=10,scoring='balanced_accuracy')) clf.fit(X,y) import pickle filename = 'clf.pickle' outfile = open(filename,'wb') pickle.dump(clf,outfile) outfile.close() filename = 'vectorizer.pickle' outfile = open(filename,'wb') pickle.dump(vectorizer_tfidf,outfile) outfile.close() #I just love this movie. Specially the climax, seriously one of the best climax I have ever seen. #I just want to say how amazing this film is from start to finish. This will take you on a emotional ride.You will not he disappointed #LITERALLY , one of the best movies i have seen in my entire life , filled with a tone of action and emotions . you will love avenger endgame . ' i love you 3000 ' ```	github_jupyter
## 最小二乘法 ``` import numpy as np import matplotlib.pyplot as plt from scipy.optimize import leastsq Xi = np.array( [157, 162, 169, 176, 188, 200, 211, 220, 230, 237, 247, 256, 268, 287, 285, 290, 301, 311, 326, 335, 337, 345, 348, 358, 384, 396, 409, 415, 432, 440, 448, 449, 461, 467, 478, 493], dtype=np.float) Yi = np.array( [143, 146, 153, 160, 169, 180, 190, 196, 207, 215, 220, 228, 242, 253, 251, 257, 271, 283, 295, 302, 301, 305, 308, 324, 341, 357, 371, 382, 397, 406, 413, 411, 422, 434, 447, 458], dtype=np.float) def func(p, x): k, b = p return k * x + b def error(p, x, y): return func(p, x) - y # k,b的初始值，可以任意设定,经过几次试验，发现p0的值会影响cost的值：Para[1] p0 = [1, 20] # 把error函数中除了p0以外的参数打包到args中(使用要求) Para = leastsq(error, p0, args=(Xi, Yi)) # 读取结果 k, b = Para[0] # 画样本点 plt.figure(figsize=(8, 6)) ##指定图像比例： 8：6 plt.scatter(Xi, Yi, color="green", linewidth=2) # 画拟合直线 # x = np.linspace(0, 12, 100) ##在0-15直接画100个连续点 # x = np.linspace(0, 500, int(500/12)100) ##在0-15直接画100个连续点 # y = k x + b ##函数式 plt.plot(Xi, k * Xi + b, color="red", linewidth=2) plt.legend(loc='lower right') # 绘制图例 plt.show() ``` ## 梯度下降法 ``` import numpy as np import matplotlib.pyplot as plt x = np.array( [157, 162, 169, 176, 188, 200, 211, 220, 230, 237, 247, 256, 268, 287, 285, 290, 301, 311, 326, 335, 337, 345, 348, 358, 384, 396, 409, 415, 432, 440, 448, 449, 461, 467, 478, 493], dtype=np.float) y = np.array( [143, 146, 153, 160, 169, 180, 190, 196, 207, 215, 220, 228, 242, 253, 251, 257, 271, 283, 295, 302, 301, 305, 308, 324, 341, 357, 371, 382, 397, 406, 413, 411, 422, 434, 447, 458], dtype=np.float) def GD(x, y, learning_rate, iteration_num=10000): theta = np.random.rand(2, 1) # 初始化参数 x = np.hstack((np.ones((len(x), 1)), x.reshape(len(x), 1))) y = y.reshape(len(y), 1) for i in range(iteration_num): # 计算梯度 grad = np.dot(x.T, (np.dot(x, theta) - y)) / x.shape[0] # 更新参数 theta -= learning_rate * grad # 计算 MSE # loss = np.linalg.norm(np.dot(x, theta) - y) plt.figure() plt.title('Learning rate: {}, iteration_num: {}'.format(learning_rate, iteration_num)) plt.scatter(x[:, 1], y.reshape(len(y))) plt.plot(x[:, 1], np.dot(x, theta), color='red', linewidth=3) GD(x, y, learning_rate=0.00001, iteration_num=1) GD(x, y, learning_rate=0.00001, iteration_num=3) GD(x, y, learning_rate=0.00001, iteration_num=10) GD(x, y, learning_rate=0.00001, iteration_num=100) GD(x, y, learning_rate=0.000001, iteration_num=1) GD(x, y, learning_rate=0.000001, iteration_num=3) GD(x, y, learning_rate=0.000001, iteration_num=10) GD(x, y, learning_rate=0.000001, iteration_num=100) ```	github_jupyter
##### Copyright 2020 The TensorFlow Authors. ``` #@title Licensed under the Apache License, Version 2.0 (the "License"); # you may not use this file except in compliance with the License. # You may obtain a copy of the License at # # https://www.apache.org/licenses/LICENSE-2.0 # # Unless required by applicable law or agreed to in writing, software # distributed under the License is distributed on an "AS IS" BASIS, # WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. # See the License for the specific language governing permissions and # limitations under the License. ``` # グラフと関数の基礎 <table class="tfo-notebook-buttons" align="left"> <td><a target="_blank" href="https://www.tensorflow.org/guide/intro_to_graphs"><img src="https://www.tensorflow.org/images/tf_logo_32px.png"> TensorFlow.orgで表示</a></td> <td><a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/ja/guide/intro_to_graphs.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png">Google Colab で実行</a></td> <td><a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/ja/guide/intro_to_graphs.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png">GitHub でソースを表示{</a></td> <td><a href="https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/ja/guide/intro_to_graphs.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png">ノートブックをダウンロード/a0}</a></td> </table> # グラフと `tf.function` の基礎このガイドは、TensorFlow の仕組みを説明するために、TensorFlow と Keras 基礎を説明します。今すぐ Keras に取り組みたい方は、[Keras のガイド一覧](keras/)を参照してください。このガイドでは、グラフ取得のための単純なコード変更、格納と表現、およびモデルの高速化とエクスポートを行うための使用方法について、TensorFlow の中核的な仕組みを説明します。注意: TensorFlow 1.x のみの知識をお持ちの場合は、このガイドでは、非常に異なるグラフビューが紹介されています。これは、基礎を概説したガイドです。これらの概念の徹底ガイドについては、[`tf.function` ガイド](function)を参照してください。 ## グラフとは？前回の 3 つのガイドでは、TensorFlow の Eager execution について説明しました。これは、TensorFlow 演算が演算ごとにPythonによって実行され、結果を Python に返すことを意味します。Eager TensorFlow は GPU を活用し、変数、テンソル、さらには演算を GPU と TPU に配置することができます。また、デバックも簡単に行えます。一部のユーザーは、Python から移動する必要はありません。ただし、TensorFlow を Python で演算ごとに実行すると、ほかの方法では得られない多数の高速化機能が利用できなくなります。Python からテンソルの計算を抽出できる場合は、グラフにすることができます。グラフとは、計算のユニットを表す一連の `tf.Operation` オブジェクトと、演算間を流れるデータのユニットを表す `tf.Tensor` オブジェクトを含むデータ構造です。 `tf.Graph` コンテキストで定義されます。これらのグラフはデータ構造であるため、元の Python コードがなくても、保存、実行、および復元することができます。次は、TensorBoard で視覚化された単純な二層グラフです。 ![a two-layer tensorflow graph](https://storage.cloud.google.com/tensorflow.org/images/two-layer-network.png) ## グラフのメリットグラフを使用すると、柔軟性が大幅に向上し、モバイルアプリケーション。組み込みデバイス、バックエンドサーバーといった Python インタプリタのない環境でも TensorFlow グラフを使用できます。TensorFlow は、Python からエクスポートされた場合に、保存されるモデルの形式としてグラフを使用します。また、グラフは最適化を簡単に行えるため、コンパイラは次のような変換を行えます。 - 計算に定数ノードを畳み込むで、テンソルの値を統計的に推論します（「定数畳み込み」）。 - 独立した計算のサブパートを分離し、スレッドまたはデバイスに分割します。 - 共通部分式を取り除き、算術演算を単純化します。これやほかの高速化を実行する [Grappler](./graph_optimization.ipynb) という総合的な最適化システムがあります。まとめると、グラフは非常に便利なもので、複数のデバイスで、TensorFlow の高速化、並列化、および効率化を期待することができます。ただし、便宜上、Python で機械学習モデル（またはその他の計算）を定義した後、必要となったときに自動的にグラフを作成することをお勧めします。 # グラフのトレース TensorFlow でグラフを作成する方法は、直接呼出しまたはデコレータのいずれかとして `tf.function` を使用することです。 ``` import tensorflow as tf import timeit from datetime import datetime # Define a Python function def function_to_get_faster(x, y, b): x = tf.matmul(x, y) x = x + b return x # Create a `Function` object that contains a graph a_function_that_uses_a_graph = tf.function(function_to_get_faster) # Make some tensors x1 = tf.constant([[1.0, 2.0]]) y1 = tf.constant([[2.0], [3.0]]) b1 = tf.constant(4.0) # It just works! a_function_that_uses_a_graph(x1, y1, b1).numpy() ``` `tf.function` 化された関数は、[Python コーラブル]()で、Python 相当と同じように機能します。特定のクラス（`python.eager.def_function.Function`）を使用しますが、ユーザーにとっては、トレースできないものと同じように動作します。 `tf.function` は、それが呼び出す Python 関数を再帰的にトレースします。 ``` def inner_function(x, y, b): x = tf.matmul(x, y) x = x + b return x # Use the decorator @tf.function def outer_function(x): y = tf.constant([[2.0], [3.0]]) b = tf.constant(4.0) return inner_function(x, y, b) # Note that the callable will create a graph that # includes inner_function() as well as outer_function() outer_function(tf.constant([[1.0, 2.0]])).numpy() ``` TensorFlow 1.x を使用したことがある場合は、`Placeholder` または `tf.Sesssion` をまったく定義する必要がないことに気づくでしょう。 ## フローの制御と副次的影響フロー制御とループは、デフォルトで `tf.autograph` によって TensorFlow に変換されます。Autograph は、ループコンストラクトの標準化、アンロール、および [AST](https://docs.python.org/3/library/ast.html) マニピュレーションなどのメソッドを組み合わせて使用します。 ``` def my_function(x): if tf.reduce_sum(x) <= 1: return x * x else: return x-1 a_function = tf.function(my_function) print("First branch, with graph:", a_function(tf.constant(1.0)).numpy()) print("Second branch, with graph:", a_function(tf.constant([5.0, 5.0])).numpy()) ``` Autograph 変換を直接呼び出して、Python が TensorFlow 演算に変換される様子を確認することができます。これはほとんど解読不能ですが、変換を確認することができます。 ``` # Don't read the output too carefully. print(tf.autograph.to_code(my_function)) ``` Autograph は、`if-then` 句、ループ、 `break`、`return`、`continue` などを自動的に変換します。ほとんどの場合、Autograph の動作に特別な考慮はいりませんが、いくつかの注意事項があり、これについては [tf.function ガイド](./function.ipynb)のほか、[Autograph 完全リファレンス](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/python/autograph/g3doc/reference/index.md)が役立ちます。 ## 高速化の確認 tensor-using 関数を `tf.function` でラッピングするだけでは、コードは高速化しません。単一のマシンで数回呼び出された小さな関数では、グラフまたはグラフの一部の呼び出しにかかるオーバーヘッドによってランタイムが占有されてしまうことがあります。また、GPU 大きな負荷をかける畳み込みのスタックなど、計算のほとんどがすでにアクセラレータで発生している場合は、グラフの高速化をあまり確認できません。複雑な計算については、グラフによって大幅な高速化を得ることができます。これは、グラフが Python からデバイスへの通信や一部の高速化の実装を減らすためです。次のコードは、小さな密のレイヤーでの数回の実行にかかる時間を計測します。 ``` # Create an oveerride model to classify pictures class SequentialModel(tf.keras.Model): def __init__(self, kwargs): super(SequentialModel, self).__init__(kwargs) self.flatten = tf.keras.layers.Flatten(input_shape=(28, 28)) self.dense_1 = tf.keras.layers.Dense(128, activation="relu") self.dropout = tf.keras.layers.Dropout(0.2) self.dense_2 = tf.keras.layers.Dense(10) def call(self, x): x = self.flatten(x) x = self.dense_1(x) x = self.dropout(x) x = self.dense_2(x) return x input_data = tf.random.uniform([60, 28, 28]) eager_model = SequentialModel() graph_model = tf.function(eager_model) print("Eager time:", timeit.timeit(lambda: eager_model(input_data), number=10000)) print("Graph time:", timeit.timeit(lambda: graph_model(input_data), number=10000)) ``` ### 多層型関数関数をトレースする場合、多層型の `Function` オブジェクトを作成します。多層型関数は Pythonコーラブルで、1つの API の背後にあるいくつかの具象関数グラフをカプセル化します。この `Function` は、あらゆる `dtypes` と形状に使用できます。新しい引数シグネチャでそれを呼び出すたびに、元の関数が新しい引数で再トレースされます。`Function` は、そのトレースに対応する `tf.Graph` を `concrete_function` に格納します。関数がすでにそのような引数でトレースされている場合は、トレース済みのグラフが取得されます。概念的に、次のようになります。 - `tf.Graph` は計算を説明する未加工のポータブルなデータ構造である - `Function` は、ConcreteFunctions のキャッシュ、トレース、およびディスパッチャーである - `ConcreteFunction` は、Python からグラフを実行できるグラフの Eager 対応ラッパーである ### 多層型関数の検査 `a_function` を検査できます。これはPython 関数 `my_function` に対して `tf.function` を呼び出した結果です。この例では、3 つの引数で `a_function` を呼び出すことで、3 つの具象関数を得られています。 ``` print(a_function) print("Calling a `Function`:") print("Int:", a_function(tf.constant(2))) print("Float:", a_function(tf.constant(2.0))) print("Rank-1 tensor of floats", a_function(tf.constant([2.0, 2.0, 2.0]))) # Get the concrete function that works on floats print("Inspecting concrete functions") print("Concrete function for float:") print(a_function.get_concrete_function(tf.TensorSpec(shape=[], dtype=tf.float32))) print("Concrete function for tensor of floats:") print(a_function.get_concrete_function(tf.constant([2.0, 2.0, 2.0]))) # Concrete functions are callable # Note: You won't normally do this, but instead just call the containing `Function` cf = a_function.get_concrete_function(tf.constant(2)) print("Directly calling a concrete function:", cf(tf.constant(2))) ``` この例では、スタックの非常に奥を調べています。具体的にトレースを管理していない限り、通常は、ここに示されるように具象関数を呼び出す必要はありません。 # Eager execution でのデバッグスタックトレースが長い場合、特に `tf.Graph` または `with tf.Graph().as_default()` の参照が含まれる場合、グラフコンテキストで実行している可能性があります。TensorFlow のコア関数は Keras の `model.fit()` などのグラフコンテキストを使用します。 Eager execution をデバッグする方がはるかに簡単であることがよくあります。スタックトレースは比較的に短く、理解しやすいからです。グラフのデバックが困難な場合は、Eager execution に戻ってデバックすることができます。 Eager で実行していることを確認するには、次を行います。 - メソッドとレイヤーを直接コーラブルとして呼び出す - Keras compile/fit を使用している場合、コンパイル時に `model.compile(run_eagerly=True)` を使用する - `tf.config.experimental_run_functions_eagerly(True)` でグローバル実行モードを設定する ### `run_eagerly=True` を使用する ``` # Define an identity layer with an eager side effect class EagerLayer(tf.keras.layers.Layer): def __init__(self, kwargs): super(EagerLayer, self).__init__(kwargs) # Do some kind of initialization here def call(self, inputs): print("\nCurrently running eagerly", str(datetime.now())) return inputs # Create an override model to classify pictures, adding the custom layer class SequentialModel(tf.keras.Model): def __init__(self): super(SequentialModel, self).__init__() self.flatten = tf.keras.layers.Flatten(input_shape=(28, 28)) self.dense_1 = tf.keras.layers.Dense(128, activation="relu") self.dropout = tf.keras.layers.Dropout(0.2) self.dense_2 = tf.keras.layers.Dense(10) self.eager = EagerLayer() def call(self, x): x = self.flatten(x) x = self.dense_1(x) x = self.dropout(x) x = self.dense_2(x) return self.eager(x) # Create an instance of this model model = SequentialModel() # Generate some nonsense pictures and labels input_data = tf.random.uniform([60, 28, 28]) labels = tf.random.uniform([60]) loss_fn = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True) ``` まず、Eager を使用せずにモデルをコンパイルします。モデルはトレースされません。名前にも関わらず、`compile` は、損失関数、最適化、およびトレーニングパラメータのセットアップしか行いません。 ``` model.compile(run_eagerly=False, loss=loss_fn) ``` ここで、`fit` を呼び出し、関数がトレース（2 回）されると Eager 効果が実行しなくなるのを確認します。 ``` model.fit(input_data, labels, epochs=3) ``` ただし、エポックを 1 つでも Eager で実行すると、Eager の副次的作用が 2 回現れます。 ``` print("Running eagerly") # When compiling the model, set it to run eagerly model.compile(run_eagerly=True, loss=loss_fn) model.fit(input_data, labels, epochs=1) ``` ### `experimental_run_functions_eagerly` を使用するまた、すべてを Eager で実行するよにグローバルに設定することができます。これは、トレースし直した場合にのみ機能することに注意してください。トレースされた関数は、トレースされたままとなり、グラフとして実行します。 ``` # Now, globally set everything to run eagerly tf.config.experimental_run_functions_eagerly(True) print("Run all functions eagerly.") # First, trace the model, triggering the side effect polymorphic_function = tf.function(model) # It was traced... print(polymorphic_function.get_concrete_function(input_data)) # But when you run the function again, the side effect happens (both times). result = polymorphic_function(input_data) result = polymorphic_function(input_data) # Don't forget to set it back when you are done tf.config.experimental_run_functions_eagerly(False) ``` # トレースとパフォーマンストレースにはある程度のオーバーヘッドがかかります。小さな関数のトレースは素早く行えますが、大規模なモデルであればかなりの時間がかかる場合があります。パフォーマンスが上昇するとこの部分の時間は迅速に取り戻されますが、大規模なモデルのトレーニングの最初の数エポックでは、トレースによって遅延が発生する可能性があることに注意しておくことが重要です。モデルの規模に関係なく、頻繁にトレースするのは避けたほうがよいでしょう。[tf.function ガイドのこのセクション](function.ipynb#when_to_retrace)では、入力仕様を設定し、テンソル引数を使用して再トレースを回避する方法について説明しています。フォーマンスが異常に低下している場合は、誤って再トレースしていないかどうかを確認することをお勧めします。 eager-only の副次的効果（Python 引数の出力など）を追加して、関数がいつトレースされているかを確認できます。ここでは、新しい Python 引数が常に再トレースをトリガするため、余分な再トレースが発生していることを確認できます。 ``` # Use @tf.function decorator @tf.function def a_function_with_python_side_effect(x): print("Tracing!") # This eager return x * x + tf.constant(2) # This is traced the first time print(a_function_with_python_side_effect(tf.constant(2))) # The second time through, you won't see the side effect print(a_function_with_python_side_effect(tf.constant(3))) # This retraces each time the Python argument chances # as a Python argument could be an epoch count or other # hyperparameter print(a_function_with_python_side_effect(2)) print(a_function_with_python_side_effect(3)) ``` # 次のステップより詳しい説明については、`tf.function` API リファレンスページと[ガイド](./function.ipynb)を参照してください。	github_jupyter
``` import warnings warnings.filterwarnings('ignore') # 実行に影響のない　warninig　を非表示にします. 非推奨. ``` # Chapter 5: 機械学習回帰問題 ## 5-1. 回帰問題を Pythonで解いてみよう 1. データセットの用意 2. モデル構築 ### 5-1-1. データセットの用意今回はwine-quality datasetを用いる. wine-quality dataset はワインのアルコール濃度や品質などの12要素の数値データ. 赤ワインと白ワイン両方あります。赤ワインの含まれるデータ数は1600ほど. まずはデータセットをダウンロードする. proxy下ではjupyter notebookに設定をしないと以下は動作しない. ``` ! wget https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv ./data/winequality-red.csv ``` jupyter notebook の設定が面倒な人へ. proxyの設定をしたshell、もしくはブラウザなどで以下のURIからダウンロードしてください. https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/ ``` import pandas as pd wine = pd.read_csv("./data/winequality-red.csv", sep=";") # sepは区切り文字の指定 display(wine.head(5)) ``` まずは説明変数１つで回帰を行ってみよう. 今回はalcoholを目的変数 $t$ に, densityを説明変数 $x$ にする. ``` X = wine[["density"]].values T = wine["alcohol"].values ``` #### 前処理データを扱いやすいように中心化する. ``` X = X - X.mean() T = T - T.mean() ``` trainとtestに分割する. ``` X_train = X[:1000, :] T_train = T[:1000] X_test = X[1000:, :] T_test = T[1000:] import matplotlib.pyplot as plt %matplotlib inline fig, axes = plt.subplots(ncols=2, figsize=(12, 4)) axes[0].scatter(X_train, T_train, marker=".") axes[0].set_title("train") axes[1].scatter(X_test, T_test, marker=".") axes[1].set_title("test") fig.show() ``` train と test の分布がかなり違う. 予め shuffle して train と test に分割する必要があるようだ. XとTの対応関係を崩さず shuffle する方法は多々あるが、その１つが以下. ``` import numpy as np np.random.seed(0) # random　の挙動を固定 p = np.random.permutation(len(X)) # random　な　index のリスト X = X[p] T = T[p] X_train = X[:1000, :] T_train = T[:1000] X_test = X[1000:, :] T_test = T[1000:] fig, axes = plt.subplots(ncols=2, figsize=(12, 4)) axes[0].scatter(X_train, T_train, marker=".") axes[0].set_title("train") axes[1].scatter(X_test, T_test, marker=".") axes[1].set_title("test") fig.show() ``` ### 5-1-2. モデルの構築今回は, 目的変数 $t$ を以下の回帰関数で予測する. $$y=ax+b$$ この時、損失が最小になるように, パラメータ$a,b$を定める必要がある. ここでは二乗損失関数を用いる. $$\mathrm{L}\left(a, b\right) =\sum^{N}_{n=1}\left(t_n - y_n\right)^2 =\sum^{N}_{n=1}\left(t_n - ax_x-b\right)^2$$ <span style="color: gray; ">※これは, 目的変数 $t$ が上記の回帰関数 $y$ を中心としたガウス分布に従うという仮定を置いて最尤推定することと等価.</span> ``` class MyLinearRegression(object): def __init__(self): """ Initialize a coefficient and an intercept. """ self.a = self.b = def fit(self, X, y): """ X: data, array-like, shape (n_samples, n_features) y: array, shape (n_samples,) Estimate a coefficient and an intercept　from data. """ return self def predict(self, X): """ Calc y from X """ return y ``` 上記の単回帰のクラスを完成させ, 以下の実行によって図の回帰直線が得られるはずだ. ``` clf = MyLinearRegression() clf.fit(X_train, T_train) # 回帰係数 print("係数: ", clf.a) # 切片 print("切片: ", clf.b) fig, axes = plt.subplots(ncols=2, figsize=(12, 4)) axes[0].scatter(X_train, T_train, marker=".") axes[0].plot(X_train, clf.predict(X_train), color="red") axes[0].set_title("train") axes[1].scatter(X_test, T_test, marker=".") axes[1].plot(X_test, clf.predict(X_test), color="red") axes[1].set_title("test") fig.show() ``` もしdatasetをshuffleせずに上記の学習を行った時, 得られる回帰直線はどうなるだろう？試してみてください. ## 5-2. scikit-learnについて ### 5-2-1. モジュールの概要 [scikit-learn](http://scikit-learn.org/stable/)のホームページに詳しい情報がある．実は scikit-learn に線形回帰のモジュールがすでにある. #### scikit-learn の特徴 - scikit-learn(sklearn)には，多くの機械学習アルゴリズムが入っており，統一した形式で書かれているため利用しやすい． - 各手法をコードで理解するだけでなく，その元となる論文も紹介されている． - チュートリアルやどのように利用するのかをまとめたページもあり，似た手法が列挙されている． ``` import sklearn print(sklearn.__version__) from sklearn.linear_model import LinearRegression clf = LinearRegression() # 予測モデルを作成 clf.fit(X_train, T_train) # 回帰係数 print("係数: ", clf.coef_) # 切片 print("切片: ", clf.intercept_) # 決定係数 print("決定係数: ", clf.score(X_train, T_train)) fig, axes = plt.subplots(ncols=2, figsize=(12, 4)) axes[0].scatter(X_train, T_train, marker=".") axes[0].plot(X_train, clf.predict(X_train), color="red") axes[0].set_title("train") axes[1].scatter(X_test, T_test, marker=".") axes[1].plot(X_test, clf.predict(X_test), color="red") axes[1].set_title("test") fig.show() ``` 自分のコードと同じ結果が出ただろうか？また, データを shuffle せず得られた回帰直線のスコアと, shuffleした時の回帰直線のスコアの比較もしてみよう. scikit-learn の linear regression のコードは [github][1] で公開されている. コーディングの参考になると思うので眺めてみるといいだろう. ### 5-2-2. 回帰モデルの評価性能を測るといっても，その目的によって指標を変える必要がある. どのような問題で，どのような指標を用いることが一般的か？という問いに対しては，先行研究を確認することを勧める．また，指標それぞれの特性(数学的な意味)を知っていることもその役に立つだろう． [参考][2] 回帰モデルの評価に用いられる指標は一般にMAE, MSE, 決定係数などが存在する. 1. MAE 2. MSE 3. 決定係数 scikit-learn はこれらの計算をするモジュールも用意されている. [1]:https://github.com/scikit-learn/scikit-learn/blob/1495f69242646d239d89a5713982946b8ffcf9d9/sklearn/linear_model/base.py#L367 [2]:https://scikit-learn.org/stable/modules/model_evaluation.html ``` from sklearn import metrics T_pred = clf.predict(X_test) print("MAE: ", metrics.mean_absolute_error(T_test, T_pred)) print("MSE: ", metrics.mean_squared_error(T_test, T_pred)) print("決定係数: ", metrics.r2_score(T_test, T_pred)) ``` ### 5-2-3. scikit-learn の他モデルを使ってみよう ``` # 1. データセットを用意する from sklearn import datasets iris = datasets.load_iris() # ここではIrisデータセットを読み込む print(iris.data[0], iris.target[0]) # 1番目のサンプルのデータとラベル # 2.学習用データとテスト用データに分割する from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target) # 3. 線形SVMという手法を用いて分類する from sklearn.svm import SVC, LinearSVC clf = LinearSVC() clf.fit(X_train, y_train) # 学習 # 4. 分類器の性能を測る y_pred = clf.predict(X_test) # 予測 print(metrics.classification_report(y_true=y_test, y_pred=y_pred)) # 予測結果の評価 ``` ### 5-2-4. 分類モデルの評価分類問題に対する指標について考えてみよう．一般的な指標だけでも以下の4つがある． 1. 正解率(accuracy) 2. 精度(precision) 3. 再現率(recall) 4. F値(F1-score) （精度，再現率，F値にはmacro, micro, weightedなどがある）今回の実験でのそれぞれの値を見てみよう． ``` print('accuracy: ', metrics.accuracy_score(y_test, y_pred)) print('precision:', metrics.precision_score(y_test, y_pred, average='macro')) print('recall: ', metrics.recall_score(y_test, y_pred, average='macro')) print('F1 score: ', metrics.f1_score(y_test, y_pred, average='macro')) ``` ## 5-3. 問題に合わせたコーディング ### 5-3-1. Irisデータの可視化 Irisデータは4次元だったので，直接可視化することはできない． 4次元のデータをPCAによって圧縮して，2次元にし可視化する． ``` from sklearn.decomposition import PCA from sklearn import datasets iris = datasets.load_iris() pca = PCA(n_components=2) X, y = iris.data, iris.target X_pca = pca.fit_transform(X) # 次元圧縮 print(X_pca.shape) import matplotlib.pyplot as plt %matplotlib inline plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y); # 次元圧縮したデータを用いて分類してみる X_train, X_test, y_train, y_test = train_test_split(X_pca, iris.target) clf = LinearSVC() clf.fit(X_train, y_train) y_pred2 = clf.predict(X_test) from sklearn import metrics print(metrics.classification_report(y_true=y_test, y_pred=y_pred2)) # 予測結果の評価 ``` ### 5-3-2. テキストに対する処理 #### テキストから特徴量を設計テキストのカウントベクトルを作成し，TF-IDFを用いて特徴ベクトルを作る．いくつかの設計ができるが，例題としてこの手法を用いる．ここでは，20newsgroupsというデータセットを利用する． ``` from sklearn.datasets import fetch_20newsgroups categories = ['alt.atheism', 'soc.religion.christian','comp.graphics', 'sci.med'] news_train = fetch_20newsgroups(subset='train', categories=categories, shuffle=True, random_state=42) from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer count_vec = CountVectorizer() X_train_counts = count_vec.fit_transform(news_train.data) tf_transformer = TfidfTransformer(use_idf=False).fit(X_train_counts) X_train_tf = tf_transformer.transform(X_train_counts) ``` #### Naive Bayseによる学習 ``` from sklearn.naive_bayes import MultinomialNB clf = MultinomialNB().fit(X_train_tf, news_train.target) docs = ["God is love.", "I study about Computer Science."] X_test_counts = count_vec.transform(docs) X_test_tf = tf_transformer.transform(X_test_counts) preds = clf.predict(X_test_tf) for d, label_id in zip(docs, preds): print("{} -> {}".format(d, news_train.target_names[label_id])) ``` このように文に対して，categoriesのうちのどれに対応するかを出力する学習器を作ることができた．この技術を応用することで，ある文がポジティブかネガティブか，スパムか否かなど自然言語の文に対する分類問題を解くことができる． ### 5-3-3. Pipelineによる結合 ``` from sklearn.pipeline import Pipeline text_clf = Pipeline([('countvec', CountVectorizer()), ('tfidf', TfidfTransformer()), ('clf', MultinomialNB())]) text_clf.fit(news_train.data, news_train.target) for d, label_id in zip(docs, text_clf.predict(docs)): print("{} -> {}".format(d, news_train.target_names[label_id])) ``` ## 5.4 scikit-learn 準拠コーディング scikit-learn　準拠でコーディングするメリットは多数存在する. 1. scikit-learn の用意するgrid search や cross validation を使える. 2. 既存のscikit-learn の他手法と入れ替えが容易になる. 3. 他の人にみてもらいやすい。使ってもらいやすい. 4. <span style="color: gray; ">本家のコミッターになれるかも？</span> 詳しくは　[Developer’s Guide][1]　に書いてある. [1]:https://scikit-learn.org/stable/developers/#rolling-your-own-estimator scikit-learn ではモデルは以下の4つのタイプに分類されている. - Classifer - Naive Bayes Classifer などの分類モデル - Clusterring - K-mearns 等のクラスタリングモデル - Regressor - Lasso, Ridge などの回帰モデル - Transformer - PCA などの変数の変換モデル *準拠コーディングでやるべきことは、* - sklearn.base.BaseEstimatorを継承する - 上記タイプに応じたMixinを多重継承する (予測モデルの場合) - fitメソッドを実装する - initでパラメータをいじる操作を入れるとgrid searchが動かなくなる（後述） - predictメソッドを実装する ### 5-4-1.　リッジ回帰のscikit-learn 準拠コーディング試しに今までにコーディングした MyLinearRegression を改造し, scikit-learn 準拠にコーディングし直してみよう. ついでにリッジ回帰の選択ができるようにもしてみよう. ``` from sklearn.base import BaseEstimator, RegressorMixin from sklearn.utils.validation import check_X_y, check_is_fitted, check_array ``` 回帰なので BaseEstimator と RegressorMixin の継承をする. さらにリッジ回帰のオプションも追加するため, initにハイパーパラメータも追加する. 入力のshapeやdtypeを整えるために```check_X_y```や```check_array```を用いる(推奨). ``` class MyLinearRegression(BaseEstimator, RegressorMixin): def __init__(self, lam = 0): """ Initialize a coefficient and an intercept. """ self.a = self.b = self.lam = lam def fit(self, X, y): """ X: array-like, shape (n_samples, n_features) y: array, shape (n_samples,) Estimate a coefficient and an intercept　from data. """ X, y = check_X_y(X, y, y_numeric=True) if self.lam != 0: pass else: pass self.a_ = self.b_ = return self def predict(self, X): """ Calc y from X """ check_is_fitted(self, "a_", "b_") # 学習済みかチェックする(推奨) X = check_array(X) return y ``` *制約* - initで宣言する変数に全て初期値を定める - また引数の変数名とクラス内の変数名は一致させる - initにデータは与えない。データの加工なども(必要なら)fit内で行う - データから推定された値はアンダースコアをつけて区別する. 今回なら、a_と b_をfit関数内で新しく定義する. - アンダースコアで終わる変数をinit内では宣言しないこと. - init内で引数の確認, 加工をしてはいけない. 例えば```self.lam=2*lam```などをするとgrid searchができなくなる. [参考][1] > As model_selection.GridSearchCV uses set_params to apply parameter setting to estimators, it is essential that calling set_params has the same effect as setting parameters using the __init__ method. The easiest and recommended way to accomplish this is to not do any parameter validation in __init__. All logic behind estimator parameters, like translating string arguments into functions, should be done in fit. [github][2]のコードをお手本にしてみるのもいいだろう. [1]:https://scikit-learn.org/stable/developers/contributing.html#coding-guidelines [2]:https://github.com/scikit-learn/scikit-learn/blob/1495f69242646d239d89a5713982946b8ffcf9d9/sklearn/linear_model/base.py#L367 ### 5-4-2. scikit-learn 準拠かどうか確認自作のコードがちゃんとscikit-learn準拠かどうか確かめるには以下を実行する. ``` from sklearn.utils.estimator_checks import check_estimator check_estimator(MyLinearRegression) ``` 問題があれば指摘してくれるはずだ. なお上記を必ずパスする必要はない. #### Grid Search 準拠モデルを作ったなら, ハイパーパラメータの決定をscikit-learnでやってみよう. ``` import numpy as np from sklearn.model_selection import GridSearchCV np.random.seed(0) # Grid search parameters = {'lam':np.exp([i for i in range(-30,1)])} reg = GridSearchCV(MyLinearRegression(),parameters,cv=5) reg.fit(X_train,T_train) best = reg.best_estimator_ # 決定係数 print("決定係数: ", best.score(X_train, T_train)) # BaseEstimatorを継承しているため使える # lambda print("lam: ", best.lam) fig, axes = plt.subplots(ncols=2, figsize=(12, 4)) axes[0].scatter(X_train, T_train, marker=".") axes[0].plot(X_train, best.predict(X_train), color="red") axes[0].set_title("train") axes[1].scatter(X_test, T_test, marker=".") axes[1].plot(X_test, best.predict(X_test), color="red") axes[1].set_title("test") fig.show() ``` ## [練習問題](./../exercise/questions.md#chapter-5)	github_jupyter
## Conditional Probability - Conditional probability has many applications, we learn it by mentioning its application in text analysis - Assume this small dataset is given: <img src="spam_ham_data_set.png" width="600" height="600"> ## Question: What is the probability that an email be spam? What is the probability that an email be ham? - $P(spam) = ?$ - $P(ham) = ?$ ## Question: We know an email is spam, what is the probability that password be a word in it? (What is the frequency of password in a spam email?) - Hint: Create the dictionary of spam where its key would be unique words in spam emails and the value shows the occurance of that word ``` spam = { "password": 2, "review": 1, "send": 3, "us": 3, "your": 3, "account": 1 } ``` $P(password \mid spam) = 2/(2+1+3+3+3+1) = 2/13$ ``` # or p_password_given_spam = spam['password']/sum(spam.values()) print(p_password_given_spam) ``` ## Question: We know an email is ham, what is the probability that password be a word in it? (What is the frequency of password in a ham email?) - Hint: Create the dictionary of ham where its key would be unique words in spam emails and the value shows the occurance of that word ``` ham = { "password": 1, "review": 2, "send": 1, "us": 1, "your": 2, "account": 0 } ``` $P(password \mid ham) = 1/(1+2+1+1+1+0) = 1/6$ ``` # or p_password_given_ham = ham['password']/sum(ham.values()) print(p_password_given_ham) ``` ## Question: Assume we have seen password in an email, what is the probability that the email be spam? - $P(spam \mid password) = ?$ - Hint: Use Bayes' rule: $P(spam \mid password) = (P(password \mid spam) P(spam))/ P(password)$ $P(password) = P(password \mid spam) P(spam) + P(password \mid ham) P(ham)$ ``` p_spam = 4/6 p_ham = 2/6 p_password = p_password_given_spamp_spam + p_password_given_hamp_ham print(p_password) p_spam_given_password = p_password_given_spamp_spam/p_password print(p_spam_given_password) ``` ## Activity: Do the above computation for each word by writing code ``` p_spam = 4/6 p_ham = 2/6 ls1 = [] ls2 = [] for i in spam: print(i) p_word_given_spam = # TODO p_word_given_ham = # TODO # obtain the probability of each word by assuming the email is spam # obtain the probability of each word by assuming the email is ham #TODO # obtain the probability that for a seen word it belongs to spam email # obtain the probability that for a seen word it belongs to ham email #TODO ``` ## Quiz: Compute the expected value of a fair dice By Definition, the expected value of random events (a random variable) like rolling a dice is computed as: $E(X) = \sum_{i=1}^{6}i P(dice = i)$ <img src="dice.jpg" width="100" height="100"> 1- For a fair dice, compute the probability that when roll the dice then 1 apprears (P(dice = 1)), compute the probability that when roll the dice then 2 apprears (P(dice = 2)), . . . compute the probability that when roll the dice then 2 apprears (P(dice = 6)) 2- Compute $E(X)$ from the above steps. ### Answer: The expected value for a fair dice is: $E(X) = (11/6) + (21/6) + (31/6)+ (41/6) + (51/6) + (61/6)$ $E(X) = 3.5$ ``` # We can show that E(X) is the mean of the random variable import numpy as np # lets roll the dice 1000 times dice = np.random.randint(low=1.0, high=7.0, size=1000) print(dice) # Compute the mean of dice list print(np.mean(dice)) print(sum(dice)/len(dice)) ```	github_jupyter
# Chapter 12 - Principal Components Analysis with scikit-learn This notebook contains code accompanying Chapter 12 Principal Components Analysis with scikit-learn in Practical Discrete Mathematics by Ryan T. White and Archana Tikayat Ray. ## Eigenvalues and eigenvectors, orthogonal bases ### Example: Pizza nutrition ``` import pandas as pd dataset = pd.read_csv('pizza.csv') dataset.head() ``` ### Example: Computing eigenvalues and eigenvectors ``` import numpy as np A = np.array([[3,1], [1,3]]) l, v = np.linalg.eig(A) print("The eigenvalues are:\n ",l) print("The eigenvectors are:\n ", v) ``` ## The scikit-learn implementation of PCA We will start by importing the dataset and then dropping the brand column from it. This is done to make sure that all our feature variables are numbers and hence can be scaled/normalized. We will then create another variable called target which will contain the names of the brands of pizzas. ``` import pandas as pd dataset = pd.read_csv('pizza.csv') #Dropping the brand name column before standardizing the data df_num = dataset.drop(["brand"], axis=1) # Setting the brand name column as the target variable target = dataset['brand'] ``` Now that we have the dataset in order, we will then normalize the columns of the dataset to make sure that the mean for a variable is 0 and the variance is 1 and then we will run PCA on the dataset. ``` #Scaling the data from sklearn.preprocessing import StandardScaler scaler = StandardScaler() scaler.fit(df_num) scaled_data = scaler.transform(df_num) #Applying PCA to the scaled data from sklearn.decomposition import PCA #Reducing the dimesions to 2 components so that we can have a 2D visualization pca = PCA(n_components = 2) pca.fit(scaled_data) #Applying to our scaled dataset scaled_data_pca = pca.transform(scaled_data) #Check the shape of the original dataset and the new dataset print("The dimensions of the original dataset is: ", scaled_data.shape) print("The dimensions of the dataset after performing PCA is: ", scaled_data_pca.shape) ``` Now we have reduced our 7-dimensional dataset to its 2 principal components as can be seen from the dimensions shown above. We will move forward with plotting the principal components to check whether 2 principal components were enough to capture the variability in the dataset – the different nutritional content of pizzas produced by different companies. ``` #Plotting the principal components import matplotlib.pyplot as plt import seaborn as sns sns.scatterplot(scaled_data_pca[:,0], scaled_data_pca[:,1], target) plt.legend(loc="best") plt.gca().set_aspect("equal") plt.xlabel("Principal Component 1") plt.ylabel("Principal Component 2") plt.show() ``` Now, we will move on to perform PCA in a way where we do not choose the number of desired principal components, rather we choose the number of principal components that add up to a certain desired variance. The Python implementation of this is very similar to the previous way with very slight changes to the code as shown below. ``` import pandas as pd dataset = pd.read_csv('pizza.csv') #Dropping the brand name column before standardizing the data df_num = dataset.drop(["brand"], axis=1) # Setting the brand name column as the target variable target = dataset['brand'] #Scaling the data (Step 1) from sklearn.preprocessing import StandardScaler scaler = StandardScaler() scaler.fit(df_num) scaled_data = scaler.transform(df_num) #Applying PCA to the scaled data from sklearn.decomposition import PCA #Setting the variance to 0.95 pca = PCA(n_components = 0.95) pca.fit(scaled_data) #Applying to our scaled dataset scaled_data_pca = pca.transform(scaled_data) #Check the shape of the original dataset and the new dataset print("The dimensions of the original dataset are: ", scaled_data.shape) print("The dimensions of the dataset after performing PCA is: ", scaled_data_pca.shape) ``` As we can see from the above output, 3 principal components are required to capture 95% of the variance in the dataset. This means that by choosing 2 principal directions previously, we were capturing < 95% of the variance in the dataset. Despite capturing < 95% of the variance, we were able to visualize the fact that the pizzas produced by different companies have different nutritional contents. ## An application to real-world data The first step is to import the data as shown below. It is going to take some time since it is a big dataset, hence hang tight. The dataset contains images of 70000 digits (0-9) where each image has 784 features. ``` #Importing the dataset from sklearn.datasets import fetch_openml mnist_data = fetch_openml('mnist_784', version = 1) # Choosing the independent (X) and dependent variables (y) X,y = mnist_data["data"], mnist_data["target"] ``` Now that we have the dataset imported, we will move on to visualize the image of a digit to get familiar with the dataset. For visualization, we will use the `matplotlib` library. We will visualize the 50000th digit image. Feel free to check out other digit images of your choice – make sure to use an index between 0 and 69999. We will set colormap to "binary" to output a grayscale image. ``` #Plotting one of the digits import matplotlib.pyplot as plt plt.figure(1) #Plotting the 50000th digit digit = X[50000] #Reshaping the 784 features into a 28x28 matrix digit_image = digit.reshape(28,28) plt.imshow(digit_image, cmap='binary') plt.show() ``` Next, we will apply PCA to this dataset to reduce its dimension from $28*28=784$ to a lower number. We will plot the proportion of the variation that is reflected by PCA-reduced dimensional data of different dimensions. ``` #Scaling the data from sklearn.preprocessing import StandardScaler scaled_mnist_data = StandardScaler().fit_transform(X) print(scaled_mnist_data.shape) #Applying PCA to ur dataset from sklearn.decomposition import PCA pca = PCA(n_components=784) mnist_data_pca = pca.fit_transform(scaled_mnist_data) #Calculating cumulative variance captured by PCs import numpy as np variance_percentage = pca.explained_variance_/np.sum(pca.explained_variance_) #Calculating cumulative variance cumulative_variance = np.cumsum(variance_percentage) #Plotting cumalative variance import matplotlib.pyplot as plt plt.figure(2) plt.plot(cumulative_variance) plt.xlabel('Number of principal components') plt.ylabel('Cumulative variance explained by PCs') plt.grid() plt.show() ```	github_jupyter
<a href="https://qworld.net" target="_blank" align="left"><img src="../qworld/images/header.jpg" align="left"></a> $ \newcommand{\bra}[1]{\langle #1\|} $ $ \newcommand{\ket}[1]{\|#1\rangle} $ $ \newcommand{\braket}[2]{\langle #1\|#2\rangle} $ $ \newcommand{\dot}[2]{ #1 \cdot #2} $ $ \newcommand{\biginner}[2]{\left\langle #1,#2\right\rangle} $ $ \newcommand{\mymatrix}[2]{\left( \begin{array}{#1} #2\end{array} \right)} $ $ \newcommand{\myvector}[1]{\mymatrix{c}{#1}} $ $ \newcommand{\myrvector}[1]{\mymatrix{r}{#1}} $ $ \newcommand{\mypar}[1]{\left( #1 \right)} $ $ \newcommand{\mybigpar}[1]{ \Big( #1 \Big)} $ $ \newcommand{\sqrttwo}{\frac{1}{\sqrt{2}}} $ $ \newcommand{\dsqrttwo}{\dfrac{1}{\sqrt{2}}} $ $ \newcommand{\onehalf}{\frac{1}{2}} $ $ \newcommand{\donehalf}{\dfrac{1}{2}} $ $ \newcommand{\hadamard}{ \mymatrix{rr}{ \sqrttwo & \sqrttwo \\ \sqrttwo & -\sqrttwo }} $ $ \newcommand{\vzero}{\myvector{1\\0}} $ $ \newcommand{\vone}{\myvector{0\\1}} $ $ \newcommand{\stateplus}{\myvector{ \sqrttwo \\ \sqrttwo } } $ $ \newcommand{\stateminus}{ \myrvector{ \sqrttwo \\ -\sqrttwo } } $ $ \newcommand{\myarray}[2]{ \begin{array}{#1}#2\end{array}} $ $ \newcommand{\X}{ \mymatrix{cc}{0 & 1 \\ 1 & 0} } $ $ \newcommand{\I}{ \mymatrix{rr}{1 & 0 \\ 0 & 1} } $ $ \newcommand{\Z}{ \mymatrix{rr}{1 & 0 \\ 0 & -1} } $ $ \newcommand{\Htwo}{ \mymatrix{rrrr}{ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} } } $ $ \newcommand{\CNOT}{ \mymatrix{cccc}{1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0} } $ $ \newcommand{\norm}[1]{ \left\lVert #1 \right\rVert } $ $ \newcommand{\pstate}[1]{ \lceil \mspace{-1mu} #1 \mspace{-1.5mu} \rfloor } $ $ \newcommand{\greenbit}[1] {\mathbf{{\color{green}#1}}} $ $ \newcommand{\bluebit}[1] {\mathbf{{\color{blue}#1}}} $ $ \newcommand{\redbit}[1] {\mathbf{{\color{red}#1}}} $ $ \newcommand{\brownbit}[1] {\mathbf{{\color{brown}#1}}} $ $ \newcommand{\blackbit}[1] {\mathbf{{\color{black}#1}}} $ <font style="font-size:28px;" align="left"><b> <font color="blue"> Solutions for </font>Phase Kickback </b></font> <br> _prepared by Abuzer Yakaryilmaz_ <br><br> <a id="task1"></a> <h3> Task 1</h3> Create a quantum circuit with two qubits, say $ q[1] $ and $ q[0] $ in the reading order of Qiskit. We start in quantum state $ \ket{01} $: - set the state of $ q[1] $ to $ \ket{0} $, and - set the state of $ q[0] $ to $ \ket{1} $. Apply Hadamard to both qubits. Apply CNOT operator, where the controller qubit is $ q[1] $ and the target qubit is $ q[0] $. Apply Hadamard to both qubits. Measure the outcomes. <h3> Solution </h3> ``` # import all necessary objects and methods for quantum circuits from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer q = QuantumRegister(2,"q") # quantum register with 2 qubits c = ClassicalRegister(2,"c") # classical register with 2 bits qc = QuantumCircuit(q,c) # quantum circuit with quantum and classical registers # the up qubit is in \|0> # set the down qubit to \|1> qc.x(q[0]) # apply x-gate (NOT operator) qc.barrier() # apply Hadamard to both qubits. qc.h(q[0]) qc.h(q[1]) # apply CNOT operator, where the controller qubit is the up qubit and the target qubit is the down qubit. qc.cx(1,0) # apply Hadamard to both qubits. qc.h(q[0]) qc.h(q[1]) # measure both qubits qc.measure(q,c) # draw the circuit in Qiskit reading order display(qc.draw(output='mpl',reverse_bits=True)) # execute the circuit 100 times in the local simulator job = execute(qc,Aer.get_backend('qasm_simulator'),shots=100) counts = job.result().get_counts(qc) print(counts) ``` <a id="task2"></a> <h3> Task 2 </h3> Create a circuit with 7 qubits, say $ q[6],\ldots,q[0] $ in the reading order of Qiskit. Set the states of the top six qubits to $ \ket{0} $. Set the state of the bottom qubit to $ \ket{1} $. Apply Hadamard operators to all qubits. Apply CNOT operator ($q[1]$,$q[0]$) <br> Apply CNOT operator ($q[4]$,$q[0]$) <br> Apply CNOT operator ($q[5]$,$q[0]$) Apply Hadamard operators to all qubits. Measure all qubits. For each CNOT operator, is there a phase-kickback effect? <h3> Solution </h3> ``` # import all necessary objects and methods for quantum circuits from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer # Create a circuit with 7 qubits. q = QuantumRegister(7,"q") # quantum register with 7 qubits c = ClassicalRegister(7) # classical register with 7 bits qc = QuantumCircuit(q,c) # quantum circuit with quantum and classical registers # the top six qubits are already in \|0> # set the bottom qubit to \|1> qc.x(0) # apply x-gate (NOT operator) # define a barrier qc.barrier() # apply Hadamard to all qubits. for i in range(7): qc.h(q[i]) # define a barrier qc.barrier() # apply CNOT operator (q[1],q[0]) # apply CNOT operator (q[4],q[0]) # apply CNOT operator (q[5],q[0]) qc.cx(q[1],q[0]) qc.cx(q[4],q[0]) qc.cx(q[5],q[0]) # define a barrier qc.barrier() # apply Hadamard to all qubits. for i in range(7): qc.h(q[i]) # define a barrier qc.barrier() # measure all qubits qc.measure(q,c) # draw the circuit in Qiskit reading order display(qc.draw(output='mpl',reverse_bits=True)) # execute the circuit 100 times in the local simulator job = execute(qc,Aer.get_backend('qasm_simulator'),shots=100) counts = job.result().get_counts(qc) print(counts) ```	github_jupyter
``` import numpy as np import torch use_cuda = torch.cuda.is_available() device = torch.device("cuda:0" if use_cuda else "cpu") device import torchvision from torchvision import models from torchvision import transforms import os import glob from PIL import Image from torch.utils.data import Dataset, DataLoader import matplotlib.pyplot as plt from torchvision import models from random import randint # tensor -> PIL image unloader = transforms.ToPILImage() # flip = transforms.RandomHorizontalFlip(p=1) class ToyDataset(Dataset): def __init__(self, dark_img_dir, light_img_dir): self.dark_img_dir = dark_img_dir self.light_img_dir = light_img_dir self.n_dark = len(os.listdir(self.dark_img_dir)) self.n_light = len(os.listdir(self.light_img_dir)) def __len__(self): return min(self.n_dark, self.n_light) def __getitem__(self, idx): filename = os.listdir(self.light_img_dir)[idx] light_img_path = f"{self.light_img_dir}{filename}" light = Image.open(light_img_path).convert("RGB") dark_img_path = f"{self.dark_img_dir}{filename}" dark = Image.open(dark_img_path).convert("RGB") # if random()>0.5: # light = transforms.functional.rotate(light, 30) # dark = transforms.functional.rotate(dark, 30) # if random()>0.5: # light = transforms.functional.rotate(light, 330) # dark = transforms.functional.rotate(dark, 330) # if random()>0.5: # light = flip(light) # dark = flip(dark) s = randint(600, 700) transform = transforms.Compose([ transforms.Resize(s), transforms.CenterCrop(512), transforms.ToTensor(), ]) light = transform(light) dark = transform(dark) return dark, light batch_size = 1 train_dark_dir = f"./data/train/dark/" train_light_dir = f"./data/train/light/" training_set = ToyDataset(train_dark_dir,train_light_dir) training_generator = DataLoader(training_set, batch_size=batch_size, shuffle=True) val_dark_dir = f"./data/test/dark/" val_light_dir = f"./data/test/light/" validation_set = ToyDataset(val_dark_dir, val_light_dir) validation_generator = DataLoader(validation_set, batch_size=batch_size, shuffle=True) # generate training images n = 1 cycle = 5 dark_save_path = "./data_augment/train/dark/" light_save_path = "./data_augment/train/light/" for i in range(cycle): for item in training_generator: dark, light = item dark = unloader(dark[0,]) light = unloader(light[0,]) dark.save(dark_save_path+f"{n}.jpg") light.save(light_save_path+f"{n}.jpg") n += 1 # generate testing images n = 1 cycle = 1 dark_save_path = "./data_augment/test/dark/" light_save_path = "./data_augment/test/light/" for i in range(cycle): for item in validation_generator: dark, light = item dark = unloader(dark[0,]) light = unloader(light[0,]) dark.save(dark_save_path+f"{n}.jpg") light.save(light_save_path+f"{n}.jpg") n += 1 ```	github_jupyter
# Global Imports ``` %matplotlib inline import matplotlib.pyplot as plt from matplotlib.pyplot import subplots ``` ### External Package Imports ``` import os as os import pickle as pickle import pandas as pd ``` ### Module Imports Here I am using a few of my own packages, they are availible on Github under [__theandygross__](https://github.com/theandygross) and should all be instalable by <code>python setup.py</code>. ``` from Stats.Scipy import * from Stats.Survival import * from Helpers.Pandas import * from Helpers.LinAlg import * from Figures.FigureHelpers import * from Figures.Pandas import * from Figures.Boxplots import * from Figures.Regression import * #from Figures.Survival import draw_survival_curve, survival_and_stats #from Figures.Survival import draw_survival_curves #from Figures.Survival import survival_stat_plot import Data.Firehose as FH from Data.Containers import get_run ``` ### Import Global Parameters * These need to be changed before you will be able to sucessfully run this code ``` import NotebookImport from Global_Parameters import * ``` ### Tweaking Display Parameters ``` pd.set_option('precision', 3) pd.set_option('display.width', 300) plt.rcParams['font.size'] = 12 '''Color schemes for paper taken from http://colorbrewer2.org/''' colors = plt.rcParams['axes.color_cycle'] colors_st = ['#CA0020', '#F4A582', '#92C5DE', '#0571B0'] colors_th = ['#E66101', '#FDB863', '#B2ABD2', '#5E3C99'] import seaborn as sns sns.set_context('paper',font_scale=1.5) sns.set_style('white') ``` ### Read in All of the Expression Data This reads in data that was pre-processed in the [./Preprocessing/init_RNA](../Notebooks/init_RNA.ipynb) notebook. ``` codes = pd.read_hdf(RNA_SUBREAD_STORE, 'codes') matched_tn = pd.read_hdf(RNA_SUBREAD_STORE, 'matched_tn') rna_df = pd.read_hdf(RNA_SUBREAD_STORE, 'all_rna') data_portal = pd.read_hdf(RNA_STORE, 'matched_tn') genes = data_portal.index.intersection(matched_tn.index) pts = data_portal.columns.intersection(matched_tn.columns) rna_df = rna_df.ix[genes] matched_tn = matched_tn.ix[genes, pts] ``` ### Read in Gene-Sets for GSEA ``` from Data.Annotations import unstack_geneset_csv gene_sets = unstack_geneset_csv(GENE_SETS) gene_sets = gene_sets.ix[rna_df.index].fillna(0) ``` Initialize function for calling model-based gene set enrichment ``` from rpy2 import robjects from rpy2.robjects import pandas2ri pandas2ri.activate() mgsa = robjects.packages.importr('mgsa') gs_r = robjects.ListVector({i: robjects.StrVector(list(ti(g>0))) for i,g in gene_sets.iteritems()}) def run_mgsa(vec): v = robjects.r.c(ti(vec)) r = mgsa.mgsa(v, gs_r) res = pandas2ri.ri2pandas(mgsa.setsResults(r)) return res ``` ### Function Tweaks Running the binomial test across 450k probes in the same test space, we rerun the same test a lot. Here I memoize the function to cache results and not recompute them. This eats up a couple GB of memory but should be reasonable. ``` from scipy.stats import binom_test def memoize(f): memo = {} def helper(x,y,z): if (x,y,z) not in memo: memo[(x,y,z)] = f(x,y,z) return memo[(x,y,z)] return helper binom_test_mem = memoize(binom_test) def binomial_test_screen(df, fc=1.5, p=.5): """ Run a binomial test on a DataFrame. df: DataFrame of measurements. Should have a multi-index with subjects on the first level and tissue type ('01' or '11') on the second level. fc: Fold-chance cutoff to use """ a, b = df.xs('01', 1, 1), df.xs('11', 1, 1) dx = a - b dx = dx[dx.abs() > np.log2(fc)] n = dx.count(1) counts = (dx > 0).sum(1) cn = pd.concat([counts, n], 1) cn = cn[cn.sum(1) > 0] b_test = cn.apply(lambda s: binom_test_mem(s[0], s[1], p), axis=1) dist = (1.cn[0] / cn[1]) tab = pd.concat([cn[0], cn[1], dist, b_test], keys=['num_ox', 'num_dx', 'frac', 'p'], axis=1) return tab ``` Added linewidth and number of bins arguments. This should get pushed eventually. ``` def draw_dist(vec, split=None, ax=None, legend=True, colors=None, lw=2, bins=300): """ Draw a smooth distribution from data with an optional splitting factor. """ _, ax = init_ax(ax) if split is None: split = pd.Series('s', index=vec.index) colors = {'s': colors} if colors is not None else None for l,v in vec.groupby(split): if colors is None: smooth_dist(v, bins=bins).plot(label=l, lw=lw, ax=ax) else: smooth_dist(v, bins=bins).plot(label=l, lw=lw, ax=ax, color=colors[l]) if legend and len(split.unique()) > 1: ax.legend(loc='upper left', frameon=False) ``` Some helper functions for fast calculation of odds ratios on matricies. ``` def odds_ratio_df(a,b): a = a.astype(int) b = b.astype(int) flip = lambda v: (v == 0).astype(int) a11 = (a.add(b) == 2).sum(axis=1) a10 = (a.add(flip(b)) == 2).sum(axis=1) a01 = (flip(a).add(b) == 2).sum(axis=1) a00 = (flip(a).add(flip(b)) == 2).sum(axis=1) odds_ratio = (1.a11 a00) / (1.a10 a01) df = pd.concat([a00, a01, a10, a11], axis=1, keys=['00','01','10','11']) return odds_ratio, df def fet(s): odds, p = stats.fisher_exact([[s['00'],s['01']], [s['10'],s['11']]]) return p ``` #### filter_pathway_hits ``` def filter_pathway_hits(hits, gs, cutoff=.00001): ''' Takes a vector of p-values and a DataFrame of binary defined gene-sets. Uses the ordering defined by hits to do a greedy filtering on the gene sets. ''' l = [hits.index[0]] for gg in hits.index: flag = 0 for g2 in l: if gg in l: flag = 1 break elif (chi2_cont_test(gs[gg], gs[g2])['p'] < cutoff): flag = 1 break if flag == 0: l.append(gg) hits_filtered = hits.ix[l] return hits_filtered ```	github_jupyter
# Advanced usage This notebook shows some more advanced features of `skorch`. More examples will be added with time. <table align="left"><td> <a target="_blank" href="https://colab.research.google.com/github/skorch-dev/skorch/blob/master/notebooks/Advanced_Usage.ipynb"> <img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a> </td><td> <a target="_blank" href="https://github.com/skorch-dev/skorch/blob/master/notebooks/Advanced_Usage.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a></td></table> ### Table of contents * [Setup](#Setup) * [Callbacks](#Callbacks) * [Writing your own callback](#Writing-a-custom-callback) * [Accessing callback parameters](#Accessing-callback-parameters) * [Working with different data types](#Working-with-different-data-types) * [Working with datasets](#Working-with-Datasets) * [Working with dicts](#Working-with-dicts) * [Multiple return values](#Multiple-return-values-from-forward) * [Implementing a simple autoencoder](#Implementing-a-simple-autoencoder) * [Training the autoencoder](#Training-the-autoencoder) * [Extracting the decoder and the encoder output](#Extracting-the-decoder-and-the-encoder-output) ``` ! [ ! -z "$COLAB_GPU" ] && pip install torch skorch import torch from torch import nn import torch.nn.functional as F torch.manual_seed(0) torch.cuda.manual_seed(0) ``` ## Setup ### A toy binary classification task We load a toy classification task from `sklearn`. ``` import numpy as np from sklearn.datasets import make_classification np.random.seed(0) X, y = make_classification(1000, 20, n_informative=10, random_state=0) X, y = X.astype(np.float32), y.astype(np.int64) X.shape, y.shape, y.mean() ``` ### Definition of the `pytorch` classification `module` We define a vanilla neural network with two hidden layers. The output layer should have 2 output units since there are two classes. In addition, it should have a softmax nonlinearity, because later, when calling `predict_proba`, the output from the `forward` call will be used. ``` from skorch import NeuralNetClassifier class ClassifierModule(nn.Module): def __init__( self, num_units=10, nonlin=F.relu, dropout=0.5, ): super(ClassifierModule, self).__init__() self.num_units = num_units self.nonlin = nonlin self.dropout = dropout self.dense0 = nn.Linear(20, num_units) self.nonlin = nonlin self.dropout = nn.Dropout(dropout) self.dense1 = nn.Linear(num_units, 10) self.output = nn.Linear(10, 2) def forward(self, X, *kwargs): X = self.nonlin(self.dense0(X)) X = self.dropout(X) X = F.relu(self.dense1(X)) X = F.softmax(self.output(X), dim=-1) return X ``` ## Callbacks Callbacks are a powerful and flexible way to customize the behavior of your neural network. They are all called at specific points during the model training, e.g. when training starts, or after each batch. Have a look at the `skorch.callbacks` module to see the callbacks that are already implemented. ### Writing a custom callback Although `skorch` comes with a handful of useful callbacks, you may find that you would like to write your own callbacks. Doing so is straightforward, just remember these rules: They should inherit from `skorch.callbacks.Callback`. * They should implement at least one of the `on_`-methods provided by the parent class (e.g. `on_batch_begin` or `on_epoch_end`). * As argument, the `on_`-methods first get the `NeuralNet` instance, and, where appropriate, the local data (e.g. the data from the current batch). The method should also have `*kwargs` in the signature for potentially unused arguments. Optional: If you have attributes that should be reset when the model is re-initialized, those attributes should be set in the `initialize` method. Here is an example of a callback that remembers at which epoch the validation accuracy reached a certain value. Then, when training is finished, it calls a mock Twitter API and tweets that epoch. We proceed as follows: * We set the desired minimum accuracy during `__init__`. * We set the critical epoch during `initialize`. * After each epoch, if the critical accuracy has not yet been reached, we check if it was reached. * When training finishes, we send a tweet informing us whether our training was successful or not. ``` from skorch.callbacks import Callback def tweet(msg): print("~" * 60) print("tweet", msg, "#skorch #pytorch") print("~" * 60) class AccuracyTweet(Callback): def __init__(self, min_accuracy): self.min_accuracy = min_accuracy def initialize(self): self.critical_epoch_ = -1 def on_epoch_end(self, net, kwargs): if self.critical_epoch_ > -1: return # look at the validation accuracy of the last epoch if net.history[-1, 'valid_acc'] >= self.min_accuracy: self.critical_epoch_ = len(net.history) def on_train_end(self, net, kwargs): if self.critical_epoch_ < 0: msg = "Accuracy never reached {} :(".format(self.min_accuracy) else: msg = "Accuracy reached {} at epoch {}!!!".format( self.min_accuracy, self.critical_epoch_) tweet(msg) ``` Now we initialize a `NeuralNetClassifier` and pass your new callback in a list to the `callbacks` argument. After that, we train the model and see what happens. ``` net = NeuralNetClassifier( ClassifierModule, max_epochs=15, lr=0.02, warm_start=True, callbacks=[AccuracyTweet(min_accuracy=0.7)], ) net.fit(X, y) ``` Oh no, our model never reached a validation accuracy of 0.7. Let's train some more (this is possible because we set `warm_start=True`): ``` net.fit(X, y) assert net.history[-1, 'valid_acc'] >= 0.7 ``` Finally, the validation score exceeded 0.7. Hooray! ### Accessing callback parameters Say you would like to use a learning rate schedule with your neural net, but you don't know what parameters are best for that schedule. Wouldn't it be nice if you could find those parameters with a grid search? With `skorch`, this is possible. Below, we show how to access the parameters of your callbacks. To simplify the access to your callback parameters, it is best if you give your callback a name. This is achieved by passing the `callbacks` parameter a list of name, callback tuples, such as: callbacks=[ ('scheduler', LearningRateScheduler)), ... ], This way, you can access your callbacks using the double underscore semantics (as, for instance, in an `sklearn` `Pipeline`): callbacks__scheduler__epoch=50, So if you would like to perform a grid search on, say, the number of units in the hidden layer and the learning rate schedule, it could look something like this: param_grid = { 'module__num_units': [50, 100, 150], 'callbacks__scheduler__epoch': [10, 50, 100], } Note: If you would like to refresh your knowledge on grid search, look [here](http://scikit-learn.org/stable/modules/grid_search.html#grid-search), [here](http://scikit-learn.org/stable/auto_examples/model_selection/grid_search_text_feature_extraction.html), or in the Basic_Usage notebok. Below, we show how accessing the callback parameters works our `AccuracyTweet` callback: ``` net = NeuralNetClassifier( ClassifierModule, max_epochs=10, lr=0.1, warm_start=True, callbacks=[ ('tweet', AccuracyTweet(min_accuracy=0.7)), ], callbacks__tweet__min_accuracy=0.6, ) net.fit(X, y) ``` As you can see, by passing `callbacks__tweet__min_accuracy=0.6`, we changed that parameter. The same can be achieved by calling the `set_params` method with the corresponding arguments: ``` net.set_params(callbacks__tweet__min_accuracy=0.75) net.fit(X, y) ``` ## Working with different data types ### Working with `Dataset`s We encourage you to not pass `Dataset`s to `net.fit` but to let skorch handle `Dataset`s internally. Nonetheless, there are situations where passing `Dataset`s to `net.fit` is hard to avoid (e.g. if you want to load the data lazily during the training). This is supported by skorch but may have some unwanted side-effects relating to sklearn. For instance, `Dataset`s cannot split into train and validation in a stratified fashion without explicit knowledge of the classification targets. Below we show what happens when you try to fit with `Dataset` and the stratified split fails: ``` class MyDataset(torch.utils.data.Dataset): def __init__(self, X, y): self.X = X self.y = y assert len(X) == len(y) def __len__(self): return len(self.X) def __getitem__(self, i): return self.X[i], self.y[i] X, y = make_classification(1000, 20, n_informative=10, random_state=0) X, y = X.astype(np.float32), y.astype(np.int64) dataset = MyDataset(X, y) net = NeuralNetClassifier(ClassifierModule) try: net.fit(dataset, y=None) except ValueError as e: print("Error:", e) net.train_split.stratified ``` As you can see, the stratified split fails since `y` is not known. There are two solutions to this: * turn off stratified splitting ( `net.train_split.stratified=False`) * pass `y` explicitly (if possible), even if it is implicitely contained in the `Dataset` The second solution is shown below: ``` net.fit(dataset, y=y) ``` ### Working with dicts #### The standard case skorch has built-in support for dictionaries as data containers. Here we show a somewhat contrived example of how to use dicts, but it should get the point across. First we create data and put it into a dictionary `X_dict` with two keys `X0` and `X1`: ``` X, y = make_classification(1000, 20, n_informative=10, random_state=0) X, y = X.astype(np.float32), y.astype(np.int64) X0, X1 = X[:, :10], X[:, 10:] X_dict = {'X0': X0, 'X1': X1} ``` When skorch passes the dict to the pytorch module, it will pass the data as keyword arguments to the forward call. That means that we should accept the two keys `XO` and `X1` in the forward method, as shown below: ``` class ClassifierWithDict(nn.Module): def __init__( self, num_units0=50, num_units1=50, nonlin=F.relu, dropout=0.5, ): super(ClassifierWithDict, self).__init__() self.num_units0 = num_units0 self.num_units1 = num_units1 self.nonlin = nonlin self.dropout = dropout self.dense0 = nn.Linear(10, num_units0) self.dense1 = nn.Linear(10, num_units1) self.nonlin = nonlin self.dropout = nn.Dropout(dropout) self.output = nn.Linear(num_units0 + num_units1, 2) # NOTE: We accept X0 and X1, the keys from the dict, as arguments def forward(self, X0, X1, kwargs): X0 = self.nonlin(self.dense0(X0)) X0 = self.dropout(X0) X1 = self.nonlin(self.dense1(X1)) X1 = self.dropout(X1) X = torch.cat((X0, X1), dim=1) X = F.relu(X) X = F.softmax(self.output(X), dim=-1) return X ``` As long as we keep this in mind, we are good to go. ``` net = NeuralNetClassifier(ClassifierWithDict, verbose=0) net.fit(X_dict, y) ``` #### Working with sklearn `Pipeline` and `GridSearchCV` ``` from sklearn.pipeline import Pipeline from sklearn.preprocessing import FunctionTransformer from sklearn.model_selection import GridSearchCV ``` sklearn makes the assumption that incoming data should be numpy/sparse arrays or something similar. This clashes with the use of dictionaries. Unfortunately, it is sometimes impossible to work around that for now (for instance using skorch with `BaggingClassifier`). Other times, there are possibilities. When we have a preprocessing pipeline that involves `FunctionTransformer`, we have to pass the parameter `validate=False` (which is the default value now) so that sklearn allows the dictionary to pass through. Everything else works: ``` pipe = Pipeline([ ('do-nothing', FunctionTransformer(validate=False)), ('net', net), ]) pipe.fit(X_dict, y) ``` When trying a grid or randomized search, it is not that easy to pass a dict. If we try, we will get an error: ``` param_grid = { 'net__module__num_units0': [10, 25, 50], 'net__module__num_units1': [10, 25, 50], 'net__lr': [0.01, 0.1], } grid_search = GridSearchCV(pipe, param_grid, scoring='accuracy', verbose=1, cv=3) try: grid_search.fit(X_dict, y) except Exception as e: print(e) ``` The error above occurs because sklearn gets the length of the input data, which is 2 for the dict, and believes that is inconsistent with the length of the target (1000). To get around that, skorch provides a helper class called `SliceDict`. It allows us to wrap our dictionaries so that they also behave like a numpy array: ``` from skorch.helper import SliceDict X_slice_dict = SliceDict(X0=X0, X1=X1) # X_slice_dict = SliceDict(X_dict) would also work ``` The SliceDict shows the correct length, shape, and is sliceable across values: ``` print("Length of dict: {}, length of SliceDict: {}".format(len(X_dict), len(X_slice_dict))) print("Shape of SliceDict: {}".format(X_slice_dict.shape)) print("Slicing the SliceDict slices across values: {}".format(X_slice_dict[:2])) ``` With this, we can call `GridSearchCV` just as expected: ``` grid_search.fit(X_slice_dict, y) grid_search.best_score_, grid_search.best_params_ ``` ## Multiple return values from `forward` Often, we want our `Module.forward` method to return more than just one value. There can be several reasons for this. Maybe, the criterion requires not one but several outputs. Or perhaps we want to inspect intermediate values to learn more about our model (say inspecting attention in a sequence-to-sequence model). Fortunately, `skorch` makes it easy to achieve this. In the following, we demonstrate how to handle multiple outputs from the `Module`. To demonstrate this, we implement a very simple autoencoder. It consists of an encoder that reduces our input of 20 units to 5 units using two linear layers, and a decoder that tries to reconstruct the original input, again using two linear layers. ### Implementing a simple autoencoder ``` from skorch import NeuralNetRegressor class Encoder(nn.Module): def __init__(self, num_units=5): super().__init__() self.num_units = num_units self.encode = nn.Sequential( nn.Linear(20, 10), nn.ReLU(), nn.Linear(10, self.num_units), nn.ReLU(), ) def forward(self, X): encoded = self.encode(X) return encoded class Decoder(nn.Module): def __init__(self, num_units): super().__init__() self.num_units = num_units self.decode = nn.Sequential( nn.Linear(self.num_units, 10), nn.ReLU(), nn.Linear(10, 20), ) def forward(self, X): decoded = self.decode(X) return decoded ``` The autoencoder module below actually returns a tuple of two values, the decoded input and the encoded input. This way, we cannot only use the decoded input to calculate the normal loss but also have access to the encoded state. ``` class AutoEncoder(nn.Module): def __init__(self, num_units): super().__init__() self.num_units = num_units self.encoder = Encoder(num_units=self.num_units) self.decoder = Decoder(num_units=self.num_units) def forward(self, X): encoded = self.encoder(X) decoded = self.decoder(encoded) return decoded, encoded # <- return a tuple of two values ``` Since the module's `forward` method returns two values, we have to adjust our objective to do the right thing with those values. If we don't do this, the criterion wouldn't know what to do with the two values and would raise an error. One strategy would be to only use the decoded state for the loss and discard the encoded state. For this demonstration, we have a different plan: We would like the encoded state to be sparse. Therefore, we add an L1 loss of the encoded state to the reconstruction loss. This way, the net will try to reconstruct the input as accurately as possible while keeping the encoded state as sparse as possible. To implement this, the right method to override is called `get_loss`, which is where `skorch` computes and returns the loss. It gets the prediction (our tuple) and the target as input, as well as other arguments and keywords that we pass through. We create a subclass of `NeuralNetRegressor` that overrides said method and implements our idea for the loss. ``` class AutoEncoderNet(NeuralNetRegressor): def get_loss(self, y_pred, y_true, args, kwargs): decoded, encoded = y_pred # <- unpack the tuple that was returned by `forward` loss_reconstruction = super().get_loss(decoded, y_true, args, *kwargs) loss_l1 = 1e-3 torch.abs(encoded).sum() return loss_reconstruction + loss_l1 ``` Note: Alternatively, we could have used an unaltered `NeuralNetRegressor` but implement a custom criterion that is responsible for unpacking the tuple and computing the loss. ### Training the autoencoder Now that everything is ready, we train the model as usual. We initialize our net subclass with the `AutoEncoder` module and call the `fit` method with `X` both as input and as target (since we want to reconstruct the original data): ``` net = AutoEncoderNet( AutoEncoder, module__num_units=5, lr=0.3, ) net.fit(X, X) ``` Voilà, the model was trained using our custom loss function that makes use of both predicted values. ### Extracting the decoder and the encoder output Sometimes, we may wish to inspect all the values returned by the `foward` method of the module. There are several ways to achieve this. In theory, we can always access the module directly by using the `net.module_` attribute. However, this is unwieldy, since this completely shortcuts the prediction loop, which takes care of important steps like casting `numpy` arrays to `pytorch` tensors and batching. Also, we cannot use the `predict` method on the net. This method will only return the first output from the forward method, in this case the decoded state. The reason for this is that `predict` is part of the `sklearn` API, which requires there to be only one output. This is shown below: ``` y_pred = net.predict(X) y_pred.shape # only the decoded state is returned ``` However, the net itself provides two methods to retrieve all outputs. The first one is the `net.forward` method, which retrieves all the predicted batches from the `Module.forward` and concatenates them. Use this to retrieve the complete decoded and encoded state: ``` decoded_pred, encoded_pred = net.forward(X) decoded_pred.shape, encoded_pred.shape ``` The other method is called `net.forward_iter`. It is similar to `net.forward` but instead of collecting all the batches, this method is lazy and only yields one batch at a time. This can be especially useful if the output doesn't fit into memory: ``` for decoded_pred, encoded_pred in net.forward_iter(X): # do something with each batch break decoded_pred.shape, encoded_pred.shape ``` Finally, let's make sure that our initial goal of having a sparse encoded state was met. We check how many activities are close to zero: ``` torch.isclose(encoded_pred, torch.zeros_like(encoded_pred)).float().mean() ``` As we had hoped, the encoded state is quite sparse, with the majority of outpus being 0.	github_jupyter
<a href="https://colab.research.google.com/github/lakshit2808/Machine-Learning-Notes/blob/master/ML_Models/Classification/KNearestNeighbor/KNN_first_try.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a> # K-Nearest Neighbor K-Nearest Neighbors is an algorithm for supervised learning. Where the data is 'trained' with data points corresponding to their classification. Once a point is to be predicted, it takes into account the 'K' nearest points to it to determine it's classification. ### Here's an visualization of the K-Nearest Neighbors algorithm. <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-ML0101EN-SkillsNetwork/labs/Module%203/images/KNN_Diagram.png"> In this case, we have data points of Class A and B. We want to predict what the star (test data point) is. If we consider a k value of 3 (3 nearest data points) we will obtain a prediction of Class B. Yet if we consider a k value of 6, we will obtain a prediction of Class A.<br><br> In this sense, it is important to consider the value of k. But hopefully from this diagram, you should get a sense of what the K-Nearest Neighbors algorithm is. It considers the 'K' Nearest Neighbors (points) when it predicts the classification of the test point. ## 1. Importing Libraries ``` import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn import preprocessing ``` ## 2. Reading Data ``` df = pd.read_csv('teleCust.csv') df.head() ``` ## 3. Data Visualization and Analysis #### Let’s see how many of each class is in our data set ``` df['custcat'].value_counts() ``` The target field, called custcat, has four possible values that correspond to the four customer groups, as follows: 1. Basic Service 2. E-Service 3. Plus Service 4. Total Service ``` df.hist(column='income' , bins=50) ``` ### Feature Set Let's Define a feature set: X ``` df.columns ``` To use scikit-learn library, we have to convert the Pandas data frame to a Numpy array: ``` X = df[['region', 'tenure', 'age', 'marital', 'address', 'income', 'ed', 'employ', 'retire', 'gender', 'reside']].values X[0:5] ``` What are our labels? ``` y = df['custcat'].values y[0:5] ``` ### Normalize Data Normalization in this case essentially means standardization. Standardization is the process of transforming data based on the mean and standard deviation for the whole set. Thus, transformed data refers to a standard distribution with a mean of 0 and a variance of 1.<br><br> Data Standardization give data zero mean and unit variance, it is good practice, especially for algorithms such as KNN which is based on distance of cases: ``` X = preprocessing.StandardScaler().fit(X).transform(X.astype(float)) X[0:5] ``` ## 4. Train/Test Split ``` from sklearn.model_selection import train_test_split X_train , X_test , y_train , y_test = train_test_split(X , y , test_size= 0.2 , random_state = 4) print ('Train set:', X_train.shape, y_train.shape) print ('Test set:', X_test.shape, y_test.shape) ``` ## 5. Classification(KNN) ``` from sklearn.neighbors import KNeighborsClassifier ``` ### Training Lets start the algorithm with k=4 for now: ``` all_acc = [] for i in range(1, 100): KNN = KNeighborsClassifier(n_neighbors=i).fit(X_train , y_train) all_acc.append(accuracy_score(y_test , KNN.predict(X_test))) best_acc = max(all_acc) best_k = all_acc.index(best_acc) + 1 KNN = KNeighborsClassifier(n_neighbors=best_k).fit(X_train , y_train) ``` ### Prediction ``` y_ = KNN.predict(X_test) y_[0:5] ``` ## 6. Accuracy Evaluation In multilabel classification, accuracy classification score is a function that computes subset accuracy. This function is equal to the jaccard_score function. Essentially, it calculates how closely the actual labels and predicted labels are matched in the test set. ``` from sklearn.metrics import accuracy_score print('Train Set Accuracy: {}'.format(accuracy_score(y_train , KNN.predict(X_train)))) print('Ttest Set Accuracy: {}'.format(accuracy_score(y_test , KNN.predict(X_test)))) ``` #### What about other K? K in KNN, is the number of nearest neighbors to examine. It is supposed to be specified by the User. So, how can we choose right value for K? The general solution is to reserve a part of your data for testing the accuracy of the model. Then chose k =1, use the training part for modeling, and calculate the accuracy of prediction using all samples in your test set. Repeat this process, increasing the k, and see which k is the best for your model. We can calculate the accuracy of KNN for different K. ``` all_acc = [] for i in range(1, 100): KNN = KNeighborsClassifier(n_neighbors=i).fit(X_train , y_train) all_acc.append(accuracy_score(y_test , KNN.predict(X_test))) best_acc = max(all_acc) best_k = all_acc.index(best_acc) + 1 ```	github_jupyter
``` %matplotlib inline %config InlineBackend.figure_format = 'svg' import scqubits as scq import scqubits.legacy.sweep_plotting as splot from scqubits import HilbertSpace, InteractionTerm, ParameterSweep import numpy as np ``` .. note:: This describes a legacy version of the `HilbertSpace` class which is deprecated with scqubits v1.4. # Composite Hilbert Spaces, QuTiP Interface The `HilbertSpace` class provides data structures and methods for handling composite Hilbert spaces which may consist of multiple qubits or qubits and oscillators coupled to each other. To harness the power of QuTiP, a toolbox for studying stationary and dynamical properties of closed and open quantum systems (and much more), `HilbertSpace` provides a convenient interface: it generates `qutip.qobj` objects which are then directly handled by QuTiP. ## Example: two transmons coupled to a harmonic mode Transmon qubits can be capacitively coupled to a common harmonic mode, realized by an LC oscillator or a transmission-line resonator. The Hamiltonian describing such a composite system is given by: \begin{equation} H=H_\text{tmon,1} + H_\text{tmon,2} + \omega_r a^\dagger a + \sum_{j=1,2}g_j n_j(a+a^\dagger), \end{equation} where $j=1,2$ enumerates the two transmon qubits, $\omega_r$ is the (angular) frequency of the resonator. Furthermore, $n_j$ is the charge number operator for qubit $j$, and $g_j$ is the coupling strength between qubit $j$ and the resonator. ### Create Hilbert space components The first step consists of creating the objects describing the individual building blocks of the full Hilbert space. Here, these will be the two transmons and one oscillator: ``` tmon1 = scq.Transmon( EJ=40.0, EC=0.2, ng=0.3, ncut=40, truncated_dim=4 # after diagonalization, we will keep 3 levels ) tmon2 = scq.Transmon( EJ=15.0, EC=0.15, ng=0.0, ncut=30, truncated_dim=4 ) resonator = scq.Oscillator( E_osc=4.5, truncated_dim=4 # up to 3 photons (0,1,2,3) ) ``` The system objects are next grouped into a Python list, and in this form used for the initialization of a `HilbertSpace` object. Once created, a print call to this object outputs a summary of the composite Hilbert space. ``` hilbertspace = scq.HilbertSpace([tmon1, tmon2, resonator]) print(hilbertspace) ``` One useful method of the `HilbertSpace` class is `.bare_hamiltonian()`. This yields the bare Hamiltonian of the non-interacting subsystems, expressed as a `qutip.Qobj`: ``` bare_hamiltonian = hilbertspace.bare_hamiltonian() bare_hamiltonian ``` ### Set up the interaction between subsystems The pairwise interactions between subsystems are assumed to have the general form $V=\sum_{i\not= j} g_{ij} A_i B_j$, where $g_{ij}$ parametrizes the interaction strength between subsystems $i$ and $j$. The operator content of the coupling is given by the two coupling operators $A_i$, $B_j$, which are operators in the two respective subsystems. This structure is captured by setting up an `InteractionTerm` object: ``` g1 = 0.1 # coupling resonator-CPB1 (without charge matrix elements) g2 = 0.2 # coupling resonator-CPB2 (without charge matrix elements) interaction1 = InteractionTerm( hilbertspace = hilbertspace, g_strength = g1, op1 = tmon1.n_operator(), subsys1 = tmon1, op2 = resonator.creation_operator() + resonator.annihilation_operator(), subsys2 =resonator ) interaction2 = InteractionTerm( hilbertspace = hilbertspace, g_strength = g2, op1 = tmon2.n_operator(), subsys1 = tmon2, op2 = resonator.creation_operator() + resonator.annihilation_operator(), subsys2 = resonator ) ``` Each `InteractionTerm` object is initialized by specifying 1. the Hilbert space object to which it will belong 2. the interaction strength coefficient $g_{ij}$ 3. `op1`, `op2`: the subsystem operators $A_i$, $B_j$ (these should be operators within the subsystems' respective Hilbert spaces only) 4. `subsys1`: the subsystem objects to which `op1` and `op2` belong Note: interaction Hamiltonians of the alternative form $V=g_{ij}A_i B_j^\dagger + g_{ij}^* A_i^\dagger B_J$ (a typical form when performing rotating-wave approximation) can be specified by setting `op1` to $A_i$ and `op2` to $B_j^\dagger$, and providing the additional keyword parameter `add_hc = True`. Now, collect all interaction terms in a list, and insert into the HilbertSpace object. ``` interaction_list = [interaction1, interaction2] hilbertspace.interaction_list = interaction_list ``` With the interactions specified, the full Hamiltonian of the coupled system can be obtained via the method `.hamiltonian()`. Again, this conveniently results in a `qubit.Qobj` operator: ``` dressed_hamiltonian = hilbertspace.hamiltonian() dressed_hamiltonian ``` ### Obtaining the eigenspectrum via QuTiP Since the Hamiltonian obtained this way is a proper `qutip.qobj`, all QuTiP routines are now available. In the first case, we are still making use of the scqubit `HilbertSpace.eigensys()` method. In the second, case, we use QuTiP's method `.eigenenergies()`: ``` evals, evecs = hilbertspace.eigensys(evals_count=4) print(evals) dressed_hamiltonian = hilbertspace.hamiltonian() dressed_hamiltonian.eigenenergies() ```	github_jupyter
# RDD basics This notebook will introduce three basic but essential Spark operations. Two of them are the transformations map and filter. The other is the action collect. At the same time we will introduce the concept of persistence in Spark. ## Getting the data and creating the RDD We will use the reduced dataset (10 percent) provided for the KDD Cup 1999, containing nearly half million network interactions. The file is provided as a Gzip file that we will download locally. ``` import urllib f = urllib.urlretrieve ("http://kdd.ics.uci.edu/databases/kddcup99/kddcup.data_10_percent.gz", "kddcup.data_10_percent.gz") ``` Now we can use this file to create our RDD. ``` data_file = "./kddcup.data_10_percent.gz" raw_data = sc.textFile(data_file) ``` ## The filter transformation This transformation can be applied to RDDs in order to keep just elements that satisfy a certain condition. More concretely, a function is evaluated on every element in the original RDD. The new resulting RDD will contain just those elements that make the function return True. For example, imagine we want to count how many normal. interactions we have in our dataset. We can filter our raw_data RDD as follows. ``` normal_raw_data = raw_data.filter(lambda x: 'normal.' in x) ``` Now we can count how many elements we have in the new RDD. ``` from time import time t0 = time() normal_count = normal_raw_data.count() tt = time() - t0 print "There are {} 'normal' interactions".format(normal_count) print "Count completed in {} seconds".format(round(tt,3)) ``` The real calculations (distributed) in Spark occur when we execute actions and not transformations. In this case counting is the action that we execute in the RDD. We can apply as many transformations as we would like in a RDD and no computation will take place until we call the first action which, in this case, takes a few seconds to complete. ## The map transformation By using the map transformation in Spark, we can apply a function to every element in our RDD. Python's lambdas are specially expressive for this particular. In this case we want to read our data file as a CSV formatted one. We can do this by applying a lambda function to each element in the RDD as follows. ``` from pprint import pprint csv_data = raw_data.map(lambda x: x.split(",")) t0 = time() head_rows = csv_data.take(5) tt = time() - t0 print "Parse completed in {} seconds".format(round(tt,3)) pprint(head_rows[0]) ``` Again, all action happens once we call the first Spark action (i.e. take in this case). What if we take a lot of elements instead of just the first few? ``` t0 = time() head_rows = csv_data.take(100000) tt = time() - t0 print "Parse completed in {} seconds".format(round(tt,3)) ``` We can see that it takes longer. The map function is applied now in a distributed way to a lot of elements on the RDD, hence the longer execution time. ## Using map and predefined functions Of course we can use predefined functions with map. Imagine we want to have each element in the RDD as a key-value pair where the key is the tag (e.g. normal) and the value is the whole list of elements that represents the row in the CSV formatted file. We could proceed as follows. ``` def parse_interaction(line): elems = line.split(",") tag = elems[41] return (tag, elems) key_csv_data = raw_data.map(parse_interaction) head_rows = key_csv_data.take(5) pprint(head_rows[0]) ``` ## The collect action Basically it will get all the elements in the RDD into memory for us to work with them. For this reason it has to be used with care, specially when working with large RDDs. An example using our raw data. ``` t0 = time() all_raw_data = raw_data.collect() tt = time() - t0 print "Data collected in {} seconds".format(round(tt,3)) ``` Every Spark worker node that has a fragment of the RDD has to be coordinated in order to retrieve its part, and then reduce everything together. As a last example combining all the previous, we want to collect all the normal interactions as key-value pairs. ``` # get data from file data_file = "./kddcup.data_10_percent.gz" raw_data = sc.textFile(data_file) # parse into key-value pairs key_csv_data = raw_data.map(parse_interaction) # filter normal key interactions normal_key_interactions = key_csv_data.filter(lambda x: x[0] == "normal.") # collect all t0 = time() all_normal = normal_key_interactions.collect() tt = time() - t0 normal_count = len(all_normal) print "Data collected in {} seconds".format(round(tt,3)) print "There are {} 'normal' interactions".format(normal_count) ``` This count matches with the previous count for normal interactions. The new procedure is more time consuming. This is because we retrieve all the data with collect and then use Python's len on the resulting list. Before we were just counting the total number of elements in the RDD by using count.	github_jupyter
#### Copyright IBM All Rights Reserved. #### SPDX-License-Identifier: Apache-2.0 # Db2 Sample For Scikit-Learn In this code sample, we will show how to use the Db2 Python driver to import data from our Db2 database. Then, we will use that data to create a machine learning model with scikit-learn. Many wine connoisseurs love to taste different wines from all over the world. Mostly importantly, they want to know how the quality differs between each wine based on the ingredients. Some of them also want to be able to predict the quality before even tasting it. In this notebook, we will be using a dataset that has collected certain attributes of many wine bottles that determines the quality of the wine. Using this dataset, we will help our wine connoisseurs predict the quality of wine. This notebook will demonstrate how to use Db2 as a data source for creating machine learning models. Prerequisites: 1. Python 3.6 and above 2. Db2 on Cloud instance (using free-tier option) 3. Data already loaded in your Db2 instance 4. Have Db2 connection credentials on hand We will be importing two libraries- `ibm_db` and `ibm_dbi`. `ibm_db` is a library with low-level functions that will directly connect to our db2 database. To make things easier for you, we will be using `ibm-dbi`, which communicates with `ibm-db` and gives us an easy interface to interact with our data and import our data as a pandas dataframe. For this example, we will be using the [winequality-red dataset](../data/winequality-red.csv), which we have loaded into our Db2 instance. NOTE: Running this notebook within a docker container. If `!easy_install ibm_db` doesn't work on your normally on jupter notebook, you may need to also run this notebook within a docker container as well. ## 1. Import Data Let's first install and import all the libraries needed for this notebook. Most important we will be installing and importing the db2 python driver `ibm_db`. ``` !pip install sklearn !easy_install ibm_db import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline # The two python ibm db2 drivers we need import ibm_db import ibm_db_dbi ``` Now let's import our data from our data source using the python db2 driver. ``` # replace only <> credentials dsn = "DRIVER={{IBM DB2 ODBC DRIVER}};" + \ "DATABASE=<DATABASE NAME>;" + \ "HOSTNAME=<HOSTNMAE>;" + \ "PORT=50000;" + \ "PROTOCOL=TCPIP;" + \ "UID=<USERNAME>;" + \ "PWD=<PWD>;" hdbc = ibm_db.connect(dsn, "", "") hdbi = ibm_db_dbi.Connection(hdbc) sql = 'SELECT * FROM <SCHEMA NAME>.<TABLE NAME>' wine = pandas.read_sql(sql,hdbi) #wine = pd.read_csv('../data/winequality-red.csv', sep=';') wine.head() ``` ## 2. Data Exploration In this step, we are going to try and explore our data inorder to gain insight. We hope to be able to make some assumptions of our data before we start modeling. ``` wine.describe() # Minimum price of the data minimum_price = np.amin(wine['quality']) # Maximum price of the data maximum_price = np.amax(wine['quality']) # Mean price of the data mean_price = np.mean(wine['quality']) # Median price of the data median_price = np.median(wine['quality']) # Standard deviation of prices of the data std_price = np.std(wine['quality']) # Show the calculated statistics print("Statistics for housing dataset:\n") print("Minimum quality: {}".format(minimum_price)) print("Maximum quality: {}".format(maximum_price)) print("Mean quality: {}".format(mean_price)) print("Median quality {}".format(median_price)) print("Standard deviation of quality: {}".format(std_price)) wine.corr() corr_matrix = wine.corr() corr_matrix["quality"].sort_values(ascending=False) ``` ## 3. Data Visualization ``` wine.hist(bins=50, figsize=(30,25)) plt.show() boxplot = wine.boxplot(column=['quality']) ``` ## 4. Creating Machine Learning Model Now that we have cleaned and explored our data. We are ready to build our model that will predict the attribute `quality`. ``` wine_value = wine['quality'] wine_attributes = wine.drop(['quality'], axis=1) from sklearn.preprocessing import StandardScaler # Let us scale our data first sc = StandardScaler() wine_attributes = sc.fit_transform(wine_attributes) from sklearn.decomposition import PCA # Apply PCA to our data pca = PCA(n_components=8) x_pca = pca.fit_transform(wine_attributes) ``` We need to split our data into train and test data. ``` from sklearn.model_selection import train_test_split # Split our data into test and train data x_train, x_test, y_train, y_test = train_test_split( wine_attributes,wine_value, test_size = 0.25) ``` We will be using Logistic Regression to model our data ``` from sklearn.linear_model import LogisticRegression from sklearn.metrics import confusion_matrix, accuracy_score lr = LogisticRegression() # Train our model lr.fit(x_train, y_train) # Predict using our trained model and our test data lr_predict = lr.predict(x_test) # Print confusion matrix and accuracy score lr_conf_matrix = confusion_matrix(y_test, lr_predict) lr_acc_score = accuracy_score(y_test, lr_predict) print(lr_conf_matrix) print(lr_acc_score*100) ```	github_jupyter
# Taylor problem 3.23 last revised: 04-Jan-2020 by Dick Furnstahl [[email protected]] This notebook is almost ready to go, except that the initial conditions and $\Delta v$ are different from the problem statement and there is no statement to print the figure. Fix these and you're done! This is a conservation of momentum problem, which in the end lets us determine the trajectories of the two masses before and after the explosion. How should we visualize that the center-of-mass of the pieces continues to follow the original parabolic path? Plan: 1. Plot the original trajectory, also continued past the explosion time. 2. Plot the two trajectories after the explosion. 3. For some specified times of the latter two trajectories, connect the points and indicate the center of mass. The implementation here could certainly be improved! Please make suggestions (and develop improved versions). ``` %matplotlib inline import numpy as np import matplotlib.pyplot as plt ``` First define some functions we think we will need. The formulas are based on our paper-and-pencil work. The trajectory starting from $t=0$ is: $ \begin{align} x(t) &= x_0 + v_{x0} t \\ y(t) &= y_0 + v_{y0} t - \frac{1}{2} g t^2 \end{align} $ ``` def trajectory(x0, y0, vx0, vy0, t_pts, g=9.8): """Calculate the x(t) and y(t) trajectories for an array of times, which must start with t=0. """ return x0 + vx0t_pts, y0 + vy0t_pts - gt_pts2/2. ``` The velocity at the final time $t_f$ is: $ \begin{align} v_{x}(t) &= v_{x0} \\ v_{y}(t) &= v_{y0} - g t_f \end{align} $ ``` def final_velocity(vx0, vy0, t_pts, g=9.8): """Calculate the vx(t) and vy(t) at the end of an array of times t_pts""" return vx0, vy0 - gt_pts[-1] # -1 gives the last element ``` The center of mass of two particles at $(x_1, y_1)$ and $(x_2, y_2)$ is: $ \begin{align} x_{cm} &= \frac{1}{2}(x_1 + x_2) \\ y_{cm} &= \frac{1}{2}(y_1 + y_2) \end{align} $ ``` def com_position(x1, y1, x2, y2): """Find the center-of-mass (com) position given two positions (x,y).""" return (x1 + x2)/2., (y1 + y2)/2. ``` 1. Calculate and plot the original trajectory up to the explosion. ``` # initial conditions x0_before, y0_before = [0., 0.] # put the origin at the starting point vx0_before, vy0_before = [6., 3.] # given in the problem statement g = 1. # as recommended # Array of times to calculate the trajectory up to the explosion at t=4 t_pts_before = np.array([0., 1., 2., 3., 4.]) x_before, y_before = trajectory(x0_before, y0_before, vx0_before, vy0_before, t_pts_before, g) fig = plt.figure() ax = fig.add_subplot(1,1,1) ax.plot(x_before, y_before, 'ro-') ax.set_xlabel('x') ax.set_ylabel('y') ``` Does it make sense so far? Note that we could use more intermediate points to make a more correct curve (rather than the piecewise straight lines) but this is fine at least for a first pass. 2. Calculate and plot the two trajectories after the explosion. For the second part of the trajectory, we reset our clock to $t=0$ because that is how our trajectory function is constructed. We'll need initial positions and velocities of the pieces just after the explosion. These are the final position of the combined piece before the explosion and the final velocity plus and minus $\Delta \mathbf{v}$. We are told $\Delta \mathbf{v}$. We have to figure out the final velocity before the explosion. ``` delta_v = np.array([2., 1.]) # change in velociy of one piece # reset time to 0 for calculating trajectories t_pts_after = np.array([0., 1., 2., 3., 4., 5.]) # Also could have used np.arange(0.,6.,1.) x0_after = x_before[-1] # -1 here means the last element of the array y0_after = y_before[-1] vxcm0_after, vycm0_after = final_velocity(vx0_before, vy0_before, t_pts_before, g) # The _1 and _2 refer to the two pieces after the explosinon vx0_after_1 = vxcm0_after + delta_v[0] vy0_after_1 = vycm0_after + delta_v[1] vx0_after_2 = vxcm0_after - delta_v[0] vy0_after_2 = vycm0_after - delta_v[1] # Given the initial conditions after the explosion, we calculate trajectories x_after_1, y_after_1 = trajectory(x0_after, y0_after, vx0_after_1, vy0_after_1, t_pts_after, g) x_after_2, y_after_2 = trajectory(x0_after, y0_after, vx0_after_2, vy0_after_2, t_pts_after, g) # This is the center-of-mass trajectory xcm_after, ycm_after = trajectory(x0_after, y0_after, vxcm0_after, vycm0_after, t_pts_after, g) # These are calculated points of the center-of-mass xcm_pts, ycm_pts = com_position(x_after_1, y_after_1, x_after_2, y_after_2) fig = plt.figure() ax = fig.add_subplot(1,1,1) ax.plot(x_before, y_before, 'ro-', label='before explosion') ax.plot(x_after_1, y_after_1, 'go-', label='piece 1 after') ax.plot(x_after_2, y_after_2, 'bo-', label='piece 2 after') ax.plot(xcm_after, ycm_after, 'r--', label='original trajectory') ax.plot(xcm_pts, ycm_pts, 'o', color='black', label='center-of-mass of 1 and 2') for i in range(len(t_pts_after)): ax.plot([x_after_1[i], x_after_2[i]], [y_after_1[i], y_after_2[i]], 'k--' ) ax.set_xlabel('x') ax.set_ylabel('y') ax.legend(); ```	github_jupyter
``` import os from pprint import pprint import torch import torch.nn as nn from transformers import BertForTokenClassification, BertTokenizer from transformers import AdamW from torch.utils.data import TensorDataset, DataLoader, RandomSampler, SequentialSampler from sklearn.model_selection import train_test_split import numpy as np from tqdm.notebook import tqdm ``` ## 读取MSRA实体识别数据集 ``` file = "../datasets/dh_msra.txt" ``` ## 检查GPU情况 ``` # GPUcheck print("CUDA Available: ", torch.cuda.is_available()) n_gpu = torch.cuda.device_count() if torch.cuda.is_available(): print("GPU numbers: ", n_gpu) print("device_name: ", torch.cuda.get_device_name(0)) device = torch.device("cuda:0") # 注意选择 torch.cuda.set_device(0) print(f"当前设备：{torch.cuda.current_device()}") else : device = torch.device("cpu") print(f"当前设备：{device}") ``` ## 配置参数规范化配置参数，方便使用。 ``` class Config(object): """配置参数""" def __init__(self): self.model_name = 'Bert_NER.bin' self.bert_path = './bert-chinese/' self.ner_file = '../datasets/dh_msra.txt' self.num_classes = 10 # 类别数(按需修改)，这里有10种实体类型 self.hidden_size = 768 # 隐藏层输出维度 self.hidden_dropout_prob = 0.1 # dropout比例 self.batch_size = 128 # mini-batch大小 self.max_len = 103 # 句子的最长padding长度 self.epochs = 3 # epoch数 self.learning_rate = 2e-5 # 学习率 self.save_path = './saved_model/' # 模型训练结果保存路径 # self.fp16 = False # self.fp16_opt_level = 'O1' # self.gradient_accumulation_steps = 1 # self.warmup_ratio = 0.06 # self.warmup_steps = 0 # self.max_grad_norm = 1.0 # self.adam_epsilon = 1e-8 # self.class_list = class_list # 类别名单 # self.require_improvement = 1000 # 若超过1000batch效果还没提升，则提前结束训练 config = Config() all_sentences_separate = [] all_letter_labels = [] label_set = set() with open(config.ner_file, encoding="utf-8") as f: single_sentence = [] single_sentence_labels = [] for s in f.readlines(): if s != "\n": word, label = s.split("\t") label = label.strip("\n") single_sentence.append(word) single_sentence_labels.append(label) label_set.add(label) elif s == "\n": all_sentences_separate.append(single_sentence) all_letter_labels.append(single_sentence_labels) single_sentence = [] single_sentence_labels = [] print(all_sentences_separate[0:2]) print(all_letter_labels[0:2]) print(f"\n所有的标签：{label_set}") # 构建 tag 到索引的字典 tag_to_ix = {"B-LOC": 0, "I-LOC": 1, "B-ORG": 2, "I-ORG": 3, "B-PER": 4, "I-PER": 5, "O": 6, "[CLS]":7, "[SEP]":8, "[PAD]":9} ix_to_tag = {0:"B-LOC", 1:"I-LOC", 2:"B-ORG", 3:"I-ORG", 4:"B-PER", 5:"I-PER", 6:"O", 7:"[CLS]", 8:"[SEP]", 9:"[PAD]"} ``` ## 数据示例这里简单查看一些数据例子，其中很多都是数字6。数字6说明是 O 类型的实体。 ``` all_sentences = [] # 句子 for one_sentence in all_sentences_separate: sentence = "".join(one_sentence) all_sentences.append(sentence) print(all_sentences[0:2]) all_labels = [] # labels for letter_labels in all_letter_labels: labels = [tag_to_ix[t] for t in letter_labels] all_labels.append(labels) print(all_labels[0:2]) print(len(all_labels[0])) print(len(all_labels)) ``` ### input数据准备 ``` # word2token tokenizer = BertTokenizer.from_pretrained('./bert-chinese/', do_lower_case=True) # 新版代码，一次性处理好输入 encoding = tokenizer(all_sentences, return_tensors='pt', # pt 指 pytorch，tf 就是 tensorflow padding='max_length', # padding 到 max_length truncation=True, # 激活并控制截断 max_length=config.max_len) input_ids = encoding['input_ids'] # 这句话的input_ids print(f"Tokenize 前的第一句话：\n{all_sentences[0]}\n") print(f"Tokenize + Padding 后的第一句话: \n{input_ids[0]}") # 新版代码 attention_masks = encoding['attention_mask'] token_type_ids = encoding['token_type_ids'] # 第一句话的 attention_masks print(attention_masks[0]) ``` ## 准备labels 由于我们的input_ids是带有`[CLS]`和`[SEP]`的，所以在准备label的同时也要考虑这些情况。 ``` # [3] 代表 O 实体 for label in all_labels: label.insert(len(label), 8) # [SEP] label.insert(0, 7) # [CLS] if config.max_len > len(label) -1: for i in range(config.max_len - len(label)): #+2的原因是扣除多出来的CLS和SEP label.append(9) # [PAD] print(len(all_labels[0])) print(all_labels[0]) # 统计最长的段落 max_len_label = 0 max_len_text = 0 for label in all_labels: if len(label) > max_len_text: max_len_label = len(label) print(max_len_label) for one_input in input_ids: if len(one_input) > max_len_text: max_len_text = len(one_input) print(max_len_text) ``` ## 切分训练和测试集 ``` # train-test-split train_inputs, validation_inputs, train_labels, validation_labels = train_test_split(input_ids, all_labels, random_state=2021, test_size=0.1) train_masks, validation_masks, _, _ = train_test_split(attention_masks, input_ids, random_state=2021, test_size=0.1) print(len(train_inputs)) print(len(validation_inputs)) print(train_inputs[0]) print(validation_inputs[0]) ``` 这里把输入的labels变为tensor形式。 ``` train_labels = torch.tensor(train_labels).clone().detach() validation_labels = torch.tensor(validation_labels).clone().detach() print(train_labels[0]) print(len(train_labels)) print(len(train_inputs)) # dataloader # 形成训练数据集 train_data = TensorDataset(train_inputs, train_masks, train_labels) # 随机采样 train_sampler = RandomSampler(train_data) # 读取数据 train_dataloader = DataLoader(train_data, sampler=train_sampler, batch_size=config.batch_size) # 形成验证数据集 validation_data = TensorDataset(validation_inputs, validation_masks, validation_labels) # 随机采样 validation_sampler = SequentialSampler(validation_data) # 读取数据 validation_dataloader = DataLoader(validation_data, sampler=validation_sampler, batch_size=config.batch_size) model = BertForTokenClassification.from_pretrained(config.bert_path, num_labels=config.num_classes) model.cuda() # 注意： # 在新版的 Transformers 中会给出警告 # 原因是我们导入的预训练参数权重是不包含模型最终的线性层权重的 # 不过我们本来就是要“微调”它，所以这个情况是符合期望的 # BERT fine-tuning parameters param_optimizer = list(model.named_parameters()) no_decay = ['bias', 'LayerNorm.weight'] # 权重衰减 optimizer_grouped_parameters = [ {'params': [p for n, p in param_optimizer if not any(nd in n for nd in no_decay)], 'weight_decay': 0.01}, {'params': [p for n, p in param_optimizer if any(nd in n for nd in no_decay)], 'weight_decay': 0.0}] # 优化器 optimizer = AdamW(optimizer_grouped_parameters, lr=5e-5) # 保存loss train_loss_set = [] # BERT training loop for _ in range(config.epochs): ## 训练 print(f"当前epoch： {_}") # 开启训练模式 model.train() tr_loss = 0 # train loss nb_tr_examples, nb_tr_steps = 0, 0 # Train the data for one epoch for step, batch in tqdm(enumerate(train_dataloader)): # 把batch放入GPU batch = tuple(t.to(device) for t in batch) # 解包batch b_input_ids, b_input_mask, b_labels = batch # 梯度归零 optimizer.zero_grad() # 前向传播loss计算 output = model(input_ids=b_input_ids, attention_mask=b_input_mask, labels=b_labels) loss = output[0] # print(loss) # 反向传播 loss.backward() # Update parameters and take a step using the computed gradient # 更新模型参数 optimizer.step() # Update tracking variables tr_loss += loss.item() nb_tr_examples += b_input_ids.size(0) nb_tr_steps += 1 print(f"当前 epoch 的 Train loss: {tr_loss/nb_tr_steps}") # 验证状态 model.eval() # 建立变量 eval_loss, eval_accuracy = 0, 0 nb_eval_steps, nb_eval_examples = 0, 0 # Evaluate data for one epoch # 验证集的读取也要batch for batch in tqdm(validation_dataloader): # 元组打包放进GPU batch = tuple(t.to(device) for t in batch) # 解开元组 b_input_ids, b_input_mask, b_labels = batch # 预测 with torch.no_grad(): # segment embeddings，如果没有就是全0，表示单句 # position embeddings，[0,句子长度-1] outputs = model(input_ids=b_input_ids, attention_mask=b_input_mask, token_type_ids=None, position_ids=None) # print(logits[0]) # Move logits and labels to CPU scores = outputs[0].detach().cpu().numpy() # 每个字的标签的概率 pred_flat = np.argmax(scores[0], axis=1).flatten() label_ids = b_labels.to('cpu').numpy() # 真实labels # print(logits, label_ids) # 保存模型 # They can then be reloaded using `from_pretrained()` # 创建文件夹 if not os.path.exists(config.save_path): os.makedirs(config.save_path) print("文件夹不存在，创建文件夹!") else: pass output_dir = config.save_path model_to_save = model.module if hasattr(model, 'module') else model # Take care of distributed/parallel training # Good practice: save your training arguments together with the trained model torch.save(model_to_save.state_dict(), os.path.join(output_dir, config.model_name)) # 读取模型 # Load a trained model and vocabulary that you have fine-tuned output_dir = config.save_path model = BertForTokenClassification.from_pretrained(output_dir) tokenizer = BertTokenizer.from_pretrained(output_dir) model.to(device) # 单句测试 # test_sententce = "在北京市朝阳区的一家网吧，我亲眼看见卢本伟和孙笑川一起开挂。" test_sententce = "史源源的房子租在滨江区南环路税友大厦附近。" # 构建 tag 到索引的字典 tag_to_ix = {"B-LOC": 0, "I-LOC": 1, "B-ORG": 2, "I-ORG": 3, "B-PER": 4, "I-PER": 5, "O": 6, "[CLS]":7, "[SEP]":8, "[PAD]":9} ix_to_tag = {0:"B-LOC", 1:"I-LOC", 2:"B-ORG", 3:"I-ORG", 4:"B-PER", 5:"I-PER", 6:"O", 7:"[CLS]", 8:"[SEP]", 9:"[PAD]"} encoding = tokenizer(test_sententce, return_tensors='pt', # pt 指 pytorch，tf 就是 tensorflow padding=True, # padding到最长的那句话 truncation=True, # 激活并控制截断 max_length=50) test_input_ids = encoding['input_ids'] # 创建attention masks test_attention_masks = encoding['attention_mask'] # 形成验证数据集 # 为了通用，这里还是用了 DataLoader 的形式 test_data = TensorDataset(test_input_ids, test_attention_masks) # 随机采样 test_sampler = SequentialSampler(test_data) # 读取数据 test_dataloader = DataLoader(test_data, sampler=test_sampler, batch_size=config.batch_size) # 验证状态 model.eval() # 建立变量 eval_loss, eval_accuracy = 0, 0 nb_eval_steps, nb_eval_examples = 0, 0 # Evaluate data for one epoch # 验证集的读取也要batch for batch in tqdm(test_dataloader): # 元组打包放进GPU batch = tuple(t.to(device) for t in batch) # 解开元组 b_input_ids, b_input_mask = batch # 预测 with torch.no_grad(): # segment embeddings，如果没有就是全0，表示单句 # position embeddings，[0,句子长度-1] outputs = model(input_ids=b_input_ids, attention_mask=None, token_type_ids=None, position_ids=None) # Move logits and labels to CPU scores = outputs[0].detach().cpu().numpy() # 每个字的标签的概率 pred_flat = np.argmax(scores[0], axis=1).flatten() # label_ids = b_labels.to('cpu').numpy() # 真实labels print(pred_flat) # 预测值 pre_labels = [ix_to_tag[n] for n in pred_flat] print(f"测试句子: {test_sententce}") print(len(test_sententce)) print(pre_labels) pre_labels_cut = pre_labels[0:len(test_sententce)+2] pre_labels_cut person = [] # 临时栈 persons = [] location = [] locations = [] for i in range(len(pre_labels_cut) - 1): # Person # 单字情况 if pre_labels[i] == 'B-PER' and pre_labels[i+1] != 'I-PER' and len(location) == 0: person.append(i) persons.append(person) person = [] # 清空 continue # 非单字 # 如果前面有连着的 PER 实体 if pre_labels[i] == 'B-PER'and pre_labels[i+1] == 'I-PER' and len(person) != 0: person.append(i) # 如果前面没有连着的 B-PER 实体 elif pre_labels[i] == 'B-PER'and pre_labels[i+1] == 'I-PER' and len(location) == 0: person.append(i) # 加入新的 B-PER elif pre_labels[i] != 'I-PER' and len(person) != 0: persons.append(person) # 临时栈内容放入正式栈 person = [] # 清空临时栈 elif pre_labels[i] == 'I-PER' and len(person) != 0: person.append(i) else: # 极少数情况会有 I-PER 开头的，不理 pass # Location # 单字情况 if pre_labels[i] == 'B-LOC' and pre_labels[i+1] != 'I-LOC' and len(location) == 0: location.append(i) locations.append(location) location = [] # 清空 continue # 非单字 # 如果前面有连着的 LOC 实体 if pre_labels[i] == 'B-LOC' and pre_labels[i+1] == 'I-LOC' and len(location) != 0: locations.append(location) location = [] # 清空栈 location.append(i) # 加入新的 B-LOC # 如果前面没有连着的 B-LOC 实体 elif pre_labels[i] == 'B-LOC' and pre_labels[i+1] == 'I-LOC' and len(location) == 0: location.append(i) # 加入新的 B-LOC elif pre_labels[i] == 'I-LOC' and len(location) != 0: location.append(i) # 结尾 elif pre_labels[i] != 'I-LOC' and len(location) != 0: locations.append(location) # 临时栈内容放入正式栈 location = [] # 清空临时栈 else: # 极少数情况会有 I-LOC 开头的，不理 pass print(persons) print(locations) # 从文字中提取 # 人物 NER_PER = [] for word_idx in persons: ONE_PER = [] for letter_idx in word_idx: ONE_PER.append(test_sententce[letter_idx - 1]) NER_PER.append(ONE_PER) NER_PER_COMBINE = [] for w in NER_PER: PER = "".join(w) NER_PER_COMBINE.append(PER) # 地点 NER_LOC = [] for word_idx in locations: ONE_LOC = [] for letter_idx in word_idx: # print(letter_idx) # print(test_sententce[letter_idx]) ONE_LOC.append(test_sententce[letter_idx - 1]) NER_LOC.append(ONE_LOC) NER_LOC_COMBINE = [] for w in NER_LOC: LOC = "".join(w) NER_LOC_COMBINE.append(LOC) # 组织 print(f"当前句子：{test_sententce}\n") print(f" 人物：{NER_PER_COMBINE}\n") print(f" 地点：{NER_LOC_COMBINE}\n") ```	github_jupyter
# Flux.pl The `Flux.pl` Perl script takes four input parameters: `Flux.pl [input file] [output file] [bin width (s)] [geometry base directory]` or, as invoked from the command line, `$ perl ./perl/Flux.pl [input file] [output file] [bin width (s)] [geometry directory]` ## Input Parameters * `[input file]` `Flux.pl` expects the first non-comment line of the input file to begin with a string of the form `<DAQ ID>.<channel>`. This is satisfied by threshold and wire delay files, as well as the outputs of data transformation scripts like `Sort.pl` and `Combine.pl` if their inputs are of the appropriate form. If the input file doesn't meet this condition, `Flux.pl` -- specifically, the `all_geo_info{}` subroutine of `CommonSubs.pl` -- won't be able to load the appropriate geometry files and execution will fail (see the `[geometry directory]` parameter below). * `[output file]` This is what the output file will be named. * `[binWidth]` In physical terms, cosmic ray _flux_ is the number of incident rays per unit area per unit time. The `[binWidth]` parameter determines the "per unit time" portion of this quantity. `Flux.pl` will sort the events in its input data into bins of the given time interval, returning the number of events per unit area recorded within each bin. * `[geometry directory]` With `[binWidth]` handling the "per unit time" portion of the flux calculation, the geometry file associated with each detector handles the "per unit area". `Flux.pl` expects geometry files to be stored in a directory structure of the form ``` geo/ ├── 6119/ │ └── 6119.geo ├── 6148/ │ └── 6148.geo └── 6203/ └── 6203.geo ``` where each DAQ has its own subdirectory whose name is the DAQ ID, and each such subdirectory has a geometry file whose name is given by the DAQ ID with the `.geo` extension. The command-line argument in this case is `geo/`, the parent directory. With this as the base directory, `Flux.pl` determines what geometry file to load by looking for the DAQ ID in the first line of data. This is why, as noted above, the first non-comment line of `[input file]` must begin with `<DAQ ID>.<channel>`. ## Flux Input Files As we mentioned above, threshold files have the appropriate first-line structure to allow `Flux.pl` to access geometry data for them. So what does `Flux.pl` do when acting on a threshold file? We'll test it using the threshold files `files/6148.2016.0109.0.thresh` and `files/6119.2016.0104.1.thresh` as input. First, take a look at the files themselves so we know what the input looks like: ``` !head -10 files/6148.2016.0109.0.thresh !wc -l files/6148.2016.0109.0.thresh !head -10 files/6119.2016.0104.1.thresh !wc -l files/6119.2016.0104.1.thresh ``` (remember, `wc -l` returns a count of the number of lines in the file). These look like fairly standard threshold files. Now we'll see what `Flux.pl` does with them. ## The Parsl Flux App For convenience, we'll wrap the UNIX command-line invocation of the `Flux.pl` script in a Parsl App, which will make it easier to work with from within the Jupyter Notebook environment. ``` # The prep work: import parsl from parsl.config import Config from parsl.executors.threads import ThreadPoolExecutor from parsl.app.app import bash_app,python_app from parsl import File config = Config( executors=[ThreadPoolExecutor()], lazy_errors=True ) parsl.load(config) # The App: @bash_app def Flux(inputs=[], outputs=[], binWidth='600', geoDir='geo/', stdout='stdout.txt', stderr='stderr.txt'): return 'perl ./perl/Flux.pl %s %s %s %s' % (inputs[0], outputs[0], binWidth, geoDir) ``` _Edit stuff below to use the App_ ## Flux Output Below is the output generated by `Flux.pl` using the threshold files `6148.2016.0109.0.thresh` and `6119.2016.0104.1.thresh` (separately) as input: ``` $ perl ./perl/Flux.pl files/6148.2016.0109.0.thresh outputs/ThreshFluxOut6148_01 600 geo/ $ head -15 outputs/ThreshFluxOut6148_01 #cf12d07ed2dfe4e4c0d52eb663dd9956 #md5_hex(1536259294 1530469616 files/6148.2016.0109.0.thresh outputs/ThreshFluxOut6148_01 600 geo/) 01/09/2016 00:06:00 59.416172 8.760437 01/09/2016 00:16:00 63.291139 9.041591 01/09/2016 00:26:00 71.041075 9.579177 01/09/2016 00:36:00 50.374580 8.066389 01/09/2016 00:46:00 55.541204 8.469954 01/09/2016 00:56:00 73.624386 9.751788 01/09/2016 01:06:00 42.624645 7.419998 01/09/2016 01:16:00 54.249548 8.370887 01/09/2016 01:26:00 45.207957 7.641539 01/09/2016 01:36:00 42.624645 7.419998 01/09/2016 01:46:00 65.874451 9.224268 01/09/2016 01:56:00 59.416172 8.760437 01/09/2016 02:06:00 94.290881 11.035913 ``` ``` $ perl ./perl/Flux.pl files/6119.2016.0104.1.thresh outputs/ThreshFluxOut6119_01 600 geo/ $ head -15 outputs/ThreshFluxOut6119_01 #84d0f02f26edb8f59da2d4011a27389d #md5_hex(1536259294 1528996902 files/6119.2016.0104.1.thresh outputs/ThreshFluxOut6119_01 600 geo/) 01/04/2016 21:00:56 12496.770860 127.049313 01/04/2016 21:10:56 12580.728494 127.475379 01/04/2016 21:20:56 12929.475588 129.230157 01/04/2016 21:30:56 12620.769827 127.678079 01/04/2016 21:40:56 12893.309222 129.049289 01/04/2016 21:50:56 12859.726169 128.881113 01/04/2016 22:00:56 12782.226815 128.492174 01/04/2016 22:10:56 12520.020666 127.167443 01/04/2016 22:20:56 12779.643503 128.479189 01/04/2016 22:30:56 12746.060449 128.310265 01/04/2016 22:40:56 12609.144924 127.619264 01/04/2016 22:50:56 12372.771894 126.417419 01/04/2016 23:00:56 12698.269181 128.069490 ``` `Flux.pl` seems to give reasonable output with a threshold file as input, provided the DAQ has a geometry file that's up to standards. Can we interpret the output? Despite the lack of a header line, some reasonable inferences will make it clear. The first column is clearly the date that the data was taken, and in both cases it agrees with the date indicated by the threshold file's filename. The second column is clearly time-of-day values, but what do they mean? We might be tempted to think of them as the full-second portion of cosmic ray event times, but we note in both cases that they occur in a regular pattern of exactly every ten minutes. Of course, that happens to be exactly what we selected as the `binWidth` parameter, 600s = 10min. These are the time bins into which the cosmic ray event data is organized. Since we're calculating flux -- muon strikes per unit area per unit time -- we expect the flux count itself to be included in the data, and in fact this is what the third column is, in units of $events/m^2/min$. Note that the "$/min$" part is always a part of the units of the third column, no matter what the size of the time bins we selected. Finally, when doing science, having a measurement means having uncertainty. The fourth column is the obligatory statistical uncertainty in the flux. ## An exercise in statistical uncertainty The general formula for flux $\Phi$ is $$\Phi = \frac{N}{AT}$$ where $N$ is the number of incident events, $A$ is the cross-sectional area over which the flux is measured, and $T$ is the time interval over which the flux is measured. By the rule of quadrature for propagating uncertainties, $$\frac{\delta \Phi}{\Phi} \approx \frac{\delta N}{N} + \frac{\delta A}{A} + \frac{\delta T}{T}$$ Here, $N$ is the raw count of muon hits in the detector, an integer with a standard statistical uncertainty of $\sqrt{N}$. In our present analysis, errors in the bin width and detector area are negligible compared to the statistical fluctuation of cosmic ray muons. Thus, we'll take $\delta A \approx \delta T \approx 0$ to leave $$\delta \Phi \approx \frac{\delta N}{N} \Phi = \frac{\Phi}{\sqrt{N}}$$ Rearranging this a bit, we find that we should be able to calculate the exact number of muon strikes for each time bin as $$N \approx \left(\frac{\Phi}{\delta\Phi}\right)^2.$$ Let's see what happens when we apply this to the data output from `Flux.pl`. For the 6148 data with `binWidth=600`, we find ``` Date Time Phi dPhi (Phi/dPhi)^2 01/09/16 12:06:00 AM 59.416172 8.760437 45.999996082 01/09/16 12:16:00 AM 63.291139 9.041591 49.0000030968 01/09/16 12:26:00 AM 71.041075 9.579177 54.9999953935 01/09/16 12:36:00 AM 50.37458 8.066389 38.9999951081 01/09/16 12:46:00 AM 55.541204 8.469954 43.0000020769 01/09/16 12:56:00 AM 73.624386 9.751788 57.000001784 01/09/16 01:06:00 AM 42.624645 7.419998 33.0000025577 01/09/16 01:16:00 AM 54.249548 8.370887 41.999999903 01/09/16 01:26:00 AM 45.207957 7.641539 35.0000040418 01/09/16 01:36:00 AM 42.624645 7.419998 33.0000025577 01/09/16 01:46:00 AM 65.874451 9.224268 51.00000197 01/09/16 01:56:00 AM 59.416172 8.760437 45.999996082 01/09/16 02:06:00 AM 94.290881 11.035913 72.9999984439 ``` The numbers we come up with are in fact integers to an excellent approximation! --- ### Exercise 1 A) Using the data table above, round the `(Phi/dPhi)^2` column to the nearest integer, calling it `N`. With $\delta N = \sqrt{N}$, calculate $\frac{\delta N}{N}$ for each row in the data. B) Using your knowledge of the cosmic ray muon detector, estimate the uncertainty $\delta A$ in the detector area $A$ and the uncertainty $\delta T$ in the time bin $T$ given as the input `binWidth` parameter. Calculate $\frac{\delta A}{A}$ and $\frac{\delta T}{T}$ for this analysis. C) Considering the results of A) and B), do you think our previous assumption that $\frac{\delta A}{A} \approx 0$ and $\frac{\delta T}{T} \approx 0$ compared to $\frac{\delta N}{N}$ is justified? --- ### Additional Exercises * Do the number of counts $N$ in one `binWidth=600s` bin match the sum of counts in the ten corresponding `binWidth=60s` bins? * Considering raw counts, do you think the "zero" bins in the above analyses are natural fluctuations in cosmic ray muon strikes? * Do the flux values shown above reasonably agree with the known average CR muon flux at sea level? If "no," what effects do you think might account for the difference? --- We can dig more information out of the `Flux.pl` output by returning to the definition of flux $$\Phi = \frac{N}{AT}.$$ Now that we know $N$ for each data point, and given that we know the bin width $T$ because we set it for the entire analysis, we should be able to calculate the area of the detector as $$A = \frac{N}{\Phi T}$$ One important comment: `Flux.pl` gives flux values in units of `events/m^2/min` - note the use of minutes instead of seconds. When substituting a numerical value for $T$, we must convert the command line parameter `binWidth=600` from $600s$ to $10min$. When we perform this calculation, we find consistent values for $A$: ``` Date Time Phi dPhi N=(Phi/dPhi)^2 A=N/Phi T 01/09/16 12:06:00 AM 59.416172 8.760437 45.999996082 0.0774199928 01/09/16 12:16:00 AM 63.291139 9.041591 49.0000030968 0.0774200052 01/09/16 12:26:00 AM 71.041075 9.579177 54.9999953935 0.0774199931 01/09/16 12:36:00 AM 50.37458 8.066389 38.9999951081 0.0774199906 01/09/16 12:46:00 AM 55.541204 8.469954 43.0000020769 0.0774200035 01/09/16 12:56:00 AM 73.624386 9.751788 57.000001784 0.0774200029 01/09/16 01:06:00 AM 42.624645 7.419998 33.0000025577 0.0774200056 01/09/16 01:16:00 AM 54.249548 8.370887 41.999999903 0.0774199997 01/09/16 01:26:00 AM 45.207957 7.641539 35.0000040418 0.0774200083 01/09/16 01:36:00 AM 42.624645 7.419998 33.0000025577 0.0774200056 01/09/16 01:46:00 AM 65.874451 9.224268 51.00000197 0.077420003 01/09/16 01:56:00 AM 59.416172 8.760437 45.999996082 0.0774199928 01/09/16 02:06:00 AM 94.290881 11.035913 72.9999984439 0.0774199983 ``` In fact, the area of one standard 6000-series QuarkNet CRMD detector panel is $0.07742m^2$. It's important to note that we're reversing only the calculations, not the physics! That is, we find $A=0.07742m^2$ because that's the value stored in the `6248.geo` file, not because we're able to determine the actual area of the detector panel from the `Flux.pl` output data using physical principles. ## Testing binWidth To verify that the third-column flux values behave as expected, we can run a quick check by manipulating the `binWidth` parameter. We'll run `Flux.pl` on the above two threshold files again, but this time we'll reduce `binWidth` by a factor of 10: ``` $ perl ./perl/Flux.pl files/6148.2016.0109.0.thresh outputs/ThreshFluxOut6148_02 60 geo/ ``` ``` !head -15 outputs/ThreshFluxOut6148_02 ``` ``` $ perl ./perl/Flux.pl files/6119.2016.0104.1.thresh outputs/ThreshFluxOut6119_02 60 geo/ ``` ``` !head -15 outputs/ThreshFluxOut6119_02 ``` In the case of the 6148 data, our new fine-grained binning reveals some sparsity in the first several minutes of the data, as all of the bins between the `2:30` bin and the `13:30` bin are empty of muon events (and therefore not reported). What happened here? It's difficult to say -- under normal statistical variations, it's possible that there were simply no recorded events during these bins. It's also possible that the experimenter adjusted the level of physical shielding around the detector during these times, or had a cable unplugged while troubleshooting.	github_jupyter
# Character-level recurrent sequence-to-sequence model Author: [fchollet](https://twitter.com/fchollet)<br> Date created: 2017/09/29<br> Last modified: 2020/04/26<br> Description: Character-level recurrent sequence-to-sequence model. ## Introduction This example demonstrates how to implement a basic character-level recurrent sequence-to-sequence model. We apply it to translating short English sentences into short French sentences, character-by-character. Note that it is fairly unusual to do character-level machine translation, as word-level models are more common in this domain. Summary of the algorithm - We start with input sequences from a domain (e.g. English sentences) and corresponding target sequences from another domain (e.g. French sentences). - An encoder LSTM turns input sequences to 2 state vectors (we keep the last LSTM state and discard the outputs). - A decoder LSTM is trained to turn the target sequences into the same sequence but offset by one timestep in the future, a training process called "teacher forcing" in this context. It uses as initial state the state vectors from the encoder. Effectively, the decoder learns to generate `targets[t+1...]` given `targets[...t]`, conditioned on the input sequence. - In inference mode, when we want to decode unknown input sequences, we: - Encode the input sequence into state vectors - Start with a target sequence of size 1 (just the start-of-sequence character) - Feed the state vectors and 1-char target sequence to the decoder to produce predictions for the next character - Sample the next character using these predictions (we simply use argmax). - Append the sampled character to the target sequence - Repeat until we generate the end-of-sequence character or we hit the character limit. ## Setup ``` import numpy as np import tensorflow as tf from tensorflow import keras ``` ## Download the data ``` !!curl -O http://www.manythings.org/anki/fra-eng.zip !!unzip fra-eng.zip ``` ## Configuration ``` batch_size = 64 # Batch size for training. epochs = 100 # Number of epochs to train for. latent_dim = 256 # Latent dimensionality of the encoding space. num_samples = 10000 # Number of samples to train on. # Path to the data txt file on disk. data_path = "fra.txt" ``` ## Prepare the data ``` # Vectorize the data. input_texts = [] target_texts = [] input_characters = set() target_characters = set() with open(data_path, "r", encoding="utf-8") as f: lines = f.read().split("\n") for line in lines[: min(num_samples, len(lines) - 1)]: input_text, target_text, _ = line.split("\t") # We use "tab" as the "start sequence" character # for the targets, and "\n" as "end sequence" character. target_text = "\t" + target_text + "\n" input_texts.append(input_text) target_texts.append(target_text) for char in input_text: if char not in input_characters: input_characters.add(char) for char in target_text: if char not in target_characters: target_characters.add(char) input_characters = sorted(list(input_characters)) target_characters = sorted(list(target_characters)) num_encoder_tokens = len(input_characters) num_decoder_tokens = len(target_characters) max_encoder_seq_length = max([len(txt) for txt in input_texts]) max_decoder_seq_length = max([len(txt) for txt in target_texts]) print("Number of samples:", len(input_texts)) print("Number of unique input tokens:", num_encoder_tokens) print("Number of unique output tokens:", num_decoder_tokens) print("Max sequence length for inputs:", max_encoder_seq_length) print("Max sequence length for outputs:", max_decoder_seq_length) input_token_index = dict([(char, i) for i, char in enumerate(input_characters)]) target_token_index = dict([(char, i) for i, char in enumerate(target_characters)]) encoder_input_data = np.zeros( (len(input_texts), max_encoder_seq_length, num_encoder_tokens), dtype="float32" ) decoder_input_data = np.zeros( (len(input_texts), max_decoder_seq_length, num_decoder_tokens), dtype="float32" ) decoder_target_data = np.zeros( (len(input_texts), max_decoder_seq_length, num_decoder_tokens), dtype="float32" ) for i, (input_text, target_text) in enumerate(zip(input_texts, target_texts)): for t, char in enumerate(input_text): encoder_input_data[i, t, input_token_index[char]] = 1.0 encoder_input_data[i, t + 1 :, input_token_index[" "]] = 1.0 for t, char in enumerate(target_text): # decoder_target_data is ahead of decoder_input_data by one timestep decoder_input_data[i, t, target_token_index[char]] = 1.0 if t > 0: # decoder_target_data will be ahead by one timestep # and will not include the start character. decoder_target_data[i, t - 1, target_token_index[char]] = 1.0 decoder_input_data[i, t + 1 :, target_token_index[" "]] = 1.0 decoder_target_data[i, t:, target_token_index[" "]] = 1.0 ``` ## Build the model ``` # Define an input sequence and process it. encoder_inputs = keras.Input(shape=(None, num_encoder_tokens)) encoder = keras.layers.LSTM(latent_dim, return_state=True) encoder_outputs, state_h, state_c = encoder(encoder_inputs) # We discard `encoder_outputs` and only keep the states. encoder_states = [state_h, state_c] # Set up the decoder, using `encoder_states` as initial state. decoder_inputs = keras.Input(shape=(None, num_decoder_tokens)) # We set up our decoder to return full output sequences, # and to return internal states as well. We don't use the # return states in the training model, but we will use them in inference. decoder_lstm = keras.layers.LSTM(latent_dim, return_sequences=True, return_state=True) decoder_outputs, _, _ = decoder_lstm(decoder_inputs, initial_state=encoder_states) decoder_dense = keras.layers.Dense(num_decoder_tokens, activation="softmax") decoder_outputs = decoder_dense(decoder_outputs) # Define the model that will turn # `encoder_input_data` & `decoder_input_data` into `decoder_target_data` model = keras.Model([encoder_inputs, decoder_inputs], decoder_outputs) ``` ## Train the model ``` model.compile( optimizer="rmsprop", loss="categorical_crossentropy", metrics=["accuracy"] ) model.fit( [encoder_input_data, decoder_input_data], decoder_target_data, batch_size=batch_size, epochs=epochs, validation_split=0.2, ) # Save model model.save("s2s") ``` ## Run inference (sampling) 1. encode input and retrieve initial decoder state 2. run one step of decoder with this initial state and a "start of sequence" token as target. Output will be the next target token. 3. Repeat with the current target token and current states ``` # Define sampling models # Restore the model and construct the encoder and decoder. model = keras.models.load_model("s2s") encoder_inputs = model.input[0] # input_1 encoder_outputs, state_h_enc, state_c_enc = model.layers[2].output # lstm_1 encoder_states = [state_h_enc, state_c_enc] encoder_model = keras.Model(encoder_inputs, encoder_states) decoder_inputs = model.input[1] # input_2 decoder_state_input_h = keras.Input(shape=(latent_dim,)) decoder_state_input_c = keras.Input(shape=(latent_dim,)) decoder_states_inputs = [decoder_state_input_h, decoder_state_input_c] decoder_lstm = model.layers[3] decoder_outputs, state_h_dec, state_c_dec = decoder_lstm( decoder_inputs, initial_state=decoder_states_inputs ) decoder_states = [state_h_dec, state_c_dec] decoder_dense = model.layers[4] decoder_outputs = decoder_dense(decoder_outputs) decoder_model = keras.Model( [decoder_inputs] + decoder_states_inputs, [decoder_outputs] + decoder_states ) # Reverse-lookup token index to decode sequences back to # something readable. reverse_input_char_index = dict((i, char) for char, i in input_token_index.items()) reverse_target_char_index = dict((i, char) for char, i in target_token_index.items()) def decode_sequence(input_seq): # Encode the input as state vectors. states_value = encoder_model.predict(input_seq) # Generate empty target sequence of length 1. target_seq = np.zeros((1, 1, num_decoder_tokens)) # Populate the first character of target sequence with the start character. target_seq[0, 0, target_token_index["\t"]] = 1.0 # Sampling loop for a batch of sequences # (to simplify, here we assume a batch of size 1). stop_condition = False decoded_sentence = "" while not stop_condition: output_tokens, h, c = decoder_model.predict([target_seq] + states_value) # Sample a token sampled_token_index = np.argmax(output_tokens[0, -1, :]) sampled_char = reverse_target_char_index[sampled_token_index] decoded_sentence += sampled_char # Exit condition: either hit max length # or find stop character. if sampled_char == "\n" or len(decoded_sentence) > max_decoder_seq_length: stop_condition = True # Update the target sequence (of length 1). target_seq = np.zeros((1, 1, num_decoder_tokens)) target_seq[0, 0, sampled_token_index] = 1.0 # Update states states_value = [h, c] return decoded_sentence ``` You can now generate decoded sentences as such: ``` for seq_index in range(20): # Take one sequence (part of the training set) # for trying out decoding. input_seq = encoder_input_data[seq_index : seq_index + 1] decoded_sentence = decode_sequence(input_seq) print("-") print("Input sentence:", input_texts[seq_index]) print("Decoded sentence:", decoded_sentence) ```	github_jupyter
Note: There are multiple ways to solve these problems in SQL. Your solution may be quite different from mine and still be correct. 1. Connect to the SQLite3 database at `data/faculty.db` in the `notebooks` folder using the `sqlite` package or `ipython-sql` magic functions. Inspect the `sql` creation statement for each tables so you know their structure. ``` %load_ext sql %sql sqlite:///../notebooks/data/faculty.db %%sql SELECT sql FROM sqlite_master WHERE type='table'; ``` 2. Find the youngest and oldest faculty member(s) of each gender. ``` %%sql SELECT min(age), max(age) FROM person %%sql SELECT first, last, age, gender FROM person INNER JOIN gender ON person.gender_id = gender.gender_id WHERE age IN (SELECT min(age) FROM person) AND gender = 'Male' UNION SELECT first, last, age, gender FROM person INNER JOIN gender ON person.gender_id = gender.gender_id WHERE age IN (SELECT min(age) FROM person) AND gender = 'Female' UNION SELECT first, last, age, gender FROM person INNER JOIN gender ON person.gender_id = gender.gender_id WHERE age IN (SELECT max(age) FROM person) AND gender = 'Male' UNION SELECT first, last, age, gender FROM person INNER JOIN gender ON person.gender_id = gender.gender_id WHERE age IN (SELECT max(age) FROM person) AND gender = 'Female' LIMIT 10 ``` 3. Find the median age of the faculty members who know Python. As SQLite3 does not provide a median function, you can create a User Defined Function (UDF) to do this. See [documentation](https://docs.python.org/2/library/sqlite3.html#sqlite3.Connection.create_function). ``` import statistics class Median: def __init__(self): self.acc = [] def step(self, value): self.acc.append(value) def finalize(self): return statistics.median(self.acc) import sqlite3 con = sqlite3.connect('../notebooks/data/faculty.db') con.create_aggregate("Median", 1, Median) cr = con.cursor() cr.execute('SELECT median(age) FROM person') cr.fetchall() ``` 4. Arrange countries by the average age of faculty in descending order. Countries are only included in the table if there are at least 3 faculty members from that country. ``` %%sql SELECT country, count(country), avg(age) FROM person INNER JOIN country ON person.country_id = country.country_id GROUP BY country HAVING count() > 3 ORDER BY age DESC LIMIT 3 ``` 5. Which country has the highest average body mass index (BMII) among the faculty? Recall that BMI is weight (kg) / (height (m))^2. ``` %%sql SELECT country, avg(weight / (heightheight)) as avg_bmi FROM person INNER JOIN country ON person.country_id = country.country_id GROUP BY country ORDER BY avg_bmi DESC LIMIT 3 ``` 6. Do obese faculty (BMI > 30) know more languages on average than non-obese faculty? ``` %%sql SELECT is_obese, avg(language) FROM ( SELECT weight / (height*height) > 30 AS is_obese, count(language_name) AS language FROM person INNER JOIN person_language ON person.person_id = person_language.person_id INNER JOIN language ON person_language.language_id = language.language_id GROUP BY person.person_id ) GROUP BY is_obese ```	github_jupyter
# Frequent opiate prescriber ``` import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns import preprocessors as pp sns.set(style="darkgrid") data = pd.read_csv('../data/prescriber-info.csv') data.head() ``` ## Variable Separation ``` uniq_cols = ['NPI'] cat_cols = list(data.columns[1:5]) cat_cols num_cols = list(data.columns[5:-1]) # print(num_cols) target = [data.columns[-1]] target ``` ## Categorical Variable Analysis & EDA ### Missing values ``` # chcking for missing values data[cat_cols].isnull().sum() # checking for missing value percentage data[cat_cols].isnull().sum()/data.shape[0] 100 # checking for null value in drugs column data[num_cols].isnull().sum().sum() data['NPI'].nunique() ``` Remarks: 1. We dont need `NPI` column it has all unique values. 2. The `Credentials` column has missing values ~3% of total. <!-- 3. All the `med_clos` are sparse in nature --> ### Basic plots ``` data[num_cols].iloc[:,2].value_counts() cat_cols for item in cat_cols[1:]: print('-'25) print(data[item].value_counts()) cat_cols # Gender analysis plt.figure(figsize=(7,5)) sns.countplot(data=data,x='Gender') plt.title('Count plot of Gender column') plt.show() # State column plt.figure(figsize=(15,5)) sns.countplot(data=data,x='State') plt.title('Count plot of State column') plt.show() # lets check out `Speciality` column data['Specialty'].nunique() plt.figure(figsize=(20,5)) sns.countplot(data=data,x='Specialty') plt.title('Count plot of Specialty column') plt.xticks(rotation=90) plt.show() data['Specialty'].value_counts()[:20] # filling missing values with mean ``` In `credentials` we can do lot more 1. The credentals column have multiple occupation in the same row. 2. \[PHD, MD\] and \[MD, PHD\] are treated differently. 3. P,A, is treated different from P.A and PA 4. MD ----- M.D. , M.D, M D, MD\` 5. This column is a mess ``` cat_cols ``` Remarks: 1. We don't need `Credentials` column which is a real mess, the `Specialty` column has the same information as of `Credentials`. 2. Cat Features to remove - `NPI`, `Credentials` 3. Cat Features to keep - `Gender`, `State`, `Speciality` 4. Cat encoder pipeline - 1. Gender - normal 1/0 encoding using category_encoders 2. State - Frequency encoding using category_encoders 3. Speciality - Frequency encoding ### Numerical Variable Analysis & Engineering ``` for item in num_cols: print('-'25) print(f'frequency - {data[item].nunique()}') print(f'Min \t Average \t Max \t Prob>0') for item in num_cols: print('-'40) prob = sum(data[item] > 0) / data[item].shape[0] print(f'{data[item].min()}\t{data[item].mean(): .4f} \t{data[item].max()} \t {prob:.4f}') print(f'Maximun of all maxs - {data[num_cols].max().max()}') print(f'Average of all maxs - {data[num_cols].max().mean()}') print(f'Minimun of all maxs - {data[num_cols].max().min()}') print(f'Maximun of all mins - {data[num_cols].min().max()}') print(f'Minimun of all mins - {data[num_cols].min().min()}') sns.distplot(data[num_cols[0]]); sns.boxplot(data = data, x = num_cols[0],orient="v"); ``` Problem: 1. All the continuous cols have large number of zeros, and other values are counting value. 2. The solutions I stumble accross are - `Two-part-models(twopm)`, `hurdle models` and `zero inflated poisson models(ZIP)` 3. These models thinks the target variable has lots of zero and the non-zero values are not 1, if they had been 1s and 0s we could use a a classification model but they are like 0s mostly and if not zeros they are continuous variable like 100,120, 234, 898, etc. 4. In our case our feature variable has lots of zeros. ``` data[data[num_cols[0]] > 0][num_cols[0]] temp = 245 sns.distplot(data[data[num_cols[temp]] > 0][num_cols[temp]]); temp = 5 sns.distplot(np.log(data[data[num_cols[temp]] > 0][num_cols[temp]])); from sklearn.preprocessing import power_transform temp = 5 # data_without_0 = data[data[num_cols[temp]] > 0][num_cols[temp]] data_without_0 = data[num_cols[temp]] data_0 = np.array(data_without_0).reshape(-1,1) data_0_trans = power_transform(data_0, method='yeo-johnson') sns.distplot(data_0_trans); temp = 5 # data_without_0 = data[data[num_cols[temp]] > 0][num_cols[temp]] data_without_0 = data[num_cols[temp]] data_0 = np.array(data_without_0).reshape(-1,1) data_0_trans = power_transform(data_0+1, method='box-cox') # data_0_trans = np.log(data_0 + 1 ) # data_0 sns.distplot(data_0_trans); from sklearn.decomposition import PCA pca = PCA(n_components=0.8,svd_solver='full') # pca = PCA(n_components='mle',svd_solver='full') pca.fit(data[num_cols]) pca_var_ratio = pca.explained_variance_ratio_ pca_var_ratio len(pca_var_ratio) plt.plot(pca_var_ratio[:],'-*'); sum(pca_var_ratio[:10]) data[num_cols].sample(2) pca.transform(data[num_cols].sample(1)) pca2 = pp.PCATransformer(cols=num_cols,n_components=0.8) pca2.fit(data) pca2.transform(data[num_cols].sample(1)) ``` ### Train test split and data saving ``` # train test split from sklearn.model_selection import train_test_split X = data.drop(target,axis=1) y = data[target] X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.20, random_state=1) pd.concat([X_train,y_train],axis=1).to_csv('../data/train.csv',index=False) pd.concat([X_test,y_test],axis=1).to_csv('../data/test.csv',index=False) ``` ## Data Engineering ``` from sklearn.preprocessing import LabelBinarizer lbin = LabelBinarizer() lbin.fit(X_train['Gender']) gen_tra = lbin.transform(X_train['Gender']) gen_tra X_train[num_cols[:5]].info(); ```	github_jupyter
# The Shared Library with GCC When your program is linked against a shared library, only a small table is created in the executable. Before the executable starts running, the operating system loads the machine code needed for the external functions - a process known as dynamic linking. * Dynamic linking makes executable files smaller and saves disk space, because `one` copy of a library can be shared between `multiple` programs. * Furthermore, most operating systems allows one copy of a shared library in memory to be used by all running programs, thus, saving memory. * The shared library codes can be upgraded without the need to recompile your program. A shared library has file extension of * `.so` (shared objects) in `Linux(Unixes)` * `.dll (dynamic link library) in `Windows`. ## 1: Building the shared library The shared library we will build consist of a single source file: `SumArray.c/h` We will compile the C file with `Position Independent Code( PIC )` into a shared library。 GCC assumes that all libraries * `start` with `lib` * `end` with `.dll`(windows) or `.so`(Linux)， so, we should name the shared library begin with `lib prefix` and the `.so/.dll` extensions. * libSumArray.dll(Windows) * libSumArray.so(Linux) #### Under Windows ``` !gcc -c -O3 -Wall -fPIC -o ./demo/bin/SumArray.o ./demo/src/SumArray.c !gcc -shared -o ./demo/bin/libSumArray.dll ./demo/bin/SumArray.o !dir .\demo\bin\libSumArray.* ``` #### under Linux ``` !gcc -c -O3 -Wall -fPIC -o ./demo/obj/SumArray.o ./demo/gcc/SumArray.c !gcc -shared -o ./cdemo/bin/libSumArray ./demo/obj/SumArray.o !ls ./demo/bin/libSumArray.* ``` * `-c`: compile into object file with default name : funs.o. By default, the object file has the same name as the source file with extension of ".o" * `-O3`: Optimize yet more. turns on all optimizations specified by -O2 and also turns on the -finline-functions, -fweb, -frename-registers and -funswitch-loops optionsturns on all optimizations * `-Wall`: prints "all" compiler's warning message. This option should always be used, in order to generate better code. * `-fPIC` : stands for `Position Independent Code`(位置无关代码) the generated machine code is `not dependent` on being located at a `specific address` in order to `work`. Position-independent code can be `executed` at `any memory address` * -shared: creating a shared library ``` %%file ./demo/makefile-SumArray-dll CC=gcc CFLAGS=-O3 -Wall -fPIC SRCDIR= ./demo/src/ OBJDIR= ./demo/obj/ BINDIR= ./demo/bin/ all: libdll libdll: obj $(CC) -shared -o $(BINDIR)libSumArray.dll $(OBJDIR)SumArray.o del .\demo\obj\SumArray.o obj: ./demo/src/SumArray.c $(CC) -c $(CFLAGS) -o $(OBJDIR)SumArray.o $(SRCDIR)SumArray.c clean: del .\demo\src\libSumArray.dll !make -f ./demo/makefile-SumArray-dll !dir .\demo\bin\libSum.dll ``` #### Under Linux ``` %%file ./code/makefile-SumArray-so CC=gcc CFLAGS=-O3 -Wall -fPIC SRCDIR= ./demo/src/ OBJDIR= ./demo/obj/ BINDIR= ./demo/bin/ all: libdll libdll: obj $(CC) -shared -o $(BINDIR)libSumArray.dll $(OBJDIR)SumArray.o rm -f ./demo/obj/SumArray.o obj: ./demo/src/SumArray.c $(CC) -c $(CFLAGS) -o $(OBJDIR)SumArray.o $(SRCDIR)SumArray.c clean: rm -f ./demo/src/libSumArray.dll !make -f ./code/makefile-SumArray-so !ls ./code/bin/libSum.so ``` ## 2 Building a client executable ### Header Files and Libraries * `Header File`: When compiling the program, the compiler needs the header files to compile the source codes; * `libraries`: the linker needs the libraries to resolve external references from other object files or libraries. The `compiler` and `linker` will not find the `headers/libraries` unless you set the appropriate options * 1 Searching for Header Files `-Idir`: The include-paths are specified via -Idir option (`uppercase` 'I' followed by the directory path or environment variable CPATH). * 2 Searching for libraries Files `-Ldir`: The library-path is specified via -Ldir option (`uppercase` 'L' followed by the directory path(or environment variable LIBRARY_PATH). * 3 Linking the library `-llibname`: Link with the library name without the `lib` prefix and the `.so/.dll` extensions. Windows ```bash -I./demo/src/ -L./demo/bin/ -lSumArray ``` Linux ```bash -I./demo/src/ -L./demo/bin/ -lSumArray -Wl,-rpath=./demo/bin/ ``` * `-Wl,option` Pass option as an option to the linker. If option contains `commas`, it is split into multiple options at the commas. You can use this syntax to pass an argument to the option. For example, -Wl,-Map,output.map passes -Map output.map to the linker. When using the GNU linker, you can also get the same effect with `-Wl,-Map=output.map'. * `-rpath=dir` Add a directory to the runtime library search path. This is used when linking an ELF executable with shared objects. All -rpath arguments are concatenated and passed to the runtime linker, which uses them to locate shared objects at runtime. The -rpath option is also used when locating shared objects which are needed by shared objects explicitly included in the link; --- The following source code `"mainSum.c"` demonstrates calling the DLL's functions: NOTE: mainSum.c is the same code in multi-source example ``` %%file ./demo/src/mainSum.c #include <stdio.h> #include "SumArray.h" int main() { int a1[] = {8, 4, 5, 3, 2}; printf("sum is %d\n", sum(a1, 5)); // sum is 22 return 0; } ``` #### Windows ``` !gcc -c -o ./demo/obj/mainSum.o ./demo/src/mainSum.c !gcc -o ./demo/bin/mainSum ./demo/obj/mainSum.o -I./demo/src/ -L./demo/bin/ -lSumArray !.\demo\bin\mainSum ``` #### Linux ``` !gcc -c -o ./demo/obj/mainSum.o ./demo/obj/mainSum.c !gcc -o ./demo/bin/mainSum ./demo/obj/mainSum.o -I./demo/obj/ -L./demo/bin/ -lSumArray -Wl,-rpath=./demo/bin/ !ldd ./demo/bin/mainSum !./code/demo/mainSum ``` #### Under Windows ``` %%file ./demo/makefile-call-dll SRCDIR= ./demo/src/ OBJDIR= ./demo/obj/ BINDIR= ./demo/bin/ all: mainexe clean: del .\demo\bin\mainSum.exe mainexe: sumobj $(SRCDIR)SumArray.h gcc -o $(BINDIR)mainSum.exe $(OBJDIR)mainSum.o -I$(SRCDIR) -L$(BINDIR) -lSumArray del .\demo\obj\mainSum.o sumobj: $(SRCDIR)mainSum.c gcc -c -o $(OBJDIR)mainSum.o $(SRCDIR)mainSum.c !make -f ./demo/makefile-call-dll !.\demo\bin\mainSum ``` #### Under Linux ``` %%file ./demo/makefile-call-so SRCDIR= ./demo/src/ OBJDIR= ./demo/obj/ BINDIR= ./demo/bin/ all: main clean: rm -f ./demo/bin/mainSum.exe main: sumobj $(SRCDIR)SumArray.h gcc -o $(BINDIR)mainSum.exe $(OBJDIR)mainSum.o -I$(SRCDIR) -L$(BINDIR) -lSumArray -Wl,-rpath=./code/bin/ rm -f ./demo/obj/mainSum.o sumobj: $(SRCDIR)mainSum.c gcc -c -o $(OBJDIR)mainSum.o $(SRCDIR)mainSum.c !make -f ./demo/makefile-call-so !./demo/bin/mainSum ``` ## 3 Building a `shared library` with `multi-source` files The shared library we will build consist of a multi-source files * funs.c/h * SumArray.c/h ``` %%file ./demo/src/funs.h #ifndef FUNS_H #define FUNS_H double dprod(double x, int n); int factorial(int n); #endif %%file ./demo/src/funs.c #include "funs.h" // x[0]x[1]...x[n-1] double dprod(double x, int n) { double y = 1.0; for (int i = 0; i < n; i++) { y = x[i]; } return y; } // The factorial of a positive integer n, denoted by n!, is the product of all positive integers less than or equal to n. // For example,5!=54321=120 // The value of 0! is 1 int factorial(int n) { if (n == 0 ) { return 1; } else { return n * factorial(n - 1); } } ``` #### Building `funs.c` and `SumArray.c` into libmultifuns.dll ``` !gcc -c -O3 -Wall -fPIC -o ./demo/obj/funs.o ./demo/src/funs.c !gcc -c -O3 -Wall -fPIC -o ./demo/obj/SumArray.o ./demo/src/SumArray.c !gcc -shared -o ./demo/bin/libmultifuns.dll ./demo/obj/funs.o ./demo/obj/SumArray.o !dir .\demo\bin\libmulti.dll ``` #### Building with makefile ``` %%file ./demo/makefile-libmultifun CC=gcc CFLAGS=-O3 -Wall -fPIC SRCDIR= ./demo/src/ OBJDIR= ./demo/obj/ BINDIR= ./demo/bin/ all: libmultifuns.dll libmultifuns.dll: multifunsobj $(CC) -shared -o $(BINDIR)libmultifuns.dll $(OBJDIR)funs.o $(OBJDIR)SumArray.o del .\demo\obj\funs.o .\demo\obj\SumArray.o multifunsobj: $(SRCDIR)funs.c $(SRCDIR)SumArray.c $(CC) -c $(CFLAGS) -o $(OBJDIR)SumArray.o $(SRCDIR)SumArray.c $(CC) -c $(CFLAGS) -o $(OBJDIR)funs.o $(SRCDIR)funs.c clean: del .\demo\bin\libmultifuns.dll !make -f ./demo/makefile-libmultifun ``` The result is a compiled shared library `libmultifuns.dll`* ##### makefile-libmultifun - more vars ``` %%file ./code/makefile-libmultifun CC=gcc CFLAGS=-O3 -Wall -fPIC SRCDIR= ./demo/src/ OBJDIR= ./demo/obj/ BINDIR= ./demo/bin/ INC = -I$(SRCDIR) SRCS= $(SRCDIR)funs.c \ $(SRCDIR)SumArray.c all: libmultifuns.dll libmultifuns.dll: multifunsobj $(CC) -shared -o $(BINDIR)libmultifuns.dll funs.o SumArray.o del funs.o SumArray.o multifunsobj: $(CC) -c $(CFLAGS) $(INC) $(SRCS) clean: del .\demo\bin\libmultifuns.dll !make -f ./code/makefile-libmultifun ``` ##### Building a client executable The following source code `"mainMultifuns.c"` demonstrates calling the DLL's functions: ``` %%file ./demo/src/mainMultifuns.c #include <stdio.h> #include "SumArray.h" #include "funs.h" int main() { int a1[] = {8, 4, 5, 3, 2}; printf("sum is %d\n", sum(a1, 5)); // sum is 22 double a2[] = {8.0, 4.0, 5.0, 3.0, 2.0}; printf("dprod is %f\n", dprod(a2, 5)); // dprod is 960 int n =5; printf("the factorial of %d is %d\n",n,factorial(n)); // 5!=120 return 0; } !gcc -c -o ./demo/obj/mainMultifuns.o ./demo/src/mainMultifuns.c !gcc -o ./demo/bin/mainMultifuns ./demo/obj/mainMultifuns.o -I./demo/src/ -L./demo/bin/ -lmultifuns !.\demo\bin\mainMultifuns ``` ## Reference * GCC (GNU compilers) http://gcc.gnu.org * GCC Manual http://gcc.gnu.org/onlinedocs * An Introduction to GCC http://www.network-theory.co.uk/docs/gccintro/index.html. * GCC and Make：Compiling, Linking and Building C/C++ Applications http://www3.ntu.edu.sg/home/ehchua/programming/cpp/gcc_make.html * MinGW-W64 (GCC) Compiler Suite: http://www.mingw-w64.org/doku.php * C/C++ for VS Code https://code.visualstudio.com/docs/languages/cpp * C/C++ Preprocessor Directives http://www.cplusplus.com/doc/tutorial/preprocessor/ * What is a DLL and How Do I Create or Use One? http://www.mingw.org/wiki/DLL	github_jupyter
# Searching the UniProt database and saving fastas: This notebook is really just to demonstrate how Andrew finds the sequences for the datasets. <br> If you do call it from within our github repository, you'll probably want to add the fastas to the `.gitignore` file. ``` # Import bioservices module, to run remote UniProt queries # (will probably need to pip install this to use) from bioservices import UniProt ``` ## Connecting to UniProt using bioservices: ``` service = UniProt() fasta_path = 'refined_query_fastas/' #optional file organization param ``` ## Query with signal_peptide ``` def data_saving_function_with_SP(organism,save_path=''): secreted_query = f'(((organism:{organism} OR host:{organism}) annotation:("signal peptide") keyword:secreted) NOT annotation:(type:transmem)) AND reviewed:yes' secreted_result = service.search(secreted_query, frmt="fasta") secreted_outfile = f'{save_path}{organism}_secreted_SP_new.fasta' with open(secreted_outfile, 'a') as ofh: ofh.write(secreted_result) cytoplasm_query = f'(((organism:{organism} OR host:{organism}) locations:(location:cytoplasm)) NOT (annotation:(type:transmem) OR annotation:("signal peptide"))) AND reviewed:yes' cytoplasm_result = service.search(cytoplasm_query, frmt="fasta") cytoplasm_outfile = f'{save_path}{organism}_cytoplasm_SP_new.fasta' with open(cytoplasm_outfile, 'a') as ofh: ofh.write(cytoplasm_result) membrane_query = f'(((organism:{organism} OR host:{organism}) annotation:(type:transmem)) annotation:("signal peptide")) AND reviewed:yes' membrane_result = service.search(membrane_query, frmt="fasta") membrane_outfile = f'{save_path}{organism}_membrane_SP_new.fasta' with open(membrane_outfile, 'a') as ofh: ofh.write(membrane_result) data_saving_function_with_SP('human',fasta_path) data_saving_function_with_SP('escherichia',fasta_path) ``` ## Query without signal_peptide ``` def data_saving_function_without_SP(organism,save_path=''): # maybe new: secreted_query = f'(((organism:{organism} OR host:{organism}) AND (keyword:secreted OR goa:("extracellular region [5576]"))) NOT (annotation:(type:transmem) OR goa:("membrane [16020]") OR locations:(location:cytoplasm) OR goa:("cytoplasm [5737]") )) AND reviewed:yes' secreted_result = service.search(secreted_query, frmt="fasta") secreted_outfile = f'{save_path}{organism}_secreted_noSP_new_new.fasta' with open(secreted_outfile, 'a') as ofh: ofh.write(secreted_result) cytoplasm_query = f'(((organism:{organism} OR host:{organism}) AND (locations:(location:cytoplasm) OR goa:("cytoplasm [5737]")) ) NOT (annotation:(type:transmem) OR goa:("membrane [16020]") OR keyword:secreted OR goa:("extracellular region [5576]") )) AND reviewed:yes' cytoplasm_result = service.search(cytoplasm_query, frmt="fasta") cytoplasm_outfile = f'{save_path}{organism}_cytoplasm_noSP_new_new.fasta' with open(cytoplasm_outfile, 'a') as ofh: ofh.write(cytoplasm_result) membrane_query= f'(((organism:{organism} OR host:{organism}) AND ( annotation:(type:transmem) OR goa:("membrane [16020]") )) NOT ( keyword:secreted OR goa:("extracellular region [5576]") OR locations:(location:cytoplasm) OR goa:("cytoplasm [5737]") )) AND reviewed:yes' membrane_result = service.search(membrane_query, frmt="fasta") membrane_outfile = f'{save_path}{organism}_membrane_noSP_new_new.fasta' with open(membrane_outfile, 'a') as ofh: ofh.write(membrane_result) data_saving_function_without_SP('human',fasta_path) data_saving_function_without_SP('yeast',fasta_path) data_saving_function_without_SP('escherichia',fasta_path) ``` ## Query ALL SHIT (warning: do not do unless you have lots of free time and computer memory) ``` def data_saving_function_without_SP_full_uniprot(save_path=''): # maybe new: secreted_query = f'((keyword:secreted OR goa:("extracellular region [5576]")) NOT (annotation:(type:transmem) OR goa:("membrane [16020]") OR locations:(location:cytoplasm) OR goa:("cytoplasm [5737]") )) AND reviewed:yes' secreted_result = service.search(secreted_query, frmt="fasta") secreted_outfile = f'{save_path}all_secreted_noSP_new_new.fasta' with open(secreted_outfile, 'a') as ofh: ofh.write(secreted_result) cytoplasm_query = f'(( locations:(location:cytoplasm) OR goa:("cytoplasm [5737]") ) NOT (annotation:(type:transmem) OR goa:("membrane [16020]") OR keyword:secreted OR goa:("extracellular region [5576]") )) AND reviewed:yes' cytoplasm_result = service.search(cytoplasm_query, frmt="fasta") cytoplasm_outfile = f'{save_path}all_cytoplasm_noSP_new_new.fasta' with open(cytoplasm_outfile, 'a') as ofh: ofh.write(cytoplasm_result) membrane_query= f'(( annotation:(type:transmem) OR goa:("membrane [16020]") ) NOT ( keyword:secreted OR goa:("extracellular region [5576]") OR locations:(location:cytoplasm) OR goa:("cytoplasm [5737]") )) AND reviewed:yes' membrane_result = service.search(membrane_query, frmt="fasta") membrane_outfile = f'{save_path}all_membrane_noSP_new_new.fasta' with open(membrane_outfile, 'a') as ofh: ofh.write(membrane_result) data_saving_function_without_SP_full_uniprot(fasta_path) ```	github_jupyter
# Introduction In this post,we will talk about some of the most important papers that have been published over the last 5 years and discuss why they’re so important.We will go through different CNN Architectures (LeNet to DenseNet) showcasing the advancements in general network architecture that made these architectures top the ILSVRC results. # What is ImageNet [ImageNet](http://www.image-net.org/) ImageNet is formally a project aimed at (manually) labeling and categorizing images into almost 22,000 separate object categories for the purpose of computer vision research. However, when we hear the term “ImageNet” in the context of deep learning and Convolutional Neural Networks, we are likely referring to the ImageNet Large Scale Visual Recognition Challenge, or ILSVRC for short. The ImageNet project runs an annual software contest, the ImageNet Large Scale Visual Recognition Challenge (ILSVRC), where software programs compete to correctly classify and detect objects and scenes. The goal of this image classification challenge is to train a model that can correctly classify an input image into 1,000 separate object categories. Models are trained on ~1.2 million training images with another 50,000 images for validation and 100,000 images for testing. These 1,000 image categories represent object classes that we encounter in our day-to-day lives, such as species of dogs, cats, various household objects, vehicle types, and much more. You can find the full list of object categories in the ILSVRC challenge When it comes to image classification, the ImageNet challenge is the de facto benchmark for computer vision classification algorithms — and the leaderboard for this challenge has been dominated by Convolutional Neural Networks and deep learning techniques since 2012. # LeNet-5(1998) [Gradient Based Learning Applied to Document Recognition](http://yann.lecun.com/exdb/publis/pdf/lecun-01a.pdf) 1. A pioneering 7-level convolutional network by LeCun that classifies digits, 2. Found its application by several banks to recognise hand-written numbers on checks (cheques) 3. These numbers were digitized in 32x32 pixel greyscale which acted as an input images. 4. The ability to process higher resolution images requires larger and more convolutional layers, so this technique is constrained by the availability of computing resources. 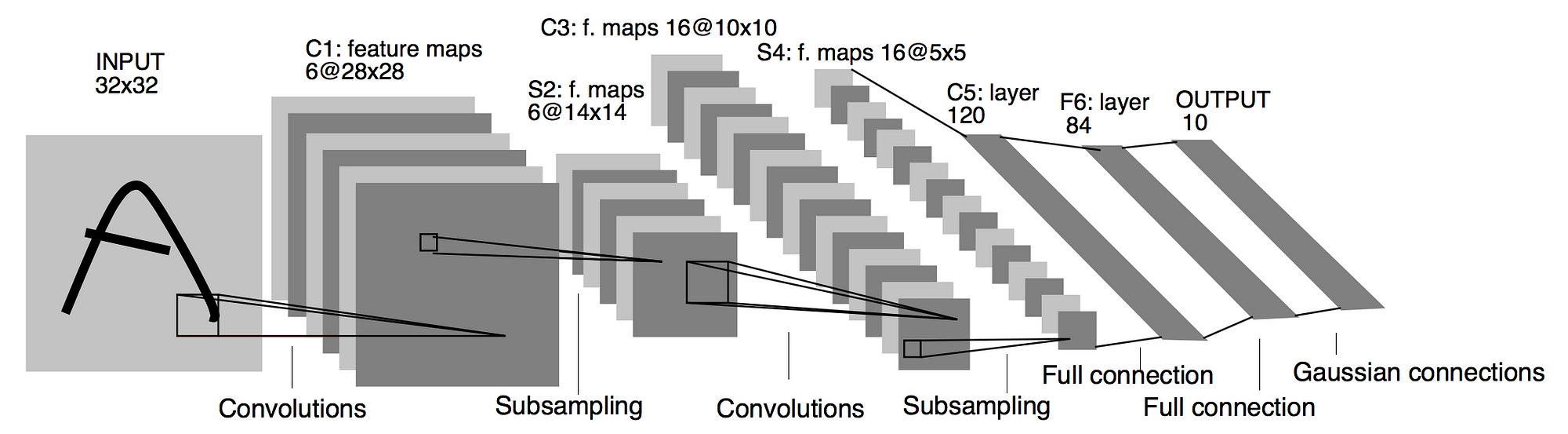![](https://cdn-images-1.medium.com/max/2000/11TI1aGBZ4dybR6__DI9dzA.png) # AlexNet(2012) [ImageNet Classification with Deep Convolutional Networks](https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf) 1. One of the most influential publications in the field by Alex Krizhevsky, Ilya Sutskever, and Geoffrey Hinton that started the revolution of CNN in Computer Vision.This was the first time a model performed so well on a historically difficult ImageNet dataset. 2. The network consisted 11x11, 5x5,3x3, convolutions and made up of 5 conv layers, max-pooling layers, dropout layers, and 3 fully connected layers. 3. Used ReLU for the nonlinearity functions (Found to decrease training time as ReLUs are several times faster than the conventional tanh function) and used SGD with momentum for training. 4. Used data augmentation techniques that consisted of image translations, horizontal reflections, and patch extractions. 5. Implemented dropout layers in order to combat the problem of overfitting to the training data. 6. Trained the model using batch stochastic gradient descent, with specific values for momentum and weight decay. 7. AlexNet was trained for 6 days simultaneously on two Nvidia Geforce GTX 580 GPUs which is the reason for why their network is split into two pipelines. 8. AlexNet significantly outperformed all the prior competitors and won the challenge by reducing the top-5 error from 26% to 15.3% ![](images/alexnet.PNG) # ZFNet(2013) [Visualizing and Understanding Convolutional Neural Networks](https://cs.nyu.edu/~fergus/papers/zeilerECCV2014.pdf) <br> This architecture was more of a fine tuning to the previous AlexNet structure by tweaking the hyper-parameters of AlexNet while maintaining the same structure but still developed some very keys ideas about improving performance.Few minor modifications done were the following: 1. AlexNet trained on 15 million images, while ZF Net trained on only 1.3 million images. 2. Instead of using 11x11 sized filters in the first layer (which is what AlexNet implemented), ZF Net used filters of size 7x7 and a decreased stride value. The reasoning behind this modification is that a smaller filter size in the first conv layer helps retain a lot of original pixel information in the input volume. A filtering of size 11x11 proved to be skipping a lot of relevant information, especially as this is the first conv layer. 3. As the network grows, we also see a rise in the number of filters used. 4. Used ReLUs for their activation functions, cross-entropy loss for the error function, and trained using batch stochastic gradient descent. 5. Trained on a GTX 580 GPU for twelve days. 6. Developed a visualization technique named Deconvolutional Network, which helps to examine different feature activations and their relation to the input space. Called deconvnet* because it maps features to pixels (the opposite of what a convolutional layer does). 7. 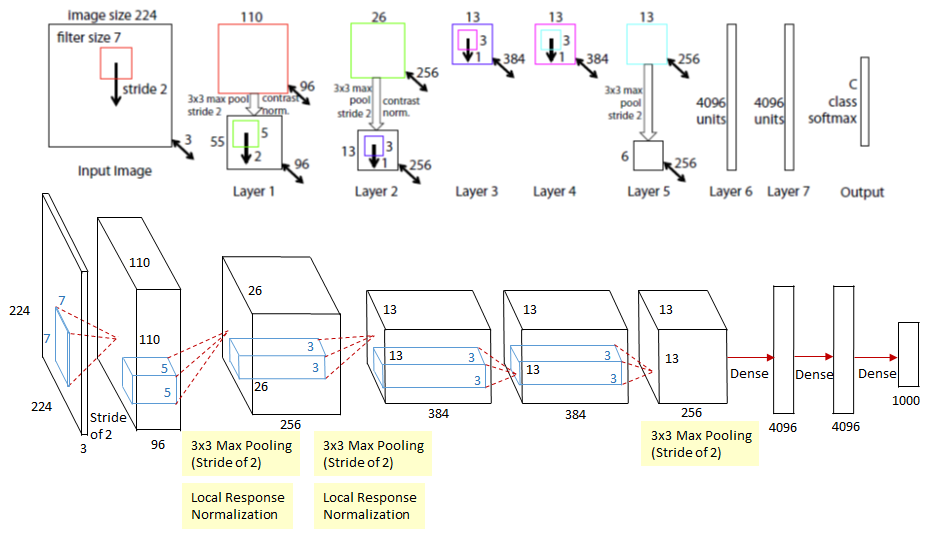It achieved a top-5 error rate of 14.8% ![](https://cdn-images-1.medium.com/max/1600/1bFjBVvUL2Po_p2mKzC4iYQ.png) # VggNet(2014) [VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION](https://arxiv.org/pdf/1409.1556v6.pdf) This architecture is well konwn for Simplicity and depth.. VGGNet is very appealing because of its very uniform architecture.They proposed 6 different variations of VggNet however 16 layer with all 3x3 convolution produced the best result. Few things to note: 1. The use of only 3x3 sized filters is quite different from AlexNet’s 11x11 filters in the first layer and ZF Net’s 7x7 filters. The authors’ reasoning is that the combination of two 3x3 conv layers has an effective receptive field of 5x5. This in turn simulates a larger filter while keeping the benefits of smaller filter sizes. One of the benefits is a decrease in the number of parameters. Also, with two conv layers, we’re able to use two ReLU layers instead of one. 2. 3 conv layers back to back have an effective receptive field of 7x7. 3. As the spatial size of the input volumes at each layer decrease (result of the conv and pool layers), the depth of the volumes increase due to the increased number of filters as you go down the network. 4. Interesting to notice that the number of filters doubles after each maxpool layer. This reinforces the idea of shrinking spatial dimensions, but growing depth. 5. Worked well on both image classification and localization tasks. The authors used a form of localization as regression (see page 10 of the paper for all details). 6. Built model with the Caffe toolbox. 7. Used scale jittering as one data augmentation technique during training. 8. Used ReLU layers after each conv layer and trained with batch gradient descent. 9. Trained on 4 Nvidia Titan Black GPUs for two to three weeks. 10. 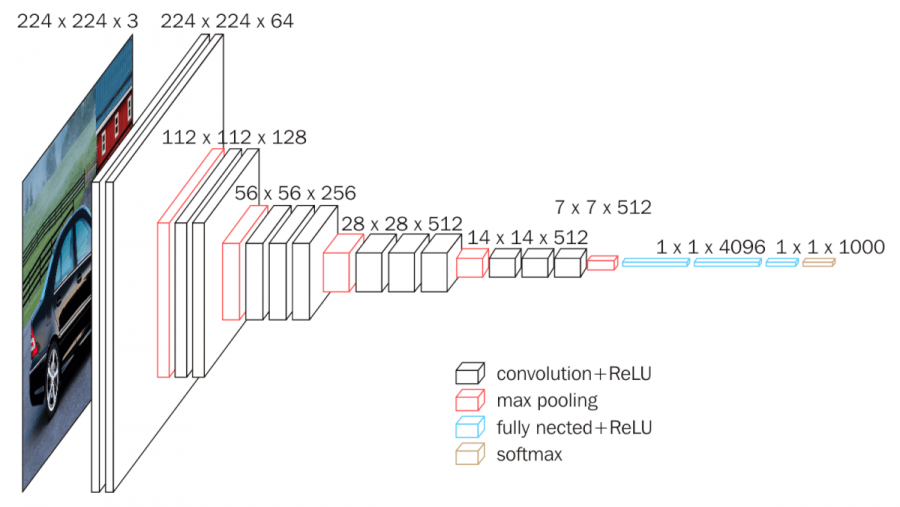It achieved a top-5 error rate of 7.3% ![](https://neurohive.io/wp-content/uploads/2018/11/vgg16-1-e1542731207177.png) ![](images/standardconvnet.PNG) In Standard ConvNet, input image goes through multiple convolution and obtain high-level features.* After Inception V1 ,the author proposed a number of upgrades which increased the accuracy and reduced the computational complexity.This lead to many new upgrades resulting in different versions of Inception Network : 1. Inception v2 2. Inception V3 # Inception Network (GoogleNet)(2014) [Going Deeper with Convolutions](https://www.cv-foundation.org/openaccess/content_cvpr_2015/papers/Szegedy_Going_Deeper_With_2015_CVPR_paper.pdf) Prior to this, most popular CNNs just stacked convolution layers deeper and deeper, hoping to get better performance,however Inception Network was one of the first CNN architectures that really strayed from the general approach of simply stacking conv and pooling layers on top of each other in a sequential structure and came up with the Inception Module.The Inception network was complex. It used a lot of tricks to push performance; both in terms of speed and accuracy. Its constant evolution lead to the creation of several versions of the network. The popular versions are as follows: 1. Inception v1. 2. Inception v2 and Inception v3. 3. Inception v4 and Inception-ResNet. <br> Each version is an iterative improvement over the previous one.Let us go ahead and explore them one by one ![](images/inception.PNG) ## Inception V1 [Inception v1](https://arxiv.org/pdf/1409.4842v1.pdf) ![](images/dog.PNG) Problems this network tried to solve: 1. What is the right kernel size for convolution <br> A larger kernel is preferred for information that is distributed more globally, and a smaller kernel is preferred for information that is distributed more locally. <br> Ans- Filters with multiple sizes.The network essentially would get a bit “wider” rather than “deeper” <br> <br> 3. How to stack convolution which can be less computationally expensive <BR> Stacking them naively computationally expensive. <br> Ans-Limit the number of input channels by adding an extra 1x1 convolution before the 3x3 and 5x5 convolutions <br> <br> 2. How to avoid overfitting in a very deep network <br> Very deep networks are prone to overfitting. It also hard to pass gradient updates through the entire network. <br> Ans-Introduce two auxiliary classifiers (The purple boxes in the image). They essentially applied softmax to the outputs of two of the inception modules, and computed an auxiliary loss over the same labels. The total loss function is a weighted sum of the auxiliary loss and the real loss. The total loss used by the inception net during training. <br> *total_loss = real_loss + 0.3 aux_loss_1 + 0.3 * aux_loss_2 <br> <br> ![](images/inception_module.PNG) Points to note 1. Used 9 Inception modules in the whole architecture, with over 100 layers in total! Now that is deep… 2. No use of fully connected layers! They use an average pool instead, to go from a 7x7x1024 volume to a 1x1x1024 volume. This saves a huge number of parameters. 3. Uses 12x fewer parameters than AlexNet. 4. Trained on “a few high-end GPUs within a week”. 5. It achieved a top-5 error rate of 6.67% ## Inception V2 [Rethinking the Inception Architecture for Computer Vision](https://arxiv.org/pdf/1512.00567v3.pdf) Upgrades were targeted towards: 1. Reducing representational bottleneck by replacing 5x5 convolution to two 3x3 convolution operations which further improves computational speed <br> The intuition was that, neural networks perform better when convolutions didn’t alter the dimensions of the input drastically. Reducing the dimensions too much may cause loss of information, known as a “representational bottleneck” <br> ![](images/inceptionv2.PNG) 2. Using smart factorization method where they factorize convolutions of filter size nxn to a combination of 1xn and nx1 convolutions. <br> For example, a 3x3 convolution is equivalent to first performing a 1x3 convolution, and then performing a 3x1 convolution on its output. They found this method to be 33% more cheaper than the single 3x3 convolution. ![](images/inceptionv2_1.PNG) # ResNet(2015) [Deep Residual Learning for Image Recognition](https://arxiv.org/pdf/1512.03385.pdf) ![](images/resnet_concept.PNG) In ResNet, identity mapping is proposed to promote the gradient propagation. Element-wise addition is used. 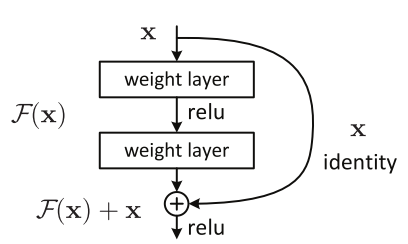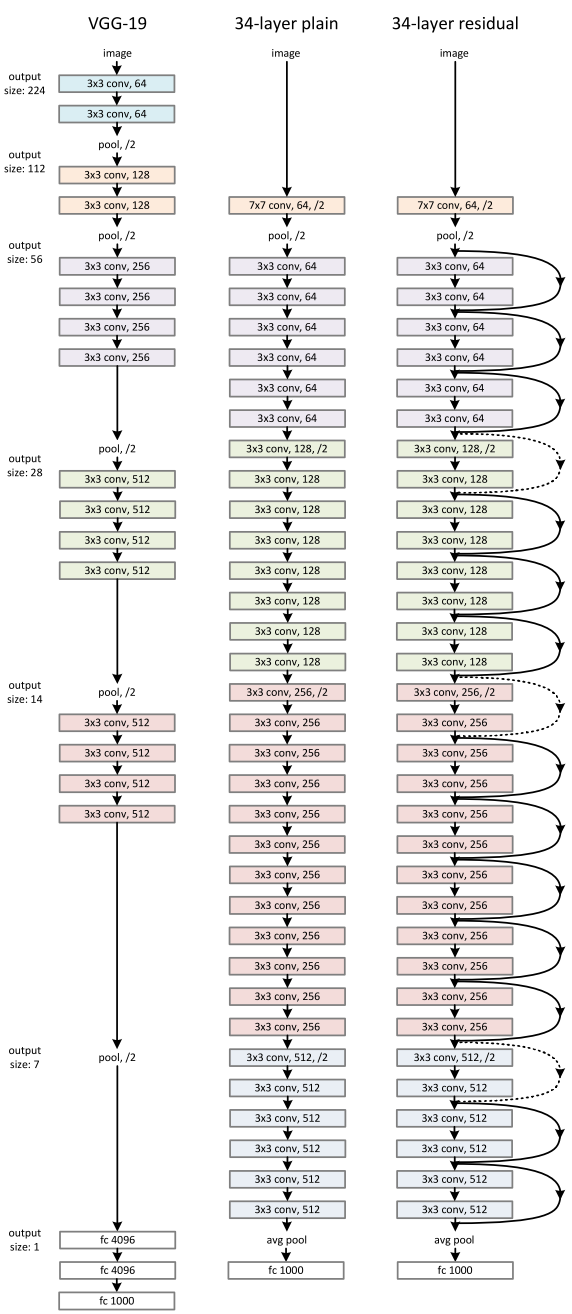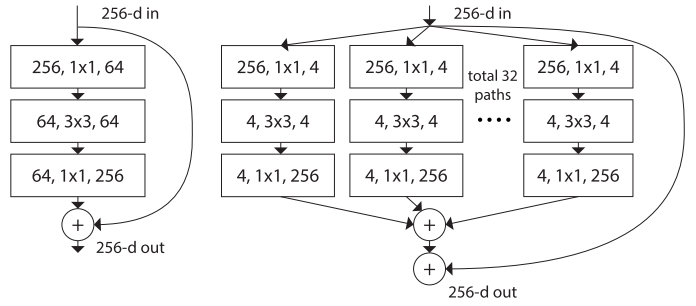It can be viewed as algorithms with a state passed from one ResNet module to another one.** ![](https://cdn-images-1.medium.com/max/720/1ByrVJspW-TefwlH7OLxNkg.png) ![](https://cdn-images-1.medium.com/max/720/12ns4ota94je5gSVjrpFq3A.png) # ResNet-Wide ![](https://cdn-images-1.medium.com/max/960/17JzJ1RGh1Y4VoG1M4dseTw.png) left: a building block of [2], right: a building block of ResNeXt with cardinality = 32 # DenseNet(2017) [Densely Connected Convolutional Networks](https://arxiv.org/pdf/1608.06993v3.pdf) <br> It is a logical extension to ResNet. From the paper:* Recent work has shown that convolutional networks can be substantially deeper, more accurate, and efficient to train if they contain shorter connections between layers close to the input and those close to the output. In this paper, we embrace this observation and introduce the Dense Convolutional Network (DenseNet), which connects each layer to every other layer in a feed-forward fashion. DenseNet Architecture ![](images/densenet_arc.PNG) Let us explore different componenets of the network <br> <br> 1. Dense Block <br> Feature map sizes are the same within the dense block so that they can be concatenated together easily. 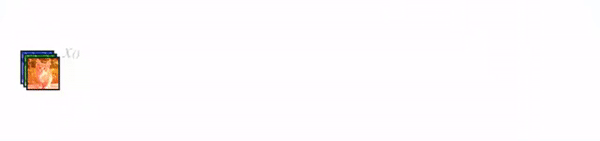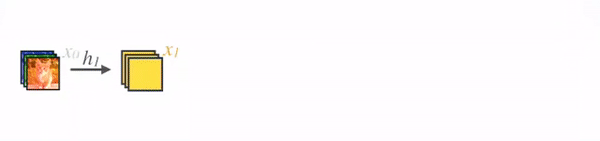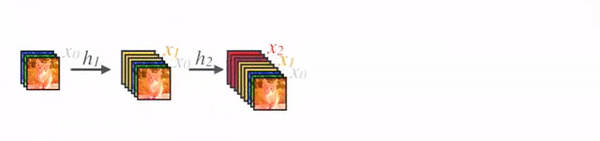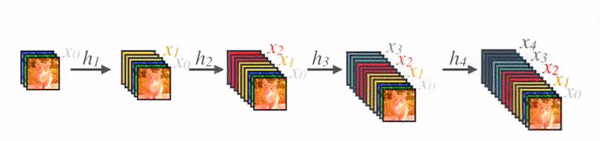![](https://cdn-images-1.medium.com/max/960/19ysRPSExk0KvXR0AhNnlAA.gif) In DenseNet, each layer obtains additional inputs from all preceding layers and passes on its own feature-maps to all subsequent layers. Concatenation is used. Each layer is receiving a “collective knowledge” from all preceding layers.* ![](images/densenet_concept.PNG) Since each layer receives feature maps from all preceding layers, network can be thinner and compact, i.e. number of channels can be fewer. The growth rate k is the additional number of channels for each layer. The paper proposed different ways to implement DenseNet with/without B/C by adding some variations in the Dense block to further reduce the complexity,size and to bring more compression in the architecture. 1. Dense Block (DenseNet) - Batch Norm (BN) - ReLU - 3×3 Convolution 2. Dense Block(DenseNet B) - Batch Norm (BN) - ReLU - 1×1 Convolution - Batch Norm (BN) - ReLU - 3×3 Convolution 3. Dense Block(DenseNet C) - If a dense block contains m feature-maps, The transition layer generate $\theta $ output feature maps, where $\theta \leq \theata \leq$ is referred to as the compression factor. - $\theta$=0.5 was used in the experiemnt which reduced the number of feature maps by 50%. 4. Dense Block(DenseNet BC) - Combination of Densenet B and Densenet C <br> 2. Trasition Layer <br> The layers between two adjacent blocks are referred to as transition layers where the following operations are done to change feature-map sizes: - 1×1 Convolution - 2×2 Average pooling Points to Note: 1. it requires fewer parameters than traditional convolutional networks 2. Traditional convolutional networks with L layers have L connections — one between each layer and its subsequent layer — our network has L(L+1)/ 2 direct connections. 3. Improved flow of information and gradients throughout the network, which makes them easy to train 4. They alleviate the vanishing-gradient problem, strengthen feature propagation, encourage feature reuse, and substantially reduce the number of parameters. 5. Concatenating feature maps instead of summing learned by different layers increases variation in the input of subsequent layers and improves efficiency. This constitutes a major difference between DenseNets and ResNets. 6. It achieved a top-5 error rate of 6.66% # MobileNet ## Spatial Seperable Convolution ![](images/separable_convolution.gif) Divides a kernel into two, smaller kernels ![](https://cdn-images-1.medium.com/max/1440/1mL53fW0tJpNWEePp54y1Sg.png) Instead of doing one convolution with 9 multiplications(parameters), we do two convolutions with 3 multiplications(parameters) each (6 in total) to achieve the same effect* ![](https://cdn-images-1.medium.com/max/1680/1o3mKhG3nHS-1dWa_plCeFw.png) 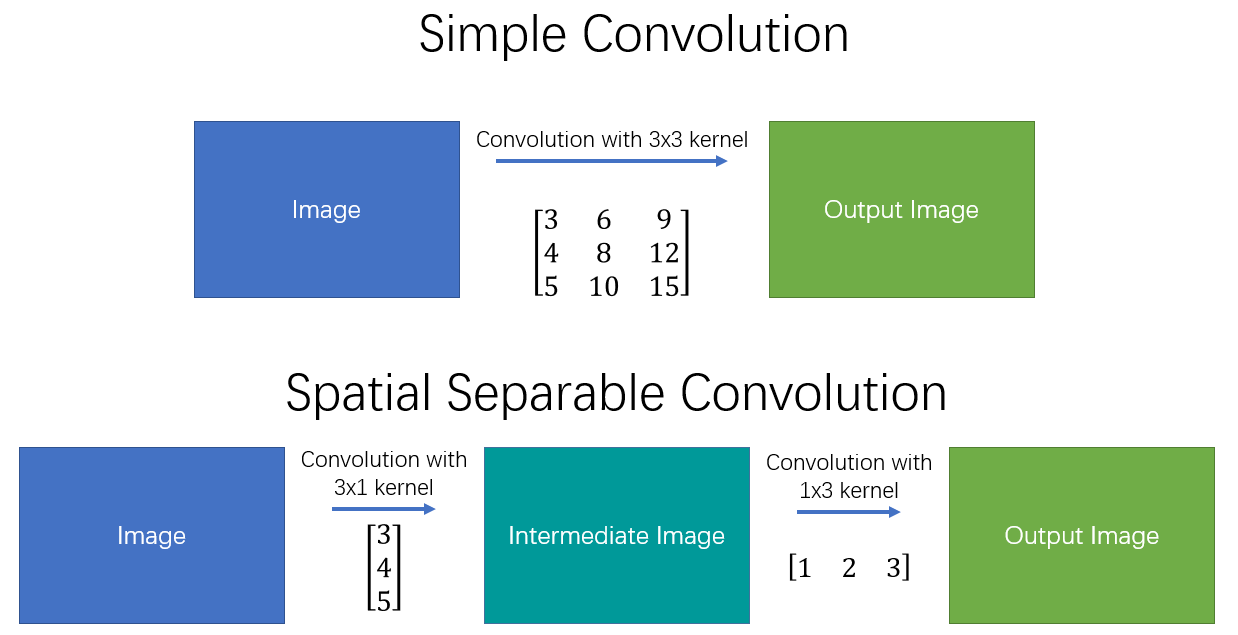With less multiplications, computational complexity goes down, and the network is able to run faster.* This was used in an architecture called [Effnet](https://arxiv.org/pdf/1801.06434v1.pdf) showing promising results. The main issue with the spatial separable convolution is that not all kernels can be “separated” into two, smaller kernels. This becomes particularly bothersome during training, since of all the possible kernels the network could have adopted, it can only end up using one of the tiny portion that can be separated into two smaller kernels. ## Depthwise Convolution ![](images/depthwise.gif) Say we need to increase the number of channels from 16 to 32 using 3x3 kernel. 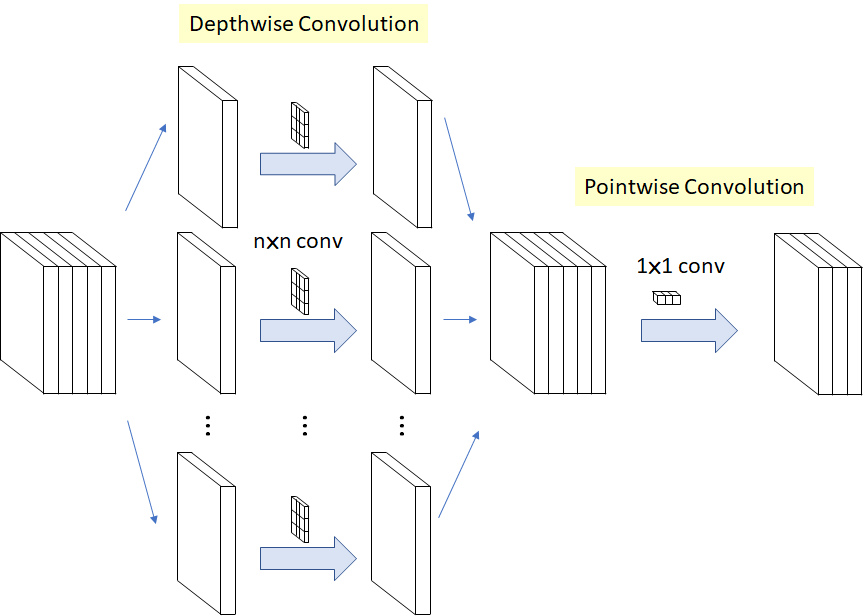<br> Normal Convolution <br> Total No of Parameters = 3 x 3 x 16 x 32 = 4608 ![](https://cdn-images-1.medium.com/max/1200/1VvBTMkVRus6bWOqrK1SlLQ.png) Depthwise Convolution* 1. DepthWise Convolution = 16 x [3 x 3 x 1] 2. PointWise Convolution = 32 x [1 x 1 x 16] Total Number of Parameters = 656 Mobile net uses depthwise seperable convolution to reduce the number of parameters # References [Standford CS231n Lecture Notes](http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture9.pdf) <br> [The 9 Deep Learning Papers You Need To Know About](https://adeshpande3.github.io/adeshpande3.github.io/The-9-Deep-Learning-Papers-You-Need-To-Know-About.html) <br> [CNN Architectures](https://medium.com/@sidereal/cnns-architectures-lenet-alexnet-vgg-googlenet-resnet-and-more-666091488df5) <br> [Lets Keep It Simple](https://arxiv.org/pdf/1608.06037.pdf) <br> [CNN Architectures Keras](https://www.pyimagesearch.com/2017/03/20/imagenet-vggnet-resnet-inception-xception-keras/) <br> [Inception Versions](https://towardsdatascience.com/a-simple-guide-to-the-versions-of-the-inception-network-7fc52b863202) <br> [DenseNet Review](https://towardsdatascience.com/review-densenet-image-classification-b6631a8ef803) <br> [DenseNet](https://towardsdatascience.com/densenet-2810936aeebb) <br> [ResNet](http://teleported.in/posts/decoding-resnet-architecture/) <br> [ResNet Versions](https://towardsdatascience.com/an-overview-of-resnet-and-its-variants-5281e2f56035) <br> [Depthwise Convolution](https://towardsdatascience.com/a-basic-introduction-to-separable-convolutions-b99ec3102728)	github_jupyter
## Probalistic Confirmed COVID19 Cases- Denmark Jorge: remember to reexecute the cell with the photo. ### Table of contents [Initialization](#Initialization) [Data Importing and Processing](#Data-Importing-and-Processing) 1. [Kalman Filter Modeling: Case of Denmark Data](#1.-Kalman-Filter-Modeling:-Case-of-Denmark-Data) 1.1. [Model with the vector c fixed as [0, 1]](#1.1.-Kalman-Filter-Model-vector-c-fixed-as-[0,-1]) 1.2. [Model with the vector c as a random variable with prior](#1.2.-Kalman-Filter-with-the-vector-c-as-a-random-variable-with-prior) 1.3. [Model without input (2 hidden variables)](#1.3.-Kalman-Filter-without-Input) 2. [Kalman Filter Modeling: Case of Norway Data](#2.-Kalman-Filter-Modeling:-Case-of-Norway-Data) 2.1. [Model with the vector c fixed as [0, 1]](#2.1.-Kalman-Filter-Model-vector-c-fixed-as-[0,-1]) 2.2. [Model with the vector c as a random variable with prior](#2.2.-Kalman-Filter-with-the-vector-c-as-a-random-variable-with-prior) 2.3. [Model without input (2 hidden variables)](#2.3.-Kalman-Filter-without-Input) 3. [Kalman Filter Modeling: Case of Sweden Data](#Kalman-Filter-Modeling:-Case-of-Sweden-Data) 3.1. [Model with the vector c fixed as [0, 1]](#3.1.-Kalman-Filter-Model-vector-c-fixed-as-[0,-1]) 3.2. [Model with the vector c as a random variable with prior](#3.2.-Kalman-Filter-with-the-vector-c-as-a-random-variable-with-prior) 3.3. [Model without input (2 hidden variables)](#3.3.-Kalman-Filter-without-Input) ## Initialization ``` from os.path import join, pardir import jax import jax.numpy as jnp import matplotlib.pyplot as plt import numpy as np import numpyro import numpyro.distributions as dist import pandas as pd import seaborn as sns from jax import lax, random, vmap from jax.scipy.special import logsumexp from numpyro import handlers from numpyro.infer import MCMC, NUTS from sklearn.preprocessing import StandardScaler np.random.seed(2103) ROOT = pardir DATA = join(ROOT, "data", "raw") # random seed np.random.seed(42) #plot style plt.style.use('ggplot') %matplotlib inline plt.rcParams['figure.figsize'] = (16, 10) ``` ## Data Importing and Processing The data in this case are the confirmed cases of the COVID-19 and the the mobility data (from Google) for three specific countries: Denmark, Sweden and Norway. ``` adress = join(ROOT, "data", "processed") data = pd.read_csv(join(adress, 'data_three_mob_cov.csv'),parse_dates=['Date']) data.info() data.head(5) ``` Handy functions to split the data, train the models and plot the results. ``` def split_forecast(df, n_train=65): """Split dataframe `df` as training, test and input mobility data.""" # just take the first 4 mobility features X = df.iloc[:, 3:7].values.astype(np.float_) # confirmed cases y = df.iloc[:,2].values.astype(np.float_) idx_train = [range(0,n_train)] idx_test = [range(n_train, len(y))] y_train = y[:n_train] y_test = y[n_train:] return X, y_train, y_test def train_kf(model, data, n_train, n_test, num_samples=9000, num_warmup=3000, kwargs): """Train a Kalman Filter model.""" rng_key = random.PRNGKey(0) rng_key, rng_key_ = random.split(rng_key) nuts_kernel = NUTS(model=model) # burn-in is still too much in comparison with the samples mcmc = MCMC( nuts_kernel, num_samples=num_samples, num_warmup=num_warmup, num_chains=1 ) mcmc.run(rng_key_, T=n_train, T_forecast=n_test, obs=data, kwargs) return mcmc def get_samples(mcmc): """Get samples from variables in MCMC.""" return {k: v for k, v in mcmc.get_samples().items()} def plot_samples(hmc_samples, nodes, dist=True): """Plot samples from the variables in `nodes`.""" for node in nodes: if len(hmc_samples[node].shape) > 1: n_vars = hmc_samples[node].shape[1] for i in range(n_vars): plt.figure(figsize=(4, 3)) if dist: sns.distplot(hmc_samples[node][:, i], label=node + "%d" % i) else: plt.plot(hmc_samples[node][:, i], label=node + "%d" % i) plt.legend() plt.show() else: plt.figure(figsize=(4, 3)) if dist: sns.distplot(hmc_samples[node], label=node) else: plt.plot(hmc_samples[node], label=node) plt.legend() plt.show() def plot_forecast(hmc_samples, idx_train, idx_test, y_train, y_test): """Plot the results of forecasting (dimension are different).""" y_hat = hmc_samples["y_pred"].mean(axis=0) y_std = hmc_samples["y_pred"].std(axis=0) y_pred_025 = y_hat - 1.96 * y_std y_pred_975 = y_hat + 1.96 * y_std plt.plot(idx_train, y_train, "b-") plt.plot(idx_test, y_test, "bx") plt.plot(idx_test[:-1], y_hat, "r-") plt.plot(idx_test[:-1], y_pred_025, "r--") plt.plot(idx_test[:-1], y_pred_975, "r--") plt.fill_between(idx_test[:-1], y_pred_025, y_pred_975, alpha=0.3) plt.legend( [ "true (train)", "true (test)", "forecast", "forecast + stddev", "forecast - stddev", ] ) plt.show() n_train = 65 # number of points to train n_test = 20 # number of points to forecast idx_train = [range(0,n_train)] idx_test = [range(n_train, n_train+n_test)] ``` ## 1. Kalman Filter Modeling: Case of Denmark Data ``` data_dk=data[data['Country'] == "Denmark"] data_dk.head(5) print("The length of the full dataset for Denmark is:" + " " ) print(len(data_dk)) ``` Prepare input of the models (we are using numpyro so the inputs are numpy arrays). ``` X, y_train, y_test = split_forecast(data_dk) ``` ### 1.1. Kalman Filter Model vector c fixed as [0, 1] First model: the sampling distribution is replaced by one fixed variable $c$. ``` def f(carry, input_t): x_t, noise_t = input_t W, beta, z_prev, tau = carry z_t = beta * z_prev + W @ x_t + noise_t z_prev = z_t return (W, beta, z_prev, tau), z_t def model_wo_c(T, T_forecast, x, obs=None): """Define KF with inputs and fixed sampling dist.""" # Define priors over beta, tau, sigma, z_1 W = numpyro.sample( name="W", fn=dist.Normal(loc=jnp.zeros((2, 4)), scale=jnp.ones((2, 4))) ) beta = numpyro.sample( name="beta", fn=dist.Normal(loc=jnp.zeros(2), scale=jnp.ones(2)) ) tau = numpyro.sample(name="tau", fn=dist.HalfCauchy(scale=jnp.ones(2))) sigma = numpyro.sample(name="sigma", fn=dist.HalfCauchy(scale=0.1)) z_prev = numpyro.sample( name="z_1", fn=dist.Normal(loc=jnp.zeros(2), scale=jnp.ones(2)) ) # Define LKJ prior L_Omega = numpyro.sample("L_Omega", dist.LKJCholesky(2, 10.0)) Sigma_lower = jnp.matmul( jnp.diag(jnp.sqrt(tau)), L_Omega ) # lower cholesky factor of the covariance matrix noises = numpyro.sample( "noises", fn=dist.MultivariateNormal(loc=jnp.zeros(2), scale_tril=Sigma_lower), sample_shape=(T + T_forecast - 2,), ) # Propagate the dynamics forward using jax.lax.scan carry = (W, beta, z_prev, tau) z_collection = [z_prev] carry, zs_exp = lax.scan(f, carry, (x, noises), T + T_forecast - 2) z_collection = jnp.concatenate((jnp.array(z_collection), zs_exp), axis=0) obs_mean = z_collection[:T, 1] pred_mean = z_collection[T:, 1] # Sample the observed y (y_obs) numpyro.sample(name="y_obs", fn=dist.Normal(loc=obs_mean, scale=sigma), obs=obs) numpyro.sample(name="y_pred", fn=dist.Normal(loc=pred_mean, scale=sigma), obs=None) mcmc = train_kf(model_wo_c, y_train, n_train, n_test, x=X[2:]) ``` Plots of the distribution of the samples for each variable. ``` hmc_samples = get_samples(mcmc) plot_samples(hmc_samples, ["beta", "tau", "sigma"]) ``` Forecasting prediction, all the datapoints in the test set are within the Confidence Interval. ``` plot_forecast(hmc_samples, idx_train, idx_test, y_train, y_test) ``` ### 1.2. Kalman Filter with the vector c as a random variable with prior Second model: the sampling distribution is a Normal distribution $c$. ``` def model_w_c(T, T_forecast, x, obs=None): # Define priors over beta, tau, sigma, z_1 (keep the shapes in mind) W = numpyro.sample( name="W", fn=dist.Normal(loc=jnp.zeros((2, 4)), scale=jnp.ones((2, 4))) ) beta = numpyro.sample( name="beta", fn=dist.Normal(loc=jnp.array([0.0, 0.0]), scale=jnp.ones(2)) ) tau = numpyro.sample(name="tau", fn=dist.HalfCauchy(scale=jnp.array([2,2]))) sigma = numpyro.sample(name="sigma", fn=dist.HalfCauchy(scale=1)) z_prev = numpyro.sample( name="z_1", fn=dist.Normal(loc=jnp.zeros(2), scale=jnp.ones(2)) ) # Define LKJ prior L_Omega = numpyro.sample("L_Omega", dist.LKJCholesky(2, 10.0)) Sigma_lower = jnp.matmul( jnp.diag(jnp.sqrt(tau)), L_Omega ) # lower cholesky factor of the covariance matrix noises = numpyro.sample( "noises", fn=dist.MultivariateNormal(loc=jnp.zeros(2), scale_tril=Sigma_lower), sample_shape=(T + T_forecast - 2,), ) # Propagate the dynamics forward using jax.lax.scan carry = (W, beta, z_prev, tau) z_collection = [z_prev] carry, zs_exp = lax.scan(f, carry, (x, noises), T + T_forecast - 2) z_collection = jnp.concatenate((jnp.array(z_collection), zs_exp), axis=0) c = numpyro.sample( name="c", fn=dist.Normal(loc=jnp.array([[0.0], [0.0]]), scale=jnp.ones((2, 1))) ) obs_mean = jnp.dot(z_collection[:T, :], c).squeeze() pred_mean = jnp.dot(z_collection[T:, :], c).squeeze() # Sample the observed y (y_obs) numpyro.sample(name="y_obs", fn=dist.Normal(loc=obs_mean, scale=sigma), obs=obs) numpyro.sample(name="y_pred", fn=dist.Normal(loc=pred_mean, scale=sigma), obs=None) mcmc2 = train_kf(model_w_c, y_train, n_train, n_test, x=X[:-2]) hmc_samples = get_samples(mcmc2) plot_samples(hmc_samples, ["beta", "tau", "sigma"]) plot_forecast(hmc_samples, idx_train, idx_test, y_train, y_test) ``` ### 1.3. Kalman Filter without Input Third model: no input mobility data, two hidden states. ``` def f_s(carry, noise_t): """Propagate forward the time series.""" beta, z_prev, tau = carry z_t = beta * z_prev + noise_t z_prev = z_t return (beta, z_prev, tau), z_t def twoh_c_kf(T, T_forecast, obs=None): """Define Kalman Filter with two hidden variates.""" # Define priors over beta, tau, sigma, z_1 # W = numpyro.sample(name="W", fn=dist.Normal(loc=jnp.zeros((2,4)), scale=jnp.ones((2,4)))) beta = numpyro.sample( name="beta", fn=dist.Normal(loc=jnp.array([0.0, 0.0]), scale=jnp.ones(2)) ) tau = numpyro.sample(name="tau", fn=dist.HalfCauchy(scale=jnp.array([10,10]))) sigma = numpyro.sample(name="sigma", fn=dist.HalfCauchy(scale=5)) z_prev = numpyro.sample( name="z_1", fn=dist.Normal(loc=jnp.zeros(2), scale=jnp.ones(2)) ) # Define LKJ prior L_Omega = numpyro.sample("L_Omega", dist.LKJCholesky(2, 10.0)) Sigma_lower = jnp.matmul( jnp.diag(jnp.sqrt(tau)), L_Omega ) # lower cholesky factor of the covariance matrix noises = numpyro.sample( "noises", fn=dist.MultivariateNormal(loc=jnp.zeros(2), scale_tril=Sigma_lower), sample_shape=(T + T_forecast - 2,), ) # Propagate the dynamics forward using jax.lax.scan carry = (beta, z_prev, tau) z_collection = [z_prev] carry, zs_exp = lax.scan(f_s, carry, noises, T + T_forecast - 2) z_collection = jnp.concatenate((jnp.array(z_collection), zs_exp), axis=0) c = numpyro.sample( name="c", fn=dist.Normal(loc=jnp.array([[0.0], [0.0]]), scale=jnp.ones((2, 1))) ) obs_mean = jnp.dot(z_collection[:T, :], c).squeeze() pred_mean = jnp.dot(z_collection[T:, :], c).squeeze() # Sample the observed y (y_obs) numpyro.sample(name="y_obs", fn=dist.Normal(loc=obs_mean, scale=sigma), obs=obs) numpyro.sample(name="y_pred", fn=dist.Normal(loc=pred_mean, scale=sigma), obs=None) mcmc3 = train_kf(twoh_c_kf, y_train, n_train, n_test, num_samples=12000, num_warmup=5000) hmc_samples = get_samples(mcmc3) plot_samples(hmc_samples, ["beta", "tau", "sigma"]) plot_forecast(hmc_samples, idx_train, idx_test, y_train, y_test) ``` ## 2. Kalman Filter Modeling: Case of Norway Data ``` data_no=data[data['Country'] == "Norway"] data_no.head(5) print("The length of the full dataset for Norway is:" + " " ) print(len(data_no)) n_train = 66 # number of points to train n_test = 20 # number of points to forecast idx_train = [range(0,n_train)] idx_test = [range(n_train, n_train+n_test)] X, y_train, y_test = split_forecast(data_no, n_train) ``` ### 2.1. Kalman Filter Model vector c fixed as [0, 1] ``` mcmc_no = train_kf(model_wo_c, y_train, n_train, n_test, x=X[:-2]) hmc_samples = get_samples(mcmc_no) plot_samples(hmc_samples, ["beta", "tau", "sigma"]) plot_forecast(hmc_samples, idx_train, idx_test, y_train, y_test) ``` ### 2.2. Kalman Filter with the vector c as a random variable with prior ``` mcmc2_no = train_kf(model_w_c, y_train, n_train, n_test, x=X[:-2]) hmc_samples = get_samples(mcmc2_no) plot_samples(hmc_samples, ["beta", "tau", "sigma"]) plot_forecast(hmc_samples, idx_train, idx_test, y_train, y_test) ``` ### 2.3. Kalman Filter without Input ``` mcmc3_no = train_kf(twoh_c_kf, y_train, n_train, n_test) hmc_samples = get_samples(mcmc3_no) plot_samples(hmc_samples, ["beta", "tau", "sigma"]) plot_forecast(hmc_samples, idx_train, idx_test, y_train, y_test) ``` ## 3. Kalman Filter Modeling: Case of Sweden Data ``` data_sw=data[data['Country'] == "Sweden"] data_sw.head(5) print("The length of the full dataset for Sweden is:" + " " ) print(len(data_sw)) n_train = 75 # number of points to train n_test = 22 # number of points to forecast idx_train = [range(0,n_train)] idx_test = [range(n_train, n_train+n_test)] X, y_train, y_test = split_forecast(data_sw, n_train) ``` ### 3.1. Kalman Filter Model vector c fixed as [0, 1] ``` mcmc_sw = train_kf(model_wo_c, y_train, n_train, n_test, x=X[:-2]) hmc_samples = get_samples(mcmc_sw) plot_samples(hmc_samples, ["beta", "tau", "sigma"]) plot_forecast(hmc_samples, idx_train, idx_test, y_train, y_test) ``` ### 3.2. Kalman Filter with the vector c as a random variable with prior ``` mcmc2_sw = train_kf(model_w_c, y_train, n_train, n_test, x=X[:-2]) hmc_samples = get_samples(mcmc2_sw) plot_samples(hmc_samples, ["beta", "tau", "sigma"]) plot_forecast(hmc_samples, idx_train, idx_test, y_train, y_test) ``` ### 3.3. Kalman Filter without Input ``` mcmc3_sw = train_kf(twoh_c_kf, y_train, n_train, n_test) hmc_samples = get_samples(mcmc3_sw) plot_samples(hmc_samples, ["beta", "tau", "sigma"]) plot_forecast(hmc_samples, idx_train, idx_test, y_train, y_test) ``` Save results to rerun the plotting functions. ``` import pickle MODELS = join(ROOT, "models") for i, mc in enumerate([mcmc3_no, mcmc_sw, mcmc2_sw, mcmc3_sw]): with open(join(MODELS, f"hmc_ok_{i}.pickle"), "wb") as f: pickle.dump(get_samples(mc),f) ``` ## Gaussian Process	github_jupyter
## Dependencies ``` import json, warnings, shutil, glob from jigsaw_utility_scripts import * from scripts_step_lr_schedulers import * from transformers import TFXLMRobertaModel, XLMRobertaConfig from tensorflow.keras.models import Model from tensorflow.keras import optimizers, metrics, losses, layers SEED = 0 seed_everything(SEED) warnings.filterwarnings("ignore") pd.set_option('max_colwidth', 120) pd.set_option('display.float_format', lambda x: '%.4f' % x) ``` ## TPU configuration ``` strategy, tpu = set_up_strategy() print("REPLICAS: ", strategy.num_replicas_in_sync) AUTO = tf.data.experimental.AUTOTUNE ``` # Load data ``` database_base_path = '/kaggle/input/jigsaw-data-split-roberta-192-ratio-1-clean-polish/' k_fold = pd.read_csv(database_base_path + '5-fold.csv') valid_df = pd.read_csv("/kaggle/input/jigsaw-multilingual-toxic-comment-classification/validation.csv", usecols=['comment_text', 'toxic', 'lang']) print('Train samples: %d' % len(k_fold)) display(k_fold.head()) print('Validation samples: %d' % len(valid_df)) display(valid_df.head()) base_data_path = 'fold_1/' fold_n = 1 # Unzip files !tar -xf /kaggle/input/jigsaw-data-split-roberta-192-ratio-1-clean-polish/fold_1.tar.gz ``` # Model parameters ``` base_path = '/kaggle/input/jigsaw-transformers/XLM-RoBERTa/' config = { "MAX_LEN": 192, "BATCH_SIZE": 128, "EPOCHS": 3, "LEARNING_RATE": 1e-5, "ES_PATIENCE": None, "base_model_path": base_path + 'tf-xlm-roberta-large-tf_model.h5', "config_path": base_path + 'xlm-roberta-large-config.json' } with open('config.json', 'w') as json_file: json.dump(json.loads(json.dumps(config)), json_file) config ``` ## Learning rate schedule ``` lr_min = 1e-7 lr_start = 0 lr_max = config['LEARNING_RATE'] step_size = (len(k_fold[k_fold[f'fold_{fold_n}'] == 'train']) * 2) // config['BATCH_SIZE'] total_steps = config['EPOCHS'] * step_size hold_max_steps = 0 warmup_steps = step_size * 1 decay = .9998 rng = [i for i in range(0, total_steps, config['BATCH_SIZE'])] y = [exponential_schedule_with_warmup(tf.cast(x, tf.float32), warmup_steps, hold_max_steps, lr_start, lr_max, lr_min, decay) for x in rng] sns.set(style="whitegrid") fig, ax = plt.subplots(figsize=(20, 6)) plt.plot(rng, y) print("Learning rate schedule: {:.3g} to {:.3g} to {:.3g}".format(y[0], max(y), y[-1])) ``` # Model ``` module_config = XLMRobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False) def model_fn(MAX_LEN): input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids') attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask') base_model = TFXLMRobertaModel.from_pretrained(config['base_model_path'], config=module_config) last_hidden_state, _ = base_model({'input_ids': input_ids, 'attention_mask': attention_mask}) cls_token = last_hidden_state[:, 0, :] output = layers.Dense(1, activation='sigmoid', name='output')(cls_token) model = Model(inputs=[input_ids, attention_mask], outputs=output) return model ``` # Train ``` # Load data x_train = np.load(base_data_path + 'x_train.npy') y_train = np.load(base_data_path + 'y_train_int.npy').reshape(x_train.shape[1], 1).astype(np.float32) x_valid = np.load(base_data_path + 'x_valid.npy') y_valid = np.load(base_data_path + 'y_valid_int.npy').reshape(x_valid.shape[1], 1).astype(np.float32) x_valid_ml = np.load(database_base_path + 'x_valid.npy') y_valid_ml = np.load(database_base_path + 'y_valid.npy').reshape(x_valid_ml.shape[1], 1).astype(np.float32) #################### ADD TAIL #################### x_train_tail = np.load(base_data_path + 'x_train_tail.npy') y_train_tail = np.load(base_data_path + 'y_train_int_tail.npy').reshape(x_train_tail.shape[1], 1).astype(np.float32) x_train = np.hstack([x_train, x_train_tail]) y_train = np.vstack([y_train, y_train_tail]) step_size = x_train.shape[1] // config['BATCH_SIZE'] valid_step_size = x_valid_ml.shape[1] // config['BATCH_SIZE'] valid_2_step_size = x_valid.shape[1] // config['BATCH_SIZE'] # Build TF datasets train_dist_ds = strategy.experimental_distribute_dataset(get_training_dataset(x_train, y_train, config['BATCH_SIZE'], AUTO, seed=SEED)) valid_dist_ds = strategy.experimental_distribute_dataset(get_validation_dataset(x_valid_ml, y_valid_ml, config['BATCH_SIZE'], AUTO, repeated=True, seed=SEED)) valid_2_dist_ds = strategy.experimental_distribute_dataset(get_validation_dataset(x_valid, y_valid, config['BATCH_SIZE'], AUTO, repeated=True, seed=SEED)) train_data_iter = iter(train_dist_ds) valid_data_iter = iter(valid_dist_ds) valid_2_data_iter = iter(valid_2_dist_ds) # Step functions @tf.function def train_step(data_iter): def train_step_fn(x, y): with tf.GradientTape() as tape: probabilities = model(x, training=True) loss = loss_fn(y, probabilities) grads = tape.gradient(loss, model.trainable_variables) optimizer.apply_gradients(zip(grads, model.trainable_variables)) train_auc.update_state(y, probabilities) train_loss.update_state(loss) for _ in tf.range(step_size): strategy.experimental_run_v2(train_step_fn, next(data_iter)) @tf.function def valid_step(data_iter): def valid_step_fn(x, y): probabilities = model(x, training=False) loss = loss_fn(y, probabilities) valid_auc.update_state(y, probabilities) valid_loss.update_state(loss) for _ in tf.range(valid_step_size): strategy.experimental_run_v2(valid_step_fn, next(data_iter)) @tf.function def valid_2_step(data_iter): def valid_step_fn(x, y): probabilities = model(x, training=False) loss = loss_fn(y, probabilities) valid_2_auc.update_state(y, probabilities) valid_2_loss.update_state(loss) for _ in tf.range(valid_2_step_size): strategy.experimental_run_v2(valid_step_fn, next(data_iter)) # Train model with strategy.scope(): model = model_fn(config['MAX_LEN']) lr = lambda: exponential_schedule_with_warmup(tf.cast(optimizer.iterations, tf.float32), warmup_steps=warmup_steps, lr_start=lr_start, lr_max=lr_max, decay=decay) optimizer = optimizers.Adam(learning_rate=lr) loss_fn = losses.binary_crossentropy train_auc = metrics.AUC() valid_auc = metrics.AUC() valid_2_auc = metrics.AUC() train_loss = metrics.Sum() valid_loss = metrics.Sum() valid_2_loss = metrics.Sum() metrics_dict = {'loss': train_loss, 'auc': train_auc, 'val_loss': valid_loss, 'val_auc': valid_auc, 'val_2_loss': valid_2_loss, 'val_2_auc': valid_2_auc} history = custom_fit_2(model, metrics_dict, train_step, valid_step, valid_2_step, train_data_iter, valid_data_iter, valid_2_data_iter, step_size, valid_step_size, valid_2_step_size, config['BATCH_SIZE'], config['EPOCHS'], config['ES_PATIENCE'], save_last=False) # model.save_weights('model.h5') # Make predictions # x_train = np.load(base_data_path + 'x_train.npy') # x_valid = np.load(base_data_path + 'x_valid.npy') x_valid_ml_eval = np.load(database_base_path + 'x_valid.npy') # train_preds = model.predict(get_test_dataset(x_train, config['BATCH_SIZE'], AUTO)) # valid_preds = model.predict(get_test_dataset(x_valid, config['BATCH_SIZE'], AUTO)) valid_ml_preds = model.predict(get_test_dataset(x_valid_ml_eval, config['BATCH_SIZE'], AUTO)) # k_fold.loc[k_fold[f'fold_{fold_n}'] == 'train', f'pred_{fold_n}'] = np.round(train_preds) # k_fold.loc[k_fold[f'fold_{fold_n}'] == 'validation', f'pred_{fold_n}'] = np.round(valid_preds) valid_df[f'pred_{fold_n}'] = valid_ml_preds # Fine-tune on validation set #################### ADD TAIL #################### x_valid_ml_tail = np.hstack([x_valid_ml, np.load(database_base_path + 'x_valid_tail.npy')]) y_valid_ml_tail = np.vstack([y_valid_ml, y_valid_ml]) valid_step_size_tail = x_valid_ml_tail.shape[1] // config['BATCH_SIZE'] # Build TF datasets train_ml_dist_ds = strategy.experimental_distribute_dataset(get_training_dataset(x_valid_ml_tail, y_valid_ml_tail, config['BATCH_SIZE'], AUTO, seed=SEED)) train_ml_data_iter = iter(train_ml_dist_ds) # Step functions @tf.function def train_ml_step(data_iter): def train_step_fn(x, y): with tf.GradientTape() as tape: probabilities = model(x, training=True) loss = loss_fn(y, probabilities) grads = tape.gradient(loss, model.trainable_variables) optimizer.apply_gradients(zip(grads, model.trainable_variables)) train_auc.update_state(y, probabilities) train_loss.update_state(loss) for _ in tf.range(valid_step_size_tail): strategy.experimental_run_v2(train_step_fn, next(data_iter)) # Fine-tune on validation set history_ml = custom_fit_2(model, metrics_dict, train_ml_step, valid_step, valid_2_step, train_ml_data_iter, valid_data_iter, valid_2_data_iter, valid_step_size_tail, valid_step_size, valid_2_step_size, config['BATCH_SIZE'], 2, config['ES_PATIENCE'], save_last=False) # Join history for key in history_ml.keys(): history[key] += history_ml[key] model.save_weights('model.h5') # Make predictions valid_ml_preds = model.predict(get_test_dataset(x_valid_ml_eval, config['BATCH_SIZE'], AUTO)) valid_df[f'pred_ml_{fold_n}'] = valid_ml_preds ### Delete data dir shutil.rmtree(base_data_path) ``` ## Model loss graph ``` plot_metrics_2(history) ``` # Model evaluation ``` # display(evaluate_model_single_fold(k_fold, fold_n, label_col='toxic_int').style.applymap(color_map)) ``` # Confusion matrix ``` # train_set = k_fold[k_fold[f'fold_{fold_n}'] == 'train'] # validation_set = k_fold[k_fold[f'fold_{fold_n}'] == 'validation'] # plot_confusion_matrix(train_set['toxic_int'], train_set[f'pred_{fold_n}'], # validation_set['toxic_int'], validation_set[f'pred_{fold_n}']) ``` # Model evaluation by language ``` display(evaluate_model_single_fold_lang(valid_df, fold_n).style.applymap(color_map)) # ML fine-tunned preds display(evaluate_model_single_fold_lang(valid_df, fold_n, pred_col='pred_ml').style.applymap(color_map)) ``` # Visualize predictions ``` print('English validation set') display(k_fold[['comment_text', 'toxic'] + [c for c in k_fold.columns if c.startswith('pred')]].head(10)) print('Multilingual validation set') display(valid_df[['comment_text', 'toxic'] + [c for c in valid_df.columns if c.startswith('pred')]].head(10)) ``` # Test set predictions ``` x_test = np.load(database_base_path + 'x_test.npy') test_preds = model.predict(get_test_dataset(x_test, config['BATCH_SIZE'], AUTO)) submission = pd.read_csv('/kaggle/input/jigsaw-multilingual-toxic-comment-classification/sample_submission.csv') submission['toxic'] = test_preds submission.to_csv('submission.csv', index=False) display(submission.describe()) display(submission.head(10)) ```	github_jupyter
``` import pandas as pd import numpy as np import matplotlib as plt from shapely.geometry import Point, Polygon from sklearn.linear_model import LogisticRegression from sklearn.ensemble import RandomForestClassifier from sklearn.model_selection import KFold import zipfile import requests import os import shutil from downloading_funcs import addr_shape, down_extract_zip from supp_funcs import * import lnks import warnings #DANGER: I triggered a ton of warnings. warnings.filterwarnings('ignore') import geopandas as gpd %matplotlib inline #Load the BBL list BBL12_17CSV = ['https://hub.arcgis.com/datasets/82ab09c9541b4eb8ba4b537e131998ce_22.csv', 'https://hub.arcgis.com/datasets/4c4d6b4defdf4561b737a594b6f2b0dd_23.csv', 'https://hub.arcgis.com/datasets/d7aa6d3a3fdc42c4b354b9e90da443b7_1.csv', 'https://hub.arcgis.com/datasets/a8434614d90e416b80fbdfe2cb2901d8_2.csv', 'https://hub.arcgis.com/datasets/714d5f8b06914b8596b34b181439e702_36.csv', 'https://hub.arcgis.com/datasets/c4368a66ce65455595a211d530facc54_3.csv',] def data_pipeline(shapetype, bbl_links, supplement=None, dex=None, ts_lst_range=None): #A pipeline for group_e dataframe operations #Test inputs -------------------------------------------------------------- if supplement: assert isinstance(supplement, list) assert isinstance(bbl_links, list) if ts_lst_range: assert isinstance(ts_lst_range, list) assert len(ts_lst_range) == 2 #Must be list of format [start-yr, end-yr] #We'll need our addresspoints and our shapefile if not dex: dex = addr_shape(shapetype) #We need a list of time_unit_of_analysis if ts_lst_range: ts_lst = [x+(i/100) for i in range(1,13,1) for x in range(1980, 2025)] ts_lst = [x for x in ts_lst if x >= ts_lst_range[0] and x <= ts_lst_range[1]] ts_lst = sorted(ts_lst) if not ts_lst_range: ts_lst = [x+(i/100) for i in range(1,13,1) for x in range(2012, 2017)] ts_lst = sorted(ts_lst) #Now we need to stack our BBL data ---------------------------------------- #Begin by forming an empty DF bbl_df = pd.DataFrame() for i in list(range(2012, 2018)): bblpth = './data/bbls/Basic_Business_License_in_'+str(i)+'.csv' #Messy hack #TODO: generalize bblpth above bbl = pd.read_csv(bblpth, low_memory=False) col_len = len(bbl.columns) bbl_df = bbl_df.append(bbl) if len(bbl.columns) != col_len: print('Column Mismatch!') del bbl bbl_df.LICENSE_START_DATE = pd.to_datetime( bbl_df.LICENSE_START_DATE) bbl_df.LICENSE_EXPIRATION_DATE = pd.to_datetime( bbl_df.LICENSE_EXPIRATION_DATE) bbl_df.LICENSE_ISSUE_DATE = pd.to_datetime( bbl_df.LICENSE_ISSUE_DATE) bbl_df.sort_values('LICENSE_START_DATE') #Set up our time unit of analysis bbl_df['month'] = 0 bbl_df['endMonth'] = 0 bbl_df['issueMonth'] = 0 bbl_df['month'] = bbl_df['LICENSE_START_DATE'].dt.year + ( bbl_df['LICENSE_START_DATE'].dt.month/100 ) bbl_df['endMonth'] = bbl_df['LICENSE_EXPIRATION_DATE'].dt.year + ( bbl_df['LICENSE_EXPIRATION_DATE'].dt.month/100 ) bbl_df['issueMonth'] = bbl_df['LICENSE_ISSUE_DATE'].dt.year + ( bbl_df['LICENSE_ISSUE_DATE'].dt.month/100 ) bbl_df.endMonth.fillna(max(ts_lst)) bbl_df['endMonth'][bbl_df['endMonth'] > max(ts_lst)] = max(ts_lst) #Sort on month bbl_df = bbl_df.dropna(subset=['month']) bbl_df = bbl_df.set_index(['MARADDRESSREPOSITORYID','month']) bbl_df = bbl_df.sort_index(ascending=True) bbl_df.reset_index(inplace=True) bbl_df = bbl_df[bbl_df['MARADDRESSREPOSITORYID'] >= 0] bbl_df = bbl_df.dropna(subset=['LICENSESTATUS', 'issueMonth', 'endMonth', 'MARADDRESSREPOSITORYID','month', 'LONGITUDE', 'LATITUDE' ]) #Now that we have the BBL data, let's create our flag and points data ----- #This is the addresspoints, passed from the dex param addr_df = dex[0] #Zip the latlongs addr_df['geometry'] = [ Point(xy) for xy in zip( addr_df.LONGITUDE.apply(float), addr_df.LATITUDE.apply(float) ) ] addr_df['Points'] = addr_df['geometry'] #Duplicate, so raw retains points addr_df['dummy_counter'] = 1 #Always one, always dropped before export crs='EPSG:4326' #Convenience assignment of crs #Now we're stacking for each month ---------------------------------------- out_gdf = pd.DataFrame() #Empty storage df for i in ts_lst: #iterate through the list of months print('Month '+ str(i)) strmfile_pth = str( './data/strm_file/' + str(i) +'_' + shapetype + '.csv') if os.path.exists(strmfile_pth): print('Skipping, ' + str(i) + ' stream file path already exists:') print(strmfile_pth) continue #dex[1] is the designated shapefile passed from the dex param, #and should match the shapetype defined in that param #Copy of the dex[1] shapefile shp_gdf = dex[1] #Active BBL in month i bbl_df['inRange'] = 0 bbl_df['inRange'][(bbl_df.endMonth > i) & (bbl_df.month <= i)] = 1 #Issued BBL in month i bbl_df['isuFlag'] = 0 bbl_df['isuFlag'][bbl_df.issueMonth == i] = 1 #Merge BBL and MAR datasets ------------------------------------------- addr = pd.merge(addr_df, bbl_df, how='left', left_on='ADDRESS_ID', right_on='MARADDRESSREPOSITORYID') addr = gpd.GeoDataFrame(addr, crs=crs, geometry=addr.geometry) shp_gdf.crs = addr.crs raw = gpd.sjoin(shp_gdf, addr, how='left', op='intersects') #A simple percent of buildings with active flags per shape, #and call it a 'utilization index' numer = raw.groupby('NAME').sum() numer = numer.inRange denom = raw.groupby('NAME').sum() denom = denom.dummy_counter issue = raw.groupby('NAME').sum() issue = issue.isuFlag flags = [] utl_inx = pd.DataFrame(numer/denom) utl_inx.columns = [ 'Util_Indx_BBL' ] flags.append(utl_inx) #This is number of buildings with an active BBL in month i bbl_count = pd.DataFrame(numer) bbl_count.columns = [ 'countBBL' ] flags.append(bbl_count) #This is number of buildings that were issued a BBL in month i isu_count = pd.DataFrame(issue) isu_count.columns = [ 'countIssued' ] flags.append(isu_count) for flag in flags: flag.crs = shp_gdf.crs shp_gdf = shp_gdf.merge(flag, how="left", left_on='NAME', right_index=True) shp_gdf['month'] = i #Head will be the list of retained columns head = ['NAME', 'Util_Indx_BBL', 'countBBL', 'countIssued', 'month', 'geometry'] shp_gdf = shp_gdf[head] print('Merging...') if supplement: #this is where your code will be fed into the pipeline. #To include time unit of analysis, pass 'i=i' as the last #item in your args list over on lnks.py, and the for-loop #will catch that. Else, it will pass your last item as an arg. #Ping CDL if you need to pass a func with more args and we #can extend this. for supp_func in supplement: if len(supp_func) == 2: if supp_func[1] == 'i=i': shp_gdf = supp_func[0](shp_gdf, raw, i=i) if supp_func[1] != 'i=i': shp_gdf = supp_func[0](shp_gdf, raw, supp_func[1]) if len(supp_func) == 3: if supp_func[2] == 'i=i': shp_gdf = supp_func[0](shp_gdf, raw, supp_func[1], i=i) if supp_func[2] != 'i=i': shp_gdf = supp_func[0](shp_gdf, raw, supp_func[1], supp_func[2]) if len(supp_func) == 4: if supp_func[3] == 'i=i': shp_gdf = supp_func[0](shp_gdf, raw, supp_func[1], supp_func[2], i=i) if supp_func[3] != 'i=i': shp_gdf = supp_func[0](shp_gdf, raw, supp_func[1], supp_func[2], supp_func[3]) print(str(supp_func[0]) + ' is done.') if not os.path.exists(strmfile_pth): shp_gdf = shp_gdf.drop('geometry', axis=1) #Save, also verify re-read works shp_gdf.to_csv(strmfile_pth, encoding='utf-8', index=False) shp_gdf = pd.read_csv(strmfile_pth, encoding='utf-8', engine='python') del shp_gdf, addr, utl_inx, numer, denom, issue, raw #Save me some memory please! #if i != 2016.12: # del raw print('Merged month:', i) print() #Done iterating through months here.... pth = './data/strm_file/' #path of the streamfiles for file in os.listdir(pth): try: filepth = str(os.path.join(pth, file)) print([os.path.getsize(filepth), filepth]) fl = pd.read_csv(filepth, encoding='utf-8', engine='python') #read the stream file out_gdf = out_gdf.append(fl) #This does the stacking del fl except IsADirectoryError: continue out_gdf.to_csv('./data/' + shapetype + '_out.csv') #Save #shutil.rmtree('./data/strm_file/') print('Done!') return [bbl_df, addr_df, out_gdf] #Remove this later, for testing now dex = addr_shape('anc') sets = data_pipeline('anc', BBL12_17CSV, supplement=lnks.supplm, dex=dex, ts_lst_range=None) sets[2].columns #Our number of rows equals our number of shapes * number of months ```	github_jupyter
# Advanced RNNs <img src="https://raw.githubusercontent.com/GokuMohandas/practicalAI/master/images/logo.png" width=150> In this notebook we're going to cover some advanced topics related to RNNs. 1. Conditioned hidden state 2. Char-level embeddings 3. Encoder and decoder 4. Attentional mechanisms 5. Implementation # Set up ``` # Load PyTorch library !pip3 install torch import os from argparse import Namespace import collections import copy import json import matplotlib.pyplot as plt import numpy as np import pandas as pd import re import torch # Set Numpy and PyTorch seeds def set_seeds(seed, cuda): np.random.seed(seed) torch.manual_seed(seed) if cuda: torch.cuda.manual_seed_all(seed) # Creating directories def create_dirs(dirpath): if not os.path.exists(dirpath): os.makedirs(dirpath) # Arguments args = Namespace( seed=1234, cuda=True, batch_size=4, condition_vocab_size=3, # vocabulary for condition possibilities embedding_dim=100, rnn_hidden_dim=100, hidden_dim=100, num_layers=1, bidirectional=False, ) # Set seeds set_seeds(seed=args.seed, cuda=args.cuda) # Check CUDA if not torch.cuda.is_available(): args.cuda = False args.device = torch.device("cuda" if args.cuda else "cpu") print("Using CUDA: {}".format(args.cuda)) ``` # Conditioned RNNs Conditioning an RNN is to add extra information that will be helpful towards a prediction. We can encode (embed it) this information and feed it along with the sequential input into our model. For example, suppose in our document classificaiton example in the previous notebook, we knew the publisher of each news article (NYTimes, ESPN, etc.). We could have encoded that information to help with the prediction. There are several different ways of creating a conditioned RNN. Note: If the conditioning information is novel for each input in the sequence, just concatenate it along with each time step's input. 1. Make the initial hidden state the encoded information instead of using the initial zerod hidden state. Make sure that the size of the encoded information is the same as the hidden state for the RNN. <img src="https://raw.githubusercontent.com/GokuMohandas/practicalAI/master/images/conditioned_rnn1.png" width=400> ``` import torch.nn as nn import torch.nn.functional as F # Condition condition = torch.LongTensor([0, 2, 1, 2]) # batch size of 4 with a vocab size of 3 condition_embeddings = nn.Embedding( embedding_dim=args.embedding_dim, # should be same as RNN hidden dim num_embeddings=args.condition_vocab_size) # of unique conditions # Initialize hidden state num_directions = 1 if args.bidirectional: num_directions = 2 # If using multiple layers and directions, the hidden state needs to match that size hidden_t = condition_embeddings(condition).unsqueeze(0).repeat( args.num_layers * num_directions, 1, 1).to(args.device) # initial state to RNN print (hidden_t.size()) # Feed into RNN # y_out, _ = self.rnn(x_embedded, hidden_t) ``` 2. Concatenate the encoded information with the hidden state at each time step. Do not replace the hidden state because the RNN needs that to learn. <img src="https://raw.githubusercontent.com/GokuMohandas/practicalAI/master/images/conditioned_rnn2.png" width=400> ``` # Initialize hidden state hidden_t = torch.zeros((args.num_layers * num_directions, args.batch_size, args.rnn_hidden_dim)) print (hidden_t.size()) def concat_condition(condition_embeddings, condition, hidden_t, num_layers, num_directions): condition_t = condition_embeddings(condition).unsqueeze(0).repeat( num_layers * num_directions, 1, 1) hidden_t = torch.cat([hidden_t, condition_t], 2) return hidden_t # Loop through the inputs time steps hiddens = [] seq_size = 1 for t in range(seq_size): hidden_t = concat_condition(condition_embeddings, condition, hidden_t, args.num_layers, num_directions).to(args.device) print (hidden_t.size()) # Feed into RNN # hidden_t = rnn_cell(x_in[t], hidden_t) ... ``` # Char-level embeddings Our conv operations will have inputs that are words in a sentence represented at the character level\| $\in \mathbb{R}^{NXSXWXE}$ and outputs are embeddings for each word (based on convlutions applied at the character level.) Word embeddings: capture the temporal correlations among adjacent tokens so that similar words have similar representations. Ex. "New Jersey" is close to "NJ" is close to "Garden State", etc. Char embeddings: create representations that map words at a character level. Ex. "toy" and "toys" will be close to each other. <img src="https://raw.githubusercontent.com/GokuMohandas/practicalAI/master/images/char_embeddings.png" width=450> ``` # Arguments args = Namespace( seed=1234, cuda=False, shuffle=True, batch_size=64, vocab_size=20, # vocabulary seq_size=10, # max length of each sentence word_size=15, # max length of each word embedding_dim=100, num_filters=100, # filters per size ) class Model(nn.Module): def __init__(self, embedding_dim, num_embeddings, num_input_channels, num_output_channels, padding_idx): super(Model, self).__init__() # Char-level embedding self.embeddings = nn.Embedding(embedding_dim=embedding_dim, num_embeddings=num_embeddings, padding_idx=padding_idx) # Conv weights self.conv = nn.ModuleList([nn.Conv1d(num_input_channels, num_output_channels, kernel_size=f) for f in [2,3,4]]) def forward(self, x, channel_first=False, apply_softmax=False): # x: (N, seq_len, word_len) input_shape = x.size() batch_size, seq_len, word_len = input_shape x = x.view(-1, word_len) # (Nseq_len, word_len) # Embedding x = self.embeddings(x) # (Nseq_len, word_len, embedding_dim) # Rearrange input so num_input_channels is in dim 1 (N, embedding_dim, word_len) if not channel_first: x = x.transpose(1, 2) # Convolution z = [F.relu(conv(x)) for conv in self.conv] # Pooling z = [F.max_pool1d(zz, zz.size(2)).squeeze(2) for zz in z] z = [zz.view(batch_size, seq_len, -1) for zz in z] # (N, seq_len, embedding_dim) # Concat to get char-level embeddings z = torch.cat(z, 2) # join conv outputs return z # Input input_size = (args.batch_size, args.seq_size, args.word_size) x_in = torch.randint(low=0, high=args.vocab_size, size=input_size).long() print (x_in.size()) # Initial char-level embedding model model = Model(embedding_dim=args.embedding_dim, num_embeddings=args.vocab_size, num_input_channels=args.embedding_dim, num_output_channels=args.num_filters, padding_idx=0) print (model.named_modules) # Forward pass to get char-level embeddings z = model(x_in) print (z.size()) ``` There are several different ways you can use these char-level embeddings: 1. Concat char-level embeddings with word-level embeddings, since we have an embedding for each word (at a char-level) and then feed it into an RNN. 2. You can feed the char-level embeddings into an RNN to processes them. # Encoder and decoder So far we've used RNNs to `encode` a sequential input and generate hidden states. We use these hidden states to `decode` the predictions. So far, the encoder was an RNN and the decoder was just a few fully connected layers followed by a softmax layer (for classification). But the encoder and decoder can assume other architectures as well. For example, the decoder could be an RNN that processes the hidden state outputs from the encoder RNN. ``` # Arguments args = Namespace( batch_size=64, embedding_dim=100, rnn_hidden_dim=100, hidden_dim=100, num_layers=1, bidirectional=False, dropout=0.1, ) class Encoder(nn.Module): def __init__(self, embedding_dim, num_embeddings, rnn_hidden_dim, num_layers, bidirectional, padding_idx=0): super(Encoder, self).__init__() # Embeddings self.word_embeddings = nn.Embedding(embedding_dim=embedding_dim, num_embeddings=num_embeddings, padding_idx=padding_idx) # GRU weights self.gru = nn.GRU(input_size=embedding_dim, hidden_size=rnn_hidden_dim, num_layers=num_layers, batch_first=True, bidirectional=bidirectional) def forward(self, x_in, x_lengths): # Word level embeddings z_word = self.word_embeddings(x_in) # Feed into RNN out, h_n = self.gru(z) # Gather the last relevant hidden state out = gather_last_relevant_hidden(out, x_lengths) return out class Decoder(nn.Module): def __init__(self, rnn_hidden_dim, hidden_dim, output_dim, dropout_p): super(Decoder, self).__init__() # FC weights self.dropout = nn.Dropout(dropout_p) self.fc1 = nn.Linear(rnn_hidden_dim, hidden_dim) self.fc2 = nn.Linear(hidden_dim, output_dim) def forward(self, encoder_output, apply_softmax=False): # FC layers z = self.dropout(encoder_output) z = self.fc1(z) z = self.dropout(z) y_pred = self.fc2(z) if apply_softmax: y_pred = F.softmax(y_pred, dim=1) return y_pred class Model(nn.Module): def __init__(self, embedding_dim, num_embeddings, rnn_hidden_dim, hidden_dim, num_layers, bidirectional, output_dim, dropout_p, padding_idx=0): super(Model, self).__init__() self.encoder = Encoder(embedding_dim, num_embeddings, rnn_hidden_dim, num_layers, bidirectional, padding_idx=0) self.decoder = Decoder(rnn_hidden_dim, hidden_dim, output_dim, dropout_p) def forward(self, x_in, x_lengths, apply_softmax=False): encoder_outputs = self.encoder(x_in, x_lengths) y_pred = self.decoder(encoder_outputs, apply_softmax) return y_pred model = Model(embedding_dim=args.embedding_dim, num_embeddings=1000, rnn_hidden_dim=args.rnn_hidden_dim, hidden_dim=args.hidden_dim, num_layers=args.num_layers, bidirectional=args.bidirectional, output_dim=4, dropout_p=args.dropout, padding_idx=0) print (model.named_parameters) ``` # Attentional mechanisms When processing an input sequence with an RNN, recall that at each time step we process the input and the hidden state at that time step. For many use cases, it's advantageous to have access to the inputs at all time steps and pay selective attention to the them at each time step. For example, in machine translation, it's advantageous to have access to all the words when translating to another language because translations aren't necessarily word for word. <img src="https://raw.githubusercontent.com/GokuMohandas/practicalAI/master/images/attention1.jpg" width=650> Attention can sound a bit confusing so let's see what happens at each time step. At time step j, the model has processed inputs $x_0, x_1, x_2, ..., x_j$ and has generted hidden states $h_0, h_1, h_2, ..., h_j$. The idea is to use all the processed hidden states to make the prediction and not just the most recent one. There are several approaches to how we can do this. With soft attention, we learn a vector of floating points (probabilities) to multiply with the hidden states to create the context vector. Ex. [0.1, 0.3, 0.1, 0.4, 0.1] With hard attention, we can learn a binary vector to multiply with the hidden states to create the context vector. Ex. [0, 0, 0, 1, 0] We're going to focus on soft attention because it's more widley used and we can visualize how much of each hidden state helps with the prediction, which is great for interpretability. <img src="https://raw.githubusercontent.com/GokuMohandas/practicalAI/master/images/attention2.jpg" width=650> We're going to implement attention in the document classification task below. # Document classification with RNNs We're going to implement the same document classification task as in the previous notebook but we're going to use an attentional interface for interpretability. Why not machine translation? Normally, machine translation is the go-to example for demonstrating attention but it's not really practical. How many situations can you think of that require a seq to generate another sequence? Instead we're going to apply attention with our document classification example to see which input tokens are more influential towards predicting the genre. ## Set up ``` from argparse import Namespace import collections import copy import json import matplotlib.pyplot as plt import numpy as np import pandas as pd import re import torch def set_seeds(seed, cuda): np.random.seed(seed) torch.manual_seed(seed) if cuda: torch.cuda.manual_seed_all(seed) # Creating directories def create_dirs(dirpath): if not os.path.exists(dirpath): os.makedirs(dirpath) args = Namespace( seed=1234, cuda=True, shuffle=True, data_file="news.csv", split_data_file="split_news.csv", vectorizer_file="vectorizer.json", model_state_file="model.pth", save_dir="news", train_size=0.7, val_size=0.15, test_size=0.15, pretrained_embeddings=None, cutoff=25, num_epochs=5, early_stopping_criteria=5, learning_rate=1e-3, batch_size=128, embedding_dim=100, kernels=[3,5], num_filters=100, rnn_hidden_dim=128, hidden_dim=200, num_layers=1, bidirectional=False, dropout_p=0.25, ) # Set seeds set_seeds(seed=args.seed, cuda=args.cuda) # Create save dir create_dirs(args.save_dir) # Expand filepaths args.vectorizer_file = os.path.join(args.save_dir, args.vectorizer_file) args.model_state_file = os.path.join(args.save_dir, args.model_state_file) # Check CUDA if not torch.cuda.is_available(): args.cuda = False args.device = torch.device("cuda" if args.cuda else "cpu") print("Using CUDA: {}".format(args.cuda)) ``` ## Data ``` import urllib url = "https://raw.githubusercontent.com/GokuMohandas/practicalAI/master/data/news.csv" response = urllib.request.urlopen(url) html = response.read() with open(args.data_file, 'wb') as fp: fp.write(html) df = pd.read_csv(args.data_file, header=0) df.head() by_category = collections.defaultdict(list) for _, row in df.iterrows(): by_category[row.category].append(row.to_dict()) for category in by_category: print ("{0}: {1}".format(category, len(by_category[category]))) final_list = [] for _, item_list in sorted(by_category.items()): if args.shuffle: np.random.shuffle(item_list) n = len(item_list) n_train = int(args.train_sizen) n_val = int(args.val_sizen) n_test = int(args.test_sizen) # Give data point a split attribute for item in item_list[:n_train]: item['split'] = 'train' for item in item_list[n_train:n_train+n_val]: item['split'] = 'val' for item in item_list[n_train+n_val:]: item['split'] = 'test' # Add to final list final_list.extend(item_list) split_df = pd.DataFrame(final_list) split_df["split"].value_counts() def preprocess_text(text): text = ' '.join(word.lower() for word in text.split(" ")) text = re.sub(r"([.,!?])", r" \1 ", text) text = re.sub(r"[^a-zA-Z.,!?]+", r" ", text) text = text.strip() return text split_df.title = split_df.title.apply(preprocess_text) split_df.to_csv(args.split_data_file, index=False) split_df.head() ``` ## Vocabulary ``` class Vocabulary(object): def __init__(self, token_to_idx=None): # Token to index if token_to_idx is None: token_to_idx = {} self.token_to_idx = token_to_idx # Index to token self.idx_to_token = {idx: token \ for token, idx in self.token_to_idx.items()} def to_serializable(self): return {'token_to_idx': self.token_to_idx} @classmethod def from_serializable(cls, contents): return cls(contents) def add_token(self, token): if token in self.token_to_idx: index = self.token_to_idx[token] else: index = len(self.token_to_idx) self.token_to_idx[token] = index self.idx_to_token[index] = token return index def add_tokens(self, tokens): return [self.add_token[token] for token in tokens] def lookup_token(self, token): return self.token_to_idx[token] def lookup_index(self, index): if index not in self.idx_to_token: raise KeyError("the index (%d) is not in the Vocabulary" % index) return self.idx_to_token[index] def __str__(self): return "<Vocabulary(size=%d)>" % len(self) def __len__(self): return len(self.token_to_idx) # Vocabulary instance category_vocab = Vocabulary() for index, row in df.iterrows(): category_vocab.add_token(row.category) print (category_vocab) # __str__ print (len(category_vocab)) # __len__ index = category_vocab.lookup_token("Business") print (index) print (category_vocab.lookup_index(index)) ``` ## Sequence vocabulary Next, we're going to create our Vocabulary classes for the article's title, which is a sequence of words. ``` from collections import Counter import string class SequenceVocabulary(Vocabulary): def __init__(self, token_to_idx=None, unk_token="<UNK>", mask_token="<MASK>", begin_seq_token="<BEGIN>", end_seq_token="<END>"): super(SequenceVocabulary, self).__init__(token_to_idx) self.mask_token = mask_token self.unk_token = unk_token self.begin_seq_token = begin_seq_token self.end_seq_token = end_seq_token self.mask_index = self.add_token(self.mask_token) self.unk_index = self.add_token(self.unk_token) self.begin_seq_index = self.add_token(self.begin_seq_token) self.end_seq_index = self.add_token(self.end_seq_token) # Index to token self.idx_to_token = {idx: token \ for token, idx in self.token_to_idx.items()} def to_serializable(self): contents = super(SequenceVocabulary, self).to_serializable() contents.update({'unk_token': self.unk_token, 'mask_token': self.mask_token, 'begin_seq_token': self.begin_seq_token, 'end_seq_token': self.end_seq_token}) return contents def lookup_token(self, token): return self.token_to_idx.get(token, self.unk_index) def lookup_index(self, index): if index not in self.idx_to_token: raise KeyError("the index (%d) is not in the SequenceVocabulary" % index) return self.idx_to_token[index] def __str__(self): return "<SequenceVocabulary(size=%d)>" % len(self.token_to_idx) def __len__(self): return len(self.token_to_idx) # Get word counts word_counts = Counter() for title in split_df.title: for token in title.split(" "): if token not in string.punctuation: word_counts[token] += 1 # Create SequenceVocabulary instance title_word_vocab = SequenceVocabulary() for word, word_count in word_counts.items(): if word_count >= args.cutoff: title_word_vocab.add_token(word) print (title_word_vocab) # __str__ print (len(title_word_vocab)) # __len__ index = title_word_vocab.lookup_token("general") print (index) print (title_word_vocab.lookup_index(index)) ``` We're also going to create an instance fo SequenceVocabulary that processes the input on a character level. ``` # Create SequenceVocabulary instance title_char_vocab = SequenceVocabulary() for title in split_df.title: for token in title: title_char_vocab.add_token(token) print (title_char_vocab) # __str__ print (len(title_char_vocab)) # __len__ index = title_char_vocab.lookup_token("g") print (index) print (title_char_vocab.lookup_index(index)) ``` ## Vectorizer Something new that we introduce in this Vectorizer is calculating the length of our input sequence. We will use this later on to extract the last relevant hidden state for each input sequence. ``` class NewsVectorizer(object): def __init__(self, title_word_vocab, title_char_vocab, category_vocab): self.title_word_vocab = title_word_vocab self.title_char_vocab = title_char_vocab self.category_vocab = category_vocab def vectorize(self, title): # Word-level vectorization word_indices = [self.title_word_vocab.lookup_token(token) for token in title.split(" ")] word_indices = [self.title_word_vocab.begin_seq_index] + word_indices + \ [self.title_word_vocab.end_seq_index] title_length = len(word_indices) word_vector = np.zeros(title_length, dtype=np.int64) word_vector[:len(word_indices)] = word_indices # Char-level vectorization word_length = max([len(word) for word in title.split(" ")]) char_vector = np.zeros((len(word_vector), word_length), dtype=np.int64) char_vector[0, :] = self.title_word_vocab.mask_index # <BEGIN> char_vector[-1, :] = self.title_word_vocab.mask_index # <END> for i, word in enumerate(title.split(" ")): char_vector[i+1,:len(word)] = [title_char_vocab.lookup_token(char) \ for char in word] # i+1 b/c of <BEGIN> token return word_vector, char_vector, len(word_indices) def unvectorize_word_vector(self, word_vector): tokens = [self.title_word_vocab.lookup_index(index) for index in word_vector] title = " ".join(token for token in tokens) return title def unvectorize_char_vector(self, char_vector): title = "" for word_vector in char_vector: for index in word_vector: if index == self.title_char_vocab.mask_index: break title += self.title_char_vocab.lookup_index(index) title += " " return title @classmethod def from_dataframe(cls, df, cutoff): # Create class vocab category_vocab = Vocabulary() for category in sorted(set(df.category)): category_vocab.add_token(category) # Get word counts word_counts = Counter() for title in df.title: for token in title.split(" "): word_counts[token] += 1 # Create title vocab (word level) title_word_vocab = SequenceVocabulary() for word, word_count in word_counts.items(): if word_count >= cutoff: title_word_vocab.add_token(word) # Create title vocab (char level) title_char_vocab = SequenceVocabulary() for title in df.title: for token in title: title_char_vocab.add_token(token) return cls(title_word_vocab, title_char_vocab, category_vocab) @classmethod def from_serializable(cls, contents): title_word_vocab = SequenceVocabulary.from_serializable(contents['title_word_vocab']) title_char_vocab = SequenceVocabulary.from_serializable(contents['title_char_vocab']) category_vocab = Vocabulary.from_serializable(contents['category_vocab']) return cls(title_word_vocab=title_word_vocab, title_char_vocab=title_char_vocab, category_vocab=category_vocab) def to_serializable(self): return {'title_word_vocab': self.title_word_vocab.to_serializable(), 'title_char_vocab': self.title_char_vocab.to_serializable(), 'category_vocab': self.category_vocab.to_serializable()} # Vectorizer instance vectorizer = NewsVectorizer.from_dataframe(split_df, cutoff=args.cutoff) print (vectorizer.title_word_vocab) print (vectorizer.title_char_vocab) print (vectorizer.category_vocab) word_vector, char_vector, title_length = vectorizer.vectorize(preprocess_text( "Roger Federer wins the Wimbledon tennis tournament.")) print ("word_vector:", np.shape(word_vector)) print ("char_vector:", np.shape(char_vector)) print ("title_length:", title_length) print (word_vector) print (char_vector) print (vectorizer.unvectorize_word_vector(word_vector)) print (vectorizer.unvectorize_char_vector(char_vector)) ``` ## Dataset ``` from torch.utils.data import Dataset, DataLoader class NewsDataset(Dataset): def __init__(self, df, vectorizer): self.df = df self.vectorizer = vectorizer # Data splits self.train_df = self.df[self.df.split=='train'] self.train_size = len(self.train_df) self.val_df = self.df[self.df.split=='val'] self.val_size = len(self.val_df) self.test_df = self.df[self.df.split=='test'] self.test_size = len(self.test_df) self.lookup_dict = {'train': (self.train_df, self.train_size), 'val': (self.val_df, self.val_size), 'test': (self.test_df, self.test_size)} self.set_split('train') # Class weights (for imbalances) class_counts = df.category.value_counts().to_dict() def sort_key(item): return self.vectorizer.category_vocab.lookup_token(item[0]) sorted_counts = sorted(class_counts.items(), key=sort_key) frequencies = [count for _, count in sorted_counts] self.class_weights = 1.0 / torch.tensor(frequencies, dtype=torch.float32) @classmethod def load_dataset_and_make_vectorizer(cls, split_data_file, cutoff): df = pd.read_csv(split_data_file, header=0) train_df = df[df.split=='train'] return cls(df, NewsVectorizer.from_dataframe(train_df, cutoff)) @classmethod def load_dataset_and_load_vectorizer(cls, split_data_file, vectorizer_filepath): df = pd.read_csv(split_data_file, header=0) vectorizer = cls.load_vectorizer_only(vectorizer_filepath) return cls(df, vectorizer) def load_vectorizer_only(vectorizer_filepath): with open(vectorizer_filepath) as fp: return NewsVectorizer.from_serializable(json.load(fp)) def save_vectorizer(self, vectorizer_filepath): with open(vectorizer_filepath, "w") as fp: json.dump(self.vectorizer.to_serializable(), fp) def set_split(self, split="train"): self.target_split = split self.target_df, self.target_size = self.lookup_dict[split] def __str__(self): return "<Dataset(split={0}, size={1})".format( self.target_split, self.target_size) def __len__(self): return self.target_size def __getitem__(self, index): row = self.target_df.iloc[index] title_word_vector, title_char_vector, title_length = \ self.vectorizer.vectorize(row.title) category_index = self.vectorizer.category_vocab.lookup_token(row.category) return {'title_word_vector': title_word_vector, 'title_char_vector': title_char_vector, 'title_length': title_length, 'category': category_index} def get_num_batches(self, batch_size): return len(self) // batch_size def generate_batches(self, batch_size, collate_fn, shuffle=True, drop_last=False, device="cpu"): dataloader = DataLoader(dataset=self, batch_size=batch_size, collate_fn=collate_fn, shuffle=shuffle, drop_last=drop_last) for data_dict in dataloader: out_data_dict = {} for name, tensor in data_dict.items(): out_data_dict[name] = data_dict[name].to(device) yield out_data_dict # Dataset instance dataset = NewsDataset.load_dataset_and_make_vectorizer(args.split_data_file, args.cutoff) print (dataset) # __str__ input_ = dataset[10] # __getitem__ print (input_['title_word_vector']) print (input_['title_char_vector']) print (input_['title_length']) print (input_['category']) print (dataset.vectorizer.unvectorize_word_vector(input_['title_word_vector'])) print (dataset.vectorizer.unvectorize_char_vector(input_['title_char_vector'])) print (dataset.class_weights) ``` ## Model embed → encoder → attend → predict ``` import torch.nn as nn import torch.nn.functional as F class NewsEncoder(nn.Module): def __init__(self, embedding_dim, num_word_embeddings, num_char_embeddings, kernels, num_input_channels, num_output_channels, rnn_hidden_dim, num_layers, bidirectional, word_padding_idx=0, char_padding_idx=0): super(NewsEncoder, self).__init__() self.num_layers = num_layers self.bidirectional = bidirectional # Embeddings self.word_embeddings = nn.Embedding(embedding_dim=embedding_dim, num_embeddings=num_word_embeddings, padding_idx=word_padding_idx) self.char_embeddings = nn.Embedding(embedding_dim=embedding_dim, num_embeddings=num_char_embeddings, padding_idx=char_padding_idx) # Conv weights self.conv = nn.ModuleList([nn.Conv1d(num_input_channels, num_output_channels, kernel_size=f) for f in kernels]) # GRU weights self.gru = nn.GRU(input_size=embedding_dim(len(kernels)+1), hidden_size=rnn_hidden_dim, num_layers=num_layers, batch_first=True, bidirectional=bidirectional) def initialize_hidden_state(self, batch_size, rnn_hidden_dim, device): """Modify this to condition the RNN.""" num_directions = 1 if self.bidirectional: num_directions = 2 hidden_t = torch.zeros(self.num_layers * num_directions, batch_size, rnn_hidden_dim).to(device) def get_char_level_embeddings(self, x): # x: (N, seq_len, word_len) input_shape = x.size() batch_size, seq_len, word_len = input_shape x = x.view(-1, word_len) # (Nseq_len, word_len) # Embedding x = self.char_embeddings(x) # (Nseq_len, word_len, embedding_dim) # Rearrange input so num_input_channels is in dim 1 (N, embedding_dim, word_len) x = x.transpose(1, 2) # Convolution z = [F.relu(conv(x)) for conv in self.conv] # Pooling z = [F.max_pool1d(zz, zz.size(2)).squeeze(2) for zz in z] z = [zz.view(batch_size, seq_len, -1) for zz in z] # (N, seq_len, embedding_dim) # Concat to get char-level embeddings z = torch.cat(z, 2) # join conv outputs return z def forward(self, x_word, x_char, x_lengths, device): """ x_word: word level representation (N, seq_size) x_char: char level representation (N, seq_size, word_len) """ # Word level embeddings z_word = self.word_embeddings(x_word) # Char level embeddings z_char = self.get_char_level_embeddings(x=x_char) # Concatenate z = torch.cat([z_word, z_char], 2) # Feed into RNN initial_h = self.initialize_hidden_state( batch_size=z.size(0), rnn_hidden_dim=self.gru.hidden_size, device=device) out, h_n = self.gru(z, initial_h) return out class NewsDecoder(nn.Module): def __init__(self, rnn_hidden_dim, hidden_dim, output_dim, dropout_p): super(NewsDecoder, self).__init__() # Attention FC layer self.fc_attn = nn.Linear(rnn_hidden_dim, rnn_hidden_dim) self.v = nn.Parameter(torch.rand(rnn_hidden_dim)) # FC weights self.dropout = nn.Dropout(dropout_p) self.fc1 = nn.Linear(rnn_hidden_dim, hidden_dim) self.fc2 = nn.Linear(hidden_dim, output_dim) def forward(self, encoder_outputs, apply_softmax=False): # Attention z = torch.tanh(self.fc_attn(encoder_outputs)) z = z.transpose(2,1) # [BHT] v = self.v.repeat(encoder_outputs.size(0),1).unsqueeze(1) #[B1H] z = torch.bmm(v,z).squeeze(1) # [BT] attn_scores = F.softmax(z, dim=1) context = torch.matmul(encoder_outputs.transpose(-2, -1), attn_scores.unsqueeze(dim=2)).squeeze() if len(context.size()) == 1: context = context.unsqueeze(0) # FC layers z = self.dropout(context) z = self.fc1(z) z = self.dropout(z) y_pred = self.fc2(z) if apply_softmax: y_pred = F.softmax(y_pred, dim=1) return attn_scores, y_pred class NewsModel(nn.Module): def __init__(self, embedding_dim, num_word_embeddings, num_char_embeddings, kernels, num_input_channels, num_output_channels, rnn_hidden_dim, hidden_dim, output_dim, num_layers, bidirectional, dropout_p, word_padding_idx, char_padding_idx): super(NewsModel, self).__init__() self.encoder = NewsEncoder(embedding_dim, num_word_embeddings, num_char_embeddings, kernels, num_input_channels, num_output_channels, rnn_hidden_dim, num_layers, bidirectional, word_padding_idx, char_padding_idx) self.decoder = NewsDecoder(rnn_hidden_dim, hidden_dim, output_dim, dropout_p) def forward(self, x_word, x_char, x_lengths, device, apply_softmax=False): encoder_outputs = self.encoder(x_word, x_char, x_lengths, device) y_pred = self.decoder(encoder_outputs, apply_softmax) return y_pred ``` ## Training ``` import torch.optim as optim class Trainer(object): def __init__(self, dataset, model, model_state_file, save_dir, device, shuffle, num_epochs, batch_size, learning_rate, early_stopping_criteria): self.dataset = dataset self.class_weights = dataset.class_weights.to(device) self.device = device self.model = model.to(device) self.save_dir = save_dir self.device = device self.shuffle = shuffle self.num_epochs = num_epochs self.batch_size = batch_size self.loss_func = nn.CrossEntropyLoss(self.class_weights) self.optimizer = optim.Adam(self.model.parameters(), lr=learning_rate) self.scheduler = optim.lr_scheduler.ReduceLROnPlateau( optimizer=self.optimizer, mode='min', factor=0.5, patience=1) self.train_state = { 'stop_early': False, 'early_stopping_step': 0, 'early_stopping_best_val': 1e8, 'early_stopping_criteria': early_stopping_criteria, 'learning_rate': learning_rate, 'epoch_index': 0, 'train_loss': [], 'train_acc': [], 'val_loss': [], 'val_acc': [], 'test_loss': -1, 'test_acc': -1, 'model_filename': model_state_file} def update_train_state(self): # Verbose print ("[EPOCH]: {0:02d} \| [LR]: {1} \| [TRAIN LOSS]: {2:.2f} \| [TRAIN ACC]: {3:.1f}% \| [VAL LOSS]: {4:.2f} \| [VAL ACC]: {5:.1f}%".format( self.train_state['epoch_index'], self.train_state['learning_rate'], self.train_state['train_loss'][-1], self.train_state['train_acc'][-1], self.train_state['val_loss'][-1], self.train_state['val_acc'][-1])) # Save one model at least if self.train_state['epoch_index'] == 0: torch.save(self.model.state_dict(), self.train_state['model_filename']) self.train_state['stop_early'] = False # Save model if performance improved elif self.train_state['epoch_index'] >= 1: loss_tm1, loss_t = self.train_state['val_loss'][-2:] # If loss worsened if loss_t >= self.train_state['early_stopping_best_val']: # Update step self.train_state['early_stopping_step'] += 1 # Loss decreased else: # Save the best model if loss_t < self.train_state['early_stopping_best_val']: torch.save(self.model.state_dict(), self.train_state['model_filename']) # Reset early stopping step self.train_state['early_stopping_step'] = 0 # Stop early ? self.train_state['stop_early'] = self.train_state['early_stopping_step'] \ >= self.train_state['early_stopping_criteria'] return self.train_state def compute_accuracy(self, y_pred, y_target): _, y_pred_indices = y_pred.max(dim=1) n_correct = torch.eq(y_pred_indices, y_target).sum().item() return n_correct / len(y_pred_indices) 100 def pad_word_seq(self, seq, length): vector = np.zeros(length, dtype=np.int64) vector[:len(seq)] = seq vector[len(seq):] = self.dataset.vectorizer.title_word_vocab.mask_index return vector def pad_char_seq(self, seq, seq_length, word_length): vector = np.zeros((seq_length, word_length), dtype=np.int64) vector.fill(self.dataset.vectorizer.title_char_vocab.mask_index) for i in range(len(seq)): char_padding = np.zeros(word_length-len(seq[i]), dtype=np.int64) vector[i] = np.concatenate((seq[i], char_padding), axis=None) return vector def collate_fn(self, batch): # Make a deep copy batch_copy = copy.deepcopy(batch) processed_batch = {"title_word_vector": [], "title_char_vector": [], "title_length": [], "category": []} # Max lengths get_seq_length = lambda sample: len(sample["title_word_vector"]) get_word_length = lambda sample: len(sample["title_char_vector"][0]) max_seq_length = max(map(get_seq_length, batch)) max_word_length = max(map(get_word_length, batch)) # Pad for i, sample in enumerate(batch_copy): padded_word_seq = self.pad_word_seq( sample["title_word_vector"], max_seq_length) padded_char_seq = self.pad_char_seq( sample["title_char_vector"], max_seq_length, max_word_length) processed_batch["title_word_vector"].append(padded_word_seq) processed_batch["title_char_vector"].append(padded_char_seq) processed_batch["title_length"].append(sample["title_length"]) processed_batch["category"].append(sample["category"]) # Convert to appropriate tensor types processed_batch["title_word_vector"] = torch.LongTensor( processed_batch["title_word_vector"]) processed_batch["title_char_vector"] = torch.LongTensor( processed_batch["title_char_vector"]) processed_batch["title_length"] = torch.LongTensor( processed_batch["title_length"]) processed_batch["category"] = torch.LongTensor( processed_batch["category"]) return processed_batch def run_train_loop(self): for epoch_index in range(self.num_epochs): self.train_state['epoch_index'] = epoch_index # Iterate over train dataset # initialize batch generator, set loss and acc to 0, set train mode on self.dataset.set_split('train') batch_generator = self.dataset.generate_batches( batch_size=self.batch_size, collate_fn=self.collate_fn, shuffle=self.shuffle, device=self.device) running_loss = 0.0 running_acc = 0.0 self.model.train() for batch_index, batch_dict in enumerate(batch_generator): # zero the gradients self.optimizer.zero_grad() # compute the output _, y_pred = self.model(x_word=batch_dict['title_word_vector'], x_char=batch_dict['title_char_vector'], x_lengths=batch_dict['title_length'], device=self.device) # compute the loss loss = self.loss_func(y_pred, batch_dict['category']) loss_t = loss.item() running_loss += (loss_t - running_loss) / (batch_index + 1) # compute gradients using loss loss.backward() # use optimizer to take a gradient step self.optimizer.step() # compute the accuracy acc_t = self.compute_accuracy(y_pred, batch_dict['category']) running_acc += (acc_t - running_acc) / (batch_index + 1) self.train_state['train_loss'].append(running_loss) self.train_state['train_acc'].append(running_acc) # Iterate over val dataset # initialize batch generator, set loss and acc to 0, set eval mode on self.dataset.set_split('val') batch_generator = self.dataset.generate_batches( batch_size=self.batch_size, collate_fn=self.collate_fn, shuffle=self.shuffle, device=self.device) running_loss = 0. running_acc = 0. self.model.eval() for batch_index, batch_dict in enumerate(batch_generator): # compute the output _, y_pred = self.model(x_word=batch_dict['title_word_vector'], x_char=batch_dict['title_char_vector'], x_lengths=batch_dict['title_length'], device=self.device) # compute the loss loss = self.loss_func(y_pred, batch_dict['category']) loss_t = loss.to("cpu").item() running_loss += (loss_t - running_loss) / (batch_index + 1) # compute the accuracy acc_t = self.compute_accuracy(y_pred, batch_dict['category']) running_acc += (acc_t - running_acc) / (batch_index + 1) self.train_state['val_loss'].append(running_loss) self.train_state['val_acc'].append(running_acc) self.train_state = self.update_train_state() self.scheduler.step(self.train_state['val_loss'][-1]) if self.train_state['stop_early']: break def run_test_loop(self): # initialize batch generator, set loss and acc to 0, set eval mode on self.dataset.set_split('test') batch_generator = self.dataset.generate_batches( batch_size=self.batch_size, collate_fn=self.collate_fn, shuffle=self.shuffle, device=self.device) running_loss = 0.0 running_acc = 0.0 self.model.eval() for batch_index, batch_dict in enumerate(batch_generator): # compute the output _, y_pred = self.model(x_word=batch_dict['title_word_vector'], x_char=batch_dict['title_char_vector'], x_lengths=batch_dict['title_length'], device=self.device) # compute the loss loss = self.loss_func(y_pred, batch_dict['category']) loss_t = loss.item() running_loss += (loss_t - running_loss) / (batch_index + 1) # compute the accuracy acc_t = self.compute_accuracy(y_pred, batch_dict['category']) running_acc += (acc_t - running_acc) / (batch_index + 1) self.train_state['test_loss'] = running_loss self.train_state['test_acc'] = running_acc def plot_performance(self): # Figure size plt.figure(figsize=(15,5)) # Plot Loss plt.subplot(1, 2, 1) plt.title("Loss") plt.plot(trainer.train_state["train_loss"], label="train") plt.plot(trainer.train_state["val_loss"], label="val") plt.legend(loc='upper right') # Plot Accuracy plt.subplot(1, 2, 2) plt.title("Accuracy") plt.plot(trainer.train_state["train_acc"], label="train") plt.plot(trainer.train_state["val_acc"], label="val") plt.legend(loc='lower right') # Save figure plt.savefig(os.path.join(self.save_dir, "performance.png")) # Show plots plt.show() def save_train_state(self): with open(os.path.join(self.save_dir, "train_state.json"), "w") as fp: json.dump(self.train_state, fp) # Initialization dataset = NewsDataset.load_dataset_and_make_vectorizer(args.split_data_file, args.cutoff) dataset.save_vectorizer(args.vectorizer_file) vectorizer = dataset.vectorizer model = NewsModel(embedding_dim=args.embedding_dim, num_word_embeddings=len(vectorizer.title_word_vocab), num_char_embeddings=len(vectorizer.title_char_vocab), kernels=args.kernels, num_input_channels=args.embedding_dim, num_output_channels=args.num_filters, rnn_hidden_dim=args.rnn_hidden_dim, hidden_dim=args.hidden_dim, output_dim=len(vectorizer.category_vocab), num_layers=args.num_layers, bidirectional=args.bidirectional, dropout_p=args.dropout_p, word_padding_idx=vectorizer.title_word_vocab.mask_index, char_padding_idx=vectorizer.title_char_vocab.mask_index) print (model.named_modules) # Train trainer = Trainer(dataset=dataset, model=model, model_state_file=args.model_state_file, save_dir=args.save_dir, device=args.device, shuffle=args.shuffle, num_epochs=args.num_epochs, batch_size=args.batch_size, learning_rate=args.learning_rate, early_stopping_criteria=args.early_stopping_criteria) trainer.run_train_loop() # Plot performance trainer.plot_performance() # Test performance trainer.run_test_loop() print("Test loss: {0:.2f}".format(trainer.train_state['test_loss'])) print("Test Accuracy: {0:.1f}%".format(trainer.train_state['test_acc'])) # Save all results trainer.save_train_state() ``` ## Inference ``` class Inference(object): def __init__(self, model, vectorizer): self.model = model self.vectorizer = vectorizer def predict_category(self, title): # Vectorize word_vector, char_vector, title_length = self.vectorizer.vectorize(title) title_word_vector = torch.tensor(word_vector).unsqueeze(0) title_char_vector = torch.tensor(char_vector).unsqueeze(0) title_length = torch.tensor([title_length]).long() # Forward pass self.model.eval() attn_scores, y_pred = self.model(x_word=title_word_vector, x_char=title_char_vector, x_lengths=title_length, device="cpu", apply_softmax=True) # Top category y_prob, indices = y_pred.max(dim=1) index = indices.item() # Predicted category category = vectorizer.category_vocab.lookup_index(index) probability = y_prob.item() return {'category': category, 'probability': probability, 'attn_scores': attn_scores} def predict_top_k(self, title, k): # Vectorize word_vector, char_vector, title_length = self.vectorizer.vectorize(title) title_word_vector = torch.tensor(word_vector).unsqueeze(0) title_char_vector = torch.tensor(char_vector).unsqueeze(0) title_length = torch.tensor([title_length]).long() # Forward pass self.model.eval() _, y_pred = self.model(x_word=title_word_vector, x_char=title_char_vector, x_lengths=title_length, device="cpu", apply_softmax=True) # Top k categories y_prob, indices = torch.topk(y_pred, k=k) probabilities = y_prob.detach().numpy()[0] indices = indices.detach().numpy()[0] # Results results = [] for probability, index in zip(probabilities, indices): category = self.vectorizer.category_vocab.lookup_index(index) results.append({'category': category, 'probability': probability}) return results # Load the model dataset = NewsDataset.load_dataset_and_load_vectorizer( args.split_data_file, args.vectorizer_file) vectorizer = dataset.vectorizer model = NewsModel(embedding_dim=args.embedding_dim, num_word_embeddings=len(vectorizer.title_word_vocab), num_char_embeddings=len(vectorizer.title_char_vocab), kernels=args.kernels, num_input_channels=args.embedding_dim, num_output_channels=args.num_filters, rnn_hidden_dim=args.rnn_hidden_dim, hidden_dim=args.hidden_dim, output_dim=len(vectorizer.category_vocab), num_layers=args.num_layers, bidirectional=args.bidirectional, dropout_p=args.dropout_p, word_padding_idx=vectorizer.title_word_vocab.mask_index, char_padding_idx=vectorizer.title_char_vocab.mask_index) model.load_state_dict(torch.load(args.model_state_file)) model = model.to("cpu") print (model.named_modules) # Inference inference = Inference(model=model, vectorizer=vectorizer) title = input("Enter a title to classify: ") prediction = inference.predict_category(preprocess_text(title)) print("{} → {} (p={:0.2f})".format(title, prediction['category'], prediction['probability'])) # Top-k inference top_k = inference.predict_top_k(preprocess_text(title), k=len(vectorizer.category_vocab)) print ("{}: ".format(title)) for result in top_k: print ("{} (p={:0.2f})".format(result['category'], result['probability'])) ``` # Interpretability We can inspect the probability vector that is generated at each time step to visualize the importance of each of the previous hidden states towards a particular time step's prediction. ``` import seaborn as sns import matplotlib.pyplot as plt attn_matrix = prediction['attn_scores'].detach().numpy() ax = sns.heatmap(attn_matrix, linewidths=2, square=True) tokens = ["<BEGIN>"]+preprocess_text(title).split(" ")+["<END>"] ax.set_xticklabels(tokens, rotation=45) ax.set_xlabel("Token") ax.set_ylabel("Importance\n") plt.show() ``` # TODO - attn visualization isn't always great - bleu score - ngram-overlap - perplexity - beamsearch - hierarchical softmax - hierarchical attention - Transformer networks - attention interpretability is hit/miss	github_jupyter
<a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content/blob/master/tutorials/W1D5_DimensionalityReduction/student/W1D5_Tutorial3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a> # Neuromatch Academy: Week 1, Day 5, Tutorial 3 # Dimensionality Reduction and reconstruction __Content creators:__ Alex Cayco Gajic, John Murray __Content reviewers:__ Roozbeh Farhoudi, Matt Krause, Spiros Chavlis, Richard Gao, Michael Waskom --- # Tutorial Objectives In this notebook we'll learn to apply PCA for dimensionality reduction, using a classic dataset that is often used to benchmark machine learning algorithms: MNIST. We'll also learn how to use PCA for reconstruction and denoising. Overview: - Perform PCA on MNIST - Calculate the variance explained - Reconstruct data with different numbers of PCs - (Bonus) Examine denoising using PCA You can learn more about MNIST dataset [here](https://en.wikipedia.org/wiki/MNIST_database). ``` # @title Video 1: PCA for dimensionality reduction from IPython.display import YouTubeVideo video = YouTubeVideo(id="oO0bbInoO_0", width=854, height=480, fs=1) print("Video available at https://youtube.com/watch?v=" + video.id) video ``` --- # Setup Run these cells to get the tutorial started. ``` # Imports import numpy as np import matplotlib.pyplot as plt # @title Figure Settings import ipywidgets as widgets # interactive display %config InlineBackend.figure_format = 'retina' plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/nma.mplstyle") # @title Helper Functions def plot_variance_explained(variance_explained): """ Plots eigenvalues. Args: variance_explained (numpy array of floats) : Vector of variance explained for each PC Returns: Nothing. """ plt.figure() plt.plot(np.arange(1, len(variance_explained) + 1), variance_explained, '--k') plt.xlabel('Number of components') plt.ylabel('Variance explained') plt.show() def plot_MNIST_reconstruction(X, X_reconstructed): """ Plots 9 images in the MNIST dataset side-by-side with the reconstructed images. Args: X (numpy array of floats) : Data matrix each column corresponds to a different random variable X_reconstructed (numpy array of floats) : Data matrix each column corresponds to a different random variable Returns: Nothing. """ plt.figure() ax = plt.subplot(121) k = 0 for k1 in range(3): for k2 in range(3): k = k + 1 plt.imshow(np.reshape(X[k, :], (28, 28)), extent=[(k1 + 1) * 28, k1 * 28, (k2 + 1) * 28, k2 * 28], vmin=0, vmax=255) plt.xlim((3 * 28, 0)) plt.ylim((3 * 28, 0)) plt.tick_params(axis='both', which='both', bottom=False, top=False, labelbottom=False) ax.set_xticks([]) ax.set_yticks([]) plt.title('Data') plt.clim([0, 250]) ax = plt.subplot(122) k = 0 for k1 in range(3): for k2 in range(3): k = k + 1 plt.imshow(np.reshape(np.real(X_reconstructed[k, :]), (28, 28)), extent=[(k1 + 1) * 28, k1 * 28, (k2 + 1) * 28, k2 * 28], vmin=0, vmax=255) plt.xlim((3 * 28, 0)) plt.ylim((3 * 28, 0)) plt.tick_params(axis='both', which='both', bottom=False, top=False, labelbottom=False) ax.set_xticks([]) ax.set_yticks([]) plt.clim([0, 250]) plt.title('Reconstructed') plt.tight_layout() def plot_MNIST_sample(X): """ Plots 9 images in the MNIST dataset. Args: X (numpy array of floats) : Data matrix each column corresponds to a different random variable Returns: Nothing. """ fig, ax = plt.subplots() k = 0 for k1 in range(3): for k2 in range(3): k = k + 1 plt.imshow(np.reshape(X[k, :], (28, 28)), extent=[(k1 + 1) * 28, k1 * 28, (k2+1) * 28, k2 * 28], vmin=0, vmax=255) plt.xlim((3 * 28, 0)) plt.ylim((3 * 28, 0)) plt.tick_params(axis='both', which='both', bottom=False, top=False, labelbottom=False) plt.clim([0, 250]) ax.set_xticks([]) ax.set_yticks([]) plt.show() def plot_MNIST_weights(weights): """ Visualize PCA basis vector weights for MNIST. Red = positive weights, blue = negative weights, white = zero weight. Args: weights (numpy array of floats) : PCA basis vector Returns: Nothing. """ fig, ax = plt.subplots() cmap = plt.cm.get_cmap('seismic') plt.imshow(np.real(np.reshape(weights, (28, 28))), cmap=cmap) plt.tick_params(axis='both', which='both', bottom=False, top=False, labelbottom=False) plt.clim(-.15, .15) plt.colorbar(ticks=[-.15, -.1, -.05, 0, .05, .1, .15]) ax.set_xticks([]) ax.set_yticks([]) plt.show() def add_noise(X, frac_noisy_pixels): """ Randomly corrupts a fraction of the pixels by setting them to random values. Args: X (numpy array of floats) : Data matrix frac_noisy_pixels (scalar) : Fraction of noisy pixels Returns: (numpy array of floats) : Data matrix + noise """ X_noisy = np.reshape(X, (X.shape[0] * X.shape[1])) N_noise_ixs = int(X_noisy.shape[0] * frac_noisy_pixels) noise_ixs = np.random.choice(X_noisy.shape[0], size=N_noise_ixs, replace=False) X_noisy[noise_ixs] = np.random.uniform(0, 255, noise_ixs.shape) X_noisy = np.reshape(X_noisy, (X.shape[0], X.shape[1])) return X_noisy def change_of_basis(X, W): """ Projects data onto a new basis. Args: X (numpy array of floats) : Data matrix each column corresponding to a different random variable W (numpy array of floats) : new orthonormal basis columns correspond to basis vectors Returns: (numpy array of floats) : Data matrix expressed in new basis """ Y = np.matmul(X, W) return Y def get_sample_cov_matrix(X): """ Returns the sample covariance matrix of data X. Args: X (numpy array of floats) : Data matrix each column corresponds to a different random variable Returns: (numpy array of floats) : Covariance matrix """ X = X - np.mean(X, 0) cov_matrix = 1 / X.shape[0] * np.matmul(X.T, X) return cov_matrix def sort_evals_descending(evals, evectors): """ Sorts eigenvalues and eigenvectors in decreasing order. Also aligns first two eigenvectors to be in first two quadrants (if 2D). Args: evals (numpy array of floats) : Vector of eigenvalues evectors (numpy array of floats) : Corresponding matrix of eigenvectors each column corresponds to a different eigenvalue Returns: (numpy array of floats) : Vector of eigenvalues after sorting (numpy array of floats) : Matrix of eigenvectors after sorting """ index = np.flip(np.argsort(evals)) evals = evals[index] evectors = evectors[:, index] if evals.shape[0] == 2: if np.arccos(np.matmul(evectors[:, 0], 1 / np.sqrt(2) * np.array([1, 1]))) > np.pi / 2: evectors[:, 0] = -evectors[:, 0] if np.arccos(np.matmul(evectors[:, 1], 1 / np.sqrt(2)np.array([-1, 1]))) > np.pi / 2: evectors[:, 1] = -evectors[:, 1] return evals, evectors def pca(X): """ Performs PCA on multivariate data. Eigenvalues are sorted in decreasing order Args: X (numpy array of floats) : Data matrix each column corresponds to a different random variable Returns: (numpy array of floats) : Data projected onto the new basis (numpy array of floats) : Vector of eigenvalues (numpy array of floats) : Corresponding matrix of eigenvectors """ X = X - np.mean(X, 0) cov_matrix = get_sample_cov_matrix(X) evals, evectors = np.linalg.eigh(cov_matrix) evals, evectors = sort_evals_descending(evals, evectors) score = change_of_basis(X, evectors) return score, evectors, evals def plot_eigenvalues(evals, limit=True): """ Plots eigenvalues. Args: (numpy array of floats) : Vector of eigenvalues Returns: Nothing. """ plt.figure() plt.plot(np.arange(1, len(evals) + 1), evals, 'o-k') plt.xlabel('Component') plt.ylabel('Eigenvalue') plt.title('Scree plot') if limit: plt.show() ``` --- # Section 1: Perform PCA on MNIST The MNIST dataset consists of a 70,000 images of individual handwritten digits. Each image is a 28x28 pixel grayscale image. For convenience, each 28x28 pixel image is often unravelled into a single 784 (=2828) element vector, so that the whole dataset is represented as a 70,000 x 784 matrix. Each row represents a different image, and each column represents a different pixel. Enter the following cell to load the MNIST dataset and plot the first nine images. ``` from sklearn.datasets import fetch_openml mnist = fetch_openml(name='mnist_784') X = mnist.data plot_MNIST_sample(X) ``` The MNIST dataset has an extrinsic dimensionality of 784, much higher than the 2-dimensional examples used in the previous tutorials! To make sense of this data, we'll use dimensionality reduction. But first, we need to determine the intrinsic dimensionality $K$ of the data. One way to do this is to look for an "elbow" in the scree plot, to determine which eigenvalues are signficant. ## Exercise 1: Scree plot of MNIST In this exercise you will examine the scree plot in the MNIST dataset. Steps: - Perform PCA on the dataset and examine the scree plot. - When do the eigenvalues appear (by eye) to reach zero? (Hint: use `plt.xlim` to zoom into a section of the plot). ``` help(pca) help(plot_eigenvalues) ################################################# ## TO DO for students: perform PCA and plot the eigenvalues ################################################# # perform PCA # score, evectors, evals = ... # plot the eigenvalues # plot_eigenvalues(evals, limit=False) # plt.xlim(...) # limit x-axis up to 100 for zooming ``` [Click for solution](https://github.com/NeuromatchAcademy/course-content/tree/master//tutorials/W1D5_DimensionalityReduction/solutions/W1D5_Tutorial3_Solution_a876e927.py) Example output: <img alt='Solution hint' align='left' width=558 height=414 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D5_DimensionalityReduction/static/W1D5_Tutorial3_Solution_a876e927_0.png> --- # Section 2: Calculate the variance explained The scree plot suggests that most of the eigenvalues are near zero, with fewer than 100 having large values. Another common way to determine the intrinsic dimensionality is by considering the variance explained. This can be examined with a cumulative plot of the fraction of the total variance explained by the top $K$ components, i.e., \begin{equation} \text{var explained} = \frac{\sum_{i=1}^K \lambda_i}{\sum_{i=1}^N \lambda_i} \end{equation} The intrinsic dimensionality is often quantified by the $K$ necessary to explain a large proportion of the total variance of the data (often a defined threshold, e.g., 90%). ## Exercise 2: Plot the explained variance In this exercise you will plot the explained variance. Steps: - Fill in the function below to calculate the fraction variance explained as a function of the number of principal componenets. Hint: use `np.cumsum`. - Plot the variance explained using `plot_variance_explained`. Questions: - How many principal components are required to explain 90% of the variance? - How does the intrinsic dimensionality of this dataset compare to its extrinsic dimensionality? ``` help(plot_variance_explained) def get_variance_explained(evals): """ Calculates variance explained from the eigenvalues. Args: evals (numpy array of floats) : Vector of eigenvalues Returns: (numpy array of floats) : Vector of variance explained """ ################################################# ## TO DO for students: calculate the explained variance using the equation ## from Section 2. # Comment once you've filled in the function raise NotImplementedError("Student excercise: calculate explaine variance!") ################################################# # cumulatively sum the eigenvalues csum = ... # normalize by the sum of eigenvalues variance_explained = ... return variance_explained ################################################# ## TO DO for students: call the function and plot the variance explained ################################################# # calculate the variance explained variance_explained = ... # Uncomment to plot the variance explained # plot_variance_explained(variance_explained) ``` [Click for solution](https://github.com/NeuromatchAcademy/course-content/tree/master//tutorials/W1D5_DimensionalityReduction/solutions/W1D5_Tutorial3_Solution_0f5f51b9.py) Example output: <img alt='Solution hint' align='left' width=560 height=416 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D5_DimensionalityReduction/static/W1D5_Tutorial3_Solution_0f5f51b9_0.png> --- # Section 3: Reconstruct data with different numbers of PCs ``` # @title Video 2: Data Reconstruction from IPython.display import YouTubeVideo video = YouTubeVideo(id="ZCUhW26AdBQ", width=854, height=480, fs=1) print("Video available at https://youtube.com/watch?v=" + video.id) video ``` Now we have seen that the top 100 or so principal components of the data can explain most of the variance. We can use this fact to perform dimensionality reduction, i.e., by storing the data using only 100 components rather than the samples of all 784 pixels. Remarkably, we will be able to reconstruct much of the structure of the data using only the top 100 components. To see this, recall that to perform PCA we projected the data $\bf X$ onto the eigenvectors of the covariance matrix: \begin{equation} \bf S = X W \end{equation} Since $\bf W$ is an orthogonal matrix, ${\bf W}^{-1} = {\bf W}^T$. So by multiplying by ${\bf W}^T$ on each side we can rewrite this equation as \begin{equation} {\bf X = S W}^T. \end{equation} This now gives us a way to reconstruct the data matrix from the scores and loadings. To reconstruct the data from a low-dimensional approximation, we just have to truncate these matrices. Let's call ${\bf S}_{1:K}$ and ${\bf W}_{1:K}$ as keeping only the first $K$ columns of this matrix. Then our reconstruction is: \begin{equation} {\bf \hat X = S}_{1:K} ({\bf W}_{1:K})^T. \end{equation} ## Exercise 3: Data reconstruction Fill in the function below to reconstruct the data using different numbers of principal components. Steps: * Fill in the following function to reconstruct the data based on the weights and scores. Don't forget to add the mean! * Make sure your function works by reconstructing the data with all $K=784$ components. The two images should look identical. ``` help(plot_MNIST_reconstruction) def reconstruct_data(score, evectors, X_mean, K): """ Reconstruct the data based on the top K components. Args: score (numpy array of floats) : Score matrix evectors (numpy array of floats) : Matrix of eigenvectors X_mean (numpy array of floats) : Vector corresponding to data mean K (scalar) : Number of components to include Returns: (numpy array of floats) : Matrix of reconstructed data """ ################################################# ## TO DO for students: Reconstruct the original data in X_reconstructed # Comment once you've filled in the function raise NotImplementedError("Student excercise: reconstructing data function!") ################################################# # Reconstruct the data from the score and eigenvectors # Don't forget to add the mean!! X_reconstructed = ... return X_reconstructed K = 784 ################################################# ## TO DO for students: Calculate the mean and call the function, then plot ## the original and the recostructed data ################################################# # Reconstruct the data based on all components X_mean = ... X_reconstructed = ... # Plot the data and reconstruction # plot_MNIST_reconstruction(X, X_reconstructed) ``` [Click for solution](https://github.com/NeuromatchAcademy/course-content/tree/master//tutorials/W1D5_DimensionalityReduction/solutions/W1D5_Tutorial3_Solution_e3395916.py) Example output: <img alt='Solution hint' align='left' width=557 height=289 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D5_DimensionalityReduction/static/W1D5_Tutorial3_Solution_e3395916_0.png> ## Interactive Demo: Reconstruct the data matrix using different numbers of PCs Now run the code below and experiment with the slider to reconstruct the data matrix using different numbers of principal components. Steps * How many principal components are necessary to reconstruct the numbers (by eye)? How does this relate to the intrinsic dimensionality of the data? * Do you see any information in the data with only a single principal component? ``` # @title # @markdown Make sure you execute this cell to enable the widget! def refresh(K=100): X_reconstructed = reconstruct_data(score, evectors, X_mean, K) plot_MNIST_reconstruction(X, X_reconstructed) plt.title('Reconstructed, K={}'.format(K)) _ = widgets.interact(refresh, K=(1, 784, 10)) ``` ## Exercise 4: Visualization of the weights Next, let's take a closer look at the first principal component by visualizing its corresponding weights. Steps: * Enter `plot_MNIST_weights` to visualize the weights of the first basis vector. * What structure do you see? Which pixels have a strong positive weighting? Which have a strong negative weighting? What kinds of images would this basis vector differentiate? * Try visualizing the second and third basis vectors. Do you see any structure? What about the 100th basis vector? 500th? 700th? ``` help(plot_MNIST_weights) ################################################# ## TO DO for students: plot the weights calling the plot_MNIST_weights function ################################################# # Plot the weights of the first principal component # plot_MNIST_weights(...) ``` [Click for solution](https://github.com/NeuromatchAcademy/course-content/tree/master//tutorials/W1D5_DimensionalityReduction/solutions/W1D5_Tutorial3_Solution_f358e413.py) Example output: <img alt='Solution hint' align='left' width=499 height=416 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D5_DimensionalityReduction/static/W1D5_Tutorial3_Solution_f358e413_0.png> --- # Summary * In this tutorial, we learned how to use PCA for dimensionality reduction by selecting the top principal components. This can be useful as the intrinsic dimensionality ($K$) is often less than the extrinsic dimensionality ($N$) in neural data. $K$ can be inferred by choosing the number of eigenvalues necessary to capture some fraction of the variance. * We also learned how to reconstruct an approximation of the original data using the top $K$ principal components. In fact, an alternate formulation of PCA is to find the $K$ dimensional space that minimizes the reconstruction error. * Noise tends to inflate the apparent intrinsic dimensionality, however the higher components reflect noise rather than new structure in the data. PCA can be used for denoising data by removing noisy higher components. * In MNIST, the weights corresponding to the first principal component appear to discriminate between a 0 and 1. We will discuss the implications of this for data visualization in the following tutorial. --- # Bonus: Examine denoising using PCA In this lecture, we saw that PCA finds an optimal low-dimensional basis to minimize the reconstruction error. Because of this property, PCA can be useful for denoising corrupted samples of the data. ## Exercise 5: Add noise to the data In this exercise you will add salt-and-pepper noise to the original data and see how that affects the eigenvalues. Steps: - Use the function `add_noise` to add noise to 20% of the pixels. - Then, perform PCA and plot the variance explained. How many principal components are required to explain 90% of the variance? How does this compare to the original data? ``` help(add_noise) ################################################################### # Insert your code here to: # Add noise to the data # Plot noise-corrupted data # Perform PCA on the noisy data # Calculate and plot the variance explained ################################################################### np.random.seed(2020) # set random seed X_noisy = ... # score_noisy, evectors_noisy, evals_noisy = ... # variance_explained_noisy = ... # plot_MNIST_sample(X_noisy) # plot_variance_explained(variance_explained_noisy) ``` [Click for solution](https://github.com/NeuromatchAcademy/course-content/tree/master//tutorials/W1D5_DimensionalityReduction/solutions/W1D5_Tutorial3_Solution_d4a41b8c.py) Example output: <img alt='Solution hint' align='left' width=424 height=416 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D5_DimensionalityReduction/static/W1D5_Tutorial3_Solution_d4a41b8c_0.png> <img alt='Solution hint' align='left' width=560 height=416 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D5_DimensionalityReduction/static/W1D5_Tutorial3_Solution_d4a41b8c_1.png> ## Exercise 6: Denoising Next, use PCA to perform denoising by projecting the noise-corrupted data onto the basis vectors found from the original dataset. By taking the top K components of this projection, we can reduce noise in dimensions orthogonal to the K-dimensional latent space. Steps: - Subtract the mean of the noise-corrupted data. - Project the data onto the basis found with the original dataset (`evectors`, not `evectors_noisy`) and take the top $K$ components. - Reconstruct the data as normal, using the top 50 components. - Play around with the amount of noise and K to build intuition. ``` ################################################################### # Insert your code here to: # Subtract the mean of the noise-corrupted data # Project onto the original basis vectors evectors # Reconstruct the data using the top 50 components # Plot the result ################################################################### X_noisy_mean = ... projX_noisy = ... X_reconstructed = ... # plot_MNIST_reconstruction(X_noisy, X_reconstructed) ``` [Click for solution](https://github.com/NeuromatchAcademy/course-content/tree/master//tutorials/W1D5_DimensionalityReduction/solutions/W1D5_Tutorial3_Solution_e3ee8262.py) Example output: <img alt='Solution hint' align='left' width=557 height=289 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W1D5_DimensionalityReduction/static/W1D5_Tutorial3_Solution_e3ee8262_0.png>	github_jupyter
Instructions: 1. For all questions after 10th, Please only use the data specified in the note given just below the question 2. You need to add answers in the same file i.e. PDS_UberDriveProject_Questions.ipynb' and rename that file as 'Name_Date.ipynb'.You can mention the date on which you will be uploading/submitting the file.For e.g. if you plan to submit your assignment on 31-March, you can rename the file as 'STUDENTNAME_31-Mar-2020' # Load the necessary libraries. Import and load the dataset with a name uber_drives . ``` import pandas as pd import numpy as np # Get the Data data_uber_driver = pd.read_csv('uberdrive-1.csv') ``` ## Q1. Show the last 10 records of the dataset. (2 point) ``` data_uber_driver.tail(10) ``` ## Q2. Show the first 10 records of the dataset. (2 points) ``` data_uber_driver.head(10) ``` ## Q3. Show the dimension(number of rows and columns) of the dataset. (2 points) ``` data_uber_driver.shape ``` ## Q4. Show the size (Total number of elements) of the dataset. (2 points) ``` data_uber_driver.size ``` ## Q5. Print the information about all the variables of the data set. (2 points) ``` data_uber_driver.info() ``` ## Q6. Check for missing values. (2 points) - Note: Output should be boolean only. ``` data_uber_driver.isna() ``` ## Q7. How many missing values are present? (2 points) ``` data_uber_driver.isna().sum().sum() ``` ## Q8. Get the summary of the original data. (2 points). Hint:Outcome will contain only numerical column. ``` data_uber_driver.describe() ``` ## Q9. Drop the missing values and store the data in a new dataframe (name it"df") (2-points) ### Note: Dataframe "df" will not contain any missing value ``` df = data_uber_driver.dropna() ``` ## Q10. Check the information of the dataframe(df). (2 points) ``` df.info() ``` ## Q11. Get the unique start destinations. (2 points) ### Note: This question is based on the dataframe with no 'NA' values ### Hint- You need to print the unique destination place names in this and not the count. ``` df['START'].unique() ``` ## Q12. What is the total number of unique start destinations? (2 points) ### Note: Use the original dataframe without dropping 'NA' values ``` data_uber_driver['START'].nunique() ``` ## Q13. Print the total number of unique stop destinations. (2 points) ### Note: Use the original dataframe without dropping 'NA' values. ``` data_uber_driver['STOP'].unique().size ``` ## Q14. Print all the Uber trips that has the starting point of San Francisco. (2 points) ### Note: Use the original dataframe without dropping the 'NA' values. ### Hint: Use the loc function ``` data_uber_driver[data_uber_driver['START']=='San Francisco'] ``` ## Q15. What is the most popular starting point for the Uber drivers? (2 points) ### Note: Use the original dataframe without dropping the 'NA' values. ### Hint:Popular means the place that is visited the most ``` data_uber_driver['START'].value_counts().idxmax() ``` ## Q16. What is the most popular dropping point for the Uber drivers? (2 points) ### Note: Use the original dataframe without dropping the 'NA' values. ### Hint: Popular means the place that is visited the most ``` data_uber_driver['STOP'].value_counts().idxmax() ``` ## Q17. List the most frequent route taken by Uber drivers. (3 points) ### Note: This question is based on the new dataframe with no 'na' values. ### Hint-Print the most frequent route taken by Uber drivers (Route= combination of START & END points present in the Data set). ``` df.groupby(['START', 'STOP']).size().sort_values(ascending=False) ``` ## Q18. Print all types of purposes for the trip in an array. (3 points) ### Note: This question is based on the new dataframe with no 'NA' values. ``` df['PURPOSE'] ``` ## Q19. Plot a bar graph of Purpose vs Miles(Distance). (3 points) ### Note: Use the original dataframe without dropping the 'NA' values. ### Hint:You have to plot total/sum miles per purpose ``` import matplotlib.pyplot as plt fig = plt.figure(figsize=(19,5)) ax = fig.add_axes([0,0,1,1]) # replacing na 'PURPOSE' values data_uber_driver["PURPOSE"].fillna("NO_PURPOSE_PROVIDED", inplace = True) # replacing na 'MILES' values data_uber_driver["MILES"].fillna("NO_MILES_PROVIDED", inplace = True) ax.bar(data_uber_driver['PURPOSE'],data_uber_driver['MILES']) plt.show() ``` ## Q20. Print a dataframe of Purposes and the distance travelled for that particular Purpose. (3 points) ### Note: Use the original dataframe without dropping "NA" values ``` data_uber_driver.groupby(by=["PURPOSE"]).sum() ``` ## Q21. Plot number of trips vs Category of trips. (3 points) ### Note: Use the original dataframe without dropping the 'NA' values. ### Hint : You can make a countplot or barplot. ``` # import seaborn as sns # sns.countplot(x='CATEGORY',data=data_uber_driver) data_uber_driver['CATEGORY'].value_counts().plot(kind='bar',figsize=(19,7),color='red'); ``` ## Q22. What is proportion of trips that is Business and what is the proportion of trips that is Personal? (3 points) ### Note:Use the original dataframe without dropping the 'NA' values. The proportion calculation is with respect to the 'miles' variable. ### Hint:Out of the category of trips, you need to find percentage wise how many are business and how many are personal on the basis of miles per category. ``` data_uber_driver['CATEGORY'].value_counts(normalize=True)100 ```	github_jupyter
# Robust Scaler - Experimento Este é um componante que dimensiona atributos usando estatísticas robustas para outliers. Este Scaler remove a mediana e dimensiona os dados de acordo com o intervalo quantil (o padrão é Amplitude interquartil). Amplitude interquartil é o intervalo entre o 1º quartil (25º quantil) e o 3º quartil (75º quantil). Faz uso da implementação do [Scikit-learn](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.RobustScaler.html). <br> Scikit-learn é uma biblioteca open source de machine learning que suporta apredizado supervisionado e não supervisionado. Também provê várias ferramentas para montagem de modelo, pré-processamento de dados, seleção e avaliação de modelos, e muitos outros utilitários. ## Declaração de parâmetros e hiperparâmetros Declare parâmetros com o botão <img src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABQAAAAUCAYAAACNiR0NAAABhWlDQ1BJQ0MgcHJvZmlsZQAAKJF9kT1Iw0AcxV9TtaIVBzuIOASpThb8QhylikWwUNoKrTqYXPohNGlIUlwcBdeCgx+LVQcXZ10dXAVB8APEydFJ0UVK/F9SaBHjwXE/3t173L0DhFqJqWbbGKBqlpGMRcVMdkUMvKID3QhiCOMSM/V4aiENz/F1Dx9f7yI8y/vcn6NHyZkM8InEs0w3LOJ14ulNS+e8TxxiRUkhPiceNeiCxI9cl11+41xwWOCZISOdnCMOEYuFFpZbmBUNlXiKOKyoGuULGZcVzluc1VKFNe7JXxjMacsprtMcRAyLiCMBETIq2EAJFiK0aqSYSNJ+1MM/4PgT5JLJtQFGjnmUoUJy/OB/8LtbMz854SYFo0D7i21/DAOBXaBete3vY9uunwD+Z+BKa/rLNWDmk/RqUwsfAb3bwMV1U5P3gMsdoP9JlwzJkfw0hXweeD+jb8oCfbdA16rbW2Mfpw9AmrpaugEODoGRAmWveby7s7W3f880+vsBocZyukMJsmwAAAAGYktHRAD/AP8A/6C9p5MAAAAJcEhZcwAADdcAAA3XAUIom3gAAAAHdElNRQfkBgsMIwnXL7c0AAACDUlEQVQ4y92UP4gTQRTGf29zJxhJZ2NxbMBKziYWlmJ/ile44Nlkd+dIYWFzItiNgoIEtFaTzF5Ac/inE/urtLWxsMqmUOwCEpt1Zmw2xxKi53XitPO9H9978+aDf/3IUQvSNG0450Yi0jXG7C/eB0cFeu9viciGiDyNoqh2KFBrHSilWstgnU7nFLBTgl+ur6/7PwK11kGe5z3n3Hul1MaiuCgKDZwALHA7z/Oe1jpYCtRaB+PxuA8kQM1aW68Kt7e3zwBp6a5b1ibj8bhfhQYVZwMRiQHrvW9nWfaqCrTWPgRWvPdvsiy7IyLXgEJE4slk8nw+T5nDgDbwE9gyxryuwpRSF5xz+0BhrT07HA4/AyRJchUYASvAbhiGaRVWLIMBYq3tAojIszkMoNRulbXtPM8HwV/sXSQi54HvQRDcO0wfhGGYArvAKjAq2wAgiqJj3vsHpbtur9f7Vi2utLx60LLW2hljEuBJOYu9OI6vAzQajRvAaeBLURSPlsBelA+VhWGYaq3dwaZvbm6+m06noYicE5ErrVbrK3AXqHvvd4bD4Ye5No7jSERGwKr3Pms2m0pr7Rb30DWbTQWYcnFvAieBT7PZbFB1V6vVfpQaU4UtDQetdTCZTC557/eA48BlY8zbRZ1SqrW2tvaxCvtt2iRJ0i9/xb4x5uJRwmNlaaaJ3AfqIvKY/+78Av++6uiSZhYMAAAAAElFTkSuQmCC" /> na barra de ferramentas.<br> A variável `dataset` possui o caminho para leitura do arquivos importados na tarefa de "Upload de dados".<br> Você também pode importar arquivos com o botão <img src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABQAAAAUCAYAAACNiR0NAAABhWlDQ1BJQ0MgcHJvZmlsZQAAKJF9kT1Iw0AcxV9TtaIVBzuIOASpThb8QhylikWwUNoKrTqYXPohNGlIUlwcBdeCgx+LVQcXZ10dXAVB8APEydFJ0UVK/F9SaBHjwXE/3t173L0DhFqJqWbbGKBqlpGMRcVMdkUMvKID3QhiCOMSM/V4aiENz/F1Dx9f7yI8y/vcn6NHyZkM8InEs0w3LOJ14ulNS+e8TxxiRUkhPiceNeiCxI9cl11+41xwWOCZISOdnCMOEYuFFpZbmBUNlXiKOKyoGuULGZcVzluc1VKFNe7JXxjMacsprtMcRAyLiCMBETIq2EAJFiK0aqSYSNJ+1MM/4PgT5JLJtQFGjnmUoUJy/OB/8LtbMz854SYFo0D7i21/DAOBXaBete3vY9uunwD+Z+BKa/rLNWDmk/RqUwsfAb3bwMV1U5P3gMsdoP9JlwzJkfw0hXweeD+jb8oCfbdA16rbW2Mfpw9AmrpaugEODoGRAmWveby7s7W3f880+vsBocZyukMJsmwAAAAGYktHRAD/AP8A/6C9p5MAAAAJcEhZcwAADdcAAA3XAUIom3gAAAAHdElNRQfkBgsOBy6ASTeXAAAC/0lEQVQ4y5WUT2gcdRTHP29m99B23Uiq6dZisgoWCxVJW0oL9dqLfyhCvGWY2YUBI95MsXgwFISirQcLhS5hfgk5CF3wJIhFI7aHNsL2VFZFik1jS1qkiZKdTTKZ3/MyDWuz0fQLc/m99/vMvDfv+4RMlUrlkKqeAAaBAWAP8DSgwJ/AXRG5rao/WWsvTU5O3qKLBMD3fSMiPluXFZEPoyj67PGAMzw83PeEMABHVT/oGpiamnoAmCcEWhH5tFsgF4bh9oWFhfeKxeJ5a+0JVT0oImWgBPQCKfAQuAvcBq67rltX1b+6ApMkKRcKhe9V9QLwbavV+qRer692Sx4ZGSnEcXw0TdP3gSrQswGYz+d/S5IkVtXTwOlCoZAGQXAfmAdagAvsAErtdnuXiDy6+023l7qNRsMODg5+CawBzwB9wFPA7mx8ns/KL2Tl3xCRz5eWlkabzebahrHxPG+v4zgnc7ncufHx8Z+Hhoa29fT0lNM03Q30ikiqqg+ttX/EcTy3WTvWgdVqtddaOw/kgXvADHBHROZVNRaRvKruUNU+EdkPfGWM+WJTYOaSt1T1LPDS/4zLWWPMaLVaPWytrYvIaBRFl/4F9H2/JCKvGmMu+76/X0QOqGoZKDmOs1NV28AicMsYc97zvFdc1/0hG6kEeNsY83UnsCwivwM3VfU7YEZE7lhr74tIK8tbnJiYWPY8b6/ruleAXR0ftQy8boyZXi85CIIICDYpc2ZgYODY3NzcHmvt1eyvP64lETkeRdE1yZyixWLx5U2c8q4x5mIQBE1g33/0d3FlZeXFR06ZttZesNZejuO4q1NE5CPgWVV9E3ij47wB1IDlJEn+ljAM86urq7+KyAtZTgqsO0VV247jnOnv7/9xbGzMViqVMVX9uANYj6LonfVtU6vVkjRNj6jqGeCXzGrPAQeA10TkuKpOz87ONrayhnIA2Qo7BZwKw3B7kiRloKSqO13Xja21C47jPNgysFO1Wi0GmtmzQap6DWgD24A1Vb3SGf8Hfstmz1CuXEIAAAAASUVORK5CYII=" /> na barra de ferramentas. ``` # parâmetros dataset = "/tmp/data/iris.csv" #@param {type:"string"} target = None #@param {type:"feature", label:"Atributo alvo", description: "Esse valor será utilizado para garantir que o alvo não seja removido."} with_centering = True #@param {type:"boolean", label:"Centralização", description:"Centralizar os dados antes de dimensionar. Ocorre exceção quando usado com matrizes esparsas"} with_scaling = True #@param {type:"boolean", label:"Dimensionamento", description:"Dimensionar os dados para um intervalo interquartil"} ``` ## Acesso ao conjunto de dados O conjunto de dados utilizado nesta etapa será o mesmo carregado através da plataforma.<br> O tipo da variável retornada depende do arquivo de origem: - [pandas.DataFrame](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.html) para CSV e compressed CSV: .csv .csv.zip .csv.gz .csv.bz2 .csv.xz - [Binary IO stream](https://docs.python.org/3/library/io.html#binary-i-o) para outros tipos de arquivo: .jpg .wav .zip .h5 .parquet etc ``` import pandas as pd df = pd.read_csv(dataset) has_target = True if target is not None and target in df.columns else False X = df.copy() if has_target: X = df.drop(target, axis=1) y = df[target] ``` ## Acesso aos metadados do conjunto de dados Utiliza a função `stat_dataset` do [SDK da PlatIAgro](https://platiagro.github.io/sdk/) para carregar metadados. <br> Por exemplo, arquivos CSV possuem `metadata['featuretypes']` para cada coluna no conjunto de dados (ex: categorical, numerical, or datetime). ``` import numpy as np from platiagro import stat_dataset metadata = stat_dataset(name=dataset) featuretypes = metadata["featuretypes"] columns = df.columns.to_numpy() featuretypes = np.array(featuretypes) if has_target: target_index = np.argwhere(columns == target) columns = np.delete(columns, target_index) featuretypes = np.delete(featuretypes, target_index) ``` ## Configuração dos atributos ``` from platiagro.featuretypes import NUMERICAL # Selects the indexes of numerical numerical_indexes = np.where(featuretypes == NUMERICAL)[0] non_numerical_indexes = np.where(~(featuretypes == NUMERICAL))[0] # After the step of the make_column_transformer, # numerical features are grouped in the beggining of the array numerical_indexes_after_first_step = np.arange(len(numerical_indexes)) ``` ## Treina um modelo usando sklearn.preprocessing.RobustScaler ``` from sklearn.compose import make_column_transformer from sklearn.impute import SimpleImputer from sklearn.pipeline import Pipeline from sklearn.preprocessing import RobustScaler pipeline = Pipeline( steps=[ ( "imputer", make_column_transformer( (SimpleImputer(), numerical_indexes), remainder="passthrough" ), ), ( "robust_scaler", make_column_transformer( ( RobustScaler( with_centering=with_centering, with_scaling=with_scaling ), numerical_indexes_after_first_step, ), remainder="passthrough", ), ), ] ) # Train model and transform dataset X = pipeline.fit_transform(X) # Put numerical features in the lowest indexes features_after_pipeline = np.concatenate( (columns[numerical_indexes], columns[non_numerical_indexes]) ) # Put data back in a pandas.DataFrame df = pd.DataFrame(data=X, columns=features_after_pipeline) if has_target: df[target] = y ``` ## Cria visualização do resultado Cria visualização do resultado como uma planilha. ``` import matplotlib.pyplot as plt from platiagro.plotting import plot_data_table ax = plot_data_table(df) plt.show() ``` ## Salva alterações no conjunto de dados O conjunto de dados será salvo (e sobrescrito com as respectivas mudanças) localmente, no container da experimentação, utilizando a função `pandas.DataFrame.to_csv`.<br> ``` # save dataset changes df.to_csv(dataset, index=False) ``` ## Salva resultados da tarefa A plataforma guarda o conteúdo de `/tmp/data/` para as tarefas subsequentes. ``` from joblib import dump artifacts = { "pipeline": pipeline, "columns": columns, "features_after_pipeline": features_after_pipeline, } dump(artifacts, "/tmp/data/robust-scaler.joblib") ```	github_jupyter
<a href="https://colab.research.google.com/github/ralsouza/python_fundamentos/blob/master/src/05_desafio/05_missao05.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a> ## Missão: Analisar o Comportamento de Compra de Consumidores. ### Nível de Dificuldade: Alto Você recebeu a tarefa de analisar os dados de compras de um web site! Os dados estão no formato JSON e disponíveis junto com este notebook. No site, cada usuário efetua login usando sua conta pessoal e pode adquirir produtos à medida que navega pela lista de produtos oferecidos. Cada produto possui um valor de venda. Dados de idade e sexo de cada usuário foram coletados e estão fornecidos no arquivo JSON. Seu trabalho é entregar uma análise de comportamento de compra dos consumidores. Esse é um tipo de atividade comum realizado por Cientistas de Dados e o resultado deste trabalho pode ser usado, por exemplo, para alimentar um modelo de Machine Learning e fazer previsões sobre comportamentos futuros. Mas nesta missão você vai analisar o comportamento de compra dos consumidores usando o pacote Pandas da linguagem Python e seu relatório final deve incluir cada um dos seguintes itens: Contagem de Consumidores * Número total de consumidores Análise Geral de Compras * Número de itens exclusivos * Preço médio de compra * Número total de compras * Rendimento total (Valor Total) Informações Demográficas Por Gênero * Porcentagem e contagem de compradores masculinos * Porcentagem e contagem de compradores do sexo feminino * Porcentagem e contagem de outros / não divulgados Análise de Compras Por Gênero * Número de compras * Preço médio de compra * Valor Total de Compra * Compras for faixa etária Identifique os 5 principais compradores pelo valor total de compra e, em seguida, liste (em uma tabela): * Login * Número de compras * Preço médio de compra * Valor Total de Compra * Itens mais populares Identifique os 5 itens mais populares por contagem de compras e, em seguida, liste (em uma tabela): * ID do item * Nome do item * Número de compras * Preço Médio do item * Valor Total de Compra * Itens mais lucrativos Identifique os 5 itens mais lucrativos pelo valor total de compra e, em seguida, liste (em uma tabela): * ID do item * Nome do item * Número de compras * Preço Médio do item * Valor Total de Compra Como considerações finais: * Seu script deve funcionar para o conjunto de dados fornecido. * Você deve usar a Biblioteca Pandas e o Jupyter Notebook. ``` # Imports import pandas as pd import numpy as np # Load file from Drive from google.colab import drive drive.mount('/content/drive') # Load file to Dataframe load_file = "/content/drive/My Drive/dados_compras.json" purchase_file = pd.read_json(load_file, orient = "records") ``` ## 1. Análise Exploratória ### 1.1 Checagem das primeiras linhas ``` # Nota-se que os logins se repetem. purchase_file.sort_values('Login') ``` ### 1.2 Checagem dos tipos dos dados ``` purchase_file.dtypes ``` ### 1.3 Checagem de valores nulos ``` purchase_file.isnull().sum().sort_values(ascending = False) ``` ### 1.4 Checagem de valores zero ``` (purchase_file == 0).sum() ``` ### 1.5 Distribuição de idades O público mais representativo desta amostra encontra-se entre 19 há 26 anos de idade. ``` plt.hist(purchase_file['Idade'], histtype='bar', rwidth=0.8) plt.title('Distribuição de vendas por idade') plt.xlabel('Idade') plt.ylabel('Quantidade de compradores') plt.show() ``` ### 1.6 Distribuição dos valores A maioria das vendas são dos produtos de `R$ 2,30`, `R$ 3,40` e `R$ 4,20`. ``` plt.hist(purchase_file['Valor'], histtype='bar', rwidth=0.8) plt.title('Distribuição por Valores') plt.xlabel('Reais R$') plt.ylabel('Quantidade de vendas') plt.show() ``` ## 2. Informações Sobre os Consumidores * Número total de consumidores ``` # Contar a quantidade de logins, removendo as linhas com dados duplicados. total_consumidores = purchase_file['Login'].drop_duplicates().count() print('O total de consumidores na amostra são: {}'.format(total_consumidores)) ``` ## 3. Análise Geral de Compras * Número de itens exclusivos * Preço médio de compra * Número total de compras * Rendimento total (Valor Total) ``` # Número de itens exclusivos itens_exclusivos = purchase_file['Item ID'].drop_duplicates().count() preco_medio = np.average(purchase_file['Valor']) total_compras = purchase_file['Nome do Item'].count() valor_total = np.sum(purchase_file['Valor']) analise_geral = pd.DataFrame({ 'Itens Exclusivos':[itens_exclusivos], 'Preço Médio (R$)':[np.round(preco_medio, decimals=2)], 'Qtd. Compras':[total_compras], 'Valor Total (R$)':[valor_total] }) analise_geral ``` ## 4. Análise Demográfica por Genêro * Porcentagem e contagem de compradores masculinos * Porcentagem e contagem de compradores do sexo feminino * Porcentagem e contagem de outros / não divulgados ``` # Selecionar os dados únicos do compradores para deduplicação info_compradores = purchase_file.loc[:,['Login','Sexo','Idade']] # Deduplicar os dados info_compradores = info_compradores.drop_duplicates() # Quantidade de compradores por genêro qtd_compradores = info_compradores['Sexo'].value_counts() # Percentual de compradores por genêro perc_compradores = round(info_compradores['Sexo'].value_counts(normalize=True) * 100, 2) # Armazenar dados no Dataframe analise_demografica = pd.DataFrame( {'Percentual':perc_compradores, 'Qtd. Compradores':qtd_compradores } ) # Impressão da tabela analise_demografica plot = analise_demografica['Percentual'].plot(kind='pie', title='Percentual de Compras por Genêro', autopct='%.2f') plot = analise_demografica['Qtd. Compradores'].plot(kind='barh', title='Quantidade de Compradores por Genêro') # Add labels for i in plot.patches: plot.text(i.get_width()+.1, i.get_y()+.31, \ str(round((i.get_width()), 2)), fontsize=10) ``` ## 5. Análise de Compras Por Gênero * Número de compras * Preço médio de compra * Valor Total de Compra * Compras for faixa etária ``` # Número de compras por genêro nro_compras_gen = purchase_file['Sexo'].value_counts() # Preço médio de compra por genêro media_compras_gen = round(purchase_file.groupby('Sexo')['Valor'].mean(), 2) # Total de compras por genêro total_compras_gen = purchase_file.groupby('Sexo')['Valor'].sum() analise_compras = pd.DataFrame( {'Qtd. de Compras':nro_compras_gen, 'Preço Médio (R$)':media_compras_gen, 'Total Compras (R$)':total_compras_gen} ) # Impressão da tabela analise_compras # Usar dataframe deduplicado info_compradores # Compras por faixa etária age_bins = [0, 9.99, 14.99, 19.99, 24.99, 29.99, 34.99, 39.99, 999] seg_idade = ['Menor de 10', '10-14', '15-19', '20-24', '25-29', '30-34', '35-39', 'Maior de 39'] info_compradores['Intervalo Idades'] = pd.cut(info_compradores['Idade'], age_bins, labels=seg_idade) df_hist_compras = pd.DataFrame(info_compradores['Intervalo Idades'].value_counts(), index=seg_idade) hist = df_hist_compras.plot(kind='bar', legend=False) hist.set_title('Compras for faixa etária', fontsize=15) hist.set_ylabel('Frequência') hist.set_xlabel('Faixas de Idades') ``` ## 6. Consumidores Mais Populares (Top 5) Identifique os 5 principais compradores pelo valor total de compra e, em seguida, liste (em uma tabela): * Login * Número de compras * Preço médio de compra * Valor Total de Compra * Itens mais populares ``` consumidores_populares = purchase_file[['Login','Nome do Item','Valor']] consumidores_populares.head(5) top_por_compras = consumidores_populares.groupby(['Login']).count()['Nome do Item'] top_por_valor_medio = round(consumidores_populares.groupby('Login').mean()['Valor'], 2) top_por_valor_total = consumidores_populares.groupby('Login').sum()['Valor'] top_consumidores = pd.DataFrame({'Número de Compras': top_por_compras, 'Preço Médio(R$)': top_por_valor_medio, 'Valor Total(R$)': top_por_valor_total}) \ .sort_values(by=['Valor Total(R$)'], ascending=False) \ .head(5) top_itens = consumidores_populares['Nome do Item'].value_counts().head(5) top_consumidores itens_populares = pd.DataFrame(consumidores_populares['Nome do Item'].value_counts().head(5)) itens_populares ``` ## 7. Itens Mais Populares Identifique os 5 itens mais populares por contagem de compras e, em seguida, liste (em uma tabela): * ID do item * Nome do item * Número de compras * Preço Médio do item * Valor Total de Compra * Itens mais lucrativos ``` itens_populares = purchase_file[['Item ID','Nome do Item','Valor']] num_compras = itens_populares.groupby('Nome do Item').count()['Item ID'] media_preco = round(itens_populares.groupby('Nome do Item').mean()['Valor'], 2) total_preco = itens_populares.groupby('Nome do Item').sum()['Valor'] df_itens_populares = pd.DataFrame({ 'Numero de Compras': num_compras, 'Preço Médio do Item': media_preco, 'Valor Total da Compra': total_preco}) df_itens_populares.sort_values(by=['Numero de Compras'], ascending=False).head(5) ``` ## 8. Itens Mais Lucrativos Identifique os 5 itens mais lucrativos pelo valor total de compra e, em seguida, liste (em uma tabela): * ID do item * Nome do item * Número de compras * Preço Médio do item * Valor Total de Compra ``` itens_lucrativos = purchase_file[['Item ID','Nome do Item','Valor']] itens_lucrativos.head(5) qtd_compras = itens_lucrativos.groupby(['Nome do Item']).count()['Valor'] avg_compras = itens_lucrativos.groupby(['Nome do Item']).mean()['Valor'] sum_compras = itens_lucrativos.groupby(['Nome do Item']).sum()['Valor'] df_itens_lucrativos = pd.DataFrame({ 'Número de Compras': qtd_compras, 'Preço Médio do Item (R$)': round(avg_compras, 2), 'Valor Total de Compra (R$)': sum_compras }) df_itens_lucrativos.sort_values(by='Valor Total de Compra (R$)', ascending=False).head(5) itens_lucrativos.sort_values('Nome do Item') itens_lucrativos.sort_values(by='Nome do Item') ```	github_jupyter
# Criminology in Portugal (2011) ## Introduction > In this _study case_, it will be analysed the _crimes occurred_ in _Portugal_, during the civil year of _2011_. It will analysed all the _categories_ or _natures_ of this _crimes_, _building some statistics and making some filtering of data related to them_. > It will be applied some _filtering_ and made some _analysis_ on the data related to _Portugal_ as _country_, like the following: * _Crimes by Nature/Category_ * _Crimes by Geographical Zone_ * _Crimes by Region/City (only considered th 5 more populated regions/cities in Portugal)_ * _Conclusions_ > It will be applied some _filtering_ and made some _analysis_ on the data related to the _5 biggest/more populated regions/cities_ (_Metropolitan Area of Lisbon_, _North_, _Center_, _Metropolitan Area of Porto_, and _Algarve_) of _Portugal_, like the following: * _Metropolitan Area of Lisbon_ * _Crimes by Nature/Category_ * _Crimes by Locality/Village_ * _Conclusions_ * _North_ * _Crimes by Nature/Category_ * _Crimes by Locality/Village_ * _Conclusions_ * _Center_ * _Crimes by Nature/Category_ * _Crimes by Locality/Village_ * _Conclusions_ * _Metropolitan Area of Porto_ * _Crimes by Nature/Category_ * _Crimes by Locality/Village_ * _Conclusions_ * _Algarve_ * _Crimes by Nature/Category_ * _Crimes by Locality/Village_ * _Conclusions_ ``` # Importing pandas library import pandas as pd import matplotlib.pyplot as plt %matplotlib inline crimes_by_geozone_2011 = pd.read_csv("datasets/ine.pt/2011/dataset-crimes-portugal-2011-by-geozone-2.csv" , header=1) crimes_by_geozone_2011 = crimes_by_geozone_2011.rename(columns={'Unnamed: 0': 'Zona Geográfica'}) crimes_by_geozone_2011 = crimes_by_geozone_2011.set_index("Zona Geográfica", drop = True) ``` #### Data Available in the Dataset > All the data available and used for this _study case_ can be found in the following _hyperlink_: * [dataset-crimes-portugal-2011-by-geozone-2.csv](datasets/ine.pt/2011/dataset-crimes-portugal-2011-by-geozone-2.csv) ##### Note: > If you pretend to see all the data available and used for this _study case_, uncomment the following line. ``` # Just for debug #crimes_by_geozone_2011 ``` ## Starting the Study Case ### Criminology in _Metropolitan Area of Lisbon_ (_2011_) #### Analysing the _crimes occurred_ in _Metropolitan Area of Lisbon_, during _2011_ * The total of _crime occurrences_ in _Metropolitan Area of Lisbon_, during _2011_, filtered by _category or nature of the crime_: ``` crimes_lisbon_2011 = crimes_by_geozone_2011.loc["170: Área Metropolitana de Lisboa", : ] crimes_lisbon_2011 ``` * The total number of _crime occurrences_ in _Metropolitan Area of Lisbon_, during _2011_, filtered by _category or nature of the crime_ (_organised as a Data Frame_): ``` crimes_lisbon_2011 = pd.DataFrame(crimes_lisbon_2011).T crimes_lisbon_2011 = crimes_lisbon_2011.iloc[:,1:8] crimes_lisbon_2011 # Just for debug #crimes_lisbon_2011.columns crimes_lisbon_2011.values[0,3] = 0 crimes_lisbon_2011.values[0,6] = 0 crimes_lisbon_2011.values[0,0] = int(crimes_lisbon_2011.values[0,0]) crimes_lisbon_2011.values[0,1] = int(float(crimes_lisbon_2011.values[0,1])) crimes_lisbon_2011.values[0,2] = int(crimes_lisbon_2011.values[0,2]) crimes_lisbon_2011.values[0,4] = int(float(crimes_lisbon_2011.values[0,4])) crimes_lisbon_2011.values[0,5] = int(float(crimes_lisbon_2011.values[0,5])) # Just for debug #crimes_lisbon_2011.values # Just for debug #crimes_lisbon_2011 ``` * The total number of _crime occurrences_ in _Metropolitan Area of Lisbon_, during _2011_, filtered by _category or nature of the crime_ (_organised as a Data Frame_ and excluding some _redundant fields and data_): ``` del crimes_lisbon_2011['Crimes contra a identidade cultural e integridade pessoal'] del crimes_lisbon_2011['Crimes contra animais de companhia'] crimes_lisbon_2011 crimes_lisbon_2011_categories = crimes_lisbon_2011.columns.tolist() # Just for debug #crimes_lisbon_2011_categories crimes_lisbon_2011_values = crimes_lisbon_2011.values[0].tolist() # Just for debug #crimes_lisbon_2011_values ``` * A _plot_ of a representation of the total of _crime occurrences_ in _Metropolitan Area of Lisbon_, during _2011_, filtered by _category or nature of the crime_ (_organised as a Data Frame_ and excluding some _redundant fields and data_): ``` plt.bar(crimes_lisbon_2011_categories, crimes_lisbon_2011_values) plt.xticks(crimes_lisbon_2011_categories, rotation='vertical') plt.xlabel('\nCrime Category/Nature\n') plt.ylabel('\nNum. Occurrences\n') plt.title('Crimes in Metropolitan Area of Lisbon, during 2011 (by Crime Category/Nature) - Bars Chart\n') print('\n') plt.show() plt.pie(crimes_lisbon_2011_values, labels=crimes_lisbon_2011_categories, autopct='%.2f%%') plt.title('Crimes in Metropolitan Area of Lisbon, during 2011 (by Crime Category/Nature) - Pie Chart\n\n') plt.axis('equal') print('\n') plt.show() ``` * The total number of _crime occurrences_ in all the _localities/villages_ of the _Metropolitan Area of Lisbon_, during _2011_, filtered by _category or nature of the crime_ (_organised as a Data Frame_): ``` crimes_lisbon_2011_by_locality = crimes_by_geozone_2011.loc["1701502: Alcochete":"1701114: Vila Franca de Xira", : ] crimes_lisbon_2011_by_locality ``` * The total number of _crime occurrences_ in all the _localities/villages_ of the _Metropolitan Area of Lisbon_, during _2011_, filtered by _category or nature of the crime_ (_organised as a Data Frame_ and excluding some _redundant fields and data_): ``` del crimes_lisbon_2011_by_locality['Crimes de homicídio voluntário consumado'] del crimes_lisbon_2011_by_locality['Crimes contra a identidade cultural e integridade pessoal'] del crimes_lisbon_2011_by_locality['Crimes contra animais de companhia'] crimes_lisbon_2011_by_locality top_6_crimes_lisbon_2011_by_locality = crimes_lisbon_2011_by_locality.sort_values(by='Total', ascending=False).head(6) top_6_crimes_lisbon_2011_by_locality top_6_crimes_lisbon_2011_by_locality_total = top_6_crimes_lisbon_2011_by_locality.loc[:,"Total"] top_6_crimes_lisbon_2011_by_locality_total top_6_crimes_lisbon_2011_by_locality_total = pd.DataFrame(top_6_crimes_lisbon_2011_by_locality_total).T top_6_crimes_lisbon_2011_by_locality_total = top_6_crimes_lisbon_2011_by_locality_total.iloc[:,0:6] top_6_crimes_lisbon_2011_by_locality_total top_6_crimes_lisbon_2011_by_locality_total_localities = top_6_crimes_lisbon_2011_by_locality_total.columns.tolist() # Just for debug #top_6_crimes_lisbon_2011_by_locality_total_localities top_6_crimes_lisbon_2011_by_locality_total_values = top_6_crimes_lisbon_2011_by_locality_total.values[0].tolist() # Just for debug #top_6_crimes_lisbon_2011_by_locality_total_values plt.bar(top_6_crimes_lisbon_2011_by_locality_total_localities, top_6_crimes_lisbon_2011_by_locality_total_values) plt.xticks(top_6_crimes_lisbon_2011_by_locality_total_localities, rotation='vertical') plt.xlabel('\nLocality/Village') plt.ylabel('\nNum. Occurrences\n') plt.title('Crimes in Metropolitan Area of Lisbon, during 2011 (by Locality/Village in Top 6) - Bars Chart\n') print('\n') plt.show() plt.pie(top_6_crimes_lisbon_2011_by_locality_total_values, labels=top_6_crimes_lisbon_2011_by_locality_total_localities, autopct='%.2f%%') plt.title('Crimes in Metropolitan Area of Lisbon, during 2011 (by Locality/Village in Top 6) - Pie Chart\n\n') plt.axis('equal') print('\n') plt.show() ``` #### Conclusion of the _crimes occurred_ in _Metropolitan Area of Lisbon_, during _2011_ * After studying all the perspectives about the _crimes occurred_ in _Metropolitan Area of Lisbon_, during _2011_, it's possible to conclude the following: * a) The most of the _crimes_ occurred was against: > 1) The _country's patrimony_ (68.52%) > 2) The _people_, at general (20.35%) > 3) The _life in society_ (9.32%) Thank you, and I hope you enjoy it! Sincerely, > Rúben André Barreiro.	github_jupyter
##### Copyright 2021 The Cirq Developers ``` #@title Licensed under the Apache License, Version 2.0 (the "License"); # you may not use this file except in compliance with the License. # You may obtain a copy of the License at # # https://www.apache.org/licenses/LICENSE-2.0 # # Unless required by applicable law or agreed to in writing, software # distributed under the License is distributed on an "AS IS" BASIS, # WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. # See the License for the specific language governing permissions and # limitations under the License. ``` <table class="tfo-notebook-buttons" align="left"> <td> <a target="_blank" href="https://quantumai.google/cirq/qcvv/xeb_theory>"><img src="https://quantumai.google/site-assets/images/buttons/quantumai_logo_1x.png" />View on QuantumAI</a> </td> <td> <a target="_blank" href="https://colab.research.google.com/github/quantumlib/Cirq/blob/master/docs/qcvv/xeb_theory.ipynb"><img src="https://quantumai.google/site-assets/images/buttons/colab_logo_1x.png" />Run in Google Colab</a> </td> <td> <a target="_blank" href="https://github.com/quantumlib/Cirq/blob/master/docs/qcvv/xeb_theory.ipynb"><img src="https://quantumai.google/site-assets/images/buttons/github_logo_1x.png" />View source on GitHub</a> </td> <td> <a href="https://storage.googleapis.com/tensorflow_docs/Cirq/docs/qcvv/xeb_theory.ipynb"><img src="https://quantumai.google/site-assets/images/buttons/download_icon_1x.png" />Download notebook</a> </td> </table> ``` try: import cirq except ImportError: print("installing cirq...") !pip install --quiet cirq print("installed cirq.") ``` # Cross Entropy Benchmarking Theory Cross entropy benchmarking uses the properties of random quantum programs to determine the fidelity of a wide variety of circuits. When applied to circuits with many qubits, XEB can characterize the performance of a large device. When applied to deep, two-qubit circuits it can be used to accurately characterize a two-qubit interaction potentially leading to better calibration. ``` # Standard imports import numpy as np import cirq from cirq.contrib.svg import SVGCircuit ``` ## The action of random circuits with noise An XEB experiment collects data from the execution of random circuits subject to noise. The effect of applying a random circuit with unitary $U$ is modeled as $U$ followed by a depolarizing channel. The result is that the initial state $\|𝜓⟩$ is mapped to a density matrix $ρ_U$ as follows: $$ \|𝜓⟩ → ρ_U = f \|𝜓_U⟩⟨𝜓_U\| + (1 - f) I / D $$ where $\|𝜓_U⟩ = U\|𝜓⟩$, $D$ is the dimension of the Hilbert space, $I / D$ is the maximally mixed state, and $f$ is the fidelity with which the circuit is applied. For this model to be accurate, we require $U$ to be a random circuit that scrambles errors. In practice, we use a particular circuit ansatz consisting of random single-qubit rotations interleaved with entangling gates. ### Possible single-qubit rotations These 88 possible rotations are chosen randomly when constructing the circuit. Geometrically, we choose 8 axes in the XY plane to perform a quarter-turn (pi/2 rotation) around. This is followed by a rotation around the Z axis of 8 different magnitudes. ``` exponents = np.linspace(0, 7/4, 8) exponents import itertools SINGLE_QUBIT_GATES = [ cirq.PhasedXZGate(x_exponent=0.5, z_exponent=z, axis_phase_exponent=a) for a, z in itertools.product(exponents, repeat=2) ] SINGLE_QUBIT_GATES[:10], '...' ``` ### Random circuit We use `random_rotations_between_two_qubit_circuit` to generate a random two-qubit circuit. Note that we provide the possible single-qubit rotations from above and declare that our two-qubit operation is the $\sqrt{i\mathrm{SWAP}}$ gate. ``` import cirq_google as cg from cirq.experiments import random_quantum_circuit_generation as rqcg q0, q1 = cirq.LineQubit.range(2) circuit = rqcg.random_rotations_between_two_qubit_circuit( q0, q1, depth=4, two_qubit_op_factory=lambda a, b, _: cirq.SQRT_ISWAP(a, b), single_qubit_gates=SINGLE_QUBIT_GATES ) SVGCircuit(circuit) ``` ## Estimating fidelity Let $O_U$ be an observable that is diagonal in the computational basis. Then the expectation value of $O_U$ on $ρ_U$ is given by $$ Tr(ρ_U O_U) = f ⟨𝜓_U\|O_U\|𝜓_U⟩ + (1 - f) Tr(O_U / D). $$ This equation shows how $f$ can be estimated, since $Tr(ρ_U O_U)$ can be estimated from experimental data, and $⟨𝜓_U\|O_U\|𝜓_U⟩$ and $Tr(O_U / D)$ can be computed. Let $e_U = ⟨𝜓_U\|O_U\|𝜓_U⟩$, $u_U = Tr(O_U / D)$, and $m_U$ denote the experimental estimate of $Tr(ρ_U O_U)$. We can write the following linear equation (equivalent to the expression above): $$ m_U = f e_U + (1-f) u_U \\ m_U - u_U = f (e_U - u_U) $$ ``` # Make long circuits (which we will truncate) MAX_DEPTH = 100 N_CIRCUITS = 10 circuits = [ rqcg.random_rotations_between_two_qubit_circuit( q0, q1, depth=MAX_DEPTH, two_qubit_op_factory=lambda a, b, _: cirq.SQRT_ISWAP(a, b), single_qubit_gates=SINGLE_QUBIT_GATES) for _ in range(N_CIRCUITS) ] # We will truncate to these lengths cycle_depths = np.arange(1, MAX_DEPTH + 1, 9) cycle_depths ``` ### Execute circuits Cross entropy benchmarking requires sampled bitstrings from the device being benchmarked as well as* the true probabilities from a noiseless simulation. We find these quantities for all `(cycle_depth, circuit)` permutations. ``` pure_sim = cirq.Simulator() # Pauli Error. If there is an error, it is either X, Y, or Z # with probability E_PAULI / 3 E_PAULI = 5e-3 noisy_sim = cirq.DensityMatrixSimulator(noise=cirq.depolarize(E_PAULI)) # These two qubit circuits have 2^2 = 4 probabilities DIM = 4 records = [] for cycle_depth in cycle_depths: for circuit_i, circuit in enumerate(circuits): # Truncate the long circuit to the requested cycle_depth circuit_depth = cycle_depth * 2 + 1 assert circuit_depth <= len(circuit) trunc_circuit = circuit[:circuit_depth] # Pure-state simulation psi = pure_sim.simulate(trunc_circuit) psi = psi.final_state_vector pure_probs = np.abs(psi)*2 # Noisy execution meas_circuit = trunc_circuit + cirq.measure(q0, q1) sampled_inds = noisy_sim.sample(meas_circuit, repetitions=10_000).values[:,0] sampled_probs = np.bincount(sampled_inds, minlength=DIM) / len(sampled_inds) # Save the results records += [{ 'circuit_i': circuit_i, 'cycle_depth': cycle_depth, 'circuit_depth': circuit_depth, 'pure_probs': pure_probs, 'sampled_probs': sampled_probs, }] print('.', end='', flush=True) ``` ## What's the observable What is $O_U$? Let's define it to be the observable that gives the sum of all probabilities, i.e. $$ O_U \|x \rangle = p(x) \|x \rangle $$ for any bitstring $x$. We can use this to derive expressions for our quantities of interest. $$ e_U = \langle \psi_U \| O_U \| \psi_U \rangle \\ = \sum_x a_x^ \langle x \| O_U \| x \rangle a_x \\ = \sum_x p(x) \langle x \| O_U \| x \rangle \\ = \sum_x p(x) p(x) $$ $e_U$ is simply the sum of squared ideal probabilities. $u_U$ is a normalizing factor that only depends on the operator. Since this operator has the true probabilities in the definition, they show up here anyways. $$ u_U = \mathrm{Tr}[O_U / D] \\ = 1/D \sum_x \langle x \| O_U \| x \rangle \\ = 1/D \sum_x p(x) $$ For the measured values, we use the definition of an expectation value $$ \langle f(x) \rangle_\rho = \sum_x p(x) f(x) $$ It becomes notationally confusing because remember: our operator on basis states returns the ideal probability of that basis state $p(x)$. The probability of observing a measured basis state is estimated from samples and denoted $p_\mathrm{est}(x)$ here. $$ m_U = \mathrm{Tr}[\rho_U O_U] \\ = \langle O_U \rangle_{\rho_U} = \sum_{x} p_\mathrm{est}(x) p(x) $$ ``` for record in records: e_u = np.sum(record['pure_probs']*2) u_u = np.sum(record['pure_probs']) / DIM m_u = np.sum(record['pure_probs'] record['sampled_probs']) record.update( e_u=e_u, u_u=u_u, m_u=m_u, ) ``` Remember: $$ m_U - u_U = f (e_U - u_U) $$ We estimate f by performing least squares minimization of the sum of squared residuals $$ \sum_U \left(f (e_U - u_U) - (m_U - u_U)\right)^2 $$ over different random circuits. The solution to the least squares problem is given by $$ f = (∑_U (m_U - u_U) * (e_U - u_U)) / (∑_U (e_U - u_U)^2) $$ ``` import pandas as pd df = pd.DataFrame(records) df['y'] = df['m_u'] - df['u_u'] df['x'] = df['e_u'] - df['u_u'] df['numerator'] = df['x'] * df['y'] df['denominator'] = df['x'] ** 2 df.head() ``` ### Fit We'll plot the linear relationship and least-squares fit while we transform the raw DataFrame into one containing fidelities. ``` %matplotlib inline from matplotlib import pyplot as plt # Color by cycle depth import seaborn as sns colors = sns.cubehelix_palette(n_colors=len(cycle_depths)) colors = {k: colors[i] for i, k in enumerate(cycle_depths)} _lines = [] def per_cycle_depth(df): fid_lsq = df['numerator'].sum() / df['denominator'].sum() cycle_depth = df.name xx = np.linspace(0, df['x'].max()) l, = plt.plot(xx, fid_lsqxx, color=colors[cycle_depth]) plt.scatter(df['x'], df['y'], color=colors[cycle_depth]) global _lines _lines += [l] # for legend return pd.Series({'fidelity': fid_lsq}) fids = df.groupby('cycle_depth').apply(per_cycle_depth).reset_index() plt.xlabel(r'$e_U - u_U$', fontsize=18) plt.ylabel(r'$m_U - u_U$', fontsize=18) _lines = np.asarray(_lines) plt.legend(_lines[[0,-1]], cycle_depths[[0,-1]], loc='best', title='Cycle depth') plt.tight_layout() ``` ### Fidelities ``` plt.plot( fids['cycle_depth'], fids['fidelity'], marker='o', label='Least Squares') xx = np.linspace(0, fids['cycle_depth'].max()) # In XEB, we extract the depolarizing fidelity, which is # related to (but not equal to) the Pauli error. # For the latter, an error involves doing X, Y, or Z with E_PAULI/3 # but for the former, an error involves doing I, X, Y, or Z with e_depol/4 e_depol = E_PAULI / (1 - 1/DIM2) # The additional factor of four in the exponent is because each layer # involves two moments of two qubits (so each layer has four applications # of a single-qubit single-moment depolarizing channel). plt.plot(xx, (1-e_depol)(4xx), label=r'$(1-\mathrm{e\_depol})^{4d}$') plt.ylabel('Circuit fidelity', fontsize=18) plt.xlabel('Cycle Depth $d$', fontsize=18) plt.legend(loc='best') plt.yscale('log') plt.tight_layout() from cirq.experiments.xeb_fitting import fit_exponential_decays # Ordinarily, we'd use this function to fit curves for multiple pairs. # We add our qubit pair as a column. fids['pair'] = [(q0, q1)] * len(fids) fit_df = fit_exponential_decays(fids) fit_row = fit_df.iloc[0] print(f"Noise model fidelity: {(1-e_depol)**4:.3e}") print(f"XEB layer fidelity: {fit_row['layer_fid']:.3e} +- {fit_row['layer_fid_std']:.2e}") ```	github_jupyter
<a href="https://colab.research.google.com/github/Shubham0Rajput/Feature-Detection-with-AKAZE/blob/master/AKAZE_code.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a> ``` #IMPORT FILES import matplotlib.pyplot as plt import cv2 #matplotlib inline #MOUNTIING DRIVE from google.colab import drive drive.mount('/content/drive') from __future__ import print_function import cv2 as cv import numpy as np import argparse from math import sqrt import matplotlib.pyplot as plt imge1 = cv.imread('/content/drive/My Drive/e2.jpg') img1 = cv.cvtColor(imge1, cv.COLOR_BGR2GRAY) # queryImage imge2 = cv.imread('/content/drive/My Drive/e1.jpg') img2 = cv.cvtColor(imge2, cv.COLOR_BGR2GRAY) # trainImage if img1 is None or img2 is None: print('Could not open or find the images!') exit(0) fs = cv.FileStorage('/content/drive/My Drive/H1to3p.xml', cv.FILE_STORAGE_READ) homography = fs.getFirstTopLevelNode().mat() ## [AKAZE] akaze = cv.AKAZE_create() kpts1, desc1 = akaze.detectAndCompute(img1, None) kpts2, desc2 = akaze.detectAndCompute(img2, None) ## [AKAZE] ## [2-nn matching] matcher = cv.DescriptorMatcher_create(cv.DescriptorMatcher_BRUTEFORCE_HAMMING) nn_matches = matcher.knnMatch(desc1, desc2, 2) ## [2-nn matching] ## [ratio test filtering] matched1 = [] matched2 = [] nn_match_ratio = 0.8 # Nearest neighbor matching ratio for m, n in nn_matches: if m.distance < nn_match_ratio * n.distance: matched1.append(kpts1[m.queryIdx]) matched2.append(kpts2[m.trainIdx]) ## [homography check] inliers1 = [] inliers2 = [] good_matches = [] inlier_threshold = 2.5 # Distance threshold to identify inliers with homography check for i, m in enumerate(matched1): col = np.ones((3,1), dtype=np.float64) col[0:2,0] = m.pt col = np.dot(homography, col) col /= col[2,0] dist = sqrt(pow(col[0,0] - matched2[i].pt[0], 2) +\ pow(col[1,0] - matched2[i].pt[1], 2)) if dist > inlier_threshold: good_matches.append(cv.DMatch(len(inliers1), len(inliers2), 0)) inliers1.append(matched1[i]) inliers2.append(matched2[i]) ## [homography check] ## [draw final matches] res = np.empty((max(img1.shape[0], img2.shape[0]), img1.shape[1]+img2.shape[1], 3), dtype=np.uint8) img0 = cv.drawMatches(img1, inliers1, img2, inliers2, good_matches, res) #img0 = cv.drawMatchesKnn(img1,inliers1,img2,inliers2,res,None,flags=cv.DrawMatchesFlags_NOT_DRAW_SINGLE_POINTS) cv.imwrite("akaze_result.png", res) inlier_ratio = len(inliers1) / float(len(matched1)) print('A-KAZE Matching Results') print('*******************************') print('# Keypoints 1: \t', len(kpts1)) print('# Keypoints 2: \t', len(kpts2)) print('# Matches: \t', len(matched1)) print('# Inliers: \t', len(inliers1)) print('# Inliers Ratio: \t', inlier_ratio) print('# Dist: \t', dist) plt.imshow(img0),plt.show() ## [draw final matches] ```	github_jupyter
# Entities Recognition <div class="alert alert-info"> This tutorial is available as an IPython notebook at [Malaya/example/entities](https://github.com/huseinzol05/Malaya/tree/master/example/entities). </div> <div class="alert alert-warning"> This module only trained on standard language structure, so it is not save to use it for local language structure. </div> ``` %%time import malaya ``` ### Models accuracy We use `sklearn.metrics.classification_report` for accuracy reporting, check at https://malaya.readthedocs.io/en/latest/models-accuracy.html#entities-recognition and https://malaya.readthedocs.io/en/latest/models-accuracy.html#entities-recognition-ontonotes5 ### Describe supported entities ``` import pandas as pd pd.set_option('display.max_colwidth', -1) malaya.entity.describe() ``` ### Describe supported Ontonotes 5 entities ``` malaya.entity.describe_ontonotes5() ``` ### List available Transformer NER models ``` malaya.entity.available_transformer() ``` ### List available Transformer NER Ontonotes 5 models ``` malaya.entity.available_transformer_ontonotes5() string = 'KUALA LUMPUR: Sempena sambutan Aidilfitri minggu depan, Perdana Menteri Tun Dr Mahathir Mohamad dan Menteri Pengangkutan Anthony Loke Siew Fook menitipkan pesanan khas kepada orang ramai yang mahu pulang ke kampung halaman masing-masing. Dalam video pendek terbitan Jabatan Keselamatan Jalan Raya (JKJR) itu, Dr Mahathir menasihati mereka supaya berhenti berehat dan tidur sebentar sekiranya mengantuk ketika memandu.' string1 = 'memperkenalkan Husein, dia sangat comel, berumur 25 tahun, bangsa melayu, agama islam, tinggal di cyberjaya malaysia, bercakap bahasa melayu, semua membaca buku undang-undang kewangan, dengar laju Siti Nurhaliza - Seluruh Cinta sambil makan ayam goreng KFC' ``` ### Load Transformer model ```python def transformer(model: str = 'xlnet', quantized: bool = False, *kwargs): """ Load Transformer Entity Tagging model trained on Malaya Entity, transfer learning Transformer + CRF. Parameters ---------- model : str, optional (default='bert') Model architecture supported. Allowed values: ``'bert'`` - Google BERT BASE parameters. * ``'tiny-bert'`` - Google BERT TINY parameters. * ``'albert'`` - Google ALBERT BASE parameters. * ``'tiny-albert'`` - Google ALBERT TINY parameters. * ``'xlnet'`` - Google XLNET BASE parameters. * ``'alxlnet'`` - Malaya ALXLNET BASE parameters. * ``'fastformer'`` - FastFormer BASE parameters. * ``'tiny-fastformer'`` - FastFormer TINY parameters. quantized : bool, optional (default=False) if True, will load 8-bit quantized model. Quantized model not necessary faster, totally depends on the machine. Returns ------- result: model List of model classes: * if `bert` in model, will return `malaya.model.bert.TaggingBERT`. * if `xlnet` in model, will return `malaya.model.xlnet.TaggingXLNET`. * if `fastformer` in model, will return `malaya.model.fastformer.TaggingFastFormer`. """ ``` ``` model = malaya.entity.transformer(model = 'alxlnet') ``` #### Load Quantized model To load 8-bit quantized model, simply pass `quantized = True`, default is `False`. We can expect slightly accuracy drop from quantized model, and not necessary faster than normal 32-bit float model, totally depends on machine. ``` quantized_model = malaya.entity.transformer(model = 'alxlnet', quantized = True) ``` #### Predict ```python def predict(self, string: str): """ Tag a string. Parameters ---------- string : str Returns ------- result: Tuple[str, str] """ ``` ``` model.predict(string) model.predict(string1) quantized_model.predict(string) quantized_model.predict(string1) ``` #### Group similar tags ```python def analyze(self, string: str): """ Analyze a string. Parameters ---------- string : str Returns ------- result: {'words': List[str], 'tags': [{'text': 'text', 'type': 'location', 'score': 1.0, 'beginOffset': 0, 'endOffset': 1}]} """ ``` ``` model.analyze(string) model.analyze(string1) ``` #### Vectorize Let say you want to visualize word level in lower dimension, you can use `model.vectorize`, ```python def vectorize(self, string: str): """ vectorize a string. Parameters ---------- string: List[str] Returns ------- result: np.array """ ``` ``` strings = [string, 'Husein baca buku Perlembagaan yang berharga 3k ringgit dekat kfc sungai petani minggu lepas, 2 ptg 2 oktober 2019 , suhu 32 celcius, sambil makan ayam goreng dan milo o ais', 'contact Husein at [email protected]', 'tolong tempahkan meja makan makan nasi dagang dan jus apple, milo tarik esok dekat Restoran Sebulek'] r = [quantized_model.vectorize(string) for string in strings] x, y = [], [] for row in r: x.extend([i[0] for i in row]) y.extend([i[1] for i in row]) from sklearn.manifold import TSNE import matplotlib.pyplot as plt tsne = TSNE().fit_transform(y) tsne.shape plt.figure(figsize = (7, 7)) plt.scatter(tsne[:, 0], tsne[:, 1]) labels = x for label, x, y in zip( labels, tsne[:, 0], tsne[:, 1] ): label = ( '%s, %.3f' % (label[0], label[1]) if isinstance(label, list) else label ) plt.annotate( label, xy = (x, y), xytext = (0, 0), textcoords = 'offset points', ) ``` Pretty good, the model able to know cluster similar entities. ### Load Transformer Ontonotes 5 model ```python def transformer_ontonotes5( model: str = 'xlnet', quantized: bool = False, *kwargs ): """ Load Transformer Entity Tagging model trained on Ontonotes 5 Bahasa, transfer learning Transformer + CRF. Parameters ---------- model : str, optional (default='bert') Model architecture supported. Allowed values: ``'bert'`` - Google BERT BASE parameters. * ``'tiny-bert'`` - Google BERT TINY parameters. * ``'albert'`` - Google ALBERT BASE parameters. * ``'tiny-albert'`` - Google ALBERT TINY parameters. * ``'xlnet'`` - Google XLNET BASE parameters. * ``'alxlnet'`` - Malaya ALXLNET BASE parameters. * ``'fastformer'`` - FastFormer BASE parameters. * ``'tiny-fastformer'`` - FastFormer TINY parameters. quantized : bool, optional (default=False) if True, will load 8-bit quantized model. Quantized model not necessary faster, totally depends on the machine. Returns ------- result: model List of model classes: * if `bert` in model, will return `malaya.model.bert.TaggingBERT`. * if `xlnet` in model, will return `malaya.model.xlnet.TaggingXLNET`. * if `fastformer` in model, will return `malaya.model.fastformer.TaggingFastFormer`. """ ``` ``` albert = malaya.entity.transformer_ontonotes5(model = 'albert') alxlnet = malaya.entity.transformer_ontonotes5(model = 'alxlnet') ``` #### Load Quantized model To load 8-bit quantized model, simply pass `quantized = True`, default is `False`. We can expect slightly accuracy drop from quantized model, and not necessary faster than normal 32-bit float model, totally depends on machine. ``` quantized_albert = malaya.entity.transformer_ontonotes5(model = 'albert', quantized = True) quantized_alxlnet = malaya.entity.transformer_ontonotes5(model = 'alxlnet', quantized = True) ``` #### Predict ```python def predict(self, string: str): """ Tag a string. Parameters ---------- string : str Returns ------- result: Tuple[str, str] """ ``` ``` albert.predict(string) alxlnet.predict(string) albert.predict(string1) alxlnet.predict(string1) quantized_albert.predict(string) quantized_alxlnet.predict(string1) ``` #### Group similar tags ```python def analyze(self, string: str): """ Analyze a string. Parameters ---------- string : str Returns ------- result: {'words': List[str], 'tags': [{'text': 'text', 'type': 'location', 'score': 1.0, 'beginOffset': 0, 'endOffset': 1}]} """ ``` ``` alxlnet.analyze(string1) ``` #### Vectorize Let say you want to visualize word level in lower dimension, you can use `model.vectorize`, ```python def vectorize(self, string: str): """ vectorize a string. Parameters ---------- string: List[str] Returns ------- result: np.array """ ``` ``` strings = [string, string1] r = [quantized_model.vectorize(string) for string in strings] x, y = [], [] for row in r: x.extend([i[0] for i in row]) y.extend([i[1] for i in row]) tsne = TSNE().fit_transform(y) tsne.shape plt.figure(figsize = (7, 7)) plt.scatter(tsne[:, 0], tsne[:, 1]) labels = x for label, x, y in zip( labels, tsne[:, 0], tsne[:, 1] ): label = ( '%s, %.3f' % (label[0], label[1]) if isinstance(label, list) else label ) plt.annotate( label, xy = (x, y), xytext = (0, 0), textcoords = 'offset points', ) ``` Pretty good, the model able to know cluster similar entities. ### Load general Malaya entity model This model able to classify, 1. date 2. money 3. temperature 4. distance 5. volume 6. duration 7. phone 8. email 9. url 10. time 11. datetime 12. local and generic foods, can check available rules in malaya.texts._food 13. local and generic drinks, can check available rules in malaya.texts._food We can insert BERT or any deep learning model by passing `malaya.entity.general_entity(model = model)`, as long the model has `predict` method and return `[(string, label), (string, label)]`. This is an optional. ``` entity = malaya.entity.general_entity(model = model) entity.predict('Husein baca buku Perlembagaan yang berharga 3k ringgit dekat kfc sungai petani minggu lepas, 2 ptg 2 oktober 2019 , suhu 32 celcius, sambil makan ayam goreng dan milo o ais') entity.predict('contact Husein at [email protected]') entity.predict('tolong tempahkan meja makan makan nasi dagang dan jus apple, milo tarik esok dekat Restoran Sebulek') ``` ### Voting stack model ``` malaya.stack.voting_stack([albert, alxlnet, alxlnet], string1) ```	github_jupyter
# Shallow regression for vector data This script reads zip code data produced by vectorDataPreparations and creates different machine learning models for predicting the average zip code income from population and spatial variables. It assesses the model accuracy with a test dataset but also predicts the number to all zip codes and writes it to a geopackage for closer inspection # 1. Read the data ``` import time import geopandas as gpd import pandas as pd from math import sqrt import os import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor, RandomForestRegressor, BaggingRegressor,ExtraTreesRegressor, AdaBoostRegressor from sklearn.model_selection import train_test_split from sklearn.metrics import mean_squared_error, mean_absolute_error,r2_score ``` ### 1.1 Input and output file paths ``` paavo_data = "../data/paavo" ### Relative path to the zip code geopackage file that was prepared by vectorDataPreparations.py input_geopackage_path = os.path.join(paavo_data,"zip_code_data_after_preparation.gpkg") ### Output file. You can change the name to identify different regression models output_geopackage_path = os.path.join(paavo_data,"median_income_per_zipcode_shallow_model.gpkg") ``` ### 1.2 Read the input data to a Geopandas dataframe ``` original_gdf = gpd.read_file(input_geopackage_path) original_gdf.head() ``` # 2. Train the model Here we try training different models. We encourage you to dive into the documentation of different models a bit and try different parameters. Which one is the best model? Can you figure out how to improve it even more? ### 2.1 Split the dataset to train and test datasets ``` ### Split the gdf to x (the predictor attributes) and y (the attribute to be predicted) y = original_gdf['hr_mtu'] # Average income ### Remove geometry and textual fields x = original_gdf.drop(['geometry','postinumer','nimi','hr_mtu'],axis=1) ### Split the both datasets to train (80%) and test (20%) datasets x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=.2, random_state=42) ``` ### 2.2 These are the functions used for training, estimating and predicting. ``` def trainModel(x_train, y_train, model): start_time = time.time() print(model) model.fit(x_train,y_train) print('Model training took: ', round((time.time() - start_time), 2), ' seconds') return model def estimateModel(x_test,y_test, model): ### Predict the unemployed number to the test dataset prediction = model.predict(x_test) ### Assess the accuracy of the model with root mean squared error, mean absolute error and coefficient of determination r2 rmse = sqrt(mean_squared_error(y_test, prediction)) mae = mean_absolute_error(y_test, prediction) r2 = r2_score(y_test, prediction) print(f"\nMODEL ACCURACY METRICS WITH TEST DATASET: \n" + f"\t Root mean squared error: {round(rmse)} \n" + f"\t Mean absolute error: {round(mae)} \n" + f"\t Coefficient of determination: {round(r2,4)} \n") ``` ### 2.3 Run different models ### Gradient Boosting Regressor * https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html * https://scikit-learn.org/stable/modules/ensemble.html#regression ``` model = GradientBoostingRegressor(n_estimators=30, learning_rate=0.1,verbose=1) model_name = "Gradient Boosting Regressor" trainModel(x_train, y_train,model) estimateModel(x_test,y_test, model) ``` ### Random Forest Regressor * https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestRegressor.html * https://scikit-learn.org/stable/modules/ensemble.html#forest ``` model = RandomForestRegressor(n_estimators=30,verbose=1) model_name = "Random Forest Regressor" trainModel(x_train, y_train,model) estimateModel(x_test,y_test, model) ``` ### Extra Trees Regressor * https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.ExtraTreesRegressor.html ``` model = ExtraTreesRegressor(n_estimators=30,verbose=1) model_name = "Extra Trees Regressor" trainModel(x_train, y_train,model) estimateModel(x_test,y_test, model) ``` ### Bagging Regressor * https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.BaggingRegressor.html * https://scikit-learn.org/stable/modules/ensemble.html#bagging ``` model = BaggingRegressor(n_estimators=30,verbose=1) model_name = "Bagging Regressor" trainModel(x_train, y_train,model) estimateModel(x_test,y_test, model) ``` ### AdaBoost Regressor * https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.AdaBoostRegressor.html * https://scikit-learn.org/stable/modules/ensemble.html#adaboost ``` model = AdaBoostRegressor(n_estimators=30) model_name = "AdaBoost Regressor" trainModel(x_train, y_train,model) estimateModel(x_test,y_test, model) ``` # 3. Predict average income to all zip codes Here we predict the average income to the whole dataset. Prediction is done with the model you have stored in the model variable - the one you ran last ``` ### Print chosen model (the one you ran last) print(model) ### Drop the not-used columns from original_gdf as done before model training. x = original_gdf.drop(['geometry','postinumer','nimi','hr_mtu'],axis=1) ### Predict the median income with already trained model prediction = model.predict(x) ### Join the predictions to the original geodataframe and pick only interesting columns for results original_gdf['predicted_hr_mtu'] = prediction.round(0) original_gdf['difference'] = original_gdf['predicted_hr_mtu'] - original_gdf['hr_mtu'] resulting_gdf = original_gdf[['postinumer','nimi','hr_mtu','predicted_hr_mtu','difference','geometry']] fig, ax = plt.subplots(figsize=(20, 10)) ax.set_title("Predicted average income by zip code " + model_name, fontsize=25) ax.set_axis_off() resulting_gdf.plot(column='predicted_hr_mtu', ax=ax, legend=True, cmap="magma") ``` # 4. EXERCISE: Calculate the difference between real and predicted incomes Calculate the difference of real and predicted income amounts by zip code level and plot a map of it * original_gdf is the original dataframe * resulting_gdf is the predicted one	github_jupyter
# RNN Sentiment Classifier In this notebook, we use an RNN to classify IMDB movie reviews by their sentiment. [![Open In Colab](https://colab.research.google.com/assets/colab-badge.svg)](https://colab.research.google.com/github/the-deep-learners/deep-learning-illustrated/blob/master/notebooks/rnn_sentiment_classifier.ipynb) #### Load dependencies ``` import keras from keras.datasets import imdb from keras.preprocessing.sequence import pad_sequences from keras.models import Sequential from keras.layers import Dense, Dropout, Embedding, SpatialDropout1D from keras.layers import SimpleRNN # new! from keras.callbacks import ModelCheckpoint import os from sklearn.metrics import roc_auc_score import matplotlib.pyplot as plt %matplotlib inline ``` #### Set hyperparameters ``` # output directory name: output_dir = 'model_output/rnn' # training: epochs = 16 # way more! batch_size = 128 # vector-space embedding: n_dim = 64 n_unique_words = 10000 max_review_length = 100 # lowered due to vanishing gradient over time pad_type = trunc_type = 'pre' drop_embed = 0.2 # RNN layer architecture: n_rnn = 256 drop_rnn = 0.2 # dense layer architecture: # n_dense = 256 # dropout = 0.2 ``` #### Load data ``` (x_train, y_train), (x_valid, y_valid) = imdb.load_data(num_words=n_unique_words) # removed n_words_to_skip ``` #### Preprocess data ``` x_train = pad_sequences(x_train, maxlen=max_review_length, padding=pad_type, truncating=trunc_type, value=0) x_valid = pad_sequences(x_valid, maxlen=max_review_length, padding=pad_type, truncating=trunc_type, value=0) ``` #### Design neural network architecture ``` model = Sequential() model.add(Embedding(n_unique_words, n_dim, input_length=max_review_length)) model.add(SpatialDropout1D(drop_embed)) model.add(SimpleRNN(n_rnn, dropout=drop_rnn)) # model.add(Dense(n_dense, activation='relu')) # typically don't see top dense layer in NLP like in # model.add(Dropout(dropout)) model.add(Dense(1, activation='sigmoid')) model.summary() ``` #### Configure model ``` model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy']) modelcheckpoint = ModelCheckpoint(filepath=output_dir+"/weights.{epoch:02d}.hdf5") if not os.path.exists(output_dir): os.makedirs(output_dir) ``` #### Train! ``` model.fit(x_train, y_train, batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(x_valid, y_valid), callbacks=[modelcheckpoint]) ``` #### Evaluate ``` model.load_weights(output_dir+"/weights.07.hdf5") y_hat = model.predict_proba(x_valid) plt.hist(y_hat) _ = plt.axvline(x=0.5, color='orange') "{:0.2f}".format(roc_auc_score(y_valid, y_hat)*100.0) ```	github_jupyter
# Intro to Jupyter Notebooks ### `Jupyter` is a project for developing open-source software ### `Jupyter Notebooks` is a `web` application to create scripts ### `Jupyter Lab` is the new generation of web user interface for Jypyter ### But it is more than that #### It lets you insert and save text, equations & visualizations ... in the same page! ![jupyternotebook_imageexample.png](attachment:jupyternotebook_imageexample.png) * # Notebook dashboard When you launch the Jupyter notebook server in your computer, you would see a dashboard like this: ![jupyter_dashboard.png](attachment:jupyter_dashboard.png) # Saving your own script All scripts we are showing here today are running online & we will make changes through the workshop. To keep your modified script for further reference, you will need to save a copy on your own computer at the end. <div class="alert alert-block alert-info"> <b>Try it out! </b> <br><br> Go to <b>File</b> in the top menu -> Download As -> Notebook </div> <br> Any changes made online, even if saved (not downloaded) will be lost once the binder connection is closed. * ## Two type of cells ### `Code` Cells: execute code ### `Markdown` Cells: show formated text There are two ways to change the type on a cell: - Cliking on the scroll-down menu on the top - using the shortcut `Esc-y` for code and `Esc-m` for markdown types <br> <div class="alert alert-block alert-info"><b>Try it out! </b> <bR> <br>- Click on the next cell <br>- Change the type using the scroll-down menu & select <b>Code</b> <br>- Change it back to <b>Markdown</b> </div> ## This is a simple operation y = 4 + 6 print(y) ## <i>Note the change in format of the first line & the text color in the second line</i> <div class="alert alert-block alert-info"><b>Try it out!</br> <br><br>In the next cell: <br>- Double-Click on the next cell <br>- Press <b> Esc</b> (note to blue color of the left border) <br>- Type <b>y</b> to change it to <b>Code</b> type <br>- Use <b>m</b> to change it back to <b>Markdown</b> type </div> ``` # This is a simple operation y = 4 + 6 print(y) ``` * # To execute commands ## - `Shift-Enter` : executes cell & advance to next ## - `Control-enter` : executes cell & stay in the same cell <div class="alert alert-block alert-info"><b>Try it out!</b> <br> <br>In the previous cell: <br>- Double-Click on the previous cell <br>- Use <b>Shift-Enter</b> to execute <br>- Double-Click on the in the previous cell again <br>- This time use <b>Control-Enter</b> to execute <br> <br>- Now change the type to <b>Code</b> & execute the cell </div> ## You could also execute the entire script use the `Run` tab in the top menu ## Or even the entire script from the `Cell` menu at the top * ## Other commands ### From the icon menu: ### Save, Add Cell, Cut Cell, Copy Cell, Paste Cell, Move Cell Up, Move Cell Down ![jupyter_iconmenu.png](attachment:jupyter_iconmenu.png) ### or the drop down menu 'command palette' <div class="alert alert-block alert-info"><b>Try them out!</b> ## Now, the keyboard shortcuts #### First press `Esc`, then: - `s` : save changes <br> - `a`, `b` : create cell above and below <br> - `dd` : delete cell <br> - `x`, `c`, `v` : cut, copy and paste cell <br> - `z` undo last change <div class="alert alert-block alert-info"> <b> Let's practice!</b> <br> <br>- Create a cell bellow with <b>Esc-b</b>, and click on it <br>- Type print('Hello world!') and execute it using <b>Control-Enter</b> <br>- Copy-paste the cell to make a duplicate by typing <b>Esc-c</b> & <b>Esc-v</b> <br>- Cut the first cell using <b>Esc-x</b> </div> ## And the last one: adding line numbers - `Esc-l` : in Jupyter Notebooks - `Esc-Shift-l`: in Jupyter Lab <div class="alert alert-block alert-info"> <b>Try it out!</b> <br><br> - Try it in a code cell <br>- And now try it in the markdown cell </div> ``` y = 5 print(y + 4) x = 8 print(yx) ``` ** ## Last note about the `Kernel` #### That little program that is running in the background & let you run your notebook <div class="alert alert-block alert-danger"> Once in a while the <b>kernel</b> will die or your program will get stucked, & like everything else in the computer world.... you'll have to restart it. </div> ### You can do this by going to the `Kernel` menu -> Restart, & then you'll have to run all your cells (or at least the ones above the one you're working on (use `Cell` menu -> Run all Above.	github_jupyter
# Introduction to geospatial vector data in Python ``` %matplotlib inline import pandas as pd import geopandas pd.options.display.max_rows = 10 ``` ## Importing geospatial data Geospatial data is often available from specific GIS file formats or data stores, like ESRI shapefiles, GeoJSON files, geopackage files, PostGIS (PostgreSQL) database, ... We can use the GeoPandas library to read many of those GIS file formats (relying on the `fiona` library under the hood, which is an interface to GDAL/OGR), using the `geopandas.read_file` function. For example, let's start by reading a shapefile with all the countries of the world (adapted from http://www.naturalearthdata.com/downloads/110m-cultural-vectors/110m-admin-0-countries/, zip file is available in the `/data` directory), and inspect the data: ``` countries = geopandas.read_file("zip://./data/ne_110m_admin_0_countries.zip") # or if the archive is unpacked: # countries = geopandas.read_file("data/ne_110m_admin_0_countries/ne_110m_admin_0_countries.shp") countries.head() countries.plot() ``` What can we observe: - Using `.head()` we can see the first rows of the dataset, just like we can do with Pandas. - There is a 'geometry' column and the different countries are represented as polygons - We can use the `.plot()` method to quickly get a basic visualization of the data ## What's a GeoDataFrame? We used the GeoPandas library to read in the geospatial data, and this returned us a `GeoDataFrame`: ``` type(countries) ``` A GeoDataFrame contains a tabular, geospatial dataset: * It has a 'geometry' column that holds the geometry information (or features in GeoJSON). * The other columns are the attributes (or properties in GeoJSON) that describe each of the geometries Such a `GeoDataFrame` is just like a pandas `DataFrame`, but with some additional functionality for working with geospatial data: * A `.geometry` attribute that always returns the column with the geometry information (returning a GeoSeries). The column name itself does not necessarily need to be 'geometry', but it will always be accessible as the `.geometry` attribute. * It has some extra methods for working with spatial data (area, distance, buffer, intersection, ...), which we will see in later notebooks ``` countries.geometry type(countries.geometry) countries.geometry.area ``` It's still a DataFrame, so we have all the pandas functionality available to use on the geospatial dataset, and to do data manipulations with the attributes and geometry information together. For example, we can calculate average population number over all countries (by accessing the 'pop_est' column, and calling the `mean` method on it): ``` countries['pop_est'].mean() ``` Or, we can use boolean filtering to select a subset of the dataframe based on a condition: ``` africa = countries[countries['continent'] == 'Africa'] africa.plot() ``` --- Exercise: create a plot of South America <!-- countries[countries['continent'] == 'South America'].plot() --> --- ``` countries.head() ``` --- The rest of the tutorial is going to assume you already know some pandas basics, but we will try to give hints for that part for those that are not familiar. A few resources in case you want to learn more about pandas: - Pandas docs: https://pandas.pydata.org/pandas-docs/stable/10min.html - Other tutorials: chapter from pandas in https://jakevdp.github.io/PythonDataScienceHandbook/, https://github.com/jorisvandenbossche/pandas-tutorial, https://github.com/TomAugspurger/pandas-head-to-tail, ... <div class="alert alert-info" style="font-size:120%"> <b>REMEMBER</b>: <br> <ul> <li>A `GeoDataFrame` allows to perform typical tabular data analysis together with spatial operations</li> <li>A `GeoDataFrame` (or Feature Collection) consists of: <ul> <li>Geometries or features: the spatial objects</li> <li>Attributes or properties: columns with information about each spatial object</li> </ul> </li> </ul> </div> ## Geometries: Points, Linestrings and Polygons Spatial vector data can consist of different types, and the 3 fundamental types are: * Point data: represents a single point in space. * Line data ("LineString"): represents a sequence of points that form a line. * Polygon data: represents a filled area. And each of them can also be combined in multi-part geometries (See https://shapely.readthedocs.io/en/stable/manual.html#geometric-objects for extensive overview). For the example we have seen up to now, the individual geometry objects are Polygons: ``` print(countries.geometry[2]) ``` Let's import some other datasets with different types of geometry objects. A dateset about cities in the world (adapted from http://www.naturalearthdata.com/downloads/110m-cultural-vectors/110m-populated-places/, zip file is available in the `/data` directory), consisting of Point data: ``` cities = geopandas.read_file("zip://./data/ne_110m_populated_places.zip") print(cities.geometry[0]) ``` And a dataset of rivers in the world (from http://www.naturalearthdata.com/downloads/50m-physical-vectors/50m-rivers-lake-centerlines/, zip file is available in the `/data` directory) where each river is a (multi-)line: ``` rivers = geopandas.read_file("zip://./data/ne_50m_rivers_lake_centerlines.zip") print(rivers.geometry[0]) ``` ### The `shapely` library The individual geometry objects are provided by the [`shapely`](https://shapely.readthedocs.io/en/stable/) library ``` type(countries.geometry[0]) ``` To construct one ourselves: ``` from shapely.geometry import Point, Polygon, LineString p = Point(1, 1) print(p) polygon = Polygon([(1, 1), (2,2), (2, 1)]) ``` <div class="alert alert-info" style="font-size:120%"> <b>REMEMBER</b>: <br><br> Single geometries are represented by `shapely` objects: <ul> <li>If you access a single geometry of a GeoDataFrame, you get a shapely geometry object</li> <li>Those objects have similar functionality as geopandas objects (GeoDataFrame/GeoSeries). For example: <ul> <li>`single_shapely_object.distance(other_point)` -> distance between two points</li> <li>`geodataframe.distance(other_point)` -> distance for each point in the geodataframe to the other point</li> </ul> </li> </ul> </div> ## Coordinate reference systems A coordinate reference system (CRS) determines how the two-dimensional (planar) coordinates of the geometry objects should be related to actual places on the (non-planar) earth. For a nice in-depth explanation, see https://docs.qgis.org/2.8/en/docs/gentle_gis_introduction/coordinate_reference_systems.html A GeoDataFrame or GeoSeries has a `.crs` attribute which holds (optionally) a description of the coordinate reference system of the geometries: ``` countries.crs ``` For the `countries` dataframe, it indicates that it used the EPSG 4326 / WGS84 lon/lat reference system, which is one of the most used. It uses coordinates as latitude and longitude in degrees, as can you be seen from the x/y labels on the plot: ``` countries.plot() ``` The `.crs` attribute is given as a dictionary. In this case, it only indicates the EPSG code, but it can also contain the full "proj4" string (in dictionary form). Under the hood, GeoPandas uses the `pyproj` / `proj4` libraries to deal with the re-projections. For more information, see also http://geopandas.readthedocs.io/en/latest/projections.html. --- There are sometimes good reasons you want to change the coordinate references system of your dataset, for example: - different sources with different crs -> need to convert to the same crs - distance-based operations -> if you a crs that has meter units (not degrees) - plotting in a certain crs (eg to preserve area) We can convert a GeoDataFrame to another reference system using the `to_crs` function. For example, let's convert the countries to the World Mercator projection (http://epsg.io/3395): ``` # remove Antartica, as the Mercator projection cannot deal with the poles countries = countries[(countries['name'] != "Antarctica")] countries_mercator = countries.to_crs(epsg=3395) # or .to_crs({'init': 'epsg:3395'}) countries_mercator.plot() ``` Note the different scale of x and y. --- Exercise: project the countries to [Web Mercator](http://epsg.io/3857), the CRS used by Google Maps, OpenStreetMap and most web providers. <!-- countries.to_crs(epsg=3857) --> --- ## Plotting our different layers together ``` ax = countries.plot(edgecolor='k', facecolor='none', figsize=(15, 10)) rivers.plot(ax=ax) cities.plot(ax=ax, color='red') ax.set(xlim=(-20, 60), ylim=(-40, 40)) ``` See the [04-more-on-visualization.ipynb](04-more-on-visualization.ipynb) notebook for more details on visualizing geospatial datasets. --- Exercise: replicate the figure above by coloring the countries in black and cities in yellow <!-- ax = countries.plot(edgecolor='w', facecolor='k', figsize=(15, 10)) rivers.plot(ax=ax) cities.plot(ax=ax, color='yellow') ax.set(xlim=(-20, 60), ylim=(-40, 40)) --> --- ## A bit more on importing and creating GeoDataFrames ### Note on `fiona` Under the hood, GeoPandas uses the [Fiona library](http://toblerity.org/fiona/) (pythonic interface to GDAL/OGR) to read and write data. GeoPandas provides a more user-friendly wrapper, which is sufficient for most use cases. But sometimes you want more control, and in that case, to read a file with fiona you can do the following: ``` import fiona from shapely.geometry import shape with fiona.drivers(): with fiona.open("data/ne_110m_admin_0_countries/ne_110m_admin_0_countries.shp") as collection: for feature in collection: # ... do something with geometry geom = shape(feature['geometry']) # ... do something with properties print(feature['properties']['name']) ``` ### Constructing a GeoDataFrame manually ``` geopandas.GeoDataFrame({ 'geometry': [Point(1, 1), Point(2, 2)], 'attribute1': [1, 2], 'attribute2': [0.1, 0.2]}) ``` ### Creating a GeoDataFrame from an existing dataframe For example, if you have lat/lon coordinates in two columns: ``` df = pd.DataFrame( {'City': ['Buenos Aires', 'Brasilia', 'Santiago', 'Bogota', 'Caracas'], 'Country': ['Argentina', 'Brazil', 'Chile', 'Colombia', 'Venezuela'], 'Latitude': [-34.58, -15.78, -33.45, 4.60, 10.48], 'Longitude': [-58.66, -47.91, -70.66, -74.08, -66.86]}) df['Coordinates'] = list(zip(df.Longitude, df.Latitude)) df['Coordinates'] = df['Coordinates'].apply(Point) gdf = geopandas.GeoDataFrame(df, geometry='Coordinates') gdf ``` See http://geopandas.readthedocs.io/en/latest/gallery/create_geopandas_from_pandas.html#sphx-glr-gallery-create-geopandas-from-pandas-py for full example --- Exercise: use [geojson.io](http://geojson.io) to mark five points, and create a `GeoDataFrame` with it. Note that coordinates will be expressed in longitude and latitude, so you'll have to set the CRS accordingly. <!-- df = pd.DataFrame( {'Name': ['Hotel', 'Capitol', 'Barton Springs'], 'Latitude': [30.28195889019179, 30.274782936992608, 30.263728440902543], 'Longitude': [-97.74006128311157, -97.74038314819336, -97.77013421058655]}) df['Coordinates'] = list(zip(df.Longitude, df.Latitude)) df['Coordinates'] = df['Coordinates'].apply(Point) gdf = geopandas.GeoDataFrame(df, geometry='Coordinates', crs={'init': 'epsg:4326'}) --> ---	github_jupyter
## Computer Vision Learner [`vision.learner`](/vision.learner.html#vision.learner) is the module that defines the [`cnn_learner`](/vision.learner.html#cnn_learner) method, to easily get a model suitable for transfer learning. ``` from fastai.gen_doc.nbdoc import * from fastai.vision import * ``` ## Transfer learning Transfer learning is a technique where you use a model trained on a very large dataset (usually [ImageNet](http://image-net.org/) in computer vision) and then adapt it to your own dataset. The idea is that it has learned to recognize many features on all of this data, and that you will benefit from this knowledge, especially if your dataset is small, compared to starting from a randomly initialized model. It has been proved in [this article](https://arxiv.org/abs/1805.08974) on a wide range of tasks that transfer learning nearly always give better results. In practice, you need to change the last part of your model to be adapted to your own number of classes. Most convolutional models end with a few linear layers (a part will call head). The last convolutional layer will have analyzed features in the image that went through the model, and the job of the head is to convert those in predictions for each of our classes. In transfer learning we will keep all the convolutional layers (called the body or the backbone of the model) with their weights pretrained on ImageNet but will define a new head initialized randomly. Then we will train the model we obtain in two phases: first we freeze the body weights and only train the head (to convert those analyzed features into predictions for our own data), then we unfreeze the layers of the backbone (gradually if necessary) and fine-tune the whole model (possibly using differential learning rates). The [`cnn_learner`](/vision.learner.html#cnn_learner) factory method helps you to automatically get a pretrained model from a given architecture with a custom head that is suitable for your data. ``` show_doc(cnn_learner) ``` This method creates a [`Learner`](/basic_train.html#Learner) object from the [`data`](/vision.data.html#vision.data) object and model inferred from it with the backbone given in `arch`. Specifically, it will cut the model defined by `arch` (randomly initialized if `pretrained` is False) at the last convolutional layer by default (or as defined in `cut`, see below) and add: - an [`AdaptiveConcatPool2d`](/layers.html#AdaptiveConcatPool2d) layer, - a [`Flatten`](/layers.html#Flatten) layer, - blocks of \[[`nn.BatchNorm1d`](https://pytorch.org/docs/stable/nn.html#torch.nn.BatchNorm1d), [`nn.Dropout`](https://pytorch.org/docs/stable/nn.html#torch.nn.Dropout), [`nn.Linear`](https://pytorch.org/docs/stable/nn.html#torch.nn.Linear), [`nn.ReLU`](https://pytorch.org/docs/stable/nn.html#torch.nn.ReLU)\] layers. The blocks are defined by the `lin_ftrs` and `ps` arguments. Specifically, the first block will have a number of inputs inferred from the backbone `arch` and the last one will have a number of outputs equal to `data.c` (which contains the number of classes of the data) and the intermediate blocks have a number of inputs/outputs determined by `lin_frts` (of course a block has a number of inputs equal to the number of outputs of the previous block). The default is to have an intermediate hidden size of 512 (which makes two blocks `model_activation` -> 512 -> `n_classes`). If you pass a float then the final dropout layer will have the value `ps`, and the remaining will be `ps/2`. If you pass a list then the values are used for dropout probabilities directly. Note that the very last block doesn't have a [`nn.ReLU`](https://pytorch.org/docs/stable/nn.html#torch.nn.ReLU) activation, to allow you to use any final activation you want (generally included in the loss function in pytorch). Also, the backbone will be frozen if you choose `pretrained=True` (so only the head will train if you call [`fit`](/basic_train.html#fit)) so that you can immediately start phase one of training as described above. Alternatively, you can define your own `custom_head` to put on top of the backbone. If you want to specify where to split `arch` you should so in the argument `cut` which can either be the index of a specific layer (the result will not include that layer) or a function that, when passed the model, will return the backbone you want. The final model obtained by stacking the backbone and the head (custom or defined as we saw) is then separated in groups for gradual unfreezing or differential learning rates. You can specify how to split the backbone in groups with the optional argument `split_on` (should be a function that returns those groups when given the backbone). The `kwargs` will be passed on to [`Learner`](/basic_train.html#Learner), so you can put here anything that [`Learner`](/basic_train.html#Learner) will accept ([`metrics`](/metrics.html#metrics), `loss_func`, `opt_func`...) ``` path = untar_data(URLs.MNIST_SAMPLE) data = ImageDataBunch.from_folder(path) learner = cnn_learner(data, models.resnet18, metrics=[accuracy]) learner.fit_one_cycle(1,1e-3) learner.save('one_epoch') show_doc(unet_learner) ``` This time the model will be a [`DynamicUnet`](/vision.models.unet.html#DynamicUnet) with an encoder based on `arch` (maybe `pretrained`) that is cut depending on `split_on`. `blur_final`, `norm_type`, `blur`, `self_attention`, `y_range`, `last_cross` and `bottle` are passed to unet constructor, the `kwargs` are passed to the initialization of the [`Learner`](/basic_train.html#Learner). ``` jekyll_warn("The models created with this function won't work with pytorch `nn.DataParallel`, you have to use distributed training instead!") ``` ### Get predictions Once you've actually trained your model, you may want to use it on a single image. This is done by using the following method. ``` show_doc(Learner.predict) img = learner.data.train_ds[0][0] learner.predict(img) ``` Here the predict class for our image is '3', which corresponds to a label of 0. The probabilities the model found for each class are 99.65% and 0.35% respectively, so its confidence is pretty high. Note that if you want to load your trained model and use it on inference mode with the previous function, you should export your [`Learner`](/basic_train.html#Learner). ``` learner.export() ``` And then you can load it with an empty data object that has the same internal state like this: ``` learn = load_learner(path) ``` ### Customize your model You can customize [`cnn_learner`](/vision.learner.html#cnn_learner) for your own model's default `cut` and `split_on` functions by adding them to the dictionary `model_meta`. The key should be your model and the value should be a dictionary with the keys `cut` and `split_on` (see the source code for examples). The constructor will call [`create_body`](/vision.learner.html#create_body) and [`create_head`](/vision.learner.html#create_head) for you based on `cut`; you can also call them yourself, which is particularly useful for testing. ``` show_doc(create_body) show_doc(create_head, doc_string=False) ``` Model head that takes `nf` features, runs through `lin_ftrs`, and ends with `nc` classes. `ps` is the probability of the dropouts, as documented above in [`cnn_learner`](/vision.learner.html#cnn_learner). ``` show_doc(ClassificationInterpretation, title_level=3) ``` This provides a confusion matrix and visualization of the most incorrect images. Pass in your [`data`](/vision.data.html#vision.data), calculated `preds`, actual `y`, and your `losses`, and then use the methods below to view the model interpretation results. For instance: ``` learn = cnn_learner(data, models.resnet18) learn.fit(1) preds,y,losses = learn.get_preds(with_loss=True) interp = ClassificationInterpretation(learn, preds, y, losses) ``` The following factory method gives a more convenient way to create an instance of this class: ``` show_doc(ClassificationInterpretation.from_learner, full_name='from_learner') ``` You can also use a shortcut `learn.interpret()` to do the same. ``` show_doc(Learner.interpret, full_name='interpret') ``` Note that this shortcut is a [`Learner`](/basic_train.html#Learner) object/class method that can be called as: `learn.interpret()`. ``` show_doc(ClassificationInterpretation.plot_top_losses, full_name='plot_top_losses') ``` The `k` items are arranged as a square, so it will look best if `k` is a square number (4, 9, 16, etc). The title of each image shows: prediction, actual, loss, probability of actual class. When `heatmap` is True (by default it's True) , Grad-CAM heatmaps (http://openaccess.thecvf.com/content_ICCV_2017/papers/Selvaraju_Grad-CAM_Visual_Explanations_ICCV_2017_paper.pdf) are overlaid on each image. `plot_top_losses` should be used with single-labeled datasets. See `plot_multi_top_losses` below for a version capable of handling multi-labeled datasets. ``` interp.plot_top_losses(9, figsize=(7,7)) show_doc(ClassificationInterpretation.top_losses) ``` Returns tuple of (losses,indices). ``` interp.top_losses(9) show_doc(ClassificationInterpretation.plot_multi_top_losses, full_name='plot_multi_top_losses') ``` Similar to `plot_top_losses()` but aimed at multi-labeled datasets. It plots misclassified samples sorted by their respective loss. Since you can have multiple labels for a single sample, they can easily overlap in a grid plot. So it plots just one sample per row. Note that you can pass `save_misclassified=True` (by default it's `False`). In such case, the method will return a list containing the misclassified images which you can use to debug your model and/or tune its hyperparameters. ``` show_doc(ClassificationInterpretation.plot_confusion_matrix) ``` If [`normalize`](/vision.data.html#normalize), plots the percentages with `norm_dec` digits. `slice_size` can be used to avoid out of memory error if your set is too big. `kwargs` are passed to `plt.figure`. ``` interp.plot_confusion_matrix() show_doc(ClassificationInterpretation.confusion_matrix) interp.confusion_matrix() show_doc(ClassificationInterpretation.most_confused) ``` #### Working with large datasets When working with large datasets, memory problems can arise when computing the confusion matrix. For example, an error can look like this: RuntimeError: $ Torch: not enough memory: you tried to allocate 64GB. Buy new RAM! In this case it is possible to force [`ClassificationInterpretation`](/train.html#ClassificationInterpretation) to compute the confusion matrix for data slices and then aggregate the result by specifying slice_size parameter. ``` interp.confusion_matrix(slice_size=10) interp.plot_confusion_matrix(slice_size=10) interp.most_confused(slice_size=10) ``` ## Undocumented Methods - Methods moved below this line will intentionally be hidden ## New Methods - Please document or move to the undocumented section	github_jupyter
# Trax : Ungraded Lecture Notebook In this notebook you'll get to know about the Trax framework and learn about some of its basic building blocks. ## Background ### Why Trax and not TensorFlow or PyTorch? TensorFlow and PyTorch are both extensive frameworks that can do almost anything in deep learning. They offer a lot of flexibility, but that often means verbosity of syntax and extra time to code. Trax is much more concise. It runs on a TensorFlow backend but allows you to train models with 1 line commands. Trax also runs end to end, allowing you to get data, model and train all with a single terse statements. This means you can focus on learning, instead of spending hours on the idiosyncrasies of big framework implementation. ### Why not Keras then? Keras is now part of Tensorflow itself from 2.0 onwards. Also, trax is good for implementing new state of the art algorithms like Transformers, Reformers, BERT because it is actively maintained by Google Brain Team for advanced deep learning tasks. It runs smoothly on CPUs,GPUs and TPUs as well with comparatively lesser modifications in code. ### How to Code in Trax Building models in Trax relies on 2 key concepts:- layers and combinators. Trax layers are simple objects that process data and perform computations. They can be chained together into composite layers using Trax combinators, allowing you to build layers and models of any complexity. ### Trax, JAX, TensorFlow and Tensor2Tensor You already know that Trax uses Tensorflow as a backend, but it also uses the JAX library to speed up computation too. You can view JAX as an enhanced and optimized version of numpy. Watch out for assignments which import `import trax.fastmath.numpy as np`. If you see this line, remember that when calling `np` you are really calling Trax’s version of numpy that is compatible with JAX. As a result of this, where you used to encounter the type `numpy.ndarray` now you will find the type `jax.interpreters.xla.DeviceArray`. Tensor2Tensor is another name you might have heard. It started as an end to end solution much like how Trax is designed, but it grew unwieldy and complicated. So you can view Trax as the new improved version that operates much faster and simpler. ### Resources - Trax source code can be found on Github: [Trax](https://github.com/google/trax) - JAX library: [JAX](https://jax.readthedocs.io/en/latest/index.html) ## Installing Trax Trax has dependencies on JAX and some libraries like JAX which are yet to be supported in [Windows](https://github.com/google/jax/blob/1bc5896ee4eab5d7bb4ec6f161d8b2abb30557be/README.md#installation) but work well in Ubuntu and MacOS. We would suggest that if you are working on Windows, try to install Trax on WSL2. Official maintained documentation - [trax-ml](https://trax-ml.readthedocs.io/en/latest/) not to be confused with this [TraX](https://trax.readthedocs.io/en/latest/index.html) ``` #!pip install trax==1.3.1 Use this version for this notebook ``` ## Imports ``` import numpy as np # regular ol' numpy from trax import layers as tl # core building block from trax import shapes # data signatures: dimensionality and type from trax import fastmath # uses jax, offers numpy on steroids # Trax version 1.3.1 or better !pip list \| grep trax ``` ## Layers Layers are the core building blocks in Trax or as mentioned in the lectures, they are the base classes. They take inputs, compute functions/custom calculations and return outputs. You can also inspect layer properties. Let me show you some examples. ### Relu Layer First I'll show you how to build a relu activation function as a layer. A layer like this is one of the simplest types. Notice there is no object initialization so it works just like a math function. Note: Activation functions are also layers in Trax, which might look odd if you have been using other frameworks for a longer time. ``` # Layers # Create a relu trax layer relu = tl.Relu() # Inspect properties print("-- Properties --") print("name :", relu.name) print("expected inputs :", relu.n_in) print("promised outputs :", relu.n_out, "\n") # Inputs x = np.array([-2, -1, 0, 1, 2]) print("-- Inputs --") print("x :", x, "\n") # Outputs y = relu(x) print("-- Outputs --") print("y :", y) ``` ### Concatenate Layer Now I'll show you how to build a layer that takes 2 inputs. Notice the change in the expected inputs property from 1 to 2. ``` # Create a concatenate trax layer concat = tl.Concatenate() print("-- Properties --") print("name :", concat.name) print("expected inputs :", concat.n_in) print("promised outputs :", concat.n_out, "\n") # Inputs x1 = np.array([-10, -20, -30]) x2 = x1 / -10 print("-- Inputs --") print("x1 :", x1) print("x2 :", x2, "\n") # Outputs y = concat([x1, x2]) print("-- Outputs --") print("y :", y) ``` ## Layers are Configurable You can change the default settings of layers. For example, you can change the expected inputs for a concatenate layer from 2 to 3 using the optional parameter `n_items`. ``` # Configure a concatenate layer concat_3 = tl.Concatenate(n_items=3) # configure the layer's expected inputs print("-- Properties --") print("name :", concat_3.name) print("expected inputs :", concat_3.n_in) print("promised outputs :", concat_3.n_out, "\n") # Inputs x1 = np.array([-10, -20, -30]) x2 = x1 / -10 x3 = x2 * 0.99 print("-- Inputs --") print("x1 :", x1) print("x2 :", x2) print("x3 :", x3, "\n") # Outputs y = concat_3([x1, x2, x3]) print("-- Outputs --") print("y :", y) ``` Note: At any point,if you want to refer the function help/ look up the [documentation](https://trax-ml.readthedocs.io/en/latest/) or use help function. ``` #help(tl.Concatenate) #Uncomment this to see the function docstring with explaination ``` ## Layers can have Weights Some layer types include mutable weights and biases that are used in computation and training. Layers of this type require initialization before use. For example the `LayerNorm` layer calculates normalized data, that is also scaled by weights and biases. During initialization you pass the data shape and data type of the inputs, so the layer can initialize compatible arrays of weights and biases. ``` # Uncomment any of them to see information regarding the function # help(tl.LayerNorm) # help(shapes.signature) # Layer initialization norm = tl.LayerNorm() # You first must know what the input data will look like x = np.array([0, 1, 2, 3], dtype="float") # Use the input data signature to get shape and type for initializing weights and biases norm.init(shapes.signature(x)) # We need to convert the input datatype from usual tuple to trax ShapeDtype print("Normal shape:",x.shape, "Data Type:",type(x.shape)) print("Shapes Trax:",shapes.signature(x),"Data Type:",type(shapes.signature(x))) # Inspect properties print("-- Properties --") print("name :", norm.name) print("expected inputs :", norm.n_in) print("promised outputs :", norm.n_out) # Weights and biases print("weights :", norm.weights[0]) print("biases :", norm.weights[1], "\n") # Inputs print("-- Inputs --") print("x :", x) # Outputs y = norm(x) print("-- Outputs --") print("y :", y) ``` ## Custom Layers This is where things start getting more interesting! You can create your own custom layers too and define custom functions for computations by using `tl.Fn`. Let me show you how. ``` help(tl.Fn) # Define a custom layer # In this example you will create a layer to calculate the input times 2 def TimesTwo(): layer_name = "TimesTwo" #don't forget to give your custom layer a name to identify # Custom function for the custom layer def func(x): return x * 2 return tl.Fn(layer_name, func) # Test it times_two = TimesTwo() # Inspect properties print("-- Properties --") print("name :", times_two.name) print("expected inputs :", times_two.n_in) print("promised outputs :", times_two.n_out, "\n") # Inputs x = np.array([1, 2, 3]) print("-- Inputs --") print("x :", x, "\n") # Outputs y = times_two(x) print("-- Outputs --") print("y :", y) ``` ## Combinators You can combine layers to build more complex layers. Trax provides a set of objects named combinator layers to make this happen. Combinators are themselves layers, so behavior commutes. ### Serial Combinator This is the most common and easiest to use. For example could build a simple neural network by combining layers into a single layer using the `Serial` combinator. This new layer then acts just like a single layer, so you can inspect intputs, outputs and weights. Or even combine it into another layer! Combinators can then be used as trainable models. _Try adding more layers_ Note:As you must have guessed, if there is serial combinator, there must be a parallel combinator as well. Do try to explore about combinators and other layers from the trax documentation and look at the repo to understand how these layers are written. ``` # help(tl.Serial) # help(tl.Parallel) # Serial combinator serial = tl.Serial( tl.LayerNorm(), # normalize input tl.Relu(), # convert negative values to zero times_two, # the custom layer you created above, multiplies the input recieved from above by 2 ### START CODE HERE # tl.Dense(n_units=2), # try adding more layers. eg uncomment these lines # tl.Dense(n_units=1), # Binary classification, maybe? uncomment at your own peril # tl.LogSoftmax() # Yes, LogSoftmax is also a layer ### END CODE HERE ) # Initialization x = np.array([-2, -1, 0, 1, 2]) #input serial.init(shapes.signature(x)) #initialising serial instance print("-- Serial Model --") print(serial,"\n") print("-- Properties --") print("name :", serial.name) print("sublayers :", serial.sublayers) print("expected inputs :", serial.n_in) print("promised outputs :", serial.n_out) print("weights & biases:", serial.weights, "\n") # Inputs print("-- Inputs --") print("x :", x, "\n") # Outputs y = serial(x) print("-- Outputs --") print("y :", y) ``` ## JAX Just remember to lookout for which numpy you are using, the regular ol' numpy or Trax's JAX compatible numpy. Both tend to use the alias np so watch those import blocks. Note:There are certain things which are still not possible in fastmath.numpy which can be done in numpy so you will see in assignments we will switch between them to get our work done. ``` # Numpy vs fastmath.numpy have different data types # Regular ol' numpy x_numpy = np.array([1, 2, 3]) print("good old numpy : ", type(x_numpy), "\n") # Fastmath and jax numpy x_jax = fastmath.numpy.array([1, 2, 3]) print("jax trax numpy : ", type(x_jax)) ``` ## Summary Trax is a concise framework, built on TensorFlow, for end to end machine learning. The key building blocks are layers and combinators. This notebook is just a taste, but sets you up with some key inuitions to take forward into the rest of the course and assignments where you will build end to end models.	github_jupyter
<h1>Data Exploration</h1> <p>In this notebook we will perform a broad data exploration on the <code>Hitters</code> data set. Note that the aim of this exploration is not to be completely thorough; instead we would like to gain quick insights to help develop a first prototype. Upon analyzing the output of the prototype, we can analyze the data further to gain more insight.</p> ``` import pandas as pd import numpy as np import matplotlib.pyplot as plt %run ../../customModules/DataQualityReports.ipynb # https://stackoverflow.com/questions/34398054/ipython-notebook-cell-multiple-outputs from IPython.core.interactiveshell import InteractiveShell InteractiveShell.ast_node_interactivity = "all" ``` <p>We first read the comma-separated values (csv) <code>Hitters</code> file into a pandas DataFrame. To get a feeling for the data we display the top five rows of the DataFrame using the <code>head()</code> method and we show how many rows and columns the DataFrame has by using the <code>shape</code> attribute. We also show the <code>dtypes</code> attribute, which returns a pandas Series with the data type of each column.</p> ``` df = pd.read_csv("Hitters.csv", index_col = 0) df.head() df.shape df.dtypes ``` <p>Is appears that all the columns have the data type we would expect. We can perform another check to see if any values are missing in the DataFrame using its <code>isnull</code> method.</p> ``` df.reset_index()[df.reset_index().isnull().any(axis=1)] df[df.isnull().any(axis=1)].shape ``` <p>This shows that there are $59$ missing values in total that seem pretty randomly distributed accross the $322$ total rows. So the next step to be able to produce the data quality reports with our custom <code>createDataQualityReports</code> function is to organize our DataFrame by quantitative and categorical variables using hierarchical indexing.</p> ``` df.columns = pd.MultiIndex.from_tuples([('quantitative', 'AtBat'), ('quantitative', 'Hits'), ('quantitative', 'HmRun'), ('quantitative', 'Runs'), ('quantitative', 'RBI'), ('quantitative', 'Walks'), ('quantitative', 'Years'), ('quantitative', 'CAtBat'), ('quantitative', 'CHits'), ('quantitative', 'CHmRun'), ('quantitative', 'CRuns'), ('quantitative', 'CRBI'), ('quantitative', 'CWalks'), ('categorical', 'League'), ('categorical', 'Division'), ('quantitative', 'PutOuts'), ('quantitative', 'Assists'), ('quantitative', 'Errors'), ('quantitative', 'Salary'), ('categorical', 'NewLeague')], names=['type of variable', 'variable']) df.sort_index(axis=1, level='type of variable', inplace=True) df.head() ``` <p>We are now in the position to use our own <code>createDataQualityReports</code> function to create a data quality report for both the categorical and the quantitative variables.</p> ``` df_qr_quantitative, df_qr_categorical = createDataQualityReports(df) df_qr_quantitative.name + ':' df_qr_quantitative.round(2) df_qr_categorical.name + ':' df_qr_categorical.round(2) ``` <p>To further gain insight into the data, we use the <code>plotQuantitativeVariables</code> and <code>plotCategoricalVariables</code> functions the produce the frequency plots for each quantitative and categorical variable.</p> ``` plotQuantitativeVariables(df.xs('quantitative', axis=1), height=3, width=7) plotCategoricalVariables(df.xs('categorical', axis=1), height=3, width=7) ``` <p>We also compute the correlation matrix of the variables.</p> ``` corr = df.corr() corr.style.background_gradient(cmap='coolwarm').set_precision(2) ```	github_jupyter
<a href="https://colab.research.google.com/github/choderalab/pinot/blob/master/scripts/adlala_mol_graph.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a> # import ``` ! rm -rf pinot ! git clone https://github.com/choderalab/pinot.git ! pip install dgl ! wget -c https://repo.continuum.io/miniconda/Miniconda3-latest-Linux-x86_64.sh ! chmod +x Miniconda3-latest-Linux-x86_64.sh ! time bash ./Miniconda3-latest-Linux-x86_64.sh -b -f -p /usr/local ! time conda install -q -y -c conda-forge rdkit import sys sys.path.append('/usr/local/lib/python3.7/site-packages/') sys.path.append('/content/pinot/') ``` # data ``` import pinot dir(pinot) ds = pinot.data.esol() ds = pinot.data.utils.batch(ds, 32) ds_tr, ds_te = pinot.data.utils.split(ds, [4, 1]) ``` # network ``` net = pinot.representation.Sequential( lambda in_feat, out_feat: pinot.representation.dgl_legacy.GN(in_feat, out_feat, 'SAGEConv'), [32, 'tanh', 32, 'tanh', 32, 'tanh', 1]) ``` # Adam ``` import torch import numpy as np opt = torch.optim.Adam(net.parameters(), 1e-3) loss_fn = torch.nn.functional.mse_loss rmse_tr = [] rmse_te = [] for _ in range(100): for g, y in ds_tr: opt.zero_grad() y_hat = net(g) loss = loss_fn(y, y_hat) loss.backward() opt.step() rmse_tr.append(np.mean([np.sqrt(loss_fn(y, net(g)).detach().numpy()) for g, y in ds_tr])) rmse_te.append(np.mean([np.sqrt(loss_fn(y, net(g)).detach().numpy()) for g, y in ds_te])) import matplotlib from matplotlib import pyplot as plt plt.rc('font', size=16) plt.plot(rmse_tr, label='training $RMSE$', linewidth=5, alpha=0.8) plt.plot(rmse_te, label='test $RMSE$', linewidth=5, alpha=0.8) plt.xlabel('epochs') plt.ylabel('$RMSE (\log (\mathtt{mol/L}))$') plt.legend() ``` # Langevin ``` net = pinot.representation.Sequential( lambda in_feat, out_feat: pinot.representation.dgl_legacy.GN(in_feat, out_feat, 'SAGEConv'), [32, 'tanh', 32, 'tanh', 32, 'tanh', 1]) opt = pinot.inference.adlala.AdLaLa(net.parameters(), partition='La', h=1e-3) rmse_tr = [] rmse_te = [] for _ in range(100): for g, y in ds_tr: def l(): opt.zero_grad() y_hat = net(g) loss = loss_fn(y, y_hat) loss.backward() print(loss) return loss opt.step(l) rmse_tr.append(np.mean([np.sqrt(loss_fn(y, net(g)).detach().numpy()) for g, y in ds_tr])) rmse_te.append(np.mean([np.sqrt(loss_fn(y, net(g)).detach().numpy()) for g, y in ds_te])) import matplotlib from matplotlib import pyplot as plt plt.rc('font', size=16) plt.plot(rmse_tr, label='training $RMSE$', linewidth=5, alpha=0.8) plt.plot(rmse_te, label='test $RMSE$', linewidth=5, alpha=0.8) plt.xlabel('epochs') plt.ylabel('$RMSE (\log (\mathtt{mol/L}))$') plt.legend() ``` # Adaptive Langevin ``` net = pinot.representation.Sequential( lambda in_feat, out_feat: pinot.representation.dgl_legacy.GN(in_feat, out_feat, 'SAGEConv'), [32, 'tanh', 32, 'tanh', 32, 'tanh', 1]) opt = pinot.inference.adlala.AdLaLa(net.parameters(), partition='AdLa', h=1e-3) rmse_tr = [] rmse_te = [] for _ in range(100): for g, y in ds_tr: def l(): opt.zero_grad() y_hat = net(g) loss = loss_fn(y, y_hat) loss.backward() print(loss) return loss opt.step(l) rmse_tr.append(np.mean([np.sqrt(loss_fn(y, net(g)).detach().numpy()) for g, y in ds_tr])) rmse_te.append(np.mean([np.sqrt(loss_fn(y, net(g)).detach().numpy()) for g, y in ds_te])) import matplotlib from matplotlib import pyplot as plt plt.rc('font', size=16) plt.plot(rmse_tr, label='training $RMSE$', linewidth=5, alpha=0.8) plt.plot(rmse_te, label='test $RMSE$', linewidth=5, alpha=0.8) plt.xlabel('epochs') plt.ylabel('$RMSE (\log (\mathtt{mol/L}))$') plt.legend() ``` # AdLaLa: AdLa for GN, La for last layer ``` net = pinot.representation.Sequential( lambda in_feat, out_feat: pinot.representation.dgl_legacy.GN(in_feat, out_feat, 'SAGEConv'), [32, 'tanh', 32, 'tanh', 32, 'tanh', 1]) net opt = pinot.inference.adlala.AdLaLa( [ {'params': list(net.f_in.parameters())\ + list(net.d0.parameters())\ + list(net.d2.parameters())\ + list(net.d4.parameters()), 'partition': 'AdLa', 'h': torch.tensor(1e-3)}, { 'params': list(net.d6.parameters()) + list(net.f_out.parameters()), 'partition': 'La', 'h': torch.tensor(1e-3) } ]) rmse_tr = [] rmse_te = [] for _ in range(100): for g, y in ds_tr: def l(): opt.zero_grad() y_hat = net(g) loss = loss_fn(y, y_hat) loss.backward() print(loss) return loss opt.step(l) rmse_tr.append(np.mean([np.sqrt(loss_fn(y, net(g)).detach().numpy()) for g, y in ds_tr])) rmse_te.append(np.mean([np.sqrt(loss_fn(y, net(g)).detach().numpy()) for g, y in ds_te])) import matplotlib from matplotlib import pyplot as plt plt.rc('font', size=16) plt.plot(rmse_tr, label='training $RMSE$', linewidth=5, alpha=0.8) plt.plot(rmse_te, label='test $RMSE$', linewidth=5, alpha=0.8) plt.xlabel('epochs') plt.ylabel('$RMSE (\log (\mathtt{mol/L}))$') plt.legend() ```	github_jupyter
# Data Loading Tutorial ``` cd ../.. save_path = 'data/' from scvi.dataset import LoomDataset, CsvDataset, Dataset10X, AnnDataset import urllib.request import os from scvi.dataset import BrainLargeDataset, CortexDataset, PbmcDataset, RetinaDataset, HematoDataset, CbmcDataset, BrainSmallDataset, SmfishDataset ``` ## Generic Datasets `scvi v0.1.3` supports dataset loading for the following three generic file formats: * `.loom` files * `.csv` files * `.h5ad` files * datasets from `10x` website Most of the dataset loading instances implemented in scvi use a positional argument `filename` and an optional argument `save_path` (value by default: `data/`). Files will be downloaded or searched for at the location `os.path.join(save_path, filename)`, make sure this path is valid when you specify the arguments. ### Loading a `.loom` file Any `.loom` file can be loaded with initializing `LoomDataset` with `filename`. Optional parameters: * `save_path`: save path (default to be `data/`) of the file * `url`: url the dataset if the file needs to be downloaded from the web * `new_n_genes`: the number of subsampling genes - set it to be `False` to turn off subsampling * `subset_genes`: a list of gene names for subsampling ``` # Loading a remote dataset remote_loom_dataset = LoomDataset("osmFISH_SScortex_mouse_all_cell.loom", save_path=save_path, url='http://linnarssonlab.org/osmFISH/osmFISH_SScortex_mouse_all_cells.loom') # Loading a local dataset local_loom_dataset = LoomDataset("osmFISH_SScortex_mouse_all_cell.loom", save_path=save_path) ``` ### Loading a `.csv` file Any `.csv` file can be loaded with initializing `CsvDataset` with `filename`. Optional parameters: * `save_path`: save path (default to be `data/`) of the file * `url`: url of the dataset if the file needs to be downloaded from the web * `compression`: set `compression` as `.gz`, `.bz2`, `.zip`, or `.xz` to load a zipped `csv` file * `new_n_genes`: the number of subsampling genes - set it to be `False` to turn off subsampling * `subset_genes`: a list of gene names for subsampling Note: `CsvDataset` currently only supoorts `.csv` files that are genes by cells. If the dataset has already been downloaded at the location `save_path`, it will not be downloaded again. ``` # Loading a remote dataset remote_csv_dataset = CsvDataset("GSE100866_CBMC_8K_13AB_10X-RNA_umi.csv.gz", save_path=save_path, compression='gzip', url = "https://www.ncbi.nlm.nih.gov/geo/download/?acc=GSE100866&format=file&file=GSE100866%5FCBMC%5F8K%5F13AB%5F10X%2DRNA%5Fumi%2Ecsv%2Egz") # Loading a local dataset local_csv_dataset = CsvDataset("GSE100866_CBMC_8K_13AB_10X-RNA_umi.csv.gz", save_path=save_path, compression='gzip') ``` ### Loading a `.h5ad` file [AnnData](http://anndata.readthedocs.io/en/latest/) objects can be stored in `.h5ad` format. Any `.h5ad` file can be loaded with initializing `AnnDataset` with `filename`. Optional parameters: * `save_path`: save path (default to be `data/`) of the file * `url`: url the dataset if the file needs to be downloaded from the web * `new_n_genes`: the number of subsampling genes - set it to be `False` to turn off subsampling * `subset_genes`: a list of gene names for subsampling ``` # Loading a local dataset local_ann_dataset = AnnDataset("TM_droplet_mat.h5ad", save_path = save_path) ``` ### Loading a file from `10x` website If the dataset has already been downloaded at the location `save_path`, it will not be downloaded again. `10x` has published several datasets on their [website](https://www.10xgenomics.com). Initialize `Dataset10X` by passing in the dataset name of one of the following datasets that `scvi` currently supports: `frozen_pbmc_donor_a`, `frozen_pbmc_donor_b`, `frozen_pbmc_donor_c`, `pbmc8k`, `pbmc4k`, `t_3k`, `t_4k`, and `neuron_9k`. Optional parameters: * `save_path`: save path (default to be `data/`) of the file * `type`: set `type` (default to be `filtered`) to be `filtered` or `raw` to choose one from the two datasets that's available on `10X` * `new_n_genes`: the number of subsampling genes - set it to be `False` to turn off subsampling ``` tenX_dataset = Dataset10X("neuron_9k", save_path=save_path) ``` ### Loading local `10x` data It is also possible to create a Dataset object from 10X data saved locally. Initialize Dataset10X by passing in the optional remote argument as False to specify you're loading local data and give the name of the directory that contains the gene expression matrix and gene names of the data as well as the path to this directory. If your data (the genes.tsv and matrix.mtx files) is located inside the directory 'mm10' which is located at 'data/10X/neuron_9k/filtered_gene_bc_matrices/'. Then filename should have the value 'mm10' and save_path should be the path to the directory containing 'mm10'. ``` local_10X_dataset = Dataset10X('mm10', save_path=os.path.join(save_path, '10X/neuron_9k/filtered_gene_bc_matrices/'), remote=False) ``` ## Built-In Datasets We've also implemented seven built-in datasets to make it easier to reproduce results from the scVI paper. * PBMC: 12,039 human peripheral blood mononuclear cells profiled with 10x; * RETINA: 27,499 mouse retinal bipolar neurons, profiled in two batches using the Drop-Seq technology; * HEMATO: 4,016 cells from two batches that were profiled using in-drop; * CBMC: 8,617 cord blood mononuclear cells profiled using 10x along with, for each cell, 13 well-characterized mononuclear antibodies; * BRAIN SMALL: 9,128 mouse brain cells profiled using 10x. * BRAIN LARGE: 1.3 million mouse brain cells profiled using 10x; * CORTEX: 3,005 mouse Cortex cells profiled using the Smart-seq2 protocol, with the addition of UMI * SMFISH: 4,462 mouse Cortex cells profiled using the osmFISH protocol * DROPSEQ: 71,639 mouse Cortex cells profiled using the Drop-Seq technology * STARMAP: 3,722 mouse Cortex cells profiled using the STARmap technology ### Loading `STARMAP` dataset `StarmapDataset` consists of 3722 cells profiled in 3 batches. The cells come with spatial coordinates of their location inside the tissue from which they were extracted and cell type labels retrieved by the authors ofthe original publication. Reference: X.Wang et al., Science10.1126/science.aat5691 (2018) ### Loading `DROPSEQ` dataset `DropseqDataset` consists of 71,639 mouse Cortex cells profiled using the Drop-Seq technology. To facilitate comparison with other methods we use a random filtered set of 15000 cells and then keep only a filtered set of 6000 highly variable genes. Cells have cell type annotaions and even sub-cell type annotations inferred by the authors of the original publication. Reference: https://www.biorxiv.org/content/biorxiv/early/2018/04/10/299081.full.pdf ### Loading `SMFISH` dataset `SmfishDataset` consists of 4,462 mouse cortex cells profiled using the OsmFISH protocol. The cells come with spatial coordinates of their location inside the tissue from which they were extracted and cell type labels retrieved by the authors of the original publication. Reference: Simone Codeluppi, Lars E Borm, Amit Zeisel, Gioele La Manno, Josina A van Lunteren, Camilla I Svensson, and Sten Linnarsson. Spatial organization of the somatosensory cortex revealed by cyclic smFISH. bioRxiv, 2018. ``` smfish_dataset = SmfishDataset(save_path=save_path) ``` ### Loading `BRAIN-LARGE` dataset <font color='red'>Loading BRAIN-LARGE requires at least 32 GB memory!</font> `BrainLargeDataset` consists of 1.3 million mouse brain cells, spanning the cortex, hippocampus and subventricular zone, and profiled with 10x chromium. We use this dataset to demonstrate the scalability of scVI. It can be used to demonstrate the scalability of scVI. Reference: 10x genomics (2017). URL https://support.10xgenomics.com/single-cell-gene-expression/datasets. ``` brain_large_dataset = BrainLargeDataset(save_path=save_path) ``` ### Loading `CORTEX` dataset `CortexDataset` consists of 3,005 mouse cortex cells profiled with the Smart-seq2 protocol, with the addition of UMI. To facilitate com- parison with other methods, we use a filtered set of 558 highly variable genes. The `CortexDataset` exhibits a clear high-level subpopulation struc- ture, which has been inferred by the authors of the original publication using computational tools and annotated by inspection of specific genes or transcriptional programs. Similar levels of annotation are provided with the `PbmcDataset` and `RetinaDataset`. Reference: Zeisel, A. et al. Cell types in the mouse cortex and hippocampus revealed by single-cell rna-seq. Science 347, 1138–1142 (2015). ``` cortex_dataset = CortexDataset(save_path=save_path) ``` ### Loading `PBMC` dataset `PbmcDataset` consists of 12,039 human peripheral blood mononu- clear cells profiled with 10x. Reference: Zheng, G. X. Y. et al. Massively parallel digital transcriptional profiling of single cells. Nature Communications 8, 14049 (2017). ``` pbmc_dataset = PbmcDataset(save_path=save_path) ``` ### Loading `RETINA` dataset `RetinaDataset` includes 27,499 mouse retinal bipolar neu- rons, profiled in two batches using the Drop-Seq technology. Reference: Shekhar, K. et al. Comprehensive classification of retinal bipolar neurons by single-cell transcriptomics. Cell 166, 1308–1323.e30 (2017). ``` retina_dataset = RetinaDataset(save_path=save_path) ``` ### Loading `HEMATO` dataset `HematoDataset` includes 4,016 cells from two batches that were profiled using in-drop. This data provides a snapshot of hematopoietic progenitor cells differentiating into various lineages. We use this dataset as an example for cases where gene expression varies in a continuous fashion (along pseudo-temporal axes) rather than forming discrete subpopulations. Reference: Tusi, B. K. et al. Population snapshots predict early haematopoietic and erythroid hierarchies. Nature 555, 54–60 (2018). ``` hemato_dataset = HematoDataset(save_path=os.path.join(save_path, 'HEMATO/')) ``` ### Loading `CBMC` dataset `CbmcDataset` includes 8,617 cord blood mononuclear cells pro- filed using 10x along with, for each cell, 13 well-characterized mononuclear antibodies. We used this dataset to analyze how the latent spaces inferred by dimensionality-reduction algorithms summarize protein marker abundance. Reference: Stoeckius, M. et al. Simultaneous epitope and transcriptome measurement in single cells. Nature Methods 14, 865–868 (2017). ``` cbmc_dataset = CbmcDataset(save_path=os.path.join(save_path, "citeSeq/")) ``` ### Loading `BRAIN-SMALL` dataset `BrainSmallDataset` consists of 9,128 mouse brain cells profiled using 10x. This dataset is used as a complement to PBMC for our study of zero abundance and quality control metrics correlation with our generative posterior parameters. Reference: ``` brain_small_dataset = BrainSmallDataset(save_path=save_path) def allow_notebook_for_test(): print("Testing the data loading notebook") ```	github_jupyter
<script async src="https://www.googletagmanager.com/gtag/js?id=UA-59152712-8"></script> <script> window.dataLayer = window.dataLayer \|\| []; function gtag(){dataLayer.push(arguments);} gtag('js', new Date()); gtag('config', 'UA-59152712-8'); </script> # Indexed Expressions: Representing and manipulating tensors, pseudotensors, etc. in NRPy+ ## Author: Zach Etienne ### Formatting improvements courtesy Brandon Clark ### NRPy+ Source Code for this module: [indexedexp.py](../edit/indexedexp.py) <a id='toc'></a> # Table of Contents $$\label{toc}$$ This notebook is organized as follows 1. [Step 1](#initializenrpy): Initialize core Python/NRPy+ modules 1. [Step 2](#idx1): Rank-1 Indexed Expressions 1. [Step 2.a](#dot): Performing a Dot Product 1. [Step 3](#idx2): Rank-2 and Higher Indexed Expressions 1. [Step 3.a](#con): Creating C Code for the contraction variable 1. [Step 3.b](#simd): Enable SIMD support 1. [Step 4](#exc): Exercise 1. [Step 5](#latex_pdf_output): Output this notebook to $\LaTeX$-formatted PDF file <a id='initializenrpy'></a> # Step 1: Initialize core NRPy+ modules \[Back to [top](#toc)\] $$\label{initializenrpy}$$ Let's start by importing all the needed modules from NRPy+ for dealing with indexed expressions and ouputting C code. ``` # The NRPy_param_funcs module sets up global structures that manage free parameters within NRPy+ import NRPy_param_funcs as par # NRPy+: Parameter interface # The indexedexp module defines various functions for defining and managing indexed quantities like tensors and pseudotensors import indexedexp as ixp # NRPy+: Symbolic indexed expression (e.g., tensors, vectors, etc.) support # The grid module defines various parameters related to a numerical grid or the dimensionality of indexed expressions # For example, it declares the parameter DIM, which specifies the dimensionality of the indexed expression import grid as gri # NRPy+: Functions having to do with numerical grids from outputC import outputC # NRPy+: Basic C code output functionality ``` <a id='idx1'></a> # Step 2: Rank-1 Indexed Expressions \[Back to [top](#toc)\] $$\label{idx1}$$ Indexed expressions of rank 1 are stored as [Python lists](https://www.tutorialspoint.com/python/python_lists.htm). There are two standard ways to declare indexed expressions: + Initialize indexed expression to zero: + zerorank1(DIM=-1) $\leftarrow$ As we will see below, initializing to zero is useful if the indexed expression depends entirely on some other indexed or non-indexed expressions. + DIM is an optional parameter that, if set to -1, will default to the dimension as set in the grid module: `par.parval_from_str("grid::DIM")`. Otherwise the rank-1 indexed expression will have dimension DIM. + Initialize indexed expression symbolically: + declarerank1(symbol, DIM=-1). + As in `zerorank1()`, DIM** is an optional parameter that, if set to -1, will default to the dimension as set in the grid module: `par.parval_from_str("grid::DIM")`. Otherwise the rank-1 indexed expression will have dimension DIM. `zerorank1()` and `declarerank1()` are both wrapper functions for the more general function `declare_indexedexp()`. + declare_indexedexp(rank, symbol=None, symmetry=None, dimension=None). + The following are optional parameters: symbol, symmetry, and dimension. If symbol is not specified, then `declare_indexedexp()` will initialize an indexed expression to zero. If symmetry is not specified or has value "nosym", then an indexed expression will not be symmetrized, which has no relevance for an indexed expression of rank 1. If dimension is not specified or has value -1, then dimension will default to the dimension as set in the grid module: `par.parval_from_str("grid::DIM")`. For example, the 3-vector $\beta^i$ (upper index denotes contravariant) can be initialized to zero as follows: ``` # Declare rank-1 contravariant ("U") vector betaU = ixp.zerorank1() # Print the result. It's a list of zeros! print(betaU) ``` Next set $\beta^i = \sum_{j=0}^i j = \{0,1,3\}$ ``` # Get the dimension we just set, so we know how many indices to loop over DIM = par.parval_from_str("grid::DIM") for i in range(DIM): # sum i from 0 to DIM-1, inclusive for j in range(i+1): # sum j from 0 to i, inclusive betaU[i] += j print("The 3-vector betaU is now set to: "+str(betaU)) ``` Alternatively, the 3-vector $\beta^i$ can be initialized symbolically as follows: ``` # Set the dimension to 3 par.set_parval_from_str("grid::DIM",3) # Declare rank-1 contravariant ("U") vector betaU = ixp.declarerank1("betaU") # Print the result. It's a list! print(betaU) ``` Declaring $\beta^i$ symbolically is standard in case `betaU0`, `betaU1`, and `betaU2` are defined elsewhere (e.g., read in from main memory as a gridfunction. As can be seen, NRPy+'s standard naming convention for indexed rank-1 expressions is + \[base variable name\]+\["U" for contravariant (up index) or "D" for covariant (down index)\] Caution: After declaring the vector, `betaU0`, `betaU1`, and `betaU2` can only be accessed or manipulated through list access; i.e., via `betaU[0]`, `betaU[1]`, and `betaU[2]`, respectively. Attempts to access `betaU0` directly will fail. Knowing this, let's multiply `betaU1` by 2: ``` betaU[1] = 2 print("The 3-vector betaU is now set to "+str(betaU)) print("The component betaU[1] is now set to "+str(betaU[1])) ``` <a id='dot'></a> ## Step 2.a: Performing a Dot Product \[Back to [top](#toc)\] $$\label{dot}$$ Next, let's declare the variable $\beta_j$ and perform the dot product $\beta^i \beta_i$: ``` # First set betaU back to its initial value betaU = ixp.declarerank1("betaU") # Declare beta_j: betaD = ixp.declarerank1("betaD") # Get the dimension we just set, so we know how many indices to loop over DIM = par.parval_from_str("grid::DIM") # Initialize dot product to zero dotprod = 0 # Perform dot product beta^i beta_i for i in range(DIM): dotprod += betaU[i]betaD[i] # Print result! print(dotprod) ``` <a id='idx2'></a> # Step 3: Rank-2 and Higher Indexed Expressions \[Back to [top](#toc)\] $$\label{idx2}$$ Moving to higher ranks, rank-2 indexed expressions are stored as lists of lists, rank-3 indexed expressions as lists of lists of lists, etc. For example + the covariant rank-2 tensor $g_{ij}$ is declared as `gDD[i][j]` in NRPy+, so that e.g., `gDD[0][2]` is stored with name `gDD02` and + the rank-2 tensor $T^{\mu}{}_{\nu}$ is declared as `TUD[m][n]` in NRPy+ (index names are of course arbitrary). Caveat: Note that it is currently up to the user to determine whether the combination of indexed expressions makes sense; NRPy+ does not track whether up and down indices are written consistently. NRPy+ supports symmetries in indexed expressions (above rank 1), so that if $h_{ij} = h_{ji}$, then declaring `hDD[i][j]` to be symmetric in NRPy+ will result in both `hDD[0][2]` and `hDD[2][0]` mapping to the single SymPy variable `hDD02`. To see how this works in NRPy+, let's define in NRPy+ a symmetric, rank-2 tensor $h_{ij}$ in three dimensions, and then compute the contraction, which should be given by $$con = h^{ij}h_{ij} = h_{00} h^{00} + h_{11} h^{11} + h_{22} h^{22} + 2 (h_{01} h^{01} + h_{02} h^{02} + h_{12} h^{12}).$$ ``` # Get the dimension we just set (should be set to 3). DIM = par.parval_from_str("grid::DIM") # Declare h_{ij}=hDD[i][j] and h^{ij}=hUU[i][j] hUU = ixp.declarerank2("hUU","sym01") hDD = ixp.declarerank2("hDD","sym01") # Perform sum h^{ij} h_{ij}, initializing contraction result to zero con = 0 for i in range(DIM): for j in range(DIM): con += hUU[i][j]hDD[i][j] # Print result print(con) ``` <a id='con'></a> ## Step 3.a: Creating C Code for the contraction variable $\text{con}$ \[Back to [top](#toc)\] $$\label{con}$$ Next let's create the C code for the contraction variable $\text{con}$, without CSE (common subexpression elimination) ``` outputC(con,"con") ``` <a id='simd'></a> ## Step 3.b: Enable SIMD support \[Back to [top](#toc)\] $$\label{simd}$$ Finally, let's see how it looks with SIMD support enabled ``` outputC(con,"con",params="enable_SIMD=True") ``` <a id='exc'></a> # Step 4: Exercise \[Back to [top](#toc)\] $$\label{exc}$$ Setting $\beta^i$ via the declarerank1(), write the NRPy+ code required to generate the needed C code for the lowering operator: $g_{ij} \beta^i$, and set the result to C variables `betaD0out`, `betaD1out`, and `betaD2out` [solution](Tutorial-Indexed_Expressions_soln.ipynb). Hint: You will want to use the `zerorank1()` function* To complete this exercise, you must first reset all variables in the notebook: ``` # Uncomment the below %reset command and then press <Shift>+<Enter>. # Respond with "y" in the dialog box to reset all variables. # %reset ``` Write your solution below: <a id='latex_pdf_output'></a> # Step 5: Output this notebook to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\] $$\label{latex_pdf_output}$$ The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename [Tutorial-Indexed_Expressions.pdf](Tutorial-Indexed_Expressions.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means.) ``` import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface cmd.output_Jupyter_notebook_to_LaTeXed_PDF("Tutorial-Indexed_Expressions") ```	github_jupyter
``` %matplotlib inline # Importing standard Qiskit libraries and configuring account from qiskit import QuantumCircuit, execute, Aer, IBMQ from qiskit.compiler import transpile, assemble from qiskit.tools.jupyter import * from qiskit.visualization import * # Loading your IBM Q account(s) provider = IBMQ.load_account() ``` # Chapter 11 - Ignis ``` # Import plot and math libraries import numpy as np import matplotlib.pyplot as plt # Import the noise models and some standard error methods from qiskit.providers.aer.noise import NoiseModel from qiskit.providers.aer.noise.errors.standard_errors import amplitude_damping_error, phase_damping_error # Import all three coherence circuits generators and fitters from qiskit.ignis.characterization.coherence import t1_circuits, t2_circuits, t2star_circuits from qiskit.ignis.characterization.coherence import T1Fitter, T2Fitter, T2StarFitter # Generate the T1 test circuits # Generate a list of number of gates to add to each circuit # using np.linspace so that the number of gates increases linearly # and append with a large span at the end of the list (200-4000) num_of_gates = np.append((np.linspace(1, 100, 12)).astype(int), np.array([200, 400, 800, 1000, 2000, 4000])) #Define the gate time for each Identity gate gate_time = 0.1 # Select the first qubit as the one we wish to measure T1 qubits = [0] # Generate the test circuits given the above parameters test_circuits, delay_times = t1_circuits(num_of_gates, gate_time, qubits) # The number of I gates appended for each circuit print('Number of gates per test circuit: \n', num_of_gates, '\n') # The gate time of each circuit (number of I gates * gate_time) print('Delay times for each test circuit created, respectively:\n', delay_times) print('Total test circuits created: ', len(test_circuits)) print('Test circuit 1 with 1 Identity gate:') test_circuits[0].draw() print('Test circuit 2 with 10 Identity gates:') test_circuits[1].draw() # Set the simulator with amplitude damping noise # Set the amplitude damping noise channel parameters T1 and Lambda t1 = 20 lam = np.exp(-gate_time/t1) # Generate the amplitude dampling error channel error = amplitude_damping_error(1 - lam) noise_model = NoiseModel() # Set the dampling error to the ID gate on qubit 0. noise_model.add_quantum_error(error, 'id', [0]) # Run the simulator with the generated noise model backend = Aer.get_backend('qasm_simulator') shots = 200 backend_result = execute(test_circuits, backend, shots=shots, noise_model=noise_model).result() # Plot the noisy results of the largest (last in the list) circuit plot_histogram(backend_result.get_counts(test_circuits[0])) # Plot the noisy results of the largest (last in the list) circuit plot_histogram(backend_result.get_counts(test_circuits[len(test_circuits)-1])) # Initialize the parameters for the T1Fitter, A, T1, and B param_t1 = t11.2 param_a = 1.0 param_b = 0.0 # Generate the T1Fitter for our test circuit results fit = T1Fitter(backend_result, delay_times, qubits, fit_p0=[param_a, param_t1, param_b], fit_bounds=([0, 0, -1], [2, param_t12, 1])) # Plot the fitter results for T1 over each test circuit's delay time fit.plot(0) # Import the thermal relaxation error we will use to create our error from qiskit.providers.aer.noise.errors.standard_errors import thermal_relaxation_error # Import the T2Fitter Class and t2_circuits method from qiskit.ignis.characterization.coherence import T2Fitter from qiskit.ignis.characterization.coherence import t2_circuits num_of_gates = (np.linspace(1, 300, 50)).astype(int) gate_time = 0.1 # Note that it is possible to measure several qubits in parallel qubits = [0] t2echo_test_circuits, t2echo_delay_times = t2_circuits(num_of_gates, gate_time, qubits) # The number of I gates appended for each circuit print('Number of gates per test circuit: \n', num_of_gates, '\n') # The gate time of each circuit (number of I gates * gate_time) print('Delay times for T2 echo test circuits:\n', t2echo_delay_times) # Draw the first T2 test circuit t2echo_test_circuits[0].draw() # We'll create a noise model on the backend simulator backend = Aer.get_backend('qasm_simulator') shots = 400 # set the t2 decay time t2 = 25.0 # Define the T2 noise model based on the thermal relaxation error model t2_noise_model = NoiseModel() t2_noise_model.add_quantum_error(thermal_relaxation_error(np.inf, t2, gate_time, 0.5), 'id', [0]) # Execute the circuit on the noisy backend t2echo_backend_result = execute(t2echo_test_circuits, backend, shots=shots, noise_model=t2_noise_model, optimization_level=0).result() plot_histogram(t2echo_backend_result.get_counts(t2echo_test_circuits[0])) plot_histogram(t2echo_backend_result.get_counts(t2echo_test_circuits[len(t2echo_test_circuits)-1])) ``` # T2 Decoherence Time ``` # Generate the T2Fitter class using similar parameters as the T1Fitter t2echo_fit = T2Fitter(t2echo_backend_result, t2echo_delay_times, qubits, fit_p0=[0.5, t2, 0.5], fit_bounds=([-0.5, 0, -0.5], [1.5, 40, 1.5])) # Print and plot the results print(t2echo_fit.params) t2echo_fit.plot(0) plt.show() # 50 total linearly spaced number of gates # 30 from 10->150, 20 from 160->450 num_of_gates = np.append((np.linspace(1, 150, 30)).astype(int), (np.linspace(160,450,20)).astype(int)) # Set the Identity gate delay time gate_time = 0.1 # Select the qubit to measure T2* qubits = [0] # Generate the 50 test circuits with number of oscillations set to 4 test_circuits, delay_times, osc_freq = t2star_circuits(num_of_gates, gate_time, qubits, nosc=4) print('Circuits generated: ', len(test_circuits)) print('Delay times: ', delay_times) print('Oscillating frequency: ', osc_freq) print(test_circuits[0].count_ops()) test_circuits[0].draw() print(test_circuits[1].count_ops()) test_circuits[1].draw() # Get the backend to execute the test circuits backend = Aer.get_backend('qasm_simulator') # Set the T2* value to 10 t2Star = 10 # Set the phase damping error and add it to the noise model to the Identity gates error = phase_damping_error(1 - np.exp(-2gate_time/t2Star)) noise_model = NoiseModel() noise_model.add_quantum_error(error, 'id', [0]) # Run the simulator shots = 1024 backend_result = execute(test_circuits, backend, shots=shots, noise_model=noise_model).result() # Plot the noisy results of the shortest (first in the list) circuit plot_histogram(backend_result.get_counts(test_circuits[0])) # Plot the noisy results of the largest (last in the list) circuit plot_histogram(backend_result.get_counts(test_circuits[len(test_circuits)-1])) # Set the initial values of the T2StarFitter parameters param_T2Star = t2Star1.1 param_A = 0.5 param_B = 0.5 # Generate the T2StarFitter with the given parameters and bounds fit = T2StarFitter(backend_result, delay_times, qubits, fit_p0=[0.5, t2Star, osc_freq, 0, 0.5], fit_bounds=([-0.5, 0, 0, -np.pi, -0.5], [1.5, 40, 2*osc_freq, np.pi, 1.5])) # Plot the qubit characterization from the T2StarFitter fit.plot(0) ``` # Mitigating Readout errors ``` # Import Qiskit classes from qiskit.providers.aer import noise from qiskit.tools.visualization import plot_histogram # Import measurement calibration functions from qiskit.ignis.mitigation.measurement import complete_meas_cal, CompleteMeasFitter # Generate the calibration circuits # Set the number of qubits num_qubits = 5 # Set the qubit list to generate the measurement calibration circuits qubit_list = [0,1,2,3,4] # Generate the measurement calibrations circuits and state labels meas_calibs, state_labels = complete_meas_cal(qubit_list=qubit_list, qr=num_qubits, circlabel='mcal') # Print the number of measurement calibration circuits generated print(len(meas_calibs)) # Draw any of the generated calibration circuits, 0-31. # In this example we will draw the last one. meas_calibs[31].draw() state_labels # Execute the calibration circuits without noise on the qasm simulator backend = Aer.get_backend('qasm_simulator') job = execute(meas_calibs, backend=backend, shots=1000) # Obtain the measurement calibration results cal_results = job.result() # The calibration matrix without noise is the identity matrix meas_fitter = CompleteMeasFitter(cal_results, state_labels, circlabel='mcal') print(meas_fitter.cal_matrix) meas_fitter.plot_calibration() # Create a 5 qubit circuit qc = QuantumCircuit(5,5) # Place the first qubit in superpostion qc.h(0) # Entangle all other qubits together qc.cx(0, 1) qc.cx(1, 2) qc.cx(2, 3) qc.cx(3, 4) # Include a barrier just to ease visualization of the circuit qc.barrier() # Measure and draw the final circuit qc.measure([0,1,2,3,4], [0,1,2,3,4]) qc.draw() # Obtain the least busy backend device, not a simulator from qiskit.providers.ibmq import least_busy # Find the least busy operational quantum device with 5 or more qubits backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 4 and not x.configuration().simulator and x.status().operational==True)) # Print the least busy backend print("least busy backend: ", backend) # Execute the quantum circuit on the backend job = execute(qc, backend=backend, shots=1024) results = job.result() # Results from backend without mitigating the noise noisy_counts = results.get_counts() # Obtain the measurement fitter object measurement_filter = meas_fitter.filter # Mitigate the results by applying the measurement fitter filtered_results = measurement_filter.apply(results) # Get the mitigated result counts filtered_counts = filtered_results.get_counts(0) plot_histogram(noisy_counts) plot_histogram(filtered_counts) import qiskit.tools.jupyter %qiskit_version_table ```	github_jupyter
``` import wget, json, os, math from pathlib import Path from string import capwords from pybtex.database import parse_string import pybtex.errors from mpcontribs.client import Client from bravado.exception import HTTPNotFound from pymatgen.core import Structure from pymatgen.ext.matproj import MPRester from tqdm.notebook import tqdm from matminer.datasets import load_dataset from monty.json import MontyEncoder, MontyDecoder ``` ### Configuration and Initialization ``` BENCHMARK_FULL_SET = [ { "name": "log_kvrh", "data_file": "matbench_log_kvrh.json.gz", "target": "log10(K_VRH)", "clf_pos_label": None, "unit": None, "has_structure": True, }, { "name": "log_gvrh", "data_file": "matbench_log_gvrh.json.gz", "target": "log10(G_VRH)", "clf_pos_label": None, "unit": None, "has_structure": True, }, { "name": "dielectric", "data_file": "matbench_dielectric.json.gz", "target": "n", "clf_pos_label": None, "unit": None, "has_structure": True, }, { "name": "jdft2d", "data_file": "matbench_jdft2d.json.gz", "target": "exfoliation_en", "clf_pos_label": None, "unit": "meV/atom", "has_structure": True, }, { "name": "mp_gap", "data_file": "matbench_mp_gap.json.gz", "target": "gap pbe", "clf_pos_label": None, "unit": "eV", "has_structure": True, }, { "name": "mp_is_metal", "data_file": "matbench_mp_is_metal.json.gz", "target": "is_metal", "clf_pos_label": True, "unit": None, "has_structure": True, }, { "name": "mp_e_form", "data_file": "matbench_mp_e_form.json.gz", "target": "e_form", "clf_pos_label": None, "unit": "eV/atom", "has_structure": True, }, { "name": "perovskites", "data_file": "matbench_perovskites.json.gz", "target": "e_form", "clf_pos_label": None, "unit": "eV", "has_structure": True, }, { "name": "glass", "data_file": "matbench_glass.json.gz", "target": "gfa", "clf_pos_label": True, "unit": None, "has_structure": False, }, { "name": "expt_is_metal", "data_file": "matbench_expt_is_metal.json.gz", "target": "is_metal", "clf_pos_label": True, "unit": None, "has_structure": False, }, { "name": "expt_gap", "data_file": "matbench_expt_gap.json.gz", "target": "gap expt", "clf_pos_label": None, "unit": "eV", "has_structure": False, }, { "name": "phonons", "data_file": "matbench_phonons.json.gz", "target": "last phdos peak", "clf_pos_label": None, "unit": "cm^-1", "has_structure": True, }, { "name": "steels", "data_file": "matbench_steels.json.gz", "target": "yield strength", "clf_pos_label": None, "unit": "MPa", "has_structure": False, } ] # Map of canonical yet non-mpcontribs-compatible tagret nams to compatible (unicode, no punctuation) target names target_map = { "yield strength": "σᵧ", "log10(K_VRH)": "log₁₀Kᵛʳʰ", "log10(G_VRH)": "log₁₀Gᵛʳʰ", "n": "𝑛", "exfoliation_en": "Eˣ", "gap pbe": "Eᵍ", "is_metal": "metallic", "e_form": "Eᶠ", "gfa": "glass", "gap expt": "Eᵍ", "last phdos peak": "ωᵐᵃˣ", } pybtex.errors.set_strict_mode(False) mprester = MPRester() client = Client(host='ml-api.materialsproject.org') datadir = Path('/Users/patrick/gitrepos/mp/mpcontribs-data/') fn = Path('dataset_metadata.json') fp = datadir / fn if not fp.exists(): prefix = "https://raw.githubusercontent.com/hackingmaterials/matminer" url = f'{prefix}/master/matminer/datasets/{fn}' wget.download(url) fn.rename(fp) metadata = json.load(open(fp, 'r')) ``` ### Prepare and create/update Projects ``` for ds in BENCHMARK_FULL_SET: name = "matbench_" + ds["name"] primitive_key = "structure" if ds["has_structure"] else "composition" target = ds["target"] columns = { target_map[target]: metadata[name]["columns"][target], primitive_key: metadata[name]["columns"][primitive_key] } project = { 'name': name, 'is_public': True, 'owner': '[email protected]', 'title': name, # TODO update and set long_title 'authors': 'A. Dunn, A. Jain', 'description': metadata[name]['description'] + \ " If you are viewing this on MPContribs-ML interactively, please ensure the order of the" f"identifiers is sequential (mb-{ds['name']}-0001, mb-{ds['name']}-0002, etc.) before benchmarking.", 'other': { 'columns': columns, 'entries': metadata[name]['num_entries'] }, 'references': [ {'label': 'RawData', 'url': metadata["name"]["url"]} ] } for ref in metadata[name]['bibtex_refs']: if name == "matbench_phonons": ref = ref.replace( "petretto_dwaraknath_miranda_winston_giantomassi_rignanese_van setten_gonze_persson_hautier_2018", "petretto2018" ) bib = parse_string(ref, 'bibtex') for key, entry in bib.entries.items(): key_is_doi = key.startswith('doi:') url = 'https://doi.org/' + key.split(':', 1)[-1] if key_is_doi else entry.fields.get('url') k = 'Zhuo2018' if key_is_doi else capwords(key.replace('_', '')) if k.startswith('C2'): k = 'Castelli2012' elif k.startswith('Landolt'): k = 'LB1997' elif k == 'Citrine': url = 'https://www.citrination.com' if len(k) > 8: k = k[:4] + k[-4:] project['references'].append( {'label': k, 'url': url} ) try: client.projects.get_entry(pk=name, _fields=["name"]).result() except HTTPNotFound: client.projects.create_entry(project=project).result() print(name, "created") else: project.pop("name") client.projects.update_entry(pk=name, project=project).result() print(name, "updated") ``` ### Prepare Contributions ``` structure_filename = "/Users/patrick/Downloads/outfile.cif" for ds in BENCHMARK_FULL_SET: name = "matbench_" + ds["name"] fn = datadir / f"{name}.json" if fn.exists(): continue target = ds["target"] unit = f" {ds['unit']}" if ds["unit"] else "" df = load_dataset(name) contributions = [] id_prefix = df.shape[0] id_n_zeros = math.floor(math.log(df.shape[0], 10)) + 1 for i, row in tqdm(enumerate(df.iterrows()), total=df.shape[0]): entry = row[1] contrib = {'project': name, 'is_public': True} if "structure" in entry.index: s = entry.loc["structure"] s.to("cif", structure_filename) s = Structure.from_file(structure_filename) c = s.composition.get_integer_formula_and_factor()[0] contrib["structures"] = [s] else: c = entry["composition"] id_number = f"{i+1:0{id_n_zeros}d}" identifier = f"mb-{ds['name']}-{id_number}" contrib["identifier"] = identifier contrib["data"] = {target_map[target]: f"{entry.loc[target]}{unit}"} contrib["formula"] = c contributions.append(contrib) with open(fn, "w") as f: json.dump(contributions, f, cls=MontyEncoder) print("saved to", fn) ``` ### Submit Contributions ``` name = "matbench_log_gvrh" fn = datadir / f"{name}.json" with open(fn, "r") as f: contributions = json.load(f, cls=MontyDecoder) # client.delete_contributions(name) client.submit_contributions(contributions, ignore_dupes=True) ```	github_jupyter
# DeepDreaming with TensorFlow >[Loading and displaying the model graph](#loading) >[Naive feature visualization](#naive) >[Multiscale image generation](#multiscale) >[Laplacian Pyramid Gradient Normalization](#laplacian) >[Playing with feature visualzations](#playing) >[DeepDream](#deepdream) This notebook demonstrates a number of Convolutional Neural Network image generation techniques implemented with TensorFlow for fun and science: - visualize individual feature channels and their combinations to explore the space of patterns learned by the neural network (see [GoogLeNet](http://storage.googleapis.com/deepdream/visualz/tensorflow_inception/index.html) and [VGG16](http://storage.googleapis.com/deepdream/visualz/vgg16/index.html) galleries) - embed TensorBoard graph visualizations into Jupyter notebooks - produce high-resolution images with tiled computation ([example](http://storage.googleapis.com/deepdream/pilatus_flowers.jpg)) - use Laplacian Pyramid Gradient Normalization to produce smooth and colorful visuals at low cost - generate DeepDream-like images with TensorFlow (DogSlugs included) The network under examination is the [GoogLeNet architecture](http://arxiv.org/abs/1409.4842), trained to classify images into one of 1000 categories of the [ImageNet](http://image-net.org/) dataset. It consists of a set of layers that apply a sequence of transformations to the input image. The parameters of these transformations were determined during the training process by a variant of gradient descent algorithm. The internal image representations may seem obscure, but it is possible to visualize and interpret them. In this notebook we are going to present a few tricks that allow to make these visualizations both efficient to generate and even beautiful. Impatient readers can start with exploring the full galleries of images generated by the method described here for [GoogLeNet](http://storage.googleapis.com/deepdream/visualz/tensorflow_inception/index.html) and [VGG16](http://storage.googleapis.com/deepdream/visualz/vgg16/index.html) architectures. ``` # boilerplate code from __future__ import print_function import os from io import BytesIO import numpy as np from functools import partial import PIL.Image from IPython.display import clear_output, Image, display, HTML import tensorflow as tf ``` <a id='loading'></a> ## Loading and displaying the model graph The pretrained network can be downloaded [here](https://storage.googleapis.com/download.tensorflow.org/models/inception5h.zip). Unpack the `tensorflow_inception_graph.pb` file from the archive and set its path to `model_fn` variable. Alternatively you can uncomment and run the following cell to download the network: ``` #!wget https://storage.googleapis.com/download.tensorflow.org/models/inception5h.zip && unzip inception5h.zip model_fn = 'tensorflow_inception_graph.pb' # creating TensorFlow session and loading the model graph = tf.Graph() sess = tf.InteractiveSession(graph=graph) with tf.gfile.FastGFile(model_fn, 'rb') as f: graph_def = tf.GraphDef() graph_def.ParseFromString(f.read()) t_input = tf.placeholder(np.float32, name='input') # define the input tensor imagenet_mean = 117.0 t_preprocessed = tf.expand_dims(t_input-imagenet_mean, 0) tf.import_graph_def(graph_def, {'input':t_preprocessed}) ``` To take a glimpse into the kinds of patterns that the network learned to recognize, we will try to generate images that maximize the sum of activations of particular channel of a particular convolutional layer of the neural network. The network we explore contains many convolutional layers, each of which outputs tens to hundreds of feature channels, so we have plenty of patterns to explore. ``` layers = [op.name for op in graph.get_operations() if op.type=='Conv2D' and 'import/' in op.name] feature_nums = [int(graph.get_tensor_by_name(name+':0').get_shape()[-1]) for name in layers] print('Number of layers', len(layers)) print('Total number of feature channels:', sum(feature_nums)) # Helper functions for TF Graph visualization def strip_consts(graph_def, max_const_size=32): """Strip large constant values from graph_def.""" strip_def = tf.GraphDef() for n0 in graph_def.node: n = strip_def.node.add() n.MergeFrom(n0) if n.op == 'Const': tensor = n.attr['value'].tensor size = len(tensor.tensor_content) if size > max_const_size: tensor.tensor_content = bytes("<stripped %d bytes>"%size, 'utf-8') return strip_def def rename_nodes(graph_def, rename_func): res_def = tf.GraphDef() for n0 in graph_def.node: n = res_def.node.add() n.MergeFrom(n0) n.name = rename_func(n.name) for i, s in enumerate(n.input): n.input[i] = rename_func(s) if s[0]!='^' else '^'+rename_func(s[1:]) return res_def def show_graph(graph_def, max_const_size=32): """Visualize TensorFlow graph.""" if hasattr(graph_def, 'as_graph_def'): graph_def = graph_def.as_graph_def() strip_def = strip_consts(graph_def, max_const_size=max_const_size) code = """ <script> function load() {{ document.getElementById("{id}").pbtxt = {data}; }} </script> <link rel="import" href="https://tensorboard.appspot.com/tf-graph-basic.build.html" onload=load()> <div style="height:600px"> <tf-graph-basic id="{id}"></tf-graph-basic> </div> """.format(data=repr(str(strip_def)), id='graph'+str(np.random.rand())) iframe = """ <iframe seamless style="width:800px;height:620px;border:0" srcdoc="{}"></iframe> """.format(code.replace('"', '"')) display(HTML(iframe)) # Visualizing the network graph. Be sure expand the "mixed" nodes to see their # internal structure. We are going to visualize "Conv2D" nodes. tmp_def = rename_nodes(graph_def, lambda s:"/".join(s.split('_',1))) show_graph(tmp_def) ``` <a id='naive'></a> ## Naive feature visualization Let's start with a naive way of visualizing these. Image-space gradient ascent! ``` # Picking some internal layer. Note that we use outputs before applying the ReLU nonlinearity # to have non-zero gradients for features with negative initial activations. layer = 'mixed4d_3x3_bottleneck_pre_relu' channel = 139 # picking some feature channel to visualize # start with a gray image with a little noise img_noise = np.random.uniform(size=(224,224,3)) + 100.0 def showarray(a, fmt='jpeg'): a = np.uint8(np.clip(a, 0, 1)255) f = BytesIO() PIL.Image.fromarray(a).save(f, fmt) display(Image(data=f.getvalue())) def visstd(a, s=0.1): '''Normalize the image range for visualization''' return (a-a.mean())/max(a.std(), 1e-4)s + 0.5 def T(layer): '''Helper for getting layer output tensor''' return graph.get_tensor_by_name("import/%s:0"%layer) def render_naive(t_obj, img0=img_noise, iter_n=20, step=1.0): t_score = tf.reduce_mean(t_obj) # defining the optimization objective t_grad = tf.gradients(t_score, t_input)[0] # behold the power of automatic differentiation! img = img0.copy() for i in range(iter_n): g, score = sess.run([t_grad, t_score], {t_input:img}) # normalizing the gradient, so the same step size should work g /= g.std()+1e-8 # for different layers and networks img += gstep print(score, end = ' ') clear_output() showarray(visstd(img)) render_naive(T(layer)[:,:,:,channel]) ``` <a id="multiscale"></a> ## Multiscale image generation Looks like the network wants to show us something interesting! Let's help it. We are going to apply gradient ascent on multiple scales. Details formed on smaller scale will be upscaled and augmented with additional details on the next scale. With multiscale image generation it may be tempting to set the number of octaves to some high value to produce wallpaper-sized images. Storing network activations and backprop values will quickly run out of GPU memory in this case. There is a simple trick to avoid this: split the image into smaller tiles and compute each tile gradient independently. Applying random shifts to the image before every iteration helps avoid tile seams and improves the overall image quality. ``` def tffunc(argtypes): '''Helper that transforms TF-graph generating function into a regular one. See "resize" function below. ''' placeholders = list(map(tf.placeholder, argtypes)) def wrap(f): out = f(placeholders) def wrapper(args, *kw): return out.eval(dict(zip(placeholders, args)), session=kw.get('session')) return wrapper return wrap # Helper function that uses TF to resize an image def resize(img, size): img = tf.expand_dims(img, 0) return tf.image.resize_bilinear(img, size)[0,:,:,:] resize = tffunc(np.float32, np.int32)(resize) def calc_grad_tiled(img, t_grad, tile_size=512): '''Compute the value of tensor t_grad over the image in a tiled way. Random shifts are applied to the image to blur tile boundaries over multiple iterations.''' sz = tile_size h, w = img.shape[:2] sx, sy = np.random.randint(sz, size=2) img_shift = np.roll(np.roll(img, sx, 1), sy, 0) grad = np.zeros_like(img) for y in range(0, max(h-sz//2, sz),sz): for x in range(0, max(w-sz//2, sz),sz): sub = img_shift[y:y+sz,x:x+sz] g = sess.run(t_grad, {t_input:sub}) grad[y:y+sz,x:x+sz] = g return np.roll(np.roll(grad, -sx, 1), -sy, 0) def render_multiscale(t_obj, img0=img_noise, iter_n=10, step=1.0, octave_n=3, octave_scale=1.4): t_score = tf.reduce_mean(t_obj) # defining the optimization objective t_grad = tf.gradients(t_score, t_input)[0] # behold the power of automatic differentiation! img = img0.copy() for octave in range(octave_n): if octave>0: hw = np.float32(img.shape[:2])octave_scale img = resize(img, np.int32(hw)) for i in range(iter_n): g = calc_grad_tiled(img, t_grad) # normalizing the gradient, so the same step size should work g /= g.std()+1e-8 # for different layers and networks img += gstep print('.', end = ' ') clear_output() showarray(visstd(img)) render_multiscale(T(layer)[:,:,:,channel]) ``` <a id="laplacian"></a> ## Laplacian Pyramid Gradient Normalization This looks better, but the resulting images mostly contain high frequencies. Can we improve it? One way is to add a smoothness prior into the optimization objective. This will effectively blur the image a little every iteration, suppressing the higher frequencies, so that the lower frequencies can catch up. This will require more iterations to produce a nice image. Why don't we just boost lower frequencies of the gradient instead? One way to achieve this is through the [Laplacian pyramid](https://en.wikipedia.org/wiki/Pyramid_%28image_processing%29#Laplacian_pyramid) decomposition. We call the resulting technique _Laplacian Pyramid Gradient Normalization_. ``` k = np.float32([1,4,6,4,1]) k = np.outer(k, k) k5x5 = k[:,:,None,None]/k.sum()np.eye(3, dtype=np.float32) def lap_split(img): '''Split the image into lo and hi frequency components''' with tf.name_scope('split'): lo = tf.nn.conv2d(img, k5x5, [1,2,2,1], 'SAME') lo2 = tf.nn.conv2d_transpose(lo, k5x54, tf.shape(img), [1,2,2,1]) hi = img-lo2 return lo, hi def lap_split_n(img, n): '''Build Laplacian pyramid with n splits''' levels = [] for i in range(n): img, hi = lap_split(img) levels.append(hi) levels.append(img) return levels[::-1] def lap_merge(levels): '''Merge Laplacian pyramid''' img = levels[0] for hi in levels[1:]: with tf.name_scope('merge'): img = tf.nn.conv2d_transpose(img, k5x54, tf.shape(hi), [1,2,2,1]) + hi return img def normalize_std(img, eps=1e-10): '''Normalize image by making its standard deviation = 1.0''' with tf.name_scope('normalize'): std = tf.sqrt(tf.reduce_mean(tf.square(img))) return img/tf.maximum(std, eps) def lap_normalize(img, scale_n=4): '''Perform the Laplacian pyramid normalization.''' img = tf.expand_dims(img,0) tlevels = lap_split_n(img, scale_n) tlevels = list(map(normalize_std, tlevels)) out = lap_merge(tlevels) return out[0,:,:,:] # Showing the lap_normalize graph with TensorBoard lap_graph = tf.Graph() with lap_graph.as_default(): lap_in = tf.placeholder(np.float32, name='lap_in') lap_out = lap_normalize(lap_in) show_graph(lap_graph) def render_lapnorm(t_obj, img0=img_noise, visfunc=visstd, iter_n=10, step=1.0, octave_n=3, octave_scale=1.4, lap_n=4): t_score = tf.reduce_mean(t_obj) # defining the optimization objective t_grad = tf.gradients(t_score, t_input)[0] # behold the power of automatic differentiation! # build the laplacian normalization graph lap_norm_func = tffunc(np.float32)(partial(lap_normalize, scale_n=lap_n)) img = img0.copy() for octave in range(octave_n): if octave>0: hw = np.float32(img.shape[:2])octave_scale img = resize(img, np.int32(hw)) for i in range(iter_n): g = calc_grad_tiled(img, t_grad) g = lap_norm_func(g) img += gstep print('.', end = ' ') clear_output() showarray(visfunc(img)) render_lapnorm(T(layer)[:,:,:,channel]) ``` <a id="playing"></a> ## Playing with feature visualizations We got a nice smooth image using only 10 iterations per octave. In case of running on GPU this takes just a few seconds. Let's try to visualize another channel from the same layer. The network can generate wide diversity of patterns. ``` render_lapnorm(T(layer)[:,:,:,65]) ``` Lower layers produce features of lower complexity. ``` render_lapnorm(T('mixed3b_1x1_pre_relu')[:,:,:,101]) ``` There are many interesting things one may try. For example, optimizing a linear combination of features often gives a "mixture" pattern. ``` render_lapnorm(T(layer)[:,:,:,65]+T(layer)[:,:,:,139], octave_n=4) ``` <a id="deepdream"></a> ## DeepDream Now let's reproduce the [DeepDream algorithm](https://github.com/google/deepdream/blob/master/dream.ipynb) with TensorFlow. ``` def render_deepdream(t_obj, img0=img_noise, iter_n=10, step=1.5, octave_n=4, octave_scale=1.4): t_score = tf.reduce_mean(t_obj) # defining the optimization objective t_grad = tf.gradients(t_score, t_input)[0] # behold the power of automatic differentiation! # split the image into a number of octaves img = img0 octaves = [] for i in range(octave_n-1): hw = img.shape[:2] lo = resize(img, np.int32(np.float32(hw)/octave_scale)) hi = img-resize(lo, hw) img = lo octaves.append(hi) # generate details octave by octave for octave in range(octave_n): if octave>0: hi = octaves[-octave] img = resize(img, hi.shape[:2])+hi for i in range(iter_n): g = calc_grad_tiled(img, t_grad) img += g*(step / (np.abs(g).mean()+1e-7)) print('.',end = ' ') clear_output() showarray(img/255.0) ``` Let's load some image and populate it with DogSlugs (in case you've missed them). ``` img0 = PIL.Image.open('pilatus800.jpg') img0 = np.float32(img0) showarray(img0/255.0) render_deepdream(tf.square(T('mixed4c')), img0) ``` Note that results can differ from the [Caffe](https://github.com/BVLC/caffe)'s implementation, as we are using an independently trained network. Still, the network seems to like dogs and animal-like features due to the nature of the ImageNet dataset. Using an arbitrary optimization objective still works: ``` render_deepdream(T(layer)[:,:,:,139], img0) ``` Don't hesitate to use higher resolution inputs (also increase the number of octaves)! Here is an [example](http://storage.googleapis.com/deepdream/pilatus_flowers.jpg) of running the flower dream over the bigger image. We hope that the visualization tricks described here may be helpful for analyzing representations learned by neural networks or find their use in various artistic applications.	github_jupyter
``` # reload packages %load_ext autoreload %autoreload 2 ``` ### Choose GPU ``` %env CUDA_DEVICE_ORDER=PCI_BUS_ID %env CUDA_VISIBLE_DEVICES=3 import tensorflow as tf gpu_devices = tf.config.experimental.list_physical_devices('GPU') if len(gpu_devices)>0: tf.config.experimental.set_memory_growth(gpu_devices[0], True) print(gpu_devices) tf.keras.backend.clear_session() ``` ### Load packages ``` import tensorflow as tf import numpy as np import matplotlib.pyplot as plt from tqdm.autonotebook import tqdm from IPython import display import pandas as pd import umap import copy import os, tempfile import tensorflow_addons as tfa import pickle ``` ### parameters ``` dataset = "fmnist" labels_per_class = 256 # 'full' n_latent_dims = 1024 confidence_threshold = 0.0 # minimum confidence to include in UMAP graph for learned metric learned_metric = True # whether to use a learned metric, or Euclidean distance between datapoints augmented = False # min_dist= 0.001 # min_dist parameter for UMAP negative_sample_rate = 5 # how many negative samples per positive sample batch_size = 128 # batch size optimizer = tf.keras.optimizers.Adam(1e-3) # the optimizer to train optimizer = tfa.optimizers.MovingAverage(optimizer) label_smoothing = 0.2 # how much label smoothing to apply to categorical crossentropy max_umap_iterations = 500 # how many times, maximum, to recompute UMAP max_epochs_per_graph = 10 # how many epochs maximum each graph trains for (without early stopping) graph_patience = 10 # how many times without improvement to train a new graph min_graph_delta = 0.0025 # minimum improvement on validation acc to consider an improvement for training from datetime import datetime datestring = datetime.now().strftime("%Y_%m_%d_%H_%M_%S_%f") datestring = ( str(dataset) + "_" + str(confidence_threshold) + "_" + str(labels_per_class) + "____" + datestring + '_umap_augmented' ) print(datestring) ``` #### Load dataset ``` from tfumap.semisupervised_keras import load_dataset ( X_train, X_test, X_labeled, Y_labeled, Y_masked, X_valid, Y_train, Y_test, Y_valid, Y_valid_one_hot, Y_labeled_one_hot, num_classes, dims ) = load_dataset(dataset, labels_per_class) ``` ### load architecture ``` from tfumap.semisupervised_keras import load_architecture encoder, classifier, embedder = load_architecture(dataset, n_latent_dims) ``` ### load pretrained weights ``` from tfumap.semisupervised_keras import load_pretrained_weights encoder, classifier = load_pretrained_weights(dataset, augmented, labels_per_class, encoder, classifier) ``` #### compute pretrained accuracy ``` # test current acc pretrained_predictions = classifier.predict(encoder.predict(X_test, verbose=True), verbose=True) pretrained_predictions = np.argmax(pretrained_predictions, axis=1) pretrained_acc = np.mean(pretrained_predictions == Y_test) print('pretrained acc: {}'.format(pretrained_acc)) ``` ### get a, b parameters for embeddings ``` from tfumap.semisupervised_keras import find_a_b a_param, b_param = find_a_b(min_dist=min_dist) ``` ### build network ``` from tfumap.semisupervised_keras import build_model model = build_model( batch_size=batch_size, a_param=a_param, b_param=b_param, dims=dims, encoder=encoder, classifier=classifier, negative_sample_rate=negative_sample_rate, optimizer=optimizer, label_smoothing=label_smoothing, embedder = embedder, ) ``` ### build labeled iterator ``` from tfumap.semisupervised_keras import build_labeled_iterator labeled_dataset = build_labeled_iterator(X_labeled, Y_labeled_one_hot, augmented, dims) ``` ### training ``` from livelossplot import PlotLossesKerasTF from tfumap.semisupervised_keras import get_edge_dataset from tfumap.semisupervised_keras import zip_datasets ``` #### callbacks ``` # plot losses callback groups = {'acccuracy': ['classifier_accuracy', 'val_classifier_accuracy'], 'loss': ['classifier_loss', 'val_classifier_loss']} plotlosses = PlotLossesKerasTF(groups=groups) history_list = [] current_validation_acc = 0 batches_per_epoch = np.floor(len(X_train)/batch_size).astype(int) epochs_since_last_improvement = 0 current_umap_iterations = 0 current_epoch = 0 from tfumap.paths import MODEL_DIR, ensure_dir save_folder = MODEL_DIR / 'semisupervised-keras' / dataset / str(labels_per_class) / datestring ensure_dir(save_folder / 'test_loss.npy') for cui in tqdm(np.arange(current_epoch, max_umap_iterations)): if len(history_list) > graph_patience+1: previous_history = [np.mean(i.history['val_classifier_accuracy']) for i in history_list] best_of_patience = np.max(previous_history[-graph_patience:]) best_of_previous = np.max(previous_history[:-graph_patience]) if (best_of_previous + min_graph_delta) > best_of_patience: print('Early stopping') break # make dataset edge_dataset = get_edge_dataset( model, augmented, classifier, encoder, X_train, Y_masked, batch_size, confidence_threshold, labeled_dataset, dims, learned_metric = learned_metric ) # zip dataset zipped_ds = zip_datasets(labeled_dataset, edge_dataset, batch_size) # train dataset history = model.fit( zipped_ds, epochs= current_epoch + max_epochs_per_graph, initial_epoch = current_epoch, validation_data=( (X_valid, tf.zeros_like(X_valid), tf.zeros_like(X_valid)), {"classifier": Y_valid_one_hot}, ), callbacks = [plotlosses], max_queue_size = 100, steps_per_epoch = batches_per_epoch, #verbose=0 ) current_epoch+=len(history.history['loss']) history_list.append(history) # save score class_pred = classifier.predict(encoder.predict(X_test)) class_acc = np.mean(np.argmax(class_pred, axis=1) == Y_test) np.save(save_folder / 'test_loss.npy', (np.nan, class_acc)) # save weights encoder.save_weights((save_folder / "encoder").as_posix()) classifier.save_weights((save_folder / "classifier").as_posix()) # save history with open(save_folder / 'history.pickle', 'wb') as file_pi: pickle.dump([i.history for i in history_list], file_pi) current_umap_iterations += 1 if len(history_list) > graph_patience+1: previous_history = [np.mean(i.history['val_classifier_accuracy']) for i in history_list] best_of_patience = np.max(previous_history[-graph_patience:]) best_of_previous = np.max(previous_history[:-graph_patience]) if (best_of_previous + min_graph_delta) > best_of_patience: print('Early stopping') #break plt.plot(previous_history) ``` ### save embedding ``` z = encoder.predict(X_train) reducer = umap.UMAP(verbose=True) embedding = reducer.fit_transform(z.reshape(len(z), np.product(np.shape(z)[1:]))) plt.scatter(embedding[:, 0], embedding[:, 1], c=Y_train.flatten(), s= 1, alpha = 0.1, cmap = plt.cm.tab10) plt.scatter(embedding[:, 0], embedding[:, 1], c=Y_train.flatten(), s= 1, alpha = 0.1, cmap = plt.cm.tab10) np.save(save_folder / 'train_embedding.npy', embedding) ```	github_jupyter
``` import sys sys.path.append('../scripts/') from robot import * from scipy.stats import multivariate_normal import random #追加 import copy class Particle: def __init__(self, init_pose, weight): self.pose = init_pose self.weight = weight def motion_update(self, nu, omega, time, noise_rate_pdf): ns = noise_rate_pdf.rvs() pnu = nu + ns[0]math.sqrt(abs(nu)/time) + ns[1]math.sqrt(abs(omega)/time) pomega = omega + ns[2]math.sqrt(abs(nu)/time) + ns[3]math.sqrt(abs(omega)/time) self.pose = IdealRobot.state_transition(pnu, pomega, time, self.pose) def observation_update(self, observation, envmap, distance_dev_rate, direction_dev): #変更 for d in observation: obs_pos = d[0] obs_id = d[1] ##パーティクルの位置と地図からランドマークの距離と方角を算出## pos_on_map = envmap.landmarks[obs_id].pos particle_suggest_pos = IdealCamera.observation_function(self.pose, pos_on_map) ##尤度の計算## distance_dev = distance_dev_rateparticle_suggest_pos[0] cov = np.diag(np.array([distance_dev2, direction_dev2])) self.weight = multivariate_normal(mean=particle_suggest_pos, cov=cov).pdf(obs_pos) class Mcl: def __init__(self, envmap, init_pose, num, motion_noise_stds={"nn":0.19, "no":0.001, "on":0.13, "oo":0.2}, \ distance_dev_rate=0.14, direction_dev=0.05): self.particles = [Particle(init_pose, 1.0/num) for i in range(num)] self.map = envmap self.distance_dev_rate = distance_dev_rate self.direction_dev = direction_dev v = motion_noise_stds c = np.diag([v["nn"]2, v["no"]2, v["on"]2, v["oo"]2]) self.motion_noise_rate_pdf = multivariate_normal(cov=c) def motion_update(self, nu, omega, time): for p in self.particles: p.motion_update(nu, omega, time, self.motion_noise_rate_pdf) def observation_update(self, observation): for p in self.particles: p.observation_update(observation, self.map, self.distance_dev_rate, self.direction_dev) self.resampling() def resampling(self): ###systematicsampling ws = np.cumsum([e.weight for e in self.particles]) #重みを累積して足していく（最後の要素が重みの合計になる） if ws[-1] < 1e-100: ws = [e + 1e-100 for e in ws] #重みの合計が0のときの処理 step = ws[-1]/len(self.particles) #正規化されていない場合はステップが「重みの合計値/N」になる r = np.random.uniform(0.0, step) cur_pos = 0 ps = [] #抽出するパーティクルのリスト while(len(ps) < len(self.particles)): if r < ws[cur_pos]: ps.append(self.particles[cur_pos]) #もしかしたらcur_posがはみ出るかもしれませんが例外処理は割愛で r += step else: cur_pos += 1 self.particles = [copy.deepcopy(e) for e in ps] #以下の処理は前の実装と同じ for p in self.particles: p.weight = 1.0/len(self.particles) def draw(self, ax, elems): xs = [p.pose[0] for p in self.particles] ys = [p.pose[1] for p in self.particles] vxs = [math.cos(p.pose[2])p.weightlen(self.particles) for p in self.particles] #重みを要素に反映 vys = [math.sin(p.pose[2])p.weightlen(self.particles) for p in self.particles] #重みを要素に反映 elems.append(ax.quiver(xs, ys, vxs, vys, \ angles='xy', scale_units='xy', scale=1.5, color="blue", alpha=0.5)) #変更 class EstimationAgent(Agent): def __init__(self, time_interval, nu, omega, estimator): super().__init__(nu, omega) self.estimator = estimator self.time_interval = time_interval self.prev_nu = 0.0 self.prev_omega = 0.0 def decision(self, observation=None): self.estimator.motion_update(self.prev_nu, self.prev_omega, self.time_interval) self.prev_nu, self.prev_omega = self.nu, self.omega self.estimator.observation_update(observation) return self.nu, self.omega def draw(self, ax, elems): self.estimator.draw(ax, elems) def trial(): time_interval = 0.1 world = World(30, time_interval, debug=False) ### 地図を生成して3つランドマークを追加 ### m = Map() for ln in [(-4,2), (2,-3), (3,3)]: m.append_landmark(Landmark(ln)) world.append(m) ### ロボットを作る ### initial_pose = np.array([0, 0, 0]).T estimator = Mcl(m, initial_pose, 100) #地図mを渡す a = EstimationAgent(time_interval, 0.2, 10.0/180math.pi, estimator) r = Robot(initial_pose, sensor=Camera(m), agent=a, color="red") world.append(r) world.draw() trial() ```	github_jupyter

Subsets and Splits

No community queries yet

The top public SQL queries from the community will appear here once available.