text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
# Sentiment Identification
## BACKGROUND
A large multinational corporation is seeking to automatically identify the sentiment that their customer base talks
about on social media. They would like to expand this capability into multiple languages. Many 3rd party tools exist for sentiment analysis, however, they need help with under-resourced languages.
## GOAL
Train a sentiment classifier (Positive, Negative, Neutral) on a corpus of the provided documents. Your goal is to
maximize accuracy. There is special interest in being able to accurately detect negative sentiment. The training data
includes documents from a wide variety of sources, not merely social media, and some of it may be inconsistently
labeled. Please describe the business outcomes in your work sample including how data limitations impact your results
and how these limitations could be addressed in a larger project.
## DATA
Link to data: http://archive.ics.uci.edu/ml/datasets/Roman+Urdu+Data+Set
```
import pandas as pd
pd.set_option('display.max_rows', 500)
pd.set_option('display.max_columns', 500)
pd.set_option('display.max_colwidth', None)
```
## Data Exploration
```
import emoji
import functools
import operator
import re
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import nltk
import spacy
import string
import re
import os
import tensorflow as tf
from tensorflow import keras
from imblearn.over_sampling import SMOTE
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_classif
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_classif
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import plot_confusion_matrix
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn.preprocessing import LabelEncoder
from sklearn.pipeline import Pipeline
DATA_DIR = os.path.abspath('../data/raw')
data_path = os.path.join(DATA_DIR, 'Roman Urdu Dataset.csv')
raw_df = pd.read_csv(data_path, skipinitialspace=True, names=['comment', 'sentiment', 'nan'], encoding='utf-8')
raw_df.tail()
#Print a concise summary of a DataFrame.
raw_df.info()
# Check missing data
raw_df.isnull().sum()
# For each column of the dataframe, we want to know numbers of unique attributes and the attributes values.
for column in raw_df.columns:
unique_attribute = (raw_df[column].unique())
print('{0:20s} {1:5d}\t'.format(column, len(unique_attribute)), unique_attribute[0:10])
```
## Initial Data Preprocessing
-- Drop the NaN column
-- Replace "Neative" - > "Negative"
```
cleaned_df = raw_df.copy()
cleaned_df.drop('nan',axis=1,inplace=True)
cleaned_df.dropna(axis=0, subset = ['comment'], inplace=True)
cleaned_df.replace(to_replace='Neative', value='Negative', inplace=True)
cleaned_df.dropna(subset=['sentiment'], inplace=True)
cleaned_df.head(5)
```
## Examine the class label imbalance
```
print(f'There are total {cleaned_df.shape[0]} comments')
print(f'There are {cleaned_df[cleaned_df["sentiment"] == "Positive"].shape[0]} Positive comments')
print(f'There are {cleaned_df[cleaned_df["sentiment"] == "Neutral"].shape[0]} Neutral comments')
print(f'There are {cleaned_df[cleaned_df["sentiment"] == "Negative"].shape[0]} Negative comments')
```
# Data Preprocessing:
### 1. Encode the Labels
### 2. Tokenization:
-- Applied lower case for each token
-- remove 0-9 numeric
-- remove the punctuation
-- (TO DO) Remove stop words
### 3. Train, Val, Test split
```
# Encode the output labels:
# Negative -> 0
# Neutral -> 1
# Positive -> 2
le = LabelEncoder()
le.fit(cleaned_df['sentiment'])
cleaned_df['sentiment']= le.transform(cleaned_df['sentiment'])
# tokenize for a single document
def tokenizer(doc):
""" Tokenize a single document"""
tokens = [word.lower() for word in nltk.word_tokenize(doc)]
tokens = [re.sub(r'[0-9]', '', word) for word in tokens]
tokens = [re.sub(r'['+string.punctuation+']', '', word) for word in tokens]
tokens = ' '.join(tokens)
em_split_emoji = emoji.get_emoji_regexp().split(tokens)
em_split_whitespace = [substr.split() for substr in em_split_emoji]
em_split = functools.reduce(operator.concat, em_split_whitespace)
tokens = ' '.join(em_split)
return tokens
cleaned_df['comment'] = cleaned_df['comment'].apply(lambda x: tokenizer(x))
train_df, test_df = train_test_split(cleaned_df, test_size=0.2,random_state=40)
train_labels = train_df['sentiment']
test_labels = test_df['sentiment']
train_features = train_df['comment']
test_features = test_df['comment']
```
# Gridsearch Pipeline: LogisticRegression
### TF-IDF
```
from typing import Any, List, Tuple
def vectorize(train_texts: List[str], train_labels, test_texts: List[str]) -> Tuple[Any, Any]:
""" Convert the document into word n-grams and vectorize it
:param train_texts: of training texts
:param train_labels: An array of labels from the training dataset
:param test_texts: List of test texts
:return: A tuple of vectorize training_text and vectorize test texts
"""
kwargs = {
'ngram_range': (1, 2),
'analyzer': 'word',
'min_df': MIN_DOCUMENT_FREQUENCY
}
# Use TfidfVectorizer to convert the raw documents to a matrix of TF-IDF features
#
vectorizer = TfidfVectorizer(**kwargs)
X_train = vectorizer.fit_transform(train_texts)
X_test = vectorizer.transform(test_texts)
selector = SelectKBest(f_classif, k=min(30000, X_train.shape[1]))
selector.fit(X_train, train_labels)
X_train = selector.transform(X_train)
X_test = selector.transform(X_test)
return X_train, X_test
from sklearn.ensemble import GradientBoostingClassifier
NGRAM_RANGE = (1, 2)
TOKEN_MODE = 'word'
MIN_DOCUMENT_FREQUENCY = 2
X_train, X_test = vectorize(train_features, train_labels, test_features)
# gridsearch
lr_tfidf = Pipeline([
('clf', LogisticRegression(random_state=40, solver = 'saga'))
])
C_OPTIONS = [1, 3, 5, 7, 10]
param_grid = [
{
'clf__penalty': ['l1', 'l2'],
'clf__C': C_OPTIONS
}
]
gs_lr_tfidf = GridSearchCV(lr_tfidf, param_grid,
scoring='accuracy',
cv=5,
verbose=2,
n_jobs=-1)
gs_lr_tfidf.fit(X_train, train_labels)
print('Best parameter set: %s ' % gs_lr_tfidf.best_params_)
print('CV Accuracy: %.3f' % gs_lr_tfidf.best_score_)
clf_lr = gs_lr_tfidf.best_estimator_
print('Test Accuracy: %.3f' % clf_lr.score(X_test, test_labels))
from sklearn.metrics import roc_auc_score, f1_score, precision_score, recall_score, confusion_matrix
y_pred_lr_tfidf = gs_lr_tfidf.predict(X_test)
y_test_exp = test_labels.to_numpy()
print('Precision Test for model: {}' .format(precision_score(y_test_exp, y_pred_lr_tfidf, average=None)))
print('Recall Test for model: {}' .format(recall_score(test_labels, y_pred_lr_tfidf, average=None)))
print('F1 Test for model: {}' .format(f1_score(test_labels, y_pred_lr_tfidf, average=None)))
print('Confusion matrix (Test):')
print(confusion_matrix(test_labels, y_pred_lr_tfidf))
title_options = [("Confusion matrix, without normalization", None),
("Normalization confusion matrix", 'true')]
classes_names = np.array(['Negative', 'Neutral', 'Positive'])
fig = plt.figure(figsize=(18,9))
nrows=1
ncols=2
for idx,value in enumerate(title_options):
ax = fig.add_subplot(nrows, ncols, idx+1)
disp= plot_confusion_matrix(clf_lr, X_test, test_labels,
display_labels=classes_names,
cmap=plt.cm.Blues,
normalize=value[1],
ax = ax)
disp.ax_.set_title(value[0])
```
# Multiclass Classification - > Binary Clasification
Since the model can only accurately predict negative sentiment about ~50% of time, I want to see if I can improve upon this result. One idea is to combine neutral sentiment and positive sentiment into one label and turn this analysis into a binary classification problem.
Since we have class imbalance issues when reforumlate to binary classifiaiton problems, use SMOTE to generate synthetic data within the minority class to have both classes have equal numbers of samples in training. The test accuracy improves from ~50% to ~70% on <b>negative sentiment </b>!
```
from imblearn.pipeline import Pipeline
# Combine the neutral/positive labels into one label -> 1
train_labels_binary = train_labels.map(lambda x: 1 if (x==2 or x==1) else 0)
test_labels_binary = test_labels.map(lambda x: 1 if (x==2 or x==1) else 0)
train_labels_binary.value_counts()
# Class Imbalance Issues
print(f'There are {train_labels_binary.value_counts()[0]} that can be classified as negative sentiments')
print(f'There are {train_labels_binary.value_counts()[1]} that can be classified as non-negative sentiments' )
# tfidf = TfidfVectorizer(strip_accents=None,
# lowercase=False,
# preprocessor=None)
param_grid = [{'clf__penalty': ['l1', 'l2'],
'clf__C': [0, 1, 3, 5, 7, 10]},
]
lr_tfidf = Pipeline([
('smote', SMOTE(sampling_strategy=1.0, random_state=5, k_neighbors=10)),
('clf', LogisticRegression(random_state=1, solver = 'saga'))
])
gs_lr_tfidf = GridSearchCV(lr_tfidf, param_grid,
scoring='accuracy',
cv=5,
verbose=2,
n_jobs=-1)
gs_lr_tfidf.fit(X_train, train_labels_binary)
print('Best parameter set: %s ' % gs_lr_tfidf.best_params_)
print('CV Accuracy: %.3f' % gs_lr_tfidf.best_score_)
clf_lr = gs_lr_tfidf.best_estimator_
print('Test Accuracy: %.3f' % clf_lr.score(X_test, test_labels_binary))
from sklearn.metrics import roc_auc_score, f1_score, precision_score, recall_score, confusion_matrix
y_pred_lr_tfidf = gs_lr_tfidf.predict(X_test)
y_test_exp_binary = test_labels_binary.to_numpy()
print('Precision Test for model: {}' .format(precision_score(y_test_exp_binary, y_pred_lr_tfidf, average=None)))
print('Recall Test for model: {}' .format(recall_score(test_labels_binary, y_pred_lr_tfidf, average=None)))
print('F1 Test for model: {}' .format(f1_score(test_labels_binary, y_pred_lr_tfidf, average=None)))
print('ROC AUC Train: %.3f for Logistic Regression' % roc_auc_score(y_test_exp_binary, y_pred_lr_tfidf, average=None))
print('Confusion matrix (Test):')
print(confusion_matrix(test_labels_binary, y_pred_lr_tfidf))
title_options = [("Confusion matrix, without normalization", None),
("Normalization confusion matrix", 'true')]
classes_names = np.array(['Negative', 'Positive/Neutral'])
fig = plt.figure(figsize=(18,9))
nrows=1
ncols=2
for idx,value in enumerate(title_options):
ax = fig.add_subplot(nrows, ncols, idx+1)
disp= plot_confusion_matrix(clf_lr, X_test, test_labels_binary,
display_labels=classes_names,
cmap=plt.cm.Blues,
normalize=value[1],
ax = ax)
disp.ax_.set_title(value[0])
```
# Gridsearch Pipeline: Naive Bayes
```
tfidf = TfidfVectorizer(strip_accents=None,
lowercase=False,
preprocessor=None)
param_grid = [
{
'clf__alpha': [0.25, 0.3, 0.35, 0.4, 0.45, 0.50]
},
]
nb_tfidf = Pipeline([
#('vect', tfidf),
('smote', SMOTE(sampling_strategy=1.0, random_state=5, k_neighbors=3)),
('clf', MultinomialNB())
])
gs_nb_tfidf = GridSearchCV(nb_tfidf, param_grid,
scoring='accuracy',
cv=5,
verbose=2,
n_jobs=-1)
gs_nb_tfidf.fit(X_train, train_labels_binary)
print('Best parameter set: %s ' % gs_nb_tfidf.best_params_)
print('CV Accuracy: %.3f' % gs_nb_tfidf.best_score_)
clf_nb = gs_nb_tfidf.best_estimator_
print('Test Accuracy: %.3f' % clf_nb.score(X_test, test_labels_binary))
from sklearn.metrics import roc_auc_score, f1_score, precision_score, recall_score, confusion_matrix
y_pred_nb_tfidf = gs_nb_tfidf.predict(X_test)
y_test_exp_binary = test_labels_binary.to_numpy()
print('Precision Test for model: {}' .format(precision_score(y_test_exp_binary, y_pred_nb_tfidf, average=None)))
print('Recall Test for model: {}' .format(recall_score(test_labels_binary, y_pred_nb_tfidf, average=None)))
print('F1 Test for model: {}' .format(f1_score(test_labels_binary, y_pred_nb_tfidf, average=None)))
print('ROC AUC Train: %.3f for Naive Bayes' % roc_auc_score(y_test_exp_binary, y_pred_nb_tfidf, average=None))
print('Confusion matrix (Test):')
print(confusion_matrix(test_labels_binary, y_pred_nb_tfidf))
title_options = [("Confusion matrix, without normalization", None),
("Normalization confusion matrix", 'true')]
classes_names = np.array(['Negative', 'Positive/Neutral'])
fig = plt.figure(figsize=(18,9))
nrows=1
ncols=2
for idx,value in enumerate(title_options):
ax = fig.add_subplot(nrows, ncols, idx+1)
disp= plot_confusion_matrix(clf_nb, X_test, test_labels_binary,
#display_labels=sorted(test_labels_binary.unique()),
cmap=plt.cm.Blues,
display_labels=classes_names,
normalize=value[1],
ax = ax)
disp.ax_.set_title(value[0])
```
|
github_jupyter
|
# Feature Engineering

## Objective
Data preprocessing and engineering techniques generally refer to the addition, deletion, or transformation of data.
The time spent on identifying data engineering needs can be significant and requires you to spend substantial time understanding your data...
> _"Live with your data before you plunge into modeling"_ - Leo Breiman
In this module we introduce:
- an example of preprocessing numerical features,
- two common ways to preprocess categorical features,
- using a scikit-learn pipeline to chain preprocessing and model training.
## Basic prerequisites
Let's go ahead and import a couple required libraries and import our data.
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;"><b>Note</b></p>
<p class="last">We will import additional libraries and functions as we proceed but we do so at the time of using the libraries and functions as that provides better learning context.</p>
</div>
```
import pandas as pd
# to display nice model diagram
from sklearn import set_config
set_config(display='diagram')
# import data
adult_census = pd.read_csv('../data/adult-census.csv')
# separate feature & target data
target = adult_census['class']
features = adult_census.drop(columns='class')
```
## Selection based on data types
Typically, data types fall into two categories:
* __Numeric__: a quantity represented by a real or integer number.
* __Categorical__: a discrete value, typically represented by string labels (but not only) taken from a finite list of possible choices.
```
features.dtypes
```
<div class="admonition warning alert alert-danger">
<p class="first admonition-title" style="font-weight: bold;"><b>Warning</b></p>
<p class="last">Do not take dtype output at face value! It is possible to have categorical data represented by numbers (i.e. <tt class="docutils literal">education_num</tt>. And <tt class="docutils literal">object</tt> dtypes can represent data that would be better represented as continuous numbers (i.e. dates).
Bottom line, always understand how your data is representing your features!
</p>
</div>
We can separate categorical and numerical variables using their data types to identify them.
There are a few ways we can do this. Here, we make use of [`make_column_selector`](https://scikit-learn.org/stable/modules/generated/sklearn.compose.make_column_selector.html) helper to select the corresponding columns.
```
from sklearn.compose import make_column_selector as selector
# create selector object based on data type
numerical_columns_selector = selector(dtype_exclude=object)
categorical_columns_selector = selector(dtype_include=object)
# get columns of interest
numerical_columns = numerical_columns_selector(features)
categorical_columns = categorical_columns_selector(features)
# results in a list containing relevant column names
numerical_columns
```
## Preprocessing numerical data
Scikit-learn works "out of the box" with numeric features. However, some algorithms make some assumptions regarding the distribution of our features.
We see that our numeric features span across different ranges:
```
numerical_features = features[numerical_columns]
numerical_features.describe()
```
Normalizing our features so that they have mean = 0 and standard deviation = 1, helps to ensure our features align to algorithm assumptions.
<div class="admonition tip alert alert-warning">
<p class="first admonition-title" style="font-weight: bold;"><b>Tip</b></p>
<p>Here are some reasons for scaling features:</p>
<ul class="last simple">
<li>Models that rely on the distance between a pair of samples, for instance
k-nearest neighbors, should be trained on normalized features to make each
feature contribute approximately equally to the distance computations.</li>
<li>Many models such as logistic regression use a numerical solver (based on
gradient descent) to find their optimal parameters. This solver converges
faster when the features are scaled.</li>
</ul>
</div>
Whether or not a machine learning model requires normalization of the features depends on the model family. Linear models such as logistic regression generally benefit from scaling the features while other models such as tree-based models (i.e. decision trees, random forests) do not need such preprocessing (but will not suffer from it).
We can apply such normalization using a scikit-learn transformer called [`StandardScaler`](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html).
```
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(numerical_features)
```
The `fit` method for transformers is similar to the `fit` method for
predictors. The main difference is that the former has a single argument (the
feature matrix), whereas the latter has two arguments (the feature matrix and the
target).

In this case, the algorithm needs to compute the mean and standard deviation
for each feature and store them into some NumPy arrays. Here, these
statistics are the model states.
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;"><b>Note</b></p>
<p class="last">The fact that the model states of this scaler are arrays of means and
standard deviations is specific to the <tt class="docutils literal">StandardScaler</tt>. Other
scikit-learn transformers will compute different statistics and store them
as model states, in the same fashion.</p>
</div>
We can inspect the computed means and standard deviations.
```
scaler.mean_
scaler.scale_
```
<div class="admonition tip alert alert-warning">
<p class="first admonition-title" style="font-weight: bold;"><b>Tip</b></p>
<p class="last">Scikit-learn convention: if an attribute is learned from the data, its name
ends with an underscore (i.e. <tt class="docutils literal">_</tt>), as in <tt class="docutils literal">mean_</tt> and <tt class="docutils literal">scale_</tt> for the
<tt class="docutils literal">StandardScaler</tt>.</p>
</ul>
</div>
Once we have called the `fit` method, we can perform data transformation by
calling the method `transform`.
```
numerical_features_scaled = scaler.transform(numerical_features)
numerical_features_scaled
```
Let's illustrate the internal mechanism of the `transform` method and put it
to perspective with what we already saw with predictors.

The `transform` method for transformers is similar to the `predict` method
for predictors. It uses a predefined function, called a **transformation
function**, and uses the model states and the input data. However, instead of
outputting predictions, the job of the `transform` method is to output a
transformed version of the input data.
Finally, the method `fit_transform` is a shorthand method to call
successively `fit` and then `transform`.

```
# fitting and transforming in one step
scaler.fit_transform(numerical_features)
```
Notice that the mean of all the columns is close to 0 and the standard deviation in all cases is close to 1:
```
numerical_features = pd.DataFrame(
numerical_features_scaled,
columns=numerical_columns
)
numerical_features.describe()
```
## Model pipelines
We can easily combine sequential operations with a scikit-learn
[`Pipeline`](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html), which chains together operations and is used as any other
classifier or regressor. The helper function [`make_pipeline`](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.make_pipeline.html#sklearn.pipeline.make_pipeline) will create a
`Pipeline`: it takes as arguments the successive transformations to perform,
followed by the classifier or regressor model.
```
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
model = make_pipeline(StandardScaler(), LogisticRegression())
model
```
Let's divide our data into train and test sets and then apply and score our logistic regression model:
```
from sklearn.model_selection import train_test_split
# split our data into train & test
X_train, X_test, y_train, y_test = train_test_split(numerical_features, target, random_state=123)
# fit our pipeline model
model.fit(X_train, y_train)
# score our model on the test data
model.score(X_test, y_test)
```
## Preprocessing categorical data
Unfortunately, Scikit-learn does not accept categorical features in their raw form. Consequently, we need to transform them into numerical representations.
The following presents typical ways of dealing with categorical variables by encoding them, namely **ordinal encoding** and **one-hot encoding**.
### Encoding ordinal categories
The most intuitive strategy is to encode each category with a different
number. The [`OrdinalEncoder`](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.OrdinalEncoder.html) will transform the data in such manner.
We will start by encoding a single column to understand how the encoding
works.
```
from sklearn.preprocessing import OrdinalEncoder
# let's illustrate with the 'education' feature
education_column = features[["education"]]
encoder = OrdinalEncoder()
education_encoded = encoder.fit_transform(education_column)
education_encoded
```
We see that each category in `"education"` has been replaced by a numeric
value. We could check the mapping between the categories and the numerical
values by checking the fitted attribute `categories_`.
```
encoder.categories_
```
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;"><b>Note</b></p>
<p class="last"><tt class="docutils literal">OrindalEncoder</tt> transforms the category value into the corresponding index value of <tt class="docutils literal">encoder.categories_</tt>.</p>
</div>
However, be careful when applying this encoding strategy:
using this integer representation leads downstream predictive models
to assume that the values are ordered (0 < 1 < 2 < 3... for instance).
By default, `OrdinalEncoder` uses a lexicographical strategy to map string
category labels to integers. This strategy is arbitrary and often
meaningless. For instance, suppose the dataset has a categorical variable
named `"size"` with categories such as "S", "M", "L", "XL". We would like the
integer representation to respect the meaning of the sizes by mapping them to
increasing integers such as `0, 1, 2, 3`.
However, the lexicographical strategy used by default would map the labels
"S", "M", "L", "XL" to 2, 1, 0, 3, by following the alphabetical order.
The `OrdinalEncoder` class accepts a `categories` argument to
pass categories in the expected ordering explicitly (`categories[i]` holds the categories expected in the ith column).
```
ed_levels = [' Preschool', ' 1st-4th', ' 5th-6th', ' 7th-8th', ' 9th', ' 10th', ' 11th',
' 12th', ' HS-grad', ' Prof-school', ' Some-college', ' Assoc-acdm',
' Assoc-voc', ' Bachelors', ' Masters', ' Doctorate']
encoder = OrdinalEncoder(categories=[ed_levels])
education_encoded = encoder.fit_transform(education_column)
education_encoded
encoder.categories_
```
If a categorical variable does not carry any meaningful order information
then this encoding might be misleading to downstream statistical models and
you might consider using one-hot encoding instead (discussed next).
### Ecoding nominal categories
[`OneHotEncoder`](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.OneHotEncoder.html) is an alternative encoder that converts the categorical levels into new columns.
We will start by encoding a single feature (e.g. `"education"`) to illustrate
how the encoding works.
```
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder(sparse=False)
education_encoded = encoder.fit_transform(education_column)
education_encoded
```
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;"><b>Note</b></p>
<p><tt class="docutils literal">sparse=False</tt> is used in the <tt class="docutils literal">OneHotEncoder</tt> for didactic purposes, namely
easier visualization of the data.</p>
<p class="last">Sparse matrices are efficient data structures when most of your matrix
elements are zero. They won't be covered in detail in this workshop. If you
want more details about them, you can look at
<a class="reference external" href="https://scipy-lectures.org/advanced/scipy_sparse/introduction.html#why-sparse-matrices">this</a>.</p>
</div>
Viewing this as a data frame provides a more intuitive illustration:
```
feature_names = encoder.get_feature_names(input_features=["education"])
pd.DataFrame(education_encoded, columns=feature_names)
```
As we can see, each category (unique value) became a column; the encoding
returned, for each sample, a 1 to specify which category it belongs to.
Let's apply this encoding to all the categorical features:
```
# get all categorical features
categorical_features = features[categorical_columns]
# one-hot encode all features
categorical_features_encoded = encoder.fit_transform(categorical_features)
# view as a data frame
columns_encoded = encoder.get_feature_names(categorical_features.columns)
pd.DataFrame(categorical_features_encoded, columns=columns_encoded).head()
```
<div class="admonition warning alert alert-danger">
<p class="first admonition-title" style="font-weight: bold;"><b>Warning</b></p>
<p class="last">One-hot encoding can significantly increase the number of features in our data. In this case we went from 8 features to 102! If you have a data set with many categorical variables and those categorical variables in turn have many unique levels, the number of features can explode. In these cases you may want to explore ordinal encoding or some other alternative.</p>
</ul>
</div>
### Choosing an encoding strategy
Choosing an encoding strategy will depend on the underlying models and the
type of categories (i.e. ordinal vs. nominal).
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;"><b>Tip</b></p>
<p class="last">In general <tt class="docutils literal">OneHotEncoder</tt> is the encoding strategy used when the
downstream models are <strong>linear models</strong> while <tt class="docutils literal">OrdinalEncoder</tt> is often a
good strategy with <strong>tree-based models</strong>.</p>
</div>
Using an `OrdinalEncoder` will output ordinal categories. This means
that there is an order in the resulting categories (e.g. `0 < 1 < 2`). The
impact of violating this ordering assumption is really dependent on the
downstream models. Linear models will be impacted by misordered categories
while tree-based models will not.
You can still use an `OrdinalEncoder` with linear models but you need to be
sure that:
- the original categories (before encoding) have an ordering;
- the encoded categories follow the same ordering than the original
categories.
One-hot encoding categorical variables with high cardinality can cause
computational inefficiency in tree-based models. Because of this, it is not recommended
to use `OneHotEncoder` in such cases even if the original categories do not
have a given order.
## Using numerical and categorical variables together
Now let's look at how to combine some of these tasks so we can preprocess both numeric and categorical data.
First, let's get our train & test data established:
```
# drop the duplicated column `"education-num"` as stated in the data exploration notebook
features = features.drop(columns='education-num')
# create selector object based on data type
numerical_columns_selector = selector(dtype_exclude=object)
categorical_columns_selector = selector(dtype_include=object)
# get columns of interest
numerical_columns = numerical_columns_selector(features)
categorical_columns = categorical_columns_selector(features)
# split into train & test sets
X_train, X_test, y_train, y_test = train_test_split(features, target, random_state=123)
```
Scikit-learn provides a [`ColumnTransformer`](https://scikit-learn.org/stable/modules/generated/sklearn.compose.ColumnTransformer.html) class which will send specific
columns to a specific transformer, making it easy to fit a single predictive
model on a dataset that combines both kinds of variables together.
We first define the columns depending on their data type:
* **one-hot encoding** will be applied to categorical columns.
* **numerical scaling** numerical features which will be standardized.
We then create our `ColumnTransfomer` by specifying three values:
1. the preprocessor name,
2. the transformer, and
3. the columns.
First, let's create the preprocessors for the numerical and categorical
parts.
```
categorical_preprocessor = OneHotEncoder(handle_unknown="ignore")
numerical_preprocessor = StandardScaler()
```
<div class="admonition tip alert alert-warning">
<p class="first admonition-title" style="font-weight: bold;"><b>Tip</b></p>
<p class="last">We can use the <tt class="docutils literal">handle_unknown</tt> parameter to ignore rare categories that may show up in test data but were not present in the training data.</p>
</ul>
</div>
Now, we create the transformer and associate each of these preprocessors
with their respective columns.
```
from sklearn.compose import ColumnTransformer
preprocessor = ColumnTransformer([
('one-hot-encoder', categorical_preprocessor, categorical_columns),
('standard_scaler', numerical_preprocessor, numerical_columns)
])
```
We can take a minute to represent graphically the structure of a
`ColumnTransformer`:

A `ColumnTransformer` does the following:
* It **splits the columns** of the original dataset based on the column names
or indices provided. We will obtain as many subsets as the number of
transformers passed into the `ColumnTransformer`.
* It **transforms each subset**. A specific transformer is applied to
each subset: it will internally call `fit_transform` or `transform`. The
output of this step is a set of transformed datasets.
* It then **concatenates the transformed datasets** into a single dataset.
The important thing is that `ColumnTransformer` is like any other
scikit-learn transformer. In particular it can be combined with a classifier
in a `Pipeline`:
```
model = make_pipeline(preprocessor, LogisticRegression(max_iter=500))
model
```
<div class="admonition warning alert alert-danger">
<p class="first admonition-title" style="font-weight: bold;"><b>Warning</b></p>
<p class="last">Including non-scaled data can cause some algorithms to iterate
longer in order to converge. Since our categorical features are not scaled it's often recommended to increase the number of allowed iterations for linear models.</p>
</div>
```
# fit our model
_ = model.fit(X_train, y_train)
# score on test set
model.score(X_test, y_test)
```
## Wrapping up
Unfortunately, we only have time to scratch the surface of feature engineering in this workshop. However, this module should provide you with a strong foundation of how to apply the more common feature preprocessing tasks.
<div class="admonition tip alert alert-warning">
<p class="first admonition-title" style="font-weight: bold;"><b>Tip</b></p>
<p class="last">Scikit-learn provides many feature engineering options. Learn more here: <a href="https://scikit-learn.org/stable/modules/preprocessing.html">https://scikit-learn.org/stable/modules/preprocessing.html</a></p>
</ul>
</div>
In this module we learned how to:
- normalize numerical features with `StandardScaler`,
- ordinal and one-hot encode categorical features with `OrdinalEncoder` and `OneHotEncoder`, and
- chain feature preprocessing and model training steps together with `ColumnTransformer` and `make_pipeline`.
|
github_jupyter
|
ERROR: type should be string, got "https://keras.io/examples/structured_data/structured_data_classification_from_scratch/\n\nmudar nome das coisas. Editar como quero // para de servir de exemplo pra o futuro..\n\n```\nimport tensorflow as tf\nimport numpy as np\nimport pandas as pd\nfrom tensorflow import keras\nfrom tensorflow.keras import layers\nimport pydot\nfile_url = \"http://storage.googleapis.com/download.tensorflow.org/data/heart.csv\"\ndataframe = pd.read_csv(file_url)\ndataframe.head()\nval_dataframe = dataframe.sample(frac=0.2, random_state=1337)\ntrain_dataframe = dataframe.drop(val_dataframe.index)\ndef dataframe_to_dataset(dataframe):\n dataframe = dataframe.copy()\n labels = dataframe.pop(\"target\")\n ds = tf.data.Dataset.from_tensor_slices((dict(dataframe), labels))\n ds = ds.shuffle(buffer_size=len(dataframe))\n return ds\n\n\ntrain_ds = dataframe_to_dataset(train_dataframe)\nval_ds = dataframe_to_dataset(val_dataframe)\n```\n\nfor x, y in train_ds.take(1):\n print(\"Input:\", x)\n print(\"Target:\", y)\n \n |||||| entender isto melhor\n\n```\ntrain_ds = train_ds.batch(32)\nval_ds = val_ds.batch(32)\nfrom tensorflow.keras.layers.experimental.preprocessing import Normalization\nfrom tensorflow.keras.layers.experimental.preprocessing import CategoryEncoding\nfrom tensorflow.keras.layers.experimental.preprocessing import StringLookup\n\n\ndef encode_numerical_feature(feature, name, dataset):\n # Create a Normalization layer for our feature\n normalizer = Normalization()\n\n # Prepare a Dataset that only yields our feature\n feature_ds = dataset.map(lambda x, y: x[name])\n feature_ds = feature_ds.map(lambda x: tf.expand_dims(x, -1))\n\n # Learn the statistics of the data\n normalizer.adapt(feature_ds)\n\n # Normalize the input feature\n encoded_feature = normalizer(feature)\n return encoded_feature\n\n\ndef encode_string_categorical_feature(feature, name, dataset):\n # Create a StringLookup layer which will turn strings into integer indices\n index = StringLookup()\n\n # Prepare a Dataset that only yields our feature\n feature_ds = dataset.map(lambda x, y: x[name])\n feature_ds = feature_ds.map(lambda x: tf.expand_dims(x, -1))\n\n # Learn the set of possible string values and assign them a fixed integer index\n index.adapt(feature_ds)\n\n # Turn the string input into integer indices\n encoded_feature = index(feature)\n\n # Create a CategoryEncoding for our integer indices\n encoder = CategoryEncoding(output_mode=\"binary\")\n\n # Prepare a dataset of indices\n feature_ds = feature_ds.map(index)\n\n # Learn the space of possible indices\n encoder.adapt(feature_ds)\n\n # Apply one-hot encoding to our indices\n encoded_feature = encoder(encoded_feature)\n return encoded_feature\n\n\ndef encode_integer_categorical_feature(feature, name, dataset):\n # Create a CategoryEncoding for our integer indices\n encoder = CategoryEncoding(output_mode=\"binary\")\n\n # Prepare a Dataset that only yields our feature\n feature_ds = dataset.map(lambda x, y: x[name])\n feature_ds = feature_ds.map(lambda x: tf.expand_dims(x, -1))\n\n # Learn the space of possible indices\n encoder.adapt(feature_ds)\n\n # Apply one-hot encoding to our indices\n encoded_feature = encoder(feature)\n return encoded_feature\n# Categorical features encoded as integers\nsex = keras.Input(shape=(1,), name=\"sex\", dtype=\"int64\")\ncp = keras.Input(shape=(1,), name=\"cp\", dtype=\"int64\")\nfbs = keras.Input(shape=(1,), name=\"fbs\", dtype=\"int64\")\nrestecg = keras.Input(shape=(1,), name=\"restecg\", dtype=\"int64\")\nexang = keras.Input(shape=(1,), name=\"exang\", dtype=\"int64\")\nca = keras.Input(shape=(1,), name=\"ca\", dtype=\"int64\")\n\n# Categorical feature encoded as string\nthal = keras.Input(shape=(1,), name=\"thal\", dtype=\"string\")\n\n# Numerical features\nage = keras.Input(shape=(1,), name=\"age\")\ntrestbps = keras.Input(shape=(1,), name=\"trestbps\")\nchol = keras.Input(shape=(1,), name=\"chol\")\nthalach = keras.Input(shape=(1,), name=\"thalach\")\noldpeak = keras.Input(shape=(1,), name=\"oldpeak\")\nslope = keras.Input(shape=(1,), name=\"slope\")\n\nall_inputs = [\n sex,\n cp,\n fbs,\n restecg,\n exang,\n ca,\n thal,\n age,\n trestbps,\n chol,\n thalach,\n oldpeak,\n slope,\n]\n\n# Integer categorical features\nsex_encoded = encode_integer_categorical_feature(sex, \"sex\", train_ds)\ncp_encoded = encode_integer_categorical_feature(cp, \"cp\", train_ds)\nfbs_encoded = encode_integer_categorical_feature(fbs, \"fbs\", train_ds)\nrestecg_encoded = encode_integer_categorical_feature(restecg, \"restecg\", train_ds)\nexang_encoded = encode_integer_categorical_feature(exang, \"exang\", train_ds)\nca_encoded = encode_integer_categorical_feature(ca, \"ca\", train_ds)\n\n# String categorical features\nthal_encoded = encode_string_categorical_feature(thal, \"thal\", train_ds)\n\n# Numerical features\nage_encoded = encode_numerical_feature(age, \"age\", train_ds)\ntrestbps_encoded = encode_numerical_feature(trestbps, \"trestbps\", train_ds)\nchol_encoded = encode_numerical_feature(chol, \"chol\", train_ds)\nthalach_encoded = encode_numerical_feature(thalach, \"thalach\", train_ds)\noldpeak_encoded = encode_numerical_feature(oldpeak, \"oldpeak\", train_ds)\nslope_encoded = encode_numerical_feature(slope, \"slope\", train_ds)\n\nall_features = layers.concatenate(\n [\n sex_encoded,\n cp_encoded,\n fbs_encoded,\n restecg_encoded,\n exang_encoded,\n slope_encoded,\n ca_encoded,\n thal_encoded,\n age_encoded,\n trestbps_encoded,\n chol_encoded,\n thalach_encoded,\n oldpeak_encoded,\n ]\n)\nx = layers.Dense(32, activation=\"relu\")(all_features)\nx = layers.Dropout(0.5)(x)\noutput = layers.Dense(1, activation=\"sigmoid\")(x)\nmodel = keras.Model(all_inputs, output)\nmodel.compile(\"adam\", \"binary_crossentropy\", metrics=[\"accuracy\"])\nmodel.fit(train_ds, epochs=50, validation_data=val_ds)\nsample = {\n \"age\": 60,\n \"sex\": 1,\n \"cp\": 1,\n \"trestbps\": 145,\n \"chol\": 233,\n \"fbs\": 1,\n \"restecg\": 2,\n \"thalach\": 150,\n \"exang\": 0,\n \"oldpeak\": 2.3,\n \"slope\": 3,\n \"ca\": 0,\n \"thal\": \"fixed\",\n}\n\ninput_dict = {name: tf.convert_to_tensor([value]) for name, value in sample.items()}\npredictions = model.predict(input_dict)\n\nprint(\n \"This particular patient had a %.1f percent probability \"\n \"of having a heart disease, as evaluated by our model.\" % (100 * predictions[0][0],)\n)\n```\n\n" |
github_jupyter
|
Greyscale ℓ1-TV Denoising
=========================
This example demonstrates the use of class [tvl1.TVL1Denoise](http://sporco.rtfd.org/en/latest/modules/sporco.admm.tvl1.html#sporco.admm.tvl1.TVL1Denoise) for removing salt & pepper noise from a greyscale image using Total Variation regularization with an ℓ1 data fidelity term (ℓ1-TV denoising).
```
from __future__ import print_function
from builtins import input
import numpy as np
from sporco.admm import tvl1
from sporco import util
from sporco import signal
from sporco import metric
from sporco import plot
plot.config_notebook_plotting()
```
Load reference image.
```
img = util.ExampleImages().image('monarch.png', scaled=True,
idxexp=np.s_[:,160:672], gray=True)
```
Construct test image corrupted by 20% salt & pepper noise.
```
np.random.seed(12345)
imgn = signal.spnoise(img, 0.2)
```
Set regularization parameter and options for ℓ1-TV denoising solver. The regularization parameter used here has been manually selected for good performance.
```
lmbda = 8e-1
opt = tvl1.TVL1Denoise.Options({'Verbose': True, 'MaxMainIter': 200,
'RelStopTol': 5e-3, 'gEvalY': False,
'AutoRho': {'Enabled': True}})
```
Create solver object and solve, returning the the denoised image ``imgr``.
```
b = tvl1.TVL1Denoise(imgn, lmbda, opt)
imgr = b.solve()
```
Display solve time and denoising performance.
```
print("TVL1Denoise solve time: %5.2f s" % b.timer.elapsed('solve'))
print("Noisy image PSNR: %5.2f dB" % metric.psnr(img, imgn))
print("Denoised image PSNR: %5.2f dB" % metric.psnr(img, imgr))
```
Display reference, corrupted, and denoised images.
```
fig = plot.figure(figsize=(20, 5))
plot.subplot(1, 3, 1)
plot.imview(img, title='Reference', fig=fig)
plot.subplot(1, 3, 2)
plot.imview(imgn, title='Corrupted', fig=fig)
plot.subplot(1, 3, 3)
plot.imview(imgr, title=r'Restored ($\ell_1$-TV)', fig=fig)
fig.show()
```
Get iterations statistics from solver object and plot functional value, ADMM primary and dual residuals, and automatically adjusted ADMM penalty parameter against the iteration number.
```
its = b.getitstat()
fig = plot.figure(figsize=(20, 5))
plot.subplot(1, 3, 1)
plot.plot(its.ObjFun, xlbl='Iterations', ylbl='Functional', fig=fig)
plot.subplot(1, 3, 2)
plot.plot(np.vstack((its.PrimalRsdl, its.DualRsdl)).T,
ptyp='semilogy', xlbl='Iterations', ylbl='Residual',
lgnd=['Primal', 'Dual'], fig=fig)
plot.subplot(1, 3, 3)
plot.plot(its.Rho, xlbl='Iterations', ylbl='Penalty Parameter', fig=fig)
fig.show()
```
|
github_jupyter
|
```
%matplotlib inline
```
# Out-of-core classification of text documents
This is an example showing how scikit-learn can be used for classification
using an out-of-core approach: learning from data that doesn't fit into main
memory. We make use of an online classifier, i.e., one that supports the
partial_fit method, that will be fed with batches of examples. To guarantee
that the features space remains the same over time we leverage a
HashingVectorizer that will project each example into the same feature space.
This is especially useful in the case of text classification where new
features (words) may appear in each batch.
```
# Authors: Eustache Diemert <[email protected]>
# @FedericoV <https://github.com/FedericoV/>
# License: BSD 3 clause
from glob import glob
import itertools
import os.path
import re
import tarfile
import time
import sys
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
from html.parser import HTMLParser
from urllib.request import urlretrieve
from sklearn.datasets import get_data_home
from sklearn.feature_extraction.text import HashingVectorizer
from sklearn.linear_model import SGDClassifier
from sklearn.linear_model import PassiveAggressiveClassifier
from sklearn.linear_model import Perceptron
from sklearn.naive_bayes import MultinomialNB
def _not_in_sphinx():
# Hack to detect whether we are running by the sphinx builder
return '__file__' in globals()
```
Reuters Dataset related routines
--------------------------------
The dataset used in this example is Reuters-21578 as provided by the UCI ML
repository. It will be automatically downloaded and uncompressed on first
run.
```
class ReutersParser(HTMLParser):
"""Utility class to parse a SGML file and yield documents one at a time."""
def __init__(self, encoding='latin-1'):
HTMLParser.__init__(self)
self._reset()
self.encoding = encoding
def handle_starttag(self, tag, attrs):
method = 'start_' + tag
getattr(self, method, lambda x: None)(attrs)
def handle_endtag(self, tag):
method = 'end_' + tag
getattr(self, method, lambda: None)()
def _reset(self):
self.in_title = 0
self.in_body = 0
self.in_topics = 0
self.in_topic_d = 0
self.title = ""
self.body = ""
self.topics = []
self.topic_d = ""
def parse(self, fd):
self.docs = []
for chunk in fd:
self.feed(chunk.decode(self.encoding))
for doc in self.docs:
yield doc
self.docs = []
self.close()
def handle_data(self, data):
if self.in_body:
self.body += data
elif self.in_title:
self.title += data
elif self.in_topic_d:
self.topic_d += data
def start_reuters(self, attributes):
pass
def end_reuters(self):
self.body = re.sub(r'\s+', r' ', self.body)
self.docs.append({'title': self.title,
'body': self.body,
'topics': self.topics})
self._reset()
def start_title(self, attributes):
self.in_title = 1
def end_title(self):
self.in_title = 0
def start_body(self, attributes):
self.in_body = 1
def end_body(self):
self.in_body = 0
def start_topics(self, attributes):
self.in_topics = 1
def end_topics(self):
self.in_topics = 0
def start_d(self, attributes):
self.in_topic_d = 1
def end_d(self):
self.in_topic_d = 0
self.topics.append(self.topic_d)
self.topic_d = ""
def stream_reuters_documents(data_path=None):
"""Iterate over documents of the Reuters dataset.
The Reuters archive will automatically be downloaded and uncompressed if
the `data_path` directory does not exist.
Documents are represented as dictionaries with 'body' (str),
'title' (str), 'topics' (list(str)) keys.
"""
DOWNLOAD_URL = ('http://archive.ics.uci.edu/ml/machine-learning-databases/'
'reuters21578-mld/reuters21578.tar.gz')
ARCHIVE_FILENAME = 'reuters21578.tar.gz'
if data_path is None:
data_path = os.path.join(get_data_home(), "reuters")
if not os.path.exists(data_path):
"""Download the dataset."""
print("downloading dataset (once and for all) into %s" %
data_path)
os.mkdir(data_path)
def progress(blocknum, bs, size):
total_sz_mb = '%.2f MB' % (size / 1e6)
current_sz_mb = '%.2f MB' % ((blocknum * bs) / 1e6)
if _not_in_sphinx():
sys.stdout.write(
'\rdownloaded %s / %s' % (current_sz_mb, total_sz_mb))
archive_path = os.path.join(data_path, ARCHIVE_FILENAME)
urlretrieve(DOWNLOAD_URL, filename=archive_path,
reporthook=progress)
if _not_in_sphinx():
sys.stdout.write('\r')
print("untarring Reuters dataset...")
tarfile.open(archive_path, 'r:gz').extractall(data_path)
print("done.")
parser = ReutersParser()
for filename in glob(os.path.join(data_path, "*.sgm")):
for doc in parser.parse(open(filename, 'rb')):
yield doc
```
Main
----
Create the vectorizer and limit the number of features to a reasonable
maximum
```
vectorizer = HashingVectorizer(decode_error='ignore', n_features=2 ** 18,
alternate_sign=False)
# Iterator over parsed Reuters SGML files.
data_stream = stream_reuters_documents()
# We learn a binary classification between the "acq" class and all the others.
# "acq" was chosen as it is more or less evenly distributed in the Reuters
# files. For other datasets, one should take care of creating a test set with
# a realistic portion of positive instances.
all_classes = np.array([0, 1])
positive_class = 'acq'
# Here are some classifiers that support the `partial_fit` method
partial_fit_classifiers = {
'SGD': SGDClassifier(max_iter=5),
'Perceptron': Perceptron(),
'NB Multinomial': MultinomialNB(alpha=0.01),
'Passive-Aggressive': PassiveAggressiveClassifier(),
}
def get_minibatch(doc_iter, size, pos_class=positive_class):
"""Extract a minibatch of examples, return a tuple X_text, y.
Note: size is before excluding invalid docs with no topics assigned.
"""
data = [('{title}\n\n{body}'.format(**doc), pos_class in doc['topics'])
for doc in itertools.islice(doc_iter, size)
if doc['topics']]
if not len(data):
return np.asarray([], dtype=int), np.asarray([], dtype=int)
X_text, y = zip(*data)
return X_text, np.asarray(y, dtype=int)
def iter_minibatches(doc_iter, minibatch_size):
"""Generator of minibatches."""
X_text, y = get_minibatch(doc_iter, minibatch_size)
while len(X_text):
yield X_text, y
X_text, y = get_minibatch(doc_iter, minibatch_size)
# test data statistics
test_stats = {'n_test': 0, 'n_test_pos': 0}
# First we hold out a number of examples to estimate accuracy
n_test_documents = 1000
tick = time.time()
X_test_text, y_test = get_minibatch(data_stream, 1000)
parsing_time = time.time() - tick
tick = time.time()
X_test = vectorizer.transform(X_test_text)
vectorizing_time = time.time() - tick
test_stats['n_test'] += len(y_test)
test_stats['n_test_pos'] += sum(y_test)
print("Test set is %d documents (%d positive)" % (len(y_test), sum(y_test)))
def progress(cls_name, stats):
"""Report progress information, return a string."""
duration = time.time() - stats['t0']
s = "%20s classifier : \t" % cls_name
s += "%(n_train)6d train docs (%(n_train_pos)6d positive) " % stats
s += "%(n_test)6d test docs (%(n_test_pos)6d positive) " % test_stats
s += "accuracy: %(accuracy).3f " % stats
s += "in %.2fs (%5d docs/s)" % (duration, stats['n_train'] / duration)
return s
cls_stats = {}
for cls_name in partial_fit_classifiers:
stats = {'n_train': 0, 'n_train_pos': 0,
'accuracy': 0.0, 'accuracy_history': [(0, 0)], 't0': time.time(),
'runtime_history': [(0, 0)], 'total_fit_time': 0.0}
cls_stats[cls_name] = stats
get_minibatch(data_stream, n_test_documents)
# Discard test set
# We will feed the classifier with mini-batches of 1000 documents; this means
# we have at most 1000 docs in memory at any time. The smaller the document
# batch, the bigger the relative overhead of the partial fit methods.
minibatch_size = 1000
# Create the data_stream that parses Reuters SGML files and iterates on
# documents as a stream.
minibatch_iterators = iter_minibatches(data_stream, minibatch_size)
total_vect_time = 0.0
# Main loop : iterate on mini-batches of examples
for i, (X_train_text, y_train) in enumerate(minibatch_iterators):
tick = time.time()
X_train = vectorizer.transform(X_train_text)
total_vect_time += time.time() - tick
for cls_name, cls in partial_fit_classifiers.items():
tick = time.time()
# update estimator with examples in the current mini-batch
cls.partial_fit(X_train, y_train, classes=all_classes)
# accumulate test accuracy stats
cls_stats[cls_name]['total_fit_time'] += time.time() - tick
cls_stats[cls_name]['n_train'] += X_train.shape[0]
cls_stats[cls_name]['n_train_pos'] += sum(y_train)
tick = time.time()
cls_stats[cls_name]['accuracy'] = cls.score(X_test, y_test)
cls_stats[cls_name]['prediction_time'] = time.time() - tick
acc_history = (cls_stats[cls_name]['accuracy'],
cls_stats[cls_name]['n_train'])
cls_stats[cls_name]['accuracy_history'].append(acc_history)
run_history = (cls_stats[cls_name]['accuracy'],
total_vect_time + cls_stats[cls_name]['total_fit_time'])
cls_stats[cls_name]['runtime_history'].append(run_history)
if i % 3 == 0:
print(progress(cls_name, cls_stats[cls_name]))
if i % 3 == 0:
print('\n')
```
Plot results
------------
The plot represents the learning curve of the classifier: the evolution
of classification accuracy over the course of the mini-batches. Accuracy is
measured on the first 1000 samples, held out as a validation set.
To limit the memory consumption, we queue examples up to a fixed amount
before feeding them to the learner.
```
def plot_accuracy(x, y, x_legend):
"""Plot accuracy as a function of x."""
x = np.array(x)
y = np.array(y)
plt.title('Classification accuracy as a function of %s' % x_legend)
plt.xlabel('%s' % x_legend)
plt.ylabel('Accuracy')
plt.grid(True)
plt.plot(x, y)
rcParams['legend.fontsize'] = 10
cls_names = list(sorted(cls_stats.keys()))
# Plot accuracy evolution
plt.figure()
for _, stats in sorted(cls_stats.items()):
# Plot accuracy evolution with #examples
accuracy, n_examples = zip(*stats['accuracy_history'])
plot_accuracy(n_examples, accuracy, "training examples (#)")
ax = plt.gca()
ax.set_ylim((0.8, 1))
plt.legend(cls_names, loc='best')
plt.figure()
for _, stats in sorted(cls_stats.items()):
# Plot accuracy evolution with runtime
accuracy, runtime = zip(*stats['runtime_history'])
plot_accuracy(runtime, accuracy, 'runtime (s)')
ax = plt.gca()
ax.set_ylim((0.8, 1))
plt.legend(cls_names, loc='best')
# Plot fitting times
plt.figure()
fig = plt.gcf()
cls_runtime = [stats['total_fit_time']
for cls_name, stats in sorted(cls_stats.items())]
cls_runtime.append(total_vect_time)
cls_names.append('Vectorization')
bar_colors = ['b', 'g', 'r', 'c', 'm', 'y']
ax = plt.subplot(111)
rectangles = plt.bar(range(len(cls_names)), cls_runtime, width=0.5,
color=bar_colors)
ax.set_xticks(np.linspace(0, len(cls_names) - 1, len(cls_names)))
ax.set_xticklabels(cls_names, fontsize=10)
ymax = max(cls_runtime) * 1.2
ax.set_ylim((0, ymax))
ax.set_ylabel('runtime (s)')
ax.set_title('Training Times')
def autolabel(rectangles):
"""attach some text vi autolabel on rectangles."""
for rect in rectangles:
height = rect.get_height()
ax.text(rect.get_x() + rect.get_width() / 2.,
1.05 * height, '%.4f' % height,
ha='center', va='bottom')
plt.setp(plt.xticks()[1], rotation=30)
autolabel(rectangles)
plt.tight_layout()
plt.show()
# Plot prediction times
plt.figure()
cls_runtime = []
cls_names = list(sorted(cls_stats.keys()))
for cls_name, stats in sorted(cls_stats.items()):
cls_runtime.append(stats['prediction_time'])
cls_runtime.append(parsing_time)
cls_names.append('Read/Parse\n+Feat.Extr.')
cls_runtime.append(vectorizing_time)
cls_names.append('Hashing\n+Vect.')
ax = plt.subplot(111)
rectangles = plt.bar(range(len(cls_names)), cls_runtime, width=0.5,
color=bar_colors)
ax.set_xticks(np.linspace(0, len(cls_names) - 1, len(cls_names)))
ax.set_xticklabels(cls_names, fontsize=8)
plt.setp(plt.xticks()[1], rotation=30)
ymax = max(cls_runtime) * 1.2
ax.set_ylim((0, ymax))
ax.set_ylabel('runtime (s)')
ax.set_title('Prediction Times (%d instances)' % n_test_documents)
autolabel(rectangles)
plt.tight_layout()
plt.show()
```
|
github_jupyter
|
# Basic objects
A `striplog` depends on a hierarchy of objects. This notebook shows the objects and their basic functionality.
- [Lexicon](#Lexicon): A dictionary containing the words and word categories to use for rock descriptions.
- [Component](#Component): A set of attributes.
- [Interval](#Interval): One element from a Striplog — consists of a top, base, a description, one or more Components, and a source.
Striplogs (a set of `Interval`s) are described in [a separate notebook](Striplog_object.ipynb).
Decors and Legends are also described in [another notebook](Display_objects.ipynb).
```
import striplog
striplog.__version__
# If you get a lot of warnings here, just run it again.
```
<hr />
## Lexicon
```
from striplog import Lexicon
print(Lexicon.__doc__)
lexicon = Lexicon.default()
lexicon
lexicon.synonyms
```
Most of the lexicon works 'behind the scenes' when processing descriptions into `Rock` components.
```
lexicon.find_synonym('Halite')
s = "grysh gn ss w/ sp gy sh"
lexicon.expand_abbreviations(s)
```
<hr />
## Component
A set of attributes. All are optional.
```
from striplog import Component
print(Component.__doc__)
```
We define a new rock with a Python `dict` object:
```
r = {'colour': 'grey',
'grainsize': 'vf-f',
'lithology': 'sand'}
rock = Component(r)
rock
```
The Rock has a colour:
```
rock['colour']
```
And it has a summary, which is generated from its attributes.
```
rock.summary()
```
We can format the summary if we wish:
```
rock.summary(fmt="My rock: {lithology} ({colour}, {grainsize!u})")
```
The formatting supports the usual `s`, `r`, and `a`:
* `s`: `str`
* `r`: `repr`
* `a`: `ascii`
Also some string functions:
* `u`: `str.upper`
* `l`: `str.lower`
* `c`: `str.capitalize`
* `t`: `str.title`
And some numerical ones, for arrays of numbers:
* `+` or `∑`: `np.sum`
* `m` or `µ`: `np.mean`
* `v`: `np.var`
* `d`: `np.std`
* `x`: `np.product`
```
x = {'colour': ['Grey', 'Brown'],
'bogosity': [0.45, 0.51, 0.66],
'porosity': [0.2003, 0.1998, 0.2112, 0.2013, 0.1990],
'grainsize': 'VF-F',
'lithology': 'Sand',
}
X = Component(x)
# This is not working at the moment.
#fmt = 'The {colour[0]!u} {lithology!u} has a total of {bogosity!∑:.2f} bogons'
#fmt += 'and a mean porosity of {porosity!µ:2.0%}.'
fmt = 'The {lithology!u} is {colour[0]!u}.'
X.summary(fmt)
X.json()
```
We can compare rocks with the usual `==` operator:
```
rock2 = Component({'grainsize': 'VF-F',
'colour': 'Grey',
'lithology': 'Sand'})
rock == rock2
rock
```
In order to create a Component object from text, we need a lexicon to compare the text against. The lexicon describes the language we want to extract, and what it means.
```
rock3 = Component.from_text('Grey fine sandstone.', lexicon)
rock3
```
Components support double-star-unpacking:
```
"My rock: {lithology} ({colour}, {grainsize})".format(**rock3)
```
<hr />
## Position
Positions define points in the earth, like a top, but with uncertainty. You can define:
* `upper` — the highest possible location
* `middle` — the most likely location
* `lower` — the lowest possible location
* `units` — the units of measurement
* `x` and `y` — the _x_ and _y_ location (these don't have uncertainty, sorry)
* `meta` — a Python dictionary containing anything you want
Positions don't have a 'way up'.
```
from striplog import Position
print(Position.__doc__)
params = {'upper': 95,
'middle': 100,
'lower': 110,
'meta': {'kind': 'erosive', 'source': 'DOE'}
}
p = Position(**params)
p
```
Even if you don't give a `middle`, you can always get `z`: the central, most likely position:
```
params = {'upper': 75, 'lower': 85}
p = Position(**params)
p
p.z
```
<hr />
## Interval
Intervals are where it gets interesting. An interval can have:
* a top
* a base
* a description (in natural language)
* a list of `Component`s
Intervals don't have a 'way up', it's implied by the order of `top` and `base`.
```
from striplog import Interval
print(Interval.__doc__)
```
I might make an `Interval` explicitly from a Component...
```
Interval(10, 20, components=[rock])
```
... or I might pass a description and a `lexicon` and Striplog will parse the description and attempt to extract structured `Component` objects from it.
```
Interval(20, 40, "Grey sandstone with shale flakes.", lexicon=lexicon).__repr__()
```
Notice I only got one `Component`, even though the description contains a subordinate lithology. This is the default behaviour, we have to ask for more components:
```
interval = Interval(20, 40, "Grey sandstone with black shale flakes.", lexicon=lexicon, max_component=2)
print(interval)
```
`Interval`s have a `primary` attribute, which holds the first component, no matter how many components there are.
```
interval.primary
```
Ask for the summary to see the thickness and a `Rock` summary of the primary component. Note that the format code only applies to the `Rock` part of the summary.
```
interval.summary(fmt="{colour} {lithology}")
```
We can change an interval's properties:
```
interval.top = 18
interval
interval.top
```
<hr />
## Comparing and combining intervals
```
# Depth ordered
i1 = Interval(top=61, base=62.5, components=[Component({'lithology': 'limestone'})])
i2 = Interval(top=62, base=63, components=[Component({'lithology': 'sandstone'})])
i3 = Interval(top=62.5, base=63.5, components=[Component({'lithology': 'siltstone'})])
i4 = Interval(top=63, base=64, components=[Component({'lithology': 'shale'})])
i5 = Interval(top=63.1, base=63.4, components=[Component({'lithology': 'dolomite'})])
# Elevation ordered
i8 = Interval(top=200, base=100, components=[Component({'lithology': 'sandstone'})])
i7 = Interval(top=150, base=50, components=[Component({'lithology': 'limestone'})])
i6 = Interval(top=100, base=0, components=[Component({'lithology': 'siltstone'})])
i2.order
```
**Technical aside:** The `Interval` class is a `functools.total_ordering`, so providing `__eq__` and one other comparison (such as `__lt__`) in the class definition means that instances of the class have implicit order. So you can use `sorted` on a Striplog, for example.
It wasn't clear to me whether this should compare tops (say), so that '>' might mean 'above', or if it should be keyed on thickness. I chose the former, and implemented other comparisons instead.
```
print(i3 == i2) # False, they don't have the same top
print(i1 > i4) # True, i1 is above i4
print(min(i1, i2, i5).summary()) # 0.3 m of dolomite
i2 > i4 > i5 # True
```
We can combine intervals with the `+` operator. (However, you cannot subtract intervals.)
```
i2 + i3
```
Adding a rock adds a (minor) component and adds to the description.
```
interval + rock3
i6.relationship(i7), i5.relationship(i4)
print(i1.partially_overlaps(i2)) # True
print(i2.partially_overlaps(i3)) # True
print(i2.partially_overlaps(i4)) # False
print()
print(i6.partially_overlaps(i7)) # True
print(i7.partially_overlaps(i6)) # True
print(i6.partially_overlaps(i8)) # False
print()
print(i5.is_contained_by(i3)) # True
print(i5.is_contained_by(i4)) # True
print(i5.is_contained_by(i2)) # False
x = i4.merge(i5)
x[-1].base = 65
x
i1.intersect(i2, blend=False)
i1.intersect(i2)
i1.union(i3)
i3.difference(i5)
```
<hr />
<p style="color:gray">©2015 Agile Geoscience. Licensed CC-BY. <a href="https://github.com/agile-geoscience/striplog">striplog.py</a></p>
|
github_jupyter
|
# Import Modules
```
import warnings
warnings.filterwarnings('ignore')
from src import detect_faces, show_bboxes
from PIL import Image
import torch
from torchvision import transforms, datasets
import numpy as np
import os
```
# Path Definition
```
dataset_path = '../Dataset/emotiw/'
face_coordinates_directory = '../Dataset/FaceCoordinates/'
processed_dataset_path = '../Dataset/CroppedFaces/'
```
# Load Train and Val Dataset
```
image_datasets = {x : datasets.ImageFolder(os.path.join(dataset_path, x))
for x in ['train', 'val']}
class_names = image_datasets['train'].classes
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
class_names
training_dataset = image_datasets['train']
validation_dataset = image_datasets['val']
neg_train = sorted(os.listdir(dataset_path + 'train/Negative/'))
neu_train = sorted(os.listdir(dataset_path + 'train/Neutral/'))
pos_train = sorted(os.listdir(dataset_path + 'train/Positive/'))
neg_val = sorted(os.listdir(dataset_path + 'val/Negative/'))
neu_val = sorted(os.listdir(dataset_path + 'val/Neutral/'))
pos_val = sorted(os.listdir(dataset_path + 'val/Positive/'))
neg_train_filelist = [x.split('.')[0] for x in neg_train]
neu_train_filelist = [x.split('.')[0] for x in neu_train]
pos_train_filelist = [x.split('.')[0] for x in pos_train]
neg_val_filelist = [x.split('.')[0] for x in neg_val]
neu_val_filelist = [x.split('.')[0] for x in neu_val]
pos_val_filelist = [x.split('.')[0] for x in pos_val]
print(neg_train_filelist[:10])
print(neu_train_filelist[:10])
print(pos_train_filelist[:10])
print(neg_val_filelist[:10])
print(neu_val_filelist[:10])
print(pos_val_filelist[:10])
train_filelist = neg_train_filelist + neu_train_filelist + pos_train_filelist
val_filelist = neg_val_filelist + neu_val_filelist + pos_val_filelist
print(len(training_dataset))
print(len(validation_dataset))
```
# Crop Faces
```
for i in range(len(training_dataset)):
try:
image, label = training_dataset[i]
face_list = []
landmarks_new_coordinates = []
if label == 0:
if os.path.isfile(processed_dataset_path + 'train/Negative/' + train_filelist[i] + '.npz'):
print(train_filelist[i] + ' Already present')
continue
bbox_lm = np.load(face_coordinates_directory + 'train/Negative/' + train_filelist[i] +'.npz')
bounding_boxes = bbox_lm['a']
if bounding_boxes.size == 0 or (bounding_boxes[0] == 0).all():
print("No bounding boxes for " + train_filelist[i] + ". Adding empty file for the same")
np.savez(processed_dataset_path + 'train/Negative/' + train_filelist[i], a = np.zeros(1), b = np.zeros(1))
continue
landmarks = bbox_lm['b']
for j in range(len(bounding_boxes)):
bbox_coordinates = bounding_boxes[j]
landmark = landmarks[j]
img_face = image.crop((bbox_coordinates[0], bbox_coordinates[1], bbox_coordinates[2], bbox_coordinates[3]))
x = bbox_coordinates[0]
y = bbox_coordinates[1]
for k in range(5):
landmark[k] -= x
landmark[k+5] -= y
img_face = np.array(img_face)
landmark = np.array(landmark)
if len(face_list) != 0:
if img_face.shape[0] == face_list[-1].shape[0]:
img_face = image.crop((bbox_coordinates[0] - 1, bbox_coordinates[1] - 1, bbox_coordinates[2], bbox_coordinates[3]))
img_face = np.array(img_face)
landmark +=1
face_list.append(img_face)
landmarks_new_coordinates.append(landmark)
face_list = np.asarray(face_list)
landmarks_new_coordinates = np.asarray(landmarks_new_coordinates)
np.savez(processed_dataset_path + 'train/Negative/' + train_filelist[i], a = face_list, b = landmarks_new_coordinates)
elif label == 1:
if os.path.isfile(processed_dataset_path + 'train/Neutral/' + train_filelist[i] + '.npz'):
print(train_filelist[i] + ' Already present')
continue
bbox_lm = np.load(face_coordinates_directory + 'train/Neutral/' + train_filelist[i] +'.npz')
bounding_boxes = bbox_lm['a']
if bounding_boxes.size == 0 or (bounding_boxes[0] == 0).all():
print("No bounding boxes for " + train_filelist[i] + ". Adding empty file for the same")
np.savez(processed_dataset_path + 'train/Neutral/' + train_filelist[i], a = np.zeros(1), b = np.zeros(1))
continue
landmarks = bbox_lm['b']
for j in range(len(bounding_boxes)):
bbox_coordinates = bounding_boxes[j]
landmark = landmarks[j]
img_face = image.crop((bbox_coordinates[0], bbox_coordinates[1], bbox_coordinates[2], bbox_coordinates[3]))
x = bbox_coordinates[0]
y = bbox_coordinates[1]
for k in range(5):
landmark[k] -= x
landmark[k+5] -= y
img_face = np.array(img_face)
landmark = np.array(landmark)
if len(face_list) != 0:
if img_face.shape[0] == face_list[-1].shape[0]:
img_face = image.crop((bbox_coordinates[0] - 1, bbox_coordinates[1] - 1, bbox_coordinates[2], bbox_coordinates[3]))
img_face = np.array(img_face)
landmark += 1
face_list.append(img_face)
landmarks_new_coordinates.append(landmark)
face_list = np.asarray(face_list)
landmarks_new_coordinates = np.asarray(landmarks_new_coordinates)
np.savez(processed_dataset_path + 'train/Neutral/' + train_filelist[i], a = face_list, b = landmarks_new_coordinates)
else:
if os.path.isfile(processed_dataset_path + 'train/Positive/' + train_filelist[i] + '.npz'):
print(train_filelist[i] + ' Already present')
continue
bbox_lm = np.load(face_coordinates_directory + 'train/Positive/' + train_filelist[i] +'.npz')
bounding_boxes = bbox_lm['a']
if bounding_boxes.size == 0 or (bounding_boxes[0] == 0).all():
print("No bounding boxes for " + train_filelist[i] + ". Adding empty file for the same")
np.savez(processed_dataset_path + 'train/Positive/' + train_filelist[i], a = np.zeros(1), b = np.zeros(1))
continue
landmarks = bbox_lm['b']
for j in range(len(bounding_boxes)):
bbox_coordinates = bounding_boxes[j]
landmark = landmarks[j]
img_face = image.crop((bbox_coordinates[0], bbox_coordinates[1], bbox_coordinates[2], bbox_coordinates[3]))
x = bbox_coordinates[0]
y = bbox_coordinates[1]
for k in range(5):
landmark[k] -= x
landmark[k+5] -= y
img_face = np.array(img_face)
landmark = np.array(landmark)
if len(face_list) != 0:
if img_face.shape[0] == face_list[-1].shape[0]:
img_face = image.crop((bbox_coordinates[0] - 1, bbox_coordinates[1] - 1, bbox_coordinates[2], bbox_coordinates[3]))
img_face = np.array(img_face)
landmark += 1
face_list.append(img_face)
landmarks_new_coordinates.append(landmark)
face_list = np.asarray(face_list)
landmarks_new_coordinates = np.asarray(landmarks_new_coordinates)
np.savez(processed_dataset_path + 'train/Positive/' + train_filelist[i], a = face_list, b = landmarks_new_coordinates)
if i % 100 == 0:
print(i)
except:
print("Error/interrput at validation dataset file " + val_filelist[i])
print(bounding_boxes)
print(landmarks)
print(bounding_boxes.shape)
print(landmarks.shape)
break
```
|
github_jupyter
|
```
# !pip install plotly
import pandas as pd
import numpy as np
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import keras
from keras.models import Sequential
from keras.layers import Dense, Dropout
from sklearn.metrics import confusion_matrix
import sys
%matplotlib inline
import matplotlib.pyplot as plt
import plotly.express as px
!ls data
def genesis_train(file):
data = pd.read_csv(file)
del data['Unnamed: 32']
print('Number of datapoints in Training dataset: ',len(data))
X_train = data.iloc[:, 2:].values
y_train = data.iloc[:, 1].values
test = pd.read_csv('./data/test.csv')
del test['Unnamed: 32']
print('Number of datapoints in Testing dataset: ',len(test))
X_test = test.iloc[:, 2:].values
y_test = test.iloc[:, 1].values
labelencoder = LabelEncoder()
y_train = labelencoder.fit_transform(y_train)
y_test = labelencoder.fit_transform(y_test)
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
model = Sequential()
model.add(Dense(16, activation='relu', input_dim=30))
model.add(Dropout(0.1))
model.add(Dense(16, activation='relu'))
model.add(Dropout(0.1))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
model.fit(X_train, y_train, batch_size=100, epochs=5)
scores = model.evaluate(X_test, y_test)
print("Loss: ", scores[0]) #Loss
print("Accuracy: ", scores[1]) #Accuracy
#Saving Model
model.save("./output.h5")
return scores[1]
def update_train(file):
data = pd.read_csv(file)
del data['Unnamed: 32']
X_train = data.iloc[:, 2:].values
y_train = data.iloc[:, 1].values
test = pd.read_csv('./data/test.csv')
del test['Unnamed: 32']
print('Number of datapoints in Testing dataset: ',len(test))
X_test = test.iloc[:, 2:].values
y_test = test.iloc[:, 1].values
labelencoder = LabelEncoder()
y_train = labelencoder.fit_transform(y_train)
y_test = labelencoder.fit_transform(y_test)
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
model = Sequential()
model.add(Dense(16, activation='relu', input_dim=30))
model.add(Dropout(0.1))
model.add(Dense(16, activation='relu'))
model.add(Dropout(0.1))
model.add(Dense(1, activation='sigmoid'))
model.load_weights("./output.h5")
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
model.fit(X_train, y_train, batch_size=100, epochs=5)
scores = model.evaluate(X_test, y_test)
print("Loss: ", scores[0]) #Loss
print("Accuracy: ", scores[1]) #Accuracy
#Saving Model
model.save("./output.h5")
return scores[1]
datasetAccuracy = {}
datasetAccuracy['Complete Dataset'] = genesis_train('./data/data.csv')
datasetAccuracy['A'] = genesis_train('./data/dataA.csv')
datasetAccuracy['B'] = genesis_train('./data/dataB.csv')
datasetAccuracy['C'] = genesis_train('./data/dataC.csv')
datasetAccuracy['D'] = genesis_train('./data/dataD.csv')
datasetAccuracy['E'] = genesis_train('./data/dataE.csv')
datasetAccuracy['F'] = genesis_train('./data/dataF.csv')
datasetAccuracy['G'] = genesis_train('./data/dataG.csv')
datasetAccuracy['H'] = genesis_train('./data/dataH.csv')
datasetAccuracy['I'] = genesis_train('./data/dataI.csv')
px.bar(pd.DataFrame.from_dict(datasetAccuracy, orient='index'))
FLAccuracy = {}
FLAccuracy['A'] = update_train('./data/dataA.csv')
FLAccuracy['B'] = update_train('./data/dataB.csv')
FLAccuracy['C'] = update_train('./data/dataC.csv')
FLAccuracy['D'] = update_train('./data/dataD.csv')
FLAccuracy['E'] = update_train('./data/dataE.csv')
FLAccuracy['F'] = update_train('./data/dataF.csv')
FLAccuracy['G'] = update_train('./data/dataG.csv')
FLAccuracy['H'] = update_train('./data/dataH.csv')
FLAccuracy['I'] = update_train('./data/dataI.csv')
px.bar(pd.DataFrame.from_dict(FLAccuracy, orient='index'))
#################################################################################################################
FLAccuracy
```
|
github_jupyter
|
```
# change to root directory of project
import os
os.chdir('/home/tm/sciebo/corona/twitter_analysis/')
from bld.project_paths import project_paths_join as ppj
from IPython.display import display
import numpy as np
import pandas as pd
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.preprocessing import LabelEncoder
from textblob import TextBlob
from vaderSentiment.vaderSentiment import SentimentIntensityAnalyzer
#import requests
#import json
#import argparse
#from google.cloud import language
#from google.oauth2 import service_account
#from google.cloud.language import enums
#from google.cloud.language import types
```
## Data management
```
data = pd.read_csv(
ppj("IN_DATA", "training_data/data_clean_translated.csv")
).iloc[:, 1:]
data_processed = pd.read_csv(
ppj("IN_DATA", "training_data/data_processed_translated.csv"),
).iloc[:, 1:]
df = data.copy()
df["processed"] = data_processed.text
df['sentiment_score'] = df.sentiment.replace({'neutral': 0, 'negative': -1, 'positive': 1})
df = df.dropna()
```
## Functions
```
def classify_sentiment(list_of_text, method):
"""Classify sentiment for each item in ``list_of_text``.
Args:
list_of_text (list): List of strings for which the sentiment
should be classified.
method (str): Name of method that should be used. Possible
values are 'google', 'vader', 'textblob'.
Returns:
sentiments (list): List of respective sentiment score
for each item in ``list_of_text``.
"""
analyzer = return_sentiment_analyzer(method)
sentiments = analyzer(list_of_text)
return sentiments
def return_sentiment_analyzer(method):
"""Return specific sentiment analyzer function.
Args:
method (str): Name of method that should be used. Possible
values are 'google', 'vader', 'textblob'.
Returns:
analyzer (function): Function which return a sentiment score
given text input. Inner workings depend on ``method``.
"""
functions = {
'google': analyze_google,
'textblob': analyze_textblob,
'vader': analyze_vader,
}
analyzer = functions[method]
return analyzer
def analyze_google(list_of_text):
"""Return sentiment for each text in ``list_of_text``.
Sentiments are analyzed using googles cloud natural language
api.
Args:
list_of_text (list): List of strings for which the sentiment
should be classified.
Returns:
sentiments (list): List of respective sentiment score
for each item in ``list_of_text``, where the sentiment score
is computed using google cloud natural language.
"""
client = language.LanguageServiceClient.from_service_account_json(
'src/keys/ose-twitter-analysis-8508806b2efb.json'
)
sentiments = []
for text in list_of_text:
document = types.Document(
content=text,
type=enums.Document.Type.PLAIN_TEXT
)
annotations = client.analyze_sentiment(document=document)
sentiments.append(annotations.document_sentiment.score)
return sentiments
def analyze_textblob(list_of_text):
"""Return sentiment for each text in ``list_of_text`` using ``textblob``.
Args:
list_of_text (list): List of strings for which the sentiment
should be classified.
Returns:
sentiments (list): List of respective sentiment score
for each item in ``list_of_text``, where the sentiment score
is computed using the package ``textblob``.
"""
sentiments = [
TextBlob(text).sentiment.polarity for text in list_of_text
]
return sentiments
def analyze_vader(list_of_text):
"""Return sentiment for each text in ``list_of_text`` using ``vaderSentiment``.
Args:
list_of_text (list): List of strings for which the sentiment
should be classified.
Returns:
sentiments (list): List of respective sentiment score
for each item in ``list_of_text``, where the sentiment score
is computed using the package ``vaderSentiment``.
"""
analyzer = SentimentIntensityAnalyzer()
sentiments = [
analyzer.polarity_scores(text)['compound'] for text in list_of_text
]
return sentiments
```
## Analysis
```
analyzers = ['textblob', 'vader'] #, 'google']
for col in ['text', 'processed']:
for m in analyzers:
df[m + "_" + col] = classify_sentiment(df[col].to_list(), method=m)
def continuous_to_class(score):
new_score = np.zeros(score.shape)
new_score[score < -0.33] = -1
new_score[score > 0.33] = 1
new_score = pd.Series(new_score).replace(
{-1: 'negative', 0: 'neutral', 1: 'positive'}
)
return new_score
def confusion_matrix_to_readable(cmat, labels):
columns = ['pred_' + lab for lab in labels]
rows = ['true_' + lab for lab in labels]
df = pd.DataFrame(cmat, columns=columns, index=rows)
return df
def absolute_to_freq(cmat):
total = cmat.sum(axis=1)
return cmat / total[:, np.newaxis]
le = LabelEncoder()
le = le.fit(df["sentiment"])
y_true = le.transform(df["sentiment"])
columns = [
'textblob_text',
'vader_text',
'textblob_processed',
'vader_processed'
]
predictions = [
le.transform(continuous_to_class(df[col])) for col in columns
]
cmats = [
confusion_matrix(y_true, pred) for pred in predictions
]
cmats_freq = [absolute_to_freq(cmat) for cmat in cmats]
df_cmats = [
confusion_matrix_to_readable(cmat, le.classes_) for cmat in cmats_freq
]
```
## Benchmark
```
weights = pd.Series(y_true).value_counts() / len(y_true)
weights = weights.reindex(le.transform(['negative', 'neutral', 'positive']))
weights
```
### Evaluation
```
for col, df_tmp in zip(columns, df_cmats):
print(col)
display(df_tmp)
print(f"Percent correctly classified: {df_tmp.values.diagonal().dot(weights)}")
```
|
github_jupyter
|
# Table of Contents
<p><div class="lev2 toc-item"><a href="#Common-Layers" data-toc-modified-id="Common-Layers-01"><span class="toc-item-num">0.1 </span>Common Layers</a></div><div class="lev3 toc-item"><a href="#Convolution-Layers" data-toc-modified-id="Convolution-Layers-011"><span class="toc-item-num">0.1.1 </span>Convolution Layers</a></div><div class="lev4 toc-item"><a href="#tf.nn.depthwise_conv2d" data-toc-modified-id="tf.nn.depthwise_conv2d-0111"><span class="toc-item-num">0.1.1.1 </span>tf.nn.depthwise_conv2d</a></div><div class="lev4 toc-item"><a href="#tf.nn.separable_conv2d" data-toc-modified-id="tf.nn.separable_conv2d-0112"><span class="toc-item-num">0.1.1.2 </span>tf.nn.separable_conv2d</a></div><div class="lev4 toc-item"><a href="#tf.nn.conv2d_transpose" data-toc-modified-id="tf.nn.conv2d_transpose-0113"><span class="toc-item-num">0.1.1.3 </span>tf.nn.conv2d_transpose</a></div><div class="lev3 toc-item"><a href="#Activation-Functions" data-toc-modified-id="Activation-Functions-012"><span class="toc-item-num">0.1.2 </span>Activation Functions</a></div><div class="lev4 toc-item"><a href="#tf.nn.relu" data-toc-modified-id="tf.nn.relu-0121"><span class="toc-item-num">0.1.2.1 </span>tf.nn.relu</a></div><div class="lev4 toc-item"><a href="#tf.sigmoid" data-toc-modified-id="tf.sigmoid-0122"><span class="toc-item-num">0.1.2.2 </span>tf.sigmoid</a></div><div class="lev4 toc-item"><a href="#tf.tanh" data-toc-modified-id="tf.tanh-0123"><span class="toc-item-num">0.1.2.3 </span>tf.tanh</a></div><div class="lev4 toc-item"><a href="#tf.nn.dropout" data-toc-modified-id="tf.nn.dropout-0124"><span class="toc-item-num">0.1.2.4 </span>tf.nn.dropout</a></div><div class="lev3 toc-item"><a href="#Pooling-Layers" data-toc-modified-id="Pooling-Layers-013"><span class="toc-item-num">0.1.3 </span>Pooling Layers</a></div><div class="lev4 toc-item"><a href="#tf.nn.max_pool" data-toc-modified-id="tf.nn.max_pool-0131"><span class="toc-item-num">0.1.3.1 </span>tf.nn.max_pool</a></div><div class="lev4 toc-item"><a href="#tf.nn.avg_pool" data-toc-modified-id="tf.nn.avg_pool-0132"><span class="toc-item-num">0.1.3.2 </span>tf.nn.avg_pool</a></div><div class="lev3 toc-item"><a href="#Normalization" data-toc-modified-id="Normalization-014"><span class="toc-item-num">0.1.4 </span>Normalization</a></div><div class="lev4 toc-item"><a href="#tf.nn.local_response_normalization-(tf.nn.lrn)" data-toc-modified-id="tf.nn.local_response_normalization-(tf.nn.lrn)-0141"><span class="toc-item-num">0.1.4.1 </span>tf.nn.local_response_normalization (tf.nn.lrn)</a></div><div class="lev3 toc-item"><a href="#High-Level-Layers" data-toc-modified-id="High-Level-Layers-015"><span class="toc-item-num">0.1.5 </span>High Level Layers</a></div><div class="lev4 toc-item"><a href="#tf.contrib.layers.convolution2d" data-toc-modified-id="tf.contrib.layers.convolution2d-0151"><span class="toc-item-num">0.1.5.1 </span>tf.contrib.layers.convolution2d</a></div><div class="lev4 toc-item"><a href="#tf.contrib.layers.fully_connected" data-toc-modified-id="tf.contrib.layers.fully_connected-0152"><span class="toc-item-num">0.1.5.2 </span>tf.contrib.layers.fully_connected</a></div><div class="lev4 toc-item"><a href="#Layer-Input" data-toc-modified-id="Layer-Input-0153"><span class="toc-item-num">0.1.5.3 </span>Layer Input</a></div>
## Common Layers
For a neural network architecture to be considered a CNN, it requires at least one convolution layer (`tf.nn.conv2d`). There are practical uses for a single layer CNN (edge detection), for image recognition and categorization it is common to use different layer types to support a convolution layer. These layers help reduce over-fitting, speed up training and decrease memory usage.
The layers covered in this chapter are focused on layers commonly used in a CNN architecture. A CNN isn't limited to use only these layers, they can be mixed with layers designed for other network architectures.
```
# setup-only-ignore
import tensorflow as tf
import numpy as np
# setup-only-ignore
sess = tf.InteractiveSession()
```
### Convolution Layers
One type of convolution layer has been covered in detail (`tf.nn.conv2d`) but there are a few notes which are useful to advanced users. The convolution layers in TensorFlow don't do a full convolution, details can be found in [the TensorFlow API documentation](https://www.tensorflow.org/versions/r0.8/api_docs/python/nn.html#convolution). In practice, the difference between a convolution and the operation TensorFlow uses is performance. TensorFlow uses a technique to speed up the convolution operation in all the different types of convolution layers.
There are use cases for each type of convolution layer but for `tf.nn.conv2d` is a good place to start. The other types of convolutions are useful but not required in building a network capable of object recognition and classification. A brief summary of each is included.
#### tf.nn.depthwise_conv2d
Used when attaching the output of one convolution to the input of another convolution layer. An advanced use case is using a `tf.nn.depthwise_conv2d` to create a network following the [inception architecture](http://arxiv.org/abs/1512.00567).
#### tf.nn.separable_conv2d
Similar to `tf.nn.conv2d` but not a replacement. For large models, it speeds up training without sacrificing accuracy. For small models, it will converge quickly with worse accuracy.
#### tf.nn.conv2d_transpose
Applies a kernel to a new feature map where each section is filled with the same values as the kernel. As the kernel strides over the new image, any overlapping sections are summed together. There is a great explanation on how `tf.nn.conv2d_transpose` is used for learnable upsampling in [Stanford's CS231n Winter 2016: Lecture 13](https://www.youtube.com/watch?v=ByjaPdWXKJ4&t=20m00s).
### Activation Functions
These functions are used in combination with the output of other layers to generate a feature map. They're used to smooth (or differentiate) the results of certain operations. The goal is to introduce non-linearity into the neural network. Non-linearity means that the input is a curve instead of a straight line. Curves are capable of representing more complex changes in input. For example, non-linear input is capable of describing input which stays small for the majority of the time but periodically has a single point at an extreme. Introduction of non-linearity in a neural network allows it to train on the complex patterns found in data.
TensorFlow has [multiple activation functions](https://www.tensorflow.org/versions/r0.8/api_docs/python/nn.html#activation-functions) available. With CNNs, `tf.nn.relu` is primarily used because of its performance although it sacrifices information. When starting out, using `tf.nn.relu` is recommended but advanced users may create their own. When considering if an activation function is useful there are a few primary considerations.
1. The function is [**monotonic**](https://en.wikipedia.org/wiki/Monotonic_function), so its output should always be increasing or decreasing along with the input. This allows gradient descent optimization to search for local minima.
2. The function is [**differentiable**](https://en.wikipedia.org/wiki/Differentiable_function), so there must be a derivative at any point in the function's domain. This allows gradient descent optimization to properly work using the output from this style of activation function.
Any functions which satisfy those considerations could be used as activation functions. In TensorFlow there are a few worth highlighting which are common to see in CNN architectures. A brief summary of each is included with a small sample code illustrating their usage.
#### tf.nn.relu
A rectifier (rectified linear unit) called a ramp function in some documentation and looks like a skateboard ramp when plotted. ReLU is linear and keeps the same input values for any positive numbers while setting all negative numbers to be 0. It has the benefits that it doesn't suffer from [gradient vanishing](https://en.wikipedia.org/wiki/Vanishing_gradient_problem) and has a range of <span class="math-tex" data-type="tex">\\([0,+\infty)\\)</span>. A drawback of ReLU is that it can suffer from neurons becoming saturated when too high of a learning rate is used.
```
features = tf.range(-2, 3)
# Keep note of the value for negative features
sess.run([features, tf.nn.relu(features)])
```
In this example, the input in a rank one tensor (vector) of integer values between <span class="math-tex" data-type="tex">\\([-2, 3]\\)</span>. A `tf.nn.relu` is ran over the values the output highlights that any value less than 0 is set to be 0. The other input values are left untouched.
#### tf.sigmoid
A sigmoid function returns a value in the range of <span class="math-tex" data-type="tex">\\([0.0, 1.0]\\)</span>. Larger values sent into a `tf.sigmoid` will trend closer to 1.0 while smaller values will trend towards 0.0. The ability for sigmoids to keep a values between <span class="math-tex" data-type="tex">\\([0.0, 1.0]\\)</span> is useful in networks which train on probabilities which are in the range of <span class="math-tex" data-type="tex">\\([0.0, 1.0]\\)</span>. The reduced range of output values can cause trouble with input becoming saturated and changes in input becoming exaggerated.
```
# Note, tf.sigmoid (tf.nn.sigmoid) is currently limited to float values
features = tf.to_float(tf.range(-1, 3))
sess.run([features, tf.sigmoid(features)])
```
In this example, a range of integers is converted to be float values (`1` becomes `1.0`) and a sigmoid function is ran over the input features. The result highlights that when a value of 0.0 is passed through a sigmoid, the result is 0.5 which is the midpoint of the simoid's domain. It's useful to note that with 0.5 being the sigmoid's midpoint, negative values can be used as input to a sigmoid.
#### tf.tanh
A hyperbolic tangent function (tanh) is a close relative to `tf.sigmoid` with some of the same benefits and drawbacks. The main difference between `tf.sigmoid` and `tf.tanh` is that `tf.tanh` has a range of <span class="math-tex" data-type="tex">\\([-1.0, 1.0]\\)</span>. The ability to output negative values may be useful in certain network architectures.
```
# Note, tf.tanh (tf.nn.tanh) is currently limited to float values
features = tf.to_float(tf.range(-1, 3))
sess.run([features, tf.tanh(features)])
```
In this example, all the setup is the same as the `tf.sigmoid` example but the output shows an important difference. In the output of `tf.tanh` the midpoint is 0.0 with negative values. This can cause trouble if the next layer in the network isn't expecting negative input or input of 0.0.
#### tf.nn.dropout
Set the output to be 0.0 based on a configurable probability. This layer performs well in scenarios where a little randomness helps training. An example scenario is when there are patterns being learned which are too tied to their neighboring features. This layer will add a little noise to the output being learned.
**NOTE**: This layer should only be used during training because the random noise it adds will give misleading results while testing.
```
features = tf.constant([-0.1, 0.0, 0.1, 0.2])
# Note, the output should be different on almost ever execution. Your numbers won't match
# this output.
sess.run([features, tf.nn.dropout(features, keep_prob=0.5)])
```
In this example, the output has a 50% probability of being kept. Each execution of this layer will have different output (most likely, it's somewhat random). When an output is dropped, its value is set to 0.0.
### Pooling Layers
Pooling layers reduce over-fitting and improving performance by reducing the size of the input. They're used to scale down input while keeping important information for the next layer. It's possible to reduce the size of the input using a `tf.nn.conv2d` alone but these layers execute much faster.
#### tf.nn.max_pool
Strides over a tensor and chooses the maximum value found within a certain kernel size. Useful when the intensity of the input data is relevant to importance in the image.

The same example is modeled using example code below. The goal is to find the largest value within the tensor.
```
# Usually the input would be output from a previous layer and not an image directly.
batch_size=1
input_height = 3
input_width = 3
input_channels = 1
layer_input = tf.constant([
[
[[1.0], [0.2], [1.5]],
[[0.1], [1.2], [1.4]],
[[1.1], [0.4], [0.4]]
]
])
# The strides will look at the entire input by using the image_height and image_width
kernel = [batch_size, input_height, input_width, input_channels]
max_pool = tf.nn.max_pool(layer_input, kernel, [1, 1, 1, 1], "VALID")
sess.run(max_pool)
```
The `layer_input` is a tensor with a shape similar to the output of `tf.nn.conv2d` or an activation function. The goal is to keep only one value, the largest value in the tensor. In this case, the largest value of the tensor is `1.5` and is returned in the same format as the input. If the `kernel` were set to be smaller, it would choose the largest value in each kernel size as it strides over the image.
Max-pooling will commonly be done using `2x2` receptive field (kernel with a height of 2 and width of 2) which is often written as a "2x2 max-pooling operation". One reason to use a `2x2` receptive field is that it's the smallest amount of downsampling which can be done in a single pass. If a `1x1` receptive field were used then the output would be the same as the input.
#### tf.nn.avg_pool
Strides over a tensor and averages all the values at each depth found within a kernel size. Useful when reducing values where the entire kernel is important, for example, input tensors with a large width and height but small depth.

The same example is modeled using example code below. The goal is to find the average of all the values within the tensor.
```
batch_size=1
input_height = 3
input_width = 3
input_channels = 1
layer_input = tf.constant([
[
[[1.0], [1.0], [1.0]],
[[1.0], [0.5], [0.0]],
[[0.0], [0.0], [0.0]]
]
])
# The strides will look at the entire input by using the image_height and image_width
kernel = [batch_size, input_height, input_width, input_channels]
max_pool = tf.nn.avg_pool(layer_input, kernel, [1, 1, 1, 1], "VALID")
sess.run(max_pool)
```
Doing a summation of all the values in the tensor, then divide them by the size of the number of scalars in the tensor:
<br />
<span class="math-tex" data-type="tex">\\(\dfrac{1.0 + 1.0 + 1.0 + 1.0 + 0.5 + 0.0 + 0.0 + 0.0 + 0.0}{9.0}\\)</span>
This is exactly what the example code did above but by reducing the size of the kernel, it's possible to adjust the size of the output.
### Normalization
Normalization layers are not unique to CNNs and aren't used as often. When using `tf.nn.relu`, it is useful to consider normalization of the output. Since ReLU is unbounded, it's often useful to utilize some form of normalization to identify high-frequency features.
#### tf.nn.local_response_normalization (tf.nn.lrn)
Local response normalization is a function which shapes the output based on a summation operation best explained in [TensorFlow's documentation](https://www.tensorflow.org/versions/master/api_docs/python/nn.html#local_response_normalization).
> ... Within a given vector, each component is divided by the weighted, squared sum of inputs within depth_radius.
One goal of normalization is to keep the input in a range of acceptable numbers. For instance, normalizing input in the range of <span class="math-tex" data-type="tex">\\([0.0,1.0]\\)</span> where the full range of possible values is normalized to be represented by a number greater than or equal to `0.0` and less than or equal to `1.0`. Local response normalization normalizes values while taking into account the significance of each value.
[Cuda-Convnet](https://code.google.com/p/cuda-convnet/wiki/LayerParams) includes further details on why using local response normalization is useful in some CNN architectures. [ImageNet](https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf) uses this layer to normalize the output from `tf.nn.relu`.
```
# Create a range of 3 floats.
# TensorShape([batch, image_height, image_width, image_channels])
layer_input = tf.constant([
[[[ 1.]], [[ 2.]], [[ 3.]]]
])
lrn = tf.nn.local_response_normalization(layer_input)
sess.run([layer_input, lrn])
```
In this example code, the layer input is in the format `[batch, image_height, image_width, image_channels]`. The normalization reduced the output to be in the range of <span class="math-tex" data-type="tex">\\([-1.0, 1.0]\\)</span>. For `tf.nn.relu`, this layer will reduce its unbounded output to be in the same range.
### High Level Layers
TensorFlow has introduced high level layers designed to make it easier to create fairly standard layer definitions. These aren't required to use but they help avoid duplicate code while following best practices. While getting started, these layers add a number of non-essential nodes to the graph. It's worth waiting until the basics are comfortable before using these layers.
#### tf.contrib.layers.convolution2d
The `convolution2d` layer will do the same logic as `tf.nn.conv2d` while including weight initialization, bias initialization, trainable variable output, bias addition and adding an activation function. Many of these steps haven't been covered for CNNs yet but should be familiar. A kernel is a trainable variable (the CNN's goal is to train this variable), weight initialization is used to fill the kernel with values (`tf.truncated_normal`) on its first run. The rest of the parameters are similar to what have been used before except they are reduced to short-hand version. Instead of declaring the full kernel, now it's a simple tuple `(1,1)` for the kernel's height and width.
```
image_input = tf.constant([
[
[[0., 0., 0.], [255., 255., 255.], [254., 0., 0.]],
[[0., 191., 0.], [3., 108., 233.], [0., 191., 0.]],
[[254., 0., 0.], [255., 255., 255.], [0., 0., 0.]]
]
])
conv2d = tf.contrib.layers.convolution2d(
image_input,
num_outputs=4,
kernel_size=(1,1), # It's only the filter height and width.
activation_fn=tf.nn.relu,
stride=(1, 1), # Skips the stride values for image_batch and input_channels.
trainable=True)
# It's required to initialize the variables used in convolution2d's setup.
sess.run(tf.global_variables_initializer())
sess.run(conv2d)
```
This example setup a full convolution against a batch of a single image. All the parameters are based off of the steps done throughout this chapter. The main difference is that `tf.contrib.layers.convolution2d` does a large amount of setup without having to write it all again. This can be a great time saving layer for advanced users.
**NOTE**: `tf.to_float` should not be used if the input is an image, instead use `tf.image.convert_image_dtype` which will properly change the range of values used to describe colors. In this example code, float values of `255.` were used which aren't what TensorFlow expects when is sees an image using float values. TensorFlow expects an image with colors described as floats to stay in the range of <span class="math-tex" data-type="tex">\\([0,1]\\)</span>.
#### tf.contrib.layers.fully_connected
A fully connected layer is one where every input is connected to every output. This is a fairly common layer in many architectures but for CNNs, the last layer is quite often fully connected. The `tf.contrib.layers.fully_connected` layer offers a great short-hand to create this last layer while following best practices.
Typical fully connected layers in TensorFlow are often in the format of `tf.matmul(features, weight) + bias` where `feature`, `weight` and `bias` are all tensors. This short-hand layer will do the same thing while taking care of the intricacies involved in managing the `weight` and `bias` tensors.
```
features = tf.constant([
[[1.2], [3.4]]
])
fc = tf.contrib.layers.fully_connected(features, num_outputs=2)
# It's required to initialize all the variables first or there'll be an error about precondition failures.
sess.run(tf.global_variables_initializer())
sess.run(fc)
```
This example created a fully connected layer and associated the input tensor with each neuron of the output. There are plenty of other parameters to tweak for different fully connected layers.
#### Layer Input
Each layer serves a purpose in a CNN architecture. It's important to understand them at a high level (at least) but without practice they're easy to forget. A crucial layer in any neural network is the input layer, where raw input is sent to be trained and tested. For object recognition and classification, the input layer is a `tf.nn.conv2d` layer which accepts images. The next step is to use real images in training instead of example input in the form of `tf.constant` or `tf.range` variables.
|
github_jupyter
|
```
import numpy as np # biblioteca utilizada para tratar com número/vetores/matrizes
import matplotlib.pyplot as plt # utilizada para plotar gráficos ao "estilo" matlab
import pandas as pd #biblioteca utilizada para realizar operações sobre dataframes
from google.colab import files #biblioteca do google colab utilizada para importar arquivos
uploaded=files.upload() #importa os arquivos
import io #biblioteca utilizada para tratar os comandos de entrada e saida
data = pd.read_csv(io.BytesIO(uploaded['AAPL.csv'])) # utilizado para importar o arquivo CSV que contém o banco de dados
data.head() #comando utilizado para mostrar as 5 primeiras colunas do dataframe
plt.plot(data["Date"],data["Open"])
plt.ylabel("Preço")
plt.xlabel("Data")
#comando utilizado para gerar o boxplot
#boxplot é empregado para ver se existem outlier
data.boxplot(column='Open')
#comando utilizado para verificar se existem dados nulos, numéricos ou não
data.info()
#preparando os dados para a entrada
entradas=data.iloc[:,1:2].values # retira do dataframe apenas a coluna relativa ao preço de abertura das ações
entradas[:5] #utilizada para realiar um print apenas das 5 primeiras linhas (pode ser visto que esse é um array, não um dataframe)
#normalizando os dados (os algoritmos de ML, em geral, não trabalham bem com dados em escalas diferentes)
from sklearn.preprocessing import MinMaxScaler #biblioteca utilizada para realizar o preprocessamento dos dados
scaler = MinMaxScaler(feature_range = (0, 1)) #cria o objeto que será utilizado para realizar a normalização dos dados
# feaure_range = define o intervalo de escala dos dados
dados_normalizados = scaler.fit_transform(entradas) # aplica o método de transformação dos dados
dados_normalizados[:5]
#Como as redes recorrentes utilizam dados no tempo T e valores passados (T-n), a entrada da rede deve conter os
#valores presentes e os (T-n). Assim, é necessário realizar uma modificação nos dados
features_set = []
labels = []
for i in range(60, 1259):
features_set.append(dados_normalizados[i-60:i, 0])
labels.append(dados_normalizados[i, 0])
#transformando os dados em um array para serem utilizados como entrada
features_set, labels = np.array(features_set), np.array(labels)
#conferindo a dimensão dos dados
print(features_set.shape) # método utilizado para retornar a dimensão dos dados
print(labels.shape)
#transformando os dados para o formato aceito pelas redes recorrentes do Keras
# 1 - formato em 3D
# (a,b,c) -> a = número de linhas do dataset
# -> b = número de steps (entradas) da rede
# -> c = número de saídas (indicators)
# método da biblioteca numpy que é utilizado para converter os dados de entrada (1199,60) em (1199,60,1)
features_set = np.reshape(features_set, (features_set.shape[0], features_set.shape[1], 1)) #
print(features_set.shape)
from keras.models import Sequential #classe utilizada para criar o modelo sequencial utilizando o keras
from keras.layers import Dense # Classe utilizada para criar as camadas que são completamente conectadas
from keras.layers import LSTM # Classe para a rede recorrente utilizando Long Shor Term Memory
from keras.layers import Dropout # Classe utilizada para a camada de dropout (utilizada para evitar o overfiting)
model = Sequential() # objeto para a criação do modelo keras sequencial
model.add(LSTM(units=50, return_sequences=True, input_shape=(features_set.shape[1], 1))) #cria a camada de entrada
# como pode ser visto, ela é adicionada como uma pilha, cada nova camada é adicionada com o método add
# na camada de entrada, é necessário definir o tamanho do vetor de entrada (input_shape)
# units=50 indica que na camada de entrada devem existir 50 neurônios
# return_sequences= True indica que devem ser adicionadas novas camadas
#adição da camada de dropout
model.add(Dropout(0.2)) # o valor de 0.2 indica que 20% dos neurônios dessa camada serão perdidos para cada interação
#Adicionando mais camadas ao modelo
model.add(LSTM(units=50, return_sequences=True))
model.add(Dropout(0.2))
model.add(LSTM(units=50, return_sequences=True))
model.add(Dropout(0.2))
model.add(LSTM(units=50)) # como essa é a última camada LSTM utilizada, a variável return_sequences=False
model.add(Dropout(0.2))
#adiciona a camada de saída com apenas 1 neurônio, pois vamos realizar a previsão de apenas uma variável (Previsão do valor de abertura)
model.add(Dense(units = 1))
#comando utilizado para ver a configuração do nosso modelo
model.summary()
#definição do tipo de função perda a ser utilizada e do tipo do otimizador
# o otimizador é utilizado para minimizar a função perda
# a função perda indica como deve ser calculado o erro do modelo (valor real - valor previsto)
model.compile(optimizer = 'adam', loss = 'mean_squared_error')
#treinamento do modelo
model.fit(features_set, labels, epochs = 100, batch_size = 32)
# valores de entrada
# saída
# número épocas para o treinamento (vezes em que vamos realizar interações durante o treinamento)
#batch_size = quantidade de dados utilizados por vez para realizar o treinamento
uploaded2=files.upload() #importa os arquivos para o teste dos dados
data_test = pd.read_csv(io.BytesIO(uploaded2['AAPL_previsao.csv'])) # utilizado para importar o arquivo CSV que contém o banco de dados para teste
data_test.head() #verifica as 5 primeiras linhas do dataframe utilizado para teste
plt.plot(data_test.Date,data_test.Open) #plot para os dados a serem utilizados como teste
df_data_apple=data_test.iloc[:, 1:2].values
df_data_apple = pd.concat((data['Open'], data_test['Open']), axis=0) # concatena os dados utilizados para teste e os utilizados para treinamento, tudo em um mesmo dataframe de 1 coluna
df_data_apple.head()
test_inputs = df_data_apple[len(df_data_apple) - len(data_test) - 60:].values
#normalização dos dados para teste, como fizemos com os dados de treinamento
test_inputs = test_inputs.reshape(-1,1)
test_inputs = scaler.transform(test_inputs)
#preparação dos 60 dados a setem utilizado
test_features = []
for i in range(60, 80):
test_features.append(test_inputs[i-60:i, 0])
#preparando os dados como entrada para o modelo de previsão
test_features = np.array(test_features)
test_features = np.reshape(test_features, (test_features.shape[0], test_features.shape[1], 1))
#previsão utilizando o modelo gerado
previsao = model.predict(test_features)
#inverte a transformação (normalização) dos dados de previsão
previsao = scaler.inverse_transform(previsao)
#plot do resultado da previsão e do real
plt.figure(figsize=(10,6))
plt.plot(data_test.Open, color='blue', label='Preço Real das Ações da Apple')
plt.plot(previsao , color='red', label='Previsão do Preço das Ações da Apple')
plt.title('Previsão do Preço de Abertura das Ações da Apple')
plt.xlabel('Data')
plt.ylabel('Preço')
plt.legend()
plt.show()
```
|
github_jupyter
|
# Twitter Sentiment Analysis for Indian Election 2019
**Abstract**<br>
The goal of this project is to do sentiment analysis for the Indian Elections. The data used is the tweets that are extracted from Twitter. The BJP and Congress are the two major political parties that will be contesting the election. The dataset will consist of tweets for both the parties. The tweets will be labeled as positive or negative based on the sentiment score obtained using Textblob library. This data will be used to build models that can classify new tweets as positive or negative. The models built are a Bidirectional RNN and GloVe word embedding model.
**Implementation**<br>
```
import os
import pandas as pd
import tweepy
import re
import string
from textblob import TextBlob
import preprocessor as p
from nltk.corpus import stopwords
from nltk.tokenize import word_tokenize
import nltk
nltk.download('punkt')
import pandas as pd
from nltk.tokenize import word_tokenize
from string import punctuation
from nltk.corpus import stopwords
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
from keras.layers import Embedding, SimpleRNN,Input
from keras.models import Sequential,Model
from keras.preprocessing import sequence
from keras.layers import Dense,Dropout
from keras.layers import Embedding, Flatten, Dense,Conv1D,MaxPooling1D
from sklearn import preprocessing
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import itertools
import seaborn as sns
from sklearn.metrics import confusion_matrix
from keras.utils import to_categorical
from collections import Counter
import tensorflow as tf
from keras.layers import LSTM, Bidirectional, Dropout
```
**Data Creation**
We use Tweepy API to access Twitter and download tweets. Tweepy supports accessing Twitter via Basic Authentication and the newer method, OAuth. Twitter has stopped accepting Basic Authentication so OAuth is now the only way to use the Twitter API.
The below code downloads the tweets from Twitter based on the keyword that we pass. The tweets sentiment score is obtained using the textblog library. The Tweets are then preprocessed. The preprocessing involved removing emoticons, removing stopwords.
```
consumer_key= '9oO3eQOBkuvCRPqMsFvnShRrq'
consumer_secret= 'BMWGbdC05jDcsWU5oI7AouWvwWmi46b2bD8zlnWXaaRC7832ep'
access_token='313324341-yQa0jL5IWmUKT15M6qM53uGeGW7FGcy1xAgx5Usy'
access_token_secret='OyjmhcMCbxGqBQAWzq12S0zrGYUvjChsZKavMYmPCAlrE'
auth = tweepy.OAuthHandler(consumer_key, consumer_secret)
auth.set_access_token(access_token, access_token_secret)
api = tweepy.API(auth)
#file location changed to "data/telemedicine_data_extraction/" for clearer path
congress_tweets = "C:/Users/Abhishek/Election Twitter Sentiment analysis/congress_test.csv"
bjp_tweets = "C:/Users/Abhishek/Election Twitter Sentiment analysis/bjp_test_new.csv"
#set two date variables for date range
start_date = '2019-04-1'
end_date = '2019-04-20'
```
**Data cleaning scripts**
```
# Happy Emoticons
emoticons_happy = set([
':-)', ':)', ';)', ':o)', ':]', ':3', ':c)', ':>', '=]', '8)', '=)', ':}',
':^)', ':-D', ':D', '8-D', '8D', 'x-D', 'xD', 'X-D', 'XD', '=-D', '=D',
'=-3', '=3', ':-))', ":'-)", ":')", ':*', ':^*', '>:P', ':-P', ':P', 'X-P',
'x-p', 'xp', 'XP', ':-p', ':p', '=p', ':-b', ':b', '>:)', '>;)', '>:-)',
'<3'
])
# Sad Emoticons
emoticons_sad = set([
':L', ':-/', '>:/', ':S', '>:[', ':@', ':-(', ':[', ':-||', '=L', ':<',
':-[', ':-<', '=\\', '=/', '>:(', ':(', '>.<', ":'-(", ":'(", ':\\', ':-c',
':c', ':{', '>:\\', ';('
])
#Emoji patterns
emoji_pattern = re.compile("["
u"\U0001F600-\U0001F64F" # emoticons
u"\U0001F300-\U0001F5FF" # symbols & pictographs
u"\U0001F680-\U0001F6FF" # transport & map symbols
u"\U0001F1E0-\U0001F1FF" # flags (iOS)
u"\U00002702-\U000027B0"
u"\U000024C2-\U0001F251"
"]+", flags=re.UNICODE)
#combine sad and happy emoticons
emoticons = emoticons_happy.union(emoticons_sad)
#mrhod clean_tweets()
def clean_tweets(tweet):
stop_words = set(stopwords.words('english'))
word_tokens = word_tokenize(tweet)
#after tweepy preprocessing the colon left remain after removing mentions
#or RT sign in the beginning of the tweet
tweet = re.sub(r':', '', tweet)
tweet = re.sub(r'…', '', tweet)
#replace consecutive non-ASCII characters with a space
tweet = re.sub(r'[^\x00-\x7F]+',' ', tweet)
#remove emojis from tweet
tweet = emoji_pattern.sub(r'', tweet)
#filter using NLTK library append it to a string
filtered_tweet = [w for w in word_tokens if not w in stop_words]
filtered_tweet = []
#looping through conditions
for w in word_tokens:
#check tokens against stop words , emoticons and punctuations
if w not in stop_words and w not in emoticons and w not in string.punctuation:
filtered_tweet.append(w)
return ' '.join(filtered_tweet)
#print(word_tokens)
#print(filtered_sentence)
#method write_tweets()
def write_tweets(keyword, file):
# If the file exists, then read the existing data from the CSV file.
if os.path.exists(file):
df = pd.read_csv(file, header=0)
else:
df = pd.DataFrame(columns=COLS)
#page attribute in tweepy.cursor and iteration
for page in tweepy.Cursor(api.search, q=keyword,
count=200, include_rts=False, since=start_date).pages(50):
for status in page:
new_entry = []
status = status._json
## check whether the tweet is in english or skip to the next tweet
if status['lang'] != 'en':
continue
#when run the code, below code replaces the retweet amount and
#no of favorires that are changed since last download.
if status['created_at'] in df['created_at'].values:
i = df.loc[df['created_at'] == status['created_at']].index[0]
if status['favorite_count'] != df.at[i, 'favorite_count'] or \
status['retweet_count'] != df.at[i, 'retweet_count']:
df.at[i, 'favorite_count'] = status['favorite_count']
df.at[i, 'retweet_count'] = status['retweet_count']
continue
#tweepy preprocessing called for basic preprocessing
#clean_text = p.clean(status['text'])
#call clean_tweet method for extra preprocessing
filtered_tweet=clean_tweets(status['text'])
#pass textBlob method for sentiment calculations
blob = TextBlob(filtered_tweet)
Sentiment = blob.sentiment
#seperate polarity and subjectivity in to two variables
polarity = Sentiment.polarity
subjectivity = Sentiment.subjectivity
#new entry append
new_entry += [status['id'], status['created_at'],
status['source'], status['text'],filtered_tweet, Sentiment,polarity,subjectivity, status['lang'],
status['favorite_count'], status['retweet_count']]
#to append original author of the tweet
new_entry.append(status['user']['screen_name'])
try:
is_sensitive = status['possibly_sensitive']
except KeyError:
is_sensitive = None
new_entry.append(is_sensitive)
# hashtagas and mentiones are saved using comma separted
hashtags = ", ".join([hashtag_item['text'] for hashtag_item in status['entities']['hashtags']])
new_entry.append(hashtags)
mentions = ", ".join([mention['screen_name'] for mention in status['entities']['user_mentions']])
new_entry.append(mentions)
#get location of the tweet if possible
try:
location = status['user']['location']
except TypeError:
location = ''
new_entry.append(location)
try:
coordinates = [coord for loc in status['place']['bounding_box']['coordinates'] for coord in loc]
except TypeError:
coordinates = None
new_entry.append(coordinates)
single_tweet_df = pd.DataFrame([new_entry], columns=COLS)
df = df.append(single_tweet_df, ignore_index=True)
csvFile = open(file, 'a' ,encoding='utf-8')
df.to_csv(csvFile, mode='a', columns=COLS, index=False, encoding="utf-8")
#declare keywords as a query for three categories
Congress_keywords = '#IndianNationalCongress OR #RahulGandhi OR #SoniaGandhi OR #INC'
BJP_keywords = '#BJP OR #Modi OR #AmitShah OR #BhartiyaJantaParty'
```
Creates two CSV files. First saves tweets for BJP and second saves tweets for Congress.
```
#call main method passing keywords and file path
write_tweets(Congress_keywords, congress_tweets)
write_tweets(BJP_keywords, bjp_tweets)
```
**LABELING TWEETS AS POSITIVE NEGATIVE**<br>
The tweepy libary gives out sentiment polarity in the range of -1 to +1. For our topic of election prediction the neutral tweets would be of no use as they will not provide any valuable information. Thus for simplicity purpose I have labeled tweets as only positive and negative. Tweets with polarity less than 0 will be labelled negative(0) and greater than 0 will be positive(1)
```
bjp_df['polarity'] = bjp_df['polarity'].apply(lambda x: 1 if x > 0 else 0)
congress_df['polarity'] = congress_df['polarity'].apply(lambda x: 1 if x > 0 else 0)
bjp_df['polarity'].value_counts()
```

```
congress_df['polarity'].value_counts()
```

## **RESAMPLING THE DATA** <br>
Since the ratio of the negative tweets to positive tweets is not proportional. Our data set is not balanced. This will create a bias while training the model. To avoid this I have resampled the data. New data was downloaded from twitter using the above procedure. For both the parties only positive tweets were sampled and appened to the main files to balance the data. After balancing the data. The count of positive and negative tweets for both the parties is as follows. The code for the resampling procedure can be found in the notebook Data_Labeling.ipynb

**CREATING FINAL DATASET**
```
frames = [bjp, congress]
election_data = pd.concat(frames)
```
The final dataset that will be used for our analysis saved in a csv file. That file can be loaded used to run our models. The final dataset looks as follows.

**TOKENIZING DATA**
We tokenize the text and keep the maximum length of the the vector 1000.

**TRAIN TEST SPLIT WITH 80:20 RATIO**
```
indices = np.arange(data.shape[0])
np.random.shuffle(indices)
data = data[indices]
labels = labels[indices]
nb_validation_samples = int(.20 * data.shape[0])
x_train = data[:-nb_validation_samples]
y_train = labels[:-nb_validation_samples]
x_val = data[-nb_validation_samples:]
y_val = labels[-nb_validation_samples:]
```
**CREATING EMBEDDING MATRIX WITH HELP OF PRETRAINED MODEL: GLOVE**
Word Embeddings are text converted into numbers. There are number of ways to represent the numeric forms.<br>
Types of embeddings: Frequency based, Prediction based.<br>Frequency Based: Tf-idf, Co-occurrence matrix<br>
Prediction-Based: BOW, Skip-gram model
Using Pre-trained word vectors: Word2vec, Glove
Word Embedding is done for the experiment with the pre trained word vector Glove.
Glove version used : 100-dimensional GloVe embeddings of 400k words computed on a 2014 dump of English Wikipedia. Training is performed on an aggregated global word-word co-occurrence matrix, giving us a vector space with meaningful substructures

```
embedding_matrix = np.zeros((len(word_index) + 1, 100))
for word, i in word_index.items():
embedding_vector = embeddings_index.get(word)
if embedding_vector is not None:
# words not found in embedding index will be all-zeros.
embedding_matrix[i] = embedding_vector
```
Creating an embedding layer using GloVe
```
embedding_layer = Embedding(len(word_index) + 1,
100,
weights=[embedding_matrix],
input_length=1000,
trainable=False)
```
# Model 1
**Glove Word Embedding model**
GloVe is an unsupervised learning algorithm for obtaining vector representations for words. Training is performed on aggregated global word-word co-occurrence statistics from a corpus, and the resulting representations showcase inter-esting linear substructures of the word vector space. GloVe can be used to find relations between words like synonyms, company - product relations, zip codes, and cities etc. It is also used by the spaCy model to build semantic word em-beddings/feature vectors while computing the top list words that match with distance measures such as Cosine Similar-ity and Euclidean distance approach.
```
def model_creation():
input_layer = Input(shape=(1000,), dtype='int32')
embed_layer = embedding_layer(input_layer)
x = Dense(100,activation='relu')(embed_layer)
x = Dense(50,activation='relu', kernel_regularizer=keras.regularizers.l2(0.002))(x)
x = Flatten()(x)
x = Dense(50,activation='relu', kernel_regularizer=keras.regularizers.l2(0.002))(x)
x = Dropout(0.5)(x)
x = Dense(50, activation='relu')(x)
x = Dropout(0.5)(x)
#x = Dense(512, activation='relu')(x)
#x = Dropout(0.4)(x)
final_layer = Dense(1, activation='sigmoid')(x)
opt = keras.optimizers.Adam(lr= learning_rate, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=False)
model = Model(input_layer,final_layer)
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['acc'])
return model
```
**MODEL 1 Architecture**
```
learning_rate = 0.0001
batch_size = 1024
epochs = 10
model_glove = model_creation()
```


**SAVE BEST MODEL AND WEIGHTS for Model1**
```
# serialize model to JSON
model_json = model_glove.to_json()
with open(".\\SavedModels\\Model_glove.h5", "w") as json_file:
json_file.write(model_json)
# serialize weights to HDF5
model_glove.save_weights(".\\SavedModels\\Weights_glove.h5")
```
**MODEL1 LOSS AND ACCURAY**

**MODEL1 PERFORMANCE**
```
def plot_modelacc(fit_model):
with plt.style.context('ggplot'):
plt.plot(fit_model.history['acc'])
plt.plot(fit_model.history['val_acc'])
plt.ylim(0,1)
plt.title("MODEL ACCURACY")
plt.xlabel("# of EPOCHS")
plt.ylabel("ACCURACY")
plt.legend(['train', 'test'], loc='upper left')
return plt.show()
def plot_model_loss(fit_model):
with plt.style.context('ggplot'):
plt.plot(fit_model.history['loss'])
plt.plot(fit_model.history['val_loss'])
plt.title("MODEL LOSS")
plt.xlabel("# of EPOCHS")
plt.ylabel("LOSS")
plt.legend(['train', 'test'], loc='upper left')
return plt.show()
```

**CONFUSION MATRIX**<br>
A confusion matrix will show us the how the model predicted with respect to the acutal output.

True Positives: 870 (Predicted True and True in reality)<br>
True Negative: 1141(Predicted False and False in realtity)<br>
False Positive: 33 (Predicted Positve but Negative in reality)<br>
False Negative: 29 (Predicted Negative but Positive in reality)
# Model 2
**Bidirectional RNN model**
Bidirectional Recurrent Neural Networks (BRNN) connect two hidden layers of opposite directions to the same output. With this form of generative deep learning, the output layer can get information from past (backwards) and future (forward) states simultaneously.Invented in 1997 by Schuster and Paliwal,BRNNs were introduced to increase the amount of input information available to the network. For example, multilayer perceptron (MLPs) and time delay neural network (TDNNs) have limitations on the input data flexibility, as they require their input data to be fixed. Standard recurrent neural network (RNNs) also have restrictions as the future input information cannot be reached from the current state. On the contrary, BRNNs do not require their input data to be fixed. Moreover, their future input information is reachable from the current state.
BRNN are especially useful when the context of the input is needed. For example, in handwriting recognition, the performance can be enhanced by knowledge of the letters located before and after the current letter.
**MODEL 1 Architecture**


**SAVING BEST MODEL2 AND ITS WEIGHTS**
```
# serialize model to JSON
model_json = model.to_json()
with open(".\\SavedModels\\Model_Bidir_LSTM.h5", "w") as json_file:
json_file.write(model_json)
# serialize weights to HDF5
model.save_weights(".\\SavedModels\\Weights_bidir_LSTM.h5")
print("Saved model to disk")
```
**MODEL 2 LOSS AND ACCURACY**


**MODEL 2 CONFUSION MATRIX**

True Positives: 887(Predicted True and True in reality)
True Negative: 1140(Predicted False and False in realtity)
False Positive: 35 (Predicted Positve but Negative in reality)
False Negative: 11 (Predicted Negative but Positive in reality)
**PREDICTION USING THE BEST MODEL**
The models were compared based on the Test loss and Test Accuracy. The Bidirectional RNN performed slightly better than the GloVe model. The RNN despite its simple architec-ture performed better than the Glove model. We use the Bidirectional RNN to make the predictions for the tweets that will be used to infer election results.
Load the test data on which the predictions will be made using our best model. The data for both the parties was collected using the same procedure like above.
```
congress_test = pd.read_csv('congress_test.csv')
bjp_test = pd.read_csv('bjp_test.csv')
```
We took equal samples for both the files. We took 2000 tweets for Congress and 2000 for BJP. The party that gets the most number of positive votes can be infered to have the higest probablity of winning the 2019 English.
```
congress_test =congress_test[:2000]
bjp_test = bjp_test[0:2000]
```
Tokenize the tweets in the same was that were used for the Bidirectional RNN model.
```
congress_inputs = tokenze_data(congress_inputs)
bjp_inputs = tokenze_data(bjp_inputs)
```
**LOAD THE BEST MODEL (BIDIRECTIONAL LSTM)**
```
from keras.models import model_from_json
# load json and create model
json_file = open(".\\SavedModels\\Model_Bidir_LSTM.h5", 'r')
loaded_model_json = json_file.read()
json_file.close()
loaded_model = model_from_json(loaded_model_json)
# load weights into new model
loaded_model.load_weights(".\\SavedModels\\Weights_bidir_LSTM.h5")
print("Loaded model from disk")
```
**SENTIMENT PREDICTION USING THE MODEL**
```
congress_prediction = loaded_model.predict(congress_inputs)
bjp_prediction = loaded_model.predict(bjp_inputs)
```
If the probabilty of the outcome is greater than 0.5 for any class then the sentiment belongs to that particular class. Since we are concerned with only the count of positive sentiments. We will check the second column variables for our inference.
```
congress_pred = (congress_prediction>0.5)
bjp_pred = (bjp_prediction>0.5)
def get_predictions(party_pred):
x = 0
for i in party_pred:
if(i[1]==True):
x+=1
return x
```

**CONCLUSION**
Just like the training data the majority of the tweets have a negative sentiment attached to them. After feeding 2000 tweets for both the Congress and BJP. The model predicted that BJP has 660 positive tweets while Congress has 416 positive tweets.<br><br> This indicated that the contest this year would be close and the chances of BJP winning on Majority like the 2015 elections are less. This has been corraborated by the poor perfomace of the BJP in the recent state elections where the lost power in three Major Hindi speaking states Rajasthan, Madhya Pradesh and Chattishgarh. <br><br>
**FUTURE SCOPE**
For this project only, a small sample of twitter data was considered for the analysis. It is difficult to give an estimate based on the limited amount of information we had access to. For future work, we can start by increasing the size of our dataset. In addition to Twitter, data can also be obtained from websites like Facebook, News websites. Apart from these we can try different models like Bidirectional RNN with attention mechanism. We can implement BERT which is currently the state of the art for solving various Natural Language Pro-cessing problems.
**LISCENCE**
**REFERENCES**
[1] Sepp Hochreiter and Jurgen Schmidhuber, “Long short- ¨ term memory,” Neural computation, vol. 9, no. 8, pp. 1735–1780,1997.<br>
[2] Mike Schuster and Kuldip K Paliwal, “Bidirectional recurrentneural networks,” Signal Processing, IEEE Transactions on, vol. 45, no. 11, pp. 2673–2681, 1997.<br>
[3] Jeffrey Pennington, Richard Socher, Christopher D. Manning.GloVe: Global Vectors for Word Representation <br>
[4] Apoorv Agarwal Boyi Xie Ilia Vovsha Owen Rambow Rebecca Passonneau Sentiment Analysis of Twitter Data <br>
[5] Alex Graves and Jurgen Schmidhuber, “Framewise ¨ phoneme classification with bidirectional LSTM and other neural network
architectures,” Neural Networks, vol. 18, no. 5, pp. 602–610,2005
|
github_jupyter
|
# Using geoprocessing tools
In ArcGIS API for Python, geoprocessing toolboxes and tools within them are represented as Python module and functions within that module. To learn more about this organization, refer to the page titled [Accessing geoprocessing tools](https://developers.arcgis.com/python/guide/accessing-geoprocessing-tools/).In this part of the guide, we will observe:
- [Invoking geoprocessing tools](#invoking-geoprocessing-tools)
- [Understanding tool input parameter and output return types](#understanding-tool-input-parameter-and-output-return-types)
- [Using helper types](#using-helper-types)
- [Using strings as input](#using-strings-as-input)
- [Tools with multiple outputs](#tools-with-multiple-outputs)
- [Invoking tools that create multiple outputs](#invoking-tools-that-create-multiple-outputs)
- [Using named tuple to access multiple outputs](#using-named-tuple-to-access-multiple-outputs)
- [Tools that export map image layer as output](#tools-that-export-map-image-layer-as-output)
<a id="invoking-geoprocessing-tools"></a>
## Invoking Geoprocessing Tools
You can execute a geoprocessing tool easily by importing its toolbox as a module and calling the function for the tool. Let us see how to execute the `extract_zion_data` tool from the Zion toolbox URL:
```
# connect to ArcGIS Online
from arcgis.gis import GIS
from arcgis.geoprocessing import import_toolbox
gis = GIS()
# import the Zion toolbox
zion_toolbox_url = 'http://gis.ices.dk/gis/rest/services/Tools/ExtractZionData/GPServer'
zion = import_toolbox(zion_toolbox_url)
result = zion.extract_zion_data()
```
Thus, executing a geoprocessing tool is that simple. Let us learn a few more concepts that will help in using these tools efficiently.
<a id="understanding-tool-input-parameter-and-output-return-types"></a>
## Understanding tool input parameter and output return types
The functions for calling geoprocessing tools can accept and return built-in Python types such as str, int, bool, float, dicts, datetime.datetime as well as some helper types defined in the ArcGIS API for Python such as the following:
* `arcgis.features.FeatureSet` - a set of features
* `arcgis.geoprocessing.LinearUnit` - linear distance with specified units
* `arcgis.geoprocessing.DataFile` - a url or item id referencing data
* `arcgis.geoprocessing.RasterData` - url or item id and format of raster data
The tools can also accept lists of the above types.
**Note**: When the helper types are used an input, the function also accepts strings in their place. For example '5 Miles' can be passed as an input instead of LinearUnit(5, 'Miles') and a URL can be passed instead of a `DataFile` or `RasterData` input.
Some geoprocessing tools are configured to return an `arcgis.mapping.MapImageLayer` for visualizing the results of the tool.
In all cases, the documentation of the tool function indicates the type of input parameters and the output values.
<a id="using-helper-types"></a>
### Using helper types
The helper types (`LinearUnit`, `DataFile` and `RasterData`) defined in the `arcgis.geoprocessing` module are simple classes that hold strings or URLs and have a dictionary representation.
The `extract_zion_data()` tool invoked above returns an output zip file as a `DataFile`:
```
type(result)
```
The output `Datafile` can be queried as shown in the snippet below.
```
result
```
The value types such as `DataFile` include helpful methods such as download:
```
result.download()
```
<a id="using-strings-as-input"></a>
### Using strings as input
Strings can also be used as inputs in place of the helper types such as `LinearUnit`, `RasterData` and `DataFile`.
The example below calls the viewshed tool to compute and display the geographical area that is visible from a clicked location on the map. The function accepts an observation point as a `FeatureSet` and a viewshed distance as a `LinearUnit`, and returns a `FeatureSet`:
```
viewshed = import_toolbox('http://sampleserver1.arcgisonline.com/ArcGIS/rest/services/Elevation/ESRI_Elevation_World/GPServer')
help(viewshed.viewshed)
import arcgis
arcgis.env.out_spatial_reference = 4326
map = gis.map('South San Francisco', zoomlevel=12)
map
```

The code snippet below adds an event listener to the map, such that when clicked, `get_viewshed()` is called with the map widget and clicked point geometry as inputs. The event handler creates a `FeatureSet` from the clicked point geometry, and uses the string '5 Miles' as input for the viewshed_distance parameter instead of creating a `LinearUnit` object. These are passed into the viewshed function that returns the viewshed from the observation point. The map widget is able to draw the returned `FeatureSet` using its `draw()` method:
```
from arcgis.features import Feature, FeatureSet
def get_viewshed(m, g):
res = viewshed.viewshed(FeatureSet([Feature(g)]),"5 Miles") # "5 Miles" or LinearUnit(5, 'Miles') can be passed as input
m.draw(res)
map.on_click(get_viewshed)
```
<a id="tools-with-multiple-outputs"></a>
## Tools with multiple outputs
Some Geoprocessing tools can return multiple results. For these tools, the corresponding function returns the multiple output values as a [named tuple](https://docs.python.org/3/library/collections.html#namedtuple-factory-function-for-tuples-with-named-fields).
The example below uses a tool that returns multiple outputs:
```
sandiego_toolbox_url = 'https://gis-public.co.san-diego.ca.us/arcgis/rest/services/InitialResearchPacketCSV_Phase2/GPServer'
multioutput_tbx = import_toolbox(sandiego_toolbox_url)
help(multioutput_tbx.initial_research_packet_csv)
```
<a id="invoking-tools-that-create-multiple-outputs"></a>
### Invoking tools that create multple outputs
The code snippet below shows how multiple outputs returned from a tool can be automatically unpacked by Python into multiple variables. Also, since we're not interested in the job status output, we can discard it using "_" as the variable name:
```
report_output_csv_file, output_map_flags_file, soil_output_file, _ = multioutput_tbx.initial_research_packet_csv()
report_output_csv_file
output_map_flags_file
soil_output_file
```
<a id="using-named-tuple-to-access-multiple-outputs"></a>
### Using named tuple to access multiple tool outputs
The code snippet below shows using a named tuple to access the multiple outputs returned from the tool:
```
results = multioutput_tbx.initial_research_packet_csv()
results.report_output_csv_file
results.job_status
```
<a id="tools-that-export-map-image-layer-as-output"></a>
## Tools that export MapImageLayer as output
Some Geoprocessing tools are configured to return their output as MapImageLayer for easier visualization of the results. The resultant layer can be added to a map or queried.
An example of such a tool is below:
```
hotspots = import_toolbox('https://sampleserver6.arcgisonline.com/arcgis/rest/services/911CallsHotspot/GPServer')
help(hotspots.execute_911_calls_hotspot)
result_layer, output_features, hotspot_raster = hotspots.execute_911_calls_hotspot()
result_layer
hotspot_raster
```
The resultant hotspot raster can be visualized in the Jupyter Notebook using the code snippet below:
```
from IPython.display import Image
Image(hotspot_raster['mapImage']['href'])
```
|
github_jupyter
|
### Creating Data Frames
documentation: http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html
DataFrame is a 2-dimensional labeled data structure with columns of potentially different types. You can think of it
like a spreadsheet or SQL table, or a dict of Series objects.
You can create a data frame using:
- Dict of 1D ndarrays, lists, dicts, or Series
- 2-D numpy.ndarray
- Structured or record ndarray
- A Series
- Another DataFrame
### Data Frame attributes
| T | Transpose index and columns | |
|---------|-------------------------------------------------------------------------------------------------------------------|---|
| at | Fast label-based scalar accessor | |
| axes | Return a list with the row axis labels and column axis labels as the only members. | |
| blocks | Internal property, property synonym for as_blocks() | |
| dtypes | Return the dtypes in this object. | |
| empty | True if NDFrame is entirely empty [no items], meaning any of the axes are of length 0. | |
| ftypes | Return the ftypes (indication of sparse/dense and dtype) in this object. | |
| iat | Fast integer location scalar accessor. | |
| iloc | Purely integer-location based indexing for selection by position. | |
| is_copy | | |
| ix | A primarily label-location based indexer, with integer position fallback. | |
| loc | Purely label-location based indexer for selection by label. | |
| ndim | Number of axes / array dimensions | |
| shape | Return a tuple representing the dimensionality of the DataFrame. | |
| size | number of elements in the NDFrame | |
| style | Property returning a Styler object containing methods for building a styled HTML representation fo the DataFrame. | |
| values | Numpy representation of NDFrame | |
```
import pandas as pd
import numpy as np
```
### Creating data frames from various data types
documentation: http://pandas.pydata.org/pandas-docs/stable/dsintro.html
cookbook: http://pandas.pydata.org/pandas-docs/stable/cookbook.html
##### create data frame from Python dictionary
```
my_dictionary = {'a' : 45., 'b' : -19.5, 'c' : 4444}
print(my_dictionary.keys())
print(my_dictionary.values())
```
##### constructor without explicit index
```
cookbook_df = pd.DataFrame({'AAA' : [4,5,6,7], 'BBB' : [10,20,30,40],'CCC' : [100,50,-30,-50]})
cookbook_df
```
##### constructor contains dictionary with Series as values
```
series_dict = {'one' : pd.Series([1., 2., 3.], index=['a', 'b', 'c']),
'two' : pd.Series([1., 2., 3., 4.], index=['a', 'b', 'c', 'd'])}
series_df = pd.DataFrame(series_dict)
series_df
```
##### dictionary of lists
```
produce_dict = {'veggies': ['potatoes', 'onions', 'peppers', 'carrots'],
'fruits': ['apples', 'bananas', 'pineapple', 'berries']}
produce_dict
```
##### list of dictionaries
```
data2 = [{'a': 1, 'b': 2}, {'a': 5, 'b': 10, 'c': 20}]
pd.DataFrame(data2)
```
##### dictionary of tuples, with multi index
```
pd.DataFrame({('a', 'b'): {('A', 'B'): 1, ('A', 'C'): 2},
('a', 'a'): {('A', 'C'): 3, ('A', 'B'): 4},
('a', 'c'): {('A', 'B'): 5, ('A', 'C'): 6},
('b', 'a'): {('A', 'C'): 7, ('A', 'B'): 8},
('b', 'b'): {('A', 'D'): 9, ('A', 'B'): 10}})
```
|
github_jupyter
|
# Chapter 10 - Predicting Continuous Target Variables with Regression Analysis
### Overview
- [Introducing a simple linear regression model](#Introducing-a-simple-linear-regression-model)
- [Exploring the Housing Dataset](#Exploring-the-Housing-Dataset)
- [Visualizing the important characteristics of a dataset](#Visualizing-the-important-characteristics-of-a-dataset)
- [Implementing an ordinary least squares linear regression model](#Implementing-an-ordinary-least-squares-linear-regression-model)
- [Solving regression for regression parameters with gradient descent](#Solving-regression-for-regression-parameters-with-gradient-descent)
- [Estimating the coefficient of a regression model via scikit-learn](#Estimating-the-coefficient-of-a-regression-model-via-scikit-learn)
- [Fitting a robust regression model using RANSAC](#Fitting-a-robust-regression-model-using-RANSAC)
- [Evaluating the performance of linear regression models](#Evaluating-the-performance-of-linear-regression-models)
- [Using regularized methods for regression](#Using-regularized-methods-for-regression)
- [Turning a linear regression model into a curve - polynomial regression](#Turning-a-linear-regression-model-into-a-curve---polynomial-regression)
- [Modeling nonlinear relationships in the Housing Dataset](#Modeling-nonlinear-relationships-in-the-Housing-Dataset)
- [Dealing with nonlinear relationships using random forests](#Dealing-with-nonlinear-relationships-using-random-forests)
- [Decision tree regression](#Decision-tree-regression)
- [Random forest regression](#Random-forest-regression)
- [Summary](#Summary)
<br>
<br>
```
from IPython.display import Image
%matplotlib inline
```
# Introducing a simple linear regression model
#### Univariate Model
$$
y = w_0 + w_1 x
$$
Relationship between
- a single feature (**explanatory variable**) $x$
- a continous target (**response**) variable $y$
```
Image(filename='./images/10_01.png', width=500)
```
- **regression line** : the best-fit line
- **offsets** or **residuals**: the gap between the regression line and the sample points
#### Multivariate Model
$$
y = w_0 + w_1 x_1 + \dots + w_m x_m
$$
<br>
<br>
# Exploring the Housing dataset
- Information about houses in the suburbs of Boston
- Collected by D. Harrison and D.L. Rubinfeld in 1978
- 506 samples
Source: [https://archive.ics.uci.edu/ml/datasets/Housing](https://archive.ics.uci.edu/ml/datasets/Housing)
Attributes:
<pre>
1. CRIM per capita crime rate by town
2. ZN proportion of residential land zoned for lots over
25,000 sq.ft.
3. INDUS proportion of non-retail business acres per town
4. CHAS Charles River dummy variable (= 1 if tract bounds
river; 0 otherwise)
5. NOX nitric oxides concentration (parts per 10 million)
6. RM average number of rooms per dwelling
7. AGE proportion of owner-occupied units built prior to 1940
8. DIS weighted distances to five Boston employment centres
9. RAD index of accessibility to radial highways
10. TAX full-value property-tax rate per $10,000
11. PTRATIO pupil-teacher ratio by town
12. B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks
by town
13. LSTAT % lower status of the population
14. MEDV Median value of owner-occupied homes in $1000's
</pre>
We'll consider **MEDV** as our target variable.
```
import pandas as pd
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/'
'housing/housing.data',
header=None,
sep='\s+')
df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS',
'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
df.head()
```
<br>
<br>
## Visualizing the important characteristics of a dataset
#### Scatter plot matrix
```
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style='whitegrid', context='notebook')
cols = ['LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']
sns.pairplot(df[cols], size=2.5)
plt.tight_layout()
# plt.savefig('./figures/scatter.png', dpi=300)
plt.show()
```
#### Correlation Matrix
- a scaled version of the covariance matrix
- each entry contains the **Pearson product-moment correlation coefficients** (**Pearson's r**)
- quantifies **linear** relationship between features
- ranges in $[-1,1]$
- $r=1$ perfect positive correlation
- $r=0$ no correlation
- $r=-1$ perfect negative correlation
$$
r = \frac{
\sum_{i=1}^n [(x^{(i)}-\mu_x)(y^{(i)}-\mu_y)]
}{
\sqrt{\sum_{i=1}^n (x^{(i)}-\mu_x)^2}
\sqrt{\sum_{i=1}^n (y^{(i)}-\mu_y)^2}
} =
\frac{\sigma_{xy}}{\sigma_x\sigma_y}
$$
```
import numpy as np
cm = np.corrcoef(df[cols].values.T)
sns.set(font_scale=1.5)
hm = sns.heatmap(cm,
cbar=True,
annot=True,
square=True,
fmt='.2f',
annot_kws={'size': 15},
yticklabels=cols,
xticklabels=cols)
# plt.tight_layout()
# plt.savefig('./figures/corr_mat.png', dpi=300)
plt.show()
```
- MEDV has large correlation with LSTAT and RM
- The relation between MEDV ~ LSTAT may not be linear
- The relation between MEDV ~ RM looks liinear
```
sns.reset_orig()
%matplotlib inline
```
<br>
<br>
# Implementing an ordinary least squares (OLS) linear regression model
## Solving regression for regression parameters with gradient descent
#### OLS Cost Function (Sum of Squred Errors, SSE)
$$
J(w) = \frac12 \sum_{i=1}^n (y^{(i)} - \hat y^{(i)})^2 = \frac12 \| y - Xw - \mathbb{1}w_0\|^2
$$
- $\hat y^{(i)} = w^T x^{(i)} $ is the predicted value
- OLS linear regression can be understood as Adaline without the step function, which converts the linear response $w^T x$ into $\{-1,1\}$.
#### Gradient Descent (refresh)
$$
w_{k+1} = w_k - \eta_k \nabla J(w_k), \;\; k=1,2,\dots
$$
- $\eta_k>0$ is the learning rate
- $$
\nabla J(w_k) =
\begin{bmatrix} -X^T(y-Xw- \mathbb{1}w_0) \\
-\mathbb{1}^T(y-Xw- \mathbb{1}w_0)
\end{bmatrix}
$$
```
class LinearRegressionGD(object):
def __init__(self, eta=0.001, n_iter=20):
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
self.w_ = np.zeros(1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
output = self.net_input(X)
errors = (y - output)
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
cost = (errors**2).sum() / 2.0
self.cost_.append(cost)
return self
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
def predict(self, X):
return self.net_input(X)
X = df[['RM']].values
y = df[['MEDV']].values
y.shape
from sklearn.preprocessing import StandardScaler
sc_x = StandardScaler()
sc_y = StandardScaler()
X_std = sc_x.fit_transform(X)
#y_std = sc_y.fit_transform(y[:, np.newaxis]).flatten()
y_std = sc_y.fit_transform(y).flatten()
y_std.shape
lr = LinearRegressionGD()
lr.fit(X_std, y_std)
plt.plot(range(1, lr.n_iter+1), lr.cost_)
plt.ylabel('SSE')
plt.xlabel('Epoch')
plt.tight_layout()
# plt.savefig('./figures/cost.png', dpi=300)
plt.show()
def lin_regplot(X, y, model):
plt.scatter(X, y, c='lightblue')
plt.plot(X, model.predict(X), color='red', linewidth=2)
return
lin_regplot(X_std, y_std, lr)
plt.xlabel('Average number of rooms [RM] (standardized)')
plt.ylabel('Price in $1000\'s [MEDV] (standardized)')
plt.tight_layout()
# plt.savefig('./figures/gradient_fit.png', dpi=300)
plt.show()
print('Slope: %.3f' % lr.w_[1])
print('Intercept: %.3f' % lr.w_[0])
num_rooms_std = sc_x.transform(np.array([[5.0]]))
price_std = lr.predict(num_rooms_std)
print("Price in $1000's: %.3f" % sc_y.inverse_transform(price_std))
```
<br>
<br>
## Estimating the coefficient of a regression model via scikit-learn
```
from sklearn.linear_model import LinearRegression
slr = LinearRegression()
slr.fit(X, y)
y_pred = slr.predict(X)
print('Slope: %.3f' % slr.coef_[0])
print('Intercept: %.3f' % slr.intercept_)
```
The solution is different from the previous result, since the data is **not** normalized here.
```
lin_regplot(X, y, slr)
plt.xlabel('Average number of rooms [RM]')
plt.ylabel('Price in $1000\'s [MEDV]')
plt.tight_layout()
# plt.savefig('./figures/scikit_lr_fit.png', dpi=300)
plt.show()
```
<br>
<br>
# Fitting a robust regression model using RANSAC (RANdom SAmple Consensus)
- Linear regression models can be heavily affected by outliers
- A very small subset of data can have a big impact on the estimated model coefficients
- Removing outliers is not easy
RANSAC algorithm:
1. Select a random subset of samples to be *inliers* and fit the model
2. Test all other data points against the fitted model, and add those points that fall within a user-defined tolerance to inliers
3. Refit the model using all inliers.
4. Estimate the error of the fitted model vs. the inliers
5. Terminate if the performance meets a user-defined threshold, or if a fixed number of iterations has been reached.
```
from sklearn.linear_model import RANSACRegressor
ransac = RANSACRegressor(LinearRegression(),
max_trials=100,
min_samples=50,
loss='absolute_loss',
residual_threshold=5.0, # problem-specific
random_state=0)
ransac.fit(X, y)
inlier_mask = ransac.inlier_mask_
outlier_mask = np.logical_not(inlier_mask)
line_X = np.arange(3, 10, 1)
line_y_ransac = ransac.predict(line_X[:, np.newaxis])
plt.scatter(X[inlier_mask], y[inlier_mask],
c='blue', marker='o', label='Inliers')
plt.scatter(X[outlier_mask], y[outlier_mask],
c='lightgreen', marker='s', label='Outliers')
plt.plot(line_X, line_y_ransac, color='red')
plt.xlabel('Average number of rooms [RM]')
plt.ylabel('Price in $1000\'s [MEDV]')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('./figures/ransac_fit.png', dpi=300)
plt.show()
print('Slope: %.3f' % ransac.estimator_.coef_[0])
print('Intercept: %.3f' % ransac.estimator_.intercept_)
```
<br>
<br>
# Evaluating the performance of linear regression models
```
from sklearn.model_selection import train_test_split
X = df.iloc[:, :-1].values
y = df['MEDV'].values
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)
slr = LinearRegression()
slr.fit(X_train, y_train)
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)
```
#### Residual Plot
- It's not easy to plot linear regression line in general, since the model uses multiple explanatory variables
- Residual plots are used for:
- detect nonlinearity
- detect outliers
- check if errors are randomly distributed
```
plt.scatter(y_train_pred, y_train_pred - y_train,
c='blue', marker='o', label='Training data')
plt.scatter(y_test_pred, y_test_pred - y_test,
c='lightgreen', marker='s', label='Test data')
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, lw=2, color='red')
plt.xlim([-10, 50])
plt.tight_layout()
# plt.savefig('./figures/slr_residuals.png', dpi=300)
plt.show()
```
If we see patterns in residual plot, it implies that our model didn't capture some explanatory information which leaked into the pattern.
#### MSE (Mean-Square Error)
$$
\text{MSE} = \frac{1}{n} \sum_{i=1}^n \left( y^{(i)} - \hat y^{(i)} \right)^2
$$
#### $R^2$ score
- The fraction of variance captured by the model
- $R^2=1$ : the model fits the data perfectly
$$
R^2 = 1 - \frac{SSE}{SST}, \;\; SST = \sum_{i=1}^n \left( y^{(i)}-\mu_y\right)^2
$$
$$
R^2 = 1 - \frac{MSE}{Var(y)}
$$
```
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
print('MSE train: %.3f, test: %.3f' % (
mean_squared_error(y_train, y_train_pred),
mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (
r2_score(y_train, y_train_pred),
r2_score(y_test, y_test_pred)))
```
The gap in MSE (between train and test) indicates overfitting
<br>
<br>
# Using regularized methods for regression
#### Ridge Regression
$$
J(w) = \frac12 \sum_{i=1}^n (y^{(i)}-\hat y^{(i)})^2 + \lambda \|w\|_2^2
$$
#### LASSO (Least Absolute Shrinkage and Selection Operator)
$$
J(w) = \frac12 \sum_{i=1}^n (y^{(i)}-\hat y^{(i)})^2 + \lambda \|w\|_1
$$
#### Elastic-Net
$$
J(w) = \frac12 \sum_{i=1}^n (y^{(i)}-\hat y^{(i)})^2 + \lambda_1 \|w\|_2^2 + \lambda_2 \|w\|_1
$$
```
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.linear_model import ElasticNet
ridge = Ridge(alpha=1.0)
lasso = Lasso(alpha=1.0)
enet = ElasticNet(alpha=1.0, l1_ratio=0.5)
ridge.fit(X_train, y_train)
lasso.fit(X_train, y_train)
enet.fit(X_train, y_train)
#y_train_pred = lasso.predict(X_train)
y_test_pred_r = ridge.predict(X_test)
y_test_pred_l = lasso.predict(X_test)
y_test_pred_e = enet.predict(X_test)
print("Ridge = ", ridge.coef_)
print("LASSO = ", lasso.coef_)
print("ENET = ",enet.coef_)
print('MSE train: %.3f, test: %.3f' % (
mean_squared_error(y_train, y_train_pred),
mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (
r2_score(y_train, y_train_pred),
r2_score(y_test, y_test_pred)))
```
<br>
<br>
# Turning a linear regression model into a curve - polynomial regression
$$
y = w_0 + w_1 x + w_2 x^2 + \dots + w_d x^d
$$
```
X = np.array([258.0, 270.0, 294.0,
320.0, 342.0, 368.0,
396.0, 446.0, 480.0, 586.0])[:, np.newaxis]
y = np.array([236.4, 234.4, 252.8,
298.6, 314.2, 342.2,
360.8, 368.0, 391.2,
390.8])
from sklearn.preprocessing import PolynomialFeatures
lr = LinearRegression()
pr = LinearRegression()
quadratic = PolynomialFeatures(degree=2)
X_quad = quadratic.fit_transform(X)
# fit linear features
lr.fit(X, y)
X_fit = np.arange(250, 600, 10)[:, np.newaxis]
y_lin_fit = lr.predict(X_fit)
# fit quadratic features
pr.fit(X_quad, y)
y_quad_fit = pr.predict(quadratic.fit_transform(X_fit))
# plot results
plt.scatter(X, y, label='training points')
plt.plot(X_fit, y_lin_fit, label='linear fit', linestyle='--')
plt.plot(X_fit, y_quad_fit, label='quadratic fit')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('./figures/poly_example.png', dpi=300)
plt.show()
y_lin_pred = lr.predict(X)
y_quad_pred = pr.predict(X_quad)
print('Training MSE linear: %.3f, quadratic: %.3f' % (
mean_squared_error(y, y_lin_pred),
mean_squared_error(y, y_quad_pred)))
print('Training R^2 linear: %.3f, quadratic: %.3f' % (
r2_score(y, y_lin_pred),
r2_score(y, y_quad_pred)))
```
<br>
<br>
## Modeling nonlinear relationships in the Housing Dataset
```
X = df[['LSTAT']].values
y = df['MEDV'].values
regr = LinearRegression()
# create quadratic features
quadratic = PolynomialFeatures(degree=2)
cubic = PolynomialFeatures(degree=3)
X_quad = quadratic.fit_transform(X)
X_cubic = cubic.fit_transform(X)
# fit features
X_fit = np.arange(X.min(), X.max(), 1)[:, np.newaxis]
regr = regr.fit(X, y)
y_lin_fit = regr.predict(X_fit)
linear_r2 = r2_score(y, regr.predict(X))
regr = regr.fit(X_quad, y)
y_quad_fit = regr.predict(quadratic.fit_transform(X_fit))
quadratic_r2 = r2_score(y, regr.predict(X_quad))
regr = regr.fit(X_cubic, y)
y_cubic_fit = regr.predict(cubic.fit_transform(X_fit))
cubic_r2 = r2_score(y, regr.predict(X_cubic))
# plot results
plt.scatter(X, y, label='training points', color='lightgray')
plt.plot(X_fit, y_lin_fit,
label='linear (d=1), $R^2=%.2f$' % linear_r2,
color='blue',
lw=2,
linestyle=':')
plt.plot(X_fit, y_quad_fit,
label='quadratic (d=2), $R^2=%.2f$' % quadratic_r2,
color='red',
lw=2,
linestyle='-')
plt.plot(X_fit, y_cubic_fit,
label='cubic (d=3), $R^2=%.2f$' % cubic_r2,
color='green',
lw=2,
linestyle='--')
plt.xlabel('% lower status of the population [LSTAT]')
plt.ylabel('Price in $1000\'s [MEDV]')
plt.legend(loc='upper right')
plt.tight_layout()
# plt.savefig('./figures/polyhouse_example.png', dpi=300)
plt.show()
```
As the model complexity increases, the chance of overfitting increases as well
Transforming the dataset:
```
X = df[['LSTAT']].values
y = df['MEDV'].values
# transform features
X_log = np.log(X)
y_sqrt = np.sqrt(y)
# fit features
X_fit = np.arange(X_log.min()-1, X_log.max()+1, 1)[:, np.newaxis]
regr = regr.fit(X_log, y_sqrt)
y_lin_fit = regr.predict(X_fit)
linear_r2 = r2_score(y_sqrt, regr.predict(X_log))
# plot results
plt.scatter(X_log, y_sqrt, label='training points', color='lightgray')
plt.plot(X_fit, y_lin_fit,
label='linear (d=1), $R^2=%.2f$' % linear_r2,
color='blue',
lw=2)
plt.xlabel('log(% lower status of the population [LSTAT])')
plt.ylabel('$\sqrt{Price \; in \; \$1000\'s [MEDV]}$')
plt.legend(loc='lower left')
plt.tight_layout()
# plt.savefig('./figures/transform_example.png', dpi=300)
plt.show()
```
<br>
<br>
# Dealing with nonlinear relationships using random forests
We use Information Gain (IG) to find the feature to split, which will lead to the maximal IG:
$$
IG(D_p, x_i) = I(D_p) - \frac{N_{left}}{N_p} I(D_{left}) - \frac{N_{right}}{N_p} I(D_{right})
$$
where $I$ is the impurity measure.
We've used e.g. entropy for discrete features. Here, we use MSE at node $t$ instead for continuous features:
$$
I(t) = MSE(t) = \frac{1}{N_t} \sum_{i \in D_t} (y^{(i)} - \bar y_t)^2
$$
where $\bar y_t$ is the sample mean,
$$
\bar y_t = \frac{1}{N_t} \sum_{i \in D_t} y^{(i)}
$$
## Decision tree regression
```
from sklearn.tree import DecisionTreeRegressor
X = df[['LSTAT']].values
y = df['MEDV'].values
tree = DecisionTreeRegressor(max_depth=3)
tree.fit(X, y)
sort_idx = X.flatten().argsort()
lin_regplot(X[sort_idx], y[sort_idx], tree)
plt.xlabel('% lower status of the population [LSTAT]')
plt.ylabel('Price in $1000\'s [MEDV]')
# plt.savefig('./figures/tree_regression.png', dpi=300)
plt.show()
r2 = r2_score(y, tree.predict(X))
print("R^2 = ", r2)
```
Disadvantage: it does not capture the continuity and differentiability of the desired prediction
<br>
<br>
## Random forest regression
Advantages:
- better generalization than individual trees
- less sensitive to outliers in the dataset
- don't require much parameter tuning
```
X = df.iloc[:, :-1].values
y = df['MEDV'].values
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.4, random_state=1)
from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor(n_estimators=1000,
criterion='mse',
random_state=1,
n_jobs=-1)
forest.fit(X_train, y_train)
y_train_pred = forest.predict(X_train)
y_test_pred = forest.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (
mean_squared_error(y_train, y_train_pred),
mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (
r2_score(y_train, y_train_pred),
r2_score(y_test, y_test_pred)))
plt.scatter(y_train_pred,
y_train_pred - y_train,
c='black',
marker='o',
s=35,
alpha=0.5,
label='Training data')
plt.scatter(y_test_pred,
y_test_pred - y_test,
c='lightgreen',
marker='s',
s=35,
alpha=0.7,
label='Test data')
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, lw=2, color='red')
plt.xlim([-10, 50])
plt.tight_layout()
# plt.savefig('./figures/slr_residuals.png', dpi=300)
plt.show()
```
<br>
<br>
# Summary
- Univariate and multivariate linear models
- RANSAC to deal with outliers
- Regularization: control model complexity to avoid overfitting
|
github_jupyter
|
# Loss Functions
This python script illustrates the different loss functions for regression and classification.
We start by loading the ncessary libraries and resetting the computational graph.
```
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.python.framework import ops
ops.reset_default_graph()
```
### Create a Graph Session
```
sess = tf.Session()
```
## Numerical Predictions
---------------------------------
To start with our investigation of loss functions, we begin by looking at numerical loss functions. To do so, we must create a sequence of predictions around a target. For this exercise, we consider the target to be zero.
```
# Various Predicted X-values
x_vals = tf.linspace(-1., 1., 500)
# Create our target of zero
target = tf.constant(0.)
```
### L2 Loss
The L2 loss is one of the most common regression loss functions. Here we show how to create it in TensorFlow and we evaluate it for plotting later.
```
# L2 loss
# L = (pred - actual)^2
l2_y_vals = tf.square(target - x_vals)
l2_y_out = sess.run(l2_y_vals)
```
### L1 Loss
An alternative loss function to consider is the L1 loss. This is very similar to L2 except that we take the `absolute value` of the difference instead of squaring it.
```
# L1 loss
# L = abs(pred - actual)
l1_y_vals = tf.abs(target - x_vals)
l1_y_out = sess.run(l1_y_vals)
```
### Pseudo-Huber Loss
The psuedo-huber loss function is a smooth approximation to the L1 loss as the (predicted - target) values get larger. When the predicted values are close to the target, the pseudo-huber loss behaves similar to the L2 loss.
```
# L = delta^2 * (sqrt(1 + ((pred - actual)/delta)^2) - 1)
# Pseudo-Huber with delta = 0.25
delta1 = tf.constant(0.25)
phuber1_y_vals = tf.multiply(tf.square(delta1), tf.sqrt(1. + tf.square((target - x_vals)/delta1)) - 1.)
phuber1_y_out = sess.run(phuber1_y_vals)
# Pseudo-Huber with delta = 5
delta2 = tf.constant(5.)
phuber2_y_vals = tf.multiply(tf.square(delta2), tf.sqrt(1. + tf.square((target - x_vals)/delta2)) - 1.)
phuber2_y_out = sess.run(phuber2_y_vals)
```
### Plot the Regression Losses
Here we use Matplotlib to plot the L1, L2, and Pseudo-Huber Losses.
```
x_array = sess.run(x_vals)
plt.plot(x_array, l2_y_out, 'b-', label='L2 Loss')
plt.plot(x_array, l1_y_out, 'r--', label='L1 Loss')
plt.plot(x_array, phuber1_y_out, 'k-.', label='P-Huber Loss (0.25)')
plt.plot(x_array, phuber2_y_out, 'g:', label='P-Huber Loss (5.0)')
plt.ylim(-0.2, 0.4)
plt.legend(loc='lower right', prop={'size': 11})
plt.show()
```
## Categorical Predictions
-------------------------------
We now consider categorical loss functions. Here, the predictions will be around the target of 1.
```
# Various predicted X values
x_vals = tf.linspace(-3., 5., 500)
# Target of 1.0
target = tf.constant(1.)
targets = tf.fill([500,], 1.)
```
### Hinge Loss
The hinge loss is useful for categorical predictions. Here is is the `max(0, 1-(pred*actual))`.
```
# Hinge loss
# Use for predicting binary (-1, 1) classes
# L = max(0, 1 - (pred * actual))
hinge_y_vals = tf.maximum(0., 1. - tf.multiply(target, x_vals))
hinge_y_out = sess.run(hinge_y_vals)
```
### Cross Entropy Loss
The cross entropy loss is a very popular way to measure the loss between categorical targets and output model logits. You can read about the details more here: https://en.wikipedia.org/wiki/Cross_entropy
```
# Cross entropy loss
# L = -actual * (log(pred)) - (1-actual)(log(1-pred))
xentropy_y_vals = - tf.multiply(target, tf.log(x_vals)) - tf.multiply((1. - target), tf.log(1. - x_vals))
xentropy_y_out = sess.run(xentropy_y_vals)
```
### Sigmoid Entropy Loss
TensorFlow also has a sigmoid-entropy loss function. This is very similar to the above cross-entropy function except that we take the sigmoid of the predictions in the function.
```
# L = -actual * (log(sigmoid(pred))) - (1-actual)(log(1-sigmoid(pred)))
# or
# L = max(actual, 0) - actual * pred + log(1 + exp(-abs(actual)))
x_val_input = tf.expand_dims(x_vals, 1)
target_input = tf.expand_dims(targets, 1)
xentropy_sigmoid_y_vals = tf.nn.softmax_cross_entropy_with_logits(logits=x_val_input, labels=target_input)
xentropy_sigmoid_y_out = sess.run(xentropy_sigmoid_y_vals)
```
### Weighted (Softmax) Cross Entropy Loss
Tensorflow also has a similar function to the `sigmoid cross entropy` loss function above, but we take the softmax of the actuals and weight the predicted output instead.
```
# Weighted (softmax) cross entropy loss
# L = -actual * (log(pred)) * weights - (1-actual)(log(1-pred))
# or
# L = (1 - pred) * actual + (1 + (weights - 1) * pred) * log(1 + exp(-actual))
weight = tf.constant(0.5)
xentropy_weighted_y_vals = tf.nn.weighted_cross_entropy_with_logits(x_vals, targets, weight)
xentropy_weighted_y_out = sess.run(xentropy_weighted_y_vals)
```
### Plot the Categorical Losses
```
# Plot the output
x_array = sess.run(x_vals)
plt.plot(x_array, hinge_y_out, 'b-', label='Hinge Loss')
plt.plot(x_array, xentropy_y_out, 'r--', label='Cross Entropy Loss')
plt.plot(x_array, xentropy_sigmoid_y_out, 'k-.', label='Cross Entropy Sigmoid Loss')
plt.plot(x_array, xentropy_weighted_y_out, 'g:', label='Weighted Cross Entropy Loss (x0.5)')
plt.ylim(-1.5, 3)
#plt.xlim(-1, 3)
plt.legend(loc='lower right', prop={'size': 11})
plt.show()
```
### Softmax entropy and Sparse Entropy
Since it is hard to graph mutliclass loss functions, we will show how to get the output instead
```
# Softmax entropy loss
# L = -actual * (log(softmax(pred))) - (1-actual)(log(1-softmax(pred)))
unscaled_logits = tf.constant([[1., -3., 10.]])
target_dist = tf.constant([[0.1, 0.02, 0.88]])
softmax_xentropy = tf.nn.softmax_cross_entropy_with_logits(logits=unscaled_logits,
labels=target_dist)
print(sess.run(softmax_xentropy))
# Sparse entropy loss
# Use when classes and targets have to be mutually exclusive
# L = sum( -actual * log(pred) )
unscaled_logits = tf.constant([[1., -3., 10.]])
sparse_target_dist = tf.constant([2])
sparse_xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=unscaled_logits,
labels=sparse_target_dist)
print(sess.run(sparse_xentropy))
```
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# 정형 데이터 다루기
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/structured_data/feature_columns">
<img src="https://www.tensorflow.org/images/tf_logo_32px.png" />
TensorFlow.org에서 보기</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/ko/tutorials/structured_data/feature_columns.ipynb">
<img src="https://www.tensorflow.org/images/colab_logo_32px.png" />
구글 코랩(Colab)에서 실행하기</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/ko/tutorials/structured_data/feature_columns.ipynb">
<img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />
깃허브(GitHub) 소스 보기</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/ko/tutorials/structured_data/feature_columns.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
Note: 이 문서는 텐서플로 커뮤니티에서 번역했습니다. 커뮤니티 번역 활동의 특성상 정확한 번역과 최신 내용을 반영하기 위해 노력함에도
불구하고 [공식 영문 문서](https://www.tensorflow.org/?hl=en)의 내용과 일치하지 않을 수 있습니다.
이 번역에 개선할 부분이 있다면
[tensorflow/docs-l10n](https://github.com/tensorflow/docs-l10n/) 깃헙 저장소로 풀 리퀘스트를 보내주시기 바랍니다.
문서 번역이나 리뷰에 참여하려면
[[email protected]](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-ko)로
메일을 보내주시기 바랍니다.
이 튜토리얼은 정형 데이터(structured data)를 다루는 방법을 소개합니다(예를 들어 CSV에서 읽은 표 형식의 데이터). [케라스](https://www.tensorflow.org/guide/keras)를 사용하여 모델을 정의하고 [특성 열](https://www.tensorflow.org/guide/feature_columns)(feature column)을 사용하여 CSV의 열을 모델 훈련에 필요한 특성으로 매핑하겠습니다. 이 튜토리얼은 다음 내용을 포함합니다:
* [판다스](https://pandas.pydata.org/)(Pandas)를 사용하여 CSV 파일을 읽기
* [tf.data](https://www.tensorflow.org/guide/datasets)를 사용하여 행을 섞고 배치로 나누는 입력 파이프라인(pipeline)을 만들기
* CSV의 열을 feature_column을 사용해 모델 훈련에 필요한 특성으로 매핑하기
* 케라스를 사용하여 모델 구축, 훈련, 평가하기
## 데이터셋
클리블랜드(Cleveland) 심장병 재단에서 제공한 작은 [데이터셋](https://archive.ics.uci.edu/ml/datasets/heart+Disease)을 사용하겠습니다. 이 CSV 파일은 수백 개의 행으로 이루어져 있습니다. 각 행은 환자 한 명을 나타내고 각 열은 환자에 대한 속성 값입니다. 이 정보를 사용해 환자의 심장병 발병 여부를 예측해 보겠습니다. 즉 이 데이터셋은 이진 분류 문제입니다.
다음은 이 데이터셋에 대한 [설명](https://archive.ics.uci.edu/ml/machine-learning-databases/heart-disease/heart-disease.names)입니다. 수치형과 범주형 열이 모두 있다는 점을 주목하세요.
>열| 설명| 특성 타입 | 데이터 타입
>------------|--------------------|----------------------|-----------------
>Age | 나이 | 수치형 | 정수
>Sex | (1 = 남성; 0 = 여성) | 범주형 | 정수
>CP | 가슴 통증 유형 (0, 1, 2, 3, 4) | 범주형 | 정수
>Trestbpd | 안정 혈압 (병원 입원시 mm Hg) | 수치형 | 정수
>Chol | 혈청 콜레스테롤 (mg/dl) | 수치형 | 정수
>FBS | (공복 혈당 > 120 mg/dl) (1 = true; 0 = false) | 범주형 | 정수
>RestECG | 안정 심전도 결과 (0, 1, 2) | 범주형 | 정수
>Thalach | 최대 심박동수 | 수치형 | 정수
>Exang | 협심증 유발 운동 (1 = yes; 0 = no) | 범주형 | 정수
>Oldpeak | 비교적 안정되기까지 운동으로 유발되는 ST depression | 수치형 | 정수
>Slope | 최대 운동 ST segment의 기울기 | 수치형 | 실수
>CA | 형광 투시된 주요 혈관의 수 (0-3) | 수치형 | 정수
>Thal | 3 = 보통; 6 = 해결된 결함; 7 = 해결가능한 결함 | 범주형 | 문자열
>Target | 심장병 진단 (1 = true; 0 = false) | 분류 | 정수
## 텐서플로와 필요한 라이브러리 임포트하기
```
!pip install sklearn
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow import feature_column
from tensorflow.keras import layers
from sklearn.model_selection import train_test_split
```
## 판다스로 데이터프레임 만들기
[판다스](https://pandas.pydata.org/)는 정형 데이터를 읽고 조작하는데 유용한 유틸리티 함수를 많이 제공하는 파이썬 라이브러리입니다. 판다스를 이용해 URL로부터 데이터를 다운로드하여 읽은 다음 데이터프레임으로 변환하겠습니다.
```
URL = 'https://storage.googleapis.com/applied-dl/heart.csv'
dataframe = pd.read_csv(URL)
dataframe.head()
```
## 데이터프레임을 훈련 세트, 검증 세트, 테스트 세트로 나누기
하나의 CSV 파일에서 데이터셋을 다운로드했습니다. 이를 훈련 세트, 검증 세트, 테스트 세트로 나누겠습니다.
```
train, test = train_test_split(dataframe, test_size=0.2)
train, val = train_test_split(train, test_size=0.2)
print(len(train), '훈련 샘플')
print(len(val), '검증 샘플')
print(len(test), '테스트 샘플')
```
## tf.data를 사용하여 입력 파이프라인 만들기
그다음 [tf.data](https://www.tensorflow.org/guide/datasets)를 사용하여 데이터프레임을 감싸겠습니다. 이렇게 하면 특성 열을 사용하여 판다스 데이터프레임의 열을 모델 훈련에 필요한 특성으로 매핑할 수 있습니다. 아주 큰 CSV 파일(메모리에 들어갈 수 없을 정도로 큰 파일)을 다룬다면 tf.data로 디스크 디렉토리에서 데이터를 읽을 수 있습니다. 이런 내용은 이 튜토리얼에 포함되어 있지 않습니다.
```
# 판다스 데이터프레임으로부터 tf.data 데이터셋을 만들기 위한 함수
def df_to_dataset(dataframe, shuffle=True, batch_size=32):
dataframe = dataframe.copy()
labels = dataframe.pop('target')
ds = tf.data.Dataset.from_tensor_slices((dict(dataframe), labels))
if shuffle:
ds = ds.shuffle(buffer_size=len(dataframe))
ds = ds.batch(batch_size)
return ds
batch_size = 5 # 예제를 위해 작은 배치 크기를 사용합니다.
train_ds = df_to_dataset(train, batch_size=batch_size)
val_ds = df_to_dataset(val, shuffle=False, batch_size=batch_size)
test_ds = df_to_dataset(test, shuffle=False, batch_size=batch_size)
```
## 입력 파이프라인 이해하기
앞서 만든 입력 파이프라인을 호출하여 반환되는 데이터 포맷을 확인해 보겠습니다. 간단하게 출력하기 위해 작은 배치 크기를 사용합니다.
```
for feature_batch, label_batch in train_ds.take(1):
print('전체 특성:', list(feature_batch.keys()))
print('나이 특성의 배치:', feature_batch['age'])
print('타깃의 배치:', label_batch )
```
이 데이터셋은 (데이터프레임의) 열 이름을 키로 갖는 딕셔너리를 반환합니다. 데이터프레임 열의 값이 매핑되어 있습니다.
## 여러 종류의 특성 열 알아 보기
텐서플로는 여러 종류의 특성 열을 제공합니다. 이 절에서 몇 가지 특성 열을 만들어서 데이터프레임의 열을 변환하는 방법을 알아 보겠습니다.
```
# 특성 열을 시험해 보기 위해 샘플 배치를 만듭니다.
example_batch = next(iter(train_ds))[0]
# 특성 열을 만들고 배치 데이터를 변환하는 함수
def demo(feature_column):
feature_layer = layers.DenseFeatures(feature_column)
print(feature_layer(example_batch).numpy())
```
### 수치형 열
특성 열의 출력은 모델의 입력이 됩니다(앞서 정의한 함수를 사용하여 데이터프레임의 각 열이 어떻게 변환되는지 알아 볼 것입니다). [수치형 열](https://www.tensorflow.org/api_docs/python/tf/feature_column/numeric_column)은 가장 간단한 종류의 열입니다. 이 열은 실수 특성을 표현하는데 사용됩니다. 이 열을 사용하면 모델은 데이터프레임 열의 값을 변형시키지 않고 그대로 전달 받습니다.
```
age = feature_column.numeric_column("age")
demo(age)
```
심장병 데이터셋 데이터프레임의 대부분 열은 수치형입니다.
### 버킷형 열
종종 모델에 수치 값을 바로 주입하기 원치 않을 때가 있습니다. 대신 수치 값의 구간을 나누어 이를 기반으로 범주형으로 변환합니다. 원본 데이터가 사람의 나이를 표현한다고 가정해 보죠. 나이를 수치형 열로 표현하는 대신 [버킷형 열](https://www.tensorflow.org/api_docs/python/tf/feature_column/bucketized_column)(bucketized column)을 사용하여 나이를 몇 개의 버킷(bucket)으로 분할할 수 있습니다. 다음에 원-핫 인코딩(one-hot encoding)된 값은 각 열이 매칭되는 나이 범위를 나타냅니다.
```
age_buckets = feature_column.bucketized_column(age, boundaries=[18, 25, 30, 35, 40, 45, 50, 55, 60, 65])
demo(age_buckets)
```
### 범주형 열
이 데이터셋에서 thal 열은 문자열입니다(예를 들어 'fixed', 'normal', 'reversible'). 모델에 문자열을 바로 주입할 수 없습니다. 대신 문자열을 먼저 수치형으로 매핑해야 합니다. 범주형 열(categorical column)을 사용하여 문자열을 원-핫 벡터로 표현할 수 있습니다. 문자열 목록은 [categorical_column_with_vocabulary_list](https://www.tensorflow.org/api_docs/python/tf/feature_column/categorical_column_with_vocabulary_list)를 사용하여 리스트로 전달하거나 [categorical_column_with_vocabulary_file](https://www.tensorflow.org/api_docs/python/tf/feature_column/categorical_column_with_vocabulary_file)을 사용하여 파일에서 읽을 수 있습니다.
```
thal = feature_column.categorical_column_with_vocabulary_list(
'thal', ['fixed', 'normal', 'reversible'])
thal_one_hot = feature_column.indicator_column(thal)
demo(thal_one_hot)
```
더 복잡한 데이터셋에는 범주형(예를 들면 문자열)인 열이 많을 수 있습니다. 특성 열은 범주형 데이터를 다룰 때 진가가 발휘됩니다. 이 데이터셋에는 범주형 열이 하나 뿐이지만 다른 데이터셋에서 사용할 수 있는 여러 종류의 특성 열을 소개하겠습니다.
### 임베딩 열
가능한 문자열이 몇 개가 있는 것이 아니라 범주마다 수천 개 이상의 값이 있는 경우를 상상해 보겠습니다. 여러 가지 이유로 범주의 개수가 늘어남에 따라 원-핫 인코딩을 사용하여 신경망을 훈련시키는 것이 불가능해집니다. 임베딩 열(embedding column)을 사용하면 이런 제한을 극복할 수 있습니다. 고차원 원-핫 벡터로 데이터를 표현하는 대신 [임베딩 열](https://www.tensorflow.org/api_docs/python/tf/feature_column/embedding_column)을 사용하여 저차원으로 데이터를 표현합니다. 이 벡터는 0 또는 1이 아니라 각 원소에 어떤 숫자도 넣을 수 있는 밀집 벡터(dense vector)입니다. 임베딩의 크기(아래 예제에서는 8입니다)는 튜닝 대상 파라미터입니다.
핵심 포인트: 범주형 열에 가능한 값이 많을 때는 임베딩 열을 사용하는 것이 최선입니다. 여기에서는 예시를 목적으로 하나를 사용하지만 완전한 예제이므로 나중에 다른 데이터셋에 수정하여 적용할 수 있습니다.
```
# 임베딩 열의 입력은 앞서 만든 범주형 열입니다.
thal_embedding = feature_column.embedding_column(thal, dimension=8)
demo(thal_embedding)
```
### 해시 특성 열
가능한 값이 많은 범주형 열을 표현하는 또 다른 방법은 [categorical_column_with_hash_bucket](https://www.tensorflow.org/api_docs/python/tf/feature_column/categorical_column_with_hash_bucket)을 사용하는 것입니다. 이 특성 열은 입력의 해시(hash) 값을 계산한 다음 `hash_bucket_size` 크기의 버킷 중 하나를 선택하여 문자열을 인코딩합니다. 이 열을 사용할 때는 어휘 목록을 제공할 필요가 없고 공간을 절약하기 위해 실제 범주의 개수보다 훨씬 작게 해시 버킷(bucket)의 크기를 정할 수 있습니다.
핵심 포인트: 이 기법의 큰 단점은 다른 문자열이 같은 버킷에 매핑될 수 있다는 것입니다. 그럼에도 실전에서는 일부 데이터셋에서 잘 작동합니다.
```
thal_hashed = feature_column.categorical_column_with_hash_bucket(
'thal', hash_bucket_size=1000)
demo(feature_column.indicator_column(thal_hashed))
```
### 교차 특성 열
여러 특성을 연결하여 하나의 특성으로 만드는 것을 [교차 특성](https://developers.google.com/machine-learning/glossary/#feature_cross)(feature cross)이라고 합니다. 모델이 특성의 조합에 대한 가중치를 학습할 수 있습니다. 이 예제에서는 age와 thal의 교차 특성을 만들어 보겠습니다. `crossed_column`은 모든 가능한 조합에 대한 해시 테이블을 만들지 않고 `hashed_column` 매개변수를 사용하여 해시 테이블의 크기를 선택합니다.
```
crossed_feature = feature_column.crossed_column([age_buckets, thal], hash_bucket_size=1000)
demo(feature_column.indicator_column(crossed_feature))
```
## 사용할 열 선택하기
여러 가지 특성 열을 사용하는 방법을 보았으므로 이제 이를 사용하여 모델을 훈련하겠습니다. 이 튜토리얼의 목적은 특성 열을 사용하는 완전한 코드(예를 들면 작동 방식)를 제시하는 것이므로 임의로 몇 개의 열을 선택하여 모델을 훈련하겠습니다.
핵심 포인트: 제대로 된 모델을 만들어야 한다면 대용량의 데이터셋을 사용하고 어떤 특성을 포함하는 것이 가장 의미있는지, 또 어떻게 표현해야 할지 신중하게 생각하세요.
```
feature_columns = []
# 수치형 열
for header in ['age', 'trestbps', 'chol', 'thalach', 'oldpeak', 'slope', 'ca']:
feature_columns.append(feature_column.numeric_column(header))
# 버킷형 열
age_buckets = feature_column.bucketized_column(age, boundaries=[18, 25, 30, 35, 40, 45, 50, 55, 60, 65])
feature_columns.append(age_buckets)
# 범주형 열
thal = feature_column.categorical_column_with_vocabulary_list(
'thal', ['fixed', 'normal', 'reversible'])
thal_one_hot = feature_column.indicator_column(thal)
feature_columns.append(thal_one_hot)
# 임베딩 열
thal_embedding = feature_column.embedding_column(thal, dimension=8)
feature_columns.append(thal_embedding)
# 교차 특성 열
crossed_feature = feature_column.crossed_column([age_buckets, thal], hash_bucket_size=1000)
crossed_feature = feature_column.indicator_column(crossed_feature)
feature_columns.append(crossed_feature)
```
### 특성 층 만들기
특성 열을 정의하고 나면 [DenseFeatures](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/layers/DenseFeatures) 층을 사용해 케라스 모델에 주입할 수 있습니다.
```
feature_layer = tf.keras.layers.DenseFeatures(feature_columns)
```
앞서 특성 열의 작동 예를 보이기 위해 작은 배치 크기를 사용했습니다. 여기에서는 조금 더 큰 배치 크기로 입력 파이프라인을 만듭니다.
```
batch_size = 32
train_ds = df_to_dataset(train, batch_size=batch_size)
val_ds = df_to_dataset(val, shuffle=False, batch_size=batch_size)
test_ds = df_to_dataset(test, shuffle=False, batch_size=batch_size)
```
## 모델 생성, 컴파일, 훈련
```
model = tf.keras.Sequential([
feature_layer,
layers.Dense(128, activation='relu'),
layers.Dense(128, activation='relu'),
layers.Dense(1, activation='sigmoid')
])
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy'])
model.fit(train_ds,
validation_data=val_ds,
epochs=5)
loss, accuracy = model.evaluate(test_ds)
print("정확도", accuracy)
```
핵심 포인트: 일반적으로 크고 복잡한 데이터셋일 경우 딥러닝 모델에서 최선의 결과를 얻습니다. 이런 작은 데이터셋에서는 기본 모델로 결정 트리(decision tree)나 랜덤 포레스트(random forest)를 사용하는 것이 권장됩니다. 이 튜토리얼의 목적은 정확한 모델을 훈련하는 것이 아니라 정형 데이터를 다루는 방식을 설명하는 것입니다. 실전 데이터셋을 다룰 때 이 코드를 시작점으로 사용하세요.
## 그 다음엔
정형 데이터를 사용한 분류 작업에 대해 배우는 가장 좋은 방법은 직접 실습하는 것입니다. 실험해 볼 다른 데이터셋을 찾아서 위와 비슷한 코드를 사용해 모델을 훈련해 보세요. 정확도를 향상시키려면 모델에 포함할 특성과 표현 방법을 신중하게 생각하세요.
|
github_jupyter
|
### Entrepreneurial Competency Analysis and Predict
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib as mat
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
data = pd.read_csv('entrepreneurial competency.csv')
data.head()
data.describe()
data.corr()
list(data)
data.shape
data_reasons = pd.DataFrame(data.ReasonsForLack.value_counts())
data_reasons
data.ReasonsForLack.value_counts().idxmax()
data.isnull().sum()[data.isnull().sum()>0]
data['ReasonsForLack'] = data.ReasonsForLack.fillna('Desconhecido')
fill_na = pd.DataFrame(data.ReasonsForLack.value_counts())
fill_na.head(5)
edu_sector = data.EducationSector.value_counts().sort_values(ascending=False)
edu_sector
edu_sector_pd = pd.DataFrame(edu_sector, columns = ['Sector', 'Amount'])
edu_sector_pd.Sector = edu_sector.index
edu_sector_pd.Amount = edu_sector.values
edu_sector_pd
perc_sec = round(data.EducationSector.value_counts()/data.EducationSector.shape[0],2)
edu_sector_pd['Percentual'] = perc_sec.values *100
edu_sector_pd
labels = [str(edu_sector_pd['Sector'][i])+' '+'['+str(round(edu_sector_pd['Percentual'][i],2)) +'%'+']' for i in edu_sector_pd.index]
from matplotlib import cm
cs = cm.Set3(np.arange(100))
f = plt.figure()
plt.pie(edu_sector_pd['Amount'], labeldistance = 1, radius = 3, colors = cs, wedgeprops = dict(width = 0.8))
plt.legend(labels = labels, loc = 'center', prop = {'size':12})
plt.title("Students distribution based on Education Sector - General Analysis", loc = 'Center', fontdict = {'fontsize':20,'fontweight':20})
plt.show()
rank_edu_sec = data.EducationSector.value_counts().sort_values(ascending=False)
rank = pd.DataFrame(rank_edu_sec, columns=['Sector', 'Amount'])
rank.Sector = rank_edu_sec.index
rank.Amount = rank_edu_sec.values
rank_3 = rank.head(3)
rank_3
fig, ax = plt.subplots(figsize=(8,5))
colors = ["#00e600", "#ff8c1a", "#a180cc"]
sns.barplot(x="Sector", y="Amount", palette=colors, data=rank_3)
ax.set_title("Sectors with largest students number",fontdict= {'size':12})
ax.xaxis.set_label_text("Sectors",fontdict= {'size':12})
ax.yaxis.set_label_text("Students amount",fontdict= {'size':12})
plt.show()
fig, ax = plt.subplots(figsize=(8,6))
sns.histplot(data["Age"], color="#33cc33",kde=True, ax=ax)
ax.set_title('Students distribution based on Age', fontsize= 15)
plt.ylabel("Density (KDE)", fontsize= 15)
plt.xlabel("Age", fontsize= 15)
plt.show()
fig = plt.figure(figsize=(10,5))
plt.boxplot(data.Age)
plt.show()
gender = data.Gender.value_counts()
gender
perc_gender = round((data.Gender.value_counts()/data.Gender.shape[0])*100, 2)
perc_gender
df_gender = pd.DataFrame(gender, columns=['Gender','Absolut_Value', 'Percent_Value'])
df_gender.Gender = gender.index
df_gender.Absolut_Value = gender.values
df_gender.Percent_Value = perc_gender.values
df_gender
fig, ax = plt.subplots(figsize=(8,6))
sns.histplot(data["Gender"], color="#33cc33", ax=ax)
ax.set_title('Students distribution by gender', fontsize= 15)
plt.ylabel("Amount", fontsize= 15)
plt.xlabel("Gender", fontsize= 15)
plt.show()
```
# Education Sector, Gender and Age Analyses, where Target = 1
```
data_y = data[data.y == 1]
data_y.head()
data_y.shape
edu_sector_y = data_y.EducationSector.value_counts().sort_values(ascending=False)
edu_sector_y
edu_sector_ypd = pd.DataFrame(edu_sector_y, columns = ['Sector', 'Amount'])
edu_sector_ypd.Sector = edu_sector_y.index
edu_sector_ypd.Amount = edu_sector_y.values
edu_sector_ypd
perc_sec_y = round(data_y.EducationSector.value_counts()/data_y.EducationSector.shape[0],2)
edu_sector_ypd['Percent'] = perc_sec_y.values *100
edu_sector_ypd
labels = [str(edu_sector_ypd['Sector'][i])+' '+'['+str(round(edu_sector_ypd['Percent'][i],2)) +'%'+']' for i in edu_sector_ypd.index]
cs = cm.Set3(np.arange(100))
f = plt.figure()
plt.pie(edu_sector_ypd['Amount'], labeldistance = 1, radius = 3, colors = cs, wedgeprops = dict(width = 0.8))
plt.legend(labels = labels, loc = 'center', prop = {'size':12})
plt.title("Students distribution based on Education Sector - Target Analysis", loc = 'Center', fontdict = {'fontsize':20,'fontweight':20})
plt.show()
fig, ax = plt.subplots(figsize=(8,6))
sns.histplot(data_y["Age"], color="#1f77b4",kde=True, ax=ax)
ax.set_title('Students distribution based on Age - Target Analysis', fontsize= 15)
plt.ylabel("Density (KDE)", fontsize= 15)
plt.xlabel("Age", fontsize= 15)
plt.show()
gender_y = data_y.Gender.value_counts()
perc_gender_y = round((data_y.Gender.value_counts()/data_y.Gender.shape[0])*100, 2)
df_gender_y = pd.DataFrame(gender_y, columns=['Gender','Absolut_Value', 'Percent_Value'])
df_gender_y.Gender = gender_y.index
df_gender_y.Absolut_Value = gender_y.values
df_gender_y.Percent_Value = perc_gender_y.values
df_gender_y
fig, ax = plt.subplots(figsize=(8,6))
sns.histplot(data_y["Gender"], color="#9467bd", ax=ax)
ax.set_title('Students distribution by gender', fontsize= 15)
plt.ylabel("Amount", fontsize= 15)
plt.xlabel("Gender", fontsize= 15)
plt.show()
pcy= round(data_y.IndividualProject.value_counts()/data_y.IndividualProject.shape[0]*100,2)
pcy
pc= round(data.IndividualProject.value_counts()/data.IndividualProject.shape[0]*100,2)
pc
fig = plt.figure(figsize=(15,5)) #tamanho do frame
plt.subplots_adjust(wspace= 0.5) #espaço entre os graficos
plt.suptitle('Comparation between Idividual Project on "y general" and "y == 1"')
plt.subplot(1,2,2)
plt.bar(data_y.IndividualProject.unique(), pcy, color = 'green')
plt.title("Individual Project Distribution - y==1")
plt.subplot(1,2,1)
plt.bar(data.IndividualProject.unique(), pc, color = 'grey')
plt.title("Individual Project Distribution - Full dataset")
plt.show()
round(data.Influenced.value_counts()/data.Influenced.shape[0],2)*100
round(data_y.Influenced.value_counts()/data_y.Influenced.shape[0],2)*100
```
Here we can observe that the categoric features have no influence on Target. Each feature measure almost haven´t any impact when compared on 'y general' and 'y == 1'. In other words, we must take the numerical features as predict parameters.
```
data.head()
list(data)
data_num = data.drop(['EducationSector', 'Age', 'Gender', 'City','MentalDisorder'], axis = 1)
data_num.head()
data_num.corr()
plt.hist(data_num.GoodPhysicalHealth, bins = 30)
plt.title("Good Physical Health distribution")
plt.show()
data_num_fil1 = data_num[data_num.y == 1]
plt.hist(data_num_fil1.GoodPhysicalHealth, bins = 30)
plt.title("Good Physical Health distribution, where target == 1")
plt.show()
pers_fil = round(data_num.GoodPhysicalHealth.value_counts()/data_num.GoodPhysicalHealth.shape[0],2)
pers_fil1 = round(data_num_fil1.GoodPhysicalHealth.value_counts()/data_num_fil1.GoodPhysicalHealth.shape[0],2)
pers_fil
pers_fil1
list(data_num)
def plot_features(df, df_filtered, columns):
df_original = df.copy()
df2 = df_filtered.copy()
for column in columns:
a = df_original[column]
b = df2[column]
fig = plt.figure(figsize=(15,5)) #tamanho do frame
plt.subplots_adjust(wspace= 0.5) #espaço entre os graficos
plt.suptitle('Comparation between Different Features on "y general" and "y == 1"')
plt.subplot(1,2,2)
plt.bar(a.unique(), round(a.value_counts()/a.shape[0],2), color = 'green')
plt.title("Comparation between " + column + " on 'y == 1'")
plt.subplot(1,2,1)
plt.bar(b.unique(), round(a.value_counts()/b.shape[0],2), color = 'grey')
plt.title("Comparation between " + column + " Full dataset")
plt.show()
plot_features(data_num,data_num_fil1,columns=['Influenced',
'Perseverance',
'DesireToTakeInitiative',
'Competitiveness',
'SelfReliance',
'StrongNeedToAchieve',
'SelfConfidence'])
```
### Data Transformation and Preprocessing
```
data_num.shape
data_num.dtypes
from sklearn.preprocessing import OneHotEncoder
X = data_num.drop(['y', 'Influenced', 'ReasonsForLack'], axis = 1)
def ohe_drop(data, columns):
df = data.copy()
ohe = OneHotEncoder()
for column in columns:
var_ohe = df[column].values.reshape(-1,1)
ohe.fit(var_ohe)
ohe.transform(var_ohe)
OHE = pd.DataFrame(ohe.transform(var_ohe).toarray(),
columns = ohe.categories_[0].tolist())
df = pd.concat([df, OHE], axis = 1)
df = df.drop([column],axis = 1)
return df
X = ohe_drop(data_num, columns =['Perseverance',
'DesireToTakeInitiative',
'Competitiveness',
'SelfReliance',
'StrongNeedToAchieve',
'SelfConfidence',
'GoodPhysicalHealth',
'Influenced',
'KeyTraits'] )
X
X = X.drop(['y', 'ReasonsForLack', 'IndividualProject'], axis = 1)
y = np.array(data_num.y)
X.shape
y.shape
X = np.array(X)
type(X)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size = 0.30, random_state = 0)
X_train.shape
X_test.shape
y_train.shape
y_test.shape
```
### Logistic Regression
```
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
logreg.predict(X_train)
logreg.predict(X_train)[:20]
y_train[:20]
```
### Performance metrics calculation
Accuracy Score
Transformar df em matrix
```
from sklearn.metrics import accuracy_score
accuracy_score(y_true = y_train, y_pred = logreg.predict(X_train))
```
Cross Validation
```
from sklearn.model_selection import KFold
kf = KFold(n_splits = 3)
classif= LogisticRegression()
train_accuracy_list = []
val_accuracy_list = []
for train_idx, val_idx in kf.split(X_train, y_train):
Xtrain_folds = X_train[train_idx]
ytrain_folds = y_train[train_idx]
Xval_fold = X_train[val_idx]
yval_fold = y_train[val_idx]
classif.fit(Xtrain_folds,ytrain_folds)
train_pred = classif.predict(Xtrain_folds)
pred_validacao = classif.predict(Xval_fold)
train_accuracy_list.append(accuracy_score(y_pred = train_pred, y_true = ytrain_folds))
val_accuracy_list.append(accuracy_score(y_pred = pred_validacao, y_true = yval_fold))
print("acurácias em treino: \n", train_accuracy_list, " \n| média: ", np.mean(train_accuracy_list))
print()
print("acurácias em validação: \n", val_accuracy_list, " \n| média: ", np.mean(val_accuracy_list))
from sklearn.metrics import confusion_matrix
confusion_matrix(y_true = y_train, y_pred = logreg.predict(X_train))
cm = confusion_matrix(y_true = y_train, y_pred = logreg.predict(X_train))
cm[1,1] / cm[1, :].sum()
cm[1,1] / cm[:, 1].sum()
from sklearn.metrics import precision_score, recall_score
from sklearn.metrics import f1_score
f1_score(y_true = y_train, y_pred = logreg.predict(X_train))
```
### Y test Predict
```
logreg.predict(X_test)
f1_score(y_true = y_test, y_pred = logreg.predict(X_test))
```
The predict of "y_test" is too low, so I'll optimize the model
### Model Optimization
```
from sklearn.feature_selection import SelectKBest, chi2
def try_k(x, y, n):
the_best = SelectKBest(score_func = chi2, k =n)
fit = the_best.fit(x, y)
features = fit.transform(x)
logreg.fit(features,y)
preds = logreg.predict(features)
f1 = f1_score(y_true = y, y_pred = preds)
precision = precision_score(y_true = y, y_pred = preds)
recall = recall_score(y_true = y, y_pred = preds)
return preds, f1, precision, recall
for n in n_list:
preds,f1, precision, recall = try_k(X_test, y_test, n)
f1
precision
recall
from sklearn.metrics import classification_report, plot_confusion_matrix,plot_roc_curve
the_best = SelectKBest(score_func = chi2, k =30)
fit = the_best.fit(X_test, y_test)
feature = fit.transform(X_test)
preds = logreg.predict(feature)
plot_confusion_matrix(logreg,features,y_test)
plot_roc_curve(logreg,features,y_test)
print(classification_report(y_test, preds))
```
|
github_jupyter
|
# Mean Shift using Standard Scaler
This Code template is for the Cluster analysis using a simple Mean Shift(Centroid-Based Clustering using a flat kernel) Clustering algorithm along with feature scaling using Standard Scaler and includes 2D and 3D cluster visualization of the Clusters.
### Required Packages
```
!pip install plotly
import operator
import warnings
import itertools
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.preprocessing import StandardScaler
import plotly.express as px
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
import plotly.graph_objects as go
from sklearn.cluster import MeanShift, estimate_bandwidth
warnings.filterwarnings("ignore")
```
### Initialization
Filepath of CSV file
```
file_path = ""
```
List of features which are required for model training
```
features=[]
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X.
```
X = df[features]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
X.head()
```
####Feature Scaling
Standard Scaler - Standardize features by removing the mean and scaling to unit variance
Centering and scaling happen independently on each feature by computing the relevant statistics on the samples in the training set. Mean and standard deviation are then stored to be used on later data using transform.<br>
[For more information click here](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html)
```
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
```
### Model
Mean shift clustering using a flat kernel.
Mean shift clustering aims to discover “blobs” in a smooth density of samples. It is a centroid-based algorithm, which works by updating candidates for centroids to be the mean of the points within a given region. These candidates are then filtered in a post-processing stage to eliminate near-duplicates to form the final set of centroids.
Seeding is performed using a binning technique for scalability.
[More information](https://analyticsindiamag.com/hands-on-tutorial-on-mean-shift-clustering-algorithm/)
#### Tuning Parameters
1. bandwidthfloat, default=None
> Bandwidth used in the RBF kernel.
If not given, the bandwidth is estimated using sklearn.cluster.estimate_bandwidth
2. seedsarray-like of shape (n_samples, n_features), default=None
> Seeds used to initialize kernels. If not set, the seeds are calculated by clustering.get_bin_seeds with bandwidth as the grid size and default values for other parameters.
3. bin_seedingbool, default=False
> If true, initial kernel locations are not locations of all points, but rather the location of the discretized version of points, where points are binned onto a grid whose coarseness corresponds to the bandwidth.
4. min_bin_freqint, default=1
> To speed up the algorithm, accept only those bins with at least min_bin_freq points as seeds.
5. cluster_allbool, default=True
> If true, then all points are clustered, even those orphans that are not within any kernel. Orphans are assigned to the nearest kernel. If false, then orphans are given cluster label -1
6. n_jobsint, default=None
> The number of jobs to use for the computation. This works by computing each of the n_init runs in parallel. None means 1 unless in a joblib.parallel_backend context. -1 means using all processors.
7. max_iterint, default=300
> Maximum number of iterations, per seed point before the clustering operation terminates
[For more detail on API](https://scikit-learn.org/stable/modules/generated/sklearn.cluster.MeanShift.html)
<br>
<br>
####Estimate Bandwidth
Estimate the bandwidth to use with the mean-shift algorithm.
That this function takes time at least quadratic in n_samples. For large datasets, it’s wise to set that parameter to a small value.
```
bandwidth = estimate_bandwidth(X_scaled, quantile=0.15)
ms = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms.fit(X_scaled)
y_pred = ms.predict(X_scaled)
```
### Cluster Analysis
First, we add the cluster labels from the trained model into the copy of the data frame for cluster analysis/visualization.
```
ClusterDF = X.copy()
ClusterDF['ClusterID'] = y_pred
ClusterDF.head()
```
#### Cluster Records
The below bar graphs show the number of data points in each available cluster.
```
ClusterDF['ClusterID'].value_counts().plot(kind='bar')
```
#### Cluster Plots
Below written functions get utilized to plot 2-Dimensional and 3-Dimensional cluster plots on the available set of features in the dataset. Plots include different available clusters along with cluster centroid.
```
def Plot2DCluster(X_Cols,df):
for i in list(itertools.combinations(X_Cols, 2)):
plt.rcParams["figure.figsize"] = (8,6)
xi,yi=df.columns.get_loc(i[0]),df.columns.get_loc(i[1])
for j in df['ClusterID'].unique():
DFC=df[df.ClusterID==j]
plt.scatter(DFC[i[0]],DFC[i[1]],cmap=plt.cm.Accent,label=j)
plt.scatter(ms.cluster_centers_[:,xi],ms.cluster_centers_[:,yi],marker="^",color="black",label="centroid")
plt.xlabel(i[0])
plt.ylabel(i[1])
plt.legend()
plt.show()
def Plot3DCluster(X_Cols,df):
for i in list(itertools.combinations(X_Cols, 3)):
xi,yi,zi=df.columns.get_loc(i[0]),df.columns.get_loc(i[1]),df.columns.get_loc(i[2])
fig,ax = plt.figure(figsize = (16, 10)),plt.axes(projection ="3d")
ax.grid(b = True, color ='grey',linestyle ='-.',linewidth = 0.3,alpha = 0.2)
for j in df['ClusterID'].unique():
DFC=df[df.ClusterID==j]
ax.scatter3D(DFC[i[0]],DFC[i[1]],DFC[i[2]],alpha = 0.8,cmap=plt.cm.Accent,label=j)
ax.scatter3D(ms.cluster_centers_[:,xi],ms.cluster_centers_[:,yi],ms.cluster_centers_[:,zi],
marker="^",color="black",label="centroid")
ax.set_xlabel(i[0])
ax.set_ylabel(i[1])
ax.set_zlabel(i[2])
plt.legend()
plt.show()
def Plotly3D(X_Cols,df):
for i in list(itertools.combinations(X_Cols,3)):
xi,yi,zi=df.columns.get_loc(i[0]),df.columns.get_loc(i[1]),df.columns.get_loc(i[2])
fig1 = px.scatter_3d(ms.cluster_centers_,x=ms.cluster_centers_[:,xi],y=ms.cluster_centers_[:,yi],
z=ms.cluster_centers_[:,zi])
fig2=px.scatter_3d(df, x=i[0], y=i[1],z=i[2],color=df['ClusterID'])
fig3 = go.Figure(data=fig1.data + fig2.data,
layout=go.Layout(title=go.layout.Title(text="x:{}, y:{}, z:{}".format(i[0],i[1],i[2])))
)
fig3.show()
sns.set_style("whitegrid")
sns.set_context("talk")
plt.rcParams["lines.markeredgewidth"] = 1
sns.pairplot(data=ClusterDF, hue='ClusterID', palette='Dark2', height=5)
Plot2DCluster(X.columns,ClusterDF)
Plot3DCluster(X.columns,ClusterDF)
Plotly3D(X.columns,ClusterDF)
```
#### [Created by Anu Rithiga](https://github.com/iamgrootsh7)
|
github_jupyter
|
```
import pickle
import matplotlib.pyplot as plt
from scipy.stats.mstats import gmean
import seaborn as sns
from statistics import stdev
from math import log
import numpy as np
from scipy import stats
%matplotlib inline
price_100c = pickle.load(open("total_price_non.p","rb"))
price_100 = pickle.load(open("C:\\Users\\ymamo\Google Drive\\1. PhD\\Dissertation\\SugarScape\Initial\\NetScape_Elegant\\total_price1.p", "rb"))
from collections import defaultdict
def make_distro(price_100):
all_stds =[]
total_log = defaultdict(list)
for run, output in price_100.items():
for step, prices in output.items():
log_pr = [log(p) for p in prices]
if len(log_pr) <2:
pass
else:
out = stdev(log_pr)
total_log[run].append(out)
all_stds.append(out)
return all_stds
price_cluster = make_distro(price_100c)
price_norm = make_distro(price_100)
fig7, ax7 = plt.subplots(figsize = (7,7))
ax7.hist(price_cluster, 500, label = "Hierarchy")
ax7.hist(price_norm, 500, label = "No Hierarchy")
plt.title("Network Approach:\nPrice Distribution of SDLM of 100 Runs", fontsize = 20, fontweight = "bold")
plt.xlabel("SDLM of Step", fontsize = 15, fontweight = "bold")
plt.ylabel("Frequency of SDLM", fontsize = 15, fontweight = "bold")
#plt.xlim(.75,2)
#plt.ylim(0,5)
plt.legend()
from statistics import mean
stan_multi_s = pickle.load(open("C:\\Users\\ymamo\\Google Drive\\1. PhD\\Dissertation\\SugarScape\\NetScape_Standard\\stan_multi_sur.p", "rb"))
stan_multi_t = pickle.load(open("C:\\Users\\ymamo\\Google Drive\\1. PhD\\Dissertation\\SugarScape\\NetScape_Standard\\stan_multi_time.p", "rb"))
brute_multi_s = pickle.load(open("C:\\Users\\ymamo\\Google Drive\\1. PhD\\Dissertation\\SugarScape\\NetScape_Brute\\brute_multi_sur.p", "rb"))
brute_multi_t = pickle.load(open("C:\\Users\\ymamo\\Google Drive\\1. PhD\\Dissertation\\SugarScape\\NetScape_Brute\\brute_multi_time.p", "rb"))
net_multi_s = pickle.load(open("net_multi_sur_non.p", "rb"))
net_multi_t =pickle.load(open("net_multi_time_non.p", "rb"))
net_mean = mean(net_multi_s)
brute_mean = mean(brute_multi_s)
stan_mean = mean(stan_multi_s)
net_time = round(mean(net_multi_t),2)
brute_time = round(mean(brute_multi_t),2)
stan_time = round(mean(stan_multi_t),2)
t, p = stats.ttest_ind(stan_multi_s,brute_multi_s)
brute_p = round(p * 2, 3)
t2, p2 = stats.ttest_ind(stan_multi_s,net_multi_s)
net_p = round(p * 2, 3)
print (net_p, brute_p)
fig5, ax5 = plt.subplots(figsize=(7,7))
plt.hist(net_multi_s, label = "Network Approach")
plt.hist(stan_multi_s, label = "Standard Approach")
plt.hist(brute_multi_s, label = "Explicit Approach")
plt.text(56.5, 28.5, "Network mean: "+str(net_mean) +"\nStandard mean: " + str(stan_mean)+ "\nExplicit mean: "+str(stan_mean))
plt.legend()
plt.title("Survivor Histogram of 100 Runs, 1000 Steps \nLink Threshold 10; with Hierarchy", fontweight = "bold", fontsize = 15)
t, p = stats.ttest_ind(stan_multi_t,brute_multi_t)
brute_t_p = (p * 2,10)
t2, p2 = stats.ttest_ind(stan_multi_t,net_multi_t)
net_t_p = (p * 2, 10)
print (net_t_p, brute_t_p)
fig6, ax6 = plt.subplots(figsize=(7,7))
plt.hist(net_multi_t, label = "Network Approach")
plt.hist(stan_multi_t, label = "Standard Approach")
plt.hist(brute_multi_t, label = "Explicit Approach")
#plt.text(78, 25, "Network p-value: "+str(net_t_p) +"\nExplicit p-value: "+str(brute_t_p))
plt.legend()
plt.title("Time Histogram of 100 Runs, 1000 steps \nLink Threshold 10; with Hierarchy", fontweight = "bold", fontsize = 15)
plt.text(70, 24, "\nNetwork Mean: "+str(net_time) +"\nStandard Mean: "+str(stan_time) + "\nExplicit Approach: "+str(brute_time))
ind_e = price_100c["Run95"]
## Calculate price
x = []
y =[]
for st, pr in ind_e.items():
#if step <=400:
x.append(st)
y.append(gmean(pr))
y[0]
fig, ax = plt.subplots(figsize = (7,7))
ax.scatter(x,y)
plt.title("Network Approach with Hierarchy:\nMean Trade Price", fontsize = 20, fontweight = "bold")
plt.xlabel("Time", fontsize = 15, fontweight = "bold")
plt.ylabel("Price", fontsize = 15, fontweight = "bold")
x_vol = []
y_vol = []
total = 0
for s, p in ind_e.items():
#if step <=400:
x_vol.append(s)
y_vol.append(len(p))
total += len(p)
total
fig2, ax2 = plt.subplots(figsize = (7,7))
ax2.hist(y_vol, 100)
plt.title("Network Approach with Hierarchy:\nTrade Volume Histogram", fontsize = 20, fontweight = "bold")
plt.xlabel("Trade Volume of Step", fontsize = 15, fontweight = "bold")
plt.ylabel("Frequency Trade Volume", fontsize = 15, fontweight = "bold")
#plt.ylim(0,400)
fig2, ax2 = plt.subplots(figsize = (7,7))
ax2.plot(x_vol, y_vol)
plt.title("Network Approach with Hierarchy:\nTrade Volume", fontsize = 20, fontweight = "bold")
plt.xlabel("Time", fontsize = 15, fontweight = "bold")
plt.ylabel("Volume", fontsize = 15, fontweight = "bold")
#ax2.text(600,300, "Total Trade Volume: \n "+str(total), fontsize = 15, fontweight = 'bold')
#plt.ylim(0,400)
from statistics import stdev
from math import log
x_dev =[]
y_dev = []
x_all = []
y_all = []
log_prices = {}
for step, prices in ind_e.items():
log_prices[step] = [log(p) for p in prices]
for step, log_p in log_prices.items():
#if step <= 400:
if len(log_p) <2:
pass
else:
for each in log_p:
x_all.append(step)
y_all.append(each)
x_dev.append(step)
y_dev.append(stdev(log_p))
from numpy.polynomial.polynomial import polyfit
fig3, ax3 = plt.subplots(figsize=(7,7))
ax3.scatter(x_all,y_all)
plt.plot(x_dev,y_dev,'-', color ='red')
plt.title("Network Approach with Hierarchy:\nStandard Deviation of Logarithmic Mean", fontsize = 20, fontweight = "bold")
plt.xlabel("Time", fontsize = 15, fontweight = "bold")
plt.ylabel("Logarithmic Price", fontsize = 15, fontweight = "bold")
net_emergent =pickle.load(open("type_df_non.p", "rb"))
net_emergent["Run67"][999]
```
|
github_jupyter
|
# Learning a LJ potential [](https://colab.research.google.com/github/Teoroo-CMC/PiNN/blob/master/docs/notebooks/Learn_LJ_potential.ipynb)
This notebook showcases the usage of PiNN with a toy problem of learning a Lennard-Jones
potential with a hand-generated dataset.
It serves as a basic test, and demonstration of the workflow with PiNN.
```
# Install PiNN
!pip install git+https://github.com/Teoroo-CMC/PiNN
%matplotlib inline
import os, warnings
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from ase import Atoms
from ase.calculators.lj import LennardJones
os.environ['CUDA_VISIBLE_DEVICES'] = ''
index_warning = 'Converting sparse IndexedSlices'
warnings.filterwarnings('ignore', index_warning)
```
## Reference data
```
# Helper function: get the position given PES dimension(s)
def three_body_sample(atoms, a, r):
x = a * np.pi / 180
pos = [[0, 0, 0],
[0, 2, 0],
[0, r*np.cos(x), r*np.sin(x)]]
atoms.set_positions(pos)
return atoms
atoms = Atoms('H3', calculator=LennardJones())
na, nr = 50, 50
arange = np.linspace(30,180,na)
rrange = np.linspace(1,3,nr)
# Truth
agrid, rgrid = np.meshgrid(arange, rrange)
egrid = np.zeros([na, nr])
for i in range(na):
for j in range(nr):
atoms = three_body_sample(atoms, arange[i], rrange[j])
egrid[i,j] = atoms.get_potential_energy()
# Samples
nsample = 100
asample, rsample = [], []
distsample = []
data = {'e_data':[], 'f_data':[], 'elems':[], 'coord':[]}
for i in range(nsample):
a, r = np.random.choice(arange), np.random.choice(rrange)
atoms = three_body_sample(atoms, a, r)
dist = atoms.get_all_distances()
dist = dist[np.nonzero(dist)]
data['e_data'].append(atoms.get_potential_energy())
data['f_data'].append(atoms.get_forces())
data['coord'].append(atoms.get_positions())
data['elems'].append(atoms.numbers)
asample.append(a)
rsample.append(r)
distsample.append(dist)
plt.pcolormesh(agrid, rgrid, egrid, shading='auto')
plt.plot(asample, rsample, 'rx')
plt.colorbar()
```
## Dataset from numpy arrays
```
from pinn.io import sparse_batch, load_numpy
data = {k:np.array(v) for k,v in data.items()}
dataset = lambda: load_numpy(data, splits={'train':8, 'test':2})
train = lambda: dataset()['train'].shuffle(100).repeat().apply(sparse_batch(100))
test = lambda: dataset()['test'].repeat().apply(sparse_batch(100))
```
## Training
### Model specification
```
import pinn
params={
'model_dir': '/tmp/PiNet',
'network': {
'name': 'PiNet',
'params': {
'ii_nodes':[8,8],
'pi_nodes':[8,8],
'pp_nodes':[8,8],
'out_nodes':[8,8],
'depth': 4,
'rc': 3.0,
'atom_types':[1]}},
'model':{
'name': 'potential_model',
'params': {
'e_dress': {1:-0.3}, # element-specific energy dress
'e_scale': 2, # energy scale for prediction
'e_unit': 1.0, # output unit of energy dur
'log_e_per_atom': True, # log e_per_atom and its distribution
'use_force': True}}} # include force in Loss function
model = pinn.get_model(params)
%rm -rf /tmp/PiNet
train_spec = tf.estimator.TrainSpec(input_fn=train, max_steps=5e3)
eval_spec = tf.estimator.EvalSpec(input_fn=test, steps=10)
tf.estimator.train_and_evaluate(model, train_spec, eval_spec)
```
## Validate the results
### PES analysis
```
atoms = Atoms('H3', calculator=pinn.get_calc(model))
epred = np.zeros([na, nr])
for i in range(na):
for j in range(nr):
a, r = arange[i], rrange[j]
atoms = three_body_sample(atoms, a, r)
epred[i,j] = atoms.get_potential_energy()
plt.pcolormesh(agrid, rgrid, epred, shading='auto')
plt.colorbar()
plt.title('NN predicted PES')
plt.figure()
plt.pcolormesh(agrid, rgrid, np.abs(egrid-epred), shading='auto')
plt.plot(asample, rsample, 'rx')
plt.title('NN Prediction error and sampled points')
plt.colorbar()
```
### Pairwise potential analysis
```
atoms1 = Atoms('H2', calculator=pinn.get_calc(model))
atoms2 = Atoms('H2', calculator=LennardJones())
nr2 = 100
rrange2 = np.linspace(1,1.9,nr2)
epred = np.zeros(nr2)
etrue = np.zeros(nr2)
for i in range(nr2):
pos = [[0, 0, 0],
[rrange2[i], 0, 0]]
atoms1.set_positions(pos)
atoms2.set_positions(pos)
epred[i] = atoms1.get_potential_energy()
etrue[i] = atoms2.get_potential_energy()
f, (ax1, ax2) = plt.subplots(2,1, gridspec_kw = {'height_ratios':[3, 1]})
ax1.plot(rrange2, epred)
ax1.plot(rrange2, etrue,'--')
ax1.legend(['Prediction', 'Truth'], loc=4)
_=ax2.hist(np.concatenate(distsample,0), 20, range=(1,1.9))
```
## Molecular dynamics with ASE
```
from ase import units
from ase.io import Trajectory
from ase.md.nvtberendsen import NVTBerendsen
from ase.md.velocitydistribution import MaxwellBoltzmannDistribution
atoms = Atoms('H', cell=[2, 2, 2], pbc=True)
atoms = atoms.repeat([5,5,5])
atoms.rattle()
atoms.set_calculator(pinn.get_calc(model))
MaxwellBoltzmannDistribution(atoms, 300*units.kB)
dyn = NVTBerendsen(atoms, 0.5 * units.fs, 300, taut=0.5*100*units.fs)
dyn.attach(Trajectory('ase_nvt.traj', 'w', atoms).write, interval=10)
dyn.run(5000)
```
|
github_jupyter
|
<h1><center>Assessmet 5 on Advanced Data Analysis using Pandas</center></h1>
## **Project 2: Correlation Between the GDP Rate and Unemployment Rate (2019)**
```
import warnings
warnings.simplefilter('ignore', FutureWarning)
import pandas as pd
pip install pandas_datareader
```
# Getting the Datasets
We got the two datasets we will be considering in this project from the Worldbank website. The first one dataset, available at http://data.worldbank.org/indicator/NY.GDP.MKTP.CD, lists the GDP of the world's countries in current US dollars, for various years. The use of a common currency allows us to compare GDP values across countries. The other dataset, available at https://data.worldbank.org/indicator/SL.UEM.TOTL.NE.ZS, lists the unemployment rate of the world's countries. The datasets were downloaded as Excel files in June 2021.
```
GDP_INDICATOR = 'NY.GDP.MKTP.CD'
#below is the first five rows of the first dataset, GDP Indicator.
gdpReset= pd.read_excel("API_NY.GDP.MKTP.CD.xls")
gdpReset.head()
#below is the last five rows of the first dataset, GDP Indicator.
gdpReset.tail()
UNEMPLOYMENT_INDICATORS = 'SL.UEM.TOTL.NE.ZS'
#below is the first five rows of the second dataset, Uemployment Rate Indicator.
UnemployReset= pd.read_excel('API_SL.UEM.TOTL.NE.ZS.xls')
UnemployReset.head()
#below is the last five rows of the second dataset, Unemployment Rate Indicator.
UnemployReset.tail()
```
# Cleaning the data
Inspecting the data with head() and tail() methods shows that for some countries the GDP and unemploymet rate values are missing. The data is, therefore, cleaned by removing the rows with unavailable values using the drop() method.
```
gdpCountries = gdpReset[0:].dropna()
gdpCountries
UnemployCountries = UnemployReset[0:].dropna()
UnemployCountries
```
# Transforming the data
The World Bank reports GDP in US dollars and cents. To make the data easier to read, the GDP is converted to millions of British pounds with the following auxiliary functions, using the average 2020 dollar-to-pound conversion rate provided by http://www.ukforex.co.uk/forex-tools/historical-rate-tools/yearly-average-rates..
```
def roundToMillions (value):
return round(value / 1000000)
def usdToGBP (usd):
return usd / 1.284145
GDP = 'GDP (£m)'
gdpCountries[GDP] = gdpCountries[GDP_INDICATOR].apply(usdToGBP).apply(roundToMillions)
gdpCountries.head()
```
The unnecessary columns can be dropped.
```
COUNTRY = 'Country Name'
headings = [COUNTRY, GDP]
gdpClean = gdpCountries[headings]
gdpClean.head()
```
```
UNEMPLOYMENT = 'Unemploymet Rate'
UnemployCountries[UNEMPLOYMENT] = UnemployCountries[UNEMPLOYMENT_INDICATORS].apply(round)
headings = [COUNTRY, UNEMPLOYMENT]
UnempClean = UnemployCountries[headings]
UnempClean.head()
```
# Combining the data
The tables are combined through an inner join merge method on the common 'Country Name' column.
```
gdpVsUnemp = pd.merge(gdpClean, UnempClean, on=COUNTRY, how='inner')
gdpVsUnemp.head()
```
# Calculating the correlation
To measure if the unemployment rate and the GDP grow together or not, the Spearman rank correlation coefficient is used.
```
from scipy.stats import spearmanr
gdpColumn = gdpVsUnemp[GDP]
UnemployColumn = gdpVsUnemp[UNEMPLOYMENT]
(correlation, pValue) = spearmanr(gdpColumn, UnemployColumn)
print('The correlation is', correlation)
if pValue < 0.05:
print('It is statistically significant.')
else:
print('It is not statistically significant.')
```
The value shows an indirect correlation, i.e. richer countries tend to have lower unemployment rate. A rise by one percentage point of unemployment will reduce real GDP growth by 0.26 percentage points with a delay of 7 lags. Studies have shown that the higher the GDP growth rate of a country, the higher the employment rate. Thus, resulting to a lower unemployment rate. Besides, a negative or inverse correlation, between two variables, indicates that one variable increases while the other decreases, and vice-versa.
# Visualizing the Data
Measures of correlation can be misleading, so it is best to view the overall picture with a scatterplot. The GDP axis uses a logarithmic scale to better display the vast range of GDP values, from a few million to several billion (million of million) pounds.
```
%matplotlib inline
gdpVsUnemp.plot(x=GDP, y=UNEMPLOYMENT, kind='scatter', grid=True, logx=True, figsize=(10, 4))
```
The plot shows there is no clear correlation: there are some poor countries with a low unemployment rate and very few averagely rich countries with a high employment rate. Hpwever, most extremely rich countries have a low unemployment rate. Besides, countries with around 10 thousand (10^4) to (10^6) million pounds GDP have almost the full range of values, from below 5 to over 10 percentage but there are still some countries with more than 10 thousand (10^5) million pounds GDP with a high unemployment rate.
Comparing the 10 poorest countries and the 10 countries with the lowest unemployment rate shows that total GDP is a rather crude measure. The population size should be taken into consideration for a more precise definiton of what 'poor' and 'rich' means.
```
# the 10 countries with lowest GDP
gdpVsUnemp.sort_values(GDP).head(10)
# the 10 countries with the lowest unemployment rate
gdpVsUnemp.sort_values(UNEMPLOYMENT).head(10)
```
# Conclusion
The correlation between real GDP growth and unemployment is very important for policy makers in order to obtain a sustainable rise in living standards. If GDP growth rate is below its natural rate it is indicated to promote employment because this rise in total income will note generate inflationary pressures. In contrast, if the GDP growth is above its natural level, policy makers will decide not to intensively promote the creation of new jobs in order to obtain a sustainable growth rate which will not generate inflation. The correlation coefficient shows that the variables are negatively correlated as predicted by the theory. These values are particularly important for policy makers in order to obtain an optimal relation between unemployment and real GDP growth.
|
github_jupyter
|
# T1557.001 - LLMNR/NBT-NS Poisoning and SMB Relay
By responding to LLMNR/NBT-NS network traffic, adversaries may spoof an authoritative source for name resolution to force communication with an adversary controlled system. This activity may be used to collect or relay authentication materials.
Link-Local Multicast Name Resolution (LLMNR) and NetBIOS Name Service (NBT-NS) are Microsoft Windows components that serve as alternate methods of host identification. LLMNR is based upon the Domain Name System (DNS) format and allows hosts on the same local link to perform name resolution for other hosts. NBT-NS identifies systems on a local network by their NetBIOS name. (Citation: Wikipedia LLMNR) (Citation: TechNet NetBIOS)
Adversaries can spoof an authoritative source for name resolution on a victim network by responding to LLMNR (UDP 5355)/NBT-NS (UDP 137) traffic as if they know the identity of the requested host, effectively poisoning the service so that the victims will communicate with the adversary controlled system. If the requested host belongs to a resource that requires identification/authentication, the username and NTLMv2 hash will then be sent to the adversary controlled system. The adversary can then collect the hash information sent over the wire through tools that monitor the ports for traffic or through [Network Sniffing](https://attack.mitre.org/techniques/T1040) and crack the hashes offline through [Brute Force](https://attack.mitre.org/techniques/T1110) to obtain the plaintext passwords. In some cases where an adversary has access to a system that is in the authentication path between systems or when automated scans that use credentials attempt to authenticate to an adversary controlled system, the NTLMv2 hashes can be intercepted and relayed to access and execute code against a target system. The relay step can happen in conjunction with poisoning but may also be independent of it. (Citation: byt3bl33d3r NTLM Relaying)(Citation: Secure Ideas SMB Relay)
Several tools exist that can be used to poison name services within local networks such as NBNSpoof, Metasploit, and [Responder](https://attack.mitre.org/software/S0174). (Citation: GitHub NBNSpoof) (Citation: Rapid7 LLMNR Spoofer) (Citation: GitHub Responder)
## Atomic Tests:
Currently, no tests are available for this technique.
## Detection
Monitor <code>HKLM\Software\Policies\Microsoft\Windows NT\DNSClient</code> for changes to the "EnableMulticast" DWORD value. A value of “0” indicates LLMNR is disabled. (Citation: Sternsecurity LLMNR-NBTNS)
Monitor for traffic on ports UDP 5355 and UDP 137 if LLMNR/NetBIOS is disabled by security policy.
Deploy an LLMNR/NBT-NS spoofing detection tool.(Citation: GitHub Conveigh) Monitoring of Windows event logs for event IDs 4697 and 7045 may help in detecting successful relay techniques.(Citation: Secure Ideas SMB Relay)
|
github_jupyter
|
<a href="https://colab.research.google.com/github/yohanesnuwara/66DaysOfData/blob/main/D01_PCA.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Principal Component Analysis
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.decomposition import PCA
from sklearn.datasets import load_digits, fetch_lfw_people
from sklearn.preprocessing import StandardScaler
rng = np.random.RandomState(1)
X = np.dot(rng.rand(2, 5), rng.randn(5, 200)).T
plt.scatter(X[:, 0], X[:, 1])
plt.axis('equal')
plt.show()
pca = PCA(n_components=2)
pca.fit(X)
```
PCA components are called eigenvectors.
```
print(pca.components_)
print(pca.explained_variance_)
def draw_vector(v0, v1, ax=None):
ax = ax or plt.gca()
arrowprops=dict(arrowstyle='->',
linewidth=2,
shrinkA=0, shrinkB=0)
ax.annotate('', v1, v0, arrowprops=arrowprops)
# plot data
plt.scatter(X[:, 0], X[:, 1])
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length)
draw_vector(pca.mean_, pca.mean_ + v)
plt.axis('equal');
```
## PCA to reduce dimension.
```
pca = PCA(n_components=1)
pca.fit(X)
X_pca = pca.transform(X)
print("original shape: ", X.shape)
print("transformed shape:", X_pca.shape)
X_new = pca.inverse_transform(X_pca)
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.8)
plt.axis('equal')
plt.show()
```
## PCA for digit classification.
```
digits = load_digits()
print(digits.data.shape)
pca = PCA(2) # project from 64 to 2 dimensions
projected = pca.fit_transform(digits.data)
print(digits.data.shape)
print(projected.shape)
plt.scatter(projected[:, 0], projected[:, 1],
c=digits.target, edgecolor='none', alpha=0.5,
cmap=plt.cm.get_cmap('jet', 10))
plt.xlabel('component 1')
plt.ylabel('component 2')
plt.colorbar()
plt.show()
```
Here, PCA can be used to approximate a digit. For instance, a 64-pixel image can be approximated by a dimensionality reduced 8-pixel image. Reconstructing using PCA as a basis function:
$$image(x)=mean+x1⋅(basis 1)+x2⋅(basis 2)+x3⋅(basis 3)⋯$$
```
def plot_pca_components(x, coefficients=None, mean=0, components=None,
imshape=(8, 8), n_components=8, fontsize=12,
show_mean=True):
if coefficients is None:
coefficients = x
if components is None:
components = np.eye(len(coefficients), len(x))
mean = np.zeros_like(x) + mean
fig = plt.figure(figsize=(1.2 * (5 + n_components), 1.2 * 2))
g = plt.GridSpec(2, 4 + bool(show_mean) + n_components, hspace=0.3)
def show(i, j, x, title=None):
ax = fig.add_subplot(g[i, j], xticks=[], yticks=[])
ax.imshow(x.reshape(imshape), interpolation='nearest', cmap='binary')
if title:
ax.set_title(title, fontsize=fontsize)
show(slice(2), slice(2), x, "True")
approx = mean.copy()
counter = 2
if show_mean:
show(0, 2, np.zeros_like(x) + mean, r'$\mu$')
show(1, 2, approx, r'$1 \cdot \mu$')
counter += 1
for i in range(n_components):
approx = approx + coefficients[i] * components[i]
show(0, i + counter, components[i], r'$c_{0}$'.format(i + 1))
show(1, i + counter, approx,
r"${0:.2f} \cdot c_{1}$".format(coefficients[i], i + 1))
if show_mean or i > 0:
plt.gca().text(0, 1.05, '$+$', ha='right', va='bottom',
transform=plt.gca().transAxes, fontsize=fontsize)
show(slice(2), slice(-2, None), approx, "Approx")
return fig
pca = PCA(n_components=8)
Xproj = pca.fit_transform(digits.data)
fig = plot_pca_components(digits.data[3], Xproj[3],
pca.mean_, pca.components_, show_mean=False)
```
Choose the optimum number of components. 20 is good to account over 90% of variance.
```
pca = PCA().fit(digits.data)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance')
plt.show()
```
## PCA for noise filtering
```
def plot_digits(data):
fig, axes = plt.subplots(4, 10, figsize=(10, 4),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(8, 8),
cmap='binary', interpolation='nearest',
clim=(0, 16))
plot_digits(digits.data)
```
Add random noise.
```
np.random.seed(42)
noisy = np.random.normal(digits.data, 5) # Tweak this number as level of noise
plot_digits(noisy)
```
Make the PCA preserve 50% of the variance. There are 12 components the most fit one.
```
pca = PCA(0.50).fit(noisy)
print(pca.n_components_)
# See the number of components given % preservations
x = np.linspace(0.1, 0.9, 19)
comp = [(PCA(i).fit(noisy)).n_components_ for i in x]
plt.plot(x, comp)
plt.xlabel('Preservation')
plt.ylabel('Number of components fit')
plt.show()
components = pca.transform(noisy)
filtered = pca.inverse_transform(components)
plot_digits(filtered)
```
## Eigenfaces
```
faces = fetch_lfw_people(min_faces_per_person=60)
print(faces.target_names)
print(faces.images.shape)
```
There are 3,000 dimensions. Take a look at first 150 components.
```
pca = PCA(150)
pca.fit(faces.data)
```
Look at the first 24 components (eigenvectors or "eigenfaces").
```
fig, axes = plt.subplots(3, 8, figsize=(9, 4),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(pca.components_[i].reshape(62, 47), cmap='bone')
```
150 is good to account for 90% of variance. Using these 150 components, we would recover most of the essential characteristics of the data.
```
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');
# Compute the components and projected faces
pca = PCA(150).fit(faces.data)
components = pca.transform(faces.data)
projected = pca.inverse_transform(components)
```
Reconstructing the full 3,000 pixel input image reduced to 150.
```
# Plot the results
fig, ax = plt.subplots(2, 10, figsize=(10, 2.5),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i in range(10):
ax[0, i].imshow(faces.data[i].reshape(62, 47), cmap='binary_r')
ax[1, i].imshow(projected[i].reshape(62, 47), cmap='binary_r')
ax[0, 0].set_ylabel('full-dim\ninput')
ax[1, 0].set_ylabel('150-dim\nreconstruction');
```
## Feature selection
```
df = pd.read_csv('https://archive.ics.uci.edu/ml/'
'machine-learning-databases/wine/wine.data',
header=None)
df.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash',
'Alcalinity of ash', 'Magnesium', 'Total phenols',
'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins',
'Color intensity', 'Hue',
'OD280/OD315 of diluted wines', 'Proline']
df.head()
X, y = df.iloc[:, 1:], df.iloc[:, 0]
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
pca=PCA()
Xt = pca.fit_transform(X_std)
pca.explained_variance_ratio_
```
From the bar plot below, 6 features are important, until it reach 90% of variance (red curve).
```
plt.bar(range(1,14),pca.explained_variance_ratio_,label='Variance Explained')
plt.step(range(1,14),np.cumsum(pca.explained_variance_ratio_),label='CumSum Variance Explained',c='r')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal component index')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
```
References:
* https://jakevdp.github.io/PythonDataScienceHandbook/05.10-manifold-learning.html
* https://github.com/dishaaagarwal/Dimensionality-Reduction-Techniques
* Other resources:
* https://www.ritchieng.com/machine-learning-dimensionality-reduction-feature-transform/
* https://medium.com/analytics-vidhya/implementing-pca-in-python-with-sklearn-4f757fb4429e
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Custom training: basics
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/customization/custom_training"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/customization/custom_training.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/customization/custom_training.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/customization/custom_training.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
In the previous tutorial, you covered the TensorFlow APIs for automatic differentiation—a basic building block for machine learning.
In this tutorial, you will use the TensorFlow primitives introduced in the prior tutorials to do some simple machine learning.
TensorFlow also includes `tf.keras`—a high-level neural network API that provides useful abstractions to reduce boilerplate and makes TensorFlow easier to use without sacrificing flexibility and performance. We strongly recommend the [tf.Keras API](../../guide/keras/overview.ipynb) for development. However, in this short tutorial you will learn how to train a neural network from first principles to establish a strong foundation.
## Setup
```
import tensorflow as tf
```
## Variables
Tensors in TensorFlow are immutable stateless objects. Machine learning models, however, must have changing state: as your model trains, the same code to compute predictions should behave differently over time (hopefully with a lower loss!). To represent this state, which needs to change over the course of your computation, you can choose to rely on the fact that Python is a stateful programming language:
```
# Using Python state
x = tf.zeros([10, 10])
x += 2 # This is equivalent to x = x + 2, which does not mutate the original
# value of x
print(x)
```
TensorFlow has stateful operations built-in, and these are often easier than using low-level Python representations for your state. Use `tf.Variable` to represent weights in a model.
A `tf.Variable` object stores a value and implicitly reads from this stored value. There are operations (`tf.assign_sub`, `tf.scatter_update`, etc.) that manipulate the value stored in a TensorFlow variable.
```
v = tf.Variable(1.0)
# Use Python's `assert` as a debugging statement to test the condition
assert v.numpy() == 1.0
# Reassign the value `v`
v.assign(3.0)
assert v.numpy() == 3.0
# Use `v` in a TensorFlow `tf.square()` operation and reassign
v.assign(tf.square(v))
assert v.numpy() == 9.0
```
Computations using `tf.Variable` are automatically traced when computing gradients. For variables that represent embeddings, TensorFlow will do sparse updates by default, which are more computation and memory efficient.
A `tf.Variable` is also a way to show a reader of your code that a piece of state is mutable.
## Fit a linear model
Let's use the concepts you have learned so far—`Tensor`, `Variable`, and `GradientTape`—to build and train a simple model. This typically involves a few steps:
1. Define the model.
2. Define a loss function.
3. Obtain training data.
4. Run through the training data and use an "optimizer" to adjust the variables to fit the data.
Here, you'll create a simple linear model, `f(x) = x * W + b`, which has two variables: `W` (weights) and `b` (bias). You'll synthesize data such that a well trained model would have `W = 3.0` and `b = 2.0`.
### Define the model
Let's define a simple class to encapsulate the variables and the computation:
```
class Model(object):
def __init__(self):
# Initialize the weights to `5.0` and the bias to `0.0`
# In practice, these should be initialized to random values (for example, with `tf.random.normal`)
self.W = tf.Variable(5.0)
self.b = tf.Variable(0.0)
def __call__(self, x):
return self.W * x + self.b
model = Model()
assert model(3.0).numpy() == 15.0
```
### Define a loss function
A loss function measures how well the output of a model for a given input matches the target output. The goal is to minimize this difference during training. Let's use the standard L2 loss, also known as the least square errors:
```
def loss(target_y, predicted_y):
return tf.reduce_mean(tf.square(target_y - predicted_y))
```
### Obtain training data
First, synthesize the training data by adding random Gaussian (Normal) noise to the inputs:
```
TRUE_W = 3.0
TRUE_b = 2.0
NUM_EXAMPLES = 1000
inputs = tf.random.normal(shape=[NUM_EXAMPLES])
noise = tf.random.normal(shape=[NUM_EXAMPLES])
outputs = inputs * TRUE_W + TRUE_b + noise
```
Before training the model, visualize the loss value by plotting the model's predictions in red and the training data in blue:
```
import matplotlib.pyplot as plt
plt.scatter(inputs, outputs, c='b')
plt.scatter(inputs, model(inputs), c='r')
plt.show()
print('Current loss: %1.6f' % loss(model(inputs), outputs).numpy())
```
### Define a training loop
With the network and training data, train the model using [gradient descent](https://en.wikipedia.org/wiki/Gradient_descent) to update the weights variable (`W`) and the bias variable (`b`) to reduce the loss. There are many variants of the gradient descent scheme that are captured in `tf.train.Optimizer`—our recommended implementation. But in the spirit of building from first principles, here you will implement the basic math yourself with the help of `tf.GradientTape` for automatic differentiation and `tf.assign_sub` for decrementing a value (which combines `tf.assign` and `tf.sub`):
```
def train(model, inputs, outputs, learning_rate):
with tf.GradientTape() as t:
current_loss = loss(outputs, model(inputs))
dW, db = t.gradient(current_loss, [model.W, model.b])
model.W.assign_sub(learning_rate * dW)
model.b.assign_sub(learning_rate * db)
```
Finally, let's repeatedly run through the training data and see how `W` and `b` evolve.
```
model = Model()
# Collect the history of W-values and b-values to plot later
Ws, bs = [], []
epochs = range(10)
for epoch in epochs:
Ws.append(model.W.numpy())
bs.append(model.b.numpy())
current_loss = loss(outputs, model(inputs))
train(model, inputs, outputs, learning_rate=0.1)
print('Epoch %2d: W=%1.2f b=%1.2f, loss=%2.5f' %
(epoch, Ws[-1], bs[-1], current_loss))
# Let's plot it all
plt.plot(epochs, Ws, 'r',
epochs, bs, 'b')
plt.plot([TRUE_W] * len(epochs), 'r--',
[TRUE_b] * len(epochs), 'b--')
plt.legend(['W', 'b', 'True W', 'True b'])
plt.show()
```
## Next steps
This tutorial used `tf.Variable` to build and train a simple linear model.
In practice, the high-level APIs—such as `tf.keras`—are much more convenient to build neural networks. `tf.keras` provides higher level building blocks (called "layers"), utilities to save and restore state, a suite of loss functions, a suite of optimization strategies, and more. Read the [TensorFlow Keras guide](../../guide/keras/overview.ipynb) to learn more.
|
github_jupyter
|
# Lecture 10 - eigenvalues and eigenvectors
An eigenvector $\boldsymbol{x}$ and corrsponding eigenvalue $\lambda$ of a square matrix $\boldsymbol{A}$ satisfy
$$
\boldsymbol{A} \boldsymbol{x} = \lambda \boldsymbol{x}
$$
Rearranging this expression,
$$
\left( \boldsymbol{A} - \lambda \boldsymbol{I}\right) \boldsymbol{x} = \boldsymbol{0}
$$
The above equation has solutions (other than $\boldsymbol{x} = \boldsymbol{0}$) if
$$
\det \left( \boldsymbol{A} - \lambda \boldsymbol{I}\right) = 0
$$
Computing the determinant of an $n \times n$ matrix requires solution of an $n$th degree polynomial. It is known how to compute roots of polynomials up to and including degree four (e.g., see <http://en.wikipedia.org/wiki/Quartic_function>). For matrices with $n > 4$, numerical methods must be used to compute eigenvalues and eigenvectors.
An $n \times n$ will have $n$ eigenvalue/eigenvector pairs (eigenpairs).
## Computing eigenvalues with NumPy
NumPy provides a function to compute eigenvalues and eigenvectors. To demonstrate how to compute eigpairs, we first create a $5 \times 5$ symmetric matrix:
```
# Import NumPy and seed random number generator to make generated matrices deterministic
import numpy as np
np.random.seed(1)
# Create a symmetric matrix with random entries
A = np.random.rand(5, 5)
A = A + A.T
print(A)
```
We can compute the eigenvectors and eigenvalues using the NumPy function `linalg.eig`
```
# Compute eigenvectors of A
evalues, evectors = np.linalg.eig(A)
print("Eigenvalues: {}".format(evalues))
print("Eigenvectors: {}".format(evectors))
```
The $i$th column of `evectors` is the $i$th eigenvector.
## Symmetric matrices
Note that the above eigenvalues and the eigenvectors are real valued. This is always the case for symmetric matrices. Another features of symmetric matrices is that the eigenvectors are orthogonal. We can verify this for the above matrix:
We can also check that the second eigenpair is indeed an eigenpair (Python/NumPy use base 0, so the second eiegenpair has index 1):
```
import itertools
# Build pairs (0,0), (0,1), . . . (0, n-1), (1, 2), (1, 3), . . .
pairs = itertools.combinations_with_replacement(range(len(evectors)), 2)
# Compute dot product of eigenvectors x_{i} \cdot x_{j}
for p in pairs:
e0, e1 = p[0], p[1]
print ("Dot product of eigenvectors {}, {}: {}".format(e0, e1, evectors[:, e0].dot(evectors[:, e1])))
print("Testing Ax and (lambda)x: \n {}, \n {}".format(A.dot(evectors[:,1]), evalues[1]*evectors[:,1]))
```
## Non-symmetric matrices
In general, the eigenvalues and eigenvectors of a non-symmetric, real-valued matrix are complex. We can see this by example:
```
B = np.random.rand(5, 5)
evalues, evectors = np.linalg.eig(B)
print("Eigenvalues: {}".format(evalues))
print("Eigenvectors: {}".format(evectors))
```
Unlike symmetric matrices, the eigenvectors are in general not orthogonal, which we can test:
```
# Compute dot product of eigenvectors x_{i} \cdot x_{j}
pairs = itertools.combinations_with_replacement(range(len(evectors)), 2)
for p in pairs:
e0, e1 = p[0], p[1]
print ("Dot product of eigenvectors {}, {}: {}".format(e0, e1, evectors[:, e0].dot(evectors[:, e1])))
```
|
github_jupyter
|
<a href="http://landlab.github.io"><img style="float: left" src="../../../landlab_header.png"></a>
# Components for modeling overland flow erosion
*(G.E. Tucker, July 2021)*
There are two related components that calculate erosion resulting from surface-water flow, a.k.a. overland flow: `DepthSlopeProductErosion` and `DetachmentLtdErosion`. They were originally created by Jordan Adams to work with the `OverlandFlow` component, which solves for water depth across the terrain. They are similar to the `StreamPowerEroder` and `FastscapeEroder` components in that they calculate erosion resulting from water flow across a topographic surface, but whereas these components require a flow-routing algorithm to create a list of node "receivers", the `DepthSlopeProductErosion` and `DetachmentLtdErosion` components only require a user-identified slope field together with an at-node depth or discharge field (respectively).
## `DepthSlopeProductErosion`
This component represents the rate of erosion, $E$, by surface water flow as:
$$E = k_e (\tau^a - \tau_c^a)$$
where $k_e$ is an erodibility coefficient (with dimensions of velocity per stress$^a$), $\tau$ is bed shear stress, $\tau_c$ is a minimum bed shear stress for any erosion to occur, and $a$ is a parameter that is commonly treated as unity.
For steady, uniform flow,
$$\tau = \rho g H S$$,
with $\rho$ being fluid density, $g$ gravitational acceleration, $H$ local water depth, and $S$ the (postive-downhill) slope gradient (an approximation of the sine of the slope angle).
The component uses a user-supplied slope field (at nodes) together with the water-depth field `surface_water__depth` to calculate $\tau$, and then the above equation to calculate $E$. The component will then modify the `topographic__elevation` field accordingly. If the user wishes to apply material uplift relative to baselevel, an `uplift_rate` parameter can be passed on initialization.
We can learn more about this component by examining its internal documentation. To get an overview of the component, we can examine its *header docstring*: internal documentation provided in the form of a Python docstring that sits just below the class declaration in the source code. This text can be displayed as shown here:
```
from landlab.components import DepthSlopeProductErosion
print(DepthSlopeProductErosion.__doc__)
```
A second useful source of internal documentation for this component is its *init docstring*: a Python docstring that describes the component's class `__init__` method. In Landlab, the init docstrings for components normally provide a list of that component's parameters. Here's how to display the init docstring:
```
print(DepthSlopeProductErosion.__init__.__doc__)
```
### Example
In this example, we load the topography of a small drainage basin, calculate a water-depth field by running overland flow over the topography using the `KinwaveImplicitOverlandFlow` component, and then calculating the resulting erosion.
Note that in order to accomplish this, we need to identify which variable we wish to use for slope gradient. This is not quite as simple as it may sound. An easy way to define slope is as the slope between two adjacent grid nodes. But using this approach means that slope is defined on the grid *links* rathter than *nodes*. To calculate slope magnitude at *nodes*, we'll define a little function below that uses Landlab's `calc_grad_at_link` method to calculate gradients at grid links, then use the `map_link_vector_components_to_node` method to calculate the $x$ and $y$ vector components at each node. With that in hand, we just use the Pythagorean theorem to find the slope magnitude from its vector components.
First, though, some imports we'll need:
```
import copy
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from landlab import imshow_grid
from landlab.components import KinwaveImplicitOverlandFlow
from landlab.grid.mappers import map_link_vector_components_to_node
from landlab.io import read_esri_ascii
def slope_magnitude_at_node(grid, elev):
# calculate gradient in elevation at each link
grad_at_link = grid.calc_grad_at_link(elev)
# set the gradient to zero for any inactive links
# (those attached to a closed-boundaries node at either end,
# or connecting two boundary nodes of any type)
grad_at_link[grid.status_at_link != grid.BC_LINK_IS_ACTIVE] = 0.0
# map slope vector components from links to their adjacent nodes
slp_x, slp_y = map_link_vector_components_to_node(grid, grad_at_link)
# use the Pythagorean theorem to calculate the slope magnitude
# from the x and y components
slp_mag = (slp_x * slp_x + slp_y * slp_y) ** 0.5
return slp_mag, slp_x, slp_y
```
(See [here](https://landlab.readthedocs.io/en/latest/reference/grid/gradients.html#landlab.grid.gradients.calc_grad_at_link) to learn how `calc_grad_at_link` works, and [here](https://landlab.readthedocs.io/en/latest/reference/grid/raster_mappers.html#landlab.grid.raster_mappers.map_link_vector_components_to_node_raster) to learn how
`map_link_vector_components_to_node` works.)
Next, define some parameters we'll need.
To estimate the erodibility coefficient $k_e$, one source is:
[http://milford.nserl.purdue.edu/weppdocs/comperod/](http://milford.nserl.purdue.edu/weppdocs/comperod/)
which reports experiments in rill erosion on agricultural soils. Converting their data into $k_e$, its values are on the order of 1 to 10 $\times 10^{-6}$ (m / s Pa), with threshold ($\tau_c$) values on the order of a few Pa.
```
# Process parameters
n = 0.1 # roughness coefficient, (s/m^(1/3))
dep_exp = 5.0 / 3.0 # depth exponent
R = 72.0 # runoff rate, mm/hr
k_e = 4.0e-6 # erosion coefficient (m/s)/(kg/ms^2)
tau_c = 3.0 # erosion threshold shear stress, Pa
# Run-control parameters
rain_duration = 240.0 # duration of rainfall, s
run_time = 480.0 # duration of run, s
dt = 10.0 # time-step size, s
dem_filename = "../hugo_site_filled.asc"
# Derived parameters
num_steps = int(run_time / dt)
# set up arrays to hold discharge and time
time_since_storm_start = np.arange(0.0, dt * (2 * num_steps + 1), dt)
discharge = np.zeros(2 * num_steps + 1)
```
Read an example digital elevation model (DEM) into a Landlab grid and set up the boundaries so that water can only exit out the right edge, representing the watershed outlet.
```
# Read the DEM file as a grid with a 'topographic__elevation' field
(grid, elev) = read_esri_ascii(dem_filename, name="topographic__elevation")
# Configure the boundaries: valid right-edge nodes will be open;
# all NODATA (= -9999) nodes will be closed.
grid.status_at_node[grid.nodes_at_right_edge] = grid.BC_NODE_IS_FIXED_VALUE
grid.status_at_node[np.isclose(elev, -9999.0)] = grid.BC_NODE_IS_CLOSED
```
Now we'll calculate the slope vector components and magnitude, and plot the vectors as quivers on top of a shaded image of the topography:
```
slp_mag, slp_x, slp_y = slope_magnitude_at_node(grid, elev)
imshow_grid(grid, elev)
plt.quiver(grid.x_of_node, grid.y_of_node, slp_x, slp_y)
```
Let's take a look at the slope magnitudes:
```
imshow_grid(grid, slp_mag, colorbar_label="Slope gradient (m/m)")
```
Now we're ready to instantiate a `KinwaveImplicitOverlandFlow` component, with a specified runoff rate and roughness:
```
# Instantiate the component
olflow = KinwaveImplicitOverlandFlow(
grid, runoff_rate=R, roughness=n, depth_exp=dep_exp
)
```
The `DepthSlopeProductErosion` component requires there to be a field called `slope_magnitude` that contains our slope-gradient values, so we will we will create this field and assign `slp_mag` to it (the `clobber` keyword says it's ok to overwrite this field if it already exists, which prevents generating an error message if you run this cell more than once):
```
grid.add_field("slope_magnitude", slp_mag, at="node", clobber=True)
```
Now we're ready to instantiate a `DepthSlopeProductErosion` component:
```
dspe = DepthSlopeProductErosion(grid, k_e=k_e, tau_crit=tau_c, slope="slope_magnitude")
```
Next, we'll make a copy of the starting terrain for later comparison, then run overland flow and erosion:
```
starting_elev = elev.copy()
for i in range(num_steps):
olflow.run_one_step(dt)
dspe.run_one_step(dt)
slp_mag[:], slp_x, slp_y = slope_magnitude_at_node(grid, elev)
```
We can visualize the instantaneous erosion rate at the end of the run, in m/s:
```
imshow_grid(grid, dspe._E, colorbar_label="erosion rate (m/s)")
```
We can also inspect the cumulative erosion during the event by differencing the before and after terrain:
```
imshow_grid(grid, starting_elev - elev, colorbar_label="cumulative erosion (m)")
```
Note that because this is a bumpy DEM, much of the erosion has occurred on (probably digital) steps in the channels. But we can see some erosion across the slopes as well.
## `DetachmentLtdErosion`
This component is similar to `DepthSlopeProductErosion` except that it calculates erosion rate from discharge and slope rather than depth and slope. The vertical incision rate, $I$ (equivalent to $E$ in the above; here we are following the notation in the component's documentation) is:
$$I = K Q^m S^n - I_c$$
where $K$ is an erodibility coefficient (with dimensions of velocity per discharge$^m$; specified by parameter `K_sp`), $Q$ is volumetric discharge, $I_c$ is a threshold with dimensions of velocity, and $m$ and $n$ are exponents. (In the erosion literature, the exponents are sometimes treated as empirical parameters, and sometimes set to particular values on theoretical grounds; here we'll just set them to unity.)
The component uses the fields `surface_water__discharge` and `topographic__slope` for $Q$ and $S$, respectively. The component will modify the `topographic__elevation` field accordingly. If the user wishes to apply material uplift relative to baselevel, an `uplift_rate` parameter can be passed on initialization.
Here are the header and constructor docstrings:
```
from landlab.components import DetachmentLtdErosion
print(DetachmentLtdErosion.__doc__)
print(DetachmentLtdErosion.__init__.__doc__)
```
The example below uses the same approach as the previous example, but now using `DetachmentLtdErosion`. Note that the value for parameter $K$ (`K_sp`) is just a guess. Use of exponents $m=n=1$ implies the use of total stream power.
```
# Process parameters
n = 0.1 # roughness coefficient, (s/m^(1/3))
dep_exp = 5.0 / 3.0 # depth exponent
R = 72.0 # runoff rate, mm/hr
K_sp = 1.0e-7 # erosion coefficient (m/s)/(m3/s)
m_sp = 1.0 # discharge exponent
n_sp = 1.0 # slope exponent
I_c = 0.0001 # erosion threshold, m/s
# Run-control parameters
rain_duration = 240.0 # duration of rainfall, s
run_time = 480.0 # duration of run, s
dt = 10.0 # time-step size, s
dem_filename = "../hugo_site_filled.asc"
# Derived parameters
num_steps = int(run_time / dt)
# set up arrays to hold discharge and time
time_since_storm_start = np.arange(0.0, dt * (2 * num_steps + 1), dt)
discharge = np.zeros(2 * num_steps + 1)
# Read the DEM file as a grid with a 'topographic__elevation' field
(grid, elev) = read_esri_ascii(dem_filename, name="topographic__elevation")
# Configure the boundaries: valid right-edge nodes will be open;
# all NODATA (= -9999) nodes will be closed.
grid.status_at_node[grid.nodes_at_right_edge] = grid.BC_NODE_IS_FIXED_VALUE
grid.status_at_node[np.isclose(elev, -9999.0)] = grid.BC_NODE_IS_CLOSED
slp_mag, slp_x, slp_y = slope_magnitude_at_node(grid, elev)
grid.add_field("topographic__slope", slp_mag, at="node", clobber=True)
# Instantiate the component
olflow = KinwaveImplicitOverlandFlow(
grid, runoff_rate=R, roughness=n, depth_exp=dep_exp
)
dle = DetachmentLtdErosion(
grid, K_sp=K_sp, m_sp=m_sp, n_sp=n_sp, entrainment_threshold=I_c
)
starting_elev = elev.copy()
for i in range(num_steps):
olflow.run_one_step(dt)
dle.run_one_step(dt)
slp_mag[:], slp_x, slp_y = slope_magnitude_at_node(grid, elev)
imshow_grid(grid, starting_elev - elev, colorbar_label="cumulative erosion (m)")
```
<hr>
<small>For more Landlab tutorials, click here: <a href="https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html">https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html</a></small>
<hr>
|
github_jupyter
|
# Evolution of CRO disclosure over time
```
import sys
import math
from datetime import date
from dateutil.relativedelta import relativedelta
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.dates
from matplotlib.ticker import MaxNLocator
import seaborn as sns
sys.path.append('../..')
from data import constants
# Setup seaborn
sns.set_theme(style="ticks", rc={'text.usetex' : True})
sns.set_context("paper")
# Read main file
df = pd.read_pickle("/Users/david/Nextcloud/Dokumente/Education/Uni Bern/Master Thesis/Analyzing Financial Climate Disclosures with NLP/Data/stoxx_inference/Firm_AnnualReport_Paragraphs_with_actual_back.pkl")
df = df.set_index(["id"])
assert df.index.is_unique, "Index is not unique. Check the data!"
# Read master for scaling
df_master = pd.read_csv("/Users/david/Nextcloud/Dokumente/Education/Uni Bern/Master Thesis/Analyzing Financial Climate Disclosures with NLP/Data/stoxx_inference/Firm_AnnualReport.csv")
df_reports_count = df_master.groupby('year')['is_inferred'].sum()
```
## Config
```
category_labels = constants.cro_category_labels
category_codes = constants.cro_category_codes
colors = sns.color_palette("GnBu", len(category_codes))
levelize_year = 2015
```
## Evolution over the years
Shows the level of *average number of predicted CRO's per report* (ACROR) over time, in 2015 *levels* (i.e. 2015 scaled to 1).
1. divide by amount of reports in each year
2. then report the levels by dividing by 2015 values
Why 2015? Paris and simply because it of missing values otherwise...
```
# Create yearly bins for each category
df_years = df.groupby('year')[[f"{c}_predicted" for c in category_codes]].sum().T
# 1. Divide by number of reports in each year
df_years = df_years / df_reports_count
df_years = df_years.T
# 2. Divide by the first column to get levels
# level_column = df_years[levelize_year]
# df_years = df_years.T / level_column
# df_years = df_years.T
df_years.rename(columns={'PR_predicted': 'Physical risks', 'TR_predicted': 'Transition risks', 'OP_predicted': 'Opportunities (rhs)'}, inplace=True)
# Plot
ax = sns.lineplot(data=df_years[['Physical risks', 'Transition risks']])
ax2 = ax.twinx()
ln2 = sns.lineplot(data=df_years[['Opportunities (rhs)']], ax=ax2, palette=["green"])
h1, l1 = ax.get_legend_handles_labels()
h2, l2 = ln2.get_legend_handles_labels()
ax.legend(h1+h2, l1+l2, loc=0)
ln2.legend_.remove()
ax.set_xlabel('')
plt.xlim()
plt.xlim(min(df_years.index), max(df_years.index))
ax.xaxis.set_major_locator(MaxNLocator(integer=True))
plt.show()
fig = ax.get_figure()
fig.savefig('/Users/david/Nextcloud/Dokumente/Education/Uni Bern/Master Thesis/Analyzing Financial Climate Disclosures with NLP/Thesis/figures/abs_acror_years.pdf', format='pdf', bbox_inches='tight')
```
## Evolution by country
```
index_id = 'country'
results = {}
pd.pivot_table(df_master, values="is_inferred", index=[index_id], columns=['year'], aggfunc=np.sum, fill_value = 0)
reports_count = pd.pivot_table(df_master, values="is_inferred", index=['country'], columns=['year'], aggfunc=np.sum, fill_value = 0)
def plot_grid_by_group(groups, group_column, y_max_values = [20, 500], no_columns=4):
reports_count = pd.pivot_table(df_master, values="is_inferred", index=[group_column], columns=['year'], aggfunc=np.sum, fill_value = 0)
rows = math.ceil(len(groups) / no_columns)
fig, axs = plt.subplots(rows, no_columns,
figsize=(12, 15 if rows > 1 else 5),
sharex=False,
sharey='row',
# constrained_layout=True
)
axs = axs.ravel()
max_y_axis_val = 0
for idx, c in enumerate(groups):
ax = axs[idx]
df_group = df.query(f"{group_column} == @c")
# Create yearly bins for each category
df_years = df_group.groupby('year')[[f"{c}_predicted" for c in category_codes]].sum().T
# 1. Divide by number of reports in each year
df_years = df_years / reports_count.loc[c]
# 2. Divide by the first column to get levels
# level_column = df_years[levelize_year]
# df_years = df_years.T / level_column
df_years = df_years.T
df_years.rename(columns={'PR_predicted': 'Physical risks', 'TR_predicted': 'Transition risks', 'OP_predicted': 'Opportunities (rhs)'}, inplace=True)
ax = sns.lineplot(data=df_years[['Physical risks', 'Transition risks']], ax=ax)
ax2 = ax.twinx()
ln2 = sns.lineplot(data=df_years[['Opportunities (rhs)']], ax=ax2, palette=["green"])
h1, l1 = ax.get_legend_handles_labels()
h2, l2 = ln2.get_legend_handles_labels()
fig.legend(h1+h2, l1+l2, loc="upper center", ncol=len(h1+h2))
ax.legend_.remove()
ln2.legend_.remove()
ax.set_ylim(0, y_max_values[0])
ax2.set_ylim(0, y_max_values[1])
ax.set_xlim(min(df_group.year), max(df_group.year))
ax.title.set_text(c.upper() if len(c) == 2 else c)
ax.set_xlabel('')
# Implement sharey also for the second y axis
if ((idx + 1) % no_columns) != 0:
ax2.set_yticklabels([])
fig.subplots_adjust(bottom=0.05 if rows > 2 else 0.25)
return fig
all_countries = sorted(df_master.country.unique())
all_countries_fig = plot_grid_by_group(all_countries, 'country', y_max_values=[20, 500])
all_countries_fig.savefig('/Users/david/Nextcloud/Dokumente/Education/Uni Bern/Master Thesis/Analyzing Financial Climate Disclosures with NLP/Thesis/figures/abs_acror_countries.pdf', format='pdf', bbox_inches='tight')
selected_countries_fig = plot_grid_by_group(["de", "ch", "fr", "gb"], 'country', y_max_values=[50, 500])
selected_countries_fig.savefig('/Users/david/Nextcloud/Dokumente/Education/Uni Bern/Master Thesis/Analyzing Financial Climate Disclosures with NLP/Thesis/figures/abs_acror_selected_countries.pdf', format='pdf', bbox_inches='tight')
```
## Industry
```
all_industries = sorted(df_master.icb_industry.unique())
all_inudustries_fig = plot_grid_by_group(all_industries, 'icb_industry', y_max_values=[50, 500])
all_inudustries_fig.savefig('/Users/david/Nextcloud/Dokumente/Education/Uni Bern/Master Thesis/Analyzing Financial Climate Disclosures with NLP/Thesis/figures/abs_acror_industries.pdf', format='pdf', bbox_inches='tight')
selected_industries_fig = plot_grid_by_group(["10 Technology", "30 Financials", "60 Energy", "65 Utilities"], 'icb_industry', y_max_values=[50, 500])
selected_industries_fig.savefig('/Users/david/Nextcloud/Dokumente/Education/Uni Bern/Master Thesis/Analyzing Financial Climate Disclosures with NLP/Thesis/figures/abs_acror_selected_industries.pdf', format='pdf', bbox_inches='tight')
```
|
github_jupyter
|
# Lesson 3. Coordinate Reference Systems (CRS) & Map Projections
Building off of what we learned in the previous notebook, we'll get to understand an integral aspect of geospatial data: Coordinate Reference Systems.
- 3.1 California County Shapefile
- 3.2 USA State Shapefile
- 3.3 Plot the Two Together
- 3.4 Coordinate Reference System (CRS)
- 3.5 Getting the CRS
- 3.6 Setting the CRS
- 3.7 Transforming or Reprojecting the CRS
- 3.8 Plotting States and Counties Togther
- 3.9 Recap
- **Exercise**: CRS Management
<br>
<font color='grey'>
<b>Instructor Notes</b>
- Datasets used
- ‘notebook_data/california_counties/CaliforniaCounties.shp’
- ‘notebook_data/us_states/us_states.shp’
- ‘notebook_data/census/Places/cb_2018_06_place_500k.zip’
- Expected time to complete
- Lecture + Questions: 45 minutes
- Exercises: 10 minutes
</font>
### Import Libraries
```
import pandas as pd
import geopandas as gpd
import matplotlib # base python plotting library
import matplotlib.pyplot as plt # submodule of matplotlib
# To display plots, maps, charts etc in the notebook
%matplotlib inline
```
## 3.1 California County shapefile
Let's go ahead and bring back in our California County shapefile. As before, we can read the file in using `gpd.read_file` and plot it straight away.
```
counties = gpd.read_file('notebook_data/california_counties/CaliforniaCounties.shp')
counties.plot(color='darkgreen')
```
Even if we have an awesome map like this, sometimes we want to have more geographical context, or we just want additional information. We're going to try **overlaying** our counties GeoDataFrame on our USA states shapefile.
## 3.2 USA State shapefile
We're going to bring in our states geodataframe, and let's do the usual operations to start exploring our data.
```
# Read in states shapefile
states = gpd.read_file('notebook_data/us_states/us_states.shp')
# Look at the first few rows
states.head()
# Count how many rows and columns we have
states.shape
# Plot our states data
states.plot()
```
You might have noticed that our plot extends beyond the 50 states (which we also saw when we executed the `shape` method). Let's double check what states we have included in our data.
```
states['STATE'].values
```
Beyond the 50 states we seem to have American Samoa, Puerto Rico, Guam, Commonwealth of the Northern Mariana Islands, and United States Virgin Islands included in this geodataframe. To make our map cleaner, let's limit the states to the contiguous states (so we'll also exclude Alaska and Hawaii).
```
# Define list of non-contiguous states
non_contiguous_us = [ 'American Samoa','Puerto Rico','Guam',
'Commonwealth of the Northern Mariana Islands',
'United States Virgin Islands', 'Alaska','Hawaii']
# Limit data according to above list
states_limited = states.loc[~states['STATE'].isin(non_contiguous_us)]
# Plot it
states_limited.plot()
```
To prepare for our mapping overlay, let's make our states a nice, light grey color.
```
states_limited.plot(color='lightgrey', figsize=(10,10))
```
## 3.3 Plot the two together
Now that we have both geodataframes in our environment, we can plot both in the same figure.
**NOTE**: To do this, note that we're getting a Matplotlib Axes object (`ax`), then explicitly adding each our layers to it
by providing the `ax=ax` argument to the `plot` method.
```
fig, ax = plt.subplots(figsize=(10,10))
counties.plot(color='darkgreen',ax=ax)
states_limited.plot(color='lightgrey', ax=ax)
```
Oh no, what happened here?
<img src="http://www.pngall.com/wp-content/uploads/2016/03/Light-Bulb-Free-PNG-Image.png" width="20" align=left > **Question** Without looking ahead, what do you think happened?
<br>
<br>
If you look at the numbers we have on the x and y axes in our two plots, you'll see that the county data has much larger numbers than our states data. It's represented in some different type of unit other than decimal degrees!
In fact, that means if we zoom in really close into our plot we'll probably see the states data plotted.
```
%matplotlib inline
fig, ax = plt.subplots(figsize=(10,10))
counties.plot(color='darkgreen',ax=ax)
states_limited.plot(color='lightgrey', ax=ax)
ax.set_xlim(-140,-50)
ax.set_ylim(20,50)
```
This is a key issue that you'll have to resolve time and time again when working with geospatial data!
It all revolves around **coordinate reference systems** and **projections**.
----------------------------
## 3.4 Coordinate Reference Systems (CRS)
<img src="http://www.pngall.com/wp-content/uploads/2016/03/Light-Bulb-Free-PNG-Image.png" width="20" align=left > **Question** Do you have experience with Coordinate Reference Systems?
<br><br>As a refresher, a CRS describes how the coordinates in a geospatial dataset relate to locations on the surface of the earth.
A `geographic CRS` consists of:
- a 3D model of the shape of the earth (a **datum**), approximated as a sphere or spheroid (aka ellipsoid)
- the **units** of the coordinate system (e.g, decimal degrees, meters, feet) and
- the **origin** (i.e. the 0,0 location), specified as the meeting of the **equator** and the **prime meridian**(
A `projected CRS` consists of
- a geographic CRS
- a **map projection** and related parameters used to transform the geographic coordinates to `2D` space.
- a map projection is a mathematical model used to transform coordinate data
### A Geographic vs Projected CRS
<img src ="https://www.e-education.psu.edu/natureofgeoinfo/sites/www.e-education.psu.edu.natureofgeoinfo/files/image/projection.gif" height="100" width="500">
#### There are many, many CRSs
Theoretically the number of CRSs is unlimited!
Why? Primariy, because there are many different definitions of the shape of the earth, multiplied by many different ways to cast its surface into 2 dimensions. Our understanding of the earth's shape and our ability to measure it has changed greatly over time.
#### Why are CRSs Important?
- You need to know the data about your data (or `metadata`) to use it appropriately.
- All projected CRSs introduce distortion in shape, area, and/or distance. So understanding what CRS best maintains the characteristics you need for your area of interest and your analysis is important.
- Some analysis methods expect geospatial data to be in a projected CRS
- For example, `geopandas` expects a geodataframe to be in a projected CRS for area or distance based analyses.
- Some Python libraries, but not all, implement dynamic reprojection from the input CRS to the required CRS and assume a specific CRS (WGS84) when a CRS is not explicitly defined.
- Most Python spatial libraries, including Geopandas, require geospatial data to be in the same CRS if they are being analysed together.
#### What you need to know when working with CRSs
- What CRSs used in your study area and their main characteristics
- How to identify, or `get`, the CRS of a geodataframe
- How to `set` the CRS of geodataframe (i.e. define the projection)
- Hot to `transform` the CRS of a geodataframe (i.e. reproject the data)
### Codes for CRSs commonly used with CA data
CRSs are typically referenced by an [EPSG code](http://wiki.gis.com/wiki/index.php/European_Petroleum_Survey_Group).
It's important to know the commonly used CRSs and their EPSG codes for your geographic area of interest.
For example, below is a list of commonly used CRSs for California geospatial data along with their EPSG codes.
##### Geographic CRSs
-`4326: WGS84` (units decimal degrees) - the most commonly used geographic CRS
-`4269: NAD83` (units decimal degrees) - the geographic CRS customized to best fit the USA. This is used by all Census geographic data.
> `NAD83 (epsg:4269)` are approximately the same as `WGS84(epsg:4326)` although locations can differ by up to 1 meter in the continental USA and elsewhere up to 3m. That is not a big issue with census tract data as these data are only accurate within +/-7meters.
##### Projected CRSs
-`5070: CONUS NAD83` (units meters) projected CRS for mapping the entire contiguous USA (CONUS)
-`3857: Web Mercator` (units meters) conformal (shape preserving) CRS used as the default in web mapping
-`3310: CA Albers Equal Area, NAD83` (units meters) projected CRS for CA statewide mapping and spatial analysis
-`26910: UTM Zone 10N, NAD83` (units meters) projected CRS for northern CA mapping & analysis
-`26911: UTM Zone 11N, NAD83` (units meters) projected CRS for Southern CA mapping & analysis
-`102641 to 102646: CA State Plane zones 1-6, NAD83` (units feet) projected CRS used for local analysis.
You can find the full CRS details on the website https://www.spatialreference.org
## 3.5 Getting the CRS
### Getting the CRS of a gdf
GeoPandas GeoDataFrames have a `crs` attribute that returns the CRS of the data.
```
counties.crs
states_limited.crs
```
As we can clearly see from those two printouts (even if we don't understand all the content!),
the CRSs of our two datasets are different! **This explains why we couldn't overlay them correctly!**
-----------------------------------------
The above CRS definition specifies
- the name of the CRS (`WGS84`),
- the axis units (`degree`)
- the shape (`datum`),
- and the origin (`Prime Meridian`, and the equator)
- and the area for which it is best suited (`World`)
> Notes:
> - `geocentric` latitude and longitude assume a spherical (round) model of the shape of the earth
> - `geodetic` latitude and longitude assume a spheriodal (ellipsoidal) model, which is closer to the true shape.
> - `geodesy` is the study of the shape of the earth.
**NOTE**: If you print a `crs` call, Python will just display the EPSG code used to initiate the CRS object. Depending on your versions of Geopandas and its dependencies, this may or may not look different from what we just saw above.
```
print(states_limited.crs)
```
## 3.6 Setting the CRS
You can also set the CRS of a gdf using the `crs` attribute. You would set the CRS if is not defined or if you think it is incorrectly defined.
> In desktop GIS terminology setting the CRS is called **defining the CRS**
As an example, let's set the CRS of our data to `None`
```
# first set the CRS to None
states_limited.crs = None
# Check it again
states_limited.crs
```
...hummm...
If a variable has a null value (None) then displaying it without printing it won't display anything!
```
# Check it again
print(states_limited.crs)
```
Now we'll set it back to its correct CRS.
```
# Set it to 4326
states_limited.crs = "epsg:4326"
# Show it
states_limited.crs
```
**NOTE**: You can set the CRS to anything you like, but **that doesn't make it correct**! This is because setting the CRS does not change the coordinate data; it just tells the software how to interpret it.
## 3.7 Transforming or Reprojecting the CRS
You can transform the CRS of a geodataframe with the `to_crs` method.
> In desktop GIS terminology transforming the CRS is called **projecting the data** (or **reprojecting the data**)
When you do this you want to save the output to a new GeoDataFrame.
```
states_limited_utm10 = states_limited.to_crs( "epsg:26910")
```
Now take a look at the CRS.
```
states_limited_utm10.crs
```
You can see the result immediately by plotting the data.
```
# plot geographic gdf
states_limited.plot();
plt.axis('square');
# plot utm gdf
states_limited_utm10.plot();
plt.axis('square')
# Your thoughts here
```
<div style="display:inline-block;vertical-align:top;">
<img src="http://www.pngall.com/wp-content/uploads/2016/03/Light-Bulb-Free-PNG-Image.png" width="30" align=left >
</div>
<div style="display:inline-block;">
#### Questions
</div>
1. What two key differences do you see between the two plots above?
1. Do either of these plotted USA maps look good?
1. Try looking at the common CRS EPSG codes above and see if any of them look better for the whole country than what we have now. Then try transforming the states data to the CRS that you think would be best and plotting it. (Use the code cell two cells below.)
```
# YOUR CODE HERE
```
**Double-click to see solution!**
<!--
#SOLUTION
states_limited_conus = states_limited.to_crs("epsg:5070")
states_limited_conus.plot();
plt.axis('square')
-->
## 3.8 Plotting states and counties together
Now that we know what a CRS is and how we can set them, let's convert our counties GeoDataFrame to match up with out states' crs.
```
# Convert counties data to NAD83
counties_utm10 = counties.to_crs("epsg:26910")
counties_utm10.plot()
# Plot it together!
fig, ax = plt.subplots(figsize=(10,10))
states_limited_utm10.plot(color='lightgrey', ax=ax)
counties_utm10.plot(color='darkgreen',ax=ax)
```
Since we know that the best CRS to plot the contiguous US from the above question is 5070, let's also transform and plot everything in that CRS.
```
counties_conus = counties.to_crs("epsg:5070")
fig, ax = plt.subplots(figsize=(10,10))
states_limited_conus.plot(color='lightgrey', ax=ax)
counties_conus.plot(color='darkgreen',ax=ax)
```
## 3.9 Recap
In this lesson we learned about...
- Coordinate Reference Systems
- Getting the CRS of a geodataframe
- `crs`
- Transforming/repojecting CRS
- `to_crs`
- Overlaying maps
## Exercise: CRS Management
Now it's time to take a crack and managing the CRS of a new dataset. In the code cell below, write code to:
1. Bring in the CA places data (`notebook_data/census/Places/cb_2018_06_place_500k.zip`)
2. Check if the CRS is EPSG code 26910. If not, transform the CRS
3. Plot the California counties and places together.
To see the solution, double-click the Markdown cell below.
```
# YOUR CODE HERE
```
## Double-click to see solution!
<!--
# SOLUTION
# 1. Bring in the CA places data
california_places = gpd.read_file('zip://notebook_data/census/Places/cb_2018_06_place_500k.zip')
california_places.head()
# 2. Check and transorm the CRS if needed
california_places.crs
california_places_utm10 = california_places.to_crs( "epsg:26910")
# 3. Plot the California counties and places together
fig, ax = plt.subplots(figsize=(10,10))
counties_utm10.plot(color='lightgrey', ax=ax)
california_places_utm10 .plot(color='purple',ax=ax)
-->
---
<div style="display:inline-block;vertical-align:middle;">
<a href="https://dlab.berkeley.edu/" target="_blank"><img src ="assets/images/dlab_logo.png" width="75" align="left">
</a>
</div>
<div style="display:inline-block;vertical-align:middle;">
<div style="font-size:larger"> D-Lab @ University of California - Berkeley</div>
<div> Team Geo<div>
</div>
|
github_jupyter
|
**Estimación puntual**
```
import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt
import random
import math
np.random.seed(2020)
population_ages_1 = stats.poisson.rvs(loc = 18, mu = 35, size = 1500000)
population_ages_2 = stats.poisson.rvs(loc = 18, mu = 10, size = 1000000)
population_ages = np.concatenate((population_ages_1, population_ages_2))
print(population_ages_1.mean())
print(population_ages_2.mean())
print(population_ages.mean())
pd.DataFrame(population_ages).hist(bins = 60, range = (17.5, 77.5), figsize = (10,10))
stats.skew(population_ages)
stats.kurtosis(population_ages)
np.random.seed(42)
sample_ages = np.random.choice(population_ages, 500)
print(sample_ages.mean())
population_ages.mean() - sample_ages.mean()
population_races = (["blanca"]*1000000) + (["negra"]*500000) + (["hispana"]*500000) + (["asiatica"]*250000) + (["otros"]*250000)
for race in set(population_races):
print("Proporción de "+race)
print(population_races.count(race) / 2500000)
random.seed(31)
race_sample = random.sample(population_races, 1000)
for race in set(race_sample):
print("Proporción de "+race)
print(race_sample.count(race) / 1000)
pd.DataFrame(population_ages).hist(bins = 60, range = (17.5, 77.5), figsize = (10,10))
pd.DataFrame(sample_ages).hist(bins = 60, range = (17.5, 77.5), figsize = (10,10))
np.random.sample(1988)
point_estimates = []
for x in range(200):
sample = np.random.choice(population_ages, size = 500)
point_estimates.append(sample.mean())
pd.DataFrame(point_estimates).plot(kind = "density", figsize = (9,9), xlim = (40, 46) )
np.array(point_estimates).mean()
```
**Si conocemos la desviación típica**
```
np.random.seed(10)
n = 1000
alpha = 0.05
sample = np.random.choice(population_ages, size = n)
sample_mean = sample.mean()
z_critical = stats.norm.ppf(q = 1-alpha/2)
sigma = population_ages.std()## sigma de la población
sample_error = z_critical * sigma / math.sqrt(n)
ci = (sample_mean - sample_error, sample_mean + sample_error)
ci
np.random.seed(10)
n = 1000
alpha = 0.05
intervals = []
sample_means = []
z_critical = stats.norm.ppf(q = 1-alpha/2)
sigma = population_ages.std()## sigma de la población
sample_error = z_critical * sigma / math.sqrt(n)
for sample in range(100):
sample = np.random.choice(population_ages, size = n)
sample_mean = sample.mean()
sample_means.append(sample_mean)
ci = (sample_mean - sample_error, sample_mean + sample_error)
intervals.append(ci)
plt.figure(figsize=(10,10))
plt.errorbar(x = np.arange(0.1, 100, 1), y = sample_means, yerr=[(top-bottom)/2 for top, bottom in intervals], fmt='o')
plt.hlines(xmin = 0, xmax = 100, y = population_ages.mean(), linewidth=2.0, color="red")
```
**Si la desviación típica no es conocida...**
```
np.random.seed(10)
n = 25
alpha = 0.05
sample = np.random.choice(population_ages, size = n)
sample_mean = sample.mean()
t_critical = stats.t.ppf(q = 1-alpha/2, df = n-1)
sample_sd = sample.std(ddof=1)## desviación estándar de la muestra
sample_error = t_critical * sample_sd / math.sqrt(n)
ci = (sample_mean - sample_error, sample_mean + sample_error)
ci
stats.t.ppf(q = 1-alpha, df = n-1) - stats.norm.ppf(1-alpha)
stats.t.ppf(q = 1-alpha, df = 999) - stats.norm.ppf(1-alpha)
stats.t.interval(alpha = 0.95, df = 24, loc = sample_mean, scale = sample_sd/math.sqrt(n))
```
**Intervalo para la proporción poblacional**
```
alpha = 0.05
n = 1000
z_critical = stats.norm.ppf(q=1-alpha/2)
p_hat = race_sample.count("blanca") / n
sample_error = z_critical * math.sqrt((p_hat*(1-p_hat)/n))
ci = (p_hat - sample_error, p_hat + sample_error)
ci
stats.norm.interval(alpha = 0.95, loc = p_hat, scale = math.sqrt(p_hat*(1-p_hat)/n))
```
**Cómo interpretar el intervalo de confianza**
```
shape, scale = 2.0, 2.0 #mean = 4, std = 2*sqrt(2)
s = np.random.gamma(shape, scale, 1000000)
mu = shape*scale
sigma = scale*np.sqrt(shape)
print(mu)
print(sigma)
meansample = []
sample_size = 500
for i in range(0,50000):
sample = random.choices(s, k=sample_size)
meansample.append(sum(sample)/len(sample))
plt.figure(figsize=(20,10))
plt.hist(meansample, 200, density=True, color="lightblue")
plt.show()
plt.figure(figsize=(20,10))
plt.hist(meansample, 200, density=True, color="lightblue")
plt.plot([mu,mu], [0, 3.5], 'k-', lw=4, color='green')
plt.plot([mu-1.96*sigma/np.sqrt(sample_size), mu-1.96*sigma/np.sqrt(sample_size)], [0, 3.5], 'k-', lw=2, color="navy")
plt.plot([mu+1.96*sigma/np.sqrt(sample_size), mu+1.96*sigma/np.sqrt(sample_size)], [0, 3.5], 'k-', lw=2, color="navy")
plt.show()
sample_data = np.random.choice(s, size = sample_size)
x_bar = sample_data.mean()
ss = sample_data.std()
plt.figure(figsize=(20,10))
plt.hist(meansample, 200, density=True, color="lightblue")
plt.plot([mu,mu], [0, 3.5], 'k-', lw=4, color='green')
plt.plot([mu-1.96*sigma/np.sqrt(sample_size), mu-1.96*sigma/np.sqrt(sample_size)], [0, 3.5], 'k-', lw=2, color="navy")
plt.plot([mu+1.96*sigma/np.sqrt(sample_size), mu+1.96*sigma/np.sqrt(sample_size)], [0, 3.5], 'k-', lw=2, color="navy")
plt.plot([x_bar, x_bar], [0,3.5], 'k-', lw=2, color="red")
plt.plot([x_bar-1.96*ss/np.sqrt(sample_size), x_bar-1.96*ss/np.sqrt(sample_size)], [0, 3.5], 'k-', lw=1, color="red")
plt.plot([x_bar+1.96*ss/np.sqrt(sample_size), x_bar+1.96*ss/np.sqrt(sample_size)], [0, 3.5], 'k-', lw=1, color="red")
plt.gca().add_patch(plt.Rectangle((x_bar-1.96*ss/np.sqrt(sample_size), 0), 2*(1.96*ss/np.sqrt(sample_size)), 3.5, fill=True, fc=(0.9, 0.1, 0.1, 0.15)))
plt.show()
interval_list = []
z_critical = 1.96 #z_0.975
sample_size = 5000
c = 0
error = z_critical*sigma/np.sqrt(sample_size)
for i in range(0,100):
rs = random.choices(s, k=sample_size)
mean = np.mean(rs)
ub = mean + error
lb = mean - error
interval_list.append([lb, mean, ub])
if ub >= mu and lb <= mu:
c += 1
c
print("Número de intervalos de confianza que contienen el valor real de mu: ",c)
plt.figure(figsize = (20, 10))
plt.boxplot(interval_list)
plt.plot([1,100], [mu, mu], 'k-', lw=2, color="red")
plt.show()
```
|
github_jupyter
|
# Approximate q-learning
In this notebook you will teach a lasagne neural network to do Q-learning.
__Frameworks__ - we'll accept this homework in any deep learning framework. For example, it translates to TensorFlow almost line-to-line. However, we recommend you to stick to theano/lasagne unless you're certain about your skills in the framework of your choice.
```
%env THEANO_FLAGS='floatX=float32'
import os
if type(os.environ.get("DISPLAY")) is not str or len(os.environ.get("DISPLAY"))==0:
!bash ../xvfb start
%env DISPLAY=:1
import gym
import numpy as np, pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
env = gym.make("CartPole-v0")
env.reset()
n_actions = env.action_space.n
state_dim = env.observation_space.shape
plt.imshow(env.render("rgb_array"))
```
# Approximate (deep) Q-learning: building the network
In this section we will build and train naive Q-learning with theano/lasagne
First step is initializing input variables
```
import theano
import theano.tensor as T
#create input variables. We'll support multiple states at once
current_states = T.matrix("states[batch,units]")
actions = T.ivector("action_ids[batch]")
rewards = T.vector("rewards[batch]")
next_states = T.matrix("next states[batch,units]")
is_end = T.ivector("vector[batch] where 1 means that session just ended")
import lasagne
from lasagne.layers import *
#input layer
l_states = InputLayer((None,)+state_dim)
<Your architecture. Please start with a single-layer network>
#output layer
l_qvalues = DenseLayer(<previous_layer>,num_units=n_actions,nonlinearity=None)
```
#### Predicting Q-values for `current_states`
```
#get q-values for ALL actions in current_states
predicted_qvalues = get_output(l_qvalues,{l_states:current_states})
#compiling agent's "GetQValues" function
get_qvalues = <compile a function that takes current_states and returns predicted_qvalues>
#select q-values for chosen actions
predicted_qvalues_for_actions = predicted_qvalues[T.arange(actions.shape[0]),actions]
```
#### Loss function and `update`
Here we write a function similar to `agent.update`.
```
#predict q-values for next states
predicted_next_qvalues = get_output(l_qvalues,{l_states:<theano input with for states>})
#Computing target q-values under
gamma = 0.99
target_qvalues_for_actions = <target Q-values using rewards and predicted_next_qvalues>
#zero-out q-values at the end
target_qvalues_for_actions = (1-is_end)*target_qvalues_for_actions
#don't compute gradient over target q-values (consider constant)
target_qvalues_for_actions = theano.gradient.disconnected_grad(target_qvalues_for_actions)
#mean squared error loss function
loss = <mean squared between target_qvalues_for_actions and predicted_qvalues_for_actions>
#all network weights
all_weights = get_all_params(l_qvalues,trainable=True)
#network updates. Note the small learning rate (for stability)
updates = lasagne.updates.sgd(loss,all_weights,learning_rate=1e-4)
#Training function that resembles agent.update(state,action,reward,next_state)
#with 1 more argument meaning is_end
train_step = theano.function([current_states,actions,rewards,next_states,is_end],
updates=updates)
```
### Playing the game
```
epsilon = 0.25 #initial epsilon
def generate_session(t_max=1000):
"""play env with approximate q-learning agent and train it at the same time"""
total_reward = 0
s = env.reset()
for t in range(t_max):
#get action q-values from the network
q_values = get_qvalues([s])[0]
a = <sample action with epsilon-greedy strategy>
new_s,r,done,info = env.step(a)
#train agent one step. Note that we use one-element arrays instead of scalars
#because that's what function accepts.
train_step([s],[a],[r],[new_s],[done])
total_reward+=r
s = new_s
if done: break
return total_reward
for i in range(100):
rewards = [generate_session() for _ in range(100)] #generate new sessions
epsilon*=0.95
print ("mean reward:%.3f\tepsilon:%.5f"%(np.mean(rewards),epsilon))
if np.mean(rewards) > 300:
print ("You Win!")
break
assert epsilon!=0, "Please explore environment"
```
### Video
```
epsilon=0 #Don't forget to reset epsilon back to initial value if you want to go on training
#record sessions
import gym.wrappers
env = gym.wrappers.Monitor(env,directory="videos",force=True)
sessions = [generate_session() for _ in range(100)]
env.close()
#unwrap
env = env.env.env
#upload to gym
#gym.upload("./videos/",api_key="<your_api_key>") #you'll need me later
#Warning! If you keep seeing error that reads something like"DoubleWrapError",
#run env=gym.make("CartPole-v0");env.reset();
#show video
from IPython.display import HTML
import os
video_names = list(filter(lambda s:s.endswith(".mp4"),os.listdir("./videos/")))
HTML("""
<video width="640" height="480" controls>
<source src="{}" type="video/mp4">
</video>
""".format("./videos/"+video_names[-1])) #this may or may not be _last_ video. Try other indices
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/dhruvsheth-ai/hydra-openvino-sensors/blob/master/hydra_openvino_pi.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
**Install the latest OpenVino for Raspberry Pi OS package from Intel OpenVino Distribution Download**
For my case, I have Installed 2020.4 version.
```
l_openvino_toolkit_runtime_raspbian_p_2020.4.28
```
This is the latest version available with the model zoo. Since the below code is executed on a Jupyter Notebook, terminal syntaxes may be different.

```
cd ~/Downloads/
!sudo mkdir -p /opt/intel/openvino
!sudo tar -xf l_openvino_toolkit_runtime_raspbian_p_<version>.tgz --strip 1 -C /opt/intel/openvino
!sudo apt install cmake
!echo "source /opt/intel/openvino/bin/setupvars.sh" >> ~/.bashrc
```
Your output on new terminal will be:
```
[setupvars.sh] OpenVINO environment initialized
```
```
!sudo usermod -a -G users "$(raspberry-pi)"
```
The below are the USB rules for Intel Neural Compute Stick 2:
```
!sh /opt/intel/openvino/install_dependencies/install_NCS_udev_rules.sh
```
Once this is set up, move to the ```
hydra-openvino-yolo.ipynb
```
file for running the model
|
github_jupyter
|
<a href="https://colab.research.google.com/github/RichardFreedman/CRIM_Collab_Notebooks/blob/main/CRIM_Data_Search.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import requests
import pandas as pd
```
# Markdown for descriptive text
## level two
### Structure notebook for various sections and TOC
Plain text is just normal
- list
- list item with dashes
or numbers
1. this
2. that
3. another
- Still other
- Still more
-And yet more
# Markdown vs Code
Pick Markdown for type of cell above. **Shift + return** to enter these
# Formatting
Italics is *before* **bold**
Escape then B to create new cells (and pick cell types later)
# Fill
Tab to auto fill within cell
# Requests
Requests in fact has several functions after the "." Like Get, or whatever
Requests.get plus (), then Shift+Tab to see all the parameters that must be passed.
Response object allows you to extract what you need, like JSON
For Obs_1_json = response.json() we **need** the parenths to run the function
# Dictionaries and Types
Dictionary= Key>Value Pairs (Key is MEI Links, value is the link)
Note that Values can themselves contain dictionary
Python Types
Dictionary (Pairs; can contain other Dictionaries)
String (thing in a quote)
List (always in square brackets, and can contain dictionaries and lists within them)
indexing of items in a list start at ZERO
last item is "-1", etc
# Get Key
To get an individual KEY from top level:
Obs_ema_1 = Obs_1_json["ema"]
This allows you to dig deeper in nested lists or dictionaries. In this case piece is top level in JSON, the MEI link is next. The number allows you to pick from items IN a list: Obs_1_json["piece"]["mei_links"][0]
```
Obs_1_url = "https://crimproject.org/data/observations/1/"
Obs_1_url
response = requests.get(Obs_1_url)
response
type(response)
Obs_1_json = response.json()
Obs_1_json
type(Obs_1_json)
example_list_1 = [5, 3, "this", "that"]
example_list_1[3]
Obs_1_json.keys()
Obs_ema_1 = Obs_1_json["ema"]
Obs_ema_1
type(Obs_ema_1)
print("here is a print statement")
Obs_1_json["musical_type"]
Obs_1_mt = Obs_1_json["musical_type"]
Obs_1_mt
Obs_1_piece = Obs_1_json["piece"]
Obs_1_piece
Obs_1_mei = Obs_1_piece["mei_links"]
Obs_1_mei
len(Obs_1_mei)
Obs_1_mei[0]
Obs_1_json["piece"]["mei_links"][0]
Obs_1_json["ema"]
```
# Loops
```
test_list = [1,5,2,5,6]
for i, observation_id in enumerate(test_list):
# do stuff
print(i, observation_id)
for number in range(1,10):
print(number)
def myfunction():
print("it is running")
myfunction
myfunction()
def adder(num_1, num_2):
return num_1 + num_2
adder(5,9)
def get_ema_for_observation_id(obs_id):
# get Obs_1_url
url = "https://crimproject.org/data/observations/{}/".format(obs_id)
return url
def get_ema_for_observation_id(obs_id):
# get Obs_1_ema
my_ema_mei_dictionary = dict()
url = "https://crimproject.org/data/observations/{}/".format(obs_id)
response = requests.get(url)
Obs_json = response.json()
# Obs_ema = Obs_json["ema"]
my_ema_mei_dictionary["id"]=Obs_json["id"]
my_ema_mei_dictionary["musical type"]=Obs_json["musical_type"]
my_ema_mei_dictionary["int"]=Obs_json["mt_fg_int"]
my_ema_mei_dictionary["tint"]=Obs_json["mt_fg_tint"]
my_ema_mei_dictionary["ema"]=Obs_json["ema"]
my_ema_mei_dictionary["mei"]=Obs_json["piece"]["mei_links"][0]
my_ema_mei_dictionary["pdf"]=Obs_json["piece"]["pdf_links"][0]
# Obs_piece = Obs_json["piece"]
# Obs_mei = Obs_piece["mei_links"]
print(f'Got: {obs_id}')
# return {"ema":Obs_ema,"mei":Obs_mei}
return my_ema_mei_dictionary
get_ema_for_observation_id(20)
output = get_ema_for_observation_id(20)
pd.Series(output).to_csv("output.csv")
# this holds the output as a LIST of DICTS
obs_data_list = []
# this is the list of IDs to call
obs_call_list = [1,3,5,17,21]
# this is the LOOP that runs through the list aboe
# for observ in obs_call_list:
for observ in range(1,11):
call_list_output = get_ema_for_observation_id(observ)
# the print command simply puts the output in the notebook terminal.
#Later we will put it in the List of Dicts.
# print(call_list_output)
obs_data_list.append(call_list_output)
# list includes APPEND function that will allow us to add one item after each loop.
# EX blank_list = [1,5,6] (note that these are in square brackets as LIST)
# blank_list.append(89)
# range would in parenths as in: range(1,11)
# here we make a LIST object that contains the Range.
# This allows it to iterate over the range
# since the range could be HUGE We can ONLY append a number to a LIST!
Obs_range = list(range(1,11))
# blank_list.append(76)
blank_list
obs_data_list
pd.Series(obs_data_list).to_csv("obs_data_list.csv")
# Pandas DataFrame interprets the series of items in each Dict
# as separate 'cells' (a tab structure)
DF_output = pd.DataFrame(obs_data_list)
DF_output
DF_output.to_csv("obs_data_list.csv")
# two = means check for equality
# for 'contains' use str.contains("letter")
# can also use regex in this (for EMA range)
# Filter_by_Type = (DF_output["musical type"]=="Fuga") & (DF_output["id"]==8)
Filter_by_Type = DF_output["musical type"].str.contains("Fuga")
#
DF_output[Filter_by_Type]
# here is a string of text with numbers in it
my_num = 5
f"here is a string of text with numbers in it: {my_num}"
```
|
github_jupyter
|
# Importing the libraries
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.metrics import roc_curve, auc
from sklearn.metrics import roc_auc_score,recall_score, precision_score, f1_score
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report, average_precision_score
```
# Load and Explore Data
```
dataset=pd.read_csv('weatherAUS.csv')
dataset.head()
dataset.describe()
# find categorical variables
categorical = [var for var in dataset.columns if dataset[var].dtype=='O']
print('There are {} categorical variables : \n'.format(len(categorical)), categorical)
# view the categorical variables
dataset[categorical].head()
# check and print categorical variables containing missing values
nullCategorical = [var for var in categorical if dataset[var].isnull().sum()!=0]
print(dataset[nullCategorical].isnull().sum())
```
Number of labels: cardinality
The number of labels within a categorical variable is known as cardinality. A high number of labels within a variable is known as high cardinality. High cardinality may pose some serious problems in the machine learning model. So, I will check for high cardinality.
```
# check for cardinality in categorical variables
for var in categorical:
print(var, ' contains ', len(dataset[var].unique()), ' labels')
# Feature Extraction
dataset['Date'].dtypes
# parse the dates, currently coded as strings, into datetime format
dataset['Date'] = pd.to_datetime(dataset['Date'])
dataset['Date'].dtypes
# extract year from date
dataset['Year'] = dataset['Date'].dt.year
# extract month from date
dataset['Month'] = dataset['Date'].dt.month
# extract day from date
dataset['Day'] = dataset['Date'].dt.day
dataset.info()
# drop the original Date variable
dataset.drop('Date', axis=1, inplace = True)
dataset.head()
```
## Explore Categorical Variables
```
# Explore Location variable
dataset.Location.unique()
# check frequency distribution of values in Location variable
dataset.Location.value_counts()
# let's do One Hot Encoding of Location variable
# get k-1 dummy variables after One Hot Encoding
pd.get_dummies(dataset.Location, drop_first=True).head()
# Explore WindGustDir variable
dataset.WindGustDir.unique()
# check frequency distribution of values in WindGustDir variable
dataset.WindGustDir.value_counts()
# let's do One Hot Encoding of WindGustDir variable
# get k-1 dummy variables after One Hot Encoding
# also add an additional dummy variable to indicate there was missing data
pd.get_dummies(dataset.WindGustDir, drop_first=True, dummy_na=True).head()
# sum the number of 1s per boolean variable over the rows of the dataset --> it will tell us how many observations we have for each category
pd.get_dummies(dataset.WindGustDir, drop_first=True, dummy_na=True).sum(axis=0)
# Explore WindDir9am variable
dataset.WindDir9am.unique()
dataset.WindDir9am.value_counts()
pd.get_dummies(dataset.WindDir9am, drop_first=True, dummy_na=True).head()
# sum the number of 1s per boolean variable over the rows of the dataset -- it will tell us how many observations we have for each category
pd.get_dummies(dataset.WindDir9am, drop_first=True, dummy_na=True).sum(axis=0)
# Explore WindDir3pm variable
dataset['WindDir3pm'].unique()
dataset['WindDir3pm'].value_counts()
pd.get_dummies(dataset.WindDir3pm, drop_first=True, dummy_na=True).head()
pd.get_dummies(dataset.WindDir3pm, drop_first=True, dummy_na=True).sum(axis=0)
# Explore RainToday variable
dataset['RainToday'].unique()
dataset.RainToday.value_counts()
pd.get_dummies(dataset.RainToday, drop_first=True, dummy_na=True).head()
pd.get_dummies(dataset.RainToday, drop_first=True, dummy_na=True).sum(axis=0)
```
## Explore Numerical Variables
```
# find numerical variables
numerical = [var for var in dataset.columns if dataset[var].dtype!='O']
print('There are {} numerical variables : \n'.format(len(numerical)), numerical)
# view the numerical variables
dataset[numerical].head()
# check missing values in numerical variables
dataset[numerical].isnull().sum()
# view summary statistics in numerical variables to check for outliers
print(round(dataset[numerical].describe()),2)
# plot box plot to check outliers
plt.figure(figsize=(10,15))
plt.subplot(2, 2, 1)
fig = sns.boxplot(y=dataset['Rainfall'])
fig.set_ylabel('Rainfall')
plt.subplot(2, 2, 2)
fig = sns.boxplot(y=dataset["Evaporation"])
fig.set_ylabel('Evaporation')
plt.subplot(2, 2, 3)
fig = sns.boxplot(y=dataset['WindSpeed9am'])
fig.set_ylabel('WindSpeed9am')
plt.subplot(2, 2, 4)
fig = sns.boxplot(y=dataset['WindSpeed3pm'])
fig.set_ylabel('WindSpeed3pm')
# plot histogram to check distribution
plt.figure(figsize=(10,15))
plt.subplot(2, 2, 1)
fig = dataset.Rainfall.hist(bins=10)
fig.set_xlabel('Rainfall')
fig.set_ylabel('RainTomorrow')
plt.subplot(2, 2, 2)
fig = dataset.Evaporation.hist(bins=10)
fig.set_xlabel('Evaporation')
fig.set_ylabel('RainTomorrow')
plt.subplot(2, 2, 3)
fig = dataset.WindSpeed9am.hist(bins=10)
fig.set_xlabel('WindSpeed9am')
fig.set_ylabel('RainTomorrow')
plt.subplot(2, 2, 4)
fig = dataset.WindSpeed3pm.hist(bins=10)
fig.set_xlabel('WindSpeed3pm')
fig.set_ylabel('RainTomorrow')
# find outliers for Rainfall variable
IQR = dataset.Rainfall.quantile(0.75) - dataset.Rainfall.quantile(0.25)
Rainfall_Lower_fence = dataset.Rainfall.quantile(0.25) - (IQR * 3)
Rainfall_Upper_fence = dataset.Rainfall.quantile(0.75) + (IQR * 3)
print('Outliers are values < {lowerboundary} or > {upperboundary}'.format(lowerboundary=Rainfall_Lower_fence, upperboundary=Rainfall_Upper_fence))
print('Number of outliers are {}'. format(dataset[(dataset.Rainfall> Rainfall_Upper_fence) | (dataset.Rainfall< Rainfall_Lower_fence)]['Rainfall'].count()))
# find outliers for Evaporation variable
IQR = dataset.Evaporation.quantile(0.75) - dataset.Evaporation.quantile(0.25)
Evaporation_Lower_fence = dataset.Evaporation.quantile(0.25) - (IQR * 3)
Evaporation_Upper_fence = dataset.Evaporation.quantile(0.75) + (IQR * 3)
print('Outliers are values < {lowerboundary} or > {upperboundary}'.format(lowerboundary=Evaporation_Lower_fence, upperboundary=Evaporation_Upper_fence))
print('Number of outliers are {}'. format(dataset[(dataset.Evaporation> Evaporation_Upper_fence) | (dataset.Evaporation< Evaporation_Lower_fence)]['Evaporation'].count()))
# find outliers for WindSpeed9am variable
IQR = dataset.WindSpeed9am.quantile(0.75) - dataset.WindSpeed9am.quantile(0.25)
WindSpeed9am_Lower_fence = dataset.WindSpeed9am.quantile(0.25) - (IQR * 3)
WindSpeed9am_Upper_fence = dataset.WindSpeed9am.quantile(0.75) + (IQR * 3)
print('Outliers are values < {lowerboundary} or > {upperboundary}'.format(lowerboundary=WindSpeed9am_Lower_fence, upperboundary=WindSpeed9am_Upper_fence))
print('Number of outliers are {}'. format(dataset[(dataset.WindSpeed9am> WindSpeed9am_Upper_fence) | (dataset.WindSpeed9am< WindSpeed9am_Lower_fence)]['WindSpeed9am'].count()))
# find outliers for WindSpeed3pm variable
IQR = dataset.WindSpeed3pm.quantile(0.75) - dataset.WindSpeed3pm.quantile(0.25)
WindSpeed3pm_Lower_fence = dataset.WindSpeed3pm.quantile(0.25) - (IQR * 3)
WindSpeed3pm_Upper_fence = dataset.WindSpeed3pm.quantile(0.75) + (IQR * 3)
print('Outliers are values < {lowerboundary} or > {upperboundary}'.format(lowerboundary=WindSpeed3pm_Lower_fence, upperboundary=WindSpeed3pm_Upper_fence))
print('Number of outliers are {}'. format(dataset[(dataset.WindSpeed3pm> WindSpeed3pm_Lower_fence) | (dataset.WindSpeed3pm< WindSpeed3pm_Upper_fence)]['WindSpeed3pm'].count()))
def max_value(dataset, variable, top):
return np.where(dataset[variable]>top, top, dataset[variable])
dataset['Rainfall'] = max_value(dataset, 'Rainfall', Rainfall_Upper_fence)
dataset['Evaporation'] = max_value(dataset, 'Evaporation', Evaporation_Upper_fence)
dataset['WindSpeed9am'] = max_value(dataset, 'WindSpeed9am', WindSpeed9am_Upper_fence)
dataset['WindSpeed3pm'] = max_value(dataset, 'WindSpeed3pm', 57)
print('Number of outliers are {}'. format(dataset[(dataset.Rainfall> Rainfall_Upper_fence) | (dataset.Rainfall< Rainfall_Lower_fence)]['Rainfall'].count()))
print('Number of outliers are {}'. format(dataset[(dataset.Evaporation> Evaporation_Upper_fence) | (dataset.Evaporation< Evaporation_Lower_fence)]['Evaporation'].count()))
print('Number of outliers are {}'. format(dataset[(dataset.WindSpeed9am> WindSpeed9am_Upper_fence) | (dataset.WindSpeed9am< WindSpeed9am_Lower_fence)]['WindSpeed9am'].count()))
print('Number of outliers are {}'. format(dataset[(dataset.WindSpeed3pm> WindSpeed3pm_Lower_fence) | (dataset.WindSpeed3pm< WindSpeed3pm_Upper_fence)]['WindSpeed3pm'].count()))
# Replace NaN with default values
nullValues = [var for var in dataset.columns if dataset[var].isnull().sum()!=0]
print(dataset[nullValues].isnull().sum())
categorical = [var for var in nullValues if dataset[var].dtype=='O']
from sklearn.impute import SimpleImputer
categoricalImputer = SimpleImputer(missing_values=np.nan,strategy='constant')
categoricalImputer.fit(dataset[categorical])
dataset[categorical]=categoricalImputer.transform(dataset[categorical])
print(dataset.head())
numerical = [var for var in dataset.columns if dataset[var].dtype!='O']
from sklearn.impute import SimpleImputer
numericalImputer = SimpleImputer(missing_values=np.nan,strategy='mean')
numericalImputer.fit(dataset[numerical])
dataset[numerical]=numericalImputer.transform(dataset[numerical])
print(dataset.head())
```
# Split data for model
```
x = dataset.drop(['RainTomorrow'], axis=1) # get all row data expect RainTomorrow
y = dataset['RainTomorrow'] # get the RainTomorrow column depentant variable data for all rows
print(x.head())
print(y[:10])
```
# Encoding categorical data
```
#encoding independent variable
x = pd.get_dummies(x)
print(x.head())
## Encoding dependent variable
# use LabelEncoder to replace purchased (dependent variable) with 0 and 1
from sklearn.preprocessing import LabelEncoder
y= LabelEncoder().fit_transform(y)
print(y[:10])
```
# Splitting the dataset into training and test set
```
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.3,random_state = 0) # func returns train and test data. It takes dataset and then split size test_size =0.3 means 30% data is for test and rest for training and random_state
print(x_train.head())
print(x_test.head())
print(y_train[:10])
print(y_test[:10])
```
# Feature scaling
```
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
x_train= scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)
print(x_train[:10,:])
print(x_test[:10,:])
```
# Build Model
```
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(solver='liblinear', random_state=0)
classifier.fit(x_train,y_train)
#predicting the test set results
y_pred = classifier.predict(x_test)
```
# Evaluate Model
```
cm = confusion_matrix(y_test,y_pred)
print(cm)
cr = classification_report(y_test,y_pred)
print(cr)
accuracy_score(y_test,y_pred)
average_precision= average_precision_score(y_test,y_pred)
print(average_precision)
recall_score(y_test,y_pred)
precision_score(y_test,y_pred)
f1_score(y_test,y_pred)
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import plot_precision_recall_curve
disp = plot_precision_recall_curve(classifier, x_test, y_test)
disp.ax_.set_title('2-class Precision-Recall curve: '
'AP={0:0.2f}'.format(average_precision))
```
|
github_jupyter
|
```
# default_exp callback.PredictionDynamics
```
# PredictionDynamics
> Callback used to visualize model predictions during training.
This is an implementation created by Ignacio Oguiza ([email protected]) based on a [blog post](http://localhost:8888/?token=83bca9180c34e1c8991886445942499ee8c1e003bc0491d0) by Andrej Karpathy I read some time ago that I really liked. One of the things he mentioned was this:
>"**visualize prediction dynamics**. I like to visualize model predictions on a fixed test batch during the course of training. The “dynamics” of how these predictions move will give you incredibly good intuition for how the training progresses. Many times it is possible to feel the network “struggle” to fit your data if it wiggles too much in some way, revealing instabilities. Very low or very high learning rates are also easily noticeable in the amount of jitter." A. Karpathy
```
#export
from fastai.callback.all import *
from tsai.imports import *
# export
class PredictionDynamics(Callback):
order, run_valid = 65, True
def __init__(self, show_perc=1., figsize=(10,6), alpha=.3, size=30, color='lime', cmap='gist_rainbow', normalize=False,
sensitivity=None, specificity=None):
"""
Args:
show_perc: percent of samples from the valid set that will be displayed. Default: 1 (all).
You can reduce it if the number is too high and the chart is too busy.
alpha: level of transparency. Default:.3. 1 means no transparency.
figsize: size of the chart. You may want to expand it if too many classes.
size: size of each sample in the chart. Default:30. You may need to decrease it a bit if too many classes/ samples.
color: color used in regression plots.
cmap: color map used in classification plots.
normalize: flag to normalize histograms displayed in binary classification.
sensitivity: (aka recall or True Positive Rate) if you pass a float between 0. and 1. the sensitivity threshold will be plotted in the chart.
Only used in binary classification.
specificity: (or True Negative Rate) if you pass a float between 0. and 1. it will be plotted in the chart. Only used in binary classification.
The red line in classification tasks indicate the average probability of true class.
"""
store_attr()
def before_fit(self):
self.run = not hasattr(self.learn, 'lr_finder') and not hasattr(self, "gather_preds")
if not self.run:
return
self.cat = True if (hasattr(self.dls, "c") and self.dls.c > 1) else False
if self.cat:
self.binary = self.dls.c == 2
if self.show_perc != 1:
valid_size = len(self.dls.valid.dataset)
self.show_idxs = np.random.choice(valid_size, int(round(self.show_perc * valid_size)), replace=False)
# Prepare ground truth container
self.y_true = []
def before_epoch(self):
# Prepare empty pred container in every epoch
self.y_pred = []
def after_pred(self):
if self.training:
return
# Get y_true in epoch 0
if self.epoch == 0:
self.y_true.extend(self.y.cpu().flatten().numpy())
# Gather y_pred for every batch
if self.cat:
if self.binary:
y_pred = F.softmax(self.pred, -1)[:, 1].reshape(-1, 1).cpu()
else:
y_pred = torch.gather(F.softmax(self.pred, -1), -1, self.y.reshape(-1, 1).long()).cpu()
else:
y_pred = self.pred.cpu()
self.y_pred.extend(y_pred.flatten().numpy())
def after_epoch(self):
# Ground truth
if self.epoch == 0:
self.y_true = np.array(self.y_true)
if self.show_perc != 1:
self.y_true = self.y_true[self.show_idxs]
self.y_bounds = (np.min(self.y_true), np.max(self.y_true))
self.min_x_bounds, self.max_x_bounds = np.min(self.y_true), np.max(self.y_true)
self.y_pred = np.array(self.y_pred)
if self.show_perc != 1:
self.y_pred = self.y_pred[self.show_idxs]
if self.cat:
neg_thr = None
pos_thr = None
if self.specificity is not None:
inp0 = self.y_pred[self.y_true == 0]
neg_thr = np.sort(inp0)[-int(len(inp0) * (1 - self.specificity))]
if self.sensitivity is not None:
inp1 = self.y_pred[self.y_true == 1]
pos_thr = np.sort(inp1)[-int(len(inp1) * self.sensitivity)]
self.update_graph(self.y_pred, self.y_true, neg_thr=neg_thr, pos_thr=pos_thr)
else:
# Adjust bounds during validation
self.min_x_bounds = min(self.min_x_bounds, np.min(self.y_pred))
self.max_x_bounds = max(self.max_x_bounds, np.max(self.y_pred))
x_bounds = (self.min_x_bounds, self.max_x_bounds)
self.update_graph(self.y_pred, self.y_true, x_bounds=x_bounds, y_bounds=self.y_bounds)
def update_graph(self, y_pred, y_true, x_bounds=None, y_bounds=None, neg_thr=None, pos_thr=None):
if not hasattr(self, 'graph_fig'):
self.df_out = display("", display_id=True)
if self.cat:
self._cl_names = self.dls.vocab
self._classes = L(self.dls.vocab.o2i.values())
self._n_classes = len(self._classes)
if self.binary:
self.bins = np.linspace(0, 1, 101)
else:
_cm = plt.get_cmap(self.cmap)
self._color = [_cm(1. * c/self._n_classes) for c in range(1, self._n_classes + 1)][::-1]
self._h_vals = np.linspace(-.5, self._n_classes - .5, self._n_classes + 1)[::-1]
self._rand = []
for i, c in enumerate(self._classes):
self._rand.append(.5 * (np.random.rand(np.sum(y_true == c)) - .5))
self.graph_fig, self.graph_ax = plt.subplots(1, figsize=self.figsize)
self.graph_out = display("", display_id=True)
self.graph_ax.clear()
if self.cat:
if self.binary:
self.graph_ax.hist(y_pred[y_true == 0], bins=self.bins, density=self.normalize, color='red', label=self._cl_names[0],
edgecolor='black', alpha=self.alpha)
self.graph_ax.hist(y_pred[y_true == 1], bins=self.bins, density=self.normalize, color='blue', label=self._cl_names[1],
edgecolor='black', alpha=self.alpha)
self.graph_ax.axvline(.5, lw=1, ls='--', color='gray')
if neg_thr is not None:
self.graph_ax.axvline(neg_thr, lw=2, ls='--', color='red', label=f'specificity={(self.specificity):.3f}')
if pos_thr is not None:
self.graph_ax.axvline(pos_thr, lw=2, ls='--', color='blue', label=f'sensitivity={self.sensitivity:.3f}')
self.graph_ax.set_xlabel(f'probability of class {self._cl_names[1]}', fontsize=12)
self.graph_ax.legend()
else:
for i, c in enumerate(self._classes):
self.graph_ax.scatter(y_pred[y_true == c], y_true[y_true == c] + self._rand[i], color=self._color[i],
edgecolor='black', alpha=self.alpha, lw=.5, s=self.size)
self.graph_ax.vlines(np.mean(y_pred[y_true == c]), i - .5, i + .5, color='r')
self.graph_ax.vlines(.5, min(self._h_vals), max(self._h_vals), lw=.5)
self.graph_ax.hlines(self._h_vals, 0, 1, lw=.5)
self.graph_ax.set_ylim(min(self._h_vals), max(self._h_vals))
self.graph_ax.set_yticks(self._classes)
self.graph_ax.set_yticklabels(self._cl_names)
self.graph_ax.set_ylabel('true class', fontsize=12)
self.graph_ax.set_xlabel('probability of true class', fontsize=12)
self.graph_ax.set_xlim(0, 1)
self.graph_ax.set_xticks(np.linspace(0, 1, 11))
self.graph_ax.grid(axis='x', color='gainsboro', lw=.2)
else:
self.graph_ax.scatter(y_pred, y_true, color=self.color, edgecolor='black', alpha=self.alpha, lw=.5, s=self.size)
self.graph_ax.set_xlim(*x_bounds)
self.graph_ax.set_ylim(*y_bounds)
self.graph_ax.plot([*x_bounds], [*x_bounds], color='gainsboro')
self.graph_ax.set_xlabel('y_pred', fontsize=12)
self.graph_ax.set_ylabel('y_true', fontsize=12)
self.graph_ax.grid(color='gainsboro', lw=.2)
self.graph_ax.set_title(f'Prediction Dynamics \nepoch: {self.epoch + 1}/{self.n_epoch}')
self.df_out.update(pd.DataFrame(np.stack(self.learn.recorder.values)[-1].reshape(1,-1),
columns=self.learn.recorder.metric_names[1:-1], index=[self.epoch]))
self.graph_out.update(self.graph_ax.figure)
if self.epoch == self.n_epoch - 1:
plt.close(self.graph_ax.figure)
from tsai.basics import *
from tsai.models.InceptionTime import *
dsid = 'NATOPS'
X, y, splits = get_UCR_data(dsid, split_data=False)
check_data(X, y, splits, False)
tfms = [None, [Categorize()]]
batch_tfms = [TSStandardize(by_var=True)]
dls = get_ts_dls(X, y, splits=splits, tfms=tfms, batch_tfms=batch_tfms)
learn = ts_learner(dls, InceptionTime, metrics=accuracy, cbs=PredictionDynamics())
learn.fit_one_cycle(2, 3e-3)
#hide
from tsai.imports import *
from tsai.export import *
nb_name = get_nb_name()
# nb_name = "064_callback.PredictionDynamics.ipynb"
create_scripts(nb_name);
```
|
github_jupyter
|
# Homework03: Topic Modeling with Latent Semantic Analysis
Latent Semantic Analysis (LSA) is a method for finding latent similarities between documents treated as a bag of words by using a low rank approximation. It is used for document classification, clustering and retrieval. For example, LSA can be used to search for prior art given a new patent application. In this homework, we will implement a small library for simple latent semantic analysis as a practical example of the application of SVD. The ideas are very similar to PCA. SVD is also used in recommender systems in an similar fashion (for an SVD-based recommender system library, see [Surpise](http://surpriselib.com).
We will implement a toy example of LSA to get familiar with the ideas. If you want to use LSA or similar methods for statistical language analysis, the most efficient Python libraries are probably [gensim](https://radimrehurek.com/gensim/) and [spaCy](https://spacy.io) - these also provide an online algorithm - i.e. the training information can be continuously updated. Other useful functions for processing natural language can be found in the [Natural Language Toolkit](http://www.nltk.org/).
**Note**: The SVD from scipy.linalg performs a full decomposition, which is inefficient since we only need to decompose until we get the first k singluar values. If the SVD from `scipy.linalg` is too slow, please use the `sparsesvd` function from the [sparsesvd](https://pypi.python.org/pypi/sparsesvd/) package to perform SVD instead. You can install in the usual way with
```
!pip install sparsesvd
```
Then import the following
```python
from sparsesvd import sparsesvd
from scipy.sparse import csc_matrix
```
and use as follows
```python
sparsesvd(csc_matrix(M), k=10)
```
**Exercise 1 (20 points)**. Calculating pairwise distance matrices.
Suppose we want to construct a distance matrix between the rows of a matrix. For example, given the matrix
```python
M = np.array([[1,2,3],[4,5,6]])
```
the distance matrix using Euclidean distance as the measure would be
```python
[[ 0.000 1.414 2.828]
[ 1.414 0.000 1.414]
[ 2.828 1.414 0.000]]
```
if $M$ was a collection of column vectors.
Write a function to calculate the pairwise-distance matrix given the matrix $M$ and some arbitrary distance function. Your functions should have the following signature:
```
def func_name(M, distance_func):
pass
```
0. Write a distance function for the Euclidean, squared Euclidean and cosine measures.
1. Write the function using looping for M as a collection of row vectors.
2. Write the function using looping for M as a collection of column vectors.
3. Wrtie the function using broadcasting for M as a collection of row vectors.
4. Write the function using broadcasting for M as a collection of column vectors.
For 3 and 4, try to avoid using transposition (but if you get stuck, there will be no penalty for using transposition). Check that all four functions give the same result when applied to the given matrix $M$.
**Exercise 2 (20 points)**.
**Exercise 2 (20 points)**. Write 3 functions to calculate the term frequency (tf), the inverse document frequency (idf) and the product (tf-idf). Each function should take a single argument `docs`, which is a dictionary of (key=identifier, value=document text) pairs, and return an appropriately sized array. Convert '-' to ' ' (space), remove punctuation, convert text to lowercase and split on whitespace to generate a collection of terms from the document text.
- tf = the number of occurrences of term $i$ in document $j$
- idf = $\log \frac{n}{1 + \text{df}_i}$ where $n$ is the total number of documents and $\text{df}_i$ is the number of documents in which term $i$ occurs.
Print the table of tf-idf values for the following document collection
```
s1 = "The quick brown fox"
s2 = "Brown fox jumps over the jumps jumps jumps"
s3 = "The the the lazy dog elephant."
s4 = "The the the the the dog peacock lion tiger elephant"
docs = {'s1': s1, 's2': s2, 's3': s3, 's4': s4}
```
**Exercise 3 (20 points)**.
1. Write a function that takes a matrix $M$ and an integer $k$ as arguments, and reconstructs a reduced matrix using only the $k$ largest singular values. Use the `scipy.linagl.svd` function to perform the decomposition. This is the least squares approximation to the matrix $M$ in $k$ dimensions.
2. Apply the function you just wrote to the following term-frequency matrix for a set of $9$ documents using $k=2$ and print the reconstructed matrix $M'$.
```
M = np.array([[1, 0, 0, 1, 0, 0, 0, 0, 0],
[1, 0, 1, 0, 0, 0, 0, 0, 0],
[1, 1, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 1, 0, 1, 0, 0, 0, 0],
[0, 1, 1, 2, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 1, 0, 0, 0, 0],
[0, 1, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 1, 1, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 1, 1, 1, 0],
[0, 0, 0, 0, 0, 0, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 1, 1]])
```
3. Calculate the pairwise correlation matrix for the original matrix M and the reconstructed matrix using $k=2$ singular values (you may use [scipy.stats.spearmanr](http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.spearmanr.html) to do the calculations). Consider the fist 5 sets of documents as one group $G1$ and the last 4 as another group $G2$ (i.e. first 5 and last 4 columns). What is the average within group correlation for $G1$, $G2$ and the average cross-group correlation for G1-G2 using either $M$ or $M'$. (Do not include self-correlation in the within-group calculations.).
**Exercise 4 (40 points)**. Clustering with LSA
1. Begin by loading a PubMed database of selected article titles using 'pickle'. With the following:
```import pickle
docs = pickle.load(open('pubmed.pic', 'rb'))```
Create a tf-idf matrix for every term that appears at least once in any of the documents. What is the shape of the tf-idf matrix?
2. Perform SVD on the tf-idf matrix to obtain $U \Sigma V^T$ (often written as $T \Sigma D^T$ in this context with $T$ representing the terms and $D$ representing the documents). If we set all but the top $k$ singular values to 0, the reconstructed matrix is essentially $U_k \Sigma_k V_k^T$, where $U_k$ is $m \times k$, $\Sigma_k$ is $k \times k$ and $V_k^T$ is $k \times n$. Terms in this reduced space are represented by $U_k \Sigma_k$ and documents by $\Sigma_k V^T_k$. Reconstruct the matrix using the first $k=10$ singular values.
3. Use agglomerative hierarchical clustering with complete linkage to plot a dendrogram and comment on the likely number of document clusters with $k = 100$. Use the dendrogram function from [SciPy ](https://docs.scipy.org/doc/scipy-0.15.1/reference/generated/scipy.cluster.hierarchy.dendrogram.html).
4. Determine how similar each of the original documents is to the new document `data/mystery.txt`. Since $A = U \Sigma V^T$, we also have $V = A^T U S^{-1}$ using orthogonality and the rule for transposing matrix products. This suggests that in order to map the new document to the same concept space, first find the tf-idf vector $v$ for the new document - this must contain all (and only) the terms present in the existing tf-idx matrix. Then the query vector $q$ is given by $v^T U_k \Sigma_k^{-1}$. Find the 10 documents most similar to the new document and the 10 most dissimilar.
**Notes on the Pubmed articles**
These were downloaded with the following script.
```python
from Bio import Entrez, Medline
Entrez.email = "YOUR EMAIL HERE"
import cPickle
try:
docs = cPickle.load(open('pubmed.pic'))
except Exception, e:
print e
docs = {}
for term in ['plasmodium', 'diabetes', 'asthma', 'cytometry']:
handle = Entrez.esearch(db="pubmed", term=term, retmax=50)
result = Entrez.read(handle)
handle.close()
idlist = result["IdList"]
handle2 = Entrez.efetch(db="pubmed", id=idlist, rettype="medline", retmode="text")
result2 = Medline.parse(handle2)
for record in result2:
title = record.get("TI", None)
abstract = record.get("AB", None)
if title is None or abstract is None:
continue
docs[title] = '\n'.join([title, abstract])
print title
handle2.close()
cPickle.dump(docs, open('pubmed.pic', 'w'))
docs.values()
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/ipavlopoulos/toxic_spans/blob/master/ToxicSpans_SemEval21.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Download the data and the code
```
from ast import literal_eval
import pandas as pd
import random
!git clone https://github.com/ipavlopoulos/toxic_spans.git
from toxic_spans.evaluation.semeval2021 import f1
tsd = pd.read_csv("toxic_spans/data/tsd_trial.csv")
tsd.spans = tsd.spans.apply(literal_eval)
tsd.head(1)
```
### Run a random baseline
* Returns random offsets as toxic per text
```
# make an example with a taboo word
taboo_word = "fucking"
template = f"This is a {taboo_word} example."
# build a random baseline (yields offsets at random)
random_baseline = lambda text: [i for i, char in enumerate(text) if random.random()>0.5]
predictions = random_baseline(template)
# find the ground truth indices and print
gold = list(range(template.index(taboo_word), template.index(taboo_word)+len(taboo_word)))
print(f"Gold\t\t: {gold}")
print(f"Predicted\t: {predictions}")
tsd["random_predictions"] = tsd.text.apply(random_baseline)
tsd["f1_scores"] = tsd.apply(lambda row: f1(row.random_predictions, row.spans), axis=1)
tsd.head()
from scipy.stats import sem
_ = tsd.f1_scores.plot(kind="box")
print (f"F1 = {tsd.f1_scores.mean():.2f} ± {sem(tsd.f1_scores):.2f}")
```
### Prepare the text file with the scores
* Name it as `spans-pred.txt`.
* Align the scores with the rows.
```
# make sure that the ids match the ones of the scores
predictions = tsd.random_predictions.to_list()
ids = tsd.index.to_list()
# write in a prediction file named "spans-pred.txt"
with open("spans-pred.txt", "w") as out:
for uid, text_scores in zip(ids, predictions):
out.write(f"{str(uid)}\t{str(text_scores)}\n")
! head spans-pred.txt
```
### Zip the predictions
* Take extra care to verify that only the predictions text file is included.
* The text file should **not** be within any directory.
* No other file should be included; the zip should only contain the txt file.
```
! zip -r random_predictions.zip ./spans-pred.*
```
###### Check by unziping it: only a `spans-pred.txt` file should be created
```
! rm spans-pred.txt
! unzip random_predictions.zip
```
### Download the zip and submit it to be assessed
```
from google.colab import files
files.download("random_predictions.zip")
```
### When the submission is finished click the `Download output from scoring step`
* The submission may take a while, so avoid late submissions.
* Download the output_file.zip and see your score in the respective file.
```
```
|
github_jupyter
|
# Quickstart
A quick introduction on how to use the OQuPy package to compute the dynamics of a quantum system that is possibly strongly coupled to a structured environment. We illustrate this by applying the TEMPO method to the strongly coupled spin boson model.
**Contents:**
* Example - The spin boson model
* 1. The model and its parameters
* 2. Create system, correlations and bath objects
* 3. TEMPO computation
First, let's import OQuPy and some other packages we are going to use
```
import sys
sys.path.insert(0,'..')
import oqupy
import numpy as np
import matplotlib.pyplot as plt
```
and check what version of tempo we are using.
```
oqupy.__version__
```
Let's also import some shorthands for the spin Pauli operators and density matrices.
```
sigma_x = oqupy.operators.sigma("x")
sigma_y = oqupy.operators.sigma("y")
sigma_z = oqupy.operators.sigma("z")
up_density_matrix = oqupy.operators.spin_dm("z+")
down_density_matrix = oqupy.operators.spin_dm("z-")
```
-------------------------------------------------
## Example - The spin boson model
As a first example let's try to reconstruct one of the lines in figure 2a of [Strathearn2018] ([Nat. Comm. 9, 3322 (2018)](https://doi.org/10.1038/s41467-018-05617-3) / [arXiv:1711.09641v3](https://arxiv.org/abs/1711.09641)). In this example we compute the time evolution of a spin which is strongly coupled to an ohmic bath (spin-boson model). Before we go through this step by step below, let's have a brief look at the script that will do the job - just to have an idea where we are going:
```
Omega = 1.0
omega_cutoff = 5.0
alpha = 0.3
system = oqupy.System(0.5 * Omega * sigma_x)
correlations = oqupy.PowerLawSD(alpha=alpha,
zeta=1,
cutoff=omega_cutoff,
cutoff_type='exponential')
bath = oqupy.Bath(0.5 * sigma_z, correlations)
tempo_parameters = oqupy.TempoParameters(dt=0.1, dkmax=30, epsrel=10**(-4))
dynamics = oqupy.tempo_compute(system=system,
bath=bath,
initial_state=up_density_matrix,
start_time=0.0,
end_time=15.0,
parameters=tempo_parameters)
t, s_z = dynamics.expectations(0.5*sigma_z, real=True)
plt.plot(t, s_z, label=r'$\alpha=0.3$')
plt.xlabel(r'$t\,\Omega$')
plt.ylabel(r'$<S_z>$')
plt.legend()
```
### 1. The model and its parameters
We consider a system Hamiltonian
$$ H_{S} = \frac{\Omega}{2} \hat{\sigma}_x \mathrm{,}$$
a bath Hamiltonian
$$ H_{B} = \sum_k \omega_k \hat{b}^\dagger_k \hat{b}_k \mathrm{,}$$
and an interaction Hamiltonian
$$ H_{I} = \frac{1}{2} \hat{\sigma}_z \sum_k \left( g_k \hat{b}^\dagger_k + g^*_k \hat{b}_k \right) \mathrm{,}$$
where $\hat{\sigma}_i$ are the Pauli operators, and the $g_k$ and $\omega_k$ are such that the spectral density $J(\omega)$ is
$$ J(\omega) = \sum_k |g_k|^2 \delta(\omega - \omega_k) = 2 \, \alpha \, \omega \, \exp\left(-\frac{\omega}{\omega_\mathrm{cutoff}}\right) \mathrm{.} $$
Also, let's assume the initial density matrix of the spin is the up state
$$ \rho(0) = \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} $$
and the bath is initially at zero temperature.
For the numerical simulation it is advisable to choose a characteristic frequency and express all other physical parameters in terms of this frequency. Here, we choose $\Omega$ for this and write:
* $\Omega = 1.0 \Omega$
* $\omega_c = 5.0 \Omega$
* $\alpha = 0.3$
```
Omega = 1.0
omega_cutoff = 5.0
alpha = 0.3
```
### 2. Create system, correlations and bath objects
#### System
$$ H_{S} = \frac{\Omega}{2} \hat{\sigma}_x \mathrm{,}$$
```
system = oqupy.System(0.5 * Omega * sigma_x)
```
#### Correlations
$$ J(\omega) = 2 \, \alpha \, \omega \, \exp\left(-\frac{\omega}{\omega_\mathrm{cutoff}}\right) $$
Because the spectral density is of the standard power-law form,
$$ J(\omega) = 2 \alpha \frac{\omega^\zeta}{\omega_c^{\zeta-1}} X(\omega,\omega_c) $$
with $\zeta=1$ and $X$ of the type ``'exponential'`` we define the spectral density with:
```
correlations = oqupy.PowerLawSD(alpha=alpha,
zeta=1,
cutoff=omega_cutoff,
cutoff_type='exponential')
```
#### Bath
The bath couples with the operator $\frac{1}{2}\hat{\sigma}_z$ to the system.
```
bath = oqupy.Bath(0.5 * sigma_z, correlations)
```
### 3. TEMPO computation
Now, that we have the system and the bath objects ready we can compute the dynamics of the spin starting in the up state, from time $t=0$ to $t=5\,\Omega^{-1}$
```
dynamics_1 = oqupy.tempo_compute(system=system,
bath=bath,
initial_state=up_density_matrix,
start_time=0.0,
end_time=5.0,
tolerance=0.01)
```
and plot the result:
```
t_1, z_1 = dynamics_1.expectations(0.5*sigma_z, real=True)
plt.plot(t_1, z_1, label=r'$\alpha=0.3$')
plt.xlabel(r'$t\,\Omega$')
plt.ylabel(r'$<S_z>$')
plt.legend()
```
Yay! This looks like the plot in figure 2a [Strathearn2018].
Let's have a look at the above warning. It said:
```
WARNING: Estimating parameters for TEMPO calculation. No guarantie that resulting TEMPO calculation converges towards the correct dynamics! Please refere to the TEMPO documentation and check convergence by varying the parameters for TEMPO manually.
```
We got this message because we didn't tell the package what parameters to use for the TEMPO computation, but instead only specified a `tolerance`. The package tries it's best by implicitly calling the function `oqupy.guess_tempo_parameters()` to find parameters that are appropriate for the spectral density and system objects given.
#### TEMPO Parameters
There are **three key parameters** to a TEMPO computation:
* `dt` - Length of a time step $\delta t$ - It should be small enough such that a trotterisation between the system Hamiltonian and the environment it valid, and the environment auto-correlation function is reasonably well sampled.
* `dkmax` - Number of time steps $K \in \mathbb{N}$ - It must be large enough such that $\delta t \times K$ is larger than the neccessary memory time $\tau_\mathrm{cut}$.
* `epsrel` - The maximal relative error $\epsilon_\mathrm{rel}$ in the singular value truncation - It must be small enough such that the numerical compression (using tensor network algorithms) does not truncate relevant correlations.
To choose the right set of initial parameters, we recommend to first use the `oqupy.guess_tempo_parameters()` function and then check with the helper function `oqupy.helpers.plot_correlations_with_parameters()` whether it satisfies the above requirements:
```
parameters = oqupy.guess_tempo_parameters(system=system,
bath=bath,
start_time=0.0,
end_time=5.0,
tolerance=0.01)
print(parameters)
fig, ax = plt.subplots(1,1)
oqupy.helpers.plot_correlations_with_parameters(bath.correlations, parameters, ax=ax)
```
In this plot you see the real and imaginary part of the environments auto-correlation as a function of the delay time $\tau$ and the sampling of it corresponding the the chosen parameters. The spacing and the number of sampling points is given by `dt` and `dkmax` respectively. We can see that the auto-correlation function is close to zero for delay times larger than approx $2 \Omega^{-1}$ and that the sampling points follow the curve reasonably well. Thus this is a reasonable set of parameters.
We can choose a set of parameters by hand and bundle them into a `TempoParameters` object,
```
tempo_parameters = oqupy.TempoParameters(dt=0.1, dkmax=30, epsrel=10**(-4), name="my rough parameters")
print(tempo_parameters)
```
and check again with the helper function:
```
fig, ax = plt.subplots(1,1)
oqupy.helpers.plot_correlations_with_parameters(bath.correlations, tempo_parameters, ax=ax)
```
We could feed this object into the `oqupy.tempo_compute()` function to get the dynamics of the system. However, instead of that, we can split up the work that `oqupy.tempo_compute()` does into several steps, which allows us to resume a computation to get later system dynamics without having to start over. For this we start with creating a `Tempo` object:
```
tempo = oqupy.Tempo(system=system,
bath=bath,
parameters=tempo_parameters,
initial_state=up_density_matrix,
start_time=0.0)
```
We can start by computing the dynamics up to time $5.0\,\Omega^{-1}$,
```
tempo.compute(end_time=5.0)
```
then get and plot the dynamics of expecatation values,
```
dynamics_2 = tempo.get_dynamics()
plt.plot(*dynamics_2.expectations(0.5*sigma_z, real=True), label=r'$\alpha=0.3$')
plt.xlabel(r'$t\,\Omega$')
plt.ylabel(r'$<S_z>$')
plt.legend()
```
then continue the computation to $15.0\,\Omega^{-1}$,
```
tempo.compute(end_time=15.0)
```
and then again get and plot the dynamics of expecatation values.
```
dynamics_2 = tempo.get_dynamics()
plt.plot(*dynamics_2.expectations(0.5*sigma_z, real=True), label=r'$\alpha=0.3$')
plt.xlabel(r'$t\,\Omega$')
plt.ylabel(r'$<S_z>$')
plt.legend()
```
Finally, we note: to validate the accuracy the result **it vital to check the convergence of such a simulation by varying all three computational parameters!** For this we recommend repeating the same simulation with slightly "better" parameters (smaller `dt`, larger `dkmax`, smaller `epsrel`) and to consider the difference of the result as an estimate of the upper bound of the accuracy of the simulation.
-------------------------------------------------
|
github_jupyter
|
<img src='./img/EU-Copernicus-EUM_3Logos.png' alt='Logo EU Copernicus EUMETSAT' align='right' width='50%'></img>
<br>
<br>
<a href="./index_ltpy.ipynb"><< Index</a><span style="float:right;"><a href="./12_ltpy_WEkEO_harmonized_data_access_api.ipynb">12 - WEkEO Harmonized Data Access API >></a></span>
# 1.1 Atmospheric composition data - Overview and data access
This module gives an overview of the following atmospheric composition data services:
* [EUMETSAT AC SAF - The EUMETSAT Satellite Application Facility on Atmospheric Composition Monitoring](#ac_saf)
* [Copernicus Sentinel-5 Precursor (Sentinel-5P)](#sentinel_5p)
* [Copernicus Sentinel-3](#sentinel3)
* [Copernicus Atmosphere Monitoring Service (CAMS)](#cams)
<br>
## <a id="ac_saf"></a>EUMETSAT AC SAF - The EUMETSAT Satellite Application Facility on Atmospheric Composition Monitoring
<span style=float:left><img src='./img/ac_saf_logo.png' alt='Logo EU Copernicus EUMETSAT' align='left' width='90%'></img></span>
The [EUMETSAT Satellite Application Facility on Atmospheric Composition Monitoring (EUMETSAT AC SAF)](http://acsaf.org/) is one of eight EUMETSAT Satellite Application Facilities (SAFs). <br>
SAFs generate and disseminate operational EUMETSAT products and services and are an integral part of the distributed EUMETSAT Application Ground Segment.
AC SAF processes data on ozone, other trace gases, aerosols and ultraviolet data, obtained from satellite instrumentation.
<br>
### Available AC SAF products
AC-SAF offers three different product types: <br>
|<font size='+0.2'><center>[Near real-time products](#nrt)</center></font> | <font size='+0.2'><center>[Offline products](#offline)</center></font> | <font size='+0.2'><center>[Data records](#records)</center></font> |
|-----|-----|------|
<img src='./img/nrt_no2_example.png' alt='Near-real time product - NO2' align='middle' width='60%'></img>|<img src='./img/offline_ozone_example.png' alt='Logo EU Copernicus EUMETSAT' align='middle' width='60%'></img>|<img src='./img/ac_saf_level3.png' alt='Logo EU Copernicus EUMETSAT' align='middle' width='100%'></img>|
<br>
Near real-time and offline products are often refered as Level 2 data. Data records are refered as Level 3 data.
AC SAF products are sensed from two instruments onboard the Metop satellites:
* [Global Ozone Monitoring Experiment-2 (GOME-2) instrument](https://acsaf.org/gome-2.html) <br>
GOME-2 can measure a range of atmospheric trace constituents, with the emphasis on global ozone distributions. Furthermore, cloud properties and intensities of ultraviolet radiation are retrieved. These data are crucial for monitoring the atmospheric composition and the detection of pollutants. <br>
* [Infrared Atmospheric Sounding Interferometer (IASI) instrument](https://acsaf.org/iasi.html)
The [Metop satellites](https://acsaf.org/metop.html) is a series of three satellites that were launched in October 2006 (Metop-A), September 2012 (Metop-B) and November 2018 (Metop-C) respectively.
All AC SAF products are disseminated under the [AC SAF Data policy](https://acsaf.org/data_policy.html).
<br>
#### <a id="nrt"></a>Near-real time (NRT) products
NRT products are Level 2 products and are available to users in 3 hours from sensing at the latest and available for the past two months. NRT products are disseminated in HDF5 format.
| <img width=100>NRT Product type name</img> | Description | Unit | <img width=80>Satellite</img> | Instrument |
| ---- | ----- | ----- | ---- | -----|
| Total Ozone (O<sub>3</sub>) column | NRT total ozone column product provided information about vertical column densities of ozone in the atmosphere | Dobson Units (DU) | Metop-A<br>Metop-B | GOME-2 |
| Total and tropospheric NO<sub>2</sub> columns | NRT total and tropospheric NO2 column products provide information about vertical column densities of nitrogen dioxide in the atmosphere. | molecules/cm2 | Metop-A<br>Metop-B | GOME-2 |
| Total SO<sub>2</sub> column | NRT total SO2 column product provides information about vertical column densities of the sulfur dioxide in the atmosphere. | Dobson Units (DU) | Metop-A<br>Metop-B | GOME-2
| Total HCHO column | NRT HCHO column product provides information about vertical column densities of formaldehyde in the atmosphere. | molecules/cm2 | Metop-A<br>Metop-B | GOME-2 |
| High-resolution vertical ozone profile | NRT high-resolution vertical ozone profile product provides an ozone profile from the GOME-2 nadir scanning mode. | Partial ozone columns in Dobson Units in 40 layers from the surface up to 0.001 hPa| Metop-A<br>Metop-B | GOME-2 |
| Global tropospheric ozone column | The global tropospheric ozone column product provides information about vertical column densities of ozone in the troposphere, <br>from the surface to the tropopause and from the surface to 500 hPa (∼5km). | Dobson Units (DU) | Metop-A<br>Metop-B | GOME-2 |
<br>
#### <a id="offline"></a>Offline products
Offline products are Level 2 products and are available to users in 15 days of sensing. Typical delay is 2-3 days. Offline products are disseminated in HDF5 format.
| Offline Product type name | Description | Unit | <img width=80>Satellite</img> | Instrument | <img width=150px>Time period</img> |
| ---- | ----- | ----- | ---- | -----|----|
| Total Ozone (O<sub>3</sub>) column | Offline total ozone column product provided information about vertical column densities of ozone in the atmosphere | Dobson Units (DU) | Metop-A<br>Metop-B | GOME-2 | 1 Jan 2008 - almost NRT<br>13 Dec 2012 - almost NRT |
| Total and tropospheric NO<sub>2</sub> columns | Offline total and tropospheric NO2 column products provide information about vertical column densities of nitrogen dioxide in the atmosphere. | molecules/cm2 | Metop-A<br>Metop-B | GOME-2 | 1 Jan 2008 - almost NRT<br>13 Dec 2012 - almost NRT |
| Total SO<sub>2</sub> column | Offline total SO2 column product provides information about vertical column densities of the sulfur dioxide in the atmosphere. | Dobson Units (DU) | Metop-A<br>Metop-B | GOME-2 | 1 Jan 2008 - almost NRT<br>13 Dec 2012 - almost NRT |
| Total HCHO column | Offline HCHO column product provides information about vertical column densities of formaldehyde in the atmosphere. | molecules/cm2 | Metop-A<br>Metop-B | GOME-2 | 1 Jan 2008 - almost NRT<br>13 Dec 2012 - almost NRT |
| High-resolution vertical ozone profile | Offline high-resolution vertical ozone profile product provides an ozone profile from the GOME-2 nadir scanning mode. | Partial ozone columns in Dobson Units in 40 layers from the surface up to 0.001 hPa| Metop-A<br>Metop-B | GOME-2 | 1 Jan 2008 - almost NRT<br>13 Dec 2012 - almost NRT |
| Global tropospheric ozone column | The offline global tropospheric ozone column product provides information about vertical column densities of ozone in the troposphere, from the surface to the tropopause and and from the surface to 500 hPa (∼5km). | Dobson Units (DU) | Metop-A<br>Metop-B | GOME-2 | 1 Jan 2008 - almost NRT<br>13 Dec 2012 - almost NRT |
<br>
#### <a id="records"></a>Data records
Data records are reprocessed, gridded Level 3 data. Data records are monthly aggregated products, regridded on a regular latitude-longitude grid. Data records are disseminated in NetCDF format.
| Data record name | Description | Unit | <img width=80>Satellite</img> | Instrument | <img width=150>Time period</img> |
| ---- | ----- | ----- | ---- | -----|----|
| Reprocessed **tropospheric O<sub>3</sub>** column data record for the Tropics | Tropospheric ozone column data record for the Tropics provides long-term information <br>about vertical densities of ozone in the atmosphere for the tropics. | Dobson Units (DU) | Metop-A<br>Metop-B | GOME-2 | Jan 2007- Dec 2018<br>Jan 2013- Jun 2019 |
| Reprocessed **total column and tropospheric NO<sub>2</sub>** data record | Total and tropospheric NO2 column data record provides long-term information about vertical column densities of nitrogen dioxide in the atmosphere. | molecules/cm2 | Metop-A<br>Metop-B | GOME-2 | Jan 2007 - Nov 2017<br>Jan 2013 - Nov 2017 |
| Reprocessed **total H<sub>2</sub>O column** data record | Total H2O column data record provides long-term information about vertical column densities of water vapour in the atmosphere. | kg/m2 | Metop-A<br>Metop-B | GOME-2 | Jan 2007 - Nov 2017<br>Jan 2013 - Nov 2017 |
<br>
### <a id="ac_saf_access"></a>How to access AC SAF products
AC SAF products can be accessed via different dissemination channels. There are channels where Level 2 and Level 3 are available for download. Other sources allow to browse through images and maps of the data. This is useful to see for what dates e.g. Level 2 data were sensed.
#### DLR ftp server
All near-real time, offline and reprocessed total column data are available at [DLR's ATMOS FTP-server](https://atmos.eoc.dlr.de/products/). Accessing data is a two step process:
1. [Register](https://acsaf.org/registration_form.html) as a user of AC SAF products
2. [Log in](https://atmos.eoc.dlr.de/products/)( (with the user name and password that is emailed to you after registration)
Once logged in, you find data folders for GOME-2 products from Metop-A in the directory *'gome2a/'* and GOME-2 products from Metop-B in the directory: *'gome2b/'* respectively. In each GOME-2 directory, you find the following sub-directories: <br>
* **`near_real_time/`**,
* **`offline/`**, and
* **`level3/`**.
<br>
<div style='text-align:center;'>
<figure><img src='./img/dlr_ftp_directory.png' width='50%'/>
<figcaption><i>Example of the directory structure of DLR's ATMOS FTP-server</i></figcaption>
</figure>
</div>
<br>
#### EUMETSAT Data Centre
The EUMETSAT Data Centre provides a long-term archive of data and generated products from EUMETSAT, which can be ordered online. Ordering data is a two step process:
1. [Create an account](https://eoportal.eumetsat.int/userMgmt/register.faces) at the EUMETSAT Earth Observation Portal
2. [Log in](https://eoportal.eumetsat.int/userMgmt/login.faces) (with the user name and password that is emailed to you after registration)
Once succesfully logged in, go to (1) Data Centre. You will be re-directed to (2) the User Services Client. Type in *'GOME'* as search term and you can get a list of all available GOME-2 products.
<div style='text-align:center;'>
<figure><img src='./img/eumetsat_data_centre.png' width='50%' />
<figcaption><i>Example of the directory structure of EUMETSAT's Data Centre</i></figcaption>
</figure>
</div>
<br>
#### Web-based services
There are two web-based services, [DLR's ATMOS webserver](https://atmos.eoc.dlr.de/app/missions/gome2) and the [TEMIS service by KNMI](http://temis.nl/index.php) that offer access to GOME-2/MetOp browse products. These services are helpful to see the availability of data for specific days, especially for AC SAF Level-2 parameters.
<br>
| <font size='+0.2'>[DLR's ATMOS webserver](https://atmos.eoc.dlr.de/app/missions/gome2)</font> | <font size='+0.2'>[TEMIS - Tropospheric Emission Monitoring Internet Service](http://temis.nl/index.php)</font> |
| - | - |
| <br>ATMOS (Atmospheric ParameTers Measured by in-Orbit Spectrosocopy is a webserver operated by DLR's Remote Sensing Technology Institute (IMF). The webserver provides access to browse products from GOME-2/Metop Products, both in NRT and offline mode. <br><br> | <br>TEMIS is a web-based service to browse and download atmospheric satellite data products maintained by KNMI. The data products consist mainly of tropospheric trace gases and aerosol concentrations, but also UV products, cloud information and surface albedo climatologies are provided. <br><br> |
| <center><img src='./img/atmos_service.png' width='70%'></img></center> | <center><img src='./img/temis_service.png' width='70%'></img></center> |
<br>
## <a id="sentinel_5p"></a>Copernicus Sentinel-5 Precursor (Sentinel-5P)
[Sentinel-5 Precursor (Sentinel-5P)](https://sentinels.copernicus.eu/web/sentinel/missions/sentinel-5p) is the first Copernicus mission dedicated to monitoring our atmosphere. The satellite carries the state-of-the-art TROPOMI instrument to map a multitude of trace gases.
Sentinel-5P was developed to reduce data gaps between the ENVISAT satellite - in particular the Sciamachy instrument - and the launch of Sentinel-5, and to complement GOME-2 on MetOp. In the future, both the geostationary Sentinel-4 and polar-orbiting Sentinel-5 missions will monitor the composition of the atmosphere for Copernicus Atmosphere Services. Both missions will be carried on meteorological satellites operated by [EUMETSAT](https://eumetsat.int).
### Available data products and trace gas information
<span style=float:right><img src='./img/sentinel_5p_data_products.jpg' alt='Sentinel-5p data prodcuts' align='right' width='90%'></img></span>
Data products from Sentinel-5P’s Tropomi instrument are distributed to users at two levels:
* `Level-1B`: provides geo-located and radiometrically corrected top of the atmosphere Earth radiances in all spectral bands, as well as solar irradiances.
* `Level-2`: provides atmospheric geophysical parameters.
`Level-2` products are disseminated within three hours after sensing. This `near-real-time`(NRT) services disseminates the following products:
* `Ozone`
* `Sulphur dioxide`
* `Nitrogen dioxide`
* `Formaldehyde`
* `Carbon monoxide`
* `Vertical profiles of ozone` and
* `Cloud / Aerosol distributions`
`Level-1B` products are disseminated within 12 hours after sensing.
`Methane`, `tropospheric ozone` and `corrected total nitrogen dioxide columns` are available withing 5 days after sensing.
<br>
### <a id="sentinel5p_access"></a>How to access Sentinel-5P data
Sentinel-5P data can be accessed via different dissemination channels. The data is accessible via the `Copernicus Open Access Hub` and `EUMETSAT's EUMETCast`.
#### Copernicus Open Access Hub
Sentinel-5P data is available for browsing and downloading via the [Copernicus Open Access Hub](https://scihub.copernicus.eu/). The Copernicus Open Access Hub provides complete, free and open access to Sentinel-1, Sentinel-2, Sentinel-3 and Sentinel-5P data.
<div style='text-align:center;'>
<figure><img src='./img/open_access_hub.png' alt='Sentinel-5p data products' align='middle' width='50%'/>
<figcaption><i>Interface of the Copernicus Open Access Hub and the Sentinel-5P Pre-Operations Data Hub</i></figcaption>
</figure>
</div>
#### EUMETSAT's EUMETCast
Since August 2019, Sentinel-5p `Level 1B` and `Level 2` are as well available on EUMETSAT's EUMETCast:
* **Level 1B** products will be distributed on EUMETCast Terrestrial
* **Level 2** products are distributed on EUMETCast Europe, High Volume Service Transponder 2 (HVS-2)
Sentinel-5P data on EUMETCast can be accessed via [EUMETSAT's Earth Observation Portal (EOP)](https://eoportal.eumetsat.int/userMgmt/login.faces).
#### TEMIS
[TEMIS - Tropospheric Emission Monitoring Internet Service](http://temis.nl/airpollution/no2.html) provides access to selected Sentinel-5P parameters, e.g. `NO`<sub>2</sub>.
<br>
## <a id='sentinel3'></a>Copernicus Sentinel-3 - Ocean and Land Colour (OLCI)
<span style=float:right><img src='./img/sentinel3.png' alt='Sentinel-5p data prodcuts' align='right' width='90%'></img></span>
The Sentinel-3 is the Copernicus mission to monitor and measure sea surface topography, sea and land surface temperature and ocean and land surface.
The Sentinel-3 mission carries five different instruments aboard the satellites: and offers four differnt data product types:
- [Ocean and Land Colour Instrument (OLCI)](https://sentinel.esa.int/web/sentinel/missions/sentinel-3/data-products/olci)
- [Sea and Land Surface Temperature Radiometer (SLSTR)](https://sentinel.esa.int/web/sentinel/missions/sentinel-3/data-products/slstr)
- [Synergy](https://sentinel.esa.int/web/sentinel/missions/sentinel-3/data-products/synergy), and
- [Altimetry](https://sentinel.esa.int/web/sentinel/missions/sentinel-3/data-products/altimetry).
The Sentinel-3 OLCI mission supports maritime monitoring, land mapping and monitoring, atmospheric monitoring and climate change monitoring.
### Available OLCI data products
OLCI product types are divided in three main categories:
- #### Level-1B products
Two different Level-1B products can be obtained:
- OL_1_EFR - output during EO processing mode for Full Resolution
- OL_1_ERR -output during EO processing mode for Reduced Resolution
The Level-1B products in EO processing mode contain calibrated, ortho-geolocated and spatially re-sampled Top Of Atmosphere (TOA) radiances for [21 OLCI spectral bands](https://sentinel.esa.int/web/sentinel/user-guides/sentinel-3-olci/resolutions/radiometric). In Full Resolution products (i.e. at native instrument spatial resolution), these parameters are provided for each re-gridded pixel on the product image and for each removed pixel. In Reduced Resolution products (i.e. at a resolution four times coarser), the parameters are only provided on the product grid.
- #### Level-2 Land products and Water products
The level-2 land product provides land and atmospheric geophysical parameters. The Level-2 water product provides water and atmospheric geophysical parameters. All products are computed for full and reduced resolution:
- OL_2_LFR - Land Full Resolution
- OL_2_LRR - Land Reduced Resolution
There are two timeframes for the delivery of the products:
- **Near-Real-Time (NRT)**: delivered to the users less than three hours after acquisition of the data by the sensor
- **Non-Time Critical (NTC)**: delivered no later than one month after acquisition or from long-term archives. Typically, the product is available within 24 or 48 hours.
The data is disseminated in .zip archive containing free-standing `NetCDF4` product files.
### How to access Sentinel-3 data
Sentinel-3 data can be accessed via different dissemination channels. The data is accessible via the `Copernicus Open Access Hub` and `WEkEO's Harmonized Data Access API`.
#### Copernicus Open Access Hub
Sentinel-3 data is available for browsing and downloading via the Copernicus Open Access Hub. The Copernicus Open Access Hub provides complete, free and open access to Sentinel-1, Sentinel-2, Sentinel-3 and Sentinel-5P data. See the an example of the Copernicus Open Access Hub interface [here](#sentinel5p_access).
#### WEkEO's Harmonized Data Access API
<span style=float:left><img src='./img/wekeo_logo2.png' alt='Logo WEkEO' align='center' width='90%'></img></span>
[WEkEO](https://www.wekeo.eu/) is the EU Copernicus DIAS (Data and Information Access Service) reference service for environmental data, virtual processing environments and skilled user support.
WEkEO offers access to a variety of data, including different parameters sensored from Sentinel-1, Sentinel-2 and Sentinel-3. It further offers access to climate reanalysis and seasonal forecast data.
The [Harmonized Data Access (HDA) API](https://www.wekeo.eu/documentation/using_jupyter_notebooks), a REST interface, allows users to subset and download datasets from WEkEO.
Please see [here](./12_ltpy_WEkEO_harmonized_access_api.ipynb) a practical example how you can retrieve Sentinel-3 data from WEkEO using the Harmonized Data Access API.
<br>
<br>
## <a id="cams"></a>Copernicus Atmosphere Monitoring Service (CAMS)
<span style=float:left><img src='./img/cams_logo_2.png' alt='Copernicus Atmosphere Monitoring Service' align='left' width='95%'></img></span>
[The Copernicus Atmosphere Monitoring Service (CAMS)](https://atmosphere.copernicus.eu/) provides consistent and quality-controlled information related to `air pollution and health`, `solar energy`, `greenhouse gases` and `climate forcing`, everywhere in the world.
CAMS is one of six services that form [Copernicus, the European Union's Earth observation programme](https://www.copernicus.eu/en).
CAMS is implemented by the [European Centre for Medium-Range Weather Forecasts (ECMWF)](http://ecmwf.int/) on behalf of the European Commission. ECMWF is an independent intergovernmental organisation supported by 34 states. It is both a research institute and a 24/7 operational service, producing and disseminating numerical weather predictions to its member states.
<br>
### Available data products
CAMS offers four different data product types:
|<font size='+0.2'><center>[CAMS Global <br>Reanalysis](#cams_reanalysis)</center></font></img> | <font size='+0.2'><center>[CAMS Global Analyses <br>and Forecasts](#cams_an_fc)</center></font> | <img width=30><font size='+0.2'><center>[CAMS Global Fire Assimilation System (GFAS)](#cams_gfas)</center></font></img> | <img width=30><font size='+0.2'><center>[CAMS Greenhouse Gases Flux Inversions](#cams_greenhouse_flux)</center></font></img> |
|-----|-----|------|------|
<img src='./img/cams_reanalysis.png' alt='CAMS reanalysis' align='middle' width='100%'></img>|<img src='./img/cams_forecast.png' alt='CAMS Forecast' align='middle' width='100%'></img>|<img src='./img/cams_gfas.png' alt='CAMS GFAS' align='middle' width='100%'></img>|<img src='./img/cams_greenhouse_fluxes.png' alt='CAMS greenhous flux inversions' align='middle' width='100%'></img>|
#### <a id="cams_reanalysis"></a>CAMS Global Reanalysis
CAMS reanalysis data set provides consistent information on aerosols and reactive gases from 2003 to 2017. CAMS global reanalysis dataset has a global horizontal resolution of approximately 80 km and a refined temporal resolution of 3 hours. CAMS reanalysis are available in GRIB and NetCDF format.
| Parameter family | Time period | <img width=80>Spatial resolution</img> | Temporal resolution |
| ---- | ----- | ----- | -----|
| [CAMS global reanalysis of total aerosol optical depth<br> at multiple wavelengths](https://atmosphere.copernicus.eu/catalogue#/product/urn:x-wmo:md:int.ecmwf::copernicus:cams:prod:rean:black-carbon-aod_dust-aod_organic-carbon-aod_sea-salt-aod_sulphate-aod_total-aod_warning_multiple_species:pid469) | 2003-2017 | ~80km | 3-hourly |
| [CAMS global reanalysis of aerosol concentrations](https://atmosphere.copernicus.eu/catalogue#/product/urn:x-wmo:md:int.ecmwf::copernicus:cams:prod:rean:black-carbon-concentration_dust-concentration_organic-carbon-concentration_pm1_pm10_pm2.5_sea-salt-concentration_sulfates-concentration_warning_multiple_species:pid467) | 2003-2017 | ~80km | 3-hourly |
| [CAMS global reanalysis chemical species](https://atmosphere.copernicus.eu/catalogue#/product/urn:x-wmo:md:int.ecmwf::copernicus:cams:prod:rean:ald2_c10h16_c2h4_c2h5oh_c2h6_c2o3_c3h6_c3h8_c5h8_ch3coch3_ch3cocho_ch3o2_ch3oh_ch3ooh_ch4_co_dms_h2o2_hcho_hcooh_hno3_ho2_ho2no2_mcooh_msa_n2o5_nh2_nh3_nh4_no_no2_no3_no3_a_nox_o3_oh_ole_onit_pan_par_pb_rooh_ror_ra_so2_so4_warning_multiple_species:pid468) | 2003-2017 | ~80km | 3-hourly |
#### <a id="cams_an_fc"></a>CAMS Global analyses and forecasts
CAMS daily global analyses and forecast data set provides daily global forecasts of atmospheric composition parameters up to five days in advance. CAMS analyses and forecast data are available in GRIB and NetCDF format.
The forecast consists of 56 reactive trace gases in the troposphere, stratospheric ozone and five different types of aersol (desert dust, sea salt, organic matter, black carbon and sulphate).
| Parameter family | Time period | <img width=80>Spatial resolution</img> | Forecast step |
| ---- | ----- | ----- | -----|
| CAMS global forecasts of aerosol optical depths | Jul 2012- 5 days in advance | ~40km | 3-hour |
| CAMS global forecasts of aerosols | Jul 2012 - 5 days in advance | ~40km | 3-hour |
| CAMS global forecasts of chemical species | Jul 2012- 5 days in advance | ~40km | 3-hour |
| CAMS global forecasts of greenhouse gases | Jul 2012- 5 days in advance | ~9km | 3-hour |
#### <a id="cams_gfas"></a>CAMS Global Fire Assimiliation System (GFAS)
CAMS GFAS assimilated fire radiative power (FRP) observations from satellite-based sensors to produce daily estimates of wildfire and biomass burning emissions. The GFAS output includes spatially gridded Fire Radiative Power (FRP), dry matter burnt and biomass burning emissions for a large set of chemical, greenhouse gas and aerosol species. CAMS GFAS data are available in GRIB and NetCDF data.
A full list of CAMS GFAS parameters can be found in the [CAMS Global Fire Assimilation System (GFAS) data documentation](https://atmosphere.copernicus.eu/sites/default/files/2018-05/CAMS%20%20Global%20Fire%20Assimilation%20System%20%28GFAS%29%20data%20documentation.pdf).
| Parameter family | Time period | <img width=80>Spatial resolution</img> | Temporal resolution |
| ---- | ----- | ----- | ---- |
| CAMS GFAS analysis surface parameters | Jan 2003 - present | ~11km | daily |
| CAMS GFAS gridded satellite parameters | Jan 2003 - present | ~11km | daily |
#### <a id="cams_greenhouse_flux"></a>CAMS Greenhouse Gases Flux Inversions
CAMS Greenhouse Gases Flux Inversion reanalysis describes the variations, in space and in time, of the surface sources and sinks (fluxes) of the three major greenhouse gases that are directly affected by human activities: `carbon dioxide (CO2)`, `methane (CH4)` and `nitrous oxide (N2O)`. CAMS Greenhouse Gases Flux data is available in GRIB and NetCDF format.
| Parameter | Time period | <img width=80>Spatial resolution</img> | Frequency | Quantity |
| ---- | ----- | ----- | ---- | -----|
| Carbon Dioxide | Jan 1979 - Dec 2018 | ??? | 3 hourly<br>Monthly average | Concentration<br>Surface flux<br> Total colum |
| Methane | Jan 1990 - Dec 2017 | ??? | 6-hourly<br>Daily average<br>Monthly average | Concentration<br>Surface flux<br>Total column
| Nitrous Oxide | Jan 1995 - Dec 2017 | ???| 3-hourly<br>Monthly average | Concentration<br>Surface flux |
<br>
### <a id="cams_access"></a>How to access CAMS data
CAMS data can be accessed in two different ways: `ECMWF data archive` and `CAMS data catalogue of data visualizations`. A more detailed description of the different data access platforms can be found [here](https://confluence.ecmwf.int/display/CKB/Access+to+CAMS+global+forecast+data).
#### ECMWF data archive
ECMWF's data archive is called Meteorological and Archival Retrieval System (MARS) and provides access to ECMWF Public Datasets. The following CAMS data can be accessed through the ECMWF MARS archive: `CAMS reanalysis`, `CAMS GFAS data` (older than one day), and `CAMS global analyses and forecasts` (older than five days).
The archive can be accessed in two ways:
* via the [web interface](https://apps.ecmwf.int/datasets/) and
* via the [ECMWF Web API](https://confluence.ecmwf.int/display/WEBAPI/Access+ECMWF+Public+Datasets).
Subsequently, an example is shown how a MARS request can be executed within Python and data in either GRIB or netCDF can be downloaded on-demand.
#### 1. Register for an ECMWF user account
- Self-register at https://apps.ecmwf.int/registration/
- Login at https://apps.ecmwf.int/auth/login
#### 2. Install the `ecmwfapi` python library
`pip install ecmwf-api-client`
#### 3. Retrieve your API key
You can retrieve your API key at https://api.ecmwf.int/v1/key/. Add the `url`, `key` and `email` information, when you define the `ECMWFDataServer` (see below).
#### 3. Execute a MARS request and download data as `netCDF` file
Below, you see the principle of a `data retrieval` request. You can use the web interface to browse through the datasets. At the end, there is the option to let generate the `data retrieval` request for the API.
Additionally, you can have a look [here](./cams_ecmwfapi_example_requests.ipynb) at some example requests for different CAMS parameters.
**NOTE**: per default, ECMWF data is stored on a grid with longitudes going from 0 to 360 degrees. It can be reprojected to a regular geographic latitude-longitude grid, by setting the keyword argument `area` and `grid`. Per default, data is retrieved in `GRIB`. If you wish to retrieve the data in `netCDF`, you have to specify it by using the keyword argument `format`.
The example requests `Organic Matter Aerosol Optical Depth at 550 nm` forecast data for 3 June 2019 in `NetCDF`.
```
#!/usr/bin/env python
from ecmwfapi import ECMWFDataServer
server = ECMWFDataServer(url="https://api.ecmwf.int/v1", key="XXXXXXXXXXXXXXXX", email="XXXXXXXXXXXXXXXX")
# Retrieve data in NetCDF format
server.retrieve({
"class": "mc",
"dataset": "cams_nrealtime",
"date": "2019-06-03/to/2019-06-03",
"expver": "0001",
"levtype": "sfc",
"param": "210.210",
"step": "3",
"stream": "oper",
"time": "00:00:00",
"type": "fc",
"format": "netcdf",
"area": "90/-180/-90/180",
"grid": "0.4/0.4",
"target": "test.nc"
})
```
#### CAMS data catalogue of data visualizations
CAMS provides an extensive [catalogue of data visualizations](https://atmosphere.copernicus.eu/data) in the form of maps and charts. Products are updated daily and are available for selected parameters of `CAMS daily analyses and forecasts`.
<hr>
## Further information
* [EUMETSAT AC SAF - The EUMETSAT Application Facility on Atmospheric Composition Monitoring](https://acsaf.org/index.html)
* [AC SAF Data policy](https://acsaf.org/data_policy.html)
* [AC SAF Algorithm Theoretical Basis Documents (atbds)](https://acsaf.org/atbds.html)
* [DLR's ATMOS webserver](https://atmos.eoc.dlr.de/app/missions/gome2)
* [TEMIS - Tropospheric Emission Monitoring Internet Service](http://temis.nl/index.php)
* [Copernicus Open Access Hub](https://scihub.copernicus.eu/)
* [EUMETSAT Earth Observation Portal](https://eoportal.eumetsat.int/userMgmt/login.faces)
* [Sentinel-5P Mission information](https://sentinels.copernicus.eu/web/sentinel/missions/sentinel-5p)
* [Sentinel-3 Mission information](https://sentinel.esa.int/web/sentinel/missions/sentinel-3)
* [Sentinel-3 OLCI User Guide](https://sentinel.esa.int/web/sentinel/user-guides/sentinel-3-olci)
* [WEkEO](https://www.wekeo.eu/)
* [Copernicus Atmosphere Monitoring Service](https://atmosphere.copernicus.eu/)
* [ECMWF Web Interface](https://apps.ecmwf.int/datasets/)
* [ECMWF Web API](https://confluence.ecmwf.int/display/WEBAPI/Access+ECMWF+Public+Datasets)
* [CAMS catalogue of data visualizations](https://atmosphere.copernicus.eu/data)
* [CAMS Service Product Portfolio](https://atmosphere.copernicus.eu/sites/default/files/2018-12/CAMS%20Service%20Product%20Portfolio%20-%20July%202018.pdf)
<br>
<a href="./index_ltpy.ipynb"><< Index</a><span style="float:right;"><a href="./12_ltpy_WEkEO_harmonized_data_access_api.ipynb">12 - WEkEO Harmonized Data Access API >></a></span>
<hr>
<p style="text-align:left;">This project is licensed under the <a href="./LICENSE">MIT License</a> <span style="float:right;"><a href="https://gitlab.eumetsat.int/eumetlab/atmosphere/atmosphere">View on GitLab</a> | <a href="https://training.eumetsat.int/">EUMETSAT Training</a> | <a href=mailto:[email protected]>Contact</a></span></p>
|
github_jupyter
|
```
from erddapy import ERDDAP
import pandas as pd
import numpy as np
## settings (move to yaml file for routines)
server_url = 'http://akutan.pmel.noaa.gov:8080/erddap'
maxdepth = 0 #keep all data above this depth
site_str = 'M8'
region = 'bs'
substring = ['bs8','bs8'] #search substring useful for M2
prelim=[]
#this elimnates bad salinity but
data_QC = True
e = ERDDAP(server=server_url)
df = pd.read_csv(e.get_search_url(response='csv', search_for=f'datasets_Mooring AND {region}'))
#print(df['Dataset ID'].values)
from requests.exceptions import HTTPError
dfs = {}
for dataset_id in sorted(df['Dataset ID'].values):
if ('1hr' in dataset_id):
continue
if any(x in dataset_id for x in substring) and not any(x in dataset_id for x in prelim) and ('final' in dataset_id):
print(dataset_id)
try:
d = ERDDAP(server=server_url,
protocol='tabledap',
response='csv'
)
d.dataset_id=dataset_id
d.variables = ['latitude',
'longitude',
'depth',
'Chlorophyll_Fluorescence',
'time',
'timeseries_id']
d.constraints = {'depth>=':maxdepth}
except HTTPError:
print('Failed to generate url {}'.format(dataset_id))
try:
df_m = d.to_pandas(
index_col='time (UTC)',
parse_dates=True,
skiprows=(1,) # units information can be dropped.
)
df_m.sort_index(inplace=True)
df_m.columns = [x[1].split()[0] for x in enumerate(df_m.columns)]
dfs.update({dataset_id:df_m})
except:
pass
if any(x in dataset_id for x in prelim) and ('preliminary' in dataset_id):
print(dataset_id)
try:
d = ERDDAP(server=server_url,
protocol='tabledap',
response='csv'
)
d.dataset_id=dataset_id
d.variables = ['latitude',
'longitude',
'depth',
'Chlorophyll_Fluorescence',
'time',
'timeseries_id']
d.constraints = {'depth>=':maxdepth}
except HTTPError:
print('Failed to generate url {}'.format(dataset_id))
try:
df_m = d.to_pandas(
index_col='time (UTC)',
parse_dates=True,
skiprows=(1,) # units information can be dropped.
)
df_m.sort_index(inplace=True)
df_m.columns = [x[1].split()[0] for x in enumerate(df_m.columns)]
#using preliminary for unfinished datasets - very simple qc
if data_QC:
#overwinter moorings
if '17bs2c' in dataset_id:
df_m=df_m['2017-10-3':'2018-5-1']
if '16bs2c' in dataset_id:
df_m=df_m['2016-10-6':'2017-4-26']
if '17bsm2a' in dataset_id:
df_m=df_m['2017-4-28':'2017-9-22']
if '18bsm2a' in dataset_id:
df_m=df_m['2018-4-30':'2018-10-01']
if '17bs8a' in dataset_id:
df_m=df_m['2017-9-30':'2018-10-1']
if '18bs8a' in dataset_id:
df_m=df_m['2018-10-12':'2019-9-23']
if '16bs4b' in dataset_id:
df_m=df_m['2016-9-26':'2017-9-24']
if '17bs4b' in dataset_id:
df_m=df_m['2017-9-30':'2018-10-1']
if '18bs4b' in dataset_id:
df_m=df_m['2018-10-12':'2018-9-23']
if '13bs5a' in dataset_id:
df_m=df_m['2013-8-18':'2014-10-16']
if '14bs5a' in dataset_id:
df_m=df_m['2014-10-16':'2015-9-24']
if '16bs5a' in dataset_id:
df_m=df_m['2016-9-26':'2017-9-24']
if '17bs5a' in dataset_id:
df_m=df_m['2017-9-30':'2018-10-1']
if '18bs5a' in dataset_id:
df_m=df_m['2018-10-12':'2018-9-23']
dfs.update({dataset_id:df_m})
except:
pass
df_merged=pd.DataFrame()
for dataset_id in dfs.keys():
df_merged = df_merged.append(dfs[dataset_id])
df_merged.describe()
df_merged = df_merged.dropna()
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.scatter(df_merged.index, y=df_merged['depth'], s=10, c=df_merged['Chlorophyll_Fluorescence'], vmin=0, vmax=10, cmap='inferno')
plt.plot(df_merged.index, df_merged['Chlorophyll_Fluorescence'])
df_merged.to_csv(f'{site_str}_nearsfc_chlor.csv')
```
|
github_jupyter
|
### Plot Comulative Distribution Of Sportive Behavior Over Time
```
%load_ext autoreload
%autoreload 2
%matplotlib notebook
from sensible_raw.loaders import loader
from world_viewer.cns_world import CNSWorld
from world_viewer.synthetic_world import SyntheticWorld
from world_viewer.glasses import Glasses
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm, PowerNorm
import math
import pandas as pd
import numpy as np
#import dask.dataframe as dd
import time
import seaborn as sns
# load data and restict timeseries
# data from "PreprocessOpinions/FitnessAsBehavior.ipynb"
data = pd.read_pickle("data/op_fitness.pkl")
#data.reset_index(inplace=True)
opinion = "op_fitness"
data = data[data.time >= CNSWorld.CNS_TIME_BEGIN]
data = data[data.time <= CNSWorld.CNS_TIME_END]
data.head()
# calc cummulative distribution function
def cdf_from_data(data, cdfx):
size_data = len(data)
y_values = []
for i in cdfx:
# all the values in data less than the ith value in x_values
temp = data[data <= i]
# fraction of that value with respect to the size of the x_values
value = temp.size / size_data
# pushing the value in the y_values
y_values.append(value)
# return both x and y values
return pd.DataFrame({'x':cdfx, 'cdf':y_values}).set_index("x")
cdfx = np.linspace(start=0,stop=4,num=400)
cdf = data.groupby("time")[opinion + "_abs"].apply(lambda d: cdf_from_data(d, cdfx))#
# load cdf if previously calculated
#cdf = pd.read_pickle("tmp/cdf_fitness.pkl")
# plot cdf as heatmap (fig.: 3.3)
fig, ax = plt.subplots(1,1)
num_ticks = 5
# the index of the position of yticks
yticks = np.linspace(0, len(cdfx)-1, num_ticks, dtype=np.int)
# the content of labels of these yticks
yticklabels = [round(cdfx[idx]) for idx in yticks]
cmap = sns.cubehelix_palette(60, hue=0.05, rot=0, light=0.9, dark=0, as_cmap=True)
ax = sns.heatmap(df2, cmap=cmap, xticklabels=80, yticklabels=yticklabels, vmin=0.4, vmax=1, cbar_kws={'label': 'cumulative distribution function'})#, norm=LogNorm(vmin=0.1, vmax=1))#, , cbar_kws={"ticks": cbar_ticks})
#ax.hlines([300], *ax.get_xlim(), linestyles="dashed")
ax.set_yticks(yticks)
ax.invert_yaxis()
plt.xticks(rotation=70)
plt.yticks(rotation=0)
plt.ylabel(r"$\bar b(t)$")
#ax.set_yscale('log')
#sns.heatmap(cdf.cdf, annot=False)
fig.savefig("test.png" , dpi=600, bbox_inches='tight')
# plot cdf for singe timestep
fig, ax = plt.subplots(1,1)
ax.plot(cdf.loc["2014-02-09"].reset_index().x, 1-cdf.loc["2014-11-30","cdf"].values)
ax.set_yscale('log')
```
|
github_jupyter
|
# PCMark benchmark on Android
The goal of this experiment is to run benchmarks on a Pixel device running Android with an EAS kernel and collect results. The analysis phase will consist in comparing EAS with other schedulers, that is comparing *sched* governor with:
- interactive
- performance
- powersave
- ondemand
The benchmark we will be using is ***PCMark*** (https://www.futuremark.com/benchmarks/pcmark-android). You will need to **manually install** the app on the Android device in order to run this Notebook.
When opinening PCMark for the first time you will need to Install the work benchmark from inside the app.
```
import logging
from conf import LisaLogging
LisaLogging.setup()
%pylab inline
import copy
import os
from time import sleep
from subprocess import Popen
import pandas as pd
# Support to access the remote target
import devlib
from env import TestEnv
# Support for trace events analysis
from trace import Trace
# Suport for FTrace events parsing and visualization
import trappy
```
## Test environment setup
For more details on this please check out **examples/utils/testenv_example.ipynb**.
In case more than one Android device are conencted to the host, you must specify the ID of the device you want to target in `my_target_conf`. Run `adb devices` on your host to get the ID. Also, you have to specify the path to your android sdk in ANDROID_HOME.
```
# Setup a target configuration
my_target_conf = {
# Target platform and board
"platform" : 'android',
# Add target support
"board" : 'pixel',
# Device ID
"device" : "HT6670300102",
"ANDROID_HOME" : "/home/vagrant/lisa/tools/android-sdk-linux/",
# Define devlib modules to load
"modules" : [
'cpufreq' # enable CPUFreq support
],
}
my_tests_conf = {
# Folder where all the results will be collected
"results_dir" : "Android_PCMark",
# Platform configurations to test
"confs" : [
{
"tag" : "pcmark",
"flags" : "ftrace", # Enable FTrace events
"sched_features" : "ENERGY_AWARE", # enable EAS
},
],
}
# Initialize a test environment using:
# the provided target configuration (my_target_conf)
# the provided test configuration (my_test_conf)
te = TestEnv(target_conf=my_target_conf, test_conf=my_tests_conf)
target = te.target
```
## Support Functions
This set of support functions will help us running the benchmark using different CPUFreq governors.
```
def set_performance():
target.cpufreq.set_all_governors('performance')
def set_powersave():
target.cpufreq.set_all_governors('powersave')
def set_interactive():
target.cpufreq.set_all_governors('interactive')
def set_sched():
target.cpufreq.set_all_governors('sched')
def set_ondemand():
target.cpufreq.set_all_governors('ondemand')
for cpu in target.list_online_cpus():
tunables = target.cpufreq.get_governor_tunables(cpu)
target.cpufreq.set_governor_tunables(
cpu,
'ondemand',
**{'sampling_rate' : tunables['sampling_rate_min']}
)
# CPUFreq configurations to test
confs = {
'performance' : {
'label' : 'prf',
'set' : set_performance,
},
#'powersave' : {
# 'label' : 'pws',
# 'set' : set_powersave,
#},
'interactive' : {
'label' : 'int',
'set' : set_interactive,
},
#'sched' : {
# 'label' : 'sch',
# 'set' : set_sched,
#},
#'ondemand' : {
# 'label' : 'odm',
# 'set' : set_ondemand,
#}
}
# The set of results for each comparison test
results = {}
#Check if PCMark si available on the device
def check_packages(pkgname):
try:
output = target.execute('pm list packages -f | grep -i {}'.format(pkgname))
except Exception:
raise RuntimeError('Package: [{}] not availabe on target'.format(pkgname))
# Check for specified PKG name being available on target
check_packages('com.futuremark.pcmark.android.benchmark')
# Function that helps run a PCMark experiment
def pcmark_run(exp_dir):
# Unlock device screen (assume no password required)
target.execute('input keyevent 82')
# Start PCMark on the target device
target.execute('monkey -p com.futuremark.pcmark.android.benchmark -c android.intent.category.LAUNCHER 1')
# Wait few seconds to make sure the app is loaded
sleep(5)
# Flush entire log
target.clear_logcat()
# Run performance workload (assume screen is vertical)
target.execute('input tap 750 1450')
# Wait for completion (10 minutes in total) and collect log
log_file = os.path.join(exp_dir, 'log.txt')
# Wait 5 minutes
sleep(300)
# Start collecting the log
with open(log_file, 'w') as log:
logcat = Popen(['adb logcat', 'com.futuremark.pcmandroid.VirtualMachineState:*', '*:S'],
stdout=log,
shell=True)
# Wait additional two minutes for benchmark to complete
sleep(300)
# Terminate logcat
logcat.kill()
# Get scores from logcat
score_file = os.path.join(exp_dir, 'score.txt')
os.popen('grep -o "PCMA_.*_SCORE .*" {} | sed "s/ = / /g" | sort -u > {}'.format(log_file, score_file))
# Close application
target.execute('am force-stop com.futuremark.pcmark.android.benchmark')
return score_file
# Function that helps run PCMark for different governors
def experiment(governor, exp_dir):
os.system('mkdir -p {}'.format(exp_dir));
logging.info('------------------------')
logging.info('Run workload using %s governor', governor)
confs[governor]['set']()
### Run the benchmark ###
score_file = pcmark_run(exp_dir)
# Save the score as a dictionary
scores = dict()
with open(score_file, 'r') as f:
lines = f.readlines()
for l in lines:
info = l.split()
scores.update({info[0] : float(info[1])})
# return all the experiment data
return {
'dir' : exp_dir,
'scores' : scores,
}
```
## Run PCMark and collect scores
```
# Run the benchmark in all the configured governors
for governor in confs:
test_dir = os.path.join(te.res_dir, governor)
res = experiment(governor, test_dir)
results[governor] = copy.deepcopy(res)
```
After running the benchmark for the specified governors we can show and plot the scores:
```
# Create results DataFrame
data = {}
for governor in confs:
data[governor] = {}
for score_name, score in results[governor]['scores'].iteritems():
data[governor][score_name] = score
df = pd.DataFrame.from_dict(data)
df
df.plot(kind='bar', rot=45, figsize=(16,8),
title='PCMark scores vs SchedFreq governors');
```
|
github_jupyter
|
## Exercise 3
In the videos you looked at how you would improve Fashion MNIST using Convolutions. For your exercise see if you can improve MNIST to 99.8% accuracy or more using only a single convolutional layer and a single MaxPooling 2D. You should stop training once the accuracy goes above this amount. It should happen in less than 20 epochs, so it's ok to hard code the number of epochs for training, but your training must end once it hits the above metric. If it doesn't, then you'll need to redesign your layers.
I've started the code for you -- you need to finish it!
When 99.8% accuracy has been hit, you should print out the string "Reached 99.8% accuracy so cancelling training!"
```
import tensorflow as tf
from os import path, getcwd, chdir
# DO NOT CHANGE THE LINE BELOW. If you are developing in a local
# environment, then grab mnist.npz from the Coursera Jupyter Notebook
# and place it inside a local folder and edit the path to that location
path = f"{getcwd()}/../tmp2/mnist.npz"
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
sess = tf.Session(config=config)
# GRADED FUNCTION: train_mnist_conv
def train_mnist_conv():
# Please write your code only where you are indicated.
# please do not remove model fitting inline comments.
# YOUR CODE STARTS HERE
class myCallback(tf.keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs={}):
# Quick solution for "older" tensorflow to get rid of TypeError: Use 'acc' instead of 'accuracy'
# The version of tf used here is 1.14.0 (old)
if(logs.get('acc') >= 0.998):
print('\nReached 99.8% accuracy so cancelling training!')
self.model.stop_training = True
# YOUR CODE ENDS HERE
mnist = tf.keras.datasets.mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data(path=path)
# YOUR CODE STARTS HERE
training_images=training_images.reshape(60000, 28, 28, 1)
training_images=training_images / 255.0
callbacks = myCallback()
# YOUR CODE ENDS HERE
model = tf.keras.models.Sequential([
# YOUR CODE STARTS HERE
tf.keras.layers.Conv2D(64, (3, 3), activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
# YOUR CODE ENDS HERE
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
# model fitting
history = model.fit(
# YOUR CODE STARTS HERE
training_images, training_labels, epochs=30, callbacks=[callbacks]
# YOUR CODE ENDS HERE
)
# model fitting
return history.epoch, history.history['acc'][-1]
_, _ = train_mnist_conv()
# Now click the 'Submit Assignment' button above.
# Once that is complete, please run the following two cells to save your work and close the notebook
%%javascript
<!-- Save the notebook -->
IPython.notebook.save_checkpoint();
%%javascript
IPython.notebook.session.delete();
window.onbeforeunload = null
setTimeout(function() { window.close(); }, 1000);
```
|
github_jupyter
|
# Distributing standardized COMBINE archives with Tellurium
<div align='center'><img src="https://raw.githubusercontent.com/vporubsky/tellurium-libroadrunner-tutorial/master/tellurium-and-libroadrunner.png" width="60%" style="padding: 20px"></div>
<div align='center' style='font-size:100%'>
Veronica L. Porubsky, BS
<div align='center' style='font-size:100%'>Sauro Lab PhD Student, Department of Bioengineering<br>
Head of Outreach, <a href="https://reproduciblebiomodels.org/dissemination-and-training/seminar/">Center for Reproducible Biomedical Modeling</a><br>
University of Washington, Seattle, WA USA
</div>
<hr>
To facilitate design and comprehension of their models, modelers should use standard systems biology formats for
model descriptions, simulation experiments, and to distribute stand-alone archives which can regenerate the modeling study. We will discuss three of these standards - the Systems Biology Markup Language (SBML), the Simulation Experiment Description Markup Language (SED-ML), and the COMBINE archive/ inline Open Modeling EXchange format (OMEX) format.
## TOC
* [Links to relevant resources](#relevant-resources)
* [Packages and Constants](#standardized-formats-packages-and-constants)
* [Import and export capabilities with Tellurium](#import-export)
* [Importing SBML directly from the BioModels Database for simulation](#import-from-biomodels)
* [Exporting SBML or Antimony models](#export-to-sbml-or-antimony)
* [Writing SED-ML with PhraSED-ML](#writing-phrasedml)
* [Exporting SED-ML](#exporting-sedml)
* [Generating a COMBINE archive](#combine-archive)
* [Exercises](#exercises)
# Links to relevant resources <a class="anchor" id="relevant-resources"></a>
<a href="http://model.caltech.edu/">SBML specification</a><br>
<a href="http://sbml.org/SBML_Software_Guide/SBML_Software_Matrix">SBML tool support</a><br>
<a href="https://sed-ml.org/">SED-ML specification</a><br>
<a href="https://sed-ml.org/showcase.html">SED-ML tool support</a><br>
<a href="http://phrasedml.sourceforge.net/phrasedml__api_8h.html">PhraSED-ML documentation</a><br>
<a href="http://phrasedml.sourceforge.net/Tutorial.html">PhraSED-ML tutorial</a><br>
<a href="https://tellurium.readthedocs.io/en/latest/">Tellurium documentation</a><br>
<a href="https://libroadrunner.readthedocs.io/en/latest/">libRoadRunner documentation</a><br>
<a href="https://tellurium.readthedocs.io/en/latest/antimony.html">Antimony documentation</a><br>
<a href="http://copasi.org/Download/">COPASI download</a><br>
# Packages and constants <a class="anchor" id="standardized-formats-packages-and-constants"></a>
```
!pip install tellurium -q
import tellurium as te
import phrasedml
```
# Import and export capabilities with Tellurium <a class="anchor" id="import-export"></a>
Models can be imported from the BioModels Database, given the appropriate BioModel ID using a standard URL format to programmatically access the model of interest.
We will use this model of respiratory oscillations in Saccharomyces cerevisae by <a href="https://www.ebi.ac.uk/biomodels/BIOMD0000000090">Jana Wolf et al. (2001)</a> </div> as an example:
<br>
<div align='center'><img src="https://raw.githubusercontent.com/vporubsky/tellurium-libroadrunner-tutorial/master/wolf_publication.PNG" width="65%" style="padding: 20px"></div>
<br>
<div align='center'><img src="https://raw.githubusercontent.com/vporubsky/tellurium-libroadrunner-tutorial/master/wolf_network.PNG" width="65%" style="padding: 20px"></div>
# Importing SBML directly from the BioModels Database for simulation <a class="anchor" id="import-from-biomodels"></a>
SBML is a software data format for describing computational biological models. Markup languages allow you to separate annotations and documentation about the content from the content itself, using standardized tags. So the model and annotations are stored in a single file, but tools that support SBML are designed to interpret these to perform tasks. SBML is independent of any particular software tool and is broadly applicable to the modeling domain. It is open and free, and widely supported. Tools might allow for writing the model, simulating the model, visualizing the network, etc.
We will demonstrate how Tellurium supports import and export of SBML model files.
```
# Import an SBML model from the BioModels Database using a url
wolf = te.loadSBMLModel("https://www.ebi.ac.uk/biomodels/model/download/BIOMD0000000090.2?filename=BIOMD0000000090_url.xml")
wolf.simulate(0, 200, 1000)
wolf.plot(figsize = (15, 10), xtitle = 'Time', ytitle = 'Concentration')
```
# Exporting SBML or Antimony models <a class="anchor" id="export-to-sbml-or-antimony"></a>
```
# Export the model you just accessed from BioModels to the current directory as an SBML string
wolf.reset()
wolf.exportToSBML('Wolf2001_Respiratory_Oscillations.xml', current = True)
# You can also export the model to the current directory as an Antimony string
# Let's take a look at the string first
print(wolf.getCurrentAntimony())
# Edit the Antimony string of Wolf et al.:
# Update model name for ease of use with PhraSED-ML
# Remove model name annotatations -- causes error with SED-ML export
wolf = te.loada("""
// Created by libAntimony v2.12.0
model wolf
// Compartments and Species:
compartment c0, c1, c2;
species $sul_ex in c0, $eth_ex in c0, $oxy_ex in c0, oxy in c2, $H2O in c2;
species A3c in c1, aps in c1, $PPi in c1, pap in c1, sul in c1, eth in c1;
species $A2c in c1, hyd in c1, cys in c1, N2 in c1, $N1 in c1, aco in c1;
species oah in c1, S1 in c2, $S2 in c2, $C1 in c2, $C2 in c2, $A2m in c2;
species A3m in c2, $Ho in c1, $Hm in c2;
// Assignment Rules:
A2c := Ac - A3c;
N1 := N - N2;
S2 := S - S1;
A2m := Am - A3m;
// Reactions:
v1: $sul_ex => sul; c0*k_v0/(1 + (cys/Kc)^n);
v13: $eth_ex => eth; c0*k_v13;
v2: sul + A3c => aps + $PPi; c1*k2*sul*A3c;
v10: $oxy_ex => oxy; c0*k_v10;
v14: oxy => $oxy_ex; c2*k14*oxy;
v3: aps + A3c => pap + $A2c; c1*k3*aps*A3c;
v4: pap + 3 N2 => hyd + 3 $N1; c1*k4*pap*N2;
v5: hyd + oah => cys; c1*k5*hyd*oah;
v6: cys => ; c1*k6*cys;
v7: eth + 2 $N1 => aco + 2 N2; c1*k7*eth*N1;
v15: aco => oah; c1*k15*aco;
v17: hyd => ; c1*k17*hyd;
v18: oah => ; c1*k18*oah;
v8: $S2 + aco => S1; c2*k8*aco*S2;
v9: S1 + 4 $N1 => $S2 + 4 N2; c2*k9*S1*N1;
v11a: $C1 + $Hm + N2 => $C2 + $Ho + $N1; c2*k11*N2*oxy/((a*N2 + oxy)*(1 + (hyd/Kh)^m));
v11a2: $C2 + oxy => $C1 + $H2O; c2*k11*N2*oxy/((a*N2 + oxy)*(1 + (hyd/Kh)^m));
v16: $A2c + A3m => $A2m + A3c; c2*k16*A3m*A2c;
v11b: $Ho + $A2m => $Hm + A3m; (c2*3*k11*N2*oxy/((a*N2 + oxy)*(1 + (hyd/Kh)^m)))*A2m/(Ka + A2m);
vLEAK: $Ho => $Hm; 0;
v12: A3c => $A2c; c1*k12*A3c;
// Species initializations:
sul_ex = 0;
eth_ex = 0;
oxy_ex = 0;
oxy = 7/c2;
oxy has substance_per_volume;
H2O = 0;
A3c = 1.5/c1;
A3c has substance_per_volume;
aps = 0.5/c1;
aps has substance_per_volume;
PPi = 0;
pap = 0.4/c1;
pap has substance_per_volume;
sul = 0.4/c1;
sul has substance_per_volume;
eth = 4/c1;
eth has substance_per_volume;
A2c has substance_per_volume;
hyd = 0.5/c1;
hyd has substance_per_volume;
cys = 0.3/c1;
cys has substance_per_volume;
N2 = 2/c1;
N2 has substance_per_volume;
N1 has substance_per_volume;
aco = 0.3/c1;
aco has substance_per_volume;
oah = 1.5/c1;
oah has substance_per_volume;
S1 = 1.5/c2;
S1 has substance_per_volume;
S2 has substance_per_volume;
C1 = 0;
C2 = 0;
A2m has substance_per_volume;
A3m = 1.5/c2;
A3m has substance_per_volume;
Ho = 0;
Hm = 0;
// Compartment initializations:
c0 = 1;
c1 = 1;
c2 = 1;
// Variable initializations:
Ac = 2;
N = 2;
S = 2;
Am = 2;
k_v0 = 1.6;
k2 = 0.2;
k3 = 0.2;
k4 = 0.2;
k5 = 0.1;
k6 = 0.12;
k7 = 10;
k8 = 10;
k9 = 10;
k_v10 = 80;
k11 = 10;
k12 = 5;
k_v13 = 4;
k14 = 10;
k15 = 5;
k16 = 10;
k17 = 0.02;
k18 = 1;
n = 4;
m = 4;
Ka = 1;
Kc = 0.1;
a = 0.1;
Kh = 0.5;
// Other declarations:
const c0, c1, c2, Ac, N, S, Am, k_v0, k2, k3, k4, k5, k6, k7, k8, k9, k_v10;
const k11, k12, k_v13, k14, k15, k16, k17, k18, n, m, Ka, Kc, a, Kh;
// Unit definitions:
unit substance = mole;
unit substance_per_volume = mole / litre;
// Display Names:
c0 is "external";
c1 is "cytosol";
c2 is "mitochondria";
sul_ex is "SO4_ex";
eth_ex is "EtOH_ex";
oxy_ex is "O2_ex";
oxy is "O2";
A3c is "ATP";
aps is "APS";
pap is "PAPS";
sul is "SO4";
eth is "EtOH";
A2c is "ADP";
hyd is "H2S";
cys is "CYS";
N2 is "NADH";
N1 is "NAD";
aco is "AcCoA";
oah is "OAH";
A2m is "ADP_mit";
A3m is "ATP_mit";
v11a is "vET1";
v11a2 is "vET2";
v11b is "vSYNT";
// CV terms:
c0 hypernym "http://identifiers.org/obo.go/GO:0005576"
c1 hypernym "http://identifiers.org/obo.go/GO:0005829"
c2 hypernym "http://identifiers.org/obo.go/GO:0005739"
sul_ex identity "http://identifiers.org/obo.chebi/CHEBI:16189"
eth_ex identity "http://identifiers.org/obo.chebi/CHEBI:16236"
oxy_ex identity "http://identifiers.org/obo.chebi/CHEBI:15379"
oxy identity "http://identifiers.org/obo.chebi/CHEBI:15379"
H2O identity "http://identifiers.org/obo.chebi/CHEBI:15377"
A3c identity "http://identifiers.org/obo.chebi/CHEBI:15422"
aps identity "http://identifiers.org/obo.chebi/CHEBI:17709"
PPi identity "http://identifiers.org/obo.chebi/CHEBI:18361"
pap identity "http://identifiers.org/obo.chebi/CHEBI:17980"
sul identity "http://identifiers.org/obo.chebi/CHEBI:16189"
eth identity "http://identifiers.org/obo.chebi/CHEBI:16236"
A2c identity "http://identifiers.org/obo.chebi/CHEBI:16761"
hyd identity "http://identifiers.org/obo.chebi/CHEBI:16136"
cys identity "http://identifiers.org/obo.chebi/CHEBI:17561"
N2 identity "http://identifiers.org/obo.chebi/CHEBI:16908"
N1 identity "http://identifiers.org/obo.chebi/CHEBI:15846"
aco identity "http://identifiers.org/obo.chebi/CHEBI:15351"
oah identity "http://identifiers.org/obo.chebi/CHEBI:16288"
S1 parthood "http://identifiers.org/obo.go/GO:0030062"
S2 parthood "http://identifiers.org/obo.go/GO:0030062"
C1 hypernym "http://identifiers.org/obo.go/GO:0005746"
C2 hypernym "http://identifiers.org/obo.go/GO:0005746"
A2m identity "http://identifiers.org/obo.chebi/CHEBI:16761"
A3m identity "http://identifiers.org/obo.chebi/CHEBI:15422"
Ho identity "http://identifiers.org/obo.chebi/CHEBI:24636"
Hm identity "http://identifiers.org/obo.chebi/CHEBI:24636"
v1 hypernym "http://identifiers.org/obo.go/GO:0015381"
v13 hypernym "http://identifiers.org/obo.go/GO:0015850"
v2 identity "http://identifiers.org/ec-code/2.7.7.4"
v3 identity "http://identifiers.org/ec-code/2.7.1.25"
v3 hypernym "http://identifiers.org/obo.go/GO:0004020"
v4 version "http://identifiers.org/ec-code/1.8.4.8",
"http://identifiers.org/ec-code/1.8.1.2"
v5 version "http://identifiers.org/ec-code/4.4.1.1",
"http://identifiers.org/ec-code/4.2.1.22",
"http://identifiers.org/ec-code/2.5.1.49"
v7 version "http://identifiers.org/ec-code/6.2.1.1",
"http://identifiers.org/ec-code/1.2.1.3",
"http://identifiers.org/ec-code/1.1.1.1"
v15 identity "http://identifiers.org/ec-code/2.3.1.31"
v8 parthood "http://identifiers.org/obo.go/GO:0006099"
v9 parthood "http://identifiers.org/obo.go/GO:0006099"
v11a identity "http://identifiers.org/obo.go/GO:0015990"
v11a parthood "http://identifiers.org/obo.go/GO:0042775"
v11a version "http://identifiers.org/obo.go/GO:0002082"
v11a2 parthood "http://identifiers.org/obo.go/GO:0042775"
v11a2 version "http://identifiers.org/obo.go/GO:0002082"
v11a2 identity "http://identifiers.org/obo.go/GO:0006123"
v16 identity "http://identifiers.org/obo.go/GO:0005471"
v11b parthood "http://identifiers.org/obo.go/GO:0042775"
v11b hypernym "http://identifiers.org/obo.go/GO:0006119"
v11b version "http://identifiers.org/obo.go/GO:0002082"
vLEAK hypernym "http://identifiers.org/obo.go/GO:0006810"
v12 hypernym "http://identifiers.org/obo.go/GO:0006200"
end
""")
# Export SBML and Antimony versions of the updated model to current working directory
wolf.exportToAntimony('wolf_antimony.txt')
wolf.exportToSBML('wolf.xml')
# Let's work with the species 'oxy'(CHEBI ID: 15379) - or dioxygen - going forward
wolf.simulate(0, 100, 1000, ['time', 'oxy']) # note that specific species can be selected for recording concentrations over the timecourse
wolf.plot(figsize = (10, 6), xtitle = 'Time', ytitle = 'Concentration')
```
# Writing SED-ML with PhraSED-ML <a class="anchor" id="writing-phrasedml"></a>
SED-ML encodes the information required by the minimal information about a simiulation experiment guidelines (MIASE) to enable reproduction of simulation experiments in a computer-readable format.
The specification includes:
* selection of experimental data for the experiment
* models used for the experiement
* which simulation to run on which models
* which results to pass to output
* how results should be output
PhraSED-ML is a language and a library that provide a text-based way to read, summarize, and create SED-ML files as part of the greater Tellurium modeling environment we have discussed.
```
# Write phraSED-ML string specifying the simulation study
wolf_phrasedml = '''
// Set model
wolf = model "wolf.xml" # model_id = model source_model
// Deterministic simulation
det_sim = simulate uniform(0, 500, 1000) # sim_id = simulate simulation_type
wolf_det_sim = run det_sim on wolf # task_id = run sim_id on model_id
plot "Wolf et al. dynamics (Model ID: BIOMD0000000090)" time vs oxy # plot title_name x vs y
'''
# Generate SED-ML string from the phraSED-ML string
wolf.resetAll()
wolf_sbml = wolf.getSBML()
phrasedml.setReferencedSBML("wolf.xml", wolf_sbml)
wolf_sedml = phrasedml.convertString(wolf_phrasedml)
print(wolf_sedml)
```
# Exporting SED-ML <a class="anchor" id="exporting-sedml"></a>
```
# Save the SED-ML simulation experiment to your current working directory
te.saveToFile('wolf_sedml.xml', wolf_sedml)
# Load and run SED-ML script
te.executeSEDML('wolf_sedml.xml')
```
# Generating a COMBINE archive <a class="anchor" id="combine-archive"></a>
COMBINE archives package SBML models and SED-ML simulation experiment descriptions together to ensure complete modeling studies or experiments can be exchangesd between software tools. Tellurium provides the inline Open Modeling EXchange format (OMEX) to edit contents of COMBINE archives in a human-readable format. Inline OMEX is essentially an Antimony description of the model joined to the PhraSED-ML experiment description.
```
# Read Antimony model into a string
wolf_antimony = te.readFromFile('wolf_antimony.txt')
# create an inline OMEX string
wolf_inline_omex = '\n'.join([wolf_antimony, wolf_phrasedml])
print(wolf_inline_omex)
# export to a COMBINE archive
te.exportInlineOmex(wolf_inline_omex, 'wolf.omex')
```
# Exercises <a class="anchor" id="exercises"></a>
## Exercise 1:
Download the <a href="http://www.ebi.ac.uk/biomodels-main/BIOMD0000000010 "> Kholodenko 2000 model</a> of ultrasensitivity and negative feedback oscillations in the MAPK cascade from the BioModels Database, and upload to your workspace. Simulate and plot simulation results for the model.
<div align='center'><img src="https://raw.githubusercontent.com/vporubsky/tellurium-libroadrunner-tutorial/master/kholodenko_publication.PNG" width="75%"></div>
```
# Write your solution here
```
## Exercise 1 Solution:
```
# Solution
r = te.loadSBMLModel(
"https://www.ebi.ac.uk/biomodels/model/download/BIOMD0000000010?filename=BIOMD0000000010_url.xml")
r.simulate(0, 5000, 1000)
r.plot()
```
# Acknowledgements
<br>
<div align='left'><img src="https://raw.githubusercontent.com/vporubsky/tellurium-libroadrunner-tutorial/master/acknowledgments.png" width="80%"></div>
<br>
<html>
<head>
</head>
<body>
<h1>Bibliography</h1>
<ol>
<li>
<p>K. Choi et al., <cite>Tellurium: An extensible python-based modeling environment for systems and synthetic biology</cite>, Biosystems, vol. 171, pp. 74–79, Sep. 2018.</p>
</li>
<li>
<p>E. T. Somogyi et al., <cite>libRoadRunner: a high performance SBML simulation and analysis library.,</cite>, Bioinformatics, vol. 31, no. 20, pp. 3315–21, Oct. 2015.</p>
<li>
<p>L. P. Smith, F. T. Bergmann, D. Chandran, and H. M. Sauro, <cite>Antimony: a modular model definition language</cite>, Bioinformatics, vol. 25, no. 18, pp. 2452–2454, Sep. 2009.</p>
</li>
<li>
<p>K. Choi, L. P. Smith, J. K. Medley, and H. M. Sauro, <cite>phraSED-ML: a paraphrased, human-readable adaptation of SED-ML</cite>, J. Bioinform. Comput. Biol., vol. 14, no. 06, Dec. 2016.</p>
</li>
<li>
<p> B.N. Kholodenko, O.V. Demin, G. Moehren, J.B. Hoek, <cite>Quantification of short term signaling by the epidermal growth factor receptor.</cite>, J Biol Chem., vol. 274, no. 42, Oct. 1999.</p>
</li>
</ol>
</body>
</html>
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#@title MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
```
# 첫 번째 신경망 훈련하기: 기초적인 분류 문제
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/keras/classification"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />TensorFlow.org에서 보기</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/ko/tutorials/keras/classification.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />구글 코랩(Colab)에서 실행하기</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/ko/tutorials/keras/classification.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />깃허브(GitHub) 소스 보기</a>
</td>
</table>
Note: 이 문서는 텐서플로 커뮤니티에서 번역했습니다. 커뮤니티 번역 활동의 특성상 정확한 번역과 최신 내용을 반영하기 위해 노력함에도
불구하고 [공식 영문 문서](https://www.tensorflow.org/?hl=en)의 내용과 일치하지 않을 수 있습니다.
이 번역에 개선할 부분이 있다면
[tensorflow/docs](https://github.com/tensorflow/docs) 깃헙 저장소로 풀 리퀘스트를 보내주시기 바랍니다.
문서 번역이나 리뷰에 참여하려면
[[email protected]](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-ko)로
메일을 보내주시기 바랍니다.
이 튜토리얼에서는 운동화나 셔츠 같은 옷 이미지를 분류하는 신경망 모델을 훈련합니다. 상세 내용을 모두 이해하지 못해도 괜찮습니다. 여기서는 완전한 텐서플로(TensorFlow) 프로그램을 빠르게 살펴 보겠습니다. 자세한 내용은 앞으로 배우면서 더 설명합니다.
여기에서는 텐서플로 모델을 만들고 훈련할 수 있는 고수준 API인 [tf.keras](https://www.tensorflow.org/guide/keras)를 사용합니다.
```
try:
# Colab only
%tensorflow_version 2.x
except Exception:
pass
from __future__ import absolute_import, division, print_function, unicode_literals, unicode_literals
# tensorflow와 tf.keras를 임포트합니다
import tensorflow as tf
from tensorflow import keras
# 헬퍼(helper) 라이브러리를 임포트합니다
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
```
## 패션 MNIST 데이터셋 임포트하기
10개의 범주(category)와 70,000개의 흑백 이미지로 구성된 [패션 MNIST](https://github.com/zalandoresearch/fashion-mnist) 데이터셋을 사용하겠습니다. 이미지는 해상도(28x28 픽셀)가 낮고 다음처럼 개별 옷 품목을 나타냅니다:
<table>
<tr><td>
<img src="https://tensorflow.org/images/fashion-mnist-sprite.png"
alt="Fashion MNIST sprite" width="600">
</td></tr>
<tr><td align="center">
<b>그림 1.</b> <a href="https://github.com/zalandoresearch/fashion-mnist">패션-MNIST 샘플</a> (Zalando, MIT License).<br/>
</td></tr>
</table>
패션 MNIST는 컴퓨터 비전 분야의 "Hello, World" 프로그램격인 고전 [MNIST](http://yann.lecun.com/exdb/mnist/) 데이터셋을 대신해서 자주 사용됩니다. MNIST 데이터셋은 손글씨 숫자(0, 1, 2 등)의 이미지로 이루어져 있습니다. 여기서 사용하려는 옷 이미지와 동일한 포맷입니다.
패션 MNIST는 일반적인 MNIST 보다 조금 더 어려운 문제이고 다양한 예제를 만들기 위해 선택했습니다. 두 데이터셋은 비교적 작기 때문에 알고리즘의 작동 여부를 확인하기 위해 사용되곤 합니다. 코드를 테스트하고 디버깅하는 용도로 좋습니다.
네트워크를 훈련하는데 60,000개의 이미지를 사용합니다. 그다음 네트워크가 얼마나 정확하게 이미지를 분류하는지 10,000개의 이미지로 평가하겠습니다. 패션 MNIST 데이터셋은 텐서플로에서 바로 임포트하여 적재할 수 있습니다:
```
fashion_mnist = keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
```
load_data() 함수를 호출하면 네 개의 넘파이(NumPy) 배열이 반환됩니다:
* `train_images`와 `train_labels` 배열은 모델 학습에 사용되는 *훈련 세트*입니다.
* `test_images`와 `test_labels` 배열은 모델 테스트에 사용되는 *테스트 세트*입니다.
이미지는 28x28 크기의 넘파이 배열이고 픽셀 값은 0과 255 사이입니다. *레이블*(label)은 0에서 9까지의 정수 배열입니다. 이 값은 이미지에 있는 옷의 *클래스*(class)를 나타냅니다:
<table>
<tr>
<th>레이블</th>
<th>클래스</th>
</tr>
<tr>
<td>0</td>
<td>T-shirt/top</td>
</tr>
<tr>
<td>1</td>
<td>Trouser</td>
</tr>
<tr>
<td>2</td>
<td>Pullover</td>
</tr>
<tr>
<td>3</td>
<td>Dress</td>
</tr>
<tr>
<td>4</td>
<td>Coat</td>
</tr>
<tr>
<td>5</td>
<td>Sandal</td>
</tr>
<tr>
<td>6</td>
<td>Shirt</td>
</tr>
<tr>
<td>7</td>
<td>Sneaker</td>
</tr>
<tr>
<td>8</td>
<td>Bag</td>
</tr>
<tr>
<td>9</td>
<td>Ankle boot</td>
</tr>
</table>
각 이미지는 하나의 레이블에 매핑되어 있습니다. 데이터셋에 *클래스 이름*이 들어있지 않기 때문에 나중에 이미지를 출력할 때 사용하기 위해 별도의 변수를 만들어 저장합니다:
```
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
```
## 데이터 탐색
모델을 훈련하기 전에 데이터셋 구조를 살펴보죠. 다음 코드는 훈련 세트에 60,000개의 이미지가 있다는 것을 보여줍니다. 각 이미지는 28x28 픽셀로 표현됩니다:
```
train_images.shape
```
비슷하게 훈련 세트에는 60,000개의 레이블이 있습니다:
```
len(train_labels)
```
각 레이블은 0과 9사이의 정수입니다:
```
train_labels
```
테스트 세트에는 10,000개의 이미지가 있습니다. 이 이미지도 28x28 픽셀로 표현됩니다:
```
test_images.shape
```
테스트 세트는 10,000개의 이미지에 대한 레이블을 가지고 있습니다:
```
len(test_labels)
```
## 데이터 전처리
네트워크를 훈련하기 전에 데이터를 전처리해야 합니다. 훈련 세트에 있는 첫 번째 이미지를 보면 픽셀 값의 범위가 0~255 사이라는 것을 알 수 있습니다:
```
plt.figure()
plt.imshow(train_images[0])
plt.colorbar()
plt.grid(False)
plt.show()
```
신경망 모델에 주입하기 전에 이 값의 범위를 0~1 사이로 조정하겠습니다. 이렇게 하려면 255로 나누어야 합니다. *훈련 세트*와 *테스트 세트*를 동일한 방식으로 전처리하는 것이 중요합니다:
```
train_images = train_images / 255.0
test_images = test_images / 255.0
```
*훈련 세트*에서 처음 25개 이미지와 그 아래 클래스 이름을 출력해 보죠. 데이터 포맷이 올바른지 확인하고 네트워크 구성과 훈련할 준비를 마칩니다.
```
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
plt.xlabel(class_names[train_labels[i]])
plt.show()
```
## 모델 구성
신경망 모델을 만들려면 모델의 층을 구성한 다음 모델을 컴파일합니다.
### 층 설정
신경망의 기본 구성 요소는 *층*(layer)입니다. 층은 주입된 데이터에서 표현을 추출합니다. 아마도 문제를 해결하는데 더 의미있는 표현이 추출될 것입니다.
대부분 딥러닝은 간단한 층을 연결하여 구성됩니다. `tf.keras.layers.Dense`와 같은 층들의 가중치(parameter)는 훈련하는 동안 학습됩니다.
```
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
```
이 네트워크의 첫 번째 층인 `tf.keras.layers.Flatten`은 2차원 배열(28 x 28 픽셀)의 이미지 포맷을 28 * 28 = 784 픽셀의 1차원 배열로 변환합니다. 이 층은 이미지에 있는 픽셀의 행을 펼쳐서 일렬로 늘립니다. 이 층에는 학습되는 가중치가 없고 데이터를 변환하기만 합니다.
픽셀을 펼친 후에는 두 개의 `tf.keras.layers.Dense` 층이 연속되어 연결됩니다. 이 층을 밀집 연결(densely-connected) 또는 완전 연결(fully-connected) 층이라고 부릅니다. 첫 번째 `Dense` 층은 128개의 노드(또는 뉴런)를 가집니다. 두 번째 (마지막) 층은 10개의 노드의 *소프트맥스*(softmax) 층입니다. 이 층은 10개의 확률을 반환하고 반환된 값의 전체 합은 1입니다. 각 노드는 현재 이미지가 10개 클래스 중 하나에 속할 확률을 출력합니다.
### 모델 컴파일
모델을 훈련하기 전에 필요한 몇 가지 설정이 모델 *컴파일* 단계에서 추가됩니다:
* *손실 함수*(Loss function)-훈련 하는 동안 모델의 오차를 측정합니다. 모델의 학습이 올바른 방향으로 향하도록 이 함수를 최소화해야 합니다.
* *옵티마이저*(Optimizer)-데이터와 손실 함수를 바탕으로 모델의 업데이트 방법을 결정합니다.
* *지표*(Metrics)-훈련 단계와 테스트 단계를 모니터링하기 위해 사용합니다. 다음 예에서는 올바르게 분류된 이미지의 비율인 *정확도*를 사용합니다.
```
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
```
## 모델 훈련
신경망 모델을 훈련하는 단계는 다음과 같습니다:
1. 훈련 데이터를 모델에 주입합니다-이 예에서는 `train_images`와 `train_labels` 배열입니다.
2. 모델이 이미지와 레이블을 매핑하는 방법을 배웁니다.
3. 테스트 세트에 대한 모델의 예측을 만듭니다-이 예에서는 `test_images` 배열입니다. 이 예측이 `test_labels` 배열의 레이블과 맞는지 확인합니다.
훈련을 시작하기 위해 `model.fit` 메서드를 호출하면 모델이 훈련 데이터를 학습합니다:
```
model.fit(train_images, train_labels, epochs=5)
```
모델이 훈련되면서 손실과 정확도 지표가 출력됩니다. 이 모델은 훈련 세트에서 약 0.88(88%) 정도의 정확도를 달성합니다.
## 정확도 평가
그다음 테스트 세트에서 모델의 성능을 비교합니다:
```
test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)
print('\n테스트 정확도:', test_acc)
```
테스트 세트의 정확도가 훈련 세트의 정확도보다 조금 낮습니다. 훈련 세트의 정확도와 테스트 세트의 정확도 사이의 차이는 *과대적합*(overfitting) 때문입니다. 과대적합은 머신러닝 모델이 훈련 데이터보다 새로운 데이터에서 성능이 낮아지는 현상을 말합니다.
## 예측 만들기
훈련된 모델을 사용하여 이미지에 대한 예측을 만들 수 있습니다.
```
predictions = model.predict(test_images)
```
여기서는 테스트 세트에 있는 각 이미지의 레이블을 예측했습니다. 첫 번째 예측을 확인해 보죠:
```
predictions[0]
```
이 예측은 10개의 숫자 배열로 나타납니다. 이 값은 10개의 옷 품목에 상응하는 모델의 신뢰도(confidence)를 나타냅니다. 가장 높은 신뢰도를 가진 레이블을 찾아보죠:
```
np.argmax(predictions[0])
```
모델은 이 이미지가 앵클 부츠(`class_name[9]`)라고 가장 확신하고 있습니다. 이 값이 맞는지 테스트 레이블을 확인해 보죠:
```
test_labels[0]
```
10개 클래스에 대한 예측을 모두 그래프로 표현해 보겠습니다:
```
def plot_image(i, predictions_array, true_label, img):
predictions_array, true_label, img = predictions_array[i], true_label[i], img[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img, cmap=plt.cm.binary)
predicted_label = np.argmax(predictions_array)
if predicted_label == true_label:
color = 'blue'
else:
color = 'red'
plt.xlabel("{} {:2.0f}% ({})".format(class_names[predicted_label],
100*np.max(predictions_array),
class_names[true_label]),
color=color)
def plot_value_array(i, predictions_array, true_label):
predictions_array, true_label = predictions_array[i], true_label[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
thisplot = plt.bar(range(10), predictions_array, color="#777777")
plt.ylim([0, 1])
predicted_label = np.argmax(predictions_array)
thisplot[predicted_label].set_color('red')
thisplot[true_label].set_color('blue')
```
0번째 원소의 이미지, 예측, 신뢰도 점수 배열을 확인해 보겠습니다.
```
i = 0
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions, test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions, test_labels)
plt.show()
i = 12
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions, test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions, test_labels)
plt.show()
```
몇 개의 이미지의 예측을 출력해 보죠. 올바르게 예측된 레이블은 파란색이고 잘못 예측된 레이블은 빨강색입니다. 숫자는 예측 레이블의 신뢰도 퍼센트(100점 만점)입니다. 신뢰도 점수가 높을 때도 잘못 예측할 수 있습니다.
```
# 처음 X 개의 테스트 이미지와 예측 레이블, 진짜 레이블을 출력합니다
# 올바른 예측은 파랑색으로 잘못된 예측은 빨강색으로 나타냅니다
num_rows = 5
num_cols = 3
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2*num_cols, 2*i+1)
plot_image(i, predictions, test_labels, test_images)
plt.subplot(num_rows, 2*num_cols, 2*i+2)
plot_value_array(i, predictions, test_labels)
plt.show()
```
마지막으로 훈련된 모델을 사용하여 한 이미지에 대한 예측을 만듭니다.
```
# 테스트 세트에서 이미지 하나를 선택합니다
img = test_images[0]
print(img.shape)
```
`tf.keras` 모델은 한 번에 샘플의 묶음 또는 *배치*(batch)로 예측을 만드는데 최적화되어 있습니다. 하나의 이미지를 사용할 때에도 2차원 배열로 만들어야 합니다:
```
# 이미지 하나만 사용할 때도 배치에 추가합니다
img = (np.expand_dims(img,0))
print(img.shape)
```
이제 이 이미지의 예측을 만듭니다:
```
predictions_single = model.predict(img)
print(predictions_single)
plot_value_array(0, predictions_single, test_labels)
_ = plt.xticks(range(10), class_names, rotation=45)
```
`model.predict`는 2차원 넘파이 배열을 반환하므로 첫 번째 이미지의 예측을 선택합니다:
```
np.argmax(predictions_single[0])
```
이전과 마찬가지로 모델의 예측은 레이블 9입니다.
|
github_jupyter
|
# Build Clause Clusters with Book Boundaries
```
from tf.app import use
bhsa = use('bhsa')
F, E, T, L = bhsa.api.F, bhsa.api.E, bhsa.api.T, bhsa.api.L
from pathlib import Path
# divide texts evenly into slices of 50 clauses
def cluster_clauses(N):
clusters = []
for book in F.otype.s('book'):
clauses = list(L.d(book,'clause'))
cluster = []
for i, clause in enumerate(clauses):
i += 1
cluster.append(clause)
# create cluster of 50
if (i and i % N == 0):
clusters.append(cluster)
cluster = []
# deal with final uneven clusters
elif i == len(clauses):
if (len(cluster) / N) < 0.6:
clusters[-1].extend(cluster) # add to last cluster
else:
clusters.append(cluster) # keep as cluster
return {
clause:i+1 for i,clust in enumerate(clusters)
for clause in clust
}
cluster_50 = cluster_clauses(50)
cluster_10 = cluster_clauses(10)
```
## Map Book-names to clause clusters
```
# map book names for visualizing
# map grouped book names
book_map = {
'Genesis':'Gen',
'Exodus':'Exod',
'Leviticus':'Lev',
'Numbers':'Num',
'Deuteronomy':'Deut',
'Joshua':'Josh',
'Judges':'Judg',
'1_Samuel':'Sam',
'2_Samuel':'Sam',
'1_Kings':'Kgs',
'2_Kings':'Kgs',
'Isaiah':'Isa',
'Jeremiah':'Jer',
'Ezekiel':'Ezek',
# 'Hosea':'Hos',
# 'Joel':'Joel',
# 'Amos':'Amos',
# 'Obadiah':'Obad',
# 'Jonah':'Jonah',
# 'Micah':'Mic',
# 'Nahum':'Nah',
# 'Habakkuk':'Hab',
# 'Zephaniah':'Zeph',
# 'Haggai':'Hag',
# 'Zechariah':'Zech',
# 'Malachi':'Mal',
'Psalms':'Pss',
'Job':'Job',
'Proverbs':'Prov',
# 'Ruth':'Ruth',
# 'Song_of_songs':'Song',
# 'Ecclesiastes':'Eccl',
# 'Lamentations':'Lam',
# 'Esther':'Esth',
# 'Daniel':'Dan',
# 'Ezra':'Ezra',
# 'Nehemiah':'Neh',
'1_Chronicles':'Chr',
'2_Chronicles':'Chr'
}
# book of 12
for book in ('Hosea', 'Joel', 'Amos', 'Obadiah',
'Jonah', 'Micah', 'Nahum', 'Habakkuk',
'Zephaniah', 'Haggai', 'Zechariah',
'Malachi'):
book_map[book] = 'Twelve'
# Megilloth
for book in ('Ruth', 'Lamentations', 'Ecclesiastes',
'Esther', 'Song_of_songs'):
book_map[book] = 'Megil'
# Dan-Neh
for book in ('Ezra', 'Nehemiah', 'Daniel'):
book_map[book] = 'Dan-Neh'
clustertypes = [cluster_50, cluster_10]
bookmaps = []
for clust in clustertypes:
bookmap = {'Gen':1}
prev_book = 'Gen'
for cl in clust:
book = T.sectionFromNode(cl)[0]
mbook = book_map.get(book, book)
if prev_book != mbook:
bookmap[mbook] = clust[cl]
prev_book = mbook
bookmaps.append(bookmap)
```
# Export
```
import json
data = {
'50': {
'clusters': cluster_50,
'bookbounds': bookmaps[0],
},
'10': {
'clusters': cluster_10,
'bookbounds': bookmaps[1]
},
}
outpath = Path('/Users/cody/github/CambridgeSemiticsLab/time_collocations/results/cl_clusters')
if not outpath.exists():
outpath.mkdir()
with open(outpath.joinpath('clusters.json'), 'w') as outfile:
json.dump(data, outfile)
```
|
github_jupyter
|
## TODO
* Add O2C and C2O seasonality
* Look at diff symbols
* Look at fund flows
## Key Takeaways
* ...
In the [first post](sell_in_may.html) of this short series, we covered several seasonality patterns for large cap equities (i.e, SPY), most of which continue to be in effect.
The findings of that exercise sparked interest in what similar seasonal patterns may exist in other asset classes. This post will pick up where that post left off, looking at "risk-off" assets which exhibit low (or negative) correlation to equities.
```
## Replace this section of imports with your preferred
## data download/access interface. This calls a
## proprietary set of methods (ie they won't work for you)
import sys
sys.path.append('/anaconda/')
import config
sys.path.append(config.REPO_ROOT+'data/')
from prices.eod import read
####### Below here are standard python packages ######
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from IPython import display
import seaborn as sns
from IPython.core.display import HTML,Image
## Load Data
symbols = ['SPY','IWM','AGG','LQD','IEF','MUB','GLD']
#symbols = ['SPY','IWM','AGG','LQD','JNK','IEF']
prices = read.get_symbols_close(symbols,adjusted=True)
returns = prices.pct_change()
log_ret = np.log(prices).diff()
```
### Month-of-year seasonality
Again, we'll start with month-of-year returns for several asset classes. Note that I'm making use of the seaborn library's excellent `clustermap()` method to both visually represent patterns in asset classes _and_ to group the assets by similarity (using Euclidean distance between the average monthly returns vectors of each column).
_Note that the values plotted are z-score values (important for accurate clustering)_.
```
by_month = log_ret.resample('BM').sum()
by_month[by_month==0.0] = None
# because months prior to fund launch are summed to 0.0000
avg_monthly = by_month.groupby(by_month.index.month).mean()
sns.clustermap(avg_monthly[symbols],row_cluster=False,z_score=True, metric='euclidean',\
cmap=sns.diverging_palette(10, 220, sep=20, n=7))
## Notes:
# should use either z_score =True or standard_scale = True for accurate clustering
# Uses Euclidean distance as metric for determining cluster
```
Clearly, the seasonal patterns we saw in the [last post](sell_in_may.html) do not generalize across all instruments - which is a very good thing! IWM (small cap equities) do more or less mimic the SPY patterns, but the "risk-off" assets generally perform well in the summer months of July and August, when equities had faltered.
We might consider a strategy of shifting from risk-on (e.g., SPY) to risk-off (e.g., IEF) for June to September.
```
rotation_results = pd.Series(index=avg_monthly.index)
rotation_results.loc[[1,2,3,4,5,10,11,12]] = avg_monthly['SPY']
rotation_results.loc[[6,7,8,9]] = avg_monthly['IEF']
#
print("Returns:")
print(avg_monthly.SPY.sum())
print(rotation_results.sum())
print()
print("Sharpe:")
print(avg_monthly.SPY.sum()/(by_month.std()['SPY']*12**0.5))
print(rotation_results.sum()/(rotation_results.std()*12**0.5))
avg_monthly.SPY.std()*12**0.5
```
Next, I'll plot the same for day-of-month.
```
avg_day_of_month = log_ret.groupby(log_ret.index.day).mean()
sns.clustermap(avg_day_of_month[symbols],row_cluster=False,z_score= True,metric='euclidean',\
cmap=sns.diverging_palette(10, 220, sep=20, n=7))
```
This is a bit messy, but I think the dominant pattern is weakness within all "risk-off" assets (treasurys, etc...) for the first 1/3 to 1/2 of the month, followed by a very strong end of month rally.
Finally, plot a clustermap for day-of-week:
```
avg_day_of_week = log_ret.groupby(log_ret.index.weekday+1).mean()
sns.clustermap(avg_day_of_week[symbols],row_cluster=False,z_score= True,metric='euclidean',\
cmap=sns.diverging_palette(10, 220, sep=20, n=7))
```
Again, a bit messy. However, the most consistent pattern is "avoid Thursday" for risk-off assets like AGG, LQD, and IEF. Anyone with a hypothesis as to why this might be, please do share!
### Observations
* Clusters form about as you'd expect. The "risk-off" assets like Treasurys (IEF), munis (MUB), gold (GLD), and long volatility (VXX) tend to cluster together. The "risk-on" assets like SPY, EEM, IXUS, and JNK tend to cluster together.
* Risk-off assets (Treasurys etc...) appear to follow the opposite of "sell in May", with weakness in November and December, when SPY and related were strongest.
* Within day-of-month, there are some _very_ strong patterns for fixed income, with negative days at the beginning of month and positive days at end of month.
* Day of week shows very strong clustering of risk-off assets (outperform on Fridays). There's an interesting clustering of underperformance on Mondays. This may be a false correlation since some of these funds have much shorter time histories than others and may be reflecting that
```
risk_off_symbols = ['IEF','MUB','AGG','LQD']
df = log_ret[symbols_1].mean(axis=1).dropna().to_frame(name='pct_chg')
by_month = df.resample('BM').sum()
by_month['month'] = by_month.index.month
title='Avg Log Return (%): by Calendar Month \nfor Risk-off Symbols {}'.format(risk_off_symbols)
s = (by_month.groupby('month').pct_chg.mean()*100)
my_colors = ['r','r','r','r','g','g','g','g','g','g','r','r',]
ax = s.plot(kind='bar',color=my_colors,title=title)
ax.axhline(y=0.00, color='grey', linestyle='--', lw=2)
```
Wow, maybe there's some truth to this myth! It appears that there is a strong difference between the summer months (June to September) and the rest.
From the above chart, it appears than we'd be well advised to sell on June 1st and buy back on September 30th. However, to follow the commonly used interpretation of selling on May 1st and repurchasing on Oct 31st. I'll group the data into those two periods and calculate the monthly average:
```
by_month['season'] = None
by_month.loc[by_month.month.between(5,10),'season'] = 'may_oct'
by_month.loc[~by_month.month.between(5,10),'season'] = 'nov_apr'
(by_month.groupby('season').pct_chg.mean()*100).plot.bar\
(title='Avg Monthly Log Return (%): \nMay-Oct vs Nov_Apr (1993-present)'\
,color='grey')
```
A significant difference. The "winter" months are more than double the average return of the summer months. But has this anomaly been taken out of the market by genius quants and vampire squid? Let's look at this breakout by year:
Of these, the most interesting patterns, to me, are the day-of-week and day-of-month cycles.
### Day of Week
I'll repeat the same analysis pattern as developed in the prior post (["Sell in May"](sell_in_may.html)), using a composite of four generally "risk-off" assets. You may choose create composites differently.
```
risk_off_symbols = ['IEF','MUB','AGG','LQD']
df = log_ret[risk_off_symbols].mean(axis=1).dropna().to_frame(name='pct_chg')
by_day = df
by_day['day_of_week'] = by_day.index.weekday+ 1
ax = (by_day.groupby('day_of_week').pct_chg.mean()*100).plot.bar\
(title='Avg Daily Log Return (%): by Day of Week \n for {}'.format(risk_off_symbols),color='grey')
plt.show()
by_day['part_of_week'] = None
by_day.loc[by_day.day_of_week ==4,'part_of_week'] = 'thurs'
by_day.loc[by_day.day_of_week !=4,'part_of_week'] = 'fri_weds'
(by_day.groupby('part_of_week').pct_chg.mean()*100).plot.bar\
(title='Avg Daily Log Return (%): Mon vs Tue-Fri \n for {}'.format(risk_off_symbols)\
,color='grey')
title='Avg Daily Log Return (%) by Part of Week\nFour Year Moving Average\n for {}'.format(risk_off_symbols)
by_day['year'] = by_day.index.year
ax = (by_day.groupby(['year','part_of_week']).pct_chg.mean().unstack().rolling(4).mean()*100).plot()
ax.axhline(y=0.00, color='grey', linestyle='--', lw=2)
ax.set_title(title)
```
The "avoid Thursday" for risk-off assets seemed to be remarkably useful until about 4 years ago, when it ceased to work. I'll call this one busted. Moving on to day-of-month, and following the same grouping and averaging approach:
```
risk_off_symbols = ['IEF','MUB','AGG','LQD']
by_day = log_ret[risk_off_symbols].mean(axis=1).dropna().to_frame(name='pct_chg')
by_day['day_of_month'] = by_day.index.day
title='Avg Daily Log Return (%): by Day of Month \nFor: {}'.format(symbols_1)
ax = (by_day.groupby('day_of_month').pct_chg.mean()*100).plot.bar(xlim=(1,31),title=title,color='grey')
ax.axhline(y=0.00, color='grey', linestyle='--', lw=2)
```
Here we see the same pattern as appeared in the clustermap. I wonder if the end of month rally is being driven by the ex-div date, which I believe is usually the 1st of the month for these funds.
_Note: this data is dividend-adjusted so there is no valid reason for this - just dividend harvesting and behavioral biases, IMO._
```
by_day['part_of_month'] = None
by_day.loc[by_day.index.day <=10,'part_of_month'] = 'first_10d'
by_day.loc[by_day.index.day >10,'part_of_month'] = 'last_20d'
(by_day.groupby('part_of_month').pct_chg.mean()*100).plot.bar\
(title='Avg Daily Log Return (%): \nDays 1-10 vs 11-31\nfor risk-off assets {}'.format(risk_off_symbols)\
,color='grey')
title='Avg Daily Log Return (%) \nDays 1-10 vs 11-31\nfor risk-off assets {}'.format(risk_off_symbols)
by_day['year'] = by_day.index.year
ax = (by_day.groupby(['year','part_of_month']).pct_chg.mean().unstack().rolling(4).mean()*100).plot(title=title)
ax.axhline(y=0.00, color='grey', linestyle='--', lw=2)
```
In contrast to the day-of-week anomaly, this day-of-month pattern seems to hold extremely well. It's also an extremely tradeable anomaly, considering that it requires only one round-trip per month.
```
baseline = by_day.resample('A').pct_chg.sum()
only_last_20 = by_day[by_day.part_of_month=='last_20d'].resample('A').pct_chg.sum()
pd.DataFrame({'baseline':baseline,'only_last_20':only_last_20}).plot.bar()
print(pd.DataFrame({'baseline':baseline,'only_last_20':only_last_20}).mean())
```
Going to cash in the first 10 days of each month actually _increased_ annualized returns (log) by about 0.60%, while simultaneously lowering capital employed and volatility of returns. Of the seasonality anomalies we've reviewed in this post and the previous, this appears to be the most robust and low risk.
## Conclusion
...
If the future looks anything like the past (insert standard disclaimer about past performance...) then rules of thumb might be:
* Sell on Labor Day and buy on Halloween - especially do this on election years! This assumes that you've got a productive use for the cash!
* Do your buying at Friday's close, do your selling at Wednesday's close
* Maximize your exposure at the end/beginning of months and during the early-middle part of the month, lighten up.
* Remember that, in most of these anomalies, _total_ return would decrease by only participating in part of the market since any positive return is better than sitting in cash. Risk-adjusted returns would be significantly improved by only participating in the most favorable periods. It's for each investor to decide what's important to them.
I had intended to extend this analysis to other asset classes, but will save that for a future post. I'd like to expand this to small caps, rest-of-world developed/emerging, fixed income, growth, value, etc...
### One last thing...
If you've found this post useful, please follow [@data2alpha](https://twitter.com/data2alpha) on twitter and forward to a friend or colleague who may also find this topic interesting.
Finally, take a minute to leave a comment below. Share your thoughts on this post or to offer an idea for future posts. Thanks for reading!
|
github_jupyter
|
## AI for Medicine Course 1 Week 1 lecture exercises
<a name="densenet"></a>
# Densenet
In this week's assignment, you'll be using a pre-trained Densenet model for image classification.
Densenet is a convolutional network where each layer is connected to all other layers that are deeper in the network
- The first layer is connected to the 2nd, 3rd, 4th etc.
- The second layer is connected to the 3rd, 4th, 5th etc.
Like this:
<img src="densenet.png" alt="U-net Image" width="400" align="middle"/>
For a detailed explanation of Densenet, check out the source of the image above, a paper by Gao Huang et al. 2018 called [Densely Connected Convolutional Networks](https://arxiv.org/pdf/1608.06993.pdf).
The cells below are set up to provide an exploration of the Keras densenet implementation that you'll be using in the assignment. Run these cells to gain some insight into the network architecture.
```
# Import Densenet from Keras
from keras.applications.densenet import DenseNet121
from keras.layers import Dense, GlobalAveragePooling2D
from keras.models import Model
from keras import backend as K
```
For your work in the assignment, you'll be loading a set of pre-trained weights to reduce training time.
```
# Create the base pre-trained model
base_model = DenseNet121(weights='./nih/densenet.hdf5', include_top=False);
```
View a summary of the model
```
# Print the model summary
base_model.summary()
# Print out the first five layers
layers_l = base_model.layers
print("First 5 layers")
layers_l[0:5]
# Print out the last five layers
print("Last 5 layers")
layers_l[-6:-1]
# Get the convolutional layers and print the first 5
conv2D_layers = [layer for layer in base_model.layers
if str(type(layer)).find('Conv2D') > -1]
print("The first five conv2D layers")
conv2D_layers[0:5]
# Print out the total number of convolutional layers
print(f"There are {len(conv2D_layers)} convolutional layers")
# Print the number of channels in the input
print("The input has 3 channels")
base_model.input
# Print the number of output channels
print("The output has 1024 channels")
x = base_model.output
x
# Add a global spatial average pooling layer
x_pool = GlobalAveragePooling2D()(x)
x_pool
# Define a set of five class labels to use as an example
labels = ['Emphysema',
'Hernia',
'Mass',
'Pneumonia',
'Edema']
n_classes = len(labels)
print(f"In this example, you want your model to identify {n_classes} classes")
# Add a logistic layer the same size as the number of classes you're trying to predict
predictions = Dense(n_classes, activation="sigmoid")(x_pool)
print(f"Predictions have {n_classes} units, one for each class")
predictions
# Create an updated model
model = Model(inputs=base_model.input, outputs=predictions)
# Compile the model
model.compile(optimizer='adam',
loss='categorical_crossentropy')
# (You'll customize the loss function in the assignment!)
```
#### This has been a brief exploration of the Densenet architecture you'll use in this week's graded assignment!
|
github_jupyter
|
Simple testing of FBT in Warp. Just transform beam in a drift. No solenoid included and no inverse transform.
```
%matplotlib notebook
import sys
del sys.argv[1:]
from warp import *
from warp.data_dumping.openpmd_diag import particle_diag
import numpy as np
import os
from copy import deepcopy
import matplotlib.pyplot as plt
diagDir = 'diags/test/hdf5'
def cleanupPrevious(outputDirectory = diagDir):
if os.path.exists(outputDirectory):
files = os.listdir(outputDirectory)
for file in files:
if file.endswith('.h5'):
os.remove(os.path.join(outputDirectory,file))
cleanupPrevious()
def setup():
pass
##########################################
### Create Beam and Set its Parameters ###
##########################################
top.lrelativ = True
top.relativity = 1
beam = Species(type=Electron, name='Electron')
beam.ekin = 55e6 #KE = 2.5 MeV
derivqty() #Sets addition derived parameters (such as beam.vbeam)
top.emitx = 4.0*800e-6 / top.gammabar # geometric emittance: emit_full = 4 * emit_rms
top.emity = 4.0*1e-6 / top.gammabar
beam.a0 = sqrt(top.emitx * 5.0)
beam.b0 = sqrt(top.emity * 5.0)
beam.ap0 = -1 * top.emitx * 0.0 / beam.a0
beam.bp0 = -1 * top.emity * 0.0 / beam.b0
beam.vthz = 0 #Sets the longitudinal thermal velocity (see iop_lin_002)
beam.ibeam = 0 # beam.ibeam/(top.gammabar**2) #Set correct current for relativity (see iop_lin_002)
top.npmax = 10000
w3d.distrbtn = "Gaussian0"
w3d.cylinder = True #Set True if running without envelope solver
#####################
### Setup Lattice ###
#####################
turnLength = 2.0e-3 #39.9682297148
steps = 2 #8000.
top.zlatstrt = 0#0. # z of lattice start (added to element z's on generate).
top.zlatperi = 10.0#turnLength # Lattice periodicity
top.dt = turnLength / steps / beam.vbeam
start = Marker()
drift1 = Drft(l=1e-3)
transform = Marker()
drift2 = Drft(l=1e-3)
end = Marker()
transformLine = start + drift1 + transform + drift2 + end
madtowarp(transformLine)
def FRBT(beta=5.0, alpha=0.0):
"""
Transforms a matched flat beam to a round 'magnetized' beam.
"""
gamma = (1. - alpha**2) / beta
R = np.zeros([6,6],dtype='float64')
R[0,0] = 1. + alpha
R[0,1] = beta
R[0,2] = 1. - alpha
R[0,3] = -beta
R[1,0] = -gamma
R[1,1] = 1. - alpha
R[1,2] = gamma
R[1,3] = 1. + alpha
R[2,0] = 1. - alpha
R[2,1] = -beta
R[2,2] = 1. + alpha
R[2,3] = beta
R[3,0] = gamma
R[3,1] = 1. + alpha
R[3,2] = -gamma
R[3,3] = 1. - alpha
R[4,4] = 2.
R[5,5] = 2.
R = 0.5 * R
x = {}
norm = {}
for i in range(6):
for j in range(6):
norm[i,j] = 1.0
norm[0,1] = norm[0,3] = norm[2,1] = norm[2,3] = 1./top.pgroup.uzp
norm[1,0] = norm[1,2] = top.pgroup.uzp
norm[3,0] = norm[3,2] = top.pgroup.uzp
x = {}
x[0] = np.copy(top.pgroup.xp)
x[1] = np.copy(top.pgroup.uxp)
x[2] = np.copy(top.pgroup.yp)
x[3] = np.copy(top.pgroup.uyp)
x[4] = np.copy(top.pgroup.zp)
x[5] = np.copy(top.pgroup.uzp)
print x[0].shape
holding = []
for i in range(6):
val = 0
for j in range(6):
val += R[i,j] * x[j] * norm[i,j]
holding.append(val)
top.pgroup.xp = holding[0]
top.pgroup.uxp = holding[1]
top.pgroup.yp = holding[2]
top.pgroup.uyp = holding[3]
top.pgroup.zp = holding[4]
top.pgroup.uzp = holding[5]
# print "Transform!"
################################
### 3D Simulation Parameters ###
################################
top.prwall = pr1 = 0.14
#Set cells
w3d.nx = 128
w3d.ny = 128
w3d.nz = 1
#Set boundaries
w3d.xmmin = -0.10
w3d.xmmax = 0.10
w3d.ymmin = -0.10
w3d.ymmax = 0.10
w3d.zmmin = -2e-3
w3d.zmmax = 2e-3
top.pboundxy = 0 # Absorbing Boundary for particles
top.ibpush = 2 # set type of pusher to vXB push without tan corrections
## 0:off, 1:fast, 2:accurate
top.fstype = -1
############################
### Particle Diagnostics ###
############################
diagP0 = particle_diag.ParticleDiagnostic( period=1, top=top, w3d=w3d,
species= { species.name : species for species in listofallspecies },
comm_world=comm_world, lparallel_output=False, write_dir = diagDir[:-4] )
diagP = particle_diag.ParticleDiagnostic( period=1, top=top, w3d=w3d,
species= { species.name : species for species in listofallspecies },
comm_world=comm_world, lparallel_output=False, write_dir = diagDir[:-4] )
installbeforestep( diagP0.write )
installafterstep( diagP.write )
#################################
### Generate and Run PIC Code ###
#################################
package("wxy")
generate()
fieldsolve()
#installafterstep(thin_lens_lattice)
#Execute First Step
installbeforestep(FRBT)
step(1)
def readparticles(filename):
"""
Reads in openPMD compliant particle file generated by Warp's ParticleDiagnostic class.
Parameters:
filename (str): Path to a ParticleDiagnostic output file.
Returns:
particle_arrays (dict): Dictionary with entry for each species in the file that contains an array
of the 6D particle coordinates.
"""
dims = ['momentum/x', 'position/y', 'momentum/y', 'position/z', 'momentum/z']
particle_arrays = {}
f = h5.File(filename, 'r')
if f.attrs.get('openPMD') is None:
print "Warning!: Not an openPMD file. This may not work."
step = f['data'].keys()[0]
species_list = f['data/%s/particles' % step].keys()
for species in species_list:
parray = f['data/%s/particles/%s/position/x' % (step, species)]
for dim in dims:
parray = np.column_stack((parray, f['data/%s/particles/%s/' % (step, species) + dim]))
particle_arrays[species] = parray
return particle_arrays
def convertunits(particlearray):
"""
Putting particle coordinate data in good ol'fashioned accelerator units:
x: m
x': ux/uz
y: m
y': uy/uz
z: m
p: MeV/c
"""
dat = deepcopy(particlearray) # Don't copy by reference
dat[:, 1] = dat[:, 1] / dat[:, 5]
dat[:, 3] = dat[:, 3] / dat[:, 5]
dat[:, 5] = dat[:, 5] / 5.344286E-22
return dat
def svecplot(array):
fig = plt.figure(figsize = (8,8))
Q = plt.quiver(array[:,0],array[:,2],array[:,1],array[:,3])
plt.quiverkey(Q,0.0, 0.92, 0.002, r'$2', labelpos='W')
xmax = np.max(array[:,0])
xmin = np.min(array[:,0])
plt.xlim(1.5*xmin,1.5*xmax)
plt.ylim(1.5*xmin,1.5*xmax)
plt.show()
init = convertunits(readparticles('diags/test/hdf5/data00000000.h5')['Electron'])
fin = convertunits(readparticles('diags/test/hdf5/data00000001.h5')['Electron'])
svecplot(init)
plt.title("Initial Flat Beam")
plt.xlabel("x (m)")
plt.ylabel("y (m)")
svecplot(fin)
plt.title("Magnetized Beam after FRBT")
plt.xlabel("x (m)")
plt.ylabel("y (m)")
def vortex_check(init):
beta = 5.0
alpha = 0
gamma = (1 - alpha**2) / beta
x1 = ((1+alpha) * init[0,0] + (beta) * init[0,1] + (1-alpha) * init[0,2] + (-beta) * init[0,3]) * 0.5
x2 = ((-gamma) * init[0,0] + (1-alpha) * init[0,1] + (gamma) * init[0,2] + (1+alpha) * init[0,3]) * 0.5
y1 = ((1-alpha) * init[0,0] + (-beta) * init[0,1] + (1+alpha) * init[0,2] + (beta) * init[0,3]) * 0.5
y2 = ((gamma) * init[0,0] + (1+alpha) * init[0,1] + (-gamma) * init[0,2] + (1-alpha) * init[0,3]) * 0.5
print x1, fin[0,0]
print x2, fin[0,1]
print y1, fin[0,2]
print y2, fin[0,3]
def calc_emittance(array):
xemit = np.sqrt(np.average(array[:,0]**2) * np.average(array[:,1]**2) - np.average(array[:,0] * array[:,1])**2 )
yemit = np.sqrt(np.average(array[:,2]**2) * np.average(array[:,3]**2) - np.average(array[:,2] * array[:,3])**2 )
return xemit,yemit
epsx0,epsy0 = calc_emittance(init)
epsxf,epsyf = calc_emittance(fin)
print "Initial:\n x-emit: %s Initial y-emit: %s" % (epsx0,epsy0)
print "After Transform:\n x-emit: %s y-emit: %s" % (epsxf,epsyf)
```
|
github_jupyter
|
### Deep learning for identifying the orientation Scanned images
First we will load the train and test data and create a CTF file
```
import os
from PIL import Image
import numpy as np
import itertools
import random
import time
import matplotlib.pyplot as plt
import cntk as C
def split_line(line):
splits = line.strip().split(',')
return (splits[0], int(splits[1]))
def load_labels_dict(labels_file):
with open(labels_file) as f:
return dict([split_line(line) for line in f.readlines()[1:]])
def load_data(data_dir, labels_dict):
for f in os.listdir(data_dir):
key = f[:-4]
label = labels_dict[key]
image = np.array(Image.open(os.path.join(data_dir, f)), dtype = np.int16).flatten()
yield np.hstack([image, int(label)])
def write_to_ctf_file(generator, test_file_name, train_file_name, pct_train = 0.9, rng_seed = 0):
random.seed(rng_seed)
labels = [l for l in map(' '.join, np.eye(4, dtype = np.int16).astype(str))]
with open(test_file_name, 'w') as testf:
with open(train_file_name, 'w') as trainf:
lines = 0
for entry in generator:
rand_num = random.random()
formatted_line = '|labels {} |features {}\n'.format(labels[int(entry[-1])], ' '.join(entry[:-1].astype(str)))
if rand_num <= pct_train:
trainf.write(formatted_line)
else:
testf.write(formatted_line)
lines += 1
if lines % 1000 == 0:
print('Processed {} entries'.format(str(lines)))
train_data_dir = os.path.join('data', 'train')
labels_file = os.path.join('data', 'train_labels.csv')
train_file = 'train_data.ctf'
test_file = 'test_data.ctf'
all_data_file = 'all_data.ctf'
labels_dict = load_labels_dict(labels_file)
if os.path.exists(train_file) and os.path.exists(test_file):
print("Test and training CTF Files exists, not recreating them again")
else:
generator = load_data(train_data_dir, labels_dict)
write_to_ctf_file(generator, test_file, train_file)
#Created only to enable testing on entire test data to hoping to improve the submission score
if os.path.exists(all_data_file):
print("All data CTF Files exists, not recreating it again")
else:
generator = load_data(train_data_dir, labels_dict)
labels = [l for l in map(' '.join, np.eye(4, dtype = np.int16).astype(str))]
with open(all_data_file, 'w') as f:
lines = 0
for entry in generator:
formatted_line = '|labels {} |features {}\n'.format(labels[int(entry[-1])], ' '.join(entry[:-1].astype(str)))
f.write(formatted_line)
lines += 1
if lines % 1000 == 0:
print('Processed {} entries'.format(str(lines)))
np.random.seed(0)
C.cntk_py.set_fixed_random_seed(1)
C.cntk_py.force_deterministic_algorithms()
num_output_classes = 4
input_dim_model = (1, 64, 64)
def create_reader(file_path, is_training):
print('Creating reader from file ' + file_path)
ctf = C.io.CTFDeserializer(file_path, C.io.StreamDefs(
labels = C.io.StreamDef(field='labels', shape = 4, is_sparse=False),
features = C.io.StreamDef(field='features', shape = 64 * 64, is_sparse=False),
))
return C.io.MinibatchSource(ctf, randomize = is_training, max_sweeps = C.io.INFINITELY_REPEAT if is_training else 1)
x = C.input_variable(input_dim_model)
y = C.input_variable(num_output_classes)
def create_model(features):
with C.layers.default_options(init = C.glorot_uniform(), activation = C.relu):
h = features
h = C.layers.Convolution2D(filter_shape=(5, 5),
num_filters = 32,
strides=(2, 2),
pad=True, name='first_conv')(h)
h = C.layers.MaxPooling(filter_shape = (5, 5), strides = (2, 2), name = 'pool1')(h)
h = C.layers.Convolution2D(filter_shape=(5, 5),
num_filters = 64,
strides=(2, 2),
pad=True, name='second_conv')(h)
h = C.layers.MaxPooling(filter_shape = (3, 3), strides = (2, 2), name = 'pool2')(h)
r = C.layers.Dense(num_output_classes, activation = None, name='classify')(h)
return r
def print_training_progress(trainer, mb, frequency, verbose=1):
training_loss = "NA"
eval_error = "NA"
if mb % frequency == 0:
training_loss = trainer.previous_minibatch_loss_average
eval_error = trainer.previous_minibatch_evaluation_average
if verbose:
print ("Minibatch: {0}, Loss: {1:.4f}, Error: {2:.2f}%".format(mb, training_loss, eval_error*100))
def train_test(train_reader, test_reader, model_func, num_sweeps_to_train_with=10):
model = model_func(x/255)
# Instantiate the loss and error function
loss = C.cross_entropy_with_softmax(model, y)
label_error = C.classification_error(model, y)
# Initialize the parameters for the trainer
minibatch_size = 64
num_samples_per_sweep = 60000
num_minibatches_to_train = (num_samples_per_sweep * num_sweeps_to_train_with) / minibatch_size
learning_rate = 0.1
lr_schedule = C.learning_rate_schedule(learning_rate, C.UnitType.minibatch)
learner = C.sgd(model.parameters, lr_schedule)
trainer = C.Trainer(model, (loss, label_error), [learner])
input_map={
y : train_reader.streams.labels,
x : train_reader.streams.features
}
training_progress_output_freq = 500
start = time.time()
for i in range(0, int(num_minibatches_to_train)):
data=train_reader.next_minibatch(minibatch_size, input_map = input_map)
trainer.train_minibatch(data)
print_training_progress(trainer, i, training_progress_output_freq, verbose=1)
print("Training took {:.1f} sec".format(time.time() - start))
test_input_map = {
y : test_reader.streams.labels,
x : test_reader.streams.features
}
test_minibatch_size = 64
num_samples = 2000
num_minibatches_to_test = num_samples // test_minibatch_size
test_result = 0.0
for i in range(num_minibatches_to_test):
data = test_reader.next_minibatch(test_minibatch_size, input_map=test_input_map)
eval_error = trainer.test_minibatch(data)
test_result = test_result + eval_error
# Average of evaluation errors of all test minibatches
print("Average test error: {0:.2f}%".format(test_result*100 / num_minibatches_to_test))
def do_train_test(model, train_on_all_data = False):
if train_on_all_data:
reader_train = create_reader(all_data_file, True)
else:
reader_train = create_reader(train_file, True)
reader_test = create_reader(test_file, False)
train_test(reader_train, reader_test, model)
C.cntk_py.set_fixed_random_seed(1)
C.cntk_py.force_deterministic_algorithms()
model = create_model(x)
print('pool2 shape is ' + str(model.pool2.shape))
C.logging.log_number_of_parameters(model)
do_train_test(model, train_on_all_data = False)
#Test data not relevant here in case we use all data, the tests won't be out of sample
#Just done as an attempt improve the submission score using all possible test data after we find the best model
#that gave minimum error on validation set
#Surprisingly, it didn't improve the score but reduced the score by a fraction.
#do_train_test(model, train_on_all_data = True)
#Accumulate and display the misclassified
#TODO: FIX this
test_reader = create_reader(test_file, False)
labels = []
predictions = []
all_images = []
for i in range(0, 2000, 500):
validation_data = test_reader.next_minibatch(500)
features = validation_data[test_reader.streams.features].as_sequences()
all_images += features
l = validation_data[test_reader.streams.labels].as_sequences()
labels += [np.argmax(i.flatten()) for i in l]
images = [i.reshape(1, 64, 64) for i in features]
preds = model(images)
predictions += [np.argmax(i.flatten()) for i in preds]
predictions = np.array(predictions)
labels = np.array(labels)
mask = predictions != labels
mismatch = np.array(all_images)[mask]
expected_label = labels[mask]
mismatch_pred = predictions[mask]
mismatch_images = np.array(all_images)[mask]
%matplotlib inline
for i in range(len(expected_label)):
fig = plt.figure(figsize = (8, 6))
ax = fig.gca()
ax.set_title('Expected label ' + str(expected_label[i]) + ', got label ' + str(mismatch_pred[i]))
image = mismatch_images[i]
plt.imshow(image.reshape(64, 64), cmap = 'gray')
plt.axis('off')
submission_data_dir = os.path.join('data', 'test')
submission_file = 'submission_data.ctf'
def file_to_ndarray(file_root, imfile):
return (imfile[:-4], np.array(Image.open(os.path.join(file_root, imfile))).reshape((-1, 64, 64)))
submission_images = [file_to_ndarray(submission_data_dir, f) for f in os.listdir(submission_data_dir)]
submission_images = sorted(submission_images, key = lambda x: x[0])
input_images = [x[1].astype(np.float32) / 255 for x in submission_images]
all_predictions = []
submission_mini_batch_size = 50
for i in range(0, 20000, submission_mini_batch_size):
predictions = model(input_images[i:(i + submission_mini_batch_size)])
all_predictions.append(np.argmax(predictions, axis = 1))
all_predictions = [item for sl in all_predictions for item in sl]
with open('submission.csv', 'w') as f:
f.write('id,orientation\n')
for i in range(20000):
f.write(submission_images[i][0] + "," + str(all_predictions[i]) + "\n")
```
|
github_jupyter
|
# Adversarial Attacks Example in PyTorch
## Import Dependencies
This section imports all necessary libraries, such as PyTorch.
```
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
from torchvision import datasets, transforms
import numpy as np
import matplotlib.pyplot as plt
import math
import torch.backends.cudnn as cudnn
import os
import argparse
```
### GPU Check
```
device = 'cuda' if torch.cuda.is_available() else 'cpu'
if torch.cuda.is_available():
print("Using GPU.")
else:
print("Using CPU.")
```
## Data Preparation
```
# MNIST dataloader declaration
print('==> Preparing data..')
# The standard output of the torchvision MNIST data set is [0,1] range, which
# is what we want for later processing. All we need for a transform, is to
# translate it to tensors.
# We first download the train and test datasets if necessary and then load them into pytorch dataloaders.
mnist_train_dataset = datasets.MNIST(root='./data', train=True, transform=transforms.ToTensor(), download=True)
mnist_test_dataset = datasets.MNIST(root='./data', train=False, transform=transforms.ToTensor(), download=True)
mnist_dataset_sizes = {'train' : mnist_train_dataset.__len__(), 'test' : mnist_test_dataset.__len__()} # a dictionary to keep both train and test datasets
mnist_train_loader = torch.utils.data.DataLoader(
dataset=mnist_train_dataset,
batch_size=256,
shuffle=True)
mnist_test_loader = torch.utils.data.DataLoader(
dataset=mnist_test_dataset,
batch_size=1,
shuffle=True)
mnist_dataloaders = {'train' : mnist_train_loader ,'test' : mnist_test_loader} # a dictionary to keep both train and test loaders
# CIFAR10 dataloader declaration
print('==> Preparing data..')
# The standard output of the torchvision CIFAR data set is [0,1] range, which
# is what we want for later processing. All we need for a transform, is to
# translate it to tensors.
# we first download the train and test datasets if necessary and then load them into pytorch dataloaders
cifar_train_dataset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transforms.ToTensor())
cifar_train_loader = torch.utils.data.DataLoader(cifar_train_dataset, batch_size=128, shuffle=True, num_workers=2)
cifar_test_dataset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=transforms.ToTensor())
cifar_test_loader = torch.utils.data.DataLoader(cifar_test_dataset, batch_size=100, shuffle=False, num_workers=2)
# these are the output categories from the CIFAR dataset
classes = ('plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
```
## Model Definition
We used LeNet model to train against MNIST dataset because the dataset is not very complex and LeNet can easily reach a high accuracy to then demonstrate an ttack. For CIFAR10 dataset, however, we used the more complex DenseNet model to reach an accuracy of 90% to then attack.
### LeNet
```
# LeNet Model definition
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.conv2_drop = nn.Dropout2d()
self.fc1 = nn.Linear(320, 50)
self.fc2 = nn.Linear(50, 10)
def forward(self, x):
x = F.relu(F.max_pool2d(self.conv1(x), 2)) #first convolutional layer
x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2)) #secon convolutional layer with dropout
x = x.view(-1, 320) #making the data flat
x = F.relu(self.fc1(x)) #fully connected layer
x = F.dropout(x, training=self.training) #final dropout
x = self.fc2(x) # last fully connected layer
return F.log_softmax(x, dim=1) #output layer
```
This is the standard implementation of the DenseNet proposed in the following paper.
[DenseNet paper](https://arxiv.org/abs/1608.06993)
The idea of Densely Connected Networks is that every layer is connected to all its previous layers and its succeeding ones, thus forming a Dense Block.

The implementation is broken to smaller parts, called a Dense Block with 5 layers. Each time there is a convolution operation of the previous layer, it is followed by concatenation of the tensors. This is allowed as the channel dimensions, height and width of the input stay the same after convolution with a kernel size 3×3 and padding 1.
In this way the feature maps produced are more diversified and tend to have richer patterns. Also, another advantage is better information flow during training.
### DenseNet
```
# This is a basic densenet model definition.
class Bottleneck(nn.Module):
def __init__(self, in_planes, growth_rate):
super(Bottleneck, self).__init__()
self.bn1 = nn.BatchNorm2d(in_planes)
self.conv1 = nn.Conv2d(in_planes, 4*growth_rate, kernel_size=1, bias=False)
self.bn2 = nn.BatchNorm2d(4*growth_rate)
self.conv2 = nn.Conv2d(4*growth_rate, growth_rate, kernel_size=3, padding=1, bias=False)
def forward(self, x):
out = self.conv1(F.relu(self.bn1(x)))
out = self.conv2(F.relu(self.bn2(out)))
out = torch.cat([out,x], 1)
return out
class Transition(nn.Module):
def __init__(self, in_planes, out_planes):
super(Transition, self).__init__()
self.bn = nn.BatchNorm2d(in_planes)
self.conv = nn.Conv2d(in_planes, out_planes, kernel_size=1, bias=False)
def forward(self, x):
out = self.conv(F.relu(self.bn(x)))
out = F.avg_pool2d(out, 2)
return out
class DenseNet(nn.Module):
def __init__(self, block, nblocks, growth_rate=12, reduction=0.5, num_classes=10):
super(DenseNet, self).__init__()
self.growth_rate = growth_rate
num_planes = 2*growth_rate
self.conv1 = nn.Conv2d(3, num_planes, kernel_size=3, padding=1, bias=False)
self.dense1 = self._make_dense_layers(block, num_planes, nblocks[0])
num_planes += nblocks[0]*growth_rate
out_planes = int(math.floor(num_planes*reduction))
self.trans1 = Transition(num_planes, out_planes)
num_planes = out_planes
self.dense2 = self._make_dense_layers(block, num_planes, nblocks[1])
num_planes += nblocks[1]*growth_rate
out_planes = int(math.floor(num_planes*reduction))
self.trans2 = Transition(num_planes, out_planes)
num_planes = out_planes
self.dense3 = self._make_dense_layers(block, num_planes, nblocks[2])
num_planes += nblocks[2]*growth_rate
out_planes = int(math.floor(num_planes*reduction))
self.trans3 = Transition(num_planes, out_planes)
num_planes = out_planes
self.dense4 = self._make_dense_layers(block, num_planes, nblocks[3])
num_planes += nblocks[3]*growth_rate
self.bn = nn.BatchNorm2d(num_planes)
self.linear = nn.Linear(num_planes, num_classes)
def _make_dense_layers(self, block, in_planes, nblock):
layers = []
for i in range(nblock):
layers.append(block(in_planes, self.growth_rate))
in_planes += self.growth_rate
return nn.Sequential(*layers)
def forward(self, x):
out = self.conv1(x)
out = self.trans1(self.dense1(out))
out = self.trans2(self.dense2(out))
out = self.trans3(self.dense3(out))
out = self.dense4(out)
out = F.avg_pool2d(F.relu(self.bn(out)), 4)
out = out.view(out.size(0), -1)
out = self.linear(out)
return out
# This creates a densenet model with basic settings for cifar.
def densenet_cifar():
return DenseNet(Bottleneck, [6,12,24,16], growth_rate=12)
#building model for MNIST data
print('==> Building the model for MNIST dataset..')
mnist_model = LeNet().to(device)
mnist_criterion = nn.CrossEntropyLoss()
mnist_optimizer = optim.Adam(mnist_model.parameters(), lr=0.001)
mnist_num_epochs= 20
#building model for CIFAR10
# Model
print('==> Building the model for CIFAR10 dataset..')
# initialize our datamodel
cifar_model = densenet_cifar()
cifar_model = cifar_model.to(device)
# use cross entropy as our objective function, since we are building a classifier
cifar_criterion = nn.CrossEntropyLoss()
# use adam as an optimizer, because it is a popular default nowadays
# (following the crowd, I know)
cifar_optimizer = optim.Adam(cifar_model.parameters(), lr=0.1)
best_acc = 0 # save the best test accuracy
start_epoch = 0 # start from epoch 0
cifar_num_epochs =20
```
##Model Training
```
#Training for MNIST dataset
def train_mnist_model(model, data_loaders, dataset_sizes, criterion, optimizer, num_epochs, device):
model = model.to(device)
model.train() # set train mode
# for each epoch
for epoch in range(num_epochs):
print('Epoch {}/{}'.format(epoch+1, num_epochs))
running_loss, running_corrects = 0.0, 0
# for each batch
for inputs, labels in data_loaders['train']:
inputs = inputs.to(device)
labels =labels.to(device)
# making sure all the gradients of parameter tensors are zero
optimizer.zero_grad() # set gradient as 0
# get the model output
outputs = model(inputs)
# get the prediction of model
_, preds = torch.max(outputs, 1)
# calculate loss of the output
loss = criterion(outputs, labels)
# backpropagation
loss.backward()
# update model parameters using optimzier
optimizer.step()
batch_loss_total = loss.item() * inputs.size(0) # total loss of the batch
running_loss += batch_loss_total # cumluative sum of loss
running_corrects += torch.sum(preds == labels.data) # cumulative sum of correct count
#calculating the loss and accuracy for the epoch
epoch_loss = running_loss / dataset_sizes['train']
epoch_acc = running_corrects.double() / dataset_sizes['train']
print('Train Loss: {:.4f} Acc: {:.4f}'.format(epoch_loss, epoch_acc))
print('-' * 10)
# after tranining epochs, test epoch starts
else:
model.eval() # set test mode
running_loss, running_corrects = 0.0, 0
# for each batch
for inputs, labels in data_loaders['test']:
inputs = inputs.to(device)
labels =labels.to(device)
# same with the training part.
outputs = model(inputs)
_, preds = torch.max(outputs, 1)
loss = criterion(outputs, labels)
running_loss += loss.item() * inputs.size(0) # cumluative sum of loss
running_corrects += torch.sum(preds == labels.data) # cumluative sum of corrects count
#calculating the loss and accuracy
test_loss = running_loss / dataset_sizes['test']
test_acc = (running_corrects.double() / dataset_sizes['test']).item()
print('<Test Loss: {:.4f} Acc: {:.4f}>'.format(test_loss, test_acc))
train_mnist_model(mnist_model, mnist_dataloaders, mnist_dataset_sizes, mnist_criterion, mnist_optimizer, mnist_num_epochs, device)
# Training for CIFAR10 dataset
def train_cifar_model(model, train_loader, criterion, optimizer, num_epochs, device):
print('\nEpoch: %d' % num_epochs)
model.train() #set the mode to train
train_loss = 0
correct = 0
total = 0
for batch_idx, (inputs, targets) in enumerate(train_loader):
inputs, targets = inputs.to(device), targets.to(device)
optimizer.zero_grad() # making sure all the gradients of parameter tensors are zero
outputs = model(inputs) #forward pass the model againt the input
loss = criterion(outputs, targets) #calculate the loss
loss.backward() #back propagation
optimizer.step() #update model parameters using the optimiser
train_loss += loss.item() #cumulative sum of loss
_, predicted = outputs.max(1) #the model prediction
total += targets.size(0)
correct += predicted.eq(targets).sum().item() #cumulative sume of corrects count
if batch_idx % 100 == 0:
#calculating and printig the loss and accuracy
print('Loss: %.3f | Acc: %.3f%% (%d/%d)' % (train_loss/(batch_idx+1), 100.*correct/total, correct, total))
#testing for CIFAR10 dataset
def test_cifar_model(model, test_loader, criterion, device, save=True):
"""Tests the model.
Taks the epoch number as a parameter.
"""
global best_acc
model.eval() # set the mode to test
test_loss = 0
correct = 0
total = 0
with torch.no_grad():
#similar to the train part
for batch_idx, (inputs, targets) in enumerate(test_loader):
inputs, targets = inputs.to(device), targets.to(device)
outputs = model(inputs)
loss = criterion(outputs, targets)
test_loss += loss.item()
_, predicted = outputs.max(1)
total += targets.size(0)
correct += predicted.eq(targets).sum().item()
if batch_idx % 100 == 0:
print('Loss: %.3f | Acc: %.3f%% (%d/%d) TEST' % (test_loss/(batch_idx+1), 100.*correct/total, correct, total))
#calculating the accuracy
acc = 100.*correct/total
if acc > best_acc and save:
best_acc = acc
for epoch in range(start_epoch, start_epoch+cifar_num_epochs):
train_cifar_model(cifar_model, cifar_train_loader, cifar_criterion, cifar_optimizer, epoch, device)
test_cifar_model(cifar_model, cifar_test_loader, cifar_criterion, device)
```
## Save and Reload the Model
```
# Mounting Google Drive
from google.colab import auth
auth.authenticate_user()
from google.colab import drive
drive.mount('/content/gdrive')
gdrive_dir = 'gdrive/My Drive/ml/' # update with your own path
# Save and reload the mnist_model
print('==> Saving model for MNIST..')
torch.save(mnist_model.state_dict(), gdrive_dir+'lenet_mnist_model.pth')
#change the directory to load your own pretrained model
print('==> Loading saved model for MNIST..')
mnist_model = LeNet().to(device)
mnist_model.load_state_dict(torch.load(gdrive_dir+'lenet_mnist_model.pth'))
mnist_model.eval()
# Save and reload the cifar_model
print('==> Saving model for CIFAR..')
torch.save(cifar_model.state_dict(), './densenet_cifar_model.pth')
#change the directory to load your own pretrained model
print('==> Loading saved model for CIFAR..')
cifar_model = densenet_cifar().to(device)
cifar_model.load_state_dict(torch.load(gdrive_dir+'densenet_cifar_model.pth'))
cifar_model.eval()
```
## Attack Definition
We used these two attack methods:
* Fast Gradient Signed Method (FGSM)
* Iterative Least Likely method (Iter.L.L.)
```
# Fast Gradient Singed Method attack (FGSM)
#Model is the trained model for the target dataset
#target is the ground truth label of the image
#epsilon is the hyper parameter which shows the degree of perturbation
def fgsm_attack(model, image, target, epsilon):
# Set requires_grad attribute of tensor. Important for Attack
image.requires_grad = True
# Forward pass the data through the model
output = model(image)
init_pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability(the prediction of the model)
# If the initial prediction is already wrong, dont bother attacking
if init_pred[0].item() != target[0].item():
#if init_pred.item() != target.item():
return image
# Calculate the loss
loss = F.nll_loss(output, target)
# Zero all existing gradients
model.zero_grad()
# Calculate gradients of model in backward pass
loss.backward()
# Collect datagrad
data_grad = image.grad.data
# Collect the element-wise sign of the data gradient
sign_data_grad = data_grad.sign()
# Create the perturbed image by adjusting each pixel of the input image
perturbed_image = image + epsilon*sign_data_grad
# Adding clipping to maintain [0,1] range
perturbed_image = torch.clamp(perturbed_image, 0, 1)
# Return the perturbed image
return perturbed_image
# Iterative least likely method
# Model is the trained model for the target dataset
# target is the ground truth label of the image
# alpha is the hyper parameter which shows the degree of perturbation in each iteration, the value is borrowed from the refrenced paper [4] according to the report file
# iters is the no. of iterations
# no. of iterations can be set manually, otherwise (if iters==0) this function will take care of it
def ill_attack(model, image, target, epsilon, alpha, iters):
# Forward passing the image through model one time to get the least likely labels
output = model(image)
ll_label = torch.min(output, 1)[1] # get the index of the min log-probability
if iters == 0 :
# In paper [4], min(epsilon + 4, 1.25*epsilon) is used as number of iterations
iters = int(min(epsilon + 4, 1.25*epsilon))
# In the original paper the images were in [0,255] range but here our data is in [0,1].
# So we need to scale the epsilon value in a way that suits our data, which is dividing by 255.
epsilon = epsilon/255
for i in range(iters) :
# Set requires_grad attribute of tensor. Important for Attack
image.requires_grad = True
# Forward pass the data through the model
output = model(image)
init_pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability(the model's prediction)
# If the current prediction is already wrong, dont bother to continue
if init_pred.item() != target.item():
return image
# Calculate the loss
loss = F.nll_loss(output, ll_label)
# Zero all existing gradients
model.zero_grad()
# Calculate gradients of model in backward pass
loss.backward()
# Collect datagrad
data_grad = image.grad.data
# Collect the element-wise sign of the data gradient
sign_data_grad = data_grad.sign()
# Create the perturbed image by adjusting each pixel of the input image
perturbed_image = image - alpha*sign_data_grad
# Updating the image for next iteration
#
# We want to keep the perturbed image in range [image-epsilon, image+epsilon]
# based on the definition of the attack. However the value of image-epsilon
# itself must not fall behind 0, as the data range is [0,1].
# And the value of image+epsilon also must not exceed 1, for the same reason.
# So we clip the perturbed image between the (image-epsilon) clipped to 0 and
# (image+epsilon) clipped to 1.
a = torch.clamp(image - epsilon, min=0)
b = (perturbed_image>=a).float()*perturbed_image + (a>perturbed_image).float()*a
c = (b > image+epsilon).float()*(image+epsilon) + (image+epsilon >= b).float()*b
image = torch.clamp(c, max=1).detach_()
return image
```
## Model Attack Design
```
# We used the same values as described in the reference paper [4] in the report.
fgsm_epsilons = [0, .05, .1, .15, .2, .25, .3] # values for epsilon hyper-parameter for FGSM attack
ill_epsilons = [0, 2, 4, 8, 16] # values for epsilon hyper-parameter for Iter.L.L attack
#This is where we test the effect of the attack on the trained model
#model is the pretrained model on your dataset
#test_loader contains the test dataset
#other parameters are set based on the type of the attack
def attack_test(model, device, test_loader, epsilon, iters, attack='fgsm', alpha=1 ):
# Accuracy counter. accumulates the number of correctly predicted exampels
correct = 0
adv_examples = [] # a list to save some of the successful adversarial examples for visualizing purpose
orig_examples = [] # this list keeps the original image before manipulation corresponding to the images in adv_examples list for comparing purpose
# Loop over all examples in test set
for data, target in test_loader:
# Send the data and label to the device
data, target = data.to(device), target.to(device)
# Forward pass the data through the model
output = model(data)
init_pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability (model prediction of the image)
# Call the Attack
if attack == 'fgsm':
perturbed_data = fgsm_attack(model, data, target, epsilon=epsilon )
else:
perturbed_data = ill_attack(model, data, target, epsilon, alpha, iters)
# Re-classify the perturbed image
output = model(perturbed_data)
# Check for success
#target refers to the ground truth label
#init_pred refers to the model prediction of the original image
#final_pred refers to the model prediction of the manipulated image
final_pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability (model prediction of the perturbed image)
if final_pred[0].item() == target[0].item(): #perturbation hasn't affected the classification
correct += 1
# Special case for saving 0 epsilon examples which is equivalent to no adversarial attack
if (epsilon == 0) and (len(adv_examples) < 5):
adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
orig_ex = data.squeeze().detach().cpu().numpy()
adv_examples.append( (init_pred[0].item(), final_pred[0].item(), adv_ex) )
orig_examples.append( (target[0].item(), init_pred[0].item(), orig_ex) )
else:
# Save some adv examples for visualization later
if len(adv_examples) < 5:
adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
orig_ex = data.squeeze().detach().cpu().numpy()
adv_examples.append( (init_pred[0].item(), final_pred[0].item(), adv_ex) )
orig_examples.append( (target[0].item(), init_pred[0].item(), orig_ex) )
# Calculate final accuracy for this epsilon
final_acc = correct/float(len(test_loader))
print("Epsilon: {}\tTest Accuracy = {} / {} = {}".format(epsilon, correct, len(test_loader), final_acc))
# Return the accuracy and an adversarial examples and their corresponding original images
return final_acc, adv_examples, orig_examples
```
##Running the Attack for MNIST dataset
```
#FGSM attack
mnist_fgsm_accuracies = [] #list to keep the model accuracy after attack for each epsilon value
mnist_fgsm_examples = [] # list to collect adversarial examples returned from the attack_test function for every epsilon values
mnist_fgsm_orig_examples = [] #list to collect original images corresponding the collected adversarial examples
# Run test for each epsilon
for eps in fgsm_epsilons:
acc, ex, orig = attack_test(mnist_model, device, mnist_test_loader, eps, attack='fgsm', alpha=1, iters=0)
mnist_fgsm_accuracies.append(acc)
mnist_fgsm_examples.append(ex)
mnist_fgsm_orig_examples.append(orig)
#Iterative_LL attack
mnist_ill_accuracies = [] #list to keep the model accuracy after attack for each epsilon value
mnist_ill_examples = [] # list to collect adversarial examples returned from the attack_test function for every epsilon values
mnist_ill_orig_examples = [] #list to collect original images corresponding the collected adversarial examples
# Run test for each epsilon
for eps in ill_epsilons:
acc, ex, orig = attack_test(mnist_model, device, mnist_test_loader, eps, attack='ill', alpha=1, iters=0)
mnist_ill_accuracies.append(acc)
mnist_ill_examples.append(ex)
mnist_ill_orig_examples.append(orig)
```
##Visualizing the results for MNIST dataset
```
#Accuracy after attack vs epsilon
plt.figure(figsize=(5,5))
plt.plot(fgsm_epsilons, mnist_fgsm_accuracies, "*-")
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.xticks(np.arange(0, .35, step=0.05))
plt.title("FSGM Attack vs MNIST Model Accuracy vs Epsilon")
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()
# Plot several examples vs their adversarial samples at each epsilon for fgms attack
cnt = 0
plt.figure(figsize=(8,20))
for i in range(len(fgsm_epsilons)):
for j in range(2):
cnt += 1
plt.subplot(len(fgsm_epsilons),2,cnt)
plt.xticks([], [])
plt.yticks([], [])
if j==0:
plt.ylabel("Eps: {}".format(fgsm_epsilons[i]), fontsize=14)
orig,adv,ex = mnist_fgsm_orig_examples[i][0]
plt.title("target "+"{} -> {}".format(orig, adv)+ " predicted")
plt.imshow(ex, cmap="gray")
else:
orig,adv,ex = mnist_fgsm_examples[i][0]
plt.title("predicted "+"{} -> {}".format(orig, adv)+ " attacked")
plt.imshow(ex, cmap="gray")
plt.tight_layout()
plt.show()
#Accuracy after attack vs epsilon
plt.figure(figsize=(5,5))
plt.plot(ill_epsilons, mnist_ill_accuracies, "*-", color='R')
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.xticks(np.arange(0, 17, step=2))
plt.title("Iterative Least Likely vs MNIST Model / Accuracy vs Epsilon")
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()
# Plot several examples vs their adversarial samples at each epsilon for ill attack
cnt = 0
plt.figure(figsize=(8,20))
for i in range(len(ill_epsilons)):
for j in range(2):
cnt += 1
plt.subplot(len(ill_epsilons),2,cnt)
plt.xticks([], [])
plt.yticks([], [])
if j==0:
plt.ylabel("Eps: {}".format(ill_epsilons[i]), fontsize=14)
orig,adv,ex = mnist_ill_orig_examples[i][0]
plt.title("target "+"{} -> {}".format(orig, adv)+ " predicted")
plt.imshow(ex, cmap="gray")
else:
orig,adv,ex = mnist_ill_examples[i][0]
plt.title("predicted "+"{} -> {}".format(orig, adv)+ " attacked")
plt.imshow(ex, cmap="gray")
plt.tight_layout()
plt.show()
```
##Running the Attack for CIFAR10 dataset
```
#FGSM attack
cifar_fgsm_accuracies = [] #list to keep the model accuracy after attack for each epsilon value
cifar_fgsm_examples = [] # list to collect adversarial examples returned from the attack_test function for every epsilon values
cifar_fgsm_orig_examples = [] #list to collect original images corresponding the collected adversarial examples
# Run test for each epsilon
for eps in fgsm_epsilons:
acc, ex, orig = attack_test(cifar_model, device, cifar_test_loader, eps, attack='fgsm', alpha=1, iters=0)
cifar_fgsm_accuracies.append(acc)
cifar_fgsm_examples.append(ex)
cifar_fgsm_orig_examples.append(orig)
#Iterative_LL attack
cifar_ill_accuracies = [] #list to keep the model accuracy after attack for each epsilon value
cifar_ill_examples = [] # list to collect adversarial examples returned from the attack_test function for every epsilon values
cifar_ill_orig_examples = [] #list to collect original images corresponding the collected adversarial examples
# Run test for each epsilon
for eps in ill_epsilons:
acc, ex, orig = attack_test(cifar_model, device, cifar_test_loader, eps, attack='ill', alpha=1, iters=0)
cifar_ill_accuracies.append(acc)
cifar_ill_examples.append(ex)
cifar_ill_orig_examples.append(orig)
```
##Visualizing the results for CIFAR10 dataset
```
#Accuracy after attack vs epsilon
plt.figure(figsize=(5,5))
plt.plot(fgsm_epsilons, cifar_fgsm_accuracies, "*-")
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.xticks(np.arange(0, .35, step=0.05))
plt.title("FSGM Attack vs CIFAR Model Accuracy vs Epsilon")
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()
# Plot several examples vs their adversarial samples at each epsilon for fgms attack
cnt = 0
# 8 is the separation between images
# 20 is the size of the printed image
plt.figure(figsize=(8,20))
for i in range(len(fgsm_epsilons)):
for j in range(2):
cnt += 1
plt.subplot(len(fgsm_epsilons),2,cnt)
plt.xticks([], [])
plt.yticks([], [])
if j==0:
plt.ylabel("Eps: {}".format(fgsm_epsilons[i]), fontsize=14)
orig,adv,ex = cifar_fgsm_orig_examples[i][0]
plt.title("target "+"{} -> {}".format(classes[orig], classes[adv])+ " predicted")
plt.imshow(ex[0].transpose(1,2,0), cmap="gray")
else:
orig,adv,ex = cifar_fgsm_examples[i][0]
plt.title("predicted "+"{} -> {}".format(classes[orig], classes[adv])+ " attacked")
plt.imshow(ex[0].transpose(1,2,0), cmap="gray")
plt.tight_layout()
plt.show()
#Accuracy after attack vs epsilon
plt.figure(figsize=(5,5))
plt.plot(ill_epsilons, cifar_ill_accuracies, "*-", color='R')
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.xticks(np.arange(0, 17, step=2))
plt.title("Iterative Least Likely vs CIFAR Model / Accuracy vs Epsilon")
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()
# Plot several examples vs their adversarial samples at each epsilon for iterative
# least likely attack.
cnt = 0
# 8 is the separation between images
# 20 is the size of the printed image
plt.figure(figsize=(8,20))
for i in range(len(ill_epsilons)):
for j in range(2):
cnt += 1
plt.subplot(len(ill_epsilons),2,cnt)
plt.xticks([], [])
plt.yticks([], [])
if j==0:
plt.ylabel("Eps: {}".format(ill_epsilons[i]), fontsize=14)
orig,adv,ex = cifar_ill_orig_examples[i][0]
plt.title("target "+"{} -> {}".format(classes[orig], classes[adv])+ " predicted")
plt.imshow(ex[0].transpose(1,2,0), cmap="gray")
else:
orig,adv,ex = cifar_ill_examples[i][0]
plt.title("predicted "+"{} -> {}".format(classes[orig], classes[adv])+ " attacked")
plt.imshow(ex[0].transpose(1,2,0), cmap="gray")
plt.tight_layout()
plt.show()
```
|
github_jupyter
|
[**Blueprints for Text Analysis Using Python**](https://github.com/blueprints-for-text-analytics-python/blueprints-text)
Jens Albrecht, Sidharth Ramachandran, Christian Winkler
**If you like the book or the code examples here, please leave a friendly comment on [Amazon.com](https://www.amazon.com/Blueprints-Text-Analytics-Using-Python/dp/149207408X)!**
<img src="../rating.png" width="100"/>
# Chapter 5:<div class='tocSkip'/>
# Feature Engineering and Syntactic Similarity
## Remark<div class='tocSkip'/>
The code in this notebook differs slightly from the printed book.
Several layout and formatting commands, like `figsize` to control figure size or subplot commands are removed in the book.
All of this is done to simplify the code in the book and put the focus on the important parts instead of formatting.
## Setup<div class='tocSkip'/>
Set directory locations. If working on Google Colab: copy files and install required libraries.
```
import sys, os
ON_COLAB = 'google.colab' in sys.modules
if ON_COLAB:
GIT_ROOT = 'https://github.com/blueprints-for-text-analytics-python/blueprints-text/raw/master'
os.system(f'wget {GIT_ROOT}/ch05/setup.py')
%run -i setup.py
```
## Load Python Settings<div class="tocSkip"/>
Common imports, defaults for formatting in Matplotlib, Pandas etc.
```
%run "$BASE_DIR/settings.py"
%reload_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = 'png'
```
# Data preparation
```
sentences = ["It was the best of times",
"it was the worst of times",
"it was the age of wisdom",
"it was the age of foolishness"]
tokenized_sentences = [[t for t in sentence.split()] for sentence in sentences]
vocabulary = set([w for s in tokenized_sentences for w in s])
import pandas as pd
[[w, i] for i,w in enumerate(vocabulary)]
```
# One-hot by hand
```
def onehot_encode(tokenized_sentence):
return [1 if w in tokenized_sentence else 0 for w in vocabulary]
onehot = [onehot_encode(tokenized_sentence) for tokenized_sentence in tokenized_sentences]
for (sentence, oh) in zip(sentences, onehot):
print("%s: %s" % (oh, sentence))
pd.DataFrame(onehot, columns=vocabulary)
sim = [onehot[0][i] & onehot[1][i] for i in range(0, len(vocabulary))]
sum(sim)
import numpy as np
np.dot(onehot[0], onehot[1])
np.dot(onehot, onehot[1])
```
## Out of vocabulary
```
onehot_encode("the age of wisdom is the best of times".split())
onehot_encode("John likes to watch movies. Mary likes movies too.".split())
```
## document term matrix
```
onehot
```
## similarities
```
import numpy as np
np.dot(onehot, np.transpose(onehot))
```
# scikit learn one-hot vectorization
```
from sklearn.preprocessing import MultiLabelBinarizer
lb = MultiLabelBinarizer()
lb.fit([vocabulary])
lb.transform(tokenized_sentences)
```
# CountVectorizer
```
from sklearn.feature_extraction.text import CountVectorizer
cv = CountVectorizer()
more_sentences = sentences + ["John likes to watch movies. Mary likes movies too.",
"Mary also likes to watch football games."]
pd.DataFrame(more_sentences)
cv.fit(more_sentences)
print(cv.get_feature_names())
dt = cv.transform(more_sentences)
dt
pd.DataFrame(dt.toarray(), columns=cv.get_feature_names())
from sklearn.metrics.pairwise import cosine_similarity
cosine_similarity(dt[0], dt[1])
len(more_sentences)
pd.DataFrame(cosine_similarity(dt, dt))
```
# TF/IDF
```
from sklearn.feature_extraction.text import TfidfTransformer
tfidf = TfidfTransformer()
tfidf_dt = tfidf.fit_transform(dt)
pd.DataFrame(tfidf_dt.toarray(), columns=cv.get_feature_names())
pd.DataFrame(cosine_similarity(tfidf_dt, tfidf_dt))
headlines = pd.read_csv(ABCNEWS_FILE, parse_dates=["publish_date"])
headlines.head()
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf = TfidfVectorizer()
dt = tfidf.fit_transform(headlines["headline_text"])
dt
dt.data.nbytes
%%time
cosine_similarity(dt[0:10000], dt[0:10000])
```
## Stopwords
```
from spacy.lang.en.stop_words import STOP_WORDS as stopwords
print(len(stopwords))
tfidf = TfidfVectorizer(stop_words=stopwords)
dt = tfidf.fit_transform(headlines["headline_text"])
dt
```
## min_df
```
tfidf = TfidfVectorizer(stop_words=stopwords, min_df=2)
dt = tfidf.fit_transform(headlines["headline_text"])
dt
tfidf = TfidfVectorizer(stop_words=stopwords, min_df=.0001)
dt = tfidf.fit_transform(headlines["headline_text"])
dt
```
## max_df
```
tfidf = TfidfVectorizer(stop_words=stopwords, max_df=0.1)
dt = tfidf.fit_transform(headlines["headline_text"])
dt
tfidf = TfidfVectorizer(max_df=0.1)
dt = tfidf.fit_transform(headlines["headline_text"])
dt
```
## n-grams
```
tfidf = TfidfVectorizer(stop_words=stopwords, ngram_range=(1,2), min_df=2)
dt = tfidf.fit_transform(headlines["headline_text"])
print(dt.shape)
print(dt.data.nbytes)
tfidf = TfidfVectorizer(stop_words=stopwords, ngram_range=(1,3), min_df=2)
dt = tfidf.fit_transform(headlines["headline_text"])
print(dt.shape)
print(dt.data.nbytes)
```
## Lemmas
```
from tqdm.auto import tqdm
import spacy
nlp = spacy.load("en")
nouns_adjectives_verbs = ["NOUN", "PROPN", "ADJ", "ADV", "VERB"]
for i, row in tqdm(headlines.iterrows(), total=len(headlines)):
doc = nlp(str(row["headline_text"]))
headlines.at[i, "lemmas"] = " ".join([token.lemma_ for token in doc])
headlines.at[i, "nav"] = " ".join([token.lemma_ for token in doc if token.pos_ in nouns_adjectives_verbs])
headlines.head()
tfidf = TfidfVectorizer(stop_words=stopwords)
dt = tfidf.fit_transform(headlines["lemmas"].map(str))
dt
tfidf = TfidfVectorizer(stop_words=stopwords)
dt = tfidf.fit_transform(headlines["nav"].map(str))
dt
```
## remove top 10,000
```
top_10000 = pd.read_csv("https://raw.githubusercontent.com/first20hours/google-10000-english/master/google-10000-english.txt", header=None)
tfidf = TfidfVectorizer(stop_words=set(top_10000.iloc[:,0].values))
dt = tfidf.fit_transform(headlines["nav"].map(str))
dt
tfidf = TfidfVectorizer(ngram_range=(1,2), stop_words=set(top_10000.iloc[:,0].values), min_df=2)
dt = tfidf.fit_transform(headlines["nav"].map(str))
dt
```
## Finding document most similar to made-up document
```
tfidf = TfidfVectorizer(stop_words=stopwords, min_df=2)
dt = tfidf.fit_transform(headlines["lemmas"].map(str))
dt
made_up = tfidf.transform(["australia and new zealand discuss optimal apple size"])
sim = cosine_similarity(made_up, dt)
sim[0]
headlines.iloc[np.argsort(sim[0])[::-1][0:5]][["publish_date", "lemmas"]]
```
# Finding the most similar documents
```
# there are "test" headlines in the corpus
stopwords.add("test")
tfidf = TfidfVectorizer(stop_words=stopwords, ngram_range=(1,2), min_df=2, norm='l2')
dt = tfidf.fit_transform(headlines["headline_text"])
```
### Timing Cosine Similarity
```
%%time
cosine_similarity(dt[0:10000], dt[0:10000], dense_output=False)
%%time
r = cosine_similarity(dt[0:10000], dt[0:10000])
r[r > 0.9999] = 0
print(np.argmax(r))
%%time
r = cosine_similarity(dt[0:10000], dt[0:10000], dense_output=False)
r[r > 0.9999] = 0
print(np.argmax(r))
```
### Timing Dot-Product
```
%%time
r = np.dot(dt[0:10000], np.transpose(dt[0:10000]))
r[r > 0.9999] = 0
print(np.argmax(r))
```
## Batch
```
%%time
batch = 10000
max_sim = 0.0
max_a = None
max_b = None
for a in range(0, dt.shape[0], batch):
for b in range(0, a+batch, batch):
print(a, b)
#r = np.dot(dt[a:a+batch], np.transpose(dt[b:b+batch]))
r = cosine_similarity(dt[a:a+batch], dt[b:b+batch], dense_output=False)
# eliminate identical vectors
# by setting their similarity to np.nan which gets sorted out
r[r > 0.9999] = 0
sim = r.max()
if sim > max_sim:
# argmax returns a single value which we have to
# map to the two dimensions
(max_a, max_b) = np.unravel_index(np.argmax(r), r.shape)
# adjust offsets in corpus (this is a submatrix)
max_a += a
max_b += b
max_sim = sim
print(max_a, max_b)
print(max_sim)
pd.set_option('max_colwidth', -1)
headlines.iloc[[max_a, max_b]][["publish_date", "headline_text"]]
```
# Finding most related words
```
tfidf_word = TfidfVectorizer(stop_words=stopwords, min_df=1000)
dt_word = tfidf_word.fit_transform(headlines["headline_text"])
r = cosine_similarity(dt_word.T, dt_word.T)
np.fill_diagonal(r, 0)
voc = tfidf_word.get_feature_names()
size = r.shape[0] # quadratic
for index in np.argsort(r.flatten())[::-1][0:40]:
a = int(index/size)
b = index%size
if a > b: # avoid repetitions
print('"%s" related to "%s"' % (voc[a], voc[b]))
```
|
github_jupyter
|
# PixelCNN
**Author:** [ADMoreau](https://github.com/ADMoreau)<br>
**Date created:** 2020/05/17<br>
**Last modified:** 2020/05/23<br>
**Description:** PixelCNN implemented in Keras.
## Introduction
PixelCNN is a generative model proposed in 2016 by van den Oord et al.
(reference: [Conditional Image Generation with PixelCNN Decoders](https://arxiv.org/abs/1606.05328)).
It is designed to generate images (or other data types) iteratively,
from an input vector where the probability distribution of prior elements dictates the
probability distribution of later elements. In the following example, images are generated
in this fashion, pixel-by-pixel, via a masked convolution kernel that only looks at data
from previously generated pixels (origin at the top left) to generate later pixels.
During inference, the output of the network is used as a probability ditribution
from which new pixel values are sampled to generate a new image
(here, with MNIST, the pixels values are either black or white).
```
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tqdm import tqdm
```
## Getting the Data
```
# Model / data parameters
num_classes = 10
input_shape = (28, 28, 1)
n_residual_blocks = 5
# The data, split between train and test sets
(x, _), (y, _) = keras.datasets.mnist.load_data()
# Concatenate all of the images together
data = np.concatenate((x, y), axis=0)
# Round all pixel values less than 33% of the max 256 value to 0
# anything above this value gets rounded up to 1 so that all values are either
# 0 or 1
data = np.where(data < (0.33 * 256), 0, 1)
data = data.astype(np.float32)
```
## Create two classes for the requisite Layers for the model
```
# The first layer is the PixelCNN layer. This layer simply
# builds on the 2D convolutional layer, but includes masking.
class PixelConvLayer(layers.Layer):
def __init__(self, mask_type, **kwargs):
super(PixelConvLayer, self).__init__()
self.mask_type = mask_type
self.conv = layers.Conv2D(**kwargs)
def build(self, input_shape):
# Build the conv2d layer to initialize kernel variables
self.conv.build(input_shape)
# Use the initialized kernel to create the mask
kernel_shape = self.conv.kernel.get_shape()
self.mask = np.zeros(shape=kernel_shape)
self.mask[: kernel_shape[0] // 2, ...] = 1.0
self.mask[kernel_shape[0] // 2, : kernel_shape[1] // 2, ...] = 1.0
if self.mask_type == "B":
self.mask[kernel_shape[0] // 2, kernel_shape[1] // 2, ...] = 1.0
def call(self, inputs):
self.conv.kernel.assign(self.conv.kernel * self.mask)
return self.conv(inputs)
# Next, we build our residual block layer.
# This is just a normal residual block, but based on the PixelConvLayer.
class ResidualBlock(keras.layers.Layer):
def __init__(self, filters, **kwargs):
super(ResidualBlock, self).__init__(**kwargs)
self.conv1 = keras.layers.Conv2D(
filters=filters, kernel_size=1, activation="relu"
)
self.pixel_conv = PixelConvLayer(
mask_type="B",
filters=filters // 2,
kernel_size=3,
activation="relu",
padding="same",
)
self.conv2 = keras.layers.Conv2D(
filters=filters, kernel_size=1, activation="relu"
)
def call(self, inputs):
x = self.conv1(inputs)
x = self.pixel_conv(x)
x = self.conv2(x)
return keras.layers.add([inputs, x])
```
## Build the model based on the original paper
```
inputs = keras.Input(shape=input_shape)
x = PixelConvLayer(
mask_type="A", filters=128, kernel_size=7, activation="relu", padding="same"
)(inputs)
for _ in range(n_residual_blocks):
x = ResidualBlock(filters=128)(x)
for _ in range(2):
x = PixelConvLayer(
mask_type="B",
filters=128,
kernel_size=1,
strides=1,
activation="relu",
padding="valid",
)(x)
out = keras.layers.Conv2D(
filters=1, kernel_size=1, strides=1, activation="sigmoid", padding="valid"
)(x)
pixel_cnn = keras.Model(inputs, out)
adam = keras.optimizers.Adam(learning_rate=0.0005)
pixel_cnn.compile(optimizer=adam, loss="binary_crossentropy")
pixel_cnn.summary()
pixel_cnn.fit(
x=data, y=data, batch_size=128, epochs=50, validation_split=0.1, verbose=2
)
```
## Demonstration
The PixelCNN cannot generate the full image at once, and must instead generate each pixel in
order, append the last generated pixel to the current image, and feed the image back into the
model to repeat the process.
```
from IPython.display import Image, display
# Create an empty array of pixels.
batch = 4
pixels = np.zeros(shape=(batch,) + (pixel_cnn.input_shape)[1:])
batch, rows, cols, channels = pixels.shape
# Iterate the pixels because generation has to be done sequentially pixel by pixel.
for row in tqdm(range(rows)):
for col in range(cols):
for channel in range(channels):
# Feed the whole array and retrieving the pixel value probabilities for the next
# pixel.
probs = pixel_cnn.predict(pixels)[:, row, col, channel]
# Use the probabilities to pick pixel values and append the values to the image
# frame.
pixels[:, row, col, channel] = tf.math.ceil(
probs - tf.random.uniform(probs.shape)
)
def deprocess_image(x):
# Stack the single channeled black and white image to rgb values.
x = np.stack((x, x, x), 2)
# Undo preprocessing
x *= 255.0
# Convert to uint8 and clip to the valid range [0, 255]
x = np.clip(x, 0, 255).astype("uint8")
return x
# Iterate the generated images and plot them with matplotlib.
for i, pic in enumerate(pixels):
keras.preprocessing.image.save_img(
"generated_image_{}.png".format(i), deprocess_image(np.squeeze(pic, -1))
)
display(Image("generated_image_0.png"))
display(Image("generated_image_1.png"))
display(Image("generated_image_2.png"))
display(Image("generated_image_3.png"))
```
|
github_jupyter
|
# "Poleval 2021 through wav2vec2"
> "Trying for pronunciation recovery"
- toc: false
- branch: master
- comments: true
- hidden: true
- categories: [wav2vec2, poleval, colab]
```
%%capture
!pip install gdown
!gdown https://drive.google.com/uc?id=1b6MyyqgA9D1U7DX3Vtgda7f9ppkxjCXJ
%%capture
!tar zxvf poleval_wav.train.tar.gz && rm poleval_wav.train.tar.gz
%%capture
!pip install librosa webrtcvad
#collapse-hide
# VAD wrapper is taken from PyTorch Speaker Verification:
# https://github.com/HarryVolek/PyTorch_Speaker_Verification
# Copyright (c) 2019, HarryVolek
# License: BSD-3-Clause
# based on https://github.com/wiseman/py-webrtcvad/blob/master/example.py
# Copyright (c) 2016 John Wiseman
# License: MIT
import collections
import contextlib
import numpy as np
import sys
import librosa
import wave
import webrtcvad
#from hparam import hparam as hp
sr = 16000
def read_wave(path, sr):
"""Reads a .wav file.
Takes the path, and returns (PCM audio data, sample rate).
Assumes sample width == 2
"""
with contextlib.closing(wave.open(path, 'rb')) as wf:
num_channels = wf.getnchannels()
assert num_channels == 1
sample_width = wf.getsampwidth()
assert sample_width == 2
sample_rate = wf.getframerate()
assert sample_rate in (8000, 16000, 32000, 48000)
pcm_data = wf.readframes(wf.getnframes())
data, _ = librosa.load(path, sr)
assert len(data.shape) == 1
assert sr in (8000, 16000, 32000, 48000)
return data, pcm_data
class Frame(object):
"""Represents a "frame" of audio data."""
def __init__(self, bytes, timestamp, duration):
self.bytes = bytes
self.timestamp = timestamp
self.duration = duration
def frame_generator(frame_duration_ms, audio, sample_rate):
"""Generates audio frames from PCM audio data.
Takes the desired frame duration in milliseconds, the PCM data, and
the sample rate.
Yields Frames of the requested duration.
"""
n = int(sample_rate * (frame_duration_ms / 1000.0) * 2)
offset = 0
timestamp = 0.0
duration = (float(n) / sample_rate) / 2.0
while offset + n < len(audio):
yield Frame(audio[offset:offset + n], timestamp, duration)
timestamp += duration
offset += n
def vad_collector(sample_rate, frame_duration_ms,
padding_duration_ms, vad, frames):
"""Filters out non-voiced audio frames.
Given a webrtcvad.Vad and a source of audio frames, yields only
the voiced audio.
Uses a padded, sliding window algorithm over the audio frames.
When more than 90% of the frames in the window are voiced (as
reported by the VAD), the collector triggers and begins yielding
audio frames. Then the collector waits until 90% of the frames in
the window are unvoiced to detrigger.
The window is padded at the front and back to provide a small
amount of silence or the beginnings/endings of speech around the
voiced frames.
Arguments:
sample_rate - The audio sample rate, in Hz.
frame_duration_ms - The frame duration in milliseconds.
padding_duration_ms - The amount to pad the window, in milliseconds.
vad - An instance of webrtcvad.Vad.
frames - a source of audio frames (sequence or generator).
Returns: A generator that yields PCM audio data.
"""
num_padding_frames = int(padding_duration_ms / frame_duration_ms)
# We use a deque for our sliding window/ring buffer.
ring_buffer = collections.deque(maxlen=num_padding_frames)
# We have two states: TRIGGERED and NOTTRIGGERED. We start in the
# NOTTRIGGERED state.
triggered = False
voiced_frames = []
for frame in frames:
is_speech = vad.is_speech(frame.bytes, sample_rate)
if not triggered:
ring_buffer.append((frame, is_speech))
num_voiced = len([f for f, speech in ring_buffer if speech])
# If we're NOTTRIGGERED and more than 90% of the frames in
# the ring buffer are voiced frames, then enter the
# TRIGGERED state.
if num_voiced > 0.9 * ring_buffer.maxlen:
triggered = True
start = ring_buffer[0][0].timestamp
# We want to yield all the audio we see from now until
# we are NOTTRIGGERED, but we have to start with the
# audio that's already in the ring buffer.
for f, s in ring_buffer:
voiced_frames.append(f)
ring_buffer.clear()
else:
# We're in the TRIGGERED state, so collect the audio data
# and add it to the ring buffer.
voiced_frames.append(frame)
ring_buffer.append((frame, is_speech))
num_unvoiced = len([f for f, speech in ring_buffer if not speech])
# If more than 90% of the frames in the ring buffer are
# unvoiced, then enter NOTTRIGGERED and yield whatever
# audio we've collected.
if num_unvoiced > 0.9 * ring_buffer.maxlen:
triggered = False
yield (start, frame.timestamp + frame.duration)
ring_buffer.clear()
voiced_frames = []
# If we have any leftover voiced audio when we run out of input,
# yield it.
if voiced_frames:
yield (start, frame.timestamp + frame.duration)
def VAD_chunk(aggressiveness, path):
audio, byte_audio = read_wave(path, sr)
vad = webrtcvad.Vad(int(aggressiveness))
frames = frame_generator(20, byte_audio, sr)
frames = list(frames)
times = vad_collector(sr, 20, 200, vad, frames)
speech_times = []
speech_segs = []
for i, time in enumerate(times):
start = np.round(time[0],decimals=2)
end = np.round(time[1],decimals=2)
j = start
while j + .4 < end:
end_j = np.round(j+.4,decimals=2)
speech_times.append((j, end_j))
speech_segs.append(audio[int(j*sr):int(end_j*sr)])
j = end_j
else:
speech_times.append((j, end))
speech_segs.append(audio[int(j*sr):int(end*sr)])
return speech_times, speech_segs
#collapse-hide
# Based on code from PyTorch Speaker Verification:
# https://github.com/HarryVolek/PyTorch_Speaker_Verification
# Copyright (c) 2019, HarryVolek
# Additions Copyright (c) 2021, Jim O'Regan
# License: MIT
import numpy as np
# wav2vec2's max duration is 40 seconds, using 39 by default
# to be a little safer
def vad_concat(times, segs, max_duration=39.0):
"""
Concatenate continuous times and their segments, where the end time
of a segment is the same as the start time of the next
Parameters:
times: list of tuple (start, end)
segs: list of segments (audio frames)
max_duration: maximum duration of the resulting concatenated
segments; the kernel size of wav2vec2 is 40 seconds, so
the default max_duration is 39, to ensure the resulting
list of segments will fit
Returns:
concat_times: list of tuple (start, end)
concat_segs: list of segments (audio frames)
"""
absolute_maximum=40.0
if max_duration > absolute_maximum:
raise Exception('`max_duration` {:.2f} larger than kernel size (40 seconds)'.format(max_duration))
# we take 0.0 to mean "don't concatenate"
do_concat = (max_duration != 0.0)
concat_seg = []
concat_times = []
seg_concat = segs[0]
time_concat = times[0]
for i in range(0, len(times)-1):
can_concat = (times[i+1][1] - time_concat[0]) < max_duration
if time_concat[1] == times[i+1][0] and do_concat and can_concat:
seg_concat = np.concatenate((seg_concat, segs[i+1]))
time_concat = (time_concat[0], times[i+1][1])
else:
concat_seg.append(seg_concat)
seg_concat = segs[i+1]
concat_times.append(time_concat)
time_concat = times[i+1]
else:
concat_seg.append(seg_concat)
concat_times.append(time_concat)
return concat_times, concat_seg
def make_dataset(concat_times, concat_segs):
starts = [s[0] for s in concat_times]
ends = [s[1] for s in concat_times]
return {'start': starts,
'end': ends,
'speech': concat_segs}
%%capture
!pip install datasets
from datasets import Dataset
def vad_to_dataset(path, max_duration):
t,s = VAD_chunk(3, path)
if max_duration > 0.0:
ct, cs = vad_concat(t, s, max_duration)
dset = make_dataset(ct, cs)
else:
dset = make_dataset(t, s)
return Dataset.from_dict(dset)
%%capture
!pip install -q transformers
%%capture
from transformers import Wav2Vec2Processor, Wav2Vec2ForCTC
# load model and tokenizer
processor = Wav2Vec2Processor.from_pretrained("mbien/wav2vec2-large-xlsr-polish")
model = Wav2Vec2ForCTC.from_pretrained("mbien/wav2vec2-large-xlsr-polish")
model.to("cuda")
def speech_file_to_array_fn(batch):
import torchaudio
speech_array, sampling_rate = torchaudio.load(batch["path"])
batch["speech"] = speech_array[0].numpy()
batch["sampling_rate"] = sampling_rate
batch["target_text"] = batch["sentence"]
return batch
def evaluate(batch):
import torch
inputs = processor(batch["speech"], sampling_rate=16_000, return_tensors="pt", padding=True)
with torch.no_grad():
logits = model(inputs.input_values.to("cuda"), attention_mask=inputs.attention_mask.to("cuda")).logits
pred_ids = torch.argmax(logits, dim=-1)
batch["pred_strings"] = processor.batch_decode(pred_ids)
return batch
import json
def process_wave(filename, duration):
import json
dataset = vad_to_dataset(filename, duration)
result = dataset.map(evaluate, batched=True, batch_size=16)
speechless = result.remove_columns(['speech'])
d=speechless.to_dict()
tlog = list()
for i in range(0, len(d['end']) - 1):
out = dict()
out['start'] = d['start'][i]
out['end'] = d['end'][i]
out['transcript'] = d['pred_strings'][i]
tlog.append(out)
with open('{}.tlog'.format(filename), 'w') as outfile:
json.dump(tlog, outfile)
import glob
for f in glob.glob('/content/poleval_final_dataset_wav/train/*.wav'):
print(f)
process_wave(f, 10.0)
!find . -name '*tlog'|zip poleval-train.zip -@
```
|
github_jupyter
|
# Tune a CNN on MNIST
This tutorial walks through using Ax to tune two hyperparameters (learning rate and momentum) for a PyTorch CNN on the MNIST dataset trained using SGD with momentum.
```
import torch
import numpy as np
from ax.plot.contour import plot_contour
from ax.plot.trace import optimization_trace_single_method
from ax.service.managed_loop import optimize
from ax.utils.notebook.plotting import render, init_notebook_plotting
from ax.utils.tutorials.cnn_utils import load_mnist, train, evaluate, CNN
init_notebook_plotting()
torch.manual_seed(12345)
dtype = torch.float
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
```
## 1. Load MNIST data
First, we need to load the MNIST data and partition it into training, validation, and test sets.
Note: this will download the dataset if necessary.
```
BATCH_SIZE = 512
train_loader, valid_loader, test_loader = load_mnist(batch_size=BATCH_SIZE)
```
## 2. Define function to optimize
In this tutorial, we want to optimize classification accuracy on the validation set as a function of the learning rate and momentum. The function takes in a parameterization (set of parameter values), computes the classification accuracy, and returns a dictionary of metric name ('accuracy') to a tuple with the mean and standard error.
```
def train_evaluate(parameterization):
net = CNN()
net = train(net=net, train_loader=train_loader, parameters=parameterization, dtype=dtype, device=device)
return evaluate(
net=net,
data_loader=valid_loader,
dtype=dtype,
device=device,
)
```
## 3. Run the optimization loop
Here, we set the bounds on the learning rate and momentum and set the parameter space for the learning rate to be on a log scale.
```
best_parameters, values, experiment, model = optimize(
parameters=[
{"name": "lr", "type": "range", "bounds": [1e-6, 0.4], "log_scale": True},
{"name": "momentum", "type": "range", "bounds": [0.0, 1.0]},
],
evaluation_function=train_evaluate,
objective_name='accuracy',
)
```
We can introspect the optimal parameters and their outcomes:
```
best_parameters
means, covariances = values
means, covariances
```
## 4. Plot response surface
Contour plot showing classification accuracy as a function of the two hyperparameters.
The black squares show points that we have actually run, notice how they are clustered in the optimal region.
```
render(plot_contour(model=model, param_x='lr', param_y='momentum', metric_name='accuracy'))
```
## 5. Plot best objective as function of the iteration
Show the model accuracy improving as we identify better hyperparameters.
```
# `plot_single_method` expects a 2-d array of means, because it expects to average means from multiple
# optimization runs, so we wrap out best objectives array in another array.
best_objectives = np.array([[trial.objective_mean*100 for trial in experiment.trials.values()]])
best_objective_plot = optimization_trace_single_method(
y=np.maximum.accumulate(best_objectives, axis=1),
title="Model performance vs. # of iterations",
ylabel="Classification Accuracy, %",
)
render(best_objective_plot)
```
## 6. Train CNN with best hyperparameters and evaluate on test set
Note that the resulting accuracy on the test set might not be exactly the same as the maximum accuracy achieved on the evaluation set throughout optimization.
```
data = experiment.fetch_data()
df = data.df
best_arm_name = df.arm_name[df['mean'] == df['mean'].max()].values[0]
best_arm = experiment.arms_by_name[best_arm_name]
best_arm
combined_train_valid_set = torch.utils.data.ConcatDataset([
train_loader.dataset.dataset,
valid_loader.dataset.dataset,
])
combined_train_valid_loader = torch.utils.data.DataLoader(
combined_train_valid_set,
batch_size=BATCH_SIZE,
shuffle=True,
)
net = train(
net=CNN(),
train_loader=combined_train_valid_loader,
parameters=best_arm.parameters,
dtype=dtype,
device=device,
)
test_accuracy = evaluate(
net=net,
data_loader=test_loader,
dtype=dtype,
device=device,
)
print(f"Classification Accuracy (test set): {round(test_accuracy*100, 2)}%")
```
|
github_jupyter
|
```
#import sys
#!{sys.executable} -m pip install --user alerce
```
# light_transient_matching
## Matches DESI observations to ALERCE and DECAM ledger objects
This code predominately takes in data from the ALERCE and DECAM ledger brokers and identifies DESI observations within 2 arcseconds of those objects, suspected to be transients. It then prepares those matches to be fed into our [CNN code](https://github.com/MatthewPortman/timedomain/blob/master/cronjobs/transient_matching/modified_cnn_classify_data_gradCAM.ipynb) which attempts to identify the class of these transients.
The main matching algorithm uses astropy's **match_coordinate_sky** to match 1-to-1 targets with the objects from the two ledgers. Wrapping functions handle data retrieval from both the ledgers as well as from DESI and prepare this data to be fed into **match_coordinate_sky**. Since ALERCE returns a small enough (pandas) dataframe, we do not need to precondition the input much. However, DECAM has many more objects to match so we use a two-stage process: an initial 2 degree match to tile RA's/DEC's and a second closer 1 arcsecond match to individual targets.
As the code is a work in progress, please forgive any redundancies. We are attempting to merge all of the above (neatly) into the same two or three matching/handling functions!
```
from astropy.io import fits
from astropy.table import Table
from astropy import units as u
from astropy.time import Time
from astropy.coordinates import SkyCoord, match_coordinates_sky, Angle
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from glob import glob
import sys
import sqlite3
import os
from desispec.io import read_spectra, write_spectra
from desispec.spectra import Spectra
# Some handy global variables
global db_filename
db_filename = '/global/cfs/cdirs/desi/science/td/daily-search/transients_search.db'
global exposure_path
exposure_path = os.environ["DESI_SPECTRO_REDUX"]
global color_band
color_band = "r"
global minDist
minDist = {}
global today
today = Time.now()
```
## Necessary functions
```
# Grabbing the file names
def all_candidate_filenames(transient_dir: str):
# This function grabs the names of all input files in the transient directory and does some python string manipulation
# to grab the names of the input files with full path and the filenames themselves.
try:
filenames_read = glob(transient_dir + "/*.fits") # Hardcoding is hopefully a temporary measure.
except:
print("Could not grab/find any fits in the transient spectra directory:")
print(transient_dir)
filenames_read = [] # Just in case
#filenames_out = [] # Just in case
raise SystemExit("Exiting.")
#else:
#filenames_out = [s.split(".")[0] for s in filenames_read]
#filenames_out = [s.split("/")[-1] for s in filenames_read]
#filenames_out = [s.replace("in", "out") for s in filenames_out]
return filenames_read #, filenames_out
#path_to_transient = "/global/cfs/cdirs/desi/science/td/daily-search/desitrip/out"
#print(all_candidate_filenames(path_to_transient)[1])
# From ALeRCE_ledgermaker https://github.com/alercebroker/alerce_client
# I have had trouble importing this before so I copy, paste it, and modify it here.
# I also leave these imports here because why not?
import requests
from alerce.core import Alerce
from alerce.exceptions import APIError
alerce_client = Alerce()
# Choose cone_radius of diameter of tile so that, whatever coord I choose for ra_in, dec_in, we cover the whole tile
def access_alerts(lastmjd_in=[], ra_in = None, dec_in = None, cone_radius = 3600*4.01, classifier='stamp_classifier', class_names=['SN', 'AGN']):
if type(class_names) is not list:
raise TypeError('Argument `class_names` must be a list.')
dataframes = []
if not lastmjd_in:
date_range = 60
lastmjd_in = [Time.now().mjd - 60, Time.now().mjd]
print('Defaulting to a lastmjd range of', str(date_range), 'days before today.')
#print("lastmjd:", lastmjd_in)
for class_name in class_names:
data = alerce_client.query_objects(classifier=classifier,
class_name=class_name,
lastmjd=lastmjd_in,
ra = ra_in,
dec = dec_in,
radius = cone_radius, # in arcseconds
page_size = 5000,
order_by='oid',
order_mode='DESC',
format='pandas')
#if lastmjd is not None:
# select = data['lastmjd'] >= lastmjd
# data = data[select]
dataframes.append(data)
#print(pd.concat(dataframes).columns)
return pd.concat(dataframes).sort_values(by = 'lastmjd')
# From https://github.com/desihub/timedomain/blob/master/too_ledgers/decam_TAMU_ledgermaker.ipynb
# Function to grab decam data
from bs4 import BeautifulSoup
import json
import requests
def access_decam_data(url, overwrite=False):
"""Download reduced DECam transient data from Texas A&M.
Cache the data to avoid lengthy and expensive downloads.
Parameters
----------
url : str
URL for accessing the data.
overwrite : bool
Download new data and overwrite the cached data.
Returns
-------
decam_transients : pandas.DataFrame
Table of transient data.
"""
folders = url.split('/')
thedate = folders[-1] if len(folders[-1]) > 0 else folders[-2]
outfile = '{}.csv'.format(thedate)
if os.path.exists(outfile) and not overwrite:
# Access cached data.
decam_transients = pd.read_csv(outfile)
else:
# Download the DECam data index.
# A try/except is needed because the datahub SSL certificate isn't playing well with URL requests.
try:
decam_dets = requests.get(url, auth=('decam','tamudecam')).text
except:
requests.packages.urllib3.disable_warnings(requests.packages.urllib3.exceptions.InsecureRequestWarning)
decam_dets = requests.get(url, verify=False, auth=('decam','tamudecam')).text
# Convert transient index page into scrapable data using BeautifulSoup.
soup = BeautifulSoup(decam_dets)
# Loop through transient object summary JSON files indexed in the main transient page.
# Download the JSONs and dump the info into a Pandas table.
decam_transients = None
j = 0
for a in soup.find_all('a', href=True):
if 'object-summary.json' in a:
link = a['href'].replace('./', '')
summary_url = url + link
summary_text = requests.get(summary_url, verify=False, auth=('decam','tamudecam')).text
summary_data = json.loads(summary_text)
j += 1
#print('Accessing {:3d} {}'.format(j, summary_url)) # Modified by Matt
if decam_transients is None:
decam_transients = pd.DataFrame(summary_data, index=[0])
else:
decam_transients = pd.concat([decam_transients, pd.DataFrame(summary_data, index=[0])])
# Cache the data for future access.
print('Saving output to {}'.format(outfile))
decam_transients.to_csv(outfile, index=False)
return decam_transients
# Function to read in fits table info, RA, DEC, MJD and targetid if so desired
# Uses control parameter tile to determine if opening tile exposure file or not since headers are different
import logging
def read_fits_info(filepath: str, transient_candidate = True):
'''
if transient_candidate:
hdu_num = 1
else:
hdu_num = 5
'''
# Disabling INFO logging temporarily to suppress INFO level output/print from read_spectra
logging.disable(logging.INFO)
try:
spec_info = read_spectra(filepath).fibermap
except:
filename = filepath.split("/")[-1]
print("Could not open or use:", filename)
#print("In path:", filepath)
#print("Trying the next file...")
return np.array([]), np.array([]), 0, 0
headers = ['TARGETID', 'TARGET_RA', 'TARGET_DEC', 'LAST_MJD']
targ_info = {}
for head in headers:
try:
targ_info[head] = spec_info[head].data
except:
if not head == 'LAST_MJD': print("Failed to read in", head, "data. Continuing...")
targ_info[head] = False
# targ_id = spec_info['TARGETID'].data
# targ_ra = spec_info['TARGET_RA'].data # Now it's a numpy array
# targ_dec = spec_info['TARGET_DEC'].data
# targ_mjd = spec_info['LAST_MJD'] #.data
if np.any(targ_info['LAST_MJD']):
targ_mjd = Time(targ_info['LAST_MJD'][0], format = 'mjd')
elif transient_candidate:
targ_mjd = filepath.split("/")[-1].split("_")[-2] #to grab the date
targ_mjd = Time(targ_mjd, format = 'mjd') #.mjd
else:
print("Unable to determine observation mjd for", filename)
print("This target will not be considered.")
return np.array([]), np.array([]), 0, 0
'''
with fits.open(filepath) as hdu1:
data_table = Table(hdu1[hdu_num].data) #columns
targ_id = data_table['TARGETID']
targ_ra = data_table['TARGET_RA'].data # Now it's a numpy array
targ_dec = data_table['TARGET_DEC'].data
#targ_mjd = data_table['MJD'][0] some have different versions of this so this is a *bad* idea... at least now I know the try except works!
if tile:
targ_mjd = hdu1[hdu_num].header['MJD-OBS']
'''
# if tile and not np.all(targ_mjd):
# print("Unable to grab mjd from spectra, taking it from the filename...")
# targ_mjd = filepath.split("/")[-1].split("_")[-2] #to grab the date
# #targ_mjd = targ_mjd[:4]+"-"+targ_mjd[4:6]+"-"+targ_mjd[6:] # Adding dashes for Time
# targ_mjd = Time(targ_mjd, format = 'mjd') #.mjd
# Re-enabling logging for future calls if necessary
logging.disable(logging.NOTSET)
return targ_info["TARGET_RA"], targ_info["TARGET_DEC"], targ_mjd, targ_info["TARGETID"] #targ_ra, targ_dec, targ_mjd, targ_id
```
## Matching function
More or less the prototype to the later rendition used for DECAM. Will not be around in later versions of this notebook as I will be able to repurpose the DECAM code to do both. Planned obsolescence?
It may not be even worth it at this point... ah well!
```
# Prototype for the later, heftier matching function
# Will be deprecated, please reference commentary in inner_matching later for operation notes
def matching(path_in: str, max_sep: float, tile = False, date_dict = {}):
max_sep *= u.arcsec
#max_sep = Angle(max_sep*u.arcsec)
#if not target_ra_dec_date:
# target_ras, target_decs, obs_mjds = read_fits_ra_dec(path_in, tile)
#else:
# target_ras, target_decs, obs_mjds = target_ra_dec_date
#Look back 60 days from the DESI observations
days_back = 60
if not date_dict:
print("No RA's/DEC's fed in. Quitting.")
return np.array([]), np.array([])
all_trans_matches = []
all_alerts_matches = []
targetid_matches = []
for obs_mjd, ra_dec in date_dict.items():
# Grab RAs and DECs from input.
target_ras = ra_dec[:, 0]
target_decs = ra_dec[:, 1]
target_ids = np.int64(ra_dec[:, 2])
# Check for NaN's and remove which don't play nice with match_coordinates_sky
nan_ra = np.isnan(target_ras)
nan_dec = np.isnan(target_decs)
if np.any(nan_ra) or np.any(nan_dec):
print("NaNs found, removing them from array (not FITS) before match.")
#print("Original length (ra, dec): ", len(target_ras), len(target_decs))
nans = np.logical_not(np.logical_and(nan_ra, nan_dec))
target_ras = target_ras[nans] # Logic masking, probably more efficient
target_decs = target_decs[nans]
#print("Reduced length (ra, dec):", len(target_ras), len(target_decs))
# Some code used to test -- please ignore ******************
# Feed average to access alerts, perhaps that will speed things up/find better results
#avg_ra = np.average(target_ras)
#avg_dec = np.average(target_decs)
# coo_trans_search = SkyCoord(target_ras*u.deg, target_decs*u.deg)
# #print(coo_trans_search)
# idxs, d2d, _ = match_coordinates_sky(coo_trans_search, coo_trans_search, nthneighbor = 2)
# # for conesearch in alerce
# max_sep = np.max(d2d).arcsec + 2.1 # to expand a bit further than the furthest neighbor
# ra_in = coo_trans_search[0].ra
# dec_in = coo_trans_search[0].dec
# Some code used to test -- please ignore ******************
#print([obs_mjd - days_back, obs_mjd])
try:
alerts = access_alerts(lastmjd_in = [obs_mjd - days_back, obs_mjd],
ra_in = target_ras[0],
dec_in = target_decs[0], #cone_radius = max_sep,
class_names = ['SN']
) # Modified Julian Day .mjd
except:
#print("No SN matches ("+str(days_back)+" day range) for", obs_mjd)
#break
continue
# For each fits file, look at one month before the observation from Alerce
# Not sure kdtrees matter
# tree_name = "kdtree_" + str(obs_mjd - days_back)
alerts_ra = alerts['meanra'].to_numpy()
#print("Length of alerts: ", len(alerts_ra))
alerts_dec = alerts['meandec'].to_numpy()
# Converting to SkyCoord type arrays (really quite handy)
coo_trans_search = SkyCoord(target_ras*u.deg, target_decs*u.deg)
coo_alerts = SkyCoord(alerts_ra*u.deg, alerts_dec*u.deg)
# Some code used to test -- please ignore ******************
#ra_range = list(zip(*[(i, j) for i,j in zip(alerts_ra,alerts_dec) if (np.min(target_ras) < i and i < np.max(target_ras) and np.min(target_decs) < j and j < np.max(target_decs))]))
#try:
# ra_range = SkyCoord(ra_range[0]*u.deg, ra_range[1]*u.deg)
#except:
# continue
#print(ra_range)
#print(coo_trans_search)
#idx_alerts, d2d_trans, d3d_trans = match_coordinates_sky(coo_trans_search, ra_range)
#for i in coo_trans_search:
#print(i.separation(ra_range[3]))
#print(idx_alerts)
#print(np.min(d2d_trans))
#break
# Some code used to test -- please ignore ******************
idx_alerts, d2d_trans, d3d_trans = match_coordinates_sky(coo_trans_search, coo_alerts)
# Filtering by maximum separation and closest match
sep_constraint = d2d_trans < max_sep
trans_matches = coo_trans_search[sep_constraint]
alerts_matches = coo_alerts[idx_alerts[sep_constraint]]
targetid_matches = target_ids[sep_constraint]
#print(d2d_trans < max_sep)
minDist[obs_mjd] = np.min(d2d_trans)
# Adding everything to lists and outputting
if trans_matches.size:
all_trans_matches.append(trans_matches)
all_alerts_matches.append(alerts_matches)
sort_dist = np.sort(d2d_trans)
#print("Minimum distance found: ", sort_dist[0])
#print()
#break
#else:
#print("No matches found...\n")
#break
return all_trans_matches, all_alerts_matches, targetid_matches
```
## Matching to ALERCE
Runs a 5 arcsecond match of DESI to Alerce objects. Since everything is handled in functions, this part is quite clean.
From back when I was going to use *if __name__ == "__main__":*... those were the days
```
# Transient dir
path_to_transient = "/global/cfs/cdirs/desi/science/td/daily-search/desitrip/out"
# Grab paths
paths_to_fits = all_candidate_filenames(path_to_transient)
#print(len(paths_to_fits))
desi_info_dict = {}
target_ras, target_decs, obs_mjd, targ_ids = read_fits_info(paths_to_fits[0], transient_candidate = True)
desi_info_dict[obs_mjd] = np.column_stack((target_ras, target_decs, targ_ids))
'''
To be used when functions are properly combined.
initial_check(ledger_df = None, ledger_type = '')
closer_check(matches_dict = {}, ledger_df = None, ledger_type = '', exclusion_list = [])
'''
fail_count = 0
# Iterate through every fits file and grab all necessary info and plop it all together
for path in paths_to_fits[1:]:
target_ras, target_decs, obs_mjd, targ_ids = read_fits_info(path, transient_candidate = True)
if not obs_mjd:
fail_count += 1
continue
#try:
if obs_mjd in desi_info_dict.keys():
np.append(desi_info_dict[obs_mjd], np.array([target_ras, target_decs, targ_ids]).T, axis = 0)
else:
desi_info_dict[obs_mjd] = np.column_stack((target_ras, target_decs, targ_ids))
#desi_info_dict[obs_mjd].extend((target_ras, target_decs, targ_ids))
#except:
# continue
#desi_info_dict[obs_mjd] = np.column_stack((target_ras, target_decs, targ_ids))
#desi_info_dict[obs_mjd].append((target_ras, target_decs, targ_ids))
#trans_matches, _ = matching(path, 5.0, (all_desi_ras, all_desi_decs, all_obs_mjd))
# if trans_matches.size:
# all_trans_matches.append(trans_matches)
# all_alerts_matches.append(alerts_matches)
#print([i.mjd for i in sorted(desi_info_dict.keys())])
print(len(paths_to_fits))
print(len(desi_info_dict))
#print(fail_count)
```
```
# I was going to prepare everything by removing duplicate target ids but it's more trouble than it's worth and match_coordinates_sky can handle it
# Takes quite a bit of time... not much more I can do to speed things up though since querying Alerce for every individual date is the hang-up.
#print(len(paths_to_fits) - ledesi_info_dictfo_dict))
#print(fail_count)
#trans_matches, _, target_id_matches = matching("", 2.0, date_dict = temp_dict)
trans_matches, _, target_id_matches = matching("", 2.0, date_dict = desi_info_dict)
print(trans_matches)
print(target_id_matches)
print(sorted(minDist.values())[:5])
#for i in minDist.values():
# print(i)
```
## Matching to DECAM functions
Overwrite *read_fits_info* with older version to accommodate *read_spectra* error
```
# Read useful data from fits file, RA, DEC, target ID, and mjd as a leftover from previous use
def read_fits_info(filepath: str, transient_candidate = False):
if transient_candidate:
hdu_num = 1
else:
hdu_num = 5
try:
with fits.open(filepath) as hdu1:
data_table = Table(hdu1[hdu_num].data) #columns
targ_ID = data_table['TARGETID']
targ_ra = data_table['TARGET_RA'].data # Now it's a numpy array
targ_dec = data_table['TARGET_DEC'].data
#targ_mjd = data_table['MJD'][0] some have different versions of this so this is a *bad* idea... at least now I know the try except works!
# if transient_candidate:
# targ_mjd = hdu1[hdu_num].header['MJD-OBS'] # This is a string
# else:
# targ_mjd = data_table['MJD'].data
# targ_mjd = Time(targ_mjd[0], format = 'mjd')
except:
filename = filepath.split("/")[-1]
print("Could not open or use:", filename)
#print("In path:", filepath)
#print("Trying the next file...")
return np.array([]), np.array([]), np.array([])
return targ_ra, targ_dec, targ_ID #targ_mjd, targ_ID
# Grabbing the frame fits files
def glob_frames(exp_d: str):
# This function grabs the names of all input files in the transient directory and does some python string manipulation
# to grab the names of the input files with full path and the filenames themselves.
try:
filenames_read = glob(exp_d + "/cframe-" + color_band + "*.fits") # Only need one of b, r, z
# sframes not flux calibrated
# May want to use tiles... coadd (will need later, but not now)
except:
try:
filenames_read = glob(exp_d + "/frame-" + color_band + "*.fits") # Only need one of b, r, z
except:
print("Could not grab/find any fits in the exposure directory:")
print(exp_d)
filenames_read = [] # Just in case
#filenames_out = [] # Just in case
raise SystemExit("Exitting.")
#else:
#filenames_out = [s.split(".")[0] for s in filenames_read]
#filenames_out = [s.split("/")[-1] for s in filenames_read]
#filenames_out = [s.replace("in", "out") for s in filenames_out]
return filenames_read #, filenames_out
#path_to_transient = "/global/cfs/cdirs/desi/science/td/daily-search/desitrip/out"
#print(all_candidate_filenames(path_to_transient)[1])
```
## Match handling routines
The two functions below perform data handling/calling for the final match step.
The first, **initial_check** grabs all the tile RAs and DECS from the exposures and tiles SQL table, does some filtering, and sends the necessary information to the matching function. Currently designed to handle ALERCE as well but work has to be done to make sure it operates correctly.
```
def initial_check(ledger_df = None, ledger_type = ''):
query_date_start = "20210301"
#today = Time.now()
smushed_YMD = today.iso.split(" ")[0].replace("-","")
query_date_end = smushed_YMD
# Handy queries for debugging/useful info
query2 = "PRAGMA table_info(exposures)"
query3 = "PRAGMA table_info(tiles)"
# Crossmatch across tiles and exposures to grab obsdate via tileid
query_match = "SELECT distinct tilera, tiledec, obsdate, obsmjd, expid, exposures.tileid from exposures INNER JOIN tiles ON exposures.tileid = tiles.tileid where obsdate BETWEEN " + \
query_date_start + " AND " + query_date_end + ";"
'''
Some handy code for debugging
#cur.execute(query2)
#row2 = cur.fetchall()
#for i in row2:
# print(i[:])
'''
# Querying sql and returning a data type called sqlite3 row, it's kind of like a namedtuple/dictionary
conn = sqlite3.connect(db_filename)
conn.row_factory = sqlite3.Row # https://docs.python.org/3/library/sqlite3.html#sqlite3.Row
cur = conn.cursor()
cur.execute(query_match)
matches_list = cur.fetchall()
cur.close()
# I knew there was a way! THANK YOU!
# https://stackoverflow.com/questions/11276473/append-to-a-dict-of-lists-with-a-dict-comprehension
# Grabbing everything by obsdate from matches_list
date_dict = {k['obsdate'] : list(filter(lambda x:x['obsdate'] == k['obsdate'], matches_list)) for k in matches_list}
alert_matches_dict = {}
all_trans_matches = []
all_alerts_matches = []
# Grabbing DECAM ledger if not already fed in
if ledger_type.upper() == 'DECAM_TAMU':
if ledger_df.empty:
ledger_df = access_decam_data('https://datahub.geos.tamu.edu:8000/decam/LCData_Legacy/')
# Iterating through the dates and checking each tile observed on each date
# It is done in this way to cut down on calls to ALERCE since we go day by day
# It's also a convenient way to organize things
for date, row in date_dict.items():
date_str = str(date)
date_str = date_str[:4]+"-"+date_str[4:6]+"-"+date_str[6:] # Adding dashes for Time
obs_mjd = Time(date_str).mjd
# This method is *technically* safer than doing a double list comprehension with set albeit slower
# The lists are small enough that speed shouldn't matter here
unique_tileid = {i['tileid']: (i['tilera'], i['tiledec']) for i in row}
exposure_ras, exposure_decs = zip(*unique_tileid.values())
# Grabbing alerce ledger if not done already
if ledger_type.upper() == 'ALERCE':
if ledger_df.empty:
ledger_df = access_alerts(lastmjd = obs_mjd - 28) # Modified Julian Day #.mjd
elif ledger_type.upper() == 'DECAM_TAMU':
pass
else:
print("Cannot use alerts broker/ledger provided. Stopping before match.")
return {}
#Reatin tileid
tileid_arr = np.array(list(unique_tileid.keys()))
# Where the magic/matching happens
trans_matches, alert_matches, trans_ids, alerts_ids, _ = \
inner_matching(target_ids_in = tileid_arr, target_ras_in = exposure_ras, target_decs_in = exposure_decs, obs_mjd_in = obs_mjd,
path_in = '', max_sep = 1.8, sep_units = 'deg', ledger_df_in = ledger_df, ledger_type_in = ledger_type)
# Add everything into one giant list for both
if trans_matches.size:
#print(date, "-", len(trans_matches), "matches")
all_trans_matches.append(trans_matches)
all_alerts_matches.append(alert_matches)
else:
#print("No matches on", date)
continue
# Prepping output
# Populating the dictionary by date (a common theme)
# Each element in the dictionary thus contains the entire sqlite3 row (all info from sql tables with said headers)
alert_matches_dict[date] = []
for tup in trans_matches:
ra = tup.ra.deg
dec = tup.dec.deg
match_rows = [i for i in row if (i['tilera'], i['tiledec']) == (ra, dec)] # Just rebuilding for populating, this shouldn't change/exclude anything
alert_matches_dict[date].extend(match_rows)
return alert_matches_dict
```
## closer_check
**closer_check** is also a handling function but operates differently in that now it is checking individual targets. This *must* be run after **initial_check** because it takes as input the dictionary **initial_check** spits out. It then grabs all the targets from the DESI files and pipes that into the matching function but this time with a much more strict matching radius (in this case 2 arcseconds).
It then preps the data for output and writing.
```
def closer_check(matches_dict = {}, ledger_df = None, ledger_type = '', exclusion_list = []):
all_exp_matches = {}
if not matches_dict:
print("No far matches fed in for nearby matching. Returning none.")
return {}
# Again just in case the dataframe isn't fed in
if ledger_type.upper() == 'DECAM_TAMU':
id_head = 'ObjectID'
ra_head = 'RA-OBJECT'
dec_head = 'DEC-OBJECT'
if ledger_df.empty:
ledger_df = access_decam_data('https://datahub.geos.tamu.edu:8000/decam/LCData_Legacy/')
count_flag=0
# Iterating through date and all tile information for that date
for date, row in matches_dict.items():
print("\n", date)
if date in exclusion_list:
continue
# Declaring some things
all_exp_matches[date] = []
alert_exp_matches = []
file_indices = {}
all_targ_ras = np.array([])
all_targ_decs = np.array([])
all_targ_ids = np.array([])
all_tileids = np.array([])
all_petals = np.array([])
# Iterating through each initial match tile for every date
for i in row:
# Grabbing the paths and iterating through them to grab the RA's/DEC's
exp_paths = '/'.join((exposure_path, "daily/exposures", str(i['obsdate']), "000"+str(i['expid'])))
#print(exp_paths)
for path in glob_frames(exp_paths):
#print(path)
targ_ras, targ_decs, targ_ids = read_fits_info(path, transient_candidate = False)
h=fits.open(path)
tileid = h[0].header['TILEID']
tileids = np.full(len(targ_ras),tileid).tolist()
petal = path.split("/")[-1].split("-")[1][-1]
petals = np.full(len(targ_ras),petal).tolist()
# This is to retain the row to debug/check the original FITS file
# And to pull the info by row direct if you feel so inclined
all_len = len(all_targ_ras)
new_len = len(targ_ras)
if all_len:
all_len -= 1
file_indices[path] = (all_len, all_len + new_len) # The start and end index, modulo number
else:
file_indices[path] = (0, new_len) # The start and end index, modulo number
if len(targ_ras) != len(targ_decs):
print("Length of all ras vs. all decs do not match.")
print("Something went wrong!")
print("Continuing but not adding those to match...")
continue
# All the ras/decs together!
all_targ_ras = np.append(all_targ_ras, targ_ras)
all_targ_decs = np.append(all_targ_decs, targ_decs)
all_targ_ids = np.append(all_targ_ids, targ_ids)
all_tileids = np.append(all_tileids, tileids)
all_petals = np.append(all_petals, petals)
date_mjd = str(date)[:4]+"-"+str(date)[4:6] + "-" + str(date)[6:] # Adding dashes for Time
date_mjd = Time(date_mjd).mjd
# Grabbing ALERCE just in case
# Slow
if ledger_type.upper() == 'ALERCE':
id_head = 'oid'
ra_head = 'meanra'
dec_head = 'meandec'
if ledger_df.empty:
ledger_df = access_alerts(lastmjd_in = obs_mjd - 45) # Modified Julian Day #.mjd
# Checking for NaNs, again doesn't play nice with match_coordinates_sky
nan_ra = np.isnan(all_targ_ras)
nan_dec = np.isnan(all_targ_decs)
if np.any(nan_ra) or np.any(nan_dec):
print("NaNs found, removing them from array before match.")
#print("Original length (ra, dec): ", len(target_ras), len(target_decs))
nans = np.logical_not(np.logical_and(nan_ra, nan_dec))
all_targ_ras = all_targ_ras[nans] # Logic masking, probably more efficient
all_targ_decs = all_targ_decs[nans]
all_targ_ids = all_targ_ids[nans]
all_tileids = all_tileids[nans]
all_petals = all_petals[nans]
# Where the magic matching happens. This time with separation 2 arcseconds.
# Will be cleaned up (eventually)
alert_exp_matches, alerts_matches, targetid_exp_matches, id_alerts_matches, exp_idx = inner_matching(target_ids_in =all_targ_ids, \
target_ras_in = all_targ_ras, target_decs_in = all_targ_decs, obs_mjd_in = date_mjd,
path_in = '', max_sep = 2, sep_units = 'arcsec', ledger_df_in = ledger_df, ledger_type_in = ledger_type)
date_arr=np.full(alerts_matches.shape[0],date)
#print(date_arr.shape,targetid_exp_matches.shape,alert_exp_matches.shape, id_alerts_matches.shape,alerts_matches.shape )
info_arr_date=np.column_stack((date_arr,all_tileids[exp_idx],all_petals[exp_idx], targetid_exp_matches,alert_exp_matches.ra.deg,alert_exp_matches.dec.deg, \
id_alerts_matches,alerts_matches.ra.deg,alerts_matches.dec.deg ))
all_exp_matches[date].append(info_arr_date)
if count_flag==0:
all_exp_matches_arr=info_arr_date
count_flag=1
else:
#print(all_exp_matches_arr,info_arr_date)
all_exp_matches_arr=np.concatenate((all_exp_matches_arr,info_arr_date))
# Does not easily output to a csv since we have multiple results for each date
# so uh... custom file output for me
return all_exp_matches_arr
```
## inner_matching
#### aka the bread & butter
**inner_matching** is what ultimately does the final match and calls **match_coordinates_sky** with everything fed in. So really it doesn't do much other than take in all the goodies and make everyone happy.
It may still be difficult to co-opt for alerce matching but that may be a project for another time.
```
def inner_matching(target_ids_in = np.array([]), target_ras_in = np.array([]), target_decs_in = np.array([]), obs_mjd_in = '', path_in = '', max_sep = 2, sep_units = 'arcsec', ledger_df_in = None, ledger_type_in = ''): # to be combined with the other matching thing in due time
# Figuring out the units
if sep_units == 'arcsec':
max_sep *= u.arcsec
elif sep_units == 'arcmin':
max_sep *= u.arcmin
elif sep_units == 'deg':
max_sep *= u.deg
else:
print("Separation unit specified is invalid for matching. Defaulting to arcsecond.")
max_sep *= u.arcsec
if not np.array(target_ras_in).size:
return np.array([]), np.array([])
# Checking for NaNs, again doesn't play nice with match_coordinates_sky
nan_ra = np.isnan(target_ras_in)
nan_dec = np.isnan(target_decs_in)
if np.any(nan_ra) or np.any(nan_dec):
print("NaNs found, removing them from array before match.")
#print("Original length (ra, dec): ", len(target_ras), len(target_decs))
nans = np.logical_not(np.logical_and(nan_ra, nan_dec))
target_ras_in = target_ras_in[nans] # Logic masking, probably more efficient
target_decs_in = target_decs_in[nans]
target_ids_in = target_ids_in[nans]
#print("Reduced length (ra, dec):", len(target_ras), len(target_decs))
# For quick matching if said kdtree actually does anything
# Supposed to speed things up on subsequent runs *shrugs*
tree_name = "_".join(("kdtree", ledger_type_in, str(obs_mjd_in)))
# Selecting header string to use with the different alert brokers/ledgers
if ledger_type_in.upper() == 'DECAM_TAMU':
id_head = 'ObjectID'
ra_head = 'RA-OBJECT'
dec_head = 'DEC-OBJECT'
elif ledger_type_in.upper() == 'ALERCE':
id_head = 'oid' #Check this is how id is called!
ra_head = 'meanra'
dec_head = 'meandec'
else:
print("No ledger type specified. Quitting.")
# lofty goals
# Will try to figure it out assuming it's a pandas dataframe.")
#print("Returning empty-handed for now until that is complete - Matthew P.")
return np.array([]), np.array([])
# Convert df RA/DEC to numpy arrays
alerts_id = ledger_df_in[id_head].to_numpy()
alerts_ra = ledger_df_in[ra_head].to_numpy()
alerts_dec = ledger_df_in[dec_head].to_numpy()
# Convert everything to SkyCoord
coo_trans_search = SkyCoord(target_ras_in*u.deg, target_decs_in*u.deg)
coo_alerts = SkyCoord(alerts_ra*u.deg, alerts_dec*u.deg)
# Do the matching!
idx_alerts, d2d_trans, d3d_trans = match_coordinates_sky(coo_trans_search, coo_alerts, storekdtree = tree_name) # store tree to speed up subsequent results
# Filter out the good stuff
sep_constraint = d2d_trans < max_sep
trans_matches = coo_trans_search[sep_constraint]
trans_matches_ids = target_ids_in[sep_constraint]
alerts_matches = coo_alerts[idx_alerts[sep_constraint]]
alerts_matches_ids = alerts_id[idx_alerts[sep_constraint]]
if trans_matches.size:
print(len(trans_matches), "matches with separation -", max_sep)
#sort_dist = np.sort(d2d_trans)
#print("Minimum distance found: ", sort_dist[0])
return trans_matches, alerts_matches, trans_matches_ids, alerts_matches_ids, sep_constraint
```
## Grab DECAM ledger as pandas dataframe
```
decam_transients = access_decam_data('https://datahub.geos.tamu.edu:8000/decam/LCData_Legacy/', overwrite = True) # If True, grabs a fresh batch
decam_transients_agn = access_decam_data('https://datahub.geos.tamu.edu:8000/decam/LCData_Legacy_AGN/', overwrite = True) # If True, grabs a fresh batch
decam_transients
```
## Run initial check (on tiles) and closer check (on targets)
```
init_matches_by_date = initial_check(ledger_df = decam_transients, ledger_type = 'DECAM_TAMU')
close_matches = closer_check(init_matches_by_date, ledger_df = decam_transients, ledger_type = 'DECAM_TAMU', exclusion_list = [])
np.save('matches_DECam',close_matches, allow_pickle=True)
init_matches_agn_by_date = initial_check(ledger_df = decam_transients_agn, ledger_type = 'DECAM_TAMU')
close_matches_agn = closer_check(init_matches_agn_by_date, ledger_df = decam_transients_agn, ledger_type = 'DECAM_TAMU', exclusion_list = [])
np.save('matches_DECam_agn',close_matches_agn, allow_pickle=True)
np.save('matches_DECam_agn',close_matches_agn, allow_pickle=True)
```
## A quick plot to see the distribution of target matches
```
plt.scatter(close_matches[:,4], close_matches[:,5],label='SN')
plt.scatter(close_matches_agn[:,4], close_matches_agn[:,5],label='AGN')
plt.legend()
```
## End notes:
Double matches are to be expected, could be worthwhile to compare the spectra of both
|
github_jupyter
|
##### Copyright 2021 The TF-Agents Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# CheckpointerとPolicySaver
<table class="tfo-notebook-buttons" align="left">
<td><a target="_blank" href="https://www.tensorflow.org/agents/tutorials/10_checkpointer_policysaver_tutorial"> <img src="https://www.tensorflow.org/images/tf_logo_32px.png"> TensorFlow.org で表示</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/ja/agents/tutorials/10_checkpointer_policysaver_tutorial.ipynb"> <img src="https://www.tensorflow.org/images/colab_logo_32px.png"> Google Colab で実行</a></td>
<td><a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/ja/agents/tutorials/10_checkpointer_policysaver_tutorial.ipynb"> <img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png"> GitHub でソースを表示</a></td>
<td><a href="https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/ja/agents/tutorials/10_checkpointer_policysaver_tutorial.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png">ノートブックをダウンロード</a></td>
</table>
## はじめに
`tf_agents.utils.common.Checkpointer`は、ローカルストレージとの間でトレーニングの状態、ポリシーの状態、およびreplay_bufferの状態を保存/読み込むユーティリティです。
`tf_agents.policies.policy_saver.PolicySaver`は、ポリシーのみを保存/読み込むツールであり、`Checkpointer`よりも軽量です。`PolicySaver`を使用すると、ポリシーを作成したコードに関する知識がなくてもモデルをデプロイできます。
このチュートリアルでは、DQNを使用してモデルをトレーニングし、次に`Checkpointer`と`PolicySaver`を使用して、状態とモデルをインタラクティブな方法で保存および読み込む方法を紹介します。`PolicySaver`では、TF2.0の新しいsaved_modelツールとフォーマットを使用することに注意してください。
## セットアップ
以下の依存関係をインストールしていない場合は、実行します。
```
#@test {"skip": true}
!sudo apt-get update
!sudo apt-get install -y xvfb ffmpeg python-opengl
!pip install pyglet
!pip install 'imageio==2.4.0'
!pip install 'xvfbwrapper==0.2.9'
!pip install tf-agents
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import base64
import imageio
import io
import matplotlib
import matplotlib.pyplot as plt
import os
import shutil
import tempfile
import tensorflow as tf
import zipfile
import IPython
try:
from google.colab import files
except ImportError:
files = None
from tf_agents.agents.dqn import dqn_agent
from tf_agents.drivers import dynamic_step_driver
from tf_agents.environments import suite_gym
from tf_agents.environments import tf_py_environment
from tf_agents.eval import metric_utils
from tf_agents.metrics import tf_metrics
from tf_agents.networks import q_network
from tf_agents.policies import policy_saver
from tf_agents.policies import py_tf_eager_policy
from tf_agents.policies import random_tf_policy
from tf_agents.replay_buffers import tf_uniform_replay_buffer
from tf_agents.trajectories import trajectory
from tf_agents.utils import common
tempdir = os.getenv("TEST_TMPDIR", tempfile.gettempdir())
#@test {"skip": true}
# Set up a virtual display for rendering OpenAI gym environments.
import xvfbwrapper
xvfbwrapper.Xvfb(1400, 900, 24).start()
```
## DQNエージェント
前のColabと同じように、DQNエージェントを設定します。 このColabでは、詳細は主な部分ではないので、デフォルトでは非表示になっていますが、「コードを表示」をクリックすると詳細を表示できます。
### ハイパーパラメーター
```
env_name = "CartPole-v1"
collect_steps_per_iteration = 100
replay_buffer_capacity = 100000
fc_layer_params = (100,)
batch_size = 64
learning_rate = 1e-3
log_interval = 5
num_eval_episodes = 10
eval_interval = 1000
```
### 環境
```
train_py_env = suite_gym.load(env_name)
eval_py_env = suite_gym.load(env_name)
train_env = tf_py_environment.TFPyEnvironment(train_py_env)
eval_env = tf_py_environment.TFPyEnvironment(eval_py_env)
```
### エージェント
```
#@title
q_net = q_network.QNetwork(
train_env.observation_spec(),
train_env.action_spec(),
fc_layer_params=fc_layer_params)
optimizer = tf.compat.v1.train.AdamOptimizer(learning_rate=learning_rate)
global_step = tf.compat.v1.train.get_or_create_global_step()
agent = dqn_agent.DqnAgent(
train_env.time_step_spec(),
train_env.action_spec(),
q_network=q_net,
optimizer=optimizer,
td_errors_loss_fn=common.element_wise_squared_loss,
train_step_counter=global_step)
agent.initialize()
```
### データ収集
```
#@title
replay_buffer = tf_uniform_replay_buffer.TFUniformReplayBuffer(
data_spec=agent.collect_data_spec,
batch_size=train_env.batch_size,
max_length=replay_buffer_capacity)
collect_driver = dynamic_step_driver.DynamicStepDriver(
train_env,
agent.collect_policy,
observers=[replay_buffer.add_batch],
num_steps=collect_steps_per_iteration)
# Initial data collection
collect_driver.run()
# Dataset generates trajectories with shape [BxTx...] where
# T = n_step_update + 1.
dataset = replay_buffer.as_dataset(
num_parallel_calls=3, sample_batch_size=batch_size,
num_steps=2).prefetch(3)
iterator = iter(dataset)
```
### エージェントのトレーニング
```
#@title
# (Optional) Optimize by wrapping some of the code in a graph using TF function.
agent.train = common.function(agent.train)
def train_one_iteration():
# Collect a few steps using collect_policy and save to the replay buffer.
collect_driver.run()
# Sample a batch of data from the buffer and update the agent's network.
experience, unused_info = next(iterator)
train_loss = agent.train(experience)
iteration = agent.train_step_counter.numpy()
print ('iteration: {0} loss: {1}'.format(iteration, train_loss.loss))
```
### ビデオ生成
```
#@title
def embed_gif(gif_buffer):
"""Embeds a gif file in the notebook."""
tag = '<img src="data:image/gif;base64,{0}"/>'.format(base64.b64encode(gif_buffer).decode())
return IPython.display.HTML(tag)
def run_episodes_and_create_video(policy, eval_tf_env, eval_py_env):
num_episodes = 3
frames = []
for _ in range(num_episodes):
time_step = eval_tf_env.reset()
frames.append(eval_py_env.render())
while not time_step.is_last():
action_step = policy.action(time_step)
time_step = eval_tf_env.step(action_step.action)
frames.append(eval_py_env.render())
gif_file = io.BytesIO()
imageio.mimsave(gif_file, frames, format='gif', fps=60)
IPython.display.display(embed_gif(gif_file.getvalue()))
```
### ビデオ生成
ビデオを生成して、ポリシーのパフォーマンスを確認します。
```
print ('global_step:')
print (global_step)
run_episodes_and_create_video(agent.policy, eval_env, eval_py_env)
```
## チェックポインタとPolicySaverのセットアップ
CheckpointerとPolicySaverを使用する準備ができました。
### Checkpointer
```
checkpoint_dir = os.path.join(tempdir, 'checkpoint')
train_checkpointer = common.Checkpointer(
ckpt_dir=checkpoint_dir,
max_to_keep=1,
agent=agent,
policy=agent.policy,
replay_buffer=replay_buffer,
global_step=global_step
)
```
### Policy Saver
```
policy_dir = os.path.join(tempdir, 'policy')
tf_policy_saver = policy_saver.PolicySaver(agent.policy)
```
### 1回のイテレーションのトレーニング
```
#@test {"skip": true}
print('Training one iteration....')
train_one_iteration()
```
### チェックポイントに保存
```
train_checkpointer.save(global_step)
```
### チェックポイントに復元
チェックポイントに復元するためには、チェックポイントが作成されたときと同じ方法でオブジェクト全体を再作成する必要があります。
```
train_checkpointer.initialize_or_restore()
global_step = tf.compat.v1.train.get_global_step()
```
また、ポリシーを保存して指定する場所にエクスポートします。
```
tf_policy_saver.save(policy_dir)
```
ポリシーの作成に使用されたエージェントまたはネットワークについての知識がなくても、ポリシーを読み込めるので、ポリシーのデプロイが非常に簡単になります。
保存されたポリシーを読み込み、それがどのように機能するかを確認します。
```
saved_policy = tf.saved_model.load(policy_dir)
run_episodes_and_create_video(saved_policy, eval_env, eval_py_env)
```
## エクスポートとインポート
以下は、後でトレーニングを続行し、再度トレーニングすることなくモデルをデプロイできるように、Checkpointer とポリシーディレクトリをエクスポート/インポートするのに役立ちます。
「1回のイテレーションのトレーニング」に戻り、後で違いを理解できるように、さらに数回トレーニングします。 結果が少し改善し始めたら、以下に進みます。
```
#@title Create zip file and upload zip file (double-click to see the code)
def create_zip_file(dirname, base_filename):
return shutil.make_archive(base_filename, 'zip', dirname)
def upload_and_unzip_file_to(dirname):
if files is None:
return
uploaded = files.upload()
for fn in uploaded.keys():
print('User uploaded file "{name}" with length {length} bytes'.format(
name=fn, length=len(uploaded[fn])))
shutil.rmtree(dirname)
zip_files = zipfile.ZipFile(io.BytesIO(uploaded[fn]), 'r')
zip_files.extractall(dirname)
zip_files.close()
```
チェックポイントディレクトリからzipファイルを作成します。
```
train_checkpointer.save(global_step)
checkpoint_zip_filename = create_zip_file(checkpoint_dir, os.path.join(tempdir, 'exported_cp'))
```
zipファイルをダウンロードします。
```
#@test {"skip": true}
if files is not None:
files.download(checkpoint_zip_filename) # try again if this fails: https://github.com/googlecolab/colabtools/issues/469
```
10〜15回ほどトレーニングした後、チェックポイントのzipファイルをダウンロードし、[ランタイム]> [再起動してすべて実行]に移動してトレーニングをリセットし、このセルに戻ります。ダウンロードしたzipファイルをアップロードして、トレーニングを続けます。
```
#@test {"skip": true}
upload_and_unzip_file_to(checkpoint_dir)
train_checkpointer.initialize_or_restore()
global_step = tf.compat.v1.train.get_global_step()
```
チェックポイントディレクトリをアップロードしたら、「1回のイテレーションのトレーニング」に戻ってトレーニングを続けるか、「ビデオ生成」に戻って読み込まれたポリシーのパフォーマンスを確認します。
または、ポリシー(モデル)を保存して復元することもできます。Checkpointerとは異なり、トレーニングを続けることはできませんが、モデルをデプロイすることはできます。ダウンロードしたファイルはCheckpointerのファイルよりも大幅に小さいことに注意してください。
```
tf_policy_saver.save(policy_dir)
policy_zip_filename = create_zip_file(policy_dir, os.path.join(tempdir, 'exported_policy'))
#@test {"skip": true}
if files is not None:
files.download(policy_zip_filename) # try again if this fails: https://github.com/googlecolab/colabtools/issues/469
```
ダウンロードしたポリシーディレクトリ(exported_policy.zip)をアップロードし、保存したポリシーの動作を確認します。
```
#@test {"skip": true}
upload_and_unzip_file_to(policy_dir)
saved_policy = tf.saved_model.load(policy_dir)
run_episodes_and_create_video(saved_policy, eval_env, eval_py_env)
```
## SavedModelPyTFEagerPolicy
TFポリシーを使用しない場合は、`py_tf_eager_policy.SavedModelPyTFEagerPolicy`を使用して、Python envでsaved_modelを直接使用することもできます。
これは、eagerモードが有効になっている場合にのみ機能することに注意してください。
```
eager_py_policy = py_tf_eager_policy.SavedModelPyTFEagerPolicy(
policy_dir, eval_py_env.time_step_spec(), eval_py_env.action_spec())
# Note that we're passing eval_py_env not eval_env.
run_episodes_and_create_video(eager_py_policy, eval_py_env, eval_py_env)
```
## ポリシーを TFLite に変換する
詳細については、「[TensorFlow Lite 推論](https://tensorflow.org/lite/guide/inference)」をご覧ください。
```
converter = tf.lite.TFLiteConverter.from_saved_model(policy_dir, signature_keys=["action"])
converter.target_spec.supported_ops = [
tf.lite.OpsSet.TFLITE_BUILTINS, # enable TensorFlow Lite ops.
tf.lite.OpsSet.SELECT_TF_OPS # enable TensorFlow ops.
]
tflite_policy = converter.convert()
with open(os.path.join(tempdir, 'policy.tflite'), 'wb') as f:
f.write(tflite_policy)
```
### TFLite モデルで推論を実行する
```
import numpy as np
interpreter = tf.lite.Interpreter(os.path.join(tempdir, 'policy.tflite'))
policy_runner = interpreter.get_signature_runner()
print(policy_runner._inputs)
policy_runner(**{
'0/discount':tf.constant(0.0),
'0/observation':tf.zeros([1,4]),
'0/reward':tf.constant(0.0),
'0/step_type':tf.constant(0)})
```
|
github_jupyter
|
# Titania = CLERK MOTEL
On Bumble, the Queen of Fairies and the Queen of Bees got together to find some other queens.
* Given
* Queen of Fairies
* Queen of Bees
* Solutions
* C [Ellery Queen](https://en.wikipedia.org/wiki/Ellery_Queen) = TDDTNW M UPZTDO
* L Queen of Hearts = THE L OF HEARTS
* E Queen Elizabeth = E ELIZABETH II
* R Steve McQueen = STEVE MC R MOVIES
* K Queen Latifah = K LATIFAH ALBUMS
* meta
```
C/M L/O
E/T R/E
K/L
```
```
import forge
from puzzle.puzzlepedia import puzzlepedia
puzzle = puzzlepedia.parse("""
LIT NPGRU IRL GWOLTNW
LIT ENTTJ MPVVFU GWOLTNW
LIT TEWYLFRU MNPOO GWOLTNW
LIT OFRGTOT LCFU GWOLTNW
LIT PNFEFU PV TZFD
""", hint="cryptogram", threshold=1)
# LIT NPGRU IRL GWOLTNW
# THE ROMAN HAT MYSTERY
# LIT ENTTJ MPVVFU GWOLTNW
# THE GREEK COFFIN MYSTERY
# LIT TEWYLFRU MNPOO GWOLTNW
# THE EGYPTIAN CROSS MYSTERY
# LIT OFRGTOT LCFU GWOLTNW
# THE SIAMESE TWIN MYSTERY
# LIT PNFEFU PV TZFD
# THE ORIGIN OF EVIL
# TDDTNW M UPZTDO
# ELLERY C NOVELS
import forge
from puzzle.puzzlepedia import puzzlepedia
puzzle = puzzlepedia.parse("""
KQLECDP
NDWSDNLSI
ZOMXFUSLDI
LZZ BFPN PNDFQ NDMWI
YOMRFUS KMQW
""", hint="cryptogram")
# Queen of Hearts
# THELOFHEARTS
# PNDOLZNDMQPI
# CROQUET
# KQLECDP
# HEDGEHOGS
# NDWSDNLSI
# FLAMINGOES
# ZOMXFUSLDI
# OFF WITH THEIR HEADS
# LZZ BFPN PNDFQ NDMWI
# BLAZING CARD
# YOMRFUS KMQW
import forge
from puzzle.puzzlepedia import puzzlepedia
puzzle = puzzlepedia.parse("""
ZOXMNRBFGP DGQGXT
XYIBNK
DINRXT XFGIQTK
QYRBTKL ITNBRNRB PYRGIXF
YXTGR QNRTI
""", hint="cryptogram")
# TQN?GZTLF
# Queen Elizabeth
# EELIZABETHII
#
# BUCKINGHAM PALACE
# ZOXMNRBFGP DGQGXT
# CORGIS
# XYIBNK
# PRINCE CHARLES
# DINRXT XFGIQTK
# LONGEST-REIGNING MONARCH
# QYRBTKL ITNBRNRB PYRGIXF
# OCEAN LINER
# YXTGR QNRTI
import forge
from puzzle.puzzlepedia import puzzlepedia
puzzle = puzzlepedia.parse("""
LUF ZTYSWDWMFSL VFQFS
LUF YEFTL FVMTRF
LUF LPXFEWSY WSDFESP
RTRWJJPS
LUF MWSMWSSTLW OWC
""", hint="cryptogram", threshold=1)
# Steve McQueen
# STEVEMCRMOVIES
# VLFQFZMEZPQWFV
# THE MAGNIFICENT SEVEN
# LUF ZTYSWDWMFSL VFQFS
# THE GREAT ESCAPE
# LUF YEFTL FVMTRF
# THE TOWERING INFERNO
# LUF LPXFEWSY WSDFESP
# PAPILLON
# RTRWJJPS
# THE CINCINNATI KID
# LUF MWSMWSSTLW OWC
import forge
from puzzle.puzzlepedia import puzzlepedia
puzzle = puzzlepedia.parse("""
HZRWPO FY Z BDBRZ
IQZVL PODTH
FPGOP DH RNO VFWPR
RNO GZHZ FXOHB ZQIWU
SOPBFHZ
""", hint="cryptogram", threshold=1)
# Queen Latifah
# LQZRDYZNZQIWUB
# KLATIFAHALBUMS
# NATURE OF A SISTA
# HZRWPO FY Z BDBRZ
# BLACK REIGN
# IQZVL PODTH
# ORDER IN THE COURT
# FPGOP DH RNO VFWPR
# THE DANA OVENS ALBUM
# RNO GZHZ FXOHB ZQIWU
# PERSONA
# SOPBFHZ
import forge
from puzzle.puzzlepedia import puzzlepedia
puzzle = puzzlepedia.parse("""
LQZRDYZNZQIWUB
PNDOLZNDMQPI
TDDTNWMUPZTDO
TTQNJGZTLFNN
VLFQFZMEZPQWFV
""", hint="cryptogram")
################
# LQZRDYZNZQIWUB
# KLATIFAHALBUMS = K / L
################
# PNDOLZNDMQPI
# THELOFHEARTS = L / O
################
# TDDTNWMUPZTDO
# ELLERYCNOVELS = C / M
################
# TTQNJGZTLFNN
# EELIZABETHII = E / T
################
# VLFQFZMEZPQWFV
# STEVEMCRMOVIES = R / E
################
```
|
github_jupyter
|
# Contrasts Overview
```
from __future__ import print_function
import numpy as np
import statsmodels.api as sm
```
This document is based heavily on this excellent resource from UCLA http://www.ats.ucla.edu/stat/r/library/contrast_coding.htm
A categorical variable of K categories, or levels, usually enters a regression as a sequence of K-1 dummy variables. This amounts to a linear hypothesis on the level means. That is, each test statistic for these variables amounts to testing whether the mean for that level is statistically significantly different from the mean of the base category. This dummy coding is called Treatment coding in R parlance, and we will follow this convention. There are, however, different coding methods that amount to different sets of linear hypotheses.
In fact, the dummy coding is not technically a contrast coding. This is because the dummy variables add to one and are not functionally independent of the model's intercept. On the other hand, a set of *contrasts* for a categorical variable with `k` levels is a set of `k-1` functionally independent linear combinations of the factor level means that are also independent of the sum of the dummy variables. The dummy coding isn't wrong *per se*. It captures all of the coefficients, but it complicates matters when the model assumes independence of the coefficients such as in ANOVA. Linear regression models do not assume independence of the coefficients and thus dummy coding is often the only coding that is taught in this context.
To have a look at the contrast matrices in Patsy, we will use data from UCLA ATS. First let's load the data.
#### Example Data
```
import pandas as pd
url = 'https://stats.idre.ucla.edu/stat/data/hsb2.csv'
hsb2 = pd.read_table(url, delimiter=",")
hsb2.head(10)
```
It will be instructive to look at the mean of the dependent variable, write, for each level of race ((1 = Hispanic, 2 = Asian, 3 = African American and 4 = Caucasian)).
```
hsb2.groupby('race')['write'].mean()
```
#### Treatment (Dummy) Coding
Dummy coding is likely the most well known coding scheme. It compares each level of the categorical variable to a base reference level. The base reference level is the value of the intercept. It is the default contrast in Patsy for unordered categorical factors. The Treatment contrast matrix for race would be
```
from patsy.contrasts import Treatment
levels = [1,2,3,4]
contrast = Treatment(reference=0).code_without_intercept(levels)
print(contrast.matrix)
```
Here we used `reference=0`, which implies that the first level, Hispanic, is the reference category against which the other level effects are measured. As mentioned above, the columns do not sum to zero and are thus not independent of the intercept. To be explicit, let's look at how this would encode the `race` variable.
```
hsb2.race.head(10)
print(contrast.matrix[hsb2.race-1, :][:20])
sm.categorical(hsb2.race.values)
```
This is a bit of a trick, as the `race` category conveniently maps to zero-based indices. If it does not, this conversion happens under the hood, so this won't work in general but nonetheless is a useful exercise to fix ideas. The below illustrates the output using the three contrasts above
```
from statsmodels.formula.api import ols
mod = ols("write ~ C(race, Treatment)", data=hsb2)
res = mod.fit()
print(res.summary())
```
We explicitly gave the contrast for race; however, since Treatment is the default, we could have omitted this.
### Simple Coding
Like Treatment Coding, Simple Coding compares each level to a fixed reference level. However, with simple coding, the intercept is the grand mean of all the levels of the factors. Patsy doesn't have the Simple contrast included, but you can easily define your own contrasts. To do so, write a class that contains a code_with_intercept and a code_without_intercept method that returns a patsy.contrast.ContrastMatrix instance
```
from patsy.contrasts import ContrastMatrix
def _name_levels(prefix, levels):
return ["[%s%s]" % (prefix, level) for level in levels]
class Simple(object):
def _simple_contrast(self, levels):
nlevels = len(levels)
contr = -1./nlevels * np.ones((nlevels, nlevels-1))
contr[1:][np.diag_indices(nlevels-1)] = (nlevels-1.)/nlevels
return contr
def code_with_intercept(self, levels):
contrast = np.column_stack((np.ones(len(levels)),
self._simple_contrast(levels)))
return ContrastMatrix(contrast, _name_levels("Simp.", levels))
def code_without_intercept(self, levels):
contrast = self._simple_contrast(levels)
return ContrastMatrix(contrast, _name_levels("Simp.", levels[:-1]))
hsb2.groupby('race')['write'].mean().mean()
contrast = Simple().code_without_intercept(levels)
print(contrast.matrix)
mod = ols("write ~ C(race, Simple)", data=hsb2)
res = mod.fit()
print(res.summary())
```
### Sum (Deviation) Coding
Sum coding compares the mean of the dependent variable for a given level to the overall mean of the dependent variable over all the levels. That is, it uses contrasts between each of the first k-1 levels and level k In this example, level 1 is compared to all the others, level 2 to all the others, and level 3 to all the others.
```
from patsy.contrasts import Sum
contrast = Sum().code_without_intercept(levels)
print(contrast.matrix)
mod = ols("write ~ C(race, Sum)", data=hsb2)
res = mod.fit()
print(res.summary())
```
This corresponds to a parameterization that forces all the coefficients to sum to zero. Notice that the intercept here is the grand mean where the grand mean is the mean of means of the dependent variable by each level.
```
hsb2.groupby('race')['write'].mean().mean()
```
### Backward Difference Coding
In backward difference coding, the mean of the dependent variable for a level is compared with the mean of the dependent variable for the prior level. This type of coding may be useful for a nominal or an ordinal variable.
```
from patsy.contrasts import Diff
contrast = Diff().code_without_intercept(levels)
print(contrast.matrix)
mod = ols("write ~ C(race, Diff)", data=hsb2)
res = mod.fit()
print(res.summary())
```
For example, here the coefficient on level 1 is the mean of `write` at level 2 compared with the mean at level 1. Ie.,
```
res.params["C(race, Diff)[D.1]"]
hsb2.groupby('race').mean()["write"][2] - \
hsb2.groupby('race').mean()["write"][1]
```
### Helmert Coding
Our version of Helmert coding is sometimes referred to as Reverse Helmert Coding. The mean of the dependent variable for a level is compared to the mean of the dependent variable over all previous levels. Hence, the name 'reverse' being sometimes applied to differentiate from forward Helmert coding. This comparison does not make much sense for a nominal variable such as race, but we would use the Helmert contrast like so:
```
from patsy.contrasts import Helmert
contrast = Helmert().code_without_intercept(levels)
print(contrast.matrix)
mod = ols("write ~ C(race, Helmert)", data=hsb2)
res = mod.fit()
print(res.summary())
```
To illustrate, the comparison on level 4 is the mean of the dependent variable at the previous three levels taken from the mean at level 4
```
grouped = hsb2.groupby('race')
grouped.mean()["write"][4] - grouped.mean()["write"][:3].mean()
```
As you can see, these are only equal up to a constant. Other versions of the Helmert contrast give the actual difference in means. Regardless, the hypothesis tests are the same.
```
k = 4
1./k * (grouped.mean()["write"][k] - grouped.mean()["write"][:k-1].mean())
k = 3
1./k * (grouped.mean()["write"][k] - grouped.mean()["write"][:k-1].mean())
```
### Orthogonal Polynomial Coding
The coefficients taken on by polynomial coding for `k=4` levels are the linear, quadratic, and cubic trends in the categorical variable. The categorical variable here is assumed to be represented by an underlying, equally spaced numeric variable. Therefore, this type of encoding is used only for ordered categorical variables with equal spacing. In general, the polynomial contrast produces polynomials of order `k-1`. Since `race` is not an ordered factor variable let's use `read` as an example. First we need to create an ordered categorical from `read`.
```
hsb2['readcat'] = np.asarray(pd.cut(hsb2.read, bins=3))
hsb2.groupby('readcat').mean()['write']
from patsy.contrasts import Poly
levels = hsb2.readcat.unique().tolist()
contrast = Poly().code_without_intercept(levels)
print(contrast.matrix)
mod = ols("write ~ C(readcat, Poly)", data=hsb2)
res = mod.fit()
print(res.summary())
```
As you can see, readcat has a significant linear effect on the dependent variable `write` but not a significant quadratic or cubic effect.
|
github_jupyter
|
# Gym environment with scikit-decide tutorial: Continuous Mountain Car
In this notebook we tackle the continuous mountain car problem taken from [OpenAI Gym](https://gym.openai.com/), a toolkit for developing environments, usually to be solved by Reinforcement Learning (RL) algorithms.
Continuous Mountain Car, a standard testing domain in RL, is a problem in which an under-powered car must drive up a steep hill.
<div align="middle">
<video controls autoplay preload
src="https://gym.openai.com/videos/2019-10-21--mqt8Qj1mwo/MountainCarContinuous-v0/original.mp4">
</video>
</div>
Note that we use here the *continuous* version of the mountain car because
it has a *shaped* or *dense* reward (i.e. not sparse) which can be used successfully when solving, as opposed to the other "Mountain Car" environments.
For reminder, a sparse reward is a reward which is null almost everywhere, whereas a dense or shaped reward has more meaningful values for most transitions.
This problem has been chosen for two reasons:
- Show how scikit-decide can be used to solve Gym environments (the de-facto standard in the RL community),
- Highlight that by doing so, you will be able to use not only solvers from the RL community (like the ones in [stable_baselines3](https://github.com/DLR-RM/stable-baselines3) for example), but also other solvers coming from other communities like genetic programming and planning/search (use of an underlying search graph) that can be very efficient.
Therefore in this notebook we will go through the following steps:
- Wrap a Gym environment in a scikit-decide domain;
- Use a classical RL algorithm like PPO to solve our problem;
- Give CGP (Cartesian Genetic Programming) a try on the same problem;
- Finally use IW (Iterated Width) coming from the planning community on the same problem.
```
import os
from time import sleep
from typing import Callable, Optional
import gym
import matplotlib.pyplot as plt
from IPython.display import clear_output
from stable_baselines3 import PPO
from skdecide import Solver
from skdecide.hub.domain.gym import (
GymDiscreteActionDomain,
GymDomain,
GymPlanningDomain,
GymWidthDomain,
)
from skdecide.hub.solver.cgp import CGP
from skdecide.hub.solver.iw import IW
from skdecide.hub.solver.stable_baselines import StableBaseline
# choose standard matplolib inline backend to render plots
%matplotlib inline
```
When running this notebook on remote servers like with Colab or Binder, rendering of gym environment will fail as no actual display device exists. Thus we need to start a virtual display to make it work.
```
if "DISPLAY" not in os.environ:
import pyvirtualdisplay
_display = pyvirtualdisplay.Display(visible=False, size=(1400, 900))
_display.start()
```
## About Continuous Mountain Car problem
In this a problem, an under-powered car must drive up a steep hill.
The agent (a car) is started at the bottom of a valley. For any given
state the agent may choose to accelerate to the left, right or cease
any acceleration.
### Observations
- Car Position [-1.2, 0.6]
- Car Velocity [-0.07, +0.07]
### Action
- the power coefficient [-1.0, 1.0]
### Goal
The car position is more than 0.45.
### Reward
Reward of 100 is awarded if the agent reached the flag (position = 0.45) on top of the mountain.
Reward is decrease based on amount of energy consumed each step.
### Starting State
The position of the car is assigned a uniform random value in [-0.6 , -0.4].
The starting velocity of the car is always assigned to 0.
## Wrap Gym environment in a scikit-decide domain
We choose the gym environment we would like to use.
```
ENV_NAME = "MountainCarContinuous-v0"
```
We define a domain factory using `GymDomain` proxy available in scikit-decide which will wrap the Gym environment.
```
domain_factory = lambda: GymDomain(gym.make(ENV_NAME))
```
Here is a screenshot of such an environment.
Note: We close the domain straight away to avoid leaving the OpenGL pop-up window open on local Jupyter sessions.
```
domain = domain_factory()
domain.reset()
plt.imshow(domain.render(mode="rgb_array"))
plt.axis("off")
domain.close()
```
## Solve with Reinforcement Learning (StableBaseline + PPO)
We first try a solver coming from the Reinforcement Learning community that is make use of OpenAI [stable_baselines3](https://github.com/DLR-RM/stable-baselines3), which give access to a lot of RL algorithms.
Here we choose [Proximal Policy Optimization (PPO)](https://stable-baselines3.readthedocs.io/en/master/modules/ppo.html) solver. It directly optimizes the weights of the policy network using stochastic gradient ascent. See more details in stable baselines [documentation](https://stable-baselines3.readthedocs.io/en/master/modules/ppo.html) and [original paper](https://arxiv.org/abs/1707.06347).
### Check compatibility
We check the compatibility of the domain with the chosen solver.
```
domain = domain_factory()
assert StableBaseline.check_domain(domain)
domain.close()
```
### Solver instantiation
```
solver = StableBaseline(
PPO, "MlpPolicy", learn_config={"total_timesteps": 10000}, verbose=True
)
```
### Training solver on domain
```
GymDomain.solve_with(solver, domain_factory)
```
### Rolling out a solution
We can use the trained solver to roll out an episode to see if this is actually solving the problem at hand.
For educative purpose, we define here our own rollout (which will probably be needed if you want to actually use the solver in a real case). If you want to take a look at the (more complex) one already implemented in the library, see the `rollout()` function in [utils.py](https://github.com/airbus/scikit-decide/blob/master/skdecide/utils.py) module.
By default we display the solution in a matplotlib figure. If you need only to check wether the goal is reached or not, you can specify `render=False`. In this case, the rollout is greatly speed up and a message is still printed at the end of process specifying success or not, with the number of steps required.
```
def rollout(
domain: GymDomain,
solver: Solver,
max_steps: int,
pause_between_steps: Optional[float] = 0.01,
render: bool = True,
):
"""Roll out one episode in a domain according to the policy of a trained solver.
Args:
domain: the maze domain to solve
solver: a trained solver
max_steps: maximum number of steps allowed to reach the goal
pause_between_steps: time (s) paused between agent movements.
No pause if None.
render: if True, the rollout is rendered in a matplotlib figure as an animation;
if False, speed up a lot the rollout.
"""
# Initialize episode
solver.reset()
observation = domain.reset()
# Initialize image
if render:
plt.ioff()
fig, ax = plt.subplots(1)
ax.axis("off")
plt.ion()
img = ax.imshow(domain.render(mode="rgb_array"))
display(fig)
# loop until max_steps or goal is reached
for i_step in range(1, max_steps + 1):
if pause_between_steps is not None:
sleep(pause_between_steps)
# choose action according to solver
action = solver.sample_action(observation)
# get corresponding action
outcome = domain.step(action)
observation = outcome.observation
# update image
if render:
img.set_data(domain.render(mode="rgb_array"))
fig.canvas.draw()
clear_output(wait=True)
display(fig)
# final state reached?
if outcome.termination:
break
# close the figure to avoid jupyter duplicating the last image
if render:
plt.close(fig)
# goal reached?
is_goal_reached = observation[0] >= 0.45
if is_goal_reached:
print(f"Goal reached in {i_step} steps!")
else:
print(f"Goal not reached after {i_step} steps!")
return is_goal_reached, i_step
```
We create a domain for the roll out and close it at the end. If not closing it, an OpenGL popup windows stays open, at least on local Jupyter sessions.
```
domain = domain_factory()
try:
rollout(
domain=domain,
solver=solver,
max_steps=999,
pause_between_steps=None,
render=True,
)
finally:
domain.close()
```
We can see that PPO does not find a solution to the problem. This is mainly due to the way the reward is computed. Indeed negative reward accumulates as long as the goal is not reached, which encourages the agent to stop moving.
Even if we increase the training time, it still occurs. (You can test that by increasing the parameter "total_timesteps" in the solver definition.)
Actually, typical RL algorithms like PPO are a good fit for domains with "well-shaped" rewards (guiding towards the goal), but can struggle in sparse or "badly-shaped" reward environment like Mountain Car Continuous.
We will see in the next sections that non-RL methods can overcome this issue.
### Cleaning up
Some solvers need proper cleaning before being deleted.
```
solver._cleanup()
```
Note that this is automatically done if you use the solver within a `with` statement. The syntax would look something like:
```python
with solver_factory() as solver:
MyDomain.solve_with(solver, domain_factory)
rollout(domain=domain, solver=solver)
```
## Solve with Cartesian Genetic Programming (CGP)
CGP (Cartesian Genetic Programming) is a form of genetic programming that uses a graph representation (2D grid of nodes) to encode computer programs.
See [Miller, Julian. (2003). Cartesian Genetic Programming. 10.1007/978-3-642-17310-3.](https://www.researchgate.net/publication/2859242_Cartesian_Genetic_Programming) for more details.
Pros:
+ ability to customize the set of atomic functions used by CPG (e.g. to inject some domain knowledge)
+ ability to inspect the final formula found by CGP (no black box)
Cons:
- the fitness function of CGP is defined by the rewards, so can be unable to solve in sparse reward scenarios
### Check compatibility
We check the compatibility of the domain with the chosen solver.
```
domain = domain_factory()
assert CGP.check_domain(domain)
domain.close()
```
### Solver instantiation
```
solver = CGP("TEMP_CGP", n_it=25, verbose=True)
```
### Training solver on domain
```
GymDomain.solve_with(solver, domain_factory)
```
### Rolling out a solution
We use the same roll out function as for PPO solver.
```
domain = domain_factory()
try:
rollout(
domain=domain,
solver=solver,
max_steps=999,
pause_between_steps=None,
render=True,
)
finally:
domain.close()
```
CGP seems doing well on this problem. Indeed the presence of periodic functions ($asin$, $acos$, and $atan$) in its base set of atomic functions makes it suitable for modelling this kind of pendular motion.
***Warning***: On some cases, it happens that CGP does not actually find a solution. As there is randomness here, this is not possible. Running multiple episodes can sometimes solve the problem. If you have bad luck, you will even have to train again the solver.
```
for i_episode in range(10):
print(f"Episode #{i_episode}")
domain = domain_factory()
try:
rollout(
domain=domain,
solver=solver,
max_steps=999,
pause_between_steps=None,
render=False,
)
finally:
domain.close()
```
### Cleaning up
```
solver._cleanup()
```
## Solve with Classical Planning (IW)
Iterated Width (IW) is a width based search algorithm that builds a graph on-demand, while pruning non-novel nodes.
In order to handle continuous domains, a state encoding specific to continuous state variables dynamically and adaptively discretizes the continuous state variables in such a way to build a compact graph based on intervals (rather than a naive grid of discrete point values).
The novelty measures discards intervals that are included in previously explored intervals, thus favoring to extend the state variable intervals.
See https://www.ijcai.org/proceedings/2020/578 for more details.
### Prepare the domain for IW
We need to wrap the Gym environment in a domain with finer charateristics so that IW can be used on it. More precisely, it needs the methods inherited from `GymPlanningDomain`, `GymDiscreteActionDomain` and `GymWidthDomain`. In addition, we will need to provide to IW a state features function to dynamically increase state variable intervals. For Gym domains, we use Boundary Extension Encoding (BEE) features as explained in the [paper](https://www.ijcai.org/proceedings/2020/578) mentioned above. This is implemented as `bee2_features()` method in `GymWidthDomain` that our domain class will inherit.
```
class D(GymPlanningDomain, GymWidthDomain, GymDiscreteActionDomain):
pass
class GymDomainForWidthSolvers(D):
def __init__(
self,
gym_env: gym.Env,
set_state: Callable[[gym.Env, D.T_memory[D.T_state]], None] = None,
get_state: Callable[[gym.Env], D.T_memory[D.T_state]] = None,
termination_is_goal: bool = True,
continuous_feature_fidelity: int = 5,
discretization_factor: int = 3,
branching_factor: int = None,
max_depth: int = 1000,
) -> None:
GymPlanningDomain.__init__(
self,
gym_env=gym_env,
set_state=set_state,
get_state=get_state,
termination_is_goal=termination_is_goal,
max_depth=max_depth,
)
GymDiscreteActionDomain.__init__(
self,
discretization_factor=discretization_factor,
branching_factor=branching_factor,
)
GymWidthDomain.__init__(
self, continuous_feature_fidelity=continuous_feature_fidelity
)
gym_env._max_episode_steps = max_depth
```
We redefine accordingly the domain factory.
```
domain4width_factory = lambda: GymDomainForWidthSolvers(gym.make(ENV_NAME))
```
### Check compatibility
We check the compatibility of the domain with the chosen solver.
```
domain = domain4width_factory()
assert IW.check_domain(domain)
domain.close()
```
### Solver instantiation
As explained earlier, we use the Boundary Extension Encoding state features `bee2_features` so that IW can dynamically increase state variable intervals. In other domains, other state features might be more suitable.
```
solver = IW(
state_features=lambda d, s: d.bee2_features(s),
node_ordering=lambda a_gscore, a_novelty, a_depth, b_gscore, b_novelty, b_depth: a_novelty
> b_novelty,
parallel=False,
debug_logs=False,
domain_factory=domain4width_factory,
)
```
### Training solver on domain
```
GymDomainForWidthSolvers.solve_with(solver, domain4width_factory)
```
### Rolling out a solution
**Disclaimer:** This roll out can be a bit painful to look on local Jupyter sessions. Indeed, IW creates copies of the environment at each step which makes pop up then close a new OpenGL window each time.
We have to slightly modify the roll out function as observations for the new domain are now wrapped in a `GymDomainProxyState` to make them serializable. So to get access to the underlying numpy array, we need to look for `observation._state`.
```
def rollout_iw(
domain: GymDomain,
solver: Solver,
max_steps: int,
pause_between_steps: Optional[float] = 0.01,
render: bool = False,
):
"""Roll out one episode in a domain according to the policy of a trained solver.
Args:
domain: the maze domain to solve
solver: a trained solver
max_steps: maximum number of steps allowed to reach the goal
pause_between_steps: time (s) paused between agent movements.
No pause if None.
render: if True, the rollout is rendered in a matplotlib figure as an animation;
if False, speed up a lot the rollout.
"""
# Initialize episode
solver.reset()
observation = domain.reset()
# Initialize image
if render:
plt.ioff()
fig, ax = plt.subplots(1)
ax.axis("off")
plt.ion()
img = ax.imshow(domain.render(mode="rgb_array"))
display(fig)
# loop until max_steps or goal is reached
for i_step in range(1, max_steps + 1):
if pause_between_steps is not None:
sleep(pause_between_steps)
# choose action according to solver
action = solver.sample_action(observation)
# get corresponding action
outcome = domain.step(action)
observation = outcome.observation
# update image
if render:
img.set_data(domain.render(mode="rgb_array"))
fig.canvas.draw()
clear_output(wait=True)
display(fig)
# final state reached?
if outcome.termination:
break
# close the figure to avoid jupyter duplicating the last image
if render:
plt.close(fig)
# goal reached?
is_goal_reached = observation._state[0] >= 0.45
if is_goal_reached:
print(f"Goal reached in {i_step} steps!")
else:
print(f"Goal not reached after {i_step} steps!")
return is_goal_reached, i_step
domain = domain4width_factory()
try:
rollout_iw(
domain=domain,
solver=solver,
max_steps=999,
pause_between_steps=None,
render=True,
)
finally:
domain.close()
```
IW works especially well in mountain car.
Indeed we need to increase the cinetic+potential energy to reach the goal, which comes to increase as much as possible the values of the state variables (position and velocity). This is exactly what IW is designed to do (trying to explore novel states, which means here with higher position or velocity).
As a consequence, IW can find an optimal strategy in a few seconds (whereas in most cases PPO and CGP can't find optimal strategies in the same computation time).
### Cleaning up
```
solver._cleanup()
```
## Conclusion
We saw that it is possible thanks to scikit-decide to apply solvers from different fields and communities (Reinforcement Learning, Genetic Programming, and Planning) on a OpenAI Gym Environment.
Even though the domain used here is more classical for RL community, the solvers from other communities performed far better. In particular the IW algorithm was able to find an efficient solution in a very short time.
|
github_jupyter
|
```
import tensorflow as tf
import numpy as np
import tsp_env
def attention(W_ref, W_q, v, enc_outputs, query):
with tf.variable_scope("attention_mask"):
u_i0s = tf.einsum('kl,itl->itk', W_ref, enc_outputs)
u_i1s = tf.expand_dims(tf.einsum('kl,il->ik', W_q, query), 1)
u_is = tf.einsum('k,itk->it', v, tf.tanh(u_i0s + u_i1s))
return tf.einsum('itk,it->ik', enc_outputs, tf.nn.softmax(u_is))
def critic_network(enc_inputs,
hidden_size = 128, embedding_size = 128,
max_time_steps = 5, input_size = 2,
batch_size = 128,
initialization_stddev = 0.1,
n_processing_steps = 5, d = 128):
# Embed inputs in larger dimensional tensors
W_embed = tf.Variable(tf.random_normal([embedding_size, input_size],
stddev=initialization_stddev))
embedded_inputs = tf.einsum('kl,itl->itk', W_embed, enc_inputs)
# Define encoder
with tf.variable_scope("encoder"):
enc_rnn_cell = tf.nn.rnn_cell.LSTMCell(hidden_size)
enc_outputs, enc_final_state = tf.nn.dynamic_rnn(cell=enc_rnn_cell,
inputs=embedded_inputs,
dtype=tf.float32)
# Define process block
with tf.variable_scope("process_block"):
process_cell = tf.nn.rnn_cell.LSTMCell(hidden_size)
first_process_block_input = tf.tile(tf.Variable(tf.random_normal([1, embedding_size]),
name='first_process_block_input'),
[batch_size, 1])
# Define attention weights
with tf.variable_scope("attention_weights", reuse=True):
W_ref = tf.Variable(tf.random_normal([embedding_size, embedding_size],
stddev=initialization_stddev),
name='W_ref')
W_q = tf.Variable(tf.random_normal([embedding_size, embedding_size],
stddev=initialization_stddev),
name='W_q')
v = tf.Variable(tf.random_normal([embedding_size], stddev=initialization_stddev),
name='v')
# Processing chain
processing_state = enc_final_state
processing_input = first_process_block_input
for t in range(n_processing_steps):
processing_cell_output, processing_state = process_cell(inputs=processing_input,
state=processing_state)
processing_input = attention(W_ref, W_q, v,
enc_outputs=enc_outputs, query=processing_cell_output)
# Apply 2 layers of ReLu for decoding the processed state
return tf.squeeze(tf.layers.dense(inputs=tf.layers.dense(inputs=processing_cell_output,
units=d, activation=tf.nn.relu),
units=1, activation=None))
batch_size = 128; max_time_steps = 5; input_size = 2
enc_inputs = tf.placeholder(tf.float32, [batch_size, max_time_steps, input_size])
bsln_value = critic_network(enc_inputs,
hidden_size = 128, embedding_size = 128,
max_time_steps = 5, input_size = 2,
batch_size = 128,
initialization_stddev = 0.1,
n_processing_steps = 5, d = 128)
tours_rewards_ph = tf.placeholder(tf.float32, [batch_size])
loss = tf.losses.mean_squared_error(labels=tours_rewards_ph,
predictions=bsln_value)
train_op = tf.train.AdamOptimizer(1e-2).minimize(loss)
##############################################################################
# Trying it out: can we learn the reward of the optimal policy for the TSP5? #
##############################################################################
def generate_batch(n_cities, batch_size):
inputs_list = []; labels_list = []
env = tsp_env.TSP_env(n_cities, use_alternative_state=True)
for i in range(batch_size):
env.reset()
s = env.reset()
coords = s.reshape([4, n_cities])[:2, ].T
inputs_list.append(coords)
labels_list.append(env.optimal_solution()[0])
return np.array(inputs_list), np.array(labels_list)
# Create tf session and initialize variables
sess = tf.InteractiveSession()
tf.global_variables_initializer().run()
# Training loop
loss_vals = []
for i in range(10000):
inputs_batch, labels_batch = generate_batch(max_time_steps, batch_size)
loss_val, _ = sess.run([loss, train_op],
feed_dict={enc_inputs: inputs_batch,
tours_rewards_ph: labels_batch})
loss_vals.append(loss_val)
if i % 50 == 0:
print(loss_val)
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(np.log(loss_vals_slow_lr))
plt.xlabel('Number of iterations')
plt.ylabel('Log of mean squared error')
len(loss_vals)
```
|
github_jupyter
|
<div align="right"><i>COM418 - Computers and Music</i></div>
<div align="right"><a href="https://people.epfl.ch/paolo.prandoni">Lucie Perrotta</a>, <a href="https://www.epfl.ch/labs/lcav/">LCAV, EPFL</a></div>
<p style="font-size: 30pt; font-weight: bold; color: #B51F1F;">Channel Vocoder</p>
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import Audio
from IPython.display import IFrame
from scipy import signal
import import_ipynb
from Helpers import *
figsize=(10,5)
import matplotlib
matplotlib.rcParams.update({'font.size': 16});
fs=44100
```
In this notebook, we will implement and test an easy **channel vocoder**. A channel vocoder is a musical device that allows to sing while playing notes on a keyboard at the same time. The vocoder blends the voice (called the modulator) with the played notes on the keyboard (called the carrier) so that the resulting voice sings the note played on the keyboard. The resulting voice has a robotic, artificial sound that is rather popular in electronic music, with notable uses by bands such as Daft Punk, or Kraftwerk.
<img src="https://www.bhphotovideo.com/images/images2000x2000/waldorf_stvc_string_synthesizer_1382081.jpg" alt="Drawing" style="width: 35%;"/>
The implementation of a Channel vocoder is in fact quite simple. It takes 2 inputs, the carrier and the modulator signals, that must be of the same length. It divides each signal into frequency bands called **channels** (hence the name) using many parallel bandpass filters. The width of each channel can be equal, or logarithmically sized to match the human ear perception of frequency. For each channel, the envelope of the modulator signal is then computed, for instance using a rectifier and a moving average. It is simply multiplied to the carrier signal for each channel, before all channels are added back together.
<img src="https://i.imgur.com/aIePutp.png" alt="Drawing" style="width: 65%;"/>
To improve the intelligibility of the speech, it is also possible to add AWGN to each to the carrier of each band, helping to produce non-voiced sounds, such as the sound s, or f.
As an example signal to test our vocoder with, we are going to use dry voice samples from the song "Nightcall" by french artist Kavinsky.

First, let's listen to the original song:
```
IFrame(src="https://www.youtube.com/embed/46qo_V1zcOM?start=30", width="560", height="315", frameborder="0", allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture")
```
## 1. The modulator and the carrier signals
We are now going to recreate the lead vocoder using 2 signals: we need a modulator signal, a voice pronouning the lyrics, and a carrier signal, a synthesizer, containing the notes for the pitch.
### 1.1. The modulator
Let's first import the modulator signal. It is simply the lyrics spoken at the right rhythm. No need to sing or pay attention to the pitch, only the prononciation and the rhythm of the text are going to matter. Note that the voice sample is available for free on **Splice**, an online resource for audio production.
```
nightcall_modulator = open_audio('snd/nightcall_modulator.wav')
Audio('snd/nightcall_modulator.wav', autoplay=False)
```
### 1.2. The carrier
Second, we import a carrier signal, which is simply a synthesizer playing the chords that are gonna be used for the vocoder. Note that the carrier signal does not need to feature silent parts, since the modulator's silences will automatically mute the final vocoded track. The carrier and the modulator simply need to be in synch with each other.
```
nightcall_carrier = open_audio('snd/nightcall_carrier.wav')
Audio("snd/nightcall_carrier.wav", autoplay=False)
```
## 2. The channel vocoder
### 2.1. The channeler
Let's now start implementing the phase vocoder. The first tool we need is an efficient filter to allow decomposing both the carrier and the modulator signals into channels (or bands). Let's call this function the **channeler** since it decomposes the input signals into frequency channels. It takes as input a signal to be filtered, a integer representing the number of bands, and a boolean for setting if we want white noise to be added to each band (used for the carrier).
```
def channeler(x, n_bands, add_noise=False):
"""
Separate a signal into log-sized frequency channels.
x: the input signal
n_bands: the number of frequency channels
add_noise: add white noise or note to each channel
"""
band_freqs = np.logspace(2, 14, n_bands+1, base=2) # get all the limits between the bands, in log space
x_bands = np.zeros((n_bands, x.size)) # Placeholder for all bands
for i in range(n_bands):
noise = 0.7*np.random.random(x.size) if add_noise else 0 # Create AWGN or not
x_bands[i] = butter_pass_filter(x + noise, np.array((band_freqs[i], band_freqs[i+1])), fs, btype="band", order=5).astype(np.float32) # Carrier + uniform noise
return x_bands
# Example plot
plt.figure(figsize=figsize)
plt.magnitude_spectrum(nightcall_carrier)
plt.title("Carrier signal before channeling")
plt.xscale("log")
plt.xlim(1e-4)
plt.show()
carrier_bands = channeler(nightcall_carrier, 8, add_noise=True)
plt.figure(figsize=figsize)
for i in range(8):
plt.magnitude_spectrum(carrier_bands[i], alpha=.7)
plt.title("Carrier channels after channeling and noise addition")
plt.xscale("log")
plt.xlim(1e-4)
plt.show()
```
### 2.2. The envelope computer
Next, we can implement a simple envelope computer. Given a signal, this function computes its temporal envelope.
```
def envelope_computer(x):
"""
Envelope computation of one channels of the modulator
x: the input signal
"""
x = np.abs(x) # Rectify the signal to positive
x = moving_average(x, 1000) # Smooth the signal
return 3*x # Normalize # Normalize
plt.figure(figsize=figsize)
plt.plot(np.abs(nightcall_modulator)[:150000] , label="Modulator")
plt.plot(envelope_computer(nightcall_modulator)[:150000], label="Modulator envelope")
plt.legend(loc="best")
plt.title("Modulator signal and its envelope")
plt.show()
```
### 2.3. The channel vocoder (itself)
We can now implement the channel vocoder itself! It takes as input both signals presented above, as well as an integer controlling the number of channels (bands) of the vocoder. A larger number of channels results in the finer grained vocoded sound, but also takes more time to compute. Some artists may voluntarily use a lower numer of bands to increase the artificial effect of the vocoder. Try playing with it!
```
def channel_vocoder(modulator, carrier, n_bands=32):
"""
Channel vocoder
modulator: the modulator signal
carrier: the carrier signal
n_bands: the number of bands of the vocoder (better to be a power of 2)
"""
# Decompose both modulation and carrier signals into frequency channels
modul_bands = channeler(modulator, n_bands, add_noise=False)
carrier_bands = channeler(carrier, n_bands, add_noise=True)
# Compute envelope of the modulator
modul_bands = np.array([envelope_computer(modul_bands[i]) for i in range(n_bands)])
# Multiply carrier and modulator
result_bands = np.prod([modul_bands, carrier_bands], axis=0)
# Merge back all channels together and normalize
result = np.sum(result_bands, axis=0)
return normalize(result) # Normalize
nightcall_vocoder = channel_vocoder(nightcall_modulator, nightcall_carrier, n_bands=32)
Audio(nightcall_vocoder, rate=fs)
```
The vocoded voice is still perfectly intelligible, and it's easy to understand the lyrics. However, the pitch of the voice is now the synthesizer playing chords! One can try to deactivate the AWGN and compare the results. We finally plot the STFT of all 3 signals. One can notice that the vocoded signal has kept the general shape of the voice (modulator) signal, but is using the frequency information from the carrier!
```
# Plot
f, t, Zxx = signal.stft(nightcall_modulator[:7*fs], fs, nperseg=1000)
plt.figure(figsize=figsize)
plt.pcolormesh(t, f[:100], np.abs(Zxx[:100,:]), cmap='nipy_spectral', shading='gouraud')
plt.title("Original voice (modulator)")
plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.show()
f, t, Zxx = signal.stft(nightcall_vocoder[:7*fs], fs, nperseg=1000)
plt.figure(figsize=figsize)
plt.pcolormesh(t, f[:100], np.abs(Zxx[:100,:]), cmap='nipy_spectral', shading='gouraud')
plt.title("Vocoded voice")
plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.show()
f, t, Zxx = signal.stft(nightcall_carrier[:7*fs], fs, nperseg=1000)
plt.figure(figsize=figsize)
plt.pcolormesh(t, f[:100], np.abs(Zxx[:100,:]), cmap='nipy_spectral', shading='gouraud')
plt.title("Carrier")
plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.show()
```
## 3. Playing it together with the music
Finally, let's try to play it with the background music to see if it sounds like the original!
```
nightcall_instru = open_audio('snd/nightcall_instrumental.wav')
nightcall_final = nightcall_vocoder + 0.6*nightcall_instru
nightcall_final = normalize(nightcall_final) # Normalize
Audio(nightcall_final, rate=fs)
```
|
github_jupyter
|
Authored by: Avani Gupta <br>
Roll: 2019121004
**Note: dataset shape is version dependent hence final answer too will be dependent of sklearn version installed on machine**
# Excercise: Eigen Face
Here, we will look into ability of PCA to perform dimensionality reduction on a set of Labeled Faces in the Wild dataset made available from scikit-learn. Our images will be of shape (62, 47). This problem is also famously known as the eigenface problem. Mathematically, we would like to find the principal components (or eigenvectors) of the covariance matrix of the set of face images. These eigenvectors are essentially a set of orthonormal features depicts the amount of variation between face images. When plotted, these eigenvectors are called eigenfaces.
#### Imports
```
import numpy as np
import matplotlib.pyplot as plt
from numpy import pi
from sklearn.datasets import fetch_lfw_people
import seaborn as sns; sns.set()
import sklearn
print(sklearn.__version__)
```
#### Setup data
```
faces = fetch_lfw_people(min_faces_per_person=8)
X = faces.data
y = faces.target
print(faces.target_names)
print(faces.images.shape)
```
Note: **images num is version dependent** <br>
I get (4822, 62, 47) in my version of sklearn which is 0.22.2. <br>
Since our images is of the shape (62, 47), we unroll each image into a single row vector of shape (1, 4822). This means that we have 4822 features defining each image. These 4822 features will result into 4822 principal components in the PCA projection space. Therefore, each image location contributes more or less to each principal component.
#### Implement Eigen Faces
```
print(faces.images.shape)
img_shape = faces.images.shape[1:]
print(img_shape)
def FindEigen(X_mat):
X_mat -= np.mean(X_mat, axis=0, keepdims=True)
temp = np.matmul(X_mat.T, X_mat)
cov_mat = 1/X_mat.shape[0]* temp
eigvals, eigvecs = np.linalg.eig(cov_mat)
ind = eigvals.argsort()[::-1]
return np.real(eigvals[ind]), np.real(eigvecs[:, ind])
def plotFace(faces, h=10, v=1):
fig, axes = plt.subplots(v, h, figsize=(10, 2.5),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(faces[i].reshape(*img_shape), cmap='gray')
def plotgraph(eigenvals):
plt.plot(range(1, eigenvals.shape[0]+1), np.cumsum(eigenvals / np.sum(eigenvals)))
plt.show()
def PrincipalComponentsNum(X, eigenvals, threshold=0.95):
num = np.argmax(np.cumsum(eigenvals / np.sum(eigenvals)) >= threshold) + 1
print(f"No. of principal components required to preserve {threshold*100} % variance is: {num}.")
```
### Q1
How many principal components are required such that 95% of the vari-
ance in the data is preserved?
```
eigenvals, eigenvecs = FindEigen(X)
plotgraph(eigenvals)
PrincipalComponentsNum(X, eigenvals)
```
### Q2
Show the reconstruction of the first 10 face images using only 100 principal
components.
```
def reconstructMat(X, eigvecs, num_c):
return (np.matmul(X,np.matmul(eigvecs[:, :num_c], eigvecs[:, :num_c].T)))
faceNum = 10
print('original faces')
plotFace(X[:faceNum, :], faceNum)
recFace = reconstructMat(X[:faceNum, :], eigenvecs, 100)
print('reconstructed faces using only 100 principal components')
plotFace(recFace, faceNum)
```
# Adding noise to images
We now add gaussian noise to the images. Will PCA be able to effectively perform dimensionality reduction?
```
def plot_noisy_faces(noisy_faces):
fig, axes = plt.subplots(2, 10, figsize=(10, 2.5),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(noisy_faces[i].reshape(62, 47), cmap='binary_r')
```
Below we plot first twenty noisy input face images.
```
np.random.seed(42)
noisy_faces = np.random.normal(X, 15)
plot_noisy_faces(noisy_faces)
noisy_faces.shape
noisy_eigenvals, noisy_eigenvecs = FindEigen(noisy_faces)
```
### Q3.1
Show the above two results for a noisy face dataset.
How many principal components are required such that 95% of the vari-
ance in the data is preserved?
```
plotgraph(noisy_eigenvals)
PrincipalComponentsNum(noisy_faces, noisy_eigenvals, 0.95)
```
### Q3.2
Show the reconstruction of the first 10 face images using only 100 principal
components.
```
faces = 10
noisy_recons = reconstructMat(noisy_faces[:faces, :], noisy_eigenvecs, 100)
print('reconstructed faces for nosiy images only 100 principal components')
plotFace(noisy_recons, faces)
```
|
github_jupyter
|
<div align="center">
<h1><img width="30" src="https://madewithml.com/static/images/rounded_logo.png"> <a href="https://madewithml.com/">Made With ML</a></h1>
Applied ML · MLOps · Production
<br>
Join 30K+ developers in learning how to responsibly <a href="https://madewithml.com/about/">deliver value</a> with ML.
<br>
</div>
<br>
<div align="center">
<a target="_blank" href="https://newsletter.madewithml.com"><img src="https://img.shields.io/badge/Subscribe-30K-brightgreen"></a>
<a target="_blank" href="https://github.com/GokuMohandas/MadeWithML"><img src="https://img.shields.io/github/stars/GokuMohandas/MadeWithML.svg?style=social&label=Star"></a>
<a target="_blank" href="https://www.linkedin.com/in/goku"><img src="https://img.shields.io/badge/style--5eba00.svg?label=LinkedIn&logo=linkedin&style=social"></a>
<a target="_blank" href="https://twitter.com/GokuMohandas"><img src="https://img.shields.io/twitter/follow/GokuMohandas.svg?label=Follow&style=social"></a>
<br>
🔥 Among the <a href="https://github.com/topics/mlops" target="_blank">top MLOps</a> repositories on GitHub
</div>
<br>
<hr>
# Optimize (GPU)
Use this notebooks to run hyperparameter optimization on Google Colab and utilize it's free GPUs.
## Clone repository
```
# Load repository
!git clone https://github.com/GokuMohandas/MLOps.git mlops
# Files
% cd mlops
!ls
```
## Setup
```
%%bash
!pip install --upgrade pip
!python -m pip install -e ".[dev]" --no-cache-dir
```
# Download data
We're going to download data directly from GitHub since our blob stores are local. But you can easily load the correct data versions from your cloud blob store using the *.json.dvc pointer files in the [data directory](https://github.com/GokuMohandas/MLOps/tree/main/data).
```
from app import cli
# Download data
cli.download_data()
# Check if data downloaded
!ls data
```
# Compute features
```
# Download data
cli.compute_features()
# Computed features
!ls data
```
## Optimize
Now we're going to perform hyperparameter optimization using the objective and parameter distributions defined in the [main script](https://github.com/GokuMohandas/MLOps/blob/main/tagifai/main.py). The best parameters will be written to [config/params.json](https://raw.githubusercontent.com/GokuMohandas/MLOps/main/config/params.json) which will be used to train the best model below.
```
# Optimize
cli.optimize(num_trials=100)
```
# Train
Once we're identified the best hyperparameters, we're ready to train our best model and save the corresponding artifacts (label encoder, tokenizer, etc.)
```
# Train best model
cli.train_model()
```
# Change metadata
In order to transfer our trained model and it's artifacts to our local model registry, we should change the metadata to match.
```
from pathlib import Path
from config import config
import yaml
def change_artifact_metadata(fp):
with open(fp) as f:
metadata = yaml.load(f)
for key in ["artifact_location", "artifact_uri"]:
if key in metadata:
metadata[key] = metadata[key].replace(
str(config.MODEL_REGISTRY), model_registry)
with open(fp, "w") as f:
yaml.dump(metadata, f)
# Change this as necessary
model_registry = "/Users/goku/Documents/madewithml/applied-ml/stores/model"
# Change metadata in all meta.yaml files
experiment_dir = Path(config.MODEL_REGISTRY, "1")
for fp in list(Path(experiment_dir).glob("**/meta.yaml")):
change_artifact_metadata(fp=fp)
```
## Download
Download and transfer the trained model's files to your local model registry. If you existing runs, just transfer that run's directory.
```
from google.colab import files
# Download
!zip -r model.zip model
!zip -r run.zip stores/model/1
files.download("run.zip")
```
|
github_jupyter
|
# Expressions and Arithmetic
**CS1302 Introduction to Computer Programming**
___
## Operators
The followings are common operators you can use to form an expression in Python:
| Operator | Operation | Example |
| --------: | :------------- | :-----: |
| unary `-` | Negation | `-y` |
| `+` | Addition | `x + y` |
| `-` | Subtraction | `x - y` |
| `*` | Multiplication | `x*y` |
| `/` | Division | `x/y` |
- `x` and `y` in the examples are called the *left and right operands* respectively.
- The first operator is a *unary operator*, which operates on just one operand.
(`+` can also be used as a unary operator, but that is not useful.)
- All other operators are *binary operators*, which operate on two operands.
Python also supports some more operators such as the followings:
| Operator | Operation | Example |
| -------: | :--------------- | :-----: |
| `//` | Integer division | `x//y` |
| `%` | Modulo | `x%y` |
| `**` | Exponentiation | `x**y` |
```
# ipywidgets to demonstrate the operations of binary operators
from ipywidgets import interact
binary_operators = {'+':' + ','-':' - ','*':'*','/':'/','//':'//','%':'%','**':'**'}
@interact(operand1=r'10',
operator=binary_operators,
operand2=r'3')
def binary_operation(operand1,operator,operand2):
expression = f"{operand1}{operator}{operand2}"
value = eval(expression)
print(f"""{'Expression:':>11} {expression}\n{'Value:':>11} {value}\n{'Type:':>11} {type(value)}""")
```
**Exercise** What is the difference between `/` and `//`?
- `/` is the usual division, and so `10/3` returns the floating-point number $3.\dot{3}$.
- `//` is integer division, and so `10//3` gives the integer quotient 3.
**What does the modulo operator `%` do?**
You can think of it as computing the remainder, but the [truth](https://docs.python.org/3/reference/expressions.html#binary-arithmetic-operations) is more complicated than required for the course.
**Exercise** What does `'abc' * 3` mean? What about `10 * 'a'`?
- The first expression means concatenating `'abc'` three times.
- The second means concatenating `'a'` ten times.
**Exercise** How can you change the default operands (`10` and `3`) for different operators so that the overall expression has type `float`.
Do you need to change all the operands to `float`?
- `/` already returns a `float`.
- For all other operators, changing at least one of the operands to `float` will return a `float`.
## Operator Precedence and Associativity
An expression can consist of a sequence of operations performed in a row such as `x + y*z`.
**How to determine which operation should be performed first?**
Like arithmetics, the order of operations is decided based on the following rules applied sequentially:
1. *grouping* by parentheses: inner grouping first
1. operator *precedence/priority*: higher precedence first
1. operator *associativity*:
- left associativity: left operand first
- right associativity: right operand first
**What are the operator precedence and associativity?**
The following table gives a concise summary:
| Operators | Associativity |
| :--------------- | :-----------: |
| `**` | right |
| `-` (unary) | right |
| `*`,`/`,`//`,`%` | left |
| `+`,`-` | left |
**Exercise** Play with the following widget to understand the precedence and associativity of different operators.
In particular, explain whether the expression `-10 ** 2*3` gives $(-10)^{2\times 3}= 10^6 = 1000000$.
```
from ipywidgets import fixed
@interact(operator1={'None':'','unary -':'-'},
operand1=fixed(r'10'),
operator2=binary_operators,
operand2=fixed(r'2'),
operator3=binary_operators,
operand3=fixed(r'3')
)
def three_operators(operator1,operand1,operator2,operand2,operator3,operand3):
expression = f"{operator1}{operand1}{operator2}{operand2}{operator3}{operand3}"
value = eval(expression)
print(f"""{'Expression:':>11} {expression}\n{'Value:':>11} {value}\n{'Type:':>11} {type(value)}""")
```
The expression evaluates to $(-(10^2))\times 3=-300$ instead because the exponentiation operator `**` has higher precedence than both the multiplication `*` and the negation operators `-`.
**Exercise** To avoid confusion in the order of operations, we should follow the [style guide](https://www.python.org/dev/peps/pep-0008/#other-recommendations) when writing expression.
What is the proper way to write `-10 ** 2*3`?
```
print(-10**2 * 3) # can use use code-prettify extension to fix incorrect styles
print((-10)**2 * 3)
```
## Augmented Assignment Operators
- For convenience, Python defines the [augmented assignment operators](https://docs.python.org/3/reference/simple_stmts.html#grammar-token-augmented-assignment-stmt) such as `+=`, where
- `x += 1` means `x = x + 1`.
The following widgets demonstrate other augmented assignment operators.
```
from ipywidgets import interact, fixed
@interact(initial_value=fixed(r'10'),
operator=['+=','-=','*=','/=','//=','%=','**='],
operand=fixed(r'2'))
def binary_operation(initial_value,operator,operand):
assignment = f"x = {initial_value}\nx {operator} {operand}"
_locals = {}
exec(assignment,None,_locals)
print(f"""Assignments:\n{assignment:>10}\nx: {_locals['x']} ({type(_locals['x'])})""")
```
**Exercise** Can we create an expression using (augmented) assignment operators? Try running the code to see the effect.
```
3*(x = 15)
```
Assignment operators are used in assignment statements, which are not expressions because they cannot be evaluated.
|
github_jupyter
|
```
%matplotlib inline
from IPython import display
import matplotlib.pyplot as plt
import torch
from torch import nn
import torchvision
import torchvision.transforms as transforms
import time
import sys
sys.path.append("../")
import d2lzh1981 as d2l
from tqdm import tqdm
print(torch.__version__)
print(torchvision.__version__)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
mnist_train = torchvision.datasets.FashionMNIST(root='/Users/nick/Documents/dataset/FashionMNIST2065',
train=True, download=False)
mnist_test = torchvision.datasets.FashionMNIST(root='/Users/nick/Documents/dataset/FashionMNIST2065',
train=False, download=False)
num_id = 0
for x, y in mnist_train:
if num_id % 1000 == 0:
print(num_id)
x.save("/Users/nick/Documents/dataset/FashionMNIST_img/train/{}_{}.png".format(y, num_id))
num_id += 1
num_id = 0
for x, y in mnist_test:
if num_id % 1000 == 0:
print(num_id)
x.save("/Users/nick/Documents/dataset/FashionMNIST_img/test/{}_{}.png".format(y, num_id))
num_id += 1
mnist_train = torchvision.datasets.FashionMNIST(root='/Users/nick/Documents/dataset/FashionMNIST2065',
train=True, download=False, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='/Users/nick/Documents/dataset/FashionMNIST2065',
train=False, download=False, transform=transforms.ToTensor())
def vgg_block(num_convs, in_channels, out_channels): #卷积层个数,输入通道数,输出通道数
blk = []
for i in range(num_convs):
if i == 0:
blk.append(nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
else:
blk.append(nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1))
blk.append(nn.ReLU())
blk.append(nn.MaxPool2d(kernel_size=2, stride=2)) # 这里会使宽高减半
return nn.Sequential(*blk)
def vgg(conv_arch, fc_features, fc_hidden_units=4096):
net = nn.Sequential()
# 卷积层部分
for i, (num_convs, in_channels, out_channels) in enumerate(conv_arch):
# 每经过一个vgg_block都会使宽高减半
net.add_module("vgg_block_" + str(i+1), vgg_block(num_convs, in_channels, out_channels))
# 全连接层部分
net.add_module("fc", nn.Sequential(d2l.FlattenLayer(),
nn.Linear(fc_features, fc_hidden_units),
nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(fc_hidden_units, fc_hidden_units),
nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(fc_hidden_units, 10)
))
return net
def evaluate_accuracy(data_iter, net, device=None):
if device is None and isinstance(net, torch.nn.Module):
# 如果没指定device就使用net的device
device = list(net.parameters())[0].device
acc_sum, n = 0.0, 0
with torch.no_grad():
for X, y in data_iter:
if isinstance(net, torch.nn.Module):
net.eval() # 评估模式, 这会关闭dropout
acc_sum += (net(X.to(device)).argmax(dim=1) == y.to(device)).float().sum().cpu().item()
net.train() # 改回训练模式
else: # 自定义的模型, 3.13节之后不会用到, 不考虑GPU
if('is_training' in net.__code__.co_varnames): # 如果有is_training这个参数
# 将is_training设置成False
acc_sum += (net(X, is_training=False).argmax(dim=1) == y).float().sum().item()
else:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum / n
batch_size = 100
if sys.platform.startswith('win'):
num_workers = 0
else:
num_workers = 4
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size,
shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size,
shuffle=False, num_workers=num_workers)
conv_arch = ((1, 1, 64), (1, 64, 128))
# 经过5个vgg_block, 宽高会减半5次, 变成 224/32 = 7
fc_features = 128 * 7 * 7 # c * w * h
fc_hidden_units = 4096 # 任意
# ratio = 8
# small_conv_arch = [(1, 1, 64//ratio), (1, 64//ratio, 128//ratio), (2, 128//ratio, 256//ratio),
# (2, 256//ratio, 512//ratio), (2, 512//ratio, 512//ratio)]
# net = vgg(small_conv_arch, fc_features // ratio, fc_hidden_units // ratio)
net = vgg(conv_arch, fc_features, fc_hidden_units)
lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
net = net.to(device)
print("training on ", device)
loss = torch.nn.CrossEntropyLoss()
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n, batch_count, start = 0.0, 0.0, 0, 0, time.time()
for X, y in tqdm(train_iter):
X = X.to(device)
y = y.to(device)
y_hat = net(X)
l = loss(y_hat, y)
optimizer.zero_grad()
l.backward()
optimizer.step()
train_l_sum += l.cpu().item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().cpu().item()
n += y.shape[0]
batch_count += 1
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f, time %.1f sec'
% (epoch + 1, train_l_sum / batch_count, train_acc_sum / n, test_acc, time.time() - start))
test_acc = evaluate_accuracy(test_iter, net)
test_acc
for X, y in train_iter:
X = X.to(device)
predict_y = net(X)
print(y)
print(predict_y.argmax(dim=1))
break
# predict_y.argmax(dim=1)
```
|
github_jupyter
|
```
import os
import numpy as np
np.random.seed(0)
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import set_config
set_config(display="diagram")
DATA_PATH = os.path.abspath(
r"C:\Users\jan\Dropbox\_Coding\UdemyML\Chapter13_CaseStudies\CaseStudyIncome\adult.xlsx"
)
```
### Dataset
```
df = pd.read_excel(DATA_PATH)
idx = np.where(df["native-country"] == "Holand-Netherlands")[0]
data = df.to_numpy()
x = data[:, :-1]
x = np.delete(x, idx, axis=0)
y = data[:, -1]
y = np.delete(y, idx, axis=0)
categorical_features = [1, 2, 3, 4, 5, 6, 7, 9]
numerical_features = [0, 8]
print(f"x shape: {x.shape}")
print(f"y shape: {y.shape}")
```
### y-Data
```
def one_hot(y):
return np.array([0 if val == "<=50K" else 1 for val in y], dtype=np.int32)
y = one_hot(y)
```
### Helper
```
def print_grid_cv_results(grid_result):
print(
f"Best model score: {grid_result.best_score_} "
f"Best model params: {grid_result.best_params_} "
)
means = grid_result.cv_results_["mean_test_score"]
stds = grid_result.cv_results_["std_test_score"]
params = grid_result.cv_results_["params"]
for mean, std, param in zip(means, stds, params):
mean = round(mean, 4)
std = round(std, 4)
print(f"{mean} (+/- {2 * std}) with: {param}")
```
### Sklearn Imports
```
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OrdinalEncoder
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)
```
### Classifier and Params
```
params = {
"classifier__n_estimators": [50, 100, 200],
"classifier__max_depth": [None, 100, 200]
}
clf = RandomForestClassifier()
```
### Ordinal Features
```
numeric_transformer = Pipeline(
steps=[
('scaler', StandardScaler())
]
)
categorical_transformer = Pipeline(
steps=[
('ordinal', OrdinalEncoder())
]
)
preprocessor_odinal = ColumnTransformer(
transformers=[
('numeric', numeric_transformer, numerical_features),
('categorical', categorical_transformer, categorical_features)
]
)
preprocessor_odinal
preprocessor_odinal.fit(x_train)
x_train_ordinal = preprocessor_odinal.transform(x_train)
x_test_ordinal = preprocessor_odinal.transform(x_test)
print(f"Shape of odinal data: {x_train_ordinal.shape}")
print(f"Shape of odinal data: {x_test_ordinal.shape}")
pipe_ordinal = Pipeline(
steps=[
('preprocessor_odinal', preprocessor_odinal),
('classifier', clf)
]
)
pipe_ordinal
grid_ordinal = GridSearchCV(pipe_ordinal, params, cv=3)
grid_results_ordinal = grid_ordinal.fit(x_train, y_train)
print_grid_cv_results(grid_results_ordinal)
```
### OneHot Features
```
numeric_transformer = Pipeline(
steps=[
('scaler', StandardScaler())
]
)
categorical_transformer = Pipeline(
steps=[
('onehot', OneHotEncoder(handle_unknown="ignore", sparse=False))
]
)
preprocessor_onehot = ColumnTransformer(
transformers=[
('numeric', numeric_transformer, numerical_features),
('categorical', categorical_transformer, categorical_features)
]
)
preprocessor_onehot
preprocessor_onehot.fit(x_train)
x_train_onehot = preprocessor_onehot.transform(x_train)
x_test_onehot = preprocessor_onehot.transform(x_test)
print(f"Shape of onehot data: {x_train_onehot.shape}")
print(f"Shape of onehot data: {x_test_onehot.shape}")
pipe_onehot = Pipeline(
steps=[
('preprocessor_onehot', preprocessor_odinal),
('classifier', clf)
]
)
pipe_onehot
grid_onehot = GridSearchCV(pipe_onehot, params, cv=3)
grid_results_onehot = grid_onehot.fit(x_train, y_train)
print_grid_cv_results(grid_results_onehot)
```
### TensorFlow Model
```
from tensorflow.keras.layers import Activation
from tensorflow.keras.layers import Dense
from tensorflow.keras.models import Sequential
from tensorflow.keras.optimizers import SGD
y_train = y_train.reshape(-1, 1)
y_test = y_test.reshape(-1, 1)
def build_model(input_dim, output_dim):
model = Sequential()
model.add(Dense(units=128, input_dim=input_dim))
model.add(Activation("relu"))
model.add(Dense(units=64))
model.add(Activation("relu"))
model.add(Dense(units=output_dim))
model.add(Activation("sigmoid"))
return model
```
### Neural Network with Ordinal Features
```
model = build_model(
input_dim=x_test_ordinal.shape[1],
output_dim=y_train.shape[1]
)
model.compile(
loss="binary_crossentropy",
optimizer=SGD(learning_rate=0.001),
metrics=["binary_accuracy"]
)
history_ordinal = model.fit(
x=x_train_ordinal,
y=y_train,
epochs=20,
validation_data=(x_test_ordinal, y_test)
)
val_binary_accuracy = history_ordinal.history["val_binary_accuracy"]
plt.plot(range(len(val_binary_accuracy)), val_binary_accuracy)
plt.show()
```
### Neural Network with OneHot Features
```
model = build_model(
input_dim=x_train_onehot.shape[1],
output_dim=y_train.shape[1]
)
model.compile(
loss="binary_crossentropy",
optimizer=SGD(learning_rate=0.001),
metrics=["binary_accuracy"]
)
history_onehot = model.fit(
x=x_train_onehot,
y=y_train,
epochs=20,
validation_data=(x_test_onehot, y_test)
)
val_binary_accuracy = history_onehot.history["val_binary_accuracy"]
plt.plot(range(len(val_binary_accuracy)), val_binary_accuracy)
plt.show()
```
### Pass in user-data
```
pipe_ordinal.fit(x_train, y_train)
score = pipe_ordinal.score(x_test, y_test)
print(f"Score: {score}")
x_sample = [
25,
"Private",
"11th",
"Never-married",
"Machine-op-inspct",
"Own-child",
"Black",
"Male",
40,
"United-States"
]
y_sample = 0
y_pred_sample = pipe_ordinal.predict([x_sample])
print(f"Pred: {y_pred_sample}")
```
|
github_jupyter
|
# UK research networks with HoloViews+Bokeh+Datashader
[Datashader](http://datashader.readthedocs.org) makes it possible to plot very large datasets in a web browser, while [Bokeh](http://bokeh.pydata.org) makes those plots interactive, and [HoloViews](http://holoviews.org) provides a convenient interface for building these plots.
Here, let's use these three programs to visualize an example dataset of 600,000 collaborations between 15000 UK research institutions, previously laid out using a force-directed algorithm by [Ian Calvert](https://www.digital-science.com/people/ian-calvert).
First, we'll import the packages we are using and set up some defaults.
```
import pandas as pd
import holoviews as hv
import fastparquet as fp
from colorcet import fire
from datashader.bundling import directly_connect_edges, hammer_bundle
from holoviews.operation.datashader import datashade, dynspread
from holoviews.operation import decimate
from dask.distributed import Client
client = Client()
hv.notebook_extension('bokeh','matplotlib')
decimate.max_samples=20000
dynspread.threshold=0.01
datashade.cmap=fire[40:]
sz = dict(width=150,height=150)
%opts RGB [xaxis=None yaxis=None show_grid=False bgcolor="black"]
```
The files are stored in the efficient Parquet format:
```
r_nodes_file = '../data/calvert_uk_research2017_nodes.snappy.parq'
r_edges_file = '../data/calvert_uk_research2017_edges.snappy.parq'
r_nodes = hv.Points(fp.ParquetFile(r_nodes_file).to_pandas(index='id'), label="Nodes")
r_edges = hv.Curve( fp.ParquetFile(r_edges_file).to_pandas(index='id'), label="Edges")
len(r_nodes),len(r_edges)
```
We can render each collaboration as a single-line direct connection, but the result is a dense tangle:
```
%%opts RGB [tools=["hover"] width=400 height=400]
%time r_direct = hv.Curve(directly_connect_edges(r_nodes.data, r_edges.data),label="Direct")
dynspread(datashade(r_nodes,cmap=["cyan"])) + \
datashade(r_direct)
```
Detailed substructure of this graph becomes visible after bundling edges using a variant of [Hurter, Ersoy, & Telea (ECV-2012)](http://www.cs.rug.nl/~alext/PAPERS/EuroVis12/kdeeb.pdf), which takes several minutes even using multiple cores with [Dask](https://dask.pydata.org):
```
%time r_bundled = hv.Curve(hammer_bundle(r_nodes.data, r_edges.data),label="Bundled")
%%opts RGB [tools=["hover"] width=400 height=400]
dynspread(datashade(r_nodes,cmap=["cyan"])) + datashade(r_bundled)
```
Zooming into these plots reveals interesting patterns (if you are running a live Python server), but immediately one then wants to ask what the various groupings of nodes might represent. With a small number of nodes or a small number of categories one could color-code the dots (using datashader's categorical color coding support), but here we just have thousands of indistinguishable dots. Instead, let's use hover information so the viewer can at least see the identity of each node on inspection.
To do that, we'll first need to pull in something useful to hover, so let's load the names of each institution in the researcher list and merge that with our existing layout data:
```
node_names = pd.read_csv("../data/calvert_uk_research2017_nodes.csv", index_col="node_id", usecols=["node_id","name"])
node_names = node_names.rename(columns={"name": "Institution"})
node_names
r_nodes_named = pd.merge(r_nodes.data, node_names, left_index=True, right_index=True)
r_nodes_named.tail()
```
We can now overlay a set of points on top of the datashaded edges, which will provide hover information for each node. Here, the entire set of 15000 nodes would be reasonably feasible to plot, but to show how to work with larger datasets we wrap the `hv.Points()` call with `decimate` so that only a finite subset of the points will be shown at any one time. If a node of interest is not visible in a particular zoom, then you can simply zoom in on that region; at some point the number of visible points will be below the specified decimate limit and the required point should be revealed.
```
%%opts Points (color="cyan") [tools=["hover"] width=900 height=650]
datashade(r_bundled, width=900, height=650) * \
decimate( hv.Points(r_nodes_named),max_samples=10000)
```
If you click around and hover, you should see interesting groups of nodes, and can then set up further interactive tools using [HoloViews' stream support](http://holoviews.org/user_guide/Responding_to_Events.html) to reveal aspects relevant to your research interests or questions.
As you can see, datashader lets you work with very large graph datasets, though there are a number of decisions to make by trial and error, you do have to be careful when doing computationally expensive operations like edge bundling, and interactive information will only be available for a limited subset of the data at any one time due to data-size limitations of current web browsers.
|
github_jupyter
|
<img src="images/utfsm.png" alt="" width="100px" align="right"/>
# USM Numérica
## Licencia y configuración del laboratorio
Ejecutar la siguiente celda mediante *`Ctr-S`*.
```
"""
IPython Notebook v4.0 para python 3.0
Librerías adicionales:
Contenido bajo licencia CC-BY 4.0. Código bajo licencia MIT.
(c) Sebastian Flores, Christopher Cooper, Alberto Rubio, Pablo Bunout.
"""
# Configuración para recargar módulos y librerías dinámicamente
%reload_ext autoreload
%autoreload 2
# Configuración para graficos en línea
%matplotlib inline
# Configuración de estilo
from IPython.core.display import HTML
HTML(open("./style/style.css", "r").read())
```
## Introducción a BASH
Antes de comenzar debemos saber que Bash es un programa informático usado como intérprete de comandos
o instrucciones dadas por un usuario, las cuales son escritas en alguna interfaz gráfica o comúnmente
una terminal. Esas instrucciones son interpretadas por Bash para luego enviar dichas órdenes al Núcleo
o Kernel del sistema operativo.
Cada sistema operativo se encuentra conformado por un Núcleo particular, que se encarga de interactuar
con la computadora siendo una especie de cerebro capaz de organizar, administrar y distribuir los recursos
físicos de esta, tales como memoria, procesador, forma de almacenamiento, entre otros.
<img src="imbash.png"width="700px">
Bash (Bourne-Again-Shell) es un lenguaje de programación basado en Bourne-Shell, el cual fue creado para
sistemas Unix en la década de los 70, siendo el sustituto natural y de acceso libre de este a partir del
año 1987 siendo compatible con la mayoría de sistemas Unix, GNU/Linux y en algunos casos con Microsoft-Windows
y Apple.
## Objetivos
1. Operaciones básicas para crear, abrir y cambiarse de directorio
2. Operaciones para crear un archivo, copiar y cambiarlo de directorio
3. Visualizador gráfico de directorios y archivos
4. Visualizador de datos y editor de un archivo de texto
5. Ejercicio de práctica
### 1. Operaciones para crear, abrir y cambiar de directorio
Este es el tipo de operaciones más básicas que un usuario ejecuta en un sistema operativo, los siguientes comandos nos permiten ubicarnos en alguna carpeta para tener acceso a algún archivo o material en específico, crear carpetas o directorios para almacenar información deseada entre otros.
La acción más simple para comenzar será ingresar a un directorio o carpeta deseada usando el comando *`cd`* como sigue:
```
cd <directorio>
```
Una extensión de este recurso es la posibilidad de colocar una secuencia de directorios para llegar a la ubicación deseada, separando los nombres por un slash del siguiente modo.
```
cd <directorio_1>/<subdirectorio_2>/<subdirectorio_3>
```
Podemos visualizar en la terminal el contenido de este directorio con el comando *`ls`* y luego crear un nuevo sub-directorio (o carpeta) dentro del directorio en el cual nos ubicamos con *`mkdir`*:
```
mkdir <subdirectorio>
```
Mencionamos además una opción con el comando anterior, que nos permite crear varios sub-directorios a la vez escribiendo sus nombres respectivos uno al lado del otro, separados por un espacio.
```
mkdir <subdirectorio_1> <subdirectorio_2> ... <subdirectorio_N>
```
Además como detalle si el nombre de nuestro directorio se conforma por palabras separadas por espacio, entonces conviene por defecto escribir el nombre completo entre comillas, puesto que de lo contrario Bash considerará cada palabra separada por un espacio como un subdirectorio diferente.
```
mkdir <"nombre subdirectorio">
```
Si queremos regresar a una ubicación anterior basta los comandos *`cd ..`* o *`cd -`* y si queremos volver al directorio original desde donde se abrió la terminal usamos *`cd ~`*.
Es posible borrar un directorio con su contenido al interior escribiendo el siguiente comando:
```Bash
rm -r <directorio>
```
Finalmente un comando que nos permite visualizar rápidamente nuestra ubicación actual y las precedentes es *`pwd`*.
### 2. Operaciones para crear, copiar y eliminar archivos
Un paso siguiente a lo visto en el punto anterior es la creación de algún tipo de archivo, realizando operaciones básicas como copiarlo de un directorio a otro, cambiarlo de ubicación o borrarlo.
Para crear un archivo debemos ingresar al directorio en el cual deseamos guardarlo con el comando *`cd`* y luego de esto podemos crear el archivo con el argumento *`>`* de la siguiente manera.
```
> <archivo.tipo>
```
Por defecto el archivo se crea en el directorio actual de nuestra ubicación, recordar que con pwd podemos visualizar la cadena de directorios y subdirectorios hasta la ubicación actual.
Debemos hacer referencia al comando *`echo`*, este consiste en una función interna del intérprete de comandos que nos permite realizar más de una acción al combinarlo de distintas maneras con otros comandos o variables. Uno de los usos más comunes es para la impresión de algún texto en la terminal.
```
echo <texto a imprimir>
```
También nos permite imprimir un texto en un archivo específico agregando *`echo <texto a imprimir> < <archivo sobre el que se imprime>`*, entre muchas otras opciones que la función *`echo`* nos permite realizar y que es posible profundizar con la práctica, pero estas las postergaremos para la siguiente sección.
Continuamos con el comando *`mv`*, que refiere a "move", el cual sirve para mover algún archivo ya creado a un nuevo directorio.
```
mv <archivo.tipo> <directorio>
```
También sirve para mover un directorio dentro de otro (mover *directorio_1* al *direcotorio_2*), para que el comando se ejecute correctamente ambos directorios deben estar en una misma ubicación.
```
mv <directorio_1> <directorio_2>
```
Una operación similar a la anterior es copiar un archivo y llevarlo a un directorio particular, con la diferencia que una vez realizada la acción se tendrán 2 copias del mismo archivo, una en el directorio original y la segunda en el nuevo directorio.
```
cp <archivo.tipo> <directorio>
```
Supongamos que queremos copiar un archivo existente en otro directorio y reemplazarlo por un archivo del directorio actual, podemos hacer esto de la siguiente manera.
```
cp ~/directorio_fuente/<archivo_fuente> <archivo_local>
```
Lo anterior se hace desde el directorio al cual deseamos copiar el archivo fuente y *~/directoiro_fuente/* hace alusión al directorio en el cual se encuentra este archivo.
Si por otra parte queremos copiar un archivo fuente y nos encontramos en el directorio en el cual este se encuentra, para realizar la copia en otro directorio, sin necesariamente hacer un reemplazo por otro archivo, se puede con:
```
cp <archivo_fuente_1> <archivo_fuente_2> ~/directorio_desitno/
```
Del mismo modo que para un directorio, si queremos borrar un archivo creado podemos hacerlo con el comando *`rm -r`*.
```
rm -r <archivo.tipo>
```
Y si queremos borrar una serie de archivos lo hacemos escribiendo consecutivamente.
```
rm -r <archivo_1.tipo> <archivo_2.tipo> ... <archivo_N.tipo>
```
### 3. Visualizador de estructura de directorios y archivos
El comando *`tree`* es una forma útil y rápida de visualizar gráficamente la estructura de directorios y archivo pudiendo ver claramente la relación entre estos. Solo debemos escribir el comando para que automáticamente aparezca esta información en pantalla (dentro de la terminal) apareciendo en orden alfabético, por defecto debe ejecutarse ubicándose en el directorio deseado visualizando la estructura dentro de este.
En caso de que este no se encuentre instalado en nuestro sistema operativo, a modo de ejercicio, primero debemos escribir los siguientes comandos.
```
sudo apt-get install <tree>
```
### 4. Visualizar, editar y concatenar un archivo de texto
Para visualizar el contenido de un texto previamente creado, pudiendo hacerlo con el comando visto anteriormente, *`echo > arhcivo.tipo`*, utilizamos el comando *`cat`*.
```
cat <archivo.tipo>
```
Luego si queremos visualizar varios archivos en la terminal, lo hacemos agregando uno al lado del otro después del comando *`cat`*.
```
cat <archivo_1.tipo> <archivo_2.tipo> ... <archivo_N.tipo>
```
Existen muchos argumentos que nos permiten visualizar de distinta forma el contenido de un archivo en la terminal, por ejemplo enumerar las filas de algún texto, *`cat -n`*, otra opción sería que solo se enumerara las filas que tienen algún contenido, *`cat -b`*.
En caso de que queramos enumerar solo las filas con texto, pero este tiene demasiadas filas en blanco y buscamos reducirlas a una sola de modo de ahorrar espacio en la terminal, podemos hacerlo agregando el argumento *-s* como sigue.
```
cat -sb <archivo.tipo>
```
Editar o imprimir un texto en un archivo es posible hacerlo usando la función *`echo`* como sigue.
```
echo <texto a imprimir> ./archivo.txt
```
Similar a sudo, less es un programa usado como visualizador de archivos de texto que funciona como un comando interpretado desde la terminal. Este permite visualizar completamente el archivo de texto usando por defecto las flechas del teclado para avanzar o retroceder en el visualizador.
Una de las ventajas de un programa como less, es que puede añadirse comandos para ejecutar acciones de forma rápida en modo de comandos que resulta por defecto al ejecutar less, a continuación presentamos algunos comandos básicos.
```
G: permite visualizar el final del texto
```
```
g: permite visualizar el inicio del texto
```
```
h: nos proporciona ayuda respecto a comandos posibles
```
```
q: permite salir de la aplicación dentro del visualizador less
```
Para modificar el texto una de las formas es cargar algún editor de texto como por ejemplo el Visual.
```
v: ejecutar el editor de texto
```
### 5. Ejercicio de práctica
Para redondear lo visto en este tutorial se dejara como ejercicio las siguientes instrucciones:
* Crear una carpeta o directorio principal
* En ella se debe copiar 2 archivos de textos provenientes de cualquier dirección
* Crear un archivo de texto el cual tenga por nombre "Texto Principal" y se imprima "concatenación de textos"
* Crear una segunda carpeta dentro de la principal
* Concatenar los 2 archivos copiados con el archivo creado
* Mover el archivo "Texto Principal" a la nueva carpeta
* Eliminar las copias de los archivos concatenados
* Visualizar con Tree la estructura y relación de archivos y directorios creados
```
%%bash
```
|
github_jupyter
|
# Prudential Life Insurance Assessment
An example of the structured data lessons from Lesson 4 on another dataset.
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
import os
from pathlib import Path
import pandas as pd
import numpy as np
import torch
from torch import nn
import torch.nn.functional as F
from fastai import structured
from fastai.column_data import ColumnarModelData
from fastai.dataset import get_cv_idxs
from sklearn.metrics import cohen_kappa_score
from ml_metrics import quadratic_weighted_kappa
from torch.nn.init import kaiming_uniform, kaiming_normal
PATH = Path('./data/prudential')
PATH.mkdir(exist_ok=True)
```
## Download dataset
```
!kaggle competitions download -c prudential-life-insurance-assessment --path={PATH}
for file in os.listdir(PATH):
if not file.endswith('zip'):
continue
!unzip -q -d {PATH} {PATH}/{file}
train_df = pd.read_csv(PATH/'train.csv')
train_df.head()
```
Extra feature engineering taken from the forum
```
train_df['Product_Info_2_char'] = train_df.Product_Info_2.str[0]
train_df['Product_Info_2_num'] = train_df.Product_Info_2.str[1]
train_df['BMI_Age'] = train_df['BMI'] * train_df['Ins_Age']
med_keyword_columns = train_df.columns[train_df.columns.str.startswith('Medical_Keyword_')]
train_df['Med_Keywords_Count'] = train_df[med_keyword_columns].sum(axis=1)
train_df['num_na'] = train_df.apply(lambda x: sum(x.isnull()), 1)
categorical_columns = 'Product_Info_1, Product_Info_2, Product_Info_3, Product_Info_5, Product_Info_6, Product_Info_7, Employment_Info_2, Employment_Info_3, Employment_Info_5, InsuredInfo_1, InsuredInfo_2, InsuredInfo_3, InsuredInfo_4, InsuredInfo_5, InsuredInfo_6, InsuredInfo_7, Insurance_History_1, Insurance_History_2, Insurance_History_3, Insurance_History_4, Insurance_History_7, Insurance_History_8, Insurance_History_9, Family_Hist_1, Medical_History_2, Medical_History_3, Medical_History_4, Medical_History_5, Medical_History_6, Medical_History_7, Medical_History_8, Medical_History_9, Medical_History_11, Medical_History_12, Medical_History_13, Medical_History_14, Medical_History_16, Medical_History_17, Medical_History_18, Medical_History_19, Medical_History_20, Medical_History_21, Medical_History_22, Medical_History_23, Medical_History_25, Medical_History_26, Medical_History_27, Medical_History_28, Medical_History_29, Medical_History_30, Medical_History_31, Medical_History_33, Medical_History_34, Medical_History_35, Medical_History_36, Medical_History_37, Medical_History_38, Medical_History_39, Medical_History_40, Medical_History_41'.split(', ')
categorical_columns += ['Product_Info_2_char', 'Product_Info_2_num']
cont_columns = 'Product_Info_4, Ins_Age, Ht, Wt, BMI, Employment_Info_1, Employment_Info_4, Employment_Info_6, Insurance_History_5, Family_Hist_2, Family_Hist_3, Family_Hist_4, Family_Hist_5, Medical_History_1, Medical_History_10, Medical_History_15, Medical_History_24, Medical_History_32'.split(', ')
cont_columns += [c for c in train_df.columns if c.startswith('Medical_Keyword_')] + ['BMI_Age', 'Med_Keywords_Count', 'num_na']
train_df[categorical_columns].head()
train_df[cont_columns].head()
train_df = train_df[categorical_columns + cont_columns + ['Response']]
len(train_df.columns)
```
### Convert to categorical
```
for col in categorical_columns:
train_df[col] = train_df[col].astype('category').cat.as_ordered()
train_df['Product_Info_1'].dtype
train_df.shape
```
### Numericalise and process DataFrame
```
df, y, nas, mapper = structured.proc_df(train_df, 'Response', do_scale=True)
y = y.astype('float')
num_targets = len(set(y))
```
### Create ColumnData object (instead of ImageClassifierData)
```
cv_idx = get_cv_idxs(len(df))
cv_idx
model_data = ColumnarModelData.from_data_frame(
PATH, cv_idx, df, y, cat_flds=categorical_columns, is_reg=True)
model_data.trn_ds[0][0].shape[0] + model_data.trn_ds[0][1].shape[0]
model_data.trn_ds[0][1].shape
```
### Get embedding sizes
The formula Jeremy uses for getting embedding sizes is: cardinality / 2 (maxed out at 50).
We reproduce that below:
```
categorical_column_sizes = [
(c, len(train_df[c].cat.categories) + 1) for c in categorical_columns]
categorical_column_sizes[:5]
embedding_sizes = [(c, min(50, (c+1)//2)) for _, c in categorical_column_sizes]
embedding_sizes[:5]
def emb_init(x):
x = x.weight.data
sc = 2/(x.size(1)+1)
x.uniform_(-sc,sc)
class MixedInputModel(nn.Module):
def __init__(self, emb_sizes, num_cont):
super().__init__()
embedding_layers = []
for size, dim in emb_sizes:
embedding_layers.append(
nn.Embedding(
num_embeddings=size, embedding_dim=dim))
self.embeddings = nn.ModuleList(embedding_layers)
for emb in self.embeddings: emb_init(emb)
self.embedding_dropout = nn.Dropout(0.04)
self.batch_norm_cont = nn.BatchNorm1d(num_cont)
num_emb = sum(e.embedding_dim for e in self.embeddings)
self.fc1 = nn.Linear(
in_features=num_emb + num_cont,
out_features=1000)
kaiming_normal(self.fc1.weight.data)
self.dropout_fc1 = nn.Dropout(p=0.01)
self.batch_norm_fc1 = nn.BatchNorm1d(1000)
self.fc2 = nn.Linear(
in_features=1000,
out_features=500)
kaiming_normal(self.fc2.weight.data)
self.dropout_fc2 = nn.Dropout(p=0.01)
self.batch_norm_fc2 = nn.BatchNorm1d(500)
self.output_fc = nn.Linear(
in_features=500,
out_features=1
)
kaiming_normal(self.output_fc.weight.data)
self.sigmoid = nn.Sigmoid()
def forward(self, categorical_input, continuous_input):
# Add categorical embeddings together
categorical_embeddings = [e(categorical_input[:,i]) for i, e in enumerate(self.embeddings)]
categorical_embeddings = torch.cat(categorical_embeddings, 1)
categorical_embeddings_dropout = self.embedding_dropout(categorical_embeddings)
# Batch normalise continuos vars
continuous_input_batch_norm = self.batch_norm_cont(continuous_input)
# Create a single vector
x = torch.cat([
categorical_embeddings_dropout, continuous_input_batch_norm
], dim=1)
# Fully-connected layer 1
fc1_output = self.fc1(x)
fc1_relu_output = F.relu(fc1_output)
fc1_dropout_output = self.dropout_fc1(fc1_relu_output)
fc1_batch_norm = self.batch_norm_fc1(fc1_dropout_output)
# Fully-connected layer 2
fc2_output = self.fc2(fc1_batch_norm)
fc2_relu_output = F.relu(fc2_output)
fc2_batch_norm = self.batch_norm_fc2(fc2_relu_output)
fc2_dropout_output = self.dropout_fc2(fc2_batch_norm)
output = self.output_fc(fc2_dropout_output)
output = self.sigmoid(output)
output = output * 7
output = output + 1
return output
num_cont = len(df.columns) - len(categorical_columns)
model = MixedInputModel(
embedding_sizes,
num_cont
)
model
from fastai.column_data import StructuredLearner
def weighted_kappa_metric(probs, y):
return quadratic_weighted_kappa(probs[:,0], y[:,0])
learner = StructuredLearner.from_model_data(model, model_data, metrics=[weighted_kappa_metric])
learner.lr_find()
learner.sched.plot()
learner.fit(0.0001, 3, use_wd_sched=True)
learner.fit(0.0001, 5, cycle_len=1, cycle_mult=2, use_wd_sched=True)
learner.fit(0.00001, 3, cycle_len=1, cycle_mult=2, use_wd_sched=True)
```
There's either a bug in my implementation, or a NN doesn't do that well at this problem.
|
github_jupyter
|
Carbon Insight: Carbon Emissions Visualization
==============================================
This tutorial aims to showcase how to visualize anthropogenic CO2 emissions with a near-global coverage and track correlations between global carbon emissions and socioeconomic factors such as COVID-19 and GDP.
```
# Requirements
%pip install numpy
%pip install pandas
%pip install matplotlib
```
# A. Process Carbon Emission Data
This notebook helps you to process and visualize carbon emission data provided by [Carbon-Monitor](https://carbonmonitor.org/), which records human-caused carbon emissions from different countries, sources, and timeframes that are of interest to you.
Overview:
- [Process carbon emission data](#a1)
- [Download data from Carbon Monitor](#a11)
- [Calculate the rate of change](#a12)
- [Expand country regions](#a13)
- [Visualize carbon emission data](#a2)
- [Observe carbon emission data from the perspective of time](#a21)
- [Compare carbon emission data of different sectors](#a22)
- [Examples](#a3)
- [World carbon emission data](#a31)
- [US carbon emission data](#a32)
```
import io
from urllib.request import urlopen
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
import os
# Optional Function: Export Data
def export_data(file_name: str, df: pd.DataFrame):
# df = country_region_name_to_code(df)
export_path = os.path.join('export_data', file_name)
print(f'Export Data to {export_path}')
if not os.path.exists('export_data'):
os.mkdir('export_data')
with open(export_path, 'w', encoding='utf-8') as f:
f.write(df.to_csv(index=None, line_terminator='\n', encoding='utf-8'))
```
## <a id="a1"></a> 1. Process Data
### <a id="a11"></a> 1.1. Download data from Carbon Monitor
We are going to download tabular carbon emission data and convert to Pandas Dataframe.
Supported data types:
- ```carbon_global``` includes carbon emission data of 11 countries and regions worldwide.
- ```carbon_us``` includes carbon emission data of 51 states of the United States.
- ```carbon_eu``` includes carbon emission data of 27 countries of the European Union.
- ```carbon_china``` includes carbon emission data of 31 cities and provinces of China.
```
def get_data_from_carbon_monitor(data_type='carbon_global'):
assert data_type in ['carbon_global', 'carbon_us', 'carbon_eu', 'carbon_china']
data_url = f'https://datas.carbonmonitor.org/API/downloadFullDataset.php?source={data_type}'
data = urlopen(data_url).read().decode('utf-8-sig')
df = pd.read_csv(io.StringIO(data))
df = df.drop(columns=['timestamp'])
df = df.loc[pd.notna(df['date'])]
df = df.rename(columns={'country': 'country_region'})
df['date'] = pd.to_datetime(df['date'], format='%d/%m/%Y')
if data_type == 'carbon_us':
df = df.loc[df['state'] != 'United States']
return df
```
### <a id="a12"></a> 1.2. Calculate the rate of change
The rate of change $\Delta(s, r, t)$ is defined as the ratio of current value and moving average of a certain window size:
$$\begin{aligned}
\Delta(s, r, t) = \left\{\begin{aligned}
&\frac{TX(s, r, t)}{\sum_{\tau=t-T}^{t-1}X(\tau)}, &t\geq T\\
&1, &0<t<T
\end{aligned}\right.
\end{aligned}$$
Where $X(s, r, t)$ is the carbon emission value of sector $s$, region $r$ and date $t$; $T$ is the window size with default value $T=14$.
```
def calculate_rate_of_change(df, window_size=14):
region_scope = 'state' if 'state' in df.columns else 'country_region'
new_df = pd.DataFrame()
for sector in set(df['sector']):
sector_mask = df['sector'] == sector
for region, values in df.loc[sector_mask].pivot(index='date', columns=region_scope, values='value').items():
values.fillna(0)
rates = values / values.rolling(window_size).mean()
rates.fillna(value=1, inplace=True)
tmp_df = pd.DataFrame(
index=values.index,
columns=['value', 'rate_of_change'],
data=np.array([values.to_numpy(), rates.to_numpy()]).T
)
tmp_df['sector'] = sector
tmp_df[region_scope] = region
new_df = new_df.append(tmp_df.reset_index())
return new_df
```
### <a id="a13"></a> 1.3. Expand country regions
*Note: This step applies only to the ```carbon_global``` dataset.*
The dataset ```carbon_global``` does not list all the countries/regions in the world. Instead, there are two groups which contains multiple countries/regions: ```ROW``` (i.e. the rest of the world) and ```EU27 & UK```.
In order to obtain the carbon emission data of countries/regions in these two groups, we can refer to [the EDGAR dataset](https://edgar.jrc.ec.europa.eu/dataset_ghg60) and use [the table of CO2 emissions of all world countries in 2019](./static_data/Baseline.csv) as the baseline.
Assume the the carbon emission of each non-listed country/region is linearly related to the carbon emission of the group it belongs to, we have:
$$\begin{aligned}
X(s, r, t) &= \frac{\sum_{r_i\in R(r)}X(s, r_i, t)}{\sum_{r_i\in R(r)}X(s, r_i, t_0)}X(s, r, t_0)\\
&= \frac{X_{Raw}(s, R(r), t)}{\sum_{r_i\in R(r)}X_{Baseline}(s, r_i)}X_{Baseline}(s, r)
\end{aligned}$$
Where
- $X(s, r, t)$ is the carbon emission value of sector $s$, country/region $r$ and date $t$.
- $t_0$ is the date of the baseline table.
- $R(r)$ is the group that contains country/region $r$.
- $X_{Raw}(s, R, t)$ is the carbon emission value of sector $s$, country/region group $R$ and date $t$ in the ```carbon_global``` dataset.
- $X_{Baseline}(s, r)$ is the carbon emission value of sector $s$ and country/region $r$ in the baseline table.
Note that the baseline table does not contain the ```International Aviation``` sector. Therefore, the data for ```International Aviation``` is only available to countries listed in the ```carbon_global``` dataset. When we expand the ```ROW``` and the ```EU27 & UK``` groups to other countries/regions of the world, only the other five sectors are considered.
```
def expand_country_regions(df):
sectors = set(df['sector'])
assert 'country_region' in df.columns
df = df.replace('US', 'United States')
df = df.replace('UK', 'United Kingdom')
original_country_regions = set(df['country_region'])
country_region_df = pd.read_csv('static_data/CountryRegion.csv')
base = {}
name_to_code = {}
for _, (name, code, source) in country_region_df.loc[:, ['Name', 'Code', 'DataSource']].iterrows():
if source.startswith('Simulated') and name not in original_country_regions:
name_to_code[name] = code
base[code] = 'ROW' if source.endswith('ROW') else 'EU27 & UK'
baseline = pd.read_csv('static_data/Baseline.csv')
baseline = baseline.set_index('CountryRegionCode')
baseline = baseline.loc[:, [sector for sector in baseline.columns if sector in sectors]]
group_baseline = {}
for group in original_country_regions & set(['ROW', 'EU27 & UK']):
group_baseline[group] = baseline.loc[[code for code, base_group in base.items() if base_group == group], :].sum()
new_df = pd.DataFrame()
sector_masks = {sector: df['sector'] == sector for sector in sectors}
for country_region in set(country_region_df['Name']):
if country_region in name_to_code:
code = name_to_code[country_region]
group = base[code]
group_mask = df['country_region'] == group
for sector, sum_value in group_baseline[group].items():
tmp_df = df.loc[sector_masks[sector] & group_mask, :].copy()
tmp_df['value'] = tmp_df['value'] / sum_value * baseline.loc[code, sector]
tmp_df['country_region'] = country_region
new_df = new_df.append(tmp_df)
elif country_region in original_country_regions:
new_df = new_df.append(df.loc[df['country_region'] == country_region])
return new_df
```
## 2. <a id="a2"></a> Visualize Data
This is a auxiliary module for displaying data, which can be modified arbitrarily.
### <a id="a21"></a> 2.1. Plot by date
In this part we are going to create a line chart, where the emission value and rate of change for given counties during the given time can be browsed.
```
def plot_by_date(df, start_date=None, end_date=None, sector=None, regions=None, title='Carbon Emission by Date'):
if start_date is None:
start_date = df['date'].min()
if end_date is None:
end_date = df['date'].max()
tmp_df = df.loc[(df['date'] >= start_date) & (df['date'] <= end_date)]
region_scope = 'state' if 'state' in tmp_df.columns else 'country_region'
if regions is None or type(regions) == int:
region_list = list(set(tmp_df[region_scope]))
sector_mask = True if sector is None else tmp_df['sector'] == sector
region_list.sort(key=lambda region: -tmp_df.loc[(tmp_df[region_scope] == region) & sector_mask, 'value'].sum())
regions = region_list[:3 if regions is None else regions]
tmp_df = pd.concat([tmp_df.loc[tmp_df[region_scope] == region] for region in regions])
if sector not in set(tmp_df['sector']):
tmp_df['rate_of_change'] = tmp_df['value'] / tmp_df['rate_of_change']
tmp_df = tmp_df.groupby(['date', region_scope]).sum().reset_index()
value_df = tmp_df.pivot(index='date', columns=region_scope, values='value')
rate_df = tmp_df.pivot(index='date', columns=region_scope, values='rate_of_change')
rate_df = value_df / rate_df
else:
tmp_df = tmp_df.loc[tmp_df['sector'] == sector, [region_scope, 'date', 'value', 'rate_of_change']]
value_df = tmp_df.pivot(index='date', columns=region_scope, values='value')
rate_df = tmp_df.pivot(index='date', columns=region_scope, values='rate_of_change')
value_df = value_df.loc[:, regions]
rate_df = rate_df.loc[:, regions]
fig = plt.figure(figsize=(10, 8))
fig.suptitle(title)
plt.subplot(2, 1, 1)
plt.plot(value_df)
plt.ylabel('Carbon Emission Value / Mt CO2')
plt.xticks(rotation=60)
plt.legend(regions, loc='upper right')
plt.subplot(2, 1, 2)
plt.plot(rate_df)
plt.ylabel('Rate of Change')
plt.xticks(rotation=60)
plt.legend(regions, loc='upper right')
plt.subplots_adjust(hspace=0.3)
```
### <a id="a22"></a> 2.2. Plot by sector
Generally, sources of emissions can be divided into five or six categories:
- Domestic Aviation
- Ground Transport
- Industry
- Power
- Residential
- International Aviation
Where the data of ```International Aviation``` are only available to ```carbon_global``` and ```carbon_us``` datasets. For ```carbon_global``` dataset, we can not expand the data for International Aviation of non-listed countries.
Let's create a pie chart and a stacked column chart, where you can focus on details of specific countiy/regions’ emission data, including quantity and percentage breakdown by above sectors.
```
def plot_by_sector(df, start_date=None, end_date=None, sectors=None, region=None, title='Carbon Emission Data by Sector'):
if start_date is None:
start_date = df['date'].min()
if end_date is None:
end_date = df['date'].max()
tmp_df = df.loc[(df['date'] >= start_date) & (df['date'] <= end_date)]
region_scope = 'state' if 'state' in df.columns else 'country_region'
if region in set(tmp_df[region_scope]):
tmp_df = tmp_df.loc[tmp_df[region_scope] == region]
if sectors is None:
sectors = list(set(tmp_df['sector']))
sectors.sort(key=lambda sector: -tmp_df.loc[tmp_df['sector'] == sector, 'value'].sum())
tmp_df = tmp_df.loc[[sector in sectors for sector in tmp_df['sector']]]
fig = plt.figure(figsize=(10, 8))
fig.suptitle(title)
plt.subplot(2, 1, 1)
data = np.array([tmp_df.loc[tmp_df['sector'] == sector, 'value'].sum() for sector in sectors])
total = tmp_df['value'].sum()
bbox_props = dict(boxstyle="square,pad=0.3", fc="w", ec="k", lw=0.72)
kw = dict(arrowprops=dict(arrowstyle="-"),
bbox=bbox_props, zorder=0, va="center")
wedges, texts = plt.pie(data, wedgeprops=dict(width=0.5), startangle=90)
for i, p in enumerate(wedges):
factor = data[i] / total * 100
if factor > 5:
ang = (p.theta2 - p.theta1)/2. + p.theta1
y = np.sin(np.deg2rad(ang))
x = np.cos(np.deg2rad(ang))
horizontalalignment = {-1: "right", 1: "left"}[int(np.sign(x))]
connectionstyle = "angle,angleA=0,angleB={}".format(ang)
kw["arrowprops"].update({"connectionstyle": connectionstyle})
text = '{}\n{:.1f} Mt CO2 ({:.1f}%)'.format(sectors[i], data[i], factor)
plt.annotate(
text,
xy=(x, y),
xytext=(1.35 * np.sign(x), 1.4 * y),
horizontalalignment=horizontalalignment,
**kw
)
plt.axis('equal')
plt.subplot(2, 1, 2)
labels = []
data = [[] for _ in sectors]
date = pd.to_datetime(start_date)
delta = pd.DateOffset(months=1)
while date <= pd.to_datetime(end_date):
sub_df = tmp_df.loc[(tmp_df['date'] >= date) & (tmp_df['date'] < date + delta)]
for i, sector in enumerate(sectors):
data[i].append(sub_df.loc[sub_df['sector'] == sector, 'value'].sum())
labels.append(date.strftime('%Y-%m'))
date += delta
data = np.array(data)
for i, sector in enumerate(sectors):
plt.bar(labels, data[i], bottom=data[:i].sum(axis=0), label=sector)
plt.xticks(rotation=60)
plt.legend()
```
## <a id="a3"></a> 3. Examples
### <a id="a31"></a> 3.1. World carbon emission data
```
data_type = 'carbon_global'
print(f'Download {data_type} data')
global_df = get_data_from_carbon_monitor(data_type)
print('Calculate rate of change')
global_df = calculate_rate_of_change(global_df)
print('Expand country / regions')
global_df = expand_country_regions(global_df)
export_data('global_carbon_emission_data.csv', global_df)
global_df
plot_by_date(
global_df,
start_date='2019-01-01',
end_date='2020-12-31',
sector='Residential',
regions=['China', 'United States'],
title='Residential Carbon Emission, China v.s. United States, 2019-2020'
)
plot_by_sector(
global_df,
start_date='2019-01-01',
end_date='2020-12-31',
sectors=None,
region=None,
title='World Carbon Emission by Sectors, 2019-2020',
)
```
### <a id="a32"></a> 3.2. US carbon emission data
```
data_type = 'carbon_us'
print(f'Download {data_type} data')
us_df = get_data_from_carbon_monitor(data_type)
print('Calculate rate of change')
us_df = calculate_rate_of_change(us_df)
export_data('us_carbon_emission_data.csv', us_df)
us_df
plot_by_date(
us_df,
start_date='2019-01-01',
end_date='2020-12-31',
sector=None,
regions=3,
title='US Carbon Emission, Top 3 States, 2019-2020'
)
plot_by_sector(
us_df,
start_date='2019-01-01',
end_date='2020-12-31',
sectors = None,
region='California',
title='California Carbon Emission by Sectors, 2019-2020',
)
```
# B. Co-Analysis of Carbon Emission Data v.s. COVID-19 Data
This section will help you to visualize the relativity between carbon emissions in different countries and the trends of the COVID-19 pandemic since January 2020 provided by [Oxford COVID-19 Government Response Tracker](https://covidtracker.bsg.ox.ac.uk/). The severity of the epidemic can be shown in three aspects: the number of new diagnoses, the number of deaths and the stringency and policy indices of governments.
Overview:
- [Download data from Oxford COVID-19 Government Response Tracker](#b1)
- [Visualize COVID-19 data and carbon emission data](#b2)
- [Example: COVID-19 cases and stringency index v.s. carbon emission in US](#b3)
```
import json
import datetime
from urllib.request import urlopen
```
## 1. <a id="b1"></a> Download COVID-19 Data
We are going to download JSON-formatted COVID-19 data and convert to Pandas Dataframe. The Oxford COVID-19 Government Response Tracker dataset provides confirmed cases, deaths and stringency index data for all countries/regions since January 2020.
- The ```confirmed``` measurement records the total number of confirmed COVID-19 cases since January 2020. We will convert it into incremental data.
- The ```deaths``` measurement records the total number of patients who died due to infection with COVID-19 since January 2020. We will convert it into incremental data.
- The ```stringency``` measurement means the Stringency Index, which is a float number from 0 to 100 that reflects how strict a country’s measures were, including lockdown, school closures, travel bans, etc. A higher score indicates a stricter response (i.e. 100 = strictest response).
```
def get_covid_data_from_oxford_covid_tracker(data_type='carbon_global'):
data = json.loads(urlopen("https://covidtrackerapi.bsg.ox.ac.uk/api/v2/stringency/date-range/{}/{}".format(
"2020-01-22",
datetime.datetime.now().strftime("%Y-%m-%d")
)).read().decode('utf-8-sig'))
country_region_df = pd.read_csv('static_data/CountryRegion.csv')
code_to_name = {code: name for _, (name, code) in country_region_df.loc[:, ['Name', 'Code']].iterrows()}
last_df = 0
df = pd.DataFrame()
for date in sorted(data['data'].keys()):
sum_df = pd.DataFrame({name: data['data'][date][code] for code, name in code_to_name.items() if code in data['data'][date]})
sum_df = sum_df.T[['confirmed', 'deaths', 'stringency']].fillna(last_df).astype(np.float32)
tmp_df = sum_df - last_df
last_df = sum_df[['confirmed', 'deaths']]
last_df['stringency'] = 0
tmp_df = tmp_df.reset_index().rename(columns={'index': 'country_region'})
tmp_df['date'] = pd.to_datetime(date)
df = df.append(tmp_df)
return df
```
## <a id="b2"></a> 2. Visualize COVID-19 Data and Carbon Emission Data
This part will guide you to create a line-column chart, where you can view the specified COVID-19 measurement (```confirmed```, ```deaths``` or ```stringency```) and carbon emissions in the specified country/region throughout time.
```
def plot_covid_data_vs_carbon_emission_data(
covid_df, carbon_df, start_date=None, end_date=None,
country_region=None, sector=None, covid_measurement='confirmed',
title='Carbon Emission v.s. COVID-19 Confirmed Cases'
):
if start_date is None:
start_date = max(covid_df['date'].min(), carbon_df['date'].min())
if end_date is None:
end_date = min(covid_df['date'].max(), carbon_df['date'].max())
x = pd.to_datetime(start_date)
dates = [x]
while x <= pd.to_datetime(end_date):
x = x.replace(year=x.year+1, month=1) if x.month == 12 else x.replace(month=x.month+1)
dates.append(x)
dates = [f'{x.year}-{x.month}' for x in dates]
plt.figure(figsize=(10, 6))
plt.title(title)
plt.xticks(rotation=60)
if sector in set(carbon_df['sector']):
carbon_df = carbon_df[carbon_df['sector'] == sector]
else:
sector = 'All Sectors'
if 'country_region' not in carbon_df.columns:
raise ValueError('The carbon emission data need to be disaggregated by countries/regions.')
if country_region in set(carbon_df['country_region']):
carbon_df = carbon_df.loc[carbon_df['country_region'] == country_region]
else:
country_region = 'World'
carbon_df = carbon_df[['date', 'value']]
carbon_df = carbon_df.loc[(carbon_df['date'] >= f'{dates[0]}-01') & (carbon_df['date'] < f'{dates[-1]}-01')].set_index('date')
carbon_df = carbon_df.groupby(carbon_df.index.year * 12 + carbon_df.index.month).sum()
plt.bar(dates[:-1], carbon_df['value'], color='C1')
plt.ylim(0)
plt.legend([f'{country_region} {sector}\nCarbon Emission / Mt CO2'], loc='upper left')
plt.twinx()
if country_region in set(covid_df['country_region']):
covid_df = covid_df.loc[covid_df['country_region'] == country_region]
covid_df = covid_df[['date', covid_measurement]]
covid_df = covid_df.loc[(covid_df['date'] >= f'{dates[0]}-01') & (covid_df['date'] < f'{dates[-1]}-01')].set_index('date')
covid_df = covid_df.groupby(covid_df.index.year * 12 + covid_df.index.month)
covid_df = covid_df.mean() if covid_measurement == 'stringency' else covid_df.sum()
plt.plot(dates[:-1], covid_df[covid_measurement])
plt.ylim(0, 100 if covid_measurement == 'stringency' else None)
plt.legend([f'COVID-19\n{covid_measurement}'], loc='upper right')
```
## <a id="b3"></a> 3. Examples
```
print(f'Download COVID-19 data')
covid_df = get_covid_data_from_oxford_covid_tracker(data_type)
export_data('covid_data.csv', covid_df)
covid_df
plot_covid_data_vs_carbon_emission_data(
covid_df,
global_df,
start_date=None,
end_date=None,
country_region='United States',
sector=None,
covid_measurement='confirmed',
title = 'US Carbon Emission v.s. COVID-19 Confirmed Cases'
)
plot_covid_data_vs_carbon_emission_data(
covid_df,
global_df,
start_date=None,
end_date=None,
country_region='United States',
sector=None,
covid_measurement='stringency',
title = 'US Carbon Emission v.s. COVID-19 Stringency Index'
)
```
# C. Co-Analysis of Historical Carbon Emission Data v.s. Population & GDP Data
This section illustrates how to compare carbon intensity and per capita emissions of different countries/regions. Refer to [the EDGAR dataset](https://edgar.jrc.ec.europa.eu/dataset_ghg60) and [World Bank Open Data](https://data.worldbank.org/), carbon emissions, population and GDP data of countries/regions in the world from 1970 to 2018 are available.
Overview:
- [Process carbon emission & social economy data](#c1)
- [Download data from EDGAR](#c11)
- [Download data from World Bank](#c12)
- [Merge datasets](#c13)
- [Visualize carbon emission & social economy data](#c2)
- [See how per capita emissions change over time in different countries/regions](#c21)
- [Observe how *carbon intensity* reduced over time](#c22)
- [Example: relationships of carbon emission and social economy in huge countries](#c3)
*Carbon intensity* is the measure of CO2 produced per US dollar GDP. In other words, it’s a measure of how much CO2 we emit when we generate one dollar of domestic economy. A rapidly decreasing carbon intensity is beneficial for the environment and economy.
```
import zipfile
```
## <a id="c1"></a> 1. Process Carbon Emission & Social Economy Data
### <a id="c11"></a> 1.1. Download 1970-2018 yearly carbon emission data from the EDGAR dataset
```
def get_historical_carbon_emission_data_from_edgar():
if not os.path.exists('download_data'):
os.mkdir('download_data')
site = 'https://cidportal.jrc.ec.europa.eu/ftp/jrc-opendata/EDGAR/datasets'
dataset = 'v60_GHG/CO2_excl_short-cycle_org_C/v60_GHG_CO2_excl_short-cycle_org_C_1970_2018.zip'
with open('download_data/historical_carbon_emission.zip', 'wb') as f:
f.write(urlopen(f'{site}/{dataset}').read())
with zipfile.ZipFile('download_data/historical_carbon_emission.zip', 'r') as zip_ref:
zip_ref.extractall('download_data/historical_carbon_emission')
hist_carbon_df = pd.read_excel(
'download_data/historical_carbon_emission/v60_CO2_excl_short-cycle_org_C_1970_2018.xls',
sheet_name='TOTALS BY COUNTRY',
index_col=2,
header=9,
).iloc[:, 4:]
hist_carbon_df.columns = hist_carbon_df.columns.map(lambda x: pd.to_datetime(f'{x[-4:]}-01-01'))
hist_carbon_df.index = hist_carbon_df.index.rename('country_region')
hist_carbon_df *= 1000
return hist_carbon_df
```
### <a id="c12"></a> 1.2. Download 1960-pressent yearly population and GDP data from World Bank
```
def read_worldbank_data(data_id):
tmp_df = pd.read_excel(
f'https://api.worldbank.org/v2/en/indicator/{data_id}?downloadformat=excel',
sheet_name='Data',
index_col=1,
header=3,
).iloc[:, 3:]
tmp_df.columns = tmp_df.columns.map(lambda x: pd.to_datetime(x, format='%Y'))
tmp_df.index = tmp_df.index.rename('country_region')
return tmp_df
def get_population_and_gdp_data_from_worldbank():
return read_worldbank_data('SP.POP.TOTL'), read_worldbank_data('NY.GDP.MKTP.CD')
```
### <a id="c13"></a> 1.3. Merge the three datasets
```
def melt_table_by_years(df, value_name, country_region_codes, code_to_name, years):
return df.loc[country_region_codes, years].rename(index=code_to_name).reset_index().melt(
id_vars=['country_region'],
value_vars=years,
var_name='date',
value_name=value_name
)
def merge_historical_data(hist_carbon_df, pop_df, gdp_df):
country_region_df = pd.read_csv('static_data/CountryRegion.csv')
code_to_name = {code: name for _, (name, code) in country_region_df.loc[:, ['Name', 'Code']].iterrows()}
country_region_codes = sorted(set(pop_df.index) & set(gdp_df.index) & set(hist_carbon_df.index) & set(code_to_name.keys()))
years = sorted(set(pop_df.columns) & set(gdp_df.columns) & set(hist_carbon_df.columns))
pop_df = melt_table_by_years(pop_df, 'population', country_region_codes, code_to_name, years)
gdp_df = melt_table_by_years(gdp_df, 'gdp', country_region_codes, code_to_name, years)
hist_carbon_df = melt_table_by_years(hist_carbon_df, 'carbon_emission', country_region_codes, code_to_name, years)
hist_carbon_df['population'] = pop_df['population']
hist_carbon_df['gdp'] = gdp_df['gdp']
return hist_carbon_df.fillna(0)
```
## <a id="c2"></a> 2. Visualize Carbon Emission & Social Economy Data
## <a id="c21"></a> 2.1. Plot changes in per capita emissions
We now will walk you through how to plot a bubble chart of per capita GDP and per capita emissions of different countries/regions for a given year.
```
def plot_carbon_emission_data_vs_gdp(df, year=None, countries_regions=None, title='Carbon Emission per Capita v.s. GDP per Capita'):
if year is None:
date = df['date'].max()
else:
date = min(max(pd.to_datetime(year, format='%Y'), df['date'].min()), df['date'].max())
df = df[df['date'] == date]
if countries_regions is None or type(countries_regions) == int:
country_region_list = list(set(df['country_region']))
country_region_list.sort(key=lambda country_region: -df.loc[df['country_region'] == country_region, 'population'].to_numpy())
countries_regions = country_region_list[:10 if countries_regions is None else countries_regions]
plt.figure(figsize=(10, 6))
plt.title(title)
max_pop = df['population'].max()
for country_region in countries_regions:
row = df.loc[df['country_region'] == country_region]
plt.scatter(
x=row['gdp'] / row['population'],
y=row['carbon_emission'] / row['population'],
s=row['population'] / max_pop * 1000,
)
for lgnd in plt.legend(countries_regions).legendHandles:
lgnd._sizes = [50]
plt.xlabel('GDP per Capita (USD)')
plt.ylabel('Carbon Emission per Capita (tCO2)')
```
## <a id="c22"></a> 2.2. Plot changes in carbon intensity
To see changes in Carbon Intensity of different countries overtime, let’s plot a line chart.
```
def plot_carbon_indensity_data(df, start_year=None, end_year=None, countries_regions=None, title='Carbon Indensity'):
start_date = df['date'].min() if start_year is None else pd.to_datetime(start_year, format='%Y')
end_date = df['date'].max() if end_year is None else pd.to_datetime(end_year, format='%Y')
df = df[(df['date'] >= start_date) & (df['date'] <= end_date)]
if countries_regions is None or type(countries_regions) == int:
country_region_list = list(set(df['country_region']))
country_region_list.sort(key=lambda country_region: -df.loc[df['country_region'] == country_region, 'population'].sum())
countries_regions = country_region_list[:3 if countries_regions is None else countries_regions]
df = pd.concat([df[df['country_region'] == country_region] for country_region in countries_regions])
df['carbon_indensity'] = df['carbon_emission'] / df['gdp']
indensity_df = df.pivot(index='date', columns='country_region', values='carbon_indensity')[countries_regions]
emission_df = df.pivot(index='date', columns='country_region', values='carbon_emission')[countries_regions]
plt.figure(figsize=(10, 8))
plt.subplot(211)
plt.title(title)
plt.plot(indensity_df)
plt.legend(countries_regions)
plt.ylabel('Carbon Emission (tCO2) per Dollar GDP')
plt.subplot(212)
plt.plot(emission_df)
plt.legend(countries_regions)
plt.ylabel('Carbon Emission (tCO2)')
```
## <a id="c3"></a> 3. Examples
```
print('Download historical carbon emission data')
hist_carbon_df = get_historical_carbon_emission_data_from_edgar()
print('Download population & GDP data')
pop_df, gdp_df = get_population_and_gdp_data_from_worldbank()
print('Merge data')
hist_carbon_df = merge_historical_data(hist_carbon_df, pop_df, gdp_df)
export_data('historical_carbon_emission_data.csv', hist_carbon_df)
hist_carbon_df
plot_carbon_emission_data_vs_gdp(
hist_carbon_df,
year=2018,
countries_regions=10,
title = 'Carbon Emission per Capita v.s. GDP per Capita, Top 10 Populous Countries/Regions, 2018'
)
plot_carbon_indensity_data(
hist_carbon_df,
start_year=None,
end_year=None,
countries_regions=['United States', 'China'],
title='Carbon Indensity & Carbon Emission, US v.s. China, 1970-2018'
)
```
|
github_jupyter
|
```
from sklearn.model_selection import train_test_split
import pandas as pd
import tensorflow as tf
import tensorflow_hub as hub
from datetime import datetime
import bert
from bert import run_classifier
from bert import optimization
from bert import tokenization
from tensorflow import keras
import os
import re
# Set the output directory for saving model file
# Optionally, set a GCP bucket location
OUTPUT_DIR = '../models'
DO_DELETE = False
USE_BUCKET = False
BUCKET = 'BUCKET_NAME'
if USE_BUCKET:
OUTPUT_DIR = 'gs://{}/{}'.format(BUCKET, OUTPUT_DIR)
from google.colab import auth
auth.authenticate_user()
if DO_DELETE:
try:
tf.gfile.DeleteRecursively(OUTPUT_DIR)
except:
pass
tf.gfile.MakeDirs(OUTPUT_DIR)
print('***** Model output directory: {} *****'.format(OUTPUT_DIR))
# Load all files from a directory in a DataFrame.
def load_directory_data(directory):
data = {}
data["sentence"] = []
data["sentiment"] = []
for file_path in os.listdir(directory):
with tf.gfile.GFile(os.path.join(directory, file_path), "r") as f:
data["sentence"].append(f.read())
data["sentiment"].append(re.match("\d+_(\d+)\.txt", file_path).group(1))
return pd.DataFrame.from_dict(data)
# Merge positive and negative examples, add a polarity column and shuffle.
def load_dataset(directory):
pos_df = load_directory_data(os.path.join(directory, "pos"))
neg_df = load_directory_data(os.path.join(directory, "neg"))
pos_df["polarity"] = 1
neg_df["polarity"] = 0
return pd.concat([pos_df, neg_df]).sample(frac=1).reset_index(drop=True)
train = load_dataset(os.path.join("../data/", "aclImdb", "train"))
test = load_dataset(os.path.join("../data/", "aclImdb", "test"))
train = train.sample(5000)
test = test.sample(5000)
DATA_COLUMN = 'sentence'
LABEL_COLUMN = 'polarity'
label_list = [0, 1]
# Use the InputExample class from BERT's run_classifier code to create examples from the data
train_InputExamples = train.apply(lambda x: bert.run_classifier.InputExample(guid=None,
text_a = x[DATA_COLUMN],
text_b = None,
label = x[LABEL_COLUMN]), axis = 1)
test_InputExamples = test.apply(lambda x: bert.run_classifier.InputExample(guid=None,
text_a = x[DATA_COLUMN],
text_b = None,
label = x[LABEL_COLUMN]), axis = 1)
# This is a path to an uncased (all lowercase) version of BERT
BERT_MODEL_HUB = "https://tfhub.dev/google/bert_uncased_L-12_H-768_A-12/1"
def create_tokenizer_from_hub_module():
"""Get the vocab file and casing info from the Hub module."""
with tf.Graph().as_default():
bert_module = hub.Module(BERT_MODEL_HUB)
tokenization_info = bert_module(signature="tokenization_info", as_dict=True)
with tf.Session() as sess:
vocab_file, do_lower_case = sess.run([tokenization_info["vocab_file"],
tokenization_info["do_lower_case"]])
return bert.tokenization.FullTokenizer(vocab_file=vocab_file, do_lower_case=do_lower_case)
tokenizer = create_tokenizer_from_hub_module()
tokenizer.tokenize("This here's an example of using the BERT tokenizer")
# We'll set sequences to be at most 128 tokens long.
MAX_SEQ_LENGTH = 128
# Convert our train and test features to InputFeatures that BERT understands.
train_features = bert.run_classifier.convert_examples_to_features(train_InputExamples,
label_list,
MAX_SEQ_LENGTH,
tokenizer)
test_features = bert.run_classifier.convert_examples_to_features(test_InputExamples,
label_list,
MAX_SEQ_LENGTH,
tokenizer)
```
|
github_jupyter
|
# Homework 2 - Deep Learning
## Liberatori Benedetta
```
import torch
import numpy as np
# A class defining the model for the Multi Layer Perceptron
class MLP(torch.nn.Module):
def __init__(self):
super().__init__()
self.layer1 = torch.nn.Linear(in_features=6, out_features=2, bias= True)
self.layer2 = torch.nn.Linear(in_features=2, out_features=1, bias= True)
def forward(self, X):
out = self.layer1(X)
out = self.layer2(out)
out = torch.nn.functional.sigmoid(out)
return out
# Initialization of weights: uniformly distributed between -0.3 and 0.3
W = (0.3 + 0.3) * torch.rand(6, 1 ) - 0.3
# Inizialization of Data: 50% symmetric randomly generated tensors
# 50% not necessarily symmetric
firsthalf= torch.rand([32,3])
secondhalf=torch.zeros([32,3])
secondhalf[:, 2:3 ]=firsthalf[:, 0:1]
secondhalf[:, 1:2 ]=firsthalf[:, 1:2]
secondhalf[:, 0:1 ]=firsthalf[:, 2:3]
y1=torch.ones([32,1])
y0=torch.zeros([32,1])
simmetric = torch.cat((firsthalf, secondhalf, y1), dim=1)
notsimmetric = torch.rand([32,6])
notsimmetric= torch.cat((notsimmetric, y0), dim=1)
data= torch.cat((notsimmetric, simmetric), dim=0)
# Permutation of the concatenated dataset
data= data[torch.randperm(data.size()[0])]
def train_epoch(model, data, loss_fn, optimizer):
X=data[:,0:6]
y=data[:,6]
# 1. reset the gradients previously accumulated by the optimizer
# this will avoid re-using gradients from previous loops
optimizer.zero_grad()
# 2. get the predictions from the current state of the model
# this is the forward pass
y_hat = model(X)
# 3. calculate the loss on the current mini-batch
loss = loss_fn(y_hat, y.unsqueeze(1))
# 4. execute the backward pass given the current loss
loss.backward()
# 5. update the value of the params
optimizer.step()
return model
def train_model(model, data, loss_fn, optimizer, num_epochs):
model.train()
for epoch in range(num_epochs):
model=train_epoch(model, data, loss_fn, optimizer)
for i in model.state_dict():
print(model.state_dict()[i])
# Parameters set as defined in the paper
learn_rate = 0.1
num_epochs = 1425
beta= 0.9
model = MLP()
# I have judged the loss function (3) reported in the paper paper a general one for the discussion
# Since the problem of interest is a binary classification and that loss is mostly suited for
# regression problems I have used instead a Binary Cross Entropy loss
loss_fn = torch.nn.BCELoss()
# Gradient descent optimizer with momentum
optimizer = torch.optim.SGD(model.parameters(), lr=learn_rate, momentum=beta)
train_model(model, data, loss_fn, optimizer, num_epochs)
```
## Some conclusions:
Even if the original protocol has been followed as deep as possible, the results obtained in the same number of epochs are fare from the ones stated in the paper. Not only the numbers, indeed those are not even near to be symmetric. I assume this could depend on the inizialization of the data, which was not reported and thus a completely autonomous choice.
|
github_jupyter
|
# Logistic Regression with a Neural Network mindset
Welcome to your first (required) programming assignment! You will build a logistic regression classifier to recognize cats. This assignment will step you through how to do this with a Neural Network mindset, and so will also hone your intuitions about deep learning.
**Instructions:**
- Do not use loops (for/while) in your code, unless the instructions explicitly ask you to do so.
**You will learn to:**
- Build the general architecture of a learning algorithm, including:
- Initializing parameters
- Calculating the cost function and its gradient
- Using an optimization algorithm (gradient descent)
- Gather all three functions above into a main model function, in the right order.
## 1 - Packages ##
First, let's run the cell below to import all the packages that you will need during this assignment.
- [numpy](https://www.numpy.org/) is the fundamental package for scientific computing with Python.
- [h5py](http://www.h5py.org) is a common package to interact with a dataset that is stored on an H5 file.
- [matplotlib](http://matplotlib.org) is a famous library to plot graphs in Python.
- [PIL](http://www.pythonware.com/products/pil/) and [scipy](https://www.scipy.org/) are used here to test your model with your own picture at the end.
```
import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage
from lr_utils import load_dataset
%matplotlib inline
```
## 2 - Overview of the Problem set ##
**Problem Statement**: You are given a dataset ("data.h5") containing:
- a training set of m_train images labeled as cat (y=1) or non-cat (y=0)
- a test set of m_test images labeled as cat or non-cat
- each image is of shape (num_px, num_px, 3) where 3 is for the 3 channels (RGB). Thus, each image is square (height = num_px) and (width = num_px).
You will build a simple image-recognition algorithm that can correctly classify pictures as cat or non-cat.
Let's get more familiar with the dataset. Load the data by running the following code.
```
# Loading the data (cat/non-cat)
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
```
We added "_orig" at the end of image datasets (train and test) because we are going to preprocess them. After preprocessing, we will end up with train_set_x and test_set_x (the labels train_set_y and test_set_y don't need any preprocessing).
Each line of your train_set_x_orig and test_set_x_orig is an array representing an image. You can visualize an example by running the following code. Feel free also to change the `index` value and re-run to see other images.
```
# Example of a picture
index = 25
plt.imshow(train_set_x_orig[index])
print ("y = " + str(train_set_y[:, index]) + ", it's a '" + classes[np.squeeze(train_set_y[:, index])].decode("utf-8") + "' picture.")
```
Many software bugs in deep learning come from having matrix/vector dimensions that don't fit. If you can keep your matrix/vector dimensions straight you will go a long way toward eliminating many bugs.
**Exercise:** Find the values for:
- m_train (number of training examples)
- m_test (number of test examples)
- num_px (= height = width of a training image)
Remember that `train_set_x_orig` is a numpy-array of shape (m_train, num_px, num_px, 3). For instance, you can access `m_train` by writing `train_set_x_orig.shape[0]`.
```
### START CODE HERE ### (≈ 3 lines of code)
m_train = train_set_x_orig.shape[0]
m_test = test_set_x_orig.shape[0]
num_px = train_set_x_orig.shape[1]
### END CODE HERE ###
print ("Number of training examples: m_train = " + str(m_train))
print ("Number of testing examples: m_test = " + str(m_test))
print ("Height/Width of each image: num_px = " + str(num_px))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_set_x shape: " + str(train_set_x_orig.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x shape: " + str(test_set_x_orig.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
```
**Expected Output for m_train, m_test and num_px**:
<table style="width:15%">
<tr>
<td>**m_train**</td>
<td> 209 </td>
</tr>
<tr>
<td>**m_test**</td>
<td> 50 </td>
</tr>
<tr>
<td>**num_px**</td>
<td> 64 </td>
</tr>
</table>
For convenience, you should now reshape images of shape (num_px, num_px, 3) in a numpy-array of shape (num_px $*$ num_px $*$ 3, 1). After this, our training (and test) dataset is a numpy-array where each column represents a flattened image. There should be m_train (respectively m_test) columns.
**Exercise:** Reshape the training and test data sets so that images of size (num_px, num_px, 3) are flattened into single vectors of shape (num\_px $*$ num\_px $*$ 3, 1).
A trick when you want to flatten a matrix X of shape (a,b,c,d) to a matrix X_flatten of shape (b$*$c$*$d, a) is to use:
```python
X_flatten = X.reshape(X.shape[0], -1).T # X.T is the transpose of X
```
```
# Reshape the training and test examples
### START CODE HERE ### (≈ 2 lines of code)
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
### END CODE HERE ###
print ("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
print ("sanity check after reshaping: " + str(train_set_x_flatten[0:5,0]))
```
**Expected Output**:
<table style="width:35%">
<tr>
<td>**train_set_x_flatten shape**</td>
<td> (12288, 209)</td>
</tr>
<tr>
<td>**train_set_y shape**</td>
<td>(1, 209)</td>
</tr>
<tr>
<td>**test_set_x_flatten shape**</td>
<td>(12288, 50)</td>
</tr>
<tr>
<td>**test_set_y shape**</td>
<td>(1, 50)</td>
</tr>
<tr>
<td>**sanity check after reshaping**</td>
<td>[17 31 56 22 33]</td>
</tr>
</table>
To represent color images, the red, green and blue channels (RGB) must be specified for each pixel, and so the pixel value is actually a vector of three numbers ranging from 0 to 255.
One common preprocessing step in machine learning is to center and standardize your dataset, meaning that you substract the mean of the whole numpy array from each example, and then divide each example by the standard deviation of the whole numpy array. But for picture datasets, it is simpler and more convenient and works almost as well to just divide every row of the dataset by 255 (the maximum value of a pixel channel).
<!-- During the training of your model, you're going to multiply weights and add biases to some initial inputs in order to observe neuron activations. Then you backpropogate with the gradients to train the model. But, it is extremely important for each feature to have a similar range such that our gradients don't explode. You will see that more in detail later in the lectures. !-->
Let's standardize our dataset.
```
train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.
```
<font color='blue'>
**What you need to remember:**
Common steps for pre-processing a new dataset are:
- Figure out the dimensions and shapes of the problem (m_train, m_test, num_px, ...)
- Reshape the datasets such that each example is now a vector of size (num_px \* num_px \* 3, 1)
- "Standardize" the data
## 3 - General Architecture of the learning algorithm ##
It's time to design a simple algorithm to distinguish cat images from non-cat images.
You will build a Logistic Regression, using a Neural Network mindset. The following Figure explains why **Logistic Regression is actually a very simple Neural Network!**
<img src="images/LogReg_kiank.png" style="width:650px;height:400px;">
**Mathematical expression of the algorithm**:
For one example $x^{(i)}$:
$$z^{(i)} = w^T x^{(i)} + b \tag{1}$$
$$\hat{y}^{(i)} = a^{(i)} = sigmoid(z^{(i)})\tag{2}$$
$$ \mathcal{L}(a^{(i)}, y^{(i)}) = - y^{(i)} \log(a^{(i)}) - (1-y^{(i)} ) \log(1-a^{(i)})\tag{3}$$
The cost is then computed by summing over all training examples:
$$ J = \frac{1}{m} \sum_{i=1}^m \mathcal{L}(a^{(i)}, y^{(i)})\tag{6}$$
**Key steps**:
In this exercise, you will carry out the following steps:
- Initialize the parameters of the model
- Learn the parameters for the model by minimizing the cost
- Use the learned parameters to make predictions (on the test set)
- Analyse the results and conclude
## 4 - Building the parts of our algorithm ##
The main steps for building a Neural Network are:
1. Define the model structure (such as number of input features)
2. Initialize the model's parameters
3. Loop:
- Calculate current loss (forward propagation)
- Calculate current gradient (backward propagation)
- Update parameters (gradient descent)
You often build 1-3 separately and integrate them into one function we call `model()`.
### 4.1 - Helper functions
**Exercise**: Using your code from "Python Basics", implement `sigmoid()`. As you've seen in the figure above, you need to compute $sigmoid( w^T x + b) = \frac{1}{1 + e^{-(w^T x + b)}}$ to make predictions. Use np.exp().
```
# GRADED FUNCTION: sigmoid
def sigmoid(z):
"""
Compute the sigmoid of z
Arguments:
z -- A scalar or numpy array of any size.
Return:
s -- sigmoid(z)
"""
### START CODE HERE ### (≈ 1 line of code)
s = 1 / (1 + np.exp(-z))
### END CODE HERE ###
return s
print ("sigmoid([0, 2]) = " + str(sigmoid(np.array([0,2]))))
```
**Expected Output**:
<table>
<tr>
<td>**sigmoid([0, 2])**</td>
<td> [ 0.5 0.88079708]</td>
</tr>
</table>
### 4.2 - Initializing parameters
**Exercise:** Implement parameter initialization in the cell below. You have to initialize w as a vector of zeros. If you don't know what numpy function to use, look up np.zeros() in the Numpy library's documentation.
```
# GRADED FUNCTION: initialize_with_zeros
def initialize_with_zeros(dim):
"""
This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
Argument:
dim -- size of the w vector we want (or number of parameters in this case)
Returns:
w -- initialized vector of shape (dim, 1)
b -- initialized scalar (corresponds to the bias)
"""
### START CODE HERE ### (≈ 1 line of code)
w = np.zeros((dim,1))
b = 0
### END CODE HERE ###
assert(w.shape == (dim, 1))
assert(isinstance(b, float) or isinstance(b, int))
return w, b
dim = 2
w, b = initialize_with_zeros(dim)
print ("w = " + str(w))
print ("b = " + str(b))
```
**Expected Output**:
<table style="width:15%">
<tr>
<td> ** w ** </td>
<td> [[ 0.]
[ 0.]] </td>
</tr>
<tr>
<td> ** b ** </td>
<td> 0 </td>
</tr>
</table>
For image inputs, w will be of shape (num_px $\times$ num_px $\times$ 3, 1).
### 4.3 - Forward and Backward propagation
Now that your parameters are initialized, you can do the "forward" and "backward" propagation steps for learning the parameters.
**Exercise:** Implement a function `propagate()` that computes the cost function and its gradient.
**Hints**:
Forward Propagation:
- You get X
- You compute $A = \sigma(w^T X + b) = (a^{(1)}, a^{(2)}, ..., a^{(m-1)}, a^{(m)})$
- You calculate the cost function: $J = -\frac{1}{m}\sum_{i=1}^{m}y^{(i)}\log(a^{(i)})+(1-y^{(i)})\log(1-a^{(i)})$
Here are the two formulas you will be using:
$$ \frac{\partial J}{\partial w} = \frac{1}{m}X(A-Y)^T\tag{7}$$
$$ \frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^m (a^{(i)}-y^{(i)})\tag{8}$$
```
# GRADED FUNCTION: propagate
def propagate(w, b, X, Y):
"""
Implement the cost function and its gradient for the propagation explained above
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat) of size (1, number of examples)
Return:
cost -- negative log-likelihood cost for logistic regression
dw -- gradient of the loss with respect to w, thus same shape as w
db -- gradient of the loss with respect to b, thus same shape as b
Tips:
- Write your code step by step for the propagation. np.log(), np.dot()
"""
m = X.shape[1]
# FORWARD PROPAGATION (FROM X TO COST)
### START CODE HERE ### (≈ 2 lines of code)
A = 1 / (1 + np.exp(-(np.dot(w.T, X) + b))) # compute activation
cost = -1 / m * np.sum(np.multiply(Y, np.log(A)) + np.multiply(1 - Y,np.log(1 - A))) # compute cost
### END CODE HERE ###
# BACKWARD PROPAGATION (TO FIND GRAD)
### START CODE HERE ### (≈ 2 lines of code)
dw = 1 / m * np.dot(X, (A - Y).T)
db = 1 / m * np.sum(A - Y)
### END CODE HERE ###
assert(dw.shape == w.shape)
assert(db.dtype == float)
cost = np.squeeze(cost)
assert(cost.shape == ())
grads = {"dw": dw,
"db": db}
return grads, cost
w, b, X, Y = np.array([[1.],[2.]]), 2., np.array([[1.,2.,-1.],[3.,4.,-3.2]]), np.array([[1,0,1]])
grads, cost = propagate(w, b, X, Y)
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
print ("cost = " + str(cost))
```
**Expected Output**:
<table style="width:50%">
<tr>
<td> ** dw ** </td>
<td> [[ 0.99845601]
[ 2.39507239]]</td>
</tr>
<tr>
<td> ** db ** </td>
<td> 0.00145557813678 </td>
</tr>
<tr>
<td> ** cost ** </td>
<td> 5.801545319394553 </td>
</tr>
</table>
### 4.4 - Optimization
- You have initialized your parameters.
- You are also able to compute a cost function and its gradient.
- Now, you want to update the parameters using gradient descent.
**Exercise:** Write down the optimization function. The goal is to learn $w$ and $b$ by minimizing the cost function $J$. For a parameter $\theta$, the update rule is $ \theta = \theta - \alpha \text{ } d\theta$, where $\alpha$ is the learning rate.
```
# GRADED FUNCTION: optimize
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
"""
This function optimizes w and b by running a gradient descent algorithm
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of shape (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat), of shape (1, number of examples)
num_iterations -- number of iterations of the optimization loop
learning_rate -- learning rate of the gradient descent update rule
print_cost -- True to print the loss every 100 steps
Returns:
params -- dictionary containing the weights w and bias b
grads -- dictionary containing the gradients of the weights and bias with respect to the cost function
costs -- list of all the costs computed during the optimization, this will be used to plot the learning curve.
Tips:
You basically need to write down two steps and iterate through them:
1) Calculate the cost and the gradient for the current parameters. Use propagate().
2) Update the parameters using gradient descent rule for w and b.
"""
costs = []
for i in range(num_iterations):
# Cost and gradient calculation (≈ 1-4 lines of code)
### START CODE HERE ###
grads, cost = propagate(w, b, X, Y)
### END CODE HERE ###
# Retrieve derivatives from grads
dw = grads["dw"]
db = grads["db"]
# update rule (≈ 2 lines of code)
### START CODE HERE ###
w = w - learning_rate * dw
b = b - learning_rate * db
### END CODE HERE ###
# Record the costs
if i % 100 == 0:
costs.append(cost)
# Print the cost every 100 training iterations
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
params = {"w": w,
"b": b}
grads = {"dw": dw,
"db": db}
return params, grads, costs
params, grads, costs = optimize(w, b, X, Y, num_iterations= 100, learning_rate = 0.009, print_cost = False)
print ("w = " + str(params["w"]))
print ("b = " + str(params["b"]))
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
```
**Expected Output**:
<table style="width:40%">
<tr>
<td> **w** </td>
<td>[[ 0.19033591]
[ 0.12259159]] </td>
</tr>
<tr>
<td> **b** </td>
<td> 1.92535983008 </td>
</tr>
<tr>
<td> **dw** </td>
<td> [[ 0.67752042]
[ 1.41625495]] </td>
</tr>
<tr>
<td> **db** </td>
<td> 0.219194504541 </td>
</tr>
</table>
**Exercise:** The previous function will output the learned w and b. We are able to use w and b to predict the labels for a dataset X. Implement the `predict()` function. There are two steps to computing predictions:
1. Calculate $\hat{Y} = A = \sigma(w^T X + b)$
2. Convert the entries of a into 0 (if activation <= 0.5) or 1 (if activation > 0.5), stores the predictions in a vector `Y_prediction`. If you wish, you can use an `if`/`else` statement in a `for` loop (though there is also a way to vectorize this).
```
# GRADED FUNCTION: predict
def predict(w, b, X):
'''
Predict whether the label is 0 or 1 using learned logistic regression parameters (w, b)
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Returns:
Y_prediction -- a numpy array (vector) containing all predictions (0/1) for the examples in X
'''
m = X.shape[1]
Y_prediction = np.zeros((1,m))
w = w.reshape(X.shape[0], 1)
# Compute vector "A" predicting the probabilities of a cat being present in the picture
### START CODE HERE ### (≈ 1 line of code)
A = sigmoid(np.dot(w.T, X) + b)
### END CODE HERE ###
for i in range(A.shape[1]):
# Convert probabilities A[0,i] to actual predictions p[0,i]
### START CODE HERE ### (≈ 4 lines of code)
Y_prediction[0][i] = 1 if A[0][i] >= 0.5 else 0
### END CODE HERE ###
assert(Y_prediction.shape == (1, m))
return Y_prediction
w = np.array([[0.1124579],[0.23106775]])
b = -0.3
X = np.array([[1.,-1.1,-3.2],[1.2,2.,0.1]])
print ("predictions = " + str(predict(w, b, X)))
```
**Expected Output**:
<table style="width:30%">
<tr>
<td>
**predictions**
</td>
<td>
[[ 1. 1. 0.]]
</td>
</tr>
</table>
<font color='blue'>
**What to remember:**
You've implemented several functions that:
- Initialize (w,b)
- Optimize the loss iteratively to learn parameters (w,b):
- computing the cost and its gradient
- updating the parameters using gradient descent
- Use the learned (w,b) to predict the labels for a given set of examples
## 5 - Merge all functions into a model ##
You will now see how the overall model is structured by putting together all the building blocks (functions implemented in the previous parts) together, in the right order.
**Exercise:** Implement the model function. Use the following notation:
- Y_prediction_test for your predictions on the test set
- Y_prediction_train for your predictions on the train set
- w, costs, grads for the outputs of optimize()
```
# GRADED FUNCTION: model
def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):
"""
Builds the logistic regression model by calling the function you've implemented previously
Arguments:
X_train -- training set represented by a numpy array of shape (num_px * num_px * 3, m_train)
Y_train -- training labels represented by a numpy array (vector) of shape (1, m_train)
X_test -- test set represented by a numpy array of shape (num_px * num_px * 3, m_test)
Y_test -- test labels represented by a numpy array (vector) of shape (1, m_test)
num_iterations -- hyperparameter representing the number of iterations to optimize the parameters
learning_rate -- hyperparameter representing the learning rate used in the update rule of optimize()
print_cost -- Set to true to print the cost every 100 iterations
Returns:
d -- dictionary containing information about the model.
"""
### START CODE HERE ###
# initialize parameters with zeros (≈ 1 line of code)
w, b = initialize_with_zeros(X_train.shape[0])
# Gradient descent (≈ 1 line of code)
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost = False)
# Retrieve parameters w and b from dictionary "parameters"
w = parameters["w"]
b = parameters["b"]
# Predict test/train set examples (≈ 2 lines of code)
Y_prediction_test = predict(w, b, X_test)
Y_prediction_train = predict(w, b, X_train)
### END CODE HERE ###
# Print train/test Errors
print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
d = {"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediction_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations}
return d
```
Run the following cell to train your model.
```
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)
```
**Expected Output**:
<table style="width:40%">
<tr>
<td> **Cost after iteration 0 ** </td>
<td> 0.693147 </td>
</tr>
<tr>
<td> <center> $\vdots$ </center> </td>
<td> <center> $\vdots$ </center> </td>
</tr>
<tr>
<td> **Train Accuracy** </td>
<td> 99.04306220095694 % </td>
</tr>
<tr>
<td>**Test Accuracy** </td>
<td> 70.0 % </td>
</tr>
</table>
**Comment**: Training accuracy is close to 100%. This is a good sanity check: your model is working and has high enough capacity to fit the training data. Test accuracy is 68%. It is actually not bad for this simple model, given the small dataset we used and that logistic regression is a linear classifier. But no worries, you'll build an even better classifier next week!
Also, you see that the model is clearly overfitting the training data. Later in this specialization you will learn how to reduce overfitting, for example by using regularization. Using the code below (and changing the `index` variable) you can look at predictions on pictures of the test set.
```
# Example of a picture that was wrongly classified.
index = 1
plt.imshow(test_set_x[:,index].reshape((num_px, num_px, 3)))
print ("y = " + str(test_set_y[0,index]) + ", you predicted that it is a \"" + classes[d["Y_prediction_test"][0,index]].decode("utf-8") + "\" picture.")
```
Let's also plot the cost function and the gradients.
```
# Plot learning curve (with costs)
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()
```
**Interpretation**:
You can see the cost decreasing. It shows that the parameters are being learned. However, you see that you could train the model even more on the training set. Try to increase the number of iterations in the cell above and rerun the cells. You might see that the training set accuracy goes up, but the test set accuracy goes down. This is called overfitting.
## 6 - Further analysis (optional/ungraded exercise) ##
Congratulations on building your first image classification model. Let's analyze it further, and examine possible choices for the learning rate $\alpha$.
#### Choice of learning rate ####
**Reminder**:
In order for Gradient Descent to work you must choose the learning rate wisely. The learning rate $\alpha$ determines how rapidly we update the parameters. If the learning rate is too large we may "overshoot" the optimal value. Similarly, if it is too small we will need too many iterations to converge to the best values. That's why it is crucial to use a well-tuned learning rate.
Let's compare the learning curve of our model with several choices of learning rates. Run the cell below. This should take about 1 minute. Feel free also to try different values than the three we have initialized the `learning_rates` variable to contain, and see what happens.
```
learning_rates = [0.01, 0.001, 0.0001]
models = {}
for i in learning_rates:
print ("learning rate is: " + str(i))
models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
print ('\n' + "-------------------------------------------------------" + '\n')
for i in learning_rates:
plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))
plt.ylabel('cost')
plt.xlabel('iterations (hundreds)')
legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()
```
**Interpretation**:
- Different learning rates give different costs and thus different predictions results.
- If the learning rate is too large (0.01), the cost may oscillate up and down. It may even diverge (though in this example, using 0.01 still eventually ends up at a good value for the cost).
- A lower cost doesn't mean a better model. You have to check if there is possibly overfitting. It happens when the training accuracy is a lot higher than the test accuracy.
- In deep learning, we usually recommend that you:
- Choose the learning rate that better minimizes the cost function.
- If your model overfits, use other techniques to reduce overfitting. (We'll talk about this in later videos.)
## 7 - Test with your own image (optional/ungraded exercise) ##
Congratulations on finishing this assignment. You can use your own image and see the output of your model. To do that:
1. Click on "File" in the upper bar of this notebook, then click "Open" to go on your Coursera Hub.
2. Add your image to this Jupyter Notebook's directory, in the "images" folder
3. Change your image's name in the following code
4. Run the code and check if the algorithm is right (1 = cat, 0 = non-cat)!
```
## START CODE HERE ## (PUT YOUR IMAGE NAME)
my_image = "my_image.jpg" # change this to the name of your image file
## END CODE HERE ##
# We preprocess the image to fit your algorithm.
fname = "images/" + my_image
image = np.array(ndimage.imread(fname, flatten=False))
image = image/255.
my_image = scipy.misc.imresize(image, size=(num_px,num_px)).reshape((1, num_px*num_px*3)).T
my_predicted_image = predict(d["w"], d["b"], my_image)
plt.imshow(image)
print("y = " + str(np.squeeze(my_predicted_image)) + ", your algorithm predicts a \"" + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") + "\" picture.")
```
<font color='blue'>
**What to remember from this assignment:**
1. Preprocessing the dataset is important.
2. You implemented each function separately: initialize(), propagate(), optimize(). Then you built a model().
3. Tuning the learning rate (which is an example of a "hyperparameter") can make a big difference to the algorithm. You will see more examples of this later in this course!
Finally, if you'd like, we invite you to try different things on this Notebook. Make sure you submit before trying anything. Once you submit, things you can play with include:
- Play with the learning rate and the number of iterations
- Try different initialization methods and compare the results
- Test other preprocessings (center the data, or divide each row by its standard deviation)
Bibliography:
- http://www.wildml.com/2015/09/implementing-a-neural-network-from-scratch/
- https://stats.stackexchange.com/questions/211436/why-do-we-normalize-images-by-subtracting-the-datasets-image-mean-and-not-the-c
|
github_jupyter
|
```
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import sys
sys.path.append('../')
from loglizer.models import SVM
from loglizer import dataloader, preprocessing
import numpy as np
struct_log = '../data/HDFS/HDFS_100k.log_structured.csv' # The structured log file
label_file = '../data/HDFS/anomaly_label.csv' # The anomaly label file
if __name__ == '__main__':
(x_train, y_train), (x_test, y_test) = dataloader.load_HDFS(struct_log,
label_file=label_file,
window='session',
train_ratio=0.5,
split_type='uniform')
feature_extractor = preprocessing.FeatureExtractor()
x_train = feature_extractor.fit_transform(x_train, term_weighting='tf-idf')
x_test = feature_extractor.transform(x_test)
print(np.array(x_train).shape)
model = SVM()
model.fit(x_train, y_train)
print(np.array(x_train).shape)
# print('Train validation:')
# precision, recall, f1 = model.evaluate(x_train, y_train)
# print('Test validation:')
# precision, recall, f1 = model.evaluate(x_test, y_test)
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import sys
sys.path.append('../')
from loglizer.models import PCA
from loglizer import dataloader, preprocessing
struct_log = '../data/HDFS/HDFS_100k.log_structured.csv' # The structured log file
label_file = '../data/HDFS/anomaly_label.csv' # The anomaly label file
if __name__ == '__main__':
(x_train, y_train), (x_test, y_test) = dataloader.load_HDFS(struct_log,
label_file=label_file,
window='session',
train_ratio=0.5,
split_type='uniform')
feature_extractor = preprocessing.FeatureExtractor()
x_train = feature_extractor.fit_transform(x_train, term_weighting='tf-idf',
normalization='zero-mean')
x_test = feature_extractor.transform(x_test)
# print("输入后的训练数据:",x_train)
# print("尺寸:",x_train.shape)
# print("输入后的测试数据:",x_test)
# print("尺寸:",x_test.shape)
model = PCA()
model.fit(x_train)
# print('Train validation:')
# precision, recall, f1 = model.evaluate(x_train, y_train)
# print('Test validation:')
# precision, recall, f1 = model.evaluate(x_test, y_test)
help(model.fit())
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
data=pd.read_csv('F:\\bank-additional-full.csv',sep=';')
data.shape
tot=len(set(data.index))
last=data.shape[0]-tot
last
data.isnull().sum()
print(data.y.value_counts())
sns.countplot(x='y', data=data)
plt.show()
cat=data.select_dtypes(include=['object']).columns
cat
for c in cat:
print(c)
print("-"*50)
print(data[c].value_counts())
print("-"*50)
from sklearn.preprocessing import LabelEncoder,OneHotEncoder
le=LabelEncoder()
data['y']=le.fit_transform(data['y'])
data.drop('poutcome',axis=1,inplace=True)
print( data['age'].quantile(q = 0.75) +
1.5*(data['age'].quantile(q = 0.75) - data['age'].quantile(q = 0.25)))
data['age']=data[data['age']<69.6]
data['age'].fillna(int(data['age'].mean()),inplace=True)
data['age'].values
data[['age','y']].groupby(['age'],as_index=False).mean().sort_values(by='y', ascending=False)
# for x in data:
# x['Sex'] = x['Sex'].map( {'female': 1, 'male': 0}).astype(int)
data['age_slice'] = pd.cut(data['age'],5)
data[['age_slice', 'y']].groupby(['age_slice'], as_index=False).mean().sort_values(by='age_slice', ascending=True)
data['age'] = data['age'].astype(int)
data.loc[(data['age'] >= 16) & (data['age'] <= 28), 'age'] = 1
data.loc[(data['age'] > 28) & (data['age'] <= 38), 'age'] = 2
data.loc[(data['age'] > 38) & (data['age'] <= 49), 'age'] = 3
data.loc[ (data['age'] > 49) & (data['age'] <= 59), 'age'] = 4
data.loc[ (data['age'] > 59 )& (data['age'] <= 69), 'age'] = 5
data.drop('age_slice',axis=1,inplace=True)
data['marital'].replace(['divorced' ,'married' , 'unknown' , 'single'] ,['single','married','unknown','single'], inplace=True)
data['marital']=le.fit_transform(data['marital'])
data
data['job'].replace(['student'] ,['unemployed'], inplace=True)
data[['education', 'y']].groupby(['education'], as_index=False).mean().sort_values(by='education', ascending=True)
fig, ax = plt.subplots()
fig.set_size_inches(20, 5)
sns.countplot(x = 'education', hue = 'loan', data = data)
ax.set_xlabel('Education', fontsize=15)
ax.set_ylabel('y', fontsize=15)
ax.set_title('Education Count Distribution', fontsize=15)
ax.tick_params(labelsize=15)
sns.despine()
fig, ax = plt.subplots()
fig.set_size_inches(20, 5)
sns.countplot(x = 'job', hue = 'loan', data = data)
ax.set_xlabel('job', fontsize=17)
ax.set_ylabel('y', fontsize=17)
ax.set_title('Education Count Distribution', fontsize=17)
ax.tick_params(labelsize=17)
sns.despine()
data['education'].replace(['basic.4y','basic.6y','basic.9y','professional.course'] ,['not_reach_highschool','not_reach_highschool','not_reach_highschool','university.degree'], inplace=True)
ohe=OneHotEncoder()
data['default']=le.fit_transform(data['default'])
data['housing']=le.fit_transform(data['housing'])
data['loan']=le.fit_transform(data['loan'])
data['month']=le.fit_transform(data['month'])
ohe=OneHotEncoder(categorical_features=data['month'])
data['contact']=le.fit_transform(data['contact'])
data['day_of_week']=le.fit_transform(data['day_of_week'])
data['job']=le.fit_transform(data['job'])
data['education']=le.fit_transform(data['education'])
cat=data.select_dtypes(include=['object']).columns
cat
def outlier_detect(data,feature):
q1 = data[feature].quantile(0.25)
q3 = data[feature].quantile(0.75)
iqr = q3-q1 #Interquartile range
lower = q1-1.5*iqr
upper = q3+1.5*iqr
data = data.loc[(data[feature] > lower) & (data[feature] < upper)]
print('lower IQR and upper IQR of',feature,"are:", lower, 'and', upper, 'respectively')
return data
data.columns
data['pdays'].unique()
data['pdays'].replace([999] ,[0], inplace=True)
data['previous'].unique()
fig, ax = plt.subplots()
fig.set_size_inches(15, 5)
sns.countplot(x = 'campaign', palette="rocket", data = data)
ax.set_xlabel('campaign', fontsize=25)
ax.set_ylabel('y', fontsize=25)
ax.set_title('campaign', fontsize=25)
sns.despine()
sns.countplot(x = 'pdays', palette="rocket", data = data)
ax.set_xlabel('pdays', fontsize=25)
ax.set_ylabel('y', fontsize=25)
ax.set_title('pdays', fontsize=25)
sns.despine()
data[['pdays', 'y']].groupby(['pdays'], as_index=False).mean().sort_values(by='pdays', ascending=True)
sns.countplot(x = 'emp.var.rate', palette="rocket", data = data)
ax.set_xlabel('emp.var.rate', fontsize=25)
ax.set_ylabel('y', fontsize=25)
ax.set_title('emp.var.rate', fontsize=25)
sns.despine()
outlier_detect(data,'duration')
#outlier_detect(data,'emp.var.rate')
outlier_detect(data,'nr.employed')
#outlier_detect(data,'euribor3m')
X = data.iloc[:,:-1]
X = X.values
y = data['y'].values
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
algo = {'LR': LogisticRegression(),
'DT':DecisionTreeClassifier(),
'RFC':RandomForestClassifier(n_estimators=100),
'SVM':SVC(gamma=0.01),
'KNN':KNeighborsClassifier(n_neighbors=10)
}
for k, v in algo.items():
model = v
model.fit(X_train, y_train)
print('Acurracy of ' + k + ' is {0:.2f}'.format(model.score(X_test, y_test)*100))
```
|
github_jupyter
|
# Revisiting Lambert's problem in Python
```
import numpy as np
import matplotlib.pyplot as plt
from cycler import cycler
from poliastro.core import iod
from poliastro.iod import izzo
plt.ion()
plt.rc('text', usetex=True)
```
## Part 1: Reproducing the original figure
```
x = np.linspace(-1, 2, num=1000)
M_list = 0, 1, 2, 3
ll_list = 1, 0.9, 0.7, 0, -0.7, -0.9, -1
fig, ax = plt.subplots(figsize=(10, 8))
ax.set_prop_cycle(cycler('linestyle', ['-', '--']) *
(cycler('color', ['black']) * len(ll_list)))
for M in M_list:
for ll in ll_list:
T_x0 = np.zeros_like(x)
for ii in range(len(x)):
y = iod._compute_y(x[ii], ll)
T_x0[ii] = iod._tof_equation(x[ii], y, 0.0, ll, M)
if M == 0 and ll == 1:
T_x0[x > 0] = np.nan
elif M > 0:
# Mask meaningless solutions
T_x0[x > 1] = np.nan
l, = ax.plot(x, T_x0)
ax.set_ylim(0, 10)
ax.set_xticks((-1, 0, 1, 2))
ax.set_yticks((0, np.pi, 2 * np.pi, 3 * np.pi))
ax.set_yticklabels(('$0$', '$\pi$', '$2 \pi$', '$3 \pi$'))
ax.vlines(1, 0, 10)
ax.text(0.65, 4.0, "elliptic")
ax.text(1.16, 4.0, "hyperbolic")
ax.text(0.05, 1.5, "$M = 0$", bbox=dict(facecolor='white'))
ax.text(0.05, 5, "$M = 1$", bbox=dict(facecolor='white'))
ax.text(0.05, 8, "$M = 2$", bbox=dict(facecolor='white'))
ax.annotate("$\lambda = 1$", xy=(-0.3, 1), xytext=(-0.75, 0.25), arrowprops=dict(arrowstyle="simple", facecolor="black"))
ax.annotate("$\lambda = -1$", xy=(0.3, 2.5), xytext=(0.65, 2.75), arrowprops=dict(arrowstyle="simple", facecolor="black"))
ax.grid()
ax.set_xlabel("$x$")
ax.set_ylabel("$T$");
```
## Part 2: Locating $T_{min}$
```
for M in M_list:
for ll in ll_list:
x_T_min, T_min = iod._compute_T_min(ll, M, 10, 1e-8)
ax.plot(x_T_min, T_min, 'kx', mew=2)
fig
```
## Part 3: Try out solution
```
T_ref = 1
ll_ref = 0
(x_ref, _), = iod._find_xy(ll_ref, T_ref, 0, 10, 1e-8)
x_ref
ax.plot(x_ref, T_ref, 'o', mew=2, mec='red', mfc='none')
fig
```
## Part 4: Run some examples
```
from astropy import units as u
from poliastro.bodies import Earth
```
### Single revolution
```
k = Earth.k
r0 = [15945.34, 0.0, 0.0] * u.km
r = [12214.83399, 10249.46731, 0.0] * u.km
tof = 76.0 * u.min
expected_va = [2.058925, 2.915956, 0.0] * u.km / u.s
expected_vb = [-3.451569, 0.910301, 0.0] * u.km / u.s
(v0, v), = izzo.lambert(k, r0, r, tof)
v
k = Earth.k
r0 = [5000.0, 10000.0, 2100.0] * u.km
r = [-14600.0, 2500.0, 7000.0] * u.km
tof = 1.0 * u.h
expected_va = [-5.9925, 1.9254, 3.2456] * u.km / u.s
expected_vb = [-3.3125, -4.1966, -0.38529] * u.km / u.s
(v0, v), = izzo.lambert(k, r0, r, tof)
v
```
### Multiple revolutions
```
k = Earth.k
r0 = [22592.145603, -1599.915239, -19783.950506] * u.km
r = [1922.067697, 4054.157051, -8925.727465] * u.km
tof = 10 * u.h
expected_va = [2.000652697, 0.387688615, -2.666947760] * u.km / u.s
expected_vb = [-3.79246619, -1.77707641, 6.856814395] * u.km / u.s
expected_va_l = [0.50335770, 0.61869408, -1.57176904] * u.km / u.s
expected_vb_l = [-4.18334626, -1.13262727, 6.13307091] * u.km / u.s
expected_va_r = [-2.45759553, 1.16945801, 0.43161258] * u.km / u.s
expected_vb_r = [-5.53841370, 0.01822220, 5.49641054] * u.km / u.s
(v0, v), = izzo.lambert(k, r0, r, tof, M=0)
v
(_, v_l), (_, v_r) = izzo.lambert(k, r0, r, tof, M=1)
v_l
v_r
```
|
github_jupyter
|
# GLM: Negative Binomial Regression
```
%matplotlib inline
import numpy as np
import pandas as pd
import pymc3 as pm
from scipy import stats
import matplotlib.pyplot as plt
plt.style.use('seaborn-darkgrid')
import seaborn as sns
import re
print('Running on PyMC3 v{}'.format(pm.__version__))
```
This notebook demos negative binomial regression using the `glm` submodule. It closely follows the GLM Poisson regression example by [Jonathan Sedar](https://github.com/jonsedar) (which is in turn inspired by [a project by Ian Osvald](http://ianozsvald.com/2016/05/07/statistically-solving-sneezes-and-sniffles-a-work-in-progress-report-at-pydatalondon-2016/)) except the data here is negative binomially distributed instead of Poisson distributed.
Negative binomial regression is used to model count data for which the variance is higher than the mean. The [negative binomial distribution](https://en.wikipedia.org/wiki/Negative_binomial_distribution) can be thought of as a Poisson distribution whose rate parameter is gamma distributed, so that rate parameter can be adjusted to account for the increased variance.
### Convenience Functions
Taken from the Poisson regression example.
```
def plot_traces(trcs, varnames=None):
'''Plot traces with overlaid means and values'''
nrows = len(trcs.varnames)
if varnames is not None:
nrows = len(varnames)
ax = pm.traceplot(trcs, varnames=varnames, figsize=(12,nrows*1.4),
lines={k: v['mean'] for k, v in
pm.summary(trcs,varnames=varnames).iterrows()})
for i, mn in enumerate(pm.summary(trcs, varnames=varnames)['mean']):
ax[i,0].annotate('{:.2f}'.format(mn), xy=(mn,0), xycoords='data',
xytext=(5,10), textcoords='offset points', rotation=90,
va='bottom', fontsize='large', color='#AA0022')
def strip_derived_rvs(rvs):
'''Remove PyMC3-generated RVs from a list'''
ret_rvs = []
for rv in rvs:
if not (re.search('_log',rv.name) or re.search('_interval',rv.name)):
ret_rvs.append(rv)
return ret_rvs
```
### Generate Data
As in the Poisson regression example, we assume that sneezing occurs at some baseline rate, and that consuming alcohol, not taking antihistamines, or doing both, increase its frequency.
#### Poisson Data
First, let's look at some Poisson distributed data from the Poisson regression example.
```
np.random.seed(123)
# Mean Poisson values
theta_noalcohol_meds = 1 # no alcohol, took an antihist
theta_alcohol_meds = 3 # alcohol, took an antihist
theta_noalcohol_nomeds = 6 # no alcohol, no antihist
theta_alcohol_nomeds = 36 # alcohol, no antihist
# Create samples
q = 1000
df_pois = pd.DataFrame({
'nsneeze': np.concatenate((np.random.poisson(theta_noalcohol_meds, q),
np.random.poisson(theta_alcohol_meds, q),
np.random.poisson(theta_noalcohol_nomeds, q),
np.random.poisson(theta_alcohol_nomeds, q))),
'alcohol': np.concatenate((np.repeat(False, q),
np.repeat(True, q),
np.repeat(False, q),
np.repeat(True, q))),
'nomeds': np.concatenate((np.repeat(False, q),
np.repeat(False, q),
np.repeat(True, q),
np.repeat(True, q)))})
df_pois.groupby(['nomeds', 'alcohol'])['nsneeze'].agg(['mean', 'var'])
```
Since the mean and variance of a Poisson distributed random variable are equal, the sample means and variances are very close.
#### Negative Binomial Data
Now, suppose every subject in the dataset had the flu, increasing the variance of their sneezing (and causing an unfortunate few to sneeze over 70 times a day). If the mean number of sneezes stays the same but variance increases, the data might follow a negative binomial distribution.
```
# Gamma shape parameter
alpha = 10
def get_nb_vals(mu, alpha, size):
"""Generate negative binomially distributed samples by
drawing a sample from a gamma distribution with mean `mu` and
shape parameter `alpha', then drawing from a Poisson
distribution whose rate parameter is given by the sampled
gamma variable.
"""
g = stats.gamma.rvs(alpha, scale=mu / alpha, size=size)
return stats.poisson.rvs(g)
# Create samples
n = 1000
df = pd.DataFrame({
'nsneeze': np.concatenate((get_nb_vals(theta_noalcohol_meds, alpha, n),
get_nb_vals(theta_alcohol_meds, alpha, n),
get_nb_vals(theta_noalcohol_nomeds, alpha, n),
get_nb_vals(theta_alcohol_nomeds, alpha, n))),
'alcohol': np.concatenate((np.repeat(False, n),
np.repeat(True, n),
np.repeat(False, n),
np.repeat(True, n))),
'nomeds': np.concatenate((np.repeat(False, n),
np.repeat(False, n),
np.repeat(True, n),
np.repeat(True, n)))})
df.groupby(['nomeds', 'alcohol'])['nsneeze'].agg(['mean', 'var'])
```
As in the Poisson regression example, we see that drinking alcohol and/or not taking antihistamines increase the sneezing rate to varying degrees. Unlike in that example, for each combination of `alcohol` and `nomeds`, the variance of `nsneeze` is higher than the mean. This suggests that a Poisson distrubution would be a poor fit for the data since the mean and variance of a Poisson distribution are equal.
### Visualize the Data
```
g = sns.factorplot(x='nsneeze', row='nomeds', col='alcohol', data=df, kind='count', aspect=1.5)
# Make x-axis ticklabels less crowded
ax = g.axes[1, 0]
labels = range(len(ax.get_xticklabels(which='both')))
ax.set_xticks(labels[::5])
ax.set_xticklabels(labels[::5]);
```
## Negative Binomial Regression
### Create GLM Model
```
fml = 'nsneeze ~ alcohol + nomeds + alcohol:nomeds'
with pm.Model() as model:
pm.glm.GLM.from_formula(formula=fml, data=df, family=pm.glm.families.NegativeBinomial())
# Old initialization
# start = pm.find_MAP(fmin=optimize.fmin_powell)
# C = pm.approx_hessian(start)
# trace = pm.sample(4000, step=pm.NUTS(scaling=C))
trace = pm.sample(1000, tune=2000, cores=2)
```
### View Results
```
rvs = [rv.name for rv in strip_derived_rvs(model.unobserved_RVs)]
plot_traces(trace, varnames=rvs);
# Transform coefficients to recover parameter values
np.exp(pm.summary(trace, varnames=rvs)[['mean','hpd_2.5','hpd_97.5']])
```
The mean values are close to the values we specified when generating the data:
- The base rate is a constant 1.
- Drinking alcohol triples the base rate.
- Not taking antihistamines increases the base rate by 6 times.
- Drinking alcohol and not taking antihistamines doubles the rate that would be expected if their rates were independent. If they were independent, then doing both would increase the base rate by 3\*6=18 times, but instead the base rate is increased by 3\*6\*2=16 times.
Finally, even though the sample for `mu` is highly skewed, its median value is close to the sample mean, and the mean of `alpha` is also quite close to its actual value of 10.
```
np.percentile(trace['mu'], [25,50,75])
df.nsneeze.mean()
trace['alpha'].mean()
```
|
github_jupyter
|
# Multi-qubit quantum circuit
In this exercise we creates a two qubit circuit, with two qubits in superposition, and then measures the individual qubits, resulting in two coin toss results with the following possible outcomes with equal probability: $|00\rangle$, $|01\rangle$, $|10\rangle$, and $|11\rangle$. This is like tossing two coins.
Import the required libraries, including the IBM Q library for working with IBM Q hardware.
```
import numpy as np
from qiskit import QuantumCircuit, execute, Aer
from qiskit.tools.monitor import job_monitor
# Import visualization
from qiskit.visualization import plot_histogram, plot_bloch_multivector, iplot_bloch_multivector, plot_state_qsphere, iplot_state_qsphere
# Add the state vector calculation function
def get_psi(circuit, vis):
global psi
backend = Aer.get_backend('statevector_simulator')
psi = execute(circuit, backend).result().get_statevector(circuit)
if vis=="IQ":
display(iplot_state_qsphere(psi))
elif vis=="Q":
display(plot_state_qsphere(psi))
elif vis=="M":
print(psi)
elif vis=="B":
display(plot_bloch_multivector(psi))
else: # vis="IB"
display(iplot_bloch_multivector(psi))
vis=""
```
How many qubits do we want to use. The notebook let's you set up multi-qubit circuits of various sizes. Keep in mind that the biggest publicly available IBM quantum computer is 14 qubits in size.
```
#n_qubits=int(input("Enter number of qubits:"))
n_qubits=2
```
Create quantum circuit that includes the quantum register and the classic register. Then add a Hadamard (super position) gate to all the qubits. Add measurement gates.
```
qc1 = QuantumCircuit(n_qubits,n_qubits)
qc_measure = QuantumCircuit(n_qubits,n_qubits)
for qubit in range (0,n_qubits):
qc1.h(qubit) #A Hadamard gate that creates a superposition
for qubit in range (0,n_qubits):
qc_measure.measure(qubit,qubit)
display(qc1.draw(output="mpl"))
```
Now that we have more than one qubit it is starting to become a bit difficult to visualize the outcomes when running the circuit. To alleviate this we can instead have the get_psi return the statevector itself by by calling it with the vis parameter set to `"M"`. We can also have it display a Qiskit-unique visualization called a Q Sphere by passing the parameter `"Q"` or `"q"`. Big Q returns an interactive Q-sphere, and little q a static one.
```
get_psi(qc1,"M")
print (abs(np.square(psi)))
get_psi(qc1,"B")
```
Now we see the statevector for multiple qubits, and can calculate the probabilities for the different outcomes by squaring the complex parameters in the vector.
The Q Sphere visualization provides the same informaton in a visual form, with |0..0> at the north pole, |1..1> at the bottom, and other combinations on latitude circles. In the dynamicc version, you can hover over the tips of the vectors to see the state, probability, and phase data. In the static version, the size of the vector tip represents the relative probability of getting that specific result, and the color represents the phase angle for that specific output. More on that later!
Now add your circuit with the measurement circuit and run a 1,000 shots to get statistics on the possible outcomes.
```
backend = Aer.get_backend('qasm_simulator')
qc_final=qc1+qc_measure
job = execute(qc_final, backend, shots=1000)
counts1 = job.result().get_counts(qc_final)
print(counts1)
plot_histogram(counts1)
```
As you might expect, with two independednt qubits ea h in a superposition, the resulting outcomes should be spread evenly accross th epossible outcomes, all the combinations of 0 and 1.
**Time for you to do some work!** To get an understanding of the probable outcomes and how these are displayed on the interactive (or static) Q Sphere, change the `n_qubits=2` value in the cell above, and run the cells again for a different number of qubits.
When you are done, set the value back to 2, and continue on.
```
n_qubits=2
```
# Entangled-qubit quantum circuit - The Bell state
Now we are going to do something different. We will entangle the qubits.
Create quantum circuit that includes the quantum register and the classic register. Then add a Hadamard (super position) gate to the first qubit. Then add a controlled-NOT gate (cx) between the first and second qubit, entangling them. Add measurement gates.
We then take a look at using the CX (Controlled-NOT) gate to entangle the two qubits in a so called Bell state. This surprisingly results in the following possible outcomes with equal probability: $|00\rangle$ and $|11\rangle$. Two entangled qubits do not at all behave like two tossed coins.
We then run the circuit a large number of times to see what the statistical behavior of the qubits are.
Finally, we run the circuit on real IBM Q hardware to see how real physical qubits behave.
In this exercise we introduce the CX gate, which creates entanglement between two qubits, by flipping the controlled qubit (q_1) if the controlling qubit (q_0) is 1.

```
qc2 = QuantumCircuit(n_qubits,n_qubits)
qc2_measure = QuantumCircuit(n_qubits, n_qubits)
for qubit in range (0,n_qubits):
qc2_measure.measure(qubit,qubit)
qc2.h(0) # A Hadamard gate that puts the first qubit in superposition
display(qc2.draw(output="mpl"))
get_psi(qc2,"M")
get_psi(qc2,"B")
for qubit in range (1,n_qubits):
qc2.cx(0,qubit) #A controlled NOT gate that entangles the qubits.
display(qc2.draw(output="mpl"))
get_psi(qc2, "B")
```
Now we notice something peculiar; after we add the CX gate, entangling the qubits the Bloch spheres display nonsense. Why is that? It turns out that once your qubits are entangled they can no longer be described individually, but only as a combined object. Let's take a look at the state vector and Q sphere.
```
get_psi(qc2,"M")
print (abs(np.square(psi)))
get_psi(qc2,"Q")
```
Set the backend to a local simulator. Then create a quantum job for the circuit, the selected backend, that runs just one shot to simulate a coin toss with two simultaneously tossed coins, then run the job. Display the result; either 0 for up (base) or 1 for down (excited) for each qubit. Display the result as a histogram. Either |00> or |11> with 100% probability.
```
backend = Aer.get_backend('qasm_simulator')
qc2_final=qc2+qc2_measure
job = execute(qc2_final, backend, shots=1)
counts2 = job.result().get_counts(qc2_final)
print(counts2)
plot_histogram(counts2)
```
Note how the qubits completely agree. They are entangled.
**Do some work..** Run the cell above a few times to verify that you only get the results 00 or 11.
Now, lets run quite a few more shots, and display the statistsics for the two results. This time, as we are no longer just talking about two qubits, but the amassed results of thousands of runs on these qubits.
```
job = execute(qc2_final, backend, shots=1000)
result = job.result()
counts = result.get_counts()
print(counts)
plot_histogram(counts)
```
And look at that, we are back at our coin toss results, fifty-fifty. Every time one of the coins comes up heads (|0>) the other one follows suit. Tossing one coin we immediately know what the other one will come up as; the coins (qubits) are entangled.
# Run your entangled circuit on an IBM quantum computer
**Important:** With the simulator we get perfect results, only |00> or |11>. On a real NISQ (Noisy Intermediate Scale Quantum computer) we do not expect perfect results like this. Let's run the Bell state once more, but on an actual IBM Q quantum computer.
**Time for some work!** Before you can run your program on IBM Q you must load your API key. If you are running this notebook in an IBM Qx environment, your API key is already stored in the system, but if you are running on your own machine you [must first store the key](https://qiskit.org/documentation/install.html#access-ibm-q-systems).
```
#Save and store API key locally.
from qiskit import IBMQ
#IBMQ.save_account('MY_API_TOKEN') <- Uncomment this line if you need to store your API key
#Load account information
IBMQ.load_account()
provider = IBMQ.get_provider()
```
Grab the least busy IBM Q backend.
```
from qiskit.providers.ibmq import least_busy
backend = least_busy(provider.backends(operational=True, simulator=False))
#backend = provider.get_backend('ibmqx2')
print("Selected backend:",backend.status().backend_name)
print("Number of qubits(n_qubits):", backend.configuration().n_qubits)
print("Pending jobs:", backend.status().pending_jobs)
```
Lets run a large number of shots, and display the statistsics for the two results: $|00\rangle$ and $|11\rangle$ on the real hardware. Monitor the job and display our place in the queue.
```
if n_qubits > backend.configuration().n_qubits:
print("Your circuit contains too many qubits (",n_qubits,"). Start over!")
else:
job = execute(qc2_final, backend, shots=1000)
job_monitor(job)
```
Get the results, and display in a histogram. Notice how we no longer just get the perfect entangled results, but also a few results that include non-entangled qubit results. At this stage, quantum computers are not perfect calculating machines, but pretty noisy.
```
result = job.result()
counts = result.get_counts(qc2_final)
print(counts)
plot_histogram(counts)
```
That was the simple readout. Let's take a look at the whole returned results:
```
print(result)
```
|
github_jupyter
|
# Twitter Mining Function & Scatter Plots
---------------------------------------------------------------
```
# Import Dependencies
%matplotlib notebook
import os
import csv
import json
import requests
from pprint import pprint
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from twython import Twython
import simplejson
import sys
import string
import glob
from pathlib import Path
# Import Twitter 'Keys' - MUST SET UP YOUR OWN 'config_twt.py' file
# You will need to create your own "config_twt.py" file using each of the Twitter authentication codes
# they provide you when you sign up for a developer account with your Twitter handle
from config_twt import (app_key_twt, app_secret_twt, oauth_token_twt, oauth_token_secret_twt)
# Set Up Consumer Keys And Secret with Twitter Keys
APP_KEY = app_key_twt
APP_SECRET = app_secret_twt
# Set up OAUTH Token and Secret With Twitter Keys
OAUTH_TOKEN = oauth_token_twt
OAUTH_TOKEN_SECRET = oauth_token_secret_twt
# Load Keys In To a Twython Function And Call It "twitter"
twitter = Twython(APP_KEY, APP_SECRET, OAUTH_TOKEN, OAUTH_TOKEN_SECRET)
# Setup Batch Counter For Phase 2
batch_counter = 0
```
___________________________
## Twitter Mining Function '(TMF)'
___________________________
### INSTRUCTIONS:
This will Twitter Query Function will:
- Perform searches for hastags (#)
- Search for "@twitter_user_acct"
- Provide mixed results of popular and most recent tweets from the last 7 days
- 'remaining' 'search/tweets (allowance of 180) rate limit status' regenerates in 15 minutes after depletion
### Final outputs are aggegrated queries in both:
- Pandas DataFrame of queried tweets
- CSV files saved in the same folder as this Jupyter Notebook
### Phase 1 - Run Query and Store The Dictionary Into a List
- Step 1) Run the 'Twitter Mining Function' cell below to begin program
Note:
- Limits have not been fully tested due to time constraint
- Search up to 180 queries where and each query yields up to 100 tweets max
- Running the TLC to see how many you have left after every csv outputs.
- Step 2) When prompted, input in EITHER: #hashtag or @Twitter_user_account
Examples: "#thuglife" or "@beyonce"
- Step 3) TMF will query Twitter and store the tweets_data, a list called "all_data"
- Step 4) Upon query search completion, it will prompt: "Perform another search query:' ('y'/'n') "
- Input 'y' to query, and the program will append the results
- Tip: Keep count of how many 'search tweets' you have, it should deduct 1 from 'remaining',
which can produce up to 100 tweets of data
- Step 5) End program by entering 'n' when prompted for 'search again'
Output: printed list of all appended query data
### Phase 2 - Converting to Pandas DataFrame and Produce a CSV Output
- Step 6) Loop Through Queried Data
- Step 7) Convert to Pandas DataFrame
- Step 8) Convert from DataFrame to CSV
### Addtional Considerations:
- Current set up uses standard search api keys, not premium
- TMF returns potentially 100 tweets at a time, and pulls from the last 7 days in random order
- More than likely will have to run multiple searches and track line items count
in each of the csv files output that will be created in the same folder
### Tweet Limit Counter (TLC)
- Run cell to see how many search queries you have available
- Your 'remaining' search tweets regenerates over 15 minutes.
```
# TLC - Run to Query Current Rate Limit on API Keys
twitter.get_application_rate_limit_status()['resources']['search']
#Twitter Mining Function (TMF)
#RUN THIS CELL TO BEGIN PROGRAM!
print('-'*80)
print("TWITTER QUERY FUNCTION - BETA")
print('-'*80)
print("INPUT PARAMETERS:")
print("- @Twitter_handle e.g. @clashofclans")
print("- Hashtags (#) e.g. #THUGLIFE")
print("NOTE: SCROLL DOWN AFTER EACH QUERY FOR ENTER INPUT")
print('-'*80)
def twitter_search(app_search):
# Store the following Twython function and parameters into variable 't'
t = Twython(app_key=APP_KEY,
app_secret=APP_SECRET,
oauth_token=OAUTH_TOKEN,
oauth_token_secret=OAUTH_TOKEN_SECRET)
# The Twitter Mining Function we will use to run searches is below
# and we're asking for it to pull 100 tweets
search = t.search(q=app_search, count=100)
tweets = search['statuses']
# This will be a list of dictionaries of each tweet where the loop below will append to
all_data = []
# From the tweets, go into each individual tweet and extract the following into a 'dictionary'
# and append it to big bucket called 'all_data'
for tweet in tweets:
try:
tweets_data = {
"Created At":tweet['created_at'],
"Text (Tweet)":tweet['text'],
"User ID":tweet['user']['id'],
"User Followers Count":tweet['user']['followers_count'],
"Screen Name":tweet['user']['name'],
"ReTweet Count":tweet['retweet_count'],
"Favorite Count":tweet['favorite_count']}
all_data.append(tweets_data)
#print(tweets_data)
except (KeyError, NameError, TypeError, AttributeError) as err:
print(f"{err} Skipping...")
#functions need to return something...
return all_data
# The On and Off Mechanisms:
search_again = 'y'
final_all_data = []
# initialize the query counter
query_counter = 0
while search_again == 'y':
query_counter += 1
start_program = str(input('Type the EXACT @twitter_acct or #hashtag to query: '))
all_data = twitter_search(start_program)
final_all_data += all_data
#print(all_data)
print(f"Completed Collecting Search Results for {start_program} . Queries Completed: {query_counter} ")
print('-'*80)
search_again = input("Would you like to run another query? Enter 'y'. Otherwise, 'n' or another response will end query mode. ")
print('-'*80)
# When you exit the program, set the query counter back to zero
query_counter = 0
print()
print(f"Phase 1 of 2 Queries Completed . Proceed to Phase 2 - Convert Collection to DF and CSV formats .")
#print("final Data", final_all_data)
#####################################################################################################
# TIPS!: # If you're searching for the same hastag or twitter_handle,
# consider copying and pasting it (e.g. @fruitninja)
# Display the total tweets the TMF successfully pulled:
print(len(final_all_data))
```
### Tweet Limit Counter (TLC)
- Run cell to see how many search queries you have available
- Your 'remaining' search tweets regenerates over 15 minutes.
```
# Run to view current rate limit status
twitter.get_application_rate_limit_status()['resources']['search']
#df = pd.DataFrame(final_all_data[0])
#df
final_all_data
```
### Step 6) Loop through the stored list of queried tweets from final_all_data and stores in designated lists
```
# Loop thru finall_all_data (list of dictionaries) and extract each item and store them into
# the respective lists
# BUCKETS
created_at = []
tweet_text = []
user_id = []
user_followers_count = []
screen_name = []
retweet_count = []
likes_count = []
# append tweets data to the buckets for each tweet
#change to final_all_data
for data in final_all_data:
#print(keys, data[keys])
created_at.append(data["Created At"]),
tweet_text.append(data['Text (Tweet)']),
user_id.append(data['User ID']),
user_followers_count.append(data['User Followers Count']),
screen_name.append(data['Screen Name']),
retweet_count.append(data['ReTweet Count']),
likes_count.append(data['Favorite Count'])
#print(created_at, tweet_text, user_id, user_followers_count, screen_name, retweet_count, likes_count)
print("Run complete. Proceed to next cell.")
```
### Step 7) Convert to Pandas DataFrame
```
# Setup DataFrame and run tweets_data_df
tweets_data_df = pd.DataFrame({
"Created At": created_at,
"Screen Name": screen_name,
"User ID": user_id,
"User Follower Count": user_followers_count,
"Likes Counts": likes_count,
"ReTweet Count": retweet_count,
"Tweet Text" : tweet_text
})
tweets_data_df.head()
```
### Step 8) Load into MySQL Database - later added this piece to display ETL potential of this project
```
# This section was added later after I reviewed and wanted to briefly reiterate on it
tweets_data_df2 = tweets_data_df.copy()
# Dropped Screen Name and Tweets Text bc would I would need to clean the 'Screen Name' and 'Tweet Text' Columns
tweets_data_df2 = tweets_data_df2.drop(["Screen Name", "Tweet Text"], axis=1).sort_values(by="User Follower Count")
# Import Dependencies 2/2:
from sqlalchemy import create_engine
from sqlalchemy.sql import select
from sqlalchemy_utils import database_exists, create_database, drop_database, has_index
import pymysql
rds_connection_string = "root:[email protected]/"
#db_name = input("What database would you like to search for?")
db_name = 'twitterAPI_data_2019_db'
# Setup engine connection string
engine = create_engine(f'mysql://{rds_connection_string}{db_name}?charset=utf8', echo=True)
# Created a function incorproating SQL Alchemy to search, create, and or drop a database:
def search_create_drop_db(db_name):
db_exist = database_exists(f'mysql://{rds_connection_string}{db_name}')
db_url = f'mysql://{rds_connection_string}{db_name}'
if db_exist == True:
drop_table_y_or_n = input(f'"{db_name}" database already exists in MySQL. Do you want you drop the table? Enter exactly: "y" or "n". ')
if drop_table_y_or_n == 'y':
drop_database(db_url)
print(f"Database {db_name} was dropped")
create_new_db = input(f"Do you want to create another database called: {db_name}? ")
if create_new_db == 'y':
create_database(db_url)
return(f"The database {db_name} was created. Next You will need to create tables for this database. ")
else:
return("No database was created. Goodbye! ")
else:
return("The database exists. No action was taken. Goodbye! ")
else:
create_database(db_url)
return(f"The queried database did not exist, and was created as: {db_name} . ")
search_create_drop_db(db_name)
tweets_data_df2.to_sql('tweets', con=engine, if_exists='append')
```
### Step 9) Convert DataFrame to CSV File and save on local drive
```
# Save Tweets Data to a CSV File (Run Cell to input filename)
# Streamline the saving of multiple queries (1 query = up to 100 tweets) into a csv file.
# E.g. input = (#fruit_ninja) will save the file as "fruit_ninja_batch1.csv" as the file result
# Note: first chracter will be slice off so you can just copy and paste
# the hastag / @twitter_handle from steps above
batch_name = str(input("Enter in batch name."))
# If you restart kernel, batch_counter resets to zero.
batch_counter = batch_counter +1
# Check if the #hastag / @twitter_handle folder exists and create the folder if it does not
Path(f"./resources/{batch_name[1:]}").mkdir(parents=True, exist_ok=True)
# Save dataframe of all queries in a csv file to a folder in the resources folder csv using the
tweets_data_df.to_csv(f"./resources/{batch_name[1:]}/{batch_name[1:]}_batch{batch_counter}.csv", encoding='utf-8')
print(f"Output saved in current folder as: {batch_name[1:]}_batch{batch_counter}.csv ")
```
# PHASE 3 - CALCULATIONS USING API DATA
```
# This prints out all of the folder titles in "resources" folder
path = './resources/*' # use your path
resources = glob.glob(path)
all_folders = []
print("All folders in the 'resources' folder:")
print("="*40)
for foldername in resources:
str(foldername)
foldername = foldername[12:]
all_folders.append(foldername)
#print(li)
print("")
print(F"Total Folders: {len(all_folders)}")
print(all_folders)
all_TopApps_df_list = []
for foldername in all_folders:
plug = foldername
path = f'./resources\\{plug}'
all_files = glob.glob(path + "/*.csv")
counter = 0
app_dataframes = []
for filename in all_files:
counter += 1
df = pd.read_csv(filename, index_col=None, header=0)
app_dataframes.append(df)
output = pd.concat(app_dataframes, axis=0, ignore_index=True)
all_TopApps_df_list.append(f"{output}_{counter}")
counter = 0
#fb_frame
```
##### Facebook Calculations
```
# Example Template of looping thru csvfiles, and concatenate all of the csv files we collected in each folder
plug = 'facebook'
path = f'./resources\\{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
fb_frame = pd.concat(li, axis=0, ignore_index=True)
fb_frame
fb_frame.describe()
# Sort to set up removal of duplicates
fb_frame.sort_values(by=['User ID','Created At'], ascending=False)
# Drop Duplicates only for matching columns omitting the index
facebook_filtered_df = fb_frame.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
# Get New Snap Shot Statistics
facebook_filtered_df.describe()
facebook_filtered_df.head()
# Count total out of Unique Tweets
facebook_total_tweets = len(facebook_filtered_df['Tweet Text'])
facebook_total_tweets
# Calculate Facebook Avg Followers - doesn't make sense to sum.
facebook_avg_followers_ct = facebook_filtered_df['User Follower Count'].mean()
facebook_avg_followers_ct
# Total Likes of all tweets
facebook_total_likes = facebook_filtered_df['Likes Counts'].sum()
#facebook_avg_likes = facebook_filtered_df['Likes Counts'].mean()
facebook_total_likes
#facebook_avg_likes
# Facebook Retweets Stats:
#facebook_sum_retweets = facebook_filtered_df['ReTweet Count'].sum()
facebook_avg_retweets = facebook_filtered_df['ReTweet Count'].mean()
#facebook_sum_retweets
facebook_avg_retweets
```
#### Instagram Calculations
```
plug = 'instagram'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
instagram_source_df = pd.concat(li, axis=0, ignore_index=True)
instagram_source_df
# Snapshot Statistics
instagram_source_df.describe()
instagram_source_df.head()
# Sort to set up removal of duplicates
instagram_source_df.sort_values(by=['User ID','Created At'], ascending=False)
# Drop Duplicates only for matching columns omitting the index
instagram_filtered_df = instagram_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
instagram_filtered_df
# Get New Snap Shot Statistics
instagram_filtered_df.describe()
# Count total out of Unique Tweets
instagram_total_tweets = len(instagram_filtered_df['Tweet Text'])
instagram_total_tweets
# Calculate Facebook Avg Followers - doesn't make sense to sum.
instagram_avg_followers_ct = instagram_filtered_df['User Follower Count'].mean()
instagram_avg_followers_ct
# Total Likes of all tweets
instagram_total_likes = instagram_filtered_df['Likes Counts'].sum()
#instagram_avg_likes = instagram_filtered_df['Likes Counts'].mean()
instagram_total_likes
#instagram_avg_likes
# Retweets Stats:
#instagram_sum_retweets = instagram_filtered_df['ReTweet Count'].sum()
instagram_avg_retweets = instagram_filtered_df['ReTweet Count'].mean()
#instagram_sum_retweets
instagram_avg_retweets
```
### Clash of Clans Calculations
```
plug = 'clashofclans'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
coc_source_df = pd.concat(li, axis=0, ignore_index=True)
coc_source_df
# Snapshot Statistics
coc_source_df.describe()
coc_source_df.head()
# Sort to set up removal of duplicates
coc_source_df.sort_values(by=['User ID','Created At'], ascending=False)
# Drop Duplicates only for matching columns omitting the index
coc_filtered_df = coc_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
coc_filtered_df.head()
# Get New Snap Shot Statistics
coc_filtered_df.describe()
# Count total out of Unique Tweets
coc_total_tweets = len(coc_filtered_df['Tweet Text'])
coc_total_tweets
# Calculate Facebook Avg Followers - doesn't make sense to sum.
coc_avg_followers_ct = coc_filtered_df['User Follower Count'].mean()
coc_avg_followers_ct
# Total Likes of all tweets
coc_total_likes = coc_filtered_df['Likes Counts'].sum()
#coc_avg_likes = coc_filtered_df['Likes Counts'].mean()
coc_total_likes
#coc_avg_likes
# Retweets Stats:
#coc_sum_retweets = coc_filtered_df['ReTweet Count'].sum()
coc_avg_retweets = coc_filtered_df['ReTweet Count'].mean()
#coc_sum_retweets
coc_avg_retweets
```
### Temple Run Calculations
```
plug = 'templerun'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
templerun_source_df = pd.concat(li, axis=0, ignore_index=True)
templerun_source_df
# Snapshot Statistics
templerun_source_df.describe()
#templerun_source_df.head()
# Sort to set up removal of duplicates
templerun_source_df.sort_values(by=['User ID','Created At'], ascending=False)
# Drop Duplicates only for matching columns omitting the index
templerun_filtered_df = templerun_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
#templerun_filtered_df
#templerun_filtered_df.describe()
# Count total out of Unique Tweets
templerun_total_tweets = len(templerun_filtered_df['Tweet Text'])
templerun_total_tweets
# Calculate Facebook Avg Followers - doesn't make sense to sum.
templerun_avg_followers_ct = templerun_filtered_df['User Follower Count'].mean()
templerun_avg_followers_ct
# Total Likes of all tweets
templerun_total_likes = templerun_filtered_df['Likes Counts'].sum()
#templerun_avg_likes = templerun_filtered_df['Likes Counts'].mean()
templerun_total_likes
#instagram_avg_likes
# Retweets Stats:
#templerun_sum_retweets = templerun_filtered_df['ReTweet Count'].sum()
templerun_avg_retweets = templerun_filtered_df['ReTweet Count'].mean()
#templerun_sum_retweets
templerun_avg_retweets
templerun_total_tweets
templerun_avg_retweets
templerun_avg_followers_ct
templerun_total_likes
```
### Pandora Calculations
```
plug = 'pandora'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
pandora_source_df = pd.concat(li, axis=0, ignore_index=True)
# Snapshot Statistics
pandora_source_df.describe()
#pandora_source_df.head()
# Sort to set up removal of duplicates
pandora_source_df.sort_values(by=['User ID','Created At'], ascending=False)
# Drop Duplicates only for matching columns omitting the index
pandora_filtered_df = pandora_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
pandora_filtered_df
pandora_filtered_df.describe()
# Count total out of Unique Tweets
pandora_total_tweets = len(pandora_filtered_df['Tweet Text'])
pandora_total_tweets
# Calculate Facebook Avg Followers - doesn't make sense to sum.
pandora_avg_followers_ct = pandora_filtered_df['User Follower Count'].mean()
pandora_avg_followers_ct
# Total Likes of all tweets
# use sum of likes.
pandora_total_likes = pandora_filtered_df['Likes Counts'].sum()
#pandora_avg_likes = pandora_filtered_df['Likes Counts'].mean()
pandora_total_likes
#pandora_avg_likes
# Retweets Stats:
#pandora_sum_retweets = pandora_filtered_df['ReTweet Count'].sum()
pandora_avg_retweets = pandora_filtered_df['ReTweet Count'].mean()
#pandora_sum_retweets
pandora_avg_retweets
```
### Pinterest Calculations
```
# Concatenate them
plug = 'pinterest'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
pinterest_source_df = pd.concat(li, axis=0, ignore_index=True)
# Snapshot Statistics
pinterest_source_df.describe()
pinterest_source_df.head()
# Sort to set up removal of duplicates
pinterest_source_df.sort_values(by=['User ID','Created At'], ascending=False)
# Drop Duplicates only for matching columns omitting the index
pinterest_filtered_df = pinterest_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
pinterest_filtered_df
pinterest_filtered_df.describe()
# Count total out of Unique Tweets
pinterest_total_tweets = len(pinterest_filtered_df['Tweet Text'])
pinterest_total_tweets
# Calculate Facebook Avg Followers - doesn't make sense to sum.
pinterest_avg_followers_ct = pinterest_filtered_df['User Follower Count'].mean()
pinterest_avg_followers_ct
# Total Likes of all tweets
pinterest_total_likes = pinterest_filtered_df['Likes Counts'].sum()
#pinterest_avg_likes = pinterest_filtered_df['Likes Counts'].mean()
pinterest_total_likes
#pinterest_avg_likes
# Retweets Stats:
#pinterest_sum_retweets = pinterest_filtered_df['ReTweet Count'].sum()
pinterest_avg_retweets = pinterest_filtered_df['ReTweet Count'].mean()
#pinterest_sum_retweets
pinterest_avg_retweets
```
### Bible (You Version) Calculations
```
plug = 'bible'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
bible_source_df = pd.concat(li, axis=0, ignore_index=True)
bible_source_df
# Snapshot Statistics
bible_source_df.describe()
bible_source_df.head()
# Sort to set up removal of duplicates
bible_source_df.sort_values(by=['User ID','Created At'], ascending=False)
# Drop Duplicates only for matching columns omitting the index
bible_filtered_df = bible_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
bible_filtered_df
bible_filtered_df.describe()
# Count total out of Unique Tweets
bible_total_tweets = len(bible_filtered_df['Tweet Text'])
bible_total_tweets
# Calculate Avg Followers - doesn't make sense to sum.
bible_avg_followers_ct = bible_filtered_df['User Follower Count'].mean()
bible_avg_followers_ct
# Total Likes of all tweets
bible_total_likes = bible_filtered_df['Likes Counts'].sum()
#bible_avg_likes = bible_filtered_df['Likes Counts'].mean()
bible_total_likes
#bible_avg_likes
# Retweets Stats:
#bible_sum_retweets = bible_filtered_df['ReTweet Count'].sum()
bible_avg_retweets = bible_filtered_df['ReTweet Count'].mean()
#bible_sum_retweets
bible_avg_retweets
```
### Candy Crush Saga Calculations
```
plug = 'candycrushsaga'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
CandyCrushSaga_source_df = pd.concat(li, axis=0, ignore_index=True)
# Snapshot Statistics
CandyCrushSaga_source_df.describe()
# has duplicates
CandyCrushSaga_source_df.sort_values(by=['User ID','Created At'], ascending=False)
CandyCrushSaga_source_df.head()
# Drop Duplicates only for matching columns omitting the index
CandyCrushSaga_filtered_df = CandyCrushSaga_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
# Get New Snap Shot Statistics
CandyCrushSaga_filtered_df.describe()
CandyCrushSaga_filtered_df.head()
# Count total out of Unique Tweets
candycrushsaga_total_tweets = len(CandyCrushSaga_filtered_df['Tweet Text'])
candycrushsaga_total_tweets
# Calculate Avg Followers - doesn't make sense to sum.
candycrushsaga_avg_followers_ct = CandyCrushSaga_filtered_df['User Follower Count'].mean()
candycrushsaga_avg_followers_ct
# Total Likes of all tweets
candycrushsaga_total_likes = CandyCrushSaga_filtered_df['Likes Counts'].sum()
#facebook_avg_likes = facebook_filtered_df['Likes Counts'].mean()
candycrushsaga_total_likes
#facebook_avg_likes
# Retweets Stats:
#facebook_sum_retweets = facebook_filtered_df['ReTweet Count'].sum()
candycrushsaga_avg_retweets = CandyCrushSaga_filtered_df['ReTweet Count'].mean()
#facebook_sum_retweets
candycrushsaga_avg_retweets
```
### Spotify Music Caculations
```
plug = 'spotify'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
spotify_source_df = pd.concat(li, axis=0, ignore_index=True)
# Snapshot Statistics
spotify_source_df.describe()
spotify_source_df.head()
# Sort to set up removal of duplicates
spotify_source_df.sort_values(by=['User ID','Created At'], ascending=False)
# Drop Duplicates only for matching columns omitting the index
spotify_filtered_df = spotify_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
spotify_filtered_df
spotify_filtered_df.describe()
# Count total out of Unique Tweets
spotify_total_tweets = len(spotify_filtered_df['Tweet Text'])
spotify_total_tweets
# Calculate Facebook Avg Followers - doesn't make sense to sum.
spotify_avg_followers_ct = spotify_filtered_df['User Follower Count'].mean()
spotify_avg_followers_ct
# Total Likes of all tweets
spotify_total_likes = spotify_filtered_df['Likes Counts'].sum()
#spotify_avg_likes = spotify_filtered_df['Likes Counts'].mean()
spotify_total_likes
#spotify_avg_likes
# Retweets Stats:
#spotify_sum_retweets = spotify_filtered_df['ReTweet Count'].sum()
spotify_avg_retweets = spotify_filtered_df['ReTweet Count'].mean()
#spotify_sum_retweets
spotify_avg_retweets
```
### Angry Birds Calculations
```
plug = 'angrybirds'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
angrybirds_source_df = pd.concat(li, axis=0, ignore_index=True)
# Snapshot Statistics
angrybirds_source_df.describe()
angrybirds_source_df.head()
# Sort to set up removal of duplicates
angrybirds_source_df.sort_values(by=['User ID','Created At'], ascending=False)
# Drop Duplicates only for matching columns omitting the index
angrybirds_filtered_df = angrybirds_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
angrybirds_filtered_df
angrybirds_filtered_df.describe()
# Count total out of Unique Tweets
angrybirds_total_tweets = len(angrybirds_filtered_df['Tweet Text'])
angrybirds_total_tweets
# Calculate angrybirds Avg Followers - doesn't make sense to sum.
angrybirds_avg_followers_ct = angrybirds_filtered_df['User Follower Count'].mean()
angrybirds_avg_followers_ct
# Total Likes of all tweets
angrybirds_total_likes = angrybirds_filtered_df['Likes Counts'].sum()
#angrybirds_avg_likes = angrybirds_filtered_df['Likes Counts'].mean()
angrybirds_total_likes
#angrybirds_avg_likes
# Retweets Stats:
#angrybirds_sum_retweets = angrybirds_filtered_df['ReTweet Count'].sum()
angrybirds_avg_retweets = angrybirds_filtered_df['ReTweet Count'].mean()
#angrybirds_sum_retweets
angrybirds_avg_retweets
```
### YouTube Calculations
```
plug = 'youtube'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
youtube_source_df = pd.concat(li, axis=0, ignore_index=True)
# Snapshot Statistics
youtube_source_df.describe()
youtube_source_df.head()
# Sort
youtube_source_df.sort_values(by=['User ID','Created At'], ascending=False)
# Drop Duplicates only for matching columns omitting the index
youtube_filtered_df = youtube_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
# Get New Snap Shot Statistics
youtube_filtered_df.describe()
youtube_filtered_df.head()
# Count total out of Unique Tweets
youtube_total_tweets = len(youtube_filtered_df['Tweet Text'])
youtube_total_tweets
# Calculate Facebook Avg Followers - doesn't make sense to sum.
youtube_avg_followers_ct = youtube_filtered_df['User Follower Count'].mean()
youtube_avg_followers_ct
# Total Likes of all tweets
# use sum of likes.
youtube_total_likes = youtube_filtered_df['Likes Counts'].sum()
#youtube_avg_likes = youtube_filtered_df['Likes Counts'].mean()
youtube_total_likes
#youtube_avg_likes
# You Tube Retweets Stats:
#youtube_sum_retweets = facebook_filtered_df['ReTweet Count'].sum()
youtube_avg_retweets = youtube_filtered_df['ReTweet Count'].mean()
#youtube_sum_retweets
youtube_avg_retweets
```
### Subway Surfers
```
plug = 'subwaysurfer'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
SubwaySurfers_source_df = pd.concat(li, axis=0, ignore_index=True)
# Snapshot Statistics
SubwaySurfers_source_df.describe()
SubwaySurfers_source_df.head()
# Sort
SubwaySurfers_source_df.sort_values(by=['User ID','Created At'], ascending=False)
SubwaySurfers_source_df.head()
# Drop Duplicates only for matching columns omitting the index
SubwaySurfers_filtered_df = SubwaySurfers_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
# Get New Snap Shot Statistics
SubwaySurfers_filtered_df.describe()
SubwaySurfers_filtered_df.head()
# Count total out of Unique Tweets
SubwaySurfers_total_tweets = len(SubwaySurfers_filtered_df['Tweet Text'])
SubwaySurfers_total_tweets
# Calculate Avg Followers - doesn't make sense to sum.
SubwaySurfers_avg_followers_ct = SubwaySurfers_filtered_df['User Follower Count'].mean()
SubwaySurfers_avg_followers_ct
# Total Likes of all tweets
SubwaySurfers_total_likes = SubwaySurfers_filtered_df['Likes Counts'].sum()
#SubwaySurfers_avg_likes = SubwaySurfers_filtered_df['Likes Counts'].mean()
SubwaySurfers_total_likes
#SubwaySurfers_avg_likes
# Subway Surfer Retweets Stats:
#SubwaySurfers_sum_retweets = SubwaySurfers_filtered_df['ReTweet Count'].sum()
SubwaySurfers_avg_retweets = SubwaySurfers_filtered_df['ReTweet Count'].mean()
#SubwaySurfers_sum_retweets
SubwaySurfers_avg_retweets
```
### Security Master - Antivirus, VPN
```
# Cheetah Mobile owns Security Master
plug = 'cheetah'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
SecurityMaster_source_df = pd.concat(li, axis=0, ignore_index=True)
# Snapshot Statistics
SecurityMaster_source_df.describe()
SecurityMaster_source_df.head()
# has duplicates
SecurityMaster_source_df.sort_values(by=['User ID','Created At'], ascending=False)
SecurityMaster_source_df.head()
# Drop Duplicates only for matching columns omitting the index
SecurityMaster_filtered_df = SecurityMaster_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
# Get New Snap Shot Statistics
SecurityMaster_filtered_df.describe()
SecurityMaster_filtered_df.head()
# Count total out of Unique Tweets
SecurityMaster_total_tweets = len(SecurityMaster_filtered_df['Tweet Text'])
SecurityMaster_total_tweets
# Calculate Avg Followers - doesn't make sense to sum.
SecurityMaster_avg_followers_ct = SecurityMaster_filtered_df['User Follower Count'].mean()
SecurityMaster_avg_followers_ct
# Total Likes of all tweets
SecurityMaster_total_likes = SecurityMaster_filtered_df['Likes Counts'].sum()
#SecurityMaster_avg_likes = SecurityMaster_filtered_df['Likes Counts'].mean()
SecurityMaster_total_likes
#SecurityMaster_avg_likes
# Security Master Retweets Stats:
#SecurityMaster_sum_retweets = SecurityMaster_filtered_df['ReTweet Count'].sum()
SecurityMaster_avg_retweets = SecurityMaster_filtered_df['ReTweet Count'].mean()
#SecurityMaster_sum_retweets
SecurityMaster_avg_retweets
```
### Clash Royale
```
plug = 'clashroyale'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
ClashRoyale_source_df = pd.concat(li, axis=0, ignore_index=True)
# Snapshot Statistics
ClashRoyale_source_df.describe()
ClashRoyale_source_df.head()
# has duplicates
ClashRoyale_source_df.sort_values(by=['User ID','Created At'], ascending=False)
# Drop Duplicates only for matching columns omitting the index
ClashRoyale_filtered_df = ClashRoyale_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
# Get New Snap Shot Statistics
ClashRoyale_filtered_df.describe()
ClashRoyale_filtered_df.head()
# Count total out of Unique Tweets
ClashRoyale_total_tweets = len(ClashRoyale_filtered_df['Tweet Text'])
ClashRoyale_total_tweets
# Calculate Avg Followers - doesn't make sense to sum.
ClashRoyale_avg_followers_ct = ClashRoyale_filtered_df['User Follower Count'].mean()
ClashRoyale_avg_followers_ct
# Total Likes of all tweets
ClashRoyale_total_likes = ClashRoyale_filtered_df['Likes Counts'].sum()
#ClashRoyale_avg_likes = ClashRoyale_filtered_df['Likes Counts'].mean()
ClashRoyale_total_likes
#ClashRoyale_avg_likes
# ClashRoyale Retweets Stats:
#ClashRoyale_sum_retweets = ClashRoyale_filtered_df['ReTweet Count'].sum()
ClashRoyale_avg_retweets = ClashRoyale_filtered_df['ReTweet Count'].mean()
#facebook_sum_retweets
ClashRoyale_avg_retweets
```
### Clean Master - Space Cleaner
```
plug = 'cleanmaster'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
CleanMaster_source_df = pd.concat(li, axis=0, ignore_index=True)
# Snapshot Statistics
CleanMaster_source_df.describe()
CleanMaster_source_df.head()
# has duplicates
CleanMaster_source_df.sort_values(by=['User ID','Created At'], ascending=False)
CleanMaster_source_df.head()
# Drop Duplicates only for matching columns omitting the index
CleanMaster_filtered_df = CleanMaster_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
# Get New Snap Shot Statistics
CleanMaster_filtered_df.describe()
CleanMaster_filtered_df.head()
# Count total out of Unique Tweets
CleanMaster_total_tweets = len(CleanMaster_filtered_df['Tweet Text'])
CleanMaster_total_tweets
# Calculate Avg Followers - doesn't make sense to sum.
CleanMaster_avg_followers_ct = CleanMaster_filtered_df['User Follower Count'].mean()
CleanMaster_avg_followers_ct
# Total Likes of all tweets
CleanMaster_total_likes = CleanMaster_filtered_df['Likes Counts'].sum()
#facebook_avg_likes = facebook_filtered_df['Likes Counts'].mean()
CleanMaster_total_likes
#facebook_avg_likes
# Clean MasterRetweets Stats:
#CleanMaster_sum_retweets = CleanMaster_filtered_df['ReTweet Count'].sum()
CleanMaster_avg_retweets = CleanMaster_filtered_df['ReTweet Count'].mean()
#facebook_sum_retweets
CleanMaster_avg_retweets
```
### What's App
```
plug = 'whatsapp'
path = f'./resources/{plug}'
all_files = glob.glob(path + "/*.csv")
li = []
for filename in all_files:
df = pd.read_csv(filename, index_col=None, header=0)
li.append(df)
whatsapp_source_df = pd.concat(li, axis=0, ignore_index=True)
# Snapshot Statistics
whatsapp_source_df.describe()
whatsapp_source_df.head()
# has duplicates
whatsapp_source_df.sort_values(by=['User ID','Created At'], ascending=False)
whatsapp_source_df.head()
# Drop Duplicates only for matching columns omitting the index
whatsapp_filtered_df = whatsapp_source_df.drop_duplicates(['Created At', 'Screen Name', 'User ID', 'User Follower Count', 'Likes Counts', 'ReTweet Count', 'Tweet Text']).sort_values(by=['User ID','Created At'], ascending=False)
# Get New Snap Shot Statistics
whatsapp_filtered_df.describe()
whatsapp_filtered_df.head()
# Count total out of Unique Tweets
whatsapp_total_tweets = len(whatsapp_filtered_df['Tweet Text'])
whatsapp_total_tweets
# Calculate Facebook Avg Followers - doesn't make sense to sum.
whatsapp_avg_followers_ct = whatsapp_filtered_df['User Follower Count'].mean()
whatsapp_avg_followers_ct
# Total Likes of all tweets.
whatsapp_total_likes = whatsapp_filtered_df['Likes Counts'].sum()
#whatsapp_avg_likes = whatsapp_filtered_df['Likes Counts'].mean()
whatsapp_total_likes
#whatsapp_avg_likes
# Whatsapp Retweets Stats:
#whatsapp_sum_retweets = whatsapp_filtered_df['ReTweet Count'].sum()
whatsapp_avg_retweets = whatsapp_filtered_df['ReTweet Count'].mean()
#whatsapp_sum_retweets
whatsapp_avg_retweets
```
# Charts and Plots
#### Scatter plot - Twitter Average Followers to Tweets
```
# Scatter Plot 1 - Tweets vs Average Followers vs Total Likes of the Top 10 Apps for both Google and Apple App Stores
fig, ax = plt.subplots(figsize=(11,11))
# Apps both on Google Play Store and Apple - 4 apps
facebook_plot = ax.scatter(facebook_total_tweets, facebook_avg_followers_ct, s=facebook_total_likes*15, color='sandybrown', label='Facebook', edgecolors='black', alpha=0.75)
instagram_plot= ax.scatter(instagram_total_tweets, instagram_avg_followers_ct, s=instagram_total_likes*15, color='saddlebrown', label='Instagram', edgecolors='black', alpha=0.5)
coc_plot= ax.scatter(coc_total_tweets, coc_avg_followers_ct, s=coc_total_likes*10, color='springgreen', label='Clash Of Clans', edgecolors='black', alpha=0.75)
candycrushsaga_plot= ax.scatter(candycrushsaga_total_tweets, candycrushsaga_avg_followers_ct, s=candycrushsaga_total_likes*5, color='limegreen', label='Candy Crush Saga', edgecolors='black')#, alpha=0.75)
# Google Play Store - 6 apps:
CleanMaster_plot= ax.scatter(CleanMaster_total_tweets, CleanMaster_avg_followers_ct, s=CleanMaster_total_likes*5, color='m', label='Clean Master Space Cleaner', edgecolors='black', alpha=0.75)
SubwaySurfers_plot= ax.scatter(SubwaySurfers_total_tweets, SubwaySurfers_avg_followers_ct, s=SubwaySurfers_total_likes*5, color='lime', label='Subway Surfers', edgecolors='black', alpha=0.75)
youtube_plot= ax.scatter(youtube_total_tweets, youtube_avg_followers_ct, s=youtube_total_likes*5, color='red', label='You Tube', edgecolors='black', alpha=0.75)
SecurityMaster_plot= ax.scatter(SecurityMaster_total_tweets, SecurityMaster_avg_followers_ct, s=SecurityMaster_total_likes*5, color='blueviolet', label='Security Master, Antivirus VPN', edgecolors='black', alpha=0.75)
ClashRoyale_plot= ax.scatter(ClashRoyale_total_tweets, ClashRoyale_avg_followers_ct, s=ClashRoyale_total_likes*5, color='darkolivegreen', label='Clash Royale', edgecolors='black', alpha=0.75)
whatsapp_plot= ax.scatter(whatsapp_total_tweets, whatsapp_avg_followers_ct, s=whatsapp_total_likes*5, color='tan', label='Whats App', edgecolors='black', alpha=0.75)
# Apple Apps Store - 6 apps
templerun_plot= ax.scatter(templerun_total_tweets, templerun_avg_followers_ct, s=templerun_total_likes*5, color='lawngreen', label='Temple Run', edgecolors='black', alpha=0.75)
pandora_plot= ax.scatter(pandora_total_tweets, pandora_avg_followers_ct, s=pandora_total_likes*5, color='coral', label='Pandora', edgecolors='black', alpha=0.75)
pinterest_plot= ax.scatter(pinterest_total_tweets, pinterest_avg_followers_ct, s=pinterest_total_likes*5, color='firebrick', label='Pinterest', edgecolors='black', alpha=0.75)
bible_plot= ax.scatter(bible_total_tweets, bible_avg_followers_ct, s=bible_total_likes*5, color='tomato', label='Bible', edgecolors='black', alpha=0.75)
spotify_plot= ax.scatter(spotify_total_tweets, spotify_avg_followers_ct, s=spotify_total_likes*5, color='orangered', label='Spotify', edgecolors='black', alpha=0.75)
angrybirds_plot= ax.scatter(angrybirds_total_tweets, angrybirds_avg_followers_ct, s=angrybirds_total_likes*5, color='forestgreen', label='Angry Birds', edgecolors='black', alpha=0.75)
# title and labels
plt.title("Tweets vs Average Followers (Mar 27 - Apr 3, 2019) \n")
plt.xlabel("Total Tweets \n Note: Circle sizes correlate with Total Likes" )
plt.ylabel("Average Number of Followers per Twitter User \n")
# set and format the legend
lgnd = plt.legend(title='Legend', loc="best")
lgnd.legendHandles[0]._sizes = [30]
lgnd.legendHandles[1]._sizes = [30]
lgnd.legendHandles[2]._sizes = [30]
lgnd.legendHandles[3]._sizes = [30]
lgnd.legendHandles[4]._sizes = [30]
lgnd.legendHandles[5]._sizes = [30]
lgnd.legendHandles[6]._sizes = [30]
lgnd.legendHandles[7]._sizes = [30]
lgnd.legendHandles[8]._sizes = [30]
lgnd.legendHandles[9]._sizes = [30]
lgnd.legendHandles[10]._sizes = [30]
lgnd.legendHandles[11]._sizes = [30]
lgnd.legendHandles[12]._sizes = [30]
lgnd.legendHandles[13]._sizes = [30]
lgnd.legendHandles[14]._sizes = [30]
lgnd.legendHandles[15]._sizes = [30]
#grid lines and show
plt.grid()
plt.show()
#plt.savefig("./TWEETS_vs__AVG_followers_Scatter.png")
# Test Cell: Tried to automate plot, but was unable to beause for the size (s), JG wanted to scale the
# the size by multiplying by a unique scale depending on the number of likes to emphasize data points
# Conclusion: was to stick with brute force method
SubwaySurfers_total_tweets,
x = [facebook_total_tweets, instagram_total_tweets, coc_total_tweets,
candycrushsaga_total_tweets, CleanMaster_total_tweets,
youtube_total_tweets, SecurityMaster_total_tweets,
ClashRoyale_total_tweets, whatsapp_total_tweets, templerun_total_tweets,
pandora_total_tweets, pinterest_total_tweets, bible_total_tweets, spotify_total_tweets,
angrybirds_total_tweets]
SubwaySurfers_avg_followers_ct,
y = [facebook_avg_followers_ct, instagram_avg_followers_ct, coc_avg_followers_ct,
candycrushsaga_avg_followers_ct, CleanMaster_avg_followers_ct,
youtube_avg_followers_ct, SecurityMaster_avg_followers_ct,
ClashRoyale_avg_followers_ct, whatsapp_avg_followers_ct, templerun_avg_followers_ct,
pandora_avg_followers_ct, pinterest_avg_followers_ct, bible_avg_followers_ct, spotify_avg_followers_ct,
angrybirds_avg_followers_ct]
"""
# Below this method doesn't work. Will go with brute force method.
s = [(facebook_total_likes*15), (instagram_total_likes*15), (coc_total_likes*10), (candycrushsaga_total_likes*5),
(CleanMaster_total_likes*5), (SubwaySurfers_total_likes*5), (youtube_total_likes*5), (SecurityMaster_total_likes*5)
(ClashRoyale_total_likes*5), (whatsapp_total_likes*5), (templerun_total_likes*5), (pandora_total_likes*5),
(pinterest_total_likes*5), (bible_total_likes*5), (spotify_total_likes*5), (angrybirds_total_likes*5)]
"""
s = [facebook_total_likes, instagram_total_likes, coc_total_likes, candycrushsaga_total_likes,
CleanMaster_total_likes, SubwaySurfers_total_likes, youtube_total_likes, SecurityMaster_total_likes,
ClashRoyale_total_likes, whatsapp_total_likes, templerun_total_likes, pandora_total_likes,
pinterest_total_likes, bible_total_likes, spotify_total_likes, angrybirds_total_likes]
colors = np.random.rand(16)
label = []
edgecolors = []
alpha = []
fig, ax = plt.subplots(figsize=(11,11))
ax.scatter(x, y, s)
plt.grid()
plt.show()
"""# Apps both on Google Play Store and Apple - 4 apps
facebook_plot = ax.scatter(, , , color='sandybrown', label='Facebook', edgecolors='black', alpha=0.75)
instagram_plot= ax.scatter(, , , color='saddlebrown', label='Instagram', edgecolors='black', alpha=0.5)
coc_plot= ax.scatter(,, , color='springgreen', label='Clash Of Clans', edgecolors='black', alpha=0.75)
candycrushsaga_plot= ax.scatter(,, , color='limegreen', label='Candy Crush Saga', edgecolors='black')#, alpha=0.75)
# Google Play Store - 6 apps:
CleanMaster_plot= ax.scatter(,, , color='m', label='Clean Master Space Cleaner', edgecolors='black', alpha=0.75)
SubwaySurfers_plot= ax.scatter(,, , color='lime', label='Subway Surfers', edgecolors='black', alpha=0.75)
youtube_plot= ax.scatter(,, , color='red', label='You Tube', edgecolors='black', alpha=0.75)
SecurityMaster_plot= ax.scatter(,, , color='blueviolet', label='Security Master, Antivirus VPN', edgecolors='black', alpha=0.75)
ClashRoyale_plot= ax.scatter(,, , color='darkolivegreen', label='Clash Royale', edgecolors='black', alpha=0.75)
whatsapp_plot= ax.scatter(,, , color='tan', label='Whats App', edgecolors='black', alpha=0.75)
# Apple Apps Store - 6 apps
templerun_plot= ax.scatter(, , , color='lawngreen', label='Temple Run', edgecolors='black', alpha=0.75)
pandora_plot= ax.scatter(, ,, color='coral', label='Pandora', edgecolors='black', alpha=0.75)
pinterest_plot= ax.scatter(, ,, color='firebrick', label='Pinterest', edgecolors='black', alpha=0.75)
bible_plot= ax.scatter(, , color='tomato', label='Bible', edgecolors='black', alpha=0.75)
spotify_plot= ax.scatter(, , color='orangered', label='Spotify', edgecolors='black', alpha=0.75)
angrybirds_plot= ax.scatter(,,, color='forestgreen', label='Angry Birds', edgecolors='black', alpha=0.75)
# title and labels
plt.title("Tweets vs Average Followers (Mar 27 - Apr 3, 2019) \n")
plt.xlabel("Total Tweets \n Note: Circle sizes correlate with Total Likes" )
plt.ylabel("Average Number of Followers per Twitter User \n")
"""
# Scatter Plot 2 - Tweets vs ReTweets vs Likes
fig, ax = plt.subplots(figsize=(11,11))
# Apps both on Google Play Store and Apple - 4 apps
facebook_plot = ax.scatter(facebook_total_tweets, facebook_avg_retweets, s=facebook_total_likes*5, color='sandybrown', label='Facebook', edgecolors='black', alpha=0.75)
instagram_plot= ax.scatter(instagram_total_tweets, instagram_avg_retweets, s=instagram_total_likes*5, color='saddlebrown', label='Instagram', edgecolors='black', alpha=0.75)
coc_plot= ax.scatter(coc_total_tweets, coc_avg_retweets, s=coc_total_likes*5, color='springgreen', label='Clash Of Clans', edgecolors='black', alpha=0.75)
candycrushsaga_plot= ax.scatter(candycrushsaga_total_tweets, candycrushsaga_avg_retweets, s=candycrushsaga_total_likes*5, color='limegreen', label='Candy Crush Saga', edgecolors='black')#, alpha=0.75)
# Google Play Store - 6 apps:
CleanMaster_plot= ax.scatter(CleanMaster_total_tweets, CleanMaster_avg_retweets, s=CleanMaster_total_likes*5, color='m', label='Clean Master Space Cleaner', edgecolors='black', alpha=0.75)
SubwaySurfers_plot= ax.scatter(SubwaySurfers_total_tweets, SubwaySurfers_avg_retweets, s=SubwaySurfers_total_likes*5, color='lime', label='Subway Surfers', edgecolors='black', alpha=0.75)
youtube_plot= ax.scatter(youtube_total_tweets, youtube_avg_retweets, s=youtube_total_likes*5, color='red', label='You Tube', edgecolors='black', alpha=0.75)
SecurityMaster_plot= ax.scatter(SecurityMaster_total_tweets, SecurityMaster_avg_retweets, s=SecurityMaster_total_likes*5, color='blueviolet', label='Security Master, Antivirus VPN', edgecolors='black', alpha=0.75)
ClashRoyale_plot= ax.scatter(ClashRoyale_total_tweets, ClashRoyale_avg_retweets, s=ClashRoyale_total_likes*5, color='darkolivegreen', label='Clash Royale', edgecolors='black', alpha=0.75)
whatsapp_plot= ax.scatter(whatsapp_total_tweets, whatsapp_avg_retweets, s=whatsapp_total_likes*5, color='tan', label='Whats App', edgecolors='black', alpha=0.75)
# Apple Apps Store - 6 apps
templerun_plot= ax.scatter(templerun_total_tweets, templerun_avg_retweets, s=templerun_total_likes*5, color='lawngreen', label='Temple Run', edgecolors='black', alpha=0.75)
pandora_plot= ax.scatter(pandora_total_tweets, pandora_avg_retweets, s=pandora_total_likes*5, color='coral', label='Pandora', edgecolors='black', alpha=0.75)
pinterest_plot= ax.scatter(pinterest_total_tweets, pinterest_avg_retweets, s=pinterest_total_likes*5, color='firebrick', label='Pinterest', edgecolors='black', alpha=0.75)
bible_plot= ax.scatter(bible_total_tweets, bible_avg_retweets, s=bible_total_likes*5, color='tomato', label='Bible', edgecolors='black', alpha=0.75)
spotify_plot= ax.scatter(spotify_total_tweets, spotify_avg_retweets, s=spotify_total_likes*5, color='orangered', label='Spotify', edgecolors='black', alpha=0.75)
angrybirds_plot= ax.scatter(angrybirds_total_tweets, angrybirds_avg_retweets, s=angrybirds_total_likes*5, color='forestgreen', label='Angry Birds', edgecolors='black', alpha=0.75)
# title and labels
plt.title("Tweets vs ReTweets (Mar 27 - Apr 3, 2019) \n")
plt.xlabel("Total Tweets \n Note: Circle sizes correlate with Total Likes \n" )
plt.ylabel("Average Number of ReTweets per Twitter User \n")
# set and format the legend
lgnd = plt.legend(title='Legend', loc="best")
lgnd.legendHandles[0]._sizes = [30]
lgnd.legendHandles[1]._sizes = [30]
lgnd.legendHandles[2]._sizes = [30]
lgnd.legendHandles[3]._sizes = [30]
lgnd.legendHandles[4]._sizes = [30]
lgnd.legendHandles[5]._sizes = [30]
lgnd.legendHandles[6]._sizes = [30]
lgnd.legendHandles[7]._sizes = [30]
lgnd.legendHandles[8]._sizes = [30]
lgnd.legendHandles[9]._sizes = [30]
lgnd.legendHandles[10]._sizes = [30]
lgnd.legendHandles[11]._sizes = [30]
lgnd.legendHandles[12]._sizes = [30]
lgnd.legendHandles[13]._sizes = [30]
lgnd.legendHandles[14]._sizes = [30]
lgnd.legendHandles[15]._sizes = [30]
#grid lines and show
plt.grid()
plt.show()
#plt.savefig('./TWEETS_VS_RETWEETS_vs_LIKES_Scatter.png')
# Scatter Plot 3 - Will not use this plot
fig, ax = plt.subplots(figsize=(8,8))
# Apps both on Google Play Store and Apple - 4 apps
facebook_plot = ax.scatter(facebook_avg_retweets, facebook_total_tweets, s=facebook_total_likes*5, color='blue', label='Facebook', edgecolors='red', alpha=0.75)
instagram_plot= ax.scatter(instagram_avg_retweets, instagram_total_tweets, s=instagram_total_likes*5, color='fuchsia', label='Instagram', edgecolors='red', alpha=0.75)
coc_plot= ax.scatter(coc_avg_retweets, coc_total_tweets, s=coc_total_likes*5, color='springgreen', label='Clash Of Clans', edgecolors='red', alpha=0.75)
candycrushsaga_plot= ax.scatter(candycrushsaga_avg_retweets, candycrushsaga_total_tweets, s=candycrushsaga_total_likes*5, color='black', label='Candy Crush Saga', edgecolors='red')#, alpha=0.75)
# Google Play Store - 6 apps:
CleanMaster_plot= ax.scatter(CleanMaster_avg_retweets, CleanMaster_total_tweets, s=CleanMaster_total_likes*5, color='olive', label='Clean Master Space Cleaner', edgecolors='lime', alpha=0.75)
SubwaySurfers_plot= ax.scatter(SubwaySurfers_avg_retweets, SubwaySurfers_total_tweets, s=SubwaySurfers_total_likes*5, color='plum', label='Subway Surfers', edgecolors='lime', alpha=0.75)
youtube_plot= ax.scatter(youtube_avg_retweets, youtube_total_tweets, s=youtube_total_likes*5, color='grey', label='You Tube', edgecolors='lime', alpha=0.75)
SecurityMaster_plot= ax.scatter(SecurityMaster_avg_retweets, SecurityMaster_total_tweets, s=SecurityMaster_total_likes*5, color='coral', label='Security Master, Antivirus VPN', edgecolors='lime', alpha=0.75)
ClashRoyale_plot= ax.scatter(ClashRoyale_avg_retweets, ClashRoyale_total_tweets, s=ClashRoyale_total_likes*5, color='orange', label='Clash Royale', edgecolors='lime', alpha=0.75)
whatsapp_plot= ax.scatter(whatsapp_avg_retweets, whatsapp_total_tweets, s=whatsapp_total_likes*5, color='green', label='Whats App', edgecolors='lime', alpha=0.75)
# Apple Apps Store - 6 apps
templerun_plot= ax.scatter(templerun_avg_retweets, templerun_total_tweets, s=templerun_total_likes*5, color='lawngreen', label='Temple Run', edgecolors='black', alpha=0.75)
pandora_plot= ax.scatter(pandora_avg_retweets, pandora_total_tweets, s=pandora_total_likes*5, color='cornflowerblue', label='Pandora', edgecolors='black', alpha=0.75)
pinterest_plot= ax.scatter(pinterest_avg_retweets, pinterest_total_tweets, s=pinterest_total_likes*5, color='firebrick', label='Pinterest', edgecolors='black', alpha=0.75)
bible_plot= ax.scatter(bible_avg_retweets, bible_total_tweets, s=bible_total_likes*5, color='brown', label='Bible', edgecolors='black', alpha=0.75)
spotify_plot= ax.scatter(spotify_avg_retweets, spotify_total_tweets, s=spotify_total_likes*5, color='darkgreen', label='Spotify', edgecolors='black', alpha=0.75)
angrybirds_plot= ax.scatter(angrybirds_avg_retweets, angrybirds_total_tweets, s=angrybirds_total_likes*5, color='salmon', label='Angry Birds', edgecolors='black', alpha=0.75)
# title and labels
plt.title("Tweets vs ReTweets (Mar 27 - Apr 3, 2019) \n")
plt.xlabel("Total Tweets \n Note: Circle sizes correlate with Total Likes \n" )
plt.ylabel("Average Number of ReTweets per Twitter User \n")
# set and format the legend
lgnd = plt.legend(title='Legend', loc="best")
lgnd.legendHandles[0]._sizes = [30]
lgnd.legendHandles[1]._sizes = [30]
lgnd.legendHandles[2]._sizes = [30]
lgnd.legendHandles[3]._sizes = [30]
lgnd.legendHandles[4]._sizes = [30]
lgnd.legendHandles[5]._sizes = [30]
lgnd.legendHandles[6]._sizes = [30]
lgnd.legendHandles[7]._sizes = [30]
lgnd.legendHandles[8]._sizes = [30]
lgnd.legendHandles[9]._sizes = [30]
lgnd.legendHandles[10]._sizes = [30]
lgnd.legendHandles[11]._sizes = [30]
lgnd.legendHandles[12]._sizes = [30]
lgnd.legendHandles[13]._sizes = [30]
lgnd.legendHandles[14]._sizes = [30]
lgnd.legendHandles[15]._sizes = [30]
#grid lines and show
plt.grid()
plt.show()
#plt.savefig('./tweets_vs__avgfollowers_Scatter.png')
# Hardcoding numbers from analysis done in Apple and Google Play Store Final Code Notebooks
# Avergage Apple, Google Ratings
facebook_avg_rating = (3.5 + 4.1)/2
instagram_avg_rating = (4.5 + 4.5)/2
coc_avg_rating = (4.5 + 4.6)/2
candycrushsaga_avg_rating = (4.5 + 4.4)/2
# Avergage Apple, Google Reviews
facebook_reviews = (2974676 + 78158306)/2
instagram_reviews = (2161558 + 66577446)/2
coc_reviews = (2130805 + 44893888)/2
candycrushsaga_reviews = (961794 + 22430188)/2
# Apple App Ratings
templerun_rating = 4.5
pandora_rating = 4.5
pinterest_rating = 4.5
bible_rating = 4.5
spotify_rating = 4.5
angrybirds_rating = 4.5
# Apple App Reviews
templerun_reviews = 1724546
pandora_reviews = 1126879
pinterest_reviews = 1061624
bible_reviews = 985920
spotify_reviews = 878563
angrybirds_reviews = 824451
# Google App Ratings
whatsapp_rating = 4.4
clean_master_rating = 4.7
subway_surfers_rating = 4.5
you_tube_rating = 4.3
security_master_rating = 4.7
clash_royale_rating = 4.6
# Google App Reviews
whatsapp_reviews = 69119316
clean_master_reviews = 42916526
subway_surfers_reviews = 27725352
you_tube_reviews = 25655305
security_master_reviews = 24900999
clash_royale_reviews = 23136735
# Scatter Plot 5 - Tweets vs Ratings vs Likes - USE THIS ONE
fig, ax = plt.subplots(figsize=(11,11))
# Apps both on Google Play Store and Apple - 4 apps
facebook_plot = ax.scatter(facebook_total_tweets, facebook_avg_rating, s=facebook_total_likes*5, color='sandybrown', label='Facebook', edgecolors='black', alpha=0.75)
instagram_plot= ax.scatter(instagram_total_tweets, instagram_avg_rating, s=instagram_total_likes*5, color='saddlebrown', label='Instagram', edgecolors='black', alpha=0.75)
coc_plot= ax.scatter(coc_total_tweets, coc_avg_rating, s=coc_total_likes*5, color='springgreen', label='Clash Of Clans', edgecolors='black', alpha=0.75)
candycrushsaga_plot= ax.scatter(candycrushsaga_total_tweets, candycrushsaga_avg_rating, s=candycrushsaga_total_likes*5, color='limegreen', label='Candy Crush Saga', edgecolors='black')#, alpha=0.75)
# Google Play Store - 6 apps:
CleanMaster_plot= ax.scatter(CleanMaster_total_tweets, clean_master_rating, s=CleanMaster_total_likes*5, color='m', label='Clean Master Space Cleaner', edgecolors='black', alpha=0.75)
SubwaySurfers_plot= ax.scatter(SubwaySurfers_total_tweets, subway_surfers_rating, s=SubwaySurfers_total_likes*5, color='lime', label='Subway Surfers', edgecolors='black', alpha=0.75)
youtube_plot= ax.scatter(youtube_total_tweets, you_tube_rating, s=youtube_total_likes*5, color='red', label='You Tube', edgecolors='black', alpha=0.75)
SecurityMaster_plot= ax.scatter(SecurityMaster_total_tweets, security_master_rating, s=SecurityMaster_total_likes*5, color='blueviolet', label='Security Master, Antivirus VPN', edgecolors='black', alpha=0.75)
ClashRoyale_plot= ax.scatter(ClashRoyale_total_tweets, clash_royale_rating, s=ClashRoyale_total_likes*5, color='darkolivegreen', label='Clash Royale', edgecolors='black', alpha=0.75)
whatsapp_plot= ax.scatter(whatsapp_total_tweets, whatsapp_rating, s=whatsapp_total_likes*5, color='tan', label='Whats App', edgecolors='black', alpha=0.75)
# Apple Apps Store - 6 apps
templerun_plot= ax.scatter(templerun_total_tweets,templerun_rating, s=templerun_total_likes*5, color='lawngreen', label='Temple Run', edgecolors='black', alpha=0.75)
pandora_plot= ax.scatter(pandora_total_tweets, pandora_rating, s=pandora_total_likes*5, color='coral', label='Pandora', edgecolors='black', alpha=0.75)
pinterest_plot= ax.scatter(pinterest_total_tweets, pinterest_rating, s=pinterest_total_likes*5, color='firebrick', label='Pinterest', edgecolors='black', alpha=0.75)
bible_plot= ax.scatter(bible_total_tweets, bible_rating, s=bible_total_likes*5, color='tomato', label='Bible', edgecolors='black', alpha=0.75)
spotify_plot= ax.scatter(spotify_total_tweets, spotify_rating, s=spotify_total_likes*5, color='orangered', label='Spotify', edgecolors='black', alpha=0.75)
angrybirds_plot= ax.scatter(angrybirds_total_tweets, angrybirds_rating, s=angrybirds_total_likes*5, color='forestgreen', label='Angry Birds', edgecolors='black', alpha=0.75)
# title and labels
plt.title("Tweets vs Ratings (Mar 27 - Apr 3, 2019) \n")
plt.xlabel("Total Tweets \n Note: Circle sizes correlate with Total Likes \n" )
plt.ylabel("App Store User Ratings (Out of 5) \n")
# set and format the legend
lgnd = plt.legend(title='Legend', loc="best")
lgnd.legendHandles[0]._sizes = [30]
lgnd.legendHandles[1]._sizes = [30]
lgnd.legendHandles[2]._sizes = [30]
lgnd.legendHandles[3]._sizes = [30]
lgnd.legendHandles[4]._sizes = [30]
lgnd.legendHandles[5]._sizes = [30]
lgnd.legendHandles[6]._sizes = [30]
lgnd.legendHandles[7]._sizes = [30]
lgnd.legendHandles[8]._sizes = [30]
lgnd.legendHandles[9]._sizes = [30]
lgnd.legendHandles[10]._sizes = [30]
lgnd.legendHandles[11]._sizes = [30]
lgnd.legendHandles[12]._sizes = [30]
lgnd.legendHandles[13]._sizes = [30]
lgnd.legendHandles[14]._sizes = [30]
lgnd.legendHandles[15]._sizes = [30]
#grid lines and show
plt.grid()
plt.show()
#plt.savefig('./TWEETS_VS_RATINGSVS LIKES_Scatter.png')
# Scatter Plot 5 - Tweets vs Reviews vs Ratings (size) - DO NOT USE
fig, ax = plt.subplots(figsize=(11,11))
# Apps both on Google Play Store and Apple - 4 apps
facebook_plot = ax.scatter(facebook_total_tweets, facebook_reviews, s=facebook_avg_rating*105, color='sandybrown', label='Facebook', edgecolors='black', alpha=0.75)
instagram_plot= ax.scatter(instagram_total_tweets, instagram_reviews, s=instagram_avg_rating*105, color='saddlebrown', label='Instagram', edgecolors='black', alpha=0.75)
coc_plot= ax.scatter(coc_total_tweets, coc_reviews, s=coc_avg_rating*105, color='springgreen', label='Clash Of Clans', edgecolors='black', alpha=0.75)
candycrushsaga_plot= ax.scatter(candycrushsaga_total_tweets, candycrushsaga_reviews, s=candycrushsaga_avg_rating*105, color='limegreen', label='Candy Crush Saga', edgecolors='black', alpha=0.75)
# Google Play Store - 6 apps:
CleanMaster_plot= ax.scatter(CleanMaster_total_tweets, clean_master_reviews, s=clean_master_rating*105, color='m', label='Clean Master Space Cleaner', edgecolors='black', alpha=0.75)
SubwaySurfers_plot= ax.scatter(SubwaySurfers_total_tweets, subway_surfers_reviews, s=subway_surfers_rating*105, color='lime', label='Subway Surfers', edgecolors='black', alpha=0.75)
youtube_plot= ax.scatter(youtube_total_tweets, you_tube_reviews, s=you_tube_rating*105, color='red', label='You Tube', edgecolors='black', alpha=0.75)
SecurityMaster_plot= ax.scatter(SecurityMaster_total_tweets, security_master_reviews, s=security_master_rating*105, color='blueviolet', label='Security Master, Antivirus VPN', edgecolors='black', alpha=0.75)
ClashRoyale_plot= ax.scatter(ClashRoyale_total_tweets, clash_royale_reviews, s=clash_royale_rating*105, color='darkolivegreen', label='Clash Royale', edgecolors='black', alpha=0.75)
whatsapp_plot= ax.scatter(whatsapp_total_tweets, whatsapp_reviews, s=whatsapp_rating*105, color='tan', label='Whats App', edgecolors='lime', alpha=0.75)
# Apple Apps Store - 6 apps
templerun_plot= ax.scatter(templerun_total_tweets,templerun_reviews, s=templerun_rating*105, color='lawngreen', label='Temple Run', edgecolors='black', alpha=0.75)
pandora_plot= ax.scatter(pandora_total_tweets, pandora_reviews, s=pandora_rating*105, color='coral', label='Pandora', edgecolors='black', alpha=0.75)
pinterest_plot= ax.scatter(pinterest_total_tweets, pinterest_reviews, s=pinterest_rating*105, color='firebrick', label='Pinterest', edgecolors='black', alpha=0.75)
bible_plot= ax.scatter(bible_total_tweets, bible_reviews, s=bible_rating*105, color='tomato', label='Bible', edgecolors='black', alpha=0.75)
spotify_plot= ax.scatter(spotify_total_tweets, spotify_reviews, s=spotify_rating*105, color='orangered', label='Spotify', edgecolors='black', alpha=0.75)
angrybirds_plot= ax.scatter(angrybirds_total_tweets, angrybirds_reviews, s=angrybirds_rating*105, color='forestgreen', label='Angry Birds', edgecolors='black', alpha=0.75)
# title and labels
plt.title("Tweets vs Reviews (Mar 27 - Apr 3, 2019) \n")
plt.xlabel("Total Tweets \n Note: Circle sizes correlate with App Ratings \n" )
plt.ylabel("App Store Reviews in Millions \n")
# set and format the legend
lgnd = plt.legend(title='Legend', loc="best")
lgnd.legendHandles[0]._sizes = [30]
lgnd.legendHandles[1]._sizes = [30]
lgnd.legendHandles[2]._sizes = [30]
lgnd.legendHandles[3]._sizes = [30]
lgnd.legendHandles[4]._sizes = [30]
lgnd.legendHandles[5]._sizes = [30]
lgnd.legendHandles[6]._sizes = [30]
lgnd.legendHandles[7]._sizes = [30]
lgnd.legendHandles[8]._sizes = [30]
lgnd.legendHandles[9]._sizes = [30]
lgnd.legendHandles[10]._sizes = [30]
lgnd.legendHandles[11]._sizes = [30]
lgnd.legendHandles[12]._sizes = [30]
lgnd.legendHandles[13]._sizes = [30]
lgnd.legendHandles[14]._sizes = [30]
lgnd.legendHandles[15]._sizes = [30]
#grid lines and show
plt.grid()
plt.show()
#plt.savefig('./tweets_vs__avgfollowers_Scatter.png')
# Scatter Plot 6 - Tweets vs Reviews vs Likes (size) -USE THIS ONE
fig, ax = plt.subplots(figsize=(11,11))
# Apps both on Google Play Store and Apple - 4 apps
facebook_plot = ax.scatter(facebook_total_tweets, facebook_reviews, s=facebook_total_likes*5, color='sandybrown', label='Facebook', edgecolors='black', alpha=0.75)
instagram_plot= ax.scatter(instagram_total_tweets, instagram_reviews, s=instagram_total_likes*5, color='saddlebrown', label='Instagram', edgecolors='black', alpha=0.75)
coc_plot= ax.scatter(coc_total_tweets, coc_reviews, s=coc_total_likes*5, color='springgreen', label='Clash Of Clans', edgecolors='black', alpha=0.75)
candycrushsaga_plot= ax.scatter(candycrushsaga_total_tweets, candycrushsaga_reviews, s=candycrushsaga_total_likes*5, color='limegreen', label='Candy Crush Saga', edgecolors='black', alpha=0.75)
# Google Play Store - 6 apps:
CleanMaster_plot= ax.scatter(CleanMaster_total_tweets, clean_master_reviews, s=CleanMaster_total_likes*5, color='m', label='Clean Master Space Cleaner', edgecolors='black', alpha=0.75)
SubwaySurfers_plot= ax.scatter(SubwaySurfers_total_tweets, subway_surfers_reviews, s=SubwaySurfers_total_likes*5, color='lime', label='Subway Surfers', edgecolors='black', alpha=0.75)
youtube_plot= ax.scatter(youtube_total_tweets, you_tube_reviews, s=youtube_total_likes*5, color='red', label='You Tube', edgecolors='black', alpha=0.75)
SecurityMaster_plot= ax.scatter(SecurityMaster_total_tweets, security_master_reviews, s=SecurityMaster_total_likes*5, color='blueviolet', label='Security Master, Antivirus VPN', edgecolors='black', alpha=0.75)
ClashRoyale_plot= ax.scatter(ClashRoyale_total_tweets, clash_royale_reviews, s=ClashRoyale_total_likes*5, color='darkolivegreen', label='Clash Royale', edgecolors='black', alpha=0.75)
whatsapp_plot= ax.scatter(whatsapp_total_tweets, whatsapp_reviews, s=whatsapp_total_likes*5, color='tan', label='Whats App', edgecolors='black', alpha=0.75)
# Apple Apps Store - 6 apps
templerun_plot= ax.scatter(templerun_total_tweets, templerun_reviews, s=templerun_total_likes*5, color='lawngreen', label='Temple Run', edgecolors='black', alpha=0.75)
pandora_plot= ax.scatter(pandora_total_tweets, pandora_reviews, s=pandora_total_likes*5, color='coral', label='Pandora', edgecolors='black', alpha=0.75)
pinterest_plot= ax.scatter(pinterest_total_tweets, pinterest_reviews, s=pinterest_total_likes*5, color='firebrick', label='Pinterest', edgecolors='black', alpha=0.75)
bible_plot= ax.scatter(bible_total_tweets, bible_reviews, s=bible_total_likes*5, color='tomato', label='Bible', edgecolors='black', alpha=0.75)
spotify_plot= ax.scatter(spotify_total_tweets, spotify_reviews, s=spotify_total_likes*5, color='orangered', label='Spotify', edgecolors='black', alpha=0.75)
angrybirds_plot= ax.scatter(angrybirds_total_tweets, angrybirds_reviews, s=angrybirds_total_likes*5, color='forestgreen', label='Angry Birds', edgecolors='black', alpha=0.75)
# title and labels
plt.title("Tweets vs Reviews (Mar 27 - Apr 3, 2019) \n")
plt.xlabel("Total Tweets \n Note: Circle sizes correlate with Likes \n" )
plt.ylabel("App Store Reviews in Millions \n")
# set and format the legend
lgnd = plt.legend(title='Legend', loc="best")
lgnd.legendHandles[0]._sizes = [30]
lgnd.legendHandles[1]._sizes = [30]
lgnd.legendHandles[2]._sizes = [30]
lgnd.legendHandles[3]._sizes = [30]
lgnd.legendHandles[4]._sizes = [30]
lgnd.legendHandles[5]._sizes = [30]
lgnd.legendHandles[6]._sizes = [30]
lgnd.legendHandles[7]._sizes = [30]
lgnd.legendHandles[8]._sizes = [30]
lgnd.legendHandles[9]._sizes = [30]
lgnd.legendHandles[10]._sizes = [30]
lgnd.legendHandles[11]._sizes = [30]
lgnd.legendHandles[12]._sizes = [30]
lgnd.legendHandles[13]._sizes = [30]
lgnd.legendHandles[14]._sizes = [30]
lgnd.legendHandles[15]._sizes = [30]
#grid lines and show
plt.grid()
plt.show()
#plt.savefig('./TWEETS_VS_REVIEWS_VSLIKES_Scatter.png')
# Scatter Plot 5 - Tweets vs Reviews vs Likes (size) - Need to do
fig, ax = plt.subplots(figsize=(8,8))
# Apps both on Google Play Store and Apple - 4 apps
facebook_plot = ax.scatter(facebook_avg_retweets, facebook_total_tweets, s=facebook_total_likes*5, color='blue', label='Facebook', edgecolors='red', alpha=0.75)
instagram_plot= ax.scatter(instagram_avg_retweets, instagram_total_tweets, s=instagram_total_likes*5, color='fuchsia', label='Instagram', edgecolors='red', alpha=0.75)
coc_plot= ax.scatter(coc_avg_retweets, coc_total_tweets, s=coc_total_likes*5, color='springgreen', label='Clash Of Clans', edgecolors='red', alpha=0.75)
candycrushsaga_plot= ax.scatter(candycrushsaga_avg_retweets, candycrushsaga_total_tweets, s=candycrushsaga_total_likes*5, color='black', label='Candy Crush Saga', edgecolors='red')#, alpha=0.75)
# Google Play Store - 6 apps:
CleanMaster_plot= ax.scatter(CleanMaster_avg_retweets, CleanMaster_total_tweets, s=CleanMaster_total_likes*5, color='olive', label='Clean Master Space Cleaner', edgecolors='lime', alpha=0.75)
SubwaySurfers_plot= ax.scatter(SubwaySurfers_avg_retweets, SubwaySurfers_total_tweets, s=SubwaySurfers_total_likes*5, color='plum', label='Subway Surfers', edgecolors='lime', alpha=0.75)
youtube_plot= ax.scatter(youtube_avg_retweets, youtube_total_tweets, s=youtube_total_likes*5, color='grey', label='You Tube', edgecolors='lime', alpha=0.75)
SecurityMaster_plot= ax.scatter(SecurityMaster_avg_retweets, SecurityMaster_total_tweets, s=SecurityMaster_total_likes*5, color='coral', label='Security Master, Antivirus VPN', edgecolors='lime', alpha=0.75)
ClashRoyale_plot= ax.scatter(ClashRoyale_avg_retweets, ClashRoyale_total_tweets, s=ClashRoyale_total_likes*5, color='orange', label='Clash Royale', edgecolors='lime', alpha=0.75)
whatsapp_plot= ax.scatter(whatsapp_avg_retweets, whatsapp_total_tweets, s=whatsapp_total_likes*5, color='green', label='Whats App', edgecolors='lime', alpha=0.75)
# Apple Apps Store - 6 apps
templerun_plot= ax.scatter(templerun_avg_retweets, templerun_total_tweets, s=templerun_total_likes*5, color='lawngreen', label='Temple Run', edgecolors='black', alpha=0.75)
pandora_plot= ax.scatter(pandora_avg_retweets, pandora_total_tweets, s=pandora_total_likes*5, color='cornflowerblue', label='Pandora', edgecolors='black', alpha=0.75)
pinterest_plot= ax.scatter(pinterest_avg_retweets, pinterest_total_tweets, s=pinterest_total_likes*5, color='firebrick', label='Pinterest', edgecolors='black', alpha=0.75)
bible_plot= ax.scatter(bible_avg_retweets, bible_total_tweets, s=bible_total_likes*5, color='brown', label='Bible', edgecolors='black', alpha=0.75)
spotify_plot= ax.scatter(spotify_avg_retweets, spotify_total_tweets, s=spotify_total_likes*5, color='darkgreen', label='Spotify', edgecolors='black', alpha=0.75)
angrybirds_plot= ax.scatter(angrybirds_avg_retweets, angrybirds_total_tweets, s=angrybirds_total_likes*5, color='salmon', label='Angry Birds', edgecolors='black', alpha=0.75)
# title and labels
plt.title("Tweets vs ReTweets (Mar 27 - Apr 3, 2019) \n")
plt.xlabel("Avg ReTweets \n Note: Circle sizes correlate with Total Likes \n" )
plt.ylabel("Total Tweets \n")
# set and format the legend
lgnd = plt.legend(title='Legend', loc="best")
lgnd.legendHandles[0]._sizes = [30]
lgnd.legendHandles[1]._sizes = [30]
lgnd.legendHandles[2]._sizes = [30]
lgnd.legendHandles[3]._sizes = [30]
lgnd.legendHandles[4]._sizes = [30]
lgnd.legendHandles[5]._sizes = [30]
lgnd.legendHandles[6]._sizes = [30]
lgnd.legendHandles[7]._sizes = [30]
lgnd.legendHandles[8]._sizes = [30]
lgnd.legendHandles[9]._sizes = [30]
lgnd.legendHandles[10]._sizes = [30]
lgnd.legendHandles[11]._sizes = [30]
lgnd.legendHandles[12]._sizes = [30]
lgnd.legendHandles[13]._sizes = [30]
lgnd.legendHandles[14]._sizes = [30]
lgnd.legendHandles[15]._sizes = [30]
#grid lines and show
plt.grid()
plt.show()
#plt.savefig('./tweets_vs__avgfollowers_Scatter.png')
```
|
github_jupyter
|
# Simulating Power Spectra
In this notebook we will explore how to simulate the data that we will use to investigate how different spectral parameters can influence band ratios.
Simulated power spectra will be created with varying aperiodic and periodic parameters, and are created using the [FOOOF](https://github.com/fooof-tools/fooof) tool.
In the first set of simulations, each set of simulated spectra will vary across a single parameter while the remaining parameters remain constant. In a secondary set of simulated power spectra, we will simulate pairs of parameters changing together.
For this part of the project, this notebook demonstrates the simulations with some examples, but does not create the actual set simulations used in the project. The full set of simulations for the project are created by the standalone scripts, available in the `scripts` folder.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from fooof.sim import *
from fooof.plts import plot_spectra
# Import custom project code
import sys
sys.path.append('../bratios')
from settings import *
from paths import DATA_PATHS as dp
# Settings
FREQ_RANGE = [1, 40]
LO_BAND = [4, 8]
HI_BAND = [13, 30]
# Define default parameters
EXP_DEF = [0, 1]
CF_LO_DEF = np.mean(LO_BAND)
CF_HI_DEF = np.mean(HI_BAND)
PW_DEF = 0.4
BW_DEF = 1
# Set a range of values for the band power to take
PW_START = 0
PW_END = 1
W_INC = .1
# Set a range of values for the aperiodic exponent to take
EXP_START = .25
EXP_END = 3
EXP_INC = .25
```
## Simulate power spectra with one parameter varying
First we will make several power spectra with varying band power.
To do so, we will continue to use the example of the theta beta ratio, and vary the power of the higher (beta) band.
```
# The Stepper object iterates through a range of values
pw_step = Stepper(PW_START, PW_END, PW_INC)
num_spectra = len(pw_step)
# `param_iter` creates a generator can be used to step across ranges of parameters
pw_iter = param_iter([[CF_LO_DEF, PW_DEF, BW_DEF], [CF_HI_DEF, pw_step, BW_DEF]])
# Simulate power spectra
pw_fs, pw_ps, pw_syns = gen_group_power_spectra(num_spectra, FREQ_RANGE, EXP_DEF, pw_iter)
# Collect together simulated data
pw_data = [pw_fs, pw_ps, pw_syns]
# Save out data, to access from other notebooks
np.save(dp.make_file_path(dp.demo, 'PW_DEMO', 'npy'), pw_data)
# Plot our series of generated power spectra, with varying high-band power
plot_spectra(pw_fs, pw_ps, log_powers=True)
```
Above, we can see each of the spectra we generated plotted, with the same properties for all parameters, except for beta power.
The same approach can be used to simulate data that vary only in one parameter, for each isolated spectral feature.
## Simulate power spectra with two parameters varying
In this section we will explore generating data in which two parameters vary simultaneously.
Specifically, we will simulate the case in which the aperiodic exponent varies while power for a higher band oscillation also varies.
The total number of trials will be: `(n_pw_changes) * (n_exp_changes)`.
```
data = []
exp_step = Stepper(EXP_START, EXP_END, EXP_INC)
for exp in exp_step:
# Low band sweeps through power range
pw_step = Stepper(PW_START, PW_END, PW_INC)
pw_iter = param_iter([[CF_LO_DEF, PW_DEF, BW_DEF],
[CF_HIGH_DEF, pw_step, BW_DEF]])
# Generates data
pw_apc_fs, pw_apc_ps, pw_apc_syns = gen_group_power_spectra(
len(pw_step), FREQ_RANGE, [0, exp], pw_iter)
# Collect together all simulated data
data.append(np.array([exp, pw_apc_fs, pw_apc_ps], dtype=object))
# Save out data, to access from other notebooks
np.save(dp.make_file_path(dp.demo, 'EXP_PW_DEMO', 'npy'), data)
# Extract some example power spectra, sub-sampling ones that vary in both exp & power
# Note: this is just a shortcut to step across the diagonal of the matrix of simulated spectra
plot_psds = [data[ii][2][ii, :] for ii in range(min(len(exp_step), len(pw_step)))]
# Plot a selection of power spectra in the paired parameter simulations
plot_spectra(pw_apc_fs, plot_psds, log_powers=True)
```
In the plot above, we can see a selection of the data we just simulated, selecting a group of power spectra that vary across both exponent and beta power.
In the next notebook we will calculate band ratios and see how changing these parameters affects ratio measures.
### Simulating the full set of data
Here we just simulated example data, to show how the simulations work.
The full set of simulations for this project are re-created with scripts, available in the `scripts` folder.
To simulate full set of single parameter simulation for this project, run this script:
`python gen_single_param_sims.py`
To simulate full set of interacting parameter simulation for this project, run this script:
`python gen_interacting_param_sims.py`
These scripts will automatically save all the regenerated data into the `data` folder.
```
# Check all the available data files for the single parameter simulations
dp.list_files('sims_single')
# Check all the available data files for the interacting parameter simulations
dp.list_files('sims_interacting')
```
|
github_jupyter
|
# Symbolic System
Create a symbolic three-state system:
```
import markoviandynamics as md
sym_system = md.SymbolicDiscreteSystem(3)
```
Get the symbolic equilibrium distribution:
```
sym_system.equilibrium()
```
Create a symbolic three-state system with potential energy barriers:
```
sym_system = md.SymbolicDiscreteSystemArrhenius(3)
```
It's the same object as the previous one, only with additional symbolic barriers:
```
sym_system.B_ij
```
We can assing values to the free parameters in the equilibrium distribution:
```
sym_system.equilibrium(energies=[0, 0.1, 1])
sym_system.equilibrium(energies=[0, 0.1, 1], temperature=1.5)
```
and create multiple equilibrium points by assigning temperature sequence:
```
import numpy as np
temperature_range = np.linspace(0.01, 10, 300)
equilibrium_line = sym_system.equilibrium([0, 0.1, 1], temperature_range)
equilibrium_line.shape
```
# Symbolic rate matrix
Create a symbolic rate matrix with Arrhenius process transitions:
```
sym_rate_matrix = md.SymbolicRateMatrixArrhenius(3)
sym_rate_matrix
```
Energies and barriers can be substituted at once:
```
energies = [0, 0.1, 1]
barriers = [[0, 0.11, 1.1],
[0.11, 0, 10],
[1.1, 10, 0]]
sym_rate_matrix.subs_symbols(energies, barriers)
sym_rate_matrix.subs_symbols(energies, barriers, temperature=2.5)
```
A symbolic rate matrix can be also lambdified (transform to lambda function):
```
rate_matrix_lambdified = sym_rate_matrix.lambdify()
```
The parameters of this function are the free symbols in the rate matrix:
```
rate_matrix_lambdified.__code__.co_varnames
```
They are positioned in ascending order. First the temperature, then the energies and the barriers. Sequence of rate matrices can be created by calling this function with a sequence for each parameter.
# Dynamics
We start by computing an initial probability distribution by assigning the energies and temperature:
```
p_initial = sym_system.equilibrium(energies, 0.5)
p_initial
```
## Trajectory - evolve by a fixed rate matrix
Compute the rate matrix by substituting free symbols:
```
rate_matrix = md.rate_matrix_arrhenius(energies, barriers, 1.2)
rate_matrix
```
Create trajectory of probability distributions in time:
```
import numpy as np
# Create time sequence
t_range = np.linspace(0, 5, 100)
trajectory = md.evolve(p_initial, rate_matrix, t_range)
trajectory.shape
import matplotlib.pyplot as plt
%matplotlib inline
for i in [0, 1, 2]:
plt.plot(t_range, trajectory[i,0,:], label='$p_{}(t)$'.format(i + 1))
plt.xlabel('$t$')
plt.legend()
```
## Trajectory - evolve by a time-dependent rate matrix
Create a temperature sequence in time:
```
temperature_time = 1.4 + np.sin(4. * t_range)
```
Create a rate matrix as a function of the temperature sequence:
```
# Array of stacked rate matrices that corresponds to ``temperature_time``
rate_matrix_time = md.rate_matrix_arrhenius(energies, barriers, temperature_time)
rate_matrix_time.shape
crazy_trajectory = md.evolve(p_initial, rate_matrix_time, t_range)
crazy_trajectory.shape
for i in [0, 1, 2]:
plt.plot(t_range, crazy_trajectory[i,0,:], label='$p_{}(t)$'.format(i + 1))
plt.xlabel('$t$')
plt.legend()
```
# Diagonalize the rate matrix
Calculate the eigenvalues, left and right eigenvectors:
```
U, eigenvalues, V = md.eigensystem(rate_matrix)
U.shape, eigenvalues.shape, V.shape
```
The eigenvalues are in descending order (the eigenvectors are ordered accordingly):
```
eigenvalues
```
We can also compute the eigensystem for multiple rate matrices at once (or evolution of a rate matrix, i.e., `rate_matrix_time`):
```
U, eigenvalues, V = md.eigensystem(rate_matrix_time)
U.shape, eigenvalues.shape, V.shape
```
# Decompose to rate matrix eigenvectors
A probability distribution, in general, can be decomposed to the right eigenvectors of the rate matrix:
$$\left|p\right\rangle = a_1\left|v_1\right\rangle + a_2\left|v_2\right\rangle + a_3\left|v_3\right\rangle$$
where $a_i$ is the coefficient of the i'th right eigenvector $\left|v_i\right\rangle$. A rate matrix that satisfies detailed balance has its first eigenvector as the equilibrium distribution $\left|\pi\right\rangle$. Therefore, *markovian-dynamics* normalizes $a_1$ to $1$ and decompose a probability distribution to
$$\left|p\right\rangle = \left|\pi\right\rangle + a_2\left|v_2\right\rangle + a_3\left|v_3\right\rangle$$
Decompose ``p_initial``:
```
md.decompose(p_initial, rate_matrix)
```
We can decompose also multiple points and/or by multiple rate matrices. For example, decompose multiple points:
```
first_decomposition = md.decompose(equilibrium_line, rate_matrix)
first_decomposition.shape
for i in [0, 1, 2]:
plt.plot(temperature_range, first_decomposition[i,:], label='$a_{}(T)$'.format(i + 1))
plt.xlabel('$T$')
plt.legend()
```
or decompose a trajectory:
```
second_decomposition = md.decompose(trajectory, rate_matrix)
second_decomposition.shape
for i in [0, 1, 2]:
plt.plot(t_range, second_decomposition[i,0,:], label='$a_{}(t)$'.format(i + 1))
plt.xlabel('$t$')
plt.legend()
```
Decompose single point using multiple rate matrices:
```
third_decomposition = md.decompose(p_initial, rate_matrix_time)
third_decomposition.shape
for i in [0, 1, 2]:
plt.plot(t_range, third_decomposition[i,0,:], label='$a_{}(t)$'.format(i + 1))
plt.legend()
```
Decompose, for every time $t$, the corresponding point $\left|p(t)\right\rangle$ using the temporal rate matrix $R(t)$
```
fourth_decomposition = md.decompose(trajectory, rate_matrix_time)
fourth_decomposition.shape
for i in [0, 1, 2]:
plt.plot(t_range, fourth_decomposition[i,0,:], label='$a_{}(t)$'.format(i + 1))
plt.legend()
```
# Plotting the 2D probability simplex for three-state system
The probability space of a three-state system is a three dimensional space. However, the normalization constraint $\sum_{i}p_i=1$ together with $0 < p_i \le 1$, form a 2D triangular plane in which all of the possible probability points reside.
We'll start by importing the plotting module:
```
import markoviandynamics.plotting.plotting2d as plt2d
# Use latex rendering
plt2d.latex()
```
Plot the probability plane:
```
plt2d.figure(figsize=(7, 5.5))
plt2d.equilibrium_line(equilibrium_line)
plt2d.legend()
```
We can plot many objects on the probability plane, such as trajectories, points, and eigenvectors of the rate matrix:
```
# Final equilibrium point
p_final = sym_system.equilibrium(energies, 1.2)
plt2d.figure(focus=True, figsize=(7, 5.5))
plt2d.equilibrium_line(equilibrium_line)
# Plot trajectory
plt2d.plot(trajectory, c='r', label=r'$\left|p(t)\right>$')
# Initial & final points
plt2d.point(p_initial, c='k', label=r'$\left|p_0\right>$')
plt2d.point(p_final, c='r', label=r'$\left|\pi\right>$')
# Eigenvectors
plt2d.eigenvectors(md.eigensystem(rate_matrix), kwargs_arrow={'zorder': 1})
plt2d.legend()
```
Plot multiple trajectories at once:
```
# Create temperature sequence
temperature_range = np.logspace(np.log10(0.01), np.log10(10), 50)
# Create the equilibrium line points
equilibrium_line = sym_system.equilibrium(energies, temperature_range)
# Create a trajectory for every point on ``equilibrium_line``
equilibrium_line_trajectory = md.evolve(equilibrium_line, rate_matrix, t_range)
plt2d.figure(focus=True, figsize=(7, 5))
plt2d.equilibrium_line(equilibrium_line)
plt2d.plot(equilibrium_line_trajectory, c='g', alpha=0.2)
plt2d.point(p_final, c='r', label=r'$\left|\pi\right>$')
plt2d.legend()
# Create a trajectory for every point on ``equilibrium_line``
equilibrium_line_crazy_trajectory = md.evolve(equilibrium_line, rate_matrix_time, t_range)
plt2d.figure(focus=True, figsize=(7, 5))
plt2d.equilibrium_line(equilibrium_line)
plt2d.plot(equilibrium_line_crazy_trajectory, c='r', alpha=0.1)
plt2d.text(p_final, r'Text $\alpha$', delta_x=0.05)
plt2d.legend()
```
|
github_jupyter
|
# Version information
```
from datetime import date
print("Running date:", date.today().strftime("%B %d, %Y"))
import pyleecan
print("Pyleecan version:" + pyleecan.__version__)
import SciDataTool
print("SciDataTool version:" + SciDataTool.__version__)
```
# How to define a machine
This tutorial shows the different ways to define electrical machine. To do so, it presents the definition of the **Toyota Prius 2004** interior magnet with distributed winding \[1\].
The notebook related to this tutorial is available on [GitHub](https://github.com/Eomys/pyleecan/tree/master/Tutorials/tuto_Machine.ipynb).
## Type of machines Pyleecan can model
Pyleecan handles the geometrical modelling of main 2D radial flux machines such as:
- surface or interior permanent magnet machines (SPMSM, IPMSM)
- synchronous reluctance machines (SynRM)
- squirrel-cage induction machines and doubly-fed induction machines (SCIM, DFIM)
- would rotor synchronous machines and salient pole synchronous machines (WSRM)
- switched reluctance machines (SRM)
The architecture of Pyleecan also enables to define other kinds of machines (with more than two laminations for instance). More information in our ICEM 2020 pyblication \[2\]
Every machine can be defined by using the **Graphical User Interface** or directly in **Python script**.
## Defining machine with Pyleecan GUI
The GUI is the easiest way to define machine in Pyleecan. Its purpose is to create or load a machine and save it in JSON format to be loaded in a python script. The interface enables to define step by step in a user-friendly way every characteristics of the machine such as:
- topology
- dimensions
- materials
- winding
Each parameter is explained by a tooltip and the machine can be previewed at each stage of the design.
## Start the GUI
The GUI can be started by running the following command in a notebook:
```python
# Start Pyleecan GUI from the Jupyter Notebook
%run -m pyleecan
```
To use it on Anaconda you may need to create the system variable:
QT_QPA_PLATFORM_PLUGIN_PATH : path\to\anaconda3\Lib\site-packages\PySide2\plugins\platforms
The GUI can also be launched in a terminal by calling one of the following commands in a terminal:
```
Path/to/python.exe -m pyleecan
Path/to/python3.exe -m pyleecan
```
## load a machine
Once the machine defined in the GUI it can be loaded with the following commands:
```
%matplotlib notebook
# Load the machine
from os.path import join
from pyleecan.Functions.load import load
from pyleecan.definitions import DATA_DIR
IPMSM_A = load(join(DATA_DIR, "Machine", "Toyota_Prius.json"))
IPMSM_A.plot()
```
## Defining Machine in scripting mode
Pyleecan also enables to define the machine in scripting mode, using different classes. Each class is defined from a csv file in the folder _pyleecan/Generator/ClasseRef_ and the documentation of every class is available on the dedicated [webpage](https://www.pyleecan.org/pyleecan.Classes.html).
The following image shows the machine classes organization :
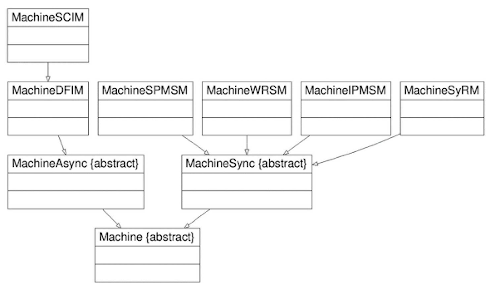
Every rotor and stator can be created with the **Lamination** class or one of its daughters.
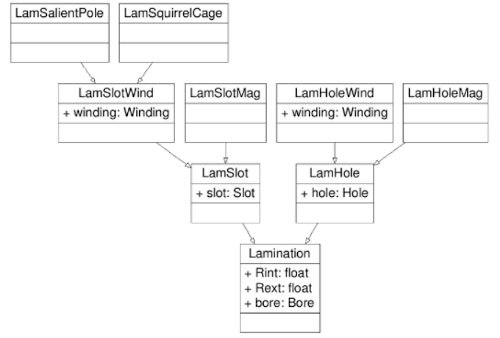
The scripting enables to define some complex and exotic machine that can't be defined in the GUI such as this one:
```
from pyleecan.Classes.MachineUD import MachineUD
from pyleecan.Classes.LamSlotWind import LamSlotWind
from pyleecan.Classes.LamSlot import LamSlot
from pyleecan.Classes.WindingCW2LT import WindingCW2LT
from pyleecan.Classes.SlotW10 import SlotW10
from pyleecan.Classes.SlotW22 import SlotW22
from numpy import pi
machine = MachineUD(name="4 laminations machine")
# Main geometry parameter
Rext = 170e-3 # Exterior radius of outter lamination
W1 = 30e-3 # Width of first lamination
A1 = 2.5e-3 # Width of the first airgap
W2 = 20e-3
A2 = 10e-3
W3 = 20e-3
A3 = 2.5e-3
W4 = 60e-3
# Outer stator
lam1 = LamSlotWind(Rext=Rext, Rint=Rext - W1, is_internal=False, is_stator=True)
lam1.slot = SlotW22(
Zs=12, W0=2 * pi / 12 * 0.75, W2=2 * pi / 12 * 0.75, H0=0, H2=W1 * 0.65
)
lam1.winding = WindingCW2LT(qs=3, p=3)
# Outer rotor
lam2 = LamSlot(
Rext=lam1.Rint - A1, Rint=lam1.Rint - A1 - W2, is_internal=True, is_stator=False
)
lam2.slot = SlotW10(Zs=22, W0=25e-3, W1=25e-3, W2=15e-3, H0=0, H1=0, H2=W2 * 0.75)
# Inner rotor
lam3 = LamSlot(
Rext=lam2.Rint - A2,
Rint=lam2.Rint - A2 - W3,
is_internal=False,
is_stator=False,
)
lam3.slot = SlotW10(
Zs=22, W0=17.5e-3, W1=17.5e-3, W2=12.5e-3, H0=0, H1=0, H2=W3 * 0.75
)
# Inner stator
lam4 = LamSlotWind(
Rext=lam3.Rint - A3, Rint=lam3.Rint - A3 - W4, is_internal=True, is_stator=True
)
lam4.slot = SlotW10(Zs=12, W0=25e-3, W1=25e-3, W2=1e-3, H0=0, H1=0, H2=W4 * 0.75)
lam4.winding = WindingCW2LT(qs=3, p=3)
# Machine definition
machine.lam_list = [lam1, lam2, lam3, lam4]
# Plot, check and save
machine.plot()
```
## Stator definition
To define the stator, we initialize a [**LamSlotWind**](http://pyleecan.org/pyleecan.Classes.LamSlotWind.html) object with the different parameters. In pyleecan, all the parameters must be set in SI units.
```
from pyleecan.Classes.LamSlotWind import LamSlotWind
mm = 1e-3 # Millimeter
# Lamination setup
stator = LamSlotWind(
Rint=80.95 * mm, # internal radius [m]
Rext=134.62 * mm, # external radius [m]
L1=83.82 * mm, # Lamination stack active length [m] without radial ventilation airducts
# but including insulation layers between lamination sheets
Nrvd=0, # Number of radial air ventilation duct
Kf1=0.95, # Lamination stacking / packing factor
is_internal=False,
is_stator=True,
)
```
Then we add 48 slots using [**SlotW11**](http://pyleecan.org/pyleecan.Classes.SlotW11.html) which is one of the 25 Slot classes:
```
from pyleecan.Classes.SlotW11 import SlotW11
# Slot setup
stator.slot = SlotW11(
Zs=48, # Slot number
H0=1.0 * mm, # Slot isthmus height
H1=0, # Height
H2=33.3 * mm, # Slot height below wedge
W0=1.93 * mm, # Slot isthmus width
W1=5 * mm, # Slot top width
W2=8 * mm, # Slot bottom width
R1=4 * mm # Slot bottom radius
)
```
As for the slot, we can define the winding and its conductor with [**WindingDW1L**](http://pyleecan.org/pyleecan.Classes.WindingDW1L.html) and [**CondType11**](http://pyleecan.org/pyleecan.Classes.CondType11.html). The conventions for winding are further explained on [pyleecan website](https://pyleecan.org/winding.convention.html)
```
from pyleecan.Classes.WindingDW1L import WindingDW1L
from pyleecan.Classes.CondType11 import CondType11
# Winding setup
stator.winding = WindingDW1L(
qs=3, # number of phases
Lewout=0, # staight length of conductor outside lamination before EW-bend
p=4, # number of pole pairs
Ntcoil=9, # number of turns per coil
Npcp=1, # number of parallel circuits per phase
Nslot_shift_wind=0, # 0 not to change the stator winding connection matrix built by pyleecan number
# of slots to shift the coils obtained with pyleecan winding algorithm
# (a, b, c becomes b, c, a with Nslot_shift_wind1=1)
is_reverse_wind=False # True to reverse the default winding algorithm along the airgap
# (c, b, a instead of a, b, c along the trigonometric direction)
)
# Conductor setup
stator.winding.conductor = CondType11(
Nwppc_tan=1, # stator winding number of preformed wires (strands)
# in parallel per coil along tangential (horizontal) direction
Nwppc_rad=1, # stator winding number of preformed wires (strands)
# in parallel per coil along radial (vertical) direction
Wwire=0.000912, # single wire width without insulation [m]
Hwire=2e-3, # single wire height without insulation [m]
Wins_wire=1e-6, # winding strand insulation thickness [m]
type_winding_shape=0, # type of winding shape for end winding length calculation
# 0 for hairpin windings
# 1 for normal windings
)
```
## Rotor definition
For this example, we use the [**LamHole**](http://www.pyleecan.org/pyleecan.Classes.LamHole.html) class to define the rotor as a lamination with holes to contain magnet.
In the same way as for the stator, we start by defining the lamination:
```
from pyleecan.Classes.LamHole import LamHole
# Rotor setup
rotor = LamHole(
Rint=55.32 * mm, # Internal radius
Rext=80.2 * mm, # external radius
is_internal=True,
is_stator=False,
L1=stator.L1 # Lamination stack active length [m]
# without radial ventilation airducts but including insulation layers between lamination sheets
)
```
After that, we can add holes with magnets to the rotor using the class [**HoleM50**](http://www.pyleecan.org/pyleecan.Classes.HoleM50.html):
```
from pyleecan.Classes.HoleM50 import HoleM50
rotor.hole = list()
rotor.hole.append(
HoleM50(
Zh=8, # Number of Hole around the circumference
W0=42.0 * mm, # Slot opening
W1=0, # Tooth width (at V bottom)
W2=0, # Distance Magnet to bottom of the V
W3=14.0 * mm, # Tooth width (at V top)
W4=18.9 * mm, # Magnet Width
H0=10.96 * mm, # Slot Depth
H1=1.5 * mm, # Distance from the lamination Bore
H2=1 * mm, # Additional depth for the magnet
H3=6.5 * mm, # Magnet Height
H4=0, # Slot top height
)
)
```
The holes are defined as a list to enable to create several layers of holes and/or to combine different kinds of holes
## Create a shaft and a frame
The classes [**Shaft**](http://www.pyleecan.org/pyleecan.Classes.Shaft.html) and [**Frame**](http://www.pyleecan.org/pyleecan.Classes.Frame.html) enable to add a shaft and a frame to the machine. For this example there is no frame:
```
from pyleecan.Classes.Shaft import Shaft
from pyleecan.Classes.Frame import Frame
# Set shaft
shaft = Shaft(Drsh=rotor.Rint * 2, # Diamater of the rotor shaft [m]
# used to estimate bearing diameter for friction losses
Lshaft=1.2 # length of the rotor shaft [m]
)
frame = None
```
## Set materials and magnets
Every Pyleecan object can be saved in JSON using the method `save` and can be loaded with the `load` function.
In this example, the materials *M400_50A* and *Copper1* are loaded and set in the corresponding properties.
```
# Loading Materials
M400_50A = load(join(DATA_DIR, "Material", "M400-50A.json"))
Copper1 = load(join(DATA_DIR, "Material", "Copper1.json"))
# Set Materials
stator.mat_type = M400_50A # Stator Lamination material
rotor.mat_type = M400_50A # Rotor Lamination material
stator.winding.conductor.cond_mat = Copper1 # Stator winding conductor material
```
A material can also be defined in scripting as any other Pyleecan object. The material *Magnet_prius* is created with the classes [**Material**](http://www.pyleecan.org/pyleecan.Classes.Material.html) and [**MatMagnetics**](http://www.pyleecan.org/pyleecan.Classes.MatMagnetics.html).
```
from pyleecan.Classes.Material import Material
from pyleecan.Classes.MatMagnetics import MatMagnetics
# Defining magnets
Magnet_prius = Material(name="Magnet_prius")
# Definition of the magnetic properties of the material
Magnet_prius.mag = MatMagnetics(
mur_lin = 1.05, # Relative magnetic permeability
Hc = 902181.163126629, # Coercitivity field [A/m]
alpha_Br = -0.001, # temperature coefficient for remanent flux density /°C compared to 20°C
Brm20 = 1.24, # magnet remanence induction at 20°C [T]
Wlam = 0, # lamination sheet width without insulation [m] (0 == not laminated)
)
# Definition of the electric properties of the material
Magnet_prius.elec.rho = 1.6e-06 # Resistivity at 20°C
# Definition of the structural properties of the material
Magnet_prius.struct.rho = 7500.0 # mass per unit volume [kg/m3]
```
The magnet materials are set with the "magnet_X" property. Pyleecan enables to define different magnetization or material for each magnets of the holes. Here both magnets are defined identical.
```
# Set magnets in the rotor hole
rotor.hole[0].magnet_0.mat_type = Magnet_prius
rotor.hole[0].magnet_1.mat_type = Magnet_prius
rotor.hole[0].magnet_0.type_magnetization = 1
rotor.hole[0].magnet_1.type_magnetization = 1
```
## Create, save and plot the machine
Finally, the Machine object can be created with [**MachineIPMSM**](http://www.pyleecan.org/pyleecan.Classes.MachineIPMSM.html) and saved using the `save` method.
```
from pyleecan.Classes.MachineIPMSM import MachineIPMSM
%matplotlib notebook
IPMSM_Prius_2004 = MachineIPMSM(
name="Toyota Prius 2004",
stator=stator,
rotor=rotor,
shaft=shaft,
frame=frame # None
)
IPMSM_Prius_2004.save('IPMSM_Toyota_Prius_2004.json')
im=IPMSM_Prius_2004.plot()
```
Note that Pyleecan also handles ventilation duct thanks to the classes :
- [**VentilationCirc**](http://www.pyleecan.org/pyleecan.Classes.VentilationCirc.html)
- [**VentilationPolar**](http://www.pyleecan.org/pyleecan.Classes.VentilationPolar.html)
- [**VentilationTrap**](http://www.pyleecan.org/pyleecan.Classes.VentilationTrap.html)
[1] Z. Yang, M. Krishnamurthy and I. P. Brown, "Electromagnetic and vibrational characteristic of IPM over full torque-speed range", *2013 International Electric Machines & Drives Conference*, Chicago, IL, 2013, pp. 295-302.
[2] P. Bonneel, J. Le Besnerais, E. Devillers, C. Marinel, and R. Pile, “Design Optimization of Innovative Electrical Machines Topologies Based on Pyleecan Opensource Object-Oriented Software,” in 24th International Conference on Electrical Machines (ICEM), 2020.
|
github_jupyter
|
## 练习 1:写程序,可由键盘读入用户姓名例如Mr. right,让用户输入出生的月份与日期,判断用户星座,假设用户是金牛座,则输出,Mr. right,你是非常有性格的金牛座!。
```
name = input('请输入你的姓名')
print('你好',name)
print('请输入出生的月份与日期')
month = int(input('月份:'))
date = int(input('日期:'))
if month == 4:
if date < 20:
print(name, '你是白羊座')
else:
print(name,'你是非常有性格的金牛座')
if month == 5:
if date < 21:
print(name, '你是非常有性格的金牛座')
else:
print(name,'你是双子座')
if month == 6:
if date < 22:
print(name, '你是双子座')
else:
print(name,'你是巨蟹座')
if month == 7:
if date < 23:
print(name, '你是巨蟹座')
else:
print(name,'你是狮子座')
if month == 8:
if date < 23:
print(name, '你是狮子座')
else:
print(name,'你是处女座')
if month == 9:
if date < 24:
print(name, '你是处女座')
else:
print(name,'你是天秤座')
if month == 10:
if date < 24:
print(name, '你是天秤座')
else:
print(name,'你是天蝎座')
if month == 11:
if date < 23:
print(name, '你是天蝎座')
else:
print(name,'你是射手座')
if month == 12:
if date < 22:
print(name, '你是射手座')
else:
print(name,'你是摩羯座')
if month == 1:
if date < 20:
print(name, '你是摩羯座')
else:
print(name,'你是水瓶座')
if month == 2:
if date < 19:
print(name, '你是水瓶座')
else:
print(name,'你是双鱼座')
if month == 3:
if date < 22:
print(name, '你是双鱼座')
else:
print(name,'你是白羊座')
```
## 练习 2:写程序,可由键盘读入两个整数m与n(n不等于0),询问用户意图,如果要求和则计算从m到n的和输出,如果要乘积则计算从m到n的积并输出,如果要求余数则计算m除以n的余数的值并输出,否则则计算m整除n的值并输出。
```
m = int(input('请输入一个整数,回车结束'))
n = int(input('请输入一个整数,不为零'))
intend = input('请输入计算意图,如 + * %')
if m<n:
min_number = m
else:
min_number = n
total = min_number
if intend == '+':
if m<n:
while m<n:
m = m + 1
total = total + m
print(total)
else:
while m > n:
n = n + 1
total = total + n
print(total)
elif intend == '*':
if m<n:
while m<n:
m = m + 1
total = total * m
print(total)
else:
while m > n:
n = n + 1
total = total * n
print(total)
elif intend == '%':
print(m % n)
else:
print(m // n)
```
## 练习 3:写程序,能够根据北京雾霾PM2.5数值给出对应的防护建议。如当PM2.5数值大于500,则应该打开空气净化器,戴防雾霾口罩等。
```
number = int(input('现在北京的PM2.5指数是多少?请输入整数'))
if number > 500:
print('应该打开空气净化器,戴防雾霾口罩')
elif 300 < number < 500:
print('尽量呆在室内不出门,出门佩戴防雾霾口罩')
elif 200 < number < 300:
print('尽量不要进行户外活动')
elif 100 < number < 200:
print('轻度污染,可进行户外活动,可不佩戴口罩')
else:
print('无须特别注意')
```
## 尝试性练习:写程序,能够在屏幕上显示空行。
```
print('空行是我')
print('空行是我')
print('空行是我')
print( )
print('我是空行')
```
## 练习 4:英文单词单数转复数,要求输入一个英文动词(单数形式),能够得到其复数形式,或给出单数转复数形式的建议
```
word = input('请输入一个单词,回车结束')
if word.endswith('s') or word.endswith('sh') or word.endswith('ch') or word.endswith('x'):
print(word,'es',sep = '')
elif word.endswith('y'):
if word.endswith('ay') or word.endswith('ey') or word.endswith('iy') or word.endswith('oy') or word.endswith('uy'):
print(word,'s',sep = '')
else:
word = word[:-1]
print(word,'ies',sep = '')
elif word.endswith('f'):
word = word[:-1]
print(word,'ves',sep = '')
elif word.endswith('fe'):
word = word[:-2]
print(word,'ves',sep = '')
elif word.endswith('o'):
print('词尾加s或者es')
else:
print(word,'s',sep = '')
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import scipy.stats as sts
import seaborn as sns
sns.set()
%matplotlib inline
```
# 01. Smooth function optimization
Рассмотрим все ту же функцию из задания по линейной алгебре:
$ f(x) = \sin{\frac{x}{5}} * e^{\frac{x}{10}} + 5 * e^{-\frac{x}{2}} $
, но теперь уже на промежутке `[1, 30]`.
В первом задании будем искать минимум этой функции на заданном промежутке с помощью `scipy.optimize`. Разумеется, в дальнейшем вы будете использовать методы оптимизации для более сложных функций, а `f(x)` мы рассмотрим как удобный учебный пример.
Напишите на Питоне функцию, вычисляющую значение `f(x)` по известному `x`. Будьте внимательны: не забывайте про то, что по умолчанию в питоне целые числа делятся нацело, и о том, что функции `sin` и `exp` нужно импортировать из модуля `math`.
```
from math import sin, exp, sqrt
def f(x):
return sin(x / 5) * exp(x / 10) + 5 * exp(-x / 2)
f(10)
xs = np.arange(41, 60, 0.1)
ys = np.array([f(x) for x in xs])
plt.plot(xs, ys)
```
Изучите примеры использования `scipy.optimize.minimize` в документации `Scipy` (см. "Материалы").
Попробуйте найти минимум, используя стандартные параметры в функции `scipy.optimize.minimize` (т.е. задав только функцию и начальное приближение). Попробуйте менять начальное приближение и изучить, меняется ли результат.
```
from scipy.optimize import minimize, rosen, rosen_der, differential_evolution
x0 = 60
minimize(f, x0)
# поиграемся с розенброком
x0 = [1., 10.]
minimize(rosen, x0, method='BFGS')
```
___
## Submission #1
Укажите в `scipy.optimize.minimize` в качестве метода `BFGS` (один из самых точных в большинстве случаев градиентных методов оптимизации), запустите из начального приближения $ x = 2 $. Градиент функции при этом указывать не нужно – он будет оценен численно. Полученное значение функции в точке минимума - ваш первый ответ по заданию 1, его надо записать с точностью до 2 знака после запятой.
Теперь измените начальное приближение на x=30. Значение функции в точке минимума - ваш второй ответ по заданию 1, его надо записать через пробел после первого, с точностью до 2 знака после запятой.
Стоит обдумать полученный результат. Почему ответ отличается в зависимости от начального приближения? Если нарисовать график функции (например, как это делалось в видео, где мы знакомились с Numpy, Scipy и Matplotlib), можно увидеть, в какие именно минимумы мы попали. В самом деле, градиентные методы обычно не решают задачу глобальной оптимизации, поэтому результаты работы ожидаемые и вполне корректные.
```
# 1. x0 = 2
x0 = 2
res1 = minimize(f, x0, method='BFGS')
# 2. x0 = 30
x0 = 30
res2 = minimize(f, x0, method='BFGS')
with open('out/06. submission1.txt', 'w') as f_out:
output = '{0:.2f} {1:.2f}'.format(res1.fun, res2.fun)
print(output)
f_out.write(output)
```
# 02. Глобальная оптимизация
Теперь попробуем применить к той же функции $ f(x) $ метод глобальной оптимизации — дифференциальную эволюцию.
Изучите документацию и примеры использования функции `scipy.optimize.differential_evolution`.
Обратите внимание, что границы значений аргументов функции представляют собой список кортежей (list, в который помещены объекты типа tuple). Даже если у вас функция одного аргумента, возьмите границы его значений в квадратные скобки, чтобы передавать в этом параметре список из одного кортежа, т.к. в реализации `scipy.optimize.differential_evolution` длина этого списка используется чтобы определить количество аргументов функции.
Запустите поиск минимума функции f(x) с помощью дифференциальной эволюции на промежутке [1, 30]. Полученное значение функции в точке минимума - ответ в задаче 2. Запишите его с точностью до второго знака после запятой. В этой задаче ответ - только одно число.
Заметьте, дифференциальная эволюция справилась с задачей поиска глобального минимума на отрезке, т.к. по своему устройству она предполагает борьбу с попаданием в локальные минимумы.
Сравните количество итераций, потребовавшихся BFGS для нахождения минимума при хорошем начальном приближении, с количеством итераций, потребовавшихся дифференциальной эволюции. При повторных запусках дифференциальной эволюции количество итераций будет меняться, но в этом примере, скорее всего, оно всегда будет сравнимым с количеством итераций BFGS. Однако в дифференциальной эволюции за одну итерацию требуется выполнить гораздо больше действий, чем в BFGS. Например, можно обратить внимание на количество вычислений значения функции (nfev) и увидеть, что у BFGS оно значительно меньше. Кроме того, время работы дифференциальной эволюции очень быстро растет с увеличением числа аргументов функции.
```
res = differential_evolution(f, [(1, 30)])
res
```
___
## Submission #2
```
res = differential_evolution(f, [(1, 30)])
with open('out/06. submission2.txt', 'w') as f_out:
output = '{0:.2f}'.format(res.fun)
print(output)
f_out.write(output)
```
# 03. Минимизация негладкой функции
Теперь рассмотрим функцию $ h(x) = int(f(x)) $ на том же отрезке `[1, 30]`, т.е. теперь каждое значение $ f(x) $ приводится к типу int и функция принимает только целые значения.
Такая функция будет негладкой и даже разрывной, а ее график будет иметь ступенчатый вид. Убедитесь в этом, построив график $ h(x) $ с помощью `matplotlib`.
```
def h(x):
return int(f(x))
xs = np.arange(0, 70, 1)
ys = [h(x) for x in xs]
plt.plot(xs, ys)
minimize(h, 40.3)
```
Попробуйте найти минимум функции $ h(x) $ с помощью BFGS, взяв в качестве начального приближения $ x = 30 $. Получившееся значение функции – ваш первый ответ в этой задаче.
```
res_bfgs = minimize(h, 30)
res_bfgs
```
Теперь попробуйте найти минимум $ h(x) $ на отрезке `[1, 30]` с помощью дифференциальной эволюции. Значение функции $ h(x) $ в точке минимума – это ваш второй ответ в этом задании. Запишите его через пробел после предыдущего.
```
res_diff_evol = differential_evolution(h, [(1, 30)])
res_diff_evol
```
Обратите внимание на то, что полученные ответы различаются. Это ожидаемый результат, ведь BFGS использует градиент (в одномерном случае – производную) и явно не пригоден для минимизации рассмотренной нами разрывной функции. Попробуйте понять, почему минимум, найденный BFGS, именно такой (возможно в этом вам поможет выбор разных начальных приближений).
Выполнив это задание, вы увидели на практике, чем поиск минимума функции отличается от глобальной оптимизации, и когда может быть полезно применить вместо градиентного метода оптимизации метод, не использующий градиент. Кроме того, вы попрактиковались в использовании библиотеки SciPy для решения оптимизационных задач, и теперь знаете, насколько это просто и удобно.
___
## Submission #3
```
with open('out/06. submission3.txt', 'w') as f_out:
output = '{0:.2f} {1:.2f}'.format(res_bfgs.fun, res_diff_evol.fun)
print(output)
f_out.write(output)
```
___
Дальше играюсь с визуализацией ф-ии розенброка
```
lb = -10
rb = 10
step = 0.2
gen_xs = np.arange(lb, rb, step)
xs = np.meshgrid(np.arange(-1, 1, 0.1), np.arange(-10, 10, 0.1))
ys = rosen(xs)
print(xs[0].shape, xs[1].shape, ys.shape)
plt.contour(xs[0], xs[1], ys, 30)
lb = 0
rb = 4
step = 0.3
gen_xs = np.arange(lb, rb, step)
#xs = np.meshgrid(gen_xs, gen_xs)
#ys = (xs[0]**2 + xs[1]**2)**0.5
xs = np.meshgrid(np.arange(-2, 2, 0.1), np.arange(-10, 10, 0.1))
ys = rosen(xs)
print(xs[0].shape, xs[1].shape, ys.shape)
cmap = sns.cubehelix_palette(light=1, as_cmap=True)
plt.contour(xs[0], xs[1], ys, 30, cmap=cmap)
#plt.plot(xs[0], xs[1], marker='.', color='k', linestyle='none', alpha=0.1)
plt.show()
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
surf = ax.plot_surface(xs[0], xs[1], ys, cmap=cmap, linewidth=0, antialiased=False)
plt.show()
x0 = [1.3, 0.7, 0.8, 1.9, 1.2]
res = minimize(rosen, x0, method='Nelder-Mead', tol=1e-6)
res.x
```
|
github_jupyter
|
# Mount Drive
```
from google.colab import drive
drive.mount('/content/drive')
!pip install -U -q PyDrive
!pip install httplib2==0.15.0
import os
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from pydrive.files import GoogleDriveFileList
from google.colab import auth
from oauth2client.client import GoogleCredentials
from getpass import getpass
import urllib
# 1. Authenticate and create the PyDrive client.
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
# Cloning PAL_2021 to access modules.
# Need password to access private repo.
if 'CLIPPER' not in os.listdir():
cmd_string = 'git clone https://github.com/PAL-ML/CLIPPER.git'
os.system(cmd_string)
```
# Installation
## Install multi label metrics dependencies
```
! pip install scikit-learn==0.24
```
## Install CLIP dependencies
```
import subprocess
CUDA_version = [s for s in subprocess.check_output(["nvcc", "--version"]).decode("UTF-8").split(", ") if s.startswith("release")][0].split(" ")[-1]
print("CUDA version:", CUDA_version)
if CUDA_version == "10.0":
torch_version_suffix = "+cu100"
elif CUDA_version == "10.1":
torch_version_suffix = "+cu101"
elif CUDA_version == "10.2":
torch_version_suffix = ""
else:
torch_version_suffix = "+cu110"
! pip install torch==1.7.1{torch_version_suffix} torchvision==0.8.2{torch_version_suffix} -f https://download.pytorch.org/whl/torch_stable.html ftfy regex
! pip install ftfy regex
! wget https://openaipublic.azureedge.net/clip/bpe_simple_vocab_16e6.txt.gz -O bpe_simple_vocab_16e6.txt.gz
!pip install git+https://github.com/Sri-vatsa/CLIP # using this fork because of visualization capabilities
```
## Install clustering dependencies
```
!pip -q install umap-learn>=0.3.7
```
## Install dataset manager dependencies
```
!pip install wget
```
# Imports
```
# ML Libraries
import tensorflow as tf
import tensorflow_hub as hub
import torch
import torch.nn as nn
import torchvision.models as models
import torchvision.transforms as transforms
import keras
# Data processing
import PIL
import base64
import imageio
import pandas as pd
import numpy as np
import json
from PIL import Image
import cv2
from sklearn.feature_extraction.image import extract_patches_2d
# Plotting
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.patches as patches
from IPython.core.display import display, HTML
from matplotlib import cm
import matplotlib.image as mpimg
# Models
import clip
# Datasets
import tensorflow_datasets as tfds
# Clustering
# import umap
from sklearn import metrics
from sklearn.cluster import KMeans
#from yellowbrick.cluster import KElbowVisualizer
# Misc
import progressbar
import logging
from abc import ABC, abstractmethod
import time
import urllib.request
import os
from sklearn.metrics import jaccard_score, hamming_loss, accuracy_score, f1_score
from sklearn.preprocessing import MultiLabelBinarizer
# Modules
from CLIPPER.code.ExperimentModules import embedding_models
from CLIPPER.code.ExperimentModules.dataset_manager import DatasetManager
from CLIPPER.code.ExperimentModules.weight_imprinting_classifier import WeightImprintingClassifier
from CLIPPER.code.ExperimentModules import simclr_data_augmentations
from CLIPPER.code.ExperimentModules.utils import (save_npy, load_npy,
get_folder_id,
create_expt_dir,
save_to_drive,
load_all_from_drive_folder,
download_file_by_name,
delete_file_by_name)
logging.getLogger('googleapicliet.discovery_cache').setLevel(logging.ERROR)
```
# Initialization & Constants
## Dataset details
```
dataset_name = "LFW"
folder_name = "LFW-Embeddings-28-02-21"
# Change parentid to match that of experiments root folder in gdrive
parentid = '1bK72W-Um20EQDEyChNhNJthUNbmoSEjD'
# Filepaths
train_labels_filename = "train_labels.npz"
train_embeddings_filename_suffix = "_embeddings_train.npz"
# Initialize sepcific experiment folder in drive
folderid = create_expt_dir(drive, parentid, folder_name)
```
## Few shot learning parameters
```
num_ways = 5 # [5, 20]
num_shot = 5 # [5, 1]
num_eval = 15 # [5, 10, 15, 19]
num_episodes = 100
shuffle = False
```
## Image embedding and augmentations
```
embedding_model = embedding_models.CLIPEmbeddingWrapper()
num_augmentations = 0 # [0, 5, 10]
trivial=False # [True, False]
```
## Training parameters
```
# List of number of epochs to train over, e.g. [5, 10, 15, 20]. [0] indicates no training.
train_epochs_arr = [0]
# Single label (softmax) parameters
multi_label= False # [True, False] i.e. sigmoid or softmax
metrics_val = ['accuracy', 'ap', 'map', 'c_f1', 'o_f1', 'c_precision', 'o_precision', 'c_recall', 'o_recall', 'top1_accuracy', 'top5_accuracy', 'classwise_accuracy', 'c_accuracy']
```
# Load data
```
def get_ndarray_from_drive(drive, folderid, filename):
download_file_by_name(drive, folderid, filename)
return np.load(filename)['data']
train_labels = get_ndarray_from_drive(drive, folderid, train_labels_filename)
train_labels = train_labels.astype(str)
dm = DatasetManager()
test_data_generator = dm.load_dataset('lfw', split='train')
class_names = dm.get_class_names()
print(class_names)
```
# Create label dictionary
```
unique_labels = np.unique(train_labels)
print(len(unique_labels))
label_dictionary = {la:[] for la in unique_labels}
for i in range(len(train_labels)):
la = train_labels[i]
label_dictionary[la].append(i)
```
# Weight Imprinting models on train data embeddings
## Function definitions
```
def start_progress_bar(bar_len):
widgets = [
' [',
progressbar.Timer(format= 'elapsed time: %(elapsed)s'),
'] ',
progressbar.Bar('*'),' (',
progressbar.ETA(), ') ',
]
pbar = progressbar.ProgressBar(
max_value=bar_len, widgets=widgets
).start()
return pbar
def prepare_indices(
num_ways,
num_shot,
num_eval,
num_episodes,
label_dictionary,
labels,
shuffle=False
):
eval_indices = []
train_indices = []
wi_y = []
eval_y = []
label_dictionary = {la:label_dictionary[la] for la in label_dictionary if len(label_dictionary[la]) >= (num_shot+num_eval)}
unique_labels = list(label_dictionary.keys())
pbar = start_progress_bar(num_episodes)
for s in range(num_episodes):
# Setting random seed for replicability
np.random.seed(s)
_train_indices = []
_eval_indices = []
selected_labels = np.random.choice(unique_labels, size=num_ways, replace=False)
for la in selected_labels:
la_indices = label_dictionary[la]
select = np.random.choice(la_indices, size = num_shot+num_eval, replace=False)
tr_idx = list(select[:num_shot])
ev_idx = list(select[num_shot:])
_train_indices = _train_indices + tr_idx
_eval_indices = _eval_indices + ev_idx
if shuffle:
np.random.shuffle(_train_indices)
np.random.shuffle(_eval_indices)
train_indices.append(_train_indices)
eval_indices.append(_eval_indices)
_wi_y = labels[_train_indices]
_eval_y = labels[_eval_indices]
wi_y.append(_wi_y)
eval_y.append(_eval_y)
pbar.update(s+1)
return train_indices, eval_indices, wi_y, eval_y
def embed_images(
embedding_model,
train_indices,
num_augmentations,
trivial=False
):
def augment_image(image, num_augmentations, trivial):
""" Perform SimCLR augmentations on the image
"""
if np.max(image) > 1:
image = image/255
augmented_images = [image]
def _run_filters(image):
width = image.shape[1]
height = image.shape[0]
image_aug = simclr_data_augmentations.random_crop_with_resize(
image,
height,
width
)
image_aug = tf.image.random_flip_left_right(image_aug)
image_aug = simclr_data_augmentations.random_color_jitter(image_aug)
image_aug = simclr_data_augmentations.random_blur(
image_aug,
height,
width
)
image_aug = tf.reshape(image_aug, [image.shape[0], image.shape[1], 3])
image_aug = tf.clip_by_value(image_aug, 0., 1.)
return image_aug.numpy()
for _ in range(num_augmentations):
if trivial:
aug_image = image
else:
aug_image = _run_filters(image)
augmented_images.append(aug_image)
augmented_images = np.stack(augmented_images)
return augmented_images
embedding_model.load_model()
unique_indices = np.unique(np.array(train_indices))
ds = dm.load_dataset('lfw', split='train')
embeddings = []
IMAGE_IDX = 'image'
pbar = start_progress_bar(unique_indices.size+1)
num_done=0
for idx, item in enumerate(ds):
if idx in unique_indices:
image = item[IMAGE_IDX]
if num_augmentations > 0:
aug_images = augment_image(image, num_augmentations, trivial)
else:
aug_images = image
processed_images = embedding_model.preprocess_data(aug_images)
embedding = embedding_model.embed_images(processed_images)
embeddings.append(embedding)
num_done += 1
pbar.update(num_done+1)
if idx == unique_indices[-1]:
break
embeddings = np.stack(embeddings)
return unique_indices, embeddings
def train_model_for_episode(
indices_and_embeddings,
train_indices,
wi_y,
num_augmentations,
train_epochs=None,
train_batch_size=5,
multi_label=True
):
train_embeddings = []
train_labels = []
ind = indices_and_embeddings[0]
emb = indices_and_embeddings[1]
for idx, tr_idx in enumerate(train_indices):
train_embeddings.append(emb[np.argwhere(ind==tr_idx)[0][0]])
train_labels += [wi_y[idx] for _ in range(num_augmentations+1)]
train_embeddings = np.concatenate(train_embeddings)
train_labels = np.array(train_labels)
train_embeddings = WeightImprintingClassifier.preprocess_input(train_embeddings)
wi_weights, label_mapping = WeightImprintingClassifier.get_imprinting_weights(
train_embeddings, train_labels, False, multi_label
)
wi_parameters = {
"num_classes": num_ways,
"input_dims": train_embeddings.shape[-1],
"scale": False,
"dense_layer_weights": wi_weights,
"multi_label": multi_label
}
wi_cls = WeightImprintingClassifier(wi_parameters)
if train_epochs:
# ep_y = train_labels
rev_label_mapping = {label_mapping[val]:val for val in label_mapping}
train_y = np.zeros((len(train_labels), num_ways))
for idx_y, l in enumerate(train_labels):
if multi_label:
for _l in l:
train_y[idx_y, rev_label_mapping[_l]] = 1
else:
train_y[idx_y, rev_label_mapping[l]] = 1
wi_cls.train(train_embeddings, train_y, train_epochs, train_batch_size)
return wi_cls, label_mapping
def evaluate_model_for_episode(
model,
eval_x,
eval_y,
label_mapping,
metrics=['hamming', 'jaccard', 'subset_accuracy', 'ap', 'map', 'c_f1', 'o_f1', 'c_precision', 'o_precision', 'c_recall', 'o_recall', 'top1_accuracy', 'top5_accuracy', 'classwise_accuracy', 'c_accuracy'],
threshold=0.7,
multi_label=True
):
eval_x = WeightImprintingClassifier.preprocess_input(eval_x)
logits = model.predict_scores(eval_x).tolist()
if multi_label:
pred_y = model.predict_multi_label(eval_x, threshold)
pred_y = [[label_mapping[v] for v in l] for l in pred_y]
met = model.evaluate_multi_label_metrics(
eval_x, eval_y, label_mapping, threshold, metrics
)
else:
pred_y = model.predict_single_label(eval_x)
pred_y = [label_mapping[l] for l in pred_y]
met = model.evaluate_single_label_metrics(
eval_x, eval_y, label_mapping, metrics
)
return pred_y, met, logits
def run_episode_through_model(
indices_and_embeddings,
train_indices,
eval_indices,
wi_y,
eval_y,
thresholds=None,
num_augmentations=0,
train_epochs=None,
train_batch_size=5,
metrics=['hamming', 'jaccard', 'subset_accuracy', 'ap', 'map', 'c_f1', 'o_f1', 'c_precision', 'o_precision', 'c_recall', 'o_recall', 'top1_accuracy', 'top5_accuracy', 'classwise_accuracy', 'c_accuracy'],
embeddings=None,
multi_label=True
):
metrics_values = {m:[] for m in metrics}
wi_cls, label_mapping = train_model_for_episode(
indices_and_embeddings,
train_indices,
wi_y,
num_augmentations,
train_epochs,
train_batch_size,
multi_label=multi_label
)
eval_x = embeddings[eval_indices]
ep_logits = []
if multi_label:
for t in thresholds:
pred_labels, met, logits = evaluate_model_for_episode(
wi_cls,
eval_x,
eval_y,
label_mapping,
threshold=t,
metrics=metrics,
multi_label=True
)
ep_logits.append(logits)
for m in metrics:
metrics_values[m].append(met[m])
else:
pred_labels, metrics_values, logits = evaluate_model_for_episode(
wi_cls,
eval_x,
eval_y,
label_mapping,
metrics=metrics,
multi_label=False
)
ep_logits = logits
return metrics_values, ep_logits
def run_evaluations(
indices_and_embeddings,
train_indices,
eval_indices,
wi_y,
eval_y,
num_episodes,
num_ways,
thresholds,
verbose=True,
normalize=True,
train_epochs=None,
train_batch_size=5,
metrics=['hamming', 'jaccard', 'subset_accuracy', 'ap', 'map', 'c_f1', 'o_f1', 'c_precision', 'o_precision', 'c_recall', 'o_recall', 'top1_accuracy', 'top5_accuracy', 'classwise_accuracy', 'c_accuracy'],
embeddings=None,
num_augmentations=0,
multi_label=True
):
metrics_values = {m:[] for m in metrics}
all_logits = []
if verbose:
pbar = start_progress_bar(num_episodes)
for idx_ep in range(num_episodes):
_train_indices = train_indices[idx_ep]
_eval_indices = eval_indices[idx_ep]
if multi_label:
_wi_y = [[label] for label in wi_y[idx_ep]]
_eval_y = [[label] for label in eval_y[idx_ep]]
else:
_wi_y = wi_y[idx_ep]
_eval_y = eval_y[idx_ep]
met, ep_logits = run_episode_through_model(
indices_and_embeddings,
_train_indices,
_eval_indices,
_wi_y,
_eval_y,
num_augmentations=num_augmentations,
train_epochs=train_epochs,
train_batch_size=train_batch_size,
embeddings=embeddings,
thresholds=thresholds,
metrics=metrics,
multi_label=multi_label
)
all_logits.append(ep_logits)
for m in metrics:
metrics_values[m].append(met[m])
if verbose:
pbar.update(idx_ep+1)
return metrics_values, all_logits
def get_max_mean_jaccard_index_by_threshold(metrics_thresholds):
max_mean_jaccard = np.max([np.mean(mt['jaccard']) for mt in metrics_thresholds])
return max_mean_jaccard
def get_max_mean_jaccard_index_with_threshold(metrics_thresholds):
arr = np.array(metrics_thresholds['jaccard'])
max_mean_jaccard = np.max(np.mean(arr, 0))
threshold = np.argmax(np.mean(arr, 0))
return max_mean_jaccard, threshold
def get_max_mean_f1_score_with_threshold(metrics_thresholds):
arr = np.array(metrics_thresholds['f1_score'])
max_mean_jaccard = np.max(np.mean(arr, 0))
threshold = np.argmax(np.mean(arr, 0))
return max_mean_jaccard, threshold
def get_mean_max_jaccard_index_by_episode(metrics_thresholds):
mean_max_jaccard = np.mean(np.max(np.array([mt['jaccard'] for mt in metrics_thresholds]), axis=0))
return mean_max_jaccard
def plot_metrics_by_threshold(
metrics_thresholds,
thresholds,
metrics=['hamming', 'jaccard', 'subset_accuracy', 'ap', 'map', 'c_f1', 'o_f1', 'c_precision', 'o_precision', 'c_recall', 'o_recall', 'top1_accuracy', 'top5_accuracy', 'classwise_accuracy', 'c_accuracy'],
title_suffix=""
):
legend = []
fig = plt.figure(figsize=(10,10))
if 'jaccard' in metrics:
mean_jaccard_threshold = np.mean(np.array(metrics_thresholds['jaccard']), axis=0)
opt_threshold_jaccard = thresholds[np.argmax(mean_jaccard_threshold)]
plt.plot(thresholds, mean_jaccard_threshold, c='blue')
plt.axvline(opt_threshold_jaccard, ls="--", c='blue')
legend.append("Jaccard Index")
legend.append(opt_threshold_jaccard)
if 'hamming' in metrics:
mean_hamming_threshold = np.mean(np.array(metrics_thresholds['hamming']), axis=0)
opt_threshold_hamming = thresholds[np.argmin(mean_hamming_threshold)]
plt.plot(thresholds, mean_hamming_threshold, c='green')
plt.axvline(opt_threshold_hamming, ls="--", c='green')
legend.append("Hamming Score")
legend.append(opt_threshold_hamming)
if 'map' in metrics:
mean_f1_score_threshold = np.mean(np.array(metrics_thresholds['map']), axis=0)
opt_threshold_f1_score = thresholds[np.argmax(mean_f1_score_threshold)]
plt.plot(thresholds, mean_f1_score_threshold, c='red')
plt.axvline(opt_threshold_f1_score, ls="--", c='red')
legend.append("mAP")
legend.append(opt_threshold_f1_score)
if 'o_f1' in metrics:
mean_f1_score_threshold = np.mean(np.array(metrics_thresholds['o_f1']), axis=0)
opt_threshold_f1_score = thresholds[np.argmax(mean_f1_score_threshold)]
plt.plot(thresholds, mean_f1_score_threshold, c='yellow')
plt.axvline(opt_threshold_f1_score, ls="--", c='yellow')
legend.append("OF1")
legend.append(opt_threshold_f1_score)
if 'c_f1' in metrics:
mean_f1_score_threshold = np.mean(np.array(metrics_thresholds['c_f1']), axis=0)
opt_threshold_f1_score = thresholds[np.argmax(mean_f1_score_threshold)]
plt.plot(thresholds, mean_f1_score_threshold, c='orange')
plt.axvline(opt_threshold_f1_score, ls="--", c='orange')
legend.append("CF1")
legend.append(opt_threshold_f1_score)
if 'o_precision' in metrics:
mean_f1_score_threshold = np.mean(np.array(metrics_thresholds['o_precision']), axis=0)
opt_threshold_f1_score = thresholds[np.argmax(mean_f1_score_threshold)]
plt.plot(thresholds, mean_f1_score_threshold, c='purple')
plt.axvline(opt_threshold_f1_score, ls="--", c='purple')
legend.append("OP")
legend.append(opt_threshold_f1_score)
if 'c_precision' in metrics:
mean_f1_score_threshold = np.mean(np.array(metrics_thresholds['c_precision']), axis=0)
opt_threshold_f1_score = thresholds[np.argmax(mean_f1_score_threshold)]
plt.plot(thresholds, mean_f1_score_threshold, c='cyan')
plt.axvline(opt_threshold_f1_score, ls="--", c='cyan')
legend.append("CP")
legend.append(opt_threshold_f1_score)
if 'o_recall' in metrics:
mean_f1_score_threshold = np.mean(np.array(metrics_thresholds['o_recall']), axis=0)
opt_threshold_f1_score = thresholds[np.argmax(mean_f1_score_threshold)]
plt.plot(thresholds, mean_f1_score_threshold, c='brown')
plt.axvline(opt_threshold_f1_score, ls="--", c='brown')
legend.append("OR")
legend.append(opt_threshold_f1_score)
if 'c_recall' in metrics:
mean_f1_score_threshold = np.mean(np.array(metrics_thresholds['c_recall']), axis=0)
opt_threshold_f1_score = thresholds[np.argmax(mean_f1_score_threshold)]
plt.plot(thresholds, mean_f1_score_threshold, c='pink')
plt.axvline(opt_threshold_f1_score, ls="--", c='pink')
legend.append("CR")
legend.append(opt_threshold_f1_score)
if 'c_accuracy' in metrics:
mean_f1_score_threshold = np.mean(np.array(metrics_thresholds['c_accuracy']), axis=0)
opt_threshold_f1_score = thresholds[np.argmax(mean_f1_score_threshold)]
plt.plot(thresholds, mean_f1_score_threshold, c='maroon')
plt.axvline(opt_threshold_f1_score, ls="--", c='maroon')
legend.append("CACC")
legend.append(opt_threshold_f1_score)
if 'top1_accuracy' in metrics:
mean_f1_score_threshold = np.mean(np.array(metrics_thresholds['top1_accuracy']), axis=0)
opt_threshold_f1_score = thresholds[np.argmax(mean_f1_score_threshold)]
plt.plot(thresholds, mean_f1_score_threshold, c='magenta')
plt.axvline(opt_threshold_f1_score, ls="--", c='magenta')
legend.append("TOP1")
legend.append(opt_threshold_f1_score)
if 'top5_accuracy' in metrics:
mean_f1_score_threshold = np.mean(np.array(metrics_thresholds['top5_accuracy']), axis=0)
opt_threshold_f1_score = thresholds[np.argmax(mean_f1_score_threshold)]
plt.plot(thresholds, mean_f1_score_threshold, c='slategray')
plt.axvline(opt_threshold_f1_score, ls="--", c='slategray')
legend.append("TOP5")
legend.append(opt_threshold_f1_score)
plt.xlabel('Threshold')
plt.ylabel('Value')
plt.legend(legend)
title = title_suffix+"\nMulti label metrics by threshold"
plt.title(title)
plt.grid()
fname = os.path.join(PLOT_DIR, title_suffix)
plt.savefig(fname)
plt.show()
```
## Setting multiple thresholds
```
# No threshold for softmax
thresholds = None
```
# Main
## Picking indices
```
train_indices, eval_indices, wi_y, eval_y = prepare_indices(
num_ways, num_shot, num_eval, num_episodes, label_dictionary, train_labels, shuffle
)
indices, embeddings = embed_images(
embedding_model,
train_indices,
num_augmentations,
trivial=trivial
)
```
## CLIP
```
clip_embeddings_train_fn = "clip" + train_embeddings_filename_suffix
clip_embeddings_train = get_ndarray_from_drive(drive, folderid, clip_embeddings_train_fn)
import warnings
warnings.filterwarnings('ignore')
if train_epochs_arr == [0]:
if trivial:
results_filename = "new_metrics"+dataset_name+"_softmax_0t"+str(num_ways)+"w"+str(num_shot)+"s"+str(num_augmentations)+"a_trivial_metrics_with_logits.json"
else:
results_filename = "new_metrics"+dataset_name+"_softmax_0t"+str(num_ways)+"w"+str(num_shot)+"s"+str(num_augmentations)+"a_metrics_with_logits.json"
else:
if trivial:
results_filename = "new_metrics"+dataset_name+"_softmax_"+str(num_ways)+"w"+str(num_shot)+"s"+str(num_augmentations)+"a_trivial_metrics_with_logits.json"
else:
results_filename = "new_metrics"+dataset_name+"_softmax_"+str(num_ways)+"w"+str(num_shot)+"s"+str(num_augmentations)+"a_metrics_with_logits.json"
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
download_file_by_name(drive, folderid, results_filename)
if results_filename in os.listdir():
with open(results_filename, 'r') as f:
json_loaded = json.load(f)
clip_metrics_over_train_epochs = json_loaded['metrics']
logits_over_train_epochs = json_loaded["logits"]
else:
clip_metrics_over_train_epochs = []
logits_over_train_epochs = []
for idx, train_epochs in enumerate(train_epochs_arr):
if idx < len(clip_metrics_over_train_epochs):
continue
print(train_epochs)
clip_metrics_thresholds, all_logits = run_evaluations(
(indices, embeddings),
train_indices,
eval_indices,
wi_y,
eval_y,
num_episodes,
num_ways,
thresholds,
train_epochs=train_epochs,
num_augmentations=num_augmentations,
embeddings=clip_embeddings_train,
multi_label=multi_label,
metrics=metrics_val
)
clip_metrics_over_train_epochs.append(clip_metrics_thresholds)
logits_over_train_epochs.append(all_logits)
fin_list = []
for a1 in wi_y:
fin_a1_list = []
for a2 in a1:
new_val = a2.decode("utf-8")
fin_a1_list.append(new_val)
fin_list.append(fin_a1_list)
with open(results_filename, 'w') as f:
results = {'metrics': clip_metrics_over_train_epochs,
"logits": logits_over_train_epochs,
"true_labels": fin_list}
json.dump(results, f)
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
delete_file_by_name(drive, folderid, results_filename)
save_to_drive(drive, folderid, results_filename)
def get_best_metric_and_threshold(mt, metric_name, thresholds, optimal='max'):
if optimal=='max':
opt_value = np.max(np.mean(np.array(mt[metric_name]), axis=0))
opt_threshold = thresholds[np.argmax(np.mean(np.array(mt[metric_name]), axis=0))]
if optimal=='min':
opt_value = np.min(np.mean(np.array(mt[metric_name]), axis=0))
opt_threshold = thresholds[np.argmin(np.mean(np.array(mt[metric_name]), axis=0))]
return opt_value, opt_threshold
def get_avg_metric(mt, metric_name):
opt_value = np.mean(np.array(mt[metric_name]), axis=0)
return opt_value
all_metrics = ['accuracy', 'map', 'c_f1', 'o_f1', 'c_precision', 'o_precision', 'c_recall', 'o_recall', 'top1_accuracy', 'top5_accuracy', 'c_accuracy']
f1_vals = []
f1_t_vals = []
jaccard_vals = []
jaccard_t_vals = []
final_dict = {}
for ind_metric in all_metrics:
vals = []
t_vals = []
final_array = []
for mt in clip_metrics_over_train_epochs:
ret_val = get_avg_metric(mt,ind_metric)
vals.append(ret_val)
final_array.append(vals)
final_dict[ind_metric] = final_array
if train_epochs_arr == [0]:
if trivial:
graph_filename = "new_metrics"+dataset_name+"_softmax_0t"+str(num_ways)+"w"+str(num_shot)+"s"+str(num_augmentations)+"a_trivial_metrics_graphs.json"
else:
graph_filename = "new_metrics"+dataset_name+"_softmax_0t"+str(num_ways)+"w"+str(num_shot)+"s"+str(num_augmentations)+"a_metrics_graphs.json"
else:
if trivial:
graph_filename = "new_metrics"+dataset_name+"_softmax_"+str(num_ways)+"w"+str(num_shot)+"s"+str(num_augmentations)+"a_trivial_metrics_graphs.json"
else:
graph_filename = "new_metrics"+dataset_name+"_softmax_"+str(num_ways)+"w"+str(num_shot)+"s"+str(num_augmentations)+"a_metrics_graphs.json"
with open(graph_filename, 'w') as f:
json.dump(final_dict, f)
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
delete_file_by_name(drive, folderid, graph_filename)
save_to_drive(drive, folderid, graph_filename)
final_dict
```
|
github_jupyter
|
# Analyzing data with Dask, SQL, and Coiled
In this notebook, we look at using [Dask-SQL](https://dask-sql.readthedocs.io/en/latest/), an exciting new open-source library which adds a SQL query layer on top of Dask. This allows you to query and transform Dask DataFrames using common SQL operations.
## Launch a cluster
Let's first start by creating a Coiled cluster which uses the `examples/dask-sql` software environment, which has `dask`, `pandas`, `s3fs`, and a few other libraries installed.
```
import coiled
cluster = coiled.Cluster(
n_workers=10,
worker_cpu=4,
worker_memory="30GiB",
software="examples/dask-sql",
)
cluster
```
and then connect Dask to our remote Coiled cluster
```
from dask.distributed import Client
client = Client(cluster)
client.wait_for_workers(10)
client
```
## Getting started with Dask-SQL
Internally, Dask-SQL uses a well-established Java library, Apache Calcite, to parse SQL and perform some initial work on your query. To help Dask-SQL locate JVM shared libraries, we set the `JAVA_HOME` environment variable.
```
import os
os.environ["JAVA_HOME"] = os.environ["CONDA_DIR"]
```
The main interface for interacting with Dask-SQL is the `dask_sql.Context` object. It allows your to register Dask DataFrames as data sources and can convert SQL queries to Dask DataFrame operations.
```
from dask_sql import Context
c = Context()
```
For this notebook, we'll use the NYC taxi dataset, which is publically accessible on AWS S3, as our data source
```
import dask.dataframe as dd
from distributed import wait
df = dd.read_csv(
"s3://nyc-tlc/trip data/yellow_tripdata_2019-*.csv",
dtype={
"payment_type": "UInt8",
"VendorID": "UInt8",
"passenger_count": "UInt8",
"RatecodeID": "UInt8",
},
storage_options={"anon": True}
)
# Load datasest into the cluster's distributed memory.
# This isn't strictly necessary, but does allow us to
# avoid repeated running the same I/O operations.
df = df.persist()
wait(df);
```
We can then use our `dask_sql.Context` to assign a table name to this DataFrame, and then use that table name within SQL queries
```
# Registers our Dask DataFrame df as a table with the name "taxi"
c.register_dask_table(df, "taxi")
# Perform a SQL operation on the "taxi" table
result = c.sql("SELECT count(1) FROM taxi")
result
```
Note that this returned another Dask DataFrame and no computation has been run yet. This is similar to other Dask DataFrame operations, which are lazily evaluated. We can call `.compute()` to run the computation on our cluster.
```
result.compute()
```
Hooray, we've run our first SQL query with Dask-SQL! Let's try out some more complex queries.
## More complex SQL examples
With Dask-SQL we can run more complex SQL statements like, for example, a groupby-aggregation:
```
c.sql('SELECT avg(tip_amount) FROM taxi GROUP BY passenger_count').compute()
```
NOTE: that the equivalent operatation using the Dask DataFrame API would be:
```python
df.groupby("passenger_count").tip_amount.mean().compute()
```
We can even make plots of our SQL query results for near-real-time interactive data exploration and visualization.
```
c.sql("""
SELECT floor(trip_distance) AS dist, avg(fare_amount) as fare
FROM taxi
WHERE trip_distance < 50 AND trip_distance >= 0
GROUP BY floor(trip_distance)
""").compute().plot(x="dist", y="fare");
```
If you would like to learn more about Dask-SQL check out the [Dask-SQL docs](https://dask-sql.readthedocs.io/) or [source code](https://github.com/nils-braun/dask-sql) on GitHub.
|
github_jupyter
|
```
# Copyright 2019 Google LLC.
#
# Licensed under the Apache License, Version 2.0 (the "License")
import tensorflow as tf
import tensorflow.keras as keras
from tensorflow.keras import layers
import tensorflow.keras.backend as keras_backend
tf.keras.backend.set_floatx('float32')
import tensorflow_probability as tfp
from tensorflow_probability.python.layers import util as tfp_layers_util
import random
import sys
import time
import os
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
print(tf.__version__) # use tensorflow version >= 2.0.0
#pip install tensorflow=2.0.0
#pip install --upgrade tensorflow-probability
exp_type = 'MAML' # choose from 'MAML', 'MR-MAML-W', 'MR-MAML-A'
class SinusoidGenerator():
def __init__(self, K=10, width=5, K_amp=20, phase=0, amps = None, amp_ind=None, amplitude =None, seed = None):
'''
Args:
K: batch size. Number of values sampled at every batch.
amplitude: Sine wave amplitude.
pahse: Sine wave phase.
'''
self.K = K
self.width = width
self.K_amp = K_amp
self.phase = phase
self.seed = seed
self.x = self._sample_x()
self.amp_ind = amp_ind if amp_ind is not None else random.randint(0,self.K_amp-5)
self.amps = amps if amps is not None else np.linspace(0.1,4,self.K_amp)
self.amplitude = amplitude if amplitude is not None else self.amps[self.amp_ind]
def _sample_x(self):
if self.seed is not None:
np.random.seed(self.seed)
return np.random.uniform(-self.width, self.width, self.K)
def batch(self, noise_scale, x = None):
'''return xa is [K, d_x+d_a], y is [K, d_y]'''
if x is None:
x = self._sample_x()
x = x[:, None]
amp = np.zeros([1, self.K_amp])
amp[0,self.amp_ind] = 1
amp = np.tile(amp, x.shape)
xa = np.concatenate([x, amp], axis = 1)
y = self.amplitude * np.sin(x - self.phase) + np.random.normal(scale = noise_scale, size = x.shape)
return xa, y
def equally_spaced_samples(self, K=None, width=None):
'''Returns K equally spaced samples.'''
if K is None:
K = self.K
if width is None:
width = self.width
return self.batch(noise_scale = 0, x=np.linspace(-width+0.5, width-0.5, K))
noise_scale = 0.1 #@param {type:"number"}
n_obs = 20 #@param {type:"number"}
n_context = 10 #@param {type:"number"}
K_amp = 20 #@param {type:"number"}
x_width = 5 #@param {type:"number"}
n_iter = 20000 #@param {type:"number"}
amps = np.linspace(0.1,4,K_amp)
lr_inner = 0.01 #@param {type:"number"}
dim_w = 5 #@param {type:"number"}
train_ds = [SinusoidGenerator(K=n_context, width = x_width, \
K_amp = K_amp, amps = amps) \
for _ in range(n_iter)]
class SineModel(keras.Model):
def __init__(self):
super(SineModel, self).__init__() # python 2 syntax
# super().__init__() # python 3 syntax
self.hidden1 = keras.layers.Dense(40)
self.hidden2 = keras.layers.Dense(40)
self.out = keras.layers.Dense(1)
def call(self, x):
x = keras.activations.relu(self.hidden1(x))
x = keras.activations.relu(self.hidden2(x))
x = self.out(x)
return x
def kl_qp_gaussian(mu_q, sigma_q, mu_p, sigma_p):
"""Kullback-Leibler KL(N(mu_q), Diag(sigma_q^2) || N(mu_p), Diag(sigma_p^2))"""
sigma2_q = tf.square(sigma_q) + 1e-16
sigma2_p = tf.square(sigma_p) + 1e-16
temp = tf.math.log(sigma2_p) - tf.math.log(sigma2_q) - 1.0 + \
sigma2_q / sigma2_p + tf.square(mu_q - mu_p) / sigma2_p #n_target * d_w
kl = 0.5 * tf.reduce_mean(temp, axis = 1)
return tf.reduce_mean(kl)
def copy_model(model, x=None, input_shape=None):
'''
Copy model weights to a new model.
Args:
model: model to be copied.
x: An input example.
'''
copied_model = SineModel()
if x is not None:
copied_model.call(tf.convert_to_tensor(x))
if input_shape is not None:
copied_model.build(tf.TensorShape([None,input_shape]))
copied_model.set_weights(model.get_weights())
return copied_model
def np_to_tensor(list_of_numpy_objs):
return (tf.convert_to_tensor(obj, dtype=tf.float32) for obj in list_of_numpy_objs)
def compute_loss(model, xa, y):
y_hat = model.call(xa)
loss = keras_backend.mean(keras.losses.mean_squared_error(y, y_hat))
return loss, y_hat
def train_batch(xa, y, model, optimizer, encoder=None):
tensor_xa, tensor_y = np_to_tensor((xa, y))
if exp_type == 'MAML':
with tf.GradientTape() as tape:
loss, _ = compute_loss(model, tensor_xa, tensor_y)
if exp_type == 'MR-MAML-W':
w = encoder(tensor_xa)
with tf.GradientTape() as tape:
y_hat = model.call(w)
loss = keras_backend.mean(keras.losses.mean_squared_error(tensor_y, y_hat))
if exp_type == 'MR-MAML-A':
_, w, _ = encoder(tensor_xa)
with tf.GradientTape() as tape:
y_hat = model.call(w)
loss = keras_backend.mean(keras.losses.mean_squared_error(y, y_hat))
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
return loss
def test_inner_loop(model, optimizer, xa_context, y_context, xa_target, y_target, num_steps, encoder=None):
inner_record = []
tensor_xa_target, tensor_y_target = np_to_tensor((xa_target, y_target))
if exp_type == 'MAML':
w_target = tensor_xa_target
if exp_type == 'MR-MAML-W':
w_target = encoder(tensor_xa_target)
if exp_type == 'MR-MAML-A':
_, w_target, _ = encoder(tensor_xa_target)
for step in range(0, np.max(num_steps) + 1):
if step in num_steps:
if exp_type == 'MAML':
loss, y_hat = compute_loss(model, w_target, tensor_y_target)
else:
y_hat = model.call(w_target)
loss = keras_backend.mean(keras.losses.mean_squared_error(tensor_y_target, y_hat))
inner_record.append((step, y_hat, loss))
loss = train_batch(xa_context, y_context, model, optimizer, encoder)
return inner_record
def eval_sinewave_for_test(model, sinusoid_generator, num_steps=(0, 1, 10), encoder=None, learning_rate = lr_inner, ax = None, legend= False):
# data for training
xa_context, y_context = sinusoid_generator.batch(noise_scale = noise_scale)
y_context = y_context + np.random.normal(scale = noise_scale, size = y_context.shape)
# data for validation
xa_target, y_target = sinusoid_generator.equally_spaced_samples(K = 200, width = 5)
y_target = y_target + np.random.normal(scale = noise_scale, size = y_target.shape)
# copy model so we can use the same model multiple times
if exp_type == 'MAML':
copied_model = copy_model(model, x = xa_context)
else:
copied_model = copy_model(model, input_shape=dim_w)
optimizer = keras.optimizers.SGD(learning_rate=learning_rate)
inner_record = test_inner_loop(copied_model, optimizer, xa_context, y_context, xa_target, y_target, num_steps, encoder)
# plot
if ax is not None:
plt.sca(ax)
x_context = xa_context[:,0,None]
x_target = xa_target[:,0,None]
train, = plt.plot(x_context, y_context, '^')
ground_truth, = plt.plot(x_target, y_target0, linewidth=2.0)
plots = [train, ground_truth]
legends = ['Context Points', 'True Function']
for n, y_hat, loss in inner_record:
cur, = plt.plot(x_target, y_hat[:, 0], '--')
plots.append(cur)
legends.append('After {} Steps'.format(n))
if legend:
plt.legend(plots, legends, loc='center left', bbox_to_anchor=(1, 0.5))
plt.ylim(-6, 6)
plt.axvline(x=-sinusoid_generator.width, linestyle='--')
plt.axvline(x=sinusoid_generator.width,linestyle='--')
return inner_record
exp_type = 'MAML'
if exp_type == 'MAML':
model = SineModel()
model.build((None, K_amp+1))
dataset = train_ds
optimizer = keras.optimizers.Adam()
total_loss = 0
n_iter = 15000
losses = []
for i, t in enumerate(random.sample(dataset, n_iter)):
xa_train, y_train = np_to_tensor(t.batch(noise_scale = noise_scale))
with tf.GradientTape(watch_accessed_variables=False) as test_tape:
test_tape.watch(model.trainable_variables)
with tf.GradientTape() as train_tape:
train_loss, _ = compute_loss(model, xa_train, y_train)
model_copy = copy_model(model, xa_train)
gradients_inner = train_tape.gradient(train_loss, model.trainable_variables) # \nabla_{\theta}
k = 0
for j in range(len(model_copy.layers)):
model_copy.layers[j].kernel = tf.subtract(model.layers[j].kernel, # \phi_t = T(\theta, \nabla_{\theta})
tf.multiply(lr_inner, gradients_inner[k]))
model_copy.layers[j].bias = tf.subtract(model.layers[j].bias,
tf.multiply(lr_inner, gradients_inner[k+1]))
k += 2
xa_validation, y_validation = np_to_tensor(t.batch(noise_scale = noise_scale))
test_loss, y_hat = compute_loss(model_copy, xa_validation, y_validation) # test_loss
gradients_outer = test_tape.gradient(test_loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients_outer, model.trainable_variables))
total_loss += test_loss
loss = total_loss / (i+1.0)
if i % 1000 == 0:
print('Step {}: loss = {}'.format(i, loss))
if exp_type == 'MAML':
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR)
n_context = 5
n_test_task = 100
errs = []
for ii in range(n_test_task):
np.random.seed(ii)
A = np.random.uniform(low = amps[0], high = amps[-1])
test_ds = SinusoidGenerator(K=n_context, seed = ii, amplitude = A, amp_ind= random.randint(0,K_amp-5))
inner_record = eval_sinewave_for_test(model, test_ds, num_steps=(0, 1, 5, 100));
errs.append(inner_record[-1][2].numpy())
print('Model is', exp_type, 'meta-test MSE is', np.mean(errs) )
```
# Training & Testing for MR-MAML(W)
```
if exp_type == 'MR-MAML-W':
model = SineModel()
dataset = train_ds
optimizer = keras.optimizers.Adam()
Beta = 5e-5
learning_rate = 1e-3
n_iter = 15000
model.build((None, dim_w))
kernel_posterior_fn=tfp_layers_util.default_mean_field_normal_fn(untransformed_scale_initializer=tf.compat.v1.initializers.random_normal(
mean=-50., stddev=0.1))
encoder_w = tf.keras.Sequential([
tfp.layers.DenseReparameterization(100, activation=tf.nn.relu, kernel_posterior_fn=kernel_posterior_fn,input_shape=(1 + K_amp,)),
tfp.layers.DenseReparameterization(dim_w,kernel_posterior_fn=kernel_posterior_fn),
])
total_loss = 0
losses = []
start = time.time()
for i, t in enumerate(random.sample(dataset, n_iter)):
xa_train, y_train = np_to_tensor(t.batch(noise_scale = noise_scale)) #[K, 1]
x_validation = np.random.uniform(-x_width, x_width, n_obs - n_context)
xa_validation, y_validation = np_to_tensor(t.batch(noise_scale = noise_scale, x = x_validation))
all_var = encoder_w.trainable_variables + model.trainable_variables
with tf.GradientTape(watch_accessed_variables=False) as test_tape:
test_tape.watch(all_var)
with tf.GradientTape() as train_tape:
w_train = encoder_w(xa_train)
y_hat_train = model.call(w_train)
train_loss = keras_backend.mean(keras.losses.mean_squared_error(y_train, y_hat_train)) # K*1
gradients_inner = train_tape.gradient(train_loss, model.trainable_variables) # \nabla_{\theta}
model_copy = copy_model(model, x = w_train)
k = 0
for j in range(len(model_copy.layers)):
model_copy.layers[j].kernel = tf.subtract(model.layers[j].kernel, # \phi_t = T(\theta, \nabla_{\theta})
tf.multiply(lr_inner, gradients_inner[k]))
model_copy.layers[j].bias = tf.subtract(model.layers[j].bias,
tf.multiply(lr_inner, gradients_inner[k+1]))
k += 2
w_validation = encoder_w(xa_validation)
y_hat_validation = model_copy.call(w_validation)
mse_loss = keras_backend.mean(keras.losses.mean_squared_error(y_validation, y_hat_validation))
kl_loss = Beta * sum(encoder_w.losses)
validation_loss = mse_loss + kl_loss
gradients_outer = test_tape.gradient(validation_loss,all_var)
keras.optimizers.Adam(learning_rate=learning_rate).apply_gradients(zip(gradients_outer, all_var))
losses.append(validation_loss.numpy())
if i % 1000 == 0 and i > 0:
print('Step {}:'.format(i), 'loss=', np.mean(losses))
losses = []
if exp_type == 'MR-MAML-W':
n_context = 5
n_test_task = 100
errs = []
for ii in range(n_test_task):
np.random.seed(ii)
A = np.random.uniform(low = amps[0], high = amps[-1])
test_ds = SinusoidGenerator(K=n_context, seed = ii, amplitude = A, amp_ind= random.randint(0,K_amp-5))
inner_record = eval_sinewave_for_test(model, test_ds, num_steps=(0, 1, 5, 100), encoder=encoder_w);
errs.append(inner_record[-1][2].numpy())
print('Model is', exp_type, ', meta-test MSE is', np.mean(errs) )
```
#Training & Testing for MR-MAML(A)
```
if exp_type == 'MR-MAML-A':
class Encoder(keras.Model):
def __init__(self, dim_w=5, name='encoder', **kwargs):
# super().__init__(name = name)
super(Encoder, self).__init__(name = name)
self.dense_proj = layers.Dense(80, activation='relu')
self.dense_mu = layers.Dense(dim_w)
self.dense_sigma_w = layers.Dense(dim_w)
def call(self, inputs):
h = self.dense_proj(inputs)
mu_w = self.dense_mu(h)
sigma_w = self.dense_sigma_w(h)
sigma_w = tf.nn.softplus(sigma_w)
ws = mu_w + tf.random.normal(tf.shape(mu_w)) * sigma_w
return ws, mu_w, sigma_w
model = SineModel()
model.build((None, dim_w))
encoder_w = Encoder(dim_w = dim_w)
encoder_w.build((None, K_amp+1))
Beta = 5.0
n_iter = 10000
dataset = train_ds
optimizer = keras.optimizers.Adam()
losses = [];
for i, t in enumerate(random.sample(dataset, n_iter)):
xa_train, y_train = np_to_tensor(t.batch(noise_scale = noise_scale)) #[K, 1]
with tf.GradientTape(watch_accessed_variables=False) as test_tape, tf.GradientTape(watch_accessed_variables=False) as encoder_test_tape:
test_tape.watch(model.trainable_variables)
encoder_test_tape.watch(encoder_w.trainable_variables)
with tf.GradientTape() as train_tape:
w_train, _, _ = encoder_w(xa_train)
y_hat = model.call(w_train)
train_loss = keras_backend.mean(keras.losses.mean_squared_error(y_train, y_hat))
model_copy = copy_model(model, x=w_train)
gradients_inner = train_tape.gradient(train_loss, model.trainable_variables) # \nabla_{\theta}
k = 0
for j in range(len(model_copy.layers)):
model_copy.layers[j].kernel = tf.subtract(model.layers[j].kernel, # \phi_t = T(\theta, \nabla_{\theta})
tf.multiply(lr_inner, gradients_inner[k]))
model_copy.layers[j].bias = tf.subtract(model.layers[j].bias,
tf.multiply(lr_inner, gradients_inner[k+1]))
k += 2
x_validation = np.random.uniform(-x_width, x_width, n_obs - n_context)
xa_validation, y_validation = np_to_tensor(t.batch(noise_scale = noise_scale, x = x_validation))
w_validation, w_mu_validation, w_sigma_validation = encoder_w(xa_validation)
test_mse, _ = compute_loss(model_copy, w_validation, y_validation)
kl_ib = kl_qp_gaussian(w_mu_validation, w_sigma_validation,
tf.zeros(tf.shape(w_mu_validation)), tf.ones(tf.shape(w_sigma_validation)))
test_loss = test_mse + Beta * kl_ib
gradients_outer = test_tape.gradient(test_mse, model.trainable_variables)
optimizer.apply_gradients(zip(gradients_outer, model.trainable_variables))
gradients = encoder_test_tape.gradient(test_loss,encoder_w.trainable_variables)
keras.optimizers.Adam(learning_rate=0.001).apply_gradients(zip(gradients, encoder_w.trainable_variables))
losses.append(test_loss)
if i % 1000 == 0 and i > 0:
print('Step {}:'.format(i), 'loss = ', np.mean(losses))
if exp_type == 'MR-MAML-A':
n_context = 5
n_test_task = 100
errs = []
for ii in range(n_test_task):
np.random.seed(ii)
A = np.random.uniform(low = amps[0], high = amps[-1])
test_ds = SinusoidGenerator(K=n_context, seed = ii, amplitude = A, amp_ind= random.randint(0,K_amp-5))
inner_record = eval_sinewave_for_test(model, test_ds, num_steps=(0, 1, 5, 100), encoder=encoder_w);
errs.append(inner_record[-1][2].numpy())
print('Model is', exp_type, ', meta-test MSE is', np.mean(errs) )
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/gpdsec/Residual-Neural-Network/blob/main/Custom_Resnet_1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
*It's custom ResNet trained demonstration purpose, not for accuracy.
Dataset used is cats_vs_dogs dataset from tensorflow_dataset with **Custom Augmentatior** for data augmentation*
---
```
from google.colab import drive
drive.mount('/content/drive')
```
### **1. Importing Libraries**
```
import tensorflow as tf
from tensorflow.keras.layers import Dense, Dropout, Flatten, Conv2D, MaxPooling2D, BatchNormalization, Input, GlobalMaxPooling2D, add, ReLU
from tensorflow.keras import layers
from tensorflow.keras import Sequential
import tensorflow_datasets as tfds
import pandas as pd
import numpy as np
from tensorflow.keras import Model
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
from PIL import Image
from tqdm.notebook import tqdm
import os
import time
%matplotlib inline
```
### **2. Loading & Processing Data**
##### **Loading Data**
```
(train_ds, val_ds, test_ds), info = tfds.load(
'cats_vs_dogs',
split=['train[:80%]', 'train[80%:90%]', 'train[90%:]'],
with_info=True,
as_supervised=True)
## Image preprocessing function
def preprocess(img, lbl):
image = tf.image.resize_with_pad(img, target_height=224, target_width=224)
image = tf.divide(image, 255)
label = [0,0]
if int(lbl) == 1:
label[1]=1
else:
label[0]=1
return image, tf.cast(label, tf.float32)
train_ds = train_ds.map(preprocess)
test_ds = test_ds.map(preprocess)
val_ds = val_ds.map(preprocess)
info
```
#### **Data Augmentation layer**
```
###### Important Variables
batch_size = 32
shape = (224, 224, 3)
training_steps = int(18610/batch_size)
validation_steps = int(2326/batch_size)
path = '/content/drive/MyDrive/Colab Notebooks/cats_v_dogs.h5'
####### Data agumentation layer
# RandomFlip and RandomRotation Suits my need for Data Agumentation
augmentation=Sequential([
layers.experimental.preprocessing.RandomFlip("horizontal_and_vertical"),
layers.experimental.preprocessing.RandomRotation(0.2),
])
####### Data Shuffle and batch Function
def shufle_batch(train_set, val_set, batch_size):
train_set=(train_set.shuffle(1000).batch(batch_size))
train_set = train_set.map(lambda x, y: (augmentation(x, training=True), y))
val_set = (val_set.shuffle(1000).batch(batch_size))
val_set = val_set.map(lambda x, y: (augmentation(x, training=True), y))
return train_set, val_set
train_set, val_set = shufle_batch(train_ds, val_ds, batch_size)
```
## **3. Creating Model**
##### **Creating Residual block**
```
def residual_block(x, feature_map, filter=(3,3) , _strides=(1,1), _network_shortcut=False):
shortcut = x
x = Conv2D(feature_map, filter, strides=_strides, activation='relu', padding='same')(x)
x = BatchNormalization()(x)
x = Conv2D(feature_map, filter, strides=_strides, activation='relu', padding='same')(x)
x = BatchNormalization()(x)
if _network_shortcut :
shortcut = Conv2D(feature_map, filter, strides=_strides, activation='relu', padding='same')(shortcut)
shortcut = BatchNormalization()(shortcut)
x = add([shortcut, x])
x = ReLU()(x)
return x
# Build the model using the functional API
i = Input(shape)
x = Conv2D(32, (3, 3), activation='relu', padding='same')(i)
x = BatchNormalization()(x)
x = residual_block(x, 32, filter=(3,3) , _strides=(1,1), _network_shortcut=False)
#x = Conv2D(32, (3, 3), activation='relu', padding='same')(x)
#x = BatchNormalization()(x)
x = MaxPooling2D((2, 2))(x)
x = Conv2D(64, (3, 3), activation='relu', padding='same')(x)
x = BatchNormalization()(x)
x = residual_block(x,64, filter=(3,3) , _strides=(1,1), _network_shortcut=False)
x = MaxPooling2D((2, 2))(x)
x = Conv2D(64, (3, 3), activation='relu', padding='same')(x)
x = BatchNormalization()(x)
x = MaxPooling2D((2, 2))(x)
x = Conv2D(128, (3, 3), activation='relu', padding='same')(x)
x = BatchNormalization()(x)
x = Conv2D(128, (3, 3), activation='relu', padding='same')(x)
x = BatchNormalization()(x)
x = MaxPooling2D((2, 2))(x)
x = Flatten()(x)
x = Dropout(0.2)(x)
x = Dense(512, activation='relu')(x)
x = Dropout(0.2)(x)
x = Dense(2, activation='sigmoid')(x)
model = Model(i, x)
model.compile()
model.summary()
```
### **4. Optimizer and loss Function**
```
loss_object = tf.keras.losses.BinaryCrossentropy(from_logits=False)
Optimiser = tf.keras.optimizers.Adam()
```
### **5. Metrics For Loss and Acuracy**
```
train_loss = tf.keras.metrics.Mean(name='train_loss')
train_accuracy = tf.keras.metrics.BinaryAccuracy(name='train_accuracy')
test_loss = tf.keras.metrics.Mean(name="test_loss")
test_accuracy = tf.keras.metrics.BinaryAccuracy(name='test_accuracy')
```
### **6. Function for training and Testing**
```
@tf.function
def train_step(images, labels):
with tf.GradientTape() as tape:
prediction = model(images, training=True)
loss = loss_object(labels,prediction)
gradient = tape.gradient(loss, model.trainable_variables)
Optimiser.apply_gradients(zip(gradient, model.trainable_variables))
train_loss(loss)
train_accuracy(labels, prediction)
@tf.function
def test_step(images, labels):
prediction = model(images, training = False)
t_loss = loss_object(labels, prediction)
test_loss(t_loss)
test_accuracy(labels, prediction)
```
### **7. Training Model**
```
EPOCHS = 25
Train_LOSS = []
TRain_Accuracy = []
Test_LOSS = []
Test_Accuracy = []
for epoch in range(EPOCHS):
train_loss.reset_states()
train_accuracy.reset_states()
test_loss.reset_states()
test_accuracy.reset_states()
print(f'Epoch : {epoch+1}')
count = 0 # variable to keep tab how much data steps of training
desc = "EPOCHS {:0>4d}".format(epoch+1)
for images, labels in tqdm(train_set, total=training_steps, desc=desc):
train_step(images, labels)
for test_images, test_labels in val_set:
test_step(test_images, test_labels)
print(
f'Loss: {train_loss.result()}, '
f'Accuracy: {train_accuracy.result()*100}, '
f'Test Loss: {test_loss.result()}, '
f'Test Accuracy: {test_accuracy.result()*100}'
)
Train_LOSS.append(train_loss.result())
TRain_Accuracy.append(train_accuracy.result()*100)
Test_LOSS.append(test_loss.result())
Test_Accuracy.append(test_accuracy.result()*100)
### Saving BestModel
if epoch==0:
min_Loss = test_loss.result()
min_Accuracy = test_accuracy.result()*100
elif (min_Loss>test_loss.result()):
if (min_Accuracy <= test_accuracy.result()*100) :
min_Loss = test_loss.result()
min_Accuracy = ( test_accuracy.result()*100)
print(f"Saving Best Model {epoch+1}")
model.save_weights(path) # Saving Model To drive
```
### **8. Ploting Loss and Accuracy Per Iteration**
```
# Plot loss per iteration
plt.plot(Train_LOSS, label='loss')
plt.plot(Test_LOSS, label='val_loss')
plt.title('Plot loss per iteration')
plt.legend()
# Plot Accuracy per iteration
plt.plot(TRain_Accuracy, label='loss')
plt.plot(Test_Accuracy, label='val_loss')
plt.title('Plot Accuracy per iteration')
plt.legend()
```
## 9. Evoluting model
##### **Note-**
Testing Accuracy of Model with Complete Unseen DataSet.
```
model.load_weights(path)
len(test_ds)
test_set = test_ds.shuffle(50).batch(2326)
for images, labels in test_set:
prediction = model.predict(images)
break
## Function For Accuracy
def accuracy(prediction, labels):
corect =0
for i in range(len(prediction)):
pred = prediction[i]
labe = labels[i]
if pred[0]>pred[1] and labe[0]>labe[1]:
corect+=1
elif pred[0]<pred[1] and labe[0]<labe[1]:
corect+=1
return (corect/len(prediction))*100
print(accuracy(prediction, labels))
```
|
github_jupyter
|
```
import geopandas as gpd
import pandas as pd
import os
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import tarfile
from discretize import TensorMesh
from SimPEG.utils import plot2Ddata, surface2ind_topo
from SimPEG.potential_fields import gravity
from SimPEG import (
maps,
data,
data_misfit,
inverse_problem,
regularization,
optimization,
directives,
inversion,
utils,
)
#sagrav = gpd.read_file(r'C:\users\rscott\Downloads\gravity_stations_shp\gravity_stations.shp') #test
print(sagrav['MGA_ZONE'].unique())
sagrav.head()
#survey_array = sagrav[['LONGITUDE','LATITUDE','AHD_ELEVAT','BA_1984_UM']].to_numpy()
survey_array = sagrav[['MGA_EAST','MGA_NORTH','AHD_ELEVAT','BA_1984_UM']].to_numpy()
dobs = survey_array
survey_array.shape
dobs.shape
#dobs_total_bounds = [sagrav['MGA_EAST'].min(),sagrav['MGA_NORTH'].min(),sagrav['MGA_EAST'].max(),sagrav['MGA_NORTH'].max()]
dobs_total_bounds = sagrav.total_bounds
print(dobs_total_bounds)
sa54 = sagrav.loc[sagrav['MGA_ZONE'] == 54]
dobs_total_bounds
minx, miny, maxx, maxy = dobs_total_bounds
minx = sa54['MGA_EAST'].min()
maxx = sa54['MGA_EAST'].max()
miny = sa54['MGA_NORTH'].min()
maxy = sa54['MGA_NORTH'].max()
minxtest = maxx - 0.045
minxtest = maxx - 5000
maxxtest = maxx
minytest = maxy - 0.045
minytest = maxy - 5000
maxytest = maxy
print(minxtest, maxxtest, minytest, maxytest)
# Define receiver locations and observed data
receiver_locations = dobs[:, 0:3]
dobs = dobs[:, -1]
#sagrav_test = sagrav.loc[(sagrav['MGA_EAST'] >= minxtest) & (sagrav['MGA_EAST'] <= maxxtest) & (sagrav['MGA_NORTH'] >= minytest) & (sagrav['MGA_NORTH'] <= maxytest) ]
from tqdm import tqdm
from time import sleep
#print(minxtest, minytest, maxxtest, maxytest)
print(minx, miny, maxx, maxy)
#maxrangey = (maxy - miny)//0.045
#maxrangex = (maxx - minx)//0.045
maxrangey = (maxy - miny)//5000
maxrangex = (maxx - minx)//5000
print(maxrangex, maxrangey)
#with tqdm(total=maxrangey) as pbar:
for i in range(int(maxrangey)):
print(i)
for j in range(int(maxrangex)):
#xmin, ymin, xmax, ymax = sagrav_test.total_bounds
#xmin = minx + j*0.045
#ymin = miny + i*0.045
#xmax = minx + (j+1)*0.045
#ymax = miny + (i+1)*0.045
xmin = minx + j*5000
ymin = miny + i*5000
xmax = minx + (j+1)*5000
ymax = miny + (i+1)*5000
print(xmin, ymin, xmax, ymax)
#sagrav_test = sagrav.loc[(sagrav['LONGITUDE'] >= xmin) & (sagrav['LATITUDE'] >= ymin) & (sagrav['LONGITUDE'] <= xmax) & (sagrav['LATITUDE'] <= ymax) ]
sagrav_test = sa54.loc[(sa54['MGA_EAST'] >= xmin) & (sa54['MGA_NORTH'] >= ymin) & (sa54['MGA_EAST'] <= xmax) & (sa54['MGA_NORTH'] <= ymax) ]
#sac_sussex = sagrav.cx[xmin:xmax, ymin:ymax]
#print(sagrav_test.shape)
if (sagrav_test.shape[0] > 0):
#print(sagrav_test)
break
if (sagrav_test.shape[0] > 3):
print(sagrav_test)
break
print(minx, miny, maxx, maxy, sagrav_test.shape)
print(sagrav_test.total_bounds)
print(xmin, xmax, ymin, ymax)
ncx = 10
ncy = 10
ncz = 5
#dx = 0.0045*2
#dy = 0.0045*2
dx = 500
dy = 500
dz = 200
x0 = xmin
y0 = ymin
z0 = -1000
hx = dx*np.ones(ncx)
hy = dy*np.ones(ncy)
hz = dz*np.ones(ncz)
mesh2 = TensorMesh([hx, hx, hz], x0 = [x0,y0,z0])
mesh2
sagrav_test
survey_array_test = sagrav_test[['LONGITUDE','LATITUDE','AHD_ELEVAT','BA_1984_UM']].to_numpy()
print(survey_array_test.shape)
dobs_test = survey_array_test
receiver_locations_test = dobs_test[:, 0:3]
dobs_test = dobs_test[:, -1]
# Plot
mpl.rcParams.update({"font.size": 12})
fig = plt.figure(figsize=(7, 5))
ax1 = fig.add_axes([0.1, 0.1, 0.73, 0.85])
plot2Ddata(receiver_locations_test, dobs_test, ax=ax1, contourOpts={"cmap": "bwr"})
ax1.set_title("Gravity Anomaly")
ax1.set_xlabel("x (m)")
ax1.set_ylabel("y (m)")
ax2 = fig.add_axes([0.8, 0.1, 0.03, 0.85])
norm = mpl.colors.Normalize(vmin=-np.max(np.abs(dobs_test)), vmax=np.max(np.abs(dobs_test)))
cbar = mpl.colorbar.ColorbarBase(
ax2, norm=norm, orientation="vertical", cmap=mpl.cm.bwr, format="%.1e"
)
cbar.set_label("$mgal$", rotation=270, labelpad=15, size=12)
plt.show()
dobs_test.shape
sagrav_test
maximum_anomaly = np.max(np.abs(dobs_test))
uncertainties = 0.01 * maximum_anomaly * np.ones(np.shape(dobs_test))
print(i)
# Define the receivers. The data consist of vertical gravity anomaly measurements.
# The set of receivers must be defined as a list.
receiver_list = gravity.receivers.Point(receiver_locations_test, components="gz")
receiver_list = [receiver_list]
# Define the source field
source_field = gravity.sources.SourceField(receiver_list=receiver_list)
# Define the survey
survey = gravity.survey.Survey(source_field)
receiver_list
data_object = data.Data(survey, dobs=dobs_test, standard_deviation=uncertainties)
data_object
mesh2
#source_field
# Define density contrast values for each unit in g/cc. Don't make this 0!
# Otherwise the gradient for the 1st iteration is zero and the inversion will
# not converge.
background_density = 1e-6
# Find the indecies of the active cells in forward model (ones below surface)
#ind_active = surface2ind_topo(mesh, xyz_topo)
topo_fake = receiver_locations_test + 399
print(receiver_locations_test)
print(topo_fake)
ind_active = surface2ind_topo(mesh2, receiver_locations_test)
#ind_active = surface2ind_topo(mesh2, topo_fake)
#ind_active = surface2ind_topo(mesh2, topo_fake)
# Define mapping from model to active cells
nC = int(ind_active.sum())
model_map = maps.IdentityMap(nP=nC) # model consists of a value for each active cell
# Define and plot starting model
starting_model = background_density * np.ones(nC)
nC
model_map
ind_active
starting_model
simulation = gravity.simulation.Simulation3DIntegral(
survey=survey, mesh=mesh2, rhoMap=model_map, actInd=ind_active
)
# Define the data misfit. Here the data misfit is the L2 norm of the weighted
# residual between the observed data and the data predicted for a given model.
# Within the data misfit, the residual between predicted and observed data are
# normalized by the data's standard deviation.
dmis = data_misfit.L2DataMisfit(data=data_object, simulation=simulation)
# Define the regularization (model objective function).
reg = regularization.Simple(mesh2, indActive=ind_active, mapping=model_map)
# Define how the optimization problem is solved. Here we will use a projected
# Gauss-Newton approach that employs the conjugate gradient solver.
opt = optimization.ProjectedGNCG(
maxIter=10, lower=-1.0, upper=1.0, maxIterLS=20, maxIterCG=10, tolCG=1e-3
)
# Here we define the inverse problem that is to be solved
inv_prob = inverse_problem.BaseInvProblem(dmis, reg, opt)
dmis.nD
# Defining a starting value for the trade-off parameter (beta) between the data
# misfit and the regularization.
starting_beta = directives.BetaEstimate_ByEig(beta0_ratio=1e0)
# Defining the fractional decrease in beta and the number of Gauss-Newton solves
# for each beta value.
beta_schedule = directives.BetaSchedule(coolingFactor=5, coolingRate=1)
# Options for outputting recovered models and predicted data for each beta.
save_iteration = directives.SaveOutputEveryIteration(save_txt=False)
# Updating the preconditionner if it is model dependent.
update_jacobi = directives.UpdatePreconditioner()
# Setting a stopping criteria for the inversion.
target_misfit = directives.TargetMisfit(chifact=1)
# Add sensitivity weights
sensitivity_weights = directives.UpdateSensitivityWeights(everyIter=False)
# The directives are defined as a list.
directives_list = [
sensitivity_weights,
starting_beta,
beta_schedule,
save_iteration,
update_jacobi,
target_misfit,
]
# Here we combine the inverse problem and the set of directives
inv = inversion.BaseInversion(inv_prob, directives_list)
# Run inversion
recovered_model = inv.run(starting_model)
# Plot Recovered Model
fig = plt.figure(figsize=(9, 4))
plotting_map = maps.InjectActiveCells(mesh2, ind_active, np.nan)
ax1 = fig.add_axes([0.1, 0.1, 0.73, 0.8])
#ax1 = fig.add_axes([10.1, 10.1, 73.73, 80.8])
mesh2.plotSlice(
plotting_map * recovered_model,
normal="Y",
ax=ax1,
ind=int(mesh2.nCy / 2),
grid=True,
clim=(np.min(recovered_model), np.max(recovered_model)),
pcolorOpts={"cmap": "viridis"},
)
ax1.set_title("Model slice at y = 0 m")
ax2 = fig.add_axes([0.85, 0.1, 0.05, 0.8])
norm = mpl.colors.Normalize(vmin=np.min(recovered_model), vmax=np.max(recovered_model))
cbar = mpl.colorbar.ColorbarBase(
ax2, norm=norm, orientation="vertical", cmap=mpl.cm.viridis
)
cbar.set_label("$g/cm^3$", rotation=270, labelpad=15, size=12)
plt.show()
dpred = inv_prob.dpred
# Observed data | Predicted data | Normalized data misfit
data_array = np.c_[dobs_test, dpred, (dobs_test - dpred) / uncertainties]
fig = plt.figure(figsize=(17, 4))
plot_title = ["Observed", "Predicted", "Normalized Misfit"]
plot_units = ["mgal", "mgal", ""]
ax1 = 3 * [None]
ax2 = 3 * [None]
norm = 3 * [None]
cbar = 3 * [None]
cplot = 3 * [None]
v_lim = [np.max(np.abs(dobs)), np.max(np.abs(dobs)), np.max(np.abs(data_array[:, 2]))]
for ii in range(0, 3):
ax1[ii] = fig.add_axes([0.33 * ii + 0.03, 0.11, 0.23, 0.84])
cplot[ii] = plot2Ddata(
receiver_list[0].locations,
data_array[:, ii],
ax=ax1[ii],
ncontour=30,
clim=(-v_lim[ii], v_lim[ii]),
contourOpts={"cmap": "bwr"},
)
ax1[ii].set_title(plot_title[ii])
ax1[ii].set_xlabel("x (m)")
ax1[ii].set_ylabel("y (m)")
ax2[ii] = fig.add_axes([0.33 * ii + 0.25, 0.11, 0.01, 0.85])
norm[ii] = mpl.colors.Normalize(vmin=-v_lim[ii], vmax=v_lim[ii])
cbar[ii] = mpl.colorbar.ColorbarBase(
ax2[ii], norm=norm[ii], orientation="vertical", cmap=mpl.cm.bwr
)
cbar[ii].set_label(plot_units[ii], rotation=270, labelpad=15, size=12)
plt.show()
dpred
data_source = "https://storage.googleapis.com/simpeg/doc-assets/gravity.tar.gz"
# download the data
downloaded_data = utils.download(data_source, overwrite=True)
# unzip the tarfile
tar = tarfile.open(downloaded_data, "r")
tar.extractall()
tar.close()
# path to the directory containing our data
dir_path = downloaded_data.split(".")[0] + os.path.sep
# files to work with
topo_filename = dir_path + "gravity_topo.txt"
data_filename = dir_path + "gravity_data.obs"
model_filename = dir_path + "true_model.txt"
xyz_topo = np.loadtxt(str(topo_filename))
xyz_topo.shape
xyzdobs = np.loadtxt(str(data_filename))
xyzdobs.shape
xyz_topo[1]
xyzdobs[0]
xyzdobs
sagrav_test
dobs_test
survey_array_test[0]
receiver_locations_test[0]
print(survey)
survey.nD
data
data.noise_floor
mesh2
xyzdobs
recovered_model
from SimPEG.utils import plot2Ddata, surface2ind_topo
```
|
github_jupyter
|
# Overview
In this project, I will build an item-based collaborative filtering system using [MovieLens Datasets](https://grouplens.org/datasets/movielens/latest/). Specically, I will train a KNN models to cluster similar movies based on user's ratings and make movie recommendation based on similarity score of previous rated movies.
## [Recommender system](https://en.wikipedia.org/wiki/Recommender_system)
A recommendation system is basically an information filtering system that seeks to predict the "rating" or "preference" a user would give to an item. It is widely used in different internet / online business such as Amazon, Netflix, Spotify, or social media like Facebook and Youtube. By using recommender systems, those companies are able to provide better or more suited products/services/contents that are personalized to a user based on his/her historical consumer behaviors
Recommender systems typically produce a list of recommendations through collaborative filtering or through content-based filtering
This project will focus on collaborative filtering and use item-based collaborative filtering systems make movie recommendation
## [Item-based Collaborative Filtering](https://beckernick.github.io/music_recommender/)
Collaborative filtering based systems use the actions of users to recommend other items. In general, they can either be user based or item based. User based collaborating filtering uses the patterns of users similar to me to recommend a product (users like me also looked at these other items). Item based collaborative filtering uses the patterns of users who browsed the same item as me to recommend me a product (users who looked at my item also looked at these other items). Item-based approach is usually prefered than user-based approach. User-based approach is often harder to scale because of the dynamic nature of users, whereas items usually don't change much, so item-based approach often can be computed offline.
## Data Sets
I use [MovieLens Datasets](https://grouplens.org/datasets/movielens/latest/).
This dataset (ml-latest.zip) describes 5-star rating and free-text tagging activity from [MovieLens](http://movielens.org), a movie recommendation service. It contains 27753444 ratings and 1108997 tag applications across 58098 movies. These data were created by 283228 users between January 09, 1995 and September 26, 2018. This dataset was generated on September 26, 2018.
Users were selected at random for inclusion. All selected users had rated at least 1 movies. No demographic information is included. Each user is represented by an id, and no other information is provided.
The data are contained in the files `genome-scores.csv`, `genome-tags.csv`, `links.csv`, `movies.csv`, `ratings.csv` and `tags.csv`.
## Project Content
1. Load data
2. Exploratory data analysis
3. Train KNN model for item-based collaborative filtering
4. Use this trained model to make movie recommendations to myself
5. Deep dive into the bottleneck of item-based collaborative filtering.
- cold start problem
- data sparsity problem
- popular bias (how to recommend products from the tail of product distribution)
- scalability bottleneck
6. Further study
```
import os
import time
# data science imports
import math
import numpy as np
import pandas as pd
from scipy.sparse import csr_matrix
from sklearn.neighbors import NearestNeighbors
# utils import
from fuzzywuzzy import fuzz
# visualization imports
import seaborn as sns
import matplotlib.pyplot as plt
plt.style.use('ggplot')
%matplotlib inline
# path config
data_path = os.path.join(os.environ['DATA_PATH'], 'MovieLens')
movies_filename = 'movies.csv'
ratings_filename = 'ratings.csv'
```
## 1. Load Data
```
df_movies = pd.read_csv(
os.path.join(data_path, movies_filename),
usecols=['movieId', 'title'],
dtype={'movieId': 'int32', 'title': 'str'})
df_ratings = pd.read_csv(
os.path.join(data_path, ratings_filename),
usecols=['userId', 'movieId', 'rating'],
dtype={'userId': 'int32', 'movieId': 'int32', 'rating': 'float32'})
df_movies.info()
df_ratings.info()
df_movies.head()
df_ratings.head()
num_users = len(df_ratings.userId.unique())
num_items = len(df_ratings.movieId.unique())
print('There are {} unique users and {} unique movies in this data set'.format(num_users, num_items))
```
## 2. Exploratory data analysis
- Plot the counts of each rating
- Plot rating frequency of each movie
#### 1. Plot the counts of each rating
we first need to get the counts of each rating from ratings data
```
# get count
df_ratings_cnt_tmp = pd.DataFrame(df_ratings.groupby('rating').size(), columns=['count'])
df_ratings_cnt_tmp
```
We can see that above table does not include counts of zero rating score. So we need to add that in rating count dataframe as well
```
# there are a lot more counts in rating of zero
total_cnt = num_users * num_items
rating_zero_cnt = total_cnt - df_ratings.shape[0]
# append counts of zero rating to df_ratings_cnt
df_ratings_cnt = df_ratings_cnt_tmp.append(
pd.DataFrame({'count': rating_zero_cnt}, index=[0.0]),
verify_integrity=True,
).sort_index()
df_ratings_cnt
```
The count for zero rating score is too big to compare with others. So let's take log transform for count values and then we can plot them to compare
```
# add log count
df_ratings_cnt['log_count'] = np.log(df_ratings_cnt['count'])
df_ratings_cnt
ax = df_ratings_cnt[['count']].reset_index().rename(columns={'index': 'rating score'}).plot(
x='rating score',
y='count',
kind='bar',
figsize=(12, 8),
title='Count for Each Rating Score (in Log Scale)',
logy=True,
fontsize=12,
)
ax.set_xlabel("movie rating score")
ax.set_ylabel("number of ratings")
```
It's interesting that there are more people giving rating score of 3 and 4 than other scores
#### 2. Plot rating frequency of all movies
```
df_ratings.head()
# get rating frequency
df_movies_cnt = pd.DataFrame(df_ratings.groupby('movieId').size(), columns=['count'])
df_movies_cnt.head()
# plot rating frequency of all movies
ax = df_movies_cnt \
.sort_values('count', ascending=False) \
.reset_index(drop=True) \
.plot(
figsize=(12, 8),
title='Rating Frequency of All Movies',
fontsize=12
)
ax.set_xlabel("movie Id")
ax.set_ylabel("number of ratings")
```
The distribution of ratings among movies often satisfies a property in real-world settings,
which is referred to as the long-tail property. According to this property, only a small
fraction of the items are rated frequently. Such items are referred to as popular items. The
vast majority of items are rated rarely. This results in a highly skewed distribution of the
underlying ratings.
Let's plot the same distribution but with log scale
```
# plot rating frequency of all movies in log scale
ax = df_movies_cnt \
.sort_values('count', ascending=False) \
.reset_index(drop=True) \
.plot(
figsize=(12, 8),
title='Rating Frequency of All Movies (in Log Scale)',
fontsize=12,
logy=True
)
ax.set_xlabel("movie Id")
ax.set_ylabel("number of ratings (log scale)")
```
We can see that roughly 10,000 out of 53,889 movies are rated more than 100 times. More interestingly, roughly 20,000 out of 53,889 movies are rated less than only 10 times. Let's look closer by displaying top quantiles of rating counts
```
df_movies_cnt['count'].quantile(np.arange(1, 0.6, -0.05))
```
So about 1% of movies have roughly 97,999 or more ratings, 5% have 1,855 or more, and 20% have 100 or more. Since we have so many movies, we'll limit it to the top 25%. This is arbitrary threshold for popularity, but it gives us about 13,500 different movies. We still have pretty good amount of movies for modeling. There are two reasons why we want to filter to roughly 13,500 movies in our dataset.
- Memory issue: we don't want to run into the “MemoryError” during model training
- Improve KNN performance: lesser known movies have ratings from fewer viewers, making the pattern more noisy. Droping out less known movies can improve recommendation quality
```
# filter data
popularity_thres = 50
popular_movies = list(set(df_movies_cnt.query('count >= @popularity_thres').index))
df_ratings_drop_movies = df_ratings[df_ratings.movieId.isin(popular_movies)]
print('shape of original ratings data: ', df_ratings.shape)
print('shape of ratings data after dropping unpopular movies: ', df_ratings_drop_movies.shape)
```
After dropping 75% of movies in our dataset, we still have a very large dataset. So next we can filter users to further reduce the size of data
```
# get number of ratings given by every user
df_users_cnt = pd.DataFrame(df_ratings_drop_movies.groupby('userId').size(), columns=['count'])
df_users_cnt.head()
# plot rating frequency of all movies
ax = df_users_cnt \
.sort_values('count', ascending=False) \
.reset_index(drop=True) \
.plot(
figsize=(12, 8),
title='Rating Frequency of All Users',
fontsize=12
)
ax.set_xlabel("user Id")
ax.set_ylabel("number of ratings")
df_users_cnt['count'].quantile(np.arange(1, 0.5, -0.05))
```
We can see that the distribution of ratings by users is very similar to the distribution of ratings among movies. They both have long-tail property. Only a very small fraction of users are very actively engaged with rating movies that they watched. Vast majority of users aren't interested in rating movies. So we can limit users to the top 40%, which is about 113,291 users.
```
# filter data
ratings_thres = 50
active_users = list(set(df_users_cnt.query('count >= @ratings_thres').index))
df_ratings_drop_users = df_ratings_drop_movies[df_ratings_drop_movies.userId.isin(active_users)]
print('shape of original ratings data: ', df_ratings.shape)
print('shape of ratings data after dropping both unpopular movies and inactive users: ', df_ratings_drop_users.shape)
```
## 3. Train KNN model for item-based collaborative filtering
- Reshaping the Data
- Fitting the Model
#### 1. Reshaping the Data
For K-Nearest Neighbors, we want the data to be in an (artist, user) array, where each row is a movie and each column is a different user. To reshape the dataframe, we'll pivot the dataframe to the wide format with movies as rows and users as columns. Then we'll fill the missing observations with 0s since we're going to be performing linear algebra operations (calculating distances between vectors). Finally, we transform the values of the dataframe into a scipy sparse matrix for more efficient calculations.
```
# pivot and create movie-user matrix
movie_user_mat = df_ratings_drop_users.pivot(index='movieId', columns='userId', values='rating').fillna(0)
# create mapper from movie title to index
movie_to_idx = {
movie: i for i, movie in
enumerate(list(df_movies.set_index('movieId').loc[movie_user_mat.index].title))
}
# transform matrix to scipy sparse matrix
movie_user_mat_sparse = csr_matrix(movie_user_mat.values)
```
#### 2. Fitting the Model
Time to implement the model. We'll initialize the NearestNeighbors class as model_knn and fit our sparse matrix to the instance. By specifying the metric = cosine, the model will measure similarity bectween artist vectors by using cosine similarity.
```
%env JOBLIB_TEMP_FOLDER=/tmp
# define model
model_knn = NearestNeighbors(metric='cosine', algorithm='brute', n_neighbors=20, n_jobs=-1)
# fit
model_knn.fit(movie_user_mat_sparse)
```
## 4. Use this trained model to make movie recommendations to myself
And we're finally ready to make some recommendations!
```
def fuzzy_matching(mapper, fav_movie, verbose=True):
"""
return the closest match via fuzzy ratio. If no match found, return None
Parameters
----------
mapper: dict, map movie title name to index of the movie in data
fav_movie: str, name of user input movie
verbose: bool, print log if True
Return
------
index of the closest match
"""
match_tuple = []
# get match
for title, idx in mapper.items():
ratio = fuzz.ratio(title.lower(), fav_movie.lower())
if ratio >= 60:
match_tuple.append((title, idx, ratio))
# sort
match_tuple = sorted(match_tuple, key=lambda x: x[2])[::-1]
if not match_tuple:
print('Oops! No match is found')
return
if verbose:
print('Found possible matches in our database: {0}\n'.format([x[0] for x in match_tuple]))
return match_tuple[0][1]
def make_recommendation(model_knn, data, mapper, fav_movie, n_recommendations):
"""
return top n similar movie recommendations based on user's input movie
Parameters
----------
model_knn: sklearn model, knn model
data: movie-user matrix
mapper: dict, map movie title name to index of the movie in data
fav_movie: str, name of user input movie
n_recommendations: int, top n recommendations
Return
------
list of top n similar movie recommendations
"""
# fit
model_knn.fit(data)
# get input movie index
print('You have input movie:', fav_movie)
idx = fuzzy_matching(mapper, fav_movie, verbose=True)
# inference
print('Recommendation system start to make inference')
print('......\n')
distances, indices = model_knn.kneighbors(data[idx], n_neighbors=n_recommendations+1)
# get list of raw idx of recommendations
raw_recommends = \
sorted(list(zip(indices.squeeze().tolist(), distances.squeeze().tolist())), key=lambda x: x[1])[:0:-1]
# get reverse mapper
reverse_mapper = {v: k for k, v in mapper.items()}
# print recommendations
print('Recommendations for {}:'.format(fav_movie))
for i, (idx, dist) in enumerate(raw_recommends):
print('{0}: {1}, with distance of {2}'.format(i+1, reverse_mapper[idx], dist))
my_favorite = 'Iron Man'
make_recommendation(
model_knn=model_knn,
data=movie_user_mat_sparse,
fav_movie=my_favorite,
mapper=movie_to_idx,
n_recommendations=10)
```
This is very interesting that my **KNN** model recommends movies that were also produced in very similar years. However, the cosine distance of all those recommendations are actually quite small. This is probabily because there is too many zero values in our movie-user matrix. With too many zero values in our data, the data sparsity becomes a real issue for **KNN** model and the distance in **KNN** model starts to fall apart. So I'd like to dig deeper and look closer inside our data.
#### (extra inspection)
Let's now look at how sparse the movie-user matrix is by calculating percentage of zero values in the data.
```
# calcuate total number of entries in the movie-user matrix
num_entries = movie_user_mat.shape[0] * movie_user_mat.shape[1]
# calculate total number of entries with zero values
num_zeros = (movie_user_mat==0).sum(axis=1).sum()
# calculate ratio of number of zeros to number of entries
ratio_zeros = num_zeros / num_entries
print('There is about {:.2%} of ratings in our data is missing'.format(ratio_zeros))
```
This result confirms my hypothesis. The vast majority of entries in our data is zero. This explains why the distance between similar items or opposite items are both pretty large.
## 5. Deep dive into the bottleneck of item-based collaborative filtering.
- cold start problem
- data sparsity problem
- popular bias (how to recommend products from the tail of product distribution)
- scalability bottleneck
We saw there is 98.35% of user-movie interactions are not yet recorded, even after I filtered out less-known movies and inactive users. Apparently, we don't even have sufficient information for the system to make reliable inferences for users or items. This is called **Cold Start** problem in recommender system.
There are three cases of cold start:
1. New community: refers to the start-up of the recommender, when, although a catalogue of items might exist, almost no users are present and the lack of user interaction makes very hard to provide reliable recommendations
2. New item: a new item is added to the system, it might have some content information but no interactions are present
3. New user: a new user registers and has not provided any interaction yet, therefore it is not possible to provide personalized recommendations
We are not concerned with the last one because we can use item-based filtering to make recommendations for new user. In our case, we are more concerned with the first two cases, especially the second case.
The item cold-start problem refers to when items added to the catalogue have either none or very little interactions. This constitutes a problem mainly for collaborative filtering algorithms due to the fact that they rely on the item's interactions to make recommendations. If no interactions are available then a pure collaborative algorithm cannot recommend the item. In case only a few interactions are available, although a collaborative algorithm will be able to recommend it, the quality of those recommendations will be poor. This arises another issue, which is not anymore related to new items, but rather to unpopular items. In some cases (e.g. movie recommendations) it might happen that a handful of items receive an extremely high number of iteractions, while most of the items only receive a fraction of them. This is also referred to as popularity bias. Please recall previous long-tail skewed distribution of movie rating frequency plot.
In addtition to that, scalability is also a big issue in KNN model too. Its time complexity is O(nd + kn), where n is the cardinality of the training set and d the dimension of each sample. And KNN takes more time in making inference than training, which increase the prediction latency
## 6. Further study
Use spark's ALS to solve above problems
|
github_jupyter
|
Quick study to investigate oscillations in reported infections in Germany. Here is the plot of the data in question:
```
import coronavirus
import numpy as np
import matplotlib.pyplot as plt
%config InlineBackend.figure_formats = ['svg']
coronavirus.display_binder_link("2020-05-10-notebook-weekly-fluctuations-in-data-from-germany.ipynb")
# get data
cases, deaths, country_label = coronavirus.get_country_data("Germany")
# plot daily changes
fig, ax = plt.subplots(figsize=(8, 4))
coronavirus.plot_daily_change(ax, cases, 'C1')
```
The working assumption is that during the weekend fewer numbers are captured or reported. The analysis below seems to confirm this.
We compute a discrete Fourier transform of the data, and expect a peak at a frequency corresponding to a period of 7 days.
## Data selection
We start with data from 1st March as numbers before were small. It is convenient to take a number of days that can be divided by seven (for alignment of the freuency axis in Fourier space, so we choose 63 days from 1st of March):
```
data = cases['2020-03-01':'2020-05-03']
# compute daily change
diff = data.diff().dropna()
# plot data points (corresponding to bars in figure above:)
fig, ax = plt.subplots()
ax.plot(diff.index, diff, '-C1',
label='daily new cases Germany')
fig.autofmt_xdate() # avoid x-labels overlap
# How many data points (=days) have we got?
diff.size
diff2 = diff.resample("24h").asfreq() # ensure we have one data point every day
diff2.size
```
## Compute the frequency spectrum
```
fig, ax = plt.subplots()
# compute power density spectrum
change_F = abs(np.fft.fft(diff2))**2
# determine appropriate frequencies
n = change_F.size
freq = np.fft.fftfreq(n, d=1)
# We skip values at indices 0, 1 and 2: these are large because we have a finite
# sequence and not substracted the mean from the data set
# We also only plot the the first n/2 frequencies as for high n, we get negative
# frequencies with the same data content as the positive ones.
ax.plot(freq[3:n//2], change_F[3:n//2], 'o-C3')
ax.set_xlabel('frequency [cycles per day]');
```
A signal with oscillations on a weekly basis would correspond to a frequency of 1/7 as frequency is measured in `per day`. We thus expect the peak above to be at 1/7 $\approx 0.1428$.
We can show this more easily by changing the frequency scale from cycles per day to cycles per week:
```
fig, ax = plt.subplots()
ax.plot(freq[3:n//2] * 7, change_F[3:n//2], 'o-C3')
ax.set_xlabel('frequency [cycles per week]');
```
In other words: there as a strong component of the data with a frequency corresponding to one week.
This is the end of the notebook.
# Fourier transform basics
A little playground to explore properties of discrete Fourier transforms.
```
time = np.linspace(0, 4, 1000)
signal_frequency = 3 # choose this freely
signal = np.sin(time * 2 * np.pi * signal_frequency)
fourier = np.abs(np.fft.fft(signal))
# compute frequencies in fourier spectrum
n = signal.size
timestep = time[1] - time[0]
freqs = np.fft.fftfreq(n, d=timestep)
fig, ax = plt.subplots()
ax.plot(time, signal, 'oC9', label=f'signal, frequency={signal_frequency}')
ax.set_xlabel('time')
ax.legend()
fig, ax = plt.subplots()
ax.plot(freqs[0:n//2][:20], fourier[0:n//2][0:20], 'o-C8', label="Fourier transform")
ax.legend()
ax.set_xlabel('frequency');
coronavirus.display_binder_link("2020-05-10-notebook-weekly-fluctuations-in-data-from-germany.ipynb")
```
|
github_jupyter
|
```
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import KFold
from sklearn.model_selection import ShuffleSplit
from sklearn.metrics import accuracy_score
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from matplotlib import pyplot as plt
import matplotlib as mpl
import seaborn as sns
import numpy as np
import pandas as pd
import category_encoders as ce
import os
import pickle
import gc
from tqdm import tqdm
import pickle
from sklearn.svm import SVR
from sklearn.linear_model import LinearRegression
from sklearn import linear_model
from sklearn.neighbors import KNeighborsRegressor
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import ExtraTreesRegressor
from sklearn import ensemble
import xgboost as xgb
def encode_text_features(encode_decode, data_frame, encoder_isa=None, encoder_mem_type=None):
# Implement Categorical OneHot encoding for ISA and mem-type
if encode_decode == 'encode':
encoder_isa = ce.one_hot.OneHotEncoder(cols=['isa'])
encoder_mem_type = ce.one_hot.OneHotEncoder(cols=['mem-type'])
encoder_isa.fit(data_frame, verbose=1)
df_new1 = encoder_isa.transform(data_frame)
encoder_mem_type.fit(df_new1, verbose=1)
df_new = encoder_mem_type.transform(df_new1)
encoded_data_frame = df_new
else:
df_new1 = encoder_isa.transform(data_frame)
df_new = encoder_mem_type.transform(df_new1)
encoded_data_frame = df_new
return encoded_data_frame, encoder_isa, encoder_mem_type
def absolute_percentage_error(Y_test, Y_pred):
error = 0
for i in range(len(Y_test)):
if(Y_test[i]!= 0 ):
error = error + (abs(Y_test[i] - Y_pred[i]))/Y_test[i]
error = error/ len(Y_test)
return error
def process_all(dataset_path, dataset_name, path_for_saving_data):
################## Data Preprocessing ######################
df = pd.read_csv(dataset_path)
encoded_data_frame, encoder_isa, encoder_mem_type = encode_text_features('encode', df,
encoder_isa = None, encoder_mem_type=None)
# total_data = encoded_data_frame.drop(columns = ['arch', 'arch1'])
total_data = encoded_data_frame.drop(columns = ['arch', 'sys','sysname','executable','PS'])
total_data = total_data.fillna(0)
X_columns = total_data.drop(columns = 'runtime').columns
X = total_data.drop(columns = ['runtime']).to_numpy()
Y = total_data['runtime'].to_numpy()
# X_columns = total_data.drop(columns = 'PS').columns
# X = total_data.drop(columns = ['runtime','PS']).to_numpy()
# Y = total_data['runtime'].to_numpy()
print('Data X and Y shape', X.shape, Y.shape)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=42)
print('Train Test Split:', X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.fit_transform(X_test)
################## Data Preprocessing ######################
# Put best models here using grid search
# 1. SVR
best_svr =SVR(C=1000, cache_size=200, coef0=0.0, degree=3, epsilon=0.1, gamma=0.1,
kernel='rbf', max_iter=-1, shrinking=True, tol=0.001, verbose=False)
# 2. LR
best_lr = LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=True)
# 3. RR
best_rr = linear_model.Ridge(alpha=10, copy_X=True, fit_intercept=True, max_iter=None, normalize=False,
random_state=None, solver='svd', tol=0.001)
# 4. KNN
best_knn = KNeighborsRegressor(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=2, p=1,
weights='distance')
# 5. GPR
best_gpr = GaussianProcessRegressor(alpha=0.01, copy_X_train=True, kernel=None,
n_restarts_optimizer=0, normalize_y=True,
optimizer='fmin_l_bfgs_b', random_state=None)
# 6. Decision Tree
best_dt = DecisionTreeRegressor(criterion='mse', max_depth=7, max_features='auto',
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best')
# 7. Random Forest
best_rf = RandomForestRegressor(bootstrap=True, criterion='friedman_mse', max_depth=7,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=10,
n_jobs=None, oob_score=False, random_state=None,
verbose=0, warm_start='False')
# 8. Extra Trees Regressor
best_etr = ExtraTreesRegressor(bootstrap=False, criterion='friedman_mse', max_depth=15,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=200, n_jobs=None,
oob_score=False, random_state=None, verbose=0,
warm_start='True')
# 9. GBR
best_gbr = ensemble.GradientBoostingRegressor(alpha=0.9, criterion='mae', init=None,
learning_rate=0.1, loss='lad', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
n_iter_no_change=None, presort='auto',
random_state=42, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0, warm_start=False)
# 10. XGB
best_xgb = xgb.XGBRegressor(alpha=10, base_score=0.5, booster='gbtree', colsample_bylevel=1,
colsample_bynode=1, colsample_bytree=0.3, gamma=0,
importance_type='gain', learning_rate=0.5, max_delta_step=0,
max_depth=10, min_child_weight=1, missing=None, n_estimators=100,
n_jobs=1, nthread=None, objective='reg:linear', random_state=0,
reg_alpha=0, reg_lambda=1, scale_pos_weight=1, seed=None,
silent=None, subsample=1, validate_parameters=False, verbosity=1)
best_models = [best_svr, best_lr, best_rr, best_knn, best_gpr, best_dt, best_rf, best_etr, best_gbr, best_xgb]
best_models_name = ['best_svr', 'best_lr', 'best_rr', 'best_knn', 'best_gpr', 'best_dt', 'best_rf', 'best_etr'
, 'best_gbr', 'best_xgb']
k = 0
df = pd.DataFrame(columns = ['model_name', 'dataset_name', 'r2', 'mse', 'mape', 'mae' ])
for model in best_models:
print('Running model number:', k+1, 'with Model Name: ', best_models_name[k])
r2_scores = []
mse_scores = []
mape_scores = []
mae_scores = []
# cv = KFold(n_splits = 10, random_state = 42, shuffle = True)
cv = ShuffleSplit(n_splits=10, random_state=0, test_size = 0.4)
# print(cv)
fold = 1
for train_index, test_index in cv.split(X):
model_orig = model
# print("Train Index: ", train_index, "\n")
# print("Test Index: ", test_index)
X_train_fold, X_test_fold, Y_train_fold, Y_test_fold = X[train_index], X[test_index], Y[train_index], Y[test_index]
# print(X_train_fold.shape, X_test_fold.shape, Y_train_fold.shape, Y_test_fold.shape)
model_orig.fit(X_train_fold, Y_train_fold)
Y_pred_fold = model_orig.predict(X_test_fold)
# save the folds to disk
data = [X_train_fold, X_test_fold, Y_train_fold, Y_test_fold]
filename = path_for_saving_data + '/folds_data/' + best_models_name[k] +'_'+ str(fold) + '.pickle'
# pickle.dump(data, open(filename, 'wb'))
# save the model to disk
# filename = path_for_saving_data + '/models_data/' + best_models_name[k] + '_' + str(fold) + '.sav'
fold = fold + 1
# pickle.dump(model_orig, open(filename, 'wb'))
# some time later...
'''
# load the model from disk
loaded_model = pickle.load(open(filename, 'rb'))
result = loaded_model.score(X_test, Y_test)
print(result)
'''
# scores.append(best_svr.score(X_test, y_test))
'''
plt.figure()
plt.plot(Y_test_fold, 'b')
plt.plot(Y_pred_fold, 'r')
'''
# print('Accuracy =',accuracy_score(Y_test, Y_pred))
r2_scores.append(r2_score(Y_test_fold, Y_pred_fold))
mse_scores.append(mean_squared_error(Y_test_fold, Y_pred_fold))
mape_scores.append(absolute_percentage_error(Y_test_fold, Y_pred_fold))
mae_scores.append(mean_absolute_error(Y_test_fold, Y_pred_fold))
df = df.append({'model_name': best_models_name[k], 'dataset_name': dataset_name
, 'r2': r2_scores, 'mse': mse_scores, 'mape': mape_scores, 'mae': mae_scores }, ignore_index=True)
k = k + 1
print(df.head())
df.to_csv(r'runtimes_final_npb_ep_60.csv')
dataset_name = 'runtimes_final_npb_ep'
dataset_path = 'C:\\Users\\Rajat\\Desktop\\DESKTOP_15_05_2020\\Evaluating-Machine-Learning-Models-for-Disparate-Computer-Systems-Performance-Prediction\\Dataset_CSV\\PhysicalSystems\\runtimes_final_npb_ep.csv'
path_for_saving_data = 'data\\' + dataset_name
process_all(dataset_path, dataset_name, path_for_saving_data)
df = pd.DataFrame(columns = ['model_name', 'dataset_name', 'r2', 'mse', 'mape', 'mae' ])
df
```
|
github_jupyter
|
---
_You are currently looking at **version 1.0** of this notebook. To download notebooks and datafiles, as well as get help on Jupyter notebooks in the Coursera platform, visit the [Jupyter Notebook FAQ](https://www.coursera.org/learn/python-text-mining/resources/d9pwm) course resource._
---
# Assignment 2 - Introduction to NLTK
In part 1 of this assignment you will use nltk to explore the Herman Melville novel Moby Dick. Then in part 2 you will create a spelling recommender function that uses nltk to find words similar to the misspelling.
## Part 1 - Analyzing Moby Dick
```
import nltk
import pandas as pd
import numpy as np
import nltk
nltk.download('punkt')
nltk.download('wordnet')
nltk.download('averaged_perceptron_tagger')
# If you would like to work with the raw text you can use 'moby_raw'
with open('moby.txt', 'r') as f:
moby_raw = f.read()
# If you would like to work with the novel in nltk.Text format you can use 'text1'
moby_tokens = nltk.word_tokenize(moby_raw)
text1 = nltk.Text(moby_tokens)
```
### Example 1
How many tokens (words and punctuation symbols) are in text1?
*This function should return an integer.*
```
def example_one():
return len(nltk.word_tokenize(moby_raw)) # or alternatively len(text1)
example_one()
```
### Example 2
How many unique tokens (unique words and punctuation) does text1 have?
*This function should return an integer.*
```
def example_two():
return len(set(nltk.word_tokenize(moby_raw))) # or alternatively len(set(text1))
example_two()
```
### Example 3
After lemmatizing the verbs, how many unique tokens does text1 have?
*This function should return an integer.*
```
from nltk.stem import WordNetLemmatizer
def example_three():
lemmatizer = WordNetLemmatizer()
lemmatized = [lemmatizer.lemmatize(w,'v') for w in text1]
return len(set(lemmatized))
example_three()
```
### Question 1
What is the lexical diversity of the given text input? (i.e. ratio of unique tokens to the total number of tokens)
*This function should return a float.*
```
def answer_one():
unique = len(set(nltk.word_tokenize(moby_raw))) # or alternatively len(set(text1))
tot = len(nltk.word_tokenize(moby_raw))
return unique/tot
answer_one()
```
### Question 2
What percentage of tokens is 'whale'or 'Whale'?
*This function should return a float.*
```
def answer_two():
tot = nltk.word_tokenize(moby_raw)
count = [w for w in tot if w == "Whale" or w == "whale"]
return 100*len(count)/len(tot)
answer_two()
```
### Question 3
What are the 20 most frequently occurring (unique) tokens in the text? What is their frequency?
*This function should return a list of 20 tuples where each tuple is of the form `(token, frequency)`. The list should be sorted in descending order of frequency.*
```
def answer_three():
tot = nltk.word_tokenize(moby_raw)
dist = nltk.FreqDist(tot)
return dist.most_common(20)
answer_three()
```
### Question 4
What tokens have a length of greater than 5 and frequency of more than 150?
*This function should return an alphabetically sorted list of the tokens that match the above constraints. To sort your list, use `sorted()`*
```
def answer_four():
tot = nltk.word_tokenize(moby_raw)
dist = nltk.FreqDist(tot)
count = [w for w in dist if len(w)>5 and dist[w]>150]
return sorted(count)
answer_four()
```
### Question 5
Find the longest word in text1 and that word's length.
*This function should return a tuple `(longest_word, length)`.*
```
def answer_five():
tot = nltk.word_tokenize(moby_raw)
dist = nltk.FreqDist(tot)
max_length = max([len(w) for w in dist])
word = [w for w in dist if len(w)==max_length]
return (word[0],max_length)
answer_five()
```
### Question 6
What unique words have a frequency of more than 2000? What is their frequency?
"Hint: you may want to use `isalpha()` to check if the token is a word and not punctuation."
*This function should return a list of tuples of the form `(frequency, word)` sorted in descending order of frequency.*
```
def answer_six():
tot = nltk.word_tokenize(moby_raw)
dist = nltk.FreqDist(tot)
words = [w for w in dist if dist[w]>2000 and w.isalpha()]
words_count = [dist[w] for w in words]
ans = list(zip(words_count,words))
ans.sort(key=lambda tup: tup[0],reverse=True)
return ans
answer_six()
```
### Question 7
What is the average number of tokens per sentence?
*This function should return a float.*
```
def answer_seven():
tot = nltk.sent_tokenize(moby_raw)
dist = nltk.FreqDist(tot)
tot1 = nltk.word_tokenize(moby_raw)
return len(tot1)/len(tot)
answer_seven()
```
### Question 8
What are the 5 most frequent parts of speech in this text? What is their frequency?
*This function should return a list of tuples of the form `(part_of_speech, frequency)` sorted in descending order of frequency.*
```
def answer_eight():
tot = nltk.word_tokenize(moby_raw)
dist1 = nltk.pos_tag(tot)
frequencies = nltk.FreqDist([tag for (word, tag) in dist1])
return frequencies.most_common(5)
answer_eight()
```
## Part 2 - Spelling Recommender
For this part of the assignment you will create three different spelling recommenders, that each take a list of misspelled words and recommends a correctly spelled word for every word in the list.
For every misspelled word, the recommender should find find the word in `correct_spellings` that has the shortest distance*, and starts with the same letter as the misspelled word, and return that word as a recommendation.
*Each of the three different recommenders will use a different distance measure (outlined below).
Each of the recommenders should provide recommendations for the three default words provided: `['cormulent', 'incendenece', 'validrate']`.
```
import pandas
from nltk.corpus import words
nltk.download('words')
from nltk.metrics.distance import (
edit_distance,
jaccard_distance,
)
from nltk.util import ngrams
correct_spellings = words.words()
spellings_series = pandas.Series(correct_spellings)
#spellings_series
```
### Question 9
For this recommender, your function should provide recommendations for the three default words provided above using the following distance metric:
**[Jaccard distance](https://en.wikipedia.org/wiki/Jaccard_index) on the trigrams of the two words.**
*This function should return a list of length three:
`['cormulent_reccomendation', 'incendenece_reccomendation', 'validrate_reccomendation']`.*
```
def Jaccard(words, n_grams):
outcomes = []
for word in words:
spellings = spellings_series[spellings_series.str.startswith(word[0])]
distances = ((jaccard_distance(set(ngrams(word, n_grams)), set(ngrams(k, n_grams))), k) for k in spellings)
closest = min(distances)
outcomes.append(closest[1])
return outcomes
def answer_nine(entries=['cormulent', 'incendenece', 'validrate']):
return Jaccard(entries,3)
answer_nine()
```
### Question 10
For this recommender, your function should provide recommendations for the three default words provided above using the following distance metric:
**[Jaccard distance](https://en.wikipedia.org/wiki/Jaccard_index) on the 4-grams of the two words.**
*This function should return a list of length three:
`['cormulent_reccomendation', 'incendenece_reccomendation', 'validrate_reccomendation']`.*
```
def answer_ten(entries=['cormulent', 'incendenece', 'validrate']):
return Jaccard(entries,4)
answer_ten()
```
### Question 11
For this recommender, your function should provide recommendations for the three default words provided above using the following distance metric:
**[Edit distance on the two words with transpositions.](https://en.wikipedia.org/wiki/Damerau%E2%80%93Levenshtein_distance)**
*This function should return a list of length three:
`['cormulent_reccomendation', 'incendenece_reccomendation', 'validrate_reccomendation']`.*
```
def Edit(words):
outcomes = []
for word in words:
spellings = spellings_series[spellings_series.str.startswith(word[0])]
distances = ((edit_distance(word,k),k) for k in spellings)
closest = min(distances)
outcomes.append(closest[1])
return outcomes
def answer_eleven(entries=['cormulent', 'incendenece', 'validrate']):
return Edit(entries)
answer_eleven()
```
|
github_jupyter
|
Evaluating performance of FFT2 and IFFT2 and checking for accuracy. <br><br>
Note that the ffts from fft_utils perform the transformation in place to save memory.<br><br>
As a rule of thumb, it's good to increase the number of threads as the size of the transform increases until one hits a limit <br><br>
pyFFTW uses lower memory and is slightly slower.(using icc to compile fftw might fix this, haven't tried it)
```
import numpy as np
import matplotlib.pyplot as plt
#from multislice import fft_utils
import pyfftw,os
import scipy.fftpack as sfft
%load_ext memory_profiler
%run obj_fft
```
Loading libraries and the profiler to be used
```
N = 15000 #size of transform
t = 12 #number of threads.
```
Creating a test signal to perform on which we will perform 2D FFT
```
a= np.random.random((N,N))+1j*np.random.random((N,N))
print('time for numpy forward')
%timeit np.fft.fft2(a)
del(a)
a = np.random.random((N,N))+1j*np.random.random((N,N))
print('time for scipy forward')
%timeit sfft.fft2(a,overwrite_x='True')
del(a)
a = np.random.random((N,N))+1j*np.random.random((N,N))
fft_obj = FFT_2d_Obj(np.shape(a),direction='FORWARD',flag='PATIENT',threads=t)
print('time for pyFFTW forward')
%timeit fft_obj.run_fft2(a)
del(a)
a = np.random.random((N,N))+1j*np.random.random((N,N))
print('Memory for numpy forward')
%memit np.fft.fft2(a)
del(a)
a = np.random.random((N,N))+1j*np.random.random((N,N))
print('Memory for scipy forward')
%memit sfft.fft2(a,overwrite_x='True')
del(a)
a = np.random.random((N,N))+1j*np.random.random((N,N))
print('Memory for pyFFTW forward')
%memit fft_obj.run_fft2(a)
del(a)
```
The results depend on how the libraries are complied. mkl linked scipy is fast but the fftw uses less memory. Also note that the fftw used in this test wasn't installed using icc.
Creating a test signal to perform on which we will perform 2D IFFT.
```
a= np.random.random((N,N))+1j*np.random.random((N,N))
print('time for numpy backward')
%timeit np.fft.ifft2(a)
del(a)
a = np.random.random((N,N))+1j*np.random.random((N,N))
print('time for scipy backward')
%timeit sfft.ifft2(a,overwrite_x='True')
del(a)
a = np.random.random((N,N))+1j*np.random.random((N,N))
del fft_obj
fft_obj = FFT_2d_Obj(np.shape(a),direction='BACKWARD',flag='PATIENT',threads=t)
print('time for pyFFTW backward')
%timeit fft_obj.run_ifft2(a)
del(a)
a = np.random.random((N,N))+1j*np.random.random((N,N))
print('Memory for numpy forward')
%memit np.fft.ifft2(a)
del(a)
a = np.random.random((N,N))+1j*np.random.random((N,N))
print('Memory for scipy forward')
%memit sfft.ifft2(a,overwrite_x='True')
del(a)
a = np.random.random((N,N))+1j*np.random.random((N,N))
print('Memory for pyFFTW backward')
%memit fft_obj.run_ifft2(a)
del(a)
```
The results depend on how the libraries are complied. mkl linked scipy is fast but the fftw uses less memory. Also note that the fftw used in this test wasn't installed using icc.
Testing for accuracy of 2D FFT:
```
N = 5000
a = np.random.random((N,N)) + 1j*np.random.random((N,N))
fft_obj = FFT_2d_Obj(np.shape(a),threads=t)
A1 = np.fft.fft2(a)
fft_obj.run_fft2(a)
np.allclose(A1,a)
```
Testing for accuracy of 2D IFFT:
```
N = 5000
a = np.random.random((N,N)) + 1j*np.random.random((N,N))
A1 = np.fft.ifft2(a)
fft_obj.run_ifft2(a)
np.allclose(A1,a)
```
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
import warnings
warnings.filterwarnings('ignore')
import math
from time import time
import pickle
import pandas as pd
import numpy as np
from time import time
from sklearn.neural_network import MLPClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.metrics import accuracy_score, f1_score
import sys
sys.path.append('../src')
from preprocessing import *
from utils import *
from plotting import *
```
# Splitting the dataset
```
features = ['R1', 'R2', 'R3', 'R4', 'R5', 'R6', 'R7', 'R8', 'Temp.', 'Humidity',
'R1_mean', 'R2_mean', 'R3_mean', 'R4_mean', 'R5_mean', 'R6_mean', 'R7_mean',
'R8_mean', 'Temp._mean', 'Humidity_mean', 'R1_std', 'R2_std', 'R3_std', 'R4_std',
'R5_std', 'R6_std', 'R7_std', 'R8_std', 'Temp._std', 'Humidity_std']
df_db = group_datafiles_byID('../datasets/preprocessed/HT_Sensor_prep_metadata.dat', '../datasets/preprocessed/HT_Sensor_prep_dataset.dat')
df_db = reclassify_series_samples(df_db)
df_db.head()
df_train, df_test = split_series_byID(0.75, df_db)
df_train, df_test = norm_train_test(df_train, df_test)
features = ['R1', 'R2', 'R3', 'R4', 'R5', 'R5', 'R6', 'R7', 'R8', 'Temp.', 'Humidity']
xtrain, ytrain = df_train[features].values, df_train['class'].values
xtest, ytest = df_test[features].values, df_test['class'].values
```
# Basic Neural Network
```
def printResults(n_hid_layers,n_neur,accuracy,elapsed):
print('========================================')
print('Number of hidden layers:', n_hid_layers)
print('Number of neurons per layer:', n_neur)
print('Accuracy:', accuracy)
print('Time (minutes):', (elapsed)/60)
def printScores(xtest,ytest,clf):
xback, yback = xtest[ytest=='background'], ytest[ytest=='background']
print('Score del background:', clf.score(xback,yback))
xrest, yrest = xtest[ytest!='background'], ytest[ytest!='background']
print('Score del resto:', clf.score(xrest,yrest))
num_back = len(yback)
num_wine = len(yrest[yrest=='wine'])
num_banana = len(yrest[yrest=='banana'])
func = lambda x: 1/num_back if x=='background' else (1/num_wine if x=='wine' else 1/num_banana)
weights = np.array([func(x) for x in ytest])
# Score donde las tres clases ponderan igual
print('Score con pesos:', clf.score(xtest,ytest,weights))
print('========================================')
# NN with 2 hidden layers and 15 neurons per layer
xtrain, ytrain, xtest, ytest = split_train_test(df_db,0.75)
start = time.time()
clf = MLPClassifier(hidden_layer_sizes=(15,15))
clf.fit(xtrain,ytrain)
score = clf.score(xtest,ytest)
final = time.time()
printResults(2,15,score,final-start)
# Adding early stopping and more iterations
xtrain, ytrain, xtest, ytest = split_train_test(df_db,0.75)
start = time.time()
clf = MLPClassifier(hidden_layer_sizes=(15,15),early_stopping=True,max_iter=2000)
clf.fit(xtrain,ytrain)
score = clf.score(xtest,ytest)
final = time.time()
printResults(2,15,score,final-start)
# Análisis del score
print('Proporcion de background:',len(ytest[ytest=='background'])/len(ytest))
printScores(xtest,ytest,clf)
```
Demasiado sesgo hacia el background, hay que reducirlo aunque el score baje
# Removing excess of background
```
# prop: ejemplos que no son background que habrá por cada ejemplo de background
def remove_bg(df,prop=2):
new_df = df[df['class']!='background'].copy()
useful_samples = new_df.shape[0]
new_df = new_df.append(df[df['class']=='background'].sample(n=int(useful_samples/2)).copy())
return new_df
# Para evitar el sesgo quitamos elementos clasificados como background, pero solo en el train set
df_train, df_test = split_series_byID(0.75, df_db)
df_train, df_test = norm_train_test(df_train, df_test)
df_train = remove_bg(df_train)
features = ['R1', 'R2', 'R3', 'R4', 'R5', 'R5', 'R6', 'R7', 'R8', 'Temp.', 'Humidity']
xtrain, ytrain = df_train[features].values, df_train['class'].values
xtest, ytest = df_test[features].values, df_test['class'].values
start = time()
clf = MLPClassifier(hidden_layer_sizes=(15,15),early_stopping=True,max_iter=2000)
clf.fit(xtrain,ytrain)
score = clf.score(xtest,ytest)
final = time()
printResults(2,15,score,final-start)
# Análisis del score
printScores(xtest,ytest,clf)
```
Aunque se ponga la misma cantidad de background que de bananas o wine sigue habiendo un sesgo hacia el background.
# Hyperparameter analysis
```
xtrain, ytrain, xtest, ytest = split_train_test(df_db,0.75)
start_total = time.time()
for n_hid_layers in range(2,5):
for n_neur in [10,20,40]:
tup = []
for i in range(n_hid_layers):
tup.append(n_neur)
tup = tuple(tup)
start = time.time()
clf_nn = MLPClassifier(
hidden_layer_sizes = tup,
max_iter=2000,
early_stopping=True
)
clf_nn.fit(xtrain, ytrain)
ypred = clf_nn.predict(xtest)
final = time.time()
metric_report(ytest, ypred)
print('\n====>Tiempo transcurrido (minutos):', (final-start)/(60))
print('Number of hidden layers:', n_hid_layers)
print('Number of neurons per layer:', n_neur)
end_total = time()
print('\n====> Total tiempo transcurrido (horas):', (end_total-start_total)/(60*60))
```
# Two Neural Networks
## 1. Classify background
```
def printScoresBack(xtest,ytest,clf):
xback, yback = xtest[ytest=='background'], ytest[ytest=='background']
print('Score del background:', clf.score(xback,yback))
xrest, yrest = xtest[ytest!='background'], ytest[ytest!='background']
print('Score del resto:', clf.score(xrest,yrest))
num_back = len(yback)
num_rest = len(ytest)-num_back
func = lambda x: 1/num_back if x=='background' else 1/num_rest
weights = np.array([func(x) for x in ytest])
# Score donde las tres clases ponderan igual
print('Score con pesos:', clf.score(xtest,ytest,weights))
print('========================================')
df_db = group_datafiles_byID('../datasets/raw/HT_Sensor_metadata.dat', '../datasets/raw/HT_Sensor_dataset.dat')
df_db = reclassify_series_samples(df_db)
df_db.loc[df_db['class']!='background','class'] = 'not-background'
df_db[df_db['class']!='background'].head()
# Primero probamos a no quitar el exceso de background
df_train, df_test = split_series_byID(0.75, df_db)
df_train, df_test = norm_train_test(df_train, df_test)
features = ['R1', 'R2', 'R3', 'R4', 'R5', 'R5', 'R6', 'R7', 'R8', 'Temp.', 'Humidity']
xtrain, ytrain = df_train[features].values, df_train['class'].values
xtest, ytest = df_test[features].values, df_test['class'].values
start_total = time.time()
for n_hid_layers in range(2,5):
for n_neur in [10,20,40]:
tup = []
for i in range(n_hid_layers):
tup.append(n_neur)
tup = tuple(tup)
start = time.time()
clf_nn = MLPClassifier(
hidden_layer_sizes = tup,
max_iter=2000,
early_stopping=True
)
clf_nn.fit(xtrain, ytrain)
ypred = clf_nn.predict(xtest)
final = time.time()
metric_report(ytest, ypred)
print('\n====>Tiempo transcurrido (minutos):', (end_total-start_total)/(60))
end_total = time.time()
print('\n====> Total tiempo transcurrido (horas):', (end_total-start_total)/(60*60))
# En más de la mitad de ocasiones aquellos datos que no son background son clasificados erroneamente.
# Veamos si es cuestión de quitar background.
# Ahora, lo mismo quitando el exceso de background
df_train, df_test = split_series_byID(0.75, df_db)
df_train = remove_bg(df_train,prop=1)
df_train, df_test = norm_train_test(df_train, df_test)
features = ['R1', 'R2', 'R3', 'R4', 'R5', 'R5', 'R6', 'R7', 'R8', 'Temp.', 'Humidity']
xtrain, ytrain = df_train[features].values, df_train['class'].values
xtest, ytest = df_test[features].values, df_test['class'].values
start_total = time()
for n_hid_layers in range(2,5):
for n_neur in [10,20,40]:
tup = []
for i in range(n_hid_layers):
tup.append(n_neur)
tup = tuple(tup)
start = time()
clf_nn = MLPClassifier(
hidden_layer_sizes = tup,
max_iter=2000,
early_stopping=True,
shuffle=True
)
clf_nn.fit(xtrain, ytrain)
score = clf_nn.score(xtest, ytest)
final = time()
printResults(n_hid_layers,n_neur,score,final-start)
printScoresBack(xtest,ytest,clf_nn)
end_total = time()
print('\n====> Total tiempo transcurrido (horas):', (end_total-start_total)/(60*60))
```
## 2. Classify wine and bananas
```
df_db = group_datafiles_byID('../datasets/raw/HT_Sensor_metadata.dat', '../datasets/raw/HT_Sensor_dataset.dat')
df_db = reclassify_series_samples(df_db)
df_db = df_db[df_db['class']!='background']
df_db.head()
xtrain, ytrain, xtest, ytest = split_train_test(df_db,0.75)
start_total = time()
for n_hid_layers in range(1,5):
for n_neur in [5,10,15,20,40]:
tup = []
for i in range(n_hid_layers):
tup.append(n_neur)
tup = tuple(tup)
start = time()
clf_nn = MLPClassifier(
hidden_layer_sizes = tup,
max_iter=2000,
early_stopping=True,
shuffle=True
)
clf_nn.fit(xtrain, ytrain)
score = clf_nn.score(xtest, ytest)
final = time()
printResults(n_hid_layers,n_neur,score,final-start)
end_total = time()
print('\n====> Total tiempo transcurrido (horas):', (end_total-start_total)/(60*60))
```
# 3. Merge the 2 NN
```
class doubleNN:
def __init__(self, n_hid_layers, n_neur):
self.hid_layers = n_hid_layers
self.neur = n_neur
tup = []
for i in range(n_hid_layers):
tup.append(n_neur)
tup = tuple(tup)
self.backNN = MLPClassifier(
hidden_layer_sizes = tup,
max_iter=2000,
early_stopping=True,
shuffle=True
)
self.wineNN = MLPClassifier(
hidden_layer_sizes = tup,
max_iter=2000,
early_stopping=True,
shuffle=True
)
def fit_bg(self, xtrain, ytrain):
ytrain_copy = np.array([x if x=='background' else 'not-background' for x in ytrain])
self.backNN.fit(xtrain, ytrain_copy)
def fit_wine(self,xtrain,ytrain):
self.wineNN.fit(xtrain, ytrain)
def predict(self,xtest):
ypred = self.backNN.predict(xtest)
ypred[ypred=='not-background'] = self.wineNN.predict(xtest[ypred=='not-background'])
return ypred
def score(self,xtest,ytest):
ypred = self.predict(ytest)
score = np.sum(np.equal(ypred,ytest))/len(ytest)
return score
# With all the background
xtrain, ytrain, xtest, ytest = split_train_test(df_db,0.75)
start_total = time.time()
for n_hid_layers in range(2,4):
for n_neur in [10,20]:
tup = []
for i in range(n_hid_layers):
tup.append(n_neur)
tup = tuple(tup)
start = time.time()
clf_nn = doubleNN(2,20)
clf_nn.fit_bg(xtrain, ytrain)
xtrain_notbg = xtrain[ytrain != 'background']
ytrain_notbg = ytrain[ytrain != 'background']
clf_nn.fit_wine(xtrain_notbg, ytrain_notbg)
ypred = clf_nn.predict(xtest)
final = time.time()
metric_report(ytest, ypred)
print('\n====>Tiempo transcurrido (minutos):', (final-start)/(60))
print('Number of hidden layers:', n_hid_layers)
print('Number of neurons per layer:', n_neur)
end_total = time.time()
print('\n====> Total tiempo transcurrido (horas):', (end_total-start_total)/(60*60))
# Removing background
df_train, df_test = split_series_byID(0.75, df_db)
df_train = remove_bg(df_train,prop=1)
features = ['R1', 'R2', 'R3', 'R4', 'R5', 'R5', 'R6', 'R7', 'R8', 'Temp.', 'Humidity']
xtrain, ytrain = df_train[features].values, df_train['class'].values
xtest, ytest = df_test[features].values, df_test['class'].values
start_total = time.time()
for n_hid_layers in range(2,4):
for n_neur in [10,20]:
tup = []
for i in range(n_hid_layers):
tup.append(n_neur)
tup = tuple(tup)
start = time.time()
clf_nn = doubleNN(2,20)
clf_nn.fit_bg(xtrain, ytrain)
xtrain_notbg = xtrain[ytrain != 'background']
ytrain_notbg = ytrain[ytrain != 'background']
clf_nn.fit_wine(xtrain_notbg, ytrain_notbg)
ypred = clf_nn.predict(xtest)
final = time.time()
metric_report(ytest, ypred)
print('\n====>Tiempo transcurrido (minutos):', (final-start)/(60))
print('Number of hidden layers:', n_hid_layers)
print('Number of neurons per layer:', n_neur)
end_total = time.time()
print('\n====> Total tiempo transcurrido (horas):', (end_total-start_total)/(60*60))
```
# Creating Windows
```
# with open('../datasets/preprocessed/window120_dataset.pkl', 'wb') as f:
# pickle.dump(win_df, f)
win_df = pd.read_pickle('../datasets/preprocessed/window120_dataset.pkl')
xtrain, ytrain, xtest, ytest = split_train_test(win_df,0.75)
start = time.time()
clf_nn = MLPClassifier(
hidden_layer_sizes = (32,16),
max_iter=2000,
early_stopping=True,
shuffle=True,
alpha=0.01,
learning_rate_init=0.01
)
clf_nn.fit(xtrain, ytrain)
ypred = clf_nn.predict(xtest)
final = time.time()
metric_report(ytest, ypred)
print('\n====>Tiempo transcurrido (minutos):', (final-start)/(60))
features = ['R1', 'R2', 'R3', 'R4', 'R5', 'R6', 'R7', 'R8', 'Temp.', 'Humidity',
'R1_mean', 'R2_mean', 'R3_mean', 'R4_mean', 'R5_mean', 'R6_mean', 'R7_mean',
'R8_mean', 'Temp._mean', 'Humidity_mean', 'R1_std', 'R2_std', 'R3_std', 'R4_std',
'R5_std', 'R6_std', 'R7_std', 'R8_std', 'Temp._std', 'Humidity_std']
# Varía ciertos hiperparámetros con ventanas e imprime los resultados más relevantes
def hyper_sim(win_df,num_val,n_hid_layers,n_neur,alpha):
errs_acc = []
errs_f1 = []
rec_ban = []
loss = []
for i in range(num_val):
df_train, df_test = split_series_byID(0.75, win_df)
df_train, df_test = norm_train_test(df_train,df_test,features_to_norm=features)
xtrain, ytrain = df_train[features].values, df_train['class'].values
xtest, ytest = df_test[features].values, df_test['class'].values
tup = []
for i in range(n_hid_layers):
tup.append(n_neur)
tup = tuple(tup)
clf_nn = MLPClassifier(
hidden_layer_sizes=tup,
max_iter=2000,
early_stopping=True,
shuffle=True,
alpha=alpha,
learning_rate='adaptive'
)
clf_nn.fit(xtrain, ytrain)
ypred = clf_nn.predict(xtest)
errs_acc.append(accuracy_score(ytest,ypred))
errs_f1.append(f1_score(ytest,ypred,average='weighted'))
rec_ban.append(np.sum(np.logical_and(ytest=='banana',ypred=='banana'))/np.sum(ytest=='banana'))
loss.append(clf_nn.loss_)
errs_acc = np.array(errs_acc)
errs_f1 = np.array(errs_f1)
rec_ban = np.array(rec_ban)
loss = np.array(loss)
print('Train loss:',np.mean(loss),'+-',np.std(loss))
print('Accuracy:',np.mean(errs_acc),'+-',np.std(errs_acc))
print('F1-score:',np.mean(errs_f1),'+-',np.std(errs_f1))
print('Recall bananas:',np.mean(rec_ban),'+-',np.std(rec_ban))
for alpha in [0.1,0.01,0.001]:
print('<<<<<<<<<<<<<<<<<<<<<<<<<<<<<>>>>>>>>>>>>>>>>>')
print('Alpha:',alpha)
for n_hid_layers in range(1,4):
print('##############################################')
print('\t Hidden layers:',n_hid_layers)
for n_neur in [4,8,16]:
print('==============================================')
print('\t \t Neurons per layer:',n_neur)
hyper_sim(win_df,3,n_hid_layers,n_neur,alpha)
print('==============================================')
# Nos quedamos con:
# alpha: 0.01
# hidden_layers: 3
# n_neurons: 4
features = ['R1', 'R2', 'R3', 'R4', 'R5', 'R6', 'R7', 'R8', 'Temp.', 'Humidity',
'R1_mean', 'R2_mean', 'R3_mean', 'R4_mean', 'R5_mean', 'R6_mean', 'R7_mean',
'R8_mean', 'Temp._mean', 'Humidity_mean', 'R1_std', 'R2_std', 'R3_std', 'R4_std',
'R5_std', 'R6_std', 'R7_std', 'R8_std', 'Temp._std', 'Humidity_std']
errs_acc = []
errs_f1 = []
rec_ban = []
for i in range(5):
df_train, df_test = split_series_byID(0.75, win_df)
df_train, df_test = norm_train_test(df_train,df_test,features_to_norm=features)
xtrain, ytrain = df_train[features].values, df_train['class'].values
xtest, ytest = df_test[features].values, df_test['class'].values
clf_nn = MLPClassifier(
hidden_layer_sizes=(4,4,4),
max_iter=2000,
early_stopping=True,
shuffle=True,
alpha=0.01,
learning_rate='adaptive'
)
bag = BaggingClassifier(base_estimator=clf_nn,n_estimators=100,n_jobs=3)
bag.fit(xtrain, ytrain)
ypred = bag.predict(xtest)
metric_report(ytest, ypred)
errs_acc.append(accuracy_score(ytest,ypred))
errs_f1.append(f1_score(ytest,ypred,average='weighted'))
rec_ban.append(np.sum(np.logical_and(ytest=='banana',ypred=='banana'))/np.sum(ytest=='banana'))
errs_acc = np.array(errs_acc)
errs_f1 = np.array(errs_f1)
rec_ban = np.array(rec_ban)
print('Accuracy:',np.mean(errs_acc),'+-',np.std(errs_acc))
print('F1-score:',np.mean(errs_f1),'+-',np.std(errs_f1))
print('Recall bananas:',np.mean(rec_ban),'+-',np.std(rec_ban))
with open('../datasets/preprocessed/nn_optimal.pkl', 'wb') as f:
pickle.dump(bag, f)
```
|
github_jupyter
|
```
import numpy as np
import tensorflow as tf
from sklearn.utils import shuffle
import re
import time
import collections
import os
def build_dataset(words, n_words, atleast=1):
count = [['PAD', 0], ['GO', 1], ['EOS', 2], ['UNK', 3]]
counter = collections.Counter(words).most_common(n_words)
counter = [i for i in counter if i[1] >= atleast]
count.extend(counter)
dictionary = dict()
for word, _ in count:
dictionary[word] = len(dictionary)
data = list()
unk_count = 0
for word in words:
index = dictionary.get(word, 0)
if index == 0:
unk_count += 1
data.append(index)
count[0][1] = unk_count
reversed_dictionary = dict(zip(dictionary.values(), dictionary.keys()))
return data, count, dictionary, reversed_dictionary
lines = open('movie_lines.txt', encoding='utf-8', errors='ignore').read().split('\n')
conv_lines = open('movie_conversations.txt', encoding='utf-8', errors='ignore').read().split('\n')
id2line = {}
for line in lines:
_line = line.split(' +++$+++ ')
if len(_line) == 5:
id2line[_line[0]] = _line[4]
convs = [ ]
for line in conv_lines[:-1]:
_line = line.split(' +++$+++ ')[-1][1:-1].replace("'","").replace(" ","")
convs.append(_line.split(','))
questions = []
answers = []
for conv in convs:
for i in range(len(conv)-1):
questions.append(id2line[conv[i]])
answers.append(id2line[conv[i+1]])
def clean_text(text):
text = text.lower()
text = re.sub(r"i'm", "i am", text)
text = re.sub(r"he's", "he is", text)
text = re.sub(r"she's", "she is", text)
text = re.sub(r"it's", "it is", text)
text = re.sub(r"that's", "that is", text)
text = re.sub(r"what's", "that is", text)
text = re.sub(r"where's", "where is", text)
text = re.sub(r"how's", "how is", text)
text = re.sub(r"\'ll", " will", text)
text = re.sub(r"\'ve", " have", text)
text = re.sub(r"\'re", " are", text)
text = re.sub(r"\'d", " would", text)
text = re.sub(r"\'re", " are", text)
text = re.sub(r"won't", "will not", text)
text = re.sub(r"can't", "cannot", text)
text = re.sub(r"n't", " not", text)
text = re.sub(r"n'", "ng", text)
text = re.sub(r"'bout", "about", text)
text = re.sub(r"'til", "until", text)
text = re.sub(r"[-()\"#/@;:<>{}`+=~|.!?,]", "", text)
return ' '.join([i.strip() for i in filter(None, text.split())])
clean_questions = []
for question in questions:
clean_questions.append(clean_text(question))
clean_answers = []
for answer in answers:
clean_answers.append(clean_text(answer))
min_line_length = 2
max_line_length = 5
short_questions_temp = []
short_answers_temp = []
i = 0
for question in clean_questions:
if len(question.split()) >= min_line_length and len(question.split()) <= max_line_length:
short_questions_temp.append(question)
short_answers_temp.append(clean_answers[i])
i += 1
short_questions = []
short_answers = []
i = 0
for answer in short_answers_temp:
if len(answer.split()) >= min_line_length and len(answer.split()) <= max_line_length:
short_answers.append(answer)
short_questions.append(short_questions_temp[i])
i += 1
question_test = short_questions[500:550]
answer_test = short_answers[500:550]
short_questions = short_questions[:500]
short_answers = short_answers[:500]
concat_from = ' '.join(short_questions+question_test).split()
vocabulary_size_from = len(list(set(concat_from)))
data_from, count_from, dictionary_from, rev_dictionary_from = build_dataset(concat_from, vocabulary_size_from)
print('vocab from size: %d'%(vocabulary_size_from))
print('Most common words', count_from[4:10])
print('Sample data', data_from[:10], [rev_dictionary_from[i] for i in data_from[:10]])
print('filtered vocab size:',len(dictionary_from))
print("% of vocab used: {}%".format(round(len(dictionary_from)/vocabulary_size_from,4)*100))
concat_to = ' '.join(short_answers+answer_test).split()
vocabulary_size_to = len(list(set(concat_to)))
data_to, count_to, dictionary_to, rev_dictionary_to = build_dataset(concat_to, vocabulary_size_to)
print('vocab from size: %d'%(vocabulary_size_to))
print('Most common words', count_to[4:10])
print('Sample data', data_to[:10], [rev_dictionary_to[i] for i in data_to[:10]])
print('filtered vocab size:',len(dictionary_to))
print("% of vocab used: {}%".format(round(len(dictionary_to)/vocabulary_size_to,4)*100))
GO = dictionary_from['GO']
PAD = dictionary_from['PAD']
EOS = dictionary_from['EOS']
UNK = dictionary_from['UNK']
for i in range(len(short_answers)):
short_answers[i] += ' EOS'
class Chatbot:
def __init__(self, size_layer, num_layers, embedded_size,
from_dict_size, to_dict_size, learning_rate,
batch_size, dropout = 0.5, beam_width = 15):
def lstm_cell(size, reuse=False):
return tf.nn.rnn_cell.GRUCell(size, reuse=reuse)
self.X = tf.placeholder(tf.int32, [None, None])
self.Y = tf.placeholder(tf.int32, [None, None])
self.X_seq_len = tf.count_nonzero(self.X, 1, dtype=tf.int32)
self.Y_seq_len = tf.count_nonzero(self.Y, 1, dtype=tf.int32)
batch_size = tf.shape(self.X)[0]
# encoder
encoder_embeddings = tf.Variable(tf.random_uniform([from_dict_size, embedded_size], -1, 1))
encoder_embedded = tf.nn.embedding_lookup(encoder_embeddings, self.X)
for n in range(num_layers):
(out_fw, out_bw), (state_fw, state_bw) = tf.nn.bidirectional_dynamic_rnn(
cell_fw = lstm_cell(size_layer // 2),
cell_bw = lstm_cell(size_layer // 2),
inputs = encoder_embedded,
sequence_length = self.X_seq_len,
dtype = tf.float32,
scope = 'bidirectional_rnn_%d'%(n))
encoder_embedded = tf.concat((out_fw, out_bw), 2)
bi_state = tf.concat((state_fw, state_bw), -1)
self.encoder_state = tuple([bi_state] * num_layers)
self.encoder_state = tuple(self.encoder_state[-1] for _ in range(num_layers))
main = tf.strided_slice(self.Y, [0, 0], [batch_size, -1], [1, 1])
decoder_input = tf.concat([tf.fill([batch_size, 1], GO), main], 1)
# decoder
decoder_embeddings = tf.Variable(tf.random_uniform([to_dict_size, embedded_size], -1, 1))
decoder_cells = tf.nn.rnn_cell.MultiRNNCell([lstm_cell(size_layer) for _ in range(num_layers)])
dense_layer = tf.layers.Dense(to_dict_size)
training_helper = tf.contrib.seq2seq.TrainingHelper(
inputs = tf.nn.embedding_lookup(decoder_embeddings, decoder_input),
sequence_length = self.Y_seq_len,
time_major = False)
training_decoder = tf.contrib.seq2seq.BasicDecoder(
cell = decoder_cells,
helper = training_helper,
initial_state = self.encoder_state,
output_layer = dense_layer)
training_decoder_output, _, _ = tf.contrib.seq2seq.dynamic_decode(
decoder = training_decoder,
impute_finished = True,
maximum_iterations = tf.reduce_max(self.Y_seq_len))
predicting_helper = tf.contrib.seq2seq.GreedyEmbeddingHelper(
embedding = decoder_embeddings,
start_tokens = tf.tile(tf.constant([GO], dtype=tf.int32), [batch_size]),
end_token = EOS)
predicting_decoder = tf.contrib.seq2seq.BasicDecoder(
cell = decoder_cells,
helper = predicting_helper,
initial_state = self.encoder_state,
output_layer = dense_layer)
predicting_decoder_output, _, _ = tf.contrib.seq2seq.dynamic_decode(
decoder = predicting_decoder,
impute_finished = True,
maximum_iterations = 2 * tf.reduce_max(self.X_seq_len))
self.training_logits = training_decoder_output.rnn_output
self.predicting_ids = predicting_decoder_output.sample_id
masks = tf.sequence_mask(self.Y_seq_len, tf.reduce_max(self.Y_seq_len), dtype=tf.float32)
self.cost = tf.contrib.seq2seq.sequence_loss(logits = self.training_logits,
targets = self.Y,
weights = masks)
self.optimizer = tf.train.AdamOptimizer(learning_rate).minimize(self.cost)
y_t = tf.argmax(self.training_logits,axis=2)
y_t = tf.cast(y_t, tf.int32)
self.prediction = tf.boolean_mask(y_t, masks)
mask_label = tf.boolean_mask(self.Y, masks)
correct_pred = tf.equal(self.prediction, mask_label)
correct_index = tf.cast(correct_pred, tf.float32)
self.accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
size_layer = 256
num_layers = 2
embedded_size = 128
learning_rate = 0.001
batch_size = 16
epoch = 20
tf.reset_default_graph()
sess = tf.InteractiveSession()
model = Chatbot(size_layer, num_layers, embedded_size, len(dictionary_from),
len(dictionary_to), learning_rate,batch_size)
sess.run(tf.global_variables_initializer())
def str_idx(corpus, dic):
X = []
for i in corpus:
ints = []
for k in i.split():
ints.append(dic.get(k,UNK))
X.append(ints)
return X
X = str_idx(short_questions, dictionary_from)
Y = str_idx(short_answers, dictionary_to)
X_test = str_idx(question_test, dictionary_from)
Y_test = str_idx(answer_test, dictionary_from)
def pad_sentence_batch(sentence_batch, pad_int):
padded_seqs = []
seq_lens = []
max_sentence_len = max([len(sentence) for sentence in sentence_batch])
for sentence in sentence_batch:
padded_seqs.append(sentence + [pad_int] * (max_sentence_len - len(sentence)))
seq_lens.append(len(sentence))
return padded_seqs, seq_lens
for i in range(epoch):
total_loss, total_accuracy = 0, 0
for k in range(0, len(short_questions), batch_size):
index = min(k+batch_size, len(short_questions))
batch_x, seq_x = pad_sentence_batch(X[k: index], PAD)
batch_y, seq_y = pad_sentence_batch(Y[k: index ], PAD)
predicted, accuracy,loss, _ = sess.run([model.predicting_ids,
model.accuracy, model.cost, model.optimizer],
feed_dict={model.X:batch_x,
model.Y:batch_y})
total_loss += loss
total_accuracy += accuracy
total_loss /= (len(short_questions) / batch_size)
total_accuracy /= (len(short_questions) / batch_size)
print('epoch: %d, avg loss: %f, avg accuracy: %f'%(i+1, total_loss, total_accuracy))
for i in range(len(batch_x)):
print('row %d'%(i+1))
print('QUESTION:',' '.join([rev_dictionary_from[n] for n in batch_x[i] if n not in [0,1,2,3]]))
print('REAL ANSWER:',' '.join([rev_dictionary_to[n] for n in batch_y[i] if n not in[0,1,2,3]]))
print('PREDICTED ANSWER:',' '.join([rev_dictionary_to[n] for n in predicted[i] if n not in[0,1,2,3]]),'\n')
batch_x, seq_x = pad_sentence_batch(X_test[:batch_size], PAD)
batch_y, seq_y = pad_sentence_batch(Y_test[:batch_size], PAD)
predicted = sess.run(model.predicting_ids, feed_dict={model.X:batch_x,model.X_seq_len:seq_x})
for i in range(len(batch_x)):
print('row %d'%(i+1))
print('QUESTION:',' '.join([rev_dictionary_from[n] for n in batch_x[i] if n not in [0,1,2,3]]))
print('REAL ANSWER:',' '.join([rev_dictionary_to[n] for n in batch_y[i] if n not in[0,1,2,3]]))
print('PREDICTED ANSWER:',' '.join([rev_dictionary_to[n] for n in predicted[i] if n not in[0,1,2,3]]),'\n')
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_12_04_atari.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# T81-558: Applications of Deep Neural Networks
**Module 12: Reinforcement Learning**
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), McKelvey School of Engineering, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# Module 12 Video Material
* Part 12.1: Introduction to the OpenAI Gym [[Video]](https://www.youtube.com/watch?v=_KbUxgyisjM&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_12_01_ai_gym.ipynb)
* Part 12.2: Introduction to Q-Learning [[Video]](https://www.youtube.com/watch?v=A3sYFcJY3lA&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_12_02_qlearningreinforcement.ipynb)
* Part 12.3: Keras Q-Learning in the OpenAI Gym [[Video]](https://www.youtube.com/watch?v=qy1SJmsRhvM&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_12_03_keras_reinforce.ipynb)
* **Part 12.4: Atari Games with Keras Neural Networks** [[Video]](https://www.youtube.com/watch?v=co0SwPWoZh0&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_12_04_atari.ipynb)
* Part 12.5: Application of Reinforcement Learning [[Video]](https://www.youtube.com/watch?v=1jQPP3RfwMI&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_12_05_apply_rl.ipynb)
# Google CoLab Instructions
The following code ensures that Google CoLab is running the correct version of TensorFlow, and has the necessary Python libraries installed.
```
try:
from google.colab import drive
%tensorflow_version 2.x
COLAB = True
print("Note: using Google CoLab")
except:
print("Note: not using Google CoLab")
COLAB = False
if COLAB:
!sudo apt-get install -y xvfb ffmpeg
!pip install -q 'gym==0.10.11'
!pip install -q 'imageio==2.4.0'
!pip install -q PILLOW
!pip install -q 'pyglet==1.3.2'
!pip install -q pyvirtualdisplay
!pip install -q --upgrade tensorflow-probability
!pip install -q tf-agents
```
# Part 12.4: Atari Games with Keras Neural Networks
The Atari 2600 is a home video game console from Atari, Inc. Released on September 11, 1977. It is credited with popularizing the use of microprocessor-based hardware and games stored on ROM cartridges instead of dedicated hardware with games physically built into the unit. The 2600 was bundled with two joystick controllers, a conjoined pair of paddle controllers, and a game cartridge: initially [Combat](https://en.wikipedia.org/wiki/Combat_(Atari_2600)), and later [Pac-Man](https://en.wikipedia.org/wiki/Pac-Man_(Atari_2600)).
Atari emulators are popular and allow many of the old Atari video games to be played on modern computers. They are even available as JavaScript.
* [Virtual Atari](http://www.virtualatari.org/listP.html)
Atari games have become popular benchmarks for AI systems, particularly reinforcement learning. OpenAI Gym internally uses the [Stella Atari Emulator](https://stella-emu.github.io/). The Atari 2600 is shown in Figure 12.ATARI.
**Figure 12.ATARI: The Atari 2600**

### Actual Atari 2600 Specs
* CPU: 1.19 MHz MOS Technology 6507
* Audio + Video processor: Television Interface Adapter (TIA)
* Playfield resolution: 40 x 192 pixels (NTSC). Uses a 20-pixel register that is mirrored or copied, left side to right side, to achieve the width of 40 pixels.
* Player sprites: 8 x 192 pixels (NTSC). Player, ball, and missile sprites use pixels that are 1/4 the width of playfield pixels (unless stretched).
* Ball and missile sprites: 1 x 192 pixels (NTSC).
* Maximum resolution: 160 x 192 pixels (NTSC). Max resolution is only somewhat achievable with programming tricks that combine sprite pixels with playfield pixels.
* 128 colors (NTSC). 128 possible on screen. Max of 4 per line: background, playfield, player0 sprite, and player1 sprite. Palette switching between lines is common. Palette switching mid line is possible but not common due to resource limitations.
* 2 channels of 1-bit monaural sound with 4-bit volume control.
### OpenAI Lab Atari Pong
OpenAI Gym can be used with Windows; however, it requires a special [installation procedure].(https://towardsdatascience.com/how-to-install-openai-gym-in-a-windows-environment-338969e24d30)
This chapter demonstrates playing [Atari Pong](https://github.com/wau/keras-rl2/blob/master/examples/dqn_atari.py). Pong is a two-dimensional sports game that simulates table tennis. The player controls an in-game paddle by moving it vertically across the left or right side of the screen. They can compete against another player controlling a second paddle on the opposing side. Players use the paddles to hit a ball back and forth. The goal is for each player to reach eleven points before the opponent; you earn points when one fails to return it to the other. For the Atari 2600 version of Pong, a computer player (controlled by the 2600) is the opposing player.
This section shows how to adapt TF-Agents to an Atari game. Some changes are necessary when compared to the pole-cart game presented earlier in this chapter. You can quickly adapt this example to any Atari game by simply changing the environment name. However, I tuned the code presented here for Pong, and it may not perform as well for other games. Some tuning will likely be necessary to produce a good agent for other games.
We begin by importing the needed Python packages.
```
import base64
import imageio
import IPython
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import PIL.Image
import pyvirtualdisplay
import tensorflow as tf
from tf_agents.agents.dqn import dqn_agent
from tf_agents.drivers import dynamic_step_driver
from tf_agents.environments import suite_gym, suite_atari
from tf_agents.environments import tf_py_environment, batched_py_environment
from tf_agents.eval import metric_utils
from tf_agents.metrics import tf_metrics
from tf_agents.networks import q_network
from tf_agents.policies import random_tf_policy
from tf_agents.replay_buffers import tf_uniform_replay_buffer
from tf_agents.trajectories import trajectory
from tf_agents.utils import common
from tf_agents.specs import tensor_spec
from tf_agents.trajectories import time_step as ts
# Set up a virtual display for rendering OpenAI gym environments.
display = pyvirtualdisplay.Display(visible=0, size=(1400, 900)).start()
```
## Hyperparameters
The hyperparameter names are the same as the previous DQN example; however, I tuned the numeric values for the more complex Atari game.
```
num_iterations = 250000
initial_collect_steps = 200
collect_steps_per_iteration = 10
replay_buffer_max_length = 100000
batch_size = 32
learning_rate = 2.5e-3
log_interval = 5000
num_eval_episodes = 5
eval_interval = 25000
```
The algorithm needs more iterations for an Atari game. I also found that increasing the number of collection steps helped the algorithm to train.
## Atari Environment's
You must handle Atari environments differently than games like cart-poll. Atari games typically use their 2D displays as the environment state. AI Gym represents Atari games as either a 3D (height by width by color) state spaced based on their screens, or a vector representing the state of the gam's computer RAM. To preprocess Atari games for greater computational efficiency, we generally skip several frames, decrease the resolution, and discard color information. The following code shows how we can set up an Atari environment.
```
#env_name = 'Breakout-v4'
env_name = 'Pong-v0'
#env_name = 'BreakoutDeterministic-v4'
#env = suite_gym.load(env_name)
# AtariPreprocessing runs 4 frames at a time, max-pooling over the last 2
# frames. We need to account for this when computing things like update
# intervals.
ATARI_FRAME_SKIP = 4
max_episode_frames=108000 # ALE frames
env = suite_atari.load(
env_name,
max_episode_steps=max_episode_frames / ATARI_FRAME_SKIP,
gym_env_wrappers=suite_atari.DEFAULT_ATARI_GYM_WRAPPERS_WITH_STACKING)
#env = batched_py_environment.BatchedPyEnvironment([env])
```
We can now reset the environment and display one step. The following image shows how the Pong game environment appears to a user.
```
env.reset()
PIL.Image.fromarray(env.render())
```
We are now ready to load and wrap the two environments for TF-Agents. The algorithm uses the first environment for evaluation, and the second to train.
```
train_py_env = suite_atari.load(
env_name,
max_episode_steps=max_episode_frames / ATARI_FRAME_SKIP,
gym_env_wrappers=suite_atari.DEFAULT_ATARI_GYM_WRAPPERS_WITH_STACKING)
eval_py_env = suite_atari.load(
env_name,
max_episode_steps=max_episode_frames / ATARI_FRAME_SKIP,
gym_env_wrappers=suite_atari.DEFAULT_ATARI_GYM_WRAPPERS_WITH_STACKING)
train_env = tf_py_environment.TFPyEnvironment(train_py_env)
eval_env = tf_py_environment.TFPyEnvironment(eval_py_env)
```
## Agent
I used the following class, from TF-Agents examples, to wrap the regular Q-network class. The AtariQNetwork class ensures that the pixel values from the Atari screen are divided by 255. This division assists the neural network by normalizing the pixel values to between 0 and 1.
```
class AtariQNetwork(q_network.QNetwork):
"""QNetwork subclass that divides observations by 255."""
def call(self,
observation,
step_type=None,
network_state=(),
training=False):
state = tf.cast(observation, tf.float32)
# We divide the grayscale pixel values by 255 here rather than storing
# normalized values beause uint8s are 4x cheaper to store than float32s.
state = state / 255
return super(AtariQNetwork, self).call(
state, step_type=step_type, network_state=network_state,
training=training)
```
Next, we introduce two hyperparameters that are specific to the neural network we are about to define.
```
fc_layer_params = (512,)
conv_layer_params=((32, (8, 8), 4), (64, (4, 4), 2), (64, (3, 3), 1))
q_net = AtariQNetwork(
train_env.observation_spec(),
train_env.action_spec(),
conv_layer_params=conv_layer_params,
fc_layer_params=fc_layer_params)
```
Convolutional neural networks usually are made up of several alternating pairs of convolution and max-pooling layers, ultimately culminating in one or more dense layers. These layers are the same types as previously seen in this course. The QNetwork accepts two parameters that define the convolutional neural network structure.
The more simple of the two parameters is **fc_layer_params**. This parameter specifies the size of each of the dense layers. A tuple specifies the size of each of the layers in a list.
The second parameter, named **conv_layer_params**, is a list of convolution layers parameters, where each item is a length-three tuple indicating (filters, kernel_size, stride). This implementation of QNetwork supports only convolution layers. If you desire a more complex convolutional neural network, you must define your variant of the QNetwork.
The QNetwork defined here is not the agent, instead, the QNetwork is used by the DQN agent to implement the actual neural network. This allows flexibility as you can set your own class if needed.
Next, we define the optimizer. For this example, I used RMSPropOptimizer. However, AdamOptimizer is another popular choice. We also create the DQN and reference the Q-network we just created.
```
optimizer = tf.compat.v1.train.RMSPropOptimizer(
learning_rate=learning_rate,
decay=0.95,
momentum=0.0,
epsilon=0.00001,
centered=True)
train_step_counter = tf.Variable(0)
observation_spec = tensor_spec.from_spec(train_env.observation_spec())
time_step_spec = ts.time_step_spec(observation_spec)
action_spec = tensor_spec.from_spec(train_env.action_spec())
target_update_period=32000 # ALE frames
update_period=16 # ALE frames
_update_period = update_period / ATARI_FRAME_SKIP
_global_step = tf.compat.v1.train.get_or_create_global_step()
agent = dqn_agent.DqnAgent(
time_step_spec,
action_spec,
q_network=q_net,
optimizer=optimizer,
epsilon_greedy=0.01,
n_step_update=1.0,
target_update_tau=1.0,
target_update_period=(
target_update_period / ATARI_FRAME_SKIP / _update_period),
td_errors_loss_fn=common.element_wise_huber_loss,
gamma=0.99,
reward_scale_factor=1.0,
gradient_clipping=None,
debug_summaries=False,
summarize_grads_and_vars=False,
train_step_counter=_global_step)
agent.initialize()
```
## Metrics and Evaluation
There are many different ways to measure the effectiveness of a model trained with reinforcement learning. The loss function of the internal Q-network is not a good measure of the entire DQN algorithm's overall fitness. The network loss function measures how close the Q-network was fit to the collected data and did not indicate how effective the DQN is in maximizing rewards. The method used for this example tracks the average reward received over several episodes.
```
def compute_avg_return(environment, policy, num_episodes=10):
total_return = 0.0
for _ in range(num_episodes):
time_step = environment.reset()
episode_return = 0.0
while not time_step.is_last():
action_step = policy.action(time_step)
time_step = environment.step(action_step.action)
episode_return += time_step.reward
total_return += episode_return
avg_return = total_return / num_episodes
return avg_return.numpy()[0]
# See also the metrics module for standard implementations of different metrics.
# https://github.com/tensorflow/agents/tree/master/tf_agents/metrics
```
## Replay Buffer
DQN works by training a neural network to predict the Q-values for every possible environment-state. A neural network needs training data, so the algorithm accumulates this training data as it runs episodes. The replay buffer is where this data is stored. Only the most recent episodes are stored, older episode data rolls off the queue as the queue accumulates new data.
```
replay_buffer = tf_uniform_replay_buffer.TFUniformReplayBuffer(
data_spec=agent.collect_data_spec,
batch_size=train_env.batch_size,
max_length=replay_buffer_max_length)
# Dataset generates trajectories with shape [Bx2x...]
dataset = replay_buffer.as_dataset(
num_parallel_calls=3,
sample_batch_size=batch_size,
num_steps=2).prefetch(3)
```
## Random Collection
The algorithm must prime the pump. Training cannot begin on an empty replay buffer. The following code performs a predefined number of steps to generate initial training data.
```
random_policy = random_tf_policy.RandomTFPolicy(train_env.time_step_spec(),
train_env.action_spec())
def collect_step(environment, policy, buffer):
time_step = environment.current_time_step()
action_step = policy.action(time_step)
next_time_step = environment.step(action_step.action)
traj = trajectory.from_transition(time_step, action_step, next_time_step)
# Add trajectory to the replay buffer
buffer.add_batch(traj)
def collect_data(env, policy, buffer, steps):
for _ in range(steps):
collect_step(env, policy, buffer)
collect_data(train_env, random_policy, replay_buffer, steps=initial_collect_steps)
```
## Training the agent
We are now ready to train the DQN. This process can take many hours, depending on how many episodes you wish to run through. As training occurs, this code will update on both the loss and average return. As training becomes more successful, the average return should increase. The losses reported reflecting the average loss for individual training batches.
```
iterator = iter(dataset)
# (Optional) Optimize by wrapping some of the code in a graph using TF function.
agent.train = common.function(agent.train)
# Reset the train step
agent.train_step_counter.assign(0)
# Evaluate the agent's policy once before training.
avg_return = compute_avg_return(eval_env, agent.policy, num_eval_episodes)
returns = [avg_return]
for _ in range(num_iterations):
# Collect a few steps using collect_policy and save to the replay buffer.
for _ in range(collect_steps_per_iteration):
collect_step(train_env, agent.collect_policy, replay_buffer)
# Sample a batch of data from the buffer and update the agent's network.
experience, unused_info = next(iterator)
train_loss = agent.train(experience).loss
step = agent.train_step_counter.numpy()
if step % log_interval == 0:
print('step = {0}: loss = {1}'.format(step, train_loss))
if step % eval_interval == 0:
avg_return = compute_avg_return(eval_env, agent.policy, num_eval_episodes)
print('step = {0}: Average Return = {1}'.format(step, avg_return))
returns.append(avg_return)
```
## Visualization
The notebook can plot the average return over training iterations. The average return should increase as the program performs more training iterations.
```
iterations = range(0, num_iterations + 1, eval_interval)
plt.plot(iterations, returns)
plt.ylabel('Average Return')
plt.xlabel('Iterations')
plt.ylim(top=10)
```
### Videos
We now have a trained model and observed its training progress on a graph. Perhaps the most compelling way to view an Atari game's results is a video that allows us to see the agent play the game. The following functions are defined so that we can watch the agent play the game in the notebook.
```
def embed_mp4(filename):
"""Embeds an mp4 file in the notebook."""
video = open(filename,'rb').read()
b64 = base64.b64encode(video)
tag = '''
<video width="640" height="480" controls>
<source src="data:video/mp4;base64,{0}" type="video/mp4">
Your browser does not support the video tag.
</video>'''.format(b64.decode())
return IPython.display.HTML(tag)
def create_policy_eval_video(policy, filename, num_episodes=5, fps=30):
filename = filename + ".mp4"
with imageio.get_writer(filename, fps=fps) as video:
for _ in range(num_episodes):
time_step = eval_env.reset()
video.append_data(eval_py_env.render())
while not time_step.is_last():
action_step = policy.action(time_step)
time_step = eval_env.step(action_step.action)
video.append_data(eval_py_env.render())
return embed_mp4(filename)
```
First, we will observe the trained agent play the game.
```
create_policy_eval_video(agent.policy, "trained-agent")
```
For comparison, we observe a random agent play. While the trained agent is far from perfect, it does outperform the random agent by a considerable amount.
```
create_policy_eval_video(random_policy, "random-agent")
```
|
github_jupyter
|
# Disclaimer
Released under the CC BY 4.0 License (https://creativecommons.org/licenses/by/4.0/)
# Purpose of this notebook
The purpose of this document is to show how I approached the presented problem and to record my learning experience in how to use Tensorflow 2 and CatBoost to perform a classification task on text data.
If, while reading this document, you think _"Why didn't you do `<this>` instead of `<that>`?"_, the answer could be simply because I don't know about `<this>`. Comments, questions and constructive criticism are of course welcome.
# Intro
This simple classification task has been developed to get familiarized with Tensorflow 2 and CatBoost handling of text data. In summary, the task is to predict the author of a short text.
To get a number of train/test examples, it is enough to create a twitter app and, using the python client library for twitter, read the user timeline of multiple accounts. This process is not covered here. If you are interested in this topic, feel free to contact me.
## Features
It is assumed the collected raw data consists of:
1. The author handle (the label that will be predicted)
2. The timestamp of the post
3. The raw text of the post
### Preparing the dataset
When preparing the dataset, the content of the post is preprocessed using these rules:
1. Newlines are replaced with a space
2. Links are replaced with a placeholder (e.g. `<link>`)
3. For each possible unicode char category, the number of chars in that category is added as a feature
4. The number of words for each tweet is added as a feature
5. Retweets (even retweets with comment) are discarded. Only responses and original tweets are taken into account
The dataset has been randomly split into three different files for train (70%), validation (10%) and test (20%). For each label, it has been verified that the same percentages hold in all three files.
Before fitting the data and before evaluation on the test dataset, the timestamp values are normalized, using the mean and standard deviation computed on the train dataset.
# TensorFlow 2 model
The model has four different input features:
1. The normalized timestamp.
2. The input text, represented as the whole sentence. This will be transformed in a 128-dimensional vector by an embedding layer.
3. The input text, this time represented as a sequence of words, expressed as indexes of tokens. This representation will be used by a LSTM layer to try to extract some meaning from the actual sequence of the used words.
4. The unicode character category usage. This should help in identify handles that use emojis, a lot of punctuation or unusual chars.
The resulting layers are concatenated, then after a sequence of two dense layers (with an applied dropout) the final layer computes the logits for the different classes. The used loss function is *sparse categorical crossentropy*, since the labels are represented as indexes of a list of twitter handles.
## Imports for the TensorFlow 2 model
```
import functools
import os
from tensorflow.keras import Input, layers
import tensorflow as tf
import tensorflow_hub as hub
from tensorflow.keras import regularizers
import pandas as pd
import numpy as np
import copy
import calendar
import datetime
import re
from tensorflow.keras.preprocessing.text import Tokenizer
import unicodedata
#masking layers and GPU don't mix
os.environ["CUDA_VISIBLE_DEVICES"] = "-1"
```
## Definitions for the TensorFlow 2 model
```
#Download size: ~446MB
hub_layer = hub.KerasLayer(
"https://tfhub.dev/google/tf2-preview/nnlm-en-dim128/1",
output_shape=[512],
input_shape=[],
dtype=tf.string,
trainable=False
)
embed = hub.load("https://tfhub.dev/google/tf2-preview/nnlm-en-dim128/1")
unicode_data_categories = [
"Cc",
"Cf",
"Cn",
"Co",
"Cs",
"LC",
"Ll",
"Lm",
"Lo",
"Lt",
"Lu",
"Mc",
"Me",
"Mn",
"Nd",
"Nl",
"No",
"Pc",
"Pd",
"Pe",
"Pf",
"Pi",
"Po",
"Ps",
"Sc",
"Sk",
"Sm",
"So",
"Zl",
"Zp",
"Zs"
]
column_names = [
"handle",
"timestamp",
"text"
]
column_names.extend(unicode_data_categories)
train_file = os.path.realpath("input.csv")
n_tokens = 100000
tokenizer = Tokenizer(n_tokens, oov_token='<OOV>')
#List of handles (labels)
#Fill with the handles you want to consider in your dataset
handles = [
]
end_token = "XEND"
train_file = os.path.realpath("data/train.csv")
val_file = os.path.realpath("data/val.csv")
test_file = os.path.realpath("data/test.csv")
```
## Preprocessing and computing dataset features
```
def get_pandas_dataset(input_file, fit_tokenizer=False, timestamp_mean=None, timestamp_std=None, pad_sequence=None):
pd_dat = pd.read_csv(input_file, names=column_names)
pd_dat = pd_dat[pd_dat.handle.isin(handles)]
if(timestamp_mean is None):
timestamp_mean = pd_dat.timestamp.mean()
if(timestamp_std is None):
timestamp_std = pd_dat.timestamp.std()
pd_dat.timestamp = (pd_dat.timestamp - timestamp_mean) / timestamp_std
pd_dat["handle_index"] = pd_dat['handle'].map(lambda x: handles.index(x))
if(fit_tokenizer):
tokenizer.fit_on_texts(pd_dat["text"])
pad_sequence = tokenizer.texts_to_sequences([[end_token]])[0][0]
pd_dat["sequence"] = tokenizer.texts_to_sequences(pd_dat["text"])
max_seq_length = 30
pd_dat = pd_dat.reset_index(drop=True)
#max length
pd_dat["sequence"] = pd.Series(el[0:max_seq_length] for el in pd_dat["sequence"])
#padding
pd_dat["sequence"] = pd.Series([el + ([pad_sequence] * (max_seq_length - len(el))) for el in pd_dat["sequence"]])
pd_dat["words_in_tweet"] = pd_dat["text"].str.strip().str.split(" ").str.len() + 1
return pd_dat, timestamp_mean, timestamp_std, pad_sequence
train_dataset, timestamp_mean, timestamp_std, pad_sequence = get_pandas_dataset(train_file, fit_tokenizer=True)
test_dataset, _, _, _= get_pandas_dataset(test_file, timestamp_mean=timestamp_mean, timestamp_std=timestamp_std, pad_sequence=pad_sequence)
val_dataset, _, _, _ = get_pandas_dataset(val_file, timestamp_mean=timestamp_mean, timestamp_std=timestamp_std, pad_sequence=pad_sequence)
#selecting as features only the unicode categories that are used in the train dataset
non_null_unicode_categories = []
for unicode_data_category in unicode_data_categories:
category_name = unicode_data_category
category_sum = train_dataset[category_name].sum()
if(category_sum > 0):
non_null_unicode_categories.append(category_name)
print("Bucketized unicode categories used as features: " + repr(non_null_unicode_categories))
```
## Defining input/output features from the datasets
```
def split_inputs_and_outputs(pd_dat):
labels = pd_dat['handle_index'].values
icolumns = pd_dat.columns
timestamps = pd_dat.loc[:, "timestamp"].astype(np.float32)
text = pd_dat.loc[:, "text"]
sequence = np.asarray([np.array(el) for el in pd_dat.loc[:, "sequence"]])
#unicode_char_ratios = pd_dat[unicode_data_categories].astype(np.float32)
unicode_char_categories = {
category_name: pd_dat[category_name] for category_name in non_null_unicode_categories
}
words_in_tweet = pd_dat['words_in_tweet']
return timestamps, text, sequence, unicode_char_categories, words_in_tweet, labels
timestamps_train, text_train, sequence_train, unicode_char_categories_train, words_in_tweet_train, labels_train = split_inputs_and_outputs(train_dataset)
timestamps_val, text_val, sequence_val, unicode_char_categories_val, words_in_tweet_val, labels_val = split_inputs_and_outputs(val_dataset)
timestamps_test, text_test, sequence_test, unicode_char_categories_test, words_in_tweet_test, labels_test = split_inputs_and_outputs(test_dataset)
```
## Input tensors
```
input_timestamp = Input(shape=(1, ), name='input_timestamp', dtype=tf.float32)
input_text = Input(shape=(1, ), name='input_text', dtype=tf.string)
input_sequence = Input(shape=(None, 1 ), name="input_sequence", dtype=tf.float32)
input_unicode_char_categories = [
Input(shape=(1, ), name="input_"+category_name, dtype=tf.float32) for category_name in non_null_unicode_categories
]
input_words_in_tweet = Input(shape=(1, ), name="input_words_in_tweet", dtype=tf.float32)
inputs_train = {
'input_timestamp': timestamps_train,
"input_text": text_train,
"input_sequence": sequence_train,
'input_words_in_tweet': words_in_tweet_train,
}
inputs_train.update({
'input_' + category_name: unicode_char_categories_train[category_name] for category_name in non_null_unicode_categories
})
outputs_train = labels_train
inputs_val = {
'input_timestamp': timestamps_val,
"input_text": text_val,
"input_sequence": sequence_val,
'input_words_in_tweet': words_in_tweet_val
}
inputs_val.update({
'input_' + category_name: unicode_char_categories_val[category_name] for category_name in non_null_unicode_categories
})
outputs_val = labels_val
inputs_test = {
'input_timestamp': timestamps_test,
"input_text": text_test,
"input_sequence": sequence_test,
'input_words_in_tweet': words_in_tweet_test
}
inputs_test.update({
'input_' + category_name: unicode_char_categories_test[category_name] for category_name in non_null_unicode_categories
})
outputs_test = labels_test
```
## TensorFlow 2 model definition
```
def get_model():
reg = None
activation = 'relu'
reshaped_text = layers.Reshape(target_shape=())(input_text)
embedded = hub_layer(reshaped_text)
x = layers.Dense(256, activation=activation)(embedded)
masking = layers.Masking(mask_value=pad_sequence)(input_sequence)
lstm_layer = layers.Bidirectional(layers.LSTM(32))(masking)
flattened_lstm_layer = layers.Flatten()(lstm_layer)
x = layers.concatenate([
input_timestamp,
flattened_lstm_layer,
*input_unicode_char_categories,
input_words_in_tweet,
x
])
x = layers.Dense(n_tokens // 30, activation=activation, kernel_regularizer=reg)(x)
x = layers.Dropout(0.1)(x)
x = layers.Dense(n_tokens // 50, activation=activation, kernel_regularizer=reg)(x)
x = layers.Dropout(0.1)(x)
x = layers.Dense(256, activation=activation, kernel_regularizer=reg)(x)
y = layers.Dense(len(handles), activation='linear')(x)
model = tf.keras.Model(
inputs=[
input_timestamp,
input_text,
input_sequence,
*input_unicode_char_categories,
input_words_in_tweet
],
outputs=[y]
)
cce = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
model.compile(
optimizer='adam',
loss=cce,
metrics=['sparse_categorical_accuracy']
)
return model
model = get_model()
tf.keras.utils.plot_model(model, to_file='twitstar.png', show_shapes=True)
```
## TensorFlow 2 model fitting
```
history = model.fit(
inputs_train,
outputs_train,
epochs=15,
batch_size=64,
verbose=True,
validation_data=(inputs_val, outputs_val),
callbacks=[
tf.keras.callbacks.ModelCheckpoint(
os.path.realpath("weights.h5"),
monitor="val_sparse_categorical_accuracy",
save_best_only=True,
verbose=2
),
tf.keras.callbacks.EarlyStopping(
patience=3,
monitor="val_sparse_categorical_accuracy"
),
]
)
```
## TensorFlow 2 model plots for train loss and accuracy
```
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Loss vs. epochs')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Training', 'Validation'], loc='upper right')
plt.show()
plt.plot(history.history['sparse_categorical_accuracy'])
plt.plot(history.history['val_sparse_categorical_accuracy'])
plt.title('Accuracy vs. epochs')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Training', 'Validation'], loc='upper right')
plt.show()
```
## TensorFlow 2 model evaluation
```
#loading the "best" weights
model.load_weights(os.path.realpath("weights.h5"))
model.evaluate(inputs_test, outputs_test)
```
### TensorFlow 2 model confusion matrix
Using predictions on the test set, a confusion matrix is produced
```
def tf2_confusion_matrix(inputs, outputs):
predictions = model.predict(inputs)
wrong_labelled_counter = np.zeros((len(handles), len(handles)))
wrong_labelled_sequences = np.empty((len(handles), len(handles)), np.object)
for i in range(len(handles)):
for j in range(len(handles)):
wrong_labelled_sequences[i][j] = []
tot_wrong = 0
for i in range(len(predictions)):
predicted = int(predictions[i].argmax())
true_value = int(outputs[i])
wrong_labelled_counter[true_value][predicted] += 1
wrong_labelled_sequences[true_value][predicted].append(inputs.get('input_text')[i])
ok = (int(true_value) == int(predicted))
if(not ok):
tot_wrong += 1
return wrong_labelled_counter, wrong_labelled_sequences, predictions
def print_confusion_matrix(wrong_labelled_counter):
the_str = "\t"
for handle in handles:
the_str += handle + "\t"
print(the_str)
ctr = 0
for row in wrong_labelled_counter:
the_str = handles[ctr] + '\t'
ctr+=1
for i in range(len(row)):
the_str += str(int(row[i]))
if(i != len(row) -1):
the_str += "\t"
print(the_str)
wrong_labelled_counter, wrong_labelled_sequences, predictions = tf2_confusion_matrix(inputs_test, outputs_test)
print_confusion_matrix(wrong_labelled_counter)
```
# CatBoost model
This CatBoost model instance was developed reusing the ideas presented in these tutorials from the official repository: [classification](https://github.com/catboost/tutorials/blob/master/classification/classification_tutorial.ipynb) and [text features](https://github.com/catboost/tutorials/blob/master/text_features/text_features_in_catboost.ipynb)
## Imports for the CatBoost model
```
import functools
import os
import pandas as pd
import numpy as np
import copy
import calendar
import datetime
import re
import unicodedata
from catboost import Pool, CatBoostClassifier
```
## Definitions for the CatBoost model
```
unicode_data_categories = [
"Cc",
"Cf",
"Cn",
"Co",
"Cs",
"LC",
"Ll",
"Lm",
"Lo",
"Lt",
"Lu",
"Mc",
"Me",
"Mn",
"Nd",
"Nl",
"No",
"Pc",
"Pd",
"Pe",
"Pf",
"Pi",
"Po",
"Ps",
"Sc",
"Sk",
"Sm",
"So",
"Zl",
"Zp",
"Zs"
]
column_names = [
"handle",
"timestamp",
"text"
]
column_names.extend(unicode_data_categories)
#List of handles (labels)
#Fill with the handles you want to consider in your dataset
handles = [
]
train_file = os.path.realpath("./data/train.csv")
val_file = os.path.realpath("./data/val.csv")
test_file = os.path.realpath("./data/test.csv")
```
## Preprocessing and computing dataset features
```
def get_pandas_dataset(input_file, timestamp_mean=None, timestamp_std=None):
pd_dat = pd.read_csv(input_file, names=column_names)
pd_dat = pd_dat[pd_dat.handle.isin(handles)]
if(timestamp_mean is None):
timestamp_mean = pd_dat.timestamp.mean()
if(timestamp_std is None):
timestamp_std = pd_dat.timestamp.std()
pd_dat.timestamp = (pd_dat.timestamp - timestamp_mean) / timestamp_std
pd_dat["handle_index"] = pd_dat['handle'].map(lambda x: handles.index(x))
pd_dat = pd_dat.reset_index(drop=True)
return pd_dat, timestamp_mean, timestamp_std
train_dataset, timestamp_mean, timestamp_std = get_pandas_dataset(train_file)
test_dataset, _, _ = get_pandas_dataset(test_file, timestamp_mean=timestamp_mean, timestamp_std=timestamp_std)
val_dataset, _, _ = get_pandas_dataset(val_file, timestamp_mean=timestamp_mean, timestamp_std=timestamp_std)
def split_inputs_and_outputs(pd_dat):
labels = pd_dat['handle_index'].values
del(pd_dat['handle'])
del(pd_dat['handle_index'])
return pd_dat, labels
X_train, labels_train = split_inputs_and_outputs(train_dataset)
X_val, labels_val = split_inputs_and_outputs(val_dataset)
X_test, labels_test = split_inputs_and_outputs(test_dataset)
```
## CatBoost model definition
```
def get_model(catboost_params={}):
cat_features = []
text_features = ['text']
catboost_default_params = {
'iterations': 1000,
'learning_rate': 0.03,
'eval_metric': 'Accuracy',
'task_type': 'GPU',
'early_stopping_rounds': 20
}
catboost_default_params.update(catboost_params)
model = CatBoostClassifier(**catboost_default_params)
return model, cat_features, text_features
model, cat_features, text_features = get_model()
```
## CatBoost model fitting
```
def fit_model(X_train, X_val, y_train, y_val, model, cat_features, text_features, verbose=100):
learn_pool = Pool(
X_train,
y_train,
cat_features=cat_features,
text_features=text_features,
feature_names=list(X_train)
)
val_pool = Pool(
X_val,
y_val,
cat_features=cat_features,
text_features=text_features,
feature_names=list(X_val)
)
model.fit(learn_pool, eval_set=val_pool, verbose=verbose)
return model
model = fit_model(X_train, X_val, labels_train, labels_val, model, cat_features, text_features)
```
## CatBoost model evaluation
Also for the CatBoost model, predictions on the test set, a confusion matrix is produced
```
def predict(X, model, cat_features, text_features):
pool = Pool(
data=X,
cat_features=cat_features,
text_features=text_features,
feature_names=list(X)
)
probs = model.predict_proba(pool)
return probs
def check_predictions_on(inputs, outputs, model, cat_features, text_features, handles):
predictions = predict(inputs, model, cat_features, text_features)
labelled_counter = np.zeros((len(handles), len(handles)))
labelled_sequences = np.empty((len(handles), len(handles)), np.object)
for i in range(len(handles)):
for j in range(len(handles)):
labelled_sequences[i][j] = []
tot_wrong = 0
for i in range(len(predictions)):
predicted = int(predictions[i].argmax())
true_value = int(outputs[i])
labelled_counter[true_value][predicted] += 1
labelled_sequences[true_value][predicted].append(inputs.get('text').values[i])
ok = (int(true_value) == int(predicted))
if(not ok):
tot_wrong += 1
return labelled_counter, labelled_sequences, predictions
def confusion_matrix(labelled_counter, handles):
the_str = "\t"
for handle in handles:
the_str += handle + "\t"
the_str += "\n"
ctr = 0
for row in labelled_counter:
the_str += handles[ctr] + '\t'
ctr+=1
for i in range(len(row)):
the_str += str(int(row[i]))
if(i != len(row) -1):
the_str += "\t"
the_str += "\n"
return the_str
labelled_counter, labelled_sequences, predictions = check_predictions_on(
X_test,
labels_test,
model,
cat_features,
text_features,
handles
)
confusion_matrix_string = confusion_matrix(labelled_counter, handles)
print(confusion_matrix_string)
```
# Evaluation
To perform some experiments and evaluate the two models, 18 Twitter users were selected and, for each user, a number of tweets and responses to other users' tweets were collected. In total 39786 tweets were collected. The difference in class representation could be eliminated, for example limiting the number of tweets for each label to the number of tweets in the less represented class. This difference, however, was not eliminated, in order to test if it represents an issue for the accuracy of the two trained models.
The division of the tweets corresponding to each twitter handle for each file (train, test, validation) is reported in the following table. To avoid policy issues (better safe than sorry), the actual user handle is masked using C_x placeholders and a brief description of the twitter user is presented instead.
|Description|Handle|Train|Test|Validation|Sum|
|-------|-------|-------|-------|-------|-------|
|UK-based labour politician|C_1|1604|492|229|2325|
|US-based democratic politician|C_2|1414|432|195|2041|
|US-based democratic politician|C_3|1672|498|273|2443|
|US-based actor|C_4|1798|501|247|2546|
|UK-based actress|C_5|847|243|110|1200|
|US-based democratic politician|C_6|2152|605|304|3061|
|US-based singer|C_7|2101|622|302|3025|
|US-based singer|C_8|1742|498|240|2480|
|Civil rights activist|C_9|314|76|58|448|
|US-based republican politician|C_10|620|159|78|857|
|US-based TV host|C_11|2022|550|259|2831|
|Parody account of C_15 |C_12|2081|624|320|3025|
|US-based democratic politician|C_13|1985|557|303|2845|
|US-based actor/director|C_14|1272|357|183|1812|
|US-based republican politician|C_15|1121|298|134|1553|
|US-based writer|C_16|1966|502|302|2770|
|US-based writer|C_17|1095|305|153|1553|
|US-based entrepreneur|C_18|2084|581|306|2971|
|Sum||27890|7900|3996|39786|
## TensorFlow 2 model
The following charts show loss and accuracy vs epochs for train and validation for a typical run of the TF2 model:


If the images do not show correctly, they can be found at these links: [loss](https://github.com/icappello/ml-predict-text-author/blob/master/img/tf2_train_val_loss.png) [accuracy](https://github.com/icappello/ml-predict-text-author/blob/master/img/tf2_train_val_accuracy.png)
After a few epochs, the model starts overfitting on the train data, and the accuracy for the validation set quickly reaches a plateau.
The obtained accuracy on the test set is 0.672
## CatBoost model
The fit procedure stopped after 303 iterations. The obtained accuracy on the test set is 0.808
## Confusion matrices
The confusion matrices for the two models are reported [here](https://docs.google.com/spreadsheets/d/17JGDXYRajnC4THrBnZrbcqQbgzgjo0Jb7KAvPYenr-w/edit?usp=sharing), since large tables are not displayed correctly in the embedded github viewer for jupyter notebooks. Rows represent the actual classes, while columns represent the predicted ones.
## Summary
The CatBoost model obtained a better accuracy overall, as well as a better accuracy on all but one label. No particular optimization was done on the definition of the CatBoost model. The TF2 model could need more data, as well as some changes to its definition, to perform better (comments and pointers on this are welcome). Some variants of the TF2 model were tried: a deeper model with more dense layers, higher dropout rate, more/less units in layers, using only a subset of features, regularization methods (L1, L2, batch regularization), different activation functions (sigmoid, tanh) but none performed significantly better than the one presented.
Looking at the results summarized in the confusion matrices, tweets from C_9 clearly represented a problem, either for the under-representation relative to the other classes or for the actual content of the tweets (some were not written in english). Also, tweets from handles C_5 and C_14 were hard to correctly classify for both models, even if they were not under-represented w.r.t other labels.
|
github_jupyter
|
## Data Description and Analysis
```
import numpy as np
import pandas as pd
pd.set_option('max_columns', 150)
import gc
import os
# matplotlib and seaborn for plotting
import matplotlib
matplotlib.rcParams['figure.dpi'] = 120 #resolution
matplotlib.rcParams['figure.figsize'] = (8,6) #figure size
import matplotlib.pyplot as plt
sns.set_style('darkgrid')
import seaborn as sns
color = sns.color_palette()
root = 'C:/Data/instacart-market-basket-analysis/'
```
The dataset contains relational set of files describing customers' orders over time. For each user, 4 to 100 orders are provided with the sequence of products purchased in each order. The data of the order's week and hour of the day as well as a relative measure of time between orders is provided.
**Files in the Dataset:**
```
os.listdir(root)
aisles = pd.read_csv(root + 'aisles.csv')
departments = pd.read_csv(root + 'departments.csv')
orders = pd.read_csv(root + 'orders.csv')
order_products_prior = pd.read_csv(root + 'order_products__prior.csv')
order_products_train = pd.read_csv(root + 'order_products__train.csv')
products = pd.read_csv(root + 'products.csv')
```
### aisles:
This file contains different aisles and there are total 134 unique aisles.
```
aisles.head()
aisles.tail()
len(aisles.aisle.unique())
aisles.aisle.unique()
```
### departments:
This file contains different departments and there are total 21 unique departments.
```
departments.head()
departments.tail()
len(departments.department.unique())
departments.department.unique()
```
### orders:
This file contains all the orders made by different users. From below analysis, we can conclude following:
- There are total 3421083 orders made by total 206209 users.
- There are three sets of orders: Prior, Train and Test. The distributions of orders in Train and Test sets are similar whereas the distribution of orders in Prior set is different.
- The total orders per customer ranges from 0 to 100.
- Based on the plot of 'Orders VS Day of Week' we can map 0 and 1 as Saturday and Sunday respectively based on the assumption that most of the people buy groceries on weekends.
- Majority of the orders are made during the day time.
- Customers order once in a week which is supported by peaks at 7, 14, 21 and 30 in 'Orders VS Days since prior order' graph.
- Based on the heatmap between 'Day of Week' and 'Hour of Day,' we can say that Saturday afternoons and Sunday mornings are prime time for orders.
```
orders.head(12)
orders.tail()
orders.info()
len(orders.order_id.unique())
len(orders.user_id.unique())
orders.eval_set.value_counts()
orders.order_number.describe().apply(lambda x: format(x, '.2f'))
order_number = orders.groupby('user_id')['order_number'].max()
order_number = order_number.value_counts()
fig, ax = plt.subplots(figsize=(15,8))
ax = sns.barplot(x = order_number.index, y = order_number.values, color = color[3])
ax.set_xlabel('Orders per customer')
ax.set_ylabel('Count')
ax.xaxis.set_tick_params(rotation=90, labelsize=10)
ax.set_title('Frequency of Total Orders by Customers')
fig.savefig('Frequency of Total Orders by Customers.png')
fig, ax = plt.subplots(figsize = (8,4))
ax = sns.kdeplot(orders.order_number[orders.eval_set == 'prior'], label = "Prior set", lw = 1)
ax = sns.kdeplot(orders.order_number[orders.eval_set == 'train'], label = "Train set", lw = 1)
ax = sns.kdeplot(orders.order_number[orders.eval_set == 'test'], label = "Test set", lw = 1)
ax.set_xlabel('Order Number')
ax.set_ylabel('Count')
ax.tick_params(axis = 'both', labelsize = 10)
ax.set_title('Distribution of Orders in Various Sets')
fig.savefig('Distribution of Orders in Various Sets.png')
plt.show()
fig, ax = plt.subplots(figsize = (5,3))
ax = sns.countplot(orders.order_dow)
ax.set_xlabel('Day of Week', size = 10)
ax.set_ylabel('Orders', size = 10)
ax.tick_params(axis = 'both', labelsize = 8)
ax.set_title('Total Orders per Day of Week')
fig.savefig('Total Orders per Day of Week.png')
plt.show()
temp_df = orders.groupby('order_dow')['user_id'].nunique()
fig, ax = plt.subplots(figsize = (5,3))
ax = sns.barplot(x = temp_df.index, y = temp_df.values)
ax.set_xlabel('Day of Week', size = 10)
ax.set_ylabel('Total Unique Users', size = 10)
ax.tick_params(axis = 'both', labelsize = 8)
ax.set_title('Total Unique Users per Day of Week')
fig.savefig('Total Unique Users per Day of Week.png')
plt.show()
fig, ax = plt.subplots(figsize = (10,5))
ax = sns.countplot(orders.order_hour_of_day, color = color[2])
ax.set_xlabel('Hour of Day', size = 10 )
ax.set_ylabel('Orders', size = 10)
ax.tick_params(axis = 'both', labelsize = 8)
ax.set_title('Total Orders per Hour of Day')
fig.savefig('Total Orders per Hour of Day.png')
plt.show()
fig, ax = plt.subplots(figsize = (10,5))
ax = sns.countplot(orders.days_since_prior_order, color = color[2])
ax.set_xlabel('Days since prior order', size = 10)
ax.set_ylabel('Orders', size = 10)
ax.tick_params(axis = 'both', labelsize = 8)
ax.set_title('Orders VS Days since prior order')
fig.savefig('Orders VS Days since prior order.png')
plt.show()
temp_df = orders.groupby(["order_dow", "order_hour_of_day"])["order_number"].aggregate("count").reset_index()
temp_df = temp_df.pivot('order_dow', 'order_hour_of_day', 'order_number')
temp_df.head()
ax = plt.subplots(figsize=(7,3))
ax = sns.heatmap(temp_df, cmap="YlGnBu", linewidths=.5)
ax.set_title("Frequency of Day of week Vs Hour of day", size = 12)
ax.set_xlabel("Hour of Day", size = 10)
ax.set_ylabel("Day of Week", size = 10)
ax.tick_params(axis = 'both', labelsize = 8)
cbar = ax.collections[0].colorbar
cbar.ax.tick_params(labelsize=10)
fig = ax.get_figure()
fig.savefig("Frequency of Day of week Vs Hour of day.png")
plt.show()
```
### order_products_prior:
This file gives information about which products were ordered and in which order they were added in the cart. It also tells us that if the product was reordered or not.
- In this file there is an information of total 3214874 orders through which total 49677 products were ordered.
- From the 'Count VS Items in cart' plot, we can say that most of the people buy 1-15 items in an order and there were a maximum of 145 items in an order.
- The percentage of reorder items in this set is 58.97%.
```
order_products_prior.head(10)
order_products_prior.tail()
len(order_products_prior.order_id.unique())
len(order_products_prior.product_id.unique())
add_to_cart_order_prior = order_products_prior.groupby('order_id')['add_to_cart_order'].count()
add_to_cart_order_prior = add_to_cart_order_prior.value_counts()
add_to_cart_order_prior.head()
add_to_cart_order_prior.tail()
add_to_cart_order_prior.index.max()
fig, ax = plt.subplots(figsize = (15,8))
ax = sns.barplot(x = add_to_cart_order_prior.index, y = add_to_cart_order_prior.values, color = color[3])
ax.set_xlabel('Items in cart')
ax.set_ylabel('Count')
ax.xaxis.set_tick_params(rotation=90, labelsize = 9)
ax.set_title('Frequency of Items in Cart in Prior set', size = 15)
fig.savefig('Frequency of Items in Cart in Prior set.png')
fig, ax = plt.subplots(figsize=(3,3))
ax = sns.barplot(x = order_products_prior.reordered.value_counts().index,
y = order_products_prior.reordered.value_counts().values, color = color[3])
ax.set_xlabel('Reorder', size = 10)
ax.set_ylabel('Count', size = 10)
ax.tick_params(axis = 'both', labelsize = 8)
ax.ticklabel_format(style='plain', axis='y')
ax.set_title('Reorder Frequency in Prior Set')
fig.savefig('Reorder Frequency in Prior Set')
plt.show()
print('Percentage of reorder in prior set:',
format(order_products_prior[order_products_prior.reordered == 1].shape[0]*100/order_products_prior.shape[0], '.2f'))
```
### order_products_train:
This file gives information about which products were ordered and in which order they were added in the cart. It also tells us that if the product was reordered or not.
- In this file there is an information of total 131209 orders through which total 39123 products were ordered.
- From the 'Count VS Items in cart' plot, we can say that most of the people buy 1-15 items in an order and there were a maximum of 145 items in an order.
- The percentage of reorder items in this set is 59.86%.
```
order_products_train.head(10)
order_products_train.tail()
len(order_products_train.order_id.unique())
len(order_products_train.product_id.unique())
add_to_cart_order_train = order_products_prior.groupby('order_id')['add_to_cart_order'].count()
add_to_cart_order_train = add_to_cart_order_train.value_counts()
add_to_cart_order_train.head()
add_to_cart_order_train.tail()
add_to_cart_order_train.index.max()
fig, ax = plt.subplots(figsize = (15,8))
ax = sns.barplot(x = add_to_cart_order_train.index, y = add_to_cart_order_train.values, color = color[2])
ax.set_xlabel('Items in cart')
ax.set_ylabel('Count')
ax.xaxis.set_tick_params(rotation=90, labelsize = 8)
ax.set_title('Frequency of Items in Cart in Train set', size = 15)
fig.savefig('Frequency of Items in Cart in Train set.png')
fig, ax = plt.subplots(figsize=(3,3))
ax = sns.barplot(x = order_products_train.reordered.value_counts().index,
y = order_products_train.reordered.value_counts().values, color = color[2])
ax.set_xlabel('Reorder', size = 10)
ax.set_ylabel('Count', size = 10)
ax.tick_params(axis = 'both', labelsize = 8)
ax.set_title('Reorder Frequency in Train Set')
fig.savefig('Reorder Frequency in Train Set')
plt.show()
print('Percentage of reorder in train set:',
format(order_products_train[order_products_train.reordered == 1].shape[0]*100/order_products_train.shape[0], '.2f'))
```
### products:
This file contains the list of total 49688 products and their aisle as well as department. The number of products in different aisles and different departments are different.
```
products.head(10)
products.tail()
len(products.product_name.unique())
len(products.aisle_id.unique())
len(products.department_id.unique())
temp_df = products.groupby('aisle_id')['product_id'].count()
fig, ax = plt.subplots(figsize = (15,6))
ax = sns.barplot(x = temp_df.index, y = temp_df.values, color = color[3])
ax.set_xlabel('Aisle Id')
ax.set_ylabel('Total products in aisle')
ax.xaxis.set_tick_params(rotation=90, labelsize = 7)
ax.set_title('Total Products in Aisle VS Aisle ID', size = 12)
fig.savefig('Total Products in Aisle VS Aisle ID.png')
temp_df = products.groupby('department_id')['product_id'].count()
fig, ax = plt.subplots(figsize = (8,5))
ax = sns.barplot(x = temp_df.index, y = temp_df.values, color = color[2])
ax.set_xlabel('Department Id')
ax.set_ylabel('Total products in department')
ax.xaxis.set_tick_params(rotation=90, labelsize = 9)
ax.set_title('Total Products in Department VS Department ID', size = 10)
fig.savefig('Total Products in Department VS Department ID.png')
temp_df = products.groupby('department_id')['aisle_id'].nunique()
fig, ax = plt.subplots(figsize = (8,5))
ax = sns.barplot(x = temp_df.index, y = temp_df.values)
ax.set_xlabel('Department Id')
ax.set_ylabel('Total Aisles in department')
ax.xaxis.set_tick_params(rotation=90, labelsize = 9)
ax.set_title('Total Aisles in Department VS Department ID', size = 10)
fig.savefig('Total Aisles in Department VS Department ID.png')
```
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.