text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
```
import numpy as np
import matplotlib.pyplot as plt
% matplotlib inline
plt.rcParams["savefig.dpi"] = 300
plt.rcParams["savefig.bbox"] = "tight"
np.set_printoptions(precision=3, suppress=True)
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import scale, StandardScaler
# toy plot
plt.plot([.3, 0, 1])
plt.xticks((0, 1, 2), ("0 (.16)", "1 (.5)", "2 (.84)"))
plt.xlabel("Bin index (expected positive)")
plt.ylabel("Observed positive in bin")
plt.savefig("images/calib_curve.png")
from sklearn.datasets import fetch_covtype
from sklearn.utils import check_array
def load_data(dtype=np.float32, order='C', random_state=13):
######################################################################
# Load covertype dataset (downloads it from the web, might take a bit)
data = fetch_covtype(download_if_missing=True, shuffle=True,
random_state=random_state)
X = check_array(data['data'], dtype=dtype, order=order)
# make it bineary classification
y = (data['target'] != 1).astype(np.int)
# Create train-test split (as [Joachims, 2006])
n_train = 522911
X_train = X[:n_train]
y_train = y[:n_train]
X_test = X[n_train:]
y_test = y[n_train:]
# Standardize first 10 features (the numerical ones)
mean = X_train.mean(axis=0)
std = X_train.std(axis=0)
mean[10:] = 0.0
std[10:] = 1.0
X_train = (X_train - mean) / std
X_test = (X_test - mean) / std
return X_train, X_test, y_train, y_test
X_train, X_test, y_train, y_test = load_data()
# subsample training set by a factor of 10:
X_train = X_train[::10]
y_train = y_train[::10]
from sklearn.linear_model import LogisticRegressionCV
print(X_train.shape)
print(np.bincount(y_train))
lr = LogisticRegressionCV().fit(X_train, y_train)
lr.C_
print(lr.predict_proba(X_test)[:10])
print(y_test[:10])
from sklearn.calibration import calibration_curve
probs = lr.predict_proba(X_test)[:, 1]
prob_true, prob_pred = calibration_curve(y_test, probs, n_bins=5)
print(prob_true)
print(prob_pred)
def plot_calibration_curve(y_true, y_prob, n_bins=5, ax=None, hist=True, normalize=False):
prob_true, prob_pred = calibration_curve(y_true, y_prob, n_bins=n_bins, normalize=normalize)
if ax is None:
ax = plt.gca()
if hist:
ax.hist(y_prob, weights=np.ones_like(y_prob) / len(y_prob), alpha=.4,
bins=np.maximum(10, n_bins))
ax.plot([0, 1], [0, 1], ':', c='k')
curve = ax.plot(prob_pred, prob_true, marker="o")
ax.set_xlabel("predicted probability")
ax.set_ylabel("fraction of positive samples")
ax.set(aspect='equal')
return curve
plot_calibration_curve(y_test, probs)
plt.title("n_bins=5")
fig, axes = plt.subplots(1, 3, figsize=(16, 6))
for ax, n_bins in zip(axes, [5, 20, 50]):
plot_calibration_curve(y_test, probs, n_bins=n_bins, ax=ax)
ax.set_title("n_bins={}".format(n_bins))
plt.savefig("images/influence_bins.png")
from sklearn.svm import LinearSVC, SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
fig, axes = plt.subplots(1, 3, figsize=(8, 8))
for ax, clf in zip(axes, [LogisticRegressionCV(), DecisionTreeClassifier(),
RandomForestClassifier(n_estimators=100)]):
# use predict_proba is the estimator has it
scores = clf.fit(X_train, y_train).predict_proba(X_test)[:, 1]
plot_calibration_curve(y_test, scores, n_bins=20, ax=ax)
ax.set_title(clf.__class__.__name__)
plt.tight_layout()
plt.savefig("images/calib_curve_models.png")
# same thing but with bier loss shown. Why do I refit the models? lol
from sklearn.metrics import brier_score_loss
fig, axes = plt.subplots(1, 3, figsize=(10, 4))
for ax, clf in zip(axes, [LogisticRegressionCV(), DecisionTreeClassifier(), RandomForestClassifier(n_estimators=100)]):
# use predict_proba is the estimator has it
scores = clf.fit(X_train, y_train).predict_proba(X_test)[:, 1]
plot_calibration_curve(y_test, scores, n_bins=20, ax=ax)
ax.set_title("{}: {:.2f}".format(clf.__class__.__name__, brier_score_loss(y_test, scores)))
plt.tight_layout()
plt.savefig("images/models_bscore.png")
from sklearn.calibration import CalibratedClassifierCV
X_train_sub, X_val, y_train_sub, y_val = train_test_split(X_train, y_train,
stratify=y_train, random_state=0)
rf = RandomForestClassifier(n_estimators=100).fit(X_train_sub, y_train_sub)
scores = rf.predict_proba(X_test)[:, 1]
plot_calibration_curve(y_test, scores, n_bins=20)
plt.title("{}: {:.3f}".format(clf.__class__.__name__, brier_score_loss(y_test, scores)))
cal_rf = CalibratedClassifierCV(rf, cv="prefit", method='sigmoid')
cal_rf.fit(X_val, y_val)
scores_sigm = cal_rf.predict_proba(X_test)[:, 1]
cal_rf_iso = CalibratedClassifierCV(rf, cv="prefit", method='isotonic')
cal_rf_iso.fit(X_val, y_val)
scores_iso = cal_rf_iso.predict_proba(X_test)[:, 1]
scores_rf = cal_rf.predict_proba(X_val)
plt.plot(scores_rf[:, 1], y_val, 'o', alpha=.01)
plt.xlabel("rf.predict_proba")
plt.ylabel("True validation label")
plt.savefig("images/calibration_val_scores.png")
sigm = cal_rf.calibrated_classifiers_[0].calibrators_[0]
scores_rf_sorted = np.sort(scores_rf[:, 1])
sigm_scores = sigm.predict(scores_rf_sorted)
iso = cal_rf_iso.calibrated_classifiers_[0].calibrators_[0]
iso_scores = iso.predict(scores_rf_sorted)
plt.plot(scores_rf[:, 1], y_val, 'o', alpha=.01)
plt.plot(scores_rf_sorted, sigm_scores, label='sigm')
plt.plot(scores_rf_sorted, iso_scores, label='iso')
plt.xlabel("rf.predict_proba")
plt.ylabel("True validation label")
plt.legend()
plt.savefig("images/calibration_val_scores_fitted.png")
fig, axes = plt.subplots(1, 3, figsize=(10, 4))
for name, s, ax in zip(['no callibration', 'sigmoid', 'isotonic'],
[scores, scores_sigm, scores_iso], axes):
plot_calibration_curve(y_test, s, n_bins=20, ax=ax)
ax.set_title("{}: {:.3f}".format(name, brier_score_loss(y_test, s)))
plt.tight_layout()
plt.savefig("images/types_callib.png")
cal_rf_iso_cv = CalibratedClassifierCV(rf, method='isotonic')
cal_rf_iso_cv.fit(X_train, y_train)
scores_iso_cv = cal_rf_iso_cv.predict_proba(X_test)[:, 1]
fig, axes = plt.subplots(1, 3, figsize=(10, 4))
for name, s, ax in zip(['no callibration', 'isotonic', 'isotonic cv'],
[scores, scores_iso, scores_iso_cv], axes):
plot_calibration_curve(y_test, s, n_bins=20, ax=ax)
ax.set_title("{}: {:.3f}".format(name, brier_score_loss(y_test, s)))
plt.tight_layout()
plt.savefig("images/types_callib_cv.png")
# http://scikit-learn.org/dev/auto_examples/calibration/plot_calibration_multiclass.html
# Author: Jan Hendrik Metzen <[email protected]>
# License: BSD Style.
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier
from sklearn.calibration import CalibratedClassifierCV
from sklearn.metrics import log_loss, brier_score_loss
np.random.seed(0)
# Generate data
X, y = make_blobs(n_samples=1000, n_features=2, random_state=42,
cluster_std=5.0)
X_train, y_train = X[:600], y[:600]
X_valid, y_valid = X[600:800], y[600:800]
X_train_valid, y_train_valid = X[:800], y[:800]
X_test, y_test = X[800:], y[800:]
# Train uncalibrated random forest classifier on whole train and validation
# data and evaluate on test data
clf = RandomForestClassifier(n_estimators=25)
clf.fit(X_train_valid, y_train_valid)
clf_probs = clf.predict_proba(X_test)
score = log_loss(y_test, clf_probs)
#score = brier_score_loss(y_test, clf_probs[:, 1])
# Train random forest classifier, calibrate on validation data and evaluate
# on test data
clf = RandomForestClassifier(n_estimators=25)
clf.fit(X_train, y_train)
clf_probs = clf.predict_proba(X_test)
sig_clf = CalibratedClassifierCV(clf, method="sigmoid", cv="prefit")
sig_clf.fit(X_valid, y_valid)
sig_clf_probs = sig_clf.predict_proba(X_test)
sig_score = log_loss(y_test, sig_clf_probs)
#sig_score = brier_score_loss(y_test, sig_clf_probs[:, 1])
# Plot changes in predicted probabilities via arrows
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
colors = ["r", "g", "b"]
for i in range(clf_probs.shape[0]):
plt.arrow(clf_probs[i, 0], clf_probs[i, 1],
sig_clf_probs[i, 0] - clf_probs[i, 0],
sig_clf_probs[i, 1] - clf_probs[i, 1],
color=colors[y_test[i]], head_width=1e-2)
# Plot perfect predictions
plt.plot([1.0], [0.0], 'ro', ms=20, label="Class 1")
plt.plot([0.0], [1.0], 'go', ms=20, label="Class 2")
plt.plot([0.0], [0.0], 'bo', ms=20, label="Class 3")
# Plot boundaries of unit simplex
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], 'k', label="Simplex")
# Annotate points on the simplex
plt.annotate(r'($\frac{1}{3}$, $\frac{1}{3}$, $\frac{1}{3}$)',
xy=(1.0/3, 1.0/3), xytext=(1.0/3, .23), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.plot([1.0/3], [1.0/3], 'ko', ms=5)
plt.annotate(r'($\frac{1}{2}$, $0$, $\frac{1}{2}$)',
xy=(.5, .0), xytext=(.5, .1), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($0$, $\frac{1}{2}$, $\frac{1}{2}$)',
xy=(.0, .5), xytext=(.1, .5), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($\frac{1}{2}$, $\frac{1}{2}$, $0$)',
xy=(.5, .5), xytext=(.6, .6), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($0$, $0$, $1$)',
xy=(0, 0), xytext=(.1, .1), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($1$, $0$, $0$)',
xy=(1, 0), xytext=(1, .1), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($0$, $1$, $0$)',
xy=(0, 1), xytext=(.1, 1), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
# Add grid
plt.grid("off")
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], 'k', alpha=0.2)
plt.plot([0, 0 + (1-x)/2], [x, x + (1-x)/2], 'k', alpha=0.2)
plt.plot([x, x + (1-x)/2], [0, 0 + (1-x)/2], 'k', alpha=0.2)
plt.title("Change of predicted probabilities after sigmoid calibration")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
plt.legend(loc="best")
print("Log-loss of")
print(" * uncalibrated classifier trained on 800 datapoints: %.3f "
% score)
print(" * classifier trained on 600 datapoints and calibrated on "
"200 datapoint: %.3f" % sig_score)
# Illustrate calibrator
plt.subplot(1, 2, 2)
# generate grid over 2-simplex
p1d = np.linspace(0, 1, 20)
p0, p1 = np.meshgrid(p1d, p1d)
p2 = 1 - p0 - p1
p = np.c_[p0.ravel(), p1.ravel(), p2.ravel()]
p = p[p[:, 2] >= 0]
calibrated_classifier = sig_clf.calibrated_classifiers_[0]
prediction = np.vstack([calibrator.predict(this_p)
for calibrator, this_p in
zip(calibrated_classifier.calibrators_, p.T)]).T
prediction /= prediction.sum(axis=1)[:, None]
# Plot modifications of calibrator
for i in range(prediction.shape[0]):
plt.arrow(p[i, 0], p[i, 1],
prediction[i, 0] - p[i, 0], prediction[i, 1] - p[i, 1],
head_width=1e-2, color=colors[np.argmax(p[i])])
# Plot boundaries of unit simplex
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], 'k', label="Simplex")
plt.grid("off")
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], 'k', alpha=0.2)
plt.plot([0, 0 + (1-x)/2], [x, x + (1-x)/2], 'k', alpha=0.2)
plt.plot([x, x + (1-x)/2], [0, 0 + (1-x)/2], 'k', alpha=0.2)
plt.title("Illustration of sigmoid calibrator")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
plt.savefig("images/multi_class_calibration.png")
```
|
github_jupyter
|
# How to setup Seven Bridges Public API python library
## Overview
Here you will learn the three possible ways to setup Seven Bridges Public API Python library.
## Prerequisites
1. You need to install _sevenbridges-python_ library. Library details are available [here](http://sevenbridges-python.readthedocs.io/en/latest/sevenbridges/)
The easiest way to install sevenbridges-python is using pip:
$ pip install sevenbridges-python
Alternatively, you can get the code. sevenbridges-python is actively developed on GitHub, where the [code](https://github.com/sbg/sevenbridges-python) is always available. To clone the public repository :
$ git clone git://github.com/sbg/sevenbridges-python.git
Once you have a copy of the source, you can embed it in your Python
package, or install it into your site-packages by invoking:
$ python setup.py install
2. You need your _authentication token_ which you can get [here](https://igor.sbgenomics.com/developer/token)
### Notes and Compatibility
Python package is intended to be used with Python 3.6+ versions.
```
# Import the library
import sevenbridges as sbg
```
### Initialize the library
You can initialize the library explicitly or by supplying the necessary information in the $HOME/.sevenbridges/credentials file
There are generally three ways to initialize the library:
1. Explicitly, when calling api constructor, like:
``` python
api = sbg.Api(url='https://api.sbgenomics.com/v2', token='MY AUTH TOKEN')
```
2. By using OS environment to store the url and authentication token
```
export AUTH_TOKEN=<MY AUTH TOKEN>
export API_ENDPOINT='https://api.sbgenomics.com/v2'
```
3. By using ini file $HOME/.sevenbridges/credentials (for MS Windows, the file should be located in \%UserProfile\%.sevenbridges\credentials) and specifying a profile to use. The format of the credentials file is standard ini file format, as shown below:
```bash
[sbpla]
api_endpoint = https://api.sbgenomics.com/v2
auth_token = 700992f7b24a470bb0b028fe813b8100
[cgc]
api_endpoint = https://cgc-api.sbgenomics.com/v2
auth_token = 910975f5b24a470bb0b028fe813b8100
```
0. to **create** this file<sup>1</sup>, use the following steps in your _Terminal_:
1.
```bash
cd ~
mkdir .sevenbridges
touch .sevenbridges/credentials
vi .sevenbridges/credentials
```
2. Press "i" then enter to go into **insert mode**
3. write the text above for each environment.
4. Press "ESC" then type ":wq" to save the file and exit vi
<sup>1</sup> If the file already exists, omit the _touch_ command
### Test if you have stored the token correctly
Below are the three options presented above, test **one** of them. Logically, if you have only done **Step 3**, then testing **Step 2** will return an error.
```
# (1.) You can also instantiate library by explicitly
# specifying API url and authentication token
api_explicitly = sbg.Api(url='https://api.sbgenomics.com/v2',
token='<MY TOKEN HERE>')
api_explicitly.users.me()
# (2.) If you have not specified profile, the python-sbg library
# will search for configuration in the environment
c = sbg.Config()
api_via_environment = sbg.Api(config=c)
api_via_environment.users.me()
# (3.) If you have credentials setup correctly, you only need to specify the profile
config_file = sbg.Config(profile='sbpla')
api_via_ini_file = sbg.Api(config=config_file)
api_via_ini_file.users.me()
```
#### PROTIP
* We _recommend_ the approach with configuration file (the **.sevenbridges/credentials** file in option #3), especially if you are using multiple environments (like SBPLA and CGC).
|
github_jupyter
|
Manipulating numbers in Python
================
**_Disclaimer_: Much of this section has been transcribed from <a href="https://pymotw.com/2/math/">https://pymotw.com/2/math/</a>**
Every computer represents numbers using the <a href="https://en.wikipedia.org/wiki/IEEE_floating_point">IEEE floating point standard</a>. The **math** module implements many of the IEEE functions that would normally be found in the native platform C libraries for complex mathematical operations using floating point values, including logarithms and trigonometric operations.
The fundamental information about number representation is contained in the module **sys**
```
import sys
sys.float_info
```
From here we can learn, for instance:
```
sys.float_info.max
```
Similarly, we can learn the limits of the IEEE 754 standard
Largest Real = 1.79769e+308, 7fefffffffffffff // -Largest Real = -1.79769e+308, ffefffffffffffff
Smallest Real = 2.22507e-308, 0010000000000000 // -Smallest Real = -2.22507e-308, 8010000000000000
Zero = 0, 0000000000000000 // -Zero = -0, 8000000000000000
eps = 2.22045e-16, 3cb0000000000000 // -eps = -2.22045e-16, bcb0000000000000
Interestingly, one could define an even larger constant (more about this below)
```
infinity = float("inf")
infinity
infinity/10000
```
## Special constants
Many math operations depend on special constants. **math** includes values for $\pi$ and $e$.
```
import math
print ('π: %.30f' % math.pi)
print ('e: %.30f' % math.e)
print('nan: {:.30f}'.format(math.nan))
print('inf: {:.30f}'.format(math.inf))
```
Both values are limited in precision only by the platform’s floating point C library.
## Testing for exceptional values
Floating point calculations can result in two types of exceptional values. INF (“infinity”) appears when the double used to hold a floating point value overflows from a value with a large absolute value.
There are several reserved bit patterns, mostly those with all ones in the exponent field. These allow for tagging special cases as Not A Number—NaN. If there are all ones and the fraction is zero, the number is Infinite.
The IEEE standard specifies:
Inf = Inf, 7ff0000000000000 // -Inf = -Inf, fff0000000000000
NaN = NaN, fff8000000000000 // -NaN = NaN, 7ff8000000000000
```
float("inf")-float("inf")
import math
print('{:^3} {:6} {:6} {:6}'.format(
'e', 'x', 'x**2', 'isinf'))
print('{:-^3} {:-^6} {:-^6} {:-^6}'.format(
'', '', '', ''))
for e in range(0, 201, 20):
x = 10.0 ** e
y = x * x
print('{:3d} {:<6g} {:<6g} {!s:6}'.format(
e, x, y, math.isinf(y),))
```
When the exponent in this example grows large enough, the square of x no longer fits inside a double, and the value is recorded as infinite. Not all floating point overflows result in INF values, however. Calculating an exponent with floating point values, in particular, raises OverflowError instead of preserving the INF result.
```
x = 10.0 ** 200
print('x =', x)
print('x*x =', x*x)
try:
print('x**2 =', x**2)
except OverflowError as err:
print(err)
```
This discrepancy is caused by an implementation difference in the library used by C Python.
Division operations using infinite values are undefined. The result of dividing a number by infinity is NaN (“not a number”).
```
import math
x = (10.0 ** 200) * (10.0 ** 200)
y = x/x
print('x =', x)
print('isnan(x) =', math.isnan(x))
print('y = x / x =', x/x)
print('y == nan =', y == float('nan'))
print('isnan(y) =', math.isnan(y))
```
## Comparing
Comparisons for floating point values can be error prone, with each step of the computation potentially introducing errors due to the numerical representation. The isclose() function uses a stable algorithm to minimize these errors and provide a way for relative as well as absolute comparisons. The formula used is equivalent to
abs(a-b) <= max(rel_tol * max(abs(a), abs(b)), abs_tol)
By default, isclose() uses relative comparison with the tolerance set to 1e-09, meaning that the difference between the values must be less than or equal to 1e-09 times the larger absolute value between a and b. Passing a keyword argument rel_tol to isclose() changes the tolerance. In this example, the values must be within 10% of each other.
The comparison between 0.1 and 0.09 fails because of the error representing 0.1.
```
import math
INPUTS = [
(1000, 900, 0.1),
(100, 90, 0.1),
(10, 9, 0.1),
(1, 0.9, 0.1),
(0.1, 0.09, 0.1),
]
print('{:^8} {:^8} {:^8} {:^8} {:^8} {:^8}'.format(
'a', 'b', 'rel_tol', 'abs(a-b)', 'tolerance', 'close')
)
print('{:-^8} {:-^8} {:-^8} {:-^8} {:-^8} {:-^8}'.format(
'-', '-', '-', '-', '-', '-'),
)
fmt = '{:8.2f} {:8.2f} {:8.2f} {:8.2f} {:8.2f} {!s:>8}'
for a, b, rel_tol in INPUTS:
close = math.isclose(a, b, rel_tol=rel_tol)
tolerance = rel_tol * max(abs(a), abs(b))
abs_diff = abs(a - b)
print(fmt.format(a, b, rel_tol, abs_diff, tolerance, close))
```
To use a fixed or "absolute" tolerance, pass abs_tol instead of rel_tol.
For an absolute tolerance, the difference between the input values must be less than the tolerance given.
```
import math
INPUTS = [
(1.0, 1.0 + 1e-07, 1e-08),
(1.0, 1.0 + 1e-08, 1e-08),
(1.0, 1.0 + 1e-09, 1e-08),
]
print('{:^8} {:^11} {:^8} {:^10} {:^8}'.format(
'a', 'b', 'abs_tol', 'abs(a-b)', 'close')
)
print('{:-^8} {:-^11} {:-^8} {:-^10} {:-^8}'.format(
'-', '-', '-', '-', '-'),
)
for a, b, abs_tol in INPUTS:
close = math.isclose(a, b, abs_tol=abs_tol)
abs_diff = abs(a - b)
print('{:8.2f} {:11} {:8} {:0.9f} {!s:>8}'.format(
a, b, abs_tol, abs_diff, close))
```
nan and inf are special cases.
nan is never close to another value, including itself. inf is only close to itself.
```
import math
print('nan, nan:', math.isclose(math.nan, math.nan))
print('nan, 1.0:', math.isclose(math.nan, 1.0))
print('inf, inf:', math.isclose(math.inf, math.inf))
print('inf, 1.0:', math.isclose(math.inf, 1.0))
```
## Converting to Integers
The math module includes three functions for converting floating point values to whole numbers. Each takes a different approach, and will be useful in different circumstances.
The simplest is trunc(), which truncates the digits following the decimal, leaving only the significant digits making up the whole number portion of the value. floor() converts its input to the largest preceding integer, and ceil() (ceiling) produces the largest integer following sequentially after the input value.
```
import math
print('{:^5} {:^5} {:^5} {:^5} {:^5}'.format('i', 'int', 'trunk', 'floor', 'ceil'))
print('{:-^5} {:-^5} {:-^5} {:-^5} {:-^5}'.format('', '', '', '', ''))
fmt = ' '.join(['{:5.1f}'] * 5)
for i in [ -1.5, -0.8, -0.5, -0.2, 0, 0.2, 0.5, 0.8, 1 ]:
print (fmt.format(i, int(i), math.trunc(i), math.floor(i), math.ceil(i)))
```
## Alternate Representations
**modf()** takes a single floating point number and returns a tuple containing the fractional and whole number parts of the input value.
```
import math
for i in range(6):
print('{}/2 = {}'.format(i, math.modf(i/2.0)))
```
**frexp()** returns the mantissa and exponent of a floating point number, and can be used to create a more portable representation of the value. It uses the formula x = m \* 2 \*\* e, and returns the values m and e.
```
import math
print('{:^7} {:^7} {:^7}'.format('x', 'm', 'e'))
print('{:-^7} {:-^7} {:-^7}'.format('', '', ''))
for x in [ 0.1, 0.5, 4.0 ]:
m, e = math.frexp(x)
print('{:7.2f} {:7.2f} {:7d}'.format(x, m, e))
```
**ldexp()** is the inverse of frexp(). Using the same formula as frexp(), ldexp() takes the mantissa and exponent values as arguments and returns a floating point number.
```
import math
print('{:^7} {:^7} {:^7}'.format('m', 'e', 'x'))
print('{:-^7} {:-^7} {:-^7}'.format('', '', ''))
for m, e in [ (0.8, -3),
(0.5, 0),
(0.5, 3),
]:
x = math.ldexp(m, e)
print('{:7.2f} {:7d} {:7.2f}'.format(m, e, x))
```
## Positive and Negative Signs
The absolute value of number is its value without a sign. Use **fabs()** to calculate the absolute value of a floating point number.
```
import math
print(math.fabs(-1.1))
print(math.fabs(-0.0))
print(math.fabs(0.0))
print(math.fabs(1.1))
```
To determine the sign of a value, either to give a set of values the same sign or simply for comparison, use **copysign()** to set the sign of a known good value. An extra function like copysign() is needed because comparing NaN and -NaN directly with other values does not work.
```
import math
print
print('{:^5} {:^5} {:^5} {:^5} {:^5}'.format('f', 's', '< 0', '> 0', '= 0'))
print('{:-^5} {:-^5} {:-^5} {:-^5} {:-^5}'.format('', '', '', '', ''))
for f in [ -1.0,
0.0,
1.0,
float('-inf'),
float('inf'),
float('-nan'),
float('nan'),
]:
s = int(math.copysign(1, f))
print('{:5.1f} {:5d} {!s:5} {!s:5} {!s:5}'.format(f, s, f < 0, f > 0, f==0))
```
## Commonly Used Calculations
Representing precise values in binary floating point memory is challenging. Some values cannot be represented exactly, and the more often a value is manipulated through repeated calculations, the more likely a representation error will be introduced. math includes a function for computing the sum of a series of floating point numbers using an efficient algorithm that minimize such errors.
```
import math
values = [ 0.1 ] * 10
print('Input values:', values)
print('sum() : {:.20f}'.format(sum(values)))
s = 0.0
for i in values:
s += i
print('for-loop : {:.20f}'.format(s))
print('math.fsum() : {:.20f}'.format(math.fsum(values)))
```
Given a sequence of ten values each equal to 0.1, the expected value for the sum of the sequence is 1.0. Since 0.1 cannot be represented exactly as a floating point value, however, errors are introduced into the sum unless it is calculated with **fsum()**.
**factorial()** is commonly used to calculate the number of permutations and combinations of a series of objects. The factorial of a positive integer n, expressed n!, is defined recursively as (n-1)! * n and stops with 0! == 1. **factorial()** only works with whole numbers, but does accept float arguments as long as they can be converted to an integer without losing value.
```
import math
for i in [ 0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.1 ]:
try:
print('{:2.0f} {:6.0f}'.format(i, math.factorial(i)))
except ValueError as err:
print('Error computing factorial(%s):' % i, err)
```
The modulo operator (%) computes the remainder of a division expression (i.e., 5 % 2 = 1). The operator built into the language works well with integers but, as with so many other floating point operations, intermediate calculations cause representational issues that result in a loss of data. fmod() provides a more accurate implementation for floating point values.
```
import math
print('{:^4} {:^4} {:^5} {:^5}'.format('x', 'y', '%', 'fmod'))
print('---- ---- ----- -----')
for x, y in [ (5, 2),
(5, -2),
(-5, 2),
]:
print('{:4.1f} {:4.1f} {:5.2f} {:5.2f}'.format(x, y, x % y, math.fmod(x, y)))
```
A potentially more frequent source of confusion is the fact that the algorithm used by fmod for computing modulo is also different from that used by %, so the sign of the result is different. mixed-sign inputs.
## Exponents and Logarithms
Exponential growth curves appear in economics, physics, and other sciences. Python has a built-in exponentiation operator (“\*\*”), but pow() can be useful when you need to pass a callable function as an argument.
```
import math
for x, y in [
# Typical uses
(2, 3),
(2.1, 3.2),
# Always 1
(1.0, 5),
(2.0, 0),
# Not-a-number
(2, float('nan')),
# Roots
(9.0, 0.5),
(27.0, 1.0/3),
]:
print('{:5.1f} ** {:5.3f} = {:6.3f}'.format(x, y, math.pow(x, y)))
```
Raising 1 to any power always returns 1.0, as does raising any value to a power of 0.0. Most operations on the not-a-number value nan return nan. If the exponent is less than 1, pow() computes a root.
Since square roots (exponent of 1/2) are used so frequently, there is a separate function for computing them.
```
import math
print(math.sqrt(9.0))
print(math.sqrt(3))
try:
print(math.sqrt(-1))
except ValueError as err:
print('Cannot compute sqrt(-1):', err)
```
Computing the square roots of negative numbers requires complex numbers, which are not handled by math. Any attempt to calculate a square root of a negative value results in a ValueError.
There are two variations of **log()**. Given floating point representation and rounding errors the computed value produced by **log(x, b)** has limited accuracy, especially for some bases. **log10()** computes **log(x, 10)**, using a more accurate algorithm than **log()**.
```
import math
print('{:2} {:^12} {:^20} {:^20} {:8}'.format('i', 'x', 'accurate', 'inaccurate', 'mismatch'))
print('{:-^2} {:-^12} {:-^20} {:-^20} {:-^8}'.format('', '', '', '', ''))
for i in range(0, 10):
x = math.pow(10, i)
accurate = math.log10(x)
inaccurate = math.log(x, 10)
match = '' if int(inaccurate) == i else '*'
print('{:2d} {:12.1f} {:20.18f} {:20.18f} {:^5}'.format(i, x, accurate, inaccurate, match))
```
The lines in the output with trailing * highlight the inaccurate values.
As with other special-case functions, the function **exp()** uses an algorithm that produces more accurate results than the general-purpose equivalent math.pow(math.e, x).
```
import math
x = 2
fmt = '%.20f'
print(fmt % (math.e ** 2))
print(fmt % math.pow(math.e, 2))
print(fmt % math.exp(2))
```
For more information about other mathematical functions, including trigonometric ones, we refer to <a href="https://pymotw.com/2/math/">https://pymotw.com/2/math/</a>
The python references can be found at <a href="https://docs.python.org/2/library/math.html">https://docs.python.org/2/library/math.html</a>
|
github_jupyter
|
```
import numpy as np
import random
twopi = 2.*np.pi
oneOver2Pi = 1./twopi
import time
def time_usage(func):
def wrapper(*args, **kwargs):
beg_ts = time.time()
retval = func(*args, **kwargs)
end_ts = time.time()
print("elapsed time: %f" % (end_ts - beg_ts))
return retval
return wrapper
#
# For the jam multiruns
# [iso, D, T, X, U, L]
mode = "edge_3"
runs = {1:"edge_3_7.00", 0:"edge_3_14.00"}
in_dir = "/home/walterms/project/walterms/mcmd/output/scratch/"+mode+"/"
trn_dir = "/home/walterms/project/walterms/mcmd/nn/data/train/"
test_dir = "/home/walterms/project/walterms/mcmd/nn/data/test/"
unlabeled_dir = "/home/walterms/project/walterms/mcmd/nn/data/unlbl/"
jidx = np.arange(2,18)
testidxs = np.arange(0,2) # want 400 ea
nblSkip = 1 # Skip first image
# noiseLvl: sigma of Gaussian in units of rod length
rodlen = 1.0
noiseLvl = 0.00*rodlen
thnoise = 0.00
noiseappend = ""
if noiseLvl > 0.0:
noiseappend = "_"+str(noiseLvl)
processTrain(noise=noiseLvl)
@time_usage
def processTrain(noise=0.):
for lbl in runs:
name = runs[lbl]
trnlim = -1
trnfnames = [name+"_"+str(i) for i in jidx]
fout = open(trn_dir+name+noiseappend,'w') #erases file
fout.close()
for f in trnfnames:
fin = open(in_dir+f,'r')
print "processing " + f + noiseappend + " for training data"
fout = open(trn_dir+name+noiseappend,'a')
# find width from file header
width, height = 0., 0.
l = fin.readline().split("|")
for ll in l:
if "boxEdge" in ll:
width = float(ll.split()[1])
height = width
fin.seek(0)
if width == 0.:
# calculate edge length based on vertices of first block
block = []
for line in fin.readlines():
if line == "\n": break
if line[0].isalpha(): continue
block.append(line)
fin.seek(0)
width, height = edgeLenCalc(block)
if not (fin.readline()[0].isalpha()): fin.seek(0)
thNorm = oneOver2Pi
normX, normY = 1./width, 1./height # normalize x and y
nbl = 0
fRot = 0. # rotation factor: 0,1,2,3. Multiplied by pi/2
block = []
for line in fin.readlines():
if line == "\n":
if nbl < nblSkip:
nbl+=1
block = []
continue
fRot = random.randint(0,3)
for l in block:
fout.write('%f %f %f\n' % (l[0], l[1], l[2]))
fout.write('label %f\n\n' % (lbl))
block = []
nbl+=1
continue
rndxy = [0.,0.]
rndth = 0.
if noise > 0.:
# Gen three random numbers
rndxy = np.random.normal(0,noise,2)
rndth = np.random.normal(0,twopi*thnoise,1)
# rndxy = [0.,0.]
# rndth = 0.
spt = [float(x) for x in line.split()]
x,y,th = spt[2],spt[3],spt[4]
# Rotate block
# note thetas should be [0,2pi] initially
th_ = fRot*twopi*0.25
th += th_ + rndth
if th > twopi: th-=twopi
th *= thNorm
x = np.cos(th_)*spt[2] - np.sin(th_)*spt[3] + rndxy[0]
y = np.sin(th_)*spt[2] + np.cos(th_)*spt[3] + rndxy[1]
# shift and normalize
x *= normX
y *= normY
block.append([x,y,th])
fout.close()
fin.close()
print "Done processing training files"
r = np.random.normal(0,noiseLvl,2)
r[0]
processTest()
@time_usage
def processTest():
for lbl in runs:
name = runs[lbl]
testfnames = [name+"_"+str(i) for i in testidxs]
fout = open(test_dir+name,'w') #erases file
fout.close()
for f in testfnames:
fin = open(in_dir+f,'r')
print "processing " + f + " for testing data"
fout = open(test_dir+name,'a')
# find width from file header
width, height = 0., 0.
l = fin.readline().split("|")
for ll in l:
if "boxEdge" in ll:
width = float(ll.split()[1])
height = width
fin.seek(0)
if width == 0.:
# calculate edge length based on vertices of first block
block = []
for line in fin.readlines():
if line == "\n": break
if line[0].isalpha(): continue
block.append(line)
fin.seek(0)
width, height = edgeLenCalc(block)
if not (fin.readline()[0].isalpha()): fin.seek(0)
thNorm = oneOver2Pi
normX, normY = 1./width, 1./height # normalize x and y
nbl = 0
fRot = 0. # rotation factor: 0,1,2,3. Multiplied by pi/2
block = []
for line in fin.readlines():
if line == "\n":
if nbl < 1:
nbl+=1
block = []
continue
fRot = random.randint(0,3)
for l in block:
fout.write('%f %f %f\n' % (l[0], l[1], l[2]))
fout.write('label %f\n\n' % (lbl))
block = []
nbl+=1
continue
spt = [float(x) for x in line.split()]
x,y,th = spt[2],spt[3],spt[4]
# Rotate block
# note thetas should be [0,2pi] initially
th_ = fRot*twopi*0.25
th += th_
if th > twopi: th-=twopi
th *= thNorm
x = np.cos(th_)*spt[2] - np.sin(th_)*spt[3]
y = np.sin(th_)*spt[2] + np.cos(th_)*spt[3]
# shift and normalize
x *= normX
y *= normY
block.append([x,y,th])
fout.close()
fin.close()
print "Done processing testing files"
edges = []
ein = open("/home/walterms/mcmd/edge_3",'r')
for line in ein.readlines():
edges.append(float(line))
unlblnames = [mode+"_"+"%.2f"%(e) for e in edges]
uidx = np.arange(0,18)
processUnlbl()
@time_usage
def processUnlbl(noise=0.):
nlimPerFile = 270+nblSkip
for run in unlblnames:
fnames = [run+"_"+str(i) for i in uidx]
fout = open(unlabeled_dir+run+noiseappend,'w') #erases file
fout.close()
for f in fnames:
fin = open(in_dir+f,'r')
print "processing " + f + noiseappend + " for training data"
fout = open(unlabeled_dir+run+noiseappend,'a')
# find width from file header
width, height = 0., 0.
l = fin.readline().split("|")
for ll in l:
if "boxEdge" in ll:
width = float(ll.split()[1])
height = width
fin.seek(0)
if width == 0.:
# calculate edge length based on vertices of first block
block = []
for line in fin.readlines():
if line == "\n": break
if line[0].isalpha(): continue
block.append(line)
fin.seek(0)
width, height = edgeLenCalc(block)
if not (fin.readline()[0].isalpha()): fin.seek(0)
thNorm = oneOver2Pi
normX, normY = 1./width, 1./height # normalize x and y
nbl = 0
fRot = 0. # rotation factor: 0,1,2,3. Multiplied by pi/2
block = []
for line in fin.readlines():
if line == "\n":
if nbl < nblSkip:
nbl+=1
block = []
continue
fRot = random.randint(0,3)
for l in block:
fout.write('%f %f %f\n' % (l[0], l[1], l[2]))
fout.write('\n')
block = []
nbl+=1
if nbl == nlimPerFile:
break
else:
continue
rndxy = [0.,0.]
rndth = 0.
if noise > 0.:
# Gen three random numbers
rndxy = np.random.normal(0,noise,2)
rndth = np.random.normal(0,twopi*thnoise,1)
# rndxy = [0.,0.]
# rndth = 0.
spt = [float(x) for x in line.split()]
x,y,th = spt[2],spt[3],spt[4]
# Rotate block
# note thetas should be [0,2pi] initially
th_ = fRot*twopi*0.25
th += th_ + rndth
if th > twopi: th-=twopi
th *= thNorm
x = np.cos(th_)*spt[2] - np.sin(th_)*spt[3] + rndxy[0]
y = np.sin(th_)*spt[2] + np.cos(th_)*spt[3] + rndxy[1]
# shift and normalize
x *= normX
y *= normY
block.append([x,y,th])
fout.close()
fin.close()
print "Done processing unlbl files"
```
|
github_jupyter
|
#### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Classification on imbalanced data
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/structured_data/imbalanced_data"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/structured_data/imbalanced_data.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/structured_data/imbalanced_data.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/structured_data/imbalanced_data.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
This tutorial demonstrates how to classify a highly imbalanced dataset in which the number of examples in one class greatly outnumbers the examples in another. You will work with the [Credit Card Fraud Detection](https://www.kaggle.com/mlg-ulb/creditcardfraud) dataset hosted on Kaggle. The aim is to detect a mere 492 fraudulent transactions from 284,807 transactions in total. You will use [Keras](../../guide/keras/overview.ipynb) to define the model and [class weights](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/Model) to help the model learn from the imbalanced data. You will display metrics for precision, recall, true positives, false positives, true negatives, false negatives, and AUC while training the model. These are more informative than accuracy when working with imbalanced datasets classification.
This tutorial contains complete code to:
* Load a CSV file using Pandas.
* Create train, validation, and test sets.
* Define and train a model using Keras (including setting class weights).
* Evaluate the model using various metrics (including precision and recall).
## Import TensorFlow and other libraries
```
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
!pip install imblearn
import tensorflow as tf
from tensorflow import keras
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from scikit_learn_contrib.imbalanced_learn.over_sampling import SMOTE
```
## Use Pandas to get the Kaggle Credit Card Fraud data set
Pandas is a Python library with many helpful utilities for loading and working with structured data and can be used to download CSVs into a dataframe.
Note: This dataset has been collected and analysed during a research collaboration of Worldline and the [Machine Learning Group](http://mlg.ulb.ac.be) of ULB (Université Libre de Bruxelles) on big data mining and fraud detection. More details on current and past projects on related topics are available [here](https://www.researchgate.net/project/Fraud-detection-5) and the page of the [DefeatFraud](https://mlg.ulb.ac.be/wordpress/portfolio_page/defeatfraud-assessment-and-validation-of-deep-feature-engineering-and-learning-solutions-for-fraud-detection/) project
```
raw_df = pd.read_csv('https://storage.googleapis.com/download.tensorflow.org/data/creditcard.csv')
raw_df.head()
```
## Split the dataframe into train, validation, and test
Split the dataset into train, validation, and test sets. The validation set is used during the model fitting to evaluate the loss and any metrics, however the model is not fit with this data. The test set is completely unused during the training phase and is only used at the end to evaluate how well the model generalizes to new data. This is especially important with imbalanced datasets where [overfitting](https://developers.google.com/machine-learning/crash-course/generalization/peril-of-overfitting) is a significant concern from the lack of training data.
```
# Use a utility from sklearn to split and shuffle our dataset.
train_df, test_df = train_test_split(raw_df, test_size=0.2)
train_df, val_df = train_test_split(train_df, test_size=0.2)
# Form np arrays of labels and features.
train_labels = np.array(train_df.pop('Class'))
val_labels = np.array(val_df.pop('Class'))
test_labels = np.array(test_df.pop('Class'))
train_features = np.array(train_df)
val_features = np.array(val_df)
test_features = np.array(test_df)
# Normalize the input features using the sklearn StandardScaler.
# This will set the mean to 0 and standard deviation to 1.
scaler = StandardScaler()
train_features = scaler.fit_transform(train_features)
val_features = scaler.transform(val_features)
test_features = scaler.transform(test_features)
print('Training labels shape:', train_labels.shape)
print('Validation labels shape:', val_labels.shape)
print('Test labels shape:', test_labels.shape)
print('Training features shape:', train_features.shape)
print('Validation features shape:', val_features.shape)
print('Test features shape:', test_features.shape)
```
## Examine the class label imbalance
Let's look at the dataset imbalance:
```
neg, pos = np.bincount(train_labels)
total = neg + pos
print('{} positive samples out of {} training samples ({:.2f}% of total)'.format(
pos, total, 100 * pos / total))
```
This shows a small fraction of positive samples.
## Define the model and metrics
Define a function that creates a simple neural network with three densely connected hidden layers, an output sigmoid layer that returns the probability of a transaction being fraudulent, and two [dropout](https://developers.google.com/machine-learning/glossary/#dropout_regularization) layers as an effective way to reduce overfitting.
```
def make_model():
model = keras.Sequential([
keras.layers.Dense(256, activation='relu',
input_shape=(train_features.shape[-1],)),
keras.layers.Dense(256, activation='relu'),
keras.layers.Dropout(0.3),
keras.layers.Dense(256, activation='relu'),
keras.layers.Dropout(0.3),
keras.layers.Dense(1, activation='sigmoid'),
])
metrics = [
keras.metrics.Accuracy(name='accuracy'),
keras.metrics.TruePositives(name='tp'),
keras.metrics.FalsePositives(name='fp'),
keras.metrics.TrueNegatives(name='tn'),
keras.metrics.FalseNegatives(name='fn'),
keras.metrics.Precision(name='precision'),
keras.metrics.Recall(name='recall'),
keras.metrics.AUC(name='auc')
]
model.compile(
optimizer='adam',
loss='binary_crossentropy',
metrics=metrics)
return model
```
## Understanding useful metrics
Notice that there are a few metrics defined above that can be computed by the model that will be helpful when evaluating the performance.
* **False** negatives and **false** positives are samples that were **incorrectly** classified
* **True** negatives and **true** positives are samples that were **correctly** classified
* **Accuracy** is the percentage of examples correctly classified
> $\frac{\text{true samples}}{\text{total samples}}$
* **Precision** is the percentage of **predicted** positives that were correctly classified
> $\frac{\text{true positives}}{\text{true positives + false positives}}$
* **Recall** is the percentage of **actual** positives that were correctly classified
> $\frac{\text{true positives}}{\text{true positives + false negatives}}$
* **AUC** refers to the Area Under the Curve of a Receiver Operating Characteristic curve (ROC-AUC). This metric is equal to the probability that a classifier will rank a random positive sample higher than than a random negative sample.
<br>
Read more:
* [True vs. False and Positive vs. Negative](https://developers.google.com/machine-learning/crash-course/classification/true-false-positive-negative)
* [Accuracy](https://developers.google.com/machine-learning/crash-course/classification/accuracy)
* [Precision and Recall](https://developers.google.com/machine-learning/crash-course/classification/precision-and-recall)
* [ROC-AUC](https://developers.google.com/machine-learning/crash-course/classification/roc-and-auc)
## Train a baseline model
Now create and train your model using the function that was defined earlier. Notice that the model is fit using a larger than default batch size of 2048, this is important to ensure that each batch has a decent chance of containing a few positive samples. If the batch size was too small, they would likely have no fraudelent transactions to learn from.
Note: this model will not handle the class imbalance well. You will improve it later in this tutorial.
```
model = make_model()
EPOCHS = 10
BATCH_SIZE = 2048
history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
validation_data=(val_features, val_labels))
```
## Plot metrics on the training and validation sets
In this section, you will produce plots of your model's accuracy and loss on the training and validation set. These are useful to check for overfitting, which you can learn more about in this [tutorial](https://www.tensorflow.org/tutorials/keras/overfit_and_underfit).
Additionally, you can produce these plots for any of the metrics you created above. False negatives are included as an example.
```
epochs = range(EPOCHS)
plt.title('Accuracy')
plt.plot(epochs, history.history['accuracy'], color='blue', label='Train')
plt.plot(epochs, history.history['val_accuracy'], color='orange', label='Val')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
_ = plt.figure()
plt.title('Loss')
plt.plot(epochs, history.history['loss'], color='blue', label='Train')
plt.plot(epochs, history.history['val_loss'], color='orange', label='Val')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
_ = plt.figure()
plt.title('False Negatives')
plt.plot(epochs, history.history['fn'], color='blue', label='Train')
plt.plot(epochs, history.history['val_fn'], color='orange', label='Val')
plt.xlabel('Epoch')
plt.ylabel('False Negatives')
plt.legend()
```
## Evaluate the baseline model
Evaluate your model on the test dataset and display results for the metrics you created above.
```
results = model.evaluate(test_features, test_labels)
for name, value in zip(model.metrics_names, results):
print(name, ': ', value)
```
It looks like the precision is relatively high, but the recall and AUC aren't as high as you might like. Classifiers often face challenges when trying to maximize both precision and recall, which is especially true when working with imbalanced datasets. However, because missing fraudulent transactions (false negatives) may have significantly worse business consequences than incorrectly flagging fraudulent transactions (false positives), recall may be more important than precision in this case.
## Examine the confusion matrix
You can use a [confusion matrix](https://developers.google.com/machine-learning/glossary/#confusion_matrix) to summarize the actual vs. predicted labels where the X axis is the predicted label and the Y axis is the actual label.
```
predicted_labels = model.predict(test_features)
cm = confusion_matrix(test_labels, np.round(predicted_labels))
plt.matshow(cm, alpha=0)
plt.title('Confusion matrix')
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
for (i, j), z in np.ndenumerate(cm):
plt.text(j, i, str(z), ha='center', va='center')
plt.show()
print('Legitimate Transactions Detected (True Negatives): ', cm[0][0])
print('Legitimate Transactions Incorrectly Detected (False Positives): ', cm[0][1])
print('Fraudulent Transactions Missed (False Negatives): ', cm[1][0])
print('Fraudulent Transactions Detected (True Positives): ', cm[1][1])
print('Total Fraudulent Transactions: ', np.sum(cm[1]))
```
If the model had predicted everything perfectly, this would be a [diagonal matrix](https://en.wikipedia.org/wiki/Diagonal_matrix) where values off the main diagonal, indicating incorrect predictions, would be zero. In this case the matrix shows that you have relatively few false positives, meaning that there were relatively few legitimate transactions that were incorrectly flagged. However, you would likely want to have even fewer false negatives despite the cost of increasing the number of false positives. This trade off may be preferable because false negatives would allow fraudulent transactions to go through, whereas false positives may cause an email to be sent to a customer to ask them to verify their card activity.
## Using class weights for the loss function
The goal is to identify fradulent transactions, but you don't have very many of those positive samples to work with, so you would want to have the classifier heavily weight the few examples that are available. You can do this by passing Keras weights for each class through a parameter. These will cause the model to "pay more attention" to examples from an under-represented class.
```
weight_for_0 = 1 / neg
weight_for_1 = 1 / pos
class_weight = {0: weight_for_0, 1: weight_for_1}
print('Weight for class 0: {:.2e}'.format(weight_for_0))
print('Weight for class 1: {:.2e}'.format(weight_for_1))
```
## Train a model with class weights
Now try re-training and evaluating the model with class weights to see how that affects the predictions.
Note: Using `class_weights` changes the range of the loss. This may affect the stability of the training depending on the optimizer. Optimizers who's step size is dependent on the magnitude of the gradient, like `optimizers.SGD`, may fail. The optimizer used here, `optimizers.Adam`, is unaffected by the scaling change. Also note that because of the weighting, the total losses are not comparable between the two models.
```
weighted_model = make_model()
weighted_history = weighted_model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
validation_data=(val_features, val_labels),
class_weight=class_weight)
weighted_results = weighted_model.evaluate(test_features, test_labels)
for name, value in zip(weighted_model.metrics_names, weighted_results):
print(name, ': ', value)
```
Here you can see that with class weights the accuracy and precision are lower because there are more false positives, but conversely the recall and AUC are higher because the model also found more true positives. Despite having lower overall accuracy, this approach may be better when considering the consequences of failing to identify fraudulent transactions driving the prioritization of recall. Depending on how bad false negatives are, you might use even more exaggerated weights to further improve recall while dropping precision.
## Oversampling the minority class
A related approach would be to resample the dataset by oversampling the minority class, which is the process of creating more positive samples using something like sklearn's [imbalanced-learn library](https://github.com/scikit-learn-contrib/imbalanced-learn). This library provides methods to create new positive samples by simply duplicating random existing samples, or by interpolating between them to generate synthetic samples using variations of [SMOTE](https://en.wikipedia.org/wiki/Oversampling_and_undersampling_in_data_analysis#Oversampling_techniques_for_classification_problems). TensorFlow also provides a way to do [Random Oversampling](https://www.tensorflow.org/api_docs/python/tf/data/experimental/sample_from_datasets).
```
# with default args this will oversample the minority class to have an equal
# number of observations
smote = SMOTE()
res_features, res_labels = smote.fit_sample(train_features, train_labels)
res_neg, res_pos = np.bincount(res_labels)
res_total = res_neg + res_pos
print('{} positive samples out of {} training samples ({:.2f}% of total)'.format(
res_pos, res_total, 100 * res_pos / res_total))
```
## Train and evaluate a model on the resampled data
Now try training the model with the resampled data set instead of using class weights to see how these methods compare.
```
resampled_model = make_model()
resampled_history = resampled_model.fit(
res_features,
res_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
validation_data=(val_features, val_labels))
resampled_results = resampled_model.evaluate(test_features, test_labels)
for name, value in zip(resampled_model.metrics_names, resampled_results):
print(name, ': ', value)
```
This approach can be worth trying, but may not provide better results than using class weights because the synthetic examples may not accurately represent the underlying data.
## Applying this tutorial to your problem
Imbalanced data classification is an inherantly difficult task since there are so few samples to learn from. You should always start with the data first and do your best to collect as many samples as possible and give substantial thought to what features may be relevant so the model can get the most out of your minority class. At some point your model may struggle to improve and yield the results you want, so it is important to keep in mind the context of the problem to evaluate how bad your false positives or negatives really are.
|
github_jupyter
|
```
pip install pyspark
pip install sklearn
pip install pandas
pip install seaborn
pip install matplotlib
import pandas as pd
import numpy as np
import os
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import LogisticRegressionCV
from sklearn import datasets
from sklearn import datasets
data = datasets.load_wine()
wine = pd.DataFrame(data = np.c_[data['data'], data['target']],
columns = data['feature_names'] + ['target'])
wine.info()
wine.head()
wine.describe()
# Gráfico que faz comparações entre as colunas que foram citadas com a coluna "target", que é representada:
# pelas cores azul (0), laranja (1) e verde (2).
sns.pairplot(wine, vars=["malic_acid", "ash", "alcalinity_of_ash", "total_phenols", "flavanoids",
"nonflavanoid_phenols"], hue='target')
# Correlacao entre as colunas da matriz
correlacao = wine.corr()
# O primeiro plot ficou impossível de entender, pois ficou muito pequeno e com muita informação
# Precisei aumentar o tamanho da heatmap
fig,ax = plt.subplots(figsize = (10, 10))
sns.heatmap(correlacao, annot = True, fmt = ".2f")
plt.show()
wine.info()
# Divisão da base em treinamento e teste
from sklearn.model_selection import train_test_split
x = wine[['alcohol', 'malic_acid', 'ash', 'alcalinity_of_ash', 'magnesium', 'total_phenols', 'flavanoids',
'nonflavanoid_phenols', 'proanthocyanins', 'color_intensity', 'hue', 'od280/od315_of_diluted_wines',
'proline']]
y = wine['target']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.30, random_state = 42)
# Normalizando a base
from sklearn.preprocessing import StandardScaler
normalize = StandardScaler()
normalize.fit(x_train)
newx_train = normalize.transform(x_train)
newx_train = pd.DataFrame(data = newx_train, columns = x.columns)
normalize.fit(x_test)
newx_test = normalize.transform(x_test)
newx_test = pd.DataFrame(newx_test)
```
## A seguir segue os modelos criados e a avaliação do compartamento na base de treinamento
## Solver: "liblinear"
```
from sklearn.model_selection import GridSearchCV
solver_list = ['liblinear']
parametros = dict(solver = solver_list)
model = LogisticRegression(random_state = 42, solver = 'liblinear', max_iter = 150)
clf = GridSearchCV(model, parametros, cv = 5)
clf.fit(x_train, y_train)
scores = clf.cv_results_["mean_test_score"]
print(solver_list,":", scores)
```
## Solver: "newton-cg"
```
solver_list = ['newton-cg']
parametros = dict(solver = solver_list)
model = LogisticRegression(random_state = 42, solver = 'newton-cg', max_iter = 150)
clf = GridSearchCV(model, parametros, cv = 5)
clf.fit(x_train, y_train)
scores = clf.cv_results_["mean_test_score"]
print(solver_list,":", scores)
```
## Solver: "lbfgs"
```
solver_list = ['lbfgs']
parametros = dict(solver = solver_list)
model = LogisticRegression(random_state = 42, solver = 'lbfgs', max_iter = 150)
clf = GridSearchCV(model, parametros, cv = 5)
clf.fit(x_train, y_train)
scores = clf.cv_results_["mean_test_score"]
print(solver_list,":", scores)
```
## Solver: "sag"
```
solver_list = ['sag']
parametros = dict(solver = solver_list)
model = LogisticRegression(random_state = 42, solver = 'sag', max_iter = 150)
clf = GridSearchCV(model, parametros, cv = 5)
clf.fit(x_train, y_train)
scores = clf.cv_results_["mean_test_score"]
print(solver_list,":", scores)
```
## Solver: "saga"
```
solver_list = ['saga']
parametros = dict(solver = solver_list)
model = LogisticRegression(random_state = 42, solver = 'saga', max_iter = 150)
clf = GridSearchCV(model, parametros, cv = 5)
clf.fit(x_train, y_train)
scores = clf.cv_results_["mean_test_score"]
print(solver_list,":", scores)
```
## Para um melhor entendimento:
#### For small datasets, ‘liblinear’ is a good choice, whereas ‘sag’ and ‘saga’ are faster for large ones.
#### For multiclass problems, only ‘newton-cg’, ‘sag’, ‘saga’ and ‘lbfgs’ handle multinomial loss; ‘liblinear’ is limited to one-versus-rest schemes.
#### ‘newton-cg’, ‘lbfgs’ and ‘sag’ only handle L2 penalty, whereas ‘liblinear’ and ‘saga’ handle L1 penalty.
#### ‘liblinear’ might be slower in LogisticRegressionCV because it does not handle warm-starting.
## Baseado nisso, o modelo que obteve a melhor avaliação, foi o "newton-cg".
```
# Treine o modelo com a melhor configuração, aplique-o na base de testes e avalie os resultados
model = LogisticRegression(random_state = 42, solver = 'newton-cg', max_iter = 150).fit(newx_train, y_train)
predictions = model.predict(newx_test)
predictions
probabilidade = model.predict_proba(newx_test)
probabilidade
# Matriz Confusão
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, model.predict(newx_test))
model.score(newx_test, y_test)
from sklearn.metrics import classification_report
print(classification_report(y_test, model.predict(newx_test)))
```
## Cross-Validation
```
# Escolher o K
from sklearn.neighbors import KNeighborsClassifier
classificador = KNeighborsClassifier(n_neighbors = 3)
# treinar
classificador.fit(newx_train, y_train)
# Fazer a predição
prediction = classificador.predict(newx_test)
# Melhor K
storage = []
for i in range(1, 100):
knn = KNeighborsClassifier(n_neighbors = i)
scores = cross_val_score(knn, x, y, cv = 12)
storage.append(scores.mean())
print(len(scores))
print(max(scores))
# Classification_report
from sklearn.metrics import classification_report
print(classification_report(y_test, classificador.predict(newx_test), zero_division = 1))
# Matriz Confusão
from sklearn.metrics import confusion_matrix
matrix_confusao = confusion_matrix(y_test, classificador.predict(newx_test))
print(matrix_confusao)
# Melhor acurácia e medindo o erro
from sklearn.model_selection import cross_val_score
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
storageK = []
error = []
for i in range(1, 30):
knn = KNeighborsClassifier(n_neighbors = i)
scores = cross_val_score(knn, x, y, cv = 5)
classificador.fit(newx_train, y_train)
prediction = classificador.predict(newx_test)
storageK = accuracy_score(y_test, prediction)
error.append(np.mean(y_test != prediction))
print("Melhor acurácia: ", storageK)
print("Taxa de erros: ", max(error))
```
## Comparando o resultado do Cross-Validation com o da Regressão Logística:
### Cross-Validation
```
# Classification_report
from sklearn.metrics import classification_report
print(classification_report(y_test, classificador.predict(newx_test)))
```
### Regressão Logística
```
from sklearn.metrics import classification_report
print(classification_report(y_test, model.predict(newx_test)))
```
|
github_jupyter
|
# GRIP_JULY - 2021 (TASK 5)
# Task Name:- Traffic sign classification/Recognition
# Domain:- Computer Vision and IOT
# Name:- Akash Singh

```
import cv2
import numpy as np
from scipy.stats import itemfreq
def get_dominant_color(image, n_colors):
pixels = np.float32(image).reshape((-1, 3))
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 200, .1)
flags = cv2.KMEANS_RANDOM_CENTERS
flags, labels, centroids = cv2.kmeans(
pixels, n_colors, None, criteria, 10, flags)
palette = np.uint8(centroids)
return palette[np.argmax(itemfreq(labels)[:, -1])]
clicked = False
def onMouse(event, x, y, flags, param):
global clicked
if event == cv2.EVENT_LBUTTONUP:
clicked = True
cameraCapture = cv2.VideoCapture(0)
cv2.namedWindow('camera')
cv2.setMouseCallback('camera', onMouse)
# Read and process frames in loop
success, frame = cameraCapture.read()
while success and not clicked:
cv2.waitKey(1)
success, frame = cameraCapture.read()
gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
img = cv2.medianBlur(gray, 37)
circles = cv2.HoughCircles(img, cv2.HOUGH_GRADIENT,
1, 50, param1=120, param2=40)
if not circles is None:
circles = np.uint16(np.around(circles))
max_r, max_i = 0, 0
for i in range(len(circles[:, :, 2][0])):
if circles[:, :, 2][0][i] > 50 and circles[:, :, 2][0][i] > max_r:
max_i = i
max_r = circles[:, :, 2][0][i]
x, y, r = circles[:, :, :][0][max_i]
if y > r and x > r:
square = frame[y-r:y+r, x-r:x+r]
dominant_color = get_dominant_color(square, 2)
if dominant_color[2] > 100:
print("STOP")
elif dominant_color[0] > 80:
zone_0 = square[square.shape[0]*3//8:square.shape[0]
* 5//8, square.shape[1]*1//8:square.shape[1]*3//8]
cv2.imshow('Zone0', zone_0)
zone_0_color = get_dominant_color(zone_0, 1)
zone_1 = square[square.shape[0]*1//8:square.shape[0]
* 3//8, square.shape[1]*3//8:square.shape[1]*5//8]
cv2.imshow('Zone1', zone_1)
zone_1_color = get_dominant_color(zone_1, 1)
zone_2 = square[square.shape[0]*3//8:square.shape[0]
* 5//8, square.shape[1]*5//8:square.shape[1]*7//8]
cv2.imshow('Zone2', zone_2)
zone_2_color = get_dominant_color(zone_2, 1)
if zone_1_color[2] < 60:
if sum(zone_0_color) > sum(zone_2_color):
print("LEFT")
else:
print("RIGHT")
else:
if sum(zone_1_color) > sum(zone_0_color) and sum(zone_1_color) > sum(zone_2_color):
print("FORWARD")
elif sum(zone_0_color) > sum(zone_2_color):
print("FORWARD AND LEFT")
else:
print("FORWARD AND RIGHT")
else:
print("N/A")
for i in circles[0, :]:
cv2.circle(frame, (i[0], i[1]), i[2], (0, 255, 0), 2)
cv2.circle(frame, (i[0], i[1]), 2, (0, 0, 255), 3)
cv2.imshow('camera', frame)
cv2.destroyAllWindows()
cameraCapture.release()
```
|
github_jupyter
|
# Markov Random Fields for Collaborative Filtering (Memory Efficient)
This notebook provides a **memory efficient version** in Python 3.7 of the algorithm outlined in the paper
"[Markov Random Fields for Collaborative Filtering](https://arxiv.org/abs/1910.09645)"
at the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, Canada.
For reproducibility, the experiments utilize publicly available [code](https://github.com/dawenl/vae_cf) for pre-processing three popular data-sets and for evaluating the learned model. That code accompanies the paper "[Variational Autoencoders for Collaborative Filtering](https://arxiv.org/abs/1802.05814)" by Dawen Liang et al. at The Web Conference 2018. While the code for the Movielens-20M data-set was made publicly available, the code for pre-processing the other two data-sets can easily be obtained by modifying their code as described in their paper.
The experiments in the paper (where an AWS instance with 64 GB RAM and 16 vCPUs was used) may be re-run by following these three steps:
- Step 1: Pre-processing the data (utilizing the publicly available [code](https://github.com/dawenl/vae_cf))
- Step 2: Learning the MRF (this code implements the new algorithm)
- Step 3: Evaluation (utilizing the publicly available [code](https://github.com/dawenl/vae_cf))
This memory efficient version is modified by Yifei Shen @ Hong Kong University of Science and Technology
## Step 1: Pre-processing the data
Utilizing the publicly available [code](https://github.com/dawenl/vae_cf), which is copied below (with kind permission of Dawen Liang):
- run their cells 1-26 for data pre-processing
- note that importing matplotlib, seaborn, and tensorflow may not be necessary for our purposes here
- run their cells 29-31 for loading the training data
Note that the following code is modified as to pre-process the [MSD data-set](https://labrosa.ee.columbia.edu/millionsong/tasteprofile). For pre-processing the [MovieLens-20M data-set](https://grouplens.org/datasets/movielens/20m/), see their original publicly-available [code](https://github.com/dawenl/vae_cf).
```
import os
import shutil
import sys
import numpy as np
from scipy import sparse
import pandas as pd
import bottleneck as bn
# change to the location of the data
DATA_DIR = 'MSD'
itemId='songId' # for MSD data
raw_data = pd.read_csv(os.path.join(DATA_DIR, 'train_triplets.txt'), sep='\t', header=None, names=['userId', 'songId', 'playCount'])
```
### Data splitting procedure
- Select 50K users as heldout users, 50K users as validation users, and the rest of the users for training
- Use all the items from the training users as item set
- For each of both validation and test user, subsample 80% as fold-in data and the rest for prediction
```
def get_count(tp, id):
playcount_groupbyid = tp[[id]].groupby(id, as_index=False)
count = playcount_groupbyid.size()
return count
def filter_triplets(tp, min_uc=5, min_sc=0):
# Only keep the triplets for items which were clicked on by at least min_sc users.
if min_sc > 0:
itemcount = get_count(tp, itemId)
tp = tp[tp[itemId].isin(itemcount.index[itemcount >= min_sc])]
# Only keep the triplets for users who clicked on at least min_uc items
# After doing this, some of the items will have less than min_uc users, but should only be a small proportion
if min_uc > 0:
usercount = get_count(tp, 'userId')
tp = tp[tp['userId'].isin(usercount.index[usercount >= min_uc])]
# Update both usercount and itemcount after filtering
usercount, itemcount = get_count(tp, 'userId'), get_count(tp, itemId)
return tp, usercount, itemcount
raw_data, user_activity, item_popularity = filter_triplets(raw_data, min_uc=20, min_sc=200) # for MSD data
sparsity = 1. * raw_data.shape[0] / (user_activity.shape[0] * item_popularity.shape[0])
print("After filtering, there are %d watching events from %d users and %d movies (sparsity: %.3f%%)" %
(raw_data.shape[0], user_activity.shape[0], item_popularity.shape[0], sparsity * 100))
unique_uid = user_activity.index
np.random.seed(98765)
idx_perm = np.random.permutation(unique_uid.size)
unique_uid = unique_uid[idx_perm]
# create train/validation/test users
n_users = unique_uid.size
n_heldout_users = 50000 # for MSD data
tr_users = unique_uid[:(n_users - n_heldout_users * 2)]
vd_users = unique_uid[(n_users - n_heldout_users * 2): (n_users - n_heldout_users)]
te_users = unique_uid[(n_users - n_heldout_users):]
train_plays = raw_data.loc[raw_data['userId'].isin(tr_users)]
unique_sid = pd.unique(train_plays[itemId])
show2id = dict((sid, i) for (i, sid) in enumerate(unique_sid))
profile2id = dict((pid, i) for (i, pid) in enumerate(unique_uid))
pro_dir = os.path.join(DATA_DIR, 'pro_sg')
if not os.path.exists(pro_dir):
os.makedirs(pro_dir)
with open(os.path.join(pro_dir, 'unique_sid.txt'), 'w') as f:
for sid in unique_sid:
f.write('%s\n' % sid)
def split_train_test_proportion(data, test_prop=0.2):
data_grouped_by_user = data.groupby('userId')
tr_list, te_list = list(), list()
np.random.seed(98765)
for i, (_, group) in enumerate(data_grouped_by_user):
n_items_u = len(group)
if n_items_u >= 5:
idx = np.zeros(n_items_u, dtype='bool')
idx[np.random.choice(n_items_u, size=int(test_prop * n_items_u), replace=False).astype('int64')] = True
tr_list.append(group[np.logical_not(idx)])
te_list.append(group[idx])
else:
tr_list.append(group)
if i % 5000 == 0:
print("%d users sampled" % i)
sys.stdout.flush()
data_tr = pd.concat(tr_list)
data_te = pd.concat(te_list)
return data_tr, data_te
vad_plays = raw_data.loc[raw_data['userId'].isin(vd_users)]
vad_plays = vad_plays.loc[vad_plays[itemId].isin(unique_sid)]
vad_plays_tr, vad_plays_te = split_train_test_proportion(vad_plays)
test_plays = raw_data.loc[raw_data['userId'].isin(te_users)]
test_plays = test_plays.loc[test_plays[itemId].isin(unique_sid)]
test_plays_tr, test_plays_te = split_train_test_proportion(test_plays)
```
### Save the data into (user_index, item_index) format
```
def numerize(tp):
uid = list(map(lambda x: profile2id[x], tp['userId']))
sid = list(map(lambda x: show2id[x], tp[itemId]))
return pd.DataFrame(data={'uid': uid, 'sid': sid}, columns=['uid', 'sid'])
train_data = numerize(train_plays)
train_data.to_csv(os.path.join(pro_dir, 'train.csv'), index=False)
vad_data_tr = numerize(vad_plays_tr)
vad_data_tr.to_csv(os.path.join(pro_dir, 'validation_tr.csv'), index=False)
vad_data_te = numerize(vad_plays_te)
vad_data_te.to_csv(os.path.join(pro_dir, 'validation_te.csv'), index=False)
test_data_tr = numerize(test_plays_tr)
test_data_tr.to_csv(os.path.join(pro_dir, 'test_tr.csv'), index=False)
test_data_te = numerize(test_plays_te)
test_data_te.to_csv(os.path.join(pro_dir, 'test_te.csv'), index=False)
```
### Load the pre-processed training and validation data
```
unique_sid = list()
with open(os.path.join(pro_dir, 'unique_sid.txt'), 'r') as f:
for line in f:
unique_sid.append(line.strip())
n_items = len(unique_sid)
def load_train_data(csv_file):
tp = pd.read_csv(csv_file)
n_users = tp['uid'].max() + 1
rows, cols = tp['uid'], tp['sid']
data = sparse.csr_matrix((np.ones_like(rows),
(rows, cols)), dtype='float64',
shape=(n_users, n_items))
return data
train_data = load_train_data(os.path.join(pro_dir, 'train.csv'))
```
## Step 2: Learning the MRF model (implementation of the new algorithm)
Now run the following code and choose to learn
- either the dense MRF model
- or the sparse MRF model
```
import time
from copy import deepcopy
class MyClock:
startTime = time.time()
def tic(self):
self.startTime = time.time()
def toc(self):
secs = time.time() - self.startTime
print("... elapsed time: {} min {} sec".format(int(secs//60), secs%60) )
myClock = MyClock()
totalClock = MyClock()
alpha = 0.75
```
### Pre-computation of the training data
```
def filter_XtX(train_data, block_size, thd4mem, thd4comp):
# To obtain and sparsify XtX at the same time to save memory
# block_size (2nd input) and threshold for memory (3rd input) controls the memory usage
# thd4comp is the threshold to control training efficiency
XtXshape = train_data.shape[1]
userCount = train_data.shape[0]
bs = block_size
blocks = train_data.shape[1]// bs + 1
flag = False
thd = thd4mem
#normalize data
mu = np.squeeze(np.array(np.sum(train_data, axis=0)))/ userCount
variance_times_userCount = (mu - mu * mu) * userCount
rescaling = np.power(variance_times_userCount, alpha / 2.0)
scaling = 1.0 / rescaling
#block multiplication
for ii in range(blocks):
for jj in range(blocks):
XtX_tmp = np.asarray(train_data[:,bs*ii : bs*(ii+1)].T.dot(train_data[:,bs*jj : bs*(jj+1)]).todense(), dtype = np.float32)
XtX_tmp -= mu[bs*ii:bs*(ii+1),None] * (mu[bs*jj : bs*(jj+1)]* userCount)
XtX_tmp = scaling[bs*ii:bs*(ii+1),None] * XtX_tmp * scaling[bs*jj : bs*(jj+1)]
# sparsification filter 1 to control memory usage
ix = np.where(np.abs(XtX_tmp) > thd)
XtX_nz = XtX_tmp[ix]
ix = np.array(ix, dtype = 'int32')
ix[0,:] += bs*ii
ix[1,:] += bs*jj
if(flag):
ixs = np.concatenate((ixs, ix), axis = 1)
XtX_nzs = np.concatenate((XtX_nzs, XtX_nz), axis = 0)
else:
ixs = ix
XtX_nzs = XtX_nz
flag = True
#sparsification filter 2 to control training time of the algorithm
ix2 = np.where(np.abs(XtX_nzs) >= thd4comp)
AA_nzs = XtX_nzs[ix2]
AA_ixs = np.squeeze(ixs[:,ix2])
print(XtX_nzs.shape, AA_nzs.shape)
XtX = sparse.csc_matrix( (XtX_nzs, ixs), shape=(XtXshape,XtXshape), dtype=np.float32)
AA = sparse.csc_matrix( (AA_nzs, AA_ixs), shape=(XtXshape,XtXshape), dtype=np.float32)
return XtX, rescaling, XtX.diagonal(), AA
XtX, rescaling, XtXdiag, AtA = filter_XtX(train_data, 10000, 0.04, 0.11)
ii_diag = np.diag_indices(XtX.shape[0])
scaling = 1/rescaling
```
### Sparse MRF model
```
def calculate_sparsity_pattern(AtA, maxInColumn):
# this implements section 3.1 in the paper.
print("sparsifying the data-matrix (section 3.1 in the paper) ...")
myClock.tic()
# apply threshold
#ix = np.where( np.abs(XtX) > threshold)
#AA = sparse.csc_matrix( (XtX[ix], ix), shape=XtX.shape, dtype=np.float32)
AA = AtA
# enforce maxInColumn, see section 3.1 in paper
countInColumns=AA.getnnz(axis=0)
iiList = np.where(countInColumns > maxInColumn)[0]
print(" number of items with more than {} entries in column: {}".format(maxInColumn, len(iiList)) )
for ii in iiList:
jj= AA[:,ii].nonzero()[0]
kk = bn.argpartition(-np.abs(np.asarray(AA[jj,ii].todense()).flatten()), maxInColumn)[maxInColumn:]
AA[ jj[kk], ii ] = 0.0
AA.eliminate_zeros()
print(" resulting sparsity of AA: {}".format( AA.nnz*1.0 / AA.shape[0] / AA.shape[0]) )
myClock.toc()
return AA
def sparse_parameter_estimation(rr, XtX, AA, XtXdiag):
# this implements section 3.2 in the paper
# list L in the paper, sorted by item-counts per column, ties broken by item-popularities as reflected by np.diag(XtX)
AAcountInColumns = AA.getnnz(axis=0)
sortedList=np.argsort(AAcountInColumns+ XtXdiag /2.0/ np.max(XtXdiag) )[::-1]
print("iterating through steps 1,2, and 4 in section 3.2 of the paper ...")
myClock.tic()
todoIndicators=np.ones(AAcountInColumns.shape[0])
blockList=[] # list of blocks. Each block is a list of item-indices, to be processed in step 3 of the paper
for ii in sortedList:
if todoIndicators[ii]==1:
nn, _, vals=sparse.find(AA[:,ii]) # step 1 in paper: set nn contains item ii and its neighbors N
kk=np.argsort(np.abs(vals))[::-1]
nn=nn[kk]
blockList.append(nn) # list of items in the block, to be processed in step 3 below
# remove possibly several items from list L, as determined by parameter rr (r in the paper)
dd_count=max(1,int(np.ceil(len(nn)*rr)))
dd=nn[:dd_count] # set D, see step 2 in the paper
todoIndicators[dd]=0 # step 4 in the paper
myClock.toc()
print("now step 3 in section 3.2 of the paper: iterating ...")
# now the (possibly heavy) computations of step 3:
# given that steps 1,2,4 are already done, the following for-loop could be implemented in parallel.
myClock.tic()
BBlist_ix1, BBlist_ix2, BBlist_val = [], [], []
for nn in blockList:
#calculate dense solution for the items in set nn
BBblock=np.linalg.inv( np.array(XtX[np.ix_(nn,nn)].todense()) )
#BBblock=np.linalg.inv( XtX[np.ix_(nn,nn)] )
BBblock/=-np.diag(BBblock)
# determine set D based on parameter rr (r in the paper)
dd_count=max(1,int(np.ceil(len(nn)*rr)))
dd=nn[:dd_count] # set D in paper
# store the solution regarding the items in D
blockix = np.meshgrid(dd,nn)
BBlist_ix1.extend(blockix[1].flatten().tolist())
BBlist_ix2.extend(blockix[0].flatten().tolist())
BBlist_val.extend(BBblock[:,:dd_count].flatten().tolist())
myClock.toc()
print("final step: obtaining the sparse matrix BB by averaging the solutions regarding the various sets D ...")
myClock.tic()
BBsum = sparse.csc_matrix( (BBlist_val, (BBlist_ix1, BBlist_ix2 ) ), shape=XtX.shape, dtype=np.float32)
BBcnt = sparse.csc_matrix( (np.ones(len(BBlist_ix1), dtype=np.float32), (BBlist_ix1,BBlist_ix2 ) ), shape=XtX.shape, dtype=np.float32)
b_div= sparse.find(BBcnt)[2]
b_3= sparse.find(BBsum)
BBavg = sparse.csc_matrix( ( b_3[2] / b_div , (b_3[0],b_3[1] ) ), shape=XtX.shape, dtype=np.float32)
BBavg[ii_diag]=0.0
myClock.toc()
print("forcing the sparsity pattern of AA onto BB ...")
myClock.tic()
BBavg = sparse.csr_matrix( ( np.asarray(BBavg[AA.nonzero()]).flatten(), AA.nonzero() ), shape=BBavg.shape, dtype=np.float32)
print(" resulting sparsity of learned BB: {}".format( BBavg.nnz * 1.0 / AA.shape[0] / AA.shape[0]) )
myClock.toc()
return BBavg
def sparse_solution(rr, maxInColumn, L2reg):
# sparsity pattern, see section 3.1 in the paper
XtX[ii_diag] = XtXdiag
AA = calculate_sparsity_pattern(AtA, maxInColumn)
# parameter-estimation, see section 3.2 in the paper
XtX[ii_diag] = XtXdiag+L2reg
BBsparse = sparse_parameter_estimation(rr, XtX, AA, XtXdiag+L2reg)
return BBsparse
```
training the sparse model:
```
maxInColumn = 1000
# hyper-parameter r in the paper, which determines the trade-off between approximation-accuracy and training-time
rr = 0.1
# L2 norm regularization
L2reg = 1.0
print("training the sparse model:\n")
totalClock.tic()
BBsparse = sparse_solution(rr, maxInColumn, L2reg)
print("\ntotal training time (including the time for determining the sparsity-pattern):")
totalClock.toc()
print("\nre-scaling BB back to the original item-popularities ...")
# assuming that mu.T.dot(BB) == mu, see Appendix in paper
myClock.tic()
BBsparse=sparse.diags(scaling).dot(BBsparse).dot(sparse.diags(rescaling))
myClock.toc()
#print("\nfor the evaluation below: converting the sparse model into a dense-matrix-representation ...")
#myClock.tic()
#BB = np.asarray(BBsparse.todense(), dtype=np.float32)
#myClock.toc()
```
## Step 3: Evaluating the MRF model
Utilizing the publicly available [code](https://github.com/dawenl/vae_cf), which is copied below (with kind permission of Dawen Liang):
- run their cell 32 for loading the test data
- run their cells 35 and 36 for the ranking metrics (for later use in evaluation)
- run their cells 45 and 46
- modify and run their cell 50:
- remove 2 lines: the one that starts with ```with``` and the line below
- remove the indentation of the line that starts with ```for```
- modify the line that starts with ```pred_val``` as follows: ```pred_val = X.dot(BB)```
- run their cell 51
```
def load_tr_te_data(csv_file_tr, csv_file_te):
tp_tr = pd.read_csv(csv_file_tr)
tp_te = pd.read_csv(csv_file_te)
start_idx = min(tp_tr['uid'].min(), tp_te['uid'].min())
end_idx = max(tp_tr['uid'].max(), tp_te['uid'].max())
rows_tr, cols_tr = tp_tr['uid'] - start_idx, tp_tr['sid']
rows_te, cols_te = tp_te['uid'] - start_idx, tp_te['sid']
data_tr = sparse.csr_matrix((np.ones_like(rows_tr),
(rows_tr, cols_tr)), dtype='float64', shape=(end_idx - start_idx + 1, n_items))
data_te = sparse.csr_matrix((np.ones_like(rows_te),
(rows_te, cols_te)), dtype='float64', shape=(end_idx - start_idx + 1, n_items))
return data_tr, data_te
def NDCG_binary_at_k_batch(X_pred, heldout_batch, k=100):
'''
normalized discounted cumulative gain@k for binary relevance
ASSUMPTIONS: all the 0's in heldout_data indicate 0 relevance
'''
batch_users = X_pred.shape[0]
idx_topk_part = bn.argpartition(-X_pred, k, axis=1)
topk_part = X_pred[np.arange(batch_users)[:, np.newaxis],
idx_topk_part[:, :k]]
idx_part = np.argsort(-topk_part, axis=1)
# X_pred[np.arange(batch_users)[:, np.newaxis], idx_topk] is the sorted
# topk predicted score
idx_topk = idx_topk_part[np.arange(batch_users)[:, np.newaxis], idx_part]
# build the discount template
tp = 1. / np.log2(np.arange(2, k + 2))
DCG = (heldout_batch[np.arange(batch_users)[:, np.newaxis],
idx_topk].toarray() * tp).sum(axis=1)
IDCG = np.array([(tp[:min(n, k)]).sum()
for n in heldout_batch.getnnz(axis=1)])
return DCG / IDCG
def Recall_at_k_batch(X_pred, heldout_batch, k=100):
batch_users = X_pred.shape[0]
idx = bn.argpartition(-X_pred, k, axis=1)
X_pred_binary = np.zeros_like(X_pred, dtype=bool)
X_pred_binary[np.arange(batch_users)[:, np.newaxis], idx[:, :k]] = True
X_true_binary = (heldout_batch > 0).toarray()
tmp = (np.logical_and(X_true_binary, X_pred_binary).sum(axis=1)).astype(
np.float32)
recall = tmp / np.minimum(k, X_true_binary.sum(axis=1))
return recall
```
### Load the test data and compute test metrics
```
test_data_tr, test_data_te = load_tr_te_data(
os.path.join(pro_dir, 'test_tr.csv'),
os.path.join(pro_dir, 'test_te.csv'))
N_test = test_data_tr.shape[0]
idxlist_test = range(N_test)
batch_size_test = 2000
n100_list, r20_list, r50_list = [], [], []
for bnum, st_idx in enumerate(range(0, N_test, batch_size_test)):
end_idx = min(st_idx + batch_size_test, N_test)
X = test_data_tr[idxlist_test[st_idx:end_idx]]
#if sparse.isspmatrix(X):
# X = X.toarray()
#X = X.astype('float32')
pred_val = np.array(X.dot(BBsparse).todense())
# exclude examples from training and validation (if any)
pred_val[X.nonzero()] = -np.inf
n100_list.append(NDCG_binary_at_k_batch(pred_val, test_data_te[idxlist_test[st_idx:end_idx]], k=100))
r20_list.append(Recall_at_k_batch(pred_val, test_data_te[idxlist_test[st_idx:end_idx]], k=20))
r50_list.append(Recall_at_k_batch(pred_val, test_data_te[idxlist_test[st_idx:end_idx]], k=50))
n100_list = np.concatenate(n100_list)
r20_list = np.concatenate(r20_list)
r50_list = np.concatenate(r50_list)
print("Test NDCG@100=%.5f (%.5f)" % (np.mean(n100_list), np.std(n100_list) / np.sqrt(len(n100_list))))
print("Test Recall@20=%.5f (%.5f)" % (np.mean(r20_list), np.std(r20_list) / np.sqrt(len(r20_list))))
print("Test Recall@50=%.5f (%.5f)" % (np.mean(r50_list), np.std(r50_list) / np.sqrt(len(r50_list))))
```
... accuracy of the sparse approximation (with sparsity 0.1% and parameter r=0.5)
|
github_jupyter
|
<a href="https://colab.research.google.com/github/emadphysics/Amsterdam_Airbnb_predictive_models/blob/main/airbnb_pytorch.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import pandas as pd
import numpy as np
from datetime import date
import matplotlib.pyplot as plt
import seaborn as sns
import os
import re
from sklearn.feature_selection import *
from sklearn.linear_model import *
from sklearn.neighbors import *
from sklearn.svm import *
from sklearn.neighbors import *
from sklearn.tree import *
from sklearn.preprocessing import *
from xgboost import *
from sklearn.metrics import *
from geopy.distance import great_circle
# Geographical analysis
import json # library to handle JSON files
from pandas.io.json import json_normalize # tranform JSON file into a pandas dataframe
from statsmodels.tsa.seasonal import seasonal_decompose
import requests
import descartes
import math
print('Libraries imported.')
from google.colab import drive
drive.mount("/content/gdrive")
df=pd.read_csv('/content/gdrive/My Drive/listingss.csv')
print(f'the numer of observations are {len(df)}')
categoricals = [var for var in df.columns if df[var].dtype=='object']
numerics = [var for var in df.columns if (df[var].dtype=='int64')|(df[var].dtype=='float64')]
dates=[var for var in df.columns if df[var].dtype=='datetime64[ns]']
#pandas data types: numeric(float,integer),object(string),category,Boolean,date
one_hot_col_names = ['host_id', 'host_location', 'host_response_time','host_is_superhost','host_neighbourhood','host_has_profile_pic','host_identity_verified',
'neighbourhood','neighbourhood_cleansed','neighbourhood_group_cleansed', 'zipcode', 'is_location_exact', 'property_type', 'room_type', 'bed_type', 'has_availability', 'requires_license', 'instant_bookable',
'is_business_travel_ready', 'cancellation_policy', 'cancellation_policy','require_guest_profile_picture', 'require_guest_phone_verification', 'calendar_updated']
text_cols = ['name', 'summary', 'space', 'description', 'neighborhood_overview', 'notes', 'transit', 'access', 'interaction', 'house_rules', 'host_name', 'host_about']
features = ['host_listings_count', 'host_total_listings_count', 'latitude', 'longitude',
'accommodates', 'bathrooms', 'bedrooms', 'beds', 'square_feet',
'guests_included', 'minimum_nights', 'maximum_nights', 'availability_30', 'availability_60',
'availability_90', 'availability_365', 'number_of_reviews', 'review_scores_rating', 'review_scores_accuracy',
'review_scores_cleanliness', 'review_scores_checkin', 'review_scores_communication', 'review_scores_location',
'review_scores_value', 'calculated_host_listings_count', 'reviews_per_month']
price_features = ['security_deposit', 'cleaning_fee', 'extra_people','price']
date_cols = ['host_since', 'first_review', 'last_review']
def host_verification(cols):
possible_words = {}
i = 0
for col in cols:
words = col.split()
for w in words:
wr = re.sub(r'\W+', '', w)
if wr != '' and wr not in possible_words:
possible_words[wr] = i
i += 1
l = len(possible_words)
new_cols = np.zeros((cols.shape[0], l))
for i, col in enumerate(cols):
words = col.split()
arr = np.zeros(l)
for w in words:
wr = re.sub(r'\W+', '', w)
if wr != '':
arr[possible_words[wr]] = 1
new_cols[i] = arr
return new_cols
def amenities(cols):
dic = {}
i = 0
for col in cols:
arr = col.split(',')
for a in arr:
ar = re.sub(r'\W+', '', a)
if len(ar) > 0:
if ar not in dic:
dic[ar] = i
i += 1
l = len(dic)
new_cols = np.zeros((cols.shape[0], l))
for i, col in enumerate(cols):
words = col.split(',')
arr = np.zeros(l)
for w in words:
wr = re.sub(r'\W+', '', w)
if wr != '':
arr[dic[wr]] = 1
new_cols[i] = arr
return new_cols
def one_hot(arr):
label_encoder = LabelEncoder()
integer_encoded = label_encoder.fit_transform(arr)
onehot_encoder = OneHotEncoder(sparse=False)
integer_encoded = integer_encoded.reshape(len(integer_encoded), 1)
onehot_encoded = onehot_encoder.fit_transform(integer_encoded)
return onehot_encoded
one_hot_col_names = ['host_response_time','host_is_superhost','host_has_profile_pic','host_identity_verified',
'neighbourhood_cleansed','neighbourhood_group_cleansed', 'zipcode', 'is_location_exact', 'property_type', 'room_type', 'bed_type', 'has_availability', 'requires_license', 'instant_bookable',
'is_business_travel_ready', 'cancellation_policy','require_guest_profile_picture', 'require_guest_phone_verification','calendar_updated']
one_hot_dict = {}
for i in one_hot_col_names:
one_hot_dict[i] = one_hot(np.array(df[i].fillna(""), dtype=str))
one_hot_dict['host_verifications'] = host_verification(df['host_verifications'])
one_hot_dict['amenities'] = amenities(df['amenities'])
ont_hot_list = []
for i in one_hot_dict.keys():
if 1<one_hot_dict[i].shape[1]<400:
ont_hot_list.append(one_hot_dict[i])
# print(i,one_hot_dict[i].shape[1])
onehot_variables = np.concatenate(ont_hot_list, axis=1)
hot_cat_variables=pd.DataFrame(onehot_variables)
hot_cat_variables.isnull().sum().sum()
hot_cat_variables.shape
def check_nan(cols):
for col in cols:
if np.isnan(col):
return True
return False
def clean_host_response_rate(host_response_rate, num_data):
total = 0
count = 0
for col in host_response_rate:
if not isinstance(col, float):
total += float(col.strip('%'))
count += 1
arr = np.zeros(num_data)
mean = total / count
for i, col in enumerate(host_response_rate):
if not isinstance(col, float):
arr[i] += float(col.strip('%'))
else:
assert(math.isnan(col))
arr[i] = mean
return arr
def clean_price(price, num_data):
arr = np.zeros(num_data)
for i, col in enumerate(price):
if not isinstance(col, float):
arr[i] += float(col.strip('$').replace(',', ''))
else:
assert(math.isnan(col))
arr[i] = 0
return arr
def to_np_array_fill_NA_mean(cols):
return np.array(cols.fillna(np.nanmean(np.array(cols))))
num_data = df.shape[0]
arr = np.zeros((len(features) + len(price_features) + 1, num_data))
host_response_rate = clean_host_response_rate(df['host_response_rate'], num_data)
arr[0] = host_response_rate
i = 0
for feature in features:
i += 1
if check_nan(df[feature]):
arr[i] = to_np_array_fill_NA_mean(df[feature])
else:
arr[i] = np.array(df[feature])
for feature in price_features:
i += 1
arr[i] = clean_price(df[feature], num_data)
target = arr[-1]
numeric_variables = arr[:-1].T
numeric_variables=pd.DataFrame(numeric_variables)
numeric_variables.isnull().sum()\
.sum()
inde_variables=np.concatenate((numeric_variables,hot_cat_variables),axis=1)
inde_variables=pd.DataFrame(inde_variables)
inde_variables.isnull().sum().sum()
mean = np.mean(inde_variables, axis = 0)
std = np.std(inde_variables, axis = 0)
inde_variables=(inde_variables-mean)/std
inde_variables.shape
import torch
from torch import nn
import torch.optim as optim
import numpy as np
import random
import copy
import torch.utils.data as data
import os
class NN229(nn.Module):
def __init__(self, input_size=355, hidden_size1=128, hidden_size2=512, hidden_size3=64, output_size=1, drop_prob=0.05):
super(NN229, self).__init__()
self.relu = nn.ReLU()
self.dropout = nn.Dropout(p=drop_prob)
self.W1 = nn.Linear(input_size, hidden_size1)
self.W2 = nn.Linear(hidden_size1, hidden_size2)
self.W3 = nn.Linear(hidden_size2, hidden_size3)
self.W4 = nn.Linear(hidden_size3, output_size)
def forward(self, x):
hidden1 = self.dropout(self.relu(self.W1(x)))
hidden2 = self.dropout(self.relu(self.W2(hidden1)))
hidden3 = self.dropout(self.relu(self.W3(hidden2)))
out = self.W4(hidden3)
return out
class AirBnb(data.Dataset):
def __init__(self, train_path, label_path):
super(AirBnb, self).__init__()
self.x = torch.from_numpy(train_path).float()
self.y = torch.from_numpy(label_path).float()
def __getitem__(self, idx):
x = self.x[idx]
y = self.y[idx]
return x, y
def __len__(self):
return self.x.shape[0]
class CSVDataset(data.Dataset):
def __init__(self, train_path, label_path):
super(CSVDataset, self).__init__()
self.x = torch.from_numpy(train_path).float()
self.y = torch.from_numpy(label_path).float()
self.y = self.y.reshape((len(self.y), 1))
def __len__(self):
return len(self.x)
def __getitem__(self, idx):
return [self.x[idx], self.y[idx]]
def get_splits(self, n_test=0.33):
test_size = round(n_test * len(self.x))
train_size = len(self.x) - test_size
return data.random_split(self, [train_size, test_size])
def load_model(model, optimizer, checkpoint_path, model_only = False):
ckpt_dict = torch.load(checkpoint_path, map_location="cuda:0")
model.load_state_dict(ckpt_dict['state_dict'])
if not model_only:
optimizer.load_state_dict(ckpt_dict['optimizer'])
epoch = ckpt_dict['epoch']
val_loss = ckpt_dict['val_loss']
else:
epoch = None
val_loss = None
return model, optimizer, epoch, val_loss
np.log(target)
def train(model, optimizer, loss_fn, epoch = 0):
train_dataset = CSVDataset(inde_variables.to_numpy(), target)
train, test = train_dataset.get_splits()
train_loader = data.DataLoader(train,
batch_size=batch_size,
shuffle=True)
dev_loader = data.DataLoader(test,
batch_size=batch_size,
shuffle=True)
model.train()
step = 0
best_model = NN229()
best_epoch = 0
best_val_loss = None
while epoch < max_epoch:
epoch += 1
stats = []
with torch.enable_grad():
for x, y in train_loader:
step += 1
# print (x)
# print (y)
# break
x = x.cuda()
y = y.cuda()
optimizer.zero_grad()
pred = model(x).reshape(-1)
loss = loss_fn(pred, y)
loss_val = loss.item()
loss.backward()
optimizer.step()
stats.append(loss_val)
# stats.append((epoch, step, loss_val))
# print ("Epoch: ", epoch, " Step: ", step, " Loss: ", loss_val)
print ("Train loss: ", sum(stats) / len(stats))
val_loss = evaluate(dev_loader, model)
if best_val_loss is None or best_val_loss > val_loss:
best_val_loss = val_loss
model.cpu()
best_model = copy.deepcopy(model)
model.cuda()
best_epoch = epoch
# print (evaluate(dev_loader, model))
return best_model, best_epoch, best_val_loss
def evaluate(dev_loader, model):
model.eval()
stats = []
with torch.no_grad():
for x, y in dev_loader:
x = x.cuda()
y = y.cuda()
pred = model(x).reshape(-1)
loss_val = loss_fn(pred, y).item()
stats.append(loss_val)
# print ("Loss: ", loss_val)
print ("Val loss: ", sum(stats) / len(stats))
return sum(stats) / len(stats)
lr = 1e-4
weight_decay = 1e-5
beta = (0.9, 0.999)
max_epoch = 100
batch_size = 64
model = NN229().cuda()
optimizer = optim.Adam(model.parameters(), lr=lr, weight_decay=weight_decay, betas=beta)
loss_fn = nn.MSELoss()
best_model, best_epoch, best_val_loss = train(model, optimizer, loss_fn, epoch = 0)
train_dataset = CSVDataset(inde_variables.to_numpy(), target)
train, test = train_dataset.get_splits()
dev_loader = data.DataLoader(test,
shuffle=True)
y_truth_list = []
for _, y_truth in dev_loader:
y_truth_list.append(y_truth[0][0].cpu().numpy())
y_pred_list = [a.squeeze().tolist() for a in y_truth_list]
y_t=np.array(y_truth_list)
y_t
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
y_pred_list = []
with torch.no_grad():
model.eval()
for X_batch, _ in dev_loader:
X_batch = X_batch.to(device)
y_test_pred = model(X_batch)
y_pred_list.append(y_test_pred.cpu().numpy())
y_pred_list = [a.squeeze().tolist() for a in y_pred_list]
y_p=np.array(y_pred_list)
y_p
import sklearn.metrics
sklearn.metrics.r2_score(y_t, y_p)
```
|
github_jupyter
|
```
import panel as pn
pn.extension()
```
One of the main design goals for Panel was that it should make it possible to seamlessly transition back and forth between interactively prototyping a dashboard in the notebook or on the commandline to deploying it as a standalone server app. This section shows how to display panels interactively, embed static output, save a snapshot, and deploy as a separate web-server app.
## Configuring output
As you may have noticed, almost all the Panel documentation is written using notebooks. Panel objects display themselves automatically in a notebook and take advantage of Jupyter Comms to support communication between the rendered app and the Jupyter kernel that backs it on the Python end. To display a Panel object in the notebook is as simple as putting it on the end of a cell. Note, however, that the ``panel.extension`` first has to be loaded to initialize the required JavaScript in the notebook context. Also, if you are working in JupyterLab, the pyviz labextension has to be installed with:
jupyter labextension install @pyviz/jupyterlab_pyviz
### Optional dependencies
Also remember that in order to use certain components such as Vega, LaTeX, and Plotly plots in a notebook, the models must be loaded using the extension. If you forget to load the extension, you should get a warning reminding you to do it. To load certain JS components, simply list them as part of the call to ``pn.extension``:
pn.extension('vega', 'katex')
Here we've ensured that the Vega and LaTeX JS dependencies will be loaded.
### Initializing JS and CSS
Additionally, any external ``css_files``, ``js_files`` and ``raw_css`` needed should be declared in the extension. The ``js_files`` should be declared as a dictionary mapping from the exported JS module name to the URL containing the JS components, while the ``css_files`` can be defined as a list:
pn.extension(js_files={'deck': https://unpkg.com/deck.gl@~5.2.0/deckgl.min.js},
css_files=['https://api.tiles.mapbox.com/mapbox-gl-js/v0.44.1/mapbox-gl.css'])
The ``raw_css`` argument allows defining a list of strings containing CSS to publish as part of the notebook and app.
Providing keyword arguments via the ``extension`` is the same as setting them on ``pn.config``, which is the preferred approach outside the notebook. ``js_files`` and ``css_files`` may be set to your chosen values as follows:
pn.config.js_files = {'deck': 'https://unpkg.com/deck.gl@~5.2.0/deckgl.min.js'}
pn.config.css_files = ['https://api.tiles.mapbox.com/mapbox-gl-js/v0.44.1/mapbox-gl.css']
## Display in the notebook
#### The repr
Once the extension is loaded, Panel objects will display themselves if placed at the end of cell in the notebook:
```
pane = pn.panel('<marquee>Here is some custom HTML</marquee>')
pane
```
To instead see a textual representation of the component, you can use the ``pprint`` method on any Panel object:
```
pane.pprint()
```
#### The ``display`` function
To avoid having to put a Panel on the last line of a notebook cell, e.g. to display it from inside a function call, you can use the IPython built-in ``display`` function:
```
def display_marquee(text):
display(pn.panel('<marquee>{text}</marquee>'.format(text=text)))
display_marquee('This Panel was displayed from within a function')
```
#### Inline apps
Lastly it is also possible to display a Panel object as a Bokeh server app inside the notebook. To do so call the ``.app`` method on the Panel object and provide the URL of your notebook server:
```
pane.app('localhost:8888')
```
The app will now run on a Bokeh server instance separate from the Jupyter notebook kernel, allowing you to quickly test that all the functionality of your app works both in a notebook and in a server context.
## Display in the Python REPL
Working from the command line will not automatically display rich representations inline as in a notebook, but you can still interact with your Panel components if you start a Bokeh server instance and open a separate browser window using the ``show`` method. The method has the following arguments:
port: int (optional)
Allows specifying a specific port (default=0 chooses an arbitrary open port)
websocket_origin: str or list(str) (optional)
A list of hosts that can connect to the websocket.
This is typically required when embedding a server app in
an external-facing web site.
If None, "localhost" is used.
threaded: boolean (optional, default=False)
Whether to launch the Server on a separate thread, allowing
interactive use.
To work with an app completely interactively you can set ``threaded=True`,` which will launch the server on a separate thread and let you interactively play with the app.
<img src='https://assets.holoviews.org/panel/gifs/commandline_show.gif'></img>
The ``show`` call will return either a Bokeh server instance (if ``threaded=False``) or a ``StoppableThread`` instance (if ``threaded=True``) which both provide a ``stop`` method to stop the server instance.
## Launching a server on the commandline
Once the app is ready for deployment it can be served using the Bokeh server. For a detailed breakdown of the design and functionality of Bokeh server, see the [Bokeh documentation](https://bokeh.pydata.org/en/latest/docs/user_guide/server.html). The most important thing to know is that Panel (and Bokeh) provide a CLI command to serve a Python script, app directory, or Jupyter notebook containing a Bokeh or Panel app. To launch a server using the CLI, simply run:
panel serve app.ipynb
The ``panel serve`` command has the following options:
positional arguments:
DIRECTORY-OR-SCRIPT The app directories or scripts or notebooks to serve
(serve empty document if not specified)
optional arguments:
-h, --help show this help message and exit
--port PORT Port to listen on
--address ADDRESS Address to listen on
--log-level LOG-LEVEL
One of: trace, debug, info, warning, error or critical
--log-format LOG-FORMAT
A standard Python logging format string (default:
'%(asctime)s %(message)s')
--log-file LOG-FILE A filename to write logs to, or None to write to the
standard stream (default: None)
--args ... Any command line arguments remaining are passed on to
the application handler
--show Open server app(s) in a browser
--allow-websocket-origin HOST[:PORT]
Public hostnames which may connect to the Bokeh
websocket
--prefix PREFIX URL prefix for Bokeh server URLs
--keep-alive MILLISECONDS
How often to send a keep-alive ping to clients, 0 to
disable.
--check-unused-sessions MILLISECONDS
How often to check for unused sessions
--unused-session-lifetime MILLISECONDS
How long unused sessions last
--stats-log-frequency MILLISECONDS
How often to log stats
--mem-log-frequency MILLISECONDS
How often to log memory usage information
--use-xheaders Prefer X-headers for IP/protocol information
--session-ids MODE One of: unsigned, signed, or external-signed
--index INDEX Path to a template to use for the site index
--disable-index Do not use the default index on the root path
--disable-index-redirect
Do not redirect to running app from root path
--num-procs N Number of worker processes for an app. Using 0 will
autodetect number of cores (defaults to 1)
--websocket-max-message-size BYTES
Set the Tornado websocket_max_message_size value
(defaults to 20MB) NOTE: This setting has effect ONLY
for Tornado>=4.5
--dev [FILES-TO-WATCH [FILES-TO-WATCH ...]]
Enable live reloading during app development.By
default it watches all *.py *.html *.css *.yaml
filesin the app directory tree. Additional files can
be passedas arguments. NOTE: This setting only works
with a single app.It also restricts the number of
processes to 1.
To turn a notebook into a deployable app simply append ``.servable()`` to one or more Panel objects, which will add the app to Bokeh's ``curdoc``, ensuring it can be discovered by Bokeh server on deployment. In this way it is trivial to build dashboards that can be used interactively in a notebook and then seamlessly deployed on Bokeh server.
### Accessing session state
Whenever a Panel app is being served the ``panel.state`` object exposes some of the internal Bokeh server components to a user.
#### Document
The current Bokeh ``Document`` can be accessed using ``panel.state.curdoc``.
#### Request arguments
When a browser makes a request to a Bokeh server a session is created for the Panel application. The request arguments are made available to be accessed on ``pn.state.session_args``. For example if your application is hosted at ``localhost:8001/app``, appending ``?phase=0.5`` to the URL will allow you to access the phase variable using the following code:
```python
try:
phase = int(pn.state.session_args.get('phase')[0])
except:
phase = 1
```
This mechanism may be used to modify the behavior of an app dependending on parameters provided in the URL.
### Accessing the Bokeh model
Since Panel is built on top of Bokeh, all Panel objects can easily be converted to a Bokeh model. The ``get_root`` method returns a model representing the contents of a Panel:
```
pn.Column('# Some markdown').get_root()
```
By default this model will be associated with Bokeh's ``curdoc()``, so if you want to associate the model with some other ``Document`` ensure you supply it explictly as the first argument.
## Embedding
Panel generally relies on either the Jupyter kernel or a Bokeh Server to be running in the background to provide interactive behavior. However for simple apps with a limited amount of state it is also possible to `embed` all the widget state, allowing the app to be used entirely from within Javascript. To demonstrate this we will create a simple app which simply takes a slider value, multiplies it by 5 and then display the result.
```
slider = pn.widgets.IntSlider(start=0, end=10)
@pn.depends(slider.param.value)
def callback(value):
return '%d * 5 = %d' % (value, value*5)
row = pn.Row(slider, callback)
```
If we displayed this the normal way it would call back into Python every time the value changed. However, the `.embed()` method will record the state of the app for the different widget configurations.
```
row.embed()
```
If you try the widget above you will note that it only has 3 different states, 0, 5 and 10. This is because by default embed will try to limit the number of options of non-discrete or semi-discrete widgets to at most three values. This can be controlled using the `max_opts` argument to the embed method. The full set of options for the embed method include:
- **max_states**: The maximum number of states to embed
- **max_opts**: The maximum number of states for a single widget
- **json** (default=True): Whether to export the data to json files
- **save_path** (default='./'): The path to save json files to
- **load_path** (default=None): The path or URL the json files will be loaded from (same as ``save_path`` if not specified)
As you might imagine if there are multiple widgets there can quickly be a combinatorial explosion of states so by default the output is limited to about 1000 states. For larger apps the states can also be exported to json files, e.g. if you want to serve the app on a website specify the ``save_path`` to declare where it will be stored and the ``load_path`` to declare where the JS code running on the website will look for the files.
## Saving
In case you don't need an actual server or simply want to export a static snapshot of a panel app, you can use the ``save`` method, which allows exporting the app to a standalone HTML or PNG file.
By default, the HTML file generated will depend on loading JavaScript code for BokehJS from the online ``CDN`` repository, to reduce the file size. If you need to work in an airgapped or no-network environment, you can declare that ``INLINE`` resources should be used instead of ``CDN``:
```python
from bokeh.resources import INLINE
panel.save('test.html', resources=INLINE)
```
Additionally the save method also allows enabling the `embed` option, which, as explained above, will embed the apps state in the app or save the state to json files which you can ship alongside the exported HTML.
Finally, if a 'png' file extension is specified, the exported plot will be rendered as a PNG, which currently requires Selenium and PhantomJS to be installed:
```python
pane.save('test.png')
```
|
github_jupyter
|
# Bias Reduction
Climate models can have biases towards different references. Commonly, biases are reduced by postprocessing before verification of forecasting skill. `climpred` provides convenience functions to do so.
```
import climpred
import xarray as xr
import matplotlib.pyplot as plt
from climpred import HindcastEnsemble
hind = climpred.tutorial.load_dataset('CESM-DP-SST') # CESM-DPLE hindcast ensemble output.
obs = climpred.tutorial.load_dataset('ERSST') # ERSST observations.
recon = climpred.tutorial.load_dataset('FOSI-SST') # Reconstruction simulation that initialized CESM-DPLE.
hind["lead"].attrs["units"] = "years"
v='SST'
alignment='same_verif'
hindcast = HindcastEnsemble(hind)
# choose one observation
hindcast = hindcast.add_observations(recon)
#hindcast = hindcast.add_observations(obs, 'ERSST') # fits hind better than reconstruction
# always only subtract a PredictionEnsemble from another PredictionEnsemble if you handle time and init at the same time
# compute anomaly with respect to 1964-2014
hindcast = hindcast - hindcast.sel(time=slice('1964', '2014')).mean('time').sel(init=slice('1964', '2014')).mean('init')
hindcast.plot()
```
The warming of the `reconstruction` is less than the `initialized`.
## Mean bias reduction
Typically, bias depends on lead-time and therefore should therefore also be removed depending on lead-time.
```
# build bias_metric by hand
from climpred.metrics import Metric
def bias_func(a,b,**kwargs):
return a-b
bias_metric = Metric('bias', bias_func, True, False,1)
bias = hindcast.verify(metric=bias_metric, comparison='e2r', dim='init', alignment=alignment).squeeze()
# equals using the pre-defined (unconditional) bias metric applied to over dimension member
xr.testing.assert_allclose(bias, hindcast.verify(metric='unconditional_bias', comparison='m2r',dim='member', alignment=alignment).squeeze())
bias[v].plot()
```
- against Reconstruction: Cold bias in early years and warm bias in later years.
- against ERSST: Overall cold bias.
### cross validatation
```
from climpred.bias_reduction import _mean_bias_reduction_quick, _mean_bias_reduction_cross_validate
_mean_bias_reduction_quick??
_mean_bias_reduction_cross_validate??
```
`climpred` wraps these functions in `HindcastEnsemble.reduce_bias(how='mean', cross_validate={bool})`.
```
hindcast.reduce_bias(how='mean', cross_validate=True, alignment=alignment).plot()
plt.title('hindcast lead timeseries reduced for unconditional mean bias')
plt.show()
```
## Skill
Distance-based accuracy metrics like (`mse`,`rmse`,`nrmse`,...) are sensitive to mean bias reduction. Correlations like (`pearson_r`, `spearman_r`) are insensitive to bias correction.
```
metric='rmse'
hindcast.verify(metric=metric, comparison='e2o', dim='init', alignment=alignment)[v].plot(label='no bias correction')
hindcast.reduce_bias(cross_validate=False, alignment=alignment).verify(metric=metric, comparison='e2o', dim='init', alignment=alignment)[v].plot(label='bias correction without cross validation')
hindcast.reduce_bias(cross_validate=True, alignment=alignment).verify(metric=metric, comparison='e2o', dim='init', alignment=alignment)[v].plot(label='formally correct bias correction with cross validation')
plt.legend()
plt.title(f"{metric} {v} evaluated against {list(hindcast._datasets['observations'].keys())[0]}")
plt.show()
```
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
import os
os.environ['CUDA_VISIBLE_DEVICES'] = "0"
import gin
import numpy as np
from matplotlib import pyplot as plt
from torch.autograd import Variable
from tqdm.auto import tqdm
import torch
from causal_util.helpers import lstdct2dctlst
from sparse_causal_model_learner_rl.sacred_gin_tune.sacred_wrapper import load_config_files
from sparse_causal_model_learner_rl.loss.losses import fit_loss_obs_space, lagrangian_granular
from sparse_causal_model_learner_rl.config import Config
from sparse_causal_model_learner_rl.learners.rl_learner import CausalModelLearnerRL
%matplotlib inline
gin.enter_interactive_mode()
import ray
ray.init('10.90.40.6:42515')
def reload_config():
load_config_files(['../sparse_causal_model_learner_rl/configs/rl_const_sparsity_obs_space.gin',
# '../keychest/config/5x5_1f_obs.gin',
# '../sparse_causal_model_learner_rl/configs/env_kc_5x5_1f_obs_quad.gin',
'../sparse_causal_model_learner_rl/configs/env_sm5_linear.gin',
# '../sparse_causal_model_learner_rl/configs/with_lagrange_dual_sparsity.gin',
'../sparse_causal_model_learner_rl/configs/with_lagrange_dual_sparsity_per_component.gin',
])
reload_config()
gin.bind_parameter('Config.collect_initial_steps', 1000)
l = CausalModelLearnerRL(Config())
l.create_trainables()
ctx = l.collect_and_get_context()
from sparse_causal_model_learner_rl.loss.losses import cache_get, maybe_item, delta_pow2_sum1, delta_01_obs, manual_switch_gradient, RunOnce
l.model.model.switch.probas.data[:, :] = 0.5
l.lagrange_multipliers.vectorized
l.lagrange_multipliers().shape
fit_loss_obs_space(**ctx,
fill_switch_grad=True, divide_by_std=True, loss_local_cache={},
return_per_component=True)
from sparse_causal_model_learner_rl.loss.losses import fit_loss_obs_space, lagrangian_granular
reload_config()
lagrangian_granular(**ctx, mode='PRIMAL')
lagrangian_granular(**ctx, mode='DUAL')
gin.clear_config()
load_config_files(['../sparse_causal_model_learner_rl/configs/rl_const_sparsity_obs_space.gin',
'../keychest/config/5x5_1f_obs.gin',
'../sparse_causal_model_learner_rl/configs/env_kc_5x5_1f_obs_quad.gin',
# '../sparse_causal_model_learner_rl/configs/env_sm5_linear.gin',
# '../sparse_causal_model_learner_rl/configs/with_lagrange_dual_sparsity.gin',
'../sparse_causal_model_learner_rl/configs/with_lagrange_dual_sparsity_per_component.gin',
])
gin.bind_parameter('Config.collect_initial_steps', 1000)
os.environ['CUDA_VISIBLE_DEVICES'] = "-1"
l = CausalModelLearnerRL(Config())
l.create_trainables()
ctx = l.collect_and_get_context()
import seaborn as sns
loss = fit_loss_obs_space(**ctx,
fill_switch_grad=True, divide_by_std=True, loss_local_cache={},
return_per_component=True)
obs_shape = l.observation_shape
l_np = loss['losses']['obs_orig'].detach().cpu().numpy().reshape(obs_shape)
l_np_1ch = np.mean(l_np, axis=2)
sns.heatmap(l_np_1ch)
obs_example = ctx['obs_x'].detach().cpu().numpy()
obs_example = obs_example[:, :, :, 2]
#obs_example = np.mean(obs_example, axis=3)
sns.heatmap(np.mean(obs_example, axis=0))
sns.heatmap(np.std(obs_example, axis=0))
```
|
github_jupyter
|
# Using `bw2landbalancer`
Notebook showing typical usage of `bw2landbalancer`
## Generating the samples
`bw2landbalancer` works with Brightway2. You only need set as current a project in which the database for which you want to balance land transformation exchanges is imported.
```
import brightway2 as bw
import numpy as np
bw.projects.set_current('ei36cutoff') # Project with ecoinvent 3.6 cut-off by classification already imported
```
The only Class you need is the `DatabaseLandBalancer`:
```
from bw2landbalancer import DatabaseLandBalancer
```
Instantiating the DatabaseLandBalancer will automatically identify land transformation biosphere activities (elementary flows).
```
dlb = DatabaseLandBalancer(
database_name="ei36_cutoff", #name the LCI db in the brightway2 project
)
```
Generating presamples for the whole database is a lengthy process. Thankfully, it only ever needs to be done once per database:
```
dlb.add_samples_for_all_acts(iterations=1000)
```
The samples and associated indices are stored as attributes:
```
dlb.matrix_samples
dlb.matrix_samples.shape
dlb.matrix_indices[0:10] # First ten indices
len(dlb.matrix_indices)
```
These can directly be used to generate [`presamples`](https://presamples.readthedocs.io/):
```
presamples_id, presamples_fp = dlb.create_presamples(
name=None, #Could have specified a string as name, not passing anything will use automatically generated random name
dirpath=None, #Could have specified a directory path to save presamples somewhere specific
id_=None, #Could have specified a string as id, not passing anything will use automatically generated random id
seed='sequential', #or None, or int.
)
```
## Using the samples
The samples are formatted for use in brighway2 via the presamples package.
The following function calculates:
- Deterministic results, using `bw.LCA`
- Stochastic results, using `bw.MonteCarloLCA`
- Stochastic results using presamples, using `bw.MonteCarloLCA` and passing `presamples=[presamples_fp]`
The ratio of stochastic results to deterministic results are then plotted for Monte Carlo results with and without presamples.
Ratios for Monte Carlo with presamples are on the order of 1.
Ratios for Monte Carlo without presamples can be multiple orders of magnitude, and can be negative or positive.
```
def check_presamples_act(act_key, ps_fp, lcia_method, iterations=1000):
"""Plot histrograms of Monte Carlo samples/det result for case w/ and w/o presamples"""
lca = bw.LCA({act_key:1}, method=m)
lca.lci()
lca.lcia()
mc_arr_wo = np.empty(shape=iterations)
mc = bw.MonteCarloLCA({act_key:1}, method=m)
for i in range(iterations):
mc_arr_wo[i] = next(mc)/lca.score
mc_arr_w = np.empty(shape=iterations)
mc_w = bw.MonteCarloLCA({act_key:1}, method=m, presamples=[ps_fp])
for i in range(iterations):
mc_arr_w[i] = next(mc_w)/lca.score
plt.hist(mc_arr_wo, histtype="step", color='orange', label="without presamples")
plt.hist(mc_arr_w, histtype="step", color='green', label="with presamples")
plt.legend()
```
Let's run this on a couple of random ecoinvent products with the ImpactWorld+ Land transformation, biodiversity LCIA method:
```
m=('IMPACTWorld+ (Default_Recommended_Midpoint 1.23)', 'Midpoint', 'Land transformation, biodiversity')
import matplotlib.pyplot as plt
%matplotlib inline
act = [act for act in bw.Database('ei36_cutoff') if act['name']=='polyester-complexed starch biopolymer production'][0]
print("Working on activity known to have non-negligeable land transformation impacts: ", act)
check_presamples_act(act.key, presamples_fp, m)
act = bw.Database('ei36_cutoff').random()
print("Randomly working on ", act)
check_presamples_act(act.key, presamples_fp, m)
act = bw.Database('ei36_cutoff').random()
print("Randomly working on ", act)
check_presamples_act(act.key, presamples_fp, m)
act = bw.Database('ei36_cutoff').random()
print("Randomly working on ", act)
check_presamples_act(act.key, presamples_fp, m)
act = bw.Database('ei36_cutoff').random()
print("Randomly working on ", act)
check_presamples_act(act.key, presamples_fp, m)
```
|
github_jupyter
|
# Analyzing volumes for word frequencies
This notebook will demonstrate some of basic functionality of the Hathi Trust FeatureReader object. We will look at a few examples of easily replicable text analysis techniques — namely word frequency and visualization.
```
%%capture
!pip install nltk
from htrc_features import FeatureReader
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
```
## Part 1 — Word frequency in novels
The following cells load a collection of nine novels from the 18th-20th centuries, chosen from an HTRC collection. Also loaded are a collection of math textbooks from the 17th-19th centuries, but the latter will be used in a later part. The collection of novels will be used as a departure point for our text analysis.
```
!rm -rf local-folder
download_output = !htid2rsync --f novels-word-use.txt | rsync -azv --files-from=- data.sharc.hathitrust.org::features/ local-folder/
suffix = '.json.bz2'
file_paths = ['local-folder/' + path for path in download_output if path.endswith(suffix)]
fr_novels = FeatureReader(file_paths)
for vol in fr_novels:
print(vol.title)
```
## Selecting volumes
The following cell is useful in choosing a volume to manipulate. Set `title_word` to any word that is contained in the title of the fr-volume you would like to work with (the string comparison is case-insensitive since some titles are lower-case). The volume will then be stored as 'vol', and can be reassigned to any variable name you would like! As an example, `title_word` is currently set to "grapes", meaning "The Grapes of Wrath" by John Steinbeck is the current volume saved under the variable name vol. You can change this cell at any time to work with a different volume.
```
title_word = 'mockingbird'
for vol in fr_novels:
if title_word.lower() in vol.title.lower():
print('Current volume:', vol.title)
break
```
## Sampling tokens from a book
The following cell will display the most common tokens (words or punctuation marks) in a given volume, alongside the number of times they appear. It will also calculate their relative frequencies (found by dividing the number of appearances over the total number of words in the book) and display the results in a `DataFrame`. We'll do this for the volume we found above, the cell may take a few seonds to run because we're looping through every word in the volume!
```
tokens = vol.tokenlist(pos=False, case=False, pages=False).sort_values('count', ascending=False)
freqs = []
for count in tokens['count']:
freqs.append(count/sum(tokens['count']))
tokens['rel_frequency'] = freqs
tokens
```
### Graphing word frequencies
The following cell outputs a bar plot of the most common tokens from the volume and their frequencies.
```
%matplotlib inline
# Build a list of frequencies and a list of tokens.
freqs_1, tokens_1 = [], []
for i in range(15): # top 8 words
freqs_1.append(freqs[i])
tokens_1.append(tokens.index.get_level_values('lowercase')[i])
# Create a range for the x-axis
x_ticks = np.arange(len(tokens_1))
# Plot!
plt.bar(x_ticks, freqs_1)
plt.xticks(x_ticks, tokens_1, rotation=90)
plt.ylabel('Frequency', fontsize=14)
plt.xlabel('Token', fontsize=14)
plt.title('Common token frequencies in "' + vol.title[:14] + '..."', fontsize=14)
```
As you can see, the most common tokens in "The Grapes of Wrath" are mostly punctuation and basic words that don't provide context. Let's see if we can narrow our search to gain some more relevant insight. We can get a list of stopwords from the `nltk` library. Punctuation is in the `string` library:
```
import nltk
nltk.download('stopwords')
from nltk.corpus import stopwords
from string import punctuation
print(stopwords.words('english'))
print()
print(punctuation)
```
Now that we have a list of words to ignore in our search, we can make a few tweaks to our plotting cell.
```
freqs_filtered, tokens_filtered, i = [], [], 0
while len(tokens_filtered) < 10:
if tokens.index.get_level_values('lowercase')[i] not in stopwords.words('english') + list(punctuation):
freqs_filtered.append(freqs[i])
tokens_filtered.append(tokens.index.get_level_values('lowercase')[i])
i += 1
# Create a range for the x-axis
x_ticks = np.arange(len(freqs_filtered))
# Plot!
plt.bar(x_ticks, freqs_filtered)
plt.xticks(x_ticks, tokens_filtered, rotation=90)
plt.ylabel('Frequency', fontsize=14)
plt.xlabel('Token', fontsize=14)
plt.title('Common token frequencies in "' + vol.title[:14] + '..."', fontsize=14)
```
That's better. No more punctuation and lower frequencies on the y-axis mean that narrowing down our search choices was effective. This is also helpful if we're trying to find distinctive words in a text, because we removed the words that most texts share.
## Sampling tokens from all books
Now we can see how relative word frequencies compare across all the books in our sample. To do this, we'll need a few useful functions.
The first finds the most common noun in a volume, with adjustable parameters for minimum length.
The second calculates the relative frequency of a token across the entirety of a volume, saving us the time of doing the calculation like in the above cell.
Finally, we'll have a visualization function to create a bar plot of relative frequencies for all volumes in our sample, so that we can easily track how word frequencies differ across titles.
```
# A function to return the most common noun of length at least word_length in the volume.
# NOTE: word_length defaults to 2.
# e.g. most_common_noun(fr_novels.first) returns 'time'.
def most_common_noun(vol, word_length=2):
# Build a table of common nouns
tokens_1 = vol.tokenlist(pages=False, case=False)
nouns_only = tokens_1.loc[(slice(None), slice(None), ['NN']),]
top_nouns = nouns_only.sort_values('count', ascending=False)
token_index = top_nouns.index.get_level_values('lowercase')
# Choose the first token at least as long as word_length with non-alphabetical characters
for i in range(max(token_index.shape)):
if (len(token_index[i]) >= word_length):
if("'", "!", ",", "?" not in token_index[i]):
return token_index[i]
print('There is no noun of this length')
return None
most_common_noun(vol, 15)
# Return the usage frequency of a given word in a given volume.
# NOTE: frequency() returns a dictionary entry of the form {'word': frequency}.
# e.g. frequency(fr_novels.first(), 'blue') returns {'blue': 0.00012}
def frequency(vol, word):
t1 = vol.tokenlist(pages=False, pos=False, case=False)
token_index = t1[t1.index.get_level_values("lowercase") == word]
if len(token_index['count'])==0:
return {word: 0}
count = token_index['count'][0]
freq = count/sum(t1['count'])
return {word: float('%.5f' % freq)}
frequency(vol, 'blue')
# Returns a plot of the usage frequencies of the given word across all volumes in the given FeatureReader collection.
# NOTE: frequencies are given as percentages rather than true ratios.
def frequency_bar_plot(word, fr):
freqs, titles = [], []
for vol in fr:
title = vol.title
short_title = title[:6] + (title[6:] and '..')
freqs.append(100*frequency(vol, word)[word])
titles.append(short_title)
# Format and plot the data
x_ticks = np.arange(len(titles))
plt.bar(x_ticks, freqs)
plt.xticks(x_ticks, titles, fontsize=10, rotation=45)
plt.ylabel('Frequency (%)', fontsize=12)
plt.title('Frequency of "' + word + '"', fontsize=14)
frequency_bar_plot('blue', fr_novels)
```
Your turn! See if you can output a bar plot of the most common noun of length at least 5 in "To Kill a Mockingbird". REMEMBER, you may have to set vol to a different value than it already has.
```
# Use the provided frequency functions to plot the most common 5-letter noun in "To Kill a Mockinbird".
# Your solution should be just one line of code.
```
## Part 2— Non-fiction volumes
Now we'll load a collection of 33 math textbooks from the 18th and 19th centuries. These volumes focus on number theory and arithmetic, and were written during the lives of Leonhard Euler and Joseph-Louis Lagrange – two of the most prolific researchers of number theory in all of history. As a result, we can expect the frequency of certain words and topics to shift over time to reflect the state of contemporary research. Let's load them and see.
```
download_output = !htid2rsync --f math-collection.txt | rsync -azv --files-from=- data.sharc.hathitrust.org::features/ local-folder/
file_paths = ['local-folder/' + path for path in download_output if path.endswith(suffix)]
fr_math = FeatureReader(file_paths)
fr_math = FeatureReader(file_paths)
for vol in fr_math:
print(vol.title)
```
### Another frequency function
The next cell contains a frequency_by_year function that takes as inputs a query word and a FeatureReader object. The function calculates relative frequencies of the query word across all volumes in the FR, then outputs them in a `DataFrame` sorted by the volume year. It then plots the frequencies and allows us to easily see trends in word usage across a time period.
```
# Returns a DF of relative frequencies, volume years, and page counts, along with a scatter plot.
# NOTE: frequencies are given in percentages rather than true ratios.
def frequency_by_year(query_word, fr):
volumes = pd.DataFrame()
years, page_counts, query_freqs = [], [], []
for vol in fr:
years.append(int(vol.year))
page_counts.append(int(vol.page_count))
query_freqs.append(100*frequency(vol, query_word)[query_word])
volumes['year'], volumes['pages'], volumes['freq'] = years, page_counts, query_freqs
volumes = volumes.sort_values('year')
# Set plot dimensions and labels
scatter_plot = volumes.plot.scatter('year', 'freq', color='black', s=50, fontsize=12)
plt.ylim(0-np.mean(query_freqs), max(query_freqs)+np.mean(query_freqs))
plt.ylabel('Frequency (%)', fontsize=12)
plt.xlabel('Year', fontsize=12)
plt.title('Frequency of "' + query_word + '"', fontsize=14)
return volumes.head(10)
```
### Checking for shifts over time
In 1744, Euler began a huge volume of work on identifying quadratic forms and progressions of primes. It follows from reason, then, that the mentions of these topics in number theory textbooks should see a discernible jump following the 1740's. The following cells call frequency_by_year on several relevant words.
```
frequency_by_year('quadratic', fr_math)
frequency_by_year('prime', fr_math)
frequency_by_year('factor', fr_math)
```
# All done!
That's all for this notebook, but it doesn't mean you can't apply what you've learned. Can you think of any words you'd like to track over time? Feel free to use the following empty cells however you'd like. An interesting challenge would be to see if you can incorporate the frequency functions from Part 1 into the scatter function from Part 2. Have fun!
|
github_jupyter
|
# Correlation and Causation
It is hard to over-emphasize the point that **correlation is not causation**!. Variables can be highly correlated for any number of reasons, none of which imply a causal relationship.
When trying to understand relationships between variables, it is worth the effort to think carefully and ask the question, does this relationship make sense? In this exercise you will explore a case where correlation appears to arise from **latent or hidden variables**.
As a first step, execute the code in the cell below to import the packages you will need.
```
import pandas as pd
import numpy as np
import numpy.random as nr
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns
#matplotlib inline
```
Is there anything you can do to improve your chances of wining a Nobel Prize? Let's have a look at some data and decide if the correlations make any sense?
Now, execute the code in the cell below and examine the first 10 rows of the data frame.
```
Nobel_chocolate = pd.read_csv('nobel-chocolate.csv', thousands=',')
print('Dimensions of the data frame = ', Nobel_chocolate.shape)
Nobel_chocolate
```
The nation of China is a bit of an outlier. While people in China win a reasonable number of Nobel prizes, the huge population skews the changes of winning per person.
To get a feel for these data, create a scatter plot of Nobel prizes vs. chocolate consumption by executing the code in the cell below.
```
## Define a figure and axes and make a scatter plot
fig = plt.figure(figsize=(8, 8)) # define plot area
ax = fig.gca() # define axis
Nobel_chocolate.plot.scatter('Chocolate', 'Laureates10_million', ax = ax) # Scatter plot
ax.set_title('Nobel Prizes vs. Chocolate Consumption') # Give the plot a main title
```
What is the correlation between Nobel prizes and chocolate consumption? To find out, execute the code in the cell below.
> Note: The Pandas corr method de-means each column before computing correlation.
```
Nobel_chocolate[['Laureates10_million', 'Chocolate']].corr()
```
There seems to be a high correlation between the number of Nobel prizes and chocolate consumption.
What about the relationship between the log of Nobel prizes and chocolate consumption? Execute the code in the cell below and examine the resulting plot.
```
Nobel_chocolate['log_Nobel'] = np.log(Nobel_chocolate.Laureates10_million)
## PLot the log Nobel vs. chocolate
fig = plt.figure(figsize=(9, 8)) # define plot area
ax = fig.gca() # define axis
Nobel_chocolate.plot.scatter('Chocolate', 'log_Nobel', ax = ax) # Scatter plot
ax.set_title('Log Nobel Prizes vs. Chocolate Consumption') # Give the plot a main title
ax.set_xlabel('Chocolate Consumption') # Set text for the x axis
ax.set_ylabel('Log Nobel Prizes per 10 Million People')# Set text for y axis
```
This looks like fairly straight line relationship, with the exception of an outlier, China.
What is the correlation between log of Nobel prizes and chocolate consumption? Execute the code in the cell below to find out.
```
Nobel_chocolate[['log_Nobel', 'Chocolate']].corr()
```
This correlation is even higher than for the untransformed relationship. But, does this make any sense in terms of a causal relationship? Can eating chocolate really improve someone's chances of winning a Nobel prize?
Perhaps some other variable makes more sense for finding a causal relationship? GDP per person could be a good choice. Execute the code in the cell below to load the GDP data.
```
GDP = pd.read_csv('GDP_Country.csv')
print(GDP)
```
There are now two data tables (Pandas data frames). These data tables must be joined and the GDP per person computed. Execute the code in the cell below to perform these operations and examine the resulting data frame.
```
Nobel_chocolate = Nobel_chocolate.merge(right=GDP, how='left', left_on='Country', right_on='Country')
Nobel_chocolate['GDP_person_thousands'] = 1000000 * np.divide(Nobel_chocolate.GDP_billions, Nobel_chocolate.Population)
Nobel_chocolate
```
Let's examine the relationship between GDP per person and the number of Nobel prizes. Execute the code in the cell below and examine the resulting plot.
```
## PLot the log Nobel vs. GDP
fig = plt.figure(figsize=(9, 8)) # define plot area
ax = fig.gca() # define axis
Nobel_chocolate.plot.scatter('GDP_person_thousands', 'log_Nobel', ax = ax) # Scatter plot
ax.set_title('Log Nobel Prizes vs. GDP per person') # Give the plot a main title
ax.set_xlabel('GDP per person') # Set text for the x axis
ax.set_ylabel('Log Nobel Prizes per 10 Million People')# Set text for y axis
```
There seems to be a reasonable relationship between the GDP per person and the log of Nobel prizes per population. There is one outlier, again China.
What is the correlation between the GDP per person and log Nobel prizes? Execute the code in the cell below and examine the results.
```
Nobel_chocolate[['log_Nobel', 'GDP_person_thousands']].corr()
```
GDP per person and the log of the number of Nobel prizes per population exhibits fairly high correlation. Does this relationship make more sense than the relationship with chocolate consumption?
Is there a relationship between chocolate consumption and GDP? This seems likely. To find out, execute the code in the cell below and examine the resulting plot.
```
## PLot the chocolate consuption vs. GDP
fig = plt.figure(figsize=(9, 8)) # define plot area
ax = fig.gca() # define axis
Nobel_chocolate.plot.scatter('Chocolate', 'GDP_person_thousands', ax = ax) # Scatter plot
ax.set_title('Chocolate consumption vs. GDP per person') # Give the plot a main title
ax.set_xlabel('GDP per person') # Set text for the x axis
ax.set_ylabel('Chocolate consumption')# Set text for y axis
```
The relationship looks fairly linear.
How correlated is chocolate consumption and GDP? To answer this question, in the cell below create and execute the code to compute the correlations between three of the variables and display the results: 'Chocolate', 'GDP_person_thousands', 'log_Nobel'. Make sure you name your correlation matrix object `corr_matrix`.
Notice the relationship between GDP per population and chocolate consumption. Do you think this relationship could be causal? What about the relationship between GDP per person and Nobel prizes?
Finally, execute the code in the cell below to display a visualization of these correlations, and examine the results?
```
sns.heatmap(corr_matrix, center=0, cmap="YlGn",
square=True, linewidths=.25)
plt.title('Correlation matrix for Nobel prize variables')
plt.yticks(rotation='horizontal')
plt.xticks(rotation='vertical')
```
Notice that the correlation coefficients between all these variables is relatively high. This example illustrates the perils of trying to extract causal relationships from correlation values alone.
Is it possible GDP has a causal relationship with both chocolate consumption and winning Nobel prizes. Are there other latent (hidden or not part of this data set) which might be important in determining causal relationships, like local tastes for chocolate, R&D spending levels in different countries?
##### Copyright 2020, Stephen F. Elston. All rights reserved.
|
github_jupyter
|
# Fraud_Detection_Using_ADASYN_OVERSAMPLING
I am able to achieve the following accuracies in the validation data. These results can be further improved by reducing the
parameter, number of frauds used to create features from category items. I have used a threshold of 100.
* Logistic Regression :
Validation Accuracy: 70.0%, ROC_AUC_Score: 70.0%
* Random Forest :
Validation Accuracy: 98.9%, ROC_AUC_Score: 98.9%
* Linear Support Vector Machine :
Validation Accuracy: 51.0%, ROC_AUC_Score: 51.1%
* K Nearest Neighbors :
Validation Accuracy: 86.7%, ROC_AUC_Score: 86.7%
* Extra Trees Classifer :
Validation Accuracy: 99.2%, ROC_AUC_Score: 99.2%
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression, Ridge, Lasso, ElasticNet
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
from sklearn import svm, neighbors
from sklearn.naive_bayes import GaussianNB
from imblearn.over_sampling import SMOTE, ADASYN
from sklearn.metrics import roc_auc_score
from sklearn.metrics import confusion_matrix
import itertools
% matplotlib inline
```
### Loading Training Transactions Data
```
tr_tr = pd.read_csv('data/train_transaction.csv', index_col='TransactionID')
print('Rows :', tr_tr.shape[0],' Columns : ',tr_tr.shape[1] )
tr_tr.tail()
print('Memory Usage : ', (tr_tr.memory_usage(deep=True).sum()/1024).round(0))
tr_tr.tail()
tr_id = pd.read_csv('data/train_identity.csv', index_col='TransactionID')
print(tr_id.shape)
tr_id.tail()
tr = tr_tr.join(tr_id)
tr['data']='train'
print(tr.shape)
tr.head()
del tr_tr
del tr_id
te_tr = pd.read_csv('data/test_transaction.csv', index_col='TransactionID')
print(te_tr.shape)
te_tr.tail()
te_id = pd.read_csv('data/test_identity.csv', index_col='TransactionID')
print(te_id.shape)
te_id.tail()
te = te_tr.join(te_id)
te['data']='test'
te['isFraud']=2
print(te.shape)
te.head()
del te_tr
del te_id
tr.isFraud.describe()
tr.isFraud.value_counts().plot(kind='bar')
tr.isFraud.value_counts()
f, (ax1, ax2) = plt.subplots(2, 1, sharex=True, figsize=(12,4))
ax1.hist(tr.TransactionAmt[tr.isFraud == 1], bins = 10)
ax1.set_title('Fraud Transactions ='+str(tr.isFraud.value_counts()[1]))
ax2.hist(tr.TransactionAmt[tr.isFraud == 0], bins = 10)
ax2.set_title('Normal Transactions ='+str(tr.isFraud.value_counts()[0]))
plt.xlabel('Amount ($)')
plt.ylabel('Number of Transactions')
plt.yscale('log')
plt.show()
sns.distplot(tr['TransactionAmt'], color='red')
sns.pairplot(tr[['TransactionAmt','isFraud']], hue='isFraud')
df = pd.concat([tr,te], sort=False)
print(df.shape)
df.head()
del tr
del te
```
### Make new category for items in Objects with A Fraud Count of more than 100
```
fraud_threshold = 100
def map_categories(*args):
columns = [col for col in args]
for column in columns:
if column == index:
return 1
else:
return 0
new_categories = []
for i in df.columns:
if i != 'data':
if df[i].dtypes == str('object'):
fraud_count = df[df.isFraud==1][i].value_counts(dropna=False)
for index, value in fraud_count.items():
if value>fraud_threshold:
df[(str(i)+'_'+str(index))]=list(map(map_categories, df[i]))
new_categories.append((str(i)+'_'+str(index)))
# else:
# tr[(str(i)+'_'+str('other'))]=list(map(map_categories, tr[i]))
# new_tr_categories.append((str(i)+'_'+str('other')))
df.drop([i], axis=1, inplace=True)
print(new_categories)
print(df.shape)
df.head()
df.isna().any().mean()
df.fillna(0, inplace=True)
df.isna().any().mean()
X = df[df['data'] == 'train'].drop(['isFraud','data'], axis=1)
y = df[df['data'] == 'train']['isFraud']
X_predict = df[df['data'] == 'test'].drop(['isFraud','data'], axis=1)
print(X.shape, y.shape, X_predict.shape)
```
### Oversampling using ADASYN
```
ada = ADASYN(random_state=91)
X_sampled,y_sampled = ada.fit_sample(X,y)
#fraudlent records in original data
y.value_counts()
#fraudlent records in oversampled data is is almost equal to normal data
np.bincount(y_sampled)
X_train, X_test, y_train, y_test = train_test_split(X_sampled,y_sampled,test_size=0.3)
class_names = ['FRAUD', 'NORMAL']
def plot_confusion_matrix(cm, classes,normalize=False,title='Confusion matrix',cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.ylabel('Ground Truth')
plt.xlabel('Predicted label')
plt.tight_layout()
plt.show()
```
### Logistic Regression
```
lr = LogisticRegression(solver='lbfgs')
clf_lr = lr.fit(X_train, y_train)
confidence_lr=clf_lr.score(X_test, y_test)
print('Accuracy on Validation Data : ', confidence_lr.round(2)*100,'%')
test_prediction = clf_lr.predict(X_test)
print('ROC_AUC_SCORE ; ', roc_auc_score(y_test, test_prediction).round(3)*100,'%')
cnf_matrix = confusion_matrix(y_test, test_prediction)
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion Matrix')
prediction_lr = clf_lr.predict(X_predict)
test = df[df['data'] == 'test']
del df
test['prediction_lr'] = prediction_lr
test.prediction_lr.value_counts()
test.prediction_lr.to_csv('adLogistic_Regression_Prediction.csv')
```
### Random Forest
```
rfor=RandomForestClassifier()
clf_rfor = rfor.fit(X_train, y_train)
confidence_rfor=clf_rfor.score(X_test, y_test)
print('Accuracy on Validation Data : ', confidence_rfor.round(3)*100,'%')
test_prediction = clf_rfor.predict(X_test)
print('ROC_AUC_SCORE ; ', roc_auc_score(y_test, test_prediction).round(3)*100,'%')
cnf_matrix = confusion_matrix(y_test, test_prediction)
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion Matrix')
prediction_rfor = clf_rfor.predict(X_predict)
test['prediction_rfor'] = prediction_rfor
test.prediction_rfor.value_counts()
test.prediction_rfor.to_csv('adRandom_Forest_Prediction.csv')
```
### Linear Support Vector Machine Algorithm
```
lsvc=svm.LinearSVC()
clf_lsvc=lsvc.fit(X_train, y_train)
confidence_lsvc=clf_lsvc.score(X_test, y_test)
print('Accuracy on Validation Data : ', confidence_lsvc.round(3)*100,'%')
test_prediction = clf_lsvc.predict(X_test)
print('ROC_AUC_SCORE ; ', roc_auc_score(y_test, test_prediction).round(3)*100,'%')
cnf_matrix = confusion_matrix(y_test, test_prediction)
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion Matrix')
```
### K-Nearest Neighbors Algorithm
```
knn=neighbors.KNeighborsClassifier(n_neighbors=10, n_jobs=-1)
clf_knn=knn.fit(X_train, y_train)
confidence_knn=clf_knn.score(X_test, y_test)
print('Accuracy on Validation Data : ', confidence_knn.round(3)*100,'%')
test_prediction = clf_knn.predict(X_test)
print('ROC_AUC_SCORE ; ', roc_auc_score(y_test, test_prediction).round(3)*100,'%')
cnf_matrix = confusion_matrix(y_test, test_prediction)
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion Matrix')
```
### Extra Trees Classifier
```
etc=ExtraTreesClassifier()
clf_etc = etc.fit(X_train, y_train)
confidence_etc=clf_etc.score(X_test, y_test)
print('Accuracy on Validation Data : ', confidence_etc.round(3)*100,'%')
test_prediction = clf_etc.predict(X_test)
print('ROC_AUC_SCORE ; ', roc_auc_score(y_test, test_prediction).round(3)*100,'%')
cnf_matrix = confusion_matrix(y_test, test_prediction)
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion Matrix')
prediction_etc = clf_etc.predict(X_predict)
test['prediction_etc'] = prediction_etc
test.prediction_etc.value_counts()
test.prediction_etc.to_csv('adExtra_Trees_Prediction.csv')
```
|
github_jupyter
|
# Boston Housing Prices Classification
```
import itertools
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from dataclasses import dataclass
from sklearn import datasets
from sklearn import svm
from sklearn import tree
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import zero_one_loss
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
import graphviz
%matplotlib inline
# Matplotlib has some built in style sheets
mpl.style.use('fivethirtyeight')
```
## Data Loading
Notice that I am loading in the data in the same way that we did for our visualization module. Time to refactor? It migth be good to abstract away some of this as functions, that way we aren't copying and pasting code between all of our notebooks.
```
boston = datasets.load_boston()
# Sklearn uses a dictionary like object to hold its datasets
X = boston['data']
y = boston['target']
feature_names = list(boston.feature_names)
X_df = pd.DataFrame(X)
X_df.columns = boston.feature_names
X_df["PRICE"] = y
X_df.describe()
def create_classes(data):
"""Create our classes using thresholds
This is used as an `apply` function for
every row in `data`.
Args:
data: pandas dataframe
"""
if data["PRICE"] < 16.:
return 0
elif data["PRICE"] >= 16. and data["PRICE"] < 22.:
return 1
else:
return 2
y = X_df.apply(create_classes, axis=1)
# Get stats for plotting
classes, counts = np.unique(y, return_counts=True)
plt.figure(figsize=(20, 10))
plt.bar(classes, counts)
plt.xlabel("Label")
plt.ylabel(r"Number of Samples")
plt.suptitle("Distribution of Classes")
plt.show()
```
## Support Vector Machine
```
def make_meshgrid(x, y, h=.02):
"""Create a mesh of points to plot in
Args:
x: data to base x-axis meshgrid on
y: data to base y-axis meshgrid on
h: stepsize for meshgrid, optional
Returns:
xx, yy : ndarray
"""
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
"""Plot the decision boundaries for a classifier.
Args:
ax: matplotlib axes object
clf: a classifier
xx: meshgrid ndarray
yy: meshgrid ndarray
params: dictionary of params to pass to contourf, optional
"""
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
# Careful, `loc` uses inclusive bounds!
X_smol = X_df.loc[:99, ['LSTAT', 'PRICE']].values
y_smol = y[:100]
C = 1.0 # SVM regularization parameter
models = [
svm.SVC(kernel='linear', C=C),
svm.LinearSVC(C=C, max_iter=10000),
svm.SVC(kernel='rbf', gamma=0.7, C=C),
svm.SVC(kernel='poly', degree=3, gamma='auto', C=C)
]
models = [clf.fit(X_smol, y_smol) for clf in models]
# title for the plots
titles = [
'SVC with linear kernel',
'LinearSVC (linear kernel)',
'SVC with RBF kernel',
'SVC with polynomial (degree 3) kernel'
]
# Set-up 2x2 grid for plotting.
fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(15, 15))
plt.subplots_adjust(wspace=0.4, hspace=0.4)
X0, X1 = X_smol[:, 0], X_smol[:, 1]
xx, yy = make_meshgrid(X0, X1)
for clf, title, ax in zip(models, titles, axs.flatten()):
plot_contours(
ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8
)
ax.scatter(
X0, X1, c=y_smol, cmap=plt.cm.coolwarm, s=20, edgecolors='k'
)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xlabel('LSTAT')
ax.set_ylabel('PRICE')
ax.set_title(title)
plt.show()
```
## Modeling with Trees and Ensembles of Trees
```
@dataclass
class Hparams:
"""Hyperparameters for our models"""
max_depth: int = 2
min_samples_leaf: int = 1
n_estimators: int = 400
learning_rate: float = 1.0
hparams = Hparams()
# Keeping price in there is cheating
#X_df = X_df.drop("PRICE", axis=1)
x_train, x_test, y_train, y_test = train_test_split(
X_df, y, test_size=0.33, random_state=42
)
dt_stump = DecisionTreeClassifier(
max_depth=hparams.max_depth,
min_samples_leaf=hparams.min_samples_leaf
)
dt_stump.fit(x_train, y_train)
dt_stump_err = 1.0 - dt_stump.score(x_test, y_test)
class_names = ['0', '1', '2']
dot_data = tree.export_graphviz(dt_stump, out_file=None,
feature_names=boston.feature_names,
class_names=class_names,
filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph
# Adding greater depth to the tree
dt = DecisionTreeClassifier(
max_depth=9, # No longer using Hparams here!
min_samples_leaf=hparams.min_samples_leaf
)
dt.fit(x_train, y_train)
dt_err = 1.0 - dt.score(x_test, y_test)
```
### A Deeper Tree
```
class_names = ['0', '1', '2']
dot_data = tree.export_graphviz(dt, out_file=None,
feature_names=boston.feature_names,
class_names=class_names,
filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph#.render("decision_tree_boston")
```
## Adaboost
An AdaBoost classifier is a meta-estimator that begins by fitting a classifier on the original dataset and then fits additional copies of the classifier on the same dataset but where the weights of incorrectly classified instances are adjusted such that subsequent classifiers focus more on difficult cases.
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.AdaBoostClassifier.html
```
ada_discrete = AdaBoostClassifier(
base_estimator=dt_stump,
learning_rate=hparams.learning_rate,
n_estimators=hparams.n_estimators,
algorithm="SAMME"
)
ada_discrete.fit(x_train, y_train)
# Notice the `algorithm` is different here.
# This is just one parameter change, but it
# makes a world of difference! Read the docs!
ada_real = AdaBoostClassifier(
base_estimator=dt_stump,
learning_rate=hparams.learning_rate,
n_estimators=hparams.n_estimators,
algorithm="SAMME.R" # <- take note!
)
ada_real.fit(x_train, y_train)
def misclassification_rate_by_ensemble_size(model, n_estimators, data, labels):
"""Get the fraction of misclassifications per ensemble size
As we increase the number of trees in the ensemble,
we often find that the performance of our model changes.
This shows us how our misclassification rate changes as
we increase the number of members in our ensemble up to
`n_estimators`
Args:
model: ensembe model that has a `staged_predict` method
n_estimators: number of models in the ensemble
data: data to be predicted over
labels: labels for the dataset
Returns:
misclassification_rate: numpy array of shape (n_estimators,)
This is the fraction of misclassifications for the `i_{th}`
number of estimators
"""
misclassification_rate = np.zeros((n_estimators,))
for i, y_pred in enumerate(model.staged_predict(data)):
# zero_one_loss returns the fraction of misclassifications
misclassification_rate[i] = zero_one_loss(y_pred, labels)
return misclassification_rate
# Get the misclassification rates for each algo on each data split
ada_discrete_err_train = misclassification_rate_by_ensemble_size(
ada_discrete, hparams.n_estimators, x_train, y_train
)
ada_discrete_err_test = misclassification_rate_by_ensemble_size(
ada_discrete, hparams.n_estimators, x_test, y_test
)
ada_real_err_train = misclassification_rate_by_ensemble_size(
ada_real, hparams.n_estimators, x_train, y_train
)
ada_real_err_test = misclassification_rate_by_ensemble_size(
ada_real, hparams.n_estimators, x_test, y_test
)
fig = plt.figure(figsize=(20,10))
ax = fig.add_subplot(111)
ax.plot([1, hparams.n_estimators], [dt_stump_err] * 2, 'k-',
label='Decision Stump Error')
ax.plot([1, hparams.n_estimators], [dt_err] * 2, 'k--',
label='Decision Tree Error')
ax.plot(np.arange(hparams.n_estimators) + 1, ada_discrete_err_test,
label='Discrete AdaBoost Test Error',
color='red')
ax.plot(np.arange(hparams.n_estimators) + 1, ada_discrete_err_train,
label='Discrete AdaBoost Train Error',
color='blue')
ax.plot(np.arange(hparams.n_estimators) + 1, ada_real_err_test,
label='Real AdaBoost Test Error',
color='orange')
ax.plot(np.arange(hparams.n_estimators) + 1, ada_real_err_train,
label='Real AdaBoost Train Error',
color='green')
ax.set_ylim((0.0, 0.5))
ax.set_xlabel('n_estimators')
ax.set_ylabel('error rate')
leg = ax.legend(loc='upper right', fancybox=True)
leg.get_frame().set_alpha(0.7)
```
## Classification Performance
How well are our classifiers doing?
```
def plot_confusion_matrix(confusion, classes, normalize=False, cmap=plt.cm.Reds):
"""Plot a confusion matrix
"""
mpl.style.use('seaborn-ticks')
fig = plt.figure(figsize=(20,10))
plt.imshow(confusion, interpolation='nearest', cmap=cmap)
plt.title("Confusion Matrix")
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = confusion.max() / 2.
for i, j in itertools.product(range(confusion.shape[0]), range(confusion.shape[1])):
plt.text(
j, i, format(confusion[i, j], fmt),
horizontalalignment="center",
color="white" if confusion[i, j] > thresh else "black"
)
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
ada_discrete_preds_test = ada_discrete.predict(x_test)
ada_real_preds_test = ada_real.predict(x_test)
```
### Accuracy
```
ada_discrete_acc = accuracy_score(y_test, ada_discrete_preds_test)
ada_real_acc = accuracy_score(y_test, ada_real_preds_test)
print(f"Adaboost discrete accuarcy: {ada_discrete_acc:.3f}")
print(f"Adaboost real accuarcy: {ada_discrete_acc:.3f}")
```
### Confusion Matrix
Accuracy, however is an overall summary. To see where our models are predicting correctly and how they could be predicting incorrectly, we can use a `confusion matrix`.
```
ada_discrete_confusion = confusion_matrix(y_test, ada_discrete_preds_test)
ada_real_confusion = confusion_matrix(y_test, ada_real_preds_test)
plot_confusion_matrix(ada_discrete_confusion, classes)
plot_confusion_matrix(ada_real_confusion, classes)
```
|
github_jupyter
|
[](http://rpi.analyticsdojo.com)
<center><h1>Intro to Tensorflow - MINST</h1></center>
<center><h3><a href = 'http://rpi.analyticsdojo.com'>rpi.analyticsdojo.com</a></h3></center>
[](https://colab.research.google.com/github/rpi-techfundamentals/fall2018-materials/blob/master/10-deep-learning/06-tensorflow-minst.ipynb)
Adopted from [Hands-On Machine Learning with Scikit-Learn and TensorFlow by Aurélien Géron](https://github.com/ageron/handson-ml).
Apache License
Version 2.0, January 2004
http://www.apache.org/licenses/
TERMS AND CONDITIONS FOR USE, REPRODUCTION, AND DISTRIBUTION
[For full license see repository.](https://github.com/ageron/handson-ml/blob/master/LICENSE)
**Chapter 10 – Introduction to Artificial Neural Networks**
_This notebook contains all the sample code and solutions to the exercices in chapter 10._
# Setup
First, let's make sure this notebook works well in both python 2 and 3, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
```
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
def reset_graph(seed=42):
tf.reset_default_graph()
tf.set_random_seed(seed)
np.random.seed(seed)
# To plot pretty figures
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# Where to save the figures
PROJECT_ROOT_DIR = "/home/jovyan/techfundamentals-fall2017-materials/classes/13-deep-learning"
def save_fig(fig_id, tight_layout=True):
path = os.path.join(PROJECT_ROOT_DIR, 'images', fig_id + ".png")
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
```
### MNIST
- Very common machine learning library with goal to classify digits.
- This example is using MNIST handwritten digits, which contains 55,000 examples for training and 10,000 examples for testing. The digits have been size-normalized and centered in a fixed-size image (28x28 pixels) with values from 0 to 1. For simplicity, each image has been flattened and converted to a 1-D numpy array of 784 features (28*28).

More info: http://yann.lecun.com/exdb/mnist/
```
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/")
X_train = mnist.train.images
X_test = mnist.test.images
y_train = mnist.train.labels.astype("int")
y_test = mnist.test.labels.astype("int")
print ("Training set: ", X_train.shape,"\nTest set: ", X_test.shape)
# List a few images and print the data to get a feel for it.
images = 2
for i in range(images):
#Reshape
x=np.reshape(X_train[i], [28, 28])
print(x)
plt.imshow(x, cmap=plt.get_cmap('gray_r'))
plt.show()
# print("Model prediction:", preds[i])
```
## TFLearn: Deep learning library featuring a higher-level API for TensorFlow
- TFlearn is a modular and transparent deep learning library built on top of Tensorflow.
- It was designed to provide a higher-level API to TensorFlow in order to facilitate and speed-up experimentations
- Fully transparent and compatible with Tensorflow
- [DNN classifier](https://www.tensorflow.org/api_docs/python/tf/contrib/learn/DNNClassifier)
- `hidden_units` list of hidden units per layer. All layers are fully connected. Ex. [64, 32] means first layer has 64 nodes and second one has 32.
- [Scikit learn wrapper for TensorFlow Learn Estimator](https://www.tensorflow.org/api_docs/python/tf/contrib/learn/SKCompat)
- See [tflearn documentation](http://tflearn.org/).
```
import tensorflow as tf
config = tf.contrib.learn.RunConfig(tf_random_seed=42) # not shown in the config
feature_cols = tf.contrib.learn.infer_real_valued_columns_from_input(X_train)
# List of hidden units per layer. All layers are fully connected. Ex. [64, 32] means first layer has 64 nodes and second one has 32.
dnn_clf = tf.contrib.learn.DNNClassifier(hidden_units=[300,100], n_classes=10,
feature_columns=feature_cols, config=config)
dnn_clf = tf.contrib.learn.SKCompat(dnn_clf) # if TensorFlow >= 1.1
dnn_clf.fit(X_train, y_train, batch_size=50, steps=4000)
#We can use the sklearn version of metrics
from sklearn import metrics
y_pred = dnn_clf.predict(X_test)
#This calculates the accuracy.
print("Accuracy score: ", metrics.accuracy_score(y_test, y_pred['classes']) )
#Log Loss is a way of score classes probabilsitically
print("Logloss: ",metrics.log_loss(y_test, y_pred['probabilities']))
```
### Tensorflow
- Direct access to Python API for Tensorflow will give more flexibility
- Like earlier, we will define the structure and then run the session.
- set placeholders
```
import tensorflow as tf
n_inputs = 28*28 # MNIST
n_hidden1 = 300 # hidden units in first layer.
n_hidden2 = 100
n_outputs = 10 # Classes of output variable.
#Placehoder
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
def neuron_layer(X, n_neurons, name, activation=None):
with tf.name_scope(name):
n_inputs = int(X.get_shape()[1])
stddev = 2 / np.sqrt(n_inputs)
init = tf.truncated_normal((n_inputs, n_neurons), stddev=stddev)
W = tf.Variable(init, name="kernel")
b = tf.Variable(tf.zeros([n_neurons]), name="bias")
Z = tf.matmul(X, W) + b
if activation is not None:
return activation(Z)
else:
return Z
with tf.name_scope("dnn"):
hidden1 = neuron_layer(X, n_hidden1, name="hidden1", activation=tf.nn.relu)
hidden2 = neuron_layer(hidden1, n_hidden2, name="hidden2", activation=tf.nn.relu)
logits = neuron_layer(hidden2, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
saver = tf.train.Saver()
```
### Running the Analysis over 40 Epocs
- 40 passes through entire dataset.
-
```
n_epochs = 40
batch_size = 50
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_test = accuracy.eval(feed_dict={X: mnist.test.images,
y: mnist.test.labels})
print("Epoc:", epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)
save_path = saver.save(sess, "./my_model_final.ckpt")
with tf.Session() as sess:
saver.restore(sess, "./my_model_final.ckpt") # or better, use save_path
X_new_scaled = mnist.test.images[:20]
Z = logits.eval(feed_dict={X: X_new_scaled})
y_pred = np.argmax(Z, axis=1)
print("Predicted classes:", y_pred)
print("Actual classes: ", mnist.test.labels[:20])
from IPython.display import clear_output, Image, display, HTML
def strip_consts(graph_def, max_const_size=32):
"""Strip large constant values from graph_def."""
strip_def = tf.GraphDef()
for n0 in graph_def.node:
n = strip_def.node.add()
n.MergeFrom(n0)
if n.op == 'Const':
tensor = n.attr['value'].tensor
size = len(tensor.tensor_content)
if size > max_const_size:
tensor.tensor_content = "<stripped %d bytes>"%size
return strip_def
def show_graph(graph_def, max_const_size=32):
"""Visualize TensorFlow graph."""
if hasattr(graph_def, 'as_graph_def'):
graph_def = graph_def.as_graph_def()
strip_def = strip_consts(graph_def, max_const_size=max_const_size)
code = """
<script>
function load() {{
document.getElementById("{id}").pbtxt = {data};
}}
</script>
<link rel="import" href="https://tensorboard.appspot.com/tf-graph-basic.build.html" onload=load()>
<div style="height:600px">
<tf-graph-basic id="{id}"></tf-graph-basic>
</div>
""".format(data=repr(str(strip_def)), id='graph'+str(np.random.rand()))
iframe = """
<iframe seamless style="width:1200px;height:620px;border:0" srcdoc="{}"></iframe>
""".format(code.replace('"', '"'))
display(HTML(iframe))
show_graph(tf.get_default_graph())
```
## Using `dense()` instead of `neuron_layer()`
Note: the book uses `tensorflow.contrib.layers.fully_connected()` rather than `tf.layers.dense()` (which did not exist when this chapter was written). It is now preferable to use `tf.layers.dense()`, because anything in the contrib module may change or be deleted without notice. The `dense()` function is almost identical to the `fully_connected()` function, except for a few minor differences:
* several parameters are renamed: `scope` becomes `name`, `activation_fn` becomes `activation` (and similarly the `_fn` suffix is removed from other parameters such as `normalizer_fn`), `weights_initializer` becomes `kernel_initializer`, etc.
* the default `activation` is now `None` rather than `tf.nn.relu`.
* a few more differences are presented in chapter 11.
```
n_inputs = 28*28 # MNIST
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1",
activation=tf.nn.relu)
hidden2 = tf.layers.dense(hidden1, n_hidden2, name="hidden2",
activation=tf.nn.relu)
logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_epochs = 20
n_batches = 50
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_test = accuracy.eval(feed_dict={X: mnist.test.images, y: mnist.test.labels})
print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)
save_path = saver.save(sess, "./my_model_final.ckpt")
show_graph(tf.get_default_graph())
```
|
github_jupyter
|
```
# Required to load webpages
from IPython.display import IFrame
```
[Table of contents](../toc.ipynb)
<img src="https://github.com/scipy/scipy/raw/master/doc/source/_static/scipyshiny_small.png" alt="Scipy" width="150" align="right">
# SciPy
* Scipy extends numpy with powerful modules in
* optimization,
* interpolation,
* linear algebra,
* fourier transformation,
* signal processing,
* image processing,
* file input output, and many more.
* Please find here the scipy reference for a complete feature list [https://docs.scipy.org/doc/scipy/reference/](https://docs.scipy.org/doc/scipy/reference/).
We will take a look at some features of scipy in the latter. Please explore the rich content of this package later on.
## Optimization
* Scipy's optimization module provides many optimization methods like least squares, gradient methods, BFGS, global optimization, and many more.
* Please find a detailed tutorial here [https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html](https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html).
* Next, we will apply one of the optimization algorithms in a simple example.
A common function to test optimization algorithms is the Rosenbrock function for $N$ variables:
$f(\boldsymbol{x}) = \sum\limits_{i=2}^N 100 \left(x_{i+1} - x_i^2\right)^2 + \left(1 - x_i^2 \right)^2$.
The optimum is at $x_i=1$, where $f(\boldsymbol{x})=0$
```
import numpy as np
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import cm
%matplotlib inline
def rosen(x):
"""The Rosenbrock function"""
return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1]**2.0)**2.0)
```
We need to generate some data in a mesh grid.
```
X = np.arange(-2, 2, 0.2)
Y = np.arange(-2, 2, 0.2)
X, Y = np.meshgrid(X, Y)
data = np.vstack([X.reshape(X.size), Y.reshape(Y.size)])
```
Let's evaluate the Rosenbrock function at the grid points.
```
Z = rosen(data)
```
And we will plot the function in a 3D plot.
```
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z.reshape(X.shape), cmap='bwr')
ax.view_init(40, 230)
```
Now, let us check that the true minimum value is at (1, 1).
```
rosen(np.array([1, 1]))
```
Finally, we will call scipy optimize and find the minimum with Nelder Mead algorithm.
```
from scipy.optimize import minimize
x0 = np.array([1.3, 0.7])
res = minimize(rosen, x0, method='nelder-mead',
options={'xatol': 1e-8, 'disp': True})
print(res.x)
```
Many more optimization examples are to find in scipy optimize tutorial [https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html](https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html).
```
IFrame(src='https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html',
width=1000, height=600)
```
## Interpolation
* Interpolation of data is very often required, for instance to replace NaNs or to fill missing values in data records.
* Scipy comes with
* 1D interpolation,
* multivariate data interpolation
* spline, and
* radial basis function interpolation.
* Please find here the link to interpolation tutorials [https://docs.scipy.org/doc/scipy/reference/tutorial/interpolate.html](https://docs.scipy.org/doc/scipy/reference/tutorial/interpolate.html).
```
from scipy.interpolate import interp1d
x = np.linspace(10, 20, 15)
y = np.sin(x) + np.cos(x**2 / 10)
f = interp1d(x, y, kind="linear")
f1 = interp1d(x, y, kind="cubic")
x_fine = np.linspace(10, 20, 200)
plt.plot(x, y, 'ko',
x_fine, f(x_fine), 'b--',
x_fine, f1(x_fine), 'r--')
plt.legend(["Data", "Linear", "Cubic"])
plt.show()
```
## Signal processing
The signal processing module is very powerful and we will have a look at its tutorial [https://docs.scipy.org/doc/scipy/reference/tutorial/signal.html](https://docs.scipy.org/doc/scipy/reference/tutorial/signal.html) for a quick overview.
```
IFrame(src='https://docs.scipy.org/doc/scipy/reference/tutorial/signal.html',
width=1000, height=600)
```
## Linear algebra
* In addition to numpy, scipy has its own linear algebra module.
* It offers more functionality than numpy's linear algebra module and is based on BLAS/LAPACK support, which makes it faster.
* The respective tutorial is here located [https://docs.scipy.org/doc/scipy/reference/tutorial/linalg.html](https://docs.scipy.org/doc/scipy/reference/tutorial/linalg.html).
```
IFrame(src='https://docs.scipy.org/doc/scipy/reference/tutorial/linalg.html',
width=1000, height=600)
```
### Total least squares as linear algebra application
<img src="ls-tls.png" alt="LS vs TLS" width="350" align="right">
We will now implement a total least squares estimator [[Markovsky2007]](../references.bib) with help of scipy's singular value decomposition (svd). The total least squares estimator provides a solution for the errors in variables problem, where model inputs and outputs are corrupted by noise.
The model becomes
$A X \approx B$, where $A \in \mathbb{R}^{m \times n}$ and $B \in \mathbb{R}^{m \times d}$ are input and output data, and $X$ is the unknown parameter vector.
More specifically, the total least squares regression becomes
$\widehat{A}X = \widehat{B}$, $\widehat{A} := A + \Delta A$, $\widehat{B} := B + \Delta B$.
The estimator can be written as pseudo code as follows.
$C = [A B] = U \Sigma V^\top$, where $U \Sigma V^\top$ is the svd of $C$.
$V:= \left[\begin{align}V_{11} &V_{12} \\
V_{21} & V_{22}\end{align}\right]$,
$\widehat{X} = -V_{12} V_{22}^{-1}$.
In Python, the implementation could be like this function.
```
from scipy import linalg
def tls(A, B):
m, n = A.shape
C = np.hstack((A, B))
U, S, V = linalg.svd(C)
V12 = V.T[0:n, n:]
V22 = V.T[n:, n:]
X = -V12 / V22
return X
```
Now we create some data where input and output are appended with noise.
```
A = np.random.rand(100, 2)
X = np.array([[3], [-7]])
B = A @ X
A += np.random.randn(100, 2) * 0.1
B += np.random.randn(100, 1) * 0.1
```
The total least squares solution becomes
```
tls(A, B)
```
And this solution is closer to correct value $X = [3 , -7]^\top$ than ordinary least squares.
```
linalg.solve((A.T @ A), (A.T @ B))
```
Finally, next function shows a "self" written least squares estimator, which uses QR decomposition and back substitution. This implementation is numerically robust in contrast to normal equations
$A ^\top A X = A^\top B$.
Please find more explanation in [[Golub2013]](../references.bib) and in section 3.11 of [[Burg2012]](../references.bib).
```
def ls(A, B):
Q, R = linalg.qr(A, mode="economic")
z = Q.T @ B
return linalg.solve_triangular(R, z)
ls(A, B)
```
## Integration
* Scipy's integration can be used for general equations as well as for ordinary differential equations.
* The integration tutorial is linked here [https://docs.scipy.org/doc/scipy/reference/tutorial/integrate.html](https://docs.scipy.org/doc/scipy/reference/tutorial/integrate.html).
### Solving a differential equation
Here, we want to use an ode solver to simulate the differential equation (ode)
$y'' + y' + 4 y = 0$.
To evaluate this second order ode, we need to convert it into a set of first order ode. The trick is to use this substitution: $x_0 = y$, $x_1 = y'$, which yields
$\begin{align}
x'_0 &= x_1 \\
x'_1 &= -4 x_0 - x_1
\end{align}$
The implementation in Python becomes.
```
def equation(t, x):
return [x[1], -4 * x[0] - x[1]]
from scipy.integrate import solve_ivp
time_span = [0, 20]
init = [1, 0]
time = np.arange(0, 20, 0.01)
sol = solve_ivp(equation, time_span, init, t_eval=time)
plt.plot(time, sol.y[0, :])
plt.plot(time, sol.y[1, :])
plt.legend(["$y$", "$y'$"])
plt.xlabel("Time")
plt.show()
```
|
github_jupyter
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Objectives" data-toc-modified-id="Objectives-1"><span class="toc-item-num">1 </span>Objectives</a></span></li><li><span><a href="#Example-Together" data-toc-modified-id="Example-Together-2"><span class="toc-item-num">2 </span>Example Together</a></span><ul class="toc-item"><li><span><a href="#Question" data-toc-modified-id="Question-2.1"><span class="toc-item-num">2.1 </span>Question</a></span></li><li><span><a href="#Considerations" data-toc-modified-id="Considerations-2.2"><span class="toc-item-num">2.2 </span>Considerations</a></span></li><li><span><a href="#Loading-the-Data" data-toc-modified-id="Loading-the-Data-2.3"><span class="toc-item-num">2.3 </span>Loading the Data</a></span></li><li><span><a href="#Some-Exploration-to-Better-Understand-our-Data" data-toc-modified-id="Some-Exploration-to-Better-Understand-our-Data-2.4"><span class="toc-item-num">2.4 </span>Some Exploration to Better Understand our Data</a></span></li><li><span><a href="#Experimental-Setup" data-toc-modified-id="Experimental-Setup-2.5"><span class="toc-item-num">2.5 </span>Experimental Setup</a></span><ul class="toc-item"><li><span><a href="#What-Test-Would-Make-Sense?" data-toc-modified-id="What-Test-Would-Make-Sense?-2.5.1"><span class="toc-item-num">2.5.1 </span>What Test Would Make Sense?</a></span></li><li><span><a href="#The-Hypotheses" data-toc-modified-id="The-Hypotheses-2.5.2"><span class="toc-item-num">2.5.2 </span>The Hypotheses</a></span></li><li><span><a href="#Setting-a-Threshold" data-toc-modified-id="Setting-a-Threshold-2.5.3"><span class="toc-item-num">2.5.3 </span>Setting a Threshold</a></span></li></ul></li><li><span><a href="#$\chi^2$-Test" data-toc-modified-id="$\chi^2$-Test-2.6"><span class="toc-item-num">2.6 </span>$\chi^2$ Test</a></span><ul class="toc-item"><li><span><a href="#Setup-the-Data" data-toc-modified-id="Setup-the-Data-2.6.1"><span class="toc-item-num">2.6.1 </span>Setup the Data</a></span></li><li><span><a href="#Calculation" data-toc-modified-id="Calculation-2.6.2"><span class="toc-item-num">2.6.2 </span>Calculation</a></span></li></ul></li><li><span><a href="#Interpretation" data-toc-modified-id="Interpretation-2.7"><span class="toc-item-num">2.7 </span>Interpretation</a></span></li></ul></li><li><span><a href="#Exercise" data-toc-modified-id="Exercise-3"><span class="toc-item-num">3 </span>Exercise</a></span></li></ul></div>
```
import numpy as np
import pandas as pd
from scipy import stats
import seaborn as sns
```
# Objectives
- Conduct an A/B test in Python
- Interpret the results of the A/B tests for a stakeholder
# Example Together
## Question
We have data about whether customers completed sales transactions, segregated by the type of ad banners to which the customers were exposed.
The question we want to answer is whether there was any difference in sales "conversions" between desktop customers who saw the sneakers banner and desktop customers who saw the accessories banner in the month of May 2019.
## Considerations
What would we need to consider when designing our experiment?
Might include:
- Who is it that we're including in our test?
- How big of an effect would make it "worth" us seeing?
- This can affect sample size
- This can give context of a statistically significant result
- Other biases or "gotchas"
## Loading the Data
First let's download the data from [kaggle](https://www.kaggle.com/podsyp/how-to-do-product-analytics) via the release page of this repo: https://github.com/flatiron-school/ds-ab_testing/releases
The code below will load it into our DataFrame:
```
# This will download the data from online so it can take some time (but relatively small download)
df = pd.read_csv('https://github.com/flatiron-school/ds-ab_testing/releases/download/v1.2/products_small.csv')
```
> Let's take a look while we're at it
```
df.head()
df.info()
```
## Some Exploration to Better Understand our Data
Lets's look at the different banner types:
```
df['product'].value_counts()
df.groupby('product')['target'].value_counts()
```
Let's look at the range of time-stamps on these data:
```
df['time'].min()
df['time'].max()
```
Let's check the counts of the different site_version values:
```
df['site_version'].value_counts()
df['title'].value_counts()
df.groupby('title').agg({'target': 'mean'})
```
## Experimental Setup
We need to filter by site_version, time, and product:
```
df_AB = df[(df['site_version'] == 'desktop') &
(df['time'] >= '2019-05-01') &
((df['product'] == 'accessories') | (df['product'] == 'sneakers'))].reset_index(drop = True)
df_AB.tail()
```
### What Test Would Make Sense?
Since we're comparing the frequency of conversions of customers who saw the "sneakers" banner against those who saw the "accessories" banner, we can use a $\chi^2$ test.
Note there are other hypothesis tests we can use but this should be fine since it should fit our criteria.
### The Hypotheses
$H_0$: Customers who saw the sneakers banner were no more or less likely to buy than customers who saw the accessories banner.
$H_1$: Customers who saw the sneakers banner were more or less likely to buy than customers who saw the accessories banner.
### Setting a Threshold
We'll set a false-positive rate of $\alpha = 0.05$.
## $\chi^2$ Test
### Setup the Data
We need our contingency table: the numbers of people who did or did not submit orders, both for the accessories banner and the sneakers banner.
```
# We have two groups
df_A = df_AB[df_AB['product'] == 'accessories']
df_B = df_AB[df_AB['product'] == 'sneakers']
accessories_orders = sum(df_A['target'])
sneakers_orders = sum(df_B['target'])
accessories_orders, sneakers_orders
```
To get the numbers of people who didn't submit orders, we get the total number of people who were shown banners and then subtract the numbers of people who did make orders.
```
accessories_total = sum(df_A['title'] == 'banner_show')
sneakers_total = sum(df_B['title'] == 'banner_show')
accessories_no_orders = accessories_total - accessories_orders
sneakers_no_orders = sneakers_total - sneakers_orders
accessories_no_orders, sneakers_no_orders
contingency_table = np.array([
(accessories_orders, accessories_no_orders),
(sneakers_orders, sneakers_no_orders)
])
contingency_table
```
### Calculation
```
stats.chi2_contingency(contingency_table)
```
This extremely low $p$-value suggests that these two groups are genuinely performing differently. In particular, the desktop customers who saw the sneakers banner in May 2019 bought at a higher rate than the desktop customers who saw the accessories banner in May 2019.
## Interpretation
```
contingency_table
# Find the difference in conversion rate
accessory_CR, sneaker_CR = contingency_table[:,0]/contingency_table[:,1]
print(f'Conversion Rate for accessory banner:\n\t{100*accessory_CR:.3f}%')
print(f'Conversion Rate for sneaker banner:\n\t{100*sneaker_CR:.3f}%')
print('')
print(f'Absolute difference of CR: {100*(sneaker_CR-accessory_CR):.3f}%')
```
So we can say:
- There was a statistically significant difference at the $\alpha$-level (confidence level)
- The difference was about $2.8\%$ in favor of the sneaker banner!
# Exercise
> The company is impressed with what you found and is now wondering if there is a difference in their other banner ads!
With your group, look at the same month (May 2019) but compare different platforms ('mobile' vs 'desktop') and or different banner types ('accessories', 'sneakers', 'clothes', 'sports_nutrition'). Just don't repeat the same test we did above 😉
Make sure you record what considerations you have for the experiment, what hypothesis test you performed ($H_0$ and $H_1$ too), and your overall conclusion/interpretation for the _business stakeholders_. Is there a follow up you'd suggest?
```
#Null: There is not a different between conversion rates for sports nutrition and clothes on the mobile site.
#Alternative: There is
df_AB = df[(df['site_version'] == 'mobile') &
(df['time'] >= '2019-05-01') &
((df['product'] == 'sports_nutrition') | (df['product'] == 'clothes'))].reset_index(drop = True)
df_A = df_AB[df_AB['product'] == 'sports_nutrition']
df_B = df_AB[df_AB['product'] == 'clothes']
sports_nutrition_orders = sum(df_A['target'])
clothes_orders = sum(df_B['target'])
sports_nutrition_total = sum(df_A['title'] == 'banner_show')
clothes_total = sum(df_B['title'] == 'banner_show')
sports_nutrition_no_orders = sports_nutrition_total - sports_nutrition_orders
clothes_no_orders = clothes_total - clothes_orders
contingency_table = np.array([
(sports_nutrition_orders, sports_nutrition_no_orders),
(clothes_orders, clothes_no_orders)
])
stats.chi2_contingency(contingency_table)
sports_nutrition_CR, clothes_CR = contingency_table[:,0]/contingency_table[:,1]
print(f'Conversion Rate for sports nutrition banner:\n\t{100*sports_nutrition_CR:.3f}%')
print(f'Conversion Rate for clothes banner:\n\t{100*clothes_CR:.3f}%')
print('')
print(f'Absolute difference of CR: {100*(sports_nutrition_CR-clothes_CR):.3f}%')
```
|
github_jupyter
|
## Dependencies
```
import json, warnings, shutil
from tweet_utility_scripts import *
from tweet_utility_preprocess_roberta_scripts import *
from transformers import TFRobertaModel, RobertaConfig
from tokenizers import ByteLevelBPETokenizer
from tensorflow.keras.models import Model
from tensorflow.keras import optimizers, metrics, losses, layers
from tensorflow.keras.callbacks import EarlyStopping, TensorBoard, ModelCheckpoint
SEED = 0
seed_everything(SEED)
warnings.filterwarnings("ignore")
class RectifiedAdam(tf.keras.optimizers.Optimizer):
"""Variant of the Adam optimizer whose adaptive learning rate is rectified
so as to have a consistent variance.
It implements the Rectified Adam (a.k.a. RAdam) proposed by
Liyuan Liu et al. in [On The Variance Of The Adaptive Learning Rate
And Beyond](https://arxiv.org/pdf/1908.03265v1.pdf).
Example of usage:
```python
opt = tfa.optimizers.RectifiedAdam(lr=1e-3)
```
Note: `amsgrad` is not described in the original paper. Use it with
caution.
RAdam is not a placement of the heuristic warmup, the settings should be
kept if warmup has already been employed and tuned in the baseline method.
You can enable warmup by setting `total_steps` and `warmup_proportion`:
```python
opt = tfa.optimizers.RectifiedAdam(
lr=1e-3,
total_steps=10000,
warmup_proportion=0.1,
min_lr=1e-5,
)
```
In the above example, the learning rate will increase linearly
from 0 to `lr` in 1000 steps, then decrease linearly from `lr` to `min_lr`
in 9000 steps.
Lookahead, proposed by Michael R. Zhang et.al in the paper
[Lookahead Optimizer: k steps forward, 1 step back]
(https://arxiv.org/abs/1907.08610v1), can be integrated with RAdam,
which is announced by Less Wright and the new combined optimizer can also
be called "Ranger". The mechanism can be enabled by using the lookahead
wrapper. For example:
```python
radam = tfa.optimizers.RectifiedAdam()
ranger = tfa.optimizers.Lookahead(radam, sync_period=6, slow_step_size=0.5)
```
"""
def __init__(self,
learning_rate=0.001,
beta_1=0.9,
beta_2=0.999,
epsilon=1e-7,
weight_decay=0.,
amsgrad=False,
sma_threshold=5.0,
total_steps=0,
warmup_proportion=0.1,
min_lr=0.,
name='RectifiedAdam',
**kwargs):
r"""Construct a new RAdam optimizer.
Args:
learning_rate: A `Tensor` or a floating point value. or a schedule
that is a `tf.keras.optimizers.schedules.LearningRateSchedule`
The learning rate.
beta_1: A float value or a constant float tensor.
The exponential decay rate for the 1st moment estimates.
beta_2: A float value or a constant float tensor.
The exponential decay rate for the 2nd moment estimates.
epsilon: A small constant for numerical stability.
weight_decay: A floating point value. Weight decay for each param.
amsgrad: boolean. Whether to apply AMSGrad variant of this
algorithm from the paper "On the Convergence of Adam and
beyond".
sma_threshold. A float value.
The threshold for simple mean average.
total_steps: An integer. Total number of training steps.
Enable warmup by setting a positive value.
warmup_proportion: A floating point value.
The proportion of increasing steps.
min_lr: A floating point value. Minimum learning rate after warmup.
name: Optional name for the operations created when applying
gradients. Defaults to "RectifiedAdam".
**kwargs: keyword arguments. Allowed to be {`clipnorm`,
`clipvalue`, `lr`, `decay`}. `clipnorm` is clip gradients
by norm; `clipvalue` is clip gradients by value, `decay` is
included for backward compatibility to allow time inverse
decay of learning rate. `lr` is included for backward
compatibility, recommended to use `learning_rate` instead.
"""
super(RectifiedAdam, self).__init__(name, **kwargs)
self._set_hyper('learning_rate', kwargs.get('lr', learning_rate))
self._set_hyper('beta_1', beta_1)
self._set_hyper('beta_2', beta_2)
self._set_hyper('decay', self._initial_decay)
self._set_hyper('weight_decay', weight_decay)
self._set_hyper('sma_threshold', sma_threshold)
self._set_hyper('total_steps', float(total_steps))
self._set_hyper('warmup_proportion', warmup_proportion)
self._set_hyper('min_lr', min_lr)
self.epsilon = epsilon or tf.keras.backend.epsilon()
self.amsgrad = amsgrad
self._initial_weight_decay = weight_decay
self._initial_total_steps = total_steps
def _create_slots(self, var_list):
for var in var_list:
self.add_slot(var, 'm')
for var in var_list:
self.add_slot(var, 'v')
if self.amsgrad:
for var in var_list:
self.add_slot(var, 'vhat')
def set_weights(self, weights):
params = self.weights
num_vars = int((len(params) - 1) / 2)
if len(weights) == 3 * num_vars + 1:
weights = weights[:len(params)]
super(RectifiedAdam, self).set_weights(weights)
def _resource_apply_dense(self, grad, var):
var_dtype = var.dtype.base_dtype
lr_t = self._decayed_lr(var_dtype)
m = self.get_slot(var, 'm')
v = self.get_slot(var, 'v')
beta_1_t = self._get_hyper('beta_1', var_dtype)
beta_2_t = self._get_hyper('beta_2', var_dtype)
epsilon_t = tf.convert_to_tensor(self.epsilon, var_dtype)
local_step = tf.cast(self.iterations + 1, var_dtype)
beta_1_power = tf.pow(beta_1_t, local_step)
beta_2_power = tf.pow(beta_2_t, local_step)
if self._initial_total_steps > 0:
total_steps = self._get_hyper('total_steps', var_dtype)
warmup_steps = total_steps *\
self._get_hyper('warmup_proportion', var_dtype)
min_lr = self._get_hyper('min_lr', var_dtype)
decay_steps = tf.maximum(total_steps - warmup_steps, 1)
decay_rate = (min_lr - lr_t) / decay_steps
lr_t = tf.where(
local_step <= warmup_steps,
lr_t * (local_step / warmup_steps),
lr_t + decay_rate * tf.minimum(local_step - warmup_steps,
decay_steps),
)
sma_inf = 2.0 / (1.0 - beta_2_t) - 1.0
sma_t = sma_inf - 2.0 * local_step * beta_2_power / (
1.0 - beta_2_power)
m_t = m.assign(
beta_1_t * m + (1.0 - beta_1_t) * grad,
use_locking=self._use_locking)
m_corr_t = m_t / (1.0 - beta_1_power)
v_t = v.assign(
beta_2_t * v + (1.0 - beta_2_t) * tf.square(grad),
use_locking=self._use_locking)
if self.amsgrad:
vhat = self.get_slot(var, 'vhat')
vhat_t = vhat.assign(
tf.maximum(vhat, v_t), use_locking=self._use_locking)
v_corr_t = tf.sqrt(vhat_t / (1.0 - beta_2_power))
else:
vhat_t = None
v_corr_t = tf.sqrt(v_t / (1.0 - beta_2_power))
r_t = tf.sqrt((sma_t - 4.0) / (sma_inf - 4.0) * (sma_t - 2.0) /
(sma_inf - 2.0) * sma_inf / sma_t)
sma_threshold = self._get_hyper('sma_threshold', var_dtype)
var_t = tf.where(sma_t >= sma_threshold,
r_t * m_corr_t / (v_corr_t + epsilon_t), m_corr_t)
if self._initial_weight_decay > 0.0:
var_t += self._get_hyper('weight_decay', var_dtype) * var
var_update = var.assign_sub(
lr_t * var_t, use_locking=self._use_locking)
updates = [var_update, m_t, v_t]
if self.amsgrad:
updates.append(vhat_t)
return tf.group(*updates)
def _resource_apply_sparse(self, grad, var, indices):
var_dtype = var.dtype.base_dtype
lr_t = self._decayed_lr(var_dtype)
beta_1_t = self._get_hyper('beta_1', var_dtype)
beta_2_t = self._get_hyper('beta_2', var_dtype)
epsilon_t = tf.convert_to_tensor(self.epsilon, var_dtype)
local_step = tf.cast(self.iterations + 1, var_dtype)
beta_1_power = tf.pow(beta_1_t, local_step)
beta_2_power = tf.pow(beta_2_t, local_step)
if self._initial_total_steps > 0:
total_steps = self._get_hyper('total_steps', var_dtype)
warmup_steps = total_steps *\
self._get_hyper('warmup_proportion', var_dtype)
min_lr = self._get_hyper('min_lr', var_dtype)
decay_steps = tf.maximum(total_steps - warmup_steps, 1)
decay_rate = (min_lr - lr_t) / decay_steps
lr_t = tf.where(
local_step <= warmup_steps,
lr_t * (local_step / warmup_steps),
lr_t + decay_rate * tf.minimum(local_step - warmup_steps,
decay_steps),
)
sma_inf = 2.0 / (1.0 - beta_2_t) - 1.0
sma_t = sma_inf - 2.0 * local_step * beta_2_power / (
1.0 - beta_2_power)
m = self.get_slot(var, 'm')
m_scaled_g_values = grad * (1 - beta_1_t)
m_t = m.assign(m * beta_1_t, use_locking=self._use_locking)
with tf.control_dependencies([m_t]):
m_t = self._resource_scatter_add(m, indices, m_scaled_g_values)
m_corr_t = m_t / (1.0 - beta_1_power)
v = self.get_slot(var, 'v')
v_scaled_g_values = (grad * grad) * (1 - beta_2_t)
v_t = v.assign(v * beta_2_t, use_locking=self._use_locking)
with tf.control_dependencies([v_t]):
v_t = self._resource_scatter_add(v, indices, v_scaled_g_values)
if self.amsgrad:
vhat = self.get_slot(var, 'vhat')
vhat_t = vhat.assign(
tf.maximum(vhat, v_t), use_locking=self._use_locking)
v_corr_t = tf.sqrt(vhat_t / (1.0 - beta_2_power))
else:
vhat_t = None
v_corr_t = tf.sqrt(v_t / (1.0 - beta_2_power))
r_t = tf.sqrt((sma_t - 4.0) / (sma_inf - 4.0) * (sma_t - 2.0) /
(sma_inf - 2.0) * sma_inf / sma_t)
sma_threshold = self._get_hyper('sma_threshold', var_dtype)
var_t = tf.where(sma_t >= sma_threshold,
r_t * m_corr_t / (v_corr_t + epsilon_t), m_corr_t)
if self._initial_weight_decay > 0.0:
var_t += self._get_hyper('weight_decay', var_dtype) * var
with tf.control_dependencies([var_t]):
var_update = self._resource_scatter_add(
var, indices, tf.gather(-lr_t * var_t, indices))
updates = [var_update, m_t, v_t]
if self.amsgrad:
updates.append(vhat_t)
return tf.group(*updates)
def get_config(self):
config = super(RectifiedAdam, self).get_config()
config.update({
'learning_rate':
self._serialize_hyperparameter('learning_rate'),
'beta_1':
self._serialize_hyperparameter('beta_1'),
'beta_2':
self._serialize_hyperparameter('beta_2'),
'decay':
self._serialize_hyperparameter('decay'),
'weight_decay':
self._serialize_hyperparameter('weight_decay'),
'sma_threshold':
self._serialize_hyperparameter('sma_threshold'),
'epsilon':
self.epsilon,
'amsgrad':
self.amsgrad,
'total_steps':
self._serialize_hyperparameter('total_steps'),
'warmup_proportion':
self._serialize_hyperparameter('warmup_proportion'),
'min_lr':
self._serialize_hyperparameter('min_lr'),
})
return config
```
# Load data
```
database_base_path = '/kaggle/input/tweet-dataset-split-roberta-base-96/'
k_fold = pd.read_csv(database_base_path + '5-fold.csv')
display(k_fold.head())
# Unzip files
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_1.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_2.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_3.tar.gz
# !tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_4.tar.gz
# !tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_5.tar.gz
```
# Model parameters
```
vocab_path = database_base_path + 'vocab.json'
merges_path = database_base_path + 'merges.txt'
base_path = '/kaggle/input/qa-transformers/roberta/'
config = {
"MAX_LEN": 96,
"BATCH_SIZE": 32,
"EPOCHS": 4,
"LEARNING_RATE": 3e-5,
"ES_PATIENCE": 1,
"question_size": 4,
"N_FOLDS": 3,
"base_model_path": base_path + 'roberta-base-tf_model.h5',
"config_path": base_path + 'roberta-base-config.json'
}
with open('config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
```
# Model
```
Model
module_config = RobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFRobertaModel.from_pretrained(config['base_model_path'], config=module_config, name="base_model")
sequence_output = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
last_state = sequence_output[0]
x_start = layers.Dropout(.1)(last_state)
x_start = layers.Conv1D(1, 1)(x_start)
x_start = layers.Flatten()(x_start)
y_start = layers.Activation('softmax', name='y_start')(x_start)
x_end = layers.Dropout(.1)(last_state)
x_end = layers.Conv1D(1, 1)(x_end)
x_end = layers.Flatten()(x_end)
y_end = layers.Activation('softmax', name='y_end')(x_end)
model = Model(inputs=[input_ids, attention_mask], outputs=[y_start, y_end])
# optimizer = optimizers.Adam(lr=config['LEARNING_RATE'])
optimizer = RectifiedAdam(lr=config['LEARNING_RATE'],
total_steps=(len(k_fold[k_fold['fold_1'] == 'train']) // config['BATCH_SIZE']) * config['EPOCHS'],
warmup_proportion=0.1,
min_lr=1e-7)
model.compile(optimizer, loss=losses.CategoricalCrossentropy(),
metrics=[metrics.CategoricalAccuracy()])
return model
```
# Tokenizer
```
tokenizer = ByteLevelBPETokenizer(vocab_file=vocab_path, merges_file=merges_path,
lowercase=True, add_prefix_space=True)
tokenizer.save('./')
```
# Train
```
history_list = []
AUTO = tf.data.experimental.AUTOTUNE
for n_fold in range(config['N_FOLDS']):
n_fold +=1
print('\nFOLD: %d' % (n_fold))
# Load data
base_data_path = 'fold_%d/' % (n_fold)
x_train = np.load(base_data_path + 'x_train.npy')
y_train = np.load(base_data_path + 'y_train.npy')
x_valid = np.load(base_data_path + 'x_valid.npy')
y_valid = np.load(base_data_path + 'y_valid.npy')
### Delete data dir
shutil.rmtree(base_data_path)
# Train model
model_path = 'model_fold_%d.h5' % (n_fold)
model = model_fn(config['MAX_LEN'])
es = EarlyStopping(monitor='val_loss', mode='min', patience=config['ES_PATIENCE'],
restore_best_weights=True, verbose=1)
checkpoint = ModelCheckpoint(model_path, monitor='val_loss', mode='min',
save_best_only=True, save_weights_only=True)
history = model.fit(list(x_train), list(y_train),
validation_data=(list(x_valid), list(y_valid)),
batch_size=config['BATCH_SIZE'],
callbacks=[checkpoint, es],
epochs=config['EPOCHS'],
verbose=1).history
history_list.append(history)
# Make predictions
train_preds = model.predict(list(x_train))
valid_preds = model.predict(list(x_valid))
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'start_fold_%d' % (n_fold)] = train_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'end_fold_%d' % (n_fold)] = train_preds[1].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'start_fold_%d' % (n_fold)] = valid_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'end_fold_%d' % (n_fold)] = valid_preds[1].argmax(axis=-1)
k_fold['end_fold_%d' % (n_fold)] = k_fold['end_fold_%d' % (n_fold)].astype(int)
k_fold['start_fold_%d' % (n_fold)] = k_fold['start_fold_%d' % (n_fold)].astype(int)
k_fold['end_fold_%d' % (n_fold)].clip(0, k_fold['text_len'], inplace=True)
k_fold['start_fold_%d' % (n_fold)].clip(0, k_fold['end_fold_%d' % (n_fold)], inplace=True)
k_fold['prediction_fold_%d' % (n_fold)] = k_fold.apply(lambda x: decode(x['start_fold_%d' % (n_fold)], x['end_fold_%d' % (n_fold)], x['text'], config['question_size'], tokenizer), axis=1)
k_fold['prediction_fold_%d' % (n_fold)].fillna(k_fold["text"], inplace=True)
k_fold['jaccard_fold_%d' % (n_fold)] = k_fold.apply(lambda x: jaccard(x['selected_text'], x['prediction_fold_%d' % (n_fold)]), axis=1)
```
# Model loss graph
```
sns.set(style="whitegrid")
for n_fold in range(config['N_FOLDS']):
print('Fold: %d' % (n_fold+1))
plot_metrics(history_list[n_fold])
```
# Model evaluation
```
display(evaluate_model_kfold(k_fold, config['N_FOLDS']).style.applymap(color_map))
```
# Visualize predictions
```
display(k_fold[[c for c in k_fold.columns if not (c.startswith('textID') or
c.startswith('text_len') or
c.startswith('selected_text_len') or
c.startswith('text_wordCnt') or
c.startswith('selected_text_wordCnt') or
c.startswith('fold_') or
c.startswith('start_fold_') or
c.startswith('end_fold_'))]].head(15))
```
|
github_jupyter
|
__This notebook__ trains resnet18 from scratch on CIFAR10 dataset.
```
%load_ext autoreload
%autoreload 2
%env CUDA_VISIBLE_DEVICES=YOURDEVICEHERE
import os, sys, time
sys.path.insert(0, '..')
import lib
import numpy as np
import torch, torch.nn as nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
%matplotlib inline
import random
random.seed(42)
np.random.seed(42)
torch.random.manual_seed(42)
import time
from resnet import ResNet18
device = 'cuda' if torch.cuda.is_available() else 'cpu'
experiment_name = 'editable_layer3'
experiment_name = '{}_{}.{:0>2d}.{:0>2d}_{:0>2d}:{:0>2d}:{:0>2d}'.format(experiment_name, *time.gmtime()[:6])
print(experiment_name)
print("PyTorch version:", torch.__version__)
from torchvision import transforms, datasets
transform_train = transforms.Compose([
transforms.RandomCrop(32, padding=4),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010)),
])
transform_test = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010)),
])
trainset = datasets.CIFAR10(root='./data', train=True, download=True, transform=transform_train)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=128, shuffle=True, num_workers=2)
testset = datasets.CIFAR10(root='./data', train=False, download=True, transform=transform_test)
testloader = torch.utils.data.DataLoader(testset, batch_size=100, shuffle=False, num_workers=2)
classes = ('plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
X_test, y_test = map(torch.cat, zip(*list(testloader)))
model = lib.Editable(
module=ResNet18(), loss_function=lib.contrastive_cross_entropy,
get_editable_parameters=lambda module: module.layer3.parameters(),
optimizer=lib.IngraphRMSProp(
learning_rate=1e-3, beta=nn.Parameter(torch.tensor(0.5, dtype=torch.float32)),
), max_steps=10,
).to(device)
trainer = lib.EditableTrainer(model, F.cross_entropy, experiment_name=experiment_name, max_norm=10)
trainer.writer.add_text("trainer", repr(trainer).replace('\n', '<br>'))
from tqdm import tqdm_notebook, tnrange
from IPython.display import clear_output
val_metrics = trainer.evaluate_metrics(X_test.to(device), y_test.to(device))
min_error, min_drawdown = val_metrics['base_error'], val_metrics['drawdown']
early_stopping_epochs = 500
number_of_epochs_without_improvement = 0
def edit_generator():
while True:
for xb, yb in torch.utils.data.DataLoader(trainset, batch_size=1, shuffle=True, num_workers=2):
yield xb.to(device), torch.randint_like(yb, low=0, high=len(classes), device=device)
edit_generator = edit_generator()
while True:
for x_batch, y_batch in tqdm_notebook(trainloader):
trainer.step(x_batch.to(device), y_batch.to(device), *next(edit_generator))
val_metrics = trainer.evaluate_metrics(X_test.to(device), y_test.to(device))
clear_output(True)
error_rate, drawdown = val_metrics['base_error'], val_metrics['drawdown']
number_of_epochs_without_improvement += 1
if error_rate < min_error:
trainer.save_checkpoint(tag='best_val_error')
min_error = error_rate
number_of_epochs_without_improvement = 0
if drawdown < min_drawdown:
trainer.save_checkpoint(tag='best_drawdown')
min_drawdown = drawdown
number_of_epochs_without_improvement = 0
trainer.save_checkpoint()
trainer.remove_old_temp_checkpoints()
if number_of_epochs_without_improvement > early_stopping_epochs:
break
from lib import evaluate_quality
np.random.seed(9)
indices = np.random.permutation(len(X_test))[:1000]
X_edit = X_test[indices].clone().to(device)
y_edit = torch.tensor(np.random.randint(0, 10, size=y_test[indices].shape), device=device)
metrics = evaluate_quality(editable_model, X_test, y_test, X_edit, y_edit, batch_size=512)
for key in sorted(metrics.keys()):
print('{}\t:{:.5}'.format(key, metrics[key]))
```
|
github_jupyter
|
## Homework-3: MNIST Classification with ConvNet
### **Deadline: 2021.04.06 23:59:00 **
### In this homework, you need to
- #### implement the forward and backward functions for ConvLayer (`layers/conv_layer.py`)
- #### implement the forward and backward functions for PoolingLayer (`layers/pooling_layer.py`)
- #### implement the forward and backward functions for DropoutLayer (`layers/dropout_layer.py`)
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import tensorflow.compat.v1 as tf
tf.disable_eager_execution()
from network import Network
from solver import train, test
from plot import plot_loss_and_acc
```
## Load MNIST Dataset
We use tensorflow tools to load dataset for convenience.
```
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
def decode_image(image):
# Normalize from [0, 255.] to [0., 1.0], and then subtract by the mean value
image = tf.cast(image, tf.float32)
image = tf.reshape(image, [1, 28, 28])
image = image / 255.0
image = image - tf.reduce_mean(image)
return image
def decode_label(label):
# Encode label with one-hot encoding
return tf.one_hot(label, depth=10)
# Data Preprocessing
x_train = tf.data.Dataset.from_tensor_slices(x_train).map(decode_image)
y_train = tf.data.Dataset.from_tensor_slices(y_train).map(decode_label)
data_train = tf.data.Dataset.zip((x_train, y_train))
x_test = tf.data.Dataset.from_tensor_slices(x_test).map(decode_image)
y_test = tf.data.Dataset.from_tensor_slices(y_test).map(decode_label)
data_test = tf.data.Dataset.zip((x_test, y_test))
```
## Set Hyperparameters
You can modify hyperparameters by yourself.
```
batch_size = 100
max_epoch = 10
init_std = 0.1
learning_rate = 0.001
weight_decay = 0.005
disp_freq = 50
```
## Criterion and Optimizer
```
from criterion import SoftmaxCrossEntropyLossLayer
from optimizer import SGD
criterion = SoftmaxCrossEntropyLossLayer()
sgd = SGD(learning_rate, weight_decay)
```
## ConvNet
```
from layers import FCLayer, ReLULayer, ConvLayer, MaxPoolingLayer, ReshapeLayer
convNet = Network()
convNet.add(ConvLayer(1, 8, 3, 1))
convNet.add(ReLULayer())
convNet.add(MaxPoolingLayer(2, 0))
convNet.add(ConvLayer(8, 16, 3, 1))
convNet.add(ReLULayer())
convNet.add(MaxPoolingLayer(2, 0))
convNet.add(ReshapeLayer((batch_size, 16, 7, 7), (batch_size, 784)))
convNet.add(FCLayer(784, 128))
convNet.add(ReLULayer())
convNet.add(FCLayer(128, 10))
# Train
convNet.is_training = True
convNet, conv_loss, conv_acc = train(convNet, criterion, sgd, data_train, max_epoch, batch_size, disp_freq)
# Test
convNet.is_training = False
test(convNet, criterion, data_test, batch_size, disp_freq)
```
## Plot
```
plot_loss_and_acc({'ConvNet': [conv_loss, conv_acc]})
```
### ~~You have finished homework3, congratulations!~~
**Next, according to the requirements (4):**
### **You need to implement the Dropout layer and train the network again.**
```
from layers import DropoutLayer
from layers import FCLayer, ReLULayer, ConvLayer, MaxPoolingLayer, ReshapeLayer, DropoutLayer
# build your network
convNet = Network()
convNet.add(ConvLayer(1, 8, 3, 1))
convNet.add(ReLULayer())
convNet.add(DropoutLayer(0.5))
convNet.add(MaxPoolingLayer(2, 0))
convNet.add(ConvLayer(8, 16, 3, 1))
convNet.add(ReLULayer())
convNet.add(MaxPoolingLayer(2, 0))
convNet.add(ReshapeLayer((batch_size, 16, 7, 7), (batch_size, 784)))
convNet.add(FCLayer(784, 128))
convNet.add(ReLULayer())
convNet.add(FCLayer(128, 10))
# training
convNet.is_training = True
convNet, conv_loss, conv_acc = train(convNet, criterion, sgd, data_train, max_epoch, batch_size, disp_freq)
# testing
convNet.is_training = False
test(convNet, criterion, data_test, batch_size, disp_freq)
plot_loss_and_acc({'ConvNet': [conv_loss, conv_acc]})
```
|
github_jupyter
|
# YOLOv5 Training on Custom Dataset
## Pre-requisite
- Make sure you read the user guide from the [repository](https://github.com/CertifaiAI/classifai-blogs/tree/sum_blogpost01/0_Complete_Guide_To_Custom_Object_Detection_Model_With_Yolov5)
- Upload this to Google Drive to run on Colab.
*This script is written primarily to run on Google Colab. If you want to run it on local jupyter notebook, modification of code is expected*
- Make sure you are running "GPU" on runtime. [tutorial](https://www.tutorialspoint.com/google_colab/google_colab_using_free_gpu.htm)
- **Make sure your `dataset.zip` file is uploaded at the right location. Click [here](https://github.com/CertifaiAI/classifai-blogs/blob/sum_blogpost01/0_Complete_Guide_To_Custom_Object_Detection_Model_With_Yolov5/ModelTraining/README.md#model-training-1) for tutorial to upload `dataset.zip` file.**
*Reference: https://github.com/ultralytics/yolov5*
## Step 1: Extract *dataset.zip* File
```
%cd /content
!unzip dataset.zip; rm dataset.zip
```
## Step 2: Clone YOLOv5 Repo and Install All Dependencies
```
# clone the repo
!git clone https://github.com/ultralytics/yolov5
# install dependencies
!pip install -qr yolov5/requirements.txt
%cd yolov5
import torch
# to display image
from IPython.display import Image, clear_output
# to download models/datasets
from utils.google_utils import gdrive_download
clear_output()
print('Setup complete. Using torch %s %s' % (torch.__version__, torch.cuda.get_device_properties(0) if torch.cuda.is_available() else 'CPU'))
```
## Step 3: *data.yaml* File Visualization
Make sure that our train and valid dataset locations are all right and the number of classes are also correct.
```
%cat /content/data.yaml
```
## Step 4: YOLOv5 Training
## Model Selection
There are 4 pre-trained models that you can choose from to start training your model and they are:
- yolov5s
- yolov5m
- yolov5l
- yolov5x
In this example, **yolov5s** is chosen for the computational speed.
For more details on these models please check out [yolov5 models](https://github.com/ultralytics/yolov5/wiki/Train-Custom-Data#4-select-a-model).
Here, we are able to pass a number of arguments including:
- **img:** Define input image size
- **batch:** Specify batch size
- **epochs:** Define the number of training epochs (note - typically we will train for more than 100 epochs)
- **data:** Set the path to our yaml file
- **weights:** Specify a custom path to weights.
- **name:** Name of training result folder
- **cache:** Cache images for faster training
```
%%time
%cd yolov5/
!python train.py --img 416 --batch 16 --epochs 100 --data '../data.yaml' --weights yolov5s.pt --name yolov5s_results --cache
```
## Step 5: Evaluate the Model Performance
Training losses and performance metrics are saved to Tensorboard. A logfile is also defined above with the **--name** flag when we train. In our case, we named this *yolov5s_results*.
### Tensorboard
```
# Start tensorboard
# Launch after you have finished training
# logs save in the folder "runs"
%load_ext tensorboard
%tensorboard --logdir runs
```
### Manual Plotting
```
Image(filename='/content/yolov5/runs/train/yolov5s_results/results.png', width=1000)
```
### Object Detection Visualization
#### Ground Truth Train Data:
```
Image(filename='/content/yolov5/runs/train/yolov5s_results/test_batch0_labels.jpg', width=900)
```
#### Model Predictions:
```
Image(filename='/content/yolov5/runs/train/yolov5s_results/test_batch0_pred.jpg', width=900)
```
## Step 6: Run Inference with Trained Model
Model is used to predict the test data
```
%cd yolov5/
!python detect.py --source '../test/images/*' --weights runs/train/yolov5s_results/weights/best.pt --img 416 --conf 0.4
```
### Inference Visualization
```
import glob
from IPython.display import Image, display
for imageName in glob.glob('/content/yolov5/runs/detect/exp/*.jpg'):
display(Image(filename=imageName))
print("\n")
```
## Step 7: Export Trained Model's Weights
```
from google.colab import files
files.download('/content/yolov5/runs/train/yolov5s_results/weights/best.pt')
```
|
github_jupyter
|
# Getting Started
## Platforms to Practice
Let us understand different platforms we can leverage to practice Apache Spark using Python.
* Local Setup
* Databricks Platform
* Setting up your own cluster
* Cloud based labs
## Setup Spark Locally - Ubuntu
Let us setup Spark Locally on Ubuntu.
* Install latest version of Anaconda
* Make sure Jupyter Notebook is setup and validated.
* Setup Spark and Validate.
* Setup Environment Variables to integrate Pyspark with Jupyter Notebook.
* Launch Jupyter Notebook using `pyspark` command.
* Setup PyCharm (IDE) for application development.
## Setup Spark Locally - Mac
### Let us setup Spark Locally on Ubuntu.
* Install latest version of Anaconda
* Make sure Jupyter Notebook is setup and validated.
* Setup Spark and Validate.
* Setup Environment Variables to integrate Pyspark with Jupyter Notebook.
* Launch Jupyter Notebook using `pyspark` command.
* Setup PyCharm (IDE) for application development.
## Signing up for ITVersity Labs
Here are the steps for signing to ITVersity labs.
* Go to https://labs.itversity.com
* Sign up to our website
* Purchase lab access
* Go to lab page and create lab account
* Login and practice
## Using ITVersity Labs
Let us understand how to submit the Spark Jobs in ITVersity Labs.
* You can either use Jupyter based environment or `pyspark` in terminal to submit jobs in ITVersity labs.
* You can also submit Spark jobs using `spark-submit` command.
* As we are using Python we can also use the help command to get the documentation - for example `help(spark.read.csv)`
## Interacting with File Systems
Let us understand how to interact with file system using %fs command from Databricks Notebook.
* We can access datasets using %fs magic command in Databricks notebook
* By default, we will see files under dbfs
* We can list the files using ls command - e. g.: `%fs ls`
* Databricks provides lot of datasets for free under databricks-datasets
* If the cluster is integrated with AWS or Azure Blob we can access files by specifying the appropriate protocol (e.g.: s3:// for s3)
* List of commands available under `%fs`
* Copying files or directories `-cp`
* Moving files or directories `-mv`
* Creating directories `-mkdirs`
* Deleting files and directories `-rm`
* We can copy or delete directories recursively using `-r` or `--recursive`
## Getting File Metadata
Let us review the source location to get number of files and the size of the data we are going to process.
* Location of airlines data /public/airlines_all/airlines
* We can get first details of files using hdfs dfs -ls /public/airlines_all/airlines
* Spark uses HDFS APIs to interact with the file system and we can access HDFS APIs using sc._jsc and sc._jvm to get file metadata.
* Here are the steps to get the file metadata.
* Get Hadoop Configuration using `sc._jsc.hadoopConfiguration()` - let's say `conf`
* We can pass conf to `sc._jvm.org.apache.hadoop.fs.FileSystem` get to get FileSystem object - let's say `fs`
* We can build `path` object by passing the path as string to `sc._jvm.org.apache.hadoop.fs.Path`
* We can invoke `listStatus` on top of fs by passing path which will return an array of FileStatus objects - let's say files.
* Each `FileStatus` object have all the metadata of each file.
* We can use `len` on files to get number of files.
* We can use `>getLen` on each `FileStatus` object to get the size of each file.
* Cumulative size of all files can be achieved using `sum(map(lambda file: file.getLen(), files))`
Let us first get list of files
```
hdfs dfs -ls /public/airlines_all/airlines
```
Here is the consolidated script to get number of files and cumulative size of all files in a given folder.
```
conf = sc._jsc.hadoopConfiguration()
fs = sc._jvm.org.apache.hadoop.fs.FileSystem.get(conf)
path = sc._jvm.org.apache.hadoop.fs.Path("/public/airlines_all/airlines")
files = fs.listStatus(path)
sum(map(lambda file: file.getLen(), files))/1024/1024/1024
```
|
github_jupyter
|
## MEG Group Analysis
Group analysis for MEG data, for the FOOOF paper.
The Data Source is from the
[Human Connectome Project](https://www.humanconnectome.org/)
This notebook is for group analysis of MEG data using the
[omapping](https://github.com/voytekresearch/omapping) module.
```
%matplotlib inline
from scipy.io import loadmat
from scipy.stats.stats import pearsonr
from om.meg.single import MegSubj
from om.meg.single import print_corrs_mat, print_corrs_vec
from om.meg.group import MegGroup
from om.meg.group import osc_space_group
from om.plts.meg import *
from om.core.db import OMDB
from om.core.osc import Osc
from om.core.io import load_obj_pickle, save_obj_pickle
```
## Settings
```
SAVE_FIG = False
```
### Setup
```
# Get database object
db = OMDB()
# Check what data is available
# Note: this function outa date (checks the wrong file folder)
sub_nums, source = db.check_data_files(dat_type='fooof', dat_source='HCP', verbose=True)
# Drop outlier subject
sub_nums = list(set(sub_nums) - set([662551]))
```
### Oscillation Band Definitions
```
# Set up oscillation band definitions to use
bands = Osc()
bands.add_band('Theta', [3, 7])
bands.add_band('Alpha', [7, 14])
bands.add_band('Beta', [15, 30])
```
### Load Data
```
# Initialize MegGroup object
meg_group = MegGroup(db, osc)
# Add subjects to meg_group
for i, subj in enumerate(sub_nums):
meg_subj = MegSubj(OMDB(), source[i], osc) # Initialize MegSubj object
meg_subj.import_fooof(subj, get_demo=True) # Import subject data
meg_subj.all_oscs(verbose=False) # Create vectors of all oscillations
meg_subj.osc_bands_vertex() # Get oscillations per band per vertex
meg_subj.peak_freq(dat='all', avg='mean') # Calculate peak frequencies
meg_group.add_subject(meg_subj, # Add subject data to group object
add_all_oscs=True, # Whether to include all-osc data
add_vertex_bands=True, # Whether to include osc-band-vertex data
add_peak_freqs=True, # Whether to include peak frequency data
add_vertex_oscs=False, # Whether to include all-osc data for each vertex
add_vertex_exponents=True, # Whether to include the aperiodic exponent per vertex
add_demo=True) # Whether to include demographic information
# OR: Check available saved files to load one of them
meg_files = db.check_res_files('meg')
# Load a pickled file
#meg_group = load_obj_pickle('meg', meg_files[2])
```
### Data Explorations
```
# Check how many subjects group includes
print('Currently analyzing ' + str(meg_group.n_subjs) + ' subjects.')
# Check data descriptions - sex
print('# of Females:\t', sum(np.array(meg_group.sex) == 'F'))
print('# of Females:\t', sum(np.array(meg_group.sex) == 'M'))
# Check some simple descriptives
print('Number of oscillations found across the whole group: \t', meg_group.n_oscs_tot)
print('Average number of oscillations per vertex: \t\t {:1.2f}'.format(np.mean(meg_group.n_oscs / 7501)))
# Plot all oscillations across the group
plot_all_oscs(meg_group.centers_all, meg_group.powers_all, meg_group.bws_all,
meg_group.comment, save_out=SAVE_FIG)
```
### Save out probabilities per frequency range
....
```
# Check for oscillations above / below fitting range
# Note: this is a quirk of older FOOOF version - fixed in fitting now
print(len(meg_group.centers_all[meg_group.centers_all < 2]))
print(len(meg_group.centers_all[meg_group.centers_all > 40]))
# Calculate probability of observing an oscillation in each frequency
bins = np.arange(0, 43, 1)
counts, freqs = np.histogram(meg_group.centers_all, bins=bins)
probs = counts / meg_group.n_oscs_tot
# Fix for the oscillation out of range
add = sum(probs[0:3]) + sum(probs[35:])
freqs = freqs[3:35]
probs = probs[3:35]
probs = probs + (add/len(probs))
# np.save('freqs.npy', freqs)
# np.save('probs.npy', probs)
```
## BACK TO NORMAL PROGRAMMING
```
# ??
print(sum(meg_group.powers_all < 0.05) / len(meg_group.powers_all))
print(sum(meg_group.bws_all < 1.0001) / len(meg_group.bws_all))
# Plot a single oscillation parameter at a time
plot_all_oscs_single(meg_group.centers_all, 0, meg_group.comment,
n_bins=150, figsize=(15, 5))
if True:
plt.savefig('meg-osc-centers.pdf', bbox_inches='tight')
```
### Exponents
```
# Plot distribution of all aperiodic exponents
plot_exponents(meg_group.exponents, meg_group.comment, save_out=SAVE_FIG)
# Check the global mean exponent value
print('Global mean exponent value is: \t{:1.4f} with st. dev of {:1.4f}'\
.format(np.mean(meg_group.exponents), np.std(meg_group.exponents)))
# Calculate Average Aperiodic Exponent value per Vertex
meg_group.group_exponent(avg='mean')
# Save out group exponent results
#meg_group.save_gr_exponent(file_name='json')
# Set group exponent results for visualization with Brainstorm
#meg_group.set_exponent_viz()
```
### Oscillation Topographies
##### Oscillation Probability
```
# Calculate probability of oscilation (band specific) across the cortex
meg_group.osc_prob()
# Correlations between probabilities of oscillatory bands.
prob_rs, prob_ps, prob_labels = meg_group.osc_map_corrs(map_type='prob')
print_corrs_mat(prob_rs, prob_ps, prob_labels)
# Plot the oscillation probability correlation matrix
#plot_corr_matrix(prob_rs, osc.labels, save_out=SAVE_FIG)
# Save group oscillation probability data for visualization with Brainstorm
meg_group.set_map_viz(map_type='prob', file_name='json')
# Save group oscillation probability data out to npz file
#meg_group.save_map(map_type='prob', file_name='json')
```
##### Oscillation Power Ratio
```
# Calculate power ratio of oscilation (band specific) across the cortex
meg_group.osc_power()
# Correlations between probabilities of oscillatory bands.
power_rs, power_ps, power_labels = meg_group.osc_map_corrs(map_type='power')
print_corrs_mat(power_rs, power_ps, power_labels)
# Plot the oscillation probability correlation matrix
#plot_corr_matrix(power_rs, osc.labels, save_out=SAVE_FIG)
# Save group oscillation probability data for visualization with Brainstorm
meg_group.set_map_viz(map_type='power', file_name='json')
# Save group oscillation probability data out to npz file
#meg_group.save_map(map_type='power', file_name='json')
```
##### Oscillation Score
```
# Calculate oscillation score
meg_group.osc_score()
# Save group oscillation probability data for visualization with Brainstorm
#meg_group.set_map_viz(map_type='score', file_name='json')
# Save group oscillation score data out to npz file
#meg_group.save_map(map_type='score', file_name='80_new_group')
# Correlations between osc-scores of oscillatory bands.
score_rs, score_ps, score_labels = meg_group.osc_map_corrs(map_type='score')
print_corrs_mat(score_rs, score_ps, score_labels)
# Plot the oscillation score correlation matrix
#plot_corr_matrix(score_rs, osc.labels, save_out=SAVE_FIG)
# Save out pickle file of current MegGroup() object
#save_obj_pickle(meg_group, 'meg', 'test')
```
#### Check correlation of aperiodic exponent with oscillation bands
```
n_bands = len(meg_group.bands)
exp_rs = np.zeros(shape=[n_bands])
exp_ps = np.zeros(shape=[n_bands])
for ind, band in enumerate(meg_group.bands):
r_val, p_val = pearsonr(meg_group.exponent_gr_avg, meg_group.osc_scores[band])
exp_rs[ind] = r_val
exp_ps[ind] = p_val
for rv, pv, label in zip(exp_rs, exp_ps, ['Theta', 'Alpha', 'Beta']):
print('Corr of {}-Exp \t is {:1.2f} \t with p-val of {:1.2f}'.format(label, rv, pv))
```
#### Plot corr matrix including bands & exponents
```
all_rs = np.zeros(shape=[n_bands+1, n_bands+1])
all_rs[0:n_bands, 0:n_bands] = score_rs
all_rs[n_bands, 0:n_bands] = exp_rs
all_rs[0:n_bands, n_bands] = exp_rs;
from copy import deepcopy
all_labels = deepcopy(osc.labels)
all_labels.append('Exps')
#plot_corr_matrix_tri(all_rs, all_labels)
#if SAVE_FIG:
# plt.savefig('Corrs.pdf')
corr_data = all_rs
labels = all_labels
# TEMP / HACK - MAKE & SAVE CORR-PLOT
# Generate a mask for the upper triangle
mask = np.zeros_like(corr_data, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
# Generate a custom diverging colormap
cmap = sns.color_palette("coolwarm", 7)
# Draw the heatmap with the mask and correct aspect ratio
sns.heatmap(corr_data, mask=mask, cmap=cmap, annot=True, square=True, annot_kws={"size":15},
vmin=-1, vmax=1, xticklabels=labels, yticklabels=labels)
plt.savefig('corr.pdf')
#plot_corr_matrix(all_rs, all_labels, save_out=SAVE_FIG)
```
|
github_jupyter
|
```
import numpy as np
import scipy
import scipy.misc
import scipy.ndimage
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import OneHotEncoder
from datetime import datetime
import resource
np.set_printoptions(suppress=True, precision=5)
%matplotlib inline
class Laptimer:
def __init__(self):
self.start = datetime.now()
self.lap = 0
def click(self, message):
td = datetime.now() - self.start
td = (td.days*86400000 + td.seconds*1000 + td.microseconds / 1000) / 1000
memory = resource.getrusage(resource.RUSAGE_SELF).ru_maxrss / (1024 ** 2)
print("[%d] %s, %.2fs, memory: %dmb" % (self.lap, message, td, memory))
self.start = datetime.now()
self.lap = self.lap + 1
return td
def reset(self):
self.__init__()
def __call__(self, message = None):
return self.click(message)
timer = Laptimer()
timer()
def normalize_fetures(X):
return X * 0.98 / 255 + 0.01
def normalize_labels(y):
y = OneHotEncoder(sparse=False).fit_transform(y)
y[y == 0] = 0.01
y[y == 1] = 0.99
return y
url = "https://raw.githubusercontent.com/makeyourownneuralnetwork/makeyourownneuralnetwork/master/mnist_dataset/mnist_train_100.csv"
train = pd.read_csv(url, header=None, dtype="float64")
train.sample(10)
X_train = normalize_fetures(train.iloc[:, 1:].values)
y_train = train.iloc[:, [0]].values.astype("int32")
y_train_ohe = normalize_labels(y_train)
fig, _ = plt.subplots(5, 6, figsize = (15, 10))
for i, ax in enumerate(fig.axes):
ax.imshow(X_train[i].reshape(28, 28), cmap="Greys", interpolation="none")
ax.set_title("T: %d" % y_train[i])
plt.tight_layout()
url = "https://raw.githubusercontent.com/makeyourownneuralnetwork/makeyourownneuralnetwork/master/mnist_dataset/mnist_test_10.csv"
test = pd.read_csv(url, header=None, dtype="float64")
test.sample(10)
X_test = normalize_fetures(test.iloc[:, 1:].values)
y_test = test.iloc[:, 0].values.astype("int32")
```
# Neural Networks Classifier
Author: Abul Basar
```
class NeuralNetwork:
def __init__(self, layers, learning_rate, random_state = None):
self.layers_ = layers
self.num_features = layers[0]
self.num_classes = layers[-1]
self.hidden = layers[1:-1]
self.learning_rate = learning_rate
if not random_state:
np.random.seed(random_state)
self.W_sets = []
for i in range(len(self.layers_) - 1):
n_prev = layers[i]
n_next = layers[i + 1]
m = np.random.normal(0.0, pow(n_next, -0.5), (n_next, n_prev))
self.W_sets.append(m)
def activation_function(self, z):
return 1 / (1 + np.exp(-z))
def fit(self, training, targets):
inputs0 = inputs = np.array(training, ndmin=2).T
assert inputs.shape[0] == self.num_features, \
"no of features {0}, it must be {1}".format(inputs.shape[0], self.num_features)
targets = np.array(targets, ndmin=2).T
assert targets.shape[0] == self.num_classes, \
"no of classes {0}, it must be {1}".format(targets.shape[0], self.num_classes)
outputs = []
for i in range(len(self.layers_) - 1):
W = self.W_sets[i]
inputs = self.activation_function(W.dot(inputs))
outputs.append(inputs)
errors = [None] * (len(self.layers_) - 1)
errors[-1] = targets - outputs[-1]
#print("Last layer", targets.shape, outputs[-1].shape, errors[-1].shape)
#print("Last layer", targets, outputs[-1])
#Back propagation
for i in range(len(self.layers_) - 1)[::-1]:
W = self.W_sets[i]
E = errors[i]
O = outputs[i]
I = outputs[i - 1] if i > 0 else inputs0
#print("i: ", i, ", E: ", E.shape, ", O:", O.shape, ", I: ", I.shape, ",W: ", W.shape)
W += self.learning_rate * (E * O * (1 - O)).dot(I.T)
if i > 0:
errors[i-1] = W.T.dot(E)
def predict(self, inputs, cls = False):
inputs = np.array(inputs, ndmin=2).T
assert inputs.shape[0] == self.num_features, \
"no of features {0}, it must be {1}".format(inputs.shape[0], self.num_features)
for i in range(len(self.layers_) - 1):
W = self.W_sets[i]
input_next = W.dot(inputs)
inputs = activated = self.activation_function(input_next)
return np.argmax(activated.T, axis=1) if cls else activated.T
def score(self, X_test, y_test):
y_test = np.array(y_test).flatten()
y_test_pred = nn.predict(X_test, cls=True)
return np.sum(y_test_pred == y_test) / y_test.shape[0]
```
# Run neural net classifier on small dataset
### Training set size: 100, testing set size 10
```
nn = NeuralNetwork([784,100,10], 0.3, random_state=0)
for i in np.arange(X_train.shape[0]):
nn.fit(X_train[i], y_train_ohe[i])
nn.predict(X_train[2]), nn.predict(X_train[2], cls=True)
print("Testing accuracy: ", nn.score(X_test, y_test), ", training accuracy: ", nn.score(X_train, y_train))
#list(zip(y_test_pred, y_test))
```
# Load full MNIST dataset.
### Training set size 60,000 and test set size 10,000
Original: http://yann.lecun.com/exdb/mnist/
CSV version:
training: https://pjreddie.com/media/files/mnist_train.csv
testing: https://pjreddie.com/media/files/mnist_test.csv
```
train = pd.read_csv("../data/MNIST/mnist_train.csv", header=None, dtype="float64")
X_train = normalize_fetures(train.iloc[:, 1:].values)
y_train = train.iloc[:, [0]].values.astype("int32")
y_train_ohe = normalize_labels(y_train)
print(y_train.shape, y_train_ohe.shape)
test = pd.read_csv("../data/MNIST/mnist_test.csv", header=None, dtype="float64")
X_test = normalize_fetures(test.iloc[:, 1:].values)
y_test = test.iloc[:, 0].values.astype("int32")
```
## Runt the Neural Network classifier and measure performance
```
timer.reset()
nn = NeuralNetwork([784,100,10], 0.3, random_state=0)
for i in range(X_train.shape[0]):
nn.fit(X_train[i], y_train_ohe[i])
timer("training time")
accuracy = nn.score(X_test, y_test)
print("Testing accuracy: ", nn.score(X_test, y_test), ", Training accuracy: ", nn.score(X_train, y_train))
```
# Effect of learning rate
```
params = 10 ** - np.linspace(0.01, 2, 10)
scores_train = []
scores_test = []
timer.reset()
for p in params:
nn = NeuralNetwork([784,100,10], p, random_state = 0)
for i in range(X_train.shape[0]):
nn.fit(X_train[i], y_train_ohe[i])
scores_train.append(nn.score(X_train, y_train))
scores_test.append(nn.score(X_test, y_test))
timer()
plt.plot(params, scores_test, label = "Test score")
plt.plot(params, scores_train, label = "Training score")
plt.xlabel("Learning Rate")
plt.ylabel("Accuracy")
plt.legend()
plt.title("Effect of learning rate")
print("Accuracy scores")
pd.DataFrame({"learning_rate": params, "train": scores_train, "test": scores_test})
```
# Effect of Epochs
```
epochs = np.arange(20)
learning_rate = 0.077
scores_train, scores_test = [], []
nn = NeuralNetwork([784,100,10], learning_rate, random_state = 0)
indices = np.arange(X_train.shape[0])
timer.reset()
for _ in epochs:
np.random.shuffle(indices)
for i in indices:
nn.fit(X_train[i], y_train_ohe[i])
scores_train.append(nn.score(X_train, y_train))
scores_test.append(nn.score(X_test, y_test))
timer("test score: %f, training score: %f" % (scores_test[-1], scores_train[-1]))
plt.plot(epochs, scores_test, label = "Test score")
plt.plot(epochs, scores_train, label = "Training score")
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend(loc = "lower right")
plt.title("Effect of Epochs")
print("Accuracy scores")
pd.DataFrame({"epochs": epochs, "train": scores_train, "test": scores_test})
```
# Effect of size (num of nodes) of the single hidden layer
```
num_layers = 50 * (np.arange(10) + 1)
learning_rate = 0.077
scores_train, scores_test = [], []
timer.reset()
for p in num_layers:
nn = NeuralNetwork([784, p,10], learning_rate, random_state = 0)
indices = np.arange(X_train.shape[0])
for i in indices:
nn.fit(X_train[i], y_train_ohe[i])
scores_train.append(nn.score(X_train, y_train))
scores_test.append(nn.score(X_test, y_test))
timer("size: %d, test score: %f, training score: %f" % (p, scores_test[-1], scores_train[-1]))
plt.plot(num_layers, scores_test, label = "Test score")
plt.plot(num_layers, scores_train, label = "Training score")
plt.xlabel("Hidden Layer Size")
plt.ylabel("Accuracy")
plt.legend(loc = "lower right")
plt.title("Effect of size (num of nodes) of the hidden layer")
print("Accuracy scores")
pd.DataFrame({"layer": num_layers, "train": scores_train, "test": scores_test})
```
# Effect of using multiple hidden layers
```
num_layers = np.arange(5) + 1
learning_rate = 0.077
scores_train, scores_test = [], []
timer.reset()
for p in num_layers:
layers = [100] * p
layers.insert(0, 784)
layers.append(10)
nn = NeuralNetwork(layers, learning_rate, random_state = 0)
indices = np.arange(X_train.shape[0])
for i in indices:
nn.fit(X_train[i], y_train_ohe[i])
scores_train.append(nn.score(X_train, y_train))
scores_test.append(nn.score(X_test, y_test))
timer("size: %d, test score: %f, training score: %f" % (p, scores_test[-1], scores_train[-1]))
plt.plot(num_layers, scores_test, label = "Test score")
plt.plot(num_layers, scores_train, label = "Training score")
plt.xlabel("No of hidden layers")
plt.ylabel("Accuracy")
plt.legend(loc = "upper right")
plt.title("Effect of using multiple hidden layers, \nNodes per layer=100")
print("Accuracy scores")
pd.DataFrame({"layer": num_layers, "train": scores_train, "test": scores_test})
```
# Rotation
```
img = scipy.ndimage.interpolation.rotate(X_train[110].reshape(28, 28), -10, reshape=False)
print(img.shape)
plt.imshow(img, interpolation=None, cmap="Greys")
epochs = np.arange(10)
learning_rate = 0.077
scores_train, scores_test = [], []
nn = NeuralNetwork([784,250,10], learning_rate, random_state = 0)
indices = np.arange(X_train.shape[0])
timer.reset()
for _ in epochs:
np.random.shuffle(indices)
for i in indices:
for rotation in [-10, 0, 10]:
img = scipy.ndimage.interpolation.rotate(X_train[i].reshape(28, 28), rotation, cval=0.01, order=1, reshape=False)
nn.fit(img.flatten(), y_train_ohe[i])
scores_train.append(nn.score(X_train, y_train))
scores_test.append(nn.score(X_test, y_test))
timer("test score: %f, training score: %f" % (scores_test[-1], scores_train[-1]))
plt.plot(epochs, scores_test, label = "Test score")
plt.plot(epochs, scores_train, label = "Training score")
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend(loc = "lower right")
plt.title("Trained with rotation (+/- 10)\n Hidden Nodes: 250, LR: 0.077")
print("Accuracy scores")
pd.DataFrame({"epochs": epochs, "train": scores_train, "test": scores_test})
```
# Which charaters NN was most wrong about?
```
missed = y_test_pred != y_test
pd.Series(y_test[missed]).value_counts().plot(kind = "bar")
plt.title("No of mis classification by digit")
plt.ylabel("No of misclassification")
plt.xlabel("Digit")
fig, _ = plt.subplots(6, 4, figsize = (15, 10))
for i, ax in enumerate(fig.axes):
ax.imshow(X_test[missed][i].reshape(28, 28), interpolation="nearest", cmap="Greys")
ax.set_title("T: %d, P: %d" % (y_test[missed][i], y_test_pred[missed][i]))
plt.tight_layout()
img = scipy.ndimage.imread("/Users/abulbasar/Downloads/9-03.png", mode="L")
print("Original size:", img.shape)
img = normalize_fetures(scipy.misc.imresize(img, (28, 28)))
img = np.abs(img - 0.99)
plt.imshow(img, cmap="Greys", interpolation="none")
print("Predicted value: ", nn.predict(img.flatten(), cls=True))
```
|
github_jupyter
|
<img src="../../images/qiskit-heading.gif" alt="Note: In order for images to show up in this jupyter notebook you need to select File => Trusted Notebook" width="500 px" align="left">
## _*Shor's Algorithm for Integer Factorization*_
The latest version of this tutorial notebook is available on https://github.com/qiskit/qiskit-tutorial.
In this tutorial, we first introduce the problem of [integer factorization](#factorization) and describe how [Shor's algorithm](#shorsalgorithm) solves it in detail. We then [implement](#implementation) a version of it in Qiskit.
### Contributors
Anna Phan
***
## Integer Factorization <a id='factorization'></a>
Integer factorization is the decomposition of an composite integer into a product of smaller integers, for example, the integer $100$ can be factored into $10 \times 10$. If these factors are restricted to prime numbers, the process is called prime factorization, for example, the prime factorization of $100$ is $2 \times 2 \times 5 \times 5$.
When the integers are very large, no efficient classical integer factorization algorithm is known. The hardest factorization problems are semiprime numbers, the product of two prime numbers. In [2009](https://link.springer.com/chapter/10.1007/978-3-642-14623-7_18), a team of researchers factored a 232 decimal digit semiprime number (768 bits), spending the computational equivalent of more than two thousand years on a single core 2.2 GHz AMD Opteron processor with 2 GB RAM:
```
RSA-768 = 12301866845301177551304949583849627207728535695953347921973224521517264005
07263657518745202199786469389956474942774063845925192557326303453731548268
50791702612214291346167042921431160222124047927473779408066535141959745985
6902143413
= 33478071698956898786044169848212690817704794983713768568912431388982883793
878002287614711652531743087737814467999489
× 36746043666799590428244633799627952632279158164343087642676032283815739666
511279233373417143396810270092798736308917
```
The presumed difficulty of this semiprime factorization problem underlines many encryption algorithms, such as [RSA](https://www.google.com/patents/US4405829), which is used in online credit card transactions, amongst other applications.
***
## Shor's Algorithm <a id='shorsalgorithm'></a>
Shor's algorithm, named after mathematician Peter Shor, is a polynomial time quantum algorithm for integer factorization formulated in [1994](http://epubs.siam.org/doi/10.1137/S0097539795293172). It is arguably the most dramatic example of how the paradigm of quantum computing changed our perception of which computational problems should be considered tractable, motivating the study of new quantum algorithms and efforts to design and construct quantum computers. It also has expedited research into new cryptosystems not based on integer factorization.
Shor's algorithm has been experimentally realised by multiple teams for specific composite integers. The composite $15$ was first factored into $3 \times 5$ in [2001](https://www.nature.com/nature/journal/v414/n6866/full/414883a.html) using seven NMR qubits, and has since been implemented using four photon qubits in 2007 by [two](https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.99.250504) [teams](https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.99.250505), three solid state qubits in [2012](https://www.nature.com/nphys/journal/v8/n10/full/nphys2385.html) and five trapped ion qubits in [2016](http://science.sciencemag.org/content/351/6277/1068). The composite $21$ has also been factored into $3 \times 7$ in [2012](http://www.nature.com/nphoton/journal/v6/n11/full/nphoton.2012.259.html) using a photon qubit and qutrit (a three level system). Note that these experimental demonstrations rely on significant optimisations of Shor's algorithm based on apriori knowledge of the expected results. In general, [$2 + \frac{3}{2}\log_2N$](https://link-springer-com.virtual.anu.edu.au/chapter/10.1007/3-540-49208-9_15) qubits are needed to factor the composite integer $N$, meaning at least $1,154$ qubits would be needed to factor $RSA-768$ above.
```
from IPython.display import HTML
HTML('<iframe width="560" height="315" src="https://www.youtube.com/embed/hOlOY7NyMfs?start=75&end=126" frameborder="0" allowfullscreen></iframe>')
```
As Peter Shor describes in the video above from [PhysicsWorld](http://physicsworld.com/cws/article/multimedia/2015/sep/30/what-is-shors-factoring-algorithm), Shor’s algorithm is composed of three parts. The first part turns the factoring problem into a period finding problem using number theory, which can be computed on a classical computer. The second part finds the period using the quantum Fourier transform and is responsible for the quantum speedup of the algorithm. The third part uses the period found to calculate the factors.
The following sections go through the algorithm in detail, for those who just want the steps, without the lengthy explanation, refer to the [blue](#stepsone) [boxes](#stepstwo) before jumping down to the [implemention](#implemention).
### From Factorization to Period Finding
The number theory that underlines Shor's algorithm relates to periodic modulo sequences. Let's have a look at an example of such a sequence. Consider the sequence of the powers of two:
$$1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, ...$$
Now let's look at the same sequence 'modulo 15', that is, the remainder after fifteen divides each of these powers of two:
$$1, 2, 4, 8, 1, 2, 4, 8, 1, 2, 4, ...$$
This is a modulo sequence that repeats every four numbers, that is, a periodic modulo sequence with a period of four.
Reduction of factorization of $N$ to the problem of finding the period of an integer $x$ less than $N$ and greater than $1$ depends on the following result from number theory:
> The function $\mathcal{F}(a) = x^a \bmod N$ is a periodic function, where $x$ is an integer coprime to $N$ and $a \ge 0$.
Note that two numbers are coprime, if the only positive integer that divides both of them is 1. This is equivalent to their greatest common divisor being 1. For example, 8 and 15 are coprime, as they don't share any common factors (other than 1). However, 9 and 15 are not coprime, since they are both divisible by 3 (and 1).
> Since $\mathcal{F}(a)$ is a periodic function, it has some period $r$. Knowing that $x^0 \bmod N = 1$, this means that $x^r \bmod N = 1$ since the function is periodic, and thus $r$ is just the first nonzero power where $x^r = 1 (\bmod N)$.
Given this information and through the following algebraic manipulation:
$$ x^r \equiv 1 \bmod N $$
$$ x^r = (x^{r/2})^2 \equiv 1 \bmod N $$
$$ (x^{r/2})^2 - 1 \equiv 0 \bmod N $$
and if $r$ is an even number:
$$ (x^{r/2} + 1)(x^{r/2} - 1) \equiv 0 \bmod N $$
From this, the product $(x^{r/2} + 1)(x^{r/2} - 1)$ is an integer multiple of $N$, the number to be factored. Thus, so long as $(x^{r/2} + 1)$ or $(x^{r/2} - 1)$ is not a multiple of $N$, then at least one of $(x^{r/2} + 1)$ or $(x^{r/2} - 1)$ must have a nontrivial factor in common with $N$.
So computing $\text{gcd}(x^{r/2} - 1, N)$ and $\text{gcd}(x^{r/2} + 1, N)$ will obtain a factor of $N$, where $\text{gcd}$ is the greatest common denominator function, which can be calculated by the polynomial time [Euclidean algorithm](https://en.wikipedia.org/wiki/Euclidean_algorithm).
#### Classical Steps to Shor's Algorithm
Let's assume for a moment that a period finding machine exists that takes as input coprime integers $x, N$ and outputs the period of $x \bmod N$, implemented by as a brute force search below. Let's show how to use the machine to find all prime factors of $N$ using the number theory described above.
```
# Brute force period finding algorithm
def find_period_classical(x, N):
n = 1
t = x
while t != 1:
t *= x
t %= N
n += 1
return n
```
For simplicity, assume that $N$ has only two distinct prime factors: $N = pq$.
<div class="alert alert-block alert-info"> <a id='stepsone'></a>
<ol>
<li>Pick a random integer $x$ between $1$ and $N$ and compute the greatest common divisor $\text{gcd}(x,N)$ using Euclid's algorithm.</li>
<li>If $x$ and $N$ have some common prime factors, $\text{gcd}(x,N)$ will equal $p$ or $q$. Otherwise $\text{gcd}(x,N) = 1$, meaning $x$ and $N$ are coprime. </li>
<li>Let $r$ be the period of $x \bmod N$ computed by the period finding machine. Repeat the above steps with different random choices of $x$ until $r$ is even.</li>
<li>Now $p$ and $q$ can be found by computing $\text{gcd}(x^{r/2} \pm 1, N)$ as long as $x^{r/2} \neq \pm 1$.</li>
</ol>
</div>
As an example, consider $N = 15$. Let's look at all values of $1 < x < 15$ where $x$ is coprime with $15$:
| $x$ | $x^a \bmod 15$ | Period $r$ |$\text{gcd}(x^{r/2}-1,15)$|$\text{gcd}(x^{r/2}+1,15)$ |
|:-----:|:----------------------------:|:----------:|:------------------------:|:-------------------------:|
| 2 | 1,2,4,8,1,2,4,8,1,2,4... | 4 | 3 | 5 |
| 4 | 1,4,1,4,1,4,1,4,1,4,1... | 2 | 3 | 5 |
| 7 | 1,7,4,13,1,7,4,13,1,7,4... | 4 | 3 | 5 |
| 8 | 1,8,4,2,1,8,4,2,1,8,4... | 4 | 3 | 5 |
| 11 | 1,11,1,11,1,11,1,11,1,11,1...| 2 | 5 | 3 |
| 13 | 1,13,4,7,1,13,4,7,1,13,4,... | 4 | 3 | 5 |
| 14 | 1,14,1,14,1,14,1,14,1,14,1,,,| 2 | 1 | 15 |
As can be seen, any value of $x$ except $14$ will return the factors of $15$, that is, $3$ and $5$. $14$ is an example of the special case where $(x^{r/2} + 1)$ or $(x^{r/2} - 1)$ is a multiple of $N$ and thus another $x$ needs to be tried.
In general, it can be shown that this special case occurs infrequently, so on average only two calls to the period finding machine are sufficient to factor $N$.
For a more interesting example, first let's find larger number N, that is semiprime that is relatively small. Using the [Sieve of Eratosthenes](https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes) [Python implementation](http://archive.oreilly.com/pub/a/python/excerpt/pythonckbk_chap1/index1.html?page=last), let's generate a list of all the prime numbers less than a thousand, randomly select two, and muliply them.
```
import random, itertools
# Sieve of Eratosthenes algorithm
def sieve( ):
D = { }
yield 2
for q in itertools.islice(itertools.count(3), 0, None, 2):
p = D.pop(q, None)
if p is None:
D[q*q] = q
yield q
else:
x = p + q
while x in D or not (x&1):
x += p
D[x] = p
# Creates a list of prime numbers up to the given argument
def get_primes_sieve(n):
return list(itertools.takewhile(lambda p: p<n, sieve()))
def get_semiprime(n):
primes = get_primes_sieve(n)
l = len(primes)
p = primes[random.randrange(l)]
q = primes[random.randrange(l)]
return p*q
N = get_semiprime(1000)
print("semiprime N =",N)
```
Now implement the [above steps](#stepsone) of Shor's Algorithm:
```
import math
def shors_algorithm_classical(N):
x = random.randint(0,N) # step one
if(math.gcd(x,N) != 1): # step two
return x,0,math.gcd(x,N),N/math.gcd(x,N)
r = find_period_classical(x,N) # step three
while(r % 2 != 0):
r = find_period_classical(x,N)
p = math.gcd(x**int(r/2)+1,N) # step four, ignoring the case where (x^(r/2) +/- 1) is a multiple of N
q = math.gcd(x**int(r/2)-1,N)
return x,r,p,q
x,r,p,q = shors_algorithm_classical(N)
print("semiprime N = ",N,", coprime x = ",x,", period r = ",r,", prime factors = ",p," and ",q,sep="")
```
### Quantum Period Finding <a id='quantumperiodfinding'></a>
Let's first describe the quantum period finding algorithm, and then go through a few of the steps in detail, before going through an example. This algorithm takes two coprime integers, $x$ and $N$, and outputs $r$, the period of $\mathcal{F}(a) = x^a\bmod N$.
<div class="alert alert-block alert-info"><a id='stepstwo'></a>
<ol>
<li> Choose $T = 2^t$ such that $N^2 \leq T \le 2N^2$. Initialise two registers of qubits, first an argument register with $t$ qubits and second a function register with $n = log_2 N$ qubits. These registers start in the initial state:
$$\vert\psi_0\rangle = \vert 0 \rangle \vert 0 \rangle$$ </li>
<li> Apply a Hadamard gate on each of the qubits in the argument register to yield an equally weighted superposition of all integers from $0$ to $T$:
$$\vert\psi_1\rangle = \frac{1}{\sqrt{T}}\sum_{a=0}^{T-1}\vert a \rangle \vert 0 \rangle$$ </li>
<li> Implement the modular exponentiation function $x^a \bmod N$ on the function register, giving the state:
$$\vert\psi_2\rangle = \frac{1}{\sqrt{T}}\sum_{a=0}^{T-1}\vert a \rangle \vert x^a \bmod N \rangle$$
This $\vert\psi_2\rangle$ is highly entangled and exhibits quantum parallism, i.e. the function entangled in parallel all the 0 to $T$ input values with the corresponding values of $x^a \bmod N$, even though the function was only executed once. </li>
<li> Perform a quantum Fourier transform on the argument register, resulting in the state:
$$\vert\psi_3\rangle = \frac{1}{T}\sum_{a=0}^{T-1}\sum_{z=0}^{T-1}e^{(2\pi i)(az/T)}\vert z \rangle \vert x^a \bmod N \rangle$$
where due to the interference, only the terms $\vert z \rangle$ with
$$z = qT/r $$
have significant amplitude where $q$ is a random integer ranging from $0$ to $r-1$ and $r$ is the period of $\mathcal{F}(a) = x^a\bmod N$. </li>
<li> Measure the argument register to obtain classical result $z$. With reasonable probability, the continued fraction approximation of $T / z$ will be an integer multiple of the period $r$. Euclid's algorithm can then be used to find $r$.</li>
</ol>
</div>
Note how quantum parallelism and constructive interference have been used to detect and measure periodicity of the modular exponentiation function. The fact that interference makes it easier to measure periodicity should not come as a big surprise. After all, physicists routinely use scattering of electromagnetic waves and interference measurements to determine periodicity of physical objects such as crystal lattices. Likewise, Shor's algorithm exploits interference to measure periodicity of arithmetic objects, a computational interferometer of sorts.
#### Modular Exponentiation
The modular exponentiation, step 3 above, that is the evaluation of $x^a \bmod N$ for $2^t$ values of $a$ in parallel, is the most demanding part of the algorithm. This can be performed using the following identity for the binary representation of any integer: $x = x_{t-1}2^{t-1} + ... x_12^1+x_02^0$, where $x_t$ are the binary digits of $x$. From this, it follows that:
\begin{aligned}
x^a \bmod N & = x^{2^{(t-1)}a_{t-1}} ... x^{2a_1}x^{a_0} \bmod N \\
& = x^{2^{(t-1)}a_{t-1}} ... [x^{2a_1}[x^{2a_0} \bmod N] \bmod N] ... \bmod N \\
\end{aligned}
This means that 1 is first multiplied by $x^1 \bmod N$ if and only if $a_0 = 1$, then the result is multiplied by $x^2 \bmod N$ if and only if $a_1 = 1$ and so forth, until finally the result is multiplied by $x^{2^{(s-1)}}\bmod N$ if and only if $a_{t-1} = 1$.
Therefore, the modular exponentiation consists of $t$ serial multiplications modulo $N$, each of them controlled by the qubit $a_t$. The values $x,x^2,...,x^{2^{(t-1)}} \bmod N$ can be found efficiently on a classical computer by repeated squaring.
#### Quantum Fourier Transform
The Fourier transform occurs in many different versions throughout classical computing, in areas ranging from signal processing to data compression to complexity theory. The quantum Fourier transform (QFT), step 4 above, is the quantum implementation of the discrete Fourier transform over the amplitudes of a wavefunction.
The classical discrete Fourier transform acts on a vector $(x_0, ..., x_{N-1})$ and maps it to the vector $(y_0, ..., y_{N-1})$ according to the formula
$$y_k = \frac{1}{\sqrt{N}}\sum_{j=0}^{N-1}x_j\omega_N^{jk}$$
where $\omega_N^{jk} = e^{2\pi i \frac{jk}{N}}$.
Similarly, the quantum Fourier transform acts on a quantum state $\sum_{i=0}^{N-1} x_i \vert i \rangle$ and maps it to the quantum state $\sum_{i=0}^{N-1} y_i \vert i \rangle$ according to the formula
$$y_k = \frac{1}{\sqrt{N}}\sum_{j=0}^{N-1}x_j\omega_N^{jk}$$
with $\omega_N^{jk}$ defined as above. Note that only the amplitudes of the state were affected by this transformation.
This can also be expressed as the map:
$$\vert x \rangle \mapsto \frac{1}{\sqrt{N}}\sum_{y=0}^{N-1}\omega_N^{xy} \vert y \rangle$$
Or the unitary matrix:
$$ U_{QFT} = \frac{1}{\sqrt{N}} \sum_{x=0}^{N-1} \sum_{y=0}^{N-1} \omega_N^{xy} \vert y \rangle \langle x \vert$$
As an example, we've actually already seen the quantum Fourier transform for when $N = 2$, it is the Hadamard operator ($H$):
$$H = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}$$
Suppose we have the single qubit state $\alpha \vert 0 \rangle + \beta \vert 1 \rangle$, if we apply the $H$ operator to this state, we obtain the new state:
$$\frac{1}{\sqrt{2}}(\alpha + \beta) \vert 0 \rangle + \frac{1}{\sqrt{2}}(\alpha - \beta) \vert 1 \rangle
\equiv \tilde{\alpha}\vert 0 \rangle + \tilde{\beta}\vert 1 \rangle$$
Notice how the Hadamard gate performs the discrete Fourier transform for $N = 2$ on the amplitudes of the state.
So what does the quantum Fourier transform look like for larger N? Let's derive a circuit for $N=2^n$, $QFT_N$ acting on the state $\vert x \rangle = \vert x_1...x_n \rangle$ where $x_1$ is the most significant bit.
\begin{aligned}
QFT_N\vert x \rangle & = \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1}\omega_N^{xy} \vert y \rangle \\
& = \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} e^{2 \pi i xy / 2^n} \vert y \rangle \:\text{since}\: \omega_N^{xy} = e^{2\pi i \frac{xy}{N}} \:\text{and}\: N = 2^n\\
& = \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} e^{2 \pi i \left(\sum_{k=1}^n y_k/2^k\right) x} \vert y_1 ... y_n \rangle \:\text{rewriting in fractional binary notation}\: y = y_1...y_k, y/2^n = \sum_{k=1}^n y_k/2^k \\
& = \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} \prod_{k=0}^n e^{2 \pi i x y_k/2^k } \vert y_1 ... y_n \rangle \:\text{after expanding the exponential of a sum to a product of exponentials} \\
& = \frac{1}{\sqrt{N}} \bigotimes_{k=1}^n \left(\vert0\rangle + e^{2 \pi i x /2^k } \vert1\rangle \right) \:\text{after rearranging the sum and products, and expanding} \\
& = \frac{1}{\sqrt{N}} \left(\vert0\rangle + e^{2 \pi i[0.x_n]} \vert1\rangle\right) \otimes...\otimes \left(\vert0\rangle + e^{2 \pi i[0.x_1.x_2...x_{n-1}.x_n]} \vert1\rangle\right) \:\text{as}\: e^{2 \pi i x/2^k} = e^{2 \pi i[0.x_k...x_n]}
\end{aligned}
This is a very useful form of the QFT for $N=2^n$ as only the last qubit depends on the the
values of all the other input qubits and each further bit depends less and less on the input qubits. Furthermore, note that $e^{2 \pi i.0.x_n}$ is either $+1$ or $-1$, which resembles the Hadamard transform.
Before we create the circuit code for general $N=2^n$, let's look at $N=8,n=3$:
$$QFT_8\vert x_1x_2x_3\rangle = \frac{1}{\sqrt{8}} \left(\vert0\rangle + e^{2 \pi i[0.x_3]} \vert1\rangle\right) \otimes \left(\vert0\rangle + e^{2 \pi i[0.x_2.x_3]} \vert1\rangle\right) \otimes \left(\vert0\rangle + e^{2 \pi i[0.x_1.x_2.x_3]} \vert1\rangle\right) $$
The steps to creating the circuit for $\vert y_1y_2x_3\rangle = QFT_8\vert x_1x_2x_3\rangle$, remembering the [controlled phase rotation gate](../tools/quantum_gates_and_linear_algebra.ipynb
) $CU_1$, would be:
1. Apply a Hadamard to $\vert x_3 \rangle$, giving the state $\frac{1}{\sqrt{2}}\left(\vert0\rangle + e^{2 \pi i.0.x_3} \vert1\rangle\right) = \frac{1}{\sqrt{2}}\left(\vert0\rangle + (-1)^{x_3} \vert1\rangle\right)$
2. Apply a Hadamard to $\vert x_2 \rangle$, then depending on $k_3$ (before the Hadamard gate) a $CU_1(\frac{\pi}{2})$, giving the state $\frac{1}{\sqrt{2}}\left(\vert0\rangle + e^{2 \pi i[0.x_2.x_3]} \vert1\rangle\right)$.
3. Apply a Hadamard to $\vert x_1 \rangle$, then $CU_1(\frac{\pi}{2})$ depending on $k_2$, and $CU_1(\frac{\pi}{4})$ depending on $k_3$.
4. Measure the bits in reverse order, that is $y_3 = x_1, y_2 = x_2, y_1 = y_3$.
In Qiskit, this is:
```
q3 = QuantumRegister(3, 'q3')
c3 = ClassicalRegister(3, 'c3')
qft3 = QuantumCircuit(q3, c3)
qft3.h(q[0])
qft3.cu1(math.pi/2.0, q3[1], q3[0])
qft3.h(q[1])
qft3.cu1(math.pi/4.0, q3[2], q3[0])
qft3.cu1(math.pi/2.0, q3[2], q3[1])
qft3.h(q[2])
```
For $N=2^n$, this can be generalised, as in the `qft` function in [tools.qi](https://github.com/Q/qiskit-terra/blob/master/qiskit/tools/qi/qi.py):
```
def qft(circ, q, n):
"""n-qubit QFT on q in circ."""
for j in range(n):
for k in range(j):
circ.cu1(math.pi/float(2**(j-k)), q[j], q[k])
circ.h(q[j])
```
#### Example
Let's factorize $N = 21$ with coprime $x=2$, following the [above steps](#stepstwo) of the quantum period finding algorithm, which should return $r = 6$. This example follows one from [this](https://arxiv.org/abs/quant-ph/0303175) tutorial.
1. Choose $T = 2^t$ such that $N^2 \leq T \le 2N^2$. For $N = 21$, the smallest value of $t$ is 9, meaning $T = 2^t = 512$. Initialise two registers of qubits, first an argument register with $t = 9$ qubits, and second a function register with $n = log_2 N = 5$ qubits:
$$\vert\psi_0\rangle = \vert 0 \rangle \vert 0 \rangle$$
2. Apply a Hadamard gate on each of the qubits in the argument register:
$$\vert\psi_1\rangle = \frac{1}{\sqrt{T}}\sum_{a=0}^{T-1}\vert a \rangle \vert 0 \rangle = \frac{1}{\sqrt{512}}\sum_{a=0}^{511}\vert a \rangle \vert 0 \rangle$$
3. Implement the modular exponentiation function $x^a \bmod N$ on the function register:
\begin{eqnarray}
\vert\psi_2\rangle
& = & \frac{1}{\sqrt{T}}\sum_{a=0}^{T-1}\vert a \rangle \vert x^a \bmod N \rangle
= \frac{1}{\sqrt{512}}\sum_{a=0}^{511}\vert a \rangle \vert 2^a \bmod 21 \rangle \\
& = & \frac{1}{\sqrt{512}} \bigg( \;\; \vert 0 \rangle \vert 1 \rangle + \vert 1 \rangle \vert 2 \rangle +
\vert 2 \rangle \vert 4 \rangle + \vert 3 \rangle \vert 8 \rangle + \;\; \vert 4 \rangle \vert 16 \rangle + \;\,
\vert 5 \rangle \vert 11 \rangle \, + \\
& & \;\;\;\;\;\;\;\;\;\;\;\;\;\, \vert 6 \rangle \vert 1 \rangle + \vert 7 \rangle \vert 2 \rangle + \vert 8 \rangle \vert 4 \rangle + \vert 9 \rangle \vert 8 \rangle + \vert 10 \rangle \vert 16 \rangle + \vert 11 \rangle \vert 11 \rangle \, +\\
& & \;\;\;\;\;\;\;\;\;\;\;\;\, \vert 12 \rangle \vert 1 \rangle + \ldots \bigg)\\
\end{eqnarray}
Notice that the above expression has the following pattern: the states of the second register of each “column” are the same. Therefore we can rearrange the terms in order to collect the second register:
\begin{eqnarray}
\vert\psi_2\rangle
& = & \frac{1}{\sqrt{512}} \bigg[ \big(\,\vert 0 \rangle + \;\vert 6 \rangle + \vert 12 \rangle \ldots + \vert 504 \rangle + \vert 510 \rangle \big) \, \vert 1 \rangle \, + \\
& & \;\;\;\;\;\;\;\;\;\;\; \big(\,\vert 1 \rangle + \;\vert 7 \rangle + \vert 13 \rangle \ldots + \vert 505 \rangle + \vert 511 \rangle \big) \, \vert 2 \rangle \, + \\
& & \;\;\;\;\;\;\;\;\;\;\; \big(\,\vert 2 \rangle + \;\vert 8 \rangle + \vert 14 \rangle \ldots + \vert 506 \rangle + \big) \, \vert 4 \rangle \, + \\
& & \;\;\;\;\;\;\;\;\;\;\; \big(\,\vert 3 \rangle + \;\vert 9 \rangle + \vert 15 \rangle \ldots + \vert 507 \rangle + \big) \, \vert 8 \rangle \, + \\
& & \;\;\;\;\;\;\;\;\;\;\; \big(\,\vert 4 \rangle + \vert 10 \rangle + \vert 16 \rangle \ldots + \vert 508 \rangle + \big) \vert 16 \rangle \, + \\
& & \;\;\;\;\;\;\;\;\;\;\; \big(\,\vert 5 \rangle + \vert 11 \rangle + \vert 17 \rangle \ldots + \vert 509 \rangle + \big) \vert 11 \rangle \, \bigg]\\
\end{eqnarray}
4. To simplify following equations, we'll measure the function register before performing a quantum Fourier transform on the argument register. This will yield one of the following numbers with equal probability: $\{1,2,4,6,8,16,11\}$. Suppose that the result of the measurement was $2$, then:
$$\vert\psi_3\rangle = \frac{1}{\sqrt{86}}(\vert 1 \rangle + \;\vert 7 \rangle + \vert 13 \rangle \ldots + \vert 505 \rangle + \vert 511 \rangle)\, \vert 2 \rangle $$
It does not matter what is the result of the measurement; what matters is the periodic pattern. The period of the states of the first register is the solution to the problem and the quantum Fourier transform can reveal the value of the period.
5. Perform a quantum Fourier transform on the argument register:
$$
\vert\psi_4\rangle
= QFT(\vert\psi_3\rangle)
= QFT(\frac{1}{\sqrt{86}}\sum_{a=0}^{85}\vert 6a+1 \rangle)\vert 2 \rangle
= \frac{1}{\sqrt{512}}\sum_{j=0}^{511}\bigg(\big[ \frac{1}{\sqrt{86}}\sum_{a=0}^{85} e^{-2 \pi i \frac{6ja}{512}} \big] e^{-2\pi i\frac{j}{512}}\vert j \rangle \bigg)\vert 2 \rangle
$$
6. Measure the argument register. The probability of measuring a result $j$ is:
$$ \rm{Probability}(j) = \frac{1}{512 \times 86} \bigg\vert \sum_{a=0}^{85}e^{-2 \pi i \frac{6ja}{512}} \bigg\vert^2$$
This peaks at $j=0,85,171,256,341,427$. Suppose that the result of the measement yielded $j = 85$, then using continued fraction approximation of $\frac{512}{85}$, we obtain $r=6$, as expected.
## Implementation <a id='implementation'></a>
```
from qiskit import Aer
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit import execute, register, get_backend, compile
from qiskit.tools.visualization import plot_histogram, circuit_drawer
```
As mentioned [earlier](#shorsalgorithm), many of the experimental demonstrations of Shor's algorithm rely on significant optimisations based on apriori knowledge of the expected results. We will follow the formulation in [this](http://science.sciencemag.org/content/351/6277/1068) paper, which demonstrates a reasonably scalable realisation of Shor's algorithm using $N = 15$. Below is the first figure from the paper, showing various quantum circuits, with the following caption: _Diagrams of Shor’s algorithm for factoring $N = 15$, using a generic textbook approach (**A**) compared with Kitaev’s approach (**B**) for a generic base $a$. (**C**) The actual implementation for factoring $15$ to base $11$, optimized for the corresponding single-input state. Here $q_i$ corresponds to the respective qubit in the computational register. (**D**) Kitaev’s approach to Shor’s algorithm for the bases ${2, 7, 8, 13}$. Here, the optimized map of the first multiplier is identical in all four cases, and the last multiplier is implemented with full modular multipliers, as depicted in (**E**). In all cases, the single QFT qubit is used three times, which, together with the four qubits in the computation register, totals seven effective qubits. (**E**) Circuit diagrams of the modular multipliers of the form $a \bmod N$ for bases $a = {2, 7, 8, 11, 13}$._
<img src="images/shoralgorithm.png" alt="Note: In order for images to show up in this jupyter notebook you need to select File => Trusted Notebook" width="500 px" align="center">
Note that we cannot run this version of Shor's algorithm on an IBM Quantum Experience device at the moment as we currently lack the ability to do measurement feedforward and qubit resetting. Thus we'll just be building the ciruits to run on the simulators for now. Based on Pinakin Padalia & Amitabh Yadav's implementation, found [here](https://github.com/amitabhyadav/Shor-Algorithm-on-IBM-Quantum-Experience)
First we'll construct the $a^1 \bmod 15$ circuits for $a = 2,7,8,11,13$ as in **E**:
```
# qc = quantum circuit, qr = quantum register, cr = classical register, a = 2, 7, 8, 11 or 13
def circuit_amod15(qc,qr,cr,a):
if a == 2:
qc.cswap(qr[4],qr[3],qr[2])
qc.cswap(qr[4],qr[2],qr[1])
qc.cswap(qr[4],qr[1],qr[0])
elif a == 7:
qc.cswap(qr[4],qr[1],qr[0])
qc.cswap(qr[4],qr[2],qr[1])
qc.cswap(qr[4],qr[3],qr[2])
qc.cx(qr[4],qr[3])
qc.cx(qr[4],qr[2])
qc.cx(qr[4],qr[1])
qc.cx(qr[4],qr[0])
elif a == 8:
qc.cswap(qr[4],qr[1],qr[0])
qc.cswap(qr[4],qr[2],qr[1])
qc.cswap(qr[4],qr[3],qr[2])
elif a == 11: # this is included for completeness
qc.cswap(qr[4],qr[2],qr[0])
qc.cswap(qr[4],qr[3],qr[1])
qc.cx(qr[4],qr[3])
qc.cx(qr[4],qr[2])
qc.cx(qr[4],qr[1])
qc.cx(qr[4],qr[0])
elif a == 13:
qc.cswap(qr[4],qr[3],qr[2])
qc.cswap(qr[4],qr[2],qr[1])
qc.cswap(qr[4],qr[1],qr[0])
qc.cx(qr[4],qr[3])
qc.cx(qr[4],qr[2])
qc.cx(qr[4],qr[1])
qc.cx(qr[4],qr[0])
```
Next we'll build the rest of the period finding circuit as in **D**:
```
# qc = quantum circuit, qr = quantum register, cr = classical register, a = 2, 7, 8, 11 or 13
def circuit_aperiod15(qc,qr,cr,a):
if a == 11:
circuit_11period15(qc,qr,cr)
return
# Initialize q[0] to |1>
qc.x(qr[0])
# Apply a**4 mod 15
qc.h(qr[4])
# controlled identity on the remaining 4 qubits, which is equivalent to doing nothing
qc.h(qr[4])
# measure
qc.measure(qr[4],cr[0])
# reinitialise q[4] to |0>
qc.reset(qr[4])
# Apply a**2 mod 15
qc.h(qr[4])
# controlled unitary
qc.cx(qr[4],qr[2])
qc.cx(qr[4],qr[0])
# feed forward
if cr[0] == 1:
qc.u1(math.pi/2.,qr[4])
qc.h(qr[4])
# measure
qc.measure(qr[4],cr[1])
# reinitialise q[4] to |0>
qc.reset(qr[4])
# Apply a mod 15
qc.h(qr[4])
# controlled unitary.
circuit_amod15(qc,qr,cr,a)
# feed forward
if cr[1] == 1:
qc.u1(math.pi/2.,qr[4])
if cr[0] == 1:
qc.u1(math.pi/4.,qr[4])
qc.h(qr[4])
# measure
qc.measure(qr[4],cr[2])
```
Next we build the optimised circuit for $11 \bmod 15$ as in **C**.
```
def circuit_11period15(qc,qr,cr):
# Initialize q[0] to |1>
qc.x(qr[0])
# Apply a**4 mod 15
qc.h(qr[4])
# controlled identity on the remaining 4 qubits, which is equivalent to doing nothing
qc.h(qr[4])
# measure
qc.measure(qr[4],cr[0])
# reinitialise q[4] to |0>
qc.reset(qr[4])
# Apply a**2 mod 15
qc.h(qr[4])
# controlled identity on the remaining 4 qubits, which is equivalent to doing nothing
# feed forward
if cr[0] == 1:
qc.u1(math.pi/2.,qr[4])
qc.h(qr[4])
# measure
qc.measure(qr[4],cr[1])
# reinitialise q[4] to |0>
qc.reset(qr[4])
# Apply 11 mod 15
qc.h(qr[4])
# controlled unitary.
qc.cx(qr[4],qr[3])
qc.cx(qr[4],qr[1])
# feed forward
if cr[1] == 1:
qc.u1(math.pi/2.,qr[4])
if cr[0] == 1:
qc.u1(math.pi/4.,qr[4])
qc.h(qr[4])
# measure
qc.measure(qr[4],cr[2])
```
Let's build and run a circuit for $a = 7$, and plot the results:
```
q = QuantumRegister(5, 'q')
c = ClassicalRegister(5, 'c')
shor = QuantumCircuit(q, c)
circuit_aperiod15(shor,q,c,7)
backend = Aer.get_backend('qasm_simulator')
sim_job = execute([shor], backend)
sim_result = sim_job.result()
sim_data = sim_result.get_counts(shor)
plot_histogram(sim_data)
```
We see here that the period, $r = 4$, and thus calculate the factors $p = \text{gcd}(a^{r/2}+1,15) = 3$ and $q = \text{gcd}(a^{r/2}-1,15) = 5$. Why don't you try seeing what you get for $a = 2, 8, 11, 13$?
|
github_jupyter
|
# A-weightening filter implementation
The A-weighting transfer function is defined in the ANSI Standards S1.4-1983 and S1.42-2001:
$$
H(s) = \frac{\omega_4^2 s^4}{(s-\omega_1)^2(s-\omega_2)(s-\omega_3)(s-\omega_4)^2}
$$
Where $\omega_i = 2\pi f_i$ are the angular frequencies defined by:
```
import numpy as np
f1 = 20.598997 # Hz
f4 = 12194.217 # Hz
f2 = 107.65265 # Hz
f3 = 737.86223 # Hz
w1 = 2*np.pi*f1 # rad/s
w2 = 2*np.pi*f2 # rad/s
w3 = 2*np.pi*f3 # rad/s
w4 = 2*np.pi*f4 # rad/s
```
In [1] ther is a method to convert this function transform to a discrete time-domain using the bilinear transform. We use a similar method, but we separate it into four filters of order one or two, in order to keep the filter stable:
$$
H(s) = \omega_4^2 H_1(s) H_2(s) H_3(s) H_4(s),
$$
where:
$$
H_i(s) = \left\{ \begin{array}{lcc}
\frac{s}{(s-\omega_i)^2} & \text{for} & i=1,4 \\
\\ \frac{s}{(s-\omega_i)} & \text{for} & i = 2,3. \\
\end{array}
\right.
$$
Now, we conver the $H_i(s)$ filters to their discrete-time implementation by using the bilinear transform:
$$
s \rightarrow 2f_s\frac{1+z^{-1}}{1-z^{-1}}.
$$
Therefore:
$$
H_i(z) = \frac{2f_s(1-z^{-2})}{(\omega_i-2f_s)^2z^{-2}+2(\omega_i^2-4f_s^2)z^{-1}+(\omega_i+2f_s)^2} \text{ for } i = 1,4
$$
$$
H_i(z) = \frac{2f_s(1-z^{-1})}{(\omega_i-2f_s)z^{-1}+(\omega_i+2f_s)} \text{ for } i = 2,3
$$
We define two python functions to calculates coefficients of both types of function transforms:
```
def filter_first_order(w,fs): #s/(s+w)
a0 = w + 2.0*fs
b = 2*fs*np.array([1, -1])/a0
a = np.array([a0, w - 2*fs])/a0
return b,a
def filter_second_order(w,fs): #s/(s+w)^2
a0 = (w + 2.0*fs)**2
b = 2*fs*np.array([1,0,-1])/a0
a = np.array([a0,2*(w**2-4*fs**2),(w-2*fs)**2])/a0
return b,a
```
Now, we calculate b and a coefficients of the four filters for some sampling rate:
```
fs = 48000 #Hz
b1,a1 = filter_second_order(w1,fs)
b2,a2 = filter_first_order(w2,fs)
b3,a3 = filter_first_order(w3,fs)
b4,a4 = filter_second_order(w4,fs)
```
Then, we calculate the impulse response of the overall filter, $h[n]$, by concatenating the four filters and using the impulse signal, $\delta[n]$, as input.
```
from scipy import signal
# generate delta[n]
N = 8192*2 #number of points
delta = np.zeros(N)
delta[0] = 1
# apply filters
x1 = signal.lfilter(b1,a1,delta)
x2 = signal.lfilter(b2,a2,x1)
x3 = signal.lfilter(b3,a3,x2)
h = signal.lfilter(b4,a4,x3)
GA = 10**(2/20.) # 0dB at 1Khz
h = h*GA*w4**2
```
Lets find the filter's frequency response, $H(e^{j\omega})$, by calcuating the FFT of $h[n]$.
```
H = np.abs(np.fft.fft(h))[:N/2]
H = 20*np.log10(H)
```
Compare the frequency response to the expresion defined in the norms:
```
eps = 10**-6
f = np.linspace(0,fs/2-fs/float(N),N/2)
curveA = f4**2*f**4/((f**2+f1**2)*np.sqrt((f**2+f2**2)*(f**2+f3**2))*(f**2+f4**2))
HA = 20*np.log10(curveA+eps)+2.0
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,10))
plt.title('Digital filter frequency response')
plt.plot(f,H, 'b',label= 'Devised filter')
plt.plot(f,HA, 'r',label= 'Norm filter')
plt.ylabel('Amplitude [dB]')
plt.xlabel('Frequency [Hz]')
plt.legend()
plt.xscale('log')
plt.xlim([10,fs/2.0])
plt.ylim([-80,3])
plt.grid()
plt.show()
```
Now we also can check if the filter designed fullfill the tolerances given in the ANSI norm [2].
```
import csv
freqs = []
tol_type0_low = []
tol_type0_high = []
tol_type1_low = []
tol_type1_high = []
with open('ANSI_tolerances.csv') as csv_file:
csv_reader = csv.reader(csv_file, delimiter=',')
line_count = 0
for row in csv_reader:
if line_count == 0:
#print('Column names are {", ".join(row)}')
line_count += 1
else:
freqs.append(float(row[0]))
Aw = float(row[1])
tol_type0_low.append(Aw + float(row[2]))
tol_type0_high.append(Aw + float(row[3]))
tol_type1_low.append(Aw + float(row[4]))
if row[5] != '':
tol_type1_high.append(Aw + float(row[5]))
else:
tol_type1_high.append(np.Inf)
line_count += 1
print('Processed %d lines.'%line_count)
fig = plt.figure(figsize=(10,10))
plt.title('Digital filter frequency response')
plt.plot(f,H, 'b',label= 'Devised filter')
plt.plot(f,HA, 'r',label= 'Norm filter')
plt.plot(freqs,tol_type0_low,'k.',label='type0 tolerances')
plt.plot(freqs,tol_type0_high,'k.')
plt.plot(freqs,tol_type1_low,'r.',label='type1 tolerances')
plt.plot(freqs,tol_type1_high,'r.')
plt.ylabel('Amplitude [dB]')
plt.xlabel('Frequency [Hz]')
plt.legend()
plt.xscale('log')
plt.xlim([10,fs/2.0])
plt.ylim([-80,3])
plt.grid()
plt.show()
```
## References
[1] Rimell, Andrew; Mansfield, Neil; Paddan, Gurmail (2015). "Design of digital filters for frequency weightings (A and C) required for risk assessments of workers exposed to noise". Industrial Health (53): 21–27.
[2] ANSI S1.4-1983. Specifications for Sound Level Meters.
|
github_jupyter
|
# Supervised baselines
Notebook with strong supervised learning baseline on cifar-10
```
%reload_ext autoreload
%autoreload 2
```
You probably need to install dependencies
```
# All things needed
!git clone https://github.com/puhsu/sssupervised
!pip install -q fastai2
!pip install -qe sssupervised
```
After running cell above you should restart your kernel
```
from sssupervised.cifar_utils import CifarFactory
from sssupervised.randaugment import RandAugment
from fastai2.data.transforms import parent_label, Categorize
from fastai2.optimizer import ranger, Adam
from fastai2.layers import LabelSmoothingCrossEntropy
from fastai2.metrics import error_rate
from fastai2.callback.all import *
from fastai2.vision.all import *
```
Baseline uses wideresnet-28-2 model with randaugment augmentation policy. It is optiimzed with RAadam with lookahead with one-cycle learning rate and momentum schedules for 200 epochs (we count epochs in number of steps on standard cifar, so we set 4000 epochs in our case, because we only have $2400$ training examples ($50000/2400 \approx 20$)
```
cifar = untar_data(URLs.CIFAR)
files, (train, test, unsup) = CifarFactory(n_same_cls=3, seed=42, n_labeled=400).splits_from_path(cifar)
sup_ds = Datasets(files, [[PILImage.create, RandAugment, ToTensor], [parent_label, Categorize]], splits=(train, test))
sup_dl = sup_ds.dataloaders(after_batch=[IntToFloatTensor, Normalize.from_stats(*cifar_stats)])
sup_dl.train.show_batch(max_n=9)
# https://github.com/uoguelph-mlrg/Cutout
import math
import torch
import torch.nn as nn
import torch.nn.functional as F
class BasicBlock(nn.Module):
def __init__(self, in_planes, out_planes, stride, dropRate=0.0):
super().__init__()
self.bn1 = nn.BatchNorm2d(in_planes)
self.relu1 = nn.ReLU(inplace=True)
self.conv1 = nn.Conv2d(in_planes, out_planes, kernel_size=3, stride=stride,
padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(out_planes)
self.relu2 = nn.ReLU(inplace=True)
self.conv2 = nn.Conv2d(out_planes, out_planes, kernel_size=3, stride=1,
padding=1, bias=False)
self.droprate = dropRate
self.equalInOut = (in_planes == out_planes)
self.convShortcut = (not self.equalInOut) and nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=stride,
padding=0, bias=False) or None
def forward(self, x):
if not self.equalInOut: x = self.relu1(self.bn1(x))
else: out = self.relu1(self.bn1(x))
out = self.relu2(self.bn2(self.conv1(out if self.equalInOut else x)))
if self.droprate > 0:
out = F.dropout(out, p=self.droprate, training=self.training)
out = self.conv2(out)
return torch.add(x if self.equalInOut else self.convShortcut(x), out)
class NetworkBlock(nn.Module):
def __init__(self, nb_layers, in_planes, out_planes, block, stride, dropRate=0.0):
super().__init__()
self.layer = self._make_layer(block, in_planes, out_planes, nb_layers, stride, dropRate)
def _make_layer(self, block, in_planes, out_planes, nb_layers, stride, dropRate):
layers = []
for i in range(nb_layers):
layers.append(block(i == 0 and in_planes or out_planes, out_planes, i == 0 and stride or 1, dropRate))
return nn.Sequential(*layers)
def forward(self, x): return self.layer(x)
class WideResNet(nn.Module):
def __init__(self, depth, num_classes, widen_factor=1, dropRate=0.0):
super().__init__()
nChannels = [16, 16*widen_factor, 32*widen_factor, 64*widen_factor]
assert((depth - 4) % 6 == 0)
n = (depth - 4) // 6
block = BasicBlock
# 1st conv before any network block
self.conv1 = nn.Conv2d(3, nChannels[0], kernel_size=3, stride=1,
padding=1, bias=False)
self.block1 = NetworkBlock(n, nChannels[0], nChannels[1], block, 1, dropRate)
self.block2 = NetworkBlock(n, nChannels[1], nChannels[2], block, 2, dropRate)
self.block3 = NetworkBlock(n, nChannels[2], nChannels[3], block, 2, dropRate)
self.bn1 = nn.BatchNorm2d(nChannels[3])
self.relu = nn.ReLU(inplace=True)
self.fc = nn.Linear(nChannels[3], num_classes)
self.nChannels = nChannels[3]
for m in self.modules():
if isinstance(m, nn.Conv2d):
n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
m.weight.data.normal_(0, math.sqrt(2. / n))
elif isinstance(m, nn.BatchNorm2d):
m.weight.data.fill_(1)
m.bias.data.zero_()
elif isinstance(m, nn.Linear): m.bias.data.zero_()
def forward(self, x):
out = self.conv1(x)
out = self.block1(out)
out = self.block2(out)
out = self.block3(out)
out = self.relu(self.bn1(out))
out = F.adaptive_avg_pool2d(out, 1)
out = out.view(-1, self.nChannels)
return self.fc(out)
def wrn_22(): return WideResNet(depth=22, num_classes=10, widen_factor=6, dropRate=0.)
def wrn_22_k8(): return WideResNet(depth=22, num_classes=10, widen_factor=8, dropRate=0.)
def wrn_22_k10(): return WideResNet(depth=22, num_classes=10, widen_factor=10, dropRate=0.)
def wrn_22_k8_p2(): return WideResNet(depth=22, num_classes=10, widen_factor=8, dropRate=0.2)
def wrn_28(): return WideResNet(depth=28, num_classes=10, widen_factor=6, dropRate=0.)
def wrn_28_k8(): return WideResNet(depth=28, num_classes=10, widen_factor=8, dropRate=0.)
def wrn_28_k8_p2(): return WideResNet(depth=28, num_classes=10, widen_factor=8, dropRate=0.2)
def wrn_28_p2(): return WideResNet(depth=28, num_classes=10, widen_factor=6, dropRate=0.2)
```
We override default callbacks (the best way I found, to pass extra arguments to callbacks)
```
defaults.callbacks = [
TrainEvalCallback(),
Recorder(train_metrics=True),
ProgressCallback(),
]
class SkipSomeValidations(Callback):
"""Perform validation regularly, but not every epoch
(usefull for small datasets, where training is quick)"""
def __init__(self, n_epochs=20): self.n_epochs=n_epochs
def begin_validate(self):
if self.train_iter % self.n_epochs != 0:
raise CancelValidException()
learner = Learner(
sup_dl,
wrn_28(),
CrossEntropyLossFlat(),
opt_func=ranger,
wd=1e-2,
metrics=error_rate,
cbs=[ShowGraphCallback(), SkipSomeValidations(n_epochs=20)]
)
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
train=pd.read_csv(r'C:\Users\prath\LoanEligibilityPrediction\Dataset\train.csv')
train.Loan_Status=train.Loan_Status.map({'Y':1,'N':0})
train.isnull().sum()
Loan_status=train.Loan_Status
train.drop('Loan_Status',axis=1,inplace=True)
test=pd.read_csv(r'C:\Users\prath\LoanEligibilityPrediction\Dataset\test.csv')
Loan_ID=test.Loan_ID
data=train.append(test)
data.head()
data.describe()
data.isnull().sum()
data.Dependents.dtypes
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
corrmat=data.corr()
f,ax=plt.subplots(figsize=(9,9))
sns.heatmap(corrmat,vmax=.8,square=True)
data.Gender=data.Gender.map({'Male':1,'Female':0})
data.Gender.value_counts()
corrmat=data.corr()
f,ax=plt.subplots(figsize=(9,9))
sns.heatmap(corrmat,vmax=.8,square=True)
data.Married=data.Married.map({'Yes':1,'No':0})
data.Married.value_counts()
data.Dependents=data.Dependents.map({'0':0,'1':1,'2':2,'3+':3})
data.Dependents.value_counts()
corrmat=data.corr()
f,ax=plt.subplots(figsize=(9,9))
sns.heatmap(corrmat,vmax=.8,square=True)
data.Education=data.Education.map({'Graduate':1,'Not Graduate':0})
data.Education.value_counts()
data.Self_Employed=data.Self_Employed.map({'Yes':1,'No':0})
data.Self_Employed.value_counts()
data.Property_Area.value_counts()
data.Property_Area=data.Property_Area.map({'Urban':2,'Rural':0,'Semiurban':1})
data.Property_Area.value_counts()
corrmat=data.corr()
f,ax=plt.subplots(figsize=(9,9))
sns.heatmap(corrmat,vmax=.8,square=True)
data.head()
data.Credit_History.size
data.Credit_History.fillna(np.random.randint(0,2),inplace=True)
data.isnull().sum()
data.Married.fillna(np.random.randint(0,2),inplace=True)
data.isnull().sum()
data.LoanAmount.fillna(data.LoanAmount.median(),inplace=True)
data.Loan_Amount_Term.fillna(data.Loan_Amount_Term.mean(),inplace=True)
data.isnull().sum()
data.Gender.value_counts()
from random import randint
data.Gender.fillna(np.random.randint(0,2),inplace=True)
data.Gender.value_counts()
data.Dependents.fillna(data.Dependents.median(),inplace=True)
data.isnull().sum()
corrmat=data.corr()
f,ax=plt.subplots(figsize=(9,9))
sns.heatmap(corrmat,vmax=.8,square=True)
data.Self_Employed.fillna(np.random.randint(0,2),inplace=True)
data.isnull().sum()
data.head()
data.drop('Loan_ID',inplace=True,axis=1)
data.isnull().sum()
train_X=data.iloc[:614,]
train_y=Loan_status
X_test=data.iloc[614:,]
seed=7
from sklearn.model_selection import train_test_split
train_X,test_X,train_y,test_y=train_test_split(train_X,train_y,random_state=seed)
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
models=[]
models.append(("logreg",LogisticRegression()))
models.append(("tree",DecisionTreeClassifier()))
models.append(("lda",LinearDiscriminantAnalysis()))
models.append(("svc",SVC()))
models.append(("knn",KNeighborsClassifier()))
models.append(("nb",GaussianNB()))
seed=7
scoring='accuracy'
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
result=[]
names=[]
for name,model in models:
#print(model)
kfold=KFold(n_splits=10,random_state=seed)
cv_result=cross_val_score(model,train_X,train_y,cv=kfold,scoring=scoring)
result.append(cv_result)
names.append(name)
print("%s %f %f" % (name,cv_result.mean(),cv_result.std()))
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
svc=LogisticRegression()
svc.fit(train_X,train_y)
pred=svc.predict(test_X)
print(accuracy_score(test_y,pred))
print(confusion_matrix(test_y,pred))
print(classification_report(test_y,pred))
df_output=pd.DataFrame()
outp=svc.predict(X_test).astype(int)
outp
df_output['Loan_ID']=Loan_ID
df_output['Loan_Status']=outp
df_output.head()
df_output[['Loan_ID','Loan_Status']].to_csv(r'C:\Users\prath\LoanEligibilityPrediction\Dataset\outputlr.csv',index=False)
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
svc=DecisionTreeClassifier()
svc.fit(train_X,train_y)
pred=svc.predict(test_X)
print(accuracy_score(test_y,pred))
print(confusion_matrix(test_y,pred))
print(classification_report(test_y,pred))
df_output=pd.DataFrame()
outp=svc.predict(X_test).astype(int)
outp
df_output['Loan_ID']=Loan_ID
df_output['Loan_Status']=outp
df_output.head()
df_output[['Loan_ID','Loan_Status']].to_csv(r'C:\Users\prath\LoanEligibilityPrediction\Dataset\outputdt.csv',index=False)
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
svc=LinearDiscriminantAnalysis()
svc.fit(train_X,train_y)
pred=svc.predict(test_X)
print(accuracy_score(test_y,pred))
print(confusion_matrix(test_y,pred))
print(classification_report(test_y,pred))
df_output=pd.DataFrame()
outp=svc.predict(X_test).astype(int)
outp
df_output['Loan_ID']=Loan_ID
df_output['Loan_Status']=outp
df_output.head()
df_output[['Loan_ID','Loan_Status']].to_csv(r'C:\Users\prath\LoanEligibilityPrediction\Dataset\outputld.csv',index=False)
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
svc=SVC()
svc.fit(train_X,train_y)
pred=svc.predict(test_X)
print(accuracy_score(test_y,pred))
print(confusion_matrix(test_y,pred))
print(classification_report(test_y,pred))
df_output=pd.DataFrame()
outp=svc.predict(X_test).astype(int)
outp
df_output['Loan_ID']=Loan_ID
df_output['Loan_Status']=outp
df_output.head()
df_output[['Loan_ID','Loan_Status']].to_csv(r'C:\Users\prath\LoanEligibilityPrediction\Dataset\outputSVC.csv',index=False)
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
svc=KNeighborsClassifier()
svc.fit(train_X,train_y)
pred=svc.predict(test_X)
print(accuracy_score(test_y,pred))
print(confusion_matrix(test_y,pred))
print(classification_report(test_y,pred))
df_output=pd.DataFrame()
outp=svc.predict(X_test).astype(int)
outp
df_output['Loan_ID']=Loan_ID
df_output['Loan_Status']=outp
df_output.head()
df_output[['Loan_ID','Loan_Status']].to_csv(r'C:\Users\prath\LoanEligibilityPrediction\Dataset\outputknn.csv',index=False)
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
svc=GaussianNB()
svc.fit(train_X,train_y)
pred=svc.predict(test_X)
print(accuracy_score(test_y,pred))
print(confusion_matrix(test_y,pred))
print(classification_report(test_y,pred))
df_output=pd.DataFrame()
outp=svc.predict(X_test).astype(int)
outp
df_output['Loan_ID']=Loan_ID
df_output['Loan_Status']=outp
df_output.head()
df_output[['Loan_ID','Loan_Status']].to_csv(r'C:\Users\prath\LoanEligibilityPrediction\Dataset\outputgnb.csv',index=False)
```
|
github_jupyter
|
# Jupyter Notebooks and CONSTELLATION
This notebook is an introduction to using Jupyter notebooks with CONSTELLATION. In part 1, we'll learn how to send data to CONSTELLATION to create and modify graphs. In part 2, we'll learn how to retrieve graph data from CONSTELLATION. Part 3 will be about getting and setting information about the graph itself. Part 4 will show how to call plugins. Part 5 is a quick look at types. Part 6 will be fun (and occasionally useful). Part 7 introduces some advanced graph usage.
This notebook uses Python libraries that are included in the [Python Anaconda3 distribution](https://www.anaconda.com/distribution/) version 2020.02, Python v3.7.6.
To run through the notebook, click on the triangular 'run cell' button in the toolbar to execute the current cell and move to the next cell.
Let's start by seeing if we can talk to CONSTELLATION. Make sure that CONSTELLATION is running, and you've started the external scripting server (which has been done for you if you started the Jupyter notebook server from CONSTELLATION). The external scripting server makes a REST HTTP API available for use by any HTTP client.
The Python ``import`` statement looks for a library with the given name. Click the 'run cell' button to execute it.
(All of the libraries used here are included in the Anaconda Python distribution.)
```
import io
import os
import pandas as pd
import PIL.Image, PIL.ImageDraw, PIL.ImageFilter, PIL.ImageFont
# Also import some of the notebook display methods so we can display nice things.
#
from IPython.display import display, HTML, Image
# This is a convenient Python interface to the REST API.
#
import constellation_client
cc = constellation_client.Constellation()
```
When the external scripting server started, it automatically downloaded ``constellation_client.py`` into your ``.ipython`` directory. It's also important that you create a client instance **after** you start the REST server, because the server creates a secret that the client needs to know to communicate with the server.
After the import succeeds, we then create a Python object that communicates with CONSTELLATION on our behalf. CONSTELLATION provides communication with the outside world using HTTP (as if it were a web server) and JSON (a common data format). The ``constellation_client`` library hides these details so you can just use Python.
## Part 1: Sending Data to CONSTELLATION
Typically you'll have some data in a CSV file. We'll use some Python tricks (in this case, ``io.StringIO``) to make it look like we have a separate CSV file that we're reading into a dataframe. (If your data is in an Excel spreadsheet, you could use ``read_excel()`` to read it it directly, rather than saving it to a CVS file first.)
```
csv_data = '''
from_address,from_country,to_address,to_country,dtg
[email protected],Brazil,[email protected],India,2017-01-01 12:34:56
[email protected],Brazil,[email protected],Zambia,2017-01-01 14:30:00
[email protected],India
'''.strip()
df = pd.read_csv(io.StringIO(csv_data))
df
```
Putting our data in a dataframe is a good idea; not only can we easily manipulate it, but it's easy to send a dataframe to CONSTELLATION, as long as we tell CONSTELLATION what data belongs where.
A dataframe is a table of data, but CONSTELLATION deals with graphs, so we need to reconcile a data table and a graph. It shouldn't be too hard to notice (especially given the column names) that a row of data in the dataframe represents a transaction: the source node has the "from" attributes, the destination node has the "to" attributes, and the transaction has the dtg attribute. The first row therefore represents a connection from `[email protected]` with country value `Brazil` to `[email protected]` with country value `India`. The last row represents a node that is not connected to any other node.
Let's massage the data to something that CONSTELLATION likes. All of the addresses are email addresses, which CONSTELLATION should be clever enough to recognise, but we'd prefer to be explicit, so let's add the types.
```
df.from_address = df.from_address + '<Email>'
df.to_address = df.to_address + '<Email>'
df
```
Dataframes are clever enough to work on a column at a time; we don't have to do our own loops.
Let's check the data types.
```
df.dtypes
```
All of the columns are of type ``object``, which in this case means "string". However, CONSTELLATION expects datetimes to actually be of ``datetime`` type; if we try and upload datetimes as strings, CONSTELLATION won't recognise them as datetimes.
Not to worry: pandas can fix that for us.
```
df.dtg = pd.to_datetime(df.dtg)
df
```
The datetimes look exactly the same, but notice that the ``Not a Number`` value in the last row has become a ``Not a Timestamp`` value. If we look at the data types again, we can see that the ``dtg`` values are now datetimes, not objects.
```
df.dtypes
```
The ``datetime64[ns]`` type means that datetimes are stored as a 64-bit number representing a number of nanoseconds from a zero timestamp. Not that we care that much about the storage: the important thing is that ``dtg`` is now
a datetime column.
CONSTELLATION recognises source, destination and transaction attributes by the prefixes of their names. It won't be too surprising to find out that the prefixes are ``source``, ``destination``, and ``transaction``, with a ``.`` separating the prefixes from the attribute names.
Let's rename the columns to match what CONSTELLATION expects. (We didn't do this first because the column headers were valid Python identifiers, it was easier to type ``df.dtg`` than ``df['transaction.DateTime']``.)
Note that we use the name ``Identifier`` for the values that uniquely identify a particular node.
```
df = df.rename(columns={
'from_address': 'source.Label',
'from_country': 'source.Geo.Country',
'to_address': 'destination.Label',
'to_country': 'destination.Geo.Country',
'dtg': 'transaction.DateTime'})
df
```
Now the dataframe is ready to be sent to CONSTELLATION. We'll create a new graph (using the ``new_graph()`` method), and send the dataframe to CONSTELLATION using the ``put_dataframe()`` method.
If you get a Python `ConnectionRefusedError` when you run this cell, you've probably forgotten to start the CONSTELLATION external scripting server in the Tools menu. If you start it now, you'll have to go back and re-execute the "`cc = constellation_client.Constellation()`" cell, then come back here.)
```
cc.new_graph()
cc.put_dataframe(df)
```
CONSTELLATION creates a new graph, accepts the contents of the dataframe, applies the schema, and automatically arranges the graph. Finally, it resets the view so you can see the complete graph.
In this simple case, it's easy to see that the first two rows of the dataframe are correctly represented as nodes with transactions between them. The third row of the dataframe does not have a destination, so there is no transaction.
If you open the `Attribute Editor` view and select a transaction, you'll see that they have the correct ``DateTime`` values.
Of course, we didn't have to create a new graph. In the same graph, let's add a new node with a transaction from an existing node (`[email protected]`). We'll use another (pretend) CSV file and modify the dataframe as we did before.
```
csv_data = '''
from_address,from_country,to_address,to_country,dtg
[email protected],Zambia,[email protected],Brazil,2017-01-02 01:22:33
'''.strip()
dfn = pd.read_csv(io.StringIO(csv_data))
dfn.from_address = dfn.from_address + '<Email>'
dfn.to_address = dfn.to_address + '<Email>'
dfn.dtg = pd.to_datetime(dfn.dtg)
dfn = dfn.rename(columns={
'from_address': 'source.Label',
'from_country': 'source.Geo.Country',
'to_address': 'destination.Label',
'to_country': 'destination.Geo.Country',
'dtg': 'transaction.DateTime'})
cc.put_dataframe(dfn)
```
## Part 2: Getting Data from CONSTELLATION
We'll use the graph that we created in Part 1 to see what happens when we get data from CONSTELLATION. Make sure that the graph is still displayed in CONSTELLATION.
```
df = cc.get_dataframe()
df.head()
```
There seems to be more data there. Let's look at the columns.
```
print(f'Number of columns: {len(df.columns)}')
df.columns
```
We added five columns in part 1, but we get 50+ columns back! (The number may vary depending on the version of CONSTELLATION and your default schema.)
What's going on?
Remember that CONSTELLATION will apply the graph's schema to your data, and do an arrangement. Those other columns are the result of applying the schema, or (in the case of the x, y, z columns) applying an arrangement. The columns are in the dataframe in no particular order.
Let's have a look at the data types in the dataframe.
```
df.dtypes
```
The various ``selected`` columns are bool (that is, ``true`` or ``false`` values): an element is either selected or not selected. The ``transaction.DateTime`` is a ``datetime64[ns]`` as expected. Everything else should be unsurprising. One thing to notice is that ``source.nradius`` may be an ``int64``, even though in CONSTELLATION it's a ``float``. This is because ``nradius`` usually has integer values (typically 1.0), so the dataframe will convert it to an ``int64``. This shouldn't be a problem for us; it's still a number. This can happen for any column that only has integral values.
We can see what the CONSTELLATION types are using ``cc``'s type attribute: the ``Constellation`` instance will remember the types after each call to ``get_dataframe()``. (Usually you won't have to worry about these.)
```
cc.types
```
CONSTELLATION types such ``boolean``, ``datetime``, ``float``, ``int``, ``string`` convert to their obvious types in a dataframe. Other types convert to reasonable string equivalents; for example, ``icon`` converts to a string containing the name of the icon.
The ``color`` type converts to a ``[red, green, blue, alpha]`` list, where each value ranges from 0 to 1. Some people are more used to web colors (in the format #RRGGBB). The following function converts a color list to a web color.
```
def to_web_color(color):
"""Convert an RGB tuple of 0..1 to a web color."""
return f'#{int(color[0]*255):02x}{int(color[1]*255):02x}{int(color[2]*255):02x}'
```
For example:
```
print(df['source.color'])
print(df['source.color'].apply(to_web_color))
```
Which allows us to display labels using their node's schema color.
```
import html
for label,color in df[['source.Label', 'source.color']].values:
h = '<span style="color:{}">{}</span>'.format(to_web_color(color), html.escape(label))
display(HTML(h))
```
### Graph elements
Calling ``get_dataframe()`` with no parameters gave us four rows representing the whole graph: one row for each transaction, and a row for the singleton node.
Sometimes we don't want all of the graph. We can ask for just the nodes.
```
df = cc.get_dataframe(vx=True)
df
```
Five rows, one for each node. Note that all of the columns use the ``source`` prefix.
We can ask for just the transactions.
```
df = cc.get_dataframe(tx=True)
df
```
Three rows, one for each transaction. Note that transactions always include the source and destination nodes.
Finally, you can get just the elements that are selected. Before you run the next cell, use your mouse to select two nodes in the current graph.
```
df = cc.get_dataframe(vx=True, selected=True)
df
```
Two rows, one for each selected node. Select some different nodes and try again. (If you don't see any rows here, it's because you didn't select any nodes. Select a couple of nodes and run the cell again.)
Generally, you'll probably want one of ``vx=True`` when you're looking at nodes, or ``tx=True`` when you're looking at transactions.
Select a couple of transactions, then run the next cell.
```
df = cc.get_dataframe(tx=True, selected=True)
df
```
When you ask for transactions, you not only get the transaction data, but the data for the modes at each end of the transaction as well.
### Choosing attributes
You generally don't want all of the attributes that CONSTELLATION knows about. For example, the x,y,z coordinates are rarely useful when you're analysing data. The ``get_dataframe()`` method allows you to specify only the attributes you want. Not only does this use less space in the dataframe, but particularly for larger graphs, it can greatly reduce the time taken to get the data from the graph into a dataframe.
First we'll find out what graph, node, and transaction attributes exist. The `get_attributes()` method returns a dictionary mapping attribute names to their CONSTELLATION types. For consistency with the other method return values, the attribute names are prefixed with `graph.`, `source.`, and `transaction.`. (Attributes that start with `graph.` are attributes of the graph itself, such as the graph's background color. You can see these in the "Graph" section of the Attribute Editor.)
```
attrs = cc.get_attributes()
attrs
```
To specify just the attributes you want, pass a list of attribute names using the ``attrs`` parameter.
```
df = cc.get_dataframe(vx=True, attrs=['source.Identifier', 'source.Type'])
df
```
### Updating the graph: nodes
There is a special attribute for each element that isn't visible in CONSTELLATION: ``source.[id]``, ``destination.[id]``, and ``transaction.[id]``. These are unique identifiers for each element. These identifiers can change whenever a graph is modified, so they can't be relied on to track an element. However, they can be used to identify a unique element when you get a dataframe, modify a value, and send the dataframe back to CONSTELLATION.
For example, suppose we want to make all nodes in the ``@example3.com`` domain larger, and color them blue. We need the ``Identifier`` attribute (for the domain name), the ``nradius`` attribute so we can modify it, and the ``source.[id]`` attribute to tell CONSTELLATION which nodes to modify. We don't need to get the color, because we don't care what it is before we change it. xx
```
df = cc.get_dataframe(vx=True, attrs=['source.Identifier', 'source.nradius', 'source.[id]'])
df
```
Let's filter out the ``example3.com`` nodes and double their radii.
```
e3 = df[df['source.Identifier'].str.endswith('@example3.com')].copy()
e3['source.nradius'] *= 2
e3
```
We don't need to send the ``source.Identifier`` column back to CONSTELLATION, so let's drop it. We'll also add the color column. (Fortunately, CONSTELLATION is quite forgiving about color values.)
```
e3 = e3.drop('source.Identifier', axis=1)
e3['source.color'] = 'blue'
e3
```
Finally, we can send this dataframe to CONSTELLATION.
```
cc.put_dataframe(e3)
```
The two ``example3.com`` nodes should be noticably larger. However, the colors didn't change. This is because one of the things that CONSTELLATION does for us is to apply the graph's schema whenever you call ``put_dataframe()``, so the color changes to blue, then is immediately overridden by the schema.
Let's put the node sizes back to 1, and call ``put_dataframe()`` again, but this time tell CONSTELLATION not to apply the schema.
```
e3['source.nradius'] = 1
cc.put_dataframe(e3, complete_with_schema=False)
```
Better.
Another thing that CONSTELLATION does for a ``put_dataframe()`` is a simple arrangement. If you want to create your own arrangement, you have to tell CONSTELLATION not to do this using the ``arrange`` parameter.
Let's arrange the nodes in a circle, just like the built-in circle arrangement. (Actually, wih only five nodes, it's more of a pentagon.) We don't need to know anything about the nodes for this one, we just need to know they exist. In particular, we don't need to know their current x, y, and z positions; we'll just create new ones.
```
df = cc.get_dataframe(vx=True, attrs=['source.[id]'])
df
n = len(df)
import numpy as np
df['source.x'] = n * np.sin(2*np.pi*(df.index/n))
df['source.y'] = n * np.cos(2*np.pi*(df.index/n))
df['source.z'] = 0
df
cc.put_dataframe(df, arrange='')
```
The empty string tells CONSTELLATION not to perform any arrangement. (You could put the name of any arrangement plugin there, but there are better ways of doing that.)
Also note that the blue nodes aren't blue any more, because the schema was applied.
### Updating the graph: transactions
The graph we created earlier has a problem: the transactions have the wrong type. More precisely, they don't have any type. Let's fix that. We'll get all of the transactions from the graph, give them a type, and update the graph.
When you run this, the transactions will turn green, indicating that schema completion has happened. You can look at the Attribute Editor to see that the transactions types are now `Communication`.
```
# Get the transactions from the graph.
#
tx_df = cc.get_dataframe(tx=True, attrs=['transaction.[id]'])
display(tx_df)
# Add the transaction type.
#
tx_df['transaction.Type'] = 'Communication'
display(tx_df)
# Update the graph.
#
cc.put_dataframe(tx_df)
```
### Updating the graph: custom attributes
Sometimes we want to add attributes that aren't defined in the graph's schema. For example, let's add an attribute called ``Country.Chars`` that shows the number of characters in each node's country name.
```
c_df = cc.get_dataframe(vx=True, attrs=['source.[id]', 'source.Geo.Country'])
c_df['source.Country.Chars'] = c_df['source.Geo.Country'].str.len()
display(c_df)
display(c_df.dtypes)
cc.put_dataframe(c_df)
```
If you look at the Attribute Editor, you'll see the new node attribute ``Country.Chars``. However, if you right-click on the attribute and select ``Modify Attribute``, you'll see that the new attribute is a string, not an integer, even though the value is an integer in the dataframe. This is because CONSTELLATION assumes that everything it doesn't recognise is a string.
We can fix this by suffixing a type indicator to the column name. Let's create a new attribute called ``Country.Length`` which we turn into an integer by adding ``<integer>`` to the name.
```
c_df = cc.get_dataframe(vx=True, attrs=['source.[id]', 'source.Geo.Country'])
c_df['source.Country.Length<integer>'] = c_df['source.Geo.Country'].str.len()
display(c_df)
cc.put_dataframe(c_df)
```
Looking at ``Country.Length`` in the Attribute Editor, we can see that it is an integer. (Click on the Edit button to see the different dialog box.)
Other useful types are ``float`` and ``datetime``. You can see the complete list of types by adding a custom attribute in the Attribute Editor and looking at the ``Attribute Type`` dropdown list.
(Note that there is currently no way to delete attributes externally, so if you want to delete the ``Country.Chars`` attribute, you'll have to do it manually.)
### Deleting nodes and vertices
The special identifier ``[delete]`` lets you delete nodes and transactions from the graph. It doesn't matter what value is in the ``source.[delete]`` column - just the fact that the column is there is sufficient to delete the graph elements. This means that all of the elements in the dataframe will be deleted, so be careful..
Let's delete all singleton nodes. These nodes have no transactions connected to them, so when we get a dataframe, the ``destination.[id]`` value will be ``NaN``.
(If we get all nodes with ``vx=True``, we won't get any data about transactions. If we get all transactions with ``tx=True``, we won't get the singleton nodes.)
```
# Get the graph. (Names are included so we can check that the dataframe matches the graph.)
#
df = cc.get_dataframe(attrs=['source.[id]', 'source.Identifier', 'destination.[id]', 'destination.Identifier'])
display(df)
# Keep the singleton rows (where the destination.[id] is null).
#
df = df[df['destination.[id]'].isnull()]
display(df)
# Create a new dataframe with a source.[id] column containing all of the values from the df source.[id] column,
# and a source.[delete] column containing any non-null value
#
del_df = pd.DataFrame({'source.[id]': df['source.[id]'], 'source.[delete]': 0})
display(del_df)
# Delete the singletons.
#
cc.put_dataframe(del_df)
```
Likewise, we can delete transactions. Let's delete all transactions originating from ``ghi`` .
```
# Get all transactions.
# We don't need all of the attributes for the delete, but we'll get them to use below.
#
df = cc.get_dataframe(tx=True)
display(df)
# Keep the transactions originating from 'ghi'.
#
df = df[df['source.Identifier'].str.startswith('ghi@')]
display(df)
# Create a new dataframe containing the transaction ids in the original dataframe.
# It doesn't matter what the value of 'transaction.[delete]' is,
# but we have to give it something.
#
del_df = pd.DataFrame({'transaction.[id]': df['transaction.[id]'], 'transaction.[delete]': 0})
display(del_df)
# Delete the transactions.
#
cc.put_dataframe(del_df)
```
And let's add a transaction that is exactly the same as the original. Remember that we originally fetched all of the attributes, so this new transaction will have the same attribute values.
```
cc.put_dataframe(df)
```
## Part 3: Graph Attributes
As well as node and transaction attributes, we can also get graph attributes. (Graph attributes can be seen in CONSTELLATION's Attribute Editor, above the node and transaction attributes.)
```
df = cc.get_graph_attributes()
df
```
There is only one set of graph attributes, so there is one row in the dataframe.
Let's display the `Geo.Country` attribute in a small size above the nodes, and the country flag as a decorator on the top-right of the node icon.
A node label is defined as *``attribute-name``*``;``*``color``*``;``*``size``*, with multiple labels separated by pipes "|".
A decorator is defined as ``"nw";"ne";"se";"sw";`` where any of the direction ordinals may be blank.
We don't care what the top labels and decorators are right now, so we'll just create a new dataframe.
```
labels = 'Geo.Country;Orange;0.5'
df = pd.DataFrame({'node_labels_top': [labels], 'decorators': [';"Geo.Country";;;']})
cc.set_graph_attributes(df)
```
(You may have to zoom in to see the smaller labels.)
To add a label on the bottom in addition to the default ``Label`` attribute, you have to specify both labels.
```
labels = 'Type;Teal;0.5|Label;LightBlue;1'
df = pd.DataFrame({'node_labels_bottom': [labels]})
cc.set_graph_attributes(df)
```
## Part 4: Types
CONSTELLATION defines many types. Use the ``describe_type()`` method to get a description of a particular type.
```
t = cc.describe_type('Communication')
t
```
## Part 5: Plugins
You can call CONSTELLATION plugins from Python (if you know what they're called). Let's arrange the graph in trees.
```
cc.run_plugin('ArrangeInTrees')
```
If we can't see all of the graph, reset the view.
```
cc.run_plugin('ResetView')
```
You can also call plugins with parameters (if you know what they are). For example, the ``AddBlaze`` plugin accepts a node id to add a blaze to.
Let's add a blaze to each ``example3.com`` node.
```
# Get all nodes and their identifiers.
#
df = cc.get_dataframe(vx=True, attrs=['source.Identifier', 'source.[id]'])
# Whioch nodes belong to the example3.com domain?
#
e3 = df[df['source.Identifier'].str.endswith('@example3.com')]
# Add a blaze to those nodes.
#
cc.run_plugin('AddBlaze', args={'BlazeUtilities.vertex_ids': list(e3['source.[id]'])})
```
Let's be neat and tidy and remove them again. We can reuse the dataframe.
```
cc.run_plugin('RemoveBlaze', args={'BlazeUtilities.vertex_ids': list(e3['source.[id]'])})
```
### Multichoice parameters
While most parameter values are quite simple (strings, integers, etc), some are a little more complex to deal with, such as the multichoice parameter. In order to pass multichoice parameter values to a plugin, you need to know the possible choices, and you need to know how to select them.
Let's use the <i>select top n</i> plugin as an example. The schema view tells us that this plugin has a multichoice parameter called <i>SelectTopNPlugin.type</i>.
Looking in the Data Access View, the type options will vary depending on the value given to the <i>SelectTopN.type_category</i> parameter. For this example we we set the type category to "Online Identifier", which will result in the possible type options being:
- Online Identifier
- Email
In order to use this parameter, we need to create a string containing all options by joining each option with '\n'. We also need to select all the options we want by prefixing them with '`✓ `' (i.e. Unicode character U+2713 (CHECK MARK) followed by character U+0020 (SPACE)).
This is obviously not an ideal system, but this is how multichoice parameters were implemented at a time when it wasn't expected that CONSTELLATION's internal workings would be exposed via scripting or a REST API.
(This plugin won't do anything on this simple graph.)
```
# Select a node.
#
cc.run_plugin('SelectSources')
# Run the "select top n" plugin with a custom multichoice parameter value.
#
CHECK = '\u2713'
options = ['Online Identifier', 'Communication', 'User Name']
checked = ['Communication']
parameters = {
'SelectTopNPlugin.mode': "Node",
'SelectTopNPlugin.type_category': 'Online Location',
'SelectTopNPlugin.type': '\n'.join([f'{CHECK} {v}' if v in checked else v for v in options]),
'SelectTopNPlugin.limit': 2
}
cc.run_plugin('SelectTopN', args=parameters)
```
So how do we know what plugins exist?
```
plugins = cc.list_plugins()
sorted(plugins)
```
Unfortunately, at the moment there is no way of using the REST API to find out what each plugin does or what parameters it takes. However, you can go the the Schema View in CONSTELLATION and look at the ``Plugins`` tab.
If you'd like to find out what a particular plugin does:
```
cc.describe_plugin('ARRANGEINGRIDGENERAL')
```
## Part 6: Data Access Plugins
Data Access plugins in CONSTELLATION are like any other plugins; they just have a different user interface. This means that they can be called from an external scripting client just like any other plugin.
One caveat is that many of these plugins use the global parameters (seen at the top of the Data Access View).
- Query Name
- Range
Let's try running a data access plugin, although to avoid connectivity problems we'll use the <i>Test Parameters</i> plugin in the <strong>Developer</strong> category of the Data Access View. This plugin doesn't actually access any external data, but rather simply exists to test the mechanisms CONSTELLATION uses to build and use plugin parameters. The plugin has many parameters, but for this example we will focus on the following:
- ``GlobalCoreParameters.query_name``: A string representing the name of the query.
- ``GlobalCoreParameters.datetime_range``: The datetime range; see below.
You might want to try running this plugin manually on an empty graph before running the code below. The plugin will create two connected nodes containing `Comment` attribute values reflecting the values specified by the plugin parameters. (You can see these in the Attribute Editor after you've run the cell.)
Note that the global parameters and plugin-specific parameters are named so they can be differentiated.
Run the plugin a few times, changing the parameters each time, to satisfy yourself that this is the case. After you've done that, let's try running it programmatically.
```
def get_data():
"""Display the results of the plugin."""
df = cc.get_dataframe()
print('query_name :', df.loc[0, 'source.Comment'])
print('datetime_range :', df.loc[0, 'destination.Comment'])
print('all_parameters :', df.loc[0, 'transaction.Comment'])
# Set up a counter.
#
counter = 0
cc.new_graph()
counter += 1
parameters = {
'CoreGlobalParameters.query_name': f'Query {counter} from a REST client',
'CoreGlobalParameters.datetime_range': 'P1D',
'TestParametersPlugin.robot': 'Bender',
'TestParametersPlugin.planets': f'{CHECK} Venus\n{CHECK} Mars'
}
cc.run_plugin('TestParameters', args=parameters)
get_data()
```
The datetime range can be an explicit range, or a duration from the current time.
### Datetime range
A range is represented by two ISO 8601 datetime values separated by a semi-colon. This represents an explicit start and end point. Examples are:
- ``2016-01-01T00:00:00Z;2016-12-31T23:59:59Z``
- ``2017-06-01T12:00:00Z;2017-06-01T13:00:00Z``
### Datetime duration
A duration is represented by a single ISO 8601 duration. This is converted to an explicit datetime range when the query is run. Examples are:
- ``P1D``: one day
- ``P7D``: 7 days
- ``P1M``: one month
- ``P1Y``: one year
- ``P1M7D``: one month and seven days
Note that only years, months, and days are supported (so ``P1H`` for one hour is not a valid period, for example.) For durations other than those, use Python to determine an explicit range.
Let's try calling the plugin again.
```
cc.new_graph()
counter += 1
parameters['CoreGlobalParameters.query_name'] = f'Query {counter} from a REST client'
parameters['CoreGlobalParameters.datetime_range'] = '2017-07-01T00:21:15Z;2017-07-14T00:21:15Z'
cc.run_plugin('TestParameters', args=parameters)
get_data()
```
### Something's wrong?
Sometimes things don't work. Like this.
```
cc.run_plugin('seletall')
```
That's not particularly helpful. Fortunately, when something goes wrong the Python client remembers the most recent response, so we can look at what the REST server is telling us.
```
HTML(cc.r.content.decode('latin1'))
```
What do you mean, "No such plugin as"... Oh, we missed a letter. Let's try that again.
```
cc.run_plugin('selectall')
```
## Part 6: Taking a Screenshot
It can be useful to include a screenshot of the graph in a notebook. It's easy to get an image encoded as data representing a PNG file.
```
buf = cc.get_graph_image()
Image(buf)
```
Here we used the built-in notebook facilities to display the image (which is returned from CONSTELLATION as a sequence of bytes, the encoding of the image in PNG format).
If another window overlaps CONSTELLATION's graph display, you might see that window in the image. One way of avoiding this is to resize the CONSTELLATION window slightly first. Another way is to add a sleep before the `get_graph_image()` call and click in the CONSTELLATION window to bring it to the top.
We can also use PIL (the Python Image Library) to turn the bytes into an image and manipulate it.
```
img = PIL.Image.open(io.BytesIO(buf))
```
You might want to resize the image to fit it into a report.
```
def resize(img, max_size):
w0 = img.width
h0 = img.height
s = max(w0, h0)/max_size
w1 = int(w0//s)
h1 = int(h0//s)
print(f'Resizing from {w0}x{h0} to {w1}x{h1}')
return img.resize((w1, h1))
small = resize(img, 512)
# PIL images know how to display themselves.
#
small
```
The image can be saved to a file. You can either write the bytes directly (remember the bytes are already in PNG format), or save the PIL image.
```
with open('my_constellation_graph.png', 'wb') as f:
f.write(buf)
img.save('my_small_constellation_graph.png')
```
PIL is fun.
```
small.filter(PIL.ImageFilter.EMBOSS)
w = small.width
h = small.height
small.crop((int(w*0.25), int(h*0.25), int(w*0.75), int(h*0.75)))
# Fonts depend on the operating system.
#
if os.name=='nt':
font = PIL.ImageFont.truetype('calibri.ttf', 20)
else:
font = PIL.ImageFont.truetype('Oxygen-Sans.ttf', 20)
draw = PIL.ImageDraw.Draw(small)
draw.text((0, 0), 'This is my graph, it is mine.', (255, 200, 40), font=font)
small
```
# Part 7: NetworkX
NetworkX is a Python package for the creation, manipulation, and study of the structure, dynamics, and functions of complex networks.
This notebook isn't going to teach you how to use NetworkX, but you can extract your CONSTELLATION graph into a NetworkX graph for further analysis.
We'll start by getting a dataframe containing the graph data.
```
cc.run_plugin('ArrangeInGridGeneral')
df = cc.get_dataframe()
df.head()
```
The ``constellation_client`` library contains a function that converts a dataframe to a NetworkX graph. You can see the documentation for it using the notebook's built-in help mechanism.
```
constellation_client.nx_from_dataframe?
```
When you've looked at the help, close the help window and create a NetworkX graph from the dataframe.
```
g = constellation_client.nx_from_dataframe(df)
g
```
We can look at a node and see that it has the expected attributes.
```
g.nodes(data=True)['0']
```
We can look at an edge and see that it has the expected attributes.
```
list(g.edges(data=True))[0]
```
NetworkX can draw its graphs using a plotting library called ``matplotlib``. We just need to tell ``matplotlib`` to draw in the notebook, and get the correct positions and colors from the node and edge attributes. (We can use a convenience function provided by ``constellation_client`` to get the positions.)
```
%matplotlib inline
import networkx as nx
pos = constellation_client.get_nx_pos(g)
node_colors = [to_web_color(g.nodes[n]['color']) for n in g.nodes()]
edge_colors = [to_web_color(g.edges[e]['color']) for e in g.edges()]
nx.draw(g, pos=pos, node_color=node_colors, edge_color=edge_colors)
```
|
github_jupyter
|
# Step 1 - Prepare Data
Data cleaning.
```
%load_ext autoreload
%autoreload 2
import pandas as pd
# Custom Functions
import sys
sys.path.append('../src')
import data as dt
import prepare as pr
import helper as he
```
### Load Data
```
dt_task = dt.Data()
data = dt_task.load('fn_clean')
fn_data = he.get_config()['path']['sample_dir'] + 'data.txt'
data = pd.read_csv(fn_data, sep='\t', encoding='utf-8')
data.columns
data = data[data.answer_markedAsAnswer == True].reset_index(drop=True).copy()
data.head().to_json()
task_params = {
1 : {
'label' : 'subcat',
'type' : 'classification',
'language' : 'en',
'prepare' : ''
},
2 : {
'label' : 'cat',
'type' : 'classification',
'language' : 'en',
'prepare' : ''
},
4 : {
'type' : 'qa',
'language' : 'en',
'prepare' : None
}
}
for t in task_params.keys():
print(t)
data.head()
cl = pr.Clean(language='en')
%%time
title_clean = cl.transform(data.question_title,
do_remove=True,
do_placeholder=True)
%%time
body_clean = cl.transform(data.question_text,
do_remove=True,
do_placeholder=True)
title_clean[0:20]
body_clean[0:20]
data['text'] = title_clean
data.head()
len(data[data.answer_markedAsAnswer == True])
tt = ['Asdas', 'asdasd sad asd', 'Asd ss asda asd']
[t.split(' ') for t in tt]
task_type_lookup = {
1 : 'classification',
2 : 'classification',
3 : 'ner',
4 : 'qa'
}
task_type_lookup[0]
task_type_lookup[1]
data[data.answer_upvotes > 1].head()
len(data)
data_red = data.drop_duplicates(subset=['text'])
data_red['text'] = data_red.text.replace('\t',' ',regex=True).replace('"','').replace("'",' ').replace('\n',' ',regex=True)
data_red['subcat'] = data_red.subcat.replace('\t',' ',regex=True).replace('"','').replace("'",' ').replace('\n',' ',regex=True)
len(data_red)
# data_red['subcat'] = data_red.subcat.str.replace(r'\D', '')
# data_red['text'] = data_red.text.str.replace(r'\D', '')
data_red.subcat.value_counts()
tt = data_red[data_red.groupby('subcat').subcat.transform('size') > 14]
tt.subcat.value_counts()
pd.DataFrame(data_red.subcat.drop_duplicates())
list(set(data.subcat.drop_duplicates()) - set(data_red.subcat.drop_duplicates()))
list(data_red.subcat.drop_duplicates())
data_red = data_red[data_red.subcat.isin(['msoffice',
'edge',
'ie',
'windows',
'insider',
'mobiledevices',
'outlook_com',
'protect',
'skype',
'surface',
'windowslive'])].copy()
len(data_red)
data_red[['text','subcat']].head(6000).reset_index(drop=True).to_csv(he.get_config()['path']['sample_dir'] + 'train.txt', sep='\t', encoding='utf-8', index=False)
data_red[['text','subcat']].tail(7733-6000).reset_index(drop=True).to_csv(he.get_config()['path']['sample_dir'] + 'test.txt', sep='\t', encoding='utf-8', index=False)
```
|
github_jupyter
|
## Create Azure Resources¶
This notebook creates relevant Azure resources. It creates a recource group where an IoT hub with an IoT edge device identity is created. It also creates an Azure container registry (ACR).
```
from dotenv import set_key, get_key, find_dotenv
from pathlib import Path
import json
import time
```
To create or access an Azure ML Workspace, you will need the following information:
* An Azure subscription id
* A resource group name
* A region for your resources
We also require you to provide variable names that will be used to create these resources in later notebooks.
```
# Azure resources
subscription_id = "<subscription_id>"
resource_group = "<resource_group>"
resource_region = "resource_region" # e.g. resource_region = "eastus"
# IoT hub name - a globally UNIQUE name is required, e.g. iot_hub_name = "myiothubplusrandomnumber".
iot_hub_name = "<iot_hub_name>"
device_id = "<device_id>" # the name you give to the edge device. e.g. device_id = "mydevice"
# azure container registry name - a globally UNIQUE name is required, e.g. arc_name = "myacrplusrandomnumber"
acr_name = '<acr_name>'
```
Create and initialize a dotenv file for storing parameters used in multiple notebooks.
```
env_path = find_dotenv()
if env_path == "":
Path(".env").touch()
env_path = find_dotenv()
set_key(env_path, "subscription_id", subscription_id)
set_key(env_path, "resource_group", resource_group)
set_key(env_path, "resource_region", resource_region)
set_key(env_path, "iot_hub_name", iot_hub_name)
set_key(env_path, "device_id", device_id)
set_key(env_path,"acr_name", acr_name)
acr_login_server = '{}.azurecr.io'.format(acr_name)
set_key(env_path,"acr_login_server", acr_login_server)
```
## Create Azure Resources
```
# login in your account
accounts = !az account list --all -o tsv
if "Please run \"az login\" to access your accounts." in accounts[0]:
!az login -o table
else:
print("Already logged in")
```
Below we will reload it just to make sure that everything is working.
```
!az account set --subscription $subscription_id
# create a new resource group
!az group create -l $resource_region -n $resource_group
```
### Create IoT Hub
```
# install az-cli iot extension - I had to use "sudo -i" to make it work
!sudo -i az extension add --name azure-cli-iot-ext
!az iot hub list --resource-group $resource_group -o table
# Command to create a Standard tier S1 hub with name `iot_hub_name` in the resource group `resource_group`.
!az iot hub create --resource-group $resource_group --name $iot_hub_name --sku S1
# Command to create a free tier F1 hub. You may encounter error "Max number of Iot Hubs exceeded for sku = Free" if quota is reached.
# !az iot hub create --resource-group $resource_group --name $iot_hub_name --sku F1
```
### Register an IoT Edge device
We create a device with name `device_id` under previously created iot hub.
```
time.sleep(30) # Wait 30 seconds to let IoT hub stable before creating a device
print("az iot hub device-identity create --hub-name {} --device-id {} --edge-enabled -g {}".format(iot_hub_name,device_id,resource_group))
!az iot hub device-identity create --hub-name $iot_hub_name --device-id $device_id --edge-enabled -g $resource_group
```
Obtain device_connection_string. It will be used in the next step.
```
print("az iot hub device-identity show-connection-string --device-id {} --hub-name {} -g {}".format(device_id, iot_hub_name,resource_group))
json_data = !az iot hub device-identity show-connection-string --device-id $device_id --hub-name $iot_hub_name -g $resource_group
print(json_data)
device_connection_string = json.loads(''.join([i for i in json_data if 'WARNING' not in i]))['connectionString']
print(device_connection_string)
set_key(env_path, "device_connection_string", device_connection_string)
```
### Create Azure Container Registry
```
!az acr create -n $acr_name -g $resource_group --sku Standard --admin-enabled
!az acr login --name $acr_name
acr_password = !az acr credential show -n $acr_name --query passwords[0].value
acr_password = "".join(acr_password)
acr_password = acr_password.strip('\"')
set_key(env_path,"acr_password", acr_password)
```
In this notebook, we created relevant Azure resources. We also created a ".env" file to save and reuse the variables needed cross all the notebooks. We can now move on to the next notebook [02_IoTEdgeConfig.ipynb](02_IoTEdgeConfig.ipynb).
|
github_jupyter
|
# Example of optimizing Xgboost XGBClassifier function
# Goal is to test the objective values found by Mango
# Benchmarking Serial Evaluation: Iterations 60
```
from mango.tuner import Tuner
from scipy.stats import uniform
def get_param_dict():
param_dict = {"learning_rate": uniform(0, 1),
"gamma": uniform(0, 5),
"max_depth": range(1,10),
"n_estimators": range(1,300),
"booster":['gbtree','gblinear','dart']
}
return param_dict
from sklearn.model_selection import cross_val_score
from xgboost import XGBClassifier
from sklearn.datasets import load_wine
X, Y = load_wine(return_X_y=True)
count_called = 1
def objfunc(args_list):
global X, Y, count_called
#print('count_called:',count_called)
count_called = count_called + 1
results = []
for hyper_par in args_list:
clf = XGBClassifier(**hyper_par)
result = cross_val_score(clf, X, Y, scoring='accuracy').mean()
results.append(result)
return results
def get_conf():
conf = dict()
conf['batch_size'] = 1
conf['initial_random'] = 5
conf['num_iteration'] = 60
conf['domain_size'] = 5000
return conf
def get_optimal_x():
param_dict = get_param_dict()
conf = get_conf()
tuner = Tuner(param_dict, objfunc,conf)
results = tuner.maximize()
return results
optimal_X = []
Results = []
num_of_tries = 100
for i in range(num_of_tries):
results = get_optimal_x()
Results.append(results)
optimal_X.append(results['best_params']['x'])
print(i,":",results['best_params']['x'])
# import numpy as np
# optimal_X = np.array(optimal_X)
# plot_optimal_X=[]
# for i in range(optimal_X.shape[0]):
# plot_optimal_X.append(optimal_X[i]['x'])
```
# Plotting the serial run results
```
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,10))
n, bins, patches = plt.hist(optimal_X, 20, facecolor='g', alpha=0.75)
def autolabel(rects):
"""
Attach a text label above each bar displaying its height
"""
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x() + rect.get_width()/2., 1.0*height,
'%d' % int(height),
ha='center', va='bottom',fontsize=15)
plt.xlabel('X-Value',fontsize=25)
plt.ylabel('Number of Occurence',fontsize=25)
plt.title('Optimal Objective: Iterations 60',fontsize=20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.grid(True)
autolabel(patches)
plt.show()
```
# Benchmarking test with different iterations for serial executions
```
from mango.tuner import Tuner
def get_param_dict():
param_dict = {
'x': range(-5000, 5000)
}
return param_dict
def objfunc(args_list):
results = []
for hyper_par in args_list:
x = hyper_par['x']
result = -(x**2)
results.append(result)
return results
def get_conf_20():
conf = dict()
conf['batch_size'] = 1
conf['initial_random'] = 5
conf['num_iteration'] = 20
conf['domain_size'] = 5000
return conf
def get_conf_30():
conf = dict()
conf['batch_size'] = 1
conf['initial_random'] = 5
conf['num_iteration'] = 30
conf['domain_size'] = 5000
return conf
def get_conf_40():
conf = dict()
conf['batch_size'] = 1
conf['initial_random'] = 5
conf['num_iteration'] = 40
conf['domain_size'] = 5000
return conf
def get_conf_60():
conf = dict()
conf['batch_size'] = 1
conf['initial_random'] = 5
conf['num_iteration'] = 60
conf['domain_size'] = 5000
return conf
def get_optimal_x():
param_dict = get_param_dict()
conf_20 = get_conf_20()
tuner_20 = Tuner(param_dict, objfunc,conf_20)
conf_30 = get_conf_30()
tuner_30 = Tuner(param_dict, objfunc,conf_30)
conf_40 = get_conf_40()
tuner_40 = Tuner(param_dict, objfunc,conf_40)
conf_60 = get_conf_60()
tuner_60 = Tuner(param_dict, objfunc,conf_60)
results_20 = tuner_20.maximize()
results_30 = tuner_30.maximize()
results_40 = tuner_40.maximize()
results_60 = tuner_60.maximize()
return results_20, results_30, results_40 , results_60
Store_Optimal_X = []
Store_Results = []
num_of_tries = 100
for i in range(num_of_tries):
results_20, results_30, results_40 , results_60 = get_optimal_x()
Store_Results.append([results_20, results_30, results_40 , results_60])
Store_Optimal_X.append([results_20['best_params']['x'],results_30['best_params']['x'],results_40['best_params']['x'],results_60['best_params']['x']])
print(i,":",[results_20['best_params']['x'],results_30['best_params']['x'],results_40['best_params']['x'],results_60['best_params']['x']])
import numpy as np
Store_Optimal_X=np.array(Store_Optimal_X)
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,10))
n, bins, patches = plt.hist(Store_Optimal_X[:,0], 20, facecolor='g', alpha=0.75)
def autolabel(rects):
"""
Attach a text label above each bar displaying its height
"""
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x() + rect.get_width()/2., 1.0*height,
'%d' % int(height),
ha='center', va='bottom',fontsize=15)
plt.xlabel('X-Value',fontsize=25)
plt.ylabel('Number of Occurence',fontsize=25)
plt.title('Optimal Objective: Iterations 20',fontsize=20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.grid(True)
autolabel(patches)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,10))
n, bins, patches = plt.hist(Store_Optimal_X[:,1], 20, facecolor='g', alpha=0.75)
def autolabel(rects):
"""
Attach a text label above each bar displaying its height
"""
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x() + rect.get_width()/2., 1.0*height,
'%d' % int(height),
ha='center', va='bottom',fontsize=15)
plt.xlabel('X-Value',fontsize=25)
plt.ylabel('Number of Occurence',fontsize=25)
plt.title('Optimal Objective: Iterations 30',fontsize=20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.grid(True)
autolabel(patches)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,10))
n, bins, patches = plt.hist(Store_Optimal_X[:,2], 20, facecolor='g', alpha=0.75)
def autolabel(rects):
"""
Attach a text label above each bar displaying its height
"""
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x() + rect.get_width()/2., 1.0*height,
'%d' % int(height),
ha='center', va='bottom',fontsize=15)
plt.xlabel('X-Value',fontsize=25)
plt.ylabel('Number of Occurence',fontsize=25)
plt.title('Optimal Objective: Iterations 40',fontsize=20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.grid(True)
autolabel(patches)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,10))
n, bins, patches = plt.hist(Store_Optimal_X[:,3], 20, facecolor='g', alpha=0.75)
def autolabel(rects):
"""
Attach a text label above each bar displaying its height
"""
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x() + rect.get_width()/2., 1.0*height,
'%d' % int(height),
ha='center', va='bottom',fontsize=15)
plt.xlabel('X-Value',fontsize=25)
plt.ylabel('Number of Occurence',fontsize=25)
plt.title('Optimal Objective: Iterations 60',fontsize=20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.grid(True)
autolabel(patches)
plt.show()
```
|
github_jupyter
|
<img src='./img/intel-logo.jpg' width=50%, Fig1>
# OpenCV 기초강좌
<font size=5><b>01. 이미지, 비디오 입출력 <b></font>
<div align='right'>성 민 석 (Minsuk Sung)</div>
<div align='right'>류 회 성 (Hoesung Ryu)</div>
<img src='./img/OpenCV_Logo_with_text.png' width=20%, Fig2>
---
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#이미지-읽기" data-toc-modified-id="이미지-읽기-1"><span class="toc-item-num">1 </span>이미지 읽기</a></span></li><li><span><a href="#Matplotlib을-이용해-이미지-시각화-하기" data-toc-modified-id="Matplotlib을-이용해-이미지-시각화-하기-2"><span class="toc-item-num">2 </span>Matplotlib을 이용해 이미지 시각화 하기</a></span></li><li><span><a href="#이미지-저장하기" data-toc-modified-id="이미지-저장하기-3"><span class="toc-item-num">3 </span>이미지 저장하기</a></span></li><li><span><a href="#웹캠을-사용하여-비디오-읽기" data-toc-modified-id="웹캠을-사용하여-비디오-읽기-4"><span class="toc-item-num">4 </span>웹캠을 사용하여 비디오 읽기</a></span></li><li><span><a href="#영상-저장" data-toc-modified-id="영상-저장-5"><span class="toc-item-num">5 </span>영상 저장</a></span></li></ul></div>
## 이미지 읽기
`cv2.imread(file, flag)`
flag에 다양한 옵션을 주어 여러가지 형태로 불러 올 수 있습니다.
1. file : 저장위치
2. flag
- cv2.IMREAD_ANYCOLOR: 원본 파일로 읽어옵니다.
- cv2.IMREAD_COLOR: 이미지 파일을 Color로 읽음. 투명한 부분은 무시하며 Default 설정입니다.
- cv2.IMREAD_GRAYSCALE: 이미지 파일을 Grayscale로 읽음. 실제 이미지 처리시 중간 단계로 많이 사용합니다
- cv2.IMREAD_UNCHAGED: 이미지 파일을 alpha channel 까지 포함해 읽음
```
import cv2
# 원본그대로 불러오기
image = cv2.imread("./img/toy.jpg")
# 회색조로 불러오기
img_gray = cv2.imread("./img/toy.jpg", cv2.IMREAD_GRAYSCALE)
```
## Matplotlib을 이용해 이미지 시각화 하기
`jupyter notebook`에서 작업하는 경우 Matplotlib을 이용하여 시각화하는 방법을 추천합니다.
```
%matplotlib inline
import matplotlib.pyplot as plt
plt.title("image")
plt.imshow(image)
plt.xticks([]) # x축 눈금 없애기
plt.yticks([]) # y축 눈금 없애기
plt.show()
plt.title("image_gray")
plt.imshow(img_gray,cmap='gray')
plt.xticks([]) # x축 눈금 없애기
plt.yticks([]) # y축 눈금 없애기
plt.show()
```
## 이미지 저장하기
```
cv2.imwrite('./data/toy_image.jpg', image)
cv2.imwrite('./data/toy_gray_image.jpg', img_gray)
```
---
## 웹캠을 사용하여 비디오 읽기
**`MAC_카탈리나` 환경에서는 창이 안닫히는 현상이 있으므로 실행하지 않는 것을 추천합니다.**
- `cv2.VideoCapture()`: 캡쳐 객체를 생성 합니다. 소유하고 있는 웹캠의 갯수많큼 인덱스가 생기며 인덱스는 0부터 시작합니다. 예를들어, 웹캠을 하나만 가지고 있다면 0 을 입력합니다. `cv2.VideoCapture(0)`
- `ret, fram = cap.read()`: 비디오의 한 프레임씩 읽습니다. 제대로 프레임을 읽으면 ret값이 True, 실패하면 False가 나타납니다. fram에 읽은 프레임이 나옵니다
- `cv2.cvtColor()`: frame을 흑백으로 변환합니다
- `cap.release()`: 오픈한 캡쳐 객체를 해제합니다
```
import cv2
OPTION = 'color' # gray: 흑백
cap = cv2.VideoCapture(0)
while True:
ret, frame = cap.read()
if ret:
if OPTION == 'gray':
gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY) # 입력 받은 화면 Gray로 변환
cv2.imshow('frame_gray', gray) # Gray 화면 출력
if cv2.waitKey(1) == ord('q'): # q 를 누를시 정지
break
elif OPTION == 'color':
cv2.imshow('frame_color', frame) # 컬러 화면 출력
if cv2.waitKey(1) == ord('q'):
break
else:
print('error')
cap.release()
cv2.destroyAllWindows()
```
## 영상 저장
영상을 저장하기 위해서는 `cv2.VideoWriter` Object를 생성해야 합니다.
```
cv2.VideoWriter(outputFile, fourcc, frame, size)
영상을 저장하기 위한 Object
Parameters:
outputFile (str) – 저장될 파일명
fourcc – Codec정보. cv2.VideoWriter_fourcc()
frame (float) – 초당 저장될 frame
size (list) – 저장될 사이즈(ex; 640, 480)
```
- `cv2.VideoWriter(outputFile, fourcc, frame, size)` : fourcc는 코덱 정보, frame은 초당 저장될 프레임, size는 저장될 사이즈를 뜻합니다.
- `cv2.VideoWriter_fourcc('D','I','V','X')` 이런식으로소 사용하곤 합니다 적용 가능한 코덱은 DIVX, XVID, MJPG, X264, WMV1, WMV2 등이 있습니다
```
import cv2
cap = cv2.VideoCapture(0)
fourcc = cv2.VideoWriter_fourcc(*'DIVX')
out = cv2.VideoWriter('./data/output.avi',
fourcc,
25.0,
(640, 480))
while (cap.isOpened()):
ret, frame = cap.read()
if ret:
out.write(frame)
cv2.imshow('frame', frame)
if cv2.waitKey(0) & 0xFF == ord('q'):
break
else:
break
cap.release()
out.release()
cv2.destroyAllWindows()
```
|
github_jupyter
|
```
import logging
import warnings
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import neurolib.optimize.exploration.explorationUtils as eu
import neurolib.utils.pypetUtils as pu
from neurolib.optimize.exploration import BoxSearch
logger = logging.getLogger()
warnings.filterwarnings("ignore")
logger.setLevel(logging.INFO)
results_path = "/Users/valery/Google_Drive/NI-Project/data/hdf/"
from neurolib.models.aln import ALNModel
from neurolib.utils.parameterSpace import ParameterSpace
model = ALNModel()
# define the parameter space to explore
parameters = ParameterSpace({"mue_ext_mean": np.linspace(0, 3, 21), # input to E
"mui_ext_mean": np.linspace(0, 3, 21)}) # input to I
# define exploration
search = BoxSearch(model, parameters)
pu.getTrajectorynamesInFile(results_path + "scz_sleep_reduce_abs_resolution-8.hdf")
search.loadResults(
filename= results_path + "scz_sleep_reduce_abs_resolution-8.hdf",
trajectoryName="results-2021-06-25-18H-59M-03S")
df = search.dfResults.copy()
search2 = BoxSearch(model, parameters)
pu.getTrajectorynamesInFile(results_path + "scz_sleep_Jei_resolution-50.hdf")
search2.loadResults(
filename=results_path + "scz_sleep_Jei_resolution-50.hdf",
trajectoryName="results-2021-06-26-00H-40M-29S")
df2 = search2.dfResults.copy()
search3 = BoxSearch(model, parameters)
pu.getTrajectorynamesInFile(results_path + "scz_sleep_resolution-50.hdf")
search3.loadResults(
filename=results_path + "scz_sleep_resolution-50.hdf",
trajectoryName="results-2021-06-25-08H-34M-46S")
df3 = search3.dfResults.copy()
search4 = BoxSearch(model, parameters)
pu.getTrajectorynamesInFile(results_path + "scz_sleep_Jii_resolution-50.hdf")
search4.loadResults(
filename=results_path + "scz_sleep_Jii_resolution-50.hdf",
trajectoryName="results-2021-06-26-04H-08M-21S")
df4 = search4.dfResults.copy()
images = "/Users/valery/Downloads/results/"
df3.loc[:, 'Global_SWS_per_min'] = df3.loc[:, 'n_global_waves']*3
eu.plotExplorationResults(
df, par1=['mue_ext_mean', 'Input to E [nA]'], par2=['Jie_max', 'Synaptic current from E to I [nA]'],
by=["Ke_gl"], plot_key='SWS_per_min', plot_clim=[0, 25],
nan_to_zero=False, plot_key_label="SWS/min", one_figure=True, savename=images + "scz_sleep1.png")
eu.plotExplorationResults(
df, par1=['mue_ext_mean', 'Input to E [nA]'], par2=['Jie_max', 'Synaptic current from E to I [nA]'],
by=["Ke_gl"], plot_key='perc_local_waves', plot_clim=[0, 100],
nan_to_zero=False, plot_key_label="'perc_local_waves'", one_figure=True, savename=images + "scz_sleep1_1.png")
eu.plotExplorationResults(
df, par1=['mue_ext_mean', 'Input to E [nA]'], par2=['Jei_max', 'Synaptic current from I to E [nA]'],
by=["Ke_gl"], plot_key='SWS_per_min', plot_clim=[0, 25],
nan_to_zero=False, plot_key_label="SWS/min", one_figure=True, savename=images + "scz_sleep2.png")
eu.plotExplorationResults(
df, par1=['mue_ext_mean', 'Input to E [nA]'], par2=['Jii_max', 'Synaptic current from I to I [nA]'],
by=["Ke_gl"], plot_key='SWS_per_min', plot_clim=[0, 25],
nan_to_zero=False, plot_key_label="SWS/min", one_figure=True, savename=images + "scz_slee3.png")
df.columns
df.describe()
df_2 = df.loc[df['Ke_gl'] == 200.0,
['mue_ext_mean', 'Ke_gl','Jie_max', 'Jei_max', 'Jii_max', 'SWS_per_min',
'perc_local_waves', 'max_output', 'normalized_up_lengths_mean', 'n_global_waves'
]].round(decimals=2)
df_2['interactions'] = False
dfdf = pd.DataFrame()
for n, (jie, jei, jii) in enumerate(zip(df_2['Jie_max'].unique(), df_2['Jei_max'].unique(), df_2['Jii_max'].unique())):
mask = (df_2['Jie_max'] == jie) & (df_2['Jei_max'] == jei) & (df_2['Jii_max'] == jii)
df_2.loc[mask, 'interactions'] = True
df_2.loc[mask, 'J'] = 8 - n
dfdf.loc[8-n, ['Jie_max', 'Jei_max', 'Jii_max']] = jie, jei, jii
df_2_interaction = df_2.loc[df_2['interactions'], :]
df_2_interaction.loc[:, 'global_SWS_per_min'] = df_2_interaction.loc[:, 'n_global_waves'] *3
dfdf
eu.plotExplorationResults(
df_2_interaction, par1=['mue_ext_mean', 'Input to E [nA]'], par2=['J', 'Decrease all J simultaneously'],
by=["Ke_gl"], plot_key='SWS_per_min', plot_clim=[0, 40],
nan_to_zero=False, plot_key_label="SWS/min", one_figure=True, savename=images + "scz_sleep4.png")
eu.plotExplorationResults(
df_2_interaction, par1=['mue_ext_mean', 'Input to E [nA]'], par2=['J', 'Decrease all J simultaneously'],
by=["Ke_gl"], plot_key='perc_local_waves', plot_clim=[0, 100],
nan_to_zero=False, plot_key_label="Fraction of the local waves %", one_figure=True, savename=images + "scz_sleep5.png")
eu.plotExplorationResults(
df_2_interaction, par1=['mue_ext_mean', 'Input to E [nA]'], par2=['J', 'Decrease all J simultaneously'],
by=["Ke_gl"], plot_key='normalized_up_lengths_mean', plot_clim=[0, 100],
nan_to_zero=False, plot_key_label="Time spent in Up state %", one_figure=True, savename=images + "scz_sleep6.png")
palette = sns.color_palette("hls", 8)
sns.relplot( # .relplot(
data=df_2_interaction[(df_2_interaction["Ke_gl"] == 200.)],
x="mue_ext_mean", y="SWS_per_min",
hue='J', # col='Jie_max', # size="choice", size_order=["T1", "T2"],
kind="line", # palette=palette,
# order=3,
height=5, aspect=1., legend=False, palette=palette
# facet_kws=dict(sharex=False),
)
plt.xlim([3.32,4.5])
plt.ylim([0, 45])
# plt.tight_layout()
# plt.title('All SW / min')
plt.gcf().subplots_adjust(bottom=0.15)
plt.savefig(images + "scz_sleep13.png", dpi=100)
palette = sns.color_palette("hls", 8)
sns.relplot(
data=df_2_interaction[(df_2_interaction["Ke_gl"] == 200.)],
x="mue_ext_mean", y="global_SWS_per_min",
hue='J', # col='Jie_max', # size="choice", size_order=["T1", "T2"],
kind="line", # palette=palette,
height=5, aspect=1., legend="full",
palette=palette
# facet_kws=dict(sharex=False),
)
plt.xlim([3.32,4.5])
plt.ylim([0, 45])
# plt.tight_layout()
plt.gcf().subplots_adjust(bottom=0.15)
# plt.title('Global SW / min')
plt.savefig(images + "scz_sleep14.png", dpi=100)
df3.columns
eu.plotExplorationResults(
df3, par1=['mue_ext_mean', 'Input to E [nA]'], par2=['Jie_max', 'Synaptic current from E to I [nA]'],
by=["Ke_gl"], plot_key='SWS_per_min', plot_clim=[0, 40], # plot_clim=[0.0, 100.0],
contour=['perc_local_waves', 'normalized_up_lengths_mean'],
contour_color=[['white'], ['red']], contour_levels=[[70], [65]], contour_alpha=[1.0, 1.0],
contour_kwargs={0: {"linewidths": (2,)}, 1: {"linewidths": (2,)}},
nan_to_zero=False, plot_key_label="SWS/min", one_figure=True, savename=images + "scz_sleep9.png")
eu.plotExplorationResults(
df3, par1=['mue_ext_mean', 'Input to E [nA]'], par2=['Jie_max', 'Synaptic current from E to I [nA]'],
by=["Ke_gl"], plot_key='frontal_SWS_per_min', plot_clim=[0, 40], # plot_clim=[0.0, 100.0],
contour=['frontal_perc_local_waves', 'frontalnormalized_up_lengths_mean'],
contour_color=[['white'], ['red']], contour_levels=[[70], [65]], contour_alpha=[1.0, 1.0],
contour_kwargs={0: {"linewidths": (2,)}, 1: {"linewidths": (2,)}},
nan_to_zero=False, plot_key_label="Frontal SWS/min", one_figure=True, savename=images + "scz_sleep9_1.png")
sns.lmplot( # .relplot(
data=df3[(df3["Ke_gl"] == 200.)&((df3['Jie_max'] < 1.4) | (df3['Jie_max'] == 2.6))].round(3),
x="mue_ext_mean", y="SWS_per_min",
hue='Jie_max', # col='Jie_max', # size="choice", size_order=["T1", "T2"],
# kind="line", # palette=palette,
order=5,
height=5, aspect=1., legend=False,
# facet_kws=dict(sharex=False),
)
plt.xlim([3.32,4.5])
plt.ylim([0, 45])
# plt.tight_layout()
# plt.title('All SW / min')
plt.gcf().subplots_adjust(bottom=0.15)
plt.savefig(images + "scz_sleep11.png", dpi=100)
sns.lmplot( # .relplot(
data=df3[(df3["Ke_gl"] == 200.)&((df3['Jie_max'] < 1.4) | (df3['Jie_max'] == 2.6))].round(3),
x="mue_ext_mean", y="Global_SWS_per_min",
hue='Jie_max', # col='Jie_max', # size="choice", size_order=["T1", "T2"],
# kind="line", # palette=palette,
order=5,
height=5, aspect=1., # legend="full"
# facet_kws=dict(sharex=False),
)
plt.xlim([3.32,4.5])
plt.ylim([0, 45])
# plt.tight_layout()
plt.gcf().subplots_adjust(bottom=0.15)
# plt.title('Global SW / min')
plt.savefig(images + "scz_sleep12.png", dpi=100)
```
|
github_jupyter
|
# Operator Upgrade Tests
## Setup Seldon Core
Follow the instructions to [Setup Cluster](https://docs.seldon.io/projects/seldon-core/en/latest/examples/seldon_core_setup.html#Setup-Cluster) with [Ambassador Ingress](https://docs.seldon.io/projects/seldon-core/en/latest/examples/seldon_core_setup.html#Ambassador) and [Install Seldon Core](https://docs.seldon.io/projects/seldon-core/en/latest/examples/seldon_core_setup.html#Install-Seldon-Core).
```
!kubectl create namespace seldon
!kubectl config set-context $(kubectl config current-context) --namespace=seldon
import json
import time
```
## Install Stable Version
```
!kubectl create namespace seldon-system
!helm upgrade seldon seldon-core-operator --repo https://storage.googleapis.com/seldon-charts --namespace seldon-system --set istio.enabled=true --wait
```
## Launch a Range of Models
```
%%writefile resources/model.yaml
apiVersion: machinelearning.seldon.io/v1
kind: SeldonDeployment
metadata:
name: seldon-model
spec:
name: test-deployment
predictors:
- componentSpecs:
- spec:
containers:
- image: seldonio/mock_classifier:1.9.1
name: classifier
graph:
name: classifier
type: MODEL
endpoint:
type: REST
name: example
replicas: 1
!kubectl create -f resources/model.yaml
%%writefile ../servers/tfserving/samples/halfplustwo_rest.yaml
apiVersion: machinelearning.seldon.io/v1alpha2
kind: SeldonDeployment
metadata:
name: hpt
spec:
name: hpt
protocol: tensorflow
transport: rest
predictors:
- graph:
name: halfplustwo
implementation: TENSORFLOW_SERVER
modelUri: gs://seldon-models/tfserving/half_plus_two
parameters:
- name: model_name
type: STRING
value: halfplustwo
name: default
replicas: 1
!kubectl create -f ../servers/tfserving/samples/halfplustwo_rest.yaml
%%writefile ../examples/models/payload_logging/model_logger.yaml
apiVersion: machinelearning.seldon.io/v1
kind: SeldonDeployment
metadata:
name: model-logs
spec:
name: model-logs
predictors:
- componentSpecs:
- spec:
containers:
- image: seldonio/mock_classifier_rest:1.3
name: classifier
imagePullPolicy: Always
graph:
name: classifier
type: MODEL
endpoint:
type: REST
logger:
url: http://logger.seldon/
mode: all
name: logging
replicas: 1
!kubectl create -f ../examples/models/payload_logging/model_logger.yaml
```
Wait for all models to be available
```
def waitStatus(desired):
for i in range(360):
allAvailable = True
failedGet = False
state = !kubectl get sdep -o json
state = json.loads("".join(state))
for model in state["items"]:
if "status" in model:
print("model", model["metadata"]["name"], model["status"]["state"])
if model["status"]["state"] != "Available":
allAvailable = False
break
else:
failedGet = True
if allAvailable == desired and not failedGet:
break
time.sleep(1)
return allAvailable
actual = waitStatus(True)
assert actual == True
```
## Count the number of resources
```
def getOwned(raw):
count = 0
for res in raw["items"]:
if (
"ownerReferences" in res["metadata"]
and res["metadata"]["ownerReferences"][0]["kind"] == "SeldonDeployment"
):
count += 1
return count
def getResourceStats():
# Get number of deployments
dps = !kubectl get deployment -o json
dps = json.loads("".join(dps))
numDps = getOwned(dps)
print("Number of deployments owned", numDps)
# Get number of services
svcs = !kubectl get svc -o json
svcs = json.loads("".join(svcs))
numSvcs = getOwned(svcs)
print("Number of services owned", numSvcs)
# Get number of virtual services
vss = !kubectl get vs -o json
vss = json.loads("".join(vss))
numVs = getOwned(vss)
print("Number of virtual services owned", numVs)
# Get number of hpas
hpas = !kubectl get hpa -o json
hpas = json.loads("".join(hpas))
numHpas = getOwned(hpas)
print("Number of hpas owned", numHpas)
return (numDps, numSvcs, numVs, numHpas)
(dp1, svc1, vs1, hpa1) = getResourceStats()
```
## Upgrade to latest
```
!helm upgrade seldon ../helm-charts/seldon-core-operator --namespace seldon-system --set istio.enabled=true --wait
actual = waitStatus(False)
assert actual == False
actual = waitStatus(True)
assert actual == True
# Give time for resources to terminate
for i in range(120):
(dp2, svc2, vs2, hpa2) = getResourceStats()
if dp1 == dp2 and svc1 == svc2 and vs1 == vs2 and hpa1 == hpa2:
break
time.sleep(1)
assert dp1 == dp2
assert svc1 == svc2
assert vs1 == vs2
assert hpa1 == hpa2
!kubectl delete sdep --all
```
|
github_jupyter
|
Comparison for decision boundary generated on iris dataset between Label Propagation and SVM.
This demonstrates Label Propagation learning a good boundary even with a small amount of labeled data.
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plot.ly/python/getting-started/) by downloading the client and [reading the primer](https://plot.ly/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plot.ly/python/getting-started/#initialization-for-online-plotting) or [offline](https://plot.ly/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plot.ly/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
### Version
```
import sklearn
sklearn.__version__
```
### Imports
```
print(__doc__)
import plotly.plotly as py
import plotly.graph_objs as go
from plotly import tools
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn import svm
from sklearn.semi_supervised import label_propagation
```
### Calculations
```
rng = np.random.RandomState(0)
iris = datasets.load_iris()
X = iris.data[:, :2]
y = iris.target
# step size in the mesh
h = .02
y_30 = np.copy(y)
y_30[rng.rand(len(y)) < 0.3] = -1
y_50 = np.copy(y)
y_50[rng.rand(len(y)) < 0.5] = -1
# we create an instance of SVM and fit out data. We do not scale our
# data since we want to plot the support vectors
ls30 = (label_propagation.LabelSpreading().fit(X, y_30),
y_30)
ls50 = (label_propagation.LabelSpreading().fit(X, y_50),
y_50)
ls100 = (label_propagation.LabelSpreading().fit(X, y), y)
rbf_svc = (svm.SVC(kernel='rbf').fit(X, y), y)
# create a mesh to plot in
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
x_ = np.arange(x_min, x_max, h)
y_ = np.arange(y_min, y_max, h)
xx, yy = np.meshgrid(x_, y_)
# title for the plots
titles = ['Label Spreading 30% data',
'Label Spreading 50% data',
'Label Spreading 100% data',
'SVC with rbf kernel']
```
### Plot Results
```
fig = tools.make_subplots(rows=2, cols=2,
subplot_titles=tuple(titles),
print_grid=False)
def matplotlib_to_plotly(cmap, pl_entries):
h = 1.0/(pl_entries-1)
pl_colorscale = []
for k in range(pl_entries):
C = map(np.uint8, np.array(cmap(k*h)[:3])*255)
pl_colorscale.append([k*h, 'rgb'+str((C[0], C[1], C[2]))])
return pl_colorscale
cmap = matplotlib_to_plotly(plt.cm.Paired, 6)
for i, (clf, y_train) in enumerate((ls30, ls50, ls100, rbf_svc)):
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
trace1 = go.Heatmap(x=x_, y=y_, z=Z,
colorscale=cmap,
showscale=False)
fig.append_trace(trace1, i/2+1, i%2+1)
# Plot also the training points
trace2 = go.Scatter(x=X[:, 0], y=X[:, 1],
mode='markers',
showlegend=False,
marker=dict(color=X[:, 0],
colorscale=cmap,
line=dict(width=1, color='black'))
)
fig.append_trace(trace2, i/2+1, i%2+1)
for i in map(str,range(1, 5)):
y = 'yaxis' + i
x = 'xaxis' + i
fig['layout'][y].update(showticklabels=False, ticks='')
fig['layout'][x].update(showticklabels=False, ticks='')
fig['layout'].update(height=700)
py.iplot(fig)
```
### License
Authors:
Clay Woolam <[email protected]>
License:
BSD
```
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'Decision Boundary of Label Propagation versus SVM on the Iris dataset.ipynb', 'scikit-learn/plot-label-propagation-versus-svm-iris/', 'Decision Boundary of Label Propagation versus SVM on the Iris dataset | plotly',
' ',
title = 'Decision Boundary of Label Propagation versus SVM on the Iris dataset | plotly',
name = 'Decision Boundary of Label Propagation versus SVM on the Iris dataset',
has_thumbnail='true', thumbnail='thumbnail/svm.jpg',
language='scikit-learn', page_type='example_index',
display_as='semi_supervised', order=3,
ipynb= '~Diksha_Gabha/3520')
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/satyajitghana/TSAI-DeepVision-EVA4.0/blob/master/05_CodingDrill/EVA4S5F1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Import Libraries
```
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
```
## Data Transformations
We first start with defining our data transformations. We need to think what our data is and how can we augment it to correct represent images which it might not see otherwise.
Here is the list of all the transformations which come pre-built with PyTorch
1. Compose
2. ToTensor
3. ToPILImage
4. Normalize
5. Resize
6. Scale
7. CenterCrop
8. Pad
9. Lambda
10. RandomApply
11. RandomChoice
12. RandomOrder
13. RandomCrop
14. RandomHorizontalFlip
15. RandomVerticalFlip
16. RandomResizedCrop
17. RandomSizedCrop
18. FiveCrop
19. TenCrop
20. LinearTransformation
21. ColorJitter
22. RandomRotation
23. RandomAffine
24. Grayscale
25. RandomGrayscale
26. RandomPerspective
27. RandomErasing
You can read more about them [here](https://pytorch.org/docs/stable/_modules/torchvision/transforms/transforms.html)
```
# Train Phase transformations
train_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)) # The mean and std have to be sequences (e.g., tuples), therefore you should add a comma after the values.
# Note the difference between (0.1307) and (0.1307,)
])
# Test Phase transformations
test_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
```
# Dataset and Creating Train/Test Split
```
train = datasets.MNIST('./data', train=True, download=True, transform=train_transforms)
test = datasets.MNIST('./data', train=False, download=True, transform=test_transforms)
```
# Dataloader Arguments & Test/Train Dataloaders
```
SEED = 1
# CUDA?
cuda = torch.cuda.is_available()
print("CUDA Available?", cuda)
# For reproducibility
torch.manual_seed(SEED)
if cuda:
torch.cuda.manual_seed(SEED)
# dataloader arguments - something you'll fetch these from cmdprmt
dataloader_args = dict(shuffle=True, batch_size=128, num_workers=4, pin_memory=True) if cuda else dict(shuffle=True, batch_size=64)
# train dataloader
train_loader = torch.utils.data.DataLoader(train, **dataloader_args)
# test dataloader
test_loader = torch.utils.data.DataLoader(test, **dataloader_args)
```
# Data Statistics
It is important to know your data very well. Let's check some of the statistics around our data and how it actually looks like
```
# We'd need to convert it into Numpy! Remember above we have converted it into tensors already
train_data = train.train_data
train_data = train.transform(train_data.numpy())
print('[Train]')
print(' - Numpy Shape:', train.train_data.cpu().numpy().shape)
print(' - Tensor Shape:', train.train_data.size())
print(' - min:', torch.min(train_data))
print(' - max:', torch.max(train_data))
print(' - mean:', torch.mean(train_data))
print(' - std:', torch.std(train_data))
print(' - var:', torch.var(train_data))
dataiter = iter(train_loader)
images, labels = dataiter.next()
print(images.shape)
print(labels.shape)
# Let's visualize some of the images
%matplotlib inline
import matplotlib.pyplot as plt
plt.imshow(images[0].numpy().squeeze(), cmap='gray_r')
```
## MORE
It is important that we view as many images as possible. This is required to get some idea on image augmentation later on
```
figure = plt.figure()
num_of_images = 60
for index in range(1, num_of_images + 1):
plt.subplot(6, 10, index)
plt.axis('off')
plt.imshow(images[index].numpy().squeeze(), cmap='gray_r')
```
# How did we get those mean and std values which we used above?
Let's run a small experiment
```
# simple transform
simple_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
# transforms.Normalize((0.1307,), (0.3081,)) # The mean and std have to be sequences (e.g., tuples), therefore you should add a comma after the values.
# Note the difference between (0.1307) and (0.1307,)
])
exp = datasets.MNIST('./data', train=True, download=True, transform=simple_transforms)
exp_data = exp.train_data
exp_data = exp.transform(exp_data.numpy())
print('[Train]')
print(' - Numpy Shape:', exp.train_data.cpu().numpy().shape)
print(' - Tensor Shape:', exp.train_data.size())
print(' - min:', torch.min(exp_data))
print(' - max:', torch.max(exp_data))
print(' - mean:', torch.mean(exp_data))
print(' - std:', torch.std(exp_data))
print(' - var:', torch.var(exp_data))
```
# The model
Let's start with the model we first saw
```
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 3, padding=1) #input -? OUtput? RF
self.conv2 = nn.Conv2d(32, 64, 3, padding=1)
self.pool1 = nn.MaxPool2d(2, 2)
self.conv3 = nn.Conv2d(64, 128, 3, padding=1)
self.conv4 = nn.Conv2d(128, 256, 3, padding=1)
self.pool2 = nn.MaxPool2d(2, 2)
self.conv5 = nn.Conv2d(256, 512, 3)
self.conv6 = nn.Conv2d(512, 1024, 3)
self.conv7 = nn.Conv2d(1024, 10, 3)
def forward(self, x):
x = self.pool1(F.relu(self.conv2(F.relu(self.conv1(x)))))
x = self.pool2(F.relu(self.conv4(F.relu(self.conv3(x)))))
x = F.relu(self.conv6(F.relu(self.conv5(x))))
# x = F.relu(self.conv7(x))
x = self.conv7(x)
x = x.view(-1, 10)
return F.log_softmax(x, dim=-1)
```
# Model Params
Can't emphasize on how important viewing Model Summary is.
Unfortunately, there is no in-built model visualizer, so we have to take external help
```
!pip install torchsummary
from torchsummary import summary
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
print(device)
model = Net().to(device)
summary(model, input_size=(1, 28, 28))
```
# Training and Testing
All right, so we have 6.3M params, and that's too many, we know that. But the purpose of this notebook is to set things right for our future experiments.
Looking at logs can be boring, so we'll introduce **tqdm** progressbar to get cooler logs.
Let's write train and test functions
```
from tqdm import tqdm
train_losses = []
test_losses = []
train_acc = []
test_acc = []
def train(model, device, train_loader, optimizer, epoch):
model.train()
pbar = tqdm(train_loader)
correct = 0
processed = 0
for batch_idx, (data, target) in enumerate(pbar):
# get samples
data, target = data.to(device), target.to(device)
# Init
optimizer.zero_grad()
# In PyTorch, we need to set the gradients to zero before starting to do backpropragation because PyTorch accumulates the gradients on subsequent backward passes.
# Because of this, when you start your training loop, ideally you should zero out the gradients so that you do the parameter update correctly.
# Predict
y_pred = model(data)
# Calculate loss
loss = F.nll_loss(y_pred, target)
train_losses.append(loss)
# Backpropagation
loss.backward()
optimizer.step()
# Update pbar-tqdm
pred = y_pred.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
processed += len(data)
pbar.set_description(desc= f'Loss={loss.item()} Batch_id={batch_idx} Accuracy={100*correct/processed:0.2f}')
train_acc.append(100*correct/processed)
def test(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
test_losses.append(test_loss)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
test_acc.append(100. * correct / len(test_loader.dataset))
```
# Let's Train and test our model
```
model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
EPOCHS = 20
for epoch in range(EPOCHS):
print("EPOCH:", epoch)
train(model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
fig, axs = plt.subplots(2,2,figsize=(15,10))
axs[0, 0].plot(train_losses)
axs[0, 0].set_title("Training Loss")
axs[1, 0].plot(train_acc)
axs[1, 0].set_title("Training Accuracy")
axs[0, 1].plot(test_losses)
axs[0, 1].set_title("Test Loss")
axs[1, 1].plot(test_acc)
axs[1, 1].set_title("Test Accuracy")
```
|
github_jupyter
|
# GPU Computing for Data Scientists
#### Using CUDA, Jupyter, PyCUDA, ArrayFire and Thrust
https://github.com/QuantScientist/Data-Science-ArrayFire-GPU
```
%reset -f
import pycuda
from pycuda import compiler
import pycuda.driver as drv
import pycuda.driver as cuda
```
# Make sure we have CUDA
```
drv.init()
print("%d device(s) found." % drv.Device.count())
for ordinal in range(drv.Device.count()):
dev = drv.Device(ordinal)
print ("Device #%d: %s" % (ordinal, dev.name()))
drv
```
## Simple addition the GPU: compilation
```
import pycuda.autoinit
import numpy
from pycuda.compiler import SourceModule
srcGPU = """
#include <stdio.h>
__global__ void multGPU(float *dest, float *a, float *b)
{
const int i = threadIdx.x;
dest[i] = a[i] * b[i];
//dest[i] = threadIdx.x + threadIdx.y + blockDim.x;
//dest[i] = blockDim.x;
//printf("I am %d.%d\\n", threadIdx.x, threadIdx.y);
}
"""
srcGPUModule = SourceModule(srcGPU)
print (srcGPUModule)
```
# Simple addition on the GPU: Host memory allocation
```
ARR_SIZE=16
a = numpy.random.randn(ARR_SIZE).astype(numpy.float32)
a=numpy.ones_like(a)*3
b = numpy.random.randn(ARR_SIZE).astype(numpy.float32)
b=numpy.ones_like(b)*2
dest = numpy.zeros_like(a)
# print dest
```
## Simple addition on the GPU: execution
```
multGPUFunc = srcGPUModule.get_function("multGPU")
print (multGPUFunc)
multGPUFunc(drv.Out(dest), drv.In(a), drv.In(b),
block=(ARR_SIZE,32,1))
print (dest)
# print "Calculating %d iterations" % (n_iter)
import timeit
rounds =3
print ('pycuda', timeit.timeit(lambda:
multGPUFunc(drv.Out(dest), drv.In(a), drv.In(b),
grid=(ARR_SIZE,1,1),
block=(1,1,1)),
number=rounds))
# print dest
# print 'pycuda', timeit.timeit(lambda:
# multGPUFunc(drv.Out(dest), drv.In(a), drv.In(b),
# block=(ARR_SIZE,1,1)),
# number=rounds)
# print dest
print ('npy', timeit.timeit(lambda:a*b , number=rounds))
```
# Threads and Blocks
```
a = numpy.random.randn(4,4)
a=numpy.ones_like(a)
a = a.astype(numpy.float32)
a_gpu = cuda.mem_alloc(a.nbytes)
cuda.memcpy_htod(a_gpu, a)
mod = SourceModule("""
#include <stdio.h>
__global__ void doublify(float *a)
{
int idx = threadIdx.x + threadIdx.y*4;
a[idx] *= 2;
//printf("I am %d.%d\\n", threadIdx.x, threadIdx.y);
printf("I am %dth thread in threadIdx.x:%d.threadIdx.y:%d blockIdx.:%d blockIdx.y:%d blockDim.x:%d blockDim.y:%d\\n",(threadIdx.x+threadIdx.y*blockDim.x+(blockIdx.x*blockDim.x*blockDim.y)+(blockIdx.y*blockDim.x*blockDim.y)),threadIdx.x, threadIdx.y,blockIdx.x,blockIdx.y,blockDim.x,blockDim.y);
}
""")
func = mod.get_function("doublify")
func(a_gpu, block=(16,1,1))
a_doubled = numpy.empty_like(a)
cuda.memcpy_dtoh(a_doubled, a_gpu)
print (a_doubled)
```
[block]

|
github_jupyter
|
# Solving Linear Systems: Iterative Methods
<a rel="license" href="http://creativecommons.org/licenses/by/4.0/"><img alt="Creative Commons License" style="border-width:0" src="https://licensebuttons.net/l/by/4.0/80x15.png" /></a><br />This notebook by Xiaozhou Li is licensed under a <a rel="license" href="http://creativecommons.org/licenses/by/4.0/">Creative Commons Attribution 4.0 International License</a>.
All code examples are also licensed under the [MIT license](http://opensource.org/licenses/MIT).
## General Form
For solving the linear system
$$
Ax = b,
$$
with the exact solution $x^{*}$. The general form based on the fixed point interation:
\begin{equation}
\begin{split}
x^{(0)} & = \text{initial guess} \\
x^{(k+1)} & = g(x^{(k)}) \quad k = 0,1,2,\ldots,
\end{split}
\end{equation}
where
$$
g(x) = x - C(Ax - b).
$$
Difficult: find a matrix $C$ such that
$$
\lim\limits_{k\rightarrow\infty}x^{(k)} = x^{*}
$$
and the algorithm needs to be converge fast and economy.
**Example 1**
\begin{equation*}
A = \left[\begin{array}{ccc} 9& -1 & -1 \\ -1 & 10 & -1 \\ -1 & -1& 15\end{array}\right],\quad b = \left[\begin{array}{c} 7 \\ 8 \\ 13\end{array}\right],
\end{equation*}
has the exact solution $x^{*} = {[1, 1, 1]}^T$
```
import numpy as np
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
from IPython.display import clear_output, display
def IterC(A, b, C, x0, x_star, iters):
x = np.copy(x0)
print ('Iteration No. Numerical Solution Max norm error ')
print (0, x, np.linalg.norm(x_star-x, np.inf))
for i in range(iters):
x = x + np.dot(C, b - np.dot(A,x))
print (i+1, x, np.linalg.norm(x_star-x,np.inf))
A = np.array([[9., -1., -1.],[-1.,10.,-1.],[-1.,-1.,15.]])
b = np.array([7.,8.,13.])
```
**Naive Choice**
Choosing $C = I$, then
$$g(x) = x - (Ax - b),$$
and the fixed-point iteration
$$x^{(k+1)} = (I - A)x^{(k)} + b \quad k = 0,1,2,\ldots. $$
Let the intial guess $x_0 = [0, 0, 0]^T$.
```
C = np.eye(3)
x0 = np.zeros(3)
x_star = np.array([1.,1.,1.])
w = interactive(IterC, A=fixed(A), b=fixed(b), C=fixed(C), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
```
**Best Choice (theoretically)**
Choosing $C = A^{-1}$, then
$$g(x) = x - A^{-1}(Ax - b),$$
and the fixed-point iteration
$$x^{(k+1)} = A^{-1}b \quad k = 0,1,2,\ldots. $$
* It equals to solve $Ax = b$ directly.
* However, it gives a hint that $C$ should be close to $A^{-1}$
**First Approach**
Let $D$ denote the main diagonal of $A$, $L$ denote the lower triangle of $A$ (entries below the main diagonal), and $U$ denote the upper triangle (entries above the main diagonal). Then $A = L + D + U$
Choosing $C = \text{diag}(A)^{-1} = D^{-1}$, then
$$g(x) = x - D^{-1}(Ax - b),$$
and the fixed-point iteration
$$Dx^{(k+1)} = (L + U)x^{(k)} + b \quad k = 0,1,2,\ldots. $$
```
C = np.diag(1./np.diag(A))
x0 = np.zeros(np.size(b))
#x0 = np.array([0,1.,0])
x_star = np.array([1.,1.,1.])
#IterC(A, b, C, x0, x_star, 10)
w = interactive(IterC, A=fixed(A), b=fixed(b), C=fixed(C), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
```
## Jacobi Method
### Matrix Form:
$$
x^{(k+1)} = x^{(k)} - D^{-1}(Ax^{(k)} - b)
$$
or
$$
Dx^{(k+1)} = b - (L+U)x^{(k)}
$$
### Algorithm
$$
x^{(k+1)}_i = \frac{b_i - \sum\limits_{j < i}a_{ij}x^{(k)}_j - \sum\limits_{j > i}a_{ij}x^{(k)}_j}{a_{ii}}
$$
```
def Jacobi(A, b, x0, x_star, iters):
x_old = np.copy(x0)
x_new = np.zeros(np.size(x0))
print (0, x_old, np.linalg.norm(x_star-x_old,np.inf))
for k in range(iters):
for i in range(np.size(x0)):
x_new[i] = (b[i] - np.dot(A[i,:i],x_old[:i]) - np.dot(A[i,i+1:],x_old[i+1:]))/A[i,i]
print (k+1, x_new, np.linalg.norm(x_star-x_new,np.inf))
x_old = np.copy(x_new)
w = interactive(Jacobi, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
```
**Second Approach**
Let $D$ denote the main diagonal of $A$, $L$ denote the lower triangle of $A$ (entries below the main diagonal), and $U$ denote the upper triangle (entries above the main diagonal). Then $A = L + D + U$
Choosing $C = (L + D)^{-1}$, then
$$g(x) = x - (L + D)^{-1}(Ax - b),$$
and the fixed-point iteration
$$(L + D)x^{(k+1)} = Ux^{(k)} + b \quad k = 0,1,2,\ldots. $$
```
def GS(A, b, x0, x_star, iters):
x = np.copy(x0)
print (0, x, np.linalg.norm(x_star-x,np.inf))
for k in range(iters):
for i in range(np.size(x0)):
x[i] = (b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i+1:],x[i+1:]))/A[i,i]
print (k+1, x, np.linalg.norm(x_star-x,np.inf))
w = interactive(GS, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
```
## Gauss-Seidel Method
### Algorithm
$$
x^{(k+1)}_i = \frac{b_i - \sum\limits_{j < i}a_{ij}x^{(k+1)}_j - \sum\limits_{j > i}a_{ij}x^{(k)}_j}{a_{ii}}
$$
### Matrix Form:
$$
x^{(k+1)} = x^{(k)} - (L+D)^{-1}(Ax^{(k)} - b)
$$
or
$$
(L+D)x^{(k+1)} = b - Ux^{(k)}
$$
**Example 2**
\begin{equation*}
A = \left[\begin{array}{ccc} 3& 1 & -1 \\ 2 & 4 & 1 \\ -1 & 2& 5\end{array}\right],\quad b = \left[\begin{array}{c} 4 \\ 1 \\ 1\end{array}\right],
\end{equation*}
has the exact solution $x^{*} = {[2, -1, 1]}^T$
```
A = np.array([[3, 1, -1],[2,4,1],[-1,2,5]])
b = np.array([4,1,1])
x0 = np.zeros(np.size(b))
x_star = np.array([2.,-1.,1.])
w = interactive(GS, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=40,value=0))
display(w)
```
**Example 3**
\begin{equation*}
A = \left[\begin{array}{ccc} 1& 2 & -2 \\ 1 & 1 & 1 \\ 2 & 2& 1\end{array}\right],\quad b = \left[\begin{array}{c} 7 \\ 8 \\ 13\end{array}\right],
\end{equation*}
has the exact solution $x^{*} = {[-3, 8, 3]}^T$
```
A = np.array([[1, 2, -2],[1,1,1],[2,2,1]])
b = np.array([7,8,13])
#x0 = np.zeros(np.size(b))
x0 = np.array([-1,1,1])
x_star = np.array([-3.,8.,3.])
w = interactive(GS, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
B = np.eye(3) - np.dot(np.diag(1./np.diag(A)),A)
print(B)
print (np.linalg.eig(B))
```
**Example 4**
\begin{equation*}
A = \left[\begin{array}{cc} 1& 2 \\ 3 & 1 \end{array}\right],\quad b = \left[\begin{array}{c} 5 \\ 5\end{array}\right],
\end{equation*}
has the exact solution $x^{*} = {[1, 2]}^T$
or
\begin{equation*}
A = \left[\begin{array}{cc} 3& 1 \\ 1 & 2 \end{array}\right],\quad b = \left[\begin{array}{c} 5 \\ 5\end{array}\right],
\end{equation*}
```
#A = np.array([[1, 2],[3,1]])
A = np.array([[3, 1],[1,2]])
b = np.array([5,5])
#x0 = np.zeros(np.size(b))
x0 = np.array([0,0])
x_star = np.array([1.,2.,])
w = interactive(GS, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
```
**Example 5**
Are Jacobi iteration and Gauss-Seidel iteration convergent for the following equations?
\begin{equation*}
A_1 = \left[\begin{array}{ccc} 3& 0 & 4 \\ 7 & 4 & 2 \\ -1 & 1 & 2\end{array}\right],\quad A_2 = \left[\begin{array}{ccc} -3& 3 & -6 \\ -4 & 7 & -8 \\ 5 & 7 & -9\end{array}\right],
\end{equation*}
* Consider the **spectral radius** of the iterative matrix
* $B_J = -D^{-1}(L+U)$ and $B_{GS} = -(L+D)^{-1}U$
```
def Is_Jacobi_Gauss(A):
L = np.tril(A,-1)
U = np.triu(A,1)
D = np.diag(np.diag(A))
B_J = np.dot(np.diag(1./np.diag(A)), L+U)
B_GS = np.dot(np.linalg.inv(L+D),U)
rho_J = np.linalg.norm(np.linalg.eigvals(B_J), np.inf)
rho_GS = np.linalg.norm(np.linalg.eigvals(B_GS), np.inf)
print ("Spectral Radius")
print ("Jacobi: ", rho_J)
print ("Gauss Sediel: ", rho_GS)
A1 = np.array([[3, 0, 4],[7, 4, 2], [-1,1,2]])
A2 = np.array([[-3, 3, -6], [-4, 7, -8], [5, 7, -9]])
Is_Jacobi_Gauss(A2)
```
## Successive Over-Relaxation (SOR)
### Algorithm
$$
x^{(k+1)}_i = x^{(k)} + \omega \frac{b_i - \sum\limits_{j < i}a_{ij}x^{(k+1)}_j - \sum\limits_{j \geq i}a_{ij}x^{(k)}_j}{a_{ii}}
$$
### Matrix Form:
$$
x^{(k+1)} = x^{(k)} - \omega(\omega L+D)^{-1}(Ax^{(k)} - b)
$$
or
$$
(\omega L+D)x^{(k+1)} = ((1-\omega)D - \omega U)x^{(k)} + \omega b
$$
```
def SOR(A, b, x0, x_star, omega, iters):
x = np.copy(x0)
print (0, x, np.linalg.norm(x_star-x,np.inf))
for k in range(iters):
for i in range(np.size(x0)):
x[i] = x[i] + omega*(b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i:],x[i:]))/A[i,i]
print (k+1, x, np.linalg.norm(x_star-x,np.inf))
def SOR2(A, b, x0, x_star, omega, iters):
x = np.copy(x0)
for k in range(iters):
for i in range(np.size(x0)):
x[i] = x[i] + omega*(b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i:],x[i:]))/A[i,i]
return (np.linalg.norm(x_star-x,np.inf))
def SOR3(A, b, x0, x_star, omega, iters):
x = np.copy(x0)
print (0, np.linalg.norm(x_star-x,np.inf))
for k in range(iters):
for i in range(np.size(x0)):
x[i] = x[i] + omega*(b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i:],x[i:]))/A[i,i]
print (k+1, np.linalg.norm(x_star-x,np.inf))
A = np.array([[9., -1., -1.],[-1.,10.,-1.],[-1.,-1.,15.]])
b = np.array([7.,8.,13.])
x0 = np.array([0.,0.,0.])
x_star = np.array([1.,1.,1.])
omega = 1.01
w = interactive(SOR, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), omega=fixed(omega), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
w = interactive(GS, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
```
**Example 6**
\begin{equation*}
A = \left[\begin{array}{ccc} 2& -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1& 2\end{array}\right],\quad b = \left[\begin{array}{c} 1 \\ 0 \\ 1.8\end{array}\right],
\end{equation*}
has the exact solution $x^{*} = {[1.2, 1.4, 1.6]}^T$
```
A = np.array([[2, -1, 0],[-1, 2, -1], [0, -1, 2]])
b = np.array([1., 0, 1.8])
x0 = np.array([1.,1.,1.])
x_star = np.array([1.2,1.4,1.6])
omega = 1.2
w = interactive(SOR, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), omega=fixed(omega), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
w = interactive(GS, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
num = 21
omega = np.linspace(0.8, 1.8, num)
err1 = np.zeros(num)
for i in range(num):
err1[i] = SOR2(A, b, x0, x_star, omega[i], 10)
print (err1)
plt.plot(omega, np.log10(err1), 'o')
```
**Example 7**
\begin{equation*}
A = \left[\begin{array}{cccc} -4& 1 & 1 & 1 \\ 1 & -4 & 1 & 1 \\ 1 & 1& -4 &1 \\ 1 & 1 &1 & -4\end{array}\right],\quad b = \left[\begin{array}{c} 1 \\ 1 \\ 1 \\ 1\end{array}\right],
\end{equation*}
has the exact solution $x^{*} = {[-1, -1, -1, -1]}^T$
```
A = np.array([[-4, 1, 1, 1],[1, -4, 1, 1], [1, 1, -4, 1], [1, 1, 1, -4]])
b = np.array([1, 1, 1, 1])
x0 = np.zeros(np.size(b))
x_star = np.array([-1,-1,-1,-1])
omega = 1.25
w = interactive(SOR, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), omega=fixed(omega), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
w = interactive(GS, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=100,value=0))
display(w)
num = 21
omega = np.linspace(0.8, 1.8, num)
err1 = np.zeros(num)
for i in range(num):
err1[i] = SOR2(A, b, x0, x_star, omega[i], 10)
print (err1)
plt.plot(omega, np.log10(err1), 'o')
```
**Example 8**
\begin{equation*}
A=\begin{pmatrix}{3} & {-1} & {0} & 0 & 0 & \frac{1}{2} \\ {-1} & {3} & {-1} & {0} & \frac{1}{2} & 0\\ {0} & {-1} & {3} & {-1} & {0} & 0 \\ 0& {0} & {-1} & {3} & {-1} & {0} \\ {0} & \frac{1}{2} & {0} & {-1} & {3} & {-1} \\ \frac{1}{2} & {0} & 0 & 0 & {-1} & {3}\end{pmatrix},\,\,b=\begin{pmatrix}\frac{5}{2} \\ \frac{3}{2} \\ 1 \\ 1 \\ \frac{3}{2} \\ \frac{5}{2} \end{pmatrix}
\end{equation*}
has the exact solution $x^{*} = {[1, 1, 1, 1, 1, 1]}^T$
```
n0 = 6
A = 3*np.eye(n0) - np.diag(np.ones(n0-1),-1) - np.diag(np.ones(n0-1),+1)
for i in range(n0):
if (abs(n0-1 - 2*i) > 1):
A[i, n0-1-i] = - 1/2
print (A)
x_star = np.ones(n0)
b = np.dot(A, x_star)
x0 = np.zeros(np.size(b))
omega = 1.25
w = interactive(SOR, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), omega=fixed(omega), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
num = 21
omega = np.linspace(0.8, 1.8, num)
err1 = np.zeros(num)
for i in range(num):
err1[i] = SOR2(A, b, x0, x_star, omega[i], 10)
print (err1)
plt.plot(omega, np.log10(err1), 'o')
w = interactive(Jacobi, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=100,value=0))
display(w)
```
## Sparse Matrix Computations
A coefficient matrix is called sparse if many of the matrix entries are known to be zero. Often, of the $n^2$ eligible entries in a sparse matrix, only $\mathcal{O}(n)$ of them are nonzero. A full matrix is the opposite, where few entries may be assumed to be zero.
**Example 9**
Consider the $n$-equation version of
\begin{equation*}
A=\begin{pmatrix}{3} & {-1} & {0} & 0 & 0 & \frac{1}{2} \\ {-1} & {3} & {-1} & {0} & \frac{1}{2} & 0\\ {0} & {-1} & {3} & {-1} & {0} & 0 \\ 0& {0} & {-1} & {3} & {-1} & {0} \\ {0} & \frac{1}{2} & {0} & {-1} & {3} & {-1} \\ \frac{1}{2} & {0} & 0 & 0 & {-1} & {3}\end{pmatrix},
\end{equation*}
has the exact solution $x^{*} = {[1, 1,\ldots, 1]}^T$ and $b = A x^{*}$
* First, let us have a look about the matrix $A$
```
n0 = 10000
A = 3*np.eye(n0) - np.diag(np.ones(n0-1),-1) - np.diag(np.ones(n0-1),+1)
for i in range(n0):
if (abs(n0-1 - 2*i) > 1):
A[i, n0-1-i] = - 1/2
#plt.spy(A)
#plt.show()
```
* How about the $PA = LU$ for the above matrix $A$?
* Are the $L$ and $U$ matrices still sparse?
```
import scipy.linalg
#P, L, U = scipy.linalg.lu(A)
#plt.spy(L)
#plt.show()
```
Gaussian elimination applied to a sparse matrix usually causes **fill-in**, where the coefficient matrix changes from sparse to full due to the necessary row operations. For this reason, the efficiency of Gaussian elimination and its $PA = LU$ implementation become questionable for sparse matrices, leaving iterative methods as a feasible alternative.
* Let us solve it with SOR method
```
x_star = np.ones(n0)
b = np.dot(A, x_star)
x0 = np.zeros(np.size(b))
omega = 1.25
w = interactive(SOR3, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), omega=fixed(omega), iters=widgets.IntSlider(min=0,max=200,value=0, step=10))
display(w)
```
## Application for Solving Laplace's Equation
### Laplace's equation
Consider the Laplace's equation given as
$$
\nabla^2 u = 0,\quad\quad (x,y) \in D,
$$
where $\nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}$, and the boundary conditions are given as

### Finite Difference Approximation
Here, we use a rectangular grid $(x_i,y_j)$, where
$$
x_i = i\Delta x, \,\,\text{for }\, i = 0,1,\ldots,N+1;\quad y_j = j\Delta y,\,\,\text{for }\, j = 0,1,\ldots,M+1.
$$
Five-points scheme:
$$
-\lambda^2 u_{i+1,j} + 2(1+\lambda^2)u_{i,j} - \lambda^2u_{i-1,j} - u_{i,j+1} - u_{i,j-1} = 0,\quad\text{for}\,\, i = 1,\ldots,N,\,\, j = 1,\ldots,M,
$$
where $\lambda = \frac{\Delta y}{\Delta x}$. The boundary conditions are
- $x = 0: u_{0,j} = g_L(y_j), \quad\text{for }\, j = 1,\ldots,M$,
- $x = a: u_{N+1,j} = g_R(y_j), \quad\text{for }\, j = 1,\ldots,M$,
- $y = 0: u_{i,0} = g_B(x_i), \quad\text{for }\, i = 1,\ldots,N$,
- $y = b: u_{i,M+1} = g_T(x_i), \quad\text{for }\, i = 1,\ldots,N$.
```
def generate_TD(N, dx, dy):
T = np.zeros([N,N])
a = - (dy/dx)**2
b = 2*(1 - a)
for i in range(N):
T[i,i] += b
if (i < N-1):
T[i,i+1] += a
if (i > 0):
T[i,i-1] += a
D = -np.identity(N)
return T, D
def assemble_matrix_A(dx, dy, N, M):
T, D = generate_TD(N, dx, dy)
A = np.zeros([N*M, N*M])
for j in range(M):
A[j*N:(j+1)*N,j*N:(j+1)*N] += T
if (j < M-1):
A[j*N:(j+1)*N,(j+1)*N:(j+2)*N] += D
if (j > 0):
A[j*N:(j+1)*N,(j-1)*N:j*N] += D
return A
N = 4
M = 4
dx = 1./(N+1)
dy = 1./(M+1)
T, D = generate_TD(N, dx, dy)
#print (T)
A = assemble_matrix_A(dx, dy, N, M)
#print (A)
plt.spy(A)
plt.show()
# Set boundary conditions
def gL(y):
return 0.
def gR(y):
return 0.
def gB(x):
return 0.
def gT(x):
return 1.
#return x*(1-x)*(4./5-x)*np.exp(6*x)
def assemble_vector_b(x, y, dx, dy, N, M, gL, gR, gB, gT):
b = np.zeros(N*M)
# Left BCs
for j in range(M):
b[(j-1)*N] += (dy/dx)**2*gL(y[j+1])
# Right BCs
# b +=
# Bottom BCs
# b +=
# Top BCs:
for i in range(N):
b[(M-1)*N+i] += gT(x[i+1])
return b
from mpl_toolkits import mplot3d
from mpl_toolkits.mplot3d import axes3d
def Laplace_solver(a, b, N, M, gL, gR, gB, gT):
dx = b/(M+1)
dy = a/(N+1)
x = np.linspace(0, a, N+2)
y = np.linspace(0, b, M+2)
A = assemble_matrix_A(dx, dy, N, M)
b = assemble_vector_b(x, y, dx, dy, N, M, gL, gR, gB, gT)
v = np.linalg.solve(A,b)
# add boundary points + plotting
u = np.zeros([(N+2),(M+2)])
#u[1:(N+1),1:(M+1)] = np.reshape(v, (N, M))
# Top BCs
for i in range(N+2):
u[i,M+1] = gT(x[i])
u = np.transpose(u)
u[1:(M+1),1:(N+1)] = np.reshape(v, (M, N))
X, Y = np.meshgrid(x, y)
#Z = np.sin(2*np.pi*X)*np.sin(2*np.pi*Y)
fig = plt.figure()
#ax = plt.axes(projection='3d')
ax = fig.add_subplot(1, 1, 1, projection='3d')
ax.plot_surface(X, Y, u, rstride=1, cstride=1,
cmap='viridis', edgecolor='none')
ax.set_title('surface')
plt.show()
Laplace_solver(1, 1, 40, 40, gL, gR, gB, gT)
def Jacobi_tol(A, b, x0, tol):
x_old = np.copy(x0)
x_new = np.zeros(np.size(x0))
for i in range(np.size(x0)):
x_new[i] = (b[i] - np.dot(A[i,:i],x_old[:i]) - np.dot(A[i,i+1:],x_old[i+1:]))/A[i,i]
iters = 1
while ((np.linalg.norm(x_new-x_old,np.inf)) > tol):
x_old = np.copy(x_new)
for i in range(np.size(x0)):
x_new[i] = (b[i] - np.dot(A[i,:i],x_old[:i]) - np.dot(A[i,i+1:],x_old[i+1:]))/A[i,i]
iters += 1
return x_new, iters
def GS_tol(A, b, x0, tol):
x_old = np.copy(x0)
x = np.copy(x0)
for i in range(np.size(x0)):
x[i] = (b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i+1:],x[i+1:]))/A[i,i]
iters = 1
while ((np.linalg.norm(x-x_old,np.inf)) > tol):
x_old = np.copy(x)
for i in range(np.size(x0)):
x[i] = (b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i+1:],x[i+1:]))/A[i,i]
iters += 1
return x, iters
def SOR_tol(A, b, x0, omega, tol):
x_old = np.copy(x0)
x = np.copy(x0)
for i in range(np.size(x0)):
x[i] = x[i] + omega*(b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i:],x[i:]))/A[i,i]
iters = 1
while ((np.linalg.norm(x-x_old,np.inf)) > tol):
x_old = np.copy(x)
for i in range(np.size(x0)):
x[i] = x[i] + omega*(b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i:],x[i:]))/A[i,i]
iters += 1
return x, iters
def CG_tol(A, b, x0, x_star, tol):
r_new = b - np.dot(A, x0)
r_old = np.copy(np.size(x0))
d_old = np.zeros(np.size(x0))
x = np.copy(x0)
iters = 0
while ((np.linalg.norm(x-x_star,np.inf)) > tol):
if (iters == 0):
d_new = np.copy(r_new)
else:
beta = np.dot(r_new,r_new)/np.dot(r_old,r_old)
d_new = r_new + beta*d_old
Ad = np.dot(A, d_new)
alpha = np.dot(r_new,r_new)/np.dot(d_new,Ad)
x += alpha*d_new
d_old = d_new
r_old = r_new
r_new = r_old - alpha*Ad
iters += 1
return x, iters
def Iterative_solver(a, b, N, M, gL, gR, gB, gT, tol):
dx = b/(M+1)
dy = a/(N+1)
x = np.linspace(0, a, N+2)
y = np.linspace(0, b, M+2)
A = assemble_matrix_A(dx, dy, N, M)
b = assemble_vector_b(x, y, dx, dy, N, M, gL, gR, gB, gT)
v = np.linalg.solve(A,b)
#tol = 1.e-8
v0 = np.zeros(np.size(b))
#v_J, iters = Jacobi_tol(A, b, v0, tol)
#print ("Jacobi Method: %4d %7.2e" %(iters, np.linalg.norm(v - v_J, np.inf)))
#v_GS, iters = GS_tol(A, b, v0, tol)
#print ("Gauss Seidel : %4d %7.2e" %(iters, np.linalg.norm(v - v_GS, np.inf)))
omega = 2./(1 + np.sin(np.pi*dx))
print ("omega = ", omega)
v_SOR, iters = SOR_tol(A, b, v0, omega, tol)
print ("SOR Method : %4d %7.2e" %(iters, np.linalg.norm(v - v_SOR, np.inf)))
v_CG, iters = CG_tol(A, b, v0, v, tol)
print ("CG Method : %4d %7.2e" %(iters, np.linalg.norm(v - v_CG, np.inf)))
Iterative_solver(1, 1, 80, 80, gL, gR, gB, gT, 1.e-4)
```
|
github_jupyter
|
```
import holoviews as hv
hv.extension('bokeh')
hv.opts.defaults(hv.opts.Curve(width=500),
hv.opts.Histogram(width=500),
hv.opts.HLine(alpha=0.5, color='r', line_dash='dashed'))
import numpy as np
import scipy.stats
```
# Cadenas de Markov
## Introducción
En la lección anterior vimos caminatas aleatorias y definimos lo que es un proceso estocástico. En lo que sigue nos restringiremos a procesos estocásticos que sólo puede tomar valores de un conjunto discreto $\mathcal{S}$ en tiempos $n>0$ que también son discretos.
Llamaremos a $\mathcal{S}=\{1, 2, \ldots, M\}$ el conjunto de **estados** del proceso. Cada estado en particular se suele denotar por un número natural.
Recordemos que para que un proceso estocástico sea considerado una **cadena de Markov** se debe cumplir
$$
P(X_{n+1}|X_{n}, X_{n-1}, \ldots, X_{1}) = P(X_{n+1}|X_{n})
$$
que se conoce como la propiedad de Markov o propiedad markoviana.
:::{important}
En una cadena de markov el estado futuro es independiente del pasado cuando conozco el presente
:::
## Matriz de transición
Si la cadena de Markov tiene estados discretos y es homogenea, podemos escribir
$$
P(X_{n+1}=j|X_{n}=i) = P_{ij},
$$
donde homogeneo quiere decir que la probabilidad de transicionar de un estado a otro no cambia con el tiempo. La probabilidad $P_{i,j}$ se suele llamar probabilidad de transición "a un paso".
El conjunto con todas las posibles combinaciones $P_{ij}$ para $i,j \in \mathcal{S}$ forma una matriz cuadrada de $M \times M$ que se conoce como matriz de transición
$$
P = \begin{pmatrix} P_{11} & P_{12} & \ldots & P_{1M} \\
P_{21} & P_{22} & \ldots & P_{2M} \\
\vdots & \vdots & \ddots & \vdots \\
P_{M1} & P_{M2} & \ldots & P_{MM}\end{pmatrix}
$$
donde siempre se debe cumplir que las filas sumen 1
$$
\sum_{j \in \mathcal{S}} P_{ij} = 1
$$
y además todos los $P_{ij} \geq 0$ y $P_{ij} \in [0, 1]$.
Una matriz de transición o matriz estocástica puede representarse como un grafo dirigido donde los vertices son los estados y las aristas las probabilidades de transición o pesos.
El siguiente es un ejemplo de grafo para un sistema de cuatro estados con todas sus transiciones equivalentes e iguales a $1/2$. Las transiciones con probabilidad $0$ no se muestran.
<img src="images/markov2.png" width="300">
Considere ahora el siguiente ejemplo
<img src="images/markov-ruin.png" width="400">
:::{note}
Si salimos del estado $0$ o del estado $3$ ya no podemos volver a ellos.
:::
Los estados a los cuales no podemos retornar se conocen como estados **transitorios** o transientes. Por el contrario los estados a los que si tenemos posibilidad de retornar se llaman estados **recurrentes**.
En general cuando se tienen estados a los que no se puede retornar se dice que cadena es **reducible**. Por el contrario si podemos regresar a todos los estados se dice que la cadena es **irreducible**.
:::{note}
Una cadena reducible puede "dividirse" para crear cadenas irreducibles.
:::
En el ejemplo de arriba podemos separar $\{0\}$, $\{1,2\}$ y $\{3\}$ en tres cadenas irreducibles [^ruina]
[^ruina]: La cadena de Markov anterior modela un problema conocido como la [ruina del apostador](https://en.wikipedia.org/wiki/Gambler%27s_ruin), puedes estudiar de que se trata [aquí](http://manjeetdahiya.com/posts/markov-chains-gamblers-ruin/)
## Ejemplo: Cadena de dos estados
Digamos que queremos predecir el clima de Valdivia por medio utilizando una cadena de Markov. Por lo tanto asumiremos que el clima de mañana es perfectamente predecible a partir del clima de hoy. Sean dos estados
- $s_A$ Luvioso
- $s_B$ Soleado
Con probabilidades condicionales $P(s_A|s_A) = 0.7$, $P(s_B|s_A) = 0.3$, $P(s_A|s_B) = 0.45$ y $P(s_B|s_B) = 0.55$. En este caso la matriz de transición es
$$
P = \begin{pmatrix} P(s_A|s_A) & P(s_B|s_A) \\ P(s_A|s_B) & P(s_B|s_B) \end{pmatrix} = \begin{pmatrix} 0.7 & 0.3 \\ 0.45 & 0.55 \end{pmatrix}
$$
que también se puede visualizar como un mapa de transición
<img src="images/markov1.png" width="500">
Si está soleado hoy, ¿Cuál es la probabilidad de que llueva mañana, en tres dias más y en una semana más?
Utilicemos `Python` y la matriz de transición para responder esta pregunta. Primero escribimos la matriz de transición como un `ndarray` de Numpy
```
P = np.array([[0.70, 0.30],
[0.45, 0.55]])
```
En segunda lugar vamos a crear un vector de estado inicial
```
s0 = np.array([0, 1]) # Estado soleado
```
Luego, las probabilidades para mañana dado que hoy esta soleado pueden calcularse como
$$
s_1 = s_0 P
$$
que se conoce como transición a un paso
```
np.dot(s0, P)
```
La probabilidad para tres días más puede calcularse como
$$
s_3 = s_2 P = s_1 P^2 = s_0 P^3
$$
que se conoce como transición a 3 pasos. Sólo necesitamos elevar la matriz al cubo y multiplicar por el estado inicial
```
np.dot(s0, np.linalg.matrix_power(P, 3))
```
El pronóstico para una semana sería entonces la transición a 7 pasos
```
np.dot(s0, np.linalg.matrix_power(P, 7))
```
Notamos que el estado de nuestro sistema comienza a converger
```
np.dot(s0, np.linalg.matrix_power(P, 1000))
```
Esto se conoce como el estado estacionario de la cadena.
## Estado estacionario de la cadena de Markov
Si la cadena de Markov converge a un estado, ese estado se llama **estado estacionario**. Una cadena puede tener más de un estado estacionario.
Por definición en un estado estacionario se cumple que
$$
s P = s
$$
Que corresponde al problema de valores y vectores propios.
:::{note}
Los estados estacionarios son los vectores propios del sistema
:::
Para el ejemplo anterior teniamos que
$$
\begin{pmatrix} s_1 & s_2 \end{pmatrix} P = \begin{pmatrix} s_1 & s_2 \end{pmatrix}
$$
Que resulta en las siguientes ecuaciones
$$
0.7 s_1 + 0.45 s_2 = s_1
$$
$$
0.3 s_1 + 0.55 s_2 = s_2
$$
Ambas nos dicen que $s_2 = \frac{2}{3} s_1$. Si además consideramos que $s_1 + s_2 = 1$ podemos despejar y obtener
- $s_1 = 3/5 = 0.6$
- $s_2 = 0.4$
Que es lo que vimos antes. Esto nos dice que en un 60\% de los días lloverá y en el restante 40% estará soleado
## Probabilidad de transición luego de n-pasos
Una pregunta interesante a responder con una cadena de Markov es
> ¿Cuál es la probabilidad de llegar al estado $j$ dado que estoy en el estado $i$ si doy exactamente $n$ pasos?
Consideremos por ejemplo
<img src="images/markov3.png" width="400">
donde la matriz de transición es claramente
$$
P = \begin{pmatrix} 1/2 & 1/4 & 1/4 \\
1/8 & 3/4 & 1/8 \\
1/4 & 1/4 & 1/2\end{pmatrix}
$$
Para este ejemplo particular
> ¿Cúal es la probabilidad de llegar al estado $2$ desde el estado $0$ en 2 pasos?
Podemos resolver esto matemáticamente como
$$
\begin{pmatrix} P_{00} & P_{01} & P_{02} \end{pmatrix} \begin{pmatrix} P_{02} \\ P_{12} \\ P_{22} \end{pmatrix} = P_{00}P_{02} + P_{01}P_{12} + P_{02}P_{22} = 0.28125
$$
Que corresponde al elemento en la fila $0$ y columna $2$ de la matriz $P^2$
```
P = np.array([[1/2, 1/4, 1/4],
[1/8, 3/4, 1/8],
[1/4, 1/4, 1/2]])
np.dot(P, P)[0, 2]
```
:::{important}
En general la probabilidad de llegar al estado $j$ desde el estado $i$ en $n$ pasos es equivalente al elemento en la fila $i$ y columna $j$ de la matriz $P^n$
:::
¿Qué ocurre cuando $n$ tiene a infinito?
```
display(np.linalg.matrix_power(P, 3),
np.linalg.matrix_power(P, 5),
np.linalg.matrix_power(P, 100))
```
Todas las filas convergen a un mismo valor. Este conjunto de probabilidades se conoce como $\pi$ la distribución estacionaria de la cadena de Markov. Notar que las filas de $P^\infty$ convergen solo si la cadena es irreducible.
El elemento $\pi_j$ (es decir $P_{ij}^\infty$) nos da la probabilidad de estar en $j$ luego de infinitos pasos. Notar que el subíndice $i$ ya no tiene importancia, es decir que el punto de partida ya no tiene relevancia.
## Algoritmo general para simular una cadena de Markov discreta
Asumiendo que tenemos un sistema con un conjunto discreto de estados $\mathcal{S}$ y que conocemos la matriz de probabilidades de transición $P$ podemos simular su evolución con el siguiente algoritmo
1. Setear $n=0$ y seleccionar un estado inicial $X_n = i$
1. Para $n = 1,2,\ldots,T$
1. Obtener la fila de $P$ que corresponde al estado actual $X_n$, es decir $P[X_n, :]$
1. Generar $X_{n+1}$ muestreando de una distribución multinomial con vector de probabilidad igual a la fila seleccionada
En este caso $T$ es el horizonte de la simulación. A continuación veremos como simular una cadena de Markov discreta usando Python
Digamos que tenemos una cadena con tres estados y que la fila de $P$ asociada a $X_n$ es $[0.7, 0.2, 0.1]$. Podemos usar `scipy.stats.multinomial` para generar una aleatoriamente una variable multinomial y luego aplicar el argumento máximo para obtener el índice del estado $X_{n+1}$
```
np.argmax(scipy.stats.multinomial.rvs(n=1, p=[0.7, 0.2, 0.1], size=1), axis=1)
```
Si repetimos esto 100 veces se obtiene la siguiente distribución para $X_{n+1}$
```
x = np.argmax(scipy.stats.multinomial.rvs(n=1, p=[0.7, 0.2, 0.1], size=100), axis=1)
edges, bins = np.histogram(x, range=(np.amin(x)-0.5, np.amax(x)+0.5), bins=len(np.unique(x)))
hv.Histogram((edges, bins), kdims='x', vdims='Frecuencia').opts(xticks=[0, 1, 2])
```
Lo cual coincide con la fila de $P$ que utilizamos
Ahora que sabemos como obtener el estado siguiente probemos algo un poco más complicado.
Consideremos el ejemplo de predicción de clima y simulemos 1000 cadenas a un horizonte de 10 pasos
```
P = np.array([[0.70, 0.30],
[0.45, 0.55]])
n_chains = 1000
horizon = 10
states = np.zeros(shape=(n_chains, horizon), dtype='int')
states[:, 0] = 1 # Estado inicial para todas las cadenas
for i in range(n_chains):
for j in range(1, horizon):
states[i, j] = np.argmax(scipy.stats.multinomial.rvs(n=1, p=P[states[i, j-1], :], size=1))
```
A continuación se muestran las tres primeras simulaciones como series de tiempo
```
p =[]
for i in range(3):
p.append(hv.Curve((states[i, :]), 'n', 'Estados').opts(yticks=[0, 1]))
hv.Overlay(p)
```
A continuación se muestra el estado más probable en cada paso
```
n_states = len(np.unique(states))
hist = np.zeros(shape=(horizon, n_states))
for j in range(horizon):
hist[j, :] = np.array([sum(states[:, j] == s) for s in range(n_states)])
hv.Curve((np.argmax(hist, axis=1)), 'n', 'Estado más probable').opts(yticks=[0, 1])
```
## Ley de los grandes números para variables no i.i.d.
Previamente vimos que el promedio de un conjunto de $N$ variables independientes e idénticamente distribuidas (iid) converge a su valor esperado cuando $N$ es grande.
Por ejemplo
$$
\lim_{N \to \infty} \frac{1}{N} \sum_{i=1}^N X_i = \mu
$$
En esta lección vimos que la cadena de markov, un proceso estocástico donde no se cumple el supuesto iid, puede tener en ciertos casos una distribución estacionaria
:::{note}
La **distribución estacionaria** $\pi$ de una cadena de Markov con matriz de transición $P$ es tal que $\pi P = \pi$
:::
**Teorema de ergodicidad:** Una cadena de Markov irreducible y aperiodica tiene una distribución estacionaria $\pi$ única, independiente de valor del estado inicial y que cumple
$$
\lim_{n\to \infty} s_j(n) = \pi_j
$$
donde los componentes de $\pi$ representan la fracción de tiempo que la cadena estará en cada uno de los estados luego de observarla por un largo tiempo
:::{important}
El límite de observar la cadena por un tiempo largo es análogo al análisis de estadísticos estáticos sobre muestras grandes. Esto es el equivalente a la ley de los grandes números para el caso de la cadena de Markov
:::
### Notas históricas
- **La primera ley de los grandes números:** [Jacob Bernoulli](https://en.wikipedia.org/wiki/Jacob_Bernoulli) mostró la primera versión de la Ley de los grandes números en su Ars Conjectandi en 1713. Esta primera versión parte del supuesto de que las VAs son iid. Bernoulli era un firme creyente del destino, se oponía al libre albedrío y abogaba por el determinismo en los fenómenos aleatorios.
- **La segunda ley de los grandes números:** En 1913 el matemático ruso [Andrei Markov](https://en.wikipedia.org/wiki/Andrey_Markov) celebró el bicentenario de la famosa prueba de Bernoulli organizando un simposio donde presentó su nueva versión de la Ley de los grandes números que aplica sobre la clase de procesos estocásticos que hoy llamamos procesos de Markov, de esta forma extendiendo el resultado de Bernoulli a un caso que no es iid.
- **La pugna de Markov y Nekrasov:** En aquellos tiempos Markov estaba en pugna con otro matemático ruso: [Pavel Nekrasov](https://en.wikipedia.org/wiki/Pavel_Nekrasov). Nekrasov había publicado previamente que "la independencia era una condición necesaria para que se cumpla la ley de los grandes números". Nekrasov mantenia que el comportamiento humano al no ser iid no podía estar guiado por la ley de los grandes números, es decir que los humanos actuan voluntariamente y con libre albedrío. Markov reaccionó a esta afirmación desarrollando un contra-ejemplo que terminó siendo lo que hoy conocemos como los procesos de Markov
|
github_jupyter
|
# The R Programming Language
1. **R**: Popular **open-source programming language** for statistical analysis
2. Widely used in statistics and econometrics
3. **User-friendly and powerful IDE**: [RStudio](https://www.rstudio.com/)
4. Basic functionalities of **R** can be extended by **packages**
5. Large number of packages available on the
[Comprehensive R Archive Network](https://cran.r-project.org/) (CRAN)
6. **Goal of this presentation:** Illustrate how to use `R` for the estimation of a
Poisson regression model
```
# install.packages("psych")
# install.packages("wooldridge")
# install.packages("xtable")
```
## Count data models
**Count data** models are used to explain dependent variables that are natural
numbers, i.e., positive integers such that $y_i \in \mathbb{N}$, where
$\mathbb{N} = \{0, 1, 2,\ldots\}$.
Count data models are frequently used in economics to study **countable events**:
Number of years of education, number of patent applications filed by companies,
number of doctor visits, number of crimes committed in a given city, etc.
The **Poisson model** is a popular count data model.
## Poisson regression model
Given a parameter $\lambda_i > 0$, the **Poisson model** assumes that the
probability of observing $Y_i=y_i$, where $y_i\in\mathbb{N}$, is equal to:
$$Prob(Y_i = y_i \mid \lambda_i) = \frac{\lambda_i^{y_i}\exp\{-\lambda_i\}}{y_i!},$$
for $i=1,\ldots,N$.
The mean and the variance of $Y_i$ are equal to the parameter $\lambda_i$:
$$E(Y_i\mid\lambda_i) = V(Y_i\mid\lambda_i) = \lambda_i,$$
implying *equi-dispersion* of the data.
To control for **observed characteristics**, the parameter $\lambda_i$ can be
parametrized as follows (implying $\lambda_i > 0$):
$$E(Y_i|X_i,\beta) \equiv \lambda_i = \exp\{X_i'\beta\},$$
where $X_i$ is a vector containing the covariates.
## Simulating data
`R` function simulating data from Poisson regression model:
```
simul_poisson <- function(n, beta) {
k <- length(beta) # number of covariates
x <- replicate(k - 1, rnorm(n)) # simulate covariates
x <- cbind(1, x) # for intercept term
lambda <- exp(x %*% beta) # individual means
y <- rpois(n, lambda) # simulate count
return(data.frame(y, x)) # return variables
}
```
Using function to generate data:
```
set.seed(123)
nobs <- 1000
beta <- c(-.5, .4, -.7)
data <- simul_poisson(nobs, beta)
```
## Data description
Descriptive statistics:
```
# extract variables of interest from data set
y <- data[, 1]
x <- as.matrix(data[, 2:4])
# descriptive statistics
library(psych)
describe(data)
```
## Data Description
Histogram of count variable:
```
barplot(table(y))
```
## Data Description
Relationship between count variable and covariates:
```
par(mfrow = c(1, 2))
plot(y, x[, 2])
plot(y, x[, 3])
```
## Likelihood Function and ML Estimator
Individual contribution to the likelihood function:
$$L_i(\beta;y_i,x_i) = \frac{\exp\{y_ix_i\beta\}\exp\{-\exp\{x_i\beta\}\}}{y_i!}$$
Individual log-Likelihood function:
$$\ell_i(\beta;y_i,x_i) = \log L_i(\beta;y_i,x_i)
= y_ix_i\beta - \exp\{x_i\beta\} - \log(y_i!)$$
Maximum Likelihood Estimator:
$$\hat{\beta}_{\text{MLE}} = \arg\max_{\beta} \sum_{i=1}^N \ell(\beta;y,X)$$
Optimization (using *minimization* of objective function):
$$\hat{\beta}_{\text{MLE}} = \arg\min_{\beta} Q(\beta;y,X) \qquad
Q(\beta;y,X) = -\frac{1}{N}\sum_{i=1}^N \ell_i(\beta;y_i,x_i)$$
## Coding the Objective Function
```
# Objective function of Poisson regression model
obj_poisson <- function(beta, y, x) {
lambda <- x %*% beta
llik <- y*lambda - exp(lambda) - lfactorial(y)
return(-mean(llik))
}
# Evaluating objective function
beta0 <- c(1, 2, 3)
obj_poisson(beta0, y, x)
```
## Maximizing the Objective Function
Set starting values:
```
beta0 <- rep(0, length(beta))
```
Optimize using quasi-Newton method (BFGS algorithm):
```
opt <- optim(beta0, obj_poisson, method = "BFGS",
y = y, x = x)
```
Show results:
```
cat("ML estimates:", opt$par,
"\nObjective function:", opt$value, "\n")
```
## Comparing Results to Built-in Function
```
opt_glm <- glm(y ~ 0 + x, family = poisson)
summary(opt_glm)
```
## Comparing Results to Built-in Function
Collect results from the two approaches to compare them:
```
res <- cbind("True" = beta, "MLE" = opt$par,
"GLM" = opt_glm$coefficients)
row.names(res) <- c("constant", "x1", "x2")
res
```
**Question:** Our results (`MLE`) are virtually the same as those obtained
with the built-in function `GLM`, but not identical. Where do the small
differences come from?
## Empirical Illustration
**Goal:** Investigate the determinants of fertility.
Poisson regression model used to estimate the relationship between explanatory
variables and count outcome variable.
Both our estimator coded from scratch and `R` built-in function will be used.
## Data
**Source:** Botswana's 1988 Demographic and Health Survey.
Data set borrowed from Wooldridge:
```
library(wooldridge)
data(fertil2)
```
Outcome variable: Total number of living children:
```
y_lab <- "children"
```
Explanatory variables: Education, age, marital status, living in urban area,
having electricity/TV at home:
```
x_lab <- c("educ", "age", "agesq", "evermarr", "urban",
"electric", "tv")
```
## Loading data
Selecting variables and removing missing values:
```
data <- fertil2[, c(y_lab, x_lab)]
data <- na.omit(data)
```
Show first 6 observations on first 8 variables:
```
head(data[, 1:8], n = 6)
```
## Descriptive Statitics
```
library(psych)
describe(data)
```
## Plot
```
attach(data)
par(mfrow = c(1, 2))
blue_transp <- adjustcolor("blue", alpha.f = 0.1)
plot(age, children, pch = 19, col = blue_transp)
plot(educ, children, pch = 19, col = blue_transp)
```
## MLE of the Poisson Model
Maximum likelihood function using built-in function `glm()`:
```
mle <- glm(children ~ educ + age + agesq + evermarr +
urban + electric + tv,
family = "poisson", data = data)
```
Maximum likelihood function using our own function:
```
y <- data[, y_lab]
x <- as.matrix(data[, x_lab])
x <- cbind(1, x) # for intercept term
beta0 <- rep(0, ncol(x)) # starting values
opt <- optim(beta0, obj_poisson, method = "BFGS",
y = y, x = x)
```
## MLE of the Poisson Model
**Results different from `glm()`?**
Optimization algorithms are iterative methods that rely on different criteria
to dertermine if/when the optimum has been reached.
**For example:** Change in the objective function, change in the parameter values,
change in the gradient, step size, etc.
*[More in Advanced Microeconometrics course].*
**Try to adjust tuning parameters**, for example add
`control = list(ndeps = rep(1e-8, ncol(x)))` to `optim()` to change step size
of gradient approximation.
## Summarizing the Empirical Results
```
summary(mle)
```
## Fitted Values
```
plot(density(mle$fitted.values),
main = "Density of fitted mean values")
```
## Formatting the results
```
library(xtable)
xtable(mle)
```
|
github_jupyter
|
```
####################################################################################################
# Copyright 2019 Srijan Verma and EMBL-European Bioinformatics Institute
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
# http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
####################################################################################################
```
# Ensembl numeric data extraction (negative)
## Below function to get Ensembl IDs from .csv and convert to a python list in JSON format
```
def csv_to_id(path):
df = pd.read_csv(path)
ids = df.TEST_neg.tolist()
for loc in ids:
loc = str(loc) #here 'nan' is converted to a string to compare with if
if loc != 'nan':
cleaned_ids.append(loc)
cleaned = json.dumps(cleaned_ids)
correct_format = "{" +'"ids": ' + cleaned + "}"
return correct_format
import pandas as pd
import numpy as np
import json
cleaned_ids = []
path = '/Training set.example.csv'
cleaned_IDs = csv_to_id(path)
#print(cleaned_IDs)
```
## Passing the list to Ensembl REST API to get JSON response
```
# Single request, multiple IDs
import requests, sys
import json, urllib
server = "https://rest.ensembl.org"
ext = '/lookup/id/?format=full;expand=1;utr=1;phenotypes=1'
#ext = '/lookup/id/?
headers = {'Content-Type' : 'application/json', "Accept" : 'application/json'}
#'{"ids" : ["ENSG00000255689", "ENSG00000254443"]}'
#cleaned_IDs = {"ids": ["ENSG00000255689", "ENSG00000254443"]}
r = requests.post(server+ext,headers=headers, data='{0}'.format(cleaned_IDs))
print(str(r))
print(type(r))
decoded = r.json()
#print(repr(decoded))
```
## Saving JSON response on local machine and then loading the .json file
```
import json
with open('/negative_data.json', 'w') as outfile:
json.dump(decoded, outfile, indent=4, sort_keys=True)
with open('/negative_data.json') as access_json:
read_content = json.load(access_json)
```
## 'read_content' variable contains the json response received
```
gene_display_name = []
gene_start = []
gene_end = []
gene_strand = []
gene_seq_region_name = []
gene_biotype = []
```
## Below function [get_gene_data() ] to extract 'gene' data. Data Extracted are :
1. gene display_name
2. gene start
3. gene end
4. gene strand
5. gene seq_region_name
6. gene biotype
```
def get_gene_data():
count = 0
for i in range(len(cleaned_ids)):
gene_display_name.append(read_content[cleaned_ids[i]]['display_name'])
gene_start.append(read_content[cleaned_ids[i]]['start'])
gene_end.append(read_content[cleaned_ids[i]]['end'])
gene_strand.append(read_content[cleaned_ids[i]]['strand'])
gene_seq_region_name.append(read_content[cleaned_ids[i]]['seq_region_name'])
gene_biotype.append(read_content[cleaned_ids[i]]['biotype'])
if cleaned_ids[i] in read_content:
count = count + 1
print(count)
get_gene_data()
print('No. of contents of gene_start is {0}'.format(len(gene_start)))
print('No. of contents of gene_end is {0}'.format(len(gene_end)))
print('No. of contents of gene_strand is {0}'.format(len(gene_strand)))
print('No. of contents of gene_seq_region_name is {0}'.format(len(gene_seq_region_name)))
print('No. of contents of gene_display_name is {0}'.format(len(gene_display_name)))
print('No. of contents of gene_biotype is {0}'.format(len(gene_biotype)))
no_of_transcripts = []
gene_ids_for_transcripts = []
```
## Below function [ get_no_of_transcripts() ] to calculate no. of transcripts in a particular gene
```
def get_no_of_transcripts():
for i in range(len(cleaned_ids)):
no_of_transcripts.append(len(read_content[cleaned_ids[i]]['Transcript']))
for k in range(len(read_content[cleaned_ids[i]]['Transcript'])):
gene_ids_for_transcripts.append(cleaned_ids[i])
for j in range(len(cleaned_ids)):
print('No. of transcripts in gene "{0}" are {1}'.format(cleaned_ids[j],no_of_transcripts[j]))
get_no_of_transcripts()
#read_content[cleaned_ids[0]]['Transcript'][0]
transcript_id = []
transcript_start = []
transcript_end = []
transcript_biotype = []
#gene_ids_for_transcripts
```
## Below function [get_transcript_data() ] to extract 'transcript' data. Data Extracted are :
1. transcript id
2. transcript start
3. transcript end
4. transcript biotype
```
def get_transcript_data():
for i in range(len(cleaned_ids)):
for j in range(len(read_content[cleaned_ids[i]]['Transcript'])):
transcript_id.append(read_content[cleaned_ids[i]]['Transcript'][j]['id'])
transcript_start.append(read_content[cleaned_ids[i]]['Transcript'][j]['start'])
transcript_end.append(read_content[cleaned_ids[i]]['Transcript'][j]['end'])
transcript_biotype.append(read_content[cleaned_ids[i]]['Transcript'][j]['biotype'])
for k in range(len(gene_ids_for_transcripts)):
print('Transcript "{0}" of gene ID "{1}" has start and end as : "{2}" & "{3}"'.format(transcript_id[k],gene_ids_for_transcripts[k],transcript_start[k],transcript_end[k]))
get_transcript_data()
print(len(transcript_id))
print(len(transcript_start))
print(len(transcript_end))
print(len(gene_ids_for_transcripts))
len(read_content[cleaned_ids[0]]['Transcript'][0]["Exon"])
no_of_exons = []
transcript_ids_for_exons = []
```
## Below function [ get_no_of_exons() ] to calculate no. of exons for a particular transcript
```
def get_no_of_exons():
for i in range(len(cleaned_ids)):
for j in range(len(read_content[cleaned_ids[i]]['Transcript'])):
no_of_exons.append(len(read_content[cleaned_ids[i]]['Transcript'][j]["Exon"]))
for k in range(len(read_content[cleaned_ids[i]]['Transcript'][j]["Exon"])):
transcript_ids_for_exons.append(read_content[cleaned_ids[i]]['Transcript'][j]['id'])
for l in range(len(cleaned_ids)):
print('No. of exons in transcript "{0}" are {1}'.format(transcript_id[l],no_of_exons[l]))
len(read_content[cleaned_ids[0]]['Transcript'][0]["Exon"])
get_no_of_exons()
sum(no_of_exons)
len(transcript_ids_for_exons)
#read_content[cleaned_ids[0]]['Transcript'][0]["Exon"][0]
exon_id = []
exon_start = []
exon_end = []
gene_ids_for_exons = []
```
## Below function [get_exon_data() ] to extract 'exon' data. Data Extracted are :
1. exon id
2. exon start
3. exon end
```
def get_exon_data():
for i in range(len(cleaned_ids)):
for j in range(len(read_content[cleaned_ids[i]]['Transcript'])):
for k in range(len(read_content[cleaned_ids[i]]['Transcript'][j]["Exon"])):
exon_id.append(read_content[cleaned_ids[i]]['Transcript'][j]["Exon"][k]['id'])
exon_start.append(read_content[cleaned_ids[i]]['Transcript'][j]["Exon"][k]['start'])
exon_end.append(read_content[cleaned_ids[i]]['Transcript'][j]["Exon"][k]['end'])
gene_ids_for_exons.append(cleaned_ids[i])
for l in range(len(transcript_ids_for_exons)):
print('Exon "{0}" of Transcript ID "{1}" having gene ID "{2}" has start and end as : "{3}" & "{4}"'.format(exon_id[l],transcript_ids_for_exons[l],gene_ids_for_exons[l],exon_start[l],exon_end[l]))
get_exon_data()
len(exon_id)
len(gene_ids_for_exons)
transcript_len = []
```
## Below function[ get_transcript_length() ] to calculate length of transcript
```
def get_transcript_length():
# for i in range(transcript_id):
# for j in range(exon)
for i in range(len(cleaned_ids)):
for j in range(len(read_content[cleaned_ids[i]]['Transcript'])):
trans_len = 0
start = 0
end = 0
total_exon_len = 0
for k in range(len(read_content[cleaned_ids[i]]['Transcript'][j]["Exon"])):
start = read_content[cleaned_ids[i]]['Transcript'][j]["Exon"][k]['start']
end = read_content[cleaned_ids[i]]['Transcript'][j]["Exon"][k]['end']
total_exon_len = total_exon_len + (end - start + 1)
transcript_len.append(total_exon_len)
for k in range(len(transcript_id)):
print('Transcript ID "{0}" has length of {1} bps'.format(transcript_id[k], transcript_len[k]))
len(transcript_id)
get_transcript_length()
len(transcript_len)
transcript_len[-1]
transcript_id[-1]
exon_len = []
```
## Below function[ get_exon_length() ] to calculate length of exon
```
def get_exon_length():
# for i in range(transcript_id):
# for j in range(exon)
#exon_id
for i in range(len(cleaned_ids)):
for j in range(len(read_content[cleaned_ids[i]]['Transcript'])):
# exon_len = 0
# start = 0
# end = 0
# exon_len = 0
for k in range(len(read_content[cleaned_ids[i]]['Transcript'][j]["Exon"])):
start = 0
end = 0
exon_len_sum = 0
start = read_content[cleaned_ids[i]]['Transcript'][j]["Exon"][k]['start']
end = read_content[cleaned_ids[i]]['Transcript'][j]["Exon"][k]['end']
exon_len_sum = (end - start + 1)
exon_len.append(exon_len_sum)
for k in range(len(exon_id)):
print('Exon ID "{0}" has length of {1} bps'.format(exon_id[k], exon_len[k]))
get_exon_length()
len(exon_len)
len(exon_id)
```
## Exporting gene data to gene_data.csv file
```
import csv
header = ['SNO', 'Gene ID', 'Display Name', 'Biotype', 'Start', 'End', 'Strand', 'Seq region Name', 'No. of Transcripts']
path = '/negative_data/gene_data.csv'
with open(path, 'wt', newline ='') as file:
writer = csv.writer(file, delimiter=',')
writer.writerow(i for i in header)
s_no = []
for i in range(len(cleaned_ids)):
s_no.append(i+1)
import pandas as pd
df = pd.read_csv(path)
df[df.columns[0]] = s_no
df[df.columns[1]] = cleaned_ids
df[df.columns[2]] = gene_display_name
df[df.columns[3]] = gene_biotype
df[df.columns[4]] = gene_start
df[df.columns[5]] = gene_end
df[df.columns[6]] = gene_strand
df[df.columns[7]] = gene_seq_region_name
df[df.columns[8]] = no_of_transcripts
df.to_csv(path)
```
## Exporting transcript data to transcript_data.csv file
```
import csv
header = ['SNO', 'Gene ID', 'Transcript ID', 'Biotype', 'Transcript Start', 'Transcript End', 'Transcript Length','No. of Exons']
path = '/negative_data/transcript_data.csv'
with open(path, 'wt', newline ='') as file:
writer = csv.writer(file, delimiter=',')
writer.writerow(i for i in header)
s_no = []
for i in range(len(transcript_id)):
s_no.append(i+1)
import pandas as pd
df = pd.read_csv(path)
df[df.columns[0]] = s_no
df[df.columns[1]] = gene_ids_for_transcripts
df[df.columns[2]] = transcript_id
df[df.columns[3]] = transcript_biotype
df[df.columns[4]] = transcript_start
df[df.columns[5]] = transcript_end
df[df.columns[6]] = transcript_len
df[df.columns[7]] = no_of_exons
df.to_csv(path)
```
## Exporting exon data to exon_data.csv file
```
import csv
header = ['SNO', 'Gene ID', 'Transcript ID', 'Exon ID', 'Exon Start', 'Exon End', 'Exon Length']
path = '/negative_data/exon_data.csv'
with open(path, 'wt', newline ='') as file:
writer = csv.writer(file, delimiter=',')
writer.writerow(i for i in header)
s_no = []
for i in range(len(exon_id)):
s_no.append(i+1)
import pandas as pd
df = pd.read_csv(path)
df[df.columns[0]] = s_no
df[df.columns[1]] = gene_ids_for_exons
df[df.columns[2]] = transcript_ids_for_exons
df[df.columns[3]] = exon_id
df[df.columns[4]] = exon_start
df[df.columns[5]] = exon_end
df[df.columns[6]] = exon_len
df.to_csv(path)
```
|
github_jupyter
|
# Running attribute inference attacks on Regression Models
In this tutorial we will show how to run black-box inference attacks on regression model. This will be demonstrated on the Nursery dataset (original dataset can be found here: https://archive.ics.uci.edu/ml/datasets/nursery).
## Preliminaries
In order to mount a successful attribute inference attack, the attacked feature must be categorical, and with a relatively small number of possible values (preferably binary).
In the case of the diabetes dataset, the sensitive feature we want to infer is the 'sex' feature, which is a binary feature.
## Load data
```
import os
import sys
sys.path.insert(0, os.path.abspath('..'))
from art.utils import load_diabetes
(x_train, y_train), (x_test, y_test), _, _ = load_diabetes(test_set=0.5)
```
## Train MLP model
```
from sklearn.tree import DecisionTreeRegressor
from art.estimators.regression.scikitlearn import ScikitlearnRegressor
model = DecisionTreeRegressor()
model.fit(x_train, y_train)
art_regressor = ScikitlearnRegressor(model)
print('Base model score: ', model.score(x_test, y_test))
```
## Attack
### Black-box attack
The black-box attack basically trains an additional classifier (called the attack model) to predict the attacked feature's value from the remaining n-1 features as well as the original (attacked) model's predictions.
#### Train attack model
```
import numpy as np
from art.attacks.inference.attribute_inference import AttributeInferenceBlackBox
attack_train_ratio = 0.5
attack_train_size = int(len(x_train) * attack_train_ratio)
attack_x_train = x_train[:attack_train_size]
attack_y_train = y_train[:attack_train_size]
attack_x_test = x_train[attack_train_size:]
attack_y_test = y_train[attack_train_size:]
attack_feature = 1 # sex
# get original model's predictions
attack_x_test_predictions = np.array([np.argmax(arr) for arr in art_regressor.predict(attack_x_test)]).reshape(-1,1)
# only attacked feature
attack_x_test_feature = attack_x_test[:, attack_feature].copy().reshape(-1, 1)
# training data without attacked feature
attack_x_test = np.delete(attack_x_test, attack_feature, 1)
bb_attack = AttributeInferenceBlackBox(art_regressor, attack_feature=attack_feature)
# train attack model
bb_attack.fit(attack_x_train)
```
#### Infer sensitive feature and check accuracy
```
# get inferred values
values = [-0.88085106, 1.]
inferred_train_bb = bb_attack.infer(attack_x_test, pred=attack_x_test_predictions, values=values)
# check accuracy
train_acc = np.sum(inferred_train_bb == np.around(attack_x_test_feature, decimals=8).reshape(1,-1)) / len(inferred_train_bb)
print(train_acc)
```
This means that for 56% of the training set, the attacked feature is inferred correctly using this attack.
Now let's check the precision and recall:
```
def calc_precision_recall(predicted, actual, positive_value=1):
score = 0 # both predicted and actual are positive
num_positive_predicted = 0 # predicted positive
num_positive_actual = 0 # actual positive
for i in range(len(predicted)):
if predicted[i] == positive_value:
num_positive_predicted += 1
if actual[i] == positive_value:
num_positive_actual += 1
if predicted[i] == actual[i]:
if predicted[i] == positive_value:
score += 1
if num_positive_predicted == 0:
precision = 1
else:
precision = score / num_positive_predicted # the fraction of predicted “Yes” responses that are correct
if num_positive_actual == 0:
recall = 1
else:
recall = score / num_positive_actual # the fraction of “Yes” responses that are predicted correctly
return precision, recall
print(calc_precision_recall(inferred_train_bb, np.around(attack_x_test_feature, decimals=8), positive_value=1.))
```
To verify the significance of these results, we now run a baseline attack that uses only the remaining features to try to predict the value of the attacked feature, with no use of the model itself.
```
from art.attacks.inference.attribute_inference import AttributeInferenceBaseline
baseline_attack = AttributeInferenceBaseline(attack_feature=attack_feature)
# train attack model
baseline_attack.fit(attack_x_train)
# infer values
inferred_train_baseline = baseline_attack.infer(attack_x_test, values=values)
# check accuracy
baseline_train_acc = np.sum(inferred_train_baseline == np.around(attack_x_test_feature, decimals=8).reshape(1,-1)) / len(inferred_train_baseline)
print(baseline_train_acc)
```
In this case, the black-box attack does not do better than the baseline.
|
github_jupyter
|
<h1><center>ERM with DNN under penalty of Equalized Odds</center></h1>
We implement here a regular Empirical Risk Minimization (ERM) of a Deep Neural Network (DNN) penalized to enforce an Equalized Odds constraint. More formally, given a dataset of size $n$ consisting of context features $x$, target $y$ and a sensitive information $z$ to protect, we want to solve
$$
\text{argmin}_{h\in\mathcal{H}}\frac{1}{n}\sum_{i=1}^n \ell(y_i, h(x_i)) + \lambda \chi^2|_1
$$
where $\ell$ is for instance the MSE and the penalty is
$$
\chi^2|_1 = \left\lVert\chi^2\left(\hat{\pi}(h(x)|y, z|y), \hat{\pi}(h(x)|y)\otimes\hat{\pi}(z|y)\right)\right\rVert_1
$$
where $\hat{\pi}$ denotes the empirical density estimated through a Gaussian KDE.
### The dataset
We use here the _communities and crimes_ dataset that can be found on the UCI Machine Learning Repository (http://archive.ics.uci.edu/ml/datasets/communities+and+crime). Non-predictive information, such as city name, state... have been removed and the file is at the arff format for ease of loading.
```
import sys, os
sys.path.append(os.path.abspath(os.path.join('../..')))
from examples.data_loading import read_dataset
x_train, y_train, z_train, x_test, y_test, z_test = read_dataset(name='crimes', fold=1)
n, d = x_train.shape
```
### The Deep Neural Network
We define a very simple DNN for regression here
```
from torch import nn
import torch.nn.functional as F
class NetRegression(nn.Module):
def __init__(self, input_size, num_classes):
super(NetRegression, self).__init__()
size = 50
self.first = nn.Linear(input_size, size)
self.fc = nn.Linear(size, size)
self.last = nn.Linear(size, num_classes)
def forward(self, x):
out = F.selu(self.first(x))
out = F.selu(self.fc(out))
out = self.last(out)
return out
```
### The fairness-inducing regularizer
We implement now the regularizer. The empirical densities $\hat{\pi}$ are estimated using a Gaussian KDE. The L1 functional norm is taken over the values of $y$.
$$
\chi^2|_1 = \left\lVert\chi^2\left(\hat{\pi}(x|z, y|z), \hat{\pi}(x|z)\otimes\hat{\pi}(y|z)\right)\right\rVert_1
$$
This used to enforce the conditional independence $X \perp Y \,|\, Z$.
Practically, we will want to enforce $\text{prediction} \perp \text{sensitive} \,|\, \text{target}$
```
from facl.independence.density_estimation.pytorch_kde import kde
from facl.independence.hgr import chi_2_cond
def chi_squared_l1_kde(X, Y, Z):
return torch.mean(chi_2_cond(X, Y, Z, kde))
```
### The fairness-penalized ERM
We now implement the full learning loop. The regression loss used is the quadratic loss with a L2 regularization and the fairness-inducing penalty.
```
import torch
import numpy as np
import torch.utils.data as data_utils
def regularized_learning(x_train, y_train, z_train, model, fairness_penalty, lr=1e-5, num_epochs=10):
# wrap dataset in torch tensors
Y = torch.tensor(y_train.astype(np.float32))
X = torch.tensor(x_train.astype(np.float32))
Z = torch.tensor(z_train.astype(np.float32))
dataset = data_utils.TensorDataset(X, Y, Z)
dataset_loader = data_utils.DataLoader(dataset=dataset, batch_size=200, shuffle=True)
# mse regression objective
data_fitting_loss = nn.MSELoss()
# stochastic optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=lr, weight_decay=0.01)
for j in range(num_epochs):
for i, (x, y, z) in enumerate(dataset_loader):
def closure():
optimizer.zero_grad()
outputs = model(x).flatten()
loss = data_fitting_loss(outputs, y)
loss += fairness_penalty(outputs, z, y)
loss.backward()
return loss
optimizer.step(closure)
return model
```
### Evaluation
For the evaluation on the test set, we compute two metrics: the MSE (accuracy) and HGR$|_\infty$ (fairness).
```
from facl.independence.hgr import hgr_cond
def evaluate(model, x, y, z):
Y = torch.tensor(y.astype(np.float32))
Z = torch.Tensor(z.astype(np.float32))
X = torch.tensor(x.astype(np.float32))
prediction = model(X).detach().flatten()
loss = nn.MSELoss()(prediction, Y)
hgr_infty = np.max(hgr_cond(prediction, Z, Y, kde))
return loss.item(), hgr_infty
```
### Running everything together
```
model = NetRegression(d, 1)
num_epochs = 20
lr = 1e-5
# $\chi^2|_1$
penalty_coefficient = 1.0
penalty = chi_squared_l1_kde
model = regularized_learning(x_train, y_train, z_train, model=model, fairness_penalty=penalty, lr=lr, \
num_epochs=num_epochs)
mse, hgr_infty = evaluate(model, x_test, y_test, z_test)
print("MSE:{} HGR_infty:{}".format(mse, hgr_infty))
```
|
github_jupyter
|
# Estimating The Mortality Rate For COVID-19
> Using Country-Level Covariates To Correct For Testing & Reporting Biases And Estimate a True Mortality Rate.
- author: Joseph Richards
- image: images/corvid-mortality.png
- comments: true
- categories: [MCMC, mortality]
- permalink: /covid-19-mortality-estimation/
- toc: true
```
#hide
# ! pip install pymc3 arviz xlrd
#hide
# Setup and imports
%matplotlib inline
import warnings
warnings.simplefilter('ignore')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc3 as pm
from IPython.display import display, Markdown
#hide
# constants
ignore_countries = [
'Others',
'Cruise Ship'
]
cpi_country_mapping = {
'United States of America': 'US',
'China': 'Mainland China'
}
wb_country_mapping = {
'United States': 'US',
'Egypt, Arab Rep.': 'Egypt',
'Hong Kong SAR, China': 'Hong Kong',
'Iran, Islamic Rep.': 'Iran',
'China': 'Mainland China',
'Russian Federation': 'Russia',
'Slovak Republic': 'Slovakia',
'Korea, Rep.': 'Korea, South'
}
wb_covariates = [
('SH.XPD.OOPC.CH.ZS',
'healthcare_oop_expenditure'),
('SH.MED.BEDS.ZS',
'hospital_beds'),
('HD.HCI.OVRL',
'hci'),
('SP.POP.65UP.TO.ZS',
'population_perc_over65'),
('SP.RUR.TOTL.ZS',
'population_perc_rural')
]
#hide
# data loading and manipulation
from datetime import datetime
import os
import numpy as np
import pandas as pd
def get_all_data():
'''
Main routine that grabs all COVID and covariate data and
returns them as a single dataframe that contains:
* count of cumulative cases and deaths by country (by today's date)
* days since first case for each country
* CPI gov't transparency index
* World Bank data on population, healthcare, etc. by country
'''
all_covid_data = _get_latest_covid_timeseries()
covid_cases_rollup = _rollup_by_country(all_covid_data['Confirmed'])
covid_deaths_rollup = _rollup_by_country(all_covid_data['Deaths'])
todays_date = covid_cases_rollup.columns.max()
# Create DataFrame with today's cumulative case and death count, by country
df_out = pd.DataFrame({'cases': covid_cases_rollup[todays_date],
'deaths': covid_deaths_rollup[todays_date]})
_clean_country_list(df_out)
_clean_country_list(covid_cases_rollup)
# Add observed death rate:
df_out['death_rate_observed'] = df_out.apply(
lambda row: row['deaths'] / float(row['cases']),
axis=1)
# Add covariate for days since first case
df_out['days_since_first_case'] = _compute_days_since_first_case(
covid_cases_rollup)
# Add CPI covariate:
_add_cpi_data(df_out)
# Add World Bank covariates:
_add_wb_data(df_out)
# Drop any country w/o covariate data:
num_null = df_out.isnull().sum(axis=1)
to_drop_idx = df_out.index[num_null > 1]
print('Dropping %i/%i countries due to lack of data' %
(len(to_drop_idx), len(df_out)))
df_out.drop(to_drop_idx, axis=0, inplace=True)
return df_out, todays_date
def _get_latest_covid_timeseries():
''' Pull latest time-series data from JHU CSSE database '''
repo = 'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/'
data_path = 'csse_covid_19_data/csse_covid_19_time_series/'
all_data = {}
for status in ['Confirmed', 'Deaths', 'Recovered']:
file_name = 'time_series_19-covid-%s.csv' % status
all_data[status] = pd.read_csv(
'%s%s%s' % (repo, data_path, file_name))
return all_data
def _rollup_by_country(df):
'''
Roll up each raw time-series by country, adding up the cases
across the individual states/provinces within the country
:param df: Pandas DataFrame of raw data from CSSE
:return: DataFrame of country counts
'''
gb = df.groupby('Country/Region')
df_rollup = gb.sum()
df_rollup.drop(['Lat', 'Long'], axis=1, inplace=True, errors='ignore')
# Drop dates with all 0 count data
df_rollup.drop(df_rollup.columns[df_rollup.sum(axis=0) == 0],
axis=1,
inplace=True)
# Convert column strings to dates:
idx_as_dt = [datetime.strptime(x, '%m/%d/%y') for x in df_rollup.columns]
df_rollup.columns = idx_as_dt
return df_rollup
def _clean_country_list(df):
''' Clean up input country list in df '''
# handle recent changes in country names:
country_rename = {
'Hong Kong SAR': 'Hong Kong',
'Taiwan*': 'Taiwan',
'Czechia': 'Czech Republic',
'Brunei': 'Brunei Darussalam',
'Iran (Islamic Republic of)': 'Iran',
'Viet Nam': 'Vietnam',
'Russian Federation': 'Russia',
'Republic of Korea': 'South Korea',
'Republic of Moldova': 'Moldova',
'China': 'Mainland China'
}
df.rename(country_rename, axis=0, inplace=True)
df.drop(ignore_countries, axis=0, inplace=True, errors='ignore')
def _compute_days_since_first_case(df_cases):
''' Compute the country-wise days since first confirmed case
:param df_cases: country-wise time-series of confirmed case counts
:return: Series of country-wise days since first case
'''
date_first_case = df_cases[df_cases > 0].idxmin(axis=1)
days_since_first_case = date_first_case.apply(
lambda x: (df_cases.columns.max() - x).days)
# Add 1 month for China, since outbreak started late 2019:
days_since_first_case.loc['Mainland China'] += 30
return days_since_first_case
def _add_cpi_data(df_input):
'''
Add the Government transparency (CPI - corruption perceptions index)
data (by country) as a column in the COVID cases dataframe.
:param df_input: COVID-19 data rolled up country-wise
:return: None, add CPI data to df_input in place
'''
cpi_data = pd.read_excel(
'https://github.com/jwrichar/COVID19-mortality/blob/master/data/CPI2019.xlsx?raw=true',
skiprows=2)
cpi_data.set_index('Country', inplace=True, drop=True)
cpi_data.rename(cpi_country_mapping, axis=0, inplace=True)
# Add CPI score to input df:
df_input['cpi_score_2019'] = cpi_data['CPI score 2019']
def _add_wb_data(df_input):
'''
Add the World Bank data covariates as columns in the COVID cases dataframe.
:param df_input: COVID-19 data rolled up country-wise
:return: None, add World Bank data to df_input in place
'''
wb_data = pd.read_csv(
'https://raw.githubusercontent.com/jwrichar/COVID19-mortality/master/data/world_bank_data.csv',
na_values='..')
for (wb_name, var_name) in wb_covariates:
wb_series = wb_data.loc[wb_data['Series Code'] == wb_name]
wb_series.set_index('Country Name', inplace=True, drop=True)
wb_series.rename(wb_country_mapping, axis=0, inplace=True)
# Add WB data:
df_input[var_name] = _get_most_recent_value(wb_series)
def _get_most_recent_value(wb_series):
'''
Get most recent non-null value for each country in the World Bank
time-series data
'''
ts_data = wb_series[wb_series.columns[3::]]
def _helper(row):
row_nn = row[row.notnull()]
if len(row_nn):
return row_nn[-1]
else:
return np.nan
return ts_data.apply(_helper, axis=1)
#hide
# Load the data (see source/data.py):
df, todays_date = get_all_data()
# Impute NA's column-wise:
df = df.apply(lambda x: x.fillna(x.mean()),axis=0)
```
# Observed mortality rates
```
#collapse-hide
display(Markdown('Data as of %s' % todays_date))
reported_mortality_rate = df['deaths'].sum() / df['cases'].sum()
display(Markdown('Overall reported mortality rate: %.2f%%' % (100.0 * reported_mortality_rate)))
df_highest = df.sort_values('cases', ascending=False).head(15)
mortality_rate = pd.Series(
data=(df_highest['deaths']/df_highest['cases']).values,
index=map(lambda x: '%s (%i cases)' % (x, df_highest.loc[x]['cases']),
df_highest.index))
ax = mortality_rate.plot.bar(
figsize=(14,7), title='Reported Mortality Rate by Country (countries w/ highest case counts)')
ax.axhline(reported_mortality_rate, color='k', ls='--')
plt.show()
```
# Model
Estimate COVID-19 mortality rate, controling for country factors.
```
#hide
import numpy as np
import pymc3 as pm
def initialize_model(df):
# Normalize input covariates in a way that is sensible:
# (1) days since first case: upper
# mu_0 to reflect asymptotic mortality rate months after outbreak
_normalize_col(df, 'days_since_first_case', how='upper')
# (2) CPI score: upper
# mu_0 to reflect scenario in absence of corrupt govts
_normalize_col(df, 'cpi_score_2019', how='upper')
# (3) healthcare OOP spending: mean
# not sure which way this will go
_normalize_col(df, 'healthcare_oop_expenditure', how='mean')
# (4) hospital beds: upper
# more beds, more healthcare and tests
_normalize_col(df, 'hospital_beds', how='mean')
# (5) hci = human capital index: upper
# HCI measures education/health; mu_0 should reflect best scenario
_normalize_col(df, 'hci', how='mean')
# (6) % over 65: mean
# mu_0 to reflect average world demographic
_normalize_col(df, 'population_perc_over65', how='mean')
# (7) % rural: mean
# mu_0 to reflect average world demographic
_normalize_col(df, 'population_perc_rural', how='mean')
n = len(df)
covid_mortality_model = pm.Model()
with covid_mortality_model:
# Priors:
mu_0 = pm.Beta('mu_0', alpha=0.3, beta=10)
sig_0 = pm.Uniform('sig_0', lower=0.0, upper=mu_0 * (1 - mu_0))
beta = pm.Normal('beta', mu=0, sigma=5, shape=7)
sigma = pm.HalfNormal('sigma', sigma=5)
# Model mu from country-wise covariates:
# Apply logit transformation so logistic regression performed
mu_0_logit = np.log(mu_0 / (1 - mu_0))
mu_est = mu_0_logit + \
beta[0] * df['days_since_first_case_normalized'].values + \
beta[1] * df['cpi_score_2019_normalized'].values + \
beta[2] * df['healthcare_oop_expenditure_normalized'].values + \
beta[3] * df['hospital_beds_normalized'].values + \
beta[4] * df['hci_normalized'].values + \
beta[5] * df['population_perc_over65_normalized'].values + \
beta[6] * df['population_perc_rural_normalized'].values
mu_model_logit = pm.Normal('mu_model_logit',
mu=mu_est,
sigma=sigma,
shape=n)
# Transform back to probability space:
mu_model = np.exp(mu_model_logit) / (np.exp(mu_model_logit) + 1)
# tau_i, mortality rate for each country
# Parametrize with (mu, sigma)
# instead of (alpha, beta) to ease interpretability.
tau = pm.Beta('tau', mu=mu_model, sigma=sig_0, shape=n)
# tau = pm.Beta('tau', mu=mu_0, sigma=sig_0, shape=n)
# Binomial likelihood:
d_obs = pm.Binomial('d_obs',
n=df['cases'].values,
p=tau,
observed=df['deaths'].values)
return covid_mortality_model
def _normalize_col(df, colname, how='mean'):
'''
Normalize an input column in one of 3 ways:
* how=mean: unit normal N(0,1)
* how=upper: normalize to [-1, 0] with highest value set to 0
* how=lower: normalize to [0, 1] with lowest value set to 0
Returns df modified in place with extra column added.
'''
colname_new = '%s_normalized' % colname
if how == 'mean':
mu = df[colname].mean()
sig = df[colname].std()
df[colname_new] = (df[colname] - mu) / sig
elif how == 'upper':
maxval = df[colname].max()
minval = df[colname].min()
df[colname_new] = (df[colname] - maxval) / (maxval - minval)
elif how == 'lower':
maxval = df[colname].max()
minval = df[colname].min()
df[colname_new] = (df[colname] - minval) / (maxval - minval)
#hide
# Initialize the model:
mod = initialize_model(df)
# Run MCMC sampler1
with mod:
trace = pm.sample(300, tune=100,
chains=3, cores=2)
#collapse-hide
n_samp = len(trace['mu_0'])
mu0_summary = pm.summary(trace).loc['mu_0']
print("COVID-19 Global Mortality Rate Estimation:")
print("Posterior mean: %0.2f%%" % (100*trace['mu_0'].mean()))
print("Posterior median: %0.2f%%" % (100*np.median(trace['mu_0'])))
lower = np.sort(trace['mu_0'])[int(n_samp*0.025)]
upper = np.sort(trace['mu_0'])[int(n_samp*0.975)]
print("95%% posterior interval: (%0.2f%%, %0.2f%%)" % (100*lower, 100*upper))
prob_lt_reported = sum(trace['mu_0'] < reported_mortality_rate) / len(trace['mu_0'])
print("Probability true rate less than reported rate (%.2f%%) = %.2f%%" %
(100*reported_mortality_rate, 100*prob_lt_reported))
print("")
# Posterior plot for mu0
print('Posterior probability density for COVID-19 mortality rate, controlling for country factors:')
ax = pm.plot_posterior(trace, var_names=['mu_0'], figsize=(18, 8), textsize=18,
credible_interval=0.95, bw=3.0, lw=3, kind='kde',
ref_val=round(reported_mortality_rate, 3))
```
## Magnitude and Significance of Factors
For bias in reported COVID-19 mortality rate
```
#collapse-hide
# Posterior summary for the beta parameters:
beta_summary = pm.summary(trace).head(7)
beta_summary.index = ['days_since_first_case', 'cpi', 'healthcare_oop', 'hospital_beds', 'hci', 'percent_over65', 'percent_rural']
beta_summary.reset_index(drop=False, inplace=True)
err_vals = ((beta_summary['hpd_3%'] - beta_summary['mean']).values,
(beta_summary['hpd_97%'] - beta_summary['mean']).values)
ax = beta_summary.plot(x='index', y='mean', kind='bar', figsize=(14, 7),
title='Posterior Distribution of Beta Parameters',
yerr=err_vals, color='lightgrey',
legend=False, grid=True,
capsize=5)
beta_summary.plot(x='index', y='mean', color='k', marker='o', linestyle='None',
ax=ax, grid=True, legend=False, xlim=plt.gca().get_xlim())
plt.savefig('../images/corvid-mortality.png')
```
# About This Analysis
This analysis was done by [Joseph Richards](https://twitter.com/joeyrichar)
In this project[^3], we attempt to estimate the true mortality rate[^1] for COVID-19 while controlling for country-level covariates[^2][^4] such as:
* age of outbreak in the country
* transparency of the country's government
* access to healthcare
* demographics such as age of population and rural vs. urban
Estimating a mortality rate lower than the overall reported rate likely implies that there has been **significant under-testing and under-reporting of cases globally**.
## Interpretation of Country-Level Parameters
1. days_since_first_case - positive (very statistically significant). As time since outbreak increases, expected mortality rate **increases**, as expected.
2. cpi - negative (statistically significant). As government transparency increases, expected mortality rate **decreases**. This may mean that less transparent governments under-report cases, hence inflating the mortality rate.
3. healthcare avg. out-of-pocket spending - no significant trend.
4. hospital beds per capita - no significant trend.
5. Human Capital Index - no significant trend (slightly negative = mortality rates decrease with increased mobilization of the country)
6. percent over 65 - positive (statistically significant). As population age increases, the mortality rate also **increases**, as expected.
7. percent rural - no significant trend.
[^1]: As of March 10, the **overall reported mortality rate is 3.5%**. However, this figure does not account for **systematic biases in case reporting and testing**. The observed mortality of COVID-19 has varied widely from country to country (as of early March 2020). For instance, as of March 10, mortality rates have ranged from < 0.1% in places like Germany (1100+ cases) to upwards of 5% in Italy (9000+ cases) and 3.9% in China (80k+ cases).
[^2]: The point of our modelling work here is to **try to understand and correct for the country-to-country differences that may cause the observed discrepancies in COVID-19 country-wide mortality rates**. That way we can "undo" those biases and try to **pin down an overall *real* mortality rate**.
[^3]: Full details about the model are available at: https://github.com/jwrichar/COVID19-mortality
[^4]: The affects of these parameters are subject to change as more data are collected.
# Appendix: Model Diagnostics
The following trace plots help to assess the convergence of the MCMC sampler.
```
#hide_input
import arviz as az
az.plot_trace(trace, compact=True);
```
|
github_jupyter
|
Building the dataset of numerical data
```
#### STOP - ONLY if needed
# Allows printing full text
import pandas as pd
pd.set_option('display.max_colwidth', None)
#mid_keywords = best_keywords(data, 1, 0.49, 0.51) # same as above, but for average papers
#low_keywords = best_keywords(data, 1, 0.03, 0.05) # same as above, but for poor papers
### PUT MAIN HERE ###
# Machine Learning Challenge
# Course: Machine Learning (880083-M-6)
# Group 58
##########################################
# Import packages #
##########################################
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import pearsonr
import yake #NOTE: with Anaconda: conda install -c conda-forge yake
##########################################
# Import self-made functions #
##########################################
from CODE.data_preprocessing.split_val import split_val
from CODE.data_preprocessing.find_outliers_tukey import find_outliers_tukey
#feature based on the title of the paper
from CODE.features.length_title import length_title
# features based on 'field_of_study' column
from CODE.features.field_variety import field_variety
from CODE.features.field_popularity import field_popularity
from CODE.features.field_citations_avarage import field_citations_avarage
# features based on the topics of the paper
from CODE.features.topic_citations_avarage import topic_citations_avarage
from CODE.features.topic_variety import topics_variety
from CODE.features.topic_popularity import topic_popularity
from CODE.features.topic_citations_avarage import topic_citations_avarage
# features based on the abstract of the paper
from CODE.features.keywords import best_keywords
from CODE.features.abst_words import abst_words
from CODE.features.abst_words import abst_count
# features based on the venue of the paper
from CODE.features.venue_popularity import venue_popularity
from CODE.features.venue_citations import venues_citations
from CODE.features.age import age
# features based on the authors of the paper
from CODE.features.author_h_index import author_h_index
from CODE.features.paper_h_index import paper_h_index
from CODE.features.team_size import team_size
from CODE.features.author_database import author_database
##########################################
# Load datasets #
##########################################
# Main datasets
data = pd.read_json('DATA/train.json') # Training set
test = pd.read_json('DATA/test.json') # Test set
# Author-centric datasets
# These datasets were made using our self-made functions 'citations_per_author' (for the author_citation_dic)
# These functions took a long time to make (ballpark ~10 minutes on a laptop in 'silent mode'), so instead we
# decided to run this function once, save the data, and reload the datasets instead of running the function again.
import pickle
with open('my_dataset1.pickle', 'rb') as dataset:
author_citation_dic = pickle.load(dataset)
with open('my_dataset2.pickle', 'rb') as dataset2:
author_db = pickle.load(dataset2)
##########################################
# Missing values handling #
##########################################
# Missing values for feature 'fields_of_study'
data.loc[data['fields_of_study'].isnull(), 'fields_of_study'] = ""
# Missing values for feature 'title'
data.loc[data['title'].isnull(), 'title'] = ""
# Missing values for feature 'abstract'
data.loc[data['abstract'].isnull(), 'abstract'] = ""
# Missing values for features 'authors'
data.loc[data['authors'].isnull(), 'authors'] = ""
# Missing values for feature 'venue'
data.loc[data['venue'].isnull(), 'venue'] = ""
# Missing values for feature 'year'
# data.loc[data['fields_of_study'].isnull(), 'fields_of_study'] = mean(year)
# Take mean by venue instead
# If venue not known, take something else?
# Missing values for feature 'references'
data.loc[data['references'].isnull(), 'references'] = ""
# Missing values for feature 'topics'
data.loc[data['topics'].isnull(), 'topics'] = ""
# Missing values for feature 'is_open_access'
#data.loc[data['is_open_access'].isnull(), 'is_open_access'] = ""
# Take most frequent occurrence for venue
# If venue not known, do something else?
##########################################
# Create basic numeric df #
##########################################
end = len(data)
num_X = data.loc[ 0:end+1 , ('doi', 'citations', 'year', 'references') ] ##REMOVE DOI
##########################################
# Feature creation #
##########################################
"""
FEATURE DATAFRAME: num_X
ALL: After writing a funtion to create a feature, please incorporate your new feature as a column on the dataframe below.
This is the dataframe we will use to train the models.
DO NOT change the order in this section if at all possible
"""
num_X['title_length'] = length_title(data) # returns a numbered series
num_X['field_variety'] = field_variety(data) # returns a numbered series
num_X['field_popularity'] = field_popularity(data) # returns a numbered series
# num_X['field_citations_avarage'] = field_citations_avarage(data) # returns a numbered series
num_X['team_sz'] = team_size(data) # returns a numbered series
num_X['topic_var'] = topics_variety(data) # returns a numbered series
num_X['topic_popularity'] = topic_popularity(data) # returns a numbered series
num_X['topic_citations_avarage'] = topic_citations_avarage(data) # returns a numbered series
num_X['venue_popularity'], num_X['venue'] = venue_popularity(data) # returns a numbered series and a pandas.Series of the 'venues' column reformatted
num_X['open_access'] = pd.get_dummies(data["is_open_access"], drop_first = True) # returns pd.df (True = 1)
num_X['age'] = age(data) # returns a numbered series. Needs to be called upon AFTER the venues have been reformed (from venue_frequency)
num_X['venPresL'] = venues_citations(data) # returns a numbered series. Needs to be called upon AFTER the venues have been reformed (from venue_frequency)
keywords = best_keywords(data, 1, 0.954, 0.955) # from [data set] get [integer] keywords from papers btw [lower bound] and [upper bound] quantiles; returns list
num_X['has_keyword'] = abst_words(data, keywords)#returns a numbered series: 1 if any of the words is present in the abstract, else 0
num_X['keyword_count'] = abst_count(data, keywords) # same as above, only a count (noot bool)
# Author H-index
author_db, reformatted_authors = author_database(data)
data['authors'] = reformatted_authors
num_X['h_index'] = paper_h_index(data, author_citation_dic) # Returns a numbered series. Must come after author names have been reformatted.
field_avg_cit = num_X.groupby('field_variety').citations.mean()
for field, field_avg in zip(field_avg_cit.index, field_avg_cit):
num_X.loc[num_X['field_variety'] == field, 'field_cit'] = field_avg
"""
END do not reorder
"""
##########################################
# Deal with specific missing values #
##########################################
# Open_access, thanks to jreback (27th of July 2016) https://github.com/pandas-dev/pandas/issues/13809
OpAc_by_venue = num_X.groupby('venue').open_access.apply(lambda x: x.mode()) # Take mode for each venue
OpAc_by_venue = OpAc_by_venue.to_dict()
missing_OpAc = num_X.loc[num_X['open_access'].isnull(),]
for i, i_paper in missing_OpAc.iterrows():
venue = i_paper['venue']
doi = i_paper['doi']
index = num_X[num_X['doi'] == doi].index[0]
if venue in OpAc_by_venue.keys(): # If a known venue, append the most frequent value for that venue
num_X[num_X['doi'] == doi]['open_access'] = OpAc_by_venue[venue] # Set most frequent occurrence
else: # Else take most occurring value in entire dataset
num_X.loc[index,'open_access'] = num_X.open_access.mode()[0] # Thanks to BENY (2nd of February, 2018) https://stackoverflow.com/questions/48590268/pandas-get-the-most-frequent-values-of-a-column
### Drop columns containing just strings
num_X = num_X.drop(['venue', 'doi', 'field_variety'], axis = 1)
num_X = num_X.dropna()
##########################################
# Train/val split #
##########################################
## train/val split
X_train, X_val, y_train, y_val = split_val(num_X, target_variable = 'citations')
"""
INSERT outlier detection on X_train here - ALBERT
"""
##########################################
# Outlier detection #
##########################################
### MODEL code for outlier detection
### names: X_train, X_val, y_train, y_val
# print(list(X_train.columns))
out_y = (find_outliers_tukey(x = y_train['citations'], top = 93, bottom = 0))[0]
out_rows = out_y
# out_X = (find_outliers_tukey(x = X_train['team_sz'], top = 99, bottom = 0))[0]
# out_rows = out_y + out_X
out_rows = sorted(list(set(out_rows)))
# print("X_train:")
# print(X_train.shape)
X_train = X_train.drop(labels = out_rows)
# print(X_train.shape)
# print()
# print("y_train:")
# print(y_train.shape)
y_train = y_train.drop(labels = out_rows)
# print(y_train.shape)
# Potential features to get rid of: team_sz
##########################################
# Model implementations #
##########################################
"""
IMPLEMENT models here
NOTE: Please do not write over X_train, X_val, y_train, y_val in your model - make new variables if needed
"""
#-----------simple regression, all columns
"""
MODEL RESULTS:
R2: 0.03724
MSE: 33.38996
"""
#-----------logistic regression, all columns
"""
MODEL RESULTS:
R2: 0.006551953988217396
MSE: 34.07342328208346
"""
#-----------SGD regression, all columns
"""
# MODEL RESULTS:
# Best outcome: ('constant', 0.01, 'squared_error', 35.74249957361433, 0.04476790061780822)
"""
#-----------polynomial regression, all columns
"""
"""
#model.fit(X_train, y_train)
#print('Best score: ', model.best_score_)
#print('Best parameters: ', model.best_params_)
#y_pred = model.predict(X_val)
#from sklearn.metrics import r2_score
#print(r2_score(y_val,y_pred))
# import json
#with open("sample.json", "w") as outfile:
#json.dump(dictionary, outfile)
"""
-----------------------------------------------------------------------------------------------------------
------------------------------ LETS EXPLORE!!! ------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------
"""
"""
"""
### FOR: exploring the new dataframe with numerical columns
# --> NOTE: it would be more efficient to combine these first and only expand the df once (per addition type)
num_X
### FOR: explore data train/val split (should be 6470 train rows and 3188 validation rows)
# names: X_train, X_val, y_train, y_val
print("number of keywords:", len(keywords))
print("total train rows:", X_train.shape)
print("numer w keyword:", sum(X_train['has_keyword']))
print()
print(keywords)
#X_val
#y_train
#y_val
#6210 of 6313
#6136 (of 6313) for 1 keyword from the top 1% of papers
#4787 for 2 keywords from top .01% of papers (correlation: 0.036)
#2917 for 1 keyword from top .01% of papers (correlation: 0.049)
"""
Look at some correlations - full num_X
"""
# names: X_train, X_val, y_train, y_val
# From: https://www.kaggle.com/ankitjha/comparing-regression-models
import seaborn as sns
corr_mat = num_X.corr(method='pearson')
plt.figure(figsize=(20,10))
sns.heatmap(corr_mat,vmax=1,square=True,annot=True,cmap='cubehelix')
"""
Look at some correlations - X_train
NOTE: there is no y here
"""
# names: X_train, X_val, y_train, y_val
#temp = y_train hstack X_train
# From: https://www.kaggle.com/ankitjha/comparing-regression-models
corr_mat = X_train.corr(method='pearson')
plt.figure(figsize=(20,10))
sns.heatmap(corr_mat,vmax=1,square=True,annot=True,cmap='cubehelix')
"""
-----------------------------------------------------------------------------------------------------------
------------------------- LETS CODE!!! --------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------
"""
"""
"""
print(list(X_train.columns))
"""
Choose your columns
"""
#X_train_small = X_train.loc[ : , 'topic_var':'h_index'].copy()
#X_val_small = X_val.loc[ : , 'topic_var':'h_index'].copy()
drops = ['year', 'team_sz', 'has_keyword']
X_train_small = X_train.copy()
X_train_small.drop(drops, inplace = True, axis=1)
X_val_small = X_val.copy()
X_val_small.drop(drops, inplace = True, axis=1)
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score, mean_absolute_error
from CODE.models.regression import simple_linear
from CODE.models.regression import log_reg
summaries = list(X_train.columns)
print(summaries)
for i in range(len(summaries)):
# fs = summaries[:i] + summaries[i+1:]
X_train_small = X_train.copy()
X_val_small = X_val.copy()
drops = summaries[i]
X_train_small.drop(drops, inplace = True, axis=1)
X_val_small.drop(drops, inplace = True, axis=1)
print("dropped:", summaries[i])
# simple_linear(X_train_small, y_train, X_val_small, y_val) #dropping venue_popularity helps a tiny bit
log_reg(X_train_small, y_train, X_val_small, y_val)
# print('r2:', r2_score(y_val, y_pred_val)) # 0.006551953988217396
# print("MAE:", mean_absolute_error(y_val, y_pred_val)) # 34.07342328208346
# print()
# helps to drop: year, field_popularity, team_size, topic_var, age, has_keyword, keyword_count
# hurts to drop: references, title length, topic_popularity, opic_citations_avarage, venue_popularity(!),
# venPresL(!), h_index(!), field_cit
X_train_small
#X_val_small
def abst_categories (the_data, keywords, mid_keywords, low_keywords):
abst = the_data['abstract']
counts = []
abst_key = []
for i in abst:
if i == None:
abst_key.append(0)
continue
else:
high = 0
for word in keywords:
if word in i.lower():
high += 1
mid = 0
for word in mid_keywords:
if word in i.lower():
mid += 1
low = 0
for word in low_keywords:
if word in i.lower():
low +=1
# abst_key = np.argmax(abst_key)
# abst_key = (max(abst_key)).index
return pd.Series(abst_key)
print(sum(abst_categories (data, keywords, mid_keywords, low_keywords))) #9499 rows
"""
Remove outliers
NOTE: can't rerun this code without restarting the kernal
"""
#names: X_train, X_val, y_train, y_val
#print(list(X_train.columns))
# print("citations:", find_outliers_tukey(x = y_train['citations'], top = 93, bottom = 0))
# print("year:", find_outliers_tukey(X_train['year'], top = 74, bottom = 25)) # seems unnecessary
# print("references:", find_outliers_tukey(X_train['references'], top = 90, bottom = 10)) # seems unnecessary
# print("team_size:", find_outliers_tukey(X_train['team_size'], top = 99, bottom = 0)) # Meh
# print("topic_variety:", find_outliers_tukey(X_train['topic_variety'], top = 75, bottom = 10)) # not much diff btw top and normal
# print("age:", find_outliers_tukey(X_train['age'], top = 90, bottom = 10)) # Meh
# print("open_access:", find_outliers_tukey(X_train['open_access'], top = 100, bottom = 0)) # Not necessary: boolean
# print("has_keyword:", find_outliers_tukey(X_train['has_keyword'], top = 100, bottom = 0)) # Not necessary: boolean
# print("title_length:", find_outliers_tukey(X_train['title_length'], top = 90, bottom = 10)) # Meh
# print("field_variety:", find_outliers_tukey(X_train['field_variety'], top = 90, bottom = 10)) # seems unnecessary
# print("venue_freq:", find_outliers_tukey(X_train['venue_freq'], top = 90, bottom = 10)) # seems unnecessary
out_y = (find_outliers_tukey(x = y_train['citations'], top = 95, bottom = 0))[0]
#out_X = (find_outliers_tukey(x = X_train['team_size'], top = 99, bottom = 0))[0]
out_rows = out_y
#out_rows = out_y + out_X
out_rows = sorted(list(set(out_rows)))
print("X_train:")
print(X_train.shape)
X_train = X_train.drop(labels = out_rows)
print(X_train.shape)
print()
print("y_train:")
print(y_train.shape)
y_train = y_train.drop(labels = out_rows)
print(y_train.shape)
X_train
# Create a mini version of the main 'data' dataframe
import pandas as pd
import numpy as np
# %pwd
# %cd C:\Users\r_noc\Desktop\Python\GIT\machinelearning
play = data.sample(100, replace = False, axis = 0, random_state = 123)
print(play.shape)
# print(play['abstract'])
print(list(play.columns))
# play['has_keyword'] = np.nan
# print(play.shape)
# play
from sklearn.linear_model import PoissonRegressor
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_z = scaler.fit_transform(X_train_small)
X_val_z =scaler.transform(X_val_small)
polynomial_features = PolynomialFeatures(degree = 2)
x_train_poly = polynomial_features.fit_transform(X_train_z)
x_val_poly = polynomial_features.transform(X_val_z)
model = LinearRegression()
model.fit(x_train_poly, y_train)
y_poly_pred = model.predict(x_val_poly)
print(r2_score(y_val, y_poly_pred)) # -0.04350391168707901
print(mean_absolute_error(y_val, y_poly_pred)) # 32.65668266590838
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_z = scaler.fit_transform(X_train_small)
X_val_z =scaler.transform(X_val_small)
model = PolynomialFeatures(degree = 2)
X_poly = model.fit_transform(X_train_z)
model.fit(X_poly, y_train)
model2 = LinearRegression()
model2.fit(X_poly, y_train)
y_pred_val = model2.predict(model.fit_transform(X_val_z))
print(r2_score(y_val, y_pred_val)) #0.03724015197555319
print(mean_absolute_error(y_val, y_pred_val)) #33.38996938585591
#names: X_train, X_val, y_train, y_val
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import SGDRegressor
scaler = StandardScaler()
X_train_z = scaler.fit_transform(X_train_small)
X_val_z =scaler.transform(X_val_small)
y_ravel = np.ravel(y_train)
lr = [ 1.1, 1, .1, .01, .001, .0001]
settings = []
for learning_rate in ['constant', 'optimal', 'invscaling']:
for loss in ['squared_error', 'huber']:
for eta0 in lr:
model = SGDRegressor(learning_rate=learning_rate, eta0=eta0, loss=loss,random_state=666, max_iter=5000)
model.fit(X_train_z, y_ravel)
y_pred = model.predict(X_val_z)
mae = mean_absolute_error(y_val, y_pred)
r2 = r2_score(y_val, y_pred)
settings.append((learning_rate, eta0, loss, mae, r2))
print(settings[-1])
# Best outcome: ('constant', 0.01, 'squared_error', 35.74249957361433, 0.04476790061780822)
# With small: ('invscaling', 1, 'squared_error', 48.92137807970932, 0.05128477811871335)
X_train
```
|
github_jupyter
|
```
import requests
import json
headers = {'content-type': 'application/json'}
url = 'https://nid.naver.com/nidlogin.login'
data = {"eventType": "AAS_PORTAL_START", "data": {"id": "lafamila", "pw": "als01060"}}
#params = {'sessionKey': '9ebbd0b25760557393a43064a92bae539d962103', 'format': 'xml', 'platformId': 1}
#requests.post(url, params=params, data=json.dumps(data), headers=headers)
source = requests.post(url, data=json.dumps(data), headers=headers)
```
<b>params</b> is for GET-style URL parameters, <b>data</b> is for POST-style body information
```
form = """
<form name="frmNIDLogin" id="frmNIDLogin" action="https://nid.naver.com/nidlogin.login" method="post" target="_top">
<input name="enctp" id="enctp" type="hidden" value="1">
<input name="encpw" id="encpw" type="hidden" value="">
<input name="encnm" id="encnm" type="hidden" value="">
<input name="svctype" id="svctype" type="hidden" value="0">
<input name="url" id="url" type="hidden" value="https://www.naver.com/">
<input name="enc_url" id="enc_url" type="hidden" value="https%3A%2F%2Fwww.naver.com%2F">
<input name="postDataKey" id="postDataKey" type="hidden" value="">
<input name="nvlong" id="nvlong" type="hidden" value="">
<input name="saveID" id="saveID" type="hidden" value="">
<input name="smart_level" id="smart_level" type="hidden" value="1">
<fieldset>
<legend class="blind">로그인</legend>
<div class="htmlarea" id="flasharea" style="visibility: hidden;"><object width="148" height="67" id="flashlogin" classid="clsid:d27cdb6e-ae6d-11cf-96b8-444553540000" codebase="https://fpdownload.macromedia.com/pub/shockwave/cabs/flash/swflash.cab#version=9,0,0,0" style="visibility: hidden;"><param name="allowScriptAccess" value="always"><param name="quality" value="high"><param name="menu" value="false"><param name="movie" value="https://static.nid.naver.com/loginv3/commonLoginF_201505.swf"><param name="wmode" value="window"><param name="bgcolor" value="#f7f7f7"><param name="FlashVars" value="null"><param name="allowFullScreen" value="false"><embed name="flashlogin" width="148" height="67" align="middle" pluginspage="https://www.macromedia.com/go/getflashplayer" src="https://static.nid.naver.com/loginv3/commonLoginF_201505.swf" type="application/x-shockwave-flash" allowscriptaccess="always" allowfullscreen="false" bgcolor="#f7f7f7" flashvars="null" menu="false" wmode="window" quality="high"></object>
<div class="error_box_v2" id="div_capslock2" style="left: -14px; top: 59px; display: none; position: absolute;">
<p><strong>Caps Lock</strong>이 켜져 있습니다.</p>
</div>
</div>
<div class="htmlarea" id="htmlarea" style="display: block;">
<div class="input_box"><label class="lbl_in" id="label_id" for="id">아이디</label><input name="id" title="아이디" class="int" id="id" accesskey="L" style="-ms-ime-mode: disabled;" type="text" maxlength="41" placeholder="아이디"></div>
<div class="input_box"><label class="lbl_in" id="label_pw" for="pw">비밀번호</label><input name="pw" title="비밀번호" class="int" id="pw" type="password" maxlength="16" placeholder="비밀번호">
<div class="error_box_v2" id="div_capslock" style="display: none;">
<p><strong>Caps Lock</strong>이 켜져 있습니다.</p>
</div>
</div>
</div>
<div class="chk_id_login">
<input title="로그인 상태유지" class="chk_login" id="chk_log" type="checkbox">
<label class="lbl_long" id="lbl_long" for="chk_log"><i class="ico_chk"></i>로그인 상태 유지</label>
</div>
<div class="login_help">
<div class="chk_ip"><a title="" id="ip_guide" href="https://static.nid.naver.com/loginv3/help_ip.html" target="_blank">IP보안</a> <span class="ip_box"><input title="IP 보안이 켜져 있습니다. IP보안을 사용하지 않으시려면 선택을 해제해주세요." class="chb_b" id="ckb_type" type="checkbox"><label class="lbl_type on" id="lbl_type" for="ckb_type">IP보안 체크</label></span></div>
</div>
<span class="btn_login"><input title="로그인" type="submit" value="로그인"></span>
<a class="btn_dis" href="https://nid.naver.com/nidlogin.login?mode=number&svctype=&logintp=&viewtype=&url=https://www.naver.com" target="_top">일회용 로그인</a>
<p class="btn_lnk">
<a class="btn_join" href="https://nid.naver.com/nidregister.form?url=https://www.naver.com" target="_blank">회원가입</a>
<a class="btn_id" href="https://nid.naver.com/user/help.nhn?todo=idinquiry" target="_blank">아이디<span class="blind">찾기</span></a>/<a href="https://nid.naver.com/nidreminder.form" target="_blank">비밀번호 찾기</a>
</p>
</fieldset>
</form>
"""
from bs4 import BeautifulSoup
soup = BeautifulSoup(form, 'html.parser')
values = soup.find_all('input')
datas = {}
for val in values:
inputs = str(val).split("\n")[0]
inp = BeautifulSoup(inputs, 'html.parser')
if "name" in str(inp):
name = inp.find('input')['name'].decode('utf-8').encode('utf-8')
if "value" not in str(inp):
datas[name] = raw_input(name)
else:
datas[name] = inp.find('input')['value'].decode('utf-8').encode('utf-8')
print datas
import requests
import json
headers = {'content-type': 'application/json'}
url = 'https://nid.naver.com/nidlogin.login'
data = {"data": datas}
#params = {'sessionKey': '9ebbd0b25760557393a43064a92bae539d962103', 'format': 'xml', 'platformId': 1}
#requests.post(url, params=params, data=json.dumps(data), headers=headers)
source = requests.post(url, data=json.dumps(data), headers=headers)
print source.text
#https://gist.github.com/blmarket/9012444
```
|
github_jupyter
|
# NumPy
NumPy is also incredibly fast, as it has bindings to C libraries. For more info on why you would want to use arrays instead of lists, check out this great [StackOverflow post](http://stackoverflow.com/questions/993984/why-numpy-instead-of-python-lists).
```
import numpy as np
```
# NumPy Arrays
NumPy arrays is the main way in which Numpy arrays are used.<br/>
NumPy arrays essentially come in two flavors: vectors and matrices.<br/>
Vectors are strictly 1-dimensional (1D) arrays and matrices are 2D (but you should note a matrix can still have only one row or one column).
## Creating NumPy Arrays
### From a Python List
We can create an array by directly converting a list or list of lists:
```
my_list = [1,2,3]
my_list
np.array(my_list)
my_matrix = [[1,2,3],[4,5,6],[7,8,9]]
my_matrix
np.array(my_matrix)
```
## Built-in Methods
There are lots of built-in ways to generate arrays.
### arange
Return evenly spaced values within a given interval. [[reference](https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.arange.html)]
```
np.arange(0,10)
np.arange(0,11,2)
```
### zeros and ones
Generate arrays of zeros or ones. [[reference](https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.zeros.html)]
```
np.zeros(3)
np.zeros((5,5))
np.ones(3)
np.ones((3,3))
```
### linspace
Return evenly spaced numbers over a specified interval. [[reference](https://www.numpy.org/devdocs/reference/generated/numpy.linspace.html)]
```
np.linspace(0,10,3)
np.linspace(0,5,20)
```
<font color=green>Note that `.linspace()` *includes* the stop value. To obtain an array of common fractions, increase the number of items:</font>
```
np.linspace(0,5,21)
```
### eye
Creates an identity matrix [[reference](https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.eye.html)]
```
np.eye(4)
```
## Random
Numpy also has lots of ways to create random number arrays:
### rand
Creates an array of the given shape and populates it with random samples from a uniform distribution over ``[0, 1)``. [[reference](https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.random.rand.html)]
```
np.random.rand(2)
np.random.rand(5,5)
```
### randn
Returns a sample (or samples) from the "standard normal" distribution [σ = 1]. Unlike **rand** which is uniform, values closer to zero are more likely to appear. [[reference](https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.random.randn.html)]
```
np.random.randn(2)
np.random.randn(5,5)
```
### randint
Returns random integers from `low` (inclusive) to `high` (exclusive). [[reference](https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.random.randint.html)]
```
np.random.randint(1,100)
np.random.randint(1,100, (10, 10))
```
### seed
Can be used to set the random state, so that the same "random" results can be reproduced. [[reference](https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.random.seed.html)]
```
np.random.seed(42)
np.random.rand(4)
np.random.seed(42)
np.random.rand(4)
```
## Array Attributes and Methods
Let's discuss some useful attributes and methods for an array:
```
arr = np.arange(25)
ranarr = np.random.randint(0,50,10)
arr
ranarr
```
## Reshape
Returns an array containing the same data with a new shape. [[reference](https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.reshape.html)]
```
arr.reshape(5,5)
```
### max, min, argmax, argmin
These are useful methods for finding max or min values. Or to find their index locations using argmin or argmax
```
ranarr
ranarr.max()
ranarr.argmax()
ranarr.min()
ranarr.argmin()
```
## Shape
Shape is an attribute that arrays have (not a method): [[reference](https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.ndarray.shape.html)]
```
# Vector
arr.shape
# Notice the two sets of brackets
arr.reshape(1,25)
arr.reshape(1,25).shape
arr.reshape(25,1)
arr.reshape(25,1).shape
```
### dtype
You can also grab the data type of the object in the array: [[reference](https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.ndarray.dtype.html)]
```
arr.dtype
arr2 = np.array([1.2, 3.4, 5.6])
arr2.dtype
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/Scott-Huston/DS-Unit-1-Sprint-2-Data-Wrangling-and-Storytelling/blob/master/LS_DS_123_Make_Explanatory_Visualizations.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
_Lambda School Data Science_
# Make Explanatory Visualizations
### Objectives
- identify misleading visualizations and how to fix them
- use Seaborn to visualize distributions and relationships with continuous and discrete variables
- add emphasis and annotations to transform visualizations from exploratory to explanatory
- remove clutter from visualizations
### Links
- [How to Spot Visualization Lies](https://flowingdata.com/2017/02/09/how-to-spot-visualization-lies/)
- [Visual Vocabulary - Vega Edition](http://ft.com/vocabulary)
- [Choosing a Python Visualization Tool flowchart](http://pbpython.com/python-vis-flowchart.html)
- [Searborn example gallery](http://seaborn.pydata.org/examples/index.html) & [tutorial](http://seaborn.pydata.org/tutorial.html)
- [Strong Titles Are The Biggest Bang for Your Buck](http://stephanieevergreen.com/strong-titles/)
- [Remove to improve (the data-ink ratio)](https://www.darkhorseanalytics.com/blog/data-looks-better-naked)
- [How to Generate FiveThirtyEight Graphs in Python](https://www.dataquest.io/blog/making-538-plots/)
# Avoid Misleading Visualizations
Did you find/discuss any interesting misleading visualizations in your Walkie Talkie?
## What makes a visualization misleading?
[5 Ways Writers Use Misleading Graphs To Manipulate You](https://venngage.com/blog/misleading-graphs/)
## Two y-axes
<img src="https://kieranhealy.org/files/misc/two-y-by-four-sm.jpg" width="800">
Other Examples:
- [Spurious Correlations](https://tylervigen.com/spurious-correlations)
- <https://blog.datawrapper.de/dualaxis/>
- <https://kieranhealy.org/blog/archives/2016/01/16/two-y-axes/>
- <http://www.storytellingwithdata.com/blog/2016/2/1/be-gone-dual-y-axis>
## Y-axis doesn't start at zero.
<img src="https://i.pinimg.com/originals/22/53/a9/2253a944f54bb61f1983bc076ff33cdd.jpg" width="600">
## Pie Charts are bad
<img src="https://i1.wp.com/flowingdata.com/wp-content/uploads/2009/11/Fox-News-pie-chart.png?fit=620%2C465&ssl=1" width="600">
## Pie charts that omit data are extra bad
- A guy makes a misleading chart that goes viral
What does this chart imply at first glance? You don't want your user to have to do a lot of work in order to be able to interpret you graph correctly. You want that first-glance conclusions to be the correct ones.
<img src="https://pbs.twimg.com/media/DiaiTLHWsAYAEEX?format=jpg&name=medium" width='600'>
<https://twitter.com/michaelbatnick/status/1019680856837849090?lang=en>
- It gets picked up by overworked journalists (assuming incompetency before malice)
<https://www.marketwatch.com/story/this-1-chart-puts-mega-techs-trillions-of-market-value-into-eye-popping-perspective-2018-07-18>
- Even after the chart's implications have been refuted, it's hard a bad (although compelling) visualization from being passed around.
<https://www.linkedin.com/pulse/good-bad-pie-charts-karthik-shashidhar/>
**["yea I understand a pie chart was probably not the best choice to present this data."](https://twitter.com/michaelbatnick/status/1037036440494985216)**
## Pie Charts that compare unrelated things are next-level extra bad
<img src="http://www.painting-with-numbers.com/download/document/186/170403+Legalizing+Marijuana+Graph.jpg" width="600">
## Be careful about how you use volume to represent quantities:
radius vs diameter vs volume
<img src="https://static1.squarespace.com/static/5bfc8dbab40b9d7dd9054f41/t/5c32d86e0ebbe80a25873249/1546836082961/5474039-25383714-thumbnail.jpg?format=1500w" width="600">
## Don't cherrypick timelines or specific subsets of your data:
<img src="https://wattsupwiththat.com/wp-content/uploads/2019/02/Figure-1-1.png" width="600">
Look how specifically the writer has selected what years to show in the legend on the right side.
<https://wattsupwiththat.com/2019/02/24/strong-arctic-sea-ice-growth-this-year/>
Try the tool that was used to make the graphic for yourself
<http://nsidc.org/arcticseaicenews/charctic-interactive-sea-ice-graph/>
## Use Relative units rather than Absolute Units
<img src="https://imgs.xkcd.com/comics/heatmap_2x.png" width="600">
## Avoid 3D graphs unless having the extra dimension is effective
Usually you can Split 3D graphs into multiple 2D graphs
3D graphs that are interactive can be very cool. (See Plotly and Bokeh)
<img src="https://thumbor.forbes.com/thumbor/1280x868/https%3A%2F%2Fblogs-images.forbes.com%2Fthumbnails%2Fblog_1855%2Fpt_1855_811_o.jpg%3Ft%3D1339592470" width="600">
## Don't go against typical conventions
<img src="http://www.callingbullshit.org/twittercards/tools_misleading_axes.png" width="600">
# Tips for choosing an appropriate visualization:
## Use Appropriate "Visual Vocabulary"
[Visual Vocabulary - Vega Edition](http://ft.com/vocabulary)
## What are the properties of your data?
- Is your primary variable of interest continuous or discrete?
- Is in wide or long (tidy) format?
- Does your visualization involve multiple variables?
- How many dimensions do you need to include on your plot?
Can you express the main idea of your visualization in a single sentence?
How hard does your visualization make the user work in order to draw the intended conclusion?
## Which Visualization tool is most appropriate?
[Choosing a Python Visualization Tool flowchart](http://pbpython.com/python-vis-flowchart.html)
## Anatomy of a Matplotlib Plot
```
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import AutoMinorLocator, MultipleLocator, FuncFormatter
np.random.seed(19680801)
X = np.linspace(0.5, 3.5, 100)
Y1 = 3+np.cos(X)
Y2 = 1+np.cos(1+X/0.75)/2
Y3 = np.random.uniform(Y1, Y2, len(X))
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 1, 1, aspect=1)
def minor_tick(x, pos):
if not x % 1.0:
return ""
return "%.2f" % x
ax.xaxis.set_major_locator(MultipleLocator(1.000))
ax.xaxis.set_minor_locator(AutoMinorLocator(4))
ax.yaxis.set_major_locator(MultipleLocator(1.000))
ax.yaxis.set_minor_locator(AutoMinorLocator(4))
ax.xaxis.set_minor_formatter(FuncFormatter(minor_tick))
ax.set_xlim(0, 4)
ax.set_ylim(0, 4)
ax.tick_params(which='major', width=1.0)
ax.tick_params(which='major', length=10)
ax.tick_params(which='minor', width=1.0, labelsize=10)
ax.tick_params(which='minor', length=5, labelsize=10, labelcolor='0.25')
ax.grid(linestyle="--", linewidth=0.5, color='.25', zorder=-10)
ax.plot(X, Y1, c=(0.25, 0.25, 1.00), lw=2, label="Blue signal", zorder=10)
ax.plot(X, Y2, c=(1.00, 0.25, 0.25), lw=2, label="Red signal")
ax.plot(X, Y3, linewidth=0,
marker='o', markerfacecolor='w', markeredgecolor='k')
ax.set_title("Anatomy of a figure", fontsize=20, verticalalignment='bottom')
ax.set_xlabel("X axis label")
ax.set_ylabel("Y axis label")
ax.legend()
def circle(x, y, radius=0.15):
from matplotlib.patches import Circle
from matplotlib.patheffects import withStroke
circle = Circle((x, y), radius, clip_on=False, zorder=10, linewidth=1,
edgecolor='black', facecolor=(0, 0, 0, .0125),
path_effects=[withStroke(linewidth=5, foreground='w')])
ax.add_artist(circle)
def text(x, y, text):
ax.text(x, y, text, backgroundcolor="white",
ha='center', va='top', weight='bold', color='blue')
# Minor tick
circle(0.50, -0.10)
text(0.50, -0.32, "Minor tick label")
# Major tick
circle(-0.03, 4.00)
text(0.03, 3.80, "Major tick")
# Minor tick
circle(0.00, 3.50)
text(0.00, 3.30, "Minor tick")
# Major tick label
circle(-0.15, 3.00)
text(-0.15, 2.80, "Major tick label")
# X Label
circle(1.80, -0.27)
text(1.80, -0.45, "X axis label")
# Y Label
circle(-0.27, 1.80)
text(-0.27, 1.6, "Y axis label")
# Title
circle(1.60, 4.13)
text(1.60, 3.93, "Title")
# Blue plot
circle(1.75, 2.80)
text(1.75, 2.60, "Line\n(line plot)")
# Red plot
circle(1.20, 0.60)
text(1.20, 0.40, "Line\n(line plot)")
# Scatter plot
circle(3.20, 1.75)
text(3.20, 1.55, "Markers\n(scatter plot)")
# Grid
circle(3.00, 3.00)
text(3.00, 2.80, "Grid")
# Legend
circle(3.70, 3.80)
text(3.70, 3.60, "Legend")
# Axes
circle(0.5, 0.5)
text(0.5, 0.3, "Axes")
# Figure
circle(-0.3, 0.65)
text(-0.3, 0.45, "Figure")
color = 'blue'
ax.annotate('Spines', xy=(4.0, 0.35), xytext=(3.3, 0.5),
weight='bold', color=color,
arrowprops=dict(arrowstyle='->',
connectionstyle="arc3",
color=color))
ax.annotate('', xy=(3.15, 0.0), xytext=(3.45, 0.45),
weight='bold', color=color,
arrowprops=dict(arrowstyle='->',
connectionstyle="arc3",
color=color))
ax.text(4.0, -0.4, "Made with http://matplotlib.org",
fontsize=10, ha="right", color='.5')
plt.show()
```
# Making Explanatory Visualizations with Seaborn
Today we will reproduce this [example by FiveThirtyEight:](https://fivethirtyeight.com/features/al-gores-new-movie-exposes-the-big-flaw-in-online-movie-ratings/)
```
from IPython.display import display, Image
url = 'https://fivethirtyeight.com/wp-content/uploads/2017/09/mehtahickey-inconvenient-0830-1.png'
example = Image(url=url, width=400)
display(example)
```
Using this data: https://github.com/fivethirtyeight/data/tree/master/inconvenient-sequel
Links
- [Strong Titles Are The Biggest Bang for Your Buck](http://stephanieevergreen.com/strong-titles/)
- [Remove to improve (the data-ink ratio)](https://www.darkhorseanalytics.com/blog/data-looks-better-naked)
- [How to Generate FiveThirtyEight Graphs in Python](https://www.dataquest.io/blog/making-538-plots/)
## Make prototypes
This helps us understand the problem
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.style.use('fivethirtyeight')
fake = pd.Series([38, 3, 2, 1, 2, 4, 6, 5, 5, 33],
index=range(1,11))
fake.plot.bar(color='C1', width=0.9);
fake2 = pd.Series(
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
2, 2, 2,
3, 3, 3,
4, 4,
5, 5, 5,
6, 6, 6, 6,
7, 7, 7, 7, 7,
8, 8, 8, 8,
9, 9, 9, 9,
10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10])
fake2.value_counts().sort_index().plot.bar(color='C1', width=0.9);
```
## Annotate with text
```
plt.style.use('fivethirtyeight')
fig = plt.figure()
fig.patch.set_facecolor('white')
ax = fake.plot.bar(color='#ED713A', width = .9)
ax.set(facecolor = 'white')
ax.text(x=-2,y = 46, s="'An Inconvenient Sequel: Truth To Power' is divisive", fontweight = 'bold')
ax.text(x=-2, y = 43, s = 'IMDb ratings for the film as of Aug. 29')
ax.set_xticklabels(range(1,11), rotation = 0, color = '#A3A3A3')
ax.set_yticklabels(['0', '10', '20', '30', '40%'], color = '#A3A3A3')
ax.set_yticks(range(0,50,10))
plt.ylabel('Percent of total votes', fontweight = 'bold', fontsize = '12')
plt.xlabel('Rating', fontweight = 'bold', fontsize = '12')
```
## Reproduce with real data
```
df = pd.read_csv('https://raw.githubusercontent.com/fivethirtyeight/data/master/inconvenient-sequel/ratings.csv')
pd.set_option('display.max_columns', 50)
print(df.shape)
df.head(20)
df.sample(1).T
df.tail()
df.dtypes
df['timestamp'] = pd.to_datetime(df['timestamp'])
df.timestamp.describe()
df.dtypes
df.set_index(df['timestamp'], inplace = True)
df['2017-08-29']
lastday = df['2017-08-29']
lastday_filtered = lastday[lastday['category']=='IMDb users']
lastday_filtered.tail(30)
df.category.value_counts()
lastday_filtered.respondents.plot()
plt.show()
final = lastday_filtered.tail(1)
final.T
pct_columns = ['1_pct', '2_pct', '3_pct', '4_pct', '5_pct','6_pct','7_pct','8_pct','9_pct','10_pct']
final = final[pct_columns]
final.T
plot_data = final.T
plot_data.index = range(1,11)
plot_data
plt.style.use('fivethirtyeight')
fig = plt.figure()
fig.patch.set_facecolor('white')
ax = plot_data.plot.bar(color='#ED713A', width = .9, legend = False)
ax.set(facecolor = 'white')
ax.text(x=-2,y = 46, s="'An Inconvenient Sequel: Truth To Power' is divisive", fontweight = 'bold')
ax.text(x=-2, y = 43, s = 'IMDb ratings for the film as of Aug. 29')
ax.set_xticklabels(range(1,11), rotation = 0, color = '#A3A3A3')
ax.set_yticklabels(['0', '10', '20', '30', '40%'], color = '#A3A3A3')
ax.set_yticks(range(0,50,10))
plt.ylabel('Percent of total votes', fontweight = 'bold', fontsize = '12')
plt.xlabel('Rating', fontweight = 'bold', fontsize = '12', labelpad = 15)
plt.show()
```
# ASSIGNMENT
Replicate the lesson code. I recommend that you [do not copy-paste](https://docs.google.com/document/d/1ubOw9B3Hfip27hF2ZFnW3a3z9xAgrUDRReOEo-FHCVs/edit).
# STRETCH OPTIONS
#### 1) Reproduce another example from [FiveThityEight's shared data repository](https://data.fivethirtyeight.com/).
#### 2) Reproduce one of the following using a library other than Seaborn or Matplotlib.
For example:
- [thanksgiving-2015](https://fivethirtyeight.com/features/heres-what-your-part-of-america-eats-on-thanksgiving/) (try the [`altair`](https://altair-viz.github.io/gallery/index.html#maps) library)
- [candy-power-ranking](https://fivethirtyeight.com/features/the-ultimate-halloween-candy-power-ranking/) (try the [`statsmodels`](https://www.statsmodels.org/stable/index.html) library)
- or another example of your choice!
#### 3) Make more charts!
Choose a chart you want to make, from [Visual Vocabulary - Vega Edition](http://ft.com/vocabulary).
Find the chart in an example gallery of a Python data visualization library:
- [Seaborn](http://seaborn.pydata.org/examples/index.html)
- [Altair](https://altair-viz.github.io/gallery/index.html)
- [Matplotlib](https://matplotlib.org/gallery.html)
- [Pandas](https://pandas.pydata.org/pandas-docs/stable/visualization.html)
Reproduce the chart. [Optionally, try the "Ben Franklin Method."](https://docs.google.com/document/d/1ubOw9B3Hfip27hF2ZFnW3a3z9xAgrUDRReOEo-FHCVs/edit) If you want, experiment and make changes.
Take notes. Consider sharing your work with your cohort!
```
# Stretch option #1
!pip install pandas==0.23.4
import pandas as pd
from IPython.display import display, Image
# url = 'https://fivethirtyeight.com/wp-content/uploads/2017/09/mehtahickey-inconvenient-0830-1.png'
# example = Image(url=url, width=400)
# example = Image(filename = '/Users/scotthuston/Desktop/FTE_image')
# display(example)
FTE = pd.read_csv('https://raw.githubusercontent.com/fivethirtyeight/checking-our-work-data/master/mlb_games.csv')
FTE.head()
prob1_bins = pd.cut(FTE['prob1'],13)
ct = pd.crosstab(FTE['prob1_outcome'], [prob1_bins])
# FTE.boxplot(column = 'prob1')
df1 = FTE[FTE['prob1'] <= .278]
df2 = FTE[(FTE['prob1'] <= .322) & (FTE['prob1']>.278)]
df3 = FTE[(FTE['prob1'] <= .367) & (FTE['prob1']>.322)]
df4 = FTE[(FTE['prob1'] <= .411) & (FTE['prob1']>.367)]
df5 = FTE[(FTE['prob1'] <= .456) & (FTE['prob1']>.411)]
df6 = FTE[(FTE['prob1'] <= .501) & (FTE['prob1']>.456)]
df7 = FTE[(FTE['prob1'] <= .545) & (FTE['prob1']>.501)]
df8 = FTE[(FTE['prob1'] <= .59) & (FTE['prob1']>.545)]
df9 = FTE[(FTE['prob1'] <= .634) & (FTE['prob1']>.59)]
df10 = FTE[(FTE['prob1'] <= .679) & (FTE['prob1']>.634)]
df11= FTE[(FTE['prob1'] <= .723) & (FTE['prob1']>.679)]
df12 = FTE[(FTE['prob1'] <= .768) & (FTE['prob1']>.723)]
df13 = FTE[(FTE['prob1'] <= .812) & (FTE['prob1']>.768)]
df1.head()
df2.head(10)
import matplotlib.pyplot as plt
import seaborn as sns
plt.errorbar(df1['prob1'],df1['prob1_outcome'], xerr = df1['prob1_outcome']-df1['prob1'])
sns.set(style="darkgrid")
lst = []
for i in len(df2.prob1_outcome):
lst.append(1)
sns.pointplot(lst, y="prob1_outcome", data=df2)
# df2['prob1_outcome']
```
|
github_jupyter
|
# Bloodmeal Calling
In this notebook, we analyze contigs from each bloodfed mosquito sample with LCA in *Vertebrata*. The potential bloodmeal call is the lowest taxonomic group consistent with the LCAs of all such contigs in a sample.
```
import pandas as pd
import numpy as np
from ete3 import NCBITaxa
import boto3
import tempfile
import subprocess
import os
import io
import re
import time
import json
ncbi = NCBITaxa()
df = pd.read_csv('../../figures/fig3/all_contigs_df.tsv', sep='\t',
dtype={'taxid': np.int})
df = df[df['group'] == 'Metazoa']
def taxid2name(taxid):
return ncbi.get_taxid_translator([taxid])[taxid]
```
There is a partial order on taxa: $a < b$ if $a$ is an ancestor of $b$. A taxon $t$ is admissible as a bloodmeal call for a given sample if it is consistent with all *Vertebrata* LCA taxa $b$: $t < b$ or $b < t$ for all $b$. That is, a taxon is admissable if t in lineage(b) or b in lineage(t) for all b.
We will report the lowest admissable taxon for each sample.
```
def get_lowest_admissable_taxon(taxa):
lineages = [ncbi.get_lineage(taxid) for taxid in taxa]
if len(lineages) == 0:
return 0
all_taxa = np.unique([taxid for lineage in lineages for taxid in lineage])
non_leaf_taxa = np.unique([taxid for lineage in lineages for taxid in lineage[:-1]])
leaf_taxa = [taxid for taxid in all_taxa if taxid not in non_leaf_taxa]
leaf_lineages = [ncbi.get_lineage(taxid) for taxid in leaf_taxa]
leaf_common_ancestors = set.intersection(*[set(l) for l in leaf_lineages])
lca = [taxid for taxid in leaf_lineages[0] if taxid in leaf_common_ancestors][-1]
return lca
def filter_taxon(taxid, exclude = [], # drop these taxa
exclude_children = [], # drop children of these taxa
parent=None # only keep children of the parent
):
if taxid in exclude:
return False
lineage = ncbi.get_lineage(taxid)
exclude_children = set(exclude_children)
if len(set(lineage) & set(exclude_children)) > 0:
return False
if parent and parent not in lineage:
return False
return True
vertebrate_taxid = 7742
primate_taxid = 9443
euarchontoglires_taxid = 314146
df['filter_taxon'] = df['taxid'].apply(lambda x: filter_taxon(x,
exclude = [euarchontoglires_taxid],
exclude_children = [primate_taxid],
parent = vertebrate_taxid))
```
How many nonprimate vertebrate contigs per sample? 1 to 11.
```
%pprint
sorted(df[df['filter_taxon']].groupby('sample').count()['taxid'])
sorted(df[df['filter_taxon']].groupby('sample')['reads'].sum())
lowest_admissable_taxa = []
for sample in df['sample'].unique():
taxid = get_lowest_admissable_taxon(df[(df['sample'] == sample) & df['filter_taxon']]['taxid'])
name = taxid2name(taxid) if taxid else "NA"
lowest_admissable_taxa.append({'sample': sample, 'name': name, 'taxid': taxid})
lowest_admissable_taxa = pd.DataFrame(lowest_admissable_taxa).sort_values('sample')
lowest_admissable_taxa = lowest_admissable_taxa[['sample', 'taxid', 'name']]
lowest_admissable_taxa.head()
partition = "Pecora Carnivora Homininae Rodentia Leporidae Aves".split()
partition = ncbi.get_name_translator(partition)
partition = {v[0]: k for k, v in partition.items()}
def get_category(taxid):
if not taxid:
return None
lineage = ncbi.get_lineage(taxid)
for k in partition:
if k in lineage:
return partition[k]
else:
return 'NA'
```
The ranks of the categories are:
```
ncbi.get_rank(partition.keys())
bloodmeal_calls = lowest_admissable_taxa
bloodmeal_calls['category'] = bloodmeal_calls['taxid'].apply(get_category)
bloodmeal_calls = bloodmeal_calls[bloodmeal_calls['category'] != 'NA']
bloodmeal_calls = bloodmeal_calls[bloodmeal_calls['name'] != 'NA']
bloodmeal_calls = bloodmeal_calls[['sample', 'category', 'name']]
bloodmeal_calls = bloodmeal_calls.sort_values('sample')
bloodmeal_calls = bloodmeal_calls.rename(columns={'sample': 'Sample',
'category': 'Bloodmeal Category',
'name': 'Bloodmeal Call'})
metadata = pd.read_csv('../../data/metadata/CMS001_CMS002_MergedAnnotations.csv')
metadata = metadata[['NewIDseqName', 'Habitat', 'collection_lat', 'collection_long', 'ska_genus', 'ska_species']].rename(
columns = {'NewIDseqName': 'Sample',
'ska_genus': 'Genus',
'ska_species': 'Species',
'collection_lat': 'Lat',
'collection_long': 'Long'})
bloodmeal_calls = bloodmeal_calls.merge(metadata, on='Sample', how='left')
bloodmeal_calls.to_csv(
'../../figures/fig4/bloodmeal_calls.csv', index=False)
```
|
github_jupyter
|
# LAB 4b: Create Keras DNN model.
**Learning Objectives**
1. Set CSV Columns, label column, and column defaults
1. Make dataset of features and label from CSV files
1. Create input layers for raw features
1. Create feature columns for inputs
1. Create DNN dense hidden layers and output layer
1. Create custom evaluation metric
1. Build DNN model tying all of the pieces together
1. Train and evaluate
## Introduction
In this notebook, we'll be using Keras to create a DNN model to predict the weight of a baby before it is born.
We'll start by defining the CSV column names, label column, and column defaults for our data inputs. Then, we'll construct a tf.data Dataset of features and the label from the CSV files and create inputs layers for the raw features. Next, we'll set up feature columns for the model inputs and build a deep neural network in Keras. We'll create a custom evaluation metric and build our DNN model. Finally, we'll train and evaluate our model.
Each learning objective will correspond to a __#TODO__ in this student lab notebook -- try to complete this notebook first and then review the [solution notebook](../solutions/4b_keras_dnn_babyweight.ipynb).
## Load necessary libraries
```
import datetime
import os
import shutil
import matplotlib.pyplot as plt
import tensorflow as tf
print(tf.__version__)
```
## Verify CSV files exist
In the seventh lab of this series [4a_sample_babyweight](../solutions/4a_sample_babyweight.ipynb), we sampled from BigQuery our train, eval, and test CSV files. Verify that they exist, otherwise go back to that lab and create them.
```
%%bash
ls *.csv
%%bash
head -5 *.csv
```
## Create Keras model
### Set CSV Columns, label column, and column defaults.
Now that we have verified that our CSV files exist, we need to set a few things that we will be using in our input function.
* `CSV_COLUMNS` are going to be our header names of our columns. Make sure that they are in the same order as in the CSV files
* `LABEL_COLUMN` is the header name of the column that is our label. We will need to know this to pop it from our features dictionary.
* `DEFAULTS` is a list with the same length as `CSV_COLUMNS`, i.e. there is a default for each column in our CSVs. Each element is a list itself with the default value for that CSV column.
```
# Determine CSV, label, and key columns
# Create list of string column headers, make sure order matches.
CSV_COLUMNS = ["weight_pounds",
"is_male",
"mother_age",
"plurality",
"gestation_weeks"]
# Add string name for label column
LABEL_COLUMN = "weight_pounds"
# Set default values for each CSV column as a list of lists.
# Treat is_male and plurality as strings.
DEFAULTS = [[0.0], ["null"], [0.0], ["null"], [0.0]]
```
### Make dataset of features and label from CSV files.
Next, we will write an input_fn to read the data. Since we are reading from CSV files we can save ourself from trying to recreate the wheel and can use `tf.data.experimental.make_csv_dataset`. This will create a CSV dataset object. However we will need to divide the columns up into features and a label. We can do this by applying the map method to our dataset and popping our label column off of our dictionary of feature tensors.
```
def features_and_labels(row_data):
"""Splits features and labels from feature dictionary.
Args:
row_data: Dictionary of CSV column names and tensor values.
Returns:
Dictionary of feature tensors and label tensor.
"""
label = row_data.pop(LABEL_COLUMN)
return row_data, label # features, label
def load_dataset(pattern, batch_size=1, mode=tf.estimator.ModeKeys.EVAL):
"""Loads dataset using the tf.data API from CSV files.
Args:
pattern: str, file pattern to glob into list of files.
batch_size: int, the number of examples per batch.
mode: tf.estimator.ModeKeys to determine if training or evaluating.
Returns:
`Dataset` object.
"""
# Make a CSV dataset
dataset = tf.data.experimental.make_csv_dataset(
file_pattern=pattern,
batch_size=batch_size,
column_names=CSV_COLUMNS,
column_defaults=DEFAULTS)
# Map dataset to features and label
dataset = dataset.map(map_func=features_and_labels) # features, label
# Shuffle and repeat for training
if mode == tf.estimator.ModeKeys.TRAIN:
dataset = dataset.shuffle(buffer_size=1000).repeat()
# Take advantage of multi-threading; 1=AUTOTUNE
dataset = dataset.prefetch(buffer_size=1)
return dataset
```
### Create input layers for raw features.
We'll need to get the data read in by our input function to our model function, but just how do we go about connecting the dots? We can use Keras input layers [(tf.Keras.layers.Input)](https://www.tensorflow.org/api_docs/python/tf/keras/Input) by defining:
* shape: A shape tuple (integers), not including the batch size. For instance, shape=(32,) indicates that the expected input will be batches of 32-dimensional vectors. Elements of this tuple can be None; 'None' elements represent dimensions where the shape is not known.
* name: An optional name string for the layer. Should be unique in a model (do not reuse the same name twice). It will be autogenerated if it isn't provided.
* dtype: The data type expected by the input, as a string (float32, float64, int32...)
```
def create_input_layers():
"""Creates dictionary of input layers for each feature.
Returns:
Dictionary of `tf.Keras.layers.Input` layers for each feature.
"""
inputs = {
colname: tf.keras.layers.Input(
name=colname, shape=(), dtype="float32")
for colname in ["mother_age", "gestation_weeks"]}
inputs.update({
colname: tf.keras.layers.Input(
name=colname, shape=(), dtype="string")
for colname in ["is_male", "plurality"]})
return inputs
```
### Create feature columns for inputs.
Next, define the feature columns. `mother_age` and `gestation_weeks` should be numeric. The others, `is_male` and `plurality`, should be categorical. Remember, only dense feature columns can be inputs to a DNN.
```
def categorical_fc(name, values):
"""Helper function to wrap categorical feature by indicator column.
Args:
name: str, name of feature.
values: list, list of strings of categorical values.
Returns:
Indicator column of categorical feature.
"""
cat_column = tf.feature_column.categorical_column_with_vocabulary_list(
key=name, vocabulary_list=values)
return tf.feature_column.indicator_column(categorical_column=cat_column)
def create_feature_columns():
"""Creates dictionary of feature columns from inputs.
Returns:
Dictionary of feature columns.
"""
feature_columns = {
colname : tf.feature_column.numeric_column(key=colname)
for colname in ["mother_age", "gestation_weeks"]
}
feature_columns["is_male"] = categorical_fc(
"is_male", ["True", "False", "Unknown"])
feature_columns["plurality"] = categorical_fc(
"plurality", ["Single(1)", "Twins(2)", "Triplets(3)",
"Quadruplets(4)", "Quintuplets(5)", "Multiple(2+)"])
return feature_columns
```
### Create DNN dense hidden layers and output layer.
So we've figured out how to get our inputs ready for machine learning but now we need to connect them to our desired output. Our model architecture is what links the two together. Let's create some hidden dense layers beginning with our inputs and end with a dense output layer. This is regression so make sure the output layer activation is correct and that the shape is right.
```
def get_model_outputs(inputs):
"""Creates model architecture and returns outputs.
Args:
inputs: Dense tensor used as inputs to model.
Returns:
Dense tensor output from the model.
"""
# Create two hidden layers of [64, 32] just in like the BQML DNN
h1 = tf.keras.layers.Dense(64, activation="relu", name="h1")(inputs)
h2 = tf.keras.layers.Dense(32, activation="relu", name="h2")(h1)
# Final output is a linear activation because this is regression
output = tf.keras.layers.Dense(
units=1, activation="linear", name="weight")(h2)
return output
```
### Create custom evaluation metric.
We want to make sure that we have some useful way to measure model performance for us. Since this is regression, we would like to know the RMSE of the model on our evaluation dataset, however, this does not exist as a standard evaluation metric, so we'll have to create our own by using the true and predicted labels.
```
def rmse(y_true, y_pred):
"""Calculates RMSE evaluation metric.
Args:
y_true: tensor, true labels.
y_pred: tensor, predicted labels.
Returns:
Tensor with value of RMSE between true and predicted labels.
"""
return tf.sqrt(tf.reduce_mean((y_pred - y_true) ** 2))
```
### Build DNN model tying all of the pieces together.
Excellent! We've assembled all of the pieces, now we just need to tie them all together into a Keras Model. This is a simple feedforward model with no branching, side inputs, etc. so we could have used Keras' Sequential Model API but just for fun we're going to use Keras' Functional Model API. Here we will build the model using [tf.keras.models.Model](https://www.tensorflow.org/api_docs/python/tf/keras/Model) giving our inputs and outputs and then compile our model with an optimizer, a loss function, and evaluation metrics.
```
def build_dnn_model():
"""Builds simple DNN using Keras Functional API.
Returns:
`tf.keras.models.Model` object.
"""
# Create input layer
inputs = create_input_layers()
# Create feature columns
feature_columns = create_feature_columns()
# The constructor for DenseFeatures takes a list of numeric columns
# The Functional API in Keras requires: LayerConstructor()(inputs)
dnn_inputs = tf.keras.layers.DenseFeatures(
feature_columns=feature_columns.values())(inputs)
# Get output of model given inputs
output = get_model_outputs(dnn_inputs)
# Build model and compile it all together
model = tf.keras.models.Model(inputs=inputs, outputs=output)
model.compile(optimizer="adam", loss="mse", metrics=[rmse, "mse"])
return model
print("Here is our DNN architecture so far:\n")
model = build_dnn_model()
print(model.summary())
```
We can visualize the DNN using the Keras plot_model utility.
```
tf.keras.utils.plot_model(
model=model, to_file="dnn_model.png", show_shapes=False, rankdir="LR")
```
## Run and evaluate model
### Train and evaluate.
We've built our Keras model using our inputs from our CSV files and the architecture we designed. Let's now run our model by training our model parameters and periodically running an evaluation to track how well we are doing on outside data as training goes on. We'll need to load both our train and eval datasets and send those to our model through the fit method. Make sure you have the right pattern, batch size, and mode when loading the data. Also, don't forget to add the callback to TensorBoard.
```
TRAIN_BATCH_SIZE = 32
NUM_TRAIN_EXAMPLES = 10000 * 5 # training dataset repeats, it'll wrap around
NUM_EVALS = 5 # how many times to evaluate
# Enough to get a reasonable sample, but not so much that it slows down
NUM_EVAL_EXAMPLES = 10000
trainds = load_dataset(
pattern="train*",
batch_size=TRAIN_BATCH_SIZE,
mode=tf.estimator.ModeKeys.TRAIN)
evalds = load_dataset(
pattern="eval*",
batch_size=1000,
mode=tf.estimator.ModeKeys.EVAL).take(count=NUM_EVAL_EXAMPLES // 1000)
steps_per_epoch = NUM_TRAIN_EXAMPLES // (TRAIN_BATCH_SIZE * NUM_EVALS)
logdir = os.path.join(
"logs", datetime.datetime.now().strftime("%Y%m%d-%H%M%S"))
tensorboard_callback = tf.keras.callbacks.TensorBoard(
log_dir=logdir, histogram_freq=1)
history = model.fit(
trainds,
validation_data=evalds,
epochs=NUM_EVALS,
steps_per_epoch=steps_per_epoch,
callbacks=[tensorboard_callback])
```
### Visualize loss curve
```
# Plot
import matplotlib.pyplot as plt
nrows = 1
ncols = 2
fig = plt.figure(figsize=(10, 5))
for idx, key in enumerate(["loss", "rmse"]):
ax = fig.add_subplot(nrows, ncols, idx+1)
plt.plot(history.history[key])
plt.plot(history.history["val_{}".format(key)])
plt.title("model {}".format(key))
plt.ylabel(key)
plt.xlabel("epoch")
plt.legend(["train", "validation"], loc="upper left");
```
### Save the model
```
OUTPUT_DIR = "babyweight_trained"
shutil.rmtree(OUTPUT_DIR, ignore_errors=True)
EXPORT_PATH = os.path.join(
OUTPUT_DIR, datetime.datetime.now().strftime("%Y%m%d%H%M%S"))
tf.saved_model.save(
obj=model, export_dir=EXPORT_PATH) # with default serving function
print("Exported trained model to {}".format(EXPORT_PATH))
!ls $EXPORT_PATH
```
## Monitor and experiment with training
To begin TensorBoard from within AI Platform Notebooks, click the + symbol in the top left corner and select the **Tensorboard** icon to create a new TensorBoard. Before you click make sure you are in the directory of your TensorBoard log_dir.
In TensorBoard, look at the learned embeddings. Are they getting clustered? How about the weights for the hidden layers? What if you run this longer? What happens if you change the batchsize?
## Lab Summary:
In this lab, we started by defining the CSV column names, label column, and column defaults for our data inputs. Then, we constructed a tf.data Dataset of features and the label from the CSV files and created inputs layers for the raw features. Next, we set up feature columns for the model inputs and built a deep neural network in Keras. We created a custom evaluation metric and built our DNN model. Finally, we trained and evaluated our model.
Copyright 2019 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
|
github_jupyter
|
```
%env CUDA_VISIBLE_DEVICES=1
DATA_DIR='/home/HDD6TB/datasets/emotions/zoom/'
import os
from PIL import Image
import cv2
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier,RandomForestRegressor
from sklearn import svm,metrics,preprocessing
from sklearn.neighbors import KNeighborsClassifier
from sklearn.decomposition import PCA
from sklearn.pipeline import Pipeline
from sklearn.metrics.pairwise import pairwise_distances
from collections import defaultdict
import os
import random
import numpy as np
from tqdm import tqdm
import time
import pickle
import pandas as pd
import matplotlib.pyplot as plt
compare_filenames=lambda x: int(os.path.splitext(x)[0])
video_path=os.path.join(DATA_DIR,'videos/4.mp4')
print(video_path)
faces_path=os.path.join(DATA_DIR,'faces/mtcnn_new/4')
```
# Face detection + OCR
```
import tensorflow as tf
print(tf.__version__)
from tensorflow.compat.v1.keras.backend import set_session
config = tf.compat.v1.ConfigProto()
config.gpu_options.allow_growth = True
sess=tf.compat.v1.Session(config=config)
set_session(sess)
from facial_analysis import FacialImageProcessing
imgProcessing=FacialImageProcessing(False)
import numpy as np
import cv2
import math
from skimage import transform as trans
def get_iou(bb1, bb2):
"""
Calculate the Intersection over Union (IoU) of two bounding boxes.
Parameters
----------
bb1 : array
order: {'x1', 'y1', 'x2', 'y2'}
The (x1, y1) position is at the top left corner,
the (x2, y2) position is at the bottom right corner
bb2 : array
order: {'x1', 'y1', 'x2', 'y2'}
The (x1, y1) position is at the top left corner,
the (x2, y2) position is at the bottom right corner
Returns
-------
float
in [0, 1]
"""
# determine the coordinates of the intersection rectangle
x_left = max(bb1[0], bb2[0])
y_top = max(bb1[1], bb2[1])
x_right = min(bb1[2], bb2[2])
y_bottom = min(bb1[3], bb2[3])
if x_right < x_left or y_bottom < y_top:
return 0.0
# The intersection of two axis-aligned bounding boxes is always an
# axis-aligned bounding box
intersection_area = (x_right - x_left) * (y_bottom - y_top)
# compute the area of both AABBs
bb1_area = (bb1[2] - bb1[0]) * (bb1[3] - bb1[1])
bb2_area = (bb2[2] - bb2[0]) * (bb2[3] - bb2[1])
# compute the intersection over union by taking the intersection
# area and dividing it by the sum of prediction + ground-truth
# areas - the interesection area
iou = intersection_area / float(bb1_area + bb2_area - intersection_area)
return iou
#print(get_iou([10,10,20,20],[15,15,25,25]))
def preprocess(img, bbox=None, landmark=None, **kwargs):
M = None
image_size = [224,224]
src = np.array([
[30.2946, 51.6963],
[65.5318, 51.5014],
[48.0252, 71.7366],
[33.5493, 92.3655],
[62.7299, 92.2041] ], dtype=np.float32 )
if image_size[1]==224:
src[:,0] += 8.0
src*=2
if landmark is not None:
dst = landmark.astype(np.float32)
tform = trans.SimilarityTransform()
#dst=dst[:3]
#src=src[:3]
#print(dst.shape,src.shape,dst,src)
tform.estimate(dst, src)
M = tform.params[0:2,:]
#M = cv2.estimateRigidTransform( dst.reshape(1,5,2), src.reshape(1,5,2), False)
#print(M)
if M is None:
if bbox is None: #use center crop
det = np.zeros(4, dtype=np.int32)
det[0] = int(img.shape[1]*0.0625)
det[1] = int(img.shape[0]*0.0625)
det[2] = img.shape[1] - det[0]
det[3] = img.shape[0] - det[1]
else:
det = bbox
margin = 0#kwargs.get('margin', 44)
bb = np.zeros(4, dtype=np.int32)
bb[0] = np.maximum(det[0]-margin//2, 0)
bb[1] = np.maximum(det[1]-margin//2, 0)
bb[2] = np.minimum(det[2]+margin//2, img.shape[1])
bb[3] = np.minimum(det[3]+margin//2, img.shape[0])
ret = img[bb[1]:bb[3],bb[0]:bb[2],:]
if len(image_size)>0:
ret = cv2.resize(ret, (image_size[1], image_size[0]))
return ret
else: #do align using landmark
assert len(image_size)==2
warped = cv2.warpAffine(img,M,(image_size[1],image_size[0]), borderValue = 0.0)
return warped
import pytesseract
if not os.path.exists(faces_path):
os.mkdir(faces_path)
cap = cv2.VideoCapture(video_path)
fps = cap.get(cv2.CAP_PROP_FPS)
total_frames = int(cap.get(cv2.CAP_PROP_FRAME_COUNT))
print('total_frames:',total_frames)
cap.set(cv2.CAP_PROP_POS_FRAMES,1)
frame_count = 0
counter=0
bboxes,all_text=[],[]
for frame_count in tqdm(range(total_frames-1)):
ret, frame_bgr = cap.read()
counter+=1
if not ret:
#cap.release()
#break
continue
frame = cv2.cvtColor(frame_bgr, cv2.COLOR_BGR2RGB)
bounding_boxes, points = imgProcessing.detect_faces(frame)
points = points.T
if len(bounding_boxes)!=0:
sorted_indices=bounding_boxes[:,0].argsort()
bounding_boxes=bounding_boxes[sorted_indices]
points=points[sorted_indices]
faces_folder=os.path.join(faces_path, str(counter))
if not os.path.exists(faces_folder):
os.mkdir(faces_folder)
for i,b in enumerate(bounding_boxes):
outfile=os.path.join(faces_folder, str(i)+'.png')
if not os.path.exists(outfile):
if True:
p=None
else:
p=points[i]
p = p.reshape((2,5)).T
face_img=preprocess(frame_bgr,b,p)
if np.prod(face_img.shape)==0:
print('Empty face ',b,' found for ',filename)
continue
cv2.imwrite(outfile, face_img)
bboxes.append(bounding_boxes)
frame = cv2.resize(frame, None, fx=2.0, fy=2.0, interpolation=cv2.INTER_LINEAR)
results=pytesseract.image_to_data(frame,lang='rus+eng',output_type=pytesseract.Output.DICT)
frame_text=[]
for i in range(0, len(results["text"])):
x = results["left"][i]
y = results["top"][i]
w = results["width"][i]
h = results["height"][i]
text = results["text"][i].strip()
conf = float(results["conf"][i])
if conf > 0 and len(text)>1:
frame_text.append((text,int(x/frame.shape[1]*frame_bgr.shape[1]),int(y/frame.shape[0]*frame_bgr.shape[0]),
int(w/frame.shape[1]*frame_bgr.shape[1]),int(h/frame.shape[0]*frame_bgr.shape[1])))
all_text.append(frame_text)
cap.release()
```
## Text processing
```
def combine_words(photo_text):
#print(photo_text)
if len(photo_text)>0:
new_text=[photo_text[0]]
for word_ind in range(1,len(photo_text)):
prev_text,x1,y1,w1,h1=new_text[-1]
center1_x,center1_y=x1+w1,y1+h1/2
cur_text,x2,y2,w2,h2=photo_text[word_ind]
center2_x,center2_y=x2,y2+h2/2
dist=abs(center1_x-center2_x)+abs(center1_y-center2_y)
#print(prev_text,cur_text,dist)
if dist>=7: #0.01:
new_text.append(photo_text[word_ind])
else:
new_text[-1]=(prev_text+' '+cur_text,x1,y1,x2+w2-x1,y2+h2-y1)
else:
new_text=[]
return new_text
def get_closest_texts(bboxes,photo_text):
best_texts,best_distances=[],[]
for (x1,y1,x2,y2,_) in bboxes:
face_x,face_y=x1,y2
#print(x1,y1,x2,y2)
best_dist=10000
best_text=''
for (text,x,y,w,h) in photo_text:
if y>y1:
dist_y=abs(face_y-y)
if face_x<x:
dist_x=x-face_x
elif face_x>x+w:
dist_x=face_x-x-w
else:
dist_x=0
#print(text,dist_x, dist_y,x,y,w,h)
if dist_x<best_dist and dist_y<1.5*(y2-y1):
best_dist=dist_x
best_text=text
#print(best_text,best_dist,(x2-x1))
if best_dist>=(x2-x1)*2:
best_text=''
if best_text!='':
for i,prev_txt in enumerate(best_texts):
if prev_txt==best_text:
if best_distances[i]<best_dist:
best_text=''
break
else:
best_texts[i]=''
best_texts.append(best_text)
best_distances.append(best_dist)
return best_texts
```
# FaceId
```
import torch
from PIL import Image
from torchvision import datasets, transforms
print(f"Torch: {torch.__version__}")
device = 'cuda'
import timm
model=timm.create_model('tf_efficientnet_b0_ns', pretrained=False)
model.classifier=torch.nn.Identity()
model.load_state_dict(torch.load('../models/pretrained_faces/state_vggface2_enet0_new.pt'))
model=model.to(device)
model.eval()
test_transforms = transforms.Compose(
[
transforms.Resize((224,224)),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])
]
)
embeddings=[]
i=0
for filename in tqdm(sorted(os.listdir(faces_path), key=compare_filenames)):
faces_dir=os.path.join(faces_path,filename)
imgs=[]
for img_name in sorted(os.listdir(faces_dir), key=compare_filenames):
img = Image.open(os.path.join(faces_dir,img_name))
img_tensor = test_transforms(img)
imgs.append(img_tensor)
if len(imgs)>0:
scores = model(torch.stack(imgs, dim=0).to(device))
scores=scores.data.cpu().numpy()
else:
scores=[]
embeddings.append(scores)
if len(scores)!=len(bboxes[i]):
print('Error',videoname,filename,i,len(scores),len(bboxes[i]))
i+=1
print(len(embeddings))
```
## Faces only
```
face_files=[]
subjects=None
X_recent_features=None
for i,filename in enumerate(sorted(os.listdir(faces_path), key=compare_filenames)):
f=preprocessing.normalize(embeddings[i],norm='l2')
if X_recent_features is None:
for face_ind in range(len(f)):
face_files.append([(i,filename,face_ind)])
X_recent_features=f
else:
dist_matrix=pairwise_distances(f,X_recent_features)
sorted_indices=dist_matrix.argsort(axis=1)
for face_ind,sorted_inds in enumerate(sorted_indices):
closest_ind=sorted_inds[0]
min_dist=dist_matrix[face_ind][closest_ind]
if min_dist<0.85 or (len(sorted_inds)>1 and min_dist<dist_matrix[face_ind][sorted_inds[1]]-0.1):
X_recent_features[closest_ind]=f[face_ind]
face_files[closest_ind].append((i,filename,face_ind))
else:
face_files.append([(i,filename,face_ind)])
X_recent_features=np.concatenate((X_recent_features,[f[face_ind]]),axis=0)
print(len(face_files), [len(files) for files in face_files])
```
## Faces+bboxes
```
def get_square(bb):
return abs((bb[2]-bb[0])*(bb[3]-bb[1]))
SQUARE_THRESHOLD=900
face_files=[]
subjects=None
X_recent_features=None
recent_bboxes=[]
for i,filename in enumerate(sorted(os.listdir(faces_path), key=compare_filenames)):
f=preprocessing.normalize(embeddings[i],norm='l2')
if X_recent_features is None:
large_face_indices=[]
for face_ind in range(len(f)):
if get_square(bboxes[i][face_ind])>SQUARE_THRESHOLD:
large_face_indices.append(face_ind)
recent_bboxes.append(bboxes[i][face_ind])
face_files.append([(i,filename,face_ind)])
if len(large_face_indices)>0:
X_recent_features=f[np.array(large_face_indices)]
#print(X_recent_features.shape)
#recent_bboxes=list(deepcopy(bboxes[i]))
else:
matched_faces=[]
for face_ind,face_bbox in enumerate(bboxes[i]):
closest_ind=-1
best_iou=0
for ind, bbox in enumerate(recent_bboxes):
iou=get_iou(face_bbox,bbox)
if iou>best_iou:
best_iou=iou
closest_ind=ind
if best_iou>0.15:
d=np.linalg.norm(f[face_ind]-X_recent_features[closest_ind])
if d<1.0:
X_recent_features[closest_ind]=f[face_ind]
face_files[closest_ind].append((i,filename,face_ind))
recent_bboxes[closest_ind]=bboxes[i][face_ind]
matched_faces.append(face_ind)
if len(matched_faces)<len(bboxes[i]):
dist_matrix=pairwise_distances(f,X_recent_features)
sorted_indices=dist_matrix.argsort(axis=1)
for face_ind,sorted_inds in enumerate(sorted_indices):
if face_ind in matched_faces or get_square(bboxes[i][face_ind])<=SQUARE_THRESHOLD:
continue
closest_ind=sorted_inds[0]
min_dist=dist_matrix[face_ind][closest_ind]
if min_dist<0.85:# or (len(sorted_inds)>1 and min_dist<dist_matrix[face_ind][sorted_inds[1]]-0.1):
X_recent_features[closest_ind]=f[face_ind]
face_files[closest_ind].append((i,filename,face_ind))
recent_bboxes[closest_ind]=bboxes[i][face_ind]
else:
face_files.append([(i,filename,face_ind)])
X_recent_features=np.concatenate((X_recent_features,[f[face_ind]]),axis=0)
recent_bboxes.append(bboxes[i][face_ind])
#print(filename,i,X_recent_features.shape,face_ind,closest_ind,dist_matrix[face_ind][closest_ind])
#print(dist_matrix)
print(len(face_files), [len(files) for files in face_files])
```
## Text + faces
```
import editdistance
def levenstein(txt1,txt2):
if txt1=='' or txt2=='':
return 1
#return editdistance.eval(txt1,txt2)
return (editdistance.eval(txt1,txt2))/(max(len(txt1),len(txt2)))
def get_name(name2count):
#print(name2count)
return max(name2count, key=name2count.get)
face_files=[]
recent_texts=[]
X_recent_features=[]
for i,filename in enumerate(sorted(os.listdir(faces_path), key=compare_filenames)):
photo_text=combine_words(all_text[i])
best_texts=get_closest_texts(bboxes[i],photo_text)
f=preprocessing.normalize(embeddings[i],norm='l2')
if len(recent_texts)==0:
for face_ind,txt in enumerate(best_texts):
if len(txt)>=4:
recent_texts.append({txt:1})
face_files.append([(i,filename,face_ind)])
X_recent_features.append(f[face_ind])
else:
for face_ind,txt in enumerate(best_texts):
if len(txt)>=4:
closest_ind=-1
best_d_txt=1
for ind,recent_text_set in enumerate(recent_texts):
d_txt=min([levenstein(txt,recent_text) for recent_text in recent_text_set])
if d_txt<best_d_txt:
best_d_txt=d_txt
closest_ind=ind
face_dist=np.linalg.norm(X_recent_features[closest_ind]-f[face_ind])
if (best_d_txt<=0.45 and face_dist<=1.0) or face_dist<=0.8:
if txt in recent_texts[closest_ind]:
recent_texts[closest_ind][txt]+=1
else:
recent_texts[closest_ind][txt]=1
face_files[closest_ind].append((i,filename,face_ind))
X_recent_features[closest_ind]=f[face_ind]
elif best_d_txt>0.45:
recent_texts.append({txt:1})
face_files.append([(i,filename,face_ind)])
X_recent_features.append(f[face_ind])
#print(videoname,filename,i,face_ind,face_dist,txt,best_d_txt,recent_texts[closest_ind])
subjects=[get_name(name2count) for name2count in recent_texts]
```
---------------
```
import random
plt_ind=1
minNoPhotos=20
min_num_files=100
no_clusters=len([i for i,files in enumerate(face_files) if len(files)>min_num_files])
plt.figure(figsize=(10,10))
for i,files in enumerate(face_files):
if len(files)>min_num_files:
print(i,len(files),files[0])
for j in range(minNoPhotos):
f=random.choice(files)
fpath=os.path.join(faces_path,f[1],str(f[2])+'.png')
plt.subplot(no_clusters,minNoPhotos,plt_ind)
if j==0 and subjects is not None:
plt.title(subjects[i])
plt.imshow(Image.open(fpath))
plt.axis('off')
plt_ind+=1
plt.show()
```
# Emotions
```
if False:
model_name='enet_b2_8'
IMG_SIZE=260 #224 #
else:
model_name='enet_b0_8_best_afew'
IMG_SIZE=224
PATH='../models/affectnet_emotions/'+model_name+'.pt'
test_transforms = transforms.Compose(
[
transforms.Resize((IMG_SIZE,IMG_SIZE)),
#transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])
]
)
feature_extractor_model = torch.load(PATH)
classifier_weights=feature_extractor_model.classifier[0].weight.cpu().data.numpy()
classifier_bias=feature_extractor_model.classifier[0].bias.cpu().data.numpy()
print(classifier_weights.shape,classifier_weights)
print(classifier_bias.shape,classifier_bias)
feature_extractor_model.classifier=torch.nn.Identity()
feature_extractor_model.eval()
def get_probab(features):
x=np.dot(features,np.transpose(classifier_weights))+classifier_bias
#print(x)
e_x = np.exp(x - np.max(x,axis=0))
return e_x / e_x.sum(axis=1)[:,None]
if len(classifier_bias)==7:
idx_to_class={0: 'Anger', 1: 'Disgust', 2: 'Fear', 3: 'Happiness', 4: 'Neutral', 5: 'Sadness', 6: 'Surprise'}
INTERESTING_STATES=[0,1,2,3,6]
else:
idx_to_class={0: 'Anger', 1: 'Contempt', 2: 'Disgust', 3: 'Fear', 4: 'Happiness', 5: 'Neutral', 6: 'Sadness', 7: 'Surprise'}
INTERESTING_STATES=[0,2,3,4,7]
print(idx_to_class)
X_global_features,X_scores=[],[]
for filename in tqdm(sorted(os.listdir(faces_path), key=compare_filenames)):
faces_dir=os.path.join(faces_path,filename)
imgs=[]
for img_name in sorted(os.listdir(faces_dir), key=compare_filenames):
img = Image.open(os.path.join(faces_dir,img_name))
img_tensor = test_transforms(img)
if img.size:
imgs.append(img_tensor)
if len(imgs)>0:
features = feature_extractor_model(torch.stack(imgs, dim=0).to(device))
features=features.data.cpu().numpy()
scores=get_probab(features)
#print(videoname,filename,features.shape,scores.shape)
X_global_features.append(features)
X_scores.append(scores)
```
# Create gifs
```
from IPython import display
from PIL import Image, ImageFont, ImageDraw
min_num_files=100
unicode_font = ImageFont.truetype("DejaVuSans.ttf", 8)
gif=[]
no_clusters=len([i for i,files in enumerate(face_files) if len(files)>min_num_files])
for subject_ind,files in enumerate(face_files):
if len(files)>min_num_files:
print(len(files),files[0])
prev_filename_ind=-1
start_i=0
current_scores,current_features=[],[]
current_emotion=-1
emotion2longest_sequence={}
for i,(file_ind,filename,face_ind) in enumerate(files):
filename_ind=int(filename)
if prev_filename_ind==-1:
prev_filename_ind=filename_ind-1
new_emotion=np.argmax(X_scores[file_ind][face_ind])
#print('check',prev_filename_ind,filename_ind-1, new_emotion,current_emotion)
if prev_filename_ind!=filename_ind-1 or new_emotion!=current_emotion or new_emotion not in INTERESTING_STATES:
if len(current_scores)>=10:
emotion=np.argmax(np.mean(current_scores,axis=0))
if emotion in emotion2longest_sequence:
if emotion2longest_sequence[emotion][0]<len(current_scores):
emotion2longest_sequence[emotion]=(len(current_scores),start_i,i-1)
else:
emotion2longest_sequence[emotion]=(len(current_scores),start_i,i-1)
#print(start_i,i-1,idx_to_class[emotion])
start_i=i
current_scores,current_features=[],[]
prev_filename_ind=filename_ind
current_emotion=new_emotion
current_scores.append(X_scores[file_ind][face_ind])
current_features.append(X_global_features[file_ind][face_ind])
if len(emotion2longest_sequence)>0:
for emotion, (_,start_i, end_i) in emotion2longest_sequence.items():
print(idx_to_class[emotion],start_i,end_i,len(files))
for i in range(start_i,min(start_i+20,end_i)+1):
#print(files[i])
fpath=os.path.join(faces_path,files[i][1],str(files[i][2])+'.png')
img=Image.open(fpath)
img = img.resize((112,112), Image.ANTIALIAS)
draw = ImageDraw.Draw(img)
draw.text((0, 0), subjects[subject_ind], align ="left", font=unicode_font,fill=(0,0,255,255))
draw.text((0, 10), idx_to_class[emotion], align ="left",font=unicode_font, fill=(0,255,0,255))
gif.append(img.convert("P",palette=Image.ADAPTIVE))
if False:
for img in gif:
display.clear_output(wait=True)
plt.axis('off')
plt.imshow(img)
plt.show()
if True and len(gif)>0:
gif[0].save('emo.gif', save_all=True,optimize=False, append_images=gif[1:],disposal=2)
```
|
github_jupyter
|
# Setup
```
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import itertools as it
import helpers_03
%matplotlib inline
```
# Neurons as Logic Gates
As an introduction to neural networks and their component neurons, we are going to look at using neurons to implement the most primitive logic computations: logic gates. Let's go!
##### The Sigmoid Function
The basic, classic activation function that we apply to neurons is a sigmoid (sometimes just called *the* sigmoid function) function: the standard logistic function.
$$
\sigma = \frac{1}{1 + e^{-x}}
$$
$\sigma$ ranges from (0, 1). When the input $x$ is negative, $\sigma$ is close to 0. When $x$ is positive, $\sigma$ is close to 1. At $x=0$, $\sigma=0.5$
We can implement this conveniently with NumPy.
```
def sigmoid(x):
"""Sigmoid function"""
return 1.0 / (1.0 + np.exp(-x))
```
And plot it with matplotlib.
```
# Plot The sigmoid function
xs = np.linspace(-10, 10, num=100, dtype=np.float32)
activation = sigmoid(xs)
fig = plt.figure(figsize=(6,4))
plt.plot(xs, activation)
plt.plot(0,.5,'ro')
plt.grid(True, which='both')
plt.axhline(y=0, color='y')
plt.axvline(x=0, color='y')
plt.ylim([-0.1, 1.15])
```
## An Example with OR
##### OR Logic
A logic gate takes in two boolean (true/false or 1/0) inputs, and returns either a 0 or 1 depending on its rule. The truth table for a logic gate shows the outputs for each combination of inputs: (0, 0), (0, 1), (1,0), and (1, 1). For example, let's look at the truth table for an Or-gate:
<table>
<tr><th colspan="3">OR gate truth table</th></tr>
<tr><th colspan="2">Input</th><th>Output</th></tr>
<tr><td>0</td><td>0</td><td>0</td></tr>
<tr><td>0</td><td>1</td><td>1</td></tr>
<tr><td>1</td><td>0</td><td>1</td></tr>
<tr><td>1</td><td>1</td><td>1</td></tr>
</table>
##### OR as a Neuron
A neuron that uses the sigmoid activation function outputs a value between (0, 1). This naturally leads us to think about boolean values. Imagine a neuron that takes in two inputs, $x_1$ and $x_2$, and a bias term:
<img src="./images/logic01.png" width=50%/>
By limiting the inputs of $x_1$ and $x_2$ to be in $\left\{0, 1\right\}$, we can simulate the effect of logic gates with our neuron. The goal is to find the weights (represented by ? marks above), such that it returns an output close to 0 or 1 depending on the inputs. What weights should we use to output the same results as OR? Remember: $\sigma(z)$ is close to 0 when $z$ is largely negative (around -10 or less), and is close to 1 when $z$ is largely positive (around +10 or greater).
$$
z = w_1 x_1 + w_2 x_2 + b
$$
Let's think this through:
* When $x_1$ and $x_2$ are both 0, the only value affecting $z$ is $b$. Because we want the result for input (0, 0) to be close to zero, $b$ should be negative (at least -10) to get the very left-hand part of the sigmoid.
* If either $x_1$ or $x_2$ is 1, we want the output to be close to 1. That means the weights associated with $x_1$ and $x_2$ should be enough to offset $b$ to the point of causing $z$ to be at least 10 (i.e., to the far right part of the sigmoid).
Let's give $b$ a value of -10. How big do we need $w_1$ and $w_2$ to be? At least +20 will get us to +10 for just one of $\{w_1, w_2\}$ being on.
So let's try out $w_1=20$, $w_2=20$, and $b=-10$:
<img src="./images/logic02.png\" width=50%/>
##### Some Utility Functions
Since we're going to be making several example logic gates (from different sets of weights and biases), here are two helpers. The first takes our weights and baises and turns them into a two-argument function that we can use like `and(a,b)`. The second is for printing a truth table for a gate.
```
def logic_gate(w1, w2, b):
''' logic_gate is a function which returns a function
the returned function take two args and (hopefully)
acts like a logic gate (and/or/not/etc.). its behavior
is determined by w1,w2,b. a longer, better name would be
make_twoarg_logic_gate_function'''
def the_gate(x1, x2):
return sigmoid(w1 * x1 + w2 * x2 + b)
return the_gate
def test(gate):
'Helper function to test out our weight functions.'
for a, b in it.product(range(2), repeat=2):
print("{}, {}: {}".format(a, b, np.round(gate(a, b))))
```
Let's see how we did. Here's the gold-standard truth table.
<table>
<tr><th colspan="3">OR gate truth table</th></tr>
<tr><th colspan="2">Input</th><th>Output</th></tr>
<tr><td>0</td><td>0</td><td>0</td></tr>
<tr><td>0</td><td>1</td><td>1</td></tr>
<tr><td>1</td><td>0</td><td>1</td></tr>
<tr><td>1</td><td>1</td><td>1</td></tr>
</table>
And our result:
```
or_gate = logic_gate(20, 20, -10)
test(or_gate)
```
This matches - great!
# Exercise 1
##### Part 1: AND Gate
Now you try finding the appropriate weight values for each truth table. Try not to guess and check. Think through it logically and try to derive values that work.
<table>
<tr><th colspan="3">AND gate truth table</th></tr>
<tr><th colspan="2">Input</th><th>Output</th></tr>
<tr><td>0</td><td>0</td><td>0</td></tr>
<tr><td>0</td><td>1</td><td>0</td></tr>
<tr><td>1</td><td>0</td><td>0</td></tr>
<tr><td>1</td><td>1</td><td>1</td></tr>
</table>
```
# Fill in the w1, w2, and b parameters such that the truth table matches
# and_gate = logic_gate()
# test(and_gate)
```
##### Part 2: NOR (Not Or) Gate
<table>
<tr><th colspan="3">NOR gate truth table</th></tr>
<tr><th colspan="2">Input</th><th>Output</th></tr>
<tr><td>0</td><td>0</td><td>1</td></tr>
<tr><td>0</td><td>1</td><td>0</td></tr>
<tr><td>1</td><td>0</td><td>0</td></tr>
<tr><td>1</td><td>1</td><td>0</td></tr>
</table>
<table>
```
# Fill in the w1, w2, and b parameters such that the truth table matches
# nor_gate = logic_gate()
# test(nor_gate)
```
##### Part 3: NAND (Not And) Gate
<table>
<tr><th colspan="3">NAND gate truth table</th></tr>
<tr><th colspan="2">Input</th><th>Output</th></tr>
<tr><td>0</td><td>0</td><td>1</td></tr>
<tr><td>0</td><td>1</td><td>1</td></tr>
<tr><td>1</td><td>0</td><td>1</td></tr>
<tr><td>1</td><td>1</td><td>0</td></tr>
</table>
```
# Fill in the w1, w2, and b parameters such that the truth table matches
# nand_gate = logic_gate()
# test(nand_gate)
```
## Solutions 1
# Limits of Single Neurons
If you've taken computer science courses, you may know that the XOR gates are the basis of computation. They can be used as half-adders, the foundation of being able to add numbers together. Here's the truth table for XOR:
##### XOR (Exclusive Or) Gate
<table>
<tr><th colspan="3">NAND gate truth table</th></tr>
<tr><th colspan="2">Input</th><th>Output</th></tr>
<tr><td>0</td><td>0</td><td>0</td></tr>
<tr><td>0</td><td>1</td><td>1</td></tr>
<tr><td>1</td><td>0</td><td>1</td></tr>
<tr><td>1</td><td>1</td><td>0</td></tr>
</table>
Now the question is, can you create a set of weights such that a single neuron can output this property? It turns out that you cannot. Single neurons can't correlate inputs, so it's just confused. So individual neurons are out. Can we still use neurons to somehow form an XOR gate?
What if we tried something more complex:
<img src="./images/logic03.png\" width=60%/>
Here, we've got the inputs going to two separate gates: the top neuron is an OR gate, and the bottom is a NAND gate. The output of these gates is passed to another neuron, which is an AND gate. If you work out the outputs at each combination of input values, you'll see that this is an XOR gate!
```
# Make sure you have or_gate, nand_gate, and and_gate working from above
def xor_gate(a, b):
c = or_gate(a, b)
d = nand_gate(a, b)
return and_gate(c, d)
test(xor_gate)
```
Thus, we can see how chaining together neurons can compose more complex models than we'd otherwise have access to.
# Learning a Logic Gate
We can use TensorFlow to try and teach a model to learn the correct weights and bias by passing in our truth table as training data.
```
# Create an empty Graph to place our operations in
logic_graph = tf.Graph()
with logic_graph.as_default():
# Placeholder inputs for our a, b, and label training data
x1 = tf.placeholder(tf.float32)
x2 = tf.placeholder(tf.float32)
label = tf.placeholder(tf.float32)
# A placeholder for our learning rate, so we can adjust it
learning_rate = tf.placeholder(tf.float32)
# The Variables we'd like to learn: weights for a and b, as well as a bias term
w1 = tf.Variable(tf.random_normal([]))
w2 = tf.Variable(tf.random_normal([]))
b = tf.Variable(0.0, dtype=tf.float32)
# Use the built-in sigmoid function for our output value
output = tf.nn.sigmoid(w1 * x1 + w2 * x2 + b)
# We'll use the mean of squared errors as our loss function
loss = tf.reduce_mean(tf.square(output - label))
correct = tf.equal(tf.round(output), label)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
# Finally, we create a gradient descent training operation and an initialization operation
train = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
init = tf.global_variables_initializer()
with tf.Session(graph=logic_graph) as sess:
sess.run(init)
# Training data for all combinations of inputs
and_table = np.array([[0,0,0],
[1,0,0],
[0,1,0],
[1,1,1]])
feed_dict={x1: and_table[:,0],
x2: and_table[:,1],
label: and_table[:,2],
learning_rate: 0.5}
for i in range(5000):
l, acc, _ = sess.run([loss, accuracy, train], feed_dict)
if i % 1000 == 0:
print('loss: {}\taccuracy: {}'.format(l, acc))
test_dict = {x1: and_table[:,0], #[0.0, 1.0, 0.0, 1.0],
x2: and_table[:,1]} # [0.0, 0.0, 1.0, 1.0]}
w1_val, w2_val, b_val, out = sess.run([w1, w2, b, output], test_dict)
print('\nLearned weight for w1:\t {}'.format(w1_val))
print('Learned weight for w2:\t {}'.format(w2_val))
print('Learned weight for bias: {}\n'.format(b_val))
print(np.column_stack((and_table[:,[0,1]], out.round().astype(np.uint8) ) ) )
# FIXME! ARGH! use real python or numpy
#idx = 0
#for i in [0, 1]:
# for j in [0, 1]:
# print('{}, {}: {}'.format(i, j, np.round(out[idx])))
# idx += 1
```
# Exercise 2
You may recall that in week 2, we built a class `class TF_GD_LinearRegression` that wrapped up the three steps of using a learning model: (1) build the model graph, (2) train/fit, and (3) test/predict. Above, we *did not* use that style of implementation. And you can see that things get a bit messy, quickly. We have model creation in one spot and then we have training, testing, and output all mixed together (along with TensorFlow helper code like sessions, etc.). We can do better. Rework the code above into a class like `TF_GD_LinearRegression`.
## Solution 2
# Learning an XOR Gate
If we compose a two stage model, we can learn the XOR gate. You'll notice that defining the model itself is starting to get messy. We'll talk about ways of dealing with that next week.
```
class XOR_Graph:
def __init__(self):
# Create an empty Graph to place our operations in
xor_graph = tf.Graph()
with xor_graph.as_default():
# Placeholder inputs for our a, b, and label training data
self.x1 = tf.placeholder(tf.float32)
self.x2 = tf.placeholder(tf.float32)
self.label = tf.placeholder(tf.float32)
# A placeholder for our learning rate, so we can adjust it
self.learning_rate = tf.placeholder(tf.float32)
# abbreviations! this section is the difference
# from the LogicGate class above
Var = tf.Variable; rn = tf.random_normal
self.weights = [[Var(rn([])), Var(rn([]))],
[Var(rn([])), Var(rn([]))],
[Var(rn([])), Var(rn([]))]]
self.biases = [Var(0.0, dtype=tf.float32),
Var(0.0, dtype=tf.float32),
Var(0.0, dtype=tf.float32)]
sig1 = tf.nn.sigmoid(self.x1 * self.weights[0][0] +
self.x2 * self.weights[0][1] +
self.biases[0])
sig2 = tf.nn.sigmoid(self.x1 * self.weights[1][0] +
self.x2 * self.weights[1][1] +
self.biases[1])
self.output = tf.nn.sigmoid(sig1 * self.weights[2][0] +
sig2 * self.weights[2][1] +
self.biases[2])
# We'll use the mean of squared errors as our loss function
self.loss = tf.reduce_mean(tf.square(self.output - self.label))
# Finally, we create a gradient descent training operation
# and an initialization operation
gdo = tf.train.GradientDescentOptimizer
self.train = gdo(self.learning_rate).minimize(self.loss)
correct = tf.equal(tf.round(self.output), self.label)
self.accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
self.sess = tf.Session(graph=xor_graph)
self.sess.run(init)
def fit(self, train_dict):
loss, acc, _ = self.sess.run([self.loss, self.accuracy, self.train],
train_dict)
return loss, acc
def predict(self, test_dict):
# make a list of organized weights:
# see tf.get_collection for more advanced ways to handle this
all_trained = (self.weights[0] + [self.biases[0]] +
self.weights[1] + [self.biases[1]] +
self.weights[2] + [self.biases[2]])
return self.sess.run(all_trained + [self.output], test_dict)
xor_table = np.array([[0,0,0],
[1,0,1],
[0,1,1],
[1,1,0]])
logic_model = XOR_Graph()
train_dict={logic_model.x1: xor_table[:,0],
logic_model.x2: xor_table[:,1],
logic_model.label: xor_table[:,2],
logic_model.learning_rate: 0.5}
print("training")
# note, I might get stuck in a local minima b/c this is a
# small problem with no noise (yes, noise helps!)
# this can converge in one round of 1000 or it might get
# stuck for all 10000
for i in range(10000):
loss, acc = logic_model.fit(train_dict)
if i % 1000 == 0:
print('loss: {}\taccuracy: {}'.format(loss, acc))
print('loss: {}\taccuracy: {}'.format(loss, acc))
print("testing")
test_dict = {logic_model.x1: xor_table[:,0],
logic_model.x2: xor_table[:,1]}
results = logic_model.predict(test_dict)
wb_lrn, predictions = results[:-1], results[-1]
print(wb_lrn)
wb_lrn = np.array(wb_lrn).reshape(3,3)
# combine the predictions with the inputs and clean up the data
# round it and convert to unsigned 8 bit ints
out_table = np.column_stack((xor_table[:,[0,1]],
predictions)).round().astype(np.uint8)
print("results")
print('Learned weights/bias (L1):', wb_lrn[0])
print('Learned weights/bias (L2):', wb_lrn[1])
print('Learned weights/bias (L3):', wb_lrn[2])
print('Testing Table:')
print(out_table)
print("Correct?", np.allclose(xor_table, out_table))
```
# An Example Neural Network
So, now that we've worked with some primitive models, let's take a look at something a bit closer to what we'll work with moving forward: an actual neural network.
The following model accepts a 100 dimensional input, has a hidden layer depth of 300, and an output layer depth of 50. We use a sigmoid activation function for the hidden layer.
```
nn1_graph = tf.Graph()
with nn1_graph.as_default():
x = tf.placeholder(tf.float32, shape=[None, 100])
y = tf.placeholder(tf.float32, shape=[None]) # Labels, not used in this model
with tf.name_scope('hidden1'):
w = tf.Variable(tf.truncated_normal([100, 300]), name='W')
b = tf.Variable(tf.zeros([300]), name='b')
z = tf.matmul(x, w) + b
a = tf.nn.sigmoid(z)
with tf.name_scope('output'):
w = tf.Variable(tf.truncated_normal([300, 50]), name='W')
b = tf.Variable(tf.zeros([50]), name='b')
z = tf.matmul(a, w) + b
output = z
with tf.name_scope('global_step'):
global_step = tf.Variable(0, trainable=False, name='global_step')
inc_step = tf.assign_add(global_step, 1, name='increment_step')
with tf.name_scope('summaries'):
for var in tf.trainable_variables():
hist_summary = tf.summary.histogram(var.op.name, var)
summary_op = tf.summary.merge_all()
init = tf.global_variables_initializer()
tb_base_path = 'tbout/nn1_graph'
tb_path = helpers_03.get_fresh_dir(tb_base_path)
sess = tf.Session(graph=nn1_graph)
writer = tf.summary.FileWriter(tb_path, graph=nn1_graph)
sess.run(init)
summaries = sess.run(summary_op)
writer.add_summary(summaries)
writer.close()
sess.close()
```
# Exercise 3
Modify the template above to create your own neural network with the following features:
* Accepts input of length 200 (and allows for variable number of examples)
* First hidden layer depth of 800
* Second hidden layer depth of 600
* Third hidden layer depth of 400
* Output layer depth of 100
* Include histogram summaries of the variables
## Solution 3
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
%aimport utils_1_1
import pandas as pd
import numpy as np
import altair as alt
from altair_saver import save
import datetime
import dateutil.parser
from os.path import join
from constants_1_1 import SITE_FILE_TYPES
from utils_1_1 import (
get_site_file_paths,
get_site_file_info,
get_site_ids,
get_visualization_subtitle,
get_country_color_map,
)
from theme import apply_theme
from web import for_website
alt.data_transformers.disable_max_rows(); # Allow using rows more than 5000
data_release='2021-04-27'
df = pd.read_csv(join("..", "data", "Phase2.1SurvivalRSummariesPublic", "ToShare", "table.beta.mice.std.toShare.csv"))
print(df.head())
# Rename columns
df = df.rename(columns={"variable": "c", "beta": "v"})
consistent_date = {
'2020-03': 'Mar - Apr',
'2020-05': 'May - Jun',
'2020-07': 'Jul - Aug',
'2020-09': 'Sep - Oct',
'2020-11': 'Since Nov'
}
colors = ['#E79F00', '#0072B2', '#D45E00', '#CB7AA7', '#029F73', '#57B4E9']
sites = ['META', 'APHP', 'FRBDX', 'ICSM', 'BIDMC', 'MGB', 'UCLA', 'UMICH', 'UPENN', 'VA1', 'VA2', 'VA3', 'VA4', 'VA5']
site_colors = ['black', '#D45E00', '#0072B2', '#CB7AA7', '#E79F00', '#029F73', '#DBD03C', '#57B4E9', '#57B4E9', '#57B4E9', '#57B4E9', '#57B4E9']
sites = ['META', 'APHP', 'FRBDX', 'ICSM', 'UKFR', 'NWU', 'BIDMC', 'MGB', 'UCLA', 'UMICH', 'UPENN', 'UPITT', 'VA1', 'VA2', 'VA3', 'VA4', 'VA5']
site_colors = ['black', '#0072B2', '#0072B2', '#0072B2', '#0072B2', '#CB7AA7', '#D45E00', '#D45E00', '#D45E00', '#D45E00', '#D45E00', '#D45E00', '#D45E00', '#D45E00', '#D45E00','#D45E00','#D45E00']
df.siteid = df.siteid.apply(lambda x: x.upper())
print(df.siteid.unique().tolist())
group_map = {
'age18to25': 'Age',
'age26to49': 'Age',
'age70to79': 'Age',
'age80plus': 'Age',
'sexfemale': 'Sex',
'raceBlack': 'Race',
'raceAsian': 'Race',
'raceHispanic.and.Other': 'Race',
'CRP': 'Lab',
'albumin': 'Lab',
'TB': 'Lab',
"LYM": 'Lab',
"neutrophil_count" : 'Lab',
"WBC" : 'Lab',
"creatinine": 'Lab',
"AST": 'Lab',
"AA": 'Lab',
"DD": 'Lab',
'mis_CRP': 'Lab Mis.',
'mis_albumin': 'Lab Mis.',
'mis_TB': 'Lab Mis.',
"mis_LYM": 'Lab Mis.',
"mis_neutrophil_count" : 'Lab Mis.',
"mis_WBC" : 'Lab Mis.',
"mis_creatinine": 'Lab Mis.',
"mis_AST": 'Lab Mis.',
"mis_AA": 'Lab Mis.',
'mis_DD': 'Lab Mis.',
'charlson_score': 'Charlson Score',
'mis_charlson_score': 'Charlson Score',
}
df['g'] = df.c.apply(lambda x: group_map[x])
consistent_c = {
'age18to25': '18 - 25',
'age26to49': '26 - 49',
'age70to79': '70 - 79',
'age80plus': '80+',
'sexfemale': 'Female',
'raceBlack': 'Black',
'raceAsian': 'Asian',
'raceHispanic.and.Other': 'Hispanic and Other',
'CRP': 'Log CRP(mg/dL)',
'albumin': 'Albumin (g/dL)',
'TB': 'Total Bilirubin (mg/dL)',
"LYM": 'Lymphocyte Count (10*3/uL)',
"neutrophil_count" : 'Neutrophil Count (10*3/uL)',
"WBC" : 'White Blood Cell (10*3/uL)',
"creatinine": 'Creatinine (mg/dL)',
"AST": 'Log AST (U/L)',
"AA": 'AST/ALT',
"DD": 'Log D-Dimer (ng/mL)',
'mis_CRP': 'CRP not tested',
'mis_albumin': 'Albumin not tested',
'mis_TB': 'Total bilirubin not tested',
"mis_LYM": 'Lymphocyte count not tested',
"mis_neutrophil_count" : 'Neutrophil count not tested',
"mis_WBC" : 'White blood cell not tested',
"mis_creatinine": 'Creatinine not tested',
"mis_AST": 'AST not tested',
"mis_AA": 'ALT/AST not available',
'mis_DD': 'D-dimer nottested',
'charlson_score': 'Charlson Comorbidity Index',
'mis_charlson_score': 'Charlson comorbidity index not available',
}
df.c = df.c.apply(lambda x: consistent_c[x])
unique_g = df.g.unique().tolist()
print(unique_g)
unique_c = df.c.unique().tolist()
print(unique_c)
df
```
# All Sites
```
point=alt.OverlayMarkDef(filled=False, fill='white', strokeWidth=2)
def plot_lab(df=None, metric='cov'):
d = df.copy()
plot = alt.Chart(
d
).mark_bar(
# point=True,
size=10,
# opacity=0.3
).encode(
y=alt.Y("c:N", title=None, axis=alt.Axis(labelAngle=0, tickCount=10), scale=alt.Scale(padding=1), sort=unique_c),
x=alt.X("v:Q", title=None, scale=alt.Scale(zero=True, domain=[-3,3], padding=2, nice=False, clamp=True)),
# color=alt.Color("siteid:N", scale=alt.Scale(domain=sites, range=site_colors)),
color=alt.Color("g:N", scale=alt.Scale(domain=unique_g, range=colors), title='Category'),
).properties(
width=150,
height=250
)
plot = plot.facet(
column=alt.Column("siteid:N", header=alt.Header(title=None), sort=sites)
).resolve_scale(color='shared')
plot = plot.properties(
title={
"text": [
f"Coefficient"
],
"dx": 120,
"subtitle": [
'Lab values are standarized by SD',
get_visualization_subtitle(data_release=data_release, with_num_sites=False)
],
"subtitleColor": "gray",
}
)
return plot
plot = plot_lab(df=df)
# plot = alt.vconcat(*(
# plot_lab(df=df, lab=lab) for lab in unique_sites
# ), spacing=30)
plot = apply_theme(
plot,
axis_y_title_font_size=16,
title_anchor='start',
legend_orient='bottom',
legend_title_orient='left',
axis_label_font_size=14,
header_label_font_size=16,
point_size=100
)
plot
```
## Final Meta
```
def plot_lab(df=None, metric='cov'):
d = df.copy()
d = d[d.siteid == 'META']
print(unique_c)
plot = alt.Chart(
d
).mark_point(
#point=True,
size=120,
filled=True,
opacity=1
).encode(
y=alt.Y("c:N", title=None, axis=alt.Axis(labelAngle=0, tickCount=10, grid=True), scale=alt.Scale(padding=1), sort=unique_c),
x=alt.X("v:Q", title="Hazard Ratio", scale=alt.Scale(zero=True, domain=[0,3.6], padding=0, nice=False, clamp=True)),
# color=alt.Color("siteid:N", scale=alt.Scale(domain=sites, range=site_colors)),
color=alt.Color("g:N", scale=alt.Scale(domain=unique_g, range=colors), title='Category',legend=None),
).properties(
width=550,
height=400
)
line = alt.Chart(pd.DataFrame({'x': [1]})).mark_rule().encode(x='x', strokeWidth=alt.value(1), strokeDash=alt.value([2, 2]))
tick = plot.mark_errorbar(
opacity=0.7 #, color='black',
#color=alt.Color("g:N", scale=alt.Scale(domain=unique_g, range=colors), title='Category')
).encode(
y=alt.Y("c:N", sort=unique_c),
x=alt.X("ci_l:Q", title="Hazard Ratio"),
x2=alt.X2("ci_u:Q"),
stroke=alt.value('black'),
strokeWidth=alt.value(1)
)
plot = (line+tick+plot)
#plot = plot.facet(
# column=alt.Column("siteid:N", header=alt.Header(title=None), sort=sites)
#).resolve_scale(color='shared')
#plot = plot.properties(
# title={
# "text": [
# f"Meta-Analysis Of Coefficient"
# ],
# "dx": 120,
# "subtitle": [
# 'Lab values are standarized by SD'#,
# #get_visualization_subtitle(data_release=data_release, with_num_sites=False)
# ],
# "subtitleColor": "gray",
# }
#)
return plot
plot = plot_lab(df=df)
# plot = alt.vconcat(*(
# plot_lab(df=df, lab=lab) for lab in unique_sites
# ), spacing=30)
plot = apply_theme(
plot,
axis_y_title_font_size=16,
title_anchor='start',
#legend_orient='bottom',
#legend_title_orient='top',
axis_label_font_size=14,
header_label_font_size=16,
point_size=100
)
plot.display()
save(plot,join("..", "result", "final-beta-std-mice-meta.png"), scalefactor=8.0)
```
## Final country
```
def plot_beta(df=None, metric='cov', country=None):
d = df.copy()
d = d[d.siteid == country]
plot = alt.Chart(
d
).mark_point(
# point=True,
size=120,
filled=True,
opacity=1
# opacity=0.3
).encode(
y=alt.Y("c:N", title=None, axis=alt.Axis(labelAngle=0, tickCount=10, grid=True), scale=alt.Scale(padding=1), sort=unique_c),
x=alt.X("v:Q", title="Hazard Ratio", scale=alt.Scale(zero=True, domain=[0,4.6], padding=0, nice=False, clamp=True)),
# color=alt.Color("siteid:N", scale=alt.Scale(domain=sites, range=site_colors)),
color=alt.Color("g:N", scale=alt.Scale(domain=unique_g, range=colors), title='Category', legend=None),
).properties(
width=750,
height=550
)
line = alt.Chart(pd.DataFrame({'x': [1]})).mark_rule().encode(x='x', strokeWidth=alt.value(1), strokeDash=alt.value([2, 2]))
tick = plot.mark_errorbar(
opacity=0.7 #, color='black'
).encode(
y=alt.Y("c:N", sort=unique_c),
x=alt.X("ci_l:Q", title="Hazard Ratio"),
x2=alt.X2("ci_u:Q"),
stroke=alt.value('black'),
strokeWidth=alt.value(1)
)
plot = (line+tick+plot)
# plot = plot.facet(
# column=alt.Column("siteid:N", header=alt.Header(title=None), sort=sites)
# ).resolve_scale(color='shared')
plot = plot.properties(
title={
"text": [
country.replace("META-","")
],
"dx": 160,
#"subtitle": [
# 'Lab values are standarized by SD'
#],
#"subtitleColor": "gray",
}
)
return plot
countrylist1 = ["META-USA", "META-FRANCE"]
countrylist2 = ["META-GERMANY", "META-SPAIN"]
plot1 = alt.hconcat(*(
plot_beta(df=df, country=country) for country in countrylist1
), spacing=30).resolve_scale(color='independent')
plot2 = alt.hconcat(*(
plot_beta(df=df, country=country) for country in countrylist2
), spacing=30).resolve_scale(color='independent')
plot=alt.vconcat(plot1, plot2)
#plot=plot1
plot = apply_theme(
plot,
axis_y_title_font_size=16,
title_anchor='start',
legend_orient='bottom',
legend_title_orient='left',
axis_label_font_size=14,
header_label_font_size=16,
point_size=100
)
plot.display()
save(plot,join("..", "result", "final-beta-std-mice-country.png"), scalefactor=8.0)
```
|
github_jupyter
|
# Session 17: Recommendation system on your own
This script should allow you to build an interactive website from your own
dataset. If you run into any issues, please let us know!
## Step 1: Select the corpus
In the block below, insert the name of your corpus. There should
be images in the directory "images". If there is metadata, it should
be in the directory "data" with the name of the corpus as the file name.
Also, if there is metadata, there must be a column called filename (with
the filename to the image) and a column called title.
```
cn = "test"
```
## Step 2: Read in the Functions
You need to read in all of the modules and functions below.
```
%pylab inline
import numpy as np
import scipy as sp
import pandas as pd
import sklearn
from sklearn import linear_model
import urllib
import os
from os.path import join
from keras.applications.vgg19 import VGG19
from keras.preprocessing import image
from keras.applications.vgg19 import preprocess_input, decode_predictions
from keras.models import Model
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"
def check_create_metadata(cn):
mdata = join("..", "data", cn + ".csv")
if not os.path.exists(mdata):
exts = [".jpg", ".JPG", ".JPEG", ".png"]
fnames = [x for x in os.listdir(join('..', 'images', cn)) if get_ext(x) in exts]
df = pd.DataFrame({'filename': fnames, 'title': fnames})
df.to_csv(mdata, index=False)
def create_embed(corpus_name):
ofile = join("..", "data", corpus_name + "_vgg19_fc2.npy")
if not os.path.exists(ofile):
vgg19_full = VGG19(weights='imagenet')
vgg_fc2 = Model(inputs=vgg19_full.input, outputs=vgg19_full.get_layer('fc2').output)
df = pd.read_csv(join("..", "data", corpus_name + ".csv"))
output = np.zeros((len(df), 224, 224, 3))
for i in range(len(df)):
img_path = join("..", "images", corpus_name, df.filename[i])
img = image.load_img(img_path, target_size=(224, 224))
x = image.img_to_array(img)
output[i, :, :, :] = x
if (i % 100) == 0:
print("Loaded image {0:03d}".format(i))
output = preprocess_input(output)
img_embed = vgg_fc2.predict(output, verbose=True)
np.save(ofile, img_embed)
def rm_ext(s):
return os.path.splitext(s)[0]
def get_ext(s):
return os.path.splitext(s)[-1]
def clean_html():
if not os.path.exists(join("..", "html")):
os.makedirs(join("..", "html"))
if not os.path.exists(join("..", "html", "pages")):
os.makedirs(join("..", "html", "pages"))
for p in [x for x in os.listdir(join('..', 'html', 'pages')) if get_ext(x) in [".html", "html"]]:
os.remove(join('..', 'html', 'pages', p))
def load_data(cn):
X = np.load(join("..", "data", cn + "_vgg19_fc2.npy"))
return X
def write_header(f, cn, index=False):
loc = ""
if not index:
loc = "../"
f.write("<html>\n")
f.write(' <link rel="icon" href="{0:s}img/favicon.ico">\n'.format(loc))
f.write(' <title>Distant Viewing Tutorial</title>\n\n')
f.write(' <link rel="stylesheet" type="text/css" href="{0:s}css/bootstrap.min.css">'.format(loc))
f.write(' <link href="https://fonts.googleapis.com/css?family=Rubik+27px" rel="stylesheet">')
f.write(' <link rel="stylesheet" type="text/css" href="{0:s}css/dv.css">\n\n'.format(loc))
f.write("<body>\n")
f.write(' <div class="d-flex flex-column flex-md-row align-items-center p-3 px-md-4')
f.write('mb-3 bg-white border-bottom box-shadow">\n')
f.write(' <h4 class="my-0 mr-md-auto font-weight-normal">Distant Viewing Tutorial Explorer')
f.write('— {0:s}</h4>\n'.format(cn.capitalize()))
f.write(' <a class="btn btn-outline-primary" href="{0:s}index.html">Back to Index</a>\n'.format(loc))
f.write(' </div>\n')
f.write('\n')
def corpus_to_html(corpus):
pd.set_option('display.max_colwidth', -1)
tc = corpus.copy()
for index in range(tc.shape[0]):
fname = rm_ext(os.path.split(tc['filename'][index])[1])
title = rm_ext(tc['filename'][index])
s = "<a href='pages/{0:s}.html'>{1:s}</a>".format(fname, title)
tc.iloc[index, tc.columns.get_loc('title')] = s
tc = tc.drop(['filename'], axis=1)
return tc.to_html(index=False, escape=False, justify='center')
def create_index(cn, corpus):
f = open(join('..', 'html', 'index.html'), 'w')
write_header(f, cn=cn, index=True)
f.write(' <div style="padding:20px; max-width:1000px">\n')
f.write(corpus_to_html(corpus))
f.write(' </div>\n')
f.write("</body>\n")
f.close()
def get_infobox(corpus, item):
infobox = []
for k, v in corpus.iloc[item].to_dict().items():
if k != "filename":
infobox = infobox + ["<p><b>" + str(k).capitalize() + ":</b> " + str(v) + "</p>"]
return infobox
def save_metadata(f, cn, corpus, X, item):
infobox = get_infobox(corpus, item)
f.write("<div style='width: 1000px;'>\n")
f.write("\n".join(infobox))
if item > 0:
link = rm_ext(os.path.split(corpus['filename'][item - 1])[-1])
f.write("<p align='center'><a href='{0:s}.html'><< previous image</a> \n".format(link))
if item + 1 < X.shape[0]:
link = rm_ext(os.path.split(corpus['filename'][item + 1])[-1])
f.write(" <a href='{0:s}.html'>next image >></a></p>\n".format(link))
f.write("</div>\n")
def save_similar_img(f, cn, corpus, X, item):
dists = np.sum(np.abs(X - X[item, :]), 1)
idx = np.argsort(dists.flatten())[1:13]
f.write("<div style='clear:both; width: 1000px; padding-top: 30px'>\n")
f.write("<h4>Similar Images:</h4>\n")
f.write("<div class='similar'>\n")
for img_path in corpus['filename'][idx].tolist():
hpath = rm_ext(os.path.split(img_path)[1])
f.write('<a href="{0:s}.html"><img src="../../images/{1:2}/{2:s}" style="max-width: 150px; padding:5px"></a>\n'.format(hpath, cn, img_path))
f.write("</div>\n")
f.write("</div>\n")
def create_image_pages(cn, corpus, X):
for item in range(X.shape[0]):
img_path = corpus['filename'][item]
url = os.path.split(img_path)[1]
f = open(join('..', 'html', 'pages', rm_ext(url) + ".html"), 'w')
write_header(f, cn, index=False)
f.write("<div style='padding:25px'>\n")
# Main image
f.write("<div style='float: left; width: 610px;'>\n")
f.write('<img src="../../images/{0:s}/{1:s}" style="max-width: 600px; max-height: 500px;">\n'.format(cn, img_path))
f.write("</div>\n\n")
# Main information box
save_metadata(f, cn, corpus, X, item)
# Similar
save_similar_img(f, cn, corpus, X, item)
f.write("</body>\n")
f.close()
```
## Step 3: Create the embeddings
The next step is create the embeddings. If there is no metadata, this code
will also create it.
```
check_create_metadata(cn)
create_embed(cn)
```
### Step 4: Create the website
Finally, create the website with the code below.
```
clean_html()
corpus = pd.read_csv(join("..", "data", cn + ".csv"))
X = load_data(cn)
create_index(cn, corpus)
create_image_pages(cn, corpus, X)
```
You should find a folder called `html`. Open that folder and double click on the
file `index.html`, opening it in a web browser (Chrome or Firefox preferred; Safari
should work too). Do not open it in Jupyter.
You will see a list of all of the available images from the corpus you selected.
Click on one and you'll get to an item page for that image. From there you can
see the image itself, available metadata, select the previous or next image in the
corpus, and view similar images from the VGG19 similarity measurement.
|
github_jupyter
|
# K-Nearest Neighbors Algorithm
In this Jupyter Notebook we will focus on $KNN-Algorithm$. KNN is a data classification algorithm that attempts to determine what group a data point is in by looking at the data points around it.
An algorithm, looking at one point on a grid, trying to determine if a point is in group A or B, looks at the states of the points that are near it. The range is arbitrarily determined, but the point is to take a sample of the data. If the majority of the points are in group A, then it is likely that the data point in question will be A rather than B, and vice versa.
<br>
<img src="knn/example 1.png" height="30%" width="30%">
# Imports
```
import numpy as np
from tqdm import tqdm_notebook
```
# How it works?
We have some labeled data set $X-train$, and a new set $X$ that we want to classify based on previous classyfications
## Seps
### 1. Calculate distance to all neightbours
### 2. Sort neightbours (based on closest distance)
### 3. Count possibilities of each class for k nearest neighbours
### 4. The class with highest possibilty is Your prediction
# 1. Calculate distance to all neighbours
Depending on the problem You should use diffrent type of count distance method.
<br>
For example we can use Euclidean distance. Euclidean distance is the "ordinary" straight-line distance between two points in D-Dimensional space
#### Definiton
$d(p, q) = d(q, p) = \sqrt{(q_1 - p_1)^2 + (q_2 - p_2)^2 + \dots + (q_D - p_D)^2} = \sum_{d=1}^{D} (p_d - q_d)^2$
#### Example
Distance in $R^2$
<img src="knn/euklidean_example.png" height="30%" width="30%">
$p = (4,6)$
<br>
$q = (1,2)$
<br>
$d(p, q) = \sqrt{(1-4)^2 + (2-6)^2} =\sqrt{9 + 16} = \sqrt{25} = 5 $
## Code
```
def get_euclidean_distance(A_matrix, B_matrix):
"""
Function computes euclidean distance between matrix A and B
Args:
A_matrix (numpy.ndarray): Matrix size N1:D
B_matrix (numpy.ndarray): Matrix size N2:D
Returns:
numpy.ndarray: Matrix size N1:N2
"""
A_square = np.reshape(np.sum(A_matrix * A_matrix, axis=1), (A_matrix.shape[0], 1))
B_square = np.reshape(np.sum(B_matrix * B_matrix, axis=1), (1, B_matrix.shape[0]))
AB = A_matrix @ B_matrix.T
C = -2 * AB + B_square + A_square
return np.sqrt(C)
```
## Example Usage
```
X = np.array([[1,2,3] , [-4,5,-6]])
X_train = np.array([[0,0,0], [1,2,3], [4,5,6], [-4, 4, -6]])
print("X: {} Exaples in {} Dimensional space".format(*X.shape))
print("X_train: {} Exaples in {} Dimensional space".format(*X_train.shape))
print()
print("X:")
print(X)
print()
print("X_train")
print(X_train)
distance_matrix = get_euclidean_distance(X, X_train)
print("Distance Matrix shape: {}".format(distance_matrix.shape))
print("Distance between first example from X and first form X_train {}".format(distance_matrix[0,0]))
print("Distance between first example from X and second form X_train {}".format(distance_matrix[0,1]))
```
# 2. Sort neightbours
In order to find best fitting class for our observations we need to find to which classes belong observation neightbours and then to sort classes based on the closest distance
## Code
```
def get_sorted_train_labels(distance_matrix, y):
"""
Function sorts y labels, based on probabilities from distances matrix
Args:
distance_matrix (numpy.ndarray): Distance Matrix, between points from X and X_train, size: N1:N2
y (numpy.ndarray): vector of classes of X points, size: N1
Returns:
numpy.ndarray: labels matrix sorted according to distances to nearest neightours, size N1:N2
"""
order = distance_matrix.argsort(kind='mergesort')
return np.squeeze(y[order])
```
## Example Usage
```
y_train = np.array([[1, 1, 2, 3]]).T
print("Labels array {} Examples in {} Dimensional Space".format(*y_train.shape))
print("Distance matrix shape {}".format(distance_matrix.shape))
sorted_train_labels = get_sorted_train_labels(distance_matrix, y_train)
print("Sorted train labels {} shape".format(sorted_train_labels.shape))
print("Closest 3 classes for first element from set X: {}".format(sorted_train_labels[0, :3]))
```
# 3. Count possibilities of each class for k nearest neighbours
In order to find best class for our observation $x$ we need to calculate the probability of belonging to each class. In our case it is quite easy. We need just to count how many from k-nearest-neighbours of observation $x$ belong to each class and then devide it by k
<br><br>
$p(y=class \space| x) = \frac{\sum_{1}^{k}(1 \space if \space N_i = class, \space else \space 0) }{k}$ Where $N_i$ is $i$ nearest neightbour
## Code
```
def get_p_y_x_using_knn(y, k):
"""
The function determines the probability distribution p (y | x)
for each of the labels for objects from the X
using the KNN classification learned on the X_train
Args:
y (numpy.ndarray): Sorted matrix of N2 nearest neighbours labels, size N1:N2
k (int): number of nearest neighbours for KNN algorithm
Returns: numpy.ndarray: Matrix of probabilities for N1 points (from set X) of belonging to each class,
size N1:C (where C is number of classes)
"""
first_k_neighbors = y[:, :k]
N1, N2 = y.shape
classes = np.unique(y)
number_of_classes = classes.shape[0]
probabilities_matrix = np.zeros(shape=(N1, number_of_classes))
for i, row in enumerate(first_k_neighbors):
for j, value in enumerate(classes):
probabilities_matrix[i][j] = list(row).count(value) / k
return probabilities_matrix
```
## Example usage
```
print("Sorted train labels:")
print(sorted_train_labels)
probabilities_matrix = get_p_y_x_using_knn(y=sorted_train_labels, k=4)
print("Probability fisrt element belongs to 1-st class: {:2f}".format(probabilities_matrix[0,0]))
print("Probability fisrt element belongs to 3-rd class: {:2f}".format(probabilities_matrix[0,2]))
```
# 4. The class with highest possibilty is Your prediction
At the end we combine all previous steps to get prediction
## Code
```
def predict(X, X_train, y_train, k, distance_function):
"""
Function returns predictions for new set X based on labels of points from X_train
Args:
X (numpy.ndarray): set of observations (points) that we want to label
X_train (numpy.ndarray): set of lalabeld bservations (points)
y_train (numpy.ndarray): labels for X_train
k (int): number of nearest neighbours for KNN algorithm
Returns:
(numpy.ndarray): label predictions for points from set X
"""
distance_matrix = distance_function(X, X_train)
sorted_labels = get_sorted_train_labels(distance_matrix=distance_matrix, y=y_train)
p_y_x = get_p_y_x_using_knn(y=sorted_labels, k=k)
number_of_classes = p_y_x.shape[1]
reversed_rows = np.fliplr(p_y_x)
prediction = number_of_classes - (np.argmax(reversed_rows, axis=1) + 1)
return prediction
```
## Example usage
```
prediction = predict(X, X_train, y_train, 3, get_euclidean_distance)
print("Predicted propabilities of classes for for first observation", probabilities_matrix[0])
print("Predicted class for for first observation", prediction[0])
print()
print("Predicted propabilities of classes for for second observation", probabilities_matrix[1])
print("Predicted class for for second observation", prediction[1])
```
# Accuracy
To find how good our knn model works we should count accuracy
## Code
```
def count_accuracy(prediction, y_true):
"""
Returns:
float: Predictions accuracy
"""
N1 = prediction.shape[0]
accuracy = np.sum(prediction == y_true) / N1
return accuracy
```
## Example usage
```
y_true = np.array([[0, 2]])
predicton = predict(X, X_train, y_train, 3, get_euclidean_distance)
print("True classes:{}, accuracy {}%".format(y_true, count_accuracy(predicton, y_true) * 100))
```
# Find best k
Best k parameter is that one for which we have highest accuracy
## Code
```
def select_knn_model(X_validation, y_validation, X_train, y_train, k_values, distance_function):
"""
Function returns k parameter that best fit Xval points
Args:
Xval (numpy.ndarray): set of Validation Data, size N1:D
Xtrain (numpy.ndarray): set of Training Data, size N2:D
yval (numpy.ndarray): set of labels for Validation data, size N1:1
ytrain (numpy.ndarray): set of labels for Training Data, size N2:1
k_values (list): list of int values of k parameter that should be checked
Returns:
int: k paprameter that best fit validation set
"""
accuracies = []
for k in tqdm_notebook(k_values):
prediction = predict(X_validation, X_train, y_train, k, distance_function)
accuracy = count_accuracy(prediction, y_validation)
accuracies.append(accuracy)
best_k = k_values[accuracies.index(max(accuracies))]
return best_k, accuracies
```
# Real World Example - Iris Dataset
<img src="knn/iris_example1.jpeg" height="60%" width="60%">
This is perhaps the best known database to be found in the pattern recognition literature. The data set contains 3 classes of 50 instances each, where each class refers to a type of iris plant. One class is linearly separable from the other 2; the latter are NOT linearly separable from each other.
Each example contains 4 attributes
1. sepal length in cm
2. sepal width in cm
3. petal length in cm
4. petal width in cm
Predicted attribute: class of iris plant.
<img src="knn/iris_example2.png" height="70%" width="70%">
```
from sklearn import datasets
import matplotlib.pyplot as plt
iris = datasets.load_iris()
iris_X = iris.data
iris_y = iris.target
print("Iris: {} examples in {} dimensional space".format(*iris_X.shape))
print("First example in dataset :\n Speal lenght: {}cm \n Speal width: {}cm \n Petal length: {}cm \n Petal width: {}cm".format(*iris_X[0]))
print("Avalible classes", np.unique(iris_y))
```
## Prepare Data
In our data set we have 150 examples (50 examples of each class), we have to divide it into 3 datasets.
1. Training data set, 90 examples. It will be used to find k - nearest neightbours
2. Validation data set, 30 examples. It will be used to find best k parameter, the one for which accuracy is highest
3. Test data set, 30 examples. It will be used to check how good our model performs
Data has to be shuffled (mixed in random order), because originally it is stored 50 examples of class 0, 50 of 1 and 50 of 2.
```
from sklearn.utils import shuffle
iris_X, iris_y = shuffle(iris_X, iris_y, random_state=134)
test_size = 30
validation_size = 30
training_size = 90
X_test = iris_X[:test_size]
X_validation = iris_X[test_size: (test_size+validation_size)]
X_train = iris_X[(test_size+validation_size):]
y_test = iris_y[:test_size]
y_validation = iris_y[test_size: (test_size+validation_size)]
y_train = iris_y[(test_size+validation_size):]
```
## Find best k parameter
```
k_values = [i for i in range(3,50)]
best_k, accuracies = select_knn_model(X_validation, y_validation, X_train, y_train, k_values, distance_function=get_euclidean_distance)
plt.plot(k_values, accuracies)
plt.xlabel('K parameter')
plt.ylabel('Accuracy')
plt.title('Accuracy for k nearest neighbors')
plt.grid()
plt.show()
```
## Count accuracy for training set
```
prediction = predict(X_test, X_train, y_train, best_k, get_euclidean_distance)
accuracy = count_accuracy(prediction, y_test)
print("Accuracy for best k={}: {:2f}%".format(best_k, accuracy*100))
```
# Real World Example - Mnist Dataset
Mnist is a popular database of handwritten images created for people who are new to machine learning. There are many courses on the internet that include classification problem using MNIST dataset.
This dataset contains 55000 images and labels. Each image is 28x28 pixels large, but for the purpose of the classification task they are flattened to 784x1 arrays $(28 \cdot 28 = 784)$. Summing up our training set is a matrix of size $[50000, 784]$ = [amount of images, size of image]. We will split it into 40000 training examples and 10000 validation examples to choose a best k
It also contains 5000 test images and labels, but for test we will use only 1000 (due to time limitations, using 5k would take 5x as much time)
<h3>Mnist Data Example</h3>
<img src="knn/mnist_example.jpg" height="70%" width="70%">
Now we are going to download this dataset and split it into test and train sets.
```
import utils
import cv2
training_size = 49_000
validation_size = 1000
test_size = 1000
train_data, test = utils.get_mnist_dataset()
train_images, train_labels = train_data
test_images, test_labels = test
validation_images = train_images[training_size:training_size + validation_size]
train_images = train_images[:training_size]
validation_labels = train_labels[training_size:training_size + validation_size]
train_labels = train_labels[:training_size]
test_images = test_images[:test_size]
test_labels = test_labels[:test_size]
print("Training images matrix size: {}".format(train_images.shape))
print("Training labels matrix size: {}".format(train_labels.shape))
print("Validation images matrix size: {}".format(validation_images.shape))
print("Validation labels matrix size: {}".format(validation_labels.shape))
print("Testing images matrix size: {}".format(test_images.shape))
print("Testing labels matrix size: {}".format(test_labels.shape))
print("Possible labels {}".format(np.unique(test_labels)))
```
## Visualisation
Visualisation isn't necessery to the problem, but it helps to understand what are we doing.
```
from matplotlib.gridspec import GridSpec
def show_first_8(images):
ax =[]
fig = plt.figure(figsize=(10, 10))
gs = GridSpec(2, 4, wspace=0.0, hspace=-0.5)
for i in range(2):
for j in range(4):
ax.append(fig.add_subplot(gs[i,j]))
for i, axis in enumerate(ax):
axis.imshow(images[i])
plt.show()
first_8_images = train_images[:8]
resized = np.reshape(first_8_images, (-1,28,28))
print('First 8 images of train set:')
show_first_8(resized)
```
## Find best k parameter
```
k_values = [i for i in range(3, 50, 5)]
best_k, accuracies = select_knn_model(validation_images, validation_labels, train_images, train_labels, k_values,
distance_function=get_euclidean_distance)
plt.plot(k_values, accuracies)
plt.xlabel('K parameter')
plt.ylabel('Accuracy')
plt.title('Accuracy for k nearest neighbors')
plt.grid()
plt.show()
prediction = np.squeeze(predict(test_images, train_images, train_labels, best_k, get_euclidean_distance))
accuracy = count_accuracy(prediction, test_labels)
print("Accuracy on test set for best k={}: {:2}%".format(best_k, accuracy * 100))
```
# Sources
https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm - first visualisation image
https://en.wikipedia.org/wiki/Euclidean_distance - euclidean distance visualisation
https://rajritvikblog.wordpress.com/2017/06/29/iris-dataset-analysis-python/ - first iris image
https://rpubs.com/wjholst/322258 - second iris image
https://www.kaggle.com/pablotab/mnistpklgz - mnist dataset
|
github_jupyter
|
# Quantization of Signals
*This jupyter notebook is part of a [collection of notebooks](../index.ipynb) on various topics of Digital Signal Processing. Please direct questions and suggestions to [[email protected]](mailto:[email protected]).*
## Spectral Shaping of the Quantization Noise
The quantized signal $x_Q[k]$ can be expressed by the continuous amplitude signal $x[k]$ and the quantization error $e[k]$ as
\begin{equation}
x_Q[k] = \mathcal{Q} \{ x[k] \} = x[k] + e[k]
\end{equation}
According to the [introduced model](linear_uniform_quantization_error.ipynb#Model-for-the-Quantization-Error), the quantization noise can be modeled as uniformly distributed white noise. Hence, the noise is distributed over the entire frequency range. The basic concept of [noise shaping](https://en.wikipedia.org/wiki/Noise_shaping) is a feedback of the quantization error to the input of the quantizer. This way the spectral characteristics of the quantization noise can be modified, i.e. spectrally shaped. Introducing a generic filter $h[k]$ into the feedback loop yields the following structure

The quantized signal can be deduced from the block diagram above as
\begin{equation}
x_Q[k] = \mathcal{Q} \{ x[k] - e[k] * h[k] \} = x[k] + e[k] - e[k] * h[k]
\end{equation}
where the additive noise model from above has been introduced and it has been assumed that the impulse response $h[k]$ is normalized such that the magnitude of $e[k] * h[k]$ is below the quantization step $Q$. The overall quantization error is then
\begin{equation}
e_H[k] = x_Q[k] - x[k] = e[k] * (\delta[k] - h[k])
\end{equation}
The power spectral density (PSD) of the quantization error with noise shaping is calculated to
\begin{equation}
\Phi_{e_H e_H}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) = \Phi_{ee}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) \cdot \left| 1 - H(\mathrm{e}^{\,\mathrm{j}\,\Omega}) \right|^2
\end{equation}
Hence the PSD $\Phi_{ee}(\mathrm{e}^{\,\mathrm{j}\,\Omega})$ of the quantizer without noise shaping is weighted by $| 1 - H(\mathrm{e}^{\,\mathrm{j}\,\Omega}) |^2$. Noise shaping allows a spectral modification of the quantization error. The desired shaping depends on the application scenario. For some applications, high-frequency noise is less disturbing as low-frequency noise.
### Example - First-Order Noise Shaping
If the feedback of the error signal is delayed by one sample we get with $h[k] = \delta[k-1]$
\begin{equation}
\Phi_{e_H e_H}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) = \Phi_{ee}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) \cdot \left| 1 - \mathrm{e}^{\,-\mathrm{j}\,\Omega} \right|^2
\end{equation}
For linear uniform quantization $\Phi_{ee}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) = \sigma_e^2$ is constant. Hence, the spectral shaping constitutes a high-pass characteristic of first order. The following simulation evaluates the noise shaping quantizer of first order.
```
import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as sig
%matplotlib inline
w = 8 # wordlength of the quantized signal
xmin = -1 # minimum of input signal
N = 32768 # number of samples
def uniform_midtread_quantizer_w_ns(x, Q):
# limiter
x = np.copy(x)
idx = np.where(x <= -1)
x[idx] = -1
idx = np.where(x > 1 - Q)
x[idx] = 1 - Q
# linear uniform quantization with noise shaping
xQ = Q * np.floor(x/Q + 1/2)
e = xQ - x
xQ = xQ - np.concatenate(([0], e[0:-1]))
return xQ[1:]
# quantization step
Q = 1/(2**(w-1))
# compute input signal
np.random.seed(5)
x = np.random.uniform(size=N, low=xmin, high=(-xmin-Q))
# quantize signal
xQ = uniform_midtread_quantizer_w_ns(x, Q)
e = xQ - x[1:]
# estimate PSD of error signal
nf, Pee = sig.welch(e, nperseg=64)
# estimate SNR
SNR = 10*np.log10((np.var(x)/np.var(e)))
print('SNR = {:2.1f} dB'.format(SNR))
plt.figure(figsize=(10, 5))
Om = nf*2*np.pi
plt.plot(Om, Pee*6/Q**2, label='estimated PSD')
plt.plot(Om, np.abs(1 - np.exp(-1j*Om))**2, label='theoretic PSD')
plt.plot(Om, np.ones(Om.shape), label='PSD w/o noise shaping')
plt.title('PSD of quantization error')
plt.xlabel(r'$\Omega$')
plt.ylabel(r'$\hat{\Phi}_{e_H e_H}(e^{j \Omega}) / \sigma_e^2$')
plt.axis([0, np.pi, 0, 4.5])
plt.legend(loc='upper left')
plt.grid()
```
**Exercise**
* The overall average SNR is lower than for the quantizer without noise shaping. Why?
Solution: The average power per frequency is lower that without noise shaping for frequencies below $\Omega \approx \pi$. However, this comes at the cost of a larger average power per frequency for frequencies above $\Omega \approx \pi$. The average power of the quantization noise is given as the integral over the PSD of the quantization noise. It is larger for noise shaping and the resulting SNR is consequently lower. Noise shaping is nevertheless beneficial in applications where a lower quantization error in a limited frequency region is desired.
**Copyright**
This notebook is provided as [Open Educational Resource](https://en.wikipedia.org/wiki/Open_educational_resources). Feel free to use the notebook for your own purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Sascha Spors, Digital Signal Processing - Lecture notes featuring computational examples*.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/MuhammedAshraf2020/DNN-using-tensorflow/blob/main/DNN_using_tensorflow_ipynb.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#import libs
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from keras.datasets.mnist import load_data
# prepare dataset
(X_train , y_train) , (X_test , y_test) = load_data()
X_train = X_train.astype("float32") / 255
X_test = X_test.astype("float32") / 255
# Make sure images have shape (28, 28, 1)
X_train = np.expand_dims(X_train, -1)
X_test = np.expand_dims(X_test, -1)
for i in range(0, 9):
plt.subplot(330 + 1 + i)
plt.imshow(X_train[i][: , : , 0], cmap=plt.get_cmap('gray'))
plt.show()
X_train = [X_train[i].ravel() for i in range(len(X_train))]
X_test = [X_test[i].ravel() for i in range(len(X_test))]
y_train = tf.keras.utils.to_categorical(y_train , num_classes = 10)
y_test = tf.keras.utils.to_categorical(y_test , num_classes = 10 )
#set parameter
n_input = 28 * 28
n_hidden_1 = 512
n_hidden_2 = 256
n_hidden_3 = 128
n_output = 10
learning_rate = 0.01
epochs = 50
batch_size = 128
tf.compat.v1.disable_eager_execution()
# weight intialization
X = tf.compat.v1.placeholder(tf.float32 , [None , n_input])
y = tf.compat.v1.placeholder(tf.float32 , [None , n_output])
def Weights_init(list_layers , stddiv):
Num_layers = len(list_layers)
weights = {}
bias = {}
for i in range( Num_layers-1):
weights["W{}".format(i+1)] = tf.Variable(tf.compat.v1.truncated_normal([list_layers[i] , list_layers[i+1]] , stddev = stddiv))
bias["b{}".format(i+1)] = tf.Variable(tf.compat.v1.truncated_normal([list_layers[i+1]]))
return weights , bias
list_param = [784 , 512 , 256 , 128 , 10]
weights , biases = Weights_init(list_param , 0.1)
def Model (X , nn_weights , nn_bias):
Z1 = tf.add(tf.matmul(X , nn_weights["W1"]) , nn_bias["b1"])
Z1_out = tf.nn.relu(Z1)
Z2 = tf.add(tf.matmul(Z1_out , nn_weights["W2"]) , nn_bias["b2"])
Z2_out = tf.nn.relu(Z2)
Z3 = tf.add(tf.matmul(Z2_out , nn_weights["W3"]) , nn_bias["b3"])
Z3_out = tf.nn.relu(Z3)
Z4 = tf.add(tf.matmul(Z3_out , nn_weights["W4"]) , nn_bias["b4"])
Z4_out = tf.nn.softmax(Z4)
return Z4_out
nn_layer_output = Model(X , weights , biases)
loss = tf.reduce_mean(tf.compat.v1.nn.softmax_cross_entropy_with_logits_v2(logits = nn_layer_output , labels = y))
optimizer = tf.compat.v1.train.GradientDescentOptimizer(learning_rate).minimize(loss)
init = tf.compat.v1.global_variables_initializer()
# Determining if the predictions are accurate
is_correct_prediction = tf.equal(tf.argmax(nn_layer_output , 1),tf.argmax(y, 1))
#Calculating prediction accuracy
accuracy = tf.reduce_mean(tf.cast(is_correct_prediction, tf.float32))
saver = tf.compat.v1.train.Saver()
with tf.compat.v1.Session() as sess:
# initializing all the variables
sess.run(init)
total_batch = int(len(X_train) / batch_size)
for epoch in range(epochs):
avg_cost = 0
for i in range(total_batch):
batch_x , batch_y = X_train[i * batch_size : (i + 1) * batch_size] , y_train[i * batch_size : (i + 1) * batch_size]
_, c = sess.run([optimizer,loss], feed_dict={X: batch_x, y: batch_y})
avg_cost += c / total_batch
if(epoch % 10 == 0):
print("Epoch:", (epoch + 1), "train_cost =", "{:.3f} ".format(avg_cost) , end = "")
print("train_acc = {:.3f} ".format(sess.run(accuracy, feed_dict={X: X_train, y:y_train})) , end = "")
print("valid_acc = {:.3f}".format(sess.run(accuracy, feed_dict={X: X_test, y:y_test})))
saver.save(sess , save_path = "/content/Model.ckpt")
```
|
github_jupyter
|
This notebook copies images and annotations from the original dataset, to perform instance detection
you can control how many images per pose (starting from some point) and how many instances to consider as well as which classes
we also edit the annotation file because initially all annotations are made by instance not category
```
import os;
from shutil import copyfile
import xml.etree.ElementTree as ET
images_per_set = 102
start_after = 100
```
the following code can be used to generate both training and testing set
```
classes = ['book1','book2','book3','book4','book5',
'cellphone1','cellphone2','cellphone3','cellphone4','cellphone5',
'mouse1','mouse2','mouse3','mouse4','mouse5',
'ringbinder1','ringbinder2','ringbinder3','ringbinder4','ringbinder5']
days = [5,5,5,5,5,3,3,3,3,3,7,7,7,7,7,3,3,3,3,3]
images_path ='C:/Users/issa/Documents/datasets/ICUB_Instance/test/'
annotations_path = 'C:/Users/issa/Documents/datasets/ICUB_Instance/test_ann/'
instances_list = [1,2,3,4,5]
for category_name,day_number in zip(classes,days):
in_pose_counter = 0;
j =0
for inst in instances_list:
j=0
dirs = ['D:\\2nd_Semester\\CV\\Project\\part1\\part1\\'+category_name+'\\'+category_name+str(inst)+'\\MIX\\day'+str(day_number)+'\\left\\',
'D:\\2nd_Semester\\CV\\Project\\part1\\part1\\'+category_name+'\\'+category_name+str(inst)+'\\ROT2D\\day'+str(day_number)+'\\left\\',
'D:\\2nd_Semester\\CV\\Project\\part1\\part1\\'+category_name+'\\'+category_name+str(inst)+'\\ROT3D\\day'+str(day_number)+'\\left\\',
'D:\\2nd_Semester\\CV\\Project\\part1\\part1\\'+category_name+'\\'+category_name+str(inst)+'\\SCALE\\day'+str(day_number)+'\\left\\',
'D:\\2nd_Semester\\CV\\Project\\part1\\part1\\'+category_name+'\\'+category_name+str(inst)+'\\TRANSL\\day'+str(day_number)+'\\left\\']
for dir in dirs:
i=0;
in_pose_counter = 0;
if(i>images_per_set):
break;
for innerSubDir,innerDirs,innerFiles in os.walk(dir):
for file in innerFiles:
i = i+1
if(i>images_per_set):
break;
in_pose_counter = in_pose_counter+1
if(in_pose_counter>start_after):
j = j+1
copyfile(dir+file,images_path+category_name+str(inst)+'_'+str(j)+'.jpg')
in_pose_counter =0
j =0
for inst in instances_list:
j=0
dirs = ['D:\\2nd_Semester\\CV\\Project\\Annotations_refined\Annotations_refined\\'+category_name+'\\'+category_name+str(inst)+'\\MIX\\day'+str(day_number)+'\\left\\',
'D:\\2nd_Semester\\CV\\Project\\Annotations_refined\Annotations_refined\\'+category_name+'\\'+category_name+str(inst)+'\\ROT2D\\day'+str(day_number)+'\\left\\',
'D:\\2nd_Semester\\CV\\Project\\Annotations_refined\Annotations_refined\\'+category_name+'\\'+category_name+str(inst)+'\\ROT3D\\day'+str(day_number)+'\\left\\',
'D:\\2nd_Semester\\CV\\Project\\Annotations_refined\Annotations_refined\\'+category_name+'\\'+category_name+str(inst)+'\\SCALE\\day'+str(day_number)+'\\left\\',
'D:\\2nd_Semester\\CV\\Project\\Annotations_refined\Annotations_refined\\'+category_name+'\\'+category_name+str(inst)+'\\TRANSL\\day'+str(day_number)+'\\left\\']
for dir in dirs:
i=0;
in_pose_counter =0
if(i>images_per_set):
break;
for innerSubDir,innerDirs,innerFiles in os.walk(dir):
for file in innerFiles:
i = i+1
if(i>images_per_set):
break;
in_pose_counter = in_pose_counter+1
if(in_pose_counter>start_after):
j = j+1
outputPath = annotations_path+category_name+str(inst)+'_'+str(j)+'.xml'
copyfile(dir+file,outputPath)
```
This part produces the train/val sets, we set the classes and the list containing the number of images per class, then we split the list and generate the files.
```
import numpy as np
from sklearn.model_selection import train_test_split
x = np.arange(1,129)
classes = ['book1','book2','book3','book4','book5',
'cellphone1','cellphone2','cellphone3','cellphone4','cellphone5',
'mouse1','mouse2','mouse3','mouse4','mouse5',
'ringbinder1','ringbinder2','ringbinder3','ringbinder4','ringbinder5']
for category in classes:
xtrain,xtest,ytrain,ytest=train_test_split(x, x, test_size=0.25)
file = open("datasets//ICUB_Instance//train.txt","a")
for i in xtrain:
file.write(category+'_'+str(i)+'\n')
file.close()
file = open("datasets//ICUB_Instance//val.txt","a")
for i in xtest:
file.write(category+'_'+str(i)+'\n')
file.close()
```
this part generates the test set list, no splitting here
```
import numpy as np
classes = ['book1','book2','book3','book4','book5',
'cellphone1','cellphone2','cellphone3','cellphone4','cellphone5',
'mouse1','mouse2','mouse3','mouse4','mouse5',
'ringbinder1','ringbinder2','ringbinder3','ringbinder4','ringbinder5']
x = np.arange(1,21)
file = open("datasets//ICUB_Instance//test.txt","a")
for category in classes:
for i in x:
file.write(category+'_'+str(i)+'\n')
file.close()
```
|
github_jupyter
|
# Validating Multi-View Spherical KMeans by Replicating Paper Results
Here we will validate the implementation of multi-view spherical kmeans by replicating the right side of figure 3 from the Multi-View Clustering paper by Bickel and Scheffer.
```
import sklearn
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
import numpy as np
import scipy as scp
from scipy import sparse
import mvlearn
from mvlearn.cluster.mv_spherical_kmeans import MultiviewSphericalKMeans
from joblib import Parallel, delayed
import matplotlib.pyplot as plt
import warnings
warnings.simplefilter('ignore') # Ignore warnings
```
### A function to recreate the artificial dataset from the paper
The experiment in the paper used the 20 Newsgroup dataset, which consists of around 18000 newsgroups posts on 20 topics. This dataset can be obtained from scikit-learn. To create the artificial dataset used in the experiment, 10 of the 20 classes from the 20 newsgroups dataset were selected and grouped into 2 groups of 5 classes, and then encoded as tfidf vectors. These now represented the 5 multi-view classes, each with 2 views (one from each group). 200 examples were randomly sampled from each of the 20 newsgroups, producing 1000 concatenated examples uniformly distributed over the 5 classes.
```
NUM_SAMPLES = 200
#Load in the vectorized news group data from scikit-learn package
news = fetch_20newsgroups(subset='all')
all_data = np.array(news.data)
all_targets = np.array(news.target)
class_names = news.target_names
#A function to get the 20 newsgroup data
def get_data():
#Set class pairings as described in the multiview clustering paper
view1_classes = ['comp.graphics','rec.motorcycles', 'sci.space', 'rec.sport.hockey', 'comp.sys.ibm.pc.hardware']
view2_classes = ['rec.autos', 'sci.med','misc.forsale', 'soc.religion.christian','comp.os.ms-windows.misc']
#Create lists to hold data and labels for each of the 5 classes across 2 different views
labels = [num for num in range(len(view1_classes)) for _ in range(NUM_SAMPLES)]
labels = np.array(labels)
view1_data = list()
view2_data = list()
#Randomly sample 200 items from each of the selected classes in view1
for ind in range(len(view1_classes)):
class_num = class_names.index(view1_classes[ind])
class_data = all_data[(all_targets == class_num)]
indices = np.random.choice(class_data.shape[0], NUM_SAMPLES)
view1_data.append(class_data[indices])
view1_data = np.concatenate(view1_data)
#Randomly sample 200 items from each of the selected classes in view2
for ind in range(len(view2_classes)):
class_num = class_names.index(view2_classes[ind])
class_data = all_data[(all_targets == class_num)]
indices = np.random.choice(class_data.shape[0], NUM_SAMPLES)
view2_data.append(class_data[indices])
view2_data = np.concatenate(view2_data)
#Vectorize the data
vectorizer = TfidfVectorizer()
view1_data = vectorizer.fit_transform(view1_data)
view2_data = vectorizer.fit_transform(view2_data)
#Shuffle and normalize vectors
shuffled_inds = np.random.permutation(NUM_SAMPLES * len(view1_classes))
view1_data = sparse.vstack(view1_data)
view2_data = sparse.vstack(view2_data)
view1_data = np.array(view1_data[shuffled_inds].todense())
view2_data = np.array(view2_data[shuffled_inds].todense())
magnitudes1 = np.linalg.norm(view1_data, axis=1)
magnitudes2 = np.linalg.norm(view2_data, axis=1)
magnitudes1[magnitudes1 == 0] = 1
magnitudes2[magnitudes2 == 0] = 1
magnitudes1 = magnitudes1.reshape((-1,1))
magnitudes2 = magnitudes2.reshape((-1,1))
view1_data /= magnitudes1
view2_data /= magnitudes2
labels = labels[shuffled_inds]
return view1_data, view2_data, labels
```
### Function to compute cluster entropy
The function below is used to calculate the total clustering entropy using the formula described in the paper.
```
def compute_entropy(partitions, labels, k, num_classes):
total_entropy = 0
num_examples = partitions.shape[0]
for part in range(k):
labs = labels[partitions == part]
part_size = labs.shape[0]
part_entropy = 0
for cl in range(num_classes):
prop = np.sum(labs == cl) * 1.0 / part_size
ent = 0
if(prop != 0):
ent = - prop * np.log2(prop)
part_entropy += ent
part_entropy = part_entropy * part_size / num_examples
total_entropy += part_entropy
return total_entropy
```
### Functions to Initialize Centroids and Run Experiment
The randSpherical function initializes the initial cluster centroids by taking a uniform random sampling of points on the surface of a unit hypersphere. The getEntropies function runs Multi-View Spherical Kmeans Clustering on the data with n_clusters from 1 to 10 once each. This function essentially runs one trial of the experiment.
```
def randSpherical(n_clusters, n_feat1, n_feat2):
c_centers1 = np.random.normal(0, 1, (n_clusters, n_feat1))
c_centers1 /= np.linalg.norm(c_centers1, axis=1).reshape((-1, 1))
c_centers2 = np.random.normal(0, 1, (n_clusters, n_feat2))
c_centers2 /= np.linalg.norm(c_centers2, axis=1).reshape((-1, 1))
return [c_centers1, c_centers2]
def getEntropies():
v1_data, v2_data, labels = get_data()
entropies = list()
for num in range(1,11):
centers = randSpherical(num, v1_data.shape[1], v2_data.shape[1])
kmeans = MultiviewSphericalKMeans(n_clusters=num, init=centers, n_init=1)
pred = kmeans.fit_predict([v1_data, v2_data])
ent = compute_entropy(pred, labels, num, 5)
entropies.append(ent)
print('done')
return entropies
```
### Running multiple trials of the experiment
It was difficult to exactly reproduce the results from the Multi-View Clustering Paper because the experimentors randomly sampled a subset of the 20 newsgroup dataset samples to create the artificial dataset, and this random subset was not reported. Therefore, in an attempt to at least replicate the overall shape of the distribution of cluster entropy over the number of clusters, we resample the dataset and recreate the artificial dataset each trial. Therefore, each trial consists of resampling and recreating the artificial dataset, and then running Multi-view Spherical KMeans clustering on that dataset for n_clusters 1 to 10 once each. We performed 80 such trials and the results of this are shown below.
```
#Do spherical kmeans and get entropy values for each k for multiple trials
n_workers = 10
n_trials = 80
mult_entropies1 = Parallel(n_jobs=n_workers)(
delayed(getEntropies)() for i in range(n_trials))
```
### Experiment Results
We see the results of this experiment below. Here, we have more or less reproduced the shape of the distribution as seen in figure 3 from the Multi-view Clustering Paper.
```
mult_entropies1 = np.array(mult_entropies1)
ave_m_entropies = np.mean(mult_entropies1, axis=0)
std_m_entropies = np.std(mult_entropies1, axis=0)
x_values = list(range(1, 11))
plt.errorbar(x_values, ave_m_entropies, std_m_entropies, capsize=5, color = '#F46C12')
plt.xlabel('k')
plt.ylabel('Entropy')
plt.legend(['2 Views'])
plt.rc('axes', labelsize=12)
plt.show()
```
|
github_jupyter
|
# StellarGraph Ensemble for link prediction
In this example, we use `stellargraph`s `BaggingEnsemble` class of [GraphSAGE](http://snap.stanford.edu/graphsage/) models to predict citation links in the Cora dataset (see below). The `BaggingEnsemble` class brings ensemble learning to `stellargraph`'s graph neural network models, e.g., `GraphSAGE`, quantifying prediction variance and potentially improving prediction accuracy.
The problem is treated as a supervised link prediction problem on a homogeneous citation network with nodes representing papers (with attributes such as binary keyword indicators and categorical subject) and links corresponding to paper-paper citations.
To address this problem, we build a a base `GraphSAGE` model with the following architecture. First we build a two-layer GraphSAGE model that takes labeled `(paper1, paper2)` node pairs corresponding to possible citation links, and outputs a pair of node embeddings for the `paper1` and `paper2` nodes of the pair. These embeddings are then fed into a link classification layer, which first applies a binary operator to those node embeddings (e.g., concatenating them) to construct the embedding of the potential link. Thus obtained link embeddings are passed through the dense link classification layer to obtain link predictions - probability for these candidate links to actually exist in the network. The entire model is trained end-to-end by minimizing the loss function of choice (e.g., binary cross-entropy between predicted link probabilities and true link labels, with true/false citation links having labels 1/0) using stochastic gradient descent (SGD) updates of the model parameters, with minibatches of 'training' links fed into the model.
Finally, using our base model, we create an ensemble with each model in the ensemble trained on a bootstrapped sample of the training data.
**References**
1. Inductive Representation Learning on Large Graphs. W.L. Hamilton, R. Ying, and J. Leskovec arXiv:1706.02216
[cs.SI], 2017.
```
import matplotlib.pyplot as plt
import networkx as nx
import pandas as pd
import numpy as np
from tensorflow import keras
import os
import stellargraph as sg
from stellargraph.data import EdgeSplitter
from stellargraph.mapper import GraphSAGELinkGenerator
from stellargraph.layer import GraphSAGE, link_classification
from stellargraph import BaggingEnsemble
from sklearn import preprocessing, feature_extraction, model_selection
from stellargraph import globalvar
%matplotlib inline
def plot_history(history):
def remove_prefix(text, prefix):
return text[text.startswith(prefix) and len(prefix):]
figsize=(7, 5)
c_train = 'b'
c_test = 'g'
metrics = sorted(set([remove_prefix(m, "val_") for m in list(history[0].history.keys())]))
for m in metrics:
# summarize history for metric m
plt.figure(figsize=figsize)
for h in history:
plt.plot(h.history[m], c=c_train)
plt.plot(h.history['val_' + m], c=c_test)
plt.title(m)
plt.ylabel(m)
plt.xlabel('epoch')
plt.legend(['train', 'validation'], loc='best')
plt.show()
def load_cora(data_dir, largest_cc=False):
g_nx = nx.read_edgelist(path=os.path.expanduser(os.path.join(data_dir, "cora.cites")))
for edge in g_nx.edges(data=True):
edge[2]['label'] = 'cites'
# load the node attribute data
cora_data_location = os.path.expanduser(os.path.join(data_dir, "cora.content"))
node_attr = pd.read_csv(cora_data_location, sep='\t', header=None)
values = { str(row.tolist()[0]): row.tolist()[-1] for _, row in node_attr.iterrows()}
nx.set_node_attributes(g_nx, values, 'subject')
if largest_cc:
# Select the largest connected component. For clarity we ignore isolated
# nodes and subgraphs; having these in the data does not prevent the
# algorithm from running and producing valid results.
g_nx_ccs = (g_nx.subgraph(c).copy() for c in nx.connected_components(g_nx))
g_nx = max(g_nx_ccs, key=len)
print("Largest subgraph statistics: {} nodes, {} edges".format(
g_nx.number_of_nodes(), g_nx.number_of_edges()))
feature_names = ["w_{}".format(ii) for ii in range(1433)]
column_names = feature_names + ["subject"]
node_data = pd.read_csv(os.path.join(data_dir, "cora.content"), sep='\t', header=None, names=column_names)
node_data.index = node_data.index.map(str)
node_data = node_data[node_data.index.isin(list(g_nx.nodes()))]
return g_nx, node_data, feature_names
```
### Loading the CORA network data
**Downloading the CORA dataset:**
The dataset used in this demo can be downloaded from https://linqs-data.soe.ucsc.edu/public/lbc/cora.tgz
The following is the description of the dataset:
> The Cora dataset consists of 2708 scientific publications classified into one of seven classes.
> The citation network consists of 5429 links. Each publication in the dataset is described by a
> 0/1-valued word vector indicating the absence/presence of the corresponding word from the dictionary.
> The dictionary consists of 1433 unique words. The README file in the dataset provides more details.
Download and unzip the cora.tgz file to a location on your computer and set the `data_dir` variable to
point to the location of the dataset (the directory containing "cora.cites" and "cora.content").
```
data_dir = os.path.expanduser("~/data/cora")
```
Load the dataset
```
G, node_data, feature_names = load_cora(data_dir)
```
We need to convert node features that will be used by the model to numeric values that are required for GraphSAGE input. Note that all node features in the Cora dataset, except the categorical "subject" feature, are already numeric, and don't require the conversion.
```
if "subject" in feature_names:
# Convert node features to numeric vectors
feature_encoding = feature_extraction.DictVectorizer(sparse=False)
node_features = feature_encoding.fit_transform(
node_data[feature_names].to_dict("records")
)
else: # node features are already numeric, no further conversion is needed
node_features = node_data[feature_names].values
```
Add node data to G:
```
for nid, f in zip(node_data.index, node_features):
G.nodes[nid][globalvar.TYPE_ATTR_NAME] = "paper" # specify node type
G.nodes[nid]["feature"] = f
```
We aim to train a link prediction model, hence we need to prepare the train and test sets of links and the corresponding graphs with those links removed.
We are going to split our input graph into train and test graphs using the `EdgeSplitter` class in `stellargraph.data`. We will use the train graph for training the model (a binary classifier that, given two nodes, predicts whether a link between these two nodes should exist or not) and the test graph for evaluating the model's performance on hold out data.
Each of these graphs will have the same number of nodes as the input graph, but the number of links will differ (be reduced) as some of the links will be removed during each split and used as the positive samples for training/testing the link prediction classifier.
From the original graph G, extract a randomly sampled subset of test edges (true and false citation links) and the reduced graph G_test with the positive test edges removed:
```
# Define an edge splitter on the original graph G:
edge_splitter_test = EdgeSplitter(G)
# Randomly sample a fraction p=0.1 of all positive links, and same number of negative links, from G, and obtain the
# reduced graph G_test with the sampled links removed:
G_test, edge_ids_test, edge_labels_test = edge_splitter_test.train_test_split(
p=0.1, method="global", keep_connected=True, seed=42
)
```
The reduced graph G_test, together with the test ground truth set of links (edge_ids_test, edge_labels_test), will be used for testing the model.
Now, repeat this procedure to obtain validation data that we are going to use for early stopping in order to prevent overfitting. From the reduced graph G_test, extract a randomly sampled subset of validation edges (true and false citation links) and the reduced graph G_val with the positive validation edges removed.
```
# Define an edge splitter on the reduced graph G_test:
edge_splitter_val = EdgeSplitter(G_test)
# Randomly sample a fraction p=0.1 of all positive links, and same number of negative links, from G_test, and obtain the
# reduced graph G_train with the sampled links removed:
G_val, edge_ids_val, edge_labels_val = edge_splitter_val.train_test_split(
p=0.1, method="global", keep_connected=True, seed=100
)
```
We repeat this procedure one last time in order to obtain the training data for the model.
From the reduced graph G_val, extract a randomly sampled subset of train edges (true and false citation links) and the reduced graph G_train with the positive train edges removed:
```
# Define an edge splitter on the reduced graph G_test:
edge_splitter_train = EdgeSplitter(G_test)
# Randomly sample a fraction p=0.1 of all positive links, and same number of negative links, from G_test, and obtain the
# reduced graph G_train with the sampled links removed:
G_train, edge_ids_train, edge_labels_train = edge_splitter_train.train_test_split(
p=0.1, method="global", keep_connected=True, seed=42
)
```
G_train, together with the train ground truth set of links (edge_ids_train, edge_labels_train), will be used for training the model.
Convert G_train, G_val, and G_test to StellarGraph objects (undirected, as required by GraphSAGE) for ML:
```
G_train = sg.StellarGraph(G_train, node_features="feature")
G_test = sg.StellarGraph(G_test, node_features="feature")
G_val = sg.StellarGraph(G_val, node_features="feature")
```
Summary of G_train and G_test - note that they have the same set of nodes, only differing in their edge sets:
```
print(G_train.info())
print(G_test.info())
print(G_val.info())
```
### Specify global parameters
Here we specify some important parameters that control the type of ensemble model we are going to use. For example, we specify the number of models in the ensemble and the number of predictions per query point per model.
```
n_estimators = 5 # Number of models in the ensemble
n_predictions = 10 # Number of predictions per query point per model
```
Next, we create link generators for sampling and streaming train and test link examples to the model. The link generators essentially "map" pairs of nodes `(paper1, paper2)` to the input of GraphSAGE: they take minibatches of node pairs, sample 2-hop subgraphs with `(paper1, paper2)` head nodes extracted from those pairs, and feed them, together with the corresponding binary labels indicating whether those pairs represent true or false citation links, to the input layer of the GraphSAGE model, for SGD updates of the model parameters.
Specify the minibatch size (number of node pairs per minibatch) and the number of epochs for training the model:
```
batch_size = 20
epochs = 20
```
Specify the sizes of 1- and 2-hop neighbour samples for GraphSAGE. Note that the length of `num_samples` list defines the number of layers/iterations in the GraphSAGE model. In this example, we are defining a 2-layer GraphSAGE model:
```
num_samples = [20, 10]
```
### Create the generators for training
For training we create a generator on the `G_train` graph. The `shuffle=True` argument is given to the `flow` method to improve training.
```
generator = GraphSAGELinkGenerator(G_train, batch_size, num_samples)
train_gen = generator.flow(edge_ids_train,
edge_labels_train,
shuffle=True)
```
At test time we use the `G_test` graph and don't specify the `shuffle` argument (it defaults to `False`).
```
test_gen = GraphSAGELinkGenerator(G_test, batch_size, num_samples).flow(edge_ids_test,
edge_labels_test)
val_gen = GraphSAGELinkGenerator(G_val, batch_size, num_samples).flow(edge_ids_val,
edge_labels_val)
```
### Create the base GraphSAGE model
Build the model: a 2-layer GraphSAGE model acting as node representation learner, with a link classification layer on concatenated `(paper1, paper2)` node embeddings.
GraphSAGE part of the model, with hidden layer sizes of 20 for both GraphSAGE layers, a bias term, and no dropout. (Dropout can be switched on by specifying a positive dropout rate, 0 < dropout < 1)
Note that the length of layer_sizes list must be equal to the length of num_samples, as len(num_samples) defines the number of hops (layers) in the GraphSAGE model.
```
layer_sizes = [20, 20]
assert len(layer_sizes) == len(num_samples)
graphsage = GraphSAGE(
layer_sizes=layer_sizes, generator=generator, bias=True, dropout=0.5
)
# Build the model and expose the input and output tensors.
x_inp, x_out = graphsage.build()
```
Final link classification layer that takes a pair of node embeddings produced by graphsage, applies a binary operator to them to produce the corresponding link embedding ('ip' for inner product; other options for the binary operator can be seen by running a cell with `?link_classification` in it), and passes it through a dense layer:
```
prediction = link_classification(
output_dim=1, output_act="relu", edge_embedding_method='ip'
)(x_out)
```
Stack the GraphSAGE and prediction layers into a Keras model.
```
base_model = keras.Model(inputs=x_inp, outputs=prediction)
```
Now we create the ensemble based on `base_model` we just created.
```
model = BaggingEnsemble(model=base_model, n_estimators=n_estimators, n_predictions=n_predictions)
```
We need to `compile` the model specifying the optimiser, loss function, and metrics to use.
```
model.compile(
optimizer=keras.optimizers.Adam(lr=1e-3),
loss=keras.losses.binary_crossentropy,
weighted_metrics=["acc"],
)
```
Evaluate the initial (untrained) ensemble of models on the train and test set:
```
init_train_metrics_mean, init_train_metrics_std = model.evaluate_generator(train_gen)
init_test_metrics_mean, init_test_metrics_std = model.evaluate_generator(test_gen)
print("\nTrain Set Metrics of the initial (untrained) model:")
for name, m, s in zip(model.metrics_names, init_train_metrics_mean, init_train_metrics_std):
print("\t{}: {:0.4f}±{:0.4f}".format(name, m, s))
print("\nTest Set Metrics of the initial (untrained) model:")
for name, m, s in zip(model.metrics_names, init_test_metrics_mean, init_test_metrics_std):
print("\t{}: {:0.4f}±{:0.4f}".format(name, m, s))
```
### Train the ensemble model
We are going to use **bootstrap samples** of the training dataset to train each model in the ensemble. For this purpose, we need to pass `generator`, `edge_ids_train`, and `edge_labels_train` to the `fit_generator` method.
Note that training time will vary based on computer speed. Set `verbose=1` for reporting of training progress.
```
history = model.fit_generator(
generator=generator,
train_data = edge_ids_train,
train_targets = edge_labels_train,
epochs=epochs,
validation_data=val_gen,
verbose=0,
use_early_stopping=True, # Enable early stopping
early_stopping_monitor="val_weighted_acc",
)
```
Plot the training history:
```
plot_history(history)
```
Evaluate the trained model on test citation links. After training the model, performance should be better than before training (shown above):
```
train_metrics_mean, train_metrics_std = model.evaluate_generator(train_gen)
test_metrics_mean, test_metrics_std = model.evaluate_generator(test_gen)
print("\nTrain Set Metrics of the trained model:")
for name, m, s in zip(model.metrics_names, train_metrics_mean, train_metrics_std):
print("\t{}: {:0.4f}±{:0.4f}".format(name, m, s))
print("\nTest Set Metrics of the trained model:")
for name, m, s in zip(model.metrics_names, test_metrics_mean, test_metrics_std):
print("\t{}: {:0.4f}±{:0.4f}".format(name, m, s))
```
### Make predictions with the model
Now let's get the predictions for all the edges in the test set.
```
test_predictions = model.predict_generator(generator=test_gen)
```
These predictions will be the output of the last layer in the model with `sigmoid` activation.
The array `test_predictions` has dimensionality $MxKxNxF$ where $M$ is the number of estimators in the ensemble (`n_estimators`); $K$ is the number of predictions per query point per estimator (`n_predictions`); $N$ is the number of query points (`len(test_predictions)`); and $F$ is the output dimensionality of the specified layer determined by the shape of the output layer (in this case it is equal to 1 since we are performing binary classification).
```
type(test_predictions), test_predictions.shape
```
For demonstration, we are going to select one of the edges in the test set, and plot the ensemble's predictions for that edge.
Change the value of `selected_query_point` (valid values are in the range of `0` to `len(test_predictions)`) to visualise the results for another test point.
```
selected_query_point = -10
# Select the predictios for the point specified by selected_query_point
qp_predictions = test_predictions[:, :, selected_query_point, :]
# The shape should be n_estimators x n_predictions x size_output_layer
qp_predictions.shape
```
Next, to facilitate plotting the predictions using either a density plot or a box plot, we are going to reshape `qp_predictions` to $R\times F$ where $R$ is equal to $M\times K$ as above and $F$ is the output dimensionality of the output layer.
```
qp_predictions = qp_predictions.reshape(np.product(qp_predictions.shape[0:-1]),
qp_predictions.shape[-1])
qp_predictions.shape
```
The model returns the probability of edge, the class to predict. The probability of no edge is just the complement of the latter. Let's calculate it so that we can plot the distribution of predictions for both outcomes.
```
qp_predictions=np.hstack((qp_predictions, 1.-qp_predictions,))
```
We'd like to assess the ensemble's confidence in its predictions in order to decide if we can trust them or not. Utilising a box plot, we can visually inspect the ensemble's distribution of prediction probabilities for a point in the test set.
If the spread of values for the predicted point class is well separated from those of the other class with little overlap then we can be confident that the prediction is correct.
```
correct_label = "Edge"
if edge_labels_test[selected_query_point] == 0:
correct_label = "No Edge"
fig, ax = plt.subplots(figsize=(12,6))
ax.boxplot(x=qp_predictions)
ax.set_xticklabels(["Edge", "No Edge"])
ax.tick_params(axis='x', rotation=45)
plt.title("Correct label is "+ correct_label)
plt.ylabel("Predicted Probability")
plt.xlabel("Class")
```
For the selected pair of nodes (query point), the ensemble is not certain as to whether an edge between these two nodes should exist. This can be inferred by the large spread of values as indicated in the above figure.
(Note that due to the stochastic nature of training neural network algorithms, the above conclusion may not be valid if you re-run the notebook; however, the general conclusion that the use of ensemble learning can be used to quantify the model's uncertainty about its prediction still holds.)
The below image shows an example of the classifier making a correct prediction with higher confidence than the above example. The results is for the setting `selected_query_point=0`.

|
github_jupyter
|
# `kmeans(data)`
#### `def kmeans_more(data, nk=10, niter=100)`
- `returns 3 items : best_k, vector of corresponding labels for each given sample, centroids for each cluster`
#### `def kmeans(data, nk=10, niter=100)`
- `returns 2 items: best_k, vector of corresponding labels for each given sample`
# Requirements
- where data is an MxN numpy array
- This should return
- an integer K, which should be programmatically identified
- a vector of length M containing the cluster labels
- `nk` is predefined as 10, which is the max number of clusters our program will test. So given a data set, the best k would be less than or equal to nk but greater than 1.
- `niter` is the number of iterations before our algorithm "gives up", if it doesn't converge to a centroid after 100 iterations, it will just use the centroids it has computed the most recently
- `kmeans_more()` is just `kmeans` but also returns the set of centroids. This is useful for visualization or plotting purposes.
```
# x_kmeans returns error per k
# kmeans returns k and data labels
from KMeans import kmeans, kmeans_more, get_angle_between_3points
# A list of four sets of 2d points
from oldsamplesgen import gen_set1
# helper plotting functions visualize what kmeans is doing
from kmeansplottinghelper import initial_plots, colored_plots, eval_plots
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Load 4 data sets of 2d points with clusters [2, 3, 4, 5] respectively
pointset = gen_set1()
# let's get one of them to test for our k means
samples = pointset[3]
# Make sure to shuffle the data, as they sorted by label
np.random.shuffle(samples)
print()
print("(M x N) row = M (number of samples) columns = N (number of features per sample)")
print("Shape of array:", samples.shape)
print()
print("Which means there are", samples.shape[0], "samples and", samples.shape[1], "features per sample")
print()
print("Let's run our kmeans implementation")
#----------------------------------------------
k, labels = kmeans(samples)
#----------------------------------------------
print()
print()
print("Proposed number of clusters:", k)
print("Labels shape:")
print(labels.shape)
print("Print all the labels:")
print(labels)
# The synthetic dataset looks like this
# They look like this
initial_plots(pointset)
# Plot a kmeans implementation given 4 sets of points
def plot_sample_kmeans_more(pointset):
idata, ilabels, icentroids, inclusters = [], [], [], []
for points in pointset:
data = points
np.random.shuffle(data)
nclusters, labels, centroids = kmeans_more(data)
idata.append(data)
ilabels.append(labels)
icentroids.append(centroids)
inclusters.append(nclusters)
colored_plots(idata, ilabels, icentroids, inclusters)
# returns the set the evaluated ks for each set
def test_final_kmeans(pointset):
ks = []
for i, points in enumerate(pointset):
data = pointset[i]
#Make sure to shuffle the data, as they sorted by label
np.random.shuffle(data)
k, _ = kmeans(data)
ks.append(k)
return ks
ks = test_final_kmeans(pointset)
print()
# Should be [2, 3, 4, 5]
print("Proposed k for each set:", ks)
plot_sample_kmeans_more(pointset)
# test if our "compute angle between three points" function is working
a = get_angle_between_3points([1, 2], [1, 1], [2, 1])
b = get_angle_between_3points([1, 1], [2, 1], [3, 1])
assert a, 90.0
assert b, 180.0
```
|
github_jupyter
|
```
%load_ext autoreload
%autoreload
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import math
import sys
sys.path.append("..")
import physics
sys.path.append("../..")
from spec.spectrum import *
import spec.spectools as spectools
import xsecs
class Rates(object):
def __init__(self, E_spec, n, den=[1,1,1], dNdW=np.zeros((2,1)), rates=np.zeros(4)):
self.energy = E_spec.eng[n]
self.n = n
self.dNdE = E_spec.dNdE[n]
self.den = den
self.rates = rates
self.v = np.sqrt(2*np.array([E_spec.eng[n]])/physics.me)*physics.c #units?
self.mult = self.den*self.v
self.dNdW = np.zeros((2, self.n ))
def ion_dNdW_calc_H(self): #uses new integration method
'''Fills *self.dNdW[0,:]* with the discretized singly differential xsec in rate form
'''
eng_temp = E_spec.eng[0:self.n]
ion_s_rates = xsecs.ionize_s_cs_H_2(self.energy, eng_temp) #possible problem with np type
self.dNdW[0] = ion_s_rates *self.mult[0] #dNdE? ;also, [0,:]?
return self.dNdW
def ion_rate_calc(self):
'''Fills *self.rate[1:3]* vector by calculating total xsec and then converting to rate
'''
ion_rates = xsecs.ionize_cs(self.energy*np.ones(3),np.array([1,2,3]))*self.mult
self.rates[1:4] = ion_rates
return self.rates
def heat_rate_calc(self, x_e, rs):
'''Fills *self.rate[0]* vector with fraction going to heating
x_e and rs...
'''
dE = xsecs.heating_dE(self.energy, x_e, rs, nH=physics.nH)
delta_dNdE = np.zeros(len(E_spec.dNdE))
np.put(delta_dNdE, self.n, self.dNdE)
delta = Spectrum(E_spec.eng, delta_dNdE, rs)
shift_delta_eng = E_spec.eng+dE
delta.shift_eng(shift_delta_eng)
delta.rebin(E_spec.eng)
heating_frac = delta.dNdE[self.n]/self.dNdE
self.rates[0] = 1-heating_frac #units?
return(self.rates)
def E_loss(self):
'''loss fraction
'''
E_loss_ion=13.6*self.rates[1]
E_loss_heat=(E_spec.eng[self.n]-E_spec.eng[self.n-1])*self.rates[0]
E_frac = E_loss_ion/E_loss_heat
return(E_frac)
def ion_int_calc(self):
'''gives total ionization rate
'''
bin_width = get_log_bin_width(E_spec.eng[0:self.n])
integ = 0
for i in range(self.n):
integ += self.dNdW[0,i-1]*bin_width[i]*E_spec.eng[i]
return integ
def electron_low_e(E_spec, rs, ion_frac=[0.01,0.01,0.01], den=[1,1,1], dt=1 ,all_outputs=False):
N = len(E_spec.eng)
den[0]=(physics.nH*(1-ion_frac[0]))*(rs)**3 #units?
R = np.zeros((2,N))
R[1,0] = 1
R[1,1] = 1
R[1,2] = 1
for n in range(3,N):
e_rates = Rates(E_spec, n, den)
e_rates.ion_rate_calc()
e_rates.heat_rate_calc(ion_frac[0], rs)
e_rates.ion_dNdW_calc_H()
delta_E_spec = np.ediff1d(E_spec.eng)[0:(n)] #bin widths
discrete_dN_dEdt_i = e_rates.dNdW[0]
h_init=np.zeros(n)
h_init[n-2] = e_rates.rates[0]
h_init[n-1] = 1 - e_rates.rates[0]
discrete_dN_dEdt_h = h_init/delta_E_spec
R_in = ((13.6*e_rates.rates[1]) + np.sum(E_spec.eng[0:n-1]*discrete_dN_dEdt_i[0:n-1]*R[0,0:n-1]*delta_E_spec[0:n-1]) \
+ np.sum(E_spec.eng[0:n-1]*discrete_dN_dEdt_h[0:n-1]*R[0,0:n-1]*delta_E_spec[0:n-1])) \
/(e_rates.energy*(np.sum(discrete_dN_dEdt_i[0:n-1])+np.sum(discrete_dN_dEdt_h[0:n-1])))
R_hn = ((e_rates.energy*e_rates.rates[0]-np.sum(E_spec.eng[0:n-1]*discrete_dN_dEdt_h[0:n-1]*delta_E_spec[0:n-1])) \
+ np.sum(E_spec.eng[0:n-1]*discrete_dN_dEdt_i[0:n-1]*R[1,0:n-1]*delta_E_spec[0:n-1]) \
+ np.sum(E_spec.eng[0:n-1]*discrete_dN_dEdt_h[0:n-1]*R[1,0:n-1]*delta_E_spec[0:n-1])) \
/(e_rates.energy*(np.sum(discrete_dN_dEdt_i[0:n-1])+np.sum(discrete_dN_dEdt_h[0:n-1])))
R[0,n] = R_in/(R_in+R_hn)
R[1,n] = R_hn/(R_in+R_hn)
if n==100 or n == 325 or n == 400:
print('energy')
print(e_rates.energy)
print('rs')
print(rs)
print('ion')
print(13.6*e_rates.rates[1])
print(np.sum(E_spec.eng[0:n-1]*discrete_dN_dEdt_i[0:n-1]*R[0,0:n-1]*delta_E_spec[0:n-1]))
print(np.sum(E_spec.eng[0:n-1]*discrete_dN_dEdt_h[0:n-1]*R[0,0:n-1]*delta_E_spec[0:n-1]))
print('heat')
print(e_rates.energy*e_rates.rates[0]-np.sum(E_spec.eng[0:n-1]*discrete_dN_dEdt_h[0:n-1]*delta_E_spec[0:n-1]))
print(np.sum(E_spec.eng[0:n-1]*discrete_dN_dEdt_i[0:n-1]*R[1,0:n-1]*delta_E_spec[0:n-1]))
print(np.sum(E_spec.eng[0:n-1]*discrete_dN_dEdt_h[0:n-1]*R[1,0:n-1]*delta_E_spec[0:n-1]))
print('denominator')
print((e_rates.energy*(np.sum(discrete_dN_dEdt_i[0:n-1])+np.sum(discrete_dN_dEdt_h[0:n-1]))))
#R[0,n] = R_in
#R[1,n] = R_hn
#print(n, e_rates.energy,R_in,R_hn)
#print(e_rates.energy*e_rates.rates[0], np.sum(E_spec.eng[0:n-1]*discrete_dN_dEdt_h[0:n-1]*delta_E_spec[0:n-1]), np.sum(E_spec.eng[0:n-1]*discrete_dN_dEdt_i[0:n-1]*R[1,0:n-1]*delta_E_spec[0:n-1]),np.sum(E_spec.eng[0:n-1]*discrete_dN_dEdt_h[0:n-1]*R[1,0:n-1]*delta_E_spec[0:n-1]) )
return R
```
<h1>Testing specific spectra:</h1>
```
eng1 = np.logspace(-4.,4.,num = 500)
#dNdE1 = np.logspace(0.,5.,num = 500)
dNdE1 = np.ones(500)
rs=1
E_spec = Spectrum(eng1,dNdE1,rs)
%%capture
results_ion_frac_0 = electron_low_e(E_spec,10**3)
%%capture
results_ion_frac_1 = electron_low_e(E_spec,10**1)
x=np.linspace(10,100,num = 10)
y=np.zeros((10,1))
for k,rs in enumerate(x):
y[k] = electron_low_e(E_spec, rs)[1,400]
print(k)
plt.plot(x,y, 'r')
plt.show()
#heat rate versus redshift
np.set_printoptions(threshold = np.nan)
#print(np.transpose([E_spec.eng, results_ion_frac_0[0,:],results_ion_frac_0[1,:]]))
plt.plot(E_spec.eng, results_ion_frac_0[0,:], 'r') #10**3
plt.plot(E_spec.eng, results_ion_frac_1[0,:], 'r--') #10**1
plt.plot(E_spec.eng, results_ion_frac_0[1,:], 'b')
plt.plot(E_spec.eng, results_ion_frac_1[1,:], 'b--')
plt.xscale('log')
plt.yscale('log')
plt.show()
#%%capture
results_ion_frac_t = electron_low_e(E_spec,1)
plt.plot(E_spec.eng, results_ion_frac_t[0,:], 'r') #10**3
plt.plot(E_spec.eng, results_ion_frac_t[1,:], 'b')
plt.xscale('log')
plt.yscale('log')
plt.show()
```
|
github_jupyter
|
# Applied Process Mining Module
This notebook is part of an Applied Process Mining module. The collection of notebooks is a *living document* and subject to change.
# Lecture 1 - 'Event Logs and Process Visualization' (R / bupaR)
## Setup
<img src="http://bupar.net/images/logo_text.PNG" alt="bupaR" style="width: 200px;"/>
In this notebook, we are going to need the `tidyverse` and the `bupaR` packages.
```
## Perform the commented out commands below in a separate R session
# install.packages("tidyverse")
# install.packages("bupaR")
# for larger and readable plots
options(jupyter.plot_scale=1.25)
# the initial execution of these may give you warnings that you can safely ignore
library(tidyverse)
library(bupaR)
library(processanimateR)
```
## Event Logs
This part introduces event logs and their unique properties that provide the basis for any Process Mining method. Together with `bupaR` several event logs are distributed that can be loaded without further processing.
In this lecture we are going to make use of the following datasets:
* Patients, a synthetically generated example event log in a hospital setting.
* Sepsis, a real-life event log taken from a Dutch hospital. The event log is publicly available here: https://doi.org/10.4121/uuid:915d2bfb-7e84-49ad-a286-dc35f063a460 and has been used in many Process Mining related publications.
### Exploring Event Data
Let us first explore the event data without any prior knowledge about event log structure or properties. We convert the `patients` event log below to a standard `tibble` (https://tibble.tidyverse.org/) and inspect the first rows.
```
patients %>%
as_tibble() %>%
head()
```
The most important ingredient of an event log is the timestamps column `time`. This allows us to establish a sequence of events.
```
patients %>%
filter(time < '2017-01-31') %>%
ggplot(aes(time, "Event")) +
geom_point() +
theme_bw()
patients %>%
as_tibble() %>%
distinct(handling)
patients %>%
as_tibble() %>%
distinct(patient) %>%
head()
patients %>%
as_tibble() %>%
count(patient) %>%
head()
patients %>%
filter(time < '2017-01-31') %>%
ggplot(aes(time, patient, color = handling)) +
geom_point() +
theme_bw()
patients %>%
as_tibble() %>%
arrange(patient, time) %>%
head()
```
### Further resources
* [XES Standard](http://xes-standard.org/)
* [Creating event logs from CSV files in bupaR](http://bupar.net/creating_eventlogs.html)
* [Changing the case, activity notiions in bupaR](http://bupar.net/mapping.html)
### Reflection Questions
* What could be the reason a column `.order` is included in this dataset?
* How could the column `employee` be used?
* What is the use of the column `handling_id` and in which situation is it required?
## Basic Process Visualization
### Set of Traces
```
patients %>%
trace_explorer(coverage = 1.0, .abbreviate = T) # abbreviated here due to poor Jupyter notebook output scaling
```
### Dotted Chart
```
patients %>%
filter(time < '2017-01-31') %>%
dotted_chart(add_end_events = T)
patients %>%
dotted_chart("relative", add_end_events = T)
```
We can also use `plotly` to get an interactive visualization:
```
patients %>%
plotly_dotted_chart("relative", add_end_events = T)
sepsis %>%
dotted_chart("relative_day",
sort = "start_day",
units = "hours")
```
Check out other process visualization options using bupaR:
* [Further Dotted Charts](http://bupar.net/dotted_chart.html)
* [Exploring Time, Resources, Structuredness](http://bupar.net/exploring.html)
## Process Map Visualization
```
patients %>%
precedence_matrix() %>%
plot()
patients %>%
process_map()
patients %>%
process_map(type = performance(units = "hours"))
```
#### Challenge 1
Use some other attribute to be shown in the `patients` dataset.
```
#patients %>%
# process_map(type = custom(...))
patients %>%
animate_process(mode = "relative")
```
#### Challenge 2
Reproduce the example shown on the lecture slides by animating some other attribute from the `traffic_fines` dataset.
```
traffic_fines %>%
head()
traffic_fines %>%
# WARNING: don't animate the full log in Jupyter (at least not on Firefox - it will really slow down your browser the library does not scale well)
bupaR::sample_n(1000) %>%
edeaR::filter_trace_frequency(percentage=0.95) %>%
animate_process(mode = "relative")
# traffic_fines %>%
```
## Real-life Processes
```
sepsis %>%
precedence_matrix() %>%
plot()
```
# Exercises - 1st Hands-on Session
In the first hands-on session, you are going to explore a real-life dataset (see the Assignment notebook) and apply what was presented in the lecture about event logs and basic process mining visualizations. The objective is to explore your dataset and as an event log and with the learned process mining visualizations in mind.
* Analyse basic properties of the the process (business process or other process) that has generated it.
* What are possible case notions / what is the or what are the case identifiers?
* What are the activities? Are all activities on the same abstraction level? Can activities be derived from other data?
* Can activities or actions be derived from other (non-activity) data?
* Discovery a map of the process (or a sub-process) behind it.
* Are there multiple processes that can be discovered?
* What is the effect of taking a subset of the data?
*Hint*: You may use/copy the code from this notebook to have a starting point.
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#@title MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
```
# 回帰:燃費を予測する
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/keras/regression"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/ja/tutorials/keras/regression.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/ja/tutorials/keras/regression.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/ja/tutorials/keras/regression.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
Note: これらのドキュメントは私たちTensorFlowコミュニティが翻訳したものです。コミュニティによる 翻訳は**ベストエフォート**であるため、この翻訳が正確であることや[英語の公式ドキュメント](https://www.tensorflow.org/?hl=en)の 最新の状態を反映したものであることを保証することはできません。 この翻訳の品質を向上させるためのご意見をお持ちの方は、GitHubリポジトリ[tensorflow/docs](https://github.com/tensorflow/docs)にプルリクエストをお送りください。 コミュニティによる翻訳やレビューに参加していただける方は、 [[email protected] メーリングリスト](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-ja)にご連絡ください。
回帰問題では、価格や確率といった連続的な値の出力を予測することが目的となります。これは、分類問題の目的が、(たとえば、写真にリンゴが写っているかオレンジが写っているかといった)離散的なラベルを予測することであるのとは対照的です。
このノートブックでは、古典的な[Auto MPG](https://archive.ics.uci.edu/ml/datasets/auto+mpg)データセットを使用し、1970年代後半から1980年台初めの自動車の燃費を予測するモデルを構築します。この目的のため、モデルにはこの時期の多数の自動車の仕様を読み込ませます。仕様には、気筒数、排気量、馬力、重量などが含まれています。
このサンプルでは`tf.keras` APIを使用しています。詳細は[このガイド](https://www.tensorflow.org/guide/keras)を参照してください。
```
# ペアプロットのためseabornを使用します
!pip install seaborn
import pathlib
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
print(tf.__version__)
```
## Auto MPG データセット
このデータセットは[UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/)から入手可能です。
### データの取得
まず、データセットをダウンロードします。
```
dataset_path = keras.utils.get_file("auto-mpg.data", "https://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")
dataset_path
```
pandasを使ってデータをインポートします。
```
column_names = ['MPG','Cylinders','Displacement','Horsepower','Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(dataset_path, names=column_names,
na_values = "?", comment='\t',
sep=" ", skipinitialspace=True)
dataset = raw_dataset.copy()
dataset.tail()
```
### データのクレンジング
このデータには、いくつか欠損値があります。
```
dataset.isna().sum()
```
この最初のチュートリアルでは簡単化のためこれらの行を削除します。
```
dataset = dataset.dropna()
```
`"Origin"`の列は数値ではなくカテゴリーです。このため、ワンホットエンコーディングを行います。
```
origin = dataset.pop('Origin')
dataset['USA'] = (origin == 1)*1.0
dataset['Europe'] = (origin == 2)*1.0
dataset['Japan'] = (origin == 3)*1.0
dataset.tail()
```
### データを訓練用セットとテスト用セットに分割
データセットを訓練用セットとテスト用セットに分割しましょう。
テスト用データセットは、作成したモデルの最終評価に使用します。
```
train_dataset = dataset.sample(frac=0.8,random_state=0)
test_dataset = dataset.drop(train_dataset.index)
```
### データの観察
訓練用セットのいくつかの列の組み合わせの同時分布を見てみましょう。
```
sns.pairplot(train_dataset[["MPG", "Cylinders", "Displacement", "Weight"]], diag_kind="kde")
```
全体の統計値も見てみましょう。
```
train_stats = train_dataset.describe()
train_stats.pop("MPG")
train_stats = train_stats.transpose()
train_stats
```
### ラベルと特徴量の分離
ラベル、すなわち目的変数を特徴量から切り離しましょう。このラベルは、モデルに予測させたい数量です。
```
train_labels = train_dataset.pop('MPG')
test_labels = test_dataset.pop('MPG')
```
### データの正規化
上の`train_stats`のブロックをもう一度見て、それぞれの特徴量の範囲がどれほど違っているかに注目してください。
スケールや値の範囲が異なる特徴量を正規化するのはよい習慣です。特徴量の正規化なしでもモデルは収束する**かもしれませんが**、モデルの訓練はより難しくなり、結果として得られたモデルも入力で使われる単位に依存することになります。
注:(正規化に使用する)統計量は意図的に訓練用データセットだけを使って算出していますが、これらはテスト用データセットの正規化にも使うことになります。テスト用のデータセットを、モデルの訓練に使用した分布とおなじ分布に射影する必要があるのです。
```
def norm(x):
return (x - train_stats['mean']) / train_stats['std']
normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)
```
この正規化したデータを使ってモデルを訓練することになります。
注意:ここで入力の正規化に使った統計量(平均と標準偏差)は、さきほど実施したワンホットエンコーディングとともに、モデルに供給するほかのどんなデータにも適用する必要があります。テスト用データセットだけでなく、モデルをプロダクション環境で使用する際の生のデータについても同様です。
## モデル
### モデルの構築
それではモデルを構築しましょう。ここでは、2つの全結合の隠れ層と、1つの連続値を返す出力層からなる、`Sequential`モデルを使います。モデルを構築するステップは`build_model`という1つの関数の中に組み込みます。あとから2つ目のモデルを構築するためです。
```
def build_model():
model = keras.Sequential([
layers.Dense(64, activation='relu', input_shape=[len(train_dataset.keys())]),
layers.Dense(64, activation='relu'),
layers.Dense(1)
])
optimizer = tf.keras.optimizers.RMSprop(0.001)
model.compile(loss='mse',
optimizer=optimizer,
metrics=['mae', 'mse'])
return model
model = build_model()
```
### モデルの検証
`.summary`メソッドを使って、モデルの簡単な説明を表示します。
```
model.summary()
```
では、モデルを試してみましょう。訓練用データのうち`10`個のサンプルからなるバッチを取り出し、それを使って`model.predict`メソッドを呼び出します。
```
example_batch = normed_train_data[:10]
example_result = model.predict(example_batch)
example_result
```
うまく動作しているようです。予定どおりの型と形状の出力が得られています。
### モデルの訓練
モデルを1000エポック訓練し、訓練と検証の正解率を`history`オブジェクトに記録します。
```
# エポックが終わるごとにドットを一つ出力することで進捗を表示
class PrintDot(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
if epoch % 100 == 0: print('')
print('.', end='')
EPOCHS = 1000
history = model.fit(
normed_train_data, train_labels,
epochs=EPOCHS, validation_split = 0.2, verbose=0,
callbacks=[PrintDot()])
```
`history`オブジェクトに保存された数値を使ってモデルの訓練の様子を可視化します。
```
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
def plot_history(history):
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Abs Error [MPG]')
plt.plot(hist['epoch'], hist['mae'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mae'],
label = 'Val Error')
plt.ylim([0,5])
plt.legend()
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Square Error [$MPG^2$]')
plt.plot(hist['epoch'], hist['mse'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mse'],
label = 'Val Error')
plt.ylim([0,20])
plt.legend()
plt.show()
plot_history(history)
```
このグラフを見ると、検証エラーは100エポックを過ぎたあたりで改善が見られなくなり、むしろ悪化しているようです。検証スコアの改善が見られなくなったら自動的に訓練を停止するように、`model.fit`メソッド呼び出しを変更します。ここでは、エポック毎に訓練状態をチェックする*EarlyStopping*コールバックを使用します。設定したエポック数の間に改善が見られない場合、訓練を自動的に停止します。
このコールバックについての詳細は[ここ](https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/EarlyStopping)を参照ください。
```
model = build_model()
# patience は改善が見られるかを監視するエポック数を表すパラメーター
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
history = model.fit(normed_train_data, train_labels, epochs=EPOCHS,
validation_split = 0.2, verbose=0, callbacks=[early_stop, PrintDot()])
plot_history(history)
```
検証用データセットでのグラフを見ると、平均誤差は+/- 2 MPG(マイル/ガロン)前後です。これはよい精度でしょうか?その判断はおまかせします。
モデルの訓練に使用していない**テスト用**データセットを使って、モデルがどれくらい汎化できているか見てみましょう。これによって、モデルが実際の現場でどれくらい正確に予測できるかがわかります。
```
loss, mae, mse = model.evaluate(normed_test_data, test_labels, verbose=2)
print("Testing set Mean Abs Error: {:5.2f} MPG".format(mae))
```
### モデルを使った予測
最後に、テストデータを使ってMPG値を予測します。
```
test_predictions = model.predict(normed_test_data).flatten()
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
plt.axis('equal')
plt.axis('square')
plt.xlim([0,plt.xlim()[1]])
plt.ylim([0,plt.ylim()[1]])
_ = plt.plot([-100, 100], [-100, 100])
```
そこそこよい予測ができているように見えます。誤差の分布を見てみましょう。
```
error = test_predictions - test_labels
plt.hist(error, bins = 25)
plt.xlabel("Prediction Error [MPG]")
_ = plt.ylabel("Count")
```
とても正規分布には見えませんが、サンプル数が非常に小さいからだと考えられます。
## 結論
このノートブックでは、回帰問題を扱うためのテクニックをいくつか紹介しました。
* 平均二乗誤差(MSE: Mean Squared Error)は回帰問題に使われる一般的な損失関数です(分類問題には異なる損失関数が使われます)。
* 同様に、回帰問題に使われる評価指標も分類問題とは異なります。回帰問題の一般的な評価指標は平均絶対誤差(MAE: Mean Absolute Error)です。
* 入力数値特徴量の範囲が異なっている場合、特徴量ごとにおなじ範囲に正規化するべきです。
* 訓練用データが多くない場合、過学習を避けるために少ない隠れ層をもつ小さいネットワークを使うというのがよい方策の1つです。
* Early Stoppingは過学習を防止するための便利な手法の一つです。
|
github_jupyter
|
# Eaton method with well log
Pore pressure prediction with Eaton's method using well log data.
Steps:
1. Calculate Velocity Normal Compaction Trend
2. Optimize for Eaton's exponent n
3. Predict pore pressure using Eaton's method
```
import warnings
warnings.filterwarnings(action='ignore')
# for python 2 and 3 compatibility
# from builtins import str
# try:
# from pathlib import Path
# except:
# from pathlib2 import Path
#--------------------------------------------
import sys
ppath = "../.."
if ppath not in sys.path:
sys.path.append(ppath)
#--------------------------------------------
from __future__ import print_function, division, unicode_literals
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use(['seaborn-paper', 'seaborn-whitegrid'])
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
import numpy as np
import pygeopressure as ppp
```
## 1. Calculate Velocity Normal Compaction Trend
Create survey with the example survey `CUG`:
```
# set to the directory on your computer
SURVEY_FOLDER = "C:/Users/yuhao/Desktop/CUG_depth"
survey = ppp.Survey(SURVEY_FOLDER)
```
Retrieve well `CUG1`:
```
well_cug1 = survey.wells['CUG1']
```
Get velocity log:
```
vel_log = well_cug1.get_log("Velocity")
```
View velocity log:
```
fig_vel, ax_vel = plt.subplots()
ax_vel.invert_yaxis()
vel_log.plot(ax_vel)
well_cug1.plot_horizons(ax_vel)
# set fig style
ax_vel.set(ylim=(5000,0), aspect=(5000/4600)*2)
ax_vel.set_aspect(2)
fig_vel.set_figheight(8)
```
Optimize for NCT coefficients a, b:
`well.params['horizon']['T20']` returns the depth of horizon T20.
```
a, b = ppp.optimize_nct(
vel_log=well_cug1.get_log("Velocity"),
fit_start=well_cug1.params['horizon']["T16"],
fit_stop=well_cug1.params['horizon']["T20"])
```
And use a, b to calculate normal velocity trend
```
from pygeopressure.velocity.extrapolate import normal_log
nct_log = normal_log(vel_log, a=a, b=b)
```
View fitted NCT:
```
fig_vel, ax_vel = plt.subplots()
ax_vel.invert_yaxis()
# plot velocity
vel_log.plot(ax_vel, label='Velocity')
# plot horizon
well_cug1.plot_horizons(ax_vel)
# plot fitted nct
nct_log.plot(ax_vel, color='r', zorder=2, label='NCT')
# set fig style
ax_vel.set(ylim=(5000,0), aspect=(5000/4600)*2)
ax_vel.set_aspect(2)
ax_vel.legend()
fig_vel.set_figheight(8)
```
Save fitted nct:
```
# well_cug1.params['nct'] = {"a": a, "b": b}
# well_cug1.save_params()
```
## 2. Optimize for Eaton's exponent n
First, we need to preprocess velocity.
Velocity log processing (filtering and smoothing):
```
vel_log_filter = ppp.upscale_log(vel_log, freq=20)
vel_log_filter_smooth = ppp.smooth_log(vel_log_filter, window=1501)
```
Veiw processed velocity:
```
fig_vel, ax_vel = plt.subplots()
ax_vel.invert_yaxis()
# plot velocity
vel_log.plot(ax_vel, label='Velocity')
# plot horizon
well_cug1.plot_horizons(ax_vel)
# plot processed velocity
vel_log_filter_smooth.plot(ax_vel, color='g', zorder=2, label='Processed', linewidth=1)
# set fig style
ax_vel.set(ylim=(5000,0), aspect=(5000/4600)*2)
ax_vel.set_aspect(2)
ax_vel.legend()
fig_vel.set_figheight(8)
```
We will use the processed velocity data for pressure prediction.
Optimize Eaton's exponential `n`:
```
n = ppp.optimize_eaton(
well=well_cug1,
vel_log=vel_log_filter_smooth,
obp_log="Overburden_Pressure",
a=a, b=b)
```
See the RMS error variation with `n`:
```
from pygeopressure.basic.plots import plot_eaton_error
fig_err, ax_err = plt.subplots()
plot_eaton_error(
ax=ax_err,
well=well_cug1,
vel_log=vel_log_filter_smooth,
obp_log="Overburden_Pressure",
a=a, b=b)
```
Save optimized n:
```
# well_cug1.params['nct'] = {"a": a, "b": b}
# well_cug1.save_params()
```
## 3.Predict pore pressure using Eaton's method
Calculate pore pressure using Eaton's method requires velocity, Eaton's exponential, normal velocity, hydrostatic pressure and overburden pressure.
`Well.eaton()` will try to read saved data, users only need to specify them when they are different from the saved ones.
```
pres_eaton_log = well_cug1.eaton(vel_log_filter_smooth, n=n)
```
View predicted pressure:
```
fig_pres, ax_pres = plt.subplots()
ax_pres.invert_yaxis()
well_cug1.get_log("Overburden_Pressure").plot(ax_pres, 'g', label='Lithostatic')
ax_pres.plot(well_cug1.hydrostatic, well_cug1.depth, 'g', linestyle='--', label="Hydrostatic")
pres_eaton_log.plot(ax_pres, color='blue', label='Pressure_Eaton')
well_cug1.plot_horizons(ax_pres)
# set figure and axis size
ax_pres.set_aspect(2/50)
ax_pres.legend()
fig_pres.set_figheight(8)
```
|
github_jupyter
|
### Details on the hardware used to gather the performance data
```
import pandas as pd
from collections import OrderedDict as odict
#name, cache-size (in kB)
hardware = odict({})
hardware['i5'] = ('Intel Core i5-6600 @ 3.30GHz (2x 8GB DDR4, 4 cores)',6144,
'1 MPI task x 4 OpenMP threads (1 per core)')
hardware['skl'] = ('2x Intel Xeon 8160 (Skylake) at 2.10 GHz (12x 16GB DDR4, 2x 24 cores)',2*33000,
'2 MPI tasks (1 per socket) x 24 OpenMP threads (1 per core)')
hardware['knl'] = ('Intel Xeon Phi 7250 (Knights Landing) at 1.40 GHz (16GB MCDRAM, 68 cores)',34000,
'1 MPI task x 136 OpenMP hyperthreads (2 per core)')
hardware['gtx1060'] = ('Nvidia GeForce GTX 1060 (6GB global memory)',1572.864, '1 MPI task per GPU')
hardware['p100'] = ('Nvidia Tesla P100-PCIe (16GB global memory)',4194.304, '1 MPI task per GPU')
hardware['v100'] = ('Nvidia Tesla V100-PCIe (16GB global memory)',6291.456, '1 MPI task per GPU')
hardware['p100nv'] = ('Nvidia Tesla P100-Power8 (16GB global memory)',4194.304, '1 MPI task per GPU')
hardware['v100nv'] = ('Nvidia Tesla V100-Power9 (16GB global memory)',6291.456, '1 MPI task per GPU')
memory =odict({}) #find with 'dmidecode --type 17'
#name, I/O bus clockrate (MHz) , buswidth (bit), size (MB),
memory['i5'] = ('2x 8GB Kingston DDR4', 1066, 2*64, 2*8192) #ECC: no (actually it is DDR4-2400 but i5 has max DDR4-2133)
memory['skl'] = ('12x 16GB DDR4',1333,12*64,12*16000) #ECC: ?
memory['knl'] = ('MCDRAM',None,None,16000) #ECC: ?
memory['gtx1060'] = ('on-card global memory',4004,192,6069) #ECC: no
memory['p100'] = ('on-card global memory',715,4096,16276) # ECC: yes
memory['v100'] = ('on-card global memory',877,4096,16152) # ECC: yes
compiler=odict({})
compiler['i5'] = ('mpic++ (gcc-5.4) -mavx -mfma -O3 -fopenmp')
compiler['skl'] = ('mpiicc-17.0.4 -mt_mpi -xCORE-AVX512 -mtune=skylake -O3 -restrict -fp-model precise -fimf-arch-consistency=true -qopenmp')
compiler['knl'] = ('mpiicc-17.0.4 -mt_mpi -xMIC-AVX512 -O3 -restrict -fp-model precise -fimf-arch-consistency=true -qopenmp')
compiler['gtx1060'] = ('nvcc-7.0 --compiler-bindir mpic++ (gcc-5.4) -O3 -arch sm_35')
compiler['p100'] = ('nvcc-8.0 --compiler-bindir mpic++ (gcc-5.4) -O3 -arch sm_60 -Xcompiler "-O3 -mavx -mfma"')
compiler['v100'] = ('nvcc-8.0 --compiler-bindir mpic++ (gcc-5.4) -O3 -arch sm_60 -Xcompiler "-O3 -mavx -mfma"')
df = pd.DataFrame(hardware)
df = df.transpose()
df.columns= ['device-name', 'cache-size-kB','single-node configuration']
com = pd.DataFrame(compiler, index=['compiler flags'])
com = com.transpose()
com
df = df.join(com)
mem = pd.DataFrame(memory)
mem = mem.transpose()
mem.columns = ['mem-description', 'clockrate-MHz', 'buswidth-bit', 'size-MB']
df=df.join(mem)
#df
```
From the available data we can compute the theoretical memory bandwidth via $$bw = 2*clockrate*buswidth$$ where the '2' is for double data rate (DDR)
```
df['bandwidth'] = 2*df['clockrate-MHz']*1e6*df['buswidth-bit']/8/1e9
#df
```
Let us compare the theoretical bandwidth with our previously measured peak bandwidth from axpby
```
exp = pd.read_csv('performance.csv',delimiter=' ')
exp.set_index('arch',inplace=True)
exp.index.name = None
df = df.join(exp['axpby_bw'])
df['mem_efficiency']=df['axpby_bw']/df['bandwidth']*100
pd.set_option('display.float_format', lambda x: '%.2f' % x)
df
```
Let us write a summarized LateX table to be used for publication
```
pd.set_option('precision',3)
file = df.loc[:,['device-name','single-node configuration']]#,'bandwidth']]
#file.loc['knl','bandwidth'] = '>400'
file.columns = ['device description', 'single-node configuration']#, 'bandwidth [GB/s]']
filename='hardware.tex'
df.loc['knl','bandwidth'] = '$>$400'
pd.set_option('display.max_colwidth', 200)
with open(filename, 'wb') as f:
f.write(bytes(file.to_latex(
column_format='@{}lp{6.5cm}p{5cm}@{}',
bold_rows=True),'UTF-8'))
file
```
|
github_jupyter
|
## setup and notebook configuration
```
# scientific python stack
import numpy as np
import scipy as sp
import sympy as sym
import orthopy, quadpy
# matplotlib, plotting setup
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.tri as mtri # delaunay triangulation
from mpl_toolkits.mplot3d import Axes3D # surface plotting
import seaborn as sns # nice plotting defaults
import cmocean as cmo # ocean colormaps
sym.init_printing(use_latex='mathjax')
sns.set()
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
%load_ext autoreload
%autoreload 2
# local imports
import src.fem_base.master.mk_basis_nodal as mbn
import src.fem_base.master.mk_master as mkm
import src.fem_maps.fem_map as fem_map
```
# creation of 1D nodal bases
We define the master 1D element as $I\in[-1, 1]$
```
b = mbn.Basis_nodal(order=1, dim=1, element=0)
b.plot_elm()
fig, ax = plt.subplots(1, 5, figsize = (10, 1))
xx = np.linspace(-1, 1, 100)
pts = [[x, 0, 0] for x in xx]
for order in range(5):
b = mbn.Basis_nodal(order=order, dim=1, element=0)
yy = b.eval_at_pts(pts=pts)
for basis_fn in range(b.nb):
ax[order].plot(xx, yy[:, basis_fn])
ax[order].set_title(r'$p = {}$'.format(order))
```
## construction of vandermonde matrices
```
x = np.linspace(-1, 1, 100)
n_polys = 4
vals = orthopy.line_segment.tree_jacobi(x, n=n_polys, alpha=0, beta=0, standardization='normal')
for i in range(n_polys):
plt.plot(x, vals[i], label='P_{}'.format(i))
plt.legend()
plt.title('normalized Legendre polynomials')
plt.show()
```
These polynomials agree with the explicitly listed polynomials in Hesthaven, so we know that they are orthonormalized correctly.
```
def Jacobi_Poly(r, alpha, beta, N):
""" wraps orthopy to return Jacobi polynomial """
return orthopy.line_segment.tree_jacobi(r, n=N-1, alpha=alpha, beta=beta, standardization='normal')
def P_tilde(r, N):
P = np.zeros((len(r), N))
polyvals = Jacobi_Poly(r, alpha=0, beta=0, N=N)
for j in range(N):
P[:, j] = polyvals[j]
return P.T
def Vandermonde1D(N, x):
""" initialize 1D vandermonde Matrix Vij = phi_j(x_i)"""
V1D = np.zeros((len(x), N))
JacobiP = Jacobi_Poly(x, alpha=0, beta=0, N=N)
for j, polyvals in enumerate(JacobiP):
V1D[:, j] = polyvals
return V1D
def LegendreGaussLobatto(N):
GL = quadpy.line_segment.GaussLobatto(N, a=0., b=0.)
return GL.points, GL.weights
def GaussLegendre(N):
GL = quadpy.line_segment.GaussLegendre(N)
return GL.points, GL.weights
```
An important conceptual point is that the Vandermonde matrix here is NOT the shape function matrix, it's the Vandermonde matrix of the Orthonormal polynomial basis. We will see this later as we have to create the shape function matrices.
## properties / conditioning of vandermonde matrices
```
equi_det, LGL_det = [], []
for N in range(2, 35):
nb = N + 1
equi_pts = np.linspace(-1, 1, nb)
V = Vandermonde1D(nb, equi_pts)
equi_det.append(np.linalg.det(V))
LGL_pts, _ = LegendreGaussLobatto(nb)
V = Vandermonde1D(nb, LGL_pts)
LGL_det.append(np.linalg.det(V))
plt.semilogy(list(range(2, 35)), equi_det, label='equidistant')
plt.semilogy(list(range(2, 35)), LGL_det, label='LGL nodes')
plt.legend()
plt.show()
```
This result agrees with Hesthaven.
```
# construct generic lagrange interpolant
from scipy.interpolate import lagrange
def lagrange_polys(pts):
lagrange_polys = []
for i, pt in enumerate(pts):
data = np.zeros_like(pts)
data[i] = 1
lagrange_polys.append(lagrange(pts, data))
return lagrange_polys
def lagrange_basis_at_pts(lagrange_polys, eval_pts):
""" evaluates lagrange polynomials at eval_pts"""
result = np.zeros((len(lagrange_polys) ,len(eval_pts)))
for i, poly in enumerate(lagrange_polys):
result[i, :] = lagrange_polys[i](eval_pts)
return result
```
plot lagrange polys over equally spaced vs LGL points
```
N = 5
lp = np.linspace(-1, 1, N)
lpolys = lagrange_polys(lp)
vN = 100
view_pts = np.linspace(-1, 1, vN)
li = lagrange_basis_at_pts(lpolys, view_pts)
plt.plot(view_pts, li.T)
plt.title('lagrange polynomials over equally spaced points')
plt.show()
N = 5
lp, _ = LegendreGaussLobatto(N)
lpolys = lagrange_polys(lp)
vN = 100
view_pts = np.linspace(-1, 1, vN)
li = lagrange_basis_at_pts(lpolys, view_pts)
plt.plot(view_pts, li.T)
plt.title('lagrange polynomials over LGL points')
plt.show()
```
So beautiful! By moving the lagrange data points to the nodal points, our basis functions don't exceed 1, unlike in the above plot, where we are already seeing a slight Runge phenomenon.
## vandermonde relations
### relationship between vandermonde $V$, basis polynomials $\tilde{\mathbf{P}}$, and lagrange basis functions (shape functions) $\ell$
Hesthaven makes the claim that $V^T \mathbf{\ell}(r) = \tilde{\mathbf{P}}(r)$ in (3.3).
In Hesthaven's notation, $N$ denotes the polynomial order, $N_p$ denotes the number of nodal points (we would call $nb$), and let's call the number of "view points" `xx`, which are arbitrary.
Then the shapes of the Hesthaven structures are:
- $\mathbf{\ell}$, $\tilde{\mathbf{P}}$, $V$ are all (`nb`, `xx`)
- $V^T \ell$ is (`xx`, `nb`) x (`nb`, `xx`) $\rightarrow$ (`xx`, `xx`) where rows contain the values of polynomials $\tilde{\mathbf{P}}$
This works for either equidistant points or the LGL points.
```
N = 5
lp, _ = LegendreGaussLobatto(N)
#lp = np.linspace(-1, 1, N)
view_pts = np.linspace(-1, 1, 50)
l_polys = lagrange_polys(pts=lp)
ℓ = lagrange_basis_at_pts(l_polys, eval_pts=view_pts)
V = Vandermonde1D(N=len(view_pts), x=lp)
P = np.dot(V.T, ℓ)
# plot the result
plt.plot(view_pts, ℓ.T, '--')
plt.plot(view_pts, P[0:3,:].T)
plt.show()
```
We see that indeed we recover the Legendre polynomials.
More directly, we can invert the relation to find that
$$\ell = (V^T)^{-1} \tilde{\mathbf{P}}$$
which allows us to create our nodal shape functions.
```
nb = 4
nodal_pts, _ = LegendreGaussLobatto(nb)
view_pts = np.linspace(-1, 1, 50)
# create the Vandermonde, P matrices
V = Vandermonde1D(N=nb, x=nodal_pts)
Vti = np.linalg.inv(V.T)
P = P_tilde(r=view_pts, N=nb)
print('shape of Vandermonde: {}'.format(V.shape))
print('shape of P: {}'.format(P.shape))
yy = np.dot(Vti, P)
plt.plot(view_pts, yy.T)
plt.title('nodal shape functions generated from orthogonal basis polynomials')
plt.show()
```
### relationship between vandermonde $V$ and mass matrix
We can build on the relationship developed in the section above to form the mass matrix for a nodal basis. We note that
$M_{ij} = \int_{-1}^{1}\ell_i(r)\, \ell_j(r) \,dr = (\ell_i, \ell_j)_I$, and if we expand out $\ell = (V^T)^{-1}\tilde{\mathbf{P}}$, it turns out (page 51)
$$M = (V V^T)^{-1}$$
because of the orthogonal nature of our choice of basis function; the implication is that we can compute the integrals over the master element without the explicit need for quadrature points or weights. Note first that $\phi_i(\xi) = \sum_{n=1}^{nb} (V^T)_{in}^{-1} \tilde{P}_{n-1}(\xi)$. Then
\begin{align}
M_{ij} &= \int^{1}_{-1} \phi_i(\xi)\,\phi_j(\xi)\,d\xi
= \int^{1}_{-1}\left[\sum_{k=1}^{nb} (V^T)_{ik}^{-1} \tilde{P}_{k-1}(\xi)
\sum_{m=1}^{nb} (V^T)_{jm}^{-1} \tilde{P}_{m-1}(\xi) \right]\, d\xi \\
&= \sum_{k=1}^{nb} \sum_{m=1}^{nb} (V^T)_{ik}^{-1}
(V^T)_{jm}^{-1} \int^{1}_{-1}\tilde{P}_{k-1}(\xi) \tilde{P}_{m-1}(\xi)
=\sum_{k=1}^{nb} \sum_{m=1}^{nb} (V^T)_{ik}^{-1}
(V^T)_{jm}^{-1} \delta_{km} \\
&=\sum_{k=1}^{nb} (V^T)_{im}^{-1}
(V^T)_{jm}^{-1} = \sum_{k=1}^{nb} (V^T)_{mi}^{-1} (V)_{mj}^{-1} \\
&= (V^{T})^{-1} V^{-1} = (VV^T)^{-1}
\end{align}
Where note we've used the cute trick that $\int_{-1}^1 \tilde{P}_m \tilde{P}_n = \delta_{mn}$, since we chose an __orthonormal__ modal basis. Orthogonal wouldn't have done it, but an orthonormal modal basis has this property.
We can check this relation against the more traditional way of constructing the mass matrix with quadrature. `master.shap` has dimensions of (`n_quad`, `nb`)
```
order = 3
m1d = mkm.Master_nodal(order=order, dim=1, element=0)
xq, wq = m1d.cube_pts, m1d.cube_wghts
shap = m1d.shap
shapw = np.dot(np.diag(wq), m1d.shap)
M_quadrature = np.dot(shap.T, shapw)
Np = order + 1
nodal_points, _ = LegendreGaussLobatto(Np)
V = Vandermonde1D(N=Np, x=nodal_points)
M_vand = np.linalg.inv(np.dot(V, V.T))
# this will throw an error if not correct
assert(np.allclose(M_quadrature, M_vand))
```
## efficient computation of derivatives of the basis functions
### derivatives of Legendre polynomials
In order to compute the derivatives of the shape functions (which are expressed via the vandermonde matrix $V$), we must take the derivatives with respect to the orthogonal basis polynomials. There is an identity (Hesthaven, p. 52)
$$ \frac{d \tilde{P}_n}{d r} = \sqrt{n(n+1)}\,\tilde{P}^{(1,1)}_{n-1}$$
This is in contrast to directly differentiating either the coefficients of $\tilde{P}$ or more directly the nodal shape functions $\ell$ if the explicit polynomial form is known (like in `scipy`, but this becomes trickier in multiple dimensions). As it turns out, the first approach is a very efficient way to compute these operators.
```
def Jacobi_Poly_Derivative(r, alpha, beta, N):
""" take a derivative of Jacobi Poly, more general than above
copy the format of orthopy (list of arrays)
"""
dp = [np.zeros_like(r)]
Jacobi_P = Jacobi_Poly(r, alpha + 1, beta + 1, N)
for n in range(1, N+1):
gamma = np.sqrt(n * (n + alpha + beta + 1))
dp.append(gamma * Jacobi_P[n-1])
return dp
#def dP_tilde(r, N):
# P = np.zeros((len(r), N))
# polyvals = Jacobi_Poly_Derivative(r, alpha=0, beta=0, N=N)
# for j in range(N):
# P[:, j] = polyvals[j]
# return P
```
We can examine some of the derivatives of the Legendre polynomials.
```
# some unit testing
# first jacobi poly is const, so der should be 0
xx = np.linspace(-1, 1, 50)
jpd = Jacobi_Poly_Derivative(xx, alpha=0, beta=0, N=3)
for i, polyder in enumerate(jpd):
plt.plot(xx, polyder, label=r'$P_{}^\prime(x)$'.format(i))
plt.legend()
plt.show()
```
These look good. The derivative of the first Legendre polynomial is analytically 0, $P_1^\prime = \sqrt{3/2}$, $P_2^\prime$ should be linear, $P_3^\prime$ should be quadratic.
### discrete derivative operators
We can declare the derivative Vandermonde matrix, and invert it in the same manner to obtain the derivatives of the nodal shape functions.
This works because
$$V^T \ell = P \Rightarrow V^T \frac{d}{dx} \ell = \frac{d}{dx}P$$
Hence $$V_r\equiv V^T D_r^T, \qquad {V_r}_{(ij)} = \frac{d \tilde{P}_j(r_i)}{d x} $$
and finally $D_r = V_r V^{-1}$ (see Hesthaven, p. 53), as well as $S = M D_r $, where $S_{ij} = \left(\phi_i, \frac{d\phi_j}{dx}\right)_I$, and where $M$ is the mass matrix.
```
def GradVandermonde1D(N, x):
Vr = np.zeros((len(x), N))
dJacobi_P = Jacobi_Poly_Derivative(x, alpha=0, beta=0, N=N-1)
for j, polyder in enumerate(dJacobi_P):
Vr[:,j] = polyder
return Vr
p = 3
nb = p+1
nodal_pts, _ = LegendreGaussLobatto(nb)
#nodal_pts = np.linspace(-1, 1, nb)
view_pts = np.linspace(-1, 1, 50)
# grad vandermonde
V = Vandermonde1D(N=nb, x=nodal_pts)
Vr = GradVandermonde1D(N=nb, x=view_pts)
Vi = np.linalg.inv(V)
Dr = np.dot(Vr, Vi)
print('shape Vr: {}'.format(Vr.shape))
print('shape V inv: {}'.format(Vi.shape))
print('shape Dr: {}'.format(Dr.shape))
# shape functions
V = Vandermonde1D(N=nb, x=nodal_pts)
Vti = np.linalg.inv(V.T)
P = P_tilde(r=view_pts, N=nb)
shap = np.dot(Vti, P)
# shape functions at view points
fig, ax = plt.subplots(1, 2, figsize=(8, 4))
ax[0].plot(view_pts, shap.T, '--')
ax[0].set_title(r'nodal shape functions $\phi$')
ax[1].plot(view_pts, Dr)
ax[1].set_title(r'derivatives of nodal shape functions $\frac{d \phi}{dx}$')
plt.show()
```
As a remark, we can once again show the effect of using Legendre Gauss Lobatto points vs equally spaced nodal points.
```
N = 8
nb = N+1
nodal_pts_LGL, _ = LegendreGaussLobatto(nb)
nodal_pts_equi = np.linspace(-1, 1, nb)
view_pts = np.linspace(-1, 1, 100)
# shape functions at view points
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_yticks([])
ax.set_xticks([])
labels = ['LGL nodes', 'uniform nodes']
for idx, nodal_pts in enumerate([nodal_pts_LGL, nodal_pts_equi]):
# grad vandermonde
V = Vandermonde1D(N=nb, x=nodal_pts)
Vr = GradVandermonde1D(N=nb, x=view_pts)
Vi = np.linalg.inv(V)
Dr = np.dot(Vr, Vi)
# shape functions
V = Vandermonde1D(N=nb, x=nodal_pts)
Vti = np.linalg.inv(V.T)
P = P_tilde(r=view_pts, N=nb)
shap = np.dot(Vti, P)
# plot
ax = fig.add_subplot(2, 2, idx*2+1)
ax.plot(view_pts, shap.T)
ax.set_yticks([0, 1])
ax.set_title(r' $\phi$, {}'.format(labels[idx]))
ax = fig.add_subplot(2, 2, idx*2+2)
ax.plot(view_pts, Dr)
ax.set_title(r'$\f{}$, {}'.format('rac{d \phi}{dx}',labels[idx]))
plt.subplots_adjust(wspace=0.2, hspace=0.2)
fig.suptitle(r'$\phi$ and $\frac{d\phi}{d x}$, LGL vs uniformly-spaced nodes')
plt.show()
```
### remarks on discrete derivative operators
Suppose we compute the derivative matrix $D_r$ at the nodal points for some order $p$. There are some interesting properties to understand about these derivative matrices.
#### annihilation of constant vectors
Note that if we represent a function nodally, i.e., $u = c_i \phi_i(x)$, then
$$ \frac{du}{dx} = \frac{d}{dx}(c_i \phi_i(x)) = c_i \frac{d\phi_i}{dx} $$
Therefore, if we want to discretely take a derivative of a function (we'll represent the function on the master element for now, but trivially, we could map it to some other region), it suffices to multiply the derivative operator with the nodal vector $D_r u$. It should be clear, then, that $D_r$ will annihilate any constant vector.
```
p = 2
nb = p+1
nodal_pts, _ = LegendreGaussLobatto(nb)
u = np.ones_like(nodal_pts)
# grad vandermonde
V = Vandermonde1D(N=nb, x=nodal_pts)
Vr = GradVandermonde1D(N=nb, x=nodal_pts)
Vi = np.linalg.inv(V)
Dr = np.dot(Vr, Vi)
duh = np.dot(Dr, u)
print(np.max(np.abs(duh)))
```
#### exponential convergence in $p$ for smooth functions
If the function of which we are attempting to take the discrete derivative is smooth (in the sense of infinitely differentiable), then we will see exponential convergence to the analytical solution w/r/t polynomial order of the nodal basis.
```
ps = [1, 2, 3, 4, 8, 12, 16, 18, 24, 32]
errs = []
fig, ax = plt.subplots(1, 3, figsize=(8, 3))
for p in ps:
nb = p+1
nodal_pts, _ = LegendreGaussLobatto(nb)
view_pts = np.linspace(-1, 1, 100)
# grad vandermonde
V = Vandermonde1D(N=nb, x=nodal_pts)
Vr = GradVandermonde1D(N=nb, x=nodal_pts)
Vi = np.linalg.inv(V)
Dr = np.dot(Vr, Vi)
# nodal shap
V = Vandermonde1D(N=nb, x=nodal_pts)
Vti = np.linalg.inv(V.T)
P = P_tilde(r=view_pts, N=nb)
view_shap = np.dot(Vti, P)
u = np.sin(nodal_pts-np.pi/4.)
du = np.cos(view_pts-np.pi/4)
duh = np.dot(Dr, u)
view_duh = np.dot(duh, view_shap)
err = np.max(np.abs(view_duh - du))
errs.append(err)
# plot first few
if p < 4:
ax[p-1].plot(view_pts, np.sin(view_pts), label=r'$u$')
ax[p-1].plot(view_pts, du, label=r'$u^\prime$')
ax[p-1].plot(view_pts, view_duh, '--', label=r'$du_h$')
ax[p-1].set_title(r'$p={}$'.format(p))
ax[p-1].legend()
plt.show()
fig, ax = plt.subplots()
ax.semilogy(ps, errs)
ax.set_xticks(ps)
ax.set_ylabel(r'$||du - du_h||_{L_\infty}$')
ax.set_xlabel('polynomial order p')
ax.set_title('exponential convergence of discrete derivative')
plt.show()
```
# creation of a 1D master element
Define a simple nodal basis object for 1D problems -- no need to be fancy, pretty much the only thing we need this for is to get nodal shape functions and their derivatives efficiently. The underlying orthonormal Legendre polynomial basis is hidden to the user.
```
class NodalBasis1D(object):
""" minimalist nodal basis object:
efficiently computes shape functions and their derivatives
"""
def __init__(self, p, node_spacing='GAUSS_LOBATTO'):
self.nb = p + 1
if node_spacing == 'GAUSS_LOBATTO':
self.nodal_pts, _ = LegendreGaussLobatto(self.nb)
elif node_spacing == 'EQUIDISTANT':
self.nodal_pts = np.linspace(-1, 1, self.nb)
else: raise ValueError('node_spacing {} not recognized'.format(node_spacing))
def shape_functions_at_pts(self, pts):
""" computes shape functions evaluated at pts on [-1, 1]
@retval shap (len(pts), nb) phi_j(pts[i])
"""
V = Vandermonde1D(N=self.nb, x=self.nodal_pts)
VTinv = np.linalg.inv(V.T)
P = P_tilde(r=pts, N=self.nb)
shap = np.dot(VTinv, P)
return shap.T
def shape_function_derivatives_at_pts(self, pts):
""" computes shape function derivatives w/r/t x on [-1, 1]
@retval shap_der, (Dr in Hesthaven), (len(pts), nb) d/dx phi_j(pts[i])
"""
V = Vandermonde1D(N=self.nb, x=self.nodal_pts)
Vx = GradVandermonde1D(N=self.nb, x=pts)
Vinv = np.linalg.inv(V)
shap_der = np.dot(Vx, Vinv)
return shap_der
```
Define a 1D master element, which is built on top of the 1D basis.
- Precompute shape functions at the nodal points and Gauss Legendre quadrature points, both are useful for different types of schemes. We use Gauss Legendre points instead of Gauss Lobatto points because they can integrate degree $2n-1$ polynomials exactly instead of $2n - 3$, where $n$ is the number of integration points. We would like to integrate $(\phi_i, \phi_j)_{\hat{K}}$, which is order 2$p$, so to integrate the mass matrix exactly, we need $2p + 1$ points, and common practice is $2p+2$. Since quadrature in 1D is cheap, we opt for the latter.
- Precompute mass matrix $M_{ij} = (\phi_i, \phi_j)$ and stiffness matrices $S_{ij} = \left(\phi_i, \frac{d\phi_j}{dx}\right)$, $K_{ij} = \left(\frac{d\phi_i}{dx}, \frac{d\phi_j}{dx}\right)$. Additionally, store $M^{-1}$, as it is commonly used. Although Hesthaven's method for mass and stiffness matrices are elegant, they rely on the underlying choice of an orthanormal modal basis. Since this class could be overloaded to work with other choices of basis, better to simply compute these matrices with quadrature.
```
class Master1D(object):
""" minimalist 1D master object """
def __init__(self, p, nquad_pts=None, *args, **kwargs):
self.p, self.nb = p, p+1
self.basis = NodalBasis1D(p=p, **kwargs)
self.nodal_pts = self.basis.nodal_pts
self.nq = 2*self.p + 2 if nquad_pts is None else nquad_pts
self.quad_pts, self.wghts = GaussLegendre(self.nq)
# shape functions at nodal and quadrature points
self.shap_nodal, self.dshap_nodal = self.mk_shap_and_dshap_at_pts(self.nodal_pts)
self.shap_quad, self.dshap_quad = self.mk_shap_and_dshap_at_pts(self.quad_pts)
# mass, stiffness matrices
self.M, self.S, self.K = self.mk_M(), self.mk_S(), self.mk_K()
self.Minv = np.linalg.inv(self.M)
# lifting permuatation matrix L (0s, 1s)
self.L = self.mk_L()
def mk_shap_and_dshap_at_pts(self, pts):
shap = self.basis.shape_functions_at_pts(pts)
dshap = self.basis.shape_function_derivatives_at_pts(pts)
return shap, dshap
def mk_M(self):
shapw = np.dot(np.diag(self.wghts), self.shap_quad)
M = np.dot(self.shap_quad.T, shapw)
return M
def mk_S(self):
dshapw = np.dot(np.diag(self.wghts), self.dshap_quad)
S = np.dot(self.shap_quad.T, dshapw)
return S
def mk_K(self):
dshapw = np.dot(np.diag(self.wghts), self.dshap_quad)
K = np.dot(self.dshap_quad.T, dshapw)
return K
def mk_L(self):
L = np.zeros((self.nb, 2))
L[0, 0] = 1
L[-1, 1] = 1
return L
@property
def shap_der(self):
""" return the shape derivatives for apps expecting 2, 3D"""
return [self.dshap_quad]
```
# creation of 1D mesh and DOF handler
## 1D mappings
For 1D problems, the mapping from the master element to physical space elements is somewhat trivial, since there's no reason for the transformation to be anything except affine. Note though, that when the 1D elements are embedded in 2D, then the transformations may be non-affine, in which case we must handle isoparametric mappings and the like. We defer this until later. For an affine mapping, we have the simple mapping
$$x(\xi) = x_L^k + \frac{1 + \xi}{2}(x_R^k - x_L^k)$$
With which we can move the nodal master points to their physical space coordinates.
```
# build T and P arrays
P = np.linspace(2, 4, 5)
class Mesh1D(object):
def __init__(self, P):
""" @param P vertex points, sorted by x position """
self.verts = P
self.nElm, self.nEdges = len(self.verts) - 1, len(self.verts)
self.connectivity = self.build_T()
connected_one_side = np.bincount(self.connectivity.ravel()) == 1
self.boundary_verts = np.where(connected_one_side)[0]
def build_T(self):
""" element connectivity array from 1D vertex list """
T = np.zeros((self.nElm, 2), dtype=int)
T[:,0] = np.arange(self.nElm)
T[:,1] = np.arange(self.nElm) + 1
return T
class dofh_1D(object): pass
class DG_dofh_1D(dofh_1D):
def __init__(self, mesh, master):
self.mesh, self.master = mesh, master
self.n_dof = self.master.nb * self.mesh.nElm
self.dgnodes = self.mk_dgnodes()
self.lg = self.mk_lg()
self.lg_PM = self.mk_minus_plus_lg()
self.nb, self.nElm = self.master.nb, self.mesh.nElm
self.ed2elm = self.mk_ed2elm()
def mk_dgnodes(self):
""" map master nodal pts to element vertices def'd in self.mesh """
dgn = np.zeros((self.master.nb, self.mesh.nElm))
master_nodal_pts = np.squeeze(self.master.nodal_pts)
for elm, elm_verts in enumerate(self.mesh.connectivity):
elm_vert_pts = self.mesh.verts[elm_verts]
elm_width = elm_vert_pts[1] - elm_vert_pts[0]
mapped_pts = elm_vert_pts[0] + (1+master_nodal_pts)/2.*(elm_width)
dgn[:, elm] = mapped_pts
return dgn
def mk_lg(self):
""" number all dof sequentially by dgnodes """
node_numbers = np.arange(np.size(self.dgnodes))
lg = node_numbers.reshape(self.dgnodes.shape, order='F')
return lg
def mk_minus_plus_lg(self):
""" (-) denotes element interior, (+) denotes exterior"""
lg_PM = dict()
lg_PM['-'] = self.lg[[0, -1], :].ravel(order='F')
lgP = self.lg[[0, -1],:]
lgP[0, 1: ] -= 1 # shift nodes to left of first
lgP[1, :-1] += 1 # shift nodes to right of last
lg_PM['+'] = lgP.ravel(order='F')
return lg_PM
def mk_ed2elm(self):
""" internal map holding the indicies to reshape vector of values on faces to
element edge space (2, nElm), duplicating the values on either side of interior faces
"""
f2elm = np.zeros((2, self.nElm))
faces = np.arange(self.mesh.nEdges)
# numpy magic is doing the following:
#
# [[0, 1, 2, 3]
# [0, 1, 2, 3]] - ravel('F') -> [0, 0, 1, 1, 2, 2, 3, 3]
#
# close, but ends duplicated. => trim the ends and reshape to f2elm shape
#
# [[0, 1, 2]
# [1, 2, 3]]
#
f2elm = np.vstack((faces, faces)).ravel(
order='F')[1:-1].reshape(f2elm.shape, order='F')
return f2elm
def edge2elm_ed(self, arr):
""" internal method to move edge values (defined on the interfaces)
to values on the "element edge space", the edge dof interior to each element
@param arr array formatted on edge space (nFaces,)
@retval elmEdArr array formatted on "element edge space" (2, nElm)
"""
return arr[self.ed2elm]
```
# computation of fluxes
The 'back end' of an explicit DG computation is the unrolled vector of all the problem unknowns. The front end that we'd like to interact with is the dgnodes data structure
```
def plot_solution(ax, u, dofh):
""" u formatted like dgnodes """
for elm in range(dofh.nElm):
nodal_pts = dofh.dgnodes[:, elm]
nodal_values = u[:, elm]
ax.plot(nodal_pts, nodal_values)
return ax
# Low storage Runge-Kutta coefficients LSERK
rk4a = np.array([
0.0,
-567301805773.0/1357537059087.0,
-2404267990393.0/2016746695238.0,
-3550918686646.0/2091501179385.0,
-1275806237668.0/842570457699.0])
rk4b = np.array([
1432997174477.0/9575080441755.0,
5161836677717.0/13612068292357.0,
1720146321549.0/2090206949498.0,
3134564353537.0/4481467310338.0,
2277821191437.0/14882151754819.0])
rk4c = np.array([
0.0,
1432997174477.0/9575080441755.0,
2526269341429.0/6820363962896.0,
2006345519317.0/3224310063776.0,
2802321613138.0/2924317926251.0])
# constants
π = np.pi
# geometry set up
P = np.linspace(0, 2*π, 10)
mesh1d = Mesh1D(P)
master = Master1D(p=2)
dofh = DG_dofh_1D(mesh1d, master)
mapdgn = np.zeros((dofh.dgnodes.shape[0], 1, dofh.dgnodes.shape[1]))
mapdgn[:,0,:] = dofh.dgnodes
_map = fem_map.Affine_Mapping(master=[master], dgnodes=[mapdgn])
```
We choose numerical fluxes of the form
$$\widehat{au} =\left\{\!\!\left\{au\right\}\!\!\right\} + (1-\alpha)\frac{|a|}{2} \left[\!\!\left[u\right]\!\!\right]$$
Where $\alpha = 0$ represents an upwinded flux and $\alpha=1$ represents a central flux. These are shown in Hesthaven to be stable for the equation we are interested in solving.
```
def compute_interior_flux(u, norm, dofh, α):
""" computes the numerical flux at all of the element interfaces
@param u the current solution u, unrolled to a vector
NOTE: boundary interfaces will be filled with garbage, and must be corrected
"""
pm = dofh.lg_PM
# equivalent to the flux
# \hat{au} = {{au}} + (1-α) * |a|/2 * [[u]]
# at element interfaces. First and last interface will have garbage.
flux = a/2*(u[pm['-']] + u[pm['+']]) + (1-α)*np.abs(norm*a)/2.*(u[pm['+']] - u[pm['-']])
return flux
```
# semi-discrete scheme
Considering the "weak" DG-FEM form, we have the semi-discrete element local equation
\begin{align}
\int_K \frac{\partial u_h}{\partial t} v \, dK
+\int_{K} (au_h) \frac{\partial v}{\partial x} \, dK =
-\int_{\partial K} \hat{n}\cdot \widehat{au} v \, d\partial K
\end{align}
Choosing a representation $u=u_i\phi_i$ piecewise polynomial over each element, and the same test space, we have, for a given choice of numerical flux $\widehat{au}$, and noting that in 1D, the normal vectors are simply (-1, +1):
\begin{align}
\int_K \frac{\partial}{\partial t} (u_i(t) \phi_i(x)) \phi_j(x) \, dx
+\int_{K} a(u_i(t)\phi_i(x)) \frac{\partial \phi_j(x)}{\partial x} \, dx =
-(\widehat{au}(x_R) - \widehat{au}(x_L))
\end{align}
transforming the integrals to the reference element:
\begin{align}
\int_{\hat{K}} \frac{\partial}{\partial t} (u_i(t) \phi_i(\xi)) \phi_j(\xi) \,|det(J)|\, d\xi
+\int_{\hat{K}} a(u_i(t)\phi_i(\xi)) \frac{\partial \phi_j(\xi)}{\partial \xi} \, |det(J)|\, d\xi =
-(\widehat{au}(x_R) - \widehat{au}(x_L))
\end{align}
This completes the description of the semi-discrete scheme, and we have a choice as to how to compute these integrals. The important part is that since the coefficients $u_i$ vary in time but are constants with respect to space, we can write
\begin{align}
&\frac{\partial u_i(t)}{\partial t} \int_{\hat{K}} \phi_i(\xi) \phi_j(\xi) \,|det(J)|\, d\xi
+au_i\int_{\hat{K}} \phi_i(\xi) \left(\frac{d\xi}{dx}\right)\frac{\partial \phi_j(\xi)}{\partial \xi} \, |det(J)|\, d\xi =
-(\widehat{au}(x_R) - \widehat{au}(x_L)) \\
&\Rightarrow M_K \vec{\frac{du_h}{dt}} + a S_K \vec{u_h}
= - L\, (\widehat{au}(x_R) - \widehat{au}(x_L))
\end{align}
Where we have computed $M_K$ and $S_K$, the mass and stiffness matrices for element $K$. Although we would normally do this with a quadrature rule, we can take advantage of the fact that in 1D (and indeed under any affine mapping from reference to physical element), $J^{-1}$ and $|\det(J)|$ will be constant over the entire element (also note that in 1D, $J^{-1}$ is a 1x1 matrix)<sup>1</sup>. In that case, we can treat both as constants, precompute $M_{\hat{K}}, S_{\hat{K}}$, and multiply the entire element-local equation by $M^{-1}$, giving
\begin{align}
\vec{\frac{du_h}{dt}} &= - a \frac{\det(J)_K}{\det(J)_K}\, J^{-1}_K M_{\hat{K}}^{-1}S^T_{\hat{K}} \vec{u_h}
- \frac{1}{\det(J)_K} M^{-1}_K L\, (\widehat{au}(x_R) - \widehat{au}(x_L)) \\
&= - a \, J^{-1}_K M_{\hat{K}}^{-1}S^T_{\hat{K}} \vec{u_h}
- \frac{1}{\det(J)_K} M^{-1}_K L\, (\widehat{au}(x_R) - \widehat{au}(x_L))
\end{align}
Which is a good form for a black box integrator, since we have a "naked" $\frac{du_h}{dt}$, and because the scheme is explicit.
note<sup>1</sup>: $J, J^{-1}$ are 1x1 matrices, and $\det{J}$ is simply $J_{11}$; $J^{-1} = 1/J_{11}$. It's important for the clarity of explicit schemes to understand where these cancellations occur.
```
def advect_rhs_1D(u, t_local, a, dofh, _map, master, flux_fn, gD, norm):
return u
# final time
T = 10
# compute time step size, irrelevant for backward euler
CFL = 0.75
Δx = dofh.dgnodes[1,0] - dofh.dgnodes[0,0]
Δt = CFL/(2*π)*Δx
Δt = Δt / 2
# number of timesteps needed
steps = int(np.ceil(T/Δt))
# initial condition, advection speed
solution = np.zeros((steps, *dofh.dgnodes.shape))
a = 2 * np.pi
solution[0,::] = np.sin(dofh.dgnodes)
LSERK_stages = [0, 1, 2, 3, 4]
t = 0
gD = lambda t: -np.sin(a*t)
# normal vectors, all positive
norm = np.ones((2, dofh.nElm))
norm[0,:] *= -1
# function pointer to something that can compute fluxes
flux_fn = compute_interior_flux
# time loop
RK_resid = np.zeros_like(dofh.dgnodes)
for tstep in range(3):
u = solution[tstep, ::]
for s in LSERK_stages:
t_local = t + rk4c[s]*Δt
rhsu = advect_rhs_1D(u, t_local, a, dofh, _map, master, flux_fn, gD, norm)
RK_resid = rk4a[s]*RK_resid + Δt*rhsu
u += rk4b[s]*RK_resid
t += Δt
u0 = solution[0,:,:]
fix, ax = plt.subplots()
ax = plot_solution(ax, u0, dofh)
pm = dofh.lg_PM
u = u0.ravel()
# normal vectors on interfaces, all positive
norm_faces = np.ones(pm['-'].shape[0])
α = 0
# compute interior fluxes
flux = compute_interior_flux(u, norm_faces, dofh, α)
# compute boundary fluxes
flux[0] = gD(t_local)
flux[-1] = flux[0]
dofh.edge2elm_ed(flux)
```
|
github_jupyter
|
```
import os
import numpy as np
from tqdm import tqdm
from src.data.loaders.ascad import ASCADData
from src.dlla.berg import make_mlp
from src.dlla.hw import prepare_traces_dl, dlla_known_p
from src.pollution.gaussian_noise import gaussian_noise
from src.tools.cache import cache_np
from src.trace_set.database import Database
from src.trace_set.pollution import Pollution, PollutionType
from src.trace_set.set_hw import TraceSetHW
from src.trace_set.window import get_windows, extract_traces
# Source [EDIT]
DB = Database.ascad_none
# Limit number of traces [EDIT]
LIMIT_PROF = None
LIMIT_ATT = 1000
# Select targets and noise parameters
RAW_TRACES, WINDOW_JITTER_PARAMS, GAUSS_PARAMS, LIMIT_RAW = [None] * 4
if DB is Database.ascad_none or DB is Database.ascad:
TARGET_ROUND = 0
TARGET_BYTE = 0
WINDOW_JITTER_PARAMS = np.arange(0, 205, 5)
GAUSS_PARAMS = np.arange(0, 205, 5)
RAW_TRACES = ASCADData.raw()['traces']
LIMIT_RAW = -1
if DB is Database.ascad:
TARGET_BYTE = 2
WINDOW_JITTER_PARAMS = np.arange(0, 2.05, .05)
GAUSS_PARAMS = np.arange(0, 5.1, .1)
if DB is Database.aisy:
TARGET_ROUND = 4
TARGET_BYTE = 0
WINDOW_JITTER_PARAMS = np.arange(0, 460, 10)
GAUSS_PARAMS = np.arange(0, 4100, 100)
RAW_TRACES = cache_np("aisy_traces")
# Select targets
TRACE_SET = TraceSetHW(DB)
SAMPLE_TRACE = TRACE_SET.profile()[0][0]
WINDOW, WINDOW_CXT = get_windows(RAW_TRACES, SAMPLE_TRACE)
# Isolate context trace for window jitter.
# Gets cached, as this procedure takes some time (depending on disk read speed)
X_CXT = cache_np(f"{DB.name}_x_cxt", extract_traces, RAW_TRACES, WINDOW_CXT)[:LIMIT_RAW]
PROFILING_MASK = np.ones(len(X_CXT), dtype=bool)
PROFILING_MASK[2::3] = 0
X_PROF, Y_PROF = TRACE_SET.profile_states()
X_ATT, Y_ATT = TRACE_SET.attack_states()
X_PROF_CXT = X_CXT[PROFILING_MASK]
X_ATT_CXT = X_CXT[~PROFILING_MASK]
def verify(db: Database, pollution: Pollution):
"""
Assess leakage from database by
"""
trace_set = TraceSetHW(db, pollution, (LIMIT_PROF, LIMIT_ATT))
x9, y9, x9_att, y9_att = prepare_traces_dl(*trace_set.profile(), *trace_set.attack())
mdl9 = make_mlp(x9, y9, progress=False)
dlla9_p = dlla_known_p(mdl9, x9_att, y9_att)
print(f"Pollution {pollution.type} ({pollution.parameter}): p-value ({dlla9_p}).")
def desync(traces: np.ndarray, window: (int, int), sigma: float):
start, end = window
num_traces = len(traces)
num_sample_points = end - start
permutations = np.round(np.random.normal(scale=sigma, size=num_traces)).astype(int)
if np.max(np.abs(permutations)) >= num_sample_points:
raise Exception(f"Window jitter parameter ({sigma}) too high. PoI is not always within the resulting traces.")
permutations += start
res = np.ones((num_traces, num_sample_points), dtype=traces.dtype)
for ix in tqdm(range(num_traces), f"Trace desynchronization, sigma={sigma}"):
permutation = permutations[ix]
res[ix] = traces[ix, permutation:permutation + num_sample_points]
return res
def apply_desync(db, x_prof_cxt, y_prof, x_att_cxt, y_att, window: (int, int), params: list):
for param in params:
pollution = Pollution(PollutionType.desync, param)
out = TraceSetHW(db, pollution, (LIMIT_PROF, LIMIT_ATT))
if not os.path.exists(out.path):
xn = desync(x_prof_cxt, window, param)
xn_att = desync(x_att_cxt, window, param)
out.create(xn, y_prof, xn_att, y_att)
verify(db, pollution)
apply_desync(DB, X_PROF_CXT, Y_PROF, X_ATT_CXT, Y_ATT, WINDOW, WINDOW_JITTER_PARAMS)
def apply_gauss(db, params: list):
for param in params:
pollution = Pollution(PollutionType.gauss, param)
default = TraceSetHW(db)
out = TraceSetHW(db, pollution, (LIMIT_PROF, LIMIT_ATT))
x_prof, y_prof = default.profile_states()
x_att, y_att = default.attack_states()
if not os.path.exists(out.path):
xn = gaussian_noise(x_prof, param)
xn_att = gaussian_noise(x_att, param)
out.create(xn, y_prof, xn_att, y_att)
verify(db, pollution)
apply_gauss(DB, GAUSS_PARAMS)
```
|
github_jupyter
|
# Import necessary depencencies
```
import pandas as pd
import numpy as np
import text_normalizer as tn
import model_evaluation_utils as meu
np.set_printoptions(precision=2, linewidth=80)
```
# Load and normalize data
```
dataset = pd.read_csv(r'movie_reviews.csv')
reviews = np.array(dataset['review'])
sentiments = np.array(dataset['sentiment'])
# extract data for model evaluation
test_reviews = reviews[35000:]
test_sentiments = sentiments[35000:]
sample_review_ids = [7626, 3533, 13010]
# normalize dataset
norm_test_reviews = tn.normalize_corpus(test_reviews)
```
# Sentiment Analysis with AFINN
```
from afinn import Afinn
afn = Afinn(emoticons=True)
```
## Predict sentiment for sample reviews
```
for review, sentiment in zip(test_reviews[sample_review_ids], test_sentiments[sample_review_ids]):
print('REVIEW:', review)
print('Actual Sentiment:', sentiment)
print('Predicted Sentiment polarity:', afn.score(review))
print('-'*60)
```
## Predict sentiment for test dataset
```
sentiment_polarity = [afn.score(review) for review in test_reviews]
predicted_sentiments = ['positive' if score >= 1.0 else 'negative' for score in sentiment_polarity]
```
## Evaluate model performance
```
meu.display_model_performance_metrics(true_labels=test_sentiments, predicted_labels=predicted_sentiments,
classes=['positive', 'negative'])
```
# Sentiment Analysis with SentiWordNet
```
from nltk.corpus import sentiwordnet as swn
awesome = list(swn.senti_synsets('awesome', 'a'))[0]
print('Positive Polarity Score:', awesome.pos_score())
print('Negative Polarity Score:', awesome.neg_score())
print('Objective Score:', awesome.obj_score())
```
## Build model
```
def analyze_sentiment_sentiwordnet_lexicon(review,
verbose=False):
# tokenize and POS tag text tokens
tagged_text = [(token.text, token.tag_) for token in tn.nlp(review)]
pos_score = neg_score = token_count = obj_score = 0
# get wordnet synsets based on POS tags
# get sentiment scores if synsets are found
for word, tag in tagged_text:
ss_set = None
if 'NN' in tag and list(swn.senti_synsets(word, 'n')):
ss_set = list(swn.senti_synsets(word, 'n'))[0]
elif 'VB' in tag and list(swn.senti_synsets(word, 'v')):
ss_set = list(swn.senti_synsets(word, 'v'))[0]
elif 'JJ' in tag and list(swn.senti_synsets(word, 'a')):
ss_set = list(swn.senti_synsets(word, 'a'))[0]
elif 'RB' in tag and list(swn.senti_synsets(word, 'r')):
ss_set = list(swn.senti_synsets(word, 'r'))[0]
# if senti-synset is found
if ss_set:
# add scores for all found synsets
pos_score += ss_set.pos_score()
neg_score += ss_set.neg_score()
obj_score += ss_set.obj_score()
token_count += 1
# aggregate final scores
final_score = pos_score - neg_score
norm_final_score = round(float(final_score) / token_count, 2)
final_sentiment = 'positive' if norm_final_score >= 0 else 'negative'
if verbose:
norm_obj_score = round(float(obj_score) / token_count, 2)
norm_pos_score = round(float(pos_score) / token_count, 2)
norm_neg_score = round(float(neg_score) / token_count, 2)
# to display results in a nice table
sentiment_frame = pd.DataFrame([[final_sentiment, norm_obj_score, norm_pos_score,
norm_neg_score, norm_final_score]],
columns=pd.MultiIndex(levels=[['SENTIMENT STATS:'],
['Predicted Sentiment', 'Objectivity',
'Positive', 'Negative', 'Overall']],
labels=[[0,0,0,0,0],[0,1,2,3,4]]))
print(sentiment_frame)
return final_sentiment
```
## Predict sentiment for sample reviews
```
for review, sentiment in zip(test_reviews[sample_review_ids], test_sentiments[sample_review_ids]):
print('REVIEW:', review)
print('Actual Sentiment:', sentiment)
pred = analyze_sentiment_sentiwordnet_lexicon(review, verbose=True)
print('-'*60)
```
## Predict sentiment for test dataset
```
predicted_sentiments = [analyze_sentiment_sentiwordnet_lexicon(review, verbose=False) for review in norm_test_reviews]
```
## Evaluate model performance
```
meu.display_model_performance_metrics(true_labels=test_sentiments, predicted_labels=predicted_sentiments,
classes=['positive', 'negative'])
```
# Sentiment Analysis with VADER
```
from nltk.sentiment.vader import SentimentIntensityAnalyzer
```
## Build model
```
def analyze_sentiment_vader_lexicon(review,
threshold=0.1,
verbose=False):
# pre-process text
review = tn.strip_html_tags(review)
review = tn.remove_accented_chars(review)
review = tn.expand_contractions(review)
# analyze the sentiment for review
analyzer = SentimentIntensityAnalyzer()
scores = analyzer.polarity_scores(review)
# get aggregate scores and final sentiment
agg_score = scores['compound']
final_sentiment = 'positive' if agg_score >= threshold\
else 'negative'
if verbose:
# display detailed sentiment statistics
positive = str(round(scores['pos'], 2)*100)+'%'
final = round(agg_score, 2)
negative = str(round(scores['neg'], 2)*100)+'%'
neutral = str(round(scores['neu'], 2)*100)+'%'
sentiment_frame = pd.DataFrame([[final_sentiment, final, positive,
negative, neutral]],
columns=pd.MultiIndex(levels=[['SENTIMENT STATS:'],
['Predicted Sentiment', 'Polarity Score',
'Positive', 'Negative', 'Neutral']],
labels=[[0,0,0,0,0],[0,1,2,3,4]]))
print(sentiment_frame)
return final_sentiment
```
## Predict sentiment for sample reviews
```
for review, sentiment in zip(test_reviews[sample_review_ids], test_sentiments[sample_review_ids]):
print('REVIEW:', review)
print('Actual Sentiment:', sentiment)
pred = analyze_sentiment_vader_lexicon(review, threshold=0.4, verbose=True)
print('-'*60)
```
## Predict sentiment for test dataset
```
predicted_sentiments = [analyze_sentiment_vader_lexicon(review, threshold=0.4, verbose=False) for review in test_reviews]
```
## Evaluate model performance
```
meu.display_model_performance_metrics(true_labels=test_sentiments, predicted_labels=predicted_sentiments,
classes=['positive', 'negative'])
```
|
github_jupyter
|
# RadarCOVID-Report
## Data Extraction
```
import datetime
import json
import logging
import os
import shutil
import tempfile
import textwrap
import uuid
import matplotlib.pyplot as plt
import matplotlib.ticker
import numpy as np
import pandas as pd
import retry
import seaborn as sns
%matplotlib inline
current_working_directory = os.environ.get("PWD")
if current_working_directory:
os.chdir(current_working_directory)
sns.set()
matplotlib.rcParams["figure.figsize"] = (15, 6)
extraction_datetime = datetime.datetime.utcnow()
extraction_date = extraction_datetime.strftime("%Y-%m-%d")
extraction_previous_datetime = extraction_datetime - datetime.timedelta(days=1)
extraction_previous_date = extraction_previous_datetime.strftime("%Y-%m-%d")
extraction_date_with_hour = datetime.datetime.utcnow().strftime("%Y-%m-%d@%H")
current_hour = datetime.datetime.utcnow().hour
are_today_results_partial = current_hour != 23
```
### Constants
```
from Modules.ExposureNotification import exposure_notification_io
spain_region_country_code = "ES"
germany_region_country_code = "DE"
default_backend_identifier = spain_region_country_code
backend_generation_days = 7 * 2
daily_summary_days = 7 * 4 * 3
daily_plot_days = 7 * 4
tek_dumps_load_limit = daily_summary_days + 1
```
### Parameters
```
environment_backend_identifier = os.environ.get("RADARCOVID_REPORT__BACKEND_IDENTIFIER")
if environment_backend_identifier:
report_backend_identifier = environment_backend_identifier
else:
report_backend_identifier = default_backend_identifier
report_backend_identifier
environment_enable_multi_backend_download = \
os.environ.get("RADARCOVID_REPORT__ENABLE_MULTI_BACKEND_DOWNLOAD")
if environment_enable_multi_backend_download:
report_backend_identifiers = None
else:
report_backend_identifiers = [report_backend_identifier]
report_backend_identifiers
environment_invalid_shared_diagnoses_dates = \
os.environ.get("RADARCOVID_REPORT__INVALID_SHARED_DIAGNOSES_DATES")
if environment_invalid_shared_diagnoses_dates:
invalid_shared_diagnoses_dates = environment_invalid_shared_diagnoses_dates.split(",")
else:
invalid_shared_diagnoses_dates = []
invalid_shared_diagnoses_dates
```
### COVID-19 Cases
```
report_backend_client = \
exposure_notification_io.get_backend_client_with_identifier(
backend_identifier=report_backend_identifier)
@retry.retry(tries=10, delay=10, backoff=1.1, jitter=(0, 10))
def download_cases_dataframe_from_ecdc():
return pd.read_csv(
"https://opendata.ecdc.europa.eu/covid19/casedistribution/csv/data.csv")
confirmed_df_ = download_cases_dataframe_from_ecdc()
confirmed_df = confirmed_df_.copy()
confirmed_df = confirmed_df[["dateRep", "cases", "geoId"]]
confirmed_df.rename(
columns={
"dateRep":"sample_date",
"cases": "new_cases",
"geoId": "country_code",
},
inplace=True)
confirmed_df["sample_date"] = pd.to_datetime(confirmed_df.sample_date, dayfirst=True)
confirmed_df["sample_date"] = confirmed_df.sample_date.dt.strftime("%Y-%m-%d")
confirmed_df.sort_values("sample_date", inplace=True)
confirmed_df.tail()
def sort_source_regions_for_display(source_regions: list) -> list:
if report_backend_identifier in source_regions:
source_regions = [report_backend_identifier] + \
list(sorted(set(source_regions).difference([report_backend_identifier])))
else:
source_regions = list(sorted(source_regions))
return source_regions
report_source_regions = report_backend_client.source_regions_for_date(
date=extraction_datetime.date())
report_source_regions = sort_source_regions_for_display(
source_regions=report_source_regions)
report_source_regions
confirmed_days = pd.date_range(
start=confirmed_df.iloc[0].sample_date,
end=extraction_datetime)
confirmed_days_df = pd.DataFrame(data=confirmed_days, columns=["sample_date"])
confirmed_days_df["sample_date_string"] = \
confirmed_days_df.sample_date.dt.strftime("%Y-%m-%d")
confirmed_days_df.tail()
source_regions_at_date_df = confirmed_days_df.copy()
source_regions_at_date_df["source_regions_at_date"] = \
source_regions_at_date_df.sample_date.apply(
lambda x: report_backend_client.source_regions_for_date(date=x))
source_regions_at_date_df.sort_values("sample_date", inplace=True)
source_regions_at_date_df["_source_regions_group"] = source_regions_at_date_df. \
source_regions_at_date.apply(lambda x: ",".join(sort_source_regions_for_display(x)))
source_regions_at_date_df.tail()
source_regions_for_summary_df = \
source_regions_at_date_df[["sample_date", "_source_regions_group"]].copy()
source_regions_for_summary_df.rename(columns={"_source_regions_group": "source_regions"}, inplace=True)
source_regions_for_summary_df.tail()
confirmed_output_columns = ["sample_date", "new_cases", "covid_cases"]
confirmed_output_df = pd.DataFrame(columns=confirmed_output_columns)
for source_regions_group, source_regions_group_series in \
source_regions_at_date_df.groupby("_source_regions_group"):
source_regions_set = set(source_regions_group.split(","))
confirmed_source_regions_set_df = \
confirmed_df[confirmed_df.country_code.isin(source_regions_set)].copy()
confirmed_source_regions_group_df = \
confirmed_source_regions_set_df.groupby("sample_date").new_cases.sum() \
.reset_index().sort_values("sample_date")
confirmed_source_regions_group_df["covid_cases"] = \
confirmed_source_regions_group_df.new_cases.rolling(7, min_periods=0).mean().round()
confirmed_source_regions_group_df = \
confirmed_source_regions_group_df[confirmed_output_columns]
confirmed_source_regions_group_df.fillna(method="ffill", inplace=True)
confirmed_source_regions_group_df = \
confirmed_source_regions_group_df[
confirmed_source_regions_group_df.sample_date.isin(
source_regions_group_series.sample_date_string)]
confirmed_output_df = confirmed_output_df.append(confirmed_source_regions_group_df)
confirmed_df = confirmed_output_df.copy()
confirmed_df.tail()
confirmed_df.rename(columns={"sample_date": "sample_date_string"}, inplace=True)
confirmed_df = confirmed_days_df[["sample_date_string"]].merge(confirmed_df, how="left")
confirmed_df.sort_values("sample_date_string", inplace=True)
confirmed_df.fillna(method="ffill", inplace=True)
confirmed_df.tail()
confirmed_df[["new_cases", "covid_cases"]].plot()
```
### Extract API TEKs
```
raw_zip_path_prefix = "Data/TEKs/Raw/"
fail_on_error_backend_identifiers = [report_backend_identifier]
multi_backend_exposure_keys_df = \
exposure_notification_io.download_exposure_keys_from_backends(
backend_identifiers=report_backend_identifiers,
generation_days=backend_generation_days,
fail_on_error_backend_identifiers=fail_on_error_backend_identifiers,
save_raw_zip_path_prefix=raw_zip_path_prefix)
multi_backend_exposure_keys_df["region"] = multi_backend_exposure_keys_df["backend_identifier"]
multi_backend_exposure_keys_df.rename(
columns={
"generation_datetime": "sample_datetime",
"generation_date_string": "sample_date_string",
},
inplace=True)
multi_backend_exposure_keys_df.head()
early_teks_df = multi_backend_exposure_keys_df[
multi_backend_exposure_keys_df.rolling_period < 144].copy()
early_teks_df["rolling_period_in_hours"] = early_teks_df.rolling_period / 6
early_teks_df[early_teks_df.sample_date_string != extraction_date] \
.rolling_period_in_hours.hist(bins=list(range(24)))
early_teks_df[early_teks_df.sample_date_string == extraction_date] \
.rolling_period_in_hours.hist(bins=list(range(24)))
multi_backend_exposure_keys_df = multi_backend_exposure_keys_df[[
"sample_date_string", "region", "key_data"]]
multi_backend_exposure_keys_df.head()
active_regions = \
multi_backend_exposure_keys_df.groupby("region").key_data.nunique().sort_values().index.unique().tolist()
active_regions
multi_backend_summary_df = multi_backend_exposure_keys_df.groupby(
["sample_date_string", "region"]).key_data.nunique().reset_index() \
.pivot(index="sample_date_string", columns="region") \
.sort_index(ascending=False)
multi_backend_summary_df.rename(
columns={"key_data": "shared_teks_by_generation_date"},
inplace=True)
multi_backend_summary_df.rename_axis("sample_date", inplace=True)
multi_backend_summary_df = multi_backend_summary_df.fillna(0).astype(int)
multi_backend_summary_df = multi_backend_summary_df.head(backend_generation_days)
multi_backend_summary_df.head()
def compute_keys_cross_sharing(x):
teks_x = x.key_data_x.item()
common_teks = set(teks_x).intersection(x.key_data_y.item())
common_teks_fraction = len(common_teks) / len(teks_x)
return pd.Series(dict(
common_teks=common_teks,
common_teks_fraction=common_teks_fraction,
))
multi_backend_exposure_keys_by_region_df = \
multi_backend_exposure_keys_df.groupby("region").key_data.unique().reset_index()
multi_backend_exposure_keys_by_region_df["_merge"] = True
multi_backend_exposure_keys_by_region_combination_df = \
multi_backend_exposure_keys_by_region_df.merge(
multi_backend_exposure_keys_by_region_df, on="_merge")
multi_backend_exposure_keys_by_region_combination_df.drop(
columns=["_merge"], inplace=True)
if multi_backend_exposure_keys_by_region_combination_df.region_x.nunique() > 1:
multi_backend_exposure_keys_by_region_combination_df = \
multi_backend_exposure_keys_by_region_combination_df[
multi_backend_exposure_keys_by_region_combination_df.region_x !=
multi_backend_exposure_keys_by_region_combination_df.region_y]
multi_backend_exposure_keys_cross_sharing_df = \
multi_backend_exposure_keys_by_region_combination_df \
.groupby(["region_x", "region_y"]) \
.apply(compute_keys_cross_sharing) \
.reset_index()
multi_backend_cross_sharing_summary_df = \
multi_backend_exposure_keys_cross_sharing_df.pivot_table(
values=["common_teks_fraction"],
columns="region_x",
index="region_y",
aggfunc=lambda x: x.item())
multi_backend_cross_sharing_summary_df
multi_backend_without_active_region_exposure_keys_df = \
multi_backend_exposure_keys_df[multi_backend_exposure_keys_df.region != report_backend_identifier]
multi_backend_without_active_region = \
multi_backend_without_active_region_exposure_keys_df.groupby("region").key_data.nunique().sort_values().index.unique().tolist()
multi_backend_without_active_region
exposure_keys_summary_df = multi_backend_exposure_keys_df[
multi_backend_exposure_keys_df.region == report_backend_identifier]
exposure_keys_summary_df.drop(columns=["region"], inplace=True)
exposure_keys_summary_df = \
exposure_keys_summary_df.groupby(["sample_date_string"]).key_data.nunique().to_frame()
exposure_keys_summary_df = \
exposure_keys_summary_df.reset_index().set_index("sample_date_string")
exposure_keys_summary_df.sort_index(ascending=False, inplace=True)
exposure_keys_summary_df.rename(columns={"key_data": "shared_teks_by_generation_date"}, inplace=True)
exposure_keys_summary_df.head()
```
### Dump API TEKs
```
tek_list_df = multi_backend_exposure_keys_df[
["sample_date_string", "region", "key_data"]].copy()
tek_list_df["key_data"] = tek_list_df["key_data"].apply(str)
tek_list_df.rename(columns={
"sample_date_string": "sample_date",
"key_data": "tek_list"}, inplace=True)
tek_list_df = tek_list_df.groupby(
["sample_date", "region"]).tek_list.unique().reset_index()
tek_list_df["extraction_date"] = extraction_date
tek_list_df["extraction_date_with_hour"] = extraction_date_with_hour
tek_list_path_prefix = "Data/TEKs/"
tek_list_current_path = tek_list_path_prefix + f"/Current/RadarCOVID-TEKs.json"
tek_list_daily_path = tek_list_path_prefix + f"Daily/RadarCOVID-TEKs-{extraction_date}.json"
tek_list_hourly_path = tek_list_path_prefix + f"Hourly/RadarCOVID-TEKs-{extraction_date_with_hour}.json"
for path in [tek_list_current_path, tek_list_daily_path, tek_list_hourly_path]:
os.makedirs(os.path.dirname(path), exist_ok=True)
tek_list_df.drop(columns=["extraction_date", "extraction_date_with_hour"]).to_json(
tek_list_current_path,
lines=True, orient="records")
tek_list_df.drop(columns=["extraction_date_with_hour"]).to_json(
tek_list_daily_path,
lines=True, orient="records")
tek_list_df.to_json(
tek_list_hourly_path,
lines=True, orient="records")
tek_list_df.head()
```
### Load TEK Dumps
```
import glob
def load_extracted_teks(mode, region=None, limit=None) -> pd.DataFrame:
extracted_teks_df = pd.DataFrame(columns=["region"])
file_paths = list(reversed(sorted(glob.glob(tek_list_path_prefix + mode + "/RadarCOVID-TEKs-*.json"))))
if limit:
file_paths = file_paths[:limit]
for file_path in file_paths:
logging.info(f"Loading TEKs from '{file_path}'...")
iteration_extracted_teks_df = pd.read_json(file_path, lines=True)
extracted_teks_df = extracted_teks_df.append(
iteration_extracted_teks_df, sort=False)
extracted_teks_df["region"] = \
extracted_teks_df.region.fillna(spain_region_country_code).copy()
if region:
extracted_teks_df = \
extracted_teks_df[extracted_teks_df.region == region]
return extracted_teks_df
daily_extracted_teks_df = load_extracted_teks(
mode="Daily",
region=report_backend_identifier,
limit=tek_dumps_load_limit)
daily_extracted_teks_df.head()
exposure_keys_summary_df_ = daily_extracted_teks_df \
.sort_values("extraction_date", ascending=False) \
.groupby("sample_date").tek_list.first() \
.to_frame()
exposure_keys_summary_df_.index.name = "sample_date_string"
exposure_keys_summary_df_["tek_list"] = \
exposure_keys_summary_df_.tek_list.apply(len)
exposure_keys_summary_df_ = exposure_keys_summary_df_ \
.rename(columns={"tek_list": "shared_teks_by_generation_date"}) \
.sort_index(ascending=False)
exposure_keys_summary_df = exposure_keys_summary_df_
exposure_keys_summary_df.head()
```
### Daily New TEKs
```
tek_list_df = daily_extracted_teks_df.groupby("extraction_date").tek_list.apply(
lambda x: set(sum(x, []))).reset_index()
tek_list_df = tek_list_df.set_index("extraction_date").sort_index(ascending=True)
tek_list_df.head()
def compute_teks_by_generation_and_upload_date(date):
day_new_teks_set_df = tek_list_df.copy().diff()
try:
day_new_teks_set = day_new_teks_set_df[
day_new_teks_set_df.index == date].tek_list.item()
except ValueError:
day_new_teks_set = None
if pd.isna(day_new_teks_set):
day_new_teks_set = set()
day_new_teks_df = daily_extracted_teks_df[
daily_extracted_teks_df.extraction_date == date].copy()
day_new_teks_df["shared_teks"] = \
day_new_teks_df.tek_list.apply(lambda x: set(x).intersection(day_new_teks_set))
day_new_teks_df["shared_teks"] = \
day_new_teks_df.shared_teks.apply(len)
day_new_teks_df["upload_date"] = date
day_new_teks_df.rename(columns={"sample_date": "generation_date"}, inplace=True)
day_new_teks_df = day_new_teks_df[
["upload_date", "generation_date", "shared_teks"]]
day_new_teks_df["generation_to_upload_days"] = \
(pd.to_datetime(day_new_teks_df.upload_date) -
pd.to_datetime(day_new_teks_df.generation_date)).dt.days
day_new_teks_df = day_new_teks_df[day_new_teks_df.shared_teks > 0]
return day_new_teks_df
shared_teks_generation_to_upload_df = pd.DataFrame()
for upload_date in daily_extracted_teks_df.extraction_date.unique():
shared_teks_generation_to_upload_df = \
shared_teks_generation_to_upload_df.append(
compute_teks_by_generation_and_upload_date(date=upload_date))
shared_teks_generation_to_upload_df \
.sort_values(["upload_date", "generation_date"], ascending=False, inplace=True)
shared_teks_generation_to_upload_df.tail()
today_new_teks_df = \
shared_teks_generation_to_upload_df[
shared_teks_generation_to_upload_df.upload_date == extraction_date].copy()
today_new_teks_df.tail()
if not today_new_teks_df.empty:
today_new_teks_df.set_index("generation_to_upload_days") \
.sort_index().shared_teks.plot.bar()
generation_to_upload_period_pivot_df = \
shared_teks_generation_to_upload_df[
["upload_date", "generation_to_upload_days", "shared_teks"]] \
.pivot(index="upload_date", columns="generation_to_upload_days") \
.sort_index(ascending=False).fillna(0).astype(int) \
.droplevel(level=0, axis=1)
generation_to_upload_period_pivot_df.head()
new_tek_df = tek_list_df.diff().tek_list.apply(
lambda x: len(x) if not pd.isna(x) else None).to_frame().reset_index()
new_tek_df.rename(columns={
"tek_list": "shared_teks_by_upload_date",
"extraction_date": "sample_date_string",}, inplace=True)
new_tek_df.tail()
shared_teks_uploaded_on_generation_date_df = shared_teks_generation_to_upload_df[
shared_teks_generation_to_upload_df.generation_to_upload_days == 0] \
[["upload_date", "shared_teks"]].rename(
columns={
"upload_date": "sample_date_string",
"shared_teks": "shared_teks_uploaded_on_generation_date",
})
shared_teks_uploaded_on_generation_date_df.head()
estimated_shared_diagnoses_df = shared_teks_generation_to_upload_df \
.groupby(["upload_date"]).shared_teks.max().reset_index() \
.sort_values(["upload_date"], ascending=False) \
.rename(columns={
"upload_date": "sample_date_string",
"shared_teks": "shared_diagnoses",
})
invalid_shared_diagnoses_dates_mask = \
estimated_shared_diagnoses_df.sample_date_string.isin(invalid_shared_diagnoses_dates)
estimated_shared_diagnoses_df[invalid_shared_diagnoses_dates_mask] = 0
estimated_shared_diagnoses_df.head()
```
### Hourly New TEKs
```
hourly_extracted_teks_df = load_extracted_teks(
mode="Hourly", region=report_backend_identifier, limit=25)
hourly_extracted_teks_df.head()
hourly_new_tek_count_df = hourly_extracted_teks_df \
.groupby("extraction_date_with_hour").tek_list. \
apply(lambda x: set(sum(x, []))).reset_index().copy()
hourly_new_tek_count_df = hourly_new_tek_count_df.set_index("extraction_date_with_hour") \
.sort_index(ascending=True)
hourly_new_tek_count_df["new_tek_list"] = hourly_new_tek_count_df.tek_list.diff()
hourly_new_tek_count_df["new_tek_count"] = hourly_new_tek_count_df.new_tek_list.apply(
lambda x: len(x) if not pd.isna(x) else 0)
hourly_new_tek_count_df.rename(columns={
"new_tek_count": "shared_teks_by_upload_date"}, inplace=True)
hourly_new_tek_count_df = hourly_new_tek_count_df.reset_index()[[
"extraction_date_with_hour", "shared_teks_by_upload_date"]]
hourly_new_tek_count_df.head()
hourly_summary_df = hourly_new_tek_count_df.copy()
hourly_summary_df.set_index("extraction_date_with_hour", inplace=True)
hourly_summary_df = hourly_summary_df.fillna(0).astype(int).reset_index()
hourly_summary_df["datetime_utc"] = pd.to_datetime(
hourly_summary_df.extraction_date_with_hour, format="%Y-%m-%d@%H")
hourly_summary_df.set_index("datetime_utc", inplace=True)
hourly_summary_df = hourly_summary_df.tail(-1)
hourly_summary_df.head()
```
### Data Merge
```
result_summary_df = exposure_keys_summary_df.merge(
new_tek_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = result_summary_df.merge(
shared_teks_uploaded_on_generation_date_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = result_summary_df.merge(
estimated_shared_diagnoses_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = confirmed_df.tail(daily_summary_days).merge(
result_summary_df, on=["sample_date_string"], how="left")
result_summary_df.head()
result_summary_df["sample_date"] = pd.to_datetime(result_summary_df.sample_date_string)
result_summary_df = result_summary_df.merge(source_regions_for_summary_df, how="left")
result_summary_df.set_index(["sample_date", "source_regions"], inplace=True)
result_summary_df.drop(columns=["sample_date_string"], inplace=True)
result_summary_df.sort_index(ascending=False, inplace=True)
result_summary_df.head()
with pd.option_context("mode.use_inf_as_na", True):
result_summary_df = result_summary_df.fillna(0).astype(int)
result_summary_df["teks_per_shared_diagnosis"] = \
(result_summary_df.shared_teks_by_upload_date / result_summary_df.shared_diagnoses).fillna(0)
result_summary_df["shared_diagnoses_per_covid_case"] = \
(result_summary_df.shared_diagnoses / result_summary_df.covid_cases).fillna(0)
result_summary_df.head(daily_plot_days)
weekly_result_summary_df = result_summary_df \
.sort_index(ascending=True).fillna(0).rolling(7).agg({
"covid_cases": "sum",
"shared_teks_by_generation_date": "sum",
"shared_teks_by_upload_date": "sum",
"shared_diagnoses": "sum"
}).sort_index(ascending=False)
with pd.option_context("mode.use_inf_as_na", True):
weekly_result_summary_df = weekly_result_summary_df.fillna(0).astype(int)
weekly_result_summary_df["teks_per_shared_diagnosis"] = \
(weekly_result_summary_df.shared_teks_by_upload_date / weekly_result_summary_df.shared_diagnoses).fillna(0)
weekly_result_summary_df["shared_diagnoses_per_covid_case"] = \
(weekly_result_summary_df.shared_diagnoses / weekly_result_summary_df.covid_cases).fillna(0)
weekly_result_summary_df.head()
last_7_days_summary = weekly_result_summary_df.to_dict(orient="records")[1]
last_7_days_summary
```
## Report Results
```
display_column_name_mapping = {
"sample_date": "Sample\u00A0Date\u00A0(UTC)",
"source_regions": "Source Countries",
"datetime_utc": "Timestamp (UTC)",
"upload_date": "Upload Date (UTC)",
"generation_to_upload_days": "Generation to Upload Period in Days",
"region": "Backend",
"region_x": "Backend\u00A0(A)",
"region_y": "Backend\u00A0(B)",
"common_teks": "Common TEKs Shared Between Backends",
"common_teks_fraction": "Fraction of TEKs in Backend (A) Available in Backend (B)",
"covid_cases": "COVID-19 Cases in Source Countries (7-day Rolling Average)",
"shared_teks_by_generation_date": "Shared TEKs by Generation Date",
"shared_teks_by_upload_date": "Shared TEKs by Upload Date",
"shared_diagnoses": "Shared Diagnoses (Estimation)",
"teks_per_shared_diagnosis": "TEKs Uploaded per Shared Diagnosis",
"shared_diagnoses_per_covid_case": "Usage Ratio (Fraction of Cases in Source Countries Which Shared Diagnosis)",
"shared_teks_uploaded_on_generation_date": "Shared TEKs Uploaded on Generation Date",
}
summary_columns = [
"covid_cases",
"shared_teks_by_generation_date",
"shared_teks_by_upload_date",
"shared_teks_uploaded_on_generation_date",
"shared_diagnoses",
"teks_per_shared_diagnosis",
"shared_diagnoses_per_covid_case",
]
```
### Daily Summary Table
```
result_summary_df_ = result_summary_df.copy()
result_summary_df = result_summary_df[summary_columns]
result_summary_with_display_names_df = result_summary_df \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping)
result_summary_with_display_names_df
```
### Daily Summary Plots
```
result_plot_summary_df = result_summary_df.head(daily_plot_days)[summary_columns] \
.droplevel(level=["source_regions"]) \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping)
summary_ax_list = result_plot_summary_df.sort_index(ascending=True).plot.bar(
title=f"Daily Summary",
rot=45, subplots=True, figsize=(15, 22), legend=False)
ax_ = summary_ax_list[-1]
ax_.get_figure().tight_layout()
ax_.get_figure().subplots_adjust(top=0.95)
ax_.yaxis.set_major_formatter(matplotlib.ticker.PercentFormatter(1.0))
_ = ax_.set_xticklabels(sorted(result_plot_summary_df.index.strftime("%Y-%m-%d").tolist()))
```
### Daily Generation to Upload Period Table
```
display_generation_to_upload_period_pivot_df = \
generation_to_upload_period_pivot_df \
.head(backend_generation_days)
display_generation_to_upload_period_pivot_df \
.head(backend_generation_days) \
.rename_axis(columns=display_column_name_mapping) \
.rename_axis(index=display_column_name_mapping)
fig, generation_to_upload_period_pivot_table_ax = plt.subplots(
figsize=(12, 1 + 0.6 * len(display_generation_to_upload_period_pivot_df)))
generation_to_upload_period_pivot_table_ax.set_title(
"Shared TEKs Generation to Upload Period Table")
sns.heatmap(
data=display_generation_to_upload_period_pivot_df
.rename_axis(columns=display_column_name_mapping)
.rename_axis(index=display_column_name_mapping),
fmt=".0f",
annot=True,
ax=generation_to_upload_period_pivot_table_ax)
generation_to_upload_period_pivot_table_ax.get_figure().tight_layout()
```
### Hourly Summary Plots
```
hourly_summary_ax_list = hourly_summary_df \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.plot.bar(
title=f"Last 24h Summary",
rot=45, subplots=True, legend=False)
ax_ = hourly_summary_ax_list[-1]
ax_.get_figure().tight_layout()
ax_.get_figure().subplots_adjust(top=0.9)
_ = ax_.set_xticklabels(sorted(hourly_summary_df.index.strftime("%Y-%m-%d@%H").tolist()))
```
### Publish Results
```
def get_temporary_image_path() -> str:
return os.path.join(tempfile.gettempdir(), str(uuid.uuid4()) + ".png")
def save_temporary_plot_image(ax):
if isinstance(ax, np.ndarray):
ax = ax[0]
media_path = get_temporary_image_path()
ax.get_figure().savefig(media_path)
return media_path
def save_temporary_dataframe_image(df):
import dataframe_image as dfi
media_path = get_temporary_image_path()
dfi.export(df, media_path)
return media_path
github_repository = os.environ.get("GITHUB_REPOSITORY")
if github_repository is None:
github_repository = "pvieito/Radar-STATS"
github_project_base_url = "https://github.com/" + github_repository
display_formatters = {
display_column_name_mapping["teks_per_shared_diagnosis"]: lambda x: f"{x:.2f}",
display_column_name_mapping["shared_diagnoses_per_covid_case"]: lambda x: f"{x:.2%}",
}
daily_summary_table_html = result_summary_with_display_names_df \
.head(daily_plot_days) \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.to_html(formatters=display_formatters)
multi_backend_summary_table_html = multi_backend_summary_df \
.head(daily_plot_days) \
.rename_axis(columns=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.rename_axis(index=display_column_name_mapping) \
.to_html(formatters=display_formatters)
def format_multi_backend_cross_sharing_fraction(x):
if pd.isna(x):
return "-"
elif round(x * 100, 1) == 0:
return ""
else:
return f"{x:.1%}"
multi_backend_cross_sharing_summary_table_html = multi_backend_cross_sharing_summary_df \
.rename_axis(columns=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.rename_axis(index=display_column_name_mapping) \
.to_html(
classes="table-center",
formatters=display_formatters,
float_format=format_multi_backend_cross_sharing_fraction)
multi_backend_cross_sharing_summary_table_html = \
multi_backend_cross_sharing_summary_table_html \
.replace("<tr>","<tr style=\"text-align: center;\">")
extraction_date_result_summary_df = \
result_summary_df[result_summary_df.index.get_level_values("sample_date") == extraction_date]
extraction_date_result_hourly_summary_df = \
hourly_summary_df[hourly_summary_df.extraction_date_with_hour == extraction_date_with_hour]
covid_cases = \
extraction_date_result_summary_df.covid_cases.item()
shared_teks_by_generation_date = \
extraction_date_result_summary_df.shared_teks_by_generation_date.item()
shared_teks_by_upload_date = \
extraction_date_result_summary_df.shared_teks_by_upload_date.item()
shared_diagnoses = \
extraction_date_result_summary_df.shared_diagnoses.item()
teks_per_shared_diagnosis = \
extraction_date_result_summary_df.teks_per_shared_diagnosis.item()
shared_diagnoses_per_covid_case = \
extraction_date_result_summary_df.shared_diagnoses_per_covid_case.item()
shared_teks_by_upload_date_last_hour = \
extraction_date_result_hourly_summary_df.shared_teks_by_upload_date.sum().astype(int)
display_source_regions = ", ".join(report_source_regions)
if len(report_source_regions) == 1:
display_brief_source_regions = report_source_regions[0]
else:
display_brief_source_regions = f"{len(report_source_regions)} 🇪🇺"
summary_plots_image_path = save_temporary_plot_image(
ax=summary_ax_list)
summary_table_image_path = save_temporary_dataframe_image(
df=result_summary_with_display_names_df)
hourly_summary_plots_image_path = save_temporary_plot_image(
ax=hourly_summary_ax_list)
multi_backend_summary_table_image_path = save_temporary_dataframe_image(
df=multi_backend_summary_df)
generation_to_upload_period_pivot_table_image_path = save_temporary_plot_image(
ax=generation_to_upload_period_pivot_table_ax)
```
### Save Results
```
report_resources_path_prefix = "Data/Resources/Current/RadarCOVID-Report-"
result_summary_df.to_csv(
report_resources_path_prefix + "Summary-Table.csv")
result_summary_df.to_html(
report_resources_path_prefix + "Summary-Table.html")
hourly_summary_df.to_csv(
report_resources_path_prefix + "Hourly-Summary-Table.csv")
multi_backend_summary_df.to_csv(
report_resources_path_prefix + "Multi-Backend-Summary-Table.csv")
multi_backend_cross_sharing_summary_df.to_csv(
report_resources_path_prefix + "Multi-Backend-Cross-Sharing-Summary-Table.csv")
generation_to_upload_period_pivot_df.to_csv(
report_resources_path_prefix + "Generation-Upload-Period-Table.csv")
_ = shutil.copyfile(
summary_plots_image_path,
report_resources_path_prefix + "Summary-Plots.png")
_ = shutil.copyfile(
summary_table_image_path,
report_resources_path_prefix + "Summary-Table.png")
_ = shutil.copyfile(
hourly_summary_plots_image_path,
report_resources_path_prefix + "Hourly-Summary-Plots.png")
_ = shutil.copyfile(
multi_backend_summary_table_image_path,
report_resources_path_prefix + "Multi-Backend-Summary-Table.png")
_ = shutil.copyfile(
generation_to_upload_period_pivot_table_image_path,
report_resources_path_prefix + "Generation-Upload-Period-Table.png")
```
### Publish Results as JSON
```
def generate_summary_api_results(df: pd.DataFrame) -> list:
api_df = df.reset_index().copy()
api_df["sample_date_string"] = \
api_df["sample_date"].dt.strftime("%Y-%m-%d")
api_df["source_regions"] = \
api_df["source_regions"].apply(lambda x: x.split(","))
return api_df.to_dict(orient="records")
summary_api_results = \
generate_summary_api_results(df=result_summary_df)
today_summary_api_results = \
generate_summary_api_results(df=extraction_date_result_summary_df)[0]
summary_results = dict(
backend_identifier=report_backend_identifier,
source_regions=report_source_regions,
extraction_datetime=extraction_datetime,
extraction_date=extraction_date,
extraction_date_with_hour=extraction_date_with_hour,
last_hour=dict(
shared_teks_by_upload_date=shared_teks_by_upload_date_last_hour,
shared_diagnoses=0,
),
today=today_summary_api_results,
last_7_days=last_7_days_summary,
daily_results=summary_api_results)
summary_results = \
json.loads(pd.Series([summary_results]).to_json(orient="records"))[0]
with open(report_resources_path_prefix + "Summary-Results.json", "w") as f:
json.dump(summary_results, f, indent=4)
```
### Publish on README
```
with open("Data/Templates/README.md", "r") as f:
readme_contents = f.read()
readme_contents = readme_contents.format(
extraction_date_with_hour=extraction_date_with_hour,
github_project_base_url=github_project_base_url,
daily_summary_table_html=daily_summary_table_html,
multi_backend_summary_table_html=multi_backend_summary_table_html,
multi_backend_cross_sharing_summary_table_html=multi_backend_cross_sharing_summary_table_html,
display_source_regions=display_source_regions)
with open("README.md", "w") as f:
f.write(readme_contents)
```
### Publish on Twitter
```
enable_share_to_twitter = os.environ.get("RADARCOVID_REPORT__ENABLE_PUBLISH_ON_TWITTER")
github_event_name = os.environ.get("GITHUB_EVENT_NAME")
if enable_share_to_twitter and github_event_name == "schedule" and \
(shared_teks_by_upload_date_last_hour or not are_today_results_partial):
import tweepy
twitter_api_auth_keys = os.environ["RADARCOVID_REPORT__TWITTER_API_AUTH_KEYS"]
twitter_api_auth_keys = twitter_api_auth_keys.split(":")
auth = tweepy.OAuthHandler(twitter_api_auth_keys[0], twitter_api_auth_keys[1])
auth.set_access_token(twitter_api_auth_keys[2], twitter_api_auth_keys[3])
api = tweepy.API(auth)
summary_plots_media = api.media_upload(summary_plots_image_path)
summary_table_media = api.media_upload(summary_table_image_path)
generation_to_upload_period_pivot_table_image_media = api.media_upload(generation_to_upload_period_pivot_table_image_path)
media_ids = [
summary_plots_media.media_id,
summary_table_media.media_id,
generation_to_upload_period_pivot_table_image_media.media_id,
]
if are_today_results_partial:
today_addendum = " (Partial)"
else:
today_addendum = ""
status = textwrap.dedent(f"""
#RadarCOVID – {extraction_date_with_hour}
Source Countries: {display_brief_source_regions}
Today{today_addendum}:
- Uploaded TEKs: {shared_teks_by_upload_date:.0f} ({shared_teks_by_upload_date_last_hour:+d} last hour)
- Shared Diagnoses: ≤{shared_diagnoses:.0f}
- Usage Ratio: ≤{shared_diagnoses_per_covid_case:.2%}
Last 7 Days:
- Shared Diagnoses: ≤{last_7_days_summary["shared_diagnoses"]:.0f}
- Usage Ratio: ≤{last_7_days_summary["shared_diagnoses_per_covid_case"]:.2%}
Info: {github_project_base_url}#documentation
""")
status = status.encode(encoding="utf-8")
api.update_status(status=status, media_ids=media_ids)
```
|
github_jupyter
|
# Plotting the Correlation between Air Quality and Weather
```
# If done right, this program should
# Shoutout to my bois at StackOverflow - you da real MVPs
# Shoutout to my bois over at StackOverflow - couldn't've done it without you
import pandas as pd
import numpy as np
from bokeh.plotting import figure
from bokeh.io import show
from bokeh.models import HoverTool, Label
import scipy.stats
weatherfile = input("Which weather file would you like to use? ")
df = pd.read_csv(weatherfile)
temp = df.as_matrix(columns=df.columns[3:4])
temp = temp.ravel()
humidity = df.as_matrix(columns=df.columns[4:5])
humidity = humidity.ravel()
pressure = df.as_matrix(columns=df.columns[5:])
pressure = pressure.ravel()
unix_timeweather = df.as_matrix(columns=df.columns[2:3])
i = 0
w_used = eval(raw_input("Which data set do you want? temp, humidity, or pressure? "))
######################################################################################
aqfile = input("Which air quality file would you like to use? ")
df2 = pd.read_csv(aqfile)
PM25 = df2.as_matrix(columns=df2.columns[4:5])
PM1 = df2.as_matrix(columns=df2.columns[3:4])
PM10 = df2.as_matrix(columns=df2.columns[5:])
unix_timeaq = df2.as_matrix(columns=df2.columns[2:3])
aq_used = eval(raw_input("Which data set do you want? PM1, PM25, or PM10? "))
######################################################################################
def find_nearest(array, value):
array = np.asarray(array)
idx = (np.abs(array - value)).argmin()
if np.abs(array[idx]-value) <= 30:
# print str(value) + "Vs" + str(array[idx])
return idx
else:
return None
#######################################################################################
def make_usable(array1, array):
i = len(array1) - 1
while i > 0:
if np.isnan(array[i]) or np.isnan(array1[i]):
del array[i]
del array1[i]
i = i - 1
#######################################################################################
weatherarr = []
aqarr = []
i = 0
while i < len(aq_used):
aqarr.append(float(aq_used[i]))
nearest_time = find_nearest(unix_timeweather, unix_timeaq[i])
if nearest_time is None:
weatherarr.append(np.nan)
else:
weatherarr.append(float(w_used[nearest_time]))
i = i+1
# Plot the arrays #####################################################################
make_usable(weatherarr,aqarr)
hoverp = HoverTool(tooltips=[("(x,y)", "($x, $y)")])
p = figure(tools = [hoverp])
correlation = Label(x=50, y=50, x_units='screen', y_units='screen', text="Pearson r and p: "+ str(scipy.stats.pearsonr(weatherarr, aqarr)),render_mode='css',
border_line_color='black', border_line_alpha=1.0,
background_fill_color='white', background_fill_alpha=1.0)
p.add_layout(correlation)
p.circle(x = weatherarr, y = aqarr, color = "firebrick")
show(p)
```
|
github_jupyter
|
# Prosper Loan Data Exploration
## By Abhishek Tiwari
# Preliminary Wrangling
This data set contains information on peer to peer loans facilitated by credit company Prosper
```
# import all packages
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
df = pd.read_csv('prosperLoanData.csv')
df.head()
df.info()
df.describe()
df.sample(10)
```
Note that this data set contains 81 columns. For the purpose of this analysis I’ve took the following columns (variables):
```
target_columns = [
'Term', 'LoanStatus', 'BorrowerRate', 'ProsperRating (Alpha)', 'ListingCategory (numeric)', 'EmploymentStatus',
'DelinquenciesLast7Years', 'StatedMonthlyIncome', 'TotalProsperLoans', 'LoanOriginalAmount',
'LoanOriginationDate', 'Recommendations', 'Investors'
]
target_df = df[target_columns]
target_df.sample(10)
```
Since Prosper use their own proprietary Prosper Rating only since 2009, we have a lot of missing values in ProsperRating column. Let's drop these missing values:
```
target_df.info()
target_df.describe()
```
Since Prosper use their own proprietary Prosper Rating only since 2009, we have a lot of missing values in ProsperRating column. Let's drop these missing values:
```
target_df = target_df.dropna(subset=['ProsperRating (Alpha)']).reset_index()
```
Convert LoanOriginationDate to datetime datatype:
```
target_df['LoanOriginationDate'] = pd.to_datetime(target_df['LoanOriginationDate'])
target_df['TotalProsperLoans'] = target_df['TotalProsperLoans'].fillna(0)
target_df.info()
```
### What is/are the main feature(s) of interest in your dataset?
> Trying to figure out what features can be used to predict default on credit. Also i would like to check what are major factors connected with prosper credit rating.
### What features in the dataset do you think will help support your investigation into your feature(s) of interest?
> I think that the borrowers Prosper rating will have the highest impact on chances of default. Also I expect that loan amount will play a major role and maybe the category of credit. Prosper rating will depend on stated income and employment status.
## Univariate Exploration
### Loan status
```
# setting color
base_color = sns.color_palette()[0]
plt.xticks(rotation=90)
sns.countplot(data = target_df, x = 'LoanStatus', color = base_color);
```
Observation 1:
* Most of the loans in the data set are actually current loans.
* Past due loans are split in several groups based on the length of payment delay.
* Other big part is completed loans, defaulted loans compromise a minority, however chargedoff loans also comporomise a substanial amount.
### Employment Status
```
sns.countplot(data = target_df, x = 'EmploymentStatus', color = base_color);
plt.xticks(rotation = 90);
```
Observation 2:
* The majority of borrowers are employed and all other categories as small part of borrowers.
* In small Group full time has highest, after that self empolyed are there and so on.
### Stated Monthly Income
```
plt.hist(data=target_df, x='StatedMonthlyIncome', bins=1000);
```
(**Note**: Distribution of stated monthly income is highly skewed to the right. so, we have to check how many outliers are there)
```
income_std = target_df['StatedMonthlyIncome'].std()
income_mean = target_df['StatedMonthlyIncome'].mean()
boundary = income_mean + income_std * 3
len(target_df[target_df['StatedMonthlyIncome'] >= boundary])
```
**After Zooming the Graph We Get This**
```
plt.hist(data=target_df, x='StatedMonthlyIncome', bins=1000);
plt.xlim(0, boundary);
```
Observation 3:
* With a boundary of mean and 3 times standard deviations distribution of monthly income still has noticeable right skew but now we can see that mode is about 5000.
### Discuss the distribution(s) of your variable(s) of interest. Were there any unusual points? Did you need to perform any transformations?
> Distribution of monthly stated income is very awkward: with a lot of outliers and very large range but still it was right skew. The majority of borrowers are employed and all other categories as small part of borrowers and most of the loans in the data set are actually current loans.
### Of the features you investigated, were there any unusual distributions? Did you perform any operations on the data to tidy, adjust, or change the form of the data? If so, why did you do this?
> The majority of loans are actually current loans. Since our main goal is to define driving factors of outcome of loan we are not interested in any current loans.
## Bivariate Exploration
```
#I'm just adjusting the form of data
condition = (target_df['LoanStatus'] == 'Completed') | (target_df['LoanStatus'] == 'Defaulted') |\
(target_df['LoanStatus'] == 'Chargedoff')
target_df = target_df[condition]
def change_to_defaulted(row):
if row['LoanStatus'] == 'Chargedoff':
return 'Defaulted'
else:
return row['LoanStatus']
target_df['LoanStatus'] = target_df.apply(change_to_defaulted, axis=1)
target_df['LoanStatus'].value_counts()
```
**After transforming dataset we have 19664 completed loans and 6341 defaulted.**
```
categories = {1: 'Debt Consolidation', 2: 'Home Improvement', 3: 'Business', 6: 'Auto', 7: 'Other'}
def reduce_categorie(row):
loan_category = row['ListingCategory (numeric)']
if loan_category in categories:
return categories[loan_category]
else:
return categories[7]
target_df['ListingCategory (numeric)'] = target_df.apply(reduce_categorie, axis=1)
target_df['ListingCategory (numeric)'].value_counts()
```
Variable Listing Category is set up as numeric and most of the values have very `low frequency`, for the easier visualization so we have change it to `categorical and reduce the number of categories`.
### Status and Prosper Rating:
```
sns.countplot(data = target_df, x = 'LoanStatus', hue = 'ProsperRating (Alpha)', palette = 'Blues')
```
Observation 1:
* The `most frequent` rating among defaulted loans is actually `D`.
* And the `most frequent` rating among Completed is also` D `and second highest is A and so on.
### Credit Start with Listing Category:
```
sns.countplot(data = target_df, x = 'LoanStatus', hue = 'ListingCategory (numeric)', palette = 'Blues');
```
Observation 2:
* In both of the Graphs the `debt Consolidation` have `most frequency among all of them`.
## Loan Status and Loan Amount
```
sns.boxplot(data = target_df, x = 'LoanStatus', y = 'LoanOriginalAmount', color = base_color);
```
Observation 3:
* As from Above Graph we can state that `defaulted credits` tend to be `smaller` than `completed credits` onces.
## Prosper Rating and Employment Status
```
plt.figure(figsize = [12, 10])
sns.countplot(data = target_df, x = 'ProsperRating (Alpha)', hue = 'EmploymentStatus', palette = 'Blues');
```
Observation 4:
* Lower ratings seem to have greater proportions of individuals with employment status Not Employed, Self-employed, Retired and Part-Time.
## Talk about some of the relationships you observed in this part of the investigation. How did the feature(s) of interest vary with other features in the dataset?
> In Loan status vs Loan amount defaulted credits tend to be smaller than completed credits onces. Employment status of individuals with lower ratings tends to be 'Not employed', 'Self-employed', 'Retired' or 'Part-time'.
## Did you observe any interesting relationships between the other features (not the main feature(s) of interest)?
> Prosper rating D is the most frequent rating among defaulted credits.
## Multivariate Exploration
## Rating, Loan Amount and Loan Status
```
plt.figure(figsize = [12, 8])
sns.boxplot(data=target_df, x='ProsperRating (Alpha)', y='LoanOriginalAmount', hue='LoanStatus');
```
Observation 1:
* Except for the lowest ratings defaulted credits tend to be larger than completed.
* Most of the defaulted credits comes from individuals with low Prosper rating.
## Relationships between Credit category, Credit rating and outcome of Credit.
```
sns.catplot(x = 'ProsperRating (Alpha)', hue = 'LoanStatus', col = 'ListingCategory (numeric)',
data = target_df, kind = 'count', palette = 'Blues', col_wrap = 3);
```
Observation 2:
* There are 5 graphs in the second one has much up and downs in it other than all of them.
* There is no substantial difference for default rates in different categories broken up by ratings.
## Amount, Listing Category Loan and Loan Status Interact
```
plt.figure(figsize = [12, 8])
sns.violinplot(data=target_df, x='ListingCategory (numeric)', y='LoanOriginalAmount', hue='LoanStatus');
```
Observation 3:
* Except for Auto, Business and Home Improvemrnt dont have nearly equal mean amoong all of them.
* Business category tend to have larger amount.
## Talk about some of the relationships you observed in this part of the investigation. Were there features that strengthened each other in terms of looking at your feature(s) of interest?
> Our initial assumptions were strengthened. Most of the defaulted credits comes from individuals with low Prosper rating and Business category tend to have larger amount.
## Were there any interesting or surprising interactions between features?
> Interesting find was that defaulted credits for individuals with high Prosper ratings tend to be larger than completed credits.
|
github_jupyter
|
## Compile per MOA p value for shuffled comparison
```
import pathlib
import numpy as np
import pandas as pd
import scipy.stats
# Load L2 distances per MOA
cp_l2_file = pathlib.Path("..", "cell-painting", "3.application", "L2_distances_with_moas.csv")
cp_l2_df = pd.read_csv(cp_l2_file).assign(shuffled="real")
cp_l2_df.loc[cp_l2_df.Model.str.contains("Shuffled"), "shuffled"] = "shuffled"
cp_l2_df = cp_l2_df.assign(
architecture=[x[-1] for x in cp_l2_df.Model.str.split(" ")],
assay="CellPainting",
metric="L2 distance"
).rename(columns={"L2 Distance": "metric_value"})
print(cp_l2_df.shape)
cp_l2_df.head()
# Load Pearson correlations per MOA
cp_file = pathlib.Path("..", "cell-painting", "3.application", "pearson_with_moas.csv")
cp_pearson_df = pd.read_csv(cp_file).assign(shuffled="real")
cp_pearson_df.loc[cp_pearson_df.Model.str.contains("Shuffled"), "shuffled"] = "shuffled"
cp_pearson_df = cp_pearson_df.assign(
architecture=[x[-1] for x in cp_pearson_df.Model.str.split(" ")],
assay="CellPainting",
metric="Pearson correlation"
).rename(columns={"Pearson": "metric_value"})
print(cp_pearson_df.shape)
cp_pearson_df.head()
# Combine data
cp_df = pd.concat([cp_l2_df, cp_pearson_df]).reset_index(drop=True)
print(cp_df.shape)
cp_df.head()
all_moas = cp_df.MOA.unique().tolist()
print(len(all_moas))
all_metrics = cp_df.metric.unique().tolist()
all_architectures = cp_df.architecture.unique().tolist()
all_architectures
results_df = []
for metric in all_metrics:
for moa in all_moas:
for arch in all_architectures:
# subset data to include moa per architecture
sub_cp_df = (
cp_df
.query(f"metric == '{metric}'")
.query(f"architecture == '{arch}'")
.query(f"MOA == '{moa}'")
.reset_index(drop=True)
)
real_ = sub_cp_df.query("shuffled == 'real'").loc[:, "metric_value"].tolist()
shuff_ = sub_cp_df.query("shuffled != 'real'").loc[:, "metric_value"].tolist()
# Calculate zscore consistently with other experiments
zscore_result = scipy.stats.zscore(shuff_ + real_)[-1]
results_df.append([moa, arch, zscore_result, metric])
# Compile results
results_df = pd.DataFrame(results_df, columns=["MOA", "model", "zscore", "metric"])
print(results_df.shape)
results_df.head()
# Output data
output_file = pathlib.Path("data", "MOA_LSA_metrics.tsv")
results_df.to_csv(output_file, sep="\t", index=False)
```
|
github_jupyter
|
# Image similarity estimation using a Siamese Network with a contrastive loss
**Author:** Mehdi<br>
**Date created:** 2021/05/06<br>
**Last modified:** 2021/05/06<br>
**ORIGINAL SOURCE:** https://github.com/keras-team/keras-io/blob/master/examples/vision/ipynb/siamese_contrastive.ipynb<br>
**Description:** Similarity learning using a siamese network trained with a contrastive loss.
### NOTE:
**We adapted the code for 1D data.**
## Introduction
[Siamese Networks](https://en.wikipedia.org/wiki/Siamese_neural_network)
are neural networks which share weights between two or more sister networks,
each producing embedding vectors of its respective inputs.
In supervised similarity learning, the networks are then trained to maximize the
contrast (distance) between embeddings of inputs of different classes, while minimizing the distance between
embeddings of similar classes, resulting in embedding spaces that reflect
the class segmentation of the training inputs.
## Setup
```
import random
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import matplotlib.pyplot as plt
```
## Load the MNIST dataset
```
(x_train_val, y_train_val), (x_test_2D, y_test) = keras.datasets.mnist.load_data()
# Change the data type to a floating point format
x_train_val = x_train_val.astype("float32")
x_test_2D = x_test_2D.astype("float32")
```
## Define training and validation sets
```
# Keep 50% of train_val in validation set
x_train_2D, x_val_2D = x_train_val[:30000], x_train_val[30000:]
y_train, y_val = y_train_val[:30000], y_train_val[30000:]
del x_train_val, y_train_val
```
## Convert 2D to 1D
```
print(x_train_2D.shape, x_val_2D.shape, x_test_2D.shape)
# convert 2D image to 1D image
size = 28*28
x_train = x_train_2D.reshape(x_train_2D.shape[0], size)
x_val = x_val_2D.reshape(x_val_2D.shape[0], size)
x_test = x_test_2D.reshape(x_test_2D.shape[0], size)
print(x_train.shape, x_val.shape, x_test.shape)
```
## Create pairs of images
We will train the model to differentiate between digits of different classes. For
example, digit `0` needs to be differentiated from the rest of the
digits (`1` through `9`), digit `1` - from `0` and `2` through `9`, and so on.
To carry this out, we will select N random images from class A (for example,
for digit `0`) and pair them with N random images from another class B
(for example, for digit `1`). Then, we can repeat this process for all classes
of digits (until digit `9`). Once we have paired digit `0` with other digits,
we can repeat this process for the remaining classes for the rest of the digits
(from `1` until `9`).
```
def make_pairs(x, y):
"""Creates a tuple containing image pairs with corresponding label.
Arguments:
x: List containing images, each index in this list corresponds to one image.
y: List containing labels, each label with datatype of `int`.
Returns:
Tuple containing two numpy arrays as (pairs_of_samples, labels),
where pairs_of_samples' shape is (2len(x), 2,n_features_dims) and
labels are a binary array of shape (2len(x)).
"""
num_classes = max(y) + 1
digit_indices = [np.where(y == i)[0] for i in range(num_classes)]
pairs = []
labels = []
for idx1 in range(len(x)):
# add a matching example
x1 = x[idx1]
label1 = y[idx1]
idx2 = random.choice(digit_indices[label1])
x2 = x[idx2]
pairs += [[x1, x2]]
labels += [1]
# add a non-matching example
label2 = random.randint(0, num_classes - 1)
while label2 == label1:
label2 = random.randint(0, num_classes - 1)
idx2 = random.choice(digit_indices[label2])
x2 = x[idx2]
pairs += [[x1, x2]]
labels += [0]
return np.array(pairs), np.array(labels).astype("float32")
# make train pairs
pairs_train, labels_train = make_pairs(x_train, y_train)
# make validation pairs
pairs_val, labels_val = make_pairs(x_val, y_val)
# make test pairs
pairs_test, labels_test = make_pairs(x_test, y_test)
print(pairs_train.shape, pairs_val.shape, pairs_test.shape)
```
We get:
- We have 60,000 pairs
- Each pair contains 2 images
- Each image has shape `(784)`
Split the training pairs
```
x_train_1 = pairs_train[:, 0]
x_train_2 = pairs_train[:, 1]
```
Split the validation pairs
```
x_val_1 = pairs_val[:, 0]
x_val_2 = pairs_val[:, 1]
```
Split the test pairs
```
x_test_1 = pairs_test[:, 0] # x_test_1.shape = (20000, 784)
x_test_2 = pairs_test[:, 1]
```
## Visualize pairs and their labels
```
def visualize(pairs, labels, to_show=6, num_col=3, predictions=None, test=False):
"""Creates a plot of pairs and labels, and prediction if it's test dataset.
Arguments:
pairs: Numpy Array, of pairs to visualize, having shape
(Number of pairs, 2, 28, 28).
to_show: Int, number of examples to visualize (default is 6)
`to_show` must be an integral multiple of `num_col`.
Otherwise it will be trimmed if it is greater than num_col,
and incremented if if it is less then num_col.
num_col: Int, number of images in one row - (default is 3)
For test and train respectively, it should not exceed 3 and 7.
predictions: Numpy Array of predictions with shape (to_show, 1) -
(default is None)
Must be passed when test=True.
test: Boolean telling whether the dataset being visualized is
train dataset or test dataset - (default False).
Returns:
None.
"""
# Define num_row
# If to_show % num_col != 0
# trim to_show,
# to trim to_show limit num_row to the point where
# to_show % num_col == 0
#
# If to_show//num_col == 0
# then it means num_col is greater then to_show
# increment to_show
# to increment to_show set num_row to 1
num_row = to_show // num_col if to_show // num_col != 0 else 1
# `to_show` must be an integral multiple of `num_col`
# we found num_row and we have num_col
# to increment or decrement to_show
# to make it integral multiple of `num_col`
# simply set it equal to num_row * num_col
to_show = num_row * num_col
# Plot the images
fig, axes = plt.subplots(num_row, num_col, figsize=(5, 5))
for i in range(to_show):
# If the number of rows is 1, the axes array is one-dimensional
if num_row == 1:
ax = axes[i % num_col]
else:
ax = axes[i // num_col, i % num_col]
ax.imshow(tf.concat([pairs[i][0].reshape(28,28), pairs[i][1].reshape(28,28)], axis=1), cmap="gray")
ax.set_axis_off()
if test:
ax.set_title("True: {} | Pred: {:.5f}".format(labels[i], predictions[i][0][0])) # TODO: check shape of predictions
else:
ax.set_title("Label: {}".format(labels[i]))
if test:
plt.tight_layout(rect=(0, 0, 1.9, 1.9), w_pad=0.0)
else:
plt.tight_layout(rect=(0, 0, 1.5, 1.5))
plt.show()
```
Inspect training pairs
```
visualize(pairs_train[:-1], labels_train[:-1], to_show=4, num_col=4)
```
Inspect validation pairs
```
visualize(pairs_val[:-1], labels_val[:-1], to_show=4, num_col=4)
```
Inspect test pairs
```
visualize(pairs_test[:-1], labels_test[:-1], to_show=4, num_col=4)
```
## Define the model
There are be two input layers, each leading to its own network, which
produces embeddings. A `Lambda` layer then merges them using an
[Euclidean distance](https://en.wikipedia.org/wiki/Euclidean_distance) and the
merged output is fed to the final network.
```
# Provided two tensors t1 and t2
# Euclidean distance = sqrt(sum(square(t1-t2)))
def euclidean_distance(vects):
"""Find the Euclidean distance between two vectors.
Arguments:
vects: List containing two tensors of same length.
Returns:
Tensor containing euclidean distance
(as floating point value) between vectors.
"""
x, y = vects
sum_square = tf.math.reduce_sum(tf.math.square(x - y), axis=1, keepdims=True)
return tf.math.sqrt(tf.math.maximum(sum_square, tf.keras.backend.epsilon()))
def make_model(input_shape):
input = layers.Input(input_shape)
x = tf.keras.layers.BatchNormalization()(input)
x = layers.Conv1D(4, 5, activation="tanh")(x)
x = layers.AveragePooling1D(pool_size=2)(x)
x = layers.Conv1D(16, 5, activation="tanh")(x)
x = layers.AveragePooling1D(pool_size=2)(x)
x = layers.Conv1D(32, 5, activation="tanh")(x)
x = layers.AveragePooling1D(pool_size=2)(x)
x = tf.keras.layers.BatchNormalization()(x)
x = layers.Dense(10, activation="tanh")(x)
embedding_network = keras.Model(input, x)
input_1 = layers.Input(input_shape)
input_2 = layers.Input(input_shape)
# As mentioned above, Siamese Network share weights between
# tower networks (sister networks). To allow this, we will use
# same embedding network for both tower networks.
tower_1 = embedding_network(input_1)
tower_2 = embedding_network(input_2)
merge_layer = layers.Lambda(euclidean_distance)([tower_1, tower_2])
normal_layer = tf.keras.layers.BatchNormalization()(merge_layer)
output_layer = layers.Dense(1, activation="sigmoid")(normal_layer)
siamese = keras.Model(inputs=[input_1, input_2], outputs=output_layer)
return siamese, embedding_network
siamese, embedding_network = make_model((784,1))
embedding_network.summary()
siamese.summary()
```
## Define the constrastive Loss
```
def loss(margin=1):
"""Provides 'constrastive_loss' an enclosing scope with variable 'margin'.
Arguments:
margin: Integer, defines the baseline for distance for which pairs
should be classified as dissimilar. - (default is 1).
Returns:
'constrastive_loss' function with data ('margin') attached.
"""
# Contrastive loss = mean( (1-true_value) * square(prediction) +
# true_value * square( max(margin-prediction, 0) ))
def contrastive_loss(y_true, y_pred):
"""Calculates the constrastive loss.
Arguments:
y_true: List of labels, each label is of type float32.
y_pred: List of predictions of same length as of y_true,
each label is of type float32.
Returns:
A tensor containing constrastive loss as floating point value.
"""
square_pred = tf.math.square(y_pred)
margin_square = tf.math.square(tf.math.maximum(margin - (y_pred), 0))
return tf.math.reduce_mean(
(1 - y_true) * square_pred + (y_true) * margin_square
)
return contrastive_loss
```
## Hyperparameters
```
epochs = 10
batch_size = 16
margin = 1 # Margin for constrastive loss.
```
## Compile the model with the contrastive loss
```
siamese.compile(loss=loss(margin=margin), optimizer="RMSprop", metrics=["accuracy"])
```
## Train the model
```
history = siamese.fit(
[x_train_1, x_train_2],
labels_train,
validation_data=([x_val_1, x_val_2], labels_val),
batch_size=batch_size,
epochs=epochs,
)
```
## Visualize results
```
def plt_metric(history, metric, title, has_valid=True):
"""Plots the given 'metric' from 'history'.
Arguments:
history: history attribute of History object returned from Model.fit.
metric: Metric to plot, a string value present as key in 'history'.
title: A string to be used as title of plot.
has_valid: Boolean, true if valid data was passed to Model.fit else false.
Returns:
None.
"""
plt.plot(history[metric])
if has_valid:
plt.plot(history["val_" + metric])
plt.legend(["train", "validation"], loc="upper left")
plt.title(title)
plt.ylabel(metric)
plt.xlabel("epoch")
plt.show()
# Plot the accuracy
plt_metric(history=history.history, metric="accuracy", title="Model accuracy")
# Plot the constrastive loss
plt_metric(history=history.history, metric="loss", title="Constrastive Loss")
```
## Evaluate the model
```
results = siamese.evaluate([x_test_1, x_test_2], labels_test)
print("test loss, test acc:", results)
```
## Visualize the predictions
```
predictions = siamese.predict([x_test_1, x_test_2])
visualize(pairs_test, labels_test, to_show=3, predictions=predictions, test=True)
```
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Ragged Tensors
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/beta/guide/ragged_tensors"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/r2/guide/ragged_tensors.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/r2/guide/ragged_tensors.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/site/en/r2/guide/ragged_tensors.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
## Setup
```
from __future__ import absolute_import, division, print_function, unicode_literals
import math
!pip install tensorflow==2.0.0-beta0
import tensorflow as tf
```
## Overview
Your data comes in many shapes; your tensors should too.
*Ragged tensors* are the TensorFlow equivalent of nested variable-length
lists. They make it easy to store and process data with non-uniform shapes,
including:
* Variable-length features, such as the set of actors in a movie.
* Batches of variable-length sequential inputs, such as sentences or video
clips.
* Hierarchical inputs, such as text documents that are subdivided into
sections, paragraphs, sentences, and words.
* Individual fields in structured inputs, such as protocol buffers.
### What you can do with a ragged tensor
Ragged tensors are supported by more than a hundred TensorFlow operations,
including math operations (such as `tf.add` and `tf.reduce_mean`), array operations
(such as `tf.concat` and `tf.tile`), string manipulation ops (such as
`tf.substr`), and many others:
```
digits = tf.ragged.constant([[3, 1, 4, 1], [], [5, 9, 2], [6], []])
words = tf.ragged.constant([["So", "long"], ["thanks", "for", "all", "the", "fish"]])
print(tf.add(digits, 3))
print(tf.reduce_mean(digits, axis=1))
print(tf.concat([digits, [[5, 3]]], axis=0))
print(tf.tile(digits, [1, 2]))
print(tf.strings.substr(words, 0, 2))
```
There are also a number of methods and operations that are
specific to ragged tensors, including factory methods, conversion methods,
and value-mapping operations.
For a list of supported ops, see the `tf.ragged` package
documentation.
As with normal tensors, you can use Python-style indexing to access specific
slices of a ragged tensor. For more information, see the section on
**Indexing** below.
```
print(digits[0]) # First row
print(digits[:, :2]) # First two values in each row.
print(digits[:, -2:]) # Last two values in each row.
```
And just like normal tensors, you can use Python arithmetic and comparison
operators to perform elementwise operations. For more information, see the section on
**Overloaded Operators** below.
```
print(digits + 3)
print(digits + tf.ragged.constant([[1, 2, 3, 4], [], [5, 6, 7], [8], []]))
```
If you need to perform an elementwise transformation to the values of a `RaggedTensor`, you can use `tf.ragged.map_flat_values`, which takes a function plus one or more arguments, and applies the function to transform the `RaggedTensor`'s values.
```
times_two_plus_one = lambda x: x * 2 + 1
print(tf.ragged.map_flat_values(times_two_plus_one, digits))
```
### Constructing a ragged tensor
The simplest way to construct a ragged tensor is using
`tf.ragged.constant`, which builds the
`RaggedTensor` corresponding to a given nested Python `list`:
```
sentences = tf.ragged.constant([
["Let's", "build", "some", "ragged", "tensors", "!"],
["We", "can", "use", "tf.ragged.constant", "."]])
print(sentences)
paragraphs = tf.ragged.constant([
[['I', 'have', 'a', 'cat'], ['His', 'name', 'is', 'Mat']],
[['Do', 'you', 'want', 'to', 'come', 'visit'], ["I'm", 'free', 'tomorrow']],
])
print(paragraphs)
```
Ragged tensors can also be constructed by pairing flat *values* tensors with
*row-partitioning* tensors indicating how those values should be divided into
rows, using factory classmethods such as `tf.RaggedTensor.from_value_rowids`,
`tf.RaggedTensor.from_row_lengths`, and
`tf.RaggedTensor.from_row_splits`.
#### `tf.RaggedTensor.from_value_rowids`
If you know which row each value belongs in, then you can build a `RaggedTensor` using a `value_rowids` row-partitioning tensor:
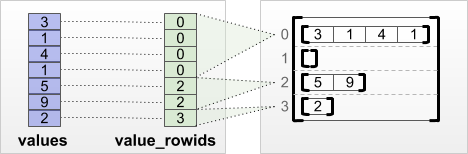
```
print(tf.RaggedTensor.from_value_rowids(
values=[3, 1, 4, 1, 5, 9, 2, 6],
value_rowids=[0, 0, 0, 0, 2, 2, 2, 3]))
```
#### `tf.RaggedTensor.from_row_lengths`
If you know how long each row is, then you can use a `row_lengths` row-partitioning tensor:
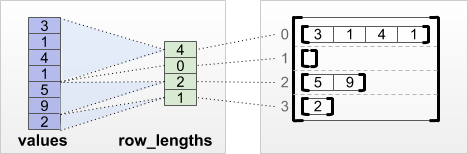
```
print(tf.RaggedTensor.from_row_lengths(
values=[3, 1, 4, 1, 5, 9, 2, 6],
row_lengths=[4, 0, 3, 1]))
```
#### `tf.RaggedTensor.from_row_splits`
If you know the index where each row starts and ends, then you can use a `row_splits` row-partitioning tensor:
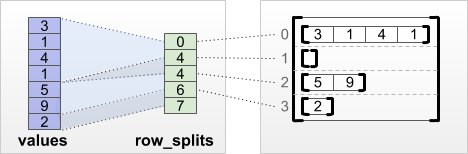
```
print(tf.RaggedTensor.from_row_splits(
values=[3, 1, 4, 1, 5, 9, 2, 6],
row_splits=[0, 4, 4, 7, 8]))
```
See the `tf.RaggedTensor` class documentation for a full list of factory methods.
### What you can store in a ragged tensor
As with normal `Tensor`s, the values in a `RaggedTensor` must all have the same
type; and the values must all be at the same nesting depth (the *rank* of the
tensor):
```
print(tf.ragged.constant([["Hi"], ["How", "are", "you"]])) # ok: type=string, rank=2
print(tf.ragged.constant([[[1, 2], [3]], [[4, 5]]])) # ok: type=int32, rank=3
try:
tf.ragged.constant([["one", "two"], [3, 4]]) # bad: multiple types
except ValueError as exception:
print(exception)
try:
tf.ragged.constant(["A", ["B", "C"]]) # bad: multiple nesting depths
except ValueError as exception:
print(exception)
```
### Example use case
The following example demonstrates how `RaggedTensor`s can be used to construct
and combine unigram and bigram embeddings for a batch of variable-length
queries, using special markers for the beginning and end of each sentence.
For more details on the ops used in this example, see the `tf.ragged` package documentation.
```
queries = tf.ragged.constant([['Who', 'is', 'Dan', 'Smith'],
['Pause'],
['Will', 'it', 'rain', 'later', 'today']])
# Create an embedding table.
num_buckets = 1024
embedding_size = 4
embedding_table = tf.Variable(
tf.random.truncated_normal([num_buckets, embedding_size],
stddev=1.0 / math.sqrt(embedding_size)))
# Look up the embedding for each word.
word_buckets = tf.strings.to_hash_bucket_fast(queries, num_buckets)
word_embeddings = tf.ragged.map_flat_values(
tf.nn.embedding_lookup, embedding_table, word_buckets) # ①
# Add markers to the beginning and end of each sentence.
marker = tf.fill([queries.nrows(), 1], '#')
padded = tf.concat([marker, queries, marker], axis=1) # ②
# Build word bigrams & look up embeddings.
bigrams = tf.strings.join([padded[:, :-1],
padded[:, 1:]],
separator='+') # ③
bigram_buckets = tf.strings.to_hash_bucket_fast(bigrams, num_buckets)
bigram_embeddings = tf.ragged.map_flat_values(
tf.nn.embedding_lookup, embedding_table, bigram_buckets) # ④
# Find the average embedding for each sentence
all_embeddings = tf.concat([word_embeddings, bigram_embeddings], axis=1) # ⑤
avg_embedding = tf.reduce_mean(all_embeddings, axis=1) # ⑥
print(avg_embedding)
```
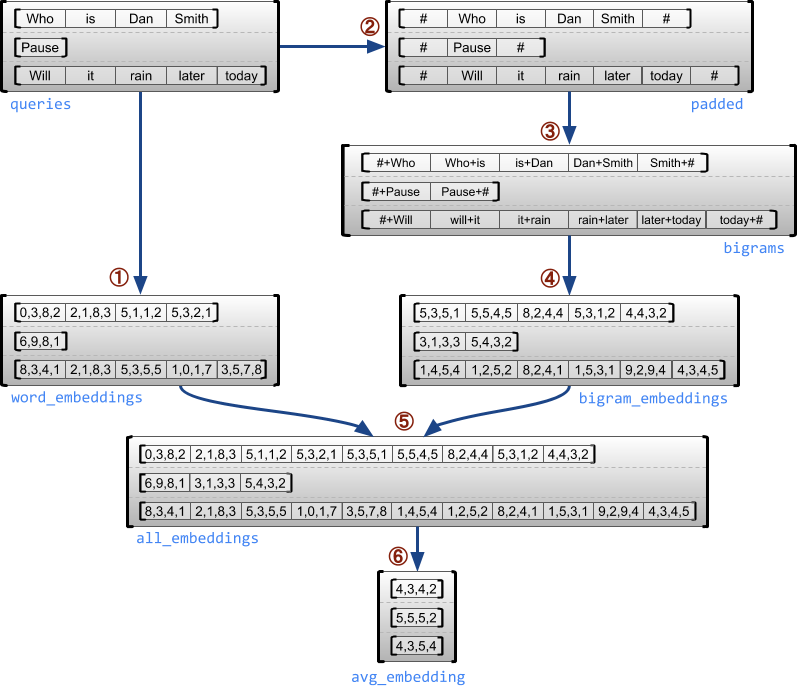
## Ragged tensors: definitions
### Ragged and uniform dimensions
A *ragged tensor* is a tensor with one or more *ragged dimensions*,
which are dimensions whose slices may have different lengths. For example, the
inner (column) dimension of `rt=[[3, 1, 4, 1], [], [5, 9, 2], [6], []]` is
ragged, since the column slices (`rt[0, :]`, ..., `rt[4, :]`) have different
lengths. Dimensions whose slices all have the same length are called *uniform
dimensions*.
The outermost dimension of a ragged tensor is always uniform, since it consists
of a single slice (and so there is no possibility for differing slice lengths).
In addition to the uniform outermost dimension, ragged tensors may also have
uniform inner dimensions. For example, we might store the word embeddings for
each word in a batch of sentences using a ragged tensor with shape
`[num_sentences, (num_words), embedding_size]`, where the parentheses around
`(num_words)` indicate that the dimension is ragged.
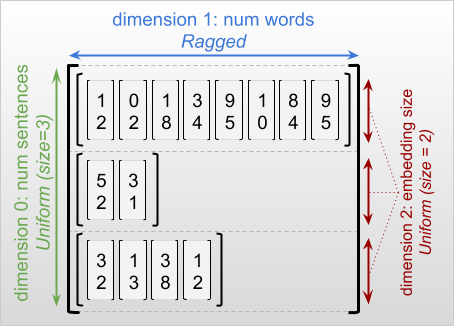
Ragged tensors may have multiple ragged dimensions. For example, we could store
a batch of structured text documents using a tensor with shape `[num_documents,
(num_paragraphs), (num_sentences), (num_words)]` (where again parentheses are
used to indicate ragged dimensions).
#### Ragged tensor shape restrictions
The shape of a ragged tensor is currently restricted to have the following form:
* A single uniform dimension
* Followed by one or more ragged dimensions
* Followed by zero or more uniform dimensions.
Note: These restrictions are a consequence of the current implementation, and we
may relax them in the future.
### Rank and ragged rank
The total number of dimensions in a ragged tensor is called its ***rank***, and
the number of ragged dimensions in a ragged tensor is called its ***ragged
rank***. In graph execution mode (i.e., non-eager mode), a tensor's ragged rank
is fixed at creation time: it can't depend
on runtime values, and can't vary dynamically for different session runs.
A ***potentially ragged tensor*** is a value that might be
either a `tf.Tensor` or a `tf.RaggedTensor`. The
ragged rank of a `tf.Tensor` is defined to be zero.
### RaggedTensor shapes
When describing the shape of a RaggedTensor, ragged dimensions are indicated by
enclosing them in parentheses. For example, as we saw above, the shape of a 3-D
RaggedTensor that stores word embeddings for each word in a batch of sentences
can be written as `[num_sentences, (num_words), embedding_size]`.
The `RaggedTensor.shape` attribute returns a `tf.TensorShape` for a
ragged tensor, where ragged dimensions have size `None`:
```
tf.ragged.constant([["Hi"], ["How", "are", "you"]]).shape
```
The method `tf.RaggedTensor.bounding_shape` can be used to find a tight
bounding shape for a given `RaggedTensor`:
```
print(tf.ragged.constant([["Hi"], ["How", "are", "you"]]).bounding_shape())
```
## Ragged vs sparse tensors
A ragged tensor should *not* be thought of as a type of sparse tensor, but
rather as a dense tensor with an irregular shape.
As an illustrative example, consider how array operations such as `concat`,
`stack`, and `tile` are defined for ragged vs. sparse tensors. Concatenating
ragged tensors joins each row to form a single row with the combined length:

```
ragged_x = tf.ragged.constant([["John"], ["a", "big", "dog"], ["my", "cat"]])
ragged_y = tf.ragged.constant([["fell", "asleep"], ["barked"], ["is", "fuzzy"]])
print(tf.concat([ragged_x, ragged_y], axis=1))
```
But concatenating sparse tensors is equivalent to concatenating the corresponding dense tensors,
as illustrated by the following example (where Ø indicates missing values):
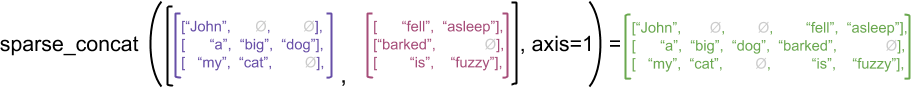
```
sparse_x = ragged_x.to_sparse()
sparse_y = ragged_y.to_sparse()
sparse_result = tf.sparse.concat(sp_inputs=[sparse_x, sparse_y], axis=1)
print(tf.sparse.to_dense(sparse_result, ''))
```
For another example of why this distinction is important, consider the
definition of “the mean value of each row” for an op such as `tf.reduce_mean`.
For a ragged tensor, the mean value for a row is the sum of the
row’s values divided by the row’s width.
But for a sparse tensor, the mean value for a row is the sum of the
row’s values divided by the sparse tensor’s overall width (which is
greater than or equal to the width of the longest row).
## Overloaded operators
The `RaggedTensor` class overloads the standard Python arithmetic and comparison
operators, making it easy to perform basic elementwise math:
```
x = tf.ragged.constant([[1, 2], [3], [4, 5, 6]])
y = tf.ragged.constant([[1, 1], [2], [3, 3, 3]])
print(x + y)
```
Since the overloaded operators perform elementwise computations, the inputs to
all binary operations must have the same shape, or be broadcastable to the same
shape. In the simplest broadcasting case, a single scalar is combined
elementwise with each value in a ragged tensor:
```
x = tf.ragged.constant([[1, 2], [3], [4, 5, 6]])
print(x + 3)
```
For a discussion of more advanced cases, see the section on
**Broadcasting**.
Ragged tensors overload the same set of operators as normal `Tensor`s: the unary
operators `-`, `~`, and `abs()`; and the binary operators `+`, `-`, `*`, `/`,
`//`, `%`, `**`, `&`, `|`, `^`, `<`, `<=`, `>`, and `>=`. Note that, as with
standard `Tensor`s, binary `==` is not overloaded; you can use
`tf.equal()` to check elementwise equality.
## Indexing
Ragged tensors support Python-style indexing, including multidimensional
indexing and slicing. The following examples demonstrate ragged tensor indexing
with a 2-D and a 3-D ragged tensor.
### Indexing a 2-D ragged tensor with 1 ragged dimension
```
queries = tf.ragged.constant(
[['Who', 'is', 'George', 'Washington'],
['What', 'is', 'the', 'weather', 'tomorrow'],
['Goodnight']])
print(queries[1])
print(queries[1, 2]) # A single word
print(queries[1:]) # Everything but the first row
print(queries[:, :3]) # The first 3 words of each query
print(queries[:, -2:]) # The last 2 words of each query
```
### Indexing a 3-D ragged tensor with 2 ragged dimensions
```
rt = tf.ragged.constant([[[1, 2, 3], [4]],
[[5], [], [6]],
[[7]],
[[8, 9], [10]]])
print(rt[1]) # Second row (2-D RaggedTensor)
print(rt[3, 0]) # First element of fourth row (1-D Tensor)
print(rt[:, 1:3]) # Items 1-3 of each row (3-D RaggedTensor)
print(rt[:, -1:]) # Last item of each row (3-D RaggedTensor)
```
`RaggedTensor`s supports multidimensional indexing and slicing, with one
restriction: indexing into a ragged dimension is not allowed. This case is
problematic because the indicated value may exist in some rows but not others.
In such cases, it's not obvious whether we should (1) raise an `IndexError`; (2)
use a default value; or (3) skip that value and return a tensor with fewer rows
than we started with. Following the
[guiding principles of Python](https://www.python.org/dev/peps/pep-0020/)
("In the face
of ambiguity, refuse the temptation to guess" ), we currently disallow this
operation.
## Tensor Type Conversion
The `RaggedTensor` class defines methods that can be used to convert
between `RaggedTensor`s and `tf.Tensor`s or `tf.SparseTensors`:
```
ragged_sentences = tf.ragged.constant([
['Hi'], ['Welcome', 'to', 'the', 'fair'], ['Have', 'fun']])
print(ragged_sentences.to_tensor(default_value=''))
print(ragged_sentences.to_sparse())
x = [[1, 3, -1, -1], [2, -1, -1, -1], [4, 5, 8, 9]]
print(tf.RaggedTensor.from_tensor(x, padding=-1))
st = tf.SparseTensor(indices=[[0, 0], [2, 0], [2, 1]],
values=['a', 'b', 'c'],
dense_shape=[3, 3])
print(tf.RaggedTensor.from_sparse(st))
```
## Evaluating ragged tensors
### Eager execution
In eager execution mode, ragged tensors are evaluated immediately. To access the
values they contain, you can:
* Use the
`tf.RaggedTensor.to_list()`
method, which converts the ragged tensor to a Python `list`.
```
rt = tf.ragged.constant([[1, 2], [3, 4, 5], [6], [], [7]])
print(rt.to_list())
```
* Use Python indexing. If the tensor piece you select contains no ragged
dimensions, then it will be returned as an `EagerTensor`. You can then use
the `numpy()` method to access the value directly.
```
print(rt[1].numpy())
```
* Decompose the ragged tensor into its components, using the
`tf.RaggedTensor.values`
and
`tf.RaggedTensor.row_splits`
properties, or row-paritioning methods such as `tf.RaggedTensor.row_lengths()`
and `tf.RaggedTensor.value_rowids()`.
```
print(rt.values)
print(rt.row_splits)
```
### Broadcasting
Broadcasting is the process of making tensors with different shapes have
compatible shapes for elementwise operations. For more background on
broadcasting, see:
* [Numpy: Broadcasting](https://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
* `tf.broadcast_dynamic_shape`
* `tf.broadcast_to`
The basic steps for broadcasting two inputs `x` and `y` to have compatible
shapes are:
1. If `x` and `y` do not have the same number of dimensions, then add outer
dimensions (with size 1) until they do.
2. For each dimension where `x` and `y` have different sizes:
* If `x` or `y` have size `1` in dimension `d`, then repeat its values
across dimension `d` to match the other input's size.
* Otherwise, raise an exception (`x` and `y` are not broadcast
compatible).
Where the size of a tensor in a uniform dimension is a single number (the size
of slices across that dimension); and the size of a tensor in a ragged dimension
is a list of slice lengths (for all slices across that dimension).
#### Broadcasting examples
```
# x (2D ragged): 2 x (num_rows)
# y (scalar)
# result (2D ragged): 2 x (num_rows)
x = tf.ragged.constant([[1, 2], [3]])
y = 3
print(x + y)
# x (2d ragged): 3 x (num_rows)
# y (2d tensor): 3 x 1
# Result (2d ragged): 3 x (num_rows)
x = tf.ragged.constant(
[[10, 87, 12],
[19, 53],
[12, 32]])
y = [[1000], [2000], [3000]]
print(x + y)
# x (3d ragged): 2 x (r1) x 2
# y (2d ragged): 1 x 1
# Result (3d ragged): 2 x (r1) x 2
x = tf.ragged.constant(
[[[1, 2], [3, 4], [5, 6]],
[[7, 8]]],
ragged_rank=1)
y = tf.constant([[10]])
print(x + y)
# x (3d ragged): 2 x (r1) x (r2) x 1
# y (1d tensor): 3
# Result (3d ragged): 2 x (r1) x (r2) x 3
x = tf.ragged.constant(
[
[
[[1], [2]],
[],
[[3]],
[[4]],
],
[
[[5], [6]],
[[7]]
]
],
ragged_rank=2)
y = tf.constant([10, 20, 30])
print(x + y)
```
Here are some examples of shapes that do not broadcast:
```
# x (2d ragged): 3 x (r1)
# y (2d tensor): 3 x 4 # trailing dimensions do not match
x = tf.ragged.constant([[1, 2], [3, 4, 5, 6], [7]])
y = tf.constant([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
try:
x + y
except tf.errors.InvalidArgumentError as exception:
print(exception)
# x (2d ragged): 3 x (r1)
# y (2d ragged): 3 x (r2) # ragged dimensions do not match.
x = tf.ragged.constant([[1, 2, 3], [4], [5, 6]])
y = tf.ragged.constant([[10, 20], [30, 40], [50]])
try:
x + y
except tf.errors.InvalidArgumentError as exception:
print(exception)
# x (3d ragged): 3 x (r1) x 2
# y (3d ragged): 3 x (r1) x 3 # trailing dimensions do not match
x = tf.ragged.constant([[[1, 2], [3, 4], [5, 6]],
[[7, 8], [9, 10]]])
y = tf.ragged.constant([[[1, 2, 0], [3, 4, 0], [5, 6, 0]],
[[7, 8, 0], [9, 10, 0]]])
try:
x + y
except tf.errors.InvalidArgumentError as exception:
print(exception)
```
## RaggedTensor encoding
Ragged tensors are encoded using the `RaggedTensor` class. Internally, each
`RaggedTensor` consists of:
* A `values` tensor, which concatenates the variable-length rows into a
flattened list.
* A `row_splits` vector, which indicates how those flattened values are
divided into rows. In particular, the values for row `rt[i]` are stored in
the slice `rt.values[rt.row_splits[i]:rt.row_splits[i+1]]`.

```
rt = tf.RaggedTensor.from_row_splits(
values=[3, 1, 4, 1, 5, 9, 2],
row_splits=[0, 4, 4, 6, 7])
print(rt)
```
### Multiple ragged dimensions
A ragged tensor with multiple ragged dimensions is encoded by using a nested
`RaggedTensor` for the `values` tensor. Each nested `RaggedTensor` adds a single
ragged dimension.
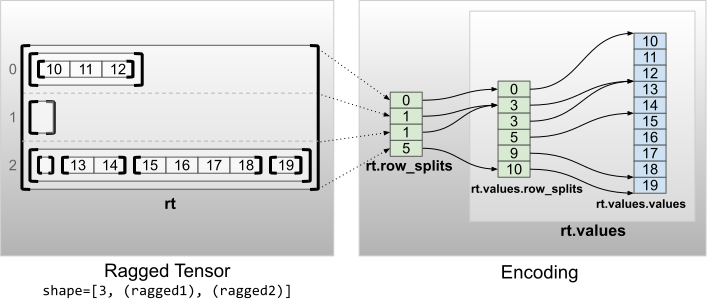
```
rt = tf.RaggedTensor.from_row_splits(
values=tf.RaggedTensor.from_row_splits(
values=[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
row_splits=[0, 3, 3, 5, 9, 10]),
row_splits=[0, 1, 1, 5])
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of ragged dimensions: {}".format(rt.ragged_rank))
```
The factory function `tf.RaggedTensor.from_nested_row_splits` may be used to construct a
RaggedTensor with multiple ragged dimensions directly, by providing a list of
`row_splits` tensors:
```
rt = tf.RaggedTensor.from_nested_row_splits(
flat_values=[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
nested_row_splits=([0, 1, 1, 5], [0, 3, 3, 5, 9, 10]))
print(rt)
```
### Uniform Inner Dimensions
Ragged tensors with uniform inner dimensions are encoded by using a
multidimensional `tf.Tensor` for `values`.
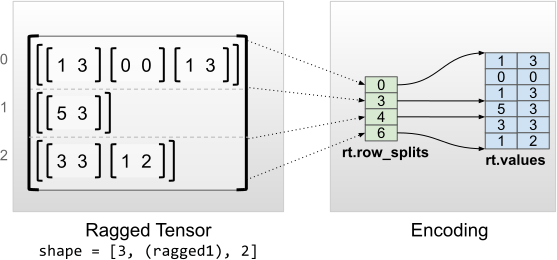
```
rt = tf.RaggedTensor.from_row_splits(
values=[[1, 3], [0, 0], [1, 3], [5, 3], [3, 3], [1, 2]],
row_splits=[0, 3, 4, 6])
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of ragged dimensions: {}".format(rt.ragged_rank))
```
### Alternative row-partitioning schemes
The `RaggedTensor` class uses `row_splits` as the primary mechanism to store
information about how the values are partitioned into rows. However,
`RaggedTensor` also provides support for four alternative row-partitioning
schemes, which can be more convenient to use depending on how your data is
formatted. Internally, `RaggedTensor` uses these additional schemes to improve
efficiency in some contexts.
<dl>
<dt>Row lengths</dt>
<dd>`row_lengths` is a vector with shape `[nrows]`, which specifies the
length of each row.</dd>
<dt>Row starts</dt>
<dd>`row_starts` is a vector with shape `[nrows]`, which specifies the start
offset of each row. Equivalent to `row_splits[:-1]`.</dd>
<dt>Row limits</dt>
<dd>`row_limits` is a vector with shape `[nrows]`, which specifies the stop
offset of each row. Equivalent to `row_splits[1:]`.</dd>
<dt>Row indices and number of rows</dt>
<dd>`value_rowids` is a vector with shape `[nvals]`, corresponding
one-to-one with values, which specifies each value's row index. In
particular, the row `rt[row]` consists of the values `rt.values[j]` where
`value_rowids[j]==row`. \
`nrows` is an integer that specifies the number of rows in the
`RaggedTensor`. In particular, `nrows` is used to indicate trailing empty
rows.</dd>
</dl>
For example, the following ragged tensors are equivalent:
```
values = [3, 1, 4, 1, 5, 9, 2, 6]
print(tf.RaggedTensor.from_row_splits(values, row_splits=[0, 4, 4, 7, 8, 8]))
print(tf.RaggedTensor.from_row_lengths(values, row_lengths=[4, 0, 3, 1, 0]))
print(tf.RaggedTensor.from_row_starts(values, row_starts=[0, 4, 4, 7, 8]))
print(tf.RaggedTensor.from_row_limits(values, row_limits=[4, 4, 7, 8, 8]))
print(tf.RaggedTensor.from_value_rowids(
values, value_rowids=[0, 0, 0, 0, 2, 2, 2, 3], nrows=5))
```
The RaggedTensor class defines methods which can be used to construct
each of these row-partitioning tensors.
```
rt = tf.ragged.constant([[3, 1, 4, 1], [], [5, 9, 2], [6], []])
print(" values: {}".format(rt.values))
print(" row_splits: {}".format(rt.row_splits))
print(" row_lengths: {}".format(rt.row_lengths()))
print(" row_starts: {}".format(rt.row_starts()))
print(" row_limits: {}".format(rt.row_limits()))
print("value_rowids: {}".format(rt.value_rowids()))
```
(Note that `tf.RaggedTensor.values` and `tf.RaggedTensors.row_splits` are properties, while the remaining row-partitioning accessors are all methods. This reflects the fact that the `row_splits` are the primary underlying representation, and the other row-partitioning tensors must be computed.)
Some of the advantages and disadvantages of the different row-partitioning
schemes are:
+ **Efficient indexing**:
The `row_splits`, `row_starts`, and `row_limits` schemes all enable
constant-time indexing into ragged tensors. The `value_rowids` and
`row_lengths` schemes do not.
+ **Small encoding size**:
The `value_rowids` scheme is more efficient when storing ragged tensors that
have a large number of empty rows, since the size of the tensor depends only
on the total number of values. On the other hand, the other four encodings
are more efficient when storing ragged tensors with longer rows, since they
require only one scalar value for each row.
+ **Efficient concatenation**:
The `row_lengths` scheme is more efficient when concatenating ragged
tensors, since row lengths do not change when two tensors are concatenated
together (but row splits and row indices do).
+ **Compatibility**:
The `value_rowids` scheme matches the
[segmentation](../api_guides/python/math_ops.md#Segmentation)
format used by operations such as `tf.segment_sum`. The `row_limits` scheme
matches the format used by ops such as `tf.sequence_mask`.
```
```
|
github_jupyter
|
```
# Copyright 2019 The TensorFlow Hub Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# ==============================================================================
```
# Text-to-Video retrieval with S3D MIL-NCE
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/hub/tutorials/text_to_video_retrieval_with_s3d_milnce"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/hub/blob/master/examples/colab/text_to_video_retrieval_with_s3d_milnce.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/hub/blob/master/examples/colab/text_to_video_retrieval_with_s3d_milnce.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/hub/examples/colab/text_to_video_retrieval_with_s3d_milnce.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
```
!pip install -q opencv-python
import os
import tensorflow.compat.v2 as tf
import tensorflow_hub as hub
import numpy as np
import cv2
from IPython import display
import math
```
## Import TF-Hub model
This tutorial demonstrates how to use the [S3D MIL-NCE model](https://tfhub.dev/deepmind/mil-nce/s3d/1) from TensorFlow Hub to do **text-to-video retrieval** to find the most similar videos for a given text query.
The model has 2 signatures, one for generating *video embeddings* and one for generating *text embeddings*. We will use these embedding to find the nearest neighbors in the embedding space.
```
# Load the model once from TF-Hub.
hub_handle = 'https://tfhub.dev/deepmind/mil-nce/s3d/1'
hub_model = hub.load(hub_handle)
def generate_embeddings(model, input_frames, input_words):
"""Generate embeddings from the model from video frames and input words."""
# Input_frames must be normalized in [0, 1] and of the shape Batch x T x H x W x 3
vision_output = model.signatures['video'](tf.constant(tf.cast(input_frames, dtype=tf.float32)))
text_output = model.signatures['text'](tf.constant(input_words))
return vision_output['video_embedding'], text_output['text_embedding']
# @title Define video loading and visualization functions { display-mode: "form" }
# Utilities to open video files using CV2
def crop_center_square(frame):
y, x = frame.shape[0:2]
min_dim = min(y, x)
start_x = (x // 2) - (min_dim // 2)
start_y = (y // 2) - (min_dim // 2)
return frame[start_y:start_y+min_dim,start_x:start_x+min_dim]
def load_video(video_url, max_frames=32, resize=(224, 224)):
path = tf.keras.utils.get_file(os.path.basename(video_url)[-128:], video_url)
cap = cv2.VideoCapture(path)
frames = []
try:
while True:
ret, frame = cap.read()
if not ret:
break
frame = crop_center_square(frame)
frame = cv2.resize(frame, resize)
frame = frame[:, :, [2, 1, 0]]
frames.append(frame)
if len(frames) == max_frames:
break
finally:
cap.release()
frames = np.array(frames)
if len(frames) < max_frames:
n_repeat = int(math.ceil(max_frames / float(len(frames))))
frames = frames.repeat(n_repeat, axis=0)
frames = frames[:max_frames]
return frames / 255.0
def display_video(urls):
html = '<table>'
html += '<tr><th>Video 1</th><th>Video 2</th><th>Video 3</th></tr><tr>'
for url in urls:
html += '<td>'
html += '<img src="{}" height="224">'.format(url)
html += '</td>'
html += '</tr></table>'
return display.HTML(html)
def display_query_and_results_video(query, urls, scores):
"""Display a text query and the top result videos and scores."""
sorted_ix = np.argsort(-scores)
html = ''
html += '<h2>Input query: <i>{}</i> </h2><div>'.format(query)
html += 'Results: <div>'
html += '<table>'
html += '<tr><th>Rank #1, Score:{:.2f}</th>'.format(scores[sorted_ix[0]])
html += '<th>Rank #2, Score:{:.2f}</th>'.format(scores[sorted_ix[1]])
html += '<th>Rank #3, Score:{:.2f}</th></tr><tr>'.format(scores[sorted_ix[2]])
for i, idx in enumerate(sorted_ix):
url = urls[sorted_ix[i]];
html += '<td>'
html += '<img src="{}" height="224">'.format(url)
html += '</td>'
html += '</tr></table>'
return html
# @title Load example videos and define text queries { display-mode: "form" }
video_1_url = 'https://upload.wikimedia.org/wikipedia/commons/b/b0/YosriAirTerjun.gif' # @param {type:"string"}
video_2_url = 'https://upload.wikimedia.org/wikipedia/commons/e/e6/Guitar_solo_gif.gif' # @param {type:"string"}
video_3_url = 'https://upload.wikimedia.org/wikipedia/commons/3/30/2009-08-16-autodrift-by-RalfR-gif-by-wau.gif' # @param {type:"string"}
video_1 = load_video(video_1_url)
video_2 = load_video(video_2_url)
video_3 = load_video(video_3_url)
all_videos = [video_1, video_2, video_3]
query_1_video = 'waterfall' # @param {type:"string"}
query_2_video = 'playing guitar' # @param {type:"string"}
query_3_video = 'car drifting' # @param {type:"string"}
all_queries_video = [query_1_video, query_2_video, query_3_video]
all_videos_urls = [video_1_url, video_2_url, video_3_url]
display_video(all_videos_urls)
```
## Demonstrate text to video retrieval
```
# Prepare video inputs.
videos_np = np.stack(all_videos, axis=0)
# Prepare text input.
words_np = np.array(all_queries_video)
# Generate the video and text embeddings.
video_embd, text_embd = generate_embeddings(hub_model, videos_np, words_np)
# Scores between video and text is computed by dot products.
all_scores = np.dot(text_embd, tf.transpose(video_embd))
# Display results.
html = ''
for i, words in enumerate(words_np):
html += display_query_and_results_video(words, all_videos_urls, all_scores[i, :])
html += '<br>'
display.HTML(html)
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/thomascong121/SocialDistance/blob/master/model_camera_colibration.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from google.colab import drive
drive.mount('/content/drive')
%%capture
!pip install gluoncv
!pip install mxnet-cu101
import gluoncv
from gluoncv import model_zoo, data, utils
from matplotlib import pyplot as plt
import numpy as np
from collections import defaultdict
from mxnet import nd
import mxnet as mx
from skimage import io
import cv2
import os
from copy import deepcopy
from tqdm import tqdm
!ls '/content/drive/My Drive/social distance/0.png'
!nvidia-smi
!nvcc --version
img_path = '/content/drive/My Drive/social distance/0.png'
img = io.imread(img_path)
video_path = '/content/drive/My Drive/social distance/TownCentreXVID.avi'
io.imshow(img)
io.show()
class Bird_eye_view_Transformer:
def __init__(self, keypoints, keypoints_birds_eye_view, actual_length, actual_width):
'''
keypoints input order
0 1
3 2
'''
self.keypoint = np.float32(keypoints)
self.keypoints_birds_eye_view = np.float32(keypoints_birds_eye_view)
self.M = cv2.getPerspectiveTransform(self.keypoint, self.keypoints_birds_eye_view)
self.length_ratio = actual_width/(keypoints_birds_eye_view[3][1] - keypoints_birds_eye_view[0][1])
self.width_ratio = actual_length/(keypoints_birds_eye_view[1][0] - keypoints_birds_eye_view[0][0])
print(self.length_ratio, self.width_ratio)
def imshow(self, img):
dst_img = cv2.warpPerspective(img, self.M, (img.shape[1], img.shape[0]))
plt.imshow(dst_img)
plt.show()
def __call__(self, points):
h = points.shape[0]
points = np.concatenate([points, np.ones((h, 1))], axis = 1)
temp = self.M.dot(points.T)
return (temp[:2]/temp[2]).T
def distance(self, p0, p1):
return ((p0[0] - p1[0])*self.width_ratio)**2 \
+ ((p0[1] - p1[1])*self.length_ratio)**2
keypoints = [(1175, 189), (1574, 235), (976, 831), (364, 694)]
keypoints_birds_eye_view = [(700, 400), (1200, 400), (1200, 900), (700, 900)]
actual_length = 10
actual_width = 5
transformer = Bird_eye_view_Transformer(keypoints, keypoints_birds_eye_view, actual_length, actual_width)
transformer.imshow(img)
'''
step0 install gluoncv
pip install --upgrade mxnet gluoncv
'''
class Model_Zoo:
def __init__(self,selected_model, transformer, device):
self.device = device
self.transformer = transformer
self.net = model_zoo.get_model(selected_model, pretrained=True, ctx = self.device)
def __call__(self,image,display=False):
'''get bbox for input image'''
image = nd.array(image)
x, orig_img = data.transforms.presets.yolo.transform_test(image)
self.shape = orig_img.shape[:2]
self.benchmark = max(orig_img.shape[:2])
x = x.copyto(self.device)
box_ids, scores, bboxes = self.net(x)
bboxes = bboxes * (image.shape[0]/orig_img.shape[0])
person_index = []
#check person class
for i in range(box_ids.shape[1]):
if box_ids[0][i][0] == 14 and scores[0][i][0] > 0.7:
person_index.append(i)
#select bbox of person
#p1:bbox id of person
#p2:confidence score
#p3:bbox location
# print('======{0} bbox of persons are detected===='.format(len(person_index)))
p1,p2,p3 = box_ids[0][[person_index],:],scores[0][[person_index],:],bboxes[0][[person_index],:]
#calaulate bbox coordinate
bbox_center = self.bbox_center(p3)
#img with bbox
img_with_bbox = utils.viz.cv_plot_bbox(image.astype('uint8'), p3[0], p2[0], p1[0], colors={14: (0,255,0)},class_names = self.net.classes, linewidth=1)
result_img = self.bbox_distance(bbox_center,img_with_bbox)
if display:
plt.imshow(result_img)
plt.show()
return result_img, p1, p2, p3, bbox_center
def show(self, img, p1, p2, p3, bbox_center, resize = None):
if resize is not None:
img = mx.image.imresize(nd.array(img).astype('uint8'), self.shape[1], self.shape[0])
else:
img = nd.array(img).astype('uint8')
img_with_bbox = utils.viz.cv_plot_bbox(img, p3[0], p2[0], p1[0], colors={14: (0,255,0)},class_names = self.net.classes, linewidth=1)
return self.bbox_distance(bbox_center,img_with_bbox)
def bbox_center(self,bbox_location):
'''calculate center coordinate for each bbox'''
rst = None
for loc in range(bbox_location[0].shape[0]):
(xmin, ymin, xmax, ymax) = bbox_location[0][loc].copyto(mx.cpu())
center_x = (xmin+xmax)/2
center_y = ymax
if rst is not None:
rst = nd.concatenate([rst, nd.stack(center_x, center_y, axis = 1)])
else:
rst = nd.stack(center_x, center_y, axis = 1)
return rst.asnumpy()
def bbox_distance(self,bbox_coord,img, max_detect = 4, safe=2):
'''
calculate distance between each bbox,
if distance < safe, draw a red line
'''
#draw the center
safe = safe**2
max_detect = max_detect**2
for coor in range(len(bbox_coord)):
cv2.circle(img,(int(bbox_coord[coor][0]),int(bbox_coord[coor][1])),5,(0, 0, 255),-1)
bird_eye_view = self.transformer(deepcopy(bbox_coord))
# print(bird_eye_view)
# self.transformer.imshow(img)
for i in range(0, len(bbox_coord)):
for j in range(i+1, len(bbox_coord)):
dist = self.transformer.distance(bird_eye_view[i], bird_eye_view [j])
# print(bird_eye_view[i], bird_eye_view [j],dist)
if dist < safe:
cv2.line(img,(bbox_coord[i][0],bbox_coord[i][1]),(bbox_coord[j][0],bbox_coord[j][1]),(255, 0, 0), 2)
elif dist < max_detect:
cv2.line(img,(bbox_coord[i][0],bbox_coord[i][1]),(bbox_coord[j][0],bbox_coord[j][1]),(0, 255, 0), 2)
return img
pretrained_models = 'yolo3_darknet53_voc'
detect_model = Model_Zoo(pretrained_models, transformer, mx.gpu())
%%time
rst = detect_model(img,display=True)
rst
class Detector:
def __init__(self, model, save_path = './detections', batch_size = 60, interval = None):
self.detector = model
self.save_path = save_path
self.interval = interval
self.batch_size = batch_size
def __call__(self, filename):
v_cap = cv2.VideoCapture(filename)
v_len = int(v_cap.get(cv2.CAP_PROP_FRAME_COUNT))
frame_size = (v_cap.get(cv2.CAP_PROP_FRAME_WIDTH), v_cap.get(cv2.CAP_PROP_FRAME_HEIGHT))
fourcc = cv2.VideoWriter_fourcc(*'MP4V')
fps = v_cap.get(cv2.CAP_PROP_FPS)
if not os.path.exists(self.save_path):
os.mkdir(self.save_path)
print(f'{self.save_path}/{filename.split("/")[-1]}')
out = cv2.VideoWriter(f'{self.save_path}/{filename.split("/")[-1]}', fourcc, fps,\
(int(frame_size[0]), int(frame_size[1])))
if self.interval is None:
sample = np.arange(0, v_len)
else:
sample = np.arange(0, v_len, self.interval)
frame = p1 = p2 = p3 = bbox_center =None
for i in tqdm(range(v_len)):
success = v_cap.grab()
success, frame = v_cap.retrieve()
if not success:
continue
frame = cv2.cvtColor(frame, cv2.COLOR_BGR2RGB)
if i in sample:
frame, p1, p2, p3, bbox_center = self.detector(frame)
else:
frame = self.detector.show(frame, p1, p2, p3, bbox_center)
# plt.imshow(frame)
# plt.show()
frame = cv2.cvtColor(frame, cv2.COLOR_RGB2BGR)
out.write(frame)
v_cap.release()
return out
detector = Detector(detect_model, interval = 10)
%%time
detector(video_path)
!ls ./detections
```
|
github_jupyter
|
# Azure Machine Learning Setup
To begin, you will need to provide the following information about your Azure Subscription.
**If you are using your own Azure subscription, please provide names for subscription_id, resource_group, workspace_name and workspace_region to use.** Note that the workspace needs to be of type [Machine Learning Workspace](https://docs.microsoft.com/en-us/azure/machine-learning/service/setup-create-workspace).
**If an enviorment is provided to you be sure to replace XXXXX in the values below with your unique identifier.**
In the following cell, be sure to set the values for `subscription_id`, `resource_group`, `workspace_name` and `workspace_region` as directed by the comments (*these values can be acquired from the Azure Portal*).
To get these values, do the following:
1. Navigate to the Azure Portal and login with the credentials provided.
2. From the left hand menu, under Favorites, select `Resource Groups`.
3. In the list, select the resource group with the name similar to `XXXXX`.
4. From the Overview tab, capture the desired values.
Execute the following cell by selecting the `>|Run` button in the command bar above.
```
#Provide the Subscription ID of your existing Azure subscription
subscription_id = "" #"<your-azure-subscription-id>"
#Provide a name for the Resource Group that will contain Azure ML related services
resource_group = "mcw-ai-lab-XXXXX" #"<your-subscription-group-name>"
# Provide the name and region for the Azure Machine Learning Workspace that will be created
workspace_name = "mcw-ai-lab-ws-XXXXX"
workspace_region = "eastus" # eastus2, eastus, westcentralus, southeastasia, australiaeast, westeurope
```
## Create and connect to an Azure Machine Learning Workspace
The Azure Machine Learning Python SDK is required for leveraging the experimentation, model management and model deployment capabilities of Azure Machine Learning services. Run the following cell to create a new Azure Machine Learning **Workspace** and save the configuration to disk. The configuration file named `config.json` is saved in a folder named `.azureml`.
**Important Note**: You will be prompted to login in the text that is output below the cell. Be sure to navigate to the URL displayed and enter the code that is provided. Once you have entered the code, return to this notebook and wait for the output to read `Workspace configuration succeeded`.
```
import azureml.core
print('azureml.core.VERSION: ', azureml.core.VERSION)
# import the Workspace class and check the azureml SDK version
from azureml.core import Workspace
ws = Workspace.create(
name = workspace_name,
subscription_id = subscription_id,
resource_group = resource_group,
location = workspace_region,
exist_ok = True)
ws.write_config()
print('Workspace configuration succeeded')
```
Take a look at the contents of the generated configuration file by running the following cell:
```
!cat .azureml/config.json
```
# Deploy model to Azure Container Instance (ACI)
In this section, you will deploy a web service that uses Gensim as shown in `01 Summarize` to summarize text. The web service will be hosted in Azure Container Service.
## Create the scoring web service
When deploying models for scoring with Azure Machine Learning services, you need to define the code for a simple web service that will load your model and use it for scoring. By convention this service has two methods init which loads the model and run which scores data using the loaded model.
This scoring service code will later be deployed inside of a specially prepared Docker container.
```
%%writefile summarizer_service.py
import re
import nltk
import unicodedata
from gensim.summarization import summarize, keywords
def clean_and_parse_document(document):
if isinstance(document, str):
document = document
elif isinstance(document, unicode):
return unicodedata.normalize('NFKD', document).encode('ascii', 'ignore')
else:
raise ValueError("Document is not string or unicode.")
document = document.strip()
sentences = nltk.sent_tokenize(document)
sentences = [sentence.strip() for sentence in sentences]
return sentences
def summarize_text(text, summary_ratio=None, word_count=30):
sentences = clean_and_parse_document(text)
cleaned_text = ' '.join(sentences)
summary = summarize(cleaned_text, split=True, ratio=summary_ratio, word_count=word_count)
return summary
def init():
nltk.download('all')
return
def run(input_str):
try:
return summarize_text(input_str)
except Exception as e:
return (str(e))
```
## Create a Conda dependencies environment file
Your web service can have dependencies installed by using a Conda environment file. Items listed in this file will be conda or pip installed within the Docker container that is created and thus be available to your scoring web service logic.
```
from azureml.core.conda_dependencies import CondaDependencies
myacienv = CondaDependencies.create(pip_packages=['gensim','nltk'])
with open("mydeployenv.yml","w") as f:
f.write(myacienv.serialize_to_string())
```
## Deployment
In the following cells you will use the Azure Machine Learning SDK to package the model and scoring script in a container, and deploy that container to an Azure Container Instance.
Run the following cells.
```
from azureml.core.webservice import AciWebservice, Webservice
aci_config = AciWebservice.deploy_configuration(
cpu_cores = 1,
memory_gb = 1,
tags = {'name':'Summarization'},
description = 'Summarizes text.')
```
Next, build up a container image configuration that names the scoring service script, the runtime, and provides the conda file.
```
service_name = "summarizer"
runtime = "python"
driver_file = "summarizer_service.py"
conda_file = "mydeployenv.yml"
from azureml.core.image import ContainerImage
image_config = ContainerImage.image_configuration(execution_script = driver_file,
runtime = runtime,
conda_file = conda_file)
```
Now you are ready to begin your deployment to the Azure Container Instance.
Run the following cell. This may take between 5-15 minutes to complete.
You will see output similar to the following when your web service is ready: `SucceededACI service creation operation finished, operation "Succeeded"`
```
webservice = Webservice.deploy(
workspace=ws,
name=service_name,
model_paths=[],
deployment_config=aci_config,
image_config=image_config,
)
webservice.wait_for_deployment(show_output=True)
```
## Test the deployed service
Now you are ready to test scoring using the deployed web service. The following cell invokes the web service.
Run the following cells to test scoring using a single input row against the deployed web service.
```
example_document = """
I was driving down El Camino and stopped at a red light.
It was about 3pm in the afternoon.
The sun was bright and shining just behind the stoplight.
This made it hard to see the lights.
There was a car on my left in the left turn lane.
A few moments later another car, a black sedan pulled up behind me.
When the left turn light changed green, the black sedan hit me thinking
that the light had changed for us, but I had not moved because the light
was still red.
After hitting my car, the black sedan backed up and then sped past me.
I did manage to catch its license plate.
The license plate of the black sedan was ABC123.
"""
result = webservice.run(input_data = example_document)
print(result)
```
## Capture the scoring URI
In order to call the service from a REST client, you need to acquire the scoring URI. Run the following cell to retrieve the scoring URI and take note of this value, you will need it in the last notebook.
```
webservice.scoring_uri
```
The default settings used in deploying this service result in a service that does not require authentication, so the scoring URI is the only value you need to call this service.
|
github_jupyter
|
SAM001a - Query Storage Pool from SQL Server Master Pool (1 of 3) - Load sample data
====================================================================================
Description
-----------
In this 3 part tutorial, load data into the Storage Pool (HDFS) using
`azdata`, convert it into Parquet (using Spark) and the in the 3rd part,
query the data using the Master Pool (SQL Server)
### Common functions
Define helper functions used in this notebook.
```
# Define `run` function for transient fault handling, suggestions on error, and scrolling updates on Windows
import sys
import os
import re
import json
import platform
import shlex
import shutil
import datetime
from subprocess import Popen, PIPE
from IPython.display import Markdown
retry_hints = {} # Output in stderr known to be transient, therefore automatically retry
error_hints = {} # Output in stderr where a known SOP/TSG exists which will be HINTed for further help
install_hint = {} # The SOP to help install the executable if it cannot be found
first_run = True
rules = None
debug_logging = False
def run(cmd, return_output=False, no_output=False, retry_count=0, base64_decode=False, return_as_json=False):
"""Run shell command, stream stdout, print stderr and optionally return output
NOTES:
1. Commands that need this kind of ' quoting on Windows e.g.:
kubectl get nodes -o jsonpath={.items[?(@.metadata.annotations.pv-candidate=='data-pool')].metadata.name}
Need to actually pass in as '"':
kubectl get nodes -o jsonpath={.items[?(@.metadata.annotations.pv-candidate=='"'data-pool'"')].metadata.name}
The ' quote approach, although correct when pasting into Windows cmd, will hang at the line:
`iter(p.stdout.readline, b'')`
The shlex.split call does the right thing for each platform, just use the '"' pattern for a '
"""
MAX_RETRIES = 5
output = ""
retry = False
global first_run
global rules
if first_run:
first_run = False
rules = load_rules()
# When running `azdata sql query` on Windows, replace any \n in """ strings, with " ", otherwise we see:
#
# ('HY090', '[HY090] [Microsoft][ODBC Driver Manager] Invalid string or buffer length (0) (SQLExecDirectW)')
#
if platform.system() == "Windows" and cmd.startswith("azdata sql query"):
cmd = cmd.replace("\n", " ")
# shlex.split is required on bash and for Windows paths with spaces
#
cmd_actual = shlex.split(cmd)
# Store this (i.e. kubectl, python etc.) to support binary context aware error_hints and retries
#
user_provided_exe_name = cmd_actual[0].lower()
# When running python, use the python in the ADS sandbox ({sys.executable})
#
if cmd.startswith("python "):
cmd_actual[0] = cmd_actual[0].replace("python", sys.executable)
# On Mac, when ADS is not launched from terminal, LC_ALL may not be set, which causes pip installs to fail
# with:
#
# UnicodeDecodeError: 'ascii' codec can't decode byte 0xc5 in position 4969: ordinal not in range(128)
#
# Setting it to a default value of "en_US.UTF-8" enables pip install to complete
#
if platform.system() == "Darwin" and "LC_ALL" not in os.environ:
os.environ["LC_ALL"] = "en_US.UTF-8"
# When running `kubectl`, if AZDATA_OPENSHIFT is set, use `oc`
#
if cmd.startswith("kubectl ") and "AZDATA_OPENSHIFT" in os.environ:
cmd_actual[0] = cmd_actual[0].replace("kubectl", "oc")
# To aid supportability, determine which binary file will actually be executed on the machine
#
which_binary = None
# Special case for CURL on Windows. The version of CURL in Windows System32 does not work to
# get JWT tokens, it returns "(56) Failure when receiving data from the peer". If another instance
# of CURL exists on the machine use that one. (Unfortunately the curl.exe in System32 is almost
# always the first curl.exe in the path, and it can't be uninstalled from System32, so here we
# look for the 2nd installation of CURL in the path)
if platform.system() == "Windows" and cmd.startswith("curl "):
path = os.getenv('PATH')
for p in path.split(os.path.pathsep):
p = os.path.join(p, "curl.exe")
if os.path.exists(p) and os.access(p, os.X_OK):
if p.lower().find("system32") == -1:
cmd_actual[0] = p
which_binary = p
break
# Find the path based location (shutil.which) of the executable that will be run (and display it to aid supportability), this
# seems to be required for .msi installs of azdata.cmd/az.cmd. (otherwise Popen returns FileNotFound)
#
# NOTE: Bash needs cmd to be the list of the space separated values hence shlex.split.
#
if which_binary == None:
which_binary = shutil.which(cmd_actual[0])
# Display an install HINT, so the user can click on a SOP to install the missing binary
#
if which_binary == None:
print(f"The path used to search for '{cmd_actual[0]}' was:")
print(sys.path)
if user_provided_exe_name in install_hint and install_hint[user_provided_exe_name] is not None:
display(Markdown(f'HINT: Use [{install_hint[user_provided_exe_name][0]}]({install_hint[user_provided_exe_name][1]}) to resolve this issue.'))
raise FileNotFoundError(f"Executable '{cmd_actual[0]}' not found in path (where/which)")
else:
cmd_actual[0] = which_binary
start_time = datetime.datetime.now().replace(microsecond=0)
print(f"START: {cmd} @ {start_time} ({datetime.datetime.utcnow().replace(microsecond=0)} UTC)")
print(f" using: {which_binary} ({platform.system()} {platform.release()} on {platform.machine()})")
print(f" cwd: {os.getcwd()}")
# Command-line tools such as CURL and AZDATA HDFS commands output
# scrolling progress bars, which causes Jupyter to hang forever, to
# workaround this, use no_output=True
#
# Work around a infinite hang when a notebook generates a non-zero return code, break out, and do not wait
#
wait = True
try:
if no_output:
p = Popen(cmd_actual)
else:
p = Popen(cmd_actual, stdout=PIPE, stderr=PIPE, bufsize=1)
with p.stdout:
for line in iter(p.stdout.readline, b''):
line = line.decode()
if return_output:
output = output + line
else:
if cmd.startswith("azdata notebook run"): # Hyperlink the .ipynb file
regex = re.compile(' "(.*)"\: "(.*)"')
match = regex.match(line)
if match:
if match.group(1).find("HTML") != -1:
display(Markdown(f' - "{match.group(1)}": "{match.group(2)}"'))
else:
display(Markdown(f' - "{match.group(1)}": "[{match.group(2)}]({match.group(2)})"'))
wait = False
break # otherwise infinite hang, have not worked out why yet.
else:
print(line, end='')
if rules is not None:
apply_expert_rules(line)
if wait:
p.wait()
except FileNotFoundError as e:
if install_hint is not None:
display(Markdown(f'HINT: Use {install_hint} to resolve this issue.'))
raise FileNotFoundError(f"Executable '{cmd_actual[0]}' not found in path (where/which)") from e
exit_code_workaround = 0 # WORKAROUND: azdata hangs on exception from notebook on p.wait()
if not no_output:
for line in iter(p.stderr.readline, b''):
try:
line_decoded = line.decode()
except UnicodeDecodeError:
# NOTE: Sometimes we get characters back that cannot be decoded(), e.g.
#
# \xa0
#
# For example see this in the response from `az group create`:
#
# ERROR: Get Token request returned http error: 400 and server
# response: {"error":"invalid_grant",# "error_description":"AADSTS700082:
# The refresh token has expired due to inactivity.\xa0The token was
# issued on 2018-10-25T23:35:11.9832872Z
#
# which generates the exception:
#
# UnicodeDecodeError: 'utf-8' codec can't decode byte 0xa0 in position 179: invalid start byte
#
print("WARNING: Unable to decode stderr line, printing raw bytes:")
print(line)
line_decoded = ""
pass
else:
# azdata emits a single empty line to stderr when doing an hdfs cp, don't
# print this empty "ERR:" as it confuses.
#
if line_decoded == "":
continue
print(f"STDERR: {line_decoded}", end='')
if line_decoded.startswith("An exception has occurred") or line_decoded.startswith("ERROR: An error occurred while executing the following cell"):
exit_code_workaround = 1
# inject HINTs to next TSG/SOP based on output in stderr
#
if user_provided_exe_name in error_hints:
for error_hint in error_hints[user_provided_exe_name]:
if line_decoded.find(error_hint[0]) != -1:
display(Markdown(f'HINT: Use [{error_hint[1]}]({error_hint[2]}) to resolve this issue.'))
# apply expert rules (to run follow-on notebooks), based on output
#
if rules is not None:
apply_expert_rules(line_decoded)
# Verify if a transient error, if so automatically retry (recursive)
#
if user_provided_exe_name in retry_hints:
for retry_hint in retry_hints[user_provided_exe_name]:
if line_decoded.find(retry_hint) != -1:
if retry_count < MAX_RETRIES:
print(f"RETRY: {retry_count} (due to: {retry_hint})")
retry_count = retry_count + 1
output = run(cmd, return_output=return_output, retry_count=retry_count)
if return_output:
if base64_decode:
import base64
return base64.b64decode(output).decode('utf-8')
else:
return output
elapsed = datetime.datetime.now().replace(microsecond=0) - start_time
# WORKAROUND: We avoid infinite hang above in the `azdata notebook run` failure case, by inferring success (from stdout output), so
# don't wait here, if success known above
#
if wait:
if p.returncode != 0:
raise SystemExit(f'Shell command:\n\n\t{cmd} ({elapsed}s elapsed)\n\nreturned non-zero exit code: {str(p.returncode)}.\n')
else:
if exit_code_workaround !=0 :
raise SystemExit(f'Shell command:\n\n\t{cmd} ({elapsed}s elapsed)\n\nreturned non-zero exit code: {str(exit_code_workaround)}.\n')
print(f'\nSUCCESS: {elapsed}s elapsed.\n')
if return_output:
if base64_decode:
import base64
return base64.b64decode(output).decode('utf-8')
else:
return output
def load_json(filename):
"""Load a json file from disk and return the contents"""
with open(filename, encoding="utf8") as json_file:
return json.load(json_file)
def load_rules():
"""Load any 'expert rules' from the metadata of this notebook (.ipynb) that should be applied to the stderr of the running executable"""
# Load this notebook as json to get access to the expert rules in the notebook metadata.
#
try:
j = load_json("sam001a-load-sample-data-into-bdc.ipynb")
except:
pass # If the user has renamed the book, we can't load ourself. NOTE: Is there a way in Jupyter, to know your own filename?
else:
if "metadata" in j and \
"azdata" in j["metadata"] and \
"expert" in j["metadata"]["azdata"] and \
"expanded_rules" in j["metadata"]["azdata"]["expert"]:
rules = j["metadata"]["azdata"]["expert"]["expanded_rules"]
rules.sort() # Sort rules, so they run in priority order (the [0] element). Lowest value first.
# print (f"EXPERT: There are {len(rules)} rules to evaluate.")
return rules
def apply_expert_rules(line):
"""Determine if the stderr line passed in, matches the regular expressions for any of the 'expert rules', if so
inject a 'HINT' to the follow-on SOP/TSG to run"""
global rules
for rule in rules:
notebook = rule[1]
cell_type = rule[2]
output_type = rule[3] # i.e. stream or error
output_type_name = rule[4] # i.e. ename or name
output_type_value = rule[5] # i.e. SystemExit or stdout
details_name = rule[6] # i.e. evalue or text
expression = rule[7].replace("\\*", "*") # Something escaped *, and put a \ in front of it!
if debug_logging:
print(f"EXPERT: If rule '{expression}' satisfied', run '{notebook}'.")
if re.match(expression, line, re.DOTALL):
if debug_logging:
print("EXPERT: MATCH: name = value: '{0}' = '{1}' matched expression '{2}', therefore HINT '{4}'".format(output_type_name, output_type_value, expression, notebook))
match_found = True
display(Markdown(f'HINT: Use [{notebook}]({notebook}) to resolve this issue.'))
print('Common functions defined successfully.')
# Hints for binary (transient fault) retry, (known) error and install guide
#
retry_hints = {'kubectl': ['A connection attempt failed because the connected party did not properly respond after a period of time, or established connection failed because connected host has failed to respond'], 'azdata': ['Endpoint sql-server-master does not exist', 'Endpoint livy does not exist', 'Failed to get state for cluster', 'Endpoint webhdfs does not exist', 'Adaptive Server is unavailable or does not exist', 'Error: Address already in use', 'Login timeout expired (0) (SQLDriverConnect)', 'SSPI Provider: No Kerberos credentials available', 'ERROR: No credentials were supplied, or the credentials were unavailable or inaccessible.']}
error_hints = {'kubectl': [['no such host', 'TSG010 - Get configuration contexts', '../monitor-k8s/tsg010-get-kubernetes-contexts.ipynb'], ['No connection could be made because the target machine actively refused it', 'TSG056 - Kubectl fails with No connection could be made because the target machine actively refused it', '../repair/tsg056-kubectl-no-connection-could-be-made.ipynb']], 'azdata': [['The token is expired', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['Reason: Unauthorized', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['Max retries exceeded with url: /api/v1/bdc/endpoints', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['Look at the controller logs for more details', 'TSG027 - Observe cluster deployment', '../diagnose/tsg027-observe-bdc-create.ipynb'], ['provided port is already allocated', 'TSG062 - Get tail of all previous container logs for pods in BDC namespace', '../log-files/tsg062-tail-bdc-previous-container-logs.ipynb'], ['Create cluster failed since the existing namespace', 'SOP061 - Delete a big data cluster', '../install/sop061-delete-bdc.ipynb'], ['Failed to complete kube config setup', 'TSG067 - Failed to complete kube config setup', '../repair/tsg067-failed-to-complete-kube-config-setup.ipynb'], ['Error processing command: "ApiError', 'TSG110 - Azdata returns ApiError', '../repair/tsg110-azdata-returns-apierror.ipynb'], ['Error processing command: "ControllerError', 'TSG036 - Controller logs', '../log-analyzers/tsg036-get-controller-logs.ipynb'], ['ERROR: 500', 'TSG046 - Knox gateway logs', '../log-analyzers/tsg046-get-knox-logs.ipynb'], ['Data source name not found and no default driver specified', 'SOP069 - Install ODBC for SQL Server', '../install/sop069-install-odbc-driver-for-sql-server.ipynb'], ["Can't open lib 'ODBC Driver 17 for SQL Server", 'SOP069 - Install ODBC for SQL Server', '../install/sop069-install-odbc-driver-for-sql-server.ipynb'], ['Control plane upgrade failed. Failed to upgrade controller.', 'TSG108 - View the controller upgrade config map', '../diagnose/tsg108-controller-failed-to-upgrade.ipynb'], ["[Errno 2] No such file or directory: '..\\\\", 'TSG053 - ADS Provided Books must be saved before use', '../repair/tsg053-save-book-first.ipynb'], ["NameError: name 'azdata_login_secret_name' is not defined", 'SOP013 - Create secret for azdata login (inside cluster)', '../common/sop013-create-secret-for-azdata-login.ipynb'], ['ERROR: No credentials were supplied, or the credentials were unavailable or inaccessible.', "TSG124 - 'No credentials were supplied' error from azdata login", '../repair/tsg124-no-credentials-were-supplied.ipynb'], ['Please accept the license terms to use this product through', "TSG126 - azdata fails with 'accept the license terms to use this product'", '../repair/tsg126-accept-license-terms.ipynb']]}
install_hint = {'kubectl': ['SOP036 - Install kubectl command line interface', '../install/sop036-install-kubectl.ipynb'], 'azdata': ['SOP063 - Install azdata CLI (using package manager)', '../install/sop063-packman-install-azdata.ipynb']}
```
### Get the Kubernetes namespace for the big data cluster
Get the namespace of the Big Data Cluster use the kubectl command line
interface .
**NOTE:**
If there is more than one Big Data Cluster in the target Kubernetes
cluster, then either:
- set \[0\] to the correct value for the big data cluster.
- set the environment variable AZDATA\_NAMESPACE, before starting
Azure Data Studio.
```
# Place Kubernetes namespace name for BDC into 'namespace' variable
if "AZDATA_NAMESPACE" in os.environ:
namespace = os.environ["AZDATA_NAMESPACE"]
else:
try:
namespace = run(f'kubectl get namespace --selector=MSSQL_CLUSTER -o jsonpath={{.items[0].metadata.name}}', return_output=True)
except:
from IPython.display import Markdown
print(f"ERROR: Unable to find a Kubernetes namespace with label 'MSSQL_CLUSTER'. SQL Server Big Data Cluster Kubernetes namespaces contain the label 'MSSQL_CLUSTER'.")
display(Markdown(f'HINT: Use [TSG081 - Get namespaces (Kubernetes)](../monitor-k8s/tsg081-get-kubernetes-namespaces.ipynb) to resolve this issue.'))
display(Markdown(f'HINT: Use [TSG010 - Get configuration contexts](../monitor-k8s/tsg010-get-kubernetes-contexts.ipynb) to resolve this issue.'))
display(Markdown(f'HINT: Use [SOP011 - Set kubernetes configuration context](../common/sop011-set-kubernetes-context.ipynb) to resolve this issue.'))
raise
print(f'The SQL Server Big Data Cluster Kubernetes namespace is: {namespace}')
```
### Create a temporary directory to stage files
```
# Create a temporary directory to hold configuration files
import tempfile
temp_dir = tempfile.mkdtemp()
print(f"Temporary directory created: {temp_dir}")
```
### Helper function to save configuration files to disk
```
# Define helper function 'save_file' to save configuration files to the temporary directory created above
import os
import io
def save_file(filename, contents):
with io.open(os.path.join(temp_dir, filename), "w", encoding='utf8', newline='\n') as text_file:
text_file.write(contents)
print("File saved: " + os.path.join(temp_dir, filename))
print("Function `save_file` defined successfully.")
```
### Get the controller username and password
Get the controller username and password from the Kubernetes Secret
Store and place in the required AZDATA\_USERNAME and AZDATA\_PASSWORD
environment variables.
```
# Place controller secret in AZDATA_USERNAME/AZDATA_PASSWORD environment variables
import os, base64
os.environ["AZDATA_USERNAME"] = run(f'kubectl get secret/controller-login-secret -n {namespace} -o jsonpath={{.data.username}}', return_output=True, base64_decode=True)
os.environ["AZDATA_PASSWORD"] = run(f'kubectl get secret/controller-login-secret -n {namespace} -o jsonpath={{.data.password}}', return_output=True, base64_decode=True)
print(f"Controller username '{os.environ['AZDATA_USERNAME']}' and password stored in environment variables")
```
### Steps
Upload this data into HDFS.
```
import os
items = [
[1, "Eldon Base for stackable storage shelf platinum", "Muhammed MacIntyre", 3, -213.25, 38.94, 35, "Nunavut", "Storage & Organization", 0.8],
[2, "1.7 Cubic Foot Compact ""Cube"" Office Refrigerators", "Barry French", 293, 457.81, 208.16, 68.02, "Nunavut", "Appliances", 0.58],
[3, "Cardinal Slant-D Ring Binder Heavy Gauge Vinyl", "Barry French", 293,46.71, 8.69, 2.99, "Nunavut", "Binders and Binder Accessories", 0.39],
[4, "R380", "Clay Rozendal", 483, 1198.97, 195.99, 3.99, "Nunavut", "Telephones and Communication", 0.58],
[5, "Holmes HEPA Air Purifier", "Carlos Soltero", 515, 30.94, 21.78, 5.94, "Nunavut", "Appliances", 0.5],
[6, "G.E. Longer-Life Indoor Recessed Floodlight Bulbs", "Carlos Soltero", 515, 4.43, 6.64, 4.95, "Nunavut", "Office Furnishings", 0.37],
[7, "Angle-D Binders with Locking Rings Label Holders", "Carl Jackson", 613, -54.04, 7.3, 7.72, "Nunavut", "Binders and Binder Accessories", 0.38],
[8, "SAFCO Mobile Desk Side File Wire Frame", "Carl Jackson", 613, 127.7, 42.76, 6.22, "Nunavut", "Storage & Organization", ],
[9, "SAFCO Commercial Wire Shelving Black", "Monica Federle", 643, -695.26, 138.14, 35, "Nunavut", "Storage & Organization", ],
[10, "Xerox 198", "Dorothy Badders", 678, -226.36, 4.98, 8.33, "Nunavut", "Paper", 0.38]
]
src = os.path.join(temp_dir, "items.csv")
dest = "/tmp/clickstream_data/datasampleCS.csv"
s = ""
for item in items:
s = s + str(item)[1:-1] + "\n"
save_file(src, s)
run(f'azdata bdc hdfs rm --path {dest}')
src = src.replace("\\", "\\\\")
run(f'azdata bdc hdfs rm --path hdfs:{dest}')
run(f'azdata bdc hdfs cp --from-path {src} --to-path hdfs:{dest}')
print (f"CSV uploaded to HDFS: {dest}")
```
### Clean up temporary directory for staging configuration files
```
# Delete the temporary directory used to hold configuration files
import shutil
shutil.rmtree(temp_dir)
print(f'Temporary directory deleted: {temp_dir}')
print('Notebook execution complete.')
```
|
github_jupyter
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Image/composite_bands.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Image/composite_bands.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Image/composite_bands.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Image/composite_bands.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
**Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
```
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
# There are many fine places to look here is one. Comment
# this out if you want to twiddle knobs while panning around.
Map.setCenter(-61.61625, -11.64273, 14)
# Grab a sample L7 image and pull out the RGB and pan bands
# in the range (0, 1). (The range of the pan band values was
# chosen to roughly match the other bands.)
image1 = ee.Image('LANDSAT/LE7/LE72300681999227EDC00')
rgb = image1.select('B3', 'B2', 'B1').unitScale(0, 255)
gray = image1.select('B8').unitScale(0, 155)
# Convert to HSV, swap in the pan band, and convert back to RGB.
huesat = rgb.rgbToHsv().select('hue', 'saturation')
upres = ee.Image.cat(huesat, gray).hsvToRgb()
# Display before and after layers using the same vis parameters.
visparams = {'min': [.15, .15, .25], 'max': [1, .9, .9], 'gamma': 1.6}
Map.addLayer(rgb, visparams, 'Orignal')
Map.addLayer(upres, visparams, 'Pansharpened')
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
|
github_jupyter
|
# Florida Single Weekly Predictions, trained on historical flu data and temperature
> Once again, just like before in the USA flu model, I am going to index COVID weekly cases by Wednesdays
```
import tensorflow as tf
physical_devices = tf.config.list_physical_devices('GPU')
tf.config.experimental.set_memory_growth(physical_devices[0], enable=True)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import sklearn
from sklearn import preprocessing
```
### getting historical flu data
```
system = "Windows"
if system == "Windows":
flu_dir = "..\\..\\..\\cdc-fludata\\us_national\\"
else:
flu_dir = "../../../cdc-fludata/us_national/"
flu_dictionary = {}
for year in range(1997, 2019):
filepath = "usflu_"
year_string = str(year) + "-" + str(year + 1)
filepath = flu_dir + filepath + year_string + ".csv"
temp_df = pd.read_csv(filepath)
flu_dictionary[year] = temp_df
```
### combining flu data into one chronological series of total cases
```
# getting total cases and putting them in a series by week
flu_series_dict = {}
for year in flu_dictionary:
temp_df = flu_dictionary[year]
temp_df = temp_df.set_index("WEEK")
abridged_df = temp_df.iloc[:, 2:]
try:
abridged_df = abridged_df.drop(columns="PERCENT POSITIVE")
except:
pass
total_cases_series = abridged_df.sum(axis=1)
flu_series_dict[year] = total_cases_series
all_cases_series = pd.Series(dtype="int64")
for year in flu_series_dict:
temp_series = flu_series_dict[year]
all_cases_series = all_cases_series.append(temp_series, ignore_index=True)
all_cases_series
all_cases_series.plot(grid=True, figsize=(60,20))
```
### Now, making a normalized series between 0, 1
```
norm_flu_series_dict = {}
for year in flu_series_dict:
temp_series = flu_series_dict[year]
temp_list = preprocessing.minmax_scale(temp_series)
temp_series = pd.Series(temp_list)
norm_flu_series_dict[year] = temp_series
all_cases_norm_series = pd.Series(dtype="int64")
for year in norm_flu_series_dict:
temp_series = norm_flu_series_dict[year]
all_cases_norm_series = all_cases_norm_series.append(temp_series, ignore_index=True)
all_cases_norm_series.plot(grid=True, figsize=(60,5))
all_cases_norm_series
```
## Getting COVID-19 Case Data
```
if system == "Windows":
datapath = "..\\..\\..\\COVID-19\\csse_covid_19_data\\csse_covid_19_time_series\\"
else:
datapath = "../../../COVID-19/csse_covid_19_data/csse_covid_19_time_series/"
# Choose from "US Cases", "US Deaths", "World Cases", "World Deaths", "World Recoveries"
key = "US Cases"
if key == "US Cases":
datapath = datapath + "time_series_covid19_confirmed_US.csv"
elif key == "US Deaths":
datapath = datapath + "time_series_covid19_deaths_US.csv"
elif key == "World Cases":
datapath = datapath + "time_series_covid19_confirmed_global.csv"
elif key == "World Deaths":
datapath = datapath + "time_series_covid19_deaths_global.csv"
elif key == "World Recoveries":
datapath = datapath + "time_series_covid19_recovered_global.csv"
covid_df = pd.read_csv(datapath)
covid_df
florida_data = covid_df.loc[covid_df["Province_State"] == "Florida"]
florida_cases = florida_data.iloc[:,11:]
florida_cases_total = florida_cases.sum(axis=0)
florida_cases_total.plot()
```
### convert daily data to weekly data
```
florida_weekly_cases = florida_cases_total.iloc[::7]
florida_weekly_cases
florida_weekly_cases.plot()
```
### Converting cumulative series to non-cumulative series
```
florida_wnew_cases = florida_weekly_cases.diff()
florida_wnew_cases[0] = 1.0
florida_wnew_cases
florida_wnew_cases.plot()
```
### normalizing weekly case data
> This is going to be different for texas. This is because, the peak number of weekly new infections probably has not been reached yet. We need to divide everything by a guess for the peak number of predictions instead of min-max scaling.
```
# I'm guessing that the peak number of weekly cases will be about 60,000. Could definitely be wrong.
peak_guess = 60000
florida_wnew_cases_norm = florida_wnew_cases / peak_guess
florida_wnew_cases_norm.plot()
florida_wnew_cases_norm
```
## getting temperature data
> At the moment, this will be dummy data
```
flu_temp_data = np.full(len(all_cases_norm_series), 0.5)
training_data_df = pd.DataFrame({
"Temperature" : flu_temp_data,
"Flu Cases" : all_cases_norm_series
})
training_data_df
covid_temp_data = np.full(len(florida_wnew_cases_norm), 0.5)
testing_data_df = pd.DataFrame({
"Temperature" : covid_temp_data,
"COVID Cases" : florida_wnew_cases_norm
})
testing_data_df
testing_data_df.shape
training_data_np = training_data_df.values
testing_data_np = testing_data_df.values
```
## Building Neural Net Model
### preparing model data
```
# this code is directly from https://www.tensorflow.org/tutorials/structured_data/time_series
# much of below data formatting code is derived straight from same link
def multivariate_data(dataset, target, start_index, end_index, history_size,
target_size, step, single_step=False):
data = []
labels = []
start_index = start_index + history_size
if end_index is None:
end_index = len(dataset) - target_size
for i in range(start_index, end_index):
indices = range(i-history_size, i, step)
data.append(dataset[indices])
if single_step:
labels.append(target[i+target_size])
else:
labels.append(target[i:i+target_size])
return np.array(data), np.array(labels)
past_history = 22
future_target = 0
STEP = 1
x_train_single, y_train_single = multivariate_data(training_data_np, training_data_np[:, 1], 0,
None, past_history,
future_target, STEP,
single_step=True)
x_test_single, y_test_single = multivariate_data(testing_data_np, testing_data_np[:, 1],
0, None, past_history,
future_target, STEP,
single_step=True)
BATCH_SIZE = 300
BUFFER_SIZE = 1000
train_data_single = tf.data.Dataset.from_tensor_slices((x_train_single, y_train_single))
train_data_single = train_data_single.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()
test_data_single = tf.data.Dataset.from_tensor_slices((x_test_single, y_test_single))
test_data_single = test_data_single.batch(1).repeat()
```
### designing actual model
```
# creating the neural network model
lstm_prediction_model = tf.keras.Sequential([
tf.keras.layers.LSTM(32, input_shape=x_train_single.shape[-2:]),
tf.keras.layers.Dense(32),
tf.keras.layers.Dense(1)
])
lstm_prediction_model.compile(optimizer=tf.keras.optimizers.RMSprop(), loss="mae")
single_step_history = lstm_prediction_model.fit(train_data_single, epochs=10,
steps_per_epoch=250,
validation_data=test_data_single,
validation_steps=50)
def create_time_steps(length):
return list(range(-length, 0))
def show_plot(plot_data, delta, title):
labels = ['History', 'True Future', 'Model Prediction']
marker = ['.-', 'rx', 'go']
time_steps = create_time_steps(plot_data[0].shape[0])
if delta:
future = delta
else:
future = 0
plt.title(title)
for i, x in enumerate(plot_data):
if i:
plt.plot(future, plot_data[i], marker[i], markersize=10,
label=labels[i])
else:
plt.plot(time_steps, plot_data[i].flatten(), marker[i], label=labels[i])
plt.legend()
plt.xlim([time_steps[0], (future+5)*2])
plt.xlabel('Week (defined by Wednesdays)')
plt.ylabel('Normalized Cases')
return plt
for x, y in train_data_single.take(10):
#print(lstm_prediction_model.predict(x))
plot = show_plot([x[0][:, 1].numpy(), y[0].numpy(),
lstm_prediction_model.predict(x)[0]], 0,
'Training Data Prediction')
plot.show()
for x, y in test_data_single.take(1):
plot = show_plot([x[0][:, 1].numpy(), y[0].numpy(),
lstm_prediction_model.predict(x)[0]], 0,
'Florida COVID Case Prediction, Single Week')
plot.show()
```
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Writing layers and models with TensorFlow Keras
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/alpha/guide/keras/custom_layers_and_models"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/r2/guide/keras/custom_layers_and_models.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/r2/guide/keras/custom_layers_and_models.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
### Setup
```
from __future__ import absolute_import, division, print_function
!pip install tensorflow-gpu==2.0.0-alpha0
import tensorflow as tf
tf.keras.backend.clear_session() # For easy reset of notebook state.
```
## The Layer class
### Layers encapsulate a state (weights) and some computation
The main data structure you'll work with is the `Layer`.
A layer encapsulates both a state (the layer's "weights")
and a transformation from inputs to outputs (a "call", the layer's
forward pass).
Here's a densely-connected layer. It has a state: the variables `w` and `b`.
```
from tensorflow.keras import layers
class Linear(layers.Layer):
def __init__(self, units=32, input_dim=32):
super(Linear, self).__init__()
w_init = tf.random_normal_initializer()
self.w = tf.Variable(initial_value=w_init(shape=(input_dim, units),
dtype='float32'),
trainable=True)
b_init = tf.zeros_initializer()
self.b = tf.Variable(initial_value=b_init(shape=(units,),
dtype='float32'),
trainable=True)
def call(self, inputs):
return tf.matmul(inputs, self.w) + self.b
x = tf.ones((2, 2))
linear_layer = Linear(4, 2)
y = linear_layer(x)
print(y)
```
Note that the weights `w` and `b` are automatically tracked by the layer upon
being set as layer attributes:
```
assert linear_layer.weights == [linear_layer.w, linear_layer.b]
```
Note you also have access to a quicker shortcut for adding weight to a layer: the `add_weight` method:
```
class Linear(layers.Layer):
def __init__(self, units=32, input_dim=32):
super(Linear, self).__init__()
self.w = self.add_weight(shape=(input_dim, units),
initializer='random_normal',
trainable=True)
self.b = self.add_weight(shape=(units,),
initializer='zeros',
trainable=True)
def call(self, inputs):
return tf.matmul(inputs, self.w) + self.b
x = tf.ones((2, 2))
linear_layer = Linear(4, 2)
y = linear_layer(x)
print(y)
```
#### Layers can have non-trainable weights
Besides trainable weights, you can add non-trainable weights to a layer as well.
Such weights are meant not to be taken into account during backpropagation,
when you are training the layer.
Here's how to add and use a non-trainable weight:
```
class ComputeSum(layers.Layer):
def __init__(self, input_dim):
super(ComputeSum, self).__init__()
self.total = tf.Variable(initial_value=tf.zeros((input_dim,)),
trainable=False)
def call(self, inputs):
self.total.assign_add(tf.reduce_sum(inputs, axis=0))
return self.total
x = tf.ones((2, 2))
my_sum = ComputeSum(2)
y = my_sum(x)
print(y.numpy())
y = my_sum(x)
print(y.numpy())
```
It's part of `layer.weights`, but it gets categorized as a non-trainable weight:
```
print('weights:', len(my_sum.weights))
print('non-trainable weights:', len(my_sum.non_trainable_weights))
# It's not included in the trainable weights:
print('trainable_weights:', my_sum.trainable_weights)
```
### Best practice: deferring weight creation until the shape of the inputs is known
In the logistic regression example above, our `Linear` layer took an `input_dim` argument
that was used to compute the shape of the weights `w` and `b` in `__init__`:
```
class Linear(layers.Layer):
def __init__(self, units=32, input_dim=32):
super(Linear, self).__init__()
self.w = self.add_weight(shape=(input_dim, units),
initializer='random_normal',
trainable=True)
self.b = self.add_weight(shape=(units,),
initializer='random_normal',
trainable=True)
```
In many cases, you may not know in advance the size of your inputs, and you would
like to lazily create weights when that value becomes known,
some time after instantiating the layer.
In the Keras API, we recommend creating layer weights in the `build(inputs_shape)` method of your layer.
Like this:
```
class Linear(layers.Layer):
def __init__(self, units=32):
super(Linear, self).__init__()
self.units = units
def build(self, input_shape):
self.w = self.add_weight(shape=(input_shape[-1], self.units),
initializer='random_normal',
trainable=True)
self.b = self.add_weight(shape=(self.units,),
initializer='random_normal',
trainable=True)
def call(self, inputs):
return tf.matmul(inputs, self.w) + self.b
```
The `__call__` method of your layer will automatically run `build` the first time it is called.
You now have a layer that's lazy and easy to use:
```
linear_layer = Linear(32) # At instantiation, we don't know on what inputs this is going to get called
y = linear_layer(x) # The layer's weights are created dynamically the first time the layer is called
```
### Layers are recursively composable
If you assign a Layer instance as attribute of another Layer,
the outer layer will start tracking the weights of the inner layer.
We recommend creating such sublayers in the `__init__` method (since the sublayers will typically have a `build` method, they will be built when the outer layer gets built).
```
# Let's assume we are reusing the Linear class
# with a `build` method that we defined above.
class MLPBlock(layers.Layer):
def __init__(self):
super(MLPBlock, self).__init__()
self.linear_1 = Linear(32)
self.linear_2 = Linear(32)
self.linear_3 = Linear(1)
def call(self, inputs):
x = self.linear_1(inputs)
x = tf.nn.relu(x)
x = self.linear_2(x)
x = tf.nn.relu(x)
return self.linear_3(x)
mlp = MLPBlock()
y = mlp(tf.ones(shape=(3, 64))) # The first call to the `mlp` will create the weights
print('weights:', len(mlp.weights))
print('trainable weights:', len(mlp.trainable_weights))
```
### Layers recursively collect losses created during the forward pass
When writing the `call` method of a layer, you can create loss tensors that you will want to use later, when writing your training loop. This is doable by calling `self.add_loss(value)`:
```
# A layer that creates an activity regularization loss
class ActivityRegularizationLayer(layers.Layer):
def __init__(self, rate=1e-2):
super(ActivityRegularizationLayer, self).__init__()
self.rate = rate
def call(self, inputs):
self.add_loss(self.rate * tf.reduce_sum(inputs))
return inputs
```
These losses (including those created by any inner layer) can be retrieved via `layer.losses`.
This property is reset at the start of every `__call__` to the top-level layer, so that `layer.losses` always contains the loss values created during the last forward pass.
```
class OuterLayer(layers.Layer):
def __init__(self):
super(OuterLayer, self).__init__()
self.activity_reg = ActivityRegularizationLayer(1e-2)
def call(self, inputs):
return self.activity_reg(inputs)
layer = OuterLayer()
assert len(layer.losses) == 0 # No losses yet since the layer has never been called
_ = layer(tf.zeros(1, 1))
assert len(layer.losses) == 1 # We created one loss value
# `layer.losses` gets reset at the start of each __call__
_ = layer(tf.zeros(1, 1))
assert len(layer.losses) == 1 # This is the loss created during the call above
```
In addition, the `loss` property also contains regularization losses created for the weights of any inner layer:
```
class OuterLayer(layers.Layer):
def __init__(self):
super(OuterLayer, self).__init__()
self.dense = layers.Dense(32, kernel_regularizer=tf.keras.regularizers.l2(1e-3))
def call(self, inputs):
return self.dense(inputs)
layer = OuterLayer()
_ = layer(tf.zeros((1, 1)))
# This is `1e-3 * sum(layer.dense.kernel)`,
# created by the `kernel_regularizer` above.
print(layer.losses)
```
These losses are meant to be taken into account when writing training loops, like this:
```python
# Instantiate an optimizer.
optimizer = tf.keras.optimizers.SGD(learning_rate=1e-3)
loss_fn = keras.losses.SparseCategoricalCrossentropy(from_logits=True)
# Iterate over the batches of a dataset.
for x_batch_train, y_batch_train in train_dataset:
with tf.GradientTape() as tape:
logits = layer(x_batch_train) # Logits for this minibatch
# Loss value for this minibatch
loss_value = loss_fn(y_batch_train, logits))
# Add extra losses created during this forward pass:
loss_value += sum(model.losses)
grads = tape.gradient(loss_value, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
```
For a detailed guide about writing training loops, see the second section of the [Guide to Training & Evaluation](./training_and_evaluation.ipynb).
### You can optionally enable serialization on your layers
If you need your custom layers to be serializable as part of a [Functional model](./functional.ipynb), you can optionally implement a `get_config` method:
```
class Linear(layers.Layer):
def __init__(self, units=32):
super(Linear, self).__init__()
self.units = units
def build(self, input_shape):
self.w = self.add_weight(shape=(input_shape[-1], self.units),
initializer='random_normal',
trainable=True)
self.b = self.add_weight(shape=(self.units,),
initializer='random_normal',
trainable=True)
def call(self, inputs):
return tf.matmul(inputs, self.w) + self.b
def get_config(self):
return {'units': self.units}
# Now you can recreate the layer from its config:
layer = Linear(64)
config = layer.get_config()
print(config)
new_layer = Linear.from_config(config)
```
Note that the `__init__` method of the base `Layer` class takes some keyword arguments, in particular a `name` and a `dtype`. It's good practice to pass these arguments to the parent class in `__init__` and to include them in the layer config:
```
class Linear(layers.Layer):
def __init__(self, units=32, **kwargs):
super(Linear, self).__init__(**kwargs)
self.units = units
def build(self, input_shape):
self.w = self.add_weight(shape=(input_shape[-1], self.units),
initializer='random_normal',
trainable=True)
self.b = self.add_weight(shape=(self.units,),
initializer='random_normal',
trainable=True)
def call(self, inputs):
return tf.matmul(inputs, self.w) + self.b
def get_config(self):
config = super(Linear, self).get_config()
config.update({'units': self.units})
return config
layer = Linear(64)
config = layer.get_config()
print(config)
new_layer = Linear.from_config(config)
```
If you need more flexibility when deserializing the layer from its config, you can also override the `from_config` class method. This is the base implementation of `from_config`:
```python
def from_config(cls, config):
return cls(**config)
```
To learn more about serialization and saving, see the complete [Guide to Saving and Serializing Models](./saving_and_serializing.ipynb).
### Privileged `training` argument in the `call` method
Some layers, in particular the `BatchNormalization` layer and the `Dropout` layer, have different behaviors during training and inference. For such layers, it is standard practice to expose a `training` (boolean) argument in the `call` method.
By exposing this argument in `call`, you enable the built-in training and evaluation loops (e.g. `fit`) to correctly use the layer in training and inference.
```
class CustomDropout(layers.Layer):
def __init__(self, rate, **kwargs):
super(CustomDropout, self).__init__(**kwargs)
self.rate = rate
def call(self, inputs, training=None):
return tf.cond(training,
lambda: tf.nn.dropout(inputs, rate=self.rate),
lambda: inputs)
```
## Building Models
### The Model class
In general, you will use the `Layer` class to define inner computation blocks,
and will use the `Model` class to define the outer model -- the object you will train.
For instance, in a ResNet50 model, you would have several ResNet blocks subclassing `Layer`,
and a single `Model` encompassing the entire ResNet50 network.
The `Model` class has the same API as `Layer`, with the following differences:
- It exposes built-in training, evaluation, and prediction loops (`model.fit()`, `model.evaluate()`, `model.predict()`).
- It exposes the list of its inner layers, via the `model.layers` property.
- It exposes saving and serialization APIs.
Effectively, the "Layer" class corresponds to what we refer to in the literature
as a "layer" (as in "convolution layer" or "recurrent layer") or as a "block" (as in "ResNet block" or "Inception block").
Meanwhile, the "Model" class corresponds to what is referred to in the literature
as a "model" (as in "deep learning model") or as a "network" (as in "deep neural network").
For instance, we could take our mini-resnet example above, and use it to build a `Model` that we could
train with `fit()`, and that we could save with `save_weights`:
```python
class ResNet(tf.keras.Model):
def __init__(self):
super(ResNet, self).__init__()
self.block_1 = ResNetBlock()
self.block_2 = ResNetBlock()
self.global_pool = layers.GlobalAveragePooling2D()
self.classifier = Dense(num_classes)
def call(self, inputs):
x = self.block_1(inputs)
x = self.block_2(x)
x = self.global_pool(x)
return self.classifier(x)
resnet = ResNet()
dataset = ...
resnet.fit(dataset, epochs=10)
resnet.save_weights(filepath)
```
### Putting it all together: an end-to-end example
Here's what you've learned so far:
- A `Layer` encapsulate a state (created in `__init__` or `build`) and some computation (in `call`).
- Layers can be recursively nested to create new, bigger computation blocks.
- Layers can create and track losses (typically regularization losses).
- The outer container, the thing you want to train, is a `Model`. A `Model` is just like a `Layer`, but with added training and serialization utilities.
Let's put all of these things together into an end-to-end example: we're going to implement a Variational AutoEncoder (VAE). We'll train it on MNIST digits.
Our VAE will be a subclass of `Model`, built as a nested composition of layers that subclass `Layer`. It will feature a regularization loss (KL divergence).
```
class Sampling(layers.Layer):
"""Uses (z_mean, z_log_var) to sample z, the vector encoding a digit."""
def call(self, inputs):
z_mean, z_log_var = inputs
batch = tf.shape(z_mean)[0]
dim = tf.shape(z_mean)[1]
epsilon = tf.keras.backend.random_normal(shape=(batch, dim))
return z_mean + tf.exp(0.5 * z_log_var) * epsilon
class Encoder(layers.Layer):
"""Maps MNIST digits to a triplet (z_mean, z_log_var, z)."""
def __init__(self,
latent_dim=32,
intermediate_dim=64,
name='encoder',
**kwargs):
super(Encoder, self).__init__(name=name, **kwargs)
self.dense_proj = layers.Dense(intermediate_dim, activation='relu')
self.dense_mean = layers.Dense(latent_dim)
self.dense_log_var = layers.Dense(latent_dim)
self.sampling = Sampling()
def call(self, inputs):
x = self.dense_proj(inputs)
z_mean = self.dense_mean(x)
z_log_var = self.dense_log_var(x)
z = self.sampling((z_mean, z_log_var))
return z_mean, z_log_var, z
class Decoder(layers.Layer):
"""Converts z, the encoded digit vector, back into a readable digit."""
def __init__(self,
original_dim,
intermediate_dim=64,
name='decoder',
**kwargs):
super(Decoder, self).__init__(name=name, **kwargs)
self.dense_proj = layers.Dense(intermediate_dim, activation='relu')
self.dense_output = layers.Dense(original_dim, activation='sigmoid')
def call(self, inputs):
x = self.dense_proj(inputs)
return self.dense_output(x)
class VariationalAutoEncoder(tf.keras.Model):
"""Combines the encoder and decoder into an end-to-end model for training."""
def __init__(self,
original_dim,
intermediate_dim=64,
latent_dim=32,
name='autoencoder',
**kwargs):
super(VariationalAutoEncoder, self).__init__(name=name, **kwargs)
self.original_dim = original_dim
self.encoder = Encoder(latent_dim=latent_dim,
intermediate_dim=intermediate_dim)
self.decoder = Decoder(original_dim, intermediate_dim=intermediate_dim)
def call(self, inputs):
z_mean, z_log_var, z = self.encoder(inputs)
reconstructed = self.decoder(z)
# Add KL divergence regularization loss.
kl_loss = - 0.5 * tf.reduce_mean(
z_log_var - tf.square(z_mean) - tf.exp(z_log_var) + 1)
self.add_loss(kl_loss)
return reconstructed
original_dim = 784
vae = VariationalAutoEncoder(original_dim, 64, 32)
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-3)
mse_loss_fn = tf.keras.losses.MeanSquaredError()
loss_metric = tf.keras.metrics.Mean()
(x_train, _), _ = tf.keras.datasets.mnist.load_data()
x_train = x_train.reshape(60000, 784).astype('float32') / 255
train_dataset = tf.data.Dataset.from_tensor_slices(x_train)
train_dataset = train_dataset.shuffle(buffer_size=1024).batch(64)
# Iterate over epochs.
for epoch in range(3):
print('Start of epoch %d' % (epoch,))
# Iterate over the batches of the dataset.
for step, x_batch_train in enumerate(train_dataset):
with tf.GradientTape() as tape:
reconstructed = vae(x_batch_train)
# Compute reconstruction loss
loss = mse_loss_fn(x_batch_train, reconstructed)
loss += sum(vae.losses) # Add KLD regularization loss
grads = tape.gradient(loss, vae.trainable_variables)
optimizer.apply_gradients(zip(grads, vae.trainable_variables))
loss_metric(loss)
if step % 100 == 0:
print('step %s: mean loss = %s' % (step, loss_metric.result()))
```
Note that since the VAE is subclassing `Model`, it features built-in training loops. So you could also have trained it like this:
```
vae = VariationalAutoEncoder(784, 64, 32)
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-3)
vae.compile(optimizer, loss=tf.keras.losses.MeanSquaredError())
vae.fit(x_train, x_train, epochs=3, batch_size=64)
```
### Beyond object-oriented development: the Functional API
Was this example too much object-oriented development for you? You can also build models using [the Functional API](./functional.ipynb). Importantly, choosing one style or another does not prevent you from leveraging components written in the other style: you can always mix-and-match.
For instance, the Functional API example below reuses the same `Sampling` layer we defined in the example above.
```
original_dim = 784
intermediate_dim = 64
latent_dim = 32
# Define encoder model.
original_inputs = tf.keras.Input(shape=(original_dim,), name='encoder_input')
x = layers.Dense(intermediate_dim, activation='relu')(original_inputs)
z_mean = layers.Dense(latent_dim, name='z_mean')(x)
z_log_var = layers.Dense(latent_dim, name='z_log_var')(x)
z = Sampling()((z_mean, z_log_var))
encoder = tf.keras.Model(inputs=original_inputs, outputs=z, name='encoder')
# Define decoder model.
latent_inputs = tf.keras.Input(shape=(latent_dim,), name='z_sampling')
x = layers.Dense(intermediate_dim, activation='relu')(latent_inputs)
outputs = layers.Dense(original_dim, activation='sigmoid')(x)
decoder = tf.keras.Model(inputs=latent_inputs, outputs=outputs, name='decoder')
# Define VAE model.
outputs = decoder(z)
vae = tf.keras.Model(inputs=original_inputs, outputs=outputs, name='vae')
# Add KL divergence regularization loss.
kl_loss = - 0.5 * tf.reduce_mean(
z_log_var - tf.square(z_mean) - tf.exp(z_log_var) + 1)
vae.add_loss(kl_loss)
# Train.
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-3)
vae.compile(optimizer, loss=tf.keras.losses.MeanSquaredError())
vae.fit(x_train, x_train, epochs=3, batch_size=64)
```
|
github_jupyter
|
# MALDI acquisition of predefined areas
author: Alex Mattausch
version: 0.1.0
```
%load_ext autoreload
%autoreload 2
# "%matplotlib widget" is slightly better, but sometimes doesn't work
# "%matplotlib notebook" or "%matplotlib inline" can be used as alternatives
%matplotlib widget
import matplotlib.pyplot as plt
import remote_control.control as rc
import remote_control.utils as utils
#from IPython.display import set_matplotlib_formats
#set_matplotlib_formats('svg')
from remote_control import acquisition
from remote_control.control import configure_fly_at_fixed_z
from itertools import product
CONFIG_FN = 'remote_config.json'
### IN CASE OF ERROR, make sure Jupyter is set to use the "Python [conda env:maldi-control-notebooks]" kernel
qa = acquisition.QueueAquisition(
config_fn = CONFIG_FN,
datadir="./data" # will save spatial position file here
)
# For plates with recessed wells, configure this to move the slide away when moving between wells.
# If the stage needs to move in the X/Y plane more than "distance", it will move the stage's Z axis
# to the value of the "z" parameter.
# configure_fly_at_fixed_z(distance=2000, z=3000) # Enable
configure_fly_at_fixed_z(distance=None, z=None) # Disable
```
### 1. Define slide area
```
# Set up safety bounds (optional - comment this out if they're unwanted)
qa.set_image_bounds(
min_x=-15000,
max_x=15000,
min_y=-25000,
max_y=25000,
)
```
### 2. Add acquisition areas
Run this cell to clear areas and start over:
```
qa.clear_areas()
qa.add_area(
name="well_1", # <- Optional!
line_start=(-10649, -18704, 3444),
line_end=(-4149, -18704, 3444),
perpendicular=(-9399, -24204, 3444),
step_size_x=500,
step_size_y=1000
)
qa.add_area(
name="well_2",
line_start=(-10729, -6580, 3444),
line_end=(-8229, -6580, 3444),
perpendicular=(-9479, -9080, 3444),
step_size_x=25,
step_size_y=25
)
qa.add_area(
name="well_4",
line_start=(-10729, 22000, 3444),
line_end=(-8229, 22000, 3444),
perpendicular=(-9479, 18000, 3444),
step_size_x=250,
step_size_y=250
)
qa.plot_areas()
```
**NOTE:** numbers in boxes indicate acquisition order!
### 3. Generate measurement positions from areas
```
qa.generate_targets()
plt.close('all')
qa.plot_targets(annotate=True)
```
### 4. Run acquistion
Once you are happy with plots above:
- Launch Telnet in apsmaldi software
- Press START on TUNE somputer
- Run the following cell with dummy=True to test coordinates
- Run the following cell with dummy=Fase, measure=True to perform acquisition
```
OUTPUT_DIR = 'D:\\imagingMS\\2021_08\\your name\\'
IMZML_PREFIX = OUTPUT_DIR + '01052019_Mouse_DHB_pos_mz200-800_px50x50_LR'
qa.acquire(
filename=IMZML_PREFIX, # Prefix for output coordinates file used in ImzML conversion
dummy=True, # False - send commands to MALDI, True - don't connect, just print commands
measure=False, # False - move stage only, True - move stage & acquire data
email_on_success='[email protected]', # Set to None to suppress
email_on_failure='[email protected]', # Set to None to suppress
)
```
### 5. Cleanup
After imaging run the following cell to terminate Telnet
```
rc.close(quit=True)
```
|
github_jupyter
|
<a href="https://practicalai.me"><img src="https://raw.githubusercontent.com/practicalAI/images/master/images/rounded_logo.png" width="100" align="left" hspace="20px" vspace="20px"></a>
<img src="https://raw.githubusercontent.com/practicalAI/images/master/basic_ml/06_Multilayer_Perceptron/nn.png" width="200" vspace="10px" align="right">
<div align="left">
<h1>Multilayer Perceptron (MLP)</h1>
In this lesson, we will explore multilayer perceptrons (MLPs) which are a basic type of neural network. We will implement them using Tensorflow with Keras.
<table align="center">
<td>
<img src="https://raw.githubusercontent.com/practicalAI/images/master/images/rounded_logo.png" width="25"><a target="_blank" href="https://practicalai.me"> View on practicalAI</a>
</td>
<td>
<img src="https://raw.githubusercontent.com/practicalAI/images/master/images/colab_logo.png" width="25"><a target="_blank" href="https://colab.research.google.com/github/practicalAI/practicalAI/blob/master/notebooks/06_Multilayer_Perceptron.ipynb"> Run in Google Colab</a>
</td>
<td>
<img src="https://raw.githubusercontent.com/practicalAI/images/master/images/github_logo.png" width="22"><a target="_blank" href="https://github.com/practicalAI/practicalAI/blob/master/notebooks/basic_ml/06_Multilayer_Perceptron.ipynb"> View code on GitHub</a>
</td>
</table>
# Overview
* **Objective:** Predict the probability of class $y$ given the inputs $X$. Non-linearity is introduced to model the complex, non-linear data.
* **Advantages:**
* Can model non-linear patterns in the data really well.
* **Disadvantages:**
* Overfits easily.
* Computationally intensive as network increases in size.
* Not easily interpretable.
* **Miscellaneous:** Future neural network architectures that we'll see use the MLP as a modular unit for feed forward operations (affine transformation (XW) followed by a non-linear operation).
Our goal is to learn a model 𝑦̂ that models 𝑦 given 𝑋 . You'll notice that neural networks are just extensions of the generalized linear methods we've seen so far but with non-linear activation functions since our data will be highly non-linear.
<img src="https://raw.githubusercontent.com/practicalAI/images/master/basic_ml/06_Multilayer_Perceptron/nn.png" width="550">
$z_1 = XW_1$
$a_1 = f(z_1)$
$z_2 = a_1W_2$
$\hat{y} = softmax(z_2)$ # classification
* $X$ = inputs | $\in \mathbb{R}^{NXD}$ ($D$ is the number of features)
* $W_1$ = 1st layer weights | $\in \mathbb{R}^{DXH}$ ($H$ is the number of hidden units in layer 1)
* $z_1$ = outputs from first layer $\in \mathbb{R}^{NXH}$
* $f$ = non-linear activation function
*nn $a_1$ = activation applied first layer's outputs | $\in \mathbb{R}^{NXH}$
* $W_2$ = 2nd layer weights | $\in \mathbb{R}^{HXC}$ ($C$ is the number of classes)
* $z_2$ = outputs from second layer $\in \mathbb{R}^{NXH}$
* $\hat{y}$ = prediction | $\in \mathbb{R}^{NXC}$ ($N$ is the number of samples)
**Note**: We're going to leave out the bias terms $\beta$ to avoid further crowding the backpropagation calculations.
### Training
1. Randomly initialize the model's weights $W$ (we'll cover more effective initalization strategies later in this lesson).
2. Feed inputs $X$ into the model to do the forward pass and receive the probabilities.
* $z_1 = XW_1$
* $a_1 = f(z_1)$
* $z_2 = a_1W_2$
* $\hat{y} = softmax(z_2)$
3. Compare the predictions $\hat{y}$ (ex. [0.3, 0.3, 0.4]]) with the actual target values $y$ (ex. class 2 would look like [0, 0, 1]) with the objective (cost) function to determine loss $J$. A common objective function for classification tasks is cross-entropy loss.
* $J(\theta) = - \sum_i y_i ln (\hat{y_i}) $
* Since each input maps to exactly one class, our cross-entropy loss simplifies to:
* $J(\theta) = - \sum_i ln(\hat{y_i}) = - \sum_i ln (\frac{e^{X_iW_y}}{\sum_j e^{X_iW}}) $
4. Calculate the gradient of loss $J(\theta)$ w.r.t to the model weights.
* $\frac{\partial{J}}{\partial{W_{2j}}} = \frac{\partial{J}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{W_{2j}}} = - \frac{1}{\hat{y}}\frac{\partial{\hat{y}}}{\partial{W_{2j}}} = - \frac{1}{\frac{e^{W_{2y}a_1}}{\sum_j e^{a_1W}}}\frac{\sum_j e^{a_1W}e^{a_1W_{2y}}0 - e^{a_1W_{2y}}e^{a_1W_{2j}}a_1}{(\sum_j e^{a_1W})^2} = \frac{a_1e^{a_1W_{2j}}}{\sum_j e^{a_1W}} = a_1\hat{y}$
* $\frac{\partial{J}}{\partial{W_{2y}}} = \frac{\partial{J}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{W_{2y}}} = - \frac{1}{\hat{y}}\frac{\partial{\hat{y}}}{\partial{W_{2y}}} = - \frac{1}{\frac{e^{W_{2y}a_1}}{\sum_j e^{a_1W}}}\frac{\sum_j e^{a_1W}e^{a_1W_{2y}}a_1 - e^{a_1W_{2y}}e^{a_1W_{2y}}a_1}{(\sum_j e^{a_1W})^2} = \frac{1}{\hat{y}}(a_1\hat{y} - a_1\hat{y}^2) = a_1(\hat{y}-1)$
* $ \frac{\partial{J}}{\partial{W_1}} = \frac{\partial{J}}{\partial{\hat{y}}} \frac{\partial{\hat{y}}}{\partial{a_2}} \frac{\partial{a_2}}{\partial{z_2}} \frac{\partial{z_2}}{\partial{W_1}} = W_2(\partial{scores})(\partial{ReLU})X $
5. Update the weights $W$ using a small learning rate $\alpha$. The updates will penalize the probabiltiy for the incorrect classes (j) and encourage a higher probability for the correct class (y).
* $W_i = W_i - \alpha\frac{\partial{J}}{\partial{W_i}}$
6. Repeat steps 2 - 4 until model performs well.
# Set up
```
# Use TensorFlow 2.x
%tensorflow_version 2.x
import os
import numpy as np
import tensorflow as tf
# Arguments
SEED = 1234
SHUFFLE = True
DATA_FILE = "spiral.csv"
INPUT_DIM = 2
NUM_CLASSES = 3
NUM_SAMPLES_PER_CLASS = 500
TRAIN_SIZE = 0.7
VAL_SIZE = 0.15
TEST_SIZE = 0.15
NUM_EPOCHS = 10
BATCH_SIZE = 32
HIDDEN_DIM = 100
LEARNING_RATE = 1e-2
# Set seed for reproducability
np.random.seed(SEED)
tf.random.set_seed(SEED)
```
# Data
Download non-linear spiral data for a classification task.
```
import matplotlib.pyplot as plt
import pandas as pd
import urllib
# Upload data from GitHub to notebook's local drive
url = "https://raw.githubusercontent.com/practicalAI/practicalAI/master/data/spiral.csv"
response = urllib.request.urlopen(url)
html = response.read()
with open(DATA_FILE, 'wb') as fp:
fp.write(html)
# Load data
df = pd.read_csv(DATA_FILE, header=0)
X = df[['X1', 'X2']].values
y = df['color'].values
df.head(5)
print ("X: ", np.shape(X))
print ("y: ", np.shape(y))
# Visualize data
plt.title("Generated non-linear data")
colors = {'c1': 'red', 'c2': 'yellow', 'c3': 'blue'}
plt.scatter(X[:, 0], X[:, 1], c=[colors[_y] for _y in y], edgecolors='k', s=25)
plt.show()
```
# Split data
```
import collections
import json
from sklearn.model_selection import train_test_split
```
### Components
```
def train_val_test_split(X, y, val_size, test_size, shuffle):
"""Split data into train/val/test datasets.
"""
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=test_size, stratify=y, shuffle=shuffle)
X_train, X_val, y_train, y_val = train_test_split(
X_train, y_train, test_size=val_size, stratify=y_train, shuffle=shuffle)
return X_train, X_val, X_test, y_train, y_val, y_test
```
### Operations
```
# Create data splits
X_train, X_val, X_test, y_train, y_val, y_test = train_val_test_split(
X=X, y=y, val_size=VAL_SIZE, test_size=TEST_SIZE, shuffle=SHUFFLE)
class_counts = dict(collections.Counter(y))
print (f"X_train: {X_train.shape}, y_train: {y_train.shape}")
print (f"X_val: {X_val.shape}, y_val: {y_val.shape}")
print (f"X_test: {X_test.shape}, y_test: {y_test.shape}")
print (f"X_train[0]: {X_train[0]}")
print (f"y_train[0]: {y_train[0]}")
print (f"Classes: {class_counts}")
```
# Label encoder
```
import json
from sklearn.preprocessing import LabelEncoder
# Output vectorizer
y_tokenizer = LabelEncoder()
# Fit on train data
y_tokenizer = y_tokenizer.fit(y_train)
classes = list(y_tokenizer.classes_)
print (f"classes: {classes}")
# Convert labels to tokens
print (f"y_train[0]: {y_train[0]}")
y_train = y_tokenizer.transform(y_train)
y_val = y_tokenizer.transform(y_val)
y_test = y_tokenizer.transform(y_test)
print (f"y_train[0]: {y_train[0]}")
# Class weights
counts = collections.Counter(y_train)
class_weights = {_class: 1.0/count for _class, count in counts.items()}
print (f"class counts: {counts},\nclass weights: {class_weights}")
```
# Standardize data
We need to standardize our data (zero mean and unit variance) in order to optimize quickly. We're only going to standardize the inputs X because out outputs y are class values.
```
from sklearn.preprocessing import StandardScaler
# Standardize the data (mean=0, std=1) using training data
X_scaler = StandardScaler().fit(X_train)
# Apply scaler on training and test data (don't standardize outputs for classification)
standardized_X_train = X_scaler.transform(X_train)
standardized_X_val = X_scaler.transform(X_val)
standardized_X_test = X_scaler.transform(X_test)
# Check
print (f"standardized_X_train: mean: {np.mean(standardized_X_train, axis=0)[0]}, std: {np.std(standardized_X_train, axis=0)[0]}")
print (f"standardized_X_val: mean: {np.mean(standardized_X_val, axis=0)[0]}, std: {np.std(standardized_X_val, axis=0)[0]}")
print (f"standardized_X_test: mean: {np.mean(standardized_X_test, axis=0)[0]}, std: {np.std(standardized_X_test, axis=0)[0]}")
```
# Linear model
Before we get to our neural network, we're going to implement a generalized linear model (logistic regression) first to see why linear models won't suffice for our dataset. We will use Tensorflow with Keras to do this.
```
import itertools
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Input
from tensorflow.keras.losses import SparseCategoricalCrossentropy
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam
```
### Components
```
# Linear model
class LogisticClassifier(Model):
def __init__(self, hidden_dim, num_classes):
super(LogisticClassifier, self).__init__()
self.fc1 = Dense(units=hidden_dim, activation='linear') # linear = no activation function
self.fc2 = Dense(units=num_classes, activation='softmax')
def call(self, x_in, training=False):
"""Forward pass."""
z = self.fc1(x_in)
y_pred = self.fc2(z)
return y_pred
def sample(self, input_shape):
x_in = Input(shape=input_shape)
return Model(inputs=x_in, outputs=self.call(x_in)).summary()
def plot_confusion_matrix(y_true, y_pred, classes, cmap=plt.cm.Blues):
"""Plot a confusion matrix using ground truth and predictions."""
# Confusion matrix
cm = confusion_matrix(y_true, y_pred)
cm_norm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
# Figure
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(cm, cmap=plt.cm.Blues)
fig.colorbar(cax)
# Axis
plt.title("Confusion matrix")
plt.ylabel("True label")
plt.xlabel("Predicted label")
ax.set_xticklabels([''] + classes)
ax.set_yticklabels([''] + classes)
ax.xaxis.set_label_position('bottom')
ax.xaxis.tick_bottom()
# Values
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, f"{cm[i, j]:d} ({cm_norm[i, j]*100:.1f}%)",
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
# Display
plt.show()
def plot_multiclass_decision_boundary(model, X, y, savefig_fp=None):
"""Plot the multiclass decision boundary for a model that accepts 2D inputs.
Arguments:
model {function} -- trained model with function model.predict(x_in).
X {numpy.ndarray} -- 2D inputs with shape (N, 2).
y {numpy.ndarray} -- 1D outputs with shape (N,).
"""
# Axis boundaries
x_min, x_max = X[:, 0].min() - 0.1, X[:, 0].max() + 0.1
y_min, y_max = X[:, 1].min() - 0.1, X[:, 1].max() + 0.1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 101),
np.linspace(y_min, y_max, 101))
# Create predictions
x_in = np.c_[xx.ravel(), yy.ravel()]
y_pred = model.predict(x_in)
y_pred = np.argmax(y_pred, axis=1).reshape(xx.shape)
# Plot decision boundary
plt.contourf(xx, yy, y_pred, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.RdYlBu)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
# Plot
if savefig_fp:
plt.savefig(savefig_fp, format='png')
```
### Operations
```
# Initialize the model
model = LogisticClassifier(hidden_dim=HIDDEN_DIM,
num_classes=NUM_CLASSES)
model.sample(input_shape=(INPUT_DIM,))
# Compile
model.compile(optimizer=Adam(lr=LEARNING_RATE),
loss=SparseCategoricalCrossentropy(),
metrics=['accuracy'])
# Training
model.fit(x=standardized_X_train,
y=y_train,
validation_data=(standardized_X_val, y_val),
epochs=NUM_EPOCHS,
batch_size=BATCH_SIZE,
class_weight=class_weights,
shuffle=False,
verbose=1)
# Predictions
pred_train = model.predict(standardized_X_train)
pred_test = model.predict(standardized_X_test)
print (f"sample probability: {pred_test[0]}")
pred_train = np.argmax(pred_train, axis=1)
pred_test = np.argmax(pred_test, axis=1)
print (f"sample class: {pred_test[0]}")
# Accuracy
train_acc = accuracy_score(y_train, pred_train)
test_acc = accuracy_score(y_test, pred_test)
print (f"train acc: {train_acc:.2f}, test acc: {test_acc:.2f}")
# Metrics
plot_confusion_matrix(y_test, pred_test, classes=classes)
print (classification_report(y_test, pred_test))
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=standardized_X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=standardized_X_test, y=y_test)
plt.show()
```
# Activation functions
Using the generalized linear method (logistic regression) yielded poor results because of the non-linearity present in our data. We need to use an activation function that can allow our model to learn and map the non-linearity in our data. There are many different options so let's explore a few.
```
from tensorflow.keras.activations import relu
from tensorflow.keras.activations import sigmoid
from tensorflow.keras.activations import tanh
# Fig size
plt.figure(figsize=(12,3))
# Data
x = np.arange(-5., 5., 0.1)
# Sigmoid activation (constrain a value between 0 and 1.)
plt.subplot(1, 3, 1)
plt.title("Sigmoid activation")
y = sigmoid(x)
plt.plot(x, y)
# Tanh activation (constrain a value between -1 and 1.)
plt.subplot(1, 3, 2)
y = tanh(x)
plt.title("Tanh activation")
plt.plot(x, y)
# Relu (clip the negative values to 0)
plt.subplot(1, 3, 3)
y = relu(x)
plt.title("ReLU activation")
plt.plot(x, y)
# Show plots
plt.show()
```
The ReLU activation function ($max(0,z)$) is by far the most widely used activation function for neural networks. But as you can see, each activation function has it's own contraints so there are circumstances where you'll want to use different ones. For example, if we need to constrain our outputs between 0 and 1, then the sigmoid activation is the best choice.
<img height="45" src="http://bestanimations.com/HomeOffice/Lights/Bulbs/animated-light-bulb-gif-29.gif" align="left" vspace="20px" hspace="10px">
In some cases, using a ReLU activation function may not be sufficient. For instance, when the outputs from our neurons are mostly negative, the activation function will produce zeros. This effectively creates a "dying ReLU" and a recovery is unlikely. To mitigate this effect, we could lower the learning rate or use [alternative ReLU activations](https://medium.com/tinymind/a-practical-guide-to-relu-b83ca804f1f7), ex. leaky ReLU or parametric ReLU (PReLU), which have a small slope for negative neuron outputs.
# From scratch
Now let's create our multilayer perceptron (MLP) which is going to be exactly like the logistic regression model but with the activation function to map the non-linearity in our data. Before we use TensorFlow 2.0 + Keras we will implement our neural network from scratch using NumPy so we can:
1. Absorb the fundamental concepts by implementing from scratch
2. Appreciate the level of abstraction TensorFlow provides
<div align="left">
<img src="https://raw.githubusercontent.com/practicalAI/images/master/images/lightbulb.gif" width="45px" align="left" hspace="10px">
</div>
It's normal to find the math and code in this section slightly complex. You can still read each of the steps to build intuition for when we implement this using TensorFlow + Keras.
```
print (f"X: {standardized_X_train.shape}")
print (f"y: {y_train.shape}")
```
Our goal is to learn a model 𝑦̂ that models 𝑦 given 𝑋 . You'll notice that neural networks are just extensions of the generalized linear methods we've seen so far but with non-linear activation functions since our data will be highly non-linear.
$z_1 = XW_1$
$a_1 = f(z_1)$
$z_2 = a_1W_2$
$\hat{y} = softmax(z_2)$ # classification
* $X$ = inputs | $\in \mathbb{R}^{NXD}$ ($D$ is the number of features)
* $W_1$ = 1st layer weights | $\in \mathbb{R}^{DXH}$ ($H$ is the number of hidden units in layer 1)
* $z_1$ = outputs from first layer $\in \mathbb{R}^{NXH}$
* $f$ = non-linear activation function
* $a_1$ = activation applied first layer's outputs | $\in \mathbb{R}^{NXH}$
* $W_2$ = 2nd layer weights | $\in \mathbb{R}^{HXC}$ ($C$ is the number of classes)
* $z_2$ = outputs from second layer $\in \mathbb{R}^{NXH}$
* $\hat{y}$ = prediction | $\in \mathbb{R}^{NXC}$ ($N$ is the number of samples)
1. Randomly initialize the model's weights $W$ (we'll cover more effective initalization strategies later in this lesson).
```
# Initialize first layer's weights
W1 = 0.01 * np.random.randn(INPUT_DIM, HIDDEN_DIM)
b1 = np.zeros((1, HIDDEN_DIM))
print (f"W1: {W1.shape}")
print (f"b1: {b1.shape}")
```
2. Feed inputs $X$ into the model to do the forward pass and receive the probabilities.
First we pass the inputs into the first layer.
* $z_1 = XW_1$
```
# z1 = [NX2] · [2X100] + [1X100] = [NX100]
z1 = np.dot(standardized_X_train, W1) + b1
print (f"z1: {z1.shape}")
```
Next we apply the non-linear activation function, ReLU ($max(0,z)$) in this case.
* $a_1 = f(z_1)$
```
# Apply activation function
a1 = np.maximum(0, z1) # ReLU
print (f"a_1: {a1.shape}")
```
We pass the activations to the second layer to get our logits.
* $z_2 = a_1W_2$
```
# Initialize second layer's weights
W2 = 0.01 * np.random.randn(HIDDEN_DIM, NUM_CLASSES)
b2 = np.zeros((1, NUM_CLASSES))
print (f"W2: {W2.shape}")
print (f"b2: {b2.shape}")
# z2 = logits = [NX100] · [100X3] + [1X3] = [NX3]
logits = np.dot(a1, W2) + b2
print (f"logits: {logits.shape}")
print (f"sample: {logits[0]}")
```
We'll apply the softmax function to normalize the logits and btain class probabilities.
* $\hat{y} = softmax(z_2)$
```
# Normalization via softmax to obtain class probabilities
exp_logits = np.exp(logits)
y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
print (f"y_hat: {y_hat.shape}")
print (f"sample: {y_hat[0]}")
```
3. Compare the predictions $\hat{y}$ (ex. [0.3, 0.3, 0.4]]) with the actual target values $y$ (ex. class 2 would look like [0, 0, 1]) with the objective (cost) function to determine loss $J$. A common objective function for classification tasks is cross-entropy loss.
* $J(\theta) = - \sum_i ln(\hat{y_i}) = - \sum_i ln (\frac{e^{X_iW_y}}{\sum_j e^{X_iW}}) $
```
# Loss
correct_class_logprobs = -np.log(y_hat[range(len(y_hat)), y_train])
loss = np.sum(correct_class_logprobs) / len(y_train)
```
4. Calculate the gradient of loss $J(\theta)$ w.r.t to the model weights.
The gradient of the loss w.r.t to W2 is the same as the gradients from logistic regression since $\hat{y} = softmax(z_2)$.
* $\frac{\partial{J}}{\partial{W_{2j}}} = \frac{\partial{J}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{W_{2j}}} = - \frac{1}{\hat{y}}\frac{\partial{\hat{y}}}{\partial{W_{2j}}} = - \frac{1}{\frac{e^{W_{2y}a_1}}{\sum_j e^{a_1W}}}\frac{\sum_j e^{a_1W}e^{a_1W_{2y}}0 - e^{a_1W_{2y}}e^{a_1W_{2j}}a_1}{(\sum_j e^{a_1W})^2} = \frac{a_1e^{a_1W_{2j}}}{\sum_j e^{a_1W}} = a_1\hat{y}$
* $\frac{\partial{J}}{\partial{W_{2y}}} = \frac{\partial{J}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{W_{2y}}} = - \frac{1}{\hat{y}}\frac{\partial{\hat{y}}}{\partial{W_{2y}}} = - \frac{1}{\frac{e^{W_{2y}a_1}}{\sum_j e^{a_1W}}}\frac{\sum_j e^{a_1W}e^{a_1W_{2y}}a_1 - e^{a_1W_{2y}}e^{a_1W_{2y}}a_1}{(\sum_j e^{a_1W})^2} = \frac{1}{\hat{y}}(a_1\hat{y} - a_1\hat{y}^2) = a_1(\hat{y}-1)$
The gradient of the loss w.r.t W1 is a bit trickier since we have to backpropagate through two sets of weights.
* $ \frac{\partial{J}}{\partial{W_1}} = \frac{\partial{J}}{\partial{\hat{y}}} \frac{\partial{\hat{y}}}{\partial{a_1}} \frac{\partial{a_1}}{\partial{z_1}} \frac{\partial{z_1}}{\partial{W_1}} = W_2(\partial{scores})(\partial{ReLU})X $
```
# dJ/dW2
dscores = y_hat
dscores[range(len(y_hat)), y_train] -= 1
dscores /= len(y_train)
dW2 = np.dot(a1.T, dscores)
db2 = np.sum(dscores, axis=0, keepdims=True)
# dJ/dW1
dhidden = np.dot(dscores, W2.T)
dhidden[a1 <= 0] = 0 # ReLu backprop
dW1 = np.dot(standardized_X_train.T, dhidden)
db1 = np.sum(dhidden, axis=0, keepdims=True)
```
5. Update the weights $W$ using a small learning rate $\alpha$. The updates will penalize the probabiltiy for the incorrect classes (j) and encourage a higher probability for the correct class (y).
* $W_i = W_i - \alpha\frac{\partial{J}}{\partial{W_i}}$
```
# Update weights
W1 += -LEARNING_RATE * dW1
b1 += -LEARNING_RATE * db1
W2 += -LEARNING_RATE * dW2
b2 += -LEARNING_RATE * db2
```
6. Repeat steps 2 - 4 until model performs well.
```
# Initialize random weights
W1 = 0.01 * np.random.randn(INPUT_DIM, HIDDEN_DIM)
b1 = np.zeros((1, HIDDEN_DIM))
W2 = 0.01 * np.random.randn(HIDDEN_DIM, NUM_CLASSES)
b2 = np.zeros((1, NUM_CLASSES))
# Training loop
for epoch_num in range(1000):
# First layer forward pass [NX2] · [2X100] = [NX100]
z1 = np.dot(standardized_X_train, W1) + b1
# Apply activation function
a1 = np.maximum(0, z1) # ReLU
# z2 = logits = [NX100] · [100X3] = [NX3]
logits = np.dot(a1, W2) + b2
# Normalization via softmax to obtain class probabilities
exp_logits = np.exp(logits)
y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
# Loss
correct_class_logprobs = -np.log(y_hat[range(len(y_hat)), y_train])
loss = np.sum(correct_class_logprobs) / len(y_train)
# show progress
if epoch_num%100 == 0:
# Accuracy
y_pred = np.argmax(logits, axis=1)
accuracy = np.mean(np.equal(y_train, y_pred))
print (f"Epoch: {epoch_num}, loss: {loss:.3f}, accuracy: {accuracy:.3f}")
# dJ/dW2
dscores = y_hat
dscores[range(len(y_hat)), y_train] -= 1
dscores /= len(y_train)
dW2 = np.dot(a1.T, dscores)
db2 = np.sum(dscores, axis=0, keepdims=True)
# dJ/dW1
dhidden = np.dot(dscores, W2.T)
dhidden[a1 <= 0] = 0 # ReLu backprop
dW1 = np.dot(standardized_X_train.T, dhidden)
db1 = np.sum(dhidden, axis=0, keepdims=True)
# Update weights
W1 += -1e0 * dW1
b1 += -1e0 * db1
W2 += -1e0 * dW2
b2 += -1e0 * db2
class MLPFromScratch():
def predict(self, x):
z1 = np.dot(x, W1) + b1
a1 = np.maximum(0, z1)
logits = np.dot(a1, W2) + b2
exp_logits = np.exp(logits)
y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
return y_hat
# Evaluation
model = MLPFromScratch()
logits_train = model.predict(standardized_X_train)
pred_train = np.argmax(logits_train, axis=1)
logits_test = model.predict(standardized_X_test)
pred_test = np.argmax(logits_test, axis=1)
# Training and test accuracy
train_acc = np.mean(np.equal(y_train, pred_train))
test_acc = np.mean(np.equal(y_test, pred_test))
print (f"train acc: {train_acc:.2f}, test acc: {test_acc:.2f}")
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=standardized_X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=standardized_X_test, y=y_test)
plt.show()
```
Credit for the plotting functions and the intuition behind all this is due to [CS231n](http://cs231n.github.io/neural-networks-case-study/), one of the best courses for machine learning. Now let's implement the MLP with TensorFlow + Keras.
# TensorFlow + Keras
### Components
```
# MLP
class MLP(Model):
def __init__(self, hidden_dim, num_classes):
super(MLP, self).__init__()
self.fc1 = Dense(units=hidden_dim, activation='relu') # replaced linear with relu
self.fc2 = Dense(units=num_classes, activation='softmax')
def call(self, x_in, training=False):
"""Forward pass."""
z = self.fc1(x_in)
y_pred = self.fc2(z)
return y_pred
def sample(self, input_shape):
x_in = Input(shape=input_shape)
return Model(inputs=x_in, outputs=self.call(x_in)).summary()
```
### Operations
```
# Initialize the model
model = MLP(hidden_dim=HIDDEN_DIM,
num_classes=NUM_CLASSES)
model.sample(input_shape=(INPUT_DIM,))
# Compile
optimizer = Adam(lr=LEARNING_RATE)
model.compile(optimizer=optimizer,
loss=SparseCategoricalCrossentropy(),
metrics=['accuracy'])
# Training
model.fit(x=standardized_X_train,
y=y_train,
validation_data=(standardized_X_val, y_val),
epochs=NUM_EPOCHS,
batch_size=BATCH_SIZE,
class_weight=class_weights,
shuffle=False,
verbose=1)
# Predictions
pred_train = model.predict(standardized_X_train)
pred_test = model.predict(standardized_X_test)
print (f"sample probability: {pred_test[0]}")
pred_train = np.argmax(pred_train, axis=1)
pred_test = np.argmax(pred_test, axis=1)
print (f"sample class: {pred_test[0]}")
# Accuracy
train_acc = accuracy_score(y_train, pred_train)
test_acc = accuracy_score(y_test, pred_test)
print (f"train acc: {train_acc:.2f}, test acc: {test_acc:.2f}")
# Metrics
plot_confusion_matrix(y_test, pred_test, classes=classes)
print (classification_report(y_test, pred_test))
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=standardized_X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=standardized_X_test, y=y_test)
plt.show()
```
# Inference
```
# Inputs for inference
X_infer = pd.DataFrame([{'X1': 0.1, 'X2': 0.1}])
X_infer.head()
# Standardize
standardized_X_infer = X_scaler.transform(X_infer)
print (standardized_X_infer)
# Predict
y_infer = model.predict(standardized_X_infer)
_class = np.argmax(y_infer)
print (f"The probability that you have a class {classes[_class]} is {y_infer[0][_class]*100.0:.0f}%")
```
# Initializing weights
So far we have been initializing weights with small random values and this isn't optimal for convergence during training. The objective is to have weights that are able to produce outputs that follow a similar distribution across all neurons. We can do this by enforcing weights to have unit variance prior the affine and non-linear operations.
<img height="45" src="http://bestanimations.com/HomeOffice/Lights/Bulbs/animated-light-bulb-gif-29.gif" align="left" vspace="20px" hspace="10px">
A popular method is to apply [xavier initialization](http://andyljones.tumblr.com/post/110998971763/an-explanation-of-xavier-initialization), which essentially initializes the weights to allow the signal from the data to reach deep into the network. You may be wondering why we don't do this for every forward pass and that's a great question. We'll look at more advanced strategies that help with optimization like batch/layer normalization, etc. in future lessons. Meanwhile you can check out other initializers [here](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/initializers).
```
from tensorflow.keras.initializers import glorot_normal
# MLP
class MLP(Model):
def __init__(self, hidden_dim, num_classes):
super(MLP, self).__init__()
xavier_initializer = glorot_normal() # xavier glorot initiailization
self.fc1 = Dense(units=hidden_dim,
kernel_initializer=xavier_initializer,
activation='relu')
self.fc2 = Dense(units=num_classes,
activation='softmax')
def call(self, x_in, training=False):
"""Forward pass."""
z = self.fc1(x_in)
y_pred = self.fc2(z)
return y_pred
def sample(self, input_shape):
x_in = Input(shape=input_shape)
return Model(inputs=x_in, outputs=self.call(x_in)).summary()
```
# Dropout
A great technique to overcome overfitting is to increase the size of your data but this isn't always an option. Fortuntely, there are methods like regularization and dropout that can help create a more robust model.
Dropout is a technique (used only during training) that allows us to zero the outputs of neurons. We do this for `dropout_p`% of the total neurons in each layer and it changes every batch. Dropout prevents units from co-adapting too much to the data and acts as a sampling strategy since we drop a different set of neurons each time.
<img src="https://raw.githubusercontent.com/practicalAI/images/master/basic_ml/06_Multilayer_Perceptron/dropout.png" width="350">
* [Dropout: A Simple Way to Prevent Neural Networks from
Overfitting](http://jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf)
```
from tensorflow.keras.layers import Dropout
from tensorflow.keras.regularizers import l2
```
### Components
```
# MLP
class MLP(Model):
def __init__(self, hidden_dim, lambda_l2, dropout_p, num_classes):
super(MLP, self).__init__()
self.fc1 = Dense(units=hidden_dim,
kernel_regularizer=l2(lambda_l2), # adding L2 regularization
activation='relu')
self.dropout = Dropout(rate=dropout_p)
self.fc2 = Dense(units=num_classes,
activation='softmax')
def call(self, x_in, training=False):
"""Forward pass."""
z = self.fc1(x_in)
if training:
z = self.dropout(z, training=training) # adding dropout
y_pred = self.fc2(z)
return y_pred
def sample(self, input_shape):
x_in = Input(shape=input_shape)
return Model(inputs=x_in, outputs=self.call(x_in)).summary()
```
### Operations
```
# Arguments
DROPOUT_P = 0.1 # % of the neurons that are dropped each pass
LAMBDA_L2 = 1e-4 # L2 regularization
# Initialize the model
model = MLP(hidden_dim=HIDDEN_DIM,
lambda_l2=LAMBDA_L2,
dropout_p=DROPOUT_P,
num_classes=NUM_CLASSES)
model.sample(input_shape=(INPUT_DIM,))
```
# Overfitting
Though neural networks are great at capturing non-linear relationships they are highly susceptible to overfitting to the training data and failing to generalize on test data. Just take a look at the example below where we generate completely random data and are able to fit a model with [$2*N*C + D$](https://arxiv.org/abs/1611.03530) hidden units. The training performance is good (~70%) but the overfitting leads to very poor test performance. We'll be covering strategies to tackle overfitting in future lessons.
```
# Arguments
NUM_EPOCHS = 500
NUM_SAMPLES_PER_CLASS = 50
LEARNING_RATE = 1e-1
HIDDEN_DIM = 2 * NUM_SAMPLES_PER_CLASS * NUM_CLASSES + INPUT_DIM # 2*N*C + D
# Generate random data
X = np.random.rand(NUM_SAMPLES_PER_CLASS * NUM_CLASSES, INPUT_DIM)
y = np.array([[i]*NUM_SAMPLES_PER_CLASS for i in range(NUM_CLASSES)]).reshape(-1)
print ("X: ", format(np.shape(X)))
print ("y: ", format(np.shape(y)))
# Create data splits
X_train, X_val, X_test, y_train, y_val, y_test = train_val_test_split(
X, y, val_size=VAL_SIZE, test_size=TEST_SIZE, shuffle=SHUFFLE)
print ("X_train:", X_train.shape)
print ("y_train:", y_train.shape)
print ("X_val:", X_val.shape)
print ("y_val:", y_val.shape)
print ("X_test:", X_test.shape)
print ("y_test:", y_test.shape)
# Standardize the inputs (mean=0, std=1) using training data
X_scaler = StandardScaler().fit(X_train)
# Apply scaler on training and test data (don't standardize outputs for classification)
standardized_X_train = X_scaler.transform(X_train)
standardized_X_val = X_scaler.transform(X_val)
standardized_X_test = X_scaler.transform(X_test)
# Initialize the model
model = MLP(hidden_dim=HIDDEN_DIM,
lambda_l2=0.0,
dropout_p=0.0,
num_classes=NUM_CLASSES)
model.sample(input_shape=(INPUT_DIM,))
# Compile
optimizer = Adam(lr=LEARNING_RATE)
model.compile(optimizer=optimizer,
loss=SparseCategoricalCrossentropy(),
metrics=['accuracy'])
# Training
model.fit(x=standardized_X_train,
y=y_train,
validation_data=(standardized_X_val, y_val),
epochs=NUM_EPOCHS,
batch_size=BATCH_SIZE,
class_weight=class_weights,
shuffle=False,
verbose=1)
# Predictions
pred_train = model.predict(standardized_X_train)
pred_test = model.predict(standardized_X_test)
print (f"sample probability: {pred_test[0]}")
pred_train = np.argmax(pred_train, axis=1)
pred_test = np.argmax(pred_test, axis=1)
print (f"sample class: {pred_test[0]}")
# Accuracy
train_acc = accuracy_score(y_train, pred_train)
test_acc = accuracy_score(y_test, pred_test)
print (f"train acc: {train_acc:.2f}, test acc: {test_acc:.2f}")
# Classification report
plot_confusion_matrix(y_true=y_test, y_pred=pred_test, classes=classes)
print (classification_report(y_test, pred_test))
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=standardized_X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=standardized_X_test, y=y_test)
plt.show()
```
It's important that we experiment, starting with simple models that underfit (high bias) and improve it towards a good fit. Starting with simple models (linear/logistic regression) let's us catch errors without the added complexity of more sophisticated models (neural networks).
<img src="https://raw.githubusercontent.com/practicalAI/images/master/basic_ml/06_Multilayer_Perceptron/fit.png" width="700">
---
<div align="center">
Subscribe to our <a href="https://practicalai.me/#newsletter">newsletter</a> and follow us on social media to get the latest updates!
<a class="ai-header-badge" target="_blank" href="https://github.com/practicalAI/practicalAI">
<img src="https://img.shields.io/github/stars/practicalAI/practicalAI.svg?style=social&label=Star"></a>
<a class="ai-header-badge" target="_blank" href="https://www.linkedin.com/company/practicalai-me">
<img src="https://img.shields.io/badge/style--5eba00.svg?label=LinkedIn&logo=linkedin&style=social"></a>
<a class="ai-header-badge" target="_blank" href="https://twitter.com/practicalAIme">
<img src="https://img.shields.io/twitter/follow/practicalAIme.svg?label=Follow&style=social">
</a>
</div>
</div>
|
github_jupyter
|

---
# Pandas Introduction
**Author list:** Ikhlaq Sidhu & Alexander Fred Ojala
**References / Sources:**
Includes examples from Wes McKinney and the 10 min intro to Pandas
**License Agreement:** Feel free to do whatever you want with this code
___
### Topics:
1. Dataframe creation
2. Reading data in DataFrames
3. Data Manipulation
## Import package
```
# pandas
import pandas as pd
# Extra packages
import numpy as np
import matplotlib.pyplot as plt # for plotting
# jupyter notebook magic to display plots in output
%matplotlib inline
plt.rcParams['figure.figsize'] = (10,6) # make the plots bigger
```
# Part 1: Creation of Pandas dataframes
**Key Points:** Main data types in Pandas:
* Series (similar to numpy arrays, but with index)
* DataFrames (table or spreadsheet with Series in the columns)
### We use `pd.DataFrame()` and can insert almost any data type as an argument
**Function:** `pd.DataFrame(data=None, index=None, columns=None, dtype=None, copy=False)`
Input data can be a numpy ndarray (structured or homogeneous), dictionary, or DataFrame.
### 1.1 Create Dataframe using an array
```
# Try it with an array
np.random.seed(0) # set seed for reproducibility
a1 = np.random.randn(3)
a2 = np.random.randn(3)
a3 = np.random.randn(3)
print (a1)
print (a2)
print (a3)
# Create our first DataFrame w/ an np.array - it becomes a column
# Check type
# DataFrame from list of np.arrays
# notice that there is no column label, only integer values,
# and the index is set automatically
# We can set column and index names
# Add more columns to dataframe, like a dictionary, dimensions must match
# DataFrame from 2D np.array
np.random.seed(0)
array_2d = np.array(np.random.randn(9)).reshape(3,3)
# Create df with labeled columns
```
### 1.2 Create Dataframe using an dictionary
```
# DataFrame from a Dictionary
dict1 = {'a1': a1, 'a2':a2, 'a3':a3}
# Note that we now have columns without assignment
# We can add a list with strings and ints as a column
```
### Pandas Series object
Every column is a Series. Like an np.array, but we can combine data types and it has its own index
```
# Check type
# Dtype object
# Create a Series from a Python list, automatic index
# Specific index
# We can add the Series s to the DataFrame above as column Series
# Remember to match indices
# We can also rename columns
# We can delete columns
# or drop columns, see axis = 1
# does not change df1 if we don't set inplace=True
# Print df1
# Or drop rows
```
### 1.3 Indexing / Slicing a Pandas Datframe
```
# Example: view only one column
# Or view several column
# Slice of the DataFrame returned
# this slices the first three rows first followed by first 2 rows of the sliced frame
# Lets print the five first 2 elements of column a1
# This is a new Series (like a new table)
# Lets print the 2 column, and top 2 values- note the list of columns
```
### Instead of double indexing, we can use loc, iloc
##### loc gets rows (or columns) with particular labels from the index.
#### iloc gets rows (or columns) at particular positions in the index (so it only takes integers).
### .iloc()
```
# iloc
# Slice
# iloc will also accept 2 'lists' of position numbers
# Data only from row with index value '1'
```
### .loc()
```
# Usually we want to grab values by column names
# Note: You have to know indices and columns
# Boolean indexing
# Return full rows where a2>0
# Return column a3 values where a2 >0
# If you want the values in an np array
```
### More Basic Statistics
```
# Get basic statistics using .describe()
# Get specific statistics
# We can change the index sorting
```
#### For more functionalities check this notebook
https://github.com/ikhlaqsidhu/data-x/blob/master/02b-tools-pandas_intro-mplib_afo/legacy/10-minutes-to-pandas-w-data-x.ipynb
# Part 2: Reading data in pandas Dataframe
### Now, lets get some data in CSV format.
#### Description:
Aggregate data on applicants to graduate school at Berkeley for the six largest departments in 1973 classified by admission and sex.
https://vincentarelbundock.github.io/Rdatasets/doc/datasets/UCBAdmissions.html
```
# Read in the file
# Check statistics
# Columns
# Head
# Tail
# Groupby
# Describe
# Info
# Unique
# Total number of applicants to Dept A
# Groupby
# Plot using a bar graph
```
|
github_jupyter
|
```
import json
import bz2
import regex
from tqdm import tqdm
from scipy import sparse
import pandas as pd
import numpy as np
import nltk
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
%pylab inline
responses = []
with bz2.BZ2File('banki_responses.json.bz2', 'r') as thefile:
for row in tqdm(thefile):
resp = json.loads(row)
if not resp['rating_not_checked'] and (len(resp['text'].split()) > 0):
responses.append(resp)
```
# Домашнее задание по NLP # 1 [100 баллов]
## Классификация по тональности
В этом домашнем задании вам предстоит классифицировать по тональности отзывы на банки с сайта banki.ru. [Ссылка на данные](https://drive.google.com/open?id=1CPKtX5HcgGWRpzbWZ2fMCyqgHGgk21l2).
Данные содержат непосредственно тексты отзывов, некоторую дополнительную информацию, а также оценку по шкале от 1 до 5.
Тексты хранятся в json-ах в массиве responses.
Посмотрим на пример отзыва:
```
responses[99]
```
## Часть 1. Анализ текстов [40/100]
1. Посчитайте количество отзывов в разных городах и на разные банки
2. Постройте гистограмы длин слов в символах и в словах (не обязательно)
3. Найдите 10 самых частых:
* слов
* слов без стоп-слов
* лемм
* существительных
4. Постройте кривую Ципфа
5. Ответьте на следующие вопросы:
* какое слово встречается чаще, "сотрудник" или "клиент"?
* сколько раз встречается слова "мошенничество" и "доверие"?
6. В поле "rating_grade" записана оценка отзыва по шкале от 1 до 5. Используйте меру $tf-idf$, для того, чтобы найти ключевые слова и биграмы для положительных отзывов (с оценкой 5) и отрицательных отзывов (с оценкой 1)
## Часть 2. Тематическое моделирование [20/100]
1. Постройте несколько тематических моделей коллекции документов с разным числом тем. Приведите примеры понятных (интерпретируемых) тем.
2. Найдите темы, в которых упомянуты конкретные банки (Сбербанк, ВТБ, другой банк). Можете ли вы их прокомментировать / объяснить?
Эта часть задания может быть сделана с использованием gensim.
## Часть 3. Классификация текстов [40/100]
Сформулируем для простоты задачу бинарной классификации: будем классифицировать на два класса, то есть, различать резко отрицательные отзывы (с оценкой 1) и положительные отзывы (с оценкой 5).
1. Составьте обучающее и тестовое множество: выберите из всего набора данных N1 отзывов с оценкой 1 и N2 отзывов с оценкой 5 (значение N1 и N2 – на ваше усмотрение). Используйте ```sklearn.model_selection.train_test_split``` для разделения множества отобранных документов на обучающее и тестовое.
2. Используйте любой известный вам алгоритм классификации текстов для решения задачи и получите baseline. Сравните разные варианты векторизации текста: использование только униграм, пар или троек слов или с использованием символьных $n$-грам.
3. Сравните, как изменяется качество решения задачи при использовании скрытых тем в качестве признаков:
* 1-ый вариант: $tf-idf$ преобразование (```sklearn.feature_extraction.text.TfidfTransformer```) и сингулярное разложение (оно же – латентый семантический анализ) (```sklearn.decomposition.TruncatedSVD```),
* 2-ой вариант: тематические модели LDA (```sklearn.decomposition.LatentDirichletAllocation```).
Используйте accuracy и F-measure для оценки качества классификации.
Ниже написан примерный Pipeline для классификации текстов.
Эта часть задания может быть сделана с использованием sklearn.
```
from sklearn.pipeline import Pipeline
from sklearn.ensemble import RandomForestClassifier
# !!! На каждом этапе Pipeline нужно указать свои параметры
# 1-ый вариант: tf-idf + LSI
# 2-ой вариант: LDA
# clf = Pipeline([
# ('vect', CountVectorizer(analyzer = 'char', ngram_range={4,6})),
# ('clf', RandomForestClassifier()),
# ])
clf = Pipeline([
('vect', CountVectorizer()),
('tfidf', TfidfTransformer()),
('tm', TruncatedSVD()),
('clf', RandomForestClassifier())
])
```
## Бонус [20]
Используйте для классификации эмбеддинги слов. Улучшилось ли качество?
|
github_jupyter
|
```
_= """
ref https://www.reddit.com/r/algotrading/comments/e44pdd/list_of_stock_tickers_from_yahoo/
https://old.nasdaq.com/screening/companies-by-name.aspx?letter=0&exchange=nasdaq&render=download
AMEX
https://old.nasdaq.com/screening/companies-by-name.aspx?letter=0&exchange=amex&render=download
NYSE
https://old.nasdaq.com/screening/companies-by-name.aspx?letter=0&exchange=nyse&render=download
"""
# look for high vol high vol.
# assume option would be too.
# compute historical implied volatility?
# suggest trading ideas.
# depending on: vol and mean ret are relatively high or low points and their dp and ddp.
### Can you actually apply any of this to gain an edge when trading?
+ Now I don't really buy technical analysis, but the immediate indicator that comes to mind is "relative strength index", obviously when you mention TA, we are implying trying to forcast a price trend, using historical data and pattern which has been proven to not be successful, albeit many successful traders swear by TAs. Thus here we will demonstrate how well/badly our 2 mean reverting time series can forecasting future price changes compared to buy-and-hold.
+ Perhaps if you split the 2D distribution plot of rolling ret mean and hist volatility into 4 quandrants (show below) you can opt to deploy different option strategies accordingly.
```
lets contrain ourselves to the below per BAT's talk linked below!
Short Strangle, Iron Condors, Credit Spread, Diagnal Spread, Ratio Spread, Broken Wing Butterfly
```
+ Tony Battisa, Tastytrade, How to Use Options Strategies & Key Mechanics https://www.youtube.com/watch?v=T6uA_XHunRc
#
# ^
# high vol | high vol
# low ret | high ret
# -----------|---------->
# low vol | low vol
# low ret | high ret
#
#
# high vol, low ret -> short put (or credit spread)
# high vol, high ret -> short call (or credit spread)
# high vol, mid ret -> short strangle (or iron condor)
# mid vol, low ret -> Ratio Spread (sell 2 otm puts, buy 1 atm put)
# mid vol, high ret -> Ratio Spread (sell 2 otm call, buy 1 atm call)
# low vol, low ret -> Broken Wing Butter Fly
# low vol, high ret -> Broken Wing Butter Fly
# low vol, mid ret -> Diagnal to bet on vol increase.
#
# product idea. deploy below as a website, earn ad revenue.
# since both signals are likely mean reverting
# and assuming realized volatility tracks implied volatilityvol_change
#
# by sectioning the 2 changes to zones, we can accordingly decide what strategy to deploy
# if vol increase, price increase - diagonal - short front month call, long back month call
# if vol increase, price no-change - diagonal - short call strangle, long back month?
# if vol increase, price decrease - diagonal - short front month put, long back month put
# if vol decrease, price increase - short put
# if vol decrease, price no-change - iron condor
# if vol decrease, price decrease - short call
# https://www.youtube.com/watch?v=T6uA_XHunRc, ratios spreads or broken wing butter fly
# if vol no-change, price increase - short put ratio spread
# if vol no-change, price no-change - iron condor ratio spreads?
# if vol no-change, price decrease - short call ratio spread
# to simplify backtesting. we will just see if we can predict the trend
# a win for each trade gets a +1 a loss for each trade gets a -1
# for the same period, for buy and hold, +1 means price ret in that period is > 0.
np.random.rand(10,10)
```
|
github_jupyter
|
_Lambda School Data Science — Tree Ensembles_
# Decision Trees — with ipywidgets!
### Notebook requirements
- [ipywidgets](https://ipywidgets.readthedocs.io/en/stable/examples/Using%20Interact.html): works in Jupyter but [doesn't work on Google Colab](https://github.com/googlecolab/colabtools/issues/60#issuecomment-462529981)
- [mlxtend.plotting.plot_decision_regions](http://rasbt.github.io/mlxtend/user_guide/plotting/plot_decision_regions/): `pip install mlxtend`
## Regressing a wave
```
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
# Example from http://scikit-learn.org/stable/auto_examples/tree/plot_tree_regression.html
def make_data():
import numpy as np
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 2 * (0.5 - rng.rand(16))
return X, y
X, y = make_data()
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.25, random_state=42)
plt.scatter(X_train, y_train)
plt.scatter(X_test, y_test);
from sklearn.tree import DecisionTreeRegressor
def regress_wave(max_depth):
tree = DecisionTreeRegressor(max_depth=max_depth)
tree.fit(X_train, y_train)
print('Train R^2 score:', tree.score(X_train, y_train))
print('Test R^2 score:', tree.score(X_test, y_test))
plt.scatter(X_train, y_train)
plt.scatter(X_test, y_test)
plt.step(X, tree.predict(X))
plt.show()
from ipywidgets import interact
interact(regress_wave, max_depth=(1,8,1));
```
## Classifying a curve
```
import numpy as np
curve_X = np.random.rand(1000, 2)
curve_y = np.square(curve_X[:,0]) + np.square(curve_X[:,1]) < 1.0
curve_y = curve_y.astype(int)
from sklearn.linear_model import LogisticRegression
from mlxtend.plotting import plot_decision_regions
lr = LogisticRegression(solver='lbfgs')
lr.fit(curve_X, curve_y)
plot_decision_regions(curve_X, curve_y, lr, legend=False)
plt.axis((0,1,0,1));
from sklearn.tree import DecisionTreeClassifier
def classify_curve(max_depth):
tree = DecisionTreeClassifier(max_depth=max_depth)
tree.fit(curve_X, curve_y)
plot_decision_regions(curve_X, curve_y, tree, legend=False)
plt.axis((0,1,0,1))
plt.show()
interact(classify_curve, max_depth=(1,8,1));
```
## Titanic survival, by age & fare
```
import seaborn as sns
from sklearn.impute import SimpleImputer
titanic = sns.load_dataset('titanic')
imputer = SimpleImputer()
titanic_X = imputer.fit_transform(titanic[['age', 'fare']])
titanic_y = titanic['survived'].values
from sklearn.linear_model import LogisticRegression
from mlxtend.plotting import plot_decision_regions
lr = LogisticRegression(solver='lbfgs')
lr.fit(titanic_X, titanic_y)
plot_decision_regions(titanic_X, titanic_y, lr, legend=False);
plt.axis((0,75,0,175));
def classify_titanic(max_depth):
tree = DecisionTreeClassifier(max_depth=max_depth)
tree.fit(titanic_X, titanic_y)
plot_decision_regions(titanic_X, titanic_y, tree, legend=False)
plt.axis((0,75,0,175))
plt.show()
interact(classify_titanic, max_depth=(1,8,1));
```
|
github_jupyter
|
# Nature of signals
In the context of this class, a signal is the data acquired by the measurement system. It contains much information that we need to be able to identify to extract knowledge about the system being tested and how to optimize the measurements. A signal caries also messages and information. We will use the content of this module for the other modules seen in the rest of the class.
## Signal classification
A signal can be characterized by its amplitude and frequency. __Amplitude__ is related to the strength of the signal and __frequency__ to the extent or duration of the signal. The time series of a signal is called a __waveform__. Multipe collection of the waveform is called an __ensemble__.
Signals can be either __deterministic__ or __random__.
Deterministic signals can be either __static__ (do not change in time) or __dynamic__. Dynamic signals can be decomposed into __periodic__ or __aperiodic__. A periodic signal repeats itself at regular interval. The smallest value over whih it repeats itself is the __fundamental period__, with an associated __fundamental frequency__. A __simple__ periodic signal has one period; it is a sine wave. A __complex__ has multiple periods and can be thought as the sum of several sinusoids (more on this in the next section). Aperiodic signals are typically __transient__ (such as step, ramp, or pulse responses).
Nondeterministic signals are an important class of signals that are often encountered in nature (think of turbulence, stock market, etc). They must be analyzed with satistical tools. They are classified as __nonstationary__ and __stationary__. This classification enables to select the proper statistical theory to analyze them. The properties of nondeterministic signals are computed with ensemble statistics of instantaneous properties. In particular, one computes the ensemble average, $\mu(t_1)$, and ensemble autocorrelation function (more on the physical meaning of this function later), $R(t_1,t_1+\tau)$.
\begin{align*}
\mu(t_1) & = \frac{1}{N} \sum_{i=0}^{N-1} x_i(t_1) \\
R(t_1,t_1+\tau) & = \frac{1}{N} \sum_{i=0}^{N-1} x_i(t_1)x_i(t_1+\tau)
\end{align*}
The term ensemble means that we take N time series and perform statistics with the ensemble of the values at recorded time $t_1$.
If $\mu(t_1) = \mu$ and $R(t_1,t_1+\tau) = R(\tau)$, then the signal is considered (weakly) __stationary__ and nonstationary, otherwise. Stationarity introdcues a lot of simplification in the statistical analysis of the data (by using a lot of tools developed for time series analysis) and one should always start by checking for signal stationarity. Stationarity implies that signal ensemble-averaged statistical properties are independent of $t_1$.
For most stationary signals, the temporal and ensemble statistical properties are identical. The signal is then __ergodic__. Thus, from a _single_ time history of length $T_r$ one can calculate $\mu$ and $R(\tau)$ (which saves time in the acquisition and analysis):
\begin{align*}
\mu & = \frac{1}{T_r} \int_{0}^{T_r} x(t) dt \\
R(\tau) & = \frac{1}{T_r} \int_{0}^{T_r} x(t)x(t+\tau) dt
\end{align*}
Thanks to statistical tools for ergodic processes, from a finite recording length of the signal, one can estimate population mean with confidence level.
## Signal variables
Most signals can be decomposed as a sum of sines and cosines (more on this in the next module). Let's start with a simple periodic signal:
\begin{align*}
y(t) = C \sin (n \omega t + \phi) = C \sin (n 2\pi f t + \phi)
\end{align*}
When several sine and cosine waves are added, complext waveforms result. For example for second order dynamic system, the system response could take the form:
\begin{align*}
y(t) = A \cos (\omega t) + B \sin (\omega t)
\end{align*}
This sum of a cosine and sine of same frequency can be rearranged as:
\begin{align*}
y(t) = C \cos (\omega t - \phi) = C \cos (\omega t - \phi + \pi/2) = C \sin (\omega t + \phi')
\end{align*}
with:
\begin{align*}
C & = \sqrt{A^2 + B^2}\\
\phi & = \tan^{-1} (B/A)\\
\phi' & = \pi/2 - \phi = \tan^{-1} (A/B)
\end{align*}
Let's look at some examples of simple and complex periodic signals.
First a simple function:
\begin{align*}
y (t) = 2 \sin (2\pi t)
\end{align*}
```
import numpy
from matplotlib import pyplot
%matplotlib inline
t=numpy.linspace(0.0,5.0,num=1000) # (s)
y = 2 * numpy.sin(2*numpy.pi*t)
pyplot.plot(t, y, color='b', linestyle='-');
```
Now a complex function made of two frequencies (harmonics):
\begin{align*}
y (t) = 2 \sin (2\pi t) + 1.2 \sin (6 \pi t)
\end{align*}
The signal has two frequencies: 1 and 3 Hz. 1 Hz is the lowest frequency and is the fundamental frequency with period 1 s. So the signal will repeat itself every second.
```
y = 2 * numpy.sin(2*numpy.pi*t) + 1.2 * numpy.sin(6*numpy.pi*t)
pyplot.plot(t, y, color='b', linestyle='-');
```
Let's now look at two sinusoidal with very close frequencies $\Delta f$.
\begin{align*}
y (t) = 2 \sin (2\pi t) + 1.2 \sin ((2+0.2) \pi t)
\end{align*}
```
t=numpy.linspace(0.0,20.0,num=1000) # (s)
y = 2 * numpy.sin(2*numpy.pi*t) + 1.2 * numpy.sin((2+0.2)*numpy.pi*t)
pyplot.plot(t, y, color='b', linestyle='-');
```
Here the frequency difference is $\Delta f = 0.2/2 = 0.1 Hz$. The resulting signal has a slow beat with __beat__ frequency $\Delta f)$ or beat period $1/\Delta f = 10$ s, i.e. the signal repepats itself every 10 s. Analytically (using trigonometric relations), one can show that the sum of two sine waves with close frequencies results in a signal modulated by $\cos(\Delta f/2)$.
## Detection schemes
The mixing of two signals to produce a signal (wave) with a new frequency is called heterodyning and is commonly used in instrumentation to obtain very accurate measurements. __Heterodyne detection__ shifts the frequency content of a signal into a new range where it is easier to detected; in communucation it is called _frequency conversion_. Heterodyning is used in laser Doppler velocimetry, tuning of musical instruments, radio receivers, etc.
In contrast, __homodyne detection__ uses a single (homo) frequency and compares the signal with a standard oscillation that would be identical to the signal if it carried null information. and measures the amplitude and phase of a signal to gain information. It enables to extract information encoded as modulation of the phase and/or frequency of the signal. In optics, this results in interferometry. It is also the fundation behind lock-in amplifier to extract information for very weak or noisy signals.
Finally in __magnitude detection__ one only records the amplitude of signals. This is the most common detection scheme used.
## Statistical description of signals
|
github_jupyter
|
# Navigation
---
You are welcome to use this coding environment to train your agent for the project. Follow the instructions below to get started!
### 1. Start the Environment
Run the next code cell to install a few packages. This line will take a few minutes to run!
```
!pip -q install ./python
```
The environment is already saved in the Workspace and can be accessed at the file path provided below. Please run the next code cell without making any changes.
```
from unityagents import UnityEnvironment
import numpy as np
# please do not modify the line below
env = UnityEnvironment(file_name="/data/Banana_Linux_NoVis/Banana.x86_64")
import gym
!pip3 install box2d
import random
import torch
import numpy as np
from collections import deque
import matplotlib.pyplot as plt
%matplotlib inline
!python -m pip install pyvirtualdisplay
from pyvirtualdisplay import Display
display = Display(visible=0, size=(1400, 900))
display.start()
is_ipython = 'inline' in plt.get_backend()
if is_ipython:
from IPython import display
plt.ion()
```
Environments contain **_brains_** which are responsible for deciding the actions of their associated agents. Here we check for the first brain available, and set it as the default brain we will be controlling from Python.
```
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
```
### 2. Examine the State and Action Spaces
Run the code cell below to print some information about the environment.
```
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents in the environment
print('Number of agents:', len(env_info.agents))
# number of actions
action_size = brain.vector_action_space_size
print('Number of actions:', action_size)
# examine the state space
state = env_info.vector_observations[0]
print('States look like:', state)
state_size = len(state)
print('States have length:', state_size)
```
### 3. Take Random Actions in the Environment
In the next code cell, you will learn how to use the Python API to control the agent and receive feedback from the environment.
Note that **in this coding environment, you will not be able to watch the agent while it is training**, and you should set `train_mode=True` to restart the environment.
```
env_info = env.reset(train_mode=True)[brain_name] # reset the environment
state = env_info.vector_observations[0] # get the current state
score = 0 # initialize the score
while True:
action = np.random.randint(action_size) # select an action
env_info = env.step(action)[brain_name] # send the action to the environment
next_state = env_info.vector_observations[0] # get the next state
reward = env_info.rewards[0] # get the reward
done = env_info.local_done[0] # see if episode has finished
score += reward # update the score
state = next_state # roll over the state to next time step
if done: # exit loop if episode finished
break
print("Score: {}".format(score))
```
When finished, you can close the environment.
### 4. It's Your Turn!
Now it's your turn to train your own agent to solve the environment! A few **important notes**:
- When training the environment, set `train_mode=True`, so that the line for resetting the environment looks like the following:
```python
env_info = env.reset(train_mode=True)[brain_name]
```
- To structure your work, you're welcome to work directly in this Jupyter notebook, or you might like to start over with a new file! You can see the list of files in the workspace by clicking on **_Jupyter_** in the top left corner of the notebook.
- In this coding environment, you will not be able to watch the agent while it is training. However, **_after training the agent_**, you can download the saved model weights to watch the agent on your own machine!
# Training the netowrk
```
from dqn_agent import Agent
agent = Agent(state_size=37, action_size=4, seed=42)
print(type(state))
def dqn(n_episodes=2000, max_t=1000, eps_start=1.0, eps_end=0.01, eps_decay=0.995):
"""Deep Q-Learning.
Params
======
n_episodes (int): maximum number of training episodes
max_t (int): maximum number of timesteps per episode
eps_start (float): starting value of epsilon, for epsilon-greedy action selection
eps_end (float): minimum value of epsilon
eps_decay (float): multiplicative factor (per episode) for decreasing epsilon
"""
scores = [] # list containing scores from each episode
scores_window = deque(maxlen=100) # last 100 scores
eps = eps_start # initialize epsilon
for i_episode in range(1, n_episodes+1):
env_info = env.reset(train_mode=True)[brain_name]
state = env_info.vector_observations[0]
score = 0
for t in range(max_t):
action = agent.act(state, eps)
env_info = env.step(action)[brain_name]
next_state = env_info.vector_observations[0]
reward = env_info.rewards[0]
done = env_info.local_done[0]
agent.step(state, action, reward, next_state, done)
state = next_state
score += reward
if done:
break
scores_window.append(score) # save most recent score
scores.append(score) # save most recent score
eps = max(eps_end, eps_decay*eps) # decrease epsilon
print('\rEpisode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_window)), end="")
if i_episode % 100 == 0:
print('\rEpisode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_window)))
if np.mean(scores_window)>=15.0:
print('\nEnvironment solved in {:d} episodes!\tAverage Score: {:.2f}'.format(i_episode-100, np.mean(scores_window)))
torch.save(agent.qnetwork_local.state_dict(), 'checkpoint.pth')
break
return scores
scores = dqn()
# plot the scores
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(len(scores)), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
env.close()
```
|
github_jupyter
|
# Objects
*Python* is an object oriented language. As such it allows the definition of classes.
For instance lists are also classes, that's why there are methods associated with them (i.e. `append()`). Here we will see how to create classes and assign them attributes and methods.
## Definition and initialization
A class gathers functions (called methods) and variables (called attributes).
The main of goal of having this kind of structure is that the methods can share a common
set of inputs to operate and get the desired outcome by the programmer.
In *Python* classes are defined with the word `class` and are always initialized
with the method ``__init__``, which is a function that *always* must have as input argument the
word `self`. The arguments that come after `self` are used to initialize the class attributes.
In the following example we create a class called ``Circle``.
```
class Circle:
def __init__(self, radius):
self.radius = radius #all attributes must be preceded by "self."
```
To create an instance of this class we do it as follows
```
A = Circle(5.0)
```
We can check that the initialization worked out fine by printing its attributes
```
print(A.radius)
```
We now redefine the class to add new method called `area` that computes the area of the circle
```
class Circle:
def __init__(self, radius):
self.radius = radius #all attributes must be preceded by "self."
def area(self):
import math
return math.pi * self.radius * self.radius
A = Circle(1.0)
print(A.radius)
print(A.area())
```
### Exercise 3.1
Redefine the class `Circle` to include a new method called `perimeter` that returns the value of the circle's perimeter.
We now want to define a method that returns a new Circle with twice the radius of the input Circle.
```
class Circle:
def __init__(self, radius):
self.radius = radius #all attributes must be preceded by "self."
def area(self):
import math
return math.pi * self.radius * self.radius
def enlarge(self):
return Circle(2.0*self.radius)
A = Circle(5.0) # Create a first circle
B = A.enlarge() # Use the method to create a new Circle
print(B.radius) # Check that the radius is twice as the original one.
```
We now add a new method that takes as an input another element of the class `Circle`
and returns the total area of the two circles
```
class Circle:
def __init__(self, radius):
self.radius = radius #all attributes must be preceded by "self."
def area(self):
import math
return math.pi * self.radius * self.radius
def enlarge(self):
return Circle(2.0*self.radius)
def add_area(self, c):
return self.area() + c.area()
A = Circle(1.0)
B = Circle(2.0)
print(A.add_area(B))
print(B.add_area(A))
```
### Exercise 3.2
Define the class `Vector3D` to represent vectors in 3D.
The class must have
* Three attributes: `x`, `y`, and `z`, to store the coordinates.
* A method called `dot` that computes the dot product
$$\vec{v} \cdot \vec{w} = v_{x}w_{x} + v_{y}w_{y} + v_{z}w_{z}$$
The method could then be used as follows
```python
v = Vector3D(2, 0, 1)
w = Vector3D(1, -1, 3)
```
```python
v.dot(w)
5
```
|
github_jupyter
|
# IntegratedML applied to biomedical data, using PyODBC
This notebook demonstrates the following:
- Connecting to InterSystems IRIS via PyODBC connection
- Creating, Training and Executing (PREDICT() function) an IntegratedML machine learning model, applied to breast cancer tumor diagnoses
- INSERTING machine learning predictions into a new SQL table
- Executing a relatively complex SQL query containing IntegratedML PREDICT() and PROBABILITY() functions, and flexibly using the results to filter and sort the output
### ODBC and pyODBC Resources
Often, connecting to a database is more than half the battle when developing SQL-heavy applications, especially if you are not familiar with the tools, or more importantly the particular database system. If this is the case, and you are just getting started using PyODBC and InterSystems IRIS, this notebook and these resources below may help you get up to speed!
https://gettingstarted.intersystems.com/development-setup/odbc-connections/
https://irisdocs.intersystems.com/irislatest/csp/docbook/DocBook.UI.Page.cls?KEY=BNETODBC_support#BNETODBC_support_pyodbc
https://stackoverflow.com/questions/46405777/connect-docker-python-to-sql-server-with-pyodbc
https://stackoverflow.com/questions/44527452/cant-open-lib-odbc-driver-13-for-sql-server-sym-linking-issue
```
# make the notebook full screen
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:100% !important; }</style>"))
```
### 1. Install system packages for ODBC
```
!apt-get update
!apt-get install gcc
!apt-get install -y tdsodbc unixodbc-dev
!apt install unixodbc-bin -y
!apt-get clean
```
#### Use this command to troubleshoot a failed pyodbc installation:
!pip install --upgrade --global-option=build_ext --global-option="-I/usr/local/include" --global-option="-L/usr/local/lib" pyodbc
```
!pip install pyodbc
!rm /etc/odbcinst.ini
!rm /etc/odbc.ini
!ln -s /tf/odbcinst.ini /etc/odbcinst.ini
!ln -s /tf/odbc.ini /etc/odbc.ini
!cat /tf/odbcinst.ini
!cat /tf/odbc.ini
!odbcinst -j
```
### 2. Verify you see "InterSystems ODBC35" in the drivers list
```
import pyodbc
print(pyodbc.drivers())
```
### 3. Get an ODBC connection
```
import pyodbc
import time
#input("Hit any key to start")
dsn = 'IRIS QuickML demo via PyODBC'
server = 'irisimlsvr' #'192.168.99.101'
port = '51773' #'9091'
database = 'USER'
username = 'SUPERUSER'
password = 'SYS'
cnxn = pyodbc.connect('DRIVER={InterSystems ODBC35};SERVER='+server+';PORT='+port+';DATABASE='+database+';UID='+username+';PWD='+ password)
### Ensure it read strings correctly.
cnxn.setdecoding(pyodbc.SQL_CHAR, encoding='utf8')
cnxn.setdecoding(pyodbc.SQL_WCHAR, encoding='utf8')
cnxn.setencoding(encoding='utf8')
```
### 4. Get a cursor; start the timer
```
cursor = cnxn.cursor()
start= time.clock()
```
### 5. specify the training data, and give a model name
```
dataTable = 'SQLUser.BreastCancer'
dataTablePredict = 'Result02'
dataColumn = 'Diagnosis'
dataColumnPredict = "PredictedDiagnosis"
modelName = "bc" #chose a name - must be unique in server end
```
### 6. Train and predict
```
cursor.execute("CREATE MODEL %s PREDICTING (%s) FROM %s" % (modelName, dataColumn, dataTable))
cursor.execute("TRAIN MODEL %s FROM %s" % (modelName, dataTable))
cursor.execute("Create Table %s (%s VARCHAR(100), %s VARCHAR(100))" % (dataTablePredict, dataColumnPredict, dataColumn))
cursor.execute("INSERT INTO %s SELECT TOP 20 PREDICT(%s) AS %s, %s FROM %s" % (dataTablePredict, modelName, dataColumnPredict, dataColumn, dataTable))
cnxn.commit()
```
### 7. Show the predict result
```
import pandas as pd
from IPython.display import display
df1 = pd.read_sql("SELECT * from %s ORDER BY ID" % dataTablePredict, cnxn)
display(df1)
```
### 8. Show a complicated query
IntegratedML function PREDICT() and PROBABILITY() can appear virtually anywhere in a SQL query, for maximal flexibility!
Below we are SELECTing columns as well as the result of the PROBABILITY function, and then filtering on the result of the PREDICT function. To top it off, ORDER BY is using the output of PROBSBILITY for sorting.
```
df2 = pd.read_sql("SELECT ID, PROBABILITY(bc FOR 'M') AS Probability, Diagnosis FROM %s \
WHERE MeanArea BETWEEN 300 AND 600 AND MeanRadius > 5 AND PREDICT(%s) = 'M' \
ORDER BY Probability" % (dataTable, modelName),cnxn)
display(df2)
```
### 9. Close and clean
```
cnxn.close()
end= time.clock()
print ("Total elapsed time: ")
print (end-start)
#input("Hit any key to end")
```
|
github_jupyter
|
# Advanced Data Wrangling with Pandas
```
import pandas as pd
import numpy as np
```
## Formas não usuais de se ler um dataset
Você não precisa que o arquivo com os seus dados esteja no seu disco local, o pandas está preparado para adquirir arquivos via http, s3, gs...
```
diamonds = pd.read_csv("https://raw.githubusercontent.com/mwaskom/seaborn-data/master/diamonds.csv")
diamonds.head()
```
Você também pode crawlear uma tabela de uma página da internet de forma simples
```
clarity = pd.read_html("https://www.brilliantearth.com/diamond-clarity/")
clarity
clarity = clarity[0]
clarity
clarity.columns = ['clarity', 'clarity_description']
clarity
```
## Como explodir a coluna de um dataframe
```
clarity['clarity'] = clarity['clarity'].str.split()
clarity
type(clarity.loc[0, 'clarity'])
clarity = clarity.explode("clarity")
clarity
```
## Como validar o merge
Esse parametro serve para validar a relação entre as duas tabelas que você está juntando. Por exemplo, se a relação é 1 para 1, 1 para muitos, muitos para 1 ou muitos para muitos.
```
diamonds.merge(clarity, on='clarity', validate="m:1")
clarity_with_problem = clarity.append(pd.Series({"clarity": "SI2", "clarity_description": "slightly included"}), ignore_index=True)
clarity_with_problem
diamonds.merge(clarity_with_problem, on='clarity', validate="m:1")
diamonds.merge(clarity_with_problem, on='clarity')
```
### Por que isso é importante?
O que aconteceria seu tivesse keys duplicadas no meu depara. Ele duplicou as minhas linhas que tinham a key duplicada, o dataset foi de 53,940 linhas para 63,134 linhas
## Como usar o método `.assign`
Para adicionar ou modificar colunas do dataframe. Você pode passar como argumento uma constante para a coluna ou um função que tenha como input um `pd.DataFrame` e output uma `pd.Series`.
```
diamonds.assign(foo="bar", bar="foo")
diamonds.assign(volume=lambda df: df['x'] * df['y'] * df['z'])
def calculate_volume(df):
return df['x'] * df['y'] * df['z']
diamonds.assign(volume=calculate_volume)
diamonds['volume'] = diamonds['x'] * diamonds['y'] * diamonds['z']
diamonds
```
## Como usar o método `.query`
Para filtrar. Tende a ser util quando você quer filtrar o dataframe baseado em algum estado intermediário
```
diamonds = pd.read_csv("https://raw.githubusercontent.com/mwaskom/seaborn-data/master/diamonds.csv")
diamonds.head()
diamonds.describe()
diamonds[(diamonds['x'] == 0) | (diamonds['y'] == 0) | (diamonds['z'] == 0)]
diamonds.query("x == 0 | y == 0 | z == 0")
x = diamonds \
.assign(volume=lambda df: df['x'] * df['y'] * df['z'])
x = x[x['volume'] > 0]
diamonds = diamonds \
.assign(volume=lambda df: df['x'] * df['y'] * df['z']) \
.query("volume > 0")
diamonds
```
Você também pode usar variáveis externas ao dataframe dentro da sua query, basta usar @ como marcador.
```
selected_cut = "Premium"
diamonds.query("cut == @selected_cut")
```
Quase qualquer string que seria um código python válido, vai ser uma query valida
```
diamonds.query("clarity.str.startswith('SI')")
```
Porém o parser do pandas tem algumas particularidades, como o `==` que também pode ser um `isin`
```
diamonds.query("color == ['E', 'J']")
diamonds = diamonds.query("x != 0 & y != 0 & z != 0")
```
Exemplo de que precisamos do estado intermediário para fazer um filtro. Você cria uma nova coluna e quer filtrar baseado nela sem precisar salvar esse resultado em uma variável intermerdiária
## Como usar o método `.loc` e `.iloc`
Uma das desvantagens do `.query` é que fica mais difícil fazer análise estática do código, os editores geralmente não suportam syntax highlighting. Um jeito de solucionar esse problemas é usando o `.loc` ou `.iloc`, que além de aceitarem mascaras, eles aceitam funções também.
```
diamonds.loc[[0, 1, 2], ['clarity', 'depth']]
diamonds.iloc[[0, 1, 2], [3, 4]]
diamonds.sort_values("depth")
diamonds.sort_values("depth").loc[[0, 1, 2]]
diamonds.sort_values("depth").iloc[[0, 1, 2]]
diamonds.loc[diamonds["price"] > 6000]
diamonds["price"] > 6000
diamonds.loc[lambda x: x['price'] > 6000]
diamonds[diamonds['price'] > 10000]['price'] = 10000
diamonds.query("price > 10000")
diamonds.loc[diamonds['price'] > 10000, 'price'] = 10000
diamonds.query("price > 10000")
```
## O que o `.groupby(...) retorna`
```
diamonds = pd.read_csv("https://raw.githubusercontent.com/mwaskom/seaborn-data/master/diamonds.csv") \
.assign(volume=lambda x: x['x'] * x['y'] * x['z']) \
.query("volume > 0")
diamonds.head()
grouped_diamonds = diamonds.groupby("cut")
grouped_diamonds
list(grouped_diamonds)
```
## Os N formatos de agregação do pandas
A função `.agg` é um *alias* da função `.aggregate`, então elas tem o mesmo resultado.
O Pandas tem algumas funções padrão que permitem que você passe só o nome delas, ao invés do *callable*:
* "all"
* "any"
* "count"
* "first"
* "idxmax"
* "idxmin"
* "last"
* "mad"
* "max"
* "mean"
* "median"
* "min"
* "nunique"
* "prod"
* "sem"
* "size"
* "skew"
* "std"
* "sum"
* "var"
Você pode passar uma lista de callable e o pandas vai aplicar todas as funções para todas as colunas. Faz sentido se são muitas funções e poucas colunas. Um problema é que ele vai nomear as novas colunas com base na coluna anterior e na função, quando você usa uma lambda isso causa um problema.
```
diamonds.groupby('clarity').agg(['mean', 'sum', np.max, lambda x: x.min()])
```
Você também pode passar um dicionário de listas, assim você pode escolher qual função será aplicada em cada coluna, você ainda tem o problema de nome das novas colunas ao usar uma função anônima.
```
diamonds.groupby('clarity').agg({"x": 'mean', 'price': [np.max, 'max', max, lambda x: x.max()]})
```
A terceira opção é o NamedAgg foi lançada recentemente. Ela resolve o problema de nomes de colunas. Você passa como parâmetro uma tupla para cada agregação que você quer. O primeiro elemento é o nome da coluna e o segundo é a função.
\* *O Dask ainda não aceita esse tipo de agregação*
```
diamonds.groupby('clarity').agg(max_price=('price', 'max'), total_cost=('price', lambda x: x.sum()))
```
## `.groupby(...).apply(...)`
Um problema comum a todas essas abordagens é que você não consegue fazer uma agregação que depende de duas colunas. Para a maior parte dos casos existe uma forma razoável de resolver esse problema criando uma nova coluna e aplicando a agregação nela. Porém, se isso não foi possível, dá para usar o `.groupby(...).apply()`.
```
# Nesse caso ao invés da função de agregação receber a pd.Series relativa ao grupo,
# ela vai receber o subset do grupo. Aqui vamos printar cada grupo do df de forma
# separada
diamonds.groupby('cut').apply(lambda x: print(x.head().to_string() + "\n"))
```
Esse formato de agregação introduz algumas complexidades, porque sua função pode retornar tanto um pd.DataFrame, pd.Series ou um escalar. O pandas vai tentar fazer um broadcasting do que você retorna para algo que ele acha que faz sentido. Exemplos:
Se você retornar um escalar, o apply vai retornar uma `pd.Series` em que cada elemento corresponde a um grupo do .groupby
```
# Retornando um escalar
def returning_scalar(df: pd.DataFrame) -> float:
return (df["x"] * df["y"] * df['z']).mean()
diamonds.groupby("cut").apply(returning_scalar)
```
Se você retornar uma `pd.Series` nomeada, o apply vai retornar um `pd.DataFrame` em que cada linha corresponde a um grupo do `.groupby` e cada coluna corresponde a uma key do pd.Series que você retorna na sua função de agregação
```
def returning_named_series(df: pd.DataFrame) -> pd.Series:
volume = (df["x"] * df["y"] * df['z'])
price_to_volume = df['price'] / volume
return pd.Series({"mean_volume": volume.mean(), "mean_price_to_volume": price_to_volume.mean()})
diamonds.groupby("cut").apply(returning_named_series)
```
Se você retornar um `pd.DataFrame`, o apply vai retornar uma concatenação dos desses `pd.DataFrame`
```
def returning_dataframe(df: pd.DataFrame) -> pd.DataFrame:
return df[df['volume'] >= df['volume'].median()]
diamonds.groupby("cut").apply(returning_dataframe)
```
Se você retornar uma `pd.Series` não nomeada, o apply vai retornar uma `pd.Series` que é uma concatenação das `pd.Series` que você retorna da sua função
```
def returning_unnamed_series(df: pd.DataFrame) -> pd.Series:
return df.loc[df['volume'] >= df['volume'].median(), 'volume']
diamonds.groupby("cut").apply(returning_unnamed_series)
```
De forma resumida, o `.groupby(...).apply(...)` é extremamente flexível, ele consegue filtrar, agregar e tranformar. Mas é mais complicado de usar e é bem lento se comparado aos outros métodos de agregação. Só use se necessário.
| Saída da Função | Saída do apply |
|-----------------------|--------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| Escalar | Uma pd.Series em que cada elemento corresponde a um grupo do .groupby |
| pd.Series nomeada | Um pd.DataFrame em que cada linha corresponde a um grupo do .groupby e cada coluna corresponde a uma key do pd.Series que você retorna na sua função de agregação |
| pd.Series não nomeada | Uma `pd.Series` que é uma concatenação das `pd.Series` que você retorna da sua função |
| pd.DataFrame | Uma concatenação dos desses `pd.DataFrame` |
## Como usar o método `.pipe`
O `.pipe` aplica uma função ao dataframe
```
def change_basis(df: pd.DataFrame, factor=10):
df[['x', 'y', 'z']] = df[['x', 'y', 'z']] * factor
return df
diamonds.pipe(change_basis)
```
Nós não atribuimos o resultado da nossa operação a nenhuma variável, então teoricamente se rodarmos de novo, o resultado vai ser o mesmo.
```
diamonds.pipe(change_basis)
```
Isso acontece porque a sua função está alterando o `pd.DataFrame` original ao invés de criar uma cópia, isso é um pouco contra intuitivo porque o Pandas por padrão faz as suas operações em copias da tabela. Para evitar isso podemos fazer uma cópia do dataframe manualmente
```
diamonds = pd.read_csv("https://raw.githubusercontent.com/mwaskom/seaborn-data/master/diamonds.csv")
def change_basis(df: pd.DataFrame, factor=10):
df = df.copy()
df[['x', 'y', 'z']] = df[['x', 'y', 'z']] * factor
return df
diamonds.pipe(change_basis, factor=10)
diamonds
```
## Como combinar o `.assign`, `.pipe`, `.query` e `.loc` para um Pandas mais idiomático
Os métodos mais importantes para *Method Chaining* são
* `.assign`
* `.query`
* `.loc`
* `.pipe`
```
diamonds = pd.read_csv("https://raw.githubusercontent.com/mwaskom/seaborn-data/master/diamonds.csv")
diamonds.head()
diamonds_cp = diamonds.copy()
diamonds_cp[['x', 'y', 'z']] = diamonds_cp[['x', 'y', 'z']] * 10
diamonds_cp['volume'] = diamonds_cp['x'] * diamonds_cp['y'] * diamonds_cp['z']
diamonds_cp = diamonds_cp[diamonds_cp['volume'] > 0]
diamonds_cp = pd.merge(diamonds_cp, clarity, on='clarity', how='left')
diamonds_cp
def change_basis(df: pd.DataFrame, factor=10):
df = df.copy()
df[['x', 'y', 'z']] = df[['x', 'y', 'z']] * factor
return df
diamonds \
.copy() \
.pipe(change_basis, factor=10) \
.assign(volume=lambda df: df['x'] * df['y'] * df['z']) \
.query("volume > 0") \
.merge(clarity, on='clarity', how='left')
```
Um problema que pode acontecer quando você usa o method chaining é você acabar com um bloco gigantesco que é impossível de debugar, uma boa prática é quebrar seus blocos por objetivos
## Como mandar um dataframe para a sua clipboard
Geralmente isso não é uma boa pratica, mas as vezes é útil para enviar uma parte do dado por mensagem ou para colar em alguma planilha.
```
df = pd.DataFrame({'a':list('abc'), 'b':np.random.randn(3)})
df
df.to_clipboard()
df.to_csv("df.csv")
```
Você também pode ler da sua *clipboard* com `pd.read_clipboard(...)`. O que é uma prática pior ainda, mas em alguns casos pode ser útil.
## Recursos
https://pandas.pydata.org/docs/user_guide/cookbook.html
https://tomaugspurger.github.io/modern-1-intro.html
|
github_jupyter
|
```
# Libraries needed for NLP
import nltk
nltk.download('punkt')
from nltk.stem.lancaster import LancasterStemmer
stemmer = LancasterStemmer()
# Libraries needed for Tensorflow processing
import tensorflow as tf
import numpy as np
import tflearn
import random
import json
from google.colab import files
files.upload()
# import our chat-bot intents file
with open('intents.json') as json_data:
intents = json.load(json_data)
intents
words = []
classes = []
documents = []
ignore = ['?']
# loop through each sentence in the intent's patterns
for intent in intents['intents']:
for pattern in intent['patterns']:
# tokenize each and every word in the sentence
w = nltk.word_tokenize(pattern)
# add word to the words list
words.extend(w)
# add word(s) to documents
documents.append((w, intent['tag']))
# add tags to our classes list
if intent['tag'] not in classes:
classes.append(intent['tag'])
# Perform stemming and lower each word as well as remove duplicates
words = [stemmer.stem(w.lower()) for w in words if w not in ignore]
words = sorted(list(set(words)))
# remove duplicate classes
classes = sorted(list(set(classes)))
print (len(documents), "documents")
print (len(classes), "classes", classes)
print (len(words), "unique stemmed words", words)
# create training data
training = []
output = []
# create an empty array for output
output_empty = [0] * len(classes)
# create training set, bag of words for each sentence
for doc in documents:
# initialize bag of words
bag = []
# list of tokenized words for the pattern
pattern_words = doc[0]
# stemming each word
pattern_words = [stemmer.stem(word.lower()) for word in pattern_words]
# create bag of words array
for w in words:
bag.append(1) if w in pattern_words else bag.append(0)
# output is '1' for current tag and '0' for rest of other tags
output_row = list(output_empty)
output_row[classes.index(doc[1])] = 1
training.append([bag, output_row])
# shuffling features and turning it into np.array
random.shuffle(training)
training = np.array(training)
# creating training lists
train_x = list(training[:,0])
train_y = list(training[:,1])
# resetting underlying graph data
tf.reset_default_graph()
# Building neural network
net = tflearn.input_data(shape=[None, len(train_x[0])])
net = tflearn.fully_connected(net, 10)
net = tflearn.fully_connected(net, 10)
net = tflearn.fully_connected(net, len(train_y[0]), activation='softmax')
net = tflearn.regression(net)
# Defining model and setting up tensorboard
model = tflearn.DNN(net, tensorboard_dir='tflearn_logs')
# Start training
model.fit(train_x, train_y, n_epoch=1000, batch_size=8, show_metric=True)
model.save('model.tflearn')
import pickle
pickle.dump( {'words':words, 'classes':classes, 'train_x':train_x, 'train_y':train_y}, open( "training_data", "wb" ) )
# restoring all the data structures
data = pickle.load( open( "training_data", "rb" ) )
words = data['words']
classes = data['classes']
train_x = data['train_x']
train_y = data['train_y']
with open('intents.json') as json_data:
intents = json.load(json_data)
# load the saved model
model.load('./model.tflearn')
def clean_up_sentence(sentence):
# tokenizing the pattern
sentence_words = nltk.word_tokenize(sentence)
# stemming each word
sentence_words = [stemmer.stem(word.lower()) for word in sentence_words]
return sentence_words
# returning bag of words array: 0 or 1 for each word in the bag that exists in the sentence
def bow(sentence, words, show_details=False):
# tokenizing the pattern
sentence_words = clean_up_sentence(sentence)
# generating bag of words
bag = [0]*len(words)
for s in sentence_words:
for i,w in enumerate(words):
if w == s:
bag[i] = 1
if show_details:
print ("found in bag: %s" % w)
return(np.array(bag))
ERROR_THRESHOLD = 0.30
def classify(sentence):
# generate probabilities from the model
results = model.predict([bow(sentence, words)])[0]
# filter out predictions below a threshold
results = [[i,r] for i,r in enumerate(results) if r>ERROR_THRESHOLD]
# sort by strength of probability
results.sort(key=lambda x: x[1], reverse=True)
return_list = []
for r in results:
return_list.append((classes[r[0]], r[1]))
# return tuple of intent and probability
return return_list
def response(sentence, userID='123', show_details=False):
results = classify(sentence)
# if we have a classification then find the matching intent tag
if results:
# loop as long as there are matches to process
while results:
for i in intents['intents']:
# find a tag matching the first result
if i['tag'] == results[0][0]:
# a random response from the intent
return print(random.choice(i['responses']))
results.pop(0)
classify('What are you hours of operation?')
response('What are you hours of operation?')
response('What is menu for today?')
#Some of other context free responses.
response('Do you accept Credit Card?')
response('Where can we locate you?')
response('That is helpful')
response('Bye')
#Adding some context to the conversation i.e. Contexualization for altering question and intents etc.
# create a data structure to hold user context
context = {}
ERROR_THRESHOLD = 0.25
def classify(sentence):
# generate probabilities from the model
results = model.predict([bow(sentence, words)])[0]
# filter out predictions below a threshold
results = [[i,r] for i,r in enumerate(results) if r>ERROR_THRESHOLD]
# sort by strength of probability
results.sort(key=lambda x: x[1], reverse=True)
return_list = []
for r in results:
return_list.append((classes[r[0]], r[1]))
# return tuple of intent and probability
return return_list
def response(sentence, userID='123', show_details=False):
results = classify(sentence)
# if we have a classification then find the matching intent tag
if results:
# loop as long as there are matches to process
while results:
for i in intents['intents']:
# find a tag matching the first result
if i['tag'] == results[0][0]:
# set context for this intent if necessary
if 'context_set' in i:
if show_details: print ('context:', i['context_set'])
context[userID] = i['context_set']
# check if this intent is contextual and applies to this user's conversation
if not 'context_filter' in i or \
(userID in context and 'context_filter' in i and i['context_filter'] == context[userID]):
if show_details: print ('tag:', i['tag'])
# a random response from the intent
return print(random.choice(i['responses']))
results.pop(0)
response('Can you please let me know the delivery options?')
response('What is menu for today?')
context
response("Hi there!", show_details=True)
response('What is menu for today?')
```
|
github_jupyter
|
## Dependencies
```
import json, warnings, shutil, glob
from jigsaw_utility_scripts import *
from scripts_step_lr_schedulers import *
from transformers import TFXLMRobertaModel, XLMRobertaConfig
from tensorflow.keras.models import Model
from tensorflow.keras import optimizers, metrics, losses, layers
SEED = 0
seed_everything(SEED)
warnings.filterwarnings("ignore")
pd.set_option('max_colwidth', 120)
pd.set_option('display.float_format', lambda x: '%.4f' % x)
```
## TPU configuration
```
strategy, tpu = set_up_strategy()
print("REPLICAS: ", strategy.num_replicas_in_sync)
AUTO = tf.data.experimental.AUTOTUNE
```
# Load data
```
database_base_path = '/kaggle/input/jigsaw-data-split-roberta-192-ratio-1-clean-polish/'
k_fold = pd.read_csv(database_base_path + '5-fold.csv')
valid_df = pd.read_csv("/kaggle/input/jigsaw-multilingual-toxic-comment-classification/validation.csv",
usecols=['comment_text', 'toxic', 'lang'])
print('Train samples: %d' % len(k_fold))
display(k_fold.head())
print('Validation samples: %d' % len(valid_df))
display(valid_df.head())
base_data_path = 'fold_1/'
fold_n = 1
# Unzip files
!tar -xf /kaggle/input/jigsaw-data-split-roberta-192-ratio-1-clean-polish/fold_1.tar.gz
```
# Model parameters
```
base_path = '/kaggle/input/jigsaw-transformers/XLM-RoBERTa/'
config = {
"MAX_LEN": 192,
"BATCH_SIZE": 128,
"EPOCHS": 3,
"LEARNING_RATE": 1e-5,
"ES_PATIENCE": None,
"base_model_path": base_path + 'tf-xlm-roberta-large-tf_model.h5',
"config_path": base_path + 'xlm-roberta-large-config.json'
}
with open('config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
config
```
## Learning rate schedule
```
lr_min = 1e-7
lr_start = 0
lr_max = config['LEARNING_RATE']
step_size = (len(k_fold[k_fold[f'fold_{fold_n}'] == 'train']) * 2) // config['BATCH_SIZE']
total_steps = config['EPOCHS'] * step_size
hold_max_steps = 0
warmup_steps = total_steps * 0.1
decay = .9998
rng = [i for i in range(0, total_steps, config['BATCH_SIZE'])]
y = [exponential_schedule_with_warmup(tf.cast(x, tf.float32), warmup_steps=warmup_steps,
hold_max_steps=hold_max_steps, lr_start=lr_start,
lr_max=lr_max, lr_min=lr_min, decay=decay) for x in rng]
sns.set(style="whitegrid")
fig, ax = plt.subplots(figsize=(20, 6))
plt.plot(rng, y)
print("Learning rate schedule: {:.3g} to {:.3g} to {:.3g}".format(y[0], max(y), y[-1]))
```
# Model
```
module_config = XLMRobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFXLMRobertaModel.from_pretrained(config['base_model_path'], config=module_config)
last_hidden_state, _ = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
cls_token = last_hidden_state[:, 0, :]
output = layers.Dense(1, activation='sigmoid', name='output')(cls_token)
model = Model(inputs=[input_ids, attention_mask], outputs=output)
return model
```
# Train
```
# Load data
x_train = np.load(base_data_path + 'x_train.npy')
y_train = np.load(base_data_path + 'y_train_int.npy').reshape(x_train.shape[1], 1).astype(np.float32)
x_valid = np.load(base_data_path + 'x_valid.npy')
y_valid = np.load(base_data_path + 'y_valid_int.npy').reshape(x_valid.shape[1], 1).astype(np.float32)
x_valid_ml = np.load(database_base_path + 'x_valid.npy')
y_valid_ml = np.load(database_base_path + 'y_valid.npy').reshape(x_valid_ml.shape[1], 1).astype(np.float32)
#################### ADD TAIL ####################
x_train_tail = np.load(base_data_path + 'x_train_tail.npy')
y_train_tail = np.load(base_data_path + 'y_train_int_tail.npy').reshape(x_train_tail.shape[1], 1).astype(np.float32)
x_train = np.hstack([x_train, x_train_tail])
y_train = np.vstack([y_train, y_train_tail])
step_size = x_train.shape[1] // config['BATCH_SIZE']
valid_step_size = x_valid_ml.shape[1] // config['BATCH_SIZE']
valid_2_step_size = x_valid.shape[1] // config['BATCH_SIZE']
# Build TF datasets
train_dist_ds = strategy.experimental_distribute_dataset(get_training_dataset(x_train, y_train, config['BATCH_SIZE'], AUTO, seed=SEED))
valid_dist_ds = strategy.experimental_distribute_dataset(get_validation_dataset(x_valid_ml, y_valid_ml, config['BATCH_SIZE'], AUTO, repeated=True, seed=SEED))
valid_2_dist_ds = strategy.experimental_distribute_dataset(get_validation_dataset(x_valid, y_valid, config['BATCH_SIZE'], AUTO, repeated=True, seed=SEED))
train_data_iter = iter(train_dist_ds)
valid_data_iter = iter(valid_dist_ds)
valid_2_data_iter = iter(valid_2_dist_ds)
# Step functions
@tf.function
def train_step(data_iter):
def train_step_fn(x, y):
with tf.GradientTape() as tape:
probabilities = model(x, training=True)
loss = loss_fn(y, probabilities)
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
train_auc.update_state(y, probabilities)
train_loss.update_state(loss)
for _ in tf.range(step_size):
strategy.experimental_run_v2(train_step_fn, next(data_iter))
@tf.function
def valid_step(data_iter):
def valid_step_fn(x, y):
probabilities = model(x, training=False)
loss = loss_fn(y, probabilities)
valid_auc.update_state(y, probabilities)
valid_loss.update_state(loss)
for _ in tf.range(valid_step_size):
strategy.experimental_run_v2(valid_step_fn, next(data_iter))
@tf.function
def valid_2_step(data_iter):
def valid_step_fn(x, y):
probabilities = model(x, training=False)
loss = loss_fn(y, probabilities)
valid_2_auc.update_state(y, probabilities)
valid_2_loss.update_state(loss)
for _ in tf.range(valid_2_step_size):
strategy.experimental_run_v2(valid_step_fn, next(data_iter))
# Train model
with strategy.scope():
model = model_fn(config['MAX_LEN'])
lr = lambda: exponential_schedule_with_warmup(tf.cast(optimizer.iterations, tf.float32),
warmup_steps=warmup_steps, hold_max_steps=hold_max_steps,
lr_start=lr_start, lr_max=lr_max, lr_min=lr_min, decay=decay)
optimizer = optimizers.Adam(learning_rate=lr)
loss_fn = losses.binary_crossentropy
train_auc = metrics.AUC()
valid_auc = metrics.AUC()
valid_2_auc = metrics.AUC()
train_loss = metrics.Sum()
valid_loss = metrics.Sum()
valid_2_loss = metrics.Sum()
metrics_dict = {'loss': train_loss, 'auc': train_auc,
'val_loss': valid_loss, 'val_auc': valid_auc,
'val_2_loss': valid_2_loss, 'val_2_auc': valid_2_auc}
history = custom_fit_2(model, metrics_dict, train_step, valid_step, valid_2_step, train_data_iter,
valid_data_iter, valid_2_data_iter, step_size, valid_step_size, valid_2_step_size,
config['BATCH_SIZE'], config['EPOCHS'], config['ES_PATIENCE'], save_last=False)
# model.save_weights('model.h5')
# Make predictions
# x_train = np.load(base_data_path + 'x_train.npy')
# x_valid = np.load(base_data_path + 'x_valid.npy')
x_valid_ml_eval = np.load(database_base_path + 'x_valid.npy')
# train_preds = model.predict(get_test_dataset(x_train, config['BATCH_SIZE'], AUTO))
# valid_preds = model.predict(get_test_dataset(x_valid, config['BATCH_SIZE'], AUTO))
valid_ml_preds = model.predict(get_test_dataset(x_valid_ml_eval, config['BATCH_SIZE'], AUTO))
# k_fold.loc[k_fold[f'fold_{fold_n}'] == 'train', f'pred_{fold_n}'] = np.round(train_preds)
# k_fold.loc[k_fold[f'fold_{fold_n}'] == 'validation', f'pred_{fold_n}'] = np.round(valid_preds)
valid_df[f'pred_{fold_n}'] = valid_ml_preds
# Fine-tune on validation set
#################### ADD TAIL ####################
x_valid_ml_tail = np.hstack([x_valid_ml, np.load(database_base_path + 'x_valid_tail.npy')])
y_valid_ml_tail = np.vstack([y_valid_ml, y_valid_ml])
valid_step_size_tail = x_valid_ml_tail.shape[1] // config['BATCH_SIZE']
# Build TF datasets
train_ml_dist_ds = strategy.experimental_distribute_dataset(get_training_dataset(x_valid_ml_tail, y_valid_ml_tail, config['BATCH_SIZE'], AUTO, seed=SEED))
train_ml_data_iter = iter(train_ml_dist_ds)
# Step functions
@tf.function
def train_ml_step(data_iter):
def train_step_fn(x, y):
with tf.GradientTape() as tape:
probabilities = model(x, training=True)
loss = loss_fn(y, probabilities)
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
train_auc.update_state(y, probabilities)
train_loss.update_state(loss)
for _ in tf.range(valid_step_size_tail):
strategy.experimental_run_v2(train_step_fn, next(data_iter))
# Fine-tune on validation set
optimizer = optimizers.Adam(learning_rate=config['LEARNING_RATE'])
history_ml = custom_fit_2(model, metrics_dict, train_ml_step, valid_step, valid_2_step, train_ml_data_iter,
valid_data_iter, valid_2_data_iter, valid_step_size_tail, valid_step_size, valid_2_step_size,
config['BATCH_SIZE'], 2, config['ES_PATIENCE'], save_last=False)
# Join history
for key in history_ml.keys():
history[key] += history_ml[key]
model.save_weights('model.h5')
# Make predictions
valid_ml_preds = model.predict(get_test_dataset(x_valid_ml_eval, config['BATCH_SIZE'], AUTO))
valid_df[f'pred_ml_{fold_n}'] = valid_ml_preds
### Delete data dir
shutil.rmtree(base_data_path)
```
## Model loss graph
```
plot_metrics_2(history)
```
# Model evaluation
```
# display(evaluate_model_single_fold(k_fold, fold_n, label_col='toxic_int').style.applymap(color_map))
```
# Confusion matrix
```
# train_set = k_fold[k_fold[f'fold_{fold_n}'] == 'train']
# validation_set = k_fold[k_fold[f'fold_{fold_n}'] == 'validation']
# plot_confusion_matrix(train_set['toxic_int'], train_set[f'pred_{fold_n}'],
# validation_set['toxic_int'], validation_set[f'pred_{fold_n}'])
```
# Model evaluation by language
```
display(evaluate_model_single_fold_lang(valid_df, fold_n).style.applymap(color_map))
# ML fine-tunned preds
display(evaluate_model_single_fold_lang(valid_df, fold_n, pred_col='pred_ml').style.applymap(color_map))
```
# Visualize predictions
```
print('English validation set')
display(k_fold[['comment_text', 'toxic'] + [c for c in k_fold.columns if c.startswith('pred')]].head(10))
print('Multilingual validation set')
display(valid_df[['comment_text', 'toxic'] + [c for c in valid_df.columns if c.startswith('pred')]].head(10))
```
# Test set predictions
```
x_test = np.load(database_base_path + 'x_test.npy')
test_preds = model.predict(get_test_dataset(x_test, config['BATCH_SIZE'], AUTO))
submission = pd.read_csv('/kaggle/input/jigsaw-multilingual-toxic-comment-classification/sample_submission.csv')
submission['toxic'] = test_preds
submission.to_csv('submission.csv', index=False)
display(submission.describe())
display(submission.head(10))
```
|
github_jupyter
|
## 1. 데이터 불러오기
```
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import random
data1 = pd.read_csv('C:/Users/Soyoung Cho/Desktop/NMT Project/dataset/train.csv')
data2 = pd.read_csv('C:/Users/Soyoung Cho/Desktop/NMT Project/dataset/test.csv')
data3 = pd.read_csv('C:/Users/Soyoung Cho/Desktop/NMT Project/dataset/tatoeba_data.csv')
print("data1: ", len(data1))
print("data2: ", len(data2))
print("data3: ", len(data3))
data = pd.concat([data1, data2, data3])
data = data.reset_index(drop=True) # 0~20만, 0~20만 이런 인덱스까지 concat 되었던 것을 초기화, 다시 인덱스 주었다
data
Kor_list = list(data['Korean']) #모든 한글 문장이 담긴 리스트
Eng_list = list(data['English']) #모든 영어 문장이 담긴 리스트
print(Kor_list[:5])
print("\n")
print(Eng_list[:5])
result = list(zip(Kor_list,Eng_list))
random.shuffle(result)
result
Kor_list, Eng_list = zip(*result)
dict_ = {"Korean": [], "English" : []}
dict_["Korean"] = Kor_list
dict_["English"] = Eng_list
data = pd.DataFrame(dict_)
data
```
## 2. 데이터 중복 검사 및 제거
```
data.describe()
data.duplicated().sum()
data = data.drop_duplicates()
data.duplicated().sum()
data = data.reset_index(drop=True) # 0~20만, 0~20만 이런 인덱스까지 concat 되었던 것을 초기화, 다시 인덱스 주었다
data
#data.to_csv("datalist.csv", encoding = 'utf-8-sig', index = False, mode = "w")
```
## 3. 문장별 단어 개수 파악 & 문제 파악
```
kor_word_cnt = []
eng_word_cnt = []
for i in range(len(data)):
kor_word_cnt.append(len(data['Korean'][i].split(" ")))
eng_word_cnt.append(len(data['English'][i].split(" ")))
data["Korean_word_count"] = kor_word_cnt
data["English_word_count"] = eng_word_cnt
```
### (1) 단어 개수 별 정렬해 데이터 확인 & 문제 수정
```
kor_sorted = data.sort_values(by=['Korean_word_count'], axis=0, ascending=False)
kor_sorted = kor_sorted.reset_index(drop=True)
kor_sorted.head()
kor_sorted[0:10]
kor_sorted[-10:]
```
#### 문제 발견 및 수정, 데이터 재저장
```
kor_sorted["Korean"][1603523]
kor_sorted["Korean"][1603524]
kor_sorted["Korean"][1603515]
```
중간의 \xa0 때문에 한 문장이 한 단어로 인식 되었었다. 전체 dataset의 \xa0 를 " " 로 대체해준다.
다시 word를 카운트 해준다.
```
data.replace("\xa0", " ", regex=True, inplace=True)
#data
```
---
---
### (2) 한글 문장 단어 개수 파악
```
kor_sorted = data.sort_values(by=['Korean_word_count'], axis=0, ascending=False)
kor_sorted = kor_sorted.reset_index(drop=True)
kor_sorted.head()
kor_sorted[-110:-90]
kor_sorted["Korean"][1603427]
kor_sorted[-130:-110]
```
위와 같이 띄어쓰기가 아예 이루어지지 않은 문장은 어떻게 해야할지 고민 필요.
```
kor_sorted[0:20]
```
### (3) 영어 문장 단어 개수 파악
```
eng_sorted = data.sort_values(by=['English_word_count'], axis=0, ascending=False)
eng_sorted = eng_sorted.reset_index(drop=True)
eng_sorted[:20]
eng_sorted['English'][0]
eng_sorted['English'][1]
eng_sorted['English'][2]
eng_sorted['English'][3]
len(eng_sorted['English'][3].split(" "))
len('"We will play the role of a hub for inter-Korean exchanges of performing arts and culture," said Kim Cheol-ho, 66, the new director of the National Theater of Korea, at an inaugural press conference held at a restaurant in Jongro-gu, Seoul on the 8th and he said, "We can invite North Korean national art troupe for the festival that will be held in 2020 for the 70th anniversary of our foundation." '.split(" "))
eng_sorted[-30:]
```
한글 데이터는 짧은 문장의 경우 띄어쓰기가 잘 안 이루어져 있음.
영어 데이터는 긴 문장의 경우 띄어쓰기가 지나치게 많이 들어가 있음.
짧은 문장의 경우 검수 안된 문장들 . 혹은 x 등 많음.
## 4. 박스플롯 그려보기
```
print("한글 문장 중 가장 적은 단어 개수 가진 문장은 ", min(kor_word_cnt))
print("한글 문장 중 가장 많은 단어 개수 가진 문장은 ", max(kor_word_cnt))
print("영어 문장 중 가장 적은 단어 개수 가진 문장은 ", min(eng_word_cnt))
print("영어 문장 중 가장 많은 단어 개수 가진 문장은 ", max(eng_word_cnt))
fig, ax = plt.subplots(figsize = (12,8))
sns.boxplot(kor_word_cnt)
plt.show()
fig, ax = plt.subplots(figsize = (12,8))
sns.boxplot(eng_word_cnt)
plt.show()
```
## 5. 데이터 저장하기
```
del data['Korean_word_count']
del data['English_word_count']
#data.to_csv("C:/Users/Soyoung Cho/Desktop/NMT Project/dataset/datalist_modified.csv", encoding = 'utf-8-sig', index = False, mode = "w")
```
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.