prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# Introduction to NumPy
Forked from [Lecture 2](https://github.com/jrjohansson/scientific-python-lectures/blob/master/Lecture-2-Numpy.ipynb) of [Scientific Python Lectures](http://github.com/jrjohansson/scientific-python-lectures) by [J.R. Johansson](http://jrjohansson.github.io/)
```
%matplotlib inline
import traceback
import matplotlib.pyplot as plt
import numpy as np
```
### Why NumPy?
```
%%time
total = 0
for i in range(100000):
total += i
%%time
total = np.arange(100000).sum()
%%time
l = list(range(0, 1000000))
ltimes5 = [x * 5 for x in l]
%%time
l = np.arange(1000000)
ltimes5 = l * 5
```
## Introduction
The `numpy` package (module) is used in almost all numerical computation using Python. It is a package that provide high-performance vector, matrix and higher-dimensional data structures for Python. It is implemented in C and Fortran so when calculations are vectorized (formulated with vectors and matrices), performance is very good.
To use `numpy` you need to import the module, using for example:
```
import numpy as np
```
In the `numpy` package the terminology used for vectors, matrices and higher-dimensional data sets is *array*.
## Creating `numpy` arrays
There are a number of ways to initialize new numpy arrays, for example from
* a Python list or tuples
* using functions that are dedicated to generating numpy arrays, such as `arange`, `linspace`, etc.
* reading data from files
### From lists
For example, to create new vector and matrix arrays from Python lists we can use the `numpy.array` function.
```
# a vector: the argument to the array function is a Python list
v = np.array([1,2,3,4])
v
# a matrix: the argument to the array function is a nested Python list
M = np.array([[1, 2], [3, 4]])
M
```
The `v` and `M` objects are both of the type `ndarray` that the `numpy` module provides.
```
type(v), type(M)
```
The difference between the `v` and `M` arrays is only their shapes. We can get information about the shape of an array by using the `ndarray.shape` property.
```
v.shape
M.shape
```
The number of elements in the array is available through the `ndarray.size` property:
```
M.size
```
Equivalently, we could use the function `numpy.shape` and `numpy.size`
```
np.shape(M)
np.size(M)
```
So far the `numpy.ndarray` looks awefully much like a Python list (or nested list). Why not simply use Python lists for computations instead of creating a new array type?
There are several reasons:
* Python lists are very general. They can contain any kind of object. They are dynamically typed. They do not support mathematical functions such as matrix and dot multiplications, etc. Implementing such functions for Python lists would not be very efficient because of the dynamic typing.
* Numpy arrays are **statically typed** and **homogeneous**. The type of the elements is determined when the array is created.
* Numpy arrays are memory efficient.
* Because of the static typing, fast implementation of mathematical functions such as multiplication and addition of `numpy` arrays can be implemented in a compiled language (C and Fortran is used).
Using the `dtype` (data type) property of an `ndarray`, we can see what type the data of an array has:
```
M.dtype
```
We get an error if we try to assign a value of the wrong type to an element in a numpy array:
```
try:
M[0,0] = "hello"
except ValueError as e:
print(traceback.format_exc())
```
If we want, we can explicitly define the type of the array data when we create it, using the `dtype` keyword argument:
```
M = np.array([[1, 2], [3, 4]], dtype=complex)
M
```
Common data types that can be used with `dtype` are: `int`, `float`, `complex`, `bool`, `object`, etc.
We can also explicitly define the bit size of the data types, for example: `int64`, `int16`, `float128`, `complex128`.
### Using array-generating functions
For larger arrays it is inpractical to initialize the data manually, using explicit python lists. Instead we can use one of the many functions in `numpy` that generate arrays of different forms. Some of the more common are:
#### arange
```
# create a range
x = np.arange(0, 10, 1) # arguments: start, stop, step
x
x = np.arange(-1, 1, 0.1)
x
```
#### linspace and logspace
```
# using linspace, both end points ARE included
np.linspace(0, 10, 25)
np.logspace(0, 10, 10, base=np.e)
```
#### mgrid
```
x, y = np.mgrid[0:5, 0:5] # similar to meshgrid in MATLAB
x
y
```
#### random data
```
# uniform random numbers in [0,1]
np.random.rand(5,5)
# standard normal distributed random numbers
np.random.randn(5,5)
```
#### diag
```
# a diagonal matrix
np.diag([1,2,3])
# diagonal with offset from the main diagonal
np.diag([1,2,3], k=1)
```
#### zeros and ones
```
np.zeros((3,3))
np.ones((3,3))
```
## File I/O
### Comma-separated values (CSV)
A very common file format for data files is comma-separated values (CSV), or related formats such as TSV (tab-separated values). To read data from such files into Numpy arrays we can use the `numpy.genfromtxt` function. For example,
```
!head ../data/stockholm_td_adj.dat
data = np.genfromtxt('../data/stockholm_td_adj.dat')
data.shape
fig, ax = plt.subplots(figsize=(14,4))
ax.plot(data[:,0]+data[:,1]/12.0+data[:,2]/365, data[:,5])
ax.axis('tight')
ax.set_title('tempeatures in Stockholm')
ax.set_xlabel('year')
ax.set_ylabel('temperature (C)');
```
Using `numpy.savetxt` we can store a Numpy array to a file in CSV format:
```
M = np.random.rand(3,3)
M
np.savetxt("../data/random-matrix.csv", M)
!cat ../data/random-matrix.csv
np.savetxt("../data/random-matrix.csv", M, fmt='%.5f') # fmt specifies the format
!cat ../data/random-matrix.csv
```
### Numpy's native file format
Useful when storing and reading back numpy array data. Use the functions `numpy.save` and `numpy.load`:
```
np.save("../data/random-matrix.npy", M)
!file ../data/random-matrix.npy
np.load("../data/random-matrix.npy")
```
## More properties of the numpy arrays
```
M.itemsize # bytes per element
M.nbytes # number of bytes
M.ndim # number of dimensions
```
## Manipulating arrays
### Indexing
We can index elements in an array using square brackets and indices:
```
# v is a vector, and has only one dimension, taking one index
v[0]
# M is a matrix, or a 2 dimensional array, taking two indices
M[1,1]
```
If we omit an index of a multidimensional array it returns the whole row (or, in general, a N-1 dimensional array)
```
M
M[1]
```
The same thing can be achieved with using `:` instead of an index:
```
M[1,:] # row 1
M[:,1] # column 1
```
We can assign new values to elements in an array using indexing:
```
M[0,0] = 1
M
# also works for rows and columns
M[1,:] = 0
M[:,2] = -1
M
```
### Index slicing
Index slicing is the technical name for the syntax `M[lower:upper:step]` to extract part of an array:
```
A = np.array([1,2,3,4,5])
A
A[1:3]
```
Array slices are *mutable*: if they are assigned a new value the original array from which the slice was extracted is modified:
```
A[1:3] = [-2,-3]
A
```
We can omit any of the three parameters in `M[lower:upper:step]`:
```
A[::] # lower, upper, step all take the default values
A[::2] # step is 2, lower and upper defaults to the beginning and end of the array
A[:3] # first three elements
A[3:] # elements from index 3
```
Negative indices counts from the end of the array (positive index from the begining):
```
A = np.array([1,2,3,4,5])
A[-1] # the last element in the array
A[-3:] # the last three elements
```
Index slicing works exactly the same way for multidimensional arrays:
```
A = np.array([[n+m*10 for n in range(5)] for m in range(5)])
A
# a block from the original array
A[1:4, 1:4]
# strides
A[::2, ::2]
```
### Fancy indexing
Fancy indexing is the name for when an array or list is used in-place of an index:
```
row_indices = [1, 2, 3]
A[row_indices]
col_indices = [1, 2, -1] # remember, index -1 means the last element
A[row_indices, col_indices]
```
We can also use index masks: If the index mask is an Numpy array of data type `bool`, then an element is selected (True) or not (False) depending on the value of the index mask at the position of each element:
```
B = np.array([n for n in range(5)])
B
row_mask = np.array([True, False, True, False, False])
B[row_mask]
# same thing
row_mask = np.array([1,0,1,0,0], dtype=bool)
B[row_mask]
```
This feature is very useful to conditionally select elements from an array, using for example comparison operators:
```
x = np.arange(0, 10, 0.5)
x
mask = (5 < x) * (x < 7.5)
mask
x[mask]
```
## Functions for extracting data from arrays and creating arrays
### where
The index mask can be converted to position index using the `where` function
```
indices = np.where(mask)
indices
x[indices] # this indexing is equivalent to the fancy indexing x[mask]
```
### diag
With the diag function we can also extract the diagonal and subdiagonals of an array:
```
np.diag(A)
np.diag(A, -1)
```
### take
The `take` function is similar to fancy indexing described above:
```
v2 = np.arange(-3,3)
v2
row_indices = [1, 3, 5]
v2[row_indices] # fancy indexing
v2.take(row_indices)
```
But `take` also works on lists and other objects:
```
np.take([-3, -2, -1, 0, 1, 2], row_indices)
```
### choose
Constructs an array by picking elements from several arrays:
```
which = [1, 0, 1, 0]
choices = [[-2,-2,-2,-2], [5,5,5,5]]
np.choose(which, choices)
```
## Linear algebra
Vectorizing code is the key to writing efficient numerical calculation with Python/Numpy. That means that as much as possible of a program should be formulated in terms of matrix and vector operations, like matrix-matrix multiplication.
### Scalar-array operations
We can use the usual arithmetic operators to multiply, add, subtract, and divide arrays with scalar numbers.
```
v1 = np.arange(0, 5)
v1 * 2
v1 + 2
A * 2, A + 2
```
### Element-wise array-array operations
When we add, subtract, multiply and divide arrays with each other, the default behaviour is **element-wise** operations:
```
A * A # element-wise multiplication
v1 * v1
```
If we multiply arrays with compatible shapes, we get an element-wise multiplication of each row:
```
A.shape, v1.shape
A * v1
```
### Matrix algebra
What about matrix mutiplication? There are two ways. We can either use the `dot` function, which applies a matrix-matrix, matrix-vector, or inner vector multiplication to its two arguments:
```
np.dot(A, A)
```
Python 3 has a new operator for using infix notation with matrix multiplication.
```
A @ A
np.dot(A, v1)
np.dot(v1, v1)
```
Alternatively, we can cast the array objects to the type `matrix`. This changes the behavior of the standard arithmetic operators `+, -, *` to use matrix algebra.
```
M = np.matrix(A)
v = np.matrix(v1).T # make it a column vector
v
M * M
M * v
# inner product
v.T * v
# with matrix objects, standard matrix algebra applies
v + M*v
```
If we try to add, subtract or multiply objects with incomplatible shapes we get an error:
```
v = np.matrix([1,2,3,4,5,6]).T
M.shape, v.shape
import traceback
try:
M * v
except ValueError as e:
print(traceback.format_exc())
```
See also the related functions: `inner`, `outer`, `cross`, `kron`, `tensordot`. Try for example `help(np.kron)`.
### Array/Matrix transformations
Above we have used the `.T` to transpose the matrix object `v`. We could also have used the `transpose` function to accomplish the same thing.
Other mathematical functions that transform matrix objects are:
```
C = np.matrix([[1j, 2j], [3j, 4j]])
C
np.conjugate(C)
```
Hermitian conjugate: transpose + conjugate
```
C.H
```
We can extract the real and imaginary parts of complex-valued arrays using `real` and `imag`:
```
np.real(C) # same as: C.real
np.imag(C) # same as: C.imag
```
Or the complex argument and absolute value
```
np.angle(C+1) # heads up MATLAB Users, angle is used instead of arg
abs(C)
```
### Matrix computations
#### Inverse
```
np.linalg.inv(C) # equivalent to C.I
C.I * C
```
#### Determinant
```
np.linalg.det(C)
np.linalg.det(C.I)
```
### Data processing
Often it is useful to store datasets in Numpy arrays. Numpy provides a number of functions to calculate statistics of datasets in arrays.
For example, let's calculate some properties from the Stockholm temperature dataset used above.
```
# reminder, the tempeature dataset is stored in the data variable:
np.shape(data)
```
#### mean
```
# the temperature data is in column 3
np.mean(data[:,3])
```
The daily mean temperature in Stockholm over the last 200 years has been about 6.2 C.
#### standard deviations and variance
```
np.std(data[:,3]), np.var(data[:,3])
```
#### min and max
```
# lowest daily average temperature
data[:,3].min()
# highest daily average temperature
data[:,3].max()
```
#### sum, prod, and trace
```
d = np.arange(0, 10)
d
# sum up all elements
np.sum(d)
# product of all elements
np.prod(d+1)
# cummulative sum
np.cumsum(d)
# cummulative product
np.cumprod(d+1)
# same as: diag(A).sum()
np.trace(A)
```
### Computations on subsets of arrays
We can compute with subsets of the data in an array using indexing, fancy indexing, and the other methods of extracting data from an array (described above).
For example, let's go back to the temperature dataset:
```
!head -n 3 ../data/stockholm_td_adj.dat
```
The dataformat is: year, month, day, daily average temperature, low, high, location.
If we are interested in the average temperature only in a particular month, say February, then we can create a index mask and use it to select only the data for that month using:
```
np.unique(data[:,1]) # the month column takes values from 1 to 12
mask_feb = data[:,1] == 2
# the temperature data is in column 3
np.mean(data[mask_feb,3])
```
With these tools we have very powerful data processing capabilities at our disposal. For example, to extract the average monthly average temperatures for each month of the year only takes a few lines of code:
```
months = np.arange(1,13)
monthly_mean = [np.mean(data[data[:,1] == month, 3]) for month in months]
fig, ax = plt.subplots()
ax.bar(months, monthly_mean)
ax.set_xlabel("Month")
ax.set_ylabel("Monthly avg. temp.");
```
### Calculations with higher-dimensional data
When functions such as `min`, `max`, etc. are applied to a multidimensional arrays, it is sometimes useful to apply the calculation to the entire array, and sometimes only on a row or column basis. Using the `axis` argument we can specify how these functions should behave:
```
m = np.random.rand(3,3)
m
# global max
m.max()
# max in each column
m.max(axis=0)
# max in each row
m.max(axis=1)
```
Many other functions and methods in the `array` and `matrix` classes accept the same (optional) `axis` keyword argument.
## Reshaping, resizing and stacking arrays
The shape of an Numpy array can be modified without copying the underlaying data, which makes it a fast operation even for large arrays.
```
A
n, m = A.shape
B = A.reshape((1,n*m))
B
B[0,0:5] = 5 # modify the array
B
A # and the original variable is also changed. B is only a different view of the same data
```
We can also use the function `flatten` to make a higher-dimensional array into a vector. But this function create a copy of the data.
```
B = A.flatten()
B
B[0:5] = 10
B
A # now A has not changed, because B's data is a copy of A's, not refering to the same data
```
## Adding a new dimension: newaxis
With `newaxis`, we can insert new dimensions in an array, for example converting a vector to a column or row matrix:
```
v = np.array([1,2,3])
v.shape
# make a column matrix of the vector v
v[:, np.newaxis]
# column matrix
v[:, np.newaxis].shape
# row matrix
v[np.newaxis, :].shape
```
## Stacking and repeating arrays
Using function `repeat`, `tile`, `vstack`, `hstack`, and `concatenate` we can create larger vectors and matrices from smaller ones:
### tile and repeat
```
a = np.array([[1, 2], [3, 4]])
# repeat each element 3 times
np.repeat(a, 3)
# tile the matrix 3 times
np.tile(a, 3)
```
### concatenate
```
b = np.array([[5, 6]])
np.concatenate((a, b), axis=0)
np.concatenate((a, b.T), axis=1)
```
### hstack and vstack
```
np.vstack((a,b))
np.hstack((a,b.T))
```
## Copy and "deep copy"
To achieve high performance, assignments in Python usually do not copy the underlaying objects. This is important for example when objects are passed between functions, to avoid an excessive amount of memory copying when it is not necessary (technical term: pass by reference).
```
A = np.array([[1, 2], [3, 4]])
A
# now B is referring to the same array data as A
B = A
# changing B affects A
B[0,0] = 10
B
A
```
If we want to avoid this behavior, so that when we get a new completely independent object `B` copied from `A`, then we need to do a so-called "deep copy" using the function `copy`:
```
B = np.copy(A)
# now, if we modify B, A is not affected
B[0,0] = -5
B
A
```
## Iterating over array elements
Generally, we want to avoid iterating over the elements of arrays whenever we can (at all costs). The reason is that in a interpreted language like Python (or MATLAB/R), iterations are really slow compared to vectorized operations.
However, sometimes iterations are unavoidable. For such cases, the Python `for` loop is the most convenient way to iterate over an array:
```
v = np.array([1,2,3,4])
for element in v:
print(element)
M = np.array([[1,2], [3,4]])
for row in M:
print("row", row)
for element in row:
print(element)
```
When we need to iterate over each element of an array and modify its elements, it is convenient to use the `enumerate` function to obtain both the element and its index in the `for` loop:
```
for row_idx, row in enumerate(M):
print("row_idx", row_idx, "row", row)
for col_idx, element in enumerate(row):
print("col_idx", col_idx, "element", element)
# update the matrix M: square each element
M[row_idx, col_idx] = element ** 2
# each element in M is now squared
M
```
## Vectorizing functions
As mentioned several times by now, to get good performance we should try to avoid looping over elements in our vectors and matrices, and instead use vectorized algorithms. The first step in converting a scalar algorithm to a vectorized algorithm is to make sure that the functions we write work with vector inputs.
```
def theta(x):
"""
Scalar implemenation of the Heaviside step function.
"""
if x >= 0:
return 1
else:
return 0
try:
theta(np.array([-3,-2,-1,0,1,2,3]))
except Exception as e:
print(traceback.format_exc())
```
OK, that didn't work because we didn't write the `Theta` function so that it can handle a vector input...
To get a vectorized version of Theta we can use the Numpy function `vectorize`. In many cases it can automatically vectorize a function:
```
theta_vec = np.vectorize(theta)
%%time
theta_vec(np.array([-3,-2,-1,0,1,2,3]))
```
We can also implement the function to accept a vector input from the beginning (requires more effort but might give better performance):
```
def theta(x):
"""
Vector-aware implemenation of the Heaviside step function.
"""
return 1 * (x >= 0)
%%time
theta(np.array([-3,-2,-1,0,1,2,3]))
# still works for scalars as well
theta(-1.2), theta(2.6)
```
## Using arrays in conditions
When using arrays in conditions,for example `if` statements and other boolean expressions, one needs to use `any` or `all`, which requires that any or all elements in the array evalutes to `True`:
```
M
if (M > 5).any():
print("at least one element in M is larger than 5")
else:
print("no element in M is larger than 5")
if (M > 5).all():
print("all elements in M are larger than 5")
else:
print("all elements in M are not larger than 5")
```
## Type casting
Since Numpy arrays are *statically typed*, the type of an array does not change once created. But we can explicitly cast an array of some type to another using the `astype` functions (see also the similar `asarray` function). This always create a new array of new type:
```
M.dtype
M2 = M.astype(float)
M2
M2.dtype
M3 = M.astype(bool)
M3
```
## Further reading
* http://numpy.scipy.org - Official Numpy Documentation
* http://scipy.org/Tentative_NumPy_Tutorial - Official Numpy Quickstart Tutorial (highly recommended)
* http://www.scipy-lectures.org/intro/numpy/index.html - Scipy Lectures: Lecture 1.3
## Versions
```
%reload_ext version_information
%version_information numpy
```
| true |
code
| 0.471041 | null | null | null | null |
|
# Importing libaries
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression, BayesianRidge
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
from sklearn import linear_model
```
# Importing first databases
Radars.csv contains all cars, trucks, motorcycles and buses that comes thru São Paulo's radar system
```
df_base = pd.read_csv(r"D:\\Users\\guilh\\Documents\\GitHub\\Dados_CET\\Marco_2018_nAg\\2_nAg.csv", index_col= "Data")
df_base.head()
```
### Reading the columns
* **Radar** is the number of identification of a street section
* **Lane** goes from 1 to 6 in most radars, low lane number are closer to the center of the freeway, high lane numbers are "local" lanes, to the right
* **Register** represents each vehicle
* **Types** are: motorcycle = 0, car = 1, bus = 2 ou truck = 3
* **Classes** are: *light* (motorcycle and car) = 0 ou *heavy* (bus and truck) = 1
* **Speeds** are in kilometer per hour
* **Radar_Lane** comes to identify each lane on a single radar (will be usefull to merge dataframes)
```
# Preprocessing
df = df_base[["Numero Agrupado", "Faixa", "Registro", "Especie", "Classe", "Velocidade"]]
# turns speed from dm/s to km/h
df["Velocidade"] = df["Velocidade"] * 0.36
df.index.names = ["Date"]
df["Radar_Lane"] = df["Numero Agrupado"].astype(str) + df["Faixa"].astype(str)
# renaming columns to english
df.columns = ["Radar", "Lane", "Register", "Type", "Class", "Speed [km/h]", "Radar_Lane"]
df.head()
```
### Lane types database
Helps to tell the **use of each lane** .
"Tipo" contains the information of lanes where all types of vehicycles can use ( *mix_use* ) and other that are for buses only ( *exclusive_bus* )
```
lane_types = pd.read_excel(r"D:\Users\guilh\Documents\[POLI]_6_Semestre\IC\2021\codigos olimpio\\Faixa Tipo.xlsx", usecols = ["Num_agrupado","faixa", "Num_fx","tipo"],engine='openpyxl')
lane_types.head()
```
### Merge dataframes
To identify the type of the lane, if it is exclusive for buses, or multipurpose
```
df_merged = lane_types[["Num_fx", "tipo"]].merge(df, left_on = "Num_fx", right_on = "Radar_Lane", how="right")
df_merged["Lane_use"] = df_merged["tipo"].map({"mista":"mix_use", "onibus": "exclusive_bus"})
df_merged = df_merged[["Radar", "Lane", "Register", "Type", "Class", "Speed [km/h]", "Lane_use"]]
df_merged.head()
```
### Looking for NaNs
As shown below, NaNs are less than 1% (actually, less than 0,2%)
With this information, there will be low loss in dropping NaNs
```
print(df_merged.isna().mean() *100)
df_merged.dropna(inplace=True)
```
### Selection of Lanes
Using only the data from mix_use lanes, select for each lane to create comparison
The max numper of lanes is 6, but only few roads have all 6, so it can be excluded from the analysis
```
lanes = df_merged.loc[df_merged["Lane_use"] == "mix_use"]
lane_1 = lanes.loc[lanes["Lane"] == 1]
lane_2 = lanes.loc[lanes["Lane"] == 2]
lane_3 = lanes.loc[lanes["Lane"] == 3]
lane_4 = lanes.loc[lanes["Lane"] == 4]
lane_5 = lanes.loc[lanes["Lane"] == 5]
lane_6 = lanes.loc[lanes["Lane"] == 6]
print(lane_1.shape, lane_2.shape, lane_3.shape, lane_4.shape, lane_5.shape, lane_6.shape)
```
### Plotting the means
```
means = []
for lane in [lane_1,lane_2,lane_3,lane_4,lane_5]:
means.append(lane["Speed [km/h]"].mean())
means = [ round(elem, 2) for elem in means ]
fig, ax = plt.subplots()
rects = ax.bar([1,2,3,4,5],means, width= 0.5)
ax.set_ylabel("Speed [km/h]")
ax.set_xlabel("Lanes")
ax.set_title('Speeds per lane')
def autolabel(rects):
"""Attach a text label above each bar in *rects*, displaying its height."""
for rect in rects:
height = rect.get_height()
ax.annotate('{}'.format(height),
xy=(rect.get_x() + rect.get_width() / 2, height),
xytext=(0, 3), # 3 points vertical offset
textcoords="offset points",
ha='center', va='bottom')
autolabel(rects)
plt.show()
```
# How can we predicti a new car?
```
df_regression = df_base[["Numero Agrupado", "Faixa", "Registro", "Especie", "Classe", "Velocidade", "Comprimento"]]
df_regression.loc[:,"Comprimento"] = df_regression.loc[:,"Comprimento"] /10
df_regression.loc[:,"Velocidade"] = df_regression.loc[:,"Velocidade"] * 0.36
```
### Reading the columns refazerrrrrrrrrrrrrrrr
* **Radar** is the number of identification of a street section
* **Lane** goes from 1 to 6 in most radars, low lane number are closer to the center of the freeway, high lane numbers are "local" lanes, to the right
* **Register** represents each vehicle
* **Types** are: motorcycle = 0, car = 1, bus = 2 ou truck = 3
* **Classes** are: *light* (motorcycle and car) = 0 ou *heavy* (bus and truck) = 1
* **Speeds** are in kilometer per hour
* **Radar_Lane** comes to identify each lane on a single radar (will be usefull to merge dataframes)
```
df_regression.columns = ["Radar", "Lane", "Register", "Type", "Class", "Speed [km/h]", "Length"]
Validation = df_regression.loc[df_regression["Speed [km/h]"].isna()]
X = df_regression[["Lane", "Type", "Class", "Length"]].dropna()
X = pd.concat([pd.get_dummies(X[["Lane", "Type", "Class"]].astype("object")),X["Length"]], axis=1)
y = df_regression["Speed [km/h]"].dropna()
X.head()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
lr = LinearRegression(normalize=True)
lr.fit(X_train, y_train)
pred = lr.predict(X_test)
print(lr.score(X_train, y_train),lr.score(X_test, y_test))
corrMatrix = df_regression[["Lane", "Type", "Speed [km/h]","Length"]].corr()
display (corrMatrix)
sns.heatmap(corrMatrix, annot=True)
plt.show()
```
| true |
code
| 0.610773 | null | null | null | null |
|
Copyright 2020 Verily Life Sciences LLC
Use of this source code is governed by a BSD-style
license that can be found in the LICENSE file or at
https://developers.google.com/open-source/licenses/bsd
# Trial Specification Demo
The first step to use the Baseline Site Selection Tool is to specify your trial.
All data in the Baseline Site Selection Tool is stored in [xarray.DataArray](http://xarray.pydata.org/en/stable/generated/xarray.DataArray.html) datasets. This is a [convenient datastructure](http://xarray.pydata.org/en/stable/why-xarray.html) for storing multidimensional arrays with different labels, coordinates or attributes. You don't need to have any expertise with xr.Datasets to use the Baseline Site Selection Tool. The goal of this notebook is to walk you through the construction of the dataset that contains the specification of your trial.
This notebook has several sections:
1. **Define the Trial**. In this section you will load all aspects of your trial, including the trial sites, the expected recruitment demographics for each trial site (e.g. from a census) as well as the rules for how the trial will be carried out.
2. **Load Incidence Forecasts**. In this section you will load forecasts for covid incidence at the locations of your trial. We highly recommend using forecasts that are as local as possible for the sites of the trial. There is significant variation in covid incidence among counties in the same state, and taking the state (province) average can be highly misleading. Here we include code to preload forecasts for county level forecasts from the US Center for Disease Control. The trial planner should include whatever forecasts they find most compelling.
3. **Simulate the Trial** Given the incidence forecasts and the trial rules, the third section will simulate the trial.
4. **Optimize the Trial** Given the parameters of the trial within our control, the next section asks whether we can set those parameters to make the trial meet our objective criteria, for example most likely to succeed or to succeed as quickly as possible. We have written a set of optimization routines for optimizing different types of trials.
We write out different trial plans, which you can then examine interactively in the second notebook in the Baseline Site Selection Tool. That notebook lets you visualize how the trial is proceeding at a per site level and experiment with what will happen when you turn up or down different sites.
If you have questions about how to implement these steps for your clinical trial, or there are variations in the trial specification that are not captured with this framework, please contact [email protected] for additional help.
## Imports
```
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('ticks')
import functools
import importlib.resources
import numpy as np
import os
import pandas as pd
pd.plotting.register_matplotlib_converters()
import xarray as xr
from IPython.display import display
# bsst imports
from bsst import demo_data
from bsst import io as bsst_io
from bsst import util
from bsst import optimization
from bsst import sim
from bsst import sim_scenarios
from bsst import public_data
```
## Helper methods for visualization
```
def plot_participants(participants):
time = participants.time.values
util.sum_all_but_dims(['time'], participants).cumsum('time').plot()
plt.title('Participants recruited (both control and treatment arm)')
plt.xlim(time[0], time[-1])
plt.ylim(bottom=0)
plt.show()
def plot_events(events):
time = events.time.values
events.cumsum('time').plot.line(x='time', color='k', alpha=.02, add_legend=False)
for analysis, num_events in c.needed_control_arm_events.to_series().items():
plt.axhline(num_events, linestyle='--')
plt.text(time[0], num_events, analysis, ha='left', va='bottom')
plt.ylim(0, 120)
plt.xlim(time[0], time[-1])
plt.title(f'Control arm events\n{events.scenario.size} simulated scenarios')
plt.show()
def plot_success(c, events):
time = c.time.values
success_day = xr.DataArray(util.success_day(c.needed_control_arm_events, events),
coords=(events.scenario, c.analysis))
fig, axes = plt.subplots(c.analysis.size, 1, sharex=True)
step = max(1, int(np.timedelta64(3, 'D') / (time[1] - time[0])))
bins = mpl.units.registry[np.datetime64].convert(time[::step], None, None)
for analysis, ax in zip(c.analysis.values, axes):
success_days = success_day.sel(analysis=analysis).values
np.where(np.isnat(success_days), np.datetime64('2050-06-01'), success_days)
ax.hist(success_days, bins=bins, density=True)
ax.yaxis.set_visible(False)
# subtract time[0] to make into timedelta64s so that we can take a mean/median
median = np.median(success_days - time[0]) + time[0]
median = pd.to_datetime(median).date()
ax.axvline(median, color='r')
ax.text(time[0], 0, f'{analysis}\n{median} median', ha='left', va='bottom')
plt.xlabel('Date when sufficient statistical power is achieved')
plt.xlim(time[0], time[-1])
plt.xticks(rotation=35)
plt.show()
```
# 1. Define the trial
## Choose the sites
A trial specification consists a list of sites, together with various properties of the sites.
For this demo, we read demonstration data embedded in the Baseline Site Selection Tool Python package. Specifically, this information is loaded from the file `demo_data/site_list1.csv`. Each row of this file contains the name of a site, as well as the detailed information about the trial. In this illustrative example, we pick sites in real US counties. Each column contains the following information:
* `opencovid_key` . This is a key that specifies location within [COVID-19 Open Data](https://github.com/GoogleCloudPlatform/covid-19-open-data). It is required by this schema because it is the way we join the incidence forecasts to the site locations.
* `capacity`, the number of participants the site can recruit each week, including both control arm and treatment arms. For simplicity, we assume this is constant over time, but variable recruitment rates are also supported. (See the construction of the `site_capacity` array below).
* `start_date`. This is the first date on which the site can recruit participants.
* The proportion of the population in various demographic categories. For this example, we consider categories for age (`over_60`), ethnicity (`black`, `hisp_lat`), and comorbidities (`smokers`, `diabetes`, `obese`). **Here we just fill in demographic information with random numbers.** We assume different categories are independent, but the data structure supports complex beliefs about how different categories intersect, how much each site can enrich for different categories, and different infection risks for different categories. These are represented in the factors `population_fraction`, `participant_fraction`, `incidence_scaler`, and `incidence_to_event_factor` below. In a practical situation, we recommend that the trial planner uses accurate estimates of the populations for the different sites they are drawing from.
```
with importlib.resources.path(demo_data, 'site_list1.csv') as p:
demo_data_file_path = os.fspath(p)
site_df = pd.read_csv(demo_data_file_path, index_col=0)
site_df.index.name = 'location'
site_df['start_date'] = pd.to_datetime(site_df['start_date'])
display(site_df)
# Add in information we have about each county.
site_df = pd.concat([site_df, public_data.us_county_data().loc[site_df.opencovid_key].set_index(site_df.index)], axis=1)
```
## Choose trial parameters
The trial requires a number of parameters that have to be specified to be able to simulate what will happen in the trial: These include:
* `trial_size_cap`: the maximum number of participants in the trial (includes both control and treatment arms)
* `start_day` and `end_day`: the boundaries of the time period we will simulate.
* `proportion_control_arm`: what proportion of participants are in the control arm. It's assumed that the control arm is as uniformly distributed across locations and time (e.g. at each location on each day, half of the recruited participants are assigned to the control arm).
* `needed_control_arm_events`: the number of events required in the *control* arm of the trial at various intermediate analysis points. For this example we assume intermediate analyses which would demonstrate a vaccine efficacy of about 55%, 65%, 75%, 85%, or 95%.
* `observation_delay`: how long after a participant is recruited before they contribute an event. This is measured in the same time units as your incidence forecasts. Here we assume 28 days.
* `site_capacity` and `site_activation`: the number of participants each site could recruit *if* it were activated, and whether each site is activated at any given time. Here we assume each site as a constant weekly capacity, but time dependence can be included (e.g. to model ramp up of recruitment).
* `population_fraction`, `participant_fraction`, and `incidence_scaler`: the proportion of the general population and the proportion of participants who fall into different demographic categories at each location, and the infection risk factor for each category. These three are required to translate an overall incidence forecast for the population into the incidence forecast for your control arm.
* `incidence_to_event_factor`: what proportion of infections lead to a clinical event. We assume a constant 0.6, but you can specify different values for different demographic categories.
These factors are specified in the datastructure below.
```
start_day = np.datetime64('2021-05-15')
end_day = np.datetime64('2021-10-01')
time_resolution = np.timedelta64(1, 'D')
time = np.arange(start_day, end_day + time_resolution, time_resolution)
c = xr.Dataset(coords=dict(time=time))
c['proportion_control_arm'] = 0.5
# Assume some intermediate analyses.
frac_control = float(c.proportion_control_arm)
efficacy = np.array([.55, .65, .75, .85, .95])
ctrl_events = util.needed_control_arm_events(efficacy, frac_control)
vaccine_events = (1 - efficacy) * ctrl_events * (1 - frac_control) / frac_control
ctrl_events, vaccine_events = np.round(ctrl_events), np.round(vaccine_events)
efficacy = 1 - (vaccine_events / ctrl_events)
total_events = ctrl_events + vaccine_events
analysis_names = [
f'{int(t)} total events @{int(100 * e)}% VE' for t, e in zip(total_events, efficacy)
]
c['needed_control_arm_events'] = xr.DataArray(
ctrl_events, dims=('analysis',)).assign_coords(analysis=analysis_names)
c['recruitment_type'] = 'default'
c['observation_delay'] = int(np.timedelta64(28, 'D') / time_resolution) # 28 days
c['trial_size_cap'] = 30000
# convert weekly capacity to capacity per time step
site_capacity = site_df.capacity.to_xarray() * time_resolution / np.timedelta64(7, 'D')
site_capacity = site_capacity.broadcast_like(c.time).astype('float')
# Can't recruit before the activation date
activation_date = site_df.start_date.to_xarray()
for l in activation_date.location.values:
date = activation_date.loc[l]
site_capacity.loc[site_capacity.time < date, l] = 0.0
c['site_capacity'] = site_capacity.transpose('location', 'time')
c['site_activation'] = xr.ones_like(c.site_capacity)
# For the sake of simplicity, this code assumes black and hisp_lat are
# non-overlapping, and that obese/smokers/diabetes are non-overlapping.
frac_and_scalar = util.fraction_and_incidence_scaler
fraction_scalers = [
frac_and_scalar(site_df, 'age', ['over_60'], [1], 'under_60'),
frac_and_scalar(site_df, 'ethnicity', ['black', 'hisp_lat'], [1, 1],
'other'),
frac_and_scalar(site_df, 'comorbidity', ['smokers', 'diabetes', 'obese'],
[1, 1, 1], 'none')
]
fractions, incidence_scalers = zip(*fraction_scalers)
# We assume that different categories are independent (e.g. the proportion of
# smokers over 60 is the same as the proportion of smokers under 60)
c['population_fraction'] = functools.reduce(lambda x, y: x * y, fractions)
# We assume the participants are drawn uniformly from the population.
c['participant_fraction'] = c['population_fraction']
# Assume some boosted incidence risk for subpopulations. We pick random numbers
# here, but in actual use you'd put your best estimate for the incidence risk
# of each demographic category.
# Since we assume participants are uniformly drawn from the county population,
# this actually doesn't end up affecting the estimated number of clinical events.
c['incidence_scaler'] = functools.reduce(lambda x, y: x * y,
incidence_scalers)
c.incidence_scaler.loc[dict(age='over_60')] = 1 + 2 * np.random.random()
c.incidence_scaler.loc[dict(comorbidity=['smokers', 'diabetes', 'obese'])] = 1 + 2 * np.random.random()
c.incidence_scaler.loc[dict(ethnicity=['black', 'hisp_lat'])] = 1 + 2 * np.random.random()
# We assume a constant incidence_to_event_factor.
c['incidence_to_event_factor'] = 0.6 * xr.ones_like(c.incidence_scaler)
util.add_empty_history(c)
```
# 2. Load incidence forecasts
We load historical incidence data from [COVID-19 Open Data](https://github.com/GoogleCloudPlatform/covid-19-open-data) and forecasts from [COVID-19 Forecast Hub](https://github.com/reichlab/covid19-forecast-hub).
We note that there are a set of caveats when using the CDC models that should be considered when using these for trial planning:
* Forecasts are only available for US counties. Hence, these forecasts will only work for US-only trials. Trials with sites outside the US will need to supplement these forecasts.
* Forecasts only go out for four weeks. Trials take much longer than four weeks to complete, when measured from site selection to logging the required number of cases in the control arm. For simplicity, here we extrapolate incidence as *constant* after the last point of the forecast. Here we extrapolate out to October 1, 2021.
* The forecasts from the CDC are provided with quantile estimates. Our method depends on getting *representative forecasts* from the model: we need a set of sample forecasts for each site which represent the set of scenarios that can occur. Ideally these scenarios will be equally probable so that we can compute probabilities by averaging over samples. To get samples from quantiles, we interpolate/extrapolate to get 100 evenly spaced quantile estimates, which we treat as representative samples.
You can of course replace these forecasts with whatever represents your beliefs and uncertainty about what will happen.
```
# Extrapolate out a bit extra to ensure we're within bounds when we interpolate later.
full_pred = public_data.fetch_cdc_forecasts([('COVIDhub-ensemble', '2021-05-10'),
('COVIDhub-baseline', '2021-05-10')],
end_date=c.time.values[-1] + np.timedelta64(15, 'D'),
num_samples=50)
full_gt = public_data.fetch_opencovid_incidence()
# Suppose we only have ground truth through 2021-05-09.
full_gt = full_gt.sel(time=slice(None, np.datetime64('2021-05-09')))
# Include more historical incidence here for context. It will be trimmed off when
# we construct scenarios to simulate. The funny backwards range is to ensure that if
# we use weekly instead of daily resolution, we use the same day of the week as c.
time = np.arange(c.time.values[-1], np.datetime64('2021-04-01'), -time_resolution)[::-1]
incidence_model = public_data.assemble_forecast(full_gt, full_pred, site_df, time)
locs = np.random.choice(c.location.values, size=5, replace=False)
incidence_model.sel(location=locs).plot.line(x='time', color='k', alpha=.1, add_legend=False, col='location', row='model')
plt.ylim(0.0, 1e-3)
plt.suptitle('Forecast incidence at a sampling of sites', y=1.0)
pass
```
# 3. Simulate the trial
Now that we've specified how the trial works, we can compute how the trial will turn out given the incidence forecasts you've specified. We do this by first imagining what sampling what incidence will be at all locations simultaneously. For any given fully-specified scenario, we compute how many participants will be under observation at any given time in any given location (in any given combination of demographic buckets), then based on the specified local incidence we compute how many will become infected, and how many will produce clinical events.
Here we assume that the incidence trajectories of different locations are drawn at random from the available forecasts. Other scenario-generation methods in `sim_scenarios` support more complex approaches. For example, we may be highly uncertain about the incidence at each site, but believe that if incidence is high at a site, then it will also be high at geographically nearby sites. If this is the case then the simulation should not choose forecasts independently at each site but instead should take these correlations into account. The code scenario-generating methods in `sim_scenarios` allows us to do that.
```
# incidence_flattened: rolls together all the models you've included in your ensemble, treating them as independent samples.
incidence_flattened = sim_scenarios.get_incidence_flattened(incidence_model, c)
# incidence_scenarios: chooses scenarios given the incidence curves and your chosen method of scenario-generation.
incidence_scenarios = sim_scenarios.generate_scenarios_independently(incidence_flattened, num_scenarios=100)
# compute the number of participants recruited under your trial rule
participants = sim.recruitment(c)
# compute the number of control arm events under your trial rules and incidence_scenarios.
events = sim.control_arm_events(c, participants, incidence_scenarios)
plot_participants(participants)
# plot events and label different vaccine efficacies
plot_events(events)
# plot histograms of time to success
plot_success(c, events)
sim.add_stuff_to_ville(c, incidence_model, site_df, num_scenarios=100)
!mkdir -p demo_data
bsst_io.write_ville_to_netcdf(c, 'demo_data/site_list1_all_site_on.nc')
```
# 4. Optimize the trial
The simulations above supposed that all sites are activated as soon as possible (i.e. `site_activation` is identically 1). Now that we have shown the ability to simulate the outcome of the trial, we can turn it into a mathematical optimization problem.
**Given the parameters of the trial within our control, how can we set those parameters to make the trial most likely to succeed or to succeed as quickly as possible?**
We imagine the main levers of control are which sites to activate or which sites to prioritize activating, and this is what is implemented here.
However, the framework we have developed is very general and could be extended to just about anything you control which you can predict the impact of. For example,
* If you can estimate the impact of money spent boosting recruitment of high-risk participants, we could use those estimates to help figure out how to best allocate a fixed budget.
* If you had requirements for the number of people infected in different demographic groups, we could use those to help figure out how to best allocate doses between sites with different population characteristics.
The optimization algorithms are implemented in [JAX](https://github.com/google/jax), a python library that makes it possible to differentiate through native python and numpy functions. The flexibility of the language makes it possible to compose a variety of trial optimization scenarios and then to write algorithms that find optima. There are a number of technical details in how the optimization algorithms are written that will be discussed elsewhere.
### Example: Optimizing Static site activations
Suppose that the only variable we can control is which sites should be activated, and we have to make this decision at the beginning of the trial. This decision is then set in stone for the duration of the trial. To calculate this we proceed as follows:
The optimizer takes in the trial plan, encoded in the xarray `c` as well as the `incidence_scenarios`, and then calls the optimizer to find the sites that should be activated to minimize the time to success of the trial. The algorithm modifies `c` *in place*, so that after the algorithm runs, it returns the trial plan `c` but with the site activations chosen to be on or off in accordance with the optimizion.
```
%time optimization.optimize_static_activation(c, incidence_scenarios)
```
#### Plot the resulting sites
Now we can plot the activations for the resulting sites. Only a subset of the original sites are activated in the optimized plan. Comparing the distributions for the time to success for the optimized sites to those in the original trial plan (all sites activated), the optimized plan will save a bit of time if the vaccine efficacy is low. If the vaccine efficacy is high, then just getting as many participants as possible as quickly as possible is optimal.
```
all_sites = c.location.values
activated_sites = c.location.values[c.site_activation.mean('time') == 1]
# Simulate the results with this activation scheme.
print(f'\n\n{len(activated_sites)} of {len(all_sites)} activated')
participants = sim.recruitment(c)
events = sim.control_arm_events(c, participants, incidence_scenarios)
plot_participants(participants)
plot_events(events)
plot_success(c, events)
df = (participants.sum(['location', 'time', 'comorbidity']) / participants.sum()).to_pandas()
display(df.style.set_caption('Proportion of participants by age and ethnicity'))
sim.add_stuff_to_ville(c, incidence_model, site_df, num_scenarios=100)
!mkdir -p demo_data
bsst_io.write_ville_to_netcdf(c, 'demo_data/site_list1_optimized_static.nc')
```
### Example: Custom loss penalizing site activation and promoting diverse participants
Suppose we want to factor in considerations aside from how quickly the trial succeeds. In this example, we assume that activating sites is expensive, so we'd like to activate as few of them as possible, so long as it doesn't delay the success of the trial too much. Similarly, we assume that it's valuable to have a larger proportion of elderly, black, or hispanic participants, and we're willing to activate sites which can recruit from these demographic groups, even if doing so delays success a bit.
```
def loss_fn(c):
# sum over location, time, comorbidity
# remaining dimensions are [age, ethnicity]
participants = c.participants.sum(axis=0).sum(axis=0).sum(axis=-1)
total_participants = participants.sum()
return (
optimization.negative_mean_successiness(c) # demonstrate efficacy fast
+ 0.2 * c.site_activation.mean() # turning on sites is costly
- 0.5 * participants[1:, :].sum() / total_participants # we want people over 60
- 0.5 * participants[:, 1:].sum() / total_participants # we want blacks and hispanics
)
%time optimization.optimize_static_activation(c, incidence_scenarios, loss_fn)
```
#### Plot the resulting sites
This time only 53 of 146 sites are activated. The slower recruitment costs us 1-2 weeks until the trial succeeds (depending on vaccine efficacy). In exchange, we don't need to activate as many sites, and we end up with a greater proportion of participants who are elderly, black, or hispanic (dropping from 55.7% to 45.6% young white).
```
all_sites = c.location.values
activated_sites = c.location.values[c.site_activation.mean('time') == 1]
# Simulate the results with this activation scheme.
print(f'\n\n{len(activated_sites)} of {len(all_sites)} activated')
participants = sim.recruitment(c)
events = sim.control_arm_events(c, participants, incidence_scenarios)
plot_participants(participants)
plot_events(events)
plot_success(c, events)
df = (participants.sum(['location', 'time', 'comorbidity']) / participants.sum()).to_pandas()
display(df.style.set_caption('Proportion of participants by age and ethnicity'))
```
### Example: prioritizing sites
Suppose we can activate up to 20 sites each week for 10 weeks. How do we prioritize them?
```
# We put all sites in on group. We also support prioritizing sites within groupings.
# For example, if you can activate 2 sites per state per week, sites would be grouped
# according to the state they're in.
site_to_group = pd.Series(['all_sites'] * len(site_df), index=site_df.index)
decision_dates = c.time.values[:70:7]
allowed_activations = pd.DataFrame([[20] * len(decision_dates)], index=['all_sites'], columns=decision_dates)
parameterizer = optimization.PivotTableActivation(c, site_to_group, allowed_activations, can_deactivate=False)
optimization.optimize_params(c, incidence_scenarios, parameterizer)
c['site_activation'] = c.site_activation.round() # each site has to be on or off at each time
df = c.site_activation.to_pandas()
df.columns = [pd.to_datetime(x).date() for x in df.columns]
sns.heatmap(df, cbar=False)
plt.title('Which sites are activated when')
plt.show()
participants = sim.recruitment(c)
events = sim.control_arm_events(c, participants, incidence_scenarios)
plot_participants(participants)
plot_events(events)
plot_success(c, events)
sim.add_stuff_to_ville(c, incidence_model, site_df, num_scenarios=100)
!mkdir -p demo_data
bsst_io.write_ville_to_netcdf(c, 'demo_data/site_list1_prioritized.nc')
```
| true |
code
| 0.592313 | null | null | null | null |
|
# Poisson Regression, Gradient Descent
In this notebook, we will show how to use gradient descent to solve a [Poisson regression model](https://en.wikipedia.org/wiki/Poisson_regression). A Poisson regression model takes on the following form.
$\operatorname{E}(Y\mid\mathbf{x})=e^{\boldsymbol{\theta}' \mathbf{x}}$
where
* $x$ is a vector of input values
* $\theta$ is a vector weights (the coefficients)
* $y$ is the expected value of the parameter for a [Poisson distribution](https://en.wikipedia.org/wiki/Poisson_distribution), typically, denoted as $\lambda$
Note that [Scikit-Learn](http://scikit-learn.org/stable/modules/classes.html#module-sklearn.linear_model) does not provide a solver a Poisson regression model, but [statsmodels](http://www.statsmodels.org/dev/generated/statsmodels.discrete.discrete_model.Poisson.html) does, though examples for the latter is [thin](https://datascience.stackexchange.com/questions/23143/poisson-regression-options-in-python).
## Simulate data
Now, let's simulate the data. Note that the coefficients are $[1, 0.5, 0.2]$ and that there is error $\epsilon \sim \mathcal{N}(0, 1)$ added to the simulated data.
$y=e^{1 + 0.5x_1 + 0.2x_2 + \epsilon}$
In this notebook, the score is denoted as $z$ and $z = 1 + 0.5x_1 + 0.2x_2 + \epsilon$. Additionally, $y$ is the mean for a Poisson distribution. The variables $X_1$ and $X_2$ are independently sampled from their own normal distribution $\mathcal{N}(0, 1)$.
After we simulate the data, we will plot the distribution of the scores and means. Note that the expected value of the output $y$ is 5.2.
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from numpy.random import normal
from scipy.stats import poisson
np.random.seed(37)
sns.set(color_codes=True)
n = 10000
X = np.hstack([
np.array([1 for _ in range(n)]).reshape(n, 1),
normal(0.0, 1.0, n).reshape(n, 1),
normal(0.0, 1.0, n).reshape(n, 1)
])
z = np.dot(X, np.array([1.0, 0.5, 0.2])) + normal(0.0, 1.0, n)
y = np.exp(z)
```
## Visualize data
```
fig, ax = plt.subplots(1, 2, figsize=(20, 5))
sns.kdeplot(z, ax=ax[0])
ax[0].set_title(r'Distribution of Scores')
ax[0].set_xlabel('score')
ax[0].set_ylabel('probability')
sns.kdeplot(y, ax=ax[1])
ax[1].set_title(r'Distribution of Means')
ax[1].set_xlabel('mean')
ax[1].set_ylabel('probability')
```
## Solve for the Poisson regression model weights
Now we learn the weights of the Poisson regression model using gradient descent. Notice that the loss function of a Poisson regression model is identical to an Ordinary Least Square (OLS) regression model?
$L(\theta) = \frac{1}{n} (\hat{y} - y)^2$
We do not have to worry about writing out the gradient of the loss function since we are using [Autograd](https://github.com/HIPS/autograd).
```
import autograd.numpy as np
from autograd import grad
from autograd.numpy import exp, log, sqrt
# define the loss function
def loss(w, X, y):
y_pred = np.exp(np.dot(X, w))
loss = ((y_pred - y) ** 2.0)
return loss.mean(axis=None)
#the magic line that gives you the gradient of the loss function
loss_grad = grad(loss)
def learn_weights(X, y, alpha=0.05, max_iter=30000, debug=False):
w = np.array([0.0 for _ in range(X.shape[1])])
if debug is True:
print('initial weights = {}'.format(w))
loss_trace = []
weight_trace = []
for i in range(max_iter):
loss = loss_grad(w, X, y)
w = w - (loss * alpha)
if i % 2000 == 0 and debug is True:
print('{}: loss = {}, weights = {}'.format(i, loss, w))
loss_trace.append(loss)
weight_trace.append(w)
if debug is True:
print('intercept + weights: {}'.format(w))
loss_trace = np.array(loss_trace)
weight_trace = np.array(weight_trace)
return w, loss_trace, weight_trace
def plot_traces(w, loss_trace, weight_trace, alpha):
fig, ax = plt.subplots(1, 2, figsize=(20, 5))
ax[0].set_title(r'Log-loss of the weights over iterations, $\alpha=${}'.format(alpha))
ax[0].set_xlabel('iteration')
ax[0].set_ylabel('log-loss')
ax[0].plot(loss_trace[:, 0], label=r'$\beta$')
ax[0].plot(loss_trace[:, 1], label=r'$x_0$')
ax[0].plot(loss_trace[:, 2], label=r'$x_1$')
ax[0].legend()
ax[1].set_title(r'Weight learning over iterations, $\alpha=${}'.format(alpha))
ax[1].set_xlabel('iteration')
ax[1].set_ylabel('weight')
ax[1].plot(weight_trace[:, 0], label=r'$\beta={:.2f}$'.format(w[0]))
ax[1].plot(weight_trace[:, 1], label=r'$x_0={:.2f}$'.format(w[1]))
ax[1].plot(weight_trace[:, 2], label=r'$x_1={:.2f}$'.format(w[2]))
ax[1].legend()
```
We try learning the coefficients with different learning weights $\alpha$. Note the behavior of the traces of the loss and weights for different $\alpha$? The loss function was the same one used for OLS regression, but the loss function for Poisson regression is defined differently. Nevertheless, we still get acceptable results.
### Use gradient descent with $\alpha=0.001$
```
alpha = 0.001
w, loss_trace, weight_trace = learn_weights(X, y, alpha=alpha, max_iter=1000)
plot_traces(w, loss_trace, weight_trace, alpha=alpha)
print(w)
```
### Use gradient descent with $\alpha=0.005$
```
alpha = 0.005
w, loss_trace, weight_trace = learn_weights(X, y, alpha=alpha, max_iter=200)
plot_traces(w, loss_trace, weight_trace, alpha=alpha)
print(w)
```
### Use gradient descent with $\alpha=0.01$
```
alpha = 0.01
w, loss_trace, weight_trace = learn_weights(X, y, alpha=alpha, max_iter=200)
plot_traces(w, loss_trace, weight_trace, alpha=alpha)
print(w)
```
| true |
code
| 0.650356 | null | null | null | null |
|
## KF Basics - Part I
### Introduction
#### What is the need to describe belief in terms of PDF's?
This is because robot environments are stochastic. A robot environment may have cows with Tesla by side. That is a robot and it's environment cannot be deterministically modelled(e.g as a function of something like time t). In the real world sensors are also error prone, and hence there'll be a set of values with a mean and variance that it can take. Hence, we always have to model around some mean and variances associated.
#### What is Expectation of a Random Variables?
Expectation is nothing but an average of the probabilites
$$\mathbb E[X] = \sum_{i=1}^n p_ix_i$$
In the continous form,
$$\mathbb E[X] = \int_{-\infty}^\infty x\, f(x) \,dx$$
```
import numpy as np
import random
x=[3,1,2]
p=[0.1,0.3,0.4]
E_x=np.sum(np.multiply(x,p))
print(E_x)
```
#### What is the advantage of representing the belief as a unimodal as opposed to multimodal?
Obviously, it makes sense because we can't multiple probabilities to a car moving for two locations. This would be too confusing and the information will not be useful.
### Variance, Covariance and Correlation
#### Variance
Variance is the spread of the data. The mean does'nt tell much **about** the data. Therefore the variance tells us about the **story** about the data meaning the spread of the data.
$$\mathit{VAR}(X) = \frac{1}{n}\sum_{i=1}^n (x_i - \mu)^2$$
```
x=np.random.randn(10)
np.var(x)
```
#### Covariance
This is for a multivariate distribution. For example, a robot in 2-D space can take values in both x and y. To describe them, a normal distribution with mean in both x and y is needed.
For a multivariate distribution, mean $\mu$ can be represented as a matrix,
$$
\mu = \begin{bmatrix}\mu_1\\\mu_2\\ \vdots \\\mu_n\end{bmatrix}
$$
Similarly, variance can also be represented.
But an important concept is that in the same way as every variable or dimension has a variation in its values, it is also possible that there will be values on how they **together vary**. This is also a measure of how two datasets are related to each other or **correlation**.
For example, as height increases weight also generally increases. These variables are correlated. They are positively correlated because as one variable gets larger so does the other.
We use a **covariance matrix** to denote covariances of a multivariate normal distribution:
$$
\Sigma = \begin{bmatrix}
\sigma_1^2 & \sigma_{12} & \cdots & \sigma_{1n} \\
\sigma_{21} &\sigma_2^2 & \cdots & \sigma_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
\sigma_{n1} & \sigma_{n2} & \cdots & \sigma_n^2
\end{bmatrix}
$$
**Diagonal** - Variance of each variable associated.
**Off-Diagonal** - covariance between ith and jth variables.
$$\begin{aligned}VAR(X) = \sigma_x^2 &= \frac{1}{n}\sum_{i=1}^n(X - \mu)^2\\
COV(X, Y) = \sigma_{xy} &= \frac{1}{n}\sum_{i=1}^n[(X-\mu_x)(Y-\mu_y)\big]\end{aligned}$$
```
x=np.random.random((3,3))
np.cov(x)
```
Covariance taking the data as **sample** with $\frac{1}{N-1}$
```
x_cor=np.random.rand(1,10)
y_cor=np.random.rand(1,10)
np.cov(x_cor,y_cor)
```
Covariance taking the data as **population** with $\frac{1}{N}$
```
np.cov(x_cor,y_cor,bias=1)
```
### Gaussians
#### Central Limit Theorem
According to this theorem, the average of n samples of random and independent variables tends to follow a normal distribution as we increase the sample size.(Generally, for n>=30)
```
import matplotlib.pyplot as plt
import random
a=np.zeros((100,))
for i in range(100):
x=[random.uniform(1,10) for _ in range(1000)]
a[i]=np.sum(x,axis=0)/1000
plt.hist(a)
```
#### Gaussian Distribution
A Gaussian is a *continuous probability distribution* that is completely described with two parameters, the mean ($\mu$) and the variance ($\sigma^2$). It is defined as:
$$
f(x, \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}} \exp\big [{-\frac{(x-\mu)^2}{2\sigma^2} }\big ]
$$
Range is $$[-\inf,\inf] $$
This is just a function of mean($\mu$) and standard deviation ($\sigma$) and what gives the normal distribution the charecteristic **bell curve**.
```
import matplotlib.mlab as mlab
import math
import scipy.stats
mu = 0
variance = 5
sigma = math.sqrt(variance)
x = np.linspace(mu - 5*sigma, mu + 5*sigma, 100)
plt.plot(x,scipy.stats.norm.pdf(x, mu, sigma))
plt.show()
```
#### Why do we need Gaussian distributions?
Since it becomes really difficult in the real world to deal with multimodal distribution as we cannot put the belief in two seperate location of the robots. This becomes really confusing and in practice impossible to comprehend.
Gaussian probability distribution allows us to drive the robots using only one mode with peak at the mean with some variance.
### Gaussian Properties
**Multiplication**
For the measurement update in a Bayes Filter, the algorithm tells us to multiply the Prior P(X_t) and measurement P(Z_t|X_t) to calculate the posterior:
$$P(X \mid Z) = \frac{P(Z \mid X)P(X)}{P(Z)}$$
Here for the numerator, $P(Z \mid X),P(X)$ both are gaussian.
$N(\mu_1, \sigma_1^2)$ and $N(\mu_2, \sigma_2^2)$ are their mean and variances.
New mean is
$$\mu_\mathtt{new} = \frac{\mu_1 \sigma_2^2 + \mu_2 \sigma_1^2}{\sigma_1^2+\sigma_2^2}$$
New variance is
$$\sigma_\mathtt{new} = \frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2}$$
```
import matplotlib.mlab as mlab
import math
mu1 = 0
variance1 = 2
sigma = math.sqrt(variance1)
x1 = np.linspace(mu1 - 3*sigma, mu1 + 3*sigma, 100)
plt.plot(x1,scipy.stats.norm.pdf(x1, mu1, sigma),label='prior')
mu2 = 10
variance2 = 2
sigma = math.sqrt(variance2)
x2 = np.linspace(mu2 - 3*sigma, mu2 + 3*sigma, 100)
plt.plot(x2,scipy.stats.norm.pdf(x2, mu2, sigma),"g-",label='measurement')
mu_new=(mu1*variance2+mu2*variance1)/(variance1+variance2)
print("New mean is at: ",mu_new)
var_new=(variance1*variance2)/(variance1+variance2)
print("New variance is: ",var_new)
sigma = math.sqrt(var_new)
x3 = np.linspace(mu_new - 3*sigma, mu_new + 3*sigma, 100)
plt.plot(x3,scipy.stats.norm.pdf(x3, mu_new, var_new),label="posterior")
plt.legend(loc='upper left')
plt.xlim(-10,20)
plt.show()
```
**Addition**
The motion step involves a case of adding up probability (Since it has to abide the Law of Total Probability). This means their beliefs are to be added and hence two gaussians. They are simply arithmetic additions of the two.
$$\begin{gathered}\mu_x = \mu_p + \mu_z \\
\sigma_x^2 = \sigma_z^2+\sigma_p^2\, \square\end{gathered}$$
```
import matplotlib.mlab as mlab
import math
mu1 = 5
variance1 = 1
sigma = math.sqrt(variance1)
x1 = np.linspace(mu1 - 3*sigma, mu1 + 3*sigma, 100)
plt.plot(x1,scipy.stats.norm.pdf(x1, mu1, sigma),label='prior')
mu2 = 10
variance2 = 1
sigma = math.sqrt(variance2)
x2 = np.linspace(mu2 - 3*sigma, mu2 + 3*sigma, 100)
plt.plot(x2,scipy.stats.norm.pdf(x2, mu2, sigma),"g-",label='measurement')
mu_new=mu1+mu2
print("New mean is at: ",mu_new)
var_new=(variance1+variance2)
print("New variance is: ",var_new)
sigma = math.sqrt(var_new)
x3 = np.linspace(mu_new - 3*sigma, mu_new + 3*sigma, 100)
plt.plot(x3,scipy.stats.norm.pdf(x3, mu_new, var_new),label="posterior")
plt.legend(loc='upper left')
plt.xlim(-10,20)
plt.show()
#Example from:
#https://scipython.com/blog/visualizing-the-bivariate-gaussian-distribution/
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
# Our 2-dimensional distribution will be over variables X and Y
N = 60
X = np.linspace(-3, 3, N)
Y = np.linspace(-3, 4, N)
X, Y = np.meshgrid(X, Y)
# Mean vector and covariance matrix
mu = np.array([0., 1.])
Sigma = np.array([[ 1. , -0.5], [-0.5, 1.5]])
# Pack X and Y into a single 3-dimensional array
pos = np.empty(X.shape + (2,))
pos[:, :, 0] = X
pos[:, :, 1] = Y
def multivariate_gaussian(pos, mu, Sigma):
"""Return the multivariate Gaussian distribution on array pos.
pos is an array constructed by packing the meshed arrays of variables
x_1, x_2, x_3, ..., x_k into its _last_ dimension.
"""
n = mu.shape[0]
Sigma_det = np.linalg.det(Sigma)
Sigma_inv = np.linalg.inv(Sigma)
N = np.sqrt((2*np.pi)**n * Sigma_det)
# This einsum call calculates (x-mu)T.Sigma-1.(x-mu) in a vectorized
# way across all the input variables.
fac = np.einsum('...k,kl,...l->...', pos-mu, Sigma_inv, pos-mu)
return np.exp(-fac / 2) / N
# The distribution on the variables X, Y packed into pos.
Z = multivariate_gaussian(pos, mu, Sigma)
# Create a surface plot and projected filled contour plot under it.
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, Z, rstride=3, cstride=3, linewidth=1, antialiased=True,
cmap=cm.viridis)
cset = ax.contourf(X, Y, Z, zdir='z', offset=-0.15, cmap=cm.viridis)
# Adjust the limits, ticks and view angle
ax.set_zlim(-0.15,0.2)
ax.set_zticks(np.linspace(0,0.2,5))
ax.view_init(27, -21)
plt.show()
```
This is a 3D projection of the gaussians involved with the lower surface showing the 2D projection of the 3D projection above. The innermost ellipse represents the highest peak, that is the maximum probability for a given (X,Y) value.
** numpy einsum examples **
```
a = np.arange(25).reshape(5,5)
b = np.arange(5)
c = np.arange(6).reshape(2,3)
print(a)
print(b)
print(c)
#this is the diagonal sum, i repeated means the diagonal
np.einsum('ij', a)
#this takes the output ii which is the diagonal and outputs to a
np.einsum('ii->i',a)
#this takes in the array A represented by their axes 'ij' and B by its only axes'j'
#and multiples them element wise
np.einsum('ij,j',a, b)
A = np.arange(3).reshape(3,1)
B = np.array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
C=np.multiply(A,B)
np.sum(C,axis=1)
D = np.array([0,1,2])
E = np.array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
np.einsum('i,ij->i',D,E)
from scipy.stats import multivariate_normal
x, y = np.mgrid[-5:5:.1, -5:5:.1]
pos = np.empty(x.shape + (2,))
pos[:, :, 0] = x; pos[:, :, 1] = y
rv = multivariate_normal([0.5, -0.2], [[2.0, 0.9], [0.9, 0.5]])
plt.contourf(x, y, rv.pdf(pos))
```
### References:
1. Roger Labbe's [repo](https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python) on Kalman Filters. (Majority of the examples in the notes are from this)
2. Probabilistic Robotics by Sebastian Thrun, Wolfram Burgard and Dieter Fox, MIT Press.
3. Scipy [Documentation](https://scipython.com/blog/visualizing-the-bivariate-gaussian-distribution/)
| true |
code
| 0.665872 | null | null | null | null |
|
```
from warnings import filterwarnings
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
from sklearn.linear_model import LinearRegression
%load_ext lab_black
%load_ext watermark
filterwarnings("ignore")
```
# A Simple Regression
From [Codes for Unit 1](https://www2.isye.gatech.edu/isye6420/supporting.html).
Associated lecture video: Unit 1 Lesson 4
You don't usually need to set inits in PyMC. The default method of generating inits is 'jitter+adapt_diag', which chooses them based on the model and input data while adding some randomness.
If you do want to set an initial value, pass a dictionary to the start parameter of pm.sample.
```python
inits = {
"alpha": np.array(0.0),
"beta": np.array(0.0)
}
trace = pm.sample(2000, start=inits)
```
```
X = np.array([1, 2, 3, 4, 5])
y = np.array([1, 3, 3, 3, 5])
x_bar = np.mean(X)
with pm.Model() as m:
# priors
alpha = pm.Normal("alpha", sigma=100)
beta = pm.Normal("beta", sigma=100)
# using precision for direct comparison with BUGS output
tau = pm.Gamma("tau", alpha=0.001, beta=0.001)
sigma = 1 / pm.math.sqrt(tau)
mu = alpha + beta * (X - x_bar)
likelihood = pm.Normal("likelihood", mu=mu, sigma=sigma, observed=y)
# start sampling
trace = pm.sample(
3000, # samples
chains=4,
tune=500,
init="jitter+adapt_diag",
random_seed=1,
cores=4, # parallel processing of chains
return_inferencedata=True, # return arviz inferencedata object
)
```
PyMC3 uses the tuning step specified in the pm.sample call to adjust various parameters in the No-U-Turn Sampler [(NUTS) algorithm](https://arxiv.org/abs/1111.4246), which is a form of Hamiltonian Monte Carlo. BUGS also silently uses different types of tuning depending on the algorithm it [chooses](https://www.york.ac.uk/depts/maths/histstat/pml1/bayes/winbugsinfo/cowles_winbugs.pdf). The professor often burns some number of samples in his examples. Note that this is separate from the tuning phase for both programs!
For some more detail on tuning, see [this post](https://colcarroll.github.io/hmc_tuning_talk/).
```
# this burns the first 500 samples
trace_burned = trace.sel(draw=slice(500, None))
```
Arviz has a variety of functions to view the results of the model. One of the most useful is az.summary. Professor Vidakovic arbitrarily asks for the 95% credible set (also called the highest density interval), so we can specify hdi_prob=.95 to get that. This is the HPD, or minimum-width, credible set.
```
az.summary(trace_burned, hdi_prob=0.95)
```
You can also get the HDIs directly:
```
az.hdi(trace_burned, hdi_prob=0.95)["beta"].values
```
There are a variety of plots available. Commonly used to diagnose problems are the trace (see [When Traceplots go Bad](https://jpreszler.rbind.io/post/2019-09-28-bad-traceplots/)) and rank plots (see the Maybe it's time to let traceplots die section from [this post](https://statmodeling.stat.columbia.edu/2019/03/19/maybe-its-time-to-let-the-old-ways-die-or-we-broke-r-hat-so-now-we-have-to-fix-it/)).
```
az.plot_trace(trace_burned)
plt.show()
az.plot_rank(trace_burned)
plt.show()
```
There are many ways to manipulate Arviz [InferenceData](https://arviz-devs.github.io/arviz/api/generated/arviz.InferenceData.html) objects to calculate statistics after sampling is complete.
```
# alpha - beta * x.bar
intercept = (
trace_burned.posterior.alpha.mean() - trace_burned.posterior.beta.mean() * x_bar
)
intercept.values
```
OpenBugs results:
| | mean | sd | MC_error | val2.5pc | median | val97.5pc | start | sample |
|-------|--------|--------|----------|----------|--------|-----------|-------|--------|
| alpha | 2.995 | 0.5388 | 0.005863 | 1.947 | 3.008 | 4.015 | 1000 | 9001 |
| beta | 0.7963 | 0.3669 | 0.003795 | 0.08055 | 0.7936 | 1.526 | 1000 | 9001 |
| tau | 1.88 | 1.524 | 0.02414 | 0.1416 | 1.484 | 5.79 | 1000 | 9001 |
Sometimes you might want to do a sanity check with classical regression. If your Bayesian regression has noninformative priors, the results should be close.
```
reg = LinearRegression().fit(X.reshape(-1, 1), y)
# compare with intercept and beta from above
reg.intercept_, reg.coef_
%watermark --iversions -v
```
| true |
code
| 0.761957 | null | null | null | null |
|
# CSX46
## Class session 6: BFS
Objective: write and test a function that can compute single-vertex shortest paths in an unweighted simple graph. Compare to the results that we get using `igraph.Graph.get_shortest_paths()`.
We're going to need several packages for this notebook; let's import them first
```
import random
import igraph
import numpy as np
import math
import collections
```
Let's set the random number seed using `random.seed` and with seed value 1337, so that we are all starting with the same graph structure. Make a simple 10-vertex random (Barabasi-Albert model) graph. Set the random number seed so that the graph is always the same, for purposes of reproducibility (we want to know that the "hub" vertex will be vertex 2, and we will test your BFS function starting at that "hub" vertex).
Let's plot the graph, using `bbox=[0,0,200,200]` so it is not huge, and using `vertex_label=` to display the vertex IDs.
Let's look at an adjacency list representation of the graph, using the method `igraph.Graph.get_adjlist`
Let's look at the degrees of the vertices using the `igraph.Graph.degree` method and the `enumerate` built-in function and list comprehension:
OK, let's implement a function to compute shortest-path (geodesic path) distances to all vertices in the graph, starting at a single vertex `p_vertex`. We'll implement the
breadth-first search (BFS) algorithm in order to compute these geodesic path distances.
We'll start by implementing the queue data structure "by hand" with our own `read_ptr` and `write_ptr` exactly as described on page 320 of Newman's book. Newman says to use an "array" to implement the queue. As it turns out, Python's native `list` data type is internally implemented as a (resizeable) array, so we can just use a `list` here. We'll call our function `bfs_single_vertex_newman`.
```
# compute N, the number of vertices by calling len() on the VertexSet obtained from graph.vs()
# initialize "queue" array (length N, containing np.nan)
# initialize distances array (length N, containing np.nan)
# set "p_vertex" entry of distances array to be 0
# while write_ptr is gerater than read_ptr:
# obtain the vertex ID of the entry at index "read_ptr" in the queue array, as cur_vertex_num
# increment read_ptr
# get the distance to cur_vertex_num, from the "distances" array
# get the neighbors of vertex cur_vertex_num in the graph, using the igraph "neighbors" func
# for each vertex_neighbor in the array vertex_neighbors
# if the distances[vertex_neighbor] is nan:
# (1) set the distance to vertex_neighbor (in "distances" vector) to the distance to
# cur_vertex_num, plus one
# (2) add neighbor to the queue
# put vertex_neighbor at position write_ptr in the queue array
# increment write_ptr
# end-while
# return "distances"
```
Let's test out our implementation of `bfs_single_vertex_newman`, on vertex 0 of the graph. Do the results make sense?
Now let's re-implement the single-vertex BFS distance function using a convenient queue data structure, `collections.deque` (note, `deque` is actually a *double-ended* queue, so it is a bit more fancy than we need, but that's OK, we just will only be using its methods `popleft` and `append`)
```
# compute N, the number of vertices by calling len() on the VertexSet obtained from graph.vs()
# create a deque data structure called "queue" and initialize it to contain p_vertex
# while the queue is not empty:
# pop vertex_id off of the left of the queue
# get the vertex_id entry of the distances vector, call it "vertex_dist"
# for each neighbor_id of vertex_id:
# if the neighbor_id entry of the distances vector is nan:
# set the neighbor_id entry of the distances vector to vertex_dist + 1
# append neighbor_id to the queue
# return "distances"
```
Compare the code implementations of `bfs_single_vertex_newman` and `bfs_single_vertex`. Which is easier to read and understand?
Test out your function `bfs_single_vertex` on vertex 0. Do we get the same result as when we used `bfs_single_vertex_newman`?
If the graph was a lot bigger, how could we systematically check that the results of `bfs_single_vertex` (from vertex 0) are correctly calculated? We can use the `igraph.Graph.get_shortest_paths` method, and specify `v=0`. Let's look at the results of calling `get_shortest_paths` with `v=0`:
So, clearly, we need to calculate the length of the list of vertices in each entry of this ragged list. But the *path* length is one less than the length of the list of vertices, so we have to subtract one in order to get the correct path length. Now we are ready to compare our BFS-based single-vertex geodesic distances with the results from calling `igraph.Graph.get_shortest_paths`:
Now let's implement a function that can compute a numpy.matrix of geodesic path distances for all pairs of vertices. The pythonic way to do this is probably to use the list-of-lists constructor for np.array, and to use list comprehension.
```
def sp_matrix(p_graph):
return FILL IN HERE
```
How about if we want to implement it using a plain old for loop?
```
def sp_matrix_forloop(p_graph):
N = FILL IN HERE
geo_dists = FILL IN HERE
FILL IN HERE
return geo_dists
```
Let's run it on our little ten-vertex graph:
| true |
code
| 0.520374 | null | null | null | null |
|
# 2.3 Least Squares and Nearest Neighbors
### 2.3.3 From Least Squares to Nearest Neighbors
1. Generates 10 means $m_k$ from a bivariate Gaussian distrubition for each color:
- $N((1, 0)^T, \textbf{I})$ for <span style="color: blue">BLUE</span>
- $N((0, 1)^T, \textbf{I})$ for <span style="color: orange">ORANGE</span>
2. For each color generates 100 observations as following:
- For each observation it picks $m_k$ at random with probability 1/10.
- Then generates a $N(m_k,\textbf{I}/5)$
```
%matplotlib inline
import random
import numpy as np
import matplotlib.pyplot as plt
sample_size = 100
def generate_data(size, mean):
identity = np.identity(2)
m = np.random.multivariate_normal(mean, identity, 10)
return np.array([
np.random.multivariate_normal(random.choice(m), identity / 5)
for _ in range(size)
])
def plot_data(orange_data, blue_data):
axes.plot(orange_data[:, 0], orange_data[:, 1], 'o', color='orange')
axes.plot(blue_data[:, 0], blue_data[:, 1], 'o', color='blue')
blue_data = generate_data(sample_size, [1, 0])
orange_data = generate_data(sample_size, [0, 1])
data_x = np.r_[blue_data, orange_data]
data_y = np.r_[np.zeros(sample_size), np.ones(sample_size)]
# plotting
fig = plt.figure(figsize = (8, 8))
axes = fig.add_subplot(1, 1, 1)
plot_data(orange_data, blue_data)
plt.show()
```
### 2.3.1 Linear Models and Least Squares
$$\hat{Y} = \hat{\beta_0} + \sum_{j=1}^{p} X_j\hat{\beta_j}$$
where $\hat{\beta_0}$ is the intercept, also know as the *bias*. It is convenient to include the constant variable 1 in X and $\hat{\beta_0}$ in the vector of coefficients $\hat{\beta}$, and then write as:
$$\hat{Y} = X^T\hat{\beta} $$
#### Residual sum of squares
How to fit the linear model to a set of training data? Pick the coefficients $\beta$ to minimize the *residual sum of squares*:
$$RSS(\beta) = \sum_{i=1}^{N} (y_i - x_i^T\beta) ^ 2 = (\textbf{y} - \textbf{X}\beta)^T (\textbf{y} - \textbf{X}\beta)$$
where $\textbf{X}$ is an $N \times p$ matrix with each row an input vector, and $\textbf{y}$ is an N-vector of the outputs in the training set. Differentiating w.r.t. β we get the normal equations:
$$\mathbf{X}^T(\mathbf{y} - \mathbf{X}\beta) = 0$$
If $\mathbf{X}^T\mathbf{X}$ is nonsingular, then the unique solution is given by:
$$\hat{\beta} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}$$
```
class LinearRegression:
def fit(self, X, y):
X = np.c_[np.ones((X.shape[0], 1)), X]
self.beta = np.linalg.inv(X.T @ X) @ X.T @ y
return self
def predict(self, x):
return np.dot(self.beta, np.r_[1, x])
model = LinearRegression().fit(data_x, data_y)
print("beta = ", model.beta)
```
#### Example of the linear model in a classification context
The fitted values $\hat{Y}$ are converted to a fitted class variable $\hat{G}$ according to the rule:
$$
\begin{equation}
\hat{G} = \begin{cases}
\text{ORANGE} & \text{ if } \hat{Y} \gt 0.5 \\
\text{BLUE } & \text{ if } \hat{Y} \leq 0.5
\end{cases}
\end{equation}
$$
```
from itertools import filterfalse, product
def plot_grid(orange_grid, blue_grid):
axes.plot(orange_grid[:, 0], orange_grid[:, 1], '.', zorder = 0.001,
color='orange', alpha = 0.3, scalex = False, scaley = False)
axes.plot(blue_grid[:, 0], blue_grid[:, 1], '.', zorder = 0.001,
color='blue', alpha = 0.3, scalex = False, scaley = False)
plot_xlim = axes.get_xlim()
plot_ylim = axes.get_ylim()
grid = np.array([*product(np.linspace(*plot_xlim, 50), np.linspace(*plot_ylim, 50))])
is_orange = lambda x: model.predict(x) > 0.5
orange_grid = np.array([*filter(is_orange, grid)])
blue_grid = np.array([*filterfalse(is_orange, grid)])
axes.clear()
axes.set_title("Linear Regression of 0/1 Response")
plot_data(orange_data, blue_data)
plot_grid(orange_grid, blue_grid)
find_y = lambda x: (0.5 - model.beta[0] - x * model.beta[1]) / model.beta[2]
axes.plot(plot_xlim, [*map(find_y, plot_xlim)], color = 'black',
scalex = False, scaley = False)
fig
```
### 2.3.2 Nearest-Neighbor Methods
$$\hat{Y}(x) = \frac{1}{k} \sum_{x_i \in N_k(x)} y_i$$
where $N_k(x)$ is the neighborhood of $x$ defined by the $k$ closest points $x_i$ in the training sample.
```
class KNeighborsRegressor:
def __init__(self, k):
self._k = k
def fit(self, X, y):
self._X = X
self._y = y
return self
def predict(self, x):
X, y, k = self._X, self._y, self._k
distances = ((X - x) ** 2).sum(axis=1)
return np.mean(y[distances.argpartition(k)[:k]])
def plot_k_nearest_neighbors(k):
model = KNeighborsRegressor(k).fit(data_x, data_y)
is_orange = lambda x: model.predict(x) > 0.5
orange_grid = np.array([*filter(is_orange, grid)])
blue_grid = np.array([*filterfalse(is_orange, grid)])
axes.clear()
axes.set_title(str(k) + "-Nearest Neighbor Classifier")
plot_data(orange_data, blue_data)
plot_grid(orange_grid, blue_grid)
plot_k_nearest_neighbors(1)
fig
```
It appears that k-nearest-neighbor have a single parameter (*k*), however the effective number of parameters is N/k and is generally bigger than the p parameters in least-squares fits. **Note:** if the neighborhoods
were nonoverlapping, there would be N/k neighborhoods and we would fit one parameter (a mean) in each neighborhood.
```
plot_k_nearest_neighbors(15)
fig
```
| true |
code
| 0.798658 | null | null | null | null |
|
# Using an external master clock for hardware control of a stage-scanning high NA oblique plane microscope
Tutorial provided by [qi2lab](https://www.shepherdlaboratory.org).
This tutorial uses Pycro-Manager to rapidly acquire terabyte-scale volumetric images using external hardware triggering of a stage scan optimized, high numerical aperture (NA) oblique plane microscope (OPM). The microscope that this notebook controls is described in detail in this [preprint](https://www.biorxiv.org/content/10.1101/2020.04.07.030569v2), under the *stage scan OPM* section in the methods.
This high NA OPM allows for versatile, high-resolution, and large field-of-view single molecule imaging. The main application is quantifying 3D spatial gene expression in millions of cells or large pieces of intact tissue using interative RNA-FISH (see examples [here](https://www.nature.com/articles/s41598-018-22297-7) and [here](https://www.nature.com/articles/s41598-019-43943-8)). Because the fluidics controller for the iterative labeling is also controlled via Python (code not provided here), using Pycro-Manager greatly simplifies controlling these complex experiments.
The tutorial highlights the use of the `post_camera_hook_fn` and `post_hardware_hook_fn` functionality to allow an external controller to synchronize the microscope acquisition (external master). This is different from the standard hardware sequencing functionality in Pycro-Manager, where the acquisition engine sets up sequencable hardware and the camera serves as the master clock.
The tutorial also discusses how to structure the events and avoid timeouts to acquire >10 million of events per acquistion.
## Microscope hardware
Briefly, the stage scan high NA OPM is built around a [bespoke tertiary objective](https://andrewgyork.github.io/high_na_single_objective_lightsheet/) designed by Alfred Millet-Sikking and Andrew York at Calico Labs. Stage scanning is performed by an ASI scan optimized XY stage, an ASI FTP Z stage, and an ASI Tiger controller with a programmable logic card. Excitation light is provided by a Coherent OBIS Laser Box. A custom Teensy based DAC synchronizes laser emission and a galvanometer mirror to the scan stage motion to eliminate motion blur. Emitted fluorescence is imaged by a Photometrics Prime BSI.
The ASI Tiger controller is the master clock in this experiment. The custom Teensy DAC is setup in a closed loop with the Photometrics camera. This controller is detailed in a previous [publication](https://www.nature.com/articles/s41467-017-00514-7) on adaptive light sheet microscopy.
The code to orthogonally deskew the acquired data and place it into a BigDataViewer HDF5 file that can be read stitched and fused using BigStitcher is found at the qi2lab (www.github.com/qi2lab/OPM/).
## Initial setup
### Imports
```
from pycromanager import Bridge, Acquisition
import numpy as np
from pathlib import Path
from time import sleep
```
### Create bridge to Micro-Manager
```
with Bridge() as bridge:
core = bridge.get_core()
```
## Define pycromanager specific hook functions for externally controlled hardware acquisition
### Post camera hook function to start external controller
This is run once after the camera is put into active mode in the sequence acquisition. The stage starts moving on this command and outputs a TTL pulse to the camera when it passes the preset initial position. This TTL starts the camera running at the set exposure time using internal timing. The camera acts the master signal for the galvo/laser controller using its own "exposure out" signal.
```
def post_camera_hook_(event,bridge,event_queue):
"""
Run a set of commands after the camera is started
:param event: current list of events, each a dictionary, to run in this hardware sequence
:type event: list
:param bridge: pycro-manager java bridge
:type bridge: pycromanager.core.Bridge
:param event_queue: thread-safe event queue
:type event_queue: multiprocessing.Queue
:return: event_queue
"""
# acquire core from bridge
core=bridge.get_core()
# send Tiger command to start constant speed scan
command='1SCAN'
core.set_property('TigerCommHub','SerialCommand',command)
return event
```
### Post hardware setup function to make sure external controller is ready
This is run once after the acquisition engine sets up the hardware for the non-sequencable hardware, such as the height axis stage and channel.
```
def post_hardware_hook(event,bridge,event_queue):
"""
Run a set of commands after the hardware setup calls by acquisition engine are finished
:param event: current list of events, each a dictionary, to run in this hardware sequence
:type event: list
:param bridge: pycro-manager java bridge
:type bridge: pycromanager.core.Bridge
:param event_queue: thread-safe event queue
:type event_queue: multiprocessing.Queue
:return: event_queue
"""
# acquire core from bridge
core = bridge.get_core()
# turn on 'transmit repeated commands' for Tiger
core.set_property('TigerCommHub','OnlySendSerialCommandOnChange','No')
# check to make sure Tiger is not busy
ready='B'
while(ready!='N'):
command = 'STATUS'
core.set_property('TigerCommHub','SerialCommand',command)
ready = core.get_property('TigerCommHub','SerialResponse')
sleep(.500)
# turn off 'transmit repeated commands' for Tiger
core.set_property('TigerCommHub','OnlySendSerialCommandOnChange','Yes')
return event
```
## Acquistion parameters set by user
### Select laser channels and powers
```
# lasers to use
# 0 -> inactive
# 1 -> active
state_405 = 0
state_488 = 0
state_561 = 1
state_635 = 0
state_730 = 0
# laser powers (0 -> 100%)
power_405 = 0
power_488 = 0
power_561 = 0
power_635 = 0
power_730 = 0
# construct arrays for laser informaton
channel_states = [state_405,state_488,state_561,state_635,state_730]
channel_powers = [power_405,power_488,power_561,power_635,power_730]
```
### Camera parameters
```
# FOV parameters.
# x size (256) is the Rayleigh length of oblique light sheet excitation
# y size (1600) is the high quality lateral extent of the remote image system (~180 microns)
# camera is oriented so that cropping the x size limits the number of readout rows and therefore lowering readout time
ROI = [1024, 0, 256, 1600] #unit: pixels
# camera exposure
exposure_ms = 5 #unit: ms
# camera pixel size
pixel_size_um = .115 #unit: um
```
### Stage scan parameters
The user defines these by interactively moving the XY and Z stages around the sample. At the edges of the sample, the user records the positions.
```
# distance between adjacent images.
scan_axis_step_um = 0.2 #unit: um
# scan axis limits. Use stage positions reported by Micromanager
scan_axis_start_um = 0. #unit: um
scan_axis_end_um = 5000. #unit: um
# tile axis limits. Use stage positions reported by Micromanager
tile_axis_start_um = 0. #unit: um
tile_axis_end_um = 5000. #unit: um
# height axis limits. Use stage positions reported by Micromanager
height_axis_start_um = 0.#unit: um
height_axis_end_um = 30. #unit: um
```
### Path to save acquistion data
```
save_directory = Path('/path/to/save')
save_name = 'test'
```
## Setup hardware for stage scanning sample through oblique digitally scanned light sheet
### Calculate stage limits and speeds from user provided scan parameters
Here, the number of events along the scan (x) axis in each acquisition, the overlap between adajcent strips along the tile (y) axis, and the overlap between adajacent strips along the height (z) axis are all calculated.
```
# scan axis setup
scan_axis_step_mm = scan_axis_step_um / 1000. #unit: mm
scan_axis_start_mm = scan_axis_start_um / 1000. #unit: mm
scan_axis_end_mm = scan_axis_end_um / 1000. #unit: mm
scan_axis_range_um = np.abs(scan_axis_end_um-scan_axis_start_um) # unit: um
scan_axis_range_mm = scan_axis_range_um / 1000 #unit: mm
actual_exposure_s = actual_readout_ms / 1000. #unit: s
scan_axis_speed = np.round(scan_axis_step_mm / actual_exposure_s,2) #unit: mm/s
scan_axis_positions = np.rint(scan_axis_range_mm / scan_axis_step_mm).astype(int) #unit: number of positions
# tile axis setup
tile_axis_overlap=0.2 #unit: percentage
tile_axis_range_um = np.abs(tile_axis_end_um - tile_axis_start_um) #unit: um
tile_axis_range_mm = tile_axis_range_um / 1000 #unit: mm
tile_axis_ROI = ROI[3]*pixel_size_um #unit: um
tile_axis_step_um = np.round((tile_axis_ROI) * (1-tile_axis_overlap),2) #unit: um
tile_axis_step_mm = tile_axis_step_um / 1000 #unit: mm
tile_axis_positions = np.rint(tile_axis_range_mm / tile_axis_step_mm).astype(int) #unit: number of positions
# if tile_axis_positions rounded to zero, make sure acquisition visits at least one position
if tile_axis_positions == 0:
tile_axis_positions=1
# height axis setup
# this is more complicated, because the excitation is an oblique light sheet
# the height of the scan is the length of the ROI in the tilted direction * sin(tilt angle)
height_axis_overlap=0.2 #unit: percentage
height_axis_range_um = np.abs(height_axis_end_um-height_axis_start_um) #unit: um
height_axis_range_mm = height_axis_range_um / 1000 #unit: mm
height_axis_ROI = ROI[2]*pixel_size_um*np.sin(30*(np.pi/180.)) #unit: um
height_axis_step_um = np.round((height_axis_ROI)*(1-height_axis_overlap),2) #unit: um
height_axis_step_mm = height_axis_step_um / 1000 #unit: mm
height_axis_positions = np.rint(height_axis_range_mm / height_axis_step_mm).astype(int) #unit: number of positions
# if height_axis_positions rounded to zero, make sure acquisition visits at least one position
if height_axis_positions==0:
height_axis_positions=1
```
### Setup Coherent laser box from user provided laser parameters
```
with Bridge() as bridge:
core = bridge.get_core()
# turn off lasers
# this relies on a Micro-Manager configuration group that sets all lasers to "off" state
core.set_config('Coherent-State','off')
core.wait_for_config('Coherent-State','off')
# set lasers to user defined power
core.set_property('Coherent-Scientific Remote','Laser 405-100C - PowerSetpoint (%)',channel_powers[0])
core.set_property('Coherent-Scientific Remote','Laser 488-150C - PowerSetpoint (%)',channel_powers[1])
core.set_property('Coherent-Scientific Remote','Laser OBIS LS 561-150 - PowerSetpoint (%)',channel_powers[2])
core.set_property('Coherent-Scientific Remote','Laser 637-140C - PowerSetpoint (%)',channel_powers[3])
core.set_property('Coherent-Scientific Remote','Laser 730-30C - PowerSetpoint (%)',channel_powers[4])
```
### Setup Photometrics camera for low-noise readout and triggering
The camera input trigger is set to `Trigger first` mode to allow for external control and the output trigger is set to `Rolling Shutter` mode to ensure that laser light is only delivered when the entire chip is exposed. The custom Teensy DAC waits for the signal from the camera to go HIGH and then sweeps a Gaussian pencil beam once across the field-of-view. It then rapidly resets and scans again upon the next trigger. The Teensy additionally blanks the Coherent laser box emission between frames.
```
with Bridge() as bridge:
core = bridge.get_core()
# set camera into 16bit readout mode
core.set_property('Camera','ReadoutRate','100MHz 16bit')
# give camera time to change modes
sleep(5)
# set camera into low noise readout mode
core.set_property('Camera','Gain','2-CMS')
# give camera time to change modes
sleep(5)
# set camera to give an exposure out signal
# this signal is used by the custom DAC to synchronize blanking and a digitally swept light sheet
core.set_property('Camera','ExposureOut','Rolling Shutter')
# give camera time to change modes
sleep(5)
# change camera timeout.
# this is necessary because the acquisition engine can take a long time to setup with millions of events
# on the first run
core.set_property('Camera','Trigger Timeout (secs)',300)
# give camera time to change modes
sleep(5)
# set camera to internal trigger
core.set_property('Camera','TriggerMode','Internal Trigger')
# give camera time to change modes
sleep(5)
```
### Setup ASI stage control cards and programmable logic card in the Tiger controller
Hardware is setup for a constant-speed scan along the `x` direction, lateral tiling along the `y` direction, and height tiling along the `z` direction. The programmable logic card sends a signal to the camera to start acquiring once the scan (x) axis reaches the desired speed and crosses the user defined start position.
Documentation for the specific commands to setup the constant speed stage scan on the Tiger controller is at the following links,
- [SCAN](http://asiimaging.com/docs/commands/scan)
- [SCANR](http://asiimaging.com/docs/commands/scanr)
- [SCANV](http://www.asiimaging.com/docs/commands/scanv)
Documentation for the programmable logic card is found [here](http://www.asiimaging.com/docs/tiger_programmable_logic_card?s[]=plc).
The Tiger is polled after each command to make sure that it is ready to receive another command.
```
with Bridge() as bridge:
core = bridge.get_core()
# Setup the PLC to output external TTL when an internal signal is received from the stage scanning card
plcName = 'PLogic:E:36'
propPosition = 'PointerPosition'
propCellConfig = 'EditCellConfig'
addrOutputBNC3 = 35
addrStageSync = 46 # TTL5 on Tiger backplane = stage sync signal
core.set_property(plcName, propPosition, addrOutputBNC3)
core.set_property(plcName, propCellConfig, addrStageSync)
# turn on 'transmit repeated commands' for Tiger
core.set_property('TigerCommHub','OnlySendSerialCommandOnChange','No')
# set tile (y) axis speed to 25% of maximum for all moves
command = 'SPEED Y=.25'
core.set_property('TigerCommHub','SerialCommand',command)
# check to make sure Tiger is not busy
ready='B'
while(ready!='N'):
command = 'STATUS'
core.set_property('TigerCommHub','SerialCommand',command)
ready = core.get_property('TigerCommHub','SerialResponse')
sleep(.500)
# set scan (x) axis speed to 25% of maximum for non-sequenced moves
command = 'SPEED X=.25'
core.set_property('TigerCommHub','SerialCommand',command)
# check to make sure Tiger is not busy
ready='B'
while(ready!='N'):
command = 'STATUS'
core.set_property('TigerCommHub','SerialCommand',command)
ready = core.get_property('TigerCommHub','SerialResponse')
sleep(.500)
# turn off 'transmit repeated commands' for Tiger
core.set_property('TigerCommHub','OnlySendSerialCommandOnChange','Yes')
# turn on 'transmit repeated commands' for Tiger
core.set_property('TigerCommHub','OnlySendSerialCommandOnChange','No')
# set scan (x) axis speed to correct speed for constant speed movement of scan (x) axis
# expects mm/s
command = 'SPEED X='+str(scan_axis_speed)
core.set_property('TigerCommHub','SerialCommand',command)
# check to make sure Tiger is not busy
ready='B'
while(ready!='N'):
command = 'STATUS'
core.set_property('TigerCommHub','SerialCommand',command)
ready = core.get_property('TigerCommHub','SerialResponse')
sleep(.500)
# set scan (x) axis to true 1D scan with no backlash
command = '1SCAN X? Y=0 Z=9 F=0'
core.set_property('TigerCommHub','SerialCommand',command)
# check to make sure Tiger is not busy
ready='B'
while(ready!='N'):
command = 'STATUS'
core.set_property('TigerCommHub','SerialCommand',command)
ready = core.get_property('TigerCommHub','SerialResponse')
sleep(.500)
# set range and return speed (25% of max) for constant speed movement of scan (x) axis
# expects mm
command = '1SCANR X='+str(scan_axis_start_mm)+' Y='+str(scan_axis_end_mm)+' R=25'
core.set_property('TigerCommHub','SerialCommand',command)
# check to make sure Tiger is not busy
ready='B'
while(ready!='N'):
command = 'STATUS'
core.set_property('TigerCommHub','SerialCommand',command)
ready = core.get_property('TigerCommHub','SerialResponse')
sleep(.500)
# turn off 'transmit repeated commands' for Tiger
core.set_property('TigerCommHub','OnlySendSerialCommandOnChange','Yes')
```
## Setup and run the acquisition
### Change core timeout
This is necessary because of the large, slow XY stage moves.
```
with Bridge() as bridge:
core = bridge.get_core()
# change core timeout for long stage moves
core.set_property('Core','TimeoutMs',20000)
```
### Move stage hardware to initial positions
```
with Bridge() as bridge:
core = bridge.get_core()
# move scan (x) and tile (y) stages to starting positions
core.set_xy_position(scan_axis_start_um,tile_axis_start_um)
core.wait_for_device(xy_stage)
# move height (z) stage to starting position
core.set_position(height_position_um)
core.wait_for_device(z_stage)
```
### Create event structure
The external controller handles all of the events in `x` for a given `yzc` position. To make sure that pycro-manager structures the acquistion this way, the value of the stage positions for `x` are kept constant for all events at a given `yzc` position. This gives the order of the loops to create the event structure as `yzcx`.
```
# empty event dictionary
events = []
# loop over all tile (y) positions.
for y in range(tile_axis_positions):
# update tile (y) axis position
tile_position_um = tile_axis_start_um+(tile_axis_step_um*y)
# loop over all height (z) positions
for z in range(height_axis_positions):
# update height (z) axis position
height_position_um = height_axis_start_um+(height_axis_step_um*z)
# loop over all channels (c)
for c in range(len(channel_states)):
# create events for all scan (x) axis positions.
# The acquistion engine knows that this is a hardware triggered sequence because
# the physical x position does not change when specifying the large number of x events
for x in range(scan_axis_positions):
# only create events if user sets laser to active
# this relies on a Micromanager group 'Coherent-State' that has individual entries that correspond
# the correct on/off state of each laser. Laser blanking and synchronization are handled by the
# custom Teensy DAC controller.
if channel_states[c]==1:
if (c==0):
evt = { 'axes': {'x': x, 'y':y, 'z':z}, 'x': scan_axis_start_um, 'y': tile_position_um,
'z': height_position_um, 'channel' : {'group': 'Coherent-State', 'config': '405nm'}}
elif (c==1):
evt = { 'axes': {'x': x, 'y':y, 'z':z}, 'x': scan_axis_start_um, 'y': tile_position_um,
'z': height_position_um, 'channel' : {'group': 'Coherent-State', 'config': '488nm'}}
elif (c==2):
evt = { 'axes': {'x': x, 'y':y, 'z':z}, 'x': scan_axis_start_um, 'y': tile_position_um,
'z': height_position_um, 'channel' : {'group': 'Coherent-State', 'config': '561nm'}}
elif (c==3):
evt = { 'axes': {'x': x, 'y':y, 'z':z}, 'x': scan_axis_start_um, 'y': tile_position_um,
'z': height_position_um, 'channel' : {'group': 'Coherent-State', 'config': '637nm'}}
elif (c==4):
evt = { 'axes': {'x': x, 'y':y, 'z':z}, 'x': scan_axis_start_um, 'y': tile_position_um,
'z': height_position_um, 'channel' : {'group': 'Coherent-State', 'config': '730nm'}}
events.append(evt)
```
### Run acquisition
- The camera is set to `Trigger first` mode. In this mode, the camera waits for an external trigger and then runs using the internal timing.
- The acquisition is setup and started. The initial acquisition setup by Pycro-manager and the Java acquisition engine takes a few minutes and requires at significant amount of RAM allocated to ImageJ. 40 GB of RAM seems acceptable. The circular buffer is only allocated 2 GB, because the computer for this experiment has an SSD array capable of writing up to 600 MBps.
- At each `yzc` position, the ASI Tiger controller supplies the external master signal when the the (scan) axis has ramped up to the correct constant speed and crossed `scan_axis_start_um`. The speed is defined by `scan_axis_speed = scan_axis_step_um / camera_exposure_ms`. Acquired images are placed into the `x` axis of the Acquisition without Pycro-Manager interacting with the hardware.
- Once the full acquisition is completed, all lasers are set to `off` and the camera is placed back in `Internal Trigger` mode.
```
with Bridge() as bridge:
core = bridge.get_core()
# set camera to trigger first mode for stage synchronization
# give camera time to change modes
core.set_property('Camera','TriggerMode','Trigger first')
sleep(5)
# run acquisition
# the acquisition needs to write data at roughly 100-500 MBps depending on frame rate and ROI
# so the display is set to off and no multi-resolution calculations are done
with Acquisition(directory=save_directory, name=save_name, post_hardware_hook_fn=post_hardware_hook,
post_camera_hook_fn=post_camera_hook, show_display=False, max_multi_res_index=0) as acq:
acq.acquire(events)
# turn off lasers
core.set_config('Coherent-State','off')
core.wait_for_config('Coherent-State','off')
# set camera to internal trigger
core.set_property('Camera','TriggerMode','Internal Trigger')
# give camera time to change modes
sleep(5)
```
| true |
code
| 0.671821 | null | null | null | null |
|
# Direct Grib Read
If you have installed more recent versions of pygrib, you can ingest grib mosaics directly without conversion to netCDF. This speeds up the ingest by ~15-20 seconds. This notebook will also demonstrate how to use MMM-Py with cartopy, and how to download near-realtime data from NCEP.
```
from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
import datetime as dt
import pandas as pd
import glob
import mmmpy
import cartopy.crs as ccrs
import cartopy.feature as cfeature
from cartopy.io.img_tiles import StamenTerrain
import pygrib
import os
import pyart
%matplotlib inline
```
### Download MRMS directly from NCEP
```
def download_files(input_dt, max_seconds=300):
"""
This function takes an input datetime object, and will try to match with the closest mosaics in time
that are available at NCEP. Note that NCEP does not archive much beyond 24 hours of data.
Parameters
----------
input_dt : datetime.datetime object
input datetime object, will try to find closest file in time on NCEP server
Other Parameters
----------------
max_seconds : int or float
Maximum number of seconds difference tolerated between input and selected datetimes,
before file matching will fail
Returns
-------
files : 1-D ndarray of strings
Array of mosaic file names, ready for ingest into MMM-Py
"""
baseurl = 'http://mrms.ncep.noaa.gov/data/3DReflPlus/'
page1 = pd.read_html(baseurl)
directories = np.array(page1[0][0][3:-1]) # May need to change indices depending on pandas version
urllist = []
files = []
for i, d in enumerate(directories):
print(baseurl + d)
page2 = pd.read_html(baseurl + d)
filelist = np.array(page2[0][0][3:-1]) # May need to change indices depending on pandas version
dts = []
for filen in filelist:
# Will need to change in event of a name change
dts.append(dt.datetime.strptime(filen[32:47], '%Y%m%d-%H%M%S'))
dts = np.array(dts)
diff = np.abs((dts - input_dt))
if np.min(diff).total_seconds() <= max_seconds:
urllist.append(baseurl + d + filelist[np.argmin(diff)])
files.append(filelist[np.argmin(diff)])
for url in urllist:
print(url)
os.system('wget ' + url)
return np.array(files)
files = download_files(dt.datetime.utcnow())
```
### Direct ingest of grib into MMM-Py
```
mosaic = mmmpy.MosaicTile(files)
mosaic.diag()
```
### Plot with cartopy
```
tiler = StamenTerrain()
ext = [-130, -65, 20, 50]
fig = plt.figure(figsize=(12, 6))
projection = ccrs.PlateCarree() # ShadedReliefESRI().crs
ax = plt.axes(projection=projection)
ax.set_extent(ext)
ax.add_image(tiler, 3)
# Create a feature for States/Admin 1 regions at 1:10m from Natural Earth
states_provinces = cfeature.NaturalEarthFeature(
category='cultural',
name='admin_1_states_provinces_lines',
scale='50m',
facecolor='none')
ax.add_feature(states_provinces, edgecolor='gray')
# Create a feature for Countries 0 regions at 1:10m from Natural Earth
countries = cfeature.NaturalEarthFeature(
category='cultural',
name='admin_0_boundary_lines_land',
scale='50m',
facecolor='none')
ax.add_feature(countries, edgecolor='k')
ax.coastlines(resolution='50m')
mosaic.get_comp()
valmask = np.ma.masked_where(mosaic.mrefl3d_comp <= 0, mosaic.mrefl3d_comp)
cs = plt.pcolormesh(mosaic.Longitude, mosaic.Latitude, valmask, vmin=0, vmax=55,
cmap='pyart_Carbone42', transform=projection)
plt.colorbar(cs, label='Composite Reflectivity (dBZ)',
orientation='horizontal', pad=0.05, shrink=0.75, fraction=0.05, aspect=30)
plt.title(dt.datetime.utcfromtimestamp(mosaic.Time).strftime('%m/%d/%Y %H:%M UTC'))
```
| true |
code
| 0.68941 | null | null | null | null |
|
```
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
np.random.seed(0)
from statistics import mean
```
今回はアルゴリズムの評価が中心の章なので,学習アルゴリズム実装は後に回し、sklearnを学習アルゴリズムとして使用する。
```
import sklearn
```
今回、学習に使うデータはsin関数に正規分布$N(\varepsilon|0,0.05)$ノイズ項を加えたデータを使う
```
size = 100
max_degree = 11
x_data = np.random.rand(size) * np.pi * 2
var_data = np.random.normal(loc=0,scale=0.1,size=size)
sin_data = np.sin(x_data) + var_data
plt.ylim(-1.2,1.2)
plt.scatter(x_data,sin_data)
```
学習用のアルゴリズムは多項式回帰を使います。
```
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
```
2.2.2:**MSE**:近似の良さの評価手法。
$$MSE=\int (y(x;D) - h(x))^2p(x)dx=E\{(y(x;D)-h(x))^2\}$$
```
def MSE(y,t):
return np.sum(np.square(y-t))/y.size
MSE(np.array([10,3,3]),np.array([1,2,3]))
```
2.2.1 (1)**ホールドアウト法**:
手元のデータを2つに分割し、片方をトレーニングに使い、片方をテストに使う手法。
テストデータの数が必要
```
%%time
def holdout_method(x,y,per=0.8,value_func=MSE,degree=11):
index = np.random.permutation(x.size)
index_train,index_test = np.split(index,[int(x.size*per)])
#plt.scatter(x_data[index_train],sin_data[index_train])
test_score_list = []
train_score_list = []
for i in range(1,degree):
pf = PolynomialFeatures(degree=i, include_bias=False)
lr = LinearRegression()
pl = Pipeline([("PF", pf), ("LR", lr)])
pl.fit(x[index_train].reshape(-1,1), y[index_train])
pred_y_test = pl.predict(x[index_test].reshape(-1,1))
pred_y_train = pl.predict(x[index_train].reshape(-1,1))
score_train = value_func(pred_y_train,y[index_train])
score_test = value_func(pred_y_test,y[index_test])
train_score_list.append(score_train)
test_score_list.append(score_test)
return train_score_list,test_score_list
hold_train_score_list,hold_test_score_list = holdout_method(x_data,sin_data,degree=max_degree)
plt.plot(np.array(range(1,max_degree)),np.array(hold_train_score_list),color='b')
plt.plot(np.array(range(1,max_degree)),np.array(hold_test_score_list),color='r')
```
(2)**交差確認法**:手元の各クラスをn分割して、n-1のグループで学習して、残りの1つのグループのデータでテストをし、その平均を誤り率とした性能評価を行う。
```
def cross_validation(x,y,value_func=MSE,split_num=5,degree=1):
assert x.size % split_num==0,"You must use divisible number"
n = x.size / split_num
train_scores =[]
test_scores =[]
for i in range(split_num):
indices = [int(i*n),int(i*n+n)]
train_x_1,test_x,train_x_2=np.split(x,indices)
train_y_1,test_y,train_y_2=np.split(y,indices)
train_x = np.concatenate([train_x_1,train_x_2])
train_y = np.concatenate([train_y_1,train_y_2])
pf = PolynomialFeatures(degree=degree, include_bias=False)
lr = LinearRegression()
pl = Pipeline([("PF", pf), ("LR", lr)])
pl.fit(train_x.reshape(-1,1), train_y)
pred_y_test = pl.predict(np.array(test_x).reshape(-1,1))
pred_y_train = pl.predict(np.array(train_x).reshape(-1,1))
score_train = value_func(pred_y_train,train_y)
#print(score_train)
score_test = value_func(pred_y_test,test_y)
#print(len(test_y))
train_scores.append(score_train)
test_scores.append(score_test)
return mean(train_scores),mean(test_scores)
cross_test_score_list = []
cross_train_score_list = []
for i in range(1,max_degree):
tra,tes = cross_validation(x_data,sin_data,degree=i)
cross_train_score_list.append(tra)
cross_test_score_list.append(tes)
plt.plot(np.array(range(1,max_degree)),np.array(cross_train_score_list),color='b')
plt.plot(np.array(range(1,max_degree)),np.array(cross_test_score_list),color='r')
```
(3)**一つ抜き法**:交差確認法の特別な場合で、データ数=グループの数としたものである。
```
def leave_one_out(x,y,value_func=MSE,size=size,degree=1):
return cross_validation(x,y,value_func,split_num=size,degree=degree)
leave_test_score_list = []
leave_train_score_list = []
for i in range(1,max_degree):
tra,tes = leave_one_out(x_data,sin_data,degree=i)
leave_train_score_list.append(tra)
leave_test_score_list.append(tes)
plt.plot(np.array(range(1,max_degree)),np.array(leave_train_score_list),color='b')
plt.plot(np.array(range(1,max_degree)),np.array(leave_test_score_list),color='r')
plt.plot(np.array(range(1,max_degree)),np.array(hold_train_score_list),color='y')
plt.plot(np.array(range(1,max_degree)),np.array(hold_test_score_list),color='m')
plt.plot(np.array(range(1,max_degree)),np.array(cross_train_score_list),color='k')
plt.plot(np.array(range(1,max_degree)),np.array(cross_test_score_list),color='c')
plt.plot(np.array(range(1,max_degree)),np.array(leave_train_score_list),color='b')
plt.plot(np.array(range(1,max_degree)),np.array(leave_test_score_list),color='r')
```
(4)**ブートストラップ法**:N個の復元抽出をしてブートストラップサンプルを作り、そこから
$bias=\varepsilon(N^*,N^*)-N(N^*,N)$
を推定して、それをいくつか計算してその平均でバイアスを推定する。
その推定値を$\overline{bias}$として、その推定値を
$\varepsilon = \varepsilon(N,N)-\overline{bias}$
とする。
```
def bootstrap(x,y,value_func=MSE,trial=50,degree=1):
biases=[]
for i in range(trial):
boot_ind = np.random.choice(range(x.size),size=x.size,replace=True)
pf = PolynomialFeatures(degree=degree, include_bias=False)
lr = LinearRegression()
pl = Pipeline([("PF", pf), ("LR", lr)])
pl.fit(x[boot_ind].reshape(-1,1), y[boot_ind])
pred_y_boot = pl.predict(x[boot_ind].reshape(-1,1))
pred_y_base = pl.predict(x.reshape(-1,1))
score_boot = value_func(pred_y_boot,y[boot_ind])
#print(score_train)
score_base = value_func(pred_y_base,y)
bias = score_base - score_boot
#print(bias)
biases.append(bias)
pf = PolynomialFeatures(degree=degree, include_bias=False)
lr = LinearRegression()
pl = Pipeline([("PF", pf), ("LR", lr)])
pl.fit(x.reshape(-1,1), y)
pred_y_base = pl.predict(x.reshape(-1,1))
score_base = value_func(pred_y_base,y)
return score_base + mean(biases)
boot_score_list = []
for i in range(1,max_degree):
boot_score = bootstrap(x_data,sin_data,degree=i)
boot_score_list.append(boot_score)
plt.plot(np.array(range(1,max_degree)),np.array(boot_score_list),color='b')
```
| true |
code
| 0.468304 | null | null | null | null |
|
Check coefficients for integration schemes - they should all line up nicely for values in the middle and vary smoothly
```
from bokeh import plotting, io, models, palettes
io.output_notebook()
import numpy
from maxr.integrator import history
nmax = 5
figures = []
palette = palettes.Category10[3]
for n in range(1, nmax):
fig = plotting.figure(height=100, width=600,
active_drag='pan', active_scroll='wheel_zoom')
for order, color in zip((1, 2, 3), palette):
try:
coeffs = history.coefficients(n, order=order)
ticks = range(len(coeffs))
fig.line(ticks, coeffs, alpha=0.9, color=color)
fig.circle(ticks, coeffs, alpha=0.9, color=color)
except ValueError:
# Skip orders if we don't have enough coefficients to calculate these
continue
fig.yaxis.axis_label = 'n={0}'.format(n)
fig.toolbar.logo = None
fig.toolbar_location = None
figures.append(fig)
# Set up scaling
if len(figures) == 1:
figures[0].x_range = models.Range1d(0, nmax - 1)
figures[0].y_range = models.Range1d(0, 2)
else:
figures[-1].x_range = figures[0].x_range
figures[-1].y_range = figures[0].y_range
io.show(models.Column(*figures))
```
Define some timesteps to integrate over
```
tmin, tmax = 0, 30
ts = numpy.linspace(tmin, tmax, 1000)
```
Check we can integrate things!
```
expected = -1.2492166377597749
history.integrator(numpy.sin(ts), ts) - expected < 1e-5
```
Turn this into a history integrator for a python function
```
def evaluate_history_integral(f, ts, order=1):
""" Evaluate the history integral for a given driving function f
"""
return numpy.array([0] + [
history.integrator(f(ts[:idx+1]), ts[:idx+1], order=order)
for idx in range(1, len(ts))])
results = evaluate_history_integral(numpy.sin, ts)
figure = plotting.figure(height=300)
figure.line(ts, results)
figure.title.text = "∫sin(t)/√(t-𝜏)d𝜏"
io.show(figure)
```
Check accuracy of convergence. We use a sinusoidal forcing and plot the response
$$
\int_0^{t} \frac{\sin{(\tau)}}{\sqrt{t - \tau}}d\tau = \sqrt{2 \pi}\left[C{\left(\sqrt{\frac{2t}{\pi}}\right)}\sin{t} - S{\left(\sqrt{\frac{2t}{\pi}}\right)}\cos{t}\right]
$$
where $C$ is the Fresnel C (cos) integral, and $S$ is the Fresnel $S$ (sin) integral. Note the solution in the paper is **WRONG**
```
from scipy.special import fresnel
def solution(t):
ssc, csc = fresnel(numpy.sqrt(2 * t / numpy.pi))
return numpy.sqrt(2 * numpy.pi) * (
csc * numpy.sin(t) - ssc * numpy.cos(t))
```
Show the solution
```
figure = plotting.figure(height=300)
figure.line(ts, numpy.sin(ts), legend='Source function sin(t)', color=palette[1], alpha=0.7)
figure.line(ts, solution(ts), legend='Analytic ∫sin(t)/√(t-𝜏)d𝜏', color=palette[0], alpha=0.7)
figure.line(ts, evaluate_history_integral(numpy.sin, ts), legend='Numerical ∫sin(t)/√(t-𝜏)d𝜏', color=palette[2], alpha=0.7)
io.show(figure)
```
and try integration numerically
```
nsteps = 30
order = 3
tmin = 0
tmax = 40
# Evaluate solution
ts = numpy.linspace(tmin, tmax, nsteps)
numeric = evaluate_history_integral(numpy.sin, ts, order=order)
exact = solution(ts)
figure = plotting.figure(height=300)
figure.line(ts, exact, legend='Analytic', color=palette[0], alpha=0.7)
figure.line(ts, numeric, legend='Numerical', color=palette[2], alpha=0.7)
io.show(figure)
numpy.mean(numeric - exact)
```
Now we loop through by order and computer the error
```
from collections import defaultdict
# Set up steps
nstepstep = 50
nsteps = numpy.arange(nstepstep, 500, nstepstep)
spacing = 10 / (nsteps - 1)
# Calculate error
error = defaultdict(list)
for order in (1, 2, 3):
for N in nsteps:
ts = numpy.linspace(0, tmax, N)
err = evaluate_history_integral(numpy.sin, ts, order=order) - solution(ts)
error[order].append(abs(err).max())
# Convert to arrays
for key, value in error.items():
error[key] = numpy.asarray(value)
```
We can plot how the error changes with spacing
```
figure = plotting.figure(height=300, x_axis_type='log', y_axis_type='log')
for order, color in zip((1, 2, 3), palette):
figure.line(spacing, error[order], legend='Order = {0}'.format(order),
color=color, alpha=0.9)
figure.xaxis.axis_label = 'Timestep (𝛿t)'
figure.yaxis.axis_label = 'Error (𝜀)'
figure.legend.location = 'bottom_right'
io.show(figure)
```
check that we get reasonable scaling (should be about $\epsilon\sim\delta t ^{\text{order} + 1}$)
```
def slope(rise, run):
return (rise[1:] - rise[0]) / (run[1:] - run[0])
figure = plotting.figure(height=300, x_axis_type='log')
for order, color in zip((1, 2, 3), palette):
figure.line(spacing[1:],
slope(numpy.log(error[order]), numpy.log(spacing)),
legend='Order = {0}'.format(order),
color=color, alpha=0.9)
figure.xaxis.axis_label = 'Timestep (𝛿t)'
figure.yaxis.axis_label = 'Scaling exponent'
figure.legend.location = 'center_right'
io.show(figure)
```
| true |
code
| 0.802246 | null | null | null | null |
|
### Notebook for the Udacity Project "Write A Data Science Blog Post"
#### Dataset used: "TripAdvisor Restaurants Info for 31 Euro-Cities"
https://www.kaggle.com/damienbeneschi/krakow-ta-restaurans-data-raw
https://www.kaggle.com/damienbeneschi/krakow-ta-restaurans-data-raw/downloads/krakow-ta-restaurans-data-raw.zip/5
## 1.: Business Understanding according to CRISP-DM
I was in south-western Poland recently and while searching for a good place to eat on Google Maps I noticed, that there were a lot of restaurants that had really good ratings and reviews in the 4+ region, in cities as well as at the countryside. This made me thinking, because in my hometown Munich there is also many great places, but also a lot that are in not-so-good-region around 3 stars. In general, ratings seemed to be better there compared to what I know. So I thought, maybe people just rate more mildly there. Then I had my first lunch at one of those 4+ places and not only the staff was so friendly and the food looked really nicely, it also tasted amazing at a decent pricetag. Okay, I was lucky I thought. On the evening of the same day I tried another place and had the same great experience.
I had even more great eats. So is the quality of the polish restaurants on average better than the quality of the bavarian ones? Subjectively… Yes, it seemed so. But what does data science say? Are there differences in average ratings and number of ratings between regions? To answer this question, I used the TripAdvisor Restaurants Info for 31 Euro-Cities from Kaggle. This dataset contains the TripAdvisor reviews and ratings for 111927 restaurants in 31 European cities.
## Problem Definition / Research Questions:
- RQ 1: Are there differences in average ratings and number of ratings between cities?
- RQ 2: Are there more vegetarian-friendly cities and if so, are they locally concentrated?
- RQ 3: Is local cuisine rated better than foreign cusine and if so, is there a difference between cities?
```
# Import Statements
import pandas as pd
import numpy as np
# Load in dataset
data_raw = pd.read_csv("TA_restaurants_curated.csv")
```
## 2.: Data Understanding according to CRISP-DM
In the following, we have a look at the raw data of the dataset.
```
# Having a first look at the data
data_raw.head()
data_raw.describe()
# Which cities are included in the dataset?
cities = data_raw.City.unique()
cities
# Manually add the name of the local cuisines into an array (needed for RQ3)
local_cuisine = ['Dutch', 'Greek', 'Spanish', 'German', 'Eastern European', 'Belgian', 'Hungarian', 'Danish', 'Irish', 'Scottish', 'Swiss', 'German', 'Scandinavian', 'Polish', 'Portuguese', 'Slovenian', 'British', 'European', 'French', 'Spanish', 'Italian', 'German', 'Portuguese', 'Norwegian', 'French', 'Czech', 'Italian', 'Swedish', 'Austrian', 'Polish', 'Swiss']
```
As I live in Munich, I will want to have a closer look on the data for the city of Munich. So I will filter for the Munich data and have a first look on it.
```
# Function to return data for a specific city
def getRawData(city):
'''Returns the data for a specific city, which is given to the function via the city argument.'''
data_raw_city = data_raw[(data_raw.City == "Munich")]
return data_raw_city
# Filter for Munich data and have a first look
city = "Munich"
data_raw_city = getRawData(city)
data_raw_city.head(10)
data_raw_city.tail(10)
data_raw_city.describe()
```
### Dealing with missing data:
It can be seen, that some restaurants, especially the last ones, don't have any Ranking, Rating, Price Ranges or reviews. How to deal with that data? I have chosen to ignore those restaurants in the relevant questions. If, for example, the average rating of a cities restaurant is needed, I only use that restaurants, that actually have a rating. The other restaurants without rating are ignored.
## 3. and 4.: Data Preparation and Modeling according to CRISP-DM
### Calculate the data for RQ 1 - 3
In the following code, the data is first prepared by only selecting relevant and non-NaN data. Afterwards, data is modelled by calculating the relevant statistical numbers.
```
# Loop through entries for each city
# Create empty lists
num_entries = []
num_rated = []
perc_rated = []
avg_num_ratings = []
avg_rating = []
avg_veg_available = []
avg_loc_available = []
avg_loc_rating = []
avg_non_loc_rating = []
diff_loc_rating = []
total_local_rating = []
total_non_local_rating = []
# Initialize city number
n_city = -1
for city in cities:
n_city = n_city + 1
# Compute Data for RQ1
# Select data for one city
data_1city = data_raw[(data_raw.City == city)]
ratings = data_1city.Rating
data_1city_non_NaN = data_1city[data_1city['Rating'].notnull()]
ratings_non_NaN = data_1city_non_NaN.Rating
# Compute Data for RQ2 & RQ3
# Initialize lists for the current city
veg_available = []
loc_available = []
rating_local = []
rating_non_local = []
data_1city_stl_non_Nan = data_1city[data_1city['Cuisine Style'].notnull()]
# Iterate through every restaurant and check if they offer vegetarian/vegan food.
for i in range(len(data_1city_stl_non_Nan)):
veg_true = 0
styles = data_1city_stl_non_Nan.iloc[i, 3]
if 'Vegetarian' in styles:
veg_true = 1
#print('Veg Found')
elif 'Vegan' in styles:
veg_true = 1
veg_available.append(veg_true)
# For RQ3 check if the current restaurant offers local food and add the rating to the respective list.
loc_true = 0
if local_cuisine[n_city] in styles:
loc_true = 1
if ~np.isnan(data_1city_stl_non_Nan.iloc[i, 5]):
rating_local.append(data_1city_stl_non_Nan.iloc[i, 5])
total_local_rating.append(data_1city_stl_non_Nan.iloc[i, 5])
else:
if ~np.isnan(data_1city_stl_non_Nan.iloc[i, 5]):
rating_non_local.append(data_1city_stl_non_Nan.iloc[i, 5])
total_non_local_rating.append(data_1city_stl_non_Nan.iloc[i, 5])
loc_available.append(loc_true)
# Add to lists / caluclate aggregated values
num_entries.append(len(data_1city))
num_rated.append(len(data_1city_non_NaN))
perc_rated.append(len(data_1city_non_NaN) / len(data_1city))
avg_num_ratings.append(np.mean(data_1city_non_NaN['Number of Reviews']))
avg_rating.append(np.mean(data_1city_non_NaN['Rating']))
avg_veg_available.append(np.mean(veg_available))
avg_loc_available.append(np.mean(loc_available))
avg_loc_rating.append(np.mean(rating_local))
avg_non_loc_rating.append(np.mean(rating_non_local))
diff_loc_rating.append(np.mean(rating_local) - np.mean(rating_non_local))
# Create Dataframe
data_RQ1 = pd.DataFrame({'City': cities, 'Local_Cuisine': local_cuisine, 'Num_Entries': num_entries, 'Num_Rated': num_rated, 'Perc_Rated': perc_rated, 'Avg_Num_Ratings': avg_num_ratings, 'Avg_Rating': avg_rating, 'Avg_Veg_Av': avg_veg_available, 'Avg_Loc_Av': avg_loc_available, 'Avg_loc_rating': avg_loc_rating, 'Avg_non_loc_rating': avg_non_loc_rating, 'Diff_loc_rating': diff_loc_rating})
# Show the before computed data for RQ 1, 2 and 3.
data_RQ1.head(31)
```
## 5.: Evaluate the Results according to CRISP-DM
In the following, for every research questions relevant plots and statistical numbers are plotted to interpret the results. Afterward the plots, results are discussed.
### RQ 1: Are there differences in average ratings and number of ratings between cities?
```
data_RQ1.plot.bar(x='City', y='Avg_Rating', rot=0, figsize=(30,6))
print('Lowest Average Rating: {:.3f}'.format(min(data_RQ1.Avg_Rating)))
print('Highest Average Rating: {:.3f}'.format(max(data_RQ1.Avg_Rating)))
print('Difference from lowest to highest average Rating: {:.3f}'.format(max(data_RQ1.Avg_Rating) - min(data_RQ1.Avg_Rating)))
```
#### As it can clearly be seen, there is a difference in average ratings by citiy. The highest average rating is 4.232 for the city of Rome and 3.797 for the city of Madrid. An interesting follow-up question would be, wether the general quality of restaurants is better in Rome or if reviewers give better ratings in Rome compared to Madrid. Another more vague explaination would be that Tripadvisor is more often used by Tourists than locals, and that tourists rate Italian food better, as they are better used to it since it is better known in the world compared to spanish food.
```
data_RQ1.plot.bar(x='City', y='Avg_Num_Ratings', rot=0, figsize=(30,6))
print('Lowest Average Number of Ratings: {:.3f}'.format(min(data_RQ1.Avg_Num_Ratings)))
print('Highest Average Number of Ratings: {:.3f}'.format(max(data_RQ1.Avg_Num_Ratings)))
print('Difference from lowest to highest number of Ratings: {:.3f}'.format(max(data_RQ1.Avg_Num_Ratings) - min(data_RQ1.Avg_Num_Ratings)))
```
#### Also with the number of ratings it can be noted, that there definitely is a a difference in number of ratings. The highest average number of ratings with 293.896 is (again) seen in the city of Rome, while Hamburg with 45.942 has the lowest average number of ratings, which makes up of a difference of close to 248 in average ratings - that means rome has 6 times the average number of ratings as Hamburg, which can't be explained by the difference in inhabitants, which is 2.872.800 for Rome (Wikipedia) and 1.841.179 for Hamburg (Wikipedia). Other explainations would be that certain regions are more rating-friendly, prefer Tripadvisor or other tools such as Google Maps or that the probably higher number of tourists in Rome uses Tripadvisor more often.
### RQ 2: Are there more vegetarian-friendly cities and if so, are they locally concentrated?
```
data_RQ1.plot.bar(x='City', y='Avg_Veg_Av', rot=0, figsize=(30,6))
print('Lowest Average Number of Vegetarian/Vegan Available: {:.3f}'.format(min(data_RQ1.Avg_Veg_Av)))
print('Highest Average Number of Vegetarian/Vegan Available: {:.3f}'.format(max(data_RQ1.Avg_Veg_Av)))
print('Difference from lowest to highest number: {:.3f}'.format(max(data_RQ1.Avg_Veg_Av) - min(data_RQ1.Avg_Veg_Av)))
```
#### It seems that there are also great differences in average number of restaurants with vegetarian/vegan option available: Edinburgh has the highest number of restaurants that offer veg, with 56.9%, Lyon on the other hand with 12,9% is a lot less veg-friendly. A clear local pattern can not be distinguished.
### RQ 3: Is local cuisine rated better than foreign cusine and if so, is there a difference between cities?
```
data_RQ1.plot.bar(x='City', y='Avg_Loc_Av', rot=0, figsize=(30,6))
data_RQ1.plot.bar(x='City', y='Avg_loc_rating', rot=0, figsize=(30,6))
data_RQ1.plot.bar(x='City', y='Avg_non_loc_rating', rot=0, figsize=(30,6))
data_RQ1.plot.bar(x='City', y='Diff_loc_rating', rot=0, figsize=(30,6))
print('Lowest Rating Difference: {:.3f}'.format(min(data_RQ1.Diff_loc_rating)))
print('Highest Rating Difference: {:.3f}'.format(max(data_RQ1.Diff_loc_rating)))
print('Average Total Rating Difference: {:.3f}'.format(np.mean(data_RQ1.Diff_loc_rating)))
print()
print('Total Local Ratings: {}'.format(len(total_local_rating)))
print('Total Local Rating Mean: {}'.format(np.mean(total_local_rating)))
print('Total Non-Local Ratings: {}'.format(len(total_non_local_rating)))
print('Total Non-Local Rating Mean: {}'.format(np.mean(total_non_local_rating)))
print('Total Non-Local Rating Mean Difference: {}'.format(np.mean(total_local_rating) - np.mean(total_non_local_rating)))
```
#### Although there is a difference with local restaurants being rated better than restaurants not serving local food (aggregated difference is 0.026 / total difference is 0.0155), it is quite small and not neccessarily statistically significant in general. Yet it is interesting to notive, that for some cities the hypothesis is true. Especially Copenhagen, Edicnburgh, Helsinki, Ljubliana and Lyana show more significant differences with local restaurants being favored and cities like Barcelona, Berlin, Bratislava, Brussels and Prahgue, where local restaurants are rated less good, in the case of Bratislava the difference is greater than 0.2.
So, again, this can have multiple reasons. It is possible that people who use Tripadvisor, which are often tourists, prefer certain cousines that they are familiar to. Also it is possible, that certain local cuisines are "easier" for the non local. Other reasons are thinkable.
| true |
code
| 0.414247 | null | null | null | null |
|
# How to setup Seven Bridges Public API python library
## Overview
Here you will learn the three possible ways to setup Seven Bridges Public API Python library.
## Prerequisites
1. You need to install _sevenbridges-python_ library. Library details are available [here](http://sevenbridges-python.readthedocs.io/en/latest/sevenbridges/)
The easiest way to install sevenbridges-python is using pip:
$ pip install sevenbridges-python
Alternatively, you can get the code. sevenbridges-python is actively developed on GitHub, where the [code](https://github.com/sbg/sevenbridges-python) is always available. To clone the public repository :
$ git clone git://github.com/sbg/sevenbridges-python.git
Once you have a copy of the source, you can embed it in your Python
package, or install it into your site-packages by invoking:
$ python setup.py install
2. You need your _authentication token_ which you can get [here](https://igor.sbgenomics.com/developer/token)
### Notes and Compatibility
Python package is intended to be used with Python 3.6+ versions.
```
# Import the library
import sevenbridges as sbg
```
### Initialize the library
You can initialize the library explicitly or by supplying the necessary information in the $HOME/.sevenbridges/credentials file
There are generally three ways to initialize the library:
1. Explicitly, when calling api constructor, like:
``` python
api = sbg.Api(url='https://api.sbgenomics.com/v2', token='MY AUTH TOKEN')
```
2. By using OS environment to store the url and authentication token
```
export AUTH_TOKEN=<MY AUTH TOKEN>
export API_ENDPOINT='https://api.sbgenomics.com/v2'
```
3. By using ini file $HOME/.sevenbridges/credentials (for MS Windows, the file should be located in \%UserProfile\%.sevenbridges\credentials) and specifying a profile to use. The format of the credentials file is standard ini file format, as shown below:
```bash
[sbpla]
api_endpoint = https://api.sbgenomics.com/v2
auth_token = 700992f7b24a470bb0b028fe813b8100
[cgc]
api_endpoint = https://cgc-api.sbgenomics.com/v2
auth_token = 910975f5b24a470bb0b028fe813b8100
```
0. to **create** this file<sup>1</sup>, use the following steps in your _Terminal_:
1.
```bash
cd ~
mkdir .sevenbridges
touch .sevenbridges/credentials
vi .sevenbridges/credentials
```
2. Press "i" then enter to go into **insert mode**
3. write the text above for each environment.
4. Press "ESC" then type ":wq" to save the file and exit vi
<sup>1</sup> If the file already exists, omit the _touch_ command
### Test if you have stored the token correctly
Below are the three options presented above, test **one** of them. Logically, if you have only done **Step 3**, then testing **Step 2** will return an error.
```
# (1.) You can also instantiate library by explicitly
# specifying API url and authentication token
api_explicitly = sbg.Api(url='https://api.sbgenomics.com/v2',
token='<MY TOKEN HERE>')
api_explicitly.users.me()
# (2.) If you have not specified profile, the python-sbg library
# will search for configuration in the environment
c = sbg.Config()
api_via_environment = sbg.Api(config=c)
api_via_environment.users.me()
# (3.) If you have credentials setup correctly, you only need to specify the profile
config_file = sbg.Config(profile='sbpla')
api_via_ini_file = sbg.Api(config=config_file)
api_via_ini_file.users.me()
```
#### PROTIP
* We _recommend_ the approach with configuration file (the **.sevenbridges/credentials** file in option #3), especially if you are using multiple environments (like SBPLA and CGC).
| true |
code
| 0.622172 | null | null | null | null |
|
# Markov Random Fields for Collaborative Filtering (Memory Efficient)
This notebook provides a **memory efficient version** in Python 3.7 of the algorithm outlined in the paper
"[Markov Random Fields for Collaborative Filtering](https://arxiv.org/abs/1910.09645)"
at the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, Canada.
For reproducibility, the experiments utilize publicly available [code](https://github.com/dawenl/vae_cf) for pre-processing three popular data-sets and for evaluating the learned model. That code accompanies the paper "[Variational Autoencoders for Collaborative Filtering](https://arxiv.org/abs/1802.05814)" by Dawen Liang et al. at The Web Conference 2018. While the code for the Movielens-20M data-set was made publicly available, the code for pre-processing the other two data-sets can easily be obtained by modifying their code as described in their paper.
The experiments in the paper (where an AWS instance with 64 GB RAM and 16 vCPUs was used) may be re-run by following these three steps:
- Step 1: Pre-processing the data (utilizing the publicly available [code](https://github.com/dawenl/vae_cf))
- Step 2: Learning the MRF (this code implements the new algorithm)
- Step 3: Evaluation (utilizing the publicly available [code](https://github.com/dawenl/vae_cf))
This memory efficient version is modified by Yifei Shen @ Hong Kong University of Science and Technology
## Step 1: Pre-processing the data
Utilizing the publicly available [code](https://github.com/dawenl/vae_cf), which is copied below (with kind permission of Dawen Liang):
- run their cells 1-26 for data pre-processing
- note that importing matplotlib, seaborn, and tensorflow may not be necessary for our purposes here
- run their cells 29-31 for loading the training data
Note that the following code is modified as to pre-process the [MSD data-set](https://labrosa.ee.columbia.edu/millionsong/tasteprofile). For pre-processing the [MovieLens-20M data-set](https://grouplens.org/datasets/movielens/20m/), see their original publicly-available [code](https://github.com/dawenl/vae_cf).
```
import os
import shutil
import sys
import numpy as np
from scipy import sparse
import pandas as pd
import bottleneck as bn
# change to the location of the data
DATA_DIR = 'MSD'
itemId='songId' # for MSD data
raw_data = pd.read_csv(os.path.join(DATA_DIR, 'train_triplets.txt'), sep='\t', header=None, names=['userId', 'songId', 'playCount'])
```
### Data splitting procedure
- Select 50K users as heldout users, 50K users as validation users, and the rest of the users for training
- Use all the items from the training users as item set
- For each of both validation and test user, subsample 80% as fold-in data and the rest for prediction
```
def get_count(tp, id):
playcount_groupbyid = tp[[id]].groupby(id, as_index=False)
count = playcount_groupbyid.size()
return count
def filter_triplets(tp, min_uc=5, min_sc=0):
# Only keep the triplets for items which were clicked on by at least min_sc users.
if min_sc > 0:
itemcount = get_count(tp, itemId)
tp = tp[tp[itemId].isin(itemcount.index[itemcount >= min_sc])]
# Only keep the triplets for users who clicked on at least min_uc items
# After doing this, some of the items will have less than min_uc users, but should only be a small proportion
if min_uc > 0:
usercount = get_count(tp, 'userId')
tp = tp[tp['userId'].isin(usercount.index[usercount >= min_uc])]
# Update both usercount and itemcount after filtering
usercount, itemcount = get_count(tp, 'userId'), get_count(tp, itemId)
return tp, usercount, itemcount
raw_data, user_activity, item_popularity = filter_triplets(raw_data, min_uc=20, min_sc=200) # for MSD data
sparsity = 1. * raw_data.shape[0] / (user_activity.shape[0] * item_popularity.shape[0])
print("After filtering, there are %d watching events from %d users and %d movies (sparsity: %.3f%%)" %
(raw_data.shape[0], user_activity.shape[0], item_popularity.shape[0], sparsity * 100))
unique_uid = user_activity.index
np.random.seed(98765)
idx_perm = np.random.permutation(unique_uid.size)
unique_uid = unique_uid[idx_perm]
# create train/validation/test users
n_users = unique_uid.size
n_heldout_users = 50000 # for MSD data
tr_users = unique_uid[:(n_users - n_heldout_users * 2)]
vd_users = unique_uid[(n_users - n_heldout_users * 2): (n_users - n_heldout_users)]
te_users = unique_uid[(n_users - n_heldout_users):]
train_plays = raw_data.loc[raw_data['userId'].isin(tr_users)]
unique_sid = pd.unique(train_plays[itemId])
show2id = dict((sid, i) for (i, sid) in enumerate(unique_sid))
profile2id = dict((pid, i) for (i, pid) in enumerate(unique_uid))
pro_dir = os.path.join(DATA_DIR, 'pro_sg')
if not os.path.exists(pro_dir):
os.makedirs(pro_dir)
with open(os.path.join(pro_dir, 'unique_sid.txt'), 'w') as f:
for sid in unique_sid:
f.write('%s\n' % sid)
def split_train_test_proportion(data, test_prop=0.2):
data_grouped_by_user = data.groupby('userId')
tr_list, te_list = list(), list()
np.random.seed(98765)
for i, (_, group) in enumerate(data_grouped_by_user):
n_items_u = len(group)
if n_items_u >= 5:
idx = np.zeros(n_items_u, dtype='bool')
idx[np.random.choice(n_items_u, size=int(test_prop * n_items_u), replace=False).astype('int64')] = True
tr_list.append(group[np.logical_not(idx)])
te_list.append(group[idx])
else:
tr_list.append(group)
if i % 5000 == 0:
print("%d users sampled" % i)
sys.stdout.flush()
data_tr = pd.concat(tr_list)
data_te = pd.concat(te_list)
return data_tr, data_te
vad_plays = raw_data.loc[raw_data['userId'].isin(vd_users)]
vad_plays = vad_plays.loc[vad_plays[itemId].isin(unique_sid)]
vad_plays_tr, vad_plays_te = split_train_test_proportion(vad_plays)
test_plays = raw_data.loc[raw_data['userId'].isin(te_users)]
test_plays = test_plays.loc[test_plays[itemId].isin(unique_sid)]
test_plays_tr, test_plays_te = split_train_test_proportion(test_plays)
```
### Save the data into (user_index, item_index) format
```
def numerize(tp):
uid = list(map(lambda x: profile2id[x], tp['userId']))
sid = list(map(lambda x: show2id[x], tp[itemId]))
return pd.DataFrame(data={'uid': uid, 'sid': sid}, columns=['uid', 'sid'])
train_data = numerize(train_plays)
train_data.to_csv(os.path.join(pro_dir, 'train.csv'), index=False)
vad_data_tr = numerize(vad_plays_tr)
vad_data_tr.to_csv(os.path.join(pro_dir, 'validation_tr.csv'), index=False)
vad_data_te = numerize(vad_plays_te)
vad_data_te.to_csv(os.path.join(pro_dir, 'validation_te.csv'), index=False)
test_data_tr = numerize(test_plays_tr)
test_data_tr.to_csv(os.path.join(pro_dir, 'test_tr.csv'), index=False)
test_data_te = numerize(test_plays_te)
test_data_te.to_csv(os.path.join(pro_dir, 'test_te.csv'), index=False)
```
### Load the pre-processed training and validation data
```
unique_sid = list()
with open(os.path.join(pro_dir, 'unique_sid.txt'), 'r') as f:
for line in f:
unique_sid.append(line.strip())
n_items = len(unique_sid)
def load_train_data(csv_file):
tp = pd.read_csv(csv_file)
n_users = tp['uid'].max() + 1
rows, cols = tp['uid'], tp['sid']
data = sparse.csr_matrix((np.ones_like(rows),
(rows, cols)), dtype='float64',
shape=(n_users, n_items))
return data
train_data = load_train_data(os.path.join(pro_dir, 'train.csv'))
```
## Step 2: Learning the MRF model (implementation of the new algorithm)
Now run the following code and choose to learn
- either the dense MRF model
- or the sparse MRF model
```
import time
from copy import deepcopy
class MyClock:
startTime = time.time()
def tic(self):
self.startTime = time.time()
def toc(self):
secs = time.time() - self.startTime
print("... elapsed time: {} min {} sec".format(int(secs//60), secs%60) )
myClock = MyClock()
totalClock = MyClock()
alpha = 0.75
```
### Pre-computation of the training data
```
def filter_XtX(train_data, block_size, thd4mem, thd4comp):
# To obtain and sparsify XtX at the same time to save memory
# block_size (2nd input) and threshold for memory (3rd input) controls the memory usage
# thd4comp is the threshold to control training efficiency
XtXshape = train_data.shape[1]
userCount = train_data.shape[0]
bs = block_size
blocks = train_data.shape[1]// bs + 1
flag = False
thd = thd4mem
#normalize data
mu = np.squeeze(np.array(np.sum(train_data, axis=0)))/ userCount
variance_times_userCount = (mu - mu * mu) * userCount
rescaling = np.power(variance_times_userCount, alpha / 2.0)
scaling = 1.0 / rescaling
#block multiplication
for ii in range(blocks):
for jj in range(blocks):
XtX_tmp = np.asarray(train_data[:,bs*ii : bs*(ii+1)].T.dot(train_data[:,bs*jj : bs*(jj+1)]).todense(), dtype = np.float32)
XtX_tmp -= mu[bs*ii:bs*(ii+1),None] * (mu[bs*jj : bs*(jj+1)]* userCount)
XtX_tmp = scaling[bs*ii:bs*(ii+1),None] * XtX_tmp * scaling[bs*jj : bs*(jj+1)]
# sparsification filter 1 to control memory usage
ix = np.where(np.abs(XtX_tmp) > thd)
XtX_nz = XtX_tmp[ix]
ix = np.array(ix, dtype = 'int32')
ix[0,:] += bs*ii
ix[1,:] += bs*jj
if(flag):
ixs = np.concatenate((ixs, ix), axis = 1)
XtX_nzs = np.concatenate((XtX_nzs, XtX_nz), axis = 0)
else:
ixs = ix
XtX_nzs = XtX_nz
flag = True
#sparsification filter 2 to control training time of the algorithm
ix2 = np.where(np.abs(XtX_nzs) >= thd4comp)
AA_nzs = XtX_nzs[ix2]
AA_ixs = np.squeeze(ixs[:,ix2])
print(XtX_nzs.shape, AA_nzs.shape)
XtX = sparse.csc_matrix( (XtX_nzs, ixs), shape=(XtXshape,XtXshape), dtype=np.float32)
AA = sparse.csc_matrix( (AA_nzs, AA_ixs), shape=(XtXshape,XtXshape), dtype=np.float32)
return XtX, rescaling, XtX.diagonal(), AA
XtX, rescaling, XtXdiag, AtA = filter_XtX(train_data, 10000, 0.04, 0.11)
ii_diag = np.diag_indices(XtX.shape[0])
scaling = 1/rescaling
```
### Sparse MRF model
```
def calculate_sparsity_pattern(AtA, maxInColumn):
# this implements section 3.1 in the paper.
print("sparsifying the data-matrix (section 3.1 in the paper) ...")
myClock.tic()
# apply threshold
#ix = np.where( np.abs(XtX) > threshold)
#AA = sparse.csc_matrix( (XtX[ix], ix), shape=XtX.shape, dtype=np.float32)
AA = AtA
# enforce maxInColumn, see section 3.1 in paper
countInColumns=AA.getnnz(axis=0)
iiList = np.where(countInColumns > maxInColumn)[0]
print(" number of items with more than {} entries in column: {}".format(maxInColumn, len(iiList)) )
for ii in iiList:
jj= AA[:,ii].nonzero()[0]
kk = bn.argpartition(-np.abs(np.asarray(AA[jj,ii].todense()).flatten()), maxInColumn)[maxInColumn:]
AA[ jj[kk], ii ] = 0.0
AA.eliminate_zeros()
print(" resulting sparsity of AA: {}".format( AA.nnz*1.0 / AA.shape[0] / AA.shape[0]) )
myClock.toc()
return AA
def sparse_parameter_estimation(rr, XtX, AA, XtXdiag):
# this implements section 3.2 in the paper
# list L in the paper, sorted by item-counts per column, ties broken by item-popularities as reflected by np.diag(XtX)
AAcountInColumns = AA.getnnz(axis=0)
sortedList=np.argsort(AAcountInColumns+ XtXdiag /2.0/ np.max(XtXdiag) )[::-1]
print("iterating through steps 1,2, and 4 in section 3.2 of the paper ...")
myClock.tic()
todoIndicators=np.ones(AAcountInColumns.shape[0])
blockList=[] # list of blocks. Each block is a list of item-indices, to be processed in step 3 of the paper
for ii in sortedList:
if todoIndicators[ii]==1:
nn, _, vals=sparse.find(AA[:,ii]) # step 1 in paper: set nn contains item ii and its neighbors N
kk=np.argsort(np.abs(vals))[::-1]
nn=nn[kk]
blockList.append(nn) # list of items in the block, to be processed in step 3 below
# remove possibly several items from list L, as determined by parameter rr (r in the paper)
dd_count=max(1,int(np.ceil(len(nn)*rr)))
dd=nn[:dd_count] # set D, see step 2 in the paper
todoIndicators[dd]=0 # step 4 in the paper
myClock.toc()
print("now step 3 in section 3.2 of the paper: iterating ...")
# now the (possibly heavy) computations of step 3:
# given that steps 1,2,4 are already done, the following for-loop could be implemented in parallel.
myClock.tic()
BBlist_ix1, BBlist_ix2, BBlist_val = [], [], []
for nn in blockList:
#calculate dense solution for the items in set nn
BBblock=np.linalg.inv( np.array(XtX[np.ix_(nn,nn)].todense()) )
#BBblock=np.linalg.inv( XtX[np.ix_(nn,nn)] )
BBblock/=-np.diag(BBblock)
# determine set D based on parameter rr (r in the paper)
dd_count=max(1,int(np.ceil(len(nn)*rr)))
dd=nn[:dd_count] # set D in paper
# store the solution regarding the items in D
blockix = np.meshgrid(dd,nn)
BBlist_ix1.extend(blockix[1].flatten().tolist())
BBlist_ix2.extend(blockix[0].flatten().tolist())
BBlist_val.extend(BBblock[:,:dd_count].flatten().tolist())
myClock.toc()
print("final step: obtaining the sparse matrix BB by averaging the solutions regarding the various sets D ...")
myClock.tic()
BBsum = sparse.csc_matrix( (BBlist_val, (BBlist_ix1, BBlist_ix2 ) ), shape=XtX.shape, dtype=np.float32)
BBcnt = sparse.csc_matrix( (np.ones(len(BBlist_ix1), dtype=np.float32), (BBlist_ix1,BBlist_ix2 ) ), shape=XtX.shape, dtype=np.float32)
b_div= sparse.find(BBcnt)[2]
b_3= sparse.find(BBsum)
BBavg = sparse.csc_matrix( ( b_3[2] / b_div , (b_3[0],b_3[1] ) ), shape=XtX.shape, dtype=np.float32)
BBavg[ii_diag]=0.0
myClock.toc()
print("forcing the sparsity pattern of AA onto BB ...")
myClock.tic()
BBavg = sparse.csr_matrix( ( np.asarray(BBavg[AA.nonzero()]).flatten(), AA.nonzero() ), shape=BBavg.shape, dtype=np.float32)
print(" resulting sparsity of learned BB: {}".format( BBavg.nnz * 1.0 / AA.shape[0] / AA.shape[0]) )
myClock.toc()
return BBavg
def sparse_solution(rr, maxInColumn, L2reg):
# sparsity pattern, see section 3.1 in the paper
XtX[ii_diag] = XtXdiag
AA = calculate_sparsity_pattern(AtA, maxInColumn)
# parameter-estimation, see section 3.2 in the paper
XtX[ii_diag] = XtXdiag+L2reg
BBsparse = sparse_parameter_estimation(rr, XtX, AA, XtXdiag+L2reg)
return BBsparse
```
training the sparse model:
```
maxInColumn = 1000
# hyper-parameter r in the paper, which determines the trade-off between approximation-accuracy and training-time
rr = 0.1
# L2 norm regularization
L2reg = 1.0
print("training the sparse model:\n")
totalClock.tic()
BBsparse = sparse_solution(rr, maxInColumn, L2reg)
print("\ntotal training time (including the time for determining the sparsity-pattern):")
totalClock.toc()
print("\nre-scaling BB back to the original item-popularities ...")
# assuming that mu.T.dot(BB) == mu, see Appendix in paper
myClock.tic()
BBsparse=sparse.diags(scaling).dot(BBsparse).dot(sparse.diags(rescaling))
myClock.toc()
#print("\nfor the evaluation below: converting the sparse model into a dense-matrix-representation ...")
#myClock.tic()
#BB = np.asarray(BBsparse.todense(), dtype=np.float32)
#myClock.toc()
```
## Step 3: Evaluating the MRF model
Utilizing the publicly available [code](https://github.com/dawenl/vae_cf), which is copied below (with kind permission of Dawen Liang):
- run their cell 32 for loading the test data
- run their cells 35 and 36 for the ranking metrics (for later use in evaluation)
- run their cells 45 and 46
- modify and run their cell 50:
- remove 2 lines: the one that starts with ```with``` and the line below
- remove the indentation of the line that starts with ```for```
- modify the line that starts with ```pred_val``` as follows: ```pred_val = X.dot(BB)```
- run their cell 51
```
def load_tr_te_data(csv_file_tr, csv_file_te):
tp_tr = pd.read_csv(csv_file_tr)
tp_te = pd.read_csv(csv_file_te)
start_idx = min(tp_tr['uid'].min(), tp_te['uid'].min())
end_idx = max(tp_tr['uid'].max(), tp_te['uid'].max())
rows_tr, cols_tr = tp_tr['uid'] - start_idx, tp_tr['sid']
rows_te, cols_te = tp_te['uid'] - start_idx, tp_te['sid']
data_tr = sparse.csr_matrix((np.ones_like(rows_tr),
(rows_tr, cols_tr)), dtype='float64', shape=(end_idx - start_idx + 1, n_items))
data_te = sparse.csr_matrix((np.ones_like(rows_te),
(rows_te, cols_te)), dtype='float64', shape=(end_idx - start_idx + 1, n_items))
return data_tr, data_te
def NDCG_binary_at_k_batch(X_pred, heldout_batch, k=100):
'''
normalized discounted cumulative gain@k for binary relevance
ASSUMPTIONS: all the 0's in heldout_data indicate 0 relevance
'''
batch_users = X_pred.shape[0]
idx_topk_part = bn.argpartition(-X_pred, k, axis=1)
topk_part = X_pred[np.arange(batch_users)[:, np.newaxis],
idx_topk_part[:, :k]]
idx_part = np.argsort(-topk_part, axis=1)
# X_pred[np.arange(batch_users)[:, np.newaxis], idx_topk] is the sorted
# topk predicted score
idx_topk = idx_topk_part[np.arange(batch_users)[:, np.newaxis], idx_part]
# build the discount template
tp = 1. / np.log2(np.arange(2, k + 2))
DCG = (heldout_batch[np.arange(batch_users)[:, np.newaxis],
idx_topk].toarray() * tp).sum(axis=1)
IDCG = np.array([(tp[:min(n, k)]).sum()
for n in heldout_batch.getnnz(axis=1)])
return DCG / IDCG
def Recall_at_k_batch(X_pred, heldout_batch, k=100):
batch_users = X_pred.shape[0]
idx = bn.argpartition(-X_pred, k, axis=1)
X_pred_binary = np.zeros_like(X_pred, dtype=bool)
X_pred_binary[np.arange(batch_users)[:, np.newaxis], idx[:, :k]] = True
X_true_binary = (heldout_batch > 0).toarray()
tmp = (np.logical_and(X_true_binary, X_pred_binary).sum(axis=1)).astype(
np.float32)
recall = tmp / np.minimum(k, X_true_binary.sum(axis=1))
return recall
```
### Load the test data and compute test metrics
```
test_data_tr, test_data_te = load_tr_te_data(
os.path.join(pro_dir, 'test_tr.csv'),
os.path.join(pro_dir, 'test_te.csv'))
N_test = test_data_tr.shape[0]
idxlist_test = range(N_test)
batch_size_test = 2000
n100_list, r20_list, r50_list = [], [], []
for bnum, st_idx in enumerate(range(0, N_test, batch_size_test)):
end_idx = min(st_idx + batch_size_test, N_test)
X = test_data_tr[idxlist_test[st_idx:end_idx]]
#if sparse.isspmatrix(X):
# X = X.toarray()
#X = X.astype('float32')
pred_val = np.array(X.dot(BBsparse).todense())
# exclude examples from training and validation (if any)
pred_val[X.nonzero()] = -np.inf
n100_list.append(NDCG_binary_at_k_batch(pred_val, test_data_te[idxlist_test[st_idx:end_idx]], k=100))
r20_list.append(Recall_at_k_batch(pred_val, test_data_te[idxlist_test[st_idx:end_idx]], k=20))
r50_list.append(Recall_at_k_batch(pred_val, test_data_te[idxlist_test[st_idx:end_idx]], k=50))
n100_list = np.concatenate(n100_list)
r20_list = np.concatenate(r20_list)
r50_list = np.concatenate(r50_list)
print("Test NDCG@100=%.5f (%.5f)" % (np.mean(n100_list), np.std(n100_list) / np.sqrt(len(n100_list))))
print("Test Recall@20=%.5f (%.5f)" % (np.mean(r20_list), np.std(r20_list) / np.sqrt(len(r20_list))))
print("Test Recall@50=%.5f (%.5f)" % (np.mean(r50_list), np.std(r50_list) / np.sqrt(len(r50_list))))
```
... accuracy of the sparse approximation (with sparsity 0.1% and parameter r=0.5)
| true |
code
| 0.214691 | null | null | null | null |
|
```
import panel as pn
pn.extension()
```
One of the main design goals for Panel was that it should make it possible to seamlessly transition back and forth between interactively prototyping a dashboard in the notebook or on the commandline to deploying it as a standalone server app. This section shows how to display panels interactively, embed static output, save a snapshot, and deploy as a separate web-server app.
## Configuring output
As you may have noticed, almost all the Panel documentation is written using notebooks. Panel objects display themselves automatically in a notebook and take advantage of Jupyter Comms to support communication between the rendered app and the Jupyter kernel that backs it on the Python end. To display a Panel object in the notebook is as simple as putting it on the end of a cell. Note, however, that the ``panel.extension`` first has to be loaded to initialize the required JavaScript in the notebook context. Also, if you are working in JupyterLab, the pyviz labextension has to be installed with:
jupyter labextension install @pyviz/jupyterlab_pyviz
### Optional dependencies
Also remember that in order to use certain components such as Vega, LaTeX, and Plotly plots in a notebook, the models must be loaded using the extension. If you forget to load the extension, you should get a warning reminding you to do it. To load certain JS components, simply list them as part of the call to ``pn.extension``:
pn.extension('vega', 'katex')
Here we've ensured that the Vega and LaTeX JS dependencies will be loaded.
### Initializing JS and CSS
Additionally, any external ``css_files``, ``js_files`` and ``raw_css`` needed should be declared in the extension. The ``js_files`` should be declared as a dictionary mapping from the exported JS module name to the URL containing the JS components, while the ``css_files`` can be defined as a list:
pn.extension(js_files={'deck': https://unpkg.com/deck.gl@~5.2.0/deckgl.min.js},
css_files=['https://api.tiles.mapbox.com/mapbox-gl-js/v0.44.1/mapbox-gl.css'])
The ``raw_css`` argument allows defining a list of strings containing CSS to publish as part of the notebook and app.
Providing keyword arguments via the ``extension`` is the same as setting them on ``pn.config``, which is the preferred approach outside the notebook. ``js_files`` and ``css_files`` may be set to your chosen values as follows:
pn.config.js_files = {'deck': 'https://unpkg.com/deck.gl@~5.2.0/deckgl.min.js'}
pn.config.css_files = ['https://api.tiles.mapbox.com/mapbox-gl-js/v0.44.1/mapbox-gl.css']
## Display in the notebook
#### The repr
Once the extension is loaded, Panel objects will display themselves if placed at the end of cell in the notebook:
```
pane = pn.panel('<marquee>Here is some custom HTML</marquee>')
pane
```
To instead see a textual representation of the component, you can use the ``pprint`` method on any Panel object:
```
pane.pprint()
```
#### The ``display`` function
To avoid having to put a Panel on the last line of a notebook cell, e.g. to display it from inside a function call, you can use the IPython built-in ``display`` function:
```
def display_marquee(text):
display(pn.panel('<marquee>{text}</marquee>'.format(text=text)))
display_marquee('This Panel was displayed from within a function')
```
#### Inline apps
Lastly it is also possible to display a Panel object as a Bokeh server app inside the notebook. To do so call the ``.app`` method on the Panel object and provide the URL of your notebook server:
```
pane.app('localhost:8888')
```
The app will now run on a Bokeh server instance separate from the Jupyter notebook kernel, allowing you to quickly test that all the functionality of your app works both in a notebook and in a server context.
## Display in the Python REPL
Working from the command line will not automatically display rich representations inline as in a notebook, but you can still interact with your Panel components if you start a Bokeh server instance and open a separate browser window using the ``show`` method. The method has the following arguments:
port: int (optional)
Allows specifying a specific port (default=0 chooses an arbitrary open port)
websocket_origin: str or list(str) (optional)
A list of hosts that can connect to the websocket.
This is typically required when embedding a server app in
an external-facing web site.
If None, "localhost" is used.
threaded: boolean (optional, default=False)
Whether to launch the Server on a separate thread, allowing
interactive use.
To work with an app completely interactively you can set ``threaded=True`,` which will launch the server on a separate thread and let you interactively play with the app.
<img src='https://assets.holoviews.org/panel/gifs/commandline_show.gif'></img>
The ``show`` call will return either a Bokeh server instance (if ``threaded=False``) or a ``StoppableThread`` instance (if ``threaded=True``) which both provide a ``stop`` method to stop the server instance.
## Launching a server on the commandline
Once the app is ready for deployment it can be served using the Bokeh server. For a detailed breakdown of the design and functionality of Bokeh server, see the [Bokeh documentation](https://bokeh.pydata.org/en/latest/docs/user_guide/server.html). The most important thing to know is that Panel (and Bokeh) provide a CLI command to serve a Python script, app directory, or Jupyter notebook containing a Bokeh or Panel app. To launch a server using the CLI, simply run:
panel serve app.ipynb
The ``panel serve`` command has the following options:
positional arguments:
DIRECTORY-OR-SCRIPT The app directories or scripts or notebooks to serve
(serve empty document if not specified)
optional arguments:
-h, --help show this help message and exit
--port PORT Port to listen on
--address ADDRESS Address to listen on
--log-level LOG-LEVEL
One of: trace, debug, info, warning, error or critical
--log-format LOG-FORMAT
A standard Python logging format string (default:
'%(asctime)s %(message)s')
--log-file LOG-FILE A filename to write logs to, or None to write to the
standard stream (default: None)
--args ... Any command line arguments remaining are passed on to
the application handler
--show Open server app(s) in a browser
--allow-websocket-origin HOST[:PORT]
Public hostnames which may connect to the Bokeh
websocket
--prefix PREFIX URL prefix for Bokeh server URLs
--keep-alive MILLISECONDS
How often to send a keep-alive ping to clients, 0 to
disable.
--check-unused-sessions MILLISECONDS
How often to check for unused sessions
--unused-session-lifetime MILLISECONDS
How long unused sessions last
--stats-log-frequency MILLISECONDS
How often to log stats
--mem-log-frequency MILLISECONDS
How often to log memory usage information
--use-xheaders Prefer X-headers for IP/protocol information
--session-ids MODE One of: unsigned, signed, or external-signed
--index INDEX Path to a template to use for the site index
--disable-index Do not use the default index on the root path
--disable-index-redirect
Do not redirect to running app from root path
--num-procs N Number of worker processes for an app. Using 0 will
autodetect number of cores (defaults to 1)
--websocket-max-message-size BYTES
Set the Tornado websocket_max_message_size value
(defaults to 20MB) NOTE: This setting has effect ONLY
for Tornado>=4.5
--dev [FILES-TO-WATCH [FILES-TO-WATCH ...]]
Enable live reloading during app development.By
default it watches all *.py *.html *.css *.yaml
filesin the app directory tree. Additional files can
be passedas arguments. NOTE: This setting only works
with a single app.It also restricts the number of
processes to 1.
To turn a notebook into a deployable app simply append ``.servable()`` to one or more Panel objects, which will add the app to Bokeh's ``curdoc``, ensuring it can be discovered by Bokeh server on deployment. In this way it is trivial to build dashboards that can be used interactively in a notebook and then seamlessly deployed on Bokeh server.
### Accessing session state
Whenever a Panel app is being served the ``panel.state`` object exposes some of the internal Bokeh server components to a user.
#### Document
The current Bokeh ``Document`` can be accessed using ``panel.state.curdoc``.
#### Request arguments
When a browser makes a request to a Bokeh server a session is created for the Panel application. The request arguments are made available to be accessed on ``pn.state.session_args``. For example if your application is hosted at ``localhost:8001/app``, appending ``?phase=0.5`` to the URL will allow you to access the phase variable using the following code:
```python
try:
phase = int(pn.state.session_args.get('phase')[0])
except:
phase = 1
```
This mechanism may be used to modify the behavior of an app dependending on parameters provided in the URL.
### Accessing the Bokeh model
Since Panel is built on top of Bokeh, all Panel objects can easily be converted to a Bokeh model. The ``get_root`` method returns a model representing the contents of a Panel:
```
pn.Column('# Some markdown').get_root()
```
By default this model will be associated with Bokeh's ``curdoc()``, so if you want to associate the model with some other ``Document`` ensure you supply it explictly as the first argument.
## Embedding
Panel generally relies on either the Jupyter kernel or a Bokeh Server to be running in the background to provide interactive behavior. However for simple apps with a limited amount of state it is also possible to `embed` all the widget state, allowing the app to be used entirely from within Javascript. To demonstrate this we will create a simple app which simply takes a slider value, multiplies it by 5 and then display the result.
```
slider = pn.widgets.IntSlider(start=0, end=10)
@pn.depends(slider.param.value)
def callback(value):
return '%d * 5 = %d' % (value, value*5)
row = pn.Row(slider, callback)
```
If we displayed this the normal way it would call back into Python every time the value changed. However, the `.embed()` method will record the state of the app for the different widget configurations.
```
row.embed()
```
If you try the widget above you will note that it only has 3 different states, 0, 5 and 10. This is because by default embed will try to limit the number of options of non-discrete or semi-discrete widgets to at most three values. This can be controlled using the `max_opts` argument to the embed method. The full set of options for the embed method include:
- **max_states**: The maximum number of states to embed
- **max_opts**: The maximum number of states for a single widget
- **json** (default=True): Whether to export the data to json files
- **save_path** (default='./'): The path to save json files to
- **load_path** (default=None): The path or URL the json files will be loaded from (same as ``save_path`` if not specified)
As you might imagine if there are multiple widgets there can quickly be a combinatorial explosion of states so by default the output is limited to about 1000 states. For larger apps the states can also be exported to json files, e.g. if you want to serve the app on a website specify the ``save_path`` to declare where it will be stored and the ``load_path`` to declare where the JS code running on the website will look for the files.
## Saving
In case you don't need an actual server or simply want to export a static snapshot of a panel app, you can use the ``save`` method, which allows exporting the app to a standalone HTML or PNG file.
By default, the HTML file generated will depend on loading JavaScript code for BokehJS from the online ``CDN`` repository, to reduce the file size. If you need to work in an airgapped or no-network environment, you can declare that ``INLINE`` resources should be used instead of ``CDN``:
```python
from bokeh.resources import INLINE
panel.save('test.html', resources=INLINE)
```
Additionally the save method also allows enabling the `embed` option, which, as explained above, will embed the apps state in the app or save the state to json files which you can ship alongside the exported HTML.
Finally, if a 'png' file extension is specified, the exported plot will be rendered as a PNG, which currently requires Selenium and PhantomJS to be installed:
```python
pane.save('test.png')
```
| true |
code
| 0.343232 | null | null | null | null |
|
# Bias Reduction
Climate models can have biases towards different references. Commonly, biases are reduced by postprocessing before verification of forecasting skill. `climpred` provides convenience functions to do so.
```
import climpred
import xarray as xr
import matplotlib.pyplot as plt
from climpred import HindcastEnsemble
hind = climpred.tutorial.load_dataset('CESM-DP-SST') # CESM-DPLE hindcast ensemble output.
obs = climpred.tutorial.load_dataset('ERSST') # ERSST observations.
recon = climpred.tutorial.load_dataset('FOSI-SST') # Reconstruction simulation that initialized CESM-DPLE.
hind["lead"].attrs["units"] = "years"
v='SST'
alignment='same_verif'
hindcast = HindcastEnsemble(hind)
# choose one observation
hindcast = hindcast.add_observations(recon)
#hindcast = hindcast.add_observations(obs, 'ERSST') # fits hind better than reconstruction
# always only subtract a PredictionEnsemble from another PredictionEnsemble if you handle time and init at the same time
# compute anomaly with respect to 1964-2014
hindcast = hindcast - hindcast.sel(time=slice('1964', '2014')).mean('time').sel(init=slice('1964', '2014')).mean('init')
hindcast.plot()
```
The warming of the `reconstruction` is less than the `initialized`.
## Mean bias reduction
Typically, bias depends on lead-time and therefore should therefore also be removed depending on lead-time.
```
# build bias_metric by hand
from climpred.metrics import Metric
def bias_func(a,b,**kwargs):
return a-b
bias_metric = Metric('bias', bias_func, True, False,1)
bias = hindcast.verify(metric=bias_metric, comparison='e2r', dim='init', alignment=alignment).squeeze()
# equals using the pre-defined (unconditional) bias metric applied to over dimension member
xr.testing.assert_allclose(bias, hindcast.verify(metric='unconditional_bias', comparison='m2r',dim='member', alignment=alignment).squeeze())
bias[v].plot()
```
- against Reconstruction: Cold bias in early years and warm bias in later years.
- against ERSST: Overall cold bias.
### cross validatation
```
from climpred.bias_reduction import _mean_bias_reduction_quick, _mean_bias_reduction_cross_validate
_mean_bias_reduction_quick??
_mean_bias_reduction_cross_validate??
```
`climpred` wraps these functions in `HindcastEnsemble.reduce_bias(how='mean', cross_validate={bool})`.
```
hindcast.reduce_bias(how='mean', cross_validate=True, alignment=alignment).plot()
plt.title('hindcast lead timeseries reduced for unconditional mean bias')
plt.show()
```
## Skill
Distance-based accuracy metrics like (`mse`,`rmse`,`nrmse`,...) are sensitive to mean bias reduction. Correlations like (`pearson_r`, `spearman_r`) are insensitive to bias correction.
```
metric='rmse'
hindcast.verify(metric=metric, comparison='e2o', dim='init', alignment=alignment)[v].plot(label='no bias correction')
hindcast.reduce_bias(cross_validate=False, alignment=alignment).verify(metric=metric, comparison='e2o', dim='init', alignment=alignment)[v].plot(label='bias correction without cross validation')
hindcast.reduce_bias(cross_validate=True, alignment=alignment).verify(metric=metric, comparison='e2o', dim='init', alignment=alignment)[v].plot(label='formally correct bias correction with cross validation')
plt.legend()
plt.title(f"{metric} {v} evaluated against {list(hindcast._datasets['observations'].keys())[0]}")
plt.show()
```
| true |
code
| 0.722068 | null | null | null | null |
|
# Using `bw2landbalancer`
Notebook showing typical usage of `bw2landbalancer`
## Generating the samples
`bw2landbalancer` works with Brightway2. You only need set as current a project in which the database for which you want to balance land transformation exchanges is imported.
```
import brightway2 as bw
import numpy as np
bw.projects.set_current('ei36cutoff') # Project with ecoinvent 3.6 cut-off by classification already imported
```
The only Class you need is the `DatabaseLandBalancer`:
```
from bw2landbalancer import DatabaseLandBalancer
```
Instantiating the DatabaseLandBalancer will automatically identify land transformation biosphere activities (elementary flows).
```
dlb = DatabaseLandBalancer(
database_name="ei36_cutoff", #name the LCI db in the brightway2 project
)
```
Generating presamples for the whole database is a lengthy process. Thankfully, it only ever needs to be done once per database:
```
dlb.add_samples_for_all_acts(iterations=1000)
```
The samples and associated indices are stored as attributes:
```
dlb.matrix_samples
dlb.matrix_samples.shape
dlb.matrix_indices[0:10] # First ten indices
len(dlb.matrix_indices)
```
These can directly be used to generate [`presamples`](https://presamples.readthedocs.io/):
```
presamples_id, presamples_fp = dlb.create_presamples(
name=None, #Could have specified a string as name, not passing anything will use automatically generated random name
dirpath=None, #Could have specified a directory path to save presamples somewhere specific
id_=None, #Could have specified a string as id, not passing anything will use automatically generated random id
seed='sequential', #or None, or int.
)
```
## Using the samples
The samples are formatted for use in brighway2 via the presamples package.
The following function calculates:
- Deterministic results, using `bw.LCA`
- Stochastic results, using `bw.MonteCarloLCA`
- Stochastic results using presamples, using `bw.MonteCarloLCA` and passing `presamples=[presamples_fp]`
The ratio of stochastic results to deterministic results are then plotted for Monte Carlo results with and without presamples.
Ratios for Monte Carlo with presamples are on the order of 1.
Ratios for Monte Carlo without presamples can be multiple orders of magnitude, and can be negative or positive.
```
def check_presamples_act(act_key, ps_fp, lcia_method, iterations=1000):
"""Plot histrograms of Monte Carlo samples/det result for case w/ and w/o presamples"""
lca = bw.LCA({act_key:1}, method=m)
lca.lci()
lca.lcia()
mc_arr_wo = np.empty(shape=iterations)
mc = bw.MonteCarloLCA({act_key:1}, method=m)
for i in range(iterations):
mc_arr_wo[i] = next(mc)/lca.score
mc_arr_w = np.empty(shape=iterations)
mc_w = bw.MonteCarloLCA({act_key:1}, method=m, presamples=[ps_fp])
for i in range(iterations):
mc_arr_w[i] = next(mc_w)/lca.score
plt.hist(mc_arr_wo, histtype="step", color='orange', label="without presamples")
plt.hist(mc_arr_w, histtype="step", color='green', label="with presamples")
plt.legend()
```
Let's run this on a couple of random ecoinvent products with the ImpactWorld+ Land transformation, biodiversity LCIA method:
```
m=('IMPACTWorld+ (Default_Recommended_Midpoint 1.23)', 'Midpoint', 'Land transformation, biodiversity')
import matplotlib.pyplot as plt
%matplotlib inline
act = [act for act in bw.Database('ei36_cutoff') if act['name']=='polyester-complexed starch biopolymer production'][0]
print("Working on activity known to have non-negligeable land transformation impacts: ", act)
check_presamples_act(act.key, presamples_fp, m)
act = bw.Database('ei36_cutoff').random()
print("Randomly working on ", act)
check_presamples_act(act.key, presamples_fp, m)
act = bw.Database('ei36_cutoff').random()
print("Randomly working on ", act)
check_presamples_act(act.key, presamples_fp, m)
act = bw.Database('ei36_cutoff').random()
print("Randomly working on ", act)
check_presamples_act(act.key, presamples_fp, m)
act = bw.Database('ei36_cutoff').random()
print("Randomly working on ", act)
check_presamples_act(act.key, presamples_fp, m)
```
| true |
code
| 0.600247 | null | null | null | null |
|
# Fraud_Detection_Using_ADASYN_OVERSAMPLING
I am able to achieve the following accuracies in the validation data. These results can be further improved by reducing the
parameter, number of frauds used to create features from category items. I have used a threshold of 100.
* Logistic Regression :
Validation Accuracy: 70.0%, ROC_AUC_Score: 70.0%
* Random Forest :
Validation Accuracy: 98.9%, ROC_AUC_Score: 98.9%
* Linear Support Vector Machine :
Validation Accuracy: 51.0%, ROC_AUC_Score: 51.1%
* K Nearest Neighbors :
Validation Accuracy: 86.7%, ROC_AUC_Score: 86.7%
* Extra Trees Classifer :
Validation Accuracy: 99.2%, ROC_AUC_Score: 99.2%
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression, Ridge, Lasso, ElasticNet
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
from sklearn import svm, neighbors
from sklearn.naive_bayes import GaussianNB
from imblearn.over_sampling import SMOTE, ADASYN
from sklearn.metrics import roc_auc_score
from sklearn.metrics import confusion_matrix
import itertools
% matplotlib inline
```
### Loading Training Transactions Data
```
tr_tr = pd.read_csv('data/train_transaction.csv', index_col='TransactionID')
print('Rows :', tr_tr.shape[0],' Columns : ',tr_tr.shape[1] )
tr_tr.tail()
print('Memory Usage : ', (tr_tr.memory_usage(deep=True).sum()/1024).round(0))
tr_tr.tail()
tr_id = pd.read_csv('data/train_identity.csv', index_col='TransactionID')
print(tr_id.shape)
tr_id.tail()
tr = tr_tr.join(tr_id)
tr['data']='train'
print(tr.shape)
tr.head()
del tr_tr
del tr_id
te_tr = pd.read_csv('data/test_transaction.csv', index_col='TransactionID')
print(te_tr.shape)
te_tr.tail()
te_id = pd.read_csv('data/test_identity.csv', index_col='TransactionID')
print(te_id.shape)
te_id.tail()
te = te_tr.join(te_id)
te['data']='test'
te['isFraud']=2
print(te.shape)
te.head()
del te_tr
del te_id
tr.isFraud.describe()
tr.isFraud.value_counts().plot(kind='bar')
tr.isFraud.value_counts()
f, (ax1, ax2) = plt.subplots(2, 1, sharex=True, figsize=(12,4))
ax1.hist(tr.TransactionAmt[tr.isFraud == 1], bins = 10)
ax1.set_title('Fraud Transactions ='+str(tr.isFraud.value_counts()[1]))
ax2.hist(tr.TransactionAmt[tr.isFraud == 0], bins = 10)
ax2.set_title('Normal Transactions ='+str(tr.isFraud.value_counts()[0]))
plt.xlabel('Amount ($)')
plt.ylabel('Number of Transactions')
plt.yscale('log')
plt.show()
sns.distplot(tr['TransactionAmt'], color='red')
sns.pairplot(tr[['TransactionAmt','isFraud']], hue='isFraud')
df = pd.concat([tr,te], sort=False)
print(df.shape)
df.head()
del tr
del te
```
### Make new category for items in Objects with A Fraud Count of more than 100
```
fraud_threshold = 100
def map_categories(*args):
columns = [col for col in args]
for column in columns:
if column == index:
return 1
else:
return 0
new_categories = []
for i in df.columns:
if i != 'data':
if df[i].dtypes == str('object'):
fraud_count = df[df.isFraud==1][i].value_counts(dropna=False)
for index, value in fraud_count.items():
if value>fraud_threshold:
df[(str(i)+'_'+str(index))]=list(map(map_categories, df[i]))
new_categories.append((str(i)+'_'+str(index)))
# else:
# tr[(str(i)+'_'+str('other'))]=list(map(map_categories, tr[i]))
# new_tr_categories.append((str(i)+'_'+str('other')))
df.drop([i], axis=1, inplace=True)
print(new_categories)
print(df.shape)
df.head()
df.isna().any().mean()
df.fillna(0, inplace=True)
df.isna().any().mean()
X = df[df['data'] == 'train'].drop(['isFraud','data'], axis=1)
y = df[df['data'] == 'train']['isFraud']
X_predict = df[df['data'] == 'test'].drop(['isFraud','data'], axis=1)
print(X.shape, y.shape, X_predict.shape)
```
### Oversampling using ADASYN
```
ada = ADASYN(random_state=91)
X_sampled,y_sampled = ada.fit_sample(X,y)
#fraudlent records in original data
y.value_counts()
#fraudlent records in oversampled data is is almost equal to normal data
np.bincount(y_sampled)
X_train, X_test, y_train, y_test = train_test_split(X_sampled,y_sampled,test_size=0.3)
class_names = ['FRAUD', 'NORMAL']
def plot_confusion_matrix(cm, classes,normalize=False,title='Confusion matrix',cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.ylabel('Ground Truth')
plt.xlabel('Predicted label')
plt.tight_layout()
plt.show()
```
### Logistic Regression
```
lr = LogisticRegression(solver='lbfgs')
clf_lr = lr.fit(X_train, y_train)
confidence_lr=clf_lr.score(X_test, y_test)
print('Accuracy on Validation Data : ', confidence_lr.round(2)*100,'%')
test_prediction = clf_lr.predict(X_test)
print('ROC_AUC_SCORE ; ', roc_auc_score(y_test, test_prediction).round(3)*100,'%')
cnf_matrix = confusion_matrix(y_test, test_prediction)
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion Matrix')
prediction_lr = clf_lr.predict(X_predict)
test = df[df['data'] == 'test']
del df
test['prediction_lr'] = prediction_lr
test.prediction_lr.value_counts()
test.prediction_lr.to_csv('adLogistic_Regression_Prediction.csv')
```
### Random Forest
```
rfor=RandomForestClassifier()
clf_rfor = rfor.fit(X_train, y_train)
confidence_rfor=clf_rfor.score(X_test, y_test)
print('Accuracy on Validation Data : ', confidence_rfor.round(3)*100,'%')
test_prediction = clf_rfor.predict(X_test)
print('ROC_AUC_SCORE ; ', roc_auc_score(y_test, test_prediction).round(3)*100,'%')
cnf_matrix = confusion_matrix(y_test, test_prediction)
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion Matrix')
prediction_rfor = clf_rfor.predict(X_predict)
test['prediction_rfor'] = prediction_rfor
test.prediction_rfor.value_counts()
test.prediction_rfor.to_csv('adRandom_Forest_Prediction.csv')
```
### Linear Support Vector Machine Algorithm
```
lsvc=svm.LinearSVC()
clf_lsvc=lsvc.fit(X_train, y_train)
confidence_lsvc=clf_lsvc.score(X_test, y_test)
print('Accuracy on Validation Data : ', confidence_lsvc.round(3)*100,'%')
test_prediction = clf_lsvc.predict(X_test)
print('ROC_AUC_SCORE ; ', roc_auc_score(y_test, test_prediction).round(3)*100,'%')
cnf_matrix = confusion_matrix(y_test, test_prediction)
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion Matrix')
```
### K-Nearest Neighbors Algorithm
```
knn=neighbors.KNeighborsClassifier(n_neighbors=10, n_jobs=-1)
clf_knn=knn.fit(X_train, y_train)
confidence_knn=clf_knn.score(X_test, y_test)
print('Accuracy on Validation Data : ', confidence_knn.round(3)*100,'%')
test_prediction = clf_knn.predict(X_test)
print('ROC_AUC_SCORE ; ', roc_auc_score(y_test, test_prediction).round(3)*100,'%')
cnf_matrix = confusion_matrix(y_test, test_prediction)
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion Matrix')
```
### Extra Trees Classifier
```
etc=ExtraTreesClassifier()
clf_etc = etc.fit(X_train, y_train)
confidence_etc=clf_etc.score(X_test, y_test)
print('Accuracy on Validation Data : ', confidence_etc.round(3)*100,'%')
test_prediction = clf_etc.predict(X_test)
print('ROC_AUC_SCORE ; ', roc_auc_score(y_test, test_prediction).round(3)*100,'%')
cnf_matrix = confusion_matrix(y_test, test_prediction)
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion Matrix')
prediction_etc = clf_etc.predict(X_predict)
test['prediction_etc'] = prediction_etc
test.prediction_etc.value_counts()
test.prediction_etc.to_csv('adExtra_Trees_Prediction.csv')
```
| true |
code
| 0.500793 | null | null | null | null |
|
# Boston Housing Prices Classification
```
import itertools
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from dataclasses import dataclass
from sklearn import datasets
from sklearn import svm
from sklearn import tree
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import zero_one_loss
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
import graphviz
%matplotlib inline
# Matplotlib has some built in style sheets
mpl.style.use('fivethirtyeight')
```
## Data Loading
Notice that I am loading in the data in the same way that we did for our visualization module. Time to refactor? It migth be good to abstract away some of this as functions, that way we aren't copying and pasting code between all of our notebooks.
```
boston = datasets.load_boston()
# Sklearn uses a dictionary like object to hold its datasets
X = boston['data']
y = boston['target']
feature_names = list(boston.feature_names)
X_df = pd.DataFrame(X)
X_df.columns = boston.feature_names
X_df["PRICE"] = y
X_df.describe()
def create_classes(data):
"""Create our classes using thresholds
This is used as an `apply` function for
every row in `data`.
Args:
data: pandas dataframe
"""
if data["PRICE"] < 16.:
return 0
elif data["PRICE"] >= 16. and data["PRICE"] < 22.:
return 1
else:
return 2
y = X_df.apply(create_classes, axis=1)
# Get stats for plotting
classes, counts = np.unique(y, return_counts=True)
plt.figure(figsize=(20, 10))
plt.bar(classes, counts)
plt.xlabel("Label")
plt.ylabel(r"Number of Samples")
plt.suptitle("Distribution of Classes")
plt.show()
```
## Support Vector Machine
```
def make_meshgrid(x, y, h=.02):
"""Create a mesh of points to plot in
Args:
x: data to base x-axis meshgrid on
y: data to base y-axis meshgrid on
h: stepsize for meshgrid, optional
Returns:
xx, yy : ndarray
"""
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
"""Plot the decision boundaries for a classifier.
Args:
ax: matplotlib axes object
clf: a classifier
xx: meshgrid ndarray
yy: meshgrid ndarray
params: dictionary of params to pass to contourf, optional
"""
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
# Careful, `loc` uses inclusive bounds!
X_smol = X_df.loc[:99, ['LSTAT', 'PRICE']].values
y_smol = y[:100]
C = 1.0 # SVM regularization parameter
models = [
svm.SVC(kernel='linear', C=C),
svm.LinearSVC(C=C, max_iter=10000),
svm.SVC(kernel='rbf', gamma=0.7, C=C),
svm.SVC(kernel='poly', degree=3, gamma='auto', C=C)
]
models = [clf.fit(X_smol, y_smol) for clf in models]
# title for the plots
titles = [
'SVC with linear kernel',
'LinearSVC (linear kernel)',
'SVC with RBF kernel',
'SVC with polynomial (degree 3) kernel'
]
# Set-up 2x2 grid for plotting.
fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(15, 15))
plt.subplots_adjust(wspace=0.4, hspace=0.4)
X0, X1 = X_smol[:, 0], X_smol[:, 1]
xx, yy = make_meshgrid(X0, X1)
for clf, title, ax in zip(models, titles, axs.flatten()):
plot_contours(
ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8
)
ax.scatter(
X0, X1, c=y_smol, cmap=plt.cm.coolwarm, s=20, edgecolors='k'
)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xlabel('LSTAT')
ax.set_ylabel('PRICE')
ax.set_title(title)
plt.show()
```
## Modeling with Trees and Ensembles of Trees
```
@dataclass
class Hparams:
"""Hyperparameters for our models"""
max_depth: int = 2
min_samples_leaf: int = 1
n_estimators: int = 400
learning_rate: float = 1.0
hparams = Hparams()
# Keeping price in there is cheating
#X_df = X_df.drop("PRICE", axis=1)
x_train, x_test, y_train, y_test = train_test_split(
X_df, y, test_size=0.33, random_state=42
)
dt_stump = DecisionTreeClassifier(
max_depth=hparams.max_depth,
min_samples_leaf=hparams.min_samples_leaf
)
dt_stump.fit(x_train, y_train)
dt_stump_err = 1.0 - dt_stump.score(x_test, y_test)
class_names = ['0', '1', '2']
dot_data = tree.export_graphviz(dt_stump, out_file=None,
feature_names=boston.feature_names,
class_names=class_names,
filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph
# Adding greater depth to the tree
dt = DecisionTreeClassifier(
max_depth=9, # No longer using Hparams here!
min_samples_leaf=hparams.min_samples_leaf
)
dt.fit(x_train, y_train)
dt_err = 1.0 - dt.score(x_test, y_test)
```
### A Deeper Tree
```
class_names = ['0', '1', '2']
dot_data = tree.export_graphviz(dt, out_file=None,
feature_names=boston.feature_names,
class_names=class_names,
filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph#.render("decision_tree_boston")
```
## Adaboost
An AdaBoost classifier is a meta-estimator that begins by fitting a classifier on the original dataset and then fits additional copies of the classifier on the same dataset but where the weights of incorrectly classified instances are adjusted such that subsequent classifiers focus more on difficult cases.
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.AdaBoostClassifier.html
```
ada_discrete = AdaBoostClassifier(
base_estimator=dt_stump,
learning_rate=hparams.learning_rate,
n_estimators=hparams.n_estimators,
algorithm="SAMME"
)
ada_discrete.fit(x_train, y_train)
# Notice the `algorithm` is different here.
# This is just one parameter change, but it
# makes a world of difference! Read the docs!
ada_real = AdaBoostClassifier(
base_estimator=dt_stump,
learning_rate=hparams.learning_rate,
n_estimators=hparams.n_estimators,
algorithm="SAMME.R" # <- take note!
)
ada_real.fit(x_train, y_train)
def misclassification_rate_by_ensemble_size(model, n_estimators, data, labels):
"""Get the fraction of misclassifications per ensemble size
As we increase the number of trees in the ensemble,
we often find that the performance of our model changes.
This shows us how our misclassification rate changes as
we increase the number of members in our ensemble up to
`n_estimators`
Args:
model: ensembe model that has a `staged_predict` method
n_estimators: number of models in the ensemble
data: data to be predicted over
labels: labels for the dataset
Returns:
misclassification_rate: numpy array of shape (n_estimators,)
This is the fraction of misclassifications for the `i_{th}`
number of estimators
"""
misclassification_rate = np.zeros((n_estimators,))
for i, y_pred in enumerate(model.staged_predict(data)):
# zero_one_loss returns the fraction of misclassifications
misclassification_rate[i] = zero_one_loss(y_pred, labels)
return misclassification_rate
# Get the misclassification rates for each algo on each data split
ada_discrete_err_train = misclassification_rate_by_ensemble_size(
ada_discrete, hparams.n_estimators, x_train, y_train
)
ada_discrete_err_test = misclassification_rate_by_ensemble_size(
ada_discrete, hparams.n_estimators, x_test, y_test
)
ada_real_err_train = misclassification_rate_by_ensemble_size(
ada_real, hparams.n_estimators, x_train, y_train
)
ada_real_err_test = misclassification_rate_by_ensemble_size(
ada_real, hparams.n_estimators, x_test, y_test
)
fig = plt.figure(figsize=(20,10))
ax = fig.add_subplot(111)
ax.plot([1, hparams.n_estimators], [dt_stump_err] * 2, 'k-',
label='Decision Stump Error')
ax.plot([1, hparams.n_estimators], [dt_err] * 2, 'k--',
label='Decision Tree Error')
ax.plot(np.arange(hparams.n_estimators) + 1, ada_discrete_err_test,
label='Discrete AdaBoost Test Error',
color='red')
ax.plot(np.arange(hparams.n_estimators) + 1, ada_discrete_err_train,
label='Discrete AdaBoost Train Error',
color='blue')
ax.plot(np.arange(hparams.n_estimators) + 1, ada_real_err_test,
label='Real AdaBoost Test Error',
color='orange')
ax.plot(np.arange(hparams.n_estimators) + 1, ada_real_err_train,
label='Real AdaBoost Train Error',
color='green')
ax.set_ylim((0.0, 0.5))
ax.set_xlabel('n_estimators')
ax.set_ylabel('error rate')
leg = ax.legend(loc='upper right', fancybox=True)
leg.get_frame().set_alpha(0.7)
```
## Classification Performance
How well are our classifiers doing?
```
def plot_confusion_matrix(confusion, classes, normalize=False, cmap=plt.cm.Reds):
"""Plot a confusion matrix
"""
mpl.style.use('seaborn-ticks')
fig = plt.figure(figsize=(20,10))
plt.imshow(confusion, interpolation='nearest', cmap=cmap)
plt.title("Confusion Matrix")
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = confusion.max() / 2.
for i, j in itertools.product(range(confusion.shape[0]), range(confusion.shape[1])):
plt.text(
j, i, format(confusion[i, j], fmt),
horizontalalignment="center",
color="white" if confusion[i, j] > thresh else "black"
)
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
ada_discrete_preds_test = ada_discrete.predict(x_test)
ada_real_preds_test = ada_real.predict(x_test)
```
### Accuracy
```
ada_discrete_acc = accuracy_score(y_test, ada_discrete_preds_test)
ada_real_acc = accuracy_score(y_test, ada_real_preds_test)
print(f"Adaboost discrete accuarcy: {ada_discrete_acc:.3f}")
print(f"Adaboost real accuarcy: {ada_discrete_acc:.3f}")
```
### Confusion Matrix
Accuracy, however is an overall summary. To see where our models are predicting correctly and how they could be predicting incorrectly, we can use a `confusion matrix`.
```
ada_discrete_confusion = confusion_matrix(y_test, ada_discrete_preds_test)
ada_real_confusion = confusion_matrix(y_test, ada_real_preds_test)
plot_confusion_matrix(ada_discrete_confusion, classes)
plot_confusion_matrix(ada_real_confusion, classes)
```
| true |
code
| 0.793666 | null | null | null | null |
|
[](http://rpi.analyticsdojo.com)
<center><h1>Intro to Tensorflow - MINST</h1></center>
<center><h3><a href = 'http://rpi.analyticsdojo.com'>rpi.analyticsdojo.com</a></h3></center>
[](https://colab.research.google.com/github/rpi-techfundamentals/fall2018-materials/blob/master/10-deep-learning/06-tensorflow-minst.ipynb)
Adopted from [Hands-On Machine Learning with Scikit-Learn and TensorFlow by Aurélien Géron](https://github.com/ageron/handson-ml).
Apache License
Version 2.0, January 2004
http://www.apache.org/licenses/
TERMS AND CONDITIONS FOR USE, REPRODUCTION, AND DISTRIBUTION
[For full license see repository.](https://github.com/ageron/handson-ml/blob/master/LICENSE)
**Chapter 10 – Introduction to Artificial Neural Networks**
_This notebook contains all the sample code and solutions to the exercices in chapter 10._
# Setup
First, let's make sure this notebook works well in both python 2 and 3, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
```
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
def reset_graph(seed=42):
tf.reset_default_graph()
tf.set_random_seed(seed)
np.random.seed(seed)
# To plot pretty figures
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# Where to save the figures
PROJECT_ROOT_DIR = "/home/jovyan/techfundamentals-fall2017-materials/classes/13-deep-learning"
def save_fig(fig_id, tight_layout=True):
path = os.path.join(PROJECT_ROOT_DIR, 'images', fig_id + ".png")
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
```
### MNIST
- Very common machine learning library with goal to classify digits.
- This example is using MNIST handwritten digits, which contains 55,000 examples for training and 10,000 examples for testing. The digits have been size-normalized and centered in a fixed-size image (28x28 pixels) with values from 0 to 1. For simplicity, each image has been flattened and converted to a 1-D numpy array of 784 features (28*28).

More info: http://yann.lecun.com/exdb/mnist/
```
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/")
X_train = mnist.train.images
X_test = mnist.test.images
y_train = mnist.train.labels.astype("int")
y_test = mnist.test.labels.astype("int")
print ("Training set: ", X_train.shape,"\nTest set: ", X_test.shape)
# List a few images and print the data to get a feel for it.
images = 2
for i in range(images):
#Reshape
x=np.reshape(X_train[i], [28, 28])
print(x)
plt.imshow(x, cmap=plt.get_cmap('gray_r'))
plt.show()
# print("Model prediction:", preds[i])
```
## TFLearn: Deep learning library featuring a higher-level API for TensorFlow
- TFlearn is a modular and transparent deep learning library built on top of Tensorflow.
- It was designed to provide a higher-level API to TensorFlow in order to facilitate and speed-up experimentations
- Fully transparent and compatible with Tensorflow
- [DNN classifier](https://www.tensorflow.org/api_docs/python/tf/contrib/learn/DNNClassifier)
- `hidden_units` list of hidden units per layer. All layers are fully connected. Ex. [64, 32] means first layer has 64 nodes and second one has 32.
- [Scikit learn wrapper for TensorFlow Learn Estimator](https://www.tensorflow.org/api_docs/python/tf/contrib/learn/SKCompat)
- See [tflearn documentation](http://tflearn.org/).
```
import tensorflow as tf
config = tf.contrib.learn.RunConfig(tf_random_seed=42) # not shown in the config
feature_cols = tf.contrib.learn.infer_real_valued_columns_from_input(X_train)
# List of hidden units per layer. All layers are fully connected. Ex. [64, 32] means first layer has 64 nodes and second one has 32.
dnn_clf = tf.contrib.learn.DNNClassifier(hidden_units=[300,100], n_classes=10,
feature_columns=feature_cols, config=config)
dnn_clf = tf.contrib.learn.SKCompat(dnn_clf) # if TensorFlow >= 1.1
dnn_clf.fit(X_train, y_train, batch_size=50, steps=4000)
#We can use the sklearn version of metrics
from sklearn import metrics
y_pred = dnn_clf.predict(X_test)
#This calculates the accuracy.
print("Accuracy score: ", metrics.accuracy_score(y_test, y_pred['classes']) )
#Log Loss is a way of score classes probabilsitically
print("Logloss: ",metrics.log_loss(y_test, y_pred['probabilities']))
```
### Tensorflow
- Direct access to Python API for Tensorflow will give more flexibility
- Like earlier, we will define the structure and then run the session.
- set placeholders
```
import tensorflow as tf
n_inputs = 28*28 # MNIST
n_hidden1 = 300 # hidden units in first layer.
n_hidden2 = 100
n_outputs = 10 # Classes of output variable.
#Placehoder
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
def neuron_layer(X, n_neurons, name, activation=None):
with tf.name_scope(name):
n_inputs = int(X.get_shape()[1])
stddev = 2 / np.sqrt(n_inputs)
init = tf.truncated_normal((n_inputs, n_neurons), stddev=stddev)
W = tf.Variable(init, name="kernel")
b = tf.Variable(tf.zeros([n_neurons]), name="bias")
Z = tf.matmul(X, W) + b
if activation is not None:
return activation(Z)
else:
return Z
with tf.name_scope("dnn"):
hidden1 = neuron_layer(X, n_hidden1, name="hidden1", activation=tf.nn.relu)
hidden2 = neuron_layer(hidden1, n_hidden2, name="hidden2", activation=tf.nn.relu)
logits = neuron_layer(hidden2, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
saver = tf.train.Saver()
```
### Running the Analysis over 40 Epocs
- 40 passes through entire dataset.
-
```
n_epochs = 40
batch_size = 50
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_test = accuracy.eval(feed_dict={X: mnist.test.images,
y: mnist.test.labels})
print("Epoc:", epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)
save_path = saver.save(sess, "./my_model_final.ckpt")
with tf.Session() as sess:
saver.restore(sess, "./my_model_final.ckpt") # or better, use save_path
X_new_scaled = mnist.test.images[:20]
Z = logits.eval(feed_dict={X: X_new_scaled})
y_pred = np.argmax(Z, axis=1)
print("Predicted classes:", y_pred)
print("Actual classes: ", mnist.test.labels[:20])
from IPython.display import clear_output, Image, display, HTML
def strip_consts(graph_def, max_const_size=32):
"""Strip large constant values from graph_def."""
strip_def = tf.GraphDef()
for n0 in graph_def.node:
n = strip_def.node.add()
n.MergeFrom(n0)
if n.op == 'Const':
tensor = n.attr['value'].tensor
size = len(tensor.tensor_content)
if size > max_const_size:
tensor.tensor_content = "<stripped %d bytes>"%size
return strip_def
def show_graph(graph_def, max_const_size=32):
"""Visualize TensorFlow graph."""
if hasattr(graph_def, 'as_graph_def'):
graph_def = graph_def.as_graph_def()
strip_def = strip_consts(graph_def, max_const_size=max_const_size)
code = """
<script>
function load() {{
document.getElementById("{id}").pbtxt = {data};
}}
</script>
<link rel="import" href="https://tensorboard.appspot.com/tf-graph-basic.build.html" onload=load()>
<div style="height:600px">
<tf-graph-basic id="{id}"></tf-graph-basic>
</div>
""".format(data=repr(str(strip_def)), id='graph'+str(np.random.rand()))
iframe = """
<iframe seamless style="width:1200px;height:620px;border:0" srcdoc="{}"></iframe>
""".format(code.replace('"', '"'))
display(HTML(iframe))
show_graph(tf.get_default_graph())
```
## Using `dense()` instead of `neuron_layer()`
Note: the book uses `tensorflow.contrib.layers.fully_connected()` rather than `tf.layers.dense()` (which did not exist when this chapter was written). It is now preferable to use `tf.layers.dense()`, because anything in the contrib module may change or be deleted without notice. The `dense()` function is almost identical to the `fully_connected()` function, except for a few minor differences:
* several parameters are renamed: `scope` becomes `name`, `activation_fn` becomes `activation` (and similarly the `_fn` suffix is removed from other parameters such as `normalizer_fn`), `weights_initializer` becomes `kernel_initializer`, etc.
* the default `activation` is now `None` rather than `tf.nn.relu`.
* a few more differences are presented in chapter 11.
```
n_inputs = 28*28 # MNIST
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int64, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1",
activation=tf.nn.relu)
hidden2 = tf.layers.dense(hidden1, n_hidden2, name="hidden2",
activation=tf.nn.relu)
logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_epochs = 20
n_batches = 50
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_test = accuracy.eval(feed_dict={X: mnist.test.images, y: mnist.test.labels})
print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)
save_path = saver.save(sess, "./my_model_final.ckpt")
show_graph(tf.get_default_graph())
```
| true |
code
| 0.659844 | null | null | null | null |
|
```
# Required to load webpages
from IPython.display import IFrame
```
[Table of contents](../toc.ipynb)
<img src="https://github.com/scipy/scipy/raw/master/doc/source/_static/scipyshiny_small.png" alt="Scipy" width="150" align="right">
# SciPy
* Scipy extends numpy with powerful modules in
* optimization,
* interpolation,
* linear algebra,
* fourier transformation,
* signal processing,
* image processing,
* file input output, and many more.
* Please find here the scipy reference for a complete feature list [https://docs.scipy.org/doc/scipy/reference/](https://docs.scipy.org/doc/scipy/reference/).
We will take a look at some features of scipy in the latter. Please explore the rich content of this package later on.
## Optimization
* Scipy's optimization module provides many optimization methods like least squares, gradient methods, BFGS, global optimization, and many more.
* Please find a detailed tutorial here [https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html](https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html).
* Next, we will apply one of the optimization algorithms in a simple example.
A common function to test optimization algorithms is the Rosenbrock function for $N$ variables:
$f(\boldsymbol{x}) = \sum\limits_{i=2}^N 100 \left(x_{i+1} - x_i^2\right)^2 + \left(1 - x_i^2 \right)^2$.
The optimum is at $x_i=1$, where $f(\boldsymbol{x})=0$
```
import numpy as np
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import cm
%matplotlib inline
def rosen(x):
"""The Rosenbrock function"""
return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1]**2.0)**2.0)
```
We need to generate some data in a mesh grid.
```
X = np.arange(-2, 2, 0.2)
Y = np.arange(-2, 2, 0.2)
X, Y = np.meshgrid(X, Y)
data = np.vstack([X.reshape(X.size), Y.reshape(Y.size)])
```
Let's evaluate the Rosenbrock function at the grid points.
```
Z = rosen(data)
```
And we will plot the function in a 3D plot.
```
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z.reshape(X.shape), cmap='bwr')
ax.view_init(40, 230)
```
Now, let us check that the true minimum value is at (1, 1).
```
rosen(np.array([1, 1]))
```
Finally, we will call scipy optimize and find the minimum with Nelder Mead algorithm.
```
from scipy.optimize import minimize
x0 = np.array([1.3, 0.7])
res = minimize(rosen, x0, method='nelder-mead',
options={'xatol': 1e-8, 'disp': True})
print(res.x)
```
Many more optimization examples are to find in scipy optimize tutorial [https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html](https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html).
```
IFrame(src='https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html',
width=1000, height=600)
```
## Interpolation
* Interpolation of data is very often required, for instance to replace NaNs or to fill missing values in data records.
* Scipy comes with
* 1D interpolation,
* multivariate data interpolation
* spline, and
* radial basis function interpolation.
* Please find here the link to interpolation tutorials [https://docs.scipy.org/doc/scipy/reference/tutorial/interpolate.html](https://docs.scipy.org/doc/scipy/reference/tutorial/interpolate.html).
```
from scipy.interpolate import interp1d
x = np.linspace(10, 20, 15)
y = np.sin(x) + np.cos(x**2 / 10)
f = interp1d(x, y, kind="linear")
f1 = interp1d(x, y, kind="cubic")
x_fine = np.linspace(10, 20, 200)
plt.plot(x, y, 'ko',
x_fine, f(x_fine), 'b--',
x_fine, f1(x_fine), 'r--')
plt.legend(["Data", "Linear", "Cubic"])
plt.show()
```
## Signal processing
The signal processing module is very powerful and we will have a look at its tutorial [https://docs.scipy.org/doc/scipy/reference/tutorial/signal.html](https://docs.scipy.org/doc/scipy/reference/tutorial/signal.html) for a quick overview.
```
IFrame(src='https://docs.scipy.org/doc/scipy/reference/tutorial/signal.html',
width=1000, height=600)
```
## Linear algebra
* In addition to numpy, scipy has its own linear algebra module.
* It offers more functionality than numpy's linear algebra module and is based on BLAS/LAPACK support, which makes it faster.
* The respective tutorial is here located [https://docs.scipy.org/doc/scipy/reference/tutorial/linalg.html](https://docs.scipy.org/doc/scipy/reference/tutorial/linalg.html).
```
IFrame(src='https://docs.scipy.org/doc/scipy/reference/tutorial/linalg.html',
width=1000, height=600)
```
### Total least squares as linear algebra application
<img src="ls-tls.png" alt="LS vs TLS" width="350" align="right">
We will now implement a total least squares estimator [[Markovsky2007]](../references.bib) with help of scipy's singular value decomposition (svd). The total least squares estimator provides a solution for the errors in variables problem, where model inputs and outputs are corrupted by noise.
The model becomes
$A X \approx B$, where $A \in \mathbb{R}^{m \times n}$ and $B \in \mathbb{R}^{m \times d}$ are input and output data, and $X$ is the unknown parameter vector.
More specifically, the total least squares regression becomes
$\widehat{A}X = \widehat{B}$, $\widehat{A} := A + \Delta A$, $\widehat{B} := B + \Delta B$.
The estimator can be written as pseudo code as follows.
$C = [A B] = U \Sigma V^\top$, where $U \Sigma V^\top$ is the svd of $C$.
$V:= \left[\begin{align}V_{11} &V_{12} \\
V_{21} & V_{22}\end{align}\right]$,
$\widehat{X} = -V_{12} V_{22}^{-1}$.
In Python, the implementation could be like this function.
```
from scipy import linalg
def tls(A, B):
m, n = A.shape
C = np.hstack((A, B))
U, S, V = linalg.svd(C)
V12 = V.T[0:n, n:]
V22 = V.T[n:, n:]
X = -V12 / V22
return X
```
Now we create some data where input and output are appended with noise.
```
A = np.random.rand(100, 2)
X = np.array([[3], [-7]])
B = A @ X
A += np.random.randn(100, 2) * 0.1
B += np.random.randn(100, 1) * 0.1
```
The total least squares solution becomes
```
tls(A, B)
```
And this solution is closer to correct value $X = [3 , -7]^\top$ than ordinary least squares.
```
linalg.solve((A.T @ A), (A.T @ B))
```
Finally, next function shows a "self" written least squares estimator, which uses QR decomposition and back substitution. This implementation is numerically robust in contrast to normal equations
$A ^\top A X = A^\top B$.
Please find more explanation in [[Golub2013]](../references.bib) and in section 3.11 of [[Burg2012]](../references.bib).
```
def ls(A, B):
Q, R = linalg.qr(A, mode="economic")
z = Q.T @ B
return linalg.solve_triangular(R, z)
ls(A, B)
```
## Integration
* Scipy's integration can be used for general equations as well as for ordinary differential equations.
* The integration tutorial is linked here [https://docs.scipy.org/doc/scipy/reference/tutorial/integrate.html](https://docs.scipy.org/doc/scipy/reference/tutorial/integrate.html).
### Solving a differential equation
Here, we want to use an ode solver to simulate the differential equation (ode)
$y'' + y' + 4 y = 0$.
To evaluate this second order ode, we need to convert it into a set of first order ode. The trick is to use this substitution: $x_0 = y$, $x_1 = y'$, which yields
$\begin{align}
x'_0 &= x_1 \\
x'_1 &= -4 x_0 - x_1
\end{align}$
The implementation in Python becomes.
```
def equation(t, x):
return [x[1], -4 * x[0] - x[1]]
from scipy.integrate import solve_ivp
time_span = [0, 20]
init = [1, 0]
time = np.arange(0, 20, 0.01)
sol = solve_ivp(equation, time_span, init, t_eval=time)
plt.plot(time, sol.y[0, :])
plt.plot(time, sol.y[1, :])
plt.legend(["$y$", "$y'$"])
plt.xlabel("Time")
plt.show()
```
| true |
code
| 0.694536 | null | null | null | null |
|
## Dependencies
```
import json, warnings, shutil
from tweet_utility_scripts import *
from tweet_utility_preprocess_roberta_scripts import *
from transformers import TFRobertaModel, RobertaConfig
from tokenizers import ByteLevelBPETokenizer
from tensorflow.keras.models import Model
from tensorflow.keras import optimizers, metrics, losses, layers
from tensorflow.keras.callbacks import EarlyStopping, TensorBoard, ModelCheckpoint
SEED = 0
seed_everything(SEED)
warnings.filterwarnings("ignore")
class RectifiedAdam(tf.keras.optimizers.Optimizer):
"""Variant of the Adam optimizer whose adaptive learning rate is rectified
so as to have a consistent variance.
It implements the Rectified Adam (a.k.a. RAdam) proposed by
Liyuan Liu et al. in [On The Variance Of The Adaptive Learning Rate
And Beyond](https://arxiv.org/pdf/1908.03265v1.pdf).
Example of usage:
```python
opt = tfa.optimizers.RectifiedAdam(lr=1e-3)
```
Note: `amsgrad` is not described in the original paper. Use it with
caution.
RAdam is not a placement of the heuristic warmup, the settings should be
kept if warmup has already been employed and tuned in the baseline method.
You can enable warmup by setting `total_steps` and `warmup_proportion`:
```python
opt = tfa.optimizers.RectifiedAdam(
lr=1e-3,
total_steps=10000,
warmup_proportion=0.1,
min_lr=1e-5,
)
```
In the above example, the learning rate will increase linearly
from 0 to `lr` in 1000 steps, then decrease linearly from `lr` to `min_lr`
in 9000 steps.
Lookahead, proposed by Michael R. Zhang et.al in the paper
[Lookahead Optimizer: k steps forward, 1 step back]
(https://arxiv.org/abs/1907.08610v1), can be integrated with RAdam,
which is announced by Less Wright and the new combined optimizer can also
be called "Ranger". The mechanism can be enabled by using the lookahead
wrapper. For example:
```python
radam = tfa.optimizers.RectifiedAdam()
ranger = tfa.optimizers.Lookahead(radam, sync_period=6, slow_step_size=0.5)
```
"""
def __init__(self,
learning_rate=0.001,
beta_1=0.9,
beta_2=0.999,
epsilon=1e-7,
weight_decay=0.,
amsgrad=False,
sma_threshold=5.0,
total_steps=0,
warmup_proportion=0.1,
min_lr=0.,
name='RectifiedAdam',
**kwargs):
r"""Construct a new RAdam optimizer.
Args:
learning_rate: A `Tensor` or a floating point value. or a schedule
that is a `tf.keras.optimizers.schedules.LearningRateSchedule`
The learning rate.
beta_1: A float value or a constant float tensor.
The exponential decay rate for the 1st moment estimates.
beta_2: A float value or a constant float tensor.
The exponential decay rate for the 2nd moment estimates.
epsilon: A small constant for numerical stability.
weight_decay: A floating point value. Weight decay for each param.
amsgrad: boolean. Whether to apply AMSGrad variant of this
algorithm from the paper "On the Convergence of Adam and
beyond".
sma_threshold. A float value.
The threshold for simple mean average.
total_steps: An integer. Total number of training steps.
Enable warmup by setting a positive value.
warmup_proportion: A floating point value.
The proportion of increasing steps.
min_lr: A floating point value. Minimum learning rate after warmup.
name: Optional name for the operations created when applying
gradients. Defaults to "RectifiedAdam".
**kwargs: keyword arguments. Allowed to be {`clipnorm`,
`clipvalue`, `lr`, `decay`}. `clipnorm` is clip gradients
by norm; `clipvalue` is clip gradients by value, `decay` is
included for backward compatibility to allow time inverse
decay of learning rate. `lr` is included for backward
compatibility, recommended to use `learning_rate` instead.
"""
super(RectifiedAdam, self).__init__(name, **kwargs)
self._set_hyper('learning_rate', kwargs.get('lr', learning_rate))
self._set_hyper('beta_1', beta_1)
self._set_hyper('beta_2', beta_2)
self._set_hyper('decay', self._initial_decay)
self._set_hyper('weight_decay', weight_decay)
self._set_hyper('sma_threshold', sma_threshold)
self._set_hyper('total_steps', float(total_steps))
self._set_hyper('warmup_proportion', warmup_proportion)
self._set_hyper('min_lr', min_lr)
self.epsilon = epsilon or tf.keras.backend.epsilon()
self.amsgrad = amsgrad
self._initial_weight_decay = weight_decay
self._initial_total_steps = total_steps
def _create_slots(self, var_list):
for var in var_list:
self.add_slot(var, 'm')
for var in var_list:
self.add_slot(var, 'v')
if self.amsgrad:
for var in var_list:
self.add_slot(var, 'vhat')
def set_weights(self, weights):
params = self.weights
num_vars = int((len(params) - 1) / 2)
if len(weights) == 3 * num_vars + 1:
weights = weights[:len(params)]
super(RectifiedAdam, self).set_weights(weights)
def _resource_apply_dense(self, grad, var):
var_dtype = var.dtype.base_dtype
lr_t = self._decayed_lr(var_dtype)
m = self.get_slot(var, 'm')
v = self.get_slot(var, 'v')
beta_1_t = self._get_hyper('beta_1', var_dtype)
beta_2_t = self._get_hyper('beta_2', var_dtype)
epsilon_t = tf.convert_to_tensor(self.epsilon, var_dtype)
local_step = tf.cast(self.iterations + 1, var_dtype)
beta_1_power = tf.pow(beta_1_t, local_step)
beta_2_power = tf.pow(beta_2_t, local_step)
if self._initial_total_steps > 0:
total_steps = self._get_hyper('total_steps', var_dtype)
warmup_steps = total_steps *\
self._get_hyper('warmup_proportion', var_dtype)
min_lr = self._get_hyper('min_lr', var_dtype)
decay_steps = tf.maximum(total_steps - warmup_steps, 1)
decay_rate = (min_lr - lr_t) / decay_steps
lr_t = tf.where(
local_step <= warmup_steps,
lr_t * (local_step / warmup_steps),
lr_t + decay_rate * tf.minimum(local_step - warmup_steps,
decay_steps),
)
sma_inf = 2.0 / (1.0 - beta_2_t) - 1.0
sma_t = sma_inf - 2.0 * local_step * beta_2_power / (
1.0 - beta_2_power)
m_t = m.assign(
beta_1_t * m + (1.0 - beta_1_t) * grad,
use_locking=self._use_locking)
m_corr_t = m_t / (1.0 - beta_1_power)
v_t = v.assign(
beta_2_t * v + (1.0 - beta_2_t) * tf.square(grad),
use_locking=self._use_locking)
if self.amsgrad:
vhat = self.get_slot(var, 'vhat')
vhat_t = vhat.assign(
tf.maximum(vhat, v_t), use_locking=self._use_locking)
v_corr_t = tf.sqrt(vhat_t / (1.0 - beta_2_power))
else:
vhat_t = None
v_corr_t = tf.sqrt(v_t / (1.0 - beta_2_power))
r_t = tf.sqrt((sma_t - 4.0) / (sma_inf - 4.0) * (sma_t - 2.0) /
(sma_inf - 2.0) * sma_inf / sma_t)
sma_threshold = self._get_hyper('sma_threshold', var_dtype)
var_t = tf.where(sma_t >= sma_threshold,
r_t * m_corr_t / (v_corr_t + epsilon_t), m_corr_t)
if self._initial_weight_decay > 0.0:
var_t += self._get_hyper('weight_decay', var_dtype) * var
var_update = var.assign_sub(
lr_t * var_t, use_locking=self._use_locking)
updates = [var_update, m_t, v_t]
if self.amsgrad:
updates.append(vhat_t)
return tf.group(*updates)
def _resource_apply_sparse(self, grad, var, indices):
var_dtype = var.dtype.base_dtype
lr_t = self._decayed_lr(var_dtype)
beta_1_t = self._get_hyper('beta_1', var_dtype)
beta_2_t = self._get_hyper('beta_2', var_dtype)
epsilon_t = tf.convert_to_tensor(self.epsilon, var_dtype)
local_step = tf.cast(self.iterations + 1, var_dtype)
beta_1_power = tf.pow(beta_1_t, local_step)
beta_2_power = tf.pow(beta_2_t, local_step)
if self._initial_total_steps > 0:
total_steps = self._get_hyper('total_steps', var_dtype)
warmup_steps = total_steps *\
self._get_hyper('warmup_proportion', var_dtype)
min_lr = self._get_hyper('min_lr', var_dtype)
decay_steps = tf.maximum(total_steps - warmup_steps, 1)
decay_rate = (min_lr - lr_t) / decay_steps
lr_t = tf.where(
local_step <= warmup_steps,
lr_t * (local_step / warmup_steps),
lr_t + decay_rate * tf.minimum(local_step - warmup_steps,
decay_steps),
)
sma_inf = 2.0 / (1.0 - beta_2_t) - 1.0
sma_t = sma_inf - 2.0 * local_step * beta_2_power / (
1.0 - beta_2_power)
m = self.get_slot(var, 'm')
m_scaled_g_values = grad * (1 - beta_1_t)
m_t = m.assign(m * beta_1_t, use_locking=self._use_locking)
with tf.control_dependencies([m_t]):
m_t = self._resource_scatter_add(m, indices, m_scaled_g_values)
m_corr_t = m_t / (1.0 - beta_1_power)
v = self.get_slot(var, 'v')
v_scaled_g_values = (grad * grad) * (1 - beta_2_t)
v_t = v.assign(v * beta_2_t, use_locking=self._use_locking)
with tf.control_dependencies([v_t]):
v_t = self._resource_scatter_add(v, indices, v_scaled_g_values)
if self.amsgrad:
vhat = self.get_slot(var, 'vhat')
vhat_t = vhat.assign(
tf.maximum(vhat, v_t), use_locking=self._use_locking)
v_corr_t = tf.sqrt(vhat_t / (1.0 - beta_2_power))
else:
vhat_t = None
v_corr_t = tf.sqrt(v_t / (1.0 - beta_2_power))
r_t = tf.sqrt((sma_t - 4.0) / (sma_inf - 4.0) * (sma_t - 2.0) /
(sma_inf - 2.0) * sma_inf / sma_t)
sma_threshold = self._get_hyper('sma_threshold', var_dtype)
var_t = tf.where(sma_t >= sma_threshold,
r_t * m_corr_t / (v_corr_t + epsilon_t), m_corr_t)
if self._initial_weight_decay > 0.0:
var_t += self._get_hyper('weight_decay', var_dtype) * var
with tf.control_dependencies([var_t]):
var_update = self._resource_scatter_add(
var, indices, tf.gather(-lr_t * var_t, indices))
updates = [var_update, m_t, v_t]
if self.amsgrad:
updates.append(vhat_t)
return tf.group(*updates)
def get_config(self):
config = super(RectifiedAdam, self).get_config()
config.update({
'learning_rate':
self._serialize_hyperparameter('learning_rate'),
'beta_1':
self._serialize_hyperparameter('beta_1'),
'beta_2':
self._serialize_hyperparameter('beta_2'),
'decay':
self._serialize_hyperparameter('decay'),
'weight_decay':
self._serialize_hyperparameter('weight_decay'),
'sma_threshold':
self._serialize_hyperparameter('sma_threshold'),
'epsilon':
self.epsilon,
'amsgrad':
self.amsgrad,
'total_steps':
self._serialize_hyperparameter('total_steps'),
'warmup_proportion':
self._serialize_hyperparameter('warmup_proportion'),
'min_lr':
self._serialize_hyperparameter('min_lr'),
})
return config
```
# Load data
```
database_base_path = '/kaggle/input/tweet-dataset-split-roberta-base-96/'
k_fold = pd.read_csv(database_base_path + '5-fold.csv')
display(k_fold.head())
# Unzip files
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_1.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_2.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_3.tar.gz
# !tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_4.tar.gz
# !tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_5.tar.gz
```
# Model parameters
```
vocab_path = database_base_path + 'vocab.json'
merges_path = database_base_path + 'merges.txt'
base_path = '/kaggle/input/qa-transformers/roberta/'
config = {
"MAX_LEN": 96,
"BATCH_SIZE": 32,
"EPOCHS": 4,
"LEARNING_RATE": 3e-5,
"ES_PATIENCE": 1,
"question_size": 4,
"N_FOLDS": 3,
"base_model_path": base_path + 'roberta-base-tf_model.h5',
"config_path": base_path + 'roberta-base-config.json'
}
with open('config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
```
# Model
```
Model
module_config = RobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFRobertaModel.from_pretrained(config['base_model_path'], config=module_config, name="base_model")
sequence_output = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
last_state = sequence_output[0]
x_start = layers.Dropout(.1)(last_state)
x_start = layers.Conv1D(1, 1)(x_start)
x_start = layers.Flatten()(x_start)
y_start = layers.Activation('softmax', name='y_start')(x_start)
x_end = layers.Dropout(.1)(last_state)
x_end = layers.Conv1D(1, 1)(x_end)
x_end = layers.Flatten()(x_end)
y_end = layers.Activation('softmax', name='y_end')(x_end)
model = Model(inputs=[input_ids, attention_mask], outputs=[y_start, y_end])
# optimizer = optimizers.Adam(lr=config['LEARNING_RATE'])
optimizer = RectifiedAdam(lr=config['LEARNING_RATE'],
total_steps=(len(k_fold[k_fold['fold_1'] == 'train']) // config['BATCH_SIZE']) * config['EPOCHS'],
warmup_proportion=0.1,
min_lr=1e-7)
model.compile(optimizer, loss=losses.CategoricalCrossentropy(),
metrics=[metrics.CategoricalAccuracy()])
return model
```
# Tokenizer
```
tokenizer = ByteLevelBPETokenizer(vocab_file=vocab_path, merges_file=merges_path,
lowercase=True, add_prefix_space=True)
tokenizer.save('./')
```
# Train
```
history_list = []
AUTO = tf.data.experimental.AUTOTUNE
for n_fold in range(config['N_FOLDS']):
n_fold +=1
print('\nFOLD: %d' % (n_fold))
# Load data
base_data_path = 'fold_%d/' % (n_fold)
x_train = np.load(base_data_path + 'x_train.npy')
y_train = np.load(base_data_path + 'y_train.npy')
x_valid = np.load(base_data_path + 'x_valid.npy')
y_valid = np.load(base_data_path + 'y_valid.npy')
### Delete data dir
shutil.rmtree(base_data_path)
# Train model
model_path = 'model_fold_%d.h5' % (n_fold)
model = model_fn(config['MAX_LEN'])
es = EarlyStopping(monitor='val_loss', mode='min', patience=config['ES_PATIENCE'],
restore_best_weights=True, verbose=1)
checkpoint = ModelCheckpoint(model_path, monitor='val_loss', mode='min',
save_best_only=True, save_weights_only=True)
history = model.fit(list(x_train), list(y_train),
validation_data=(list(x_valid), list(y_valid)),
batch_size=config['BATCH_SIZE'],
callbacks=[checkpoint, es],
epochs=config['EPOCHS'],
verbose=1).history
history_list.append(history)
# Make predictions
train_preds = model.predict(list(x_train))
valid_preds = model.predict(list(x_valid))
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'start_fold_%d' % (n_fold)] = train_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'end_fold_%d' % (n_fold)] = train_preds[1].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'start_fold_%d' % (n_fold)] = valid_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'end_fold_%d' % (n_fold)] = valid_preds[1].argmax(axis=-1)
k_fold['end_fold_%d' % (n_fold)] = k_fold['end_fold_%d' % (n_fold)].astype(int)
k_fold['start_fold_%d' % (n_fold)] = k_fold['start_fold_%d' % (n_fold)].astype(int)
k_fold['end_fold_%d' % (n_fold)].clip(0, k_fold['text_len'], inplace=True)
k_fold['start_fold_%d' % (n_fold)].clip(0, k_fold['end_fold_%d' % (n_fold)], inplace=True)
k_fold['prediction_fold_%d' % (n_fold)] = k_fold.apply(lambda x: decode(x['start_fold_%d' % (n_fold)], x['end_fold_%d' % (n_fold)], x['text'], config['question_size'], tokenizer), axis=1)
k_fold['prediction_fold_%d' % (n_fold)].fillna(k_fold["text"], inplace=True)
k_fold['jaccard_fold_%d' % (n_fold)] = k_fold.apply(lambda x: jaccard(x['selected_text'], x['prediction_fold_%d' % (n_fold)]), axis=1)
```
# Model loss graph
```
sns.set(style="whitegrid")
for n_fold in range(config['N_FOLDS']):
print('Fold: %d' % (n_fold+1))
plot_metrics(history_list[n_fold])
```
# Model evaluation
```
display(evaluate_model_kfold(k_fold, config['N_FOLDS']).style.applymap(color_map))
```
# Visualize predictions
```
display(k_fold[[c for c in k_fold.columns if not (c.startswith('textID') or
c.startswith('text_len') or
c.startswith('selected_text_len') or
c.startswith('text_wordCnt') or
c.startswith('selected_text_wordCnt') or
c.startswith('fold_') or
c.startswith('start_fold_') or
c.startswith('end_fold_'))]].head(15))
```
| true |
code
| 0.835332 | null | null | null | null |
|
## Homework-3: MNIST Classification with ConvNet
### **Deadline: 2021.04.06 23:59:00 **
### In this homework, you need to
- #### implement the forward and backward functions for ConvLayer (`layers/conv_layer.py`)
- #### implement the forward and backward functions for PoolingLayer (`layers/pooling_layer.py`)
- #### implement the forward and backward functions for DropoutLayer (`layers/dropout_layer.py`)
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import tensorflow.compat.v1 as tf
tf.disable_eager_execution()
from network import Network
from solver import train, test
from plot import plot_loss_and_acc
```
## Load MNIST Dataset
We use tensorflow tools to load dataset for convenience.
```
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
def decode_image(image):
# Normalize from [0, 255.] to [0., 1.0], and then subtract by the mean value
image = tf.cast(image, tf.float32)
image = tf.reshape(image, [1, 28, 28])
image = image / 255.0
image = image - tf.reduce_mean(image)
return image
def decode_label(label):
# Encode label with one-hot encoding
return tf.one_hot(label, depth=10)
# Data Preprocessing
x_train = tf.data.Dataset.from_tensor_slices(x_train).map(decode_image)
y_train = tf.data.Dataset.from_tensor_slices(y_train).map(decode_label)
data_train = tf.data.Dataset.zip((x_train, y_train))
x_test = tf.data.Dataset.from_tensor_slices(x_test).map(decode_image)
y_test = tf.data.Dataset.from_tensor_slices(y_test).map(decode_label)
data_test = tf.data.Dataset.zip((x_test, y_test))
```
## Set Hyperparameters
You can modify hyperparameters by yourself.
```
batch_size = 100
max_epoch = 10
init_std = 0.1
learning_rate = 0.001
weight_decay = 0.005
disp_freq = 50
```
## Criterion and Optimizer
```
from criterion import SoftmaxCrossEntropyLossLayer
from optimizer import SGD
criterion = SoftmaxCrossEntropyLossLayer()
sgd = SGD(learning_rate, weight_decay)
```
## ConvNet
```
from layers import FCLayer, ReLULayer, ConvLayer, MaxPoolingLayer, ReshapeLayer
convNet = Network()
convNet.add(ConvLayer(1, 8, 3, 1))
convNet.add(ReLULayer())
convNet.add(MaxPoolingLayer(2, 0))
convNet.add(ConvLayer(8, 16, 3, 1))
convNet.add(ReLULayer())
convNet.add(MaxPoolingLayer(2, 0))
convNet.add(ReshapeLayer((batch_size, 16, 7, 7), (batch_size, 784)))
convNet.add(FCLayer(784, 128))
convNet.add(ReLULayer())
convNet.add(FCLayer(128, 10))
# Train
convNet.is_training = True
convNet, conv_loss, conv_acc = train(convNet, criterion, sgd, data_train, max_epoch, batch_size, disp_freq)
# Test
convNet.is_training = False
test(convNet, criterion, data_test, batch_size, disp_freq)
```
## Plot
```
plot_loss_and_acc({'ConvNet': [conv_loss, conv_acc]})
```
### ~~You have finished homework3, congratulations!~~
**Next, according to the requirements (4):**
### **You need to implement the Dropout layer and train the network again.**
```
from layers import DropoutLayer
from layers import FCLayer, ReLULayer, ConvLayer, MaxPoolingLayer, ReshapeLayer, DropoutLayer
# build your network
convNet = Network()
convNet.add(ConvLayer(1, 8, 3, 1))
convNet.add(ReLULayer())
convNet.add(DropoutLayer(0.5))
convNet.add(MaxPoolingLayer(2, 0))
convNet.add(ConvLayer(8, 16, 3, 1))
convNet.add(ReLULayer())
convNet.add(MaxPoolingLayer(2, 0))
convNet.add(ReshapeLayer((batch_size, 16, 7, 7), (batch_size, 784)))
convNet.add(FCLayer(784, 128))
convNet.add(ReLULayer())
convNet.add(FCLayer(128, 10))
# training
convNet.is_training = True
convNet, conv_loss, conv_acc = train(convNet, criterion, sgd, data_train, max_epoch, batch_size, disp_freq)
# testing
convNet.is_training = False
test(convNet, criterion, data_test, batch_size, disp_freq)
plot_loss_and_acc({'ConvNet': [conv_loss, conv_acc]})
```
| true |
code
| 0.678247 | null | null | null | null |
|
## MEG Group Analysis
Group analysis for MEG data, for the FOOOF paper.
The Data Source is from the
[Human Connectome Project](https://www.humanconnectome.org/)
This notebook is for group analysis of MEG data using the
[omapping](https://github.com/voytekresearch/omapping) module.
```
%matplotlib inline
from scipy.io import loadmat
from scipy.stats.stats import pearsonr
from om.meg.single import MegSubj
from om.meg.single import print_corrs_mat, print_corrs_vec
from om.meg.group import MegGroup
from om.meg.group import osc_space_group
from om.plts.meg import *
from om.core.db import OMDB
from om.core.osc import Osc
from om.core.io import load_obj_pickle, save_obj_pickle
```
## Settings
```
SAVE_FIG = False
```
### Setup
```
# Get database object
db = OMDB()
# Check what data is available
# Note: this function outa date (checks the wrong file folder)
sub_nums, source = db.check_data_files(dat_type='fooof', dat_source='HCP', verbose=True)
# Drop outlier subject
sub_nums = list(set(sub_nums) - set([662551]))
```
### Oscillation Band Definitions
```
# Set up oscillation band definitions to use
bands = Osc()
bands.add_band('Theta', [3, 7])
bands.add_band('Alpha', [7, 14])
bands.add_band('Beta', [15, 30])
```
### Load Data
```
# Initialize MegGroup object
meg_group = MegGroup(db, osc)
# Add subjects to meg_group
for i, subj in enumerate(sub_nums):
meg_subj = MegSubj(OMDB(), source[i], osc) # Initialize MegSubj object
meg_subj.import_fooof(subj, get_demo=True) # Import subject data
meg_subj.all_oscs(verbose=False) # Create vectors of all oscillations
meg_subj.osc_bands_vertex() # Get oscillations per band per vertex
meg_subj.peak_freq(dat='all', avg='mean') # Calculate peak frequencies
meg_group.add_subject(meg_subj, # Add subject data to group object
add_all_oscs=True, # Whether to include all-osc data
add_vertex_bands=True, # Whether to include osc-band-vertex data
add_peak_freqs=True, # Whether to include peak frequency data
add_vertex_oscs=False, # Whether to include all-osc data for each vertex
add_vertex_exponents=True, # Whether to include the aperiodic exponent per vertex
add_demo=True) # Whether to include demographic information
# OR: Check available saved files to load one of them
meg_files = db.check_res_files('meg')
# Load a pickled file
#meg_group = load_obj_pickle('meg', meg_files[2])
```
### Data Explorations
```
# Check how many subjects group includes
print('Currently analyzing ' + str(meg_group.n_subjs) + ' subjects.')
# Check data descriptions - sex
print('# of Females:\t', sum(np.array(meg_group.sex) == 'F'))
print('# of Females:\t', sum(np.array(meg_group.sex) == 'M'))
# Check some simple descriptives
print('Number of oscillations found across the whole group: \t', meg_group.n_oscs_tot)
print('Average number of oscillations per vertex: \t\t {:1.2f}'.format(np.mean(meg_group.n_oscs / 7501)))
# Plot all oscillations across the group
plot_all_oscs(meg_group.centers_all, meg_group.powers_all, meg_group.bws_all,
meg_group.comment, save_out=SAVE_FIG)
```
### Save out probabilities per frequency range
....
```
# Check for oscillations above / below fitting range
# Note: this is a quirk of older FOOOF version - fixed in fitting now
print(len(meg_group.centers_all[meg_group.centers_all < 2]))
print(len(meg_group.centers_all[meg_group.centers_all > 40]))
# Calculate probability of observing an oscillation in each frequency
bins = np.arange(0, 43, 1)
counts, freqs = np.histogram(meg_group.centers_all, bins=bins)
probs = counts / meg_group.n_oscs_tot
# Fix for the oscillation out of range
add = sum(probs[0:3]) + sum(probs[35:])
freqs = freqs[3:35]
probs = probs[3:35]
probs = probs + (add/len(probs))
# np.save('freqs.npy', freqs)
# np.save('probs.npy', probs)
```
## BACK TO NORMAL PROGRAMMING
```
# ??
print(sum(meg_group.powers_all < 0.05) / len(meg_group.powers_all))
print(sum(meg_group.bws_all < 1.0001) / len(meg_group.bws_all))
# Plot a single oscillation parameter at a time
plot_all_oscs_single(meg_group.centers_all, 0, meg_group.comment,
n_bins=150, figsize=(15, 5))
if True:
plt.savefig('meg-osc-centers.pdf', bbox_inches='tight')
```
### Exponents
```
# Plot distribution of all aperiodic exponents
plot_exponents(meg_group.exponents, meg_group.comment, save_out=SAVE_FIG)
# Check the global mean exponent value
print('Global mean exponent value is: \t{:1.4f} with st. dev of {:1.4f}'\
.format(np.mean(meg_group.exponents), np.std(meg_group.exponents)))
# Calculate Average Aperiodic Exponent value per Vertex
meg_group.group_exponent(avg='mean')
# Save out group exponent results
#meg_group.save_gr_exponent(file_name='json')
# Set group exponent results for visualization with Brainstorm
#meg_group.set_exponent_viz()
```
### Oscillation Topographies
##### Oscillation Probability
```
# Calculate probability of oscilation (band specific) across the cortex
meg_group.osc_prob()
# Correlations between probabilities of oscillatory bands.
prob_rs, prob_ps, prob_labels = meg_group.osc_map_corrs(map_type='prob')
print_corrs_mat(prob_rs, prob_ps, prob_labels)
# Plot the oscillation probability correlation matrix
#plot_corr_matrix(prob_rs, osc.labels, save_out=SAVE_FIG)
# Save group oscillation probability data for visualization with Brainstorm
meg_group.set_map_viz(map_type='prob', file_name='json')
# Save group oscillation probability data out to npz file
#meg_group.save_map(map_type='prob', file_name='json')
```
##### Oscillation Power Ratio
```
# Calculate power ratio of oscilation (band specific) across the cortex
meg_group.osc_power()
# Correlations between probabilities of oscillatory bands.
power_rs, power_ps, power_labels = meg_group.osc_map_corrs(map_type='power')
print_corrs_mat(power_rs, power_ps, power_labels)
# Plot the oscillation probability correlation matrix
#plot_corr_matrix(power_rs, osc.labels, save_out=SAVE_FIG)
# Save group oscillation probability data for visualization with Brainstorm
meg_group.set_map_viz(map_type='power', file_name='json')
# Save group oscillation probability data out to npz file
#meg_group.save_map(map_type='power', file_name='json')
```
##### Oscillation Score
```
# Calculate oscillation score
meg_group.osc_score()
# Save group oscillation probability data for visualization with Brainstorm
#meg_group.set_map_viz(map_type='score', file_name='json')
# Save group oscillation score data out to npz file
#meg_group.save_map(map_type='score', file_name='80_new_group')
# Correlations between osc-scores of oscillatory bands.
score_rs, score_ps, score_labels = meg_group.osc_map_corrs(map_type='score')
print_corrs_mat(score_rs, score_ps, score_labels)
# Plot the oscillation score correlation matrix
#plot_corr_matrix(score_rs, osc.labels, save_out=SAVE_FIG)
# Save out pickle file of current MegGroup() object
#save_obj_pickle(meg_group, 'meg', 'test')
```
#### Check correlation of aperiodic exponent with oscillation bands
```
n_bands = len(meg_group.bands)
exp_rs = np.zeros(shape=[n_bands])
exp_ps = np.zeros(shape=[n_bands])
for ind, band in enumerate(meg_group.bands):
r_val, p_val = pearsonr(meg_group.exponent_gr_avg, meg_group.osc_scores[band])
exp_rs[ind] = r_val
exp_ps[ind] = p_val
for rv, pv, label in zip(exp_rs, exp_ps, ['Theta', 'Alpha', 'Beta']):
print('Corr of {}-Exp \t is {:1.2f} \t with p-val of {:1.2f}'.format(label, rv, pv))
```
#### Plot corr matrix including bands & exponents
```
all_rs = np.zeros(shape=[n_bands+1, n_bands+1])
all_rs[0:n_bands, 0:n_bands] = score_rs
all_rs[n_bands, 0:n_bands] = exp_rs
all_rs[0:n_bands, n_bands] = exp_rs;
from copy import deepcopy
all_labels = deepcopy(osc.labels)
all_labels.append('Exps')
#plot_corr_matrix_tri(all_rs, all_labels)
#if SAVE_FIG:
# plt.savefig('Corrs.pdf')
corr_data = all_rs
labels = all_labels
# TEMP / HACK - MAKE & SAVE CORR-PLOT
# Generate a mask for the upper triangle
mask = np.zeros_like(corr_data, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
# Generate a custom diverging colormap
cmap = sns.color_palette("coolwarm", 7)
# Draw the heatmap with the mask and correct aspect ratio
sns.heatmap(corr_data, mask=mask, cmap=cmap, annot=True, square=True, annot_kws={"size":15},
vmin=-1, vmax=1, xticklabels=labels, yticklabels=labels)
plt.savefig('corr.pdf')
#plot_corr_matrix(all_rs, all_labels, save_out=SAVE_FIG)
```
| true |
code
| 0.615203 | null | null | null | null |
|
# A-weightening filter implementation
The A-weighting transfer function is defined in the ANSI Standards S1.4-1983 and S1.42-2001:
$$
H(s) = \frac{\omega_4^2 s^4}{(s-\omega_1)^2(s-\omega_2)(s-\omega_3)(s-\omega_4)^2}
$$
Where $\omega_i = 2\pi f_i$ are the angular frequencies defined by:
```
import numpy as np
f1 = 20.598997 # Hz
f4 = 12194.217 # Hz
f2 = 107.65265 # Hz
f3 = 737.86223 # Hz
w1 = 2*np.pi*f1 # rad/s
w2 = 2*np.pi*f2 # rad/s
w3 = 2*np.pi*f3 # rad/s
w4 = 2*np.pi*f4 # rad/s
```
In [1] ther is a method to convert this function transform to a discrete time-domain using the bilinear transform. We use a similar method, but we separate it into four filters of order one or two, in order to keep the filter stable:
$$
H(s) = \omega_4^2 H_1(s) H_2(s) H_3(s) H_4(s),
$$
where:
$$
H_i(s) = \left\{ \begin{array}{lcc}
\frac{s}{(s-\omega_i)^2} & \text{for} & i=1,4 \\
\\ \frac{s}{(s-\omega_i)} & \text{for} & i = 2,3. \\
\end{array}
\right.
$$
Now, we conver the $H_i(s)$ filters to their discrete-time implementation by using the bilinear transform:
$$
s \rightarrow 2f_s\frac{1+z^{-1}}{1-z^{-1}}.
$$
Therefore:
$$
H_i(z) = \frac{2f_s(1-z^{-2})}{(\omega_i-2f_s)^2z^{-2}+2(\omega_i^2-4f_s^2)z^{-1}+(\omega_i+2f_s)^2} \text{ for } i = 1,4
$$
$$
H_i(z) = \frac{2f_s(1-z^{-1})}{(\omega_i-2f_s)z^{-1}+(\omega_i+2f_s)} \text{ for } i = 2,3
$$
We define two python functions to calculates coefficients of both types of function transforms:
```
def filter_first_order(w,fs): #s/(s+w)
a0 = w + 2.0*fs
b = 2*fs*np.array([1, -1])/a0
a = np.array([a0, w - 2*fs])/a0
return b,a
def filter_second_order(w,fs): #s/(s+w)^2
a0 = (w + 2.0*fs)**2
b = 2*fs*np.array([1,0,-1])/a0
a = np.array([a0,2*(w**2-4*fs**2),(w-2*fs)**2])/a0
return b,a
```
Now, we calculate b and a coefficients of the four filters for some sampling rate:
```
fs = 48000 #Hz
b1,a1 = filter_second_order(w1,fs)
b2,a2 = filter_first_order(w2,fs)
b3,a3 = filter_first_order(w3,fs)
b4,a4 = filter_second_order(w4,fs)
```
Then, we calculate the impulse response of the overall filter, $h[n]$, by concatenating the four filters and using the impulse signal, $\delta[n]$, as input.
```
from scipy import signal
# generate delta[n]
N = 8192*2 #number of points
delta = np.zeros(N)
delta[0] = 1
# apply filters
x1 = signal.lfilter(b1,a1,delta)
x2 = signal.lfilter(b2,a2,x1)
x3 = signal.lfilter(b3,a3,x2)
h = signal.lfilter(b4,a4,x3)
GA = 10**(2/20.) # 0dB at 1Khz
h = h*GA*w4**2
```
Lets find the filter's frequency response, $H(e^{j\omega})$, by calcuating the FFT of $h[n]$.
```
H = np.abs(np.fft.fft(h))[:N/2]
H = 20*np.log10(H)
```
Compare the frequency response to the expresion defined in the norms:
```
eps = 10**-6
f = np.linspace(0,fs/2-fs/float(N),N/2)
curveA = f4**2*f**4/((f**2+f1**2)*np.sqrt((f**2+f2**2)*(f**2+f3**2))*(f**2+f4**2))
HA = 20*np.log10(curveA+eps)+2.0
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,10))
plt.title('Digital filter frequency response')
plt.plot(f,H, 'b',label= 'Devised filter')
plt.plot(f,HA, 'r',label= 'Norm filter')
plt.ylabel('Amplitude [dB]')
plt.xlabel('Frequency [Hz]')
plt.legend()
plt.xscale('log')
plt.xlim([10,fs/2.0])
plt.ylim([-80,3])
plt.grid()
plt.show()
```
Now we also can check if the filter designed fullfill the tolerances given in the ANSI norm [2].
```
import csv
freqs = []
tol_type0_low = []
tol_type0_high = []
tol_type1_low = []
tol_type1_high = []
with open('ANSI_tolerances.csv') as csv_file:
csv_reader = csv.reader(csv_file, delimiter=',')
line_count = 0
for row in csv_reader:
if line_count == 0:
#print('Column names are {", ".join(row)}')
line_count += 1
else:
freqs.append(float(row[0]))
Aw = float(row[1])
tol_type0_low.append(Aw + float(row[2]))
tol_type0_high.append(Aw + float(row[3]))
tol_type1_low.append(Aw + float(row[4]))
if row[5] != '':
tol_type1_high.append(Aw + float(row[5]))
else:
tol_type1_high.append(np.Inf)
line_count += 1
print('Processed %d lines.'%line_count)
fig = plt.figure(figsize=(10,10))
plt.title('Digital filter frequency response')
plt.plot(f,H, 'b',label= 'Devised filter')
plt.plot(f,HA, 'r',label= 'Norm filter')
plt.plot(freqs,tol_type0_low,'k.',label='type0 tolerances')
plt.plot(freqs,tol_type0_high,'k.')
plt.plot(freqs,tol_type1_low,'r.',label='type1 tolerances')
plt.plot(freqs,tol_type1_high,'r.')
plt.ylabel('Amplitude [dB]')
plt.xlabel('Frequency [Hz]')
plt.legend()
plt.xscale('log')
plt.xlim([10,fs/2.0])
plt.ylim([-80,3])
plt.grid()
plt.show()
```
## References
[1] Rimell, Andrew; Mansfield, Neil; Paddan, Gurmail (2015). "Design of digital filters for frequency weightings (A and C) required for risk assessments of workers exposed to noise". Industrial Health (53): 21–27.
[2] ANSI S1.4-1983. Specifications for Sound Level Meters.
| true |
code
| 0.470797 | null | null | null | null |
|
# Supervised baselines
Notebook with strong supervised learning baseline on cifar-10
```
%reload_ext autoreload
%autoreload 2
```
You probably need to install dependencies
```
# All things needed
!git clone https://github.com/puhsu/sssupervised
!pip install -q fastai2
!pip install -qe sssupervised
```
After running cell above you should restart your kernel
```
from sssupervised.cifar_utils import CifarFactory
from sssupervised.randaugment import RandAugment
from fastai2.data.transforms import parent_label, Categorize
from fastai2.optimizer import ranger, Adam
from fastai2.layers import LabelSmoothingCrossEntropy
from fastai2.metrics import error_rate
from fastai2.callback.all import *
from fastai2.vision.all import *
```
Baseline uses wideresnet-28-2 model with randaugment augmentation policy. It is optiimzed with RAadam with lookahead with one-cycle learning rate and momentum schedules for 200 epochs (we count epochs in number of steps on standard cifar, so we set 4000 epochs in our case, because we only have $2400$ training examples ($50000/2400 \approx 20$)
```
cifar = untar_data(URLs.CIFAR)
files, (train, test, unsup) = CifarFactory(n_same_cls=3, seed=42, n_labeled=400).splits_from_path(cifar)
sup_ds = Datasets(files, [[PILImage.create, RandAugment, ToTensor], [parent_label, Categorize]], splits=(train, test))
sup_dl = sup_ds.dataloaders(after_batch=[IntToFloatTensor, Normalize.from_stats(*cifar_stats)])
sup_dl.train.show_batch(max_n=9)
# https://github.com/uoguelph-mlrg/Cutout
import math
import torch
import torch.nn as nn
import torch.nn.functional as F
class BasicBlock(nn.Module):
def __init__(self, in_planes, out_planes, stride, dropRate=0.0):
super().__init__()
self.bn1 = nn.BatchNorm2d(in_planes)
self.relu1 = nn.ReLU(inplace=True)
self.conv1 = nn.Conv2d(in_planes, out_planes, kernel_size=3, stride=stride,
padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(out_planes)
self.relu2 = nn.ReLU(inplace=True)
self.conv2 = nn.Conv2d(out_planes, out_planes, kernel_size=3, stride=1,
padding=1, bias=False)
self.droprate = dropRate
self.equalInOut = (in_planes == out_planes)
self.convShortcut = (not self.equalInOut) and nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=stride,
padding=0, bias=False) or None
def forward(self, x):
if not self.equalInOut: x = self.relu1(self.bn1(x))
else: out = self.relu1(self.bn1(x))
out = self.relu2(self.bn2(self.conv1(out if self.equalInOut else x)))
if self.droprate > 0:
out = F.dropout(out, p=self.droprate, training=self.training)
out = self.conv2(out)
return torch.add(x if self.equalInOut else self.convShortcut(x), out)
class NetworkBlock(nn.Module):
def __init__(self, nb_layers, in_planes, out_planes, block, stride, dropRate=0.0):
super().__init__()
self.layer = self._make_layer(block, in_planes, out_planes, nb_layers, stride, dropRate)
def _make_layer(self, block, in_planes, out_planes, nb_layers, stride, dropRate):
layers = []
for i in range(nb_layers):
layers.append(block(i == 0 and in_planes or out_planes, out_planes, i == 0 and stride or 1, dropRate))
return nn.Sequential(*layers)
def forward(self, x): return self.layer(x)
class WideResNet(nn.Module):
def __init__(self, depth, num_classes, widen_factor=1, dropRate=0.0):
super().__init__()
nChannels = [16, 16*widen_factor, 32*widen_factor, 64*widen_factor]
assert((depth - 4) % 6 == 0)
n = (depth - 4) // 6
block = BasicBlock
# 1st conv before any network block
self.conv1 = nn.Conv2d(3, nChannels[0], kernel_size=3, stride=1,
padding=1, bias=False)
self.block1 = NetworkBlock(n, nChannels[0], nChannels[1], block, 1, dropRate)
self.block2 = NetworkBlock(n, nChannels[1], nChannels[2], block, 2, dropRate)
self.block3 = NetworkBlock(n, nChannels[2], nChannels[3], block, 2, dropRate)
self.bn1 = nn.BatchNorm2d(nChannels[3])
self.relu = nn.ReLU(inplace=True)
self.fc = nn.Linear(nChannels[3], num_classes)
self.nChannels = nChannels[3]
for m in self.modules():
if isinstance(m, nn.Conv2d):
n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
m.weight.data.normal_(0, math.sqrt(2. / n))
elif isinstance(m, nn.BatchNorm2d):
m.weight.data.fill_(1)
m.bias.data.zero_()
elif isinstance(m, nn.Linear): m.bias.data.zero_()
def forward(self, x):
out = self.conv1(x)
out = self.block1(out)
out = self.block2(out)
out = self.block3(out)
out = self.relu(self.bn1(out))
out = F.adaptive_avg_pool2d(out, 1)
out = out.view(-1, self.nChannels)
return self.fc(out)
def wrn_22(): return WideResNet(depth=22, num_classes=10, widen_factor=6, dropRate=0.)
def wrn_22_k8(): return WideResNet(depth=22, num_classes=10, widen_factor=8, dropRate=0.)
def wrn_22_k10(): return WideResNet(depth=22, num_classes=10, widen_factor=10, dropRate=0.)
def wrn_22_k8_p2(): return WideResNet(depth=22, num_classes=10, widen_factor=8, dropRate=0.2)
def wrn_28(): return WideResNet(depth=28, num_classes=10, widen_factor=6, dropRate=0.)
def wrn_28_k8(): return WideResNet(depth=28, num_classes=10, widen_factor=8, dropRate=0.)
def wrn_28_k8_p2(): return WideResNet(depth=28, num_classes=10, widen_factor=8, dropRate=0.2)
def wrn_28_p2(): return WideResNet(depth=28, num_classes=10, widen_factor=6, dropRate=0.2)
```
We override default callbacks (the best way I found, to pass extra arguments to callbacks)
```
defaults.callbacks = [
TrainEvalCallback(),
Recorder(train_metrics=True),
ProgressCallback(),
]
class SkipSomeValidations(Callback):
"""Perform validation regularly, but not every epoch
(usefull for small datasets, where training is quick)"""
def __init__(self, n_epochs=20): self.n_epochs=n_epochs
def begin_validate(self):
if self.train_iter % self.n_epochs != 0:
raise CancelValidException()
learner = Learner(
sup_dl,
wrn_28(),
CrossEntropyLossFlat(),
opt_func=ranger,
wd=1e-2,
metrics=error_rate,
cbs=[ShowGraphCallback(), SkipSomeValidations(n_epochs=20)]
)
```
| true |
code
| 0.821725 | null | null | null | null |
|
# Example of optimizing Xgboost XGBClassifier function
# Goal is to test the objective values found by Mango
# Benchmarking Serial Evaluation: Iterations 60
```
from mango.tuner import Tuner
from scipy.stats import uniform
def get_param_dict():
param_dict = {"learning_rate": uniform(0, 1),
"gamma": uniform(0, 5),
"max_depth": range(1,10),
"n_estimators": range(1,300),
"booster":['gbtree','gblinear','dart']
}
return param_dict
from sklearn.model_selection import cross_val_score
from xgboost import XGBClassifier
from sklearn.datasets import load_wine
X, Y = load_wine(return_X_y=True)
count_called = 1
def objfunc(args_list):
global X, Y, count_called
#print('count_called:',count_called)
count_called = count_called + 1
results = []
for hyper_par in args_list:
clf = XGBClassifier(**hyper_par)
result = cross_val_score(clf, X, Y, scoring='accuracy').mean()
results.append(result)
return results
def get_conf():
conf = dict()
conf['batch_size'] = 1
conf['initial_random'] = 5
conf['num_iteration'] = 60
conf['domain_size'] = 5000
return conf
def get_optimal_x():
param_dict = get_param_dict()
conf = get_conf()
tuner = Tuner(param_dict, objfunc,conf)
results = tuner.maximize()
return results
optimal_X = []
Results = []
num_of_tries = 100
for i in range(num_of_tries):
results = get_optimal_x()
Results.append(results)
optimal_X.append(results['best_params']['x'])
print(i,":",results['best_params']['x'])
# import numpy as np
# optimal_X = np.array(optimal_X)
# plot_optimal_X=[]
# for i in range(optimal_X.shape[0]):
# plot_optimal_X.append(optimal_X[i]['x'])
```
# Plotting the serial run results
```
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,10))
n, bins, patches = plt.hist(optimal_X, 20, facecolor='g', alpha=0.75)
def autolabel(rects):
"""
Attach a text label above each bar displaying its height
"""
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x() + rect.get_width()/2., 1.0*height,
'%d' % int(height),
ha='center', va='bottom',fontsize=15)
plt.xlabel('X-Value',fontsize=25)
plt.ylabel('Number of Occurence',fontsize=25)
plt.title('Optimal Objective: Iterations 60',fontsize=20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.grid(True)
autolabel(patches)
plt.show()
```
# Benchmarking test with different iterations for serial executions
```
from mango.tuner import Tuner
def get_param_dict():
param_dict = {
'x': range(-5000, 5000)
}
return param_dict
def objfunc(args_list):
results = []
for hyper_par in args_list:
x = hyper_par['x']
result = -(x**2)
results.append(result)
return results
def get_conf_20():
conf = dict()
conf['batch_size'] = 1
conf['initial_random'] = 5
conf['num_iteration'] = 20
conf['domain_size'] = 5000
return conf
def get_conf_30():
conf = dict()
conf['batch_size'] = 1
conf['initial_random'] = 5
conf['num_iteration'] = 30
conf['domain_size'] = 5000
return conf
def get_conf_40():
conf = dict()
conf['batch_size'] = 1
conf['initial_random'] = 5
conf['num_iteration'] = 40
conf['domain_size'] = 5000
return conf
def get_conf_60():
conf = dict()
conf['batch_size'] = 1
conf['initial_random'] = 5
conf['num_iteration'] = 60
conf['domain_size'] = 5000
return conf
def get_optimal_x():
param_dict = get_param_dict()
conf_20 = get_conf_20()
tuner_20 = Tuner(param_dict, objfunc,conf_20)
conf_30 = get_conf_30()
tuner_30 = Tuner(param_dict, objfunc,conf_30)
conf_40 = get_conf_40()
tuner_40 = Tuner(param_dict, objfunc,conf_40)
conf_60 = get_conf_60()
tuner_60 = Tuner(param_dict, objfunc,conf_60)
results_20 = tuner_20.maximize()
results_30 = tuner_30.maximize()
results_40 = tuner_40.maximize()
results_60 = tuner_60.maximize()
return results_20, results_30, results_40 , results_60
Store_Optimal_X = []
Store_Results = []
num_of_tries = 100
for i in range(num_of_tries):
results_20, results_30, results_40 , results_60 = get_optimal_x()
Store_Results.append([results_20, results_30, results_40 , results_60])
Store_Optimal_X.append([results_20['best_params']['x'],results_30['best_params']['x'],results_40['best_params']['x'],results_60['best_params']['x']])
print(i,":",[results_20['best_params']['x'],results_30['best_params']['x'],results_40['best_params']['x'],results_60['best_params']['x']])
import numpy as np
Store_Optimal_X=np.array(Store_Optimal_X)
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,10))
n, bins, patches = plt.hist(Store_Optimal_X[:,0], 20, facecolor='g', alpha=0.75)
def autolabel(rects):
"""
Attach a text label above each bar displaying its height
"""
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x() + rect.get_width()/2., 1.0*height,
'%d' % int(height),
ha='center', va='bottom',fontsize=15)
plt.xlabel('X-Value',fontsize=25)
plt.ylabel('Number of Occurence',fontsize=25)
plt.title('Optimal Objective: Iterations 20',fontsize=20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.grid(True)
autolabel(patches)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,10))
n, bins, patches = plt.hist(Store_Optimal_X[:,1], 20, facecolor='g', alpha=0.75)
def autolabel(rects):
"""
Attach a text label above each bar displaying its height
"""
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x() + rect.get_width()/2., 1.0*height,
'%d' % int(height),
ha='center', va='bottom',fontsize=15)
plt.xlabel('X-Value',fontsize=25)
plt.ylabel('Number of Occurence',fontsize=25)
plt.title('Optimal Objective: Iterations 30',fontsize=20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.grid(True)
autolabel(patches)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,10))
n, bins, patches = plt.hist(Store_Optimal_X[:,2], 20, facecolor='g', alpha=0.75)
def autolabel(rects):
"""
Attach a text label above each bar displaying its height
"""
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x() + rect.get_width()/2., 1.0*height,
'%d' % int(height),
ha='center', va='bottom',fontsize=15)
plt.xlabel('X-Value',fontsize=25)
plt.ylabel('Number of Occurence',fontsize=25)
plt.title('Optimal Objective: Iterations 40',fontsize=20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.grid(True)
autolabel(patches)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,10))
n, bins, patches = plt.hist(Store_Optimal_X[:,3], 20, facecolor='g', alpha=0.75)
def autolabel(rects):
"""
Attach a text label above each bar displaying its height
"""
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x() + rect.get_width()/2., 1.0*height,
'%d' % int(height),
ha='center', va='bottom',fontsize=15)
plt.xlabel('X-Value',fontsize=25)
plt.ylabel('Number of Occurence',fontsize=25)
plt.title('Optimal Objective: Iterations 60',fontsize=20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.grid(True)
autolabel(patches)
plt.show()
```
| true |
code
| 0.579698 | null | null | null | null |
|
Comparison for decision boundary generated on iris dataset between Label Propagation and SVM.
This demonstrates Label Propagation learning a good boundary even with a small amount of labeled data.
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plot.ly/python/getting-started/) by downloading the client and [reading the primer](https://plot.ly/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plot.ly/python/getting-started/#initialization-for-online-plotting) or [offline](https://plot.ly/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plot.ly/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
### Version
```
import sklearn
sklearn.__version__
```
### Imports
```
print(__doc__)
import plotly.plotly as py
import plotly.graph_objs as go
from plotly import tools
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn import svm
from sklearn.semi_supervised import label_propagation
```
### Calculations
```
rng = np.random.RandomState(0)
iris = datasets.load_iris()
X = iris.data[:, :2]
y = iris.target
# step size in the mesh
h = .02
y_30 = np.copy(y)
y_30[rng.rand(len(y)) < 0.3] = -1
y_50 = np.copy(y)
y_50[rng.rand(len(y)) < 0.5] = -1
# we create an instance of SVM and fit out data. We do not scale our
# data since we want to plot the support vectors
ls30 = (label_propagation.LabelSpreading().fit(X, y_30),
y_30)
ls50 = (label_propagation.LabelSpreading().fit(X, y_50),
y_50)
ls100 = (label_propagation.LabelSpreading().fit(X, y), y)
rbf_svc = (svm.SVC(kernel='rbf').fit(X, y), y)
# create a mesh to plot in
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
x_ = np.arange(x_min, x_max, h)
y_ = np.arange(y_min, y_max, h)
xx, yy = np.meshgrid(x_, y_)
# title for the plots
titles = ['Label Spreading 30% data',
'Label Spreading 50% data',
'Label Spreading 100% data',
'SVC with rbf kernel']
```
### Plot Results
```
fig = tools.make_subplots(rows=2, cols=2,
subplot_titles=tuple(titles),
print_grid=False)
def matplotlib_to_plotly(cmap, pl_entries):
h = 1.0/(pl_entries-1)
pl_colorscale = []
for k in range(pl_entries):
C = map(np.uint8, np.array(cmap(k*h)[:3])*255)
pl_colorscale.append([k*h, 'rgb'+str((C[0], C[1], C[2]))])
return pl_colorscale
cmap = matplotlib_to_plotly(plt.cm.Paired, 6)
for i, (clf, y_train) in enumerate((ls30, ls50, ls100, rbf_svc)):
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
trace1 = go.Heatmap(x=x_, y=y_, z=Z,
colorscale=cmap,
showscale=False)
fig.append_trace(trace1, i/2+1, i%2+1)
# Plot also the training points
trace2 = go.Scatter(x=X[:, 0], y=X[:, 1],
mode='markers',
showlegend=False,
marker=dict(color=X[:, 0],
colorscale=cmap,
line=dict(width=1, color='black'))
)
fig.append_trace(trace2, i/2+1, i%2+1)
for i in map(str,range(1, 5)):
y = 'yaxis' + i
x = 'xaxis' + i
fig['layout'][y].update(showticklabels=False, ticks='')
fig['layout'][x].update(showticklabels=False, ticks='')
fig['layout'].update(height=700)
py.iplot(fig)
```
### License
Authors:
Clay Woolam <[email protected]>
License:
BSD
```
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'Decision Boundary of Label Propagation versus SVM on the Iris dataset.ipynb', 'scikit-learn/plot-label-propagation-versus-svm-iris/', 'Decision Boundary of Label Propagation versus SVM on the Iris dataset | plotly',
' ',
title = 'Decision Boundary of Label Propagation versus SVM on the Iris dataset | plotly',
name = 'Decision Boundary of Label Propagation versus SVM on the Iris dataset',
has_thumbnail='true', thumbnail='thumbnail/svm.jpg',
language='scikit-learn', page_type='example_index',
display_as='semi_supervised', order=3,
ipynb= '~Diksha_Gabha/3520')
```
| true |
code
| 0.610076 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/satyajitghana/TSAI-DeepVision-EVA4.0/blob/master/05_CodingDrill/EVA4S5F1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Import Libraries
```
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
```
## Data Transformations
We first start with defining our data transformations. We need to think what our data is and how can we augment it to correct represent images which it might not see otherwise.
Here is the list of all the transformations which come pre-built with PyTorch
1. Compose
2. ToTensor
3. ToPILImage
4. Normalize
5. Resize
6. Scale
7. CenterCrop
8. Pad
9. Lambda
10. RandomApply
11. RandomChoice
12. RandomOrder
13. RandomCrop
14. RandomHorizontalFlip
15. RandomVerticalFlip
16. RandomResizedCrop
17. RandomSizedCrop
18. FiveCrop
19. TenCrop
20. LinearTransformation
21. ColorJitter
22. RandomRotation
23. RandomAffine
24. Grayscale
25. RandomGrayscale
26. RandomPerspective
27. RandomErasing
You can read more about them [here](https://pytorch.org/docs/stable/_modules/torchvision/transforms/transforms.html)
```
# Train Phase transformations
train_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)) # The mean and std have to be sequences (e.g., tuples), therefore you should add a comma after the values.
# Note the difference between (0.1307) and (0.1307,)
])
# Test Phase transformations
test_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
```
# Dataset and Creating Train/Test Split
```
train = datasets.MNIST('./data', train=True, download=True, transform=train_transforms)
test = datasets.MNIST('./data', train=False, download=True, transform=test_transforms)
```
# Dataloader Arguments & Test/Train Dataloaders
```
SEED = 1
# CUDA?
cuda = torch.cuda.is_available()
print("CUDA Available?", cuda)
# For reproducibility
torch.manual_seed(SEED)
if cuda:
torch.cuda.manual_seed(SEED)
# dataloader arguments - something you'll fetch these from cmdprmt
dataloader_args = dict(shuffle=True, batch_size=128, num_workers=4, pin_memory=True) if cuda else dict(shuffle=True, batch_size=64)
# train dataloader
train_loader = torch.utils.data.DataLoader(train, **dataloader_args)
# test dataloader
test_loader = torch.utils.data.DataLoader(test, **dataloader_args)
```
# Data Statistics
It is important to know your data very well. Let's check some of the statistics around our data and how it actually looks like
```
# We'd need to convert it into Numpy! Remember above we have converted it into tensors already
train_data = train.train_data
train_data = train.transform(train_data.numpy())
print('[Train]')
print(' - Numpy Shape:', train.train_data.cpu().numpy().shape)
print(' - Tensor Shape:', train.train_data.size())
print(' - min:', torch.min(train_data))
print(' - max:', torch.max(train_data))
print(' - mean:', torch.mean(train_data))
print(' - std:', torch.std(train_data))
print(' - var:', torch.var(train_data))
dataiter = iter(train_loader)
images, labels = dataiter.next()
print(images.shape)
print(labels.shape)
# Let's visualize some of the images
%matplotlib inline
import matplotlib.pyplot as plt
plt.imshow(images[0].numpy().squeeze(), cmap='gray_r')
```
## MORE
It is important that we view as many images as possible. This is required to get some idea on image augmentation later on
```
figure = plt.figure()
num_of_images = 60
for index in range(1, num_of_images + 1):
plt.subplot(6, 10, index)
plt.axis('off')
plt.imshow(images[index].numpy().squeeze(), cmap='gray_r')
```
# How did we get those mean and std values which we used above?
Let's run a small experiment
```
# simple transform
simple_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
# transforms.Normalize((0.1307,), (0.3081,)) # The mean and std have to be sequences (e.g., tuples), therefore you should add a comma after the values.
# Note the difference between (0.1307) and (0.1307,)
])
exp = datasets.MNIST('./data', train=True, download=True, transform=simple_transforms)
exp_data = exp.train_data
exp_data = exp.transform(exp_data.numpy())
print('[Train]')
print(' - Numpy Shape:', exp.train_data.cpu().numpy().shape)
print(' - Tensor Shape:', exp.train_data.size())
print(' - min:', torch.min(exp_data))
print(' - max:', torch.max(exp_data))
print(' - mean:', torch.mean(exp_data))
print(' - std:', torch.std(exp_data))
print(' - var:', torch.var(exp_data))
```
# The model
Let's start with the model we first saw
```
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 3, padding=1) #input -? OUtput? RF
self.conv2 = nn.Conv2d(32, 64, 3, padding=1)
self.pool1 = nn.MaxPool2d(2, 2)
self.conv3 = nn.Conv2d(64, 128, 3, padding=1)
self.conv4 = nn.Conv2d(128, 256, 3, padding=1)
self.pool2 = nn.MaxPool2d(2, 2)
self.conv5 = nn.Conv2d(256, 512, 3)
self.conv6 = nn.Conv2d(512, 1024, 3)
self.conv7 = nn.Conv2d(1024, 10, 3)
def forward(self, x):
x = self.pool1(F.relu(self.conv2(F.relu(self.conv1(x)))))
x = self.pool2(F.relu(self.conv4(F.relu(self.conv3(x)))))
x = F.relu(self.conv6(F.relu(self.conv5(x))))
# x = F.relu(self.conv7(x))
x = self.conv7(x)
x = x.view(-1, 10)
return F.log_softmax(x, dim=-1)
```
# Model Params
Can't emphasize on how important viewing Model Summary is.
Unfortunately, there is no in-built model visualizer, so we have to take external help
```
!pip install torchsummary
from torchsummary import summary
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
print(device)
model = Net().to(device)
summary(model, input_size=(1, 28, 28))
```
# Training and Testing
All right, so we have 6.3M params, and that's too many, we know that. But the purpose of this notebook is to set things right for our future experiments.
Looking at logs can be boring, so we'll introduce **tqdm** progressbar to get cooler logs.
Let's write train and test functions
```
from tqdm import tqdm
train_losses = []
test_losses = []
train_acc = []
test_acc = []
def train(model, device, train_loader, optimizer, epoch):
model.train()
pbar = tqdm(train_loader)
correct = 0
processed = 0
for batch_idx, (data, target) in enumerate(pbar):
# get samples
data, target = data.to(device), target.to(device)
# Init
optimizer.zero_grad()
# In PyTorch, we need to set the gradients to zero before starting to do backpropragation because PyTorch accumulates the gradients on subsequent backward passes.
# Because of this, when you start your training loop, ideally you should zero out the gradients so that you do the parameter update correctly.
# Predict
y_pred = model(data)
# Calculate loss
loss = F.nll_loss(y_pred, target)
train_losses.append(loss)
# Backpropagation
loss.backward()
optimizer.step()
# Update pbar-tqdm
pred = y_pred.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
processed += len(data)
pbar.set_description(desc= f'Loss={loss.item()} Batch_id={batch_idx} Accuracy={100*correct/processed:0.2f}')
train_acc.append(100*correct/processed)
def test(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
test_losses.append(test_loss)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
test_acc.append(100. * correct / len(test_loader.dataset))
```
# Let's Train and test our model
```
model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
EPOCHS = 20
for epoch in range(EPOCHS):
print("EPOCH:", epoch)
train(model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
fig, axs = plt.subplots(2,2,figsize=(15,10))
axs[0, 0].plot(train_losses)
axs[0, 0].set_title("Training Loss")
axs[1, 0].plot(train_acc)
axs[1, 0].set_title("Training Accuracy")
axs[0, 1].plot(test_losses)
axs[0, 1].set_title("Test Loss")
axs[1, 1].plot(test_acc)
axs[1, 1].set_title("Test Accuracy")
```
| true |
code
| 0.881564 | null | null | null | null |
|
# Solving Linear Systems: Iterative Methods
<a rel="license" href="http://creativecommons.org/licenses/by/4.0/"><img alt="Creative Commons License" style="border-width:0" src="https://licensebuttons.net/l/by/4.0/80x15.png" /></a><br />This notebook by Xiaozhou Li is licensed under a <a rel="license" href="http://creativecommons.org/licenses/by/4.0/">Creative Commons Attribution 4.0 International License</a>.
All code examples are also licensed under the [MIT license](http://opensource.org/licenses/MIT).
## General Form
For solving the linear system
$$
Ax = b,
$$
with the exact solution $x^{*}$. The general form based on the fixed point interation:
\begin{equation}
\begin{split}
x^{(0)} & = \text{initial guess} \\
x^{(k+1)} & = g(x^{(k)}) \quad k = 0,1,2,\ldots,
\end{split}
\end{equation}
where
$$
g(x) = x - C(Ax - b).
$$
Difficult: find a matrix $C$ such that
$$
\lim\limits_{k\rightarrow\infty}x^{(k)} = x^{*}
$$
and the algorithm needs to be converge fast and economy.
**Example 1**
\begin{equation*}
A = \left[\begin{array}{ccc} 9& -1 & -1 \\ -1 & 10 & -1 \\ -1 & -1& 15\end{array}\right],\quad b = \left[\begin{array}{c} 7 \\ 8 \\ 13\end{array}\right],
\end{equation*}
has the exact solution $x^{*} = {[1, 1, 1]}^T$
```
import numpy as np
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
from IPython.display import clear_output, display
def IterC(A, b, C, x0, x_star, iters):
x = np.copy(x0)
print ('Iteration No. Numerical Solution Max norm error ')
print (0, x, np.linalg.norm(x_star-x, np.inf))
for i in range(iters):
x = x + np.dot(C, b - np.dot(A,x))
print (i+1, x, np.linalg.norm(x_star-x,np.inf))
A = np.array([[9., -1., -1.],[-1.,10.,-1.],[-1.,-1.,15.]])
b = np.array([7.,8.,13.])
```
**Naive Choice**
Choosing $C = I$, then
$$g(x) = x - (Ax - b),$$
and the fixed-point iteration
$$x^{(k+1)} = (I - A)x^{(k)} + b \quad k = 0,1,2,\ldots. $$
Let the intial guess $x_0 = [0, 0, 0]^T$.
```
C = np.eye(3)
x0 = np.zeros(3)
x_star = np.array([1.,1.,1.])
w = interactive(IterC, A=fixed(A), b=fixed(b), C=fixed(C), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
```
**Best Choice (theoretically)**
Choosing $C = A^{-1}$, then
$$g(x) = x - A^{-1}(Ax - b),$$
and the fixed-point iteration
$$x^{(k+1)} = A^{-1}b \quad k = 0,1,2,\ldots. $$
* It equals to solve $Ax = b$ directly.
* However, it gives a hint that $C$ should be close to $A^{-1}$
**First Approach**
Let $D$ denote the main diagonal of $A$, $L$ denote the lower triangle of $A$ (entries below the main diagonal), and $U$ denote the upper triangle (entries above the main diagonal). Then $A = L + D + U$
Choosing $C = \text{diag}(A)^{-1} = D^{-1}$, then
$$g(x) = x - D^{-1}(Ax - b),$$
and the fixed-point iteration
$$Dx^{(k+1)} = (L + U)x^{(k)} + b \quad k = 0,1,2,\ldots. $$
```
C = np.diag(1./np.diag(A))
x0 = np.zeros(np.size(b))
#x0 = np.array([0,1.,0])
x_star = np.array([1.,1.,1.])
#IterC(A, b, C, x0, x_star, 10)
w = interactive(IterC, A=fixed(A), b=fixed(b), C=fixed(C), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
```
## Jacobi Method
### Matrix Form:
$$
x^{(k+1)} = x^{(k)} - D^{-1}(Ax^{(k)} - b)
$$
or
$$
Dx^{(k+1)} = b - (L+U)x^{(k)}
$$
### Algorithm
$$
x^{(k+1)}_i = \frac{b_i - \sum\limits_{j < i}a_{ij}x^{(k)}_j - \sum\limits_{j > i}a_{ij}x^{(k)}_j}{a_{ii}}
$$
```
def Jacobi(A, b, x0, x_star, iters):
x_old = np.copy(x0)
x_new = np.zeros(np.size(x0))
print (0, x_old, np.linalg.norm(x_star-x_old,np.inf))
for k in range(iters):
for i in range(np.size(x0)):
x_new[i] = (b[i] - np.dot(A[i,:i],x_old[:i]) - np.dot(A[i,i+1:],x_old[i+1:]))/A[i,i]
print (k+1, x_new, np.linalg.norm(x_star-x_new,np.inf))
x_old = np.copy(x_new)
w = interactive(Jacobi, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
```
**Second Approach**
Let $D$ denote the main diagonal of $A$, $L$ denote the lower triangle of $A$ (entries below the main diagonal), and $U$ denote the upper triangle (entries above the main diagonal). Then $A = L + D + U$
Choosing $C = (L + D)^{-1}$, then
$$g(x) = x - (L + D)^{-1}(Ax - b),$$
and the fixed-point iteration
$$(L + D)x^{(k+1)} = Ux^{(k)} + b \quad k = 0,1,2,\ldots. $$
```
def GS(A, b, x0, x_star, iters):
x = np.copy(x0)
print (0, x, np.linalg.norm(x_star-x,np.inf))
for k in range(iters):
for i in range(np.size(x0)):
x[i] = (b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i+1:],x[i+1:]))/A[i,i]
print (k+1, x, np.linalg.norm(x_star-x,np.inf))
w = interactive(GS, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
```
## Gauss-Seidel Method
### Algorithm
$$
x^{(k+1)}_i = \frac{b_i - \sum\limits_{j < i}a_{ij}x^{(k+1)}_j - \sum\limits_{j > i}a_{ij}x^{(k)}_j}{a_{ii}}
$$
### Matrix Form:
$$
x^{(k+1)} = x^{(k)} - (L+D)^{-1}(Ax^{(k)} - b)
$$
or
$$
(L+D)x^{(k+1)} = b - Ux^{(k)}
$$
**Example 2**
\begin{equation*}
A = \left[\begin{array}{ccc} 3& 1 & -1 \\ 2 & 4 & 1 \\ -1 & 2& 5\end{array}\right],\quad b = \left[\begin{array}{c} 4 \\ 1 \\ 1\end{array}\right],
\end{equation*}
has the exact solution $x^{*} = {[2, -1, 1]}^T$
```
A = np.array([[3, 1, -1],[2,4,1],[-1,2,5]])
b = np.array([4,1,1])
x0 = np.zeros(np.size(b))
x_star = np.array([2.,-1.,1.])
w = interactive(GS, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=40,value=0))
display(w)
```
**Example 3**
\begin{equation*}
A = \left[\begin{array}{ccc} 1& 2 & -2 \\ 1 & 1 & 1 \\ 2 & 2& 1\end{array}\right],\quad b = \left[\begin{array}{c} 7 \\ 8 \\ 13\end{array}\right],
\end{equation*}
has the exact solution $x^{*} = {[-3, 8, 3]}^T$
```
A = np.array([[1, 2, -2],[1,1,1],[2,2,1]])
b = np.array([7,8,13])
#x0 = np.zeros(np.size(b))
x0 = np.array([-1,1,1])
x_star = np.array([-3.,8.,3.])
w = interactive(GS, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
B = np.eye(3) - np.dot(np.diag(1./np.diag(A)),A)
print(B)
print (np.linalg.eig(B))
```
**Example 4**
\begin{equation*}
A = \left[\begin{array}{cc} 1& 2 \\ 3 & 1 \end{array}\right],\quad b = \left[\begin{array}{c} 5 \\ 5\end{array}\right],
\end{equation*}
has the exact solution $x^{*} = {[1, 2]}^T$
or
\begin{equation*}
A = \left[\begin{array}{cc} 3& 1 \\ 1 & 2 \end{array}\right],\quad b = \left[\begin{array}{c} 5 \\ 5\end{array}\right],
\end{equation*}
```
#A = np.array([[1, 2],[3,1]])
A = np.array([[3, 1],[1,2]])
b = np.array([5,5])
#x0 = np.zeros(np.size(b))
x0 = np.array([0,0])
x_star = np.array([1.,2.,])
w = interactive(GS, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
```
**Example 5**
Are Jacobi iteration and Gauss-Seidel iteration convergent for the following equations?
\begin{equation*}
A_1 = \left[\begin{array}{ccc} 3& 0 & 4 \\ 7 & 4 & 2 \\ -1 & 1 & 2\end{array}\right],\quad A_2 = \left[\begin{array}{ccc} -3& 3 & -6 \\ -4 & 7 & -8 \\ 5 & 7 & -9\end{array}\right],
\end{equation*}
* Consider the **spectral radius** of the iterative matrix
* $B_J = -D^{-1}(L+U)$ and $B_{GS} = -(L+D)^{-1}U$
```
def Is_Jacobi_Gauss(A):
L = np.tril(A,-1)
U = np.triu(A,1)
D = np.diag(np.diag(A))
B_J = np.dot(np.diag(1./np.diag(A)), L+U)
B_GS = np.dot(np.linalg.inv(L+D),U)
rho_J = np.linalg.norm(np.linalg.eigvals(B_J), np.inf)
rho_GS = np.linalg.norm(np.linalg.eigvals(B_GS), np.inf)
print ("Spectral Radius")
print ("Jacobi: ", rho_J)
print ("Gauss Sediel: ", rho_GS)
A1 = np.array([[3, 0, 4],[7, 4, 2], [-1,1,2]])
A2 = np.array([[-3, 3, -6], [-4, 7, -8], [5, 7, -9]])
Is_Jacobi_Gauss(A2)
```
## Successive Over-Relaxation (SOR)
### Algorithm
$$
x^{(k+1)}_i = x^{(k)} + \omega \frac{b_i - \sum\limits_{j < i}a_{ij}x^{(k+1)}_j - \sum\limits_{j \geq i}a_{ij}x^{(k)}_j}{a_{ii}}
$$
### Matrix Form:
$$
x^{(k+1)} = x^{(k)} - \omega(\omega L+D)^{-1}(Ax^{(k)} - b)
$$
or
$$
(\omega L+D)x^{(k+1)} = ((1-\omega)D - \omega U)x^{(k)} + \omega b
$$
```
def SOR(A, b, x0, x_star, omega, iters):
x = np.copy(x0)
print (0, x, np.linalg.norm(x_star-x,np.inf))
for k in range(iters):
for i in range(np.size(x0)):
x[i] = x[i] + omega*(b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i:],x[i:]))/A[i,i]
print (k+1, x, np.linalg.norm(x_star-x,np.inf))
def SOR2(A, b, x0, x_star, omega, iters):
x = np.copy(x0)
for k in range(iters):
for i in range(np.size(x0)):
x[i] = x[i] + omega*(b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i:],x[i:]))/A[i,i]
return (np.linalg.norm(x_star-x,np.inf))
def SOR3(A, b, x0, x_star, omega, iters):
x = np.copy(x0)
print (0, np.linalg.norm(x_star-x,np.inf))
for k in range(iters):
for i in range(np.size(x0)):
x[i] = x[i] + omega*(b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i:],x[i:]))/A[i,i]
print (k+1, np.linalg.norm(x_star-x,np.inf))
A = np.array([[9., -1., -1.],[-1.,10.,-1.],[-1.,-1.,15.]])
b = np.array([7.,8.,13.])
x0 = np.array([0.,0.,0.])
x_star = np.array([1.,1.,1.])
omega = 1.01
w = interactive(SOR, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), omega=fixed(omega), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
w = interactive(GS, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
```
**Example 6**
\begin{equation*}
A = \left[\begin{array}{ccc} 2& -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1& 2\end{array}\right],\quad b = \left[\begin{array}{c} 1 \\ 0 \\ 1.8\end{array}\right],
\end{equation*}
has the exact solution $x^{*} = {[1.2, 1.4, 1.6]}^T$
```
A = np.array([[2, -1, 0],[-1, 2, -1], [0, -1, 2]])
b = np.array([1., 0, 1.8])
x0 = np.array([1.,1.,1.])
x_star = np.array([1.2,1.4,1.6])
omega = 1.2
w = interactive(SOR, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), omega=fixed(omega), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
w = interactive(GS, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
num = 21
omega = np.linspace(0.8, 1.8, num)
err1 = np.zeros(num)
for i in range(num):
err1[i] = SOR2(A, b, x0, x_star, omega[i], 10)
print (err1)
plt.plot(omega, np.log10(err1), 'o')
```
**Example 7**
\begin{equation*}
A = \left[\begin{array}{cccc} -4& 1 & 1 & 1 \\ 1 & -4 & 1 & 1 \\ 1 & 1& -4 &1 \\ 1 & 1 &1 & -4\end{array}\right],\quad b = \left[\begin{array}{c} 1 \\ 1 \\ 1 \\ 1\end{array}\right],
\end{equation*}
has the exact solution $x^{*} = {[-1, -1, -1, -1]}^T$
```
A = np.array([[-4, 1, 1, 1],[1, -4, 1, 1], [1, 1, -4, 1], [1, 1, 1, -4]])
b = np.array([1, 1, 1, 1])
x0 = np.zeros(np.size(b))
x_star = np.array([-1,-1,-1,-1])
omega = 1.25
w = interactive(SOR, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), omega=fixed(omega), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
w = interactive(GS, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=100,value=0))
display(w)
num = 21
omega = np.linspace(0.8, 1.8, num)
err1 = np.zeros(num)
for i in range(num):
err1[i] = SOR2(A, b, x0, x_star, omega[i], 10)
print (err1)
plt.plot(omega, np.log10(err1), 'o')
```
**Example 8**
\begin{equation*}
A=\begin{pmatrix}{3} & {-1} & {0} & 0 & 0 & \frac{1}{2} \\ {-1} & {3} & {-1} & {0} & \frac{1}{2} & 0\\ {0} & {-1} & {3} & {-1} & {0} & 0 \\ 0& {0} & {-1} & {3} & {-1} & {0} \\ {0} & \frac{1}{2} & {0} & {-1} & {3} & {-1} \\ \frac{1}{2} & {0} & 0 & 0 & {-1} & {3}\end{pmatrix},\,\,b=\begin{pmatrix}\frac{5}{2} \\ \frac{3}{2} \\ 1 \\ 1 \\ \frac{3}{2} \\ \frac{5}{2} \end{pmatrix}
\end{equation*}
has the exact solution $x^{*} = {[1, 1, 1, 1, 1, 1]}^T$
```
n0 = 6
A = 3*np.eye(n0) - np.diag(np.ones(n0-1),-1) - np.diag(np.ones(n0-1),+1)
for i in range(n0):
if (abs(n0-1 - 2*i) > 1):
A[i, n0-1-i] = - 1/2
print (A)
x_star = np.ones(n0)
b = np.dot(A, x_star)
x0 = np.zeros(np.size(b))
omega = 1.25
w = interactive(SOR, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), omega=fixed(omega), iters=widgets.IntSlider(min=0,max=20,value=0))
display(w)
num = 21
omega = np.linspace(0.8, 1.8, num)
err1 = np.zeros(num)
for i in range(num):
err1[i] = SOR2(A, b, x0, x_star, omega[i], 10)
print (err1)
plt.plot(omega, np.log10(err1), 'o')
w = interactive(Jacobi, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), iters=widgets.IntSlider(min=0,max=100,value=0))
display(w)
```
## Sparse Matrix Computations
A coefficient matrix is called sparse if many of the matrix entries are known to be zero. Often, of the $n^2$ eligible entries in a sparse matrix, only $\mathcal{O}(n)$ of them are nonzero. A full matrix is the opposite, where few entries may be assumed to be zero.
**Example 9**
Consider the $n$-equation version of
\begin{equation*}
A=\begin{pmatrix}{3} & {-1} & {0} & 0 & 0 & \frac{1}{2} \\ {-1} & {3} & {-1} & {0} & \frac{1}{2} & 0\\ {0} & {-1} & {3} & {-1} & {0} & 0 \\ 0& {0} & {-1} & {3} & {-1} & {0} \\ {0} & \frac{1}{2} & {0} & {-1} & {3} & {-1} \\ \frac{1}{2} & {0} & 0 & 0 & {-1} & {3}\end{pmatrix},
\end{equation*}
has the exact solution $x^{*} = {[1, 1,\ldots, 1]}^T$ and $b = A x^{*}$
* First, let us have a look about the matrix $A$
```
n0 = 10000
A = 3*np.eye(n0) - np.diag(np.ones(n0-1),-1) - np.diag(np.ones(n0-1),+1)
for i in range(n0):
if (abs(n0-1 - 2*i) > 1):
A[i, n0-1-i] = - 1/2
#plt.spy(A)
#plt.show()
```
* How about the $PA = LU$ for the above matrix $A$?
* Are the $L$ and $U$ matrices still sparse?
```
import scipy.linalg
#P, L, U = scipy.linalg.lu(A)
#plt.spy(L)
#plt.show()
```
Gaussian elimination applied to a sparse matrix usually causes **fill-in**, where the coefficient matrix changes from sparse to full due to the necessary row operations. For this reason, the efficiency of Gaussian elimination and its $PA = LU$ implementation become questionable for sparse matrices, leaving iterative methods as a feasible alternative.
* Let us solve it with SOR method
```
x_star = np.ones(n0)
b = np.dot(A, x_star)
x0 = np.zeros(np.size(b))
omega = 1.25
w = interactive(SOR3, A=fixed(A), b=fixed(b), x0=fixed(x0), x_star=fixed(x_star), omega=fixed(omega), iters=widgets.IntSlider(min=0,max=200,value=0, step=10))
display(w)
```
## Application for Solving Laplace's Equation
### Laplace's equation
Consider the Laplace's equation given as
$$
\nabla^2 u = 0,\quad\quad (x,y) \in D,
$$
where $\nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}$, and the boundary conditions are given as

### Finite Difference Approximation
Here, we use a rectangular grid $(x_i,y_j)$, where
$$
x_i = i\Delta x, \,\,\text{for }\, i = 0,1,\ldots,N+1;\quad y_j = j\Delta y,\,\,\text{for }\, j = 0,1,\ldots,M+1.
$$
Five-points scheme:
$$
-\lambda^2 u_{i+1,j} + 2(1+\lambda^2)u_{i,j} - \lambda^2u_{i-1,j} - u_{i,j+1} - u_{i,j-1} = 0,\quad\text{for}\,\, i = 1,\ldots,N,\,\, j = 1,\ldots,M,
$$
where $\lambda = \frac{\Delta y}{\Delta x}$. The boundary conditions are
- $x = 0: u_{0,j} = g_L(y_j), \quad\text{for }\, j = 1,\ldots,M$,
- $x = a: u_{N+1,j} = g_R(y_j), \quad\text{for }\, j = 1,\ldots,M$,
- $y = 0: u_{i,0} = g_B(x_i), \quad\text{for }\, i = 1,\ldots,N$,
- $y = b: u_{i,M+1} = g_T(x_i), \quad\text{for }\, i = 1,\ldots,N$.
```
def generate_TD(N, dx, dy):
T = np.zeros([N,N])
a = - (dy/dx)**2
b = 2*(1 - a)
for i in range(N):
T[i,i] += b
if (i < N-1):
T[i,i+1] += a
if (i > 0):
T[i,i-1] += a
D = -np.identity(N)
return T, D
def assemble_matrix_A(dx, dy, N, M):
T, D = generate_TD(N, dx, dy)
A = np.zeros([N*M, N*M])
for j in range(M):
A[j*N:(j+1)*N,j*N:(j+1)*N] += T
if (j < M-1):
A[j*N:(j+1)*N,(j+1)*N:(j+2)*N] += D
if (j > 0):
A[j*N:(j+1)*N,(j-1)*N:j*N] += D
return A
N = 4
M = 4
dx = 1./(N+1)
dy = 1./(M+1)
T, D = generate_TD(N, dx, dy)
#print (T)
A = assemble_matrix_A(dx, dy, N, M)
#print (A)
plt.spy(A)
plt.show()
# Set boundary conditions
def gL(y):
return 0.
def gR(y):
return 0.
def gB(x):
return 0.
def gT(x):
return 1.
#return x*(1-x)*(4./5-x)*np.exp(6*x)
def assemble_vector_b(x, y, dx, dy, N, M, gL, gR, gB, gT):
b = np.zeros(N*M)
# Left BCs
for j in range(M):
b[(j-1)*N] += (dy/dx)**2*gL(y[j+1])
# Right BCs
# b +=
# Bottom BCs
# b +=
# Top BCs:
for i in range(N):
b[(M-1)*N+i] += gT(x[i+1])
return b
from mpl_toolkits import mplot3d
from mpl_toolkits.mplot3d import axes3d
def Laplace_solver(a, b, N, M, gL, gR, gB, gT):
dx = b/(M+1)
dy = a/(N+1)
x = np.linspace(0, a, N+2)
y = np.linspace(0, b, M+2)
A = assemble_matrix_A(dx, dy, N, M)
b = assemble_vector_b(x, y, dx, dy, N, M, gL, gR, gB, gT)
v = np.linalg.solve(A,b)
# add boundary points + plotting
u = np.zeros([(N+2),(M+2)])
#u[1:(N+1),1:(M+1)] = np.reshape(v, (N, M))
# Top BCs
for i in range(N+2):
u[i,M+1] = gT(x[i])
u = np.transpose(u)
u[1:(M+1),1:(N+1)] = np.reshape(v, (M, N))
X, Y = np.meshgrid(x, y)
#Z = np.sin(2*np.pi*X)*np.sin(2*np.pi*Y)
fig = plt.figure()
#ax = plt.axes(projection='3d')
ax = fig.add_subplot(1, 1, 1, projection='3d')
ax.plot_surface(X, Y, u, rstride=1, cstride=1,
cmap='viridis', edgecolor='none')
ax.set_title('surface')
plt.show()
Laplace_solver(1, 1, 40, 40, gL, gR, gB, gT)
def Jacobi_tol(A, b, x0, tol):
x_old = np.copy(x0)
x_new = np.zeros(np.size(x0))
for i in range(np.size(x0)):
x_new[i] = (b[i] - np.dot(A[i,:i],x_old[:i]) - np.dot(A[i,i+1:],x_old[i+1:]))/A[i,i]
iters = 1
while ((np.linalg.norm(x_new-x_old,np.inf)) > tol):
x_old = np.copy(x_new)
for i in range(np.size(x0)):
x_new[i] = (b[i] - np.dot(A[i,:i],x_old[:i]) - np.dot(A[i,i+1:],x_old[i+1:]))/A[i,i]
iters += 1
return x_new, iters
def GS_tol(A, b, x0, tol):
x_old = np.copy(x0)
x = np.copy(x0)
for i in range(np.size(x0)):
x[i] = (b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i+1:],x[i+1:]))/A[i,i]
iters = 1
while ((np.linalg.norm(x-x_old,np.inf)) > tol):
x_old = np.copy(x)
for i in range(np.size(x0)):
x[i] = (b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i+1:],x[i+1:]))/A[i,i]
iters += 1
return x, iters
def SOR_tol(A, b, x0, omega, tol):
x_old = np.copy(x0)
x = np.copy(x0)
for i in range(np.size(x0)):
x[i] = x[i] + omega*(b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i:],x[i:]))/A[i,i]
iters = 1
while ((np.linalg.norm(x-x_old,np.inf)) > tol):
x_old = np.copy(x)
for i in range(np.size(x0)):
x[i] = x[i] + omega*(b[i] - np.dot(A[i,:i],x[:i]) - np.dot(A[i,i:],x[i:]))/A[i,i]
iters += 1
return x, iters
def CG_tol(A, b, x0, x_star, tol):
r_new = b - np.dot(A, x0)
r_old = np.copy(np.size(x0))
d_old = np.zeros(np.size(x0))
x = np.copy(x0)
iters = 0
while ((np.linalg.norm(x-x_star,np.inf)) > tol):
if (iters == 0):
d_new = np.copy(r_new)
else:
beta = np.dot(r_new,r_new)/np.dot(r_old,r_old)
d_new = r_new + beta*d_old
Ad = np.dot(A, d_new)
alpha = np.dot(r_new,r_new)/np.dot(d_new,Ad)
x += alpha*d_new
d_old = d_new
r_old = r_new
r_new = r_old - alpha*Ad
iters += 1
return x, iters
def Iterative_solver(a, b, N, M, gL, gR, gB, gT, tol):
dx = b/(M+1)
dy = a/(N+1)
x = np.linspace(0, a, N+2)
y = np.linspace(0, b, M+2)
A = assemble_matrix_A(dx, dy, N, M)
b = assemble_vector_b(x, y, dx, dy, N, M, gL, gR, gB, gT)
v = np.linalg.solve(A,b)
#tol = 1.e-8
v0 = np.zeros(np.size(b))
#v_J, iters = Jacobi_tol(A, b, v0, tol)
#print ("Jacobi Method: %4d %7.2e" %(iters, np.linalg.norm(v - v_J, np.inf)))
#v_GS, iters = GS_tol(A, b, v0, tol)
#print ("Gauss Seidel : %4d %7.2e" %(iters, np.linalg.norm(v - v_GS, np.inf)))
omega = 2./(1 + np.sin(np.pi*dx))
print ("omega = ", omega)
v_SOR, iters = SOR_tol(A, b, v0, omega, tol)
print ("SOR Method : %4d %7.2e" %(iters, np.linalg.norm(v - v_SOR, np.inf)))
v_CG, iters = CG_tol(A, b, v0, v, tol)
print ("CG Method : %4d %7.2e" %(iters, np.linalg.norm(v - v_CG, np.inf)))
Iterative_solver(1, 1, 80, 80, gL, gR, gB, gT, 1.e-4)
```
| true |
code
| 0.274327 | null | null | null | null |
|
# Running attribute inference attacks on Regression Models
In this tutorial we will show how to run black-box inference attacks on regression model. This will be demonstrated on the Nursery dataset (original dataset can be found here: https://archive.ics.uci.edu/ml/datasets/nursery).
## Preliminaries
In order to mount a successful attribute inference attack, the attacked feature must be categorical, and with a relatively small number of possible values (preferably binary).
In the case of the diabetes dataset, the sensitive feature we want to infer is the 'sex' feature, which is a binary feature.
## Load data
```
import os
import sys
sys.path.insert(0, os.path.abspath('..'))
from art.utils import load_diabetes
(x_train, y_train), (x_test, y_test), _, _ = load_diabetes(test_set=0.5)
```
## Train MLP model
```
from sklearn.tree import DecisionTreeRegressor
from art.estimators.regression.scikitlearn import ScikitlearnRegressor
model = DecisionTreeRegressor()
model.fit(x_train, y_train)
art_regressor = ScikitlearnRegressor(model)
print('Base model score: ', model.score(x_test, y_test))
```
## Attack
### Black-box attack
The black-box attack basically trains an additional classifier (called the attack model) to predict the attacked feature's value from the remaining n-1 features as well as the original (attacked) model's predictions.
#### Train attack model
```
import numpy as np
from art.attacks.inference.attribute_inference import AttributeInferenceBlackBox
attack_train_ratio = 0.5
attack_train_size = int(len(x_train) * attack_train_ratio)
attack_x_train = x_train[:attack_train_size]
attack_y_train = y_train[:attack_train_size]
attack_x_test = x_train[attack_train_size:]
attack_y_test = y_train[attack_train_size:]
attack_feature = 1 # sex
# get original model's predictions
attack_x_test_predictions = np.array([np.argmax(arr) for arr in art_regressor.predict(attack_x_test)]).reshape(-1,1)
# only attacked feature
attack_x_test_feature = attack_x_test[:, attack_feature].copy().reshape(-1, 1)
# training data without attacked feature
attack_x_test = np.delete(attack_x_test, attack_feature, 1)
bb_attack = AttributeInferenceBlackBox(art_regressor, attack_feature=attack_feature)
# train attack model
bb_attack.fit(attack_x_train)
```
#### Infer sensitive feature and check accuracy
```
# get inferred values
values = [-0.88085106, 1.]
inferred_train_bb = bb_attack.infer(attack_x_test, pred=attack_x_test_predictions, values=values)
# check accuracy
train_acc = np.sum(inferred_train_bb == np.around(attack_x_test_feature, decimals=8).reshape(1,-1)) / len(inferred_train_bb)
print(train_acc)
```
This means that for 56% of the training set, the attacked feature is inferred correctly using this attack.
Now let's check the precision and recall:
```
def calc_precision_recall(predicted, actual, positive_value=1):
score = 0 # both predicted and actual are positive
num_positive_predicted = 0 # predicted positive
num_positive_actual = 0 # actual positive
for i in range(len(predicted)):
if predicted[i] == positive_value:
num_positive_predicted += 1
if actual[i] == positive_value:
num_positive_actual += 1
if predicted[i] == actual[i]:
if predicted[i] == positive_value:
score += 1
if num_positive_predicted == 0:
precision = 1
else:
precision = score / num_positive_predicted # the fraction of predicted “Yes” responses that are correct
if num_positive_actual == 0:
recall = 1
else:
recall = score / num_positive_actual # the fraction of “Yes” responses that are predicted correctly
return precision, recall
print(calc_precision_recall(inferred_train_bb, np.around(attack_x_test_feature, decimals=8), positive_value=1.))
```
To verify the significance of these results, we now run a baseline attack that uses only the remaining features to try to predict the value of the attacked feature, with no use of the model itself.
```
from art.attacks.inference.attribute_inference import AttributeInferenceBaseline
baseline_attack = AttributeInferenceBaseline(attack_feature=attack_feature)
# train attack model
baseline_attack.fit(attack_x_train)
# infer values
inferred_train_baseline = baseline_attack.infer(attack_x_test, values=values)
# check accuracy
baseline_train_acc = np.sum(inferred_train_baseline == np.around(attack_x_test_feature, decimals=8).reshape(1,-1)) / len(inferred_train_baseline)
print(baseline_train_acc)
```
In this case, the black-box attack does not do better than the baseline.
| true |
code
| 0.468851 | null | null | null | null |
|
<h1><center>ERM with DNN under penalty of Equalized Odds</center></h1>
We implement here a regular Empirical Risk Minimization (ERM) of a Deep Neural Network (DNN) penalized to enforce an Equalized Odds constraint. More formally, given a dataset of size $n$ consisting of context features $x$, target $y$ and a sensitive information $z$ to protect, we want to solve
$$
\text{argmin}_{h\in\mathcal{H}}\frac{1}{n}\sum_{i=1}^n \ell(y_i, h(x_i)) + \lambda \chi^2|_1
$$
where $\ell$ is for instance the MSE and the penalty is
$$
\chi^2|_1 = \left\lVert\chi^2\left(\hat{\pi}(h(x)|y, z|y), \hat{\pi}(h(x)|y)\otimes\hat{\pi}(z|y)\right)\right\rVert_1
$$
where $\hat{\pi}$ denotes the empirical density estimated through a Gaussian KDE.
### The dataset
We use here the _communities and crimes_ dataset that can be found on the UCI Machine Learning Repository (http://archive.ics.uci.edu/ml/datasets/communities+and+crime). Non-predictive information, such as city name, state... have been removed and the file is at the arff format for ease of loading.
```
import sys, os
sys.path.append(os.path.abspath(os.path.join('../..')))
from examples.data_loading import read_dataset
x_train, y_train, z_train, x_test, y_test, z_test = read_dataset(name='crimes', fold=1)
n, d = x_train.shape
```
### The Deep Neural Network
We define a very simple DNN for regression here
```
from torch import nn
import torch.nn.functional as F
class NetRegression(nn.Module):
def __init__(self, input_size, num_classes):
super(NetRegression, self).__init__()
size = 50
self.first = nn.Linear(input_size, size)
self.fc = nn.Linear(size, size)
self.last = nn.Linear(size, num_classes)
def forward(self, x):
out = F.selu(self.first(x))
out = F.selu(self.fc(out))
out = self.last(out)
return out
```
### The fairness-inducing regularizer
We implement now the regularizer. The empirical densities $\hat{\pi}$ are estimated using a Gaussian KDE. The L1 functional norm is taken over the values of $y$.
$$
\chi^2|_1 = \left\lVert\chi^2\left(\hat{\pi}(x|z, y|z), \hat{\pi}(x|z)\otimes\hat{\pi}(y|z)\right)\right\rVert_1
$$
This used to enforce the conditional independence $X \perp Y \,|\, Z$.
Practically, we will want to enforce $\text{prediction} \perp \text{sensitive} \,|\, \text{target}$
```
from facl.independence.density_estimation.pytorch_kde import kde
from facl.independence.hgr import chi_2_cond
def chi_squared_l1_kde(X, Y, Z):
return torch.mean(chi_2_cond(X, Y, Z, kde))
```
### The fairness-penalized ERM
We now implement the full learning loop. The regression loss used is the quadratic loss with a L2 regularization and the fairness-inducing penalty.
```
import torch
import numpy as np
import torch.utils.data as data_utils
def regularized_learning(x_train, y_train, z_train, model, fairness_penalty, lr=1e-5, num_epochs=10):
# wrap dataset in torch tensors
Y = torch.tensor(y_train.astype(np.float32))
X = torch.tensor(x_train.astype(np.float32))
Z = torch.tensor(z_train.astype(np.float32))
dataset = data_utils.TensorDataset(X, Y, Z)
dataset_loader = data_utils.DataLoader(dataset=dataset, batch_size=200, shuffle=True)
# mse regression objective
data_fitting_loss = nn.MSELoss()
# stochastic optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=lr, weight_decay=0.01)
for j in range(num_epochs):
for i, (x, y, z) in enumerate(dataset_loader):
def closure():
optimizer.zero_grad()
outputs = model(x).flatten()
loss = data_fitting_loss(outputs, y)
loss += fairness_penalty(outputs, z, y)
loss.backward()
return loss
optimizer.step(closure)
return model
```
### Evaluation
For the evaluation on the test set, we compute two metrics: the MSE (accuracy) and HGR$|_\infty$ (fairness).
```
from facl.independence.hgr import hgr_cond
def evaluate(model, x, y, z):
Y = torch.tensor(y.astype(np.float32))
Z = torch.Tensor(z.astype(np.float32))
X = torch.tensor(x.astype(np.float32))
prediction = model(X).detach().flatten()
loss = nn.MSELoss()(prediction, Y)
hgr_infty = np.max(hgr_cond(prediction, Z, Y, kde))
return loss.item(), hgr_infty
```
### Running everything together
```
model = NetRegression(d, 1)
num_epochs = 20
lr = 1e-5
# $\chi^2|_1$
penalty_coefficient = 1.0
penalty = chi_squared_l1_kde
model = regularized_learning(x_train, y_train, z_train, model=model, fairness_penalty=penalty, lr=lr, \
num_epochs=num_epochs)
mse, hgr_infty = evaluate(model, x_test, y_test, z_test)
print("MSE:{} HGR_infty:{}".format(mse, hgr_infty))
```
| true |
code
| 0.737078 | null | null | null | null |
|
# Estimating The Mortality Rate For COVID-19
> Using Country-Level Covariates To Correct For Testing & Reporting Biases And Estimate a True Mortality Rate.
- author: Joseph Richards
- image: images/corvid-mortality.png
- comments: true
- categories: [MCMC, mortality]
- permalink: /covid-19-mortality-estimation/
- toc: true
```
#hide
# ! pip install pymc3 arviz xlrd
#hide
# Setup and imports
%matplotlib inline
import warnings
warnings.simplefilter('ignore')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc3 as pm
from IPython.display import display, Markdown
#hide
# constants
ignore_countries = [
'Others',
'Cruise Ship'
]
cpi_country_mapping = {
'United States of America': 'US',
'China': 'Mainland China'
}
wb_country_mapping = {
'United States': 'US',
'Egypt, Arab Rep.': 'Egypt',
'Hong Kong SAR, China': 'Hong Kong',
'Iran, Islamic Rep.': 'Iran',
'China': 'Mainland China',
'Russian Federation': 'Russia',
'Slovak Republic': 'Slovakia',
'Korea, Rep.': 'Korea, South'
}
wb_covariates = [
('SH.XPD.OOPC.CH.ZS',
'healthcare_oop_expenditure'),
('SH.MED.BEDS.ZS',
'hospital_beds'),
('HD.HCI.OVRL',
'hci'),
('SP.POP.65UP.TO.ZS',
'population_perc_over65'),
('SP.RUR.TOTL.ZS',
'population_perc_rural')
]
#hide
# data loading and manipulation
from datetime import datetime
import os
import numpy as np
import pandas as pd
def get_all_data():
'''
Main routine that grabs all COVID and covariate data and
returns them as a single dataframe that contains:
* count of cumulative cases and deaths by country (by today's date)
* days since first case for each country
* CPI gov't transparency index
* World Bank data on population, healthcare, etc. by country
'''
all_covid_data = _get_latest_covid_timeseries()
covid_cases_rollup = _rollup_by_country(all_covid_data['Confirmed'])
covid_deaths_rollup = _rollup_by_country(all_covid_data['Deaths'])
todays_date = covid_cases_rollup.columns.max()
# Create DataFrame with today's cumulative case and death count, by country
df_out = pd.DataFrame({'cases': covid_cases_rollup[todays_date],
'deaths': covid_deaths_rollup[todays_date]})
_clean_country_list(df_out)
_clean_country_list(covid_cases_rollup)
# Add observed death rate:
df_out['death_rate_observed'] = df_out.apply(
lambda row: row['deaths'] / float(row['cases']),
axis=1)
# Add covariate for days since first case
df_out['days_since_first_case'] = _compute_days_since_first_case(
covid_cases_rollup)
# Add CPI covariate:
_add_cpi_data(df_out)
# Add World Bank covariates:
_add_wb_data(df_out)
# Drop any country w/o covariate data:
num_null = df_out.isnull().sum(axis=1)
to_drop_idx = df_out.index[num_null > 1]
print('Dropping %i/%i countries due to lack of data' %
(len(to_drop_idx), len(df_out)))
df_out.drop(to_drop_idx, axis=0, inplace=True)
return df_out, todays_date
def _get_latest_covid_timeseries():
''' Pull latest time-series data from JHU CSSE database '''
repo = 'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/'
data_path = 'csse_covid_19_data/csse_covid_19_time_series/'
all_data = {}
for status in ['Confirmed', 'Deaths', 'Recovered']:
file_name = 'time_series_19-covid-%s.csv' % status
all_data[status] = pd.read_csv(
'%s%s%s' % (repo, data_path, file_name))
return all_data
def _rollup_by_country(df):
'''
Roll up each raw time-series by country, adding up the cases
across the individual states/provinces within the country
:param df: Pandas DataFrame of raw data from CSSE
:return: DataFrame of country counts
'''
gb = df.groupby('Country/Region')
df_rollup = gb.sum()
df_rollup.drop(['Lat', 'Long'], axis=1, inplace=True, errors='ignore')
# Drop dates with all 0 count data
df_rollup.drop(df_rollup.columns[df_rollup.sum(axis=0) == 0],
axis=1,
inplace=True)
# Convert column strings to dates:
idx_as_dt = [datetime.strptime(x, '%m/%d/%y') for x in df_rollup.columns]
df_rollup.columns = idx_as_dt
return df_rollup
def _clean_country_list(df):
''' Clean up input country list in df '''
# handle recent changes in country names:
country_rename = {
'Hong Kong SAR': 'Hong Kong',
'Taiwan*': 'Taiwan',
'Czechia': 'Czech Republic',
'Brunei': 'Brunei Darussalam',
'Iran (Islamic Republic of)': 'Iran',
'Viet Nam': 'Vietnam',
'Russian Federation': 'Russia',
'Republic of Korea': 'South Korea',
'Republic of Moldova': 'Moldova',
'China': 'Mainland China'
}
df.rename(country_rename, axis=0, inplace=True)
df.drop(ignore_countries, axis=0, inplace=True, errors='ignore')
def _compute_days_since_first_case(df_cases):
''' Compute the country-wise days since first confirmed case
:param df_cases: country-wise time-series of confirmed case counts
:return: Series of country-wise days since first case
'''
date_first_case = df_cases[df_cases > 0].idxmin(axis=1)
days_since_first_case = date_first_case.apply(
lambda x: (df_cases.columns.max() - x).days)
# Add 1 month for China, since outbreak started late 2019:
days_since_first_case.loc['Mainland China'] += 30
return days_since_first_case
def _add_cpi_data(df_input):
'''
Add the Government transparency (CPI - corruption perceptions index)
data (by country) as a column in the COVID cases dataframe.
:param df_input: COVID-19 data rolled up country-wise
:return: None, add CPI data to df_input in place
'''
cpi_data = pd.read_excel(
'https://github.com/jwrichar/COVID19-mortality/blob/master/data/CPI2019.xlsx?raw=true',
skiprows=2)
cpi_data.set_index('Country', inplace=True, drop=True)
cpi_data.rename(cpi_country_mapping, axis=0, inplace=True)
# Add CPI score to input df:
df_input['cpi_score_2019'] = cpi_data['CPI score 2019']
def _add_wb_data(df_input):
'''
Add the World Bank data covariates as columns in the COVID cases dataframe.
:param df_input: COVID-19 data rolled up country-wise
:return: None, add World Bank data to df_input in place
'''
wb_data = pd.read_csv(
'https://raw.githubusercontent.com/jwrichar/COVID19-mortality/master/data/world_bank_data.csv',
na_values='..')
for (wb_name, var_name) in wb_covariates:
wb_series = wb_data.loc[wb_data['Series Code'] == wb_name]
wb_series.set_index('Country Name', inplace=True, drop=True)
wb_series.rename(wb_country_mapping, axis=0, inplace=True)
# Add WB data:
df_input[var_name] = _get_most_recent_value(wb_series)
def _get_most_recent_value(wb_series):
'''
Get most recent non-null value for each country in the World Bank
time-series data
'''
ts_data = wb_series[wb_series.columns[3::]]
def _helper(row):
row_nn = row[row.notnull()]
if len(row_nn):
return row_nn[-1]
else:
return np.nan
return ts_data.apply(_helper, axis=1)
#hide
# Load the data (see source/data.py):
df, todays_date = get_all_data()
# Impute NA's column-wise:
df = df.apply(lambda x: x.fillna(x.mean()),axis=0)
```
# Observed mortality rates
```
#collapse-hide
display(Markdown('Data as of %s' % todays_date))
reported_mortality_rate = df['deaths'].sum() / df['cases'].sum()
display(Markdown('Overall reported mortality rate: %.2f%%' % (100.0 * reported_mortality_rate)))
df_highest = df.sort_values('cases', ascending=False).head(15)
mortality_rate = pd.Series(
data=(df_highest['deaths']/df_highest['cases']).values,
index=map(lambda x: '%s (%i cases)' % (x, df_highest.loc[x]['cases']),
df_highest.index))
ax = mortality_rate.plot.bar(
figsize=(14,7), title='Reported Mortality Rate by Country (countries w/ highest case counts)')
ax.axhline(reported_mortality_rate, color='k', ls='--')
plt.show()
```
# Model
Estimate COVID-19 mortality rate, controling for country factors.
```
#hide
import numpy as np
import pymc3 as pm
def initialize_model(df):
# Normalize input covariates in a way that is sensible:
# (1) days since first case: upper
# mu_0 to reflect asymptotic mortality rate months after outbreak
_normalize_col(df, 'days_since_first_case', how='upper')
# (2) CPI score: upper
# mu_0 to reflect scenario in absence of corrupt govts
_normalize_col(df, 'cpi_score_2019', how='upper')
# (3) healthcare OOP spending: mean
# not sure which way this will go
_normalize_col(df, 'healthcare_oop_expenditure', how='mean')
# (4) hospital beds: upper
# more beds, more healthcare and tests
_normalize_col(df, 'hospital_beds', how='mean')
# (5) hci = human capital index: upper
# HCI measures education/health; mu_0 should reflect best scenario
_normalize_col(df, 'hci', how='mean')
# (6) % over 65: mean
# mu_0 to reflect average world demographic
_normalize_col(df, 'population_perc_over65', how='mean')
# (7) % rural: mean
# mu_0 to reflect average world demographic
_normalize_col(df, 'population_perc_rural', how='mean')
n = len(df)
covid_mortality_model = pm.Model()
with covid_mortality_model:
# Priors:
mu_0 = pm.Beta('mu_0', alpha=0.3, beta=10)
sig_0 = pm.Uniform('sig_0', lower=0.0, upper=mu_0 * (1 - mu_0))
beta = pm.Normal('beta', mu=0, sigma=5, shape=7)
sigma = pm.HalfNormal('sigma', sigma=5)
# Model mu from country-wise covariates:
# Apply logit transformation so logistic regression performed
mu_0_logit = np.log(mu_0 / (1 - mu_0))
mu_est = mu_0_logit + \
beta[0] * df['days_since_first_case_normalized'].values + \
beta[1] * df['cpi_score_2019_normalized'].values + \
beta[2] * df['healthcare_oop_expenditure_normalized'].values + \
beta[3] * df['hospital_beds_normalized'].values + \
beta[4] * df['hci_normalized'].values + \
beta[5] * df['population_perc_over65_normalized'].values + \
beta[6] * df['population_perc_rural_normalized'].values
mu_model_logit = pm.Normal('mu_model_logit',
mu=mu_est,
sigma=sigma,
shape=n)
# Transform back to probability space:
mu_model = np.exp(mu_model_logit) / (np.exp(mu_model_logit) + 1)
# tau_i, mortality rate for each country
# Parametrize with (mu, sigma)
# instead of (alpha, beta) to ease interpretability.
tau = pm.Beta('tau', mu=mu_model, sigma=sig_0, shape=n)
# tau = pm.Beta('tau', mu=mu_0, sigma=sig_0, shape=n)
# Binomial likelihood:
d_obs = pm.Binomial('d_obs',
n=df['cases'].values,
p=tau,
observed=df['deaths'].values)
return covid_mortality_model
def _normalize_col(df, colname, how='mean'):
'''
Normalize an input column in one of 3 ways:
* how=mean: unit normal N(0,1)
* how=upper: normalize to [-1, 0] with highest value set to 0
* how=lower: normalize to [0, 1] with lowest value set to 0
Returns df modified in place with extra column added.
'''
colname_new = '%s_normalized' % colname
if how == 'mean':
mu = df[colname].mean()
sig = df[colname].std()
df[colname_new] = (df[colname] - mu) / sig
elif how == 'upper':
maxval = df[colname].max()
minval = df[colname].min()
df[colname_new] = (df[colname] - maxval) / (maxval - minval)
elif how == 'lower':
maxval = df[colname].max()
minval = df[colname].min()
df[colname_new] = (df[colname] - minval) / (maxval - minval)
#hide
# Initialize the model:
mod = initialize_model(df)
# Run MCMC sampler1
with mod:
trace = pm.sample(300, tune=100,
chains=3, cores=2)
#collapse-hide
n_samp = len(trace['mu_0'])
mu0_summary = pm.summary(trace).loc['mu_0']
print("COVID-19 Global Mortality Rate Estimation:")
print("Posterior mean: %0.2f%%" % (100*trace['mu_0'].mean()))
print("Posterior median: %0.2f%%" % (100*np.median(trace['mu_0'])))
lower = np.sort(trace['mu_0'])[int(n_samp*0.025)]
upper = np.sort(trace['mu_0'])[int(n_samp*0.975)]
print("95%% posterior interval: (%0.2f%%, %0.2f%%)" % (100*lower, 100*upper))
prob_lt_reported = sum(trace['mu_0'] < reported_mortality_rate) / len(trace['mu_0'])
print("Probability true rate less than reported rate (%.2f%%) = %.2f%%" %
(100*reported_mortality_rate, 100*prob_lt_reported))
print("")
# Posterior plot for mu0
print('Posterior probability density for COVID-19 mortality rate, controlling for country factors:')
ax = pm.plot_posterior(trace, var_names=['mu_0'], figsize=(18, 8), textsize=18,
credible_interval=0.95, bw=3.0, lw=3, kind='kde',
ref_val=round(reported_mortality_rate, 3))
```
## Magnitude and Significance of Factors
For bias in reported COVID-19 mortality rate
```
#collapse-hide
# Posterior summary for the beta parameters:
beta_summary = pm.summary(trace).head(7)
beta_summary.index = ['days_since_first_case', 'cpi', 'healthcare_oop', 'hospital_beds', 'hci', 'percent_over65', 'percent_rural']
beta_summary.reset_index(drop=False, inplace=True)
err_vals = ((beta_summary['hpd_3%'] - beta_summary['mean']).values,
(beta_summary['hpd_97%'] - beta_summary['mean']).values)
ax = beta_summary.plot(x='index', y='mean', kind='bar', figsize=(14, 7),
title='Posterior Distribution of Beta Parameters',
yerr=err_vals, color='lightgrey',
legend=False, grid=True,
capsize=5)
beta_summary.plot(x='index', y='mean', color='k', marker='o', linestyle='None',
ax=ax, grid=True, legend=False, xlim=plt.gca().get_xlim())
plt.savefig('../images/corvid-mortality.png')
```
# About This Analysis
This analysis was done by [Joseph Richards](https://twitter.com/joeyrichar)
In this project[^3], we attempt to estimate the true mortality rate[^1] for COVID-19 while controlling for country-level covariates[^2][^4] such as:
* age of outbreak in the country
* transparency of the country's government
* access to healthcare
* demographics such as age of population and rural vs. urban
Estimating a mortality rate lower than the overall reported rate likely implies that there has been **significant under-testing and under-reporting of cases globally**.
## Interpretation of Country-Level Parameters
1. days_since_first_case - positive (very statistically significant). As time since outbreak increases, expected mortality rate **increases**, as expected.
2. cpi - negative (statistically significant). As government transparency increases, expected mortality rate **decreases**. This may mean that less transparent governments under-report cases, hence inflating the mortality rate.
3. healthcare avg. out-of-pocket spending - no significant trend.
4. hospital beds per capita - no significant trend.
5. Human Capital Index - no significant trend (slightly negative = mortality rates decrease with increased mobilization of the country)
6. percent over 65 - positive (statistically significant). As population age increases, the mortality rate also **increases**, as expected.
7. percent rural - no significant trend.
[^1]: As of March 10, the **overall reported mortality rate is 3.5%**. However, this figure does not account for **systematic biases in case reporting and testing**. The observed mortality of COVID-19 has varied widely from country to country (as of early March 2020). For instance, as of March 10, mortality rates have ranged from < 0.1% in places like Germany (1100+ cases) to upwards of 5% in Italy (9000+ cases) and 3.9% in China (80k+ cases).
[^2]: The point of our modelling work here is to **try to understand and correct for the country-to-country differences that may cause the observed discrepancies in COVID-19 country-wide mortality rates**. That way we can "undo" those biases and try to **pin down an overall *real* mortality rate**.
[^3]: Full details about the model are available at: https://github.com/jwrichar/COVID19-mortality
[^4]: The affects of these parameters are subject to change as more data are collected.
# Appendix: Model Diagnostics
The following trace plots help to assess the convergence of the MCMC sampler.
```
#hide_input
import arviz as az
az.plot_trace(trace, compact=True);
```
| true |
code
| 0.549641 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/Scott-Huston/DS-Unit-1-Sprint-2-Data-Wrangling-and-Storytelling/blob/master/LS_DS_123_Make_Explanatory_Visualizations.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
_Lambda School Data Science_
# Make Explanatory Visualizations
### Objectives
- identify misleading visualizations and how to fix them
- use Seaborn to visualize distributions and relationships with continuous and discrete variables
- add emphasis and annotations to transform visualizations from exploratory to explanatory
- remove clutter from visualizations
### Links
- [How to Spot Visualization Lies](https://flowingdata.com/2017/02/09/how-to-spot-visualization-lies/)
- [Visual Vocabulary - Vega Edition](http://ft.com/vocabulary)
- [Choosing a Python Visualization Tool flowchart](http://pbpython.com/python-vis-flowchart.html)
- [Searborn example gallery](http://seaborn.pydata.org/examples/index.html) & [tutorial](http://seaborn.pydata.org/tutorial.html)
- [Strong Titles Are The Biggest Bang for Your Buck](http://stephanieevergreen.com/strong-titles/)
- [Remove to improve (the data-ink ratio)](https://www.darkhorseanalytics.com/blog/data-looks-better-naked)
- [How to Generate FiveThirtyEight Graphs in Python](https://www.dataquest.io/blog/making-538-plots/)
# Avoid Misleading Visualizations
Did you find/discuss any interesting misleading visualizations in your Walkie Talkie?
## What makes a visualization misleading?
[5 Ways Writers Use Misleading Graphs To Manipulate You](https://venngage.com/blog/misleading-graphs/)
## Two y-axes
<img src="https://kieranhealy.org/files/misc/two-y-by-four-sm.jpg" width="800">
Other Examples:
- [Spurious Correlations](https://tylervigen.com/spurious-correlations)
- <https://blog.datawrapper.de/dualaxis/>
- <https://kieranhealy.org/blog/archives/2016/01/16/two-y-axes/>
- <http://www.storytellingwithdata.com/blog/2016/2/1/be-gone-dual-y-axis>
## Y-axis doesn't start at zero.
<img src="https://i.pinimg.com/originals/22/53/a9/2253a944f54bb61f1983bc076ff33cdd.jpg" width="600">
## Pie Charts are bad
<img src="https://i1.wp.com/flowingdata.com/wp-content/uploads/2009/11/Fox-News-pie-chart.png?fit=620%2C465&ssl=1" width="600">
## Pie charts that omit data are extra bad
- A guy makes a misleading chart that goes viral
What does this chart imply at first glance? You don't want your user to have to do a lot of work in order to be able to interpret you graph correctly. You want that first-glance conclusions to be the correct ones.
<img src="https://pbs.twimg.com/media/DiaiTLHWsAYAEEX?format=jpg&name=medium" width='600'>
<https://twitter.com/michaelbatnick/status/1019680856837849090?lang=en>
- It gets picked up by overworked journalists (assuming incompetency before malice)
<https://www.marketwatch.com/story/this-1-chart-puts-mega-techs-trillions-of-market-value-into-eye-popping-perspective-2018-07-18>
- Even after the chart's implications have been refuted, it's hard a bad (although compelling) visualization from being passed around.
<https://www.linkedin.com/pulse/good-bad-pie-charts-karthik-shashidhar/>
**["yea I understand a pie chart was probably not the best choice to present this data."](https://twitter.com/michaelbatnick/status/1037036440494985216)**
## Pie Charts that compare unrelated things are next-level extra bad
<img src="http://www.painting-with-numbers.com/download/document/186/170403+Legalizing+Marijuana+Graph.jpg" width="600">
## Be careful about how you use volume to represent quantities:
radius vs diameter vs volume
<img src="https://static1.squarespace.com/static/5bfc8dbab40b9d7dd9054f41/t/5c32d86e0ebbe80a25873249/1546836082961/5474039-25383714-thumbnail.jpg?format=1500w" width="600">
## Don't cherrypick timelines or specific subsets of your data:
<img src="https://wattsupwiththat.com/wp-content/uploads/2019/02/Figure-1-1.png" width="600">
Look how specifically the writer has selected what years to show in the legend on the right side.
<https://wattsupwiththat.com/2019/02/24/strong-arctic-sea-ice-growth-this-year/>
Try the tool that was used to make the graphic for yourself
<http://nsidc.org/arcticseaicenews/charctic-interactive-sea-ice-graph/>
## Use Relative units rather than Absolute Units
<img src="https://imgs.xkcd.com/comics/heatmap_2x.png" width="600">
## Avoid 3D graphs unless having the extra dimension is effective
Usually you can Split 3D graphs into multiple 2D graphs
3D graphs that are interactive can be very cool. (See Plotly and Bokeh)
<img src="https://thumbor.forbes.com/thumbor/1280x868/https%3A%2F%2Fblogs-images.forbes.com%2Fthumbnails%2Fblog_1855%2Fpt_1855_811_o.jpg%3Ft%3D1339592470" width="600">
## Don't go against typical conventions
<img src="http://www.callingbullshit.org/twittercards/tools_misleading_axes.png" width="600">
# Tips for choosing an appropriate visualization:
## Use Appropriate "Visual Vocabulary"
[Visual Vocabulary - Vega Edition](http://ft.com/vocabulary)
## What are the properties of your data?
- Is your primary variable of interest continuous or discrete?
- Is in wide or long (tidy) format?
- Does your visualization involve multiple variables?
- How many dimensions do you need to include on your plot?
Can you express the main idea of your visualization in a single sentence?
How hard does your visualization make the user work in order to draw the intended conclusion?
## Which Visualization tool is most appropriate?
[Choosing a Python Visualization Tool flowchart](http://pbpython.com/python-vis-flowchart.html)
## Anatomy of a Matplotlib Plot
```
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import AutoMinorLocator, MultipleLocator, FuncFormatter
np.random.seed(19680801)
X = np.linspace(0.5, 3.5, 100)
Y1 = 3+np.cos(X)
Y2 = 1+np.cos(1+X/0.75)/2
Y3 = np.random.uniform(Y1, Y2, len(X))
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 1, 1, aspect=1)
def minor_tick(x, pos):
if not x % 1.0:
return ""
return "%.2f" % x
ax.xaxis.set_major_locator(MultipleLocator(1.000))
ax.xaxis.set_minor_locator(AutoMinorLocator(4))
ax.yaxis.set_major_locator(MultipleLocator(1.000))
ax.yaxis.set_minor_locator(AutoMinorLocator(4))
ax.xaxis.set_minor_formatter(FuncFormatter(minor_tick))
ax.set_xlim(0, 4)
ax.set_ylim(0, 4)
ax.tick_params(which='major', width=1.0)
ax.tick_params(which='major', length=10)
ax.tick_params(which='minor', width=1.0, labelsize=10)
ax.tick_params(which='minor', length=5, labelsize=10, labelcolor='0.25')
ax.grid(linestyle="--", linewidth=0.5, color='.25', zorder=-10)
ax.plot(X, Y1, c=(0.25, 0.25, 1.00), lw=2, label="Blue signal", zorder=10)
ax.plot(X, Y2, c=(1.00, 0.25, 0.25), lw=2, label="Red signal")
ax.plot(X, Y3, linewidth=0,
marker='o', markerfacecolor='w', markeredgecolor='k')
ax.set_title("Anatomy of a figure", fontsize=20, verticalalignment='bottom')
ax.set_xlabel("X axis label")
ax.set_ylabel("Y axis label")
ax.legend()
def circle(x, y, radius=0.15):
from matplotlib.patches import Circle
from matplotlib.patheffects import withStroke
circle = Circle((x, y), radius, clip_on=False, zorder=10, linewidth=1,
edgecolor='black', facecolor=(0, 0, 0, .0125),
path_effects=[withStroke(linewidth=5, foreground='w')])
ax.add_artist(circle)
def text(x, y, text):
ax.text(x, y, text, backgroundcolor="white",
ha='center', va='top', weight='bold', color='blue')
# Minor tick
circle(0.50, -0.10)
text(0.50, -0.32, "Minor tick label")
# Major tick
circle(-0.03, 4.00)
text(0.03, 3.80, "Major tick")
# Minor tick
circle(0.00, 3.50)
text(0.00, 3.30, "Minor tick")
# Major tick label
circle(-0.15, 3.00)
text(-0.15, 2.80, "Major tick label")
# X Label
circle(1.80, -0.27)
text(1.80, -0.45, "X axis label")
# Y Label
circle(-0.27, 1.80)
text(-0.27, 1.6, "Y axis label")
# Title
circle(1.60, 4.13)
text(1.60, 3.93, "Title")
# Blue plot
circle(1.75, 2.80)
text(1.75, 2.60, "Line\n(line plot)")
# Red plot
circle(1.20, 0.60)
text(1.20, 0.40, "Line\n(line plot)")
# Scatter plot
circle(3.20, 1.75)
text(3.20, 1.55, "Markers\n(scatter plot)")
# Grid
circle(3.00, 3.00)
text(3.00, 2.80, "Grid")
# Legend
circle(3.70, 3.80)
text(3.70, 3.60, "Legend")
# Axes
circle(0.5, 0.5)
text(0.5, 0.3, "Axes")
# Figure
circle(-0.3, 0.65)
text(-0.3, 0.45, "Figure")
color = 'blue'
ax.annotate('Spines', xy=(4.0, 0.35), xytext=(3.3, 0.5),
weight='bold', color=color,
arrowprops=dict(arrowstyle='->',
connectionstyle="arc3",
color=color))
ax.annotate('', xy=(3.15, 0.0), xytext=(3.45, 0.45),
weight='bold', color=color,
arrowprops=dict(arrowstyle='->',
connectionstyle="arc3",
color=color))
ax.text(4.0, -0.4, "Made with http://matplotlib.org",
fontsize=10, ha="right", color='.5')
plt.show()
```
# Making Explanatory Visualizations with Seaborn
Today we will reproduce this [example by FiveThirtyEight:](https://fivethirtyeight.com/features/al-gores-new-movie-exposes-the-big-flaw-in-online-movie-ratings/)
```
from IPython.display import display, Image
url = 'https://fivethirtyeight.com/wp-content/uploads/2017/09/mehtahickey-inconvenient-0830-1.png'
example = Image(url=url, width=400)
display(example)
```
Using this data: https://github.com/fivethirtyeight/data/tree/master/inconvenient-sequel
Links
- [Strong Titles Are The Biggest Bang for Your Buck](http://stephanieevergreen.com/strong-titles/)
- [Remove to improve (the data-ink ratio)](https://www.darkhorseanalytics.com/blog/data-looks-better-naked)
- [How to Generate FiveThirtyEight Graphs in Python](https://www.dataquest.io/blog/making-538-plots/)
## Make prototypes
This helps us understand the problem
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.style.use('fivethirtyeight')
fake = pd.Series([38, 3, 2, 1, 2, 4, 6, 5, 5, 33],
index=range(1,11))
fake.plot.bar(color='C1', width=0.9);
fake2 = pd.Series(
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
2, 2, 2,
3, 3, 3,
4, 4,
5, 5, 5,
6, 6, 6, 6,
7, 7, 7, 7, 7,
8, 8, 8, 8,
9, 9, 9, 9,
10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10])
fake2.value_counts().sort_index().plot.bar(color='C1', width=0.9);
```
## Annotate with text
```
plt.style.use('fivethirtyeight')
fig = plt.figure()
fig.patch.set_facecolor('white')
ax = fake.plot.bar(color='#ED713A', width = .9)
ax.set(facecolor = 'white')
ax.text(x=-2,y = 46, s="'An Inconvenient Sequel: Truth To Power' is divisive", fontweight = 'bold')
ax.text(x=-2, y = 43, s = 'IMDb ratings for the film as of Aug. 29')
ax.set_xticklabels(range(1,11), rotation = 0, color = '#A3A3A3')
ax.set_yticklabels(['0', '10', '20', '30', '40%'], color = '#A3A3A3')
ax.set_yticks(range(0,50,10))
plt.ylabel('Percent of total votes', fontweight = 'bold', fontsize = '12')
plt.xlabel('Rating', fontweight = 'bold', fontsize = '12')
```
## Reproduce with real data
```
df = pd.read_csv('https://raw.githubusercontent.com/fivethirtyeight/data/master/inconvenient-sequel/ratings.csv')
pd.set_option('display.max_columns', 50)
print(df.shape)
df.head(20)
df.sample(1).T
df.tail()
df.dtypes
df['timestamp'] = pd.to_datetime(df['timestamp'])
df.timestamp.describe()
df.dtypes
df.set_index(df['timestamp'], inplace = True)
df['2017-08-29']
lastday = df['2017-08-29']
lastday_filtered = lastday[lastday['category']=='IMDb users']
lastday_filtered.tail(30)
df.category.value_counts()
lastday_filtered.respondents.plot()
plt.show()
final = lastday_filtered.tail(1)
final.T
pct_columns = ['1_pct', '2_pct', '3_pct', '4_pct', '5_pct','6_pct','7_pct','8_pct','9_pct','10_pct']
final = final[pct_columns]
final.T
plot_data = final.T
plot_data.index = range(1,11)
plot_data
plt.style.use('fivethirtyeight')
fig = plt.figure()
fig.patch.set_facecolor('white')
ax = plot_data.plot.bar(color='#ED713A', width = .9, legend = False)
ax.set(facecolor = 'white')
ax.text(x=-2,y = 46, s="'An Inconvenient Sequel: Truth To Power' is divisive", fontweight = 'bold')
ax.text(x=-2, y = 43, s = 'IMDb ratings for the film as of Aug. 29')
ax.set_xticklabels(range(1,11), rotation = 0, color = '#A3A3A3')
ax.set_yticklabels(['0', '10', '20', '30', '40%'], color = '#A3A3A3')
ax.set_yticks(range(0,50,10))
plt.ylabel('Percent of total votes', fontweight = 'bold', fontsize = '12')
plt.xlabel('Rating', fontweight = 'bold', fontsize = '12', labelpad = 15)
plt.show()
```
# ASSIGNMENT
Replicate the lesson code. I recommend that you [do not copy-paste](https://docs.google.com/document/d/1ubOw9B3Hfip27hF2ZFnW3a3z9xAgrUDRReOEo-FHCVs/edit).
# STRETCH OPTIONS
#### 1) Reproduce another example from [FiveThityEight's shared data repository](https://data.fivethirtyeight.com/).
#### 2) Reproduce one of the following using a library other than Seaborn or Matplotlib.
For example:
- [thanksgiving-2015](https://fivethirtyeight.com/features/heres-what-your-part-of-america-eats-on-thanksgiving/) (try the [`altair`](https://altair-viz.github.io/gallery/index.html#maps) library)
- [candy-power-ranking](https://fivethirtyeight.com/features/the-ultimate-halloween-candy-power-ranking/) (try the [`statsmodels`](https://www.statsmodels.org/stable/index.html) library)
- or another example of your choice!
#### 3) Make more charts!
Choose a chart you want to make, from [Visual Vocabulary - Vega Edition](http://ft.com/vocabulary).
Find the chart in an example gallery of a Python data visualization library:
- [Seaborn](http://seaborn.pydata.org/examples/index.html)
- [Altair](https://altair-viz.github.io/gallery/index.html)
- [Matplotlib](https://matplotlib.org/gallery.html)
- [Pandas](https://pandas.pydata.org/pandas-docs/stable/visualization.html)
Reproduce the chart. [Optionally, try the "Ben Franklin Method."](https://docs.google.com/document/d/1ubOw9B3Hfip27hF2ZFnW3a3z9xAgrUDRReOEo-FHCVs/edit) If you want, experiment and make changes.
Take notes. Consider sharing your work with your cohort!
```
# Stretch option #1
!pip install pandas==0.23.4
import pandas as pd
from IPython.display import display, Image
# url = 'https://fivethirtyeight.com/wp-content/uploads/2017/09/mehtahickey-inconvenient-0830-1.png'
# example = Image(url=url, width=400)
# example = Image(filename = '/Users/scotthuston/Desktop/FTE_image')
# display(example)
FTE = pd.read_csv('https://raw.githubusercontent.com/fivethirtyeight/checking-our-work-data/master/mlb_games.csv')
FTE.head()
prob1_bins = pd.cut(FTE['prob1'],13)
ct = pd.crosstab(FTE['prob1_outcome'], [prob1_bins])
# FTE.boxplot(column = 'prob1')
df1 = FTE[FTE['prob1'] <= .278]
df2 = FTE[(FTE['prob1'] <= .322) & (FTE['prob1']>.278)]
df3 = FTE[(FTE['prob1'] <= .367) & (FTE['prob1']>.322)]
df4 = FTE[(FTE['prob1'] <= .411) & (FTE['prob1']>.367)]
df5 = FTE[(FTE['prob1'] <= .456) & (FTE['prob1']>.411)]
df6 = FTE[(FTE['prob1'] <= .501) & (FTE['prob1']>.456)]
df7 = FTE[(FTE['prob1'] <= .545) & (FTE['prob1']>.501)]
df8 = FTE[(FTE['prob1'] <= .59) & (FTE['prob1']>.545)]
df9 = FTE[(FTE['prob1'] <= .634) & (FTE['prob1']>.59)]
df10 = FTE[(FTE['prob1'] <= .679) & (FTE['prob1']>.634)]
df11= FTE[(FTE['prob1'] <= .723) & (FTE['prob1']>.679)]
df12 = FTE[(FTE['prob1'] <= .768) & (FTE['prob1']>.723)]
df13 = FTE[(FTE['prob1'] <= .812) & (FTE['prob1']>.768)]
df1.head()
df2.head(10)
import matplotlib.pyplot as plt
import seaborn as sns
plt.errorbar(df1['prob1'],df1['prob1_outcome'], xerr = df1['prob1_outcome']-df1['prob1'])
sns.set(style="darkgrid")
lst = []
for i in len(df2.prob1_outcome):
lst.append(1)
sns.pointplot(lst, y="prob1_outcome", data=df2)
# df2['prob1_outcome']
```
| true |
code
| 0.594728 | null | null | null | null |
|
# LAB 4b: Create Keras DNN model.
**Learning Objectives**
1. Set CSV Columns, label column, and column defaults
1. Make dataset of features and label from CSV files
1. Create input layers for raw features
1. Create feature columns for inputs
1. Create DNN dense hidden layers and output layer
1. Create custom evaluation metric
1. Build DNN model tying all of the pieces together
1. Train and evaluate
## Introduction
In this notebook, we'll be using Keras to create a DNN model to predict the weight of a baby before it is born.
We'll start by defining the CSV column names, label column, and column defaults for our data inputs. Then, we'll construct a tf.data Dataset of features and the label from the CSV files and create inputs layers for the raw features. Next, we'll set up feature columns for the model inputs and build a deep neural network in Keras. We'll create a custom evaluation metric and build our DNN model. Finally, we'll train and evaluate our model.
Each learning objective will correspond to a __#TODO__ in this student lab notebook -- try to complete this notebook first and then review the [solution notebook](../solutions/4b_keras_dnn_babyweight.ipynb).
## Load necessary libraries
```
import datetime
import os
import shutil
import matplotlib.pyplot as plt
import tensorflow as tf
print(tf.__version__)
```
## Verify CSV files exist
In the seventh lab of this series [4a_sample_babyweight](../solutions/4a_sample_babyweight.ipynb), we sampled from BigQuery our train, eval, and test CSV files. Verify that they exist, otherwise go back to that lab and create them.
```
%%bash
ls *.csv
%%bash
head -5 *.csv
```
## Create Keras model
### Set CSV Columns, label column, and column defaults.
Now that we have verified that our CSV files exist, we need to set a few things that we will be using in our input function.
* `CSV_COLUMNS` are going to be our header names of our columns. Make sure that they are in the same order as in the CSV files
* `LABEL_COLUMN` is the header name of the column that is our label. We will need to know this to pop it from our features dictionary.
* `DEFAULTS` is a list with the same length as `CSV_COLUMNS`, i.e. there is a default for each column in our CSVs. Each element is a list itself with the default value for that CSV column.
```
# Determine CSV, label, and key columns
# Create list of string column headers, make sure order matches.
CSV_COLUMNS = ["weight_pounds",
"is_male",
"mother_age",
"plurality",
"gestation_weeks"]
# Add string name for label column
LABEL_COLUMN = "weight_pounds"
# Set default values for each CSV column as a list of lists.
# Treat is_male and plurality as strings.
DEFAULTS = [[0.0], ["null"], [0.0], ["null"], [0.0]]
```
### Make dataset of features and label from CSV files.
Next, we will write an input_fn to read the data. Since we are reading from CSV files we can save ourself from trying to recreate the wheel and can use `tf.data.experimental.make_csv_dataset`. This will create a CSV dataset object. However we will need to divide the columns up into features and a label. We can do this by applying the map method to our dataset and popping our label column off of our dictionary of feature tensors.
```
def features_and_labels(row_data):
"""Splits features and labels from feature dictionary.
Args:
row_data: Dictionary of CSV column names and tensor values.
Returns:
Dictionary of feature tensors and label tensor.
"""
label = row_data.pop(LABEL_COLUMN)
return row_data, label # features, label
def load_dataset(pattern, batch_size=1, mode=tf.estimator.ModeKeys.EVAL):
"""Loads dataset using the tf.data API from CSV files.
Args:
pattern: str, file pattern to glob into list of files.
batch_size: int, the number of examples per batch.
mode: tf.estimator.ModeKeys to determine if training or evaluating.
Returns:
`Dataset` object.
"""
# Make a CSV dataset
dataset = tf.data.experimental.make_csv_dataset(
file_pattern=pattern,
batch_size=batch_size,
column_names=CSV_COLUMNS,
column_defaults=DEFAULTS)
# Map dataset to features and label
dataset = dataset.map(map_func=features_and_labels) # features, label
# Shuffle and repeat for training
if mode == tf.estimator.ModeKeys.TRAIN:
dataset = dataset.shuffle(buffer_size=1000).repeat()
# Take advantage of multi-threading; 1=AUTOTUNE
dataset = dataset.prefetch(buffer_size=1)
return dataset
```
### Create input layers for raw features.
We'll need to get the data read in by our input function to our model function, but just how do we go about connecting the dots? We can use Keras input layers [(tf.Keras.layers.Input)](https://www.tensorflow.org/api_docs/python/tf/keras/Input) by defining:
* shape: A shape tuple (integers), not including the batch size. For instance, shape=(32,) indicates that the expected input will be batches of 32-dimensional vectors. Elements of this tuple can be None; 'None' elements represent dimensions where the shape is not known.
* name: An optional name string for the layer. Should be unique in a model (do not reuse the same name twice). It will be autogenerated if it isn't provided.
* dtype: The data type expected by the input, as a string (float32, float64, int32...)
```
def create_input_layers():
"""Creates dictionary of input layers for each feature.
Returns:
Dictionary of `tf.Keras.layers.Input` layers for each feature.
"""
inputs = {
colname: tf.keras.layers.Input(
name=colname, shape=(), dtype="float32")
for colname in ["mother_age", "gestation_weeks"]}
inputs.update({
colname: tf.keras.layers.Input(
name=colname, shape=(), dtype="string")
for colname in ["is_male", "plurality"]})
return inputs
```
### Create feature columns for inputs.
Next, define the feature columns. `mother_age` and `gestation_weeks` should be numeric. The others, `is_male` and `plurality`, should be categorical. Remember, only dense feature columns can be inputs to a DNN.
```
def categorical_fc(name, values):
"""Helper function to wrap categorical feature by indicator column.
Args:
name: str, name of feature.
values: list, list of strings of categorical values.
Returns:
Indicator column of categorical feature.
"""
cat_column = tf.feature_column.categorical_column_with_vocabulary_list(
key=name, vocabulary_list=values)
return tf.feature_column.indicator_column(categorical_column=cat_column)
def create_feature_columns():
"""Creates dictionary of feature columns from inputs.
Returns:
Dictionary of feature columns.
"""
feature_columns = {
colname : tf.feature_column.numeric_column(key=colname)
for colname in ["mother_age", "gestation_weeks"]
}
feature_columns["is_male"] = categorical_fc(
"is_male", ["True", "False", "Unknown"])
feature_columns["plurality"] = categorical_fc(
"plurality", ["Single(1)", "Twins(2)", "Triplets(3)",
"Quadruplets(4)", "Quintuplets(5)", "Multiple(2+)"])
return feature_columns
```
### Create DNN dense hidden layers and output layer.
So we've figured out how to get our inputs ready for machine learning but now we need to connect them to our desired output. Our model architecture is what links the two together. Let's create some hidden dense layers beginning with our inputs and end with a dense output layer. This is regression so make sure the output layer activation is correct and that the shape is right.
```
def get_model_outputs(inputs):
"""Creates model architecture and returns outputs.
Args:
inputs: Dense tensor used as inputs to model.
Returns:
Dense tensor output from the model.
"""
# Create two hidden layers of [64, 32] just in like the BQML DNN
h1 = tf.keras.layers.Dense(64, activation="relu", name="h1")(inputs)
h2 = tf.keras.layers.Dense(32, activation="relu", name="h2")(h1)
# Final output is a linear activation because this is regression
output = tf.keras.layers.Dense(
units=1, activation="linear", name="weight")(h2)
return output
```
### Create custom evaluation metric.
We want to make sure that we have some useful way to measure model performance for us. Since this is regression, we would like to know the RMSE of the model on our evaluation dataset, however, this does not exist as a standard evaluation metric, so we'll have to create our own by using the true and predicted labels.
```
def rmse(y_true, y_pred):
"""Calculates RMSE evaluation metric.
Args:
y_true: tensor, true labels.
y_pred: tensor, predicted labels.
Returns:
Tensor with value of RMSE between true and predicted labels.
"""
return tf.sqrt(tf.reduce_mean((y_pred - y_true) ** 2))
```
### Build DNN model tying all of the pieces together.
Excellent! We've assembled all of the pieces, now we just need to tie them all together into a Keras Model. This is a simple feedforward model with no branching, side inputs, etc. so we could have used Keras' Sequential Model API but just for fun we're going to use Keras' Functional Model API. Here we will build the model using [tf.keras.models.Model](https://www.tensorflow.org/api_docs/python/tf/keras/Model) giving our inputs and outputs and then compile our model with an optimizer, a loss function, and evaluation metrics.
```
def build_dnn_model():
"""Builds simple DNN using Keras Functional API.
Returns:
`tf.keras.models.Model` object.
"""
# Create input layer
inputs = create_input_layers()
# Create feature columns
feature_columns = create_feature_columns()
# The constructor for DenseFeatures takes a list of numeric columns
# The Functional API in Keras requires: LayerConstructor()(inputs)
dnn_inputs = tf.keras.layers.DenseFeatures(
feature_columns=feature_columns.values())(inputs)
# Get output of model given inputs
output = get_model_outputs(dnn_inputs)
# Build model and compile it all together
model = tf.keras.models.Model(inputs=inputs, outputs=output)
model.compile(optimizer="adam", loss="mse", metrics=[rmse, "mse"])
return model
print("Here is our DNN architecture so far:\n")
model = build_dnn_model()
print(model.summary())
```
We can visualize the DNN using the Keras plot_model utility.
```
tf.keras.utils.plot_model(
model=model, to_file="dnn_model.png", show_shapes=False, rankdir="LR")
```
## Run and evaluate model
### Train and evaluate.
We've built our Keras model using our inputs from our CSV files and the architecture we designed. Let's now run our model by training our model parameters and periodically running an evaluation to track how well we are doing on outside data as training goes on. We'll need to load both our train and eval datasets and send those to our model through the fit method. Make sure you have the right pattern, batch size, and mode when loading the data. Also, don't forget to add the callback to TensorBoard.
```
TRAIN_BATCH_SIZE = 32
NUM_TRAIN_EXAMPLES = 10000 * 5 # training dataset repeats, it'll wrap around
NUM_EVALS = 5 # how many times to evaluate
# Enough to get a reasonable sample, but not so much that it slows down
NUM_EVAL_EXAMPLES = 10000
trainds = load_dataset(
pattern="train*",
batch_size=TRAIN_BATCH_SIZE,
mode=tf.estimator.ModeKeys.TRAIN)
evalds = load_dataset(
pattern="eval*",
batch_size=1000,
mode=tf.estimator.ModeKeys.EVAL).take(count=NUM_EVAL_EXAMPLES // 1000)
steps_per_epoch = NUM_TRAIN_EXAMPLES // (TRAIN_BATCH_SIZE * NUM_EVALS)
logdir = os.path.join(
"logs", datetime.datetime.now().strftime("%Y%m%d-%H%M%S"))
tensorboard_callback = tf.keras.callbacks.TensorBoard(
log_dir=logdir, histogram_freq=1)
history = model.fit(
trainds,
validation_data=evalds,
epochs=NUM_EVALS,
steps_per_epoch=steps_per_epoch,
callbacks=[tensorboard_callback])
```
### Visualize loss curve
```
# Plot
import matplotlib.pyplot as plt
nrows = 1
ncols = 2
fig = plt.figure(figsize=(10, 5))
for idx, key in enumerate(["loss", "rmse"]):
ax = fig.add_subplot(nrows, ncols, idx+1)
plt.plot(history.history[key])
plt.plot(history.history["val_{}".format(key)])
plt.title("model {}".format(key))
plt.ylabel(key)
plt.xlabel("epoch")
plt.legend(["train", "validation"], loc="upper left");
```
### Save the model
```
OUTPUT_DIR = "babyweight_trained"
shutil.rmtree(OUTPUT_DIR, ignore_errors=True)
EXPORT_PATH = os.path.join(
OUTPUT_DIR, datetime.datetime.now().strftime("%Y%m%d%H%M%S"))
tf.saved_model.save(
obj=model, export_dir=EXPORT_PATH) # with default serving function
print("Exported trained model to {}".format(EXPORT_PATH))
!ls $EXPORT_PATH
```
## Monitor and experiment with training
To begin TensorBoard from within AI Platform Notebooks, click the + symbol in the top left corner and select the **Tensorboard** icon to create a new TensorBoard. Before you click make sure you are in the directory of your TensorBoard log_dir.
In TensorBoard, look at the learned embeddings. Are they getting clustered? How about the weights for the hidden layers? What if you run this longer? What happens if you change the batchsize?
## Lab Summary:
In this lab, we started by defining the CSV column names, label column, and column defaults for our data inputs. Then, we constructed a tf.data Dataset of features and the label from the CSV files and created inputs layers for the raw features. Next, we set up feature columns for the model inputs and built a deep neural network in Keras. We created a custom evaluation metric and built our DNN model. Finally, we trained and evaluated our model.
Copyright 2019 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
| true |
code
| 0.78537 | null | null | null | null |
|
# Setup
```
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import itertools as it
import helpers_03
%matplotlib inline
```
# Neurons as Logic Gates
As an introduction to neural networks and their component neurons, we are going to look at using neurons to implement the most primitive logic computations: logic gates. Let's go!
##### The Sigmoid Function
The basic, classic activation function that we apply to neurons is a sigmoid (sometimes just called *the* sigmoid function) function: the standard logistic function.
$$
\sigma = \frac{1}{1 + e^{-x}}
$$
$\sigma$ ranges from (0, 1). When the input $x$ is negative, $\sigma$ is close to 0. When $x$ is positive, $\sigma$ is close to 1. At $x=0$, $\sigma=0.5$
We can implement this conveniently with NumPy.
```
def sigmoid(x):
"""Sigmoid function"""
return 1.0 / (1.0 + np.exp(-x))
```
And plot it with matplotlib.
```
# Plot The sigmoid function
xs = np.linspace(-10, 10, num=100, dtype=np.float32)
activation = sigmoid(xs)
fig = plt.figure(figsize=(6,4))
plt.plot(xs, activation)
plt.plot(0,.5,'ro')
plt.grid(True, which='both')
plt.axhline(y=0, color='y')
plt.axvline(x=0, color='y')
plt.ylim([-0.1, 1.15])
```
## An Example with OR
##### OR Logic
A logic gate takes in two boolean (true/false or 1/0) inputs, and returns either a 0 or 1 depending on its rule. The truth table for a logic gate shows the outputs for each combination of inputs: (0, 0), (0, 1), (1,0), and (1, 1). For example, let's look at the truth table for an Or-gate:
<table>
<tr><th colspan="3">OR gate truth table</th></tr>
<tr><th colspan="2">Input</th><th>Output</th></tr>
<tr><td>0</td><td>0</td><td>0</td></tr>
<tr><td>0</td><td>1</td><td>1</td></tr>
<tr><td>1</td><td>0</td><td>1</td></tr>
<tr><td>1</td><td>1</td><td>1</td></tr>
</table>
##### OR as a Neuron
A neuron that uses the sigmoid activation function outputs a value between (0, 1). This naturally leads us to think about boolean values. Imagine a neuron that takes in two inputs, $x_1$ and $x_2$, and a bias term:
<img src="./images/logic01.png" width=50%/>
By limiting the inputs of $x_1$ and $x_2$ to be in $\left\{0, 1\right\}$, we can simulate the effect of logic gates with our neuron. The goal is to find the weights (represented by ? marks above), such that it returns an output close to 0 or 1 depending on the inputs. What weights should we use to output the same results as OR? Remember: $\sigma(z)$ is close to 0 when $z$ is largely negative (around -10 or less), and is close to 1 when $z$ is largely positive (around +10 or greater).
$$
z = w_1 x_1 + w_2 x_2 + b
$$
Let's think this through:
* When $x_1$ and $x_2$ are both 0, the only value affecting $z$ is $b$. Because we want the result for input (0, 0) to be close to zero, $b$ should be negative (at least -10) to get the very left-hand part of the sigmoid.
* If either $x_1$ or $x_2$ is 1, we want the output to be close to 1. That means the weights associated with $x_1$ and $x_2$ should be enough to offset $b$ to the point of causing $z$ to be at least 10 (i.e., to the far right part of the sigmoid).
Let's give $b$ a value of -10. How big do we need $w_1$ and $w_2$ to be? At least +20 will get us to +10 for just one of $\{w_1, w_2\}$ being on.
So let's try out $w_1=20$, $w_2=20$, and $b=-10$:
<img src="./images/logic02.png\" width=50%/>
##### Some Utility Functions
Since we're going to be making several example logic gates (from different sets of weights and biases), here are two helpers. The first takes our weights and baises and turns them into a two-argument function that we can use like `and(a,b)`. The second is for printing a truth table for a gate.
```
def logic_gate(w1, w2, b):
''' logic_gate is a function which returns a function
the returned function take two args and (hopefully)
acts like a logic gate (and/or/not/etc.). its behavior
is determined by w1,w2,b. a longer, better name would be
make_twoarg_logic_gate_function'''
def the_gate(x1, x2):
return sigmoid(w1 * x1 + w2 * x2 + b)
return the_gate
def test(gate):
'Helper function to test out our weight functions.'
for a, b in it.product(range(2), repeat=2):
print("{}, {}: {}".format(a, b, np.round(gate(a, b))))
```
Let's see how we did. Here's the gold-standard truth table.
<table>
<tr><th colspan="3">OR gate truth table</th></tr>
<tr><th colspan="2">Input</th><th>Output</th></tr>
<tr><td>0</td><td>0</td><td>0</td></tr>
<tr><td>0</td><td>1</td><td>1</td></tr>
<tr><td>1</td><td>0</td><td>1</td></tr>
<tr><td>1</td><td>1</td><td>1</td></tr>
</table>
And our result:
```
or_gate = logic_gate(20, 20, -10)
test(or_gate)
```
This matches - great!
# Exercise 1
##### Part 1: AND Gate
Now you try finding the appropriate weight values for each truth table. Try not to guess and check. Think through it logically and try to derive values that work.
<table>
<tr><th colspan="3">AND gate truth table</th></tr>
<tr><th colspan="2">Input</th><th>Output</th></tr>
<tr><td>0</td><td>0</td><td>0</td></tr>
<tr><td>0</td><td>1</td><td>0</td></tr>
<tr><td>1</td><td>0</td><td>0</td></tr>
<tr><td>1</td><td>1</td><td>1</td></tr>
</table>
```
# Fill in the w1, w2, and b parameters such that the truth table matches
# and_gate = logic_gate()
# test(and_gate)
```
##### Part 2: NOR (Not Or) Gate
<table>
<tr><th colspan="3">NOR gate truth table</th></tr>
<tr><th colspan="2">Input</th><th>Output</th></tr>
<tr><td>0</td><td>0</td><td>1</td></tr>
<tr><td>0</td><td>1</td><td>0</td></tr>
<tr><td>1</td><td>0</td><td>0</td></tr>
<tr><td>1</td><td>1</td><td>0</td></tr>
</table>
<table>
```
# Fill in the w1, w2, and b parameters such that the truth table matches
# nor_gate = logic_gate()
# test(nor_gate)
```
##### Part 3: NAND (Not And) Gate
<table>
<tr><th colspan="3">NAND gate truth table</th></tr>
<tr><th colspan="2">Input</th><th>Output</th></tr>
<tr><td>0</td><td>0</td><td>1</td></tr>
<tr><td>0</td><td>1</td><td>1</td></tr>
<tr><td>1</td><td>0</td><td>1</td></tr>
<tr><td>1</td><td>1</td><td>0</td></tr>
</table>
```
# Fill in the w1, w2, and b parameters such that the truth table matches
# nand_gate = logic_gate()
# test(nand_gate)
```
## Solutions 1
# Limits of Single Neurons
If you've taken computer science courses, you may know that the XOR gates are the basis of computation. They can be used as half-adders, the foundation of being able to add numbers together. Here's the truth table for XOR:
##### XOR (Exclusive Or) Gate
<table>
<tr><th colspan="3">NAND gate truth table</th></tr>
<tr><th colspan="2">Input</th><th>Output</th></tr>
<tr><td>0</td><td>0</td><td>0</td></tr>
<tr><td>0</td><td>1</td><td>1</td></tr>
<tr><td>1</td><td>0</td><td>1</td></tr>
<tr><td>1</td><td>1</td><td>0</td></tr>
</table>
Now the question is, can you create a set of weights such that a single neuron can output this property? It turns out that you cannot. Single neurons can't correlate inputs, so it's just confused. So individual neurons are out. Can we still use neurons to somehow form an XOR gate?
What if we tried something more complex:
<img src="./images/logic03.png\" width=60%/>
Here, we've got the inputs going to two separate gates: the top neuron is an OR gate, and the bottom is a NAND gate. The output of these gates is passed to another neuron, which is an AND gate. If you work out the outputs at each combination of input values, you'll see that this is an XOR gate!
```
# Make sure you have or_gate, nand_gate, and and_gate working from above
def xor_gate(a, b):
c = or_gate(a, b)
d = nand_gate(a, b)
return and_gate(c, d)
test(xor_gate)
```
Thus, we can see how chaining together neurons can compose more complex models than we'd otherwise have access to.
# Learning a Logic Gate
We can use TensorFlow to try and teach a model to learn the correct weights and bias by passing in our truth table as training data.
```
# Create an empty Graph to place our operations in
logic_graph = tf.Graph()
with logic_graph.as_default():
# Placeholder inputs for our a, b, and label training data
x1 = tf.placeholder(tf.float32)
x2 = tf.placeholder(tf.float32)
label = tf.placeholder(tf.float32)
# A placeholder for our learning rate, so we can adjust it
learning_rate = tf.placeholder(tf.float32)
# The Variables we'd like to learn: weights for a and b, as well as a bias term
w1 = tf.Variable(tf.random_normal([]))
w2 = tf.Variable(tf.random_normal([]))
b = tf.Variable(0.0, dtype=tf.float32)
# Use the built-in sigmoid function for our output value
output = tf.nn.sigmoid(w1 * x1 + w2 * x2 + b)
# We'll use the mean of squared errors as our loss function
loss = tf.reduce_mean(tf.square(output - label))
correct = tf.equal(tf.round(output), label)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
# Finally, we create a gradient descent training operation and an initialization operation
train = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
init = tf.global_variables_initializer()
with tf.Session(graph=logic_graph) as sess:
sess.run(init)
# Training data for all combinations of inputs
and_table = np.array([[0,0,0],
[1,0,0],
[0,1,0],
[1,1,1]])
feed_dict={x1: and_table[:,0],
x2: and_table[:,1],
label: and_table[:,2],
learning_rate: 0.5}
for i in range(5000):
l, acc, _ = sess.run([loss, accuracy, train], feed_dict)
if i % 1000 == 0:
print('loss: {}\taccuracy: {}'.format(l, acc))
test_dict = {x1: and_table[:,0], #[0.0, 1.0, 0.0, 1.0],
x2: and_table[:,1]} # [0.0, 0.0, 1.0, 1.0]}
w1_val, w2_val, b_val, out = sess.run([w1, w2, b, output], test_dict)
print('\nLearned weight for w1:\t {}'.format(w1_val))
print('Learned weight for w2:\t {}'.format(w2_val))
print('Learned weight for bias: {}\n'.format(b_val))
print(np.column_stack((and_table[:,[0,1]], out.round().astype(np.uint8) ) ) )
# FIXME! ARGH! use real python or numpy
#idx = 0
#for i in [0, 1]:
# for j in [0, 1]:
# print('{}, {}: {}'.format(i, j, np.round(out[idx])))
# idx += 1
```
# Exercise 2
You may recall that in week 2, we built a class `class TF_GD_LinearRegression` that wrapped up the three steps of using a learning model: (1) build the model graph, (2) train/fit, and (3) test/predict. Above, we *did not* use that style of implementation. And you can see that things get a bit messy, quickly. We have model creation in one spot and then we have training, testing, and output all mixed together (along with TensorFlow helper code like sessions, etc.). We can do better. Rework the code above into a class like `TF_GD_LinearRegression`.
## Solution 2
# Learning an XOR Gate
If we compose a two stage model, we can learn the XOR gate. You'll notice that defining the model itself is starting to get messy. We'll talk about ways of dealing with that next week.
```
class XOR_Graph:
def __init__(self):
# Create an empty Graph to place our operations in
xor_graph = tf.Graph()
with xor_graph.as_default():
# Placeholder inputs for our a, b, and label training data
self.x1 = tf.placeholder(tf.float32)
self.x2 = tf.placeholder(tf.float32)
self.label = tf.placeholder(tf.float32)
# A placeholder for our learning rate, so we can adjust it
self.learning_rate = tf.placeholder(tf.float32)
# abbreviations! this section is the difference
# from the LogicGate class above
Var = tf.Variable; rn = tf.random_normal
self.weights = [[Var(rn([])), Var(rn([]))],
[Var(rn([])), Var(rn([]))],
[Var(rn([])), Var(rn([]))]]
self.biases = [Var(0.0, dtype=tf.float32),
Var(0.0, dtype=tf.float32),
Var(0.0, dtype=tf.float32)]
sig1 = tf.nn.sigmoid(self.x1 * self.weights[0][0] +
self.x2 * self.weights[0][1] +
self.biases[0])
sig2 = tf.nn.sigmoid(self.x1 * self.weights[1][0] +
self.x2 * self.weights[1][1] +
self.biases[1])
self.output = tf.nn.sigmoid(sig1 * self.weights[2][0] +
sig2 * self.weights[2][1] +
self.biases[2])
# We'll use the mean of squared errors as our loss function
self.loss = tf.reduce_mean(tf.square(self.output - self.label))
# Finally, we create a gradient descent training operation
# and an initialization operation
gdo = tf.train.GradientDescentOptimizer
self.train = gdo(self.learning_rate).minimize(self.loss)
correct = tf.equal(tf.round(self.output), self.label)
self.accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
self.sess = tf.Session(graph=xor_graph)
self.sess.run(init)
def fit(self, train_dict):
loss, acc, _ = self.sess.run([self.loss, self.accuracy, self.train],
train_dict)
return loss, acc
def predict(self, test_dict):
# make a list of organized weights:
# see tf.get_collection for more advanced ways to handle this
all_trained = (self.weights[0] + [self.biases[0]] +
self.weights[1] + [self.biases[1]] +
self.weights[2] + [self.biases[2]])
return self.sess.run(all_trained + [self.output], test_dict)
xor_table = np.array([[0,0,0],
[1,0,1],
[0,1,1],
[1,1,0]])
logic_model = XOR_Graph()
train_dict={logic_model.x1: xor_table[:,0],
logic_model.x2: xor_table[:,1],
logic_model.label: xor_table[:,2],
logic_model.learning_rate: 0.5}
print("training")
# note, I might get stuck in a local minima b/c this is a
# small problem with no noise (yes, noise helps!)
# this can converge in one round of 1000 or it might get
# stuck for all 10000
for i in range(10000):
loss, acc = logic_model.fit(train_dict)
if i % 1000 == 0:
print('loss: {}\taccuracy: {}'.format(loss, acc))
print('loss: {}\taccuracy: {}'.format(loss, acc))
print("testing")
test_dict = {logic_model.x1: xor_table[:,0],
logic_model.x2: xor_table[:,1]}
results = logic_model.predict(test_dict)
wb_lrn, predictions = results[:-1], results[-1]
print(wb_lrn)
wb_lrn = np.array(wb_lrn).reshape(3,3)
# combine the predictions with the inputs and clean up the data
# round it and convert to unsigned 8 bit ints
out_table = np.column_stack((xor_table[:,[0,1]],
predictions)).round().astype(np.uint8)
print("results")
print('Learned weights/bias (L1):', wb_lrn[0])
print('Learned weights/bias (L2):', wb_lrn[1])
print('Learned weights/bias (L3):', wb_lrn[2])
print('Testing Table:')
print(out_table)
print("Correct?", np.allclose(xor_table, out_table))
```
# An Example Neural Network
So, now that we've worked with some primitive models, let's take a look at something a bit closer to what we'll work with moving forward: an actual neural network.
The following model accepts a 100 dimensional input, has a hidden layer depth of 300, and an output layer depth of 50. We use a sigmoid activation function for the hidden layer.
```
nn1_graph = tf.Graph()
with nn1_graph.as_default():
x = tf.placeholder(tf.float32, shape=[None, 100])
y = tf.placeholder(tf.float32, shape=[None]) # Labels, not used in this model
with tf.name_scope('hidden1'):
w = tf.Variable(tf.truncated_normal([100, 300]), name='W')
b = tf.Variable(tf.zeros([300]), name='b')
z = tf.matmul(x, w) + b
a = tf.nn.sigmoid(z)
with tf.name_scope('output'):
w = tf.Variable(tf.truncated_normal([300, 50]), name='W')
b = tf.Variable(tf.zeros([50]), name='b')
z = tf.matmul(a, w) + b
output = z
with tf.name_scope('global_step'):
global_step = tf.Variable(0, trainable=False, name='global_step')
inc_step = tf.assign_add(global_step, 1, name='increment_step')
with tf.name_scope('summaries'):
for var in tf.trainable_variables():
hist_summary = tf.summary.histogram(var.op.name, var)
summary_op = tf.summary.merge_all()
init = tf.global_variables_initializer()
tb_base_path = 'tbout/nn1_graph'
tb_path = helpers_03.get_fresh_dir(tb_base_path)
sess = tf.Session(graph=nn1_graph)
writer = tf.summary.FileWriter(tb_path, graph=nn1_graph)
sess.run(init)
summaries = sess.run(summary_op)
writer.add_summary(summaries)
writer.close()
sess.close()
```
# Exercise 3
Modify the template above to create your own neural network with the following features:
* Accepts input of length 200 (and allows for variable number of examples)
* First hidden layer depth of 800
* Second hidden layer depth of 600
* Third hidden layer depth of 400
* Output layer depth of 100
* Include histogram summaries of the variables
## Solution 3
| true |
code
| 0.54692 | null | null | null | null |
|
# Session 17: Recommendation system on your own
This script should allow you to build an interactive website from your own
dataset. If you run into any issues, please let us know!
## Step 1: Select the corpus
In the block below, insert the name of your corpus. There should
be images in the directory "images". If there is metadata, it should
be in the directory "data" with the name of the corpus as the file name.
Also, if there is metadata, there must be a column called filename (with
the filename to the image) and a column called title.
```
cn = "test"
```
## Step 2: Read in the Functions
You need to read in all of the modules and functions below.
```
%pylab inline
import numpy as np
import scipy as sp
import pandas as pd
import sklearn
from sklearn import linear_model
import urllib
import os
from os.path import join
from keras.applications.vgg19 import VGG19
from keras.preprocessing import image
from keras.applications.vgg19 import preprocess_input, decode_predictions
from keras.models import Model
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"
def check_create_metadata(cn):
mdata = join("..", "data", cn + ".csv")
if not os.path.exists(mdata):
exts = [".jpg", ".JPG", ".JPEG", ".png"]
fnames = [x for x in os.listdir(join('..', 'images', cn)) if get_ext(x) in exts]
df = pd.DataFrame({'filename': fnames, 'title': fnames})
df.to_csv(mdata, index=False)
def create_embed(corpus_name):
ofile = join("..", "data", corpus_name + "_vgg19_fc2.npy")
if not os.path.exists(ofile):
vgg19_full = VGG19(weights='imagenet')
vgg_fc2 = Model(inputs=vgg19_full.input, outputs=vgg19_full.get_layer('fc2').output)
df = pd.read_csv(join("..", "data", corpus_name + ".csv"))
output = np.zeros((len(df), 224, 224, 3))
for i in range(len(df)):
img_path = join("..", "images", corpus_name, df.filename[i])
img = image.load_img(img_path, target_size=(224, 224))
x = image.img_to_array(img)
output[i, :, :, :] = x
if (i % 100) == 0:
print("Loaded image {0:03d}".format(i))
output = preprocess_input(output)
img_embed = vgg_fc2.predict(output, verbose=True)
np.save(ofile, img_embed)
def rm_ext(s):
return os.path.splitext(s)[0]
def get_ext(s):
return os.path.splitext(s)[-1]
def clean_html():
if not os.path.exists(join("..", "html")):
os.makedirs(join("..", "html"))
if not os.path.exists(join("..", "html", "pages")):
os.makedirs(join("..", "html", "pages"))
for p in [x for x in os.listdir(join('..', 'html', 'pages')) if get_ext(x) in [".html", "html"]]:
os.remove(join('..', 'html', 'pages', p))
def load_data(cn):
X = np.load(join("..", "data", cn + "_vgg19_fc2.npy"))
return X
def write_header(f, cn, index=False):
loc = ""
if not index:
loc = "../"
f.write("<html>\n")
f.write(' <link rel="icon" href="{0:s}img/favicon.ico">\n'.format(loc))
f.write(' <title>Distant Viewing Tutorial</title>\n\n')
f.write(' <link rel="stylesheet" type="text/css" href="{0:s}css/bootstrap.min.css">'.format(loc))
f.write(' <link href="https://fonts.googleapis.com/css?family=Rubik+27px" rel="stylesheet">')
f.write(' <link rel="stylesheet" type="text/css" href="{0:s}css/dv.css">\n\n'.format(loc))
f.write("<body>\n")
f.write(' <div class="d-flex flex-column flex-md-row align-items-center p-3 px-md-4')
f.write('mb-3 bg-white border-bottom box-shadow">\n')
f.write(' <h4 class="my-0 mr-md-auto font-weight-normal">Distant Viewing Tutorial Explorer')
f.write('— {0:s}</h4>\n'.format(cn.capitalize()))
f.write(' <a class="btn btn-outline-primary" href="{0:s}index.html">Back to Index</a>\n'.format(loc))
f.write(' </div>\n')
f.write('\n')
def corpus_to_html(corpus):
pd.set_option('display.max_colwidth', -1)
tc = corpus.copy()
for index in range(tc.shape[0]):
fname = rm_ext(os.path.split(tc['filename'][index])[1])
title = rm_ext(tc['filename'][index])
s = "<a href='pages/{0:s}.html'>{1:s}</a>".format(fname, title)
tc.iloc[index, tc.columns.get_loc('title')] = s
tc = tc.drop(['filename'], axis=1)
return tc.to_html(index=False, escape=False, justify='center')
def create_index(cn, corpus):
f = open(join('..', 'html', 'index.html'), 'w')
write_header(f, cn=cn, index=True)
f.write(' <div style="padding:20px; max-width:1000px">\n')
f.write(corpus_to_html(corpus))
f.write(' </div>\n')
f.write("</body>\n")
f.close()
def get_infobox(corpus, item):
infobox = []
for k, v in corpus.iloc[item].to_dict().items():
if k != "filename":
infobox = infobox + ["<p><b>" + str(k).capitalize() + ":</b> " + str(v) + "</p>"]
return infobox
def save_metadata(f, cn, corpus, X, item):
infobox = get_infobox(corpus, item)
f.write("<div style='width: 1000px;'>\n")
f.write("\n".join(infobox))
if item > 0:
link = rm_ext(os.path.split(corpus['filename'][item - 1])[-1])
f.write("<p align='center'><a href='{0:s}.html'><< previous image</a> \n".format(link))
if item + 1 < X.shape[0]:
link = rm_ext(os.path.split(corpus['filename'][item + 1])[-1])
f.write(" <a href='{0:s}.html'>next image >></a></p>\n".format(link))
f.write("</div>\n")
def save_similar_img(f, cn, corpus, X, item):
dists = np.sum(np.abs(X - X[item, :]), 1)
idx = np.argsort(dists.flatten())[1:13]
f.write("<div style='clear:both; width: 1000px; padding-top: 30px'>\n")
f.write("<h4>Similar Images:</h4>\n")
f.write("<div class='similar'>\n")
for img_path in corpus['filename'][idx].tolist():
hpath = rm_ext(os.path.split(img_path)[1])
f.write('<a href="{0:s}.html"><img src="../../images/{1:2}/{2:s}" style="max-width: 150px; padding:5px"></a>\n'.format(hpath, cn, img_path))
f.write("</div>\n")
f.write("</div>\n")
def create_image_pages(cn, corpus, X):
for item in range(X.shape[0]):
img_path = corpus['filename'][item]
url = os.path.split(img_path)[1]
f = open(join('..', 'html', 'pages', rm_ext(url) + ".html"), 'w')
write_header(f, cn, index=False)
f.write("<div style='padding:25px'>\n")
# Main image
f.write("<div style='float: left; width: 610px;'>\n")
f.write('<img src="../../images/{0:s}/{1:s}" style="max-width: 600px; max-height: 500px;">\n'.format(cn, img_path))
f.write("</div>\n\n")
# Main information box
save_metadata(f, cn, corpus, X, item)
# Similar
save_similar_img(f, cn, corpus, X, item)
f.write("</body>\n")
f.close()
```
## Step 3: Create the embeddings
The next step is create the embeddings. If there is no metadata, this code
will also create it.
```
check_create_metadata(cn)
create_embed(cn)
```
### Step 4: Create the website
Finally, create the website with the code below.
```
clean_html()
corpus = pd.read_csv(join("..", "data", cn + ".csv"))
X = load_data(cn)
create_index(cn, corpus)
create_image_pages(cn, corpus, X)
```
You should find a folder called `html`. Open that folder and double click on the
file `index.html`, opening it in a web browser (Chrome or Firefox preferred; Safari
should work too). Do not open it in Jupyter.
You will see a list of all of the available images from the corpus you selected.
Click on one and you'll get to an item page for that image. From there you can
see the image itself, available metadata, select the previous or next image in the
corpus, and view similar images from the VGG19 similarity measurement.
| true |
code
| 0.31357 | null | null | null | null |
|
# K-Nearest Neighbors Algorithm
In this Jupyter Notebook we will focus on $KNN-Algorithm$. KNN is a data classification algorithm that attempts to determine what group a data point is in by looking at the data points around it.
An algorithm, looking at one point on a grid, trying to determine if a point is in group A or B, looks at the states of the points that are near it. The range is arbitrarily determined, but the point is to take a sample of the data. If the majority of the points are in group A, then it is likely that the data point in question will be A rather than B, and vice versa.
<br>
<img src="knn/example 1.png" height="30%" width="30%">
# Imports
```
import numpy as np
from tqdm import tqdm_notebook
```
# How it works?
We have some labeled data set $X-train$, and a new set $X$ that we want to classify based on previous classyfications
## Seps
### 1. Calculate distance to all neightbours
### 2. Sort neightbours (based on closest distance)
### 3. Count possibilities of each class for k nearest neighbours
### 4. The class with highest possibilty is Your prediction
# 1. Calculate distance to all neighbours
Depending on the problem You should use diffrent type of count distance method.
<br>
For example we can use Euclidean distance. Euclidean distance is the "ordinary" straight-line distance between two points in D-Dimensional space
#### Definiton
$d(p, q) = d(q, p) = \sqrt{(q_1 - p_1)^2 + (q_2 - p_2)^2 + \dots + (q_D - p_D)^2} = \sum_{d=1}^{D} (p_d - q_d)^2$
#### Example
Distance in $R^2$
<img src="knn/euklidean_example.png" height="30%" width="30%">
$p = (4,6)$
<br>
$q = (1,2)$
<br>
$d(p, q) = \sqrt{(1-4)^2 + (2-6)^2} =\sqrt{9 + 16} = \sqrt{25} = 5 $
## Code
```
def get_euclidean_distance(A_matrix, B_matrix):
"""
Function computes euclidean distance between matrix A and B
Args:
A_matrix (numpy.ndarray): Matrix size N1:D
B_matrix (numpy.ndarray): Matrix size N2:D
Returns:
numpy.ndarray: Matrix size N1:N2
"""
A_square = np.reshape(np.sum(A_matrix * A_matrix, axis=1), (A_matrix.shape[0], 1))
B_square = np.reshape(np.sum(B_matrix * B_matrix, axis=1), (1, B_matrix.shape[0]))
AB = A_matrix @ B_matrix.T
C = -2 * AB + B_square + A_square
return np.sqrt(C)
```
## Example Usage
```
X = np.array([[1,2,3] , [-4,5,-6]])
X_train = np.array([[0,0,0], [1,2,3], [4,5,6], [-4, 4, -6]])
print("X: {} Exaples in {} Dimensional space".format(*X.shape))
print("X_train: {} Exaples in {} Dimensional space".format(*X_train.shape))
print()
print("X:")
print(X)
print()
print("X_train")
print(X_train)
distance_matrix = get_euclidean_distance(X, X_train)
print("Distance Matrix shape: {}".format(distance_matrix.shape))
print("Distance between first example from X and first form X_train {}".format(distance_matrix[0,0]))
print("Distance between first example from X and second form X_train {}".format(distance_matrix[0,1]))
```
# 2. Sort neightbours
In order to find best fitting class for our observations we need to find to which classes belong observation neightbours and then to sort classes based on the closest distance
## Code
```
def get_sorted_train_labels(distance_matrix, y):
"""
Function sorts y labels, based on probabilities from distances matrix
Args:
distance_matrix (numpy.ndarray): Distance Matrix, between points from X and X_train, size: N1:N2
y (numpy.ndarray): vector of classes of X points, size: N1
Returns:
numpy.ndarray: labels matrix sorted according to distances to nearest neightours, size N1:N2
"""
order = distance_matrix.argsort(kind='mergesort')
return np.squeeze(y[order])
```
## Example Usage
```
y_train = np.array([[1, 1, 2, 3]]).T
print("Labels array {} Examples in {} Dimensional Space".format(*y_train.shape))
print("Distance matrix shape {}".format(distance_matrix.shape))
sorted_train_labels = get_sorted_train_labels(distance_matrix, y_train)
print("Sorted train labels {} shape".format(sorted_train_labels.shape))
print("Closest 3 classes for first element from set X: {}".format(sorted_train_labels[0, :3]))
```
# 3. Count possibilities of each class for k nearest neighbours
In order to find best class for our observation $x$ we need to calculate the probability of belonging to each class. In our case it is quite easy. We need just to count how many from k-nearest-neighbours of observation $x$ belong to each class and then devide it by k
<br><br>
$p(y=class \space| x) = \frac{\sum_{1}^{k}(1 \space if \space N_i = class, \space else \space 0) }{k}$ Where $N_i$ is $i$ nearest neightbour
## Code
```
def get_p_y_x_using_knn(y, k):
"""
The function determines the probability distribution p (y | x)
for each of the labels for objects from the X
using the KNN classification learned on the X_train
Args:
y (numpy.ndarray): Sorted matrix of N2 nearest neighbours labels, size N1:N2
k (int): number of nearest neighbours for KNN algorithm
Returns: numpy.ndarray: Matrix of probabilities for N1 points (from set X) of belonging to each class,
size N1:C (where C is number of classes)
"""
first_k_neighbors = y[:, :k]
N1, N2 = y.shape
classes = np.unique(y)
number_of_classes = classes.shape[0]
probabilities_matrix = np.zeros(shape=(N1, number_of_classes))
for i, row in enumerate(first_k_neighbors):
for j, value in enumerate(classes):
probabilities_matrix[i][j] = list(row).count(value) / k
return probabilities_matrix
```
## Example usage
```
print("Sorted train labels:")
print(sorted_train_labels)
probabilities_matrix = get_p_y_x_using_knn(y=sorted_train_labels, k=4)
print("Probability fisrt element belongs to 1-st class: {:2f}".format(probabilities_matrix[0,0]))
print("Probability fisrt element belongs to 3-rd class: {:2f}".format(probabilities_matrix[0,2]))
```
# 4. The class with highest possibilty is Your prediction
At the end we combine all previous steps to get prediction
## Code
```
def predict(X, X_train, y_train, k, distance_function):
"""
Function returns predictions for new set X based on labels of points from X_train
Args:
X (numpy.ndarray): set of observations (points) that we want to label
X_train (numpy.ndarray): set of lalabeld bservations (points)
y_train (numpy.ndarray): labels for X_train
k (int): number of nearest neighbours for KNN algorithm
Returns:
(numpy.ndarray): label predictions for points from set X
"""
distance_matrix = distance_function(X, X_train)
sorted_labels = get_sorted_train_labels(distance_matrix=distance_matrix, y=y_train)
p_y_x = get_p_y_x_using_knn(y=sorted_labels, k=k)
number_of_classes = p_y_x.shape[1]
reversed_rows = np.fliplr(p_y_x)
prediction = number_of_classes - (np.argmax(reversed_rows, axis=1) + 1)
return prediction
```
## Example usage
```
prediction = predict(X, X_train, y_train, 3, get_euclidean_distance)
print("Predicted propabilities of classes for for first observation", probabilities_matrix[0])
print("Predicted class for for first observation", prediction[0])
print()
print("Predicted propabilities of classes for for second observation", probabilities_matrix[1])
print("Predicted class for for second observation", prediction[1])
```
# Accuracy
To find how good our knn model works we should count accuracy
## Code
```
def count_accuracy(prediction, y_true):
"""
Returns:
float: Predictions accuracy
"""
N1 = prediction.shape[0]
accuracy = np.sum(prediction == y_true) / N1
return accuracy
```
## Example usage
```
y_true = np.array([[0, 2]])
predicton = predict(X, X_train, y_train, 3, get_euclidean_distance)
print("True classes:{}, accuracy {}%".format(y_true, count_accuracy(predicton, y_true) * 100))
```
# Find best k
Best k parameter is that one for which we have highest accuracy
## Code
```
def select_knn_model(X_validation, y_validation, X_train, y_train, k_values, distance_function):
"""
Function returns k parameter that best fit Xval points
Args:
Xval (numpy.ndarray): set of Validation Data, size N1:D
Xtrain (numpy.ndarray): set of Training Data, size N2:D
yval (numpy.ndarray): set of labels for Validation data, size N1:1
ytrain (numpy.ndarray): set of labels for Training Data, size N2:1
k_values (list): list of int values of k parameter that should be checked
Returns:
int: k paprameter that best fit validation set
"""
accuracies = []
for k in tqdm_notebook(k_values):
prediction = predict(X_validation, X_train, y_train, k, distance_function)
accuracy = count_accuracy(prediction, y_validation)
accuracies.append(accuracy)
best_k = k_values[accuracies.index(max(accuracies))]
return best_k, accuracies
```
# Real World Example - Iris Dataset
<img src="knn/iris_example1.jpeg" height="60%" width="60%">
This is perhaps the best known database to be found in the pattern recognition literature. The data set contains 3 classes of 50 instances each, where each class refers to a type of iris plant. One class is linearly separable from the other 2; the latter are NOT linearly separable from each other.
Each example contains 4 attributes
1. sepal length in cm
2. sepal width in cm
3. petal length in cm
4. petal width in cm
Predicted attribute: class of iris plant.
<img src="knn/iris_example2.png" height="70%" width="70%">
```
from sklearn import datasets
import matplotlib.pyplot as plt
iris = datasets.load_iris()
iris_X = iris.data
iris_y = iris.target
print("Iris: {} examples in {} dimensional space".format(*iris_X.shape))
print("First example in dataset :\n Speal lenght: {}cm \n Speal width: {}cm \n Petal length: {}cm \n Petal width: {}cm".format(*iris_X[0]))
print("Avalible classes", np.unique(iris_y))
```
## Prepare Data
In our data set we have 150 examples (50 examples of each class), we have to divide it into 3 datasets.
1. Training data set, 90 examples. It will be used to find k - nearest neightbours
2. Validation data set, 30 examples. It will be used to find best k parameter, the one for which accuracy is highest
3. Test data set, 30 examples. It will be used to check how good our model performs
Data has to be shuffled (mixed in random order), because originally it is stored 50 examples of class 0, 50 of 1 and 50 of 2.
```
from sklearn.utils import shuffle
iris_X, iris_y = shuffle(iris_X, iris_y, random_state=134)
test_size = 30
validation_size = 30
training_size = 90
X_test = iris_X[:test_size]
X_validation = iris_X[test_size: (test_size+validation_size)]
X_train = iris_X[(test_size+validation_size):]
y_test = iris_y[:test_size]
y_validation = iris_y[test_size: (test_size+validation_size)]
y_train = iris_y[(test_size+validation_size):]
```
## Find best k parameter
```
k_values = [i for i in range(3,50)]
best_k, accuracies = select_knn_model(X_validation, y_validation, X_train, y_train, k_values, distance_function=get_euclidean_distance)
plt.plot(k_values, accuracies)
plt.xlabel('K parameter')
plt.ylabel('Accuracy')
plt.title('Accuracy for k nearest neighbors')
plt.grid()
plt.show()
```
## Count accuracy for training set
```
prediction = predict(X_test, X_train, y_train, best_k, get_euclidean_distance)
accuracy = count_accuracy(prediction, y_test)
print("Accuracy for best k={}: {:2f}%".format(best_k, accuracy*100))
```
# Real World Example - Mnist Dataset
Mnist is a popular database of handwritten images created for people who are new to machine learning. There are many courses on the internet that include classification problem using MNIST dataset.
This dataset contains 55000 images and labels. Each image is 28x28 pixels large, but for the purpose of the classification task they are flattened to 784x1 arrays $(28 \cdot 28 = 784)$. Summing up our training set is a matrix of size $[50000, 784]$ = [amount of images, size of image]. We will split it into 40000 training examples and 10000 validation examples to choose a best k
It also contains 5000 test images and labels, but for test we will use only 1000 (due to time limitations, using 5k would take 5x as much time)
<h3>Mnist Data Example</h3>
<img src="knn/mnist_example.jpg" height="70%" width="70%">
Now we are going to download this dataset and split it into test and train sets.
```
import utils
import cv2
training_size = 49_000
validation_size = 1000
test_size = 1000
train_data, test = utils.get_mnist_dataset()
train_images, train_labels = train_data
test_images, test_labels = test
validation_images = train_images[training_size:training_size + validation_size]
train_images = train_images[:training_size]
validation_labels = train_labels[training_size:training_size + validation_size]
train_labels = train_labels[:training_size]
test_images = test_images[:test_size]
test_labels = test_labels[:test_size]
print("Training images matrix size: {}".format(train_images.shape))
print("Training labels matrix size: {}".format(train_labels.shape))
print("Validation images matrix size: {}".format(validation_images.shape))
print("Validation labels matrix size: {}".format(validation_labels.shape))
print("Testing images matrix size: {}".format(test_images.shape))
print("Testing labels matrix size: {}".format(test_labels.shape))
print("Possible labels {}".format(np.unique(test_labels)))
```
## Visualisation
Visualisation isn't necessery to the problem, but it helps to understand what are we doing.
```
from matplotlib.gridspec import GridSpec
def show_first_8(images):
ax =[]
fig = plt.figure(figsize=(10, 10))
gs = GridSpec(2, 4, wspace=0.0, hspace=-0.5)
for i in range(2):
for j in range(4):
ax.append(fig.add_subplot(gs[i,j]))
for i, axis in enumerate(ax):
axis.imshow(images[i])
plt.show()
first_8_images = train_images[:8]
resized = np.reshape(first_8_images, (-1,28,28))
print('First 8 images of train set:')
show_first_8(resized)
```
## Find best k parameter
```
k_values = [i for i in range(3, 50, 5)]
best_k, accuracies = select_knn_model(validation_images, validation_labels, train_images, train_labels, k_values,
distance_function=get_euclidean_distance)
plt.plot(k_values, accuracies)
plt.xlabel('K parameter')
plt.ylabel('Accuracy')
plt.title('Accuracy for k nearest neighbors')
plt.grid()
plt.show()
prediction = np.squeeze(predict(test_images, train_images, train_labels, best_k, get_euclidean_distance))
accuracy = count_accuracy(prediction, test_labels)
print("Accuracy on test set for best k={}: {:2}%".format(best_k, accuracy * 100))
```
# Sources
https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm - first visualisation image
https://en.wikipedia.org/wiki/Euclidean_distance - euclidean distance visualisation
https://rajritvikblog.wordpress.com/2017/06/29/iris-dataset-analysis-python/ - first iris image
https://rpubs.com/wjholst/322258 - second iris image
https://www.kaggle.com/pablotab/mnistpklgz - mnist dataset
| true |
code
| 0.777564 | null | null | null | null |
|
# Quantization of Signals
*This jupyter notebook is part of a [collection of notebooks](../index.ipynb) on various topics of Digital Signal Processing. Please direct questions and suggestions to [[email protected]](mailto:[email protected]).*
## Spectral Shaping of the Quantization Noise
The quantized signal $x_Q[k]$ can be expressed by the continuous amplitude signal $x[k]$ and the quantization error $e[k]$ as
\begin{equation}
x_Q[k] = \mathcal{Q} \{ x[k] \} = x[k] + e[k]
\end{equation}
According to the [introduced model](linear_uniform_quantization_error.ipynb#Model-for-the-Quantization-Error), the quantization noise can be modeled as uniformly distributed white noise. Hence, the noise is distributed over the entire frequency range. The basic concept of [noise shaping](https://en.wikipedia.org/wiki/Noise_shaping) is a feedback of the quantization error to the input of the quantizer. This way the spectral characteristics of the quantization noise can be modified, i.e. spectrally shaped. Introducing a generic filter $h[k]$ into the feedback loop yields the following structure

The quantized signal can be deduced from the block diagram above as
\begin{equation}
x_Q[k] = \mathcal{Q} \{ x[k] - e[k] * h[k] \} = x[k] + e[k] - e[k] * h[k]
\end{equation}
where the additive noise model from above has been introduced and it has been assumed that the impulse response $h[k]$ is normalized such that the magnitude of $e[k] * h[k]$ is below the quantization step $Q$. The overall quantization error is then
\begin{equation}
e_H[k] = x_Q[k] - x[k] = e[k] * (\delta[k] - h[k])
\end{equation}
The power spectral density (PSD) of the quantization error with noise shaping is calculated to
\begin{equation}
\Phi_{e_H e_H}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) = \Phi_{ee}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) \cdot \left| 1 - H(\mathrm{e}^{\,\mathrm{j}\,\Omega}) \right|^2
\end{equation}
Hence the PSD $\Phi_{ee}(\mathrm{e}^{\,\mathrm{j}\,\Omega})$ of the quantizer without noise shaping is weighted by $| 1 - H(\mathrm{e}^{\,\mathrm{j}\,\Omega}) |^2$. Noise shaping allows a spectral modification of the quantization error. The desired shaping depends on the application scenario. For some applications, high-frequency noise is less disturbing as low-frequency noise.
### Example - First-Order Noise Shaping
If the feedback of the error signal is delayed by one sample we get with $h[k] = \delta[k-1]$
\begin{equation}
\Phi_{e_H e_H}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) = \Phi_{ee}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) \cdot \left| 1 - \mathrm{e}^{\,-\mathrm{j}\,\Omega} \right|^2
\end{equation}
For linear uniform quantization $\Phi_{ee}(\mathrm{e}^{\,\mathrm{j}\,\Omega}) = \sigma_e^2$ is constant. Hence, the spectral shaping constitutes a high-pass characteristic of first order. The following simulation evaluates the noise shaping quantizer of first order.
```
import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as sig
%matplotlib inline
w = 8 # wordlength of the quantized signal
xmin = -1 # minimum of input signal
N = 32768 # number of samples
def uniform_midtread_quantizer_w_ns(x, Q):
# limiter
x = np.copy(x)
idx = np.where(x <= -1)
x[idx] = -1
idx = np.where(x > 1 - Q)
x[idx] = 1 - Q
# linear uniform quantization with noise shaping
xQ = Q * np.floor(x/Q + 1/2)
e = xQ - x
xQ = xQ - np.concatenate(([0], e[0:-1]))
return xQ[1:]
# quantization step
Q = 1/(2**(w-1))
# compute input signal
np.random.seed(5)
x = np.random.uniform(size=N, low=xmin, high=(-xmin-Q))
# quantize signal
xQ = uniform_midtread_quantizer_w_ns(x, Q)
e = xQ - x[1:]
# estimate PSD of error signal
nf, Pee = sig.welch(e, nperseg=64)
# estimate SNR
SNR = 10*np.log10((np.var(x)/np.var(e)))
print('SNR = {:2.1f} dB'.format(SNR))
plt.figure(figsize=(10, 5))
Om = nf*2*np.pi
plt.plot(Om, Pee*6/Q**2, label='estimated PSD')
plt.plot(Om, np.abs(1 - np.exp(-1j*Om))**2, label='theoretic PSD')
plt.plot(Om, np.ones(Om.shape), label='PSD w/o noise shaping')
plt.title('PSD of quantization error')
plt.xlabel(r'$\Omega$')
plt.ylabel(r'$\hat{\Phi}_{e_H e_H}(e^{j \Omega}) / \sigma_e^2$')
plt.axis([0, np.pi, 0, 4.5])
plt.legend(loc='upper left')
plt.grid()
```
**Exercise**
* The overall average SNR is lower than for the quantizer without noise shaping. Why?
Solution: The average power per frequency is lower that without noise shaping for frequencies below $\Omega \approx \pi$. However, this comes at the cost of a larger average power per frequency for frequencies above $\Omega \approx \pi$. The average power of the quantization noise is given as the integral over the PSD of the quantization noise. It is larger for noise shaping and the resulting SNR is consequently lower. Noise shaping is nevertheless beneficial in applications where a lower quantization error in a limited frequency region is desired.
**Copyright**
This notebook is provided as [Open Educational Resource](https://en.wikipedia.org/wiki/Open_educational_resources). Feel free to use the notebook for your own purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Sascha Spors, Digital Signal Processing - Lecture notes featuring computational examples*.
| true |
code
| 0.72046 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/MuhammedAshraf2020/DNN-using-tensorflow/blob/main/DNN_using_tensorflow_ipynb.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#import libs
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from keras.datasets.mnist import load_data
# prepare dataset
(X_train , y_train) , (X_test , y_test) = load_data()
X_train = X_train.astype("float32") / 255
X_test = X_test.astype("float32") / 255
# Make sure images have shape (28, 28, 1)
X_train = np.expand_dims(X_train, -1)
X_test = np.expand_dims(X_test, -1)
for i in range(0, 9):
plt.subplot(330 + 1 + i)
plt.imshow(X_train[i][: , : , 0], cmap=plt.get_cmap('gray'))
plt.show()
X_train = [X_train[i].ravel() for i in range(len(X_train))]
X_test = [X_test[i].ravel() for i in range(len(X_test))]
y_train = tf.keras.utils.to_categorical(y_train , num_classes = 10)
y_test = tf.keras.utils.to_categorical(y_test , num_classes = 10 )
#set parameter
n_input = 28 * 28
n_hidden_1 = 512
n_hidden_2 = 256
n_hidden_3 = 128
n_output = 10
learning_rate = 0.01
epochs = 50
batch_size = 128
tf.compat.v1.disable_eager_execution()
# weight intialization
X = tf.compat.v1.placeholder(tf.float32 , [None , n_input])
y = tf.compat.v1.placeholder(tf.float32 , [None , n_output])
def Weights_init(list_layers , stddiv):
Num_layers = len(list_layers)
weights = {}
bias = {}
for i in range( Num_layers-1):
weights["W{}".format(i+1)] = tf.Variable(tf.compat.v1.truncated_normal([list_layers[i] , list_layers[i+1]] , stddev = stddiv))
bias["b{}".format(i+1)] = tf.Variable(tf.compat.v1.truncated_normal([list_layers[i+1]]))
return weights , bias
list_param = [784 , 512 , 256 , 128 , 10]
weights , biases = Weights_init(list_param , 0.1)
def Model (X , nn_weights , nn_bias):
Z1 = tf.add(tf.matmul(X , nn_weights["W1"]) , nn_bias["b1"])
Z1_out = tf.nn.relu(Z1)
Z2 = tf.add(tf.matmul(Z1_out , nn_weights["W2"]) , nn_bias["b2"])
Z2_out = tf.nn.relu(Z2)
Z3 = tf.add(tf.matmul(Z2_out , nn_weights["W3"]) , nn_bias["b3"])
Z3_out = tf.nn.relu(Z3)
Z4 = tf.add(tf.matmul(Z3_out , nn_weights["W4"]) , nn_bias["b4"])
Z4_out = tf.nn.softmax(Z4)
return Z4_out
nn_layer_output = Model(X , weights , biases)
loss = tf.reduce_mean(tf.compat.v1.nn.softmax_cross_entropy_with_logits_v2(logits = nn_layer_output , labels = y))
optimizer = tf.compat.v1.train.GradientDescentOptimizer(learning_rate).minimize(loss)
init = tf.compat.v1.global_variables_initializer()
# Determining if the predictions are accurate
is_correct_prediction = tf.equal(tf.argmax(nn_layer_output , 1),tf.argmax(y, 1))
#Calculating prediction accuracy
accuracy = tf.reduce_mean(tf.cast(is_correct_prediction, tf.float32))
saver = tf.compat.v1.train.Saver()
with tf.compat.v1.Session() as sess:
# initializing all the variables
sess.run(init)
total_batch = int(len(X_train) / batch_size)
for epoch in range(epochs):
avg_cost = 0
for i in range(total_batch):
batch_x , batch_y = X_train[i * batch_size : (i + 1) * batch_size] , y_train[i * batch_size : (i + 1) * batch_size]
_, c = sess.run([optimizer,loss], feed_dict={X: batch_x, y: batch_y})
avg_cost += c / total_batch
if(epoch % 10 == 0):
print("Epoch:", (epoch + 1), "train_cost =", "{:.3f} ".format(avg_cost) , end = "")
print("train_acc = {:.3f} ".format(sess.run(accuracy, feed_dict={X: X_train, y:y_train})) , end = "")
print("valid_acc = {:.3f}".format(sess.run(accuracy, feed_dict={X: X_test, y:y_test})))
saver.save(sess , save_path = "/content/Model.ckpt")
```
| true |
code
| 0.646934 | null | null | null | null |
|
# Validating Multi-View Spherical KMeans by Replicating Paper Results
Here we will validate the implementation of multi-view spherical kmeans by replicating the right side of figure 3 from the Multi-View Clustering paper by Bickel and Scheffer.
```
import sklearn
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
import numpy as np
import scipy as scp
from scipy import sparse
import mvlearn
from mvlearn.cluster.mv_spherical_kmeans import MultiviewSphericalKMeans
from joblib import Parallel, delayed
import matplotlib.pyplot as plt
import warnings
warnings.simplefilter('ignore') # Ignore warnings
```
### A function to recreate the artificial dataset from the paper
The experiment in the paper used the 20 Newsgroup dataset, which consists of around 18000 newsgroups posts on 20 topics. This dataset can be obtained from scikit-learn. To create the artificial dataset used in the experiment, 10 of the 20 classes from the 20 newsgroups dataset were selected and grouped into 2 groups of 5 classes, and then encoded as tfidf vectors. These now represented the 5 multi-view classes, each with 2 views (one from each group). 200 examples were randomly sampled from each of the 20 newsgroups, producing 1000 concatenated examples uniformly distributed over the 5 classes.
```
NUM_SAMPLES = 200
#Load in the vectorized news group data from scikit-learn package
news = fetch_20newsgroups(subset='all')
all_data = np.array(news.data)
all_targets = np.array(news.target)
class_names = news.target_names
#A function to get the 20 newsgroup data
def get_data():
#Set class pairings as described in the multiview clustering paper
view1_classes = ['comp.graphics','rec.motorcycles', 'sci.space', 'rec.sport.hockey', 'comp.sys.ibm.pc.hardware']
view2_classes = ['rec.autos', 'sci.med','misc.forsale', 'soc.religion.christian','comp.os.ms-windows.misc']
#Create lists to hold data and labels for each of the 5 classes across 2 different views
labels = [num for num in range(len(view1_classes)) for _ in range(NUM_SAMPLES)]
labels = np.array(labels)
view1_data = list()
view2_data = list()
#Randomly sample 200 items from each of the selected classes in view1
for ind in range(len(view1_classes)):
class_num = class_names.index(view1_classes[ind])
class_data = all_data[(all_targets == class_num)]
indices = np.random.choice(class_data.shape[0], NUM_SAMPLES)
view1_data.append(class_data[indices])
view1_data = np.concatenate(view1_data)
#Randomly sample 200 items from each of the selected classes in view2
for ind in range(len(view2_classes)):
class_num = class_names.index(view2_classes[ind])
class_data = all_data[(all_targets == class_num)]
indices = np.random.choice(class_data.shape[0], NUM_SAMPLES)
view2_data.append(class_data[indices])
view2_data = np.concatenate(view2_data)
#Vectorize the data
vectorizer = TfidfVectorizer()
view1_data = vectorizer.fit_transform(view1_data)
view2_data = vectorizer.fit_transform(view2_data)
#Shuffle and normalize vectors
shuffled_inds = np.random.permutation(NUM_SAMPLES * len(view1_classes))
view1_data = sparse.vstack(view1_data)
view2_data = sparse.vstack(view2_data)
view1_data = np.array(view1_data[shuffled_inds].todense())
view2_data = np.array(view2_data[shuffled_inds].todense())
magnitudes1 = np.linalg.norm(view1_data, axis=1)
magnitudes2 = np.linalg.norm(view2_data, axis=1)
magnitudes1[magnitudes1 == 0] = 1
magnitudes2[magnitudes2 == 0] = 1
magnitudes1 = magnitudes1.reshape((-1,1))
magnitudes2 = magnitudes2.reshape((-1,1))
view1_data /= magnitudes1
view2_data /= magnitudes2
labels = labels[shuffled_inds]
return view1_data, view2_data, labels
```
### Function to compute cluster entropy
The function below is used to calculate the total clustering entropy using the formula described in the paper.
```
def compute_entropy(partitions, labels, k, num_classes):
total_entropy = 0
num_examples = partitions.shape[0]
for part in range(k):
labs = labels[partitions == part]
part_size = labs.shape[0]
part_entropy = 0
for cl in range(num_classes):
prop = np.sum(labs == cl) * 1.0 / part_size
ent = 0
if(prop != 0):
ent = - prop * np.log2(prop)
part_entropy += ent
part_entropy = part_entropy * part_size / num_examples
total_entropy += part_entropy
return total_entropy
```
### Functions to Initialize Centroids and Run Experiment
The randSpherical function initializes the initial cluster centroids by taking a uniform random sampling of points on the surface of a unit hypersphere. The getEntropies function runs Multi-View Spherical Kmeans Clustering on the data with n_clusters from 1 to 10 once each. This function essentially runs one trial of the experiment.
```
def randSpherical(n_clusters, n_feat1, n_feat2):
c_centers1 = np.random.normal(0, 1, (n_clusters, n_feat1))
c_centers1 /= np.linalg.norm(c_centers1, axis=1).reshape((-1, 1))
c_centers2 = np.random.normal(0, 1, (n_clusters, n_feat2))
c_centers2 /= np.linalg.norm(c_centers2, axis=1).reshape((-1, 1))
return [c_centers1, c_centers2]
def getEntropies():
v1_data, v2_data, labels = get_data()
entropies = list()
for num in range(1,11):
centers = randSpherical(num, v1_data.shape[1], v2_data.shape[1])
kmeans = MultiviewSphericalKMeans(n_clusters=num, init=centers, n_init=1)
pred = kmeans.fit_predict([v1_data, v2_data])
ent = compute_entropy(pred, labels, num, 5)
entropies.append(ent)
print('done')
return entropies
```
### Running multiple trials of the experiment
It was difficult to exactly reproduce the results from the Multi-View Clustering Paper because the experimentors randomly sampled a subset of the 20 newsgroup dataset samples to create the artificial dataset, and this random subset was not reported. Therefore, in an attempt to at least replicate the overall shape of the distribution of cluster entropy over the number of clusters, we resample the dataset and recreate the artificial dataset each trial. Therefore, each trial consists of resampling and recreating the artificial dataset, and then running Multi-view Spherical KMeans clustering on that dataset for n_clusters 1 to 10 once each. We performed 80 such trials and the results of this are shown below.
```
#Do spherical kmeans and get entropy values for each k for multiple trials
n_workers = 10
n_trials = 80
mult_entropies1 = Parallel(n_jobs=n_workers)(
delayed(getEntropies)() for i in range(n_trials))
```
### Experiment Results
We see the results of this experiment below. Here, we have more or less reproduced the shape of the distribution as seen in figure 3 from the Multi-view Clustering Paper.
```
mult_entropies1 = np.array(mult_entropies1)
ave_m_entropies = np.mean(mult_entropies1, axis=0)
std_m_entropies = np.std(mult_entropies1, axis=0)
x_values = list(range(1, 11))
plt.errorbar(x_values, ave_m_entropies, std_m_entropies, capsize=5, color = '#F46C12')
plt.xlabel('k')
plt.ylabel('Entropy')
plt.legend(['2 Views'])
plt.rc('axes', labelsize=12)
plt.show()
```
| true |
code
| 0.658115 | null | null | null | null |
|
# StellarGraph Ensemble for link prediction
In this example, we use `stellargraph`s `BaggingEnsemble` class of [GraphSAGE](http://snap.stanford.edu/graphsage/) models to predict citation links in the Cora dataset (see below). The `BaggingEnsemble` class brings ensemble learning to `stellargraph`'s graph neural network models, e.g., `GraphSAGE`, quantifying prediction variance and potentially improving prediction accuracy.
The problem is treated as a supervised link prediction problem on a homogeneous citation network with nodes representing papers (with attributes such as binary keyword indicators and categorical subject) and links corresponding to paper-paper citations.
To address this problem, we build a a base `GraphSAGE` model with the following architecture. First we build a two-layer GraphSAGE model that takes labeled `(paper1, paper2)` node pairs corresponding to possible citation links, and outputs a pair of node embeddings for the `paper1` and `paper2` nodes of the pair. These embeddings are then fed into a link classification layer, which first applies a binary operator to those node embeddings (e.g., concatenating them) to construct the embedding of the potential link. Thus obtained link embeddings are passed through the dense link classification layer to obtain link predictions - probability for these candidate links to actually exist in the network. The entire model is trained end-to-end by minimizing the loss function of choice (e.g., binary cross-entropy between predicted link probabilities and true link labels, with true/false citation links having labels 1/0) using stochastic gradient descent (SGD) updates of the model parameters, with minibatches of 'training' links fed into the model.
Finally, using our base model, we create an ensemble with each model in the ensemble trained on a bootstrapped sample of the training data.
**References**
1. Inductive Representation Learning on Large Graphs. W.L. Hamilton, R. Ying, and J. Leskovec arXiv:1706.02216
[cs.SI], 2017.
```
import matplotlib.pyplot as plt
import networkx as nx
import pandas as pd
import numpy as np
from tensorflow import keras
import os
import stellargraph as sg
from stellargraph.data import EdgeSplitter
from stellargraph.mapper import GraphSAGELinkGenerator
from stellargraph.layer import GraphSAGE, link_classification
from stellargraph import BaggingEnsemble
from sklearn import preprocessing, feature_extraction, model_selection
from stellargraph import globalvar
%matplotlib inline
def plot_history(history):
def remove_prefix(text, prefix):
return text[text.startswith(prefix) and len(prefix):]
figsize=(7, 5)
c_train = 'b'
c_test = 'g'
metrics = sorted(set([remove_prefix(m, "val_") for m in list(history[0].history.keys())]))
for m in metrics:
# summarize history for metric m
plt.figure(figsize=figsize)
for h in history:
plt.plot(h.history[m], c=c_train)
plt.plot(h.history['val_' + m], c=c_test)
plt.title(m)
plt.ylabel(m)
plt.xlabel('epoch')
plt.legend(['train', 'validation'], loc='best')
plt.show()
def load_cora(data_dir, largest_cc=False):
g_nx = nx.read_edgelist(path=os.path.expanduser(os.path.join(data_dir, "cora.cites")))
for edge in g_nx.edges(data=True):
edge[2]['label'] = 'cites'
# load the node attribute data
cora_data_location = os.path.expanduser(os.path.join(data_dir, "cora.content"))
node_attr = pd.read_csv(cora_data_location, sep='\t', header=None)
values = { str(row.tolist()[0]): row.tolist()[-1] for _, row in node_attr.iterrows()}
nx.set_node_attributes(g_nx, values, 'subject')
if largest_cc:
# Select the largest connected component. For clarity we ignore isolated
# nodes and subgraphs; having these in the data does not prevent the
# algorithm from running and producing valid results.
g_nx_ccs = (g_nx.subgraph(c).copy() for c in nx.connected_components(g_nx))
g_nx = max(g_nx_ccs, key=len)
print("Largest subgraph statistics: {} nodes, {} edges".format(
g_nx.number_of_nodes(), g_nx.number_of_edges()))
feature_names = ["w_{}".format(ii) for ii in range(1433)]
column_names = feature_names + ["subject"]
node_data = pd.read_csv(os.path.join(data_dir, "cora.content"), sep='\t', header=None, names=column_names)
node_data.index = node_data.index.map(str)
node_data = node_data[node_data.index.isin(list(g_nx.nodes()))]
return g_nx, node_data, feature_names
```
### Loading the CORA network data
**Downloading the CORA dataset:**
The dataset used in this demo can be downloaded from https://linqs-data.soe.ucsc.edu/public/lbc/cora.tgz
The following is the description of the dataset:
> The Cora dataset consists of 2708 scientific publications classified into one of seven classes.
> The citation network consists of 5429 links. Each publication in the dataset is described by a
> 0/1-valued word vector indicating the absence/presence of the corresponding word from the dictionary.
> The dictionary consists of 1433 unique words. The README file in the dataset provides more details.
Download and unzip the cora.tgz file to a location on your computer and set the `data_dir` variable to
point to the location of the dataset (the directory containing "cora.cites" and "cora.content").
```
data_dir = os.path.expanduser("~/data/cora")
```
Load the dataset
```
G, node_data, feature_names = load_cora(data_dir)
```
We need to convert node features that will be used by the model to numeric values that are required for GraphSAGE input. Note that all node features in the Cora dataset, except the categorical "subject" feature, are already numeric, and don't require the conversion.
```
if "subject" in feature_names:
# Convert node features to numeric vectors
feature_encoding = feature_extraction.DictVectorizer(sparse=False)
node_features = feature_encoding.fit_transform(
node_data[feature_names].to_dict("records")
)
else: # node features are already numeric, no further conversion is needed
node_features = node_data[feature_names].values
```
Add node data to G:
```
for nid, f in zip(node_data.index, node_features):
G.nodes[nid][globalvar.TYPE_ATTR_NAME] = "paper" # specify node type
G.nodes[nid]["feature"] = f
```
We aim to train a link prediction model, hence we need to prepare the train and test sets of links and the corresponding graphs with those links removed.
We are going to split our input graph into train and test graphs using the `EdgeSplitter` class in `stellargraph.data`. We will use the train graph for training the model (a binary classifier that, given two nodes, predicts whether a link between these two nodes should exist or not) and the test graph for evaluating the model's performance on hold out data.
Each of these graphs will have the same number of nodes as the input graph, but the number of links will differ (be reduced) as some of the links will be removed during each split and used as the positive samples for training/testing the link prediction classifier.
From the original graph G, extract a randomly sampled subset of test edges (true and false citation links) and the reduced graph G_test with the positive test edges removed:
```
# Define an edge splitter on the original graph G:
edge_splitter_test = EdgeSplitter(G)
# Randomly sample a fraction p=0.1 of all positive links, and same number of negative links, from G, and obtain the
# reduced graph G_test with the sampled links removed:
G_test, edge_ids_test, edge_labels_test = edge_splitter_test.train_test_split(
p=0.1, method="global", keep_connected=True, seed=42
)
```
The reduced graph G_test, together with the test ground truth set of links (edge_ids_test, edge_labels_test), will be used for testing the model.
Now, repeat this procedure to obtain validation data that we are going to use for early stopping in order to prevent overfitting. From the reduced graph G_test, extract a randomly sampled subset of validation edges (true and false citation links) and the reduced graph G_val with the positive validation edges removed.
```
# Define an edge splitter on the reduced graph G_test:
edge_splitter_val = EdgeSplitter(G_test)
# Randomly sample a fraction p=0.1 of all positive links, and same number of negative links, from G_test, and obtain the
# reduced graph G_train with the sampled links removed:
G_val, edge_ids_val, edge_labels_val = edge_splitter_val.train_test_split(
p=0.1, method="global", keep_connected=True, seed=100
)
```
We repeat this procedure one last time in order to obtain the training data for the model.
From the reduced graph G_val, extract a randomly sampled subset of train edges (true and false citation links) and the reduced graph G_train with the positive train edges removed:
```
# Define an edge splitter on the reduced graph G_test:
edge_splitter_train = EdgeSplitter(G_test)
# Randomly sample a fraction p=0.1 of all positive links, and same number of negative links, from G_test, and obtain the
# reduced graph G_train with the sampled links removed:
G_train, edge_ids_train, edge_labels_train = edge_splitter_train.train_test_split(
p=0.1, method="global", keep_connected=True, seed=42
)
```
G_train, together with the train ground truth set of links (edge_ids_train, edge_labels_train), will be used for training the model.
Convert G_train, G_val, and G_test to StellarGraph objects (undirected, as required by GraphSAGE) for ML:
```
G_train = sg.StellarGraph(G_train, node_features="feature")
G_test = sg.StellarGraph(G_test, node_features="feature")
G_val = sg.StellarGraph(G_val, node_features="feature")
```
Summary of G_train and G_test - note that they have the same set of nodes, only differing in their edge sets:
```
print(G_train.info())
print(G_test.info())
print(G_val.info())
```
### Specify global parameters
Here we specify some important parameters that control the type of ensemble model we are going to use. For example, we specify the number of models in the ensemble and the number of predictions per query point per model.
```
n_estimators = 5 # Number of models in the ensemble
n_predictions = 10 # Number of predictions per query point per model
```
Next, we create link generators for sampling and streaming train and test link examples to the model. The link generators essentially "map" pairs of nodes `(paper1, paper2)` to the input of GraphSAGE: they take minibatches of node pairs, sample 2-hop subgraphs with `(paper1, paper2)` head nodes extracted from those pairs, and feed them, together with the corresponding binary labels indicating whether those pairs represent true or false citation links, to the input layer of the GraphSAGE model, for SGD updates of the model parameters.
Specify the minibatch size (number of node pairs per minibatch) and the number of epochs for training the model:
```
batch_size = 20
epochs = 20
```
Specify the sizes of 1- and 2-hop neighbour samples for GraphSAGE. Note that the length of `num_samples` list defines the number of layers/iterations in the GraphSAGE model. In this example, we are defining a 2-layer GraphSAGE model:
```
num_samples = [20, 10]
```
### Create the generators for training
For training we create a generator on the `G_train` graph. The `shuffle=True` argument is given to the `flow` method to improve training.
```
generator = GraphSAGELinkGenerator(G_train, batch_size, num_samples)
train_gen = generator.flow(edge_ids_train,
edge_labels_train,
shuffle=True)
```
At test time we use the `G_test` graph and don't specify the `shuffle` argument (it defaults to `False`).
```
test_gen = GraphSAGELinkGenerator(G_test, batch_size, num_samples).flow(edge_ids_test,
edge_labels_test)
val_gen = GraphSAGELinkGenerator(G_val, batch_size, num_samples).flow(edge_ids_val,
edge_labels_val)
```
### Create the base GraphSAGE model
Build the model: a 2-layer GraphSAGE model acting as node representation learner, with a link classification layer on concatenated `(paper1, paper2)` node embeddings.
GraphSAGE part of the model, with hidden layer sizes of 20 for both GraphSAGE layers, a bias term, and no dropout. (Dropout can be switched on by specifying a positive dropout rate, 0 < dropout < 1)
Note that the length of layer_sizes list must be equal to the length of num_samples, as len(num_samples) defines the number of hops (layers) in the GraphSAGE model.
```
layer_sizes = [20, 20]
assert len(layer_sizes) == len(num_samples)
graphsage = GraphSAGE(
layer_sizes=layer_sizes, generator=generator, bias=True, dropout=0.5
)
# Build the model and expose the input and output tensors.
x_inp, x_out = graphsage.build()
```
Final link classification layer that takes a pair of node embeddings produced by graphsage, applies a binary operator to them to produce the corresponding link embedding ('ip' for inner product; other options for the binary operator can be seen by running a cell with `?link_classification` in it), and passes it through a dense layer:
```
prediction = link_classification(
output_dim=1, output_act="relu", edge_embedding_method='ip'
)(x_out)
```
Stack the GraphSAGE and prediction layers into a Keras model.
```
base_model = keras.Model(inputs=x_inp, outputs=prediction)
```
Now we create the ensemble based on `base_model` we just created.
```
model = BaggingEnsemble(model=base_model, n_estimators=n_estimators, n_predictions=n_predictions)
```
We need to `compile` the model specifying the optimiser, loss function, and metrics to use.
```
model.compile(
optimizer=keras.optimizers.Adam(lr=1e-3),
loss=keras.losses.binary_crossentropy,
weighted_metrics=["acc"],
)
```
Evaluate the initial (untrained) ensemble of models on the train and test set:
```
init_train_metrics_mean, init_train_metrics_std = model.evaluate_generator(train_gen)
init_test_metrics_mean, init_test_metrics_std = model.evaluate_generator(test_gen)
print("\nTrain Set Metrics of the initial (untrained) model:")
for name, m, s in zip(model.metrics_names, init_train_metrics_mean, init_train_metrics_std):
print("\t{}: {:0.4f}±{:0.4f}".format(name, m, s))
print("\nTest Set Metrics of the initial (untrained) model:")
for name, m, s in zip(model.metrics_names, init_test_metrics_mean, init_test_metrics_std):
print("\t{}: {:0.4f}±{:0.4f}".format(name, m, s))
```
### Train the ensemble model
We are going to use **bootstrap samples** of the training dataset to train each model in the ensemble. For this purpose, we need to pass `generator`, `edge_ids_train`, and `edge_labels_train` to the `fit_generator` method.
Note that training time will vary based on computer speed. Set `verbose=1` for reporting of training progress.
```
history = model.fit_generator(
generator=generator,
train_data = edge_ids_train,
train_targets = edge_labels_train,
epochs=epochs,
validation_data=val_gen,
verbose=0,
use_early_stopping=True, # Enable early stopping
early_stopping_monitor="val_weighted_acc",
)
```
Plot the training history:
```
plot_history(history)
```
Evaluate the trained model on test citation links. After training the model, performance should be better than before training (shown above):
```
train_metrics_mean, train_metrics_std = model.evaluate_generator(train_gen)
test_metrics_mean, test_metrics_std = model.evaluate_generator(test_gen)
print("\nTrain Set Metrics of the trained model:")
for name, m, s in zip(model.metrics_names, train_metrics_mean, train_metrics_std):
print("\t{}: {:0.4f}±{:0.4f}".format(name, m, s))
print("\nTest Set Metrics of the trained model:")
for name, m, s in zip(model.metrics_names, test_metrics_mean, test_metrics_std):
print("\t{}: {:0.4f}±{:0.4f}".format(name, m, s))
```
### Make predictions with the model
Now let's get the predictions for all the edges in the test set.
```
test_predictions = model.predict_generator(generator=test_gen)
```
These predictions will be the output of the last layer in the model with `sigmoid` activation.
The array `test_predictions` has dimensionality $MxKxNxF$ where $M$ is the number of estimators in the ensemble (`n_estimators`); $K$ is the number of predictions per query point per estimator (`n_predictions`); $N$ is the number of query points (`len(test_predictions)`); and $F$ is the output dimensionality of the specified layer determined by the shape of the output layer (in this case it is equal to 1 since we are performing binary classification).
```
type(test_predictions), test_predictions.shape
```
For demonstration, we are going to select one of the edges in the test set, and plot the ensemble's predictions for that edge.
Change the value of `selected_query_point` (valid values are in the range of `0` to `len(test_predictions)`) to visualise the results for another test point.
```
selected_query_point = -10
# Select the predictios for the point specified by selected_query_point
qp_predictions = test_predictions[:, :, selected_query_point, :]
# The shape should be n_estimators x n_predictions x size_output_layer
qp_predictions.shape
```
Next, to facilitate plotting the predictions using either a density plot or a box plot, we are going to reshape `qp_predictions` to $R\times F$ where $R$ is equal to $M\times K$ as above and $F$ is the output dimensionality of the output layer.
```
qp_predictions = qp_predictions.reshape(np.product(qp_predictions.shape[0:-1]),
qp_predictions.shape[-1])
qp_predictions.shape
```
The model returns the probability of edge, the class to predict. The probability of no edge is just the complement of the latter. Let's calculate it so that we can plot the distribution of predictions for both outcomes.
```
qp_predictions=np.hstack((qp_predictions, 1.-qp_predictions,))
```
We'd like to assess the ensemble's confidence in its predictions in order to decide if we can trust them or not. Utilising a box plot, we can visually inspect the ensemble's distribution of prediction probabilities for a point in the test set.
If the spread of values for the predicted point class is well separated from those of the other class with little overlap then we can be confident that the prediction is correct.
```
correct_label = "Edge"
if edge_labels_test[selected_query_point] == 0:
correct_label = "No Edge"
fig, ax = plt.subplots(figsize=(12,6))
ax.boxplot(x=qp_predictions)
ax.set_xticklabels(["Edge", "No Edge"])
ax.tick_params(axis='x', rotation=45)
plt.title("Correct label is "+ correct_label)
plt.ylabel("Predicted Probability")
plt.xlabel("Class")
```
For the selected pair of nodes (query point), the ensemble is not certain as to whether an edge between these two nodes should exist. This can be inferred by the large spread of values as indicated in the above figure.
(Note that due to the stochastic nature of training neural network algorithms, the above conclusion may not be valid if you re-run the notebook; however, the general conclusion that the use of ensemble learning can be used to quantify the model's uncertainty about its prediction still holds.)
The below image shows an example of the classifier making a correct prediction with higher confidence than the above example. The results is for the setting `selected_query_point=0`.

| true |
code
| 0.682097 | null | null | null | null |
|
# `kmeans(data)`
#### `def kmeans_more(data, nk=10, niter=100)`
- `returns 3 items : best_k, vector of corresponding labels for each given sample, centroids for each cluster`
#### `def kmeans(data, nk=10, niter=100)`
- `returns 2 items: best_k, vector of corresponding labels for each given sample`
# Requirements
- where data is an MxN numpy array
- This should return
- an integer K, which should be programmatically identified
- a vector of length M containing the cluster labels
- `nk` is predefined as 10, which is the max number of clusters our program will test. So given a data set, the best k would be less than or equal to nk but greater than 1.
- `niter` is the number of iterations before our algorithm "gives up", if it doesn't converge to a centroid after 100 iterations, it will just use the centroids it has computed the most recently
- `kmeans_more()` is just `kmeans` but also returns the set of centroids. This is useful for visualization or plotting purposes.
```
# x_kmeans returns error per k
# kmeans returns k and data labels
from KMeans import kmeans, kmeans_more, get_angle_between_3points
# A list of four sets of 2d points
from oldsamplesgen import gen_set1
# helper plotting functions visualize what kmeans is doing
from kmeansplottinghelper import initial_plots, colored_plots, eval_plots
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Load 4 data sets of 2d points with clusters [2, 3, 4, 5] respectively
pointset = gen_set1()
# let's get one of them to test for our k means
samples = pointset[3]
# Make sure to shuffle the data, as they sorted by label
np.random.shuffle(samples)
print()
print("(M x N) row = M (number of samples) columns = N (number of features per sample)")
print("Shape of array:", samples.shape)
print()
print("Which means there are", samples.shape[0], "samples and", samples.shape[1], "features per sample")
print()
print("Let's run our kmeans implementation")
#----------------------------------------------
k, labels = kmeans(samples)
#----------------------------------------------
print()
print()
print("Proposed number of clusters:", k)
print("Labels shape:")
print(labels.shape)
print("Print all the labels:")
print(labels)
# The synthetic dataset looks like this
# They look like this
initial_plots(pointset)
# Plot a kmeans implementation given 4 sets of points
def plot_sample_kmeans_more(pointset):
idata, ilabels, icentroids, inclusters = [], [], [], []
for points in pointset:
data = points
np.random.shuffle(data)
nclusters, labels, centroids = kmeans_more(data)
idata.append(data)
ilabels.append(labels)
icentroids.append(centroids)
inclusters.append(nclusters)
colored_plots(idata, ilabels, icentroids, inclusters)
# returns the set the evaluated ks for each set
def test_final_kmeans(pointset):
ks = []
for i, points in enumerate(pointset):
data = pointset[i]
#Make sure to shuffle the data, as they sorted by label
np.random.shuffle(data)
k, _ = kmeans(data)
ks.append(k)
return ks
ks = test_final_kmeans(pointset)
print()
# Should be [2, 3, 4, 5]
print("Proposed k for each set:", ks)
plot_sample_kmeans_more(pointset)
# test if our "compute angle between three points" function is working
a = get_angle_between_3points([1, 2], [1, 1], [2, 1])
b = get_angle_between_3points([1, 1], [2, 1], [3, 1])
assert a, 90.0
assert b, 180.0
```
| true |
code
| 0.55447 | null | null | null | null |
|
# Eaton method with well log
Pore pressure prediction with Eaton's method using well log data.
Steps:
1. Calculate Velocity Normal Compaction Trend
2. Optimize for Eaton's exponent n
3. Predict pore pressure using Eaton's method
```
import warnings
warnings.filterwarnings(action='ignore')
# for python 2 and 3 compatibility
# from builtins import str
# try:
# from pathlib import Path
# except:
# from pathlib2 import Path
#--------------------------------------------
import sys
ppath = "../.."
if ppath not in sys.path:
sys.path.append(ppath)
#--------------------------------------------
from __future__ import print_function, division, unicode_literals
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use(['seaborn-paper', 'seaborn-whitegrid'])
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
import numpy as np
import pygeopressure as ppp
```
## 1. Calculate Velocity Normal Compaction Trend
Create survey with the example survey `CUG`:
```
# set to the directory on your computer
SURVEY_FOLDER = "C:/Users/yuhao/Desktop/CUG_depth"
survey = ppp.Survey(SURVEY_FOLDER)
```
Retrieve well `CUG1`:
```
well_cug1 = survey.wells['CUG1']
```
Get velocity log:
```
vel_log = well_cug1.get_log("Velocity")
```
View velocity log:
```
fig_vel, ax_vel = plt.subplots()
ax_vel.invert_yaxis()
vel_log.plot(ax_vel)
well_cug1.plot_horizons(ax_vel)
# set fig style
ax_vel.set(ylim=(5000,0), aspect=(5000/4600)*2)
ax_vel.set_aspect(2)
fig_vel.set_figheight(8)
```
Optimize for NCT coefficients a, b:
`well.params['horizon']['T20']` returns the depth of horizon T20.
```
a, b = ppp.optimize_nct(
vel_log=well_cug1.get_log("Velocity"),
fit_start=well_cug1.params['horizon']["T16"],
fit_stop=well_cug1.params['horizon']["T20"])
```
And use a, b to calculate normal velocity trend
```
from pygeopressure.velocity.extrapolate import normal_log
nct_log = normal_log(vel_log, a=a, b=b)
```
View fitted NCT:
```
fig_vel, ax_vel = plt.subplots()
ax_vel.invert_yaxis()
# plot velocity
vel_log.plot(ax_vel, label='Velocity')
# plot horizon
well_cug1.plot_horizons(ax_vel)
# plot fitted nct
nct_log.plot(ax_vel, color='r', zorder=2, label='NCT')
# set fig style
ax_vel.set(ylim=(5000,0), aspect=(5000/4600)*2)
ax_vel.set_aspect(2)
ax_vel.legend()
fig_vel.set_figheight(8)
```
Save fitted nct:
```
# well_cug1.params['nct'] = {"a": a, "b": b}
# well_cug1.save_params()
```
## 2. Optimize for Eaton's exponent n
First, we need to preprocess velocity.
Velocity log processing (filtering and smoothing):
```
vel_log_filter = ppp.upscale_log(vel_log, freq=20)
vel_log_filter_smooth = ppp.smooth_log(vel_log_filter, window=1501)
```
Veiw processed velocity:
```
fig_vel, ax_vel = plt.subplots()
ax_vel.invert_yaxis()
# plot velocity
vel_log.plot(ax_vel, label='Velocity')
# plot horizon
well_cug1.plot_horizons(ax_vel)
# plot processed velocity
vel_log_filter_smooth.plot(ax_vel, color='g', zorder=2, label='Processed', linewidth=1)
# set fig style
ax_vel.set(ylim=(5000,0), aspect=(5000/4600)*2)
ax_vel.set_aspect(2)
ax_vel.legend()
fig_vel.set_figheight(8)
```
We will use the processed velocity data for pressure prediction.
Optimize Eaton's exponential `n`:
```
n = ppp.optimize_eaton(
well=well_cug1,
vel_log=vel_log_filter_smooth,
obp_log="Overburden_Pressure",
a=a, b=b)
```
See the RMS error variation with `n`:
```
from pygeopressure.basic.plots import plot_eaton_error
fig_err, ax_err = plt.subplots()
plot_eaton_error(
ax=ax_err,
well=well_cug1,
vel_log=vel_log_filter_smooth,
obp_log="Overburden_Pressure",
a=a, b=b)
```
Save optimized n:
```
# well_cug1.params['nct'] = {"a": a, "b": b}
# well_cug1.save_params()
```
## 3.Predict pore pressure using Eaton's method
Calculate pore pressure using Eaton's method requires velocity, Eaton's exponential, normal velocity, hydrostatic pressure and overburden pressure.
`Well.eaton()` will try to read saved data, users only need to specify them when they are different from the saved ones.
```
pres_eaton_log = well_cug1.eaton(vel_log_filter_smooth, n=n)
```
View predicted pressure:
```
fig_pres, ax_pres = plt.subplots()
ax_pres.invert_yaxis()
well_cug1.get_log("Overburden_Pressure").plot(ax_pres, 'g', label='Lithostatic')
ax_pres.plot(well_cug1.hydrostatic, well_cug1.depth, 'g', linestyle='--', label="Hydrostatic")
pres_eaton_log.plot(ax_pres, color='blue', label='Pressure_Eaton')
well_cug1.plot_horizons(ax_pres)
# set figure and axis size
ax_pres.set_aspect(2/50)
ax_pres.legend()
fig_pres.set_figheight(8)
```
| true |
code
| 0.608041 | null | null | null | null |
|
# Import necessary depencencies
```
import pandas as pd
import numpy as np
import text_normalizer as tn
import model_evaluation_utils as meu
np.set_printoptions(precision=2, linewidth=80)
```
# Load and normalize data
```
dataset = pd.read_csv(r'movie_reviews.csv')
reviews = np.array(dataset['review'])
sentiments = np.array(dataset['sentiment'])
# extract data for model evaluation
test_reviews = reviews[35000:]
test_sentiments = sentiments[35000:]
sample_review_ids = [7626, 3533, 13010]
# normalize dataset
norm_test_reviews = tn.normalize_corpus(test_reviews)
```
# Sentiment Analysis with AFINN
```
from afinn import Afinn
afn = Afinn(emoticons=True)
```
## Predict sentiment for sample reviews
```
for review, sentiment in zip(test_reviews[sample_review_ids], test_sentiments[sample_review_ids]):
print('REVIEW:', review)
print('Actual Sentiment:', sentiment)
print('Predicted Sentiment polarity:', afn.score(review))
print('-'*60)
```
## Predict sentiment for test dataset
```
sentiment_polarity = [afn.score(review) for review in test_reviews]
predicted_sentiments = ['positive' if score >= 1.0 else 'negative' for score in sentiment_polarity]
```
## Evaluate model performance
```
meu.display_model_performance_metrics(true_labels=test_sentiments, predicted_labels=predicted_sentiments,
classes=['positive', 'negative'])
```
# Sentiment Analysis with SentiWordNet
```
from nltk.corpus import sentiwordnet as swn
awesome = list(swn.senti_synsets('awesome', 'a'))[0]
print('Positive Polarity Score:', awesome.pos_score())
print('Negative Polarity Score:', awesome.neg_score())
print('Objective Score:', awesome.obj_score())
```
## Build model
```
def analyze_sentiment_sentiwordnet_lexicon(review,
verbose=False):
# tokenize and POS tag text tokens
tagged_text = [(token.text, token.tag_) for token in tn.nlp(review)]
pos_score = neg_score = token_count = obj_score = 0
# get wordnet synsets based on POS tags
# get sentiment scores if synsets are found
for word, tag in tagged_text:
ss_set = None
if 'NN' in tag and list(swn.senti_synsets(word, 'n')):
ss_set = list(swn.senti_synsets(word, 'n'))[0]
elif 'VB' in tag and list(swn.senti_synsets(word, 'v')):
ss_set = list(swn.senti_synsets(word, 'v'))[0]
elif 'JJ' in tag and list(swn.senti_synsets(word, 'a')):
ss_set = list(swn.senti_synsets(word, 'a'))[0]
elif 'RB' in tag and list(swn.senti_synsets(word, 'r')):
ss_set = list(swn.senti_synsets(word, 'r'))[0]
# if senti-synset is found
if ss_set:
# add scores for all found synsets
pos_score += ss_set.pos_score()
neg_score += ss_set.neg_score()
obj_score += ss_set.obj_score()
token_count += 1
# aggregate final scores
final_score = pos_score - neg_score
norm_final_score = round(float(final_score) / token_count, 2)
final_sentiment = 'positive' if norm_final_score >= 0 else 'negative'
if verbose:
norm_obj_score = round(float(obj_score) / token_count, 2)
norm_pos_score = round(float(pos_score) / token_count, 2)
norm_neg_score = round(float(neg_score) / token_count, 2)
# to display results in a nice table
sentiment_frame = pd.DataFrame([[final_sentiment, norm_obj_score, norm_pos_score,
norm_neg_score, norm_final_score]],
columns=pd.MultiIndex(levels=[['SENTIMENT STATS:'],
['Predicted Sentiment', 'Objectivity',
'Positive', 'Negative', 'Overall']],
labels=[[0,0,0,0,0],[0,1,2,3,4]]))
print(sentiment_frame)
return final_sentiment
```
## Predict sentiment for sample reviews
```
for review, sentiment in zip(test_reviews[sample_review_ids], test_sentiments[sample_review_ids]):
print('REVIEW:', review)
print('Actual Sentiment:', sentiment)
pred = analyze_sentiment_sentiwordnet_lexicon(review, verbose=True)
print('-'*60)
```
## Predict sentiment for test dataset
```
predicted_sentiments = [analyze_sentiment_sentiwordnet_lexicon(review, verbose=False) for review in norm_test_reviews]
```
## Evaluate model performance
```
meu.display_model_performance_metrics(true_labels=test_sentiments, predicted_labels=predicted_sentiments,
classes=['positive', 'negative'])
```
# Sentiment Analysis with VADER
```
from nltk.sentiment.vader import SentimentIntensityAnalyzer
```
## Build model
```
def analyze_sentiment_vader_lexicon(review,
threshold=0.1,
verbose=False):
# pre-process text
review = tn.strip_html_tags(review)
review = tn.remove_accented_chars(review)
review = tn.expand_contractions(review)
# analyze the sentiment for review
analyzer = SentimentIntensityAnalyzer()
scores = analyzer.polarity_scores(review)
# get aggregate scores and final sentiment
agg_score = scores['compound']
final_sentiment = 'positive' if agg_score >= threshold\
else 'negative'
if verbose:
# display detailed sentiment statistics
positive = str(round(scores['pos'], 2)*100)+'%'
final = round(agg_score, 2)
negative = str(round(scores['neg'], 2)*100)+'%'
neutral = str(round(scores['neu'], 2)*100)+'%'
sentiment_frame = pd.DataFrame([[final_sentiment, final, positive,
negative, neutral]],
columns=pd.MultiIndex(levels=[['SENTIMENT STATS:'],
['Predicted Sentiment', 'Polarity Score',
'Positive', 'Negative', 'Neutral']],
labels=[[0,0,0,0,0],[0,1,2,3,4]]))
print(sentiment_frame)
return final_sentiment
```
## Predict sentiment for sample reviews
```
for review, sentiment in zip(test_reviews[sample_review_ids], test_sentiments[sample_review_ids]):
print('REVIEW:', review)
print('Actual Sentiment:', sentiment)
pred = analyze_sentiment_vader_lexicon(review, threshold=0.4, verbose=True)
print('-'*60)
```
## Predict sentiment for test dataset
```
predicted_sentiments = [analyze_sentiment_vader_lexicon(review, threshold=0.4, verbose=False) for review in test_reviews]
```
## Evaluate model performance
```
meu.display_model_performance_metrics(true_labels=test_sentiments, predicted_labels=predicted_sentiments,
classes=['positive', 'negative'])
```
| true |
code
| 0.397354 | null | null | null | null |
|
# Prosper Loan Data Exploration
## By Abhishek Tiwari
# Preliminary Wrangling
This data set contains information on peer to peer loans facilitated by credit company Prosper
```
# import all packages
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
df = pd.read_csv('prosperLoanData.csv')
df.head()
df.info()
df.describe()
df.sample(10)
```
Note that this data set contains 81 columns. For the purpose of this analysis I’ve took the following columns (variables):
```
target_columns = [
'Term', 'LoanStatus', 'BorrowerRate', 'ProsperRating (Alpha)', 'ListingCategory (numeric)', 'EmploymentStatus',
'DelinquenciesLast7Years', 'StatedMonthlyIncome', 'TotalProsperLoans', 'LoanOriginalAmount',
'LoanOriginationDate', 'Recommendations', 'Investors'
]
target_df = df[target_columns]
target_df.sample(10)
```
Since Prosper use their own proprietary Prosper Rating only since 2009, we have a lot of missing values in ProsperRating column. Let's drop these missing values:
```
target_df.info()
target_df.describe()
```
Since Prosper use their own proprietary Prosper Rating only since 2009, we have a lot of missing values in ProsperRating column. Let's drop these missing values:
```
target_df = target_df.dropna(subset=['ProsperRating (Alpha)']).reset_index()
```
Convert LoanOriginationDate to datetime datatype:
```
target_df['LoanOriginationDate'] = pd.to_datetime(target_df['LoanOriginationDate'])
target_df['TotalProsperLoans'] = target_df['TotalProsperLoans'].fillna(0)
target_df.info()
```
### What is/are the main feature(s) of interest in your dataset?
> Trying to figure out what features can be used to predict default on credit. Also i would like to check what are major factors connected with prosper credit rating.
### What features in the dataset do you think will help support your investigation into your feature(s) of interest?
> I think that the borrowers Prosper rating will have the highest impact on chances of default. Also I expect that loan amount will play a major role and maybe the category of credit. Prosper rating will depend on stated income and employment status.
## Univariate Exploration
### Loan status
```
# setting color
base_color = sns.color_palette()[0]
plt.xticks(rotation=90)
sns.countplot(data = target_df, x = 'LoanStatus', color = base_color);
```
Observation 1:
* Most of the loans in the data set are actually current loans.
* Past due loans are split in several groups based on the length of payment delay.
* Other big part is completed loans, defaulted loans compromise a minority, however chargedoff loans also comporomise a substanial amount.
### Employment Status
```
sns.countplot(data = target_df, x = 'EmploymentStatus', color = base_color);
plt.xticks(rotation = 90);
```
Observation 2:
* The majority of borrowers are employed and all other categories as small part of borrowers.
* In small Group full time has highest, after that self empolyed are there and so on.
### Stated Monthly Income
```
plt.hist(data=target_df, x='StatedMonthlyIncome', bins=1000);
```
(**Note**: Distribution of stated monthly income is highly skewed to the right. so, we have to check how many outliers are there)
```
income_std = target_df['StatedMonthlyIncome'].std()
income_mean = target_df['StatedMonthlyIncome'].mean()
boundary = income_mean + income_std * 3
len(target_df[target_df['StatedMonthlyIncome'] >= boundary])
```
**After Zooming the Graph We Get This**
```
plt.hist(data=target_df, x='StatedMonthlyIncome', bins=1000);
plt.xlim(0, boundary);
```
Observation 3:
* With a boundary of mean and 3 times standard deviations distribution of monthly income still has noticeable right skew but now we can see that mode is about 5000.
### Discuss the distribution(s) of your variable(s) of interest. Were there any unusual points? Did you need to perform any transformations?
> Distribution of monthly stated income is very awkward: with a lot of outliers and very large range but still it was right skew. The majority of borrowers are employed and all other categories as small part of borrowers and most of the loans in the data set are actually current loans.
### Of the features you investigated, were there any unusual distributions? Did you perform any operations on the data to tidy, adjust, or change the form of the data? If so, why did you do this?
> The majority of loans are actually current loans. Since our main goal is to define driving factors of outcome of loan we are not interested in any current loans.
## Bivariate Exploration
```
#I'm just adjusting the form of data
condition = (target_df['LoanStatus'] == 'Completed') | (target_df['LoanStatus'] == 'Defaulted') |\
(target_df['LoanStatus'] == 'Chargedoff')
target_df = target_df[condition]
def change_to_defaulted(row):
if row['LoanStatus'] == 'Chargedoff':
return 'Defaulted'
else:
return row['LoanStatus']
target_df['LoanStatus'] = target_df.apply(change_to_defaulted, axis=1)
target_df['LoanStatus'].value_counts()
```
**After transforming dataset we have 19664 completed loans and 6341 defaulted.**
```
categories = {1: 'Debt Consolidation', 2: 'Home Improvement', 3: 'Business', 6: 'Auto', 7: 'Other'}
def reduce_categorie(row):
loan_category = row['ListingCategory (numeric)']
if loan_category in categories:
return categories[loan_category]
else:
return categories[7]
target_df['ListingCategory (numeric)'] = target_df.apply(reduce_categorie, axis=1)
target_df['ListingCategory (numeric)'].value_counts()
```
Variable Listing Category is set up as numeric and most of the values have very `low frequency`, for the easier visualization so we have change it to `categorical and reduce the number of categories`.
### Status and Prosper Rating:
```
sns.countplot(data = target_df, x = 'LoanStatus', hue = 'ProsperRating (Alpha)', palette = 'Blues')
```
Observation 1:
* The `most frequent` rating among defaulted loans is actually `D`.
* And the `most frequent` rating among Completed is also` D `and second highest is A and so on.
### Credit Start with Listing Category:
```
sns.countplot(data = target_df, x = 'LoanStatus', hue = 'ListingCategory (numeric)', palette = 'Blues');
```
Observation 2:
* In both of the Graphs the `debt Consolidation` have `most frequency among all of them`.
## Loan Status and Loan Amount
```
sns.boxplot(data = target_df, x = 'LoanStatus', y = 'LoanOriginalAmount', color = base_color);
```
Observation 3:
* As from Above Graph we can state that `defaulted credits` tend to be `smaller` than `completed credits` onces.
## Prosper Rating and Employment Status
```
plt.figure(figsize = [12, 10])
sns.countplot(data = target_df, x = 'ProsperRating (Alpha)', hue = 'EmploymentStatus', palette = 'Blues');
```
Observation 4:
* Lower ratings seem to have greater proportions of individuals with employment status Not Employed, Self-employed, Retired and Part-Time.
## Talk about some of the relationships you observed in this part of the investigation. How did the feature(s) of interest vary with other features in the dataset?
> In Loan status vs Loan amount defaulted credits tend to be smaller than completed credits onces. Employment status of individuals with lower ratings tends to be 'Not employed', 'Self-employed', 'Retired' or 'Part-time'.
## Did you observe any interesting relationships between the other features (not the main feature(s) of interest)?
> Prosper rating D is the most frequent rating among defaulted credits.
## Multivariate Exploration
## Rating, Loan Amount and Loan Status
```
plt.figure(figsize = [12, 8])
sns.boxplot(data=target_df, x='ProsperRating (Alpha)', y='LoanOriginalAmount', hue='LoanStatus');
```
Observation 1:
* Except for the lowest ratings defaulted credits tend to be larger than completed.
* Most of the defaulted credits comes from individuals with low Prosper rating.
## Relationships between Credit category, Credit rating and outcome of Credit.
```
sns.catplot(x = 'ProsperRating (Alpha)', hue = 'LoanStatus', col = 'ListingCategory (numeric)',
data = target_df, kind = 'count', palette = 'Blues', col_wrap = 3);
```
Observation 2:
* There are 5 graphs in the second one has much up and downs in it other than all of them.
* There is no substantial difference for default rates in different categories broken up by ratings.
## Amount, Listing Category Loan and Loan Status Interact
```
plt.figure(figsize = [12, 8])
sns.violinplot(data=target_df, x='ListingCategory (numeric)', y='LoanOriginalAmount', hue='LoanStatus');
```
Observation 3:
* Except for Auto, Business and Home Improvemrnt dont have nearly equal mean amoong all of them.
* Business category tend to have larger amount.
## Talk about some of the relationships you observed in this part of the investigation. Were there features that strengthened each other in terms of looking at your feature(s) of interest?
> Our initial assumptions were strengthened. Most of the defaulted credits comes from individuals with low Prosper rating and Business category tend to have larger amount.
## Were there any interesting or surprising interactions between features?
> Interesting find was that defaulted credits for individuals with high Prosper ratings tend to be larger than completed credits.
| true |
code
| 0.431944 | null | null | null | null |
|
# Azure Machine Learning Setup
To begin, you will need to provide the following information about your Azure Subscription.
**If you are using your own Azure subscription, please provide names for subscription_id, resource_group, workspace_name and workspace_region to use.** Note that the workspace needs to be of type [Machine Learning Workspace](https://docs.microsoft.com/en-us/azure/machine-learning/service/setup-create-workspace).
**If an enviorment is provided to you be sure to replace XXXXX in the values below with your unique identifier.**
In the following cell, be sure to set the values for `subscription_id`, `resource_group`, `workspace_name` and `workspace_region` as directed by the comments (*these values can be acquired from the Azure Portal*).
To get these values, do the following:
1. Navigate to the Azure Portal and login with the credentials provided.
2. From the left hand menu, under Favorites, select `Resource Groups`.
3. In the list, select the resource group with the name similar to `XXXXX`.
4. From the Overview tab, capture the desired values.
Execute the following cell by selecting the `>|Run` button in the command bar above.
```
#Provide the Subscription ID of your existing Azure subscription
subscription_id = "" #"<your-azure-subscription-id>"
#Provide a name for the Resource Group that will contain Azure ML related services
resource_group = "mcw-ai-lab-XXXXX" #"<your-subscription-group-name>"
# Provide the name and region for the Azure Machine Learning Workspace that will be created
workspace_name = "mcw-ai-lab-ws-XXXXX"
workspace_region = "eastus" # eastus2, eastus, westcentralus, southeastasia, australiaeast, westeurope
```
## Create and connect to an Azure Machine Learning Workspace
The Azure Machine Learning Python SDK is required for leveraging the experimentation, model management and model deployment capabilities of Azure Machine Learning services. Run the following cell to create a new Azure Machine Learning **Workspace** and save the configuration to disk. The configuration file named `config.json` is saved in a folder named `.azureml`.
**Important Note**: You will be prompted to login in the text that is output below the cell. Be sure to navigate to the URL displayed and enter the code that is provided. Once you have entered the code, return to this notebook and wait for the output to read `Workspace configuration succeeded`.
```
import azureml.core
print('azureml.core.VERSION: ', azureml.core.VERSION)
# import the Workspace class and check the azureml SDK version
from azureml.core import Workspace
ws = Workspace.create(
name = workspace_name,
subscription_id = subscription_id,
resource_group = resource_group,
location = workspace_region,
exist_ok = True)
ws.write_config()
print('Workspace configuration succeeded')
```
Take a look at the contents of the generated configuration file by running the following cell:
```
!cat .azureml/config.json
```
# Deploy model to Azure Container Instance (ACI)
In this section, you will deploy a web service that uses Gensim as shown in `01 Summarize` to summarize text. The web service will be hosted in Azure Container Service.
## Create the scoring web service
When deploying models for scoring with Azure Machine Learning services, you need to define the code for a simple web service that will load your model and use it for scoring. By convention this service has two methods init which loads the model and run which scores data using the loaded model.
This scoring service code will later be deployed inside of a specially prepared Docker container.
```
%%writefile summarizer_service.py
import re
import nltk
import unicodedata
from gensim.summarization import summarize, keywords
def clean_and_parse_document(document):
if isinstance(document, str):
document = document
elif isinstance(document, unicode):
return unicodedata.normalize('NFKD', document).encode('ascii', 'ignore')
else:
raise ValueError("Document is not string or unicode.")
document = document.strip()
sentences = nltk.sent_tokenize(document)
sentences = [sentence.strip() for sentence in sentences]
return sentences
def summarize_text(text, summary_ratio=None, word_count=30):
sentences = clean_and_parse_document(text)
cleaned_text = ' '.join(sentences)
summary = summarize(cleaned_text, split=True, ratio=summary_ratio, word_count=word_count)
return summary
def init():
nltk.download('all')
return
def run(input_str):
try:
return summarize_text(input_str)
except Exception as e:
return (str(e))
```
## Create a Conda dependencies environment file
Your web service can have dependencies installed by using a Conda environment file. Items listed in this file will be conda or pip installed within the Docker container that is created and thus be available to your scoring web service logic.
```
from azureml.core.conda_dependencies import CondaDependencies
myacienv = CondaDependencies.create(pip_packages=['gensim','nltk'])
with open("mydeployenv.yml","w") as f:
f.write(myacienv.serialize_to_string())
```
## Deployment
In the following cells you will use the Azure Machine Learning SDK to package the model and scoring script in a container, and deploy that container to an Azure Container Instance.
Run the following cells.
```
from azureml.core.webservice import AciWebservice, Webservice
aci_config = AciWebservice.deploy_configuration(
cpu_cores = 1,
memory_gb = 1,
tags = {'name':'Summarization'},
description = 'Summarizes text.')
```
Next, build up a container image configuration that names the scoring service script, the runtime, and provides the conda file.
```
service_name = "summarizer"
runtime = "python"
driver_file = "summarizer_service.py"
conda_file = "mydeployenv.yml"
from azureml.core.image import ContainerImage
image_config = ContainerImage.image_configuration(execution_script = driver_file,
runtime = runtime,
conda_file = conda_file)
```
Now you are ready to begin your deployment to the Azure Container Instance.
Run the following cell. This may take between 5-15 minutes to complete.
You will see output similar to the following when your web service is ready: `SucceededACI service creation operation finished, operation "Succeeded"`
```
webservice = Webservice.deploy(
workspace=ws,
name=service_name,
model_paths=[],
deployment_config=aci_config,
image_config=image_config,
)
webservice.wait_for_deployment(show_output=True)
```
## Test the deployed service
Now you are ready to test scoring using the deployed web service. The following cell invokes the web service.
Run the following cells to test scoring using a single input row against the deployed web service.
```
example_document = """
I was driving down El Camino and stopped at a red light.
It was about 3pm in the afternoon.
The sun was bright and shining just behind the stoplight.
This made it hard to see the lights.
There was a car on my left in the left turn lane.
A few moments later another car, a black sedan pulled up behind me.
When the left turn light changed green, the black sedan hit me thinking
that the light had changed for us, but I had not moved because the light
was still red.
After hitting my car, the black sedan backed up and then sped past me.
I did manage to catch its license plate.
The license plate of the black sedan was ABC123.
"""
result = webservice.run(input_data = example_document)
print(result)
```
## Capture the scoring URI
In order to call the service from a REST client, you need to acquire the scoring URI. Run the following cell to retrieve the scoring URI and take note of this value, you will need it in the last notebook.
```
webservice.scoring_uri
```
The default settings used in deploying this service result in a service that does not require authentication, so the scoring URI is the only value you need to call this service.
| true |
code
| 0.363308 | null | null | null | null |
|
# Florida Single Weekly Predictions, trained on historical flu data and temperature
> Once again, just like before in the USA flu model, I am going to index COVID weekly cases by Wednesdays
```
import tensorflow as tf
physical_devices = tf.config.list_physical_devices('GPU')
tf.config.experimental.set_memory_growth(physical_devices[0], enable=True)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import sklearn
from sklearn import preprocessing
```
### getting historical flu data
```
system = "Windows"
if system == "Windows":
flu_dir = "..\\..\\..\\cdc-fludata\\us_national\\"
else:
flu_dir = "../../../cdc-fludata/us_national/"
flu_dictionary = {}
for year in range(1997, 2019):
filepath = "usflu_"
year_string = str(year) + "-" + str(year + 1)
filepath = flu_dir + filepath + year_string + ".csv"
temp_df = pd.read_csv(filepath)
flu_dictionary[year] = temp_df
```
### combining flu data into one chronological series of total cases
```
# getting total cases and putting them in a series by week
flu_series_dict = {}
for year in flu_dictionary:
temp_df = flu_dictionary[year]
temp_df = temp_df.set_index("WEEK")
abridged_df = temp_df.iloc[:, 2:]
try:
abridged_df = abridged_df.drop(columns="PERCENT POSITIVE")
except:
pass
total_cases_series = abridged_df.sum(axis=1)
flu_series_dict[year] = total_cases_series
all_cases_series = pd.Series(dtype="int64")
for year in flu_series_dict:
temp_series = flu_series_dict[year]
all_cases_series = all_cases_series.append(temp_series, ignore_index=True)
all_cases_series
all_cases_series.plot(grid=True, figsize=(60,20))
```
### Now, making a normalized series between 0, 1
```
norm_flu_series_dict = {}
for year in flu_series_dict:
temp_series = flu_series_dict[year]
temp_list = preprocessing.minmax_scale(temp_series)
temp_series = pd.Series(temp_list)
norm_flu_series_dict[year] = temp_series
all_cases_norm_series = pd.Series(dtype="int64")
for year in norm_flu_series_dict:
temp_series = norm_flu_series_dict[year]
all_cases_norm_series = all_cases_norm_series.append(temp_series, ignore_index=True)
all_cases_norm_series.plot(grid=True, figsize=(60,5))
all_cases_norm_series
```
## Getting COVID-19 Case Data
```
if system == "Windows":
datapath = "..\\..\\..\\COVID-19\\csse_covid_19_data\\csse_covid_19_time_series\\"
else:
datapath = "../../../COVID-19/csse_covid_19_data/csse_covid_19_time_series/"
# Choose from "US Cases", "US Deaths", "World Cases", "World Deaths", "World Recoveries"
key = "US Cases"
if key == "US Cases":
datapath = datapath + "time_series_covid19_confirmed_US.csv"
elif key == "US Deaths":
datapath = datapath + "time_series_covid19_deaths_US.csv"
elif key == "World Cases":
datapath = datapath + "time_series_covid19_confirmed_global.csv"
elif key == "World Deaths":
datapath = datapath + "time_series_covid19_deaths_global.csv"
elif key == "World Recoveries":
datapath = datapath + "time_series_covid19_recovered_global.csv"
covid_df = pd.read_csv(datapath)
covid_df
florida_data = covid_df.loc[covid_df["Province_State"] == "Florida"]
florida_cases = florida_data.iloc[:,11:]
florida_cases_total = florida_cases.sum(axis=0)
florida_cases_total.plot()
```
### convert daily data to weekly data
```
florida_weekly_cases = florida_cases_total.iloc[::7]
florida_weekly_cases
florida_weekly_cases.plot()
```
### Converting cumulative series to non-cumulative series
```
florida_wnew_cases = florida_weekly_cases.diff()
florida_wnew_cases[0] = 1.0
florida_wnew_cases
florida_wnew_cases.plot()
```
### normalizing weekly case data
> This is going to be different for texas. This is because, the peak number of weekly new infections probably has not been reached yet. We need to divide everything by a guess for the peak number of predictions instead of min-max scaling.
```
# I'm guessing that the peak number of weekly cases will be about 60,000. Could definitely be wrong.
peak_guess = 60000
florida_wnew_cases_norm = florida_wnew_cases / peak_guess
florida_wnew_cases_norm.plot()
florida_wnew_cases_norm
```
## getting temperature data
> At the moment, this will be dummy data
```
flu_temp_data = np.full(len(all_cases_norm_series), 0.5)
training_data_df = pd.DataFrame({
"Temperature" : flu_temp_data,
"Flu Cases" : all_cases_norm_series
})
training_data_df
covid_temp_data = np.full(len(florida_wnew_cases_norm), 0.5)
testing_data_df = pd.DataFrame({
"Temperature" : covid_temp_data,
"COVID Cases" : florida_wnew_cases_norm
})
testing_data_df
testing_data_df.shape
training_data_np = training_data_df.values
testing_data_np = testing_data_df.values
```
## Building Neural Net Model
### preparing model data
```
# this code is directly from https://www.tensorflow.org/tutorials/structured_data/time_series
# much of below data formatting code is derived straight from same link
def multivariate_data(dataset, target, start_index, end_index, history_size,
target_size, step, single_step=False):
data = []
labels = []
start_index = start_index + history_size
if end_index is None:
end_index = len(dataset) - target_size
for i in range(start_index, end_index):
indices = range(i-history_size, i, step)
data.append(dataset[indices])
if single_step:
labels.append(target[i+target_size])
else:
labels.append(target[i:i+target_size])
return np.array(data), np.array(labels)
past_history = 22
future_target = 0
STEP = 1
x_train_single, y_train_single = multivariate_data(training_data_np, training_data_np[:, 1], 0,
None, past_history,
future_target, STEP,
single_step=True)
x_test_single, y_test_single = multivariate_data(testing_data_np, testing_data_np[:, 1],
0, None, past_history,
future_target, STEP,
single_step=True)
BATCH_SIZE = 300
BUFFER_SIZE = 1000
train_data_single = tf.data.Dataset.from_tensor_slices((x_train_single, y_train_single))
train_data_single = train_data_single.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()
test_data_single = tf.data.Dataset.from_tensor_slices((x_test_single, y_test_single))
test_data_single = test_data_single.batch(1).repeat()
```
### designing actual model
```
# creating the neural network model
lstm_prediction_model = tf.keras.Sequential([
tf.keras.layers.LSTM(32, input_shape=x_train_single.shape[-2:]),
tf.keras.layers.Dense(32),
tf.keras.layers.Dense(1)
])
lstm_prediction_model.compile(optimizer=tf.keras.optimizers.RMSprop(), loss="mae")
single_step_history = lstm_prediction_model.fit(train_data_single, epochs=10,
steps_per_epoch=250,
validation_data=test_data_single,
validation_steps=50)
def create_time_steps(length):
return list(range(-length, 0))
def show_plot(plot_data, delta, title):
labels = ['History', 'True Future', 'Model Prediction']
marker = ['.-', 'rx', 'go']
time_steps = create_time_steps(plot_data[0].shape[0])
if delta:
future = delta
else:
future = 0
plt.title(title)
for i, x in enumerate(plot_data):
if i:
plt.plot(future, plot_data[i], marker[i], markersize=10,
label=labels[i])
else:
plt.plot(time_steps, plot_data[i].flatten(), marker[i], label=labels[i])
plt.legend()
plt.xlim([time_steps[0], (future+5)*2])
plt.xlabel('Week (defined by Wednesdays)')
plt.ylabel('Normalized Cases')
return plt
for x, y in train_data_single.take(10):
#print(lstm_prediction_model.predict(x))
plot = show_plot([x[0][:, 1].numpy(), y[0].numpy(),
lstm_prediction_model.predict(x)[0]], 0,
'Training Data Prediction')
plot.show()
for x, y in test_data_single.take(1):
plot = show_plot([x[0][:, 1].numpy(), y[0].numpy(),
lstm_prediction_model.predict(x)[0]], 0,
'Florida COVID Case Prediction, Single Week')
plot.show()
```
| true |
code
| 0.363788 | null | null | null | null |
|
<a href="https://practicalai.me"><img src="https://raw.githubusercontent.com/practicalAI/images/master/images/rounded_logo.png" width="100" align="left" hspace="20px" vspace="20px"></a>
<img src="https://raw.githubusercontent.com/practicalAI/images/master/basic_ml/06_Multilayer_Perceptron/nn.png" width="200" vspace="10px" align="right">
<div align="left">
<h1>Multilayer Perceptron (MLP)</h1>
In this lesson, we will explore multilayer perceptrons (MLPs) which are a basic type of neural network. We will implement them using Tensorflow with Keras.
<table align="center">
<td>
<img src="https://raw.githubusercontent.com/practicalAI/images/master/images/rounded_logo.png" width="25"><a target="_blank" href="https://practicalai.me"> View on practicalAI</a>
</td>
<td>
<img src="https://raw.githubusercontent.com/practicalAI/images/master/images/colab_logo.png" width="25"><a target="_blank" href="https://colab.research.google.com/github/practicalAI/practicalAI/blob/master/notebooks/06_Multilayer_Perceptron.ipynb"> Run in Google Colab</a>
</td>
<td>
<img src="https://raw.githubusercontent.com/practicalAI/images/master/images/github_logo.png" width="22"><a target="_blank" href="https://github.com/practicalAI/practicalAI/blob/master/notebooks/basic_ml/06_Multilayer_Perceptron.ipynb"> View code on GitHub</a>
</td>
</table>
# Overview
* **Objective:** Predict the probability of class $y$ given the inputs $X$. Non-linearity is introduced to model the complex, non-linear data.
* **Advantages:**
* Can model non-linear patterns in the data really well.
* **Disadvantages:**
* Overfits easily.
* Computationally intensive as network increases in size.
* Not easily interpretable.
* **Miscellaneous:** Future neural network architectures that we'll see use the MLP as a modular unit for feed forward operations (affine transformation (XW) followed by a non-linear operation).
Our goal is to learn a model 𝑦̂ that models 𝑦 given 𝑋 . You'll notice that neural networks are just extensions of the generalized linear methods we've seen so far but with non-linear activation functions since our data will be highly non-linear.
<img src="https://raw.githubusercontent.com/practicalAI/images/master/basic_ml/06_Multilayer_Perceptron/nn.png" width="550">
$z_1 = XW_1$
$a_1 = f(z_1)$
$z_2 = a_1W_2$
$\hat{y} = softmax(z_2)$ # classification
* $X$ = inputs | $\in \mathbb{R}^{NXD}$ ($D$ is the number of features)
* $W_1$ = 1st layer weights | $\in \mathbb{R}^{DXH}$ ($H$ is the number of hidden units in layer 1)
* $z_1$ = outputs from first layer $\in \mathbb{R}^{NXH}$
* $f$ = non-linear activation function
*nn $a_1$ = activation applied first layer's outputs | $\in \mathbb{R}^{NXH}$
* $W_2$ = 2nd layer weights | $\in \mathbb{R}^{HXC}$ ($C$ is the number of classes)
* $z_2$ = outputs from second layer $\in \mathbb{R}^{NXH}$
* $\hat{y}$ = prediction | $\in \mathbb{R}^{NXC}$ ($N$ is the number of samples)
**Note**: We're going to leave out the bias terms $\beta$ to avoid further crowding the backpropagation calculations.
### Training
1. Randomly initialize the model's weights $W$ (we'll cover more effective initalization strategies later in this lesson).
2. Feed inputs $X$ into the model to do the forward pass and receive the probabilities.
* $z_1 = XW_1$
* $a_1 = f(z_1)$
* $z_2 = a_1W_2$
* $\hat{y} = softmax(z_2)$
3. Compare the predictions $\hat{y}$ (ex. [0.3, 0.3, 0.4]]) with the actual target values $y$ (ex. class 2 would look like [0, 0, 1]) with the objective (cost) function to determine loss $J$. A common objective function for classification tasks is cross-entropy loss.
* $J(\theta) = - \sum_i y_i ln (\hat{y_i}) $
* Since each input maps to exactly one class, our cross-entropy loss simplifies to:
* $J(\theta) = - \sum_i ln(\hat{y_i}) = - \sum_i ln (\frac{e^{X_iW_y}}{\sum_j e^{X_iW}}) $
4. Calculate the gradient of loss $J(\theta)$ w.r.t to the model weights.
* $\frac{\partial{J}}{\partial{W_{2j}}} = \frac{\partial{J}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{W_{2j}}} = - \frac{1}{\hat{y}}\frac{\partial{\hat{y}}}{\partial{W_{2j}}} = - \frac{1}{\frac{e^{W_{2y}a_1}}{\sum_j e^{a_1W}}}\frac{\sum_j e^{a_1W}e^{a_1W_{2y}}0 - e^{a_1W_{2y}}e^{a_1W_{2j}}a_1}{(\sum_j e^{a_1W})^2} = \frac{a_1e^{a_1W_{2j}}}{\sum_j e^{a_1W}} = a_1\hat{y}$
* $\frac{\partial{J}}{\partial{W_{2y}}} = \frac{\partial{J}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{W_{2y}}} = - \frac{1}{\hat{y}}\frac{\partial{\hat{y}}}{\partial{W_{2y}}} = - \frac{1}{\frac{e^{W_{2y}a_1}}{\sum_j e^{a_1W}}}\frac{\sum_j e^{a_1W}e^{a_1W_{2y}}a_1 - e^{a_1W_{2y}}e^{a_1W_{2y}}a_1}{(\sum_j e^{a_1W})^2} = \frac{1}{\hat{y}}(a_1\hat{y} - a_1\hat{y}^2) = a_1(\hat{y}-1)$
* $ \frac{\partial{J}}{\partial{W_1}} = \frac{\partial{J}}{\partial{\hat{y}}} \frac{\partial{\hat{y}}}{\partial{a_2}} \frac{\partial{a_2}}{\partial{z_2}} \frac{\partial{z_2}}{\partial{W_1}} = W_2(\partial{scores})(\partial{ReLU})X $
5. Update the weights $W$ using a small learning rate $\alpha$. The updates will penalize the probabiltiy for the incorrect classes (j) and encourage a higher probability for the correct class (y).
* $W_i = W_i - \alpha\frac{\partial{J}}{\partial{W_i}}$
6. Repeat steps 2 - 4 until model performs well.
# Set up
```
# Use TensorFlow 2.x
%tensorflow_version 2.x
import os
import numpy as np
import tensorflow as tf
# Arguments
SEED = 1234
SHUFFLE = True
DATA_FILE = "spiral.csv"
INPUT_DIM = 2
NUM_CLASSES = 3
NUM_SAMPLES_PER_CLASS = 500
TRAIN_SIZE = 0.7
VAL_SIZE = 0.15
TEST_SIZE = 0.15
NUM_EPOCHS = 10
BATCH_SIZE = 32
HIDDEN_DIM = 100
LEARNING_RATE = 1e-2
# Set seed for reproducability
np.random.seed(SEED)
tf.random.set_seed(SEED)
```
# Data
Download non-linear spiral data for a classification task.
```
import matplotlib.pyplot as plt
import pandas as pd
import urllib
# Upload data from GitHub to notebook's local drive
url = "https://raw.githubusercontent.com/practicalAI/practicalAI/master/data/spiral.csv"
response = urllib.request.urlopen(url)
html = response.read()
with open(DATA_FILE, 'wb') as fp:
fp.write(html)
# Load data
df = pd.read_csv(DATA_FILE, header=0)
X = df[['X1', 'X2']].values
y = df['color'].values
df.head(5)
print ("X: ", np.shape(X))
print ("y: ", np.shape(y))
# Visualize data
plt.title("Generated non-linear data")
colors = {'c1': 'red', 'c2': 'yellow', 'c3': 'blue'}
plt.scatter(X[:, 0], X[:, 1], c=[colors[_y] for _y in y], edgecolors='k', s=25)
plt.show()
```
# Split data
```
import collections
import json
from sklearn.model_selection import train_test_split
```
### Components
```
def train_val_test_split(X, y, val_size, test_size, shuffle):
"""Split data into train/val/test datasets.
"""
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=test_size, stratify=y, shuffle=shuffle)
X_train, X_val, y_train, y_val = train_test_split(
X_train, y_train, test_size=val_size, stratify=y_train, shuffle=shuffle)
return X_train, X_val, X_test, y_train, y_val, y_test
```
### Operations
```
# Create data splits
X_train, X_val, X_test, y_train, y_val, y_test = train_val_test_split(
X=X, y=y, val_size=VAL_SIZE, test_size=TEST_SIZE, shuffle=SHUFFLE)
class_counts = dict(collections.Counter(y))
print (f"X_train: {X_train.shape}, y_train: {y_train.shape}")
print (f"X_val: {X_val.shape}, y_val: {y_val.shape}")
print (f"X_test: {X_test.shape}, y_test: {y_test.shape}")
print (f"X_train[0]: {X_train[0]}")
print (f"y_train[0]: {y_train[0]}")
print (f"Classes: {class_counts}")
```
# Label encoder
```
import json
from sklearn.preprocessing import LabelEncoder
# Output vectorizer
y_tokenizer = LabelEncoder()
# Fit on train data
y_tokenizer = y_tokenizer.fit(y_train)
classes = list(y_tokenizer.classes_)
print (f"classes: {classes}")
# Convert labels to tokens
print (f"y_train[0]: {y_train[0]}")
y_train = y_tokenizer.transform(y_train)
y_val = y_tokenizer.transform(y_val)
y_test = y_tokenizer.transform(y_test)
print (f"y_train[0]: {y_train[0]}")
# Class weights
counts = collections.Counter(y_train)
class_weights = {_class: 1.0/count for _class, count in counts.items()}
print (f"class counts: {counts},\nclass weights: {class_weights}")
```
# Standardize data
We need to standardize our data (zero mean and unit variance) in order to optimize quickly. We're only going to standardize the inputs X because out outputs y are class values.
```
from sklearn.preprocessing import StandardScaler
# Standardize the data (mean=0, std=1) using training data
X_scaler = StandardScaler().fit(X_train)
# Apply scaler on training and test data (don't standardize outputs for classification)
standardized_X_train = X_scaler.transform(X_train)
standardized_X_val = X_scaler.transform(X_val)
standardized_X_test = X_scaler.transform(X_test)
# Check
print (f"standardized_X_train: mean: {np.mean(standardized_X_train, axis=0)[0]}, std: {np.std(standardized_X_train, axis=0)[0]}")
print (f"standardized_X_val: mean: {np.mean(standardized_X_val, axis=0)[0]}, std: {np.std(standardized_X_val, axis=0)[0]}")
print (f"standardized_X_test: mean: {np.mean(standardized_X_test, axis=0)[0]}, std: {np.std(standardized_X_test, axis=0)[0]}")
```
# Linear model
Before we get to our neural network, we're going to implement a generalized linear model (logistic regression) first to see why linear models won't suffice for our dataset. We will use Tensorflow with Keras to do this.
```
import itertools
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Input
from tensorflow.keras.losses import SparseCategoricalCrossentropy
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam
```
### Components
```
# Linear model
class LogisticClassifier(Model):
def __init__(self, hidden_dim, num_classes):
super(LogisticClassifier, self).__init__()
self.fc1 = Dense(units=hidden_dim, activation='linear') # linear = no activation function
self.fc2 = Dense(units=num_classes, activation='softmax')
def call(self, x_in, training=False):
"""Forward pass."""
z = self.fc1(x_in)
y_pred = self.fc2(z)
return y_pred
def sample(self, input_shape):
x_in = Input(shape=input_shape)
return Model(inputs=x_in, outputs=self.call(x_in)).summary()
def plot_confusion_matrix(y_true, y_pred, classes, cmap=plt.cm.Blues):
"""Plot a confusion matrix using ground truth and predictions."""
# Confusion matrix
cm = confusion_matrix(y_true, y_pred)
cm_norm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
# Figure
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(cm, cmap=plt.cm.Blues)
fig.colorbar(cax)
# Axis
plt.title("Confusion matrix")
plt.ylabel("True label")
plt.xlabel("Predicted label")
ax.set_xticklabels([''] + classes)
ax.set_yticklabels([''] + classes)
ax.xaxis.set_label_position('bottom')
ax.xaxis.tick_bottom()
# Values
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, f"{cm[i, j]:d} ({cm_norm[i, j]*100:.1f}%)",
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
# Display
plt.show()
def plot_multiclass_decision_boundary(model, X, y, savefig_fp=None):
"""Plot the multiclass decision boundary for a model that accepts 2D inputs.
Arguments:
model {function} -- trained model with function model.predict(x_in).
X {numpy.ndarray} -- 2D inputs with shape (N, 2).
y {numpy.ndarray} -- 1D outputs with shape (N,).
"""
# Axis boundaries
x_min, x_max = X[:, 0].min() - 0.1, X[:, 0].max() + 0.1
y_min, y_max = X[:, 1].min() - 0.1, X[:, 1].max() + 0.1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 101),
np.linspace(y_min, y_max, 101))
# Create predictions
x_in = np.c_[xx.ravel(), yy.ravel()]
y_pred = model.predict(x_in)
y_pred = np.argmax(y_pred, axis=1).reshape(xx.shape)
# Plot decision boundary
plt.contourf(xx, yy, y_pred, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.RdYlBu)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
# Plot
if savefig_fp:
plt.savefig(savefig_fp, format='png')
```
### Operations
```
# Initialize the model
model = LogisticClassifier(hidden_dim=HIDDEN_DIM,
num_classes=NUM_CLASSES)
model.sample(input_shape=(INPUT_DIM,))
# Compile
model.compile(optimizer=Adam(lr=LEARNING_RATE),
loss=SparseCategoricalCrossentropy(),
metrics=['accuracy'])
# Training
model.fit(x=standardized_X_train,
y=y_train,
validation_data=(standardized_X_val, y_val),
epochs=NUM_EPOCHS,
batch_size=BATCH_SIZE,
class_weight=class_weights,
shuffle=False,
verbose=1)
# Predictions
pred_train = model.predict(standardized_X_train)
pred_test = model.predict(standardized_X_test)
print (f"sample probability: {pred_test[0]}")
pred_train = np.argmax(pred_train, axis=1)
pred_test = np.argmax(pred_test, axis=1)
print (f"sample class: {pred_test[0]}")
# Accuracy
train_acc = accuracy_score(y_train, pred_train)
test_acc = accuracy_score(y_test, pred_test)
print (f"train acc: {train_acc:.2f}, test acc: {test_acc:.2f}")
# Metrics
plot_confusion_matrix(y_test, pred_test, classes=classes)
print (classification_report(y_test, pred_test))
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=standardized_X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=standardized_X_test, y=y_test)
plt.show()
```
# Activation functions
Using the generalized linear method (logistic regression) yielded poor results because of the non-linearity present in our data. We need to use an activation function that can allow our model to learn and map the non-linearity in our data. There are many different options so let's explore a few.
```
from tensorflow.keras.activations import relu
from tensorflow.keras.activations import sigmoid
from tensorflow.keras.activations import tanh
# Fig size
plt.figure(figsize=(12,3))
# Data
x = np.arange(-5., 5., 0.1)
# Sigmoid activation (constrain a value between 0 and 1.)
plt.subplot(1, 3, 1)
plt.title("Sigmoid activation")
y = sigmoid(x)
plt.plot(x, y)
# Tanh activation (constrain a value between -1 and 1.)
plt.subplot(1, 3, 2)
y = tanh(x)
plt.title("Tanh activation")
plt.plot(x, y)
# Relu (clip the negative values to 0)
plt.subplot(1, 3, 3)
y = relu(x)
plt.title("ReLU activation")
plt.plot(x, y)
# Show plots
plt.show()
```
The ReLU activation function ($max(0,z)$) is by far the most widely used activation function for neural networks. But as you can see, each activation function has it's own contraints so there are circumstances where you'll want to use different ones. For example, if we need to constrain our outputs between 0 and 1, then the sigmoid activation is the best choice.
<img height="45" src="http://bestanimations.com/HomeOffice/Lights/Bulbs/animated-light-bulb-gif-29.gif" align="left" vspace="20px" hspace="10px">
In some cases, using a ReLU activation function may not be sufficient. For instance, when the outputs from our neurons are mostly negative, the activation function will produce zeros. This effectively creates a "dying ReLU" and a recovery is unlikely. To mitigate this effect, we could lower the learning rate or use [alternative ReLU activations](https://medium.com/tinymind/a-practical-guide-to-relu-b83ca804f1f7), ex. leaky ReLU or parametric ReLU (PReLU), which have a small slope for negative neuron outputs.
# From scratch
Now let's create our multilayer perceptron (MLP) which is going to be exactly like the logistic regression model but with the activation function to map the non-linearity in our data. Before we use TensorFlow 2.0 + Keras we will implement our neural network from scratch using NumPy so we can:
1. Absorb the fundamental concepts by implementing from scratch
2. Appreciate the level of abstraction TensorFlow provides
<div align="left">
<img src="https://raw.githubusercontent.com/practicalAI/images/master/images/lightbulb.gif" width="45px" align="left" hspace="10px">
</div>
It's normal to find the math and code in this section slightly complex. You can still read each of the steps to build intuition for when we implement this using TensorFlow + Keras.
```
print (f"X: {standardized_X_train.shape}")
print (f"y: {y_train.shape}")
```
Our goal is to learn a model 𝑦̂ that models 𝑦 given 𝑋 . You'll notice that neural networks are just extensions of the generalized linear methods we've seen so far but with non-linear activation functions since our data will be highly non-linear.
$z_1 = XW_1$
$a_1 = f(z_1)$
$z_2 = a_1W_2$
$\hat{y} = softmax(z_2)$ # classification
* $X$ = inputs | $\in \mathbb{R}^{NXD}$ ($D$ is the number of features)
* $W_1$ = 1st layer weights | $\in \mathbb{R}^{DXH}$ ($H$ is the number of hidden units in layer 1)
* $z_1$ = outputs from first layer $\in \mathbb{R}^{NXH}$
* $f$ = non-linear activation function
* $a_1$ = activation applied first layer's outputs | $\in \mathbb{R}^{NXH}$
* $W_2$ = 2nd layer weights | $\in \mathbb{R}^{HXC}$ ($C$ is the number of classes)
* $z_2$ = outputs from second layer $\in \mathbb{R}^{NXH}$
* $\hat{y}$ = prediction | $\in \mathbb{R}^{NXC}$ ($N$ is the number of samples)
1. Randomly initialize the model's weights $W$ (we'll cover more effective initalization strategies later in this lesson).
```
# Initialize first layer's weights
W1 = 0.01 * np.random.randn(INPUT_DIM, HIDDEN_DIM)
b1 = np.zeros((1, HIDDEN_DIM))
print (f"W1: {W1.shape}")
print (f"b1: {b1.shape}")
```
2. Feed inputs $X$ into the model to do the forward pass and receive the probabilities.
First we pass the inputs into the first layer.
* $z_1 = XW_1$
```
# z1 = [NX2] · [2X100] + [1X100] = [NX100]
z1 = np.dot(standardized_X_train, W1) + b1
print (f"z1: {z1.shape}")
```
Next we apply the non-linear activation function, ReLU ($max(0,z)$) in this case.
* $a_1 = f(z_1)$
```
# Apply activation function
a1 = np.maximum(0, z1) # ReLU
print (f"a_1: {a1.shape}")
```
We pass the activations to the second layer to get our logits.
* $z_2 = a_1W_2$
```
# Initialize second layer's weights
W2 = 0.01 * np.random.randn(HIDDEN_DIM, NUM_CLASSES)
b2 = np.zeros((1, NUM_CLASSES))
print (f"W2: {W2.shape}")
print (f"b2: {b2.shape}")
# z2 = logits = [NX100] · [100X3] + [1X3] = [NX3]
logits = np.dot(a1, W2) + b2
print (f"logits: {logits.shape}")
print (f"sample: {logits[0]}")
```
We'll apply the softmax function to normalize the logits and btain class probabilities.
* $\hat{y} = softmax(z_2)$
```
# Normalization via softmax to obtain class probabilities
exp_logits = np.exp(logits)
y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
print (f"y_hat: {y_hat.shape}")
print (f"sample: {y_hat[0]}")
```
3. Compare the predictions $\hat{y}$ (ex. [0.3, 0.3, 0.4]]) with the actual target values $y$ (ex. class 2 would look like [0, 0, 1]) with the objective (cost) function to determine loss $J$. A common objective function for classification tasks is cross-entropy loss.
* $J(\theta) = - \sum_i ln(\hat{y_i}) = - \sum_i ln (\frac{e^{X_iW_y}}{\sum_j e^{X_iW}}) $
```
# Loss
correct_class_logprobs = -np.log(y_hat[range(len(y_hat)), y_train])
loss = np.sum(correct_class_logprobs) / len(y_train)
```
4. Calculate the gradient of loss $J(\theta)$ w.r.t to the model weights.
The gradient of the loss w.r.t to W2 is the same as the gradients from logistic regression since $\hat{y} = softmax(z_2)$.
* $\frac{\partial{J}}{\partial{W_{2j}}} = \frac{\partial{J}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{W_{2j}}} = - \frac{1}{\hat{y}}\frac{\partial{\hat{y}}}{\partial{W_{2j}}} = - \frac{1}{\frac{e^{W_{2y}a_1}}{\sum_j e^{a_1W}}}\frac{\sum_j e^{a_1W}e^{a_1W_{2y}}0 - e^{a_1W_{2y}}e^{a_1W_{2j}}a_1}{(\sum_j e^{a_1W})^2} = \frac{a_1e^{a_1W_{2j}}}{\sum_j e^{a_1W}} = a_1\hat{y}$
* $\frac{\partial{J}}{\partial{W_{2y}}} = \frac{\partial{J}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{W_{2y}}} = - \frac{1}{\hat{y}}\frac{\partial{\hat{y}}}{\partial{W_{2y}}} = - \frac{1}{\frac{e^{W_{2y}a_1}}{\sum_j e^{a_1W}}}\frac{\sum_j e^{a_1W}e^{a_1W_{2y}}a_1 - e^{a_1W_{2y}}e^{a_1W_{2y}}a_1}{(\sum_j e^{a_1W})^2} = \frac{1}{\hat{y}}(a_1\hat{y} - a_1\hat{y}^2) = a_1(\hat{y}-1)$
The gradient of the loss w.r.t W1 is a bit trickier since we have to backpropagate through two sets of weights.
* $ \frac{\partial{J}}{\partial{W_1}} = \frac{\partial{J}}{\partial{\hat{y}}} \frac{\partial{\hat{y}}}{\partial{a_1}} \frac{\partial{a_1}}{\partial{z_1}} \frac{\partial{z_1}}{\partial{W_1}} = W_2(\partial{scores})(\partial{ReLU})X $
```
# dJ/dW2
dscores = y_hat
dscores[range(len(y_hat)), y_train] -= 1
dscores /= len(y_train)
dW2 = np.dot(a1.T, dscores)
db2 = np.sum(dscores, axis=0, keepdims=True)
# dJ/dW1
dhidden = np.dot(dscores, W2.T)
dhidden[a1 <= 0] = 0 # ReLu backprop
dW1 = np.dot(standardized_X_train.T, dhidden)
db1 = np.sum(dhidden, axis=0, keepdims=True)
```
5. Update the weights $W$ using a small learning rate $\alpha$. The updates will penalize the probabiltiy for the incorrect classes (j) and encourage a higher probability for the correct class (y).
* $W_i = W_i - \alpha\frac{\partial{J}}{\partial{W_i}}$
```
# Update weights
W1 += -LEARNING_RATE * dW1
b1 += -LEARNING_RATE * db1
W2 += -LEARNING_RATE * dW2
b2 += -LEARNING_RATE * db2
```
6. Repeat steps 2 - 4 until model performs well.
```
# Initialize random weights
W1 = 0.01 * np.random.randn(INPUT_DIM, HIDDEN_DIM)
b1 = np.zeros((1, HIDDEN_DIM))
W2 = 0.01 * np.random.randn(HIDDEN_DIM, NUM_CLASSES)
b2 = np.zeros((1, NUM_CLASSES))
# Training loop
for epoch_num in range(1000):
# First layer forward pass [NX2] · [2X100] = [NX100]
z1 = np.dot(standardized_X_train, W1) + b1
# Apply activation function
a1 = np.maximum(0, z1) # ReLU
# z2 = logits = [NX100] · [100X3] = [NX3]
logits = np.dot(a1, W2) + b2
# Normalization via softmax to obtain class probabilities
exp_logits = np.exp(logits)
y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
# Loss
correct_class_logprobs = -np.log(y_hat[range(len(y_hat)), y_train])
loss = np.sum(correct_class_logprobs) / len(y_train)
# show progress
if epoch_num%100 == 0:
# Accuracy
y_pred = np.argmax(logits, axis=1)
accuracy = np.mean(np.equal(y_train, y_pred))
print (f"Epoch: {epoch_num}, loss: {loss:.3f}, accuracy: {accuracy:.3f}")
# dJ/dW2
dscores = y_hat
dscores[range(len(y_hat)), y_train] -= 1
dscores /= len(y_train)
dW2 = np.dot(a1.T, dscores)
db2 = np.sum(dscores, axis=0, keepdims=True)
# dJ/dW1
dhidden = np.dot(dscores, W2.T)
dhidden[a1 <= 0] = 0 # ReLu backprop
dW1 = np.dot(standardized_X_train.T, dhidden)
db1 = np.sum(dhidden, axis=0, keepdims=True)
# Update weights
W1 += -1e0 * dW1
b1 += -1e0 * db1
W2 += -1e0 * dW2
b2 += -1e0 * db2
class MLPFromScratch():
def predict(self, x):
z1 = np.dot(x, W1) + b1
a1 = np.maximum(0, z1)
logits = np.dot(a1, W2) + b2
exp_logits = np.exp(logits)
y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
return y_hat
# Evaluation
model = MLPFromScratch()
logits_train = model.predict(standardized_X_train)
pred_train = np.argmax(logits_train, axis=1)
logits_test = model.predict(standardized_X_test)
pred_test = np.argmax(logits_test, axis=1)
# Training and test accuracy
train_acc = np.mean(np.equal(y_train, pred_train))
test_acc = np.mean(np.equal(y_test, pred_test))
print (f"train acc: {train_acc:.2f}, test acc: {test_acc:.2f}")
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=standardized_X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=standardized_X_test, y=y_test)
plt.show()
```
Credit for the plotting functions and the intuition behind all this is due to [CS231n](http://cs231n.github.io/neural-networks-case-study/), one of the best courses for machine learning. Now let's implement the MLP with TensorFlow + Keras.
# TensorFlow + Keras
### Components
```
# MLP
class MLP(Model):
def __init__(self, hidden_dim, num_classes):
super(MLP, self).__init__()
self.fc1 = Dense(units=hidden_dim, activation='relu') # replaced linear with relu
self.fc2 = Dense(units=num_classes, activation='softmax')
def call(self, x_in, training=False):
"""Forward pass."""
z = self.fc1(x_in)
y_pred = self.fc2(z)
return y_pred
def sample(self, input_shape):
x_in = Input(shape=input_shape)
return Model(inputs=x_in, outputs=self.call(x_in)).summary()
```
### Operations
```
# Initialize the model
model = MLP(hidden_dim=HIDDEN_DIM,
num_classes=NUM_CLASSES)
model.sample(input_shape=(INPUT_DIM,))
# Compile
optimizer = Adam(lr=LEARNING_RATE)
model.compile(optimizer=optimizer,
loss=SparseCategoricalCrossentropy(),
metrics=['accuracy'])
# Training
model.fit(x=standardized_X_train,
y=y_train,
validation_data=(standardized_X_val, y_val),
epochs=NUM_EPOCHS,
batch_size=BATCH_SIZE,
class_weight=class_weights,
shuffle=False,
verbose=1)
# Predictions
pred_train = model.predict(standardized_X_train)
pred_test = model.predict(standardized_X_test)
print (f"sample probability: {pred_test[0]}")
pred_train = np.argmax(pred_train, axis=1)
pred_test = np.argmax(pred_test, axis=1)
print (f"sample class: {pred_test[0]}")
# Accuracy
train_acc = accuracy_score(y_train, pred_train)
test_acc = accuracy_score(y_test, pred_test)
print (f"train acc: {train_acc:.2f}, test acc: {test_acc:.2f}")
# Metrics
plot_confusion_matrix(y_test, pred_test, classes=classes)
print (classification_report(y_test, pred_test))
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=standardized_X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=standardized_X_test, y=y_test)
plt.show()
```
# Inference
```
# Inputs for inference
X_infer = pd.DataFrame([{'X1': 0.1, 'X2': 0.1}])
X_infer.head()
# Standardize
standardized_X_infer = X_scaler.transform(X_infer)
print (standardized_X_infer)
# Predict
y_infer = model.predict(standardized_X_infer)
_class = np.argmax(y_infer)
print (f"The probability that you have a class {classes[_class]} is {y_infer[0][_class]*100.0:.0f}%")
```
# Initializing weights
So far we have been initializing weights with small random values and this isn't optimal for convergence during training. The objective is to have weights that are able to produce outputs that follow a similar distribution across all neurons. We can do this by enforcing weights to have unit variance prior the affine and non-linear operations.
<img height="45" src="http://bestanimations.com/HomeOffice/Lights/Bulbs/animated-light-bulb-gif-29.gif" align="left" vspace="20px" hspace="10px">
A popular method is to apply [xavier initialization](http://andyljones.tumblr.com/post/110998971763/an-explanation-of-xavier-initialization), which essentially initializes the weights to allow the signal from the data to reach deep into the network. You may be wondering why we don't do this for every forward pass and that's a great question. We'll look at more advanced strategies that help with optimization like batch/layer normalization, etc. in future lessons. Meanwhile you can check out other initializers [here](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/initializers).
```
from tensorflow.keras.initializers import glorot_normal
# MLP
class MLP(Model):
def __init__(self, hidden_dim, num_classes):
super(MLP, self).__init__()
xavier_initializer = glorot_normal() # xavier glorot initiailization
self.fc1 = Dense(units=hidden_dim,
kernel_initializer=xavier_initializer,
activation='relu')
self.fc2 = Dense(units=num_classes,
activation='softmax')
def call(self, x_in, training=False):
"""Forward pass."""
z = self.fc1(x_in)
y_pred = self.fc2(z)
return y_pred
def sample(self, input_shape):
x_in = Input(shape=input_shape)
return Model(inputs=x_in, outputs=self.call(x_in)).summary()
```
# Dropout
A great technique to overcome overfitting is to increase the size of your data but this isn't always an option. Fortuntely, there are methods like regularization and dropout that can help create a more robust model.
Dropout is a technique (used only during training) that allows us to zero the outputs of neurons. We do this for `dropout_p`% of the total neurons in each layer and it changes every batch. Dropout prevents units from co-adapting too much to the data and acts as a sampling strategy since we drop a different set of neurons each time.
<img src="https://raw.githubusercontent.com/practicalAI/images/master/basic_ml/06_Multilayer_Perceptron/dropout.png" width="350">
* [Dropout: A Simple Way to Prevent Neural Networks from
Overfitting](http://jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf)
```
from tensorflow.keras.layers import Dropout
from tensorflow.keras.regularizers import l2
```
### Components
```
# MLP
class MLP(Model):
def __init__(self, hidden_dim, lambda_l2, dropout_p, num_classes):
super(MLP, self).__init__()
self.fc1 = Dense(units=hidden_dim,
kernel_regularizer=l2(lambda_l2), # adding L2 regularization
activation='relu')
self.dropout = Dropout(rate=dropout_p)
self.fc2 = Dense(units=num_classes,
activation='softmax')
def call(self, x_in, training=False):
"""Forward pass."""
z = self.fc1(x_in)
if training:
z = self.dropout(z, training=training) # adding dropout
y_pred = self.fc2(z)
return y_pred
def sample(self, input_shape):
x_in = Input(shape=input_shape)
return Model(inputs=x_in, outputs=self.call(x_in)).summary()
```
### Operations
```
# Arguments
DROPOUT_P = 0.1 # % of the neurons that are dropped each pass
LAMBDA_L2 = 1e-4 # L2 regularization
# Initialize the model
model = MLP(hidden_dim=HIDDEN_DIM,
lambda_l2=LAMBDA_L2,
dropout_p=DROPOUT_P,
num_classes=NUM_CLASSES)
model.sample(input_shape=(INPUT_DIM,))
```
# Overfitting
Though neural networks are great at capturing non-linear relationships they are highly susceptible to overfitting to the training data and failing to generalize on test data. Just take a look at the example below where we generate completely random data and are able to fit a model with [$2*N*C + D$](https://arxiv.org/abs/1611.03530) hidden units. The training performance is good (~70%) but the overfitting leads to very poor test performance. We'll be covering strategies to tackle overfitting in future lessons.
```
# Arguments
NUM_EPOCHS = 500
NUM_SAMPLES_PER_CLASS = 50
LEARNING_RATE = 1e-1
HIDDEN_DIM = 2 * NUM_SAMPLES_PER_CLASS * NUM_CLASSES + INPUT_DIM # 2*N*C + D
# Generate random data
X = np.random.rand(NUM_SAMPLES_PER_CLASS * NUM_CLASSES, INPUT_DIM)
y = np.array([[i]*NUM_SAMPLES_PER_CLASS for i in range(NUM_CLASSES)]).reshape(-1)
print ("X: ", format(np.shape(X)))
print ("y: ", format(np.shape(y)))
# Create data splits
X_train, X_val, X_test, y_train, y_val, y_test = train_val_test_split(
X, y, val_size=VAL_SIZE, test_size=TEST_SIZE, shuffle=SHUFFLE)
print ("X_train:", X_train.shape)
print ("y_train:", y_train.shape)
print ("X_val:", X_val.shape)
print ("y_val:", y_val.shape)
print ("X_test:", X_test.shape)
print ("y_test:", y_test.shape)
# Standardize the inputs (mean=0, std=1) using training data
X_scaler = StandardScaler().fit(X_train)
# Apply scaler on training and test data (don't standardize outputs for classification)
standardized_X_train = X_scaler.transform(X_train)
standardized_X_val = X_scaler.transform(X_val)
standardized_X_test = X_scaler.transform(X_test)
# Initialize the model
model = MLP(hidden_dim=HIDDEN_DIM,
lambda_l2=0.0,
dropout_p=0.0,
num_classes=NUM_CLASSES)
model.sample(input_shape=(INPUT_DIM,))
# Compile
optimizer = Adam(lr=LEARNING_RATE)
model.compile(optimizer=optimizer,
loss=SparseCategoricalCrossentropy(),
metrics=['accuracy'])
# Training
model.fit(x=standardized_X_train,
y=y_train,
validation_data=(standardized_X_val, y_val),
epochs=NUM_EPOCHS,
batch_size=BATCH_SIZE,
class_weight=class_weights,
shuffle=False,
verbose=1)
# Predictions
pred_train = model.predict(standardized_X_train)
pred_test = model.predict(standardized_X_test)
print (f"sample probability: {pred_test[0]}")
pred_train = np.argmax(pred_train, axis=1)
pred_test = np.argmax(pred_test, axis=1)
print (f"sample class: {pred_test[0]}")
# Accuracy
train_acc = accuracy_score(y_train, pred_train)
test_acc = accuracy_score(y_test, pred_test)
print (f"train acc: {train_acc:.2f}, test acc: {test_acc:.2f}")
# Classification report
plot_confusion_matrix(y_true=y_test, y_pred=pred_test, classes=classes)
print (classification_report(y_test, pred_test))
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=standardized_X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=standardized_X_test, y=y_test)
plt.show()
```
It's important that we experiment, starting with simple models that underfit (high bias) and improve it towards a good fit. Starting with simple models (linear/logistic regression) let's us catch errors without the added complexity of more sophisticated models (neural networks).
<img src="https://raw.githubusercontent.com/practicalAI/images/master/basic_ml/06_Multilayer_Perceptron/fit.png" width="700">
---
<div align="center">
Subscribe to our <a href="https://practicalai.me/#newsletter">newsletter</a> and follow us on social media to get the latest updates!
<a class="ai-header-badge" target="_blank" href="https://github.com/practicalAI/practicalAI">
<img src="https://img.shields.io/github/stars/practicalAI/practicalAI.svg?style=social&label=Star"></a>
<a class="ai-header-badge" target="_blank" href="https://www.linkedin.com/company/practicalai-me">
<img src="https://img.shields.io/badge/style--5eba00.svg?label=LinkedIn&logo=linkedin&style=social"></a>
<a class="ai-header-badge" target="_blank" href="https://twitter.com/practicalAIme">
<img src="https://img.shields.io/twitter/follow/practicalAIme.svg?label=Follow&style=social">
</a>
</div>
</div>
| true |
code
| 0.746183 | null | null | null | null |
|
_Lambda School Data Science — Tree Ensembles_
# Decision Trees — with ipywidgets!
### Notebook requirements
- [ipywidgets](https://ipywidgets.readthedocs.io/en/stable/examples/Using%20Interact.html): works in Jupyter but [doesn't work on Google Colab](https://github.com/googlecolab/colabtools/issues/60#issuecomment-462529981)
- [mlxtend.plotting.plot_decision_regions](http://rasbt.github.io/mlxtend/user_guide/plotting/plot_decision_regions/): `pip install mlxtend`
## Regressing a wave
```
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
# Example from http://scikit-learn.org/stable/auto_examples/tree/plot_tree_regression.html
def make_data():
import numpy as np
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 2 * (0.5 - rng.rand(16))
return X, y
X, y = make_data()
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.25, random_state=42)
plt.scatter(X_train, y_train)
plt.scatter(X_test, y_test);
from sklearn.tree import DecisionTreeRegressor
def regress_wave(max_depth):
tree = DecisionTreeRegressor(max_depth=max_depth)
tree.fit(X_train, y_train)
print('Train R^2 score:', tree.score(X_train, y_train))
print('Test R^2 score:', tree.score(X_test, y_test))
plt.scatter(X_train, y_train)
plt.scatter(X_test, y_test)
plt.step(X, tree.predict(X))
plt.show()
from ipywidgets import interact
interact(regress_wave, max_depth=(1,8,1));
```
## Classifying a curve
```
import numpy as np
curve_X = np.random.rand(1000, 2)
curve_y = np.square(curve_X[:,0]) + np.square(curve_X[:,1]) < 1.0
curve_y = curve_y.astype(int)
from sklearn.linear_model import LogisticRegression
from mlxtend.plotting import plot_decision_regions
lr = LogisticRegression(solver='lbfgs')
lr.fit(curve_X, curve_y)
plot_decision_regions(curve_X, curve_y, lr, legend=False)
plt.axis((0,1,0,1));
from sklearn.tree import DecisionTreeClassifier
def classify_curve(max_depth):
tree = DecisionTreeClassifier(max_depth=max_depth)
tree.fit(curve_X, curve_y)
plot_decision_regions(curve_X, curve_y, tree, legend=False)
plt.axis((0,1,0,1))
plt.show()
interact(classify_curve, max_depth=(1,8,1));
```
## Titanic survival, by age & fare
```
import seaborn as sns
from sklearn.impute import SimpleImputer
titanic = sns.load_dataset('titanic')
imputer = SimpleImputer()
titanic_X = imputer.fit_transform(titanic[['age', 'fare']])
titanic_y = titanic['survived'].values
from sklearn.linear_model import LogisticRegression
from mlxtend.plotting import plot_decision_regions
lr = LogisticRegression(solver='lbfgs')
lr.fit(titanic_X, titanic_y)
plot_decision_regions(titanic_X, titanic_y, lr, legend=False);
plt.axis((0,75,0,175));
def classify_titanic(max_depth):
tree = DecisionTreeClassifier(max_depth=max_depth)
tree.fit(titanic_X, titanic_y)
plot_decision_regions(titanic_X, titanic_y, tree, legend=False)
plt.axis((0,75,0,175))
plt.show()
interact(classify_titanic, max_depth=(1,8,1));
```
| true |
code
| 0.751209 | null | null | null | null |
|
# Objects
*Python* is an object oriented language. As such it allows the definition of classes.
For instance lists are also classes, that's why there are methods associated with them (i.e. `append()`). Here we will see how to create classes and assign them attributes and methods.
## Definition and initialization
A class gathers functions (called methods) and variables (called attributes).
The main of goal of having this kind of structure is that the methods can share a common
set of inputs to operate and get the desired outcome by the programmer.
In *Python* classes are defined with the word `class` and are always initialized
with the method ``__init__``, which is a function that *always* must have as input argument the
word `self`. The arguments that come after `self` are used to initialize the class attributes.
In the following example we create a class called ``Circle``.
```
class Circle:
def __init__(self, radius):
self.radius = radius #all attributes must be preceded by "self."
```
To create an instance of this class we do it as follows
```
A = Circle(5.0)
```
We can check that the initialization worked out fine by printing its attributes
```
print(A.radius)
```
We now redefine the class to add new method called `area` that computes the area of the circle
```
class Circle:
def __init__(self, radius):
self.radius = radius #all attributes must be preceded by "self."
def area(self):
import math
return math.pi * self.radius * self.radius
A = Circle(1.0)
print(A.radius)
print(A.area())
```
### Exercise 3.1
Redefine the class `Circle` to include a new method called `perimeter` that returns the value of the circle's perimeter.
We now want to define a method that returns a new Circle with twice the radius of the input Circle.
```
class Circle:
def __init__(self, radius):
self.radius = radius #all attributes must be preceded by "self."
def area(self):
import math
return math.pi * self.radius * self.radius
def enlarge(self):
return Circle(2.0*self.radius)
A = Circle(5.0) # Create a first circle
B = A.enlarge() # Use the method to create a new Circle
print(B.radius) # Check that the radius is twice as the original one.
```
We now add a new method that takes as an input another element of the class `Circle`
and returns the total area of the two circles
```
class Circle:
def __init__(self, radius):
self.radius = radius #all attributes must be preceded by "self."
def area(self):
import math
return math.pi * self.radius * self.radius
def enlarge(self):
return Circle(2.0*self.radius)
def add_area(self, c):
return self.area() + c.area()
A = Circle(1.0)
B = Circle(2.0)
print(A.add_area(B))
print(B.add_area(A))
```
### Exercise 3.2
Define the class `Vector3D` to represent vectors in 3D.
The class must have
* Three attributes: `x`, `y`, and `z`, to store the coordinates.
* A method called `dot` that computes the dot product
$$\vec{v} \cdot \vec{w} = v_{x}w_{x} + v_{y}w_{y} + v_{z}w_{z}$$
The method could then be used as follows
```python
v = Vector3D(2, 0, 1)
w = Vector3D(1, -1, 3)
```
```python
v.dot(w)
5
```
| true |
code
| 0.70854 | null | null | null | null |
|
# Advanced Data Wrangling with Pandas
```
import pandas as pd
import numpy as np
```
## Formas não usuais de se ler um dataset
Você não precisa que o arquivo com os seus dados esteja no seu disco local, o pandas está preparado para adquirir arquivos via http, s3, gs...
```
diamonds = pd.read_csv("https://raw.githubusercontent.com/mwaskom/seaborn-data/master/diamonds.csv")
diamonds.head()
```
Você também pode crawlear uma tabela de uma página da internet de forma simples
```
clarity = pd.read_html("https://www.brilliantearth.com/diamond-clarity/")
clarity
clarity = clarity[0]
clarity
clarity.columns = ['clarity', 'clarity_description']
clarity
```
## Como explodir a coluna de um dataframe
```
clarity['clarity'] = clarity['clarity'].str.split()
clarity
type(clarity.loc[0, 'clarity'])
clarity = clarity.explode("clarity")
clarity
```
## Como validar o merge
Esse parametro serve para validar a relação entre as duas tabelas que você está juntando. Por exemplo, se a relação é 1 para 1, 1 para muitos, muitos para 1 ou muitos para muitos.
```
diamonds.merge(clarity, on='clarity', validate="m:1")
clarity_with_problem = clarity.append(pd.Series({"clarity": "SI2", "clarity_description": "slightly included"}), ignore_index=True)
clarity_with_problem
diamonds.merge(clarity_with_problem, on='clarity', validate="m:1")
diamonds.merge(clarity_with_problem, on='clarity')
```
### Por que isso é importante?
O que aconteceria seu tivesse keys duplicadas no meu depara. Ele duplicou as minhas linhas que tinham a key duplicada, o dataset foi de 53,940 linhas para 63,134 linhas
## Como usar o método `.assign`
Para adicionar ou modificar colunas do dataframe. Você pode passar como argumento uma constante para a coluna ou um função que tenha como input um `pd.DataFrame` e output uma `pd.Series`.
```
diamonds.assign(foo="bar", bar="foo")
diamonds.assign(volume=lambda df: df['x'] * df['y'] * df['z'])
def calculate_volume(df):
return df['x'] * df['y'] * df['z']
diamonds.assign(volume=calculate_volume)
diamonds['volume'] = diamonds['x'] * diamonds['y'] * diamonds['z']
diamonds
```
## Como usar o método `.query`
Para filtrar. Tende a ser util quando você quer filtrar o dataframe baseado em algum estado intermediário
```
diamonds = pd.read_csv("https://raw.githubusercontent.com/mwaskom/seaborn-data/master/diamonds.csv")
diamonds.head()
diamonds.describe()
diamonds[(diamonds['x'] == 0) | (diamonds['y'] == 0) | (diamonds['z'] == 0)]
diamonds.query("x == 0 | y == 0 | z == 0")
x = diamonds \
.assign(volume=lambda df: df['x'] * df['y'] * df['z'])
x = x[x['volume'] > 0]
diamonds = diamonds \
.assign(volume=lambda df: df['x'] * df['y'] * df['z']) \
.query("volume > 0")
diamonds
```
Você também pode usar variáveis externas ao dataframe dentro da sua query, basta usar @ como marcador.
```
selected_cut = "Premium"
diamonds.query("cut == @selected_cut")
```
Quase qualquer string que seria um código python válido, vai ser uma query valida
```
diamonds.query("clarity.str.startswith('SI')")
```
Porém o parser do pandas tem algumas particularidades, como o `==` que também pode ser um `isin`
```
diamonds.query("color == ['E', 'J']")
diamonds = diamonds.query("x != 0 & y != 0 & z != 0")
```
Exemplo de que precisamos do estado intermediário para fazer um filtro. Você cria uma nova coluna e quer filtrar baseado nela sem precisar salvar esse resultado em uma variável intermerdiária
## Como usar o método `.loc` e `.iloc`
Uma das desvantagens do `.query` é que fica mais difícil fazer análise estática do código, os editores geralmente não suportam syntax highlighting. Um jeito de solucionar esse problemas é usando o `.loc` ou `.iloc`, que além de aceitarem mascaras, eles aceitam funções também.
```
diamonds.loc[[0, 1, 2], ['clarity', 'depth']]
diamonds.iloc[[0, 1, 2], [3, 4]]
diamonds.sort_values("depth")
diamonds.sort_values("depth").loc[[0, 1, 2]]
diamonds.sort_values("depth").iloc[[0, 1, 2]]
diamonds.loc[diamonds["price"] > 6000]
diamonds["price"] > 6000
diamonds.loc[lambda x: x['price'] > 6000]
diamonds[diamonds['price'] > 10000]['price'] = 10000
diamonds.query("price > 10000")
diamonds.loc[diamonds['price'] > 10000, 'price'] = 10000
diamonds.query("price > 10000")
```
## O que o `.groupby(...) retorna`
```
diamonds = pd.read_csv("https://raw.githubusercontent.com/mwaskom/seaborn-data/master/diamonds.csv") \
.assign(volume=lambda x: x['x'] * x['y'] * x['z']) \
.query("volume > 0")
diamonds.head()
grouped_diamonds = diamonds.groupby("cut")
grouped_diamonds
list(grouped_diamonds)
```
## Os N formatos de agregação do pandas
A função `.agg` é um *alias* da função `.aggregate`, então elas tem o mesmo resultado.
O Pandas tem algumas funções padrão que permitem que você passe só o nome delas, ao invés do *callable*:
* "all"
* "any"
* "count"
* "first"
* "idxmax"
* "idxmin"
* "last"
* "mad"
* "max"
* "mean"
* "median"
* "min"
* "nunique"
* "prod"
* "sem"
* "size"
* "skew"
* "std"
* "sum"
* "var"
Você pode passar uma lista de callable e o pandas vai aplicar todas as funções para todas as colunas. Faz sentido se são muitas funções e poucas colunas. Um problema é que ele vai nomear as novas colunas com base na coluna anterior e na função, quando você usa uma lambda isso causa um problema.
```
diamonds.groupby('clarity').agg(['mean', 'sum', np.max, lambda x: x.min()])
```
Você também pode passar um dicionário de listas, assim você pode escolher qual função será aplicada em cada coluna, você ainda tem o problema de nome das novas colunas ao usar uma função anônima.
```
diamonds.groupby('clarity').agg({"x": 'mean', 'price': [np.max, 'max', max, lambda x: x.max()]})
```
A terceira opção é o NamedAgg foi lançada recentemente. Ela resolve o problema de nomes de colunas. Você passa como parâmetro uma tupla para cada agregação que você quer. O primeiro elemento é o nome da coluna e o segundo é a função.
\* *O Dask ainda não aceita esse tipo de agregação*
```
diamonds.groupby('clarity').agg(max_price=('price', 'max'), total_cost=('price', lambda x: x.sum()))
```
## `.groupby(...).apply(...)`
Um problema comum a todas essas abordagens é que você não consegue fazer uma agregação que depende de duas colunas. Para a maior parte dos casos existe uma forma razoável de resolver esse problema criando uma nova coluna e aplicando a agregação nela. Porém, se isso não foi possível, dá para usar o `.groupby(...).apply()`.
```
# Nesse caso ao invés da função de agregação receber a pd.Series relativa ao grupo,
# ela vai receber o subset do grupo. Aqui vamos printar cada grupo do df de forma
# separada
diamonds.groupby('cut').apply(lambda x: print(x.head().to_string() + "\n"))
```
Esse formato de agregação introduz algumas complexidades, porque sua função pode retornar tanto um pd.DataFrame, pd.Series ou um escalar. O pandas vai tentar fazer um broadcasting do que você retorna para algo que ele acha que faz sentido. Exemplos:
Se você retornar um escalar, o apply vai retornar uma `pd.Series` em que cada elemento corresponde a um grupo do .groupby
```
# Retornando um escalar
def returning_scalar(df: pd.DataFrame) -> float:
return (df["x"] * df["y"] * df['z']).mean()
diamonds.groupby("cut").apply(returning_scalar)
```
Se você retornar uma `pd.Series` nomeada, o apply vai retornar um `pd.DataFrame` em que cada linha corresponde a um grupo do `.groupby` e cada coluna corresponde a uma key do pd.Series que você retorna na sua função de agregação
```
def returning_named_series(df: pd.DataFrame) -> pd.Series:
volume = (df["x"] * df["y"] * df['z'])
price_to_volume = df['price'] / volume
return pd.Series({"mean_volume": volume.mean(), "mean_price_to_volume": price_to_volume.mean()})
diamonds.groupby("cut").apply(returning_named_series)
```
Se você retornar um `pd.DataFrame`, o apply vai retornar uma concatenação dos desses `pd.DataFrame`
```
def returning_dataframe(df: pd.DataFrame) -> pd.DataFrame:
return df[df['volume'] >= df['volume'].median()]
diamonds.groupby("cut").apply(returning_dataframe)
```
Se você retornar uma `pd.Series` não nomeada, o apply vai retornar uma `pd.Series` que é uma concatenação das `pd.Series` que você retorna da sua função
```
def returning_unnamed_series(df: pd.DataFrame) -> pd.Series:
return df.loc[df['volume'] >= df['volume'].median(), 'volume']
diamonds.groupby("cut").apply(returning_unnamed_series)
```
De forma resumida, o `.groupby(...).apply(...)` é extremamente flexível, ele consegue filtrar, agregar e tranformar. Mas é mais complicado de usar e é bem lento se comparado aos outros métodos de agregação. Só use se necessário.
| Saída da Função | Saída do apply |
|-----------------------|--------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| Escalar | Uma pd.Series em que cada elemento corresponde a um grupo do .groupby |
| pd.Series nomeada | Um pd.DataFrame em que cada linha corresponde a um grupo do .groupby e cada coluna corresponde a uma key do pd.Series que você retorna na sua função de agregação |
| pd.Series não nomeada | Uma `pd.Series` que é uma concatenação das `pd.Series` que você retorna da sua função |
| pd.DataFrame | Uma concatenação dos desses `pd.DataFrame` |
## Como usar o método `.pipe`
O `.pipe` aplica uma função ao dataframe
```
def change_basis(df: pd.DataFrame, factor=10):
df[['x', 'y', 'z']] = df[['x', 'y', 'z']] * factor
return df
diamonds.pipe(change_basis)
```
Nós não atribuimos o resultado da nossa operação a nenhuma variável, então teoricamente se rodarmos de novo, o resultado vai ser o mesmo.
```
diamonds.pipe(change_basis)
```
Isso acontece porque a sua função está alterando o `pd.DataFrame` original ao invés de criar uma cópia, isso é um pouco contra intuitivo porque o Pandas por padrão faz as suas operações em copias da tabela. Para evitar isso podemos fazer uma cópia do dataframe manualmente
```
diamonds = pd.read_csv("https://raw.githubusercontent.com/mwaskom/seaborn-data/master/diamonds.csv")
def change_basis(df: pd.DataFrame, factor=10):
df = df.copy()
df[['x', 'y', 'z']] = df[['x', 'y', 'z']] * factor
return df
diamonds.pipe(change_basis, factor=10)
diamonds
```
## Como combinar o `.assign`, `.pipe`, `.query` e `.loc` para um Pandas mais idiomático
Os métodos mais importantes para *Method Chaining* são
* `.assign`
* `.query`
* `.loc`
* `.pipe`
```
diamonds = pd.read_csv("https://raw.githubusercontent.com/mwaskom/seaborn-data/master/diamonds.csv")
diamonds.head()
diamonds_cp = diamonds.copy()
diamonds_cp[['x', 'y', 'z']] = diamonds_cp[['x', 'y', 'z']] * 10
diamonds_cp['volume'] = diamonds_cp['x'] * diamonds_cp['y'] * diamonds_cp['z']
diamonds_cp = diamonds_cp[diamonds_cp['volume'] > 0]
diamonds_cp = pd.merge(diamonds_cp, clarity, on='clarity', how='left')
diamonds_cp
def change_basis(df: pd.DataFrame, factor=10):
df = df.copy()
df[['x', 'y', 'z']] = df[['x', 'y', 'z']] * factor
return df
diamonds \
.copy() \
.pipe(change_basis, factor=10) \
.assign(volume=lambda df: df['x'] * df['y'] * df['z']) \
.query("volume > 0") \
.merge(clarity, on='clarity', how='left')
```
Um problema que pode acontecer quando você usa o method chaining é você acabar com um bloco gigantesco que é impossível de debugar, uma boa prática é quebrar seus blocos por objetivos
## Como mandar um dataframe para a sua clipboard
Geralmente isso não é uma boa pratica, mas as vezes é útil para enviar uma parte do dado por mensagem ou para colar em alguma planilha.
```
df = pd.DataFrame({'a':list('abc'), 'b':np.random.randn(3)})
df
df.to_clipboard()
df.to_csv("df.csv")
```
Você também pode ler da sua *clipboard* com `pd.read_clipboard(...)`. O que é uma prática pior ainda, mas em alguns casos pode ser útil.
## Recursos
https://pandas.pydata.org/docs/user_guide/cookbook.html
https://tomaugspurger.github.io/modern-1-intro.html
| true |
code
| 0.40866 | null | null | null | null |
|
```
import sys
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KDTree
from sklearn.decomposition import PCA
#### Visulization imports
import pandas_profiling
import plotly.express as px
import seaborn as sns
import plotly.graph_objs as go
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
df_april_19 = pd.read_csv('../data/SpotifyAudioFeaturesApril2019.csv')
df_nov_18 = pd.read_csv('../data/SpotifyAudioFeaturesNov2018.csv')
df = pd.concat([df_april_19, df_nov_18], ignore_index=True)
print(df.shape)
assert df.shape[0] == (df_april_19.shape[0] + df_nov_18.shape[0])
df = df.drop_duplicates(subset = 'track_id', keep='first')
print(df.shape)
# number_of_songs = 200
# remove categoricals
df_numerics = df.drop(columns=['track_id', 'track_name', 'artist_name'])
# Scale Data To Cluster More Accurately, and fit clustering model
df_scaled = StandardScaler().fit_transform(df_numerics)
df_modeled = KDTree(df_scaled)
# Querying the model for the 15 Nearest Neighbors
dist, ind = df_modeled.query(df_scaled, k=(number_of_songs+1))
# Putting the Results into a Dataframe
dist_df = pd.DataFrame(dist)
# Calculating the Distances
scores = (1 - ((dist - dist.min()) / (dist.max() - dist.min()))) * 100
# Creating A New Dataframe for the Distances
columns = ['Searched_Song']
for i in range(number_of_songs):
columns.append(f'Nearest_Song{i}')
dist_score = pd.DataFrame(scores.tolist(), columns = columns)
# An Array of all indices of the nearest neighbors
ind[:(number_of_songs+1)]
# Making an array of the Track IDs
song_ids = np.array(df.track_id)
# A function that creates list of the each song with its nearest neighbors
def find_similars(song_ids, ind):
similars = []
for row in ind:
ids = [song_ids[i] for i in row]
similars.append(ids)
return similars
# using the above function
nearest_neighbors = find_similars(song_ids, ind)
# putting the results into a dataframe
nearest_neighbors_df = pd.DataFrame(nearest_neighbors, columns=columns)
```
## 3D Representation of a Random Sample From Dataset, Visualized Spacially
```
fig = px.scatter_3d(df.sample(n=5000, random_state=69), x='acousticness', y='liveness', z='tempo', color='loudness', size='popularity',
opacity=.7, hover_name='track_name', color_discrete_sequence=px.colors.sequential.Plasma[-2::-1],
template="plotly_dark")
fig.show()
```
# A variety of Song Selections along with 200 Song recommendations
## Notice how they generally follow the same trajectory along the path across the features
This helping to Visually convey how Songs are recommended based on songs nearest to in terms of quantifable Audio Features such as accoustiness, danceability, energy etc.
```
id_numbers = ''' 16UKw34UY9w40Vc7TOkPpA 7LYb6OuJcmMsBXnBHacrZE 0Lpsmg0pmlm1h1SJyWPGN2 6T8CFjCR5G83Ew3EILL60q 5ba3vTyegTVbMoLDniANWy 6VK3ZdppJW3Q6I1plyADxX 47nZUjQa9NZb7Nheg8gSj0 5P42OvFcCn5hZm8lzXqNJZ 77RsQL1RDECVnB3LL7zhTF 2vqZnmBn0REOMmNp5pMTJz 1dLHaoG70esepC2eC0ykV4 4SUQbrebZgvSX8i3aYHMB6 4D0Xgaln0O8K8LK2gjwpr8 5ipjhrirlnBV7BMY7QV3H5 2lvkak4Ik64c4vlAQyek12 0t4JgAUj8ZCbWOwSU9h4nt 1RjYRvWpZeh9vMjjKzpH3w 0YELRuijk4XsKWvyoWY7jI 3Xn791JUhuITZdLsIuKuQQ 1Y2wWhbLCHW0WfTczmuA2X 65CE7YGQzGY4p1MqnfWYZt 6a6zG2o8geJvBVJkDkFCHQ 4Vcqv8zsfoNpxr7dWEJi48 2sfcE3uPqDObs5COsvk7QJ 2gz8HI5hZew7abJ9gcLY7J 2UFpXorq5JOIctCwcmDyZ5 7pNNFcYN2N1T0lOKMHL8u9 7deuaj4pjJqxWVky0jcFrd 2eCdpRpnYLp4fj0iMNra3p 5WyXaXmMpo1fJds5pzmS4c 2HLNwAHYH7Ejs2rZLLyrmj 0wXjzthQdMd7SZu2kNwsVC 3EnzqTwdFWe68x0OTxR9T5 50rPhDfxSL2kmEovmXqTNf 3VY3JjW7T0f49JqdFlvqIV 458Cn793jgrNc6miDUSAiK 40XOJ16Zc7pqgqYq9o7wjS 0QuuDvOB9fZ49pZ2cIdEdw 1f5aQjgYy4mKjA7EgJJvLY 1QJjIWHLf05mUQPq3N2hxZ 0wrhAauh8QSw2DFDi6ZHFV 2K55wT0q49n54mZmA3hqS8 6glST22VPJZRTKvxecHSp6 0lvEyZrkTDg0vK9luhcjZg 5YaV62mxj62GSlXvwzgG3J 6yC44aQAf9AALUyJPimZ11 1frCKo4D3lktaPHfkyEuHo 3hXsGl1WdOuKye1aHo6pF7 40NAjxDw25daUXVt1b0A0D 0bkPHOwWOIG6ffwJISGNUr 6w3401sQAMkeKdQ3z3RPXt 56UwCbkvU1p3vHTnlbv3kS 04MkdoV7vxprPhtYA0Cx5y 7AesCHBrKOy4Npkxt907mG 5B7w6neMDX6BYPJdb6ikRE 4AowP9TvejSnEpxxJigpyn 4M9onsaj8IxHJEFVezMRoA 2DRNLTuiZr3MdFNfEHzWfz 4Wo5LyWddbPCogBIBrkhlt 0UJmSMFB05CyY3dTps6g2c 7nZR4x2aHeIyzAtrMi4Wua 6UZVW9DjfRKrcIVco5uwc1 2O1FwU85kgG0SJGJhszkB0 4OK4tHSUnCXpBfIusCOdAo 0MfWpTp3GrJ51bNxLanyy1 5DVsV3ZetLbmDUak9z0d1E 3ki056t9qL4g9GHWkPFJYe 4WCNiW7DJFE6h94q5NPZmZ 3N0Q5ce0Q3v6MmcNwaGG2p 7rQFDOKqUEaXE6X6Of4HTw 0wi0Hn8puUPmYdZ0JvpG2H 5wMD46niyehV3y5HfeQpNf 1nTn4pZhcgfRPobs43xrvL 0NxPZvt6UYWLgTbvjCJd2n 7fdHvtur1uLx5crFzAfWJ2 5AZt6HoqpUdHyhia36Khtc 1exbNAnvvYLYsEFESsCjDO 27ZfYwqic7RnwuitxJZiE9 2iPvO3ctXFGlkzOsx6iWyn 2w8g5LJzKqez8mENuk2pbL 3aBmFnfx9QfLB3knrKr1Mo 4UUA76EBTJzcICr2nNyhnV 4aV1txuotqBFGLB2jwiogo 7ASmnEp32JgxgH76TAaWwo 344WuUSk6SRQd9849fkAct 7aXH7YjPAixvHIPxCKxwIo 1CakWoqY0bPK9Ov8UocFTR 2B9VQlYlq6CUH0VXdQqB4y 3gCPlZpymjidx564rWcPHX 691J2jGivJasVLkWU11dpU 0ulEzQTIdtZGvYH3mkK84G 2XpxTgvloEbIIVfEt4XUKt 4dqcedp9451K9DvxYugrTt 2Y6IAs1aCdb4rzFfGjONUo 7LDtRLCz9D5DOR31jQZ65m 0oliuZWC43aafuxqNlGuxy 0Ks2NJH2PCxyWAFPlI4p9B 7oLqoswT2hfCG90crbiToe 11wZ39zESerUTPXKWhx7QE 4HWfA0iD0gXuL6gVreNYTL 5EFw2MVleUknhnPzfrCrTq 2drp4ajf2V2xUvV79EmzMw 6KL8uR3Y3JjFpzzLQFBzQa 0SYo2aRh2MYfBoJAFOYtNs 6Iq5a3BvMSx6X7auul0yDE 6TZUjNnW4qHI9wPrO54L5o 4v3s1AdtPSBxFK93PNMFSg 7FM6VwHNF3EWQTyiloogTV 3FNbf1Qt2ycepS4fasCuOm 2qK9xZkbBrTRiDw2dnJul8 5ozbdCZw5MZmJryCOyDYO1 0M82DdRxHFedS7fg7Gk2qB 6k1Epe9JbePsbdq0EZCc4i 63TMt7zR9YLpNBpzRYLG5I 6tbdFaJWas52BT8DZH76Xj 4V7gH33fKlEhX4d1uk2xYB 6jY7PeOZ4P6ww8XuzCyGfO 3m4nvQbC1n3dm6SbYIDbDR 6J5ArwJqeLHFKNfHcDP6OG 4RlzULwFEYBjTJNhc7frWm 1kZ0mav2lhlhXf4fWjw5Nc 0gJBsp5q8Ro6zXxKzT4DiQ 0CWuF6SrEXmfM0EDIERBS1 0ogRPfqHhhZuaeeVt02L0Z 4AEJ6dqjb3uo7K9R2xKGJ0 0b4akisi6edx4RkU3VO1XW 2xLzmImDWvk0jw92tTsnHk 2PFvERcsENO2mSXV2abmMW 57miVDdQOiOx7ZNaEjGaFC 0LdkVfBGmZUOKf8sway0tM 5GtQkJTQ01zxZ9xRuIBRyY 1LX7SGrc4FIE6LnzV498Ow 2l3OlYqGIiJrPByZNx8Ll6 1yCb0FSeO48efDRg80Turo 3r5OR32RDkcp3eIQ2ylF5o 3grKLoUX87NaEkvouW0vmz 7ts8ZBKNCtJvd0ijGxTgCw 6LSlTgBUF1T8rBrTKtzbWB 0VCTFk3PtHHTbCdiI2SNf6 5flKCotkqTK0SRHyu9ywOE 7FNVvZKIFb5VIwyY4tCMXt 1mc6PrRRhSipTHKSLRuv5B 1s7X6ZKOMhP2luohWVXNNP 5WPjMN7nxk2HqcPfewseyz 2rX3PbfV6OrObng2YL9Osd 6ahWJqh8GQag4OWmyRbcnE 3ZYN2cfyCFn4NuWxEW9tuh 3DchJOgF4JUzQJyoAVePa7 1fhnlsDdCLs1Oi5X3oVCTD 3T0UOBcMTeytq7RmFDZMbu 14gtLymOStY8niLakJlbf8 677SnHIc0M92Nb6XUnaSCT 1t2hs48AduLr9wik6nF0pw 3QavdjzqIxMUPeSXgoA4Di 4LK5o7buDJB9A3aL86y5dR 1JAGP2PPls6WXahoN9IM14 0uteQpEpt2XpZ99ZT7m0eA 0zm5v1li5HwBcFJZzXz2Iq 7epZd4ZUwXGq5CTOwW9EO7 1R8ihhEOnbscF8kheDNC0H 5gYUBAE3o6k5yBv2Ni7KwQ 4EuW6g3eq56jUDqdNbUryM 727FY7suhFAVmwP3tsg6uG 2j9tX4ubo2WISo9GIJLySx 3QUtbFgjjnAHTtLup31xVa 6viaOSezCxDApUQlIc8mhA 3J0ZbecfqYszqlQJKYswVV 10aAr61dsWKA9RRdAmk2CM 7gE8QvR9Pxl7G2ey8XFtwa 6RF6zRVTz1FUYzBhop3jen 2stJA4LcpvwPHIRa1Gxp2P 0yrFVbIvtPU6bb4YMD2Vcr 68Hwxn8KEb3cXjv3w3eHtV 6aTdoiCwo5eYrl6ik4jRYH 3FWU0Aq3QHHkslDWD5sXvJ 3ckyP4jOXNBskOGeM1E4WY 137Lgw0gey9uw6hDKI6Los 4FrbvIGxud4J9DeWC5OYrd 0d29ZVNUaxWOtUFzElL3B9 7AvTgaX6gs7L0f1O0qSlDf 3C3pZzGJJR8wwuh6npPvHv 3YcmUK7BiWMBJoRWC5p0vi 3gBPhTsYDm9xtuOt4iFjMW 6QotxMJ0VE8eh1rvm2alsC 1fh5YKCSpo4OvC6usURns4 11bs6ROtD5D1VfDcCje9Sy 2DLcXvfFrQRm9D1GzMbgMg 1HqOKMf8bNLaEPvd8NXx3c 3tN1favTAEXAadxfygjNmG 7F8ip8rt5cfD18wUTgE7us 08pFqsZZZYeFbiTGPQj1J8 512JyhHrndIxZ81JmYZLmP 5Df1IuQ5AqKIrK1Rplsr9p 52MsPDozAb8oy9IjsndB6v 4tYja8TMtjBAejK7pzP2y4 3s9BUjzYDIesX8PXqcWno3 4jAbuuhObXbHrJP5ShVOZ8 7ezSDJfiOAmSt5nYe00VaQ 1p6BhKjxF03jOd00W6io6O 56b6kZuturLKiFl9v29tEp 3YGG0dmOCgA60bQts3J0C2 '''.split(' ')
to_be_parallel_coordinated = df.query('track_id == @id_numbers')
len(to_be_parallel_coordinated)
px.parallel_coordinates(to_be_parallel_coordinated, template="plotly_dark")
id_numbers = ''' 3Rx1zM3nDFQzAOYg9Hd0D4 67AHtK2jFq8dlOLSSSbQ7T 2ystp6xiBASPJkFR16gJON 5VNGj3qgKC1n28B9etIoJv 6OarwT6HBT8jW6MsnVwn58 61VbbeUd8bXxzyZYrg4djH 21rvKibsH3WmojUZh5H3Gm 11wxWExHmqBNKIo6zK9NEn 5ZGXAHp0YPYFUMbyMqDQH9 4BMPGmOzi4H3S31B2Ckx0u 1VcVGJ4sqRv2Iruxc8CfYf 1xOoqWTv2wLhUeLtXZTm9q 4SV8h3RlcuQc9jE9MUQfFF 5c1Hz72Bc8VMbghi4MJQus 0iZOviuGDLFc8vSrB4RI2T 7JRV17HtiiXksxDdTdpYTy 7apGuGr4Zf6t9JkATkolAI 0Mw9dLno600aQgA0Gf9Usr 6jUXJaXtxOhBLeWbpR2kN5 1nASmYf1d9HiiIgEOPhYQR 5LAe0lSl7rMle11o6Et9WI 5LZu2syDoQNaA0NptU1YIs 0lz57CGwAyuYdMk7BO72XI 3MDnGMGGC00nbpkLP1r6cN 4QZpmKzjC5t1OxEKCvL7Ft 15sVDXzpwJLfHM99VeP7mR 3Yeb5nDeWTvXfJ4TdlTtIP 56Tuc3GqQrByXDZu82TfN2 2jyrDZbZoScSdiTxVRlzb3 5RHZg80sV4QFq3alySZABa 3IYkFudbmV1sgbz4riV73P 0xtEwGTNW1fjQVJM6PZ3U2 5zllzp3gvXWq2cmyBZReij 43hjTh4WF2cICX1JhwfE9x 7BCPy7FIt6MIZwIYjgwHUc 3HRLlKWdmzXfAmbcrOkevH 5zTE3LjI0vXoNs5sXe1wBd 5ijr9nCHXMTb9qYvn3taSg 0R9HIKNmfmn44AYsSux8Qs 4AtiPcMHA5VPbNlO4EdB4T 0Ica23299eon0SQ5GMcJYc 2xkcKjB8CYW1wXiZ4haZfu 1kcNoS77udN6sSUWq9mI60 2kWUZwAhXDQmEvxv6zAxsx 6a5vpD5O3gMZH7G8xwOv5X 2mg15L7RUwpaymfobUFHOM 6HMKAeNDeWkPaHVEwvf6OJ 6zZeZcCSnugaVt5mCiCCP0 58xiGZhGtgJGCBDlXwCTbe 5O4MkYjbKpC3UH7oE7YRQa 6NBheB7uq3KuwjrriafhSy 6Tdyv7xZrcnHmO9iQoysKS 6GJh9XXO7e9D16Eyw0RIuz 3ayOojGZYT6wNtFC0NDQTm 79wTeGSVlONiNfZTdyGUNq 43w1mfDBN6MHueSkUjN7D8 4HqgpQdgUT12xACerT4yS6 3XRfdbb65XE1bfrAwlRu28 3Cv56grsf8F5iWn4BHtZx8 3YG5WGhUOj8Qzj4q9hF4TE 2MpCXZtBR02QWKP6xwRqy8 1WmKw3lMhA5YU869ilylyn 0vOSZ7hAUxocDU7qPh0VCo 3rnjAdt1duHuVV5AjavYk2 3uUzHjzRxKewzg1bE4TJwq 7M3e3QMHiGgWaGqwaRS0oH 6JtZVLdOzT6GeTgPzSoGAA 5u7UqEwOyaEIoA1TLLFpz9 0TWdTb7si8hunDhLmynRsr 0fzEYa7EiGDTU9wz976bAX 1HybrAhpKs9bm4ol6UR8bZ 4dp22919ccLK9SpvAEfTbA 4dhR3lLe5XLiR1TDNuGJ25 2Ovrl3OYjw4Ys4UJJQZaVT 0KU1n705y9CXC2F6fBOWej 4sPQHt3Tk3zz2TxBv6iSwu 1IdFop8kheQ8DF0rFhHiqa 4Ex2Fk2vc5JOsYptDUBtJA 1slZlNfFpMAfNiqtf9uYto 5ykg5P1kKcYCVqF5cHXjYu 6IGRNK7vC8fuhncF7YXXg9 1gZRSXSFGgZ2FfTClxI2A9 46BanJsjr1hqamrvLBYkng 5IwncSTQf2nC5aTktUNJFQ 58iaGunPax6nehU5K3AlCO 5vEwDx78onSExtBl8Q44Qf 65fd6IOZZjFYkuApCdbGxR 0G69NybuKLFtOulxwW348d 1z0b8KGrWldcZLakynC9Hc 2iaJ69ql68l3uCFtP6Rz0w 525g3ZvALoI6eTwOnE0dvh 54Amn3maW5gDB20vIkOzMK 3ZSj7F0vNEUmr0pJX3ROcD 0DbubpYjXBCGCrbcVl6YCY 6gdYVynIAdcSMWIaK3x7lW 23NI7LEZNcNgqMQ4MtNZPf 3sVNfmjOawrMVBxZ5HR992 4CCFVqakDhrAqEBbIeebgw 4VRoNouo8soGhl3GaFLmdr 5Mtb2rpcBkZEbNqLx06qfp 2m2Si8RtoOGPfbIjDx9Ug7 64SrUvSXvi2DCqwnScNQ87 7boSAJxzyyCJbP3LcDzssT 0SgncrTJSvH5xrvkllBZWj 23ptyiin2PKgaHZW6F0mMa 6gpomTTKog3SU0if4XT8E3 71jN5pqWqS1Gq2UXg8IabB 0yItuTAWCQ4JRvo9a081uD 0TSzNyWeCGVz9VdwFLWc2k 4gq34v5gzCtdaL4o8drPBx 3IR6Za6YHTAeikVF8w1DvK 2pkluglrMGfygP1yVADsX6 6sQyFRXaDU3MmLORr6EdNv 4QtS332yh4ex5KFgcMA40E 5t6GgWRjcigpk0pXpcwzSO 1bHaP4ZOPgtpoZ3CN6bIML 2zT9xdBcvSo1CO8RZ8Tcqj 0GgFwGjaAdqVga8j3ZKCtl 7m5LVVSaWzik4h332VqvbN 1P3RGzIqmcHKvH68e5nkBW 6uIYA3RVNgr1btPAtr1XXy 79pqKla5Q9IiAQfK4jalAO 3KDZxrjgFLKWs7ds2rvVcW 3yiT9hyDinSAvubb3XZ8S5 4byppJf1BVIEYj0FV48uN7 1PihJ1fLjU2wkTatRudSyE 1rVYJMGey3MZapQwCx6xXn 3X1MK1cg0in1bV5s8BvI4O 6xDEZCZm0Ehbzgj1HAqLIe 5fDXSKPlZQlaq1jC3izCkd 3JOdpt3Msi1e20Nxmor4o5 7gLSX6HlNso7WkoWPCGNGr 0PswjCzT2lZY8EDjVRPrPc 3XXbyMFA9F4adfcnEjMKHM 5jM3bDFV7UuyhHA5264QAs 1KRiMLHjthCAhWqDunAJOV 79ojwy5zomoWoQNuaOWbKh 7qbUjczokcnGFIwx68aBqV 5IKtH5C078QBjDSniwdTXj 2LfM9NwbQkBFV8XKAwhuTo 7A2lPmhXhtlZlsRMz0ShNs 3nSvqC1W3IEhdubx1538g6 5pFoVXWo5sCBfC5pLZu1Gg 1XCccHjyDRUdOVrEOpLzoH 6LeiYw9DsrS6fTGG329tK4 7md22n0LputBo41lYOG7tA 6YPafAdayjyjcoPoKIxn6y 5Tpbw8WbGEwI2pzjxXrGvm 6ummA8cVxCDnjT9382Ui8G 3m9yfMVIpEYvNLQZl2f8YF 37S7watyULcdUTc7z8Opha 2uOPEftUSMDJK4UpsUjGPO 2Xv0TmNKxLIV0cVRwM2HFz 246dN8gCiMv5nHi5wR2Anr 6i05cmZT3PHtSriKFWxTPn 06M77pQeFWvFiVn1Be6XsI 6WW4VgC1CHJjrWxYOtvayZ 06qD1C1Tcd0mYdRBBmYuTx 02ZFCSXPFgFPEahuN88kOQ 06QqCHpEStp7fwJYK4qoB1 3XuQifZguMGzjZJ7zHw7O8 7bXHynjjhieyUVyq8PfjHg 5WGOhaEiVJzjeUbjgPK2ww 4FXamUtTru5LlMNoCjlBRH 5oi0T9CsacaGLVECLBKWq5 5ulm5IhULY27ehqTSrQeLB 4L0RXCGs4SP8CkrBbZxsfS 5jYACoLz1e0r07W9G7oqOi 5PbIFyF34gCASgnG7yi0AG 0iZU8XzmveXaRiWBpE1ZTI 4pvwyXkwtXdrKIXpOc0keI 4wILZuKMKmJZIQxW30u960 3DrjcLyxLSG3aOh3MvXnUF 6Zm6DJFgghFMnMw7xBIwyn 02MMgyaLCvnIBw4skXmZ9V 1kVyvQzqxOZz4BgAWOY8ps 6U3j5OkhwwHlVeVgZlyl7n 6wdOphejlm1hNfFhXmzT0l 5rNFuymSOcCW8nTfd3vYJn 7kfZsjQgEApwNuceCzJIp8 4AhUSi91kDdC4G51qwvDlD 5Oi4T8e7vZK1xfJgBEWDdd 5Q5POfYGAdWGSSYLtkVQ4T 1KgOw1rCe9YWTFbFJYuYjD 2Z40xmLbAGbv1vQno1YMvJ 4PgpYEtlH6VfWmds9jVDoT 0ERjKxvwU91tthphZGgLFn 45b5fAvIFHBWmEcBGytul1 5biNqsTCkccqUfmzRFVIPO 1fdwOBuqrsjf95i8rAMUCC 0Sm76b6hQobYvHebmCa49H 73A5MOZ2MJyKw5sigQe64R 56rBa1McCcF8Q6cyPOAWji 76B1zH5bbarUGH4CYLfvbS 1bUQorCYDuyQhIyDYWzNyz 0eOAeqbD5sxU77qdHSYLOY 26VXbBYVzPXvl0wAAEppnr 5DK7vMKUkq3ejNQK1SP2I0 1E3e15pztQETb3hysHnuDy 6yl56wrtGJVrnhFJjQvIVS 1xWDs7mhV3YbENkbEkmvH8 '''.split(' ')
to_be_parallel_coordinated = df.query('track_id == @id_numbers')
len(to_be_parallel_coordinated)
px.parallel_coordinates(to_be_parallel_coordinated, template="plotly_dark")
id_numbers = ''' 6bwTuNxmVEOQw0dXdmgLjC 4rTVdzMKkbRtcJtbHCtTKm 09m4moKIXDyQNZDkoDqjNk 74VJWMSZHMcvkHQhyFmsXk 6CE0gR4USBQnxKj9vWiotk 3REJFRU6OZmqWk5neOLPXd 1jEH3K14qOijd64Sa052fn 5Z5YYYAFiSsfwOm3EMmWJY 58bs4VQUlgyZcMKJVjpZ6o 78EsU5Njik3K2b1Os6zwLV 0BdUgqNA6b63BXGDu4PeKN 4PdEXwNLZrPK0BxuJwr0nJ 4kKREED4rj50B72mZFuIip 14houuG4FrK5ZHlzVccj3I 5gH7dn57qXFVoeY2IKULtY 2bJs4cwj40fPxm3m94ORe7 0KE6mugI11bbF8kBYC41R3 2PWUpPMK2GeLxLm6boZjto 60bhcR1KCbE3KXx0zDv0XY 1zl1cnISd42IeaGjcnQNAD 07jABQKHpIpXKCOcqWtDpV 1kdgim6R7kqUAOOakjyWGq 5NiqIB4BwRpoU1V6U195OU 1oNvNkTsX2YtpPpYQHL9Zv 038Cff0ZD16m5byH6ohfVM 0dgHfb4WaQAzBdS7n4SPmN 2Us0EFBMreM3VlE8AS9srv 6K3E77Wxm5oH9kEI7Qb6rv 2IAvDrAdvPDiz7Z9ABphO5 2m0pE0vX5h4NahhFsPMwnr 2jaKU9jN3X2auwOGjukuE3 5MtAIjUBeWqQ4ZUsb66vEZ 4CvRCtSjUTYksvMiHsT0CV 537UFrFPasLdnwe4Rk0ROO 2UBg1GC3tMTnw0VzwmLelz 4dVWz5zq7XXigjOfrAfI19 3Ek6sWpamhmmtk032Uhg2V 7oYH3VjR13Kmtj7o7xLEZr 5wZxmzrLNDTcw2JNyaKHS1 7EsGSHSaobePkf3Lsqre6s 1pe3AGBuipdklcKbJKDP9u 4IDNf4oDocAj6dufznifao 0rjX0ul1dfUmtNDAUXIPup 46Pk9K4Ta26lFiUs5thsU0 2OP7W1lsZkSWGBPdnO3mgk 3jrcoA3eEMZGKzF11VzxO2 1XbzwdyDW4YohbntjCdso4 78XVcxI67oXSzfV6YAODtr 3BWTnYtojgn68TZSkGeaZw 6pVGYwDiMSfrEAMdIVSoLt 0S3f2G3nuCWHmmSbck4i9C 58yF5Yqokn4NxABBmpK8Yi 0cEL1Cg68zorMS2hFq0JJI 536PcP6LHChvhsH64QVBhq 4gRH3vcS741pSZW66LQK4P 6ULiCxVUaWBG0Gw2UAg8Dz 5QkHEhAJcVrsTKSZFJDzwX 5bQygUkLEUYEWSk6rA59QU 4XdhTfbWbD11U3fTW4EHcj 1rS24VudoY628mdFumzVcI 32iYiowgoEfTsWQkcwTRlX 7HcbJJxIaZbbPIRb1CyZ3m 27do8NxmUa0D1O9Mfi7qJN 4MpCSQSpk2yLnfrOSHsZxq 0PkKfT55z3nNSVhII0tZdN 20QnKWlncgqaX5NYOybhgy 5gFjlxAUKTqM1GUlFNKw0S 0CkMQnSzNWzx30BaLnllr9 30ZIabSNa8EbZT49b6HdFO 0hrdCoV5LPC0ni1ahSbAID 3FfWjwjwjVDZWlddoQ7jP9 1RDif5mDdaGro37AxOVYoJ 5rfLztZGbpbF2qC2sU0LZq 6bcIIzSu0niVuplUk7t7LB 4khYVmGHZz4JWpFlOMXanb 3xXqlPnnVXRsxfz7UGVi71 5a26fblCJE2O4kEJSJxU5h 3up1JsYa4JNZBakiWP41s0 3WOFMQnYvfcGFxA13J1e55 6On8OnESrMsfScviCLu0ac 2vVVMFMLolbasmvpkyEF8K 2GgiRBztrAUC3SHmBxAgdB 0aCwjJMzkOdxUZfAjKtmuY 5k3DQ5XZGBc5a0Rwbwc8hW 3DOm109bpm8LVlGrPj8601 6uSQ61RK297rMcatNDbUqW 4kcM8vye44jgsRMus1UjER 3umDgMGgONpKVH6KzpCcho 6CqEVY16aBgIMzKmHOBLAy 3x2Xk59n3Ey2703JJX8ss7 0ajlXtd6JWlrEGt1Cb2gRH 5YE0jwzEgR55ngUvtAzEG3 31Z3tkTDOaYAIJt37DG7lW 0v5tTD8cCbNsuSPdZq4ppU 62tQ11UnK9za7j0dyqT7Hs 5h53e771faNluczmIdNTqd 2lhWPS4vdx7F0kkwfLmAwG 7oLLKRFfOyE6FnIbbpXsyR 16Hf2J1HuPbNPWFvNZzYPs 6i1fuTteHcDcO64tGAnGeh 0URolWwoi4SSkoNHXDrTpO 6KiZqNhZtkdB219BIJkxNJ 1XKMWyhXlzu54mHfQuLUlf 064OyTlK7wUeK3D0OcCNcp 53APvcivoxGrAmK2b0Givf 2qKCyrQ61bmJqoV0cCl6eW 2mpINSrBUHvmP5oYSZ1ZFV 5K7gKm344eKOkDPHQPKAzd 0utSnGPZthEAuKH2kUfTcj 1FC2CEy48qcygiudnhS11x 2uGcDgpKyKBIIOfGwTd6bu 3CgPWIPgiLM0fuYQSPV3Vb 3cQCiT1PvddSKI8pRk4ygK 7rPm8nyaZMDzrt7HDFC1IA 6FS6mOlzpyIWMz9o7pZoWo 5bOGB5m6V5yWR0tGhbBhX6 6HnJLuczohJYWkDGgYmm0u 1BZe0OJ0eEjJloBAvg6aJJ 5avuMjb46hBDucxFvxn0zo 2Z0q1138jfn6aSMB7O8o4w 1sVtiUcsOJTWYjucbPoVnN 1QSdwCcfv00YVFjlMFzlo9 4IRGT4KQBDfevJfYgUuZvP 3zM11n3Po3s6eBH9QAqcNr 5w6y38iH5HdSNk0EtjAdW9 5BZNTeEo1t1HXVucObfYSp 66bWbHHVd9Zi5xNAKQjTmS 4NlYgUpDS3K7m7mw4lsTM0 1NBksoTuYxMACF2v9OVDMB 4jomQr6ARl89f4ZguNlIQm 3lQ1IPdzulBHfTrqLYH4vX 7gsd2pg4vXfmAnMuXRxTEE 56Sz3MTf0cGyjYwTJOZVRY 7aw7h5j6BK5KvzSPNpKNRj 3woUcMUIeew0PfIlEAGUcH 3j1jNAZIgr4vhBfI6sgfxC 7zhc7NI9JHyPmcOaDcHCVn 6lGe38gKVRfF6cKeXmhidF 0XUZDGgOioOehdcstP1hU6 4aILeLn5yHT6AsB1W7bEHG 6DdGyHy8hlqylxfaDRpVcK 2Kt3W0rl0PjPCOjAsf9mjX 0sAuFhtMq2SKZ3jZeU59Yn 6ldSXWJYVt1Qig7mDm3fXv 2YlIQsylMAOcqI7aLas6zj 4G96MmIt9XmoVPn9XzgtSy 4gPw3HZ18KN0UOniw4UEm3 5n0mpjpvR5iWWkiQL4kgRX 2pX3YMabAIjH2yQxb56n9l 4p3zss13iYj3TcxUgjmrKM 3QuoES16r0kfiewaKeYYnJ 6Cz0v9MHjAdviUGTtzO3Dq 0DdCjDmCzioT6W6nIhMOgA 4ZNj2L44lvkGZ58SaSql7O 04ENoZKEACEkrcc7v9EjnY 3xYgJpdnAuKPBSA0LHtg4I 4Xds70hJW0HNo0K7OKJbl7 1AIYotQAJnVXpyfAznXK8y 1Ez2SpFr05CspgDgHSja91 0si5v3WiNFDgQUcbkgRp3o 0HRQMiz9Ua969JXOPVLlcB 51XnpBsO8S8utaHscyhOnP 5myMjEVTHoBQrvatNM0kyy 58b7PzFbREarz0Os8GRBZK 4sX6evSOdSL04HR40EcEN1 4fubn0dRFW1WMa7yiYIZSs 1OKVJpL9RPeLjFGJUzeXv6 33gjPr3rzp1dylPMPgvLYV 2qeEyuDUaucAe63BoqJqoS 5v44Md1bcJYN0rL5kpWfd7 6PSyaM5jEbwLXm1RsKZyWE 0hLPDVYwODPeJfkHSol5aI 4OPPSKaowfmIiUEVNyh0l2 682gIKe9M4YJeDbw0Uqimn 5aGZpag8gyQf8bYu1RhYZe 42o454bTsMf9g1A0cwGxke 40vqauqc0VQpvTGYYH8ad1 6oxVrlxeTwhmOroYJkrAad 3AVBA0GTpnMFh1Rv6Xqymu 1VZmjJ3WV1nc3ojykNVxFa 4Nclo8xnQeuX54AGKOybbM 7Dba82QckMfi9xvgeePc72 6PFiq41950kSI58ILz7uGO 2jJUHXFaFdvtxCOVW7q8bd 2lEmjaR8rQqsQqe6CLXtdz 3lPO5WuqFNY12UGkZzZ4Xf 1o1tRS1Vzt9RZDJSDJUzSC 5D7erlQmTndO42J9VuvBW0 1kjxPdNwFKldrMVxlO7lio 3l7DVkePu6bBxBXTl8cIDc 6pTMJuynSqNQXuGar4Skno 7oGEP1UfFPnJOFeE38Erjr 6tIXXMXvOi3XNHdRTwYFOl 5lYAexg45DfNm7LfJNYMva 2wgL4gIm8InPw4IPaOBp8h 1CzXfJbCKcHb33F28SyGv2 4nHMoGnvsDsCMHmwfSVWop 2R3ifU5sK0FygVOZpk1yJW 7yeO78qI0fxnz6gjTZEp7i 68SS7wcjzSTXcifbplZztH 6fbTH5few6yjRaQuD0tqfA '''.split(' ')
to_be_parallel_coordinated = df.query('track_id == @id_numbers')
len(to_be_parallel_coordinated)
px.parallel_coordinates(to_be_parallel_coordinated, template="plotly_dark")
id_numbers = ''' 16VsMwJDmhKf8rzvIHB1lJ 4DdgOzDiK3VocRlOpgyZvI 5smmdqbHwTdVJI1VlnBizP 6lyFgQE2nJwT34DYJO0gr9 6C7oT5ZSNyy7ljnkgwRH6E 4YSO3y5EkzXDiBW2JSsXyk 2PktIwDOLDNRntJHjghIZj 2OKbnAB4LIw93b8IXJr34m 6drCDhqlK6cZ7LKDi3SB18 0ZsWvJXGaHqKUHrvBjZxSy 4hnq2TnTGgiLG1qFAFQtQG 40OCjuNPJQUTjSnTqFc9u5 2J3vblLOe0NKOJvHXxmvuu 2NGl2ljBxtvl5duT5U0Rgc 07iwjTrXQsfQRJ65rEConJ 4Mjn1iv3fhTtDt1ZRnUvn7 77MM047j6loQsPsUFntTiC 1oTmjppGp1ITPZCKsYNqs9 1DJUNsDTNuMWGrxfJmNGnm 5ZTiNyy1YtvyBEwDWoVOsa 20iBwNgEMH8b63MZ7wmN2F 6HgNAjt5zvGy3YQfib9hbC 4zG58gSipyazhsiVdS84lM 4NDw0ExQPFKQNkkFKvPh32 5ghFFUCCEspRulW23d3Awc 6FCl5VIhI3c6StmRgieLKu 1IeEYWlLBatGhtSTVRdOgJ 5MzQStKKOo666peyPoltxh 6D2KvMGxjFMk47D6CbCEaT 0DVnlsmBltpcWafM3TScIu 6jwmlu44QMMDesyUIFLQS9 4lUz3IxMsXYpsrbV6SVQAM 01y9jiO8FHCzv9iLmYpw4F 5XIkSMJ9sODfZoHUJYoi1g 7atUBpdQv34PNmYix84wzR 6vhOg0jBNyCzQo7nlotVeH 0m0ndzeNd7bTNWpgeGoQcP 1NBBs5Ym76El2gojyE4EvP 0R5S8PHmsl3TzHdMUx1oiM 1b35m5XbZpyNAx9atEDaDH 3aCIbAoc0CTE46enUrDmuu 2Y88xiM3oe4DFYX0jLLSON 7DcVWzeud5tqtNTZKQWvhz 6DdG99q2hNKrSHZ7hL6pBt 7ESz0yGdmhiWp85j5z09Ub 3xmwsqwkhI9gbvmapDO9S0 2N9LsBQMtLyMZL0LeydiLW 1sGGodtsPFq1JC2w3vXZLv 150NZIcOF5CtN93dp72A6g 1COgmyz8tnpvBoZvqqZqCL 314QsKiXd2SgDXPYNsKu0N 57p3QcWwIjVwvAcQpu4hkr 5IYNm9xiOZkLjGJYH0kqsR 6z2Rtx1CjQGaEEC1xzqtIT 247ye33xXOEhnjN2rCdj8I 32ccjDeiYYtombISVtse9U 5eEZLIu17HRBwt0Beldd0j 30DnQCN64v8xBpGZpLgb6l 0PrPfp5FbP87rTk39MUKcc 14EblrVdzyjpAWaedKO7x8 1l5CriNdYpEL3NoJxKA9uA 45ZTQl9GbmdM418qgLZvQZ 3dgf8JT9Ya3QAfWaJTNuI6 6ga6wioJAkB7MtOwremcSe 3HUsmE6j4afm7zWM3bprkW 7Jcf74UJvImsHrGOqSS0tG 7he1eOKQBxz1JK66afUzzD 2jtaAeW1k3qgbpQxT8Y4lm 3C9ZhZSSd2ki6Ko4Zj4sOo 3KuP7KttXAKmsjCLx9gKeM 6I5FyefGR36b9OF8rFkxVK 6YNIvsHK5fdy0ROHDuFpm4 0M7ZzCZ75sAUBq6Rkwpu09 5soDoRuEEmx9BriBtoWbr4 0zjLqMGvY7j7TuBkh2MIVd 4YfWZTRKOt0Lp1x1TkgsJz 3xhxhvEYDY0Txl8jUqbH0p 05FSDW170E4Brk3Et2Tsn9 64sixBk8xj9Eaz1VmdbenU 2KcO2wBpD9kfEUq7K5L8NU 5lpIW3pxLBGZ47LhXmHuH7 3aayFmSl21VgL3vybq2EAe 1nhZ34zdByR7TKRNLi6jXH 1WU3fG5GlEsQSsxj4SlGn2 6mAMDridbMDlW2ovdyPDUy 4yKqq31wiiTYlzsTspc9bF 5BgjDdJGaa7iB3kQfj6QMh 0AYTA3nevKu9S6LpeJwG7B 2q1mQzjkmrUINRWiyvctSi 2OIGt6nkvpYyTCsgqgosut 4nHpPnnYddn9KhXWKcVcPS 1aeKIPo431ykCa62MFpVxO 6J0LsDeQEMbXNCJCsPEnPx 4U4UKccQf96YM2pVVehbDd 0iInUMrkWaGGUkPwIY1Ntk 5kM4TGc7A3VyX1AmnIznGx 5ByZw9BY1See6eYgqUiB1x 1odwlrTdOkOVUoJhlE25Dx 4zsYOCkDiS14hdCc7gJX1Q 3XnpqyDY1Jo53Tgod58Mxf 5w3peXuUoDQIRWJbtK4kYi 1LWhjl461aekeNdmQk2JuJ 18zmtkXBaSHd7G3xobWIEJ 45vdRv1YwLbpbVeJ8BO2pR 1K6WHHqLXlqyGxX2lUMQr3 7gIS4JjropHYqNq3UzjHNB 2wklaFrsGnIfvLggxQhwQB 68WhMF4gKml7wKQcpILei6 2NVoGLBsrbQrH9c8bRDQu7 5gxxz91fYTlkR2cqmDkPWP 0tewjlNbotxqF2obibsg36 55hoUnXPjk2xma2eYSbltW 2iGTayx2t62y1J0XOInyfX 6ScbJrUjGIWS76VXsK8UEp 6M1W8DojBHXnjenYcn7H7M 4VyvzQoIfG49xiNuYVYBiv 1dMabx7tqxUpeDYQAu8c7S 2bQN2bSNXxpGTnVKpKXl2R 1FCueyFK8jtU0zmxQZyVtJ 0sMph7dbpLD4DlzEEfJlpX 5rW3anmLNKDA81nVJvW50H 0w71NjrPNzBsa6yO0of2CZ 76hmKWewz3vGnKLbY2nPRh 3BIyzKK2U5O4Ij19G9z51J 5OLQw1i9uk8Je39V0SJ2GR 6FAPlqbXTuXOPM1UmJj1X3 1kAJBuEhXnXHNA64DDO0Bq 2H5cbxbGjC00Zqe8IqKHm7 6wd1MrcFIjgblPkTvm0veJ 2BfTod61ST4H3K9jxPg9mp 4Uq8jQxsADt7piVcuwYgVJ 3z8VNabIASkrBxq94cP3TL 4c86vSmmzcIO4x21LuD7XM 6gqoJC9MUub1AbISMFCuWr 7s4SSLsUwBjEJzNVODbV8z 1zXA806qSJVWnHpGWQ3UUC 57E1gf3WclWxUuLcwYYyU4 33azw14HJcaClFGZ5kW6Nn 1izLAQzCTkTCTpu3l9TFzB 754UYs1LuDtaEKKfaDkx7Y 6sNMSl0MAqzvlGEt4Y072v 4aAZVfU1M4cm7XqTnzhCnr 28Val6Yko2x2iJQ9YlG789 4RwLQseJrBm0Pjl6vQcY5D 4TZvXowrJenK3OCEbmJzUT 1I3iCPuCId7Vkg5rlqYDrp 7hWa53fOj9Fh0X790Bl32B 1JMkYhhLa7KPDd8i3sPGOL 355ezvqbe2QtgMf70xXBE6 0KlGGlCwuBw9cPcjq7xjgf 5kwDBRZrCvDtN27XtT2wzA 7oMJTXLhm8TAkk6K3j8u1E 0ELWm49HJEJqIvqzTdZK3n 6VziOL8abdt5gchEEBCMRg 0XUHYxHOOctkSXReILAaJV 3wMVhcD7YbfOFqhgYiN9hp 30VCkYXm8pkZ1rOg5yC4LL 1NE1ljBeJzmk6wZZ4uUdRT 6FWhcFQApH24r8AgaOLrFw 5z4mf1xZt0z0u89ntbWN5z 05Tz6QuSWq66WaqpHGK6iw 6xq7BAoiGiXC27rW6RH3ww 47AJA4geNelnpulvvfZjdn 0BOhco72YhbPpJIqDEZNmA 1ciJCLzKzezhHbBtii28UD 63IkPNf3Z4xHLASIyhxS1R 0BNWj55u3tfVB3hozoC5lY 55FD4r3EgXRMKP79hDbt5y 3SatXFFuUyX2IlV9JbaWp2 0L4u2qg18ieitQkA2HBXgq 5OmUVlZP8zQ5zGCX9wsD3p 38ueylzenb5JK5JHDGnWuO 7FLUgR5esAR2m8kl6CSQ32 7KOOHzDAxzl87i8VYk1iO2 47jAQrNH7CLIcYu1lqE7pZ 7ve96Lk22N2ZGVqVq8EJOf 6F6MrtUbHqf7AASOXDMlMp 78E3QFSTlLijRUrukdbXK8 5wMlr2ncg0SoPOKEs0Pc85 0rfSwqjq0k20rVZLzATVwP 0PYPlbP5Vdz5ivIfC0jAmf 4UWkS1obHdt123rtx5v9cx 5RpMFAJcf116DGFBcK5Ny8 6i4o7jn033PDiNab3Yc3jY 6FCWOKBTjzHsHpa0cF0br6 2b3Xo30P9KFEqBvsTRQTM6 1b903k5gadxEFXhbGHAoWD 5tA3oQh58iYSdJWhSw0yJV 4f01YssEopYUrYIO6YZmjZ 3960gvUO5yuDJtI6VtPqYS 7fc3kOECAsJoCbsV2p64rt 3CboU4vdisSItbjfbx6SqO 745VS3h8id3zcLh7Gd6gGa 5JQlQR9REVJmP34AqI7Tpc 5K4LPGFKqKO7YSbUdSQAZH 18vjAkuAMaSxfAf2EAcjP5 7is6wEBQ4zPEcjust2rB7u 1PxJV79Px9gFHPLvFO9ZOS 7cgt4TZJH3HDdmHQhfVmzx 3bl6n1sBma0Lp7etqjx5j6 76rLK2XhT6waumcLkLNTID '''.split(' ')
to_be_parallel_coordinated = df.query('track_id == @id_numbers')
len(to_be_parallel_coordinated)
px.parallel_coordinates(to_be_parallel_coordinated, template="plotly_dark")
id_numbers = ''' 6eZ4ivJPxbK7I6QToXVPTU 6V37apVtCiUpEKcAUyUjoA 5SxlhL1idBgsfYBfR1KEcR 0C0XJ2JYr9jEGAt89JyZqJ 1XsqZ0mMrIRMAktdnEuFF8 5SUMNsXNVtR4ujz84sWEWe 1xfTdLDg10CJfhcR4Yis0z 5zHgA4J4CrOaUvQ9UD219j 1XO9zgpDMkwhmAijuYBCxb 1U6vwXAvc7VvbhqNyedGEG 2T9ZyRnW6omzsVDLo4I72l 0UBDke5y1kqTgTkgmyHiwj 23tftAc7uJnxEfy5AGS9lr 0n2gtAOGT6Pxu5cEeaugym 0nqRtO4jdv4K6AJ7hYmDW6 2wsVeO1Hqx6IqM48UXGWSO 7mmqxoKWTFZB8tHXfQpmk4 336ihMIODpi6nlL1ytSEm6 4w2lb0V0qHGwj1GR2f52c5 7cKSdtwLEayFd8MuLdZR85 44q1XQgawoP50HHMiMMWCq 4iPaNKCg8kY3rwUK3CnUw3 5EvsUz8wsUh0dP7HaixMh8 6A1prRyHlB113go9En4cX7 7iylYXaOUTO3BixPecSjhP 52pvmjSRaV7k0TCqJK5sKn 5ATIMj2gOKsj06UvoTkFxe 6Isu6pTUwBa3ftiyOpKf7s 6lajHnTKM9Fiv10kzUpD90 37VDfyF70jTo1HqGQOsrRR 3RYMOo7YF9gCkVZomhOPrK 1ZIQ5girZEdA70xIkevkrt 76C7vN5uEcuF1BXvUJMvjk 3v8Zu57HCIauve733J6PjR 0KfjaQSlDL0r7dLaXNDMv5 7sRTfvTV5EUhDY4e4LjlVS 5wI6LhywYSgmHNMVERAJpe 4K0hPQgmWzx4jGM2Q4tNQN 0WmyLH7XemypvsAHuIOCp7 2YbZbmqqxrCysQDc4AkIIX 1UegIYDIgDicEBuHhWY026 3gdHLVZqeU2mHNggC6Tzwr 1uYAog8LWWeVnqNWItZaHc 4LpsUDYp9D7VvzU0iRTCq3 2akKNicOhUSp1QHQEQDTbC 4zHo8J0WbUDDiHTAURs6kO 32Q6wqR85WhBeoqZwMRwnV 5iofFSJRoRDyiKD4kWTpf9 7owI1qTHoXGBVznJod7yuh 6rbiT8DV9h50NBjPxkDygF 5twkCu1ET6objhnLfQtgJQ 7gGLo0dwMbJhRy0JVJP00p 2ZWv2tklegv3gwKeLD35o9 7sLsIr2vhjYeR6rniJj5dj 5IOozjD7gJOOhTV1lDXrXl 2cC2PIXKFjnY8sbuS8spzw 4PHM9PG5J6IQ8fumsJuSYJ 0WcGdMWl75v33B27KafycK 6K4pZ32MorbsHeqtAwaWHW 0h0jNccol3eyMQ2mIcNcBp 2MfFjRh4gv4lU0vtYH0GaZ 3uEFKAtU1hdfcgFC60yt84 0slfqpTh3q10bNfAYb73RS 7dg0pRcn7R5VVekBryq583 082bDyzPxizG0gIqArJoQ7 73OC95krAM3n1u2LcKraBX 3qpm5w0qS99qUN0q8MzvlL 1NywSw2TUrdnpnNtGu8KL8 1zSqLFmuL6mDCVbZNj7hTR 7kPsDSN7eFLbzNF0xEchjc 2qw3xeuKWfsV8GynO2peHr 6tEeqhvdmOVU2iQqnLk2zg 5K7VRObcsBDfKnyVbVhwTx 78WeKIDpoVu6r0TziQwl3y 4ZYir67KzcmiNKTmFVqNf8 22BJjJeknJ7ff8vGGzPB98 0b81xIMQLSdUpeGv1oStXH 4u00iLhEPkbLlclQDYuIHV 1p8QusGejMBctlhsZ3jtSF 2FzI0rp4FsSvx7N1GFs4HB 1XKqzLGxhIcpEXv8SoA8tu 6T3yaivZB0v5AODCyaR67G 4WOPKEtVmSAZvWXtyApl3h 3xvtJJiFdTR6d5N8PaFb8f 4ZAjZHxvrzKZMXdHmg0DFz 3ekvh2GPv2ebjPHYKhuIXG 0bv1k0dLjgp9f9rj5dBScM 1MQio3srmAmDC0c32Xh56A 0BZ7rkI4prRAbfkO3jo2OB 5Vu5DPFMNAJc0eoq7i8skM 1zE9o1WK0Vpocnf1H5nssQ 3zdIn3IbbJAddtf9Qo6i0D 3huj9hX9ECvhipWIGNObFl 1rFMpIUb6Hs66ypS32MOOb 1Qmb5p0mK08hxMjWJvCfBw 3C6fiBrM14YAynsEeRZXWv 4t8WpwzDLTYwMulJBavljv 7vqMKsg985FFLyK5DN9uq1 5yqoXxgDIQ9fPOcSAQUjUq 2D0FmjFP7dxrin4XanSnbo 4Yuux4zVxXI0KVHil24U9L 5MzGtEojUtMsLueJ55hRn3 2RDFWx08YULhklhS0DyVtj 4yEdofTvNsL7PnBJNDN1Sf 4n9SsVwbc7Y4tn5UfPTNn4 29ldunhjkUfuB5k1gXlqFS 6VFAILGN7uOz24elIyt4vB 2361cLjSnEpolPC3Mb0yv1 0T19N334CPKgpMpxh36KiE 3RjuP7n7x8DaOVN62TXFke 3V5LrENP5AgplQwvGeTIIU 4SNbrw7KNj3rupRnXzV31d 5XdtGPF22knBwy1fAzjSCK 3GE6KLTgmCxsNzhp0nI3Zf 75iGW6GTfBU7j6ldQNAvu4 1FvxqWCDg1xYdg0eXOr9FU 3NmVag0g3N0B4nDT0ypVk4 07jMNENLpJ60ej30L1BFPD 4KVybsvg26UiPJEVynN3qE 4k304lkj8Ga9Kp0p82cii2 1HVwhAQMU71rg7GVlQVxNz 6nYTfmQEE9ZYYFzdLRWP8Z 5QdTBAXXaFZDhsBqPT0GBI 3QElxQCbZjCqAG8yLRwLsm 5yvF3kvaX2ufVt3VvWbGP2 52uwpMhSoReK5wQ3Yxr2eC 1awdo11NQFC6THLXQAaDjV 6n6Wrf6HRSgTXwyWugKDwf 5MXF8IhBY1z63VZVRvFZUK 6NjMv3rcXwyQg4Dtr3WpoE 0JsAUsmagEqYQo8FZUkpBE 36Kumm8Qj49ABflKCvltIH 078Sr3upDQIPRIAc2IpSxy 2wJdo21bsx5HfTnwPJ3p92 0WWk0UiErQiR8EAnSjll1o 1Fs2986kJPeJR94vCqRGha 5eImJYwPyrdhUqZ4gTO6Qs 6bXr647nkFkrphCoA3L2KK 1counClRuzpBxsb8gkTCmO 7yCtrkXdQEVJQyk7pFxGyq 4sGN5db8sJsecYNWoxLPky 4EbVxLV394SADIDf5zFTHY 0tZvlW8YxwnPS7Ui7pzF9q 69LAIJUcPbsw6G8F1vCv1y 4wzeevLrnqs87z6FrcFNKu 2fKvOnZPwh4gz24MjM5hWp 3Hbl4FnRkj8TK88Jg37Omt 2mSHfW689yTYIZCu0k1Frb 00MLppbVubwv4Rbf46CCfg 1MvhXhNkwRJDH94ZloFU4c 7oM8U222NuBLUun8aFjhKu 2veD2T9UElKuePBt6FW4nO 4Bulfi18OkBRXehhVg1SzI 6M9bTZutc2QtXWl2p5TQ1I 4fM8cupzQbc6qNeDK9FXu3 7xktbw9wyJyJbwS3y4LZFg 63PP8XGwgRI7gIruMO7IG3 3C0Kxh2lnOTmlSCD1rB15W 0YFoUawskWM6iKHSyQgeNZ 1HEzYfexDpgfwyceOWvNz8 2zKB5hjGfqoYZUi7B3LAK0 3mEnnPSXvKoVouByyUqhUX 0dC2glrlKpld5xY5BAX9lK 0XXvMZGbrz60taMwPbVGgK 2y2xE0gB5lVIGbdAnHNUIz 6Ech2zanuCQ2ihfXDOLtID 6rEcPr1jbReCGcT7LD2cB1 0gn77iNwUHN2pScHbqttN8 5NH0w0LSvcjiMjWnTwhm2u 19HDqVwakevUkynlB1Ztut 0g5kny7FqZlnS1bGMPQFWR 02PBxJsA9YIhdbiXMNN9Cd 0tpRok1p8ooccX7DQqy1BZ 1P5uhYSYMDxXpcYgpMYnkg 3UTt7dSBf9MG6833z9gNUV 0Si0HsULu8gFAtYm0BwqXI 4sO0deplZf1WJnXwrEVNUt 1fTuKuiLtYmckVKwtoT812 0hMOYGKQK3m2ipKTZKUbrI 6nsyzCRGHluwU3QIDSQr6d 5y3HyzqdypXCRFz2V8OpOF 0mPvAhvAA0IyrcbUh9KEQv 3n5N1ECcHzZDvAzHLpJULT 5Wo8dHK8N9pMyDdXI4WWsZ 7KvGuebu3RAtH0FSY8RG6l 6XEfmMikJLYbYZ3ZL4l7yK 5ijg8Z5M9WNI2VLXDaxrAz 0FGiZTL9LSSzdO05Vtgg9U 1tYLrptJ56VWore4o9Mj50 4EI3t79hsPIQJLdHitvB2A 0uwIsRVkvzZTzxqCQHlgiz 4dM9Vju1O76L2V79EebLsj 20XscF3HtxEGo8ghFhOgCx 0QPSeBG4P39z9KOihZARLf 7wbsdw0VnVe421V68sNwDk 75nO71NiNoIaGVIqYTqSvN 6Jk8VFFPoUyr7zCXIGcUQS 1UdTsJcI4MwzKIxCP5HHXG 53oWCQ8bcFSFzcQd0Xggl8 4iFYF17QReVxN6bQoKE4NM 4uAg8KXLiGu0kIvICmdUR0 '''.split(' ')
to_be_parallel_coordinated = df.query('track_id == @id_numbers')
len(to_be_parallel_coordinated)
px.parallel_coordinates(to_be_parallel_coordinated, template="plotly_dark")
fig = px.line_polar(df.sample(n=1000, random_state=42), theta = 'tempo',
color_discrete_sequence=px.colors.sequential.Plasma[-2::-1],
template="plotly_dark")
fig.show()
# Make a PCA like the one I did on the Iris, but make it 2d and 3d because that's cool
pd.set_option('display.max_columns', None)
nearest_neighbors_df.iloc[[69000]]
```
| true |
code
| 0.471649 | null | null | null | null |
|
# Regresión con Redes Neuronales
Empleando diferentes *funciones de pérdida* y *funciones de activación* las **redes neuronales** pueden resolver
efectivamente problemas de **regresión.**
En esta libreta se estudia el ejemplo de [California Housing](http://www.spatial-statistics.com/pace_manuscripts/spletters_ms_dir/statistics_prob_lets/html/ms_sp_lets1.html)
donde el propósito es predecir el valor medio de una casa según 8 atributos.
## Descripción general del conjunto de datos
El conjunto de datos `California Housing` está hecho de 9 variables numéricas, donde 8 son las *características* y 1 es la variable objetivo.
Este conjunto de datos fue creado en 1990 basándose en el censo poblacional realizado por el gobierno de EUA. La estructura del conjunto de datos
es simple: cada línea en el archivo de datos cuenta por un **bloque** poblacional que consta de entre 600 y 3000 personas. Por cada *bloque*
se tienen 8 características de cada casa y su costo medio.
Empleando *redes neuronales* se pretende predecir el costo de las casas por bloque.
## Atributos del conjunto de datos
Este conjunto de datos cuenta con 8 *atributos*, descritos a continuación, con la etiqueta como viene en el conjunto de datos de `scikit-learn`:
- **MedInc**, *Ingresos promedio por bloque*
- **HouseAge**, *Antigüedad promedio por casa en el bloque*
- **AveRooms**, *Número promedio de cuartos por casa en el bloque*
- **AveBedrms**, *Número promedio de recámaras por casa en el bloque*
- **Population**, *Población total del bloque*
- **AveOccup**, *Ocupancia promedio por casa en el bloque*
- **Latitude**, *Latitud del bloque*
- **Longitude**, *Longitud del bloque*
Y la *variable respuesta* es:
- **MedValue**, *Costo promedio por casa en el distrito*
```
import tensorflow as tf
from sklearn import datasets, metrics, model_selection, preprocessing
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
# Importar el conjunto de datos California Housing
cali_data = datasets.fetch_california_housing()
```
## Visualización de datos
```
# Realizar una visualización general de la relación entre atributos del conjunto de datos
sns.pairplot(pd.DataFrame(cali_data.data, columns=cali_data.feature_names))
plt.show()
```
Con estas figuras se pueden observar algunas características interesantes:
- *Primero*, todas las variables importan en el modelo. Esto significa que el modelo de regresión viene pesado por todas las
características y se requiere que el modelo sea *robusto* ante esta situación.
- *Segundo*, hay algunas características que tienen relación *lineal* entre ellas, como lo es **AveRooms** y **AveBedrms**.
Esto puede ayudar a discriminar ciertas características que no tienen mucho peso sobre el modelo y solamente utilizar
aquellas que influyen mucho más. A esta parte del *procesamiento de datos* se le conoce como **selección de características**
y es una rama específica de la *inteligencia computacional.*
- *Tercero*, la línea diagonal muestra la relación *distribución* de cada una de las características. Esto es algo importante
de estudiar dado que algunas características muestran *distribuciones* conocidas y este hecho se puede utilizar para
emplear técnicas estadísticas más avanzadas en el **análisis de regresión.**
Sin embargo, en toda esta libreta se dejarán las 8 características para que sean pesadas en el modelo final.
```
# Separar todos los datos y estandarizarlos
X = cali_data.data
y = cali_data.target
# Crear el transformador para estandarización
std = preprocessing.StandardScaler()
X = std.fit_transform(X)
X = np.array(X).astype(np.float32)
y = std.fit_transform(y.reshape(-1, 1))
y = np.array(y).astype(np.float32)
```
Dado que los datos vienen en diferentes unidades y escalas, siempre se debe estandarizar los datos de alguna forma. En particular
en esta libreta se emplea la normalización de los datos, haciendo que tengan *media* $\mu = 0$ y *desviación estándar* $\sigma = 1$.
```
# Separar en conjunto de entrenamiento y prueba
x_train, x_test, y_train, y_test = model_selection.train_test_split(
X, y, test_size=0.2, random_state=49
)
# Definir parámetros generales de la Red Neuronal
pasos_entrenamiento = 1000
tam_lote = 30
ratio_aprendizaje = 0.01
```
## Estructura o *topología* de la red neuronal
Para esta regresión se pretende utilizar una *red neuronal* de **dos capas ocultas**, con *funciones de activación* **ReLU**,
la **primera** capa oculta cuenta con 25 neuronas mientras que la **segunda** cuenta con 50.
La **capa de salida** *no* tiene función de activación, por lo que el modelo lineal queda de la siguiente forma
$$ \hat{y}(x) = \sum_{i=1}^{8} \alpha_i \cdot x_i + \beta_i$$
donde $\alpha_i$ son los *pesos* de la *capa de salida*, mientras que $\beta_i$ son los *sesgos*.
```
# Parámetros para la estructura general de la red
# Número de neuronas por capa
n_capa_oculta_1 = 25
n_capa_oculta_2 = 50
n_entrada = X.shape[1]
n_salida = 1
# Definir las entradas de la red neuronal
x_entrada = tf.placeholder(tf.float32, shape=[None, n_entrada])
y_entrada = tf.placeholder(tf.float32, shape=[None, n_salida])
# Diccionario de pesos
pesos = {
"o1": tf.Variable(tf.random_normal([n_entrada, n_capa_oculta_1])),
"o2": tf.Variable(tf.random_normal([n_capa_oculta_1, n_capa_oculta_2])),
"salida": tf.Variable(tf.random_normal([n_capa_oculta_2, n_salida])),
}
# Diccionario de sesgos
sesgos = {
"b1": tf.Variable(tf.random_normal([n_capa_oculta_1])),
"b2": tf.Variable(tf.random_normal([n_capa_oculta_2])),
"salida": tf.Variable(tf.random_normal([n_salida])),
}
def propagacion_adelante(x):
# Capa oculta 1
# Esto es la mismo que Ax + b, un modelo lineal
capa_1 = tf.add(tf.matmul(x, pesos["o1"]), sesgos["b1"])
# ReLU como función de activación
capa_1 = tf.nn.relu(capa_1)
# Capa oculta 1
# Esto es la mismo que Ax + b, un modelo lineal
capa_2 = tf.add(tf.matmul(capa_1, pesos["o2"]), sesgos["b2"])
# ReLU como función de activación
capa_2 = tf.nn.relu(capa_2)
# Capa de salida
# Nuevamente, un modelo lineal
capa_salida = tf.add(tf.matmul(capa_2, pesos["salida"]), sesgos["salida"])
return capa_salida
# Implementar el modelo y sus capas
y_prediccion = propagacion_adelante(x_entrada)
```
## Función de pérdida
Para la función de pérdida se emplea la [función de Huber](https://en.wikipedia.org/wiki/Huber_loss) definida como
\begin{equation}
L_{\delta} \left( y, f(x) \right) =
\begin{cases}
\frac{1}{2} \left( y - f(x) \right)^2 & \text{para} \vert y - f(x) \vert \leq \delta, \\
\delta \vert y - f(x) \vert - \frac{1}{2} \delta^2 & \text{en cualquier otro caso.}
\end{cases}
\end{equation}
Esta función es [robusta](https://en.wikipedia.org/wiki/Robust_regression) lo cual está hecha para erradicar el peso de posibles
valores atípicos y puede encontrar la verdadera relación entre las características sin tener que recurrir a metodologías paramétricas
y no paramétricas.
## Nota
Es importante mencionar que el valor de $\delta$ en la función de Huber es un **hiperparámetro** que debe de ser ajustado mediante *validación cruzada*
pero no es realiza en esta libreta por limitaciones de equipo y rendimiento en la ejecución de esta libreta.
```
# Definir la función de costo
f_costo = tf.reduce_mean(tf.losses.huber_loss(y_entrada, y_prediccion, delta=2.0))
# f_costo = tf.reduce_mean(tf.square(y_entrada - y_prediccion))
optimizador = tf.train.AdamOptimizer(learning_rate=ratio_aprendizaje).minimize(f_costo)
# Primero, inicializar las variables
init = tf.global_variables_initializer()
# Función para evaluar la precisión de clasificación
def precision(prediccion, real):
return tf.sqrt(tf.losses.mean_squared_error(real, prediccion))
```
## Precisión del modelo
Para evaluar la precisión del modelo se emplea la función [RMSE](https://en.wikipedia.org/wiki/Root-mean-square_deviation) (Root Mean Squared Error)
definida por la siguiente función:
$$ RMSE = \sqrt{\frac{\sum_{i=1}^{N} \left( \hat{y}_i - y_i \right)^2}{N}} $$
Para crear un mejor estimado, se empleará validación cruzada de 5 pliegues.
```
# Crear el plegador para el conjunto de datos
kf = model_selection.KFold(n_splits=5)
kf_val_score_train = []
kf_val_score_test = []
# Crear un grafo de computación
with tf.Session() as sess:
# Inicializar las variables
sess.run(init)
for tr_idx, ts_idx in kf.split(x_train):
# Comenzar los pasos de entrenamiento
# solamente con el conjunto de datos de entrenamiento
for p in range(pasos_entrenamiento):
# Minimizar la función de costo
minimizacion = sess.run(
optimizador,
feed_dict={x_entrada: x_train[tr_idx], y_entrada: y_train[tr_idx]},
)
# Cada tamaño de lote, calcular la precisión del modelo
if p % tam_lote == 0:
prec_entrenamiento = sess.run(
precision(y_prediccion, y_entrada),
feed_dict={x_entrada: x_train[tr_idx], y_entrada: y_train[tr_idx]},
)
kf_val_score_train.append(prec_entrenamiento)
prec_prueba = sess.run(
precision(y_prediccion, y_entrada),
feed_dict={x_entrada: x_train[ts_idx], y_entrada: y_train[ts_idx]},
)
kf_val_score_test.append(prec_prueba)
# Prediccion final, una vez entrenado el modelo
pred_final = sess.run(
precision(y_prediccion, y_entrada),
feed_dict={x_entrada: x_test, y_entrada: y_test},
)
pred_report = sess.run(y_prediccion, feed_dict={x_entrada: x_test})
print("Precisión final: {0}".format(pred_final))
print("Precisión RMSE para entrenamiento: {0}".format(np.mean(kf_val_score_train)))
print("Precisión RMSE para entrenamiento: {0}".format(np.mean(kf_val_score_test)))
```
Aquí se muestra el valor de *RMSE* final para cada parte, entrenamiento y prueba. Se puede observar que hay muy poco sobreajuste,
y si se quisiera corregir se puede realizar aumentando el número de neuronas, de capas, cambiando las funciones de activación,
entre muchas otras cosas.
| true |
code
| 0.483222 | null | null | null | null |
|
## Fish classification
In this notebook the fish classification is done. We are going to classify in four classes: Tuna fish (TUNA), LAG, DOL and SHARK. The detector will save the cropped image of a fish. Here we will take this image and we will use a CNN to classify it.
In the original Kaggle competition there are six classes of fish: ALB, BET, YFT, DOL, LAG and SHARK. We started trying to classify them all, but three of them are vey similar: ALB, BET and YFT. In fact, they are all different tuna species, while the other fishes come from different families. Therefore, the classification of those species was difficult and the results were not too good. We will make a small comparison of both on the presentation, but here we will only upload the clsifier with four classes.
```
from PIL import Image
import tensorflow as tf
import numpy as np
import scipy
import os
import cv2
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import log_loss
from keras.utils import np_utils
from keras.models import Sequential
from keras.layers.convolutional import Convolution2D
from keras.layers.convolutional import MaxPooling2D
from keras.layers.core import Activation
from keras.layers.core import Flatten
from keras.layers.core import Dense
from keras.layers.core import Dropout
from keras import backend as K
import matplotlib.pyplot as plt
#Define some values and constants
fish_classes = ['TUNA','DOL','SHARK','LAG']
fish_classes_test = fish_classes
number_classes = len(fish_classes)
main_path_train = '../train_cut_oversample'
main_path_test = '../test'
channels = 3
ROWS_RESIZE = 100
COLS_RESIZE = 100
```
Now we read the data from the file where the fish detection part has stored the images.
We also preprocess slightly the images to convert them to the same size (100x100). The aspect ratio of the images is important, so instead of just resizing the image, we have created the function resize(im). This function takes an image and resizes its longest side to 100, keeping the aspect ratio. In other words, the short side of the image will be smaller than 100 poixels. This image is pasted onto the middle of a white layer that is 100x100. So, our image will have white pixels on two of its sides. This is not optimum, but it is still better than changing the aspect ratio. We have also tried with other colors, but the best results were achieved with white.
```
# Get data and preproccess it
def resize(image):
rows = image.shape[0]
cols = image.shape[1]
dominant = max(rows,cols)
ratio = ROWS_RESIZE/float(dominant)
im_res = scipy.misc.imresize(image,ratio)
rows = im_res.shape[0]
cols = im_res.shape[1]
im_res = Image.fromarray(im_res)
layer = Image.new('RGB',[ROWS_RESIZE,COLS_RESIZE],(255,255,255))
if rows > cols:
layer.paste(im_res,(COLS_RESIZE/2-cols/2,0))
if cols > rows:
layer.paste(im_res,(0,ROWS_RESIZE/2-rows/2))
if rows == cols:
layer.paste(im_res,(0,0))
return np.array(layer)
X_train = []
y_labels = []
for classes in fish_classes:
path_class = os.path.join(main_path_train,classes)
y_class = np.tile(classes,len(os.listdir(path_class)))
y_labels.extend(y_class)
for image in os.listdir(path_class):
path = os.path.join(path_class,image)
im = scipy.misc.imread(path)
im = resize(im)
X_train.append(np.array(im))
X_train = np.array(X_train)
# Convert labels into one hot vectors
y_labels = LabelEncoder().fit_transform(y_labels)
y_train = np_utils.to_categorical(y_labels)
X_test = []
y_test = []
for classes in fish_classes_test:
path_class = os.path.join(main_path_test,classes)
y_class = np.tile(classes,len(os.listdir(path_class)))
y_test.extend(y_class)
for image in os.listdir(path_class):
path = os.path.join(path_class,image)
im = scipy.misc.imread(path)
im = resize(im)
X_test.append(np.array(im))
X_test = np.array(X_test)
# Convert labels into one hot vectors
y_test = LabelEncoder().fit_transform(y_test)
y_test = np_utils.to_categorical(y_test)
X_train = np.reshape(X_train,(X_train.shape[0],ROWS_RESIZE,COLS_RESIZE,channels))
X_test = np.reshape(X_test,(X_test.shape[0],ROWS_RESIZE,COLS_RESIZE,channels))
print('X_train shape: ',X_train.shape)
print('y_train shape: ',y_train.shape)
print('X_test shape: ',X_test.shape)
print('y_test shape: ',y_test.shape)
```
The data is now organized in the following way:
-The training has been done with 23581 images of size 100x100x3 (rgb).
-There are 4 possible classes: LAG, SHARK, DOL and TUNA.
-The test has been done with 400 images of the same size, 100 per class.
We are now ready to build and train the classifier. Th CNN has 7 convolutional layers, 4 pooling layers and three fully connected layers at the end. Dropout has been used in the fully connected layers to avoid overfitting. The loss function used is multi class logloss because is the one used by Kaggle in the competition. The optimizeer is gradient descent.
```
def center_normalize(x):
return (x-K.mean(x))/K.std(x)
# Convolutional net
model = Sequential()
model.add(Activation(activation=center_normalize,input_shape=(ROWS_RESIZE,COLS_RESIZE,channels)))
model.add(Convolution2D(6,20,20,border_mode='same',activation='relu',dim_ordering='tf'))
model.add(MaxPooling2D(pool_size=(2,2),dim_ordering='tf'))
model.add(Convolution2D(12,10,10,border_mode='same',activation='relu',dim_ordering='tf'))
model.add(Convolution2D(12,10,10,border_mode='same',activation='relu',dim_ordering='tf'))
model.add(MaxPooling2D(pool_size=(2,2),dim_ordering='tf'))
model.add(Convolution2D(24,5,5,border_mode='same',activation='relu',dim_ordering='tf'))
model.add(Convolution2D(24,5,5,border_mode='same',activation='relu',dim_ordering='tf'))
model.add(MaxPooling2D(pool_size=(2,2),dim_ordering='tf'))
model.add(Convolution2D(24,5,5,border_mode='same',activation='relu',dim_ordering='tf'))
model.add(Convolution2D(24,5,5,border_mode='same',activation='relu',dim_ordering='tf'))
model.add(MaxPooling2D(pool_size=(2,2),dim_ordering='tf'))
model.add(Flatten())
model.add(Dense(4092,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1024,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(number_classes))
model.add(Activation('softmax'))
print(model.summary())
model.compile(optimizer='sgd',loss='categorical_crossentropy',metrics=['accuracy'])
model.fit(X_train,y_train,nb_epoch=1,verbose=1)
```
Since there are a lot of images the training takes around one hour. Once it is done we can pass the test set to the classifier and measure its accuracy.
```
(loss,accuracy) = model.evaluate(X_test,y_test,verbose=1)
print('accuracy',accuracy)
```
| true |
code
| 0.560493 | null | null | null | null |
|
# WGAN with MNIST (or Fashion MNIST)
* `Wasserstein GAN`, [arXiv:1701.07875](https://arxiv.org/abs/1701.07875)
* Martin Arjovsky, Soumith Chintala, and L ́eon Bottou
* This code is available to tensorflow version 2.0
* Implemented by [`tf.keras.layers`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/layers) [`tf.losses`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/losses)
* Use `transposed_conv2d` and `conv2d` for Generator and Discriminator, respectively.
* I do not use `dense` layer for model architecture consistency. (So my architecture is different from original dcgan structure)
* based on DCGAN model
## Import modules
```
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
from __future__ import unicode_literals
import os
import sys
import time
import glob
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import PIL
import imageio
from IPython import display
import tensorflow as tf
from tensorflow.keras import layers
sys.path.append(os.path.dirname(os.path.abspath('.')))
from utils.image_utils import *
from utils.ops import *
os.environ["CUDA_VISIBLE_DEVICES"]="0"
```
## Setting hyperparameters
```
# Training Flags (hyperparameter configuration)
model_name = 'wgan'
train_dir = os.path.join('train', model_name, 'exp1')
dataset_name = 'mnist'
assert dataset_name in ['mnist', 'fashion_mnist']
max_epochs = 100
save_model_epochs = 10
print_steps = 200
save_images_epochs = 1
batch_size = 64
learning_rate_D = 5e-5
learning_rate_G = 5e-5
k = 5 # the number of step of learning D before learning G (Not used in this code)
num_examples_to_generate = 25
noise_dim = 100
clip_value = 0.01 # cliping value for D weights in order to implement `1-Lipshitz function`
```
## Load the MNIST dataset
```
# Load training and eval data from tf.keras
if dataset_name == 'mnist':
(train_images, train_labels), _ = \
tf.keras.datasets.mnist.load_data()
else:
(train_images, train_labels), _ = \
tf.keras.datasets.fashion_mnist.load_data()
train_images = train_images.reshape(-1, MNIST_SIZE, MNIST_SIZE, 1).astype('float32')
#train_images = train_images / 255. # Normalize the images to [0, 1]
train_images = (train_images - 127.5) / 127.5 # Normalize the images to [-1, 1]
```
## Set up dataset with `tf.data`
### create input pipeline with `tf.data.Dataset`
```
#tf.random.set_seed(219)
# for train
N = len(train_images)
train_dataset = tf.data.Dataset.from_tensor_slices(train_images)
train_dataset = train_dataset.shuffle(buffer_size=N)
train_dataset = train_dataset.batch(batch_size=batch_size, drop_remainder=True)
print(train_dataset)
```
## Create the generator and discriminator models
```
class Generator(tf.keras.Model):
"""Build a generator that maps latent space to real space.
G(z): z -> x
"""
def __init__(self):
super(Generator, self).__init__()
self.conv1 = ConvTranspose(256, 3, padding='valid')
self.conv2 = ConvTranspose(128, 3, padding='valid')
self.conv3 = ConvTranspose(64, 4)
self.conv4 = ConvTranspose(1, 4, apply_batchnorm=False, activation='tanh')
def call(self, inputs, training=True):
"""Run the model."""
# inputs: [1, 1, 100]
conv1 = self.conv1(inputs, training=training) # conv1: [3, 3, 256]
conv2 = self.conv2(conv1, training=training) # conv2: [7, 7, 128]
conv3 = self.conv3(conv2, training=training) # conv3: [14, 14, 64]
generated_images = self.conv4(conv3, training=training) # generated_images: [28, 28, 1]
return generated_images
class Discriminator(tf.keras.Model):
"""Build a discriminator that discriminate real image x whether real or fake.
D(x): x -> [0, 1]
"""
def __init__(self):
super(Discriminator, self).__init__()
self.conv1 = Conv(64, 4, 2, apply_batchnorm=False, activation='leaky_relu')
self.conv2 = Conv(128, 4, 2, activation='leaky_relu')
self.conv3 = Conv(256, 3, 2, padding='valid', activation='leaky_relu')
self.conv4 = Conv(1, 3, 1, padding='valid', apply_batchnorm=False, activation='none')
def call(self, inputs, training=True):
"""Run the model."""
# inputs: [28, 28, 1]
conv1 = self.conv1(inputs) # conv1: [14, 14, 64]
conv2 = self.conv2(conv1) # conv2: [7, 7, 128]
conv3 = self.conv3(conv2) # conv3: [3, 3, 256]
conv4 = self.conv4(conv3) # conv4: [1, 1, 1]
discriminator_logits = tf.squeeze(conv4, axis=[1, 2]) # discriminator_logits: [1,]
return discriminator_logits
generator = Generator()
discriminator = Discriminator()
```
### Plot generated image via generator network
```
noise = tf.random.normal([1, 1, 1, noise_dim])
generated_image = generator(noise, training=False)
plt.imshow(generated_image[0, :, :, 0], cmap='gray')
```
### Test discriminator network
* **CAUTION**: the outputs of discriminator is **logits** (unnormalized probability) NOT probabilites
```
decision = discriminator(generated_image)
print(decision)
```
## Define the loss functions and the optimizer
```
# use logits for consistency with previous code I made
# `tf.losses` and `tf.keras.losses` are the same API (alias)
bce = tf.losses.BinaryCrossentropy(from_logits=True)
mse = tf.losses.MeanSquaredError()
def WGANLoss(logits, is_real=True):
"""Computes Wasserstain GAN loss
Args:
logits (`2-rank Tensor`): logits
is_real (`bool`): boolean, Treu means `-` sign, False means `+` sign.
Returns:
loss (`0-rank Tensor`): the WGAN loss value.
"""
loss = tf.reduce_mean(logits)
if is_real:
loss = -loss
return loss
def GANLoss(logits, is_real=True, use_lsgan=True):
"""Computes standard GAN or LSGAN loss between `logits` and `labels`.
Args:
logits (`2-rank Tensor`): logits.
is_real (`bool`): True means `1` labeling, False means `0` labeling.
use_lsgan (`bool`): True means LSGAN loss, False means standard GAN loss.
Returns:
loss (`0-rank Tensor`): the standard GAN or LSGAN loss value. (binary_cross_entropy or mean_squared_error)
"""
if is_real:
labels = tf.ones_like(logits)
else:
labels = tf.zeros_like(logits)
if use_lsgan:
loss = mse(labels, tf.nn.sigmoid(logits))
else:
loss = bce(labels, logits)
return loss
def discriminator_loss(real_logits, fake_logits):
# losses of real with label "1"
real_loss = WGANLoss(logits=real_logits, is_real=True)
# losses of fake with label "0"
fake_loss = WGANLoss(logits=fake_logits, is_real=False)
return real_loss + fake_loss
def generator_loss(fake_logits):
# losses of Generator with label "1" that used to fool the Discriminator
return WGANLoss(logits=fake_logits, is_real=True)
discriminator_optimizer = tf.keras.optimizers.RMSprop(learning_rate_D)
generator_optimizer = tf.keras.optimizers.RMSprop(learning_rate_G)
```
## Checkpoints (Object-based saving)
```
checkpoint_dir = train_dir
if not tf.io.gfile.exists(checkpoint_dir):
tf.io.gfile.makedirs(checkpoint_dir)
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(generator_optimizer=generator_optimizer,
discriminator_optimizer=discriminator_optimizer,
generator=generator,
discriminator=discriminator)
```
## Training
```
# keeping the random vector constant for generation (prediction) so
# it will be easier to see the improvement of the gan.
# To visualize progress in the animated GIF
const_random_vector_for_saving = tf.random.uniform([num_examples_to_generate, 1, 1, noise_dim],
minval=-1.0, maxval=1.0)
```
### Define training one step function
```
# Notice the use of `tf.function`
# This annotation causes the function to be "compiled".
@tf.function
def discriminator_train_step(images):
# generating noise from a uniform distribution
noise = tf.random.uniform([batch_size, 1, 1, noise_dim], minval=-1.0, maxval=1.0)
with tf.GradientTape() as disc_tape:
generated_images = generator(noise, training=True)
real_logits = discriminator(images, training=True)
fake_logits = discriminator(generated_images, training=True)
gen_loss = generator_loss(fake_logits)
disc_loss = discriminator_loss(real_logits, fake_logits)
gradients_of_discriminator = disc_tape.gradient(disc_loss, discriminator.trainable_variables)
discriminator_optimizer.apply_gradients(zip(gradients_of_discriminator, discriminator.trainable_variables))
# clip the weights for discriminator to implement 1-Lipshitz function
for var in discriminator.trainable_variables:
var.assign(tf.clip_by_value(var, -clip_value, clip_value))
return gen_loss, disc_loss
# Notice the use of `tf.function`
# This annotation causes the function to be "compiled".
@tf.function
def generator_train_step():
# generating noise from a uniform distribution
noise = tf.random.uniform([batch_size, 1, 1, noise_dim], minval=-1.0, maxval=1.0)
with tf.GradientTape() as gen_tape:
generated_images = generator(noise, training=True)
fake_logits = discriminator(generated_images, training=True)
gen_loss = generator_loss(fake_logits)
gradients_of_generator = gen_tape.gradient(gen_loss, generator.trainable_variables)
generator_optimizer.apply_gradients(zip(gradients_of_generator, generator.trainable_variables))
```
### Train full steps
```
print('Start Training.')
num_batches_per_epoch = int(N / batch_size)
global_step = tf.Variable(0, trainable=False)
num_learning_critic = 0
for epoch in range(max_epochs):
for step, images in enumerate(train_dataset):
start_time = time.time()
if num_learning_critic < k:
gen_loss, disc_loss = discriminator_train_step(images)
num_learning_critic += 1
global_step.assign_add(1)
else:
generator_train_step()
num_learning_critic = 0
if global_step.numpy() % print_steps == 0:
epochs = epoch + step / float(num_batches_per_epoch)
duration = time.time() - start_time
examples_per_sec = batch_size / float(duration)
display.clear_output(wait=True)
print("Epochs: {:.2f} global_step: {} Wasserstein distance: {:.3g} loss_G: {:.3g} ({:.2f} examples/sec; {:.3f} sec/batch)".format(
epochs, global_step.numpy(), -disc_loss, gen_loss, examples_per_sec, duration))
random_vector_for_sampling = tf.random.uniform([num_examples_to_generate, 1, 1, noise_dim],
minval=-1.0, maxval=1.0)
sample_images = generator(random_vector_for_sampling, training=False)
print_or_save_sample_images(sample_images.numpy(), num_examples_to_generate)
if (epoch + 1) % save_images_epochs == 0:
display.clear_output(wait=True)
print("This images are saved at {} epoch".format(epoch+1))
sample_images = generator(const_random_vector_for_saving, training=False)
print_or_save_sample_images(sample_images.numpy(), num_examples_to_generate,
is_square=True, is_save=True, epoch=epoch+1,
checkpoint_dir=checkpoint_dir)
# saving (checkpoint) the model every save_epochs
if (epoch + 1) % save_model_epochs == 0:
checkpoint.save(file_prefix=checkpoint_prefix)
print('Training Done.')
# generating after the final epoch
display.clear_output(wait=True)
sample_images = generator(const_random_vector_for_saving, training=False)
print_or_save_sample_images(sample_images.numpy(), num_examples_to_generate,
is_square=True, is_save=True, epoch=epoch+1,
checkpoint_dir=checkpoint_dir)
```
## Restore the latest checkpoint
```
# restoring the latest checkpoint in checkpoint_dir
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
```
## Display an image using the epoch number
```
display_image(max_epochs, checkpoint_dir=checkpoint_dir)
```
## Generate a GIF of all the saved images.
```
filename = model_name + '_' + dataset_name + '.gif'
generate_gif(filename, checkpoint_dir)
display.Image(filename=filename + '.png')
```
| true |
code
| 0.89449 | null | null | null | null |
|
```
from keras.models import Sequential
from keras.layers import Dense
from keras.callbacks import TensorBoard
from keras.layers import *
import numpy
from sklearn.model_selection import train_test_split
#ignoring the first row (header)
# and the first column (unique experiment id, which I'm not using here)
dataset = numpy.loadtxt("/results/shadow_robot_dataset.csv", skiprows=1, usecols=range(1,30), delimiter=",")
```
# Loading the data
Each row of my dataset contains the following:
|0 | 1|2|3|4|5|6|7|8|9|10|11|12|13|14|15|16|17|18|19|20|21|22|23|24|25|26|27|28|29|
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
| experiment_number | robustness| H1_F1J2_pos | H1_F1J2_vel | H1_F1J2_effort | H1_F1J3_pos | H1_F1J3_vel | H1_F1J3_effort | H1_F1J1_pos | H1_F1J1_vel | H1_F1J1_effort | H1_F3J1_pos | H1_F3J1_vel | H1_F3J1_effort | H1_F3J2_pos | H1_F3J2_vel | H1_F3J2_effort | H1_F3J3_pos | H1_F3J3_vel | H1_F3J3_effort | H1_F2J1_pos | H1_F2J1_vel | H1_F2J1_effort | H1_F2J3_pos | H1_F2J3_vel | H1_F2J3_effort | H1_F2J2_pos | H1_F2J2_vel | H1_F2J2_effort | measurement_number|
My input vector contains the velocity and effort for each joint. I'm creating the vector `X` containing those below:
```
# Getting the header
header = ""
with open('/results/shadow_robot_dataset.csv', 'r') as f:
header = f.readline()
header = header.strip("\n").split(',')
header = [i.strip(" ") for i in header]
# only use velocity and effort, not position
saved_cols = []
for index,col in enumerate(header[1:]):
if ("vel" in col) or ("eff" in col):
saved_cols.append(index)
new_X = []
for x in dataset:
new_X.append([x[i] for i in saved_cols])
X = numpy.array(new_X)
```
My output vector is the predicted grasp robustness.
```
Y = dataset[:,0]
```
We are also splitting the dataset into a training set and a test set.
This gives us 4 sets:
* `X_train` associated to its `Y_train`
* `X_test` associated to its `Y_test`
We also discretize the output: 1 is a stable grasp and 0 is unstable. A grasp is considered stable if the robustness value is more than 100.
```
# fix random seed for reproducibility
# and splitting the dataset
seed = 7
numpy.random.seed(seed)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.20, random_state=seed)
# this is a sensible grasp threshold for stability
GOOD_GRASP_THRESHOLD = 50
# we're also storing the best and worst grasps of the test set to do some sanity checks on them
itemindex = numpy.where(Y_test>1.05*GOOD_GRASP_THRESHOLD)
best_grasps = X_test[itemindex[0]]
itemindex = numpy.where(Y_test<=0.95*GOOD_GRASP_THRESHOLD)
bad_grasps = X_test[itemindex[0]]
# discretizing the grasp quality for stable or unstable grasps
Y_train = numpy.array([int(i>GOOD_GRASP_THRESHOLD) for i in Y_train])
Y_train = numpy.reshape(Y_train, (Y_train.shape[0],))
Y_test = numpy.array([int(i>GOOD_GRASP_THRESHOLD) for i in Y_test])
Y_test = numpy.reshape(Y_test, (Y_test.shape[0],))
```
# Creating the model
I'm now creating a model to train. It's a very simple topology. Feel free to play with it and experiment with different model shapes.
```
# create model
model = Sequential()
model.add(Dense(20*len(X[0]), use_bias=True, input_dim=len(X[0]), activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1, activation='sigmoid'))
# Compile model
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
```
# Training the model
The model training should be relatively quick. To speed it up you can use a GPU :)
I'm using 80% of the data for training and 20% for validation.
```
model.fit(X_train, Y_train, validation_split=0.20, epochs=50,
batch_size=500000)
```
Now that the model is trained I'm saving it to be able to load it easily later on.
```
import h5py
model.save("./model.h5")
```
# Evaluating the model
First let's see how this model performs on the test set - which hasn't been used during the training phase.
```
scores = model.evaluate(X_test, Y_test)
print("\n%s: %.2f%%" % (model.metrics_names[1], scores[1]*100))
```
Now let's take a quick look at the good grasps we stored earlier. Are they correctly predicted as stable?
```
predictions = model.predict(best_grasps)
%matplotlib inline
import matplotlib.pyplot as plt
plt.hist(predictions,
color='#77D651',
alpha=0.5,
label='Good Grasps',
bins=np.arange(0.0, 1.0, 0.03))
plt.title('Histogram of grasp prediction')
plt.ylabel('Number of grasps')
plt.xlabel('Grasp quality prediction')
plt.legend(loc='upper right')
plt.show()
```
Most of the grasps are correctly predicted as stable (the grasp quality prediction is more than 0.5)! Looking good.
What about the unstable grasps?
```
predictions_bad_grasp = model.predict(bad_grasps)
# Plot a histogram of defender size
plt.hist(predictions_bad_grasp,
color='#D66751',
alpha=0.3,
label='Bad Grasps',
bins=np.arange(0.0, 1.0, 0.03))
plt.title('Histogram of grasp prediction')
plt.ylabel('Number of grasps')
plt.xlabel('Grasp quality prediction')
plt.legend(loc='upper right')
plt.show()
```
Most of the grasps are considered unstable - below 0.5 - with a few bad classification.
| true |
code
| 0.743178 | null | null | null | null |
|
# Gaussian Mixture Model
```
!pip install tqdm torchvision tensorboardX
from __future__ import print_function
import torch
import torch.utils.data
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
seed = 0
torch.manual_seed(seed)
if torch.cuda.is_available():
device = "cuda"
else:
device = "cpu"
```
### toy dataset
```
# https://angusturner.github.io/generative_models/2017/11/03/pytorch-gaussian-mixture-model.html
def sample(mu, var, nb_samples=500):
"""
Return a tensor of (nb_samples, features), sampled
from the parameterized gaussian.
:param mu: torch.Tensor of the means
:param var: torch.Tensor of variances (NOTE: zero covars.)
"""
out = []
for i in range(nb_samples):
out += [
torch.normal(mu, var.sqrt())
]
return torch.stack(out, dim=0)
# generate some clusters
cluster1 = sample(
torch.Tensor([1.5, 2.5]),
torch.Tensor([1.2, .8]),
nb_samples=150
)
cluster2 = sample(
torch.Tensor([7.5, 7.5]),
torch.Tensor([.75, .5]),
nb_samples=50
)
cluster3 = sample(
torch.Tensor([8, 1.5]),
torch.Tensor([.6, .8]),
nb_samples=100
)
def plot_2d_sample(sample_dict):
x = sample_dict["x"][:,0].data.numpy()
y = sample_dict["x"][:,1].data.numpy()
plt.plot(x, y, 'gx')
plt.show()
# create the dummy dataset, by combining the clusters.
samples = torch.cat([cluster1, cluster2, cluster3])
samples = (samples-samples.mean(dim=0)) / samples.std(dim=0)
samples_dict = {"x": samples}
plot_2d_sample(samples_dict)
```
## GMM
```
from pixyz.distributions import Normal, Categorical
from pixyz.distributions.mixture_distributions import MixtureModel
from pixyz.utils import print_latex
z_dim = 3 # the number of mixture
x_dim = 2
distributions = []
for i in range(z_dim):
loc = torch.randn(x_dim)
scale = torch.empty(x_dim).fill_(0.6)
distributions.append(Normal(loc=loc, scale=scale, var=["x"], name="p_%d" %i))
probs = torch.empty(z_dim).fill_(1. / z_dim)
prior = Categorical(probs=probs, var=["z"], name="p_{prior}")
p = MixtureModel(distributions=distributions, prior=prior)
print(p)
print_latex(p)
post = p.posterior()
print(post)
print_latex(post)
def get_density(N=200, x_range=(-5, 5), y_range=(-5, 5)):
x = np.linspace(*x_range, N)
y = np.linspace(*y_range, N)
x, y = np.meshgrid(x, y)
# get the design matrix
points = np.concatenate([x.reshape(-1, 1), y.reshape(-1, 1)], axis=1)
points = torch.from_numpy(points).float()
pdf = p.prob().eval({"x": points}).data.numpy().reshape([N, N])
return x, y, pdf
def plot_density_3d(x, y, loglike):
fig = plt.figure(figsize=(10, 10))
ax = fig.gca(projection='3d')
ax.plot_surface(x, y, loglike, rstride=3, cstride=3, linewidth=1, antialiased=True,
cmap=cm.inferno)
cset = ax.contourf(x, y, loglike, zdir='z', offset=-0.15, cmap=cm.inferno)
# adjust the limits, ticks and view angle
ax.set_zlim(-0.15,0.2)
ax.set_zticks(np.linspace(0,0.2,5))
ax.view_init(27, -21)
plt.show()
def plot_density_2d(x, y, pdf):
fig = plt.figure(figsize=(5, 5))
plt.plot(samples_dict["x"][:,0].data.numpy(), samples_dict["x"][:,1].data.numpy(), 'gx')
for d in distributions:
plt.scatter(d.loc[0,0], d.loc[0,1], c='r', marker='o')
cs = plt.contour(x, y, pdf, 10, colors='k', linewidths=2)
plt.show()
eps = 1e-6
min_scale = 1e-6
# plot_density_3d(*get_density())
plot_density_2d(*get_density())
print("Epoch: {}, log-likelihood: {}".format(0, p.log_prob().mean().eval(samples_dict)))
for epoch in range(20):
# E-step
posterior = post.prob().eval(samples_dict)
# M-step
N_k = posterior.sum(dim=1) # (n_mix,)
# update probs
probs = N_k / N_k.sum() # (n_mix,)
prior.probs[0] = probs
# update loc & scale
loc = (posterior[:, None] @ samples[None]).squeeze(1) # (n_mix, n_dim)
loc /= (N_k[:, None] + eps)
cov = (samples[None, :, :] - loc[:, None, :]) ** 2 # Covariances are set to 0.
var = (posterior[:, None, :] @ cov).squeeze(1) # (n_mix, n_dim)
var /= (N_k[:, None] + eps)
scale = var.sqrt()
for i, d in enumerate(distributions):
d.loc[0] = loc[i]
d.scale[0] = scale[i]
# plot_density_3d(*get_density())
plot_density_2d(*get_density())
print("Epoch: {}, log-likelihood: {}".format(epoch+1, p.log_prob().mean().eval({"x": samples}).mean()))
psudo_sample_dict = p.sample(batch_n=200)
plot_2d_sample(samples_dict)
```
| true |
code
| 0.847337 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/gdg-ml-team/ioExtended/blob/master/Lab_2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
!pip install -q tensorflow_hub
from __future__ import absolute_import, division, print_function
import matplotlib.pylab as plt
import tensorflow as tf
import tensorflow_hub as hub
from tensorflow.keras import layers
tf.VERSION
data_root = tf.keras.utils.get_file(
'flower_photos','https://storage.googleapis.com/download.tensorflow.org/example_images/flower_photos.tgz',
untar=True)
image_generator = tf.keras.preprocessing.image.ImageDataGenerator(rescale=1/255)
image_data = image_generator.flow_from_directory(str(data_root))
for image_batch,label_batch in image_data:
print("Image batch shape: ", image_batch.shape)
print("Labe batch shape: ", label_batch.shape)
break
classifier_url = "https://tfhub.dev/google/imagenet/mobilenet_v2_100_224/classification/2" #@param {type:"string"}
def classifier(x):
classifier_module = hub.Module(classifier_url)
return classifier_module(x)
IMAGE_SIZE = hub.get_expected_image_size(hub.Module(classifier_url))
classifier_layer = layers.Lambda(classifier, input_shape = IMAGE_SIZE+[3])
classifier_model = tf.keras.Sequential([classifier_layer])
classifier_model.summary()
image_data = image_generator.flow_from_directory(str(data_root), target_size=IMAGE_SIZE)
for image_batch,label_batch in image_data:
print("Image batch shape: ", image_batch.shape)
print("Labe batch shape: ", label_batch.shape)
break
import tensorflow.keras.backend as K
sess = K.get_session()
init = tf.global_variables_initializer()
sess.run(init)
import numpy as np
import PIL.Image as Image
grace_hopper = tf.keras.utils.get_file('image.jpg','https://storage.googleapis.com/download.tensorflow.org/example_images/grace_hopper.jpg')
grace_hopper = Image.open(grace_hopper).resize(IMAGE_SIZE)
grace_hopper
grace_hopper = np.array(grace_hopper)/255.0
grace_hopper.shape
result = classifier_model.predict(grace_hopper[np.newaxis, ...])
result.shape
predicted_class = np.argmax(result[0], axis=-1)
predicted_class
labels_path = tf.keras.utils.get_file('ImageNetLabels.txt','https://storage.googleapis.com/download.tensorflow.org/data/ImageNetLabels.txt')
imagenet_labels = np.array(open(labels_path).read().splitlines())
plt.imshow(grace_hopper)
plt.axis('off')
predicted_class_name = imagenet_labels[predicted_class]
_ = plt.title("Prediction: " + predicted_class_name)
```
| true |
code
| 0.80905 | null | null | null | null |
|
**This notebook is an exercise in the [Introduction to Machine Learning](https://www.kaggle.com/learn/intro-to-machine-learning) course. You can reference the tutorial at [this link](https://www.kaggle.com/dansbecker/underfitting-and-overfitting).**
---
## Recap
You've built your first model, and now it's time to optimize the size of the tree to make better predictions. Run this cell to set up your coding environment where the previous step left off.
```
# Code you have previously used to load data
import pandas as pd
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
# Path of the file to read
iowa_file_path = '../input/home-data-for-ml-course/train.csv'
home_data = pd.read_csv(iowa_file_path)
# Create target object and call it y
y = home_data.SalePrice
# Create X
features = ['LotArea', 'YearBuilt', '1stFlrSF', '2ndFlrSF', 'FullBath', 'BedroomAbvGr', 'TotRmsAbvGrd']
X = home_data[features]
# Split into validation and training data
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=1)
# Specify Model
iowa_model = DecisionTreeRegressor(random_state=1)
# Fit Model
iowa_model.fit(train_X, train_y)
# Make validation predictions and calculate mean absolute error
val_predictions = iowa_model.predict(val_X)
val_mae = mean_absolute_error(val_predictions, val_y)
print("Validation MAE: {:,.0f}".format(val_mae))
# Set up code checking
from learntools.core import binder
binder.bind(globals())
from learntools.machine_learning.ex5 import *
print("\nSetup complete")
```
# Exercises
You could write the function `get_mae` yourself. For now, we'll supply it. This is the same function you read about in the previous lesson. Just run the cell below.
```
def get_mae(max_leaf_nodes, train_X, val_X, train_y, val_y):
model = DecisionTreeRegressor(max_leaf_nodes=max_leaf_nodes, random_state=0)
model.fit(train_X, train_y)
preds_val = model.predict(val_X)
mae = mean_absolute_error(val_y, preds_val)
return(mae)
```
## Step 1: Compare Different Tree Sizes
Write a loop that tries the following values for *max_leaf_nodes* from a set of possible values.
Call the *get_mae* function on each value of max_leaf_nodes. Store the output in some way that allows you to select the value of `max_leaf_nodes` that gives the most accurate model on your data.
```
candidate_max_leaf_nodes = [5, 25, 50, 100, 250, 500]
# Write loop to find the ideal tree size from candidate_max_leaf_nodes
for max_leaf_nodes in candidate_max_leaf_nodes:
my_mae = get_mae(max_leaf_nodes, train_X, val_X, train_y, val_y)
print("Max leaf nodes: %d \t\t Mean Absolute Error: %d" %(max_leaf_nodes, my_mae))
# Store the best value of max_leaf_nodes (it will be either 5, 25, 50, 100, 250 or 500)
best_tree_size = 100
# Check your answer
step_1.check()
# The lines below will show you a hint or the solution.
# step_1.hint()
# step_1.solution()
```
## Step 2: Fit Model Using All Data
You know the best tree size. If you were going to deploy this model in practice, you would make it even more accurate by using all of the data and keeping that tree size. That is, you don't need to hold out the validation data now that you've made all your modeling decisions.
```
# Fill in argument to make optimal size and uncomment
final_model = DecisionTreeRegressor(max_leaf_nodes=100, random_state=0)
# fit the final model and uncomment the next two lines
final_model.fit(X, y)
# Check your answer
step_2.check()
# step_2.hint()
# step_2.solution()
```
You've tuned this model and improved your results. But we are still using Decision Tree models, which are not very sophisticated by modern machine learning standards. In the next step you will learn to use Random Forests to improve your models even more.
# Keep Going
You are ready for **[Random Forests](https://www.kaggle.com/dansbecker/random-forests).**
---
*Have questions or comments? Visit the [Learn Discussion forum](https://www.kaggle.com/learn-forum/161285) to chat with other Learners.*
| true |
code
| 0.464962 | null | null | null | null |
|
# Computing the Bayesian Hilbert Transform-DRT
In this tutorial example, we will show how the developed BHT-DRT method works using a simple ZARC model. The equivalent circuit consists one ZARC model, *i.e*., a resistor in parallel with a CPE element.
```
# import the libraries
import numpy as np
from math import pi, log10
import matplotlib.pyplot as plt
import seaborn as sns
# core library
import Bayes_HT
import importlib
importlib.reload(Bayes_HT)
# plot standards
plt.rc('font', family='serif', size=15)
plt.rc('text', usetex=True)
plt.rc('xtick', labelsize=15)
plt.rc('ytick', labelsize=15)
```
## 1) Define the synthetic impedance experiment $Z_{\rm exp}(\omega)$
### 1.1) Define the frequency range
```
N_freqs = 81
freq_min = 10**-4 # Hz
freq_max = 10**4 # Hz
freq_vec = np.logspace(log10(freq_min), log10(freq_max), num=N_freqs, endpoint=True)
tau_vec = np.logspace(-log10(freq_max), -log10(freq_min), num=N_freqs, endpoint=True)
omega_vec = 2.*pi*freq_vec
```
### 1.2) Define the circuit parameters for the two ZARCs
```
R_ct = 50 # Ohm
R_inf = 10. # Ohm
phi = 0.8
tau_0 = 1. # sec
```
### 1.3) Generate exact impedance $Z_{\rm exact}(\omega)$ as well as the stochastic experiment $Z_{\rm exp}(\omega)$, here $Z_{\rm exp}(\omega)=Z_{\rm exact}(\omega)+\sigma_n(\varepsilon_{\rm re}+i\varepsilon_{\rm im})$
```
# generate exact
T = tau_0**phi/R_ct
Z_exact = R_inf + 1./(1./R_ct+T*(1j*2.*pi*freq_vec)**phi)
# random
rng = np.random.seed(121295)
sigma_n_exp = 0.8 # Ohm
Z_exp = Z_exact + sigma_n_exp*(np.random.normal(0, 1, N_freqs)+1j*np.random.normal(0, 1, N_freqs))
```
### 1.4) show the impedance in Nyquist plot
```
fig, ax = plt.subplots()
plt.plot(Z_exact.real, -Z_exact.imag, linewidth=4, color='black', label='exact')
plt.plot(np.real(Z_exp), -Z_exp.imag, 'o', markersize=8, color='red', label='synth exp')
plt.plot(np.real(Z_exp[0:70:20]), -np.imag(Z_exp[0:70:20]), 's', markersize=8, color="black")
plt.plot(np.real(Z_exp[30]), -np.imag(Z_exp[30]), 's', markersize=8, color="black")
plt.annotate(r'$10^{-4}$', xy=(np.real(Z_exp[0]), -np.imag(Z_exp[0])),
xytext=(np.real(Z_exp[0])-15, -np.imag(Z_exp[0])),
arrowprops=dict(arrowstyle='-',connectionstyle='arc'))
plt.annotate(r'$10^{-1}$', xy=(np.real(Z_exp[20]), -np.imag(Z_exp[20])),
xytext=(np.real(Z_exp[20])-5, 10-np.imag(Z_exp[20])),
arrowprops=dict(arrowstyle='-',connectionstyle='arc'))
plt.annotate(r'$1$', xy=(np.real(Z_exp[30]), -np.imag(Z_exp[30])),
xytext=(np.real(Z_exp[30]), 8-np.imag(Z_exp[30])),
arrowprops=dict(arrowstyle='-',connectionstyle='arc'))
plt.annotate(r'$10$', xy=(np.real(Z_exp[40]), -np.imag(Z_exp[40])),
xytext=(np.real(Z_exp[40]), 8-np.imag(Z_exp[40])),
arrowprops=dict(arrowstyle='-',connectionstyle='arc'))
plt.annotate(r'$10^2$', xy=(np.real(Z_exp[60]), -np.imag(Z_exp[60])),
xytext=(np.real(Z_exp[60])+5, -np.imag(Z_exp[60])),
arrowprops=dict(arrowstyle='-',connectionstyle='arc'))
plt.legend(frameon=False, fontsize = 15)
plt.axis('scaled')
plt.xlim(5, 70)
plt.ylim(-2, 32)
plt.xticks(range(5, 70, 10))
plt.yticks(range(0, 40, 10))
plt.xlabel(r'$Z_{\rm re}/\Omega$', fontsize = 20)
plt.ylabel(r'$-Z_{\rm im}/\Omega$', fontsize = 20)
plt.show()
```
## 2) Calculate the DRT impedance $Z_{\rm DRT}(\omega)$ and the Hilbert transformed impedance $Z_{\rm H}(\omega)$
### 2.1) optimize the hyperparamters
```
# set the intial parameters
sigma_n = 1
sigma_beta = 20
sigma_lambda = 100
theta_0 = np.array([sigma_n, sigma_beta, sigma_lambda])
data_real, data_imag, scores = Bayes_HT.HT_est(theta_0, Z_exp, freq_vec, tau_vec)
```
### 2.2) Calculate the real part of the $Z_{\rm DRT}(\omega)$ and the imaginary part of the $Z_{\rm H}(\omega)$
#### 2.2.1) Bayesian regression to obtain the real part of impedance for both mean and covariance
```
mu_Z_re = data_real.get('mu_Z')
cov_Z_re = np.diag(data_real.get('Sigma_Z'))
# the mean and covariance of $R_\infty$
mu_R_inf = data_real.get('mu_gamma')[0]
cov_R_inf = np.diag(data_real.get('Sigma_gamma'))[0]
```
#### 2.2.2) Calculate the real part of DRT impedance for both mean and covariance
```
mu_Z_DRT_re = data_real.get('mu_Z_DRT')
cov_Z_DRT_re = np.diag(data_real.get('Sigma_Z_DRT'))
```
#### 2.2.3) Calculate the imaginary part of HT impedance for both mean and covariance
```
mu_Z_H_im = data_real.get('mu_Z_H')
cov_Z_H_im = np.diag(data_real.get('Sigma_Z_H'))
```
#### 2.2.4) Estimate the $\sigma_n$
```
sigma_n_re = data_real.get('theta')[0]
```
### 2.3) Calculate the imaginary part of the $Z_{\rm DRT}(\omega)$ and the real part of the $Z_{\rm H}(\omega)$
```
# 2.3.1 Bayesian regression
mu_Z_im = data_imag.get('mu_Z')
cov_Z_im = np.diag(data_imag.get('Sigma_Z'))
# the mean and covariance of the inductance $L_0$
mu_L_0 = data_imag.get('mu_gamma')[0]
cov_L_0 = np.diag(data_imag.get('Sigma_gamma'))[0]
# 2.3.2 DRT part
mu_Z_DRT_im = data_imag.get('mu_Z_DRT')
cov_Z_DRT_im = np.diag(data_imag.get('Sigma_Z_DRT'))
# 2.3.3 HT prediction
mu_Z_H_re = data_imag.get('mu_Z_H')
cov_Z_H_re = np.diag(data_imag.get('Sigma_Z_H'))
# 2.3.4 estimated sigma_n
sigma_n_im = data_imag.get('theta')[0]
```
## 3) Plot the BHT_DRT
### 3.1) plot the real parts of impedance for both Bayesian regression and the synthetic experiment
```
band = np.sqrt(cov_Z_re)
plt.fill_between(freq_vec, mu_Z_re-3*band, mu_Z_re+3*band, facecolor='lightgrey')
plt.semilogx(freq_vec, mu_Z_re, linewidth=4, color='black', label='mean')
plt.semilogx(freq_vec, Z_exp.real, 'o', markersize=8, color='red', label='synth exp')
plt.xlim(1E-4, 1E4)
plt.ylim(5, 65)
plt.xscale('log')
plt.yticks(range(5, 70, 10))
plt.xlabel(r'$f/{\rm Hz}$', fontsize=20)
plt.ylabel(r'$Z_{\rm re}/\Omega$', fontsize=20)
plt.legend(frameon=False, fontsize = 15)
plt.show()
```
### 3.2 plot the imaginary parts of impedance for both Bayesian regression and the synthetic experiment
```
band = np.sqrt(cov_Z_im)
plt.fill_between(freq_vec, -mu_Z_im-3*band, -mu_Z_im+3*band, facecolor='lightgrey')
plt.semilogx(freq_vec, -mu_Z_im, linewidth=4, color='black', label='mean')
plt.semilogx(freq_vec, -Z_exp.imag, 'o', markersize=8, color='red', label='synth exp')
plt.xlim(1E-4, 1E4)
plt.ylim(-3, 30)
plt.xscale('log')
plt.xlabel(r'$f/{\rm Hz}$', fontsize=20)
plt.ylabel(r'$-Z_{\rm im}/\Omega$', fontsize=20)
plt.legend(frameon=False, fontsize = 15)
plt.show()
```
### 3.3) plot the real parts of impedance for both Hilbert transform and the synthetic experiment
```
mu_Z_H_re_agm = mu_R_inf + mu_Z_H_re
band_agm = np.sqrt(cov_R_inf + cov_Z_H_re + sigma_n_im**2)
plt.fill_between(freq_vec, mu_Z_H_re_agm-3*band_agm, mu_Z_H_re_agm+3*band_agm, facecolor='lightgrey')
plt.semilogx(freq_vec, mu_Z_H_re_agm, linewidth=4, color='black', label='mean')
plt.semilogx(freq_vec, Z_exp.real, 'o', markersize=8, color='red', label='synth exp')
plt.xlim(1E-4, 1E4)
plt.ylim(-3, 70)
plt.xscale('log')
plt.xlabel(r'$f/{\rm Hz}$', fontsize=20)
plt.ylabel(r'$\left(R_\infty + Z_{\rm H, re}\right)/\Omega$', fontsize=20)
plt.legend(frameon=False, fontsize = 15)
plt.show()
```
### 3.4) plot the imaginary parts of impedance for both Hilbert transform and the synthetic experiment
```
mu_Z_H_im_agm = omega_vec*mu_L_0 + mu_Z_H_im
band_agm = np.sqrt((omega_vec**2)*cov_L_0 + cov_Z_H_im + sigma_n_re**2)
plt.fill_between(freq_vec, -mu_Z_H_im_agm-3*band_agm, -mu_Z_H_im_agm+3*band_agm, facecolor='lightgrey')
plt.semilogx(freq_vec, -mu_Z_H_im_agm, linewidth=4, color='black', label='mean')
plt.semilogx(freq_vec, -Z_exp.imag, 'o', markersize=8, color='red', label='synth exp')
plt.xlim(1E-4, 1E4)
plt.ylim(-3, 30)
plt.xscale('log')
plt.xlabel(r'$f/{\rm Hz}$', fontsize=20)
plt.ylabel(r'$-\left(\omega L_0 + Z_{\rm H, im}\right)/\Omega$', fontsize=20)
plt.legend(frameon=False, fontsize = 15)
plt.show()
```
### 3.5) plot the difference between real parts of impedance for Hilbert transform and the synthetic experiment
```
difference_re = mu_R_inf + mu_Z_H_re - Z_exp.real
band = np.sqrt(cov_R_inf + cov_Z_H_re + sigma_n_im**2)
plt.fill_between(freq_vec, -3*band, 3*band, facecolor='lightgrey')
plt.plot(freq_vec, difference_re, 'o', markersize=8, color='red')
plt.xlim(1E-4, 1E4)
plt.ylim(-10, 10)
plt.xscale('log')
plt.xlabel(r'$f/{\rm Hz}$', fontsize=20)
plt.ylabel(r'$\left(R_\infty + Z_{\rm H, re} - Z_{\rm exp, re}\right)/\Omega$', fontsize=20)
plt.show()
```
### 3.6) plot the density distribution of residuals for the real part
```
fig = plt.figure(1)
a = sns.kdeplot(difference_re, shade=True, color='grey')
a = sns.rugplot(difference_re, color='black')
a.set_xlabel(r'$\left(R_\infty + Z_{\rm H, re} - Z_{\rm exp, re}\right)/\Omega$',fontsize=20)
a.set_ylabel(r'pdf',fontsize=20)
a.tick_params(labelsize=15)
plt.xlim(-5, 5)
plt.ylim(0, 0.5)
plt.show()
```
### 3.7) plot the difference between imaginary parts of impedance for Hilbert transform and the synthetic experiment
```
difference_im = omega_vec*mu_L_0 + mu_Z_H_im - Z_exp.imag
band = np.sqrt((omega_vec**2)*cov_L_0 + cov_Z_H_im + sigma_n_re**2)
plt.fill_between(freq_vec, -3*band, 3*band, facecolor='lightgrey')
plt.plot(freq_vec, difference_im, 'o', markersize=8, color='red')
plt.xlim(1E-4, 1E4)
plt.ylim(-10, 10)
plt.xscale('log')
plt.xlabel(r'$f/{\rm Hz}$', fontsize=20)
plt.ylabel(r'$\left(\omega L_0 + Z_{\rm H, im} - Z_{\rm exp, im}\right)/\Omega$', fontsize=20)
plt.show()
```
### 3.8) plot the density distribution of residuals for the imaginary part
```
fig = plt.figure(2)
a = sns.kdeplot(difference_im, shade=True, color='grey')
a = sns.rugplot(difference_im, color='black')
a.set_xlabel(r'$\left(\omega L_0 + Z_{\rm H, im} - Z_{\rm exp, im}\right)/\Omega$',fontsize=20)
a.set_ylabel(r'pdf',fontsize=20)
a.tick_params(labelsize=15)
plt.xlim(-5, 5)
plt.ylim(0, 0.5)
plt.show()
```
| true |
code
| 0.704236 | null | null | null | null |
|
# Python Data Science
> Dataframe Wrangling with Pandas
Kuo, Yao-Jen from [DATAINPOINT](https://www.datainpoint.com/)
```
import requests
import json
from datetime import date
from datetime import timedelta
```
## TL; DR
> In this lecture, we will talk about essential data wrangling skills in `pandas`.
## Essential Data Wrangling Skills in `pandas`
## What is `pandas`?
> Flexible and powerful data analysis / manipulation library for Python, providing labeled data structures similar to R data.frame objects, statistical functions, and much more.
Source: <https://github.com/pandas-dev/pandas>
## Why `pandas`?
Python used to have a weak spot in its analysis capability due to it did not have an appropriate structure handling the common tabular datasets. Pythonists had to switch to a more data-centric language like R or Matlab during the analysis stage until the presence of `pandas`.
## Import Pandas with `import` command
Pandas is officially aliased as `pd`.
```
import pandas as pd
```
## If Pandas is not installed, we will encounter a `ModuleNotFoundError`
```
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ModuleNotFoundError: No module named 'pandas'
```
## Use `pip install` at Terminal to install pandas
```bash
pip install pandas
```
## Check version and its installation file path
- `__version__` attribute
- `__file__` attribute
```
print(pd.__version__)
print(pd.__file__)
```
## What does `pandas` mean?

Source: <https://giphy.com/>
## Turns out its naming has nothing to do with panda the animal, it refers to three primary class customed by its author [Wes McKinney](https://wesmckinney.com/)
- **Pan**el(Deprecated since version 0.20.0)
- **Da**taFrame
- **S**eries
## In order to master `pandas`, it is vital to understand the relationships between `Index`, `ndarray`, `Series`, and `DataFrame`
- An `Index` and a `ndarray` assembles a `Series`
- A couple of `Series` that sharing the same `Index` can then form a `DataFrame`
## `Index` from Pandas
The simpliest way to create an `Index` is using `pd.Index()`.
```
prime_indices = pd.Index([2, 3, 5, 7, 11, 13, 17, 19, 23, 29])
print(type(prime_indices))
```
## An `Index` is like a combination of `tuple` and `set`
- It is immutable.
- It has the characteristics of a set.
```
# It is immutable
prime_indices = pd.Index([2, 3, 5, 7, 11, 13, 17, 19, 23, 29])
#prime_indices[-1] = 31
# It has the characteristics of a set
odd_indices = pd.Index(range(1, 30, 2))
print(prime_indices.intersection(odd_indices)) # prime_indices & odd_indices
print(prime_indices.union(odd_indices)) # prime_indices | odd_indices
print(prime_indices.symmetric_difference(odd_indices)) # prime_indices ^ odd_indices
print(prime_indices.difference(odd_indices))
print(odd_indices.difference(prime_indices))
```
## `Series` from Pandas
The simpliest way to create an `Series` is using `pd.Series()`.
```
prime_series = pd.Series([2, 3, 5, 7, 11, 13, 17, 19, 23, 29])
print(type(prime_series))
```
## A `Series` is a combination of `Index` and `ndarray`
```
print(type(prime_series.index))
print(type(prime_series.values))
```
## `DataFrame` from Pandas
The simpliest way to create an `DataFrame` is using `pd.DataFrame()`.
```
movie_df = pd.DataFrame()
movie_df["title"] = ["The Shawshank Redemption", "The Dark Knight", "Schindler's List", "Forrest Gump", "Inception"]
movie_df["imdb_rating"] = [9.3, 9.0, 8.9, 8.8, 8.7]
print(type(movie_df))
```
## A `DataFrame` is a combination of multiple `Series` sharing the same `Index`
```
print(type(movie_df.index))
print(type(movie_df["title"]))
print(type(movie_df["imdb_rating"]))
```
## Review of the definition of modern data science
> Modern data science is a huge field, it invovles applications and tools like importing, tidying, transformation, visualization, modeling, and communication. Surrounding all these is programming.

Source: [R for Data Science](https://r4ds.had.co.nz/)
## Key functionalities analysts rely on `pandas` are
- Importing
- Tidying
- Transforming
## Tidying and transforming together is also known as WRANGLING
Source: <https://giphy.com/>
## Importing
## `pandas` has massive functions importing tabular data
- Flat text file
- Database table
- Spreadsheet
- Array of JSONs
- HTML `<table></table>` tags
- ...etc.
Source: <https://pandas.pydata.org/pandas-docs/stable/user_guide/io.html>
## Using `read_csv` function for flat text files
```
from datetime import date
from datetime import timedelta
def get_covid19_latest_daily_report():
"""
Get latest daily report(world) from:
https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_daily_reports
"""
data_date = date.today()
data_date_delta = timedelta(days=1)
daily_report_url_no_date = "https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_daily_reports/{}.csv"
while True:
data_date_str = date.strftime(data_date, '%m-%d-%Y')
daily_report_url = daily_report_url_no_date.format(data_date_str)
try:
print("嘗試載入{}的每日報告".format(data_date_str))
daily_report = pd.read_csv(daily_report_url)
print("檔案存在,擷取了{}的每日報告".format(data_date_str))
break
except:
print("{}的檔案還沒有上傳".format(data_date_str))
data_date -= data_date_delta # data_date = data_date - data_date_delta
return daily_report
daily_report = get_covid19_latest_daily_report()
```
## Using `read_sql` function for database tables
```python
import sqlite3
conn = sqlite3.connect('YOUR_DATABASE.db')
sql_query = """
SELECT *
FROM YOUR_TABLE
LIMIT 100;
"""
pd.read_sql(sql_query, conn)
```
## Using `read_excel` function for spreadsheets
```python
excel_file_path = "PATH/TO/YOUR/EXCEL/FILE"
pd.read_excel(excel_file_path)
```
## Using `read_json` function for array of JSONs
```python
json_file_path = "PATH/TO/YOUR/JSON/FILE"
pd.read_json(json_file_path)
```
## What is JSON?
> JSON (JavaScript Object Notation) is a lightweight data-interchange format. It is easy for humans to read and write. It is easy for machines to parse and generate. It is based on a subset of the JavaScript Programming Language. JSON is a text format that is completely language independent but uses conventions that are familiar to programmers of the C-family of languages, including C, C++, C#, Java, JavaScript, Perl, Python, and many others. These properties make JSON an ideal data-interchange language.
Source: <https://www.json.org/json-en.html>
## Using `read_html` function for HTML `<table></table>` tags
> The `<table>` tag defines an HTML table. An HTML table consists of one `<table>` element and one or more `<tr>`, `<th>`, and `<td>` elements. The `<tr>` element defines a table row, the `<th>` element defines a table header, and the `<td>` element defines a table cell.
Source: <https://www.w3schools.com/default.asp>
```
request_url = "https://www.imdb.com/chart/top"
html_tables = pd.read_html(request_url)
print(type(html_tables))
print(len(html_tables))
html_tables[0]
```
## Basic attributes and methods
## Basic attributes of a `DataFrame` object
- `shape`
- `dtypes`
- `index`
- `columns`
```
print(daily_report.shape)
print(daily_report.dtypes)
print(daily_report.index)
print(daily_report.columns)
```
## Basic methods of a `DataFrame` object
- `head(n)`
- `tail(n)`
- `describe`
- `info`
- `set_index`
- `reset_index`
## `head(n)` returns the top n observations with header
```
daily_report.head() # n is default to 5
```
## `tail(n)` returns the bottom n observations with header
```
daily_report.tail(3)
```
## `describe` returns the descriptive summary for numeric columns
```
daily_report.describe()
```
## `info` returns the concise information of the dataframe
```
daily_report.info()
```
## `set_index` replaces current `Index` with a specific variable
```
daily_report.set_index('Combined_Key')
```
## `reset_index` resets current `Index` with default `RangeIndex`
```
daily_report.set_index('Combined_Key').reset_index()
```
## Basic Dataframe Wrangling
## Basic wrangling is like writing SQL queries
- Selecting: `SELECT FROM`
- Filtering: `WHERE`
- Subsetting: `SELECT FROM WHERE`
- Indexing
- Sorting: `ORDER BY`
- Deriving
- Summarizing
- Summarizing and Grouping: `GROUP BY`
## Selecting a column as `Series`
```
print(daily_report['Country_Region'])
print(type(daily_report['Country_Region']))
```
## Selecting a column as `DataFrame`
```
print(type(daily_report[['Country_Region']]))
daily_report[['Country_Region']]
```
## Selecting multiple columns as `DataFrame`, for sure
```
cols = ['Country_Region', 'Province_State']
daily_report[cols]
```
## Filtering rows with conditional statements
```
is_taiwan = daily_report['Country_Region'] == 'Taiwan*'
daily_report[is_taiwan]
```
## Subsetting columns and rows simultaneously
```
cols_to_select = ['Country_Region', 'Confirmed']
rows_to_filter = daily_report['Country_Region'] == 'Taiwan*'
daily_report[rows_to_filter][cols_to_select]
```
## Indexing `DataFrame` with
- `loc[]`
- `iloc[]`
## `loc[]` is indexing `DataFrame` with `Index`
```
print(daily_report.loc[3388, ['Country_Region', 'Confirmed']]) # as Series
daily_report.loc[[3388], ['Country_Region', 'Confirmed']] # as DataFrame
```
## `iloc[]` is indexing `DataFrame` with absolute position
```
print(daily_report.iloc[3388, [3, 7]]) # as Series
daily_report.iloc[[3388], [3, 7]] # as DataFrame
```
## Sorting `DataFrame` with
- `sort_values`
- `sort_index`
## `sort_values` sorts `DataFrame` with specific columns
```
daily_report.sort_values(['Country_Region', 'Confirmed'])
```
## `sort_index` sorts `DataFrame` with the `Index` of `DataFrame`
```
daily_report.sort_index(ascending=False)
```
## Deriving new variables from `DataFrame`
- Simple operations
- `pd.cut`
- `map` with a `dict`
- `map` with a function(or a lambda expression)
## Deriving new variable with simple operations
```
active = daily_report['Confirmed'] - daily_report['Deaths'] - daily_report['Recovered']
print(active)
```
## Deriving categorical from numerical with `pd.cut`
```
import numpy as np
cut_bins = [0, 1000, 10000, 100000, np.Inf]
cut_labels = ['Less than 1000', 'Between 1000 and 10000', 'Between 10000 and 100000', 'Above 100000']
confirmed_categorical = pd.cut(daily_report['Confirmed'], bins=cut_bins, labels=cut_labels, right=False)
print(confirmed_categorical)
```
## Deriving categorical from categorical with `map`
- Passing a `dict`
- Passing a function(or lambda expression)
```
# Passing a dict
country_name = {
'Taiwan*': 'Taiwan'
}
daily_report_tw = daily_report[is_taiwan]
daily_report_tw['Country_Region'].map(country_name)
# Passing a function
def is_us(x):
if x == 'US':
return 'US'
else:
return 'Not US'
daily_report['Country_Region'].map(is_us)
# Passing a lambda expression)
daily_report['Country_Region'].map(lambda x: 'US' if x == 'US' else 'Not US')
```
## Summarizing `DataFrame` with aggregate methods
```
daily_report['Confirmed'].sum()
```
## Summarizing and grouping `DataFrame` with aggregate methods
```
daily_report.groupby('Country_Region')['Confirmed'].sum()
```
## More Dataframe Wrangling Operations
## Other common `Dataframe` wranglings including
- Dealing with missing values
- Dealing with text values
- Reshaping dataframes
- Merging and joining dataframes
## Dealing with missing values
- Using `isnull` or `notnull` to check if `np.NaN` exists
- Using `dropna` to drop rows with `np.NaN`
- Using `fillna` to fill `np.NaN` with specific values
```
print(daily_report['Province_State'].size)
print(daily_report['Province_State'].isnull().sum())
print(daily_report['Province_State'].notnull().sum())
print(daily_report.dropna().shape)
print(daily_report['FIPS'].fillna(0))
```
## Splitting strings with `str.split` as a `Series`
```
split_pattern = ', '
daily_report['Combined_Key'].str.split(split_pattern)
```
## Splitting strings with `str.split` as a `DataFrame`
```
split_pattern = ', '
daily_report['Combined_Key'].str.split(split_pattern, expand=True)
```
## Replacing strings with `str.replace`
```
daily_report['Combined_Key'].str.replace(", ", ';')
```
## Testing for strings that match or contain a pattern with `str.contains`
```
print(daily_report['Country_Region'].str.contains('land').sum())
daily_report[daily_report['Country_Region'].str.contains('land')]
```
## Reshaping dataframes from wide to long format with `pd.melt`
A common problem is that a dataset where some of the column names are not names of variables, but values of a variable.
```
ts_confirmed_global_url = "https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv"
ts_confirmed_global = pd.read_csv(ts_confirmed_global_url)
ts_confirmed_global
```
## We can pivot the columns into a new pair of variables
To describe that operation we need four parameters:
- The set of columns whose names are not values
- The set of columns whose names are values
- The name of the variable to move the column names to
- The name of the variable to move the column values to
## In this example, the four parameters are
- `id_vars`: `['Province/State', 'Country/Region', 'Lat', 'Long']`
- `value_vars`: The columns from `1/22/20` to the last column
- `var_name`: Let's name it `Date`
- `value_name`: Let's name it `Confirmed`
```
idVars = ['Province/State', 'Country/Region', 'Lat', 'Long']
ts_confirmed_global_long = pd.melt(ts_confirmed_global,
id_vars=idVars,
var_name='Date',
value_name='Confirmed')
ts_confirmed_global_long
```
## Merging and joining dataframes
- `merge` on column names
- `join` on index
## Using `merge` function to join dataframes on columns
```
left_df = daily_report[daily_report['Country_Region'].isin(['Taiwan*', 'Japan'])]
right_df = ts_confirmed_global_long[ts_confirmed_global_long['Country/Region'].isin(['Taiwan*', 'Korea, South'])]
# default: inner join
pd.merge(left_df, right_df, left_on='Country_Region', right_on='Country/Region')
# left join
pd.merge(left_df, right_df, left_on='Country_Region', right_on='Country/Region', how='left')
# right join
pd.merge(left_df, right_df, left_on='Country_Region', right_on='Country/Region', how='right')
```
## Using `join` method to join dataframes on index
```
left_df = daily_report[daily_report['Country_Region'].isin(['Taiwan*', 'Japan'])]
right_df = ts_confirmed_global_long[ts_confirmed_global_long['Country/Region'].isin(['Taiwan*', 'Korea, South'])]
left_df = left_df.set_index('Country_Region')
right_df = right_df.set_index('Country/Region')
# default: left join
left_df.join(right_df, lsuffix='_x', rsuffix='_y')
# inner join
left_df.join(right_df, lsuffix='_x', rsuffix='_y', how='inner')
# inner join
left_df.join(right_df, lsuffix='_x', rsuffix='_y', how='inner')
# right join
left_df.join(right_df, lsuffix='_x', rsuffix='_y', how='right')
```
| true |
code
| 0.312462 | null | null | null | null |
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.
# Part 1: Training Tensorflow 2.0 Model on Azure Machine Learning Service
## Overview of the part 1
This notebook is Part 1 (Preparing Data and Model Training) of a two part workshop that demonstrates an end-to-end workflow using Tensorflow 2.0 on Azure Machine Learning service. The different components of the workshop are as follows:
- Part 1: [Model Training](https://github.com/microsoft/bert-stack-overflow/blob/master/1-Training/AzureServiceClassifier_Training.ipynb)
- Part 2: [Inferencing and Deploying a Model](https://github.com/microsoft/bert-stack-overflow/blob/master/2-Inferencing/AzureServiceClassifier_Inferencing.ipynb)
**This notebook will cover the following topics:**
- Stackoverflow question tagging problem
- Introduction to Transformer and BERT deep learning models
- Registering cleaned up training data as a Dataset
- Training the model on GPU cluster
- Monitoring training progress with built-in Tensorboard dashboard
- Automated search of best hyper-parameters of the model
- Registering the trained model for future deployment
## Prerequisites
This notebook is designed to be run in Azure ML Notebook VM. See [readme](https://github.com/microsoft/bert-stack-overflow/blob/master/README.md) file for instructions on how to create Notebook VM and open this notebook in it.
### Check Azure Machine Learning Python SDK version
This tutorial requires version 1.0.69 or higher. Let's check the version of the SDK:
```
import azureml.core
print("Azure Machine Learning Python SDK version:", azureml.core.VERSION)
```
## Stackoverflow Question Tagging Problem
In this workshop we will use powerful language understanding model to automatically route Stackoverflow questions to the appropriate support team on the example of Azure services.
One of the key tasks to ensuring long term success of any Azure service is actively responding to related posts in online forums such as Stackoverflow. In order to keep track of these posts, Microsoft relies on the associated tags to direct questions to the appropriate support team. While Stackoverflow has different tags for each Azure service (azure-web-app-service, azure-virtual-machine-service, etc), people often use the generic **azure** tag. This makes it hard for specific teams to track down issues related to their product and as a result, many questions get left unanswered.
**In order to solve this problem, we will build a model to classify posts on Stackoverflow with the appropriate Azure service tag.**
We will be using a BERT (Bidirectional Encoder Representations from Transformers) model which was published by researchers at Google AI Reasearch. Unlike prior language representation models, BERT is designed to pre-train deep bidirectional representations from unlabeled text by jointly conditioning on both left and right context in all layers. As a result, the pre-trained BERT model can be fine-tuned with just one additional output layer to create state-of-the-art models for a wide range of natural language processing (NLP) tasks without substantial architecture modifications.
## Why use BERT model?
[Introduction of BERT model](https://arxiv.org/pdf/1810.04805.pdf) changed the world of NLP. Many NLP problems that before relied on specialized models to achive state of the art performance are now solved with BERT better and with more generic approach.
If we look at the leaderboards on such popular NLP problems as GLUE and SQUAD, most of the top models are based on BERT:
* [GLUE Benchmark Leaderboard](https://gluebenchmark.com/leaderboard/)
* [SQuAD Benchmark Leaderboard](https://rajpurkar.github.io/SQuAD-explorer/)
Recently, Allen Institue for AI announced new language understanding system called Aristo [https://allenai.org/aristo/](https://allenai.org/aristo/). The system has been developed for 20 years, but it's performance was stuck at 60% on 8th grade science test. The result jumped to 90% once researchers adopted BERT as core language understanding component. With BERT Aristo now solves the test with A grade.
## Quick Overview of How BERT model works
The foundation of BERT model is Transformer model, which was introduced in [Attention Is All You Need paper](https://arxiv.org/abs/1706.03762). Before that event the dominant way of processing language was Recurrent Neural Networks (RNNs). Let's start our overview with RNNs.
## RNNs
RNNs were powerful way of processing language due to their ability to memorize its previous state and perform sophisticated inference based on that.
<img src="https://miro.medium.com/max/400/1*L38xfe59H5tAgvuIjKoWPg.png" alt="Drawing" style="width: 100px;"/>
_Taken from [1](https://towardsdatascience.com/transformers-141e32e69591)_
Applied to language translation task, the processing dynamics looked like this.
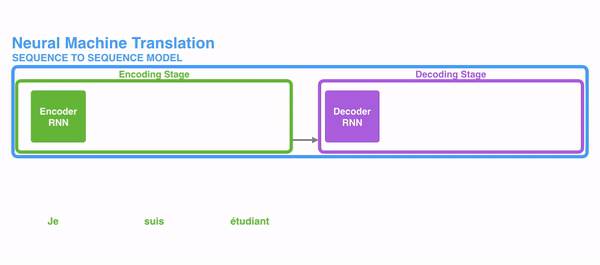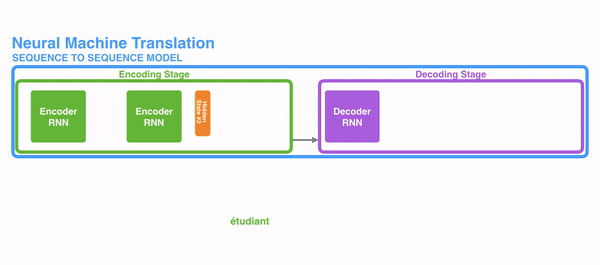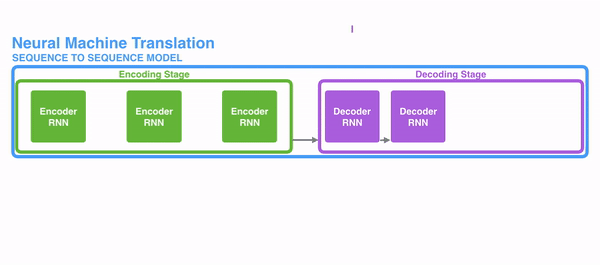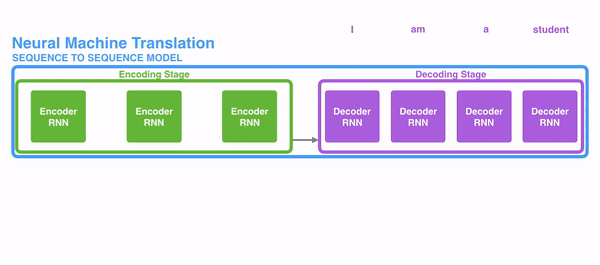
_Taken from [2](https://jalammar.github.io/visualizing-neural-machine-translation-mechanics-of-seq2seq-models-with-attention/)_
But RNNs suffered from 2 disadvantes:
1. Sequential computation put a limit on parallelization, which limited effectiveness of larger models.
2. Long term relationships between words were harder to detect.
## Transformers
Transformers were designed to address these two limitations of RNNs.
<img src="https://miro.medium.com/max/2436/1*V2435M1u0tiSOz4nRBfl4g.png" alt="Drawing" style="width: 500px;"/>
_Taken from [3](http://jalammar.github.io/illustrated-transformer/)_
In each Encoder layer Transformer performs Self-Attention operation which detects relationships between all word embeddings in one matrix multiplication operation.
<img src="https://miro.medium.com/max/2176/1*fL8arkEFVKA3_A7VBgapKA.gif" alt="Drawing" style="width: 500px;"/>
_Taken from [4](https://towardsdatascience.com/deconstructing-bert-part-2-visualizing-the-inner-workings-of-attention-60a16d86b5c1)_
## BERT Model
BERT is a very large network with multiple layers of Transformers (12 for BERT-base, and 24 for BERT-large). The model is first pre-trained on large corpus of text data (WikiPedia + books) using un-superwised training (predicting masked words in a sentence). During pre-training the model absorbs significant level of language understanding.
<img src="http://jalammar.github.io/images/bert-output-vector.png" alt="Drawing" style="width: 700px;"/>
_Taken from [5](http://jalammar.github.io/illustrated-bert/)_
Pre-trained network then can easily be fine-tuned to solve specific language task, like answering questions, or categorizing spam emails.
<img src="http://jalammar.github.io/images/bert-classifier.png" alt="Drawing" style="width: 700px;"/>
_Taken from [5](http://jalammar.github.io/illustrated-bert/)_
The end-to-end training process of the stackoverflow question tagging model looks like this:

## What is Azure Machine Learning Service?
Azure Machine Learning service is a cloud service that you can use to develop and deploy machine learning models. Using Azure Machine Learning service, you can track your models as you build, train, deploy, and manage them, all at the broad scale that the cloud provides.

#### How can we use it for training machine learning models?
Training machine learning models, particularly deep neural networks, is often a time- and compute-intensive task. Once you've finished writing your training script and running on a small subset of data on your local machine, you will likely want to scale up your workload.
To facilitate training, the Azure Machine Learning Python SDK provides a high-level abstraction, the estimator class, which allows users to easily train their models in the Azure ecosystem. You can create and use an Estimator object to submit any training code you want to run on remote compute, whether it's a single-node run or distributed training across a GPU cluster.
## Connect To Workspace
The [workspace](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.workspace(class)?view=azure-ml-py) is the top-level resource for Azure Machine Learning, providing a centralized place to work with all the artifacts you create when you use Azure Machine Learning. The workspace holds all your experiments, compute targets, models, datastores, etc.
You can [open ml.azure.com](https://ml.azure.com) to access your workspace resources through a graphical user interface of **Azure Machine Learning studio**.

**You will be asked to login in the next step. Use your Microsoft AAD credentials.**
```
from azureml.core import Workspace
workspace = Workspace.from_config()
print('Workspace name: ' + workspace.name,
'Azure region: ' + workspace.location,
'Subscription id: ' + workspace.subscription_id,
'Resource group: ' + workspace.resource_group, sep = '\n')
```
## Create Compute Target
A [compute target](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.computetarget?view=azure-ml-py) is a designated compute resource/environment where you run your training script or host your service deployment. This location may be your local machine or a cloud-based compute resource. Compute targets can be reused across the workspace for different runs and experiments.
For this tutorial, we will create an auto-scaling [Azure Machine Learning Compute](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.compute.amlcompute?view=azure-ml-py) cluster, which is a managed-compute infrastructure that allows the user to easily create a single or multi-node compute. To create the cluster, we need to specify the following parameters:
- `vm_size`: The is the type of GPUs that we want to use in our cluster. For this tutorial, we will use **Standard_NC12s_v2 (NVIDIA P100) GPU Machines** .
- `idle_seconds_before_scaledown`: This is the number of seconds before a node will scale down in our auto-scaling cluster. We will set this to **6000** seconds.
- `min_nodes`: This is the minimum numbers of nodes that the cluster will have. To avoid paying for compute while they are not being used, we will set this to **0** nodes.
- `max_modes`: This is the maximum number of nodes that the cluster will scale up to. Will will set this to **2** nodes.
**When jobs are submitted to the cluster it takes approximately 5 minutes to allocate new nodes**
```
from azureml.core.compute import AmlCompute, ComputeTarget
cluster_name = 'p100cluster'
compute_config = AmlCompute.provisioning_configuration(vm_size='Standard_NC12s_v2',
idle_seconds_before_scaledown=6000,
min_nodes=0,
max_nodes=2)
compute_target = ComputeTarget.create(workspace, cluster_name, compute_config)
compute_target.wait_for_completion(show_output=True)
```
To ensure our compute target was created successfully, we can check it's status.
```
compute_target.get_status().serialize()
```
#### If the compute target has already been created, then you (and other users in your workspace) can directly run this cell.
```
compute_target = workspace.compute_targets['p100cluster']
```
## Prepare Data Using Apache Spark
To train our model, we used the Stackoverflow data dump from [Stack exchange archive](https://archive.org/download/stackexchange). Since the Stackoverflow _posts_ dataset is 12GB, we prepared the data using [Apache Spark](https://spark.apache.org/) framework on a scalable Spark compute cluster in [Azure Databricks](https://azure.microsoft.com/en-us/services/databricks/).
For the purpose of this tutorial, we have processed the data ahead of time and uploaded it to an [Azure Blob Storage](https://azure.microsoft.com/en-us/services/storage/blobs/) container. The full data processing notebook can be found in the _spark_ folder.
* **ACTION**: Open and explore [data preparation notebook](spark/stackoverflow-data-prep.ipynb).
## Register Datastore
A [Datastore](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.datastore.datastore?view=azure-ml-py) is used to store connection information to a central data storage. This allows you to access your storage without having to hard code this (potentially confidential) information into your scripts.
In this tutorial, the data was been previously prepped and uploaded into a central [Blob Storage](https://azure.microsoft.com/en-us/services/storage/blobs/) container. We will register this container into our workspace as a datastore using a [shared access signature (SAS) token](https://docs.microsoft.com/en-us/azure/storage/common/storage-sas-overview).
```
from azureml.core import Datastore, Dataset
datastore_name = 'tfworld'
container_name = 'azureml-blobstore-7c6bdd88-21fa-453a-9c80-16998f02935f'
account_name = 'tfworld6818510241'
sas_token = '?sv=2019-02-02&ss=bfqt&srt=sco&sp=rl&se=2021-01-01T06:07:44Z&st=2020-01-11T22:00:44Z&spr=https&sig=geV1mc46gEv9yLBsWjnlJwij%2Blg4qN53KFyyK84tn3Q%3D'
datastore = Datastore.register_azure_blob_container(workspace=workspace,
datastore_name=datastore_name,
container_name=container_name,
account_name=account_name,
sas_token=sas_token)
```
#### If the datastore has already been registered, then you (and other users in your workspace) can directly run this cell.
```
datastore = workspace.datastores['tfworld']
```
#### What if my data wasn't already hosted remotely?
All workspaces also come with a blob container which is registered as a default datastore. This allows you to easily upload your own data to a remote storage location. You can access this datastore and upload files as follows:
```
datastore = workspace.get_default_datastore()
ds.upload(src_dir='<LOCAL-PATH>', target_path='<REMOTE-PATH>')
```
## Register Dataset
Azure Machine Learning service supports first class notion of a Dataset. A [Dataset](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.dataset.dataset?view=azure-ml-py) is a resource for exploring, transforming and managing data in Azure Machine Learning. The following Dataset types are supported:
* [TabularDataset](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.data.tabulardataset?view=azure-ml-py) represents data in a tabular format created by parsing the provided file or list of files.
* [FileDataset](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.data.filedataset?view=azure-ml-py) references single or multiple files in datastores or from public URLs.
We can use visual tools in Azure ML studio to register and explore dataset. In this workshop we will skip this step to save time. After the workshop please explore visual way of creating dataset as your homework. Use the guide below as guiding steps.
* **Homework**: After workshop follow [create-dataset](images/create-dataset.ipynb) guide to create Tabular Dataset from our training data using visual tools in studio.
#### Use created dataset in code
```
from azureml.core import Dataset
# Get a dataset by name
tabular_ds = Dataset.get_by_name(workspace=workspace, name='Stackoverflow dataset')
# Load a TabularDataset into pandas DataFrame
df = tabular_ds.to_pandas_dataframe()
df.head(10)
```
## Register Dataset using SDK
In addition to UI we can register datasets using SDK. In this workshop we will register second type of Datasets using code - File Dataset. File Dataset allows specific folder in our datastore that contains our data files to be registered as a Dataset.
There is a folder within our datastore called **azure-service-data** that contains all our training and testing data. We will register this as a dataset.
```
azure_dataset = Dataset.File.from_files(path=(datastore, 'azure-service-classifier/data'))
azure_dataset = azure_dataset.register(workspace=workspace,
name='Azure Services Dataset',
description='Dataset containing azure related posts on Stackoverflow')
```
#### If the dataset has already been registered, then you (and other users in your workspace) can directly run this cell.
```
azure_dataset = workspace.datasets['Azure Services Dataset']
```
## Explore Training Code
In this workshop the training code is provided in [train.py](./train.py) and [model.py](./model.py) files. The model is based on popular [huggingface/transformers](https://github.com/huggingface/transformers) libary. Transformers library provides performant implementation of BERT model with high level and easy to use APIs based on Tensorflow 2.0.

* **ACTION**: Explore _train.py_ and _model.py_ using [Azure ML studio > Notebooks tab](images/azuremlstudio-notebooks-explore.png)
* NOTE: You can also explore the files using Jupyter or Jupyter Lab UI.
## Test Locally
Let's try running the script locally to make sure it works before scaling up to use our compute cluster. To do so, you will need to install the transformers libary.
```
%pip install transformers==2.0.0
```
We have taken a small partition of the dataset and included it in this repository. Let's take a quick look at the format of the data.
```
data_dir = './data'
import os
import pandas as pd
data = pd.read_csv(os.path.join(data_dir, 'train.csv'), header=None)
data.head(5)
```
Now we know what the data looks like, let's test out our script!
```
import sys
!{sys.executable} train.py --data_dir {data_dir} --max_seq_length 128 --batch_size 16 --learning_rate 3e-5 --steps_per_epoch 5 --num_epochs 1 --export_dir ../outputs/model
```
## Homework: Debugging in TensorFlow 2.0 Eager Mode
Eager mode is new feature in TensorFlow 2.0 which makes understanding and debugging models easy. You can use VS Code Remote feature to connect to Notebook VM and perform debugging in the cloud environment.
#### More info: Configuring VS Code Remote connection to Notebook VM
* Homework: Install [Microsoft VS Code](https://code.visualstudio.com/) on your local machine.
* Homework: Follow this [configuration guide](https://github.com/danielsc/azureml-debug-training/blob/master/Setting%20up%20VSCode%20Remote%20on%20an%20AzureML%20Notebook%20VM.md) to setup VS Code Remote connection to Notebook VM.
On a CPU machine training on a full dataset will take approximatly 1.5 hours. Although it's a small dataset, it still takes a long time. Let's see how we can speed up the training by using latest NVidia V100 GPUs in the Azure cloud.
## Perform Experiment
Now that we have our compute target, dataset, and training script working locally, it is time to scale up so that the script can run faster. We will start by creating an [experiment](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.experiment.experiment?view=azure-ml-py). An experiment is a grouping of many runs from a specified script. All runs in this tutorial will be performed under the same experiment.
```
from azureml.core import Experiment
experiment_name = 'azure-service-classifier'
experiment = Experiment(workspace, name=experiment_name)
```
#### Create TensorFlow Estimator
The Azure Machine Learning Python SDK Estimator classes allow you to easily construct run configurations for your experiments. They allow you too define parameters such as the training script to run, the compute target to run it on, framework versions, additional package requirements, etc.
You can also use a generic [Estimator](https://docs.microsoft.com/en-us/python/api/azureml-train-core/azureml.train.estimator.estimator?view=azure-ml-py) to submit training scripts that use any learning framework you choose.
For popular libaries like PyTorch and Tensorflow you can use their framework specific estimators. We will use the [TensorFlow Estimator](https://docs.microsoft.com/en-us/python/api/azureml-train-core/azureml.train.dnn.tensorflow?view=azure-ml-py) for our experiment.
```
from azureml.train.dnn import TensorFlow
estimator1 = TensorFlow(source_directory='.',
entry_script='train_logging.py',
compute_target=compute_target,
script_params = {
'--data_dir': azure_dataset.as_named_input('azureservicedata').as_mount(),
'--max_seq_length': 128,
'--batch_size': 32,
'--learning_rate': 3e-5,
'--steps_per_epoch': 150,
'--num_epochs': 3,
'--export_dir':'./outputs/model'
},
framework_version='2.0',
use_gpu=True,
pip_packages=['transformers==2.0.0', 'azureml-dataprep[fuse,pandas]==1.1.29'])
```
A quick description for each of the parameters we have just defined:
- `source_directory`: This specifies the root directory of our source code.
- `entry_script`: This specifies the training script to run. It should be relative to the source_directory.
- `compute_target`: This specifies to compute target to run the job on. We will use the one created earlier.
- `script_params`: This specifies the input parameters to the training script. Please note:
1) *azure_dataset.as_named_input('azureservicedata').as_mount()* mounts the dataset to the remote compute and provides the path to the dataset on our datastore.
2) All outputs from the training script must be outputted to an './outputs' directory as this is the only directory that will be saved to the run.
- `framework_version`: This specifies the version of TensorFlow to use. Use Tensorflow.get_supported_verions() to see all supported versions.
- `use_gpu`: This will use the GPU on the compute target for training if set to True.
- `pip_packages`: This allows you to define any additional libraries to install before training.
#### 1) Submit a Run
We can now train our model by submitting the estimator object as a [run](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.run.run?view=azure-ml-py).
```
run1 = experiment.submit(estimator1)
```
We can view the current status of the run and stream the logs from within the notebook.
```
from azureml.widgets import RunDetails
RunDetails(run1).show()
```
You cancel a run at anytime which will stop the run and scale down the nodes in the compute target.
```
run1.cancel()
```
While we wait for the run to complete, let's go over how a Run is executed in Azure Machine Learning.

#### 2) Monitoring metrics with Azure ML SDK
To monitor performance of our model we log those metrics using a few lines of code in our training script:
```python
# 1) Import SDK Run object
from azureml.core.run import Run
# 2) Get current service context
run = Run.get_context()
# 3) Log the metrics that we want
run.log('val_accuracy', float(logs.get('val_accuracy')))
run.log('accuracy', float(logs.get('accuracy')))
```
#### 3) Monitoring metrics with Tensorboard
Tensorboard is a popular Deep Learning Training visualization tool and it's built-in into TensorFlow framework. We can easily add tracking of the metrics in Tensorboard format by adding Tensorboard callback to the **fit** function call.
```python
# Add callback to record Tensorboard events
model.fit(train_dataset, epochs=FLAGS.num_epochs,
steps_per_epoch=FLAGS.steps_per_epoch, validation_data=valid_dataset,
callbacks=[
AmlLogger(),
tf.keras.callbacks.TensorBoard(update_freq='batch')]
)
```
* **ACTION**: Explore _train_logging.py_ using [Azure ML studio > Notebooks tab](images/azuremlstudio-notebooks-explore.png)
#### Launch Tensorboard
Azure ML service provides built-in integration with Tensorboard through **tensorboard** package.
While the run is in progress (or after it has completed), we can start Tensorboard with the run as its target, and it will begin streaming logs.
```
from azureml.tensorboard import Tensorboard
# The Tensorboard constructor takes an array of runs, so be sure and pass it in as a single-element array here
tb = Tensorboard([run1])
# If successful, start() returns a string with the URI of the instance.
tb.start()
```
#### Stop Tensorboard
When you're done, make sure to call the stop() method of the Tensorboard object, or it will stay running even after your job completes.
```
tb.stop()
```
## Check the model performance
Last training run produced model of decent accuracy. Let's test it out and see what it does. First, let's check what files our latest training run produced and download the model files.
#### Download model files
```
run1.get_file_names()
run1.download_files(prefix='outputs/model')
# If you haven't finished training the model then just download pre-made model from datastore
datastore.download('./',prefix="azure-service-classifier/model")
```
#### Instantiate the model
Next step is to import our model class and instantiate fine-tuned model from the model file.
```
from model import TFBertForMultiClassification
from transformers import BertTokenizer
import tensorflow as tf
def encode_example(text, max_seq_length):
# Encode inputs using tokenizer
inputs = tokenizer.encode_plus(
text,
add_special_tokens=True,
max_length=max_seq_length
)
input_ids, token_type_ids = inputs["input_ids"], inputs["token_type_ids"]
# The mask has 1 for real tokens and 0 for padding tokens. Only real tokens are attended to.
attention_mask = [1] * len(input_ids)
# Zero-pad up to the sequence length.
padding_length = max_seq_length - len(input_ids)
input_ids = input_ids + ([0] * padding_length)
attention_mask = attention_mask + ([0] * padding_length)
token_type_ids = token_type_ids + ([0] * padding_length)
return input_ids, attention_mask, token_type_ids
labels = ['azure-web-app-service', 'azure-storage', 'azure-devops', 'azure-virtual-machine', 'azure-functions']
# Load model and tokenizer
loaded_model = TFBertForMultiClassification.from_pretrained('azure-service-classifier/model', num_labels=len(labels))
tokenizer = BertTokenizer.from_pretrained('bert-base-cased')
print("Model loaded from disk.")
```
#### Define prediction function
Using the model object we can interpret new questions and predict what Azure service they talk about. To do that conveniently we'll define **predict** function.
```
# Prediction function
def predict(question):
input_ids, attention_mask, token_type_ids = encode_example(question, 128)
predictions = loaded_model.predict({
'input_ids': tf.convert_to_tensor([input_ids], dtype=tf.int32),
'attention_mask': tf.convert_to_tensor([attention_mask], dtype=tf.int32),
'token_type_ids': tf.convert_to_tensor([token_type_ids], dtype=tf.int32)
})
prediction = labels[predictions[0].argmax().item()]
probability = predictions[0].max()
result = {
'prediction': str(labels[predictions[0].argmax().item()]),
'probability': str(predictions[0].max())
}
print('Prediction: {}'.format(prediction))
print('Probability: {}'.format(probability))
```
#### Experiment with our new model
Now we can easily test responses of the model to new inputs.
* **ACTION**: Invent your own input for one of the 5 services our model understands: 'azure-web-app-service', 'azure-storage', 'azure-devops', 'azure-virtual-machine', 'azure-functions'.
```
# Route question
predict("How can I specify Service Principal in devops pipeline when deploying virtual machine")
# Now more tricky case - the opposite
predict("How can virtual machine trigger devops pipeline")
```
## Distributed Training Across Multiple GPUs
Distributed training allows us to train across multiple nodes if your cluster allows it. Azure Machine Learning service helps manage the infrastructure for training distributed jobs. All we have to do is add the following parameters to our estimator object in order to enable this:
- `node_count`: The number of nodes to run this job across. Our cluster has a maximum node limit of 2, so we can set this number up to 2.
- `process_count_per_node`: The number of processes to enable per node. The nodes in our cluster have 2 GPUs each. We will set this value to 2 which will allow us to distribute the load on both GPUs. Using multi-GPUs nodes is benefitial as communication channel bandwidth on local machine is higher.
- `distributed_training`: The backend to use for our distributed job. We will be using an MPI (Message Passing Interface) backend which is used by Horovod framework.
We use [Horovod](https://github.com/horovod/horovod), which is a framework that allows us to easily modifying our existing training script to be run across multiple nodes/GPUs. The distributed training script is saved as *train_horovod.py*.
* **ACTION**: Explore _train_horovod.py_ using [Azure ML studio > Notebooks tab](images/azuremlstudio-notebooks-explore.png)
We can submit this run in the same way that we did with the others, but with the additional parameters.
```
from azureml.train.dnn import Mpi
estimator3 = TensorFlow(source_directory='./',
entry_script='train_horovod.py',compute_target=compute_target,
script_params = {
'--data_dir': azure_dataset.as_named_input('azureservicedata').as_mount(),
'--max_seq_length': 128,
'--batch_size': 32,
'--learning_rate': 3e-5,
'--steps_per_epoch': 150,
'--num_epochs': 3,
'--export_dir':'./outputs/model'
},
framework_version='2.0',
node_count=1,
distributed_training=Mpi(process_count_per_node=2),
use_gpu=True,
pip_packages=['transformers==2.0.0', 'azureml-dataprep[fuse,pandas]==1.1.29'])
run3 = experiment.submit(estimator3)
```
Once again, we can view the current details of the run.
```
from azureml.widgets import RunDetails
RunDetails(run3).show()
```
Once the run completes note the time it took. It should be around 5 minutes. As you can see, by moving to the cloud GPUs and using distibuted training we managed to reduce training time of our model from more than an hour to 5 minutes. This greatly improves speed of experimentation and innovation.
## Tune Hyperparameters Using Hyperdrive
So far we have been putting in default hyperparameter values, but in practice we would need tune these values to optimize the performance. Azure Machine Learning service provides many methods for tuning hyperparameters using different strategies.
The first step is to choose the parameter space that we want to search. We have a few choices to make here :
- **Parameter Sampling Method**: This is how we select the combinations of parameters to sample. Azure Machine Learning service offers [RandomParameterSampling](https://docs.microsoft.com/en-us/python/api/azureml-train-core/azureml.train.hyperdrive.randomparametersampling?view=azure-ml-py), [GridParameterSampling](https://docs.microsoft.com/en-us/python/api/azureml-train-core/azureml.train.hyperdrive.gridparametersampling?view=azure-ml-py), and [BayesianParameterSampling](https://docs.microsoft.com/en-us/python/api/azureml-train-core/azureml.train.hyperdrive.bayesianparametersampling?view=azure-ml-py). We will use the `GridParameterSampling` method.
- **Parameters To Search**: We will be searching for optimal combinations of `learning_rate` and `num_epochs`.
- **Parameter Expressions**: This defines the [functions that can be used to describe a hyperparameter search space](https://docs.microsoft.com/en-us/python/api/azureml-train-core/azureml.train.hyperdrive.parameter_expressions?view=azure-ml-py), which can be discrete or continuous. We will be using a `discrete set of choices`.
The following code allows us to define these options.
```
from azureml.train.hyperdrive import GridParameterSampling
from azureml.train.hyperdrive.parameter_expressions import choice
param_sampling = GridParameterSampling( {
'--learning_rate': choice(3e-5, 3e-4),
'--num_epochs': choice(3, 4)
}
)
```
The next step is to a define how we want to measure our performance. We do so by specifying two classes:
- **[PrimaryMetricGoal](https://docs.microsoft.com/en-us/python/api/azureml-train-core/azureml.train.hyperdrive.primarymetricgoal?view=azure-ml-py)**: We want to `MAXIMIZE` the `val_accuracy` that is logged in our training script.
- **[BanditPolicy](https://docs.microsoft.com/en-us/python/api/azureml-train-core/azureml.train.hyperdrive.banditpolicy?view=azure-ml-py)**: A policy for early termination so that jobs which don't show promising results will stop automatically.
```
from azureml.train.hyperdrive import BanditPolicy
from azureml.train.hyperdrive import PrimaryMetricGoal
primary_metric_name='val_accuracy'
primary_metric_goal=PrimaryMetricGoal.MAXIMIZE
early_termination_policy = BanditPolicy(slack_factor = 0.1, evaluation_interval=1, delay_evaluation=2)
```
We define an estimator as usual, but this time without the script parameters that we are planning to search.
```
estimator4 = TensorFlow(source_directory='./',
entry_script='train_logging.py',
compute_target=compute_target,
script_params = {
'--data_dir': azure_dataset.as_named_input('azureservicedata').as_mount(),
'--max_seq_length': 128,
'--batch_size': 32,
'--steps_per_epoch': 150,
'--export_dir':'./outputs/model',
},
framework_version='2.0',
use_gpu=True,
pip_packages=['transformers==2.0.0', 'azureml-dataprep[fuse,pandas]==1.1.29'])
```
Finally, we add all our parameters in a [HyperDriveConfig](https://docs.microsoft.com/en-us/python/api/azureml-train-core/azureml.train.hyperdrive.hyperdriveconfig?view=azure-ml-py) class and submit it as a run.
```
from azureml.train.hyperdrive import HyperDriveConfig
hyperdrive_run_config = HyperDriveConfig(estimator=estimator4,
hyperparameter_sampling=param_sampling,
policy=early_termination_policy,
primary_metric_name=primary_metric_name,
primary_metric_goal=PrimaryMetricGoal.MAXIMIZE,
max_total_runs=10,
max_concurrent_runs=2)
run4 = experiment.submit(hyperdrive_run_config)
```
When we view the details of our run this time, we will see information and metrics for every run in our hyperparameter tuning.
```
from azureml.widgets import RunDetails
RunDetails(run4).show()
```
We can retrieve the best run based on our defined metric.
```
best_run = run4.get_best_run_by_primary_metric()
```
## Register Model
A registered [model](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.core.model(class)?view=azure-ml-py) is a reference to the directory or file that make up your model. After registering a model, you and other people in your workspace can easily gain access to and deploy your model without having to run the training script again.
We need to define the following parameters to register a model:
- `model_name`: The name for your model. If the model name already exists in the workspace, it will create a new version for the model.
- `model_path`: The path to where the model is stored. In our case, this was the *export_dir* defined in our estimators.
- `description`: A description for the model.
Let's register the best run from our hyperparameter tuning.
```
model = best_run.register_model(model_name='azure-service-classifier',
model_path='./outputs/model',
datasets=[('train, test, validation data', azure_dataset)],
description='BERT model for classifying azure services on stackoverflow posts.')
```
We have registered the model with Dataset reference.
* **ACTION**: Check dataset to model link in **Azure ML studio > Datasets tab > Azure Service Dataset**.
In the [next tutorial](), we will perform inferencing on this model and deploy it to a web service.
| true |
code
| 0.51818 | null | null | null | null |
|
## Week 2-2 - Visualizing General Social Survey data
Your mission is to analyze a data set of social attitudes by turning it into vectors, then visualizing the result.
### 1. Choose a topic and get your data
We're going to be working with data from the General Social Survey, which asks Americans thousands of questions ever year, over decades. This is an enormous data set and there have been very many stories written from its data. The first thing you need to do is decide which questions and which years you are going to try to analyze.
Use their [data explorer](https://gssdataexplorer.norc.org/) to see what's available, and ultimately download an Excel file with the data.
- Click the `Search Varibles` button.
- You will need at least a dozen or two related variables. Try selecting some using their `Filter by Module / Subject` interface.
- When you've made your selection, click the `+ All` button to add all listed variables, then choose `Extract Data` under the `Actions` menu.
- Then you have a multi-step process. Step 1 is just naming your extract
- Step 2: select variables *again!* Click `Add All` in the upper right of the "Variable Cart" in the "Choose Variables" step.
- Step 3: Skip it. You could use this to filter the data in various ways.
- Step 4: Click `Select certain years` to pick one year of data, then check `Excel Workbook (data + metadata)` as the output format.
- Click `Create Extract` and wait a minute or two on the "Extracts" page until the spinner stops and turns into a download link.
You'll end up with an compressed file in tar.gz format, which you should be able to decompressed by double-clicking on it. Inside is an Excel file. Open it in Excel (or your favorite spreadsheet program) and resave it as a CSV.
```
import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import math
# load your data set here
gss = pd.read_csv(...)
```
### 3. Turn people into vectors
I know, it sounds cruel. We're trying to group people, but computers can only group vectors, so there we are.
Translating the spreadsheet you downloaded from GSS Explorer into vectors is a multistep process. Generally, each row of the spreadsheet is one person, and each column is one qeustion.
- First, we need to throw away any extra rows and columns: headers, questions with no data, etc.
- Many GSS questions already have numerical answers. These usually don't require any work.
- But you'll need to turn categorical variables into numbers.
Basically, you have to remove or convert every value that isn't a number. Because this is survey data, we can turn most questions into an integer scale. The cleanup might use functions like this:
```
# drop the last two rows, which are just notes and do not contain data
gss = gss.iloc[0:-2,:]
# Here's a bunch of cleanup code. It probably won't be quite right for your data.
# The goal is to convert all values to small integers, to make them easy to plot with colors below.
# First, replace all of the "Not Applicable" values with None
gss = gss.replace({'Not applicable' : None,
'No answer' : None,
'Don\'t know' : None,
'Dont know' : None})
# Manually code likert scales
gss = gss.replace({'Strongly disagree':-2, 'Disagree':-1, 'Neither agree nor disagree':0, 'Agree':1, 'Strongly agree':2})
# yes/no -> 1/-1
gss = gss.replace({'Yes':1, 'No':-1})
# Some frequency scales should have numeric coding too
gss = gss.replace({'Not at all in the past year' : 0,
'Once in the past year' : 1,
'At least 2 or 3 times in the past year' : 2,
'Once a month' : 3,
'Once a week' : 4,
'More than once a week':5})
gss = gss.replace({ 'Never or almost never' : 0,
'Once in a while' : 1,
'Some days' : 2,
'Most days' : 3,
'Every day' : 4,
'Many times a day' : 5})
# Drop some columns that don't contain useful information
gss = gss.drop(['Respondent id number',
'Ballot used for interview',
'Gss year for this respondent'], axis=1)
# Turn invalid numeric entries into zeros
gss = gss.replace({np.nan:0.0})
```
### 4. Plot those vectors!
For this assignment, we'll use the PCA projection algorithm to make 2D (or 3D!) pictures of the set of vectors. Once you have the vectors, it should be easy to make a PCA plot using the steps we followed in class.
```
# make a PCA plot here
```
### 5. Add color to help interpretation
Congratulations, you have a picture of a blob of dots. Hopefully, that blob has some structure representing clusters of similar people. To understand what the plot is telling us, it really helps to take one of the original variables and use it to assign colors to the points.
So: pick one of the questions that you think will separate people into natural groups. Use it to set the color of the dots in your scatterplot. By repeating this with different questions, or combining questions (like two binary questions giving rise to a four color scheme) you should be able to figure out what the structure of the clusters represents.
```
# map integer columns to colors
def col2colors(colvals):
# gray for zero, then a rainbow.
# This is set up so yes = 1 = red and no = -1 = indigo
my_colors = ['gray', 'red','orange','yellow','lightgreen','cyan','blue','indigo']
# We may have integers higher than len(my_colors) or less than zero
# So use the mod operator (%) to make values "wrap around" when they go off the end of the list
column_ints = colvals.astype(int) % len(my_colors)
# map each index to the corresponding color
return column_ints.apply(lambda x: my_colors[x])
# Make a plot using colors from a particular column
# Make another plot using colors from another column
# ... repeat and see if you can figure out what each axis means
```
### 6. Tell us what it means?
What did you learn from this exercise? Did you find the standard left-right divide? Or urban-rural? Early adopters vs. luddites? People with vs. without children?
What did you learn? What could end up in a story?
| true |
code
| 0.455865 | null | null | null | null |
|
```
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.ensemble import RandomForestClassifier
from sklearn import svm
from sklearn.metrics import precision_score, recall_score
import matplotlib.pyplot as plt
#reading train.csv
data = pd.read_csv('train.csv')
# show the actaul data
data
# show the first few rows
data.head(10)
# count the null values
null_values = data.isnull().sum()
null_values
plt.plot(null_values)
plt.show()
```
## Data Processing
```
def handle_non_numerical_data(df):
columns = df.columns.values
for column in columns:
text_digit_vals = {}
def convert_to_int(val):
return text_digit_vals[val]
#print(column,df[column].dtype)
if df[column].dtype != np.int64 and df[column].dtype != np.float64:
column_contents = df[column].values.tolist()
#finding just the uniques
unique_elements = set(column_contents)
# great, found them.
x = 0
for unique in unique_elements:
if unique not in text_digit_vals:
text_digit_vals[unique] = x
x+=1
df[column] = list(map(convert_to_int,df[column]))
return df
y_target = data['Survived']
# Y_target.reshape(len(Y_target),1)
x_train = data[['Pclass', 'Age', 'Sex', 'SibSp', 'Parch', 'Fare','Embarked', 'Ticket']]
x_train = handle_non_numerical_data(x_train)
x_train.head()
fare = pd.DataFrame(x_train['Fare'])
# Normalizing
min_max_scaler = preprocessing.MinMaxScaler()
newfare = min_max_scaler.fit_transform(fare)
x_train['Fare'] = newfare
x_train
null_values = x_train.isnull().sum()
null_values
plt.plot(null_values)
plt.show()
# Fill the NAN values with the median values in the datasets
x_train['Age'] = x_train['Age'].fillna(x_train['Age'].mean())
print("Number of NULL values" , x_train['Age'].isnull().sum())
print(x_train.head(3))
x_train['Sex'] = x_train['Sex'].replace('male', 0)
x_train['Sex'] = x_train['Sex'].replace('female', 1)
# print(type(x_train))
corr = x_train.corr()
corr.style.background_gradient()
def plot_corr(df,size=10):
corr = df.corr()
fig, ax = plt.subplots(figsize=(size, size))
ax.matshow(corr)
plt.xticks(range(len(corr.columns)), corr.columns);
plt.yticks(range(len(corr.columns)), corr.columns);
# plot_corr(x_train)
x_train.corr()
corr.style.background_gradient()
# Dividing the data into train and test data set
X_train, X_test, Y_train, Y_test = train_test_split(x_train, y_target, test_size = 0.4, random_state = 40)
clf = RandomForestClassifier()
clf.fit(X_train, Y_train)
print(clf.predict(X_test))
print("Accuracy: ",clf.score(X_test, Y_test))
## Testing the model.
test_data = pd.read_csv('test.csv')
test_data.head(3)
# test_data.isnull().sum()
### Preprocessing on the test data
test_data = test_data[['Pclass', 'Age', 'Sex', 'SibSp', 'Parch', 'Fare', 'Ticket', 'Embarked']]
test_data = handle_non_numerical_data(test_data)
fare = pd.DataFrame(test_data['Fare'])
min_max_scaler = preprocessing.MinMaxScaler()
newfare = min_max_scaler.fit_transform(fare)
test_data['Fare'] = newfare
test_data['Fare'] = test_data['Fare'].fillna(test_data['Fare'].median())
test_data['Age'] = test_data['Age'].fillna(test_data['Age'].median())
test_data['Sex'] = test_data['Sex'].replace('male', 0)
test_data['Sex'] = test_data['Sex'].replace('female', 1)
print(test_data.head())
print(clf.predict(test_data))
from sklearn.model_selection import cross_val_predict
predictions = cross_val_predict(clf, X_train, Y_train, cv=3)
print("Precision:", precision_score(Y_train, predictions))
print("Recall:",recall_score(Y_train, predictions))
from sklearn.metrics import precision_recall_curve
# getting the probabilities of our predictions
y_scores = clf.predict_proba(X_train)
y_scores = y_scores[:,1]
precision, recall, threshold = precision_recall_curve(Y_train, y_scores)
def plot_precision_and_recall(precision, recall, threshold):
plt.plot(threshold, precision[:-1], "r-", label="precision", linewidth=5)
plt.plot(threshold, recall[:-1], "b", label="recall", linewidth=5)
plt.xlabel("threshold", fontsize=19)
plt.legend(loc="upper right", fontsize=19)
plt.ylim([0, 1])
plt.figure(figsize=(14, 7))
plot_precision_and_recall(precision, recall, threshold)
plt.axis([0.3,0.8,0.8,1])
plt.show()
def plot_precision_vs_recall(precision, recall):
plt.plot(recall, precision, "g--", linewidth=2.5)
plt.ylabel("recall", fontsize=19)
plt.xlabel("precision", fontsize=19)
plt.axis([0, 1.5, 0, 1.5])
plt.figure(figsize=(14, 7))
plot_precision_vs_recall(precision, recall)
plt.show()
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix
predictions = cross_val_predict(clf, X_train, Y_train, cv=3)
confusion_matrix(Y_train, predictions)
```
True positive: 293 (We predicted a positive result and it was positive)
True negative: 143 (We predicted a negative result and it was negative)
False positive: 34 (We predicted a positive result and it was negative)
False negative: 64 (We predicted a negative result and it was positive)
### data v
```
import seaborn as sns
survived = 'survived'
not_survived = 'not survived'
fig, axes = plt.subplots(nrows=1, ncols=2,figsize=(10, 4))
women = data[data['Sex']=='female']
men = data[data['Sex']=='male']
ax = sns.distplot(women[women['Survived']==1].Age.dropna(), bins=18, label = survived, ax = axes[0], kde =False)
ax = sns.distplot(women[women['Survived']==0].Age.dropna(), bins=40, label = not_survived, ax = axes[0], kde =False)
ax.legend()
ax.set_title('Female')
ax = sns.distplot(men[men['Survived']==1].Age.dropna(), bins=18, label = survived, ax = axes[1], kde = False)
ax = sns.distplot(men[men['Survived']==0].Age.dropna(), bins=40, label = not_survived, ax = axes[1], kde = False)
ax.legend()
_ = ax.set_title('Male')
FacetGrid = sns.FacetGrid(data, row='Embarked', size=4.5, aspect=1.6)
FacetGrid.map(sns.pointplot, 'Pclass', 'Survived', 'Sex', palette=None, order=None, hue_order=None )
FacetGrid.add_legend()
```
#### Embarked seems to be correlated with survival, depending on the gender.
Women on port Q and on port S have a higher chance of survival. The inverse is true, if they are at port C. Men have a high survival probability if they are on port C, but a low probability if they are on port Q or S.
```
sns.barplot('Pclass', 'Survived', data=data, color="darkturquoise")
plt.show()
sns.barplot('Embarked', 'Survived', data=data, color="teal")
plt.show()
sns.barplot('Sex', 'Survived', data=data, color="aquamarine")
plt.show()
print(clf.predict(X_test))
print("Accuracy: ",clf.score(X_test, Y_test))
data
```
| true |
code
| 0.543651 | null | null | null | null |
|
# Extracting training data from the ODC <img align="right" src="../../Supplementary_data/dea_logo.jpg">
* [**Sign up to the DEA Sandbox**](https://docs.dea.ga.gov.au/setup/sandbox.html) to run this notebook interactively from a browser
* **Compatibility:** Notebook currently compatible with the `DEA Sandbox` environment
* **Products used:**
[ls8_nbart_geomedian_annual](https://explorer.sandbox.dea.ga.gov.au/products/ls8_nbart_geomedian_annual/extents),
[ls8_nbart_tmad_annual](https://explorer.sandbox.dea.ga.gov.au/products/ls8_nbart_tmad_annual/extents),
[fc_percentile_albers_annual](https://explorer.sandbox.dea.ga.gov.au/products/fc_percentile_albers_annual/extents)
## Background
**Training data** is the most important part of any supervised machine learning workflow. The quality of the training data has a greater impact on the classification than the algorithm used. Large and accurate training data sets are preferable: increasing the training sample size results in increased classification accuracy ([Maxell et al 2018](https://www.tandfonline.com/doi/full/10.1080/01431161.2018.1433343)). A review of training data methods in the context of Earth Observation is available [here](https://www.mdpi.com/2072-4292/12/6/1034)
When creating training labels, be sure to capture the **spectral variability** of the class, and to use imagery from the time period you want to classify (rather than relying on basemap composites). Another common problem with training data is **class imbalance**. This can occur when one of your classes is relatively rare and therefore the rare class will comprise a smaller proportion of the training set. When imbalanced data is used, it is common that the final classification will under-predict less abundant classes relative to their true proportion.
There are many platforms to use for gathering training labels, the best one to use depends on your application. GIS platforms are great for collection training data as they are highly flexible and mature platforms; [Geo-Wiki](https://www.geo-wiki.org/) and [Collect Earth Online](https://collect.earth/home) are two open-source websites that may also be useful depending on the reference data strategy employed. Alternatively, there are many pre-existing training datasets on the web that may be useful, e.g. [Radiant Earth](https://www.radiant.earth/) manages a growing number of reference datasets for use by anyone.
## Description
This notebook will extract training data (feature layers, in machine learning parlance) from the `open-data-cube` using labelled geometries within a geojson. The default example will use the crop/non-crop labels within the `'data/crop_training_WA.geojson'` file. This reference data was acquired and pre-processed from the USGS's Global Food Security Analysis Data portal [here](https://croplands.org/app/data/search?page=1&page_size=200) and [here](https://e4ftl01.cr.usgs.gov/MEASURES/GFSAD30VAL.001/2008.01.01/).
To do this, we rely on a custom `dea-notebooks` function called `collect_training_data`, contained within the [dea_tools.classification](../../Tools/dea_tools/classification.py) script. The principal goal of this notebook is to familarise users with this function so they can extract the appropriate data for their use-case. The default example also highlights extracting a set of useful feature layers for generating a cropland mask forWA.
1. Preview the polygons in our training data by plotting them on a basemap
2. Extract training data from the datacube using `collect_training_data`'s inbuilt feature layer parameters
3. Extract training data from the datacube using a **custom defined feature layer function** that we can pass to `collect_training_data`
4. Export the training data to disk for use in subsequent scripts
***
## Getting started
To run this analysis, run all the cells in the notebook, starting with the "Load packages" cell.
### Load packages
```
%matplotlib inline
import os
import sys
import datacube
import numpy as np
import xarray as xr
import subprocess as sp
import geopandas as gpd
from odc.io.cgroups import get_cpu_quota
from datacube.utils.geometry import assign_crs
sys.path.append('../../Scripts')
from dea_plotting import map_shapefile
from dea_bandindices import calculate_indices
from dea_classificationtools import collect_training_data
import warnings
warnings.filterwarnings("ignore")
```
## Analysis parameters
* `path`: The path to the input vector file from which we will extract training data. A default geojson is provided.
* `field`: This is the name of column in your shapefile attribute table that contains the class labels. **The class labels must be integers**
```
path = 'data/crop_training_WA.geojson'
field = 'class'
```
### Find the number of CPUs
```
ncpus = round(get_cpu_quota())
print('ncpus = ' + str(ncpus))
```
## Preview input data
We can load and preview our input data shapefile using `geopandas`. The shapefile should contain a column with class labels (e.g. 'class'). These labels will be used to train our model.
> Remember, the class labels **must** be represented by `integers`.
```
# Load input data shapefile
input_data = gpd.read_file(path)
# Plot first five rows
input_data.head()
# Plot training data in an interactive map
map_shapefile(input_data, attribute=field)
```
## Extracting training data
The function `collect_training_data` takes our geojson containing class labels and extracts training data (features) from the datacube over the locations specified by the input geometries. The function will also pre-process our training data by stacking the arrays into a useful format and removing any `NaN` or `inf` values.
`Collect_training_data` has the ability to generate many different types of **feature layers**. Relatively simple layers can be calculated using pre-defined parameters within the function, while more complex layers can be computed by passing in a `custom_func`. To begin with, let's try generating feature layers using the pre-defined methods.
The in-built feature layer parameters are described below:
* `product`: The name of the product to extract from the datacube. In this example we use a Landsat 8 geomedian composite from 2019, `'ls8_nbart_geomedian_annual'`
* `time`: The time range from which to extract data
* `calc_indices`: This parameter provides a method for calculating a number of remote sensing indices (e.g. `['NDWI', 'NDVI']`). Any of the indices found in the [dea_tools.bandindices](../../Tools/dea_tools/bandindices.py) script can be used here
* `drop`: If this variable is set to `True`, and 'calc_indices' are supplied, the spectral bands will be dropped from the dataset leaving only the band indices as data variables in the dataset.
* `reduce_func`: The classification models we're applying here require our training data to be in two dimensions (ie. `x` & `y`). If our data has a time-dimension (e.g. if we load in an annual time-series of satellite images) then we need to collapse the time dimension. `reduce_func` is simply the summary statistic used to collapse the temporal dimension. Options are 'mean', 'median', 'std', 'max', 'min', and 'geomedian'. In the default example we are loading a geomedian composite, so there is no time dimension to reduce.
* `zonal_stats`: An optional string giving the names of zonal statistics to calculate across each polygon. Default is `None` (all pixel values are returned). Supported values are 'mean', 'median', 'max', and 'min'.
* `return_coords` : If `True`, then the training data will contain two extra columns 'x_coord' and 'y_coord' corresponding to the x,y coordinate of each sample. This variable can be useful for handling spatial autocorrelation between samples later on in the ML workflow when we conduct k-fold cross validation.
> Note: `collect_training_data` also has a number of additional parameters for handling ODC I/O read failures, where polygons that return an excessive number of null values can be resubmitted to the multiprocessing queue. Check out the [docs](https://github.com/GeoscienceAustralia/dea-notebooks/blob/68d3526f73779f3316c5e28001c69f556c0d39ae/Tools/dea_tools/classification.py#L661) to learn more.
In addition to the parameters required for `collect_training_data`, we also need to set up a few parameters for the Open Data Cube query, such as `measurements` (the bands to load from the satellite), the `resolution` (the cell size), and the `output_crs` (the output projection).
```
# Set up our inputs to collect_training_data
products = ['ls8_nbart_geomedian_annual']
time = ('2014')
reduce_func = None
calc_indices = ['NDVI', 'MNDWI']
drop = False
zonal_stats = 'median'
return_coords = True
# Set up the inputs for the ODC query
measurements = ['blue', 'green', 'red', 'nir', 'swir1', 'swir2']
resolution = (-30, 30)
output_crs = 'epsg:3577'
```
Generate a datacube query object from the parameters above:
```
query = {
'time': time,
'measurements': measurements,
'resolution': resolution,
'output_crs': output_crs,
'group_by': 'solar_day',
}
```
Now let's run the `collect_training_data` function. We will limit this run to only a subset of all samples (first 100) as here we are only demonstrating the use of the function. Futher on in the notebook we will rerun this function but with all the polygons in the training data.
> **Note**: With supervised classification, its common to have many, many labelled geometries in the training data. `collect_training_data` can parallelize across the geometries in order to speed up the extracting of training data. Setting `ncpus>1` will automatically trigger the parallelization. However, its best to set `ncpus=1` to begin with to assist with debugging before triggering the parallelization. You can also limit the number of polygons to run when checking code. For example, passing in `gdf=input_data[0:5]` will only run the code over the first 5 polygons.
```
column_names, model_input = collect_training_data(gdf=input_data[0:100],
products=products,
dc_query=query,
ncpus=ncpus,
return_coords=return_coords,
field=field,
calc_indices=calc_indices,
reduce_func=reduce_func,
drop=drop,
zonal_stats=zonal_stats)
```
The function returns two numpy arrays, the first (`column_names`) contains a list of the names of the feature layers we've computed:
```
print(column_names)
```
The second array (`model_input`) contains the data from our labelled geometries. The first item in the array is the class integer (e.g. in the default example 1. 'crop', or 0. 'noncrop'), the second set of items are the values for each feature layer we computed:
```
print(np.array_str(model_input, precision=2, suppress_small=True))
```
## Custom feature layers
The feature layers that are most relevant for discriminating the classes of your classification problem may be more complicated than those provided in the `collect_training_data` function. In this case, we can pass a custom feature layer function through the `custom_func` parameter. Below, we will use a custom function to recollect training data (overwriting the previous example above).
* `custom_func`: A custom function for generating feature layers. If this parameter is set, all other options (excluding 'zonal_stats'), will be ignored. The result of the 'custom_func' must be a single xarray dataset containing 2D coordinates (i.e x and y with no time dimension). The custom function has access to the datacube dataset extracted using the `dc_query` params. To load other datasets, you can use the `like=ds.geobox` parameter in `dc.load`
First, lets define a custom feature layer function. This function is fairly basic and replicates some of what the `collect_training_data` function can do, but you can build these custom functions as complex as you like. We will calculate some band indices on the Landsat 8 geomedian, append the ternary median aboslute deviation dataset from the same year: [ls8_nbart_tmad_annual](https://explorer.sandbox.dea.ga.gov.au/products/ls8_nbart_tmad_annual/extents), and append fractional cover percentiles for the photosynthetic vegetation band, also from the same year: [fc_percentile_albers_annual](https://explorer.sandbox.dea.ga.gov.au/products/fc_percentile_albers_annual/extents).
```
def custom_reduce_function(ds):
# Calculate some band indices
da = calculate_indices(ds,
index=['NDVI', 'LAI', 'MNDWI'],
drop=False,
collection='ga_ls_2')
# Connect to datacube to add TMADs product
dc = datacube.Datacube(app='custom_feature_layers')
# Add TMADs dataset
tmad = dc.load(product='ls8_nbart_tmad_annual',
measurements=['sdev','edev','bcdev'],
like=ds.geobox, #will match geomedian extent
time='2014' #same as geomedian
)
# Add Fractional cover percentiles
fc = dc.load(product='fc_percentile_albers_annual',
measurements=['PV_PC_10','PV_PC_50','PV_PC_90'], #only the PV band
like=ds.geobox, #will match geomedian extent
time='2014' #same as geomedian
)
# Merge results into single dataset
result = xr.merge([da, tmad, fc],compat='override')
return result.squeeze()
```
Now, we can pass this function to `collect_training_data`. We will redefine our intial parameters to align with the new custom function. Remember, passing in a `custom_func` to `collect_training_data` means many of the other feature layer parameters are ignored.
```
# Set up our inputs to collect_training_data
products = ['ls8_nbart_geomedian_annual']
time = ('2014')
zonal_stats = 'median'
return_coords = True
# Set up the inputs for the ODC query
measurements = ['blue', 'green', 'red', 'nir', 'swir1', 'swir2']
resolution = (-30, 30)
output_crs = 'epsg:3577'
# Generate a new datacube query object
query = {
'time': time,
'measurements': measurements,
'resolution': resolution,
'output_crs': output_crs,
'group_by': 'solar_day',
}
```
Below we collect training data from the datacube using the custom function. This will take around 5-6 minutes to run all 430 samples on the default sandbox as it only has two cpus.
```
%%time
column_names, model_input = collect_training_data(
gdf=input_data,
products=products,
dc_query=query,
ncpus=ncpus,
return_coords=return_coords,
field=field,
zonal_stats=zonal_stats,
custom_func=custom_reduce_function)
print(column_names)
print('')
print(np.array_str(model_input, precision=2, suppress_small=True))
```
## Separate coordinate data
By setting `return_coords=True` in the `collect_training_data` function, our training data now has two extra columns called `x_coord` and `y_coord`. We need to separate these from our training dataset as they will not be used to train the machine learning model. Instead, these variables will be used to help conduct Spatial K-fold Cross validation (SKVC) in the notebook `3_Evaluate_optimize_fit_classifier`. For more information on why this is important, see this [article](https://www.tandfonline.com/doi/abs/10.1080/13658816.2017.1346255?journalCode=tgis20).
```
# Select the variables we want to use to train our model
coord_variables = ['x_coord', 'y_coord']
# Extract relevant indices from the processed shapefile
model_col_indices = [column_names.index(var_name) for var_name in coord_variables]
# Export to coordinates to file
np.savetxt("results/training_data_coordinates.txt", model_input[:, model_col_indices])
```
## Export training data
Once we've collected all the training data we require, we can write the data to disk. This will allow us to import the data in the next step(s) of the workflow.
```
# Set the name and location of the output file
output_file = "results/test_training_data.txt"
# Grab all columns except the x-y coords
model_col_indices = [column_names.index(var_name) for var_name in column_names[0:-2]]
# Export files to disk
np.savetxt(output_file, model_input[:, model_col_indices], header=" ".join(column_names[0:-2]), fmt="%4f")
```
## Recommended next steps
To continue working through the notebooks in this `Scalable Machine Learning on the ODC` workflow, go to the next notebook `2_Inspect_training_data.ipynb`.
1. **Extracting training data from the ODC (this notebook)**
2. [Inspecting training data](2_Inspect_training_data.ipynb)
3. [Evaluate, optimize, and fit a classifier](3_Evaluate_optimize_fit_classifier.ipynb)
4. [Classifying satellite data](4_Classify_satellite_data.ipynb)
5. [Object-based filtering of pixel classifications](5_Object-based_filtering.ipynb)
***
## Additional information
**License:** The code in this notebook is licensed under the [Apache License, Version 2.0](https://www.apache.org/licenses/LICENSE-2.0).
Digital Earth Australia data is licensed under the [Creative Commons by Attribution 4.0](https://creativecommons.org/licenses/by/4.0/) license.
**Contact:** If you need assistance, please post a question on the [Open Data Cube Slack channel](http://slack.opendatacube.org/) or on the [GIS Stack Exchange](https://gis.stackexchange.com/questions/ask?tags=open-data-cube) using the `open-data-cube` tag (you can view previously asked questions [here](https://gis.stackexchange.com/questions/tagged/open-data-cube)).
If you would like to report an issue with this notebook, you can file one on [Github](https://github.com/GeoscienceAustralia/dea-notebooks).
**Last modified:** March 2021
**Compatible datacube version:**
```
print(datacube.__version__)
```
## Tags
Browse all available tags on the DEA User Guide's [Tags Index](https://docs.dea.ga.gov.au/genindex.html)
| true |
code
| 0.439687 | null | null | null | null |
|
# Introduction to Band Ratios & Spectral Features
The BandRatios project explore properties of band ratio measures.
Band ratio measures are an analysis measure in which the ratio of power between frequency bands is calculated.
By 'spectral features' we mean features we can measure from the power spectra, such as periodic components (oscillations), that we can describe with their center frequency, power and bandwidth, and the aperiodic component, which we can describe with their exponent and offset value. These parameters will be further explored and explained later on.
In this introductory notebook, we walk through how band ratio measures and spectral features are calculated.
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context('poster')
from fooof import FOOOF
from fooof.sim import gen_power_spectrum
from fooof.analysis import get_band_peak_fm
from fooof.plts import plot_spectrum, plot_spectrum_shading
# Import custom project code
import sys
sys.path.append('../bratios')
from ratios import *
from paths import FIGS_PATHS as fp
from paths import DATA_PATHS as dp
# Settings
SAVE_FIG = False
```
## What is a Band Ratio
This project explores frequency band ratios, a metric used in spectral analysis since at least the 1960's to characterize cognitive functions such as vigilance, aging, memory among other. In clinical work, band ratios have also been used as a biomarker for diagnosing and monitoring of ADHD, diseases of consciousness, and nervous system disorders such as Parkinson's disease.
Given a power spectrum, a band ratio is the ratio of average power within a band between two frequency ranges.
Typically, band ratio measures are calculated as:
$ \frac{avg(low\ band\ power)}{avg(high\ band\ power} $
The following cell generates a power spectrum and highlights the frequency ranges used to calculate a theta/beta band ratio.
```
# Settings
theta_band = [4, 8]
beta_band = [20, 30]
freq_range = [1, 35]
# Define default simulation values
ap_def = [0, 1]
theta_def = [6, 0.25, 1]
alpha_def = [10, 0.4, 0.75]
beta_def = [25, 0.2, 1.5]
# Plot Settings
line_color = 'black'
shade_colors = ['#057D2E', '#0365C0']
# Generate a simulated power spectrum
fs, ps = gen_power_spectrum(freq_range, ap_def,
[theta_def, alpha_def, beta_def])
# Plot the power spectrum, shading the frequency bands used for the ratio
plot_spectrum_shading(fs, ps, [theta_band, beta_band],
color=line_color, shade_colors=shade_colors,
log_powers=True, linewidth=3.5)
# Plot aesthetics
ax = plt.gca()
for it in [ax.xaxis.label, ax.yaxis.label]:
it.set_fontsize(26)
ax.set_xlim([0, 35])
ax.set_ylim([-1.6, 0])
if SAVE_FIG: plt.savefig(fp.make_file_path(fp.demo, 'Ratio-example', 'pdf'))
```
# Calculate theta/beta ratios
### Average Power Ratio
The typical way of calculating band ratios is to take average power in the low-band and divide it by the average power from the high-band.
Average power is calculated as the sum of all discrete power values divided by number on power values in that band.
```
# Calculate the theta / beta ratio for our simulated power spectrum
ratio = calc_band_ratio(fs, ps, theta_band, beta_band)
print('Theta-beta ratio is: {:1.4f}'.format(ratio))
```
And there you have it - our first computed frequency band ratio!
# The FOOOF Model
To measure spectral features from power spectra, which we can then compare to ratio measures, we will use the [FOOOF](https://github.com/fooof-tools/fooof) library.
Briefly, the FOOOF algorithm parameterizes neural power spectra, measuring both periodic (oscillatory) and aperiodic features.
Each identified oscillation is parameterized as a peak, fit as a gaussian, which provides us with a measures of the center frequency, power and bandwidth of peak.
The aperiodic component is measured by a function of the form $ 1/f^\chi $, in which this $ \chi $ value is referred to as the aperiodic exponent.
This exponent is equivalent the the negative slope of the power spectrum, when plotted in log-log.
More details on FOOOF can be found in the associated [paper](https://doi.org/10.1101/299859) and/or on the documentation [site](https://fooof-tools.github.io/fooof/).
```
# Load power spectra from an example subject
psd = np.load(dp.make_file_path(dp.eeg_psds, 'A00051886_ec_psds', 'npz'))
# Unpack the loaded power spectra, and select a spectrum to fit
freqs = psd['arr_0']
powers = psd['arr_1'][0][50]
# Initialize a FOOOF object
fm = FOOOF(verbose=False)
# Fit the FOOOF model
fm.fit(freqs, powers)
# Plot the power spectrum, with the FOOOF model
fm.plot()
# Plot aesthetic updates
ax = plt.gca()
ax.set_ylabel('log(Power)', {'fontsize':35})
ax.set_xlabel('Frequency', {'fontsize':35})
plt.legend(prop={'size': 24})
for line, width in zip(ax.get_lines(), [3, 5, 5]):
line.set_linewidth(width)
ax.set_xlim([0, 35]);
if SAVE_FIG: plt.savefig(fp.make_file_path(fp.demo, 'FOOOF-example', 'pdf'))
```
In the plot above, the the FOOOF model fit, in red, is plotted over the original data, in black.
The blue dashed line is the fit of the aperiodic component of the data. The aperiodic exponent describes the steepness of this line.
For all future notebooks, the aperiodic exponent reflects values that are simulated and/or measured with the FOOOF model, reflecting the blue line.
Periodic spectral features are simulation values and/or model fit values from the FOOOF model that measure oscillatory peaks over and above the blue dashed line.
#### Helper settings & functions for the next section
```
# Settings
f_theta = 6
f_beta = 25
# Functions
def style_plot(ax):
"""Helper function to style plots."""
ax.get_legend().remove()
ax.grid(False)
for line in ax.get_lines():
line.set_linewidth(3.5)
ax.set_xticks([])
ax.set_yticks([])
def add_lines(ax, fs, ps, f_val):
"""Helper function to add vertical lines to power spectra plots."""
y_lims = ax.get_ylim()
ax.plot([f_val, f_val], [y_lims[0], np.log10(ps[fs==f_val][0])],
'g--', markersize=12, alpha=0.75)
ax.set_ylim(y_lims)
```
### Comparing Ratios With and Without Periodic Activity
In the next section, we will explore power spectra with and without periodic activity within specified bands.
We will use simulations to explore how ratio measures relate to the presence or absence or periodic activity, and how this relates to the analyses we will be performing, comparing ratio measures to spectral features.
```
# Generate simulated power spectrum, with and without a theta & beta oscillations
fs, ps0 = gen_power_spectrum(freq_range, ap_def,
[theta_def, alpha_def, beta_def])
fs, ps1 = gen_power_spectrum(freq_range, ap_def,
[alpha_def, beta_def])
fs, ps2 = gen_power_spectrum(freq_range, ap_def,
[theta_def, alpha_def])
fs, ps3 = gen_power_spectrum(freq_range, ap_def,
[alpha_def])
# Initialize some FOOOF models
fm0 = FOOOF(verbose=False)
fm1 = FOOOF(verbose=False)
fm2 = FOOOF(verbose=False)
fm3 = FOOOF(verbose=False)
# Fit FOOOF models
fm0.fit(fs, ps0)
fm1.fit(fs, ps1)
fm2.fit(fs, ps2)
fm3.fit(fs, ps3)
# Create a plot with the spectra
fig, axes = plt.subplots(1, 4, figsize=(18, 4))
titles = ['Theta & Beta', 'Beta Only', 'Theta Only', 'Neither']
for cur_fm, cur_ps, cur_title, cur_ax in zip(
[fm0, fm1, fm2, fm3], [ps0, ps1, ps2, ps3], titles, axes):
# Create the
cur_fm.plot(ax=cur_ax)
cur_ax.set_title(cur_title)
style_plot(cur_ax)
add_lines(cur_ax, fs, cur_ps, f_theta)
add_lines(cur_ax, fs, cur_ps, f_beta)
# Save out the FOOOF figure
if SAVE_FIG: plt.savefig(fp.make_file_path(fp.demo, 'PeakComparisons', 'pdf'))
```
Note that in the plots above, we have plotted the power spectra, with the aperiodic component parameterized in blue, and the potential location of peaks is indicated in green.
Keep in mind that under the FOOOF model idea, there is only evidence for an oscillation if there is band specific power over and above the aperiodic activity.
In the first power spectrum, for example, we see clear peaks in both theta and beta. However, in subsequent power spectra, we have created spectra without theta, without theta, and without either (or, alternatively put, spectra in which the FOOOF model would say there is no evidence of peaks in these bands).
We can actually check our model parameterizations, to see if and when theta and beta peaks were detected, over and above the aperiodic, was measured.
```
# Check if there are extracted thetas in the model parameterizations
print('Detected Theta Values:')
print('\tTheta & Beta: \t', get_band_peak_fm(fm0, theta_band))
print('\tBeta Only: \t', get_band_peak_fm(fm1, theta_band))
print('\tTheta Only: \t', get_band_peak_fm(fm2, theta_band))
print('\tNeither: \t', get_band_peak_fm(fm3, theta_band))
```
Now, just because there is no evidence of, for example, theta activity specifically, does not mean there is no power in the 4-8 Hz range.
We can see this in the power spectra, as the aperiodic component also contributes power across all frequencies.
This means that, due to the way that band ratio measures are calculated, the theta-beta ratio in power spectra without any actual theta activity (or beta) will still measure a value.
```
print('Theta / Beta Ratio of Theta & Beta: \t{:1.4f}'.format(
calc_band_ratio(fm0.freqs, fm0.power_spectrum, theta_band, beta_band)))
print('Theta / Beta Ratio of Beta Only: \t{:1.4f}'.format(
calc_band_ratio(fm1.freqs, fm1.power_spectrum, theta_band, beta_band)))
print('Theta / Beta Ratio of Theta Only: \t{:1.4f}'.format(
calc_band_ratio(fm2.freqs, fm2.power_spectrum, theta_band, beta_band)))
print('Theta / Beta Ratio of Neither: \t{:1.4f}'.format(
calc_band_ratio(fm3.freqs, fm3.power_spectrum, theta_band, beta_band)))
```
As we can see above, as compared to the 'Theta & Beta' PSD, the theta / beta ratio of the 'Beta Only' PSD is higher (which we might interpret as reflecting less theta or more beta activity), and the theta / beta ratio of the 'Theta Only' PSD is lower (which we might interpret as reflecting more theta or less beta activity).
However, we know that these are not really the best interpretations, in so far as we would like to say that these differences reflect the lack of theta and beta, and not merely a change in their power.
In the extreme case, with no theta or beta peaks at all, we still measure a (quite high) value for the theta / beta ratio, though in this case it entirely reflects aperiodic activity. It is important to note that the measure is not zero (or undefined) as we might expect or want in cases in which there is no oscillatory activity, over and above the aperiodic component.
### Summary
In this notebook, we have explored band ratio measures, and spectral features, using the FOOOF model.
One thing to keep in mind, for the upcoming analyses in this project is that when we compare a ratio value to periodic power, we do so to the isolated periodic power - periodic power over and above the aperiodic power - and we can only calculate this when there is actually power over and above the aperiodic component.
That is to say, revisiting the plots above, the periodic activity we are interested in is not the green line, which is total power, but rather is section of the green line above the blue line (the aperiodic adjusted power measured by FOOOF). This means that to compare ratio values to periodic power, we can only calculate this, and only do so, when we measure periodic power within the specified band.
| true |
code
| 0.736237 | null | null | null | null |
|
# Bayesian Curve Fitting
### Overview
The predictive distribution resulting from a Baysian treatment of polynominal curve fittting using an $M = 9$ polynominal, with the fixed parameters $\alpha = 5×10^{-3}$ and $\beta = 11.1$ (Corresponding to known noise variance), in which the red curve denotes the mean of the predictive distribution and the red region corresponds to $±1$ standard deviation around the mean.
### Procedure
1. The predictive distribution tis written in the form
\begin{equation*}
p(t| x, {\bf x}, {\bf t}) = N(t| m(x), s^2(x)) (1.69).
\end{equation*}
2. The basis function is defined as $\phi_i(x) = x^i$ for $i = 0,...M$.
3. The mean and variance are given by
\begin{equation*}m(x) = \beta\phi(x)^{\bf T}{\bf S} \sum_{n=1}^N \phi(x_n)t_n(1.70)\end{equation*}
\begin{equation*} s^2(x) = \beta^{-1} + \phi(x)^{\bf T} {\bf S} \phi(x)(1.71)\end{equation*}
\begin{equation*}{\bf S}^{-1} = \alpha {\bf I} + \beta \sum_{n=1}^N \phi(x_n)\phi(x_n)^{\bf T}(1.72)\end{equation*}
4. Inprement these equation and visualize the predictive distribution in the raneg of $0.0<x<1.0$.
```
import numpy as np
from numpy.linalg import inv
import pandas as pd
from pylab import *
import matplotlib.pyplot as plt
%matplotlib inline
#From p31 the authors define phi as following
def phi(x):
return np.array([x ** i for i in range(M + 1)]).reshape((M + 1, 1))
#(1.70) Mean of predictive distribution
def mean(x, x_train, y_train, S): #m
sum = np.array(zeros((M+1, 1)))
for n in range(len(x_train)):
sum += np.dot(phi(x_train[n]), y_train[n])
return Beta * phi(x).T.dot(S).dot(sum)
#(1.71) Variance of predictive distribution
def var(x, S): #s2
return 1.0/Beta + phi(x).T.dot(S).dot(phi(x))
#(1.72)
def S(x_train, y_train):
I = np.identity(M + 1)
Sigma = np.zeros((M + 1, M + 1))
for n in range(len(x_train)):
Sigma += np.dot(phi(x_train[n]), phi(x_train[n]).T)
S_inv = alpha * I + Beta * Sigma
return inv(S_inv)
alpha = 0.005
Beta = 11.1
M = 9
#Sine curve
x_real = np.arange(0, 1, 0.01)
y_real = np.sin(2*np.pi*x_real)
##Training Data
N=10
x_train = np.linspace(0, 1, 10)
#Set "small level of random noise having a Gaussian distribution"
loc = 0
scale = 0.3
y_train = np.sin(2* np.pi * x_train) + np.random.normal(loc, scale, N)
result = S(x_train, y_train)
#Seek predictive distribution corespponding to entire x
mu = [mean(x, x_train, y_train, result)[0,0] for x in x_real]
variance = [var(x, result)[0,0] for x in x_real]
SD = np.sqrt(variance)
upper = mu + SD
lower = mu - SD
plt.figure(figsize=(10, 7))
plot(x_train, y_train, 'bo')
plot(x_real, y_real, 'g-')
plot(x_real, mu, 'r-')
fill_between(x_real, upper, lower, color='pink')
xlim(0.0, 1.0)
ylim(-2, 2)
title("Figure 1.17")
```
| true |
code
| 0.558447 | null | null | null | null |
|
# Cavity flow with Navier-Stokes
The final two steps will both solve the Navier–Stokes equations in two dimensions, but with different boundary conditions.
The momentum equation in vector form for a velocity field v⃗
is:
$$ \frac{\partial \overrightarrow{v}}{\partial t} + (\overrightarrow{v} \cdot \nabla ) \overrightarrow{v} = -\frac{1}{\rho}\nabla p + \nu \nabla^2 \overrightarrow{v}$$
This represents three scalar equations, one for each velocity component (u,v,w). But we will solve it in two dimensions, so there will be two scalar equations.
Remember the continuity equation? This is where the Poisson equation for pressure comes in!
Here is the system of differential equations: two equations for the velocity components u,v and one equation for pressure:
$$ \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y}= -\frac{1}{\rho}\frac{\partial p}{\partial x} + \nu \left[ \frac{\partial^2 u}{\partial x^2} +\frac{\partial^2 u}{\partial y^2} \right] $$
$$ \frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y}= -\frac{1}{\rho}\frac{\partial p}{\partial y} + \nu \left[ \frac{\partial^2 v}{\partial x^2} +\frac{\partial^2 v}{\partial y^2} \right] $$
$$
\frac{\partial^2 p}{\partial x^2} +\frac{\partial^2 p}{\partial y^2} =
\rho \left[\frac{\partial}{\partial t} \left(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \right) - \left(\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y} \right) \right]
$$
From the previous steps, we already know how to discretize all these terms. Only the last equation is a little unfamiliar. But with a little patience, it will not be hard!
Our stencils look like this:
First the momentum equation in the u direction
$$
\begin{split}
u_{i,j}^{n+1} = u_{i,j}^{n} & - u_{i,j}^{n} \frac{\Delta t}{\Delta x} \left(u_{i,j}^{n}-u_{i-1,j}^{n}\right) - v_{i,j}^{n} \frac{\Delta t}{\Delta y} \left(u_{i,j}^{n}-u_{i,j-1}^{n}\right) \\
& - \frac{\Delta t}{\rho 2\Delta x} \left(p_{i+1,j}^{n}-p_{i-1,j}^{n}\right) \\
& + \nu \left(\frac{\Delta t}{\Delta x^2} \left(u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}\right) + \frac{\Delta t}{\Delta y^2} \left(u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}\right)\right)
\end{split}
$$
Second the momentum equation in the v direction
$$
\begin{split}
v_{i,j}^{n+1} = v_{i,j}^{n} & - u_{i,j}^{n} \frac{\Delta t}{\Delta x} \left(v_{i,j}^{n}-v_{i-1,j}^{n}\right) - v_{i,j}^{n} \frac{\Delta t}{\Delta y} \left(v_{i,j}^{n}-v_{i,j-1}^{n})\right) \\
& - \frac{\Delta t}{\rho 2\Delta y} \left(p_{i,j+1}^{n}-p_{i,j-1}^{n}\right) \\
& + \nu \left(\frac{\Delta t}{\Delta x^2} \left(v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}\right) + \frac{\Delta t}{\Delta y^2} \left(v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}\right)\right)
\end{split}
$$
Finally the pressure-Poisson equation
$$\begin{split}
p_{i,j}^{n} = & \frac{\left(p_{i+1,j}^{n}+p_{i-1,j}^{n}\right) \Delta y^2 + \left(p_{i,j+1}^{n}+p_{i,j-1}^{n}\right) \Delta x^2}{2\left(\Delta x^2+\Delta y^2\right)} \\
& -\frac{\rho\Delta x^2\Delta y^2}{2\left(\Delta x^2+\Delta y^2\right)} \\
& \times \left[\frac{1}{\Delta t}\left(\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}+\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\right)-\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}\frac{u_{i+1,j}-u_{i-1,j}}{2\Delta x}\right. \\
& \left. -2\frac{u_{i,j+1}-u_{i,j-1}}{2\Delta y}\frac{v_{i+1,j}-v_{i-1,j}}{2\Delta x}-\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y}\frac{v_{i,j+1}-v_{i,j-1}}{2\Delta y} \right]
\end{split}
$$
The initial condition is $u,v,p=0$
everywhere, and the boundary conditions are:
$u=1$ at $y=1$ (the "lid");
$u,v=0$ on the other boundaries;
$\frac{\partial p}{\partial y}=0$ at $y=0,1$;
$\frac{\partial p}{\partial x}=0$ at $x=0,1$
$p=0$ at $(0,0)$
Interestingly these boundary conditions describe a well known problem in the Computational Fluid Dynamics realm, where it is known as the lid driven square cavity flow problem.
## Numpy Implementation
```
import numpy as np
from matplotlib import pyplot, cm
%matplotlib inline
nx = 41
ny = 41
nt = 1000
nit = 50
c = 1
dx = 1. / (nx - 1)
dy = 1. / (ny - 1)
x = np.linspace(0, 1, nx)
y = np.linspace(0, 1, ny)
Y, X = np.meshgrid(x, y)
rho = 1
nu = .1
dt = .001
u = np.zeros((nx, ny))
v = np.zeros((nx, ny))
p = np.zeros((nx, ny))
```
The pressure Poisson equation that's written above can be hard to write out without typos. The function `build_up_b` below represents the contents of the square brackets, so that the entirety of the Poisson pressure equation is slightly more manageable.
```
def build_up_b(b, rho, dt, u, v, dx, dy):
b[1:-1, 1:-1] = (rho * (1 / dt *
((u[2:, 1:-1] - u[0:-2, 1:-1]) /
(2 * dx) + (v[1:-1, 2:] - v[1:-1, 0:-2]) / (2 * dy)) -
((u[2:, 1:-1] - u[0:-2, 1:-1]) / (2 * dx))**2 -
2 * ((u[1:-1, 2:] - u[1:-1, 0:-2]) / (2 * dy) *
(v[2:, 1:-1] - v[0:-2, 1:-1]) / (2 * dx))-
((v[1:-1, 2:] - v[1:-1, 0:-2]) / (2 * dy))**2))
return b
```
The function `pressure_poisson` is also defined to help segregate the different rounds of calculations. Note the presence of the pseudo-time variable nit. This sub-iteration in the Poisson calculation helps ensure a divergence-free field.
```
def pressure_poisson(p, dx, dy, b):
pn = np.empty_like(p)
pn = p.copy()
for q in range(nit):
pn = p.copy()
p[1:-1, 1:-1] = (((pn[2:, 1:-1] + pn[0:-2, 1:-1]) * dy**2 +
(pn[1:-1, 2:] + pn[1:-1, 0:-2]) * dx**2) /
(2 * (dx**2 + dy**2)) -
dx**2 * dy**2 / (2 * (dx**2 + dy**2)) *
b[1:-1,1:-1])
p[-1, :] = p[-2, :] # dp/dx = 0 at x = 2
p[:, 0] = p[:, 1] # dp/dy = 0 at y = 0
p[0, :] = p[1, :] # dp/dx = 0 at x = 0
p[:, -1] = p[:, -2] # p = 0 at y = 2
p[0, 0] = 0
return p, pn
```
Finally, the rest of the cavity flow equations are wrapped inside the function `cavity_flow`, allowing us to easily plot the results of the cavity flow solver for different lengths of time.
```
def cavity_flow(nt, u, v, dt, dx, dy, p, rho, nu):
un = np.empty_like(u)
vn = np.empty_like(v)
b = np.zeros((nx, ny))
for n in range(0,nt):
un = u.copy()
vn = v.copy()
b = build_up_b(b, rho, dt, u, v, dx, dy)
p = pressure_poisson(p, dx, dy, b)[0]
pn = pressure_poisson(p, dx, dy, b)[1]
u[1:-1, 1:-1] = (un[1:-1, 1:-1]-
un[1:-1, 1:-1] * dt / dx *
(un[1:-1, 1:-1] - un[0:-2, 1:-1]) -
vn[1:-1, 1:-1] * dt / dy *
(un[1:-1, 1:-1] - un[1:-1, 0:-2]) -
dt / (2 * rho * dx) * (p[2:, 1:-1] - p[0:-2, 1:-1]) +
nu * (dt / dx**2 *
(un[2:, 1:-1] - 2 * un[1:-1, 1:-1] + un[0:-2, 1:-1]) +
dt / dy**2 *
(un[1:-1, 2:] - 2 * un[1:-1, 1:-1] + un[1:-1, 0:-2])))
v[1:-1,1:-1] = (vn[1:-1, 1:-1] -
un[1:-1, 1:-1] * dt / dx *
(vn[1:-1, 1:-1] - vn[0:-2, 1:-1]) -
vn[1:-1, 1:-1] * dt / dy *
(vn[1:-1, 1:-1] - vn[1:-1, 0:-2]) -
dt / (2 * rho * dy) * (p[1:-1, 2:] - p[1:-1, 0:-2]) +
nu * (dt / dx**2 *
(vn[2:, 1:-1] - 2 * vn[1:-1, 1:-1] + vn[0:-2, 1:-1]) +
dt / dy**2 *
(vn[1:-1, 2:] - 2 * vn[1:-1, 1:-1] + vn[1:-1, 0:-2])))
u[:, 0] = 0
u[0, :] = 0
u[-1, :] = 0
u[:, -1] = 1 # Set velocity on cavity lid equal to 1
v[:, 0] = 0
v[:, -1] = 0
v[0, :] = 0
v[-1, :] = 0
return u, v, p, pn
#NBVAL_IGNORE_OUTPUT
u = np.zeros((nx, ny))
v = np.zeros((nx, ny))
p = np.zeros((nx, ny))
b = np.zeros((nx, ny))
nt = 1000
# Store the output velocity and pressure fields in the variables a, b and c.
# This is so they do not clash with the devito outputs below.
a, b, c, d = cavity_flow(nt, u, v, dt, dx, dy, p, rho, nu)
fig = pyplot.figure(figsize=(11, 7), dpi=100)
pyplot.contourf(X, Y, c, alpha=0.5, cmap=cm.viridis)
pyplot.colorbar()
pyplot.contour(X, Y, c, cmap=cm.viridis)
pyplot.quiver(X[::2, ::2], Y[::2, ::2], a[::2, ::2], b[::2, ::2])
pyplot.xlabel('X')
pyplot.ylabel('Y');
```
### Validation
Marchi et al (2009)$^1$ compared numerical implementations of the lid driven cavity problem with their solution on a 1024 x 1024 nodes grid. We will compare a solution using both NumPy and Devito with the results of their paper below.
1. https://www.scielo.br/scielo.php?pid=S1678-58782009000300004&script=sci_arttext
```
# Import u values at x=L/2 (table 6, column 2 rows 12-26) in Marchi et al.
Marchi_Re10_u = np.array([[0.0625, -3.85425800e-2],
[0.125, -6.96238561e-2],
[0.1875, -9.6983962e-2],
[0.25, -1.22721979e-1],
[0.3125, -1.47636199e-1],
[0.375, -1.71260757e-1],
[0.4375, -1.91677043e-1],
[0.5, -2.05164738e-1],
[0.5625, -2.05770198e-1],
[0.625, -1.84928116e-1],
[0.6875, -1.313892353e-1],
[0.75, -3.1879308e-2],
[0.8125, 1.26912095e-1],
[0.875, 3.54430364e-1],
[0.9375, 6.50529292e-1]])
# Import v values at y=L/2 (table 6, column 2 rows 27-41) in Marchi et al.
Marchi_Re10_v = np.array([[0.0625, 9.2970121e-2],
[0.125, 1.52547843e-1],
[0.1875, 1.78781456e-1],
[0.25, 1.76415100e-1],
[0.3125, 1.52055820e-1],
[0.375, 1.121477612e-1],
[0.4375, 6.21048147e-2],
[0.5, 6.3603620e-3],
[0.5625,-5.10417285e-2],
[0.625, -1.056157259e-1],
[0.6875,-1.51622101e-1],
[0.75, -1.81633561e-1],
[0.8125,-1.87021651e-1],
[0.875, -1.59898186e-1],
[0.9375,-9.6409942e-2]])
#NBVAL_IGNORE_OUTPUT
# Check results with Marchi et al 2009.
npgrid=[nx,ny]
x_coord = np.linspace(0, 1, npgrid[0])
y_coord = np.linspace(0, 1, npgrid[1])
fig = pyplot.figure(figsize=(12, 6))
ax1 = fig.add_subplot(121)
ax1.plot(a[int(npgrid[0]/2),:],y_coord[:])
ax1.plot(Marchi_Re10_u[:,1],Marchi_Re10_u[:,0],'ro')
ax1.set_xlabel('$u$')
ax1.set_ylabel('$y$')
ax1 = fig.add_subplot(122)
ax1.plot(x_coord[:],b[:,int(npgrid[1]/2)])
ax1.plot(Marchi_Re10_v[:,0],Marchi_Re10_v[:,1],'ro')
ax1.set_xlabel('$x$')
ax1.set_ylabel('$v$')
pyplot.show()
```
## Devito Implementation
```
from devito import Grid
grid = Grid(shape=(nx, ny), extent=(1., 1.))
x, y = grid.dimensions
t = grid.stepping_dim
```
Reminder: here are our equations
$$ \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y}= -\frac{1}{\rho}\frac{\partial p}{\partial x} + \nu \left[ \frac{\partial^2 u}{\partial x^2} +\frac{\partial^2 u}{\partial y^2} \right] $$
$$ \frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y}= -\frac{1}{\rho}\frac{\partial p}{\partial y} + \nu \left[ \frac{\partial^2 v}{\partial x^2} +\frac{\partial^2 v}{\partial y^2} \right] $$
$$
\frac{\partial^2 p}{\partial x^2} +\frac{\partial^2 p}{\partial y^2} =
\rho \left[\frac{\partial}{\partial t} \left(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \right) - \left(\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y} \right) \right]
$$
Note that p has no time dependence, so we are going to solve for p in pseudotime then move to the next time step and solve for u and v. This will require two operators, one for p (using p and pn) in pseudotime and one for u and v in time.
As shown in the Poisson equation tutorial, a TimeFunction can be used despite the lack of a time-dependence. This will cause Devito to allocate two grid buffers, which we can addressed directly via the terms pn and pn.forward. The internal time loop can be controlled by supplying the number of pseudotime steps (iterations) as a time argument to the operator.
The time steps are advanced through a Python loop where a separator operator calculates u and v.
Also note that we need to use first order spatial derivatives for the velocites and these derivatives are not the maximum spatial derivative order (2nd order) in these equations. This is the first time we have seen this in this tutorial series (previously we have only used a single spatial derivate order).
To use a first order derivative of a devito function, we use the syntax `function.dxc` or `function.dyc` for the x and y derivatives respectively.
```
from devito import TimeFunction, Function, \
Eq, solve, Operator, configuration
# Build Required Functions and derivatives:
# --------------------------------------
# |Variable | Required Derivatives |
# --------------------------------------
# | u | dt, dx, dy, dx**2, dy**2 |
# | v | dt, dx, dy, dx**2, dy**2 |
# | p | dx, dy, dx**2, dy**2 |
# | pn | dx, dy, dx**2, dy**2 |
# --------------------------------------
u = TimeFunction(name='u', grid=grid, space_order=2)
v = TimeFunction(name='v', grid=grid, space_order=2)
p = TimeFunction(name='p', grid=grid, space_order=2)
#Variables are automatically initalized at 0.
# First order derivatives will be handled with p.dxc
eq_u =Eq(u.dt + u*u.dx + v*u.dy, -1./rho * p.dxc + nu*(u.laplace), subdomain=grid.interior)
eq_v =Eq(v.dt + u*v.dx + v*v.dy, -1./rho * p.dyc + nu*(v.laplace), subdomain=grid.interior)
eq_p =Eq(p.laplace,rho*(1./dt*(u.dxc+v.dyc)-(u.dxc*u.dxc)+2*(u.dyc*v.dxc)+(v.dyc*v.dyc)), subdomain=grid.interior)
# NOTE: Pressure has no time dependence so we solve for the other pressure buffer.
stencil_u =solve(eq_u , u.forward)
stencil_v =solve(eq_v , v.forward)
stencil_p=solve(eq_p, p)
update_u =Eq(u.forward, stencil_u)
update_v =Eq(v.forward, stencil_v)
update_p =Eq(p.forward, stencil_p)
# Boundary Conds. u=v=0 for all sides
bc_u = [Eq(u[t+1, 0, y], 0)]
bc_u += [Eq(u[t+1, nx-1, y], 0)]
bc_u += [Eq(u[t+1, x, 0], 0)]
bc_u += [Eq(u[t+1, x, ny-1], 1)] # except u=1 for y=2
bc_v = [Eq(v[t+1, 0, y], 0)]
bc_v += [Eq(v[t+1, nx-1, y], 0)]
bc_v += [Eq(v[t+1, x, ny-1], 0)]
bc_v += [Eq(v[t+1, x, 0], 0)]
bc_p = [Eq(p[t+1, 0, y],p[t+1, 1,y])] # dpn/dx = 0 for x=0.
bc_p += [Eq(p[t+1,nx-1, y],p[t+1,nx-2, y])] # dpn/dx = 0 for x=2.
bc_p += [Eq(p[t+1, x, 0],p[t+1,x ,1])] # dpn/dy = 0 at y=0
bc_p += [Eq(p[t+1, x, ny-1],p[t+1, x, ny-2])] # pn=0 for y=2
bc_p += [Eq(p[t+1, 0, 0], 0)]
bc=bc_u+bc_v
optime=Operator([update_u, update_v]+bc_u+bc_v)
oppres=Operator([update_p]+bc_p)
# Silence non-essential outputs from the solver.
configuration['log-level'] = 'ERROR'
# This is the time loop.
for step in range(0,nt):
if step>0:
oppres(time_M = nit)
optime(time_m=step, time_M=step, dt=dt)
#NBVAL_IGNORE_OUTPUT
fig = pyplot.figure(figsize=(11,7), dpi=100)
# Plotting the pressure field as a contour.
pyplot.contourf(X, Y, p.data[0], alpha=0.5, cmap=cm.viridis)
pyplot.colorbar()
# Plotting the pressure field outlines.
pyplot.contour(X, Y, p.data[0], cmap=cm.viridis)
# Plotting velocity field.
pyplot.quiver(X[::2,::2], Y[::2,::2], u.data[0,::2,::2], v.data[0,::2,::2])
pyplot.xlabel('X')
pyplot.ylabel('Y');
```
### Validation
```
#NBVAL_IGNORE_OUTPUT
# Again, check results with Marchi et al 2009.
fig = pyplot.figure(figsize=(12, 6))
ax1 = fig.add_subplot(121)
ax1.plot(u.data[0,int(grid.shape[0]/2),:],y_coord[:])
ax1.plot(Marchi_Re10_u[:,1],Marchi_Re10_u[:,0],'ro')
ax1.set_xlabel('$u$')
ax1.set_ylabel('$y$')
ax1 = fig.add_subplot(122)
ax1.plot(x_coord[:],v.data[0,:,int(grid.shape[0]/2)])
ax1.plot(Marchi_Re10_v[:,0],Marchi_Re10_v[:,1],'ro')
ax1.set_xlabel('$x$')
ax1.set_ylabel('$v$')
pyplot.show()
```
The Devito implementation produces results consistent with the benchmark solution. There is a small disparity in a few of the velocity values, but this is expected as the Devito 41 x 41 node grid is much coarser than the benchmark on a 1024 x 1024 node grid.
## Comparison
```
#NBVAL_IGNORE_OUTPUT
fig = pyplot.figure(figsize=(12, 6))
ax1 = fig.add_subplot(121)
ax1.plot(a[int(npgrid[0]/2),:],y_coord[:])
ax1.plot(u.data[0,int(grid.shape[0]/2),:],y_coord[:],'--')
ax1.plot(Marchi_Re10_u[:,1],Marchi_Re10_u[:,0],'ro')
ax1.set_xlabel('$u$')
ax1.set_ylabel('$y$')
ax1 = fig.add_subplot(122)
ax1.plot(x_coord[:],b[:,int(npgrid[1]/2)])
ax1.plot(x_coord[:],v.data[0,:,int(grid.shape[0]/2)],'--')
ax1.plot(Marchi_Re10_v[:,0],Marchi_Re10_v[:,1],'ro')
ax1.set_xlabel('$x$')
ax1.set_ylabel('$v$')
ax1.legend(['numpy','devito','Marchi (2009)'])
pyplot.show()
#Pressure norm check
tol = 1e-3
assert np.sum((c[:,:]-d[:,:])**2/ np.maximum(d[:,:]**2,1e-10)) < tol
assert np.sum((p.data[0]-p.data[1])**2/np.maximum(p.data[0]**2,1e-10)) < tol
```
Overlaying all the graphs together shows how the Devito, NumPy and Marchi et al (2009)$^1$
solutions compare with each other. A final accuracy check is done which is to test whether the pressure norm has exceeded a specified tolerance.
| true |
code
| 0.323647 | null | null | null | null |
|
# Data Prep of Chicago Food Inspections Data
This notebook reads in the food inspections dataset containing records of food inspections in Chicago since 2010. This dataset is freely available through healthdata.gov, but must be provided with the odbl license linked below and provided within this repository. This notebook prepares the data for statistical analysis and modeling by creating features from categorical variables and enforcing a prevalence threshold for these categories. Note that in this way, rare features are not analyzed or used to create a model (to encourage generalizability), though the code is designed so that it would be easy to change or eliminate the prevalence threshold to run downstream analysis with a different feature set.
### References
- Data Source: https://healthdata.gov/dataset/food-inspections
- License: http://opendefinition.org/licenses/odc-odbl/
### Set Global Seed
```
SEED = 666
```
### Imports
```
import pandas as pd
```
### Read Chicago Food Inspections Data
Count records and columns.
```
food_inspections_df = pd.read_csv('../data/Food_Inspections.gz', compression='gzip')
food_inspections_df.shape
```
### Rename Columns
```
food_inspections_df.columns.tolist()
columns = ['inspection_id', 'dba_name', 'aka_name', 'license_number', 'facility_type',
'risk', 'address', 'city', 'state', 'zip', 'inspection_date', 'inspection_type',
'result', 'violation', 'latitude', 'longitude', 'location']
food_inspections_df.columns = columns
```
### Convert Zip Code to String
And take only the first five digits, chopping off the decimal from reading the column as a float.
```
food_inspections_df['zip'] = food_inspections_df['zip'].astype(str).apply(lambda x: x.split('.')[0])
```
### Normalize Casing of Chicago
Accept only proper spellings of the word Chicago with mixed casing accepted.
```
food_inspections_df['city'] = food_inspections_df['city'].apply(lambda x: 'CHICAGO'
if str(x).upper() == 'CHICAGO'
else x)
```
### Filter for Facilities in Chicago Illinois
```
loc_condition = (food_inspections_df['city'] == 'CHICAGO') & (food_inspections_df['state'] == 'IL')
```
### Drop Redundant Information
- Only Chicago is considered
- Only Illinois is considered
- Location is encoded as separate latitute and longitude columns
```
food_inspections_df = food_inspections_df[loc_condition].drop(['city', 'state', 'location'], 1)
food_inspections_df.shape
```
### Create Codes Corresponding to Each Violation Type by Parsing Violation Text
```
def create_violation_code(violation_text):
if violation_text != violation_text:
return -1
else:
return int(violation_text.split('.')[0])
food_inspections_df['violation_code'] = food_inspections_df['violation'].apply(create_violation_code)
```
### Create Attribute Dataframes with the Unique Inspection ID for Lookups if Needed
- Names
- Licenses
- Locations
- Violations
- Dates
```
names = ['inspection_id', 'dba_name', 'aka_name']
names_df = food_inspections_df[names]
licenses = ['inspection_id', 'license_number']
licenses_df = food_inspections_df[licenses]
locations = ['inspection_id', 'address', 'latitude', 'longitude']
locations_df = food_inspections_df[locations]
violations = ['inspection_id', 'violation', 'violation_code']
violations_df = food_inspections_df[violations]
dates = ['inspection_id', 'inspection_date']
dates_df = food_inspections_df[dates]
```
### Drop Features Not Used in Statistical Analysis
Features such as:
- `DBA Name`
- `AKA Name`
- `License #`
- `Address`
- `Violations`
- `Inspection Date`
May be examined following statistical analysis by joining on `Inspection ID`. **Note:** future iterations of this work may wish to consider:
- Text from the the facility name
- Street level information from the facility address
- Prior inspections of the same facility by performing a temporal analysis of the data using `Inspection Date`
```
not_considered = ['dba_name', 'aka_name', 'license_number', 'address', 'violation', 'inspection_date']
food_inspections_df = food_inspections_df.drop(not_considered, 1)
```
### Create Dataframes of Count and Prevalence for Categorical Features
- Facility types
- Violation codes
- Zip codes
- Inspection types
```
facilities = food_inspections_df['facility_type'].value_counts()
facilities_df = pd.DataFrame({'facility_type':facilities.index, 'count':facilities.values})
facilities_df['prevalence'] = facilities_df['count'] / food_inspections_df.shape[0]
facilities_df.nlargest(10, 'count')
facilities_df.nsmallest(10, 'count')
violations = food_inspections_df['violation_code'].value_counts()
violations_df = pd.DataFrame({'violation_code':violations.index, 'count':violations.values})
violations_df['prevalence'] = violations_df['count'] / food_inspections_df.shape[0]
violations_df.nlargest(10, 'count')
violations_df.nsmallest(10, 'count')
zips = food_inspections_df['zip'].value_counts()
zips_df = pd.DataFrame({'zip':zips.index, 'count':zips.values})
zips_df['prevalence'] = zips_df['count'] / food_inspections_df.shape[0]
zips_df.nlargest(10, 'count')
zips_df.nsmallest(10, 'count')
inspections = food_inspections_df['inspection_type'].value_counts()
inspections_df = pd.DataFrame({'inspection_type':inspections.index, 'count':inspections.values})
inspections_df['prevalence'] = inspections_df['count'] / food_inspections_df.shape[0]
inspections_df.nlargest(10, 'count')
inspections_df.nsmallest(10, 'count')
results = food_inspections_df['result'].value_counts()
results_df = pd.DataFrame({'result':results.index, 'count':results.values})
results_df['prevalence'] = results_df['count'] / food_inspections_df.shape[0]
results_df.nlargest(10, 'count')
```
### Drop Violation Code for Now
We can join back using the Inspection ID to learn about types of violations, but we don't want to use any information about the violation itself to predict if a food inspection will pass or fail.
```
food_inspections_df = food_inspections_df.drop('violation_code', 1)
```
### Create Risk Group Feature
If the feature cannot be found in the middle of the text string as a value 1-3, return -1.
```
def create_risk_groups(risk_text):
try:
risk = int(risk_text.split(' ')[1])
return risk
except:
return -1
food_inspections_df['risk'] = food_inspections_df['risk'].apply(create_risk_groups)
```
### Format Result
- Encode Pass and Pass w/ Conditions as 0
- Encode Fail as 1
- Encode all others as -1 and filter out these results
```
def format_results(result):
if result == 'Pass':
return 0
elif result == 'Pass w/ Conditions':
return 0
elif result == 'Fail':
return 1
else:
return -1
food_inspections_df['result'] = food_inspections_df['result'].apply(format_results)
food_inspections_df = food_inspections_df[food_inspections_df['result'] != -1]
food_inspections_df.shape
```
### Filter for Categorical Features that Pass some Prevalence Threshold
This way we only consider fairly common attributes of historical food establishments and inspections so that our analysis will generalize to new establishments and inspections. **Note:** the prevalence threshold is set to **0.1%**.
```
categorical_features = ['facility_type', 'zip', 'inspection_type']
def prev_filter(df, feature, prevalence='prevalence', prevalence_threshold=0.001):
return df[df[prevalence] > prevalence_threshold][feature].tolist()
feature_dict = dict(zip(categorical_features, [prev_filter(facilities_df, 'facility_type'),
prev_filter(zips_df, 'zip'),
prev_filter(inspections_df, 'inspection_type')]))
```
### Encode Rare Features with the 'DROP' String, to be Removed Later
Note that by mapping all rare features to the 'DROP' attribute, we avoid having to one-hot-encode all rare features and then drop them after the fact. That would create an unnecessarily large feature matrix. Instead we one-hot encode features passing the prevalence threshold and then drop all rare features that were tagged with the 'DROP' string.
```
for feature in categorical_features:
food_inspections_df[feature] = food_inspections_df[feature].apply(lambda x:
x if x in feature_dict[feature]
else 'DROP')
feature_df = pd.get_dummies(food_inspections_df,
prefix=['{}'.format(feature) for feature in categorical_features],
columns=categorical_features)
feature_df = feature_df[[col for col in feature_df.columns if 'DROP' not in col]]
feature_df.shape
```
### Drop Features with:
- Risk level not recorded as 1, 2, or 3
- Result not recorded as Pass, Pass w/ Conditions, or Fail
- NA values (Some latitudes and longitudes are NA)
```
feature_df = feature_df[feature_df['risk'] != -1]
feature_df = feature_df[feature_df['result'] != -1]
feature_df = feature_df.dropna()
feature_df.shape
```
### Write the Feature Set to a Compressed CSV File to Load for Modeling and Analysis
```
feature_df.to_csv('../data/Food_Inspection_Features.gz', compression='gzip', index=False)
```
### Write off Zip Codes to Join with Census Data
```
zips_df.to_csv('../data/Zips.csv', index=False)
```
| true |
code
| 0.231006 | null | null | null | null |
|
# Markov Decision Process (MDP)
# Discounted Future Return
$$R_t = \sum^{T}_{k=0}\gamma^{t}r_{t+k+1}$$
$$R_0 = \gamma^{0} * r_{1} + \gamma^{1} * r_{2} = r_{1} + \gamma^{1} * r_{2}\ (while\ T\ =\ 1) $$
$$R_1 = \gamma^{1} * r_{2} =\ (while\ T\ =\ 1) $$
$$so,\ R_0 = r_{1} + R_1$$
Higher $\gamma$ stands for lower discounted value, and lower $\gamma$ stands for higher discounted value (in normal, $\gamma$ value is between 0.97 and 0.99).
```
def discount_rewards(rewards, gamma=0.98):
discounted_returns = [0 for _ in rewards]
discounted_returns[-1] = rewards[-1]
for t in range(len(rewards)-2, -1, -1):
discounted_returns[t] = rewards[t] + discounted_returns[t+1]*gamma
return discounted_returns
```
If returns get higher when the time passes by, the Discounted Future Return method is not suggested.
```
print(discount_rewards([1,2,4]))
```
If returns are the same or lesser when the time passes by, the Discounted Future Return method is suggested.
```
# about 2.94 fold
# examples are like succeeding or failing
print(discount_rewards([1,1,1]))
# about 3.31 fold
# examples are like relating to the time-consuming
print(discount_rewards([1,0.9,0.8]))
```
# Explore and Exploit
## $\epsilon$-Greedy strategy
Each time the agent decides to take an action, it will consider one of which, the recommended one (exploit) or the random one (explore). The value $\epsilon$ standing for the probability of taking random actions.
```
import random
import numpy as np
def epsilon_greedy_action(action_distribution, epsilon=1e-1):
if random.random() < epsilon:
return np.argmax(np.random.random(action_distribution.shape))
else:
return np.argmax(action_distribution)
```
here we assume there are 10 actions as well as their probabilities (fixed probabilities on each step making us easier to monitor the result) for the agent to take
```
action_distribution = np.random.random((1, 10))
print(action_distribution)
print(epsilon_greedy_action(action_distribution))
```
## Annealing $\epsilon$-Greedy strategy
At the beginning of training reinforcement learning, the agent knows nothing about the environment and the state or the feedback while taking an action as well. Thus we hope the agent takes more random actions (exploring) at the beginning of training.
After a long training period, the agent knows the environment more and learns more the feedback given an action. Thus, we hope the agent takes an action based on its own experience (exploiting).
We provide a new idea to anneal (or decay) the $\epsilon$ parameter in each time the agent takes an action. The classic annealing strategy is decaying $\epsilon$ value from 0.99 to 0.01 in around 10000 steps.
```
def epsilon_greedy_annealed(action_distribution, training_percentage, epsilon_start=1.0, epsilon_end=1e-2):
annealed_epsilon = epsilon_start * (1-training_percentage) + epsilon_end * training_percentage
if random.random() < annealed_epsilon:
# take random action
return np.argmax(np.random.random(action_distribution.shape))
else:
# take the recommended action
return np.argmax(action_distribution)
```
here we assume there are 10 actions as well as their probabilities (fixed probabilities on each step making us easier to monitor the result) for the agent to take
```
action_distribution = np.random.random((1, 10))
print(action_distribution)
for i in range(1, 99, 10):
percentage = i / 100.0
action = epsilon_greedy_annealed(action_distribution, percentage)
print("percentage : {} and action is {}".format(percentage, action))
```
# Learning to Earn Max Returns
## Policy Learning
Policy learning is the policy the agent learning to earn the maximum returns. For instance, if we ride a bicycle, when the bicycle is tilt to the left we try to give more power to the right side. The above strategy is called policy learning.
### Gradient Descent in Policy Learning
$$arg\ min_\theta\ -\sum_{i}\ R_{i}\ log{p(y_{i}|x_{i}, \theta)}$$
$R_{i}$ is the discounted future return, $y_{i}$ is the action taken at time $i$.
## Value Learning
Value learning is the agent learns the value from the state while taking an action. That is, value learning is to learn the value from a pair [state, action]. For example, if we ride a bicycle, we give higher or lower values to any combinations of [state, action], such a strategy is called value learning.
```
```
| true |
code
| 0.654591 | null | null | null | null |
|
<img src="../figures/HeaDS_logo_large_withTitle.png" width="300">
<img src="../figures/tsunami_logo.PNG" width="600">
[](https://colab.research.google.com/github/Center-for-Health-Data-Science/PythonTsunami/blob/intro/Numbers_and_operators/Numbers_and_operators.ipynb)
# Numerical Operators
*Prepared by [Katarina Nastou](https://www.cpr.ku.dk/staff/?pure=en/persons/672471)*
## Objectives
- understand differences between `int`s and `float`s
- work with simple math operators
- add comments to your code
## Numbers
Two main types of numbers:
- Integers: `56, 3, -90`
- Floating Points: `5.666, 0.0, -8.9`
## Operators
- addition: `+`
- subtraction: `-`
- multiplication: `*`
- division: `/`
- exponentiation, power: `**`
- modulo: `%`
- integer division: `//` (what does it return?)
```
# playground
```
### Qestions: Ints and Floats
- Question 1: Which of the following numbers is NOT a float?
(a) 0
(b) 2.3
(c) 23.0
(d) -23.0
(e) 0.0
- Question 2: What type does the following expression result in?
```python
3.0 + 5
```
### Operators 1
- Question 3: How can we add parenthesis to the following expression to make it equal 100?
```python
1 + 9 * 10
```
- Question 4: What is the result of the following expression?
```python
3 + 14 * 2 + 4 * 5
```
- Question 5: What is the result of the following expression
```python
5 * 9 / 4 ** 3 - 6 * 7
```
```
```
### Comments
- Question 6: What is the result of running this code?
```python
15 / 3 * 2 # + 1
```
```
```
### Questions: Operators 2
- Question 7: Which of the following result in integers in Python?
(a) 8 / 2
(b) 3 // 2
(c) 4.5 * 2
- Question 8: What is the result of `18 // 3` ?
- Question 9: What is the result of `121 % 7` ?
## Exercise
Ask the user for a number using the function [input()](https://www.askpython.com/python/examples/python-user-input) and then multiply that number by 2 and print out the value. Remember to store the input value into a variable, so that you can use it afterwards in the multiplication.
Modfify your previous calculator and ask for the second number (instead of x * 2 --> x * y).
Now get the square of the number that the user inputs
### Note
Check out also the [math library](https://docs.python.org/3/library/math.html) in Python. You can use this library for more complex operations with numbers. Just import the library and try it out:
```python
import math
print(math.sqrt(25))
print(math.log10(10))
```
| true |
code
| 0.677234 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/mrdbourke/tensorflow-deep-learning/blob/main/05_transfer_learning_in_tensorflow_part_2_fine_tuning.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# 05. Transfer Learning with TensorFlow Part 2: Fine-tuning
In the previous section, we saw how we could leverage feature extraction transfer learning to get far better results on our Food Vision project than building our own models (even with less data).
Now we're going to cover another type of transfer learning: fine-tuning.
In **fine-tuning transfer learning** the pre-trained model weights from another model are unfrozen and tweaked during to better suit your own data.
For feature extraction transfer learning, you may only train the top 1-3 layers of a pre-trained model with your own data, in fine-tuning transfer learning, you might train 1-3+ layers of a pre-trained model (where the '+' indicates that many or all of the layers could be trained).
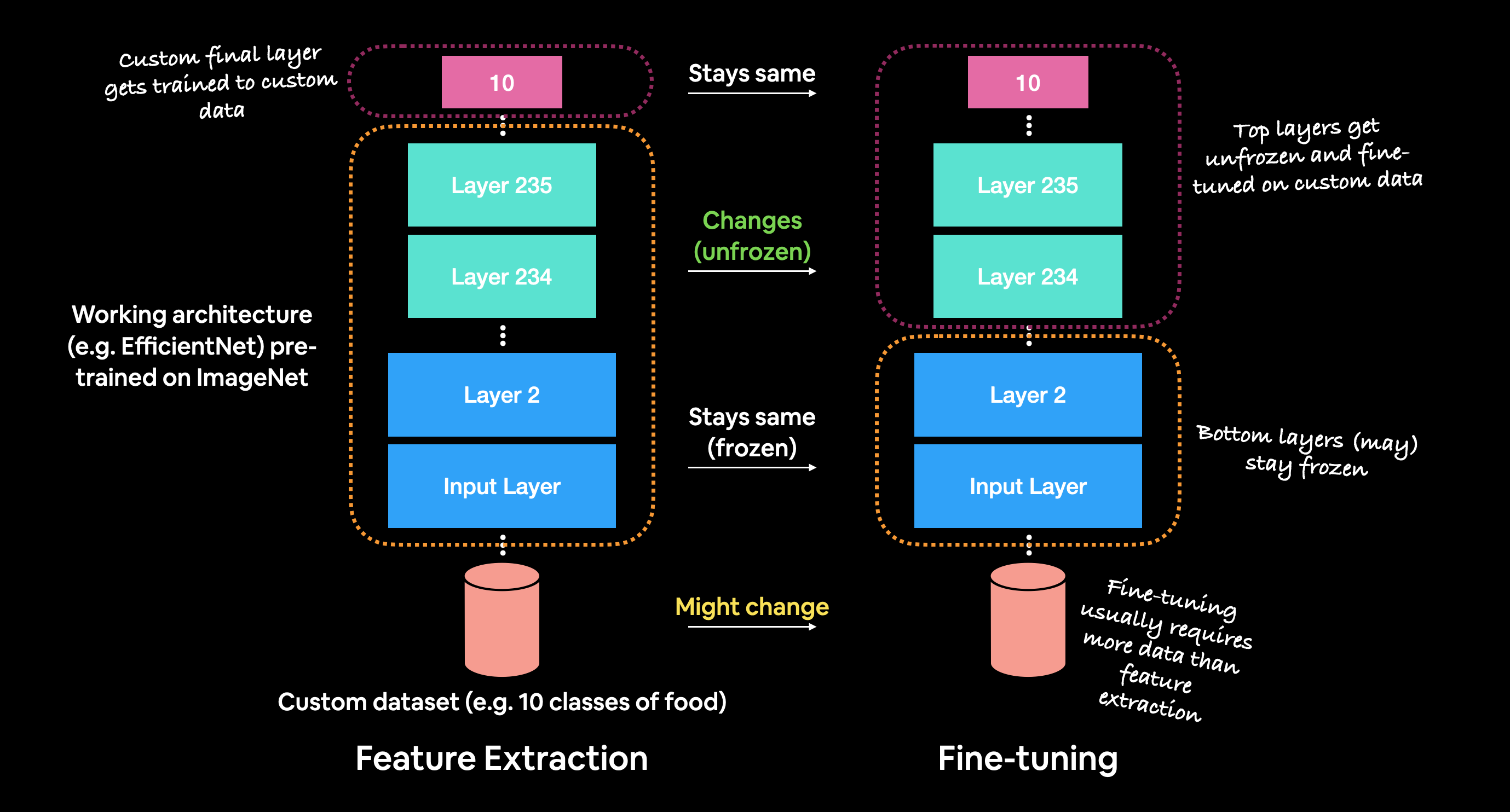
*Feature extraction transfer learning vs. fine-tuning transfer learning. The main difference between the two is that in fine-tuning, more layers of the pre-trained model get unfrozen and tuned on custom data. This fine-tuning usually takes more data than feature extraction to be effective.*
## What we're going to cover
We're going to go through the follow with TensorFlow:
- Introduce fine-tuning, a type of transfer learning to modify a pre-trained model to be more suited to your data
- Using the Keras Functional API (a differnt way to build models in Keras)
- Using a smaller dataset to experiment faster (e.g. 1-10% of training samples of 10 classes of food)
- Data augmentation (how to make your training dataset more diverse without adding more data)
- Running a series of modelling experiments on our Food Vision data
- Model 0: a transfer learning model using the Keras Functional API
- Model 1: a feature extraction transfer learning model on 1% of the data with data augmentation
- Model 2: a feature extraction transfer learning model on 10% of the data with data augmentation
- Model 3: a fine-tuned transfer learning model on 10% of the data
- Model 4: a fine-tuned transfer learning model on 100% of the data
- Introduce the ModelCheckpoint callback to save intermediate training results
- Compare model experiments results using TensorBoard
## How you can use this notebook
You can read through the descriptions and the code (it should all run, except for the cells which error on purpose), but there's a better option.
Write all of the code yourself.
Yes. I'm serious. Create a new notebook, and rewrite each line by yourself. Investigate it, see if you can break it, why does it break?
You don't have to write the text descriptions but writing the code yourself is a great way to get hands-on experience.
Don't worry if you make mistakes, we all do. The way to get better and make less mistakes is to **write more code**.
```
# Are we using a GPU? (if not & you're using Google Colab, go to Runtime -> Change Runtime Type -> Harware Accelerator: GPU )
!nvidia-smi
```
## Creating helper functions
Throughout your machine learning experiments, you'll likely come across snippets of code you want to use over and over again.
For example, a plotting function which plots a model's `history` object (see `plot_loss_curves()` below).
You could recreate these functions over and over again.
But as you might've guessed, rewritting the same functions becomes tedious.
One of the solutions is to store them in a helper script such as [`helper_functions.py`](https://github.com/mrdbourke/tensorflow-deep-learning/blob/main/extras/helper_functions.py). And then import the necesary functionality when you need it.
For example, you might write:
```
from helper_functions import plot_loss_curves
...
plot_loss_curves(history)
```
Let's see what this looks like.
```
# Get helper_functions.py script from course GitHub
!wget https://raw.githubusercontent.com/mrdbourke/tensorflow-deep-learning/main/extras/helper_functions.py
# Import helper functions we're going to use
from helper_functions import create_tensorboard_callback, plot_loss_curves, unzip_data, walk_through_dir
```
Wonderful, now we've got a bunch of helper functions we can use throughout the notebook without having to rewrite them from scratch each time.
> 🔑 **Note:** If you're running this notebook in Google Colab, when it times out Colab will delete the `helper_functions.py` file. So to use the functions imported above, you'll have to rerun the cell.
## 10 Food Classes: Working with less data
We saw in the [previous notebook](https://github.com/mrdbourke/tensorflow-deep-learning/blob/main/04_transfer_learning_in_tensorflow_part_1_feature_extraction.ipynb) that we could get great results with only 10% of the training data using transfer learning with TensorFlow Hub.
In this notebook, we're going to continue to work with smaller subsets of the data, except this time we'll have a look at how we can use the in-built pretrained models within the `tf.keras.applications` module as well as how to fine-tune them to our own custom dataset.
We'll also practice using a new but similar dataloader function to what we've used before, [`image_dataset_from_directory()`](https://www.tensorflow.org/api_docs/python/tf/keras/preprocessing/image_dataset_from_directory) which is part of the [`tf.keras.preprocessing`](https://www.tensorflow.org/api_docs/python/tf/keras/preprocessing) module.
Finally, we'll also be practicing using the [Keras Functional API](https://keras.io/guides/functional_api/) for building deep learning models. The Functional API is a more flexible way to create models than the tf.keras.Sequential API.
We'll explore each of these in more detail as we go.
Let's start by downloading some data.
```
# Get 10% of the data of the 10 classes
!wget https://storage.googleapis.com/ztm_tf_course/food_vision/10_food_classes_10_percent.zip
unzip_data("10_food_classes_10_percent.zip")
```
The dataset we're downloading is the 10 food classes dataset (from Food 101) with 10% of the training images we used in the previous notebook.
> 🔑 **Note:** You can see how this dataset was created in the [image data modification notebook](https://github.com/mrdbourke/tensorflow-deep-learning/blob/main/extras/image_data_modification.ipynb).
```
# Walk through 10 percent data directory and list number of files
walk_through_dir("10_food_classes_10_percent")
```
We can see that each of the training directories contain 75 images and each of the testing directories contain 250 images.
Let's define our training and test filepaths.
```
# Create training and test directories
train_dir = "10_food_classes_10_percent/train/"
test_dir = "10_food_classes_10_percent/test/"
```
Now we've got some image data, we need a way of loading it into a TensorFlow compatible format.
Previously, we've used the [`ImageDataGenerator`](https://www.tensorflow.org/api_docs/python/tf/keras/preprocessing/image/ImageDataGenerator) class. And while this works well and is still very commonly used, this time we're going to use the `image_data_from_directory` function.
It works much the same way as `ImageDataGenerator`'s `flow_from_directory` method meaning your images need to be in the following file format:
```
Example of file structure
10_food_classes_10_percent <- top level folder
└───train <- training images
│ └───pizza
│ │ │ 1008104.jpg
│ │ │ 1638227.jpg
│ │ │ ...
│ └───steak
│ │ 1000205.jpg
│ │ 1647351.jpg
│ │ ...
│
└───test <- testing images
│ └───pizza
│ │ │ 1001116.jpg
│ │ │ 1507019.jpg
│ │ │ ...
│ └───steak
│ │ 100274.jpg
│ │ 1653815.jpg
│ │ ...
```
One of the main benefits of using [`tf.keras.prepreprocessing.image_dataset_from_directory()`](https://www.tensorflow.org/api_docs/python/tf/keras/preprocessing/image_dataset_from_directory) rather than `ImageDataGenerator` is that it creates a [`tf.data.Dataset`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset) object rather than a generator. The main advantage of this is the `tf.data.Dataset` API is much more efficient (faster) than the `ImageDataGenerator` API which is paramount for larger datasets.
Let's see it in action.
```
# Create data inputs
import tensorflow as tf
IMG_SIZE = (224, 224) # define image size
train_data_10_percent = tf.keras.preprocessing.image_dataset_from_directory(directory=train_dir,
image_size=IMG_SIZE,
label_mode="categorical", # what type are the labels?
batch_size=32) # batch_size is 32 by default, this is generally a good number
test_data_10_percent = tf.keras.preprocessing.image_dataset_from_directory(directory=test_dir,
image_size=IMG_SIZE,
label_mode="categorical")
```
Wonderful! Looks like our dataloaders have found the correct number of images for each dataset.
For now, the main parameters we're concerned about in the `image_dataset_from_directory()` funtion are:
* `directory` - the filepath of the target directory we're loading images in from.
* `image_size` - the target size of the images we're going to load in (height, width).
* `batch_size` - the batch size of the images we're going to load in. For example if the `batch_size` is 32 (the default), batches of 32 images and labels at a time will be passed to the model.
There are more we could play around with if we needed to [in the `tf.keras.preprocessing` documentation](https://www.tensorflow.org/api_docs/python/tf/keras/preprocessing/image_dataset_from_directory).
If we check the training data datatype we should see it as a `BatchDataset` with shapes relating to our data.
```
# Check the training data datatype
train_data_10_percent
```
In the above output:
* `(None, 224, 224, 3)` refers to the tensor shape of our images where `None` is the batch size, `224` is the height (and width) and `3` is the color channels (red, green, blue).
* `(None, 10)` refers to the tensor shape of the labels where `None` is the batch size and `10` is the number of possible labels (the 10 different food classes).
* Both image tensors and labels are of the datatype `tf.float32`.
The `batch_size` is `None` due to it only being used during model training. You can think of `None` as a placeholder waiting to be filled with the `batch_size` parameter from `image_dataset_from_directory()`.
Another benefit of using the `tf.data.Dataset` API are the assosciated methods which come with it.
For example, if we want to find the name of the classes we were working with, we could use the `class_names` attribute.
```
# Check out the class names of our dataset
train_data_10_percent.class_names
```
Or if we wanted to see an example batch of data, we could use the `take()` method.
```
# See an example batch of data
for images, labels in train_data_10_percent.take(1):
print(images, labels)
```
Notice how the image arrays come out as tensors of pixel values where as the labels come out as one-hot encodings (e.g. `[0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]` for `hamburger`).
### Model 0: Building a transfer learning model using the Keras Functional API
Alright, our data is tensor-ified, let's build a model.
To do so we're going to be using the [`tf.keras.applications`](https://www.tensorflow.org/api_docs/python/tf/keras/applications) module as it contains a series of already trained (on ImageNet) computer vision models as well as the Keras Functional API to construct our model.
We're going to go through the following steps:
1. Instantiate a pre-trained base model object by choosing a target model such as [`EfficientNetB0`](https://www.tensorflow.org/api_docs/python/tf/keras/applications/EfficientNetB0) from `tf.keras.applications`, setting the `include_top` parameter to `False` (we do this because we're going to create our own top, which are the output layers for the model).
2. Set the base model's `trainable` attribute to `False` to freeze all of the weights in the pre-trained model.
3. Define an input layer for our model, for example, what shape of data should our model expect?
4. [Optional] Normalize the inputs to our model if it requires. Some computer vision models such as `ResNetV250` require their inputs to be between 0 & 1.
> 🤔 **Note:** As of writing, the `EfficientNet` models in the `tf.keras.applications` module do not require images to be normalized (pixel values between 0 and 1) on input, where as many of the other models do. I posted [an issue to the TensorFlow GitHub](https://github.com/tensorflow/tensorflow/issues/42506) about this and they confirmed this.
5. Pass the inputs to the base model.
6. Pool the outputs of the base model into a shape compatible with the output activation layer (turn base model output tensors into same shape as label tensors). This can be done using [`tf.keras.layers.GlobalAveragePooling2D()`](https://www.tensorflow.org/api_docs/python/tf/keras/layers/GlobalAveragePooling2D) or [`tf.keras.layers.GlobalMaxPooling2D()`](https://www.tensorflow.org/api_docs/python/tf/keras/layers/GlobalMaxPool2D?hl=en) though the former is more common in practice.
7. Create an output activation layer using `tf.keras.layers.Dense()` with the appropriate activation function and number of neurons.
8. Combine the inputs and outputs layer into a model using [`tf.keras.Model()`](https://www.tensorflow.org/api_docs/python/tf/keras/Model).
9. Compile the model using the appropriate loss function and choose of optimizer.
10. Fit the model for desired number of epochs and with necessary callbacks (in our case, we'll start off with the TensorBoard callback).
Woah... that sounds like a lot. Before we get ahead of ourselves, let's see it in practice.
```
# 1. Create base model with tf.keras.applications
base_model = tf.keras.applications.EfficientNetB0(include_top=False)
# 2. Freeze the base model (so the pre-learned patterns remain)
base_model.trainable = False
# 3. Create inputs into the base model
inputs = tf.keras.layers.Input(shape=(224, 224, 3), name="input_layer")
# 4. If using ResNet50V2, add this to speed up convergence, remove for EfficientNet
# x = tf.keras.layers.experimental.preprocessing.Rescaling(1./255)(inputs)
# 5. Pass the inputs to the base_model (note: using tf.keras.applications, EfficientNet inputs don't have to be normalized)
x = base_model(inputs)
# Check data shape after passing it to base_model
print(f"Shape after base_model: {x.shape}")
# 6. Average pool the outputs of the base model (aggregate all the most important information, reduce number of computations)
x = tf.keras.layers.GlobalAveragePooling2D(name="global_average_pooling_layer")(x)
print(f"After GlobalAveragePooling2D(): {x.shape}")
# 7. Create the output activation layer
outputs = tf.keras.layers.Dense(10, activation="softmax", name="output_layer")(x)
# 8. Combine the inputs with the outputs into a model
model_0 = tf.keras.Model(inputs, outputs)
# 9. Compile the model
model_0.compile(loss='categorical_crossentropy',
optimizer=tf.keras.optimizers.Adam(),
metrics=["accuracy"])
# 10. Fit the model (we use less steps for validation so it's faster)
history_10_percent = model_0.fit(train_data_10_percent,
epochs=5,
steps_per_epoch=len(train_data_10_percent),
validation_data=test_data_10_percent,
# Go through less of the validation data so epochs are faster (we want faster experiments!)
validation_steps=int(0.25 * len(test_data_10_percent)),
# Track our model's training logs for visualization later
callbacks=[create_tensorboard_callback("transfer_learning", "10_percent_feature_extract")])
```
Nice! After a minute or so of training our model performs incredibly well on both the training (87%+ accuracy) and test sets (~83% accuracy).
This is incredible. All thanks to the power of transfer learning.
It's important to note the kind of transfer learning we used here is called feature extraction transfer learning, similar to what we did with the TensorFlow Hub models.
In other words, we passed our custom data to an already pre-trained model (`EfficientNetB0`), asked it "what patterns do you see?" and then put our own output layer on top to make sure the outputs were tailored to our desired number of classes.
We also used the Keras Functional API to build our model rather than the Sequential API. For now, the benefits of this main not seem clear but when you start to build more sophisticated models, you'll probably want to use the Functional API. So it's important to have exposure to this way of building models.
> 📖 **Resource:** To see the benefits and use cases of the Functional API versus the Sequential API, check out the [TensorFlow Functional API documentation](https://www.tensorflow.org/guide/keras/functional).
Let's inspect the layers in our model, we'll start with the base.
```
# Check layers in our base model
for layer_number, layer in enumerate(base_model.layers):
print(layer_number, layer.name)
```
Wow, that's a lot of layers... to handcode all of those would've taken a fairly long time to do, yet we can still take advatange of them thanks to the power of transfer learning.
How about a summary of the base model?
```
base_model.summary()
```
You can see how each of the different layers have a certain number of parameters each. Since we are using a pre-trained model, you can think of all of these parameters are patterns the base model has learned on another dataset. And because we set `base_model.trainable = False`, these patterns remain as they are during training (they're frozen and don't get updated).
Alright that was the base model, let's see the summary of our overall model.
```
# Check summary of model constructed with Functional API
model_0.summary()
```
Our overall model has five layers but really, one of those layers (`efficientnetb0`) has 236 layers.
You can see how the output shape started out as `(None, 224, 224, 3)` for the input layer (the shape of our images) but was transformed to be `(None, 10)` by the output layer (the shape of our labels), where `None` is the placeholder for the batch size.
Notice too, the only trainable parameters in the model are those in the output layer.
How do our model's training curves look?
```
# Check out our model's training curves
plot_loss_curves(history_10_percent)
```
## Getting a feature vector from a trained model
> 🤔 **Question:** What happens with the `tf.keras.layers.GlobalAveragePooling2D()` layer? I haven't seen it before.
The [`tf.keras.layers.GlobalAveragePooling2D()`](https://www.tensorflow.org/api_docs/python/tf/keras/layers/GlobalAveragePooling2D) layer transforms a 4D tensor into a 2D tensor by averaging the values across the inner-axes.
The previous sentence is a bit of a mouthful, so let's see an example.
```
# Define input tensor shape (same number of dimensions as the output of efficientnetb0)
input_shape = (1, 4, 4, 3)
# Create a random tensor
tf.random.set_seed(42)
input_tensor = tf.random.normal(input_shape)
print(f"Random input tensor:\n {input_tensor}\n")
# Pass the random tensor through a global average pooling 2D layer
global_average_pooled_tensor = tf.keras.layers.GlobalAveragePooling2D()(input_tensor)
print(f"2D global average pooled random tensor:\n {global_average_pooled_tensor}\n")
# Check the shapes of the different tensors
print(f"Shape of input tensor: {input_tensor.shape}")
print(f"Shape of 2D global averaged pooled input tensor: {global_average_pooled_tensor.shape}")
```
You can see the `tf.keras.layers.GlobalAveragePooling2D()` layer condensed the input tensor from shape `(1, 4, 4, 3)` to `(1, 3)`. It did so by averaging the `input_tensor` across the middle two axes.
We can replicate this operation using the `tf.reduce_mean()` operation and specifying the appropriate axes.
```
# This is the same as GlobalAveragePooling2D()
tf.reduce_mean(input_tensor, axis=[1, 2]) # average across the middle axes
```
Doing this not only makes the output of the base model compatible with the input shape requirement of our output layer (`tf.keras.layers.Dense()`), it also condenses the information found by the base model into a lower dimension **feature vector**.
> 🔑 **Note:** One of the reasons feature extraction transfer learning is named how it is is because what often happens is a pretrained model outputs a **feature vector** (a long tensor of numbers, in our case, this is the output of the [`tf.keras.layers.GlobalAveragePooling2D()`](https://www.tensorflow.org/api_docs/python/tf/keras/layers/GlobalAveragePooling2D) layer) which can then be used to extract patterns out of.
> 🛠 **Practice:** Do the same as the above cell but for [`tf.keras.layers.GlobalMaxPool2D()`](https://www.tensorflow.org/api_docs/python/tf/keras/layers/GlobalMaxPool2D).
## Running a series of transfer learning experiments
We've seen the incredible results of transfer learning on 10% of the training data, what about 1% of the training data?
What kind of results do you think we can get using 100x less data than the original CNN models we built ourselves?
Why don't we answer that question while running the following modelling experiments:
1. `model_1`: Use feature extraction transfer learning on 1% of the training data with data augmentation.
2. `model_2`: Use feature extraction transfer learning on 10% of the training data with data augmentation.
3. `model_3`: Use fine-tuning transfer learning on 10% of the training data with data augmentation.
4. `model_4`: Use fine-tuning transfer learning on 100% of the training data with data augmentation.
While all of the experiments will be run on different versions of the training data, they will all be evaluated on the same test dataset, this ensures the results of each experiment are as comparable as possible.
All experiments will be done using the `EfficientNetB0` model within the `tf.keras.applications` module.
To make sure we're keeping track of our experiments, we'll use our `create_tensorboard_callback()` function to log all of the model training logs.
We'll construct each model using the Keras Functional API and instead of implementing data augmentation in the `ImageDataGenerator` class as we have previously, we're going to build it right into the model using the [`tf.keras.layers.experimental.preprocessing`](https://www.tensorflow.org/api_docs/python/tf/keras/layers/experimental/preprocessing) module.
Let's begin by downloading the data for experiment 1, using feature extraction transfer learning on 1% of the training data with data augmentation.
```
# Download and unzip data
!wget https://storage.googleapis.com/ztm_tf_course/food_vision/10_food_classes_1_percent.zip
unzip_data("10_food_classes_1_percent.zip")
# Create training and test dirs
train_dir_1_percent = "10_food_classes_1_percent/train/"
test_dir = "10_food_classes_1_percent/test/"
```
How many images are we working with?
```
# Walk through 1 percent data directory and list number of files
walk_through_dir("10_food_classes_1_percent")
```
Alright, looks like we've only got seven images of each class, this should be a bit of a challenge for our model.
> 🔑 **Note:** As with the 10% of data subset, the 1% of images were chosen at random from the original full training dataset. The test images are the same as the ones which have previously been used. If you want to see how this data was preprocessed, check out the [Food Vision Image Preprocessing notebook](https://github.com/mrdbourke/tensorflow-deep-learning/blob/main/extras/image_data_modification.ipynb).
Time to load our images in as `tf.data.Dataset` objects, to do so, we'll use the [`image_dataset_from_directory()`](https://www.tensorflow.org/api_docs/python/tf/keras/preprocessing/image_dataset_from_directory) method.
```
import tensorflow as tf
IMG_SIZE = (224, 224)
train_data_1_percent = tf.keras.preprocessing.image_dataset_from_directory(train_dir_1_percent,
label_mode="categorical",
batch_size=32, # default
image_size=IMG_SIZE)
test_data = tf.keras.preprocessing.image_dataset_from_directory(test_dir,
label_mode="categorical",
image_size=IMG_SIZE)
```
Data loaded. Time to augment it.
### Adding data augmentation right into the model
Previously we've used the different parameters of the `ImageDataGenerator` class to augment our training images, this time we're going to build data augmentation right into the model.
How?
Using the [`tf.keras.layers.experimental.preprocessing`](https://www.tensorflow.org/api_docs/python/tf/keras/layers/experimental/preprocessing) module and creating a dedicated data augmentation layer.
This a relatively new feature added to TensorFlow 2.2+ but it's very powerful. Adding a data augmentation layer to the model has the following benefits:
* Preprocessing of the images (augmenting them) happens on the GPU rather than on the CPU (much faster).
* Images are best preprocessed on the GPU where as text and structured data are more suited to be preprocessed on the CPU.
* Image data augmentation only happens during training so we can still export our whole model and use it elsewhere. And if someone else wanted to train the same model as us, including the same kind of data augmentation, they could.

*Example of using data augmentation as the first layer within a model (EfficientNetB0).*
> 🤔 **Note:** At the time of writing, the preprocessing layers we're using for data augmentation are in *experimental* status within the in TensorFlow library. This means although the layers should be considered stable, the code may change slightly in a future version of TensorFlow. For more information on the other preprocessing layers avaiable and the different methods of data augmentation, check out the [Keras preprocessing layers guide](https://keras.io/guides/preprocessing_layers/) and the [TensorFlow data augmentation guide](https://www.tensorflow.org/tutorials/images/data_augmentation).
To use data augmentation right within our model we'll create a Keras Sequential model consisting of only data preprocessing layers, we can then use this Sequential model within another Functional model.
If that sounds confusing, it'll make sense once we create it in code.
The data augmentation transformations we're going to use are:
* [RandomFlip](https://www.tensorflow.org/api_docs/python/tf/keras/layers/experimental/preprocessing/RandomFlip) - flips image on horizontal or vertical axis.
* [RandomRotation](https://www.tensorflow.org/api_docs/python/tf/keras/layers/experimental/preprocessing/RandomRotation) - randomly rotates image by a specified amount.
* [RandomZoom](https://www.tensorflow.org/api_docs/python/tf/keras/layers/experimental/preprocessing/RandomZoom) - randomly zooms into an image by specified amount.
* [RandomHeight](https://www.tensorflow.org/api_docs/python/tf/keras/layers/experimental/preprocessing/RandomHeight) - randomly shifts image height by a specified amount.
* [RandomWidth](https://www.tensorflow.org/api_docs/python/tf/keras/layers/experimental/preprocessing/RandomWidth) - randomly shifts image width by a specified amount.
* [Rescaling](https://www.tensorflow.org/api_docs/python/tf/keras/layers/experimental/preprocessing/Rescaling) - normalizes the image pixel values to be between 0 and 1, this is worth mentioning because it is required for some image models but since we're using the `tf.keras.applications` implementation of `EfficientNetB0`, it's not required.
There are more option but these will do for now.
```
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.layers.experimental import preprocessing
# Create a data augmentation stage with horizontal flipping, rotations, zooms
data_augmentation = keras.Sequential([
preprocessing.RandomFlip("horizontal"),
preprocessing.RandomRotation(0.2),
preprocessing.RandomZoom(0.2),
preprocessing.RandomHeight(0.2),
preprocessing.RandomWidth(0.2),
# preprocessing.Rescaling(1./255) # keep for ResNet50V2, remove for EfficientNetB0
], name ="data_augmentation")
```
And that's it! Our data augmentation Sequential model is ready to go. As you'll see shortly, we'll be able to slot this "model" as a layer into our transfer learning model later on.
But before we do that, let's test it out by passing random images through it.
```
# View a random image
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import os
import random
target_class = random.choice(train_data_1_percent.class_names) # choose a random class
target_dir = "10_food_classes_1_percent/train/" + target_class # create the target directory
random_image = random.choice(os.listdir(target_dir)) # choose a random image from target directory
random_image_path = target_dir + "/" + random_image # create the choosen random image path
img = mpimg.imread(random_image_path) # read in the chosen target image
plt.imshow(img) # plot the target image
plt.title(f"Original random image from class: {target_class}")
plt.axis(False); # turn off the axes
# Augment the image
augmented_img = data_augmentation(tf.expand_dims(img, axis=0)) # data augmentation model requires shape (None, height, width, 3)
plt.figure()
plt.imshow(tf.squeeze(augmented_img)/255.) # requires normalization after augmentation
plt.title(f"Augmented random image from class: {target_class}")
plt.axis(False);
```
Run the cell above a few times and you can see the different random augmentations on different classes of images. Because we're going to add the data augmentation model as a layer in our upcoming transfer learning model, it'll apply these kind of random augmentations to each of the training images which passes through it.
Doing this will make our training dataset a little more varied. You can think of it as if you were taking a photo of food in real-life, not all of the images are going to be perfect, some of them are going to be orientated in strange ways. These are the kind of images we want our model to be able to handle.
Speaking of model, let's build one with the Functional API. We'll run through all of the same steps as before except for one difference, we'll add our data augmentation Sequential model as a layer immediately after the input layer.
## Model 1: Feature extraction transfer learning on 1% of the data with data augmentation
```
# Setup input shape and base model, freezing the base model layers
input_shape = (224, 224, 3)
base_model = tf.keras.applications.EfficientNetB0(include_top=False)
base_model.trainable = False
# Create input layer
inputs = layers.Input(shape=input_shape, name="input_layer")
# Add in data augmentation Sequential model as a layer
x = data_augmentation(inputs)
# Give base_model inputs (after augmentation) and don't train it
x = base_model(x, training=False)
# Pool output features of base model
x = layers.GlobalAveragePooling2D(name="global_average_pooling_layer")(x)
# Put a dense layer on as the output
outputs = layers.Dense(10, activation="softmax", name="output_layer")(x)
# Make a model with inputs and outputs
model_1 = keras.Model(inputs, outputs)
# Compile the model
model_1.compile(loss="categorical_crossentropy",
optimizer=tf.keras.optimizers.Adam(),
metrics=["accuracy"])
# Fit the model
history_1_percent = model_1.fit(train_data_1_percent,
epochs=5,
steps_per_epoch=len(train_data_1_percent),
validation_data=test_data,
validation_steps=int(0.25* len(test_data)), # validate for less steps
# Track model training logs
callbacks=[create_tensorboard_callback("transfer_learning", "1_percent_data_aug")])
```
Wow! How cool is that? Using only 7 training images per class, using transfer learning our model was able to get ~40% accuracy on the validation set. This result is pretty amazing since the [original Food-101 paper](https://data.vision.ee.ethz.ch/cvl/datasets_extra/food-101/static/bossard_eccv14_food-101.pdf) achieved 50.67% accuracy with all the data, namely, 750 training images per class (**note:** this metric was across 101 classes, not 10, we'll get to 101 classes soon).
If we check out a summary of our model, we should see the data augmentation layer just after the input layer.
```
# Check out model summary
model_1.summary()
```
There it is. We've now got data augmentation built right into the our model. This means if we saved it and reloaded it somewhere else, the data augmentation layers would come with it.
The important thing to remember is **data augmentation only runs during training**. So if we were to evaluate or use our model for inference (predicting the class of an image) the data augmentation layers will be automatically turned off.
To see this in action, let's evaluate our model on the test data.
```
# Evaluate on the test data
results_1_percent_data_aug = model_1.evaluate(test_data)
results_1_percent_data_aug
```
The results here may be slightly better/worse than the log outputs of our model during training because during training we only evaluate our model on 25% of the test data using the line `validation_steps=int(0.25 * len(test_data))`. Doing this speeds up our epochs but still gives us enough of an idea of how our model is going.
Let's stay consistent and check out our model's loss curves.
```
# How does the model go with a data augmentation layer with 1% of data
plot_loss_curves(history_1_percent)
```
It looks like the metrics on both datasets would improve if we kept training for more epochs. But we'll leave that for now, we've got more experiments to do!
## Model 2: Feature extraction transfer learning with 10% of data and data augmentation
Alright, we've tested 1% of the training data with data augmentation, how about we try 10% of the data with data augmentation?
But wait...
> 🤔 **Question:** How do you know what experiments to run?
Great question.
The truth here is you often won't. Machine learning is still a very experimental practice. It's only after trying a fair few things that you'll start to develop an intuition of what to try.
My advice is to follow your curiosity as tenaciously as possible. If you feel like you want to try something, write the code for it and run it. See how it goes. The worst thing that'll happen is you'll figure out what doesn't work, the most valuable kind of knowledge.
From a practical standpoint, as we've talked about before, you'll want to reduce the amount of time between your initial experiments as much as possible. In other words, run a plethora of smaller experiments, using less data and less training iterations before you find something promising and then scale it up.
In the theme of scale, let's scale our 1% training data augmentation experiment up to 10% training data augmentation. That sentence doesn't really make sense but you get what I mean.
We're going to run through the exact same steps as the previous model, the only difference being using 10% of the training data instead of 1%.
```
# Get 10% of the data of the 10 classes (uncomment if you haven't gotten "10_food_classes_10_percent.zip" already)
# !wget https://storage.googleapis.com/ztm_tf_course/food_vision/10_food_classes_10_percent.zip
# unzip_data("10_food_classes_10_percent.zip")
train_dir_10_percent = "10_food_classes_10_percent/train/"
test_dir = "10_food_classes_10_percent/test/"
```
Data downloaded. Let's create the dataloaders.
```
# Setup data inputs
import tensorflow as tf
IMG_SIZE = (224, 224)
train_data_10_percent = tf.keras.preprocessing.image_dataset_from_directory(train_dir_10_percent,
label_mode="categorical",
image_size=IMG_SIZE)
# Note: the test data is the same as the previous experiment, we could
# skip creating this, but we'll leave this here to practice.
test_data = tf.keras.preprocessing.image_dataset_from_directory(test_dir,
label_mode="categorical",
image_size=IMG_SIZE)
```
Awesome! We've got 10x more images to work with, 75 per class instead of 7 per class.
Let's build a model with data augmentation built in. We could reuse the data augmentation Sequential model we created before but we'll recreate it to practice.
```
# Create a functional model with data augmentation
import tensorflow as tf
from tensorflow.keras import layers
from tensorflow.keras.layers.experimental import preprocessing
from tensorflow.keras.models import Sequential
# Build data augmentation layer
data_augmentation = Sequential([
preprocessing.RandomFlip('horizontal'),
preprocessing.RandomHeight(0.2),
preprocessing.RandomWidth(0.2),
preprocessing.RandomZoom(0.2),
preprocessing.RandomRotation(0.2),
# preprocessing.Rescaling(1./255) # keep for ResNet50V2, remove for EfficientNet
], name="data_augmentation")
# Setup the input shape to our model
input_shape = (224, 224, 3)
# Create a frozen base model
base_model = tf.keras.applications.EfficientNetB0(include_top=False)
base_model.trainable = False
# Create input and output layers
inputs = layers.Input(shape=input_shape, name="input_layer") # create input layer
x = data_augmentation(inputs) # augment our training images
x = base_model(x, training=False) # pass augmented images to base model but keep it in inference mode, so batchnorm layers don't get updated: https://keras.io/guides/transfer_learning/#build-a-model
x = layers.GlobalAveragePooling2D(name="global_average_pooling_layer")(x)
outputs = layers.Dense(10, activation="softmax", name="output_layer")(x)
model_2 = tf.keras.Model(inputs, outputs)
# Compile
model_2.compile(loss="categorical_crossentropy",
optimizer=tf.keras.optimizers.Adam(lr=0.001), # use Adam optimizer with base learning rate
metrics=["accuracy"])
```
### Creating a ModelCheckpoint callback
Our model is compiled and ready to be fit, so why haven't we fit it yet?
Well, for this experiment we're going to introduce a new callback, the `ModelCheckpoint` callback.
The [`ModelCheckpoint`](https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/ModelCheckpoint) callback gives you the ability to save your model, as a whole in the [`SavedModel`](https://www.tensorflow.org/tutorials/keras/save_and_load#save_the_entire_model) format or the [weights (patterns) only](https://www.tensorflow.org/tutorials/keras/save_and_load#manually_save_weights) to a specified directory as it trains.
This is helpful if you think your model is going to be training for a long time and you want to make backups of it as it trains. It also means if you think your model could benefit from being trained for longer, you can reload it from a specific checkpoint and continue training from there.
For example, say you fit a feature extraction transfer learning model for 5 epochs and you check the training curves and see it was still improving and you want to see if fine-tuning for another 5 epochs could help, you can load the checkpoint, unfreeze some (or all) of the base model layers and then continue training.
In fact, that's exactly what we're going to do.
But first, let's create a `ModelCheckpoint` callback. To do so, we have to specifcy a directory we'd like to save to.
```
# Setup checkpoint path
checkpoint_path = "ten_percent_model_checkpoints_weights/checkpoint.ckpt" # note: remember saving directly to Colab is temporary
# Create a ModelCheckpoint callback that saves the model's weights only
checkpoint_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_path,
save_weights_only=True, # set to False to save the entire model
save_best_only=False, # set to True to save only the best model instead of a model every epoch
save_freq="epoch", # save every epoch
verbose=1)
```
> 🤔 **Question:** What's the difference between saving the entire model (SavedModel format) and saving the weights only?
The [`SavedModel`](https://www.tensorflow.org/tutorials/keras/save_and_load#save_the_entire_model) format saves a model's architecture, weights and training configuration all in one folder. It makes it very easy to reload your model exactly how it is elsewhere. However, if you do not want to share all of these details with others, you may want to save and share the weights only (these will just be large tensors of non-human interpretable numbers). If disk space is an issue, saving the weights only is faster and takes up less space than saving the whole model.
Time to fit the model.
Because we're going to be fine-tuning it later, we'll create a variable `initial_epochs` and set it to 5 to use later.
We'll also add in our `checkpoint_callback` in our list of `callbacks`.
```
# Fit the model saving checkpoints every epoch
initial_epochs = 5
history_10_percent_data_aug = model_2.fit(train_data_10_percent,
epochs=initial_epochs,
validation_data=test_data,
validation_steps=int(0.25 * len(test_data)), # do less steps per validation (quicker)
callbacks=[create_tensorboard_callback("transfer_learning", "10_percent_data_aug"),
checkpoint_callback])
```
Would you look at that! Looks like our `ModelCheckpoint` callback worked and our model saved its weights every epoch without too much overhead (saving the whole model takes longer than just the weights).
Let's evaluate our model and check its loss curves.
```
# Evaluate on the test data
results_10_percent_data_aug = model_2.evaluate(test_data)
results_10_percent_data_aug
# Plot model loss curves
plot_loss_curves(history_10_percent_data_aug)
```
Looking at these, our model's performance with 10% of the data and data augmentation isn't as good as the model with 10% of the data without data augmentation (see `model_0` results above), however the curves are trending in the right direction, meaning if we decided to train for longer, its metrics would likely improve.
Since we checkpointed (is that a word?) our model's weights, we might as well see what it's like to load it back in. We'll be able to test if it saved correctly by evaluting it on the test data.
To load saved model weights you can use the the [`load_weights()`](https://www.tensorflow.org/tutorials/keras/save_and_load#checkpoint_callback_options) method, passing it the path where your saved weights are stored.
```
# Load in saved model weights and evaluate model
model_2.load_weights(checkpoint_path)
loaded_weights_model_results = model_2.evaluate(test_data)
```
Now let's compare the results of our previously trained model and the loaded model. These results should very close if not exactly the same. The reason for minor differences comes down to the precision level of numbers calculated.
```
# If the results from our native model and the loaded weights are the same, this should output True
results_10_percent_data_aug == loaded_weights_model_results
```
If the above cell doesn't output `True`, it's because the numbers are close but not the *exact* same (due to how computers store numbers with degrees of precision).
However, they should be *very* close...
```
import numpy as np
# Check to see if loaded model results are very close to native model results (should output True)
np.isclose(np.array(results_10_percent_data_aug), np.array(loaded_weights_model_results))
# Check the difference between the two results
print(np.array(results_10_percent_data_aug) - np.array(loaded_weights_model_results))
```
## Model 3: Fine-tuning an existing model on 10% of the data
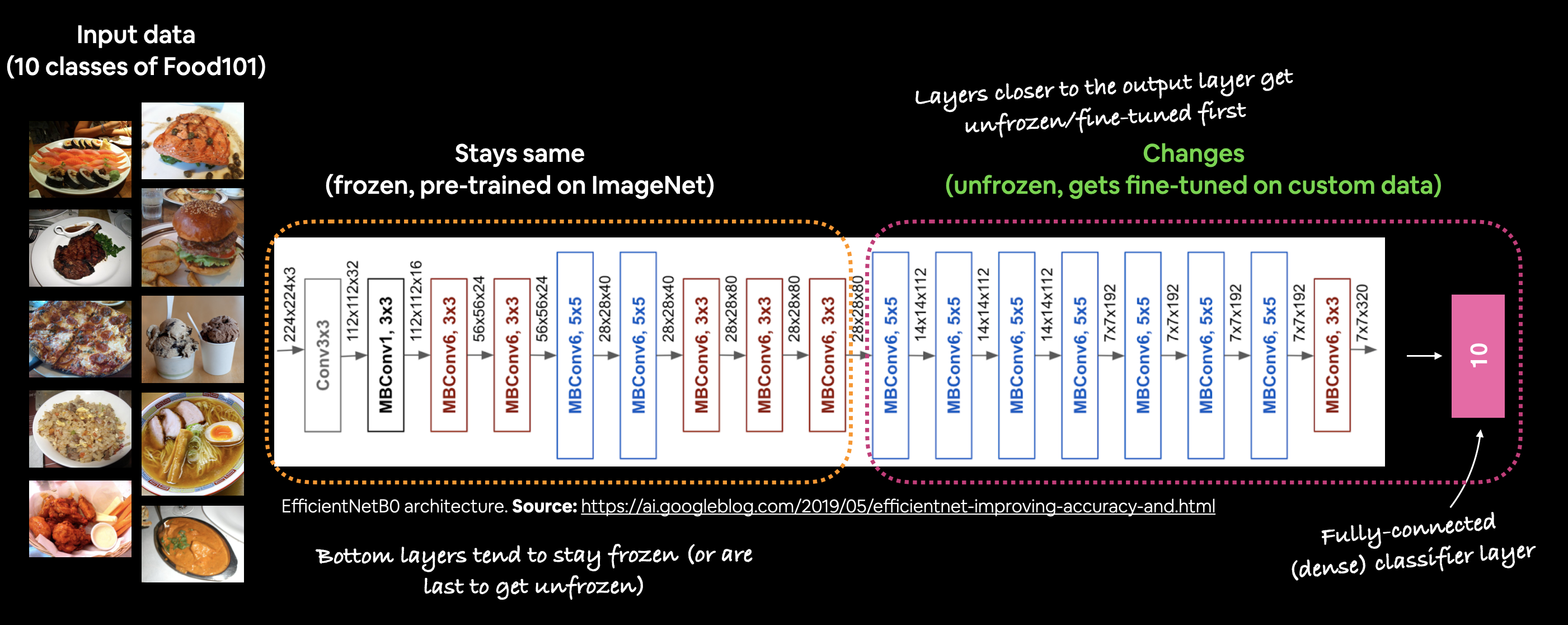
*High-level example of fine-tuning an EfficientNet model. Bottom layers (layers closer to the input data) stay frozen where as top layers (layers closer to the output data) are updated during training.*
So far our saved model has been trained using feature extraction transfer learning for 5 epochs on 10% of the training data and data augmentation.
This means all of the layers in the base model (EfficientNetB0) were frozen during training.
For our next experiment we're going to switch to fine-tuning transfer learning. This means we'll be using the same base model except we'll be unfreezing some of its layers (ones closest to the top) and running the model for a few more epochs.
The idea with fine-tuning is to start customizing the pre-trained model more to our own data.
> 🔑 **Note:** Fine-tuning usually works best *after* training a feature extraction model for a few epochs and with large amounts of data. For more on this, check out [Keras' guide on Transfer learning & fine-tuning](https://keras.io/guides/transfer_learning/).
We've verified our loaded model's performance, let's check out its layers.
```
# Layers in loaded model
model_2.layers
for layer in model_2.layers:
print(layer.trainable)
```
Looking good. We've got an input layer, a Sequential layer (the data augmentation model), a Functional layer (EfficientNetB0), a pooling layer and a Dense layer (the output layer).
How about a summary?
```
model_2.summary()
```
Alright, it looks like all of the layers in the `efficientnetb0` layer are frozen. We can confirm this using the `trainable_variables` attribute.
```
# How many layers are trainable in our base model?
print(len(model_2.layers[2].trainable_variables)) # layer at index 2 is the EfficientNetB0 layer (the base model)
```
This is the same as our base model.
```
print(len(base_model.trainable_variables))
```
We can even check layer by layer to see if the they're trainable.
```
# Check which layers are tuneable (trainable)
for layer_number, layer in enumerate(base_model.layers):
print(layer_number, layer.name, layer.trainable)
```
Beautiful. This is exactly what we're after.
Now to fine-tune the base model to our own data, we're going to unfreeze the top 10 layers and continue training our model for another 5 epochs.
This means all of the base model's layers except for the last 10 will remain frozen and untrainable. And the weights in the remaining unfrozen layers will be updated during training.
Ideally, we should see the model's performance improve.
> 🤔 **Question:** How many layers should you unfreeze when training?
There's no set rule for this. You could unfreeze every layer in the pretrained model or you could try unfreezing one layer at a time. Best to experiment with different amounts of unfreezing and fine-tuning to see what happens. Generally, the less data you have, the less layers you want to unfreeze and the more gradually you want to fine-tune.
> 📖 **Resource:** The [ULMFiT (Universal Language Model Fine-tuning for Text Classification) paper](https://arxiv.org/abs/1801.06146) has a great series of experiments on fine-tuning models.
To begin fine-tuning, we'll unfreeze the entire base model by setting its `trainable` attribute to `True`. Then we'll refreeze every layer in the base model except for the last 10 by looping through them and setting their `trainable` attribute to `False`. Finally, we'll recompile the model.
```
base_model.trainable = True
# Freeze all layers except for the
for layer in base_model.layers[:-10]:
layer.trainable = False
# Recompile the model (always recompile after any adjustments to a model)
model_2.compile(loss="categorical_crossentropy",
optimizer=tf.keras.optimizers.Adam(lr=0.0001), # lr is 10x lower than before for fine-tuning
metrics=["accuracy"])
```
Wonderful, now let's check which layers of the pretrained model are trainable.
```
# Check which layers are tuneable (trainable)
for layer_number, layer in enumerate(base_model.layers):
print(layer_number, layer.name, layer.trainable)
```
Nice! It seems all layers except for the last 10 are frozen and untrainable. This means only the last 10 layers of the base model along with the output layer will have their weights updated during training.
> 🤔 **Question:** Why did we recompile the model?
Every time you make a change to your models, you need to recompile them.
In our case, we're using the exact same loss, optimizer and metrics as before, except this time the learning rate for our optimizer will be 10x smaller than before (0.0001 instead of Adam's default of 0.001).
We do this so the model doesn't try to overwrite the existing weights in the pretrained model too fast. In other words, we want learning to be more gradual.
> 🔑 **Note:** There's no set standard for setting the learning rate during fine-tuning, though reductions of [2.6x-10x+ seem to work well in practice](https://arxiv.org/abs/1801.06146).
How many trainable variables do we have now?
```
print(len(model_2.trainable_variables))
```
Wonderful, it looks like our model has a total of 10 trainable variables, the last 10 layers of the base model and the weight and bias parameters of the Dense output layer.
Time to fine-tune!
We're going to continue training on from where our previous model finished. Since it trained for 5 epochs, our fine-tuning will begin on the epoch 5 and continue for another 5 epochs.
To do this, we can use the `initial_epoch` parameter of the [`fit()`](https://keras.rstudio.com/reference/fit.html) method. We'll pass it the last epoch of the previous model's training history (`history_10_percent_data_aug.epoch[-1]`).
```
# Fine tune for another 5 epochs
fine_tune_epochs = initial_epochs + 5
# Refit the model (same as model_2 except with more trainable layers)
history_fine_10_percent_data_aug = model_2.fit(train_data_10_percent,
epochs=fine_tune_epochs,
validation_data=test_data,
initial_epoch=history_10_percent_data_aug.epoch[-1], # start from previous last epoch
validation_steps=int(0.25 * len(test_data)),
callbacks=[create_tensorboard_callback("transfer_learning", "10_percent_fine_tune_last_10")]) # name experiment appropriately
```
> 🔑 **Note:** Fine-tuning usually takes far longer per epoch than feature extraction (due to updating more weights throughout a network).
Ho ho, looks like our model has gained a few percentage points of accuracy! Let's evalaute it.
```
# Evaluate the model on the test data
results_fine_tune_10_percent = model_2.evaluate(test_data)
```
Remember, the results from evaluating the model might be slightly different to the outputs from training since during training we only evaluate on 25% of the test data.
Alright, we need a way to evaluate our model's performance before and after fine-tuning. How about we write a function to compare the before and after?
```
def compare_historys(original_history, new_history, initial_epochs=5):
"""
Compares two model history objects.
"""
# Get original history measurements
acc = original_history.history["accuracy"]
loss = original_history.history["loss"]
print(len(acc))
val_acc = original_history.history["val_accuracy"]
val_loss = original_history.history["val_loss"]
# Combine original history with new history
total_acc = acc + new_history.history["accuracy"]
total_loss = loss + new_history.history["loss"]
total_val_acc = val_acc + new_history.history["val_accuracy"]
total_val_loss = val_loss + new_history.history["val_loss"]
print(len(total_acc))
print(total_acc)
# Make plots
plt.figure(figsize=(8, 8))
plt.subplot(2, 1, 1)
plt.plot(total_acc, label='Training Accuracy')
plt.plot(total_val_acc, label='Validation Accuracy')
plt.plot([initial_epochs-1, initial_epochs-1],
plt.ylim(), label='Start Fine Tuning') # reshift plot around epochs
plt.legend(loc='lower right')
plt.title('Training and Validation Accuracy')
plt.subplot(2, 1, 2)
plt.plot(total_loss, label='Training Loss')
plt.plot(total_val_loss, label='Validation Loss')
plt.plot([initial_epochs-1, initial_epochs-1],
plt.ylim(), label='Start Fine Tuning') # reshift plot around epochs
plt.legend(loc='upper right')
plt.title('Training and Validation Loss')
plt.xlabel('epoch')
plt.show()
```
This is where saving the history variables of our model training comes in handy. Let's see what happened after fine-tuning the last 10 layers of our model.
```
compare_historys(original_history=history_10_percent_data_aug,
new_history=history_fine_10_percent_data_aug,
initial_epochs=5)
```
Alright, alright, seems like the curves are heading in the right direction after fine-tuning. But remember, it should be noted that fine-tuning usually works best with larger amounts of data.
## Model 4: Fine-tuning an existing model all of the data
Enough talk about how fine-tuning a model usually works with more data, let's try it out.
We'll start by downloading the full version of our 10 food classes dataset.
```
# Download and unzip 10 classes of data with all images
!wget https://storage.googleapis.com/ztm_tf_course/food_vision/10_food_classes_all_data.zip
unzip_data("10_food_classes_all_data.zip")
# Setup data directories
train_dir = "10_food_classes_all_data/train/"
test_dir = "10_food_classes_all_data/test/"
# How many images are we working with now?
walk_through_dir("10_food_classes_all_data")
```
And now we'll turn the images into tensors datasets.
```
# Setup data inputs
import tensorflow as tf
IMG_SIZE = (224, 224)
train_data_10_classes_full = tf.keras.preprocessing.image_dataset_from_directory(train_dir,
label_mode="categorical",
image_size=IMG_SIZE)
# Note: this is the same test dataset we've been using for the previous modelling experiments
test_data = tf.keras.preprocessing.image_dataset_from_directory(test_dir,
label_mode="categorical",
image_size=IMG_SIZE)
```
Oh this is looking good. We've got 10x more images in of the training classes to work with.
The **test dataset is the same** we've been using for our previous experiments.
As it is now, our `model_2` has been fine-tuned on 10 percent of the data, so to begin fine-tuning on all of the data and keep our experiments consistent, we need to revert it back to the weights we checkpointed after 5 epochs of feature-extraction.
To demonstrate this, we'll first evaluate the current `model_2`.
```
# Evaluate model (this is the fine-tuned 10 percent of data version)
model_2.evaluate(test_data)
```
These are the same values as `results_fine_tune_10_percent`.
```
results_fine_tune_10_percent
```
Now we'll revert the model back to the saved weights.
```
# Load model from checkpoint, that way we can fine-tune from the same stage the 10 percent data model was fine-tuned from
model_2.load_weights(checkpoint_path) # revert model back to saved weights
```
And the results should be the same as `results_10_percent_data_aug`.
```
# After loading the weights, this should have gone down (no fine-tuning)
model_2.evaluate(test_data)
# Check to see if the above two results are the same (they should be)
results_10_percent_data_aug
```
Alright, the previous steps might seem quite confusing but all we've done is:
1. Trained a feature extraction transfer learning model for 5 epochs on 10% of the data (with all base model layers frozen) and saved the model's weights using `ModelCheckpoint`.
2. Fine-tuned the same model on the same 10% of the data for a further 5 epochs with the top 10 layers of the base model unfrozen.
3. Saved the results and training logs each time.
4. Reloaded the model from 1 to do the same steps as 2 but with all of the data.
The same steps as 2?
Yeah, we're going to fine-tune the last 10 layers of the base model with the full dataset for another 5 epochs but first let's remind ourselves which layers are trainable.
```
# Check which layers are tuneable in the whole model
for layer_number, layer in enumerate(model_2.layers):
print(layer_number, layer.name, layer.trainable)
```
Can we get a little more specific?
```
# Check which layers are tuneable in the base model
for layer_number, layer in enumerate(base_model.layers):
print(layer_number, layer.name, layer.trainable)
```
Looking good! The last 10 layers are trainable (unfrozen).
We've got one more step to do before we can begin fine-tuning.
Do you remember what it is?
I'll give you a hint. We just reloaded the weights to our model and what do we need to do every time we make a change to our models?
Recompile them!
This will be just as before.
```
# Compile
model_2.compile(loss="categorical_crossentropy",
optimizer=tf.keras.optimizers.Adam(lr=0.0001), # divide learning rate by 10 for fine-tuning
metrics=["accuracy"])
```
Alright, time to fine-tune on all of the data!
```
# Continue to train and fine-tune the model to our data
fine_tune_epochs = initial_epochs + 5
history_fine_10_classes_full = model_2.fit(train_data_10_classes_full,
epochs=fine_tune_epochs,
initial_epoch=history_10_percent_data_aug.epoch[-1],
validation_data=test_data,
validation_steps=int(0.25 * len(test_data)),
callbacks=[create_tensorboard_callback("transfer_learning", "full_10_classes_fine_tune_last_10")])
```
> 🔑 **Note:** Training took longer per epoch, but that makes sense because we're using 10x more training data than before.
Let's evaluate on all of the test data.
```
results_fine_tune_full_data = model_2.evaluate(test_data)
results_fine_tune_full_data
```
Nice! It looks like fine-tuning with all of the data has given our model a boost, how do the training curves look?
```
# How did fine-tuning go with more data?
compare_historys(original_history=history_10_percent_data_aug,
new_history=history_fine_10_classes_full,
initial_epochs=5)
```
Looks like that extra data helped! Those curves are looking great. And if we trained for longer, they might even keep improving.
## Viewing our experiment data on TensorBoard
Right now our experimental results are scattered all throughout our notebook. If we want to share them with someone, they'd be getting a bunch of different graphs and metrics... not a fun time.
But guess what?
Thanks to the TensorBoard callback we made with our helper function `create_tensorflow_callback()`, we've been tracking our modelling experiments the whole time.
How about we upload them to TensorBoard.dev and check them out?
We can do with the `tensorboard dev upload` command and passing it the directory where our experiments have been logged.
> 🔑 **Note:** Remember, whatever you upload to TensorBoard.dev becomes public. If there are training logs you don't want to share, don't upload them.
```
# View tensorboard logs of transfer learning modelling experiments (should be 4 models)
# Upload TensorBoard dev records
!tensorboard dev upload --logdir ./transfer_learning \
--name "Transfer learning experiments" \
--description "A series of different transfer learning experiments with varying amounts of data and fine-tuning" \
--one_shot # exits the uploader when upload has finished
```
Once we've uploaded the results to TensorBoard.dev we get a shareable link we can use to view and compare our experiments and share our results with others if needed.
You can view the original versions of the experiments we ran in this notebook here: https://tensorboard.dev/experiment/2O76kw3PQbKl0lByfg5B4w/
> 🤔 **Question:** Which model performed the best? Why do you think this is? How did fine-tuning go?
To find all of your previous TensorBoard.dev experiments using the command `tensorboard dev list`.
```
# View previous experiments
!tensorboard dev list
```
And if you want to remove a previous experiment (and delete it from public viewing) you can use the command:
```
tensorboard dev delete --experiment_id [INSERT_EXPERIMENT_ID_TO_DELETE]```
```
# Remove previous experiments
# !tensorboard dev delete --experiment_id OUbW0O3pRqqQgAphVBxi8Q
```
## 🛠 Exercises
1. Write a function to visualize an image from any dataset (train or test file) and any class (e.g. "steak", "pizza"... etc), visualize it and make a prediction on it using a trained model.
2. Use feature-extraction to train a transfer learning model on 10% of the Food Vision data for 10 epochs using [`tf.keras.applications.EfficientNetB0`](https://www.tensorflow.org/api_docs/python/tf/keras/applications/EfficientNetB0) as the base model. Use the [`ModelCheckpoint`](https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/ModelCheckpoint) callback to save the weights to file.
3. Fine-tune the last 20 layers of the base model you trained in 2 for another 10 epochs. How did it go?
4. Fine-tune the last 30 layers of the base model you trained in 2 for another 10 epochs. How did it go?
## 📖 Extra-curriculum
* Read the [documentation on data augmentation](https://www.tensorflow.org/tutorials/images/data_augmentation) in TensorFlow.
* Read the [ULMFit paper](https://arxiv.org/abs/1801.06146) (technical) for an introduction to the concept of freezing and unfreezing different layers.
* Read up on learning rate scheduling (there's a [TensorFlow callback](https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/LearningRateScheduler) for this), how could this influence our model training?
* If you're training for longer, you probably want to reduce the learning rate as you go... the closer you get to the bottom of the hill, the smaller steps you want to take. Imagine it like finding a coin at the bottom of your couch. In the beginning your arm movements are going to be large and the closer you get, the smaller your movements become.
| true |
code
| 0.739446 | null | null | null | null |
|
# 1. Event approach
## Reading the full stats file
```
import numpy
import pandas
full_stats_file = '/Users/irv033/Downloads/data/stats_example.csv'
df = pandas.read_csv(full_stats_file)
def date_only(x):
"""Chop a datetime64 down to date only"""
x = numpy.datetime64(x)
return numpy.datetime64(numpy.datetime_as_string(x, timezone='local')[:10])
#df.time = df.time.apply(lambda x: numpy.datetime64(x))
df.time = df.time.apply(date_only)
#print pandas.to_datetime(df['time'].values)
#df_times = df.time.apply(lambda x: x.date())
df = df.set_index('time')
```
## Read xarray data frame
```
import xray
data_file = '/Users/irv033/Downloads/data/va_ERAInterim_500hPa_2006-030day-runmean_native.nc'
dset_in = xray.open_dataset(data_file)
print dset_in
darray = dset_in['va']
print darray
times = darray.time.values
date_only(times[5])
darray_times = map(date_only, list(times))
print darray_times[0:5]
```
## Merge
### Re-index the event data
```
event_numbers = df['event_number']
event_numbers = event_numbers.reindex(darray_times)
```
### Broadcast the shape
```
print darray
print darray.shape
print type(darray)
print type(event_numbers.values)
type(darray.data)
event_data = numpy.zeros((365, 241, 480))
for i in range(0,365):
event_data[i,:,:] = event_numbers.values[i]
```
### Cobmine
```
d = {}
d['time'] = darray['time']
d['latitude'] = darray['latitude']
d['longitude'] = darray['longitude']
d['va'] = (['time', 'latitude', 'longitude'], darray.data)
d['event'] = (['time'], event_numbers.values)
ds = xray.Dataset(d)
print ds
```
## Get event averages
```
event_averages = ds.groupby('event').mean('time')
print event_averages
```
# 2. Standard autocorrelation approach
### Read data
```
tas_file = '/Users/irv033/Downloads/data/tas_ERAInterim_surface_030day-runmean-anom-wrt-all-2005-2006_native.nc'
tas_dset = xray.open_dataset(tas_file)
tas_darray = tas_dset['tas']
print tas_darray
tas_data = tas_darray[dict(longitude=130, latitude=-40)].values
print tas_data.shape
```
### Plot autocorrelation with Pandas
```
%matplotlib inline
from pandas.tools.plotting import autocorrelation_plot
pandas_test_data = pandas.Series(tas_data)
autocorrelation_plot(pandas_test_data)
```
### Calculate autocorrelation with statsmodels
```
import statsmodels
from statsmodels.tsa.stattools import acf
n = len(tas_data)
statsmodels_test_data = acf(tas_data, nlags=n-2)
import matplotlib.pyplot as plt
k = numpy.arange(1, n - 1)
plt.plot(k, statsmodels_test_data[1:])
plt.plot(k[0:40], statsmodels_test_data[1:41])
# Formula from Zieba2010, equation 12
r_k_sum = ((n - k) / float(n)) * statsmodels_test_data[1:]
n_eff = float(n) / (1 + 2 * numpy.sum(r_k_sum))
print n_eff
print numpy.sum(r_k_sum)
```
So an initial sample size of 730 has an effective sample size of 90.
### Get the p value
```
from scipy import stats
var_x = tas_data.var() / n_eff
tval = tas_data.mean() / numpy.sqrt(var_x)
pval = stats.t.sf(numpy.abs(tval), n - 1) * 2 # two-sided pvalue = Prob(abs(t)>tt)
print 't-statistic = %6.3f pvalue = %6.4f' % (tval, pval)
```
## Implementation
```
def calc_significance(data_subset, data_all, standard_name):
"""Perform significance test.
Once sample t-test, with sample size adjusted for autocorrelation.
Reference:
Zięba, A. (2010). Metrology and Measurement Systems, XVII(1), 3–16
doi:10.2478/v10178-010-0001-0
"""
# Data must be three dimensional, with time first
assert len(data_subset.shape) == 3, "Input data must be 3 dimensional"
# Define autocorrelation function
n = data_subset.shape[0]
autocorr_func = numpy.apply_along_axis(acf, 0, data_subset, nlags=n - 2)
# Calculate effective sample size (formula from Zieba2010, eq 12)
k = numpy.arange(1, n - 1)
r_k_sum = ((n - k[:, None, None]) / float(n)) * autocorr_func[1:]
n_eff = float(n) / (1 + 2 * numpy.sum(r_k_sum))
# Calculate significance
var_x = data_subset.var(axis=0) / n_eff
tvals = (data_subset.mean(axis=0) - data_all.mean(axis=0)) / numpy.sqrt(var_x)
pvals = stats.t.sf(numpy.abs(tvals), n - 1) * 2 # two-sided pvalue = Prob(abs(t)>tt)
notes = "One sample t-test, with sample size adjusted for autocorrelation (Zieba2010, eq 12)"
pval_atts = {'standard_name': standard_name,
'long_name': standard_name,
'units': ' ',
'notes': notes,}
return pvals, pval_atts
min_lon, max_lon = (130, 135)
min_lat, max_lat = (-40, -37)
subset_dict = {'time': slice('2005-03-01', '2005-05-31'),
'latitude': slice(min_lat, max_lat),
'longitude': slice(min_lon, max_lon)}
all_dict = {'latitude': slice(min_lat, max_lat),
'longitude': slice(min_lon, max_lon)}
subset_data = tas_darray.sel(**subset_dict).values
all_data = tas_darray.sel(**all_dict).values
print all_data.shape
print subset_data.shape
p, atts = calc_significance(subset_data, all_data, 'p_mam')
p.shape
print atts
```
| true |
code
| 0.456531 | null | null | null | null |
|
# The effect of steel casing in AEM data
Figures 4, 5, 6 in Kang et al. (2020) are generated using this
```
# core python packages
import numpy as np
import scipy.sparse as sp
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
from scipy.constants import mu_0, inch, foot
import ipywidgets
import properties
import time
from scipy.interpolate import interp1d
from simpegEM1D.Waveforms import piecewise_pulse_fast
# SimPEG and discretize
import discretize
from discretize import utils
from SimPEG.EM import TDEM
from SimPEG import Utils, Maps
from SimPEG.Utils import Zero
from pymatsolver import Pardiso
# casing utilities
import casingSimulations as casingSim
%matplotlib inline
```
## Model Parameters
We will two classes of examples
- permeable wells, one example is run for each $\mu_r$ in `casing_mur`. The conductivity of this well is `sigma_permeable_casing`
- conductive wells ($\mu_r$=1), one example is run for each $\sigma$ value in `sigma_casing`
To add model runs to the simulation, just add to the list
```
# permeabilities to model
casing_mur = [100]
sigma_permeable_casing = 1.45*1e6
1./1.45*1e6
# background parameters
sigma_air = 1e-6
sigma_back = 1./340.
casing_t = 10e-3 # 10mm thick casing
casing_d = 300e-3 # 30cm diameter
casing_l = 200
def get_model(mur, sigc):
model = casingSim.model.CasingInHalfspace(
directory = simDir,
sigma_air = sigma_air,
sigma_casing = sigc, # conductivity of the casing (S/m)
sigma_back = sigma_back, # conductivity of the background (S/m)
sigma_inside = sigma_back, # fluid inside the well has same conductivity as the background
casing_d = casing_d-casing_t, # 135mm is outer casing diameter
casing_l = casing_l,
casing_t = casing_t,
mur_casing = mur,
src_a = np.r_[0., 0., 30.],
src_b = np.r_[0., 0., 30.]
)
return model
```
## store the different models
```
simDir = "./"
model_names_permeable = ["casing_{}".format(mur) for mur in casing_mur]
model_dict_permeable = {
key: get_model(mur, sigma_permeable_casing) for key, mur in zip(model_names_permeable, casing_mur)
}
model_names = model_names_permeable
model_dict = {}
model_dict.update(model_dict_permeable)
model_dict["baseline"] = model_dict[model_names[0]].copy()
model_dict["baseline"].sigma_casing = model_dict["baseline"].sigma_back
model_names = ["baseline"] + model_names
model_names
```
## Create a mesh
```
# parameters defining the core region of the mesh
csx2 = 2.5 # cell size in the x-direction in the second uniform region of the mesh (where we measure data)
csz = 2.5 # cell size in the z-direction
domainx2 = 100 # go out 500m from the well
# padding parameters
npadx, npadz = 19, 17 # number of padding cells
pfx2 = 1.4 # expansion factor for the padding to infinity in the x-direction
pfz = 1.4
# set up a mesh generator which will build a mesh based on the provided parameters
# and casing geometry
def get_mesh(mod):
return casingSim.CasingMeshGenerator(
directory=simDir, # directory where we can save things
modelParameters=mod, # casing parameters
npadx=npadx, # number of padding cells in the x-direction
npadz=npadz, # number of padding cells in the z-direction
domain_x=domainx2, # extent of the second uniform region of the mesh
# hy=hy, # cell spacings in the
csx1=mod.casing_t/4., # use at least 4 cells per across the thickness of the casing
csx2=csx2, # second core cell size
csz=csz, # cell size in the z-direction
pfx2=pfx2, # padding factor to "infinity"
pfz=pfz # padding factor to "infinity" for the z-direction
)
mesh_generator = get_mesh(model_dict[model_names[0]])
mesh_generator.mesh.hx.sum()
mesh_generator.mesh.hx.min() * 1e3
mesh_generator.mesh.hz.sum()
# diffusion_distance(1e-2, 1./340.) * 2
```
## Physical Properties
```
# Assign physical properties on the mesh
physprops = {
name: casingSim.model.PhysicalProperties(mesh_generator, mod)
for name, mod in model_dict.items()
}
from matplotlib.colors import LogNorm
import matplotlib
matplotlib.rcParams['font.size'] = 14
pp = physprops['casing_100']
sigma = pp.sigma
fig, ax = plt.subplots()
out = mesh_generator.mesh.plotImage(
1./sigma, grid=True,
gridOpts={'alpha':0.2, 'color':'w'},
pcolorOpts={'norm':LogNorm(), 'cmap':'jet'},
mirror=True, ax=ax
)
cb= plt.colorbar(out[0], ax=ax)
cb.set_label("Resistivity ($\Omega$m)")
ax.set_xlabel("x (m)")
ax.set_ylabel("z (m)")
ax.set_xlim(-0.3, 0.3)
ax.set_ylim(-30, 30)
ax.set_aspect(0.008)
plt.tight_layout()
fig.savefig("./figures/figure-4", dpi=200)
from simpegEM1D import diffusion_distance
mesh_generator.mesh.plotGrid()
```
## Set up the time domain EM problem
We run a time domain EM simulation with SkyTEM geometry
```
data_dir = "./data/"
waveform_hm = np.loadtxt(data_dir+"HM_butte_312.txt")
time_gates_hm = np.loadtxt(data_dir+"HM_butte_312_gates")[7:,:] * 1e-6
waveform_lm = np.loadtxt(data_dir+"LM_butte_312.txt")
time_gates_lm = np.loadtxt(data_dir+"LM_butte_312_gates")[8:,:] * 1e-6
time_input_currents_HM = waveform_hm[:,0]
input_currents_HM = waveform_hm[:,1]
time_input_currents_LM = waveform_lm[:,0]
input_currents_LM = waveform_lm[:,1]
time_LM = time_gates_lm[:,3] - waveform_lm[:,0].max()
time_HM = time_gates_hm[:,3] - waveform_hm[:,0].max()
base_frequency_HM = 30.
base_frequency_LM = 210.
radius = 13.25
source_area = np.pi * radius**2
pico = 1e12
def run_simulation(sigma, mu, z_src):
mesh = mesh_generator.mesh
dts = np.diff(np.logspace(-6, -1, 50))
timeSteps = []
for dt in dts:
timeSteps.append((dt, 1))
prb = TDEM.Problem3D_e(
mesh=mesh, timeSteps=timeSteps,
Solver=Pardiso
)
x_rx = 0.
z_offset = 0.
rxloc = np.array([x_rx, 0., z_src+z_offset])
srcloc = np.array([0., 0., z_src])
times = np.logspace(np.log10(1e-5), np.log10(1e-2), 31)
rx = TDEM.Rx.Point_dbdt(locs=np.array([x_rx, 0., z_src+z_offset]), times=times, orientation="z")
src = TDEM.Src.CircularLoop(
[rx],
loc=np.r_[0., 0., z_src], orientation="z", radius=13.25
)
area = np.pi * src.radius**2
def bdf2(sigma):
# Operators
C = mesh.edgeCurl
Mfmui = mesh.getFaceInnerProduct(1./mu_0)
MeSigma = mesh.getEdgeInnerProduct(sigma)
n_steps = prb.timeSteps.size
Fz = mesh.getInterpolationMat(rx.locs, locType='Fz')
eps = 1e-10
def getA(dt, factor=1.):
return C.T*Mfmui*C + factor/dt * MeSigma
dt_0 = 0.
data_test = np.zeros(prb.timeSteps.size)
sol_n0 = np.zeros(mesh.nE)
sol_n1 = np.zeros(mesh.nE)
sol_n2 = np.zeros(mesh.nE)
for ii in range(n_steps):
dt = prb.timeSteps[ii]
#Factor for BDF2
factor=3/2.
if abs(dt_0-dt) > eps:
if ii != 0:
Ainv.clean()
# print (ii, factor)
A = getA(dt, factor=factor)
Ainv = prb.Solver(A)
if ii==0:
b0 = src.bInitial(prb)
s_e = C.T*Mfmui*b0
rhs = factor/dt*s_e
elif ii==1:
rhs = -factor/dt*(MeSigma*(-4/3.*sol_n1+1/3.*sol_n0) + 1./3.*s_e)
else:
rhs = -factor/dt*(MeSigma*(-4/3.*sol_n1+1/3.*sol_n0))
sol_n2 = Ainv*rhs
data_test[ii] = Fz*(-C*sol_n2)
dt_0 = dt
sol_n0 = sol_n1.copy()
sol_n1 = sol_n2.copy()
step_response = -data_test.copy()
step_func = interp1d(
np.log10(prb.times[1:]), step_response
)
period_HM = 1./base_frequency_HM
period_LM = 1./base_frequency_LM
data_hm = piecewise_pulse_fast(
step_func, time_HM,
time_input_currents_HM, input_currents_HM,
period_HM, n_pulse=1
)
data_lm = piecewise_pulse_fast(
step_func, time_LM,
time_input_currents_LM, input_currents_LM,
period_LM, n_pulse=1
)
return np.r_[data_hm, data_lm] / area * pico
return bdf2(sigma)
```
## Run the simulation
- for each permeability model we run the simulation for 2 conductivity models (casing = $10^6$S/m and $10^{-4}$S/m
- each simulation takes 15s-20s on my machine: the next cell takes ~ 4min to run
```
pp = physprops['baseline']
sigma_base = pp.sigma
pp = physprops['casing_100']
sigma = pp.sigma
mu = pp.mu
inds_half_space = sigma_base != sigma_air
inds_air = ~inds_half_space
inds_casing = sigma == sigma_permeable_casing
print (pp.mesh.hx.sum())
print (pp.mesh.hz.sum())
sigma_backgrounds = np.r_[1./1, 1./20, 1./100, 1./200, 1./340]
# start = timeit.timeit()
data_base = {}
data_casing = {}
for sigma_background in sigma_backgrounds:
sigma_base = np.ones(pp.mesh.nC) * sigma_air
sigma_base[inds_half_space] = sigma_background
sigma = np.ones(pp.mesh.nC) * sigma_air
sigma[inds_half_space] = sigma_background
sigma[inds_casing] = sigma_permeable_casing
for height in [20, 30, 40, 60, 80]:
rho = 1/sigma_background
name = str(int(rho)) + str(height)
data_base[name] = run_simulation(sigma_base, mu_0, height)
data_casing[name] = run_simulation(sigma, mu, height)
# end = timeit.timeit()
# print(("Elapsed time is %1.f")%(end - start))
rerr_max = []
for sigma_background in sigma_backgrounds:
rerr_tmp = np.zeros(5)
for ii, height in enumerate([20, 30, 40, 60, 80]):
rho = 1/sigma_background
name = str(int(rho)) + str(height)
data_casing_tmp = data_casing[name]
data_base_tmp = data_base[name]
rerr_hm = abs(data_casing_tmp[:time_HM.size]-data_base_tmp[:time_HM.size]) / abs(data_base_tmp[:time_HM.size])
rerr_lm = abs(data_casing_tmp[time_HM.size:]-data_base_tmp[time_HM.size:]) / abs(data_base_tmp[time_HM.size:])
# rerr_tmp[ii] = np.r_[rerr_hm, rerr_lm].max()
rerr_tmp[ii] = np.sqrt(((np.r_[rerr_hm, rerr_lm])**2).sum() / np.r_[rerr_hm, rerr_lm].size)
rerr_max.append(rerr_tmp)
import matplotlib
matplotlib.rcParams['font.size'] = 14
fig_dir = "./figures/"
times = np.logspace(np.log10(1e-5), np.log10(1e-2), 31)
colors = ['k', 'b', 'g', 'r']
name='2040'
fig, axs = plt.subplots(1,2, figsize=(10, 5))
axs[0].loglog(time_gates_hm[:,3]*1e3, data_base[name][:time_HM.size], 'k--')
axs[0].loglog(time_gates_lm[:,3]*1e3, data_base[name][time_HM.size:], 'b--')
axs[0].loglog(time_gates_hm[:,3]*1e3, data_casing[name][:time_HM.size], 'k-')
axs[0].loglog(time_gates_lm[:,3]*1e3, data_casing[name][time_HM.size:], 'b-')
rerr_hm = abs(data_casing[name][:time_HM.size]-data_base[name][:time_HM.size]) / abs(data_base[name][:time_HM.size])
rerr_lm = abs(data_casing[name][time_HM.size:]-data_base[name][time_HM.size:]) / abs(data_base[name][time_HM.size:])
axs[1].loglog(time_gates_hm[:,3]*1e3, rerr_hm * 100, 'k-')
axs[1].loglog(time_gates_lm[:,3]*1e3, rerr_lm * 100, 'b-')
axs[1].set_ylim(0, 100)
axs[0].legend(('HM-background', 'LM-background', 'HM-casing', 'LM-casing'))
for ax in axs:
ax.set_xlabel("Time (ms)")
ax.grid(True)
axs[0].set_title('(a) AEM response')
axs[1].set_title('(b) Percentage casing effect')
axs[0].set_ylabel("Voltage (pV/A-m$^4$)")
axs[1].set_ylabel("Percentage casing effect (%)")
ax_1 = axs[1].twinx()
xlim = axs[1].get_xlim()
ax_1.loglog(xlim, (3,3), '-', color='grey', alpha=0.8)
axs[1].set_ylim((1e-4, 100))
ax_1.set_ylim((1e-4, 100))
axs[1].set_xlim(xlim)
ax_1.set_xlim(xlim)
ax_1.set_yticks([3])
ax_1.set_yticklabels(["3%"])
plt.tight_layout()
fig.savefig("./figures/figure-5", dpi=200)
fig = plt.figure(figsize = (10,5))
ax = plt.gca()
ax_1 = ax.twinx()
markers = ['k--', 'b--', 'g--', 'r--', 'y--']
for ii, rerr in enumerate(rerr_max[::-1]):
ax.plot([20, 30, 40, 60, 80], rerr*100, markers[ii], ms=10)
ax.set_xlabel("Transmitter height (m)")
ax.set_ylabel("Total percentage casing effect (%)")
ax.legend(("340 $\Omega$m", "200 $\Omega$m", "100 $\Omega$m", "20 $\Omega$m", "1 $\Omega$m",), bbox_to_anchor=(1.4,1))
ax.set_yscale('log')
ax_1.set_yscale('log')
xlim = ax.get_xlim()
ylim = ax.get_ylim()
ax_1.plot(xlim, (3,3), '-', color='grey', alpha=0.8)
ax.set_ylim(ylim)
ax_1.set_ylim(ylim)
ax.set_xlim(xlim)
ax_1.set_yticks([3])
ax_1.set_yticklabels(["3%"])
plt.tight_layout()
fig.savefig("./figures/figure-6", dpi=200)
```
| true |
code
| 0.628236 | null | null | null | null |
|
## 2-3. 量子フーリエ変換
この節では、量子アルゴリズムの中でも最も重要なアルゴリズムの一つである量子フーリエ変換について学ぶ。
量子フーリエ変換はその名の通りフーリエ変換を行う量子アルゴリズムであり、様々な量子アルゴリズムのサブルーチンとしても用いられることが多い。
(参照:Nielsen-Chuang 5.1 `The quantum Fourier transform`)
※なお、最後のコラムでも多少述べるが、回路が少し複雑である・入力状態を用意することが難しいといった理由から、いわゆるNISQデバイスでの量子フーリエ変換の実行は難しいと考えられている。
### 定義
まず、$2^n$成分の配列 $\{x_j\}$ に対して$(j=0,\cdots,2^n-1)$、その[離散フーリエ変換](https://ja.wikipedia.org/wiki/離散フーリエ変換)である配列$\{ y_k \}$を
$$
y_k = \frac{1}{\sqrt{2^n}} \sum_{j=0}^{2^n-1} x_j e^{i\frac{2\pi kj}{2^n}} \tag{1}
$$
で定義する$(k=0, \cdots 2^n-1)$。配列 $\{x_j\}$ は$\sum_{j=0}^{2^n-1} |x_j|^2 = 1$ と規格化されているものとする。
量子フーリエ変換アルゴリズムは、入力の量子状態
$$
|x\rangle := \sum_{j=0}^{2^n-1} x_j |j\rangle
$$
を、
$$
|y \rangle := \sum_{k=0}^{2^n-1} y_k |k\rangle \tag{2}
$$
となるように変換する量子アルゴリズムである。ここで、$|i \rangle$は、整数$i$の二進数での表示$i_1 \cdots i_n$ ($i_m = 0,1$)に対応する量子状態$|i_1 \cdots i_n \rangle$の略記である。(例えば、$|2 \rangle = |0\cdots0 10 \rangle, |7 \rangle = |0\cdots0111 \rangle$となる)
ここで、式(1)を(2)に代入してみると、
$$
|y \rangle = \frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n-1} \sum_{j=0}^{2^n-1} x_j e^{i\frac{2\pi kj}{2^n}} |k\rangle
= \sum_{j=0}^{2^n-1} x_j \left( \frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n-1} e^{i\frac{2\pi kj}{2^n}} |k\rangle \right)
$$
となる。よって、量子フーリエ変換では、
$$
|j\rangle \to \frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n-1} e^{i\frac{2\pi kj}{2^n}} |k\rangle
$$
を行う量子回路(変換)$U$を見つければ良いことになる。(余裕のある読者は、これがユニタリ変換であることを実際に計算して確かめてみよう)
この式はさらに式変形できて(やや複雑なので最後の結果だけ見てもよい)
$$
\begin{eqnarray}
\sum_{k=0}^{2^n-1} e^{i\frac{2\pi kj}{2^n}} |k\rangle
&=& \sum_{k_1=0}^1 \cdots \sum_{k_n=0}^1 e^{i\frac{2\pi (k_1 2^{n-1} + \cdots k_n 2^0 )\cdot j}{2^n}} |k_1 \cdots k_n\rangle \:\:\:\: \text{(kの和を2進数表示で書き直した)} \\
&=& \sum_{k_1=0}^1 \cdots \sum_{k_n=0}^1 e^{i 2\pi j (k_1 2^{-1} + \cdots k_n 2^{-n})} |k_1 \cdots k_n\rangle \\
&=& \left( \sum_{k_1=0}^1 e^{i 2\pi j k_1 2^{-1}} |k_1 \rangle \right) \otimes \cdots \otimes \left( \sum_{k_n=0}^1 e^{i 2\pi j k_n 2^{-n}} |k_n \rangle \right) \:\:\:\: \text{("因数分解"をして、全体をテンソル積で書き直した)} \\
&=& \left( |0\rangle + e^{i 2\pi 0.j_n} |1 \rangle \right) \otimes \left( |0\rangle + e^{i 2\pi 0.j_{n-1}j_n} |1 \rangle \right) \otimes \cdots \otimes \left( |0\rangle + e^{i 2\pi 0.j_1j_2\cdots j_n} |1 \rangle \right) \:\:\:\: \text{(カッコの中の和を計算した)}
\end{eqnarray}
$$
となる。ここで、
$$
0.j_l\cdots j_n = \frac{j_l}{2} + \frac{j_{l-1}}{2^2} + \cdots + \frac{j_n}{2^{n-l+1}}
$$
は2進小数であり、$e^{i 2\pi j/2^{-l} } = e^{i 2\pi j_1 \cdots j_l . j_{l-1}\cdots j_n }
= e^{i 2\pi 0. j_{l-1}\cdots j_n }$となることを用いた。($e^{i2\pi}=1$なので、整数部分は関係ない)
まとめると、量子フーリエ変換では、
$$
|j\rangle = |j_1 \cdots j_n \rangle \to \frac{ \left( |0\rangle + e^{i 2\pi 0.j_n} |1 \rangle \right) \otimes \left( |0\rangle + e^{i 2\pi 0.j_{n-1}j_n} |1 \rangle \right) \otimes \cdots \otimes \left( |0\rangle + e^{i 2\pi 0.j_1j_2\cdots j_n} |1 \rangle \right) }{\sqrt{2^n}}
\tag{*}
$$
という変換ができればよい。
### 回路の構成
それでは、量子フーリエ変換を実行する回路を実際にどのように構成するかを見ていこう。
そのために、次のアダマールゲート$H$についての等式(計算すると合っていることが分かる)
$$
H |m \rangle = \frac{|0\rangle + e^{i 2\pi 0.m}|1\rangle }{\sqrt{2}} \:\:\: (m=0,1)
$$
と、角度 $2\pi/2^l$ の一般位相ゲート
$$
R_l =
\begin{pmatrix} 1 & 0\\ 0 & e^{i \frac{2\pi}{2^l} } \end{pmatrix}
$$
を多用する。
1. まず、状態$\left( |0\rangle + e^{i 2\pi 0.j_1j_2\cdots j_n} |1\rangle \right)$の部分をつくる。1番目の量子ビット$|j_1\rangle$にアダマールゲートをかけると
$$
|j_1 \cdots j_n \rangle \to \frac{1}{\sqrt{2}} \left( |0\rangle + e^{i2\pi 0.j_1} |1\rangle \right) |j_2 \cdots j_n \rangle
$$
となるが、ここで、2番目のビット$|j_2\rangle$を制御ビットとする一般位相ゲート$R_2$を1番目の量子ビットにかけると、$j_2=0$の時は何もせず、$j_2=1$の時のみ1番目の量子ビットの$|1\rangle$部分に位相 $2\pi/2^2 = 0.01$(二進小数)がつくから、
$$
\frac{1}{\sqrt{2}} \left( |0\rangle + e^{i2\pi 0.j_1} |1\rangle \right) |j_2 \cdots j_n \rangle
\to \frac{1}{\sqrt{2}} \left( |0\rangle + e^{i2\pi 0.j_1j_2} |1\rangle \right) |j_2 \cdots j_n \rangle
$$
となる。以下、$l$番目の量子ビット$|j_l\rangle$を制御ビットとする一般位相ゲート$R_l$をかければ($l=3,\cdots n$)、最終的に
$$
\frac{1}{\sqrt{2}} \left( |0\rangle + e^{i2\pi 0.j_1\cdots j_n} |1\rangle \right) |j_2 \cdots j_n \rangle
$$
が得られる。
2. 次に、状態$\left( |0\rangle + e^{i2\pi 0.j_2\cdots j_n} |1\rangle\right)$の部分をつくる。先ほどと同様に、2番目のビット$|j_2\rangle$にアダマールゲートをかければ
$$
\frac{1}{\sqrt{2}} \left( |0\rangle + e^{i2\pi 0.j_1\cdots j_n}|1\rangle \right) \frac{1}{\sqrt{2}} \left( |0\rangle + e^{i2\pi 0.j_2} |1\rangle \right) |j_3 \cdots j_n \rangle
$$
ができる。再び、3番目の量子ビットを制御ビット$|j_3\rangle$とする位相ゲート$R_2$をかければ
$$
\frac{1}{\sqrt{2}} \left( |0\rangle + e^{i2\pi 0.j_1\cdots j_n}|1\rangle \right) \frac{1}{\sqrt{2}} \left( |0\rangle + e^{i2\pi 0.j_2j_3}|1\rangle \right) |j_3 \cdots j_n \rangle
$$
となり、これを繰り返して
$$
\frac{1}{\sqrt{2}} \left( |0\rangle + e^{i2\pi 0.j_1\cdots j_n}|1\rangle \right) \frac{1}{\sqrt{2}} \left( |0\rangle + e^{i2\pi 0.j_2\cdots j_n}|1\rangle \right) |j_3 \cdots j_n \rangle
$$
を得る。
3. 1,2と同様の手順で、$l$番目の量子ビット$|j_l\rangle$にアダマールゲート・制御位相ゲート$R_l, R_{l+1},\cdots$をかけていく($l=3,\cdots,n$)。すると最終的に
$$
|j_1 \cdots j_n \rangle \to \left( \frac{|0\rangle + e^{i 2\pi 0.j_1\cdots j_n} |1 \rangle}{\sqrt{2}} \right) \otimes
\left( \frac{|0\rangle + e^{i 2\pi 0.j_2\cdots j_n} |1 \rangle}{\sqrt{2}} \right) \otimes \cdots \otimes
\left( \frac{|0\rangle + e^{i 2\pi 0.j_n} |1 \rangle}{\sqrt{2}} \right)
$$
が得られるので、最後にビットの順番をSWAPゲートで反転させてあげれば、量子フーリエ変換を実行する回路が構成できたことになる(式($*$)とはビットの順番が逆になっていることに注意)。
SWAPを除いた部分を回路図で書くと以下のようである。

### SymPyを用いた実装
量子フーリエ変換への理解を深めるために、SymPyを用いて$n=3$の場合の回路を実装してみよう。
```
from sympy import *
from sympy.physics.quantum import *
from sympy.physics.quantum.qubit import Qubit,QubitBra
init_printing() # ベクトルや行列を綺麗に表示するため
from sympy.physics.quantum.gate import X,Y,Z,H,S,T,CNOT,SWAP,CPHASE,CGateS
# Google Colaboratory上でのみ実行してください
from IPython.display import HTML
def setup_mathjax():
display(HTML('''
<script>
if (!window.MathJax && window.google && window.google.colab) {
window.MathJax = {
'tex2jax': {
'inlineMath': [['$', '$'], ['\\(', '\\)']],
'displayMath': [['$$', '$$'], ['\\[', '\\]']],
'processEscapes': true,
'processEnvironments': true,
'skipTags': ['script', 'noscript', 'style', 'textarea', 'code'],
'displayAlign': 'center',
},
'HTML-CSS': {
'styles': {'.MathJax_Display': {'margin': 0}},
'linebreaks': {'automatic': true},
// Disable to prevent OTF font loading, which aren't part of our
// distribution.
'imageFont': null,
},
'messageStyle': 'none'
};
var script = document.createElement("script");
script.src = "https://colab.research.google.com/static/mathjax/MathJax.js?config=TeX-AMS_HTML-full,Safe";
document.head.appendChild(script);
}
</script>
'''))
get_ipython().events.register('pre_run_cell', setup_mathjax)
```
まず、フーリエ変換される入力$|x\rangle$として、
$$
|x\rangle = \sum_{j=0}^7 \frac{1}{\sqrt{8}} |j\rangle
$$
という全ての状態の重ね合わせ状態を考える($x_0 = \cdots = x_7 = 1/\sqrt{8}$)。
```
input = 1/sqrt(8) *( Qubit("000")+Qubit("001")+Qubit("010")+Qubit("011")+Qubit("100")+Qubit("101")+Qubit("110")+Qubit("111"))
input
```
この状態に対応する配列をnumpyでフーリエ変換すると
```
import numpy as np
input_np_array = 1/np.sqrt(8)*np.ones(8)
print( input_np_array ) ## 入力
print( np.fft.ifft(input_np_array) * np.sqrt(8) ) ## 出力. ここでのフーリエ変換の定義とnumpyのifftの定義を合わせるため、sqrt(2^3)をかける
```
となり、フーリエ変換すると $y_0=1,y_1=\cdots=y_7=0$ という簡単な配列になることが分かる。これを量子フーリエ変換で確かめてみよう。
まず、$R_1, R_2, R_3$ゲートはそれぞれ$Z, S, T$ゲートに等しいことに注意する($e^{i\pi}=-1, e^{i\pi/2}=i$)。
```
represent(Z(0),nqubits=1), represent(S(0),nqubits=1), represent(T(0),nqubits=1)
```
量子フーリエ変換(Quantum Fourier TransformなのでQFTと略す)を実行回路を構成していく。
最初に、1番目(SymPyは右から0,1,2とビットを数えるので、SymPyでは2番目)の量子ビットにアダマール演算子をかけ、2番目・3番目のビットを制御ビットとする$R_2, R_3$ゲートをかける。
```
QFT_gate = H(2)
QFT_gate = CGateS(1, S(2)) * QFT_gate
QFT_gate = CGateS(0, T(2)) * QFT_gate
```
2番目(SymPyでは1番目)の量子ビットにもアダマールゲートと制御$R_2$演算を施す。
```
QFT_gate = H(1) * QFT_gate
QFT_gate = CGateS(0, S(1)) * QFT_gate
```
3番目(SymPyでは0番目)の量子ビットにはアダマールゲートのみをかければ良い。
```
QFT_gate = H(0) * QFT_gate
```
最後に、ビットの順番を合わせるためにSWAPゲートをかける。
```
QFT_gate = SWAP(0, 2) * QFT_gate
```
これで$n=3$の時の量子フーリエ変換の回路を構成できた。回路自体はやや複雑である。
```
QFT_gate
```
入力ベクトル$|x\rangle$ にこの回路を作用させると、以下のようになり、正しくフーリエ変換された状態が出力されていることが分かる。($y_0=1,y_1=\cdots=y_7=0$)
```
simplify( qapply( QFT_gate * input) )
```
読者は是非、入力を様々に変えてこの回路を実行し、フーリエ変換が正しく行われていることを確認してみてほしい。
---
### コラム:計算量について
「量子コンピュータは計算を高速に行える」とは、どういうことだろうか。本節で学んだ量子フーリエ変換を例にとって考えてみる。
量子フーリエ変換を行うために必要なゲート操作の回数は、1番目の量子ビットに$n$回、2番目の量子ビットに$n-1$回、...、$n$番目の量子ビットに1回で合計$n(n-1)/2$回、そして最後のSWAP操作が約$n/2$回であるから、全て合わせると$\mathcal{O}(n^2)$回である($\mathcal{O}$記法について詳しく知りたい人は、下記セクションを参照)。
一方、古典コンピュータでフーリエ変換を行う[高速フーリエ変換](https://ja.wikipedia.org/wiki/高速フーリエ変換)は、同じ計算を行うのに$\mathcal{O}(n2^n)$の計算量を必要とする。この意味で、量子フーリエ変換は、古典コンピュータで行う高速フーリエ変換に比べて「高速」と言える。
これは一見喜ばしいことに見えるが、落とし穴がある。フーリエ変換した結果$\{y_k\}$は量子フーリエ変換後の状態$|y\rangle$の確率振幅として埋め込まれているが、この振幅を素直に読み出そうとすると、結局は**指数関数的な回数の観測を繰り返さなくてはならない**。さらに、そもそも入力$|x\rangle$を用意する方法も簡単ではない(素直にやると、やはり指数関数的な時間がかかってしまう)。
このように、量子コンピュータや量子アルゴリズムを「実用」するのは簡単ではなく、さまざまな工夫・技術発展がまだまだ求められている。
一体どのような問題で量子コンピュータが高速だと思われているのか、理論的にはどのように扱われているのかなど、詳しく学びたい方はQmediaの記事[「量子計算機が古典計算機より優れている」とはどういうことか](https://www.qmedia.jp/computational-complexity-and-quantum-computer/)(竹嵜智之)を参照されたい。
#### オーダー記法$\mathcal{O}$についての註
そもそも、アルゴリズムの性能はどのように定量評価できるのだろうか。ここでは、アルゴリズムの実行に必要な資源、主に時間をその基準として考える。とくに問題のサイズを$n$としたとき、計算ステップ数(時間)や消費メモリなど、必要な計算資源が$n$の関数としてどう振る舞うかを考える。(問題のサイズとは、例えばソートするデータの件数、あるいは素因数分解したい数の二進数表現の桁数などである。)
例えば、問題のサイズ$n$に対し、アルゴリズムの要求する計算資源が次の$f(n)$で与えられるとする。
$$ f(n) = 2n^2 + 5n + 8 $$
$n$が十分大きいとき(例えば$n=10^{10}$)、$2n^2$に比べて$5n$や$6$は十分に小さい。したがって、このアルゴリズムの評価という観点では$5n+8$という因子は重要ではない。また、$n^2$の係数が$2$であるという情報も、$n$が十分大きいときの振る舞いには影響を与えない。こうして、計算時間$f(n)$の一番**「強い」**項の情報が重要であると考えることができる。このような考え方を漸近的評価といい、計算量のオーダー記法では次の式で表す。
$$f(n) = \mathcal{O}(n^2)$$
一般に$f(n) = \mathcal{O}(g(n))$とは、ある正の数$n_0, c$が存在して、任意の$n > n_0$に対して
$$|f(n)| \leq c |g(n)|$$
が成り立つことである。上の例では、$n_0=7, c=3$とすればこの定義の通りである(グラフを描画してみよ)。練習として、$f(n) = 6n^3 +5n$のオーダー記法$f(n) = \mathcal{O}(n^3)$を与える$n_0, c$の組を考えてみよ。
アルゴリズムの性能評価では、その入力のサイズを$n$としたときに必要な計算資源を$n$の関数として表す。特にオーダー記法による漸近評価は、入力のサイズが大きくなったときの振る舞いを把握するときに便利である。そして、こうした漸近評価に基づいた計算量理論というものを用いて、様々なアルゴリズムの分類が行われている。詳細は上記のQmedia記事を参照されたい。
| true |
code
| 0.359912 | null | null | null | null |
|
# CA Coronavirus Cases and Deaths Trends
CA's [Blueprint for a Safer Economy](https://www.cdph.ca.gov/Programs/CID/DCDC/Pages/COVID-19/COVID19CountyMonitoringOverview.aspx) assigns each county [to a tier](https://www.cdph.ca.gov/Programs/CID/DCDC/Pages/COVID-19/COVID19CountyMonitoringOverview.aspx) based on case rate and test positivity rate. What's opened / closed [under each tier](https://www.cdph.ca.gov/Programs/CID/DCDC/CDPH%20Document%20Library/COVID-19/Dimmer-Framework-September_2020.pdf).
Tiers, from most severe to least severe, categorizes coronavirus spread as <strong><span style='color:#6B1F84'>widespread; </span></strong>
<strong><span style='color:#F3324C'>substantial; </span></strong><strong><span style='color:#F7AE1D'>moderate; </span></strong><strong><span style = 'color:#D0E700'>or minimal.</span></strong>
**Counties must stay in the current tier for 3 consecutive weeks and metrics from the last 2 consecutive weeks must fall into less restrictive tier before moving into a less restrictive tier.**
We show *only* case charts labeled with each county's population-adjusted tier cut-offs.
**Related daily reports:**
1. **[US counties report on cases and deaths for select major cities](https://cityoflosangeles.github.io/covid19-indicators/us-county-trends.html)**
1. **[Los Angeles County, detailed indicators](https://cityoflosangeles.github.io/covid19-indicators/coronavirus-stats.html)**
1. **[Los Angeles County neighborhoods report on cases and deaths](https://cityoflosangeles.github.io/covid19-indicators/la-neighborhoods-trends.html)**
Code available in GitHub: [https://github.com/CityOfLosAngeles/covid19-indicators](https://github.com/CityOfLosAngeles/covid19-indicators)
<br>
Get informed with [public health research](https://github.com/CityOfLosAngeles/covid19-indicators/blob/master/reopening-sources.md)
```
import altair as alt
import altair_saver
import geopandas as gpd
import os
import pandas as pd
from processing_utils import default_parameters
from processing_utils import make_charts
from processing_utils import make_maps
from processing_utils import neighborhood_utils
from processing_utils import us_county_utils
from processing_utils import utils
from datetime import date, datetime, timedelta
from IPython.display import display_html, Markdown, HTML, Image
# For map
import branca.colormap
import ipywidgets
# There's a warning that comes up about projects, suppress
import warnings
warnings.filterwarnings("ignore")
# Default parameters
time_zone = default_parameters.time_zone
start_date = datetime(2021, 3, 1).date()
today_date = default_parameters.today_date
fulldate_format = default_parameters.fulldate_format
#alt.renderers.enable('html')
STATE = "CA"
jhu = us_county_utils.clean_jhu(start_date)
jhu = jhu[jhu.state_abbrev==STATE]
hospitalizations = us_county_utils.clean_hospitalizations(start_date)
vaccinations = utils.clean_vaccines_by_county()
vaccinations_demog = utils.clean_vaccines_by_demographics()
ca_counties = list(jhu[jhu.state_abbrev==STATE].county.unique())
# Put LA county first
ca_counties.remove("Los Angeles")
ca_counties = ["Los Angeles"] + ca_counties
data_through = jhu.date.max()
display(Markdown(
f"Report updated: {default_parameters.today_date.strftime(fulldate_format)}; "
f"data available through {data_through.strftime(fulldate_format)}."
)
)
title_font_size = 9
def plot_charts(cases_df, hospital_df, vaccine_df, vaccine_demog_df, county_name):
cases_df = cases_df[cases_df.county==county_name]
hospital_df = hospital_df[hospital_df.county==county_name]
vaccine_df = vaccine_df[vaccine_df.county==county_name]
vaccine_df2 = vaccine_demog_df[vaccine_demog_df.county==county_name]
name = cases_df.county.iloc[0]
cases_chart, deaths_chart = make_charts.setup_cases_deaths_chart(cases_df, "county", name)
hospitalizations_chart = make_charts.setup_county_covid_hospital_chart(
hospital_df.drop(columns = "date"), county_name)
vaccines_type_chart = make_charts.setup_county_vaccination_doses_chart(vaccine_df, county_name)
vaccines_pop_chart = make_charts.setup_county_vaccinated_population_chart(vaccine_df, county_name)
vaccines_age_chart = make_charts.setup_county_vaccinated_category(vaccine_df2, county_name, category="Age Group")
outbreak_chart = (alt.hconcat(
cases_chart,
deaths_chart,
make_charts.add_tooltip(hospitalizations_chart, "hospitalizations")
).configure_concat(spacing=50)
)
#https://stackoverflow.com/questions/60328943/how-to-display-two-different-legends-in-hconcat-chart-using-altair
vaccines_chart = (alt.hconcat(
make_charts.add_tooltip(vaccines_type_chart, "vaccines_type"),
make_charts.add_tooltip(vaccines_pop_chart, "vaccines_pop"),
make_charts.add_tooltip(vaccines_age_chart, "vaccines_age"),
).resolve_scale(color="independent")
.configure_view(stroke=None)
.configure_concat(spacing=0)
)
outbreak_chart = (make_charts.configure_chart(outbreak_chart)
.configure_title(fontSize=title_font_size)
)
vaccines_chart = (make_charts.configure_chart(vaccines_chart)
.configure_title(fontSize=title_font_size)
)
county_state_name = county_name + f", {STATE}"
display(Markdown(f"#### {county_state_name}"))
try:
us_county_utils.county_caption(cases_df, county_name)
except:
pass
us_county_utils.ca_hospitalizations_caption(hospital_df, county_name)
us_county_utils.ca_vaccinations_caption(vaccine_df, county_name)
make_charts.show_svg(outbreak_chart)
make_charts.show_svg(vaccines_chart)
display(Markdown("<strong>Cases chart, explained</strong>"))
Image("../notebooks/chart_parts_explained.png", width=700)
```
<a id='counties_by_region'></a>
## Counties by Region
<strong>Superior California Region: </strong> [Butte](#Butte), Colusa,
[El Dorado](#El-Dorado),
Glenn,
[Lassen](#Lassen), Modoc,
[Nevada](#Nevada),
[Placer](#Placer), Plumas,
[Sacramento](#Sacramento),
[Shasta](#Shasta), Sierra, Siskiyou,
[Sutter](#Sutter),
[Tehama](#Tehama),
[Yolo](#Yolo),
[Yuba](#Yuba)
<br>
<strong>North Coast:</strong> [Del Norte](#Del-Norte),
[Humboldt](#Humboldt),
[Lake](#Lake),
[Mendocino](#Mendocino),
[Napa](#Napa),
[Sonoma](#Sonoma), Trinity
<br>
<strong>San Francisco Bay Area:</strong> [Alameda](#Alameda),
[Contra Costa](#Contra-Costa),
[Marin](#Marin),
[San Francisco](#San-Francisco),
[San Mateo](#San-Mateo),
[Santa Clara](#Santa-Clara),
[Solano](#Solano)
<br>
<strong>Northern San Joaquin Valley:</strong> Alpine, Amador, Calaveras,
[Madera](#Madera), Mariposa,
[Merced](#Merced),
Mono,
[San Joaquin](#San-Joaquin),
[Stanislaus](#Stanislaus),
[Tuolumne](#Tuolumne)
<br>
<strong>Central Coast:</strong> [Monterey](#Monterey),
[San Benito](#San-Benito),
[San Luis Obispo](#San-Luis-Obispo),
[Santa Barbara](#Santa-Barbara),
[Santa Cruz](#Santa-Cruz),
[Ventura](#Ventura)
<br>
<strong>Southern San Joaquin Valley:</strong> [Fresno](#Fresno),
Inyo,
[Kern](#Kern),
[Kings](#Kings),
[Tulare](#Tulare)
<br>
<strong>Southern California:</strong> [Los Angeles](#Los-Angeles),
[Orange](#Orange),
[Riverside](#Riverside),
[San Bernardino](#San-Bernardino)
<br>
<strong>San Diego-Imperial:</strong> [Imperial](#Imperial),
[San Diego](#San-Diego)
<br>
<br>
[**Summary of CA County Severity Map**](#summary)
<br>
[**Vaccinations by Zip Code**](#vax_map)
Note for <i>small values</i>: If the 7-day rolling average of new cases or new deaths is under 10, the 7-day rolling average is listed for the past week, rather than a percent change. Given that it is a rolling average, decimals are possible, and are rounded to 1 decimal place. Similarly for hospitalizations.
```
for c in ca_counties:
id_anchor = c.replace(" - ", "-").replace(" ", "-")
display(HTML(f"<a id={id_anchor}></a>"))
plot_charts(jhu, hospitalizations, vaccinations, vaccinations_demog, c)
display(HTML(
"<br>"
"<a href=#counties_by_region>Return to top</a><br>"
))
```
<a id=summary></a>
## Summary of CA Counties
```
ca_boundary = gpd.read_file(f"{default_parameters.S3_FILE_PATH}ca_counties_boundary.geojson")
def grab_map_stats(df):
# Let's grab the last available date for each county
df = (df.sort_values(["county", "fips", "date2"],
ascending = [True, True, False])
.drop_duplicates(subset = ["county", "fips"], keep = "first")
.reset_index(drop=True)
)
# Calculate its severity metric
df = df.assign(
severity = (df.cases_avg7 / df.tier3_case_cutoff).round(1)
)
# Make gdf
gdf = pd.merge(ca_boundary, df,
on = ["fips", "county"], how = "left", validate = "1:1")
gdf = gdf.assign(
cases_avg7 = gdf.cases_avg7.round(1),
deaths_avg7 = gdf.deaths_avg7.round(1),
)
return gdf
gdf = grab_map_stats(jhu)
```
#### Severity by County
Severity measured as proportion relative to Tier 1 (minimal) threshold.
<br>*1 = at Tier 1 threshold*
<br>*2 = 2x higher than Tier 1 threshold*
```
MAX_SEVERITY = gdf.severity.max()
light_gray = make_charts.light_gray
#https://stackoverflow.com/questions/47846744/create-an-asymmetric-colormap
"""
Against Tier 4 cut-off
If severity = 1 when case_rate = 7 per 100k
If severity = x when case_rate = 4 per 100k
If severity = y when case_rate = 1 per 100k
x = 4/7; y = 1/7
Against Tier 1 cut-off
If severity = 1 when case_rate = 1 per 100k
If severity = x when case_rate = 4 per 100k
If severity = y when case_rate = 7 per 100k
x = 4; y = 7
"""
tier_4_colormap_cutoff = [
(1/7), (4/7), 1, 2.5, 5
]
tier_1_colormap_cutoff = [
1, 4, 7, 10, 15
]
# Note: CA reopening guidelines have diff thresholds based on how many vaccines are administered...
# We don't have vaccine info, so ignore, use original cut-offs
colormap_cutoff = tier_4_colormap_cutoff
colorscale = branca.colormap.StepColormap(
colors=["#D0E700", "#F7AE1D", "#F77889",
"#D59CE8", "#B249D4", "#6B1F84", # purples
],
index=colormap_cutoff,
vmin=0, vmax=MAX_SEVERITY,
)
popup_dict = {
"county": "County",
"severity": "Severity",
}
tooltip_dict = {
"county": "County: ",
"severity": "Severity: ",
"new_cases": "New Cases Yesterday: ",
"cases_avg7": "New Cases (7-day rolling avg): ",
"new_deaths": "New Deaths Yesterday: ",
"deaths_avg7": "New Deaths (7-day rolling avg): ",
"cases": "Cumulative Cases",
"deaths": "Cumulative Deaths",
}
fig = make_maps.make_choropleth_map(gdf.drop(columns = ["date", "date2"]),
plot_col = "severity",
popup_dict = popup_dict,
tooltip_dict = tooltip_dict,
colorscale = colorscale,
fig_width = 570, fig_height = 700,
zoom=6, centroid = [36.2, -119.1])
display(Markdown("Severity Scale"))
display(colorscale)
fig
table = (gdf[gdf.severity.notna()]
[["county", "severity"]]
.sort_values("severity", ascending = False)
.reset_index(drop=True)
)
df1_styler = (table.iloc[:14].style.format({'severity': "{:.1f}"})
.set_table_attributes("style='display:inline'")
#.set_caption('Caption table 1')
.hide_index()
)
df2_styler = (table.iloc[15:29].style.format({'severity': "{:.1f}"})
.set_table_attributes("style='display:inline'")
#.set_caption('Caption table 2')
.hide_index()
)
df3_styler = (table.iloc[30:].style.format({'severity': "{:.1f}"})
.set_table_attributes("style='display:inline'")
#.set_caption('Caption table 2')
.hide_index()
)
display(Markdown("#### Counties (in order of decreasing severity)"))
display_html(df1_styler._repr_html_() +
df2_styler._repr_html_() +
df3_styler._repr_html_(), raw=True)
```
[Return to top](#counties_by_region)
```
# Vaccination data by zip code
def select_latest_date(df):
df = (df[df.date == df.date.max()]
.sort_values(["county", "zipcode"])
.reset_index(drop=True)
)
return df
vax_by_zipcode = neighborhood_utils.clean_zipcode_vax_data()
vax_by_zipcode = select_latest_date(vax_by_zipcode)
popup_dict = {
"county": "County",
"zipcode": "Zip Code",
"fully_vaccinated_percent": "% Fully Vax"
}
tooltip_dict = {
"county": "County: ",
"zipcode": "Zip Code",
"at_least_one_dose_percent": "% 1+ dose",
"fully_vaccinated_percent": "% fully vax"
}
colormap_cutoff = [
0, 0.2, 0.4, 0.6, 0.8, 1
]
colorscale = branca.colormap.StepColormap(
colors=["#CDEAF8", "#97BFD6", "#5F84A9",
"#315174", "#17375E",
],
index=colormap_cutoff,
vmin=0, vmax=1,
)
fig = make_maps.make_choropleth_map(vax_by_zipcode.drop(columns = "date"),
plot_col = "fully_vaccinated_percent",
popup_dict = popup_dict,
tooltip_dict = tooltip_dict,
colorscale = colorscale,
fig_width = 570, fig_height = 700,
zoom=6, centroid = [36.2, -119.1])
```
<a id=vax_map></a>
#### Full Vaccination Rates by Zip Code
```
display(Markdown("% Fully Vaccinated by Zip Code"))
display(colorscale)
fig
zipcode_dropdown = ipywidgets.Dropdown(description="Zip Code",
options=sorted(vax_by_zipcode.zipcode.unique()),
value=90012)
def make_map_show_table(x):
plot_col = "fully_vaccinated_percent"
popup_dict = {
"county": "County",
"zipcode": "Zip Code",
"fully_vaccinated_percent": "% Fully Vax"
}
tooltip_dict = {
"county": "County: ",
"zipcode": "Zip Code",
"at_least_one_dose_percent": "% 1+ dose",
"fully_vaccinated_percent": "% fully vax"
}
colormap_cutoff = [
0, 0.2, 0.4, 0.6, 0.8, 1
]
colorscale = branca.colormap.StepColormap(
colors=["#CDEAF8", "#97BFD6", "#5F84A9",
"#315174", "#17375E",
],
index=colormap_cutoff,
vmin=0, vmax=1,
)
fig_width = 300
fig_height = 300
zoom = 12
df = vax_by_zipcode.copy()
subset_df = (df[df.zipcode==x]
.assign(
# When calculating centroids, use EPSG:2229, but when mapping, put it back into EPSG:4326
# https://gis.stackexchange.com/questions/372564/userwarning-when-trying-to-get-centroid-from-a-polygon-geopandas
lon = df.geometry.centroid.x,
lat = df.geometry.centroid.y,
county_partial_vax_avg = neighborhood_utils.calculate_county_avg(df,
group_by="county",
output_col = "at_least_one_dose_percent"),
county_full_vax_avg = neighborhood_utils.calculate_county_avg(df,
group_by = "county",
output_col = "fully_vaccinated_percent"),
at_least_one_dose_percent = round(df.apply(lambda x: x.at_least_one_dose_percent * 100, axis=1), 0),
fully_vaccinated_percent = round(df.apply(lambda x: x.fully_vaccinated_percent * 100, axis=1), 0),
).drop(columns = "date")
)
display_cols = ["county", "zipcode", "population",
"% 1+ dose", "% fully vax",
"county_partial_vax_avg", "county_full_vax_avg",
]
table = (subset_df.rename(columns = {
"at_least_one_dose_percent": "% 1+ dose",
"fully_vaccinated_percent": "% fully vax",})
[display_cols].style.format({
'% 1+ dose': "{:.0f}%",
'% fully vax': "{:.0f}%",
'date': '{:%-m-%d-%y}',
'population': '{:,.0f}',
'county_partial_vax_avg': '{:.0f}%',
'county_full_vax_avg': '{:.0f}%',
}).set_table_attributes("style='display:inline'")
.hide_index()
)
display_html(table)
center = [subset_df.lat, subset_df.lon]
fig = make_maps.make_choropleth_map(subset_df,
plot_col, popup_dict, tooltip_dict,
colorscale, fig_width, fig_height, zoom, center)
display(fig)
ipywidgets.interact(make_map_show_table, x=zipcode_dropdown)
```
[Return to top](#counties_by_region)
| true |
code
| 0.421492 | null | null | null | null |
|
# Simulators
## Introduction
This notebook shows how to import the *Qiskit Aer* simulator backend and use it to run ideal (noise free) Qiskit Terra circuits.
```
import numpy as np
# Import Qiskit
from qiskit import QuantumCircuit
from qiskit import Aer, transpile
from qiskit.tools.visualization import plot_histogram, plot_state_city
import qiskit.quantum_info as qi
```
## The Aer Provider
The `Aer` provider contains a variety of high performance simulator backends for a variety of simulation methods. The available backends on the current system can be viwed using `Aer.backends`
```
Aer.backends()
```
## The Aer Simulator
The main simulator backend of the Aer provider is the `AerSimulator` backend. A new simulator backend can be created using `Aer.get_backend('aer_simulator')`.
```
simulator = Aer.get_backend('aer_simulator')
```
The default behavior of teh `AerSimulator` backend is to mimic the execution of an actual device. If a `QuantumCircuit` containing measurements is run it will return a count dictionary containing the final values of any classical registers in the circuit. The circuit may contain gates, measurements, resets, conditionals, and other custom simulator instructions that will be discussed in another notebook.
### Simulating a quantum circuit
The basic operation runs a quantum circuit and returns a counts dictionary of measurement outcomes. Here we run a simple circuit that prepares a 2-qubit Bell-state $\left|\psi\right\rangle = \frac{1}{2}\left(\left|0,0\right\rangle + \left|1,1 \right\rangle\right)$ and measures both qubits.
```
# Create circuit
circ = QuantumCircuit(2)
circ.h(0)
circ.cx(0, 1)
circ.measure_all()
# Transpile for simulator
simulator = Aer.get_backend('aer_simulator')
circ = transpile(circ, simulator)
# Run and get counts
result = simulator.run(circ).result()
counts = result.get_counts(circ)
plot_histogram(counts, title='Bell-State counts')
```
### Returning measurement outcomes for each shot
The `QasmSimulator` also supports returning a list of measurement outcomes for each individual shot. This is enabled by setting the keyword argument `memory=True` in the `run`.
```
# Run and get memory
result = simulator.run(circ, shots=10, memory=True).result()
memory = result.get_memory(circ)
print(memory)
```
## Aer Simulator Options
The `AerSimulator` backend supports a variety of configurable options which can be updated using the `set_options` method. See the `AerSimulator` API documentation for additional details.
### Simulation Method
The `AerSimulator` supports a variety of simulation methods, each of which supports a different set of instructions. The method can be set manually using `simulator.set_option(method=value)` option, or a simulator backend with a preconfigured method can be obtained directly from the `Aer` provider using `Aer.get_backend`.
When simulating ideal circuits, changing the method between the exact simulation methods `stabilizer`, `statevector`, `density_matrix` and `matrix_product_state` should not change the simulation result (other than usual variations from sampling probabilities for measurement outcomes)
```
# Increase shots to reduce sampling variance
shots = 10000
# Stabilizer simulation method
sim_stabilizer = Aer.get_backend('aer_simulator_stabilizer')
job_stabilizer = sim_stabilizer.run(circ, shots=shots)
counts_stabilizer = job_stabilizer.result().get_counts(0)
# Statevector simulation method
sim_statevector = Aer.get_backend('aer_simulator_statevector')
job_statevector = sim_statevector.run(circ, shots=shots)
counts_statevector = job_statevector.result().get_counts(0)
# Density Matrix simulation method
sim_density = Aer.get_backend('aer_simulator_density_matrix')
job_density = sim_density.run(circ, shots=shots)
counts_density = job_density.result().get_counts(0)
# Matrix Product State simulation method
sim_mps = Aer.get_backend('aer_simulator_matrix_product_state')
job_mps = sim_mps.run(circ, shots=shots)
counts_mps = job_mps.result().get_counts(0)
plot_histogram([counts_stabilizer, counts_statevector, counts_density, counts_mps],
title='Counts for different simulation methods',
legend=['stabilizer', 'statevector',
'density_matrix', 'matrix_product_state'])
```
#### Automatic Simulation Method
The default simulation method is `automatic` which will automatically select a one of the other simulation methods for each circuit based on the instructions in those circuits. A fixed simualtion method can be specified by by adding the method name when getting the backend, or by setting the `method` option on the backend.
### GPU Simulation
The `statevector`, `density_matrix` and `unitary` simulators support running on a NVidia GPUs. For these methods the simulation device can also be manually set to CPU or GPU using `simulator.set_options(device='GPU')` backend option. If a GPU device is not available setting this option will raise an exception.
```
from qiskit.providers.aer import AerError
# Initialize a GPU backend
# Note that the cloud instance for tutorials does not have a GPU
# so this will raise an exception.
try:
simulator_gpu = Aer.get_backend('aer_simulator')
simulator_gpu.set_options(device='GPU')
except AerError as e:
print(e)
```
The `Aer` provider will also contain preconfigured GPU simulator backends if Qiskit Aer was installed with GPU support on a complatible system:
* `aer_simulator_statevector_gpu`
* `aer_simulator_density_matrix_gpu`
* `aer_simulator_unitary_gpu`
*Note: The GPU version of Aer can be installed using `pip install qiskit-aer-gpu`.*
### Simulation Precision
One of the available simulator options allows setting the float precision for the `statevector`, `density_matrix` `unitary` and `superop` methods. This is done using the `set_precision="single"` or `precision="double"` (default) option:
```
# Configure a single-precision statevector simulator backend
simulator = Aer.get_backend('aer_simulator_statevector')
simulator.set_options(precision='single')
# Run and get counts
result = simulator.run(circ).result()
counts = result.get_counts(circ)
print(counts)
```
Setting the simulation precesion applies to both CPU and GPU simulation devices. Single precision will halve the requried memeory and may provide performance improvements on certain systems.
## Custom Simulator Instructions
### Saving the simulator state
The state of the simulator can be saved in a variety of formats using custom simulator instructions.
| Circuit method | Description |Supported Methods |
|----------------|-------------|------------------|
| `save_state` | Save the simulator state in the native format for the simulation method | All |
| `save_statevector` | Save the simulator state as a statevector | `"automatic"`, `"statevector"`, `"matrix_product_state"`, `"extended_stabilizer"`|
| `save_stabilizer` | Save the simulator state as a Clifford stabilizer | `"automatic"`, `"stabilizer"`|
| `save_density_matrix` | Save the simulator state as a density matrix | `"automatic"`, `"statevector"`, `"matrix_product_state"`, `"density_matrix"` |
| `save_matrix_product_state` | Save the simulator state as a a matrix product state tensor | `"automatic"`, `"matrix_product_state"`|
| `save_unitary` | Save the simulator state as unitary matrix of the run circuit | `"automatic"`, `"unitary"`|
| `save_superop` | Save the simulator state as superoperator matrix of the run circuit | `"automatic"`, `"superop"`|
Note that these instructions are only supported by the Aer simulator and will result in an error if a circuit containing them is run on a non-simulator backend such as an IBM Quantum device.
#### Saving the final statevector
To save the final statevector of the simulation we can append the circuit with the `save_statevector` instruction. Note that this instruction should be applied *before* any measurements if we do not want to save the collapsed post-measurement state
```
# Construct quantum circuit without measure
circ = QuantumCircuit(2)
circ.h(0)
circ.cx(0, 1)
circ.save_statevector()
# Transpile for simulator
simulator = Aer.get_backend('aer_simulator')
circ = transpile(circ, simulator)
# Run and get statevector
result = simulator.run(circ).result()
statevector = result.get_statevector(circ)
plot_state_city(statevector, title='Bell state')
```
#### Saving the circuit unitary
To save the unitary matrix for a `QuantumCircuit` we can append the circuit with the `save_unitary` instruction. Note that this circuit cannot contain any measurements or resets since these instructions are not suppored on for the `"unitary"` simulation method
```
# Construct quantum circuit without measure
circ = QuantumCircuit(2)
circ.h(0)
circ.cx(0, 1)
circ.save_unitary()
# Transpile for simulator
simulator = Aer.get_backend('aer_simulator')
circ = transpile(circ, simulator)
# Run and get unitary
result = simulator.run(circ).result()
unitary = result.get_unitary(circ)
print("Circuit unitary:\n", unitary.round(5))
```
#### Saving multiple states
We can also apply save instructions at multiple locations in a circuit. Note that when doing this we must provide a unique label for each instruction to retrieve them from the results
```
# Construct quantum circuit without measure
steps = 5
circ = QuantumCircuit(1)
for i in range(steps):
circ.save_statevector(label=f'psi_{i}')
circ.rx(i * np.pi / steps, 0)
circ.save_statevector(label=f'psi_{steps}')
# Transpile for simulator
simulator = Aer.get_backend('aer_simulator')
circ = transpile(circ, simulator)
# Run and get saved data
result = simulator.run(circ).result()
data = result.data(0)
data
```
### Setting the simulator to a custom state
The `AerSimulator` allows setting a custom simulator state for several of its simulation methods using custom simulator instructions
| Circuit method | Description |Supported Methods |
|----------------|-------------|------------------|
| `set_statevector` | Set the simulator state to the specified statevector | `"automatic"`, `"statevector"`, `"density_matrix"`|
| `set_stabilizer` | Set the simulator state to the specified Clifford stabilizer | `"automatic"`, `"stabilizer"`|
| `set_density_matrix` | Set the simulator state to the specified density matrix | `"automatic"`, `"density_matrix"` |
| `set_unitary` | Set the simulator state to the specified unitary matrix | `"automatic"`, `"unitary"`, `"superop"`|
| `set_superop` | Set the simulator state to the specified superoperator matrix | `"automatic"`, `"superop"`|
**Notes:**
* These instructions must be applied to all qubits in a circuit, otherwise an exception will be raised.
* The input state must also be a valid state (statevector, denisty matrix, unitary etc) otherwise an exception will be raised.
* These instructions can be applied at any location in a circuit and will override the current state with the specified one. Any classical register values (eg from preceeding measurements) will be unaffected
* Set state instructions are only supported by the Aer simulator and will result in an error if a circuit containing them is run on a non-simulator backend such as an IBM Quantum device.
#### Setting a custom statevector
The `set_statevector` instruction can be used to set a custom `Statevector` state. The input statevector must be valid ($|\langle\psi|\psi\rangle|=1$)
```
# Generate a random statevector
num_qubits = 2
psi = qi.random_statevector(2 ** num_qubits, seed=100)
# Set initial state to generated statevector
circ = QuantumCircuit(num_qubits)
circ.set_statevector(psi)
circ.save_state()
# Transpile for simulator
simulator = Aer.get_backend('aer_simulator')
circ = transpile(circ, simulator)
# Run and get saved data
result = simulator.run(circ).result()
result.data(0)
```
#### Using the initialize instruction
It is also possible to initialize the simulator to a custom statevector using the `initialize` instruction. Unlike the `set_statevector` instruction this instruction is also supported on real device backends by unrolling to reset and standard gate instructions.
```
# Use initilize instruction to set initial state
circ = QuantumCircuit(num_qubits)
circ.initialize(psi, range(num_qubits))
circ.save_state()
# Transpile for simulator
simulator = Aer.get_backend('aer_simulator')
circ = transpile(circ, simulator)
# Run and get result data
result = simulator.run(circ).result()
result.data(0)
```
#### Setting a custom density matrix
The `set_density_matrix` instruction can be used to set a custom `DensityMatrix` state. The input density matrix must be valid ($Tr[\rho]=1, \rho \ge 0$)
```
num_qubits = 2
rho = qi.random_density_matrix(2 ** num_qubits, seed=100)
circ = QuantumCircuit(num_qubits)
circ.set_density_matrix(rho)
circ.save_state()
# Transpile for simulator
simulator = Aer.get_backend('aer_simulator')
circ = transpile(circ, simulator)
# Run and get saved data
result = simulator.run(circ).result()
result.data(0)
```
#### Setting a custom stabilizer state
The `set_stabilizer` instruction can be used to set a custom `Clifford` stabilizer state. The input stabilizer must be a valid `Clifford`.
```
# Generate a random Clifford C
num_qubits = 2
stab = qi.random_clifford(num_qubits, seed=100)
# Set initial state to stabilizer state C|0>
circ = QuantumCircuit(num_qubits)
circ.set_stabilizer(stab)
circ.save_state()
# Transpile for simulator
simulator = Aer.get_backend('aer_simulator')
circ = transpile(circ, simulator)
# Run and get saved data
result = simulator.run(circ).result()
result.data(0)
```
#### Setting a custom unitary
The `set_unitary` instruction can be used to set a custom unitary `Operator` state. The input unitary matrix must be valid ($U^\dagger U=\mathbb{1}$)
```
# Generate a random unitary
num_qubits = 2
unitary = qi.random_unitary(2 ** num_qubits, seed=100)
# Set initial state to unitary
circ = QuantumCircuit(num_qubits)
circ.set_unitary(unitary)
circ.save_state()
# Transpile for simulator
simulator = Aer.get_backend('aer_simulator')
circ = transpile(circ, simulator)
# Run and get saved data
result = simulator.run(circ).result()
result.data(0)
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
```
| true |
code
| 0.609582 | null | null | null | null |
|
# Distance Based Statistical Method for Planar Point Patterns
**Authors: Serge Rey <[email protected]> and Wei Kang <[email protected]>**
## Introduction
Distance based methods for point patterns are of three types:
* [Mean Nearest Neighbor Distance Statistics](#Mean-Nearest-Neighbor-Distance-Statistics)
* [Nearest Neighbor Distance Functions](#Nearest-Neighbor-Distance-Functions)
* [Interevent Distance Functions](#Interevent-Distance-Functions)
In addition, we are going to introduce a computational technique [Simulation Envelopes](#Simulation-Envelopes) to aid in making inferences about the data generating process. An [example](#CSR-Example) is used to demonstrate how to use and interpret simulation envelopes.
```
import scipy.spatial
import pysal.lib as ps
import numpy as np
from pysal.explore.pointpats import PointPattern, PoissonPointProcess, as_window, G, F, J, K, L, Genv, Fenv, Jenv, Kenv, Lenv
%matplotlib inline
import matplotlib.pyplot as plt
```
## Mean Nearest Neighbor Distance Statistics
The nearest neighbor(s) for a point $u$ is the point(s) $N(u)$ which meet the condition
$$d_{u,N(u)} \leq d_{u,j} \forall j \in S - u$$
The distance between the nearest neighbor(s) $N(u)$ and the point $u$ is nearest neighbor distance for $u$. After searching for nearest neighbor(s) for all the points and calculating the corresponding distances, we are able to calculate mean nearest neighbor distance by averaging these distances.
It was demonstrated by Clark and Evans(1954) that mean nearest neighbor distance statistics distribution is a normal distribution under null hypothesis (underlying spatial process is CSR). We can utilize the test statistics to determine whether the point pattern is the outcome of CSR. If not, is it the outcome of cluster or regular
spatial process?
Mean nearest neighbor distance statistic
$$\bar{d}_{min}=\frac{1}{n} \sum_{i=1}^n d_{min}(s_i)$$
```
points = [[66.22, 32.54], [22.52, 22.39], [31.01, 81.21],
[9.47, 31.02], [30.78, 60.10], [75.21, 58.93],
[79.26, 7.68], [8.23, 39.93], [98.73, 77.17],
[89.78, 42.53], [65.19, 92.08], [54.46, 8.48]]
pp = PointPattern(points)
pp.summary()
```
We may call the method **knn** in PointPattern class to find $k$ nearest neighbors for each point in the point pattern *pp*.
```
# one nearest neighbor (default)
pp.knn()
```
The first array is the ids of the most nearest neighbor for each point, the second array is the distance between each point and its most nearest neighbor.
```
# two nearest neighbors
pp.knn(2)
pp.max_nnd # Maximum nearest neighbor distance
pp.min_nnd # Minimum nearest neighbor distance
pp.mean_nnd # mean nearest neighbor distance
pp.nnd # Nearest neighbor distances
pp.nnd.sum()/pp.n # same as pp.mean_nnd
pp.plot()
```
## Nearest Neighbor Distance Functions
Nearest neighbour distance distribution functions (including the nearest “event-to-event” and “point-event” distance distribution functions) of a point process are cumulative distribution functions of several kinds -- $G, F, J$. By comparing the distance function of the observed point pattern with that of the point pattern from a CSR process, we are able to infer whether the underlying spatial process of the observed point pattern is CSR or not for a given confidence level.
#### $G$ function - event-to-event
The $G$ function is defined as follows: for a given distance $d$, $G(d)$ is the proportion of nearest neighbor distances that are less than $d$.
$$G(d) = \sum_{i=1}^n \frac{ \phi_i^d}{n}$$
$$
\phi_i^d =
\begin{cases}
1 & \quad \text{if } d_{min}(s_i)<d \\
0 & \quad \text{otherwise } \\
\end{cases}
$$
If the underlying point process is a CSR process, $G$ function has an expectation of:
$$
G(d) = 1-e(-\lambda \pi d^2)
$$
However, if the $G$ function plot is above the expectation this reflects clustering, while departures below expectation reflect dispersion.
```
gp1 = G(pp, intervals=20)
gp1.plot()
```
A slightly different visualization of the empirical function is the quantile-quantile plot:
```
gp1.plot(qq=True)
```
in the q-q plot the csr function is now a diagonal line which serves to make accessment of departures from csr visually easier.
It is obvious that the above $G$ increases very slowly at small distances and the line is below the expected value for a CSR process (green line). We might think that the underlying spatial process is regular point process. However, this visual inspection is not enough for a final conclusion. In [Simulation Envelopes](#Simulation-Envelopes), we are going to demonstrate how to simulate data under CSR many times and construct the $95\%$ simulation envelope for $G$.
```
gp1.d # distance domain sequence (corresponding to the x-axis)
gp1.G #cumulative nearest neighbor distance distribution over d (corresponding to the y-axis))
```
#### $F$ function - "point-event"
When the number of events in a point pattern is small, $G$ function is rough (see the $G$ function plot for the 12 size point pattern above). One way to get around this is to turn to $F$ function where a given number of randomly distributed points are generated in the domain and the nearest event neighbor distance is calculated for each point. The cumulative distribution of all nearest event neighbor distances is called $F$ function.
```
fp1 = F(pp, intervals=20) # The default is to randomly generate 100 points.
fp1.plot()
fp1.plot(qq=True)
```
We can increase the number of intervals to make $F$ more smooth.
```
fp1 = F(pp, intervals=50)
fp1.plot()
fp1.plot(qq=True)
```
$F$ function is more smooth than $G$ function.
#### $J$ function - a combination of "event-event" and "point-event"
$J$ function is defined as follows:
$$J(d) = \frac{1-G(d)}{1-F(d)}$$
If $J(d)<1$, the underlying point process is a cluster point process; if $J(d)=1$, the underlying point process is a random point process; otherwise, it is a regular point process.
```
jp1 = J(pp, intervals=20)
jp1.plot()
```
From the above figure, we can observe that $J$ function is obviously above the $J(d)=1$ horizontal line. It is approaching infinity with nearest neighbor distance increasing. We might tend to conclude that the underlying point process is a regular one.
## Interevent Distance Functions
Nearest neighbor distance functions consider only the nearest neighbor distances, "event-event", "point-event" or the combination. Thus, distances to higher order neighbors are ignored, which might reveal important information regarding the point process. Interevent distance functions, including $K$ and $L$ functions, are proposed to consider distances between all pairs of event points. Similar to $G$, $F$ and $J$ functions, $K$ and $L$ functions are also cumulative distribution function.
#### $K$ function - "interevent"
Given distance $d$, $K(d)$ is defined as:
$$K(d) = \frac{\sum_{i=1}^n \sum_{j=1}^n \psi_{ij}(d)}{n \hat{\lambda}}$$
where
$$
\psi_{ij}(d) =
\begin{cases}
1 & \quad \text{if } d_{ij}<d \\
0 & \quad \text{otherwise } \\
\end{cases}
$$
$\sum_{j=1}^n \psi_{ij}(d)$ is the number of events within a circle of radius $d$ centered on event $s_i$ .
Still, we use CSR as the benchmark (null hypothesis) and see how the $K$ function estimated from the observed point pattern deviate from that under CSR, which is $K(d)=\pi d^2$. $K(d)<\pi d^2$ indicates that the underlying point process is a regular point process. $K(d)>\pi d^2$ indicates that the underlying point process is a cluster point process.
```
kp1 = K(pp)
kp1.plot()
```
#### $L$ function - "interevent"
$L$ function is a scaled version of $K$ function, defined as:
$$L(d) = \sqrt{\frac{K(d)}{\pi}}-d$$
```
lp1 = L(pp)
lp1.plot()
```
## Simulation Envelopes
A [Simulation envelope](http://www.esajournals.org/doi/pdf/10.1890/13-2042.1) is a computer intensive technique for inferring whether an observed pattern significantly deviates from what would be expected under a specific process. Here, we always use CSR as the benchmark. In order to construct a simulation envelope for a given function, we need to simulate CSR a lot of times, say $1000$ times. Then, we can calculate the function for each simulated point pattern. For every distance $d$, we sort the function values of the $1000$ simulated point patterns. Given a confidence level, say $95\%$, we can acquire the $25$th and $975$th value for every distance $d$. Thus, a simulation envelope is constructed.
#### Simulation Envelope for G function
**Genv** class in pysal.
```
realizations = PoissonPointProcess(pp.window, pp.n, 100, asPP=True) # simulate CSR 100 times
genv = Genv(pp, intervals=20, realizations=realizations) # call Genv to generate simulation envelope
genv
genv.observed
genv.plot()
```
In the above figure, **LB** and **UB** comprise the simulation envelope. **CSR** is the mean function calculated from the simulated data. **G** is the function estimated from the observed point pattern. It is well below the simulation envelope. We can infer that the underlying point process is a regular one.
#### Simulation Envelope for F function
**Fenv** class in pysal.
```
fenv = Fenv(pp, intervals=20, realizations=realizations)
fenv.plot()
```
#### Simulation Envelope for J function
**Jenv** class in pysal.
```
jenv = Jenv(pp, intervals=20, realizations=realizations)
jenv.plot()
```
#### Simulation Envelope for K function
**Kenv** class in pysal.
```
kenv = Kenv(pp, intervals=20, realizations=realizations)
kenv.plot()
```
#### Simulation Envelope for L function
**Lenv** class in pysal.
```
lenv = Lenv(pp, intervals=20, realizations=realizations)
lenv.plot()
```
## CSR Example
In this example, we are going to generate a point pattern as the "observed" point pattern. The data generating process is CSR. Then, we will simulate CSR in the same domain for 100 times and construct a simulation envelope for each function.
```
from pysal.lib.cg import shapely_ext
from pysal.explore.pointpats import Window
import pysal.lib as ps
va = ps.io.open(ps.examples.get_path("vautm17n.shp"))
polys = [shp for shp in va]
state = shapely_ext.cascaded_union(polys)
```
Generate the point pattern **pp** (size 100) from CSR as the "observed" point pattern.
```
a = [[1],[1,2]]
np.asarray(a)
n = 100
samples = 1
pp = PoissonPointProcess(Window(state.parts), n, samples, asPP=True)
pp.realizations[0]
pp.n
```
Simulate CSR in the same domain for 100 times which would be used for constructing simulation envelope under the null hypothesis of CSR.
```
csrs = PoissonPointProcess(pp.window, 100, 100, asPP=True)
csrs
```
Construct the simulation envelope for $G$ function.
```
genv = Genv(pp.realizations[0], realizations=csrs)
genv.plot()
```
Since the "observed" $G$ is well contained by the simulation envelope, we infer that the underlying point process is a random process.
```
genv.low # lower bound of the simulation envelope for G
genv.high # higher bound of the simulation envelope for G
```
Construct the simulation envelope for $F$ function.
```
fenv = Fenv(pp.realizations[0], realizations=csrs)
fenv.plot()
```
Construct the simulation envelope for $J$ function.
```
jenv = Jenv(pp.realizations[0], realizations=csrs)
jenv.plot()
```
Construct the simulation envelope for $K$ function.
```
kenv = Kenv(pp.realizations[0], realizations=csrs)
kenv.plot()
```
Construct the simulation envelope for $L$ function.
```
lenv = Lenv(pp.realizations[0], realizations=csrs)
lenv.plot()
```
| true |
code
| 0.607896 | null | null | null | null |
|
# Loss and Regularization
```
%load_ext autoreload
%autoreload 2
import numpy as np
from numpy import linalg as nplin
from cs771 import plotData as pd
from cs771 import optLib as opt
from sklearn import linear_model
from matplotlib import pyplot as plt
from matplotlib.ticker import MaxNLocator
import random
```
**Loading Benchmark Datasets using _sklearn_**: the _sklearn_ library, along with providing methods for various ML problems like classification, regression and clustering, also gives the facility to download various datasets. We will use the _Boston Housing_ dataset that requires us to predict house prices in the city of Boston using 13 features such as crime rates, pollution levels, education facilities etc. Check this [[link]](https://scikit-learn.org/stable/datasets/index.html#boston-dataset) to learn more.
**Caution**: when executing the dataset download statement for the first time, sklearn will attempt to download this dataset from an internet source. Make sure you have a working internet connection at this point otherwise the statement will fail. Once you have downloaded the dataset once, it will be cached and you would not have to download it again and again.
```
from sklearn.datasets import load_boston
(X, y) = load_boston( return_X_y=True )
(n, d) = X.shape
print( "This dataset has %d data points and %d features" % (n,d) )
print( "The mean value of the (real-valued) labels is %.2f" % np.mean(y) )
```
**Experiments with Ridge Regression**: we first use rigde regression (that uses the least squares loss and $L_2$ regularization) to try and solve this problem. We will try out a variety of regularization parameters ranging across 15 orders of magnitude from $10^{-4}$ all the way to $10^{11}$. Note that as the regularization parameter increases, the model norm drops significantly so that at extremely high levels of regularization, the learnt model is almost a zero vector. Naturally, such a trivial model offers poor prediction hence, beyond a point, increasing the regularization parameter decreases prediction performance. We measure prediction performance in term of _mean absolute error_ (shortened to MAE).
**Regularization Path**: the concept of a regularization path traces the values different coordinates of the model take when the problem is solved using various values of the regularization parameter. Note that initially, when there is very feeble regularization (say $\alpha = 10^{-4}$), model coordinates take large magnitude values, some positive, others negative. However, as regularization increases, all model coordinate values _shrink_ towards zero.
```
alphaVals = np.concatenate( [np.linspace( 1e-4 * 10**i, 1e-4 * 10**(i+1), num = 5 )[:-1] for i in range(15)] )
MAEVals = np.zeros_like( alphaVals )
modelNorms = np.zeros_like( alphaVals )
models = np.zeros( (X.shape[1], len(alphaVals)) )
for i in range( len(alphaVals) ):
reg = linear_model.Ridge( alpha = alphaVals[i] )
reg.fit( X, y )
w = reg.coef_
b = reg.intercept_
MAEVals[i] = np.mean( np.abs( X.dot(w) + b - y ) )
modelNorms[i] = nplin.norm( w, 2 )
models[:,i] = w
bestRRMAENoCorr = min( MAEVals )
fig = pd.getFigure( 7, 7 )
ax = plt.gca()
ax.set_title( "The effect of the strength of L2 regularization on performance" )
ax.set_xlabel( "L2 Regularization Parameter Value" )
ax.set_ylabel( "Mean Absolute Error", color = "r" )
ax.semilogx( alphaVals, MAEVals, color = 'r', linestyle = '-' )
ax2 = ax.twinx()
ax2.set_ylabel( "Model Complexity (L2 Norm)", color = "b" )
ax2.semilogx( alphaVals, modelNorms, color = 'b', linestyle = '-' )
fig2 = pd.getFigure( 7, 7 )
plt.figure( fig2.number )
plt.title( "The Regularization Path for L2 regularization" )
plt.xlabel( "L2 Regularization Parameter Value" )
plt.ylabel( "Value of Various Coordinates of Models" )
for i in range(d):
plt.semilogx( alphaVals, models[i,:] )
```
**Robust Regression**: we will now investigate how to deal with cases when the data is corrupted. We will randomly choose 25% of the data points and significantly change their labels (i.e. $y$ values). We will note that ridge regression fails to offer a decent solution no matter what value of the regression parameter we choose. The best MAE offered by ridge regression in this case is 8.1 whereas it was around 3.2 when data was not corrupted. Clearly $L_2$ regularization is not a good option when data is maliciously or adversarially corrupted.
```
# How many points do we want to corrupt?
k = int( 0.25 * n )
corr = np.zeros_like( y )
idx_corr = np.random.permutation( n )[:k]
# What diff do we want to introduce in the labels of the corrupted data points?
corr[idx_corr] = 30
y_corr = y + corr
MAEVals = np.zeros_like( alphaVals )
modelNorms = np.zeros_like( alphaVals )
for i in range( len(alphaVals) ):
reg = linear_model.Ridge( alpha = alphaVals[i] )
reg.fit( X, y_corr )
w = reg.coef_
b = reg.intercept_
MAEVals[i] = np.mean( np.abs( X.dot(w) + b - y ) )
modelNorms[i] = nplin.norm( w, 2 )
bestRRMAE = min( MAEVals )
fig3 = pd.getFigure( 7, 7 )
ax = plt.gca()
ax.set_title( "L2 regularization on Corrupted Data" )
ax.set_xlabel( "L2 Regularization Parameter Value" )
ax.set_ylabel( "Mean Absolute Error", color = "r" )
ax.semilogx( alphaVals, MAEVals, color = 'r', linestyle = '-' )
ax2 = ax.twinx()
ax2.set_ylabel( "Model Complexity (L2 Norm)", color = "b" )
ax2.semilogx( alphaVals, modelNorms, color = 'b', linestyle = '-' )
```
**Alternating Minimization for Robust Regression**: a simple heuristic that works well in such corrupted data settings is to learn the model and try to identify the subset of the data that is corrupted simultaneously. A variant of this heuristic, as presented in the _TORRENT_ algorithm is implemented below. At each time step, this method takes an existing model and postulates that data points with high residuals with respect to this model may be corrupted and sets them aside. Ridge regression is then carried out with the rest of the data points to update the model.
The results show that this simple heuristic not only offers a much better MAE (of around 3.2, the same that ridge regression offered when executed with clean data) but that the method is able to identify most of the data points that were corrupted. The method converges in only a couple of iterations.
**Reference**\
Kush Bhatia, Prateek Jain and P.K., _Robust Regression via Hard Thresholding_ , Proceedings of the 29th Annual Conference on Neural Information Processing Systems (NIPS), 2015.
```
# How many iterations do we wish to run the algorithm
horizon = 10
MAEVals = np.zeros( (horizon,) )
suppErrVals = np.zeros( (horizon,) )
# Initialization
w = np.zeros( (d,) )
b = 0
reg = linear_model.Ridge( alpha = 0.005 )
# Find out how many of the corrupted data points were correctly identified by the algorithm
def getSupportIden( idx, idxAst ):
return len( set(idxAst).intersection( set(idx) ) )
# Implement the TORRENT algorithm
for t in range( horizon ):
MAEVals[t] = np.mean( np.abs( X.dot(w) + b - y ) )
# Find out the data points with largest residual -- these maybe the corrupted points
res = np.abs( X.dot(w) + b - y_corr )
idx_sorted = np.argsort( res )
idx_clean_hat = idx_sorted[0:n-k]
idx_corr_hat = idx_sorted[-k:]
suppErrVals[t] = getSupportIden( idx_corr, idx_corr_hat )
# The points with low residuals are used to update the model
XClean = X[idx_clean_hat,:]
yClean = y_corr[idx_clean_hat]
reg.fit( XClean, yClean )
w = reg.coef_
b = reg.intercept_
fig4 = pd.getFigure( 7, 7 )
plt.plot( np.arange( horizon ), bestRRMAE * np.ones_like(suppErrVals), color = 'r', linestyle = ':', label = "Best MAE achieved by Ridge Regression on Corrupted Data" )
plt.plot( np.arange( horizon ), bestRRMAENoCorr * np.ones_like(suppErrVals), color = 'g', linestyle = ':', label = "Best MAE achieved by Ridge Regression on Clean Data" )
plt.legend()
ax = plt.gca()
ax.set_title( "Alternating Minimization on Corrupted Data" )
ax.set_xlabel( "Number of Iterations" )
ax.set_ylabel( "Mean Absolute Error", color = "r" )
ax.plot( np.arange( horizon ), MAEVals, color = 'r', linestyle = '-' )
plt.ylim( np.floor(min(MAEVals)), np.ceil(bestRRMAE) )
ax2 = ax.twinx()
ax2.set_ylabel( "Number of Corrupted Indices (out of %d) Identified Correctly" % k, color = "b" )
ax2.yaxis.set_major_locator( MaxNLocator( integer = True ) )
ax2.plot( np.arange( horizon ), suppErrVals, color = 'b', linestyle = '-' )
plt.ylim( min(suppErrVals)-1, k )
```
**Spurious Features present a Sparse Recovery Problem**: in this experiment we add 500 new features to the dataset (with the new features containing nothing but pure random white noise), taking the total number of features to 513 which is greater than the total number of data points which is 506. Upon executing ridge regression on this dataset, we find something very surprising. We find that at low levels of regularization, the method offers almost zero MAE!
The above may seem paradoxical since the new features were white noise and had nothing informative to say about the problem. What happened was that these new features increased the power of the linear model and since there was not enough data, ridge regression used these new features to artificially reduce the error. This is clear from the regularization path plot.
Such a model is actually not very useful since it would not perform very well on test data. To do well on test data, the only way is to identify the truly informative features (of which there are only 13). Note that in the error plot, the blue curve demonstrates the amount of weight the model puts on the spurious features. Only when there is heavy regularization (around $\alpha = 10^4$ does the model stop placing large weights on the spurious features and error levels climb to around 3.2, where they were when spurious features were not present. Thus, L2 regularization may not be the best option when there are several irrelevant features.
```
X_spurious = np.random.normal( 0, 1, (n, 500) )
X_extend = np.hstack( (X, X_spurious) )
(n,d) = X_extend.shape
MAEVals = np.zeros_like( alphaVals )
spuriousModelNorms = np.zeros_like( alphaVals )
models = np.zeros( (d, len(alphaVals)) )
for i in range( len(alphaVals) ):
reg = linear_model.Ridge( alpha = alphaVals[i] )
reg.fit( X_extend, y )
w = reg.coef_
b = reg.intercept_
MAEVals[i] = np.mean( np.abs( X_extend.dot(w) + b - y ) )
spuriousModelNorms[i] = nplin.norm( w[13:], 2 )
models[:,i] = w
fig5 = pd.getFigure( 7, 7 )
plt.plot( alphaVals, bestRRMAENoCorr * np.ones_like(alphaVals), color = 'g', linestyle = ':', label = "Best MAE achieved by Ridge Regression on Original Data" )
plt.legend()
ax = plt.gca()
ax.set_title( "Effect of L2 regularization with Spurious Features" )
ax.set_xlabel( "L2 Regularization Parameter Value" )
ax.set_ylabel( "Mean Absolute Error", color = "r" )
ax.semilogx( alphaVals, MAEVals, color = 'r', linestyle = '-' )
ax2 = ax.twinx()
ax2.set_ylabel( "Weight on Spurious Features", color = "b" )
ax2.semilogx( alphaVals, spuriousModelNorms, color = 'b', linestyle = '-' )
fig6 = pd.getFigure( 7, 7 )
plt.figure( fig6.number )
plt.title( "The Regularization Path for L2 regularization with Spurious Features" )
plt.xlabel( "L2 Regularization Parameter Value" )
plt.ylabel( "Value of Various Coordinates of Models" )
for i in range(d):
plt.semilogx( alphaVals, models[i,:] )
```
**LASSO for Sparse Recovery**: the LASSO (Least Absolute Shrinkage and Selection Operator) performs regression using the least squares loss and the $L_1$ regularizer instead. The error plot and the regularization path plots show that LASSO offers a far quicker identification of the spurious features. LASSO is indeed a very popular technique to deal with sparse recovery when we have very less data and suspect that there may be irrelevant features.
```
MAEVals = np.zeros_like( alphaVals )
spuriousModelNorms = np.zeros_like( alphaVals )
models = np.zeros( (X_extend.shape[1], len(alphaVals)) )
for i in range( len(alphaVals) ):
reg = linear_model.Lasso( alpha = alphaVals[i] )
reg.fit( X_extend, y )
w = reg.coef_
b = reg.intercept_
MAEVals[i] = np.mean( np.abs( X_extend.dot(w) + b - y ) )
spuriousModelNorms[i] = nplin.norm( w[13:], 2 )
models[:,i] = w
fig5 = pd.getFigure( 7, 7 )
plt.plot( alphaVals, bestRRMAENoCorr * np.ones_like(alphaVals), color = 'g', linestyle = ':', label = "Best MAE achieved by Ridge Regression on Original Data" )
plt.legend()
ax = plt.gca()
ax.set_title( "Examining the effect of the strength of L1 regularization" )
ax.set_xlabel( "L1 Regularization Parameter Value" )
ax.set_ylabel( "Mean Absolute Error", color = "r" )
ax.semilogx( alphaVals, MAEVals, color = 'r', linestyle = '-' )
ax2 = ax.twinx()
ax2.set_ylabel( "Weight on Spurious Features", color = "b" )
ax2.semilogx( alphaVals, spuriousModelNorms, color = 'b', linestyle = '-' )
fig6 = pd.getFigure( 7, 7 )
plt.figure( fig6.number )
plt.title( "Plotting the Regularization Path for L1 regularization" )
plt.xlabel( "L2 Regularization Parameter Value" )
plt.ylabel( "Value of Various Coordinates of Models" )
for i in range(X_extend.shape[1]):
plt.semilogx( alphaVals, models[i,:] )
```
**Proximal Gradient Descent to solve LASSO**: we will now implement the proximal gradient descent method to minimize the LASSO objective. The _ProxGD_ method performs a usual gradient step and then applies the _prox operator_ corresponding to the regularizer. For the $L_1$ regularizer $\lambda\cdot\|\cdot\|_1$, the prox operator $\text{prox}_{\lambda\cdot\|\cdot\|_1}$ is simply the so-called _soft-thresholding_ operator described below. If $\mathbf z = \text{prox}_{\lambda\cdot\|\cdot\|_1}(\mathbf x)$, then for all $i \in [d]$, we have
$$
\mathbf z_i = \begin{cases} \mathbf x_i - \lambda & \mathbf x_i > \lambda \\ 0 & |\mathbf x_i| \leq \lambda \\ \mathbf x_i + \lambda & \mathbf x_i < -\lambda \end{cases}
$$
Applying ProxGD to the LASSO problem is often called _ISTA_ (Iterative Soft Thresholding Algorithm) for this reason. Note that at time $t$, if the step length used for the gradient step is $\eta_t$, then the prox operator corresponding to $\text{prox}_{\lambda_t\cdot\|\cdot\|_1}$ is used where $\lambda_t = \eta_t\cdot\lambda$ and $\lambda$ is the regularization parameter in the LASSO problem we are trying to solve. Thus, ISTA requires shrinkage to be smaller if we are also using small step sizes.
To speed up convergence, _acceleration_ techniques (e.g. NAG, Adam) are helpful. We will use a very straightforward acceleration technique which simply sets
$$
\mathbf w^t = \mathbf w^t + \frac {t}{t+1}\cdot(\mathbf w^t - \mathbf w^{t-1})
$$
In particular, the application of Nesterov's acceleartion i.e. NAG to ISTA gives us the so-called _FISTA_ (Fast ISTA).
```
# Get the MAE and LASSO objective
def getLASSOObj( model ):
w = model[:-1]
b = model[-1]
res = X_extend.dot(w) + b - y
objVal = alpha * nplin.norm( w, 1 ) + 1/(2*n) * ( nplin.norm( res ) ** 2 )
MAEVal = np.mean( np.abs( res ) )
return (objVal, MAEVal)
# Apply the prox operator and also apply acceleration
def doSoftThresholding( model, t ):
global modelPrev
w = model[:-1]
b = model[-1]
# Shrink all model coordinates by the effective value of alpha
idx = w < 0
alphaEff = alpha * stepFunc(t)
w = np.abs(w) - alphaEff
w[w < 0] = 0
w[idx] = w[idx] * -1
model = np.append( w, b )
# Acceleration step improves convergence rate
model = model + (t/(t+1)) * (model - modelPrev)
modelPrev = model
return model
# Get the gradient to the loss function in LASSO (just the least squares part)
# Note that gradients w.r.t the regularizer are not required in proximal gradient
# This is one reason why they are useful with non-differentiable regularizers
def getLASSOGrad( model, t ):
w = model[:-1]
b = model[-1]
samples = random.sample( range(0, n), B )
X_ = X_extend[samples,:]
y_ = y[samples]
res = X_.dot(w) + b - y_
grad = np.append( X_.T.dot(res), np.sum(res) )
return grad/B
# Set hyperparameters and initialize the model
alpha = 1
B = 10
eta = 2e-6
init = np.zeros( (d+1,) )
modelPrev = np.zeros( (d+1,) )
# A constant step length seems to work well here
stepFunc = opt.stepLengthGenerator( "constant", eta )
(modelProxGD, objProxGD, timeProxGD) = opt.doGD( getLASSOGrad, stepFunc, getLASSOObj, init, horizon = 50000, doModelAveraging = True, postGradFunc = doSoftThresholding )
objVals = [objProxGD[i][0] for i in range(len(objProxGD))]
MAEVals = [objProxGD[i][1] for i in range(len(objProxGD))]
fig7 = pd.getFigure( 7, 7 )
ax = plt.gca()
ax.set_title( "An Accelerated ProxGD Solver for LASSO" )
ax.set_xlabel( "Elapsed time (sec)" )
ax.set_ylabel( "Objective Value for LASSO", color = "r" )
ax.plot( timeProxGD, objVals, color = 'r', linestyle = ':' )
ax2 = ax.twinx()
ax2.set_ylabel( "MAE Value for LASSO", color = "b" )
ax2.plot( timeProxGD, MAEVals, color = 'b', linestyle = '--' )
plt.ylim( 2, 10 )
```
**Improving the Performance of ProxGD**: there are several steps one can adopt to get better performance
1. Use a line search method to tune the step length instead of using a fixed step length or a regular schedule
1. Perform a better implementation of the acceleration step (which may require additional hyperparameters)
1. The Boston housing problem is what is called _ill-conditioned_ (this was true even before spurious features were added). Advanced methods like conjugate gradient descent (beyond the scope of CS771) perform better for ill-conditioned problems.
1. Use better solvers -- coordinate descent solvers for the Lagrangian dual of the LASSO are known to offer superior performance.
**Data Normalization to Improve Data Conditioning**: in some cases (and fortunately, this happens to be one of them), the data conditioning can be improved somewhat by normalizing the data features. This does not change the problem (we will see below how) but it definitely makes life easier for the solvers. Professional solvers such as those used within libraries such as sklearn often attempt to normalize data themselves.
The two most common data normalization steps are
1. _Mean centering_ : we calculate the mean/average feature vector from the data set $\mathbf \mu \in \mathbb R^d$ and subtract it from each feature vector to get centered feature vectors. This has an effect of bringing the dataset feature vectors closer to the origin.
1. _Variance normalization_ : we calculate the standard deviation along each feature as a vector $\mathbf \sigma \in \mathbb R^d$ and divide each centered feature vector by this vector (in an element-wise manner). This has an effect of limiting how wildly any feature can vary.
If you are not familiar with concepts such as mean and variance, please refer to the Statistics Refresher material in the course or else consult some other external source of your liking.
Thus, we transform each feature vector as follows (let $\Sigma \in \mathbb R^{d \times d}$ denote a diagonal matrix with entries of the vector $\mathbf \sigma$ along its diagonal):
$$
\tilde{\mathbf x}^i = \Sigma^{-1}(\mathbf x^i - \mathbf \mu)
$$
We then learn our linear model, say $(\tilde{\mathbf w}, \tilde b)$ over the centered data. We will see that our solvers will thank us for normalizing our data. However, it is very easy to transform this linear model to one that works over the original data (we may want to do this since our test data would not be normalized and normalizing test data may take precious time which we may wish to save).
To transform the model to one that works over the original data features, simply notice that we have
$$
\tilde{\mathbf w}^\top\tilde{\mathbf x}^i + \tilde b = \tilde{\mathbf w}^\top\Sigma^{-1}(\mathbf x^i - \mathbf \mu) + \tilde b = \mathbf w^\top\mathbf x^i + b,
$$
where $\mathbf w = \Sigma^{-1}\tilde{\mathbf w}$ and $b = \tilde b - \tilde{\mathbf w}^\top\Sigma^{-1}\mathbf \mu$ (we exploited the fact that $\Sigma$ being a diagonal matrix, is a symmetric matrix)
```
# Normalize data
mu = np.mean( X_extend, axis = 0 )
sg = np.std( X_extend, axis = 0 )
XNorm = (X_extend - mu)/sg
# The original dataset is still recoverable from the centered data
if np.allclose( X_extend, XNorm * sg + mu, atol = 1e-7 ):
print( "Successfully recovered the original data from the normalized data" )
```
**Running ProxGD on Normalized Data**: we will have to make two simple changes. Firstly, we will need to change the gradient calculator method to perform gradient computations with normalized data. Secondly, we will change the method that calculates the objective values since we want evaluation to be still done on unnormalized data (to demonstrate that the model can be translated to work with unnormalized data).
```
# Get the MAE and LASSO objective on original data by translating the model
def getLASSOObjNorm( model ):
w = model[:-1]
b = model[-1]
# Translate the model to work with original data features
b = b - w.dot(mu / sg)
w = w / sg
res = X_extend.dot(w) + b - y
objVal = alpha * nplin.norm( w, 1 ) + 1/(2*n) * ( nplin.norm( res ) ** 2 )
MAEVal = np.mean( np.abs( res ) )
return (objVal, MAEVal)
# Get the gradient to the loss function in LASSO for normalized data
def getLASSOGradNorm( model, t ):
w = model[:-1]
b = model[-1]
samples = random.sample( range(0, n), B )
X_ = XNorm[samples,:]
y_ = y[samples]
res = X_.dot(w) + b - y_
grad = np.append( X_.T.dot(res), np.sum(res) )
return grad/B
# Set hyperparameters and initialize the model as before
# Since our normalized data is better conditioned, we are able to use a much
# bigger value of the step length parameter which leads to faster progress
alpha = 1
B = 10
eta = 1e-2
init = np.zeros( (d+1,) )
modelPrev = np.zeros( (d+1,) )
# A constant step length seems to work well here
stepFunc = opt.stepLengthGenerator( "constant", eta )
# Notice that we are running the ProxGD method for far fewer iterations (1000)
# than we did (50000) when we had badly conditioned data
(modelProxGD, objProxGD, timeProxGD) = opt.doGD( getLASSOGradNorm, stepFunc, getLASSOObjNorm, init, horizon = 1000, doModelAveraging = True, postGradFunc = doSoftThresholding )
objVals = [objProxGD[i][0] for i in range(len(objProxGD))]
MAEVals = [objProxGD[i][1] for i in range(len(objProxGD))]
fig8 = pd.getFigure( 7, 7 )
ax = plt.gca()
ax.set_title( "The Accelerated ProxGD Solver on Normalized Data" )
ax.set_xlabel( "Elapsed time (sec)" )
ax.set_ylabel( "Objective Value for LASSO", color = "r" )
ax.plot( timeProxGD, objVals, color = 'r', linestyle = ':' )
ax2 = ax.twinx()
ax2.set_ylabel( "MAE Value for LASSO", color = "b" )
ax2.plot( timeProxGD, MAEVals, color = 'b', linestyle = '--' )
plt.ylim( 2, 10 )
```
**Support Recovery**: we note that our accelerated ProxGD is able to offer good support recovery. If we look at the top 13 coordinates of the model learnt by ProxGD in terms of magnitude, we find that several of them are actually the non-spurious features. We should note that one of the features of the original data, namely the fourth coordinate called CHAS (Charles River dummy variable) is, as its name suggests, known to be a dummy variable itself (see [[link]](https://scikit-learn.org/stable/datasets/index.html#boston-dataset) to learn more) with nothing to do with the regression problem!
```
idxTop = np.argsort( np.abs(modelProxGD) )[::-1][:13]
print( "The top 13 coordinates in terms of magnitude are \n ", idxTop )
print( "These contain %d of the non-spurious coordinates" % len( set(idxTop).intersection( set(np.arange(13)) ) ) )
```
| true |
code
| 0.713469 | null | null | null | null |
|
## AutoGraph: examples of simple algorithms
This notebook shows how you can use AutoGraph to compile simple algorithms and run them in TensorFlow.
It requires the nightly build of TensorFlow, which is installed below.
```
!pip install -U -q tf-nightly-2.0-preview
import tensorflow as tf
tf = tf.compat.v2
tf.enable_v2_behavior()
```
### Fibonacci numbers
https://en.wikipedia.org/wiki/Fibonacci_number
```
@tf.function
def fib(n):
f1 = 0
f2 = 1
for i in tf.range(n):
tmp = f2
f2 = f2 + f1
f1 = tmp
tf.print(i, ': ', f2)
return f2
_ = fib(tf.constant(10))
```
#### Generated code
```
print(tf.autograph.to_code(fib.python_function))
```
### Fizz Buzz
https://en.wikipedia.org/wiki/Fizz_buzz
```
import tensorflow as tf
@tf.function(experimental_autograph_options=tf.autograph.experimental.Feature.EQUALITY_OPERATORS)
def fizzbuzz(i, n):
while i < n:
msg = ''
if i % 3 == 0:
msg += 'Fizz'
if i % 5 == 0:
msg += 'Buzz'
if msg == '':
msg = tf.as_string(i)
tf.print(msg)
i += 1
return i
_ = fizzbuzz(tf.constant(10), tf.constant(16))
```
#### Generated code
```
print(tf.autograph.to_code(fizzbuzz.python_function))
```
### Conway's Game of Life
https://en.wikipedia.org/wiki/Conway%27s_Game_of_Life
#### Testing boilerplate
```
NUM_STEPS = 1
```
#### Game of Life for AutoGraph
Note: the code may take a while to run.
```
#@test {"skip": true}
NUM_STEPS = 75
```
Note: This code uses a non-vectorized algorithm, which is quite slow. For 75 steps, it will take a few minutes to run.
```
import time
import traceback
import sys
from matplotlib import pyplot as plt
from matplotlib import animation as anim
import numpy as np
from IPython import display
@tf.autograph.experimental.do_not_convert
def render(boards):
fig = plt.figure()
ims = []
for b in boards:
im = plt.imshow(b, interpolation='none')
im.axes.get_xaxis().set_visible(False)
im.axes.get_yaxis().set_visible(False)
ims.append([im])
try:
ani = anim.ArtistAnimation(
fig, ims, interval=100, blit=True, repeat_delay=5000)
plt.close()
display.display(display.HTML(ani.to_html5_video()))
except RuntimeError:
print('Coult not render animation:')
traceback.print_exc()
return 1
return 0
def gol_episode(board):
new_board = tf.TensorArray(tf.int32, 0, dynamic_size=True)
for i in tf.range(len(board)):
for j in tf.range(len(board[i])):
num_neighbors = tf.reduce_sum(
board[tf.maximum(i-1, 0):tf.minimum(i+2, len(board)),
tf.maximum(j-1, 0):tf.minimum(j+2, len(board[i]))]
) - board[i][j]
if num_neighbors == 2:
new_cell = board[i][j]
elif num_neighbors == 3:
new_cell = 1
else:
new_cell = 0
new_board.append(new_cell)
final_board = new_board.stack()
final_board = tf.reshape(final_board, board.shape)
return final_board
@tf.function(experimental_autograph_options=(
tf.autograph.experimental.Feature.EQUALITY_OPERATORS,
tf.autograph.experimental.Feature.BUILTIN_FUNCTIONS,
tf.autograph.experimental.Feature.LISTS,
))
def gol(initial_board):
board = initial_board
boards = tf.TensorArray(tf.int32, size=0, dynamic_size=True)
i = 0
for i in tf.range(NUM_STEPS):
board = gol_episode(board)
boards.append(board)
boards = boards.stack()
tf.py_function(render, (boards,), (tf.int64,))
return i
# Gosper glider gun
# Adapted from http://www.cplusplus.com/forum/lounge/75168/
_ = 0
initial_board = tf.constant((
( _,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_ ),
( _,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,1,_,_,_,_,_,_,_,_,_,_,_,_ ),
( _,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,1,_,1,_,_,_,_,_,_,_,_,_,_,_,_ ),
( _,_,_,_,_,_,_,_,_,_,_,_,_,1,1,_,_,_,_,_,_,1,1,_,_,_,_,_,_,_,_,_,_,_,_,1,1,_ ),
( _,_,_,_,_,_,_,_,_,_,_,_,1,_,_,_,1,_,_,_,_,1,1,_,_,_,_,_,_,_,_,_,_,_,_,1,1,_ ),
( _,1,1,_,_,_,_,_,_,_,_,1,_,_,_,_,_,1,_,_,_,1,1,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_ ),
( _,1,1,_,_,_,_,_,_,_,_,1,_,_,_,1,_,1,1,_,_,_,_,1,_,1,_,_,_,_,_,_,_,_,_,_,_,_ ),
( _,_,_,_,_,_,_,_,_,_,_,1,_,_,_,_,_,1,_,_,_,_,_,_,_,1,_,_,_,_,_,_,_,_,_,_,_,_ ),
( _,_,_,_,_,_,_,_,_,_,_,_,1,_,_,_,1,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_ ),
( _,_,_,_,_,_,_,_,_,_,_,_,_,1,1,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_ ),
( _,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_ ),
( _,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_,_ ),
))
initial_board = tf.pad(initial_board, ((0, 10), (0, 5)))
_ = gol(initial_board)
```
#### Generated code
```
print(tf.autograph.to_code(gol.python_function))
```
| true |
code
| 0.340732 | null | null | null | null |
|
```
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib
import numpy as np
import utils
matplotlib.rcParams['figure.figsize'] = (0.89 * 12, 6)
matplotlib.rcParams['lines.linewidth'] = 10
matplotlib.rcParams['lines.markersize'] = 20
```
# The Dataset
$$y = x^3 + x^2 - 4x$$
```
x, y, X, transform, scale = utils.get_base_data()
utils.plotter(x, y)
```
# The Dataset
```
noise = utils.get_noise()
utils.plotter(x, y + noise)
```
# Machine Learning
$$
y = f(\mathbf{x}, \mathbf{w})
$$
$$
f(x, \mathbf{w}) = w_3 x^3 + w_2x^2 + w_1x + w_0
$$
$$
y = \mathbf{w} \cdot \mathbf{x}
$$
# Transforming Features
<center><img src="images/transform_features.png" style="height: 600px;"></img></center>
# Fitting Data with Scikit-Learn
<center><img src="images/sklearn.png"></img></center>
# Fitting Data with Scikit-Learn
Minimize
$$C(\mathbf{w}) = \sum_j (\mathbf{x}_j^T \mathbf{w} - y_j)^2$$
```
def mean_squared_error(X, y, fit_func):
return ((fit_func(X).squeeze() - y.squeeze()) ** 2).mean()
```
# Fitting Data with Scikit-Learn
```
from sklearn.linear_model import LinearRegression
reg = LinearRegression(fit_intercept=False).fit(X, y)
print(reg.coef_ / scale)
print(mean_squared_error(X, y, reg.predict))
utils.plotter(x, y, fit_fn=reg.predict, transform=transform)
```
# Fitting Data with Scikit-Learn
```
reg = LinearRegression(fit_intercept=False).fit(X, y + noise)
print(reg.coef_ / scale)
print(mean_squared_error(X, y + noise, reg.predict))
utils.plotter(x, y + noise, fit_fn=reg.predict, transform=transform)
```
# Exercise 1
# Fitting Data with Numpy
<center><img src="images/numpylogoicon.svg" style="height: 400px;"></img></center>
# Linear Algebra
<center><img src="images/linear_tweet.png" style="height: 400px;"></img></center>
# Linear Algebra!
$$X\mathbf{w} = \mathbf{y}$$
<center><img src="images/row_mult.png" style="height: 500px;"></img></center>
# Linear Algebra!
<center><img src="images/row_mult.png" style="height: 200px;"></img></center>
```
(X.dot(reg.coef_.T) == reg.predict(X)).all()
```
# Fitting Data with Numpy
$$X\mathbf{w} = \mathbf{y}$$
$$\mathbf{w} = X^{-1}\mathbf{y}$$
<center><img src="images/pete-4.jpg" style="height: 400px;"></img></center>
# Fitting Data with Numpy
$$X\mathbf{w} = \mathbf{y}$$
$$X^TX\mathbf{w} = X^T\mathbf{y}$$
$$\mathbf{w} = (X^TX)^{-1}X^T\mathbf{y}$$
# Orthogonal Projections!
$$P = X(X^TX)^{-1}X^T$$
Try to show $$P^2 = P$$
and that
$$(\mathbf{y} - P\mathbf{y})^T P\mathbf{y} = 0$$
<center><img src="images/pete-5.jpg" style="height: 350px;"></img></center>
# Fitting Data with Numpy
$$\mathbf{w} = (X^TX)^{-1}X^T\mathbf{y}$$
```
np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).T / scale
(np.linalg.inv(X.T @ X) @ X.T @ y).T / scale
np.linalg.pinv(X).dot(y).T / scale
```
# Fitting Data with Numpy
```
class NumpyLinearRegression(object):
def fit(self, X, y):
self.coef_ = np.linalg.pinv(X).dot(y)
return self
def predict(self, X):
return X.dot(self.coef_)
```
# Fitting Data with Numpy
```
linalg_reg = NumpyLinearRegression().fit(X, y)
print(linalg_reg.coef_.T / scale)
print(mean_squared_error(X, y, linalg_reg.predict))
utils.plotter(x, y, fit_fn=linalg_reg.predict, transform=transform)
```
# Fitting Data with Numpy
```
linalg_reg = NumpyLinearRegression().fit(X, y + noise)
print(linalg_reg.coef_.T / scale)
print(mean_squared_error(X, y + noise, linalg_reg.predict))
utils.plotter(x, y + noise, fit_fn=linalg_reg.predict, transform=transform)
```
# Exercise 2
# Regularization
```
x_train, x_test, y_train, y_test, X_train, X_test, transform, scale = utils.get_overfitting_data()
```
# What does overfitting look like?
```
reg = LinearRegression(fit_intercept=False).fit(X_train, y_train)
print((reg.coef_ / scale))
plt.bar(np.arange(len(reg.coef_.squeeze())), reg.coef_.squeeze() / scale);
```
# What does overfitting look like?
```
mean_squared_error(X_train, y_train, reg.predict)
utils.plotter(x_train, y_train, fit_fn=reg.predict, transform=transform)
```
# What does overfitting look like?
```
mean_squared_error(X_test, y_test, reg.predict)
utils.plotter(x_test, y_test, fit_fn=reg.predict, transform=transform)
```
# Ridge Regression
## "Penalize model complexity"
$$C(\mathbf{w}) = \sum_j (\mathbf{x}_j^T \mathbf{w} - y_j)^2$$
$$C(\mathbf{w}) = \sum_j (\mathbf{x}_j^T \mathbf{w} - y_j)^2 + \alpha \sum_j w_j^2$$
# Ridge Regression
```
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=0.02).fit(X_train, y_train)
utils.plotter(x_test, y_test, fit_fn=ridge_reg.predict, transform=transform)
```
# Ridge Regression
```
print(mean_squared_error(X_test, y_test, ridge_reg.predict))
plt.bar(np.arange(len(ridge_reg.coef_.squeeze())), ridge_reg.coef_.squeeze() / scale);
```
# Lasso Regression
```
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.005, max_iter=100000, fit_intercept=False).fit(X_train, y_train)
utils.plotter(x_test, y_test, fit_fn=lasso_reg.predict, transform=transform)
```
# Lasso Regression
```
print(mean_squared_error(X_test, y_test, lasso_reg.predict))
plt.bar(np.arange(len(lasso_reg.coef_)), lasso_reg.coef_ / scale);
```
# Exercise 3
| true |
code
| 0.66796 | null | null | null | null |
|
# Rotation Transformation
We meta-learn how to rotate images so that we can accurately classify rotated images. We use MNIST.
Import relevant packages
```
from operator import mul
from itertools import cycle
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.backends.cudnn as cudnn
import torch.nn as nn
import torch.nn.functional as F
import torchvision.datasets as datasets
import torchvision.models as models
import torchvision.transforms as transforms
import tqdm
from higher.patch import make_functional
from higher.utils import get_func_params
from sklearn.metrics import accuracy_score
%matplotlib inline
matplotlib.rcParams['pdf.fonttype'] = 42
matplotlib.rcParams['ps.fonttype'] = 42
```
Define transformations to create standard and rotated images
```
transform_basic = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
transform_rotate = transforms.Compose([
transforms.RandomRotation([30, 30]),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
```
Load the data and split the indices so that we both standard and rotated images in various sets. We also keep a part of the training data as unrotated test images in case it is useful.
```
train_set = datasets.MNIST(
'data', train=True, transform=transform_basic, target_transform=None, download=True)
train_set_rotated = datasets.MNIST(
'data', train=True, transform=transform_rotate, target_transform=None, download=True)
train_basic_indices = range(40000)
train_test_basic_indices = range(40000, 50000)
val_rotate_indices = range(50000, 60000)
train_basic_set = torch.utils.data.Subset(train_set, train_basic_indices)
train_test_basic_set = torch.utils.data.Subset(train_set, train_test_basic_indices)
val_rotate_set = torch.utils.data.Subset(
train_set_rotated, val_rotate_indices)
test_set = datasets.MNIST(
'data', train=False, transform=transform_rotate, target_transform=None, download=True)
```
Define data loaders
```
batch_size = 128
train_basic_set_loader = torch.utils.data.DataLoader(
train_basic_set, batch_size=batch_size, shuffle=True)
train_test_basic_set_loader = torch.utils.data.DataLoader(
train_test_basic_set, batch_size=batch_size, shuffle=True)
val_rotate_set_loader = torch.utils.data.DataLoader(
val_rotate_set, batch_size=batch_size, shuffle=True)
test_set_loader = torch.utils.data.DataLoader(
test_set, batch_size=batch_size, shuffle=True)
```
Set-up the device to use
```
if torch.cuda.is_available(): # checks whether a cuda gpu is available
device = torch.cuda.current_device()
print("use GPU", device)
print("GPU ID {}".format(torch.cuda.current_device()))
else:
print("use CPU")
device = torch.device('cpu') # sets the device to be CPU
```
Define a function to do rotation by angle theta (in radians). We define the function in a way that allows us to differentiate with respect to theta.
```
def rot_img(x, theta, device):
rot = torch.cat([torch.cat([torch.cos(theta), -torch.sin(theta), torch.tensor([0.], device=device)]),
torch.cat([torch.sin(theta), torch.cos(theta), torch.tensor([0.], device=device)])])
grid = F.affine_grid(rot.expand([x.size()[0], 6]).view(-1, 2, 3), x.size())
x = F.grid_sample(x, grid)
return x
```
Define the model that we use - simple LeNet that will allow us to do fast experiments
```
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
self.in_channels = 1
self.input_size = 28
self.conv1 = nn.Conv2d(self.in_channels, 6, 5,
padding=2 if self.input_size == 28 else 0)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, 2)
x = F.relu(self.conv2(x))
x = F.max_pool2d(x, 2)
x = x.view(x.size(0), -1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
```
A function to test a model on the test set
```
def test_classification_net(data_loader, model, device):
'''
This function reports classification accuracy over a dataset.
'''
model.eval()
labels_list = []
predictions_list = []
with torch.no_grad():
for i, (data, label) in enumerate(data_loader):
data = data.to(device)
label = label.to(device)
logits = model(data)
softmax = F.softmax(logits, dim=1)
_, predictions = torch.max(softmax, dim=1)
labels_list.extend(label.cpu().numpy().tolist())
predictions_list.extend(predictions.cpu().numpy().tolist())
accuracy = accuracy_score(labels_list, predictions_list)
return 100 * accuracy
```
A function to test the model on the test set while doing the rotations manually with a specified angle
```
def test_classification_net_rot(data_loader, model, device, angle=0.0):
'''
This function reports classification accuracy over a dataset.
'''
model.eval()
labels_list = []
predictions_list = []
with torch.no_grad():
for i, (data, label) in enumerate(data_loader):
data = data.to(device)
if angle != 0.0:
data = rot_img(data, angle, device)
label = label.to(device)
logits = model(data)
softmax = F.softmax(logits, dim=1)
_, predictions = torch.max(softmax, dim=1)
labels_list.extend(label.cpu().numpy().tolist())
predictions_list.extend(predictions.cpu().numpy().tolist())
accuracy = accuracy_score(labels_list, predictions_list)
return 100 * accuracy
```
Define a model to do the rotations - it has a meta-learnable parameter theta that represents the rotation angle in radians
```
class RotTransformer(nn.Module):
def __init__(self, device):
super(RotTransformer, self).__init__()
self.theta = nn.Parameter(torch.FloatTensor([0.]))
self.device = device
# Rotation transformer network forward function
def rot(self, x):
rot = torch.cat([torch.cat([torch.cos(self.theta), -torch.sin(self.theta), torch.tensor([0.], device=self.device)]),
torch.cat([torch.sin(self.theta), torch.cos(self.theta), torch.tensor([0.], device=self.device)])])
grid = F.affine_grid(rot.expand([x.size()[0], 6]).view(-1, 2, 3), x.size())
x = F.grid_sample(x, grid)
return x
def forward(self, x):
return self.rot(x)
```
We first train a simple model on standard images to see how it performs when applied to rotated images
```
acc_rotate_list = []
acc_basic_list = []
num_repetitions = 5
for e in range(num_repetitions):
print('Repetition ' + str(e + 1))
model = LeNet().to(device=device)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
criterion = nn.CrossEntropyLoss().to(device=device)
num_epochs_meta = 5
with tqdm.tqdm(total=num_epochs_meta) as pbar_epochs:
for epoch in range(0, num_epochs_meta):
for i, batch in enumerate(train_basic_set_loader):
(input_, target) = batch
input_ = input_.to(device=device)
target = target.to(device=device)
logits = model(input_)
loss = criterion(logits, target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
pbar_epochs.update(1)
# testing
acc_rotate = test_classification_net(test_set_loader, model, device)
acc_rotate_list.append(acc_rotate)
angle = torch.tensor([-np.pi/6], device=device)
acc_basic = test_classification_net_rot(test_set_loader, model, device, angle)
acc_basic_list.append(acc_basic)
```
Print statistics:
```
print('Accuracy on rotated test images: {:.2f} $\pm$ {:.2f}'.format(np.mean(acc_rotate_list), np.std(acc_rotate_list)))
print('Accuracy on standard position test images: {:.2f} $\pm$ {:.2f}'.format(np.mean(acc_basic_list), np.std(acc_basic_list)))
```
We see there is a large drop in accuracy if we apply the model on rotated images rather the same images without rotations
Now we use EvoGrad and meta-learning to train the model with images that are rotated by the rotation transformer. Rotation transformer is learned jointly alongside the base model. We will use random seeds to improve reproducibility since EvoGrad random noise perturbations depend on sampling of random numbers (but the precise accuracies may differ).
```
acc_rotate_list_evo_2mc = []
acc_basic_list_evo_2mc = []
angles_reps_2mc = []
# define the settings
num_repetitions = 5
torch_seeds = [1, 23, 345, 4567, 56789]
sigma = 0.001
temperature = 0.05
n_model_candidates = 2
num_epochs_meta = 5
for e in range(num_repetitions):
print('Repetition ' + str(e + 1))
torch.manual_seed(torch_seeds[e])
model = LeNet().to(device=device)
model_patched = make_functional(model)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
criterion = nn.CrossEntropyLoss().to(device=device)
feature_transformer = RotTransformer(device=device).to(device=device)
meta_opt = torch.optim.Adam(feature_transformer.parameters(), lr=1e-2)
angles = []
with tqdm.tqdm(total=num_epochs_meta) as pbar_epochs:
for epoch in range(0, num_epochs_meta):
loaders = zip(train_basic_set_loader, cycle(val_rotate_set_loader))
for i, batch in enumerate(loaders):
((input_, target), (input_rot, target_rot)) = batch
input_ = input_.to(device=device)
target = target.to(device=device)
input_rot = input_rot.to(device=device)
target_rot = target_rot.to(device=device)
# base model training with images rotated using the rotation transformer
logits = model(feature_transformer(input_))
loss = criterion(logits, target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# update the model parameters used for patching
model_parameter = [i.detach() for i in get_func_params(model)]
input_transformed = feature_transformer(input_)
# create multiple model copies
theta_list = [[j + sigma * torch.sign(torch.randn_like(j)) for j in model_parameter] for i in range(n_model_candidates)]
pred_list = [model_patched(input_transformed, params=theta) for theta in theta_list]
loss_list = [criterion(pred, target) for pred in pred_list]
baseline_loss = criterion(model_patched(input_transformed, params=model_parameter), target)
# calculate weights for the different model copies
weights = torch.softmax(-torch.stack(loss_list)/temperature, 0)
# merge the model copies
theta_updated = [sum(map(mul, theta, weights)) for theta in zip(*theta_list)]
pred_rot = model_patched(input_rot, params=theta_updated)
loss_rot = criterion(pred_rot, target_rot)
# update the meta-knowledge
meta_opt.zero_grad()
loss_rot.backward()
meta_opt.step()
angles.append(180 / 3.14 * feature_transformer.theta.item())
pbar_epochs.update(1)
angles_reps_2mc.append(angles)
acc = test_classification_net(test_set_loader, model, device)
acc_rotate_list_evo_2mc.append(acc)
angle = torch.tensor([-np.pi/6], device=device)
acc_basic = test_classification_net_rot(test_set_loader, model, device, angle)
acc_basic_list_evo_2mc.append(acc_basic)
```
Print statistics:
```
print('Accuracy on rotated test images: {:.2f} $\pm$ {:.2f}'.format(np.mean(acc_rotate_list_evo_2mc), np.std(acc_rotate_list_evo_2mc)))
print('Accuracy on standard position test images: {:.2f} $\pm$ {:.2f}'.format(np.mean(acc_basic_list_evo_2mc), np.std(acc_basic_list_evo_2mc)))
```
Show what the learned angles look like during training:
```
for angles_list in angles_reps_2mc:
plt.plot(range(len(angles_list)), angles_list, linewidth=2.0)
plt.ylabel('Learned angle', fontsize=14)
plt.xlabel('Number of iterations', fontsize=14)
plt.savefig("RotTransformerLearnedAngles.pdf", bbox_inches='tight')
plt.show()
```
Print the average final meta-learned angle:
```
final_angles_2mc = [angles_list[-1] for angles_list in angles_reps_2mc]
print("{:.2f} $\pm$ {:.2f}".format(np.mean(final_angles_2mc), np.std(final_angles_2mc)))
```
It's great to see the meta-learned angle is typically close to 30 degrees, which is the true value.
| true |
code
| 0.92944 | null | null | null | null |
|
## TrainingPhase and General scheduler
Creates a scheduler that lets you train a model with following different [`TrainingPhase`](/callbacks.general_sched.html#TrainingPhase).
```
from fastai.gen_doc.nbdoc import *
from fastai.callbacks.general_sched import *
from fastai.vision import *
show_doc(TrainingPhase)
```
You can then schedule any hyper-parameter you want by using the following method.
```
show_doc(TrainingPhase.schedule_hp)
```
The phase will make the hyper-parameter vary from the first value in `vals` to the second, following `anneal`. If an annealing function is specified but `vals` is a float, it will decay to 0. If no annealing function is specified, the default is a linear annealing for a tuple, a constant parameter if it's a float.
```
jekyll_note("""If you want to use discriminative values, you can pass an numpy array in `vals` (or a tuple
of them for start and stop).""")
```
The basic hyper-parameters are named:
- 'lr' for learning rate
- 'mom' for momentum (or beta1 in Adam)
- 'beta' for the beta2 in Adam or the alpha in RMSprop
- 'wd' for weight decay
You can also add any hyper-parameter that is in your optimizer (even if it's custom or a [`GeneralOptimizer`](/general_optimizer.html#GeneralOptimizer)), like 'eps' if you're using Adam.
Let's make an example by using this to code [SGD with warm restarts](https://arxiv.org/abs/1608.03983).
```
def fit_sgd_warm(learn, n_cycles, lr, mom, cycle_len, cycle_mult):
n = len(learn.data.train_dl)
phases = [(TrainingPhase(n * (cycle_len * cycle_mult**i))
.schedule_hp('lr', lr, anneal=annealing_cos)
.schedule_hp('mom', mom)) for i in range(n_cycles)]
sched = GeneralScheduler(learn, phases)
learn.callbacks.append(sched)
if cycle_mult != 1:
total_epochs = int(cycle_len * (1 - (cycle_mult)**n_cycles)/(1-cycle_mult))
else: total_epochs = n_cycles * cycle_len
learn.fit(total_epochs)
path = untar_data(URLs.MNIST_SAMPLE)
data = ImageDataBunch.from_folder(path)
learn = Learner(data, simple_cnn((3,16,16,2)), metrics=accuracy)
fit_sgd_warm(learn, 3, 1e-3, 0.9, 1, 2)
learn.recorder.plot_lr()
show_doc(GeneralScheduler)
```
### Callback methods
You don't call these yourself - they're called by fastai's [`Callback`](/callback.html#Callback) system automatically to enable the class's functionality.
```
show_doc(GeneralScheduler.on_batch_end, doc_string=False)
```
Takes a step in the current phase and prepare the hyperparameters for the next batch.
```
show_doc(GeneralScheduler.on_train_begin, doc_string=False)
```
Initiates the hyperparameters to the start values of the first phase.
## Undocumented Methods - Methods moved below this line will intentionally be hidden
| true |
code
| 0.653514 | null | null | null | null |
|
## Problem Definition
In the following different ways of loading or implementing an optimization problem in our framework are discussed.
### By Class
A very detailed description of defining a problem through a class is already provided in the [Getting Started Guide](../getting_started.ipynb).
The following definition of a simple optimization problem with **one** objective and **two** constraints is considered. The problem has two constants, *const_1* and *const_2*, which can be modified by initiating the problem with different parameters. By default, it consists of 10 variables, and the lower and upper bounds are within $[-5, 5]$ for all variables.
**Note**: The example below uses the `autograd` library, which calculates the gradients through automatic differentiation.
```
import numpy as np
import autograd.numpy as anp
from pymoo.model.problem import Problem
class MyProblem(Problem):
def __init__(self, const_1=5, const_2=0.1):
# define lower and upper bounds - 1d array with length equal to number of variable
xl = -5 * anp.ones(10)
xu = 5 * anp.ones(10)
super().__init__(n_var=10, n_obj=1, n_constr=2, xl=xl, xu=xu, evaluation_of="auto")
# store custom variables needed for evaluation
self.const_1 = const_1
self.const_2 = const_2
def _evaluate(self, x, out, *args, **kwargs):
f = anp.sum(anp.power(x, 2) - self.const_1 * anp.cos(2 * anp.pi * x), axis=1)
g1 = (x[:, 0] + x[:, 1]) - self.const_2
g2 = self.const_2 - (x[:, 2] + x[:, 3])
out["F"] = f
out["G"] = anp.column_stack([g1, g2])
```
After creating a problem object, the evaluation function can be called. The `return_values_of` parameter can be overwritten to modify the list of returned parameters. The gradients for the objectives `dF` and constraints `dG` can be obtained as follows:
```
problem = MyProblem()
F, G, CV, feasible, dF, dG = problem.evaluate(np.random.rand(100, 10),
return_values_of=["F", "G", "CV", "feasible", "dF", "dG"])
```
**Elementwise Evaluation**
If the problem can not be executed using matrix operations, a serialized evaluation can be indicated using the `elementwise_evaluation=True` flag. If the flag is set, then an outer loop is already implemented, an `x` is only a **one**-dimensional array.
```
class MyProblem(Problem):
def __init__(self, **kwargs):
super().__init__(n_var=2, n_obj=1, elementwise_evaluation=True, **kwargs)
def _evaluate(self, x, out, *args, **kwargs):
out["F"] = x.sum()
```
### By Function
Another way of defining a problem is through functions. One the one hand, many function calls need to be performed to evaluate a set of solutions, but on the other hand, it is a very intuitive way of defining a problem.
```
import numpy as np
from pymoo.model.problem import FunctionalProblem
objs = [
lambda x: np.sum((x - 2) ** 2),
lambda x: np.sum((x + 2) ** 2)
]
constr_ieq = [
lambda x: np.sum((x - 1) ** 2)
]
problem = FunctionalProblem(10,
objs,
constr_ieq=constr_ieq,
xl=np.array([-10, -5, -10]),
xu=np.array([10, 5, 10])
)
F, CV = problem.evaluate(np.random.rand(3, 10))
print(f"F: {F}\n")
print(f"CV: {CV}")
# END from_string
```
### By String
In our framework, various test problems are already implemented and available by providing the corresponding problem name we have assigned to it. A couple of problems can be further parameterized by providing the number of variables, constraints, or other problem-dependent constants.
```
from pymoo.factory import get_problem
p = get_problem("dtlz1_-1", n_var=20, n_obj=5)
# create a simple test problem from string
p = get_problem("Ackley")
# the input name is not case sensitive
p = get_problem("ackley")
# also input parameter can be provided directly
p = get_problem("dtlz1_-1", n_var=20, n_obj=5)
```
## API
| true |
code
| 0.551393 | null | null | null | null |
|
# Using AWS Lambda and PyWren for Landsat 8 Time Series
This notebook is a simple demonstration of drilling a timeseries of NDVI values from the [Landsat 8 scenes held on AWS](https://landsatonaws.com/)
### Credits
- NDVI PyWren - [Peter Scarth](mailto:[email protected]?subject=AWS%20Lambda%20and%20PyWren) (Joint Remote Sensing Research Program)
- [RemotePixel](https://github.com/RemotePixel/remotepixel-api) - Landsat 8 NDVI GeoTIFF parsing function
- [PyWren](https://github.com/pywren/pywren) - Project by BCCI and riselab. Makes it easy to executive massive parallel map queries across [AWS Lambda](https://aws.amazon.com/lambda/)
#### Additional notes
The below remotely executed function will deliver results usually in under a minute for the full timeseries of more than 100 images, and we can simply plot the resulting timeseries or do further analysis. BUT, the points may well be cloud or cloud shadow contaminated. We haven’t done any cloud masking to the imagery, but we do have the scene metadata on the probable amount of cloud across the entire scene. We use this to weight a [smoothing spline](https://docs.scipy.org/doc/scipy-0.19.1/reference/generated/scipy.interpolate.UnivariateSpline.html), such that an observation with no reported cloud over the scene has full weight, and an observation with a reported 100% of the scene with cloud has zero weight.
# Step by Step instructions
### Setup Logging (optional)
Only activate the below lines if you want to see all debug messages from PyWren. _Note: The output will be rather chatty and lengthy._
```
import logging
logger = logging.getLogger()
logger.setLevel(logging.INFO)
%env PYWREN_LOGLEVEL=INFO
```
### Setup all the necessary libraries
This will setup all the necessary libraries to properly display our results and it also imports the library that allows us to query Landsat 8 data from the [AWS Public Dataset](https://aws.amazon.com/public-datasets/landsat/):
```
import requests, json, numpy, datetime, os, boto3
from IPython.display import HTML, display, Image
import matplotlib.pyplot as plt
import l8_ndvi
from scipy.interpolate import UnivariateSpline
import pywren
# Function to return a Landsat 8 scene list given a Longitude,Latitude string
# This uses the amazing developmentseed Satellite API
# https://github.com/sat-utils/sat-api
def getSceneList(lonLat):
scenes=[]
url = "https://api.developmentseed.org/satellites/landsat"
params = dict(
contains=lonLat,
satellite_name="landsat-8",
limit="1000")
# Call the API to grab the scene metadata
sceneMetaData = json.loads(requests.get(url=url, params=params).content)
# Parse the metadata
for record in sceneMetaData["results"]:
scene = str(record['aws_index'].split('/')[-2])
# This is a bit of a hack to get around some versioning problem on the API :(
# Related to this issue https://github.com/sat-utils/sat-api/issues/18
if scene[-2:] == '01':
scene = scene[:-2] + '00'
if scene[-2:] == '02':
scene = scene[:-2] + '00'
if scene[-2:] == '03':
scene = scene[:-2] + '02'
scenes.append(scene)
return scenes
# Function to call a AWS Lambda function to drill a single pixel and compute the NDVI
def getNDVI(scene):
return l8_ndvi.point(scene, eval(lonLat))
```
### Run the code locally over a point of interest
Let's have a look at Hong Kong, an urban area with some country parks surrounding the city: [114.1095,22.3964](https://goo.gl/maps/PhDLAdLbiQT2)
First we need to retrieve the available Landsat 8 scenes from the point of interest:
```
lonLat = '114.1095,22.3964'
scenesHK = getSceneList('114.1095,22.3964')
#print(scenesHK)
display(HTML('Total scenes: <b>' + str(len(scenesHK)) + '</b>'))
```
Now let's find out the NDVI and the amount of clouds on a specific scene locally on our machine:
```
lonLat = '114.1095,22.3964'
thumbnail = l8_ndvi.thumb('LC08_L1TP_121045_20170829_20170914_01_T1', eval(lonLat))
display(Image(url=thumbnail, format='jpg'))
result = getNDVI('LC08_L1TP_121045_20170829_20170914_01_T1')
#display(result)
display(HTML('<b>Date:</b> '+result['date']))
display(HTML('<b>Amount of clouds:</b> '+str(result['cloud'])+'%'))
display(HTML('<b>NDVI:</b> '+str(result['ndvi'])))
```
Great, time to try this with an observation on a cloudier day. Please note that the NDVI drops too, as we are not able to actually receive much data fom the land surface:
```
lonLat = '114.1095,22.3964'
thumbnail = l8_ndvi.thumb('LC08_L1GT_122044_20171108_20171108_01_RT', eval(lonLat))
display(Image(url=thumbnail, format='jpg'))
result = getNDVI('LC08_L1GT_122044_20171108_20171108_01_RT')
#display(result)
display(HTML('<b>Date:</b> '+result['date']))
display(HTML('<b>Amount of clouds:</b> '+str(result['cloud'])+'%'))
display(HTML('<b>NDVI:</b> '+str(result['ndvi'])))
```
### Massively Parallel calculation with PyWren
Now let's try this with multiple scenes and send it to PyWren, however to accomplish this we need to change our PyWren AWS Lambda function to include the necessary libraries such as rasterio and GDAL. Since those libraries are compiled C code, PyWren will not be able to pickle it up and send it to the Lambda function. Hence we will update the entire PyWren function to include the necessary binaries that have been compiled on an Amazon EC2 instance with Amazon Linux. We pre-packaged this and made it available via https://s3-us-west-2.amazonaws.com/pywren-workshop/lambda_function.zip
You can simple push this code to your PyWren AWS Lambda function with below command, assuming you named the function with the default name pywren_1 and region us-west-2:
```
lambdaclient = boto3.client('lambda', 'us-west-2')
response = lambdaclient.update_function_code(
FunctionName='pywren_1',
Publish=True,
S3Bucket='pywren-workshop',
S3Key='lambda_function.zip'
)
response = lambdaclient.update_function_configuration(
FunctionName='pywren_1',
Environment={
'Variables': {
'GDAL_DATA': '/var/task/lib/gdal'
}
}
)
```
If you look at the list of available scenes, we have a rather large amount. This is a good use-case for PyWren as it will allows us to have AWS Lambda perform the calculation of NDVI and clouds for us - furthermore it will have a faster connectivity to read and write from Amazon S3. If you want to know more details about the calculation, have a look at [l8_ndvi.py](/edit/Lab-4-Landsat-NDVI/l8_ndvi.py).
Ok let's try this on the latest 200 collected Landsat 8 images GeoTIFFs of Hong Kong:
```
lonLat = '114.1095,22.3964'
pwex = pywren.default_executor()
resultsHK = pywren.get_all_results(pwex.map(getNDVI, scenesHK[:200]))
display(resultsHK)
```
### Display results
Let's try to render our results in a nice HTML table first:
```
#Remove results where we couldn't retrieve data from the scene
results = filter(None, resultsHK)
#Render a nice HTML table to display result
html = '<table><tr><td><b>Date</b></td><td><b>Clouds</b></td><td><b>NDVI</b></td></tr>'
for x in results:
html = html + '<tr>'
html = html + '<td>' + x['date'] + '</td>'
html = html + '<td>' + str(x['cloud']) + '%</td>'
html = html + '<td '
if (x['ndvi'] > 0.5):
html = html + ' bgcolor="#00FF00">'
elif (x['ndvi'] > 0.1):
html = html + ' bgcolor="#FFFF00">'
else:
html = html + ' bgcolor="#FF0000">'
html = html + str(round(abs(x['ndvi']),2)) + '</td>'
html = html + '</tr>'
html = html + '</table>'
display(HTML(html))
```
This provides us a good overview but would quickly become difficult to read as the datapoints expand - let's use [Matplotlib](https://matplotlib.org/) instead to plot this out:
```
timeSeries = filter(None,resultsHK)
# Extract the data trom the list of results
timeStamps = [datetime.datetime.strptime(obs['date'],'%Y-%m-%d') for obs in timeSeries if 'date' in obs]
ndviSeries = [obs['ndvi'] for obs in timeSeries if 'ndvi' in obs]
cloudSeries = [obs['cloud']/100 for obs in timeSeries if 'cloud' in obs]
# Create a time variable as the x axis to fit the observations
# First we convert to seconds
timeSecs = numpy.array([(obsTime-datetime.datetime(1970,1,1)).total_seconds() for obsTime in timeStamps])
# And then normalise from 0 to 1 to avoid any numerical issues in the fitting
fitTime = ((timeSecs-numpy.min(timeSecs))/(numpy.max(timeSecs)-numpy.min(timeSecs)))
# Smooth the data by fitting a spline weighted by cloud amount
smoothedNDVI=UnivariateSpline(
fitTime[numpy.argsort(fitTime)],
numpy.array(ndviSeries)[numpy.argsort(fitTime)],
w=(1.0-numpy.array(cloudSeries)[numpy.argsort(fitTime)])**2.0,
k=2,
s=0.1)(fitTime)
fig = plt.figure(figsize=(16,10))
plt.plot(timeStamps,ndviSeries, 'gx',label='Raw NDVI Data')
plt.plot(timeStamps,ndviSeries, 'y:', linewidth=1)
plt.plot(timeStamps,cloudSeries, 'b.', linewidth=1,label='Scene Cloud Percent')
plt.plot(timeStamps,cloudSeries, 'b:', linewidth=1)
#plt.plot(timeStamps,smoothedNDVI, 'r--', linewidth=3,label='Cloudfree Weighted Spline')
plt.xlabel('Date', fontsize=16)
plt.ylabel('NDVI', fontsize=16)
plt.title('AWS Lambda Landsat 8 NDVI Drill (Hong Kong)', fontsize=20)
plt.grid(True)
plt.ylim([-.1,1.0])
plt.legend(fontsize=14)
plt.show()
```
### Run the code over another location
This test site is a cotton farming area in Queensland, Australia [147.870599,-28.744617](https://goo.gl/maps/GF5szf7vZo82)
Let's first acquire some scenes:
```
lonLat = '147.870599,-28.744617'
scenesQLD = getSceneList(lonLat)
#print(scenesQLD)
display(HTML('Total scenes: <b>' + str(len(scenesQLD)) + '</b>'))
```
Let's first have a look at an individual observation first on our local machine:
```
thumbnail = l8_ndvi.thumb('LC80920802017118LGN00', eval(lonLat))
display(Image(url=thumbnail, format='jpg'))
result = getNDVI('LC80920802017118LGN00')
#display(result)
display(HTML('<b>Date:</b> '+result['date']))
display(HTML('<b>Amount of clouds:</b> '+str(result['cloud'])+'%'))
display(HTML('<b>NDVI:</b> '+str(result['ndvi'])))
```
### Pywren Time
Let's process this across all of the observations in parallel using AWS Lambda:
```
pwex = pywren.default_executor()
resultsQLD = pywren.get_all_results(pwex.map(getNDVI, scenesQLD))
display(resultsQLD)
```
Now let's plot this out again:
```
timeSeries = filter(None,resultsQLD)
# Extract the data trom the list of results
timeStamps = [datetime.datetime.strptime(obs['date'],'%Y-%m-%d') for obs in timeSeries if 'date' in obs]
ndviSeries = [obs['ndvi'] for obs in timeSeries if 'ndvi' in obs]
cloudSeries = [obs['cloud']/100 for obs in timeSeries if 'cloud' in obs]
# Create a time variable as the x axis to fit the observations
# First we convert to seconds
timeSecs = numpy.array([(obsTime-datetime.datetime(1970,1,1)).total_seconds() for obsTime in timeStamps])
# And then normalise from 0 to 1 to avoid any numerical issues in the fitting
fitTime = ((timeSecs-numpy.min(timeSecs))/(numpy.max(timeSecs)-numpy.min(timeSecs)))
# Smooth the data by fitting a spline weighted by cloud amount
smoothedNDVI=UnivariateSpline(
fitTime[numpy.argsort(fitTime)],
numpy.array(ndviSeries)[numpy.argsort(fitTime)],
w=(1.0-numpy.array(cloudSeries)[numpy.argsort(fitTime)])**2.0,
k=2,
s=0.1)(fitTime)
fig = plt.figure(figsize=(16,10))
plt.plot(timeStamps,ndviSeries, 'gx',label='Raw NDVI Data')
plt.plot(timeStamps,ndviSeries, 'g:', linewidth=1)
plt.plot(timeStamps,cloudSeries, 'b.', linewidth=1,label='Scene Cloud Percent')
plt.plot(timeStamps,smoothedNDVI, 'r--', linewidth=3,label='Cloudfree Weighted Spline')
plt.xlabel('Date', fontsize=16)
plt.ylabel('NDVI', fontsize=16)
plt.title('AWS Lambda Landsat 8 NDVI Drill (Cotton Farm QLD, Australia)', fontsize=20)
plt.grid(True)
plt.ylim([-.1,1.0])
plt.legend(fontsize=14)
plt.show()
```
| true |
code
| 0.459561 | null | null | null | null |
|
```
%tensorflow_version 2.x
import tensorflow as tf
#from tf.keras.models import Sequential
#from tf.keras.layers import Dense
import os
import io
tf.__version__
```
# Download Data
```
# Download the zip file
path_to_zip = tf.keras.utils.get_file("smsspamcollection.zip",
origin="https://archive.ics.uci.edu/ml/machine-learning-databases/00228/smsspamcollection.zip",
extract=True)
# Unzip the file into a folder
!unzip $path_to_zip -d data
# optional step - helps if colab gets disconnected
# from google.colab import drive
# drive.mount('/content/drive')
# Test data reading
# lines = io.open('/content/drive/My Drive/colab-data/SMSSpamCollection').read().strip().split('\n')
lines = io.open('/content/data/SMSSpamCollection').read().strip().split('\n')
lines[0]
```
# Pre-Process Data
```
spam_dataset = []
count = 0
for line in lines:
label, text = line.split('\t')
if label.lower().strip() == 'spam':
spam_dataset.append((1, text.strip()))
count += 1
else:
spam_dataset.append(((0, text.strip())))
print(spam_dataset[0])
print("Spam: ", count)
```
# Data Normalization
```
import pandas as pd
df = pd.DataFrame(spam_dataset, columns=['Spam', 'Message'])
import re
# Normalization functions
def message_length(x):
# returns total number of characters
return len(x)
def num_capitals(x):
_, count = re.subn(r'[A-Z]', '', x) # only works in english
return count
def num_punctuation(x):
_, count = re.subn(r'\W', '', x)
return count
df['Capitals'] = df['Message'].apply(num_capitals)
df['Punctuation'] = df['Message'].apply(num_punctuation)
df['Length'] = df['Message'].apply(message_length)
df.describe()
train=df.sample(frac=0.8,random_state=42) #random state is a seed value
test=df.drop(train.index)
train.describe()
test.describe()
```
# Model Building
```
# Basic 1-layer neural network model for evaluation
def make_model(input_dims=3, num_units=12):
model = tf.keras.Sequential()
# Adds a densely-connected layer with 12 units to the model:
model.add(tf.keras.layers.Dense(num_units,
input_dim=input_dims,
activation='relu'))
# Add a sigmoid layer with a binary output unit:
model.add(tf.keras.layers.Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam',
metrics=['accuracy'])
return model
x_train = train[['Length', 'Punctuation', 'Capitals']]
y_train = train[['Spam']]
x_test = test[['Length', 'Punctuation', 'Capitals']]
y_test = test[['Spam']]
x_train
model = make_model()
model.fit(x_train, y_train, epochs=10, batch_size=10)
model.evaluate(x_test, y_test)
y_train_pred = model.predict_classes(x_train)
# confusion matrix
tf.math.confusion_matrix(tf.constant(y_train.Spam),
y_train_pred)
sum(y_train_pred)
y_test_pred = model.predict_classes(x_test)
tf.math.confusion_matrix(tf.constant(y_test.Spam), y_test_pred)
```
# Tokenization and Stop Word Removal
```
sentence = 'Go until jurong point, crazy.. Available only in bugis n great world'
sentence.split()
!pip install stanza # StanfordNLP has become https://github.com/stanfordnlp/stanza/
import stanza
en = stanza.download('en')
en = stanza.Pipeline(lang='en')
sentence
tokenized = en(sentence)
len(tokenized.sentences)
for snt in tokenized.sentences:
for word in snt.tokens:
print(word.text)
print("<End of Sentence>")
```
## Dependency Parsing Example
```
en2 = stanza.Pipeline(lang='en')
pr2 = en2("Hari went to school")
for snt in pr2.sentences:
for word in snt.tokens:
print(word)
print("<End of Sentence>")
```
## Japanese Tokenization Example
```
jp = stanza.download('ja')
jp = stanza.Pipeline(lang='ja')
jp_line = jp("選挙管理委員会")
for snt in jp_line.sentences:
for word in snt.tokens:
print(word.text)
```
# Adding Word Count Feature
```
def word_counts(x, pipeline=en):
doc = pipeline(x)
count = sum( [ len(sentence.tokens) for sentence in doc.sentences] )
return count
#en = snlp.Pipeline(lang='en', processors='tokenize')
df['Words'] = df['Message'].apply(word_counts)
df.describe()
#train=df.sample(frac=0.8,random_state=42) #random state is a seed value
#test=df.drop(train.index)
train['Words'] = train['Message'].apply(word_counts)
test['Words'] = test['Message'].apply(word_counts)
x_train = train[['Length', 'Punctuation', 'Capitals', 'Words']]
y_train = train[['Spam']]
x_test = test[['Length', 'Punctuation', 'Capitals' , 'Words']]
y_test = test[['Spam']]
model = make_model(input_dims=4)
model.fit(x_train, y_train, epochs=10, batch_size=10)
model.evaluate(x_test, y_test)
```
## Stop Word Removal
```
!pip install stopwordsiso
import stopwordsiso as stopwords
stopwords.langs()
sorted(stopwords.stopwords('en'))
en_sw = stopwords.stopwords('en')
def word_counts(x, pipeline=en):
doc = pipeline(x)
count = 0
for sentence in doc.sentences:
for token in sentence.tokens:
if token.text.lower() not in en_sw:
count += 1
return count
train['Words'] = train['Message'].apply(word_counts)
test['Words'] = test['Message'].apply(word_counts)
x_train = train[['Length', 'Punctuation', 'Capitals', 'Words']]
y_train = train[['Spam']]
x_test = test[['Length', 'Punctuation', 'Capitals' , 'Words']]
y_test = test[['Spam']]
model = make_model(input_dims=4)
#model = make_model(input_dims=3)
model.fit(x_train, y_train, epochs=10, batch_size=10)
```
## POS Based Features
```
en = stanza.Pipeline(lang='en')
txt = "Yo you around? A friend of mine's lookin."
pos = en(txt)
def print_pos(doc):
text = ""
for sentence in doc.sentences:
for token in sentence.tokens:
text += token.words[0].text + "/" + \
token.words[0].upos + " "
text += "\n"
return text
print(print_pos(pos))
en_sw = stopwords.stopwords('en')
def word_counts_v3(x, pipeline=en):
doc = pipeline(x)
count = 0
for sentence in doc.sentences:
for token in sentence.tokens:
if token.text.lower() not in en_sw and \
token.words[0].upos not in ['PUNCT', 'SYM']:
count += 1
return count
print(word_counts(txt), word_counts_v3(txt))
train['Test'] = 0
train.describe()
def word_counts_v3(x, pipeline=en):
doc = pipeline(x)
totals = 0.
count = 0.
non_word = 0.
for sentence in doc.sentences:
totals += len(sentence.tokens) # (1)
for token in sentence.tokens:
if token.text.lower() not in en_sw:
if token.words[0].upos not in ['PUNCT', 'SYM']:
count += 1.
else:
non_word += 1.
non_word = non_word / totals
return pd.Series([count, non_word], index=['Words_NoPunct', 'Punct'])
x = train[:10]
x.describe()
train_tmp = train['Message'].apply(word_counts_v3)
train = pd.concat([train, train_tmp], axis=1)
train.describe()
test_tmp = test['Message'].apply(word_counts_v3)
test = pd.concat([test, test_tmp], axis=1)
test.describe()
z = pd.concat([x, train_tmp], axis=1)
z.describe()
z.loc[z['Spam']==0].describe()
z.loc[z['Spam']==1].describe()
aa = [word_counts_v3(y) for y in x['Message']]
ab = pd.DataFrame(aa)
ab.describe()
```
# Lemmatization
```
text = "Stemming is aimed at reducing vocabulary and aid un-derstanding of" +\
" morphological processes. This helps people un-derstand the" +\
" morphology of words and reduce size of corpus."
lemma = en(text)
lemmas = ""
for sentence in lemma.sentences:
for token in sentence.tokens:
lemmas += token.words[0].lemma +"/" + \
token.words[0].upos + " "
lemmas += "\n"
print(lemmas)
```
# TF-IDF Based Model
```
# if not installed already
!pip install sklearn
corpus = [
"I like fruits. Fruits like bananas",
"I love bananas but eat an apple",
"An apple a day keeps the doctor away"
]
```
## Count Vectorization
```
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(corpus)
vectorizer.get_feature_names()
X.toarray()
from sklearn.metrics.pairwise import cosine_similarity
cosine_similarity(X.toarray())
query = vectorizer.transform(["apple and bananas"])
cosine_similarity(X, query)
```
## TF-IDF Vectorization
```
import pandas as pd
from sklearn.feature_extraction.text import TfidfTransformer
transformer = TfidfTransformer(smooth_idf=False)
tfidf = transformer.fit_transform(X.toarray())
pd.DataFrame(tfidf.toarray(),
columns=vectorizer.get_feature_names())
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.preprocessing import LabelEncoder
tfidf = TfidfVectorizer(binary=True)
X = tfidf.fit_transform(train['Message']).astype('float32')
X_test = tfidf.transform(test['Message']).astype('float32')
X.shape
from keras.utils import np_utils
_, cols = X.shape
model2 = make_model(cols) # to match tf-idf dimensions
lb = LabelEncoder()
y = lb.fit_transform(y_train)
dummy_y_train = np_utils.to_categorical(y)
model2.fit(X.toarray(), y_train, epochs=10, batch_size=10)
model2.evaluate(X_test.toarray(), y_test)
train.loc[train.Spam == 1].describe()
```
# Word Vectors
```
# memory limit may be exceeded. Try deleting some objects before running this next section
# or copy this section to a different notebook.
!pip install gensim
from gensim.models.word2vec import Word2Vec
import gensim.downloader as api
api.info()
model_w2v = api.load("word2vec-google-news-300")
model_w2v.most_similar("cookies",topn=10)
model_w2v.doesnt_match(["USA","Canada","India","Tokyo"])
king = model_w2v['king']
man = model_w2v['man']
woman = model_w2v['woman']
queen = king - man + woman
model_w2v.similar_by_vector(queen)
```
| true |
code
| 0.590779 | null | null | null | null |
|
```
#default_exp fastai.dataloader
```
# DataLoader Errors
> Errors and exceptions for any step of the `DataLoader` process
This includes `after_item`, `after_batch`, and collating. Anything in relation to the `Datasets` or anything before the `DataLoader` process can be found in `fastdebug.fastai.dataset`
```
#export
import inflect
from fastcore.basics import patch
from fastai.data.core import TfmdDL
from fastai.data.load import DataLoader, fa_collate, fa_convert
#export
def collate_error(e:Exception, batch):
"""
Raises an explicit error when the batch could not collate, stating
what items in the batch are different sizes and their types
"""
p = inflect.engine()
err = f'Error when trying to collate the data into batches with fa_collate, '
err += 'at least two tensors in the batch are not the same size.\n\n'
# we need to iterate through the entire batch and find a mismatch
length = len(batch[0])
for idx in range(length): # for each type in the batch
for i, item in enumerate(batch):
if i == 0:
shape_a = item[idx].shape
type_a = item[idx].__class__.__name__
elif item[idx].shape != shape_a:
shape_b = item[idx].shape
if shape_a != shape_b:
err += f'Mismatch found within the {p.ordinal(idx)} axis of the batch and is of type {type_a}:\n'
err += f'The first item has shape: {shape_a}\n'
err += f'The {p.number_to_words(p.ordinal(i+1))} item has shape: {shape_b}\n\n'
err += f'Please include a transform in `after_item` that ensures all data of type {type_a} is the same size'
e.args = [err]
raise e
#export
@patch
def create_batch(self:DataLoader, b):
"Collate a list of items into a batch."
func = (fa_collate,fa_convert)[self.prebatched]
try:
return func(b)
except Exception as e:
if not self.prebatched:
collate_error(e, b)
else: raise e
```
`collate_error` is `@patch`'d into `DataLoader`'s `create_batch` function through importing this module, so if there is any possible reason why the data cannot be collated into the batch, it is presented to the user.
An example is below, where we forgot to include an item transform that resizes all our images to the same size:
```
#failing
from fastai.vision.all import *
path = untar_data(URLs.PETS)/'images'
dls = ImageDataLoaders.from_name_func(
path, get_image_files(path), valid_pct=0.2,
label_func=lambda x: x[0].isupper())
x,y = dls.train.one_batch()
#export
@patch
def new(self:TfmdDL, dataset=None, cls=None, **kwargs):
res = super(TfmdDL, self).new(dataset, cls, do_setup=False, **kwargs)
if not hasattr(self, '_n_inp') or not hasattr(self, '_types'):
try:
self._one_pass()
res._n_inp,res._types = self._n_inp,self._types
except Exception as e:
print("Could not do one pass in your dataloader, there is something wrong in it")
raise e
else: res._n_inp,res._types = self._n_inp,self._types
return res
```
| true |
code
| 0.653929 | null | null | null | null |
|
# Hertzian conatct 1
## Assumptions
When two objects are brought into contact they intially touch along a line or at a single point. If any load is transmitted throught the contact the point or line grows to an area. The size of this area, the pressure distribtion inside it and the resulting stresses in each solid require a theory of contact to describe.
The first satisfactory theory for round bodies was presented by Hertz in 1880 who worked on it during his christmas holiday at the age of twenty three. He assumed that:
The bodies could be considered as semi infinite elastic half spaces from a stress perspective as the contact area is normally much smaller than the size of the bodies, it is also assumed strains are small. This means that the normal integral equations for surface contact can be used:
The contact is also assumed to be frictionless so the contact equations reduce to:
$\Psi_1=\int_S \int p(\epsilon,\eta)ln(\rho+z)\ d\epsilon\ d\eta$ [1]
$\Psi=\int_S \int \frac{p(\epsilon,\eta)}{\rho}\ d\epsilon\ d\eta$ [2]
$u_x=-\frac{1+v}{2\pi E}\left((1-2v)\frac{\delta\Psi_1}{\delta x}+z\frac{\delta\Psi}{\delta x}\right) $ [3a]
$u_y=-\frac{1+v}{2\pi E}\left((1-2v)\frac{\delta\Psi_1}{\delta y}+z\frac{\delta\Psi}{\delta y}\right) $ [3b]
$u_z=-\frac{1+v}{2\pi E}\left(2(1-v)\Psi+z\frac{\delta\Psi}{\delta z}\right) $ [3c]
```
from IPython.display import Image
Image("figures/hertz_probelm reduction.png")
```
For the shape of the surfaces: it was asumed that they are smooth on both the micro scale and the macro scale. Assuming that they are smooth on the micro scale means that small irregulararities which would cause discontinuous contact and local pressure variations are ignored.
## Geometry
Assuming that the surfaces are smooth on the macro scale implies that the surface profiles are continuous up to their second derivative. Meaning that the surfaces can be described by polynomials:
$z_1=A_1'x+B_1'y+A_1x^2+B_1y^2+C_1xy+...$ [4]
With higher order terms being neglected. By choosing the location of the origin to be at the point of contact and the orientation of the xy plane to be inline wiht the principal radii of the surface the equation above reduces to:
$z_1=\frac{1}{2R'_1}x_1^2+\frac{1}{2R''_1}y_1^2$ [5]
Where $R'_1$ and $R''_1$ are the principal radii of the first surface at the origin.
### They are the maximum and minimum radii of curvature across all possible cross sections
The following widget allows you to change the principal radii of a surface and the angle between it an the coordinate axes
```
from matplotlib import pyplot as plt
from matplotlib.lines import Line2D
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from __future__ import print_function
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
plt.rcParams['figure.figsize'] = [15, 10]
@interact(r1=(-10,10),r2=(-10,10),theta=(0,np.pi),continuous_update=False)
def plot_surface(r1=5,r2=0,theta=0):
"""
Plots a surface given two principal radii and the angle relative to the coordinate axes
Parameters
----------
r1,r2 : float
principal radii
theta : float
Angle between the plane of the first principal radius and the coordinate axes
"""
X,Y=np.meshgrid(np.linspace(-1,1,20),np.linspace(-1,1,20))
X_dash=X*np.cos(theta)-Y*np.sin(theta)
Y_dash=Y*np.cos(theta)+X*np.sin(theta)
r1 = r1 if np.abs(r1)>=1 else float('inf')
r2 = r2 if np.abs(r2)>=1 else float('inf')
Z=0.5/r1*X_dash**2+0.5/r2*Y_dash**2
x1=np.linspace(-1.5,1.5)
y1=np.zeros_like(x1)
z1=0.5/r1*x1**2
y2=np.linspace(-1.5,1.5)
x2=np.zeros_like(y2)
z2=0.5/r2*y2**2
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z)
ax.plot((x1*np.cos(-theta)-y1*np.sin(-theta)),x1*np.sin(-theta)+y1*np.cos(-theta),z1)
ax.plot((x2*np.cos(-theta)-y2*np.sin(-theta)),x2*np.sin(-theta)+y2*np.cos(-theta),z2)
ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
ax.set_zlim(-0.5, 0.5)
```
A similar equation defines the second surface:
$z_2=-\left(\frac{1}{2R'_2}x_2^2+\frac{1}{2R''_2}y_2^2\right)$ [6]
The separation between these surfaces is then given as $h=z_1-z_2$.
by writing equation 4 and its counterpart on common axes, it is clear that the gap between the surfaces can be written as:
$h=Ax^2+By^2+Cxy$ [7]
And by a suitable choice of orientation of the xy plane the C term can be made to equal 0. As such when ever two surfaces with parabolic shape are brought into contact (with no load) the gap between them can be defined as a single parabola:
$h=Ax^2+Bx^2=\frac{1}{2R'_{gap}}x^2+\frac{1}{2R''_{gap}}y^2$ [8]
#### The values $R'_{gap}$ and $R''_{gap}$ are called the principal radii of relative curvature.
These relate to the principal radii of each of the bodies through the equations below:
$(A+B)=\frac{1}{2}\left(\frac{1}{R'_{gap}}+\frac{1}{R''_{gap}}\right)=\frac{1}{2}\left(\frac{1}{R'_1}+\frac{1}{R''_1}+\frac{1}{R'_2}+\frac{1}{R''_2}\right)$
The next widget shows the shpae of the gap between two bodies in contact allowing you to set the principal radii of each boday and the angle between them:
```
@interact(top_r1=(-10,10),top_r2=(-10,10),
bottom_r1=(-10,10),bottom_r2=(-10,10),
theta=(0,np.pi),continuous_update=False)
def plot_two_surfaces(top_r1=2,top_r2=5,bottom_r1=4,bottom_r2=-9,theta=0.3):
"""
Plots 2 surfaces and the gap between them
Parameters
----------
top_r1,top_r2,bottom_r1,bottom_r2 : float
The principal radii of the top and bottom surface
theta : float
The angel between the first principal radii of the surfaces
"""
X,Y=np.meshgrid(np.linspace(-1,1,20),np.linspace(-1,1,20))
X_dash=X*np.cos(theta)-Y*np.sin(theta)
Y_dash=Y*np.cos(theta)+X*np.sin(theta)
top_r1 = top_r1 if np.abs(top_r1)>=1 else float('inf')
top_r2 = top_r2 if np.abs(top_r2)>=1 else float('inf')
bottom_r1 = bottom_r1 if np.abs(bottom_r1)>=1 else float('inf')
bottom_r2 = bottom_r2 if np.abs(bottom_r2)>=1 else float('inf')
Z_top=0.5/top_r1*X_dash**2+0.5/top_r2*Y_dash**2
Z_bottom=-1*(0.5/bottom_r1*X**2+0.5/bottom_r2*Y**2)
fig = plt.figure()
ax = fig.add_subplot(121, projection='3d')
ax.set_title("Surfaces")
ax2 = fig.add_subplot(122)
ax2.set_title("Gap")
ax2.axis("equal")
ax2.set_adjustable("box")
ax2.set_xlim([-1,1])
ax2.set_ylim([-1,1])
ax.plot_surface(X, Y, Z_top)
ax.plot_surface(X, Y, Z_bottom)
if top_r1==top_r2==bottom_r1==bottom_r2==float('inf'):
ax2.text(s='Flat surfaces, no gap', x=-0.6, y=-0.1)
else:
ax2.contour(X,Y,Z_top-Z_bottom)
div=((1/top_r2)-(1/top_r1))
if div==0:
lam=float('inf')
else:
lam=((1/bottom_r2)-(1/bottom_r1))/div
beta=-1*np.arctan((np.sin(2*theta))/(lam+np.cos(2*theta)))/2
if beta<=(np.pi/4):
x=1
y=np.tan(beta)
else:
x=np.tan(beta)
y=1
ax2.add_line(Line2D([x,-1*x],[y,-1*y]))
beta-=np.pi/2
if beta<=(np.pi/4):
x=1
y=np.tan(beta)
else:
x=np.tan(beta)
y=1
ax2.add_line(Line2D([x,-1*x],[y,-1*y]))
```
From the form of equation 8 it is clear that the contours of constant gap (the contours plotted by the widget) are elipitcal in shape. With axes in the ratio $(R'_gap/R''_gap)^{1/2}$. In the special case of equal principal radii for each body (spherical contact) the contours of separation will be circular. From the symmetry of this problem it is clear that this will remain true when a load is applied.
Additonally, when two cylinders are brought in to contact with their axes parallel the contours of separation are straight lines parallel to the axes of the cylinders. When loaded the cylinders will also make contact along a narrow strip parallel to the axes of the cylinders.
We might expect, then that for the general case the contour of contact under load will follow the same eliptical shape as the contours of separation. This is infact the case but the proof will have to wait for the next section
| true |
code
| 0.718304 | null | null | null | null |
|
# Exercise 6
```
# Importing libs
import cv2
import numpy as np
import matplotlib.pyplot as plt
apple = cv2.imread('images/apple.jpg')
apple = cv2.cvtColor(apple, cv2.COLOR_BGR2RGB)
apple = cv2.resize(apple, (512,512))
orange = cv2.imread('images/orange.jpg')
orange = cv2.cvtColor(orange, cv2.COLOR_BGR2RGB)
orange = cv2.resize(orange, (512,512))
plt.figure(figsize=(10,10))
ax1 = plt.subplot(121)
ax1.imshow(apple)
ax2 = plt.subplot(122)
ax2.imshow(orange)
ax1.axis('off')
ax2.axis('off')
ax1.text(0.5,-0.1, "Apple", ha="center", transform=ax1.transAxes)
ax2.text(0.5,-0.1, "Orange", ha="center", transform=ax2.transAxes)
def combine(img1, img2):
result = np.zeros(img1.shape, dtype='uint')
h,w,_ = img1.shape
result[:,0:w//2,:] = img1[:,0:w//2,:]
result[:,w//2:,:] = img2[:,w//2:,:]
return result.astype('uint8')
apple_orange = combine(apple,orange)
plt.imshow(apple_orange)
plt.axis('off')
plt.figtext(0.5, 0, 'Apple + Orange', horizontalalignment='center')
plt.show()
def buildPyramid(levels, left,right=None):
lresult = left
rresult = right if type(right) is np.ndarray else left
for i in range(levels):
lresult = cv2.pyrDown(lresult)
rresult = cv2.pyrDown(rresult)
for i in range(levels):
lresult = cv2.pyrUp(lresult)
rresult = cv2.pyrUp(rresult)
return combine(lresult,rresult)
apple_orange_pyramid = buildPyramid(3, apple_orange)
plt.figure(figsize=(10,10))
ax1 = plt.subplot(121)
ax1.imshow(apple_orange)
ax2 = plt.subplot(122)
ax2.imshow(apple_orange_pyramid)
ax1.axis('off')
ax2.axis('off')
ax1.text(0.5,-0.1, "Raw", ha="center", transform=ax1.transAxes)
ax2.text(0.5,-0.1, "After Pyramid", ha="center", transform=ax2.transAxes)
apple_orange_pyramid = buildPyramid(3, apple, orange)
plt.figure(figsize=(10,10))
ax1 = plt.subplot(121)
ax1.imshow(apple_orange)
ax2 = plt.subplot(122)
ax2.imshow(apple_orange_pyramid)
ax1.axis('off')
ax2.axis('off')
ax1.text(0.5,-0.1, "Raw", ha="center", transform=ax1.transAxes)
ax2.text(0.5,-0.1, "After Pyramid", ha="center", transform=ax2.transAxes)
```
## Another implementation
```
def buildPyramid2(levels, left,right=None):
lresult = left
rresult = right if type(right) is np.ndarray else left
for i in range(levels):
lresult = cv2.pyrDown(lresult)
rresult = cv2.pyrDown(rresult)
result = combine(lresult,rresult)
for i in range(levels):
result = cv2.pyrUp(result)
return result
apple_orange_pyramid = buildPyramid2(3, apple, orange)
plt.figure(figsize=(10,10))
ax1 = plt.subplot(121)
ax1.imshow(apple_orange)
ax2 = plt.subplot(122)
ax2.imshow(apple_orange_pyramid)
ax1.axis('off')
ax2.axis('off')
ax1.text(0.5,-0.1, "Raw", ha="center", transform=ax1.transAxes)
ax2.text(0.5,-0.1, "After Pyramid", ha="center", transform=ax2.transAxes)
```
| true |
code
| 0.459925 | null | null | null | null |
|
<h1>datetime library</h1>
<li>Time is linear
<li>progresses as a straightline trajectory from the big bag
<li>to now and into the future
<li>日期库官方说明 https://docs.python.org/3.5/library/datetime.html
<h3>Reasoning about time is important in data analysis</h3>
<li>Analyzing financial timeseries data
<li>Looking at commuter transit passenger flows by time of day
<li>Understanding web traffic by time of day
<li>Examining seaonality in department store purchases
<h3>The datetime library</h3>
<li>understands the relationship between different points of time
<li>understands how to do operations on time
<h3>Example:</h3>
<li>Which is greater? "10/24/2017" or "11/24/2016"
```
d1 = "10/24/2017"
d2 = "11/24/2016"
max(d1,d2)
```
<li>How much time has passed?
```
d1 - d2
```
<h4>Obviously that's not going to work. </h4>
<h4>We can't do date operations on strings</h4>
<h4>Let's see what happens with datetime</h4>
```
import datetime
d1 = datetime.date(2016,11,24)
d2 = datetime.date(2017,10,24)
max(d1,d2)
print(d2 - d1)
```
<li>datetime objects understand time
<h3>The datetime library contains several useful types</h3>
<li>date: stores the date (month,day,year)
<li>time: stores the time (hours,minutes,seconds)
<li>datetime: stores the date as well as the time (month,day,year,hours,minutes,seconds)
<li>timedelta: duration between two datetime or date objects
<h3>datetime.date</h3>
```
import datetime
century_start = datetime.date(2000,1,1)
today = datetime.date.today()
print(century_start,today)
print("We are",today-century_start,"days into this century")
print(type(century_start))
print(type(today))
```
<h3>For a cleaner output</h3>
```
print("We are",(today-century_start).days,"days into this century")
```
<h3>datetime.datetime</h3>
```
century_start = datetime.datetime(2000,1,1,0,0,0)
time_now = datetime.datetime.now()
print(century_start,time_now)
print("we are",time_now - century_start,"days, hour, minutes and seconds into this century")
```
<h4>datetime objects can check validity</h4>
<li>A ValueError exception is raised if the object is invalid</li>
```
some_date=datetime.date(2015,2,29)
#some_date =datetime.date(2016,2,29)
#some_time=datetime.datetime(2015,2,28,23,60,0)
```
<h3>datetime.timedelta</h3>
<h4>Used to store the duration between two points in time</h4>
```
century_start = datetime.datetime(2050,1,1,0,0,0)
time_now = datetime.datetime.now()
time_since_century_start = time_now - century_start
print("days since century start",time_since_century_start.days)
print("seconds since century start",time_since_century_start.total_seconds())
print("minutes since century start",time_since_century_start.total_seconds()/60)
print("hours since century start",time_since_century_start.total_seconds()/60/60)
```
<h3>datetime.time</h3>
```
date_and_time_now = datetime.datetime.now()
time_now = date_and_time_now.time()
print(time_now)
```
<h4>You can do arithmetic operations on datetime objects</h4>
<li>You can use timedelta objects to calculate new dates or times from a given date
```
today=datetime.date.today()
five_days_later=today+datetime.timedelta(days=5)
print(five_days_later)
now=datetime.datetime.today()
five_minutes_and_five_seconds_later = now + datetime.timedelta(minutes=5,seconds=5)
print(five_minutes_and_five_seconds_later)
now=datetime.datetime.today()
five_minutes_and_five_seconds_earlier = now+datetime.timedelta(minutes=-5,seconds=-5)
print(five_minutes_and_five_seconds_earlier)
```
<li>But you can't use timedelta on time objects. If you do, you'll get a TypeError exception
```
time_now=datetime.datetime.now().time() #Returns the time component (drops the day)
print(time_now)
thirty_seconds=datetime.timedelta(seconds=30)
time_later=time_now+thirty_seconds
#Bug or feature?
#But this is Python
#And we can always get around something by writing a new function!
#Let's write a small function to get around this problem
def add_to_time(time_object,time_delta):
import datetime
temp_datetime_object = datetime.datetime(500,1,1,time_object.hour,time_object.minute,time_object.second)
print(temp_datetime_object)
return (temp_datetime_object+time_delta).time()
#And test it
time_now=datetime.datetime.now().time()
thirty_seconds=datetime.timedelta(seconds=30)
print(time_now,add_to_time(time_now,thirty_seconds))
```
<h2>datetime and strings</h2>
<h4>datetime.strptime</h4>
<li>datetime.strptime(): grabs time from a string and creates a date or datetime or time object
<li>The programmer needs to tell the function what format the string is using
<li> See http://pubs.opengroup.org/onlinepubs/009695399/functions/strptime.html for how to specify the format
```
date='01-Apr-03'
date_object=datetime.datetime.strptime(date,'%d-%b-%y')
print(date_object)
#Unfortunately, there is no similar thing for time delta
#So we have to be creative!
bus_travel_time='2:15:30'
hours,minutes,seconds=bus_travel_time.split(':')
x=datetime.timedelta(hours=int(hours),minutes=int(minutes),seconds=int(seconds))
print(x)
#Or write a function that will do this for a particular format
def get_timedelta(time_string):
hours,minutes,seconds = time_string.split(':')
import datetime
return datetime.timedelta(hours=int(hours),minutes=int(minutes),seconds=int(seconds))
```
<h4>datetime.strftime</h4>
<li>The strftime function flips the strptime function. It converts a datetime object to a string
<li>with the specified format
```
now = datetime.datetime.now()
string_now = datetime.datetime.strftime(now,'%m/%d/%y %H:%M:%S')
print(now,string_now)
print(str(now)) #Or you can use the default conversion
```
| true |
code
| 0.205735 | null | null | null | null |
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Algorithms/CloudMasking/landsat457_surface_reflectance.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Algorithms/CloudMasking/landsat457_surface_reflectance.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Algorithms/CloudMasking/landsat457_surface_reflectance.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://geemap.org). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('Installing geemap ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
import ee
import geemap
```
## Create an interactive map
The default basemap is `Google Maps`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/basemaps.py) can be added using the `Map.add_basemap()` function.
```
Map = geemap.Map(center=[40,-100], zoom=4)
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
# This example demonstrates the use of the Landsat 4, 5 or 7
# surface reflectance QA band to mask clouds.
# cloudMaskL457 = function(image) {
def cloudMaskL457(image):
qa = image.select('pixel_qa')
# If the cloud bit (5) is set and the cloud confidence (7) is high
# or the cloud shadow bit is set (3), then it's a bad pixel.
cloud = qa.bitwiseAnd(1 << 5) \
.And(qa.bitwiseAnd(1 << 7)) \
.Or(qa.bitwiseAnd(1 << 3))
# Remove edge pixels that don't occur in all bands
mask2 = image.mask().reduce(ee.Reducer.min())
return image.updateMask(cloud.Not()).updateMask(mask2)
# }
# Map the function over the collection and take the median.
collection = ee.ImageCollection('LANDSAT/LT05/C01/T1_SR') \
.filterDate('2010-04-01', '2010-07-30')
composite = collection \
.map(cloudMaskL457) \
.median()
# Display the results in a cloudy place.
Map.setCenter(-6.2622, 53.3473, 12)
Map.addLayer(composite, {'bands': ['B3', 'B2', 'B1'], 'min': 0, 'max': 3000})
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
| true |
code
| 0.59131 | null | null | null | null |
|
# LinearSVR with MinMaxScaler & Power Transformer
This Code template is for the Classification task using Support Vector Regressor (SVR) based on the Support Vector Machine algorithm with Power Transformer as Feature Transformation Technique and MinMaxScaler for Feature Scaling in a pipeline.
### Required Packages
```
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as se
from sklearn.preprocessing import PowerTransformer, MinMaxScaler
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split
from imblearn.over_sampling import RandomOverSampler
from sklearn.svm import LinearSVR
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path=""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_values
target=''
```
### Data fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X=df[features]
Y=df[target]
```
### Data preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=NullClearner(Y)
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)#performing datasplitting
```
### Model
Support vector machines (SVMs) are a set of supervised learning methods used for classification, regression and outliers detection.
A Support Vector Machine is a discriminative classifier formally defined by a separating hyperplane. In other terms, for a given known/labelled data points, the SVM outputs an appropriate hyperplane that classifies the inputted new cases based on the hyperplane. In 2-Dimensional space, this hyperplane is a line separating a plane into two segments where each class or group occupied on either side.
LinearSVR is similar to SVR with kernel=’linear’. It has more flexibility in the choice of tuning parameters and is suited for large samples.
#### Feature Transformation
PowerTransformer applies a power transform featurewise to make data more Gaussian-like.
Power transforms are a family of parametric, monotonic transformations that are applied to make data more Gaussian-like. This is useful for modeling issues related to heteroscedasticity (non-constant variance), or other situations where normality is desired.
For more information... [click here](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PowerTransformer.html)
#### Model Tuning Parameters
1. epsilon : float, default=0.0
> Epsilon parameter in the epsilon-insensitive loss function.
2. loss : {‘epsilon_insensitive’, ‘squared_epsilon_insensitive’}, default=’epsilon_insensitive’
> Specifies the loss function. ‘hinge’ is the standard SVM loss (used e.g. by the SVC class) while ‘squared_hinge’ is the square of the hinge loss. The combination of penalty='l1' and loss='hinge' is not supported.
3. C : float, default=1.0
> Regularization parameter. The strength of the regularization is inversely proportional to C. Must be strictly positive.
4. tol : float, default=1e-4
> Tolerance for stopping criteria.
5. dual : bool, default=True
> Select the algorithm to either solve the dual or primal optimization problem. Prefer dual=False when n_samples > n_features.
### Feature Scaling
#### MinMaxScalar:
Transform features by scaling each feature to a given range.
This estimator scales and translates each feature individually such that it is in the given range on the training set, e.g. between zero and one.
```
model=make_pipeline(MinMaxScaler(),PowerTransformer(),LinearSVR())
model.fit(x_train, y_train)
```
#### Model Accuracy
We will use the trained model to make a prediction on the test set.Then use the predicted value for measuring the accuracy of our model.
> **score**: The **score** function returns the coefficient of determination <code>R<sup>2</sup></code> of the prediction.
```
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
```
> **r2_score**: The **r2_score** function computes the percentage variablility explained by our model, either the fraction or the count of correct predictions.
> **mae**: The **mean abosolute error** function calculates the amount of total error(absolute average distance between the real data and the predicted data) by our model.
> **mse**: The **mean squared error** function squares the error(penalizes the model for large errors) by our model.
```
y_pred=model.predict(x_test)
print("R2 Score: {:.2f} %".format(r2_score(y_test,y_pred)*100))
print("Mean Absolute Error {:.2f}".format(mean_absolute_error(y_test,y_pred)))
print("Mean Squared Error {:.2f}".format(mean_squared_error(y_test,y_pred)))
```
#### Prediction Plot
First, we make use of a plot to plot the actual observations, with x_train on the x-axis and y_train on the y-axis.
For the regression line, we will use x_train on the x-axis and then the predictions of the x_train observations on the y-axis.
```
plt.figure(figsize=(14,10))
plt.plot(range(20),y_test[0:20], color = "green")
plt.plot(range(20),model.predict(x_test[0:20]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
```
#### Creator:Shreepad Nade , Github: [Profile](https://github.com/shreepad-nade)
| true |
code
| 0.529324 | null | null | null | null |
|
#Instalamos pytorch
```
#pip install torch===1.6.0 torchvision===0.7.0 -f https://download.pytorch.org/whl/torch_stable.html
```
#Clonamos el repositorio para obtener el dataset
```
!git clone https://github.com/joanby/deeplearning-az.git
from google.colab import drive
drive.mount('/content/drive')
```
# Importar las librerías
```
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.nn.parallel
import torch.optim as optim
import torch.utils.data
from torch.autograd import Variable
```
# Importar el dataset
```
movies = pd.read_csv("/content/deeplearning-az/datasets/Part 6 - AutoEncoders (AE)/ml-1m/movies.dat", sep = '::', header = None, engine = 'python', encoding = 'latin-1')
users = pd.read_csv("/content/deeplearning-az/datasets/Part 6 - AutoEncoders (AE)/ml-1m/users.dat", sep = '::', header = None, engine = 'python', encoding = 'latin-1')
ratings = pd.read_csv("/content/deeplearning-az/datasets/Part 6 - AutoEncoders (AE)/ml-1m/ratings.dat", sep = '::', header = None, engine = 'python', encoding = 'latin-1')
```
# Preparar el conjunto de entrenamiento y elconjunto de testing
```
training_set = pd.read_csv("/content/deeplearning-az/datasets/Part 6 - AutoEncoders (AE)/ml-100k/u1.base", sep = "\t", header = None)
training_set = np.array(training_set, dtype = "int")
test_set = pd.read_csv("/content/deeplearning-az/datasets/Part 6 - AutoEncoders (AE)/ml-100k/u1.test", sep = "\t", header = None)
test_set = np.array(test_set, dtype = "int")
```
# Obtener el número de usuarios y de películas
```
nb_users = int(max(max(training_set[:, 0]), max(test_set[:,0])))
nb_movies = int(max(max(training_set[:, 1]), max(test_set[:, 1])))
```
# Convertir los datos en un array X[u,i] con usuarios u en fila y películas i en columna
```
def convert(data):
new_data = []
for id_user in range(1, nb_users+1):
id_movies = data[:, 1][data[:, 0] == id_user]
id_ratings = data[:, 2][data[:, 0] == id_user]
ratings = np.zeros(nb_movies)
ratings[id_movies-1] = id_ratings
new_data.append(list(ratings))
return new_data
training_set = convert(training_set)
test_set = convert(test_set)
```
# Convertir los datos a tensores de Torch
```
training_set = torch.FloatTensor(training_set)
test_set = torch.FloatTensor(test_set)
```
# Crear la arquitectura de la Red Neuronal
```
class SAE(nn.Module):
def __init__(self, ):
super(SAE, self).__init__()
self.fc1 = nn.Linear(nb_movies, 20)
self.fc2 = nn.Linear(20, 10)
self.fc3 = nn.Linear(10, 20)
self.fc4 = nn.Linear(20, nb_movies)
self.activation = nn.Sigmoid()
def forward(self, x):
x = self.activation(self.fc1(x))
x = self.activation(self.fc2(x))
x = self.activation(self.fc3(x))
x = self.fc4(x)
return x
sae = SAE()
criterion = nn.MSELoss()
optimizer = optim.RMSprop(sae.parameters(), lr = 0.01, weight_decay = 0.5)
```
# Entrenar el SAE
```
nb_epoch = 200
for epoch in range(1, nb_epoch+1):
train_loss = 0
s = 0.
for id_user in range(nb_users):
input = Variable(training_set[id_user]).unsqueeze(0)
target = input.clone()
if torch.sum(target.data > 0) > 0:
output = sae.forward(input)
target.require_grad = False
output[target == 0] = 0
loss = criterion(output, target)
# la media no es sobre todas las películas, sino sobre las que realmente ha valorado
mean_corrector = nb_movies/float(torch.sum(target.data > 0)+1e-10)
loss.backward()
train_loss += np.sqrt(loss.data*mean_corrector) ## sum(errors) / n_pelis_valoradas
s += 1.
optimizer.step()
print("Epoch: "+str(epoch)+", Loss: "+str(train_loss/s))
```
# Evaluar el conjunto de test en nuestro SAE
```
test_loss = 0
s = 0.
for id_user in range(nb_users):
input = Variable(training_set[id_user]).unsqueeze(0)
target = Variable(test_set[id_user]).unsqueeze(0)
if torch.sum(target.data > 0) > 0:
output = sae.forward(input)
target.require_grad = False
output[target == 0] = 0
loss = criterion(output, target)
# la media no es sobre todas las películas, sino sobre las que realmente ha valorado
mean_corrector = nb_movies/float(torch.sum(target.data > 0)+1e-10)
test_loss += np.sqrt(loss.data*mean_corrector) ## sum(errors) / n_pelis_valoradas
s += 1.
print("Test Loss: "+str(test_loss/s))
```
| true |
code
| 0.736463 | null | null | null | null |
|
# NLP Intent Recognition
Hallo und herzlich willkommen zum codecentric.AI bootcamp!
Heute wollen wir uns mit einem fortgeschrittenen Thema aus dem Bereich _natural language processing_, kurz _NLP_, genannt, beschäftigen:
> Wie bringt man Sprachassistenten, Chatbots und ähnlichen Systemen bei, die Absicht eines Nutzers aus seinen Äußerungen zu erkennen?
Dieses Problem wird im Englischen allgemein als _intent recognition_ bezeichnet und gehört zu dem ambitionierten Gebiet des _natural language understanding_, kurz _NLU_ genannt. Einen Einstieg in dieses Thema bietet das folgende [Youtube-Video](https://www.youtube.com/watch?v=H_3R8inCOvM):
```
# lade Video
from IPython.display import IFrame
IFrame('https://www.youtube.com/embed/H_3R8inCOvM', width=850, height=650)
```
Zusammen werden wir in diesem Tutorial mit Hilfe der NLU-Bibliothek [Rasa-NLU](https://rasa.com/docs/nlu/) einem WetterBot beibringen, einfache Fragemuster zum Wetter zu verstehen und zu beantworten. Zum Beispiel wird er auf die Fragen
> `"Wie warm war es 1989?"`
mit
<img src="img/answer-1.svg" width="85%" align="middle">
und auf
> `"Welche Temperatur hatten wir in Schleswig-Holstein und in Baden-Württemberg?"`
mit
<img src="img/answer-2.svg" width="85%" align="middle">
antworten. Der folgende Screencast gibt einen Überblick über das Notebook:
```
# lade Video
from IPython.display import IFrame
IFrame('https://www.youtube.com/embed/pVwO4Brs4kY', width=850, height=650)
```
Damit es gleich richtig losgehen kann, importieren wir noch zwei Standardbibliotheken und vereinbaren das Datenverzeichnis:
```
import os
import numpy as np
DATA_DIR = 'data'
```
## Unser Ausgangspunkt
Allgemein ist die Aufgabe, aus einer Sprachäußerung die zugrunde liegende Absicht zu erkennen, selbst für Menschen manchmal nicht einfach. Soll ein Computer diese schwierige Aufgabe lösen, so muss man sich überlegen, was man zu einem gegebenen Input — also einer (unstrukturierten) Sprachäußerung — für einen Output erwarten, wie man also Absichten modelliert und strukturiert.
Weit verbreitet ist folgender Ansatz für Intent Recognition:
- jede Äußerung wird einer _Domain_, also einem Gebiet, zugeordnet,
- für jede _Domain_ gibt es einen festen Satz von _Intents_, also eine Reihe von Absichten,
- jede Absicht kann durch _Parameter_ konkretisiert werden und hat dafür eine Reihe von _Slots_, die wie Parameter einer Funktion oder Felder eines Formulares mit gewissen Werten gefüllt werden können.
Für die Äußerungen
> - `"Wie warm war es 1990 in Berlin?"`
> - `"Welche Temperatur hatten wir in Hessen im Jahr 2018?"`
> - `"Wie komme ich zum Hauptbahnhof?"`
könnte _Intent Recognition_ also zum Beispiel jeweils folgende Ergebnisse liefern:
> - `{'intent': 'Frag_Temperatur', 'slots': {'Ort': 'Berlin', 'Jahr': '1990'}}`
> - `{'intent': 'Frag_Temperatur', 'slots': {'Ort': 'Hessen', 'Jahr': '2018'}}`
> - `{'intent': 'Frag_Weg', 'slots': {'Start': None, 'Ziel': 'Hauptbahnhof'}}`
Für Python steht eine ganze von NLP-Bibliotheken zur Verfügung, die Intent Recognition in der einen oder anderen Form ermöglichen, zum Beispiel
- [Rasa NLU](https://rasa.com/docs/nlu/) („Language Understanding for chatbots and AI assistants“),
- [snips](https://snips-nlu.readthedocs.io/en/latest/) („Using Voice to Make Technology Disappear“),
- [DeepPavlov](http://deeppavlov.ai) („an open-source conversational AI library“),
- [NLP Architect](http://nlp_architect.nervanasys.com/index.html) von Intel („for exploring state-of-the-art deep learning topologies and techniques for natural language processing and natural language unterstanding“),
- [pytext](https://pytext-pytext.readthedocs-hosted.com/en/latest/index.html) von Facebook („a deep-learning based NLP modeling framework built on PyTorch“).
Wir entscheiden uns im Folgenden für die Bibliothek Rasa NLU, weil wir dafür bequem mit einem Open-Source-Tool (chatette) umfangreiche Trainingsdaten generieren können. Rasa NLU wiederum benutzt die NLP-Bibliothek [spaCy](https://spacy.io), die Machine-Learning-Bibliothek [scikit-learn](https://scikit-learn.org/stable/) und die Deep-Learning-Bibliothek [TensorFlow](https://www.tensorflow.org/).
## Intent Recognition von Anfang bis Ende mit Rasa NLU
Schauen wir uns an, wie man eine Sprach-Engine für Intent Recognition trainieren kann! Dafür beschränken wir uns zunächst auf wenige Intents und Trainingsdaten und gehen die benötigten Schritte von Anfang bis Ende durch.
### Schritt 1: Intents durch Trainingsdaten beschreiben
Als Erstes müssen wir die Intents mit Hilfe von Trainingsdaten beschreiben. _Rasa NLU_ erwartet beides zusammen in einer Datei im menschenfreundlichen [Markdown-Format](http://markdown.de/) oder im computerfreundlichen [JSON-Format](https://de.wikipedia.org/wiki/JavaScript_Object_Notation). Ein Beispiel für solche Trainingsdaten im Markdown-Format ist der folgende Python-String, den wir in die Datei `intents.md` speichern:
```
TRAIN_INTENTS = """
## intent: Frag_Temperatur
- Wie [warm](Eigenschaft) war es [1900](Zeit) in [Brandenburg](Ort)
- Wie [kalt](Eigenschaft) war es in [Hessen](Ort) [1900](Zeit)
- Was war die Temperatur [1977](Zeit) in [Sachsen](Ort)
## intent: Frag_Ort
- Wo war es [1998](Zeit) am [kältesten](Superlativ:kalt)
- Finde das [kältesten](Superlativ:kalt) Bundesland im Jahr [2004](Zeit)
- Wo war es [2010](Zeit) [kälter](Komparativ:kalt) als [1994](Zeit) in [Rheinland-Pfalz](Ort)
## intent: Frag_Zeit
- Wann war es in [Bayern](Ort) am [kühlsten](Superlativ:kalt)
- Finde das [kälteste](Superlativ:kalt) Jahr im [Saarland](Ort)
- Wann war es in [Schleswig-Holstein](Ort) [wärmer](Komparativ:warm) als in [Baden-Württemberg](Ort)
## intent: Ende
- Ende
- Auf Wiedersehen
- Tschuess
"""
INTENTS_PATH = os.path.join(DATA_DIR, 'intents.md')
def write_file(filename, text):
with open(filename, 'w', encoding='utf-8') as file:
file.write(text)
write_file(INTENTS_PATH, TRAIN_INTENTS)
```
Hier wird jeder Intent erst in der Form
> `## intent: NAME`
deklariert, wobei `NAME` durch die Bezeichnung des Intents zu ersetzen ist. Anschließend wird der Intent durch eine Liste von
Beispiel-Äußerungen beschrieben. Die Parameter beziehungsweise Slots werden in den Beispieläußerungen in der Form
> `[WERT](SLOT)`
markiert, wobei `SLOT` die Bezeichnung des Slots und `Wert` der entsprechende Teil der Äußerung ist.
### Schritt 2: Sprach-Engine konfigurieren...
Die Sprach-Engine von _Rasa NLU_ ist als Pipeline gestaltet und [sehr flexibel konfigurierbar](https://rasa.com/docs/nlu/components/#section-pipeline). Zwei [Beispiel-Konfigurationen](https://rasa.com/docs/nlu/choosing_pipeline/) sind in Rasa bereits enthalten:
- `spacy_sklearn` verwendet vortrainierte Wortvektoren, eine [scikit-learn-Implementierung](https://scikit-learn.org/stable/modules/svm.html) einer linearen [Support-vector Machine]( https://en.wikipedia.org/wiki/Support-vector_machine) für die Klassifikation und wird für kleine Trainingsmengen (<1000) empfohlen. Da diese Pipeline vortrainierte Wortvektoren und spaCy benötigt, kann sie nur für [die meisten westeuropäische Sprachen](https://rasa.com/docs/nlu/languages/#section-languages) verwendet werden. Allerdings sind die Version 0.20.1 von scikit-learn und 0.13.8 von Rasa-NLU nicht kompatibel
- `tensorflow_embedding` trainiert für die Klassifikation Einbettungen von Äußerungen und von Intents in denselben Vektorraum und wird für größere Trainingsmengen (>1000) empfohlen. Die zu Grunde liegende Idee stammt aus dem Artikel [StarSpace: Embed All The Things!](https://arxiv.org/abs/1709.03856). Sie ist sehr vielseitig anwendbar und beispielsweise auch für [Question Answering](https://en.wikipedia.org/wiki/Question_answering) geeignet. Diese Pipeline benötigt kein Vorwissen über die verwendete Sprache, ist also universell einsetzbar, und kann auch auf das Erkennen mehrerer Intents in einer Äußerung trainiert werden.
Zum Füllen der Slots verwenden beide Pipelines eine [Python-Implementierung](http://www.chokkan.org/software/crfsuite/) von [Conditional Random Fields](https://en.wikipedia.org/wiki/Conditional_random_field).
Die Konfiguration der Pipeline wird durch eine YAML-Datei beschrieben. Der folgende Python-String entspricht der Konfiguration `tensorflow_embedding`:
```
CONFIG_TF = """
pipeline:
- name: "tokenizer_whitespace"
- name: "ner_crf"
- name: "ner_synonyms"
- name: "intent_featurizer_count_vectors"
- name: "intent_classifier_tensorflow_embedding"
"""
```
### Schritt 3: ...trainieren...
Sind die Trainingsdaten und die Konfiguration der Pipeline beisammen, so kann die Sprach-Engine trainiert werden. In der Regel erfolgt dies bei Rasa mit Hilfe eines Kommandozeilen-Interface oder direkt [in Python](https://rasa.com/docs/nlu/python/). Die folgende Funktion `train` erwartet die Konfiguration als Python-String und den Namen der Datei mit den Trainingsdaten und gibt die trainierte Sprach-Engine als Instanz einer `Interpreter`-Klasse zurück:
```
import rasa_nlu.training_data
import rasa_nlu.config
from rasa_nlu.model import Trainer, Interpreter
MODEL_DIR = 'models'
def train(config=CONFIG_TF, intents_path=INTENTS_PATH):
config_path = os.path.join(DATA_DIR, 'rasa_config.yml')
write_file(config_path, config)
trainer = Trainer(rasa_nlu.config.load(config_path))
trainer.train(rasa_nlu.training_data.load_data(intents_path))
return Interpreter.load(trainer.persist(MODEL_DIR))
interpreter = train()
```
### Schritt 4: ...und testen!
Wir testen nun, ob die Sprach-Engine `interpreter` folgende Test-Äußerungen richtig versteht:
```
TEST_UTTERANCES = [
'Was war die durchschnittliche Temperatur 2004 in Mecklenburg-Vorpommern',
'Nenn mir das wärmste Bundesland 2018',
'In welchem Jahr war es in Nordrhein-Westfalen heißer als 1990',
'Wo war es 2000 am kältesten',
'Bis bald',
]
```
Die Methode `parse` von `interpreter` erwartet eine Äußerung als Python-String, wendet Intent Recognition an und liefert eine sehr detaillierte Rückgabe:
```
interpreter.parse(TEST_UTTERANCES[0])
```
Die Rückgabe umfasst im Wesentlichen
- den Namen des ermittelten Intent sowie eine Sicherheit beziehungsweise Konfidenz zwischen 0 und 1,
- für jeden ermittelten Parameter die Start- und Endposition in der Äußerung, den Wert und wieder eine Konfidenz,
- ein Ranking der möglichen Intents nach der Sicherheit/Konfidenz, mit der sie in dieser Äußerung vermutet wurden.
Für eine übersichtlichere Darstellung und leichte Weiterverarbeitung bereiten wir die Rückgabe mit Hilfe der Funktionen `extract_intent` und `extract_confidences` ein wenig auf. Anschließend gehen wir unsere Test-Äußerungen durch:
```
def extract_intent(intent):
return (intent['intent']['name'] if intent['intent'] else None,
[(ent['entity'], ent['value']) for ent in intent['entities']])
def extract_confidences(intent):
return (intent['intent']['confidence'] if intent['intent'] else None,
[ent['confidence'] for ent in intent['entities']])
def test(interpreter, utterances=TEST_UTTERANCES):
for utterance in utterances:
intent = interpreter.parse(utterance)
print('<', utterance)
print('>', extract_intent(intent))
print(' ', extract_confidences(intent))
print()
test(interpreter)
```
Das Ergebnis ist noch nicht ganz überzeugend — wir haben aber auch nur ganz wenig Trainingsdaten vorgegeben!
## Trainingsdaten generieren mit Chatette
Für ein erfolgreiches Training brauchen wir also viel mehr Trainingsdaten. Doch fängt man an, weitere Beispiele aufzuschreiben, so fallen einem schnell viele kleine Variationsmöglichkeiten ein, die sich recht frei kombinieren lassen. Zum Beispiel können wir für eine Frage nach der Temperatur in Berlin im Jahr 1990 mit jeder der Phrasen
> - "Wie warm war es..."
> - "Wie kalt war es..."
> - "Welche Temperatur hatten wir..."
beginnen und dann mit
> - "...in Berlin 1990"
> - "...1990 in Berlin"
abschließen, vor "1990" noch "im Jahr" einfügen und so weiter. Statt alle denkbaren Kombinationen aufzuschreiben, ist es sinnvoller, die Möglichkeiten mit Hilfe von Regeln zu beschreiben und daraus Trainingsdaten generieren zu lassen. Genau das ermöglicht das Python-Tool [chatette](https://github.com/SimGus/Chatette), das wir im Folgenden verwenden. Dieses Tool liest Regeln, die einer speziellen Syntax folgen müssen, aus einer Datei aus und erzeugt dann daraus Trainingsdaten für Rasa NLU im JSON-Format.
### Regeln zur Erzeugung von Trainingsdaten
Wir legen im Folgenden erst einen Grundvorrat an Regeln für die Intents `Frag_Temperatur`, `Frag_Ort`, `Frag_Zeit` und `Ende` in einem Python-Dictionary an und erläutern danach genauer, wie die Regeln aufgebaut sind:
```
RULES = {
'@[Ort]': (
'Brandenburg', 'Baden-Wuerttemberg', 'Bayern', 'Hessen',
'Rheinland-Pfalz', 'Schleswig-Holstein', 'Saarland', 'Sachsen',
),
'@[Zeit]': set(map(str, np.random.randint(1891, 2018, size=5))),
'@[Komparativ]': ('wärmer', 'kälter',),
'@[Superlativ]': ('wärmsten', 'kältesten',),
'%[Frag_Temperatur]': ('Wie {warm/kalt} war es ~[zeit_ort]',
'Welche Temperatur hatten wir ~[zeit_ort]',
'Wie war die Temperatur ~[zeit_ort]',
),
'%[Frag_Ort]': (
'~[wo_war] es @[Zeit] @[Komparativ] als {@[Zeit]/in @[Ort]}',
'~[wo_war] es @[Zeit] am @[Superlativ]',
),
'%[Frag_Jahr]': (
'~[wann_war] es in @[Ort] @[Komparativ] als {@[Zeit]/in @[Ort]}',
'~[wann_war] es in @[Ort] am @[Superlativ]',
),
'%[Ende]': ('Ende', 'Auf Wiedersehen', 'Tschuess',),
'~[finde]': ('Sag mir', 'Finde'),
'~[wie_war]': ('Wie war', '~[finde]',),
'~[was_war]': ('Was war', '~[finde]',),
'~[wo_war]': ('Wo war', 'In welchem {Bundesland|Land} war',),
'~[wann_war]': ('Wann war', 'In welchem Jahr war',),
'~[zeit_ort]': ('@[Zeit] in @[Ort]', '@[Ort] in @[Zeit]',),
'~[Bundesland]': ('Land', 'Bundesland',),
}
```
Jede Regel besteht aus einem Namen beziehungsweise Platzhalter und einer Menge von Phrasen. Je nachdem, ob der Name die Form
> `%[NAME]`, `@[NAME]` oder `~[NAME]`
hat, beschreibt die Regel einen
> _Intent_, _Slot_ oder eine _Alternative_
mit der Bezeichnung `NAME`. Jede Phrase kann ihrerseits Platzhalter für Slots und Alternativen erhalten. Diese Platzhalter werden bei der Erzeugung von Trainingsdaten von chatette jeweils durch eine der Phrasen ersetzt, die in der Regel für den jeweiligen Slot beziehungsweise die Alternativen aufgelistet sind. Außerdem können Phrasen
- Alternativen der Form `{_|_|_}`,
- optionale Teile in der Form `[_?]`
und einige weitere spezielle Konstrukte enthalten. Mehr Details finden sich in der [Syntax-Beschreibung](https://github.com/SimGus/Chatette/wiki/Syntax-specifications) von chatette.
### Erzeugung der Trainingsdaten
Die in dem Python-Dictionary kompakt abgelegten Regeln müssen nun für chatette so formatiert werden, dass bei jeder Regel der Name einen neuen Absatz einleitet und anschließend die möglichen Phrasen schön eingerückt Zeile für Zeile aufgelistet werden. Dies leistet die folgende Funktion `format_rules`. Zusätzlich fügt sie eine Vorgabe ein, wieviel Trainingsbeispiele pro Intent erzeugt werden sollen:
```
def format_rules(rules, train_samples):
train_str = "('training':'{}')".format(train_samples)
llines = [[name if (name[0] != '%') else name + train_str]
+ [' ' + val for val in rules[name]] + [''] for name in rules]
return '\n'.join((l for lines in llines for l in lines))
```
Nun wenden wir chatette an, um die Trainingsdaten zu generieren. Dafür bietet chatette ein bequemes [Kommandozeilen-Interface](https://github.com/SimGus/Chatette/wiki/Command-line-interface), aber wir verwenden direkt die zu Grunde liegenden Python-Module.
Die folgende Funktion `chatette` erwartet wie `format_rules` ein Python-Dictionary mit Regeln, schreibt diese passend formatiert in eine Datei, löscht etwaige zuvor generierte Trainingsdateien und erzeugt dann den Regeln entsprechend neue Trainingsdaten.
```
from chatette.adapters import RasaAdapter
from chatette.parsing import Parser
from chatette.generator import Generator
import glob
TRAIN_SAMPLES = 400
CHATETTE_DIR = os.path.join(DATA_DIR, 'chatette')
def chatette(rules=RULES, train_samples=TRAIN_SAMPLES):
rules_path = os.path.join(DATA_DIR, 'intents.chatette')
write_file(rules_path, format_rules(rules, train_samples))
with open(rules_path, 'r') as rule_file:
parser = Parser(rule_file)
parser.parse()
generator = Generator(parser)
for f in glob.glob(os.path.join(CHATETTE_DIR, '*')):
os.remove(f)
RasaAdapter().write(CHATETTE_DIR, list(generator.generate_train()),
generator.get_entities_synonyms())
chatette(train_samples=400)
```
### Und nun: neuer Test!
Bringen die umfangreicheren Trainingsdaten wirklich eine Verbesserung? Schauen wir's uns an! Um verschiedene Sprach-Engines zu vergleichen, nutzen wir die folgende Funktion:
```
def train_and_test(config=CONFIG_TF, utterances=TEST_UTTERANCES):
interpreter = train(config, CHATETTE_DIR)
test(interpreter, utterances)
return interpreter
interpreter = train_and_test()
```
Hier wurde nur die letzte Äußerung nicht verstanden, aber das ist auch nicht weiter verwunderlich.
## Unser kleiner WetterBot
Experimentieren macht mehr Spaß, wenn es auch mal zischt und knallt. Oder zumindest irgendeine andere Reaktion erfolgt. Und deswegen bauen wir uns einen kleinen WetterBot, der auf die erkannten Intents reagieren kann. Zuerst schreiben wir dafür eine Eingabe-Verarbeitungs-Ausgabe-Schleife. Diese erwartet als Parameter erstens die Sprach-Engine `interpreter` und zweitens ein Python-Dictionary `handlers`, welches jeder Intent-Bezeichnung einen Handler zuordnet. Der Handler wird dann mit dem erkannten Intent aufgerufen und sollte zurückgeben, ob die Schleife fortgeführt werden soll oder nicht:
```
def dialog(interpreter, handlers):
quit = False
while not quit:
intent = extract_intent(interpreter.parse(input('>')))
print('<', intent)
intent_name = intent[0]
if intent_name in handlers:
quit = handlers[intent_name](intent)
```
Wir implementieren gleich beispielhaft einen Handler für den Intent `Frag_Temperatur`und reagieren auf alle anderen Intents mit einer Standard-Antwort:
```
def message(msg, quit=False):
print(msg)
return quit
HANDLERS = {
'Ende': lambda intent: message('=> Oh, wie schade. Bis bald!', True),
'Frag_Zeit': lambda intent: message('=> Das ist eine gute Frage.'),
'Frag_Ort': lambda intent: message('=> Dafür wurde ich nicht programmiert.'),
'Frag_Temperatur': lambda intent: message('=> Das weiss ich nicht.')
}
```
Um die Fragen nach den Temperaturen zu beantworten, nutzen wir [Archiv-Daten](ftp://ftp-cdc.dwd.de/pub/CDC/regional_averages_DE/annual/air_temperature_mean/regional_averages_tm_year.txt) des [Deutschen Wetterdienstes](https://www.dwd.de), die wir schon etwas aufbereitet haben. Die Routine `show` gibt die nachgefragten Temperaturdaten je nach Anzahl der angegebenen Jahre und Bundesländer als Liniendiagramm, Balkendiagramm oder in Textform an. Der eigentliche Hander `frag_wert` prüft, ob die angegebenen Jahre und Orte auch zulässig sind und setzt, falls eine der beiden Angaben fehlt, einfach alle Jahre beziehungsweise Bundesländer ein:
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import set_matplotlib_formats
%matplotlib inline
set_matplotlib_formats('svg')
sns.set()
DATA_PATH = os.path.join(DATA_DIR, 'temperaturen.txt')
temperature = pd.read_csv(DATA_PATH, index_col=0, sep=';')
def show(times, places):
if (len(places) == 0) and (len(times) == 0):
print('Keine zulässigen Orte oder Zeiten')
elif (len(places) == 1) and (len(times) == 1):
print(temperature.loc[times, places])
else:
if (len(places) > 1) and (len(times) == 1):
temperature.loc[times[0], places].plot.barh()
if (len(places) == 1) and (len(times) > 1):
temperature.loc[times, places[0]].plot.line()
if (len(places) > 1) and (len(times) > 1):
temperature.loc[times, places].plot.line()
plt.legend(bbox_to_anchor=(1.05,1), loc=2, borderaxespad=0.)
plt.show()
def frag_temperatur(intent):
def validate(options, ent_name, fn):
chosen = [fn(value) for (name, value) in intent[1] if name == ent_name]
return list(set(options) & set(chosen)) if chosen else options
places = validate(list(temperature.columns), 'Ort', lambda x:x)
times = validate(list(temperature.index), 'Zeit', int)
show(times, places)
return False
HANDLERS['Frag_Temperatur'] = frag_temperatur
```
Nun kann der WetterBot getestet werden! Zum Beispiel mit
> "Wie warm war es in Baden-Württemberg und Sachsen?"
```
dialog(interpreter, HANDLERS)
```
## Intent Recognition selbst gemacht — ein Bi-LSTM-Netzwerk mit Keras
Im Prinzip haben wir nun gesehen, wie sich Intent Recognition mit Hilfe von Rasa NLU recht einfach anwenden lässt. Aber wie funktioniert das ganz genau? In diesem zweiten Teil des Notebooks werden wir
- ein bidirektionales rekurrentes Netz, wie es im Video vorgestellt wurde, implementieren,
- die mit chatette erstellten Trainingsdaten so aufbereiten, dass wir damit das Netz trainieren können,
und sehen, dass das ganz gut klappt und gar nicht so schwer ist!
### Intents einlesen und aufbereiten
Zuerst lesen wir die Trainings-Daten, die von chatette im JSON-Format ausgegeben in die Date `RASA_INTENTS` geschrieben wurden, aus, und schauen uns das Format der Einträge an:
```
import json
CHATETTE_DIR = os.path.join(DATA_DIR, 'chatette')
RASA_INTENTS = os.path.join(CHATETTE_DIR, 'output.json')
def load_intents():
with open(RASA_INTENTS) as intents_file:
intents = json.load(intents_file)
return intents['rasa_nlu_data']['common_examples']
sample_intent = load_intents()[0]
```
Wie bereits im [Video](https://www.youtube.com/watch?v=H_3R8inCOvM) erklärt, sind für Intent Recognition zwei Aufgaben zu lösen:
- die _Klassifikation_ des Intent anhand der gegebenen Äußerung und
- das Füllen der Slots.
Die zweite Aufgabe kann man als _Sequence Tagging_ auffassen — für jedes Token der Äußerung ist zu bestimmen, ob es den Parameter für einen Slot darstellt oder nicht. Für den Beispiel-Intent
> `{'entities': [{'end': 20, 'entity': 'Zeit', 'start': 16, 'value': '1993'},
> {'end': 35, 'entity': 'Ort', 'start': 24, 'value': 'Brandenburg'}],
> 'intent': 'Frag_Temperatur',
> 'text': 'Wie warm war es 1993 in Brandenburg'}`
wäre die Eingabe für diese beiden Aufgaben also die Token-Folge
> `['Wie', 'warm', 'war', 'es', '1993', 'in', 'Brandenburg']`
und die gewünschte Ausgabe jeweils
> `'Frag_Temperatur'`
beziehungsweise die Tag-Folge
> `['-', '-', '-', '-', 'Zeit', '-', 'Ort']`
Die folgende Funktion extrahiert aus den geladenen Beispiel-Intents die gewünschte Eingabe und die Ausgaben für diese beiden Aufgaben:
```
import spacy
from itertools import accumulate
nlp = spacy.load('de_core_news_sm')
def tokenize(text):
return [word for word in nlp(text)]
NO_ENTITY = '-'
def intent_and_sequences(intent):
def get_tag(offset):
"""Returns the tag (+slot name) for token starting at `offset`"""
ents = [ent['entity'] for ent in intent['entities'] if ent['start'] == offset]
return ents[0] if ents else NO_ENTITY
token = tokenize(intent['text'])
# `offsets` is the list of starting positions of the token
offsets = list(accumulate([0,] + [len(t.text_with_ws) for t in token]))
return (intent['intent'], token, list(map(get_tag, offsets[:-1])))
intent_and_sequences(sample_intent)
```
### Symbolische Daten in numerische Daten umwandeln
Die aufbereiteten Intents enthalten nun jeweils
1. die Folge der Token als "Eingabe"
2. den Namen des Intent als Ergebnis der Klassifikation und
3. die Folge der Slot-Namen als Ergebnis des Sequence Tagging.
Diese kategoriellen Daten müssen wir für die Weiterverarbeitung in numerische Daten umwandeln. Dafür bieten sich
- für 1. Wortvektoren und
- für 2. und 3. die One-hot-Kodierung an.
Außerdem müssen wir die Eingabe-Folge und Tag-Folge auf eine feste Länge bringen.
Beginnen wir mit der One-hot-Kodierung. Die folgende Funktion erzeug zu einer gegebenen Menge von Objekten ein Paar von Python-Dictionaries, welche jedem Objekt einen One-hot-Code und umgekehrt jedem Index das entsprechende Objekt zuordnet.
```
def ohe(s):
codes = np.eye(len(s))
numerated = list(enumerate(s))
return ({value: codes[idx] for (idx, value) in numerated},
{idx: value for (idx, value) in numerated})
```
Die nächste Hilfsfunktion erwartet eine Liste von Elementen und schneidet diese auf eine vorgegebene Länge beziehungsweise füllt sie mit einem vorgegebenen Element auf diese Länge auf.
```
def fill(items, max_len, filler):
if len(items) < max_len:
return items + [filler] * (max_len - len(items))
else:
return items[0:max_len]
```
Die Umwandlung der aufbereiteten Intent-Tripel in numerische Daten verpacken wir in einen [scikit-learn-Transformer](https://scikit-learn.org/stable/data_transforms.html), weil während der Umwandlung die One-Hot-Kodierung der Intent-Namen und Slot-Namen gelernt und eventuell später für neue Testdaten wieder gebraucht wird.
```
from sklearn.base import BaseEstimator, TransformerMixin
MAX_LEN = 20
VEC_DIM = len(list(nlp(' '))[0].vector)
class IntentNumerizer(BaseEstimator, TransformerMixin):
def __init__(self):
pass
def fit(self, X, y=None):
intent_names = set((x[0] for x in X))
self.intents_ohe, self.idx_intents = ohe(intent_names)
self.nr_intents = len(intent_names)
tag_lists = list(map(lambda x: set(x[2]), X)) + [[NO_ENTITY]]
tag_names = frozenset().union(*tag_lists)
# tag_names = set(())
self.tags_ohe, self.idx_tags = ohe(tag_names)
self.nr_tags = len(tag_names)
return self
def transform_utterance(self, token):
return np.stack(fill([tok.vector for tok in token], MAX_LEN,
np.zeros((VEC_DIM))))
def transform_tags(self, tags):
return np.stack([self.tags_ohe[t] for t in fill(tags, MAX_LEN, NO_ENTITY)])
def transform(self, X):
return (np.stack([self.transform_utterance(x[1]) for x in X]),
np.stack([self.intents_ohe[x[0]] for x in X]),
np.stack([self.transform_tags(x[2]) for x in X]))
def revert(self, intent_idx, tag_idxs):
return (self.idx_intents[intent_idx],
[self.idx_tags[t] for t in tag_idxs])
```
### Keras-Implementierung eines Bi-LSTM-Netzes für Intent Recognition
Wir implementieren nun mit Keras eine Netz-Architektur, die in [diesem Artikel]() vorgeschlagen wurde und schematisch in folgendem Diagramm dargestellt ist:
<img src="img/birnn.svg" style="background:white" width="80%" align="middle">
Hierbei wird
1. die Eingabe, wie bereits erklärt, als Folge von Wortvektoren dargestellt,
2. diese Eingabe erst durch eine rekurrente Schicht forwärts abgearbeitet,
3. der Endzustand dieser Schicht als Initialisierung einer sich anschließenden rekurrenten Schicht verwendet, welche die Eingabefolge rückwärts abarbeitet,
4. der Endzustand dieser Schicht an eine Schicht mit genau so vielen Neuronen, wie es Intent-Klassen gibt, zur Klassifikation des Intent weitergleitet,
5. die Ausgabe der beiden rekurrenten Schichten für jeden Schritt zusammengefügt und
6. die zusammengefügte Ausgabe jeweils an ein Bündel von so vielen Neuronen, wie es Slot-Arten gibt, zur Klassifikation des Tags des jeweiligen Wortes weitergeleitet.
Genau diesen Aufbau bilden wir nun mit Keras ab, wobei wir die [funktionale API]() benutzen. Als Loss-Funktion verwenden wir jeweils [kategorielle Kreuzentropie](). Für die rekurrenten Schichten verwenden wir [LSTM-Zellen](), auf die wir gleich noch eingehen.
```
from keras.models import Model
from keras.layers import Input, LSTM, Concatenate, TimeDistributed, Dense
UNITS = 256
def build_bilstm(input_dim, nr_intents, nr_tags, units=UNITS):
inputs = Input(shape=(MAX_LEN, input_dim))
lstm_params = {'units': units, 'return_sequences': True, 'return_state': True}
fwd = LSTM(**lstm_params)(inputs)
bwd = LSTM(**lstm_params)(inputs, initial_state=fwd[1:])
merged = Concatenate()([fwd[0], bwd[0]])
tags = TimeDistributed(Dense(nr_tags, activation='softmax'))(merged)
intent = Dense(nr_intents, activation='softmax')(bwd[2])
model = Model(inputs=inputs, outputs=[intent, tags])
model.compile(optimizer='Adam' ,loss='categorical_crossentropy')
return model
```
Schauen wir uns einmal genauer an, wie so eine LSTM-Zelle aufgebaut ist:
<img src="img/lstm.svg" style="background:white" width="70%" align="middle">
Die Bezeichnung 'LSTM' steht für _long short-term memory_ und rührt daher, dass solch eine Zelle neben der Eingabe des aktuellen Schrittes nicht nur die Ausgabe des vorherigen Schrittes, sondern zusätzlich auch einen Speicherwert des vorherigen Schrittes erhält. Nacheinander wird in der LSTM-Zelle dann jeweils anhand der aktuellen Eingabe und der vorherigen Ausgabe
1. in einem _forget gate_ entschieden, wieviel vom alten Speicherwert vergessen werden soll,
2. in einem _input gate_ entschieden, wieviel von der neuen Eingabe in den neuen Speicherwert aufgenommen werden soll,
3. in einem _output gate_ aus dem aktuellen Speicher die aktuelle Ausgabe gebildet.
### Training und Test des Bi-LSTM-Netzes
Schauen wir uns nun an, wie gut das funktioniert! Dazu müssen wir nun alles zusammenfügen und tun das in zwei Schritten.
Die Funktion `train_test_data` erwartet als Eingabe Regeln, wie wir sie für chatette in einem Python-Dictionary gespeichert hatten, und liefert die entsprechend erzeugten Intents in numerisch aufbereiter Form, aufgeteilt in Trainings- und Validierungsdaten, einschließlich des angepassten `IntentNumerizer`zurück.
```
TRAIN_RATIO = 0.7
def train_test_data(rules=RULES, train_ratio=TRAIN_RATIO):
structured_intents = list(map(intent_and_sequences, load_intents()))
intent_numerizer = IntentNumerizer()
X, y, Y = intent_numerizer.fit_transform(structured_intents)
nr_samples = len(y)
shuffled_indices = np.random.permutation(nr_samples)
split = int(nr_samples * train_ratio)
train_indices, test_indices = (shuffled_indices[0:split], shuffled_indices[split:])
y_train, X_train, Y_train = y[train_indices], X[train_indices], Y[train_indices]
y_test, X_test, Y_test = y[test_indices], X[test_indices], Y[test_indices]
return intent_numerizer, X_train, y_train, Y_train, X_test, y_test, Y_test
```
Mit diesen Trainings- und Testdaten trainiert beziehungsweise validiert die folgende Funktion `build_interpreter` nun das von `build_lstm` gebaute neuronale Netz und liefert einen Interpreter-Funktion zurück. Diese erwartet als Eingabe eine Äußerung, transformiert diese anschließend mit dem angepassten `IntentNumerizer` und führt mit dem zuvor trainierten Netz die Intent Recognition durch.
```
BATCH_SIZE = 128
EPOCHS = 10
def build_interpreter(rules=RULES, units=UNITS, batch_size=128, epochs=EPOCHS):
def interpreter(utterance):
x = intent_numerizer.transform_utterance(tokenize(utterance))
y, Y = model.predict(np.stack([x]))
tag_idxs = np.argmax(Y[0], axis=1)
intent_idx = np.argmax(y[0])
return intent_numerizer.revert(intent_idx, tag_idxs)
intent_numerizer, X_train, y_train, Y_train, X_test, y_test, Y_test = train_test_data(rules)
model = build_bilstm(X_train.shape[2], y_train.shape[1], Y_train.shape[2], units)
model.fit(x=X_train, y=[y_train, Y_train],
validation_data=(X_test,[y_test, Y_test]),
batch_size=batch_size, epochs=epochs)
return interpreter
```
Und nun sind wir bereit zum Testen!
```
interpreter = build_interpreter()
interpreter('Welche ungefähre Temperatur war 1992 und 2018 in Sachsen')
```
Und jetzt kannt Du loslegen — der WetterBot kann noch nicht viel, ist aber nun recht einfach zu trainieren! Und mit der selbstgebauten Intent Recognition wird er bestimmt noch besser! Ein paar Ideen dazu gibt Dir das Notebook mit Aufgaben zu Intent Recognition.
_Viel Spaß und bis bald zu einer neuen Lektion vom codecentric.AI bootcamp!_
| true |
code
| 0.455562 | null | null | null | null |
|
Copyright 2018 Google Inc.
Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at
https://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
**This tutorial is for educational purposes purposes only and is not intended for use in clinical diagnosis or clinical decision-making or for any other clinical use.**
# Training/Inference on Breast Density Classification Model on AutoML Vision
The goal of this tutorial is to train, deploy and run inference on a breast density classification model. Breast density is thought to be a factor for an increase in the risk for breast cancer. This will emphasize using the [Cloud Healthcare API](https://cloud.google.com/healthcare/) in order to store, retreive and transcode medical images (in DICOM format) in a managed and scalable way. This tutorial will focus on using [Cloud AutoML Vision](https://cloud.google.com/vision/automl/docs/beginners-guide) to scalably train and serve the model.
**Note: This is the AutoML version of the Cloud ML Engine Codelab found [here](./breast_density_cloud_ml.ipynb).**
## Requirements
- A Google Cloud project.
- Project has [Cloud Healthcare API](https://cloud.google.com/healthcare/docs/quickstart) enabled.
- Project has [Cloud AutoML API ](https://cloud.google.com/vision/automl/docs/quickstart) enabled.
- Project has [Cloud Build API](https://cloud.google.com/cloud-build/docs/quickstart-docker) enabled.
- Project has [Kubernetes engine API](https://console.developers.google.com/apis/api/container.googleapis.com/overview?project=) enabled.
- Project has [Cloud Resource Manager API](https://console.cloud.google.com/cloud-resource-manager) enabled.
## Notebook dependencies
We will need to install the hcls_imaging_ml_toolkit package found [here](./toolkit). This toolkit helps make working with DICOM objects and the Cloud Healthcare API easier.
In addition, we will install [dicomweb-client](https://dicomweb-client.readthedocs.io/en/latest/) to help us interact with the DIOCOMWeb API and [pydicom](https://pydicom.github.io/pydicom/dev/index.html) which is used to help up construct DICOM objects.
```
%%bash
pip3 install git+https://github.com/GoogleCloudPlatform/healthcare.git#subdirectory=imaging/ml/toolkit
pip3 install dicomweb-client
pip3 install pydicom
```
## Input Dataset
The dataset that will be used for training is the [TCIA CBIS-DDSM](https://wiki.cancerimagingarchive.net/display/Public/CBIS-DDSM) dataset. This dataset contains ~2500 mammography images in DICOM format. Each image is given a [BI-RADS breast density ](https://breast-cancer.ca/densitbi-rads/) score from 1 to 4. In this tutorial, we will build a binary classifier that distinguishes between breast density "2" (*scattered density*) and "3" (*heterogeneously dense*). These are the two most common and variably assigned scores. In the literature, this is said to be [particularly difficult for radiologists to consistently distinguish](https://aapm.onlinelibrary.wiley.com/doi/pdf/10.1002/mp.12683).
```
project_id = "MY_PROJECT" # @param
location = "us-central1"
dataset_id = "MY_DATASET" # @param
dicom_store_id = "MY_DICOM_STORE" # @param
# Input data used by AutoML must be in a bucket with the following format.
automl_bucket_name = "gs://" + project_id + "-vcm"
%%bash -s {project_id} {location} {automl_bucket_name}
# Create bucket.
gsutil -q mb -c regional -l $2 $3
# Allow Cloud Healthcare API to write to bucket.
PROJECT_NUMBER=`gcloud projects describe $1 | grep projectNumber | sed 's/[^0-9]//g'`
SERVICE_ACCOUNT="service-${PROJECT_NUMBER}@gcp-sa-healthcare.iam.gserviceaccount.com"
COMPUTE_ENGINE_SERVICE_ACCOUNT="${PROJECT_NUMBER}[email protected]"
gsutil -q iam ch serviceAccount:${SERVICE_ACCOUNT}:objectAdmin $3
gsutil -q iam ch serviceAccount:${COMPUTE_ENGINE_SERVICE_ACCOUNT}:objectAdmin $3
gcloud projects add-iam-policy-binding $1 --member=serviceAccount:${SERVICE_ACCOUNT} --role=roles/pubsub.publisher
gcloud projects add-iam-policy-binding $1 --member=serviceAccount:${COMPUTE_ENGINE_SERVICE_ACCOUNT} --role roles/pubsub.admin
# Allow compute service account to create datasets and dicomStores.
gcloud projects add-iam-policy-binding $1 --member=serviceAccount:${COMPUTE_ENGINE_SERVICE_ACCOUNT} --role roles/healthcare.dicomStoreAdmin
gcloud projects add-iam-policy-binding $1 --member=serviceAccount:${COMPUTE_ENGINE_SERVICE_ACCOUNT} --role roles/healthcare.datasetAdmin
import json
import os
import google.auth
from google.auth.transport.requests import AuthorizedSession
from hcls_imaging_ml_toolkit import dicom_path
credentials, project = google.auth.default()
authed_session = AuthorizedSession(credentials)
# Path to Cloud Healthcare API.
HEALTHCARE_API_URL = 'https://healthcare.googleapis.com/v1'
# Create Cloud Healthcare API dataset.
path = os.path.join(HEALTHCARE_API_URL, 'projects', project_id, 'locations', location, 'datasets?dataset_id=' + dataset_id)
headers = {'Content-Type': 'application/json'}
resp = authed_session.post(path, headers=headers)
assert resp.status_code == 200, 'error creating Dataset, code: {0}, response: {1}'.format(resp.status_code, resp.text)
print('Full response:\n{0}'.format(resp.text))
# Create Cloud Healthcare API DICOM store.
path = os.path.join(HEALTHCARE_API_URL, 'projects', project_id, 'locations', location, 'datasets', dataset_id, 'dicomStores?dicom_store_id=' + dicom_store_id)
resp = authed_session.post(path, headers=headers)
assert resp.status_code == 200, 'error creating DICOM store, code: {0}, response: {1}'.format(resp.status_code, resp.text)
print('Full response:\n{0}'.format(resp.text))
dicom_store_path = dicom_path.Path(project_id, location, dataset_id, dicom_store_id)
```
Next, we are going to transfer the DICOM instances to the Cloud Healthcare API.
Note: We are transfering >100GB of data so this will take some time to complete
```
# Store DICOM instances in Cloud Healthcare API.
path = 'https://healthcare.googleapis.com/v1/{}:import'.format(dicom_store_path)
headers = {'Content-Type': 'application/json'}
body = {
'gcsSource': {
'uri': 'gs://gcs-public-data--healthcare-tcia-cbis-ddsm/dicom/**'
}
}
resp = authed_session.post(path, headers=headers, json=body)
assert resp.status_code == 200, 'error creating Dataset, code: {0}, response: {1}'.format(resp.status_code, resp.text)
print('Full response:\n{0}'.format(resp.text))
response = json.loads(resp.text)
operation_name = response['name']
import time
def wait_for_operation_completion(path, timeout, sleep_time=30):
success = False
while time.time() < timeout:
print('Waiting for operation completion...')
resp = authed_session.get(path)
assert resp.status_code == 200, 'error polling for Operation results, code: {0}, response: {1}'.format(resp.status_code, resp.text)
response = json.loads(resp.text)
if 'done' in response:
if response['done'] == True and 'error' not in response:
success = True;
break
time.sleep(sleep_time)
print('Full response:\n{0}'.format(resp.text))
assert success, "operation did not complete successfully in time limit"
print('Success!')
return response
path = os.path.join(HEALTHCARE_API_URL, operation_name)
timeout = time.time() + 40*60 # Wait up to 40 minutes.
_ = wait_for_operation_completion(path, timeout)
```
### Explore the Cloud Healthcare DICOM dataset (optional)
This is an optional section to explore the Cloud Healthcare DICOM dataset. In the following code, we simply just list the studies that we have loaded into the Cloud Healthcare API. You can modify the *num_of_studies_to_print* parameter to print as many studies as desired.
```
num_of_studies_to_print = 2 # @param
path = os.path.join(HEALTHCARE_API_URL, dicom_store_path.dicomweb_path_str, 'studies')
resp = authed_session.get(path)
assert resp.status_code == 200, 'error querying Dataset, code: {0}, response: {1}'.format(resp.status_code, resp.text)
response = json.loads(resp.text)
print(json.dumps(response[:num_of_studies_to_print], indent=2))
```
## Convert DICOM to JPEG
The ML model that we will build requires that the dataset be in JPEG. We will leverage the Cloud Healthcare API to transcode DICOM to JPEG.
First we will create a [Google Cloud Storage](https://cloud.google.com/storage/) bucket to hold the output JPEG files. Next, we will use the ExportDicomData API to transform the DICOMs to JPEGs.
```
# Folder to store input images for AutoML Vision.
jpeg_folder = automl_bucket_name + "/images/"
```
Next we will convert the DICOMs to JPEGs using the [ExportDicomData](https://cloud.google.com/sdk/gcloud/reference/beta/healthcare/dicom-stores/export/gcs).
```
%%bash -s {jpeg_folder} {project_id} {location} {dataset_id} {dicom_store_id}
gcloud beta healthcare --project $2 dicom-stores export gcs $5 --location=$3 --dataset=$4 --mime-type="image/jpeg; transfer-syntax=1.2.840.10008.1.2.4.50" --gcs-uri-prefix=$1
```
Meanwhile, you should be able to observe the JPEG images being added to your Google Cloud Storage bucket.
Next, we will join the training data stored in Google Cloud Storage with the labels in the TCIA website. The output of this step is a [CSV file that is input to AutoML](https://cloud.google.com/vision/automl/docs/prepare). This CSV contains a list of pairs of (IMAGE_PATH, LABEL).
```
# tensorflow==1.15.0 to have same versions in all environments - dataflow, automl, ai-platform
!pip install tensorflow==1.15.0 --ignore-installed
# CSV to hold (IMAGE_PATH, LABEL) list.
input_data_csv = automl_bucket_name + "/input.csv"
import csv
import os
import re
from tensorflow.python.lib.io import file_io
import scripts.tcia_utils as tcia_utils
# Get map of study_uid -> file paths.
path_list = file_io.get_matching_files(os.path.join(jpeg_folder, '*/*/*'))
study_uid_to_file_paths = {}
pattern = r'^{0}(?P<study_uid>[^/]+)/(?P<series_uid>[^/]+)/(?P<instance_uid>.*)'.format(jpeg_folder)
for path in path_list:
match = re.search(pattern, path)
study_uid_to_file_paths[match.group('study_uid')] = path
# Get map of study_uid -> labels.
study_uid_to_labels = tcia_utils.GetStudyUIDToLabelMap()
# Join the two maps, output results to CSV in Google Cloud Storage.
with file_io.FileIO(input_data_csv, 'w') as f:
writer = csv.writer(f, delimiter=',')
for study_uid, label in study_uid_to_labels.items():
if study_uid in study_uid_to_file_paths:
writer.writerow([study_uid_to_file_paths[study_uid], label])
```
## Training
***This section will focus on using AutoML through its API. AutoML can also be used through the user interface found [here](https://console.cloud.google.com/vision/). The below steps in this section can all be done through the web UI .***
We will use [AutoML Vision ](https://cloud.google.com/automl/) to train the classification model. AutoML provides a fully managed solution for training the model. All we will do is input the list of input images and labels. The trained model in AutoML will be able to classify the mammography images as either "2" (scattered density) or "3" (heterogeneously dense).
As a first step, we will create a AutoML dataset.
```
automl_dataset_display_name = "MY_AUTOML_DATASET" # @param
import json
import os
# Path to AutoML API.
AUTOML_API_URL = 'https://automl.googleapis.com/v1beta1'
# Path to request creation of AutoML dataset.
path = os.path.join(AUTOML_API_URL, 'projects', project_id, 'locations', location, 'datasets')
# Headers (request in JSON format).
headers = {'Content-Type': 'application/json'}
# Body (encoded in JSON format).
config = {'display_name': automl_dataset_display_name, 'image_classification_dataset_metadata': {'classification_type': 'MULTICLASS'}}
resp = authed_session.post(path, headers=headers, json=config)
assert resp.status_code == 200, 'creating AutoML dataset, code: {0}, response: {1}'.format(resp.status_code, resp.text)
print('Full response:\n{0}'.format(resp.text))
# Record the AutoML dataset name.
response = json.loads(resp.text)
automl_dataset_name = response['name']
```
Next, we will import the CSV that contains the list of (IMAGE_PATH, LABEL) list into AutoML. **Please ignore errors regarding an existing ground truth.**
```
# Path to request import into AutoML dataset.
path = os.path.join(AUTOML_API_URL, automl_dataset_name + ':importData')
# Body (encoded in JSON format).
config = {'input_config': {'gcs_source': {'input_uris': [input_data_csv]}}}
resp = authed_session.post(path, headers=headers, json=config)
assert resp.status_code == 200, 'error importing AutoML dataset, code: {0}, response: {1}'.format(resp.status_code, resp.text)
print('Full response:\n{0}'.format(resp.text))
# Record operation_name so we can poll for it later.
response = json.loads(resp.text)
operation_name = response['name']
```
The output of the previous step is an [operation](https://cloud.google.com/vision/automl/docs/models#get-operation) that will need to poll the status for. We will poll until the operation's "done" field is set to true. This will take a few minutes to complete so we will wait until completion.
```
path = os.path.join(AUTOML_API_URL, operation_name)
timeout = time.time() + 40*60 # Wait up to 40 minutes.
_ = wait_for_operation_completion(path, timeout)
```
Next, we will train the model to perform classification. We will set the training budget to be a maximum of 1hr (but this can be modified below). The cost of using AutoML can be found [here](https://cloud.google.com/vision/automl/pricing). Typically, the longer the model is trained for, the more accurate it will be.
```
# Name of the model.
model_display_name = "MY_MODEL_NAME" # @param
# Training budget (1 hr).
training_budget = 1 # @param
# Path to request import into AutoML dataset.
path = os.path.join(AUTOML_API_URL, 'projects', project_id, 'locations', location, 'models')
# Headers (request in JSON format).
headers = {'Content-Type': 'application/json'}
# Body (encoded in JSON format).
automl_dataset_id = automl_dataset_name.split('/')[-1]
config = {'display_name': model_display_name, 'dataset_id': automl_dataset_id, 'image_classification_model_metadata': {'train_budget': training_budget}}
resp = authed_session.post(path, headers=headers, json=config)
assert resp.status_code == 200, 'error creating AutoML model, code: {0}, response: {1}'.format(resp.status_code, contenresp.text)
print('Full response:\n{0}'.format(resp.text))
# Record operation_name so we can poll for it later.
response = json.loads(resp.text)
operation_name = response['name']
```
The output of the previous step is also an [operation](https://cloud.google.com/vision/automl/docs/models#get-operation) that will need to poll the status of. We will poll until the operation's "done" field is set to true. This will take a few minutes to complete.
```
path = os.path.join(AUTOML_API_URL, operation_name)
timeout = time.time() + 40*60 # Wait up to 40 minutes.
sleep_time = 5*60 # Update each 5 minutes.
response = wait_for_operation_completion(path, timeout, sleep_time)
full_model_name = response['response']['name']
# google.cloud.automl to make api calls to Cloud AutoML
!pip install google-cloud-automl
from google.cloud import automl_v1
client = automl_v1.AutoMlClient()
response = client.deploy_model(full_model_name)
print(u'Model deployment finished. {}'.format(response.result()))
```
Next, we will check out the accuracy metrics for the trained model. The following command will return the [AUC (ROC)](https://developers.google.com/machine-learning/crash-course/classification/roc-and-auc), [precision](https://developers.google.com/machine-learning/crash-course/classification/precision-and-recall) and [recall](https://developers.google.com/machine-learning/crash-course/classification/precision-and-recall) for the model, for various ML classification thresholds.
```
# Path to request to get model accuracy metrics.
path = os.path.join(AUTOML_API_URL, full_model_name, 'modelEvaluations')
resp = authed_session.get(path)
assert resp.status_code == 200, 'error getting AutoML model evaluations, code: {0}, response: {1}'.format(resp.status_code, resp.text)
print('Full response:\n{0}'.format(resp.text))
```
## Inference
To allow medical imaging ML models to be easily integrated into clinical workflows, an *inference module* can be used. A standalone modality, a PACS system or a DICOM router can push DICOM instances into Cloud Healthcare [DICOM stores](https://cloud.google.com/healthcare/docs/introduction), allowing ML models to be triggered for inference. This inference results can then be structured into various DICOM formats (e.g. DICOM [structured reports](http://dicom.nema.org/MEDICAL/Dicom/2014b/output/chtml/part20/sect_A.3.html)) and stored in the Cloud Healthcare API, which can then be retrieved by the customer.
The inference module is built as a [Docker](https://www.docker.com/) container and deployed using [Kubernetes](https://kubernetes.io/), allowing you to easily scale your deployment. The dataflow for inference can look as follows (see corresponding diagram below):
1. Client application uses [STOW-RS](ftp://dicom.nema.org/medical/Dicom/2013/output/chtml/part18/sect_6.6.html) to push a new DICOM instance to the Cloud Healthcare DICOMWeb API.
2. The insertion of the DICOM instance triggers a [Cloud Pubsub](https://cloud.google.com/pubsub/) message to be published. The *inference module* will pull incoming Pubsub messages and will recieve a message for the previously inserted DICOM instance.
3. The *inference module* will retrieve the instance in JPEG format from the Cloud Healthcare API using [WADO-RS](ftp://dicom.nema.org/medical/Dicom/2013/output/chtml/part18/sect_6.5.html).
4. The *inference module* will send the JPEG bytes to the model hosted on AutoML.
5. AutoML will return the prediction back to the *inference module*.
6. The *inference module* will package the prediction into a DICOM instance. This can potentially be a DICOM structured report, [presentation state](ftp://dicom.nema.org/MEDICAL/dicom/2014b/output/chtml/part03/sect_A.33.html), or even burnt text on the image. In this codelab, we will focus on just DICOM structured reports, specifically [Comprehensive Structured Reports](http://dicom.nema.org/dicom/2013/output/chtml/part20/sect_A.3.html). The structured report is then stored back in the Cloud Healthcare API using STOW-RS.
7. The client application can query for (or retrieve) the structured report by using [QIDO-RS](http://dicom.nema.org/dicom/2013/output/chtml/part18/sect_6.7.html) or WADO-RS. Pubsub can also be used by the client application to poll for the newly created DICOM structured report instance.

To begin, we will create a new DICOM store that will store our inference source (DICOM mammography instance) and results (DICOM structured report). In order to enable Pubsub notifications to be triggered on inserted instances, we will give the DICOM store a Pubsub channel to publish on.
```
# Pubsub config.
pubsub_topic_id = "MY_PUBSUB_TOPIC_ID" # @param
pubsub_subscription_id = "MY_PUBSUB_SUBSRIPTION_ID" # @param
# DICOM Store for store DICOM used for inference.
inference_dicom_store_id = "MY_INFERENCE_DICOM_STORE" # @param
pubsub_subscription_name = "projects/" + project_id + "/subscriptions/" + pubsub_subscription_id
inference_dicom_store_path = dicom_path.FromPath(dicom_store_path, store_id=inference_dicom_store_id)
%%bash -s {pubsub_topic_id} {pubsub_subscription_id} {project_id} {location} {dataset_id} {inference_dicom_store_id}
# Create Pubsub channel.
gcloud beta pubsub topics create $1
gcloud beta pubsub subscriptions create $2 --topic $1
# Create a Cloud Healthcare DICOM store that published on given Pubsub topic.
TOKEN=`gcloud beta auth application-default print-access-token`
NOTIFICATION_CONFIG="{notification_config: {pubsub_topic: \"projects/$3/topics/$1\"}}"
curl -s -X POST -H "Content-Type: application/json" -H "Authorization: Bearer ${TOKEN}" -d "${NOTIFICATION_CONFIG}" https://healthcare.googleapis.com/v1/projects/$3/locations/$4/datasets/$5/dicomStores?dicom_store_id=$6
# Enable Cloud Healthcare API to publish on given Pubsub topic.
PROJECT_NUMBER=`gcloud projects describe $3 | grep projectNumber | sed 's/[^0-9]//g'`
SERVICE_ACCOUNT="service-${PROJECT_NUMBER}@gcp-sa-healthcare.iam.gserviceaccount.com"
gcloud beta pubsub topics add-iam-policy-binding $1 --member="serviceAccount:${SERVICE_ACCOUNT}" --role="roles/pubsub.publisher"
```
Next, we will building the *inference module* using [Cloud Build API](https://cloud.google.com/cloud-build/docs/api/reference/rest/). This will create a Docker container that will be stored in [Google Container Registry](https://cloud.google.com/container-registry/). The inference module code is found in *[inference.py](./scripts/inference/inference.py)*. The build script used to build the Docker container for this module is *[cloudbuild.yaml](./scripts/inference/cloudbuild.yaml)*. Progress of build may be found on [cloud build dashboard](https://console.cloud.google.com/cloud-build/builds?project=).
```
%%bash -s {project_id}
PROJECT_ID=$1
gcloud builds submit --config scripts/inference/cloudbuild.yaml --timeout 1h scripts/inference
```
Next, we will deploy the *inference module* to Kubernetes.
Then we create a Kubernetes Cluster and a Deployment for the *inference module*.
```
%%bash -s {project_id} {location} {pubsub_subscription_name} {full_model_name} {inference_dicom_store_path}
gcloud container clusters create inference-module --region=$2 --scopes https://www.googleapis.com/auth/cloud-platform --num-nodes=1
PROJECT_ID=$1
SUBSCRIPTION_PATH=$3
MODEL_PATH=$4
INFERENCE_DICOM_STORE_PATH=$5
cat <<EOF | kubectl create -f -
apiVersion: extensions/v1beta1
kind: Deployment
metadata:
name: inference-module
namespace: default
spec:
replicas: 1
template:
metadata:
labels:
app: inference-module
spec:
containers:
- name: inference-module
image: gcr.io/${PROJECT_ID}/inference-module:latest
command:
- "/opt/inference_module/bin/inference_module"
- "--subscription_path=${SUBSCRIPTION_PATH}"
- "--model_path=${MODEL_PATH}"
- "--dicom_store_path=${INFERENCE_DICOM_STORE_PATH}"
- "--prediction_service=AutoML"
EOF
```
Next, we will store a mammography DICOM instance from the TCIA dataset to the DICOM store. This is the image that we will request inference for. Pushing this instance to the DICOM store will result in a Pubsub message, which will trigger the *inference module*.
```
# DICOM Study/Series UID of input mammography image that we'll push for inference.
input_mammo_study_uid = "1.3.6.1.4.1.9590.100.1.2.85935434310203356712688695661986996009"
input_mammo_series_uid = "1.3.6.1.4.1.9590.100.1.2.374115997511889073021386151921807063992"
input_mammo_instance_uid = "1.3.6.1.4.1.9590.100.1.2.289923739312470966435676008311959891294"
from google.cloud import storage
from dicomweb_client.api import DICOMwebClient
from dicomweb_client import session_utils
from pydicom
storage_client = storage.Client()
bucket = storage_client.bucket('gcs-public-data--healthcare-tcia-cbis-ddsm', user_project=project_id)
blob = bucket.blob("dicom/{}/{}/{}.dcm".format(input_mammo_study_uid,input_mammo_series_uid,input_mammo_instance_uid))
blob.download_to_filename('example.dcm')
dataset = pydicom.dcmread('example.dcm')
session = session_utils.create_session_from_gcp_credentials()
study_path = dicom_path.FromPath(inference_dicom_store_path, study_uid=input_mammo_study_uid)
dicomweb_url = os.path.join(HEALTHCARE_API_URL, study_path.dicomweb_path_str)
dcm_client = DICOMwebClient(dicomweb_url, session)
dcm_client.store_instances(datasets=[dataset])
```
You should be able to observe the *inference module*'s logs by running the following command. In the logs, you should observe that the inference module successfully recieved the the Pubsub message and ran inference on the DICOM instance. The logs should also include the inference results. It can take a few minutes for the Kubernetes deployment to start up, so you many need to run this a few times. The logs should also include the inference results. It can take a few minutes for the Kubernetes deployment to start up, so you many need to run this a few times.
```
!kubectl logs -l app=inference-module
```
You can also query the Cloud Healthcare DICOMWeb API (using QIDO-RS) to see that the DICOM structured report has been inserted for the study. The structured report contents can be found under tag **"0040A730"**.
You can optionally also use WADO-RS to recieve the instance (e.g. for viewing).
```
dcm_client.search_for_instances(study_path.study_uid, fields=['all'])
```
| true |
code
| 0.433202 | null | null | null | null |
|
# Lab 2: networkX Drawing and Network Properties
```
import matplotlib.pyplot as plt
import pandas as pd
from networkx import nx
```
## TOC
1. [Q1](#Q1)
2. [Q2](#Q2)
3. [Q3](#Q3)
4. [Q4](#Q4)
```
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(11, 8))
ax = axes.flatten()
path = nx.path_graph(5)
nx.draw_networkx(path, with_labels=True, ax=ax[0])
ax[0].set_title('Path')
cycle = nx.cycle_graph(5)
nx.draw_networkx(cycle, node_color='green', with_labels=True, ax=ax[1])
ax[1].set_title('Cycle')
complete = nx.complete_graph(5)
nx.draw_networkx(complete, node_color='#A0CBE2', edge_color='red', width=2, with_labels=False, ax=ax[2])
ax[2].set_title('Complete')
star = nx.star_graph(5)
pos=nx.spring_layout(star)
nx.draw_networkx(star, pos, with_labels=True, ax=ax[3])
ax[3].set_title('Star')
for i in range(4): ax[i].set_axis_off()
plt.show()
```
### Q1:
*Use one sentence each to briefly describe the characteristics of each graph
type (its shape, edges, etc..)*
$V$ = a set of vertices, where $V \ni \{v_1, v_2, ... , v_n\}$
$E$ = a set of edges, where $E \subseteq \{\{v_x,v_y\}\mid v_x,v_y\in V\}$
Let $G$ = ($V$, $E$) be an undirected graph
- **Path Graph** := Suppose there are n vertices ($v_0, v_1, ... , v_n$) in $G$, such that $\forall e_{(v_x,v_y)} \in E $ | $0 \leq x \leq n-1$; $y = x + 1$
- **Cycle Graph** := Suppose there are n vertices ($v_0, v_1, ... , v_n$) in $G$, such that $\forall e_{(v_x,v_y)} \in E $ | $0 \leq x \leq n; \{(0 \leq x \leq n-1) \Rightarrow (y = x + 1)\} \land \{(x = n) \Rightarrow (y = 0)\}$
- **Complete Graph**:= Suppose there are n vertices ($v_0, v_1, ... , v_n$) in $G$, such that $\forall e_{(v_x,v_y)} \in E $ | $x \neq y; 0 \leq x,y \leq n$
- **Star Graph** := Suppose there are n vertices ($v_0, v_1, ... , v_n$) in $G$, such that $\forall e_{(v_x,v_y)} \in E $ | $x = 0; 1 \leq y \leq n$
```
G = nx.lollipop_graph(3,2)
nx.draw(G, with_labels=True)
plt.show()
list(nx.connected_components(G))
nx.clustering(G)
```
### Q2:
*How many connected components are there in the graph? What are they?*
There is only one connected component in the graph, it's all 5 vertices of the graph
### Q3:
*Which nodes have the highest local clustering coefficient? Explain (from the
definition) why they have high clustering coefficient.*
Node 0 and 1 have the highest local clustering coefficient of 1, because the neighbor of these two nodes are each other and node 2, $(2*1\text{ between neighbor link})\div(2\text{ degrees}*(2-1)) = 1$
```
def netMeta(net):
meta = {}
meta["radius"]= nx.radius(net)
meta["diameter"]= nx.diameter(net)
meta["eccentricity"]= nx.eccentricity(net)
meta["center"]= nx.center(net)
meta["periphery"]= nx.periphery(net)
meta["density"]= nx.density(net)
return meta
netMeta(G)
def netAna(net):
cols = ['Node name', "Betweenness centrality", "Degree centrality", "Closeness centrality", "Eigenvector centrality"]
rows =[]
print()
a = nx.betweenness_centrality(net)
b = nx.degree_centrality(net)
c = nx.closeness_centrality(net)
d = nx.eigenvector_centrality(net)
for v in net.nodes():
temp = []
temp.append(v)
temp.append(a[v])
temp.append(b[v])
temp.append(c[v])
temp.append(d[v])
rows.append(temp)
df = pd.DataFrame(rows,columns=cols)
df.set_index('Node name', inplace = True)
return df
G_stat = netAna(G)
G_stat
G_stat.sort_values(by=['Eigenvector centrality'])
```
### Q4:
*Which node(s) has the highest betweenness, degree, closeness, eigenvector
centrality? Explain using the definitions and graph structures.*
Node 2 has the highest betweenness, degree, closeness, and eigenvector centrality
Because node 2 has the most geodesics passing through, it has the highest degree of 3, it has the shortest average path length, and it has the most refferences by its neighbors
```
pathlengths = []
print("source vertex {target:length, }")
for v in G.nodes():
spl = dict(nx.single_source_shortest_path_length(G, v))
print('{} {} '.format(v, spl))
for p in spl:
pathlengths.append(spl[p])
print('')
print("average shortest path length %s" % (sum(pathlengths) / len(pathlengths)))
dist = {}
for p in pathlengths:
if p in dist: dist[p] += 1
else: dist[p] = 1
print('')
print("length #paths")
verts = dist.keys()
for d in sorted(verts):
print('%s %d' % (d, dist[d]))
mapping = {0: 'a', 1: 'b', 2: 'c', 3: 'd', 4: 'e'}
H = nx.relabel_nodes(G, mapping)
nx.draw(H, with_labels=True)
plt.show()
```
| true |
code
| 0.370524 | null | null | null | null |
|
# Tutorial
In this notebook, we will see how to pass your own encoder and decoder's architectures to your VAE model using pythae!
```
# If you run on colab uncomment the following line
#!pip install git+https://github.com/clementchadebec/benchmark_VAE.git
import torch
import torchvision.datasets as datasets
import matplotlib.pyplot as plt
import numpy as np
import os
%matplotlib inline
%load_ext autoreload
%autoreload 2
```
### Get the data
```
mnist_trainset = datasets.MNIST(root='../data', train=True, download=True, transform=None)
n_samples = 200
dataset = mnist_trainset.data[np.array(mnist_trainset.targets)==2][:n_samples].reshape(-1, 1, 28, 28) / 255.
fig, axes = plt.subplots(2, 10, figsize=(10, 2))
for i in range(2):
for j in range(10):
axes[i][j].matshow(dataset[i*10 +j].reshape(28, 28), cmap='gray')
axes[i][j].axis('off')
plt.tight_layout(pad=0.8)
```
## Let's build a custom auto-encoding architecture!
### First thing, you need to import the ``BaseEncoder`` and ``BaseDecoder`` as well as ``ModelOutput`` classes from pythae by running
```
from pythae.models.nn import BaseEncoder, BaseDecoder
from pythae.models.base.base_utils import ModelOutput
```
### Then build your own architectures
```
import torch.nn as nn
class Encoder_VAE_MNIST(BaseEncoder):
def __init__(self, args):
BaseEncoder.__init__(self)
self.input_dim = (1, 28, 28)
self.latent_dim = args.latent_dim
self.n_channels = 1
self.conv_layers = nn.Sequential(
nn.Conv2d(self.n_channels, 128, 4, 2, padding=1),
nn.BatchNorm2d(128),
nn.ReLU(),
nn.Conv2d(128, 256, 4, 2, padding=1),
nn.BatchNorm2d(256),
nn.ReLU(),
nn.Conv2d(256, 512, 4, 2, padding=1),
nn.BatchNorm2d(512),
nn.ReLU(),
nn.Conv2d(512, 1024, 4, 2, padding=1),
nn.BatchNorm2d(1024),
nn.ReLU(),
)
self.embedding = nn.Linear(1024, args.latent_dim)
self.log_var = nn.Linear(1024, args.latent_dim)
def forward(self, x: torch.Tensor):
h1 = self.conv_layers(x).reshape(x.shape[0], -1)
output = ModelOutput(
embedding=self.embedding(h1),
log_covariance=self.log_var(h1)
)
return output
class Decoder_AE_MNIST(BaseDecoder):
def __init__(self, args):
BaseDecoder.__init__(self)
self.input_dim = (1, 28, 28)
self.latent_dim = args.latent_dim
self.n_channels = 1
self.fc = nn.Linear(args.latent_dim, 1024 * 4 * 4)
self.deconv_layers = nn.Sequential(
nn.ConvTranspose2d(1024, 512, 3, 2, padding=1),
nn.BatchNorm2d(512),
nn.ReLU(),
nn.ConvTranspose2d(512, 256, 3, 2, padding=1, output_padding=1),
nn.BatchNorm2d(256),
nn.ReLU(),
nn.ConvTranspose2d(256, self.n_channels, 3, 2, padding=1, output_padding=1),
nn.Sigmoid(),
)
def forward(self, z: torch.Tensor):
h1 = self.fc(z).reshape(z.shape[0], 1024, 4, 4)
output = ModelOutput(reconstruction=self.deconv_layers(h1))
return output
```
### Define a model configuration (in which the latent will be stated). Here, we use the RHVAE model.
```
from pythae.models import VAEConfig
model_config = VAEConfig(
input_dim=(1, 28, 28),
latent_dim=10
)
```
### Build your encoder and decoder
```
encoder = Encoder_VAE_MNIST(model_config)
decoder= Decoder_AE_MNIST(model_config)
```
### Last but not least. Build you RHVAE model by passing the ``encoder`` and ``decoder`` arguments
```
from pythae.models import VAE
model = VAE(
model_config=model_config,
encoder=encoder,
decoder=decoder
)
```
### Now you can see the model that you've just built contains the custom autoencoder and decoder
```
model
```
### *note*: If you want to launch a training of such a model, try to ensure that the provided architectures are suited for the data. pythae performs a model sanity check before launching training and raises an error if the model cannot encode and decode an input data point
## Train the model !
```
from pythae.trainers import BaseTrainerConfig
from pythae.pipelines import TrainingPipeline
```
### Build the training pipeline with your ``TrainingConfig`` instance
```
training_config = BaseTrainerConfig(
output_dir='my_model_with_custom_archi',
learning_rate=1e-3,
batch_size=200,
steps_saving=None,
num_epochs=200)
pipeline = TrainingPipeline(
model=model,
training_config=training_config)
```
### Launch the ``Pipeline``
```
torch.manual_seed(8)
torch.cuda.manual_seed(8)
pipeline(
train_data=dataset
)
```
### *note 1*: You will see now that a ``encoder.pkl`` and ``decoder.pkl`` appear in the folder ``my_model_with_custom_archi/training_YYYY_MM_DD_hh_mm_ss/final_model`` to allow model rebuilding with your own architecture ``Encoder_VAE_MNIST`` and ``Decoder_AE_MNIST``.
### *note 2*: Model rebuilding is based on the [dill](https://pypi.org/project/dill/) librairy allowing to reload the class whithout importing them. Hence, you should still be able to reload the model even if the classes ``Encoder_VAE_MNIST`` or ``Decoder_AE_MNIST`` were not imported.
```
last_training = sorted(os.listdir('my_model_with_custom_archi'))[-1]
print(last_training)
```
### You can now reload the model easily using the classmethod ``VAE.load_from_folder``
```
model_rec = VAE.load_from_folder(os.path.join('my_model_with_custom_archi', last_training, 'final_model'))
model_rec
```
## The model can now be used to generate new samples !
```
from pythae.samplers import NormalSampler
sampler = NormalSampler(
model=model_rec
)
gen_data = sampler.sample(
num_samples=25
)
import matplotlib.pyplot as plt
fig, axes = plt.subplots(nrows=5, ncols=5, figsize=(10, 10))
for i in range(5):
for j in range(5):
axes[i][j].imshow(gen_data[i*5 +j].cpu().reshape(28, 28), cmap='gray')
axes[i][j].axis('off')
plt.tight_layout(pad=0.)
```
| true |
code
| 0.813442 | null | null | null | null |
|
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from ttim import *
```
### Theis
```
from scipy.special import exp1
def theis(r, t, T, S, Q):
u = r ** 2 * S / (4 * T * t)
h = -Q / (4 * np.pi * T) * exp1(u)
return h
def theisQr(r, t, T, S, Q):
u = r ** 2 * S / (4 * T * t)
return -Q / (2 * np.pi) * np.exp(-u) / r
T = 500
S = 1e-4
t = np.logspace(-5, 0, 100)
r = 30
Q = 788
htheis = theis(r, t, T, S, Q)
Qrtheis = theisQr(r, t, T, S, Q)
ml = ModelMaq(kaq=25, z=[20, 0], Saq=S/20, tmin=1e-5, tmax=1)
w = Well(ml, tsandQ=[(0, Q)], rw=1e-5)
ml.solve()
h = ml.head(r, 0, t)
Qx, Qy = ml.disvec(r, 0, t)
plt.figure(figsize=(12, 4))
plt.subplot(121)
plt.semilogx(t, htheis, 'b', label='theis')
plt.semilogx(t, h[0], 'r--', label='ttim')
plt.xlabel('time (day)')
plt.ylabel('head (m)')
plt.legend();
plt.subplot(122)
plt.semilogx(t, Qrtheis, 'b', label='theis')
plt.semilogx(t, Qx[0], 'r--', label='ttim')
plt.xlabel('time (day)')
plt.ylabel('head (m)')
plt.legend(loc='best');
def test(M=10):
ml = ModelMaq(kaq=25, z=[20, 0], Saq=S/20, tmin=1e-5, tmax=1, M=M)
w = Well(ml, tsandQ=[(0, Q)], rw=1e-5)
ml.solve(silent=True)
h = ml.head(r, 0, t)
return htheis - h[0]
enumba = test(M=10)
plt.plot(t, enumba, 'C1')
plt.xlabel('time (d)')
plt.ylabel('head difference Thies - Ttim');
plt.plot(t, Qrtheis - Qx[0])
plt.xlabel('time (d)')
plt.ylabel('Qx difference Thies - Ttim');
def compare(M=10):
ml = ModelMaq(kaq=25, z=[20, 0], Saq=S/20, tmin=1e-5, tmax=1, M=M)
w = Well(ml, tsandQ=[(0, Q)], rw=1e-5)
ml.solve(silent=True)
h = ml.head(r, 0, t)
rmse = np.sqrt(np.mean((h[0] - htheis)**2))
return rmse
Mlist = np.arange(1, 21)
rmse = np.zeros(len(Mlist))
for i, M in enumerate(Mlist):
rmse[i] = compare(M)
plt.semilogy(Mlist, rmse)
plt.xlabel('Number of terms M')
plt.xticks(np.arange(1, 21))
plt.ylabel('relative error')
plt.title('comparison between TTim solution and Theis \n solution using numba and M terms')
plt.grid()
def volume(r, t=1):
return -2 * np.pi * r * ml.head(r, 0, t) * ml.aq.Scoefaq[0]
from scipy.integrate import quad
quad(volume, 1e-5, np.inf)
from scipy.special import exp1
def theis2(r, t, T, S, Q, tend):
u1 = r ** 2 * S / (4 * T * t)
u2 = r ** 2 * S / (4 * T * (t[t > tend] - tend))
h = -Q / (4 * np.pi * T) * exp1(u1)
h[t > tend] -= -Q / (4 * np.pi * T) * exp1(u2)
return h
ml2 = ModelMaq(kaq=25, z=[20, 0], Saq=S/20, tmin=1e-5, tmax=10)
w2 = Well(ml2, tsandQ=[(0, Q), (1, 0)])
ml2.solve()
t2 = np.linspace(0.01, 2, 100)
htheis2 = theis2(r, t2, T, S, Q, tend=1)
h2 = ml2.head(r, 0, t2)
plt.plot(t2, htheis2, 'b', label='theis')
plt.plot(t2, h2[0], 'r--', label='ttim')
plt.legend(loc='best');
```
### Hantush
```
T = 500
S = 1e-4
c = 1000
t = np.logspace(-5, 0, 100)
r = 30
Q = 788
from scipy.integrate import quad
def integrand_hantush(y, r, lab):
return np.exp(-y - r ** 2 / (4 * lab ** 2 * y)) / y
def hantush(r, t, T, S, c, Q, tstart=0):
lab = np.sqrt(T * c)
u = r ** 2 * S / (4 * T * (t - tstart))
F = quad(integrand_hantush, u, np.inf, args=(r, lab))[0]
return -Q / (4 * np.pi * T) * F
hantushvec = np.vectorize(hantush)
ml = ModelMaq(kaq=25, z=[21, 20, 0], c=[1000], Saq=S/20, topboundary='semi', tmin=1e-5, tmax=1)
w = Well(ml, tsandQ=[(0, Q)])
ml.solve()
hhantush = hantushvec(30, t, T, S, c, Q)
h = ml.head(r, 0, t)
plt.semilogx(t, hhantush, 'b', label='hantush')
plt.semilogx(t, h[0], 'r--', label='ttim')
plt.legend(loc='best');
```
### Well with welbore storage
```
T = 500
S = 1e-4
t = np.logspace(-5, 0, 100)
rw = 0.3
Q = 788
ml = ModelMaq(kaq=25, z=[20, 0], Saq=S/20, tmin=1e-5, tmax=1)
w = Well(ml, rw=rw, tsandQ=[(0, Q)])
ml.solve()
hnostorage = ml.head(rw, 0, t)
ml = ModelMaq(kaq=25, z=[20, 0], Saq=S/20, tmin=1e-5, tmax=1)
w = Well(ml, rw=rw, tsandQ=[(0, Q)], rc=rw)
ml.solve()
hstorage = ml.head(rw, 0, t)
plt.semilogx(t, hnostorage[0], label='no storage')
plt.semilogx(t, hstorage[0], label='with storage')
plt.legend(loc='best')
plt.xticks([1/(24*60*60), 1/(24 * 60), 1/24, 1], ['1 sec', '1 min', '1 hr', '1 d']);
```
### Slug test
```
k = 25
H = 20
S = 1e-4 / H
t = np.logspace(-7, -1, 100)
rw = 0.2
rc = 0.2
delh = 1
ml = ModelMaq(kaq=k, z=[H, 0], Saq=S, tmin=1e-7, tmax=1)
Qslug = np.pi * rc ** 2 * delh
w = Well(ml, tsandQ=[(0, -Qslug)], rw=rw, rc=rc, wbstype='slug')
ml.solve()
h = w.headinside(t)
plt.semilogx(t, h[0])
plt.xticks([1 / (24 * 60 * 60) / 10, 1 / (24 * 60 * 60), 1 / (24 * 60), 1 / 24],
['0.1 sec', '1 sec', '1 min', '1 hr']);
```
### Slug test in 5-layer aquifer
Well in top 2 layers
```
k = 25
H = 20
Ss = 1e-4 / H
t = np.logspace(-7, -1, 100)
rw = 0.2
rc = 0.2
delh = 1
ml = Model3D(kaq=k, z=np.linspace(H, 0, 6), Saq=Ss, tmin=1e-7, tmax=1)
Qslug = np.pi * rc**2 * delh
w = Well(ml, tsandQ=[(0, -Qslug)], rw=rw, rc=rc, layers=[0, 1], wbstype='slug')
ml.solve()
hw = w.headinside(t)
plt.semilogx(t, hw[0], label='inside well')
h = ml.head(0.2 + 1e-8, 0, t)
for i in range(2, 5):
plt.semilogx(t, h[i], label='layer' + str(i))
plt.legend()
plt.xticks([1/(24*60*60)/10, 1/(24*60*60), 1/(24 * 60), 1/24], ['0.1 sec', '1 sec', '1 min', '1 hr']);
```
20 layers
```
k = 25
H = 20
S = 1e-4 / H
t = np.logspace(-7, -1, 100)
rw = 0.2
rc = 0.2
delh = 1
ml = Model3D(kaq=k, z=np.linspace(H, 0, 21), Saq=S, tmin=1e-7, tmax=1)
Qslug = np.pi * rc**2 * delh
w = Well(ml, tsandQ=[(0, -Qslug)], rw=rw, rc=rc, layers=np.arange(8), wbstype='slug')
ml.solve()
hw = w.headinside(t)
plt.semilogx(t, hw[0], label='inside well')
h = ml.head(0.2 + 1e-8, 0, t)
for i in range(8, 20):
plt.semilogx(t, h[i], label='layer' + str(i))
plt.legend()
plt.xticks([1/(24*60*60)/10, 1/(24*60*60), 1/(24 * 60), 1/24], ['0.1 sec', '1 sec', '1 min', '1 hr']);
```
### Head Well
```
ml = ModelMaq(kaq=25, z=[20, 0], Saq=1e-5, tmin=1e-3, tmax=1000)
w = HeadWell(ml, tsandh=[(0, -1)], rw=0.2)
ml.solve()
plt.figure(figsize=(12,5))
plt.subplot(1,2,1)
ml.xsection(0.2, 100, 0, 0, 100, t=[0.1, 1, 10], sstart=0.2, newfig=False)
t = np.logspace(-3, 3, 100)
dis = w.discharge(t)
plt.subplot(1,2,2)
plt.semilogx(t, dis[0], label='rw=0.2')
ml = ModelMaq(kaq=25, z=[20, 0], Saq=1e-5, tmin=1e-3, tmax=1000)
w = HeadWell(ml, tsandh=[(0, -1)], rw=0.3)
ml.solve()
dis = w.discharge(t)
plt.semilogx(t, dis[0], label='rw=0.3')
plt.xlabel('time (d)')
plt.ylabel('discharge (m3/d)')
plt.legend();
```
| true |
code
| 0.540439 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.